Prerpints.org logo
Preprint
Article

Gaming Tree Based Evaluation Model for Badminton Tactic Benefit Analysis and Prediction

Altmetrics

Downloads

149

Views

24

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

24 May 2023

Posted:

25 May 2023

You are already at the latest version

Alerts
Abstract
Badminton tactics refer to the techniques and strategies employed by players to win a match. Analyzing these tactics can help players improve their performance and outsmart their opponents. To study the tactics of top players, we use a gaming tree to analyze matches between two of the most powerful badminton players in history: Lin and Lee. By employing the Nash Equilibrium, we can discover the most beneficial strategies for both players, which reflect their most powerful techniques. Additionally, with the help of this gaming tree, we can precisely predict how players will implement their tactics. Empirical experimental results demonstrate that our proposed method not only evaluates and identifies each player's weaknesses and strengths but also has powerful capabilities to predict their tactics.
Keywords: 
Subject: Computer Science and Mathematics  -   Analysis

1. Introduction

Badminton is one of the most popular sports in the world [1,2], and is also the racquet sport with the highest speed in the world [3], with its competitive form being two single/pair athletes completing tactical implementation quickly and accurately [4,5] on an 80 square meter court. As a result, tactical strategies (strategical strokes) are one of the key factors for winning badminton matches [6].
With the rapid development of information technology, advanced statistical methods such as data mining and artificial intelligence are commonly used in tactical analysis. Such methods can mine implicit information from performance data of competitions to provide decision support for coaches and athletes, which is an important aspect of tactical strategy research for sports such as basketball [7,8], football [9,10], tennis [11,12], table tennis [13,14], badminton [15,16], and is also a promising direction for improvement and development of traditional performance diagnosis and evaluation methods [17,18]. In recent years, predicting match results (scores, wins/losses) using these methods has become a hot research topic [19,20]. Through prediction models, key tactical factors affecting match results can be analyzed. For example, Valero et al. [21] uses four data mining methods (including lazy learners, artificial neural networks, support vector machines, and decision trees) to evaluate classification-based and regression-based methods for predicting match results (home team win or lose) in Major League Baseball (MLB) regular season games over 10 years; Razali et al. [22] used Bayesian networks to predict home wins, away wins, and draws in the English Premier League; Karlis and Ntzoufras [23] constructed a bivariate Poisson model to analyze scores between two teams, etc. However, there has been no prediction research on badminton so far.
Game theory studies how rational actors make decisions and the equilibrium of such decisions under the assumption of mutual interaction and influence among relevant actors. The prediction ability, actual behavior selection and optimal selection between the two sides of the game are the research focuses of game theory. Consequently, game theory has been widely applied in the sports science, including sports teaching [24,25], tactical strategies [26,27,28], etc., while researches on its prediction in sports field has not yet been studied.
Badminton matches have strong confrontation and competition, and have obvious interactive and interdependent characteristics of tactics and strategies between opponents, which is consistent with the research object characteristics of game theory. Therefore, this study intends to use game tree method with game theory to explore the winning rate of badminton matches. By using important badminton match data in recent years, this study predicts the winning rate of the future matches through the tactics strategy of the history matches, so as to reflect the tactical winning factors in badminton matches.

2. Materials and Methods

2.1. Materials

In this paper, 29 matches of 2 most famous badminton players (i.e., Dan Lin and Chong Wei Lee) from 2006 to 2018 are selected. As men’s single players, Lin has won nine major titles in the badminton world with 2 Olympic gold medals, while Lee was ranked first worldwide for 349 weeks including a 199-week streak. Thus, the selected matches between Lin and Lee present the highest-level badminton techniques and tactics, and are worth analyzing. All match videos were from television relay or the Internet Note that, the two players have announced retirement and the selected matches are only used for analysis, i.e., no technical guidance is provided.

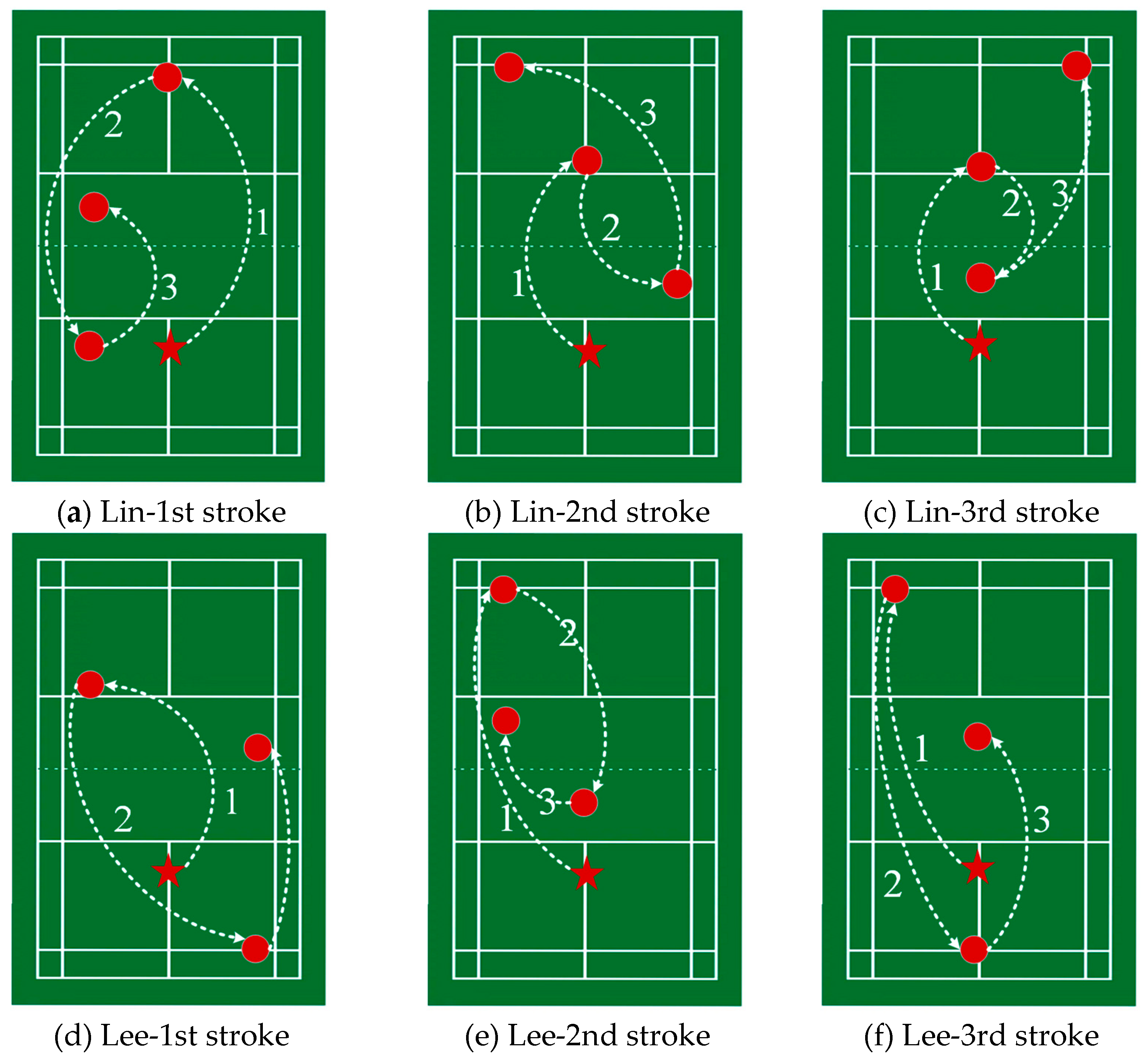
2.2. Observation indices and tactical combination

Based on the studies by Butterworth and Turner [29], and Phomsoupha and Laffaye [30], we conclude the tactical observation indices including stroke technique, stroke placement, and rally results, as follows:
  • Stroke technique: Serve, including short serve and long serve; Smash, an aggressive overhead shot with a downward trajectory; Clear, an overhead shot with a flat or rising trajectory towards the back of the opponent’s court; Drop, is a smooth shot from above the head with a downward trajectory towards the front of the court; Net shot, denoting a precise shot from near the net, including the net drop, lob and kill; Drive, a powerful shot made at middle body height and in the middle of the court with a flat trajectory;
  • Stroke placement: the start position and the target placement of each stroke. In this paper, the badminton court are evenly divided into 9 (3x3) grids, i.e., the combination of vertically three parts (front court, middle court, and back court) and horizontally three parts (left court, middle court, and right court);
  • The rally results: scoring and losing.
In fact, the speed of each stroke also contributes to the tactics. However, as the speed (including smash speed, clear shoot speed, e.t.c.) of high-level players are almost the same (especially for Lin and Lee), the influence of the stroke speed for the rally results is not considered in this paper.
Based on the above, the tactical combination is composed of the different stroke techniques and stroke placements of each strokes by two players, where each stroke has four attributes, i.e., the start position, the applied technique, the target placement and the final result for rally that this stroke belongs to.

2.3. Tactical frequency and scoring rate algorithm

In this study, the attributes of different strokes for each rally are computed first. Let P be a binary set that represent the stroking player, X be a set of stroke techniques, Y be a set of stroke placements, S be a set of strokes and D be a set of descriptive vectors of all rallies, a stroke s k i ∈ S for the k t h stroke in the i t h rally can be denoted as ( p k i , x k i , y k i , x k + 1 i ) , where p k i is the player for this stroke, x k i is the applied technique, y k i is the start place for this stroke and the destination of this stroke is denoted as y k + 1 i . Based on the s k i , a descriptive vector d i ∈ D in a given rally can be denoted as ( s 1 i , s 2 i , … , s n i ) , where n is the length of strokes in this rally. For each rally, the sign of the end of the rally is that either side has lost a point, i.e., the loser has not returned the ball to the opponent’s court, making that the stroke does not exist.
Consider all the strokes, rallies, and games in each match, the later ones are more important than the earlier ones, as the later strokes, rallies, and games decide the result of the general results of each rally, game and matches respectively. Thus, consider that each match has the total score of 1, the scores for each game g j ∈ G , each rally r i ∈ R j , and each stroke s k i ∈ S i can be calculated as follows, where R j denotes all the rallies in g j , and S i denotes all the strokes in r i .
S c o r e g j = 2 j | G | · ( G − 1 )
S c o r e r i = S c o r e g j · 2 i | R j | · ( R j − 1 )  
S c o r e s k i = S c o r e r i · 2 k | S i | · ( S i − 1 )

2.4. Evaluation model of tactical benefit

2.4.1. Tactical benefit

According to the feature of badminton match, i.e., each rally has only one result and each stroke has limited start placement and destination, the players have limited choices to conduct their techniques and tactics. Thus, if we consider each single rally is an individual game with different weights, we can count all the rallies together, and compute the benefit for each stroke. Given a number of rallies R = { r 1 , r 2 , … , r m } , we construct a gaming tree T for all the strokes S i = s 1 i , s 2 i , … , s n i in each rally r i . and compute the benefit for each node in the gaming tree. Specifically, each node of T represent a possible stroke, and all the nodes of T covers all the strokes in the selected rallies.
Figure 1 presents a simplified example (the specific technique and the destination for each stroke is not considered here) of building a gaming tree for three rallies r 1 , r 2 , r 3 , where S denotes strokes, P denotes the player, the Y denotes the placement, and N denotes the gaming tree node. To illustrate, consider the strokes { s 1 1 , s 1 2 , s 1 3 } , though they belong to different rally, they are the first stroke for each rally and share the same player and placement (player p 1 with the placement 1), leading to the same tree node position N 1 . Note that, two strokes can be classified into the same tree node if and only if their player and placement are same and their previous strokes (if exist) all have the same player and placement. For this reason, s 2 1 and s 2 3 can be classified to be node N 2 , as they succeed s 1 1 and s 1 3 separately (both can be regarded as N 1 ) and have the same player and placement. Meanwhile, though s 3 1 and s 3 3 also have the same player and placement, they belong to different tree nodes as their previous strokes are different, e.g., s 2 1 and s 2 3 have different placement.
Based on the gaming tree constructed from each stroke s k i = ( p k i , x k i , y k i , x k + 1 i ) , each tree node represent a possible stroke and we can derive all the possible strokes for each single rally, as each rally starts from the root nodes (have no predecessors) of the gaming tree and ends at leaf nodes (have no successors). Meanwhile, the benefit of each possible stroke can be obtained by considering formula 3 and the gaming tree, i.e., we summarize the score of each stroke s i that can be reduced to the same gaming tree node N (denoted as s i ∈ N ) and regard it as the benefit for that stroke. Generally, the benefit of each Node N can be computed as follows.
S c o r e N = ∑ s i ∈ N S c o r e ( s i ) · 1                   t h e   s e r v e r   p a l y e r   w i n − 1                   t h e   s e r v e r   p a l y e r   l o s e s
For example, given two strokes s k i and s k j that can be reduced to the same gaming tree node N , and s k i leads to the server player wins while s k j is the opposite, we calculate the benefit of N as S c o r e N = S c o r e s k i − S c o r e s k i . Note that, according to the formula 1-3, we can obtain that ∑ S c o r e s k i = 1 . Thus, the benefit range of each node is [-1, 1].

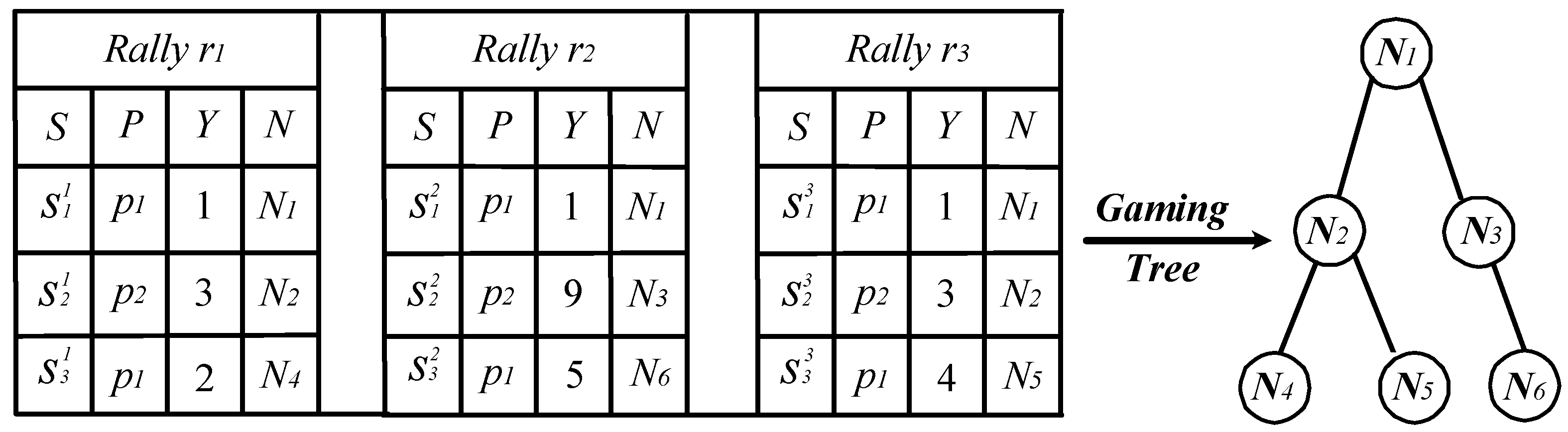
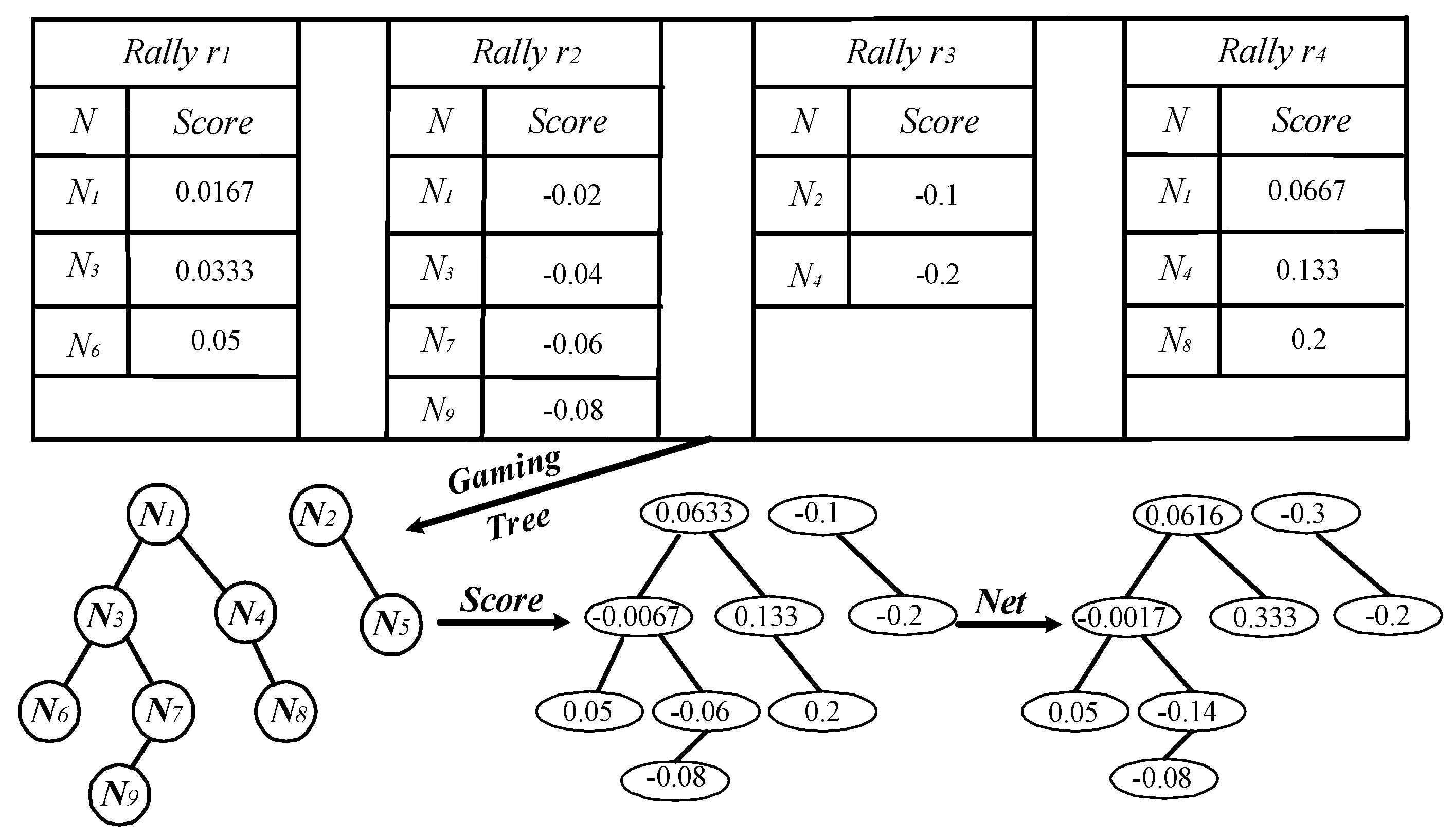
2.4.2. Evaluation Model

The evaluation model for the badminton matches include two steps, i.e., (i) constructing the gaming tree for the history strokes and evaluating the techniques and tactics for two players, and (ii) analyzing the rallies and strokes using the constructed gaming tree.
Evaluating. Given a set of existing matches, we first formulize each rally as r i = s 1 i , s 2 i , … , s n i and each stroke as s k i = ( p k i , x k i , y k i , x k + 1 i ) . Then, we add s k i into the gaming tree. For example, consider the rally r i = s 1 i , s 2 i , … , s n i , we first find if there exist a node N that has the same ( p 1 i , x 1 i , y 1 i , x 2 i ) as s 1 i . If not, we create a new node N for s 1 i into the gaming tree. After that, we update the S c o r e ( N ) with S c o r e ( s 1 i ) . Next, we check the leaves of N and check the following strokes s 2 i , s 3 i , … , s n i as s 1 i . After all the rallies and strokes are evaluated and the gaming tree is constructed, we compute the net benefit for each tree node as follows.
N e t N = S c o r e N + M a x N i i s   a   l e a f   o f   N ( S c o r e N i ) ,
where M a x i ∈ m S c o r e N i denote the function that finds the maximal value among { S c o r e ( N 1 ) , S c o r e ( N 2 ) , … , S c o r e ( N m ) }.
Consider the example shown in Figure 2, where four rallies are given and the gaming tree is constructed with nine nodes. Specifically, in the first rally r 1 , the server p 1 wins and continues to serve. In the second rally r 2 , p 1 loses and alternates the service. However, the opponent player p 2 loses the rally r 3 , and the service is alternated again. Finally, the player p 1 wins the fourth rally r 4 and the match ends. To model this match, we first build the gaming tree and compute the scores for each stroke, then the score of each tree node is obtained. Based on the above, we then compute the net benefit. Clearly, when it starts from N 2 , the serve player always loses as the net benefit is negative.
However, when it comes to start from N 1 , the tactics becomes complicated, as the opponent has two choices to play, i.e., move to N 3 with the benefit of -0.0067 or move to N 4 with the benefit of 0.333. According to the Nash Equilibrium, the opponent should move to N 3 and will win this rally. Thus, though in this example the player that serve at r 1 , r 2 , and r 4 seems to have more possibility to win the match, the opponent also has the chance to change the result. This makes our proposed gaming tree not only have the ability to evaluate how the player have performed in the existing matches by leveraging the net benefit, but also can analyze how the players use their techniques with tactics by finding Nash Equilibriums in the gaming tree.
Analysis. Based on the above, we find that the score of each stroke illustrate how much important that stroke is to the whole match. Thus, we propose the following rating strategy to find Nash Equilibriums in the gaming tree, which helps analyzing the existing strokes, rallies, games and matches.
S c o r e ' N = ∑ s i ∈ N S c o r e ( s i )
Based on equation 6, we compute the importance weight S c o r e ' N of each node N . Next, we propose the win-loss flag table to determine whether the node N leads to the server win or lose. Note that, the win-loss table is obtained by following the strategy that the player will choose the best strategy to win the game, and the opponent will make the player lose the game. To illustrate, consider a node N that is an odd stroke, there are two situations: (i) N is a leaf, the server must win when S c o r e N is positive, while the server lose if S c o r e N is negative, and the result is draw if S c o r e N =0, and (ii) N is non-leaf node, the server win when it holds that M a x N i ∈ s u c c e s s o r s o f N   ( S c o r e ' N i · F l g N i ) is positive, and the result is lose or draw if the value is negative or equal respectively. Based on the above, we can also analyze the result when N is an even stroke. The summarized table is shown below.
Table 1. Win-loss flag table.
Table 1. Win-loss flag table.
Node Win/
Lose		 Flg(N)
Odd/Even Situation
Odd Stroke Leaf node, and the S c o r e ( N ) is positive Win 1
Leaf node, and the S c o r e ( N ) is negative Lose -1
Leaf node, and the S c o r e ( N ) is 0 --- 0
Non-leaf, M a x N i ∈ s u c c e s s o r s o f N ( S c o r e ' N i · F l g N i ) >0 Win 1
Non-leaf, M a x N i ∈ s u c c e s s o r s o f N ( S c o r e ' N i · F l g N i ) <0 Lose -1
Non-leaf, M a x N i ∈ s u c c e s s o r s o f N S c o r e ' N i · F l g N i = 0 --- 0
Even Stroke Leaf node, and the S c o r e ( N ) is positive Win 1
Leaf node, and the   S c o r e ( N ) is negative Lose -1
Leaf node, and the S c o r e ( N ) is 0 --- 0
Non-leaf, M i n N i ∈ s u c c e s s o r s o f N ( S c o r e ' N i · F l g N i ) >0 Win 1
Non-leaf, M i n N i ∈ s u c c e s s o r s o f N S c o r e ' N i · F l g N i < 0 Lose -1
Non-leaf, M i n N i ∈ s u c c e s s o r s o f N S c o r e ' N i · F l g N i = 0 --- 0
Generally, based on the Win-loss flag table, the Nash Equilibrium for each tree node N can be obtained, and the F l g ( N ) correspond to rally result (win, lose, or draw). Especially, we can decide whether the server will win or lose by directly checking the F l g ( · ) function for the root node (i.e., the initial stroke).

3. Results

3.1. Basic Data

The detailed information of selected matches is shown in Table 2, with Lin winning 19 times while Lee winning 10 times in total. In Table 2, during the early period (2006 to 2009), the two players have roughly the same winning times. However, during the middle period (10-15), Lin shows a higher-level performance, and beats Lee at most of matches. In the last three year (2016-2018), the two players come back to a stalemate.

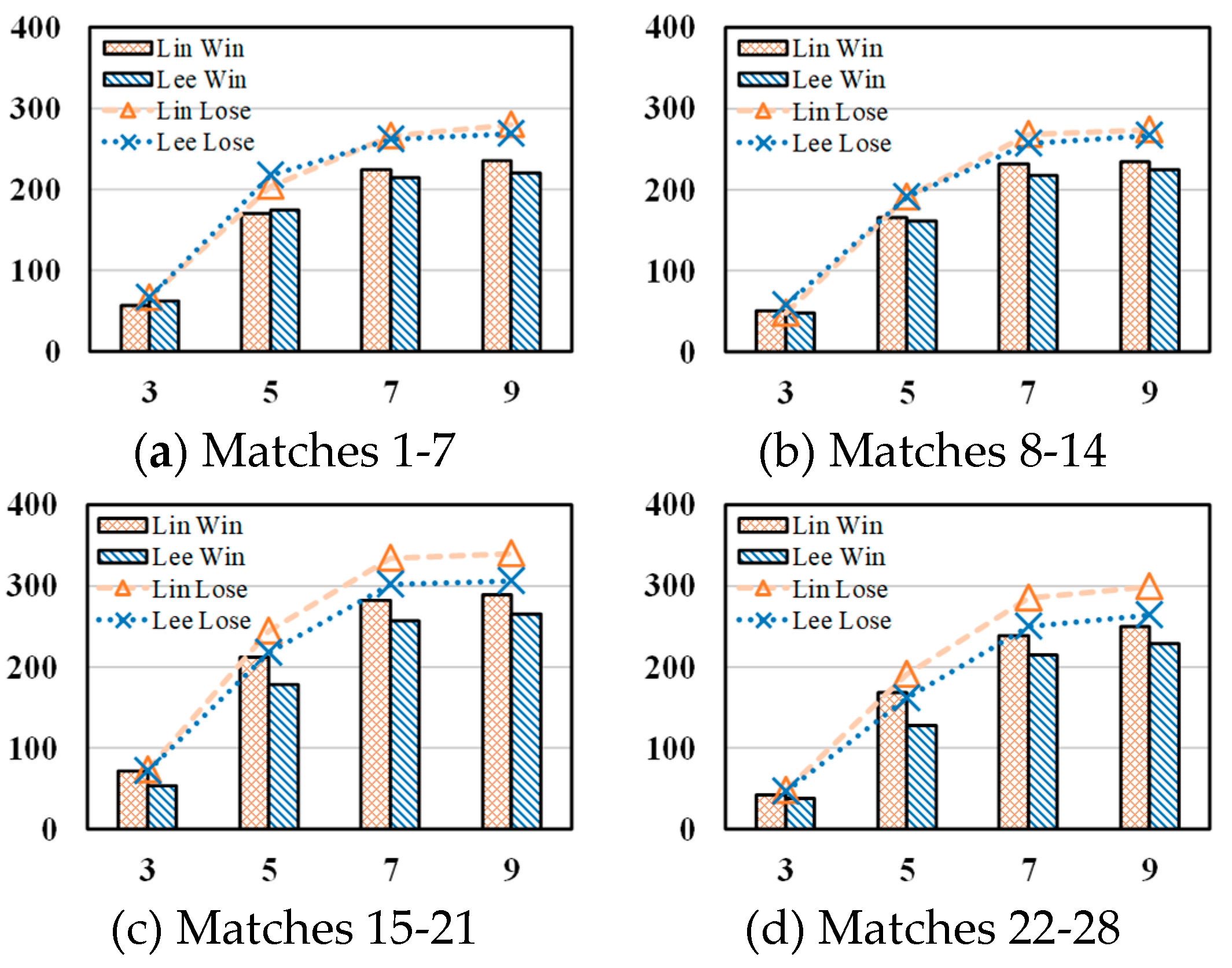
3.2. General Analysis

In this paper, we analyze the matches based of the gaming tree, while leveraging the benefit and net benefit (formulas 4 and 5) to evaluate the strokes of each player and use the Nash Equilibrium derived by gaming tree and win-loss flags to analyze the general win-loss situation.
Firstly, according to the definition of the benefit, the higher benefit value implies that the stroke leads to higher contribution for winning the game. Thus, we compute the gaming tree for all the matches, and find the strokes with the top-3 benefits during the first three beats as shown in Figure 3, aiming at illustrating the tactics of two players for the first three beat. From the figures, we find that the best choices for Lin is to hit the shuttle to the backcourt while that for Lee is to control the forecourt.
Next, we find the Nash Equilibrium based on the gaming tree, and derive the results as shown in Table 3. As can be seen from the table, with the growing beats, Lin and Lee have more choices to win or lose the match, while mostly the number of the strokes that result in losing is larger than the strokes that lead to wining the rally. This also implies that Lin and Lee have many tactics and techniques to win each other, and will lose the game with high possibility. However, during the matches, they defend the with great skills and seize the opportunity to win the match. Besides, according to the win-loss ratios, Lin has higher value than Lee, which is consistence with the results that Lin wins more matches than Lee.

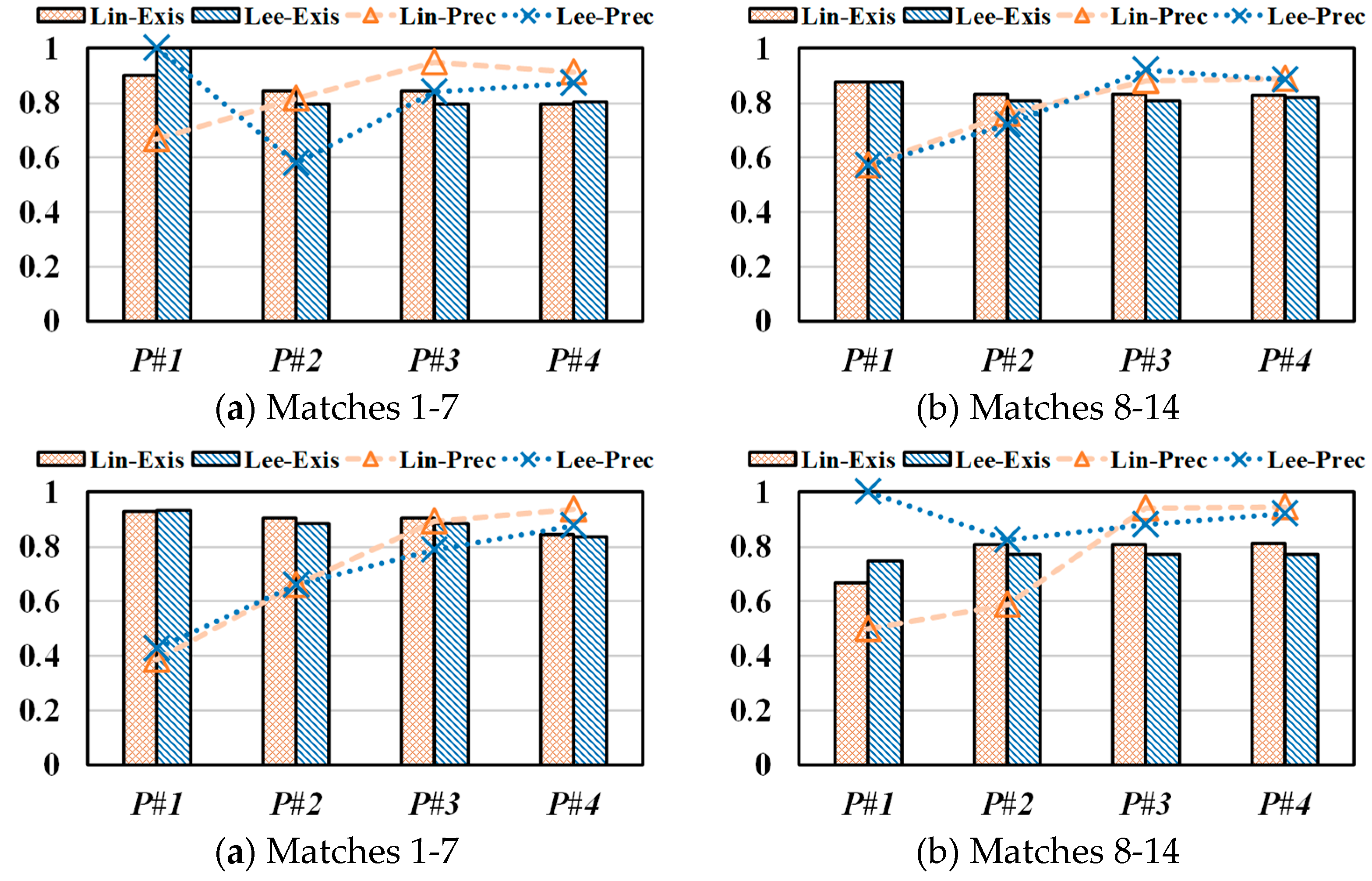
3.3. Analysis for Different Periods

In different career period, the results are different. Thus, we compute the Nash Equilibrium for different period and present the result in Figure 4. Specifically, we divide all the matches into four groups, i.e., matches 1-7, 8-14, 15-21, and 22-28. For each group, we construct an individual gaming tree and compute there Nash Equilibrium results. The results are consistent with the analysis in Sec 3.2, while there also exists a new observation that as the two players play more match, they find more ways to beat each other. However, when it comes to the last period (matches 22-28), there is a significant drop for both players. This is because they are too familiar with each other that their tactics are not efficient, and their bodies cannot support their all tactics and techniques. As a result, they try to use the most effective way to win the game, making the number of gaming strategies descend.
Besides, we compute the win-loss ratio for two players in four career periods based on the win-loss results presented in Figure 4, and the results are shown in Figure 5. For example, Lin#1 with parameter 3 denotes the win-loss ratio between the winning strokes and lose strokes for player Lin among the first three beats in the career period #1 (i.e., the matches 1-7). We find that the results are consistence with the real matches, i.e., in the first three period the win-loss ratio of Lin is larger than Lee, thus Lin has more possibility to win the game. In the last period, the ratio of Lin is larger than Lee when the beats are not larger than 5, while it becomes the opposite when the beats are 7 or more. Thus, Lin and Lee have the equal possibility to win the match.

3.4. Prediction using Top-k Benefits

This section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation, as well as the experimental conclusions that can be drawn.
As stated in Sec 2.4.1, the score and benefits imply how each stroke contribute to the match result. Thus, when the player comes to a specific node in the gaming tree, we can predict the next stroke by considering the top-k strokes with the highest benefits in the predecessors (children) of that node. For this reason, we construct the gaming tree for four different career period and use the strokes with top-k to predict the first m beats in the next match. Note that, we use four parameters group of (k, m) to demonstrate the effectiveness of gaming tree prediction capability, i.e., P#1(3, 3), P#2(5, 3), P#3(5, 5), and P#4(5, 10). For example, for predicting the first period career of (matches 1-7) with parameters P#1(3, 3), we use matches 1-6 to construct the gaming tree, and use the strokes with top-3 benefits to predict all the first 3 beats.
The results are shown in Figure 6, where the Exist. denotes that the number of real strokes that can be found in the gaming tree, and the Prec. denotes precision for correctly predicted strokes that exist in the gaming tree. As can be observed, the Exist. drops as the beats increase, while the precision generally keeps ascending, and the precision is above 90% when we use top-5 benefit strokes to predict more than 5 beats, demonstrating the effectiveness of our strategy. Meanwhile, there is also an interesting observation that during the first period and the last period, when Lin and Lee have similar win-loss result, our model performs well for the first 3 beats on Lee. However, during the middle period (matches 8-21), when Lin wins more, the precision of our method for the first 3 beats on Lee is low. Thus, we can conclude that the first 3 beats of Lin are always hard to predict, while Lee can be predicted with high accuracy at the early and late career stage.

4. Discussion

Authors should discuss the results and how they can be interpreted from the perspective of previous studies and of the working hypotheses. The findings and their implications should be discussed in the broadest context possible. Future research directions may also be highlighted. In this paper, we use gaming tree to analyze the technical and tactical strategies of Lin and Lee. Based on the analysis results, we make precise predictions for some of their matches. In addition, we analyze the different stages of their professional careers and find that they have made some adjustments to their technical and tactical strategies with their increasing ages, thus revealing some hidden factors that determine the outcome of the match. However, with the recent adjustment of competition rules and the wide application of Hawk-Eye system, badminton matches are undergoing tremendous changes. The technical and tactical analysis revealed in this paper is only for top men’s singles matches in the past decade. There are still two aspects of technical and tactical analysis to be explored.
  • Tactics combinations. Unlike male players, female players do not have such strong offensive ability, resulting in a difference in the technical and tactical skills of female singles matches. In addition, double matches require higher cooperation ability from the players, so the technical and tactical skills in doubles matches are completely different from those in singles matches, e.g., Cao et al. [31] find special tactics in mixed double table tennis matches, and Abián-Vicén et al. [32] analyze the different performance between men’s and women’s double matches. In addition, tactic length and tactic frequency are also important for players to control the match, as illustrated by Liu [33] and Zhou [34]. For instance, when a match reaches its final stage, both players face increased pressure. Therefore, using an efficient tactic combination (i.e., utilizing a smaller number of tactics) can significantly increase the chances of winning the match. Thus, the tactic combinations are worth studying;
  • Factors that are outside the tactics. In a match, the match length and the point difference also contribute to the final result. For example, based on the analysis of recent math lengths, Iizuka et al. [35] suggest badminton players to strengthen their physical capabilities to win the match; Barreira et al. [36] find that a small point difference not necessarily implies the winning of the match, while a more than 4 points lead to great possibility for winning the match; O’donoghue [37] observe the grand slam singles tennis matches and conclude that some key points determine the match results. Besides, Chu et al. [38] demonstrated the significant influence of spatial information on tactics and techniques by visualizing badminton strokes, thus helping badminton players to win the match.

5. Conclusions

In this paper, we study the problem of tactical benefit in badminton matches. To tackle this problem, we propose to a gaming tree that consider the contribution of each stroke to the result of the match, and develop an evaluation model with prediction techniques to analyze the strokes of each player. To further analyze the tactics and techniques of the two world’s top players, we leverage the Nash Equilibrium derived by the gaming tree to help analyze their tactics behind the strokes. The experiment results demonstrate that our evaluations for the strokes of two players are consistence with the real match result, and our prediction model are with high accuracy. Thus, our proposed methods are effectiveness and have the potential to help players find their strengths and weaknesses, and further improve their tactics.

Author Contributions

Conceptualization, W.L., Y.Z., W.G., X.W., Y.S. and S.Y.; methodology, Y.Z. and S.Y.; software, W.L., W.G. and X.W.; validation, W.G., Y.S. and X.W.; formal analysis, W.L. and Y.Z.; investigation, W.G., Y.S. and X.W.; resources, S.Y.; data curation, Y.Z.; writing—original draft preparation, W.L., Y.S. and Y.Z.; writing—review and editing, W.G., X.W., Y.S. and S.Y.; visualization, Y.Z..; supervision, W.L.; project administration, W.G., X.W. and S.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Publicly available videos of badminton matches in official competitions were used to analyze the data. For this purpose, we used common video platforms (e.g., youtube.com) (accessed on 25 January 2022).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Lees, A. Science and the major racket sports: a review. J Sports Sci. 2003, 21, 707–732. [Google Scholar] [CrossRef]
  2. Phomsoupha, M.; Laffaye, G. The science of badminton: game characteristics, anthropometry, physiology, visual fitness and biomechanics. Sports Med. 2015, 45, 473–95. [Google Scholar] [CrossRef]
  3. Singh, G. Technology and badminton [abstract]. Br J Sports Med. 2010, 44, i51–i51. [Google Scholar] [CrossRef]
  4. Cabello, M.D.; González-Badillo, J.J. Analysis of the characteristics of competitive badminton. Br J Sports Med. 2003, 37, 62–66. [Google Scholar] [CrossRef] [PubMed]
  5. Sonoda, T.; Tashiro, Y.; Suzuki, Y.; Kajiwara, Y.; Zeidan, H.; Yokota, Y.; Aoyama, T. Relationship between agility and lower limb muscle strength, targeting university badminton players. Journal of Physical Therapy Science 2018, 30, 320–323. [Google Scholar] [CrossRef]
  6. Ghosh, I.; Ramamurthy, S.R.; Chakma, A.; Roy, N. DeCoach: Deep Learning-based Coaching for Badminton Player Assessment. Pervasive and Mobile Computing 2022, 83, 101608. [Google Scholar] [CrossRef]
  7. Guillot, A.; Nadrowska, E.; Collet, C. Using Motor Imagery to Learn Tactical Movements in Basketball. Journal of Sport Behavior 2009, 32, 189. [Google Scholar]
  8. Figueira, B.; Mateus, N.; Esteves, P.; Dadelienė, R.; Paulauskas, R. Physiological responses and technical-tactical performance of youth basketball players: A brief comparison between 3x3 and 5x5 basketball. Journal of Sports Science & Medicine 2022, 21, 332. [Google Scholar]
  9. Moura, F.A.; Martins, L.E.B.; Cunha, S.A. Analysis of football game-related statistics using multivariate techniques. Journal of sports sciences 2014, 32, 1881–1887. [Google Scholar] [CrossRef] [PubMed]
  10. Sarmento, H.; Clemente, F.M.; Araújo, D.; Davids, K.; McRobert, A.; Figueiredo, A. What performance analysts need to know about research trends in association football (2012–2016): A systematic review. Sports medicine 2018, 48, 799–836. [Google Scholar] [CrossRef] [PubMed]
  11. Martínez-Gallego, R.; Salvador, S. M.; Luján, J.F.G.; Reid, M.; Ramón-Llin, J.; Crespo, M. Challenging serve myths in doubles tennis. International Journal of Sports Science & Coaching 2021, 16, 1305–1311. [Google Scholar]
  12. Wu, J.; Liu, D.; Guo, Z.; Xu, Q.; Wu, Y. TacticFlow: Visual analytics of ever-changing tactics in racket sports. IEEE Transactions on Visualization and Computer Graphics 2021, 28, 835–845. [Google Scholar] [CrossRef]
  13. Wang, J.; Wu, J.; Cao, A.; Zhou, Z.; Zhang, H.; Wu, Y. Tac-miner: Visual tactic mining for multiple table tennis matches. IEEE Transactions on Visualization and Computer Graphics 2021, 27, 2770–2782. [Google Scholar] [CrossRef] [PubMed]
  14. Guo, W.; Liang, M.; Xiao, D.; Hao, W. A systematic and comparative study on the line-changing strategies in top-level table tennis players. International Journal of Performance Analysis in Sport 2020, 20, 1018–1034. [Google Scholar] [CrossRef]
  15. Torres-Luque, G.; Blanca-Torres, J.C.; Giménez-Egido, J.M.; Cabello-Manrique, D.; Ortega-Toro, E. Design, validation, and reliability of an observational instrument for technical and tactical actions in singles badminton. Frontiers in psychology 2020, 11, 582693. [Google Scholar] [CrossRef] [PubMed]
  16. Carboch, J.; Smocek, P. Serve and Return in Badminton: Gender Differences of Elite Badminton Players. International Journal of Physical Education, Fitness and Sports 2020, 9, 44–48. [Google Scholar] [CrossRef]
  17. Yuan, C.; Yang, Y.; Liu, Y. Sports decision-making model based on data mining and neural network. Neural Computing and Applications 2021, 33, 3911–3924. [Google Scholar] [CrossRef]
  18. Xie, Y.; Bai, B.; Zhao, Y. Variation Factors and Dynamic Modeling Analysis of Tennis Players’ Competitive Ability Based on Big Data Mining Algorithm. Journal of Sensors 2022. [CrossRef]
  19. Thabtah, F.; Zhang, L.; Abdelhamid, N. NBA game result prediction using feature analysis and machine learning. Ann. Data Sci. 2019, 6, 103–116. [Google Scholar]
  20. Pathak, N.; Wadhwa, H. Applications of Modern Classifification Techniques to Predict the Outcome of ODI Cricket. Procedia Comput. Sci. 2016, 87, 55–60. [Google Scholar] [CrossRef]
  21. Valero, C.S. Predicting Win-Loss outcomes in MLB regular season games-A comparative study using data mining methods. Int. J. Comput. Sci. Sport 2016, 15, 91–112. [Google Scholar] [CrossRef]
  22. Razali, N.; Mustapha, A.; Yatim, F.A.; Ab Aziz, R. Predicting football matches results using bayesian networks for English Premier League (EPL). In Proceedings of the IOP Conf. Ser. Mater. Sci. Eng. 2017, 226, 012099. [Google Scholar] [CrossRef]
  23. Karlis, D.; Ntzoufras, I. Analysis of sports data using bivariate Poisson models. J. R. Stat. Soc. Ser. D Stat. 2003, 52, 381–393. [Google Scholar] [CrossRef]
  24. Fortunado, I.T. An overview to game theory, physical education and sports, its thirteen essentials and categories. Education Journal 2016, 5, 92–96. [Google Scholar] [CrossRef]
  25. Kao, C.C. Development of team cohesion and sustained collaboration skills with the sport education model. Sustainability 2019, 11, 2348. [Google Scholar] [CrossRef]
  26. Sindik, J; Vidak, N. Application of game theory in describing efficacy of decision making in sportsman’s tactical performance in team sports. Interdisciplinary Description of Complex Systems: INDECS 2008, 6, 53–66. [Google Scholar]
  27. Tuyls, K.; Omidshafiei, S.; Muller, P.; Wang, Z.; Connor, J.; Hennes, D.; Hassabis, D. Game Plan: What AI can do for Football, and What Football can do for AI. Journal of Artificial Intelligence Research 2021, 71, 41–88. [Google Scholar] [CrossRef]
  28. Orugun, J.; Nafiu, A.; Aduku, D.J. Strategy implementation and its effect on superior performance and competitive advantage of SMEs in Kogi State, Nigeria. Asian Journal of Economics, Business and Accounting 2017, 2, 1–13. [Google Scholar] [CrossRef]
  29. Butterworth, D.A.; Turner, J.D.; Johnstone, A.J. Coaches’ perceptions of the potential use of performance analysis in badminton. International Journal of Performance Analysis in Sport 2012, 12, 452–467. [Google Scholar] [CrossRef]
  30. Phomsoupha, M.; Laffaye, G. The science of badminton: game characteristics, anthropometry, physiology, visual fitness and biomechanics. Sports medicine 2015, 45, 473–495. [Google Scholar] [CrossRef] [PubMed]
  31. Cao, Y.; Peng, Y.; Shen, Z.; Chen, H.; Peng, B.; Yan, X. Application of tactics in technical and tactical analysis of table tennis mixed doubles based on artificial intelligence graph theory model. Journal of Environmental and Public Health 2022. [CrossRef] [PubMed]
  32. Abián-Vicén, J.; Sánchez, L.; Abián, P. Performance structure analysis of the men’s and women’s badminton doubles matches in the Olympic Games from 2008 to 2016 during playoffs stage. International Journal of Performance Analysis in Sport 2018, 18, 633–644. [Google Scholar] [CrossRef]
  33. Liu, W.; Zhou, Z.; Shen, Y.; Zhang, H. Stroke performance relevance model for elite table tennis matches. International Journal of Performance Analysis in Sport 2022, 22, 558–570. [Google Scholar] [CrossRef]
  34. Zhou, Z.; Zhang, H. A visible analysis approach for table tennis tactical benefit. Journal of Sports Science and Medicine 2022, 21, 517–527. [Google Scholar] [CrossRef] [PubMed]
  35. Iizuka, T.; Hirano, K.; Atomi, T.; Shimizu, M.; Atomi, Y. Changes in duration and intensity of the world’s top-level badminton matches: A consideration of the increased acute injuries among elite women’s singles players. Sports 2020, 8, 19. [Google Scholar] [CrossRef]
  36. Barreira, J.; Chiminazzo, J.G.C.; Fernandes, P.T. Analysis of point difference established by winners and losers in games of badminton. International Journal of Performance Analysis in Sport 2016, 16, 687–694. [Google Scholar] [CrossRef]
  37. O’donoghue, P.G. The most important points in grand slam singles tennis. Research quarterly for exercise and sport 2001, 72, 125–131. [Google Scholar] [CrossRef]
  38. Chu, X.; Xie, X.; Ye, S.; Lu, H.; Xiao, H.; Yuan, Z.; Wu, Y. TIVEE: Visual exploration and explanation of badminton tactics in immersive visualizations. IEEE Transactions on Visualization and Computer Graphics 2021, 28, 118–128. [Google Scholar] [CrossRef]
Preprints 74572 g001
Figure 1. Illustration of the gaming tree for rallies.
Figure 1. Illustration of the gaming tree for rallies.
Preprints 74572 g001
Preprints 74572 g002
Figure 2. Illustration of the gaming tree evaluation.
Figure 2. Illustration of the gaming tree evaluation.
Preprints 74572 g002
Preprints 74572 g003
Figure 3. The top-3 benefits strokes.
Figure 3. The top-3 benefits strokes.
Preprints 74572 g003
Preprints 74572 g004
Figure 4. The Win-Loss results for different career period.
Figure 4. The Win-Loss results for different career period.
Preprints 74572 g004
Preprints 74572 g005
Figure 5. The Win-Loss ratio for different career period.
Figure 5. The Win-Loss ratio for different career period.
Preprints 74572 g005
Preprints 74572 g006
Figure 6. The prediction results for different career period.
Figure 6. The prediction results for different career period.
Preprints 74572 g006
Table 2. Match statics.
Table 2. Match statics.
No. Year Tournament Match Round Winner
1 2006 Hong Kong Open Super Series Final Lin
2 2007 Sudirman Cup BWF tournaments Group stage Lee
3 2007 China Masters Super Series Semi-finals Lin
4 2007 Japan Open Super Series Semi-finals Lee
5 2007 Hong Kong Open Super Series Final Lin
6 2008 Swiss Open Super Series Final Lin
7 2008 Thomas Cup BWF tournaments Semi-finals Lee
8 2008 Olympic Games Multi-sport events Final Lin
9 2008 China Open Super Series Final Lin
10 2009 All England Open Super Series Final Lin
11 2009 Swiss Open Super Series Final Lee
12 2009 Sudirman Cup BWF tournaments Semi-finals Lin
13 2010 Thomas Cup BWF tournaments Semi-finals Lin
14 2010 Japan Open Super Series Final Lee
15 2010 Asian Games Multi-sport events Final Lin
16 2011 All England Open Super Series Premier Final Lee
17 2011 BWF World Championships BWF tournaments Final Lin
18 2011 China Open Super Series Premier Semi-finals Lin
19 2012 Korea Open Super Series Premier Final Lee
20 2012 Olympic Games Multi-sport events Final Lin
21 2013 BWF World Championships BWF tournaments Final Lin
22 2014 Asian Games Multi-sport events Semi-finals Lin
23 2015 Japan Open Super Series Last 16 Lin
24 2015 China Open Super Series Premier Semi-finals Lee
25 2016 Badminton Asia Championships BAC tournaments Semi-finals Lee
26 2016 Olympic Games Multi-sport events Semi-finals Lee
27 2017 Malaysia Open Super Series Premier Final Lin
28 2017 Badminton Asia Championships BAC tournaments Semi-finals Lin
29 2018 All England Open Super 1000 Quarter-finals Lin
Table 3. Win-Loss comparison for all matches.
Table 3. Win-Loss comparison for all matches.
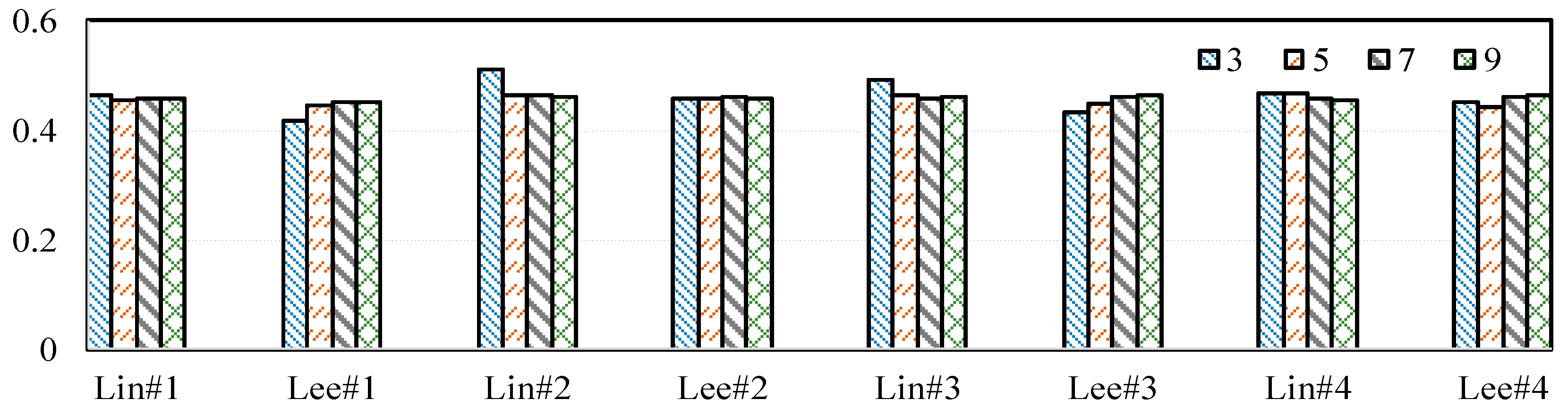
First 3 Beats First 5 Beats First 7 Beats First 9 Beats All Beats
Win Lose Win Lose Win Lose Win Lose Win Lose
Lin 122 114 487 550 830 984 906 1066 910 1071
Lee 102 119 433 539 769 925 841 999 846 1005
Win-Loss Ratio
Lin 0.517 0.47 0.458 0.459 0.459
Lee 0.462 0.445 0.454 0.457 0.457
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated