1. Introduction
With the enhancement of environmental protection awareness, electric vehicles have been widely used in many countries to alleviate global warming and energy crisis [
1,
2]. Typically, electric vehicles obtain electrical energy from the power grid through charging piles, especially direct current (DC) charging piles. Whereas, due to nonlinear components contained in the batteries of the electric vehicles and charging piles, the charging behavior of the electric vehicles, especially fast charging mode, brings a large number of harmonic and non-stationary signals, resulting in voltage and current distortion on the grid side of the charging piles, i.e. the voltage or current waveform is not standard sinusoidal [
3]. The non-sinusoidal waveform would seriously affect the accuracy of electricity metering, thus, the research on the power calculation for electric vehicles makes sense for fair trade between users and power companies, the generation, transmission, and operation of electricity.
For the power calculation under non-sinusoidal conditions, Budeanu [
4] and Fryze [
5] first proposed the definition of power quantities, commonly referred to as power theories, based on frequency-domain or time-domain analysis, respectively. After that, the definitions of various power components have been developed by many researchers [
6,
7,
8,
9,
10,
11]. Among these, IEEE Standard 1459-2010 [
12], as one of the most prominent power theories, provides definitions mainly based on Fourier-transform analysis. Although Fourier transform can provide the frequency information of analytical signals, it is only suitable to analyze the stationary and periodic signals due to the missing time-domain information. Commonly, harmonics, sudden changes, and non-stationary signals are generated during the charging processing of electric vehicles [
13]. For Fourier transform, it is not possible to extract the time-frequency information of non-stationary signals, thus it would bring large errors in power calculation.
To address the limitation of the Fourier transform, wavelet-related transforms, as one of the most widely used time-frequency analyses, have been applied to power calculation in non-sinusoidal environments. Discrete Wavelet Transform (DWT) is first applied to calculate the root mean square (RMS) and power values by decomposing the given signals into constituent frequency subbands [
14,
15]. According to the definition of IEEE Standard 1459-2010 [
12], the DWT was utilized to estimate the power components in a single system [
16] and a three-phase system [
17]. Further, for maintaining the temporal resolution of each decomposition level, Stationary Discrete Wavelet Transform (SDWT) without down-sampling was used for the power calculation [
18]. To achieve uniform frequency bandwidth for each subband, Discrete Wavelet Packet Transform (DWPT) [
19] or stationary DWPT [
20] were proposed for power calculation.
Although wavelet-related transforms can decompose the signals into frequency sub-bands through a filtering process, there is the issue of energy leakage [
21], i.e., the content of decomposed frequency sub-bands does not correspond to individual harmonics or special non-stationary signal components. If the sub-bands are used for the power calculation of individual harmonic components or special non-stationary signal components, the results cause inconsistencies from the real power. This limitation of wavelet-related transforms is not existed in adaptive chirp mode decomposition (ACMD). The ACMD extracts signal modes one by one with good adaptability and high time-frequency resolution, widely used in many fields [
22,
23,
24,
25]. However, the ACMD has not been applied for power calculation in the literature.
Thus, according to the definition of the IEEE Standard 1459-2010 [
12], this paper presents an ACMD-based method to calculate power-related quantities of the charging load of the electric vehicles through the charging piles, since the electric vehicles connect to the power grid through the charging piles. Based on a time-frequency represntation of the voltage and current using the ACMD method, the power-related quantities are calculated for the fundamental, harmonic, and non-stationary components, respectively. The proposed method is suitable for estimating harmonics or non-stationary components of voltage and current signals on the grid side of the charging piles, improving the representation of power-related quantities in non-stationary conditions.
mds
January 11, 2007
2. Proposed Method
This section first presents the general mathematical mode of the voltage and current signals, according to the principle of the charging piles of electric vehicles. And then, the ACMD method is introduced to decompose the voltage and current signals into each component. Finally, decomposed components are utilized to estimate the corresponding active power and the RMS value of the voltage and current signals for the electric vehicle charging load.
2.1. General Mathematical Mode of Charging Voltage and Current
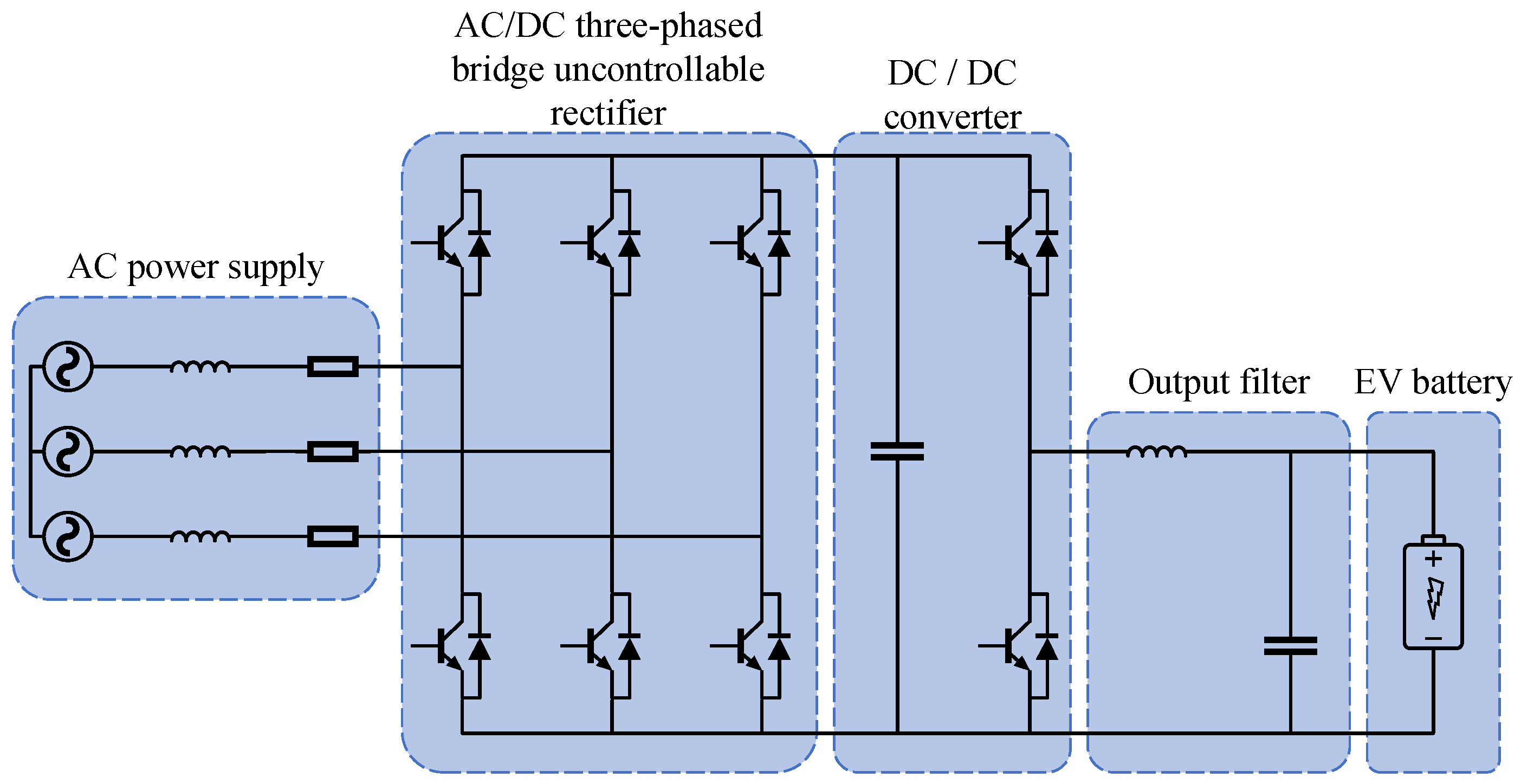
Due to the wide use of power electronic devices in the charging piles, the charging for the batteries of electric vehicles brings harmonic current and non-stationary signals to the power grid. The general structure of the charging piles is mainly composed of a rectifier circuit, a power converter, and an output filter circuit, as shown in
Figure 1. Alternating current (AC) power is rectified to DC power through a three-phase bridge uncontrollable rectifier circuit, and then provided for the DC/DC power converter to output the required DC of the electric vehicles. Finally, DC is filtered to charge the batteries of the electric vehicles.
Figure 1.
Topology of the Charging pile of electric vehicles.
Figure 1.
Topology of the Charging pile of electric vehicles.
More researches on the load characteristics of electric vehicles show that the voltage and current waveforms on the grid side of the charging piles, collected at charging stations [
13,
26], contain multiple harmonics and non-stationary signals. Typically, the current waveform mainly includes
order harmonics, and the amplitude of the harmonics gradually decreases with the increase of the harmonic order, which further can be confirmed in the simulation model in
Section 3.2.
Generally, the voltage and current on the grid side of the charging piles can be respectively expressed as
where (
,
,
) denote the fundamental, harmonic, and non-stationary components of voltage signal, respectively, and (
,
,
) denote the fundamental, harmonic, and non-stationary ones of current signal, respectively,
is the fundamental frequency in radian, (
,
,
,
) are initial phases of the fundamental voltage, the
h-th harmonic voltage, the fundamental current, the
h-th harmonic current, respectively.
To accurately calculate the charging power of charging piles for the electric vehicles, the ACMD is firstly applied to decompose the fundamental, harmonic, and non-stationary components from
and
in our work, and then the power-related quantities are calculated according to IEEE Standard 1459-2010 [
12].
2.2. ACMD-Based Power-Related Calculation
2.2.1. Adaptive Chirp Mode Decomposition (ACMD)
The ACMD, as a recursive mode decomposition technique, can adaptively extract signal components one by one using the matching pursuit method. For a nonstationary signal
with
m components, it can be modeled as
where
,
, and
denote the instantaneous amplitude, instantaneous frequency, and the initial phase of
i-th component, respectively. Based on the technique of frequency demodulation, a demodulation frequency
is introduced, and then Eq. (3) can be reformulated as
with
where
and
denote two demodulation operators, and
and
denote two demodulated signals with a phase difference of
. In particular,
and
become slowly varying baseband signals and have the narrowest bandwidth when
.
To extract the
i-th signal component
, the ACMD solve the minimization problem as follows
where
denotes
norm,
denotes the second derivative, two terms
and
are used as smoothness constraints for measuring bandwidth of the signal,
is the penalty factor, and the last term
denotes the residue energy after the currently estimated
i-th component is eliminated.
To implement ACMD decomposition in computer, the signal
is sampled st discrete time
, where
N is the number of samples. And then, the objective function of (6) can be written in a discrete form as
where
is a second-order difference matrix, given by
and
with
, where
denotes the diagonal matrix.
To solve the optimization problem in (7), an iterative algorithm is used to alternately update the demodulated signals
,
, and the frequency
. For the
m-th iteration, with the current frequency
, the solution of
and
are updated by setting
and
, given by
respectively, and then, the instantaneous frequency
is updated by
with
where
is a weighting factor, and
denotes the derivative.
Since the iterative algorithm requires the initial frequency
in advance, synchroextracting transform (SET) [
27] is adopted to estimate
in this study. The SET, as a novel postprocessing strategy of short-time Fourier transform, has the advantage of better energy concentration to provide good instantaneous initial frequency for iteration. The iterative process continues until there is little difference in the extracted signal component
in two adjacent iterations. After the signal component
is extracted from the raw signal, the residual signal is obtained by removing
from the raw signal, and then the iteration can be applied to the residual signal to extract the next signal component sequentially.
The above procedure is repeated for
M times, and the components of signal
are finally obtained as
where
denotes the residual signal after
M components are separated from the original signal. More details of the iteration algorithm can be found in [
28].
When the ACMD method is applied to the voltage and current signals of charging piles, the corresponding fundamental component, harmonic components, and non-stationary components are separated from each other, and then, the decomposed components are used to implement the calculation of the active power, the RMS values of the voltage and current.
2.2.2. Power Calculation
According to IEEE Standard 1459-2010 [
12], the active power (
P), the RMS values of the voltage (
U) and current (
I) are calculated as
respectively, where
and
are the start time and end time of measurements, respectively, and
is an integer multiple of the power system fundamental period.
Using
in (
1) and
in (2), the active power
P in (12) is expressed as
with
where
,
, and
are the fundamental, harmonic, and non-stationary active power, respectively;
,
,
,
,
, and
are the distortion active powers, generated by the different cross combinations from the fundamental/harmonic/non-stationary voltage and the fundamental/harmonic/non-stationary current, respectively.
Since
for
, we have
. And then,
,
,
, and
can be considered in statistics, although there are minor errors. Thus, according to the references [
26,
29], (
,
,
, and
) can be ignored, and then, the simplified calculation of the active power in (
15) is given by
i.e., the active power is the summation of the fundamental, harmonic, and non-stationary active power.
Accordingly, we calculate the RMS values of the voltage and current as
where (
,
, and
) are the RMS values of the fundamental, harmonic, and non-stationary voltage, respectively, and (
,
, and
) are the RMS values of the fundamental, harmonic, and non-stationary current, respectively.
In practice, the analog voltage and current are first digitalized and the continuous integration operation would be converted into the discrete ones. Thus, the active power (
,
, and
) in (17) can be calculated as
where (
,
) are the digitalized data of (
,
) at
n-th sampling index, respectively, and
N is the integration interval. Accordingly, the RMS values of the voltage and current in (18) can be calculated as
for the fundamental, harmonics and non-stationary components, respectively.
3. Experiments and Results
In this section, we evaluate the proposed ACMD-based estimation of RMS values and active power using synthetic signals and simulation tests. In the following experiments, the key parameters
and
of the ACMD method are set as
and
, respectively. The performance of the ACMD-based method is compared with the DWT-based method, since DWT is a time-frequency method widely used in signal analysis for power systems. The relative error of the estimated quantity is calculated as
where
is the reference value, and
is estimated value from ACMD or DWT method.
3.1. Non-Stationary Synthetic Signal
To demonstrate the performance of the ACMD method in signal decomposition and power-related estimation, three stationary waveforms, containing the fundamental and two harmonics, and one non-stationary component, are considered in synthetic signals of the voltage and current, expressed as
where the fundamental frequency is 50 Hz, the sampling frequency is 1500 Hz for discretizing
and
, and the time interval of the synthetic signal is 0.5 s in this experiment.
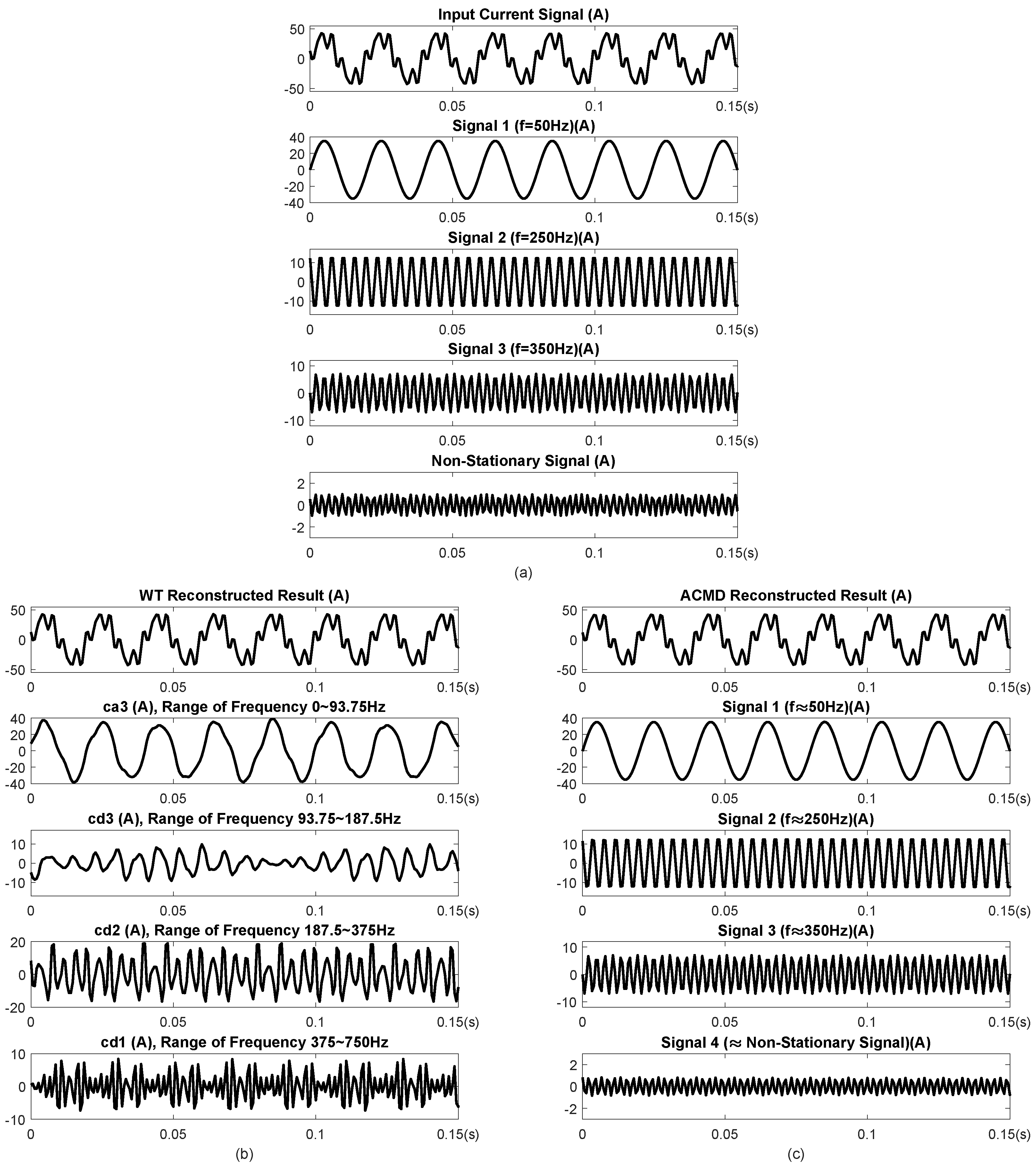
To visually evaluate the decomposition performance of ACMD and DWT methods, we show the resultant synthetic current waveform and each component in
Figure 2a as the ground-truth ones, based on (22). After the DWT with mother wavelet ’db4’ and ACMD methods are used to decompose the current
, the decomposed components and reconstructed signal are shown in
Figure 2b,c. According to the principle of the DWT method, the fundamental component can be extracted from three-level DWT decomposition, and its frequency is within that of the highest-level approximation coefficients, i.e., ca3 in
Figure 2b. From the decomposed results of the DWT method shown in
Figure 2b, we observe that there is a component that does not already exist in (22) within [93.75,187.5]Hz. In addition, the obtained components within [0, 93.75] Hz is not pure fundamental component as expected but mixed with the leakage components from other frequency ranges. Similar patterns exist in other frequency ranges. Whereas, the ACMD method obtains each component, more closely to the ground-truth ones, compared with the results from the DWT method.
Figure 2.
Current synthetic waveform and the corresponding decomposed results by using DWT and ACMD methods. (a) synthetic current and its components; (b) decomposed and reconstructed results of the DWT method, (c) decomposed and reconstructed results of the ACMD method.
Figure 2.
Current synthetic waveform and the corresponding decomposed results by using DWT and ACMD methods. (a) synthetic current and its components; (b) decomposed and reconstructed results of the DWT method, (c) decomposed and reconstructed results of the ACMD method.
The calculated quantities and relative errors (‰) of the fundamental, harmonics, and non-stationary components are shown in
Table 1, where the reference values are directly calculated from the analytic expressions in (22), agreeing with IEEE Standard 1459-2010. The estimated quantities for three-type components are calculated from the decomposed results from ACMD and DWT methods. The results in
Table 1 show that the DWT-based method causes small estimations for the fundamental and large ones for harmonics, especially for non-stationary component, resulting in bring large estimated errors for each component, the main reason is its leakage issue as above mentioned. Whereas, compared with the DWT-based method, the ACMD-based method brings quantities closer to the reference values with fewer estimation errors.
Table 1.
Comparisons of estimated quantities of ACMD-based and DWT-based methods for synthetic signal.
Table 1.
Comparisons of estimated quantities of ACMD-based and DWT-based methods for synthetic signal.
| Quantity |
Reference values |
ACMD |
DWT |
| Symbols |
Parameters |
Analytical |
Value |
Error(‰) |
Value |
Error(‰) |
| U |
Voltage RMS (V) |
220.97 |
220.82 |
0.68 |
220.87 |
0.45 |
| I |
Current RMS (A) |
27.39 |
27.38 |
0.36 |
27.38 |
0.36 |
| P |
Active power (W) |
5625.86 |
5618.00 |
1.40 |
5602.85 |
4.09 |
|
Fundamental voltage RMS (V) |
220.00 |
219.85 |
0.68 |
217.96 |
9.27 |
|
Fundamental current RMS (A) |
25.00 |
24.98 |
0.80 |
24.80 |
8.00 |
|
Fundamental active power (W) |
5500.00 |
5492.78 |
1.31 |
5399.46 |
18.28 |
|
Harmonic voltage RMS (V) |
20.62 |
20.59 |
1.45 |
35.13 |
703.68 |
|
Harmonic current RMS (A) |
11.18 |
11.17 |
0.89 |
10.85 |
29.52 |
|
Harmonic active power (W) |
125.00 |
124.66 |
2.72 |
186.88 |
495.04 |
|
Non-stationary voltage RMS (V) |
1.31 |
1.07 |
183.21 |
6.46 |
3931.29 |
|
Non-stationary current RMS (A) |
0.66 |
0.53 |
196.96 |
4.14 |
5272.72 |
|
Non-stationary active power (W) |
0.86 |
0.57 |
337.21 |
16.52 |
18209.30 |
3.2. Simulation Signal
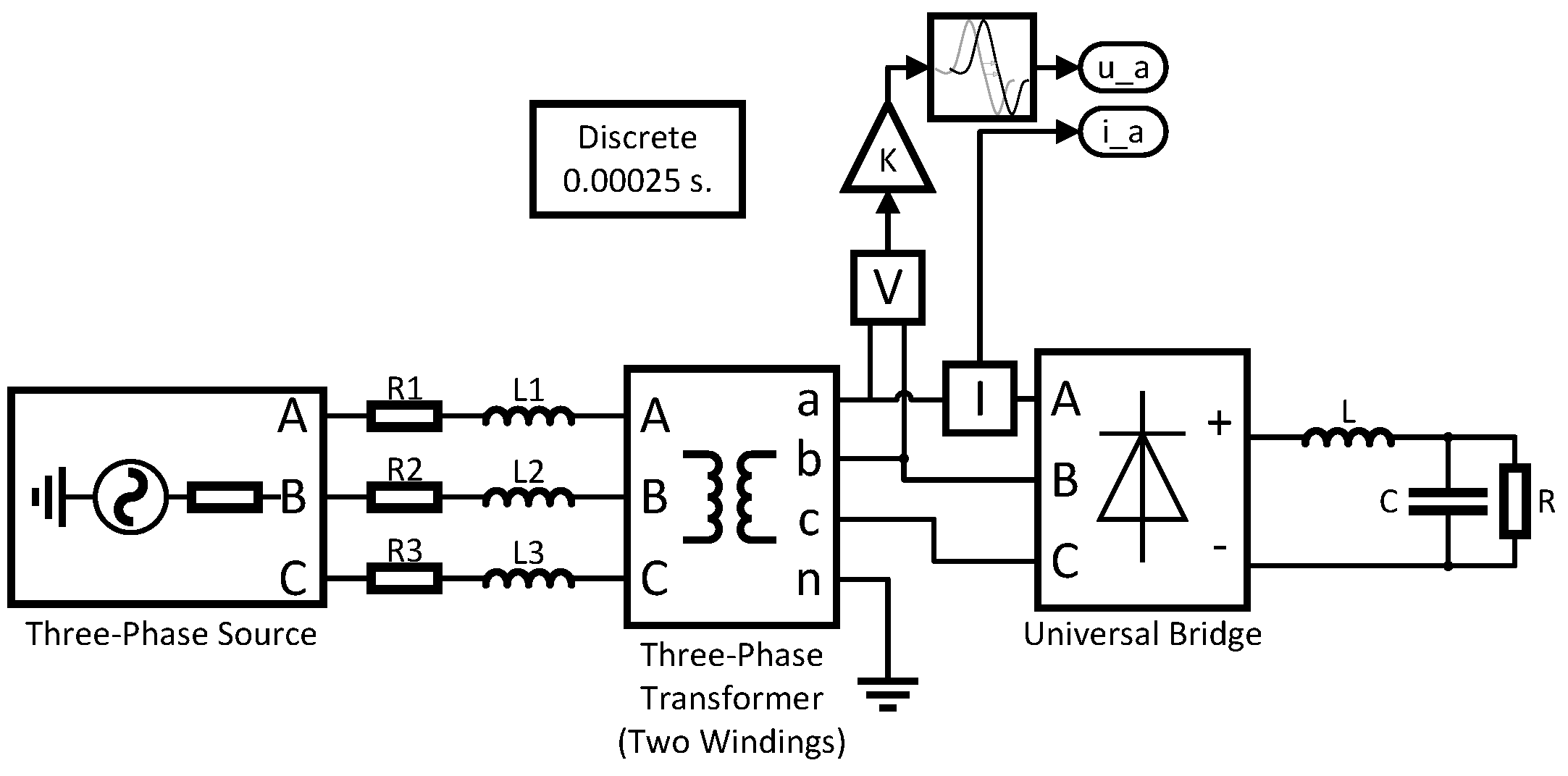
The performance of the proposed ACMD-based calculation method is further validated by using a simulation model in MATLAB/SIMULINK, as shown in
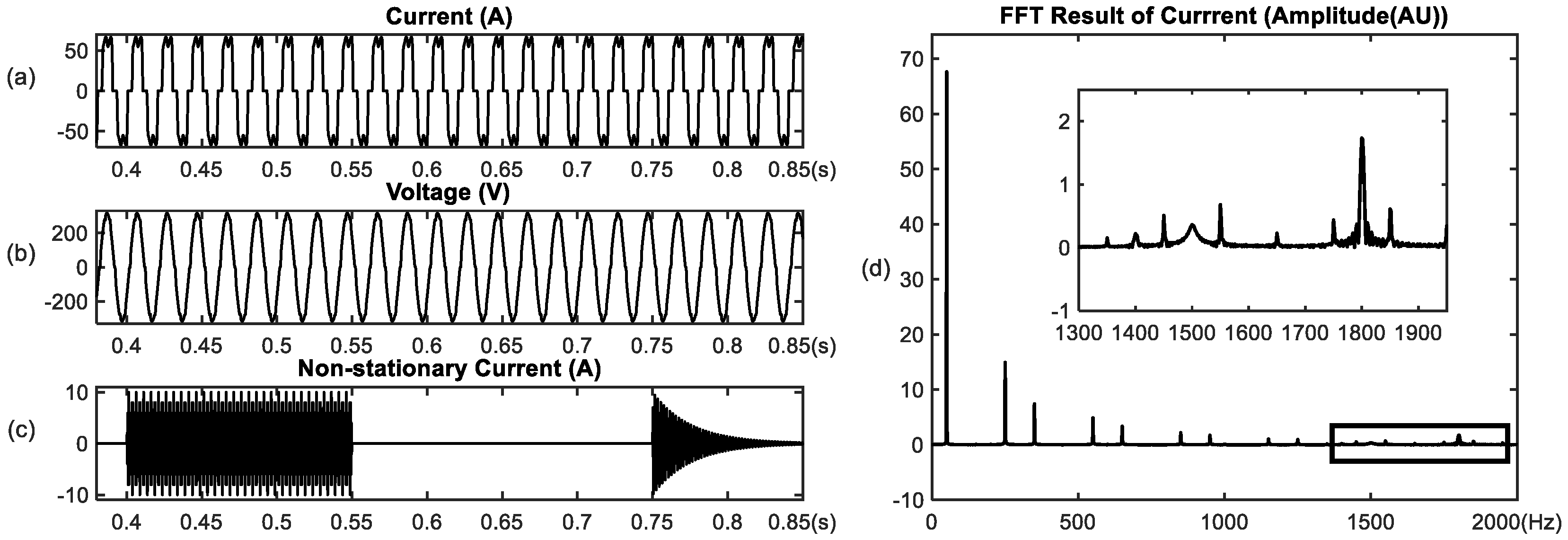
Figure 5. The current and voltage waveforms at the grid side of the charging pile are shown in
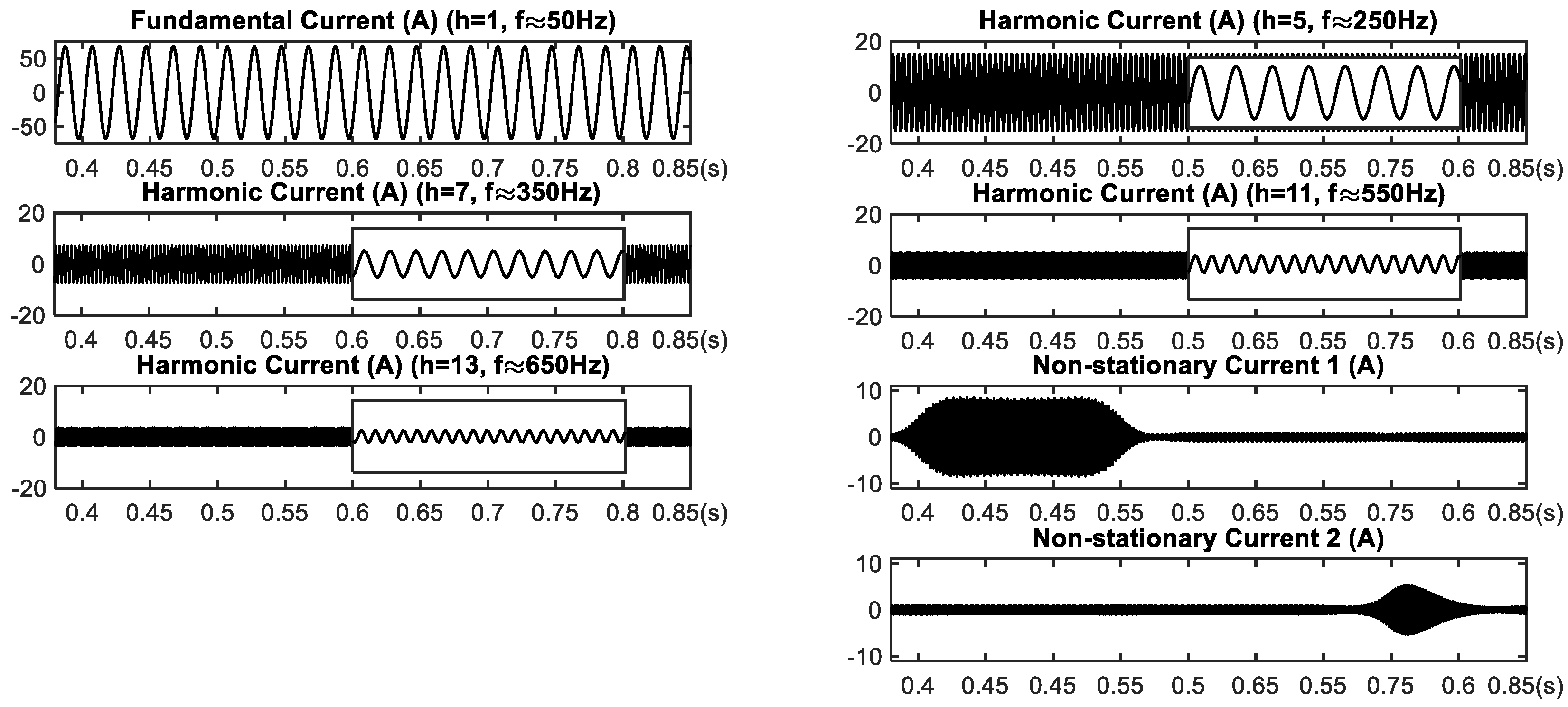
Figure 3a,b, respectively. From
Figure 3, we observe that the charging current is similar to a square wave, deviating from the standard sine signal, while the voltage contains fewer harmonics, closer to the sine signal. Further, considering there are non-linear elements in the charging piles of electric vehicles, the non-stationary signals are introduced to the current and voltage for realistically simulating the charging characteristics of electric vehicles. In this experiment, sawtooth impulse and high-frequency attenuation signals are used for the non-stationary signals
and
, expressed as
and
respectively.
Figure 3c shows the waveform of
. To observe the components of current, the spectrum of the current
is shown in
Figure 3d, which demonstrates that
order harmonics with successively attenuated amplitude appear on the corresponding spectral bins beside the fundamental, and the non-stationary signals appear on multiple high-frequency ranges, as shown in the enlarged drawing.
Figure 3.
Waveform generated from simulation model and the spectrum of current. (a) current; (b) voltage; (c) non-stationary ; (d) the spectrum of the current.
Figure 3.
Waveform generated from simulation model and the spectrum of current. (a) current; (b) voltage; (c) non-stationary ; (d) the spectrum of the current.
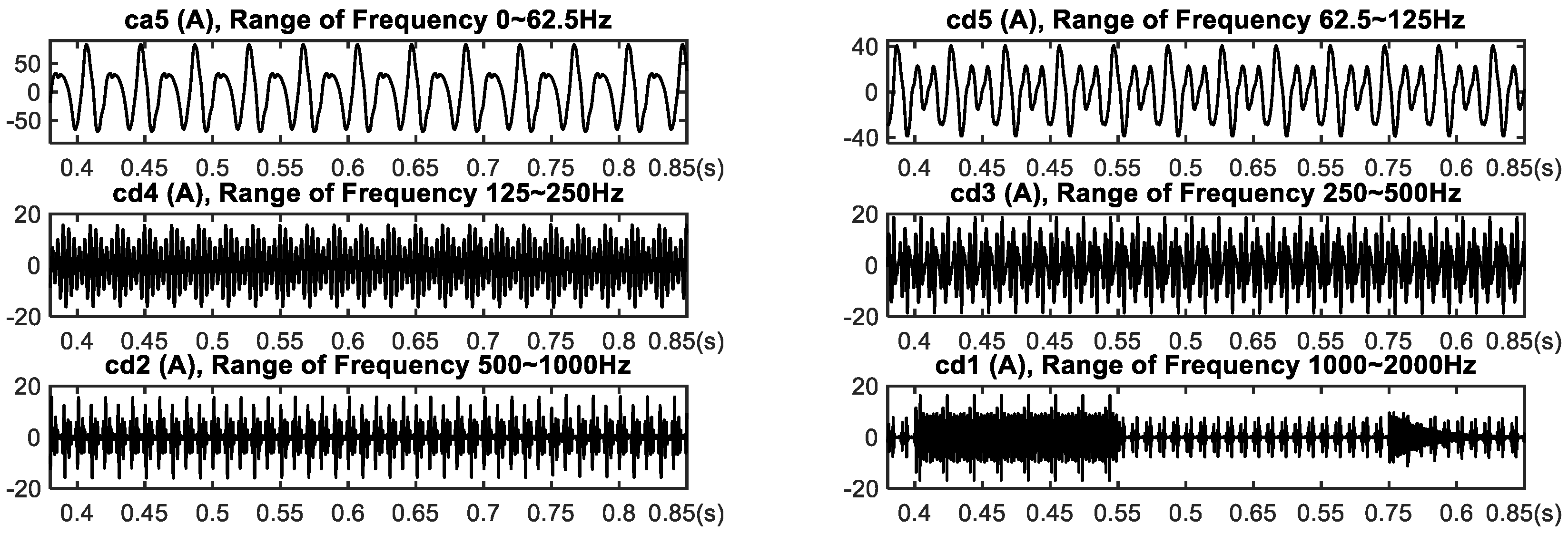
The sampling frequency is 4000 Hz in this experiment, and five-level DWT decomposition with the mother wavelet ’db4’ is applied on current and voltage, making that the highest-level frequency range corresponds to that of the fundamental component (i.e., ca5).
Figure 4 shows the decomposed results of the current. From the decomposed fundamental and non-stationary components, it is easy to discern that both of them are mixed with other frequency components. Meanwhile, the ACMD method is utilized for current and voltage, and the decomposed results for the current are shown in
Figure 6. Since the ACMD method performs decomposition recursively, two non-stationary signals are extracted separately, and close to the raw waveform in the views of waveform trend and occurrence interval. For harmonics, parts of waveform within black windows are enlarged and displayed in small attached windows for comparison. Compared with the results from the DWT method in
Figure 4, the decomposed components from the ACMD method in
Figure 6 more agree with the real ones.
Figure 4.
Decomposed results by using DWT method for current.
Figure 4.
Decomposed results by using DWT method for current.
Figure 5.
Simulation model in MATLAB/SIMULINK.
Figure 5.
Simulation model in MATLAB/SIMULINK.
Figure 6.
Decomposed results by using ACMD method for current.
Figure 6.
Decomposed results by using ACMD method for current.
Using the decomposed components from DWT and ACMD methods, the RMS values, active power, and relative error (‰) for three components are calculated and shown in
Table 2. Since the real value for each component can not be calculated directly as the case of synthetic signals done, the RMS values of the fundamental and harmonics are calculated from the corresponding information of spectral magnitude, while the quantities of the non-stationary component are calculated according to
and
in (24) and (25). Similar to the comparison results for synthetic signals, the ACMD-based method achieves better estimation for each component and total active power for simulation data, compared with the DWT-based method.
Table 2.
Comparisons of estimated quantities of ACMD-based and DWT-based methods for simulation signals in MATLAB/SIMULINK.
Table 2.
Comparisons of estimated quantities of ACMD-based and DWT-based methods for simulation signals in MATLAB/SIMULINK.
| Quantity |
Reference values |
ACMD |
DWT |
| Symbols |
Parameters |
Analytical |
Value |
Error(‰) |
Value |
Error(‰) |
| U |
Voltage RMS (V) |
224.76 |
224.77 |
0.04 |
223.88 |
3.92 |
| I |
Current RMS (A) |
49.54 |
49.62 |
1.61 |
49.49 |
1.01 |
| P |
Active power (W) |
10756.46 |
10749.33 |
0.66 |
10659.48 |
9.02 |
|
Fundamental voltage RMS (V) |
224.41 |
224.46 |
0.22 |
200.07 |
108.46 |
|
Fundamental current RMS (A) |
47.8200 |
47.83 |
0.21 |
42.74 |
106.23 |
|
Fundamental active power (W) |
10686.11 |
10691.48 |
0.50 |
8512.89 |
203.36 |
|
Harmonic voltage RMS (V) |
10.49 |
10.75 |
24.78 |
100.39 |
8570.06 |
|
Harmonic current RMS (A) |
12.60 |
12.74 |
11.11 |
24.69 |
959.52 |
|
Harmonic active power (W) |
48.48 |
51.07 |
53.42 |
2139.69 |
43135.52 |
|
Non-stationary voltage RMS (V) |
2.28 |
2.47 |
83.33 |
3.78 |
657.89 |
|
Non-stationary current RMS (A) |
2.86 |
2.82 |
13.98 |
3.69 |
290.21 |
|
Non-stationary active power (W) |
6.54 |
5.79 |
114.48 |
6.89 |
53.45 |
4. Conclusions
In this paper, a new approach based on the ACMD method was proposed to estimate the power-related quantities for electric vehicle charging load, according to the definition in the IEEE Standard 1459-2010 in the time-frequency domain. The current and voltage on the grid side of the charging piles were decomposed into the fundamental correctly, harmonic, and non-stationary components through the ACMD method. With the decomposed components, the active power and the RMS values were calculated for each component and the overall. Compared with the DWT-based method, the proposed ACMD-based method achieved better estimation of power-related quantities for the electric vehicle charging load with significantly fewer estimation errors, especially for the harmonics and non-stationary components. To further explore the advantage of the ACMD method for more applications in power system, our future works will focus on power-related estimation of three-phase systems or other electric devices (e.g., power transformer) for abnormality detection, fault diagnosis, etc.
Author Contributions
Conceptualization, Ding. H. L. and Tian. R.; methodology, Ding. H. L. and Yang. X. M.; validation, Tian. R.; investigation, Tian. R.; writing—original draft preparation, Ding. H. L. and Wang. J. F.; writing—review and editing, Yang. X. M.; visualization, Wang. J. F.; All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Technology Research Project of Ningxia Electric Power Co., Ltd. National Grid of China, "Research on the Influence of Electric Vehicle Charging Load on the Accuracy of Electric Energy Measurement"(SGTYHT/21-JS, SGNXYX002JJS2200153)
Abbreviations
The following abbreviations are used in this manuscript:
| P |
Active power |
| U |
RMS value of the voltage |
| I |
RMS value of the current |
|
and
|
Voltage and current on the grid side of the charging piles, respectively |
|
and
|
Fundamental voltage and current, respectively |
|
and
|
h-th harmonic voltage and current, respectively |
|
and
|
Non-stationary voltage and current, respectively |
|
, , and
|
Fundamental, harmoinc, and non-stationary active power, respectively |
|
, , and
|
RMS values of the fundamental, harmoinc, and non-stationary voltage, respectively |
|
, , and
|
RMS values of the fundamental, harmoinc, and non-stationary current, respectively |
References
- Zhao, H.; Wang, L.; Chen, Z.; He, X. Challenges of Fast Charging for Electric Vehicles and the Role of Red Phosphorous as Anode Material: Review. Energies 2019, 12. [Google Scholar] [CrossRef]
- Liu, S.; He, K.; Pan, X.; Hu, Y. Review of Development Trend of Transportation Energy System and Energy Usages in China Considering Influences of Intelligent Technologies. Energies 2023, 16. [Google Scholar] [CrossRef]
- Ding, X.; Shi, H.; Wang, Y.; Zhuang, Y.; Yuan, G.; Zhu, S. Research on Harmonic Management of Single-Phase AC Charging Pile Based on Active Filtering. Energies 2023, 16. [Google Scholar] [CrossRef]
- Budeanu, C. Reactive and fictitious powers. Rumanian National Institute 1927. [Google Scholar]
- Fryze, S. Active, reactive and apparent power in circuts with nonsinusoidal voltages and currents. Przglad Elektro. 1931, 1, 193–203. [Google Scholar]
- Miyasaka, G. and Silvério, E. and Xavier, G. and da Silva, H. and Braz, L. and Oliveira, R. and Lima, R. and Macedo, J.. Analysis of Reactive Energy Measurement Methods Under Non-Sinusoidal Conditions. IEEE Latin America Transactions, 2018, 16, 2521–2529. [Google Scholar] [CrossRef]
- Pajic, S. and Emanuel, A.E.. Modern apparent power definitions: theoretical versus practical Approach-the general case. IEEE Transactions on Power Delivery, 2006, 21, 1787–1792. [Google Scholar] [CrossRef]
- George, S. and Agarwal, V.. A novel, DSP based algorithm for optimizing the harmonics and reactive power under non-sinusoidal supply voltage conditions. IEEE Transactions on Power Delivery 2005, 20, 2526–2534. [Google Scholar] [CrossRef]
- oelho, Rodrigo de Almeida and Brito, Núbia Silva Dantas. Power Measurement Using Stockwell Transform. IEEE Transactions on Power Delivery, 2021, 36, 3091–3100. [CrossRef]
- Ferrero, A.; Superti-Furga, G. A new approach to the definition of power components in three-phase systems under nonsinusoidal conditions. IEEE Transactions on Instrumentation and Measurement 1991, 40, 568–577. [Google Scholar] [CrossRef]
- Peng, F.Z.; Lai, J.S. Generalized instantaneous reactive power theory for three-phase power systems. IEEE Transactions on Instrumentation and Measurement 1996, 45, 293–297. [Google Scholar] [CrossRef]
- IEEE Standard Definitions for the Measurement of Electric Power Quantities Under Sinusoidal, Nonsinusoidal, Balanced, or Unbalanced Conditions. IEEE Std 1459-2010 (Revision of IEEE Std 1459-2000) 2010, pp. 1–50.
- Liu, J.; Xu, Q.; Tian, Z.; Guo, Y.; Qi, S.; Wang, L. Feature Extraction Method for DC Charging Signal of Electric Vehicle. 3RD ANNUAL INTERNATIONAL CONFERENCE ON INFORMATION SYSTEM AND ARTIFICIAL INTELLIGENCE (ISAI2018).
- Yoon, W.K.; Devaney, M. Power measurement using the wavelet transform. IEEE Transactions on Instrumentation and Measurement 1998, 47, 1205–1210. [Google Scholar] [CrossRef]
- Yoon, W.K.; Devaney, M. Reactive power measurement using the wavelet transform. IEEE Transactions on Instrumentation and Measurement 2000, 49, 246–252. [Google Scholar] [CrossRef]
- Morsi, W.G.; El-Hawary, M.E. Reformulating Power Components Definitions Contained in the IEEE Standard 1459-2000 Using Discrete Wavelet Transform. IEEE Transactions on Power Delivery 2007, 22, 1910–1916. [Google Scholar] [CrossRef]
- Morsi, W.G.; El-Hawary, M.E. Reformulating Three-Phase Power Components Definitions Contained in the IEEE Standard 1459-2000 Using Discrete Wavelet Transform. IEEE Transactions on Power Delivery 2007, 22, 1917–1925. [Google Scholar] [CrossRef]
- Morsi, W.; El-Hawary, M. A new perspective for the IEEE standard 1459-2000 via stationary wavelet transform in the presence of nonstationary power quality disturbance. 2009 IEEE Power & Energy Society General Meeting, 2009, pp. 1–1.
- Osipov, Dmitry S. and Dolgikh, Nadezda N. and Goryunov, Vladimir N. and Kovalenko, Dmitry V.. Algorithms of packet wavelet transform for power determination under nonsinusoidal modes. 2016 Dynamics of Systems, Mechanisms and Machines (Dynamics), 2016, pp. 1–5.
- D. K. Alves, F. B. Costa, R.L.d.A.R.C.M.d.S.N.; de Oliveira Alves Rocha, T. Real-Time Power Measurement Using the Maximal Overlap Discrete Wavelet-Packet Transform. IEEE Transactions on Industrial Electronics 2017, 64, 3177–3187. [CrossRef]
- Peng, Z.K.; Jackson, M.R.; Rongong, J.A.; Chu, F.L.; Parkin, R.M. On The Energy Leakage Of Discrete Wavelet Transform. Mechanical systems and signal processing 2009, 23, 330–343. [Google Scholar] [CrossRef]
- Wang, X.; Tang, G.; Yan, X.; He, Y.; Zhang, X.; Zhang, C. Fault Diagnosis of Wind Turbine Bearing Based on Optimized Adaptive Chirp Mode Decomposition. IEEE Sensors Journal 2021, 21, 13649–13666. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Z.; Kong, Y.; Li, C. Mutual Interference Suppression Using Signal Separation and Adaptive Mode Decomposition in Noncontact Vital Sign Measurements. IEEE Transactions on Instrumentation and Measurement 2022, 71, 1–15. [Google Scholar] [CrossRef]
- Wang, H.; Chen, S.; Zhai, W. Data-driven adaptive chirp mode decomposition with application to machine fault diagnosis under non-stationary conditions. Mechanical Systems and Signal Processing 2023, 188, 109997. [Google Scholar] [CrossRef]
- Ding, C.; Wang, B. Sparsity-assisted adaptive chirp mode decomposition and its application in rub-impact fault detection. Measurement 2022, 188, 110539. [Google Scholar] [CrossRef]
- Qi, S.r. Research on the Influence of Electrical Vehicle Charging Load on Electric Energy Measurement Accuracy. Master’s thesis, Southeast University, China, 2019. [Google Scholar]
- Yu, G.; Yu, M.; Xu, C. Synchroextracting Transform. IEEE Transactions on Industrial Electronics 2017, 64, 8042–8054. [Google Scholar] [CrossRef]
- Chen, S.; Yang, Y.; Peng, Z.; Dong, X.; Zhang, W.; Meng, G. Adaptive chirp mode pursuit: Algorithm and applications. Mechanical Systems & Signal Processing 2019, 116, 566–584. [Google Scholar]
- Tong, T.; Ni, W.; Gu, D.; Cao, Y.; Yang, W. Study on the method of electric energy measurement for unsteady signal. The 16th IET International Conference on AC and DC Power Transmission (ACDC 2020), 2020, Vol. 2020, pp. 1634–1640.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).