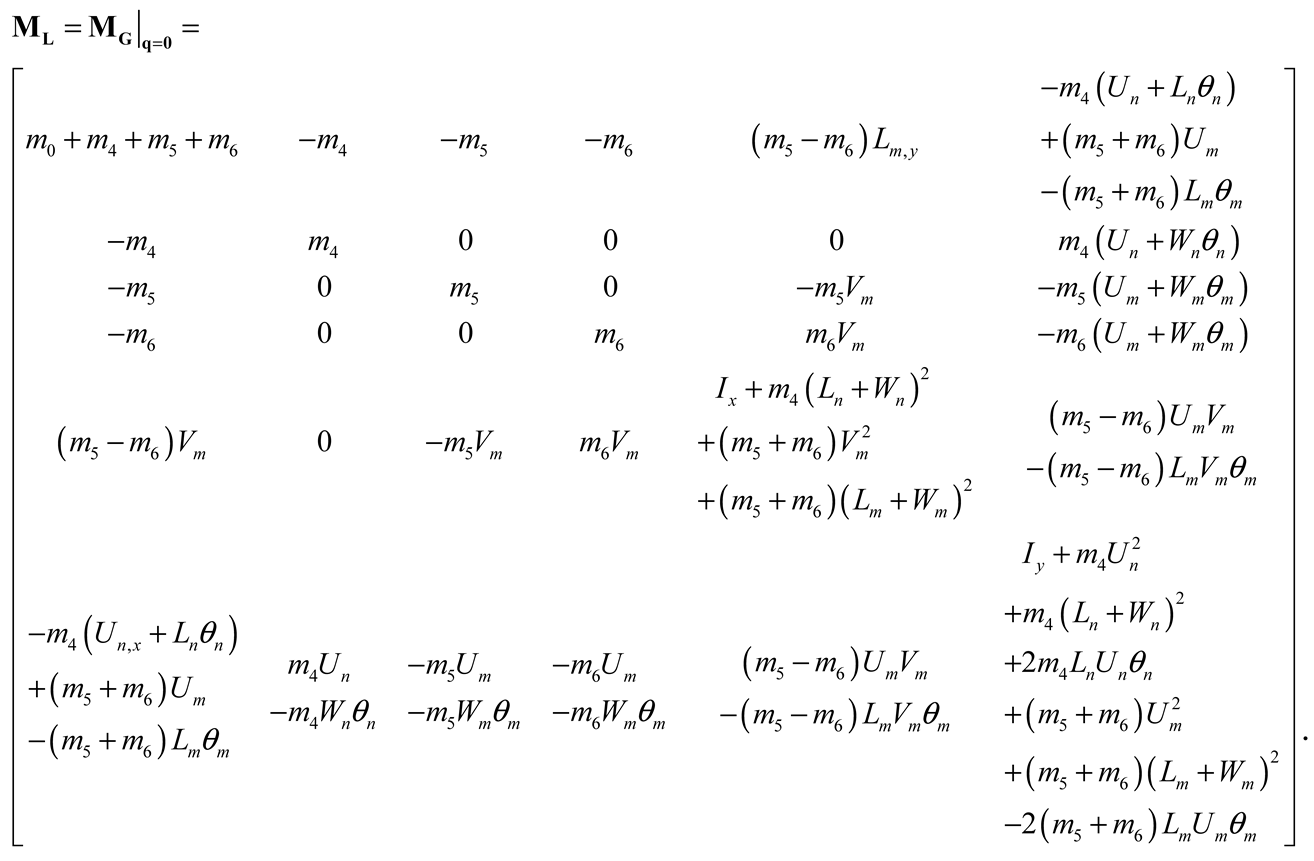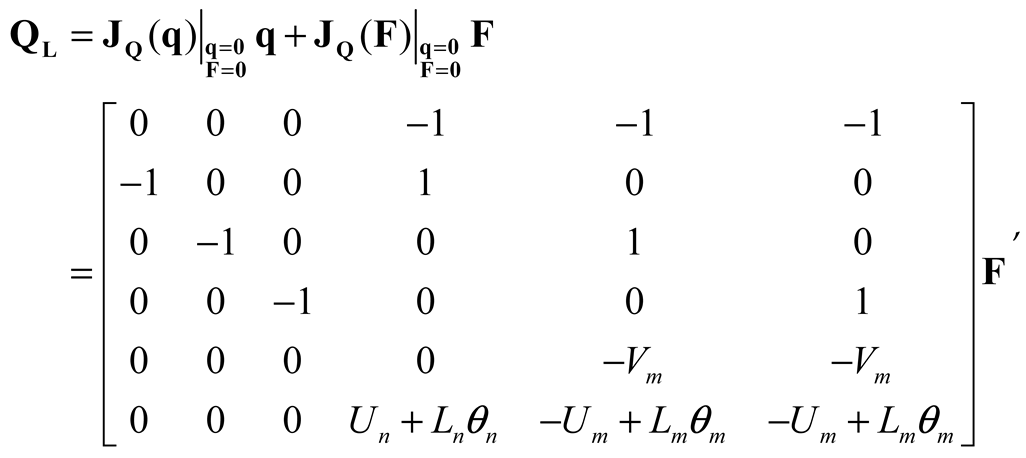Linear and Nonlinear Models for Drop Simulation of Aircraft Landing Gear System with MR Dampers

Preprint

Article

Linear and Nonlinear Models for Drop Simulation of Aircraft Landing Gear System with MR Dampers

Altmetrics

Downloads

204

Views

Comments

A peer-reviewed article of this preprint also exists.

Byung-Hyuk Kang

Bang-Hyun Jo,Bo-Gyu Kim,

Jai-Hyuk Hwang^*

Seung-Bok Choi^*

Byung-Hyuk Kang

Bang-Hyun Jo,Bo-Gyu Kim,

Jai-Hyuk Hwang^*

Seung-Bok Choi^*

This version is not peer-reviewed

Submitted:

24 May 2023

Posted:

25 May 2023

You are already at the latest version

Alerts

Abstract

In this study, the focus is on the drop test simulation of an MR (Magnetorheological) damper-based main landing gear (MRMLG), aiming to explore multi-degree-of-freedom (DOF) dynamic models during aircraft landing. Three different 6-DOF dynamic models are proposed in this work and their drop performances are compared with results achieved one of commercial softwares. The proposed models include a nonlinear aircraft model (NLAM), a linearized approximated aircraft model (LAAM) linearizing from the nonlinear equations of motion in NLAM, and a fully approximated aircraft model (FAAM) which linearizes the MRMLG's strut force model. In order to evaluate drop performance of the aircraft landing gear system with MR dampers, a 7-DOF aircraft model incorporating the nonlinear MRMLG is formulated using RecurDyn. The principal comparative param-eters are the coefficient of determination (R2) for system response of each model with Re-curDyn model and root mean square error (RMSE) which is the ensembles of CG dis-placement data for each model. In addition, the ensemble of time series data is created for diverse drop scenarios, providing valuable insights into the performance of the proposed drop test models of the aircraft landing gear system featuring MR dampers.

Keywords:

Subject: Engineering - Aerospace Engineering

1. Introduction

Drop simulation and test play a key role in the design and evaluation of aerospace landing systems [1]. Accurately predicting the behavior of the landing gear under various conditions is essential for ensuring the safety and reliability of aircraft operations [2]. Numerical modeling using computational tools has become an indispensable process in this domain, offering a cost-effective and efficient means of studying complex dynamic systems [3,4]. As aircraft technology continues to advance, there is a growing demand for more sophisticated landing gear systems that can adapt to varying landing conditions and provide precise attitude control. One promising approach is the use of magnetorheological (MR) dampers in the main landing gear to enhance their performance [5,6,7]. The MR main landing gear(MRMLG), equipped with MR dampers, offers the advantage of adjustable damping characteristics, allowing for real-time control of the landing gear response. This capability opens up new possibilities for improving landing gear behavior and enhancing aircraft safety [8,9,10]. However, to fully exploit the potential of MRMLG systems, accurate dynamic models are required to capture the complex interactions between the aircraft, landing gear, and control systems. In recent years, several modeling approaches have been developed to simulate the drop test behavior of landing gears. These approaches range from simplified analytical models to more sophisticated numerical methods that consider multiple degrees of freedom and various force components [11,12]. However, the accuracy and reliability of these models are critical factors in determining their suitability for practical applications.

The objective of this work is to develop and validate various 6-DOF dynamic models for MRMLG to enable precise dynamic drop motions during aircraft landings. We propose three different models: the Nonlinear Aircraft Model (NLAM), the Linear Approximated Aircraft Model (LAAM), and the Fully Approximated Aircraft Model (FAAM). These models are constructed based on the nonlinear equations of motion and linear approximations, considering the effect of MR dampers on the strut force. To validate the accuracy of the proposed models, RecurDyn is utilized which is known as a powerful multi-body analysis tool. A comprehensive comparison is made between the models and the RecurDyn model, considering evaluation metrics such as the coefficient of determination (R²) and root mean square error (RMSE). Additionally, an ensemble of time series data is created to analyze the performance of the models under various drop scenarios.

The outcomes of this research will contribute to the development of effective control strategies for MRMLG and also enhance the understanding of the behavior of landing gear during drop motions. The validation and analysis of NLAM, LAAM, and FAAM models will assist in selecting appropriate model for dynamic simulations which can provide accurate predictions of MRMLG performance. The findings in this work will be valuable in improving the design and implementation of MRMLG systems for enhanced aircraft landing perofemances. This research will also serve as a foundation for further advancements in modeling techniques and their application in aerospace engineering.

2. MRMLG Design and Drop Test

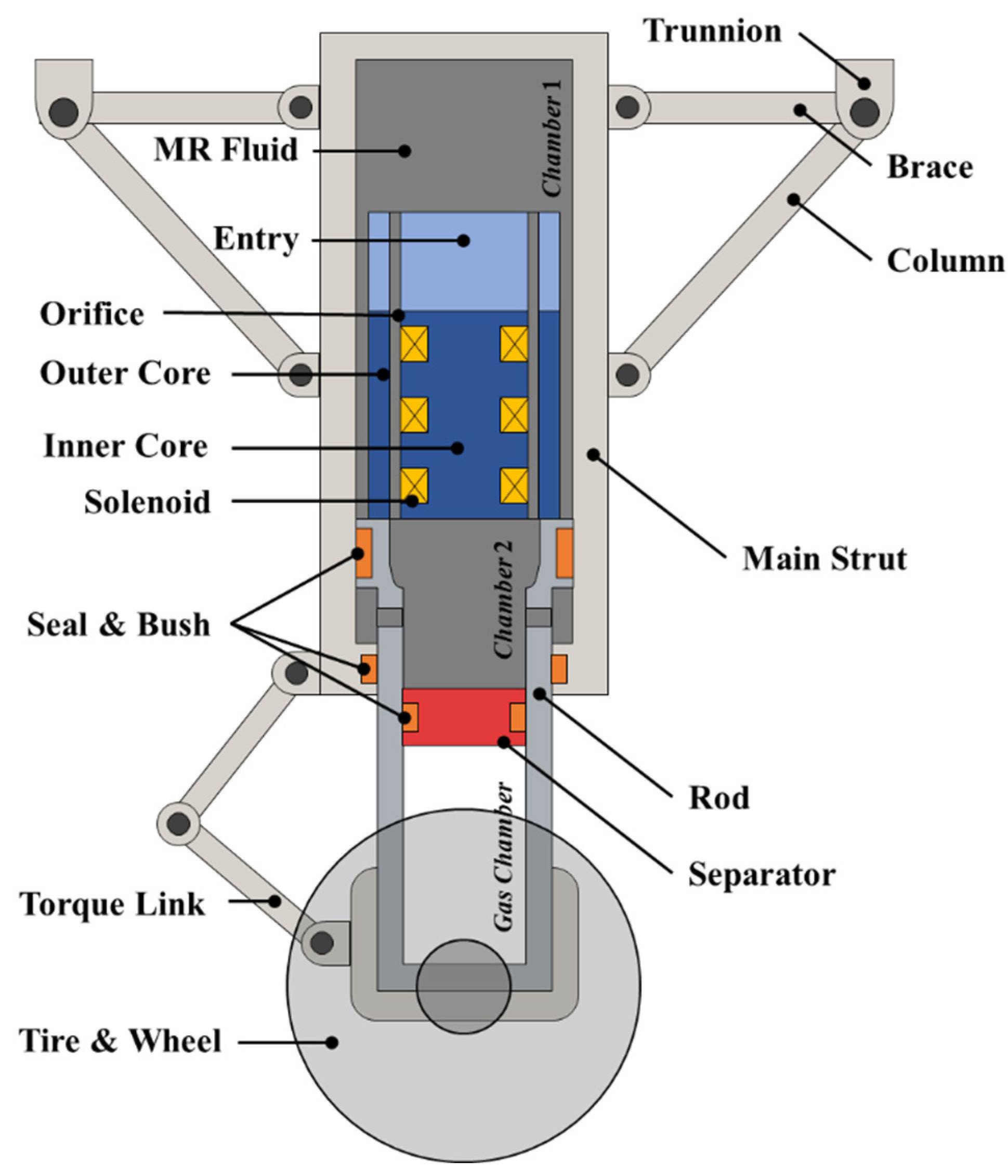
The MRMLG consists of the structure shown in Figure 1. Chambers consist of three sections; Chambers 1 and 2 and the orifice are filled with MR fluid, and the gas chamber is mainly filled with nitrogen gas. MR fluid can flow freely into chambers 1 and 2 through the orifice. The biggest feature of the MRMLG is that the flow resistance of the fluid can be controlled by the electromagnet around the orifice. The electromagnet consists of inner and outer cores. The solenoid is wound around the groove of the inner core. The orifice beside the electromagnet should be located in the fully developed region [10]. Therefore, the entry is installed on the top of the electromagnet to ensure the orifice corresponds to the entrance region. Chamber 2 and the gas chamber are separated by the separator. The gas in the gas chamber serves as a pneumatic spring that converts kinetic energy into elastic energy when the aircraft landing, creating a repulsive force depending on the stroke of the rod. Seals divide the chamber by suppressing the penetration of fluid, and Bushes mainly guarantee the linear motion of each part. The trunnion connects to the fuselage’s gearbox. During landing, most of the impact force acting on the runway transfer to the wheels and rods, and MR fluid dampens the force acting on the main strut. The braces and columns dissipate the forces acting on the fuselage so that the aircraft lands safely.

The strut force model of the MRMLG was derived in detail from previous studies, and the derived equation is as follows [10]:

F_{s} = F_{g a s} (s) + F_{h y d} (\dot{s}) + F_{m r} (\dot{s}, τ) + F_{c},

(1)

Where, Fs is the strut force, and F_gas, F_hyd, F_MR, and F_c are the pneumatic force, hydraulic force, field-dependent force, and Coulomb friction force, respectively. In this study, the Coulomb friction is ignored since it is very small compared to other forces. Each force can be calculated as:

F_{g a s} (s) = (P_{a t m} + P_{0}) A_{2} {(\frac{V_{0}}{V_{0} - A_{2} s})}^{γ} - P_{a t m} A_{2},

(2)

F_{h y d} (\dot{s}) = \frac{12 η l A_{1}}{b d^{3}} \dot{s} + K \frac{ρ A_{1}^{2}}{2 b^{2} d^{2}} {\dot{s}}^{2},

(3)

F_{m r} (\dot{s}, τ) = (2.07 + \frac{30 η A_{1} | \dot{s} |}{30 η A_{1} | \dot{s} | + b d^{2} | τ |}) \frac{l_{p}}{d} | τ | \tanh (\frac{\dot{s}}{ε}),

(4)

Where, P_atm is the atmospheric pressure; P₀ and V₀ are the initial gas pressure and volume; γ is the ratio of the specific heats; A₁ and A₂ are the inner diameter of the main strut and the outer diameter of the rod, respectively; η and ρ are the dynamic viscosity and density of the MR fluid; L, b, and d are the length, circumference, and gap, respectively; L_p is the total length of the electromagnet, except the solenoid length. K is the total sum of system losses caused by the turbulence of fluid around the orifice. K was calculated depending on the flow path gap size using computational fluid dynamics in previous work [13]. ε is a small positive value, used to adjust the rate of the hyperbolic tangent function, tanh.

s

and

\dot{s}

are the stroke and the velocity of the rod, respectively. τ is the yield stress, which is a function of the magnetic field intensity, and the yield stress characteristics are provided by the MR fluid manufacturer [14].

The MRMLG can be modeled as a two-degree-of-freedom (2-DOF) by imitating the drop test conditions. In general, the half weight of the fuselage is set as sprung mass, m_s, and the weight of the rod, electromagnet, tire, and wheel can be replaced by unsprung mass, m_u. The equations of motion for sprung and unsprung masses are:

{\ddot{z}}_{s} = g - F_{s} / m_{s},

(5)

{\ddot{z}}_{u} = g + F_{s} / m_{u} - F_{t} / m_{u},

(6)

Where, g is the gravitational acceleration, and

{\ddot{z}}_{s}

and

{\ddot{z}}_{u}

are the sprung and unsprung accelerations, respectively. F_t can be calculated in the tire force as:

F_{t} = (k_{t} z_{u} - k_{t} r) ℋ (z_{u} - r),

(7)

Where, k_t and r are the tire stiffness and ground displacement, respectively;

ℋ

is the Heaviside step function. The drop test is conducted under the condition of no ground displacement. To verify the model via the drop test, a drop simulation was performed numerically by building a 2-DOF model based on equations (5) and (6). The parameters used in the drop simulation are listed in Table 1.

The function of magnetic field intensity for the input current is obtained in the previous study through the ANSYS MAXWELL, electromagnetic analysis program [13]. Based on the determined parameters, the yield stress regarding the input current was calculated:

τ = 40.5 \tanh {(1.3 I)}^{1.8} .

(8)

The range of I in equation (8) is from 0 to 2 A and the units of τ and I are kPa and A, respectively. A drop test is performed to validate the MRMLG 2-DOF model. As a drop test condition, a current of 0 A to 2 A is applied to the MRMLG at a sink rate of 3.050 m/s just before the tire contacts the ground.

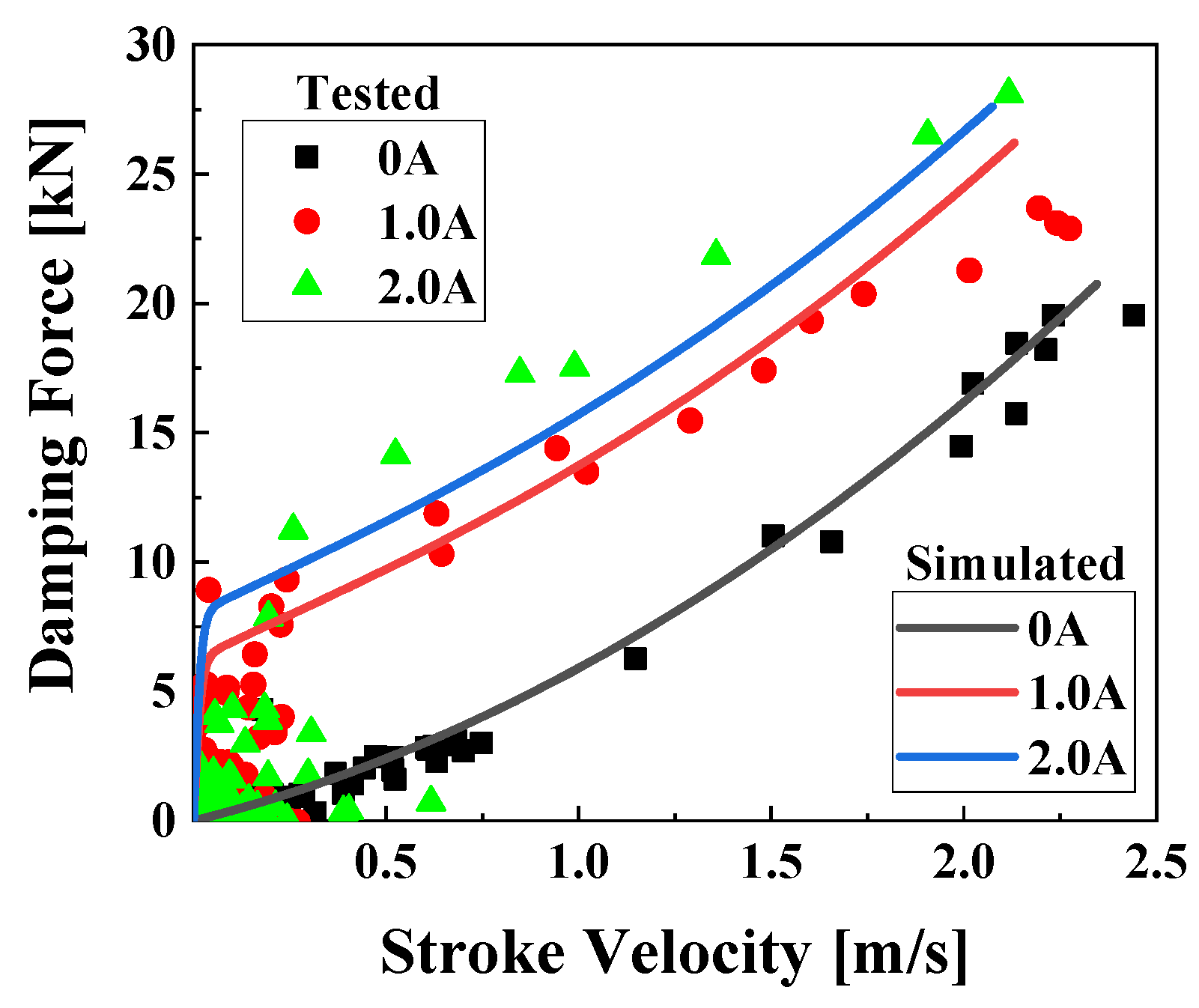
Figure 2 shows the simulation and test results of the strut force in relation to the stroke velocity. The solid line represents the simulation results, while the dots represent the test results. The measured strut force is obtained by using pressure sensors attached to chambers 1 and 2. The accuracy of the measurements and simulations is evaluated using the root mean square error (RMSE) and coefficient of determination (R²). RMSE is the square root of the mean square error of two datasets. R² measures the proportion of the variance in the dependent variable that can be explained by the independent variable, determined in the range of 0 to 1; As the value increases, the correlation between the two datasets increases. The hydraulic force model is relatively accurate when off-state since the RMSE and R² are 1.018 kN and 0.950. the RMSE and R² of 1 A are 2.179 kN and 0.844, showing some model error at high speeds. The test results of 2 A are higher than the predicted values in all velocity ranges, measured with the RMSE of 2.309 and R² of 0.746, respectively.

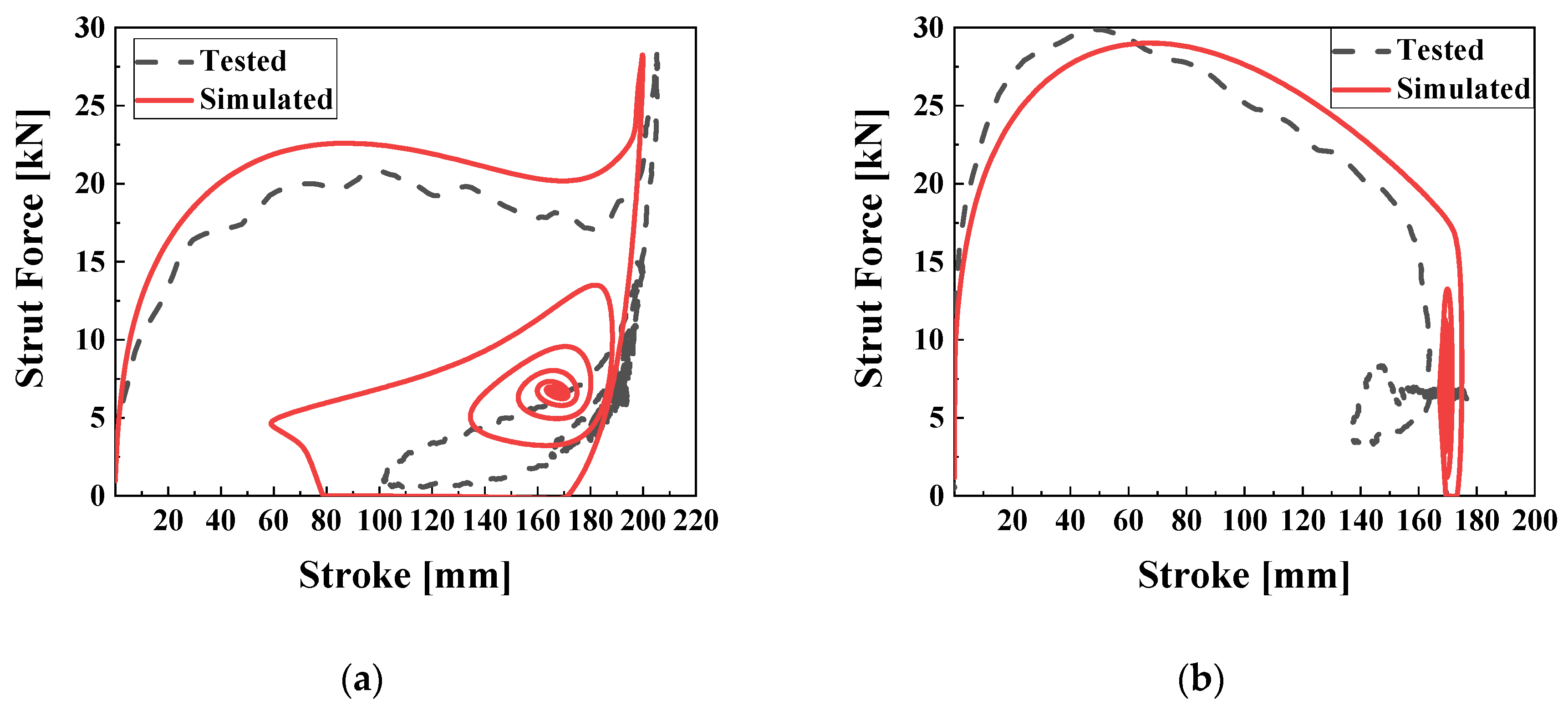
Figure 3 illustrates the spring-damping characteristics of MRMLG. Figure 3a shows the strut force exerted by the MRMLG as a function of stroke when a 0 A input current is applied. In the simulation, the maximum stroke and strut force are predicted to be 199.9 mm and 28.30 kN, respectively, while the actual measurements yield 205.6 mm and 28.24 kN. The equilibrium point in the simulation and test are determined to be 165.7 mm and 192.7 mm, respectively. The discrepancy in the equilibrium point can be attributed to the compression process of the gas chamber, which undergoes an adiabatic process during the initial impact but gradually releases heat to the surroundings, transitioning to an isothermal process over time. The RMSE values for stroke and strut force are 29.31 mm and 1.556 kN, respectively, with corresponding R² values of 0.738 and 0.889. Figure 3b describes the characteristics of 2 A input. The predicted and measured values for strut force are 29.01 kN and 29.97 kN, respectively, with corresponding stroke values of 174.9 mm and 176.53 mm. The RMSE and R² values for stroke are 10.56 mm and 0.792, respectively, while for strut force they are 2.003 kN and 0.768, respectively.

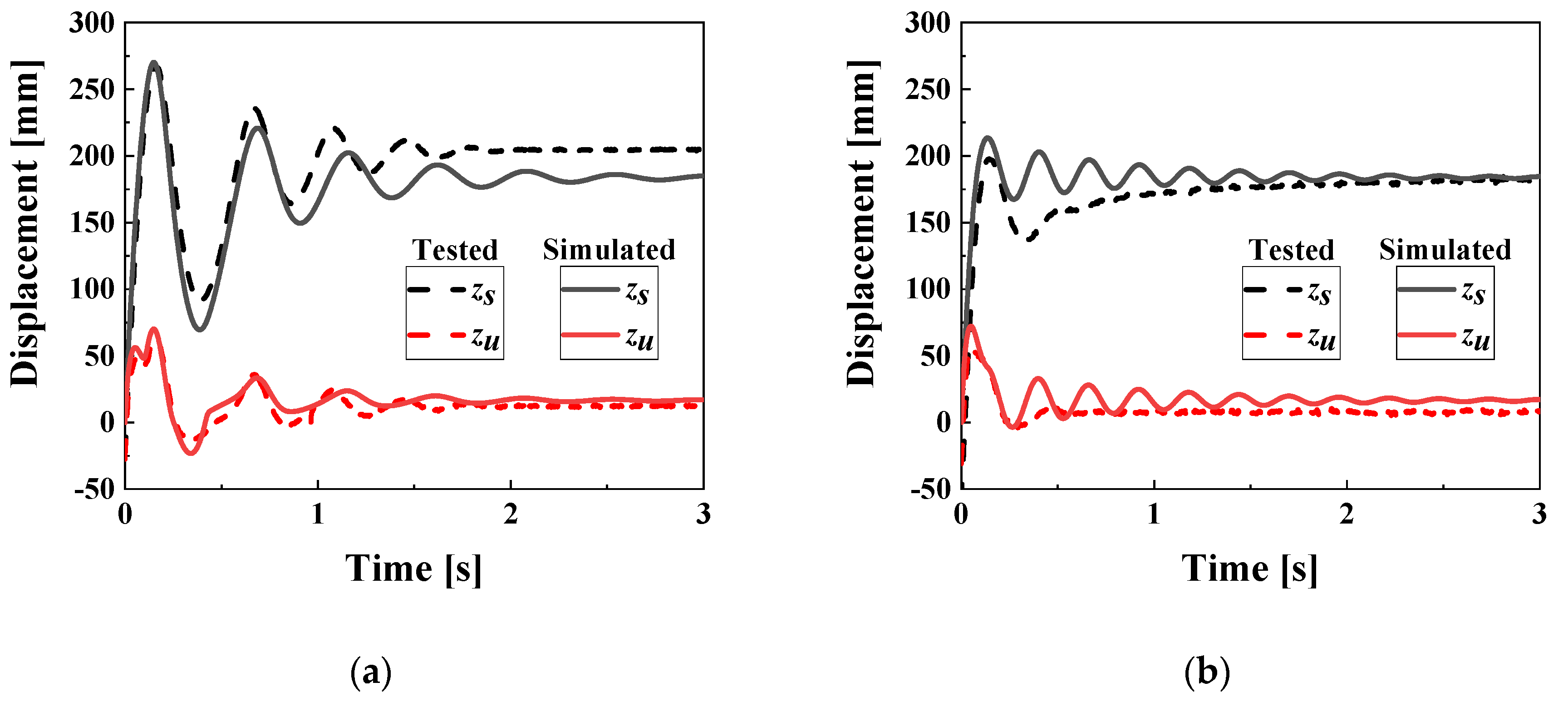
Figure 4 displays the predicted (solid line) and measured (dashed line) system response to an impact. (a) and (b) show the sprung displacement (z_u) and unsprung displacement (z_s) for 0 A and 2 A current inputs, respectively. For the off-state, the average values of z_s and z_u are predicted to be 176.1 mm and 17.50 mm, while the measured values are 193.3 mm and 13.25 mm, respectively. The predicted final values are 184.9 mm and 17.00 mm, whereas the measured final values are 11.65 mm and 204.0 mm. The RMSE values are 21.10 mm and 6.667 mm for z_s and z_u, respectively, with corresponding R² values of 0.890 and 0.851. For the on-state, the average value of z_s is 183.1 mm and 170.6 mm in simulation and test, with equilibrium points of 184.5 mm and 182.6 mm, respectively. The RMSE and R² values for z_s are 18.55 mm and 0.701. The predicted and measured average values for z_u are 18.29 mm and 9.182 mm, with final values of 17.29 mm and 8.621 mm, respectively. The RMSE and R² values for z_u are 10.78 mm and 0.693. In the simulation, the absence of friction leads to chattering in z_s and z_u, which is not observed in the actual measurements due to the presence of friction. As a result, R² is slightly lower than that of the off-state.

Figure 3. Strut force-stroke characteristics of MRMLG depending on the input current. (a) 0 A; (b) 2 A.

Figure 4. System response of MRMLG depending on the input current. (a) 0 A; (b) 2 A.

3. Nonlinear Model and Linear Approximation Model

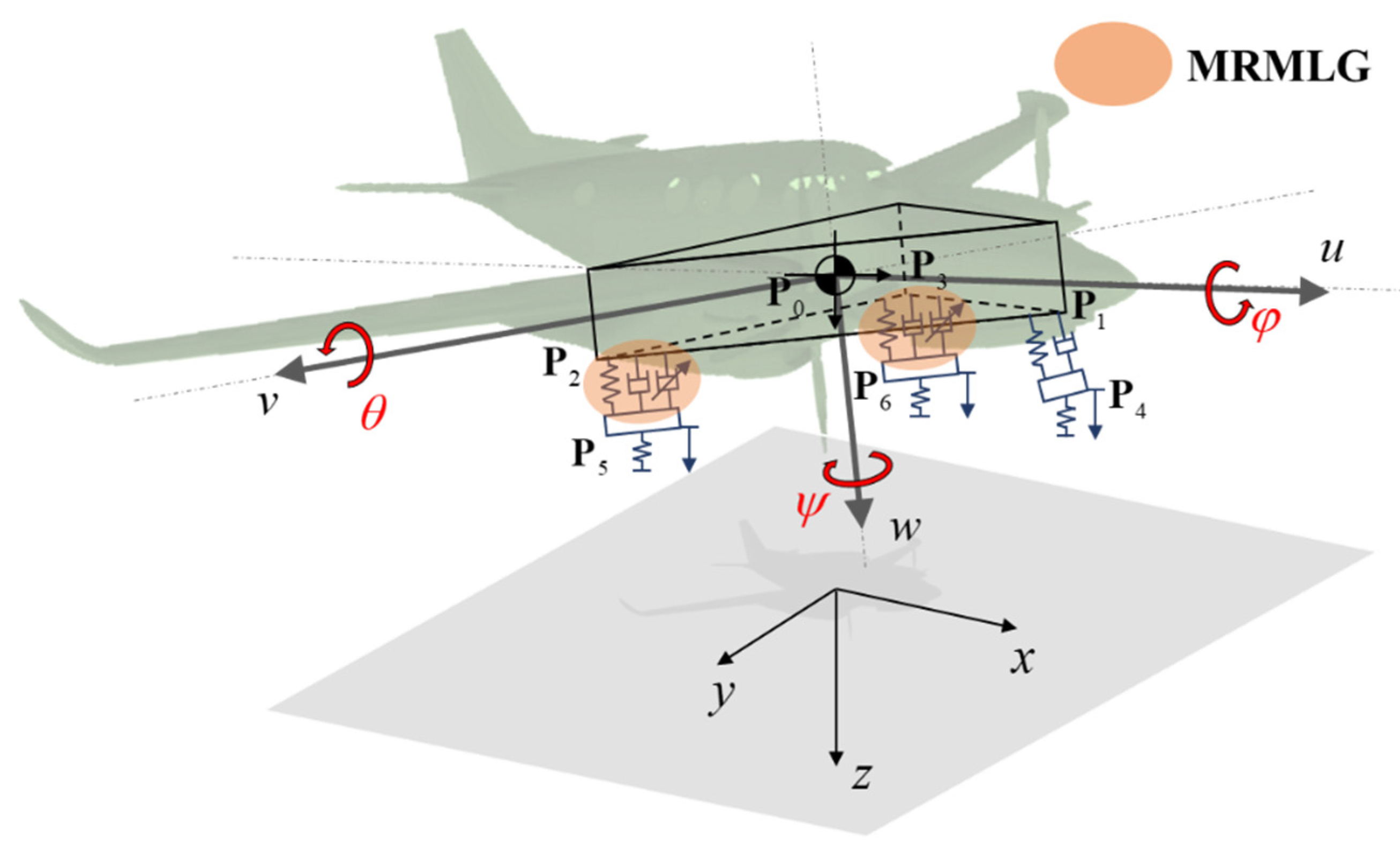
For the analysis of the aircraft’s landing motion, previous research derived the kinematics and dynamics of 6-DOF aircraft landing system [15]. Figure 5 shows the ground’s absolute coordinate system (x, y, z) and the benchmarked aircraft model’s relative coordinate system (u, v, w), position vectors, roll (φ), pitch (θ), and yaw (ψ) direction. The aircraft model’s generalized coordinate q and i-th position vector P_i were defined in the previous research:

q = {[\begin{matrix} z_{0} & s_{1} & s_{2} & s_{3} & φ & θ \end{matrix}]}^{T},

(9)

P_{i} = {[\begin{matrix} X_{i} & Y_{i} & Z_{i} \end{matrix}]}^{T},

(10)

where, s₁ represents the stroke of the nose gear, s₂ and s₃ are the strokes of the left and right main gears, and φ and θ are the roll and pitch angles, respectively. X_i, Y_i, and Z_i denote the distances along i-th x-, y-, and z-axis, respectively. ψ shown in Figure 5 is the yaw angle, which arises from the steering of the nose gear. This study assumes no yaw motion and therefore ignores it. Moreover, the equation of motion for a nonlinear aircraft model (NLAM) is as follows:

\ddot{q} = M_{G}^{- 1} (Q - (f_{ℒ} - M_{G} \ddot{q})),

(11)

Where, M_G is the generalized mass matrix, Q is the generalized force vector, and f_L is the solution of the Euler-Lagrange equation. The equation of motion in Equation (11) has a disadvantage in that the formula is complicated and it is difficult to apply the linear control logic. If the formula is simplified by linear approximation, the system analysis and linear control logic become simpler, but the accuracy of the model decreases.

The nonlinear position vectors and the equation of motion, derived from kinematics and dynamics in the previous research, are linearly approximated. During linearization, it is assumed that the perturbations in the system variables are very small. Additionally, the sinusoidal function is also linearly approximated since the perturbation of the angle is also very small. First, the position vector in Figure 5 can be approximated through the Jacobian matrix as follows:

p_{i} = {J_{P_{i}} (q) |}_{q = 0} q + {P_{i} |}_{q = 0} = {[\begin{matrix} x_{i} & y_{i} & z_{i} \end{matrix}]}^{T} .

(12)

The position vectors calculated through the linearization are:

p_{0} = {[\begin{matrix} 0 & 0 & z_{0} \end{matrix}]}^{T},

(13)

p_{1} = [\begin{matrix} U_{n} + W_{n} θ \\ - W_{n} φ \\ W_{n} + z_{0} - U_{n} θ \end{matrix}],

(14)

p_{2} = [\begin{matrix} - U_{m} + W_{m} θ \\ V_{m} - W_{m} φ \\ W_{m} + z_{0} + V_{m} φ + U_{m} θ \end{matrix}],

(15)

p_{3} = [\begin{matrix} - U_{m} + W_{m} θ \\ - V_{m} - U_{m} φ \\ W_{m} + z_{0} - V_{m} φ + U_{m} θ \end{matrix}],

(16)

p_{4} = [\begin{matrix} U_{n} + L_{n} θ_{n} - θ_{n} s_{1} + (L_{n} + W_{n}) θ \\ - (L_{n} + W_{n}) φ \\ L_{n} + W_{n} + z_{0} - s_{1} - (U_{n} + L_{n} θ_{n}) θ \end{matrix}],

(17)

p_{5} = [\begin{matrix} - U_{m} + L_{m} θ_{m} - θ_{m} s_{2} + (L_{m} + W_{m}) θ \\ V_{m} - (L_{m} + W_{m}) φ \\ L_{m} + W_{m} + z_{0} - s_{2} + V_{m} φ + (U_{m} - L_{m} θ_{m}) θ \end{matrix}],

(18)

p_{6} = [\begin{matrix} - U_{m} + L_{m} θ_{m} - θ_{m} s_{3} + (L_{m} + W_{m}) θ \\ - V_{m} - (L_{m} + W_{m}) φ \\ L_{m} + W_{m} + z_{0} - s_{3} - V_{m} φ + (U_{m} - L_{m} θ_{m}) θ \end{matrix}],

(19)

where z₀ is the distance from the origin of the absolute coordinate system to the fuselage’s center of gravity (CG). Other geometric parameters used in position vectors are listed in Table 2.

Second, assuming that the nominal initial condition and perturbation of the generalized coordinates are very small and time-invariant, M_G can be expressed as:

(20)

Third, the vectors of the equation of motion in equation (11) can be linearly approximated through the Jacobian matrix as follows [16]:

(21)

(22)

Where, F is the force vector and is:

F = [F_s,1 F_s,2 F_s,3 F_s,4 F_s,5 F_s,6]^T.

(23)

The elements of the force vector are arranged as follows, according to Equations (1)–(4) and (7)–(8), respectively:

F_{s, 1} = k_{1} s_{1} + c_{1} {\dot{s}}_{1},

(24)

F_{s, 2} = F_{g a s} (s_{2}) + F_{h y d} ({\dot{s}}_{2}) + F_{m r} ({\dot{s}}_{2}, I_{2}),

(25)

F_{s, 3} = F_{g a s} (s_{3}) + F_{h y d} ({\dot{s}}_{3}) + F_{m r} ({\dot{s}}_{3}, I_{3}),

(26)

F_{t, 4} = k_{4} (z_{4} - r_{4}) ℋ (z_{4} - r_{4}),

(27)

F_{t, 5} = k_{5} (z_{5} - r_{5}) ℋ (z_{5} - r_{5}),

(28)

F_{t, 6} = k_{6} (z_{6} - r_{6}) ℋ (z_{6} - r_{6}),

(29)

where k₁ and c₁ represent the spring coefficient and damping coefficient of the nose gear strut; I₂ and I₃ denote the control inputs (current) applied to the right and left main gears; k₄, k₅, and k₆ represent the tire stiffness of the nose, right, and left gears; r₄, r₅, and r₆ refer to the runway roughness transmitted to the tires of the nose, right, and left gears, respectively. In this study, it is assumed that the aircraft is landing on an ideal runway, so the runway roughness is neglected. As a result, the motion equation of a linear approximated aircraft model (LAAM) is:

\ddot{q} = M_{L}^{- 1} (Q_{L} - g_{L}) .

(30)

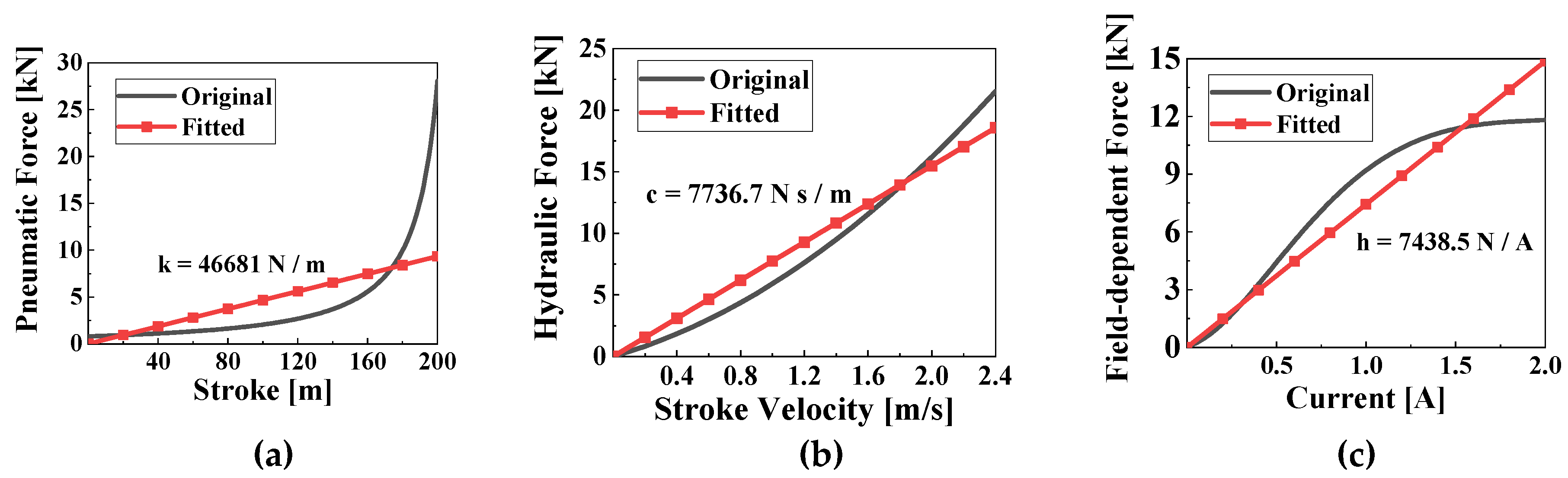
Although the affine equations of motion for the aircraft landing system have been derived, the pneumatic spring, hydraulic force, and field-dependent force of the MRMLG in Equations (2)–(4) have not been linearized. As a result, the system equation of the LAAM satisfies the linear approximation, but the elements of the generalized force vector include the nonlinear MRMLG model. Therefore, by linearizing the MRMLG, it is possible to construct a Fully Approximated Aircraft Model (FAAM). For the strut force model in Equations (2)–(4), a linearized relationship can be obtained using the Linear Regression technique, as shown in Figure 6.

In Figure 6, k, c, and h are the linearized pneumatic spring coefficient, damping coefficient, and coefficient for the input current of the MRMLG, respectively. The following linear regressed forces are used instead of Equations (25) and (26) in the FAAM model:

F_{s, 2} = k_{2} s_{2} + c_{2} {\dot{s}}_{2} + h_{2} I_{2},

(31)

F_{s, 3} = k_{3} s_{3} + c_{3} {\dot{s}}_{3} + h_{3} I_{3} .

(32)

All physical quantities used in NLAM, LAAM, and FAAM and their descriptions are summarized in Table 3.

4. Drop Simulation Comparison with RecurDyn Model

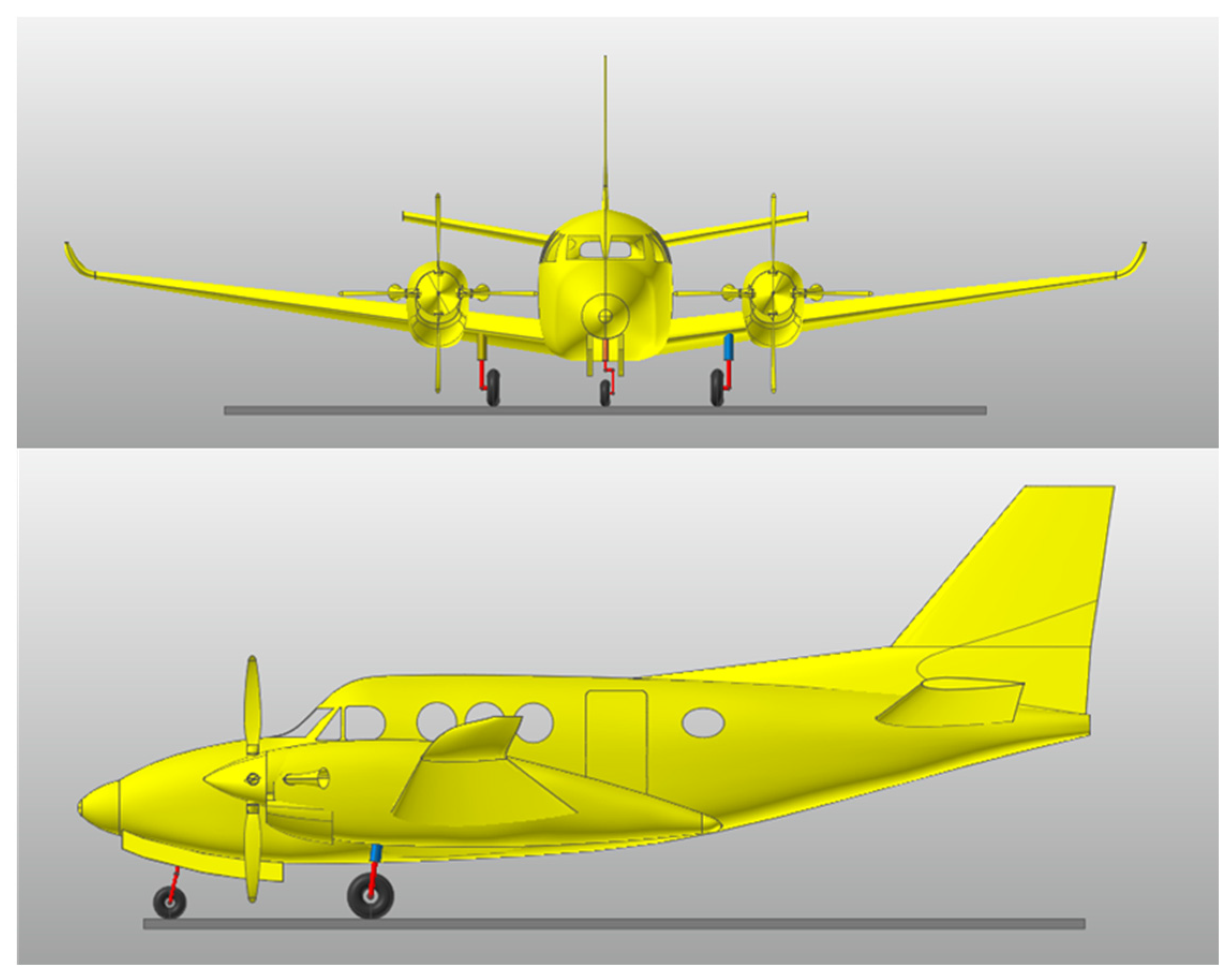
An MRMLG-based aircraft drop simulation was performed through the RecurDyn program to analyze the accuracy of the model. RecurDyn is a program that specializes in multi-body dynamics analysis. As shown in Figure 7, the aircraft model consists of the fuselage, two MRMLGs, and one nose landing gear; Each landing gear is composed of a rod, cylinder, and tire. Constraint settings are configured as follows: The fuselage, cylinder, rod, and tire were fixed; The cylinder and rod are allowed translation; The tire and ground have a frictionless planar condition. The forces acting on the tire are set to act vertically upward from the ground. The friction force in the translational condition is neglected. Damping forces, pneumatic forces, and reaction forces due to tire deflection are all applied based on the mathematical model in Equations (2)–(4). The required state variables of 7-DOF for modeling are obtained directly from the 3D model, including the CG of the aircraft and the landing gear strokes (nose, right, left gears), roll, pitch, and yaw of the landing gear.

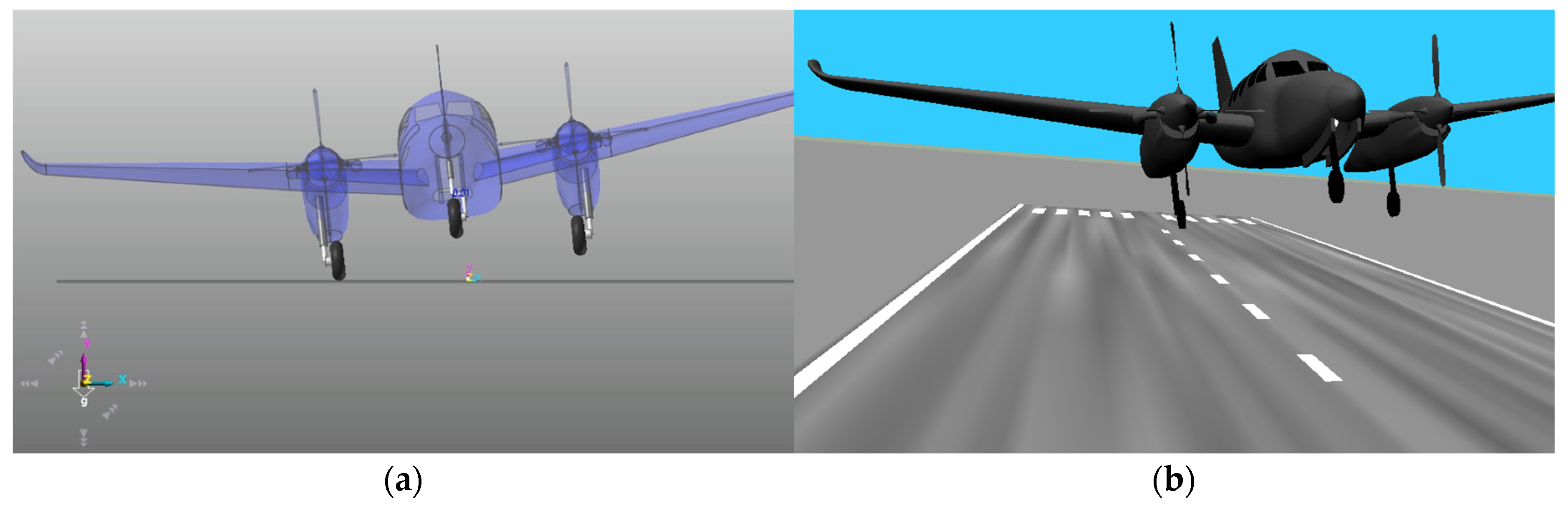
Figure 8a,b illustrate the aircraft landing behavior during the free fall simulations performed using RecurDyn and MATLAB. The simulation settings are configured with a time step of 1 ms for both RecurDyn and MATLAB, and data are recorded for a total duration of 4 seconds. The simulation solver in RecurDyn is set to dynamic analysis, and the specific parameters used are summarized in Table 2 and Table 3. The NLAM, LAAM, and FAAM models are numerically analyzed using MATLAB’s ode45 solver. For the initial conditions, the sink rate is fixed at 3.050 m/s, while the roll and pitch angles and input current are adjusted. The roll angle is set to 0°, 3°, and 6°, and the pitch angle is set to 0°, 5°, and 10°. Input currents of 0 A, 1 A, and 2 A are applied. In this study, the notation RφPθuI (pitch angle: φ degrees, roll angle: θ degrees, input current: I A) is used to define the initial conditions. For example, the notation R6P10u2 represents the initial condition with roll and pitch angles of 6° and 10°, respectively, and an input current of 2A. In the analysis, system responses and strut force characteristics are compared and analyzed for different models, including R0P0u0, R0P0u2, R6P10u0, and R6P10u2 of initial conditions. The reference model is RecurDyn, and the accuracy of the NLAM, LAAM, and FAAM models is evaluated based on R². Subsequently, ensemble processing is performed on the system responses for various initial conditions to evaluate the models. R² and RMSE are calculated with respect to RecurDyn to assess model accuracy and errors.

Figure 7. 7-DOF Aircraft landing model based on RecurDyn.

Figure 8. Aircraft drop simulation. (a) RecurDyn; (b) MATLAB Simulink 3D Animation.

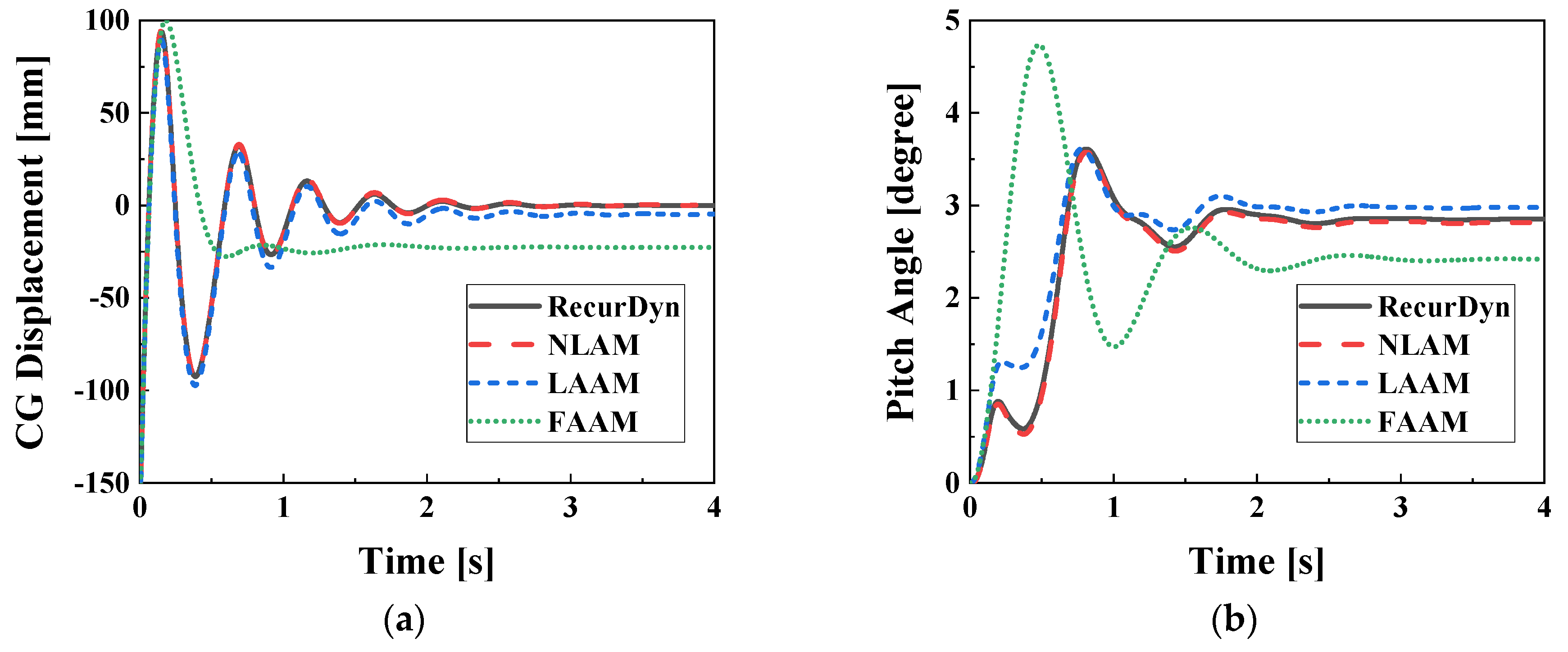
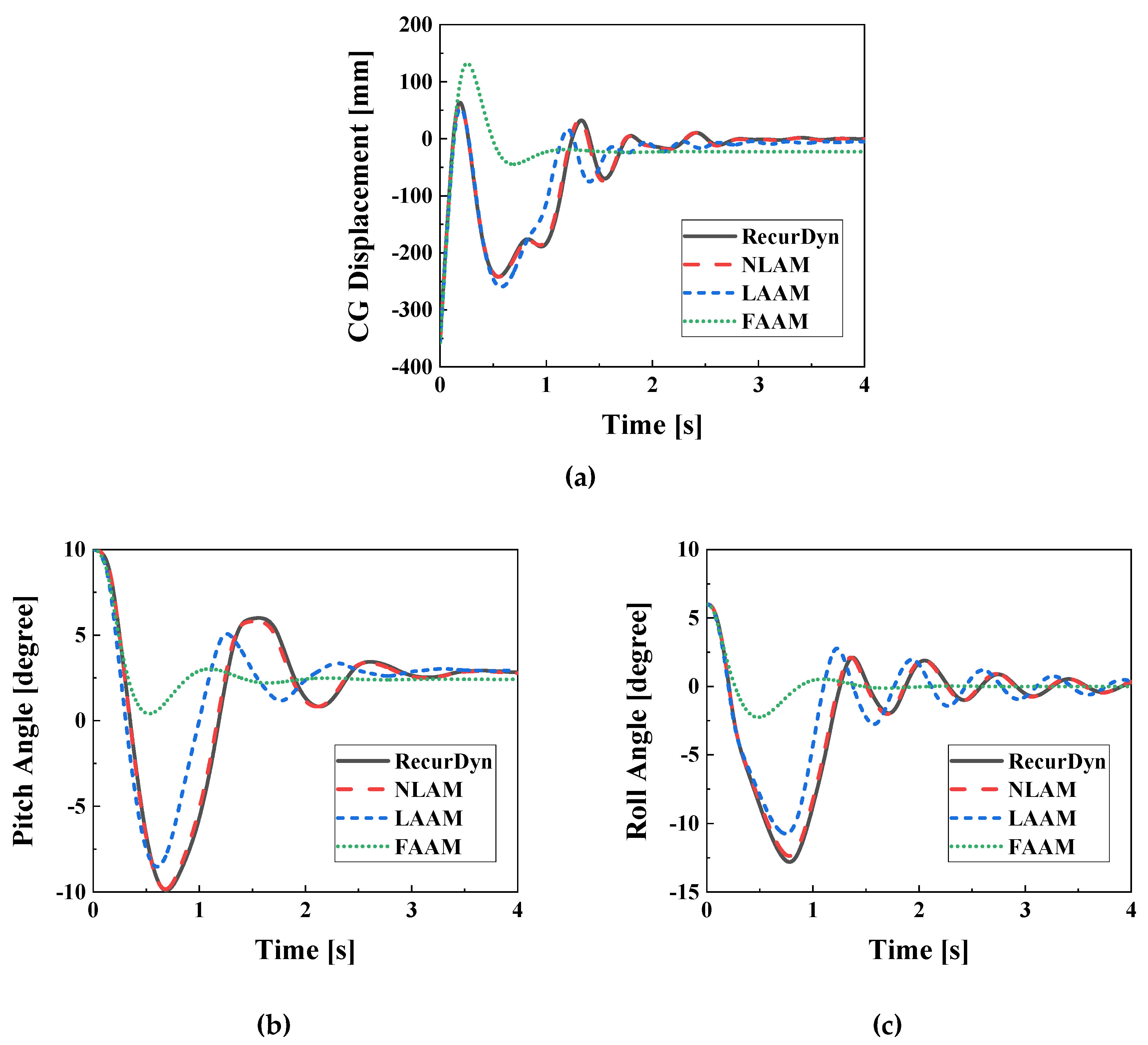
Figure 9 shows the system response to the shock under the R0P0u0 condition. Figure 9a represents the displacement of the CG, and Figure 9b shows the pitch angular displacement. The roll angle remains constant at zero for all models. The R² between the RecurDyn model and the NLAM model is calculated as 1.000 for both CG displacement and pitch angle, indicating no difference. The R2 values between the RecurDyn model and the LAAM model are 0.999 and 0.973, respectively, for CG displacement and pitch angle. However, the FAAM model shows very low R2 values of 0.119 and 0.014, indicating a lack of correlation with the reference model. Figure 10 illustrates the system response under the R0P0u2 condition. In Figure 10a, the CG displacement yields R² values of 0.998, 0.996, and 0.482 for the NLAM, LAAM, and FAAM models, respectively. In Figure 10b, the pitch angle exhibits R² values of 1.000, 0.973, and 0.941 in the same order. These results indicate an improvement in the accuracy of the FAAM model compared to the R0P0u0 condition.

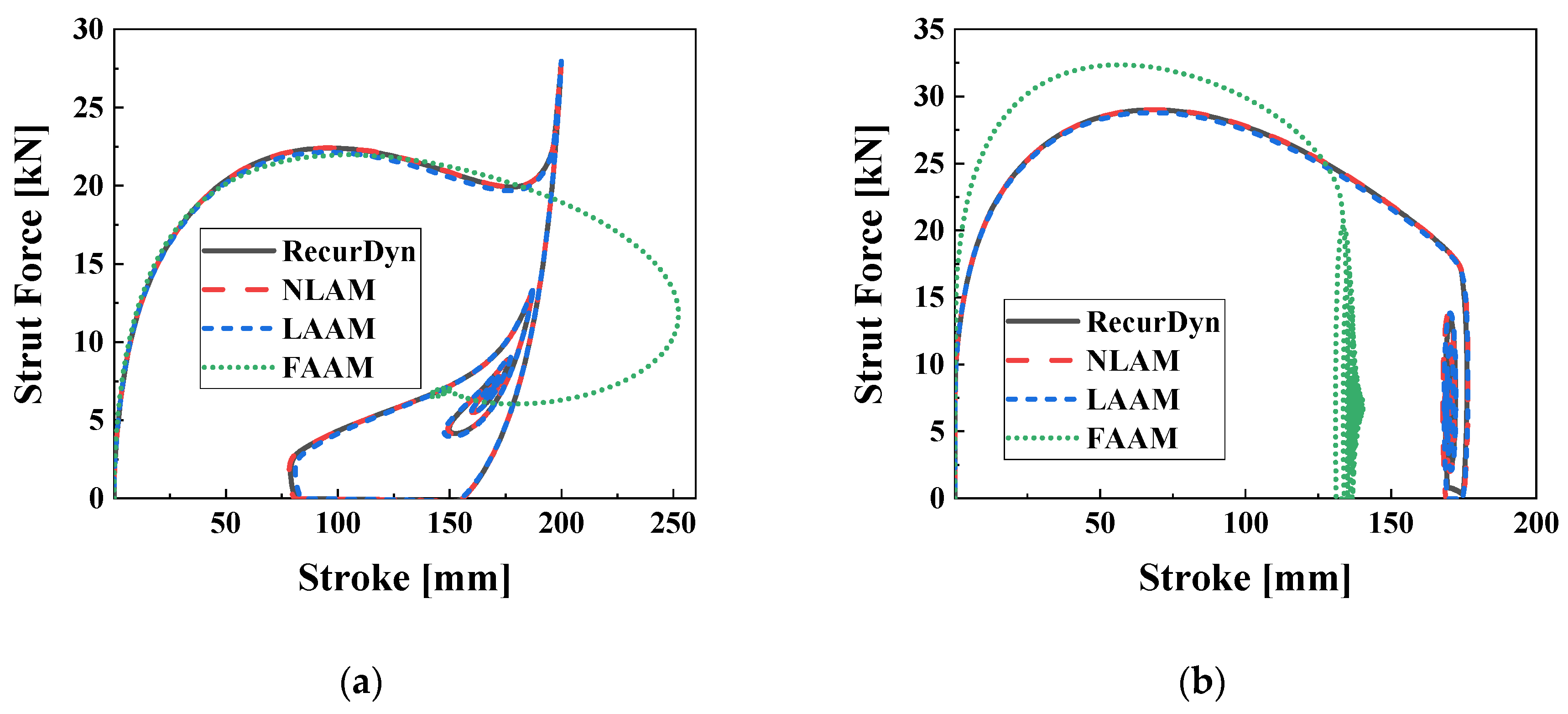
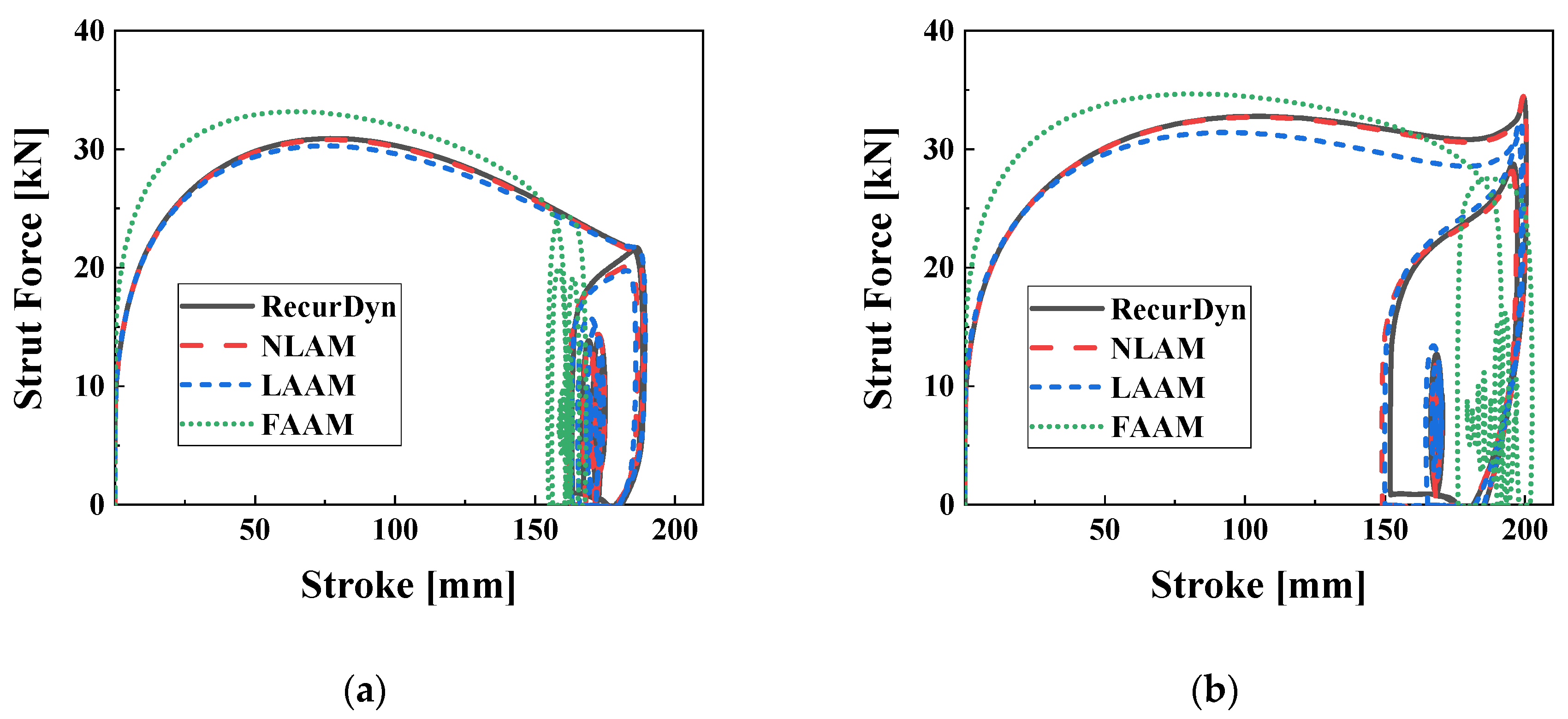
Figure 11 depicts the strut force characteristics for the stroke under the R0P0u0 and R0P0u2. It is worth noting that the results exhibit similarities to the 2-DOF drop test simulation and test results shown in Figure 3. In Figure 11a, the maximum stroke values for RecurDyn, NLAM, LAAM, and FAAM are 199.8 mm, 199.8 mm, 199.9 mm, and 252.3 mm, respectively. The corresponding maximum strut force values are 27.66 kN, 27.69 kN, 27.97 kN, and 21.98 kN. In the figure, FAAM closely matches the other models up to a stroke of 180 mm, but diverges in accuracy beyond that point. This discrepancy is due to the model error in the pneumatic model for strokes above 180 mm, as depicted in Figure 6a. In the time series analysis, the R² values for stroke, in the order of NLAM, LAAM, and FAAM, are 1.000, 0.998, and 0.050, respectively. For strut force, the R² values are 1.000, 0.998, and 0.648, respectively. These results indicate that the accuracy of the FAAM model is significantly lower compared to NLAM and LAAM. In Figure 11b under the R0P0u2 condition, the maximum stroke and strut force are approximately 176 mm and 29 kN for NLAM and LAAM, while for FAAM they are 140.3 mm and 32.35 kN, respectively. The deviation of approximately 3 kN in the maximum strut force for FAAM is attributed to the error in the input current model shown in Figure 6c, which consequently leads to a shorter maximum stroke of approximately 36 mm compared to NLAM and LAAM. The R² values for stroke and strut force in the time series analysis are 1.000 and 0.996 for NLAM, 1.000 and 0.991 for LAAM, and 0.958 and 0.587 for FAAM, indicating an overall improvement in the accuracy of the FAAM model with increasing input current.

Figure 9. System responses depending on the aircraft model (R0P0u0). (a) Displacement of CG; (b) Pitch angle.

Figure 10. System responses depending on the aircraft model (R0P0u2). (a) Displacement of CG; (b) Pitch angle.

Figure 11. Strut force-stroke characteristic curves for the aircraft model; (a) R0P0u0; (b) R0P0u2.

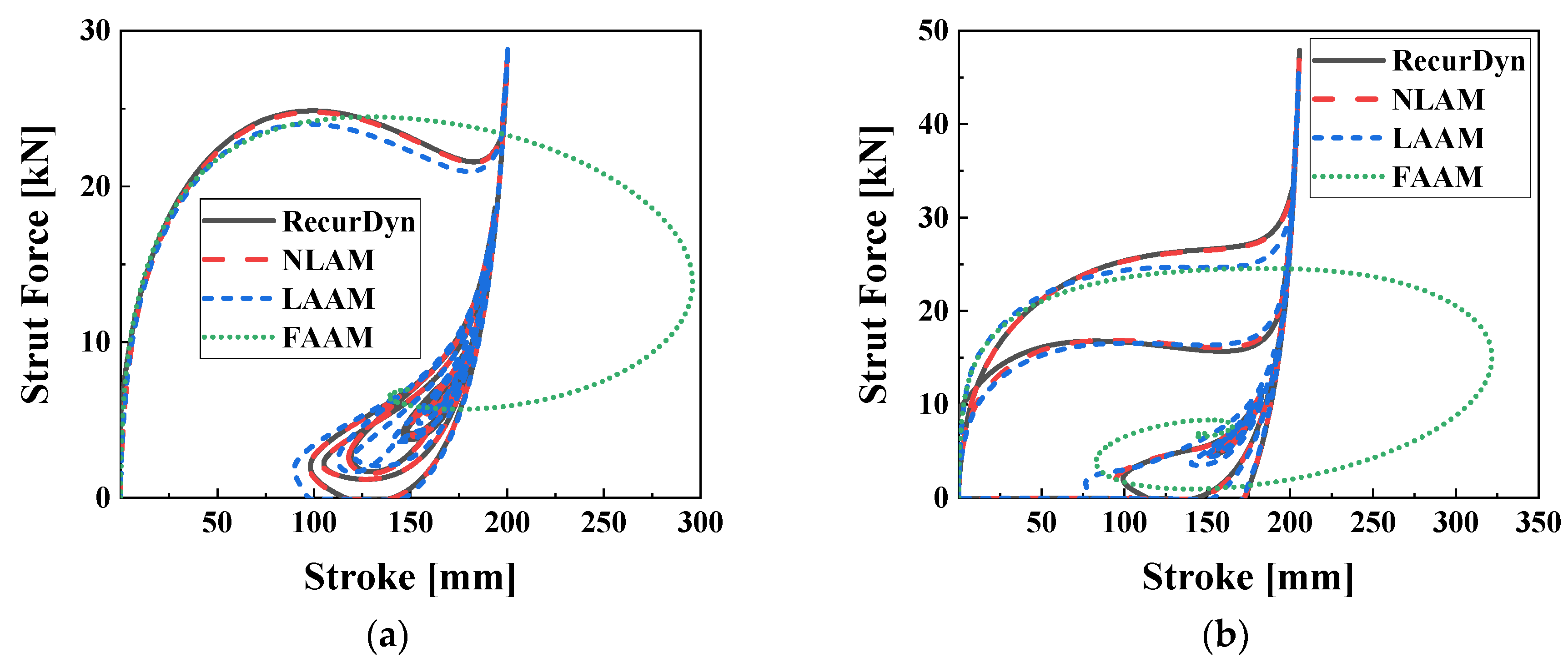
Figure 12 and Figure 13 present the model responses and strut force-stroke characteristics for the R6P10u0, respectively. Since the roll angle being non-zero leads to different responses between the right and left main gears in Figure 13. Compared to the R0P0u0, the NLAM model’s accuracy in R6P10u0 is not significantly different, with R² values above 0.98 for all variables in the time series analysis. However, the LAAM model shows a notable decrease in accuracy. FAAM exhibits unreliable model accuracy. Table 4 summarizes the R² calculations for the time series responses of each model under the R6P10u0 condition. In Figure 12a–c, the data-shifting phenomenon can be observed in LAAM, resulting in R² values below 0.9. The strut force of the right main gear has the lowest R² value of 0.510, which is also attributed to the data-shifting between the LAAM model and the time series data from RecurDyn. The R² values for the time series responses in FAAM do not exceed 0.5, with the stroke of the right main gear being the lowest at 0.116.

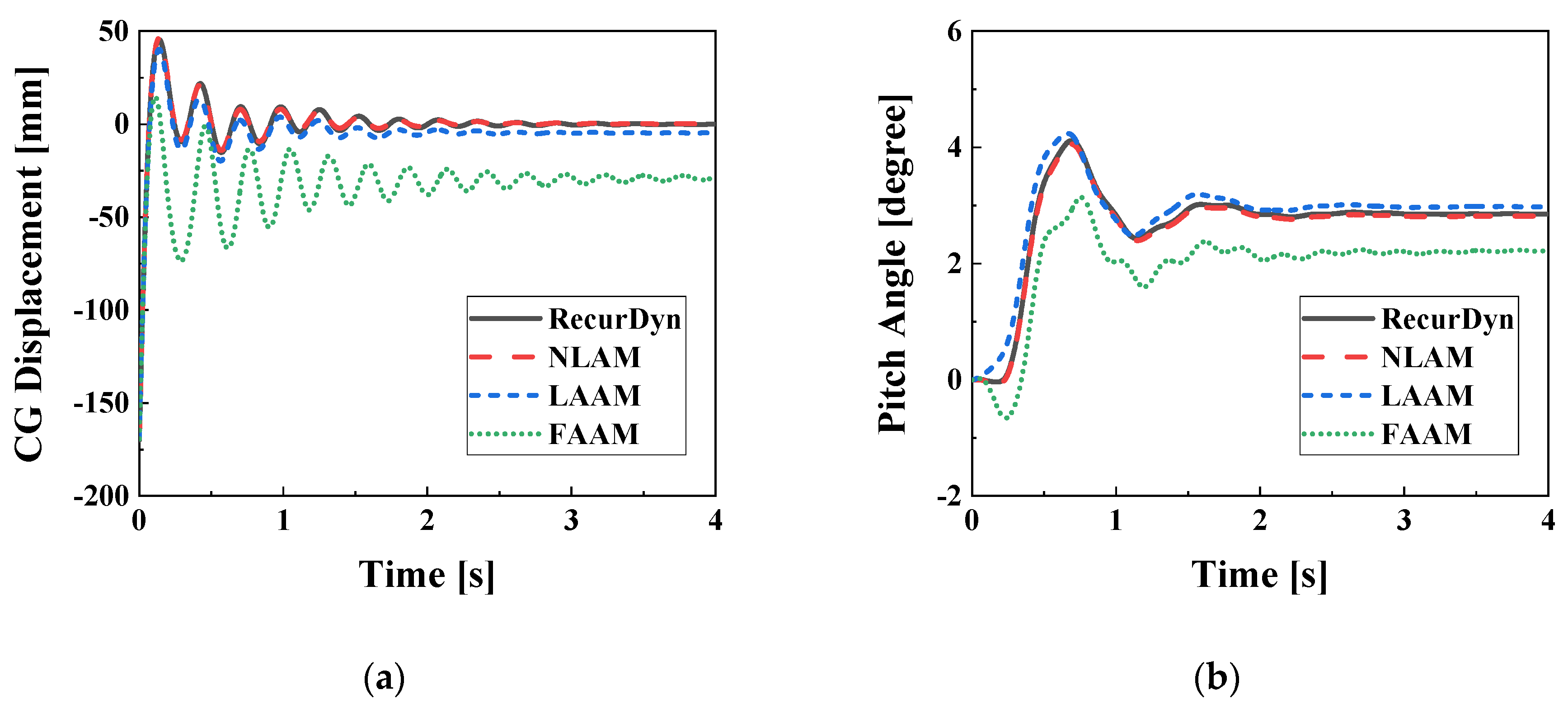
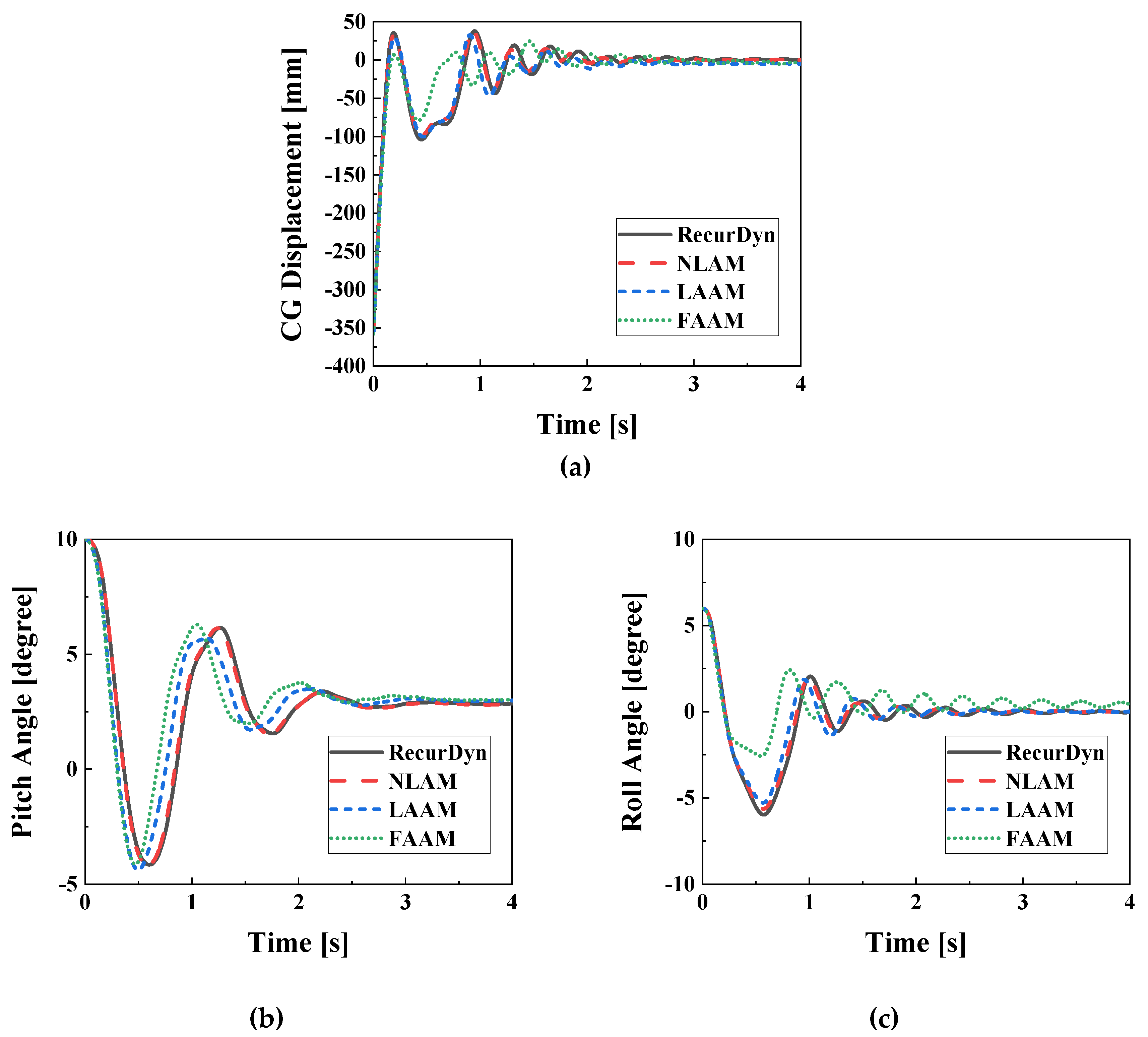
Figure 14 and Figure 15 illustrate the CG displacements, angular displacements, and left-right characteristics of the main landing gear for the R6P10u2 condition. The R² values for the time series data are summarized in Table 5. In the NLAM model, the lowest R² value in the time series data for the R6P10u2 condition is 0.861 for the force of the left main strut, which is slightly lower compared to the R0P0u2 condition. NLAM is modeled with 6-DOF, while RecurDyn utilizes a 7-DOF model including yaw. It is observed that as roll and pitch angles increase, the yaw angle fluctuates within 0.5 degrees. This fact suggests that the increase in model error may have contributed to the decrease in R² for the NLAM model. The R² values for the LAAM model range from 0.621 to 0.989 for the time series data, and the data-shifting phenomenon observed in R6P10u0 occurs only in Figure 14b. For the FAAM model, the R² values for the time series data are above 0.5 for all variables except the strut force, and data-shifting is observed in all Figure 15a–c. The minimum R² is calculated as 0.069 for the strut force.

Table 4. R² for system response of each model with RecurDyn model (R6P10u0).

Variables	NLAM	LAAM	FAAM
Displacement of CG	0.998	0.876	0.086
Roll angle	0.999	0.846	0.299
Pitch angle	0.998	0.766	0.307
Stroke of the right gear	0.994	0.686	0.116
Stroke of the left gear	0.996	0.634	0.225
Strut force of the right gear	0.987	0.510	0.486
Strut force of the left gear	0.991	0.484	0.445

Figure 12. System responses depending on the aircraft model (R6P10u0). (a) Displacement of CG; (b) Pitch; (c) Roll.

Figure 13. Strut force characteristics of main gears in regard to aircraft model (R6P10u0); (a) Left; (b) Right.

Figure 14. System responses depending on the aircraft model (R6P10u2). (a) Displacement of CG; (b) Pitch; (c) Roll.

Figure 15. Strut force characteristics of main gears regarding aircraft model (R6P10u2); (a) Left; (b) Right.

Table 5. R² for system response of each model with RecurDyn model (R6P10u2).

Variables	NLAM	LAAM	FAAM
Displacement of CG	0.988	0.960	0.681
Roll angle	0.992	0.939	0.509
Pitch angle	0.998	0.838	0.629
Stroke of the right gear	0.994	0.929	0.790
Stroke of the left gear	0.998	0.989	0.961
Strut force of the right gear	0.932	0.718	0.103
Strut force of the left gear	0.861	0.621	0.069

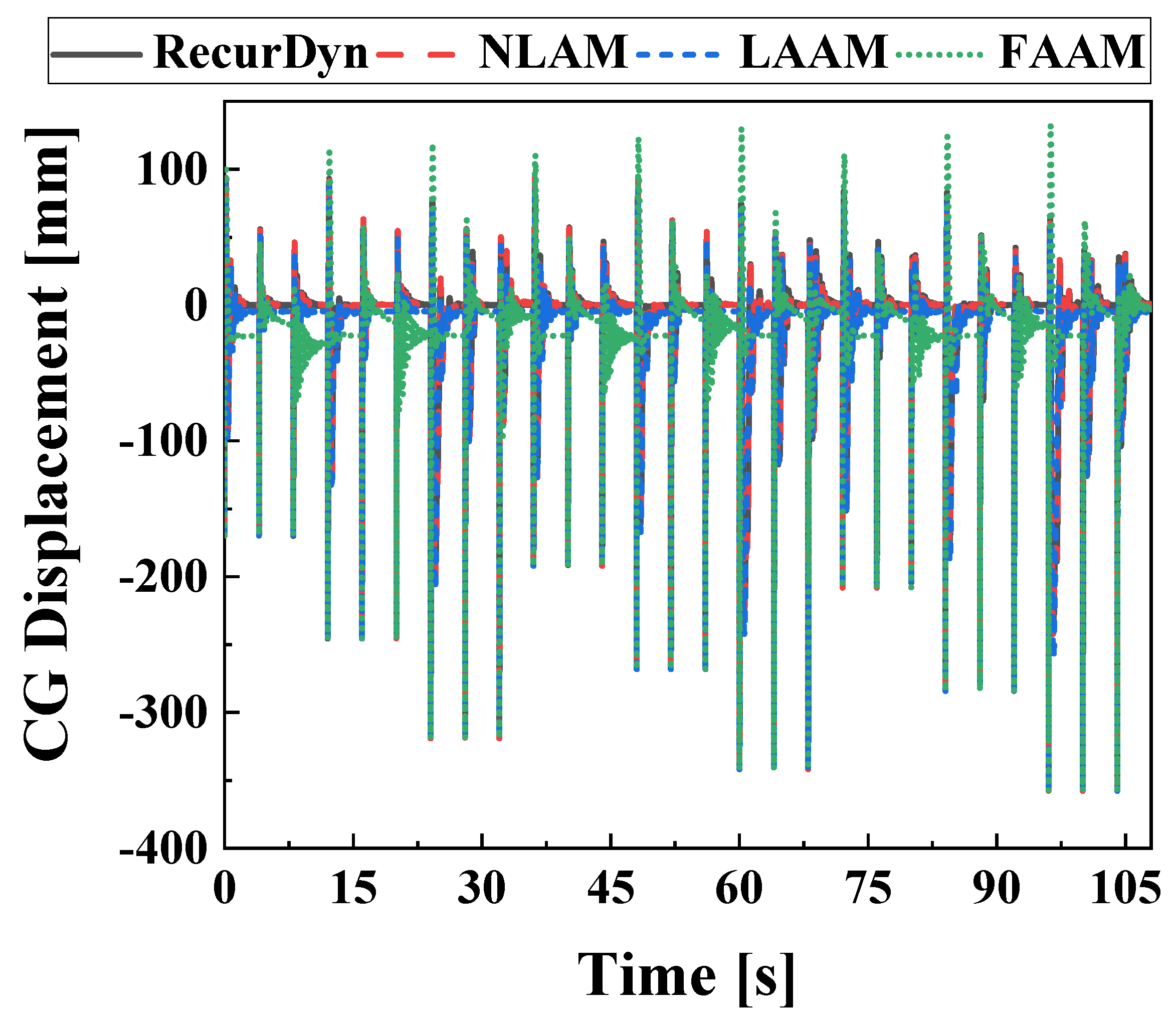
To analyze synthesized R² values of 4 seconds time series variables for various initial conditions, an ensemble of time series data was created for 27 initial conditions, resulting in a total of 108 seconds of data. Figure 16 displays the ensembles of CG displacement data for each model. The ensembles were used to perform the evaluation for the coefficient of determination and calculate the RMSE. 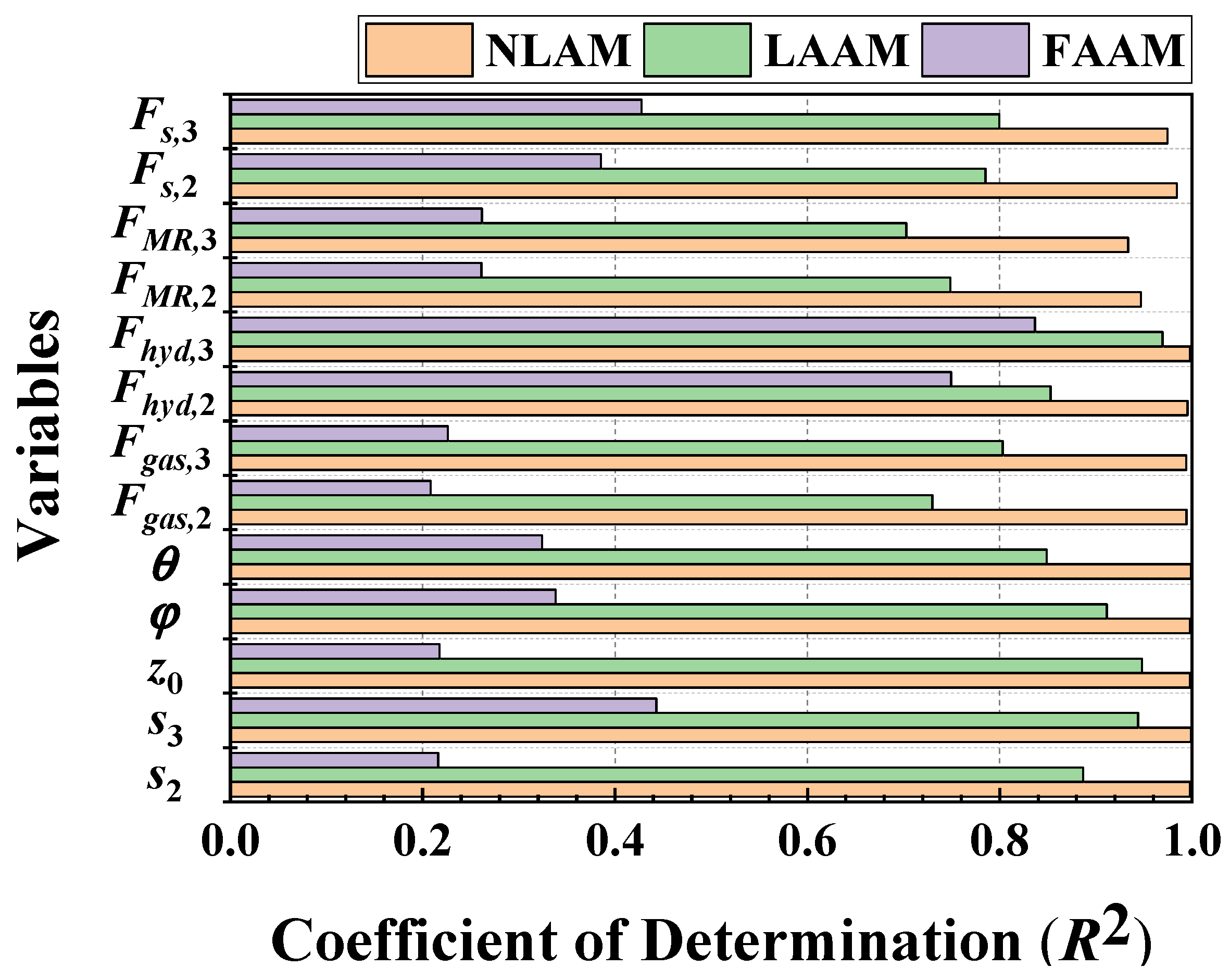Figure 17 shows the results of calculating the R² values by constructing ensembles for each time series variable and model, displayed in a bar chart format. The NLAM model shows R2 values of 0.93 or higher for all variables, which is comparable to the RecurDyn model. The LAAM exhibits displacement responses with R² values above 0.85 and force models with R² values above 0.7, indicating its suitability for the drop simulation. However, the FAAM model has R² values below 0.45 for all variables except hydraulic force. These results indicate that the FAAM is unsuitable for use as a drop simulation model.

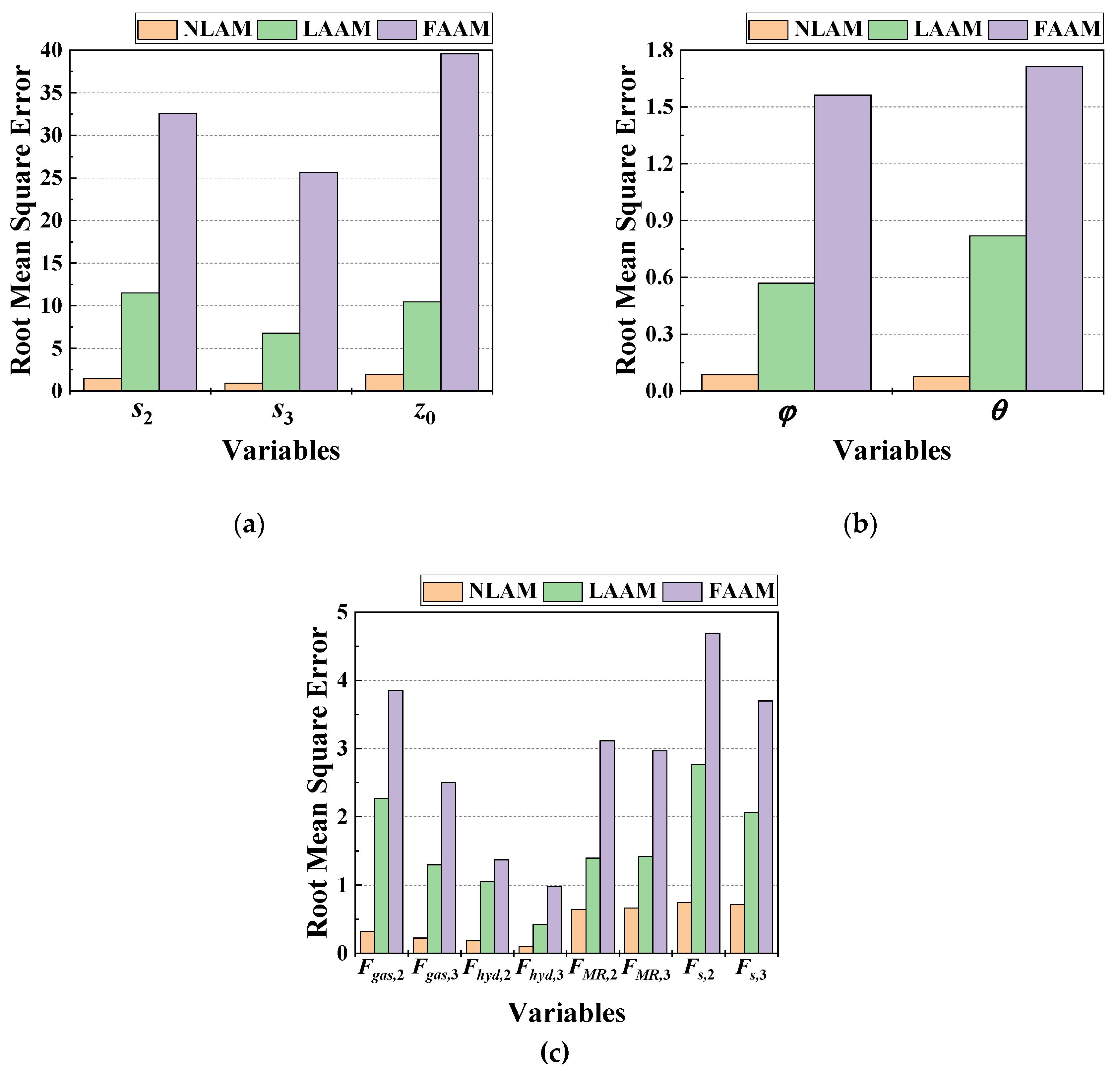
Figure 18 displays histograms analyzing the model-specific RMSE for each variable in the ensemble. It can be observed that models with high R2 values in Figure 17 exhibit relatively low RMSE values. Figure 18a displays the RMSE for strokes and CG displacement. The model-specific RMSE values are within 2 mm for NLAM, within 12 mm for LAAM, and reach a maximum of approximately 40 mm for FAAM, indicating the highest error range. Figure 18b shows the RMSE for roll and pitch angles. The RMSE for angular displacement is less than 0.1 degrees for NLAM, less than 1 degree for LAAM, and exceeds 1.5 degrees for FAAM. Figure 18c presents the RMSE for pneumatic and hydraulic forces of the right and left main gears, as well as field-dependent and strut forces. The RMSE for hydraulic force is below 1.5 kN for all models. The RMSE for pneumatic force is less than 0.4 kN for NLAM, less than 2.3 kN for LAAM, and below 4 kN for FAAM. The field-dependent and strut forces have RMSE values below 0.8 kN for NLAM, below 1.5 kN and 2.8 kN for LAAM, respectively. FAAM exhibits the highest RMSE values, approximately 3 kN for field-dependent force and a maximum of 4.691 kN for strut force, indicating the largest degree of error.

5. Conclusions

This study focuses on the dynamic drop simulation models of an aircraft landing system equipped with MR dampers. Three different 6-DOF models are proposed and their drop performances are compared with RecurDyn model in which MRMLG is incorporated. The dynamic models proposed in this work includes the nonlinear aircraft model (NLAM), which is derived from a previous study [15], the linear approximated aircraft model (LAAM), which linearizes the nonlinear equations of motion in NLAM, and the fully approximated aircraft model (FAAM), which linearizes the strut force model of the MRMLG. To validate the suitability of NLAM, LAAM, and FAAM, MRMLG integrated 7-DOF aircraft model was constructed using RecurDyn, which is a useful multi-body dynamics analysis tool. A comparison and error analysis with the RecurDyn model were performed using the coefficient of determination (R²) and root mean square error (RMSE). The calculation of R² values and RMSE provide a comprehensive evaluation of model accuracy. Furthermore, the construction of an ensemble of time series data for various drop scenarios provides valuable insights into the performance of the derived models.

It has been shown from the evaluation that the NLAM model demonstrates a high level of accuracy, with R2 values consistently above 0.93 for all variables, closely matching the results from the RecurDyn model. This indicates that NLAM is a reliable choice for simulating the system’s behavior. The LAAM model shows a satisfactory displacement response, with R2 values above 0.85 and force model accuracy above 0.7, making it suitable for drop simulation. However, there are instances of data-shifting observed in the time series data, affecting the accuracy of certain variables. On the other hand, the FAAM model exhibits poor accuracy, with R2 values below 0.45 for all variables except hydraulic force. This indicates that FAAM is not suitable for drop test modeling due to its unreliable performance.

The RMSE analysis further supports the following findings. NLAM consistently achieves low RMSE values, with displacements within 2 mm and angular displacements below 0.1 degrees. LAAM shows slightly higher RMSE values but is still within acceptable ranges for practical applications. However, FAAM displays significantly higher RMSE values, indicating large errors in its predictions. In summary, based on the ensemble analysis, NLAM emerges as the most accurate model, closely matching the results from RecurDyn. LAAM shows satisfactory performance with some limitations due to data-shifting, while FAAM demonstrates poor accuracy. These findings highlight the importance of selecting an appropriate model for drop test simulations to ensure reliable and accurate results of an aircraft landing gear system.

Author Contributions

Conceptualization, J.-H.H., S.-B.C., and B.-H.K.; methodology, B.-H.K. and B.-H.J.; data analysis, B.-H.K. and B.-H.J.; software, J.-H.H. and B.-H.J.; investigation and validation, S.-B.C., B.-G.K., and B.-H.K.; writing—original draft preparation, B.-G.K. and B.-H.K.; writing—review and editing, S.-B.C.; All authors have read and agreed to the published version of the manuscript.

Funding

This work was partially supported by the Technology Innovation Program (Intelligent landing gear with variable damping force for 1500lb class) (10073291) funded by the Ministry of Trade, Industry, and Energy (MOTIE, Korea).

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

Pecora, R. A rational numerical method for simulation of drop-impact dynamics of oleo-pneumatic landing gear. Appl. Sci. 2021, 11, 4136. [Google Scholar] [CrossRef]
Hwang, J.-H.; Kim, J.-S. On the approximate solution of aircraft landing gear under nonstationary random excitations. KSME Int. J. 2000, 14, 968–977. [Google Scholar] [CrossRef]
Luong, Q.V.; Jang, D.-S.; Hwang, J.-H. Semi-active control for a helicopter with multiple landing gears equipped with magnetorheological dampers. Appl. Sci. 2021, 11, 3667. [Google Scholar] [CrossRef]
Kang, B.H.; Yoon, J.Y.; Kim, G.W.; Choi, S.B. Landing efficiency control of a six degrees of freedom aircraft model with magneto-rheological dampers: Part 2—Control simulation. J. Intell. Mater. Syst. Struct. 2020, 12, 1303–1315. [Google Scholar] [CrossRef]
Luong, Q.V.; Jang, D.-S.; Hwang, J.-H. Robust adaptive control for an aircraft landing gear equipped with a magnetorheological damper. Appl. Sci. 2020, 10, 1459. [Google Scholar] [CrossRef]
Luong, Q.V.; Jang, D.-S.; Hwang, J.-H. Intelligent Control based on a neural network for aircraft landing gear with a magnetorheological damper in different landing scenarios. Applied Sciences 2020. 10, 5962. [CrossRef]
Jo, B.H.; Jang, D.S.; Hwang, J.H.; Choi, Y.H. Experimental validation for the performance of MR damper aircraft landing gear. Aerospace 2021, 8, 272. [Google Scholar] [CrossRef]
Han, C.; Kang, B.H.; Choi, S.B.; Tak, J.M.; Hwang, J.H. Control of landing efficiency of an aircraft landing gear system with magnetorheological dampers. J. Aircr. 2019, 56, 1980–1986. [Google Scholar] [CrossRef]
Yoon, J.Y.; Kang, B.H.; Kim, J.H.; Choi, S.B. New control logic based on mechanical energy conservation for aircraft landing gear system with magnetorheological dampers. Smart Mater. Struct. 2020, 29, 084003. [Google Scholar] [CrossRef]
Kang, B.-H.; Hwang, J.-H.; Choi, S.-B. A New Design Model of an MR Shock Absorber for Aircraft Landing Gear Systems Considering Major and Minor Pressure Losses: Experimental Validation. Appl. Sci. 2021, 11, 7895. [Google Scholar] [CrossRef]
Pirooz, M.; Mirmahdi, S.H.; Moafi, S.R. Promoting both passenger comfort and aircraft handling of 6 DOF landing gear utilizing variable mechanical admittance approach. Vibroengineering Procedia 2020, 30, 79–85. [Google Scholar] [CrossRef]
Gharapurkar, A.A.; et al. Semi-active control of aircraft landing gear system using H-infinity control approach. In Proceedings of the 2013 International Conference on Connected Vehicles and Expo (ICCVE), Las Vegas, NV, USA, 2–6 December 2013. [Google Scholar] [CrossRef]
Kang, B.-H.; Kim, B.-G.; Choi, S.-B. Aircraft landing gear system with magnetorheological shock strut: Performance evaluation via drop test. J. Intell. Mater. Syst. Struct. 2023, 1045389X221147632. [Google Scholar] [CrossRef]
Corporation, L. MRF 132DG Technical Data Sheet; Cary, NC, USA, 2019. [Google Scholar]
Kang, B.H.; Yoon, J.Y.; Kim, G.W.; Choi, S.B. Landing efficiency control of a six-degree-of-freedom aircraft model with magnetorheological dampers: Part 1—Modeling. J. Intell. Mater. Syst. Struct. 2020, 1045389X20942578. [Google Scholar] [CrossRef]
Stengel, R.F. Flight dynamics; Princeton University Press, 2005. [Google Scholar]

Figure 1. Configuration of MRMLG.

Figure 2. Damping force-velocity characteristics of MRMLG.

Figure 5. Dynamic model and position vectors of aircraft landing gear system.

Figure 6. Linear regression of MRMLG’s strut force model. (a) pneumatic characteristics and fitted stiffness, k; (b) Hydraulic force model and fitted damping coefficient, c; (c) Field-dependent model and fitted coefficient for the input current, h.

Figure 16. CG displacement’s ensemble regarding the aircraft model.

Figure 17. R² depending on the time series variables and models obtained by ensemble.

Figure 18. RMSE in conformity with the ensembles in the time domain and models. (a) Displacement; (b) Angular displacement; (c) Force.

Table 1. MRMLG parameters and physical quantities.

Parameter	Notation	Value	Unit
Atmospheric Pressure	P_atm	1.013	bar
Initial Gauge Pressure	P₀	4.000	bar
Initial Volume of the Gas Chamber	V₀	454.0	cm³
Polytropic Index of the Nitrogen	γ	1.300	-
Inner Area of the Main Strut	A₁	25.52	cm³
Outer Area of the Rod	A₂	20.19	cm³
Viscosity of MRF-132DG [14]	η	112.0	mPa s
Density of MRF-132DG [14]	ρ	3.050	g/cm³
Orifice Length	l	130.0	mm
Orifice Perimeter	b	139.4	mm
Orifice Gap	d	1.300	mm
Effective Pole Length	l_p	49.40	mm
Total Loss Coefficient	K	2.836	-
Slope Value of the Hyperbolic Tangent	ε	0.050	-
Sprung Mass	m_s	680.0	kg
Unsprung Mass	m_u	18.00	kg
Tire Stiffness	k_t	412.0	kN/m
Gravitational Acceleration	g	9.807	m/s²

Table 2. Geometric parameters for the benchmarked aircraft model.

Parameter	Notation	Value	Unit
y-angle of the nose gear	θ_n	12.8	degree
y-angle of the main gear	θ_m	6.5	degree
x-distance of the nose gear from the CG	U_n	1.652	m
z-distance of the nose gear from the CG	W_n	0.124	m
x-distance of the main gear from the CG	U_m	0.393	m
y-distance of the main gear from the CG	V_m	1.479	m
z-distance of the main gear from the CG	W_m	0.038	m
Total length of fully extended nose gear	L_n	0.756	m
Total length of fully extended main gear	L_m	0.830	m

Table 3. Physical parameters for the benchmarked aircraft model.

Parameter	Notation	Value	Unit
Sprung (fuselage) mass	m₀	1633	kg
Unsprung (nose and main gears) mass	m₄, m₅, m₆	18.00	kg
Moments of inertia about the x-axis	I_x	6132	kg m²
Moments of inertia about the y-axis	I_y	2555	kg m²
Moments of inertia about the z-axis	I_z	8595	kg m²
Stiffness of the nose gear	k₁	30.00	kN / m
Damping coefficient of the nose gear	c₁	3000	N s / m
Linearized Stiffness of the main gears	k₂, k₃	46.68	kN / m
Linearized damping coefficient of the main gears	c₂, c₃	7337	N s / m
Linearized coefficient of the control input	h₂, h₃	7439	N / A
Tire stiffness of the nose gear	k₄	200.0	kN / m
Tire stiffness of the main gears	k₅, k₆	412.0	kN / m

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Linear and Nonlinear Models for Drop Simulation of Aircraft Landing Gear System with MR Dampers

Abstract

1. Introduction

2. MRMLG Design and Drop Test

3. Nonlinear Model and Linear Approximation Model

4. Drop Simulation Comparison with RecurDyn Model

5. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe