Can the Orbital Debris Disease Be Cured Using Lasers?

1. Introduction

As an update to the usually cited prediction [1] of a possibly exponentially future increase of space debris in the low Earth orbit (LEO), known as the Kessler syndrome, which would massively endanger or even shut down space operations, the onset of this phenomenon in highly frequented altitudes around the sun-synchronous orbit has been reported recently [2]. This fact induces a paradigm shift in space situational awareness from being a sustainability issue towards an emergency question. In a certain regard, this is as well reflected in the report recently issued by the U.S. National Aeronautics and Space Administration (NASA) [3], re-assessing ground-based or space-based lasers for the removal of a multitude of small space debris objects possibly being the most efficient way to tackle the scope of space debris remediation at present. Of course, the current efforts like Clearspace-1 [4] or Active Debris Removal by Astroscale-Japan (ADRAS-J) [5] for removing inactive payloads or spent upper stages as possible sources of new fragments due to collisions and/or explosions are an adequate measure as the appropriate long-term solution for the sustainability of the space debris environment. Nevertheless, the increasing severity of – symbolically speaking – the symptoms of the orbital debris disease, i.e., fragmentation debris, of the orbit’s congestion by space debris puts into question the prevailing restriction of interest to removal of a few “pathogens”, i.e., payloads and rocket bodies, per year [6].

On top of this, the Kessler syndrome is currently on the verge of becoming evident in a variation of the theme by increasingly high debris awareness. Improving optical performance for detection and tracking allows for cataloguing more and more small objects which are the more prevalent the smaller they are [7]. Moreover, the rise of mega-constellations is anticipated to increase the number of collision warnings in the low Earth orbit by more than two orders of magnitude [8]. In combination, the future burden of collision avoidance in space debris management might encounter critical capacity limits, which renders the removal of a multitude of objects a welcome option for short-term mitigation, even if it contributes less for the space environment from a sustainability perspective. In this regard, methods for active debris removal (ADR) that comprise dedicated in-orbit missions for manipulation of specific objects using, e.g., nets, electrodynamic tethers, ion beams or robotic arms [9], appear unsuitable for de-orbiting a multitude of small debris. For them, so-called sweepers have been proposed in various conceptions orbiting with a large material pad for deceleration, break-up or capture of small debris [3]. Alternatively, as a non-contact method that can be operated remotely over great distances, recoil from high power laser ablation of the debris surface has been analyzed under various aspects as a method to stepwise de-orbit debris objects for atmospheric burn-up.

Since the first proposals dating from the 1990’s both ground-based [10] and space-based [11] high-power lasers have been investigated regarding their advantages and drawbacks in the field of laser-based space debris removal. Space-based operation facilitates beam focusing benefiting from reduced distances and possible usage of a short laser wavelength [12], however, a very compact and efficient laser unit is required [13] for space-qualified operation in a harsh environment without opportunities for on-site maintenance. Instead, ground-based laser stations benefit from a comprehensive infrastructure covering extensive power supply, tightly supervised operation and flexible maintenance without significant needs for constraining volume or mass of the laser site, which gave rise to propose technology from large high energy laser facilities as blueprints for possible removal lasers [14].

Considering existing limitations of currently available laser power, some concepts include irradiation of small debris during multiple station passes for stepwise de-orbiting [15] instead of removing the object by a single pass. But even under very optimistic assumptions on future power scaling of high energy lasers, laser-ablative momentum transfer to space debris is not limitless: Laser-induced thermal disintegration of space debris targets – experimentally observed initially in [11] but discarded afterwards in the literature for decades – emerged recently as a constraint to ensure operational safety [16], underpinned by experimental proof of solar cell fragmentation from pulsed laser irradiation in a relevant parameter range [17]. In this regard, it is no wonder that laser-based removal or even nudging of space debris is frequently associated with its potential dual use of applying directed energy as a threat for satellites [18,19]. Therefore, we consider in our study the irradiation level that presumably may not be crossed in order to keep the integrity of the irradiated debris object, which may serve as a first proxy to assess the threat level of a debris removal laser station. We hope that this approach helps to get a clearer and more realistic picture of the potential and implications of research and development of laser-based technology for the ground-based removal of space debris.

2. Methods

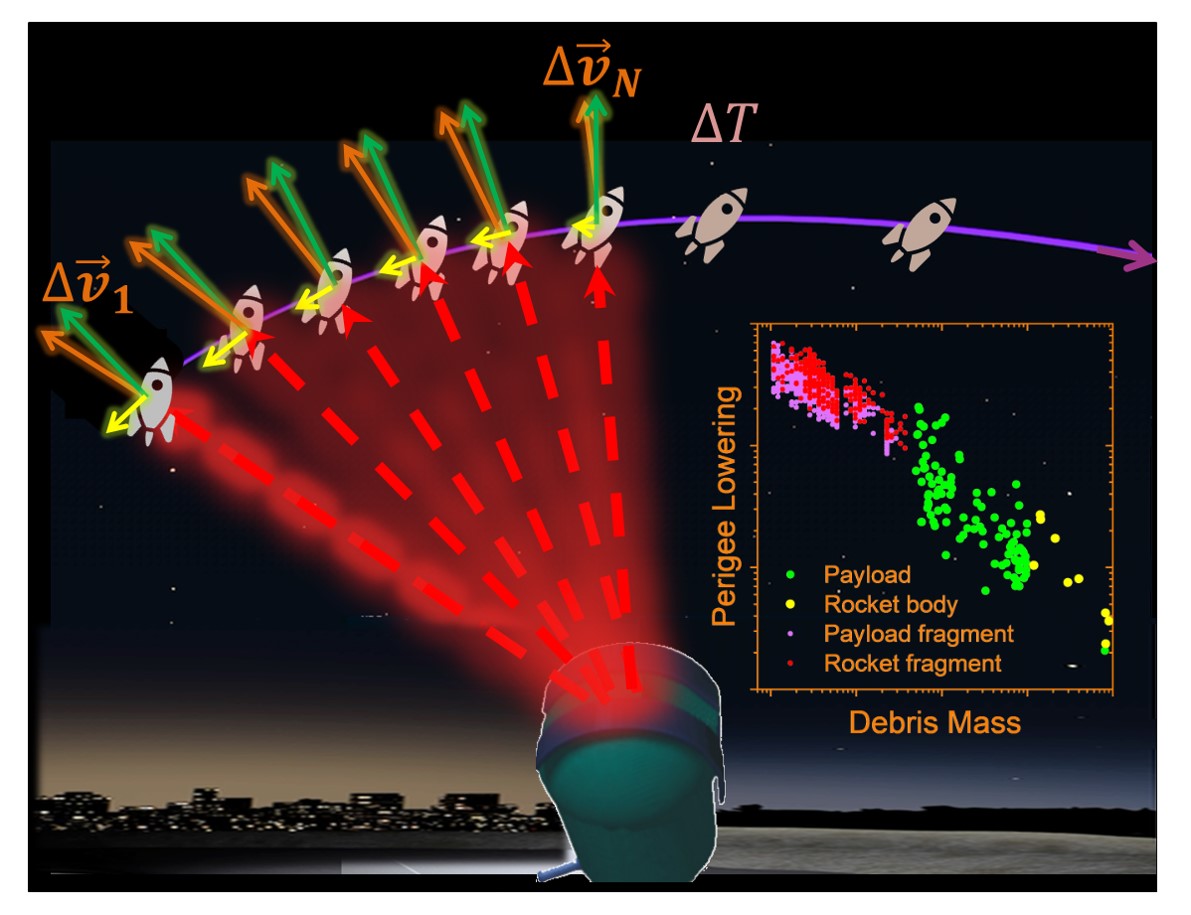
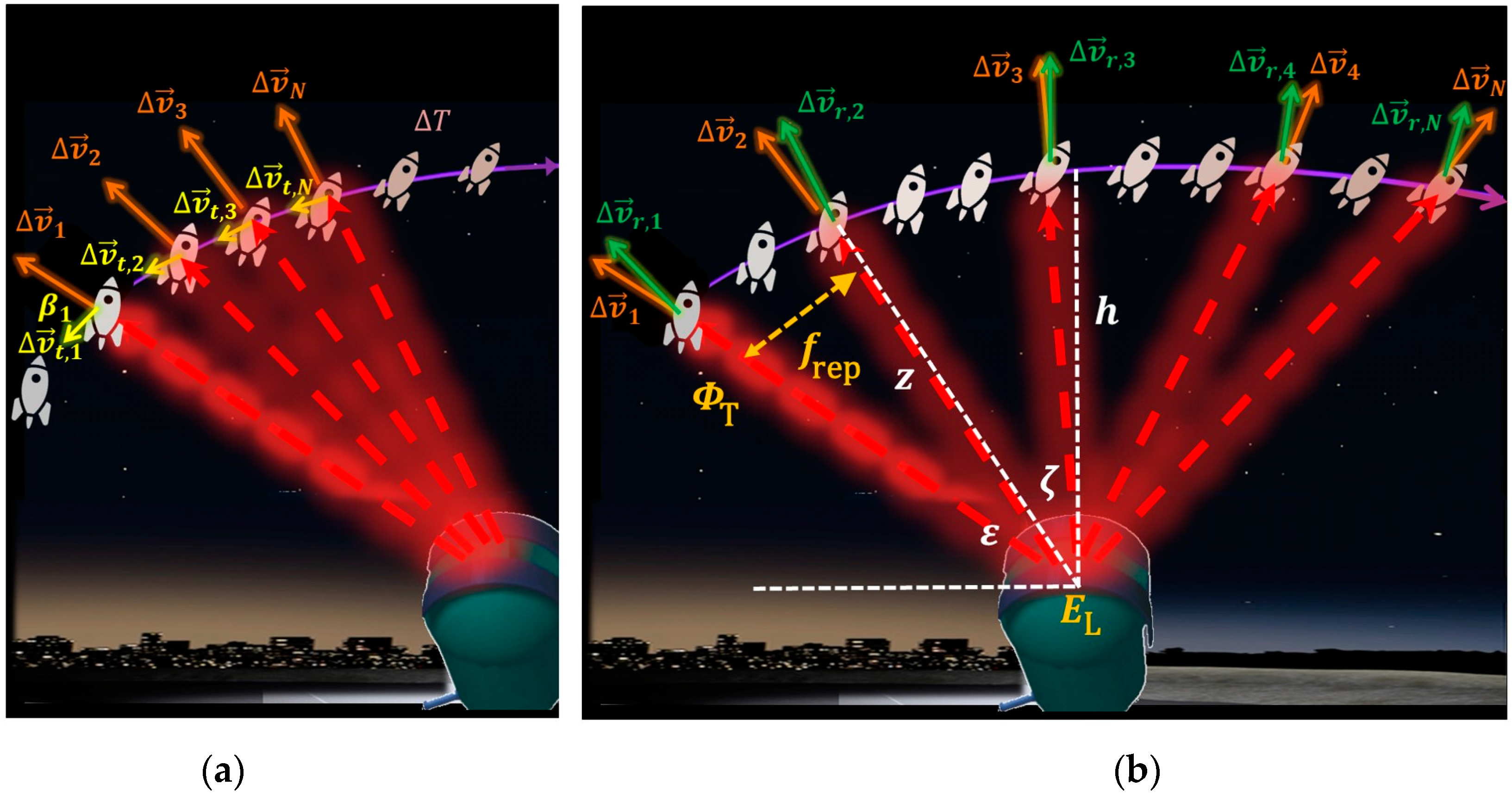
A brief overview on the computational workflow of this study can be taken from Figure 1: We analyze the orbit modification of a space debris object due to recoil from surface ablation induced by repetitively pulsed laser irradiation from a high energy laser station on ground. Head-on irradiation at rather low elevation angles, cf. Figure 1(a), is compared to outward irradiation near zenith, Figure 1(b), regarding velocity change $\mathsf{\Delta }v$ and laser-induced temperature change $\mathsf{\Delta }T$. The laser fluence ${\mathsf{\Phi }}_{\mathrm{T}}$ arriving at the debris momentary position is computed from the laser pulse energy $E_{\mathrm{L}}$ considering the distance $z$ between laser and debris with respect to the object’s orbit altitude $h$ and its current zenith angle $\zeta$ or elevation angle $\epsilon$, respectively. The impact of transmitter design, atmospheric extinction as well as turbulence compensation on ${\mathsf{\Phi }}_{\mathrm{T}}\left(t\right)$ is lined out in Sect. 2.1.

Figure 1. Scheme of repetitively pulsed laser irradiation of space debris by a high energy laser ground station for perigee lowering by (a) head-on momentum and, alternatively, (b) outward momentum.

Figure 1. Scheme of repetitively pulsed laser irradiation of space debris by a high energy laser ground station for perigee lowering by (a) head-on momentum and, alternatively, (b) outward momentum.

As a realistic computational input for the momentum-generation process of laser ablation, the dependencies of momentum coupling coefficient $c_m=\mathsf{\Delta }p/E_{\mathrm{L}}$ and the coefficient of residual heat ${\eta }_{res}=\mathsf{\Delta }Q/E_{\mathrm{L}}$ from the incident fluence ${\mathsf{\Phi }}_{\mathrm{T}}$ are discussed in Sect. 2.2. Here, $\mathsf{\Delta }p$ are the imparted momentum, $\mathsf{\Delta }Q$ is the laser-induced heat remaining in the debris object after ablation and$A$ is the irradiated area.

Section 2.3 gives an overview of the different debris target categories and geometries which are used in the raytracing computations of laser-imparted momentum and analytic estimates of laser-induced heat, as described in Sect. 2.4. Finally, the role of the laser-induced velocity change in orbit modification and de-orbiting is outlined in Sect. 2.5.

2.1 High Energy Laser Ground Station

As a conceivable laser source for debris removal we assume a system of multiple laser emitters with comparably low pulse energy organized in a phased array for coherent beam coupling. Based on the experimental work of our group outlined in [20], the single emitters are anticipated as diode-pumped Yb:YAG (Ytterbium-doped yttrium aluminum garnet) laser sources in a master oscillator power amplifier configuration (MOPA) in which an initial laser pulse energy of 100 mJ is amplified within two stages up to an overall pulse energy of 20 J with a pulse length of $\tau =5$ ns at $\lambda =1030$ nm wavelength, and a superior beam quality of $M^2=1.5$ for each laser source. Arrangement of 5000 of such emitters in a tiled aperture configuration [21] would allow for coherent beam coupling yielding an overall laser pulse energy of $E_{\mathrm{L}}=100$ kJ.

For beam transmission we assume an optical aperture with a diameter of $D_{\mathrm{T}}=4$ m and an initial radius of the effective laser beam of $w_0=0.715·D_{\mathrm{T}}/2$, which corresponds to a 2 % power loss at the transmitter from outshining. The ground station is anticipated to be operated in junction with an optical system for target acquisition and continuous laser tracking of the debris object during its station pass exhibiting a low tracking uncertainty of ${\sigma }_{\mathrm{t}}=0.1$ arcsecs enabled by adaptive optics and laser guide star (LGS) usage in downlink from the object [22]. This allows for high-precision pointing of the high energy laser beam, moreover, the real-time data from ranging can be used to dynamically adapt the focus length of the transmitter to achieve focusing of the beam at the actual position of the debris object throughout the entire pass.

Turbulence compensation is not only required in downlink but also for uplink, i.e., power beaming to the debris object. Hence, an additional LGS is employed pointing slightly ahead the debris object probing the turbulence in the solid angular segment for uplink. Real-time data analysis of corresponding measurements with a Shack-Hartmann sensor on ground allows for dynamic conjugation of turbulence-induced phase distortions by actively shifting the phases of the different laser emitters based on data from heterodyne phase detection. The overall performance of such a beam transmission system can be quantified by the Strehl ratio $Str$ [23] yielding the following expression for the laser spot radius $w$ focused at the distance $z$ from the transmitter:

$$w\left(z\right)=\frac{M^2·\lambda ·z}{\pi ·w_0·\sqrt{Str}}.$$

(1)

Here, the Strehl ratio comprises the temporal compensation, the so-called cone effect, and a spatial contribution expressed as

$$Str=S_{\mathrm{temp}}·S_{\mathrm{cone}}·S_{\mathrm{zonal}}.$$

(2)

Specifically, the factor $S_{\mathrm{temp}}$ for the temporal effects given by

$$S_{\mathrm{temp}}=\exp \left[-{\left(f_G/f_{3\mathrm{dB}}\right)}^{5/3}\right]$$

(3)

where $f_G$ is the Greenwood frequency and $f_{3\mathrm{dB}}=300$ Hz is the characteristic response frequency of the phase correction system, and the factor $S_{\mathrm{cone}}$ considers the residual atmospheric volume not covered by LGS probing:

$$S_{\mathrm{cone}}=\exp \left[-{\left(D_{\mathrm{T}}/d_0\right)}^{5/3}\right]$$

(4)

where $d_0$ is a parameter describing focus anisoplanatism. Moreover, a spatial contribution $S_{\mathrm{zonal}}\approx 0.9$ is employed stemming from the spatial configuration of the phase compensation in the tiled aperture array. Since $f_G$ and $d_0$ depend on the underlying turbulence model and, in the case of $f_G$, on the propagation length, $Str$ is a function of both orbit altitude $h$ and beam pointing zenith angle $\zeta$, cf. [22] for a detailed description.

The residual impact of atmospheric turbulence beam pointing in tip-tilt correction mode has been assessed following [24] giving a pointing jitter from ${\sigma }_{\mathrm{p}}=0.17$ arcsecs at zenith up to ${\sigma }_{\mathrm{p}}=0.63$ arcsecs at $\zeta =65$°. Regarding extinction, we have employed data from [25] for clear air at $\lambda =1.06$ µm showing an atmospheric transmissivity of $T$ $=$ $86.6$ % at zenith down to $T=71.1$ % at $\zeta =65$°. Moreover, from practical considerations on the tiled aperture concept we deem the far-field power-in-the-bucket (discarding the side lobes) to be around $S_{PIB}\approx 65$ % of the transmitted laser energy (including losses at the transmitter), which gives an overall transmitted laser pulse energy of

$$E_{\mathrm{T}}=T\left(\zeta \right)·S_{\mathrm{PIB}}·E_{\mathrm{L}}$$

(5)

at the target’s position in orbit.

2.2 Laser-Matter Interaction

For the computation of laser-based orbit modification we employ the commonly used momentum coupling coefficient $c_m$

$$c_m=∆p/E_{\mathrm{inc}}$$

(6)

where $∆p$ is the momentum change of the target due to recoil obtained from the ablation jet and $E_{\mathrm{inc}}$ is the laser pulse energy that hits the target.

Though the predominant fraction of laser-induced heat leaves the target with the plasma jet formed by heated surface material, a residual amount of heat remains in the heat affected zone below the ablated material and dissipates into the bulk. This phenomenon can be quantified using the residual heat coefficient ${\eta }_{res}$ by

$${\eta }_{res}=∆Q/E_{\mathrm{inc}}$$

(7)

where $\mathsf{\Delta }Q$ is the amount of residual heat in the target.

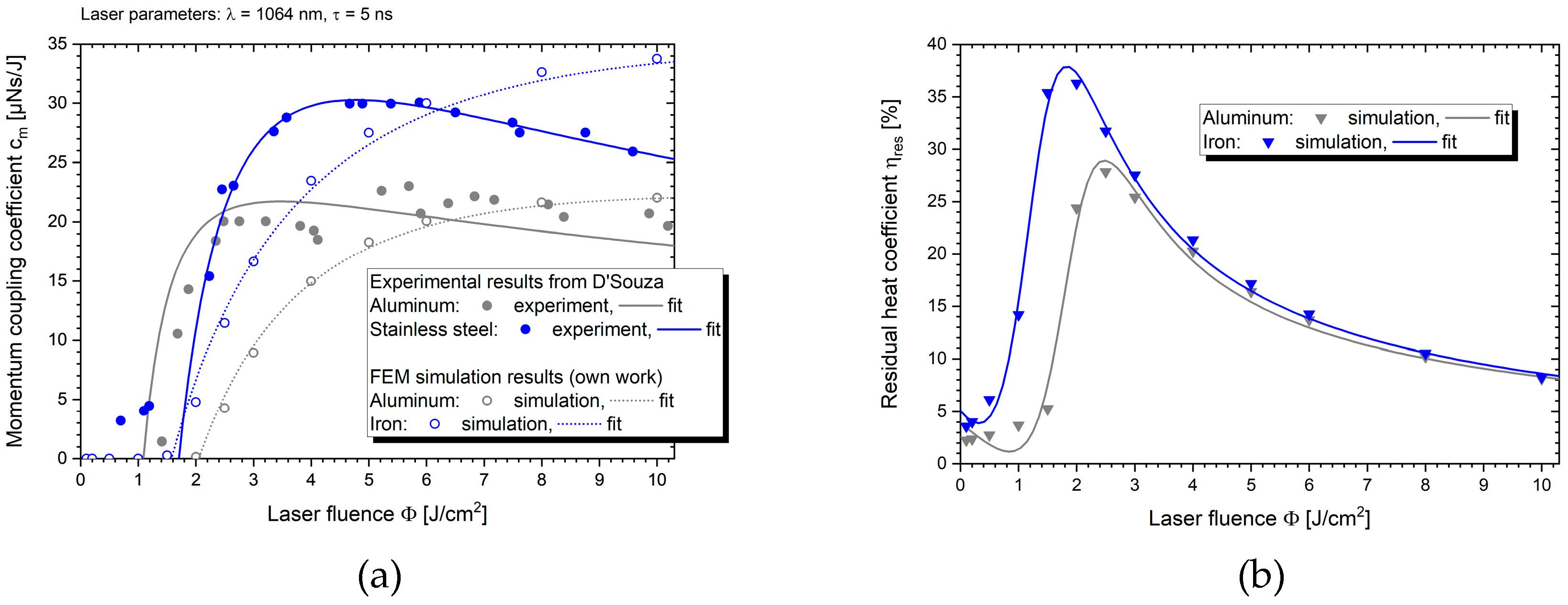
These coefficients of thermal and mechanical coupling, $c_m$ and ${\eta }_{res}$, are material-specific and depend on laser parameters such as wavelength $\lambda$ and pulse duration $\tau$. Moreover, both figures of merit show a strongly non-linear behavior regarding their dependency on the incident laser fluence $\mathsf{\Phi }$, which should be considered for a realistic simulation of a laser-based orbit modification maneuver. Taking this into account we use a parametric fit function of $c_m\left(\mathsf{\Phi }\right)$ based on experimental data for aluminum and stainless steel as relevant target materials [26]. The pronounced dependency of $c_m$ from the incident laser fluence $\mathsf{\Phi }$ can be seen from the respective data shown in Figure 2(a). Experimental data from [27] has been extracted using Image-J and an empirical fit function has been applied. The corresponding fit parameters, cf. [28], serve as input for momentum coupling computation in the raytracing simulations of laser-matter interaction described below.

Figure 2. (a) Momentum coupling as a function of incident fluence of a laser pulse with $\tau =5$ ns pulse duration at $\lambda =1064$ nm wavelength, which is close to the wavelength of our laser configuration (1030 nm). Experimental data from [27] and own simulation results for aluminum, stainless steel, and iron are shown together with corresponding data fits using the empirical fit function for $c_m\left(\mathsf{\Phi }\right)$ derived in [29]. (b) Results from finite-elements-method (FEM) simulations on thermal coupling in laser ablation of aluminum and iron, respectively, for these laser parameters.

Figure 2. (a) Momentum coupling as a function of incident fluence of a laser pulse with $\tau =5$ ns pulse duration at $\lambda =1064$ nm wavelength, which is close to the wavelength of our laser configuration (1030 nm). Experimental data from [27] and own simulation results for aluminum, stainless steel, and iron are shown together with corresponding data fits using the empirical fit function for $c_m\left(\mathsf{\Phi }\right)$ derived in [29]. (b) Results from finite-elements-method (FEM) simulations on thermal coupling in laser ablation of aluminum and iron, respectively, for these laser parameters.

Beyond momentum coupling, laser-induced heat from repetitive laser ablation is of interest regarding possible limitations of laser-based removal. However, corresponding experimental data for the residual heat coefficient ${\eta }_{res}$ was not available for the experiments described in [27]. Instead, we have used results from our own simulations of the laser ablation process, implemented in the commercial finite-elements-method (FEM) software COMSOL Multiphysics^® version 6.1, employing a modeling approach which has been developed in [30], and extended in further research. It comprises laser-induced heat transfer, evaporation cooling, material ablation, Knudsen layer formation, ablation plume gas dynamics, and plasma shielding.

As a preliminary validation for the scope of this work respective simulation results for the same laser parameters as from the experiments [27] are shown in Figure 2(a) (hollow symbols, dotted fit). Basically, there are still some discrepancies between experimental data and simulation results: Results for the ablation threshold of aluminum differ by a factor of two. Nevertheless, we deem this acceptable for our purposes, since experimental data from the literature, however, scatters as well significantly: While for aluminum we find ${\mathsf{\Phi }}_0=1.1$ J/cm² at $\tau =5$ ns [27], $3.2$ J/cm² at $6$ ns [31], and $1.5$ J/cm² at $8$ ns [32], the scatter with stainless steel is even larger exhibiting ${\mathsf{\Phi }}_0=1.7$ J/cm² at $\tau =$ $5$ ns [27], ${\mathsf{\Phi }}_0=7.3$ J/cm² at $\tau =6$ ns [31], and ${\mathsf{\Phi }}_0=0.8$ J/cm² at $\tau =10$ ns [33] whereas one would actually expect ${\mathsf{\Phi }}_0\propto \sqrt{\tau }$ [31].

Moreover, the decrease of $c_m$ due to plasma shielding is predicted at higher fluences (not shown) in the simulations than reported from the experiment. While there is still space for improvement of the simulation regards matching with experimental data, the overall rather good agreement of $c_m$ data between simulation and experiment in the relevant fluence range makes it appear reasonable to use empirical fits of simulation data of ${\eta }_{res}$, cf. Figure 2(b), for this study in order to derive a first estimate on thermal limitations in laser-based removal of space debris.

2.3 Space Debris Simulation Targets

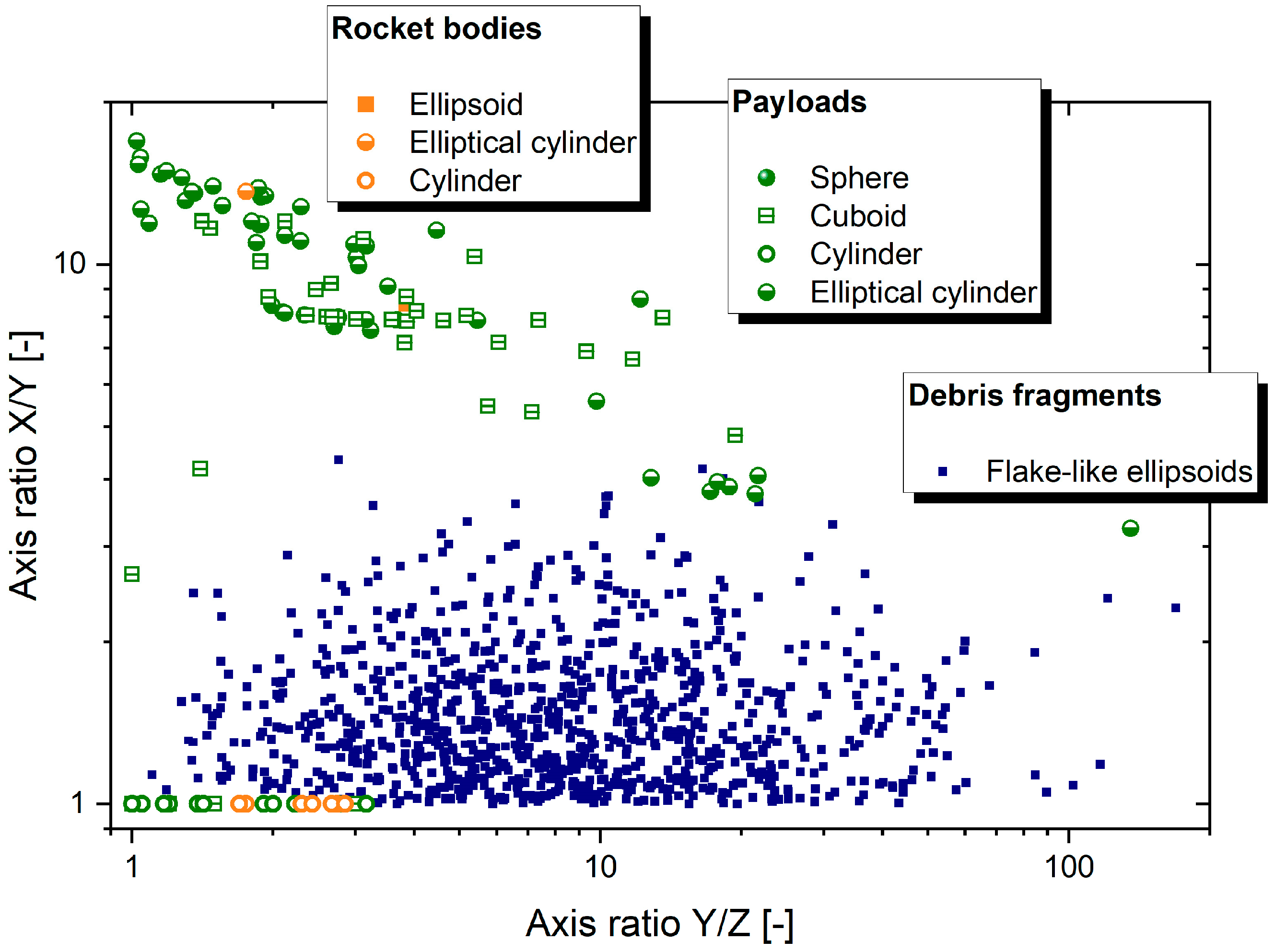
Figure 3. Axis ratios of debris simulation targets. Dimensions X, Y, and Z are defined according to the method of shadow dimensions as described in [34].

Figure 3. Axis ratios of debris simulation targets. Dimensions X, Y, and Z are defined according to the method of shadow dimensions as described in [34].

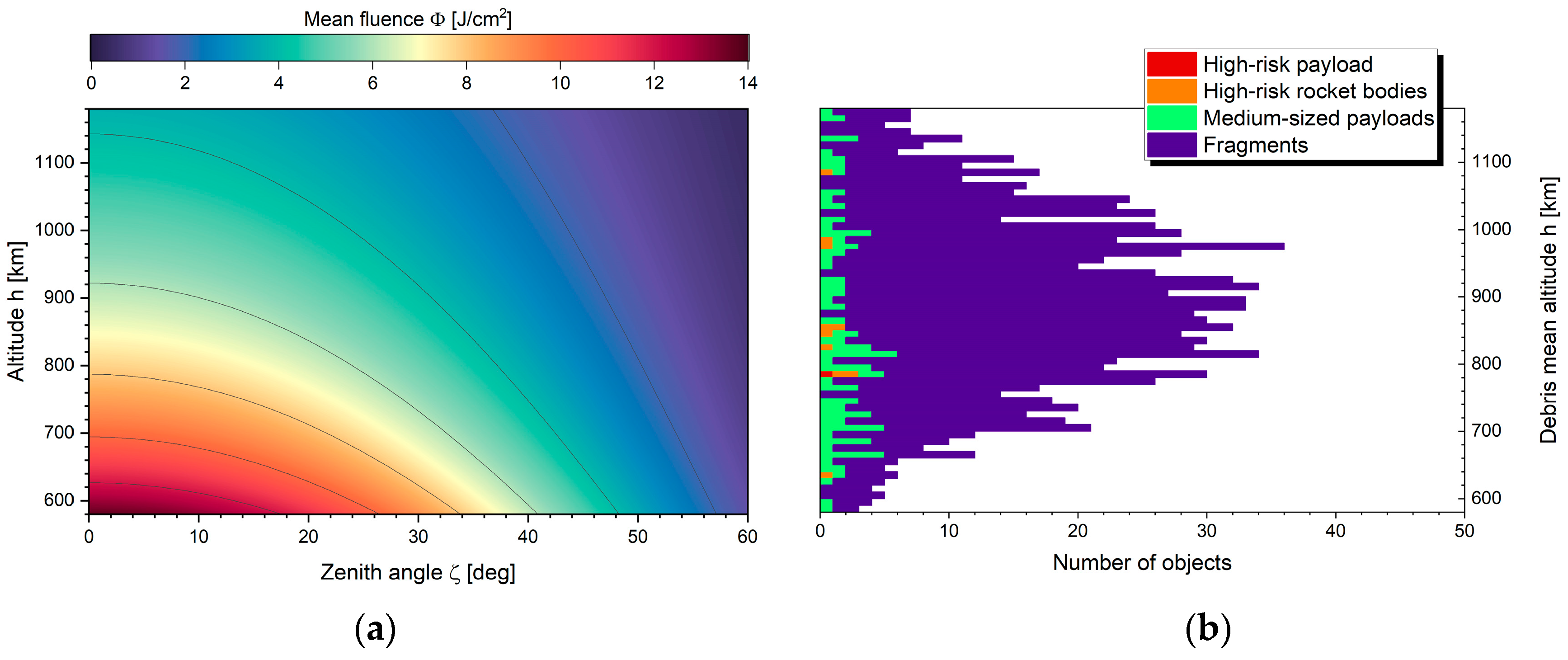
For our simulations we have chosen four different categories of catalogued debris objects: (i) 1,000 fragments from explosions and collisions with a mass ranging from 1 kg to 50 kg, (ii) 100 medium-sized payloads from 50 kg to 1,000 kg, (iii) a representative selection of 10 large-risk rocket bodies with high priority for ADR according to [35] exhibiting a mass between 1,000 kg and 10,000 kg, and (iv) Envisat, as well listed as high-risk object in [35], which is the largest known debris satellite in LEO. Fragments and medium-sized payloads have been selected from a larger debris population in LEO as of 2 July 2019 comprising objects at mean altitudes between 579 and 1179 km with an orbital eccentricity up to 0.2 and an orbit inclination between 65° and 110°. Orbital data had been retrieved from the catalogue of the United States Strategic Command (USSTRATCOM) [44]. Data on mass and geometry have been provided from the Database and Information System Characterizing Objects in Space (DISCOS) of the European Space Agency (ESA) [43], in particular allowing us for deriving geometric primitives for our simulations, cf. [22] for a description in greater detail. The scatterplot of the geometric axis ratios in Figure 3 underlines the great variety of the investigated debris objects.

Aluminum is attributed as surface material to the 101 payloads while rocket bodies are assumed to consist of stainless steel at their outer shell. Correspondingly, steel is assumed as material of the 287 rocket fragments whereas the remaining 713 payload fragments, among which 342 have arisen from tests of kinetic anti-satellite weapons (ASAT tests), aluminum is selected as simulation material for laser-matter interaction.

2.4 Laser-imparted Momentum and Heat

For the computation of momentum from laser ablation we have employed our numerical code EXPEDIT (Examination Program for Irregularly Shaped Debris Targets) [29] which is based on Liedahl’s area-matrix approach [36] that allows for consideration of arbitrarily oriented target surface elements and the corresponding implications on local fluence, momentum magnitude, and momentum direction. For this purpose, the dependency of momentum coupling on the fluence is taken as simulation input from the parametric fit functions, cf. [28], of the experimental data shown in Figure 2(a).

The laser source in our simulations is placed in the vicinity of the target and exhibits a Gaussian fluence distribution that equals the one of the focused laser spot. This allows for raytracing simulations with parallel rays. The beam waist $w\left(z\right)$ is given by Eq. 1 and the spatial resolution of the single rays is $\mathsf{\Delta }r=0.02·w\left(z\right)$ yielding a fine discretization for momentum computation. The overall laser pulse energy is given by $E_{\mathrm{T}}$ as from Eq. 5.

For our study we assume that the target orientation at the time of a laser pulse is unknown. To account for this, we use a Monte Carlo approach similar to our study on photon pressure [22] sampling the computed momentum for various orientations of the object determined by a random uniform distribution of the Eulerian angles which describe its attitude. Moreover, we comprise fluctuations of the offset between laser spot center and the target’s center of mass, denoted here as hit uncertainty ${\sigma }_{\mathrm{h}}$, in Monte Carlo sampling. The hit uncertainty can be derived from tracking uncertainty ${\sigma }_{\mathrm{t}}$, inherent beam pointing jitter ${\sigma }_{\mathrm{p}}$, cf. Sect. 2.1., and distance to target as ${\sigma }_{\mathrm{h}}=z\sqrt{{\sigma }_{\mathrm{p}}^2+{\sigma }_{\mathrm{t}}^2}$. The overall jitter ${\sigma }_{\mathrm{h}}$ then serves as the standard deviation of the Gaussian random distribution which determines the particular beam offset of the different Monte Carlo samples. For the polar angle of the offset’s position vector a uniform random distribution is employed yielding overall five degrees of freedom for attitude and position of the debris object within the beam.

Using these definitions of random beam offset and arbitrary target orientation, Monte Carlo sampling has been undertaken for each target at its particular altitude under twelve different beam pointing zenith angles $\zeta$ ranging from 0° up to 65° in steps of $\mathsf{\Delta }\zeta =$ $5°$ unless the spot’s peak fluence fell below the material’s ablation threshold. Sampling has been halted when the averaged momentum achieved convergence after at least 11 samples or, in the case slowly converging samples, 1,000 samples had been computed. Eventually, 15,257 Monte Carlo simulations comprising overall 9,130,275 samples of raytracing-based momentum computation have been employed to establish a target- and altitude-specific database with average values of laser-imparted momentum as a function of the beam pointing zenith angle.

Note that in the following only the momentum component $∆p_{ax}$ co-axial to the laser beam propagation axis was employed whereas the component perpendicular to the beam axis was discarded since those components might more or less cancel out due to a possible spinning motion of the target. Moreover, a linear interpolation was employed for intermediate values of $\zeta$.

While the imparted momentum was computed directly in EXPEDIT, we used the average of incident laser energy $〈E_{\mathrm{inc}}〉$ for deriving laser-induced heat from the parametric fit functions shown in Figure 2(b). Then, the average fluence is $〈{\mathsf{\Phi }}_{\mathrm{inc}}〉=〈E_{\mathrm{inc}}〉/A_{\mathrm{cs}}$ where $A_{\mathrm{cs}}$ is the optical cross-section of the target. Admittedly, this approach discards effects of oblique light incidence on the fluence and can only serve as a rough proxy. Nevertheless, it gives a good idea about thermo-mechanical constraints which anyway would have to be revised once detailed knowledge on target shape and surface material is available.

However, this approach only holds true for sufficiently small targets where outshining occurs. Larger targets with an optical cross-section that exceeds the beam spot size, $A_{\mathrm{s}}<$ $A_{\mathrm{cs}}$, allow for an even more simplified computation using $〈{\mathsf{\Phi }}_{\mathrm{inc}}〉=E_{\mathrm{T}}/A_{\mathrm{s}}$ where $E_{\mathrm{T}}$ is the laser pulse energy arriving in orbit after atmospheric attenuation. With small targets and $A_{\mathrm{cs}}<A_{\mathrm{s}}$, however, computation via $〈{\mathsf{\Phi }}_{\mathrm{inc}}〉=〈E_{\mathrm{inc}}〉/A_{\mathrm{cs}}$ is chosen since this accounts for effects stemming from the spatial distribution of the fluence when the target is more or less centered in the high-fluence area of the laser spot.

2.5 Prediction of Orbit Modification

The component $∆p_{ax}$ of laser-imparted momentum, which is aligned co-axial with the laser beam propagation axis and can be taken from the above-mentioned database, splits up in two subcomponents for a direct station transit, namely imparted in-track momentum $∆p_t=∆p_{ax}·\cos \beta$ and radial impulse transfer $∆p_r=∆p_{ax}·\sin \beta$ where $\beta \left(t\right)$ is the angle of attack, cf. Figure 1. As indicated there, two different options for perigee lowering are assessed: In perigee lowering by head-on momentum the object is only irradiated during its approach to the laser station, cf. Figure 1(a). The main idea here is to decelerate the target by applying a tangential thrust opposite to the direction of motion. Therefore, the target is not irradiated when its elevation angle decreases, since this would accelerate it again. In addition to tangential deceleration, the radial momentum components are considered for computation of the modified orbit as well.

As a second option for irradiation, the scope of outward momentum, cf. Figure 1(b), is to increase the apogee altitude by additional radial momentum while at the same time lowering the perigee altitude. In contrast to head-on momentum, only the imparted radial momentum is used to compute perigee lowering by outward momentum. Imparted in-track deceleration from irradiation during the ascending segment of the pass can simply be compensated for by acceleration during the same interval of elevation angles of the descending transit period.

For the computation of orbit modification, we use the semi-latus rectum $q=$ $a\left(1-e^2\right)$ of the elliptical orbit to express the tangential component $v_t$ of the debris velocity $v=\sqrt{v_t^2+v_r^2}$ by

$$v_t=\sqrt{GM/q}\left[1+e\cos \phi \right]$$

(8)

and the radial component $v_r$ via

$$v_r=\sqrt{GM/q}\left[e\sin \phi \right]$$

(9)

where $a$ is the orbit’s semi-major axis, $GM=398600.4$ km³/s² is Earth’s gravitational constant, $e$ is the numerical eccentricity of the orbit, and $\phi$ is the true anomaly [37].

The change of the orbital parameters by laser-induced momentum from a station transit is given by [38]

$$\mathsf{\Delta }e=\left[2\left(e_0+\cos {\phi }_0\right)\mathsf{\Delta }{v}_t-r_0\sin {\phi }_0·\mathsf{\Delta }{v}_r/a_0\right]/v_0,$$

(10)

$$\mathsf{\Delta }\mathrm{a}=2a_0^2{v}_0\mathsf{\Delta }{v}_t/GM,$$

(11)

where the subscript 0 denotes the orbital parameters before irradiation. From this, the change of the perigee radius can be computed using $r_p=\left(1-e\right)·a$ via

$$\mathsf{\Delta }{r}_p=\left(1-e_0\right)\mathsf{\Delta }a-\left(a_0+\mathsf{\Delta }a\right)\mathsf{\Delta }e.$$

(12)

For the irradiation pass, we use the mean altitude of the debris object and propagate the target’s motion on a corresponding circular orbit, which is a good approximation for ${\phi }_0\approx 270$°, cf. Eq. 8, and, in our case, typically low values for $e$, cf. Eq. 9. From Eqns. 10 – 12 it can be taken that in the case of the outward momentum approach, where $\mathsf{\Delta }{v}_t=0$, the minimum $\mathsf{\Delta }{r}_p$, i.e., the maximum perigee lowering, can be achieved for ${\phi }_0=$ $270$°. Hence, it would be optimal to irradiate the object at mean altitude when it descends apogee to perigee. If instead the average altitude on the ascending orbital path, i.e., ${\phi }_0=90$° was chosen, the apogee would be lowered and the perigee would be raised counterproductively.

In the head-on momentum approach, $\mathsf{\Delta }{v}_t<0$, selection of the optimum true anomaly for irradiation is significantly more complex since it additionally depends on the eccentricity. While this optimization is beyond the scope of our study, we restrain our simulations to ${\phi }_0=270$° for head-on irradiation. Note that for the sake of simplicity the laser-imparted momentum components of all $N$ laser pulses are straightforwardly summed up and attributed to the orbital point with ${\phi }_0=270$°, i.e., we have

$$\mathsf{\Delta }{v}_t={\sum }_{i=1}^N‖{\mathsf{\Delta }\overrightarrow{v}}_{t,i}‖$$

(13)

and

$$\mathsf{\Delta }{v}_r={\sum }_{i=1}^N‖{\mathsf{\Delta }\overrightarrow{v}}_{r,i}‖.$$

(14)

While the former equation for the cumulative deceleration is intuitive from Figure 1, the latter might appear questionable regarding the related error due to the different directions and positions of ${\mathsf{\Delta }\overrightarrow{v}}_{r,i}$ during the station pass. However, regarding the irradiation intervals employed in our study, cf. Sect. 3.1.2, we have only a small range of true anomalies during the pass, $\mathsf{\Delta }\phi =5.2°\pm 0.4°$ for head-on irradiation and $\mathsf{\Delta }\phi =7.8°\pm 0.7°$ for outward pointing. Hence, the angular variation of ${\mathsf{\Delta }\overrightarrow{v}}_{r,i}$ is rather marginal. Moreover, the mean true anomaly in head-on irradiation is at $\phi =266°\pm 0.3°$, which is very close to ${\phi }_0=270$°.

3. Results

3.1. Laser irradiation settings

3.1.1 Laser Fluence

Figure 4. (a) Mean fluence in the low Earth orbit (LEO) from a ground-based laser station using coherent coupling of 5,000 laser emitters at 20 J pulse energy each. Laser wavelength $\lambda$ is $1030$ nm, transmitter aperture: $D_{\mathrm{T}}=4$ m. Turbulence compensation is employed using a laser guide star and phase control. (b) Occurrence of the selected 1,111 debris objects.

Figure 4. (a) Mean fluence in the low Earth orbit (LEO) from a ground-based laser station using coherent coupling of 5,000 laser emitters at 20 J pulse energy each. Laser wavelength $\lambda$ is $1030$ nm, transmitter aperture: $D_{\mathrm{T}}=4$ m. Turbulence compensation is employed using a laser guide star and phase control. (b) Occurrence of the selected 1,111 debris objects.

It can be seen from Figure 4 that with our approach for turbulence compensation the threshold fluences for laser ablation of aluminum and steel, which are at 1 to 2 J/cm², corresponding to a beam diameter of 2 – 3 meters, cf. Figure 2(a), can be exceeded at any orbit altitude considered in our study sufficiently well. In particular for the highly frequented altitudes around 800 – 1,000 km, optimum momentum coupling, occurring around 3 to 7 J/cm², equivalent to beam diameters down to 1 meter, can be achieved for a wide range of beam pointing zenith angles. At higher altitudes certain restrictions exist for large zenith angles due to the great distance to the target and the correspondingly decreasing focusability of the beam, while at lower altitudes the momentum coupling coefficient even decreases for small zenith angles due to the high fluences where plasma shielding starts to occur. Most likely, however, this would not give reason for defocusing the beam, since the overall imparted momentum would still increase nearly proportional with the incident laser energy since $∆p=c_m·E_{\mathrm{inc}}$ and, in general, the effective fluence on the surface might be lower due to oblique beam incidence.

3.1.2. Irradiation Interval

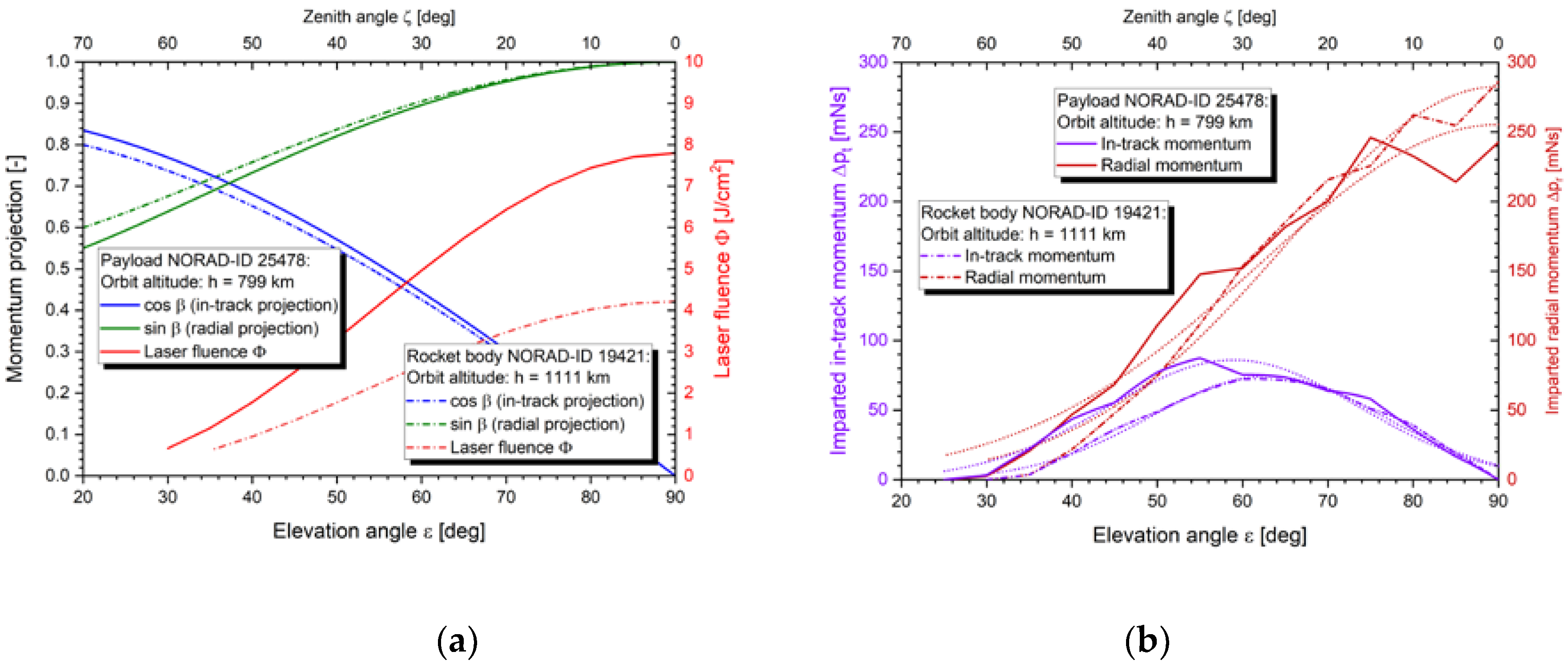
The efficiency of momentum generation strongly depends on the irradiation geometry during the station pass of the debris target. For head-on momentum, irradiation under low elevation angles is more beneficial than at small zenith angles regarding the in-track projection $∆p_t$ of the imparted momentum component, cf. Figure 5(a). However, as can be seen from Eq. 1, beam transmission constraints in principle lead to a larger spot size at greater distances between laser and target, which is the case at low elevation angles. In turn, the risk of energy losses by outshining the target increases, moreover, the fluence is significantly lower than at zenith. Hence, obtaining the maximum in-track momentum comes as a trade-off between momentum projection and laser spot size while radial momentum approaches its maximum for small zenith angles for both geometric as well as beam propagation reasons, cf. Figure 5(b).

Figure 5. Aspects of momentum changes in laser-based orbit modification for two debris target examples: (a) in-track (cos β) and radial (sin β) projection of momentum and laser fluence corresponding to the respective distance between laser and target, (b) imparted in-track and radial momentum per laser pulse. Dotted lines indicate Gaussian fit functions of the imparted momentum, see text.

Figure 5. Aspects of momentum changes in laser-based orbit modification for two debris target examples: (a) in-track (cos β) and radial (sin β) projection of momentum and laser fluence corresponding to the respective distance between laser and target, (b) imparted in-track and radial momentum per laser pulse. Dotted lines indicate Gaussian fit functions of the imparted momentum, see text.

Table 1. Fit parameters for determination of the optimum laser irradiation interval of space debris using a pulsed laser at $\lambda =1030$ nm, $\tau =5$ ns and $E_{\mathrm{L}}=100$ kJ. Note that due to the strong non-linearity of $c_m$ removal laser stations with deviating laser parameters or other power beaming performance likely demand for different settings of the irradiation interval.

Category	${\mathit{y}}_1\left[°\right]$	${\mathit{m}}_1\left[°/\mathit{k}\mathit{m}\right]$	${\mathit{y}}_2\left[°\right]$	${\mathit{m}}_2\left[°/\mathit{k}\mathit{m}\right]$	${\mathit{y}}_3\left[°\right]$	${\mathit{m}}_3\left[°/\mathit{k}\mathit{m}\right]$
Payload	59.9	-0.0145	17.4	-0.0052	41.1	-0.0105
Rocket Body	68.7	-0.0253	22.9	-0.0099	54.2	-0.0237
Payload fragment	55.7	-0.0113	13.1	-0.0024	34.6	-0.0056
Rocket fragment	57.0	-0.0158	14.9	-0.0046	36.5	-0.0092

Table 1. Fit parameters for determination of the optimum laser irradiation interval of space debris using a pulsed laser at $\lambda =1030$ nm, $\tau =5$ ns and $E_{\mathrm{L}}=100$ kJ. Note that due to the strong non-linearity of $c_m$ removal laser stations with deviating laser parameters or other power beaming performance likely demand for different settings of the irradiation interval.

Category	${\mathit{y}}_1\left[°\right]$	${\mathit{m}}_1\left[°/\mathit{k}\mathit{m}\right]$	${\mathit{y}}_2\left[°\right]$	${\mathit{m}}_2\left[°/\mathit{k}\mathit{m}\right]$	${\mathit{y}}_3\left[°\right]$	${\mathit{m}}_3\left[°/\mathit{k}\mathit{m}\right]$
Payload	59.9	-0.0145	17.4	-0.0052	41.1	-0.0105
Rocket Body	68.7	-0.0253	22.9	-0.0099	54.2	-0.0237
Payload fragment	55.7	-0.0113	13.1	-0.0024	34.6	-0.0056
Rocket fragment	57.0	-0.0158	14.9	-0.0046	36.5	-0.0092

Considering the risk of overheating the target, a restriction of the irradiation interval appears to be reasonable in order to avoid laser heating at fluences where the outcome in terms of momentum transfer is rather low. Hence, the magnitude of momentum transfer has been analyzed for the simulated targets at their different altitudes, and a Gaussian has been fitted to the data of momentum as a function of the zenith angle for each target’s pass, cf. Figure 5(b). The related fit parameters show a clear dependency on the orbit altitude, which makes sense from a geometric viewpoint. From the full width half maximum (FWHM) of the Gaussian fit functions, averaged among the different target categories, we have determined the laser irradiation interval by the parameters shown in Table 1. They allow to derive the optimum onset angle ${\zeta }_{\mathrm{in}}=y_1+m_1·h$ and termination angle ${\zeta }_{\mathrm{out}}=$ $y_2+m_2·h$ for head-on irradiation from the object’s orbital altitude $h$. For outward irradiation, a symmetric interval is chosen, i.e., ${\zeta }_{\mathrm{in}}=-{\zeta }_{\mathrm{out}}=y_3+m_3·h$.

3.1.3 Laser Pulse Repetition Rate

As a starting point for our analysis of orbit modification within a single station transit we have selected a laser pulse repetition rate of $f_{\mathrm{rep}}=100$ Hz during the irradiation interval specified in Table 1. However, the resulting number of laser pulses will presumably be too high in terms of laser-induced heat which could endanger the target’s mechanical integrity eventually worsening the space debris situation. To assess this, we analyzed fragments and mechanically intact targets separately regarding their thermal constraints.

For fragments, overheating might eventually lead to uncontrolled target melting and subsequent sphere formation from the initially typically rather flat shape, i.e., yielding a significantly lower optical cross-section and, hence, area-to-mass ratio which might be detrimental for object tracking and removal [16]. Thus, we analyzed target heating at 100 Hz repetition rate, cf. Sect. 2.4, in order to derive an upper limit for the repetition rate in the irradiation interval. For this computation enthalpies of fusion and vaporization have been discarded and the material’s specific heat has been assumed constant at its value for room temperature in order to simplify subsequent downscaling of the laser repetition rate. Moreover, an initial temperature of 273.15 K before laser irradiation has been chosen discarding the fluctuations of debris temperature during the orbital path through sunlight and Earth’s shadow. Finally, we assume that heat distributes rapidly throughout the target before the next laser pulse arrives, which at least for thin metal fragments appears reasonable regarding their high heat conductivity.

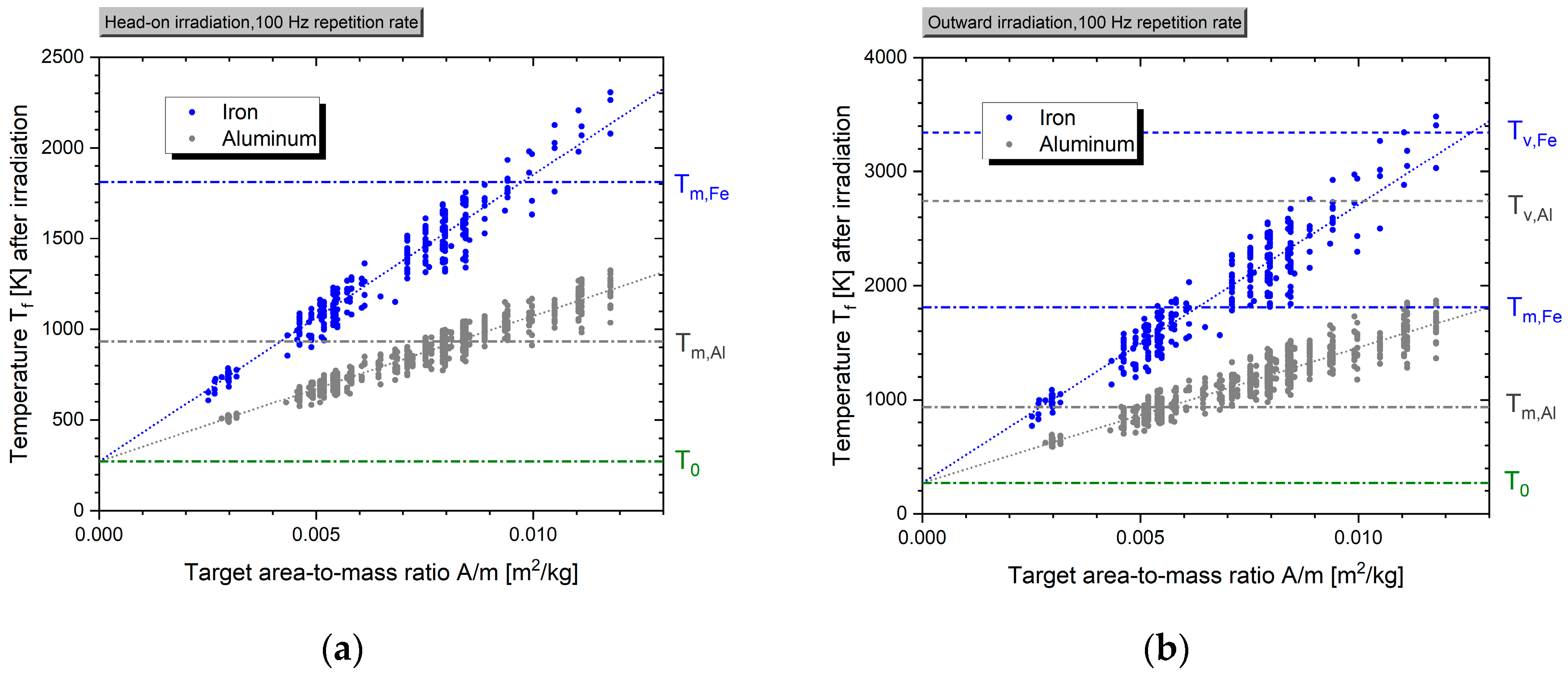
Figure 6. Simulated temperature of space debris fragments after irradiation by a 100 kJ high energy laser at 100 Hz pulse repetition rate during the zenith angle range as specified in Table 1 for (a) head-on and (b) outward irradiation, respectively.

Figure 6. Simulated temperature of space debris fragments after irradiation by a 100 kJ high energy laser at 100 Hz pulse repetition rate during the zenith angle range as specified in Table 1 for (a) head-on and (b) outward irradiation, respectively.

It can be seen from the simulation results shown in Figure 6 that the target’s temperature after irradiation increases linearly with its area-to-mass ratio, which can be deduced from Eq. 7 yielding $T_{\mathrm{f}}\approx T_0+\left(A/m\right)\left(1/c_p\right){\sum }_i^N{\eta }_{res}\left({\mathsf{\Phi }}_i\right)·{\mathsf{\Phi }}_i$ where ${\mathsf{\Phi }}_i$ is the fluence at the target surface at the $i^{th}$ pulse, $N$ is the number of laser pulses during the station pass and the heat capacity is assumed to be constant yielding $∆T=$ ${\eta }_{res}{E}_{\mathrm{L}}/\left(m·c_p\right)$. The scatter in the depicted data stems from the various altitudes of the different targets which affect the number of pulses that increases with orbit height by up to more than 80 % throughout the altitude range from 583 km to 1182 km. Moreover, the achievable fluence at higher altitudes is considerably lower, cf. Figure 5(a), which implies greater thermal coupling, cf. Figure 2(b).

Overall, it is evident that the number of laser pulses has to be limited to avoid melting or even vaporization of target in particular when their area-to-mass ratio is rather high. For that purpose, we decided to leave the angular irradiation range unchanged but to reduce the pulse repetition rate which approximately decreases the temperature increment after the pass by the same amount. Choosing a pulse repetition rate of 9 Hz in the case of head-on irradiation and 6 Hz for outward irradiation yields a maximum temperature increment of $∆T\approx 100$ K for aluminum fragments with a very high area-to-mass ratio and $∆T\approx 200$ K for the respective fragments when iron is considered as target material. This temperature increment is less than 20 % of the temperature increase which would yield target melting and seems to be a reasonable limitation of the repetition rate. Afterwards, the acquired heat can be re-radiated into space to allow target cooldown before its trajectory is modified further in a posterior laser station pass.

This assessment of thermal constraints does not hold for non-fragmented targets like payloads or rocket bodies, which are much more complex objects than a target that is treated as homogeneous bulk material. Instead, the outer shell of such an object demands for dedicated consideration. Even for a temperature rise to values substantially below the melting point, heating might already pose a high risk, e.g., in case that stored energy, i.e., not completely discharged batteries or residual propellant, is located inside the object in the vicinity to an outer wall. Since these aspects are not available for a detailed assessment, we restrain our analysis to the computation of the average laser intensity during a station pass.

As an estimate for maximum permissible average irradiation intensity we refer to [40] where an irradiance threshold for lethality against unhardened satellites significantly below $100$ W/cm² was stated. Acknowledging that heat absorbance under laser ablation might be significantly higher than for highly reflective metals, cf. Figure 2(b), we choose $I_{\max }=13.7$ W/cm² as an upper limit for the average intensity during laser irradiation, which equals the hundredfold of the solar constant. To ensure that $I_{\max }$ is not exceeded during irradiation we set the repetition rate for outward irradiation altitude-dependent to $f_{rep}\left(h\right)=I_{max}/{\mathsf{\Phi }}_0\left(h\right)$ where ${\mathsf{\Phi }}_0$ is the laser fluence focused at a target with altitude $h$ in the zenith of the laser station, i.e., $\zeta =0°$. Hence, the applicable laser repetition rate increases nearly linearly from 1.1 Hz at 600 km altitude up to 3.8 Hz at 1,200 km altitude.

While this limitation is reasonable for outward irradiation, where the object is irradiated during a relatively long timespan near zenith, i.e., at high fluences, these values are reached merely at the end of the irradiation interval in the case of head-on irradiation. Therefore, we chose an enhanced repetition rate for head-on momentum which exceeds the repetition rate of outward irradiation at the respective altitude by 50 %. While $I_{max}$ is hence exceeded at the end of the irradiation interval, this is somehow compensated since the arriving laser intensity is significantly lower in the initial phase of the irradiation interval – unlike in the case of outward irradiation, where high intensities are obtained for a relatively long timespan. Overall, this choice gives the same ratio of repetition rates as for fragments, where we had 9 Hz and 6 Hz, respectively. Hence, the selection of repetition rates should yield a nearly similar heat load ratio of the irradiated target for the different irradiation strategies.

3.2. Orbit modification

3.2.1. Orbital velocity changes

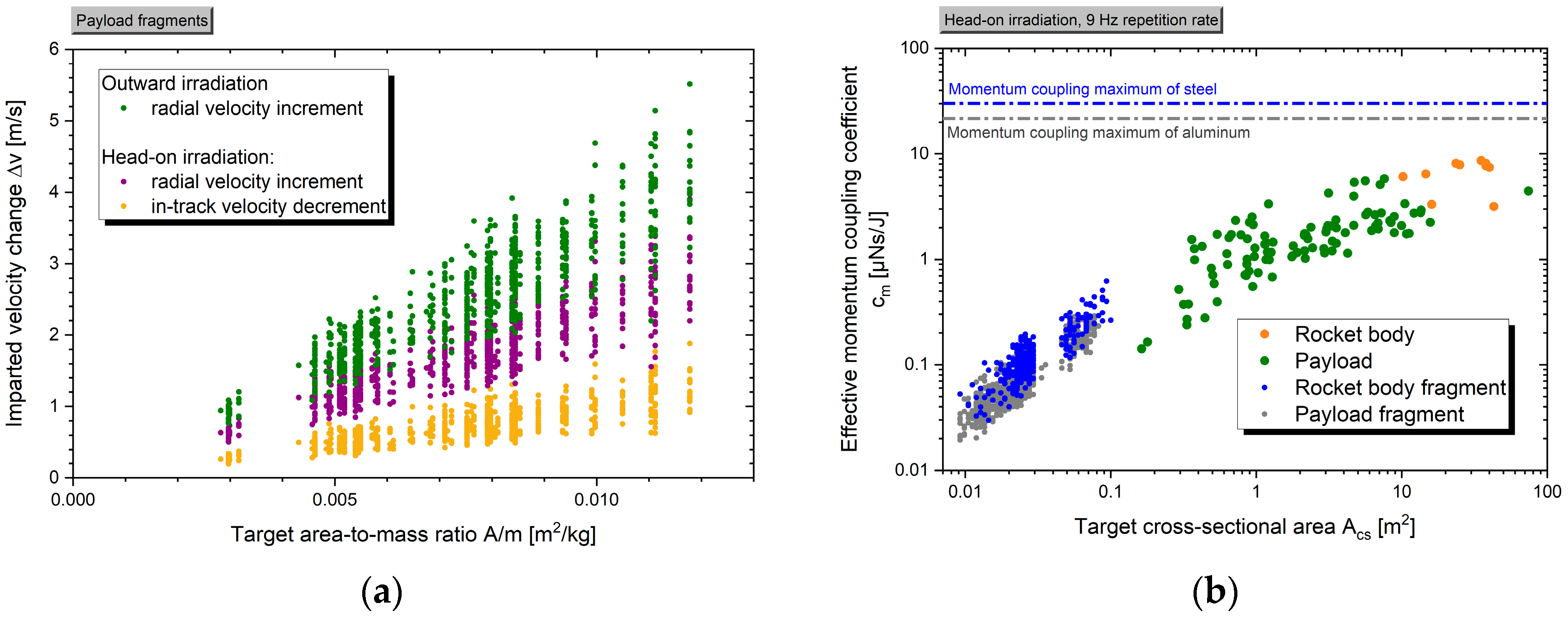
Figure 7(a) shows the simulation results for the resulting velocity change of the debris object when the restriction of the repetition rate to 6 and 9 Hz, resp., is applied. Again, a linear dependency of coupling from the object’s area-to-mass ratio is found, which here can be predicted from Eq. 6 as $\mathsf{\Delta }v=\left(A/m\right){\sum }_{i=1}^N{c}_m\left({\mathsf{\Phi }}_i\right)·{\mathsf{\Phi }}_i$. However, the data on laser-induced velocity change exhibits a larger scatter than the data on temperature increment, since beyond the altitude dependency of pulse number and fluence as well the different target shapes are reflected in the raytracing computation of imparted momentum. Overall, the resulting velocity change of a few m/s is about two orders lower than the required $\mathsf{\Delta }v$ for perigee lowering of initially circular orbits for atmospheric burn-up, cf. [39], clearly indicating the necessity of debris irradiation during a multitude of station passes.

Figure 7. Simulation results for (a) velocity change of aluminum fragments and (b) effective momentum coupling coefficient of different object types after repetitive head-on irradiation by a 100 kJ high energy laser. Laser pulse repetition rates depend from target type and irradiation mode, cf. Sect. 3.1.3. The range of irradiation angles is defined in Table 1.

Figure 7. Simulation results for (a) velocity change of aluminum fragments and (b) effective momentum coupling coefficient of different object types after repetitive head-on irradiation by a 100 kJ high energy laser. Laser pulse repetition rates depend from target type and irradiation mode, cf. Sect. 3.1.3. The range of irradiation angles is defined in Table 1.

It should be noted here that the effective momentum coupling coefficient $c_{m,\mathrm{eff}}$ significantly deviates from the experimental data on momentum coupling as of Figure 2(a). Here, we define $c_{m,\mathrm{eff}}$ as a figure of merit for the entire debris removal system, i.e.,

$$c_{m,\mathrm{eff}}=\sum ∆v/\left(N_p·E_{\mathrm{L}}\right)$$

(15)

where $E_{\mathrm{L}}$ is the initially emitted laser pulse energy and $N_{\mathrm{p}}$ is the number of applied laser pulses. Then, it can be taken from Figure 7(b) that the effective momentum coupling is around two to three orders of magnitude below the experimental data, mainly due to the large outshining losses in particular for small targets at beam diameters in the size range of 1 to 3 m. However, what seems here as a massive waste of laser energy is somehow needed for the small objects since the relatively large spot size enables momentum coupling to small objects even in the presence of significant beam pointing jitter. In any case the impact of outshining losses on the effective momentum coupling coefficient should be carefully considered in conceptual studies in order to avoid performance overestimation of any laser-based debris removal system.

3.2.2. Perigee Lowering Method

In the next step of our analysis, our findings on laser-induced velocity change from a station pass have been employed to compute the corresponding perigee change of the respective target’s orbit. The results for head-on irradiation are shown in Figure 8.

Simulation results on perigee lowering after a transit with head-on irradiation are shown in Figure 8. Note that regarding the amount of perigee lowering head-on irradiation outperforms outward irradiation by in average 23 ± 8 %, even though the true anomaly for irradiation has not been optimized for the head-on irradiation, cf. Sect. 2.5, and though outward irradiation benefits from lower zenith angles, i.e., higher fluences yielding an overall velocity change that exceeds the overall $∆v$ resulting from head-on irradiation by ca. 36 ± 5 %.

Frequently, head-on irradiation is treated i the literature as pure deceleration, i.e., $v_r=0$ and perigee lowering is computed using a Hohmann transfer from an initially circular orbit, i.e., assuming $e_0=0$ and $\phi ={\phi }_0=180°$, resulting in a required ${∆v}_t$ for perigee lowering which is about four times lower than the needed ${∆v}_r$ in outward irradiation [39]. From our simulations assuming ${\phi }_0=270°$ we can see that in-track deceleration and imparted radial momentum contribute almost in equal parts to perigee lowering, in particular since the orbit’s initial eccentricity is considered in our simulations. In conclusion, these findings disprove the view that head-on irradiation would be inefficient from ground due to the large displacement between laser source and orbital trajectory.

Figure 8. Simulation results on perigee lowering of space debris after a single station pass with head-on irradiation. Laser pulse repetition rates depend on the target type and irradiation mode, cf. Sect. 3.1.3. The range of irradiation angles is defined in Table 1.

Figure 8. Simulation results on perigee lowering of space debris after a single station pass with head-on irradiation. Laser pulse repetition rates depend on the target type and irradiation mode, cf. Sect. 3.1.3. The range of irradiation angles is defined in Table 1.

3.2.3. Multi-Pass Removal

From the results on perigee lowering in a single transit a rough estimate can be given for the number $N_{\mathrm{pass}}$ of required passes with laser irradiation to achieve the targeted perigee altitude of $h_{p,\mathrm{final}}=200$ km. For this purpose, the progress in the change of the orbit’s eccentricity, semi-major axis, and perigee altitude is monitored for a multitude of station transits until $h_p<h_{p,\mathrm{final}}$. For the sake of simplicity, laser-imparted momentum is not re-computed for each transit. Instead, for each pass the same $∆p$ is used which means that for reasons of computational effort we discard the change $∆a$ of the mean altitude where the irradiation takes place. Otherwise a new set of laser-matter interaction tables would have to be computed for each target at every pass altitude which would increase the overall computational effort of our study by several orders of magnitude. Moreover, we discard the effects of mass loss following the findings in [36].

While discarding $\mathsf{\Delta }a$ for momentum computation is no issue in outward irradiation where we have $\mathsf{\Delta }{v}_t=0\Rightarrow \mathsf{\Delta }a=0$, cf. Eq. 11, due to ${\zeta }_{\mathrm{in}}=-{\zeta }_{\mathrm{out}}$, for head-on irradiation the mean altitude is lowered significantly in a single pass, approximately $∆a/∆r_p\approx$ $0.46\pm 0.02$. Hence, a higher laser fluence and less absolute hit uncertainty is obtained the more the perigee is lowered. Therefore, the number of required passes might in principle be overestimated while, on the other hand, better momentum coupling might as well be associated with higher thermal coupling – which in turn would demand for a stronger limitation of the number of laser pulses during a single transit at a lower altitude. Eventually, this might end up in a similar overall efficiency of the laser irradiation during a single pass. At this point, a more precise assessment is left to be given by more elaborate simulations in the future.

Figure 9. Simulation results for the number of required passes for perigee lowering from LEO down to 200 km with head-on irradiation for (a) fragments and (b) non-fragmented debris objects.

Figure 9. Simulation results for the number of required passes for perigee lowering from LEO down to 200 km with head-on irradiation for (a) fragments and (b) non-fragmented debris objects.

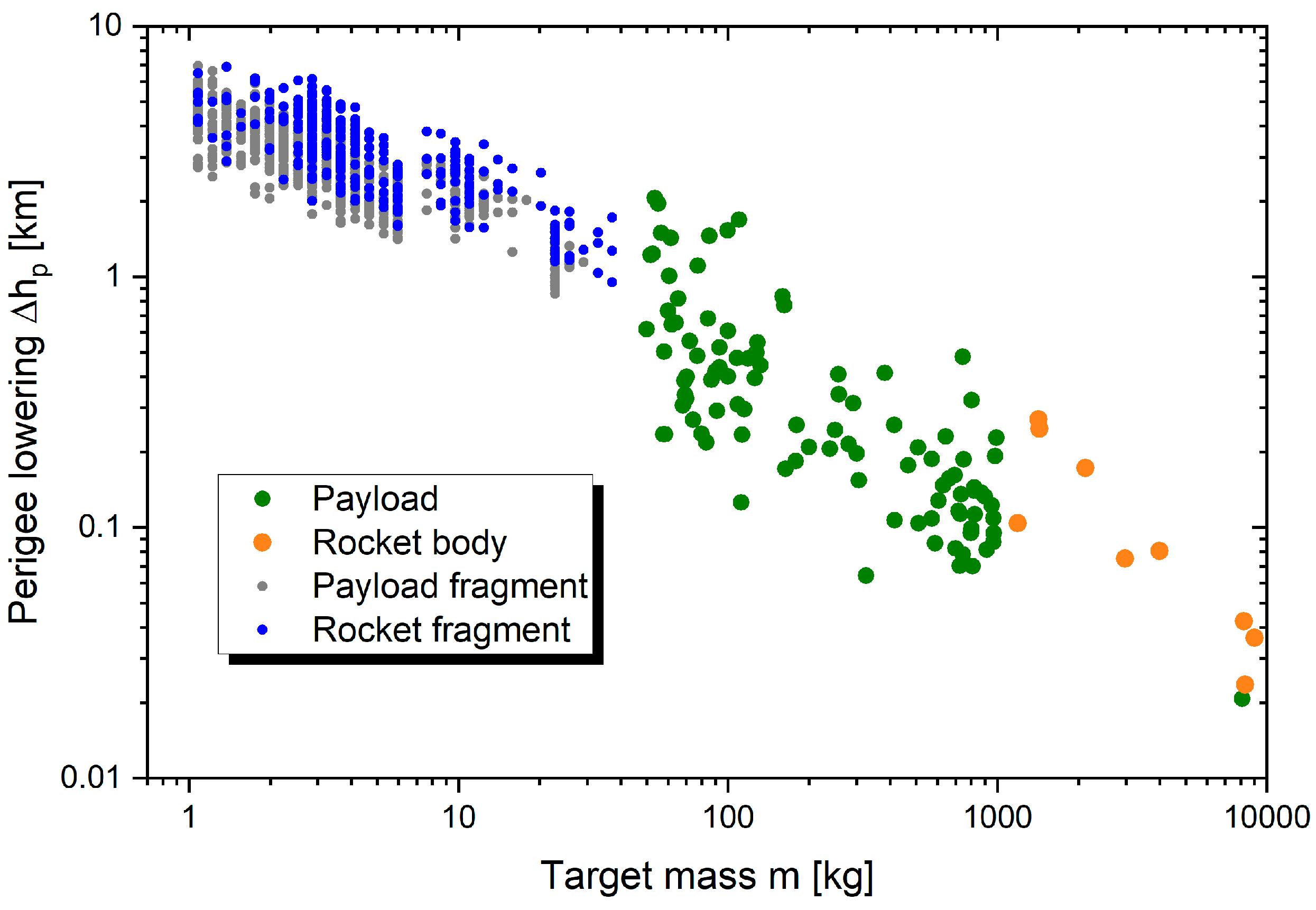
It can be seen from Figure 9(a) that the number of passes for lowering the perigee of fragments is in average 240 ± 130. The lowest values for the number of transits are achieved for targets with a low initial perigee altitude and high area-to-mass ratio, since then a relatively small change of orbital velocity is needed and a relatively large amount of laser energy can be captured for momentum transfer.

In contrast, the resulting number of station passes with laser irradiation is rather high for massive objects, as can be seen from Figure 9(b). As the targets become significantly larger than the spot size, the ratio of spot area to target mass decreases strongly, thus, lowering the capability of laser-induced deceleration. With only a few exceptions, objects larger than 2 meters demand for more than 1,000 passes with laser irradiation while for the high-risk targets between 3,000 and 30,000 irradiations would be needed which cannot be deemed a realistic perspective for their efficient removal at all. Hence, it does not seem to be recommendable to remove larger objects using lasers unless they are rather light-weight and the required perigee lowering is not too high.

4. Discussion

4.1 Thermo-Mechanical Integrity

Thermo-mechanical limitations constitute rather tight constraints for laser-based orbit modification, which cannot be easily overcome. In contrast to earlier studies, e.g., [37], it can at least be stated that small space debris in LEO is not likely to be removed during a single pass but irradiation during several passes has to be considered. It can be seen from Eqns. 6 and 7 that this issue is half-way material specific and half-way of technical nature: Combining both equations we obtain the thermo-mechanical coupling coefficient $c_{tm}$ [16]

$$c_{tm}=c_m/{\eta }_{res}\approx \frac{1}{c_p}·\frac{∆v}{∆T}$$

(16)

representing the material’s inherent thermal constraints for laser-based momentum change. From this viewpoint, optimizing orbit modification in a station pass would mean to maximize $c_{tm}$ eventually yielding a higher number of permissible laser pulses before thermal limits are experienced. In our case, this would simply mean to maximize the fluence even beyond the fluence where $c_m$ has its optimum since the benefit from the strong decrease of ${\eta }_{res}$ with the fluence predominates the performance loss of momentum coupling at high fluences, cf. Figure 2. In general, selection of a shorter laser pulse length could yield a higher thermo-mechanical coupling coefficient as well, cf. [29], in particular when ultrashort pulses were used, as, e.g., proposed in [13] for space-based operation.

The heat deposited at the debris mainly depends on the number of laser pulses, but not directly on the pulse repetition rate. Instead of choosing a low repetition rate, as undertaken in our study, the irradiation interval can as well be shortened when higher repetition rates of 100 Hz and beyond are employed which, however, might increase the requirements for target tracking due to rapid orbit modification. Note, however, that heat deposition can be significantly different for plastic fragments where high repetition rates might soon yield overheating and possible thermal decomposition of the irradiated surface due to the low heat conductivity of the object.

For mechanically intact objects preservation of thermo-mechanical integrity is even more complex, since our chosen limit of hundredfold solar irradiation is still rather generic. For removal by high energy laser radiation, thorough knowledge of such a debris object and its potential susceptibility to laser-induced thermo-mechanical stresses is mandatory, in particular regarding possible remainders of stored energy, in order to avoid its partial fragmentation or, as a worst-case scenario, detonation from laser-heated propellant residuals. Moreover, certain components like solar panels, multilayer insulation (MLI) or components from carbon-fiber reinforced plastics (CFRP) might have to be excluded in general from pulsed laser irradiation due to fragmentation risks [17] eventually constraining laser-irradiation for removal to remainders from fragmentations but avoiding objects that have not fragmented (yet).

4.2 Momentum Prediction

Safety considerations are not limited to thermal constraints but cover dynamical issues as well. The dependency of velocity change from target size and area-to-mass ratio and in particular the significant scatter of $∆v$ due to the variety of different target shapes and material, cf. Figure 7, underline that detailed target reconnaissance is mandatory for an accurate prediction of the modified trajectory to avoid harmful interference with other space missions. Moreover, we averaged over a multitude of Monte Carlo samples with different orientations discarding the large momentum scatter that might occur over time due to the object’s rotational motion. Here, debris attitude analysis by lightcurve observations might be game-changing for the selection of fortunate points of time where laser-momentum coupling is both efficient and well predictable regarding magnitude and direction. Beyond reconstruction of the rotational motion, information about the debris material could be obtained from spectral [41] and polarimetric [42] analysis of the reflected light eventually yielding a better prediction of $∆v$ as well.

Overall, predictability of momentum depends strongly on the ground station’s performance of turbulence compensation and the remaining hit uncertainty from beam pointing jitter in combination with a-priori uncertainty from target tracking. Together with the strong non-linearity of $c_m$ which is very sensitive to the incident fluence, cf. Figure 2(a), this constitutes a significant risk of overestimating the achievable $∆v$ and its potential for optimization.

4.3 Removal Efficiency of Laser Station Networks

Incorporating the above-mentioned constraints like, e.g., thermo-mechanical integrity, hit uncertainty and momentum non-linearity in our simulations, the resulting number of irradiations for removal, cf. Figure 9, is quite high compared to earlier findings from the literature, e.g., in [15,36]. Moreover, we have focused our study on irradiation of the debris at a specific point of its trajectory, ${\phi }_0\approx 270$°, where the induced orbit modification is rather fortunate for de-orbiting. In the real-world scenario, however, the apsidal line, which virtually connects apogee with perigee, naturally rotates over time, in average 2.3° ± 1.4° per day for the initial orbits of our simulation targets, thus moving the optimum geographical latitude for laser irradiation continuously. Hence, a widespread distribution of the stations’ geographical latitude might be beneficial at the end. Network simulations of multi-pass laser-based debris removal would yield a more profound assessment including considerations of, e.g., the overall impact of non-direct station transit on in-track momentum reduction and generation of cross-track momentum.

At present, we have learned from the network simulations on photon pressure carried out earlier that a laser station network with only nine globally distributed sites would – under realistic weather conditions regarding laser access to sky – be able to perform quasi-continuous laser tracking on a few-hourly or at least daily basis for approximately $N_{\mathrm{LXN}}\approx 1787$ debris objects in the low Earth orbit simultaneously [22]. Given this capacity of a station network to maintain a constantly updated “space debris laser catalogue”, adding high energy laser pulses to each and every laser ranging maneuver would result in a continuous orbit modification of those catalogued objects. Therefore, in a very simplified and optimistic guess we assume that such high-power irradiation could in principle be undertaken each time when it is required to keep the object in the high-precision catalogue from laser ranging data, i.e., when the so-called laser tracking data expiry time ${\tau }_{\mathrm{LT}}$ has passed. Since irradiation would not be reasonable for every value of the true anomaly, cf. Eq. 10 – 12 for the impact of ${\phi }_0$ on $∆r_p$, we estimate the time between two removal irradiations to amount to at least $∆T=2·{\tau }_{\mathrm{LT}}$. From the number of required passes for perigee lowering, cf. Figure 9(a) one can compute that the average time needed to de-orbit a fragment would be around 340 ± 240 days. Therefore, as a rule of thumb, the number of fragments which can be removed per year by such a network is slightly higher than the number of objects which can be tracked by it simultaneously over a long timespan, i.e., 1,937 objects in our case.

Note that this is a rather rough assessment and dedicated laser station network simulations on orbit modification would be needed to consolidate these numbers. Moreover, smaller fragments down to 1 cm size might exhibit an up to 50 % higher area-to-mass ratio [34] than the smallest objects ($L_{c,\min }\approx 10.8$ cm) in our study yielding eventually a shorter time for de-orbit. Nevertheless, this network performance is about a factor of five times lower than the assumptions of [3] considering laser-based removal of 100,000 small fragments in a timespan of 10 years, which, hence, would require a significantly larger network of ground stations.

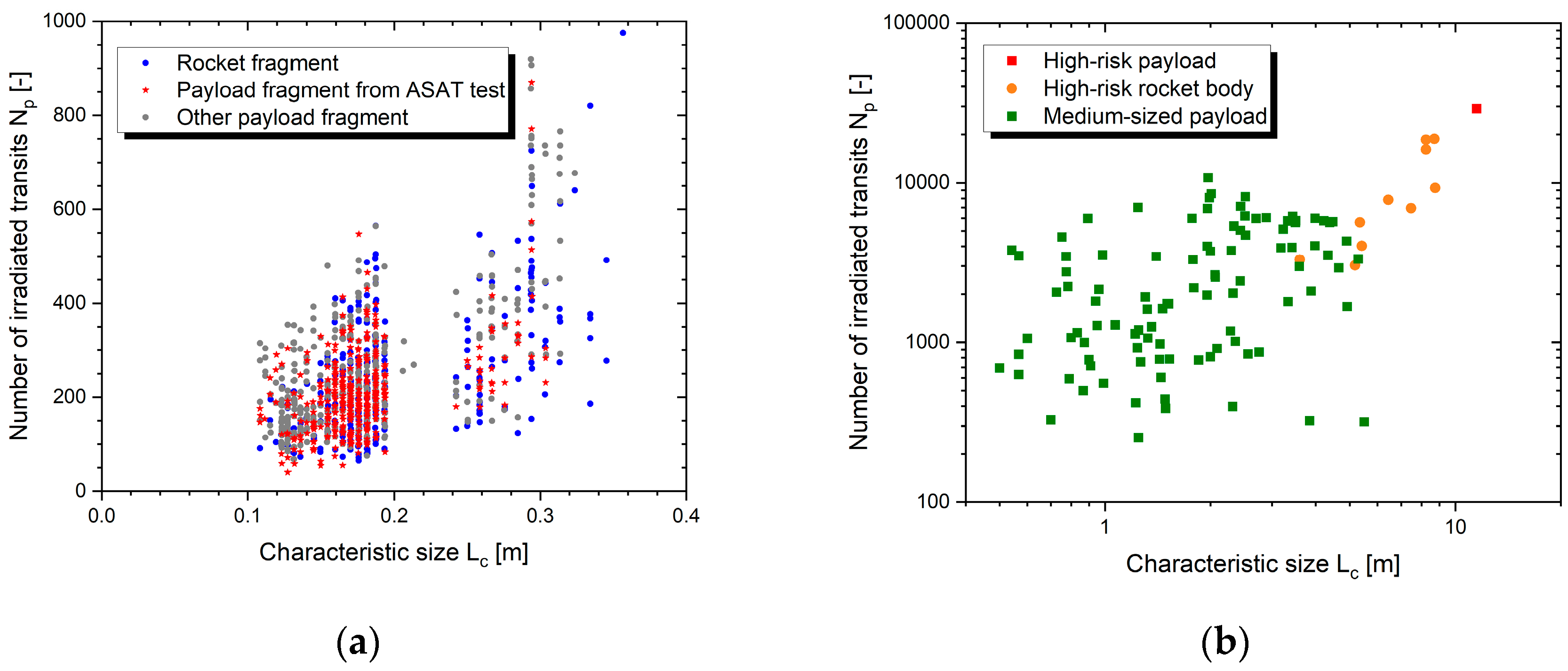
At this point one can say that the continuing testing of anti-satellite weapons impedes all efforts for the protection of the space debris environment. Removing only the currently tracked fragments created from ASAT tests in space, namely 3,472 objects [18], would already take more than a year with the above-mentioned laser network – not to mention the far greater number of smaller fragments not tracked yet.

5. Conclusions

Thermal constraints have a remarkable impact on the efficiency of laser-based debris removal by limiting laser pulse number and repetition rate for a single station pass. This has to be addressed thoroughly by well-defined irradiation maneuvers with subsequent cooldown times in advance to the next laser station transit in order to maintain the mechanical integrity of the irradiated target, which at the same time illustrates the weaponization potential of this technology. To ensure operational safety of laser-based debris removal, remote reconnaissance of material, shape, temperature, and attitude is of great importance. Moreover, not only momentum coupling but as well thermo-mechanical integrity of space-aged targets under relevant laser irradiation conditions should be investigated experimentally to derive realistic estimates for the efficacy of laser-based removal, in particular regarding astrodynamic and atmospheric constraints.

Regarding sustainability in the Earth’s orbital environment high power lasers might not be the optimum cure for the orbital disease from space debris, but – remaining in the picture of cure and disease – laser station networks could act very well as a needed painkiller significantly lowering the increasing burden of orbital collision avoidance and simultaneously supporting space sustainability by perceptibly reducing the large number of debris fragments which constitute centers of inflammation in the collisional cascade of the progressing Kessler syndrome. While high power lasers do not appear particularly suitable for the removal of the massive high priority debris objects as the presumably most sustainable debris remediation step [6], they seem to be very well suited for massive removal of small debris which is an increasingly emergent task.