Prerpints.org logo
Preprint
Article

A General Rule-Based Framework for Generating Alternatives for Forest Ecosystem Management Decision Support Systems

Altmetrics

Downloads

128

Views

41

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

24 May 2023

Posted:

26 May 2023

You are already at the latest version

Alerts
Abstract
Linear programming formulations of forest ecosystem management (FEM) problems proposed in the 60s have been adapted and improved upon over the years. Generating management alternatives for forest management planning is a key step in building these models. Global forests are diverse, and a variety of models have been developed to simulate management alternatives. Climate change has made forest management calculations even more complex, requiring flexibility, diverse parameters, models, and methods. Despite this complexity, consistent concepts can be applied in developing management alternatives for forest management planning. This work describes iGen, a flexible forest prescription generator that applies the AI technique Rule-Based System (AI-RBS). iGen projects the state and associated inputs and outputs for a set of management units using rules from its knowledge base. An Inference Engine uses the rules to simulate a set of prescriptions in a tree-like graph structure. Without needing IT specialists, forest managers can describe the potential development of their forest through variables, rules, formulas, functions, and procedures. A key feature of iGen is that it is not limited to, adapted to, or focused on any specific region, landscape, forest condition, projection method, or yield function. Instead, it aims to maximize generality, enabling it to address a broad range of FEM problems. This article introduces iGen, explaining its concepts, structure, and algorithms through two FEM problems: natural regeneration with shelterwood harvests and plantation/coppice. For data and iGen source programs, visit github.com/…/iGen.
Keywords: 
Subject: Environmental and Earth Sciences  -   Sustainable Science and Technology

1. Introduction

The forest ecosystem management (FEM) problem can be defined as characterizing the Pareto frontier for the problem of selecting a management prescription for the duration of some planning horizon for each forest management unit within a specified planning area, given a set of management and policy objectives and constraints. A management unit is defined here as either a contiguous area to be managed with a single prescription or as a collection of similar areas to which a common set of management prescriptions can be applied and for which the associated inputs and outputs for a given prescription will be sufficiently similar. While other approaches could be used to solve the FEM problem, this paper focuses on situations where the problem will be formulated as either a linear program (LP) or mixed-integer linear programming (MIP) problem. To formulate this problem, one needs to have 1) a set of forest management units, 2) a set of management prescriptions for each unit, and 3) a set of management constraints and objectives. It is also necessary to quantify the contribution of each management alternative to each constraint or objective, i.e., the relevant inputs and outputs associated with each prescription for a given management unit. For the purposes of this paper, we refer to any problem that fits this definition as a FEM problem. FEM problems are frequently quite complex, and considerable research has gone into the development of decision support systems to assist forest planners in finding efficient solutions to such problems [1,2,3,4,5,6,7,8].
A forest ecosystem management decision support system (FEMDSS) is a software system that facilitates the formulation, solution, storage, and interpretation of FEM models. It must be able to project the state, including the associated inputs and outputs, of each management unit under each possible management prescription for the entire planning horizon. It must then be able to use the information generated about the projected states (and inputs and outputs) of each management unit to formulate and solve a set of optimization models, store the solutions of these models, and use the solution information to enable decision-makers to visualize and understand the attributes of the Pareto frontier and the implied tradeoffs among objectives.
Most of the literature related to the FEMDSS problem has addressed questions related to the formulation and solution of these optimization models [1,9] or to the problem of generating and/or visualizing the Pareto frontier [10,11,12,13]. This paper focuses on the generation of alternatives for a FEMDSS, often referred to as a stand simulator module. According to Eriksson and Bergh [14], an effective stand simulator should be able to cover a broad problem domain. Eriksson and Bergh [14] describe two strategies for a prescription generation: evaluation and development. The evaluation strategy involves assessing forest states and growth based on a predefined management strategy to simulate a single preferred management prescription for each management unit. On the other hand, the development strategy generates a range of management options for each stand so that preferred management strategies for each management unit can be assessed in the context of identifying an overall optimal strategy for the forest as a whole, using either linear programming (LP), mixed-integer linear programming (MILP), or heuristic techniques. iGen is designed for the latter context. It is not designed to find an optimal solution, but rather to generate a set of feasible alternatives.
Since the 1960s, numerous forest management alternative generators have been developed [15,16,17,18]. The need for multiple generators arises due to the unique features of each FEM planning problem, which existing solutions often cannot handle [19]. Various FEM problems differ in the types of management regimes, outputs (e.g., wood, wildlife habitat, carbon storage), and production functions used to predict inputs and outputs for each management alternative. Growth and yield models, the most common production functions, vary widely, ranging from simple yield models [20,21] to more complex individual tree models [22,23] and process-based physiological models [24]. Moreover, models used in different regions frequently require different inputs (e.g., age, site class, basal area, forest type, tree list) and output variables (e.g., species mix, product mix to meet local market demand). Therefore, forest planners often develop their own alternative generators tailored to their specific FEM problem.
The alternative generation phase is the initial step of a FEMDSS; thus, it is the one that deals with the forest reality that varies most from one planning instance to another. Several authors have emphasized the use of rules to enhance the flexibility of Decision Support Systems (DSS) for FEM, addressing various problems [25,26,27,28,29,30,31,32,33]. These rules are often applied to predefined conditions, possible forest interventions, or projection methods for growth and yields [34]. Here, we propose the use of an artificial intelligence (AI) technique [35,36,37] for building a rule-based system that provides the forest planning analyst with complete flexibility and control over the alternative-generation process. This technique enables a standardized approach to generating management alternative information that enhances the efficiency of the process and produces a FEMDSS that can be applied to a broad range of forest conditions.
Furthermore, standardizing the model formulation step results in a flexible structure for the database that stores the information about the alternatives. The database can store information for all management prescriptions and facilitates easy retrieval of information for the model formulation step. The general features of this database are also outlined in this paper.
Specifically, this paper focuses on the alternative generation process within a general FEMDSS framework. To enhance flexibility and user-defined forest conditions, we build on the developer-group strategy described by Eriksson and Bergh (2022) that allows users to openly define variables that guide the simulation of possible options for their forests. The proposed approach uses an artificial intelligence (AI) rule-based technique to develop a comprehensive alternative generation framework for FEMDSS. We present iGen, an open-source software, as an implementation of this framework that can be collaboratively developed to address a wide range of FEM problems across the globe.

2. Materials and Methods

This section describes the application of an AI technique called a Rule-Based System (AI-RBS) to generate management alternatives. The approach is extremely flexible, allowing it to be applied to a wide range of FEM applications. Furthermore, it breaks down the alternative generation process into a set of fundamental components that are easily recognizable to most forest managers, which reduces the effort required by forest planners to formulate management models. We first describe the structure of the management alternative generation process, its elements, and the role of each element in the alternative generation process. Next, we describe the AI-RBS and how it has been applied to non-forestry applications. Finally, we describe iGen, an application of AI-RBS to the forest management alternative generation task.

2.1. The structure of management alternative generation component of the problem

We assume the following:
  • The initial state of a management unit, i, can be described by a vector of n attributes X i 0 = [ x i 01 , x i 02 … x i 0 n ]
  • The state of the forest can be described by aggregating the states of individual management units.
  • The initial state of each management unit is a known set of values for X i 0
  • Note that the set of attributes for a management unit at a given time is defined to include any relevant inputs and outputs associated with that management unit at that time.
To project the state of each management unit under a given management alternative, we must have equations of motion that describe how the vector of state attributes evolves over time, as a function of any interventions that may be applied to the management unit. The general specification of the equations of motion is:
X i p = f X i p − 1 , I i p   Equation   of   motion
where:
p is a period
Xip is the vector of attributes for management unit i in period p
Iip is an intervention that is applied to management unit i in period p
Every problem requires the explicit specification of these elements, i.e., the state of a management unit and the equations of motion for the management unit. Without these elements, the problem cannot be described mathematically. Note, however, that we have defined both the state space and the equations of motion very generally so that this specification can be applied to virtually any FEM problem.
The final elements needed to formulate management alternatives are a set of potential interventions and the conditions under which they can be applied. This is where the rules come in. Intervention rules are defined based on managers’ knowledge of potential interventions and the conditions under which the interventions can be applied.

2.2. AI - Rule Based System description

Rule-Based Systems (RBS) are one of the earliest AI techniques and were first developed in the 1970s [35,36,37]. These techniques are the simplest form of artificial intelligence and mimic the reasoning of a human expert in solving a knowledge-intensive problem. In other words, RBSs encode human expert knowledge about a specific topic into an automated system [38,39]. An RBS reproduces deductive reasoning mechanisms by employing logic rules made of conjunctions of conditions to verify and a set of actions to execute [40].
In the context of an RBS, a rule consists of two parts: the IF part and the THEN part. It relates the facts in the IF part to some action in the THEN part. The IF part is called antecedent (or condition), and the THEN part is called consequent (or action). Thus, a simple rule can be expressed as: IF antecedent THEN consequent. Each rule states that if certain conditions are met, then certain conclusions can be inferred [38,39] A rule base is a particular type of knowledge base that consists of three essential elements: (i) a set of facts relevant to the beginning state of the system, (ii) a set of rules describing actions that should be taken as a function of the current state, and (iii) a termination criterion that determines when a solution has been found [39]. A rule base aims to encapsulate the intelligence and information held by experts and to provide this knowledge to others through an RBS.
These elements are embedded in an information technology system that has at least the following components: (i) a knowledge base with the rules and termination conditions; (ii) a database with the beginning state; and (iii) an inference engine. The inference engine combines reasoning methods with the knowledge base to each state and applies the reasoning required by the system to reach a solution [39,41] The inference engine is designed to act based on rule conditions. It goes through the beginning states, checks the applicable rules, and executes the “consequent” of the matched rule when it finds a match. The inference engine performs this process in a loop until the termination condition is reached. At this point, the inference engine is ready to present a solution to the initial question [42].

2.3. Applications of Rule Base Systems in other fields

While the AI-RBS methodology is simple in concept, it has been used to solve complex problems. For example, AI-RBS methods have been widely applied in medicine. Health applications of AI-RBS are becoming more advanced and capable of delivering innovative services for improving the quality of life and promoting wellness and a healthy lifestyle. Minutolo et al. [40] assert that the most relevant component of such applications is the RBS. Medical diagnosis applications often use RBSs with medical image processing to select surgical strategies and for other medical tasks [43,44,45,46,47,48]. Beyond medicine, the rule-based technique, combined with other information technology methods, has been applied to a variety of research areas including electric pumps control [49,50], power distribution networks [51], floor plan analysis [52], welding process control [53], air conditioning systems [54], investment analysis [55], and many others.
AI-RBS has been widely and successfully applied because it is one of the most common and natural explainable frameworks for knowledge representation [56]. After analyzing three applications for medical image processing, Matsuyama [41] concludes that even when far from complete, this way of organizing knowledge can increase the flexibility of software systems, and it is a flexible software environment for developing image analysis systems. According to Abdullah et al. [57], rule-based technology is three times more efficient than conventional methods in the context of healthcare edits. It outperforms conventional systems by increasing the confidence in the value of the results to 95%. Moreover, al Fryan et al. [47], analyzing the use of decision trees associated with a rule-base in medical applications, recommend using these technologies in other fields of study due to the efficiency of the processes.

2.4. iGen description

Considering the structure of the FEMDSS problem described in section 2.1 we have developed a software system called iGen that applies Rule-based System principles to the problem of generating forest management alternatives in the context of an FEMDSS. This section describes the iGen elements and how they work together to generate management alternatives for each management unit of a given forest. The iGen elements are designed to enable the application to enumerate all possible ways a given forest management unit could be managed.

2.4.1. iGen elements

Set of variables and initial state

Potential management alternatives for each management unit are based on its initial state. A user-defined set of variables must first be specified in iGen to describe the initial and subsequent states of each management unit. Furthermore, the state variables must include any inputs or outputs that will be relevant in the model-building stage. If the planner expects to include an objective or constraints related to carbon storage, they must create a variable for that attribute when specifying the vector of state variables. For a typical FEM problem, the state variables could include age, basal area, forest type or species composition, site quality, standing and harvested wood or non-wood product quantities, biomass stock, carbon stock, the carbon sequestration rate, other ecosystem services indicators, equipment requirements, and cost of management activities. The state descriptor vector is flexible and can also include a matrix – for example, a tree list and the attributes of each tree in the list. The initial values of the state-descriptor variables must describe all relevant attributes of the management unit and enable the projection of the state of the management unit. The structure and attributes of the state-descriptor variables are defined by the analyst based on their specific instance of the FEM problem. Furthermore, the analyst must populate the initial state-descriptor variables based on the initial condition of each management unit in their forest. For a given instance of iGen, this defines a set of variables X i 0 =   [ x i 01   ,   x i 02   …   x i 0 n ] that describes the initial state each management unit within the forest of interest.

Set of intervention types

According to Bettinger et al. [58], human interventions are management activities that can alter the character of a forest. The stand of trees in each management unit will grow and develop according to its condition until the managers intervene. These interventions could be any silvicultural treatment, harvesting, or a business intervention like an ownership change. Also, how the forests evolve after an intervention is central to decisions because forest sustainability and growth rates can be enhanced or harmed by human interventions.
In iGen an intervention is an event that can be planned. iGen does not consider random disturbances. Also, non-intervention, where no activity is planned, is treated as a particular type of intervention in iGen and is considered a feasible management option by default, although this can be overridden in the case of a mandatory treatment.
In an instance of iGen, the analyst must define the set of valid intervention typess, I =   I 1 ,   I 2 … I n , that can occur in their forest. In addition, the initial state of a management unit must include the last intervention that happened in that unit and when it occurred. The initial state is what rule-based system principles call “the set of facts of a beginning state” [39], as described in section 2.2.

Equations of motion

Left free to grow and affected solely by the forces of nature, forests change, and understanding the change that can occur is critical for forest planning efforts [58]. Equations of motion typically mathematically describe these biological changes. Understanding and representing those changes is one of the most crucial issues of the forest planning process. Each state variable must have an equation of motion that describes how that variable evolves over time. The equation of motion for a variable x n ∈   X ( Equation 1) is a function of the vector of state variables from the previous period and the intervention type occurring in the period ( Equation 2).
x i , n ,     p = f n X i , p − 1 , I i , p   Equation   of   motion   for   a   state   variable   n
Note that the intervention I i , p can be a non-intervention, in which case the function should compute the development of the management unit in the absence of any management activity. In the case of a regular intervention, the function should calculate the result of the intervention, including any natural growth.

Rule base

In iGen, rules describe the conditions under which interventions may be applied to management units. In other words, a rule is a Boolean function that returns false when an intervention cannot be applied and true when an intervention can be applied. More specifically, rules specify the sequence under which interventions can be applied, so they are built on the last intervention that occurred in a management unit and the subsequent evolution of the state of the unit. Thus, given two intervention types I l a s t and I n e x t and I n e x t , we say that a rule r n ∈ R is a Boolean function representing the condition for the application of I n e x t given that I l a s t occurred and given the current state of the management unit.
R = r 1   ,   r 2 …     r n   Set   of   Rules
r n =   f I l a s t   ,   I n e x t   ,   X p   Rule   function
where f is a boolean function.
Since the state of the forest is evolving over time according to the equations of motion, the values of the state variables change over time, so the rules must be reevaluated in each period. So, after an occurrence of an I l a s t , a r n function can return false in a sequence of periods, until in a certain period p the r n function returns true, so the intervention I n e x t can be applied.
As described earlier, a rule has two parts: a condition and a consequent. Accordingly, once iGen has evaluated the condition for applying a rule, if the rule returns true, the consequent part is to create a branch where one branch assumes that no intervention will occur, and the other branch assumes that the corresponding active intervention will occur. For each branch, iGen will apply the equations of motion for each state variable for the given management unit, in one case with no intervention and in the other with an active intervention. If the rule returns false, the consequent part is to continue assuming that no intervention will occur. Multiple rules may apply for a management unit at a single point in time, so it is possible to create multiple branches, each representing different interventions.
In summary, an instance of iGen includes a defined set of rules R =   r 1   ,   r 2 …     r n according to the specifics of the given forest planning situation. Each instance has a unique set of rules that translate how the interventions can be sequenced to generate a complete set of alternatives. The analyst must build this rule base comprising the elements I =   I 1 ,   I 2 … I n     and =   [ x 1   ,   x 2   …   x n ] .

Network Graph

The management alternatives for each management unit are stored in a network graph. Each unit has one graph built in a non-loop-directed graph named tree-graph [59]. The first node of each graph describes the initial state of the corresponding management unit and begins with the last intervention in the unit. This last intervention may have happened in period zero or any period before period zero of the planning horizon. If the last intervention occurred prior to period zero, iGen will update the management unit’s state to time zero. The nodes of the graph represent the state of the management unit at a given point in time. All the edges of the graph have a one-period length, and the total length of the graph is the planning horizon, plus any nodes representing the state of the management unit prior to period zero.
iGen systematically processes each node in the graph until reaching an ending point, which represents the state of the management unit at the end of the planning horizon. For each node that is processed, a new non-intervention node is created for the subsequent period representing the management unit's natural development when no active intervention is planned. The state variables for the management unit are updated for the new node with the equations of motion assuming no active intervention will occur. When an active intervention can be applied, a new intervention node is also created and the state variables for the management unit are updated with the equations of motion assuming the intervention occurs. Figure 1 shows an example of the resulting graph and its elements.
The management unit graphs and the underlying database that stores them are the main output of the application. The graphs contain all simulated state data (including inputs and outputs) for all possible management alternatives for each management unit according to the rules created in the rule base. Each node of these graphs has a vector of attributes calculated according to the equations of motion. The resulting graphs show the evolution of the forest state over time.

Relational Database

All the elements of the graphs, including parameters, inputs, outputs, rule base, and equations of motion, are kept in a relational database. Table 1 shows the elements and the tables where they are stored.
As discussed above, the analyst must specify the set of state variables, the set of intervention types, the equations of motion, the initial state of each management unit, and build the rule base. Those elements are the inputs of the application. Also, the analyst must specify some general parameters such as the planning horizon, period length, name of the model, and other parameters related to the graph shape, as the graph can be visualized as a table or a graph. Examples of these inputs and outputs are presented in section Figure 2 shows a diagram of Entities and Relationships (DER) of one instance of iGen. The DER also shows how the tables described in Table 1 are related to each other.
It is important to note that this is a dynamic database. Depending on the unique characteristics of the FEM problem, the analyst defines which variables will describe the state of the individual management units. Those variables will be rows in the Variable table, and for consistency, they will be the columns of the Nodes table. Also, there must be an equation of motion for each variable. The equations of motion used to update the state of a management unit during the graph building process can be stored in the Variable table, or an external function can be specified in the case of complex equations of motion.
The analyst can define the MgmUnit attributes according to specific forest characteristics and planning needs. The table must be in the database because each graph node is related to a management unit. The Nodes table has one attribute to connect each node to its previous node (PreviousNode) and another to connect each node to the last active intervention (LiNode). Also, there is an attribute to identify the node type (NodeType). The other fields in this table are user-defined elements of the set of state variables.
The Rule table is related twice to the InterventionType table, one for the Last Intervention and one for the Next Intervention. The Rule condition function compiles all RuleExpression attributes for the same Rule when IfOrThen equals “IF.” The equations of motion for each variable and each rule (or a pair Ilast - Inext) are stored in the attribute RuleExpression in the RuleCondition table when IfOrThen equals “THEN.”

2.4.2. iGen Algorithm: The Inference Engine

The Inference Engine (I_Engine), as the algorithm of a Rule-base system is called, applies the rules to the initial nodes and builds a tree graph, as in Figure 1. The first step is to consider all initial nodes as nodes-to-be-open and put them in a list. The opening process is a recursive procedure. During the opening process, I_Engine generates new nodes, mostly non-intervention nodes plus some intervention nodes. These new intervention nodes will also need to be opened, but iGen processes an entire non-intervention path until it reaches the end of the planning horizon or until an exception occurs where two interventions are required to happen in a prescribed sequence, as shown in the Pennsylvania example below. I_Engine saves all new nodes in the graph and adds any new intervention nodes to the “node-to-open” list. When I_Engine finishes the opening process of one node, it sets it as an “opened-node.” I_Engine continues with this process until the “node-to-open” list is empty.
The node opening process involves nine steps. Figure 1 provides an example to demonstrate the opening process. Figure 3 shows the nine steps in a flow chart.
  • 1o–I_Engine gets a node from the “node-to-open” list. Initially, this node will be an initial node. This node is always an intervention node. In our example (Figure 1), an intervention I1 happens in node a:I1.
  • 2o –I_Engine creates a new non-intervention node in the following period (node #1 in Figure 1) and connects it to the current node being processed (node a:I1 initially).
  • 3o – I_Engine uses the equations of motion for each variable to update the forest state for the new node and saves the results in the recently generated node record.
  • 4o – I_Engine filters the rules to select only the ones with I1 as the last Intervention.
  • 5o – For the first rule (Ilast, Inext) = (I1, I2), I_Engine runs the Rule Boolean function.
    • If it returns True, that is a match. So, I_Engine:
      a)
      creates a node with an intervention I2 in the same period,
      b)
      connects this node to the previous node,
      c)
      evaluates the equation of motion for the Intervention I2 for each state variable to determine what happens to this specific management unit when I2 occurs, and
      d)
      unless the new node occurs at the end of the planning horizon, adds this new node to the “node-to-open” list.
    • If it returns False, I_Engine does nothing.
  • 6o – I_Engine repeats step 5o for each rule in the filtered list of rules.
  • 7o – I_Engine repeats steps 2o through 6o until the end of the planning horizon and removes the node that was processed from the “node-to-open” list.
  • 8o – I_Engine returns to the node-to-open list and picks the next one. In our example, node a:I1 will no longer be in the list, but there will be two others to open: b:I2 and c:I2.
  • 9o – I_Engine repeats steps from 1o to 8o until the node-to-open list is empty.
In summary, in our example (Figure 1), I_Engine begins by opening the node a:I1; it then
a)
generates nodes 1 to 12;
b)
finds a match at node 6, creates node c:I2, connects it to node 5 (the node previous to node 6), and sets c:I2 as a “node-to-open;”
c)
finds a match at node 7, creates node b:I2, connects it to node 6 (the node previous to node 7), and sets b:I2 as a “node-to-open;”
d)
and sets the node a:I1 as “opened.”
Next, I_Engine opens the node b:I2 and generates nodes 13 to 17 without creating any new intervention nodes to add to the “nodes to open” list. Next, it opens node c:I2 and generates nodes from 18 to 23 and the intervention node d:I2. Node d:I2 is not added to the “nodes to open” list because it is already at the end of the planning horizon.
The graph in Figure 1 represents four potential management prescriptions for this management unit that apply for the span of the planning horizon. Note that these prescriptions share at least some arcs and nodes within the graph. In fact, all four prescriptions share the same path from the initial node through node 5. Generating prescriptions this way avoids simulating shared components of each prescription multiple times. These kinds of efficiencies are crucial for FEMDSSs when there are many management units and many management alternatives for each management unit. I_Engine can efficiently generate graphs for FEM problems that have thousands of management units with potentially millions of nodes. Additionally, a multicriteria framework typically involves projecting a variety of ecosystem services indicators, production, and social indicators. In these cases, simulating state updates for many management alternatives can consume considerable computer resources. The iGen framework (Inference Engine and the representation of the problem as Graphs and Rule-bases) was developed to optimize the use of planning resources, including computer processing and analysts’ time.

3. Examples

In this section we apply the concepts of Section 2 to two FEMDSS problems: a natural regeneration problem with shelterwood harvests and a plantation/coppice problem. The data for the two examples are attached to this article in SQLite® and Excel® format. The iGen source programs that can run these examples can be found at github.com/…/iGen.

3.1. Pennsylvania Example

3.1.1. Problem description

To demonstrate how iGen generates alternatives for a management problem, consider an example of an even-aged forest managed under a natural regeneration regime; we refer to it as the Pennsylvania Example.
The Pennsylvania Example has eight management units, each with an area, age, species composition type (forest type), site quality, and the last intervention that occurred in it. Stand growth is projected with yield curves developed by Gilabert et al. [60] for natural forests in Pennsylvania. Alternatives are generated for a 110-year planning horizon comprised of eleven 10-year periods. Also, for simplicity, we consider only two site qualities and two forest types.

3.1.2. Set of state variables

The state variables chosen for the Pennsylvania Example are typical ones, including area, age, site quality, forest type, yield, yield removed, yield remaining, the last intervention in a unit, and when it occurred. Two additional variables are defined to facilitate the application of required treatment sequences. The variable named TreatReq specifies a required treatment to apply to the unit, and AfterInt tracks how many periods have elapsed since the last intervention.

3.1.3. Set of intervention types

We consider two types of interventions: a shelterwood cut (SWC) and an overstory removal (OR). In practice, most management units require a SWC prior to an OR to establish advance regeneration. An SWC can only occur after a specified minimum age. On the better site, site 1, the SWC can be done starting at 60 years old. On the poorer site, a SWC can occur only after age 70. An OR should occur immediately (one period, or 10 years) after an SWC intervention. After an OR, the regeneration process begins, and the age is set to zero. In some management units where an inventory cruise has indicated that adequate advance regeneration already exists, an OR can be made without a SWC. A management unit cannot be designated as not requiring a SWC unless it is already old enough to be harvested, and this condition is valid only for the first cycle. Subsequent regeneration cycles will assume that an SWC treatment will be required and the general rule requiring an SWC followed by an OR will apply.

3.1.4. Initial state

With these definitions, we can define the initial state for the management units. Table 2 shows the initial states of key variables for the first three management units. Note that the columns of the table match the previously defined set of state variables. The age refers to the management unit's age at the end of the period when the last intervention happened. Management unit 1 was harvested (OR) 60 years ago and requires a SWC before an OR can be conducted. Management unit 2 was harvested 50 years ago and does not require a SWC before an OR can be conducted. Management unit 3 was recently treated with a shelterwood harvest and must receive an OR in the first period.

3.1.5. Equation of motion

The equations of motion describe the evolution of the state variables over time. An equation of motion must be specified for each variable. In the Pennsylvania Example, most variables have simple equations that can be specified directly in iGen, as shown in Table 3. For more complex equations of motion, iGen can call an external function. In this example, only the yield variables require external functions to calculate updated values. The information in Table 3 is stored in the database table Variable.
The value of each variable at the previous node is accessed by writing “:variableName.” So, for example, the equation “Site = :Site” specifies that the value of the site quality variable does not change. This is also the case for MgmUnit, Area, SpcComposition, and TreatReq. The expression "Age = :Age+10" (Table 3) tells iGen to add ten years to the previous node’s Age variable value. While this seems obvious, iGen is meant to be general and flexible in the way specific meanings are assigned to variables. The analyst preparing the problem must provide meaning to each variable by writing appropriate equations of motion. The external function, PennsylvaniaYield is written in Python, and it returns standing, removed, and remaining volume based on the age, site, species composition, and stocking of the stand and the type of intervention being simulated (e.g., SWC vs. OR). A full transcript of this function is provided in Annex 1.

3.1.6 Example rules

As noted earlier, a SWC can happen a minimum of 60 or 70 years after a management unit had been regenerated, depending on the site quality. A rule can therefore be created in iGen to guide the I_Engine during the alternative generation algorithm. The rule for implementing a SWC is shown in Table 4.
The conditional part of a rule specifies when a particular intervention can be applied, in this case, an SWC. In addition, a rule must describe how the management unit’s state will be updated after an SWC occurs. This is described in the consequent part of the rule. In both the conditional and the consequent parts, the variable values refer to the new non-intervention node that is being analyzed when a new intervention node is created and not the previous node. This non-intervention node represents the state of the management unit just prior to the implementation of the intervention.
The next rule establishes the conditions for an OR occurrence following an SWC. Since the OR should occur immediately after a SWC intervention, the RuleCondtion states that when the last intervention was an SWC and AfterInt == 1 then an OR must occur (Table 5). And when the I_Engine gets a match for this rule, the consequent part is the same as the rule described in Table 4, with the following exceptions (i) age is set to five1 on average by the end of the period (Age = 5), and (ii) the treatment required will turn to SWC (TreatReq = 'SWC'); (iii) and the yield functions are called with the parameter 'OR' for the intervention type parameter.
Table 6 shows the rule for management units that do not require an SWC prior to conducting an OR, i.e., management units with LastIntervention = 'OR' and TreatReq = 'OR' (Table 6). Note that in the consequent part of this rule TreatReq is set to 'SWC', as shown in Table 6, so that in the next rotation a SWC will be required. Note that the yield functions are called with the parameter 'OR1.' This is because the yield for an OR will be greater when no SWC has been conducted prior to the OR.

3.1.7. Result

The I_Engine applies the rules to the initial state and generates one network graph containing all the alternatives for each management unit. Data related to all graphs are stored in the database table Nodes, and the results can be visualized in either of the two formats, a graph or a table. As an example, Figure 4 presents the graph for management unit 2. This management unit is one where an inventory cruise indicated that an OR can be made without a SWC. The Figure 4 shows that the last intervention in unit 2 was an OR that occurred 50 years ago. From period -5, the I_Engine grows the forest until period 0 (zero), at which point unit 2 reaches age 57. Then, according to the rules, the I_Engine opens a non-intervention node (which will leave the unit to grow one period more) and an OR node. Following the non-intervention path, the I_Engine generates the default non-intervention node and one OR node for each period until the end of the planning horizon. The program then begins opening the intervention nodes that have not been processed. After each OR node the program grows the forest until age 65, because this unit is site 1 (Table 2), and then begins creating SWC alternatives for each period until the end of the planning horizon.
When the equations of motion are applied to update the state of the forest over time, the values of each variable for each non-intervention node are stored in the Nodes table shows some rows of this table for the nodes highlighted in Figure 4. Node 43, an OR node, is the first one of the set, and the following nodes refer to it in the column LiNode (Last Intervention Node).
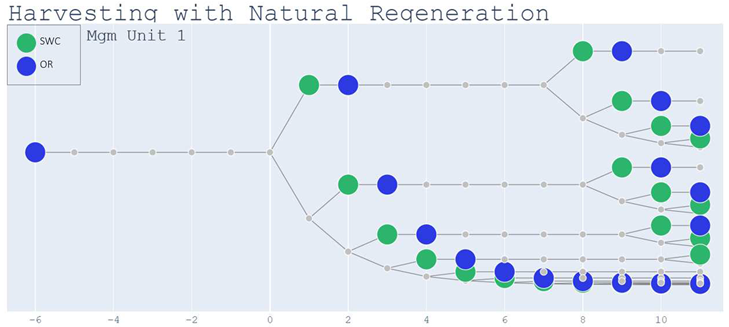
For management units 1 and 3, that have a TreatReq = “SWC”, I_Engine, according to the rules raws a similar graph with a different sequence in which the pattern observed in Figure 6 follows a second cycle. Appendix B shows the graph for management unit 1.

3.2. Plantation-Coppice Example

3.2.1. Problem description

The second FEMDSS example is a fast-growing plantation under a short-rotation coppice regime to produce biomass or pulp wood [61,62]. We call it the Plantation-Coppice Example.
The Plantation-Coppice Example has seven management units, with each belonging to a stratum and having attributes such as area, age, rotation count and the last intervention that occurred in it. Unlike the first example, the Plantation-Coppice Example has a yield table with two entries: Stratum and Age. The alternatives are generated for a 21-year horizon comprised of twenty-one 1-year periods. Also, for simplicity, we consider only two strata.

3.2.2. State variables

As with the first example, the state variables for the Plantation-Coppice Example management units are the typical ones such as area, age, stratum, rotation count, yield, the last intervention in a unit, and when it occurred. The rotation count is 1 after the initial planting, 2 after the first coppice, and so on.

3.2.3. Potential interventions

The two types of interventions are based on a regular coppice regime: a clear cut followed by a renewal planting (CCR) or a clear cut followed by sprouting from stumps (CCS). In this example only one CCS is allowed, so after a coppice harvest the next clear cut must be followed by a renewal (CCR) to plant new genetic material [63].

3.2.4. Initial state

With these definitions, we can define the initial state for each management unit. Table 8 shows the data for the first four. Note that the columns of the table match the set of state variables. The age and the yield refer to the management unit's age in the period when the last intervention happened. All ages are zero when a clear cut occurs, some are in the first rotation after the renewal, and others are in the second rotation, following a CCS intervention.

3.2.5. Equation of motion

As in the Pennsylvania Example, in the Plantation-Coppice Example most variables have simple equations of motion for no intervention, as shown in Table 9. Only the yield variable requires a function (SearchTable) to select yield coefficients from a production table. For this kind of equation of motion, I_Engine can read a table (Productivity) using the specified entries (Stratum, Age) to return the appropriate value (Volume).

3.2.6. Example Rules

There are three rules related to the two intervention types in Coppice Example. After a CCR, we can have either another CCR or a CCS. However, a CCR must follow a CCS. The rule conditions for the three possibilities are the same. The management units can only be cut at ages 6 or 7 if they have reached a minimum yield of 200 m3/ha. However, in periods 1 to 3, older ages up to 9 years can also be cut. Table 10 shows how the rules are written within the iGen context.
When any of these rules is satisfied a new intervention node is generated, and I_Engine applies the consequent part of the rules (intervention state updates). The equation of motion for all variables are identical, except for RotationCount, which assumes the value 1 when a CCR occurs and value 2 when a CCS occurs according to the logic of coppice regime. Age and Yield turn to zero; Area, MgmUnit and Stratum remain the same.

3.2.7. Results

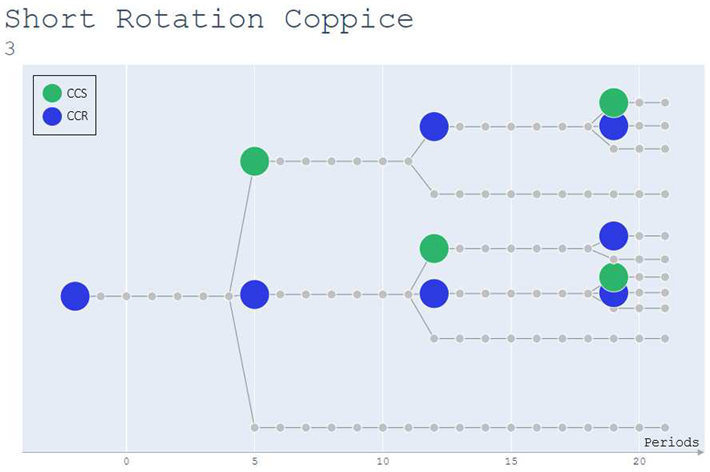
As in the Pennsylvania Example, the I_Engine generates a graph for each management unit. presents the graph for the management unit 1 of our Plantation-Coppice example. Unit 1 was clear cut two years before the beginning of the horizon; therefore, by the fourth period it will be possible to cut this unit again. This results in three alternatives for the fourth period: conducting a CCR, or a CCS, or doing nothing and letting the forest grow (no intervention). This pattern repeats in the following years according to the rules. For unit 3, located in a less productive stratum, it is impossible to have a clear cut at age six because the minimum productivity is not reached yet, making fewer alternatives for that unit, as shown in Appendix C.
As stated earlier, Inference Engine applies the equation of motion to previous states and saves each state in the Nodes table. Table 11 shows the content of part of this table regarding the nodes marked in Figure 5. The CCS node in period 4 is node #15. Nodes 218 to 219 have node 15 as the last intervention (LiNode). Note that the initial value of RotationCount for unit 1 was 1, but the CCS intervention changes this value to 2

4. Discussion and conclusions

A single set of management alternatives can be used to build multiple optimization models, for example, when finding the Pareto frontier of a multiobjective planning problem. So, in many cases, the alternative generation process only needs to be done once, while the optimization model-building process will usually need to be performed multiple times. A well-defined, flexible structure that provides an interface between the generation of management alternatives and the model formulation phase improves the transparency and clarity of the processes for the forest analyst. This visual interface allows the analyst to verify and validate the alternatives generated and better understand the relationships between the evolution of the forest state and the management prescriptions before building any optimization models.
We contend that developing a sufficiently general and comprehensive framework that applies to the majority of FEM planning situations that use linear programming (LP) or mixed-integer programming (MIP) formulations is quite challenging. Furthermore, we believe that our framework has accomplished that by identifying the common elements that define the process of generating alternatives for any FEM problem. These are: 1) the definition of the state space for the management units, 2) the specification of potential management interventions that can be applied to the management units, 3) a set of rules that define the conditions when each management intervention can be applied, and 4) equations of motion that describe how the state of a management unit will evolve over time in a no-intervention case or with an active intervention. This is the key contribution of the iGen methodology: identifying these fundamental elements of the alternative generation process and defining them in a very general way creates a framework that can be applied to most, if not all, FEM problems. While each problem is unique in terms of the specific details of these elements, the iGen modeling framework allows forest planners to specify the state description, the possible interventions, the rules for applying interventions, and the equations of motion according to the specifics of their problem.
Besides its generality, a key feature of the iGen approach to alternative generation is its efficiency. First, it efficiently simulates each possible alternative for each management unit. iGen uses a recursive algorithm for generating a graph of alternatives for each management unit, ensuring that each arc of the graph is simulated only once, and the rules specified by the user guarantee that only acceptable and feasible alternatives will be created. In addition, each node in the graph is unique, so there is no duplication of information storage and all data related to the management alternatives needed for building the LP model or MIP models are contained in the database. Furthermore, because the graph provides a natural representation of the alternatives, it makes it easy for users to visualize, interpret and verify the data generated for each alternative. Since the equations of motion and intervention rules are written by the forest planning analyst and not by the programmer, the analyst has control of the model. The analyst can verify the alternatives generated and better understand the relationships between the evolution of the forest state and the management prescriptions. They can also check the validity of the coefficients that will be used to build an LP or MIP model before the model is built to ensure that the simulations in the model are generating valid results. This is much easier than reviewing the coefficients of, for example, an LP model.
While not addressed in this paper, the network structure of the management alternative database produced by iGen provides a natural structure for constructing an LP or MIP model. Exactly how this is done will be the topic of a forthcoming paper, but it is easy to extract the information needed to build objective functions and constraints for LP and MIP models from the database. Specifically, one can easily construct area (for LP) or logical (for MIP) constraints, as well as accounting constraints for any ecosystem service that was included in the state variable definition. Furthermore, this is easily done for a variety of model structures, including Model I, Model II [64], and others. Constraints, such as flow [65], supply chain and market[66], transportation and logistics [67], adjacency [68], labor [69], and equipment constraints [70] can also be built, but will require other inputs that are not needed in the alternative generation stage and that can be input at the LP or MIP model-building stage.
The code for iGen is open source, and datasets and equations of motion sample code for different types of forests are provided on the github.com/…/iGen. We hope this system will be a valuable resource for practitioners and researchers interested in the development of FEMDSSs.

Author Contributions

Nobre, S.R., conceived the ideas, designed the study, programmed iGen, and was the primary author of the manuscript. McDill, M.E., advised in the design the study and contributed substantially to writing the manuscript. Rodriguez, L.C.E., and Diaz-Balteiro, L., contributed to the writing and connected this study to the DecisionES project and previous research projects bringing contextualization, improvements, and literature references. All the authors substantially contributed to the manuscript and agreed with the final version for submission.

Funding

This research was funded by Unión Europea-NextGenerationEU, through Ministerio de Universidades and Universidad Politécnica de Madrid, reference code UP2021-035. It also received support from DecisionES, grant agreement ID 101007950, under Excellent Science - Marie Skłodowska-Curie Actions.

Data Availability Statement

All the data generated or analyzed during this study are available at github.com/SilvanaNobre/iGen

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

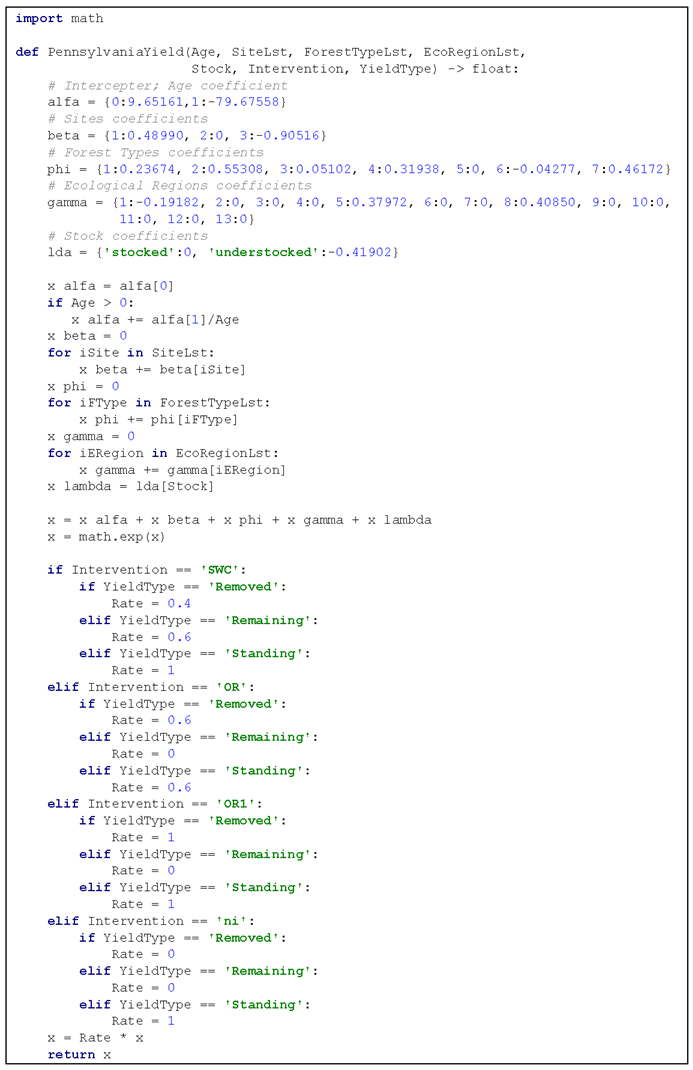
PennsylvaniaYield is an external function written in Python. All external functions must be saved in a file named ExtFunctions.py which is one of the files of iGen Python Project.
Preprints 74616 i001

Appendix B

Pennsylvania Example – Management unit 1
Preprints 74616 i002

Appendix C

Coppice Example – Management Unit 3
Preprints 74616 i003

References

  1. Borges, J.G.; Nordström, E.M.; Garcia-Gonzalo, J.; Hujala, T.; Trasobares, A. Computer-Based Tools for Supporting Forest Management. The Experience and the Expertise World-Wide; 1st ed.; Department of Forest Resource Management, Swedish University of Agricultural Sciences: Umea, 2014. [Google Scholar]
  2. Rönnqvist, M.; D’Amours, S.; Weintraub, A.; Jofre, A.; Gunn, E.; Haight, R.G.; Martell, D.; Murray, A.T.; Romero, C. Operations Research Challenges in Forestry: 33 Open Problems. Ann Oper Res 2015, 232. [Google Scholar] [CrossRef]
  3. Radke, N.; Yousefpour, R.; von Detten, R.; Reifenberg, S.; Hanewinkel, M. Adopting Robust Decision-Making to Forest Management under Climate Change. Ann For Sci 2017, 74. [Google Scholar] [CrossRef]
  4. Franca, L.C.D.; Acerbi, F.W.; Silva, C.; Monti, C.A.U.; Ferreira, T.C.; Santana, C.J.D.; Gomide, L.R. Forest Landscape Planning and Management: A State-of-the-Art Review. TREES FORESTS AND PEOPLE 2022, 8. [Google Scholar] [CrossRef]
  5. Bettinger, P.; Chung, W. The Key Literature of, and Trends in, Forest-Level Management Planning in North America, 1950-2001. INTERNATIONAL FORESTRY REVIEW 2004, 6, 40–50. [Google Scholar] [CrossRef]
  6. Hujala, T.; Khadka, C.; Wolfslehner, B.; Vacik, H. Review. Supporting Problem Structuring with Computer-Based Tools in Participatory Forest Planning. For Syst 2013, 22, 270–281. [Google Scholar] [CrossRef]
  7. Pasalodos-Tato, M.; Makinen, A.; Garcia-Gonzalo, J.; Borges, J.G.; Lamas, T.; Eriksson, L.O. Review. Assessing Uncertainty and Risk in Forest Planning and Decision Support Systems: Review of Classical Methods and Introduction of Innovative Approaches. For Syst 2013, 22, 282–303. [Google Scholar] [CrossRef]
  8. Baskent, E.Z.; Borges, J.G.; Kaspar, J.; Tahri, M. A Design for Addressing Multiple Ecosystem Services in Forest Management Planning. Forests 2020, 11. [Google Scholar] [CrossRef]
  9. Kaya, A.; Bettinger, P.; Boston, K.; Akbulut, R.; Ucar, Z.; Siry, J.; Merry, K.; Cieszewski, C. Optimisation in Forest Management. Current Forestry Reports 2016, 2, 1–17. [Google Scholar] [CrossRef]
  10. Nobre, S.R.; Diaz-Balteiro, L.; Rodriguez, L.C.E. A Compromise Programming Application to Support Forest Industrial Plantation Decision-Makers. Forests 2021, 12. [Google Scholar] [CrossRef]
  11. Xavier, A.M.D.; Freitas, M.D.C.; Fragoso, R.M.D. Management of Mediterranean Forests - A Compromise Programming Approach Considering Different Stakeholders and Different Objectives. For Policy Econ 2015, 57, 38–46. [Google Scholar] [CrossRef]
  12. Marques, S.; Bushenkov, V.A.; Lotov, A. v.; Marto, M.; Borges, J.G. Bi-Level Participatory Forest Management Planning Supported by Pareto Frontier Visualization. Forest Science 2020, 66, 490–500. [Google Scholar] [CrossRef]
  13. Marques, S.; Bushenkov, V.; Lotov, A. Building Pareto Frontiers for Ecosystem Services Tradeoff Analysis in Forest Management Planning Integer Programs. Forests 2021, 12, 1–20. [Google Scholar] [CrossRef]
  14. Eriksson, L.O.; Bergh, J. A Tool for Long-Term Forest Stand Projections of Swedish Forests. Forests 2022, 13. [Google Scholar] [CrossRef]
  15. Borges, J.G.; Falcao, A.O.; Miragaia, C.; Marques, P.; Marques, M. A Decision Support System for Forest Ecosystem Management in Portugal. In Proceedings of the SYSTEMS ANALYSIS IN FOREST RESOURCES, PROCEEDINGS; Arthaudf, G.J., Barrett, T.M., Eds.; SPRINGER: PO BOX 17, 3300 AA DORDRECHT, NETHERLANDS, 2003; Vol. 7, pp. 155–163.
  16. Marto, M.; Marques, M.; Borges, J.G.; Tomé, M. Forestry Databases to Simulators and Decision Support Systems - Technical Report No. 01/2015 (Version 2.6); Lisboa, 2015.
  17. Potter, M.W.; Kessell, S.R.; Cattelino, P.J. FORPLAN: A FORest Planning LANguage and Simulator. Environ Manage 1979, 3, 59–72. [Google Scholar] [CrossRef]
  18. Eriksson, L.O. Planning under Uncertainty at the Forest Level: A Systems Approach. Scand J For Res 2006, 21, 111–117. [Google Scholar] [CrossRef]
  19. Nobre, S.R.; Eriksson, L.O.; Trubins, R. The Use of Decision Support Systems in Forest Management: Analysis of FORSYS Country Reports. Forests 2016, 7, 72. [Google Scholar] [CrossRef]
  20. Skovsgaard, J.P.; Vanclay, J.K. Forest Site Productivity: A Review of the Evolution of Dendrometric Concepts for Even-Aged Stands. FORESTRY 2008, 81, 13–31. [Google Scholar] [CrossRef]
  21. Shifley, S.R.; He, H.S.; Lischke, H.; Wang, W.J.; Jin, W.; Gustafson, E.J.; Thompson, J.R.; Thompson, F.R.; Dijak, W.D.; Yang, J. The Past and Future of Modeling Forest Dynamics: From Growth and Yield Curves to Forest Landscape Models. Landsc Ecol 2017, 32, 1307–1325. [Google Scholar] [CrossRef]
  22. Miles, P.D. Forest Inventory and Analysis Data for FVS Modelers. In Proceedings of the THIRD FOREST VEGETATION SIMULATOR CONFERENCE; Havis, R.N., Crookston, N.L., Eds.; US DEPT AGR, FOREST SERV ROCKY MT FOREST & RANGE EXPTL STN: FT COLLINS, CO 80526 USA, 2008; Vol. 54, pp. 125– 129.
  23. de Oliveira, E.B.; de Oliveira, Y.M.M.; Hafley, W.L. Software to predict Growth and Yield for p.ellioti and p.taeda in southern Brazil. Pesqui Agropecu Bras 1991, 26, 149–151. [Google Scholar]
  24. HN Palma, J.; Hakamada, R.; Moreira, G.G.; Nobre, S.R.; Rodriguez, L.C.E. Using 3PG to Assess Climate Change Impacts on Management Plan Optimization of Eucalyptus Plantations. A Case Study in Southern Brazil. Sci Rep 2021, 11. [Google Scholar] [CrossRef]
  25. Gustafson, E.J.; Crow, T.R. Forest Management Alternatives in the Hoosier National Forest. J For 1994, 92, 28–29. [Google Scholar] [CrossRef]
  26. Næsset, E. A Spatial Decision Support System for Long-term Forest Management Planning by Means of Linear Programming and a Geographical Information System. Scand J For Res 1997, 12, 77–88. [Google Scholar] [CrossRef]
  27. Siitonen, M.; Anola-Pukkila, A.; Haara, A.; Harkonen, K.; Redsven, V.; Salminen, O.; Suokas, A. Mela Handkbook; 2000th ed.; The Finish Forest Research Institute, Project 3002.: Helsinki, Finland, 2001; Vol. 1.
  28. Wikström, P.; Edenius, L.; Elfving, B.; Eriksson, L.O.; Lämås, T.; Sonesson, J.; Öhman, K.; Wallerman, J.; Waller, C.; Klintebäck, F. The Heureka Forestry Decision Support System: An Overview. Math. Comput. For. Nat. Resour. Sci. 2011, 3, 87–95. [Google Scholar]
  29. McDill, M.E. RxWrite: An Information Management Tool for Minnesota’s Generic Environmental Impact Statement on Timber Harvesting. In Proceedings of the E4-Management Science and Operations Research session at SAF National Convention; Indianapolis - IN - USA, November 7 1993. [Google Scholar]
  30. Rodriguez, L.C.E.; Stansfield, W.F. ForXGen - A Matrix Generator for Use with ForxCel; Flagstaff, Arizona, USA, 1995.
  31. LAACKE, R.J. BUILDING A DECISION-SUPPORT SYSTEM FOR ECOSYSTEM MANAGEMENT - KLEMS. AI APPLICATIONS 1995, 9, 115–127. [Google Scholar]
  32. WILLIAMS, S.B.; ROSCHKE, D.J.; HOLTFRERICH, D.R. DESIGNING CONFIGURABLE DECISION-SUPPORT SOFTWARE - LESSONS LEARNED. AI APPLICATIONS 1995, 9, 103–114. [Google Scholar]
  33. Albert, M. Predicting the selection of elite trees in mixed-species stands - a rule-based algorithm for silvicultural decision support systems. ALLGEMEINE FORST UND JAGDZEITUNG 2002, 173, 153–161. [Google Scholar]
  34. Packalen, T.; Marques, A.F.; Rasinmäki, J.; Rosset, C.; Mounir, F.; Rodriguez, L.C.E.; Nobre, S.R. Review. A Brief Overview of Forest Management Decision Support Systems (FMDSS) Listed in the FORSYS Wiki. For Syst 2013, 22, 263–269. [Google Scholar] [CrossRef]
  35. Mcdermott, J. RI: A Rule-Based Configurer of Computer Systems*; 1982;
  36. Waterman, D.A. ; F. Hayes-Roth Pattern-Directed Inference Systems; Waterman, D.A., Ed.; 1st ed.; Academic Press: New York, 1978; ISBN 978-0-12-737550-2. [Google Scholar]
  37. Amarel, S.; Brown, J.S.; Buchanan, B.; Hart, P.; Kulikowski, C.; Martin, W.; Pople, H. Reports of Panel on Applications of Artificial Intelligence. In Proceedings of the Fifth Internat. Joint Conference on Artificial Intelligence; Cambridge - USA; 1977; pp. 994–1006. [Google Scholar]
  38. Duda, R. 0; Hart, P.E.; Nilsson, N.J.; Sutherland, G.L. NETWORK REPRESENTATIONS IN RULE-BASED INFERENCE SYSTEMS 1. In; Waterman, D.F., Ed.; Academic Press: New York, 1978 ISBN 0127375503.
  39. Grosan, C.; Abraham, A. Rule-Based Expert Systems. In Intelligent Systems; Grosan, C., Abraham, A., Eds.; Springer, Berlin, Heidelberg: Berlin, Heidelberg, 2011; pp. 149–185 ISBN 978-3-642-21004-4.
  40. Minutolo, A.; Esposito, M.; de Pietro, G. Optimization of Rule-Based Systems in MHealth Applications. Eng Appl Artif Intell 2017, 59, 103–121. [Google Scholar] [CrossRef]
  41. Matsuyama, T. Expert Systems for Image Processing: Knowledge-Based Composition of Image Analysis Processes*; 1989.
  42. Griffin, N.L.; Lewis, F.D. A Rule-Based Inference Engine Which Is Optimal and VLSI Implementable. In Proceedings of the [Proceedings 1989] IEEE International Workshop on Tools for Artificial Intelligence; 1989; pp. 246–251. [Google Scholar]
  43. Stansfield, S.A. ANGY: A Rule-Based Expert System for Automatic Segmentation of Coronary Vessels From Digital Subtracted Angiograms. IEEE Trans Pattern Anal Mach Intell, 1986; PAMI-8, 188–199. [Google Scholar] [CrossRef]
  44. Michael, D.J.; Nelson, A.C. HANDX: A Model-Based System for Automatic Segmentation of Bones from Digital Hand Radiographs. IEEE Trans Med Imaging 1989, 8, 64–69. [Google Scholar] [CrossRef]
  45. Phan, P.; Ouellet, J.; Mezghani, N.; de Guise, J.A.; Labelle, H. A Rule-Based Algorithm Can Output Valid Surgical Strategies in the Treatment of AIS. European Spine Journal 2015, 24, 1370–1381. [Google Scholar] [CrossRef]
  46. Savadjiev, P.; Chong, J.; Dohan, A.; Vakalopoulou, M.; Reinhold, C.; Paragios, N.; Gallix, B. Demystification of AI-Driven Medical Image Interpretation: Past, Present and Future. Eur Radiol 2019, 29, 1616–1624. [Google Scholar] [CrossRef]
  47. al Fryan, L.H.; Shomo, M.I.; Alazzam, M.B.; Rahman, M.A. Processing Decision Tree Data Using Internet of Things (IoT) and Artificial Intelligence Technologies with Special Reference to Medical Application. Biomed Res Int 2022, 2022, 8626234. [Google Scholar] [CrossRef] [PubMed]
  48. Hooda, R.; Joshi, V.; Shah, M. A Comprehensive Review of Approaches to Detect Fatigue Using Machine Learning Techniques. Chronic Dis Transl Med 2022, 8, 26–35. [Google Scholar] [CrossRef]
  49. Beccali, M.; Bonomolo, M.; Martorana, F.; Catrini, P.; Buscemi, A. Electrical Hybrid Heat Pumps Assisted by Natural Gas Boilers: A Review. Appl Energy 2022, 322. [Google Scholar] [CrossRef]
  50. Pean, T.Q.; Salom, J.; Costa-Castello, R. Review of Control Strategies for Improving the Energy Flexibility Provided by Heat Pump Systems in Buildings. J Process Control 2019, 74, 35–49. [Google Scholar] [CrossRef]
  51. Igder, M.A.; Liang, X.D.; Mitolo, M. Service Restoration Through Microgrid Formation in Distribution Networks: A Review. IEEE ACCESS 2022, 10, 46618–46632. [Google Scholar] [CrossRef]
  52. Pizarro, P.N.; Hitschfeld, N.; Sipiran, I.; Saavedra, J.M. Automatic Floor Plan Analysis and Recognition. Autom Constr 2022, 140. [Google Scholar] [CrossRef]
  53. Wu, C.S.; Liu, Y.C. Rule-Based Control of Weld Bead Width in Pulsed Gas Tungsten Are Welding (GTAW). PROCEEDINGS OF THE INSTITUTION OF MECHANICAL ENGINEERS PART B-JOURNAL OF ENGINEERING MANUFACTURE 1996, 210, 93–98. [Google Scholar] [CrossRef]
  54. Fu, Y.Y.; Neill, Z.O.; Wen, J.; Pertzborn, A.T.; Bushby, S. Utilizing Commercial Heating, Ventilating, and Air Conditioning Systems to Provide Grid Services: A Review. Appl Energy 2022, 307. [Google Scholar] [CrossRef]
  55. Yousefli, A.; Heydari, M.; Norouzi, R. A Data-Driven Stochastic Decision Support System to Investment Portfolio Problem under Uncertainty. Soft comput 2022, 26, 5283–5296. [Google Scholar] [CrossRef]
  56. Yang, L.H.; Liu, J.; Ye, F.F.; Wang, Y.M.; Nugent, C.; Wang, H.; Martinez, L. Highly Explainable Cumulative Belief Rule-Based System with Effective Rule-Base Modeling and Inference Scheme. Knowl Based Syst 2022, 240. [Google Scholar] [CrossRef]
  57. Abdullah, U.; Shaheen, M.; Ujager, F.S. Implementing Rule-Based Healthcare Edits. KSII TRANSACTIONS ON INTERNET AND INFORMATION SYSTEMS 2022, 16, 116–132. [Google Scholar] [CrossRef]
  58. Bettinger, P.; Boston, K.; Siry, J.P.; Grebner, D.L. Forest Management and Planning: Second Edition; Elsevier Inc., 2017; ISBN 9780128094761.
  59. Allan Bickle Fundamentals of Graph Theory; 1st ed.; American Mathematical Society, 2020; Vol. 1;
  60. Gilabert, H.; Manning, P.J.; McDill, M.E.; Sterner, S. Sawtimber Yield Tables for Pennsylvania Forest Management Planning. Northern Journal of Applied Forestry 2010, 27, 140–150. [Google Scholar] [CrossRef]
  61. Oliveira, N.; Pérez-Cruzado, C.; Cañellas, I.; Rodríguez-Soalleiro, R.; Sixto, H. Poplar Short Rotation Coppice Plantations under Mediterranean Conditions: The Case of Spain. Forests 2020, 11. [Google Scholar] [CrossRef]
  62. Leslie, A.D.; Mencuccini, M.; Perks, M.P.; Wilson, E.R. A Review of the Suitability of Eucalypts for Short Rotation Forestry for energy in the UK. New For (Dordr) 2020, 51, 1–19. [Google Scholar] [CrossRef]
  63. Amancio, M.R.; Pereira, F.B.; Zanon Paludeto, J.G.; Vergani, A.R.; Bison, O.; Bandeira Peres, F.S.; Tambarussi, E.V. Genetic Control of Coppice Regrowth in Eucalyptus Spp. Silvae Genet 2020, 69, 6–12. [Google Scholar] [CrossRef]
  64. Johnson, K.N.; Scheurman, H.L. Tequiniques for Precribing Optimal Timber Harvest and Investment under Different Objectives - Discussion and Synthesis. Forest Science 1977, 23, 1–31. [Google Scholar]
  65. Hof, J.G.; Pickens, J.B.; Barlett, E.T. A Maxmin Approach to Nondeclining Yield Timber Harvest Scheduling Problems. Forest Science 1986, 32, 653–666. [Google Scholar]
  66. D’Amours, S.; Ronnqvist, M.; Weintraub, A. Using Operational Research for Supply Chain Planning in the Forest Products Industry. INFOR 2008, 46, 265–281. [Google Scholar] [CrossRef]
  67. Malladi, K.T.; Sowlati, T. Biomass Logistics: A Review of Important Features, Optimization Modeling and the New Trends. RENEWABLE & SUSTAINABLE ENERGY REVIEWS 2018, 94, 587–599. [Google Scholar] [CrossRef]
  68. Toth, S.F.; McDill, M.E.; Konnyu, N.; George, S. Testing the Use of Lazy Constraints in Solving Area-Based Adjacency Formulations of Harvest Scheduling Models. FOREST SCIENCE 2013, 59, 157–176. [Google Scholar] [CrossRef]
  69. Kabli, M.; Gan, J.B.; Ntaimo, L. A Stochastic Programming Model for Fuel Treatment Management. Forests 2015, 6, 2148–2162. [Google Scholar] [CrossRef]
  70. Marques, A.F.; de Sousa, J.P.; Ronnqvist, M.; Jafe, R. Combining Optimization and Simulation Tools for Short-Term Planning of Forest Operations. Scand J For Res 2014, 29, 166–177. [Google Scholar] [CrossRef]
1
The age is set to five because we assume that the intervention happened at the midpoint of the period.
Preprints 74616 g001
Figure 1. An example management unit network graph.
Figure 1. An example management unit network graph.
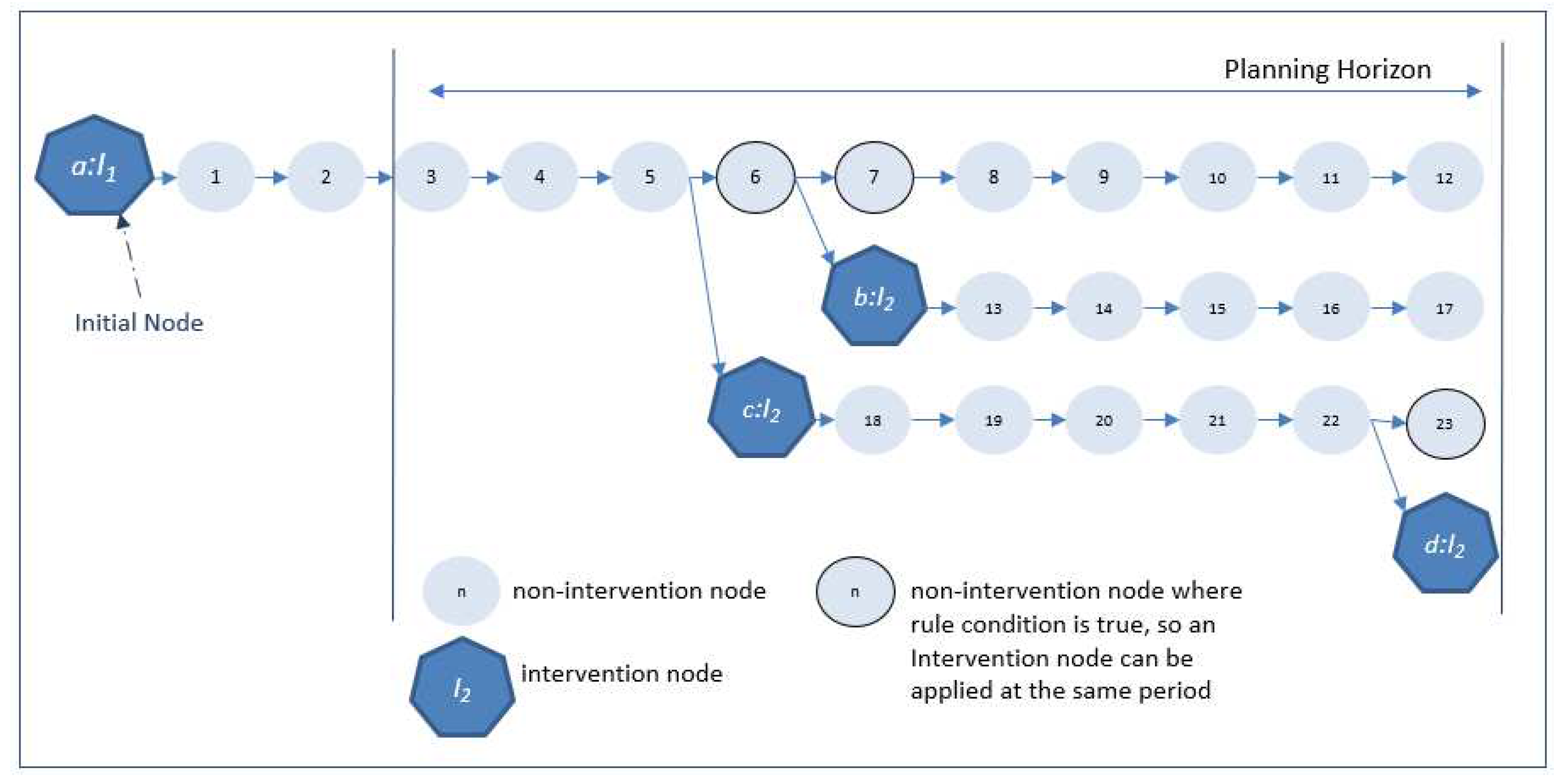
Preprints 74616 g001
Preprints 74616 g002
Figure 2. Diagram of entities and relationships of an instance of iGen.
Figure 2. Diagram of entities and relationships of an instance of iGen.
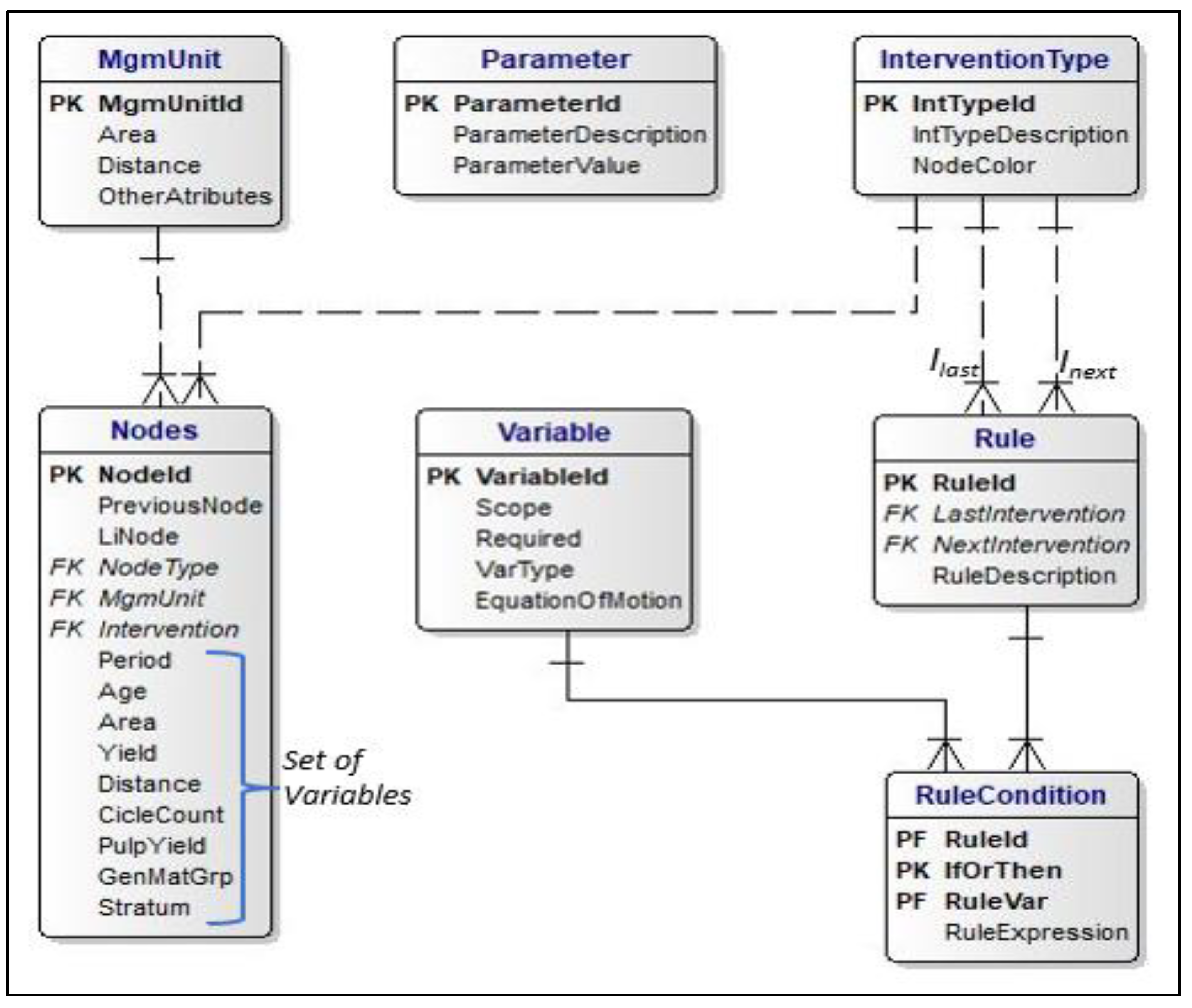
Preprints 74616 g002
Preprints 74616 g003
Figure 3. Flow chart of the inference engine algorithm.
Figure 3. Flow chart of the inference engine algorithm.
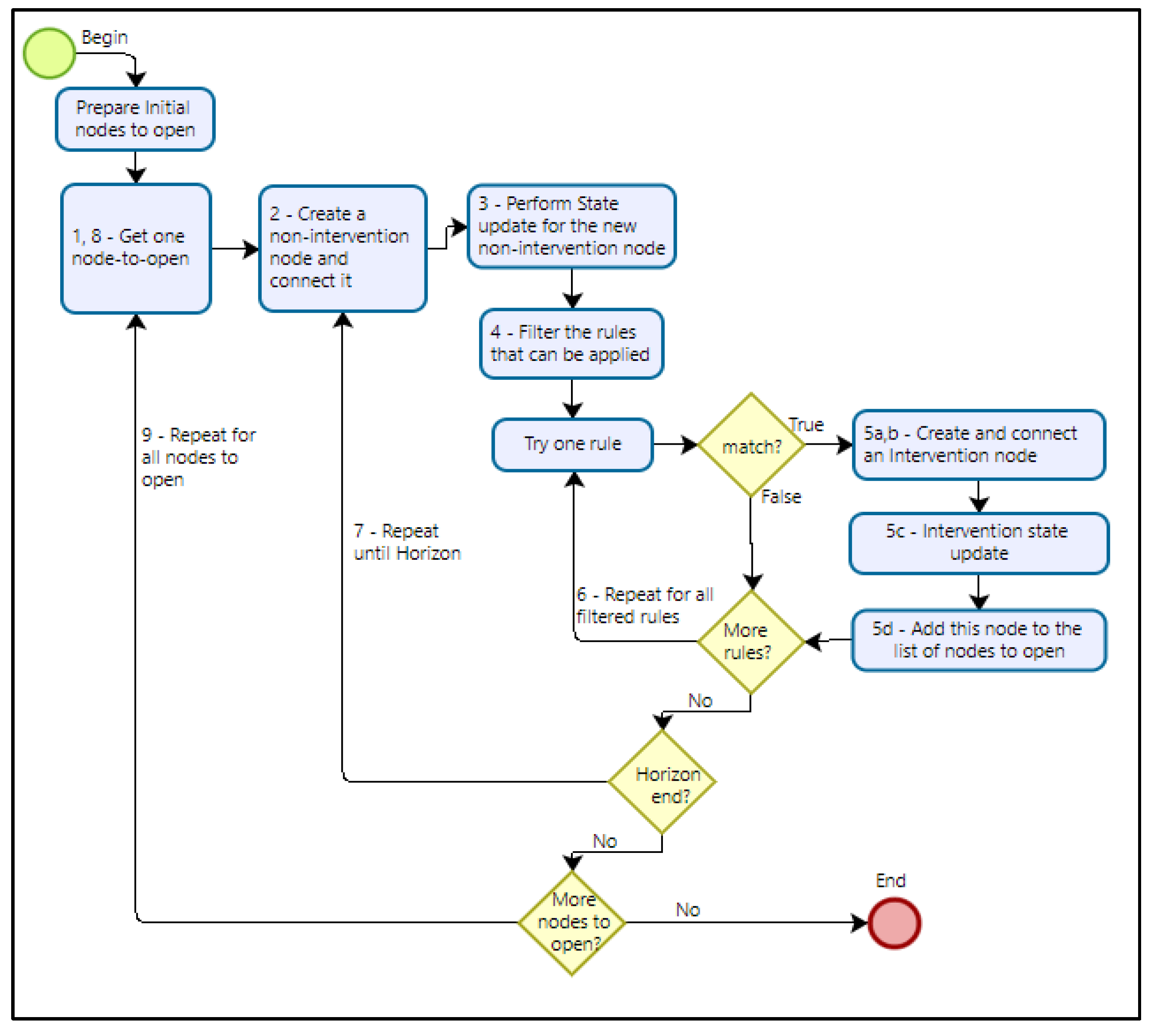
Preprints 74616 g003
Preprints 74616 g004
Figure 4. Management alternative graph for Pennsylvania Example - Management Unit 2.
Figure 4. Management alternative graph for Pennsylvania Example - Management Unit 2.
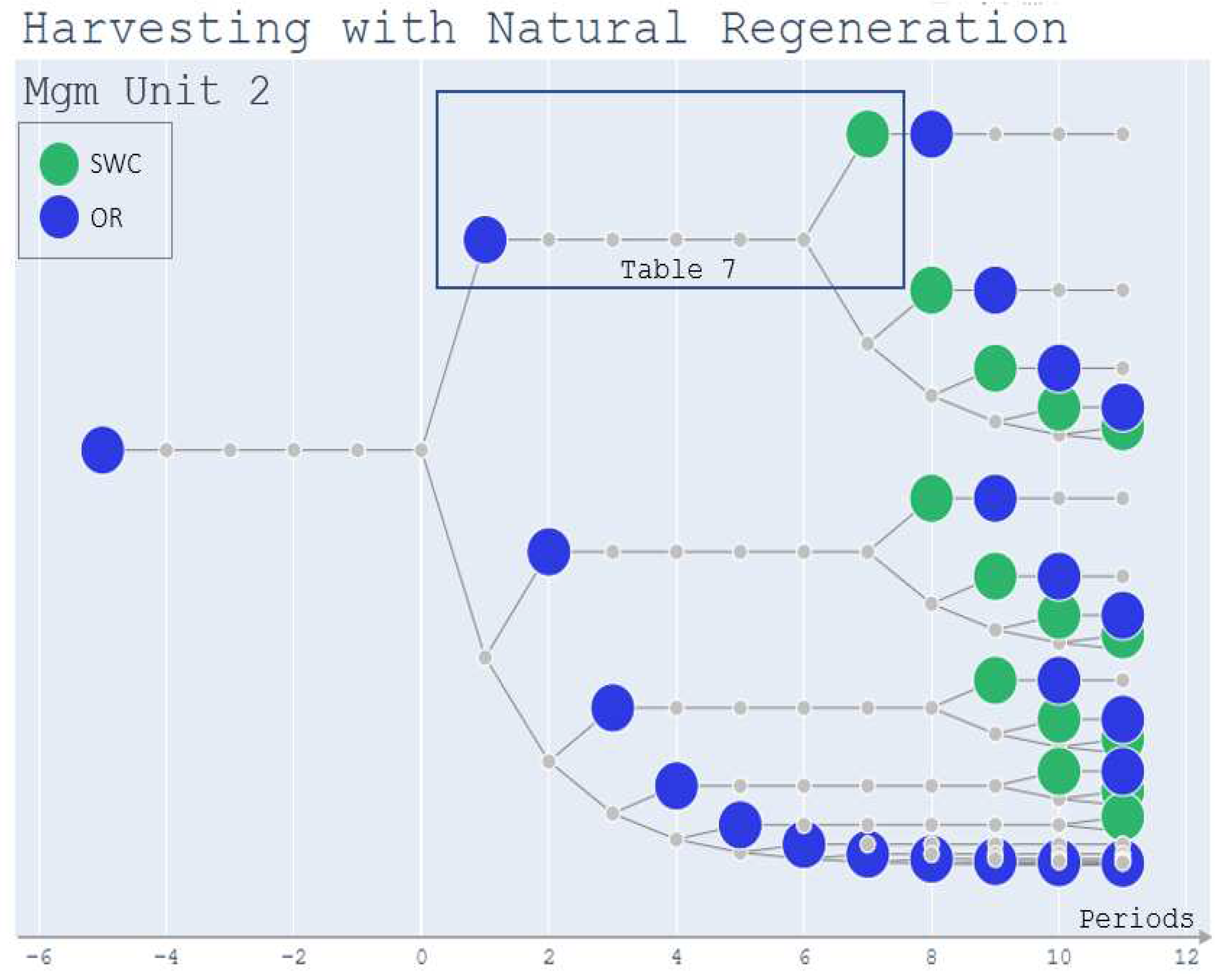
Preprints 74616 g004
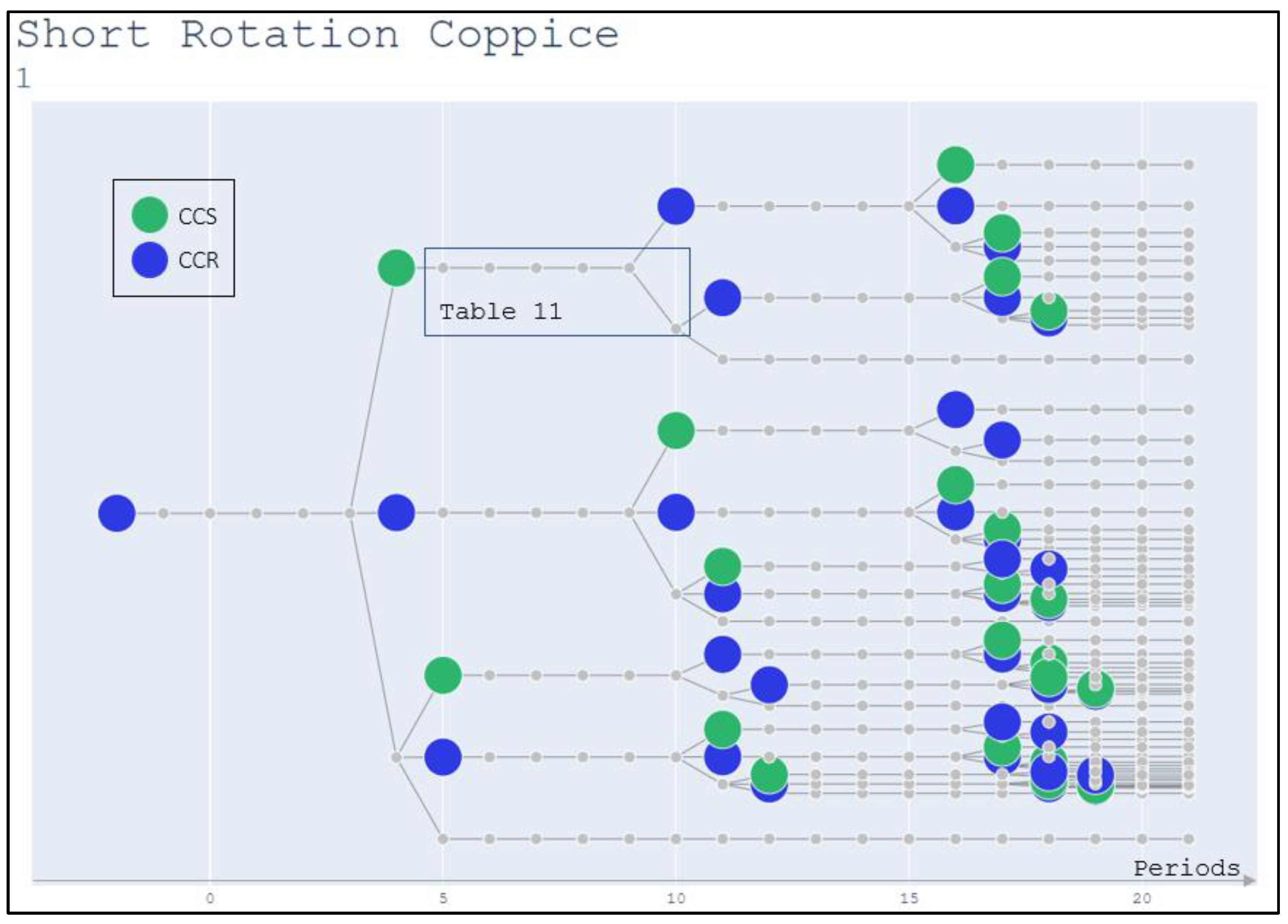
Preprints 74616 g005
Figure 5. Coppice Example - Management Unit 1.
Figure 5. Coppice Example - Management Unit 1.
Preprints 74616 g005
Table 1. iGen database tables where the elements are stored.
Table 1. iGen database tables where the elements are stored.
iGen elements Input or Output Tables where the elements are stored
Set of state variables Input Variable
Set of Intervention types Input InterventionType
Equations of motion for non-Intervention nodes Input Variable
Equations of motion for intervention nodes Input RuleCondtion
Rule base Input Rule and RuleCondtion
Initial nodes Input Nodes
Graph Output Nodes
General Parameters Input Parameter
Table 2. Initial State for three management units in the Pennsylvania Example.
Table 2. Initial State for three management units in the Pennsylvania Example.
yield
Mgm
Unit		 Site Area
(acre)		 Period Inter-vention Age
(years)		 Spc
Compo-sition		 Treat
Req		 Standing Volume
(MBF*)		 Removed Volume Remaining
Volume
1 1 100 -6 OR 8 1 SWC 0 0 0
2 1 90 -5 OR 7 2 OR 0 0 0
3 2 120 0 SWC 70 1 OR 6,311.49 2,524.59 3,786.89
(*) Thousand board feet.
Table 3. Equations of Motion for the Pennsylvania Example.
Table 3. Equations of Motion for the Pennsylvania Example.
Variable Equations of Motion Variable Equations of Motion
MgmUnit = :MgmUnit Age = :Age + 10
Site = :Site SpcComposition = :SpcComposition
Area = :Area TreatReq = :TreatReq
AfterInt = AfterInt + 1
yield =ExtFunctions.PennsylvaniaYield(:Age+10,[:Site],[:SpcComposition],[9],'stocked','ni', 'Standing')
yRemoved =ExtFunctions.PennsylvaniaYield(:Age+10,[:Site],[:SpcComposition],[9],'stocked', 'ni','Removed')
yRemaining =ExtFunctions.PennsylvaniaYield(:Age+10,[:Site],[:SpcComposition],[9],'stocked', 'ni', 'Remaining')
Table 4. The rule for shelterwood cut in the Pennsylvania Example.
Table 4. The rule for shelterwood cut in the Pennsylvania Example.
On the database table Rule:
RuleId LastIntervention NextIntervention RuleDescription
7 OR SWC A Shelterwood cut can occur after a minimum age
On the database table RuleCondition:
RuleVar RuleExpression
Conditional Part
Age, Site ((:Age >= 60) and (:Site == 1)) or ((:Age >= 70) and (:Site == 2))
TreatReq (:TreatReq == 'SWC')
Consequent Part
MgmUnit = :MgmUnit Age = :Age
Site = :Site SpcComposition = :SpcComposition
Area = :Area TreatReq = 'OR'
AfterInt = 0
Yield = ExtFunctions.PennsylvaniaYield(:Age,[:Site],[:SpcComposition],[9],'stocked','SWC', 'Standing')
YRemoved = ExtFunctions.PennsylvaniaYield(:Age,[:Site],[:SpcComposition],[9],'stocked','SWC', 'Removed')
yRemaining = ExtFunctions.PennsylvaniaYield(:Age,[:Site],[:SpcComposition],[9],'stocked','SWC', 'Remaining')
Table 5. The rule for an overstory removal following a shelterwood harvest in the Pennsylvania Example.
Table 5. The rule for an overstory removal following a shelterwood harvest in the Pennsylvania Example.
Ruletable: RuleId Last Intervention Next Intervention RuleDescription
6 SWC OR Overstory removal must occur after a Shelterwood
RuleCondition
table: 		RuleId IfOrThen RuleVar RuleExpression
6 If AfterInt (:AfterInt == 1)
Table 6. The rule for an overstory removal without a shelterwood harvest in the Pennsylvania Example.
Table 6. The rule for an overstory removal without a shelterwood harvest in the Pennsylvania Example.
On the database table Rule:
RuleId LastIntervention NextIntervention RuleDescription
8 OR OR An overstory removal can occur without a shelterwood cut
On the database table RuleCondition
RuleVar RuleExpression
Conditional Part
TreatReq (:TreatReq == ‘OR’)
Consequent Part
MgmUnit = :MgmUnit Then Age = 5
Site = :Site Then SpcComposition = :SpcComposition
Area = :Area Then TreatReq = ‘SWC’
AfterInt = 0
Yield = ExtFunctions.PennsylvaniaYield(:Age,[:Site],[:SpcComposition],[9],’stocked’,’OR1’, ‘Standing’)
YRemoved = ExtFunctions.PennsylvaniaYield(:Age,[:Site],[:SpcComposition],[9],’stocked’,’OR1’, ‘Removed’)
Yremaining = ExtFunctions.PennsylvaniaYield(:Age,[:Site],[:SpcComposition],[9],’stocked’,’OR1’, ‘Remaining’)
Table 7. Pennsylvania Example State updates.
Table 7. Pennsylvania Example State updates.
NodeId Previous
Node		 LiNode Period Inter-vention Age After-Int Yield Y
Removed		 Y
Remaning
43 41 2 1 OR 5 0 13,432.09 13,432.09
197 43 43 2 ni 15 1 217.65
198 197 43 3 ni 25 2 1,821.78
199 198 43 4 ni 35 3 4,528.49
200 199 43 5 ni 45 4 7,510.23
201 200 43 6 ni 55 5 10,362.44
203 201 43 7 SWC 65 0 12,949.49 5,179.80 7,769.70
Table 8. Plantation/Coppice example initial state for four management units.
Table 8. Plantation/Coppice example initial state for four management units.
MgmUnit Stratum Area Period Last Intervention Age Rotation Yield
1 1 40 -2 CCR 0 1 0
2 1 50 -4 CCR 0 1 0
3 2 54 -2 CCR 0 1 0
4 1 20 -1 CCS 0 2 0
Table 9. Plantation-Coppice example equations of motion for no intervention.
Table 9. Plantation-Coppice example equations of motion for no intervention.
VariableId Equation of Motion
MgmUnit =:MgmUnit
Stratum =:Stratum
Area =:Area
Age =:Age+1
RotationCount =:RotationCount
Yield =SearchTable(Productivity,(:Stratum,:Age + 1),Volume)
Table 10. The conditional part of the Plantation/Coppice Example Rules.
Table 10. The conditional part of the Plantation/Coppice Example Rules.
Intervention
Rule Id Last Next Rule Var RuleExpression
1 CCR CCR If Age (6 <= :Age <= 7) or (1 <= :Period <=3 and 6 <= :Age <=9)
Yield :Yield>=200
2 CCS CCR If Age (6 <= :Age <= 7) or (1 <= :Period <=3 and 6 <= :Age <=9)
Yield :Yield>=200
3 CCR CCS If Age (6 <= :Age <= 7) or (1 <= :Period <=3 and 6 <= :Age <=9)
Yield :Yield>=200
Table 11. Plantation/Coppice Example State Updates.
Table 11. Plantation/Coppice Example State Updates.
NodeId PreviousNode LiNode Period Age RotationCount Yield
214 15 15 5 1 2 60
215 214 15 6 2 2 100
216 215 15 7 3 2 140
217 216 15 8 4 2 190
218 217 15 9 5 2 210
219 218 15 10 6 2 230
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated