Preprint
Article
Thermodynamic and Thermal Analyze of N,N-Dimethylformamide + 1-Butanol Mixture Properties Based on Density, Sound Velocity and Heat Capacity Data
Altmetrics
Downloads
119
Views
13
Comments
0
A peer-reviewed article of this preprint also exists.
supplementary.docx (75.87KB )
This version is not peer-reviewed
Submitted:
24 May 2023
Posted:
26 May 2023
You are already at the latest version
Alerts
Abstract
The present paper contains data on the density (ρ), sound velocity (u), specific heat capacity (c_p ) of the mixture of N,N-dimethylformamide + 1-butanol (DMF + BuOH) determined in the entire concentration range of solution and in the temperature range: (293.15–318.15) K. The analysis of thermodynamic functions such as isobaric molar expansion, isentropic and isothermal molar compression, isobaric and isochoric molar heat capacity, as well as their excess functions (〖 E〗_(p,m)^E,〖 K〗_(S,m)^E,〖 K〗_(T,m)^E,〖 C〗_"p,m" ^E,〖 C〗_"V,m" ^E) and also V_m^E was undertaken. The analysis of changes in the physicochemical quantities was based on consideration of the system in an aspect of intermolecular interactions with resulting changes in the mixture structure. The results available in the literature are confusing during the analysis and became the reason for our decision to thoroughly examine the system. What is more, for a system whose components are widely used, there is no information in the literature regarding the heat capacity of the tested mixture, which was also achieved and presented in this publication. The conclusions drawn from so many data allow us to approximate and understand the changes that occur in the structure of the system due to repeatability and consistency of the obtained results
Keywords:
Subject: Chemistry and Materials Science - Physical Chemistry
1. Introduction
Thermodynamic properties are a valuable source of information on the interaction between solute and solvent molecules. In particular, the combination of techniques such as density, sound velocity, and specific heat capacity gives a range of data allowing one to analyse the changes in the structure of mixed solvent. Regarding the thermodynamic properties, it appeared that volumes, heat capacities, expansivities, and compressibilities are sensitive to structural changes and allow prediction of the type of interactions prevailing in the liquid mixtures. The density, ultrasonic, and thermodynamic studies with the change of one component of the solution are of high value and practical importance in industry. Such data are also used in manufacturing process control and other significant fields.
Alcohol-containing mixtures are gaining in popularity. Such solutions are used in the pharmaceutical and cosmetic industries, in high-energy battery technologies, or in organic synthesis [1,2]. Great interest in the product requires a better understanding of the influence of the liquid structure on its macroscopic properties, including density, speed of ultrasound propagation, and heat capacity [3,4]. 1-Butanol (BuOH) is used as a perfume ingredient and a solvent for the extraction of essential oils, an extractant in the production of antibiotics, hormones, and vitamins [5]. It is also present in the cosmetics industry, mainly in make-up removers, nail care, and shaving products [5]. BuOH is also used in the food industry as a flavouring agent in cream and baked goods [5]. N,N-dimethylformamide (DMF) has many useful properties, making it an exceptionally good cosolvent [6]. Secondary and tertiary amides play a role in constructing the backbone conformation of peptides and proteins [7]. DMF is used in the formation of pesticides and in the manufacture of synthetic leathers, fibres, films, and surface coatings [8,9]. It is also used in the production of vinyl and acrylic polymers. It is an extractant as well as an absorbent of gases [10]. The mixture of DMF with supercritical CO2 is of great interest in the extraction of supercritical fluids in separation processes [11,12,13]. It is well-known that amides interact with alcohols through hydrogen bonding, and the addition of DMF to alcohol causes characteristic changes in mixture structure. Due to this fact, it is interesting to know the properties of the DMF and 1-buthanol mixture. The available data on this mixture are often focused mainly on densimetric data, sometimes enriched with ultrasound or viscosity techniques [4,14,15,16,17,18,19,20,21].
However, the results obtained by the researchers are not entirely consistent and often cover a narrow temperature range, as well as a few points that determine the change in the composition of the mixture [4,14,15,16,17,18,19,20,21]. The heat capacity data in the available literature is very scarce [22] and there is no complete information on the value of the specific heat capacity in the entire range of the composition of the mixture and the wide temperature changes. The data obtained in this work include analysis of selected physicochemical quantities e.g. excess molar volume , also excess partial molar volume of 1-butanol and N,N-dimethylformamide , molar volume expansion , molar isentropic () and isothermal () compressibility, isobaric and isochoric molar heat capacity as well as their excess values of DMF + BuOH system at six temperatures in the whole concentration range. Data available in the literature [4,14,15,16,17,18,19,20,21]. on the tested system so far do not include small and precise changes in the concentration of the mixture and such a wide range of temperatures, as presented in our work. The change in concentration is 0.05 mole fraction, which allowed us to show characteristic changes in analysed functions not previously listed. Connecting so many data gives the opportunity to draw variety valuable conclusions regarding changes in the structure of the system [23,24]. Moreover, we determined the thermal properties of the system by taking the attempts to measure the isobaric specific heat capacity . In the literature there are no data presenting isobaric and isochoric molar heat capacities of the system. Such data in combination with density and ultrasound velocity in a temperature range (293.15–318.15) K presents worth attention and coherent results.
2. Results and Discussion
2.1. Volumetric Properties
The results obtained from the density tests of the DMF + BuOH mixture (Table S1 Supplementary Materials) show that the values increase with increasing DMF content in the mixture and decrease systematically with increasing temperature over the whole range of mixture compositions. To study the properties of real solutions, excess functions are used, which determine the difference between the magnitude of a given molar thermodynamic function in a real solution and its magnitude in an ideal solution. The excess properties were calculated using the following expression:
where is the excess quantity of the property Z and is the corresponding ideal value [25].
In this paper will be presented and analyze six excess functions calculated according to Equation (1). In order to calculate excess molar volume , the molar volume of the mixture was obtained according to Equation (2):
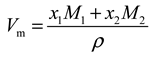 where: is the density of DMF + BuOH mixture, , and , are the mole fractions and molar masses of the mixture components, respectively, i.e. BuOH (1), DMF (2).
where: is the density of DMF + BuOH mixture, , and , are the mole fractions and molar masses of the mixture components, respectively, i.e. BuOH (1), DMF (2).
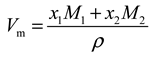
In order to determine the changes taking place in a real solution in relation to an ideal solution in a binary mixture, the values of excess molar volume (have been executed. values of the mixture in the whole composition range and at the temperature range (293.15 K–318.15 K) was calculated according to Equation (3) and presented in Figure 1:
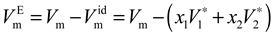 where: is the molar volume of (DMF+BuOH) mixture, is the volume of ideal mixture, , are the molar volume of pure compounds, i.e. BuOH (1), DMF (2).
where: is the molar volume of (DMF+BuOH) mixture, is the volume of ideal mixture, , are the molar volume of pure compounds, i.e. BuOH (1), DMF (2).
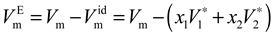
The values of excess functions and among others the of DMF + BuOH mixture were fitted to the polynomial of Redlich−Kister type:
where is the polynomial coefficient calculated by the least-squares method using Equation (5).
As can be seen in Figure 1, the excess molar volume exhibits positive values in a solution with a predominantly BuOH content in the mixture. increases when small amounts of DMF are added to pure BuOH and passes through a maximum which appears depending on the temperature among ≈ 0.3 and ≈ 0.35 values. Above this value of mole fraction, values are decreasing and reach the minimum value at ≈ 0.9. It is noteworthy that negative values for are obtained for different mixture compositions depending on the temperature. The mole fraction of DMF, in which we observe the change of sign of the function, increases with increasing temperature from the value ≈ 0.5 for 293.15 K to the value ≈ 0.9 for 318.15 K. One can notice that the volume contraction of the DMF + BuOH mixture increases when the molar fraction of DMF increases above 0.5 and decreases with increasing temperature. In the literature, you can find several reports in which an attempt was made to determine the value of for the DMF + BuOH mixture [14,15,16,19,20,21]. However, the research results presented in these articles are divergent. Similar results to ours were obtained by Rao and Reddy [14] at 303 K and Garcia et al. [21] but only at 298K. In the other works, the results diverged from each other and from our results. Moreover, some authors obtained negative values of in the whole range of compositions [15,19] which was completely inconsistent with the results obtained by other researchers, including ours. Such ambiguous data and conclusions prompted us to study the properties of this mixture with more accuracy using the three different test methods mentioned earlier.
The sign and magnitude of the excess functions may be attributed to the result of an appropriate combination of the following three major effects. The mutual dissociation of the components due to addition of the second component, the formation of hydrogen bonds between unlike molecules and steric hindrance, as well as geometry of molecular structure, which could be the reason which resist the closeness of the molecules. For DMF + PrOH according to the results obtained by us in our previous work [26], the values were negative over the entire range of the mixture composition. Excess molar volumes are more negative in systems with lower alcohols, which may be attributed to strong interactions between unlike molecules and different molecular sizes [27]. Such properties cause volume contraction in these mixtures. For the DMF + BuOH system, the small increase in the size of the alcohol molecule (extra –CH2 group in 1-butanol compared to DMF + PrOH [26]) gives completely different results and appears in volume expansion when DMF is added to BuOH. These values are positive in the BuOH rich region. Mostly for the DMF + BuOH system, the results obtained in their absolute value are 1.5 to 2 times smaller than for the DMF + PrOH mixture, however, in some compositions, they are several or ten times smaller than for the DMF + PrOH mixture.
Alcohols are strongly hydrogen-bonded in the pure state. Their molecules are self- and cross-associated [28,29]. The degree of association decreases also with increasing alcohol chain length. Thus, the addition of DMF to pure BuOH breaks the hydrogen bonds between molecules in the structure of the alcohol network, which produces a positive contribution to . The results obtained on the basis of the dielectric study prove that in a solution with a predominant content of BuOH, the largest changes in the structure of hydrogen bonds occur in the DMF + BuOH solution [30]. At the same time, an increase in the length of the alcohol chain causes a steric hindrance that also contributes to the increase in the real volume of the DMF + BuOH mixture. There is also not much difference in the molecular size of these two compounds, which also makes mutual accommodation difficult. The presence of hydrogen bonds between the components of the mixture tested was also confirmed by other researchers [4,20,30,31]. Prajapati [30] based on the analysis of parameters obtained from the dielectric study provides confirmation of the formation of hydrogen bonds between DMF and BuOH molecules and weak dipole-dipole interactions between the components of the mixture. In contrast to the DMF + PrOH mixture, it is known that the interactions between unlike molecules are very weak in DMF + BuOH solution [32]. Therefore, we observe an increase in with increasing DMF content in the mixture to ≈ 0.3. The maximum observed at this mole fraction of DMF is related to the fact that in this range of the mixture composition there are probably the weakest interactions between the components of the mixture, which also contributes positively to the [32]. Despite the fact that there is probably still the possibility to form some amount of hydrogen bonds between DMF and BuOH molecules, the excess of BuOH amount is a competitive factor in the formation of hydrogen bonds between unlike molecules. According to the researchers [32], the binding energy –O–H···O=C decreases when another alcohol molecule approaches with its oxygen atom favorablely orientated for “change”. As a consequence, instead of hydrogen bonding between DMF and BuOH molecules, the bonding appears between alcohol molecules rather more. When the amount of BuOH prevails in the DMF + BuOH system, there exists a greater tendency to create hydrogen bonds between BuOH molecules than between unlike species. As a result of the specific arrangement of neighbouring molecules around the DMF and BuOH molecules that form the bond, this interaction is weakened, which is confirmed by the negative values in the entire concentration range of the solution obtained by Prajapati [30]. This parameter assumes the largest negative deviation for a mixture with the composition ≈ 0.3, hence we observe a maximum on the relationship
= f(. Dissociation of bonding of pure components presumably became the main reason for volume expansion of the tested system. When > 0.3 values decrease and become negative when > 0.5 (293.15 K). In a solution with a predominant DMF content in the mixture, they can observe small volume contraction. The volume contraction value is similar to that observed for the DMF + PrOH system in the same concentration area of the mixture. When DMF starts to prevail in the solution, dipole-dipole interactions are most likely to begin to prevail in DMF and the creation of hydrogen bonding between DMF and BuOH molecules.
The analysis of the excess partial molar volume of both components of the mixture may help to explain the observed changes in this range of the mixture composition. The volume of the solution, in the case of a binary mixture, is the sum of the partial molar volumes of both components:
where:, – mole fraction of BuOH i DMF respectively, , – partial molar volume of BuOH i DMF respectively. and we can calculate using the following Equations (7) i (8):
where: – molar volume of the real solution (DMF + BuOH),, – mole fraction of DMF and BuOH.
Analysis of changes in the partial molar volume of the components of a mixture can be represented by the excess partial molar volume (, ). These values can be calculated using Equations (9) and (10):
where: , – excess partial molar volume of DMF and BuOH respectively,, – molar volume of pure DMF and BuOH.
The results for partial and excess partial molar volume of DMF and BuOH and are presented in Tables S4-S7 in Supplementary Materials and presented in Figure 2 at T = 293.15 K.
The values of and express the difference between the value of the partial molar volume of DMF or BuOH in the solution and the molar volume of each of the components in their pure form. Based on the analysis of Figure 2, one can notice that for DMF the values of are negative when > 0.4 at 293.15 K. This means that DMF contributes negatively to the real volume of the mixture in this composition range of the solution. Although assumes positive values in the same concentration range, however the amount of DMF prevails over the amount of BuOH when > 0.4. Having been aware that DMF is a weakly associated liquid in contrast to BuOH [30], the results obtained allow us to conclude that the negative contribution to the real volume of the mixture is made by the DMF molecules ( This is presumably one of the main factors of the slight contraction of the volume of the mixture causing that we observe < 0 when > 0.5. Analysis of data on the partial molar volume of each component in the DMF + BuOH mixture (Tables S4 and S5 Supplementary Materials) allows one to observe that the relationships and shows only little change with increasing DMF content in solution. This proves that chemical entities, such as various types of associations or complexes built of both molecules of the solution components, are most likely not formed in the system. Otherwise, we would observe characteristic changes in the course of both functions, along with an increase in the content of one of the components of the mixture, as in the case of an aqueous solution of N,N-dimethylformamide [33], which also confirms the conclusions drawn earlier. The partial molar volume of DMF decreases slightly as the DMF content of the mixture increases, with a higher temperature. Garcia et al. [19] presented a similar course of this dependence at a temperature of 298.15 K. In addition, takes the highest value at the highest temperature. Determined by Zegers and Somsen [22] value of in pure BuOH is equal to 7.779·10−5 m3·mol−1 and is close to the one obtained by us (7.749·10−5 m3·mol−1). The course of the relationship is opposite to that observed for DMF. values increase slightly with increasing DMF content. The influence of temperature on the values of is analogous to the case . Zegers and Somsen [22] determined also in pure DMF, which is equal to 9.197·10−5 m3·mol−1. The value obtained by them is close to the one determined by us (9.208·10−5 m3·mol−1).
Using the density values of the mixture at six temperatures, the coefficient of thermal expansion was calculated (αp) using Equation (11):
was calculated with Equation (12) [34]:
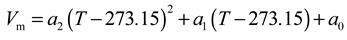
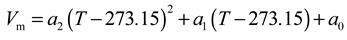
The values of molar isobaric expansion () were calculated using Equation (13) [25]:
The obtained results of as a function of the DMF molar fraction are presented in Figure 3.
The isobaric molar expansion reaches the highest value for pure BuOH and decreases with increasing DMF in the mixture. The values increase with increasing temperature over the whole composition range of the mixture which seems to be logical due to the increase in thermal movements at higher temperatures. Such a behaviour of the system in the BuOH rich region is most likely related to the breaking of hydrogen bonds in BuOH after adding DMF to the solution. This causes greater changes in volume expansion with an increase in temperature. With a high BuOH content in the mixture, a slight maximum is visible at the two lowest temperatures (293.15 K, 298.15 K). For higher temperatures on the relationship, we observe only a change in the slope of the function. A greater effect of temperature on the value of this function is observed when BuOH prevails in the mixture. As the DMF content increases, the temperature differentiates the values of the mixture increasingly less. Small changes in the value of the isobaric molar expansion in the DMF rich region show that the structure of this solvent remains only slightly associated by dipol-dipol interactions.
Using the calculated values of and Equations (14) and (15) [25] excess molar isobaric expansion was determined () and presented in Figure 4:
where: are volume fraction of BuOH and DMF and are the coefficient of thermal expansion of pure BuOH and DMF respectively.
Excess isobaric molar expansion in the entire concentration range takes positive values. A real solution has a greater ability to thermally expand relative to the ideal solution. In the range of 0.4 ≤ ≥ 0.5 (depending on the measurement temperature) a maximum appears, which proves the occurrence of characteristic changes in the interactions between molecules in this composition range. The value of is the lowest at T = 318.15 K, which means that at the highest temperature the volumetric expansion of a real solution is the smallest and increases with decreasing temperature. It should be expected that at the lowest temperatures, the interactions between molecules will be stronger in relation to the intermolecular interactions weakening with increasing temperature.
2.2. Sound Velocity and Heat Capacity
Based on density and sound velocity measurements (Tables S1 and S2 in Supplementary Material) the isentropic compressibility coefficient and molar isentropic compression were calculated according to Equations (16) and (17) in the whole temperature range:
where is the isentropic compressibility coefficient, is the molar isentropic compression, is the sound velocity of DMF + BuOH mixture, is the experimental value of solution’s density.
Based on the obtained data like isentropic compressibility coefficient , the coefficient of isobaric thermal expansibility ( and experimentally gained data of density () and specific heat capacity ( of the tested DMF+BuOH solution which (presented in Tables S1 and S3 in Supplementary Materials), the values of isothermal compressibility efficient and isothermal molar compression were calculated using Equations (18) and (19):
Obtained results of and for the whole composition and temaprature range are presented in Table S8 (Supplementary Materials). The course of changes in isentropic and isothermal molar compression as a function of concentration and temperature is very analogous. and reach similar values. Both the isentropic and isothermal molar compression decreases with increasing DMF content in the mixture. This is in agreement with the results of other researchers [35]. The highest value of and is observed for pure BuOH, due to the hydrogen bonds existing in the alcohol structure. and increases with concentration increase of alcohol. It is principally associated with an increase in compressibility due to structural changes in the mixture that lead to a decrease in ultrasonic velocity [36]. Adding DMF to BuOH breaks these bonds and creates new ones, weaker, between the DMF and BuOH molecules. This leads to a closer arrangement of the molecules. In the DMF rich region only the diop-dipol interaction prevail. Most likely, this phenomenon contributes to a decrease in the compressibility of the system with increasing mole fraction of DMF. The compressibility of the system increases with increasing temperature. A greater effect of temperature on the value of isentropic and isothermal molar compression is visible for solutions in which the content of BuOH prevails. When there is more DMF in the system, and depends on the temperature increasingly less.
In order to better understand the nature of the interactions between the components of the mixture and the nature of molecular agitation in dissimilar molecules, the excess molar isentropic compression was determined () and excess molar isothermal compressibility (). These are found to be sensitive towards differences in the size and shape of molecules [37]. For this purpose and values were calculated according to Equations (20) – (24) [25]:
where: represent excess molar isentropic and isothermal compression, and represent the molar isentropic and isothermal compression, and andtheir molar values for an ideal mixture; the isentropic and isothermal compressibility coefficients of pure components 1 (BuOH) and 2 (DMF), the volume fraction of the mixture components; represents the isobaric molar heat capacity of pure BuOH (1) and DMF (2) calculated on the basis of the obtained values (Table S3 Supplementary Materials).
The courses of both functions and in the whole temperature range are shown on Figure 5.
The excess molar isentropic and isothermal compression take negative values. The same trend can be seen in studies published by Thirumaran et al. [4], Rao and Reddy [14], and Acree [35]. This parameter takes negative values, and the minimum is observed at ≈ 0.45. It can be concluded that the real solution is less compressible than the ideal solution. At ≈ 0.45 where there is a minimum on the function curves and visible, apparently there are characteristic changes in the interactions between the particles of the real mixture in relation to the ideal solution, causing more and more difficulties in the compression of the system. With the addition of DMF to the pure BuOH, the excess compressibility rapidly decreases up to ≈ 0.45 caused by the rupture of hydrogen bonds in pure BuOH occurring during mixing. In this range of composition, we also observe probably the weakest interactions between the components of the mixture [30,32]. The lower compression in the solution is observed for systems with lower alcohols, which can be attributed to strong interactions between unlike molecules and different molecular sizes causing stronger mutual accommodation of components [26,27]. Such situation was observed for DMF + PrOH mixture [26]. Since the size of both BuOH and DMF molecules is similar, the weakening and breaking of bonds and the lack of interstitial accommodation due to similar molecular sizes may be the reason for decreasing the compressibility of the DMF + BuOH system in the BuOH rich region. In the DMF rich region, with the increasing importance of interactions of unlike molecules and dipole - dipole interaction in DMF, we can observe the decresing negative values for and . The value of decreases with increasing temperature. Thus, the lower the temperature, the greater the compressibility of a real solution relative to that of an ideal solution. At T = 293.15 K, the real system will show the least negative and of the mixture compared to the other temperatures.
The values of isobaric molar heat capacity () were calculated using specific heat capacity obtained from experiment (Table S3 Supplementary Materials). The results in the whole composition range of the mixture and for six temperatures (293.15K–318.15K) were calculated and presented on Figure 6 and in Table S9 (Supplementary Materials).
Heat capacity and thermal analysis data for the DMF + BuOH system have not been published earlier. As can be seen from the Figure 6 the values decrease with increasing DMF content. With increasing temperature values are increasing. A greater temperature differentiation is also visible in the BuOH rich region compared to the area of DMF that prevails. An analogous course of dependence with an increase in DMF content for this system DMF + BuOH and changes under the influence of temperature was visible in the course of the previously discussed functions and , which make us able to conclude that our data are coherent. The analysis of changes in the function with increasing concentration and temperature allows us to confirm the changes in the nature and strength of interactions between unlike species in the structure of the system occurring and which was discussed earlier. Based on these data, one can observe the transition from strong hydrogen bonds in the structure of BuOH to weak intermolecular interactions in the DMF rich region. With the values of and it was also possible to calculate the values of according to Equation (25) [25]:
The obtained calculation results for have been collected in Table S9 in Supplementary Materials.
Excess molar isobaric and isochoric heat capacities were calculated using Equations (26) and (27).
where: , are isobaric and isochoric molar heat capacities of the ideal mixture, , are the isothermal and isentropic compressibility coefficients for the ideal mixture and are the isobaric and isochoric molar heat capacities of pure compounds, BuOH (1) and DMF (2).
is presented as a function of mixture composition in Figure 7. The obtained relationship of is analogous to with the change of temperature. A comparison of both functions at 298.15 K is shown in Figure 8.
Excess molar isobaric ) and isochoric ) heat capacity of DMF + BuOH mixture shows negative values in the entire composition range of the mixture. The reason of reduction of is forming of interactions occurring between DMF and BuOH molecules which are presumably weaker compared to the hydrogen bonds between the molecules of these compounds existing in their pure form. As the temperature increases, we observe an increase in the negative values of both functions. With increasing DMF content, and decrease and reach a minimum value when ≈ 0.5. The obtained results confirm the changes in , and already analyzed in this paper. All analyzed excess functions, including and reach their extreme value when ≈ 0.5. The obtained results of thermal properties for the DMF + BuOH mixture confirm the characteristic change in the strength of interactions between the components of the mixture with the change in the composition of the system. Interactions in the system weaken in the BuOH rich region with an increasing amount of DMF. This allows us to confirm the conclusion that the specific arrangement of neighbouring molecules around the DMF and BuOH molecules forming the bond, this interaction is weakened [30]. Hence, we observe and negative values. Then one can notice an increase in the strength of the interaction when DMF is prevailing. Otherwise, as a result of the formation of intermolecular hydrogen bonds between unlike molecules, stronger than in their pure state, the maximum would be observed [33]. From Figure 7 the position of the minimum shifts very slightly towards lower values of the DMF with increasing temperature. An analogous course is observed for dependence.
3. Experimental
3.1. Materials
The list of compounds used in the study in this paper, as well as the suppliers, purity, purification method, and water content, is presented in Table 1.
3.2. Method
3.2.1. Density and Speed of Sound
The density and speed of sound of DMF + BuOH mixture within its entire concentration range were measured at temperatures T = (293.15, 298.15, 303.15, 308.15, 313.15, 318.15) K with the use of a DSA 5000 analyser from Anton Paar. It is a device that allows simultaneous measurement of the density and speed of sound of a liquid sample at ambient pressure by connecting the two measuring cells in a linear manner. These cells are located in the thermostat block. The repeatability of the temperature measurement declared by the manufacturer is ± 0.001 K, while its uncertainty is 0.01 K. The range of density measurement of the Anton Paar DSA 5000 M densimeter is (0 – 3) g·cm−3. The repeatability of the density measurement declared by the manufacturer is ± 1·10-3 kg·m−3 and the determined uncertainty is equal ± 2·10−2 kg·m−3 considering the formula for the combined standard uncertainty for the average density measurements proposed by Fortin et al. [38]. Each series of measurements was preceded by checking the correct device operation. The verification consisted of measuring the density and speed of ultrasound propagation of ultra-pure degassed water (Direct Q3 UV purification). Particular attention was paid to cleaning the entire system between measurements. Due to the combination of cells, this is extremely important. To avoid the appearance of gas bubbles, which would significantly disturb the entire measurement, the density of the tested solution was measured from the highest temperature (318.15 K) to the lowest temperature (293.15 K) with increments of five degrees. The speed of sound of the DMF + BuOH mixture was also measured in the temperature range (293.15 – 318.15) K. The measurement uncertainty is ± 0.5 m·s−1, and its precision is estimated to ± 0.1 m·s−1. The speed of sound is measured by measuring the propagation time of the sound signal. The sound speed cell has a circular cylindrical cavity of 8 mm diameter and 5 mm thickness. The sample is introduced between two piezoelectric ultrasonic transducers. The first transducer produces sound waves (average frequency is 3 MHz), while the second transducer receives the waves. If necessary, calibration of the measuring equipment was also carried out according to the procedure in accordance with the manufacturer’s instructions using ultra-pure, degassed water and air at 293.15 K and at 0.1002 MPa pressure. The value of water density and speed of sound amounting 998.204 kg·m−3 and 1482.63 m·s−1 at a temperature of 293.15 K is consistent with those given in our previous paper [26].
The DMF+BuOH solutions were prepared by weight using a Sartorius Quintrix 125D-1CEU balance. The readability and repeatability of the mass measurement were, respectively: 1·10−5 g and 4·10−5 g. After the weight was determined, the sample was weighed until the same result appeared three times. The uncertainty of the determined value of the mole fraction of the component in the solution is ± 5·10−5. In order to obtain a solution of a certain composition, suitable components were collected using a syringe. Solvents were degassed in an ultrasonic bath prior to use. Particular attention was paid to high accuracy weighing and thorough cleaning of the measuring cells after each measurement to maintain this level of performance. The data of solution densities and speed of sounds obtained as a function of DMF mole fraction () and temperature (T) are presented in Tables S1 and S2 (Supplementary Material). The mentioned data obtained by us for pure DMF and BuOH are compared with the data from the literature in Table 2.
The measurement of the specific heat capacity, , of DMF+BuOH mixtures as well as of pure solvents was carried out by means of a differential scanning calorimeter Micro DSC III manufactured by Setaram and based on Tian-Calvet’s principle. The detailed description of the measurement procedure has been described by Góralski et al. [78]. We recorded the heat flow during sample heating from 288.15 K to 323.15 K with a scanning rate of 0.35 K·min−1. The so-called continuous with reference method was used, with a known capacity of 1-butanol as a reference substance [79]. The uncertainty of the absolute temperature value in the measuring cell is estimated to be (0.05 K). The temperature of the external cooling system is kept constant (0.02 °K) with a HAAKE type DC30 thermostat. The measuring vessel was the standard ’batch’ type cell with volume ∼ 1.0 cm3. The uncertainty in the values can be estimated to be smaller than 0.5% excluding the effects of sample impurities [79] and with the error of the absolute temperature determination 0.05 K. The accuracy in the present investigation of value for DMF is ±0.8% and for BuOH is ±2.5% [79]. The values of the specific heat capacity as a function of the mole fraction of DMF are presented in Table S3 (Supplementary Material). The calculated molar heat capacity data obtained by us for pure DMF and BuOH are compared with literature data in Table 3.
4. Conclusions
The presented work contains data and conclusions obtained using three different research methods. The results complement each other and allow one to confirm the conclusions drawn regarding changes occurring in the solution under the influence of adding the second component of the mixture and temperature. In addition, the obtained results are enriched with cp data, so far not available in the literature for the DMF + BuOH system along with the change in composition and temperature. Based on density studies, sound velocity, and specific heat capacity of the DMF + BuOH mixture at six temperatures between 293.15 and 318.15 K, the excess functions like were calculated and analyzed in term of changes occurring in the solution structure. The analysis of changes in as a function of the DMF mole fraction showed that characteristic changes in the structure of the system appear in the tested mixture. The observed positive trends in values indicate that the effect due to the breaking up of self-associated structures of the components of the mixtures is dominant over the effect of H-bonding and dipole–dipole interaction between unlike molecules. The conclusions drawn turn out to be different from those drawn in the case of the DMF + PrOH solution. An increase in chain length by one –CH2– group in the alcohol molecule causes expansion of the mixture volume in the BuOH rich region. The obtained results show how a small change in the size of the alcohol molecule can affect the strength of interactions and show opposite to the DMF + PrOH system the tendency of the system to mutual accommodation. Additionally, the analysis of the excess partial molar volume of both components in the mixture confirms the changes in intermolecular interactions of the system, especially in the DMF-rich region. All the conclusions drawn were confirmed in the courses of the remaining excess functions, making the obtained results reliable and consistent. The extrema appearing in the course of the other analysed excess functions confirm the tendency of the system to form probably only weak hydrogen bonds between DMF and BuOH molecules and the fact that its strength changes depending on the DMF content in the mixture. Moreover, the disruption effect dominates in relation to the influence of differentiated intermolecular interactions in the studied system. Furthermore, the thermal analysis of the DMF + BuOH system () provides previously unpublished data that confirm the nature of the interactions that are forming in the mixture. Despite the commonly accepted fact that the interactions in pure DMF are weak and there are no hydrogen bonds, they seem to gain in importance in the studied system, especially when > 0.5.
Author Contributions
Conceptualization, M.T.; formal Analysis: M.T and M.J.; investigation, M.T. and A.D.; methodology, M.T.; visualisation, M.T.; writing—original draft preparation, M.T; Writing – Review & Editing: M.T. and M.J.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are grateful to the University of Lodz for partial financial support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Potvin, J.; Péringer, P. Influence of n-propanol on growth and antibiotic production by an industrial strain of streptomyces erythreus under different nutritional conditions. Biotechnol. Lett. 1993, 15, 455–460. [Google Scholar] [CrossRef]
- Rotter, M.L.; Koller, W.; Neumann, R. The influence of cosmetic additives on the acceptability of alcohol-based hand disinfectants. J. Hosp. Infect. 1991, 18, 57–63. [Google Scholar] [CrossRef] [PubMed]
- Das, R.K.; Roy, M.N. Study on solution–solution interactions prevailing in some liquid mixtures by volumetric, viscometric and acoustic measurements. Phys. Chem. Liq. 2014, 52, 55–77. [Google Scholar] [CrossRef]
- Thirumaran, S.; Alli, T.; Priya, D.; Selvi, A. Ultrasonic studies of molecular interactions in organic binary liquid mixtures, J. Chem. 2010, 7, 217–222. [Google Scholar] [CrossRef]
- Gautan, R. K.; Saharan, A.; Wilson, K.; Kaur, K. P. Properties and uses of butanol. In: Artois, A.M. [red.]. In Properties and uses of butanol; Nova Science Publishers: New York, NY, USA, 2020; pp. 1–26. [Google Scholar]
- Žagar, E.; Žigon, M. Solution properties of carboxylated polyurethanes and related ionomers in polar solvents (DMF and LiBr/DMF). Polymer 2000, 41, 3513–3521. [Google Scholar] [CrossRef]
- Kang, Y.K.; Park, H.S. Internal rotation about the C–N bond of amides. J. Mol. Struc-Theochem 2004, 676, 171–176. [Google Scholar] [CrossRef]
- Howard, P.H. Handbook of environmental fate and exposure data for organic chemicals, Solvents 2. Lewis Publishers Inc.: Chelsea, MI, USA, 1993; Volume 4. [Google Scholar]
- Gescher, A. Metabolism of N,N-dimethylformamide: key to the understanding of its toxicity. Chem. Res. Toxicol. 1993, 6, 245–251. [Google Scholar] [CrossRef]
- Jankowska, A.; Czerczak, S. N,N-dimetyloformamid. Dokumentacja dopuszczalnych wielkości narażenia zawodowego. Podstawy i metody oceny środowiska pracy, 2010, 4, 55–92. [Google Scholar]
- Jödecke, M.; Pérez-Salado Kamps, Á.; Maurer, G. An experimental investigation of the solubility of CO2 in (N,N-dimethylmethanamide + water). J. Chem. Eng. Data 2012, 57, 1249–1266. [Google Scholar] [CrossRef]
- Byun, H.-S.; Kim, N.-H.; Kwak, C. Measurements and modeling of high-pressure phase behavior of binary CO2–amides systems. Fluid Phase Equilib. 2003, 208, 53–68. [Google Scholar] [CrossRef]
- Chang, C.J.; Chen, C.-Y.; Lin, H.-C. Solubilities of carbon dioxide and nitrous oxide in cyclohexanone, toluene, and N,N-dimethylformamide at elevated pressures. J. Chem. Eng. Data 1995, 40, 850–855. [Google Scholar] [CrossRef]
- Rao, K.P.; Reddy, K.S. Excess volumes and excess isentropic compressibility of binary mixtures of N,N-dimethylformamide with n-alcohols at 303.15 K. Phys. Chem. Liq. 1985, 15, 147–154. [Google Scholar] [CrossRef]
- Iloukhani, H.; Rostami, Z. Measurement of some thermodynamic and acoustic properties of binary solutions of N,N-dimethylformamide with 1-alkanols at 30°C and comparison with theories. J. Solut. Chem. 2003, 32, 451–462. [Google Scholar] [CrossRef]
- Dakua, V.K.; Sinha, B.; Roy, M.N. Thermophysical properties of binary mixtures of N,N-dimethylformamide with isomeric butanols at 298.15, 308.15 and 318.15 K. J. Indian Chem. Soc. 2007, 84, 37–45. [Google Scholar] [CrossRef]
- El-Dossoki, F.I. Refractive index and density measurements for selected binary protic-protic, aprotic-aprotic, and aprotic-protic systems at temperatures from 298.15 K to 308.15 K. JCCS 2007, 54, 1129–1137. [Google Scholar] [CrossRef]
- Sagar, S.; Kumari, L.; Gupta, M. Thermoacoustical analysis of binary mixtures of N,N-dimethylformamide (DMF) with BAE and 1-BuOH. J. Pure Appl. Ultrason. 2017, 39, 71–78. [Google Scholar]
- Meza, M.; Lans Ceballos, E.; Cantero-López, P. Densities and volumetric properties of the mixture N,N-dimethylformamide (DMF) + 1-butanol at several temperatures. DYNA 2013, 80, 132–141. [Google Scholar]
- Uddin, H.; Khan, M.Z.H.; Rahman, H.; Shahriar, A.; Md. ; Al Mashud, A. Volumetric and viscometric properties observed for the mixtures of dmf (N,N-dimethylformamide) and other alcohols (butanol and 1-propanol). Phys. Chem. Liq. 2014, 52, 251–261. [Google Scholar] [CrossRef]
- García, B.; Alcalde, R.; Leal, J.M.; Trenzado, J.L. Volumetric behaviour of N-methylformamide–(C1–C10)alkan-1-ol and N,N-dimethylformamide–(C1–C10)alkan-1-ol solvent systems. JPOC 1997, 10, 138–144. [Google Scholar] [CrossRef]
- Zegers, H.C.; Somsen, G. Partial molar volumes and heat capacities in (dimethylformamide + an n-alkanol). J. Chem. Thermodyn. 1984, 16, 225–235. [Google Scholar] [CrossRef]
- Khursan, S.L. Heat capacity estimation using a complete set of homodesmotic reactions for organic compounds. Molecules 2022, 27, 7814. [Google Scholar] [CrossRef] [PubMed]
- Kumari, S.; Chauhan, S.; Singh, K.; Umar, A.; Fouad, H.; Alissawi, M.S.; Akhtar, M.S. Volumetric, Compressibility and viscometric approach to study the interactional behaviour of sodium cholate and sodium deoxycholate in aqueous glycyl glycine. Molecules 2022, 27, 8998. [Google Scholar] [CrossRef] [PubMed]
- Douhéret, G.; Davis, M.I.; Reis, J.C.R.; Blandamer, M.J. Isentropic compressibilities—experimental origin and the quest for their rigorous estimation in thermodynamically ideal liquid mixtures. ChemPhysChem 2001, 2, 148–161. [Google Scholar] [CrossRef] [PubMed]
- Tyczyńska, M.; Jóźwiak, M.; Komudzińska, M.; Majak, T. Effect of temperature and composition on the volumetric, acoustic and thermal properties of N,N-dimethylformamide + propan-1-ol Mixture. J. Mol. Liq. 2019, 290, 111124. [Google Scholar] [CrossRef]
- Kato, M.; Suzuki, N. Excess volumes of binary mixtures containing acetylacetone. J. Chem. Thermodyn. 1978, 10, 435–440. [Google Scholar] [CrossRef]
- Smith, F.B.I. Thermodynamic properties of alcohol + alkane mixtures. I. Theoretical results for the hydrogen bond contribution to the excess energies. Aust. J. Chem. 1973, 26, 691–704. [Google Scholar] [CrossRef]
- Franks, F.; Ives, D.J.G. The structural properties of alcohol–water mixtures. Q. Rev. Chem. Soc. 1966, 20, 1–44. [Google Scholar] [CrossRef]
- Prajapati, A.N. Dielectric study of binary mixtures of 1-butanol with N,N-dimethylformamide. AIP Conf. Proc. 2020, 2220, 040030. [Google Scholar] [CrossRef]
- Chao, J.P.; Wang, Y.X.; Dai, M. Studies of thermodynamic properties of binary mixtures containing an alcohol XVII. excess molar enthalpies of each of (one of the four butanols + N,N-dimethylacetamide or N,N-dimethylformamide or dimethyl sulfoxide) at the temperature 298.15 K. J. Chem. Thermodyn. 1991, 23, 163–168. [Google Scholar] [CrossRef]
- Sivagurunathan, P.; Ramachandran, K.; Dharmalingam, K. Hydrogen bonding between alcohols and N,N-dimethylformamide: An FTIR study. Main Group Chem. 2006, 5, 89–94. [Google Scholar] [CrossRef]
- Komudzińska, M.; Tyczyńska, M.; Jóźwiak, M.; Burakowski, A.; Gliński, J. Volumetric, acoustic and thermal properties of aqueous n,n-dimethylformamide system. effect of temperature and composition. J. Mol. Liq. 2020, 300, 112321. [Google Scholar] [CrossRef]
- Klimaszewski, K.; Stronka-Lewkowska, E.; Soliwoda, K.; Bald, A. Acoustic and volumetric studies on water+diethylene glycol mixtures in a wide temperature range. comparison with mixtures of water with tri- and tetraethylene glycol. J. Mol. Liq. 2016, 215, 520–533. [Google Scholar] [CrossRef]
- Acree, W.E. Excess Isentropic Compressibilities of binary mixtures of N,N-dimethylformamide with n-alcohols at 303.1 5 K. Phys. Chem. Liq. 1986, 16, 113–116. [Google Scholar] [CrossRef]
- Sridevi, U.; Samatha, K.; Sarma, A.V. Excess thermodynamic properties in binary liquids. J. Pure Appl. Ultrason. 2004, 26, 1–11. [Google Scholar]
- Yasmin, M.; Gupta, M.; Shukla, J.P. Acoustical study of molecular interactions in polymer solutions through various thermodynamical parameters and Flory’s theory at 298.15 K. Phys. Chem. Liq. 2010, 48, 682–697. [Google Scholar] [CrossRef]
- Fortin, T.J.; Laesecke, A.; Freund, M.; Outcalt, S. Advanced calibration, adjustment, and operation of a density and sound speed analyzer. J. Chem. Thermodyn. 2013, 57, 276–285. [Google Scholar] [CrossRef]
- Nain, A.K. Densities and volumetric properties of binary mixtures of formamide with 1-butanol, 2-butanol, 1,3-butanediol and 1,4-butanediol at temperatures between 293.15 and 318.15 K. J. Solution Chem. 2007, 36, 497–516. [Google Scholar] [CrossRef]
- Singh, S.; Parveen, S.; Shukla, D.; Gupta, M.; Shukla, J.P. Volumetric, optical, acoustical and viscometric study of molecular association in binary mixtures of butylamine with 1-butanol and tert-butanol. Acta Phys. Pol. A 2007, 111, 847–858. [Google Scholar] [CrossRef]
- Jóźwiak, M.; Tyczyńska, M. Volumetric properties of urea in the mixture of n,n-dimethylformamide with water. J. Chem. Eng. Data 2012, 57, 2067–2075. [Google Scholar] [CrossRef]
- Rodríguez, A.; Canosa, J.; Tojo, J. Density, refractive index, and speed of sound of binary mixtures (diethyl carbonate + alcohols) at several temperatures. J. Chem. Eng. Data 2001, 46, 1506–1515. [Google Scholar] [CrossRef]
- Tyczyńska, M.; Jóźwiak, M. Apparent and partial molar volumes of 18-crown-6 ether in the mixture of N,N-dimethylformamide with water. J. Mol. Liq. 2014, 195, 80–86. [Google Scholar] [CrossRef]
- Calvar, N.; González, E.J.; Domínguez, Á.; Macedo, E.A. Acoustic, volumetric and osmotic properties of binary mixtures containing the ionic liquid 1-butyl-3-methylimidazolium dicyanamide mixed with primary and secondary alcohols. J. Chem. Thermodyn. 2012, 50, 19–29. [Google Scholar] [CrossRef]
- Olivieri, G.V.; da Cunha, C.S.; dos Santos Martins, L.; Paegle, P.A.M.; Nuncio, S.D.; de Araújo Morandim-Giannetti, A.; Torres, R.B. thermodynamic and spectroscopic study of binary mixtures of n-butylammonium oleate ionic liquid + alcohol at T = 288.15–308.15 K. J. Therm. Anal. Calorim. 2018, 131, 2925–2942. [Google Scholar] [CrossRef]
- Tyczyńska, M.; Jóźwiak, M. Partial molar volumes of 15-crown-5 ether in mixtures of n,n-dimethylformamide with water. J. Solution Chem. 2014, 43, 388–403. [Google Scholar] [CrossRef] [PubMed]
- Warmińska, D.; Krakowiak, J.; Grzybkowski, W. Thermodynamic properties of inorganic salts in nonaqueous solvents. iii. apparent molar volumes and compressibilities of divalent transition-metal chlorides in N,N-dimethylformamide. J. Chem. Eng. Data 2007, 52, 2099–2104. [Google Scholar] [CrossRef]
- Płaczek, A.; Koziel, H.; Grzybkowski, W. Apparent molar compressibilities and volumes of some 1,1-electrolytes in N,N-dimethylacetamide and N,N-dimethylformamide. J. Chem. Eng. Data 2007, 52, 699–706. [Google Scholar] [CrossRef]
- Riddick, J. A.; Bunger, W. B. and Sakano, T. K. Organic solvents: Physical properties and methods of purification. Techniques of Chemistry, 1986. [Google Scholar]
- Boruń, A.; Bald, A. Conductometric studies of 1-ethyl-3-methylimidazolium tetrafluoroborate and 1-butyl-3-methylimidazolium tetrafluoroborate in N,N-dimethylformamide at temperatures from (283.15 to 318.15) K. J. Chem. Eng. Data 2012, 57, 475–481. [Google Scholar] [CrossRef]
- Iloukhani, H.; Zarei, H.A. Excess molar enthalpies of N,N-dimethylformamide + alkan-1-ols (C1−C6) at 298.15 K. J. Chem. Eng. Data 2002, 47, 195–197. [Google Scholar] [CrossRef]
- Warmińska, D.; Krakowiak, J.; Grzybkowski, W. Thermodynamic properties of inorganic salts in nonaqueous solvents. I. Apparent molar volumes and compressibilities of divalent transition-metal perchlorates in N,N-dimethylformamide. J. Chem. Eng. Data 2005, 50, 221–225. [Google Scholar] [CrossRef]
- Chabouni, Y.; Amireche, F. Some physicochemical properties of binary mixtures of glycerol with butanol isomers in the temperature range 293.15–318.15 K and ambient pressure. J. Chem. Eng. Data 2020, 65, 1679–1694. [Google Scholar] [CrossRef]
- Singh, S.; Aznar, M.; Deenadayalu, N. Densities, speeds of sound, and refractive indices for binary mixtures of 1-butyl-3-methylimidazolium methyl sulphate ionic liquid with alcohols at T = (298.15, 303.15, 308.15, and 313.15) K. J. Chem. Thermodyn. 2013, 57, 238–247. [Google Scholar] [CrossRef]
- Nain, A.K. Densities, ultrasonic speeds, viscosities and excess properties of binary mixtures of methyl methacrylate with N,N-dimethylformamide and N,N-dimethylacetamide at different temperatures. J. Chem. Thermodyn. 2013, 60, 105–116. [Google Scholar] [CrossRef]
- Papari, M.M.; Ghodrati, H.; Fadaei, F.; Sadeghi, R.; Behrouz, S.; Rad, M.N.S.; Moghadasi, J. Volumetric and ultrasonic study of mixtures of 2-phenylethanol with 1-butanol, 2-butanol, and 2-methyl-1-butanol at T = (298.15–323.15) K and atmospheric pressure: measurement and prediction. J. Mol. Liq. 2013, 180, 121–128. [Google Scholar] [CrossRef]
- AlTuwaim, M.S.; Alkhaldi, K.H.A.E.; Al-Jimaz, A.S.; Mohammad, A.A. Comparative Study of physico-chemical properties of binary mixtures of N,N-dimethylformamide with 1-alkanols at different temperatures. J. Chem. Thermodyn. 2012, 48, 39–47. [Google Scholar] [CrossRef]
- Roy, M.N.; Chanda, R.; Ghosh, G. Molar volumes, viscosity, and isentropic compressibility of some primary monoalkanols in aqueous N,N-dimethylformamide solutions. Russ. J. Phys. Chem. 2009, 83, 1331–1341. [Google Scholar] [CrossRef]
- Sharma, V.K.; Dua, R. Topological and thermodynamic investigations of mixtures containing o-chlorotoluene and lower amides. J. Chem. Thermodyn. 2014, 71, 182–195. [Google Scholar] [CrossRef]
- Segade, L.; Jiménez de Llano, J.; Domínguez-Pérez, M.; Cabeza, Ó.; Cabanas, M.; Jiménez, E. Density, surface tension, and refractive index of octane + 1-alkanol mixtures at T = 298.15 K. J. Chem. Eng. Data 2003, 48, 1251–1255. [Google Scholar] [CrossRef]
- Varfolomeev, M.A.; Zaitseva, K.V.; Rakipov, I.T.; Solomonov, B.N.; Marczak, W. Speed of sound, density, and related thermodynamic excess properties of binary mixtures of butan-2-one with C1–C4 n-alkanols and chloroform. J. Chem. Eng. Data 2014, 59, 4118–4132. [Google Scholar] [CrossRef]
- Papamatthaiakis, D.; Aroni, F.; Havredaki, V. Isentropic compressibilities of (amide+water) mixtures: A comparative study. J. Chem. Thermodyn. 2008, 40, 107–118. [Google Scholar] [CrossRef]
- Alavianmehr, M.M.; Hemmati, N.; Ghodrati, H. Excess molar volumes, excess thermal expansion coefficients and isentropic compressibility deviations for binary mixtures of benzyl alcohol + (1-butanol, 2-butanol, 2-methyl-1-butanol and tert-butanol) at T = (298.15-328.15) K and ambient pressure. Phys. Chem. Liq. 2017, 55, 85–99. [Google Scholar] [CrossRef]
- Ivanov, E.V.; Abrosimov, V.K.; Lebedeva, E.Yu. Apparent molar volumes and expansibilities of H2O and D2O in N,N-dimethylformamide and N,N-dimethylacetamide in the range of T = (278.15 to 318.15)K at p = 0.1MPa: A Comparative Analysis. J. Chem. Thermodyn. 2012, 53, 131–139. [Google Scholar] [CrossRef]
- Neeti; Jangra, S. K.; Yadav, J.S.; Dimple; Sharma, V.K. Thermodynamic investigations of ternary o-toluidine+tetrahydropyran+N,N-dimethylformamide mixture and its binaries at 298.15, 303.15 and 308.15 K. J. Mol. Liq. 2011, 163, 36–45. [Google Scholar] [CrossRef]
- Abidi, R.; Artal, M.; Hichri, M.; Lafuente, C. Experimental and modelled thermophysical behaviour of methyl levulinate (methyl 4-oxopentanoate) and n-alkanol systems. J. Mol. Liq. 2021, 339, 116739. [Google Scholar] [CrossRef]
- Iglesias, M.; Orge, B.; Canosa, J.M.; Rodrı́guez, A.; Domı́nguez, M.; Piñeiro, M.M.; Tojo, J. Thermodynamic behaviour of mixtures containing methyl acetate, methanol, and 1-butanol at 298.15 K: application of the eras model. Fluid Phase Equilib. 1998, 147, 285–300. [Google Scholar] [CrossRef]
- Zhu, L.; Li, H.; Wang, C.; Han, S. Isothermal and isobaric (vapour + liquid) equilibria of (N,N-dimethylformamide + 2-propanol+ 1-butanol). J. Chem. Thermodyn. 2001, 33, 1535–1543. [Google Scholar] [CrossRef]
- Chandra Sekhar, M.; Madhu Mohan, T.; Vijaya Krishna, T. Excess thermodynamic and ft-ir spectroscopic studies on binary liquid mixtures of 2-chloroaniline with isomeric butanols at T = (303.15 to 318.15) K. J. Mol. Liq. 2014, 200, 263–272. [Google Scholar] [CrossRef]
- Palani, R.; Geetha, A. Acoustical and excess thermodynamic studies of molecular interaction in aqueous mixed solvent systems at 303, 308 and 313 K. Phys. Chem. Liq. 2009, 47, 542–552. [Google Scholar] [CrossRef]
- Oswal, S.L.; Desai, H.S. Studies of viscosity and excess molar volume of binary mixtures: 4. 1-alkanol + tri-n-butylamine mixtures at 303.15 and 313.15 K. Fluid Phase Equilib. 2003, 204, 281–294. [Google Scholar] [CrossRef]
- Mehta, S.K.; Ram, G.; Mani, C.; Bhasin, K.K. A Comparative study of thermophysical and spectroscopic properties in mixtures of isomeric butanediol and N,N-dimethylformamide. J. Chem. Thermodyn. 2006, 38, 836–848. [Google Scholar] [CrossRef]
- Nikam, P.S.; Shirsat, L.N.; Hasan, M. Density and viscosity studies of binary mixtures of acetonitrile with methanol, ethanol, propan-1-ol, propan-2-ol, butan-1-ol, 2-methylpropan-1-ol, and 2-methylpropan-2-ol at (298.15, 303.15, 308.15, and 313.15) K. J. Chem. Eng. Data 1998, 43, 732–737. [Google Scholar] [CrossRef]
- Bebek, K.; Strugała-Wilczek, A. Acoustic and thermophysical properties of binary liquid mixtures of primary butanols with hexane and cyclohexane at 293.15 K. Int. J. Thermophys. 2010, 31, 8–15. [Google Scholar] [CrossRef]
- Bernal-García, J.M.; Guzmán-López, A.; Cabrales-Torres, A.; Estrada-Baltazar, A.; Iglesias-Silva, G.A. Densities and viscosities of (N,N-dimethylformamide + water) at atmospheric pressure from (283.15 to 353.15) K. J. Chem. Eng. Data 2008, 53, 1024–1027. [Google Scholar] [CrossRef]
- Gadžurić, S.; Tot, A.; Zec, N.; Papović, S.; Vraneš, M. Volumetric properties of binary mixtures of 1-butyl-1-methylpyrrolidinium tris(pentafluoroethyl)trifluorophosphate with N-methylformamide, N-ethylformamide, N,N-dimethylformamide, N,N-dibutylformamide, and N,N-dimethylacetamide from (293.15 to 323.15) K. J. Chem. Eng. Data 2014, 59, 1225–1231. [Google Scholar] [CrossRef]
- Scharlin, P.; Steinby, K.; Domańska, U. Volumetric properties of binary mixtures of N,N- dimethylformamide with water or water- d2 at temperatures from 277.13 K to 318.15 K. J. Chem. Thermodyn. 2002, 34, 927–957. [Google Scholar] [CrossRef]
- Góralski, P.; Tkaczyk, M.; Chora̧żewski, M. Heat capacities of α,ω-dichloroalkanes at temperatures from 284.15 K to 353.15 K and a group additivity analysis. J. Chem. Eng. Data 2003, 48, 492–496. [Google Scholar] [CrossRef]
- Zábranský, M.; Růžička, V., Jr.; Domalski, E.S. Heat capacity of liquids: critical review and recommended values. supplement I. J. Phys. Chem. Ref. Data 2001, 30, 1199–1689. [Google Scholar] [CrossRef]
- Zorębski, E.; Góralski, P. Molar heat capacities for (1-butanol+1,4-butanediol, 2,3-butanediol, 1,2-butanediol, and 2-methyl-2,4-pentanediol) as function of temperature. J. Chem. Thermodyn. 2007, 39, 1601–1607. [Google Scholar] [CrossRef]
- Smirnova, N.N.; Tsvetkova, L.Ya.; Bykova, T.A.; Marcus, Y. Thermodynamic properties of N,N-dimethylformamide and N,N-dimethylacetamide. J. Chem. Thermodyn. 2007, 39, 1508–1513. [Google Scholar] [CrossRef]
- Checoni, R.F.; Volpe, P.L.O. Measurements of the molar heat capacities and excess molar heat capacities for water + organic solvents mixtures at 288.15 K to 303.15 K and atmospheric pressure. J. Solution Chem. 2010, 39, 259–276. [Google Scholar] [CrossRef]
- Shokouhi, M.; Jalili, A.H.; Hosseini-Jenab, M.; Vahidi, M. Thermo-physical properties of aqueous solutions of N,N-dimethylformamide. J. Mol. Liq. 2013, 186, 142–146. [Google Scholar] [CrossRef]
Figure 1.
Excess molar volume () of DMF + BuOH mixture: ■ T = 293.15 K, ● T = 298.15 K, ▲ T = 303.15 K, ▼ T = 308.15 K, ◆ T = 313.15 K, ◀ T = 318.15 K. Solid lines are obtained using Redlich-Kister Equation (4).
Figure 1.
Excess molar volume () of DMF + BuOH mixture: ■ T = 293.15 K, ● T = 298.15 K, ▲ T = 303.15 K, ▼ T = 308.15 K, ◆ T = 313.15 K, ◀ T = 318.15 K. Solid lines are obtained using Redlich-Kister Equation (4).
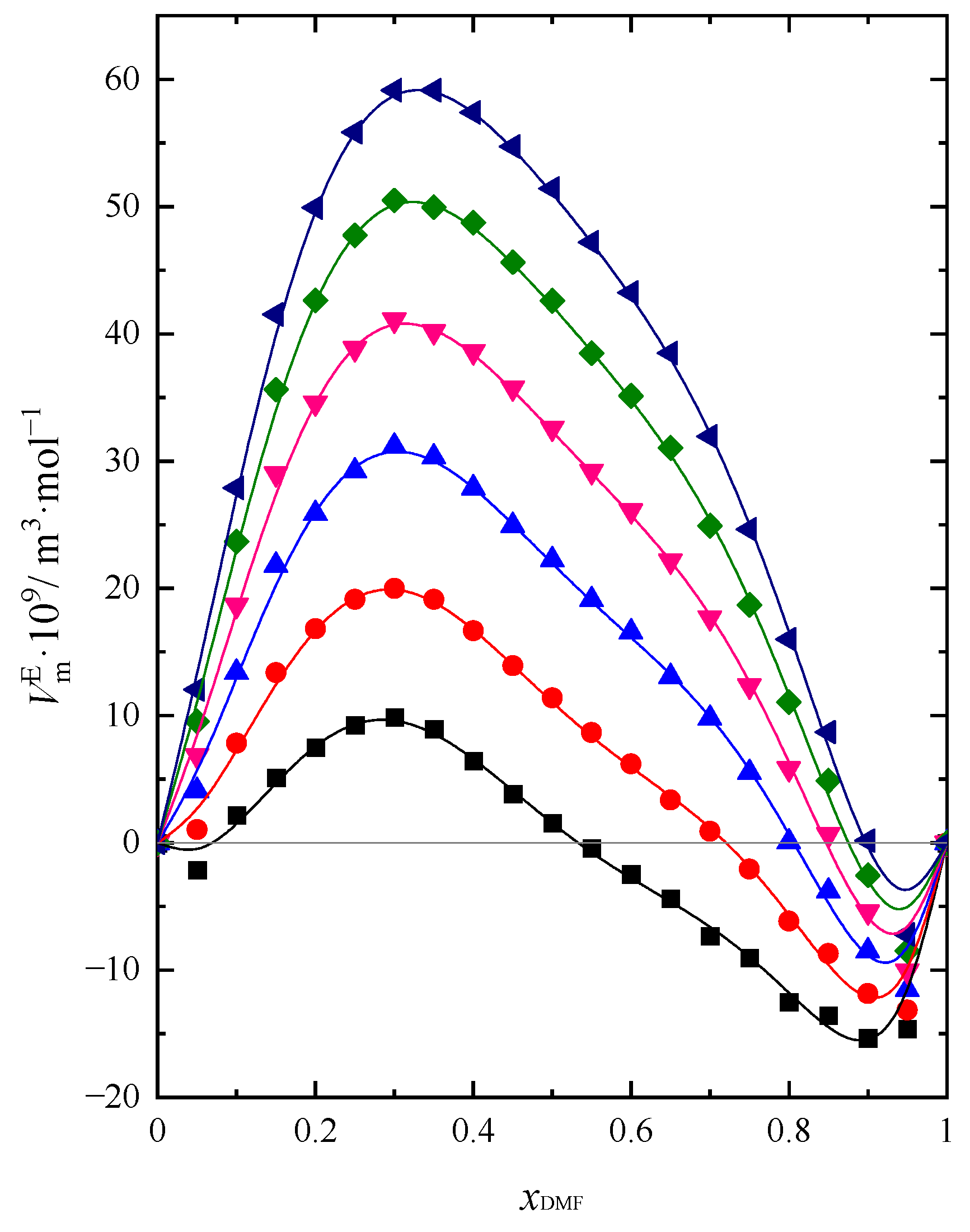
Figure 2.
Excess partial molar volume (, ) of: ● DMF, ■ BuOH in the DMF + BuOH mixture at T = 293.15 K.
Figure 2.
Excess partial molar volume (, ) of: ● DMF, ■ BuOH in the DMF + BuOH mixture at T = 293.15 K.
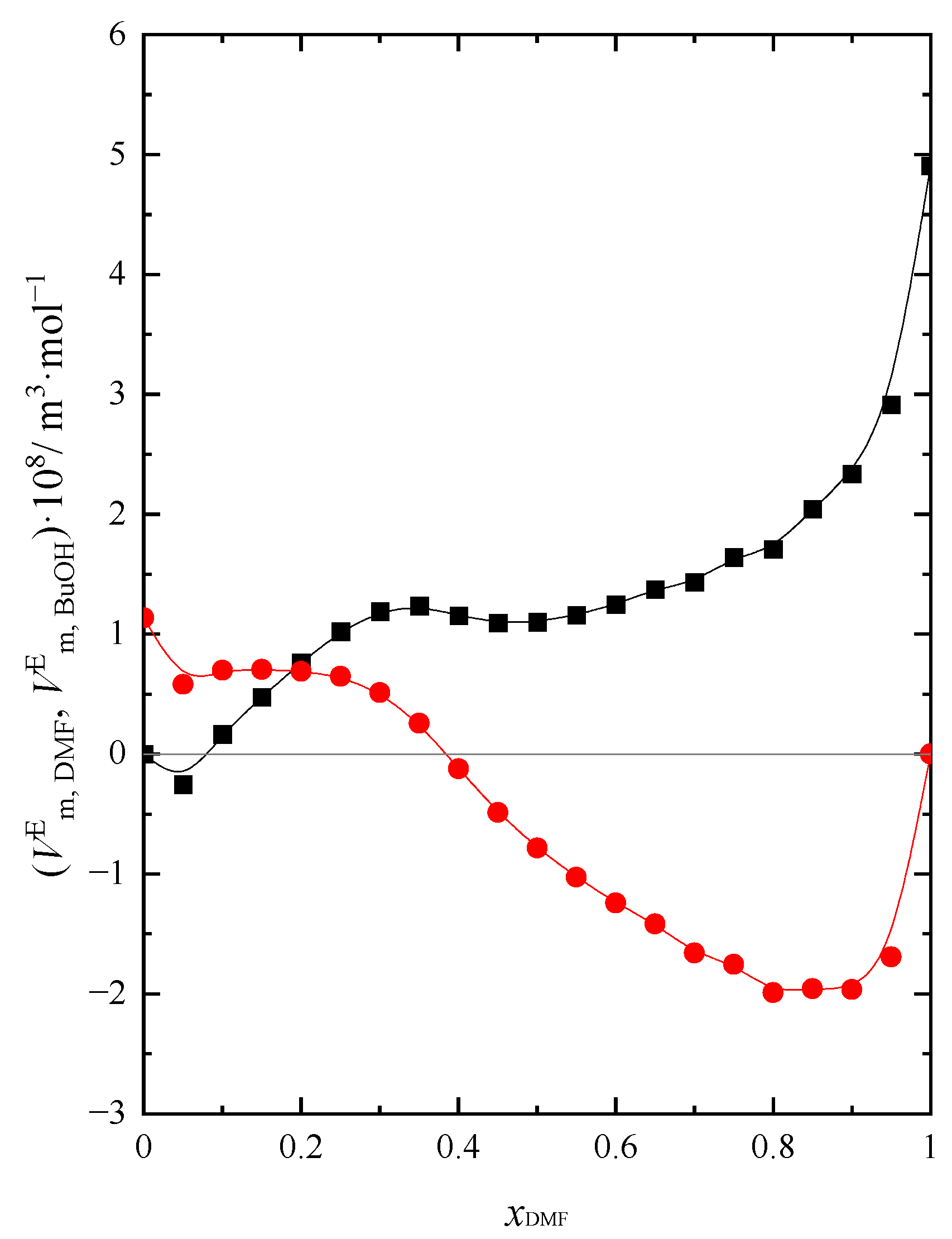
Figure 3.
Isobaric molar expansion () of DMF + BuOH mixture: ■ T = 293.15 K, ● T = 298.15 K, ▲ T = 303.15 K, ▼ T = 308.15 K, ◆ T = 313.15 K, ◀ T = 318.15 K.
Figure 3.
Isobaric molar expansion () of DMF + BuOH mixture: ■ T = 293.15 K, ● T = 298.15 K, ▲ T = 303.15 K, ▼ T = 308.15 K, ◆ T = 313.15 K, ◀ T = 318.15 K.

Figure 4.
Excess molar isobaric expansion () of (DMF+BuOH) mixture: ■ T = 293.15 K, ● T = 298.15 K, ▲ T = 303.15 K, ▼ T = 308.15 K, ◆ T = 313.15 K, ◀ T = 318.15 K. Solid lines are obtained using Redlich-Kister Equation (4).
Figure 4.
Excess molar isobaric expansion () of (DMF+BuOH) mixture: ■ T = 293.15 K, ● T = 298.15 K, ▲ T = 303.15 K, ▼ T = 308.15 K, ◆ T = 313.15 K, ◀ T = 318.15 K. Solid lines are obtained using Redlich-Kister Equation (4).
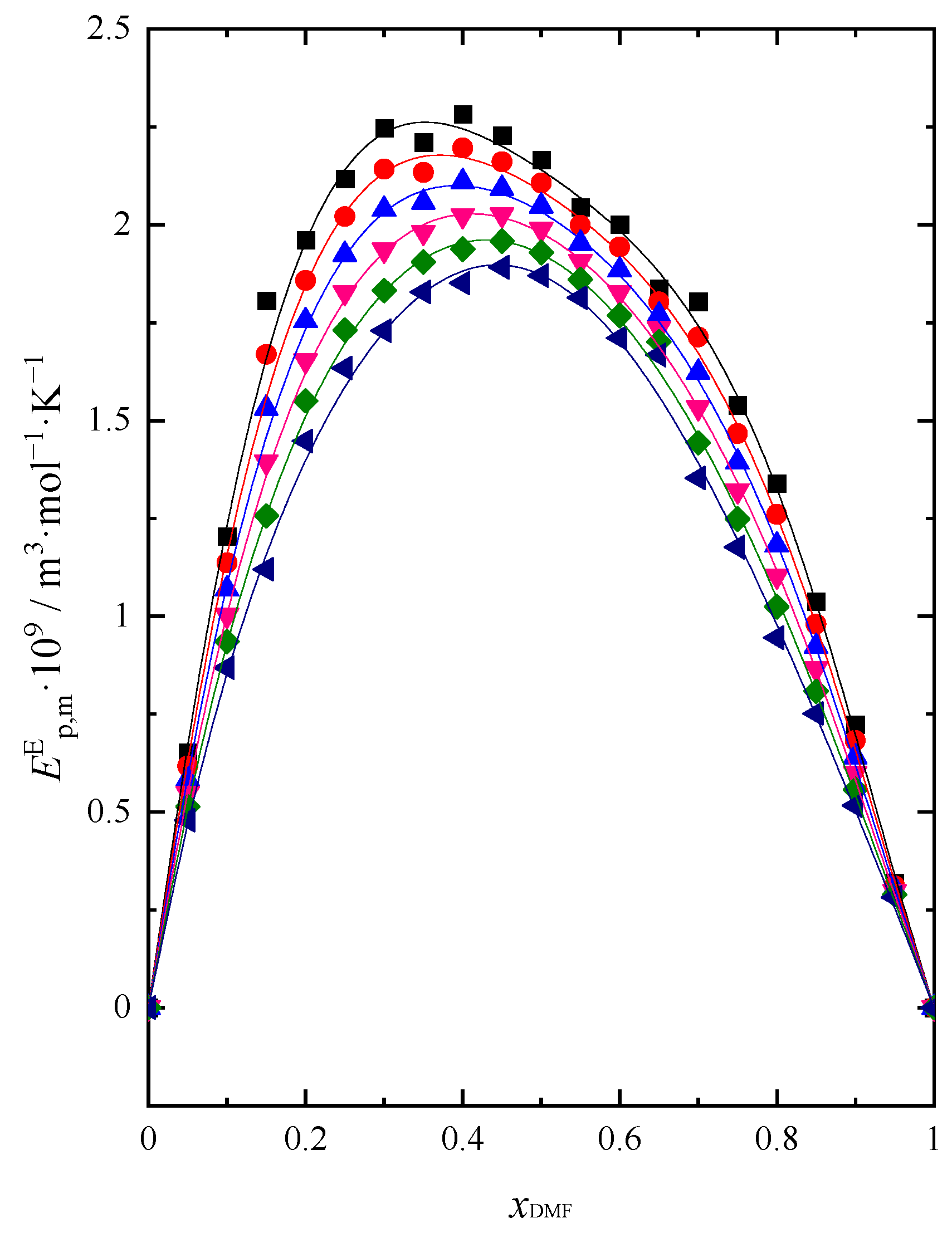
Figure 5.
Excess molar isentropic ( (full symbol) and isothermal (open symbol) compression of DMF+BuOH mixture at temperature: ■ T = 293.15 K, ● T = 298.15 K, ▲ T = 303.15 K, ▼ T = 308.15 K, ◆ T = 313.15 K, ◀ T = 318.15 K. Solid lines are obtained using Redlich-Kister Equation (4).
Figure 5.
Excess molar isentropic ( (full symbol) and isothermal (open symbol) compression of DMF+BuOH mixture at temperature: ■ T = 293.15 K, ● T = 298.15 K, ▲ T = 303.15 K, ▼ T = 308.15 K, ◆ T = 313.15 K, ◀ T = 318.15 K. Solid lines are obtained using Redlich-Kister Equation (4).
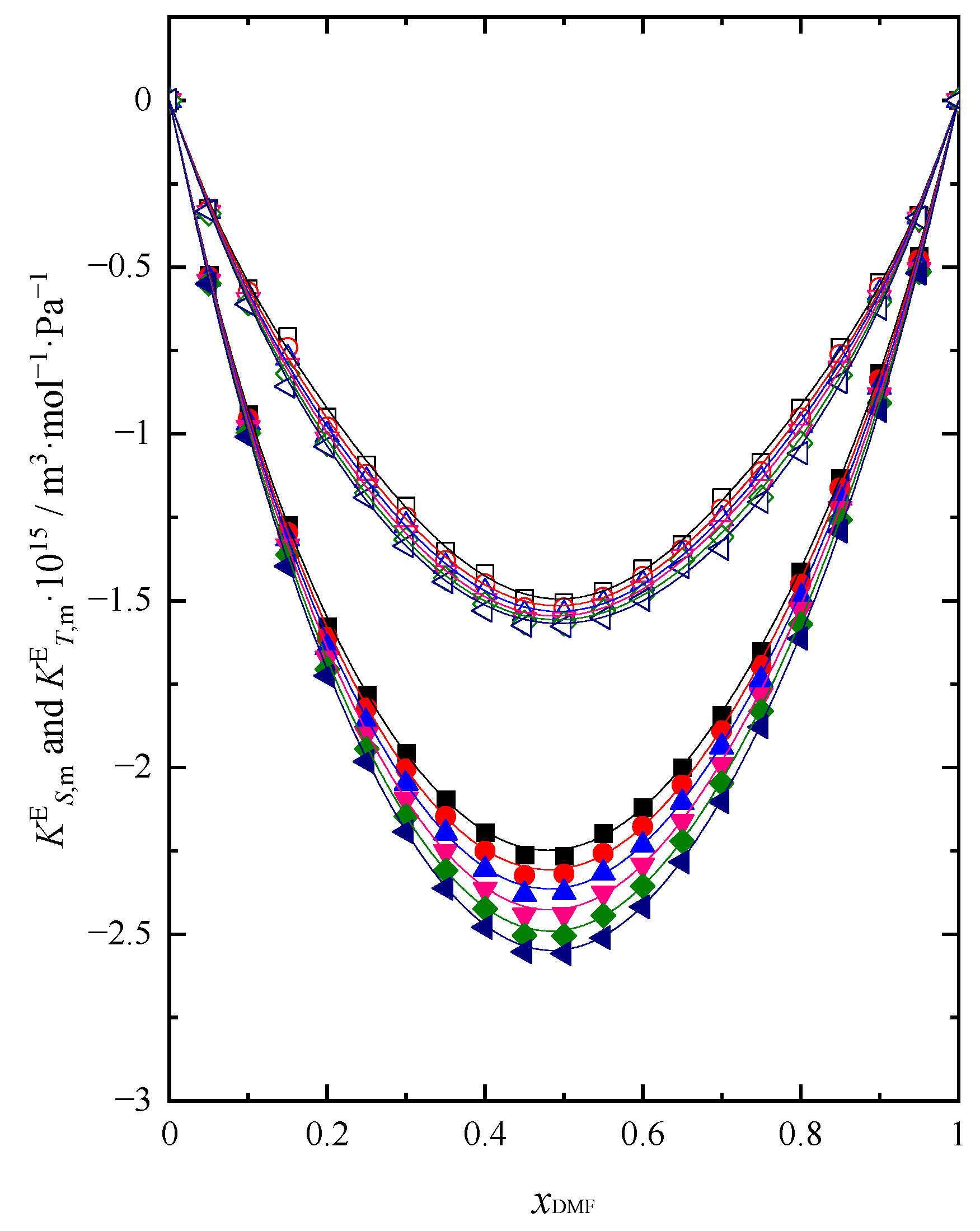
Figure 6.
Isobaric molar heat capacity () of (DMF+BuOH) mixture: ■ T = 293.15 K, ● T = 298.15 K, ▲ T = 303.15 K, ▼ T = 308.15 K, ◆ T = 313.15 K, ◀ T = 318.15 K.
Figure 6.
Isobaric molar heat capacity () of (DMF+BuOH) mixture: ■ T = 293.15 K, ● T = 298.15 K, ▲ T = 303.15 K, ▼ T = 308.15 K, ◆ T = 313.15 K, ◀ T = 318.15 K.

Figure 7.
Excess molar heat capacity () of (DMF+BuOH) mixture: ■ T = 293.15 K, ● T = 298.15 K, ▲ T = 303.15 K, ▼ T = 308.15 K, ◆ T = 313.15 K, ◀ T = 318.15 K. Solid lines are obtained using Redlich-Kister Equation (4).
Figure 7.
Excess molar heat capacity () of (DMF+BuOH) mixture: ■ T = 293.15 K, ● T = 298.15 K, ▲ T = 303.15 K, ▼ T = 308.15 K, ◆ T = 313.15 K, ◀ T = 318.15 K. Solid lines are obtained using Redlich-Kister Equation (4).
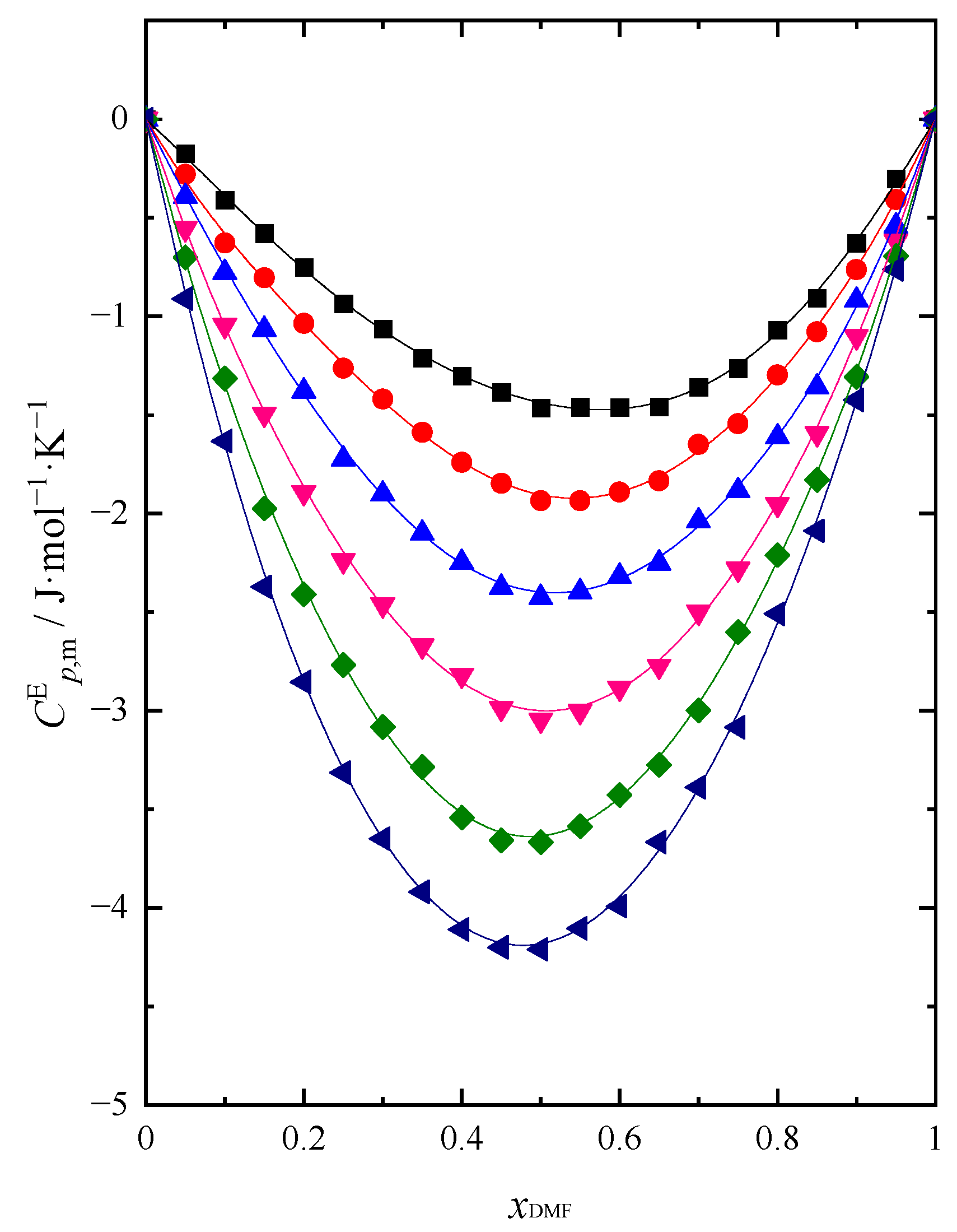
Figure 8.
Excess molar isobaric ) ● and isochoric ) ■ heat capacity of DMF + BuOH mixture at 298.15 K. Solid lines are obtained using Redlich-Kister Equation (4).
Figure 8.
Excess molar isobaric ) ● and isochoric ) ■ heat capacity of DMF + BuOH mixture at 298.15 K. Solid lines are obtained using Redlich-Kister Equation (4).
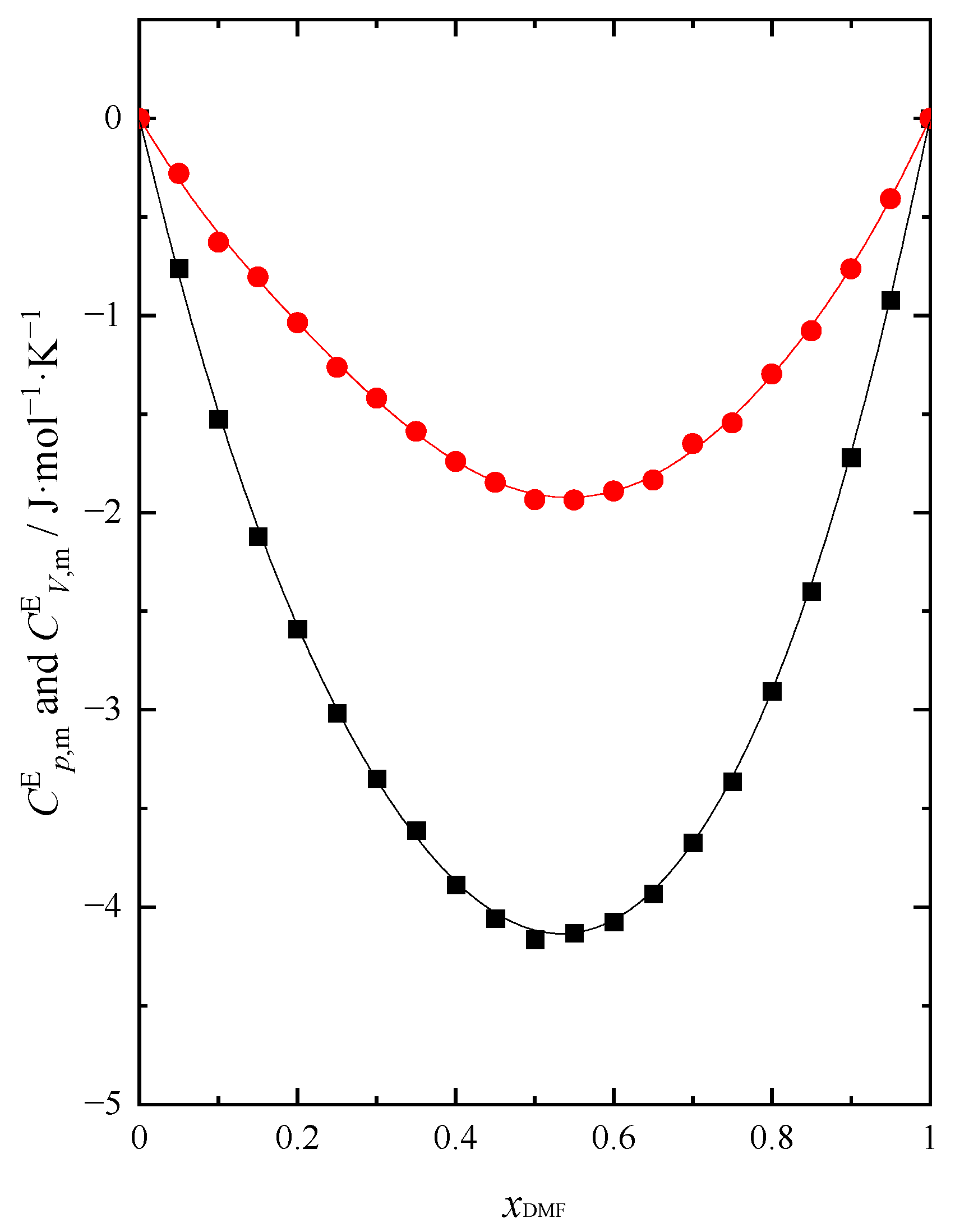
Table 1.
Materials.
| Name of Compound | Source | Purity a | Purification Method | Mass Fraction of Water b |
|---|---|---|---|---|
| 1-butanol (BuOH) | Sigma-Aldrich (Poznan-Poland) |
>0.998 | 3·10−3 | |
|
N,N-dimethylformamide (DMF) |
Sigma-Aldrich (Poznan-Poland) |
0.998 | Distillation under reduced pressure | 2·10−4 |
a Declared by the supplier. b Determined by the Karl Fischer method.
Table 2.
Densities (ρ) and sound velocities (u) of BuOH and DMF at pressure p = 0.1002 ± 0.005 MPa.a.
Table 2.
Densities (ρ) and sound velocities (u) of BuOH and DMF at pressure p = 0.1002 ± 0.005 MPa.a.
| BuOH | DMF | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| T/K | ρ (kg·m−3) | u (m·s−1) | ρ (kg·m−3) | u (m·s−1) | |||||||
| Exp. | Lit. | Exp. | Lit. | Exp. | Lit. | Exp. | Lit. | ||||
| 293.15 | 809.55 | 809.17 [39] | 1256.4 | 1256 [40] | 948.69 | 948.742 [41] | 1477.0 | 1499 [18] | |||
| 809.5 [42] | 1256 [42] | 948.747 [43] | |||||||||
| 809.53 [44] | 1256.55 [45] | 948.737 [46] | |||||||||
| 809.54 [19] | 1256.57 [44] | 948.611 [47] | |||||||||
| 809.664 [45] | 1260.4 [18] | 948.546 [48] | |||||||||
| 809.7 [49] | 948.584 [50] | ||||||||||
| 809.78 [15] | 948.67 [19] | ||||||||||
| 809.79 [51] | 948.73 [49] | ||||||||||
| 809.8 [40] | 948.653 [52] | ||||||||||
| 809.94 [53] | |||||||||||
| 298.15 | 805.74 | 805.54 [39] | 1239.5 | 1239.28 [54] | 943.92 | 943.976 [41] | 1457.4 | 1469.5 [55] | |||
| 805.6 [16] | 1240.09 [56] | 943.981 [43] | 1457.69 [57] | ||||||||
| 805.73 [19] | 1240.2 [58] | 943.971 [46] | 1458.5 [59] | ||||||||
| 805.76 [60] | 1240.37 [61] | 944.290 [57] | 1457.49 [62] | ||||||||
| 805.806 [63] | 1240.52 [45] | 943.869 [64] | 1458 [65] | ||||||||
| 805.81 [61] | 1240.55 [66] | 943.817 [50] | 1457.13 [48] | ||||||||
| 805.851 [45] | 1241 [42] | 944.603 [65] | 1478 [18] | ||||||||
| 805.89 [67] | 1241.6 [18] | 943.90 [19] | 1465.2 [58] | ||||||||
| 805.94 [68] | 943.97 [49] | ||||||||||
| 806 [49] | 944.09 [68] | ||||||||||
| 806.06 [66] | |||||||||||
| 303.15 | 801.90 | 801.90 [39] | 1222.7 | 1222.5 [69] | 939.14 | 939.201 [41] | 1438.0 | 1438.23 [57] | |||
| 801.90 [19] | 1223 [40] | 939.206 [43] | 1440.2 [59] | ||||||||
| 801.92 [69] | 1223.69 [45] | 939.196 [46] | 1476.2 [70] | ||||||||
| 801.94 [71] | 1224 [42] | 939.047 [57] | 1458.8 [18] | ||||||||
| 801.970 [63] | 1229.2 [18] | 939.073 [47] | |||||||||
| 802.009 [45] | 939.042 [50] | ||||||||||
| 802.04 [15] | 939.13 [19] | ||||||||||
| 802.28 [53] | 939.8 [71] | ||||||||||
| 802.31 [14] | |||||||||||
| 308.15 | 798.03 | 789.03 [19] | 1206.0 | 1206.5 [44] | 934.36 | 934.425 [41] | 1418.6 | 1421.95 [57] | |||
| 789.25 [39] | 1206.5 [69] | 934.430 [43] | 1420.8 [59] | ||||||||
| 798 [58] | 1206.95 [45] | 934.420 [46] | 1426.03 [72] | ||||||||
| 798.06 [44] | 1215.6 [18] | 934.721 [57] | 1464.6 [70] | ||||||||
| 798.101 [63] | 934.298 [64] | 1432.4 [18] | |||||||||
| 798.133 [45] | 934.255 [50] | ||||||||||
| 798.21 [73] | 934.34 [19] | ||||||||||
| 798.25 [39] | 941.2 [49] | ||||||||||
| 798.41 [53] | |||||||||||
| 313.15 | 794.13 | 794.12 [19] | 1189.4 | 1190.48 [66] | 929.56 | 929.478 [57] | 1399.4 | 1395.69 [57] | |||
| 794.195 [63] | 1193 [74] | 929.458 [50] | 1408.8 [18] | ||||||||
| 794.42 [66] | 1196.0 [18] | 929.55 [19] | |||||||||
| 794.49 [53] | |||||||||||
| 794.60 [39] | |||||||||||
| 318.15 | 790.18 | 790.248 [53] | 1173.2 | - | 924.76 | 924.683 [64] | 1380.4 | 1453.5 [70] | |||
| 790.5 [58] | 925.49 [75] | ||||||||||
| 790.53 [63] | 924.04 [76] | ||||||||||
| 790.97 [39] | 924.6 [77] | ||||||||||
a Standard uncertainties u are u(T) = 0.01 K, u(p) = 0.005 MPa, and the combined expanded uncertainty Uc are Uc(u) = 0.5 m·s−1 and Uc(ρ) = 2·10−2 kg·m−3 with 0.95 level of confidence (k ≈ 2).3.2.2. Heat capacity.
Table 3.
Isobaric molar heat capacities ( ) for BuOH and DMF at pressure p = 0.1001 ± 0.005 MPa.
|
T/K |
|||||
|---|---|---|---|---|---|
| BuOH | DMF | ||||
| This paper | Literature | This Paper | Literature | ||
| 293.15 | 176.3 | 173.80 [80] 176.8 [79]b 177.6 [79]a |
148.3 | 147.16 [63] 147.3 [61]a 147.5 [61]b |
|
| 298.15 | 179.3 | 177.10 [80] 180.9 [79]b 181.4 [79]a |
148.9 | 148.0 [79]b 148.1 [79]a 148.16 [81] 148.2 [81] 148.54 [59] 150.16 [82] |
|
| 303.15 | 182.7 | 180.61 [80] 185.2 [79]a 185.3 [79]b |
149.5 | 148.5 [79]b 148.9 [79]a 150.41 [59] 151.3 [83] 153.32 [82] |
|
| 308.15 | 186.3 | 184.28 [80] 189.2 [79]a 189.8 [79]b |
150.2 | 149.1 [79]b 149.8 [79]a 152.65 [59] |
|
| 313.15 | 190.1 | 188.02 [80] 193.2 [79]a 194.4 [79]b |
150.9 | 149.7 [79]b 150.7 [79]a 152.9 [83] |
|
| 318.15 | 193.9 | 192.10 [80] 197.3 [79]a 199.1 [79]b |
151.6 | 150.4 [79]b 151.5 [79]a |
|
a data calculated from recommended values of parameters of quasi-polynomial equation:
where: R – gas constant, , – critical temperature. b data calculated from recommended values of parameters of cubic spline polynomials or parameters of regression polynomials: .
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






