Preprint
Article
NMR Magnetic Shielding in Transition Metal Compounds Containing Cadmium, Platinum, and Mercury
Altmetrics
Downloads
153
Views
56
Comments
0
A peer-reviewed article of this preprint also exists.
supplementary.pdf (209.78KB )
Submitted:
25 May 2023
Posted:
26 May 2023
You are already at the latest version
Alerts
Abstract
In this article, we delve into the intricate behavior of electronic mechanisms underlying
NMR magnetic shieldings, σ, in molecules containing heavy atoms such as cadmium, platinum,
and mercury. Specifically, we explore PtXn^{−2} (X = F, Cl, Br, I; n = 4, 6) and XCl2 Te2 Y2 H6 (X = Cd,
Hg; Y = N, P) molecular systems. It is known that the leading electronic mechanisms responsible
for the relativistic effects on σ are well characterized by the linear response with elimination of
small components model (LRESC). In this study, we present results obtained from the innovative
LRESC-Loc model, which offers the same outcomes as the LRESC model but employs localized
molecular orbitals (LMOs) instead of canonical MOs. These LMOs provide a chemist’s representation
of atomic core, lone pairs, and bonds. The whole set of electronic mechanisms responsible of the
relativistic effects can be expressed in terms of both non-ligand-dependent and ligand-dependent
contributions. We elucidate the electronic origins of trends and behaviors exhibited by these di-
verse mechanisms in the aforementioned molecular systems. In PtX4^{−2} molecules, the predominant
relativistic mechanism is the well-established one-body spin-orbit (σ^SO(1) ) mechanism, while the
paramagnetic mass-velocity (σ^Mv ) and Darwin (σ^Dw ) contributing mechanisms also demand con-
sideration. However, in PtX6−2 molecules, the σ Mv+ Dw contribution surpasses that of the SO(1)
mechanism, thus influencing the overall ligand-dependent contributions. As for complexes con-
taining Cd and Hg, the ligand-dependent contributions exhibit similar magnitudes when nitrogen
is substituted with phosphorus. The only discrepancy arises from the σ^SO(1) contribution, which
changes sign between the two molecules due to the contribution of bond orbitals between the metal
and tellurium atoms.
Keywords:
Subject: Chemistry and Materials Science - Theoretical Chemistry
1. Introduction
Transition metal chemistry represents a field of study characterized by a rich historical background and ongoing advancements. A profound comprehension of organometallic complex properties and the underlying reaction mechanisms has paved the way for the development of practical methodologies widely employed in synthetic chemistry. Moreover, transition metals find utility as Lewis acids, heterogeneous catalysts, and polymerization catalysts, among other roles [1].
While the application of methods of the density functional theory (DFT) to calculate the spectroscopic parameters of the nuclear magnetic resonance (NMR) of transition metals has been previously reviewed [2,3], discussions pertaining to those calculations on heavier transition metal complexes are found within reviews that focus specifically on relativistic methodologies. This emphasis stems from the significant influence of relativistic effects on the spectroscopic parameters associated with such complexes [4,5,6,7].
In this work we wanted to explore the NMR spectroscopic parameters of some particular transition metal containing compounds. They contain Cd, Hg and Pt. In a seminal work, Gilbert and Ziegler achieved a remarkable accuracy in predicting 195Pt chemical shifts for a series of Pt(II) complexes by meticulously unraveling the contributing parameters responsible for the shielding of platinum nuclei [8]. Their study underscored the dominant influence of paramagnetic and spin-orbit contributions on the overall shielding. Building upon this results, numerous theoretical and experimental investigations have explored the chemical shifts of platinum halides in square-planar (D4h) and octahedral (Oh) complexes [8,9,10,11,12,13], with some studies employing localized molecular orbitals (LMOs) as an analytical framework [14,15]. Concerning the other two transition metals, i.e Cd and Hg, we want to point out to a computational NMR study conducted on recently synthesized complexes encompassing cadmium, mercury, tellurium, selenium, and phosphorus [16]. These complexes, known as MRE complexes, were identified as promising qubit molecules for NMR quantum information processing (QIP). Employing spin-orbit zeroth-order regular approximation (ZORA) and four-component (4C) relativistic methods, the researchers presented a comprehensive computational design strategy for screening molecules suitable for diverse and heteronuclear qubits in NMR-QIP implementations. Their investigation encompassed the influence of different conformers, basis sets, functionals, as well as methods to account for relativistic and solvent effects.
It is known that the nuclear magnetic shielding of the NMR spectroscopy, denoted as , is a highly sensitive quantity influenced by the electronic environment. Consequently, it serves as a valuable descriptor of the electronic behavior in the vicinity of the nucleus under investigation, offering insights into the nature of the involved bonding interactions [17]. When heavy atoms (HAs) are present in a molecule, they introduce relativistic effects that impact on the neighboring atoms though also on themselves. There are three well established types of relativistic effects described in the literature: i) the heavy-atom on light-atom (HALA) effect [18], the heavy-atom effect on the heavy-atom itself [19] and the heavy-atom effect on vicinal-heavy-atom (HAVHA) effect [20,21]. The HALA effect is the most studied being the basic rule of propagation of the SO effect on a molecule given more than twenty years ago [22]. It can show some characteristics of the HA-LA bond and the structure of the heavy-atom [7]. The HAHA effect is less studied due to its inclusion gives more accurate absolute values of but it does not contribute much to the chemical shift. On the other hand, the HAVHA effect is currently being more studied due to its description requires considering other mechanisms different from the SO one. Then the characteristics of the bonds between two heavy atoms are better described through including some more ligand-dependent mechanisms.
Several years ago, Autschbach introduced the London orbitals and the interface with natural bond orbitals (NBO) in the calculation of the shielding tensor that include scalar relativistic corrections [15]. In a similar vein, Marek and colleagues investigated various systems encompassing different heavy atoms across the Periodic Table, studying trends in the HALA effect. They called it SO-HALA to emphasize that HALA effects mainly arises from spin-orbit couplings. Their studies involved the inclusion of those corrections through third-order perturbation theory, revealing the increase of the HALA effect when lone pair electrons are involved [7,17,23].
Another model that has been developed over the past two decades with the objective of accurately reproduce and analyze the electronic origins of NMR spectroscopic parameters is the linear response with elimination of small component model (LRESC) [24,25,26]. This model enables a comprehensive understanding of the electronic mechanisms responsible for relativistic effects. To this end, the LRESC-Loc model is an scheme that has been recently introduced [27] to facilitate the analysis of various types of localization procedures (such as Pypek-Mezey [28] or natural bond orbitals (NBO)) [29] for getting localized molecular orbitals (LMOs) and providing a chemical representation of atomic core, lone pairs, and chemical bonds in elucidating well-known relativistic effects.
In this work, we delve into the nuclear magnetic shielding properties of cadmium, platinum, and mercury nuclei within Pt (X = F, Cl, Br, I; n = 4, 6) and Cl2XTe2H6 (X= Cd, Hg; Y= P, N) molecular systems, employing both the LRESC-Loc and the four-component (4C) relativistic methods. The primary purpose of this study is related with the understanding the origin and behavior of relativistic corrections expressed in terms of LMOs. Specifically, we investigate the influence of the chemical environment on the shielding of the transition metals under investigation through the mechanisms known as ligand-dependent and considering both, the HAHA and the HAVHA effects. We shall show how important are the electronic mechanisms involved and how much each LMO do contribute to such mechanisms. It will be shown that the SO is not the main mechanism contributing to the shielding of some of the transition metals analyzed. This is one of the results that appears when the HAVHA effects are considered.
2. Theoretical Framework
The LRESC model is a robust methodology rooted in second-order Rayleigh-Schrödinger Perturbation Theory (RSPT), which enables the transformation of four-component (4C) wave functions to two-component (2C) wave functions for describing magnetic and electric properties [24,26,30]. Within the LRESC model, the final expressions encompasses several electronic mechanisms incorporating relativistic corrections at different levels of the selected parameter (1/c) (being c the speed of light in vacuum).
Specifically, in the studies of NMR nuclear magnetic shieldings, the LRESC approach facilitates the calculation of relativistic corrections for both paramagnetic and diamagnetic nonrelativistic components. This is accomplished through a rewriting of the 4C expression while adhering to the kinetic balance condition, Pauli normalization, and incorporating relativistic corrections into the Pauli wave function. For further in-depth information, additional references can be consulted [24,25,26].
The paramagnetic component of the nuclear magnetic shielding involves several relativistic corrections which are expressed up to the order as follows:
In these expressions, and represent the paramagnetic spin-orbit and orbital-Zeeman integrals, respectively. The kinetic energy corrections for paramagnetic spin-orbit () and orbital-Zeeman () terms are also considered. The Fermi contact and the spin-dipolar operators are denoted as , while the spin-Zeeman kinetic energy correction and the magnetic field-induced spin-orbit term are represented by and , respectively. The one-body relativistic effect of spin-orbit coupling is captured by , while the scalar relativistic corrections Darwin and Mass-velocity are represented by . Detailed expressions for these Hamiltonians can be found in the supplementary information.
The relativistic corrections to the diamagnetic component of the shieldings include: i) the linear response between the NR diamagnetic-like Hamiltonian of Equation (S11) and the Mv and Dw correcting Hamiltonians and ii) the average value of given in Equation (S12). The Hamiltonian contains several terms: the average value of the Fermi contact plus spin-dipolar contributions induced by the external magnetic field, the orbital-Zeeman corrections to the paramagnetic spin-orbit term, the kinetic correction to the diamagnetic NR shielding contribution and a multiple of the Dirac delta function centered on the given [26].
Furthermore, the relativistic corrections to the shielding can be divided into two groups: ligand-dependent corrections, which depend on the chemical environment, and non-ligand-dependent (NL-dependent) corrections, which are primarily influenced by the core MOs. The ligand-dependent corrections take into account the specific interactions with surrounding ligands and their effects on the shielding. On the other hand, the NL-dependent corrections are mainly governed by the behavior of the core MOs and their contributions to the shielding. These two categories collectively contribute to the overall relativistic corrections to the nuclear magnetic shieldings.
The ligand-dependent contribution encompasses , , , and . On the other hand, the NL-dependent contribution encompasses all diamagnetic corrections and the remaining paramagnetic corrections. The clear separation of these contributions is illustrated in Table 1.
3. Materials and Methods
The molecular systems investigated in this study include Pt (X = F, Cl, Br, I; n = 4, 6) and XCl2Te2Y2H6 (X = Cd, Hg; Y = N, P).
For the , , , and geometries, geometry optimization was performed using the Dirac program package [31] with the Dirac-Hartree-Fock (DHF) Hamiltonian and the dyall.cv3z basis set [32]. The remaining geometries of the platinum-containing systems were adopted from Refs. [13,33]. In the case of Cl2XTe2Y2H6, the geometries were obtained using an analytic gradient at the same level of theory.
The calculations with the new model LRESC-Loc were carried out at the Hartree-Fock (HF) level using the dyall.cv3z basis set for all atoms. These calculations were performed with the Dalton program [34]. The 4c shielding calculations were obtained using the relativistic polarization propagator [35] within the Random Phase Approximation (4c-RPA). The dyall.cv3z basis set was employed, and the unrestricted kinetic balance prescription was applied [20]. The gauge origin was positioned at the position of the heavy atom, but for the analysis of HAVHA effects the gauge origin was placed on tellurium atom. The localization of the wave function was performed using the Pypek-Mezey methodology [28] implemented in the PySCF code [36]. The LRESC response calculations and the calculation of average values with canonical coefficients were performed using the Dalton program package. Additionally, a code developed in our group was used for the response and average value calculations with localized molecular orbitals, as described in Ref. [27].
For the chemical shift calculations of the systems, the molecule was selected as the reference. This choice was motivated by the fact that has been widely used as a reference in numerous theoretical and experimental studies [12,13]. By using as the reference, we can establish a consistent framework for comparison and the interpretation of the chemical shifts of other molecules in relation to this well-established reference system.
4. Results and Discussion
The whole set of molecules studied in this work is depicted in Figure 1, and specific geometric parameters can be found in the Supplementary Information.
Additionally, Table 2 provides the optimized bond lengths for Pt-F and Pt-Cl, whereas the Pt-Br and Pt-I distances were obtained from the literature.
The orbitals associated with lone pair MOs are indicated as and . The inner electrons of an atom are labeled as core(X), while the bonds are represented as X–Y, where X and Y are the respective atoms involved.
4.1. Platinum complexes
In Table 3, we present results of calculations of the isotropic nuclear magnetic shielding of the Pt atom, (Pt), obtained using the LRESC and 4C-RPA methods. Both the paramagnetic and diamagnetic components are shown for comparison between the two calculation schemes. Additionally, we include the chemical shifts, (Pt), with respect to the molecule, which serves as a reference for both theoretical and experimental results.
From Table 3, it can be observed that the LRESC values are not in close agreement with the 4C-RPA values. However, the overall sign of the total shielding value is consistent for the entire set of molecules, except for and . It is known that the LRESC scheme encounters some difficulties in accurately reproducing magnetic shielding for nuclei in the 6th row of the Periodic Table, although it does capture the correct trends [21,27,37].
Table 3.
Nuclear magnetic shielding and chemical shift of the Pt atom in Pt molecules (X = F, Cl, Br, I; n = 4, 6) calculated at LRESC and 4c-RPA levels. The values are reported in ppm.
Table 3.
Nuclear magnetic shielding and chemical shift of the Pt atom in Pt molecules (X = F, Cl, Br, I; n = 4, 6) calculated at LRESC and 4c-RPA levels. The values are reported in ppm.
| Total | Total | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 6548.0 | -8400.6 | -1852.6 | 7980.7 | -6728.6 | 1252.1 | -836.0 | -4624.9 | – | |
| 6628.3 | -18770.3 | -12142.0 | 8062.8 | -17612.8 | -9550.0 | 9453.2 | 6177.1 | 7325 | |
| 6644.3 | -6006.9 | 637.4 | 8076.8 | -6391.6 | 1685.2 | -3326.2 | -5058.1 | -1626 | |
| 6770.7 | -9459.3 | -2688.6 | 8203.3 | -11576.3 | -3372.9 | 0.0 | 0.0 | 0 | |
| 6906.8 | -5061.0 | 1845.8 | 8338.3 | -5957.0 | 2381.3 | -4534.6 | -5754.2 | -2676 | |
| 7147.0 | -6256.8 | 890.1 | 8585.5 | -9228.6 | -643.1 | -3578.7 | -2729.8 | -1903 | |
| 7124.8 | -2539.7 | 4585.0 | 8554.5 | -3276.6 | 5277.9 | -7273.8 | -8650.8 | -5522 | |
| 7457.3 | -2117.4 | 5339.9 | 8886.3 | -6079.4 | 2806.9 | -8028.7 | -6179.8 | -6067 |
∗) Experimental values taken from Ref. [38] in H2O solution, except for in Cl2.
A more insightful analysis can be performed by considering the chemical shifts instead of the absolute values and comparing them with experimental results. In this regard, the LRESC chemical shifts exhibit closer agreement with the experimental values compared to the 4C-RPA results. Figure 2 demonstrates that follows the same trend as across the entire set of molecules studied. However, it is important to note that these calculations were conducted under static conditions, and several effects were not taken into account.
The primary differences between LRESC and 4C-RPA total values originate from the paramagnetic component, as the diamagnetic component exhibits a nearly constant difference. Specifically, the LRESC diamagnetic component is consistently approximately 1400 ppm lower than the corresponding 4c diamagnetic contributions. The variation of the paramagnetic component is not constant and is influenced by the ligand-dependent contributions, as illustrated in Table 4 and Table 5.
The primary electronic mechanisms responsible for ligand-dependent relativistic effects are the well-known contribution and the contribution. Both of these mechanisms exhibit significant variations with the atomic number of the halogen atom, particularly in planar systems. The contribution is widely recognized as being important in numerous atomic and molecular systems. However, the contribution is also of comparable magnitude but with an opposite sign. As a result, the overall relativistic effects depend on the difference between these two contributions. In the case of the Pt molecule, the contribution is greater than the contribution, resulting in a negative value. Moreover, this negative value becomes more pronounced (in absolute value) as the influence of the halogen substituent increases. This analysis tell us that one must include the non-SO contributions to the shieldings of heavy atoms when they are bonded to heavy-atoms. As will be shown in Table 4 and Table 5 the main contribution to arises from the core(Pt) and the bonding Pt-X being X= F, Cl, Br, I. There is also a contribution from the of the atom X. When X=I, is around 4 times the contribution of . This becomes 2 times when X=F. The importance of HAVHA effects are clearly shown in this case.
Table 4 and Table 5 provide insights into the ligand-dependent and non-ligand-dependent contributions to the nuclear magnetic shieldings of the platinum atom, focusing on the localized molecular orbitals. These contributions can be categorized into core orbitals, lone pairs, and bond orbitals. It is evident that the non-ligand-dependent corrections remain unaffected by the substituent atom, with the primary contribution originating from the platinum core orbitals. On the other hand, for the ligand-dependent contribution, the core orbitals of platinum and Pt-X bond orbitals play crucial roles in the correction, while arises from the platinum core orbitals. However, when the weight of the halogen atom grows up, such a contribution is reduced and the contribution of the lone-pairs becomes important reaching the 50% of the platinum core contributions.
At the NR level, the diamagnetic component of platinum, (Pt), exhibits a similar trend for the whole set of molecules and experiences an increase of less than 600 ppm from F to I atoms. The core orbital contributions of platinum remain independent of the substituent halogen atom, constituting approximately 92% to 98% of the total . However, the core orbitals of the substituent atom play a crucial role in determining the variation in this component, ranging from 40 ppm for F to 662 ppm for I. The combination of these contributions determines the overall behavior of .
On the other hand, the NR paramagnetic component of platinum shielding, (Pt), displays a significant variation depending on the substituent halogen atom, ranging from -15838 ppm for F to -8055 ppm for I. Analysis of the molecular orbitals reveals that the core orbitals of Pt are consistently negative and dominant, ranging from -15772 ppm for F to -8754 ppm for I. The core orbitals of the halogen atoms also contribute negatively, with a negligible contribution for F but progressively increasing with the atomic weight of the halogen, accounting for up to 4% of the platinum core orbitals contribution in the case of I.
Table 4 and Table 5 further illustrate the distinct behavior of the remaining MOs. The Pt-X bond orbitals consistently contribute positively but at magnitudes one or two orders of magnitude lower than the platinum core orbitals. In contrast, the -type and -type lone pair contributions exhibit similar behavior, with negative values for F substituents that transition to positive values for the other halogens. These lone pair contributions can collectively account for up to 10% of the platinum core orbitals contribution in the case of the molecule.
In Figure 3, the contributions of localized molecular orbitals to the and relativistic corrections are presented for the entire set of molecules under study. Additionally, for , the contribution of is also shown. The mechanism originates from the core electrons of platinum, but as the weight of the halogen increases, the lone-pair orbitals become significant and change the sign from negative to positive. The primary contribution to the mechanism also arises from the core orbitals of platinum. Furthermore, the mechanism exhibits a comparable magnitude to in and molecules, with the core orbitals of platinum and Pt-X bonds playing a significant role.
We will now analyze the (Pt) in Pt (X = F, Cl, Br, I) molecules, as shown in Table 3. This allows us to observe the influence of the number of substituent halogen atoms as well as the influence of the change in geometry.
The core contributions to the paramagnetic and diamagnetic components are the same as those in Pt molecules. These contributions arise from the core orbitals of Pt and are responsible for these effects.
The diamagnetic component, (Pt), in Pt molecules is approximately 1% larger than in Pt molecules. However, the contribution of platinum core orbitals slightly decreases with an increasing number of bonds, resulting in a slightly higher contribution from the other molecular orbitals. These orbitals contribute a larger percentage to the total values compared to Pt molecules. Additionally, the core value of the halogen atoms increases by 31% when Pt is bonded to six halogen atoms. This analysis highlights the effect of the increased number of halogen substituents on the electronic mechanisms.
Regarding the paramagnetic component, Table 6 and Table 7 reveal that the relativistic correction is less significant than the corrections and has an opposite sign. As a result, the ligand-dependent corrections to the paramagnetic component have negative values with the exceptions of and .
In PtX molecules with symmetry, both and corrections decrease as the weight of the substituent halogen atom increases. However, in molecules with symmetry, the behavior is opposite, as illustrated in Fig. Figure 4.
4.2. Cadmium and mercury complexes
Table 8 presents the paramagnetic and diamagnetic contributions to (X) and (Te) in the Cl2XTe2Y2H6 (X = Cd, Hg; Y = N, P) molecular systems, calculated using both the LRESC and 4C-RPA methods. For the Cd atom, which belongs to the 5th row of the Periodic Table, the LRESC values are very close to the 4C-RPA values, with differences ranging from 0.2% to 1%. This indicates a good agreement between the two methods for Cd atom. On the other hand, for the Hg atom belonging to the 6th row of the Periodic Table, larger differences are observed between the LRESC and 4C-RPA values. The differences range from 16% to 18%, which is consistent with the expected behavior for an atom in the 6th row. In addition, the nuclear magnetic shielding of the Te atom is included in the table to analyze the HAVHA effect. When the total relativistic contribution cannot be explained by only including the SO mechanism that effect is then in action. In other words, the HAVHA effects become important when the SO mechanism does not explain the trends found for the shielding of HAs that are bonded to anoother HA.
The diamagnetic component of Cd and Hg in the Cl2XTe2Y2H6 (X = Cd, Hg; Y = N, P) molecular systems shows quite close values when the nitrogen (N) atom is replaced by the phosphorus (P) atom, both at the LRESC and 4C-RPA levels. This similarity indicates the core nature of this component. In contrast, the paramagnetic component of Cd and Hg exhibits a small variation when the N atom is replaced by the P atom due to the two-bond coupling between X and Y. However, the influence of the surrounding environment on the total value is not significant, with values of approximately 163 ppm for Cd and 380 ppm for Hg at the 4C-RPA level. This results in a relative increase of approximately 3.7% for Cd and 2.8% for Hg when the N atom is replaced by the P atom.
As mentioned above, the influence of replacing Cd with Hg on (Te) provides a measure of the HAVHA effect on this parameter. Additionally, it is interesting to analyze the replacement of the atom N with the atom P. At the 4C-RPA level, the substitution of Cd by Hg in Cl2XTe2N2H6 molecules leads to a 15% decrease in (Te), while such a substitution in Cl2XTe2P2H6 molecules results in only a 0.5% decrease. These values demonstrate a significant HAVHA effect on (Te) when nitrogen is present in the molecule, but a negligible effect when phosphorus is present. However, the most substantial change occurs when N is replaced by P, resulting in an increase of approximately 2900 ppm for Cd-centered molecules and 3230 ppm for Hg-centered molecules. This represents a variation of over 100% in (Te) from Cl2XTe2N2H6 to Cl2XTe2P2H6 molecules.
Upon analyzing the orbitals responsible for the nonrelativistic diamagnetic component () of transition metals Cd and Hg, it becomes evident that this component is primarily attributed to the contribution of core molecular orbitals. However, the core orbitals of Te contribute approximately 6% of the total value for Cd and 3% for Hg. On the other hand, the non-ligand-dependent contributions to the nonrelativistic paramagnetic component () solely originate from the core orbitals of Cd or Hg. The behavior of and the ligand-dependent contributions to this component warrant further analysis.
In Figure 5, the contributions of the most significant ligand-dependent electronic mechanisms, namely , , , and , are shown for Cd, Hg, and Te in Cl2XTe2Y2H6 systems at the LRESC level. The ligand-dependent contributions on Cd are relatively small compared to those on Hg in both analyzed molecules, but the behavior of each electronic mechanism is similar. Due to the comparable magnitudes of the main electronic mechanisms with opposite signs, the total ligand-dependent value is very small. Specifically, (Hg) amounts to only 66 ppm in the Cl2XTe2N2H6 molecule and 209 ppm in the Cl2XTe2P2H6 molecule. The difference arises from the change in sign of , which is negative in the first molecule and positive in the second.
Figure 5 also provides a clear demonstration of the HAVHA effect on (Te). As mentioned earlier, the HAVHA effect is approximately 15% in Cl2XTe2N2H6 molecules, and the contributions of each electronic mechanism to (Te) are very similar when Cd or Hg atoms are present in the molecule. However, a significant difference arises when N is replaced by P, particularly in the reduction of , , and (in absolute value) contributions. The molecular orbitals responsible for these changes are the X-Te bond orbitals, and in particular, the lone pairs of tellurium (Te), as shown in Tables provided in the Electronic Supporting Information (ESI).
Table 9 and Table 10 present the contributions of localized molecular orbitals to , , , and on Cd in Cl2CdTe2Y2H6 (Y = N, P) molecules. Similarly, Table 11 and Table 12 display the corresponding contributions on Hg atom in Cl2HgTe2Y2H6 molecules. These tables provide detailed information about the specific molecular orbitals involved in each mechanism and their respective contributions to the overall electronic behavior of the system.
For the Cd atom, the , , and relativistic electronic mechanisms show similar values in both molecules when the N atom is replaced by P. The contribution of each molecular orbital follows the same trend. However, the mechanism changes its sign between the two molecules, and the Cd-Te bond orbitals are responsible for the change in the final value. A similar behavior is observed for the Hg atom, where the major change occurs when N is replaced by P in the mechanism, attributed to the Hg-Te bond orbitals. The contributions change from -186 ppm in Cl2HgTe2N2H6 to 47 ppm in Cl2HgTe2P2H6 even including the negative increase due to the Hg-Cl bondings.
As mentioned earlier, the replacement of the p-orbital element produces significant changes in some relativistic electronic mechanisms and, consequently, in the total magnetic shielding value. This effect is more significant than the variation in the weight of the transition metal atom in this kind of molecules.
5. Conclusions
In this study, we have investigated the nuclear magnetic shielding of heavy transition metals, including cadmium, platinum, and mercury, in Pt (X = F, Cl, Br, I; n = 4, 6) and XCl2Te2Y2H6 (X = Cd, Hg; Y = N, P) molecular systems using 4C-RPA and LRESC computational methods. We employed the LRESC-Loc formalism, which enables the analysis of different electronic mechanisms responsible for relativistic effects on heavy atoms based on localized molecular orbitals. These orbitals are classified into core orbitals, lone pairs, and bond orbitals.
The calculated chemical shifts () of Pt molecules at the LRESC level exhibit a similar trend to the experimental values (). This provides valuable insights into the molecular orbitals involved in the contributions from various corrections when the weight and number of halogen atoms vary.
Among the ligand-dependent relativistic effects, the prominent electronic mechanisms are the well-known contribution and , which have opposite signs. In planar PtX systems with symmetry, both and decrease as the substituent halogen atom becomes heavier. However, in octahedral PtX systems with symmetry, the behavior is opposite. The core orbitals of platinum and Pt-X bond orbitals play crucial roles in the correction, while originates from the core orbitals of platinum.
In the case of XCl2Te2Y2H6 molecules, the variation in (X) is relatively small, ranging from 2.8 to 3.8% when a p-orbital element is changed. However, when examining (Te), the HAVHA effect resulting from the replacement of Cd with Hg is observed to be only between 0.5 and 15%. Nonetheless, when considering a fixed metal atom (Cd or Hg), there is a remarkable enhancement of more than 100% in (Te) from Cl2XTe2N2H6 to Cl2XTe2P2H6 molecules. These changes can be attributed to the molecular orbitals associated with X-Te bond orbitals, and also with the lone pairs of tellurium (Te).
Furthermore, for both Cd and Hg complexes, the electronic mechanisms exhibit similar values when the N atom is replaced by P. The only difference lies in the mechanism, which changes its sign between the two molecules. The variation in the final value can be attributed to the X-Te bond orbitals.
Author Contributions
“Conceptualization, A.F.M. and G.A.A.; methodology, A.F.M., A.D.Z. and G.A.A.; software, A.D.Z.; validation, A.F.M. and A.D.Z.; formal analysis, A.F.M., A.D.Z. and G.A.A.; resources, J.L.M.C., A.F.M. and A.D.Z.; data curation, A.D.Z.; writing—original draft preparation, A.F.M.; writing—review and editing, A.F.M., A.D.Z., J.L.M.C. and G.A.A.; supervision, A.F.M.,J.L.M.C., and G.A.A.; funding acquisition, J.L.M.C., G.A.A. All authors have read and agreed to the published version of the manuscript.”
Funding
This research was funded by the Argentinian Agency for Promotion of Science and Technology, FONCYT (Grant PICT2016-2936). J.L.M.C. acknowledge startup funds from Michigan State University
Data Availability Statement
The data that support the findings of this study are available within the article and its supplementary material.
Acknowledgments
We gratefully acknowledge support from the Argentinian Agency for Promotion of Science and Technology, FONCYT (Grant PICT2016-2936). This work was supported in part through computational resources and services provided by the Institute for Cyber-Enabled Research at Michigan State University
Conflicts of Interest
The authors declare no conflict of interest.
References
- Huang, C.Y.; Doyle, A.G. The Chemistry of Transition Metals with Three-Membered Ring Heterocycles. Chem. Rev. 2014, 114, 8153–8198. [Google Scholar] [CrossRef] [PubMed]
- Kaupp, M.; Malkin, V.G.; Malkina, O.L. Encyclopedia of computational chemistry; Wiley, Chichester, 1998; pp. 1857–1866.
- Bühl, M.; Kaupp, M.; Malkina, O.L.; Malkin, V.G. The DFT route to NMR chemical shifts. J. Comput. Chem. 1999, 20, 91–105. [Google Scholar] [CrossRef]
- Autschbach, J.; Ziegler, T. Encyclopedia of nuclear magnetic resonance; Wiley, Chichester, 2002; pp. 303–323.
- Autschbach, J.; Ziegler, T. Calculation of NMR and EPR parameters. Theory and applications; Wiley-VCH, Weinheim, 2004; pp. 249–264.
- Autschbach, J. The Calculation of NMR Parameters in Transition Metal Complexes; Springer, Berlin, Heidelberg, 2004; pp. 1–48.
- Vícha, J.; Novotny, J.; Komorovsky, S.; Straka, M.; Kaupp, M.; Marek, R. Relativistic Heavy-Neighbor-Atom Effects on NMR Shifts: Concepts and Trends Across the Periodic Table. Chem. Rev. 2020, 120, 7065–7103. [Google Scholar] [CrossRef]
- Gilbert, T.M.; Ziegler, T. Prediction of 195Pt NMR Chemical Shifts by Density Functional Theory Computations: The Importance of Magnetic Coupling and Relativistic Effects in Explaining Trends. J. Phys. Chem. A 1999, 103, 7535–7543. [Google Scholar] [CrossRef]
- Dean, R.R.; Green, J.C. Platinum-195 and phoshorus-31 nuclear magnetic resonance studies of some platinum hydrides. J. Chem. Soc. A 1968, 3047–3050. [Google Scholar] [CrossRef]
- Preetz, W.; Peters, G.; Bubitz, D. Preparation and Spectroscopic Investigations of Mixed Octahedral Complexes and Clusters. Chem. Rev. 1996, 96, 977. [Google Scholar] [CrossRef]
- Drews, H.; Preetz, W. Calculation of 19F and 195Pt NMR Shifts of Fluoro-Chloro-Bromo-Platinates(IV). Z. Naturforschung 1997, 52, 9435. [Google Scholar]
- Fowe, E.P.; Belser, P.; Daul, C.; Chermette, H. Assessment of theoretical prediction of the NMR shielding tensor of 195PtClxBr6-x2- complexes by DFT calculations: experimental and computational results. Phys. Chem. Chem. Phys. 2005, 7, 1732–1738. [Google Scholar] [CrossRef] [PubMed]
- Burger, M.R.; Kramer, J.; Chermette, H.; Koch, K.R. A comparison of experimental and DFT calculations of 195Pt NMR shielding trends for [PtXnY6-n]2- (X, Y = Cl, Br, F and I) anions. Magn. Reson. Chem. 2010, 48, S38–S47. [Google Scholar] [CrossRef]
- Malkin, V.G.; Malkina, O.L.; Erikson, L.A.; Salahub, D.R. Modern Density Functional Theory: A Tool for Chemistry; Elsevier, Amsterdam, 1995.
- Autschbach, J. Analyzing NMR shielding tensors calculated with two-component relativistic methods using spin-free localized molecular orbitals. J. Chem. Phys. 2008, 128, 164112. [Google Scholar] [CrossRef]
- dos Reis Lino, J.B.; Sauer, S.P.A.; Ramalho, T.C. Enhancing NMR Quantum Computation by Exploring Heavy Metal Complexes as Multiqubit Systems: A Theoretical Investigation. J. Chem. Phys. A. 2020, 124, 4946. [Google Scholar] [CrossRef] [PubMed]
- Vícha, J.; Komorovsky, S.; Repisky, M.; Marek, R.; Straka, M. Relativistic Spin–Orbit Heavy Atom on the Light Atom NMR Chemical Shifts: General Trends Across the Periodic Table Explained. J. Chem. Theory Comput. 2018, 14, 3025–3039. [Google Scholar] [CrossRef] [PubMed]
- Morishima, I.; Endo, K.; Yonezawa, T. Effect of the heavy atom on the nuclear shielding constant. I. The proton chemical shifts in hydrogen halides. J. Chem. Phys. 1973, 59, 3356–3364. [Google Scholar] [CrossRef]
- Edlund, U.; Lejon, T.; Pyykkö, P.; Venkatachalam, T.K.; Buncel, E. 7Li, 29Si,’ 1 9 S n, and 207PbNMR Studies of Phenyl-Substituted Group 4 Anions. J. Am. Chem. Soc. 1987, 109, 5982. [Google Scholar] [CrossRef]
- Maldonado, A.F.; Aucar, G.A. The UKB prescription and the heavy atom effects on the nuclear magnetic shielding of vicinal heavy atoms. Phys. Chem. Chem. Phys. 2009, 11, 5615. [Google Scholar] [CrossRef] [PubMed]
- Maldonado, A.F.; Melo, J.I.; Aucar, G.A. Theoretical analysis of NMR shieldings of group-11 metal halides on MX (M = Cu, Ag, Au; X = H, F, Cl, Br, I) molecular systems, and the appearance of quasi instabilities on AuF. Phys. Chem. Chem. Phys. 2015, 17, 25516–25524. [Google Scholar] [CrossRef] [PubMed]
- Kaupp, M.; Malkina, O.L.; Malkin, V.G.; Pyykkö, P. How Do Spin ± Orbit-Induced Heavy-Atom Effects on NMR Chemical Shifts Function? Validation of a Simple Analogy to Spin ± Spin Coupling by Density Functional Theory (DFT) Calculations on Some Iodo Compounds. Chem. Eur. J. 1998, 4, 118. [Google Scholar] [CrossRef]
- Novotný, J.; Vícha, J.; Bora, P.L.; Repisky, M.; Straka, M.; Komorovsky, S.; Marek, R. Linking the Character of the Metal–Ligand Bond to the Ligand NMR Shielding in Transition-Metal Complexes: NMR Contributions from Spin–Orbit Coupling. J. Chem. Theory Comput. 2017, 13, 3586–3601. [Google Scholar] [CrossRef]
- Melo, J.I.; Ruiz de Azúa, M.C.; Giribet, C.G.; Aucar, G.A.; Romero, R.H. Relativistic effects on the nuclear magnetic shielding tensor. J. Chem. Phys. 2003, 118, 471–486. [Google Scholar] [CrossRef]
- Melo, J.I.; Ruiz de Azúa, M.C.; Giribet, C.G.; Aucar, G.A.; Provasi, P.F. Relativistic effects on nuclear magnetic shielding constants in HX and CH3X(X=Br,I) based on the linear response within the elimination of small component approach. J. Chem. Phys. 2004, 121, 6798–6808. [Google Scholar] [CrossRef]
- Aucar, G.A.; Melo, J.I.; Aucar, I.A.; Maldonado, A.F. Foundations of the LRESC model for response properties and some applications. Int. J. Quantum Chem. 2018, 118, e25487. [Google Scholar] [CrossRef]
- Zapata-Escobar, A.D.; Maldonado, A.F.; Aucar, G.A. The LRESC-Loc Model to Analyze Magnetic Shieldings with Localized Molecular Orbitals. J. Phys. Chem. A 2022, 126, 9519. [Google Scholar] [CrossRef]
- Pipek, J.; Mezey, P.G. A fast intrinsic localization procedure applicable for ab-initio and semiempirical linear combination of atomic orbital wave functions. J. Chem. Phys. 1989, 90, 4916–4926. [Google Scholar] [CrossRef]
- Weinhold, F. Discovering chemistry with natural bond orbitals; John Wiley & Sons, 2012.
- Melo, J.I.; Maldonado, A.F. Relativistic corrections to the electric field gradient given by linear response elimination of the small component formalism. Int. J. Quantum Chem. 2019, 119, e25935. [Google Scholar] [CrossRef]
- Saue, T.; Bast, R.; Gomes, A.; Jensen, H.J.A.; Visscher, L.; Aucar, I.A.; Remigio, R.D.; Dyall, K.G.; Eliav, E.; Fasshauer, E.; Fleig, T.; et al. The DIRAC code for relativistic molecular calculations. J Chem. Phys. 2020, 152, 204104. [Google Scholar] [CrossRef]
- Dyall, K.G. Relativistic Quadruple-Zeta and Revised Triple-Zeta and Double-Zeta Basis Sets for the 4p, 5p, and 6p Elements. Theor. Chem. Acc. 2006, 115, 441–447. [Google Scholar] [CrossRef]
- Gilbert, T.M.; Ziegler, T. Prediction of 195Pt NMR Chemical Shifts by Density Functional Theory Computations: The Importance of Magnetic Coupling and Relativistic Effects in Explaining Trends. J. Phys. Chem. A. 1999, 103, 7535. [Google Scholar] [CrossRef]
- Dalton, a molecular electronic structure program, Release v2018.2 (2019).
- Aucar, G.A.; Maldonado, A.F.; Montero, M.D.A.; Cruz, T.S. Theoretical developments and applications of polarization propagators. Int. J. Quantum Chem. 2018, 119, e25722. [Google Scholar] [CrossRef]
- Sun, Q.; Berkelbach, T.C.; Blunt, N.S.; Booth, G.H.; Guo, S.; Li, Z.; Liu, J.; McClain, J.D.; Sayfutyarova, E.R.; Sharma, S.; Wouters, S.; Chan, G.K. PySCF: the Python-based simulations of chemistry framework. WIREs Comput. Mol. Sci. 2018, 8, e1340. [Google Scholar] [CrossRef]
- Melo, J.I.; Maldonado, A.F.; Aucar, G.A. Relativistic effects on the shielding of SnH2XY and PbH2XY (X, Y = F, Cl, Br and I) heavy atom–containing molecules. Theor. Chem. Acc. 2011, 129, 483. [Google Scholar] [CrossRef]
- Mason, J. Multinuclear NMR; Springer, Boston, MA, 1987.
Figure 1.
Representation of the molecular structures for Pt, Pt (X = Cl, Br, I), and XCl2Te2Y2H6 (X = Cd, Hg; Y = N, P) systems.
Figure 1.
Representation of the molecular structures for Pt, Pt (X = Cl, Br, I), and XCl2Te2Y2H6 (X = Cd, Hg; Y = N, P) systems.

Figure 2.
Chemical shift results for platinum, , calculated at LRESC and 4c-RPA levels. Experimental values are also included. All values are given in ppm.
Figure 2.
Chemical shift results for platinum, , calculated at LRESC and 4c-RPA levels. Experimental values are also included. All values are given in ppm.
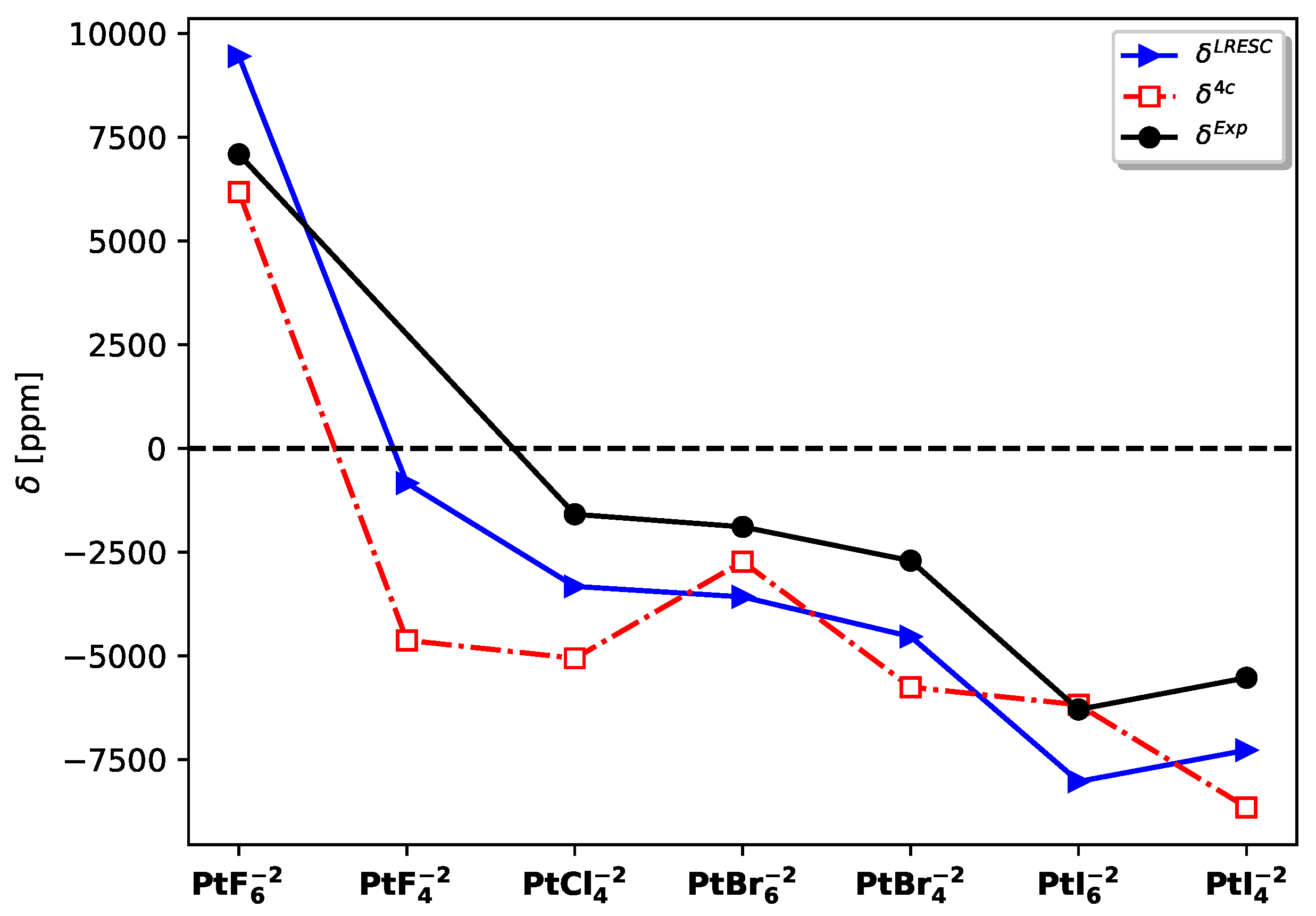
Figure 3.
Contributions of core orbitals, bond orbitals, and lone-pair orbitals to the and mechanisms on Pt in (left) and (right) molecules. The mechanism is also displayed for .
Figure 3.
Contributions of core orbitals, bond orbitals, and lone-pair orbitals to the and mechanisms on Pt in (left) and (right) molecules. The mechanism is also displayed for .
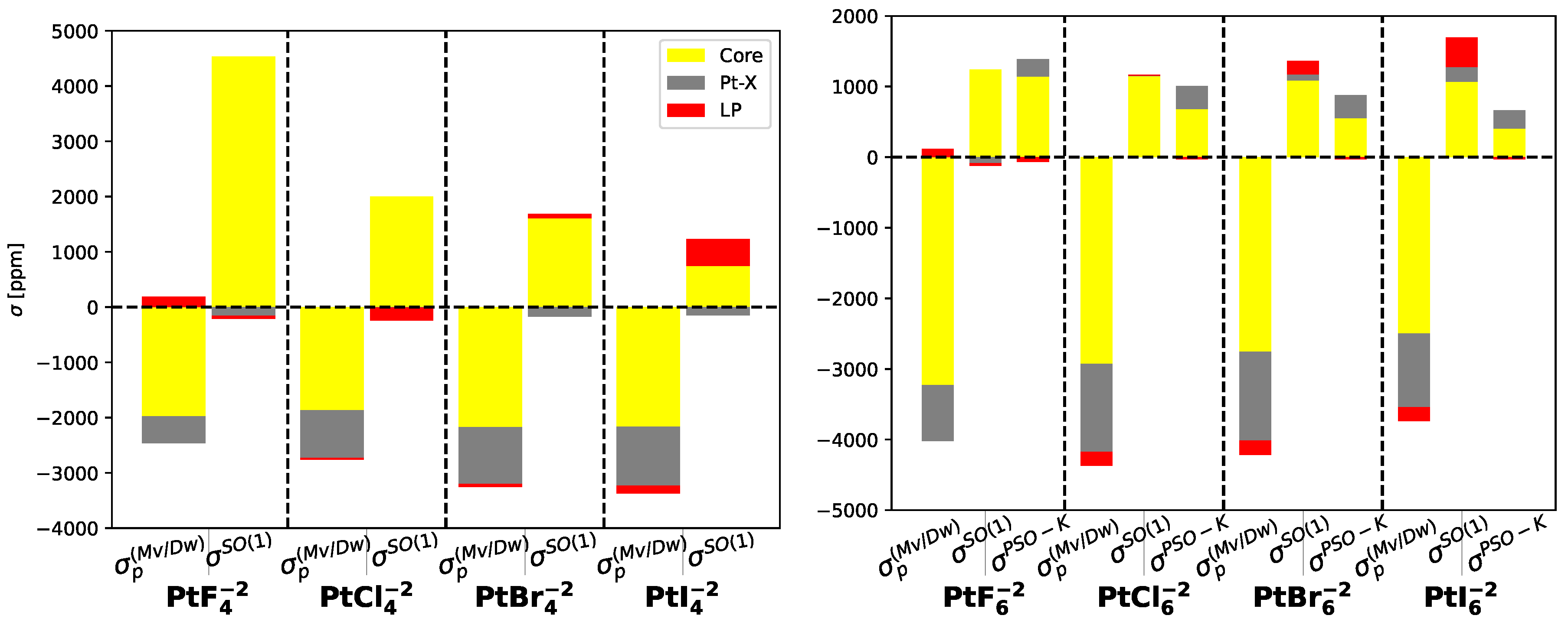
Figure 4.
Contributions of and to in (left) and (right) molecules. All values are given in ppm.
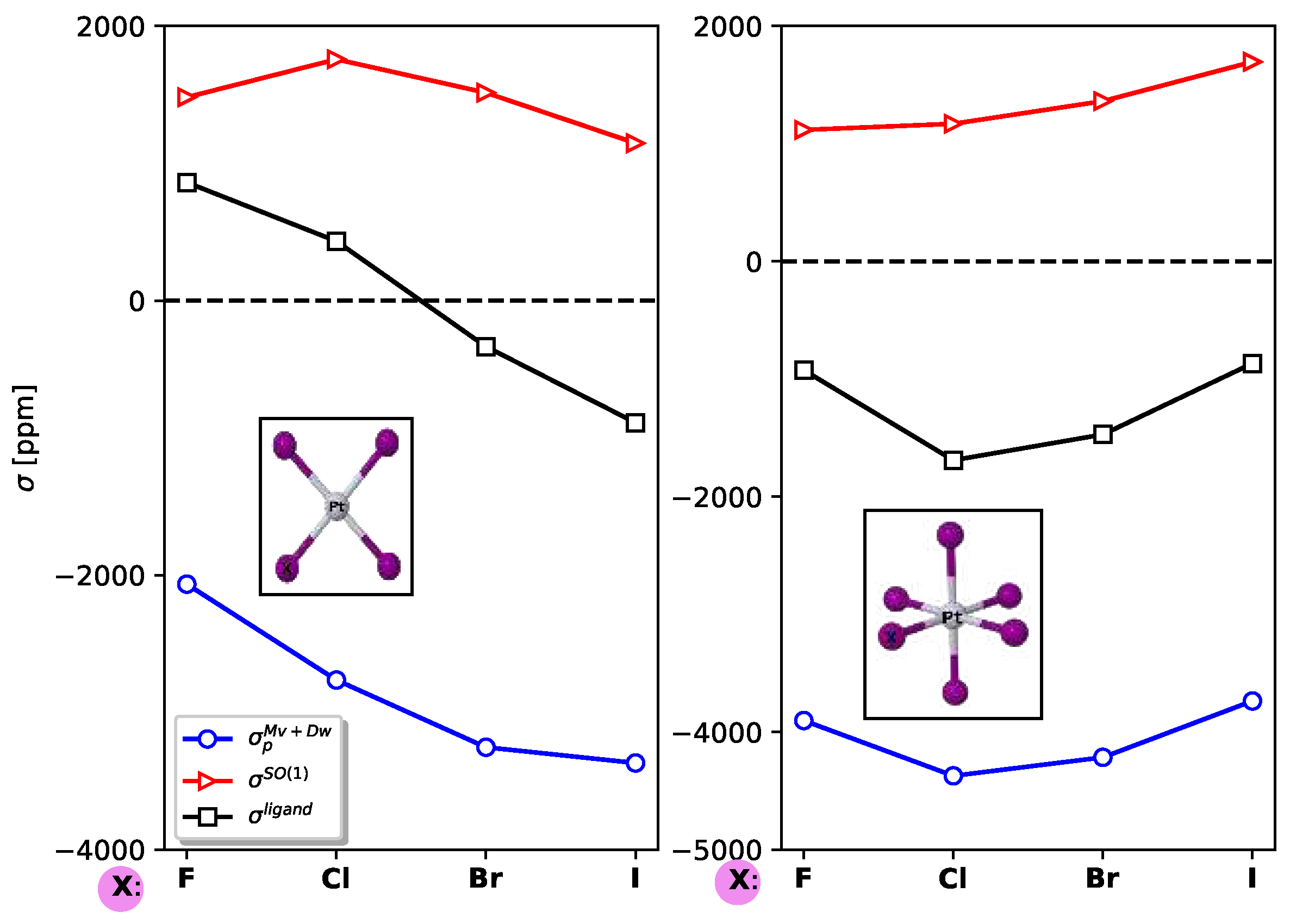
Figure 5.
Ligand-dependent contributions to (Te), (Cd), and (Hg) in the Cl2XTe2Y2H6 molecular systems using Localized Molecular Orbitals.
Figure 5.
Ligand-dependent contributions to (Te), (Cd), and (Hg) in the Cl2XTe2Y2H6 molecular systems using Localized Molecular Orbitals.
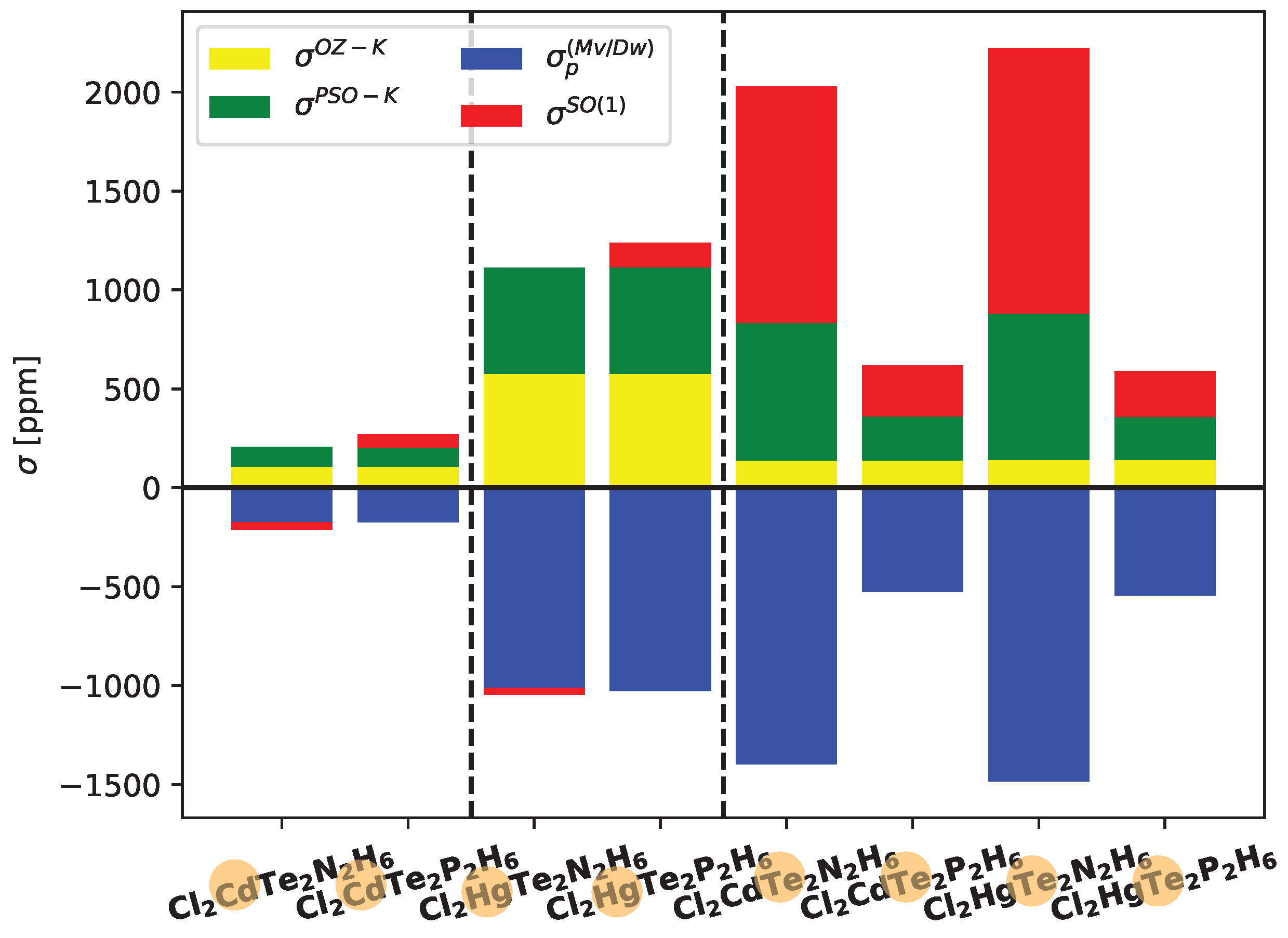
Table 1.
Comprehensive scheme of paramagnetic and diamagnetic corrections as given within the LRESC model, including ligand-dependent and non-ligand-dependent contributions.
Table 1.
Comprehensive scheme of paramagnetic and diamagnetic corrections as given within the LRESC model, including ligand-dependent and non-ligand-dependent contributions.
| paramagnetic | diamagnetic | ||||||
| ligand-dependent | non-ligand-dependent | ||||||
Table 2.
Bond lengths between Pt and X halogen atoms. All values are given in angstroms (Å).
| Pt–X [Å] | Pt–X [Å] | ||
| 1.90 | 2.43 | ||
| 1.93 | 2.56 | ||
| 2.31 | 2.61 | ||
| 2.36 | 2.71 |
Table 4.
Localized molecular orbital contributions to the electronic mechanisms in the LRESC formalism for the Pt atom in the molecule. All values are reported in ppm.
Table 4.
Localized molecular orbital contributions to the electronic mechanisms in the LRESC formalism for the Pt atom in the molecule. All values are reported in ppm.
| Core(Pt) | 4xCore(F) | 4xPt–F | F | F | ∑ | |
|---|---|---|---|---|---|---|
| -3034.7 | -0.1 | 0.0 | 0.6 | 0.0 | -3034.2 | |
| 9379.4 | 39.5 | 51.2 | 34.6 | 77.5 | 9582.2 | |
| 533.9 | 0.1 | 0.2 | 0.3 | -0.9 | 533.6 | |
| 597.4 | 0.5 | 282.7 | 34.2 | -3.9 | 910.9 | |
| -1633.5 | -0.6 | -487.7 | -67.0 | 123.7 | -2065.2 | |
| 1650.6 | -0.4 | -124.1 | -15.7 | -28.9 | 1481.6 | |
| 1148.4 | -0.4 | -328.9 | -48.3 | 90.0 | 860.9 | |
| 6575.9 | 0.0 | 0.0 | 0.0 | 0.0 | 6576.0 | |
| -15771.5 | -11.5 | 245.9 | -138.6 | -161.9 | -15837.5 |
Table 5.
Localized molecular orbital contributions to the electronic mechanisms in the LRESC formalism for the Pt atom in the PtI molecule. All values are reported in ppm.
Table 5.
Localized molecular orbital contributions to the electronic mechanisms in the LRESC formalism for the Pt atom in the PtI molecule. All values are reported in ppm.
| Core(Pt) | 4xCore(I) | 4xPt–I | I | I | ∑ | |
|---|---|---|---|---|---|---|
| -3034.2 | -5.7 | -0.2 | 0.2 | 0.0 | -3039.9 | |
| 9376.4 | 662.2 | 48.0 | 24.2 | 53.9 | 10164.7 | |
| 532.4 | 8.7 | 1.5 | 0.5 | -5.6 | 537.5 | |
| 312.9 | 12.3 | 402.8 | 37.5 | 28.4 | 793.8 | |
| -2197.7 | 33.7 | -1065.6 | -35.6 | -102.5 | -3367.7 | |
| 922.0 | -117.0 | -146.9 | 35.4 | 453.7 | 1147.2 | |
| -430.4 | -62.3 | -808.1 | 37.7 | 373.9 | -889.1 | |
| 6575.0 | 0.0 | 1.1 | -0.2 | 0.0 | 6575.8 | |
| -8754.3 | -332.7 | 714.0 | 117.2 | 200.5 | -8055.3 |
Table 6.
Localized molecular orbital contributions to the electronic mechanisms calculated using the LRESC formalism for the Pt atom in the molecule. All values are reported in ppm.
Table 6.
Localized molecular orbital contributions to the electronic mechanisms calculated using the LRESC formalism for the Pt atom in the molecule. All values are reported in ppm.
| Core(Pt) | 6xCore(F) | 6xPt–F | F | F | ∑ | |
|---|---|---|---|---|---|---|
| -3033.1 | -0.1 | -1.0 | 0.0 | 0.0 | -3034.2 | |
| 9358.3 | 58.2 | 75.8 | 55.8 | 114.4 | 9662.5 | |
| 540.0 | 0.0 | 0.4 | 0.2 | -1.9 | 538.7 | |
| 1148.1 | -3.3 | 241.1 | 2.7 | -67.7 | 1321.0 | |
| -3226.9 | -3.9 | -789.9 | 4.6 | 114.6 | -3901.5 | |
| 1242.8 | -0.6 | -84.4 | -0.4 | -39.8 | 1117.7 | |
| -296.0 | -7.7 | -632.7 | 7.1 | 5.3 | -924.0 | |
| 6574.2 | 0.0 | 0.0 | 0.0 | 0.0 | 6574.2 | |
| -27652.8 | 76.7 | 1589.3 | -113.1 | 1679.5 | -24420.5 |
Table 7.
Contributions of LMOs to the electronic mechanisms in the molecule, as calculated using the LRESC-Loc model. All values are given in ppm.
Table 7.
Contributions of LMOs to the electronic mechanisms in the molecule, as calculated using the LRESC-Loc model. All values are given in ppm.
| Core(Pt) | 6xCore(I) | 6xPt–I | I | I | ∑ | |
|---|---|---|---|---|---|---|
| -3033.5 | -8.4 | -1.1 | 0.2 | 0.0 | -3042.8 | |
| 9350.2 | 961.6 | 79.9 | 36.7 | 71.7 | 10500.1 | |
| 532.5 | 12.4 | 2.8 | 1.1 | -9.0 | 539.9 | |
| 402.8 | 4.5 | 256.4 | 6.2 | -37.0 | 632.9 | |
| -2568.4 | 72.1 | -1041.6 | 47.6 | -245.0 | -3735.3 | |
| 1146.4 | -75.5 | 204.1 | -47.5 | 468.6 | 1696.1 | |
| -486.7 | 13.5 | -578.3 | 7.5 | 177.6 | -866.4 | |
| 6573.8 | 0.0 | 2.4 | -0.8 | 0.0 | 6575.4 | |
| -10917.3 | -403.5 | 2047.1 | 133.1 | 1314.3 | -7826.3 |
Table 8.
Paramagnetic and diamagnetic contributions to (X) and (Te) in the Cl2XTe2Y2H6 (X = Cd, Hg; Y = N, P) molecular systems, calculated using the LRESC and 4C-RPA methods. All values are given in ppm.
Table 8.
Paramagnetic and diamagnetic contributions to (X) and (Te) in the Cl2XTe2Y2H6 (X = Cd, Hg; Y = N, P) molecular systems, calculated using the LRESC and 4C-RPA methods. All values are given in ppm.
| Atom | Total | Total | |||||
|---|---|---|---|---|---|---|---|
| Cl2CdTe2N2H6 | Cd | 4615.8 | -167.3 | 4448.5 | 4830.1 | -423.9 | 4406.1 |
| Te | 4848.6 | -2764.7 | 2083.9 | 5248.1 | -3109.0 | 2039.1 | |
| Cl2CdTe2P2H6 | Cd | 4646.8 | -87.1 | 4559.7 | 4861.0 | -291.8 | 4569.2 |
| Te | 4885.1 | 41.8 | 4927.0 | 5183.6 | -244.9 | 4938.8 | |
| Cl2HgTe2N2H6 | Hg | 6953.5 | 4369.0 | 11322.6 | 8526.1 | 4980.3 | 13506.3 |
| Te | 4948.2 | -3038.5 | 1909.7 | 5246.8 | -3513.7 | 1733.1 | |
| Cl2HgTe2P2H6 | Hg | 6989.0 | 4437.4 | 11426.3 | 8559.8 | 5326.5 | 13886.3 |
| Te | 4985.2 | -54.9 | 4930.3 | 5282.8 | -318.9 | 4963.9 |
Table 9.
Localized molecular orbital contributions to the electronic mechanisms on the Cd atom in the Cl2CdTe2N2H6 molecule, as computed by the LRESC formalism. All values are provided in ppm.
Table 9.
Localized molecular orbital contributions to the electronic mechanisms on the Cd atom in the Cl2CdTe2N2H6 molecule, as computed by the LRESC formalism. All values are provided in ppm.
| Core(Cd) | 2xCore(Te) | 2xCd–Te | 2xCd–Cl | 2xTe–N | Te | ∑ | |||
|---|---|---|---|---|---|---|---|---|---|
| -699.4 | -2.4 | 0.1 | 0.2 | 0.0 | 0.1 | 0.0 | -0.2 | -701.7 | |
| 4799.7 | 288.7 | 17.9 | 20.2 | 10.9 | 22.5 | 42.4 | 115.1 | 5317.5 | |
| 102.8 | 3.2 | -0.1 | 0.2 | 0.0 | 0.1 | 0.0 | 0.3 | 106.5 | |
| 2.6 | 3.5 | 38.1 | 38.7 | 0.6 | 4.0 | 11.1 | 0.3 | 98.9 | |
| -52.7 | -7.0 | -32.7 | -59.1 | -0.4 | -11.0 | -12.0 | -0.3 | -175.2 | |
| 0.8 | -20.5 | -119.6 | 2.8 | 30.1 | 53.7 | 16.3 | -0.6 | -37.0 | |
| 53.5 | -20.8 | -114.3 | -17.4 | 30.3 | 46.8 | 15.5 | -0.3 | -6.8 | |
| 1493.4 | 0.0 | 0.3 | 0.1 | 0.0 | 0.2 | 0.1 | 0.0 | 1494.0 | |
| -111.7 | -214.4 | -463.1 | -450.3 | -21.7 | -78.4 | -203.2 | -111.6 | -1654.5 |
1) Total Cl + Cl value. 2) Total core(Cl,N) + core (N,H).
Table 10.
Localized molecular orbitals contributions to the electronic mechanisms within the LRESC formalism for the Cd atom in the Cl2CdTe2P2H6 molecule. All values are given in ppm.
Table 10.
Localized molecular orbitals contributions to the electronic mechanisms within the LRESC formalism for the Cd atom in the Cl2CdTe2P2H6 molecule. All values are given in ppm.
| Core(Cd) | 2xCore(Te) | 2xCd–Te | 2xCd–Cl | 2xTe–P | Te | ∑ | |||
|---|---|---|---|---|---|---|---|---|---|
| -699.4 | -2.4 | 0.1 | 0.3 | 0.0 | 0.1 | 0.0 | -0.3 | -701.7 | |
| 4799.7 | 283.8 | 16.9 | 20.6 | 11.0 | 22.4 | 43.0 | 151.2 | 5348.5 | |
| 102.8 | 3.1 | 0.0 | 0.2 | 0.0 | 0.1 | 0.0 | 0.4 | 106.6 | |
| 2.5 | 3.4 | 33.7 | 43.1 | 0.6 | 2.3 | 10.8 | 0.3 | 96.8 | |
| -53.4 | -6.6 | -34.6 | -64.7 | -0.6 | -4.2 | -10.9 | -0.4 | -175.5 | |
| 2.6 | -18.0 | -33.4 | 0.1 | 25.2 | 66.4 | 21.4 | 2.4 | 66.7 | |
| 54.5 | -18.1 | -34.3 | -21.3 | 25.2 | 64.6 | 21.3 | 2.7 | 94.6 | |
| 1493.4 | 0.0 | 0.3 | 0.0 | 0.0 | 0.0 | 0.1 | 0.0 | 1493.7 | |
| -112.5 | -210.0 | -426.0 | -489.4 | -20.2 | -65.7 | -202.9 | -148.8 | -1675.4 |
1) Total Cl + Cl value. 2) Total core(Cl,P) + core (P,H).
Table 11.
Localized molecular orbital contributions to the electronic mechanisms based on LRESC formalism for the Hg atom in the Cl2HgTe2N2H6 molecule. All values are given in ppm.
Table 11.
Localized molecular orbital contributions to the electronic mechanisms based on LRESC formalism for the Hg atom in the Cl2HgTe2N2H6 molecule. All values are given in ppm.
| Core(Hg) | 2xCore(Te) | 2xHg–Te | 2xHg–Cl | 2xTe–N | ∑ | ||||
|---|---|---|---|---|---|---|---|---|---|
| -3275.2 | -2.4 | 0.6 | 0.7 | 0.0 | 0.1 | 0.0 | -0.2 | -3276.4 | |
| 9716.6 | 285.3 | 17.5 | 20.1 | 10.8 | 22.3 | 42.6 | 114.8 | 10230.0 | |
| 571.7 | 3.2 | -0.1 | 0.4 | 0.0 | 0.2 | 0.0 | 0.3 | 575.7 | |
| 22.3 | 5.0 | 200.2 | 238.6 | 3.1 | 16.3 | 51.2 | 0.2 | 536.8 | |
| 142.7 | -6.0 | -423.0 | -587.4 | -3.7 | -81.3 | -50.9 | -1.3 | -1011.0 | |
| 22.1 | -27.6 | -185.7 | -4.3 | 44.5 | 89.4 | 27.4 | -1.1 | -35.2 | |
| 758.9 | -25.5 | -408.7 | -352.8 | 43.9 | 24.7 | 27.7 | -1.9 | 66.2 | |
| 7105.7 | 0.0 | 0.7 | -0.3 | 0.0 | 0.0 | 0.0 | 0.0 | 7106.1 | |
| -265.7 | -216.2 | -845.8 | -913.1 | -30.5 | -96.5 | -325.0 | -110.6 | -2803.3 |
1) Total Cl + Cl value. 2) Total core(Cl,N) + core (N,H).
Table 12.
Contributions of localized molecular orbitals to the electronic mechanisms calculated using LRESC formalism on the Hg atom in the Cl2HgTe2P2H6 molecule. All values are reported in ppm.
Table 12.
Contributions of localized molecular orbitals to the electronic mechanisms calculated using LRESC formalism on the Hg atom in the Cl2HgTe2P2H6 molecule. All values are reported in ppm.
| Core(Hg) | 2xCore(Te) | 2xHg–Te | 2xHg–Cl | 2xTe–P | ∑ | ||||
|---|---|---|---|---|---|---|---|---|---|
| -3275.2 | -2.3 | 0.5 | 0.8 | 0.0 | 0.0 | 0.0 | -0.3 | -3276.5 | |
| 9716.6 | 283.9 | 16.7 | 20.3 | 11.1 | 22.5 | 42.8 | 151.5 | 10265.5 | |
| 571.7 | 3.1 | 0.0 | 0.4 | 0.0 | 0.1 | 0.0 | 0.4 | 575.8 | |
| 22.2 | 4.5 | 197.6 | 246.8 | 3.3 | 12.6 | 54.0 | -0.8 | 540.3 | |
| 130.6 | -8.7 | -457.3 | -608.9 | -4.6 | -24.7 | -54.7 | -0.1 | -1028.4 | |
| 0.1 | -27.1 | 46.7 | -136.8 | 126.9 | 52.8 | 18.6 | 40.2 | 121.4 | |
| 724.7 | -28.1 | -213.0 | -498.5 | 125.5 | 40.8 | 17.9 | 39.8 | 209.0 | |
| 7105.7 | 0.0 | 0.9 | 0.3 | 0.0 | 0.0 | 0.0 | 0.0 | 7106.9 | |
| -266.4 | -214.8 | -840.7 | -936.8 | -30.8 | -107.4 | -334.0 | -147.7 | -2878.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






