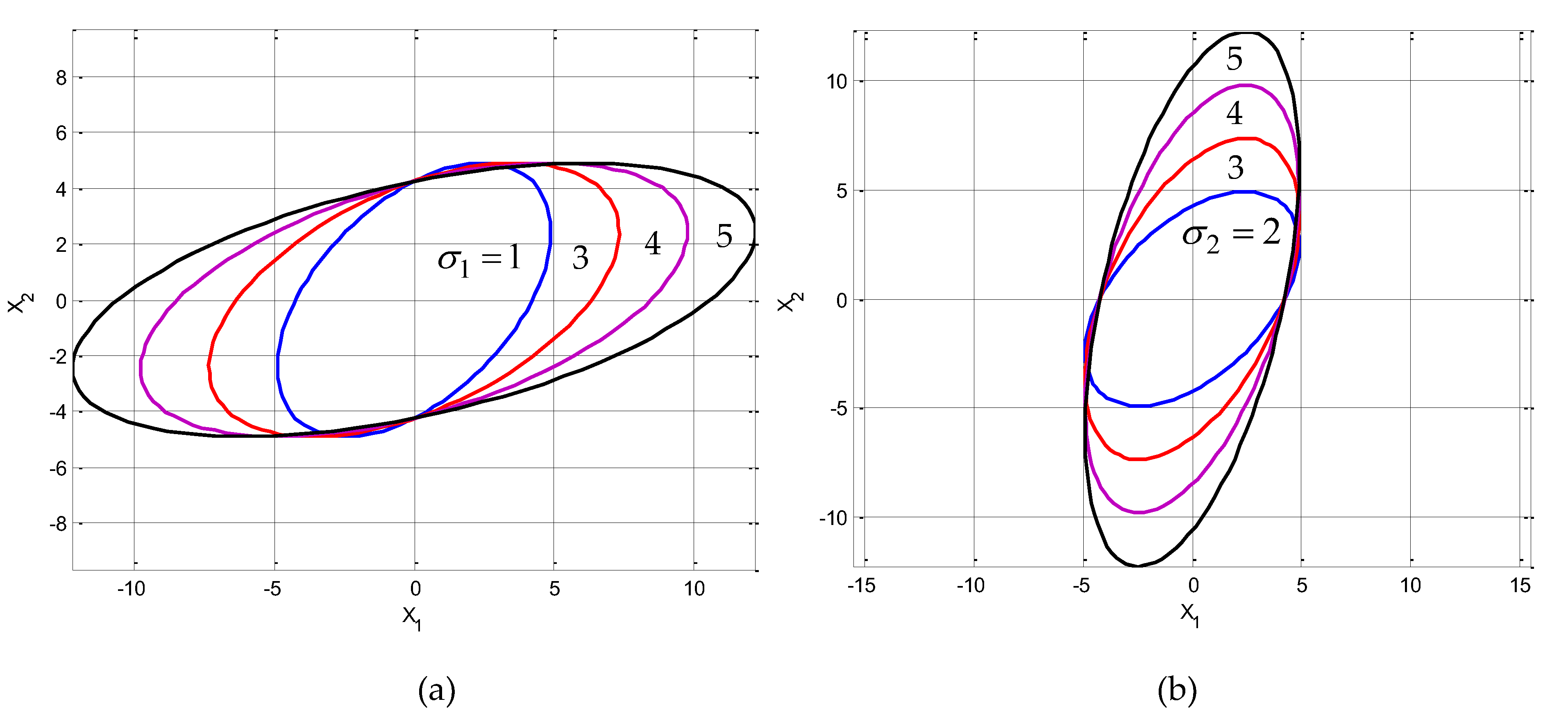1. Introduction
Understanding the ways knowledge concerning an external variable, or the reciprocal information of its parts, is distributed across the parts of a multivariate system can assist characterize and infer the underlying mechanics and function of the system. This goal has driven the development of several techniques for dissecting the elements of a set of variables’ combined entropy or for dissecting the contributions of a set of variables to the mutual information about the variable of interest. In actuality, this association and its modifications exist for any input signal and the widest range of Gaussian pathways, comprising discrete-time and continuous-time pathways in scalar or vector forms.
In a more general way, mutual information and mean-square error are the fundamental concepts of information theory and estimating theory, respectively. In contrast to the MMSE, which determines how precisely each input sample can be restored using the channel’s outcomes, the input-output mutual information is an estimation of whether the information can be consistently delivered over a channel given a specific input signal. An inactive functioning characterization for mutual information is provided by the substantial relevance of mutual information to estimate and filtering. Therefore, the significance of identity is not only obvious, but the link is also fascinating and merits an in-depth explanation [
1,
2,
3]. Relations between the MMSE of the approximation of the output given the input and the localized actions of the mutual information at diminishing SNR are presented in [
4]. [
6] gives the idea about the probabilistic ratios of geometric characteristics of signal detection in Gaussian noise. Furthermore, whether in a continuous-time [
5,
6,
7] or discrete-time setting [
8] context, the likelihood ratio is difficult in the relationship between observation and estimation [
9].
Considering the specific instance of parametric computation (or Gaussian inputs), correlations relating to causal and non-causal estimation errors have been investigated in [
10,
11], involving the limit on the loss owing to the causality restriction is specified. Knowing how data pertaining of an external parameter, or inversely related data within its parts, distributes across the parts of a multivariate system can assist categorize and determining the fundamental mechanics and functionality of the structure. This goal served as the impetus for the development of various techniques for decomposing the various elements of a set of parameters’ joint entropy [
12,
13] or to deconvolute the additions of a set of elements to the mutual information about a target variable [
14]. These techniques can be used to examine a variety of intricate systems, including those in the physical distinctions domain, such as gene networks [
15] or brain coding [
16], as well as those in the social domain, such as selection agents [
17] and community behavior [
18]. They can also be used to analyze artificial agents [
19]. Additionally, some new proposals diverge more significantly from the original framework, either through the adoption of novel principles, the consideration of the presence of detrimental elements linked to erroneous, or the implementation of joint entropy subdivisions in place of mutual information [
20,
21].
In the multivariate scenario, the challenges of breaking down mutual information into redundancy and complimentary sections have nevertheless been significantly increased. The novel redundancy determines that were initially developed are only defined for the bivariate situation [
24,
25], or allow negative components [
26], whereas measurements of coordination are more readily extended to the multivariate case, especially when using the maximum entropy architecture [
22,
23]. By either utilizing the associations between lattices formed by various numbers of parameters or utilizing the multiple interactions between redundant lattices and information loss lattices, for which collaborative efforts are more actually defined, the study in [
27] established two analogous techniques for constructing multivariate redundant metrics. The maximum entropy framework allows for a more straightforward generalization of the efficiency measurements to the multivariate case [
24,
25].
In the present study, we propose an extension of the bivariate Gaussian distribution technique to calculate multivariate redundant metrics inside the maximum entropy context. The importance of the maximum entropy approach in the bivariate scenario, where it offers constraints for the actual redundancy, unique information, and efficiency terms under logical presumptions shared by additional criteria, acts as the motivation for this particular focus [
24]. The maximum entropy measurements, specifically, offer a lower limit for the actual cooperation and redundant terms and a higher limit for the actual specific information if it is presumed that a bivariate non-negative disintegration exists and that redundancy can be calculated from the bivariate distributions of the desired outcome with every source. Furthermore, if these bivariate distributions are consistent with possibly having little interaction under the previous hypotheses, then the maximum entropy decomposition returns not only boundaries but also the precise actual terms. Here, we demonstrate that, under similar presumptions, the maximum entropy reduction also plays this dominant role in the multivariate situation.
The remainder of this paper is organized as follows. A brief review of the geometry of the Gaussian distribution is reviewed in
Section 2. The
consecutive three sections deal with various important topics on information entropy with illustrative examples with emphasis on visualization of the information and discussion. In
Section 3, continuous entropy/differential entropy is presented. In
Section 4, the relative entropy (Kullback-Leibler divergence) is presented. Mutual information is presented in
Section 5. Conclusions are given in
Section 6.
2. Geometry of the Gaussian Distribution
In this section, the background relations on Gaussian distribution for different parametric point of view has been discussed. The exploratory analysis’s fundamental objective is to identify “the framework” in multivariate datasets. Ordinary least-squares regression and principal component analysis (PCA), respectively, offer typical measurements for dependency (the predicted connection between particular components) and rigidity (the degree of prominence of the probability density function (pdf) around a low-dimensional axis) for bivariate Gaussian distributions. Mutual information, an established measure of dependency, is not an accurate indicator of rigidity since it is not invariant with an opposite rotation of the parameters. For bivariate Gaussian distributions, a suitable rotating invariant compactness measure is constructed and demonstrated to reduce the corresponding PCA measure.
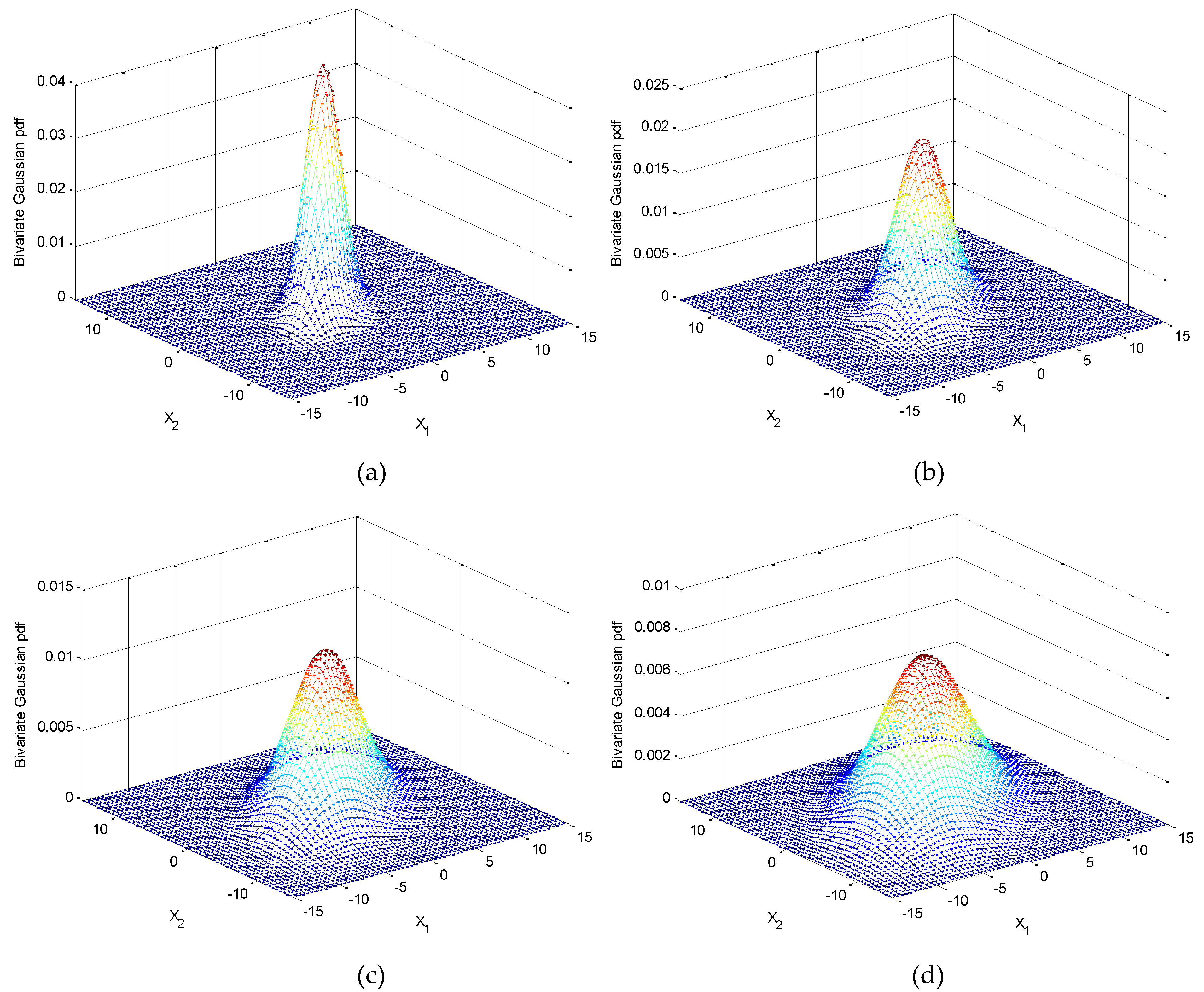
The Gaussian pdf (a) does not have a framework in either of the above-described definitions and represents the independent variables without any settling around a lower-dimensional region. The Gaussian pdf (b), on the other hand, has greater variance along one axis over another. Despite being independent, their combined pdf is small. Although the variables are associated and therefore likewise characterized by dependency, the Gaussian pdf (c) is equally focused around one dimension as is (b).
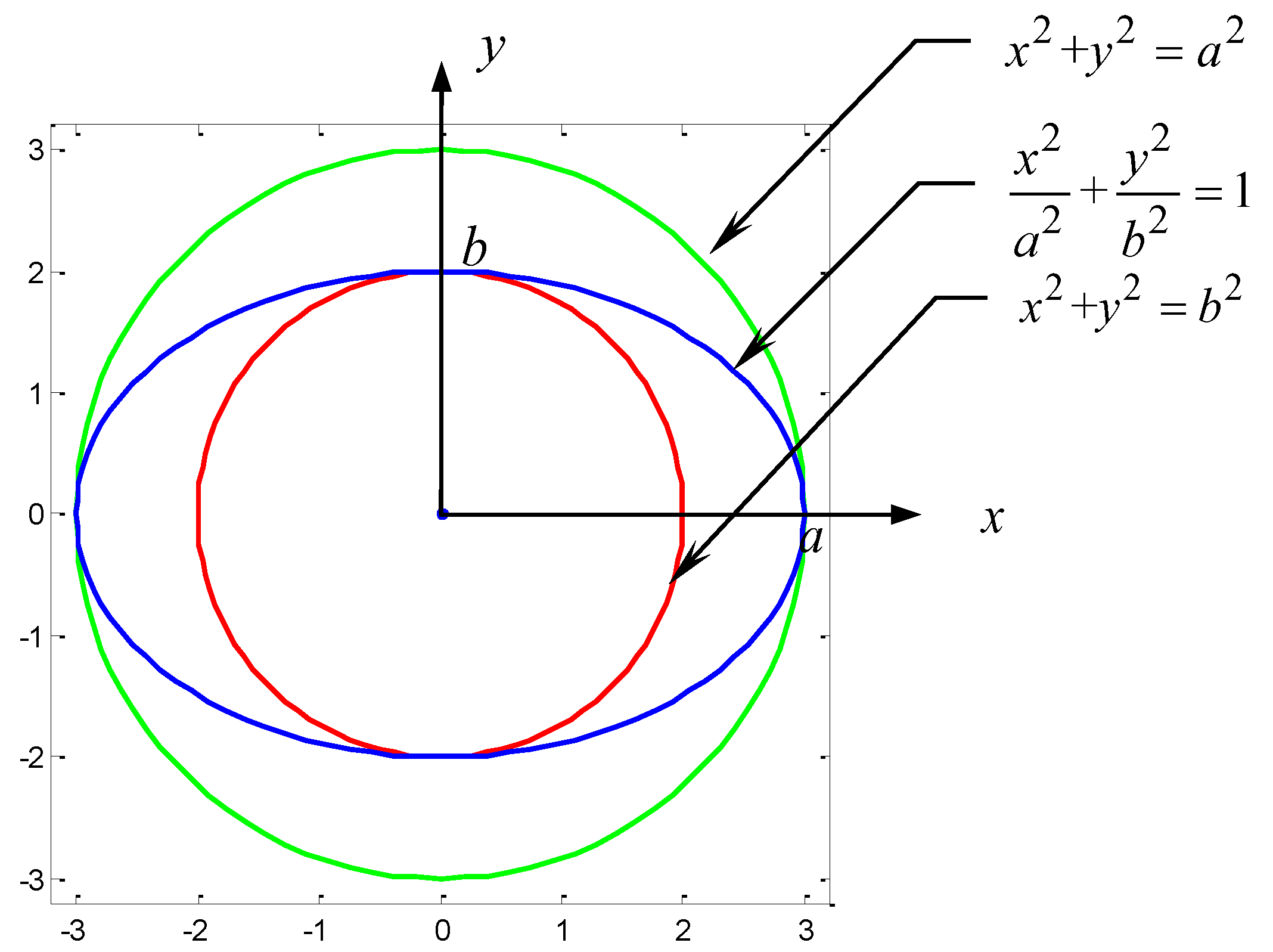
2.1. Standard Parametric Represenatation of an Ellipse
If the data is uncorrelated and therefore has zero covariance, the ellipse is not rotated and axis aligned. The radii of the ellipse in both directions are then the variances. Geometrically, a not rotated ellipse at point (0,0) and radii
and
for the
- and
-direction is described by
Figure 1 represents the construction of single points of an ellipse is due to de La Hire. It is based on the standard parametric representation.
The general probability density function for the multivariate Gaussian is given by
where
,
is symmetric, positive semi-definite matrix. If
is the identity matrix, then the Mahalanobis distance reduces to the standard Euclidean distance between
and
.
For bivariate Gaussian distributions with zero mean, the pdf can be expressed as
and mean and covariance matrix are given by
respectively, where the linear correlation coefficient
.
Variance measures the variation of a single random variable, whereas covariance is a measure of how much two random variables vary together. With the covariance we can calculate entries of the covariance matrix, which is a square matrix. In addition, the covariance matrix is symmetric. The diagonal entries of the covariance matrix are the variances, however the other entries are the covariances. Due to this cause, the covariance matrix is often called as the variance-covariance matrix.
2.2. The Confidence Ellipse
A typical way to visualize two-dimensional Gaussian distributed data is plotting a confidence ellipse. The distance
is a constant value referred to as the Mahalanobis distance, which is a random variable distributed by the chi-squared distribution, denoted as
where
is the number of degree of freedom and
is the given probability related to the confidence ellipse. For example, if
95% confidence ellipse is defined. Extension from Equation (1), the radius in each direction is the standard deviation
and
parametrized by a scale factor
s, known as the Mahalanobis radius of the ellipsoid:
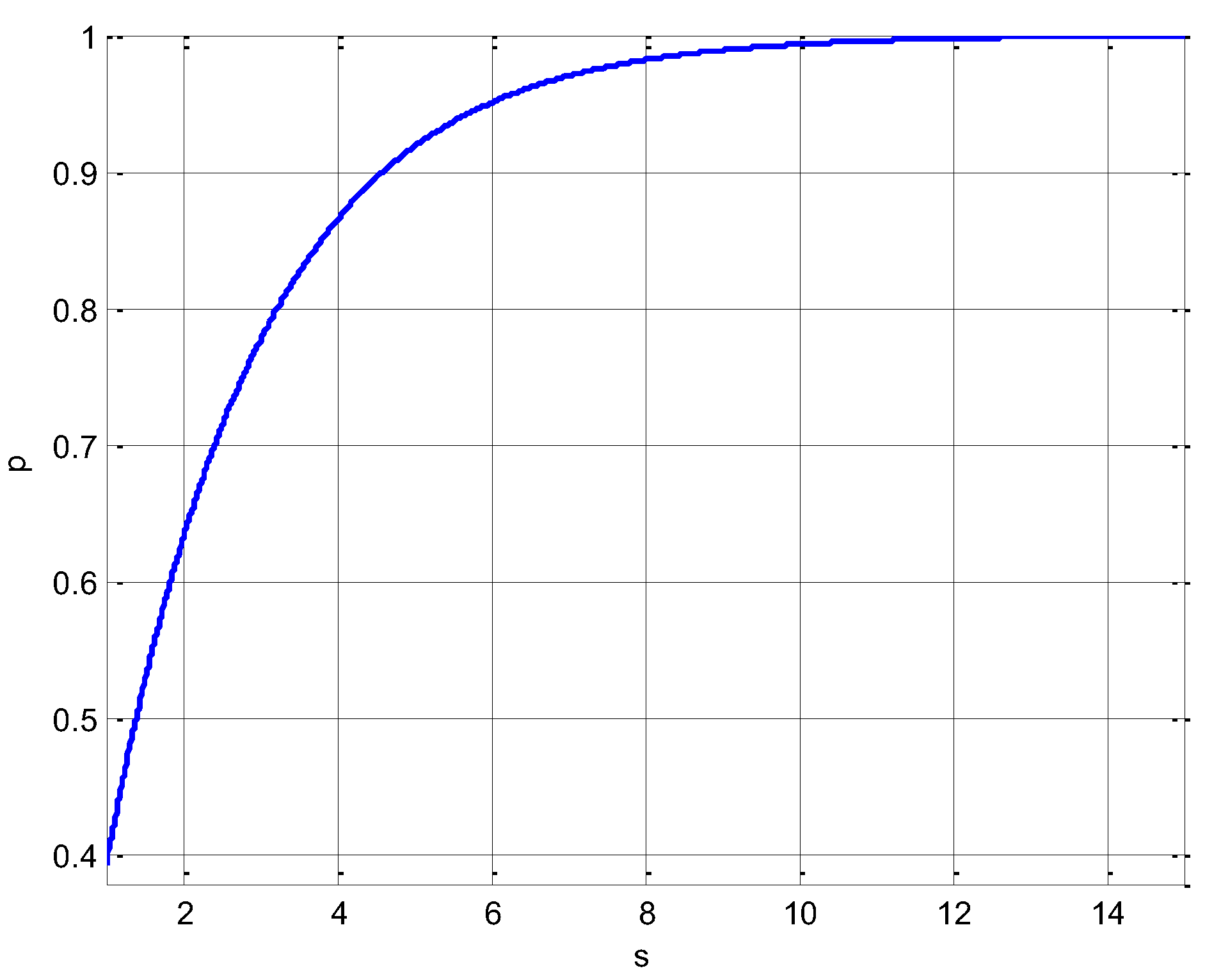
The goal must be to determine the scale s such that confidence p is met. Since the data is multivariate Gaussian distributed, the left hand side of the equation is the sum of squares of Gaussian distributed samples, which follows a χ2 distribution. A χ2 distribution is defined by the degrees of freedom and since we have two dimensions, the number of degrees of freedom is also two. We now want to know the probability that the sum and therefore s has a certain value under a χ2 distribution.
This ellipse, also a probability contour, defines the region of a minimum area (or volume in multivariate case) containing a given probability under the Gaussian assumption. This equation can be solved using a χ2 table or simply using the relation. The confidence interval can be evaluated through. For, we have. Furthermore, typical values include, , and for , , and , respectively. The ellipse can then be drawn with radii and .
Figure 2.
Relation of the confidence interval and the scale factor s.
Figure 2.
Relation of the confidence interval and the scale factor s.
The Mahalanobis distance accounts for the variance of each variable and the covariance between variables.
Geometrically, it does this by transforming the data into standardized uncorrelated data and computing the ordinary Euclidean distance for the transformed data. In this way, the Mahalanobis distance is like a univariate z-score: it provides a way to measure distances that takes into account the scale of the data.
In the general case, covariances and are not zero and therefore the ellipse-coordinate system is not axis-aligned. In such case, instead of using the variance as a spread indicator, we use the eigenvalues of the covariance matrix. The eigenvalues represent the spread in the direction of the eigenvectors, which are the variances under a rotated coordinate system. By definition a covariance matrix is positive definite therefore all eigenvalues are positive and can be seen as a linear transformation to the data. The actual radii of the ellipse are and for the two eigenvalues and of the scaled covariance matrix .
Based on Equations (3) and (7), the bivariate Gaussian distributions can be represented as
Level surface of
are concentric ellipses
where
is the Mahalanobis distance possessing the following properties:
It accounts for the fact that the variances in each direction are different.
It accounts for the covariance between variables.
It reduces to the familiar Euclidean distance for uncorrelated variables with unit variance.
The length of the ellipse axes are a function of the given probability of the chi-squared distribution with 2 degrees of freedom
, the eigenvalues
and the linear correlation coefficient
. If
95% confidence ellipse is defined by
where
As denotes a symmetric matrix, the eigenvectors of is linearly independent (or orthogonal).
2.3. Similarity Transform
The simplest similarity transformation method for eigenvalue computation is the Jacobi method which deals with the standard eigenproblems. In the multivariate Gaussian distribution, the covariance matrix
can be expressed in terms of eigenvectors
where
are the eigenvectors of
and
is the diagonal matrix of the eigenvalues
Replacing
by
, the square of the difference can be written as:
as
. Denoting
the square of the difference can then be expressed as:
If the above equation is further evaluated, the resulting equation is the equation of an ellipse aligned with the axis
and
in the new coordinate system.
The axes of the ellipse are defined by axis with a length and axis with a length .
When
, the eigenvectors are equal to
and
. Also,
matrix whose elements are the eigenvectors of
becomes an identity matrix. The final equation of an ellipse is then defined by
It is clear from the equation given above that the axes of the ellipse are parallel to the coordinate axes. The lengths of the axes of the ellipse are then defined as and .
The covariance matrix can be presented by its eigenvectors and eigenvalues: , where is the matrix whose columns are the eigenvectors of and is the diagonal matrix with diagonal elements given by the eigenvalues of . Transformation is performated based on the three steps involving scaling, rotation, and translation.
The coariance matrix can be written as , where is a diagonal scaling matrix .
- 2.
Rotation
is generalized from the normalized eigenvectors of the covariance matrix
.
Note that
is an orthogonal matrix
, and
. Define the matrix with rorartion and scaling
,
. The covariance matrix can thus be written as
and
being diagonal with eigenvalues
. Since
, we have
.
The similarity transform is applied to obtain the relation
, and the pdf of
vector can be found to be
The ellipse in the transformed frame can be represented as
where the eigenvectors are equal to
and
.
- 3.
Translation
The eigenvalues
can be calculated through
and thus
From other view point for calculation of covariance matrix
Claculation for the determinant of covariance matrix above gives the same result and the inverse is
2.4. Simulation with a Given Variance-covariance Matrix
Given the data
, an ellipse representing the confidence
p can be plotted by calculating the radii of the ellipse, its center and rotation. Specify
(by which
can be obtained) and
for generating the covariance matrix
, thus
can be derived. The inclination angle is calculated through:
which can be used in calculation of
and the covariance can be evaluated by:
if
is specified. On the other way, given the correlation coefficient
and variances for generating the covariance matrix
, thus
can be obtained.
To generate the sampling points that meet the specified correlation, the following procedure can be followed. Given two random variables
and
, their linear combination
. As for the generation of correlated random variables, if we have two Gaussian, uncorrelated random variables
,
then we can create 2 correlated random variables using the formula
and then
will have a correlation
with
:
Based on the relation:
,
, the following equation can be employed to generate the sampling points for the scatter plots using the Matlab software:
where the Cholesky decomposition of
has a lower triangular matrix for
,
and
is the vectors of mean values .
When
, the axes of the ellipse are parallel to the original coordinate system and when
, axes of the ellipse are aligned with the rotated axes in the transformed coordinate system.
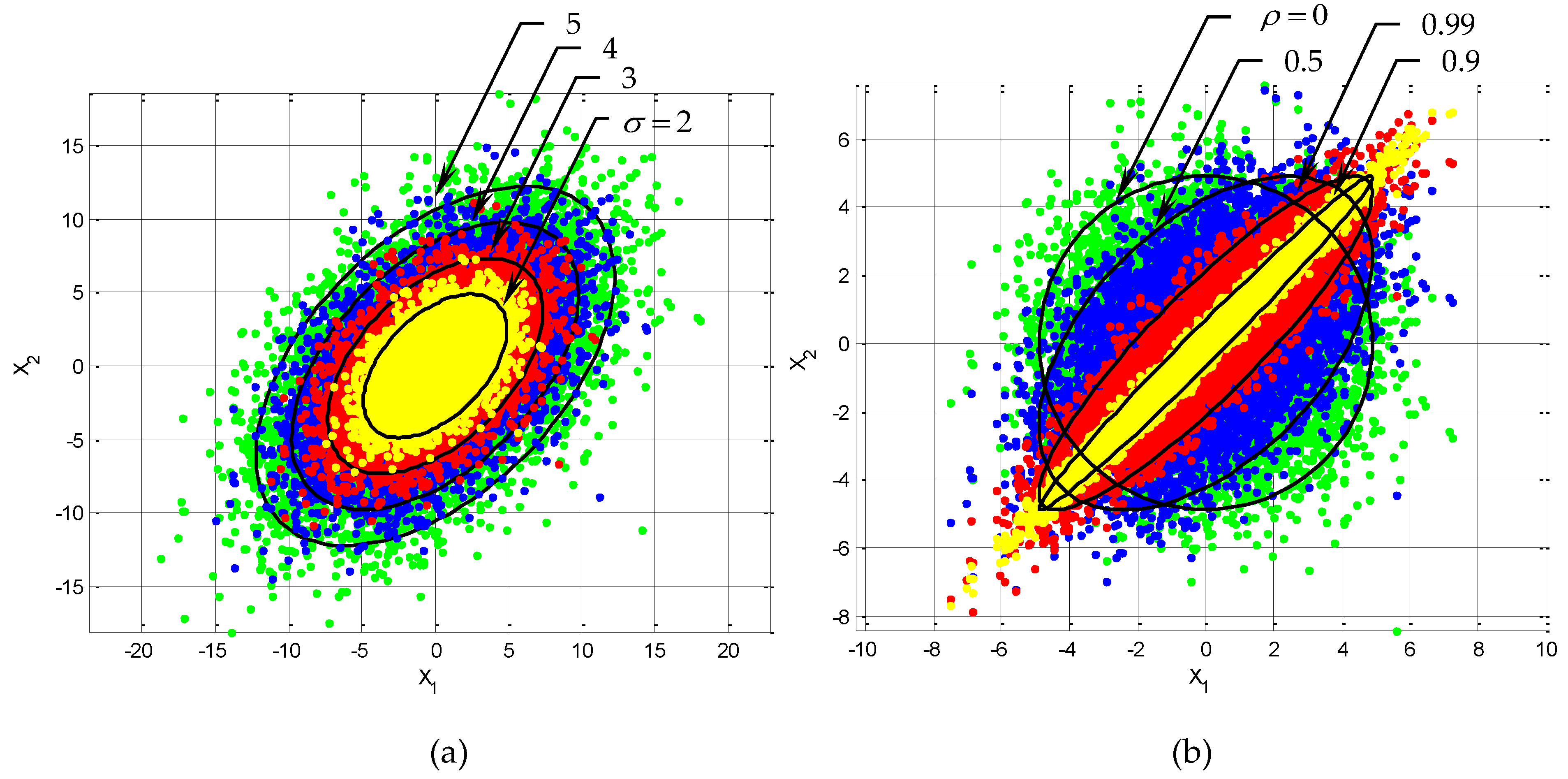
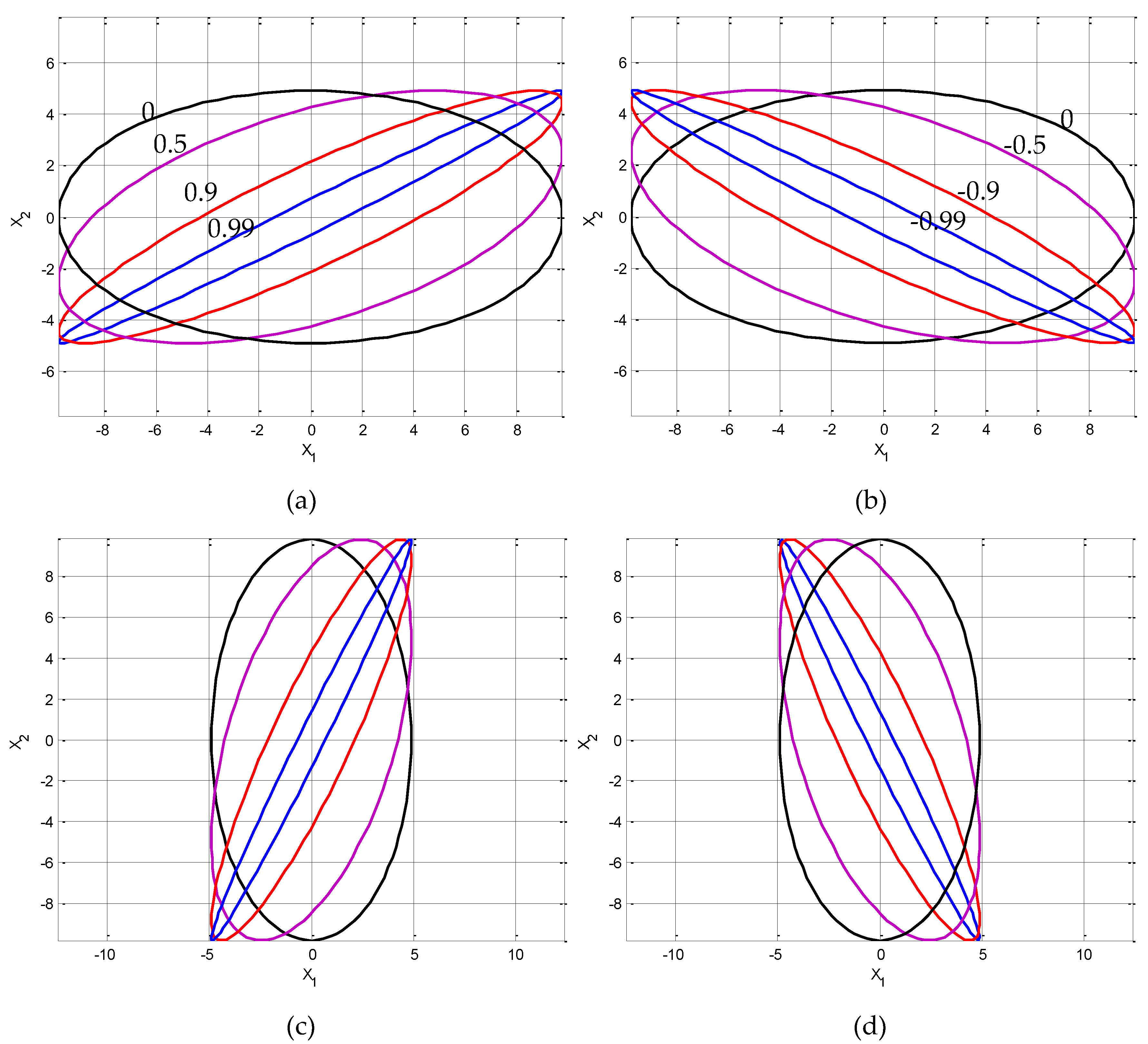
Figure 3 and
Figure 4 display ellipses drawn for various levels of confidences. The plots provide illustration of confidence (error) ellipses with different confidence levels (i.e., 68%,
; 90%,
; 95%,
; 99%,
from inner to outer ellipses), considering the cases where the random variables are (1) positively correlated
, (2) negatively correlated
, and (3) independent
. More specifically, in
Figure 3, the position of ellipse with various correlation coefficient given by the angel of inclination, specify
to obtain
,
: (a)
,
; (b)
,
; (c)
,
, respectively. On the other hand, in
Figure 4, the position of ellipse with various values of correlation constant given the angel of inclination, specify
to obtain
: (a)
,
; (b)
,
; (c)
,
, respectively. Rotation angle is measrued
with respect to the positive axis. When
, the angle is in the first quadrant and
, the angle is in the second quadrant.
In the following, two scenarios cases invloving more illustrations will be visited.
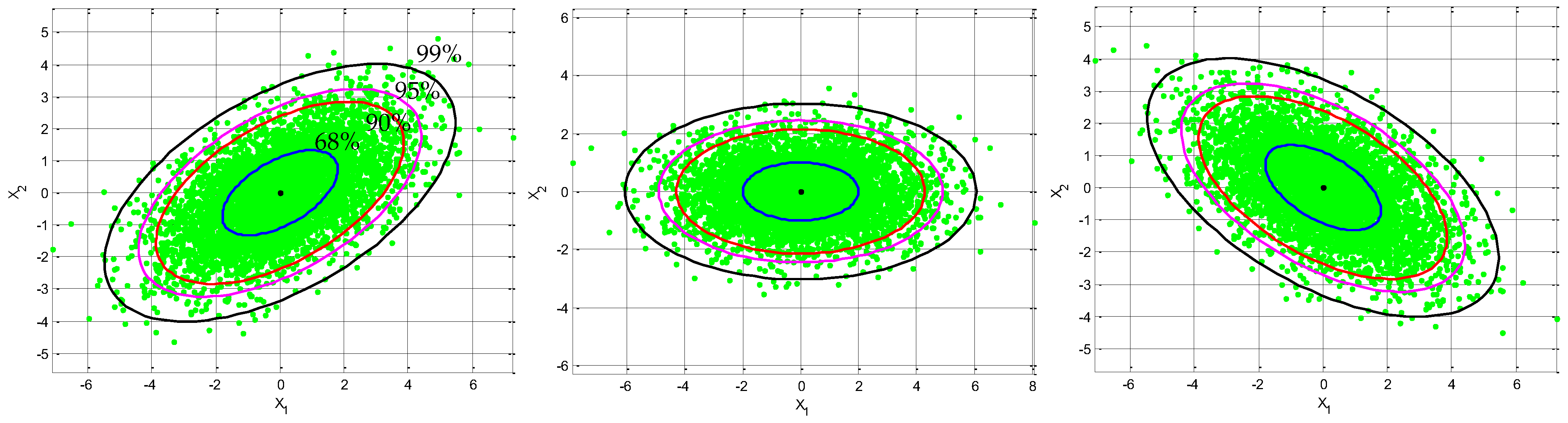
(1) Equal variances for two random variables with nonzero :
Case 1: Fixed correlation coefficient. As a example, when
, and the variances
are ranging from
, as shown in
Figure 5. As can be seen, the contours and the scatter plots are ellipses instead of circles.
Subplot (a) in
Figure 6 shows the ellipses for
with varying variances. In the present and
subsequent illustartions, 95% confidence levels are shown.
Case 2: Increasing correlation coefficient
from zero correlation. With fixed variance
, the contour will initially be a circle when
and then an ellipse as
increases when
. Sbuplot (b) in
Figure 6 provides the contours with scatter plots for
, respectively when
. The eccestricity of the ellipses increases with the increase of
.
(2) Unequal variances for two random variables,
with fixed correlation coefficient.
Case 1:
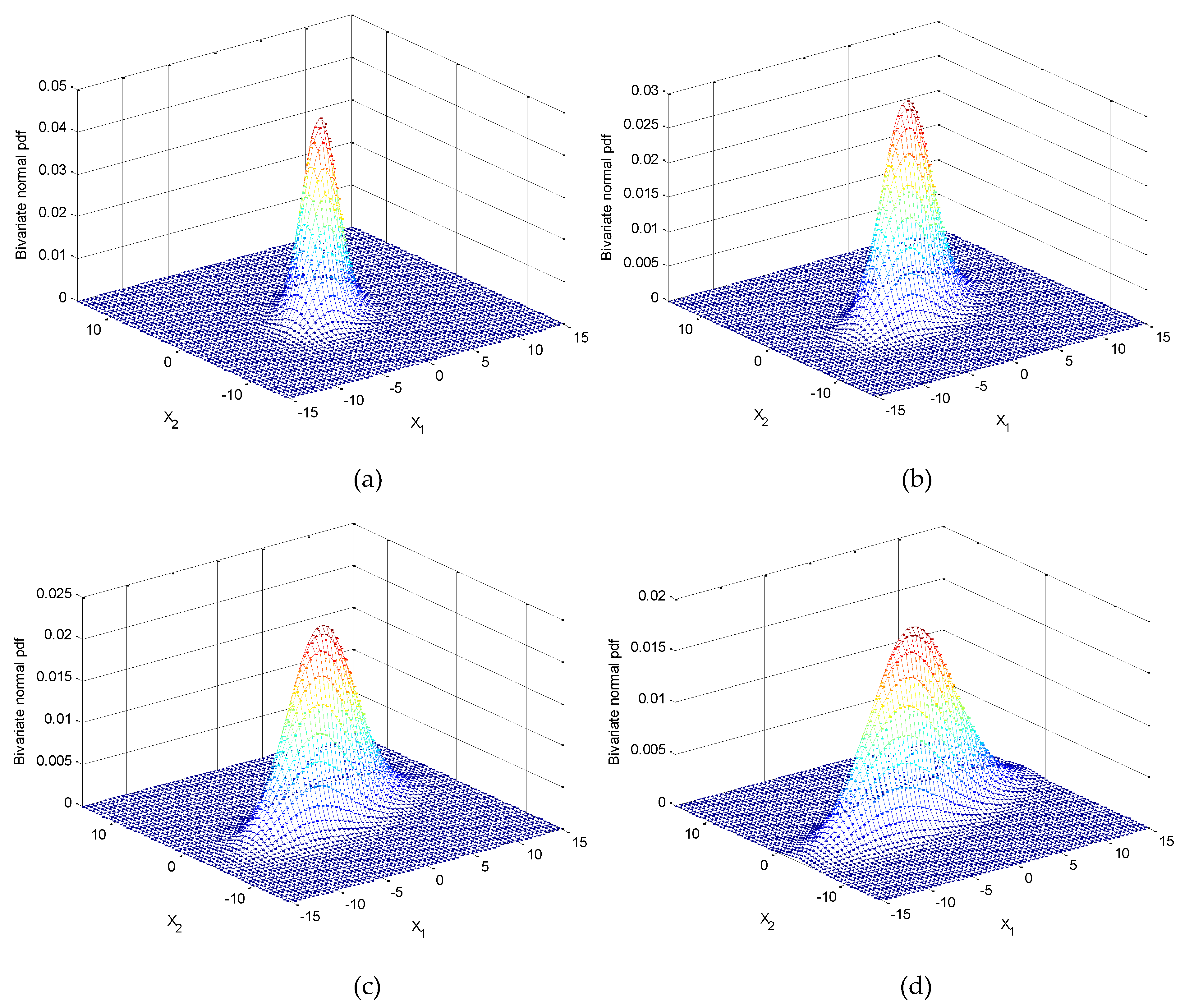
. The variation of three dimensional surfaces and ellipses are presented in
Figure 7 and
Figure 8a with the increase of
, where
and
.
Case 2:
. The variation of the ellipses are presented in
Figure 8b with the increase of
, where
and
.
Figure 9 shows the variation of inclination angle as a function of
and
, for
and
for providing further insights on the variation of inclination angle
with respect to
and
.
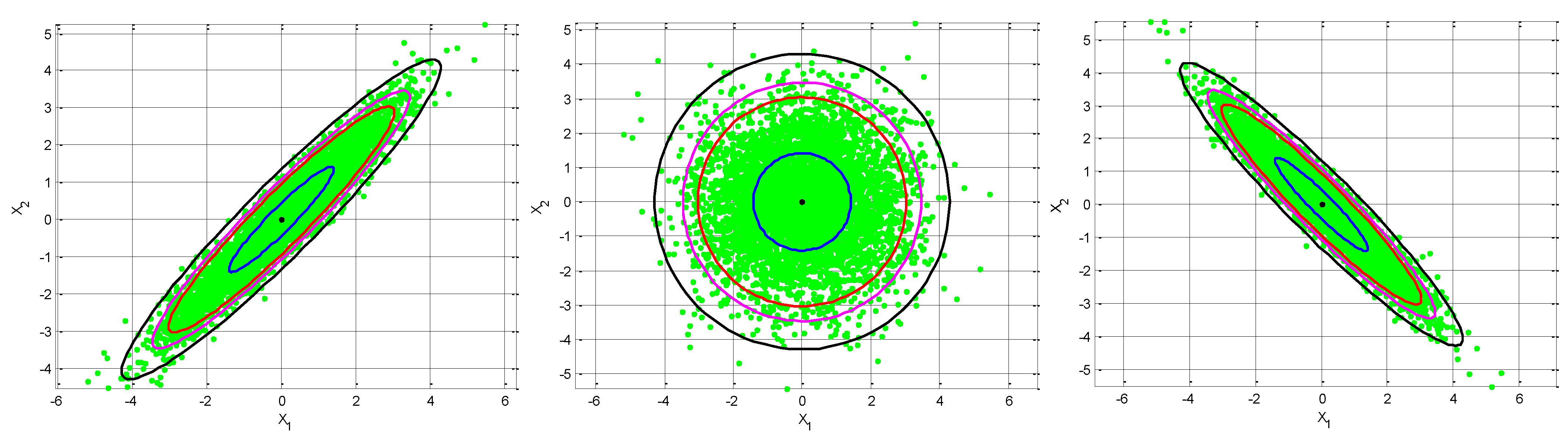
(3) Variation of the ellipses for the various positive and negaive correlation. For a given variance, when
is specified, thus the eigenvalues and the inclination angle are obtained accordingly.
Figure 10 presents results for the cases of
(
,
in this example) and
(
,
in this example) with various correlation coefficients (namely, positive, zero, and negative) including
and
. In the figure,
,
are applied for the top plots; while
,
are applied for the bottom plots. On the other hand,
are applied for the left plots; while
are applied for the left plots. Furthermore,
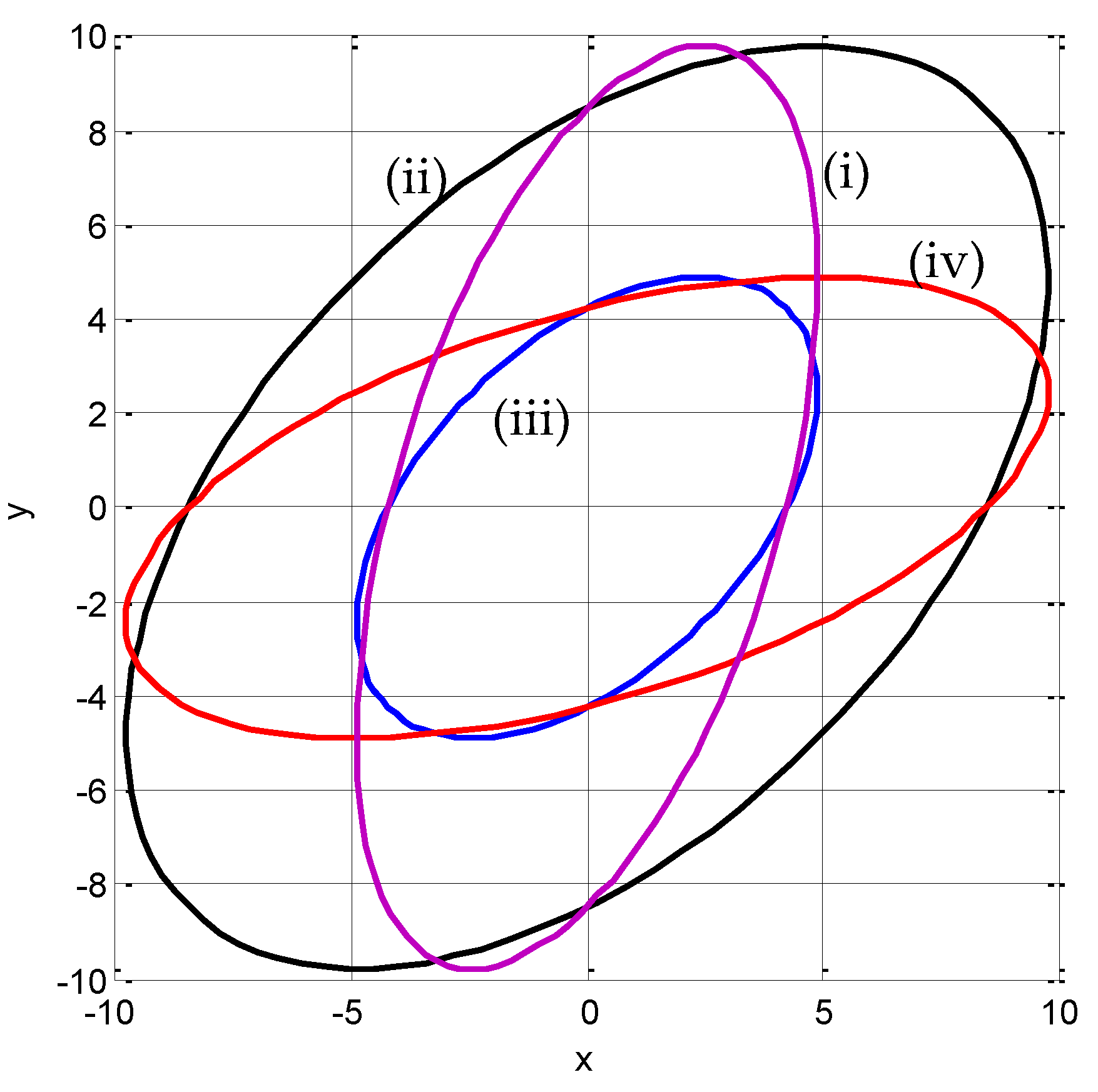
Figure 11 provides comparsion of the ellipses for various
and
for the following cases: (i)
,
; (ii)
,
; (iii)
; (iv)
, while fived
.
3. Continuous Entropy/Differential Entropy
Differential entropy (also referred to as continuous entropy) is a concept in information theory that began as an attempt by Claude Shannon to extend the idea of (Shannon) entropy, a measure of average surprisal of a random variable, to continuous probability distributions. Unfortunately, Shannon did not derive this formula and rather just assumed it was the correct continuous analog of discrete entropy, but it is not.[
1]: [181–218]. The actual continuous version of discrete entropy is the limiting density of discrete points (LDDP). Differential entropy (described here) is commonly encountered in the literature, but it is a limiting case of the LDDP and one that loses its fundamental association with discrete entropy.
In the following discussion, differential entropy, and relative entropy are measured in bits, which is used in the definition. Instead, if ln is used, it is then measured in nats, and the only difference in the expression is the factor.
3.1. Entropy of a Univariate Gaussian Distribution
If we have a continuous random variable
with a probability density function (pdf)
, the differential entropy of
in bits is expressed as
Let
be a Gaussian random varialbe
The differential entropy for this
univariate Guassian distribution can be evaluated
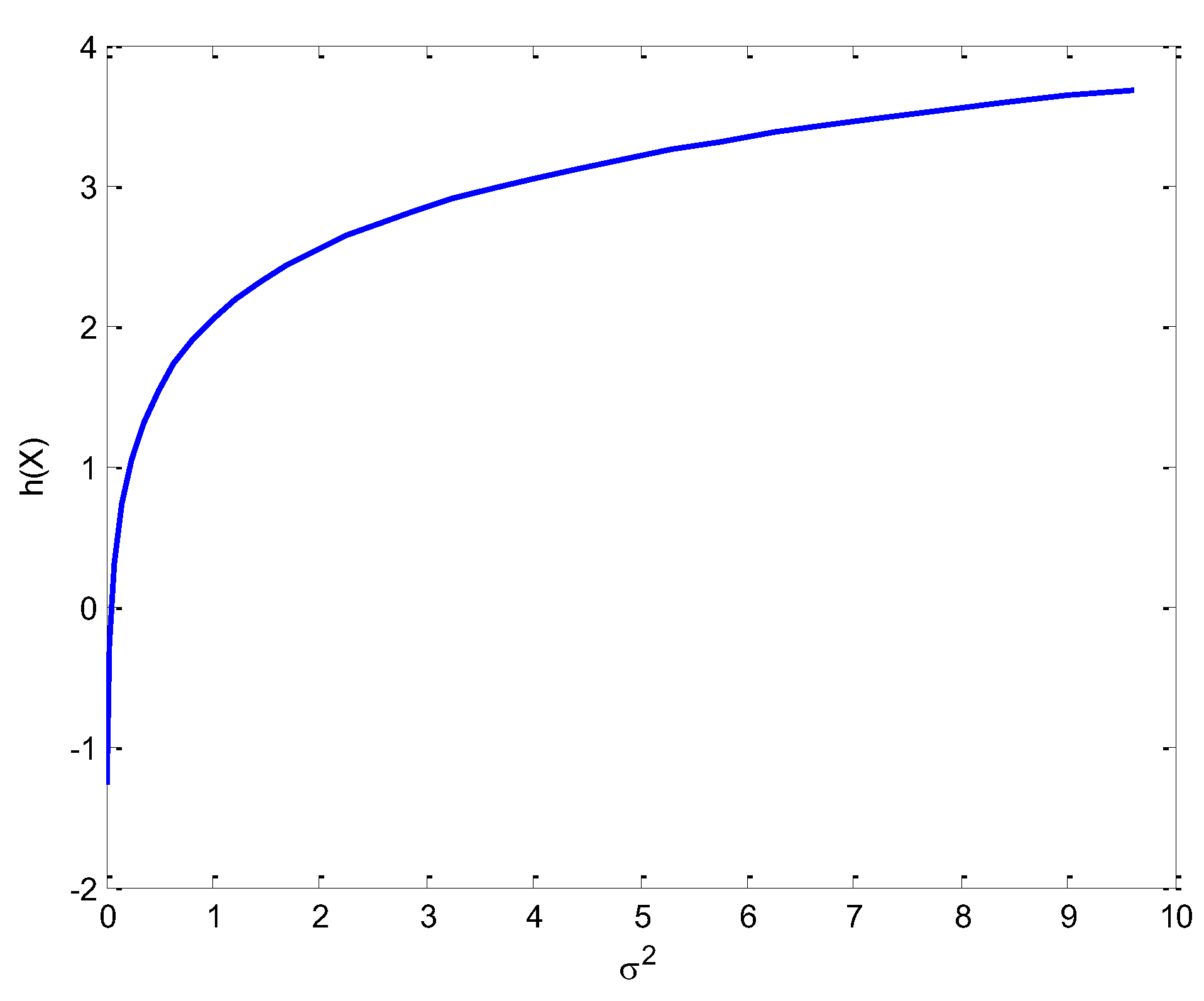
Figure 12 shows the differential entropy as a function
for the univariate Gaussian variable, which is concave downward and grows first very fast and then much slower at high values of
.
3.2. Entropy of a Multivariate Gaussian Distribution
Let
follows a
multivariate Gaussian distribution
, as given by Equation (2), then the differential entropy of
in nats is
and the differential entropy is given by (
Appendix B)
The above calculation involves the evaluation of expectation of the Mahalanobis distance as (
Appendix C)
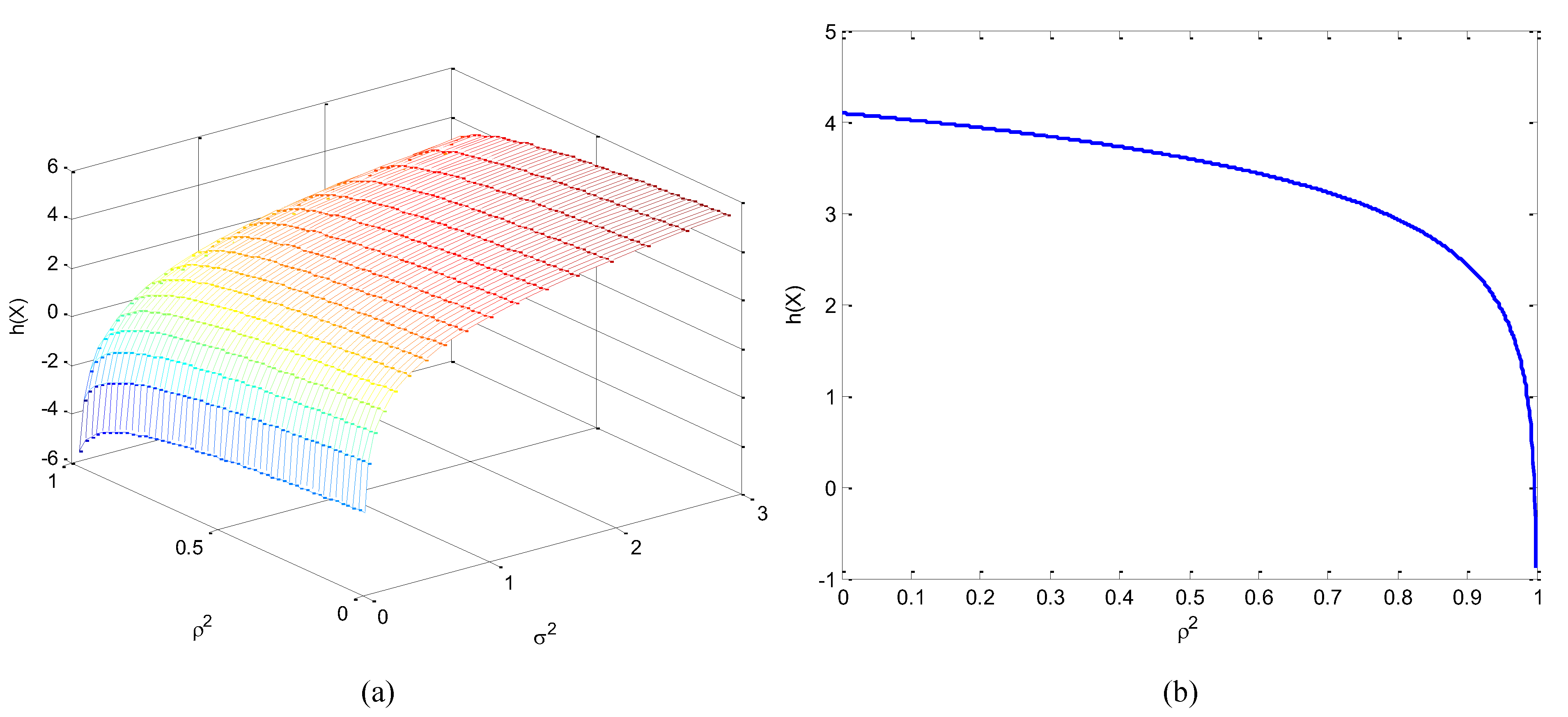
For a fixed variance, the normal distribution is the pdf that maximizes entropy. Let
be a 2D Gaussian vector, the entropy of
can be calculated to be
with covaraince matrix
If
, this becomes
which is a function of
concave downward, and grows first very fast and then much slower for high
values, shown as in
Figure 13.
3.3. The Differential Entropy in the Transformed Frame
The differential entropy is invariant to a translation (change in the mean of the pdf)
and
For a random variable vector, the differential entropy in the transformed frame remains the same as the one in the original frame. It can be shown in general that
For the case of multivariate Gaussian distribution, we have
It is known that the determinant of the covariance matrix is equal to the product of its eigenvalues:
For the case of bivariate Gaussian distribution,
, we have
It can be shown that the entropy in the transformed frame is given by
Detailed derivation are provided in
Appendix D. As discussed, the determinant of the covariance matrix is equal to the product of its eigenvalues
and thus the entropy can be presented as
The result confirms the statement that the differential entropy remains unchanged in the transformed frame.
4. Relative Entropy (Kullback-Leibler Divergence)
In this section, various important issues regarding the relative entropy (Kullback-Leibler divergence will be delivered. Despite the aforementioned flaws, there is a possibility of information theory in the continuous case. A key result is that definitions for relative entropy and mutual information follow naturally from the discrete case and retain their usefulness.
The relative entropy is a type of statistical distance that provides a measure of how one probability distribution
is different from a second, reference probability distribution
, denoted as
Detailed derivation is provided in
Appendix E. The relative entropy between two Gaussian distributions with different means and variances are given by
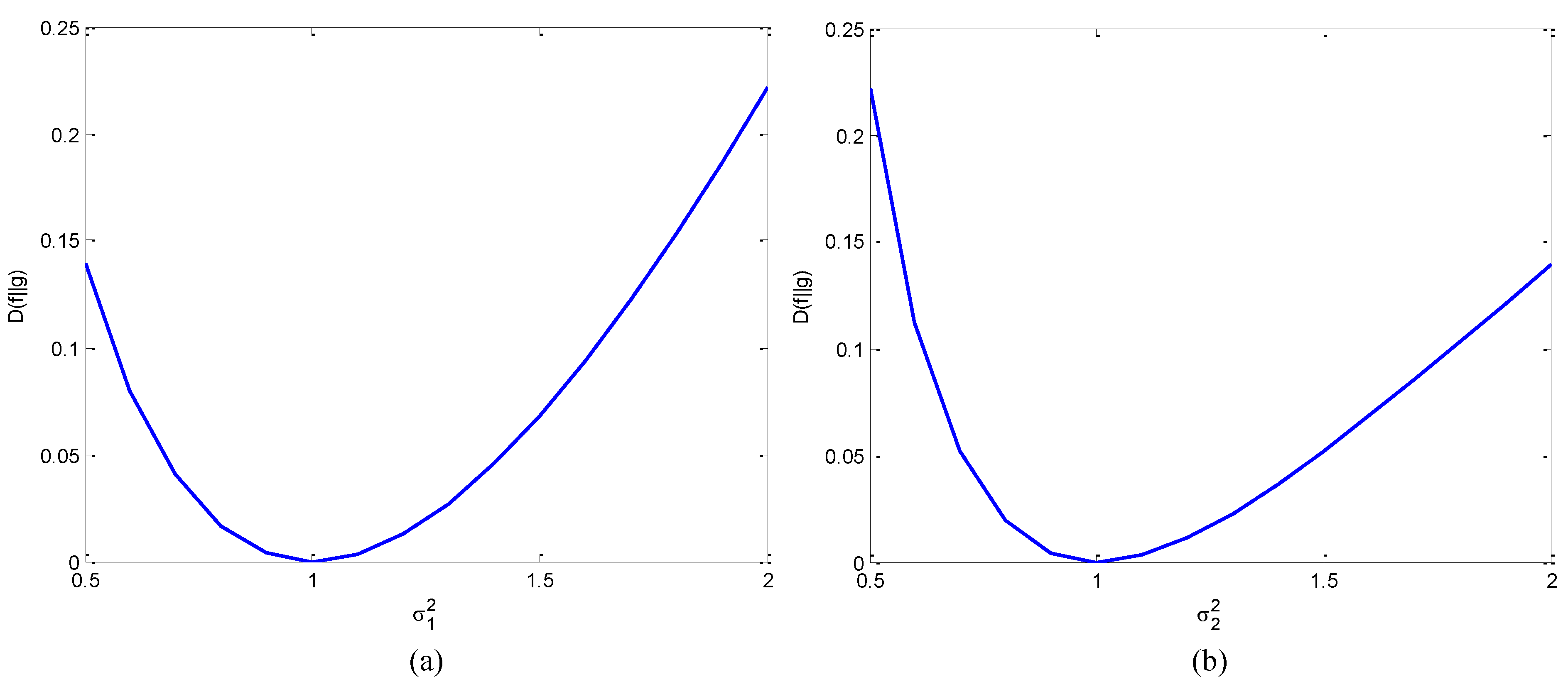
Notice that the relative entropy here is measured in bits where is used in the definition. In stead, if ln is used, it would be measured in nats. The only difference in the expression is the factor. Several conditions are discussed.
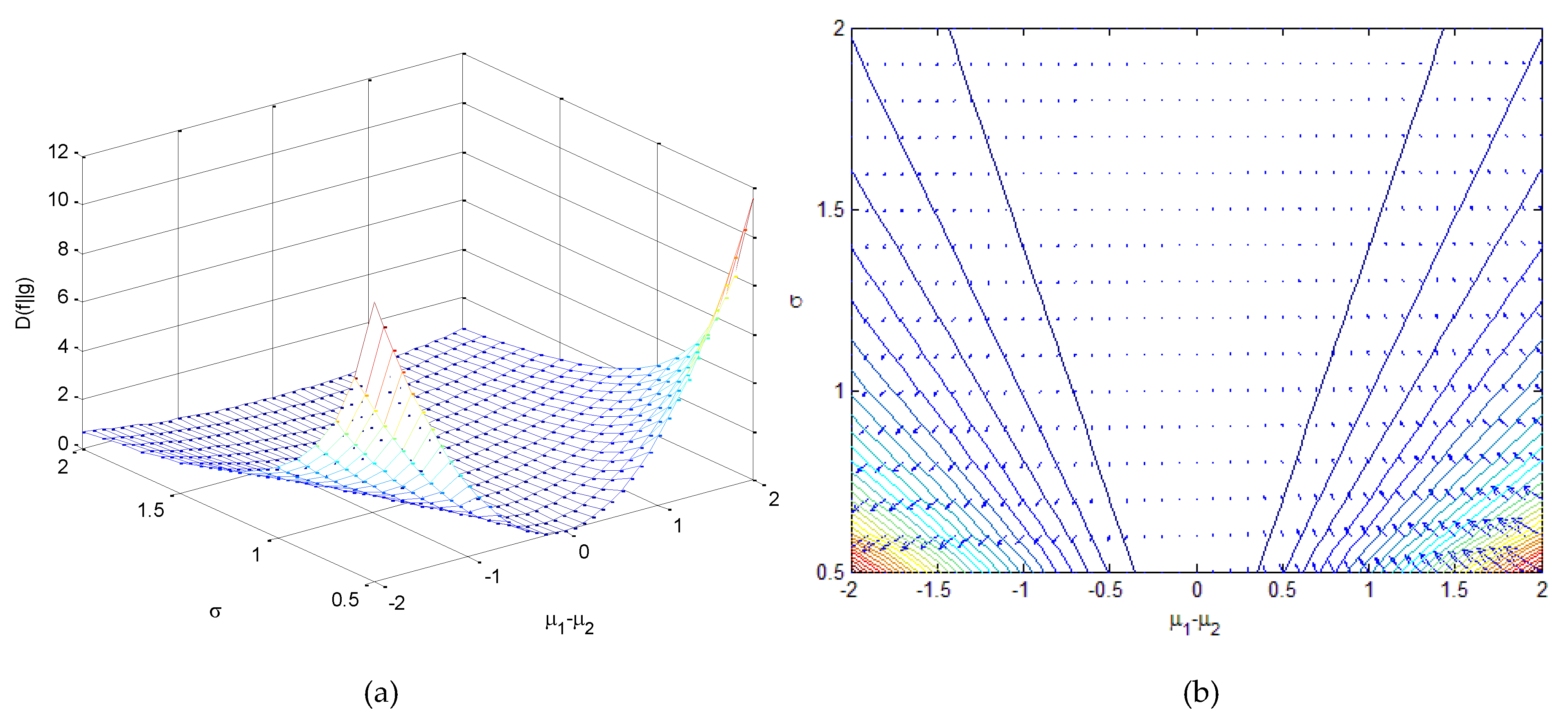
(1) If , , which is 0 when.
Figure 14.
Relative entropyas a function of and when : (a) three dimensional surface; (b) contour with entropy gradient.
Figure 14.
Relative entropyas a function of and when : (a) three dimensional surface; (b) contour with entropy gradient.
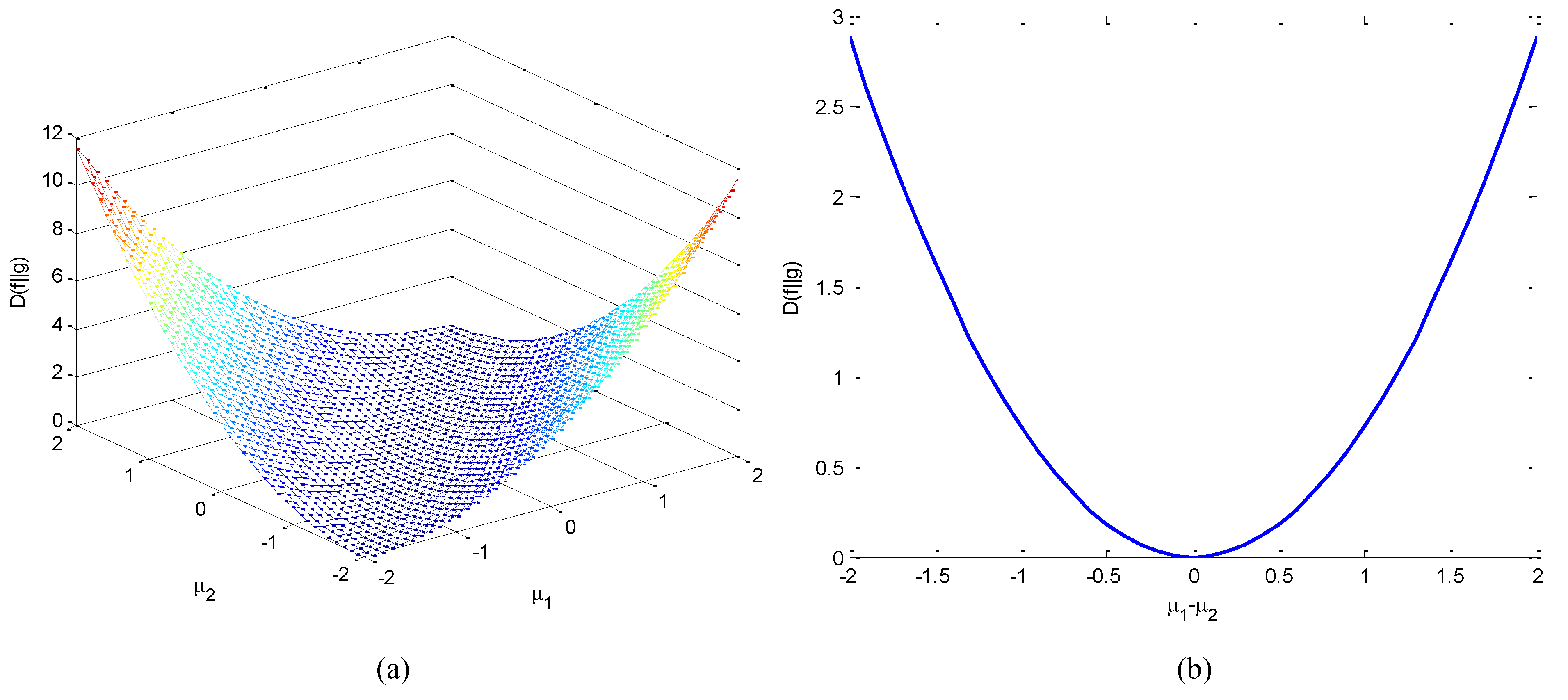
(2) If , , which is a even function with a minimum value of 0 when.
Figure 15.
Variations of relative entropy when : (a) three dimensional surface as a function of and (b) as a function of .
Figure 15.
Variations of relative entropy when : (a) three dimensional surface as a function of and (b) as a function of .
- If , , it is a function of concave upward.
- If , , it is a function of concave upward.
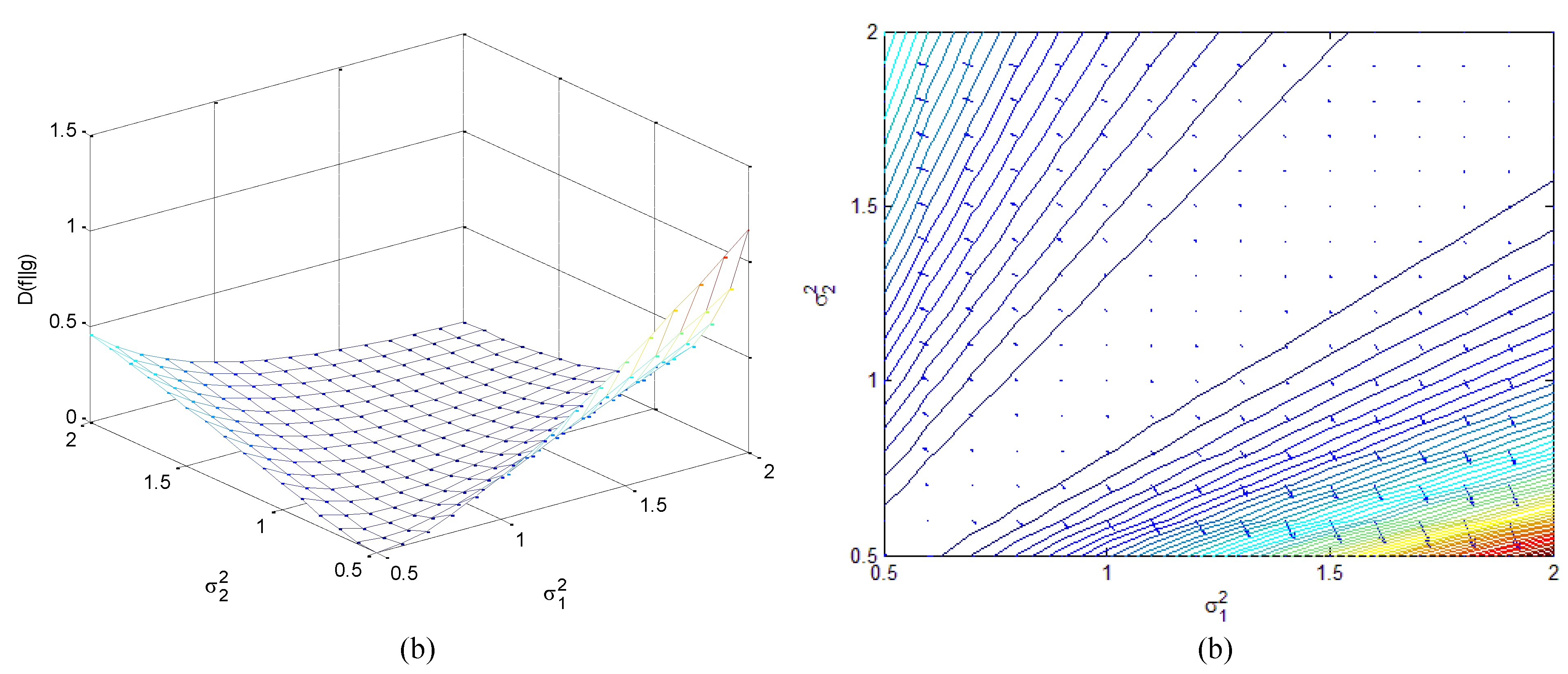
(3) If ,
Figure 17.
Relative entropy as a function of and when: (a) the three dimensional surface; (b) contour with entropy gradient.
Figure 17.
Relative entropy as a function of and when: (a) the three dimensional surface; (b) contour with entropy gradient.
- When ,
- When ,
Figure 18.
Variations of relative entropy as a function of (a) when fixed and (b) when fixed , respectively ().
Figure 18.
Variations of relative entropy as a function of (a) when fixed and (b) when fixed , respectively ().
Sensitivity analysis of the relative entropy due to change of variances and means. The gradient of
given by
can be calculated where the calculation deals with partial derivatives where the cahin rule is involved. Based on the relation
, we have
and the following derivatives are obtained.
(1)
(2)
(3)
(4)
For optimality for each of the above cases, we have
5. Mutual Information
Mutual information is one of many quantities that measures how much one random variables tells us about another. It is a dimensionless quantity with (generally) units of bits, and can be thought of as the reduction in uncertainty about one random variable given knowledge of another. The mutual information
between two variables with joint pdf
is given by
The mutual information between the random variables X and Y has the following relation
where
and
implying that
and
. The mutual information of a random variable with itself is the self information, which is the entropy. High mutual information indicates a large reduction in uncertainty; low mutual information indicates a small reduction; and zero mutual information between two random variables,
, meaning that the variables are independent. In such case,
and
.
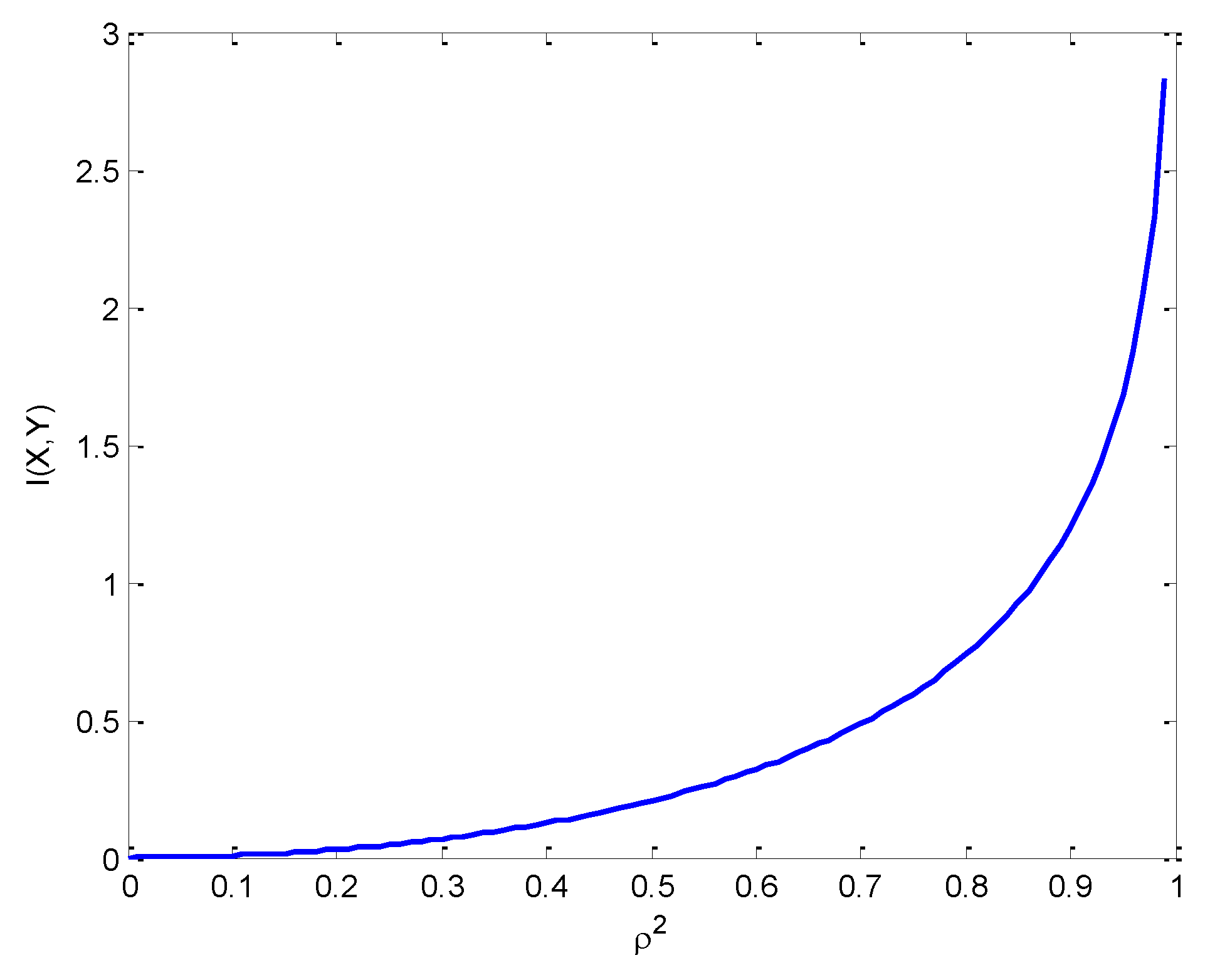
Let’s consider the mutual information between the correlated Gaussian variables
X and
Y given by
Figure 19 presents the mutual information versus
, where it grows first much slower and then very fast for high values of
. If
, the random variables X and Y are perfectly correlated, the mutually information is infinite. It can be ceen that
for
and that
for
.
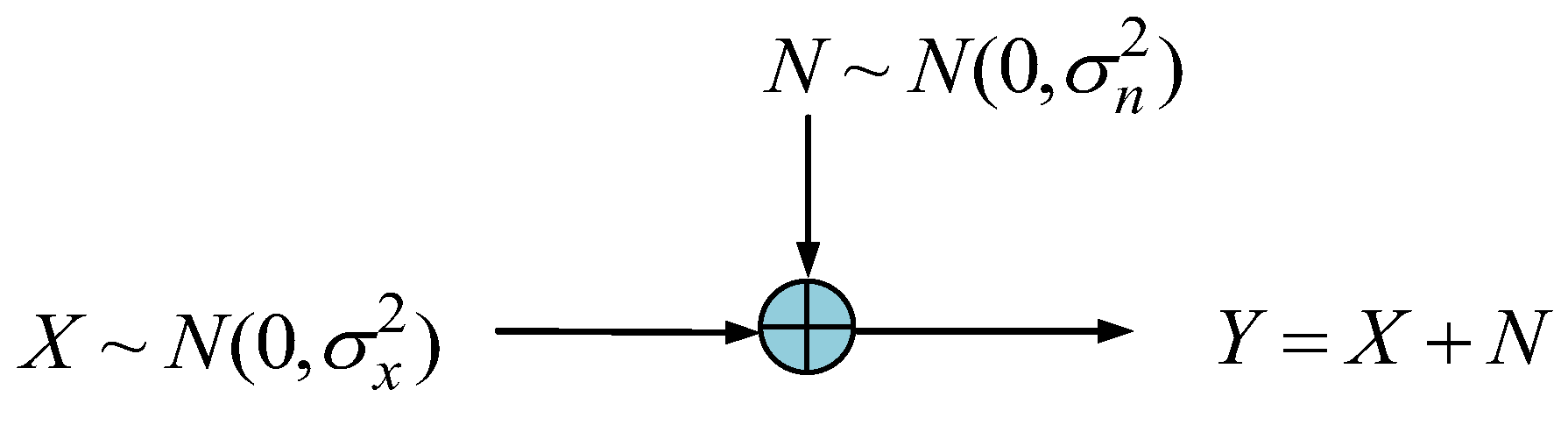
On the other hand, consider the additive white Gaussian noise (AWGN) channel shown as in
Figure 20, the mutual information is given by
where
and
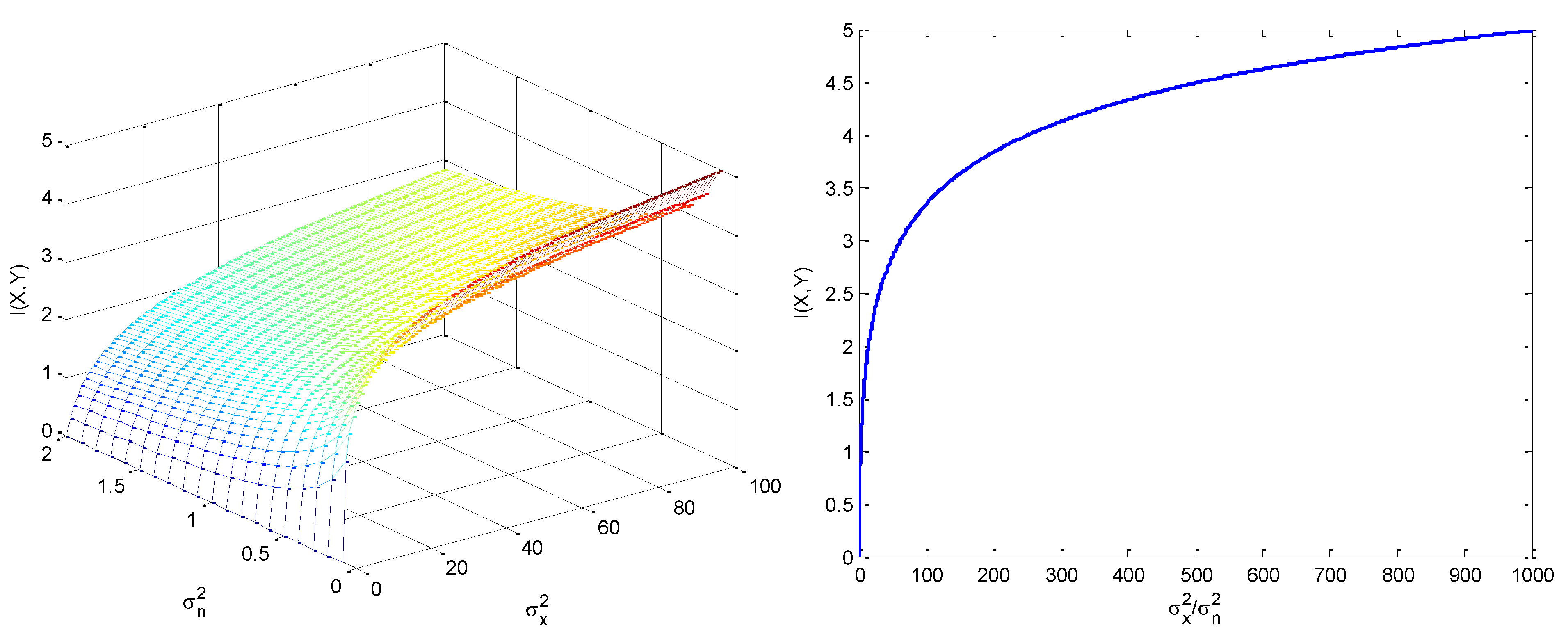
Mutual information for the additive white Gaussian noise (AWGN) channel is shown in
Figure 21, including the three-dimensional surface as a function of
and
;, and also in terms of the the signal-to-noise-ratio
. It can be seen that The mutual information grows first very fast and then much slower for high values of the signal-to-noise ratio.
6. Conclusions
This paper intends to serve to the readers as a supplement note on the geometric interpretation of the multivariate Gaussian distribution and its entropy, relative entropy, and mutual information. The illustrative examples are employed to provide further insights into the geometric interpretation of the multivariate Gaussian distribution and its entropy and mutual information, enabling the readers to correctly interpret the theory for future design. The fundamental objective is to study the application of multivariate sets of data in Gaussian distribution. This paper examines broad measurements of structure for Gaussian distributions, which shows that they can be described in terms of the information-theoretic between the given covariance matrix and correlated random variables (in terms of relative entropy). To develop the multivariate Gaussian distribution with the entropy and mutual information, several significant methodologies are presented through the discussion supported by illustrations, both technically and statistically. The content obtained allows readers to better perceive concepts, comprehend techniques, and properly execute software programs for future study on the topic’s science and implementations. It also helps readers grasp the themes’ fundamental concepts. Involving the relative entropy and mutual information as well as the potential correlated covariance analysis based on differential equations, a wide range of information is addressed, including basic to application concerns.
Author Contributions
Conceptualization, D.-J.J.; methodology, D.-J.J.; software, D.-J.J.; validation, D.-J.J. and T.-S.C.; writing—original draft preparation, D.-J.J. and T.-S.C.; writing—review and editing, D.-J.J., T.-S.C. and A. B.; supervision, D.-J.J. All authors have read and agreed to the published version of the manuscript.
Funding
The author gratefully acknowledges the support of the National Science and Technology Council, Taiwan under grant number NSTC 111-2221-E-019-047.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Derivation of the differential entropy for the univariate Gaussian distribution
Appendix B. Derivation of the differential entropy for the multivariate Gaussian distribution
The calculation involves the evaluation of expectation of the Mahalanobis distance.
Appendix C. Evaluation of expectation of the Mahalanobis distance
Appendix D. Derivation of the differential entropy in the transformed frame
The eigenvalues are the diagonal elements of the covariance matrix, namely variances, in the transformed frame. When , the eigenvectors are equal to .
Appendix E. Derivation of the Kullback–Leibler divergence between two normal distributions
where the equality was used.
References
- Verdú, S. (1990). On channel capacity per unit cost, IEEE Trans. Inf. Theory, vol. 36, no. 5, pp. 1019–1030. [CrossRef]
- Lapidoth, A. and Shamai (Shitz), S. (2002). Fading channels: How perfect need perfect side information be? IEEE Trans. Inf. Theory, vol. 48, no. 5, pp. 1118–1134.
- Verdú, S. (2002). Spectral efficiency in the wideband regime, IEEE Trans. Inf. Theory, vol. 48, no. 6, pp. 1319–1343. [CrossRef]
- Prelov, V. and Verdú, S. (2004). Second-order asymptotics of mutual information, IEEE Trans. Inf. Theory, vol. 50, no. 8, pp. 1567–1580. [CrossRef]
- Kailath, T. (1968). A note on least squares estimates from likelihood ratios, Inf. Contr., vol. 13, pp. 534–540. [CrossRef]
- Kailath, T. (1969). A general likelihood-ratio formula for random signals in Gaussian noise, IEEE Trans. Inf. Theory, vol. IT-15, no. 2, pp. 350–361. [CrossRef]
- Kailath, T. (1970). A further note on a general likelihood formula for random signals in Gaussian noise, IEEE Trans. Inf. Theory, vol. IT-16, no. 4, pp. 393–396. [CrossRef]
- Jaffer A. G. and Gupta S. C. (1972). On relations between detection and estimation of discrete time processes, Inf. Contr., vol. 20, pp. 46–54. [CrossRef]
- Jwo, D. J., Biswal, A. (2023). Implementation and Performance Analysis of Kalman Filters with Consistency Validation. Mathematics, 11, 521. [CrossRef]
- Duncan, T. E. (1970). On the calculation of mutual information, SIAM J. Applied Mathematics, vol. 19, pp. 215–220. [CrossRef]
- Kadota, T. T., Zakai, M. and Ziv, J. (1971). Mutual information of the white Gaussian channel with and without feedback, IEEE Trans. Inf. Theory, vol. IT-17, no. 4, pp. 368–371. [CrossRef]
- Amari, S. I. (2016). Information geometry and its applications, Vol. 194. Springer.
- Schneidman, E., Still, S., Berry, M. J. and Bialek, W. (2003). Network information and connected correlations. Physical review letters, 91(23), p.238701. [CrossRef]
- Timme, N., Alford, W., Flecker, B. and Beggs, J. M. (2014). Synergy, redundancy, and multivariate information measures: an experimentalist’s perspective. Journal of computational neuroscience, 36, pp.119-140.
- Liang, K. C. and Wang, X. (2008). Gene regulatory network reconstruction using conditional mutual information. EURASIP Journal on Bioinformatics and Systems Biology, 2008, pp.1-14. [CrossRef]
- Panzeri, S., Magri, C. and Logothetis, N. K. (2008). On the use of information theory for the analysis of the relationship between neural and imaging signals. Magnetic resonance imaging, 26(7), pp.1015-1025. [CrossRef]
- Katz, Y., Tunstrøm, K., Ioannou, C. C., Huepe, C. and Couzin, I. D. (2011). Inferring the structure and dynamics of interactions in schooling fish. Proceedings of the National Academy of Sciences, 108(46), pp.18720-18725. [CrossRef]
- Cutsuridis, V., Hussain, A. and Taylor, J. G. eds. (2011). Perception-action cycle: Models, architectures, and hardware. Springer Science & Business Media.
- Ay, N., Bernigau, H., Der, R. and Prokopenko, M. (2012). Information-driven self-organization: the dynamical system approach to autonomous robot behavior. Theory in Biosciences, 131, pp.161-179. [CrossRef]
- Rosas, F., Ntranos, V., Ellison, C. J., Pollin, S. and Verhelst, M. (2016). Understanding interdependency through complex information sharing. Entropy, 18(2), p.38. [CrossRef]
- Ince, R. A. (2017). The Partial Entropy Decomposition: Decomposing multivariate entropy and mutual information via pointwise common surprisal. arXiv preprint arXiv:1702.01591.
- Perrone, P. and Ay, N. (2016). Hierarchical quantification of synergy in channels. Frontiers in Robotics and AI, 2, p.35. [CrossRef]
- Bertschinger, N., Rauh, J., Olbrich, E., Jost, J. and Ay, N. (2014). Quantifying unique information. Entropy, 16(4), pp.2161-2183. [CrossRef]
- Harder, M., Salge, C. and Polani, D. (2013). Bivariate measure of redundant information. Physical Review E, 87(1), p.012130. [CrossRef]
- Rauh, J., Banerjee, P. K., Olbrich, E., Jost, J. and Bertschinger, N. (2017). On extractable shared information. Entropy, 19(7), p.328. [CrossRef]
- Ince, R. A. (2017). Measuring multivariate redundant information with pointwise common change in surprisal. Entropy, 19(7), p.318. [CrossRef]
- Chicharro, D. and Panzeri, S. (2017). Synergy and redundancy in dual decompositions of mutual information gain and information loss. Entropy, 19(2), p.71. [CrossRef]
Figure 1.
Standard parametric represenatation of ellipse followed by de La Hire’s point construction.
Figure 1.
Standard parametric represenatation of ellipse followed by de La Hire’s point construction.
Figure 3.
The position of ellipse with various correlation coefficient given by the angel of inclination, specify to obtain , : (a) , ; (b) ,; (c) , , respectively.
Figure 3.
The position of ellipse with various correlation coefficient given by the angel of inclination, specify to obtain , : (a) , ; (b) ,; (c) , , respectively.
Figure 4.
The position of ellipse with various values of correlation constant given the angel of inclination, specify to obtain : (a) , ; (b) , ; (c) , , respectively.
Figure 4.
The position of ellipse with various values of correlation constant given the angel of inclination, specify to obtain : (a) , ; (b) , ; (c) , , respectively.
Figure 5.
Equal variances for a fixed : (a) (b) (c) (d) .
Figure 5.
Equal variances for a fixed : (a) (b) (c) (d) .
Figure 6.
Ellipses for (a)
with varying variances ; (b) equal variances with varying .
Figure 6.
Ellipses for (a)
with varying variances ; (b) equal variances with varying .
Figure 7.
, increases , for a fixed .
Figure 7.
, increases , for a fixed .
Figure 8.
Ellipses for a fixed correlation coefficient when for a fixed : (a) , increases where and; (b) , increases where and .
Figure 8.
Ellipses for a fixed correlation coefficient when for a fixed : (a) , increases where and; (b) , increases where and .
Figure 9.
Variation of inclination angle as a function of and , for (a) ; (b) .
Figure 9.
Variation of inclination angle as a function of and , for (a) ; (b) .
Figure 10.
(, ) with (a) ; (b) as compared to (, ) with (c) (d) .
Figure 10.
(, ) with (a) ; (b) as compared to (, ) with (c) (d) .
Figure 11.
Comparsion of the ellipses for various (i),; (ii),; (iii); (iv), while fived.
Figure 11.
Comparsion of the ellipses for various (i),; (ii),; (iii); (iv), while fived.
Figure 12.
The differential entropy as a function for a univariate Gaussian variable.
Figure 12.
The differential entropy as a function for a univariate Gaussian variable.
Figure 13.
Differential entropy for the bivariate Gaussian distribution (a) as function of and , (b) as function of when .
Figure 13.
Differential entropy for the bivariate Gaussian distribution (a) as function of and , (b) as function of when .
Figure 19.
Mutual information versus between the correlated Gaussian variables.
Figure 19.
Mutual information versus between the correlated Gaussian variables.
Figure 20.
Schematic illustration of the additive white Gaussian noise (AWGN) channel.
Figure 20.
Schematic illustration of the additive white Gaussian noise (AWGN) channel.
Figure 21.
Mutual information for the additive white Gaussian noise (AWGN) channel: (a) the three-dimensional surface as a function of and ; (b) in terms of the the signal-to-noise-ratio.
Figure 21.
Mutual information for the additive white Gaussian noise (AWGN) channel: (a) the three-dimensional surface as a function of and ; (b) in terms of the the signal-to-noise-ratio.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).