Prerpints.org logo
Preprint
Article

Time-Varying Mechanical Analysis of Long-Span Spatial Steel Structures Integral Lifting during Construction Process

Altmetrics

Downloads

149

Views

38

Comments

0

This version is not peer-reviewed

Submitted:

24 May 2023

Posted:

26 May 2023

You are already at the latest version

Alerts
Abstract
Improper lifting measures of long-span spatial steel structures during construction process may delay the construction period and even cause safety accidents. Few studies on long-span spatial steel structures considered time-varying mechanical characteristic during construction process. In order to achieve safe and efficient installation in a long-span spatial steel structure, this research presents a time-varying mechanical analysis of the synchronous and asynchronous integral lifting and a single and interlaced point’s asynchronous integral lifting analysis method of a long-span spatial steel structure. The results showed that in the case of asynchronous lifting of single point, the displacement influence on other members is related to the distance. The closer the distance from the lifting point, the greater the influence. In asynchronous integral lifting, the lifting point with large lifting force is first installed to the specified position, and the lifting point with small lifting force is installed to the specified position.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Long-span spatial steel structures has been widely used in large-scale public building, such as airport and stadium. It is challenging to install long-span spatial steel structures on the target position accurately and efficiently especially in dynamic and congested construction site[1]. Lifting measures during construction process is risky and inefficient owing to the frequent blind lifts and the potential risks of collisions between long-span spatial steel structures and the surrounding environment[2,3].
To address the challenges of long-span spatial steel structures lifts, several studies have been conducted on lifting machine, lifting path to assist engineer in identifying an optimal lifting plan. For example, in the selection of lifting equipment, crane operation simulation can be used for automatic selection [4], or an artificial neural network can be used to establish a predictive analysis framework for crane configuration selection [5]. In terms of lifting technology, the integral lifting technology is usually adopted for the lifting of steel structures [6,7,8,9,10], combined with genetic algorithms to derive the optimal working condition combination[11,12], optimize the position of the lifting points based on the principle of minimum potential energy[13], and use computer control to lift and lower during construction[14]. Structural monitoring can also be used to output real-time parameters such as deflection, stress, strain, wind, and temperature of the large-span spatial steel structure to ensure safety during the lifting process[15]. In terms of optimizing the lifting path, in order to develop a safe and efficient lifting path, the bidirectional rapidly exploring random tree algorithm is usually used to plan the motion of the mobile crane in dynamic environments[16], combined with a virtual simulation platform to provide 3D information on obstacles, lifting modules, and site boundaries[17,18]. In addition, the Dijkstra algorithm can be used to find the shortest lifting path from the initial point to the target point[19].
However, there is a lack of an effective analysis by considering construction process-specific features during the installation of long-span spatial steel structure with integral lifting. Integral lifting of long-span spatial steel structure in construction process is critical and challenging. Therefore, this study aims to develop a time-varying mechanical analysis method with integral lifting to achieve safe and efficient installation in long-span spatial steel structure. The analysis method of long-span spatial steel structure in construction process was developed by integrating time-varying mechanical theory and displacement difference control theory. Taking the attendant hangar roof of Chengdu Tianfu Airport as background, this research presents a simulation with the synchronous and asynchronous integral lifting. Asynchronous integral lifting analysis methods with single and interlaced points are developed.
The remainder of this paper proceeds as follows, Section 2 introduces the theory of time-varying mechanics and displacement difference control equations in the lifting of large-span spatial steel structures. Section 3 analyzes the mechanical performance of the first lifting stage and the second lifting stage. Section 4 analyzes the mechanical performance of single-point asynchronous lifting and two-point asynchronous lifting.

2. Theoretical Model Establishment of Integral Lifting

2.1. Time-varying Mechanical Theory of Integral Lifting

Time-varying structural mechanics considers the influence of the structure change and the influence of subsidiary structures in construction process, and then produces the construction mechanics based on time-varying structural mechanics. Internal force and displacement are used as the objects to study the structural characteristics. The internal force and displacement of the structure are affected by many factors in the construction process and have been in dynamic change. Therefore, the study can not only consider the influence of dead load, but also take into account the construction load with obvious influence according to the construction stage of the structure. The classification of time-varying structural mechanics is based on the rate of change of structure and load. There are ultra-slow, slow and fast time-varying structural mechanics[20,21,22,23,24]. The construction period of long-span spatial steel structure generally has a long duration, especially the whole construction process of integral lifting and installation is relatively slow. The internal force and displacement of the structural system change slowly with time during the construction process. Therefore, it is more appropriate to use chronic time-varying structural mechanics to analyze the mechanical properties of long-span spatial steel structure in the construction process [25,26,27,28]. In different construction processes, the constant and construction load are added into the main unit of long-span spatial steel structure, but the change of the whole structure in a certain construction stage is ignored, and the construction influence load is considered to be constant in the process of this stage.
With the emergence of long-span spatial steel structure, several unique time-varying mechanical problems during construction process have gained importance. The long-span spatial steel structure construction process could be divided into N construction phases, and the corresponding structure is also divided into N parts, assuming that the structure in each stage is constant, and each stage is analyzed separately. First, long-span spatial steel structure is analyzed to establish the full model. At this time, the overall control equation of the structure is Eq(1):
∑ i = 1 N K i 0 δ 0 = ∑ i = 1 N F i 0
K i j represents the stiffness matrix of structure i in the jth construction section, F i j represents the load array of structure i in the jth construction section, and δ j represents the displacement of the overall structure of the jth construction section. Kill all units and make the structure in its initial state. By multiplying the stiffness matrix by the life and death element coefficient η = 10 − η , the total stiffness of the structure is close to zero, and all loads are set to zero at the same time. The governing equation is Eq(2):
η ∑ i = 1 N K i 0 δ 0 = 0
The corresponding units are activated according to the construction sequence, and then are applied with the corresponding boundary conditions and loads to obtain the force situation. The governing equation of the kth stage is Eq(3):
∑ i = 1 k K i k δ k + η ∑ i = k + 1 N K i k δ k = ∑ i = 1 k F i k
If the component is removed, the element stiffness matrix of the component should be multiplied by the life-death coefficient. At the same time, the internal force of the removed component should be applied to the structure in the opposite direction to modify the structural constraints and load array. After the displacement at each stage is calculated, the corresponding structural strain and stress can be calculated through geometric equations and physical equations.

2.2. Displacement Difference Control Theory of Integral Lifting

The whole long-span spatial steel structure is completely horizontal according to the basic construction organization design principle. Thus, all of the lifting points are synchronously fully lifted. Differences in the hydraulic jacks and measurement errors make it almost impossible to achieve complete synchronization in the actual construction process. And hence, there is an inevitable displacement difference between lifting points [29,30]. The displacement difference affects the mechanical performance of the whole long-span spatial steel structure by affecting the overall stiffness of the structure[31].
According to the structure form and boundary conditions of long-span spatial steel structure during integral lifting, the internal force solution of the structure can be regarded as the internal force solution of the statically indeterminate structure with displacement load. Therefore, the basic equation of any lifting point when the displacement difference occurs at the lifting point can be obtained in Eq(4):
{ K 11 Δ 1 + K 12 Δ 2 + ⋅ ⋅ ⋅ + K 1 n Δ n + F 1 Δ = 0 K 21 Δ 1 + K 22 Δ 2 + ⋅ ⋅ ⋅ + K 2 n Δ n + F 2 Δ = 0 K n 1 Δ 1 + K n 2 Δ 2 + ⋅ ⋅ ⋅ + K nn Δ n + F n Δ = 0
Δj is the displacement of node j. Kij is the constraint force generated at the additional constraint i under the action of node displacement Δj. FiΔ is the constraint force generated by the additional constraint i under the action of a given displacement difference at a lifting point. If the displacement of each lifting point is known, the force of all members of the whole long-span spatial steel structure can be obtained by iterative transformation when a specific displacement difference occurs at the lifting point. Constraints analysis of integral lifting can be proposed according to the above theories and the actual stress of construction process. Joints of long-span spatial steel structures can be taken as hinged connection. The force condition of construction process can be calculated according to the small deflection theory. Each long-span spatial steel structure member is in the elastic range.

3. Mechanical Performance Analysis of Synchronous Integral Lifting

3.1. Engineering Background

The roof of the maintenance hangar at Chengdu Tianfu International Airport consists of a hall space grid and a gate truss, with a total area of 13140m2. The hall space grid part is 6m high, the gate truss part is 13m high, and the weight of the whole grid is 2000t after assembling. The roof has a plan size of 146m×90m and is composed of many quadrangular cone space units connected, as shown in Figure 1(a) The quadrangular cone space unit in the structure consists of the upper chord, middle chord, lower chord, upper web and lower web, with a plan size of 6m×6m and a height of 6m, and the nodes are all welded hollow ball nodes. The lower chord center height of the hangar roof hall space grid is 25.5m, the lower chord center height of the hangar gate truss is 22m, the net height of the hangar gate is 21m, and the roof is supported by peripheral concrete columns. A gate truss is set on the opening edge.
When determining the lifting points for the structure, it is important to consider the stiffness of the structure. Whenever possible, the original supporting points of the structure should be used as lifting points, and the number of lifting points should be approximately half the number of supporting points. Additionally, since the structure is almost symmetrical, the lifting point configuration on one side can be mirrored on the other.
As can be seen from Figure 1(b), lifting points D1~D4 and D13~D10 as well as lifting points D16 and D17, are arranged symmetrically (the symmetry axis is Y-Y axis) in order to keep the balance of the spatial grid in the direction of the hangar opening. D14 and D15 are arranged near the third equilibrium point of the hangar span, and together with D5~D9, they keep the balance of the spatial grid in the direction of hangar inlet depth. Among all the lifting points, except for D14 and D15, which are arranged on the temporary tire frame, the rest of the lifting points are arranged on the concrete structure bearing column, which makes it possible to reduce the construction cost while ensuring a reasonable force of the grid structure.

3.2. Mechanical Analysis of the First Lifting Stage

After the completion of the assembly of the hall space grid part on the ground, the first lifting stage was started. Fifteen lifting points were set in the first lifting stage, numbered D1~D15, where D1~D13 were set on the nodes of the spatial grid corresponding to the temporary support frame on the top of the concrete bearing column, and D14 and D15 were set on the nodes of the spatial grid corresponding to the lattice lifting bracket within the gate span. The lifting points were set symmetrically about the centerline of the gate of the spatial grid to guarantee the balance of forces when the spatial grid was lifted. The schematic diagram of the arrangement of lifting points in the first lifting stage is shown in Figure 2.
During the first lifting stage, the lifting force was provided by the 15 lifting points from D1 to D15. Figure 3 shows the simulation results of lifting force for each lifting point.
As can be seen from Figure 3, among the 15 lifting points in the first lifting stage, the lifting force of D4 is the smallest with a value of 223kN, while the lifting force of D15 is the largest with a value of 1862kN, which is provided by the lattice lifting bracket at the gate. The lifting points D1~D4 are located on the left side of the spatial grid, and the lifting points D13~D10 are located on the right side of the spatial grid, and they are symmetrically distributed about the centerline of the gate, with D1 corresponding to D13, D2 corresponding to D12, D3 corresponding to D11, and D4 corresponding to D10. From the lifting force of the nodes, it can be seen that the lifting force values of the lifting points, which are symmetrical about the center line of the gate, are relatively close to each other. This indicates that the pressure generated by the spatial grid on the lifting points also becomes symmetrically distributed, which is consistent with the actual force characteristics of the spatial grid and verifies the reasonableness of integral lifting.
The strength stress diagram of the first lifting stage of the spatial grid is shown in Figure 4. In the first lifting stage, the overall stress of the spatial grid is symmetrical about the center line of the gate, which is related to the symmetry of the spatial grid structure and the lifting point arrangement. The stress of the members around the lifting point is relatively high, and the maximum value of stress in the mesh is 155MPa (less than 345MPa), which meets the requirements of the member bearing capacity, and the spatial grid is in a safe state.
Figure 5 shows the displacement cloud diagram of the first lifting stage of the spatial grid, and it can be seen from the figure that the displacement cloud diagram of the spatial grid is also symmetrical about the center line of the gate and shows a trend of gradually decreasing along the surrounding with the center as the starting point. The vertical displacement in the center of the spatial grid is the largest, with a maximum value of 132.9mm.
According to the requirements of the Technical Specification of Space Grid Structure JGJ 7-2010, the maximum vertical displacement of the spatial grid should meet Umax≤l0/250 (l0 is the short span of the spatial grid). In this study, the span of the spatial grid is 90m, so Umax≤90000/250=360mm. From the previous section, it is known that the maximum displacement of the spatial grid in the first lifting stage is 132.9mm (less than 360mm). Therefore, the integral lifting vertical displacement of the spatial grid in this study is within the design range and meets the specification requirements. However, it is still necessary to detect the maximum vertical direction in the center area of the spatial grid at any time during the actual spatial grid lifting construction and take certain measures to reduce the maximum vertical displacement to ensure the safety of the spatial grid lifting construction.
For the maximum horizontal displacement limit of the spatial grid, it can be determined by the horizontal displacement limit of the top of the concrete row frame column. According to Building Seismic Design Code GB50011-2010, the horizontal displacement of the top of the row frame column should be less than H/30=22100/30=737mm (H is the height of the top of the row frame column). The maximum horizontal displacement of the spatial grid at this stage is 26.3mm, which is less than 737mm and meets the requirements of the code. Obviously, compared with the vertical displacement, the horizontal displacement of the spatial grid in the lifting process is very small, so the vertical displacement is the key monitoring object. Figure 6 shows the spatial steel roof structure during the lifting process, reflecting the practicality of the method and providing a scientific reference for future design and lifting construction.

3.3. Mechanical Analysis of the Second Lifting Stage

As can be seen from Figure 7, the stress distribution of the internal members of the spatial grid is relatively uniform, and the distribution law is similar to that of the first lifting stage. The maximum stress in all the members is 165.6 MPa, which meets the code requirements. The vertical displacement cloud diagram of the second lifting stage of the spatial grid is shown in Figure 8. It can be seen that for the hall space grid part, the vertical displacement law is similar to that of the first stage. The displacement in the center of the hall space grid is the largest and shows the law of gradually decreasing from the center to the surroundings. For the gate truss part, the maximum displacement point is located in the middle of the span of the gate truss. And the maximum displacement of the roof is located in the middle of the span of the gate truss. Its maximum value is 176.5 mm (less than 360mm). Therefore, the overall design of the roof grid structure meets the specification requirements.
Similarly, the maximum horizontal displacement of the spatial grid at this stage is 30.6mm (less than 737mm), which is in line with the specification requirements. Compared with the maximum value of vertical displacement, the horizontal displacement value of the spatial grid at this stage is also smaller, and the maximum value of vertical displacement is the key monitoring object during construction.
Figure 9 compares the lifting forces of the lifting points in the two stages, and the lifting forces of each lifting point were changed during the two stages of lifting construction. During the construction of the second lifting stage, the spatial grid was deformed due to the change in the structure form and the number of lifting points, which made the internal force of the spatial grid redistributed. The lifting force of the point with a larger lifting force in the first stage gradually decreases in the second stage, while the lifting force of the point with a smaller lifting force in the first stage gradually increases in the second stage., thus making the distribution of the internal force of the spatial grid more uniform. The above analysis shows that the maximum stress and maximum displacement of the spatial grid members in both stages meet the requirements of the relevant design codes during the phased lifting construction.

4. Mechanical performance analysis of asynchronous integral lifting

During the lifting process, there are factors such as wind changes, temperature changes, construction operations, hydraulic lifting control system delays, etc., which can cause the spatial grid to be lifted out of synchronization, thus leading to uneven distribution of internal forces in the spatial grid and excessive stress or displacement in some members. This will make the stability of the grid lifting and the safety of construction workers unable to be guaranteed. Studying the asynchronous lifting situation of the spatial grid during the lifting process and providing corresponding control measures can help ensure the smooth progress of the integral lifting and installation construction.
In the process of the integral lifting of the spatial grid, the displacement difference between the lifting points is random, and there are several combinations of displacement differences, so it is necessary to determine the most unfavorable working condition of the spatial grid when the combination of displacement differences acts, and to analyze it numerically.

4.1. Mechanical Analysis of Single-Point Asynchronous Integral Lifting

According to the requirements of the penetrating jack, the allowable displacement difference between two adjacent lifting points is 1/250 of the distance between the two points and is less than 25 mm. In this study, the displacement difference of unsynchronized lifting is set to 20mm, i.e., a 20mm displacement difference is applied to the unsynchronized lifting points, while the displacement difference between the synchronized lifting points is set to 0.
A 20mm displacement difference was applied to each of the 15 lifting points during the first lifting stage of the spatial grid, and then a simulation analysis of the vertical deformation of the spatial grid was carried out. The vertical displacement cloud of the spatial grid was obtained, as shown in Figure 10, and the lifting force statistics of each lifting point are in Table 1.
From Figure 10, it can be seen that when there is a 20mm displacement difference at a single lifting point, the displacement of the members near this point is significantly affected, while the displacement of the members farther away is almost unaffected. In addition, when a single lifting point has a displacement difference of 20mm, the adjacent short members are affected to a greater extent than the long members.
As can be seen from Table 1, when a single lifting point has a displacement difference of 20mm, it has a more obvious effect on the lifting force of adjacent lifting points, while it has a smaller effect on the lifting force of more distant lifting points.

4.2. Mechanical Analysis of Double-Point Asynchronous Integral Lifting

When the spatial grid is lifted asynchronously, the main consideration is the combination of the displacement difference between the lifting point and the neighboring points and between the lifting point and the interval point. The combination of the given lifting displacement difference is studied, and the results obtained are compared and analyzed with the calculation results of the displacement difference applied to a single lifting point only, in order to find the pattern of it.
Taking the combination of neighboring points (D7 and D8) and the combination of interval points (D7 and D9) as an example, a vertical displacement of 20mm is applied to each combination of lifting points to simulate the vertical deformation of the spatial grid and the change of lifting force of lifting points under the combination action of double lifting point displacement difference.
A comparative analysis of the displacement of the spatial grid for single-point asynchronous integral lifting and double-point asynchronous integral lifting by Figure 10 and Figure 11 shows that when a 20mm displacement difference is applied to the combination of neighboring points (D7 and D8) or the combination of interval points (D7 and D9), the influence area of vertical deformation is similar to the superimposed influence area when the displacement difference is applied to two points alone.
This also indicates that the displacement difference applied to the combination of neighboring points and the combination of interval points will affect the displacement of the spatial grid members near the lifting points, and then affect the internal force of the members.
Table 2 shows the lifting point lift forces for the combination of neighboring points (D7 and D8) and the combination of interval points (D7 and D9) with the displacement difference applied simultaneously and separately. When lifting points D7 and D8 are simultaneously applied with a 20mm vertical displacement difference, the lifting force of the lifting point itself and its neighboring points (D6 and D9) are smaller than the lifting force when D7 and D8 are applied with 20mm respectively, and the difference is not negligible. Although the lifting forces of the remaining lifting points are changed, the difference is negligible compared with the overall lifting force. The change in lifting force between lifting points D7 and D9 applied simultaneously and separately with a 20mm vertical displacement difference is small. However, compared to applying the displacement difference separately, the lifting force of interval lifting point D8 was increased by 10.9% when the displacement difference was applied simultaneously. This is caused by the superimposed influence of the two lifting points, so its influence needs to be considered during the actual construction.
Thus, the influence produced by applying displacement difference to neighboring lifting points separately includes the influence of applying displacement difference at the same time, and the latter need not be considered separately. When the displacement difference is applied to the interval lifting point, the influence of the interval lifting point and its connected members cannot be ignored and should be included in the most unfavorable working conditions. The most unfavorable working conditions for asynchronous lifting of the spatial grid are shown in Table 3.
From the above analysis, it can be seen that the actual project in the construction of the safety verification should mainly consider the impact of the single-point asynchronous lifting displacement difference and the interval point asynchronous lifting combination displacement difference on the integral lifting of the spatial grid structure. Consider the impact of the most unfavorable working conditions on the asynchronous lifting of the spatial grid structure, and if the stress or displacement of the members in the most unfavorable working condition verification results do not meet the code requirements, the unqualified members should be reinforced or replaced to ensure the safety of the spatial grid structure.

5. Conclusions

This research proposes a time-varying mechanical analysis of the synchronous and asynchronous integral lifting and a single and interlaced point’s asynchronous integral lifting analysis method of a long-span spatial steel structure. The adverse effects of the displacement difference between lifting points with asynchronous integral lifting and have been displayed in construction with numerical simulation. In the case of asynchronous lifting of single point, the displacement influence on other members is related to the distance. The closer the distance from the lifting point, the greater the influence. Under the condition of the same distance, it has a great influence on the short rod and a small influence on the long rod. In the process of structural lifting, it is necessary to pay attention to the lifting order of each lifting point. The detached lifting can be carried out according to the statistical results. In the process of lifting, the lifting point with small lifting force should be lifted first, and then the lifting point with large lifting force should be lifted. In the asynchronous integral lifting, the order of lifting points should be opposite to the ascending order. The lifting point with large lifting force is first installed to the specified position, and the lifting point with small lifting force is installed to the specified position.

Author Contributions

Conceptualization, G.Y. and Y.Y.; methodology, G.Y.; software, H.D. and X.M.; validation, G.Y., Y.Y. and H.D.; formal analysis, Y.Y. and W.M.; investigation, H.D. and X.M.; resources, G.Y.; data curation, H.D. and W.M.; writing—original draft preparation, H.D. and Y.Y.; writing—review and editing, G.Y., Y.Y. and H.D.; visualization, H.D. and X.M.; supervision, G.Y.; project administration, G.Y. and H.D.; funding acquisition, G.Y. and Y.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This work was funded by the National Key R&D Program of the Ministry of Science and Technology (No. 2019YFD1101005-4).

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Tian, L.; Hao, J.; Wei, J.; Zheng, J. Integral lifting simulation of long-span spatial steel structures during construction. Automation in Construction 2016, 70, 156–166. [Google Scholar] [CrossRef]
  2. Lacey, A.W.; Chen, W.; Hao, H.; Bi, K. Structural response of modular buildings – An overview. Journal of Building Engineering 2018, 16, 45–56. [Google Scholar] [CrossRef]
  3. Kang, S.; Miranda, E. Planning and visualization for automated robotic crane erection processes in construction. Automation in Construction 2006, 15, 398–414. [Google Scholar] [CrossRef]
  4. Guo, H.; Zhou, Y.; Pan, Z.; Zhang, Z.; Yu, Y.; Li, Y. Automated Selection and Localization of Mobile Cranes in Construction Planning. Buildings 2022, 12, 580. [Google Scholar] [CrossRef]
  5. Azami, R.; Lei, Z.; Hermann, U.; Zubick, T. A Predictive Analytics Framework for Mobile Crane Configuration Selection in Heavy Industrial Construction Projects. Buildings 2022, 12, 960. [Google Scholar] [CrossRef]
  6. Guo, T.; Wu, E.; Li, A.; Wei, L.; Li, X. Integral lifting and seismic isolation retrofit of great hall of Nanjing Museum. Journal of performance of constructed facilities 2012, 26, 558–566. [Google Scholar] [CrossRef]
  7. Nianchun, D.; Jianhui, W.; Yu, D. Simulation of Construction Process Combining Steel Truss Integral Lifting with Concrete Pouring for SRC Conversion Layer Structure. In Proceedings of the 2016 International Conference on Architectural Engineering and Civil Engineering; 2016; pp. 75–79. [Google Scholar]
  8. Yaozhi, L.; Ning, H.; Xiao-guang, C. Deployable integral lifting construction technology for cylindrical latticed shells [J]. Progress in Steel Building Structures 2005, 7, 27–32. [Google Scholar]
  9. Zhang, H.; Zhang, Y.T.; Zhu, H.; Gao, J.B. Research on Integral Lifting Continuous Steel Box Girder Bridge Construction Technology. In Proceedings of the Applied Mechanics and Materials; 2013; pp. 1674–1681. [Google Scholar] [CrossRef]
  10. Zhang, H.; Zhou, R.Z. Research on Lifting Techniques of Large Segments of steel box girder of Chongqi Bridge. In Proceedings of the Advanced Materials Research; 2012; pp. 1094–1098. [Google Scholar] [CrossRef]
  11. Gwak, H.S.; Lee, H.C.; Choi, B.Y.; Mi, Y. GA-Based Optimization Method for Mobile Crane Repositioning Route Planning. Appl. Sci.-Basel 2021, 11, 18. [Google Scholar] [CrossRef]
  12. Zhao, Z.; Zhu, H.; Liu, H.; Chen, Z. Thermal and integral lifting analysis of a lattice shell lighting roof based on genetic algorithm and probabilistic design. Journal of Constructional Steel Research 2015, 112, 208–220. [Google Scholar] [CrossRef]
  13. Fan, X.C.; Chen, H.; Liu, Y.; Lv, W.C. Lifting Point Optimization of Large Steel Truss on the Principle of Minimum Potential Energy. In Proceedings of the Advanced Materials Research; 2014; pp. 158–163. [Google Scholar] [CrossRef]
  14. Cao, X.L.; Zhang, Z.F. Study on the application of computer synchronous control in lift-slab construction for steel frame structures. In Proceedings of the Advanced Materials Research; 2011; pp. 45–49. [Google Scholar] [CrossRef]
  15. Zhu, Y.; Gao, Y.; Zeng, Q.; Liao, J.; Liu, Z.; Zhou, C. Real-Time Structural Monitoring of the Multi-Point Hoisting of a Long-Span Converter Station Steel Structure. Sensors 2021, 21, 4737. [Google Scholar] [CrossRef]
  16. Zhang, C.; Hammad, A. Improving lifting motion planning and re-planning of cranes with consideration for safety and efficiency. Advanced Engineering Informatics 2012, 26, 396–410. [Google Scholar] [CrossRef]
  17. Hu, S.; Fang, Y. Automating crane lift path through integration of BIM and path finding algorithm. In Proceedings of the ISARC. Proceedings of the International Symposium on Automation and Robotics in Construction; 2020; pp. 522–529. [Google Scholar]
  18. Zhu, A.; Zhang, Z.; Pan, W. Crane-lift path planning for high-rise modular integrated construction through metaheuristic optimization and virtual prototyping. Automation in Construction 2022, 141, 104434. [Google Scholar] [CrossRef]
  19. Kayhani, N.; Taghaddos, H.; Mousaei, A.; Behzadipour, S.; Hermann, U. Heavy mobile crane lift path planning in congested modular industrial plants using a robotics approach. Automation in Construction 2021, 122, 103508. [Google Scholar] [CrossRef]
  20. Guo, Y.L.; Tian, G.Y.; Wang, X.A.; Chen, G.D.; Fan, F. Research and Application of Time-Variation Analysis and Key Control Technology in Complex Steel Structures Construction. In Proceedings of the Advanced Materials Research; 2012; pp. 2319–2326. [Google Scholar] [CrossRef]
  21. Li, Q.; Wang, C.; Ellingwood, B.R. Time-dependent reliability of aging structures in the presence of non-stationary loads and degradation. Structural Safety 2015, 52, 132–141. [Google Scholar] [CrossRef]
  22. Tian, L.; Hao, J. Nonlinear time-varying analysis algorithms for modeling the behavior of complex rigid long-span steel structures during construction processes. Steel and Composite Structures 2015, 18. [Google Scholar] [CrossRef]
  23. Tian, L.; Hao, J.; Li, C.; Wang, Y. Simulation analysis on integral lifting of large-span steel roof structures during construction process. Journal of Building Structures 2013, 34, 33–39. [Google Scholar] [CrossRef]
  24. Wang, Z.; Ren, W.; Chen, G. Time–frequency analysis and applications in time-varying/nonlinear structural systems: A state-of-the-art review. Advances in Structural Engineering 2018, 21, 1562–1584. [Google Scholar] [CrossRef]
  25. Hajjar, D.; AbouRizk, S.M. Unified modeling methodology for construction simulation. J. Constr. Eng. Manage. 2002, 128, 174–185. [Google Scholar] [CrossRef]
  26. Agkathidis, A.; Brown, A. Tree-Structure Canopy: A Case Study in Design and Fabrication of Complex Steel Structures using Digital Tools. International Journal of Architectural Computing 2013, 11, 87–104. [Google Scholar] [CrossRef]
  27. Huang, T.; Kong, C.W.; Guo, H.L.; Baldwin, A.; Li, H. A virtual prototyping system for simulating construction processes. Automation in Construction 2007, 16, 576–585. [Google Scholar] [CrossRef]
  28. Case, F.; Beinat, A.; Crosilla, F.; Alba, I.M. Virtual trial assembly of a complex steel structure by Generalized Procrustes Analysis techniques. Automation in Construction 2014, 37, 155–165. [Google Scholar] [CrossRef]
  29. Guo, Y.; Miao, Y.; Lou, J.; Lin, B.; Xu, Y.; Cui, W. Integral lift design of the main trusses in Macao Gymnasium and analysis of the latticed hoist tower. Jianzhu Jiegou Xuebao(J. Build. Struct.) 2005, 26, 17–24. [Google Scholar]
  30. Liu, Y.P.; Chan, S.L. Second-Order and Advanced Analysis of Structures Allowing for Load and Construction Sequences. Advances in Structural Engineering 2011, 14, 635–646. [Google Scholar] [CrossRef]
  31. Zheng, J.; Hao, J.P.; Zhong, W.H. The mechanics analysis and research of multi-suspension-centers integral lifting technology for long-span steel roof. In Proceedings of the Applied Mechanics and Materials; 2012; pp. 3194–3198. [Google Scholar] [CrossRef]
Preprints 74563 g001
Figure 1. Structural parameter and the spatial grid lifting point layout: (a) grid structure in place; (b) the spatial grid lifting point layout.
Figure 1. Structural parameter and the spatial grid lifting point layout: (a) grid structure in place; (b) the spatial grid lifting point layout.
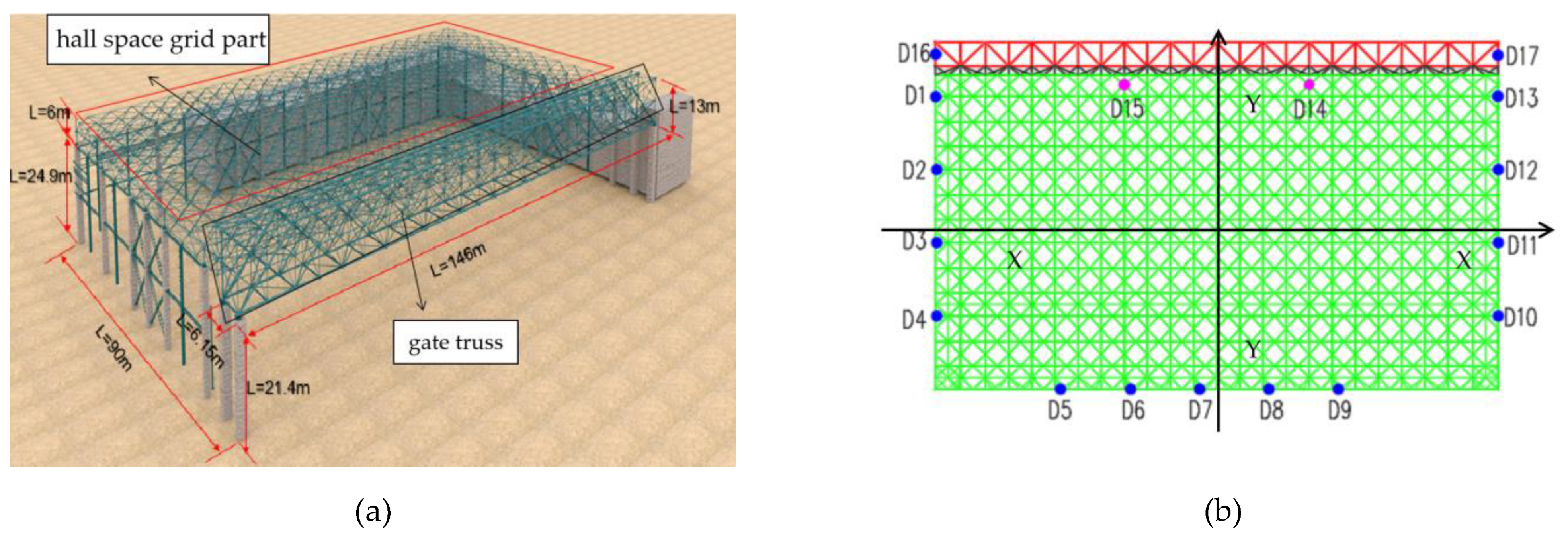
Preprints 74563 g001
Preprints 74563 g002
Figure 2. Layout of the first lifting stage point.
Figure 2. Layout of the first lifting stage point.
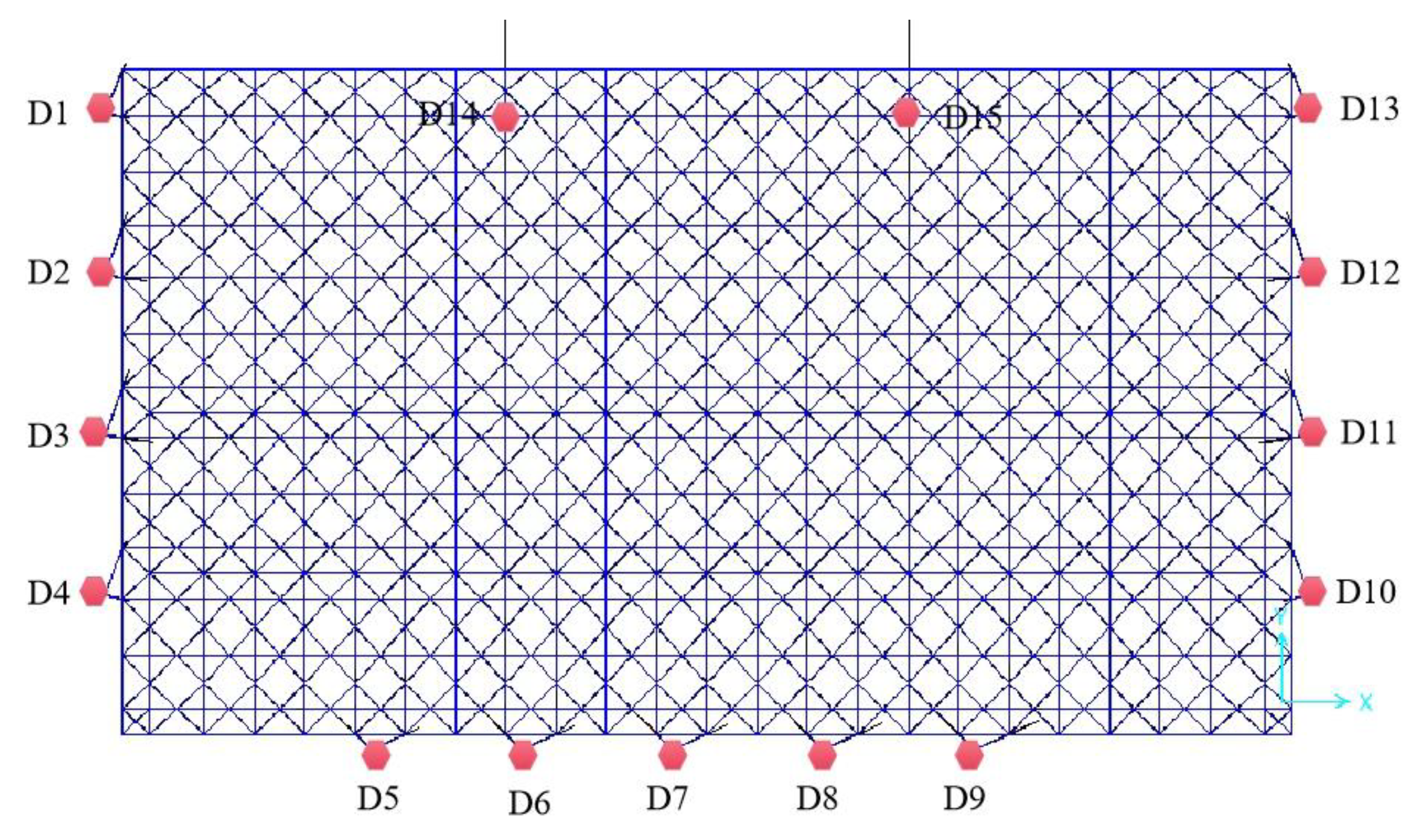
Preprints 74563 g002
Preprints 74563 g003
Figure 3. The lifting force of each point in the first lifting stage.
Figure 3. The lifting force of each point in the first lifting stage.
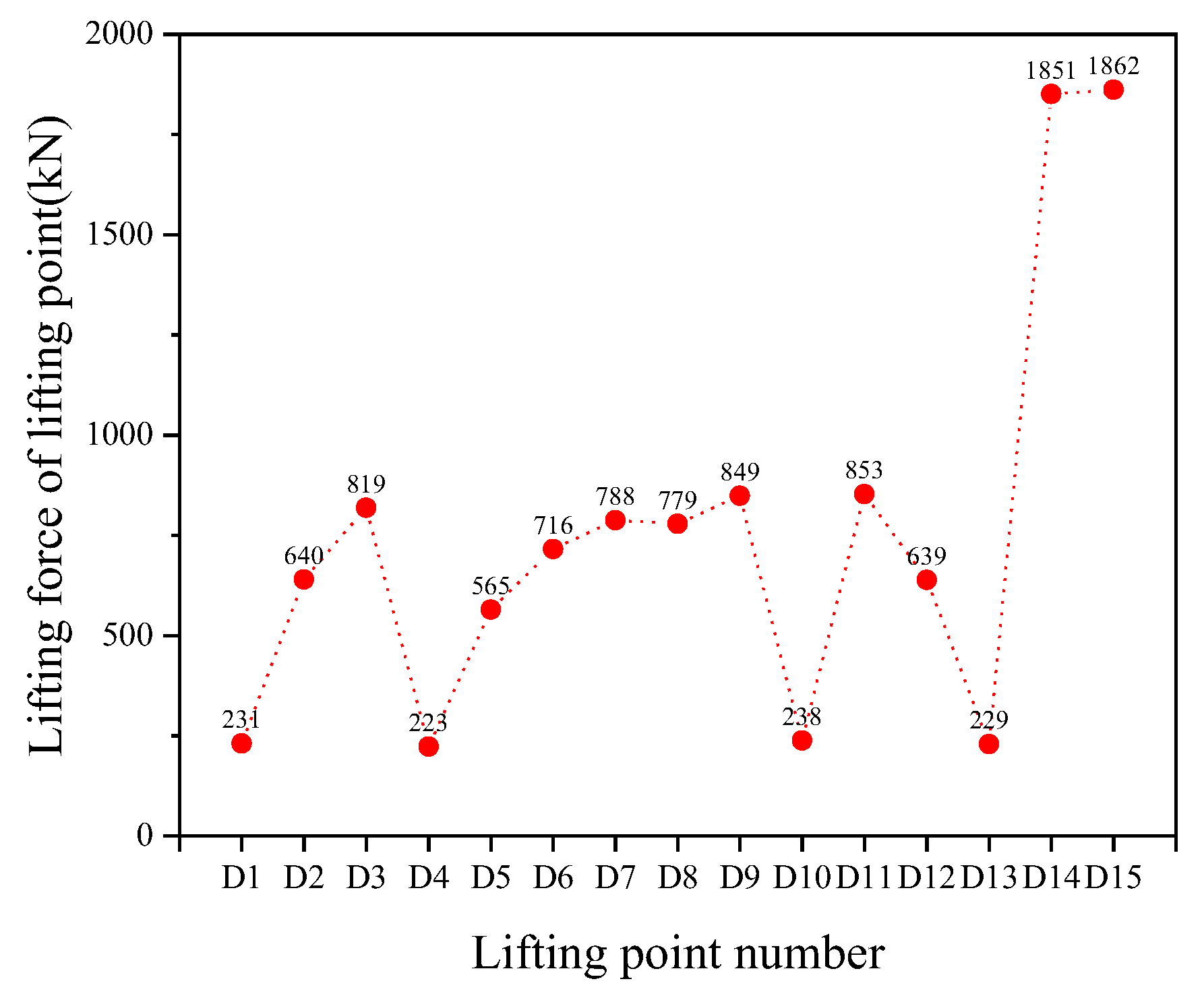
Preprints 74563 g003
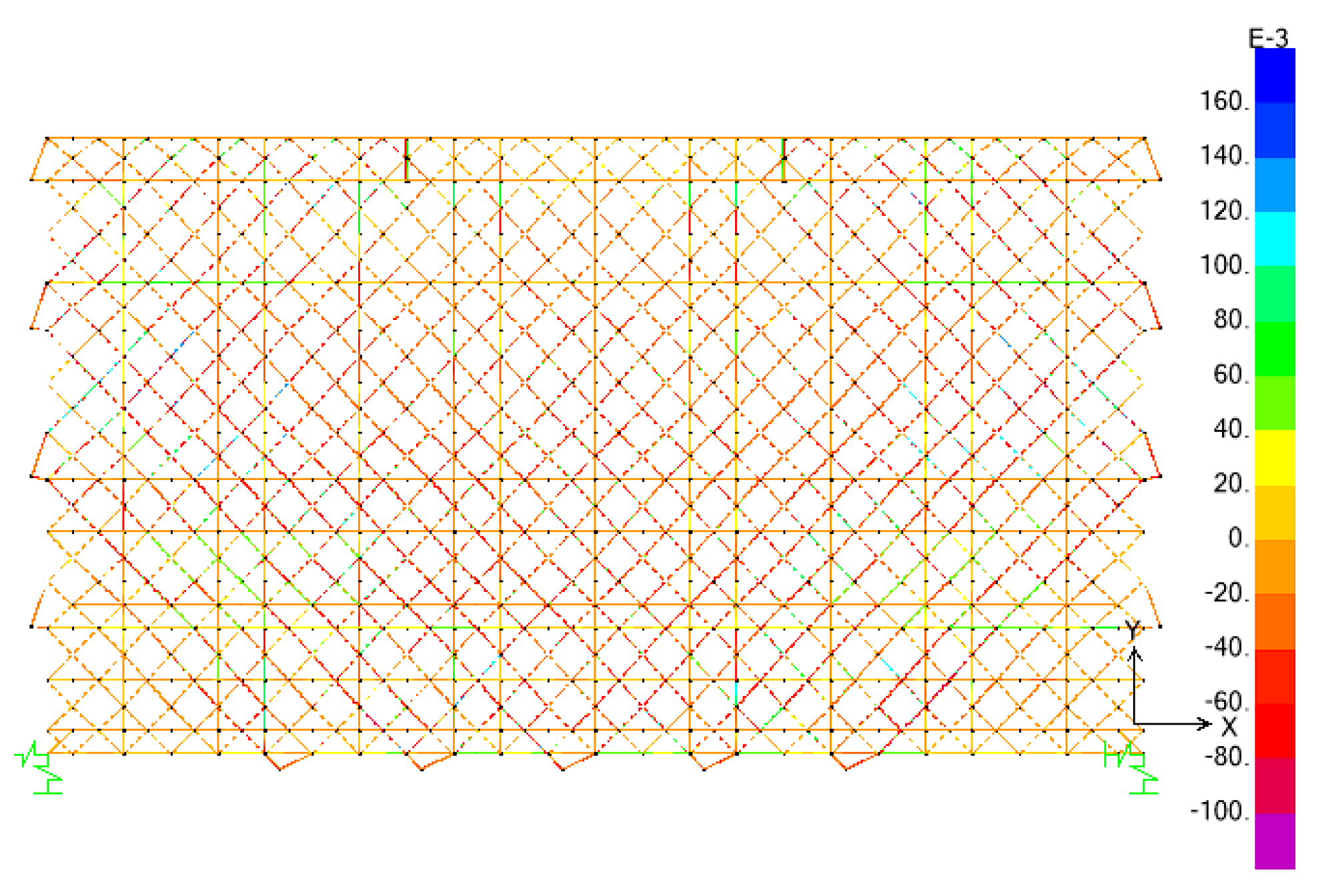
Preprints 74563 g004
Figure 4. Strength and stress cloud diagram of the first lifting stage of the spatial grid (GPa).
Figure 4. Strength and stress cloud diagram of the first lifting stage of the spatial grid (GPa).
Preprints 74563 g004
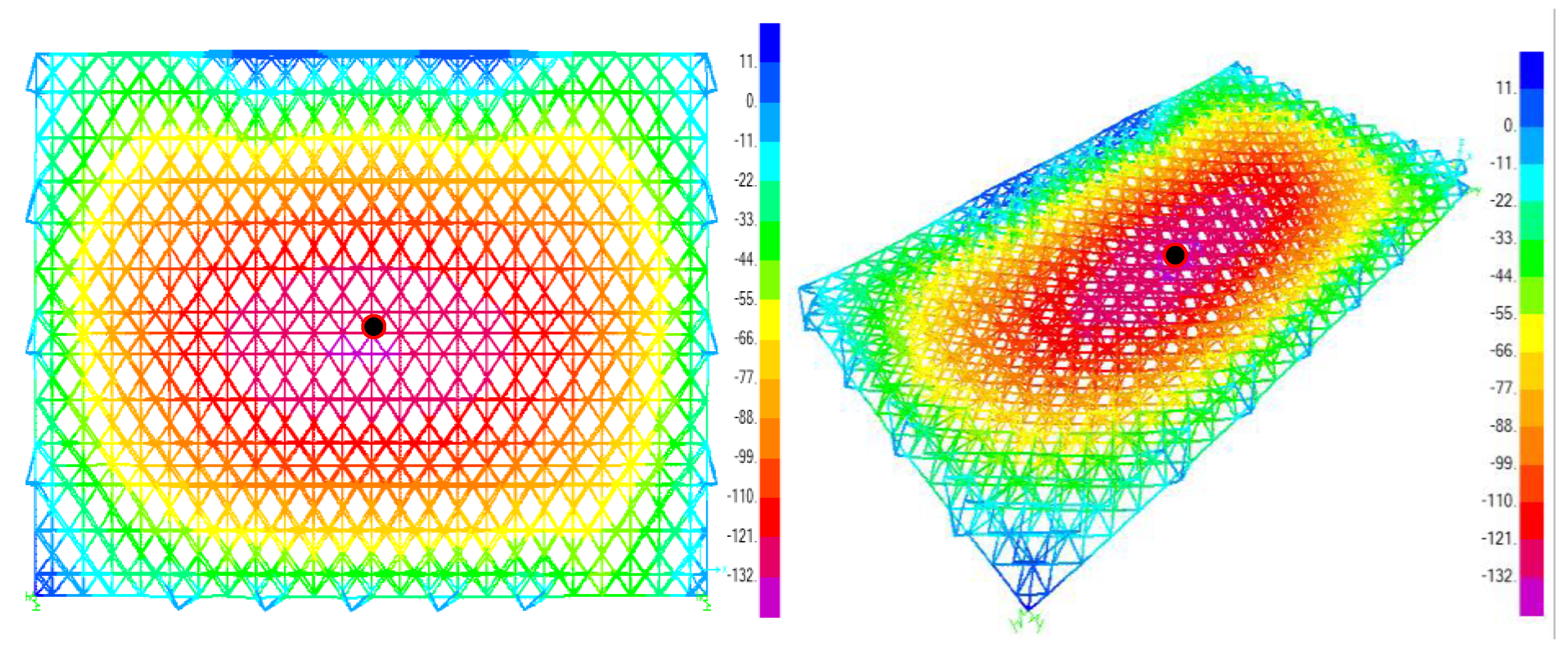
Preprints 74563 g005
Figure 5. Vertical displacement cloud map of the first lifting stage of the spatial grid (mm).
Figure 5. Vertical displacement cloud map of the first lifting stage of the spatial grid (mm).
Preprints 74563 g005
Preprints 74563 g006
Figure 6. Spatial steel roof structure in the lifting construction.
Figure 6. Spatial steel roof structure in the lifting construction.
Preprints 74563 g006
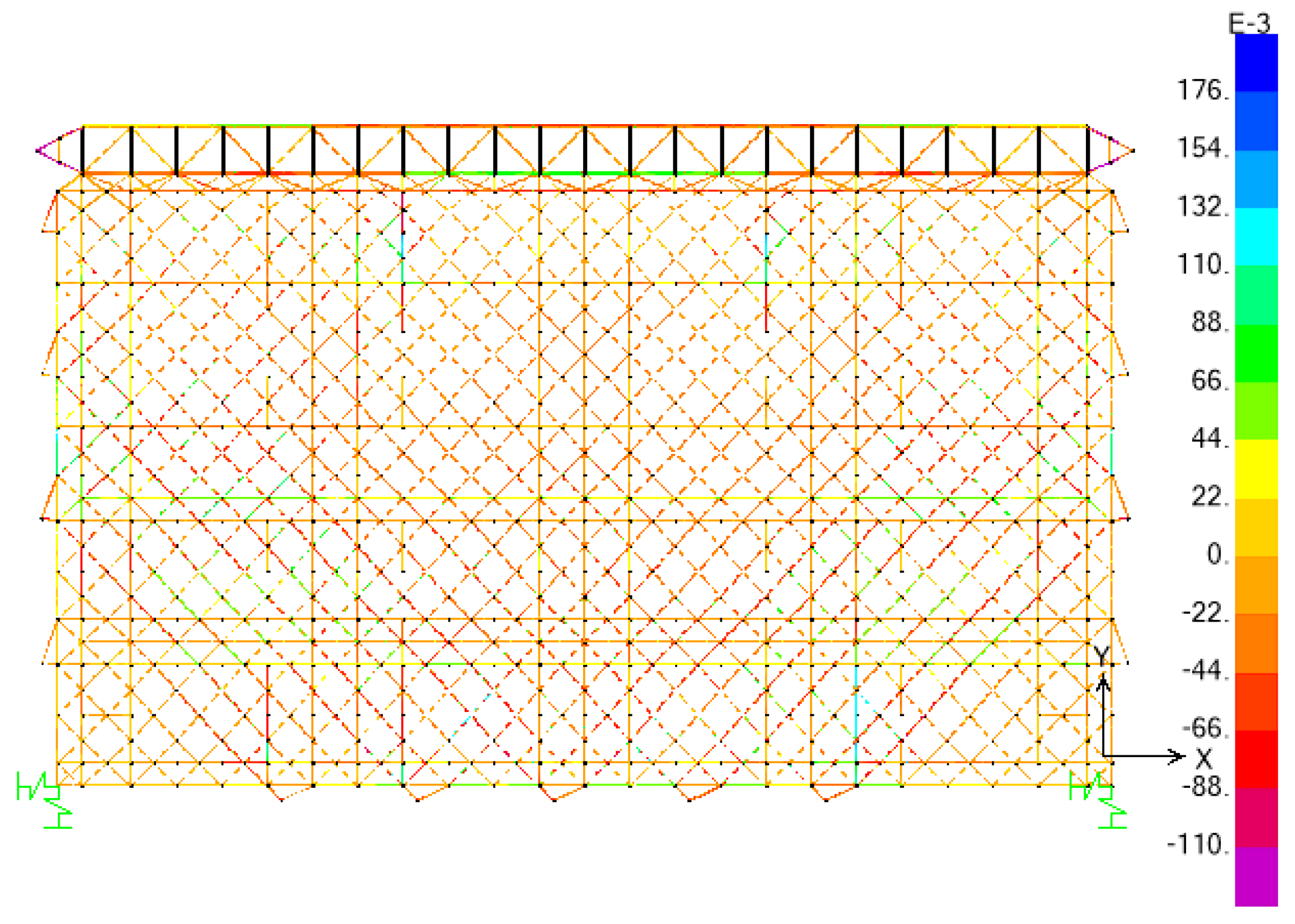
Preprints 74563 g007
Figure 7. Strength and stress cloud diagram of the second lifting stage of the spatial grid (GPa).
Figure 7. Strength and stress cloud diagram of the second lifting stage of the spatial grid (GPa).
Preprints 74563 g007
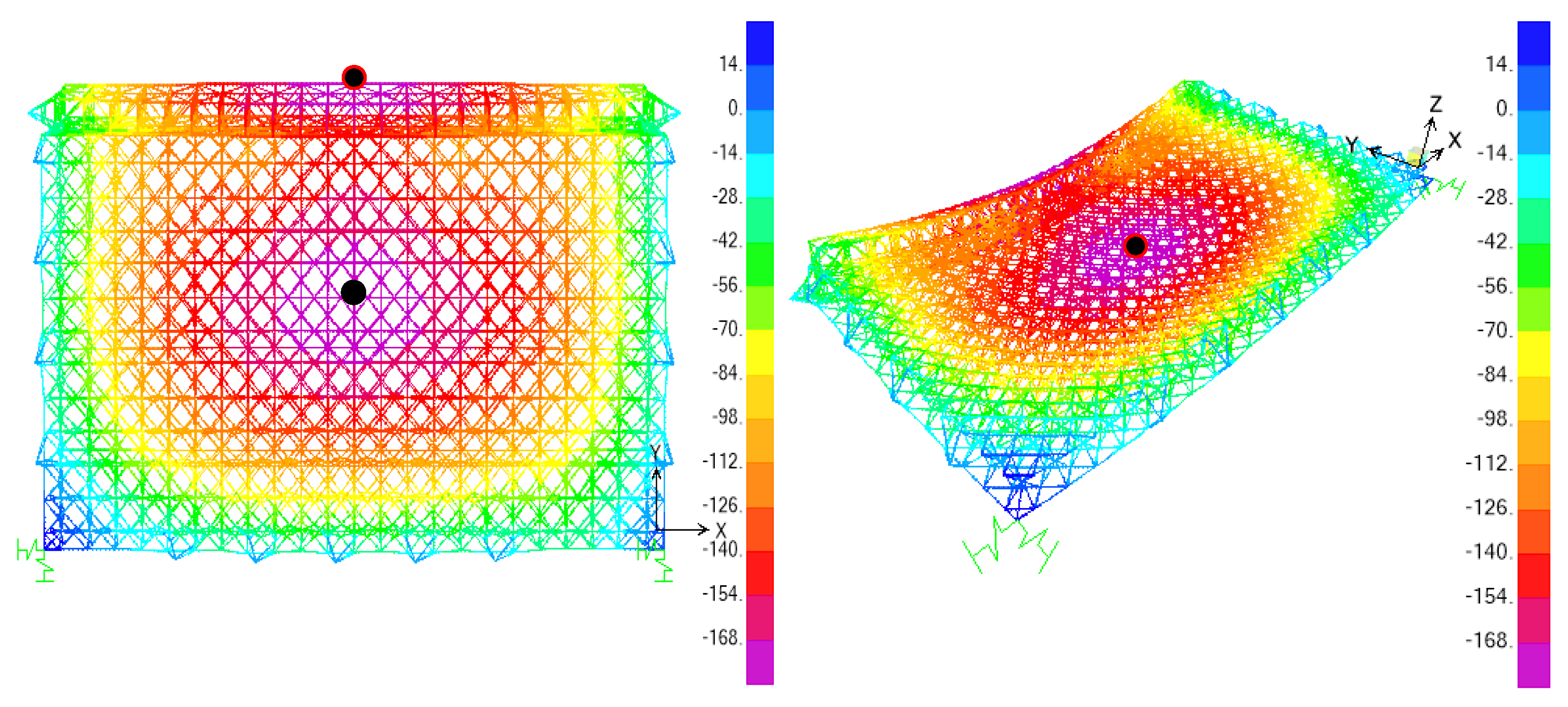
Preprints 74563 g008
Figure 8. Vertical displacement cloud map of the first lifting stage of the spatial grid (mm).
Figure 8. Vertical displacement cloud map of the first lifting stage of the spatial grid (mm).
Preprints 74563 g008
Preprints 74563 g009
Figure 9. Two-stage lifting point lifting force comparison diagram.
Figure 9. Two-stage lifting point lifting force comparison diagram.
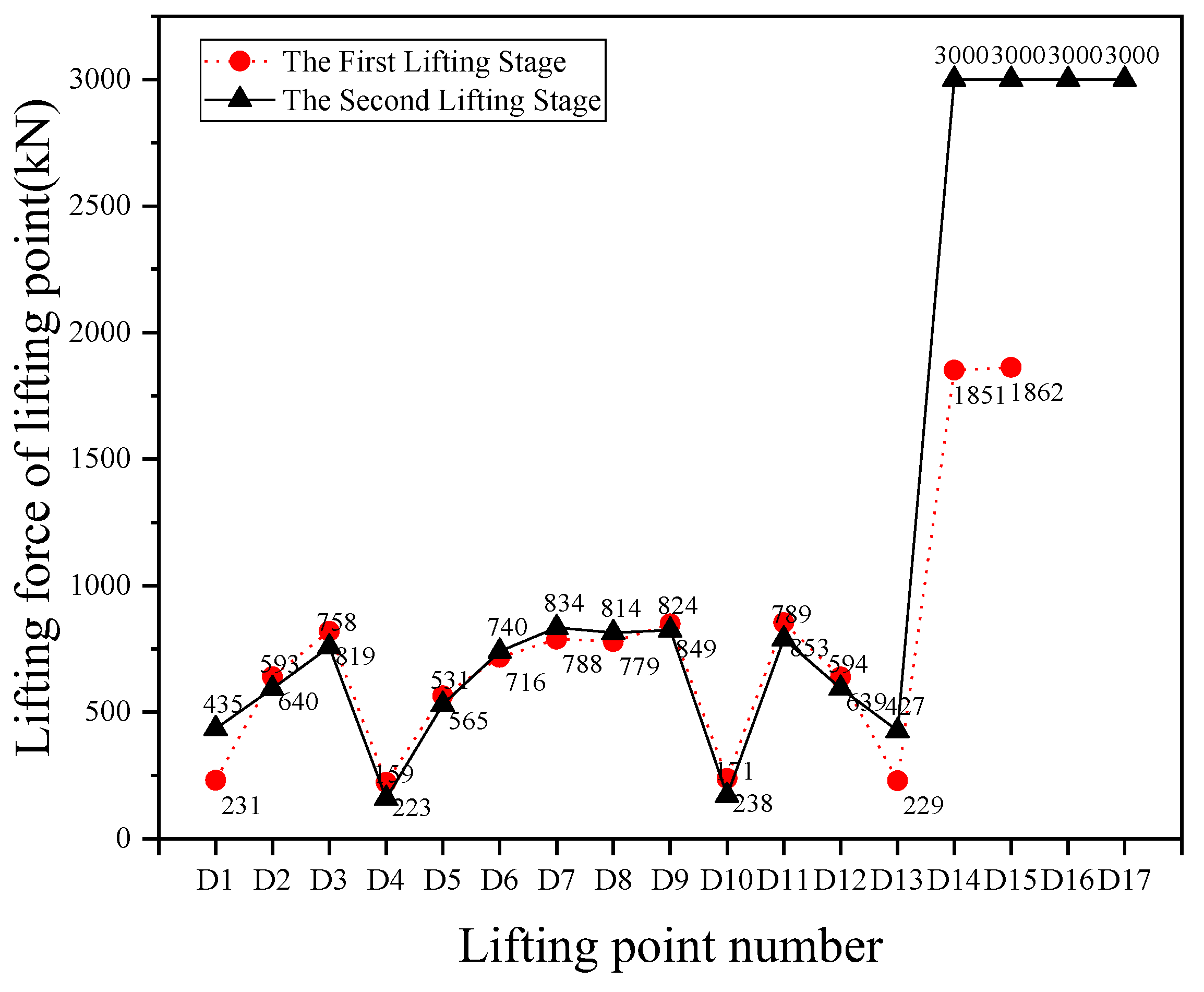
Preprints 74563 g009
Preprints 74563 g010
Figure 10. Vertical deformation cloud map of single point lifting spatial grid (mm): a 20mm displacement difference imposed on lifting point D7; a 20mm displacement difference imposed on lifting point D8; a 20mm displacement difference imposed on lifting point D9.
Figure 10. Vertical deformation cloud map of single point lifting spatial grid (mm): a 20mm displacement difference imposed on lifting point D7; a 20mm displacement difference imposed on lifting point D8; a 20mm displacement difference imposed on lifting point D9.
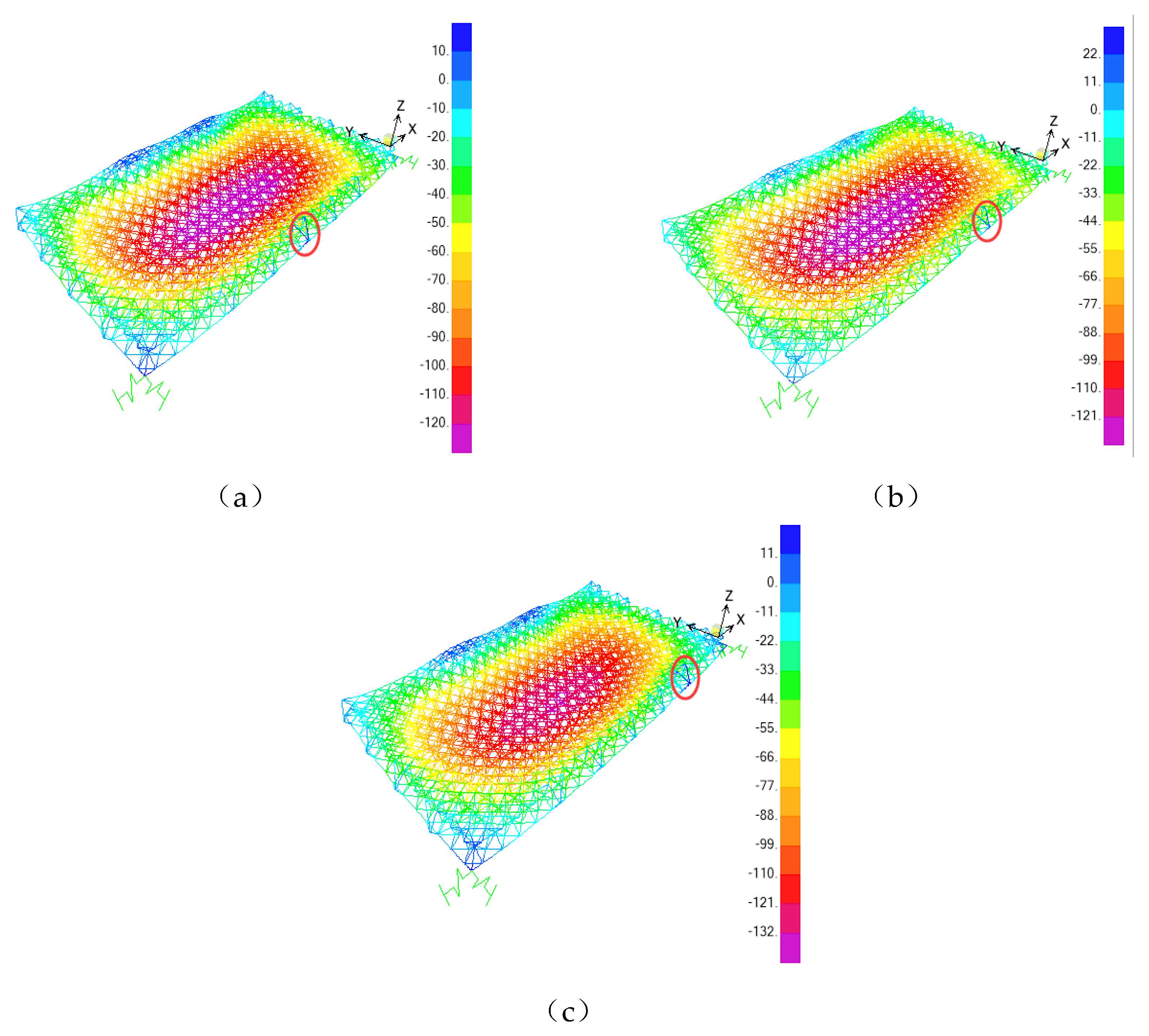
Preprints 74563 g010
Preprints 74563 g011
Figure 11. Vertical deformation cloud map of double points lifting spatial grid (mm): a 20mm displacement difference imposed on lifting points D7 and D8; a 20mm displacement difference imposed on lifting points D7 and D9.
Figure 11. Vertical deformation cloud map of double points lifting spatial grid (mm): a 20mm displacement difference imposed on lifting points D7 and D8; a 20mm displacement difference imposed on lifting points D7 and D9.
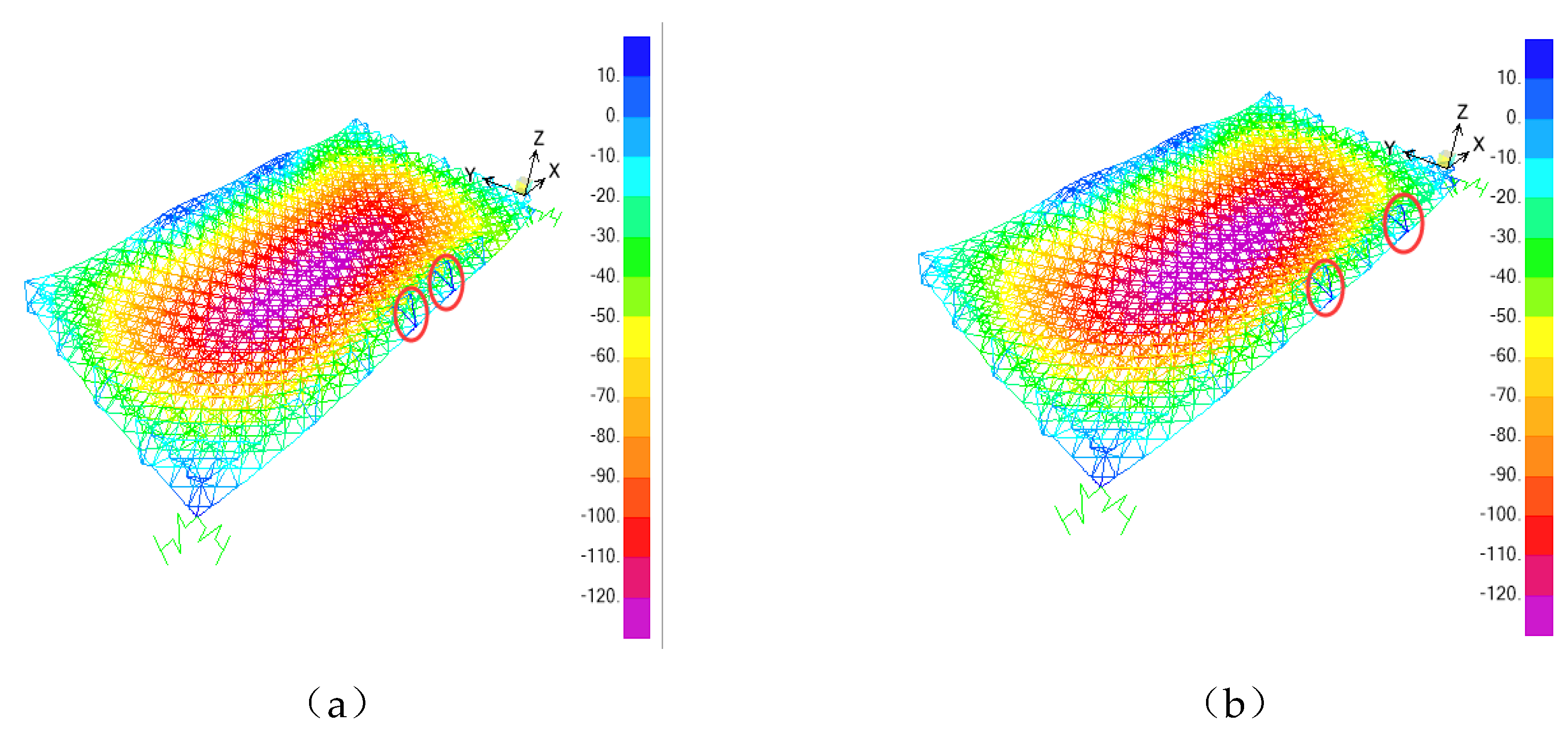
Preprints 74563 g011
Table 1. Lifting force when a 20mm displacement difference is imposed on a lifting point (kN).
Table 1. Lifting force when a 20mm displacement difference is imposed on a lifting point (kN).
Lifting point number Lifting force (kN)
D1 D2 D3 D4 D5 D6 D7 D8 D9 D10 D11 D12 D13 D14 D15
D1 303 590 816 234 564 719 795 782 849 238 854 640 228 1820 1865
D2 181 758 750 223 563 721 791 779 850 239 858 638 230 1860 1852
D3 228 571 952 157 571 718 785 777 849 239 851 638 230 1867 1855
D4 232 640 753 297 546 712 789 779 849 238 854 640 229 1875 1854
D5 229 637 825 203 646 648 786 781 850 238 854 640 229 1860 1861
D6 235 644 821 219 498 861 717 772 851 238 852 639 231 1845 1862
D7 238 643 816 223 564 645 942 701 847 239 851 641 235 1852 1850
D8 235 640 818 223 568 709 711 933 778 238 849 646 235 1870 1835
D9 232 640 819 223 566 717 786 707 934 216 863 637 228 1876 1841
D10 231 640 820 223 567 716 789 778 827 311 787 640 229 1865 1864
D11 232 638 817 223 566 714 786 774 859 172 988 568 226 1866 1856
D12 232 638 818 223 566 716 790 785 847 238 783 759 179 1863 1849
D13 230 640 820 223 565 718 794 784 848 239 850 590 300 1876 1809
D14 144 634 827 246 560 680 766 792 875 242 860 640 254 2079 1687
D15 256 640 825 226 583 735 785 743 825 262 861 633 861 1698 2068
Note: The thickened data indicate the lifting force of the lifting point with 20mm displacement difference.
Table 2. Lifting force when a 20mm displacement difference is imposed on two lifting points (kN).
Table 2. Lifting force when a 20mm displacement difference is imposed on two lifting points (kN).
Lifting point numbers Lifting force (kN)
D1 D2 D3 D4 D5 D6 D7 D8 D9 D10 D11 D12 D13 D14 D15
D7-D8 238 643 818 223 568 709 942 933 847 239 851 646 235 1870 1850
D7+D8 242 643 814 224 566 638 865 856 775 238 846 647 241 1859 1833
D7-D9 238 643 819 223 566 717 939 630 932 217 863 641 235 1876 1850
D7+D9 238 643 816 223 564 706 942 707 934 239 861 639 234 1865 1840
Note: The thickened data indicate the lifting force of the lifting point with a 20mm displacement difference. "-" indicates that the displacement difference is applied separately, and "+" indicates that the displacement difference is applied simultaneously.
Table 3. The most unfavorable conditions when the spatial grid is asynchronized lifting.
Table 3. The most unfavorable conditions when the spatial grid is asynchronized lifting.
Number Working condition Number Working condition
1 D1 9 D9
2 D2 10 D10
3 D3 11 D11
4 D4 12 D12
5 D5 13 D13
6 D6 14 D14
7 D7 15 D15
8 D8 16 D1+D3+D5+D7+D9+D11+D13
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated