Balancing Strategy for Battery Systems Based on Reconfigurable Converters

Preprint

Article

Balancing Strategy for Battery Systems Based on Reconfigurable Converters

Altmetrics

Downloads

151

Views

Comments

Guangwei Wan,

Qiang Zhang^*,Menghan Li,

Siyuan Li^*,Zehao Fu,Junjie Liu

Guangwei Wan,

Qiang Zhang^*,Menghan Li,

Siyuan Li^*,Zehao Fu,Junjie Liu

This version is not peer-reviewed

Submitted:

26 May 2023

Posted:

29 May 2023

You are already at the latest version

Alerts

Abstract

This paper proposes a new battery balancing control strategy based on state of charge (SOC) for addressing the problem of cell-to-cell differences in lithium-ion battery systems. The strategy utilizes a reconfigurable converter system to transfer energy from high-SOC battery modules to low-SOC battery modules and allows balancing the battery modules while they are powering the load. A MATLAB/Simulink simulation model with five batteries was built to validate the effectiveness of the proposed balancing strategy under unloaded and loaded conditions. The simulation results demonstrate that the proposed strategy achieves more efficient and accurate battery module balancing compared to the previous balancing modes, thus increasing the overall lifespan and safety of the battery pack.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

Due to the cell-to-cell variation in lithium-ion battery systems, individual cells may become overcharged or over-discharged during charging and discharging processes. Failure to perform timely and effective balancing may result in decreased battery pack lifespan, reduced capacity, performance degradation, and even safety hazards such as fire [1,2]. Therefore, battery balancing plays an important role in improving overall battery pack lifespan, ensuring battery safety and reliability, and increasing energy utilization efficiency [3,4].

Battery balancing methods can be classified into passive balancing and active balancing depending on whether energy dissipation is involved [5].

Passive balancing mainly utilizes resistors to bypass discharge energy from cells with higher energy levels, consuming their excess energy in the form of heat to achieve energy consistency among all cells. The advantages of passive balancing include simple and feasible circuit structure, low cost, small circuit volume, and easy control. However, since energy is dissipated in the form of heat, the overall energy utilization efficiency of the battery module is relatively low [6,7].

Active balancing mainly utilizes energy storage components such as capacitors and inductors to transfer energy between cells, which can be achieved with different circuit structures. Active balancing has high energy utilization efficiency, high balancing efficiency, and fast balancing speed. However, it usually comes with complex circuit structures and control strategies, resulting in higher implementation costs [8].

Currently, reconfigurable battery energy storage systems have attracted increasing attention due to their ability to dynamically reconfigure the battery topology in real-time to adapt to specific application requirements [2,9,10,11,12,13]. This can more effectively utilize battery resources, isolate corresponding batteries according to their current state of charge and health status without affecting the charge and discharge processes of other batteries, and extend the battery's service life while reducing the possibility of module failure [14,15].

Since the internal resistance between battery cells is different, using single-cell voltage as the balancing index would typically result in errors. Therefore, the state of charge (SOC) of the battery is usually used as the balancing index. The State of Charge (SOC) is commonly used to characterize the amount of charge in a battery cell. A battery cell’s SOC is defined by the ratio of the cell’s present amount of charge to its rated charge capacity [16]. In [17], the authors proposed an integrated reconfigurable converter structure that can be used for high-voltage battery systems. In [18,19], the authors proposed load-sharing balancing strategies and distributed balancing control for battery modules based on the circuit structure of the integrated reconfigurable converter. In [20], the authors improved the structure of the integrated reconfigurable converter system and proposed a new balancing strategy. However, this balancing strategy cannot achieve free energy exchange between battery modules.

In this paper, we propose a new charge-balancing strategy based on [20]. This balance mode enables high-charged battery modules to transfer energy to low-charged battery modules and achieve free energy exchange between battery modules.

This paper is organized as follows: Section 2 introduces the integrated system of reconfigurable battery and converter and illustrates its working principle. Section 3 describes the balancing strategy and design of the control system. Section 4 presents simulation experimental results and analysis. The last section concludes this paper.

2. Structure and Working Principle of Integrated Reconfigurable Converter

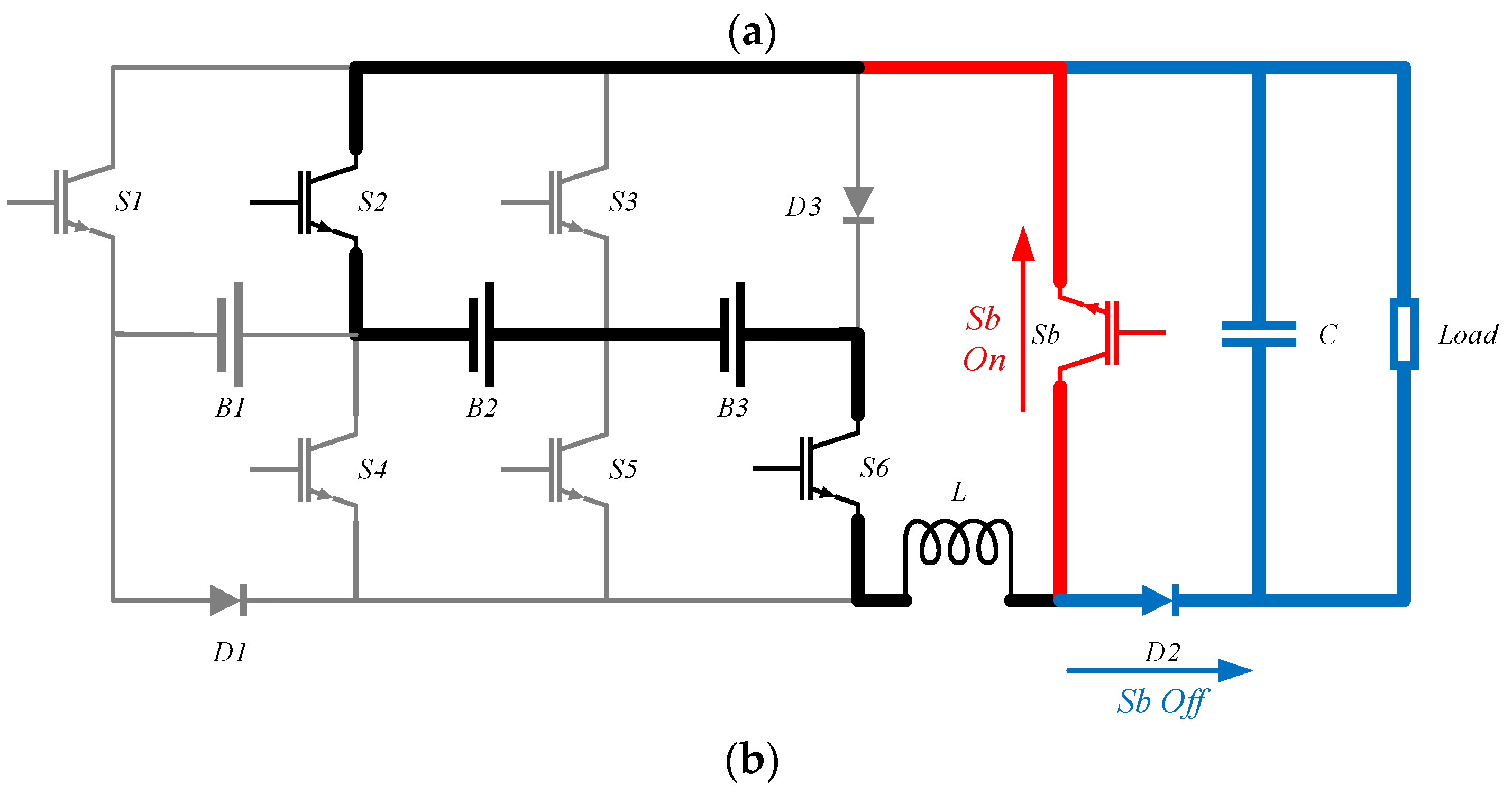
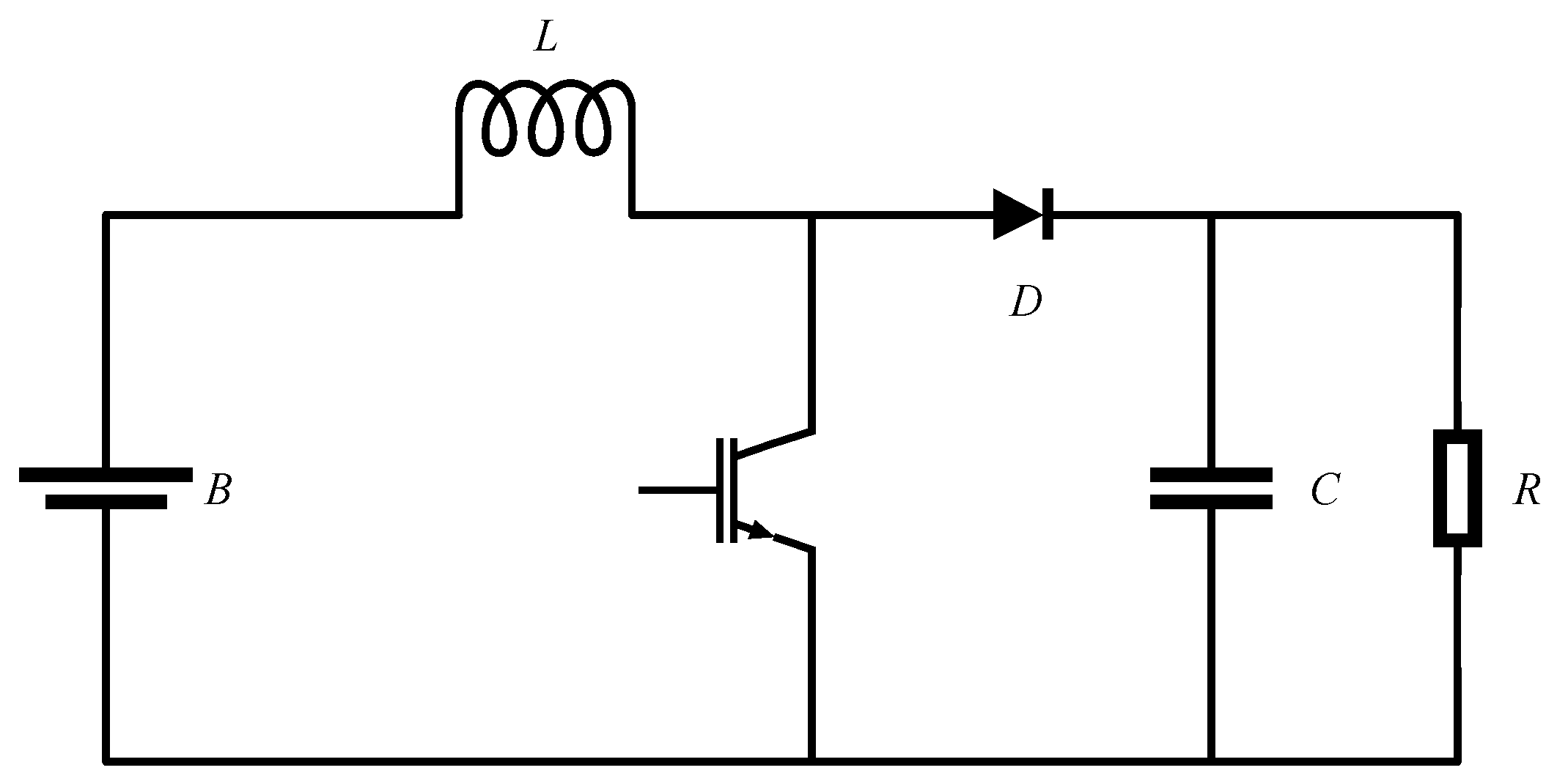
The integrated reconfigurable converter is shown in Figure 1, where three battery modules are presented for illustration purposes. However, the same configuration can be applied to systems with a higher number of battery modules. The entire system consists of a battery module selector and boost converters. The Boost converter's configuration is displayed in Figure 2. The battery modules can be dynamically reconfigured to select different input voltages. When the input voltage changes, the range of output voltage that the Boost converter can provide also changes accordingly. The relationship between the output voltage V_out, input voltage V_in, and the duty cycle D of the Boost converter is expressed in Equation (1). Table 1 shows the different battery modules that the battery module selector can choose from. It is worth noting that due to the need to reduce the number of switches, the battery module selector cannot individually connect B1 and B3 to the circuit, which can be further improved in future circuit designs.

V_{out} = \frac{1}{1 - D} V_{in}

(1)

The Battery Management System (BMS) can identify battery modules with relatively high States of Charge (SOC), and the battery module selector prioritizes their discharging by switching corresponding switches. The BMS can dynamically reconfigure battery modules to have two different working modes: power supply mode and balancing mode. These two modes will be elaborated on in detail below.

2.1. Power supply mode

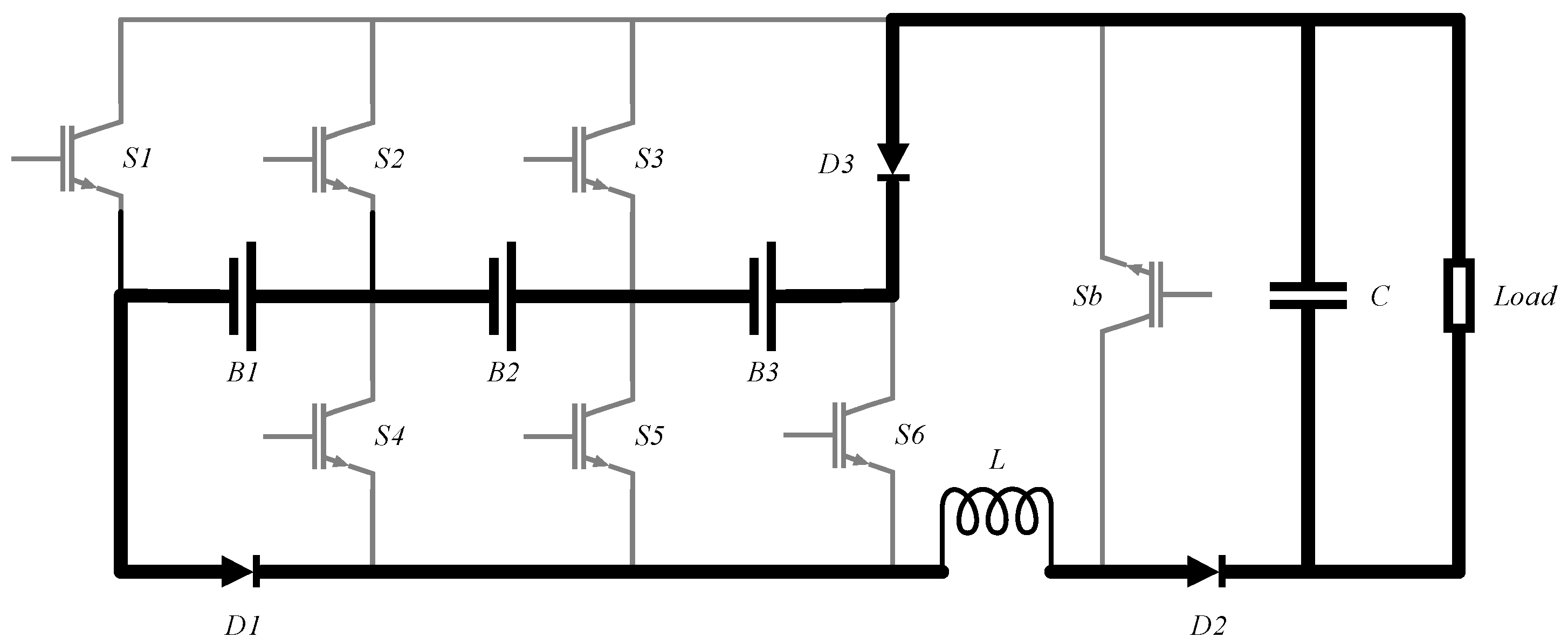
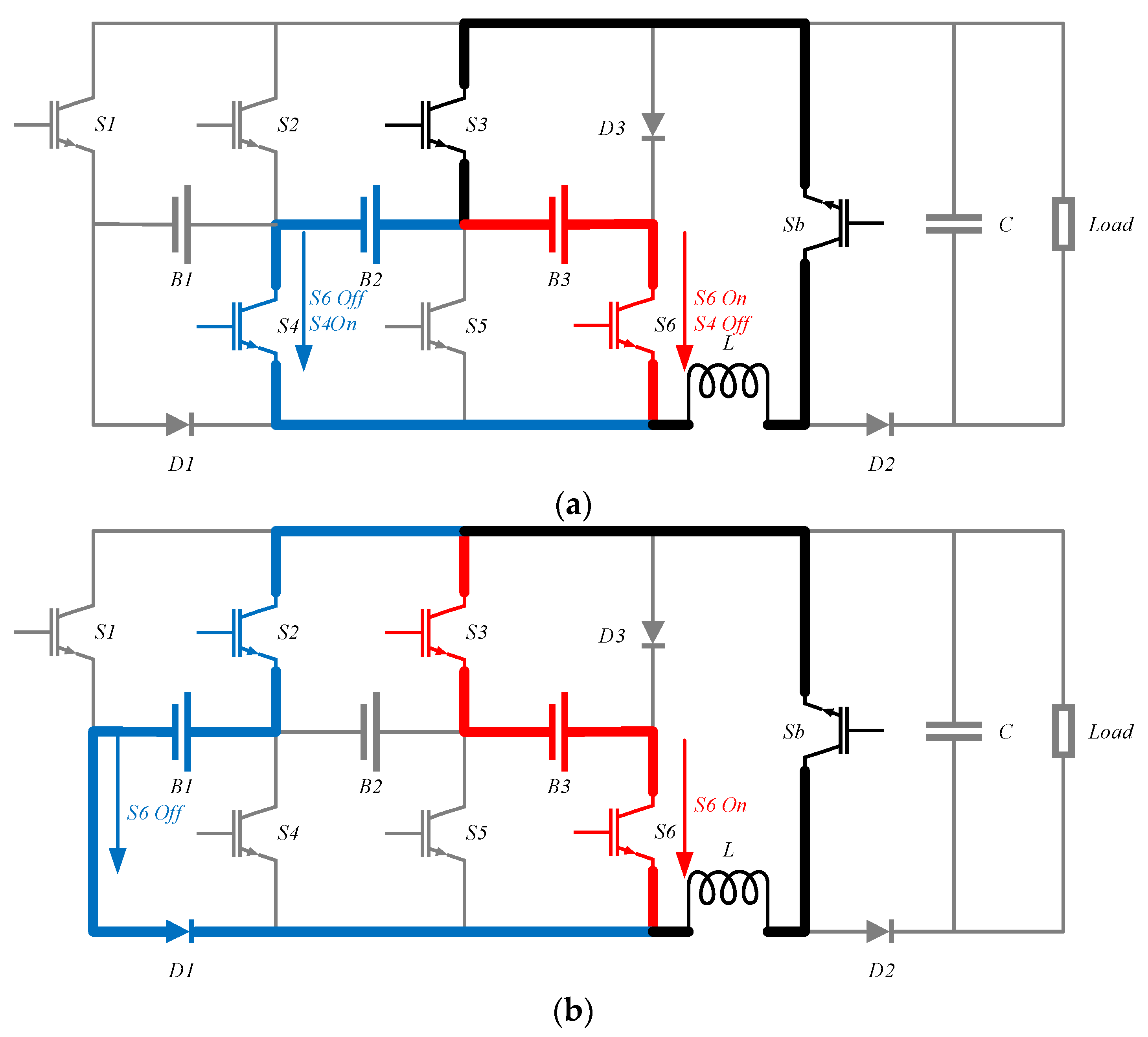
Figure 3a,b illustrate the configuration of the battery system when they are powering the load. In this mode, the converter operates in boost mode, and the control system can select different battery modules through the battery module selector to discharge at different input voltages. In case of a failure among the switches S1-S6, a flow path is required to release the energy from the inductor to protect the circuit from damage. Figure 4 shows the path where the inductor current flows. This path can also be used to return the energy from the inductor back to all battery modules, which not only protects the circuit but also avoids wasting energy.

2.2. balance mode

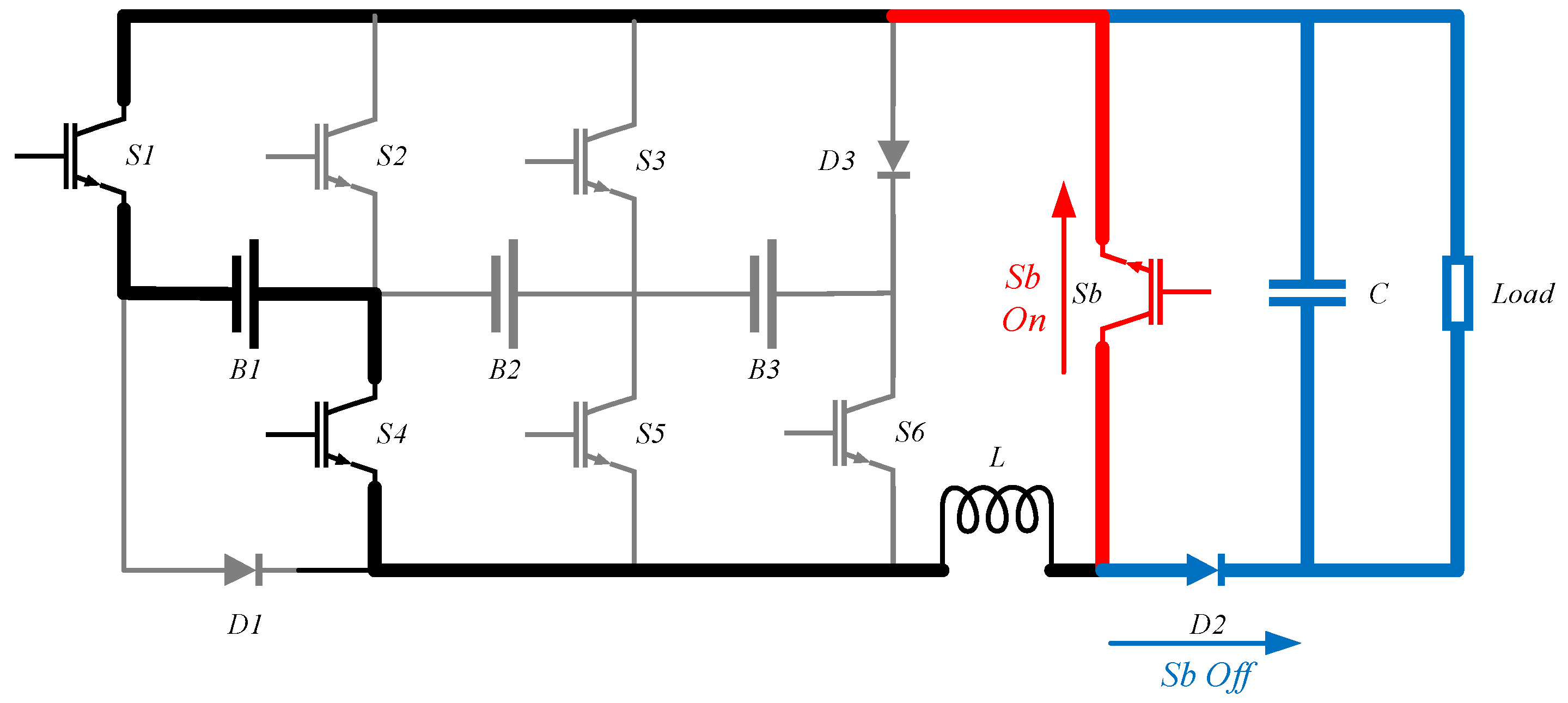
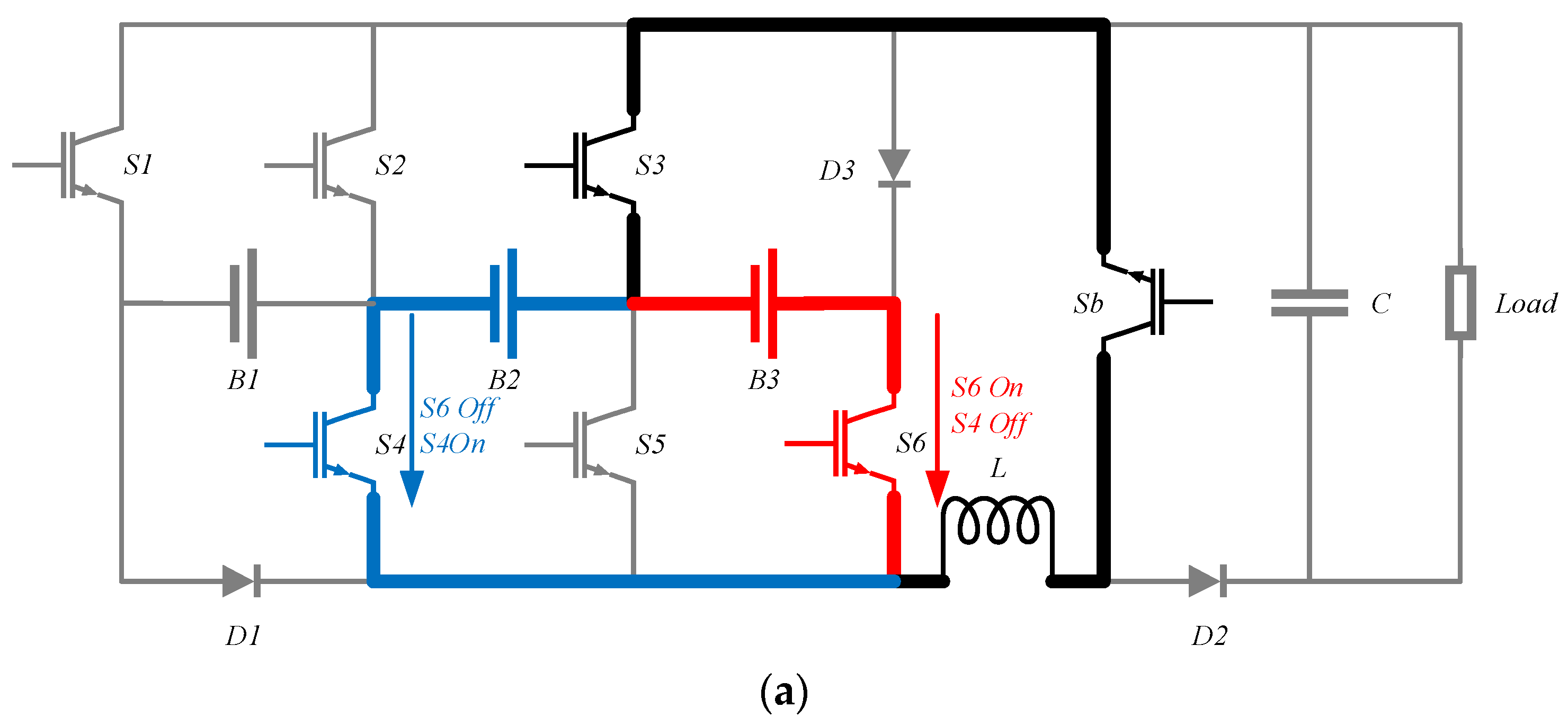
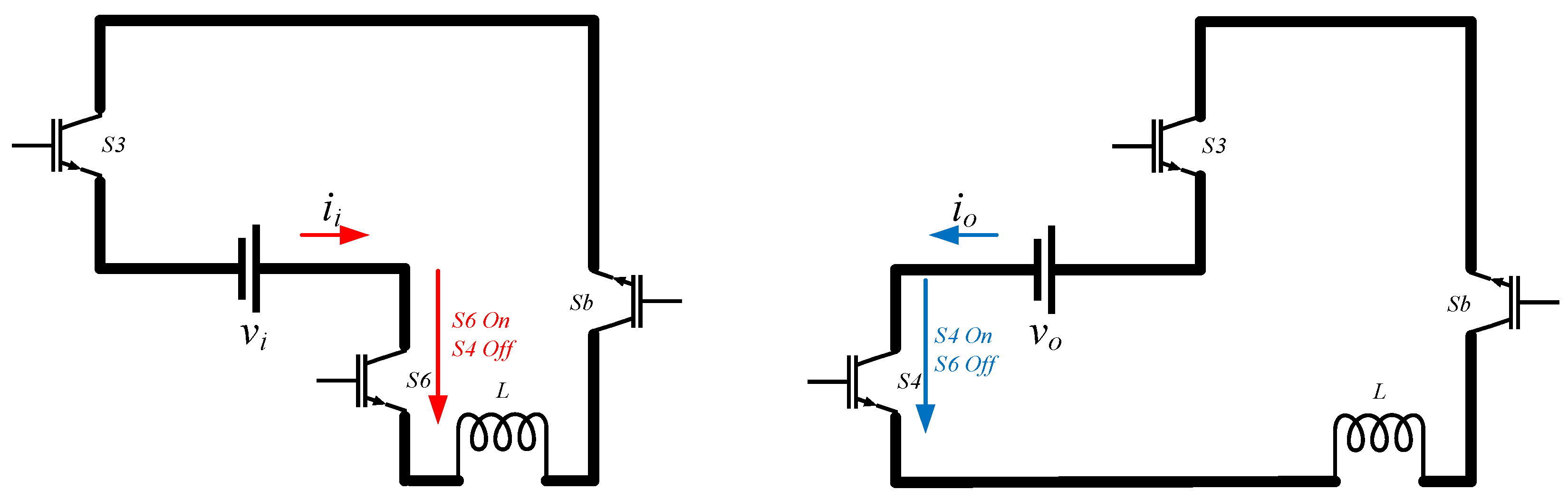
The balancing mode enables energy transfer from battery modules with high SOC to those with lower SOC, and this energy transfer is achieved by utilizing the inductor L. Figure 5a–c demonstrate the leftward energy transfer. Figure 5a shows the energy transfer between one module and another. In this figure, switches Sb and S3 are always on, and by turning on switch S6 and turning off switch S4, the energy in B3 shifts to inductor L. Then, by turning off switch S6 and turning on switch S4, the energy in inductor L is released and charges B2, achieving energy transfer from B3 to B2. The same switching cycle is repeated until the two modules reach equilibrium. 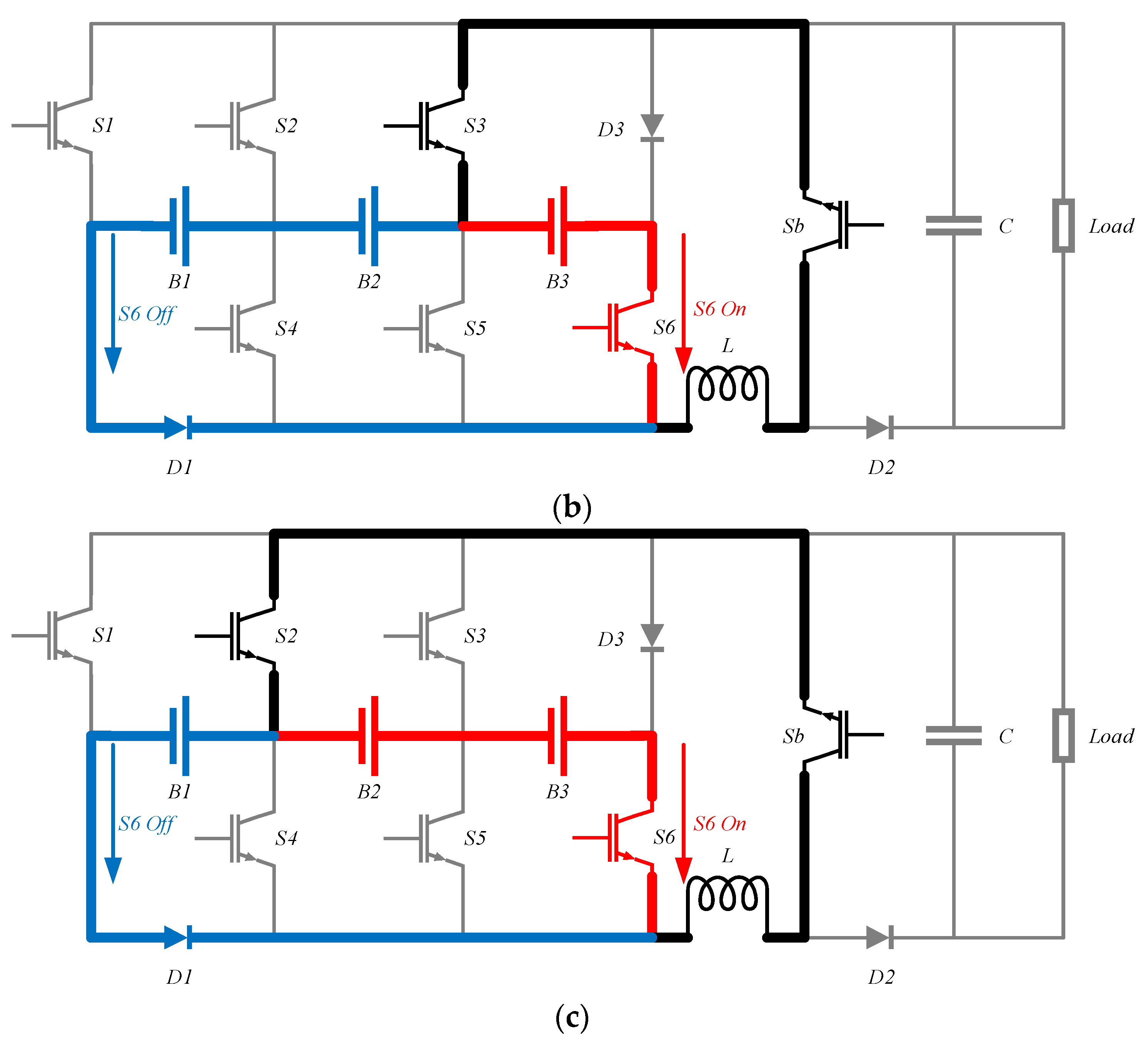Figure 5b illustrates the energy transfer from one module to two modules, and Figure 5c shows the energy transfer from two modules to one module.

3. Balancing Strategy and Control System Design

This section describes the system balancing strategy and the design of the control system.

3.1. balanced strategy

The proposed new balancing strategy first identifies the battery module with the highest SOC and charges the inductor. Since the current flowing through the inductor cannot change immediately, the energy on the inductor is transferred to the battery module with the lowest SOC by changing the switch status. This balancing strategy can accelerate the balancing speed and can also be applied during load usage. The specific balancing strategies for scenarios with and without load usage are explained below:

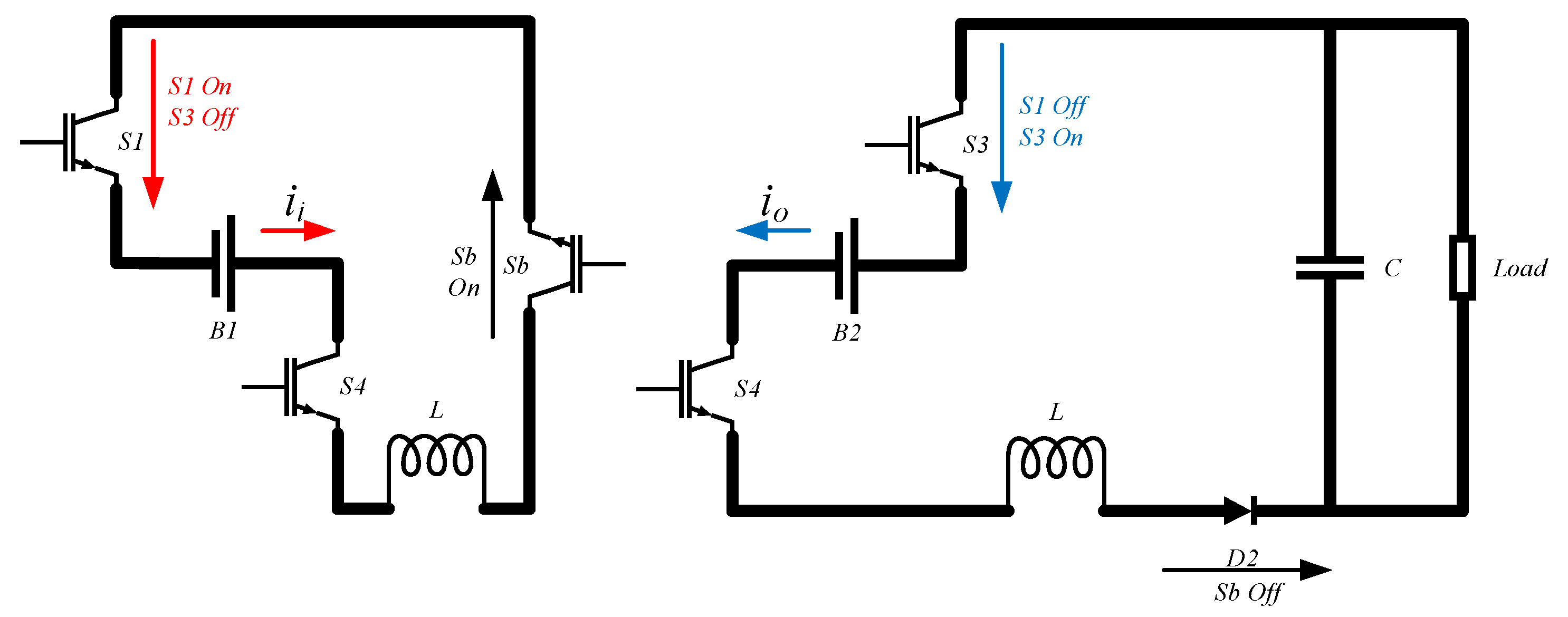
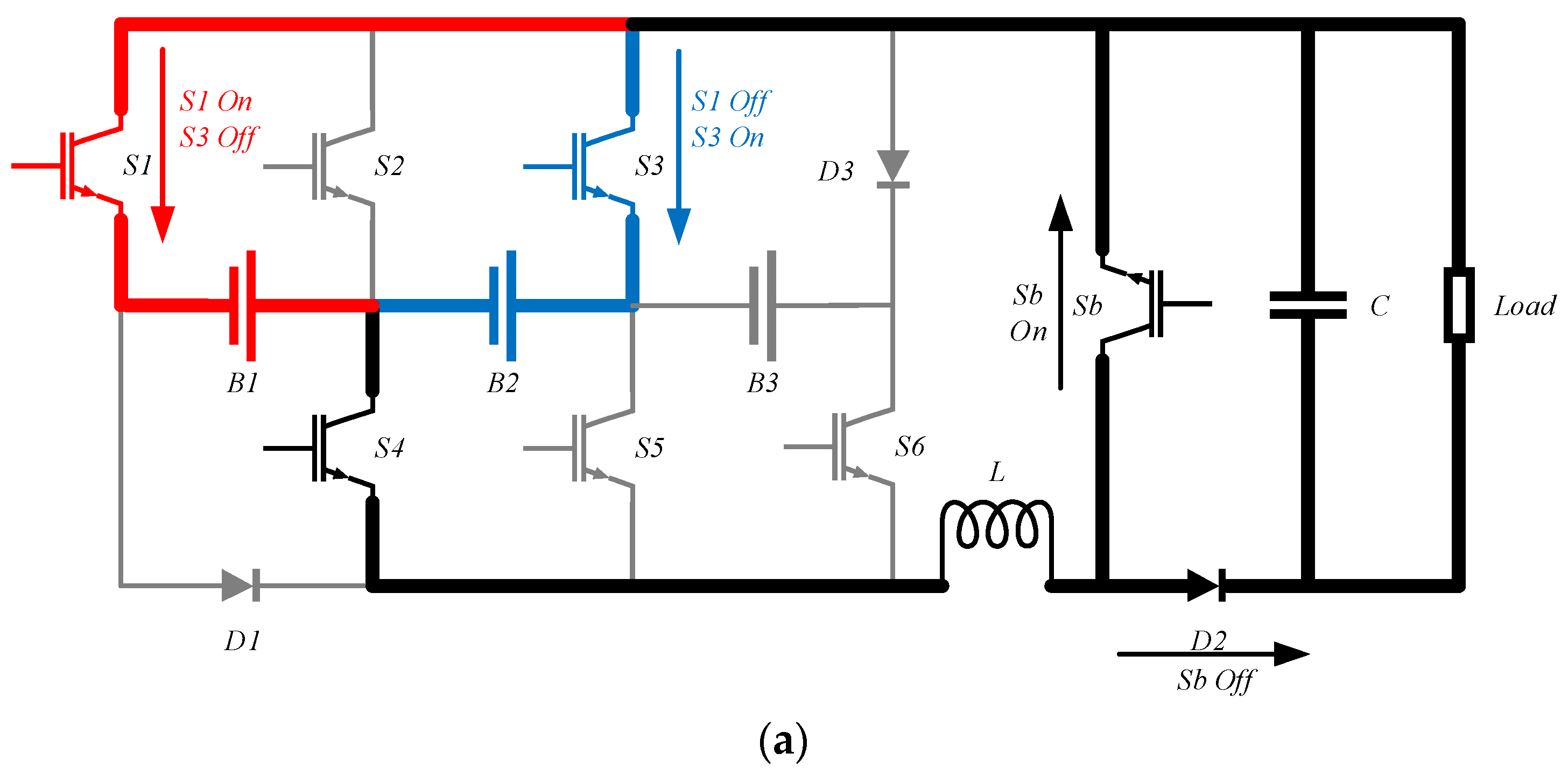
When there is no load usage, the balancing measure of the battery system is to have the battery module with the highest SOC store energy in the inductor, and then change the switch status to release the energy stored on the inductor to the battery module with the lowest SOC. As shown in Figure 6a,b, when battery module B3 has the highest charge while B2 has the lowest, the balancing strategy adjusts such that battery module B3 first charges the inductor through switches S3 and S6, then maintains the closure of switch S3 and opens switch S4 to transfer the energy from the inductor to S4. Figure 6b shows the energy transfer from battery module B3 to battery module B1 when B3 has the highest charge while B1 has the lowest.

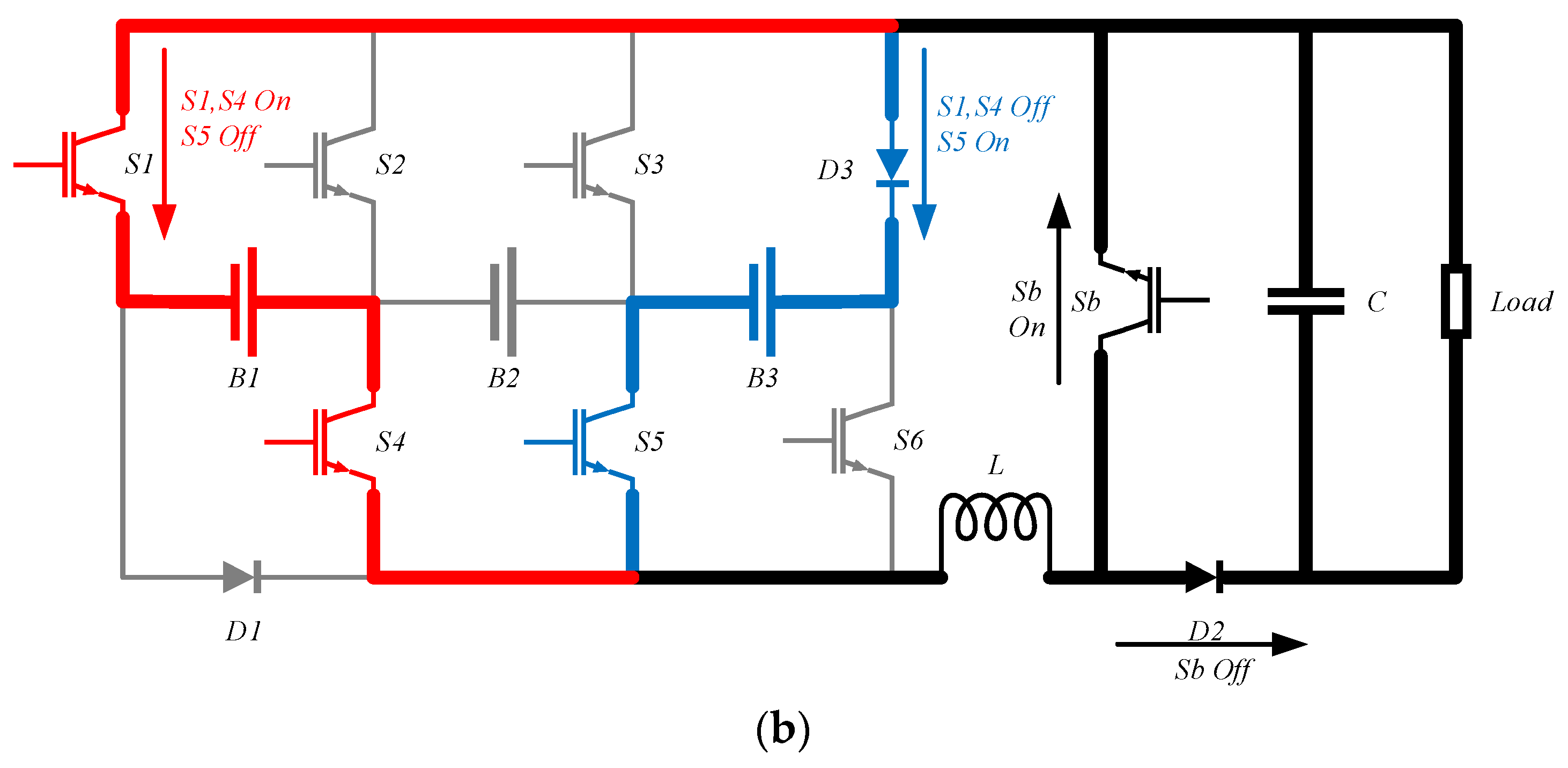
When the load needs to be used, a converter is connected, and the balancing measure of the battery system is adjusted so that the battery module with the highest charge level supplies power to both the load and the inductor, then, by changing the switch status, the energy stored on the inductor is released to the battery module with the lowest SOC. As shown in Figure 7a,b, when battery module B1 has the highest charge level while B2 has the lowest with the load operating, the balancing strategy adjusts such that battery module B1 supplies power to the inductor and the load via switches S1 and S4, then maintains the closure of switch S4 and opens switch S3 to transfer the energy from the inductor to the load and B2. Figure 7b shows the case when battery module B1 has the highest charge level while B3 has the lowest.

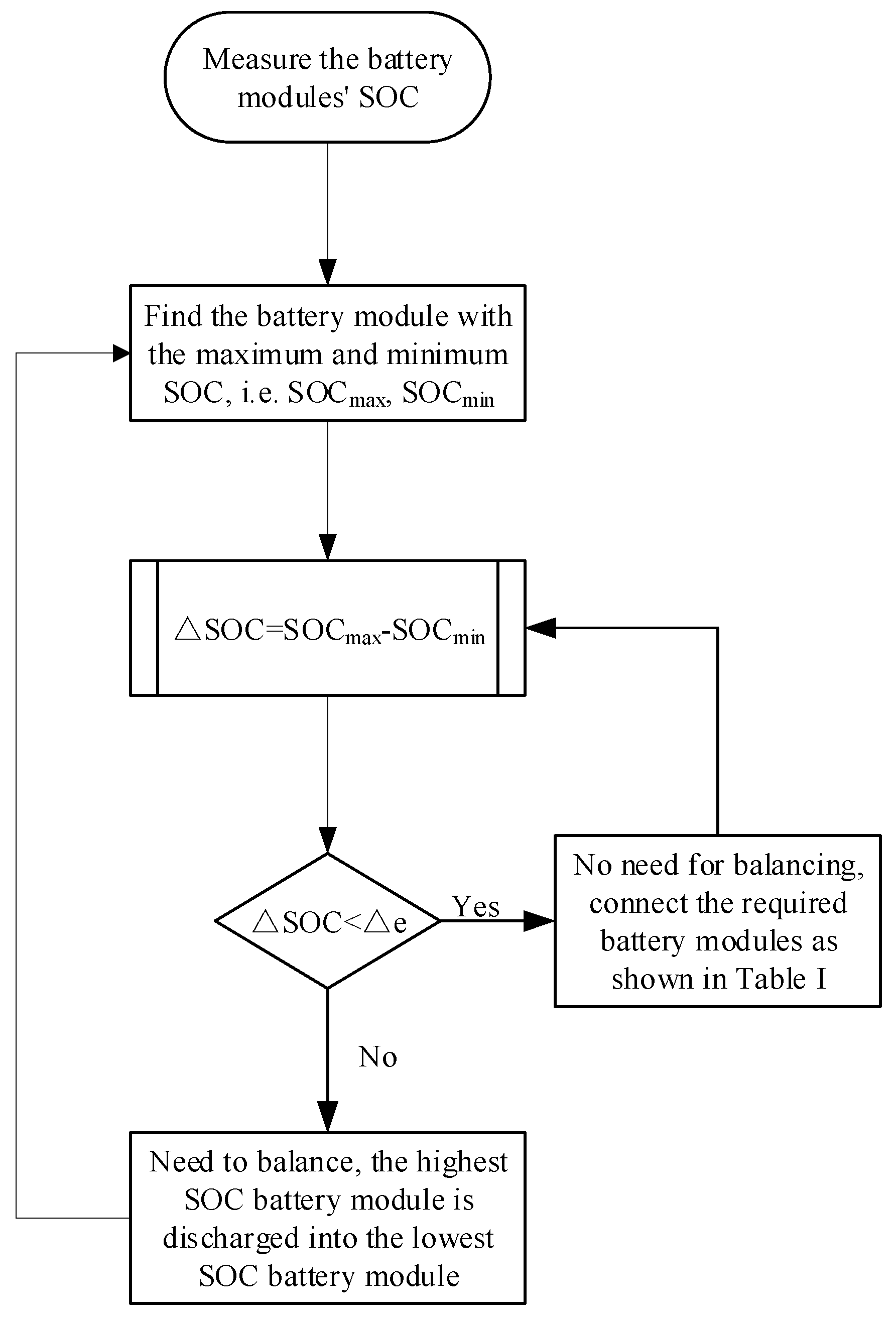
Figure 8 illustrates the flow diagram of the balancing system: First, obtain and sort all SOC values of battery modules to find the module with the highest and lowest SOC levels. If the difference in SOC between two modules exceeds the threshold value ∆e, the control system controls the corresponding switches of these two modules to transfer excess charge from the high SOC module to the low SOC module. If there is no load during the balancing process, switch Sb remains closed. If the load is used, a PWM signal is used to control the on/off state of switch Sb to connect the converter, ensuring that a single battery module can provide the required voltage. When the SOC difference between any two modules is lower than the threshold value ∆e, the balancing process ends, and the required battery modules can be connected according to Table 1 to change the working voltage range of the boost converter. Once the SOC difference exceeds the threshold value ∆e, the balancing procedure starts over. This iterative process ensures effective SOC balancing and prevents overcharging or over-discharging, thus improving the overall life and safety performance of the battery.

3.2. Control System Design

This section describes the design of a balancing system with and without load, and the balancing system controllers are both PI controlled.

3.2.1. Controller design for the balancing operation when no load is used.

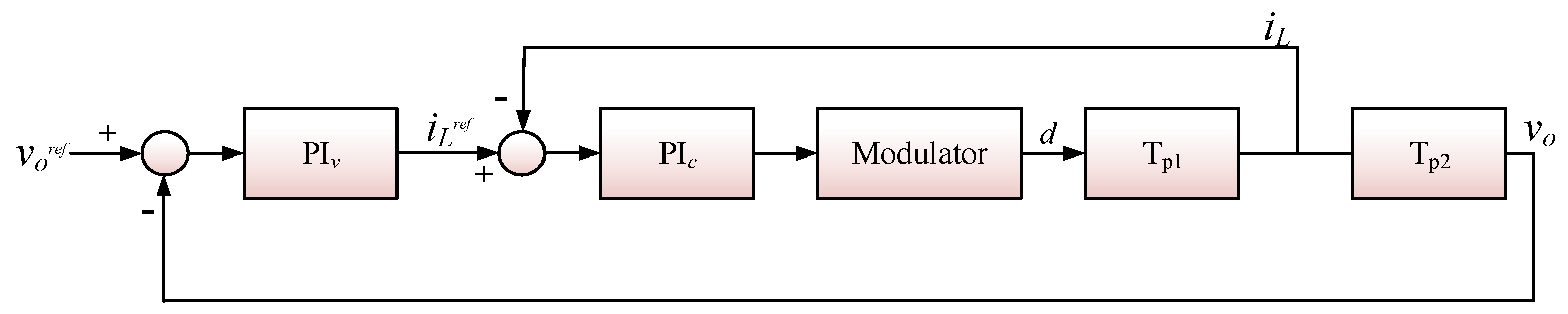
The system diagram of the PI controller without load balancing mode is shown in Figure 9. In order to design the PI controller, the small-signal modeling shown in Figure 10 is first derived

The average state equation for balancing mode without load usage is as follows:

L \frac{d i_{L}}{d t} = d v_{i} - (1 - d) v_{o}

(2)

Introducing ac perturbations into the above equation yields

L \frac{d (I_{L} + \hat{i_{L}})}{d t} = (D + \hat{d}) (V_{i} + \hat{v_{i}}) - [1 - (D + \hat{d})] (V_{o} + \hat{v_{o}})

(3)

The small-signal model can then be written as

L \frac{d \hat{i_{L}}}{d t} = \hat{d} V_{i} + D \hat{v_{i}} - (1 - D) \hat{v_{o}} + \hat{d} V_{o}

(4)

The above equation can be obtained by applying Laplace transform:

s L \hat{i_{L}} = D \hat{v_{i}} - (1 - D) \hat{v_{o}} + \hat{d} (V_{o} + V_{i})

(5)

The transfer function of the balancing mode when unused load can be obtained from equation (5):

T_{p} = \hat{\frac{i_{L}}{\hat{d}}} = \frac{V_{i} + V_{o}}{L s}

(6)

The transfer function of the PWM modulator can be modeled as:

T_{m} = \frac{1}{\hat{V}}

(7)

where

\hat{V} = 1

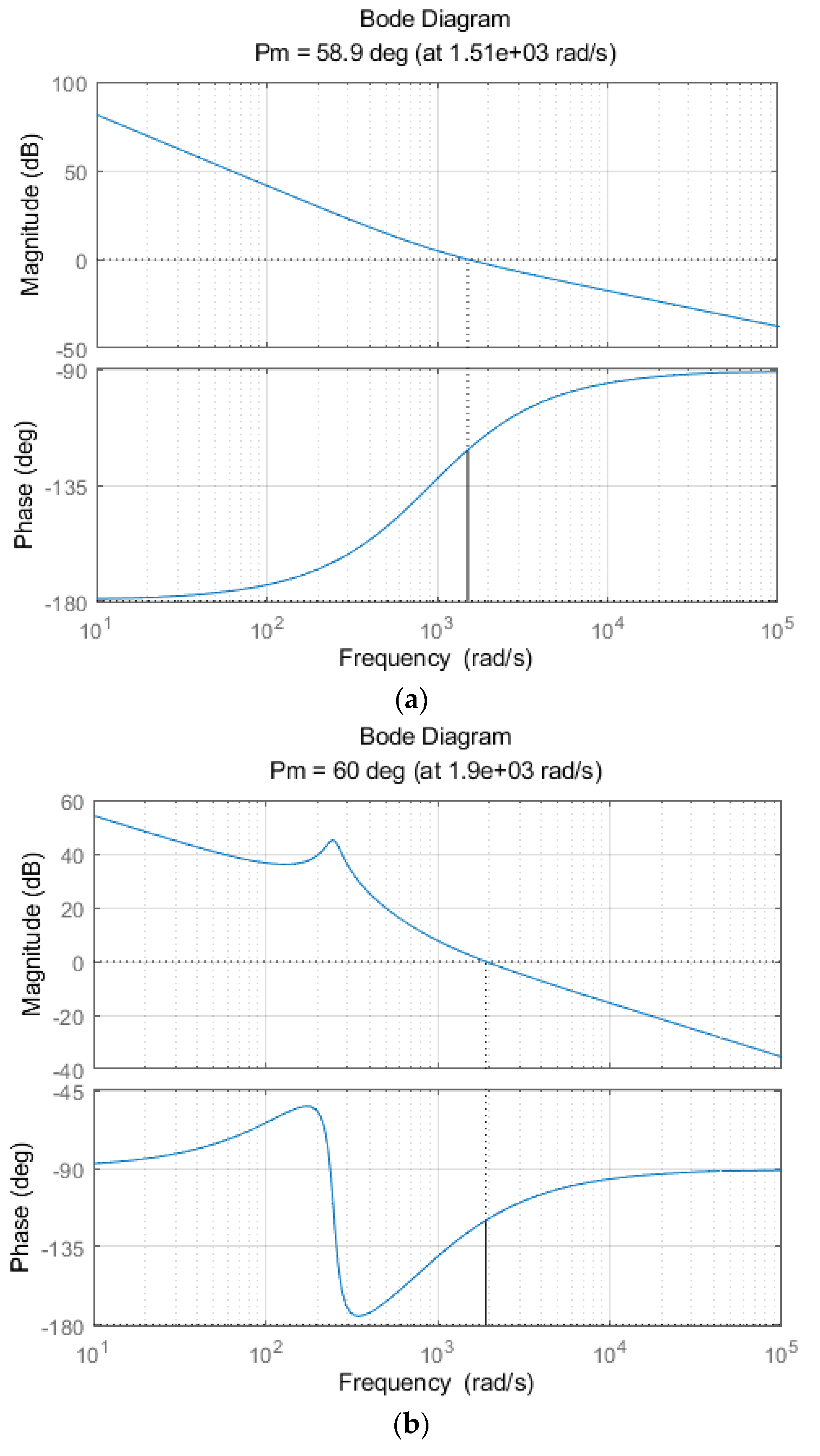
is the peak value of the sawtooth carrier signal. Using the small-signal transfer function (6), the PI controller parameters K_p and K_i were calculated to regulate the current on the inductor, namely the balancing current, for achieving the desired open-loop phase margin at the required cutoff frequency. The Bode plot of the control loop in the charging mode is shown in Figure 13a. From the Bode plot, it can be inferred that the system is stable as the open-loop phase margin (PM) at the cutoff frequency is greater than zero.

3.2.2. Controller design for the balancing operation when load is used.

In the balancing mode when load is used, the double-loop control system is adopted for regulating the Buck-Boost circuit composed of the battery pack, inductor, and diode D2, as shown in Figure 11. The inner loop is a high-bandwidth current control loop, while the outer loop is a voltage control loop with lower bandwidth and slower response compared to the inner loop. The voltage outer loop adjusts the output voltage by providing a reference current signal to the current inner loop, which regulates the current on the inductor. Owing to the faster response of the inner loop, the outer loop can be treated separately in the circuit design process, in order to simplify the controller design.

Design of internal current control loop: In order to design the PI controller, the small-signal modeling as shown in Figure 12 is first derived.

The average state equation for balancing mode when using load is as follows:

L \frac{d i_{L}}{d t} = d v_{i} - (1 - d) v_{o}

(8)

C \frac{d v_{o}}{d t} = (1 - d) i_{L} - \frac{v_{o}}{R}

(9)

Introducing ac perturbations into the above equation yields

L \frac{d (I_{L} + \hat{i_{L}})}{d t} = (D + \hat{d}) (V_{i} + \hat{v_{i}}) - [1 - (D + \hat{d})] (V_{o} + \hat{v_{o}})

(10)

C \frac{d (V_{o} + \hat{v_{o}})}{d t} = [1 - (D + \hat{d})] (I_{L} + \hat{i_{L}}) - \frac{V_{o} + \hat{v_{o}}}{R}

(11)

The small-signal model can then be written as

L \frac{d \hat{i_{L}}}{d t} = D \hat{v_{i}} - (1 - D) \hat{v_{o}} + \hat{d} (V_{o} + V_{i})

(12)

C \frac{d \hat{v_{o}}}{d t} = (1 - D) \hat{i_{L}} - \hat{d} I_{L} - \frac{\hat{v_{o}}}{R}

(13)

The above equation can be obtained by applying Laplace transform

s L \hat{i_{L}} = D \hat{v_{i}} - (1 - D) \hat{v_{o}} + \hat{d} (V_{o} + V_{i})

(14)

s C \hat{v_{o}} = (1 - D) \hat{i_{L}} - \hat{d} I_{L} - \frac{\hat{v_{o}}}{R}

(15)

The transfer function can be obtained from equations (15) and (16):

T_{p 1} = \hat{\frac{i_{L}}{\hat{d}}} = \frac{C (V_{o} + V_{i}) s + (2 - D) I_{L}}{L C s^{2} + \frac{L}{R} s + {(1 - D)}^{2}}

(16)

Next, the PI controller parameters K_pc and K_ic were calculated to obtain the desired phase margin for the inner current control loop. The Bode plot of the inner loop is shown in Figure 13b, and it indicates that the system is stable as the open-loop phase margin at the cutoff frequency is greater than zero.

2.: Design of the outer voltage control loop: Due to the high-bandwidth and fast current control characteristics of the inner loop, the transfer function of the inner current control loop can be neglected in the design of the voltage controller. Therefore, the duty cycle D can be assumed constant, and its transfer function is:

T_{p 2} = \frac{\hat{v_{o}}}{\hat{i_{L}}} = \frac{1 - D}{C s + \frac{1}{R}}

(16)

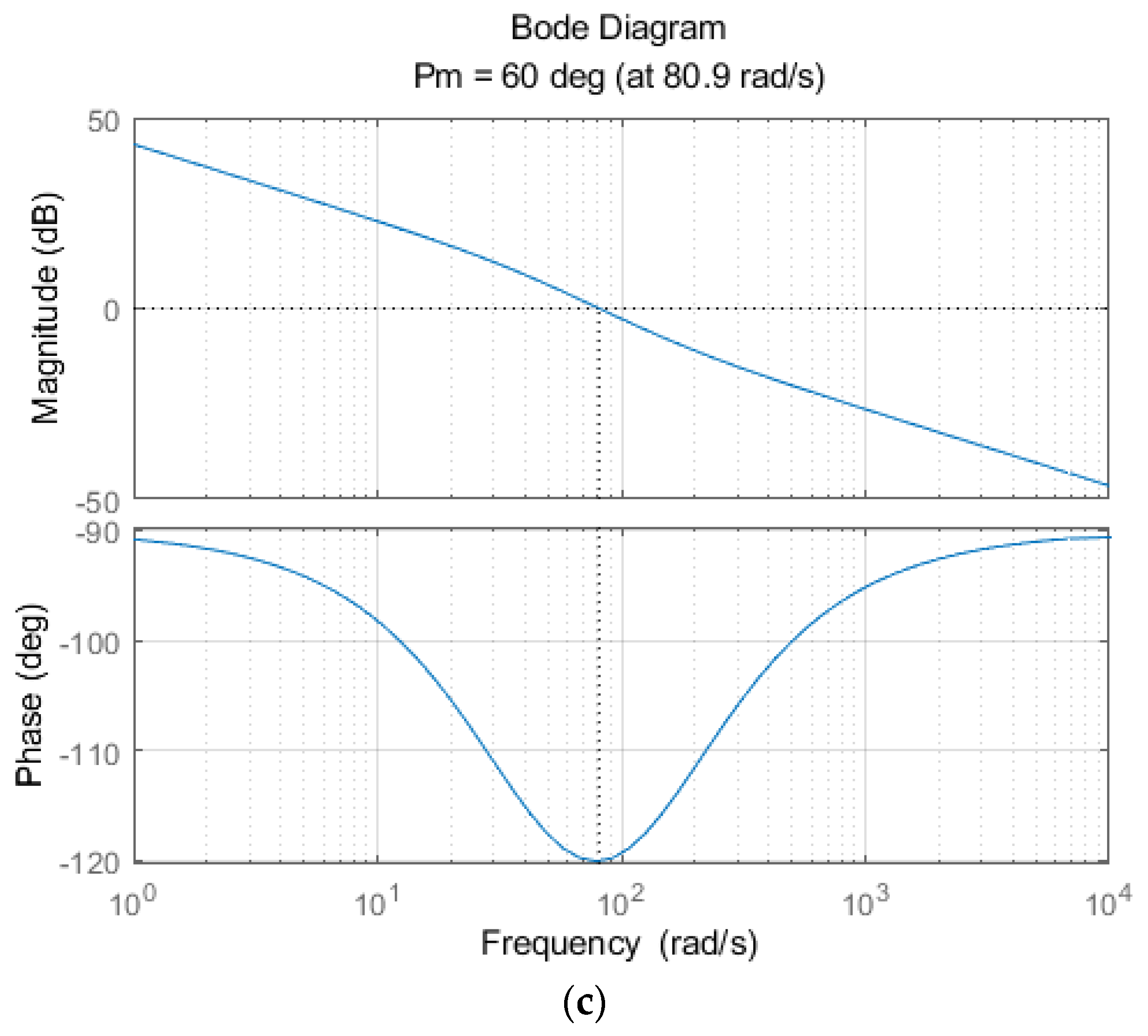
Then calculate the PI controller parameters K_pv and K_iv to obtain sufficient open-loop phase margin at the required cutoff frequency. Figure 13c shows the Bode diagram of the external voltage control circuit. The phase margin at the cut-off frequency is greater than zero, and the system is stable. Parameters of the control system designed as described in Section 3 are given in Table 2.

Figure 13. Bode diagrams of (a) Balance mode control circuit when not using load, (b) internal current control circuit when using load, (c) external voltage control circuit when using load.

4. Simulation result

To verify the effectiveness of the above SOC balancing strategy, a system model with 5 battery cells was built and simulated using Simulink for validation, and compared with the balancing strategy in [20]. The same settings can be applied to a larger number of battery modules. When the control system detects that the difference between the maximum and minimum SOC of the battery module exceeds the set value, the balancing starts until the SOC of all battery modules reaches equilibrium, and the balancing process ends. The simulation model adopts a lithium-ion battery equivalent to the 18650 batteries with a rated voltage of 3.7V and capacity of 2000mAh. The basic parameters of various devices are shown in Table 3.

4.1. Balanced simulation when unused load

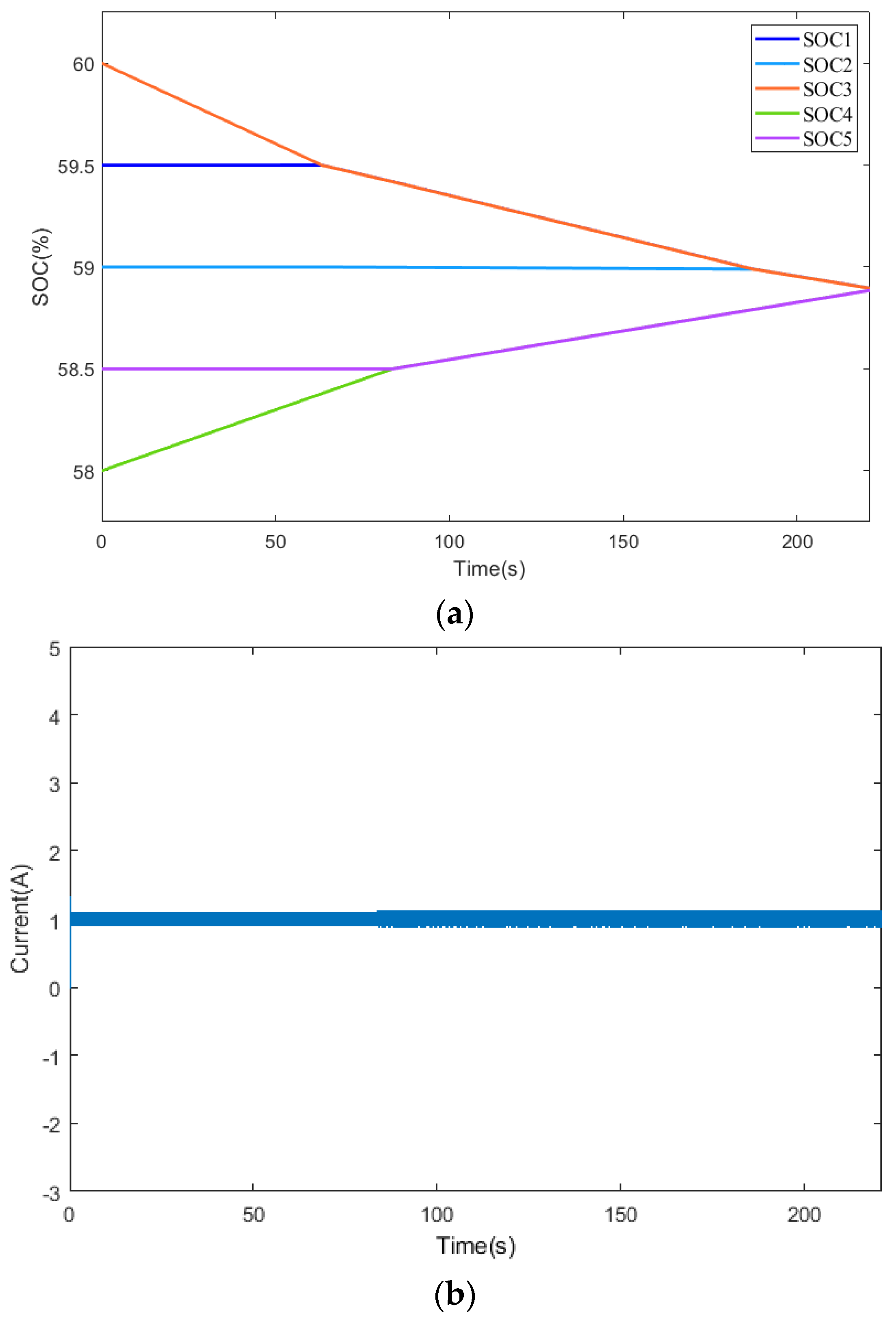
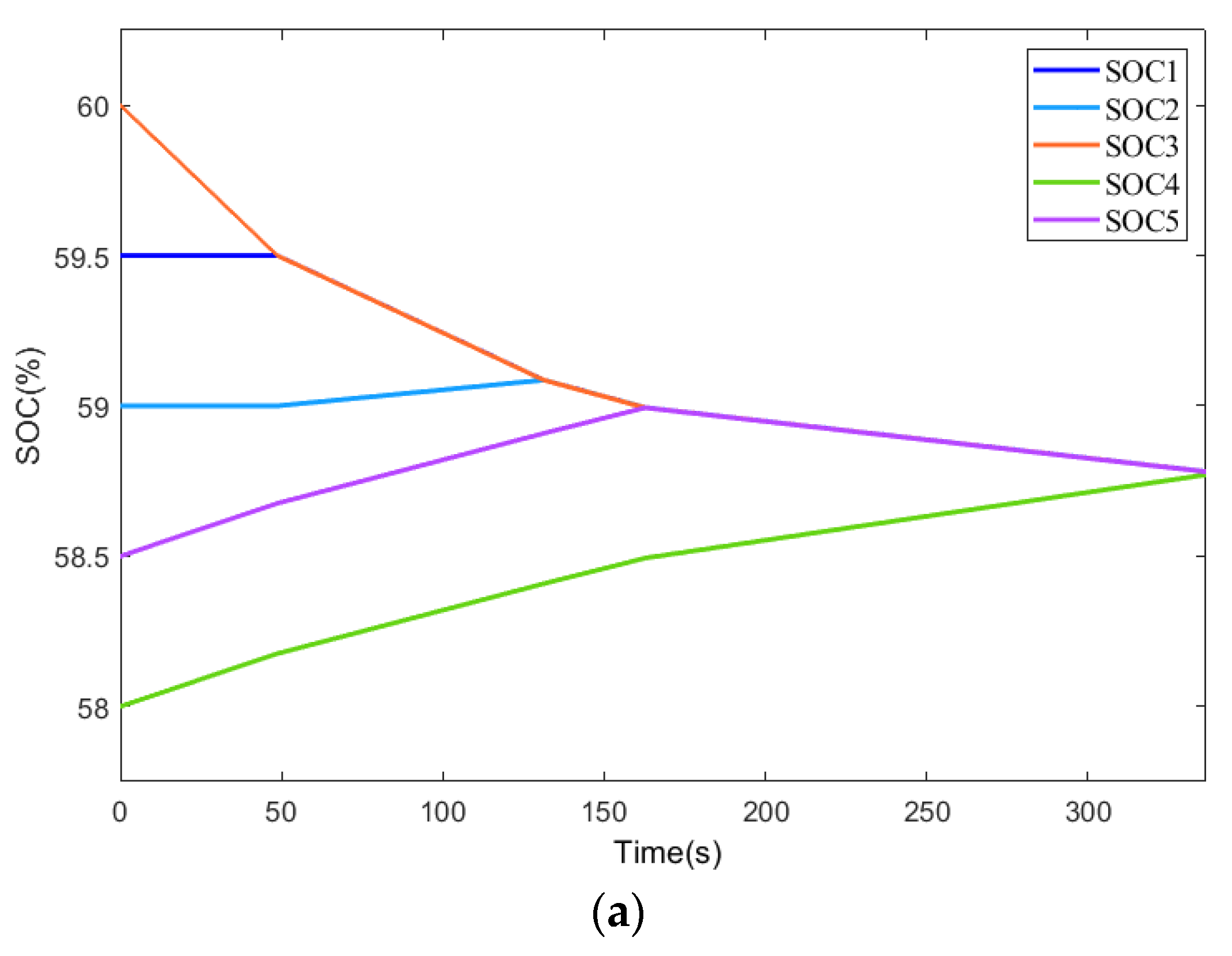
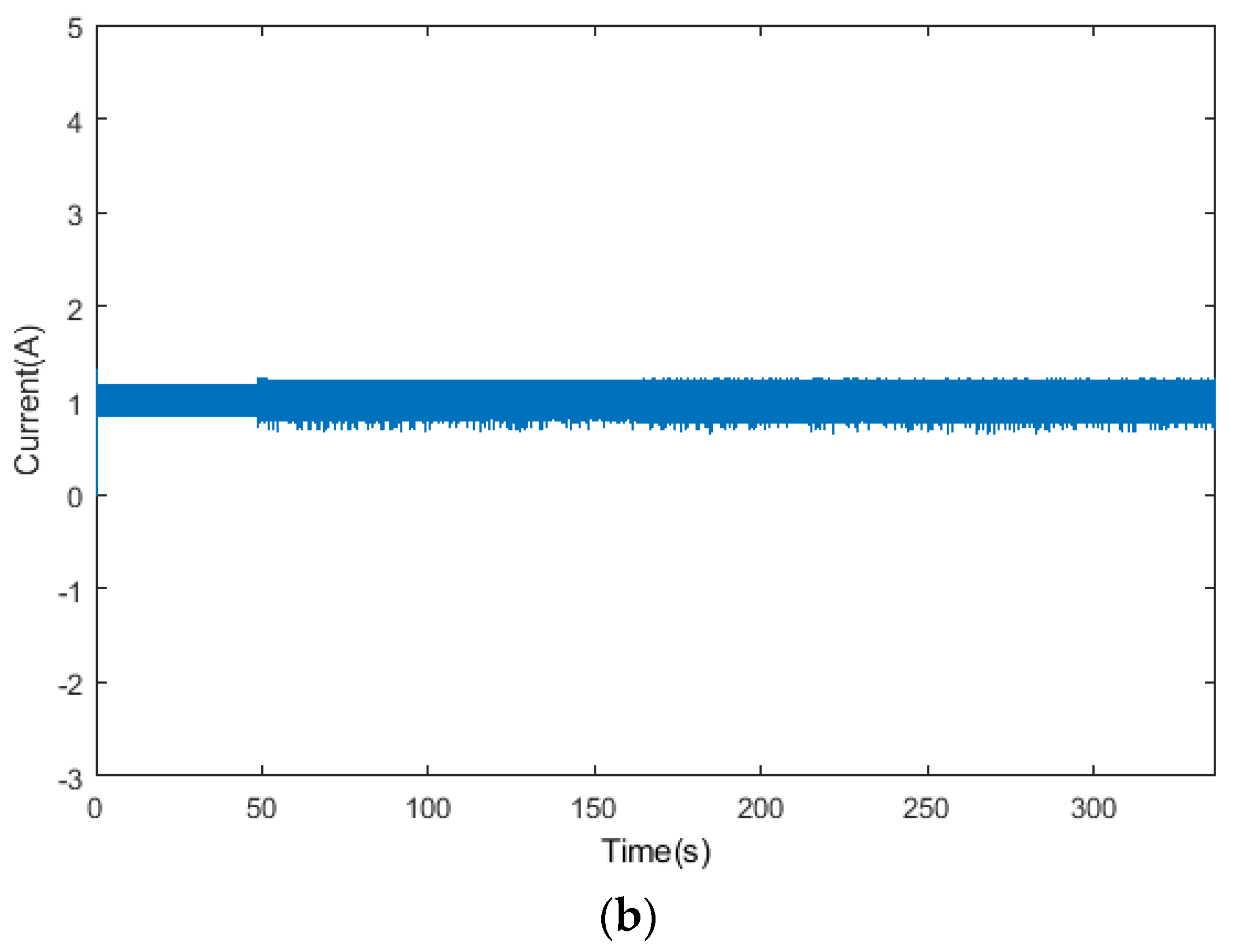
When no load is used, the balancing current was set to 1A for the simulation experiment. To verify the effectiveness of the proposed new balancing control scheme, a comparison and analysis were conducted with the balancing strategy proposed in [20]. The SOC variation and balancing current of the battery module under the proposed new balancing strategy are shown in Figure 14, where the battery module SOC reaches equilibrium at about 221s, while the balancing strategy in [20] achieves equilibrium at around 336s. The proposed balancing strategy improves the balancing speed by approximately 34.2%, with the balancing current remaining stable around 1A and its current ripple relatively small, indicating good balancing performance.

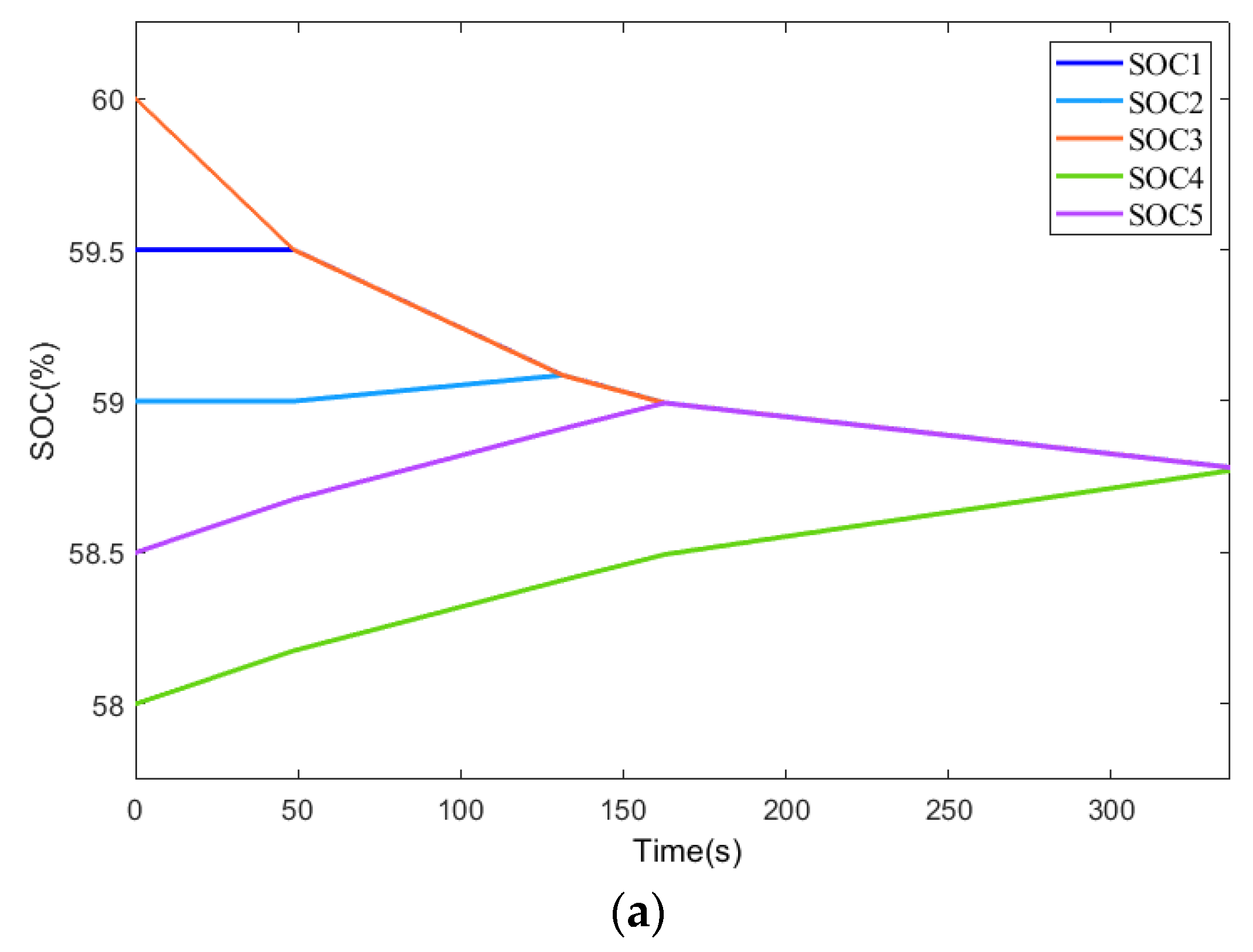
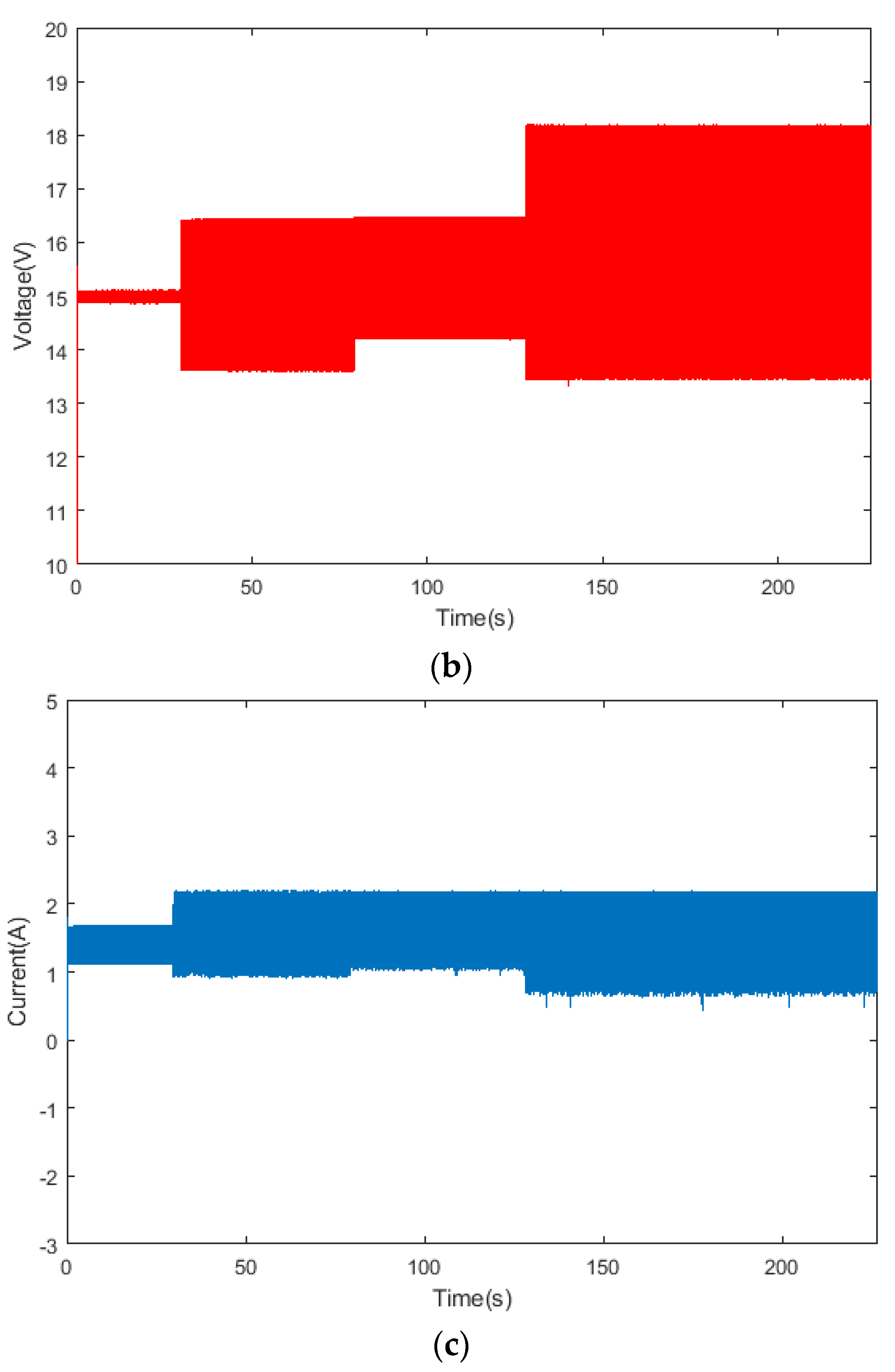
4.2. Balanced simulation when using load

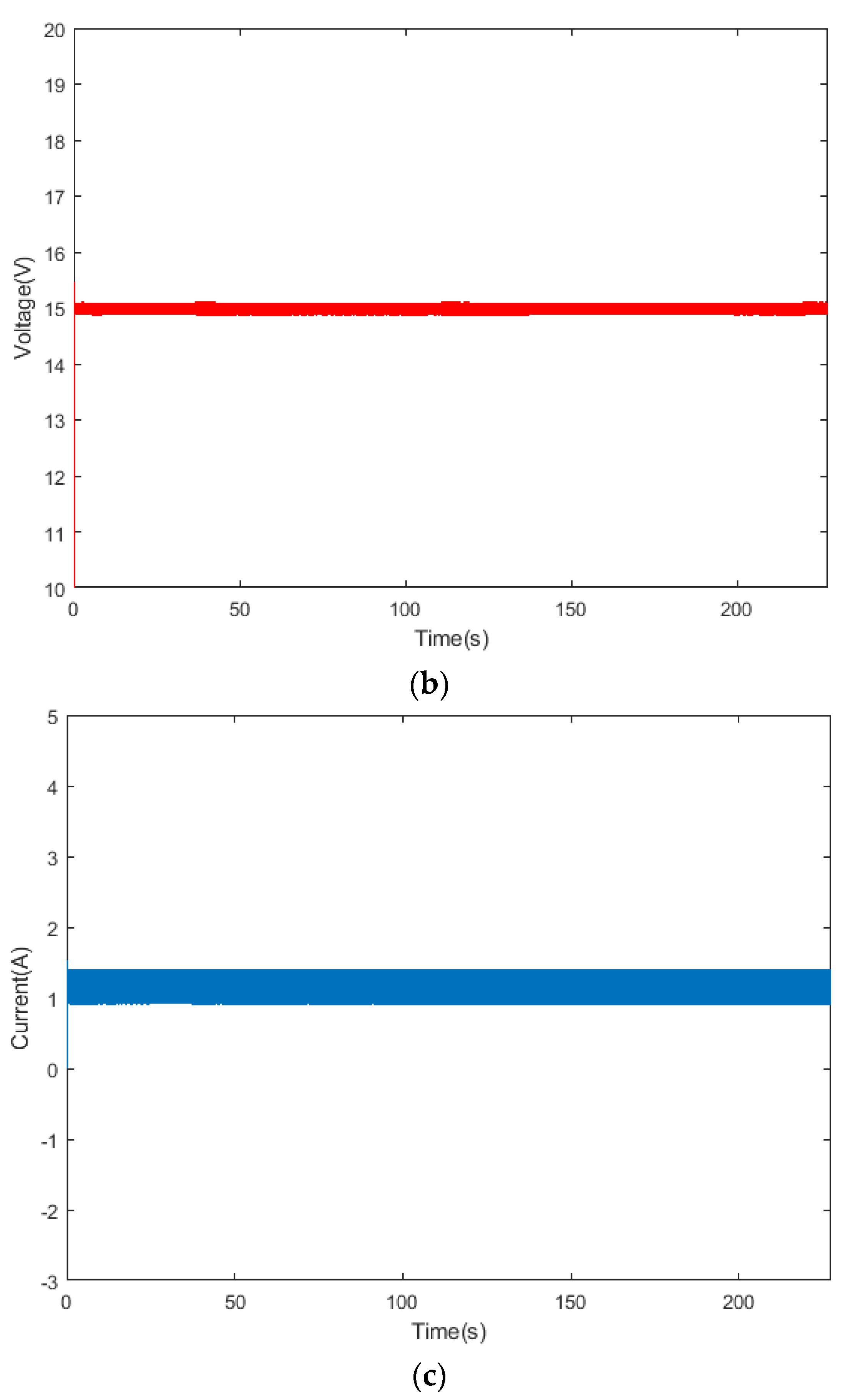
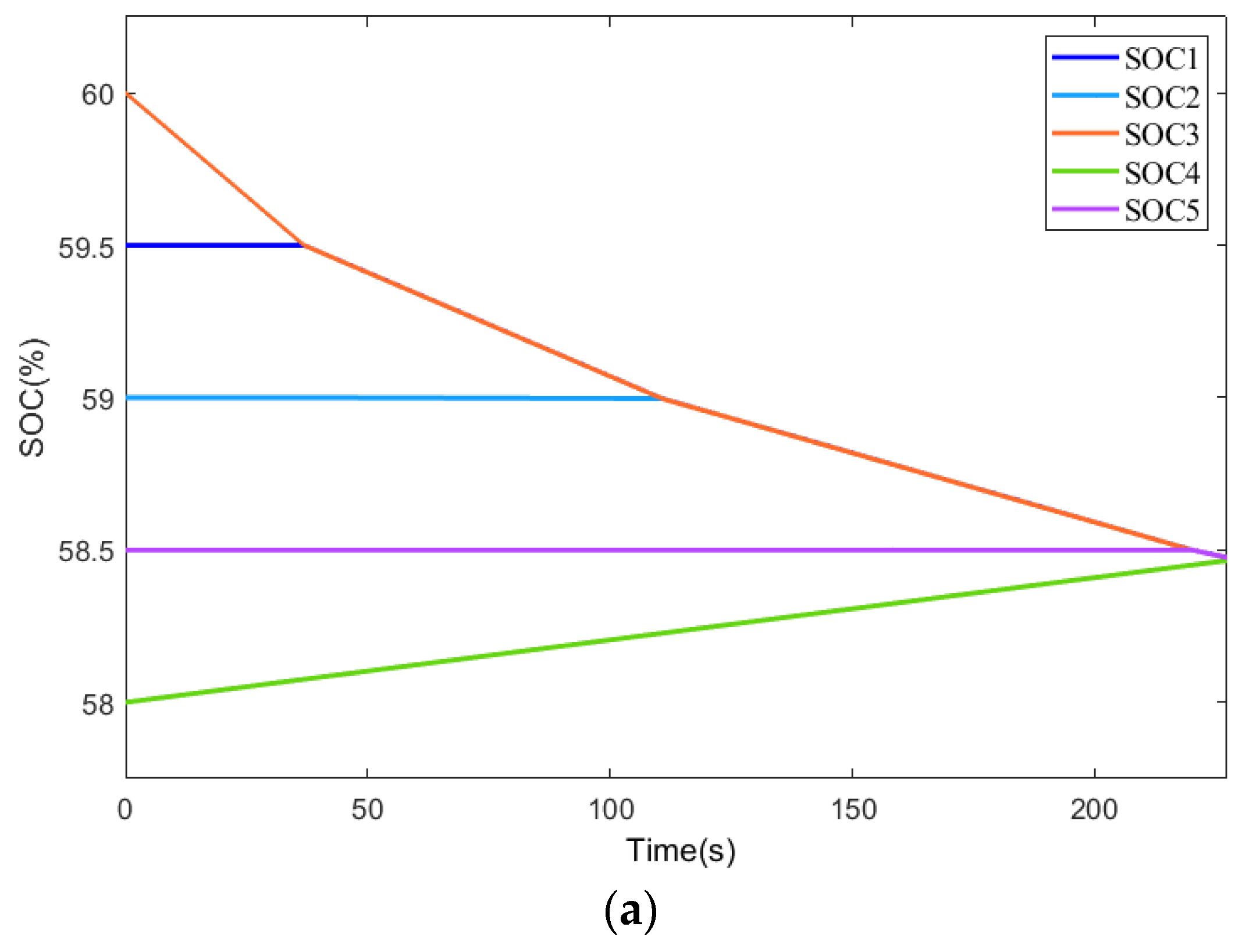
When a load is used, the output voltage was set to 15V for the simulation experiment. The SOC variation, balancing current, and output voltage of the battery module under the proposed new balancing strategy are shown in Figure 16 and Figure 17. The battery module SOC reaches equilibrium at approximately 227s with the proposed new balancing strategy, while the balancing strategy in [20] reaches equilibrium at around 226s. Their balancing speed is basically the same. However, the balancing current in the proposed new balancing strategy remains stable at around 1.2A, and the output voltage stays stable at 15V with relatively small current ripple and voltage ripple. In contrast, the balancing current in [20] is approximately 1.3A with large corresponding current and voltage ripple.

5. Conclusions

This paper described the functions of the integrated reconfigurable converter system and proposed a new balancing strategy that can be used both with and without a load. The effectiveness of the proposed balancing strategy was verified through MATLAB/SIMULINK simulations, demonstrating improved balancing speed and system stability.

Author Contributions

Conceptualization, G.W. and Z.Q.; methodology, G.W. and M.H.; software, G.W.; validation, M.H., S.Y., Z.H. and J.J.; formal analysis, Z.Q.; investigation, Z.H.; resources, J.J.; data curation, G.W.; writing—original draft preparation, G.W.; writing—review and editing, Z.Q.; visualization, M.H.; supervision, S.Y.; project administration, Z.Q.; funding acquisition, Z.Q. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Natural Science Foundation of Shandong Province, China(ZR2021ME163).

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of Interest

There are no relevant financial or non-financial competing interests to report.

References

Chen, Y.; Liu, X.; Cui, Y.; Zou, J.; Yang, S. , A multiwinding transformer cell-to-cell active equalization method for lithium-ion batteries with reduced number of driving circuits. IEEE Transactions on Power Electronics 2015, 31, 4916–4929. [Google Scholar]
Han, W.; Zhang, L. , Battery cell reconfiguration to expedite charge equalization in series-connected battery systems. IEEE Robotics and Automation Letters 2017, 3, 22–28. [Google Scholar] [CrossRef]
Omariba, Z.B.; Zhang, L.; Sun, D. , Review of battery cell balancing methodologies for optimizing battery pack performance in electric vehicles. IEEE Access 2019, 7, 129335–129352. [Google Scholar] [CrossRef]
Ren, H.; Zhao, Y.; Chen, S.; Wang, T. , Design and implementation of a battery management system with active charge balance based on the SOC and SOH online estimation. Energy 2019, 166, 908–917. [Google Scholar] [CrossRef]
Zhang, H.; Wang, Y.; Qi, H.; Zhang, J. , Active battery equalization method based on redundant battery for electric vehicles. IEEE transactions on vehicular technology 2019, 68, 7531–7543. [Google Scholar] [CrossRef]
Cao, J.; Schofield, N.; Emadi, A. In Battery balancing methods: A comprehensive review, 2008 IEEE Vehicle Power and Propulsion Conference, 2008; IEEE: 2008; pp 1-6.
Vardwaj, V.; Vishakha, V.; Jadoun, V.K.; Jayalaksmi, N.; Agarwal, A. In Various methods used for battery balancing in electric vehicles: A comprehensive review, 2020 International Conference on Power Electronics & IoT Applications in Renewable Energy and its Control (PARC), 2020; IEEE: 2020; pp 208-213.
Daowd, M.; Omar, N.; Van Den Bossche, P.; Van Mierlo, J. In Passive and active battery balancing comparison based on MATLAB simulation, 2011 IEEE Vehicle Power and Propulsion Conference, 2011; IEEE: 2011; pp 1-7.
Schmid, M.; Gebauer, E.; Endisch, C. , Structural analysis in reconfigurable battery systems for active fault diagnosis. IEEE Transactions on Power Electronics 2021, 36, 8672–8684. [Google Scholar] [CrossRef]
Schmid, M.; Gebauer, E.; Hanzl, C.; Endisch, C. , Active model-based fault diagnosis in reconfigurable battery systems. IEEE Transactions on Power Electronics 2020, 36, 2584–2597. [Google Scholar] [CrossRef]
Wang, G.; Pou, J.; Agelidis, V.G. In Reconfigurable battery energy storage system for utility-scale applications, IECON 2015-41st Annual Conference of the IEEE Industrial Electronics Society, 2015; IEEE: 2015; pp 004086-004091.
Wang, X.; Duan, B.; Shang, Y.; Xu, Y.; Yu, K.; Zhang, C. In Fast equalization for lithium ion battery packs based on reconfigurable battery structure, 2020 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), 2020; IEEE: 2020; pp 1149-1154.
Zhu, Y.; Zhang, W.; Cheng, J.; Li, Y. In A novel design of reconfigurable multicell for large-scale battery packs, 2018 International Conference on Power System Technology (POWERCON), 2018; IEEE: 2018; pp 1445-1452.
Ci, S.; Lin, N.; Wu, D. , Reconfigurable battery techniques and systems: A survey. IEEE Access 2016, 4, 1175–1189. [Google Scholar] [CrossRef]
Mashayekh, A.; Kersten, A.; Kuder, M.; Estaller, J.; Khorasani, M.; Buberger, J.; Eckerle, R.; Weyh, T. In Proactive soc balancing strategy for battery modular multilevel management (bm3) converter systems and reconfigurable batteries, 2021 23rd European Conference on Power Electronics and Applications (EPE'21 ECCE Europe), 2021; IEEE: 2021; pp P. 1-P. 10.
Han, W.; Zou, C.; Zhou, C.; Zhang, L. , Estimation of cell SOC evolution and system performance in module-based battery charge equalization systems. IEEE Transactions on Smart Grid 2018, 10, 4717–4728. [Google Scholar] [CrossRef]
Momayyezan, M.; Hredzak, B.; Agelidis, V.G. , Integrated reconfigurable converter topology for high-voltage battery systems. IEEE Transactions on Power Electronics 2015, 31, 1968–1979. [Google Scholar] [CrossRef]
Momayyezan, M.; Hredzak, B.; Agelidis, V.G. , A load-sharing strategy for the state of charge balancing between the battery modules of integrated reconfigurable converter. IEEE Transactions on power electronics 2016, 32, 4056–4063. [Google Scholar] [CrossRef]
Morstyn, T.; Momayyezan, M.; Hredzak, B.; Agelidis, V.G. , Distributed control for state-of-charge balancing between the modules of a reconfigurable battery energy storage system. IEEE Transactions on Power Electronics 2015, 31, 7986–7995. [Google Scholar] [CrossRef]
Zhao, C.; Liu, S.; Fan, B. In State of Charge Balancing Control for Battery System Based on the ReconFigurable Converter, 2021 IEEE 5th Conference on Energy Internet and Energy System Integration (EI2), 2021; IEEE: 2021; pp 4215-4220.

Figure 1. Reconfigurable Battery and Converter Integrated Structure.

Figure 2. Boost Converter.

Figure 3. Battery system power supply mode (a) B1 provides power to the load (b) B2 and B3 provide power to the load.

Figure 4. The freewheeling path for the inductor current.

Figure 5. Illustration of balancing mode during one switching cycle. (a) Module to a module (B3 is discharged into B2). (b) Module to modules (B3 is discharged into B1 and B2). (c) Modules to a module (B2 and B3 are discharged into B1).

Figure 6. Balancing strategy when not using load: (a) B3 is discharged into B2. (b) B3 is discharged into B1.

Figure 7. Balancing strategy when using load: (a) B1 is discharged into B2. (b) B1 is discharged into B3.

Figure 8. Flow diagram of the balancing management system.

Figure 9. Controller design for the balancing operation when no load is used.

Figure 10. Simplified topology of the balancing mode when unused load in small-signal modeling.

Figure 11. Controller design for the balancing operation when load is used.

Figure 12. Simplified topology of the balancing mode when using load in small-signal modeling.

Figure 14. Simulation of the proposed balancing strategy without using load(a) Changes in SOC of battery modules (b) Balanced current.

Figure 15. Balanced simulation of unused load in [20] (a) Changes in SOC of battery module (b) Balanced current.

Figure 16. Simulation of the proposed balancing strategy when using load (a) Changes in SOC of battery module (b) Output voltage (b) Balanced current.

Figure 17. Simulation of the balancing strategy when using load in [20] (a) Changes in SOC of battery module (b) Output voltage (c) Balanced current.

Table 1. Different input modes of battery modules.

Selected module	S1	S2	S3	S4	S5	S6
B1	1	0	0	1	0	0
B2	0	1	0	0	1	0
B3	0	0	1	0	0	1
B1, B2	1	0	0	0	1	0
B2, B3	0	1	0	0	0	1
B1, B2, B3	1	0	0	0	0	1

Table 2. Parameters of the control system.

Mode	PI controller parameters
Balancing mode when not using load	K_pb=0.35, K_ib=320
Balancing mode when using load	K_pc=0.15, K_ic=132 K_pv=0.063, K_iv=8.6

Table 3. Parameters of simulation experiment.

Parameters	Size
V_B1~V_B5	3.7V
C_B1~C_B5	2Ah
SOC1	59.5%
SOC2	59%
SOC3	60%
SOC4	58%
SOC5	58.5%
L	2mH
C	220uF
R	100Ω
f	20kHz

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Balancing Strategy for Battery Systems Based on Reconfigurable Converters

Abstract

1. Introduction

2. Structure and Working Principle of Integrated Reconfigurable Converter

2.1. Power supply mode

2.2. balance mode

3. Balancing Strategy and Control System Design

3.1. balanced strategy

3.2. Control System Design

3.2.1. Controller design for the balancing operation when no load is used.

3.2.2. Controller design for the balancing operation when load is used.

4. Simulation result

4.1. Balanced simulation when unused load

4.2. Balanced simulation when using load

5. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe