Preprint
Article
A Time Two-mesh Finite Difference Numerical Scheme for the Symmetric Regularized Long Wave Equation
Altmetrics
Downloads
111
Views
7
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
24 May 2023
Posted:
29 May 2023
You are already at the latest version
Alerts
Abstract
This paper proposed a time two-mesh (TT-M) finite difference numerical scheme to improve the efficiency of solving the symmetric regularized long wave (SRLW) equation. The TT-M Crank-Nicolson discretization and finite difference method are employed in time and space approximation respectively. The scheme involves three main steps: firstly, the time interval is divided into coarse and fine time meshes, then the nonlinear system is solved on the coarse time mesh; secondly, coarse numerical solutions on the fine time mesh are computed using an interpolation formula based on the solutions derived in the step one; lastly, the TT-M finite difference numerical solutions can be obtained through constructing the linearized fine time mesh system using Taylor’s formula. Compared to the currently existing TT-M numerical methods, the novelty of this study is that the nonlinear term including derivatives is linearized by Taylor’s formula for a function with three variables, whose error analysis is more complex. Finally, some numerical examples, including computational time and accuracy, preservation of conservation laws, are given to verify the efficiency of the scheme. By comparing it with the standard nonlinear finite difference scheme, this method can reduce CPU time without sacrificing accuracy.
Keywords:
Subject: Computer Science and Mathematics - Computational Mathematics
1. Introduction
The regularized long wave (RLW) equation [1,2] is a nonlinear partial differential equation that mainly describes the evolution of waves in shallow water channels and ion acoustic etc. It is a simplified version of the more complex Korteweg-de Vries (KdV) equation [3], which includes higher-order nonlinearities and dispersion effects. The symmetric regularized long wave (SRLW) equation [4] is a modified version of the RLW equation that includes a symmetry-breaking term. This term allows for the formation of asymmetric solutions, making the SRLW equation a more realistic model for waves in shallow water channels.
In this paper, the following initial boundary value problem of the SRLW equation is considered:
The SRLW equation has attracted significant attention and has been extensively studied in the literatures. Numerous methods have been developed for obtaining numerical solutions to the SRLW equation, ranging from conservative finite difference schemes to mixed finite element methods. Wang et al. [5] proposed three conservative finite difference schemes that are all of second-order accuracy in both space and time. They also proved that the energy is preserved for all schemes while the mass is preserved only for the first scheme. Yimnet et al. [6] presented a novel finite difference method for the SRLW equation that utilizes a four-level average difference technique for solving the fluid velocity independently from the density. Hu et al. [7] developed a coupled conservative three-level implicit scheme that achieves a fourth–order rate of convergence. Li [8] considered a weighted and compact conservative difference scheme that is decoupled and linearized in practical computation, thus requiring only the solution of two tridiagonal systems of linear algebraic equations at each time step. Bai et al. [9] investigated a two-layer conservative finite difference scheme for the SRLW equation with homogeneous boundary conditions and analyzed the scheme’s convergence and stability using a discrete functional analysis method. Xu et al. [10] applied a mixed finite element method to solve the dissipative SRLW equations with damping term. He et al. [11] developed a fourth-order accurate compact difference scheme for the SRLW equation for a single nonlinear velocity form and conducted theoretical analysis using the discrete energy method.
From the view of numerical calculation, the time two-mesh (TT-M) method combined with finite element method or finite difference method can also solve plenty of nonlinear partial differential equation with better computational efficiency. For instance, Liu et al. [12] proposed the fast TT-M finite element method to solve the fractional water wave model, which has also been applied to other fractional models. Yin et al. [13] developed the TT-M finite element algorithm to solve a space fractional Allen–Cahn model and discussed in detail the problem of parameter selection. The TT-M finite element method was utilized by Liu et al. [14] to numerically solve the two-dimensional Gray–Scott model with space fractional derivatives. Wen et al. [15] used the TT-M algorithm in combination with the -Galerkin mixed finite element method to numerically solve the nonlinear distributed order diffusion model. The computational efficiency of the algorithm was demonstrated, and the theoretical results were verified by numerical examples with both smooth and non-smooth solutions. Tian et al. [16] developed the finite element method combined with the TT-M technique to solve the coupled Schrödinger–Boussinesq equations. In recent years, there has been a amount of research on using the combined TT-M and finite difference methods to solve partial differential equations. Qiu and Xu et al. [17,18] developed and analyzed a TT-M algorithm based on finite difference (FD) methods for solving nonlinear fractional partial differential equations. Similarly, Niu et al. [19] used the TT-M technique to propose a fast high-order compact difference scheme for the nonlinear distributed order fractional Sobolev model appearing in porous media. He et al. [20] further extended the application of the TT-M method by studying a time two-mesh high-order compact difference scheme for solving the nonlinear Schrödinger equation and the scheme of second-order convergence rate in time as well as fourth-order in space. Despite the extensive research on the TT-M method in various fields, to the best of our knowledge, no study on the application of the TT-M method combined with finite difference to the SRLW equation has been discovered. Hence, investigations on the TT-M finite difference method’s performance when applied to the SRLW equation are still required.
The main contributions of this paper are as follows: (i) A novel TT-M finite difference numerical approach, incorporating a TT-M Crank-Nicolson algorithm for time discretization and finite difference method for space approximation, has been proposed to solve the SRLW equation. (ii) The TT-M finite difference method is used for the first time to solve partial differential equation with nonlinear term including derivatives. (iii) The detailed proofs of convergence analysis of the scheme are given, which are more complicated than existing methods. (iv) Numerical examples have been provided to demonstrate the computational speed and accuracy of the proposed method, which outperforms standard nonlinear finite difference method.
The remaining part of this article is organized as follows. In Section 2, some notations and useful lemmas are given. In Section 3, the TT-M finite difference numerical scheme is presented. In Section 4, the convergence of the scheme is analyzed. In Section 5, some numerical results are provided to test the theoretical results, computational efficiency of the scheme. Finally, in Section 6, we provide a brief conclusion.
2. Notations and Some Lemmas
As usual, the time interval and spatial interval are divided into N and J uniform partitions. The following notations will be used in this paper:
where denote the uniform time and spatial step length respectively, , , superscript n denotes a quantity associated with the time level , subscript j denotes a quantity associated with space mesh point . In this paper, M denotes general constant, which may have different value in different place.
Since for or , we may assume for simplicity, where and are ghost points. Let denote the set of mesh functions defined on with boundary conditions . For any two mesh functions , we define the discrete inner product and norms as follows:
Next, we presented some useful lemmas.
Lemma 1.
(See [11]). For any mesh functions , we have
Lemma 2.
then there has the inequality , where and τ are positive constants.
3. The TT-M Finite Difference Scheme
In this paper, we studied a TT-M finite difference fast numerical method for the SRLW equation (1). In order to give the TT-M finite difference scheme, firstly, the time interval is partitioned uniformly into P coarse time intervals and then each coarse time interval is divided into fine time intervals. The coarse time mesh with the nodes satisfying and the fine time mesh with the nodes satisfying , where and are the coarse time and the fine time step size, respectively.
Secondly, the truncation errors of the problem (1) is considered, let be the exact solutions of and in term of the point , then we have
By Taylor series expansion, we have
Next, based on equations (2) and (3), a TT-M finite difference scheme for problem (1) is constructed with three steps.
Step 1: On the coarse time mesh, let be the numerical solutions of of and in term of the point , then coarse time nonlinear finite difference scheme is given as
where
Step 2: Based on the solutions at time levels obtained from step 1, we apply the Lagrange’s linear interpolation formula to compute at time levels and , we have
Remark 1.
The equation (7) is only employed for theoretical analysis of the scheme. In numerical simulation, the coarse numerical solutions are no need to compute since it does not used in step 3.
Step 3: Based on all the coarse numerical solutions obtained in the first two steps, Taylor’s formula is used to construct a linearized system on the fine time mesh, which is expressed as follows. Let be the numerical solutions of and in term of the point on the fine time mesh, then
where and
are the three partial derivatives of with respect to .
Remark 2.
Similar to the Gauss-Seidel method applied to linear systems, we have modified our method to improve the accuracy of fine mesh solutions by using in calculation.
4. Convergence Analysis of the TT-M Finite Difference Scheme
The focus of this section is on performing convergence analysis of the nonlinear system specifically on the coarse time mesh.
Theorem 1.
Suppose that the exact solutions to the initial boundary value problem equation (1) is sufficiently smooth and let be the numerical solutions on the coarse time mesh. Then,
Proof.
The proof contains two cases. Firstly, we consider the case of , then . The initial and boundary condition satisfies
From Cauchy–Schwarz inequality, we obtain
Using Lemma 1, the equation (18) can be rewritten as
Similarly, taking the inner product (·, ·) on both sides of equation (11) with , we obtain
From Cauchy–Schwarz inequality, we have
Using Lemma 1, the equation (20) can be rewritten as
By taking small enough so that , then
From equation (24) and the initial and boundary condition, we have
Then using Lemma 3, we obtain
Secondly, we consider the case of and . Based on the Lagrange’s interpolation formula, we get
We obtain the result of Theorem 1 by synthesizing the aforementioned two cases. Next, we give the convergence analysis of the scheme on the fine time mesh. □
Theorem 2.
Suppose that the exact solutions to the initial boundary value problem equation (1) is sufficiently smooth and let be the numerical solutions on the fine time mesh. Then,
Proof.
Assume , Subtracting equation (8) from equation (2) and equation (9) from equation (3), we obtain
where
and , are the second order partial derivatives of ,
Taking the inner product (·, ·) on both sides of equation (29) with , we have
Using and , we obtain
Using Lemma 1 and Cauchy–Schwarz inequality, we have
Taking the inner product (·, ·) on both sides of equation (30) with , we obtain
Let , then
and obtain
By taking small enough so that , then
Summing from 0 to inequalities in equation (40), we obtain
Using Lemma 2, we get
From equation (42) and the initial and boundary condition, we have
Using Lemma 3, it lead to
This completes the proof of Theorem 2. □
5. Numerical Results
This section provides some numerical examples aimed at demonstrating the accuracy and computational time of the TT-M finite difference scheme that was discussed in Section 3. We consider the SRLW equation as the following form:
In this section, we chose associated with this equation, which takes the form
and consider the following initial conditions
5.1. Error and convergence rate
We define the error and convergence rate by the following formula:
where m represents the TT-M finite difference scheme or the standard nonlinear finite difference (SNFD) scheme. We set in the entire numerical illustration process.
Table 1 and Table 2 present discrete norm errors, convergence rates, and the time cost for both the TT-M finite difference scheme and the SNFD scheme. To demonstrate the accuracy of the proposed method, we computed the error of TT-M finite difference scheme at the final time for various mesh steps and compare it to the errors obtained by the SNFD scheme. The results from the new scheme show nearly identical significant digits as those obtained by the SNFD scheme. In term of the convergence rate, the results indicate that both the SNFD scheme and the TT-M finite difference scheme achieve approximately second-order convergence in space when and first-order in time when , which confirming the theoretical results.
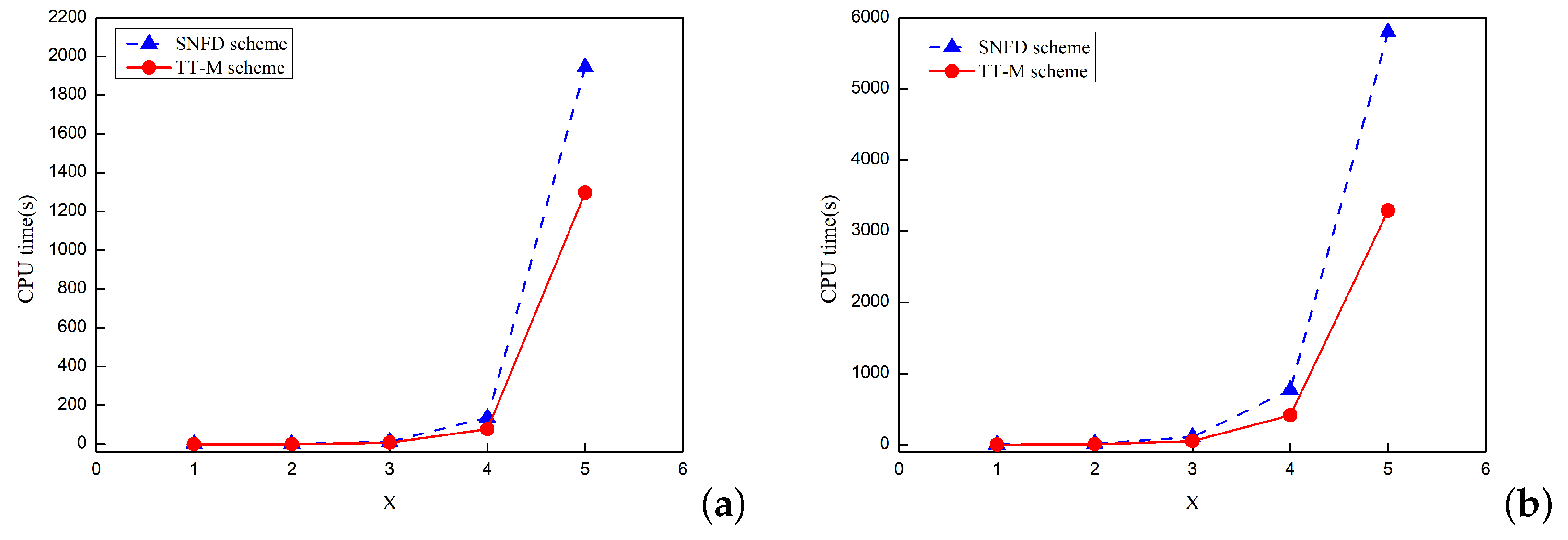
Figure 1 illustrates the exact and numerical solutions of and at obtained by the TT-M finite difference scheme. The results indicate the excellent correspondence between our numerical solution and the exact solution. Furthermore, the CPU times of the two schemes are plotted in Figure 2 under and , respectively. It is worth noting that the TT-M finite difference scheme can significantly decrease computation time. To sum up, the computational performance of the new scheme is obviously better than that of the SNFD scheme.
5.2. Conservative approximations
To further verify the accuracy of the new scheme, we calculate four conservation laws of the SRLW equation (1), such as:
Afterwards, employing discrete forms, we are able to compute four approximate conservative quantities which can be represented as
The quantities values are recorded in Table 3, Table 4, Table 5 and Table 6. In Table 3 and Table 4, regardless of the time step and grid spacing, the quantities and remain well-preserved at various times. In Table 5, for the case and , one can see that the quantity experiences a slight increase as time increases, however, as the spatial and temporal step sizes decrease, the variation of becomes extremely small. In Table 6, it has been found that for quantity , there was a minor decline under different mesh steps, but it gradually rebounded over time. Meanwhile, as the spatial and temporal step sizes decrease, the increases slightly. Figure 3 plots the variation curves of four quantities for the case and , which visually demonstrate that our scheme preserves the four conservation laws.
6. Conclusions
The paper presents a new time two-mesh finite difference scheme for the nonlinear symmetric regularized long wave equation with a nonlinear term including derivatives. The time interval is divied into coarse and fine meshes, then the Lagrange’s linear interpolation formula and Taylor’s formula are utilized to construct the three steps time two-mesh finite difference scheme. The convergence of the new scheme are also analyzed and theoretical results are verified by some numerical examples. Compared to the standard nonlinear finite difference scheme, our scheme not only maintains accuracy but also reduces CPU time. Therefore, the TT-M finite difference scheme is a promising method for solving the SRLW equation.
Author Contributions
Conceptualization, J.G.; methodology, J.G.; software, J.G. and S.H.; validation, S.H., Q.B. and J.L.; formal analysis, J.G. and S.H.; writing—original draft preparation, J.G.; writing—review and editing, J.G., S.H.; funding acquisition, S.H., Q.B and J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by National Natural Science Foundation of China (Nos. 12161034 and 11961022), Natural Science Foundation of Inner Mongolia (No. 2021MS01017), Natural Scientific Research Innovation Team of Hohhot Minzu College (No. HMTD202005).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All the data were computed using our method.
Acknowledgments
We are grateful to the anonymous reviewers for their valuable suggestions and comments.
Conflicts of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Peregrine, D. H. Calculations of the development of an undular bore. Journal of Fluid Mechanics 1966, 25, 321–330. [Google Scholar] [CrossRef]
- Peregrine, D. H. Long waves on beach. Journal of Fluid Mechanics 1967, 27, 815–827. [Google Scholar] [CrossRef]
- Korteweg, D.J.; de Vries, G. On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Philosophical Magazine 1895, 39, 422–443. [Google Scholar] [CrossRef]
- Seyler, C.E.; Fenstermacher, D.L. A symmetric regularized-long-wave equation. Physics of Fluids 1984, 27, 4–7. [Google Scholar] [CrossRef]
- Wang, T.C.; Zhang, L.M.; Chen, F.Q. Conservative schemes for the symmetric regularized long wave equations. Applied Mathematics and Computation 2007, 190, 1063–1080. [Google Scholar] [CrossRef]
- Yimnet, S.; Wongsaijai, B.; Rojsiraphisal, T.; Poochinapan, K. Numerical implementation for solving the symmetric regularized long wave equation. Applied Mathematics and Computation 2016, 273, 809–825. [Google Scholar] [CrossRef]
- Hu, J.S.; Zheng, K.L.; Zheng, M.B. Numerical simulation and convergence analysis of high-order conservative difference scheme for SRLW equation. Applied Mathematical Modelling 2014, 38, 5573–5581. [Google Scholar] [CrossRef]
- Li, S.G. Numerical study of a conservative weighted compact difference scheme for the symmetric regularized long wave equations. Numerical Methods for Partial Differential Equations 2019, 35, 60–83. [Google Scholar] [CrossRef]
- Bai, Y.; Zhang, L.M. A conservative finite difference scheme for symmetric regularized long wave equations. Acta Mathematicae Applicatae Sinica 2007, 30, 248–255. [Google Scholar]
- Xu, Y.C.; Hu, B.; Xie, X.P.; Hu, J.S. Mixed finite element analysis for dissipative SRLW equations with damping term. Physics of Fluids 2012, 218, 4788–4797. [Google Scholar] [CrossRef]
- He, Y.Y.; Wang, X.F.; Cheng, H.; Deng, Y.Q. Numerical analysis of a high-order accurate compact finite difference scheme for the SRLW equation. Applied Mathematics and Computation 2022, 418, 126837. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, Z.D.; Li, H.; Liu, F.W.; Wang, J.F. Time two-mesh algorithm combined with finite element method for time fractional water wave model. International Journal of Heat and Mass Transfer 2018, 120, 1132–1145. [Google Scholar] [CrossRef]
- Yin, B.L.; Liu, Y.; Li, H.; He, S. Fast algorithm based on TT-M FE system for space fractional Allen-Cahn equations with smooth and non-smooth solutions. Journal Of Computational Physics 2019, 379, 351–372. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, E.Y.; Yin, B.L.; Li, H.; Wang, J.F. TT-M finite element algorithm for a two-dimensional space fractional Gray-Scott model. Computers and Mathematics with Applications 2020, 80, 1793–1809. [Google Scholar] [CrossRef]
- Wen, C.; Liu, Y.; Yin, B.L.; Li, H.; Wang, J.F. Fast second-order time two-mesh mixed finite element method for a nonlinear distributed-order sub-diffusion model. Numerical Algorithms 2021, 88, 523–553. [Google Scholar] [CrossRef]
- Tian, J.L.; Sun, Z.Y.; Liu, Y.; Li, H. TT-M Finite Element Algorithm for the Coupled Schrödinger–Boussinesq Equations. Axioms 2022, 11, 314. [Google Scholar] [CrossRef]
- Qiu, W.L.; Xu, D.; Guo, J.; Zhou, J. A time two-grid algorithm based on finite difference method for the two-dimensional nonlinear time-fractional mobile/immobile transport model. Numerical Algorithms 2020, 85, 39–58. [Google Scholar] [CrossRef]
- Xu, D.; Guo, J.; Qiu, W.L. Time two-grid algorithm based on finite difference method for two-dimensional nonlinear fractional evolution equations. Applied Numerical Mathematics 2019, 152, 169–184. [Google Scholar] [CrossRef]
- Niu, Y.X.; Liu, Y.; Li, H.; Liu, F.W. Fast high-order compact difference scheme for the nonlinear distributed-order fractional Sobolev model appearing in porous media. Mathematics and Computers in Simulation 2023, 203, 387–407. [Google Scholar] [CrossRef]
- He, S.; Liu, Y.; Li, H. Numerical simulation and convergence analysis of high-order conservative difference scheme for SRLW equation. Entropy 2022, 24, 806. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.L. Application of Discrete Functional Analysis to the Finite Difference Method; International Academic Publishers: Beijing, China, 1990. [Google Scholar]
Figure 1.
Exact and numerical solution of (a) and (b) at .
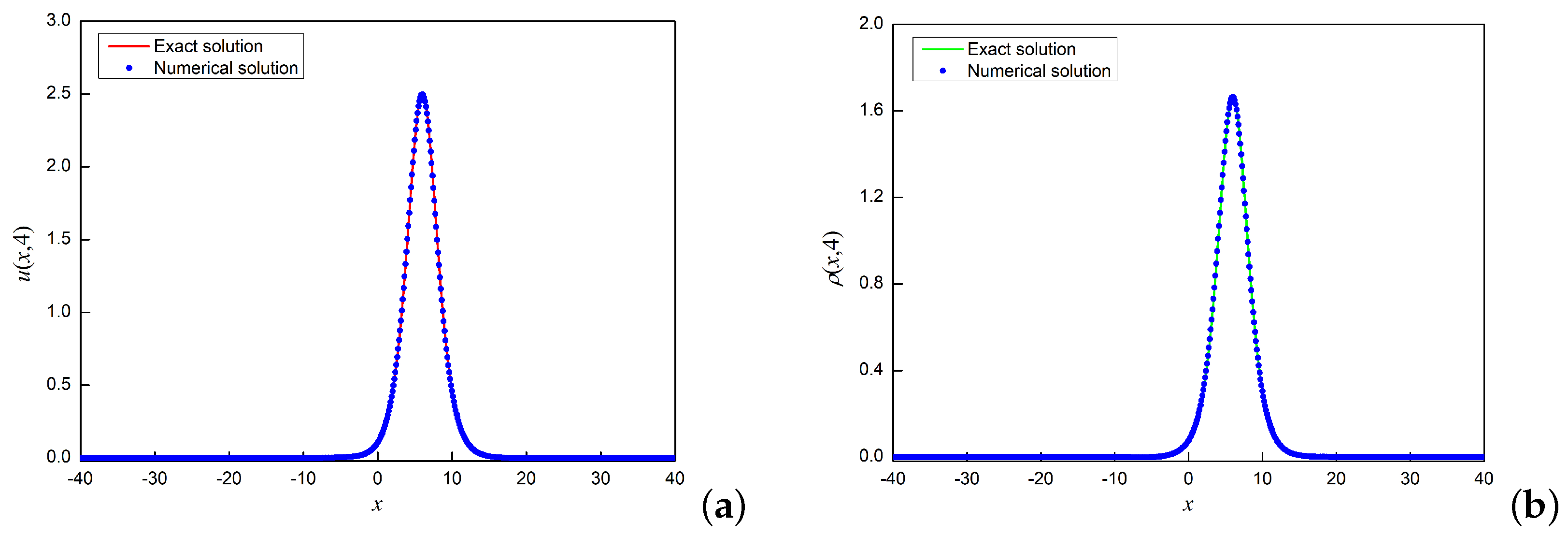
Figure 3.
Quantities (a), (b), (c) and (d) under mesh steps , .
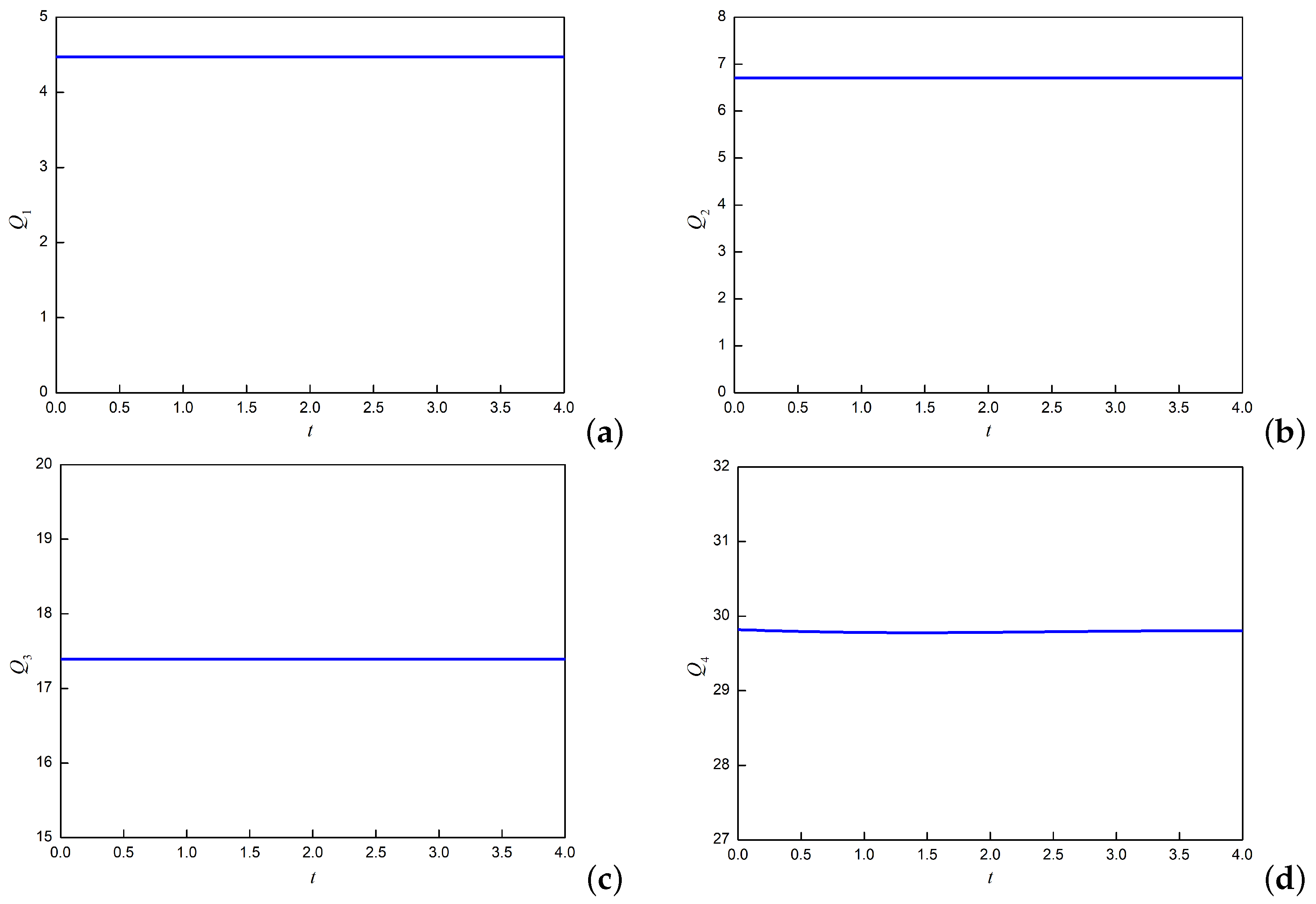
Table 1.
The errors and convergence rates with .
| SNFD scheme | |||||
|---|---|---|---|---|---|
| CPU(s) | |||||
| — | — | 0.14 | |||
| 2.02 | 2.02 | 0.51 | |||
| 2.01 | 2.01 | 12.30 | |||
| 2.00 | 2.00 | 136.31 | |||
| 2.00 | 2.00 | 1943.47 | |||
| TT-M finite difference scheme | |||||
| CPU(s) | |||||
| — | — | 0.10 | |||
| 2.04 | 2.03 | 0.30 | |||
| 2.01 | 2.01 | 7.53 | |||
| 2.00 | 2.00 | 76.99 | |||
| 2.00 | 2.00 | 1297.88 | |||
Table 2.
The errors and convergence rates with .
| SNFD scheme | |||||
|---|---|---|---|---|---|
| CPU(s) | |||||
| — | — | 2.47 | |||
| 1.04 | 1.04 | 14.09 | |||
| 1.02 | 1.02 | 109.20 | |||
| 1.01 | 1.01 | 770.01 | |||
| 1.00 | 1.00 | 5792.53 | |||
| TT-M finite difference scheme | |||||
| CPU(s) | |||||
| — | — | 1.49 | |||
| 1.04 | 1.04 | 7.10 | |||
| 1.02 | 1.02 | 51.40 | |||
| 1.01 | 1.01 | 414.33 | |||
| 1.00 | 1.01 | 3289.71 | |||
Table 3.
Quantities under different mesh steps h and at various times.
| TT-M finite difference scheme | ||||
|---|---|---|---|---|
| 4.4721359549 | 4.4721359549 | 4.4721359549 | 4.4721359549 | |
| 4.4721359549 | 4.4721359549 | 4.4721359549 | 4.4721359549 | |
| 4.4721359549 | 4.4721359549 | 4.4721359549 | 4.4721359549 | |
| 4.4721359549 | 4.4721359549 | 4.4721359549 | 4.4721359549 | |
| 4.4721359549 | 4.4721359549 | 4.4721359549 | 4.4721359549 | |
| 4.4721359549 | 4.4721359549 | 4.4721359549 | 4.4721359549 | |
| 4.4721359549 | 4.4721359549 | 4.4721359549 | 4.4721359549 | |
| 4.4721359549 | 4.4721359549 | 4.4721359549 | 4.4721359549 | |
| 4.4721359549 | 4.4721359549 | 4.4721359549 | 4.4721359549 | |
Table 4.
Quantities under different mesh steps h and at various times.
| TT-M finite difference scheme | ||||
|---|---|---|---|---|
| 6.7082039324 | 6.7082039324 | 6.7082039324 | 6.7082039324 | |
| 6.7082039324 | 6.7082039324 | 6.7082039324 | 6.7082039324 | |
| 6.7082039324 | 6.7082039324 | 6.7082039324 | 6.7082039324 | |
| 6.7082039324 | 6.7082039324 | 6.7082039324 | 6.7082039324 | |
| 6.7082039324 | 6.7082039324 | 6.7082039324 | 6.7082039324 | |
| 6.7082039324 | 6.7082039324 | 6.7082039324 | 6.7082039324 | |
| 6.7082039324 | 6.7082039324 | 6.7082039324 | 6.7082039324 | |
| 6.7082039324 | 6.7082039324 | 6.7082039324 | 6.7082039324 | |
| 6.7082039323 | 6.7082039323 | 6.7082039323 | 6.7082039323 | |
Table 5.
Quantities under different mesh steps h and at various times.
| TT-M finite difference scheme | ||||
|---|---|---|---|---|
| 17.3814360100 | 17.3890764778 | 17.3909982095 | 17.3914793723 | |
| 17.3879364459 | 17.3894925427 | 17.3910247524 | 17.3914810404 | |
| 17.4021575260 | 17.3904434452 | 17.3910850544 | 17.3914848239 | |
| 17.4178948195 | 17.3914089843 | 17.3911453660 | 17.3914885933 | |
| 17.4279575149 | 17.3919924045 | 17.3911803618 | 17.3914907570 | |
| 17.4320624736 | 17.3921089940 | 17.3911854445 | 17.3914910387 | |
| 17.4298852213 | 17.3919072419 | 17.3911710024 | 17.3914901056 | |
| 17.4257242289 | 17.3915916231 | 17.3911504036 | 17.3914888028 | |
| 17.4208004460 | 17.3913048704 | 17.3911324701 | 17.3914876800 | |
Table 6.
Quantities under different mesh steps h and at various times.
| TT-M finite difference scheme | ||||
|---|---|---|---|---|
| 29.8645685095 | 29.8270800111 | 29.8174683777 | 29.8150480627 | |
| 29.5194998279 | 29.7377964805 | 29.7949677954 | 29.8094115019 | |
| 29.2953094352 | 29.6804305056 | 29.7805099425 | 29.8057894879 | |
| 29.2373157339 | 29.6665651150 | 29.7770997278 | 29.8049405034 | |
| 29.3052034101 | 29.6864373371 | 29.7822468973 | 29.8062391542 | |
| 29.4333002603 | 29.7204018949 | 29.7909264484 | 29.8084218678 | |
| 29.5520897511 | 29.7519209103 | 29.7989376025 | 29.8104338587 | |
| 29.6355327196 | 29.7733189521 | 29.8043614200 | 29.8117950932 | |
| 29.6765644108 | 29.7843463859 | 29.8071613054 | 29.8124980105 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated