Preprint
Article
High static gain DC-DC Double Boost Quadratic Converter
Altmetrics
Downloads
201
Views
53
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
26 May 2023
Posted:
29 May 2023
You are already at the latest version
Alerts
Abstract
This paper presents a comprehensive study and the analysis of a topology of a no isolated DC-DC intituled Double Quadratic Boost converter with high static gain. This converter has the main advantage of high static gain and low voltage stress on its switches. The article will first present the theoretical analysis of the converter operating in an open loop. The objective of the work is the mathematical modeling and the control strategy of the converter, as well as the validation through closed-loop experimental results. Besides, we presented the practice test results to demonstrate the operation of the converter, such as the static gain experimental curve, the practice efficiency of the converter, and the control of the output voltage, as well as the capacitor voltage balance control. The authors designed a prototype for 1 kW, with a switching frequency of fs=50kHz, with FPGA-based command and modulation.
Keywords:
Subject: Engineering - Electrical and Electronic Engineering
1. Introduction
Currently, concern for the environment has increased with the use of new sustainable practices. In the field of energy generation, clean and renewable sources have been made available, and with that, equipment such as power converters has been required more frequently. In that regard, renewable power generation has been increasing the use of DC-DC converters in such as photovoltaic systems, as presented in [1,2], both on-grid and off-grid, [3]. To optimize the use of solar energy, it is common to use an MPPT controller (Maximum Power Point Tracking), [4]. The DC-DC converters are also used in applications with fuel cells, electric or hybrid vehicles, as in [5,6], as well as in aeronautics, [7], or even space applications, [8], in addition to uninterruptible power systems, or even powered systems by batteries that require the conversion stage. Thus, recent research study the development of low cost, high power density DC-DC converters for microgeneration applications, as presented in [9]. However, the applications of power converters are not restricted to continuous conduction, as shown by [10], which demonstrates the importance of these energy converters.
In general, one can cite the various studies in the literature on high static gain DC-DC topologies, as shown in [11,12,13], especially as showed in [14], in which the author proposed one of the first high static gain converters. In [16], presented the switching cell of quadratic DC-DC converters. Subsequently, the authors analyzed the converter in continuous, critical, and discontinuous conduction modes, according cited in [17]. The article [18] presented the quadratic boost converter. However, since it is a high static gain converter, the topology presented in the work mentioned, presented the disadvantage of applying the total output bus voltage to its single switch. To minimize the voltage stresses in the switch, besides presenting the study of the optimization of switching losses [19], the quasi-resonant converter was shown [20]. To gather several topologies of the high static gain DC-DC converters, in [21], it was performed a bibliographic review. New converters based on [16,17] were introduced in [22,23], thus highlighting the importance of studying new high gain DC-DC converters topologies. Among the various works we can mention the boost converter applied in renewable energy sources, as presented in [24].
Despite the various structures present in the literature, this paper presents a distinct topology for a high static gain converter based on the boost converter. The proposed topology has the objective of reducing semiconductor efforts through the use of two switches to support the total output bus voltage, besides having high efficiency and simple structure when compared to the other mentioned topologies, considering its symmetrical characteristic. The converter presented is called Double Boost Quadratic Converter [15].
For the theoretical analysis, presents the operating stages and waveforms of the converter operating in continuous, critical, and discontinuous conduction mode. Besides, shown the mathematical model as well as for the experimental tests, to the converter operating in continuous conduction mode. It developed dynamic modeling using a state-space model to obtain the transfer function of current and voltage plants. Also, present the experimental results for the open-loop and closed-loop converter. It is also essential to highlight the evaluation of the output capacitor voltage balance, and such characteristics may not occur naturally, with unbalanced load. Thus, it presents a control strategy aiming at equalizing these voltages.
2. Converter Topology
The Double Quadratic Boost Converter characterized by having a high static gain and low voltage efforts in its switches. Figure 1 shows the topology of the proposed converter. In this structure, the voltages on the and switches are equal to half of the total output voltage, .
An interesting question that simplifies the analysis of this converter is its symmetry since the behavior of the electrical variables in the components of the upper part of the power circuit has the same conduct of the elements in the lower part, so this converter becomes multiport converter. In this section, we will present the analyzes of the converter operating in continuous, critical, and discontinuous conduction mode.
2.1. Operation in Continuous Conduction Mode (CCM)
In this section are shown the analysis of the operating stages, the waveforms, and the static gain curve of the proposed converter for continuous conduction mode6. Figure 2 shows the operating stages of the converter in continuous conduction mode, considering the command pulses of the simultaneous switches and duty cycle of .
2.1.1. First Stage: (, )
At this stage, are turned ON the switches and . The voltage source in series with the inductor, and the intermediate capacitor in series with the inductor, are considered as current sources. The diodes and are directly polarized, isolating the output from the input source. The current equals the sum of with , and the current is null.
2.1.2. Second Stage: (, )
At this stage the switches and are turned OFF. The diodes and go into conduction and the current sources and begin to release power to the output. In this stage, the currents and are null, and .
According to the described operating stages, Figure 3a illustrates the waveforms of the converter, with their respective time intervals corresponding to each stage. This Figure shows the and switch current, which is equal to the sum of the currents in the and inductors. The voltage on the switches and is equal to the total output voltage divided by two.
For the elaboration of the ideal static gain curve, the source and the inductor are considered a constant current source . The energy applied by the source in a period of operation is given by (1).
The energy received by capacitor in the second stage of the operation is given by (2).
Considering the converter an ideal system, in a period of operation, all energy applied by the source is received by the intermediate capacitor . Thus, solving (1) and (2), supply the ideal static gain for the subcircuit A of the converter, shown in (3).
The same analysis is developed for the subcircuit B of the converter, considering the intermediate capacitor voltage , as the input voltage and the capacitor voltage , as the output voltage.
Using the superposition principle, for the subcircuits A and B of the proposed converter, according to (3), one gets the ideal static gain of the Double Boost Quadratic Converter as a function of the output voltage by input voltage, as (4):
Figure 4 shows the ideal static gain as a function of the duty cycle for the Double Boost Quadratic Converter compared to the static gain of the conventional boost converter. This comparison shows the high static gain of the proposed converter, resulting from the quadratic term in the denominator of the expression (4).
For the actual static gain of the converter the non-idealities of the components due to copper in the inductor windings are included, according to the analysis shown in [25]. The voltage drops in the semiconductors are considered not relevant for the survey of the converter’s actual static gain curve, and are not taken into account. Thus, through the developed analysis, similar to the analysis for the survey of the ideal static gain curve, the real static gain equation is developed, that is, considering in this case the losses in the components, as shown in Equation (5).
where: ().
The authors obtain actual static gain for the various ratios between inductors resistances and load resistance R. It is considered the influence of the inductor resistance value on the converter static gain curve, which coincides with the ideal curve when . However, the concern with minimizing the inductor resistance value of the Double Boost Quadratic Converter is greater since for values of , the static gain curve has a maximum value. Thus, any duty cycle increment from this maximum point of the curve may bring the output voltage to zero, as shown in Figure 4.
2.1.3. Current Ripple in Inductors and
Starting from the voltage analysis in the inductor for the 1st operation stage, analyzing the subcircuit A of the converter, is obtained the current ripple in the inductor, as shown in Equation (6):
where:
Knowing that , it is possible to calculate the maximum and minimum current values on the inductor. The average output current of the converter subcircuit A (current in the intermediate capacitors ( and ), can be called intermediate current , is given by :
Rewriting the equation regarding the current variation of the inductor as a function of the maximum current , it is obtained:
Therefore, the maximum and minimum values of the inductor current are given as a function of the current of the intermediate capacitor :
Repeating the analysis of inductor , for inductor , referring to subcircuit B of the converter. Again, from the analysis of the voltage in the inductor, for the 1st stage of operation, the current ripple in the inductor is obtained, as shown in Equation (12).
From the current ripple in the inductor , it is possible to calculate the maximum and minimum current values in the inductor . The average output current , is given by :
Rewriting the equation for current variation in the inductor as a function of the maximum current , it is obtained:
Therefore, the maximum and minimum values of the inductor current as a function of the output current , are given by:
2.1.4. Converter Component Design
Considering the principle of volt-second balance in the inductor and knowing that the Equation (11) defines the maximum and minimum values for the inductor, and still that the current ripple in the inductor is given as shown in Equation (9), the value of the inductor is calculated by isolating it in the Equation (6) and considering the 1st stage of operation of the converter. Again, based on the volt-second balance principle for the inductor, and considering that Equation (17) defines the maximum and minimum values for the inductor, the same is calculated by isolating it in Equation (12) and considering the 1st stage of operation of the converter, as shown in Table 1 respectively.
Due to the symmetry of the converter topology, the values of the inductors and are given by: and . Considering the topology of the symmetrical converter, the other components located in the lower region of the converter will not be present during the design, because they have their respective dual dimensioned.
Considering the charge balance in the intermediate capacitor, and also its voltage ripple, the capacitance value is calculated so that the capacitor is charged and discharged linearly at each operating period. Thus, the intermediate capacitor is calculated using the expression presented in Table 1. Similar to the analysis performed for the calculation of the intermediate capacitor, the output capacitor is calculated using the expression shown in Table 1. Finally, the load resistance is calculated using the power expression, as shown in Table 1.
After the component design, it is possible to calculate the efforts on the converter components for the continuous conduction mode, as shown in Table 2.
2.2. Operation in Critical Conduction Mode
In this mode of operation, the currents in inductors and are initially zero and return to this value precisely at the end of the converter operate period. Figure 3b show the waveforms of the converter operating in critical conduction mode, with the respective time intervals corresponding to each stage.
The calculation of the critical inductances and is developed by analyzing the current ripple in the inductors. The average input current is equal to the average diode current , and the output current is the average diode current .
Through from the maximum and minimum values obtained from the input current and as a function of capacitor current for continuous conduction , the critical inductance is determined by setting the value of current to zero.
Repeating the same analysis for the inductor, given the maximum and minimum values for the input current and as a function of capacitor output current to the subcircuit B (), in continuous conduction mode, it is determined the critical inductance by setting the value of current to zero. In this case, the input voltage becomes the voltage on the intermediate capacitors ().
2.3. Operation in Discontinuous Conduction Mode
This converter presents consider two situations that operate in discontinuous conduction mode. The first occurs when only the current is in discontinuous mode, characterized in the third operation stage. Thus, in this situation, the converter operates in the first, second, and third stages of operation.
The second situation presenting the discontinuous conduction mode occurs when the currents and have discontinuity during the same interval, thus characterizing the fourth stage of operation. Therefore, only in this situation does the converter operate in the first, second, third, and fourth stages.
The following describes the operating stages in discontinuous conduction mode. The first and second operating stages are identical at continuous conduction mode, so they will not be described again.
2.3.1. Three Stage: (, )
This stage transfer all energy stored in to the load. Therefore, the diode blocks, and the capacitors and maintain the voltage of the load. The inductor continues to supply power to the and capacitors.
2.3.2. Fourth Stage: (, )
This last stage, all energy stored in the inductor is transferred, and the diode is blocked. In this stage only the capacitors and feed the load. Figure 5 and Figure 3c show the operating stages and the main waveforms of the converter, respectively. As shown in Figure 3c, the voltage value at switch in the third and fourth operating stages is equal to half of the total output voltage less diode voltage .
To analyze the static gain, in discontinuous conduction mode, the current ripple of inductor is considered. By analyzing the inductor currents and diode for the subcircuit A of the converter as shown in Figure 5, one can obtain (20).
Assuming that the input power of the converter is equal to the sum of the powers in the intermediate capacitors, it is shown (21) for the ideal static gain and belonging to the subcircuit A:
Figure 6.
External characteristic of the proposed converter showing the boundary of the curve between CCM and DCM.
Figure 6.
External characteristic of the proposed converter showing the boundary of the curve between CCM and DCM.
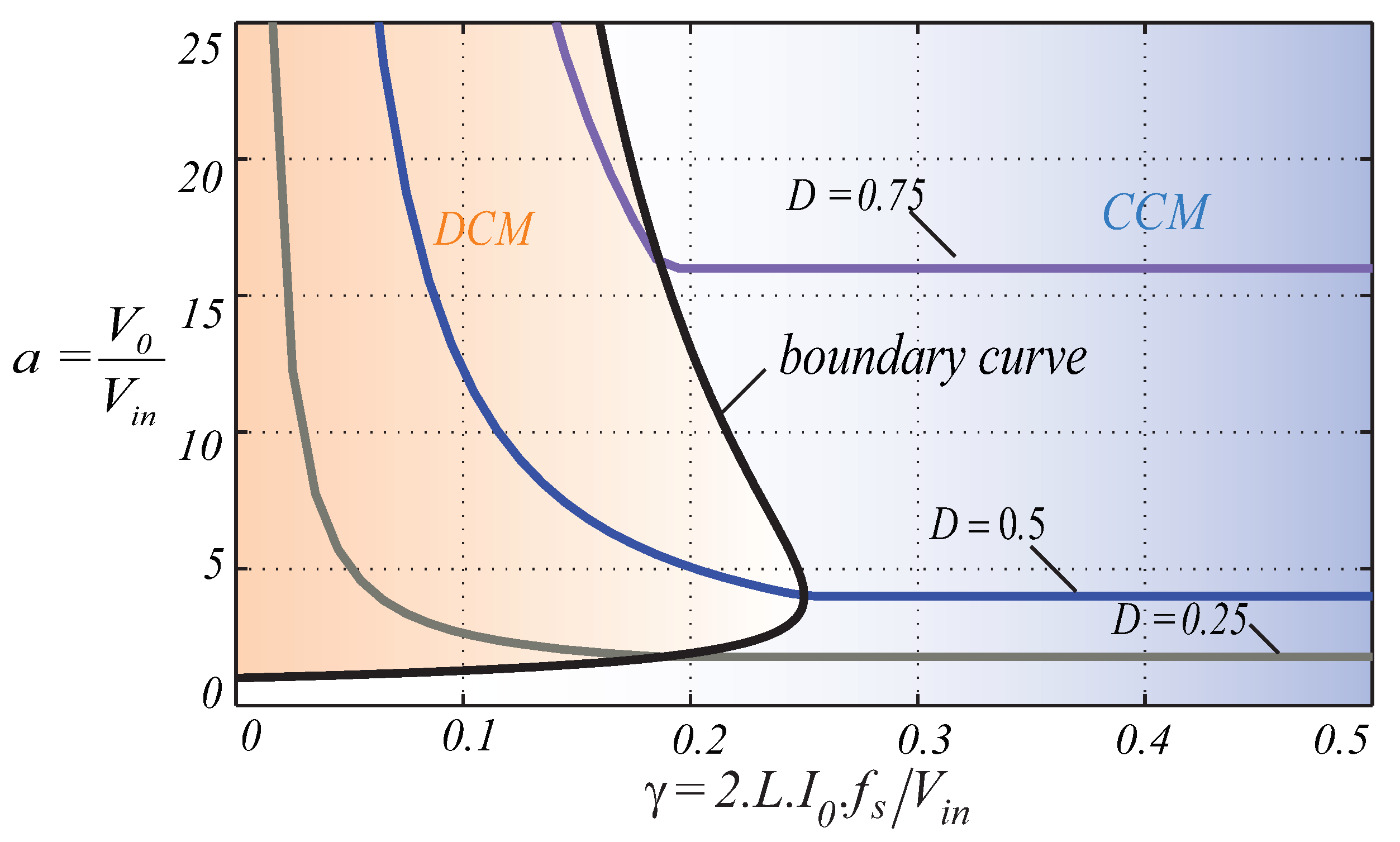
To develop the total ideal static gain of the converter, the is used superposition principle, it is added the Equation (21) for the subcircuit A and the Equation (23) referring to the subcircuit B, getting the Equation (22). For simplicity, is also considered:
In the discontinuous conduction mode, the equations for the design can be obtained through the waveforms in each component of the circuit or by making and , in the equations for design in continuous conduction mode.
Repeating the analysis for the inductor its obtains the ideal static gain equation for the subcircuit B:
To develop the total ideal static gain of the converter, the is used superposition principle, it is added the Equation (21) for the subcircuit A and the Equation (23) referring to the subcircuit B, getting the Equation (22). For simplicity, is also considered:
In the discontinuous conduction mode, the equations for the design can be obtained through the waveforms in each component of the circuit or by making and , in the equations for design in continuous conduction mode.
3. Dynamic Modeling and Converter Control
The authors obtained the mathematical model of systems with multiple inputs and outputs employing the state-space modeling, achieving more accurate mathematical models and representing the system precisely, as presented in [25,26]. The system can then be described by input and output equations, as shown in (25).
where:
For the dynamic modeling of small signals by the state space method of the Double Boost Quadratic Converter takes into account the operating stages, converter symmetry and continuous conduction mode, as follows:
3.1. First Stage: ()
3.2. Second Stage:
The circuit illustrated in Figure 2b represents the converter operation during this stage, as shown in (27). The C and E arrays vary depending on the choice of output variable.
where:
The next step is to obtain the equation that determines the average model of smalls signals for the two stages of the converter. The average matrix is given by:
Similarly, we can find the value of the matrix B. With the values of the DC components, we can define the smalls signals AC model:
where: and , are small variations on the point of operation and and are the values of states and input in steady state.
By obtaining the matrices of the first and second stages of operation, as well as the equations that define the state-space system, the circuit transfer function is accomplished through mathematical software [27]. Through the functions of transferring the input current by the duty cycle and the output voltage by the input current obtain the mathematical model of the converter. Therefore, Equation (30) shows the transfer functions of plants to the current and voltage control loops, respectively.
Besides, for the converter to be able to reject variations in output voltage and input current peaks at instants of load variations, the controllers in the voltage and current loops are designed, as presented in [28]. For the internal control of the current loop, the linear controller (PI + pole) is used to clear the error in steady state, meeting the following specifications:
The higher the compensator zero, the faster the transient response. However, the phase margin decreases, bringing the system closer to instability. The compensator pole serves to reduce the effect of the switching frequency on the current loop. It is usually positioned at half the switching frequency. Compensator gain is set to ensure the specified zero-crossing frequency (usually limited to a decade below the switching frequency). Equation (31), presents the transfer function current compensator [29]. The block diagram illustrating the projected loops is shown in Figure 7.
where:
- is positioned at half the switching frequency;
- is positioned a decade below the crossover frequency, in other words, a decade below the switching frequency;
- is designed so that the system has a low phase margin (higher than and less than ) at the crossover frequency.
For control of the external voltage loop, it adds an integral proportional compensator (PI). In first-order systems, it is usual to position the zero of the compensator PI over the plant pole, canceling it. Thus, the feedback system presents the first-order behavior.
It set the compensator gain to ensure the specified zero-crossing frequency, around 30 Hz. Typically, the voltage loop crossing frequency in DC-DC converters is related to the frequency of the drained pulsed current by the load, if an inverter is used as a load. Since this pulsed current is 120 Hz, it defines that the voltage loop crossing frequency is of the value of this frequency. The reference (32) shows the transfer function of the projected voltage control.
As shown in Figure 7, in addition to the controllers employed in the current and voltage loops, a discrete control system typically includes a delay resulting basically from the sum of two parcel, the signal sampling delay and the computational delay, totaling in this project a sampling period and a half, represented by .
The internal loop current signal conditioning transfer function, , equals the association of the current sensor gain (), the ADC gain () and the gain of the instrumentation circuits (), as expressed in (33). Voltage conditioning is equivalent, represented by the transfer function , and given by (33). In the instrumentation circuits, a low pass 1st order filter with cutoff frequency was used, being half of the switching frequency, .
Finally, the ADC gain is represented by the number of discrete ADC levels divided by the maximum ADC excursion value, in this case, given by:
In the converter model considered the inclusion of the PWM modulator given by the maximum value of excursion of signal of analogic digital converter divided by a value representing the peak of the triangular carrier, in others words, dividing the frequency of operation of the FPGA by the sampling frequency, . The Equation (35) represent the transfer function of the PWM modulator.
4. Voltage Equilibrium on the Output capacitors
Due to the converter multiports [30], the studied converter has advantages for application in photovoltaic systems, or in situations where the output voltage bus must be bipolar. In this configuration, it is possible, among others, to reduce the stresses of the switches, making it possible to couple a particular load with total bus voltage by joining two loads, each with half of the total required voltage [31,32].
Thus, when the voltage balance in the output capacitors is necessary, the voltage-balancing technique of these capacitors with a shared loop can be used, that is, the midpoint current can be controlled independently of the input current control. Thus, in addition to full control of the output voltage loop, the system features control of the voltage loop responsible for keeping the midpoint balanced, [33]. The technique is based on rejecting slight variations in output voltage, so as not to overload one of the capacitors that can assume higher voltage values or total voltage the bus while the voltage of the other capacitor becomes zero.
The main difference between the loops with separated voltage control and shared voltage control is that the latter uses control for the full voltage loop of the converter and a second control for the voltage loop of one of the capacitors to ensure the voltage balance at the midpoint. Figure 8 shows, in block diagram, the voltage balance control of the output capacitors. The blocks presented in the schematic of Figure 8 follow the similar model for the current and voltage loops shown in Figure 7.
The technique with shared voltage control loops has as its primary function to quickly correct the load disturbance at the transient instant. For this, it is used the characteristic that the total output voltage does not present high ripples. Therefore, the voltage loop that regulates the midpoint between the output capacitors must have relatively slow dynamics, and with a cut-off frequency much lower than the cut-off frequency of voltage control with separate loops.
The transfer function required for midpoint voltage control is obtained through the state space model by analyzing (27) for the first and second operating stages. When the converter has its load balanced, its midpoint current is zero. However, when the load is unbalanced, the midpoint current is responsible for the output voltage balance.
5. Experimental Results
In this section, the authors present the experimental results of the Double Boost Quadratic converter. Table 3 shows the parameters and values of the components used in the implementation of the converter. Laboratory tests were performed with a 1 kW power prototype, as shown in Figure 9. The current and voltage sensor models used were the LTSR-25-NP and the LV-25NP from LEM.
In the development of the experimental tests was used the Altera development kit, model ,34]. This Kit features a FPGA chip, which contains an intrinsic ADC block with 18 channels, and 12 bits resolution with up to 1 MHz sampling rate. Converter digital control has been implemented in the FPGA employing the VHDL hardware description language (VHSIC HDL - Very High-Speed Integrated Circuit Hardware Description Language).
The FPGA has some advantages such as the real-time processing feature and high processing density, in addition it is different from microcontrollers because it has a large number of PWM outputs, but the main difference is the parallel processing feature, in other words, it is possible to process digital signals simultaneously without interaction with other processes, [34,35]. The flowchart in Figure 10 shows the parallel processing adopted for the control of the Double Quadratic Boost Converter. Each block represents a code responsible for generating the hardware description. Thus, several processes with distinct functions work simultaneously.
In this work, the FPGA does the acquisition, filtering, and processing of data, in addition to modulation and protection of the circuit. As presented in the Figure 10, the hardware description was divided and organized in different logic blocks interconnected by a flag responsible for synchronism. Data collection happens when there is no switching, in order to avoid noise. Subsequently, the reading data are filtered and sent to the control loop. Finally, they are available for use in the logic block responsible for modulation.
5.1. Converter Operating Open Loop
Figure Figure 11a shows input and output voltages and Figure Figure 11b it is observed that the voltage at the switches is halved compared to similar topologies in the literature [19].
Comparing the experimental waveforms of the total output voltage and the input voltage , it verifies the high static gain of the converter (four times for ). Although the experimental results are presented only for the total output voltage , these results can be obtained by summing the voltage of the output capacitors and .
The current in the inductors is significant in the analysis of the converter operating mode. However, it developed the theoretical analysis for continuous, critical, and discontinuous conduction modes; the practical implementation was performed only in continuous driving mode, where these converters generally operate in most applications because of its presented lower current peaks in their semiconductors. The currents in the and inductors are shown in Figure 12. The current ripple in the inductor is greater than in the inductor as designed. The project considered a ripple of in the value of their respective nominal currents.
Converter efficiency is an important parameter and must be taken into consideration. Therefore, Figure 13 presents the comparison of the converter performance obtained via simulation in PSIM, using the Device Database Editor tool through the semiconductor models specified in Table 3 and the efficiency obtained through the experimental tests, in this case, the power analyzer, Yokogawa wt500, was used. Therefore, it is seen in Figure 13, that the proposed converter has high efficiency, proven through simulation and experimental tests.
Moreover, as presented in the theoretical analysis through Equations (4) and (5), the Double Boost Quadratic converter has a high static gain. Figure 14 shows the static gain curve obtained by simulation using the Matlab software compared to the experimental curve. For the experimental tests, it was possible to vary the duty cycle D ( - ). This value was limited by the power at which the converter was designed and built, according to Table 3. It chose low power value, allowing for a greater range of the duty cycle.
As shown in Figure 14, the static converter gain reached the ratio of 12 times of output voltage to the input voltage, as proposed in the theoretical analysis. For the tests, limited the input inductor current was in the function of the design current. It performed the test at 15% of the rated power of the converter.
5.2. Converter Operating in Closed Loop
Considering the converter operating in the closed-loop with current, voltage, and voltage balance control on the output capacitors, Figure 15 presents the input current, midpoint current, and output capacitor voltages. It develops the tests for a load step of 50% of rated power to 75% of rated power. It noticed that at the moment of load variation to the input current increase () is proportional to the power variation, as shown in Figure 15, and in this case the overshoot of one of the output capacitors is similar, but with the opposite signal, characterizing their balance control.
In order to complement the load variation test shown in Figure 15 and Figure 16a presents the same waveforms, replacing the input current with the total output voltage. In this case, despite the variation of the input current shown in Figure 15, there is no variation of the output capacitor voltage and just than a small overshoot at the time the load steps occurred.
In Figure 16a, it is noticed that the over voltage at the total voltage is lower when compared to the over voltage at the output capacitors and , proving that the balance control can balance the voltage values in the capacitors, even with load imbalance. To keep the voltage on the output capacitors unchanged despite load imbalance, the midpoint current is responsible for absorbing this imbalance through this current variation.
In order to introduce the operation of the converter against the imbalances in the output capacitor voltages, besides the load variation, Figure 16b presents the midpoint current, the output capacitor voltages and the total output voltage at four different times: a) In load imbalance (); b) In total load disturbance (); c) In load disturbance (removal of 50% total load); d) In removal of load imbalance ().
6. Discussion
It verifies that the control of the output capacitors voltage balance presents a good response in the instant of capacitors voltage unbalance and in the moment of load variation. While the output voltage remains unchanged, except for a small transient at these times, allowing compensation for this variation. Finally, the midpoint current has significantly varied at times of load imbalance, as expected in the voltage balance control of the output capacitor, because it is through the current midpoint variation that capacitors voltages are balanced.
7. Conclusions
Considering that energy generation is fundamental for world economic development, combined with care for the environment and sustainable practices, the generation of energy through renewable sources plays an important role. Thus, research related to applications in the field of electricity is fundamental to technological development.
Therefore, thinking about optimizing power converters for these applications, in this work was presented the study of a new non-isolated high static gain converter DC-DC. The operating stages and waveforms of the converter have been shown for continuous, critical, and discontinuous conduction mode in addition to the ideal static gain curves, actual static gain for the various load resistance values, and the curve representing the boundary between the conduction modes. For the development of the dynamic mathematical model, the state space technique was used.
Due to the symmetry of the converter, it was possible to reduce the stresses on the switches. Moreover, its symmetry also simplified its mathematical model, as presented in the paper, in which an eighth-order system can be simplified by a fourth-order system, making it easier to obtain its transfer function. In this configuration, this converter can be used, for example, in conjunction with a multi-level inverter coupled to its output for photovoltaic generation, grid-connected applications, or coupled to AC loads requiring low harmonic distortion rates.
The experimental results were presented confirming the theoretical analysis. Thus, it was possible to verify the high static gain (greater than twelve times) experimentally through the practical tests of the duty cycle variation, where the results were obtained as expected. Also, it was possible to verify the reduced voltage efforts on the converter switches when compared to existing converters in the literature. As it is an important parameter, the efficiency curve of the converter was presented in the experimental results, proving the high efficiency of the proposed converter.
Finally, the results show that this converter has a great natural potential for application in renewable energies, being this an excellent option in the conditioning of power generation through photovoltaic panels.
Author Contributions
Conceptualization, D.R. and S.A.; methodology, S.A.; software, F.L.; validation, F.L.; formal analysis, F.L.; investigation, F.L. and C.D.; resources, F.L. and C.D.; data curation, F.L.; writing original draft preparation, F.L. and C.D.; writing review and editing, F.L. and W.S.; visualization, F.L. and W.S.; supervision, S.A.; project administration, S.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data sharing is not applicable to this article.
Acknowledgments
We would like to thank the Institute of Power Electronics INEP - UFSC, for the equipment and laboratory provided for the development of practical experiments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Danielis, R.; Scorrano, M.; Massi Pavan, A.; Blasuttigh, N. ’Simulating the Diffusion of Residential Rooftop Photovoltaic, Battery Storage Systems and Electric Cars in Italy. An Exploratory Study Combining a Discrete Choice and Agent-Based Modelling Approach. Enegies, 2023, 16, 557. [Google Scholar] [CrossRef]
- Sumathy, P.; Navamani, J.D.; Lavanya, A.; Sathik, J.; Zahira, R.; Essa, F.A. : ’PV Powered High Voltage Pulse Converter with Switching Cells for Food Processing Application’. Energies 2023, 16, 1010. [Google Scholar] [CrossRef]
- Karbowniczak, A.; Latała, H.; Ne˛cka, K.; Kurpaska, S.; Ksia˛z˙ ek, L. : ’Modelling of Energy Storage System from Photoelectric Conversion in a Phase Change Battery’. Energies 2022, 15, 1132. [Google Scholar] [CrossRef]
- Khodair, D.; Motahhir, S.; Mostafa, H.H.; Shaker, A.; Munim, H.A.E.; Abouelatta, M.; Saeed, A. : ’Modeling and Simulation of Modified MPPT Techniques under Varying Operating Climatic Conditions’. Energies 2023, 16, 549. [Google Scholar] [CrossRef]
- Pellitteri, F.; Di Dio, V.; Puccio, C.; Miceli, R. : ’A Model of DC-DC Converter with Switched-Capacitor Structure for Electric Vehicle Applications’. Energies 2022, 15, 1224. [Google Scholar] [CrossRef]
- Yalla, N., Agarwal, P., Venkata, J. S. P. A., Bussa, V. K.: ’Reduced switching state multilevel improved power factor converter for level-3 electric vehicle applications’, IET Power Electronics, 2020, 13, (4), pp. 693–702.
- Russo, A.; Cavallo, A. : ’Stability and Control for Buck–Boost Converter for Aeronautic Power Management’. Energies 2023, 16, 988. [Google Scholar] [CrossRef]
- Li, H.; Gu, Y.; Zhang, X.; Liu, Z.; Zhang, L.; Zeng, Y. : ’A Fault-Tolerant Strategy for Three-Level Flying-Capacitor DC/DC Converter in Spacecraft Power System’. Energies 2023, 16, 556. [Google Scholar] [CrossRef]
- Zhou, G., Tian, Q. Leng, M., Fan, X., Bi, Q.: ’Energy management and control strategy for DC microgrid based on DMPPT technique’, IET Power Electronics, 2020, 13, (4), pp. 658–668.
- Kumar, R.; Wu, C.-C.; Liu, C.-Y.; Hsiao, Y.-L.; Chieng, W.-H.; Chang, E.-Y. : ’Discontinuous Current Mode Modeling and Zero Current Switching of Flyback Converter’. Energies 2021, 14, 5996. [Google Scholar] [CrossRef]
- Farakhor, A., Abapour, M., Sabahi, M.: ’Study on the derivation of the continuous input current high-voltage gain DC/DC converters’, IET Power Electronics, 2018, 11, (10), pp. 1–9.
- Sedaghati, F., Pourfajar, S.: ’Analysis and implementation of a boost DC– DC converter with high voltage gain and continuous input current’. IET Power Electronics, 2020, 13, 798–807. [CrossRef]
- Samuel, V. J., Keerthi, G., Mahalingam, P.: ’Coupled inductor-based DC–DC converter with high voltage conversion ratio and smooth input current’. IET Power Electronics, 2020, 13, 733–743. [CrossRef]
- Middlebrook, R. D.: ’Transformerless DC-to-DC converters with large conversion ratios’, Power Electronics. IEEE Transactions on 1988, 3, 484–488.
- F. L. de Sá, D. Ruiz-Caballero and S. A. Mussa, "A new DC-DC double Boost Quadratic converter," 2013 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2013, pp. 1-10. -10. [CrossRef]
- Maksimovic, D., Cuk, S.: ’General properties and synthesis of PWM DC-to-DC converters’. Power Electronics Specialists Conference, 1989. PESC ’89 Record., 20th Annual IEEE, 1989, pp. 515–525 vol.2.
- Maksimovic, D., Cuk, S.: ’Switching converters with wide DC conversion range’. Power Electronics, IEEE Transactions on, 1991, 6, 151–157. [CrossRef]
- Wu, T. F., Yu, T. H.: ’Unified approach to developing single-stage power converters’. Aerospace and Electronic Systems, IEEE Transactions on, 1998, 34, 211–223. [CrossRef]
- Barreto, L.H.S.C., Coelho, E.A.A., Farias, V.J., de Freitas, L.C., Vieira, J.B., Jr.: ’An optimal lossless commutation quadratic PWM Boost converter’. Applied Power Electronics Conference and Exposition. APEC 2002. Seventeenth Annual IEEE, 2002, pp. 624–629 vol.2.
- Barreto, L. H. S. C., Coelho, E. A. A., Farias, V. J., de Oliveira, J. C., de Freitas, L. C., Vieira, J. B.: ’A quasi-resonant quadratic boost converter using a single resonant network. Industrial Electronics, IEEE Transactions on 2005, 58, 552–557.
- Li, W., He, X.: ’Review of Nonisolated High-Step-Up DC/DC Converters in Photovoltaic Grid-Connected Applications. Industrial Electronics, IEEE Transactions on, 2011, 52, 1239–1250.
- Novaes, Y. R., Barbi, I., Rufer, A.: ’A New Three-Level Quadratic (T-LQ) DC/DC Converter Suitable for Fuel Cell Applications’. Power Conversion Conference - Nagoya, 2007. PCC ’07, 2007, pp. 1–10.
- Fiori, M., Barbosa, L. R.: ’Three-Level Boost Quadratic G Converter. Power Electronics, IEEE Transactions on, 2017, 22, 131–138.
- Kishore, P. M., Bhimasingu, R.: ’Dual-input and triple-output boost hybrid converter suitable for grid-connected renewable energy sources. IET Power Electronics, 2020, 13, 808–820. [CrossRef]
- Erickson, R. W.: ’Fundamentals of Power electronics’, Lectures on Power Electronics (USA: Chapman & Hall, 1997, 1st ed.).
- Silva, G. V., Coelho, R. F., Lazzarin, T. B.: ’Modeling the Switched Capacitor Cell Boost Converter Using a Reduced Order Equivalent Converter. Power Electronics, IEEE Transactions on, 2017, 22, 288–297.
- Sun, J., Bass, R. M.: ’Modeling and practical design issues for average current control’. Applied Power Electronics Conference and Exposition, 1999. APEC ’99. Fourteenth Annual, 1999, pp. 980–986 vol.2.
- Guepfrih, M. F., Waltrich, G., Lazzarin, T. B.: ’Quadratic-boost-double-flyback converter’. IET Power Electronics, 2019, 12, 1–12.
- Silva Junior, E. T.: ’Boost Converter Analysis and Design of the compensators’. Masters dissertation, University Federal of Santa Catarina UFSC, INEP, 1994.
- Brockveld, S. L., Waltrich, G.: ’Boost–flyback converter with interleaved input current and output voltage series connection’. IET Power Electronics, 2018, 11, 1–9.
- Martins, A. S., Kassick, E. V., Barbi, I.: ’Control strategy for the double-boost converter in continuous conduction mode applied to power factor correction’. Power Electronics Specialists Conference, 1996. PESC ’96 Record., 27th Annual IEEE, 1996, pp. 1066–1072 vol.2.
- Padilha, F. J. C., Bellar, M. D.: ’Modeling and control of the half bridge voltage doubler boost converter’. Industrial Electronics, 2003. ISIE ’03. 2003 IEEE International Symposium on, 2003, pp. 741–745 vol.2.
- Zhou, J., Cheng, S., Hu, Z. and Liu, J.: ’Balancing control of neutral-point voltage for three-level T-type inverter based on hybrid variable virtual space vector’. IET Power Electronics, 2020, 13, 744–750. [CrossRef]
- `BeMicro Max10, FPGA Evaluation Kit’, Altera, Analog Devices, 2014.
- Lahari, MV. P., Vedula, S. V., Rao, V. U.: ’Real time models for FPGA based control of power electronic converters: A graphical programming approach’. IEEE IAS Joint Industrial and Commercial Power Systems/ Petroleum and Chemical Industry Conference (ICPSPCIC), 2015, pp. 60–65.
Figure 1.
Double Boost Quadratic Converter, represented in two subcircuits called ’A’ and ’B’.
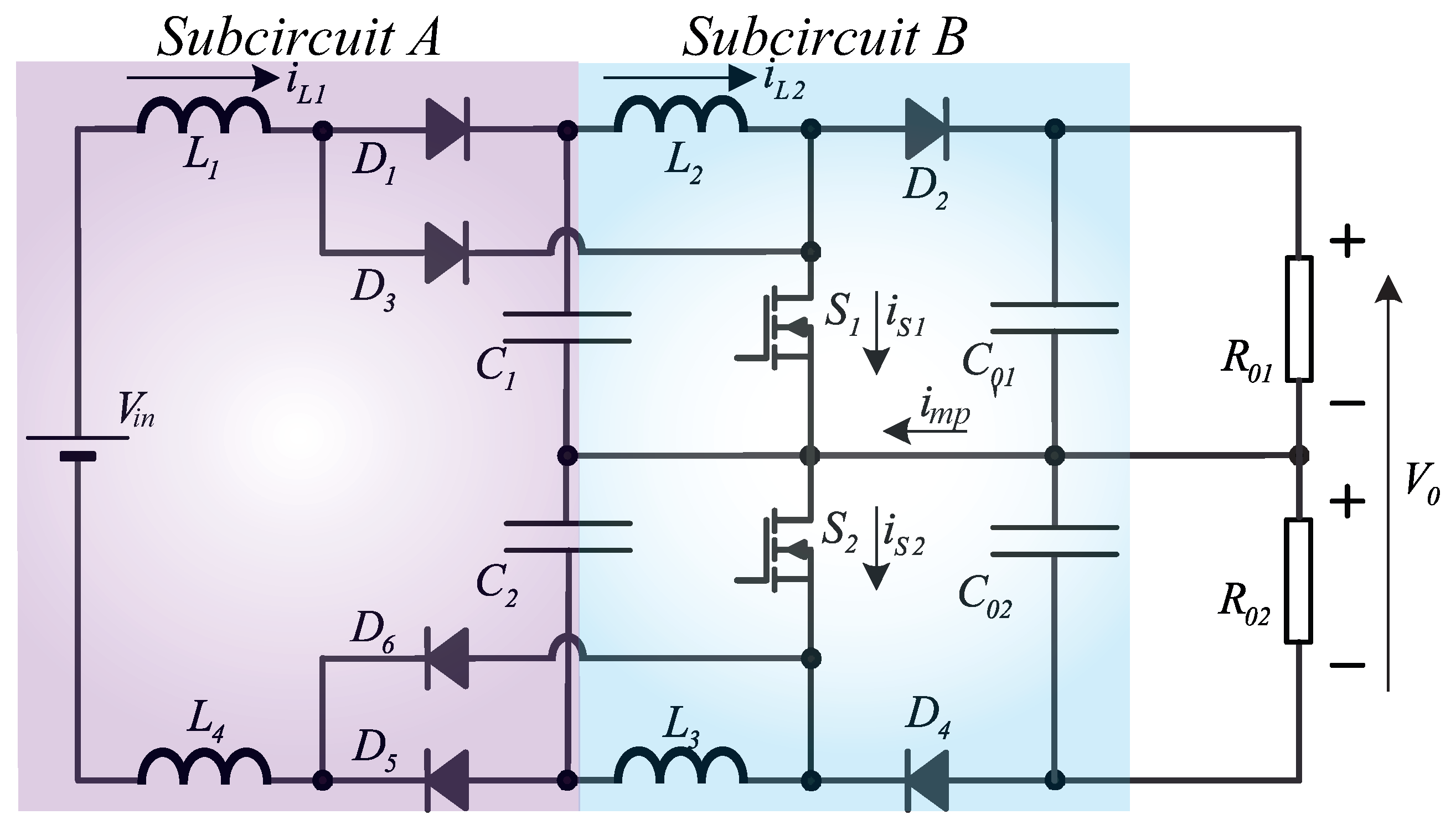
Figure 2.
Operating stages of the converter in continuous conduction mode: (a) First stage; b) Second stage.
Figure 2.
Operating stages of the converter in continuous conduction mode: (a) First stage; b) Second stage.
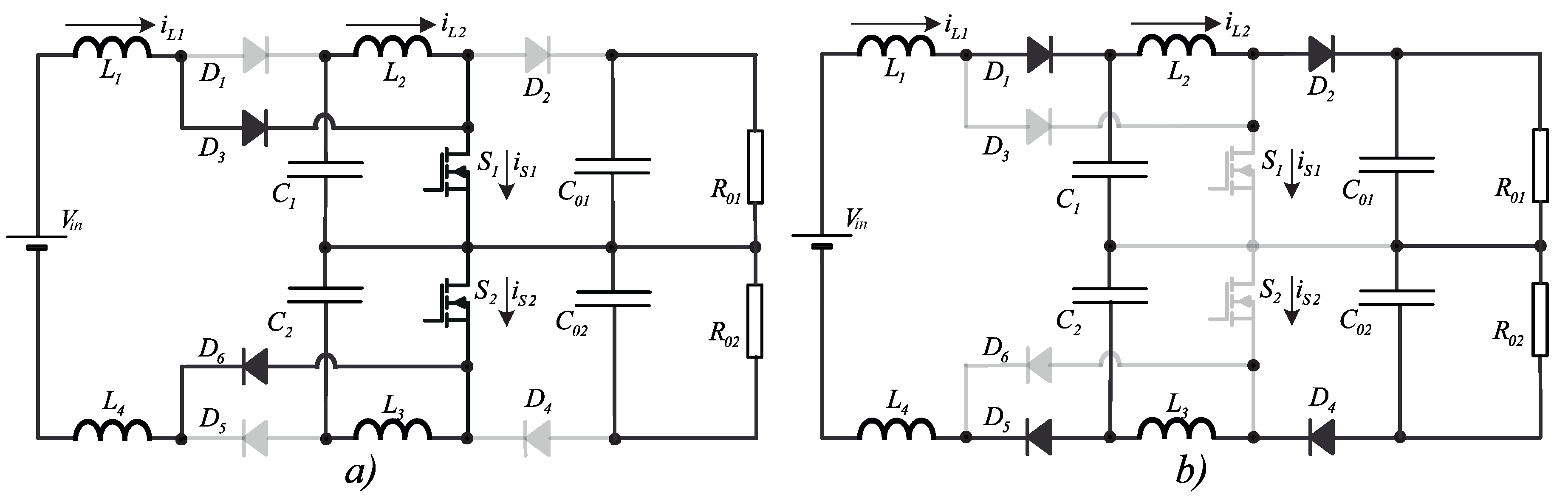
Figure 3.
Quadratic Double Boost Converter waveforms operating in conduction mode: a) Continuous; b) Critical and c) Discontinuous.
Figure 3.
Quadratic Double Boost Converter waveforms operating in conduction mode: a) Continuous; b) Critical and c) Discontinuous.
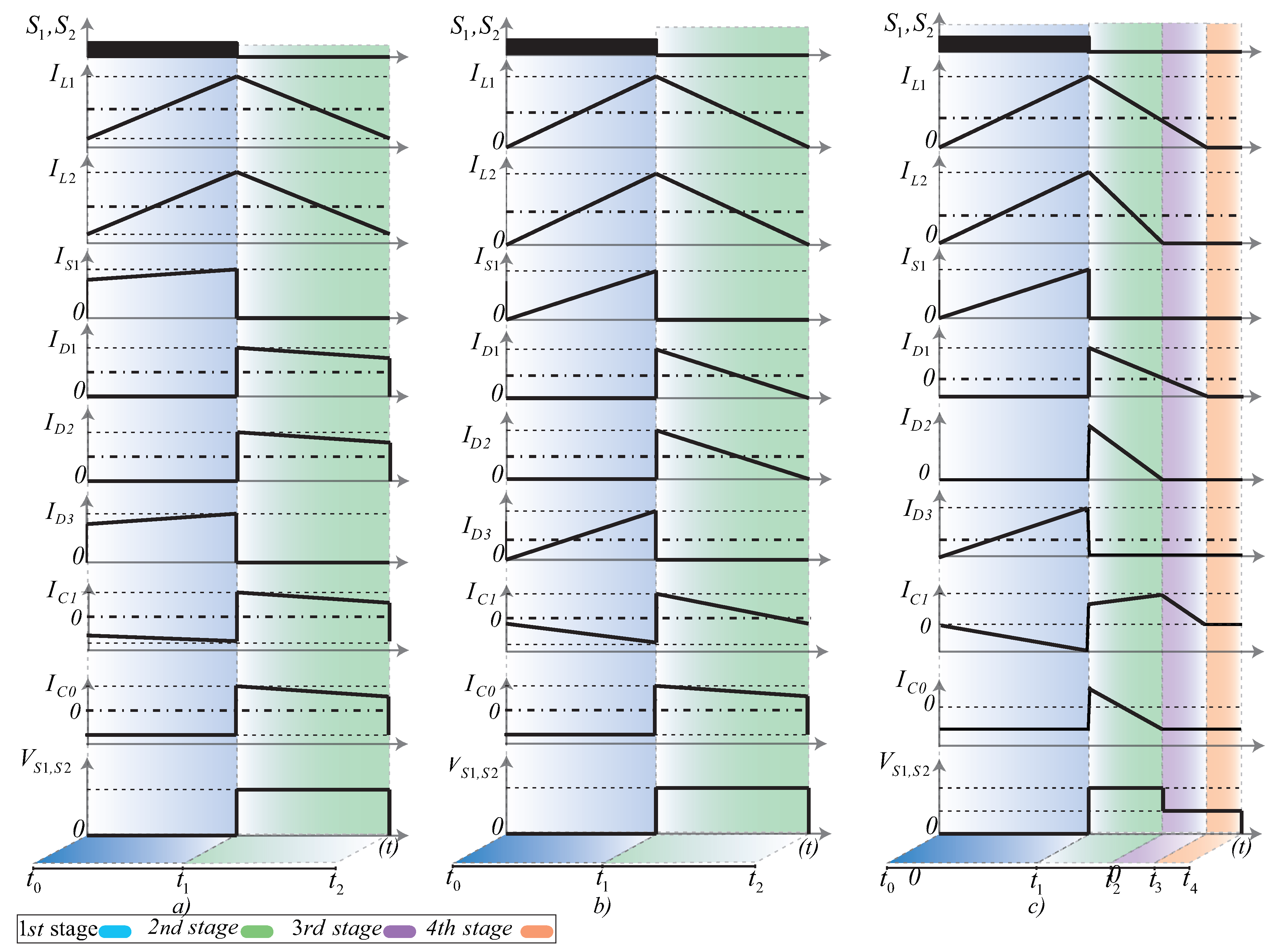
Figure 4.
Ideal and real static gain of Double Boost Quadratic Converter for various values of .

Figure 5.
Operating stages in discontinuous conduction mode: (a) First stage; b) Second stage; c) Third stage; d) Fourth stage.
Figure 5.
Operating stages in discontinuous conduction mode: (a) First stage; b) Second stage; c) Third stage; d) Fourth stage.
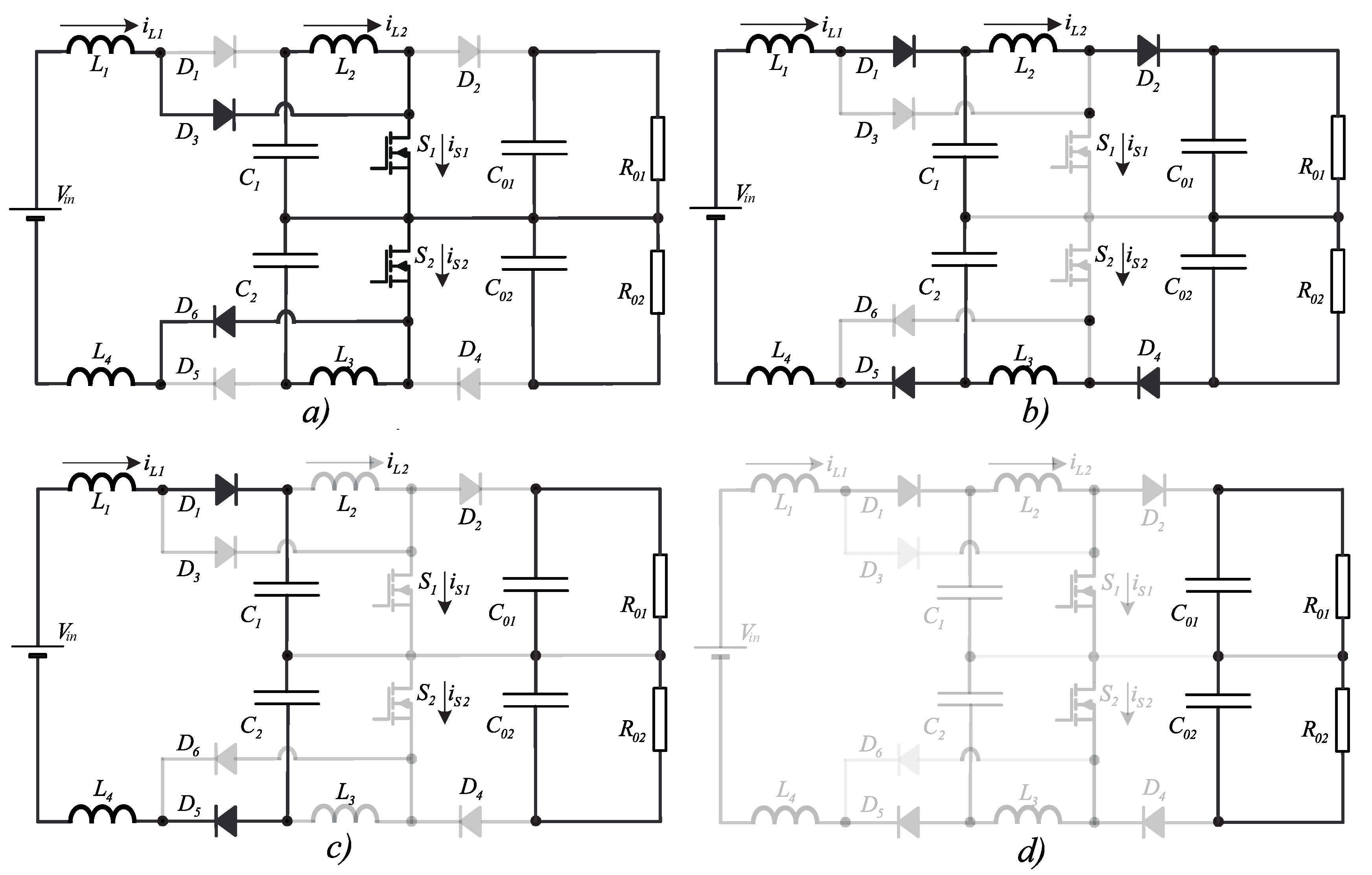
Figure 7.
Block Diagram representing the internal current loop and the external voltage loop - represents the complete converter model, is the reference voltage and represents the reference current. The and variables refer to the converter control variables.
Figure 7.
Block Diagram representing the internal current loop and the external voltage loop - represents the complete converter model, is the reference voltage and represents the reference current. The and variables refer to the converter control variables.
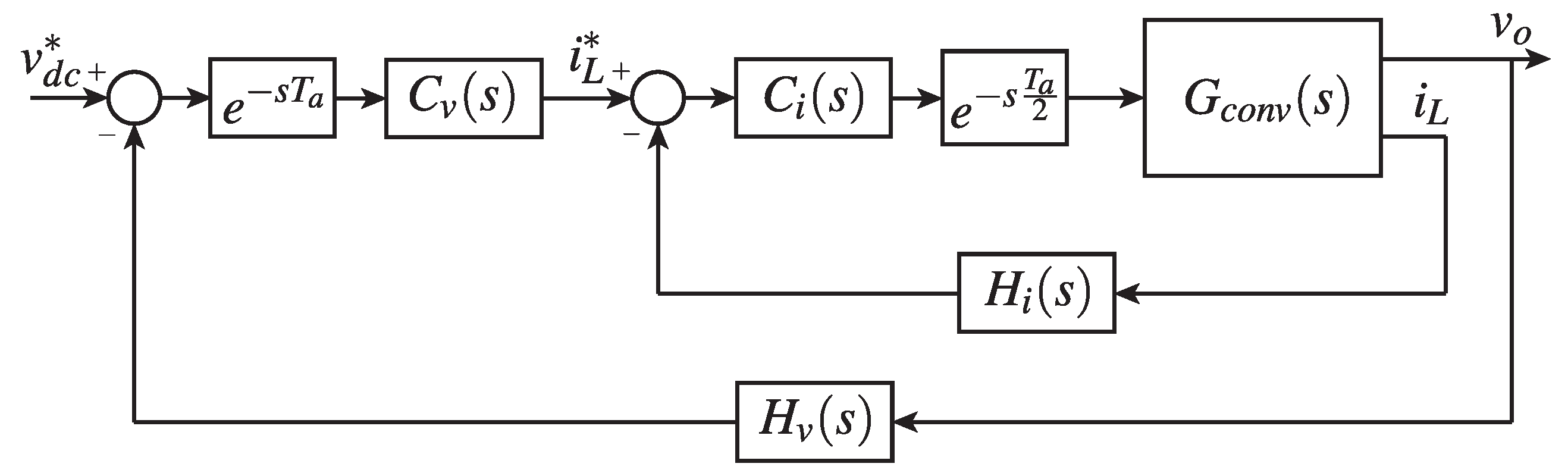
Figure 8.
Schematic of the Double Boost Quadratic Converter with voltage balance loops, on output capacitors, and total.
Figure 8.
Schematic of the Double Boost Quadratic Converter with voltage balance loops, on output capacitors, and total.
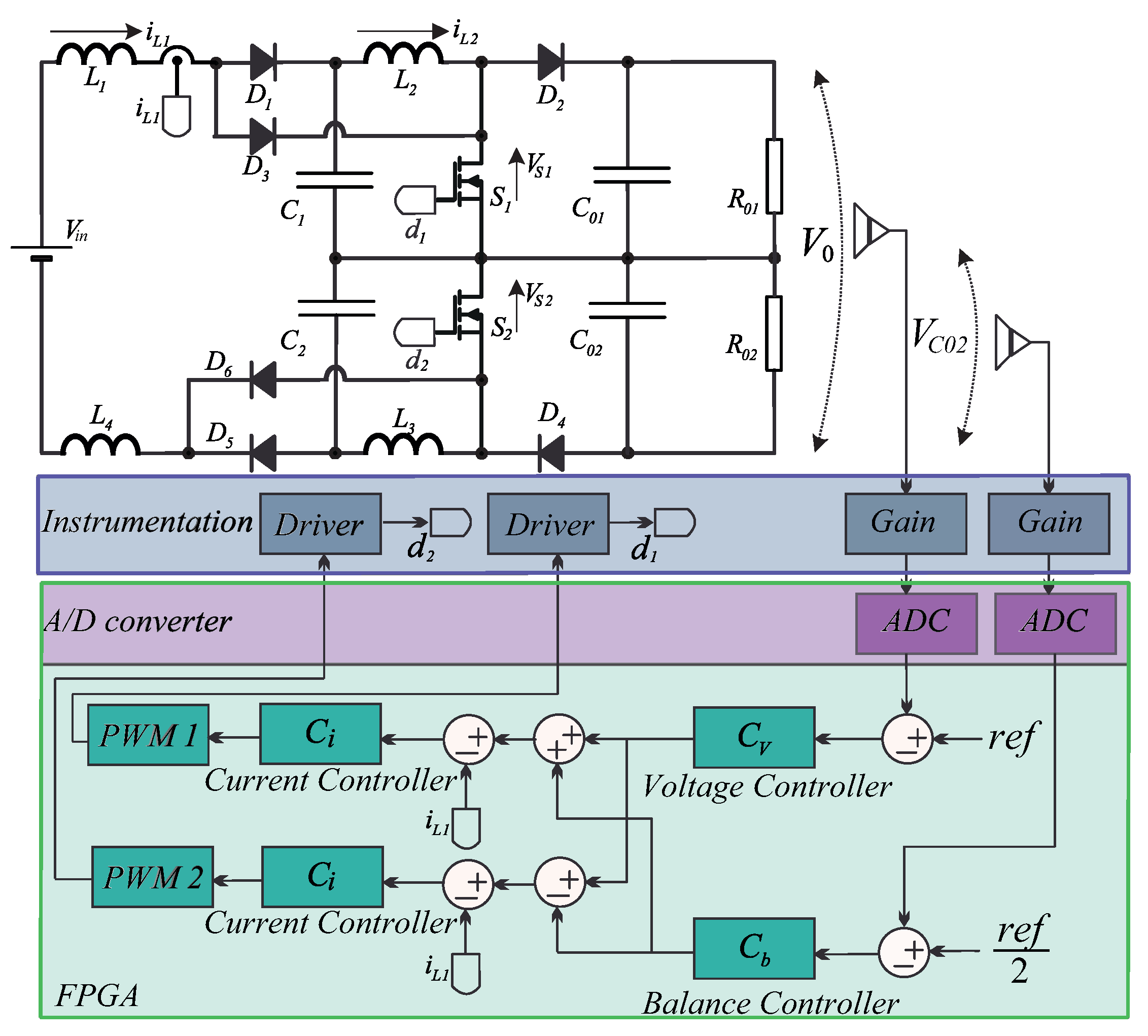
Figure 9.
Double Boost Quadratic Converter Prototype, power 1 kW.

Figure 10.
Digital control flowchart.
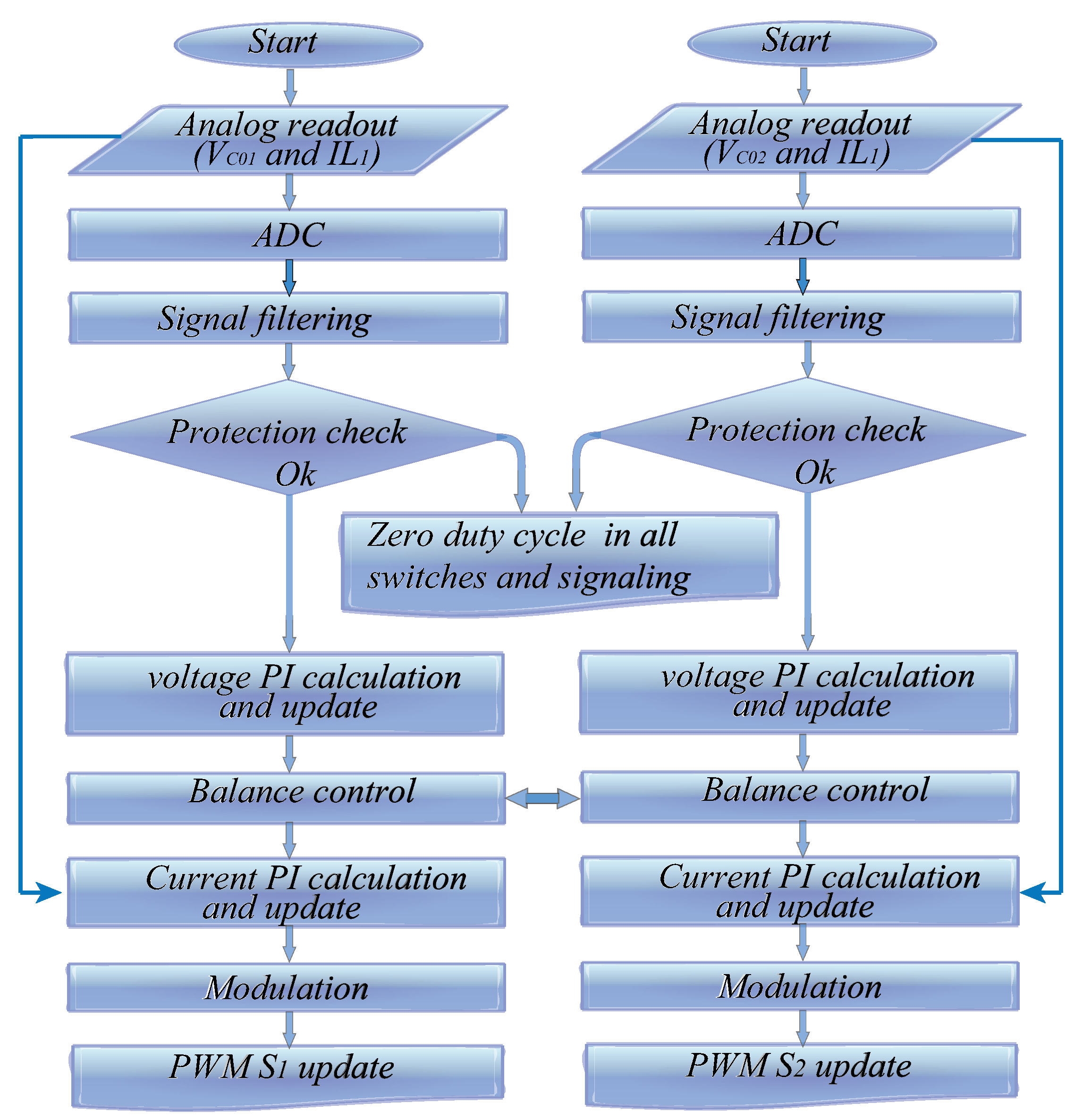
Figure 11.
(a) Input voltage () and total output voltage (). (b) Voltage at switches and , using and a scale of by division.
Figure 11.
(a) Input voltage () and total output voltage (). (b) Voltage at switches and , using and a scale of by division.
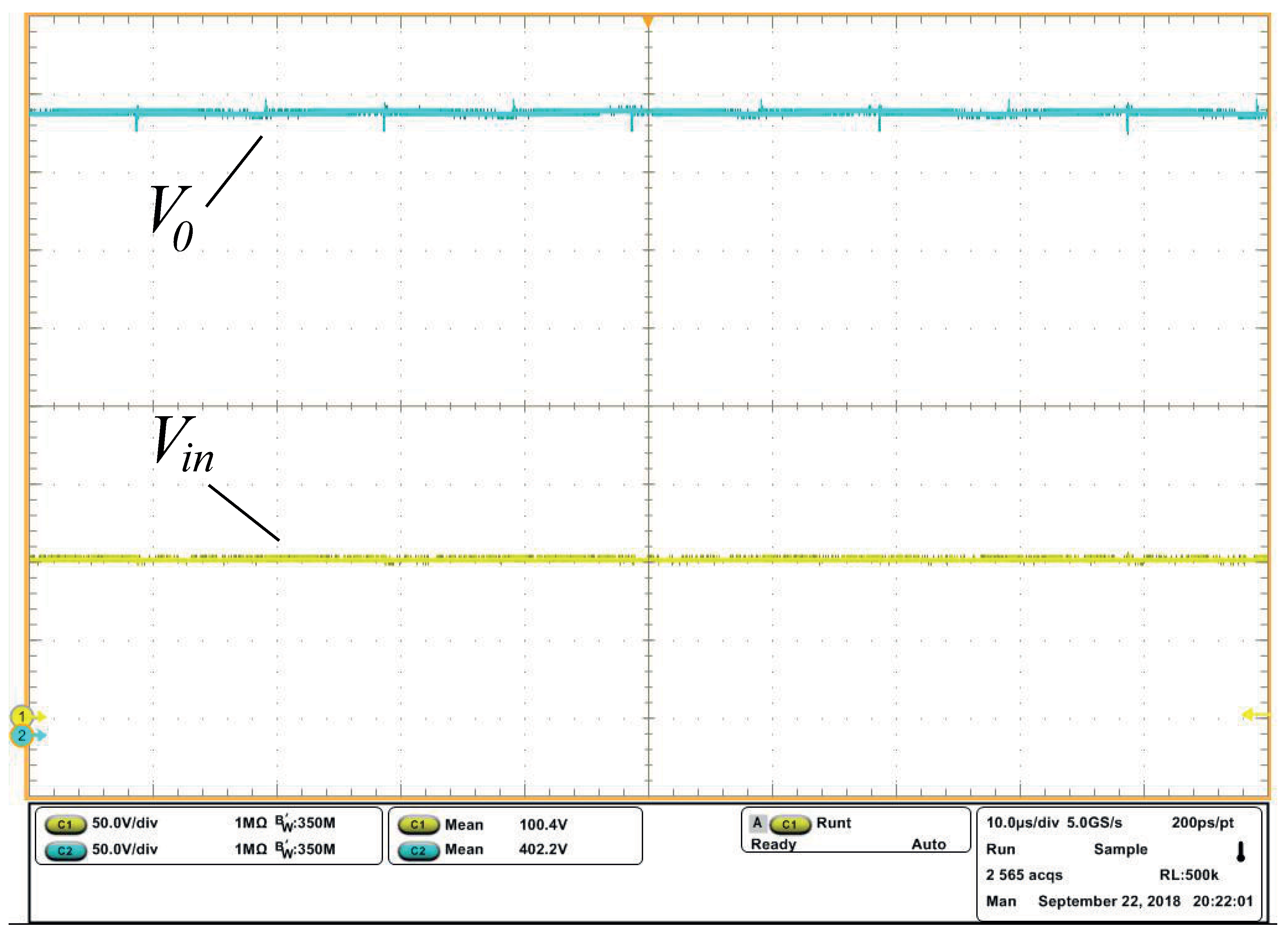
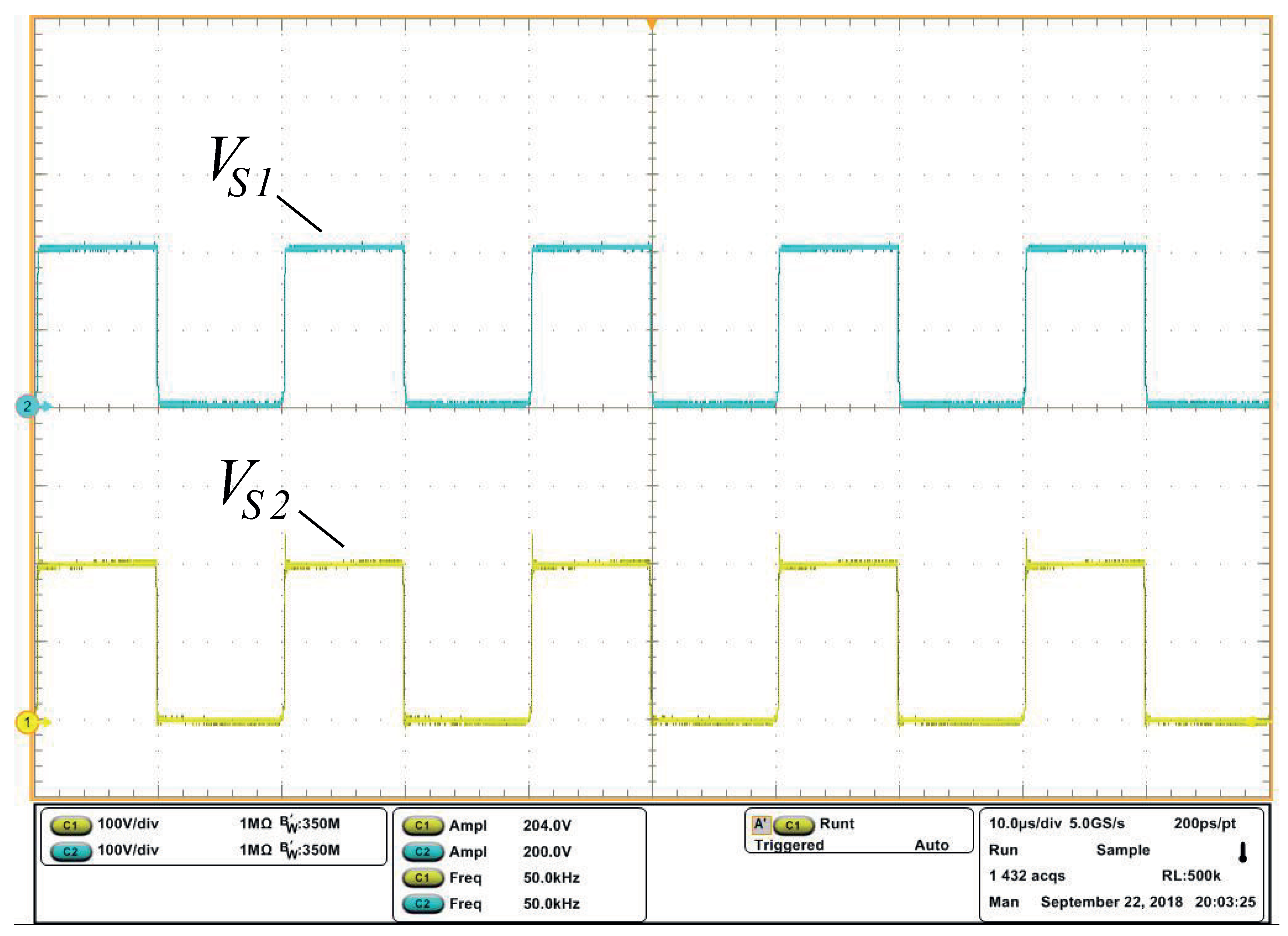
Figure 12.
Current in inductors and , in scale per division. Average values: e , with current ripple of .
Figure 12.
Current in inductors and , in scale per division. Average values: e , with current ripple of .
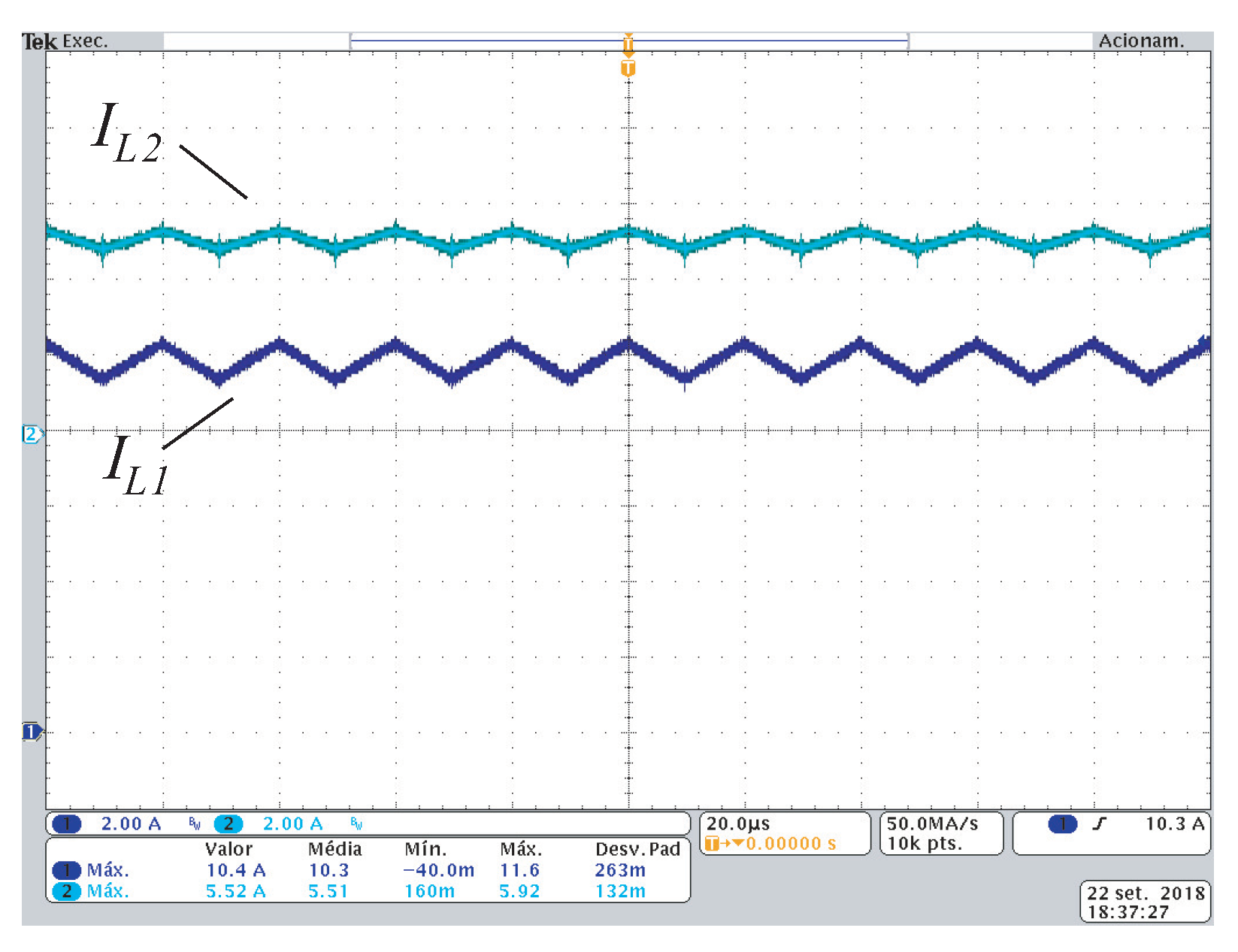
Figure 13.
Converter efficiency: simulation result compared to the experimental result.
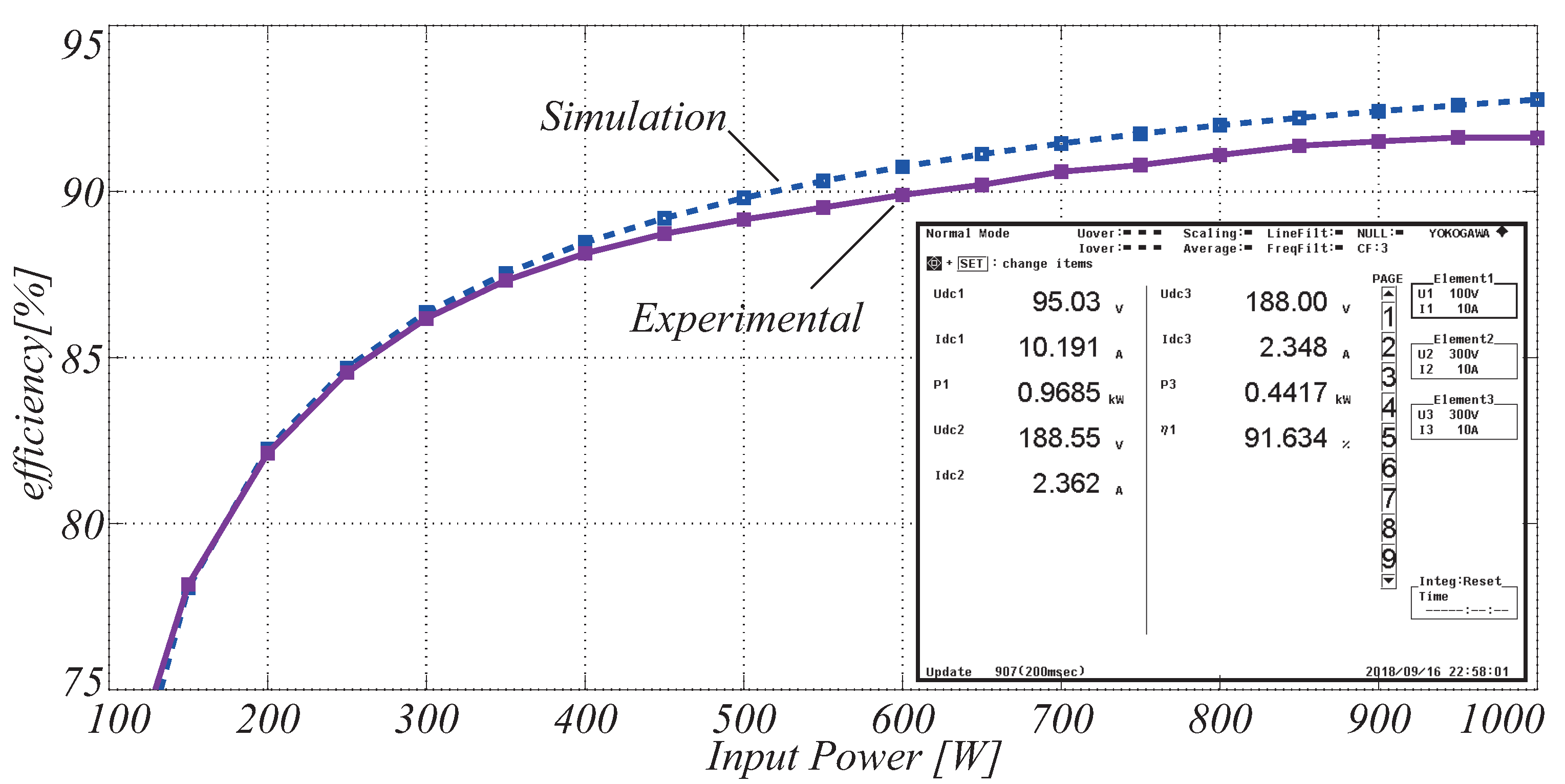
Figure 14.
Real static gain: simulation result (dashed) compared to experimental result.
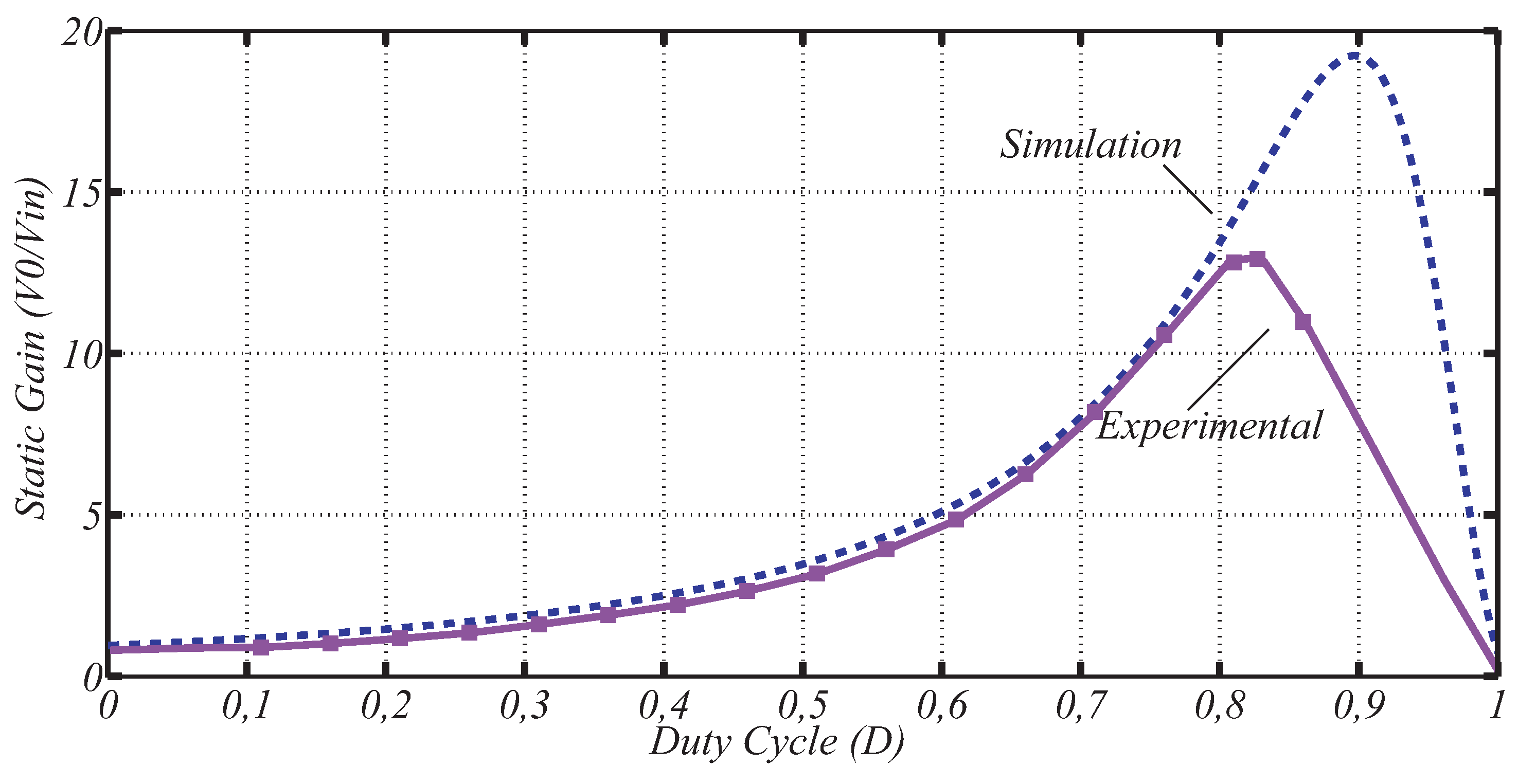
Figure 15.
Input current , midpoint current and voltage on output capacitors and , at times of charge variation ().
Figure 15.
Input current , midpoint current and voltage on output capacitors and , at times of charge variation ().
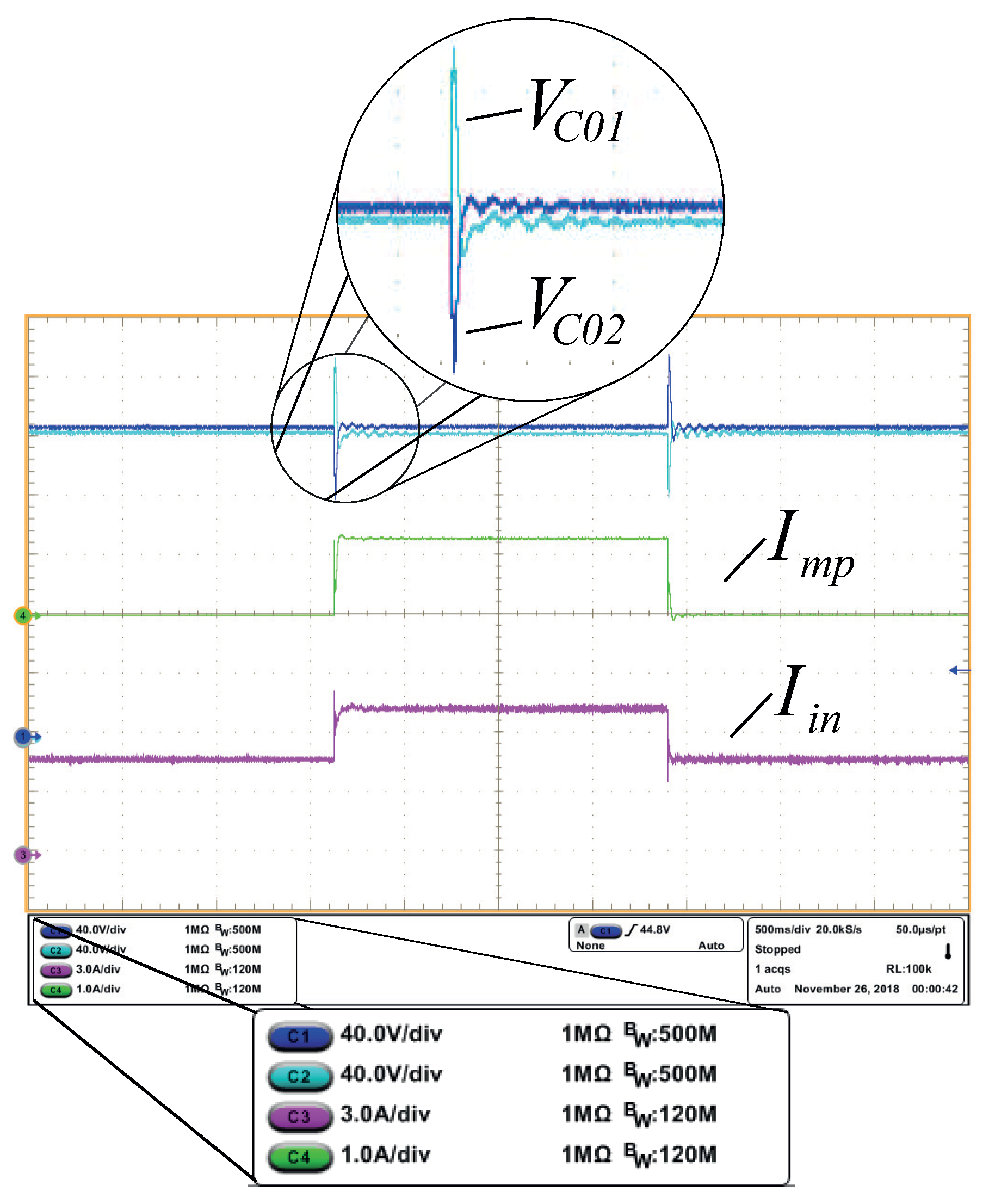
Figure 16.
Midpoint current , voltage at output capacitors , and total output voltage .
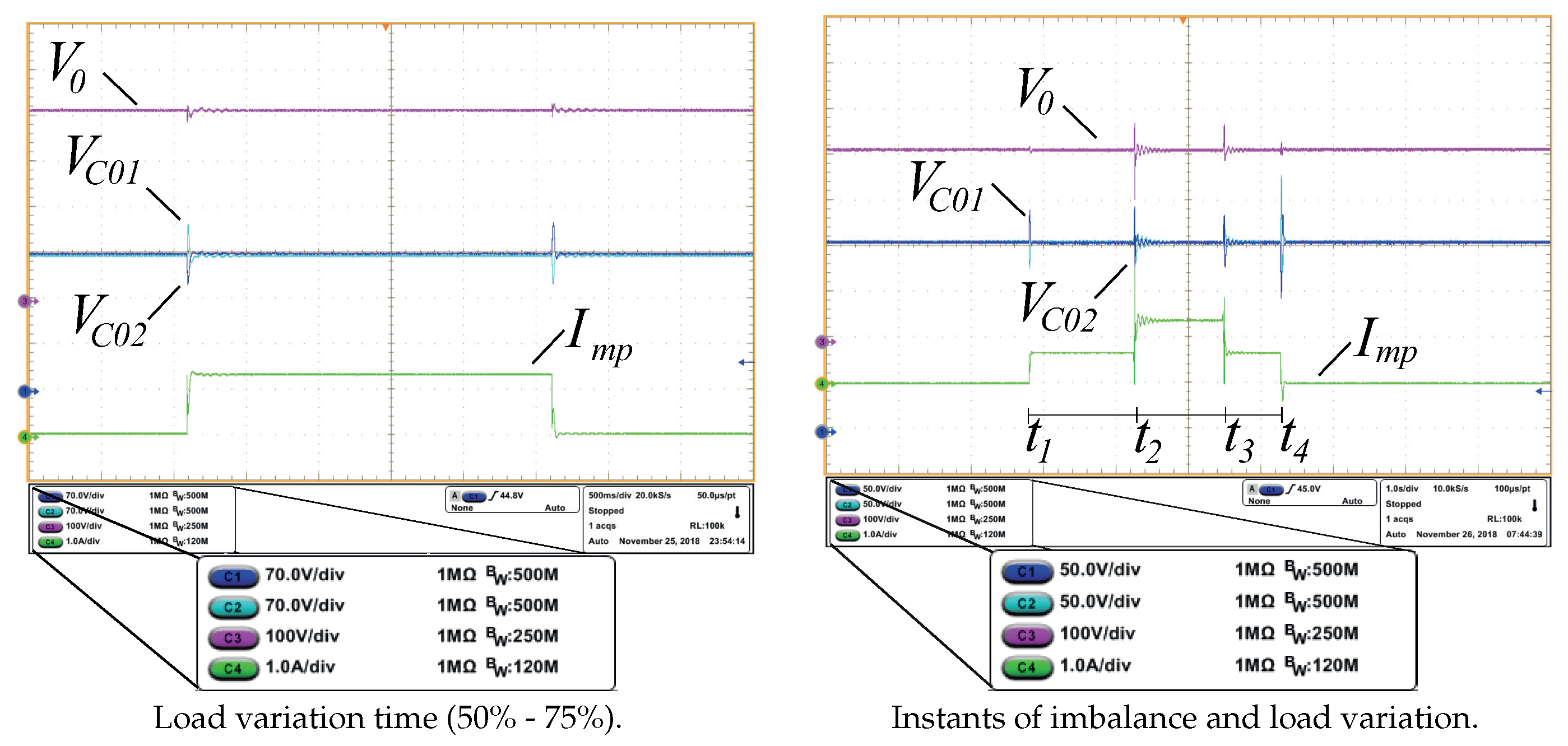
Table 1.
Converter Component Design.
| Component | Calculation to obtain parameters |
|---|---|
| Inductor | |
| Inductor | |
| Intermediate Capacitor | |
| Output Capacitor | |
| Load Resistance R |
Table 2.
Calculation of Efforts on Components of the Converter operating in CCM.
| Component | Description | Equating efforts |
|---|---|---|
| Switch | Average Current | |
| RMS current | ||
| Maximum Current | ||
| Maximum voltage | ||
| Diode | Average Current | |
| RMS current | ||
| Maximum Current | ||
| Maximum voltage | ||
| Diode | Average Current | |
| RMS current | ||
| Maximum Current | ||
| Maximum voltage | ||
| Diode | Average Current | |
| RMS current | ||
| Maximum Current | ||
| Maximum voltage | ||
| Inductor | Average Current | |
| RMS current | ||
| Maximum Current | ||
| Maximum voltage | ||
| Inductor | Average Current | |
| RMS current | ||
| Maximum Current | ||
| Maximum voltage | ||
| Capacitor | Average Current | |
| RMS current | ||
| Capacitor | Average Current | |
| RMS current |
Table 3.
Parameters used in the prototype of .
| Description | Parameters |
|---|---|
| Output Voltage | |
| Input Voltage | |
| Intermediate Capacitor | |
| Output Capacitor | |
| Load Resistance | |
| Switching Frequency | |
| Duty Cycle | |
| Input Inductance | |
| Intermediate Inductance | |
| Switch Models (Mosfets)- | |
| Diodes Models (Ultrafast) - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






