Prerpints.org logo
Preprint
Article

Design of Intelligent Nonlinear H2/H∞ Robust Control Strategy of Diesel Generator Based CPSOGSA Optimization Algorithm

Altmetrics

Downloads

133

Views

26

Comments

0

A peer-reviewed article of this preprint also exists.

  † These authors contributed equally to the work.

This version is not peer-reviewed

Submitted:

26 May 2023

Posted:

29 May 2023

You are already at the latest version

Alerts
Abstract
In today's human society, diesel generators (DGs) are highly applied into the human energy and electricity supply system due to its technical, operational and economic advantages. This paper proposes an intelligent nonlinear $H_2/H_{\infty}$ robust controller based on the chaos particle swarm gravity search optimization algorithm (CPSOGSA), which controls the speed and excitation of a DG. In this method, firstly, establish the nonlinear mathematical model of the DG and then design the nonlinear $H_2/H_{\infty}$ robust controller based on this. The direct feedback linearization and the $H_2/H_{\infty}$ robust control theory are combined and applied. Based on the design of the integrated controller for DG speed and excitation, the system's performance requirements are transformed into a standard robust $H_2/H_{\infty}$ control problem. The parameters of the proposed solution controller are optimized by using the proposed CPSOGSA. The introduction of CPSOGSA completes the design of an intelligent nonlinear $H_2/H_{\infty}$ robust controller for DG. The simulation is implemented in MATLAB/Simulink, and the results are compared with the PID control method. The obtained results prove that the proposed method can effectively improve the dynamic accuracy of the system and the ability to suppress disturbances and improve the stability of the system.
Keywords: 
Subject: Engineering  -   Energy and Fuel Technology

1. Introduction

The diesel generator (DG) is a typical energy and power equipment widely used in the human industrial system [1]. In particular, In areas with weak grids and high cost of long-distance power transmission, and some particular power supply scenarios (such as military emergency power supply and disaster relief power supply), traditional large power grids cannot provide the adequate and timely power supply [2,3,4]. In this case, DGs and their systems can work well.
The system consisting of DGs and the various types of loads connected can be considered a micro-grid (MG) [5]. The MG is an effective way to accelerate renewable energy development and solve the shortcomings of large grids [6,7]. The complementation of photovoltaic panels, wind turbines and DGs in MG is one of the development trends of power generation and distribution in the future power system [8]. With the continuous improvement and perfection of DG technology, more and more people will also benefit from it, especially far away from the large grid. Therefore, the DG research work has a progressive significance for energy supply of human society.
In some MGs, the DG is usually configured as the primary power source to maintain the safe and stable operation of the MG [9,10]. For most MGs, DGs account for a large proportion of their capacity, and their control performance dramatically impacts the MG’s stability [11]. Therefore, the research on the control of the DG is fundamental. However, from the current research status, the comprehensive disturbance characteristics of voltage and frequency of distributed MG are rarely considered in the control research process of conventional DGs [12,13].
The speed control system composed of the diesel engine (DE) and the governor determines the frequency of the synchronous generator, and the frequency stability of the MG system depends on the characteristics of the DE governor system [14,15]. When the load in the MG system changes, the power flow of the system and the output power of each generator will also change suddenly, which will destroy the power balance between the generator and the prime mover. Unbalanced torque occurs, and thus relative motion occurs between the rotors of the generators [16]. The frequency fluctuation of the MG system not only affects users but also deteriorates the operation of the entire system. Therefore, frequency adjustment of the prime mover is necessary [17,18]. Most of the work focuses on optimizing the speed controller. Valenzuela et al. [19] proposed a conventional PI speed controller with a reduced bandwidth to suppress any excitation at the resonant frequency. This slow dynamic performance is also undesirable. Mahmoud et al. [20] analyzed the optimal tuning method of PI/PID controller to improve system performance. The main limitation of this technique is that it is ineffective when the inertia of the driving machine is comparable to that of the loading device [21]. In addition, speed controller optimization using advanced control strategies such as sliding mode controller [22], model predictive control [23], fuzzy logic [24,25], neural networks [26] and optimization algorithm [27]. These proposed solutions show improved dynamic properties and robustness to parameter changes, but these works do not consider the effects of the excitation regulation process. In some extreme cases, these methods may not apply to DG.
We hope that the mechanical power of the prime mover is balanced with the electromagnetic power of the generator. Otherwise, it will cause the rotor of the generator to sway and also cause the electromagnetic transient process and the dynamic process of excitation regulation caused by the voltage and current changes at the generator terminal [28,29]. Since the electrical equipment in the DG system is a mostly inductive load, the load current has a demagnetizing effect on the synchronous generator, and the change of the current size and power factor will cause the change of the terminal voltage of the generator, so the synchronous generator must be equipped with excitation control device [30]. At the same time, in order to improve the reliability of the power supply and generate electricity economically and reasonably, some systems will have several generator sets running in parallel according to different working conditions. In order to make the parallel system run stably, the reactive power between the generators must be reasonably assigned, and this task is also regulated by the excitation control [31,32]. In the study of the excitation control problem, Patel et al. [33] proposed an alternative method that follows the principle of command filtered backstepping to control the terminal voltage and stabilize the DG through the excitation system. In addition, many researchers have proposed to introduce other advanced control techniques into excitation control, such as: decentralized improved cooperative excitation controller [34], excitation controller based on linear matrix inequality (LMI) [35], robust control [36,37], Model Predictive Control [38] for better performance. However, some controllers in these methods are developed based on the linear approximation and bounded operating range of the system, so their performance may degrade significantly when the system is subjected to large disturbances [39].
The dynamic process of DGs in the system includes both electromagnetic dynamic process and dynamic mechanical process, and the two are related to each other [40]. The comprehensive control of speed and excitation can be used as an effective measure to improve the transient stability of the MG system [41]. However, most of the existing DG strategies only consider one of these methods while ignoring the dual control functions of voltage regulation and prime mover speed regulation. In the above studies, stable islanded MGs based on nonlinear control techniques for speed regulation and excitation robust controllers for DGs have been studied [42]. However, the speed regulation and robust excitation controller they designed is not intelligent; that is, the user manually selects the parameters of the robust controller, and no optimization is used to optimize the adjustable parameters.
This paper proposes a robust control method for DG speed and excitation based on the intelligent CPSOGSA, which is used in island MG with multiple load types. The CPSOGSA optimizes the parameters of the robust controller, and the CPSOGSA is introduced for the robust control of DG speed and excitation. Simulation results show that the method effectively suppressed oscillations under severe disturbances and uncertain conditions. The main innovations of this paper can be divided into the following categories:
-
Based on the theory of direct feedback linearization, a nonlinear speed and excitation robust controller of a DG is designed;
-
Applying the intelligent CPSOGSA to optimize the dynamic output function parameters of the robust controller, thus introducing the CPSOGSA for this problem solving multi-objective mixed H 2 / H ∞ robust controller
-
The proposed method effectively suppresses frequency and voltage oscillations under various load disturbances and uncertainties;
-
Excellent damping efficiency, especially low overshoot, steady-state error, and settling time.
Preprints 74838 g001
Figure 1. Widely used energy power device —- diesel generator.
Figure 1. Widely used energy power device —- diesel generator.
Preprints 74838 g001
This paper is organized as follows: In Section 2, the isolated MG structure supplied by DG studied in this paper is introduced, and the dynamic mathematical model of the DG is established in detail, respectively. Then, in Section 3, a speed and excitation robust controller is designed for the MG system’s primary power source-DG. Section 4 presents the CPSOGSA and its application to robust controller optimization problems. Simulation studies are conducted in Section 5 to demonstrate the advantages of the new method. Finally, Section 6 concludes this paper.

2. Modeling of diesel generator and its loads

This section briefly introduces the nonlinear mathematical model of DG, which mainly consists of two parts: speed regulation and excitation system of DG.

2.1. Modeling of speed control part

As shown in Figure 2, the diesel in the DG is a kind of power machine, which can convert the heat energy in the diesel fuel into the mechanical energy required by the generator [43]. Since the main driving output torque M 1 of the diesel is a pulsating torque [44], it can be decomposed into a mathematical expression in the form of a Fourier series, which can be described as:
M 1 = M p + ∑ f = 1 ∞ M f 0 s i n ( f ω 0 t + φ f )
where M 1 is the DE pulsating torque; M p is the average torque of one cycle; M f 0 is the fth harmonic torque amplitude; ω 0 is the harmonic torque angular velocity; φ f is the fth harmonic torque initial phase angle.
As shown in Figure 3, a flywheel with a significant moment of inertia is installed on the main shaft of the diesel to keep the output torque of the diesel within the allowable range , which can make the flywheel rotation unevenness between 0 . 0033 0 . 0067 [45]. During operation, the enormous flywheel torque ensures that the output torque of the diesel is uniform. Therefore, the output torque’s unevenness can be ignored in the diesel’s regular operation. In other words, the first constant in Eq. (1) can be retained, and the rest of the harmonic torque composed of amplitude, phase, and frequency can be ignored, and Eq. (2) can be derived
M 1 = M p
The driving torque and rotating speed characteristics of DE are smooth curves, approximating several linear segments [46]. Divide the driving torque and rotating speed characteristics of the diesel into m sections; then each section can be written as
M 1 j = k j n d + b j
where n d is the DE rotational speed; the constant value of k j and b j is determined by the positions of different segments ( j = 1 , 2 , ⋯ , m ).
It can be seen from the adjustment characteristics of the diesel that the relationship between the main driving torque M 1 of the DE and the output throttle displacement L of the actuator presents a specific linear relationship [48]. At the same time, the driving torque of the diesel has a certain lag, then the adjustment characteristic of the diesel can be expressed as
M 1 = M 1 e L e − L 0 ( L ( t − T d ) − L 0 )
where M 1 e is the torque at rated oil supply; L e is the rated stroke of the DE actuator; L 0 is the no-load stroke of the DE actuator; T d is the DE torque lag time.
Through the above analysis and derivation, the rotating speed characteristic and adjustment characteristic of the integrated the DE can be obtained as the expression of the driving torque M 1 :
M 1 = k j n d + b j + M 1 e L e − L 0 ( L ( t − T d ) − L 0 )
When the DE is running at the rated speed, the segment described in Eq. (5) can be described as
M 1 = k 1 n d + b 1 + M 1 e L e − L 0 ( L ( t − T d ) − L 0 )
Define d 1 = b 1 − ( M 1 e L 0 ) / ( L e − L 0 ) , then Eq. (6) can be written as
M 1 = k 1 n d + d 1 + M 1 e L e − L 0 L ( t − T d )
The rotational speed, the number of cylinders, and the number of strokes of the diesel determine the torque lag time T d of the diesel [47]. Generally, the following equation can be used to estimate the value range
15 n d < T d < 15 n d + 60 τ n d l s
where τ is the DE stroke coefficient; l s is the number of DE cylinders.
The diesel parameters studied in this paper are: the value of rated speed n d = 1500 r / m i n , the number of cylinders is 16, and the stroke coefficient τ = 2 . According to Eq. (8), the value range of T d can be calculated as 0 . 01 s < T d < 0 . 015 . The speed transition time of the diesel is 2 seconds, and T d is very small compared with it and can be ignored. Therefore, Eq. (7) can become
M 1 = k 1 n d + d 1 + M 1 e L e − L 0 L
where L is the throttle actuator displacement.
The relationship between the rotational speed of the diesel n d and the angular velocity of the crank shaft ω g is
n d = 60 ω g 2 π
where ω g is the angular velocity of the crankshaft shaft.
Eq. (9) can be written as:
M 1 = 60 k 1 ω g 2 π + d 1 + M 1 e L e − L 0 L
The dynamic motion equation of the main shaft of the DG set can be expressed as
J ω ˙ g = M 1 − M 2 − M d
where J is the DE rotational moment of inertia; ω g is the DE spindle angular velocity; M 1 is the DE output shaft torque; M 2 is the DE load torque; and M d is the generator damping torque.
The damping torque M d is generated by the damping winding of the synchronous generator, and its characteristic is that it is proportional to the electrical angular speed of the generator rotor, which can be calculated by Eq. (13).
M d = D p ω g
where D is the damping factor; p is the number of synchronous generator pole pairs.
Substituting Eq. (11) and Eq. (13) into Eq. (12) get
J ω ˙ g + D p ω g = 60 k 1 ω g 2 π + d 1 + M 1 e L e − L 0 L − M 2
General variables are marked per unit value in the research and analysis of electric power systems. In order to unify the form, Eq. (14) can be standardized as per unit value. This paper converts the mechanical angular speed into electrical angular speed and then standardizes the power, torque, and angular speed to study the speed response of the diesel. This paper defines the rated apparent power S B of the DG as the reference value of power and defines ω 0 = 100 π as the reference value of the angular speed. Therefore, in standardized form, Eq. (14) can be written as
J ω g 0 2 S B ω ˙ = 60 k 1 ω g 0 2 − 2 π D p ω g 0 2 2 π S B ω + d 1 ω g 0 S B + a ω g 0 S B L − M 2
where ω g 0 is 100 π .
Ignoring the no-load torque and the winding loss, M 2 is equal to the output torque of the synchronous generator. In the stability analysis or control system design, for the convenience of calculation, or it is considered that the angular speed ω does not change much during the transient process, approximately equal to the synchronous speed, that is, ω ≈ 1 . Therefore, Eq. (15) can be derived as
J ω g 0 2 S B ω ˙ = 60 k 1 ω g 0 2 − 2 π D p ω g 0 2 2 π S B ω + d 1 ω g 0 S B + a ω g 0 S B L − P e
The output power P e of the salient-pole synchronous generator can be described as
P e = E q ′ U X d ′ sin δ + U 2 2 X d ′ − X q X d ′ X q s i n ( 2 δ )
where E q ′ is the q-axis transient potential; U is the DG terminal voltage; X is the generator winding reactance.
The relationship between generator rotor angle δ and electrical angular velocity ω be described as
δ ˙ = ( ω − 1 ) ω 0
where ω g 0 is the diesel generator idle angular speed.
From Eq. (16), (17) and (18), the mathematical model of the electrical transient process of DGs is
δ ˙ = ( ω − 1 ) ω 0 ω ˙ = T b T a ω + 1 T a c 1 + c 2 T a L − 1 T a E q ′ U X d ′ sin δ − 1 T a U 2 2 X d ′ − X q X d ′ X q sin ( 2 δ )
in the above, the definitions of T a , T b , c 1 , c 2 , and a are as follows
T a = J ω g 0 2 S B T b = 60 k 1 ω g 0 2 − 2 π D p ω g 0 2 2 π S B c 1 = d 1 ω g 0 S B c 2 = a ω g 0 S B a = M 1 e L e − L 0

2.2. Modeling of excitation control part

During the operation of DGs, excitation control is the most basic and indispensable. The synchronous generator is the control object of the excitation control system [48]. Studying the dynamic characteristics of the excitation system is inseparable from the analysis of the dynamic characteristics of the synchronous generator. The mathematical model of the electromagnetic transient process of the DG includes the stator voltage balance equation of the generator and the transient electromagnetic equation of each winding of the rotor [49]. The standard form of the transient electromagnetic equation of the synchronous generator can be described as
E ˙ q ′ = 1 T d 0 E f d − 1 T d 0 E q ′ − X d − X d ′ T d 0 E ˙ q ′ ′ = 1 T d 0 X d ′ ′ − X l X d ′ − X l E f d + 1 T d 0 ′ ′ − X d ′ ′ − X l X d ′ − X 1 1 T d 0 E q ′ − 1 T d 0 ′ ′ E q ′ ′ − X d ′ − X d ′ ′ T d 0 ′ ′ + X d ′ ′ − X l X d ′ − X l X d − X d ′ T d 0 I d E ˙ d ′ ′ = − 1 T q 0 ′ ′ E d ′ ′ + X q − X q ′ ′ T q 0 ′ ′ I q U d = − R I d + ω X q ′ ′ I q + ω E d ′ ′ U q = − R I q − ω X d ′ ′ I d + ω E q ′ ′ U = U d 2 + U q 2
where U is the stator winding terminal voltage; U d and U q are the d-axis and q-axis components of the stator winding terminal voltage; R is the stator winding resistance; X is the winding reactance; I is the winding current; T is the winding time constant; E d ′ ′ is the d-axis subtransitory potential; E q ′ is the q-axis transient potential; E q ′ ′ is the q-axis subtransitory potential; E d f is the excitation winding voltage.
Combining Eq. (19) and Eq. (20), a nonlinear mathematical model of the DG is obtained. This model reflects the interaction and mutual influence of speed and voltage and more accurately describes the change law of speed and voltage.

3. Design of nonliear H 2 / H ∞ synthetic controller

3.1. Multi-objective state-feedback theory

The control system shown in Figure 4 defines the closed-loop transfer function T ∞ ( s ) from disturbance w to H ∞ control performance output vector z ∞ , and the closed-loop transfer function T 2 ( s ) from disturbance w to H 2 control performance output vector z 2 . The control goal is to design a state feedback control law u = K x to stabilize the closed-loop system progressively. In addition, it needs to meet:
-
Keep the RMS gain ( H ∞ norm) of T ∞ ( s ) below a certain specified value γ 0 > 0 ;
-
Maintain the H 2 norm (LQG cost) of T 2 ( s ) below a certain specified value υ 0 > 0 ;
-
Minimized form of H 2 / H ∞ trade-off standard α T 2 ( s ) + β T ∞ ( s ) ;
-
Place the closed-loop pole in the designated area of the open left half-plane.
The mixed H 2 / H ∞ standard considers both the interference suppression aspect (RMS gain from w to z ∞ ) and the LQG aspect ( H 2 norm from w to z 2 ). In addition, the closed-loop pole can be forced into a specific part of the stable half-plane to obtain a well-damped transient response. Such control problems are called H 2 / H ∞ control design problems [49,50].
The linear system shown in Figure (Figure 4) can be expressed as:
x ˙ = A x + B 1 w + B 2 u z ∞ = C 1 x + D 11 w + D 12 u z 2 = C 2 x + D 21 w + D 22 u
where the first term in Eq. (21) is a dynamic linear state-space differential equation, and the second and third terms are its dynamic performance evaluation signals.
The closed-loop system formed after adding the controller K x can be described in the form of state-space as:
x ˙ = A c l x + B 1 w z ∞ = C c l 1 x + D 11 w z 2 = C c l 2 x + D 21 w
where A c l = A + B 2 K ; C c l 1 = C 1 + D 12 K ; C c l 2 = C 2 + D 22 K .
Taken separately, the two design goals have the following LMI formulation:
H ∞ performance: the closed-loop RMS gain from w to z ∞ does not exceed γ if and only if there exists a symmetric matrix X ∞ such that
A c l X ∞ + X ∞ A c l T B 1 X ∞ C c l 1 T B 1 T − γ I D 11 T C c l 1 X ∞ D 11 − γ I < 0 X ∞ > 0
H 2 performance: the closed-loop H 2 norm of T 2 ( s ) does not exceed υ if there exist two symmetric matrices X 2 and Q such that
A c l X 2 + X 2 A c l T B 1 B 1 T − I < 0 Q C c l 2 X 2 X 2 C c l 2 T X 2 > 0 T r a c e ( Q ) < υ 2
The mixed H 2 / H ∞ performance: The pole of the closed-loop system is located in the left half-open complex plane, and the performance index α ∥ T ( s ) ∞ ∥ ∞ 2 + β ∥ T 2 ( s ) ∥ 2 2 is minimized.
To solve the mixed objective, the two sets of conditions add up to a non-convex optimization problem with variables Q , K , X ∞ , and X 2 . In order to facilitate the processing of this problem in the LMI framework, we seek a single Lyapunov matrix X : = X ∞ = X 2 to force the solution of the two goals. With the change of variable Y : = K X , this leads to the multi-objective state feedback synthesis problem, which the following sub-optimal LMI formula can express:
Minimize α γ 2 + β T r a c e ( Q ) over Y , X , Q , and γ 2 satisfying:
A X + X A T + B 2 Y + Y T B 2 T B 1 X C 1 T + Y T D 12 T B 1 T − γ I D 11 T C 1 X + D 12 Y D 11 − γ I < 0 Q C 2 X + D 22 Y X C 2 T + Y T D 22 T X < 0 T r a c e ( Q ) < υ 0 2 γ 0 < γ 0 2
Denoting the optimal solution by ( X * , Y * , Q * , γ * ), the corresponding state-feedback gain is given by:
K * = Y * ( X * ) − 1
this gain guarantees the worst-case performances:
∥ T ( s ) ∞ ∥ ∞ ≤ γ * ∥ T ( s ) 2 ∥ 2 ≤ T r a c e ( Q * )
The solution of the mixed H 2 / H ∞ controller is usually configured with α = 0 . 5 and β = 0 . 5 to obtain ([48]). The robust controller obtained by this method can improve and optimize the control performance of the related system.

3.2. Design of speed controller

The schematic diagram of the DG integrated control system based on the nonlinear H 2 / H ∞ integrated controller is shown in Figure 5. The DG integrated control system comprises a diesel, generator, nonlinear H 2 / H ∞ integrated controller, actuator, fuel supply mechanism, and exciter. The nonlinear H 2 / H ∞ integrated controller consists of two parts, one part is the nonlinear H 2 / H ∞ speed controller, and the other is the nonlinear H 2 / H ∞ voltage controller. The nonlinear H 2 / H ∞ integrated controller should consider the coupling effect of speed and voltage, comprehensively control the speed and voltage, and control the mutual influence between the two to a minimum. Further, improve the stability of the frequency and voltage of the independent MG system.
The differential equation expression of the actuator is:
L ˙ = − 1 T 1 L + K 1 T 1 u 1
where T 1 is the actuator time constant; K 1 is the actuator gain.
The expression of the differential equation of the exciter is
E ˙ f d = − 1 T 2 E f d + K 2 T 2 u 2
where T 2 is the exciter time constant; K 2 is the exciter gain.
Combining Eq. (19) and Eq. (28) can get the nonlinear mathematical model of the DG’s speed control system:
δ ˙ = ( ω − 1 ) ω 0 L ˙ = − 1 T 1 L + K 1 T 1 u 1 ω ˙ = T b T a ω + 1 T a c 1 + c 2 T a L − 1 T a E q ′ U X d ′ sin δ − 1 T a U 2 2 X d ′ − X q X d ′ X q sin ( 2 δ )
Eq. (30) has apparent nonlinear terms. In order to be able to apply the above mixed H 2 / H ∞ control theory, this paper uses the direct feedback linearization method to linearize the nonlinear mathematical model of the diesel generator speed system described in Eq. (30) to obtain its linear model and then obtain the corresponding nonlinear speed control law.
Three variables X 1 , X 2 and X 3 are defined in this paper, which can be expressed as:
X 1 = δ X 2 = ( ω − 1 ) ω 0 X 3 = T b T a ω + 1 T a c 1 + c 2 T a L − 1 T a E q ′ U X d ′ sin δ 1 T a U 2 2 X d ′ − X q X d ′ X q sin ( 2 δ )
According to the definitions of X 1 , X 2 and X 3 , the nonlinear differential equations described by Eq. (30) can be rewritten as:
X ˙ 1 = X 2 X ˙ 2 = ω 0 X 3 + d 1 W X ˙ 3 = T b T a X 3 + c 2 K 1 T a T 1 u 1 − c 2 T a T 1 L − E q ′ U ω 0 T a X d ′ cos δ ( ω − 1 ) − U 2 ω 0 X d ′ − X q T a X d ′ X d cos ( 2 δ ) ( ω − 1 )
where d 1 W is the disturbance signal set when the mixed H 2 / H ∞ control method is adopted, including equivalent disturbances caused by disturbance torque and modelling errors.
For speed control, this paper defines virtual control variables V as:
V = c 2 K 1 T a T 1 u 1 − c 2 T a T 1 L − E q ′ U ω 0 T a X d ′ cos δ ( ω − 1 ) − U 2 ω 0 ( X d ′ − X q ) T a X d ′ X q cos ( 2 δ ) ( ω − 1 )
By introducing virtual control variables V, Eq. (30) is described by linear state-space differential equations as:
X ˙ = A s X + B 1 s W + B 2 s V
where X, A s , B 1 s and B 2 s are defined as follows:
X = X 1 X 2 X 3 ; A s = 0 1 0 0 0 ω 0 0 0 T b T a ; B 1 s = 0 d 1 0 ; B 2 s = 0 0 1 .
Add the dynamic performance evaluation signal described by Eq. (35) to this system.
Z ∞ s = C 1 s X + D 11 s W + D 12 s V Z 2 s = C 2 s X + D 21 s W + D 22 s V
where
C 1 s = q 11 0 0 0 q 12 0 0 0 q 13 ; D 12 s = 0 0 r 1 ; C 2 s = q 21 0 0 0 q 22 0 0 0 q 23 ; D 22 s = 0 0 r 2 ; D 11 s = D 21 s = 0 0 0 .
C 1 s , C 2 s , D 11 s , D 12 s , D 21 s , D 22 s are weighting matrices, q i j > 0 ( i = 1 , 2 ; j = 1 , 2 , 3 ) and r i > 0 ( i = 1 , 2 ) are weighting coefficients. A controller that meets the optimal performance requirements can be obtained by selecting different weighting coefficients. The performance requirements include independent power system stability, frequency adjustment accuracy, and low energy consumption of the speed control system.
From Eqs. (34) and (35), the augmented controlled object based on the mixed H 2 / H ∞ control theory can be obtained as
P s = A s B 1 s B 2 s C 1 s D 11 s D 12 s C 2 s D 21 s D 22 s
Bring the augmented controlled object P s into the framework shown in Figure 4 and meet the design requirements of the multi-objective H 2 / H ∞ state-feedback controller at the same time, and then the H 2 / H ∞ state feedback controller can be obtained as:
V = F s X = f 1 s f 2 s f 3 s X 1 X 2 X 3 = f 1 s X 1 + f 2 s X 2 + f 3 s X 3
From Eq. (33) and Eq. (37), the speed control law u 1 can be solved as:
u 1 = 1 K 1 L + T a T 1 c 2 K 1 F s X + E q ′ U ω 0 T 1 c 2 K 1 X d ′ cos δ ( ω − 1 ) + U 2 ω 0 T 1 ( X d ′ − X q ) c 2 K 1 X d ′ X q cos ( 2 δ ) ( ω − 1 )
Substituting X 1 , X 2 , and X 3 into Eq. (38), the DE nonlinear H 2 / H ∞ speed control law in the usable form shown in Eq. (39) can be obtained.
u 1 = 1 K 1 L + T a T 1 c 2 K 1 f 1 s δ + T a T 1 c 2 K 1 f 2 s ( ω − 1 ) ω 0 + T b T 1 c 2 K 1 f 3 s ω − T 1 c 2 K 1 E q ′ U X d ′ f 3 s sin δ − T 1 c 2 K 1 U 2 2 X d ′ − X q X d ′ X q f 3 s sin ( 2 δ ) + T 1 c 2 K 1 f 3 s c 1 + T 1 K 1 f 3 s L + E q ′ U ω 0 T 1 c 2 K 1 X d ′ cos δ ( ω − 1 ) + U 2 ω 0 T 1 ( X d ′ − X q ) c 2 K 1 X d ′ X q cos ( 2 δ ) ( ω − 1 )

3.3. Design of excitation control controller

Combining Eq. (29) and Eq. (20) of the first three terms can get the nonlinear mathematical model of the synchronous generator voltage regulation system, which is shown in Eq. (40).
E ˙ f d = − 1 T 2 E f d + K 2 T 2 u 2 E ˙ q ′ = 1 T d 0 E f d − 1 T d 0 E q ′ − X d − X d ′ T d I d δ ˙ = ( ω − 1 ) ω 0 ω ˙ = T b T a ω 0 ω + 1 T a ω 0 c 1 + c 2 T a ω 0 L − 1 T a ω 0 E q ′ U X d ′ sin δ − 1 T a ω 0 U 2 2 X d ′ − X q X d ′ X q sin ( 2 δ )
Since the damper winding of the synchronous generator has a weak influence on the excitation control, the fourth and fifth terms of Eq. (20) can be ignored when designing the voltage controller. Regarding the electromagnetic power P e as an external disturbance, Eq. (40) becomes
E ˙ f d = − 1 T 2 E f d + K 2 T 2 u 2 E ˙ q ′ = 1 T d 0 E f d − 1 T d 0 E q ′ − X d − X d ′ T d 0 I d δ ˙ = ω − 1 ω ˙ = T b T a ω 0 ω + 1 T a ω 0 c 1 + c 2 T a ω 0 L − 1 T a ω 0 P e
Since E q ′ is not easy to measure, it is not conducive to designing a state feedback controller. Therefore, the voltage error Δ U is selected as the state variable, so this paper converts E q ′ in Eq. (41) into Δ U by a constant c 3 . According to the relationship between variable data:
U = E q ′ − c 3 δ
Through the relationship between U and the voltage U 0 at the stator winding end of the generator, it can be derived:
E q ′ = U 0 + Δ U + c 3 δ
According to the relationship described in Eq. (43), the state-space differential equation expressed by Eq. (41) can be rewritten as
E ˙ f d = − 1 T 2 E f d + K 2 T 2 u 2 Δ U ˙ = 1 T d 0 E f d − 1 T d 0 Δ U − 1 T d 0 c 3 δ − c 3 ω + ( c 3 − 1 T d 0 ) − X d − X d ′ T d 0 I d δ ˙ = ω − 1 ω ˙ = T b T a ω 0 ω + 1 T a ω 0 c 1 + c 2 T a ω 0 L − 1 T a ω 0 P e
Eq. (44) is written as a linear state-space differential equation in the form
X ˙ ′ = A e X ′ + B 1 e W ′ + B 2 e u 2
where
X ′ ( t ) = E f d Δ U δ ω ; W ′ = I d L P e 1 ; B 2 e = K 2 T 2 0 0 0 ; A e = − 1 T 2 0 0 0 1 T d 0 − 1 T d 0 − c 3 T d 0 − c 3 0 0 0 1 0 0 0 T b T a ω 0 ; B 1 e = 0 0 0 0 X d − X d ′ 0 0 c 3 − 1 T d 0 − T d 0 0 0 0 − 1 0 c 2 T a ω 0 − 1 T a ω 0 c 1 T a ω 0 .
Similarly, the dynamic performance evaluation signal of the system described in Eq. (45) is defined as
Z ∞ e = C 1 e X ′ + D 11 e W ′ + D 12 e u 2 Z 2 e = C 2 e X ′ + D 21 e W ′ + D 22 e u 2
where
C 1 e = q 14 0 0 0 0 q 15 0 0 0 0 q 16 0 0 0 0 q 17 ; D 12 e = r 3 r 4 r 5 r 6 ; C 2 e = q 24 0 0 0 0 q 25 0 0 0 0 q 26 0 0 0 0 q 27 ; D 22 e = r 7 r 8 r 9 r 10 ; D 11 e = D 21 e = 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 .
C 1 e , C 2 e , D 11 e , D 12 e , D 21 e , and D 22 e are weighting matrices, q i j > 0 ( i = 1 , 2 ; j = 4 , 5 , 6 , 7 ) and r i > 0 ( i = 3 , 4 , ⋯ , 10 ) are weighting coefficients. The voltage controller that meets the optimal performance is solved by combining different weighting coefficients. The performance includes system stability, voltage regulation accuracy and low energy loss of the excitation system.
From Eqs. (45) and (46), the augmented controlled object P e used to solve the mixed H 2 / H ∞ robust controller can be obtained, which can be expressed as:
P e = A e B 1 e B 2 e C 1 e D 11 e D 12 e C 2 e D 21 e D 22 e
Similarly, the augmented controlled object P e is brought into the solution framework shown in Figure 4, and the voltage H 2 / H ∞ state feedback controller of the diesel generator is obtained to satisfy the LMI. The nonlinear H 2 / H ∞ voltage control law of the DG is
u 2 = F e X ′ = f 1 e f 2 e f 3 e f 4 e E f d Δ U δ ω = f 1 e E f d + f 2 e Δ U + f 3 e δ + f 4 e ω
Combining the Eq. (39) and Eq. (48) derived above, the diesel generator’s nonlinear robust H 2 / H ∞ integrated controller is obtained.
u 1 = 1 K 1 L + T a T 1 c 2 K 1 f 1 s δ + T a T 1 c 2 K 1 f 2 s ( ω − 1 ) ω 0 + T b T 1 c 2 K 1 f 3 s ω − T 1 c 2 K 1 E q ′ U X d ′ f 3 s sin δ − T 1 c 2 K 1 U 2 2 X d ′ − X q X d ′ X q f 3 s sin ( 2 δ ) + T 1 c 2 K 1 f 3 s c 1 + T 1 K 1 f 3 s L + E q ′ U ω 0 T 1 c 2 K 1 X d ′ cos δ ( ω − 1 ) + U 2 ω 0 T 1 ( X d ′ − X q ) c 2 K 1 X d ′ X q cos ( 2 δ ) ( ω − 1 ) u 2 = f 1 e E f d + f 2 e Δ U + f 3 e δ + f 4 e ω
It can be found from Eq. (49) that the designed nonlinear control law considers the coupling effect of the DG’s speed and voltage and comprehensively controls the two, which can improve the dynamic accuracy of the DG’s speed and voltage. Further, improve the stability of the MG system connected to the DG.

4. Artificial hybrid PSOGSA with chaotic maps approach and its application to multi-objective H 2 / H ∞ robust problem

4.1. The proposed CPSOGSA algorithm

The artificial intelligence CPSOGSA algorithm is a hybrid particle swarm optimization and gravitational search algorithm combined with chaotic mapping [51]. Besides, the CPSOGSA is superior and more robust than other methods (such as MSA, GWO, WOA and so on) [52]. Therefore, this paper also adopts CPSOGSA to optimize the robust controller. This subsection provides the necessary description of the algorithm.

4.1.1. Particle swarm optimization

The PSO consists of three crucial operators, which are the inertia weight vector w p , the personal particle best (pbest), and the global particle best (gbest). The inertia weight gives diversification (exploration) capability, and <pbest, gbest> provides intensification (exploitation) power to PSO, respectively [53]. The velocity v i ( k ) and position p i ( k ) of each particle in the PSO algorithm are updated as follows
v i ( k + 1 ) = w p v i ( k ) + c 1 × rand × pbest i − p i ( k ) + c 2 × rand × gbest i − p i ( k ) p i ( k + 1 ) = p i ( k ) + v i ( k + 1 )
where c 1 and c 2 are the acceleration coefficient; rand is a uniform random variable between O and 1.

4.1.2. Gravitational search algorithm

GSA is an optimization algorithm inspired by Newton’s theories of gravity and motion. The operation steps of GSA are briefly summarized as follows [54].
Positions of N agents constituting the initialization population P i in GSA are listed in Eq. (51). The best and worst fitness values are computed for each iteration. Best and worst fitness values are defined as in Eq. (52) for the problem.
P i = p 1 1 , … , p i d , … , p i n , i = 1 , 2 , … , N
where p i d is the ith agent of the dth dimensions.
best ( k ) = min fit i ( k ) i ∈ { 1 , 2 , … , N } worst ( k ) = max fit i ( k ) i ∈ { 1 , 2 , … , N }
where fit i ( k ) denotes the fitness value of the ith individual.
The gravitational constant G ( k ) for each iteration and inertial masses are calculated as follows
G ( k ) = G 0 e − a k K M a i = M p i = M i i = M i i = 1 , 2 , 3 , … , N m i ( k ) = fit i ( k ) − worst ( k ) best ( k ) − worst ( k ) M i ( k ) = m i ( k ) ∑ j = 1 N m j ( k )
where G 0 is the initial value of gravitational constant; k and K are the index and the total number of iterations; M a i is the active mass at kth iteration for the ith agent; M p i is the passive mass at kth iteration for the ith agent; M i i is the the inertial mass at kth iteration for the ith agent; M i is the mass at kth iteration for the ith agent.
The force F i j d ( k ) acting on the ith mass from the jth mass, the total force F i d ( k ) , and the acceleration value σ i d ( k ) at iteration k are calculated as follows
F i j d ( k ) = G ( k ) M p i ( k ) × M a j ( k ) R i j ( k ) + ε p j d ( k ) − p i d ( k ) F i d ( k ) = ∑ j ∈ ( k ) best , j ≠ i rand j F i j d ( k ) σ i d ( k ) = F i d ( k ) M i i ( k )
where R i j is the euclidean distance between the ith mass and the jth mass.
The velocity V i d ( k ) and position p i d ( k ) of the ith agent at the dth dimension of the next iteration are updated as follows
V i d ( k + 1 ) = rand × V i d ( k ) + σ i d ( k ) p i d ( k + 1 ) = p i d ( k ) + V i d ( k + 1 )

4.1.3. Modified hybrid particle swarm optimization and gravitational search algorithm with chaotic maps

The hybrid PSOGSA combines the advantages of PSO and GSA algorithms. The algorithm can be explained a follows
V i ( k + 1 ) = w p × V i ( k ) + c 1 ′ × rand × σ i ( k ) + c 2 ′ × rand × gbest − p i ( k ) p i ( k + 1 ) = p i ( k ) + V i ( k + 1 )
When the chaotic map is used in the optimization algorithm, the optimization algorithm can quickly converge to the optimal solution and get rid of the optimal local solution [55]. Therefore, the one-dimensional and irreversible chaotic mapping method with this advantage is applied to the PSOGSA optimization algorithm so that the performance of PSOGSA can be further improved. The chaotic map equation gives these characteristics of the chaotic map. In [56], ten chaotic mapping methods are given to improve the performance of the hybrid PSOGSA algorithm, and the change curve of the chaotic map with the number of iterations is shown in Figure 6. From the figure, it can be found that there is no random value in any chaotic map.
In the proposed CPSOGSA algorithm, the chaotic map method is used to improve the local search ability of GSA. Eqs. (54) calculates the total force, while a random number between 0 and 1 is used as a weight. In other words, this parameter will impact the local search ability of the algorithm. If this situation is considered, using chaotic map methods instead of the random number could increase the convergence ability of the PSOGSA algorithm in an optimization process. Although each chaotic map follows the order in Table, Eq. (57) is applied instead of using a random parameter for calculating the total force in Eqs. (54). The application of chaotic map methods to the total force value is shown in Eq. (57). After the total force value is calculated, the acceleration value is determined using Eqs. (53), while Eqs. (56) updates the velocities and positions of all agents in the population.
F i d ( k ) = ∑ j ∈ k best , j ≠ i C ( k ) F i j d ( k )
where C ( k ) is the chaotic sequence constant for the kth iteration.

4.2. Applying CPSOGSA to multi-objective robust H 2 / H ∞ problem

In subsection 3.2, the dynamic performance evaluation function and its weighting matrix for solving the robust controller of DG speed are proposed. The value of the weighting coefficient in these weighting matrices dramatically influences the performance of the speed controller. Therefore, These parameters need to be sufficient, and there are ten weighting coefficients for solving the speed robust controller, including the values of q i j > 0 ( i = 1 , 2 ; j = 1 , 2 , 3 ) , r i ( i = 1 , 2 ) . This paper uses the CPSOGSA algorithm to optimize and adjust these parameters. In optimizing the speed controller, the objective optimization function of CPSOGSA is O F 1 . The function described by Eq. (58) is used to calculate the fitness value passed in the optimization process, aiming to minimize the absolute value of the change in the absolute value of the DG speed during this period.
O F 1 = ∫ | Δ ω | 2 d t
where Δ ω is the speed deviation of DG.
Similarly, CPSOGSA is used to adjust the dynamic performance evaluation function of the DG excitation controller proposed in subsection 3.3 and the weighting coefficients in the weighting matrix. For the solution of the excitation controller, the weighting coefficients include q i j ( i = 1 , 2 ; j = 4 , 5 , 6 , 7 ) , r i ( i = 3 , 4 , ⋯ , 10 ) . In the optimization process, the objective optimization function of CPSOGSA is O F 2 . The function described by Eq. (59) is used to calculate the fitness value of the excitation controller during the optimization process, aiming to minimize the absolute value of the DG voltage in time.
O F 2 = ∫ | Δ U | 2 d t
where Δ U is the voltage deviation of DG.
In conclusion, these parameters need to be adequately tuned. The number of parameters to be adjusted is 16. These parameters are optimally adjusted using the CPSOGSA algorithm, whose overall optimal objective function is considered to be Eq. (60) as the weighted sum of O F 1 and O F 2 given by Eqs. (58) and (58). Therefore, the optimization objective can be described as
O F = m i n O F 1 + O F 2

5. Numerical study

5.1. Simulation parameters

The MG system composed of DG is shown in Figure 7. Among them, the rated power of the DE is 1250kW, the rated speed is 1500r/min, the rated torque is 11.9kNm, and the moment of inertia is 71.82; while the rated voltage of the generator is 380V, the rated current is 2310A, the power factor is 0.8, and the rated frequency is 50Hz; in addition, there are static and dynamic loads in this MG. The static load is mainly composed of electric heaters and lighting equipment, which accounts for a small proportion of the total loads; the dynamic loads refers to PMSM and driving devices, such as washing machines, water pumps, and fans, which account for a large proportion of the total load. Some parameters are also used for simulation, as shown in Table 1.
The selection of the relevant coefficients in the weighting function is a difficult point in multi-objective H 2 / H ∞ control and must be selected through repeated trials. After each trial selection, use the LMI toolbox to find the state feedback coefficient, substitute it into the simulation model, and then conduct the characteristic test to obtain the best comprehensive performance index. Simulations are carried out in MATLAB/Simulink and its programming environment interface. The parameters generated by the CPSOGSA algorithm are brought into the weighting function, and the state feedback control matrix F s of the speed regulation part of the DG and the state feedback control matrix F e of the excitation control part are calculated by the LMI and sent to Simulink. Simulink then iteratively evaluates the performance of the DG based on the adjusted parameters. In general, the flowchart of Figure 8 can be thought of as an optimization process. The number of iterative optimizations in this paper is 100 times.
As shown in Figure 9, under the optimization objective described in Eq. (60), the fitness value (OF value) change curve in different algorithm iterations for 100 times. The optimization range of each parameter is [ 11 e − 3 ] . It is not difficult to find from the figure that the CPSOGSA algorithm only needs about ten iterations to complete the optimization. On the contrary, the traditional algorithms are insufficient in convergence and optimization efficiency. For example, the particle swarm algorithm PSO needs nearly 80 generations to converge, while the gravitational search algorithm falls into the local optimum at the beginning, and after introducing the chaotic sequence, GSA can avoid falling into the local optimum.
For the design of the speed control part of the nonlinear integrated controller based on the mixed H 2 / H ∞ control theory, after the optimization of the CPSOGSA optimization algorithm, the weighting matrixs in Eq. (35) are
C 1 s = C 2 s 0.4788 0 0 0 0.0015 0 0 0 0.1105 D 12 s = D 22 s 0 0 0.0011
Combining these matrices and using the Linear Matrix Inequality Toolbox in MATLAB, find the feedback coefficients in Eq. (37) as f 1 s = − 1 . 9188 , f 2 s = − 1 . 8738 , and f 3 s = 35 . 604 .
Similarly, for the weighting matrix in Eq. (46), These matrix are
C 1 e = C 2 e = 0.7817 0 0 0 0 3.824 × 10 3 0 0 0 0 0.0256 0 0 0 0 0.1270 D 12 e = D 22 e = 0.1038 0.1143 0.1043 0.1417
Using the LMI toolbox in Matlab, get the coefficients of state-feedback controller in Eq. (48): f 1 e = − 2 . 227 , f 2 e = − 7 . 516 × 10 3 , f 3 e − 8 . 328 × 10 − 4 and f 4 e = − 9 . 495 × 10 − 5 .

5.2. Simulation results

In MATLAB/SIMULINK, the simulation experiment of a diesel generator with the mixed H 2 / H ∞ robust integrated controller is established to complete the effect verification of the controller described by Eq. (49). The relevant simulation parameters are shown in Table 1. In the comparative simulation process, the diesel generator adopts the optimized PID parameters K p = 20 , K i = 0 . 02 , K d = 5 .
Firstly, the comparison simulation experiment of diesel generator no-load starting characteristics is carried out. When no load is connected, the diesel generator start-up process is controlled by the controller and PID controller proposed in this paper, respectively. The simulation results are shown in Figure 10 and Figure 11. It can be seen from the speed curve diagram in Figure 10: from 0 to the establishment of the speed of 1 p.u, the proposed controller is about 3s faster than the PID controller. From the voltage change curve in Figure 11, it can be seen that from 0 to 1 p.u of the machine terminal voltage, our controller is 10s faster than the PID controller and has better start-up performance.
Then the computer simulation of the designed system with sudden static loads is carried out. Figure 12 and Figure 13 show the dynamic characteristic curves of speed and voltage of the system after sudden static loads, and the two variables are per unit value. Among them, the blue curve represents the action result of the intelligent nonlinear H 2 / H ∞ integrated controller, and the red curve represents the action result of the conventional PID controller.
From the simulation results, the dynamic performance of the proposed controller is excellent. The dynamic regulation rate is minimal, the stabilization time is about 2 seconds, the dynamic voltage regulation rate is only about 0.05, and the stabilization time is 4 seconds. Then, when the conventional PID controller is applied, the dynamic regulation rate of the system is significant, and the stabilization time takes 5 seconds. The dynamic regulation rate of the system exceeds 0.15, and the stabilization time takes a long time. It can be seen through computer simulation that after using the proposed controller, the rate and voltage rate are both decreased, and the stabilization time is shortened.
Finally, a simulation is performed that introduces a simulation of a dynamic loads such as PMSM in the system. The dynamic loads greatly influences the grid voltage, especially when the grid is unloaded. The simulation runs for 55 seconds to connect to a PMSM with a size of 90 kW. The simulation results are shown in Figure 14 and Figure 15. From the situation of the speed change in Figure 14, when the controller proposed in this paper is used, the system shows very little oscillation, while when the PID controller is used, the number of speed oscillations of the system exceeds five times. Figure 15 shows the response process of the terminal voltage under this working condition, and the controller proposed in this paper also shows better performance.
In this paper, the intelligent nonlinear integrated controller effectively improves the dynamic accuracy of speed control and excitation control. The improvement of dynamic accuracy weakens the mutual influence and interaction between speed and voltage and solves the comprehensive control problem of speed and voltage. The method improves the stability of the MG system.

6. Conclusion

This paper first establishes a DG’s nonlinear dynamic model. Then, the DG’s speed and excitation controller are designed, respectively. The direct feedback linearization method and the multi-objective robust control theory are applied in the design process. Given the difficulty in determining the weighting parameters in the design process, this paper introduces the artificial intelligence CPSOGSA optimization algorithm to optimize the relevant weighting parameters that affect the controller’s performance. In order to verify the effectiveness of the proposed controller in improving the MG system supplied by DG, a MG model driven by a DG was built in Simulink. The relevant simulation results show that, compared with the traditional PID controller, the proposed controller can effectively improve the dynamic accuracy of the system and the ability to suppress disturbances and reduce the fluctuation of the MG system in the process of sudden load change and operating condition switching. The stability of the independent MG is improved.

Author Contributions

Conceptualization, Y.Z.; methodology, Y.Z. and B.X.; software, B.X.; validation, Y.Z. and B.X.; formal analysis, Y.Z.; investigation, Y.Z.; resources, Z.X.; data curation, Z.X. and J.Q.; writing—original draft preparation, Y.Z. and B.X.; writing—review and editing, Y.Z. and B.X.; visualization, J.Q.; supervision, Z.X.; project administration, Z.X. and J.Q.; funding acquisition, Z.X. and J.Q.; All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (No. 51869007 and 51979204)

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data sharing is not applicable to this article as no datasets were generated or analysed during the current study.

Acknowledgments

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

Sample Availability

Not applicable.

References

  1. Muresan C I, Birs I, Ionescu C, et al. A review of recent developments in autotuning methods for fractional-order controllers[J]. Fractal and Fractional, 2022, 6(1): 37.
  2. Belboul Z, Toual B, Kouzou A, et al. Multiobjective optimization of a hybrid PV/Wind/Battery/Diesel generator system integrated in microgrid: A case study in Djelfa, Algeria[J]. Energies, 2022, 15(10): 3579.
  3. Amiryar M E, Pullen K R. Assessment of the carbon and cost savings of a combined diesel generator, solar photovoltaic, and flywheel energy storage islanded grid system[J]. Energies, 2019, 12(17): 3356.
  4. Hemeida A M, Omer A S, Bahaa-Eldin A M, et al. Multi-objective multi-verse optimization of renewable energy sources-based micro-grid system: Real case[J]. Ain Shams Engineering Journal, 2022, 13(1): 101543.
  5. Yu W, Li S, Zhu Y, et al. Management and distribution strategies for dynamic power in a ship’s micro-grid system based on photovoltaic cell, diesel generator, and lithium battery[J]. Energies, 2019, 12(23): 4505.
  6. Hasankhani A, Hakimi S M. Stochastic energy management of smart microgrid with intermittent renewable energy resources in electricity market[J]. Energy, 2021, 219: 119668.
  7. Hakimi S M, Hasankhani A, Shafie-khah M, et al. Stochastic planning of a multi-microgrid considering integration of renewable energy resources and real-time electricity market[J]. Applied Energy, 2021, 298: 117215.
  8. Hu J, Shan Y, Guerrero J M, et al. Model predictive control of microgrids–An overview[J]. Renewable and Sustainable Energy Reviews, 2021, 136: 110422.
  9. Marqusee J, Becker W, Ericson S. Resilience and economics of microgrids with PV, battery storage, and networked diesel generators[J]. Advances in Applied Energy, 2021, 3: 100049.
  10. Bouchekara H R E H, Javaid M S, Shaaban Y A, et al. Decomposition based multiobjective evolutionary algorithm for PV/Wind/Diesel Hybrid Microgrid System design considering load uncertainty[J]. Energy Reports, 2021, 7: 52-69.
  11. Guo Y, Lei X, Wang Q. Capacity coordination planning of isolated microgrid and battery swapping station based on the quantum behavior particle swarm optimization algorithm[J]. International Transactions on Electrical Energy Systems, 2021, 31(3): e12804.
  12. Rameshar V, Sharma G, Bokoro P N, et al. Frequency Support Studies of a Diesel–Wind Generation System Using Snake Optimizer-Oriented PID with UC and RFB[J]. Energies, 2023, 16(8): 3417.
  13. Ahmed M, Meegahapola L, Vahidnia A, et al. Stability and control aspects of microgrid architectures–a comprehensive review[J]. IEEE access, 2020, 8: 144730-144766.
  14. McGowan D J, Morrow D J, Fox B. Multiple input governor control for a diesel generating set[J]. IEEE transactions on Energy Conversion, 2008, 23(3): 851-859.
  15. Zou Y, Qian J, Zeng Y, et al. Optimized Robust Controller Design Based on CPSOGSA Optimization Algorithm and H-two/H-infty Weights Distribution Method for Load Frequency Control of Micro-Grid[J]. IEEE Access, 2021, 9: 162093-162107.
  16. Qian J, Guo Y, Zou Y, et al. Hamiltonian Modeling and Structure Modified Control of Diesel Engine[J]. Energies, 2021, 14(7): 2011.
  17. Latif A, Hussain S M S, Das D C, et al. Double stage controller optimization for load frequency stabilization in hybrid wind-ocean wave energy based maritime microgrid system[J]. Applied Energy, 2021, 282: 116171.
  18. Ali H, Magdy G, Xu D. A new optimal robust controller for frequency stability of interconnected hybrid microgrids considering non-inertia sources and uncertainties[J]. International Journal of Electrical Power & Energy Systems, 2021, 128: 106651.
  19. Valenzuela M A, Bentley J M, Lorenz R D. Evaluation of torsional oscillations in paper machine sections[J]. IEEE Transactions on Industry Applications, 2005, 41(2): 493-501.
  20. Al-Suod M M S, Oleksandr U. Optimization of the Speed Controller in Gas Diesel Device Including in the Autonomous Electric Power System[J]. WSEAS Transactions on Circuits and Systems, 2019, 18: 135-140.
  21. Iwanski G, Bigorajski Ł, Koczara W. Speed control with incremental algorithm of minimum fuel consumption tracking for variable speed diesel generator[J]. Energy Conversion and Management, 2018, 161: 182-192.
  22. Afzal Thoker Z, Ahmad Lone S. Dynamic performance improvement of wind-diesel power system through robust sliding mode control of hybrid energy storage system[J]. Wind Engineering, 2022, 46(4): 1065-1079.
  23. Wang R, Li X, Ahmed Q, et al. Speed control of a marine engine using predictive functional control based PID controller[C]//2018 Annual American control conference (ACC). IEEE, 2018: 3908-3914.
  24. Tran T A. The optimization of marine diesel engine rotational speed control process by fuzzy logic control based on particle swarm optimization algorithm[J]. Future Internet, 2018, 10(10): 99.
  25. Tran T A, Haidara G. A research on marine diesel engine speed controller by fuzzy logic control theory based on experimental investigation[J]. world, 2019, 17: 19.
  26. Ding Y, Shi W, Zhang Y, et al. Design of Neural Network Speed Controller for Marine Diesel Generator Set[J]. International Core Journal of Engineering, 2021, 7(6): 586-592.
  27. Asgari S, Suratgar A A, Kazemi M G. Feedforward fractional order PID load frequency control of microgrid using harmony search algorithm[J]. Iranian Journal of Science and Technology, Transactions of Electrical Engineering, 2021, 45(4): 1369-1381.
  28. He Y, Fan A, Wang Z, et al. Two-phase energy efficiency optimisation for ships using parallel hybrid electric propulsion system[J]. Ocean engineering, 2021, 238: 109733.
  29. Li J. Design and application of modern synchronous generator excitation systems[M]. John Wiley & Sons, 2019.
  30. Chakraborty C, Basak S, Rao Y T. Synchronous generator with embedded brushless synchronous exciter[J]. IEEE Transactions on Energy Conversion, 2019, 34(3): 1242-1254.
  31. Krishnamurthy S, Jahns T M, Lasseter R H. The operation of diesel gensets in a CERTS microgrid[C]//2008 IEEE Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century. IEEE, 2008: 1-8.
  32. Gayatri M T L, Parimi A M, Kumar A V P. A review of reactive power compensation techniques in microgrids[J]. Renewable and Sustainable Energy Reviews, 2018, 81: 1030-1036.
  33. Patel R, Hafiz F, Swain A, et al. Nonlinear excitation control of diesel generator: A command filter backstepping approach[J]. IEEE Transactions on Industrial Informatics, 2020, 17(7): 4809-4817.
  34. Zhao P, Yao W, Wen J, et al. Improved synergetic excitation control for transient stability enhancement and voltage regulation of power systems[J]. International Journal of Electrical Power & Energy Systems, 2015, 68: 44-51.
  35. Ramakrishnan K. Delay-dependent stability of networked generator-excitation control systems: An LMI based approach[J]. IFAC-PapersOnLine, 2016, 49(1): 431-436.
  36. Berkoune K, Sedrine E B, Vido L, et al. Robust control of hybrid excitation synchronous generator for wind applications[J]. Mathematics and Computers in Simulation, 2017, 131: 55-75.
  37. Pramanik M A H, Roy T K, Ghosh S K, et al. Robust partial feedback linearizing excitation controller design for higher-order synchronous generator in smib systems to improve the transient stability[C]//2021 IEEE Texas Power and Energy Conference (TPEC). IEEE, 2021: 1-6.
  38. Orchi T F, Roy T K, Mahmud M A, et al. Feedback linearizing model predictive excitation controller design for multimachine power systems[J]. IEEE Access, 2017, 6: 2310-2319.
  39. Roy T K, Mahmud M A, Shen W, et al. Robust nonlinear adaptive backstepping excitation controller design for rejecting external disturbances in multimachine power systems[J]. International Journal of Electrical Power & Energy Systems, 2017, 84: 76-86.
  40. Mobarra M, Rezkallah M, Ilinca A. Variable speed diesel generators: Performance and characteristic comparison[J]. Energies, 2022, 15(2): 592.
  41. Mobarra M, Tremblay B, Rezkallah M, et al. Advanced control of a compensator motor driving a variable speed diesel generator with rotating stator[J]. Energies, 2020, 13(9): 2224.
  42. Huang M L, Song K M, Wei Z D. Nonlinear H-two/H-infinity synthetic controller for diesel-generator set[J]. Control Theory & Applications, 2011, 28(6): 885-893.
  43. Issa M, Ibrahim H, Lepage R, et al. A review and comparison on recent optimization methodologies for diesel engines and diesel power generators[J]. Journal of Power and Energy Engineering, 2019, 7(06): 31.
  44. Ramstedt M. Cylinder-by-Cylinder Diesel Engine Modelling: A Torque-based Approach[J]. 2004.
  45. Zhang Y, Zhang X, Qian T, et al. Modeling and simulation of a passive variable inertia flywheel for diesel generator[J]. Energy Reports, 2020, 6: 58-68.
  46. Huang M, Wang C. Nonlinear mathematical model of diesel generator sets in marine power stations[J]. Journal of Harbin Engineering University,2006(01):15-19+47.
  47. Huang M,Wang C. Nonlinear H-infty governor for diesel engines in marine power stations[J]. Journal of Electrical Engineering Technology,2006(10):56-61.
  48. Huang M.L.,Wei Z.D.,Song K.M.. Synchronous generator state feedback H-infty regulator for marine power plants[J]. Journal of Power Systems and Automation,2011,23(04):15-20.
  49. Zou Y, Hu W, Xiao Z, et al. Design of intelligent nonlinear robust controller for hydro-turbine governing system based on state-dynamic-measurement hybrid feedback linearization method[J]. Renewable Energy, 2023.
  50. Dao F, Zou Y, Zeng Y, et al. An intelligent CPSOGSA-based mixed H-two/H-infty robust controller for the multi-hydro-turbine governing system with sharing common penstock[J]. Renewable Energy, 2023.
  51. Li L, Qian J, Zou Y, et al. Optimized Takagi–Sugeno Fuzzy Mixed H-two/H-infty Robust Controller Design Based on CPSOGSA Optimization Algorithm for Hydraulic Turbine Governing System[J]. Energies, 2022, 15(13): 4771.
  52. Duman S, Li J, Wu L, et al. Optimal power flow with stochastic wind power and FACTS devices: a modified hybrid PSOGSA with chaotic maps approach[J]. Neural Computing and Applications, 2020, 32: 8463-8492.
  53. Rather S A, Bala P S. Constriction coefficient based particle swarm optimization and gravitational search algorithm for multilevel image thresholding[J]. Expert Systems, 2021, 38(7): e12717.
  54. Rather S A, Bala P S. A hybrid constriction coefficient-based particle swarm optimization and gravitational search algorithm for training multi-layer perceptron[J]. International Journal of Intelligent Computing and Cybernetics, 2020, 13(2): 129-165.
  55. Rather S A, Bala P S. Swarm-based chaotic gravitational search algorithm for solving mechanical engineering design problems[J]. World Journal of Engineering, 2020.
  56. Rather S A, Bala P S. Hybridization of constriction coefficient-based particle swarm optimization and chaotic gravitational search algorithm for solving engineering design problems[J]. Applied Soft Computing and Communication Networks: Proceedings of ACN 2019, 2020: 95-115.
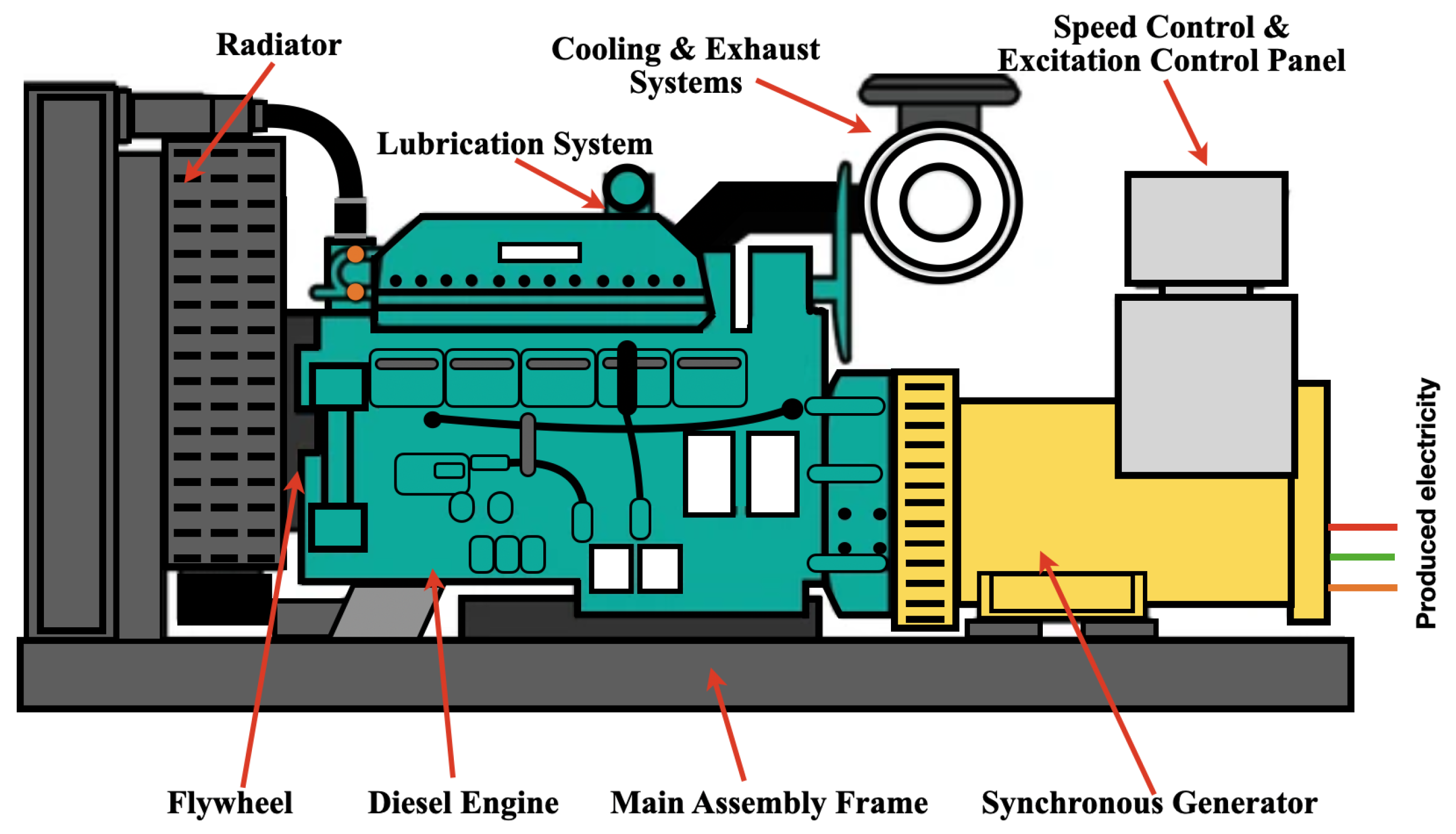
Preprints 74838 g002
Figure 2. Principle diagram of DE speed regulation system.
Figure 2. Principle diagram of DE speed regulation system.
Preprints 74838 g002
Preprints 74838 g003
Figure 3. Flywheel of diesel.
Figure 3. Flywheel of diesel.
Preprints 74838 g003
Preprints 74838 g004
Figure 4. State-feedback control.
Figure 4. State-feedback control.
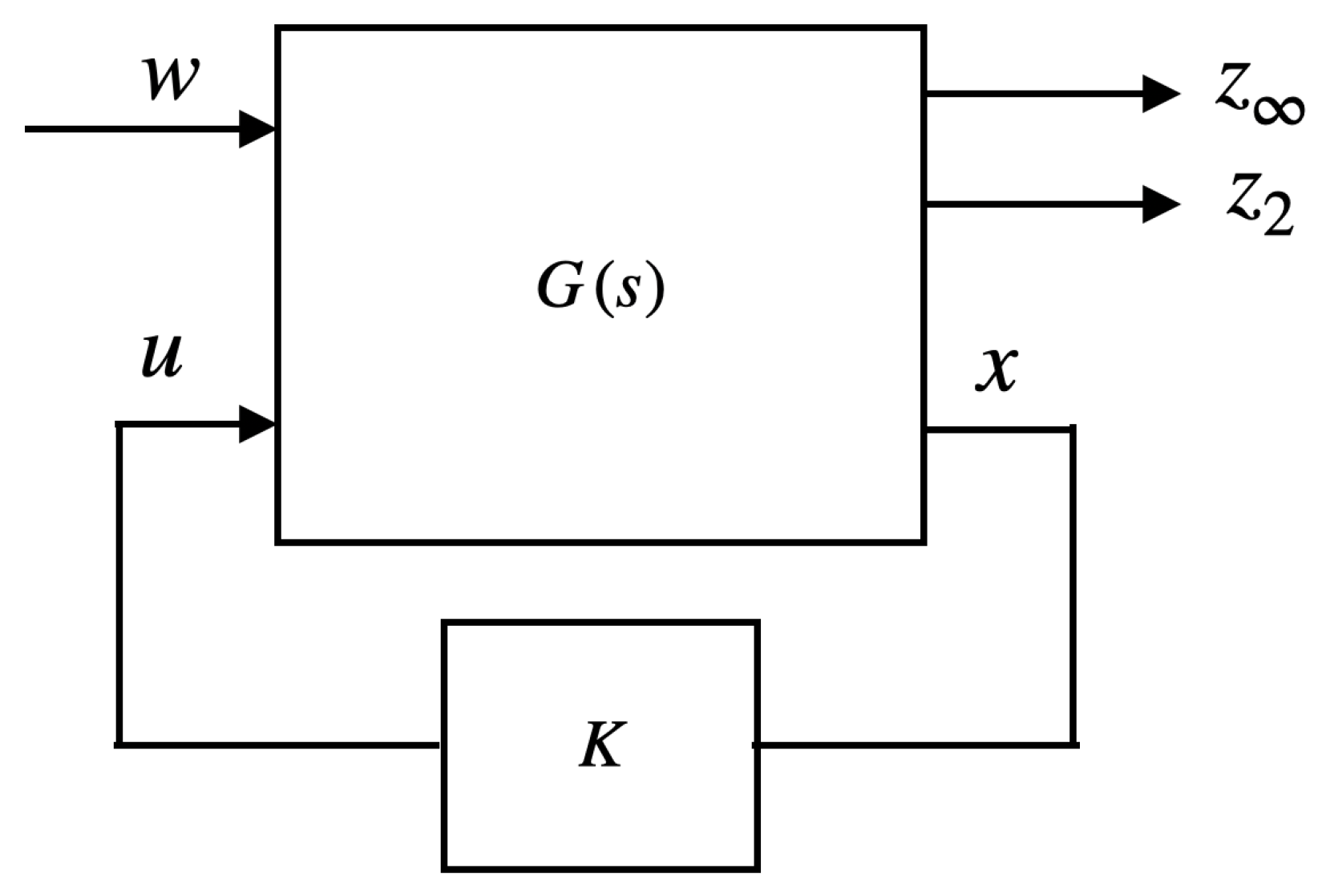
Preprints 74838 g004
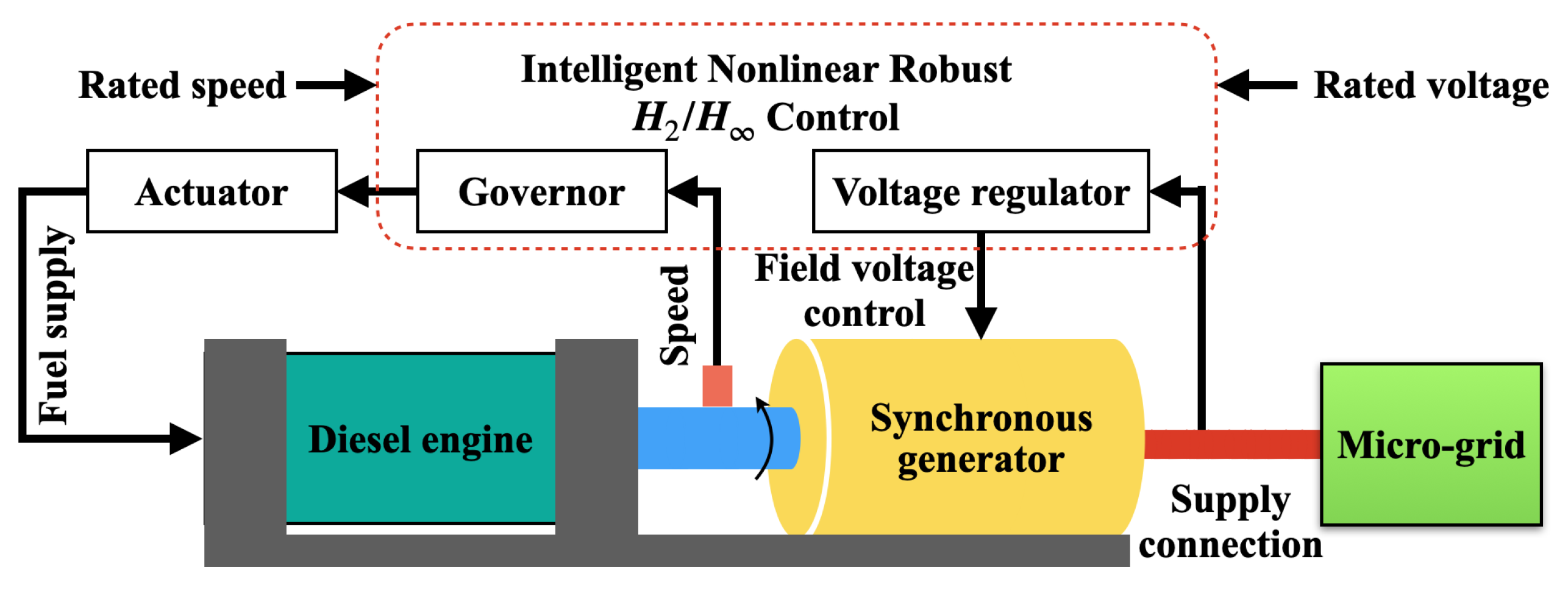
Preprints 74838 g005
Figure 5. Principle diagram of diesel-generator set synthetic control system.
Figure 5. Principle diagram of diesel-generator set synthetic control system.
Preprints 74838 g005
Preprints 74838 g006
Figure 6. Curves of chaotic maps.
Figure 6. Curves of chaotic maps.
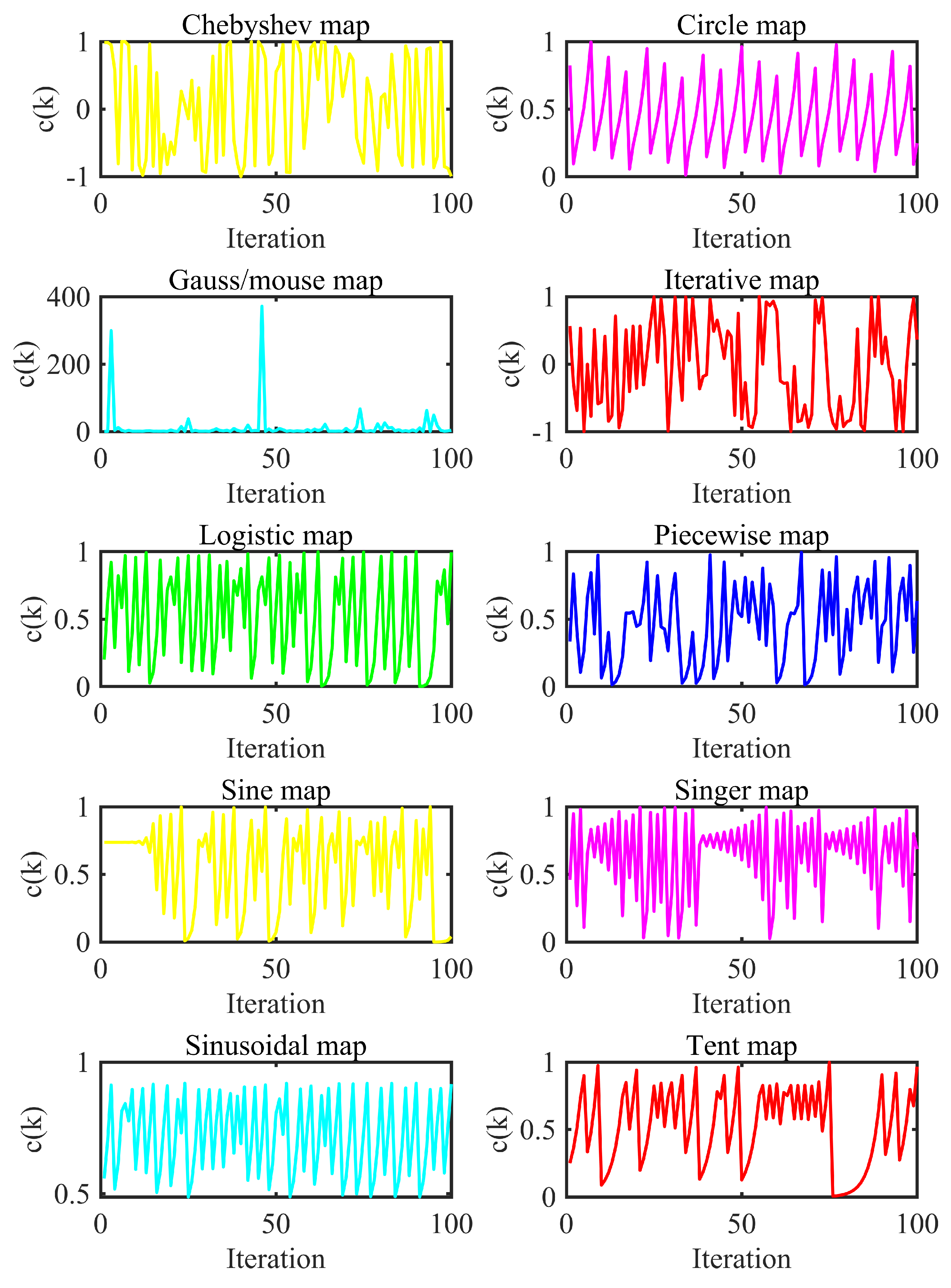
Preprints 74838 g006
Preprints 74838 g007
Figure 7. Diesel generator and its microgrid Simulink model.
Figure 7. Diesel generator and its microgrid Simulink model.
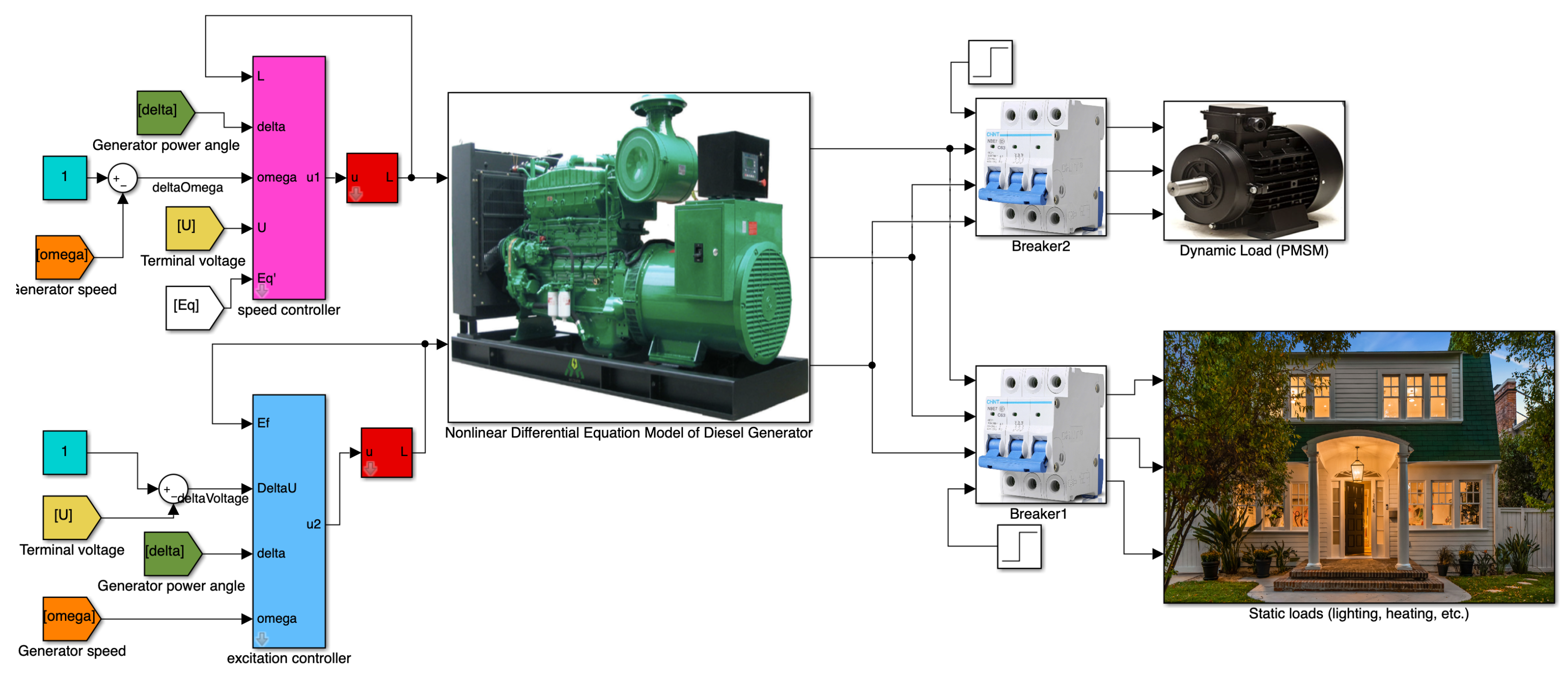
Preprints 74838 g007
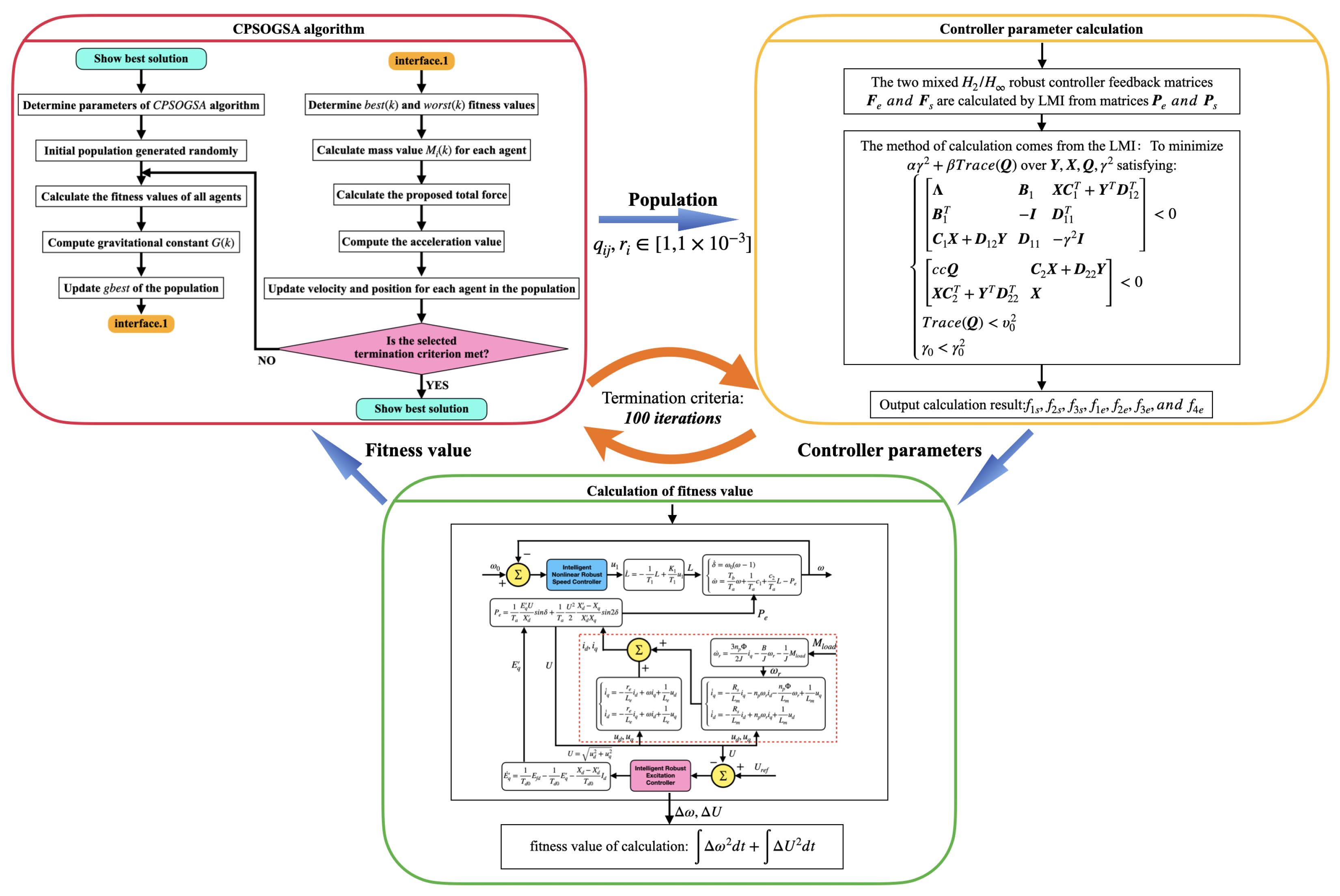
Preprints 74838 g008
Figure 8. The flowchart of optimization process.
Figure 8. The flowchart of optimization process.
Preprints 74838 g008
Preprints 74838 g009
Figure 9. Iterative graph of the optimization process.
Figure 9. Iterative graph of the optimization process.
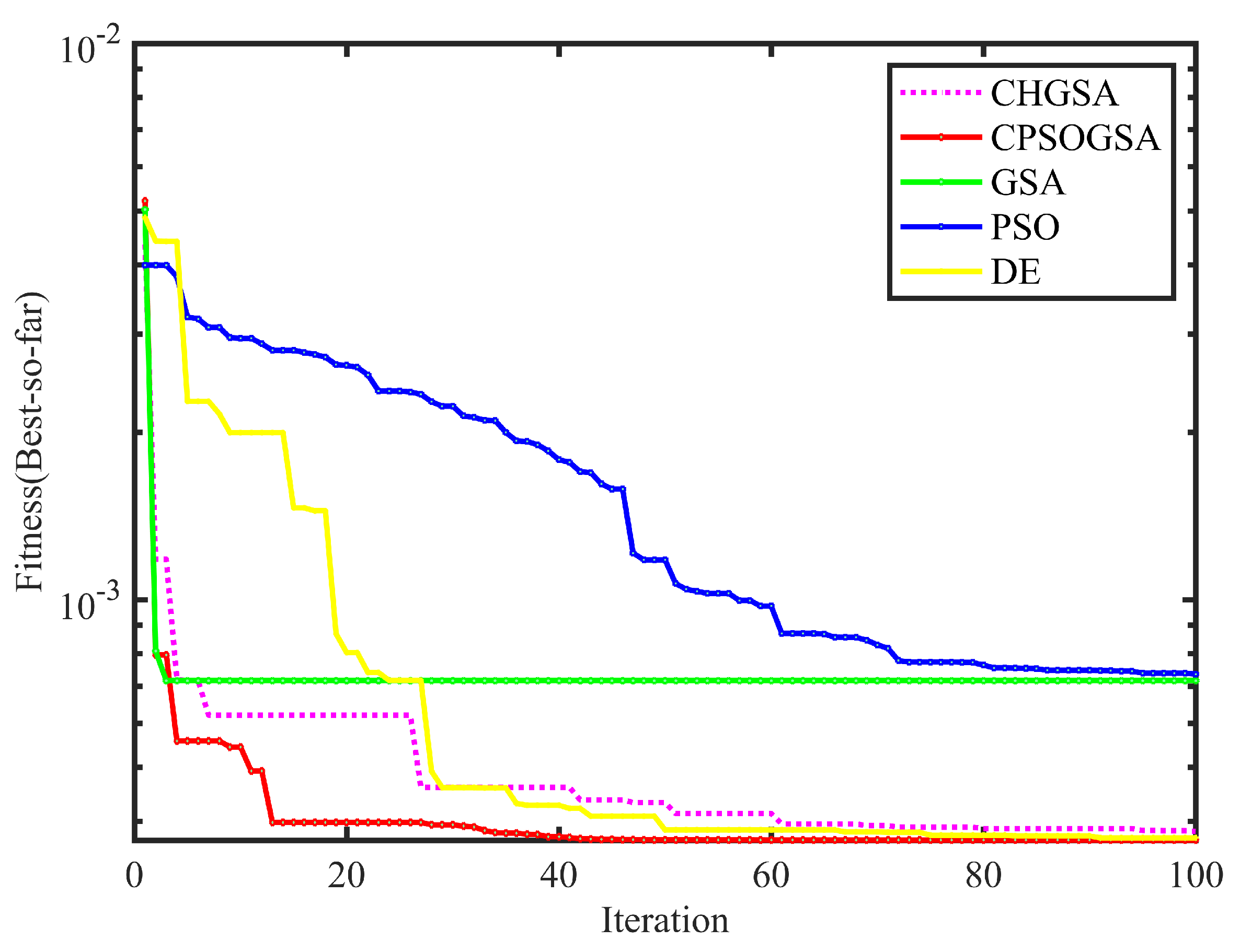
Preprints 74838 g009
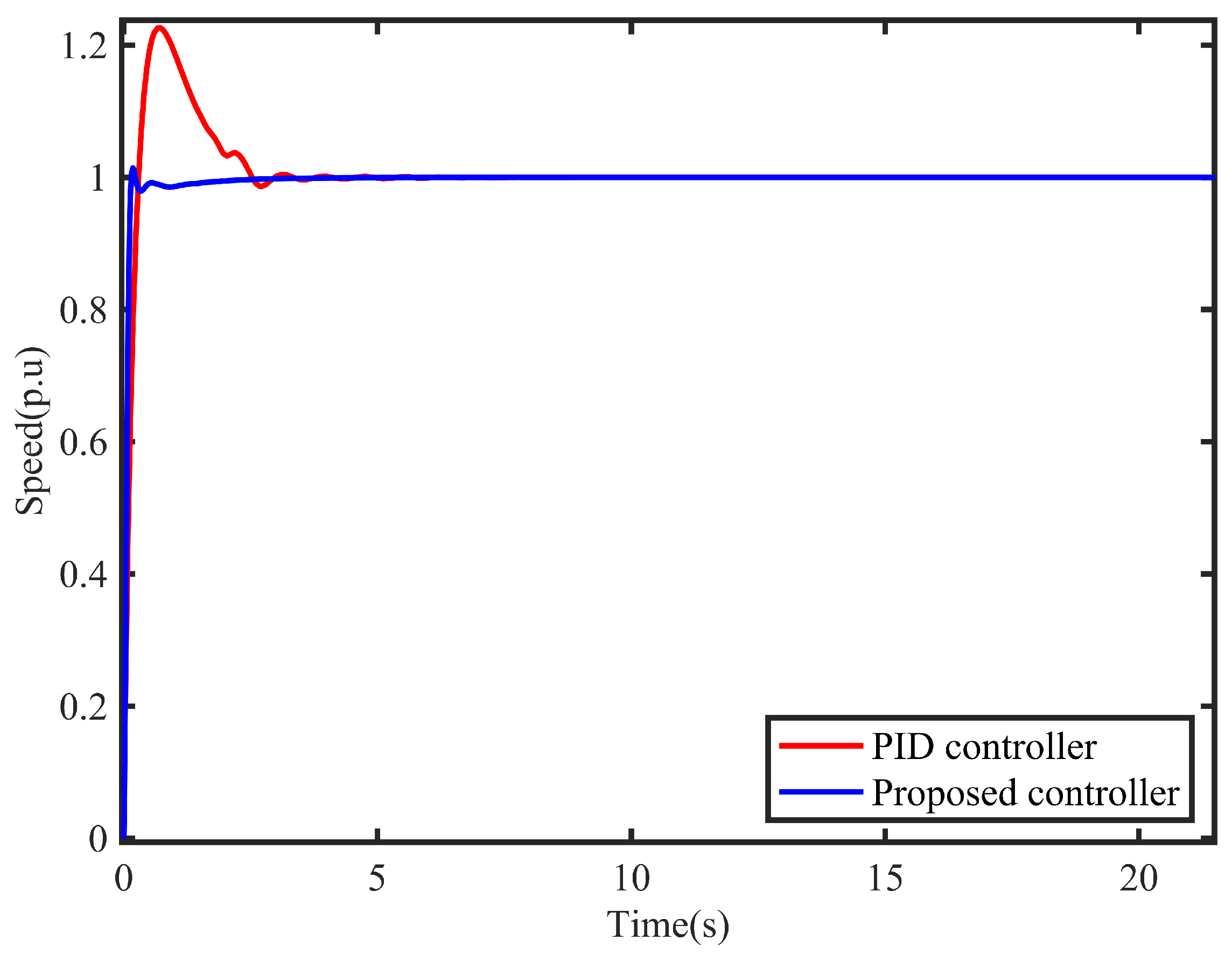
Preprints 74838 g010
Figure 10. Variation curve of speed at no-load start-up.
Figure 10. Variation curve of speed at no-load start-up.
Preprints 74838 g010
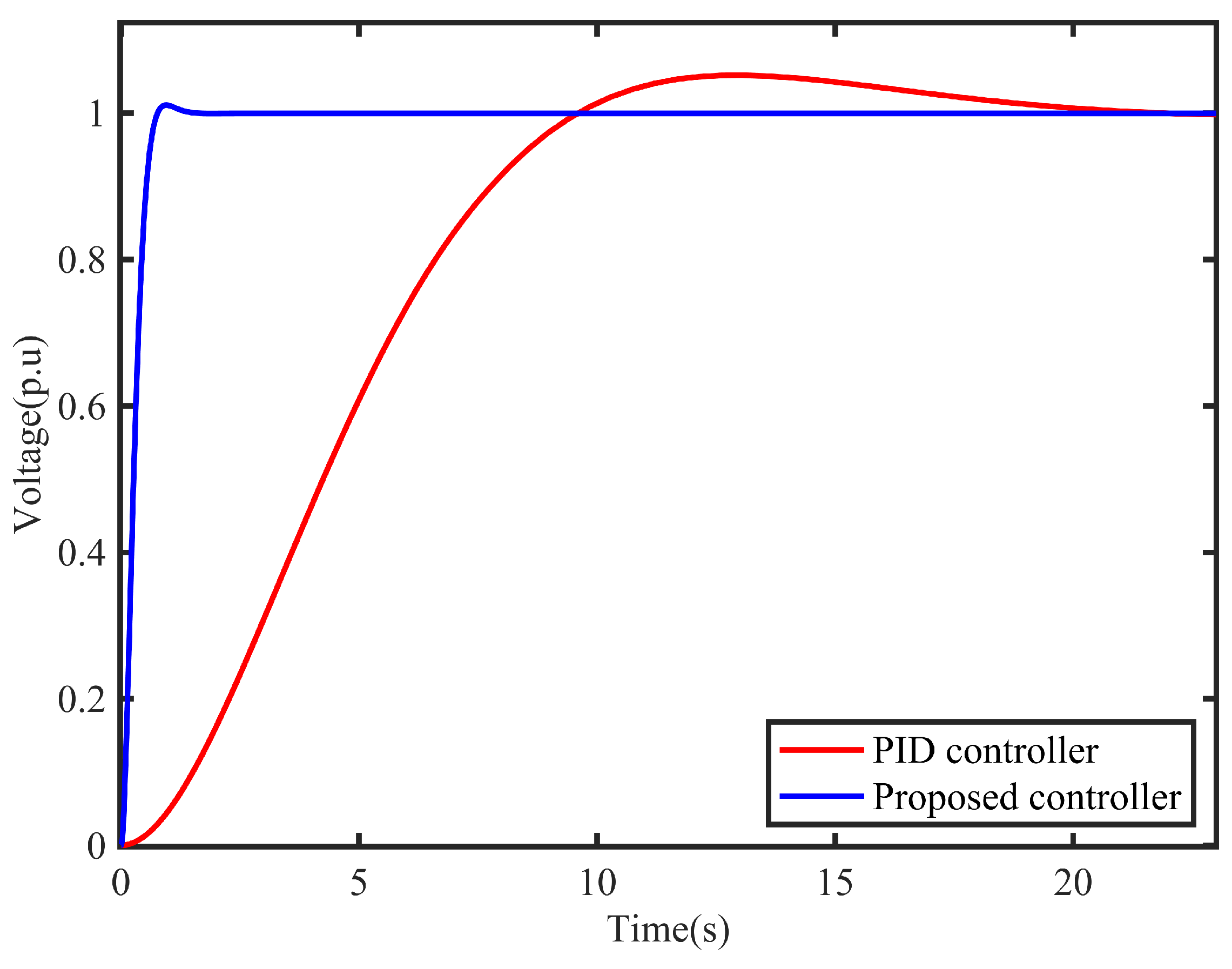
Preprints 74838 g011
Figure 11. Variation curve of voltage at no-load start-up.
Figure 11. Variation curve of voltage at no-load start-up.
Preprints 74838 g011
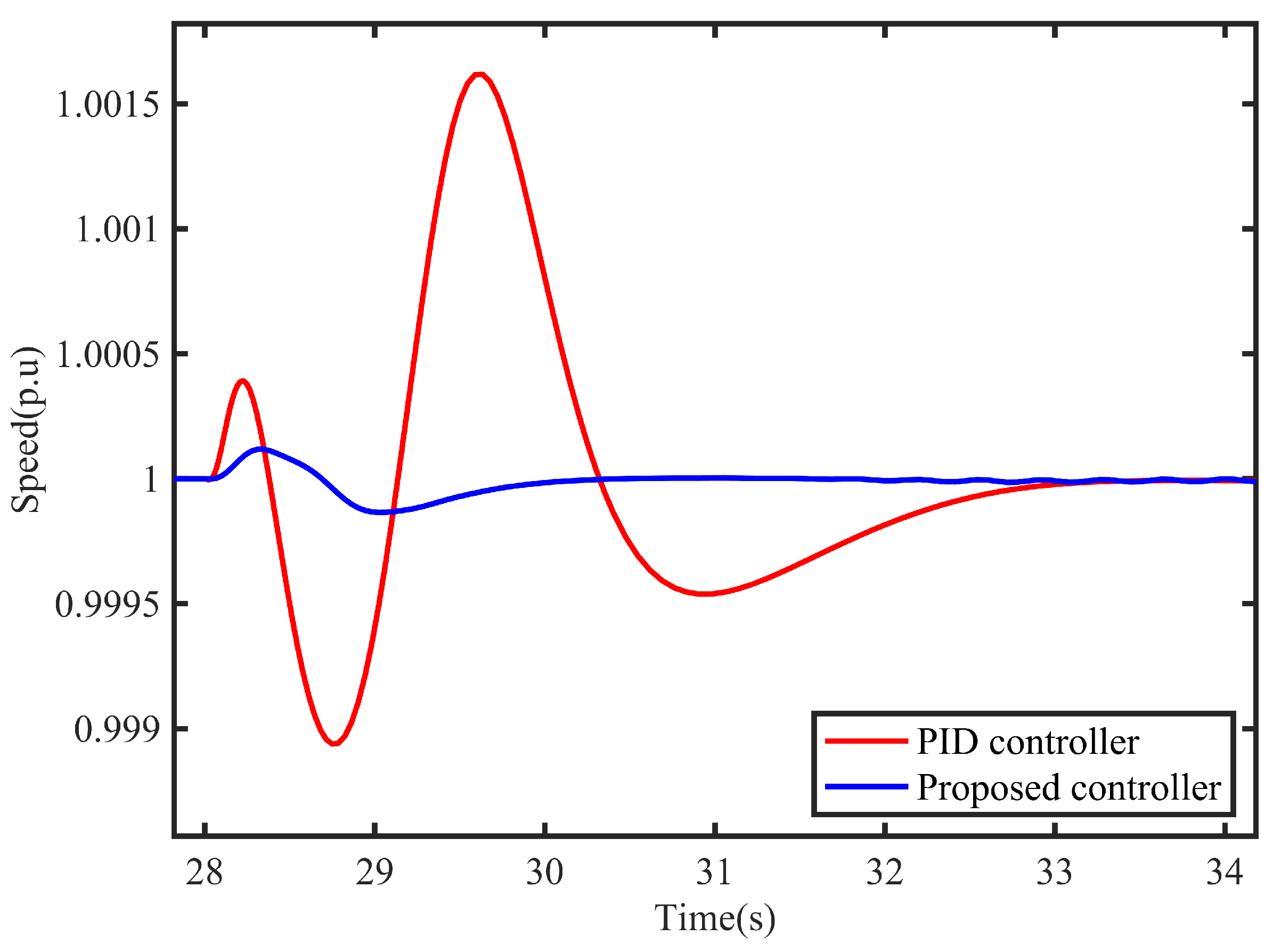
Preprints 74838 g012
Figure 12. Speed response of system on suddenly increasing static load.
Figure 12. Speed response of system on suddenly increasing static load.
Preprints 74838 g012
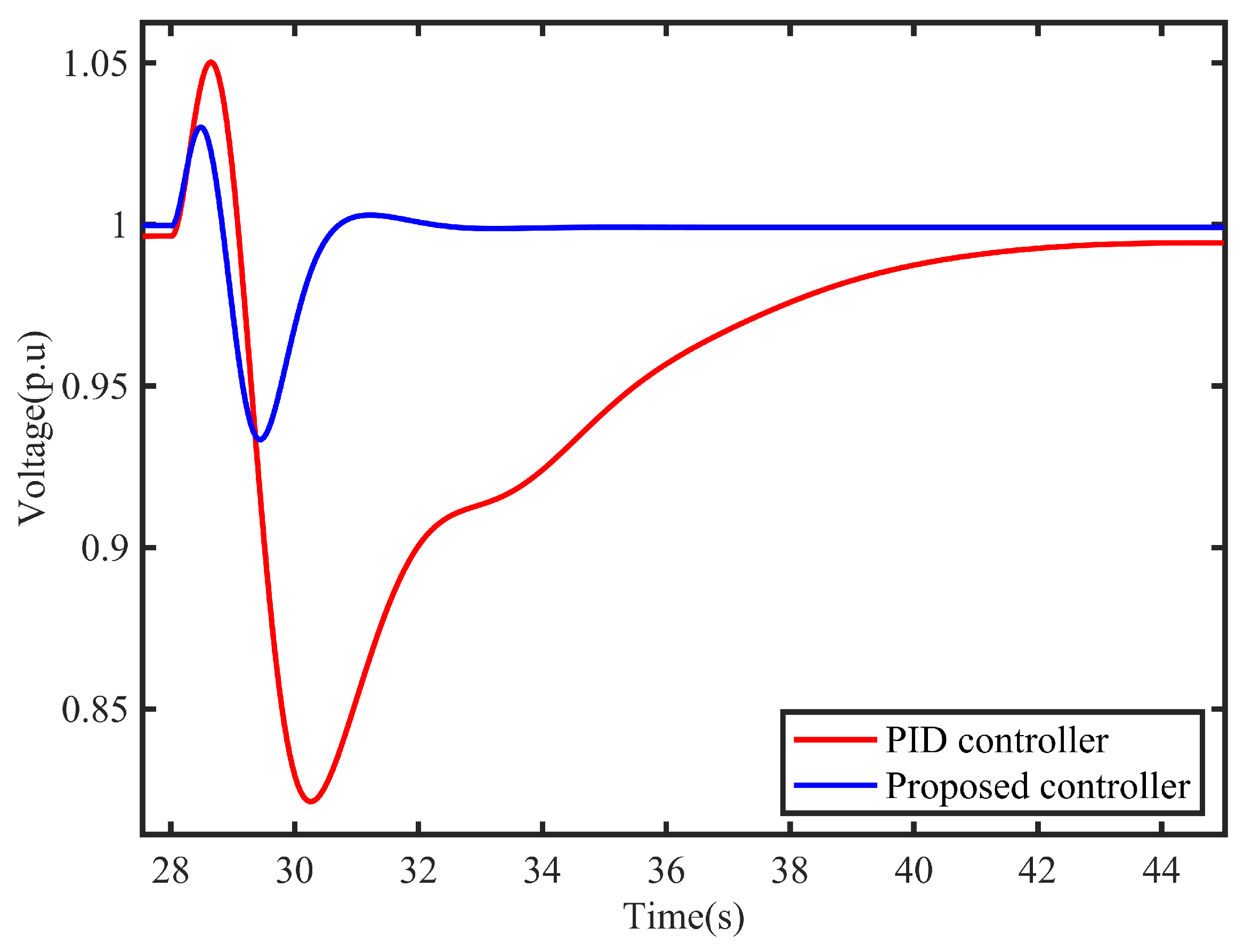
Preprints 74838 g013
Figure 13. Voltage dynamic response of system on suddenly static load.
Figure 13. Voltage dynamic response of system on suddenly static load.
Preprints 74838 g013
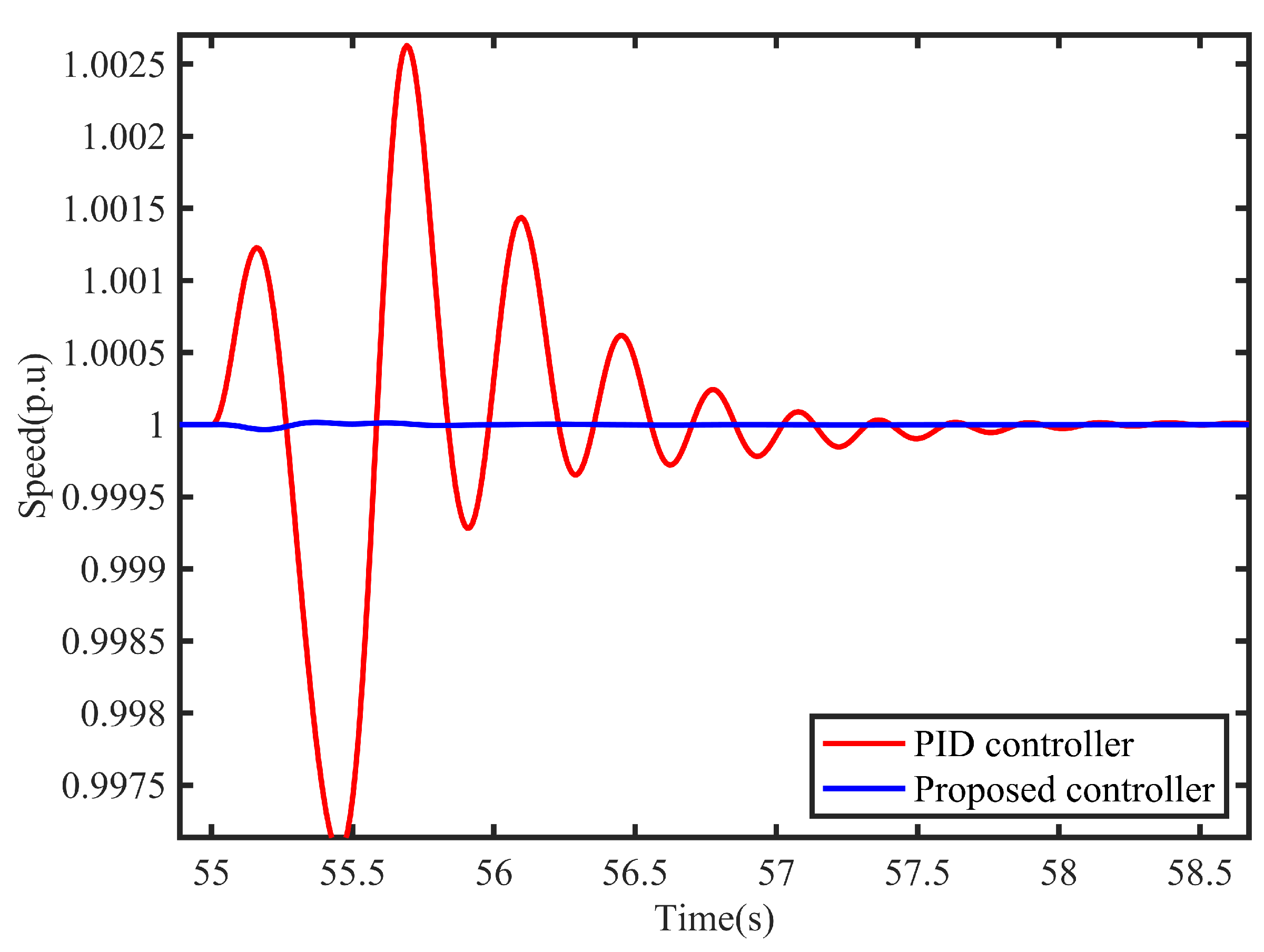
Preprints 74838 g014
Figure 14. Speed response of system on suddenly increasing dynamic load.
Figure 14. Speed response of system on suddenly increasing dynamic load.
Preprints 74838 g014
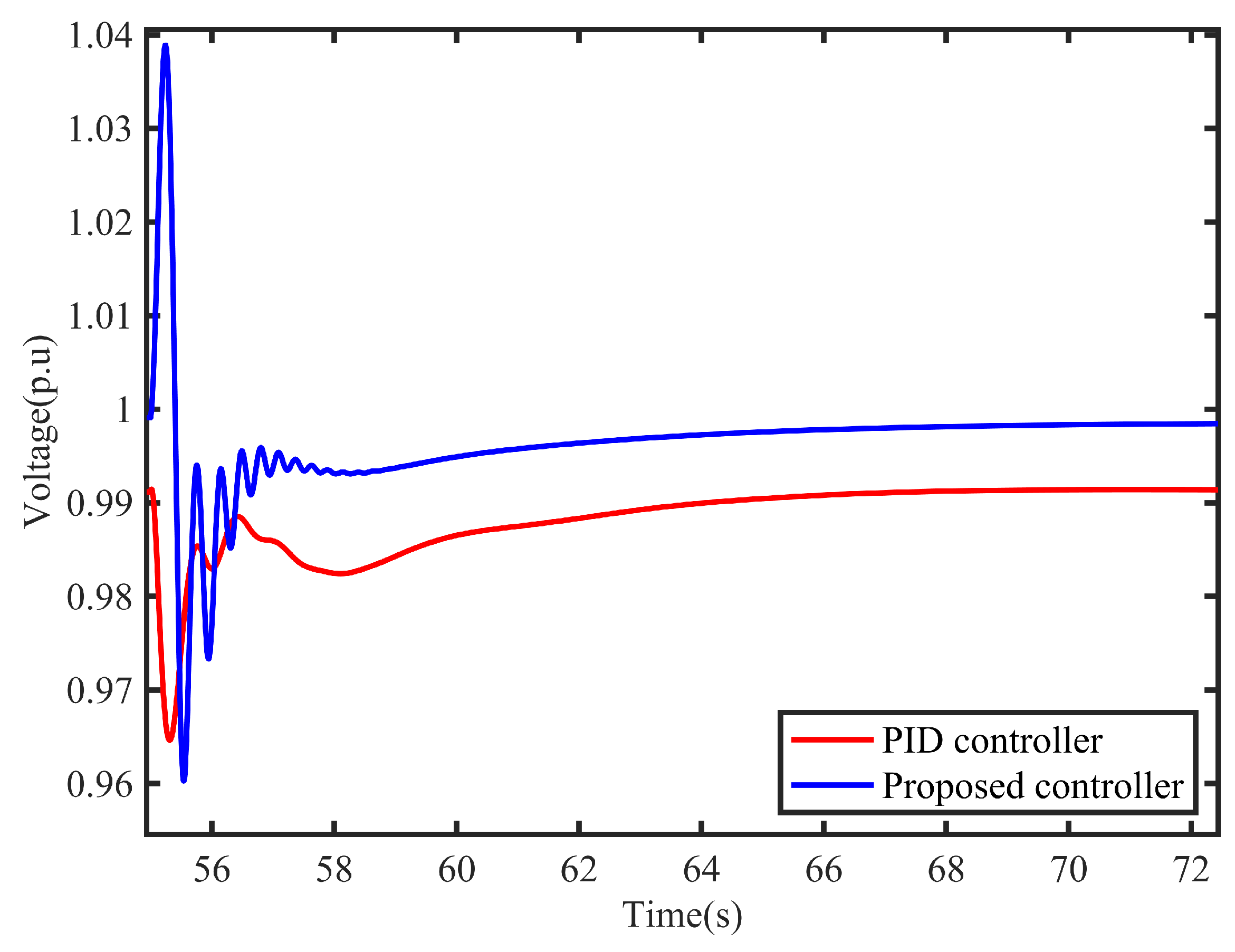
Preprints 74838 g015
Figure 15. Voltage dynamic response of system on suddenly dynamic load.
Figure 15. Voltage dynamic response of system on suddenly dynamic load.
Preprints 74838 g015
Table 1. Relevant parameters for simulation.
Table 1. Relevant parameters for simulation.
T a T b c 1 c 2 X d X d ′
1.136 -0.492 1.515 -0.215 2.053 0.213
X q T 1 R T d 0 K 1 d 1
1.003 0.050 0.011 2.200 0.200 0.1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated