Proficient Optimization for Precise control of Rehabilitation Robots using Machine Learning Algorithms: PSO and Firefly Comparison

Diversified techniques have been applied in many research papers for the optimization of rehabilitation robotic movements in order to maintain smoothness and accuracy. Smooth and precise control is needed necessarily for upper limb rehabilitation robotic applications having five degree of freedom. The preferred parameters which are used for the controlling were validated by mathematical model and these tuning parameters were optimized. Designing optimization algorithms to control complex physical robots has been a challenging task. In this study, a number of optimization techniques will be analyzed to determine the optimal parameters of a PID controller with a dynamic model of the upper limb rehabilitation system. For determining optimal control parameters for PID, there exists a number of tuning methods such as Zeigler Nichols and fuzzy logic which are classical methods. Swarm intelligence-based optimization algorithms are inspired by the behaviors of living things in nature. Several researchers have reported the optimal design of PID controller parameters using optimization techniques. The proposed control technique has been implemented on a 5-DOF RAX hardware and before any clinical trials, six healthy subjects went for trials under strict protocol. It has been discovered that the proposed control technique rejects the external unwanted disturbances as well as keeps the system stable under extreme perturbed and harsh conditions. In this research paper mathematical models have been validated to determine the PID parameters for the optimization. The comparative study is carried out with four different cost functions since a well-designed objective function leads to better performance of the system and indicates control design expectations. These objective functions are an integral squared error (ISE) and integral absolute error (IAE). In this research work, the effects of different cost functions on optimization techniques for controller parameters were analyzed. The performance of the controller with different cost functions has examined for robustness analysis. The cost function of particle swarm optimization, Firefly, Ant Bee Colony and Ant Colony optimization were developed for the better optimization results.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

Rehabilitation Robotics can be described as a type of robotics which aims to reduce most of the demerits of classical rehabilitation and focuses on technology which may assist people to recover from severe physical trauma or assist them in activities of daily living [1]. Utilizing robotics to design machines for rehabilitation increases the number of the training session with consistent repetitions which enables the opportunity to assign one therapist to train more patients at a time [2]. It also permits to assess the objective and quantitative evaluation of the patients during and after the therapy sessions which is not possible with conventional therapy. In addition, augmenting gaming and virtual reality with therapy creates an exaggerated environment which can intensify motivation during sessions [3]. Rehabilitation therapy devices use different control algorithms based on the control strategy and training modes. The control algorithm reviewed in this section can generally be divided into three categories; conventional position controllers, model-based controllers and advance intelligent controllers.

1.1. Recent Traditional Position Controllers

Traditional position controller’s motive is to control the position of the set point of the system. In rehabilitation robotics, position control is the primary objective to perform an exercise. Mostly PID, PD or PI controllers are used to control the position of a rehabilitation robot. ARM-Guide [6], a stationary end-effector based 4-DOF system which was developed for physical therapy. The researchers utilized the Proportional Derivative (PD) control algorithm while input parameters were position and forced to perform shoulder and elbow movements for training. Motion ARM [7], based on MIT Manus was developed which is also a stationary end-effector based system with 3-DOF in which two are active and one is passive. It uses brushless DC motors to actuate the motion. The system is utilized to perform shoulder and elbow exercises. Impedance controller alongside with gravity compensation is used as controllers. NeReBot [8] is also a stationary end-effector based system which is a 3-DOF cable-driven system for physical therapy. The system utilized the proportional derivative (PD) controller to perform therapy for the shoulder joint and elbow joint using three DC motors.

Another researcher in 2008 developed a 3-DOF rehabilitation system[9]. Proportion Integral (PI) and Proportional Derivative (PD) control algorithms were utilized as controllers using position and force as input parameters while impedance control strategy was used. MIME-RiceWrist [10], is a 9-DOF exoskeleton system perform shoulder, elbow, forearm and wrist exercises. Maxon electric motors and a capstan drive transmission system are used to actuate the system. Furthermore, impedance control is used in the system while an inverse kinematics-based task-space position controller is utilized with a proportional derivative (PD) trajectory controller. The passive and active-assistance training modes on the RiceWrist are executed utilizing joint-level PD control while the constrained mode is applied by an impedance controller. MEMOS [11], another end-effector based 2-DOF stationary system was developed for rehabilitation. With the assistance of two DC motors, the planner motion for shoulder and elbow joints were achieved. Force impedance controller is used to control the system. Position and force were the two important control parameters used. ArmeoPower from Hocoma [12] is a 7-DOF with six active and one passive DOF system is capable of performing Shoulder, elbow, forearm and wrist exercises. The stationary exoskeleton system uses six DC motor actuators to achieve the desired motion. The rehabilitation system utilizes impedance controller with gravity and friction compensation. Calculated torque PD controller is used for the system with gravity compensation. MUNDUS [13] is a wheelchair mounted exoskeleton system. A sequential feedback controller is used for simultaneous feedback control of the 3 DOFs implemented with a biomimetic feed forward controller. The use of a sequential controller alone can lessen the calculation time and guarantee a very robust accuracy in achieving the target. Gentle/G [14] is a 9-DOF stationary rehabilitation system which can perform Shoulder, elbow, forearm, wrist, thumb and other fingers together to perform grasp motion. The parameters of Gentle/G are endpoint torque, position and velocity and for haptic master, the parameters are joint angles and endpoint forces. Gentle/G uses admittance control and is used as a reach and grasp system.

1.2. Model Based Controllers

Model-based controllers are mostly used in process control or where the system model is defined. These controllers can also be used in rehabilitation robotics for precise control and chattering removal. A researcher used a Model Predictive Control (MPC) strategy to control a single DOF robot [15]. The robot used the AAN control strategy for rehabilitation exercise. EMG is used to muscle condition and assist in the form of provided torque.

A fully assistive 2-DOF robot prototype was developed [16]. MPC as a controller was used with brain and arm model along with scented Kalman filter to control the robot angular position. The joint angle is the control parameter used in this system. Another researcher also used MPC and H∞ control to control the 6-DOF upper limb robot. Joint angle as input parameters were used of the system [17].

Reha-Maus [18], a mobile rehabilitation system developed for upper limb rehabilitation uses position and speed are the control parameters of the system. Linear Quadratic Regulator (LQR) to control techniques is used and the Maxon brushed DC motors are used to actuate the system. A prototype was developed for rehabilitation purposes where hybrid LQR and H∞ control was used by utilizing Markovian theory [19].

A 3-DOF upper extremity rehabilitation robot for capable of performing Shoulder, elbow (forearm) and wrist exercises were developed. For the system, a model-based nonlinear control was used which shifts from PD controller, force PI controller and impedance controller depending on the category of training, using fuzzy to choose between them. Device joint angle, endpoint force are the parameters of the system [9].

1.3. Latest Metaheuristics Approaches for smooth Controlling of Parameters

Out of the existing tuning methods, recently swarm intelligent algorithms have gained increasing popularity amongst researchers on account of their outstanding performance on many practical issues [20].

Gaing proposed a novel design method for determining the optimal PID controller parameters of an AVR system using Particle Swarm Optimization (PSO). In that research, the performance of the system improved and was more efficient as compared with the genetic algorithm (GA) [21]. Extension of this work with a similar system with PID as the controller was optimized using Artificial Bee Colony (ABC). It was reported for AVR type systems ABC produces better results than PSO [22]. Ayas [23] used PSO optimization method to determine PID controller parameters for 2 DOF rehabilitation robot. In that study, the author used an Integral squared error as a performance parameter. Mehdi [24] used a 3-DOF planar robotic manipulator system and utilized PSO for offline tuning of the impedance controller. Aminizar [25] developed a 2 DOF robotic system for rehabilitation. The neural network was used in this study as a controller and genetic algorithm was used for optimization. Mandava [26] used Invasive weed optimization (IWO) for tuning PID for a biped robot. Weed Optimization (IWO)-tuned PID controller is compared in terms of error and the torque required at various joints. Further IWO tuned PID controller was tested with 18-DOF biped robot. Ali [27] worked on 2 DOF upper limb robotic arm which used Fuzzy inference system for online tuning of parameters of PID. The system was simulated and had positive results. Khoury [28], developed a 5-DOF system and applied fuzzy PID control for trajectory tracking problem. A systematic study was presented for optimizing the tuning parameters of the controller. The performance of the proposed controller was validated with a comparative evaluation to torque and direct adaptive control methods. Ayas [29]worked on a 2 DOF ankle rehabilitation robot and used a cuckoo search algorithm to determine the optimal control parameters for fractional-order PID control. ITAE, ISE and IAE as an objective function were used to evaluate performance criteria. Mahanta [30] used Artificial Bee Colony for predicting inverse kinematics problem for a 6 DOF industrial robot. Inverse kinematic problem is one of the important issues in end effector-based robots where the location of the end-effector position is not easy to determine. Two approaches are usually adopted which include a geometric approach that is much easier than using a heuristic approach to determine 12 unknown elements of the kinematic matrix. In real-time, the geometric approach is a much more realistic approach as it has simplified non-iterative equations. Ayala [31], developed a 2-DOF robotic manipulator. PID control technique was used as independent joint control where the tuning of parameters of PID were found using multiple objective evolutionary algorithm using a non-dominated sorting genetic algorithm. The proposed method was found to be robust and good closed-loop tracking performance. Kadiyala [32], claimed to use evolutionary soft computing tools such as PSO and bacterial foraging optimization algorithms for electromagnetic actuator system for aero fin control. The algorithms were used to tune PID controllers. Geetha [33], used PSO and Ant Colony Optimization techniques to determine near-optimal parameters of virtual feedback PID controller for the CSTR system using soft computing algorithms using integral squared error as the objective function.

2. Proposed Control Algorithm Implementation

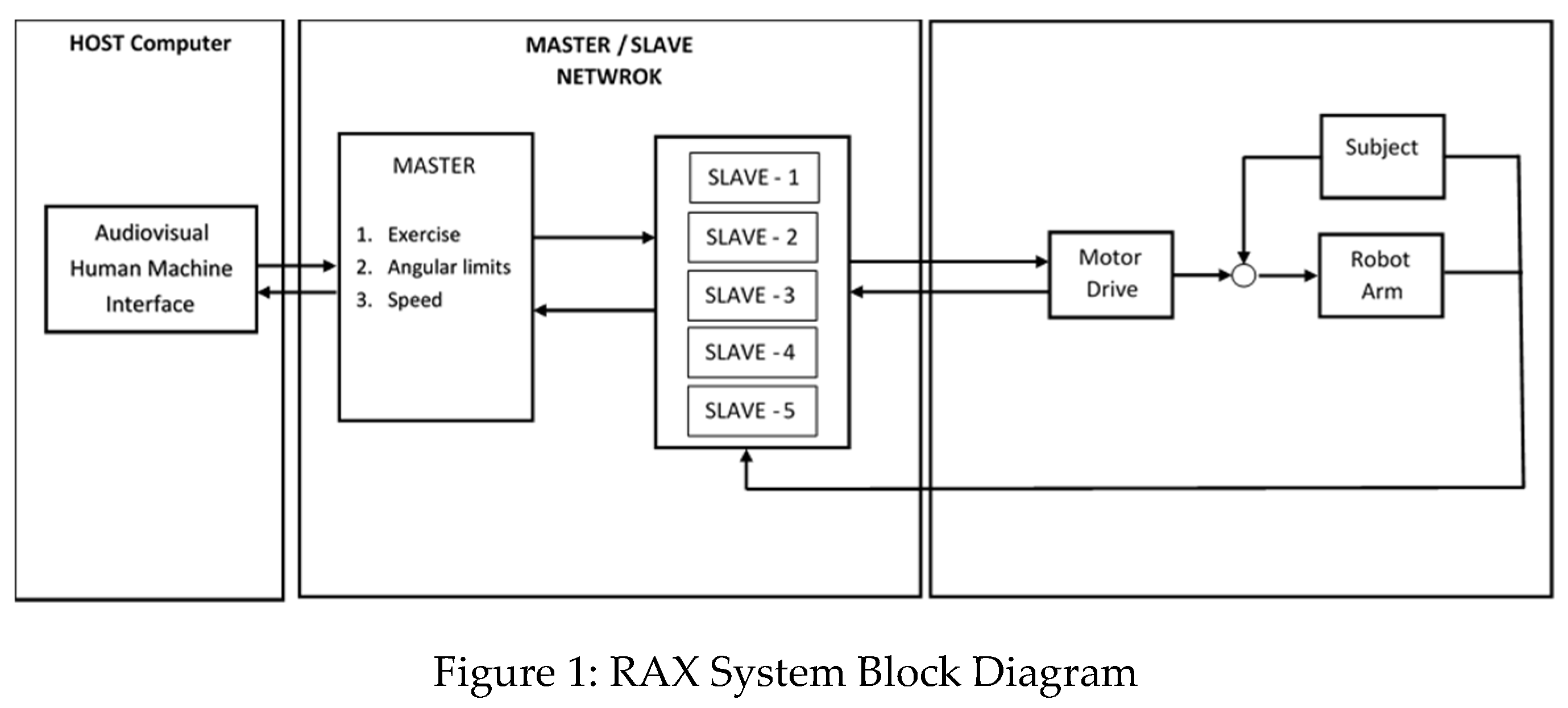
A master/slave network based on I2C is designed to interconnect user with the system where each joint in the system is a slave. CC3200 from Texas Instrument is used as a peripheral device which controls the angular movement. CC3200 is equipped with ARM Cortex-M4 processor specifically designed for IoT applications which means it incorporates all the features and communication protocols required for RAX. The HMI as a graphical user interface created for the user is shown in Figure 1. The master is instructed by the user to select the exercise, repetitions and set angular movement through HMI which is then communicated to slaves for further implementation of the task as provided in Figure 1. The overall system block diagram is given in Figure 1.

Figure 1: RAX System Block Diagram

The system transfer functions for each joint is given. To imply the control algorithm, it is important to know the open-loop response of the system. For open-loop stability, pole-zero map and root locus can provide whether the system is stable or not. To meet the stability criteria, all the poles of the open-loop transfer function must be in the left half-plane. The pole-zero response for all five joints is presented and discussed.

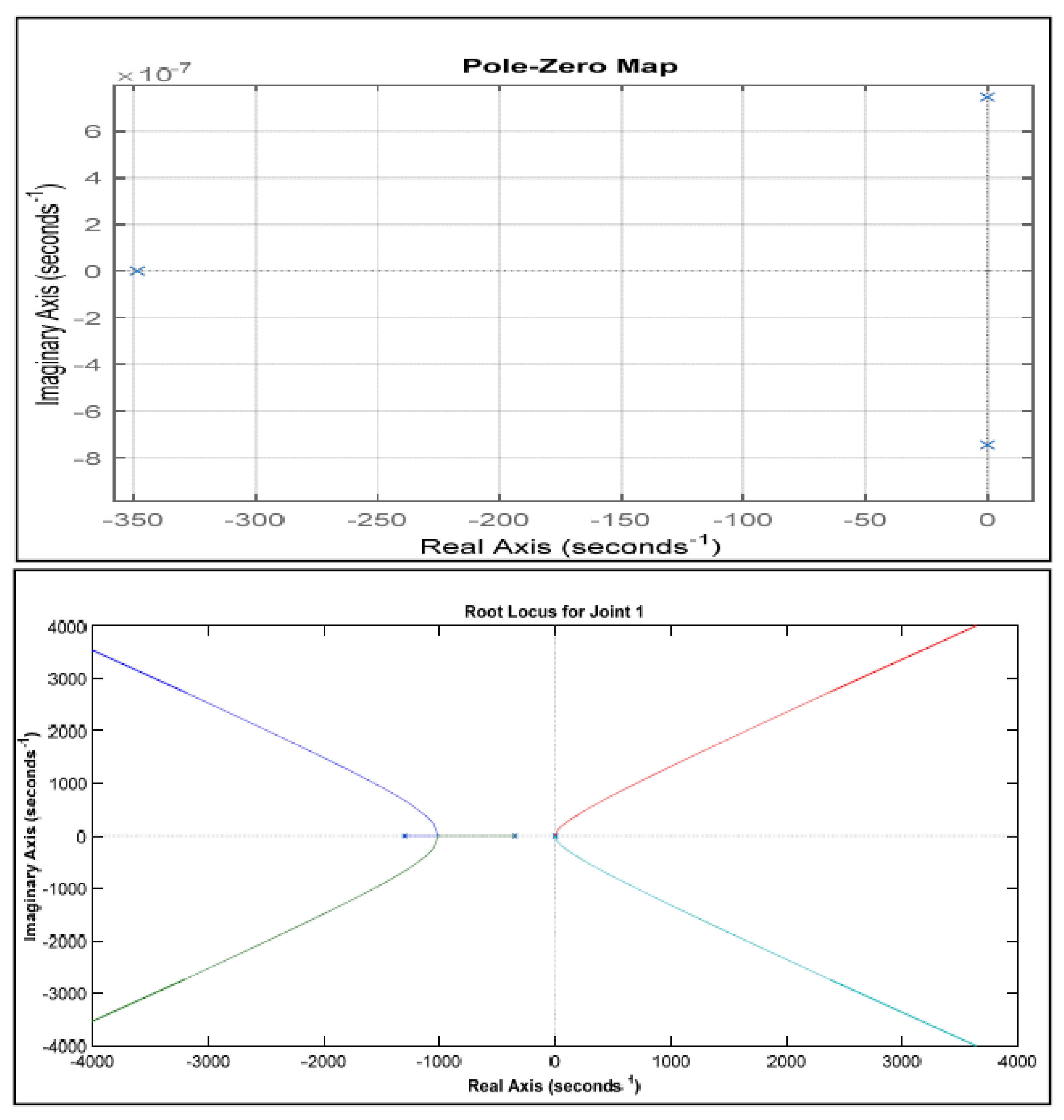
Pole zero map shown in Figure 3 shows that all the poles of joint 1 are either on the left-hand side plane or on the origin line of the imaginary axis. The map shows that the system is marginally stable. The other part of Figure 3 is the root locus of joint 1 in which the poles at origin are driving toward instability as it is moving towards the right-hand side.

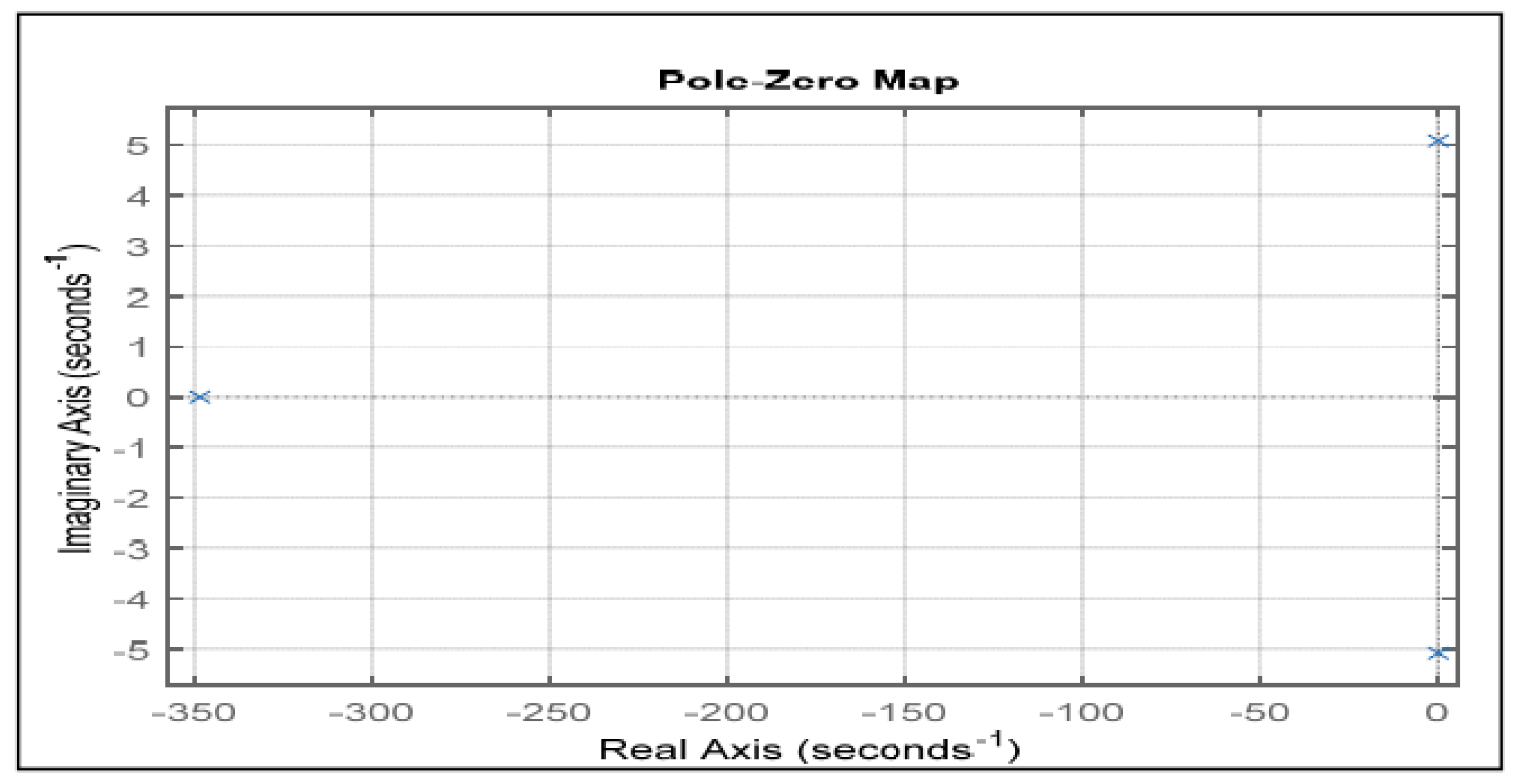
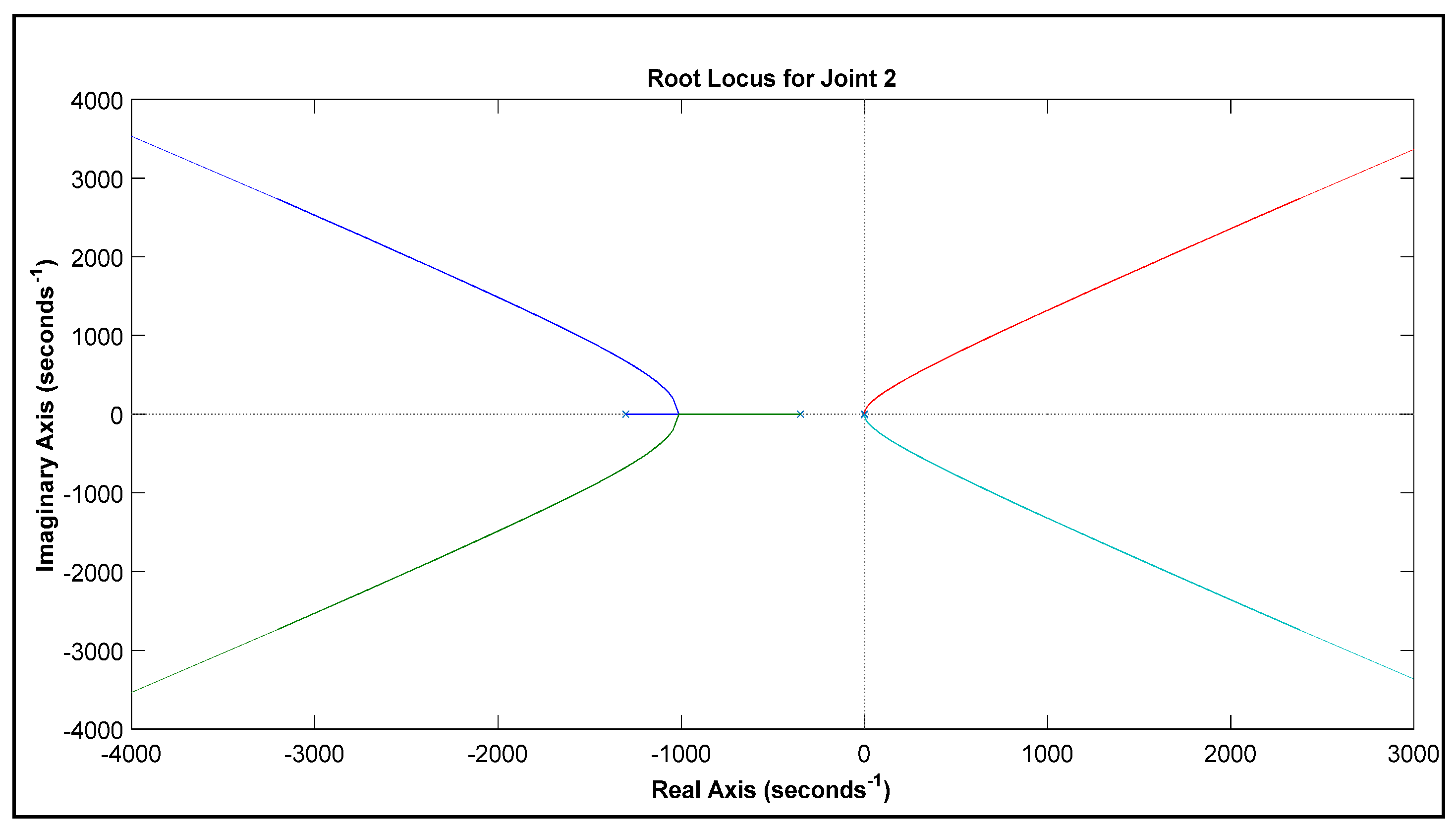
For joint 2, the pole-zero map is shown in Figure 4 which shows that all the poles either on the left-hand side plane or on the origin line of the imaginary axis. The map shows that the system is marginally stable. The second part of Figure 4 is the root locus of joint 2 in which the poles at origin are driving toward instability as it is moving towards the right-hand side.

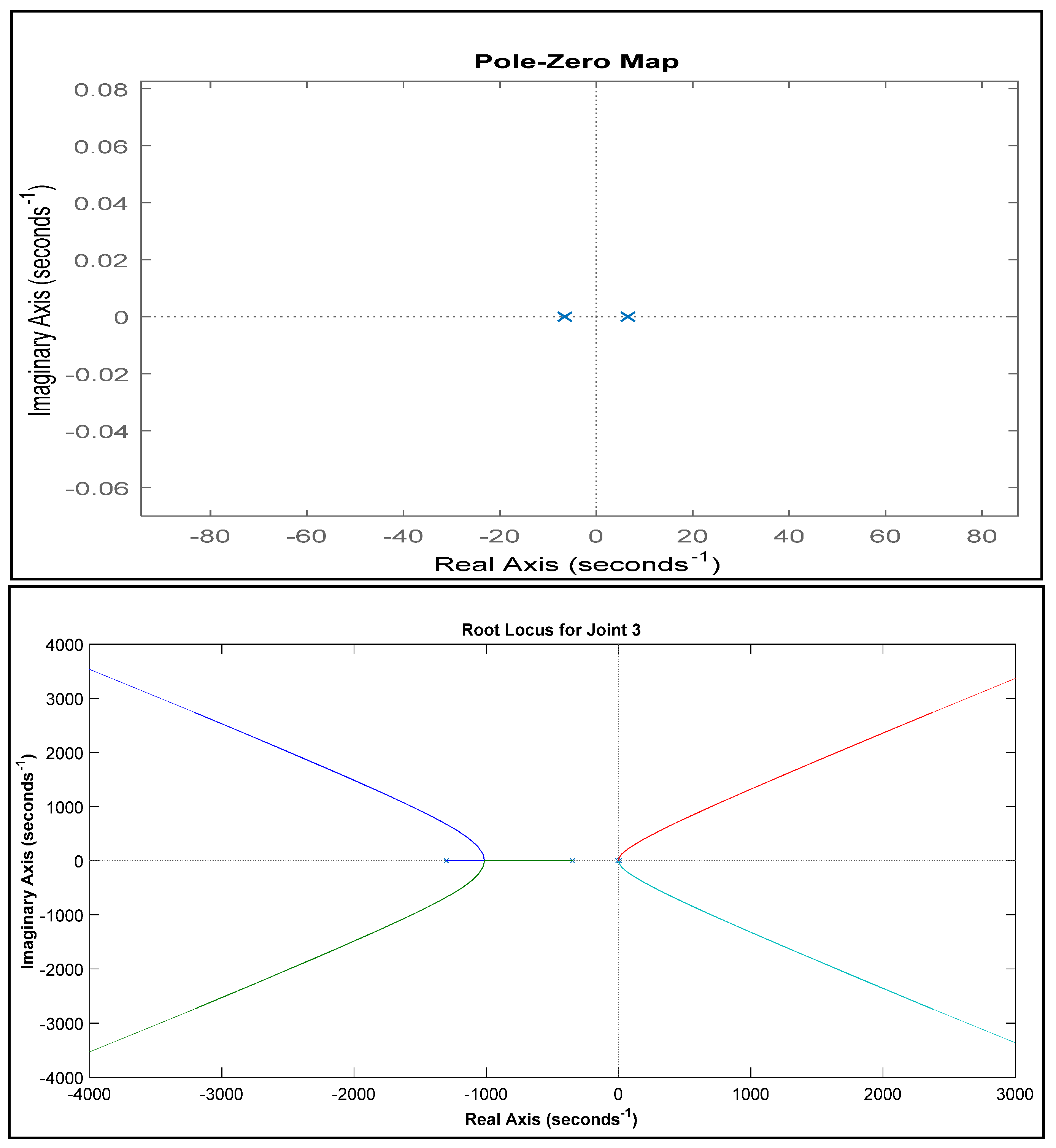
For joint 3, the pole-zero map is shown in Figure 5, which shows that all the poles on the left-hand side plane except one. The map shows that the system is not stable. The second part of Figure 5 is the root locus of joint 3 in which the poles at origin and at right-hand side are driving toward instability as it is moving towards the right-hand side.

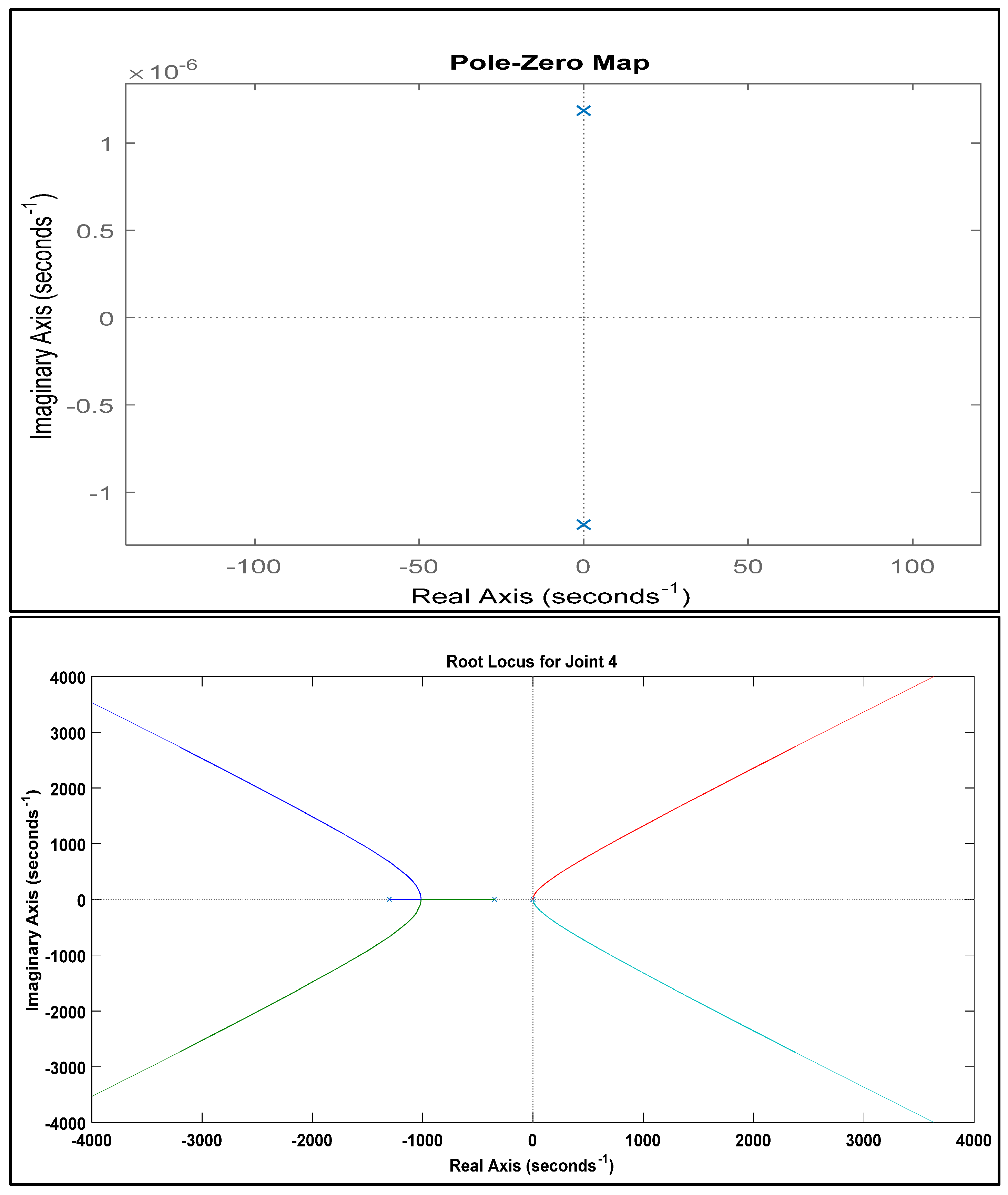
For joint 4, the pole-zero map is shown in Figure 6 which shows that all the poles either on the left-hand side plane or on the origin line of the imaginary axis. The map shows that the system is marginally stable. The other part of Figure 6 is the root locus of joint 4 in which the poles at origin are driving toward instability as it is moving towards the right-hand side.

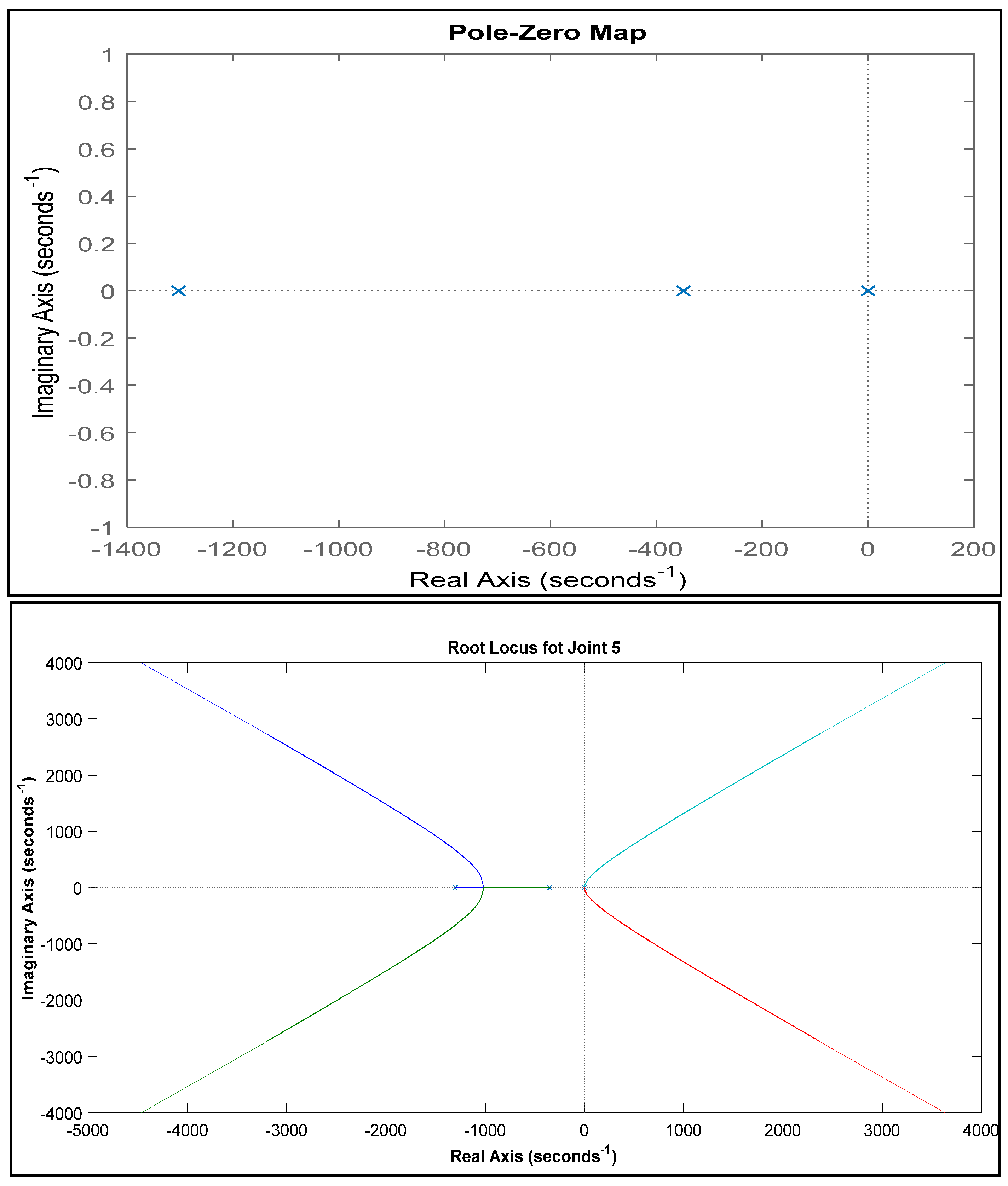
For joint 5, the pole-zero map is shown in Figure 7 which shows that all the poles either on the left-hand side plane or on the origin line of the imaginary axis. The map shows that the system is marginally stable. The second part of Figure 7 is the root locus of joint 5 in which the poles at origin are driving toward instability as it is moving towards the right-hand side. Stability analysis of the sub-systems shows that the systems are either marginally stable or can go towards the instability. Therefore, the need for the controller to control the system is imminent.

4. PID Optimization Results

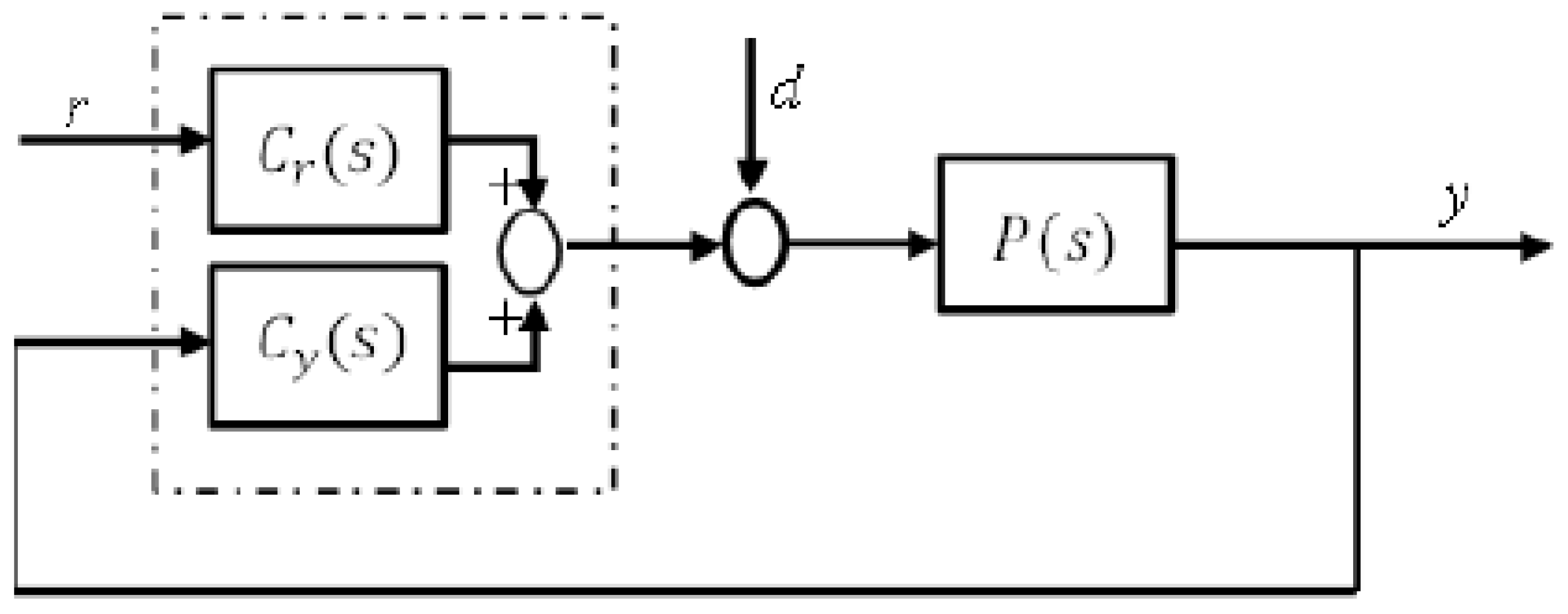
Figure 8. General Structure of the proposed control System Diagram.

The comparative study is carried out with four different cost functions since a well-designed objective function leads to better performance of the system and indicates control design expectations. These objective functions are an integral squared error (ISE) and integral absolute error (IAE). In this research work, the effects of different cost functions on optimization techniques for controller parameters were analysed. The performance of the controller with different cost functions has examined for robustness analysis. The cost function of the food source of PSO, Firefly, ABC and ACO are defined as:

I n t e g r a l S q u a r e d E r r o r (I S E) = \int e^{2} d t

(1)

I n t e g r a l A b s o l u t e E r r o r (I A E) = \int |e| d t

(2)

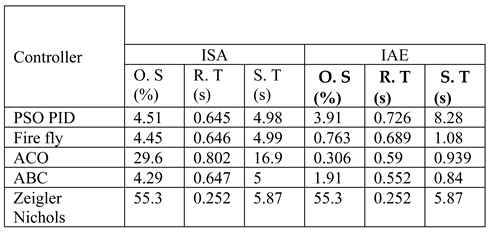
The parameters of applied optimization algorithms for joint 1 are defined in Table 1. Starting with Zeigler-Nichols (ZN) which is a classical criterion to find the gains for PID-ZN requires only two parameters to determine the gains of PID. The parameters of ZN are ‘K_u’ and ‘T_u’ and are given in Table 1.

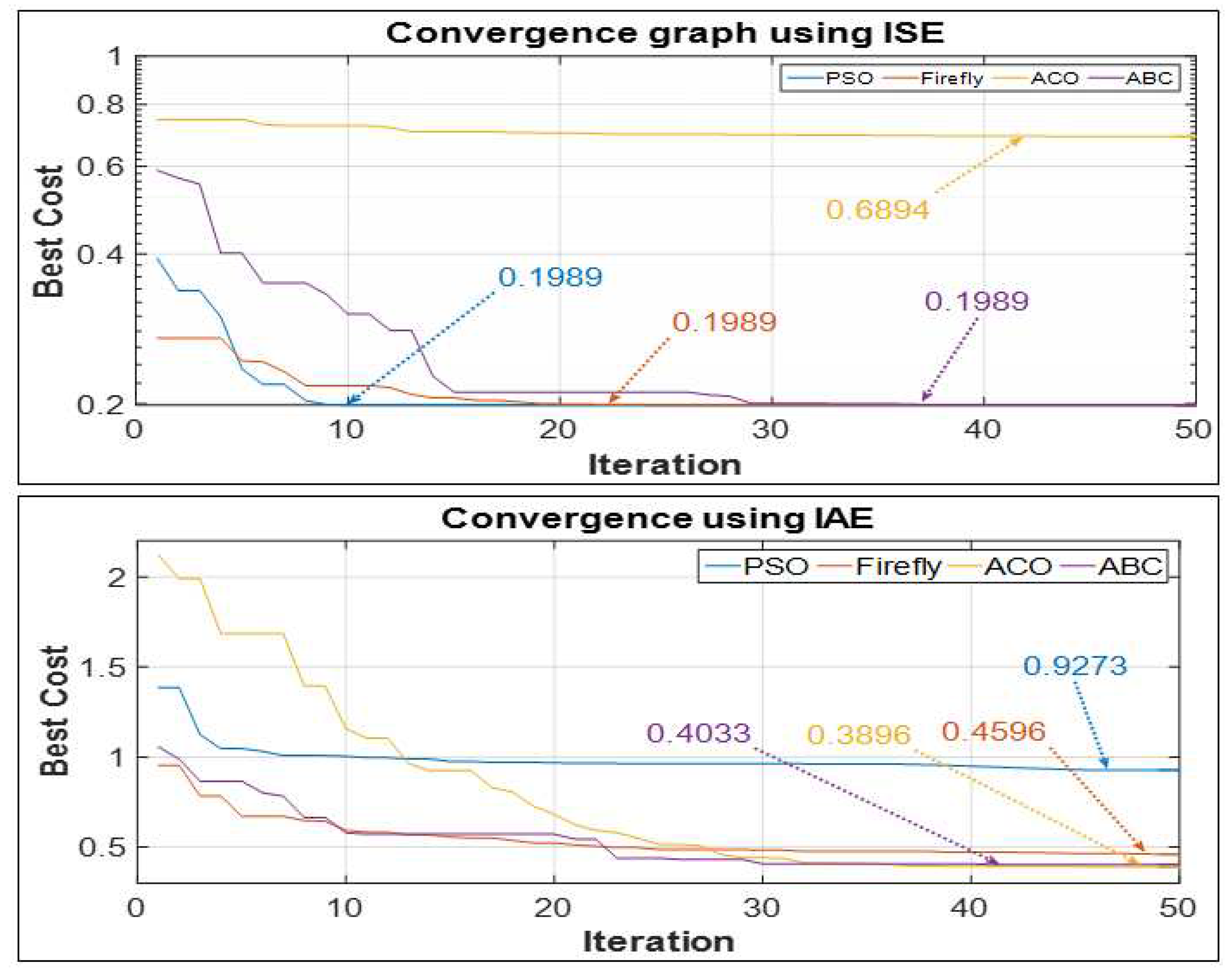
The convergence behaviour towards ISE and IAE cost functions for joint-1 during the tuning for 50 iterations are given in Figure 9. The graphs show convergence values of cost functions versus iterations for joint-1. It is evident from the graph that PSO converges much faster than other optimization techniques while using ISE and IAE as the objective function as shown in Figure 9(a) and Figure 9(b) respectively. When using IAE and ISE as an objective function, ABC converges faster than other optimization techniques as shown in Figure 9(a) and Figure 9(b) respectively. ACO converges faster while using ISE and IAE. Firefly converges faster for all objective functions. It can be seen from the graphs that PSO, Firefly and ABC have less cost value of the functions as compared to ACO while using ISE and IAE. For IAE and ISE, PSO has the high-cost value of the functions as compared to others.

The step response is carried out for Joint-1 with 2-DOF PID controller tuned by above-discussed optimization algorithms using all four cost functions. From the graph, it is evident that ZN response has large overshoots as the approach is designed based on systems oscillatory output due to which overshoot is obvious in the system and there is an occurrence of larger steady-state. While dealing with subjects undergoing rehabilitation, such kind of fast and quick response is avoided to lessen the occurrence of overshoot and jerking which may harm the patient. Therefore, optimal parameter selection is necessary for such systems.

Table 2. Optimal PID control parameters obtained from PSO, Firefly, ACO, ABC and Zeigler Nichols.

Controller	Objective Function	K_p	K_i	K_d	b	c	N
PID-PSO	ISE	0.8000	0.4497	0.8000	0.8000	0.8000	63.1232
PID-PSO	IAE	0.8000	0.2058	0.6315	0.8000	0.8000	2000
PID-Firefly	ISE	0.8000	0.4474	0.8000	0.8000	0.8000	63.2117
PID-Firefly	IAE	0.5701	0.2534	0.6833	0.8000	0.6810	7.5324
PID-ACO	ISE	0.1152	0.0562	0.8000	0.8000	0.8000	1
PID-ACO	IAE	0.7452	0.5184	0.7999	0.7320	0.7080	8.7665
PID-ABC	ISE	0.8000	0.4415	0.8000	0.8000	0.8000	62.8749
PID-ABC	IAE	0.7417	0.4215	0.8000	0.7861	0.7311	8.9157
Zeigler-Nichols	-	2.7	2.5714	0.70875	1	1	100

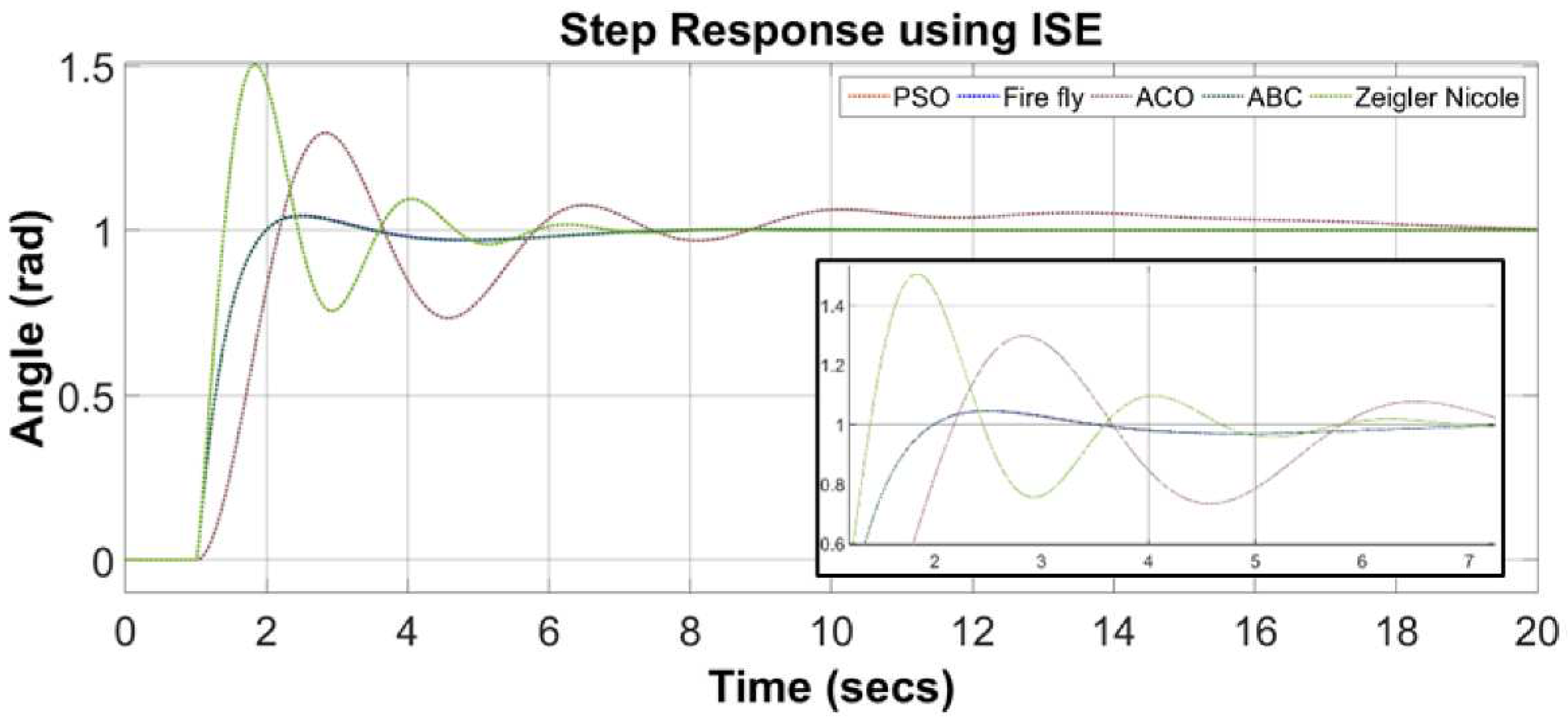
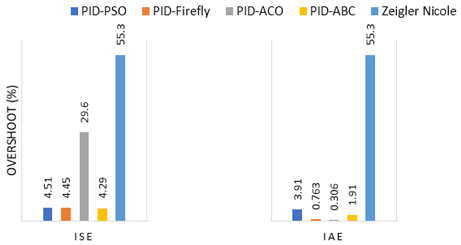
The performance of Joint 1 increases when tuned with the optimization algorithm. It is evident from Figure 10 that ACO’s response has less overshoot than Zeigler-Nicole. However, while using ISE as an objective function ACO’s response is not good as compared to PSO, Firefly or ABC. When tuned with PSO, Firefly or ABC, the response of Joint 1 is approximately similar. However, in terms of statistics, ABC has the shortest overshoot of all and PSO has the shortest settling time and Zeigler-Nicole has the quickest rise time.

Figure 10. demonstrated that all optimization algorithms produce a decent result. The response of the system has less overshoot due to the presence of the time variable in the objective function which puts extra penalties to minimize the error.

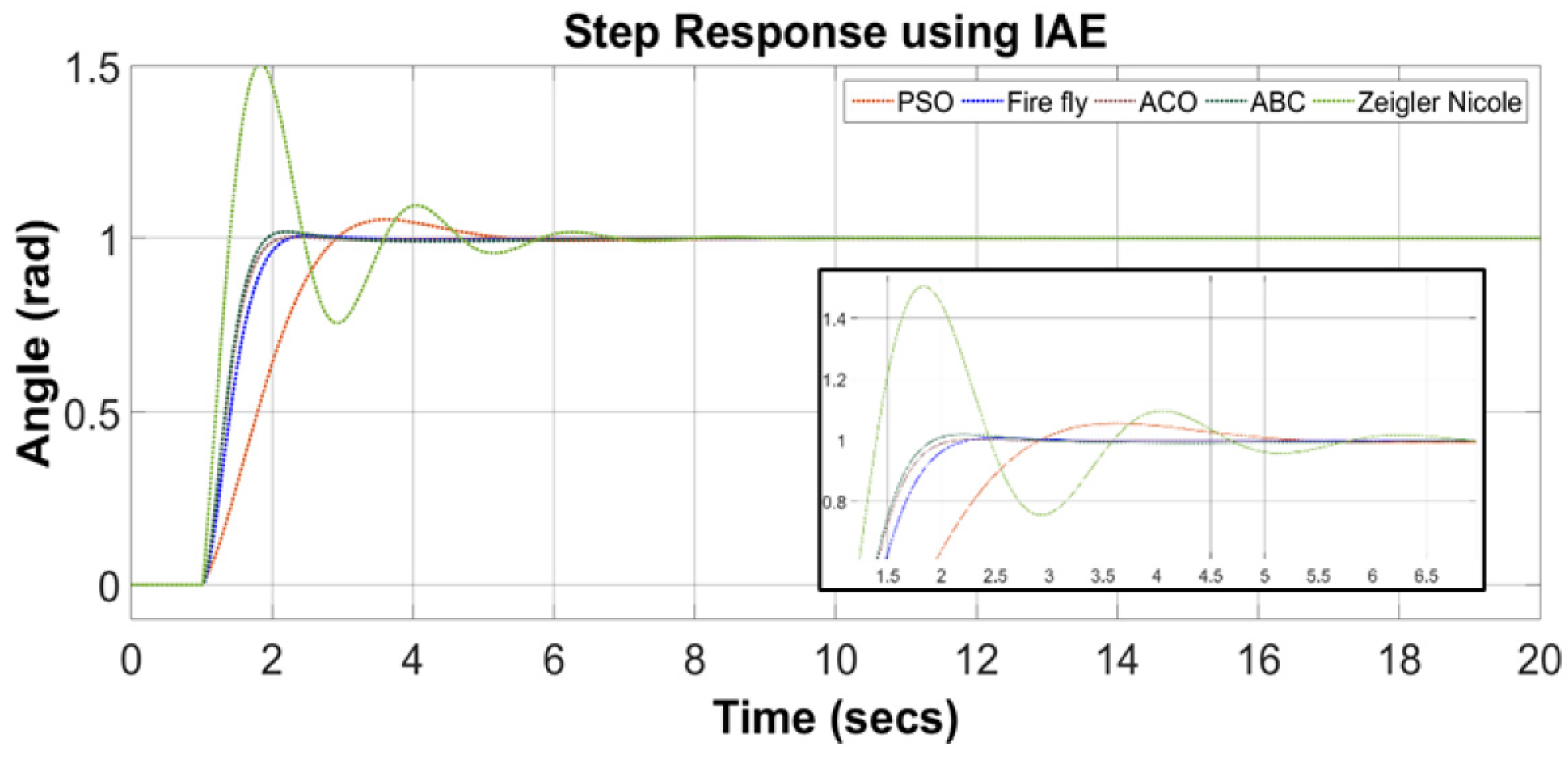
Step response for all optimization algorithms using IAE as a cost function is given in Figure 11. It is evident from the graph that all optimization algorithms produce a decent result. However, the response of PSO is slower and has larger overshoot then other optimization algorithms. Firefly algorithm has less overshoot, quicker rise time and requires less time to settle than PSO. ACO and ABC have better performance in all optimization techniques while using IAE.

5. Conclusions

PID controller is commonly used controller because of a number of features of this algorithm such as simplicity, robustness and wide range of applications. A PID controller continuously calculates an error value as the difference between the desired set point and a measured process variable and applies a correction based on proportional, integral, and derivative terms. In this research paper mathematical models have been validated to determine the PID parameters for the optimization. In the next phase the parameters would be optimized with the better optimization algorithms as a future work. It can be concluded from the results that proposed techniques show less overshoot as compared to other described techniques. For all five joints, the proposed technique shows less overshoot as compared to other techniques. Moreover, the controller tracks the position trajectory precisely and shows no steady-state error. The proposed controller was able to overcome the disturbance effect applied by the subject with an intent to oppose the motion. The proposed technique performs better in terms of overshoot, settling time and steady-state error by satisfying control objectives.

Funding

The APC was funded by Universiti Kuala Lumpur, Malaysia.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data set was collected by 10 to 12 persons. That persons wore that and moved the robotic arm and the values were measured. The proposed control technique has been implemented on a 5-DOF RAX hardware and before any clinical trials, six healthy subjects went for trials under strict protocol. It has been discovered that the proposed control technique rejects the external disturbances as well as keeps the system stable under extreme perturbed conditions.

Conflicts of Interest

The authors declare no conflict of interest.

References

C. Frumento, E. Messier, and V. Montero, "History and future of rehabilitation robotics," 2010.
C. Senanayake and S. A. Senanayake, "Emerging robotics devices for therapeutic rehabilitation of the lower extremity," in Advanced Intelligent Mechatronics, 2009. AIM 2009. IEEE/ASME International Conference on, 2009, pp. 1142-1147.
A. Frisoli, L. Borelli, A. Montagner, S. Marcheschi, C. Procopio, F. Salsedo, et al., "Arm rehabilitation with a robotic exoskeleleton in Virtual Reality," in Rehabilitation Robotics, 2007. ICORR 2007. IEEE 10th International Conference on, 2007, pp. 631-642.
(2014). The Atlas of Heart Disease and Stroke. Available: http://www.who.int/cardiovascular_diseases/resources/atlas/en/.
(2014, August 05, 2014). Available: http://www.who.int/en/news-room/factsheets/detail/cardiovascular-diseases-(cvds).
H. Satoh, T. Kawabata, and Y. Sankai, "Bathing care assistance with robot suit HAL," in Robotics and Biomimetics (ROBIO), 2009 IEEE International Conference on, 2009, pp. 498-503.
H. I. Krebs, N. Hogan, M. L. Aisen, and B. T. Volpe, "Robot-aided neurorehabilitation," IEEE transactions on rehabilitation engineering, vol. 6, pp. 75-87, 1998.
G. Rosati, P. Gallina, and S. Masiero, "Design, implementation and clinical tests of a wire-based robot for neurorehabilitation," IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 15, pp. 560-569, 2007. [CrossRef]
A. Denève, S. Moughamir, L. Afilal, and J. Zaytoon, "Control system design of a 3-DOF upper limbs rehabilitation robot," Computer methods and programs in biomedicine, vol. 89, pp. 202-214, 2008. [CrossRef]
A. Gupta, M. K. O'Malley, V. Patoglu, and C. Burgar, "Design, control and performance of RiceWrist: a force feedback wrist exoskeleton for rehabilitation and training," The International Journal of Robotics Research, vol. 27, pp. 233-251, 2008. [CrossRef]
S. Micera, M. C. Carrozza, E. Guglielmelli, G. Cappiello, F. Zaccone, C. Freschi, et al., "A simple robotic system for neurorehabilitation," Autonomous Robots, vol. 19, p. 271, 2005. [CrossRef]
T. Nef, M. Guidali, V. Klamroth-Marganska, and R. Riener, "ARMin-exoskeleton robot for stroke rehabilitation," in World Congress on Medical Physics and Biomedical Engineering, September 7-12, 2009, Munich, Germany, 2009, pp. 127-130.
A. Pedrocchi, S. Ferrante, E. Ambrosini, M. Gandolla, C. Casellato, T. Schauer, et al., "MUNDUS project: MUltimodal Neuroprosthesis for daily Upper limb Support," Journal of neuroengineering and rehabilitation, vol. 10, p. 66, 2013. [CrossRef]
R. C. Loureiro and W. S. Harwin, "Reach & grasp therapy: design and control of a 9-DOF robotic neuro-rehabilitation system," in Rehabilitation Robotics, 2007. ICORR 2007. IEEE 10th International Conference on, 2007, pp. 757-763. [CrossRef]
T. Teramae, T. Noda, and J. Morimoto, "EMG-based model predictive control for physical human–robot interaction: application for assist-as-needed control," IEEE Robotics and Automation Letters, vol. 3, pp. 210-217, 2018. [CrossRef]
S. M. Sketch, C. S. Simpson, F. Crevecoeur, and A. M. Okamura, "Simulating the impact of sensorimotor deficits on reaching performance," bioRxiv, p. 139857, 2017. [CrossRef]
J. Iqbal, R. U. Islam, and H. Khan, "Modeling and analysis of a 6 DOF robotic arm manipulator," Canadian Journal on Electrical and Electronics Engineering, vol. 3, pp. 300-306, 2012.
D. Luo, M. Roth, C. Wiesener, T. Schauer, H. Schmidt, and J. Raisch, "Reha-Maus: A Novel Robot for Upper Limb Rehabilitation," in Workshop Automatisierungstechnische Verfahren fur die Medizin (AUTOMED), 2010, pp. 33-34.
C. M. Mitschka, M. H. Terra, and A. A. Siqueira, "Markovian theory applied for the development of control strategies in rehabilitation robotics," in American Control Conference (ACC), 2017, 2017, pp. 1797-1802.
A. Sikander, P. Thakur, R. Bansal, and S. Rajasekar, "A novel technique to design cuckoo search based FOPID controller for AVR in power systems," Computers & Electrical Engineering, vol. 70, pp. 261-274, 2018. [CrossRef]
Z.-L. Gaing, "A particle swarm optimization approach for optimum design of PID controller in AVR system," IEEE transactions on energy conversion, vol. 19, pp. 384-391, 2004. [CrossRef]
Z. Bingul and O. Karahan, "Comparison of PID and FOPID controllers tuned by PSO and ABC algorithms for unstable and integrating systems with time delay," Optimal Control Applications and Methods, vol. 39, pp. 1431-1450, 2018. [CrossRef]
M. S. Ayas, E. Sahin, and I. H. Altas, "Optimized control of a parallel mechanism rehabilitation robot," in IASTED International Conference on Robotic Applications, Switzerland, DOI, 2014, pp. 2014.817-014.
H. Mehdi and O. Boubaker, "Impedance controller tuned by particle swarm optimization for robotic arms," International Journal of Advanced Robotic Systems, vol. 8, p. 57, 2011. [CrossRef]
W. Aminiazar, F. Najafi, and M. A. Nekoui, "Optimized intelligent control of a 2-degree of freedom robot for rehabilitation of lower limbs using neural network and genetic algorithm," Journal of neuroengineering and rehabilitation, vol. 10, p. 96, 2013. [CrossRef]
R. K. Mandava and P. R. Vundavilli, "Tuning of PID Controller Parameters of a Biped Robot using IWO Algorithm," in Proceedings of the 2018 4th International Conference on Mechatronics and Robotics Engineering, 2018, pp. 90-94.
A. Ali, S. F. Ahmed, K. A. Kadir, M. K. Joyo, and R. S. Yarooq, "Fuzzy PID controller for upper limb rehabilitation robotic system," in Innovative Research and Development (ICIRD), 2018 IEEE International Conference on, 2018, pp. 1-5. [CrossRef]
G. Khoury, M. Saad, H. Y. Kanaan, and C. Asmar, "Fuzzy PID control of a five DOF robot arm," Journal of Intelligent and Robotic systems, vol. 40, pp. 299-320, 2004.
M. S. Ayas, I. H. Altas, and E. Sahin, "Fractional order based trajectory tracking control of an ankle rehabilitation robot," Transactions of the Institute of Measurement and Control, vol. 40, pp. 550-564, 2018. [CrossRef]
G. B. Mahanta, B. Deepak, M. Dileep, B. Biswal, and S. Pattanayak, "Prediction of Inverse Kinematics for a 6-DOF Industrial Robot Arm Using Soft Computing Techniques," in Soft Computing for Problem Solving, ed: Springer, 2019, pp. 519-530.
H. V. H. Ayala and L. dos Santos Coelho, "Tuning of PID controller based on a multiobjective genetic algorithm applied to a robotic manipulator," Expert Systems with Applications, vol. 39, pp. 8968-8974, 2012. [CrossRef]
V. K. Kadiyala, R. K. Jatoth, and S. Pothalaiah, "Evolutionary soft computing tools based tuning of PID controller for EMA-AFC," in TENCON 2009-2009 IEEE Region 10 Conference, 2009, pp. 1-6.
M. Geetha, P. Manikandan, and J. Jerome, "Soft computing techniques based optimal tuning of virtual feedback PID controller for chemical tank reactor," in Evolutionary Computation (CEC), 2014 IEEE Congress on, 2014, pp. 1922-1928.

Figure 1. represents the controller card used for RAX which consists of Master/Slave network and drivers used for motors.

Figure 2. Control Board.

Figure 3. The pole-zero response and root locus for joint 1.

Figure 4. The pole-zero response and root locus for joint 2.

Figure 5. The pole-zero response and root locus for joint 3.

Figure 6. The pole-zero response and root locus for joint 4.

Figure 7. The pole-zero response and root locus for joint 5.

Figure 9. Convergence behavior of PSO, Firefly, ACO and ABC: (a) ISE, (b) IAE.

Figure 10. Step Response of Joint 1 using ISE as a cost function.

Figure 11. Step Response of Joint using IAE as a cost function.

Table 1. Internal Parameters of optimization algorithms.

Controller	Parameter	Value
Particle Swarm Optimization	Particles number	20
	Iterations number	50
	(Inertial term)	0.4
	$w_{m a x}$ (Inertial term)	0.9
	$c_{1}$ (Acceleration coefficient)	2
	$c_{2}$ (Acceleration coefficient)	2
Firefly	Swarm Size	20
	Number of iterations	50
	$γ$ (Light absorption coefficient)	1
	$β$ (Attraction Coefficient)	2
	$α$ (Damping ratio)	0.2
	$δ$ ( Uniform Mutation Range)	0.039
Ant Colony	Archive Size	20
	Number of iterations	50
	Sample Size	10
	$q$ (Selection pressure)	0.5
	$ζ$ (Deviation distance ration)	1
Artificial Bee Colony	Colony Size	20
	Number of iterations	50
	$L$ (Abandonment Limit)	72
	$a$ (Acceleration coefficient)	1
Zeigler Nichols	K_u	4.5
Zeigler Nichols	T_u	2.1

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer