Prerpints.org logo
Preprint
Article

Superconducting Gravimeters: A Novel Tool for Validating Remote Sensing Evapotranspiration Products

Altmetrics

Downloads

144

Views

295

Comments

3

A peer-reviewed article of this preprint also exists.

Submitted:

29 May 2023

Posted:

30 May 2023

You are already at the latest version

Alerts
Abstract
The practical utility of remote sensing techniques relies on validating them with ground-truth data. Validation requires similar spatial-temporal scales for ground measurements and remote sensing resolution. Evapotranspiration (ET) estimates are commonly compared to weighing lysimeter data, which provide precise but localized measurements. To address this limitation, we propose using superconducting gravimeters (SG) to obtain ground-truth ET data at larger spatial scales. SG measure gravity acceleration with high resolution (tenths of nm/s2) within a few hundred meters. Similar to lysimeters, gravimeters provide direct estimates of water mass changes for determining ET without soil disturbance. To demonstrate the practical applicability of SG data, we conducted a case study in Buenos Aires Province, Argentina (-34.87, -58.14). We estimated cumulative ET values for 8-day and monthly intervals using gravity and precipitation data from the study site. Comparing these values with MODIS-based ET products (MOD16A2), we found a very good agreement at the monthly scale, with an RMSE of 32.6 mm/month (1.1 mm/day). This study represents progress in using SG for hydrogeological applications. The future development of lighter and smaller gravimeters is expected to further expand their use.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

The evapotranspiration (ET) is one of the major components of the global water cycle and provides a critical nexus between terrestrial water, carbon and surface energy exchanges. Accurate estimation of ET is essential for agrometeorological studies, understanding hydrological and ecological processes, and developing effective water management strategies. Nevertheless, ET is inherently difficult to measure and predict especially at large spatial scales as its spatio-temporal patterns depend on vegetation types, soil properties, and the meteorological conditions at the study site [1].
Most methods to estimate ET are based on the water balance equation. This equation, also known as the continuity equation, accounts for water storage changes in a given water system and time interval caused by inputs and outputs of water flow (i.e., rainfall, ET, and surface and subsurface runoff). Water storage is probably the most difficult component of the water balance equation to quantify due to two main reasons. First, water storage is composed of different contributions like soil moisture, groundwater, and surface water bodies (including snow and ice) that are usually monitored individually. Secondly, the high spatial heterogeneity observed in both the hydraulic properties and the scales of the flow processes involved, makes it difficult to obtain representative values of water storage changes for the whole system [2]. Thus, the estimate of ET from the water balance equation is largely conditioned by the accuracy in determining water storage changes.
At point scale, weighable lysimeters provide accurate measurements of water storage changes in the unsaturated zone by recording mass changes of a soil profile. Based on these measurements and an independent record of the flux across the lower boundary of the lysimeter, ET can be easily calculated from the mass balance equation [3]. It is important to remark that weighable lysimeters are considered the only device to directly measure the actual ET [4,5]. However, lysimeter data describe the ET in a single point of the field and do not consider water storage changes in deeper zones of the soil [6].
Water storage changes can also be estimated at regional and global scales using data from the Gravity Recovery and Climate Experiment (GRACE) and GRACE Follow-On (GRACE-FO) satellite missions [7]. These missions provide time-variable measurements of the Earth’s gravity field with high accuracy that have been used in many studies of mass variation in different components of the climate system, including terrestrial water storage changes, groundwater depletion, ice sheets and glaciers changes, and ET [8,9,10,11]. Unfortunately, the application of GRACE data in local water resources is greatly limited because of the coarse spatial resolution. Swenson et al. [12] show that the accuracy of GRACE-derived water storage increases with the study area and they estimate an accuracy of less than 1 cm for study areas larger than 400000 km2. Based on this result, the spatial resolution of GRACE data is not expected to be better than a few hundred km.
Despite the above-mentioned methods, the determination of water storage changes at the mesoscale (tens to hundreds of meters) remains a challenge for the hydrological community. Measurements of water system components at this spatial resolution are useful for validating remote sensing estimates [13,14,15]. A promising method to estimate water storage at mesoscale is to use data from superconducting gravimeters (SG) [2,16]. Similar to GRACE and GRACE-FO satellite missions, these terrestrial instruments measure temporal variations of gravity with unprecedented accuracy and a spatial resolution estimated between 50 and 4000 m [16]. From these gravity measurements, it is possible to estimate the integrated water storage changes with an accuracy of the order of a few mm. Due to these characteristics, SG have been used as hydrological sensors to calibrate and validate hydrological models [17], monitor the artificial recharge of an aquifer [18], and specific yield estimates [19]. In addition, SG data can be used to estimate ET in the mesoscale [2,20,21,22].
The main objective of this work is to show the potential of the SG as a novel tool for the validation of ET estimates from satellite data. Ground-truth ET is obtained from the water balance equation using SG data recorded at the Argentine-German Geodetic Observatory (AGGO) located in the Buenos Aires Province, Argentina. ET is a key hydrological parameter at the study site since it is the main water loss mechanism and it is strongly associated with water availability. Nevertheless, there are few ground stations to estimate ET in the Buenos Aires Province. In this context, remote sensing methods represent a valuable tool to monitor ET since they allow mapping the patterns of this hydrological variable at different spatial scales. Particularly, the Moderate Resolution Imaging Spectroradiometer (MODIS) global terrestrial ET product (MOD16A2) is widely used in different ecosystems due to its high spatio-temporal resolution. The practical utility of the MOD16A2 ET product depends on validation by ground-truth data at similar temporal and spatial scales [23,24,25]. In the Pampas region, Degano et al. [26] evaluated the performance of the MOD16A2 version 6 ET product against ET values based on soil water balance data from seven ground stations. They concluded that the MOD16A2 product underestimates ET values in humid-subhumid areas. Therefore, in this work, MOD16A2 product is validated using the gravity-based method for an annual period from May 2017 to May 2018 at 8-day and monthly scales.

2. Study Site and Methodology

2.2. Study Site

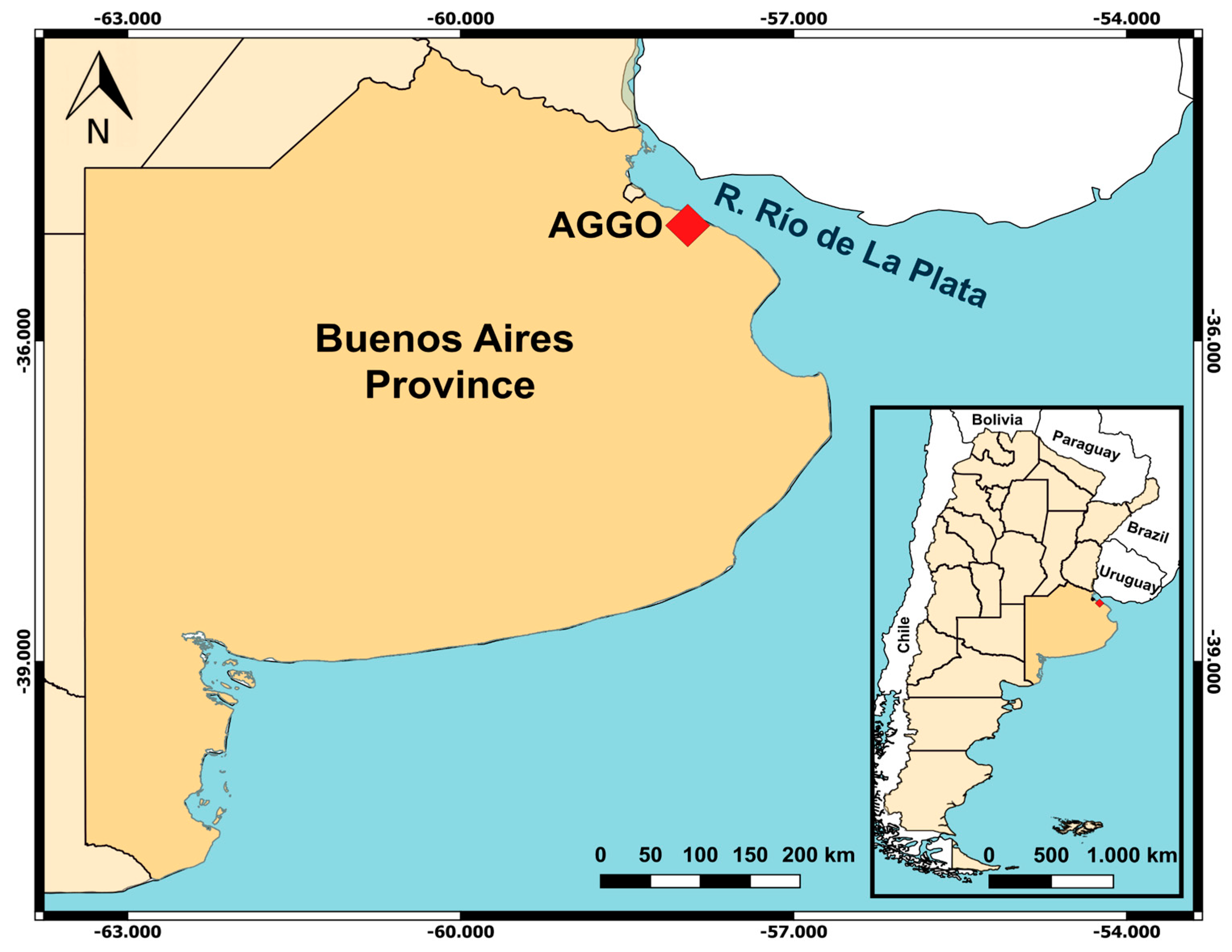
The AGGO is a fundamental geodetic observatory located in Parque Pereyra Iraola, Berazategui, Argentina (Figure 1). AGGO is equipped with the main geodetic techniques such as VLBI, SRL, GNSS, absolute gravimetry, and a superconducting gravimeter (SG038) which continuously measures the temporal gravity changes since December 2015 [27]. It is worth noting that the SG038 is currently the only SG operating in Latin America and the Caribbean. In addition to geodetic techniques, hydrometeorological sensors have been installed at AGGO. A weather station with sensors for air temperature, relative humidity, short and long wave radiation, wind speed, and two rain gauges were installed in April 2016. In addition, soil moisture sensors have been installed in several profiles between 5 and 450 cm depth. These instruments are located in the vicinity of the SG038. The hydrometeorological dataset is available in Mikolaj et al. [28].
AGGO is located in the Pampas region, one of the largest plains in the world (approximately 520000 km2) being an important food-producing region due to its fertile land suitable for livestock and agricultural production [29]. In this region, vertical water flow predominates over horizontal ones with a strong interaction between surface water and groundwater.
The AGGO site is covered by natural grass and surrounded by a small forest of eucalyptus. The mean annual temperature, relative humidity, and precipitation of the study site are 15.8°C, 74.3%, and 1007 mm, respectively. Furthermore, the soil is composed of silty and clayey sediments and the mean groundwater level is approximately 13 m depth.

2.2. Superconducting Gravimeter

SG are the most precise and long-term stable relative instrument to monitor temporal gravity variations. The measurement resolution of SG is in the range of 0.1 – 0.3 nm s-2 with a temporal resolution of 1 second. The principle of measurement is based on the levitation of a superconducting sphere in a stable magnetic field generated with a pair of niobium coils [30]. In order to maintain the superconducting state, the gravity sensor is inside a liquid helium Dewar with a refrigeration system which keeps the temperature close to absolute zero (4.2 K). Any change in gravity produces an external force that affects the levitation of the sphere. To compensate for that external force and keep the sphere at a fixed position, an electrical current is injected by an auxiliary feedback coil inducing a change in the magnetic field intensity and consequently, in the voltage. The SG output signal is provided in voltage units, and then, it is converted to gravity values using a calibration factor.
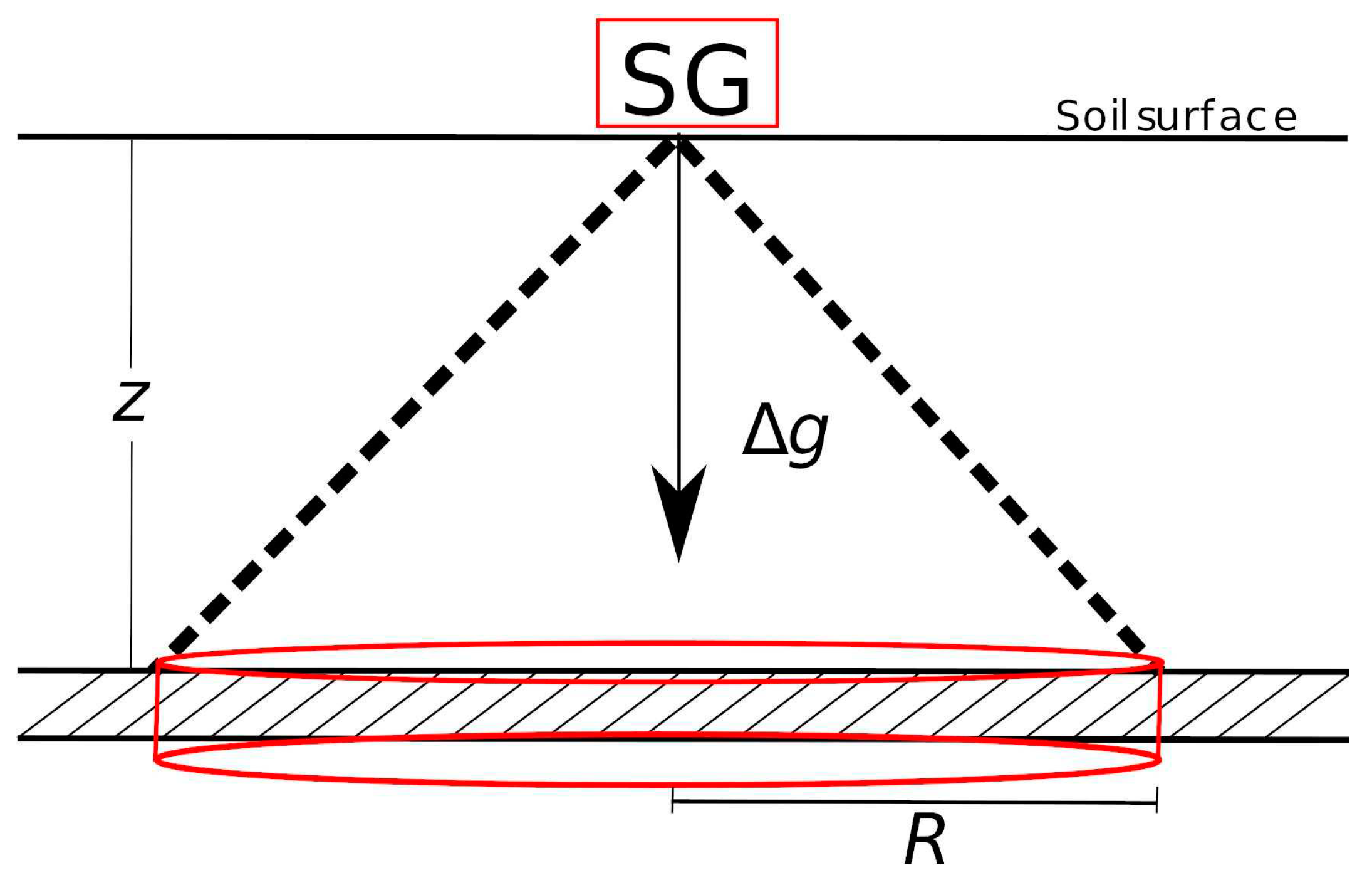
As it is well known from Newton's law, the gravimetric signal attenuates with the square of the distance. Then the SG is more sensitive to nearby mass variations. To define the radius of influence R of the SG, we will consider the gravimetric effect of an infinite horizontal layer of water at depth z. The gravity response of 1 mm thick layer water is 0.42 nm s-2 which is usually called water admittance [31] and is independent of the depth z [32]. As SG accuracy is in the range 0.1 – 0.3 nm s-2, these devices can detect water layers with thicknesses from 0.2 to 0.7 mm.
The radius of influence or footprint of SG can be inferred from the comparison between the water admittance value and the gravity effect of a vertical cylinder of 1 mm thickness and radius R at a depth z below the SG, as shown in Figure 2.
The gravity effect (Δg) of a vertical cylinder of radius R and 1 mm thickness is estimated from the following equation [33]:
Δ g ( z , R ) = 1 − z z 2 + R 2   0.42
nm s-2
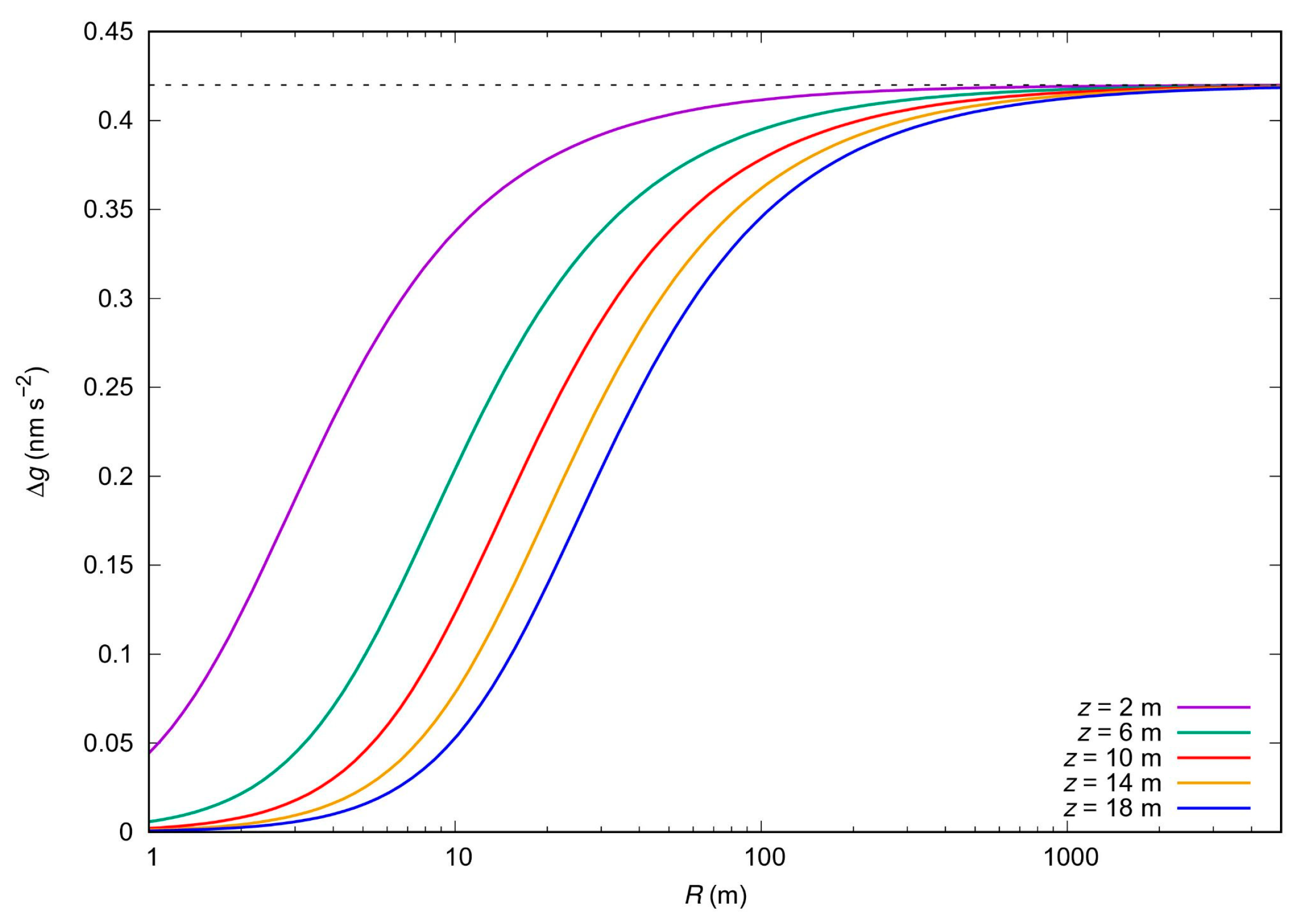
Figure 3 shows the gravity effect (Δg) as a function of R for different depths. Note that when R tends to infinity in Equation (1), we obtain the value of the water admittance (0.42 nm s-2). However, 99% of the gravity signal comes from an area of radius 200 to 2000 m, depending on the depth. Moreover, from Equation (1) it can be shown that approximately 99% of the signal is originated within a radius:
R = 100   z
Equation (2) defines the radius of influence of the SG, which depends on the depth z. The dependence on depth explains why different radius of influence ranging from 50 to 4000 m are reported in literature (i.e., [2,5,34]). Since the mean groundwater depth in the study site is 13 m, a radius of influence less than 1300 m would be expected.
It is important to mention that Equation (1) is valid for flat terrain. When the topography is not smooth, specific site effects on gravity measurement must be considered to compute R.

2.3. Ground-Truth ET Estimates Using SG Data

ET water balance-based approach is usually used as a benchmark for evaluating other ET products. This approach is based on the principle of mass conservation and contemplates the difference between incoming and outgoing hydrological fluxes at different temporal and spatial scales. The classical water balance equation can be expressed as:
E T = P − R s − Δ S
where ET, P and Rs are cumulative ET, precipitation, and runoff (in mm) during an arbitrary period of time Δt = ti - ti-1, respectively, and Δ S represents the water storage changes. In this study, Δt periods of 8-day, which is the temporal resolution of the MOD16A2 product, and 1 month are considered. The estimated ET values using Equation (6) are representative within an area defined by the SG radius of influence whose value is approximately 1300 m in the study site (see Section 2.2).
As previously mentioned, the study site is characterized by very low topographic slopes. Then, runoff (Rs) can be estimated as:
R s = α P
where α is a model parameter which is assumed to be constant. Several studies performed in Buenos Aires Province report a value of α = 0.05.
Water storage changes ΔS are estimated from SG data (Δg) using a factor C to convert gravity variations into equivalent water storage changes as follow:
Δ S = C Δ g
The value of C depends on the topography and the size of the building that houses the SG. The building impedes the processes of ET and natural infiltration, affecting the gravity measurements. This phenomenon is known as the umbrella effect [35]. When the topography of the study site is flat and the umbrella effect is negligible, the conversion factor C is 2.38 mm (nm s-2)-1 [31]. At the AGGO study site, Pendiuk [22] estimated a site-specific C of 2.57 mm (nm s-2)-1 from a regression analysis between gravity residuals and water storage changes computed by soil moisture data.
Combining Equations (3) – (5) an expression for computing ET is obtained:
E T = ( 1 − α ) P − C Δ g
Note that Equation (6) only depends on precipitation and gravity residuals so no additional data about physiological properties of canopy is required. In section 3, ET values estimated from Equation (6) are used as ground-truth data to validate the global terrestrial ET products MOD16A2.

2.4. Description of the data Set

In this work, an annual period from May 1, 2017 to April 30, 2018 is considered. Gravity residuals and precipitation time series are available on the GFZ database [28]. The MODIS global terrestrial ET (MOD16A2) data is obtained from the Google Earth Engine platform.

2.4.1. Gravity Residuals and Water Storage Changes Time Series

Gravity residuals (Δg) with an hourly time resolution are provided by the GFZ database [28]. These residuals are obtained from SG038 data after subtraction for the Earth tides, atmospheric and oceanic loading, polar motion effects, instrumental drift, and global both atmospheric and hydrological effects [36]. Additionally, a moving average filter with a window length of 6 days is applied to the data series in order to reduce the non-hydrological effects that can be distinguished in gravity residuals. 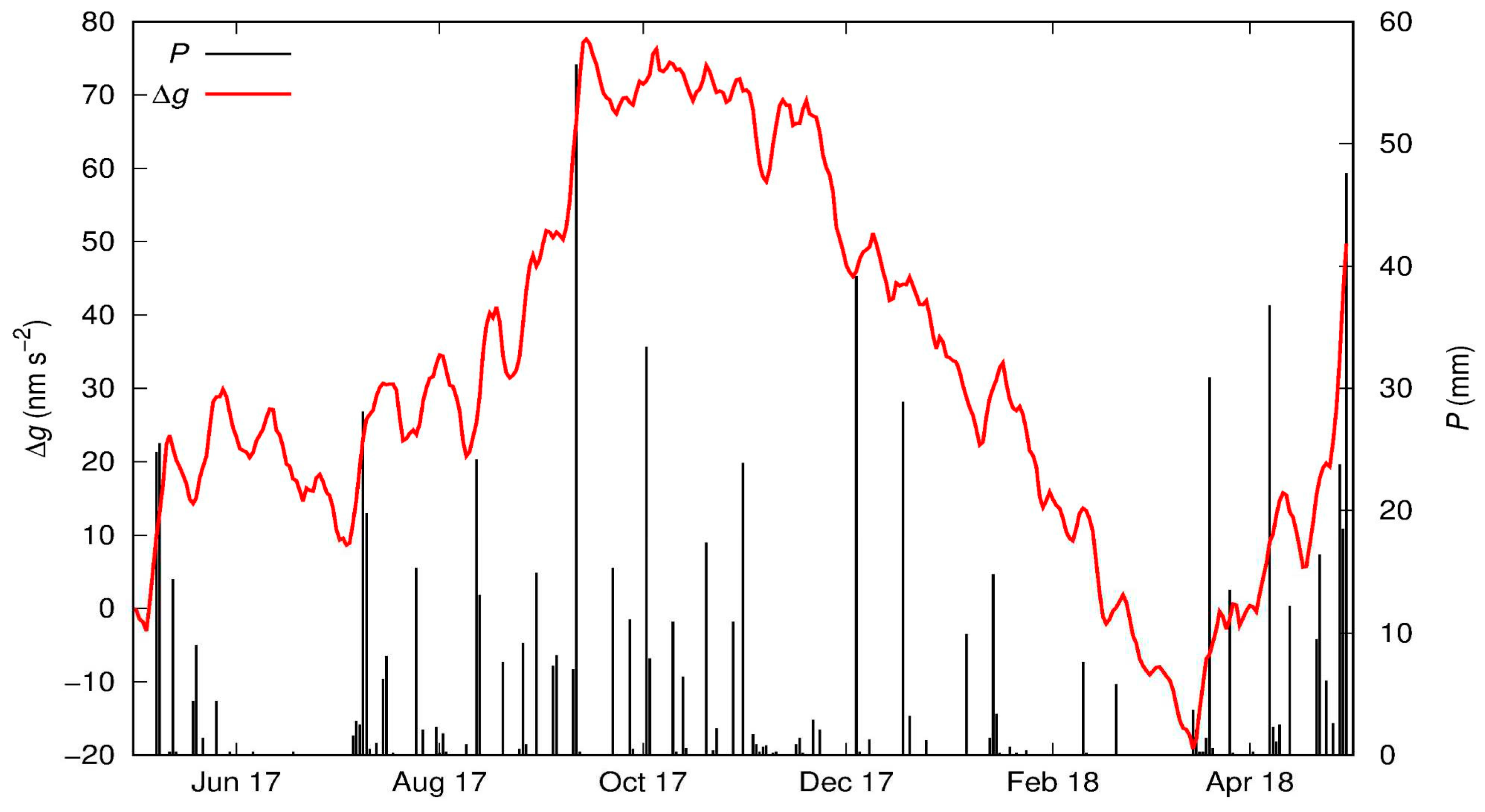Figure 4 shows gravity residual time series which is assumed to reflect the main local water storage changes in the surroundings of SG038. For the period November 2017 - March 2018, it is assumed that the water storages decrease significantly since the gravity residual is directly proportional to water storage changes (see Equation (5)).
Note that, despite the filtering applied to the gravity data, a non-hydrologic signal with a period of approximately 14 days persists, identified from a spectral analysis.

2.4.2. Precipitation

Precipitation (P) is recorded in hourly time steps by two rain gauges. They are located at a distance of 10.9 m from each other near the SG038. Both time series are pre-processed and then merged to obtain a precipitation series without missing values [36]. Figure 4 shows the precipitation series for the study period. The cumulative precipitation is 838 mm, which is less than the mean annual value (1007 mm). April 2018 is the rainiest month of the study period (P = 180 mm), followed by September and October 2017, while June is the driest month (P = 1.1 mm).

2.4.3. Satellite Data (MOD16A2)

MOD16 is selected for this study since to our knowledge it is the most widely used remote-sensing-based ET data set at the global scale. MOD16 is usually used to evaluate modelled ET due to its high spatial resolution, extensive historical data availability, and global coverage. However, it is not applicable in ice-driven catchments, desert areas, and water bodies where the MOD16 algorithm cannot derive ET [37]. The MOD16 product has been evaluated against ground measurements derived from eddy flux towers in several parts of the world, resulting in varying levels of accuracy across different regions, including North America, Europe, South America, and Asia [37,38,39,40]. In all of these comparisons, it is important to highlight that the ground measurements themselves have inherent uncertainties, typically ranging from 10% to 30% when ET is estimated by eddy flux towers.
The MOD16A2 version 6 data is provided by Earth Data-National Aeronautics and Space Administration (NASA). The algorithm to calculate ET is based on the Penman-Monteith equation [41]. Inputs come from the reanalysis global daily meteorological dataset Modern-Era Retrospective analysis for Research and Applications (MERRA), and from MODIS data: land cover (MOD12Q1) product, Leaf Area Index/Fraction of Photosynthetically Active Radiation (LAI/FPAR MOD15) product, and Albedo (MCD43A2/A3) product. MOD16A2 is based on the algorithm first proposed by Mu et al. [37]. The actual ET is retrieved from remote sensing data as the sum of evaporation losses from the wet canopy, actual plant transpiration, and actual soil evaporation [37,42]. The MOD16A2 estimates ET in 8-day time intervals. This time period allows capturing changes in ET patterns on a global scale. Additionally, the 8-day interval is also related to the satellite data acquisition used in the product, resulting in good accuracy. However, some updates have been implemented in the operational code to fix some issues. These updates are detailed in Running et al. [43].
The MOD16A2 version 6 product is provided with a spatial resolution of 500 m per pixel. To obtain representative ET values for the study site, average values are computed for a 3x3 pixel grid with the SG as the central point. Note that the grid size of 3x3 pixel (1500 m) is similar to the radius of influence of the SG, which is approximately 1300 m (see Equation (2)).

2.5. Statistical Performance Metrics

To compare the performance of MOD16A2 products in relation to the ET estimated by the gravity-based approach, three statistics metrics are computed: (1) Mean Absolute Error (MAE), (2) Root Mean Square Error (RMSE), and (3) Pearson correlation coefficient (r):
M A E = ∑ j = 1 N E T M j − E T j N
R M S E = ∑ j = 1 N E T M j − E T j 2 N  
r = ∑ j = 1 N ( E T M j − < E T M > ) ( E T j − < E T > ) ∑ j = 1 N E T M j − < E T M > 2 E T j − < E T > 2  
where N represent the number of total observations, E T M j and E T j are MOD16A2 data and ET gravity-based approach at time period j, respectively. The symbol <> indicates the mean value of the variable for the whole period of the analysis.

3. Results

3.1. ET Estimates on an 8-Day Timescale

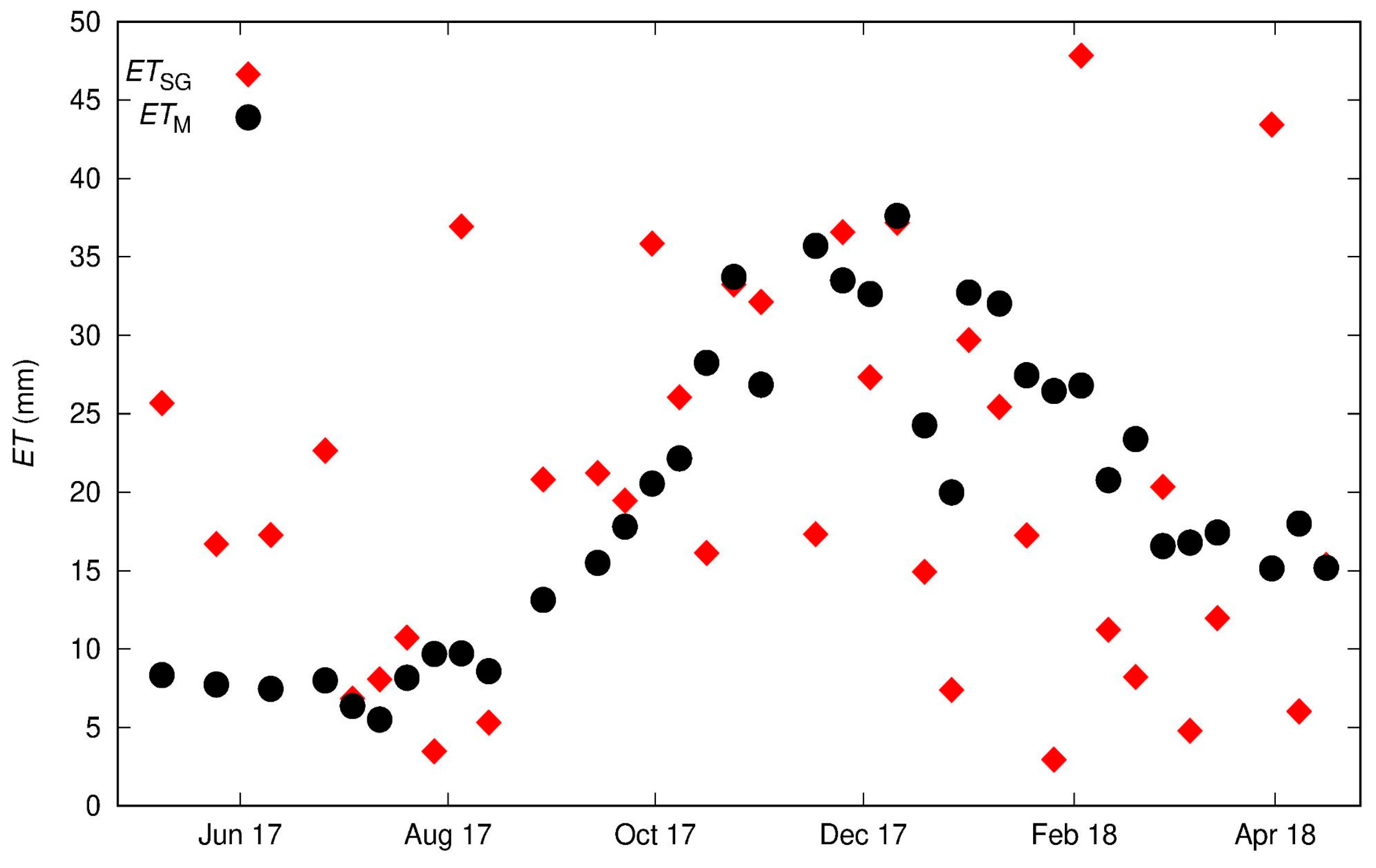
ET is estimated by the gravity-based method using Equation (6) on an 8-day time scale and compared to the MOD16A2 product (ETM). Figure 5 shows ET gravity-based approach (ETSG) and ETM time series. Negative values of ETSG estimated by the gravity-based technique are not realistic and were removed from this analysis. ETM shows a clear seasonal pattern where the maximum values are observed in the period November 2017 - December 2018, whereas, values of ETSG show dispersion. Moreover, the gravity-based technique yields high ET values for the cold period May 2017 - June 2017. Statistical metrics are calculated using Equations (7)–(9) and the obtained values are listed in Table 1. The estimated MAE and RMSE values are 9.32 (1.2 mm day-1) and 11.9 mm (1.5 mm day-1), respectively. In addition, the estimated value of the correlation coefficient is r = 0.4, indicating a weak correlation due to the significant dispersion of ETSG.
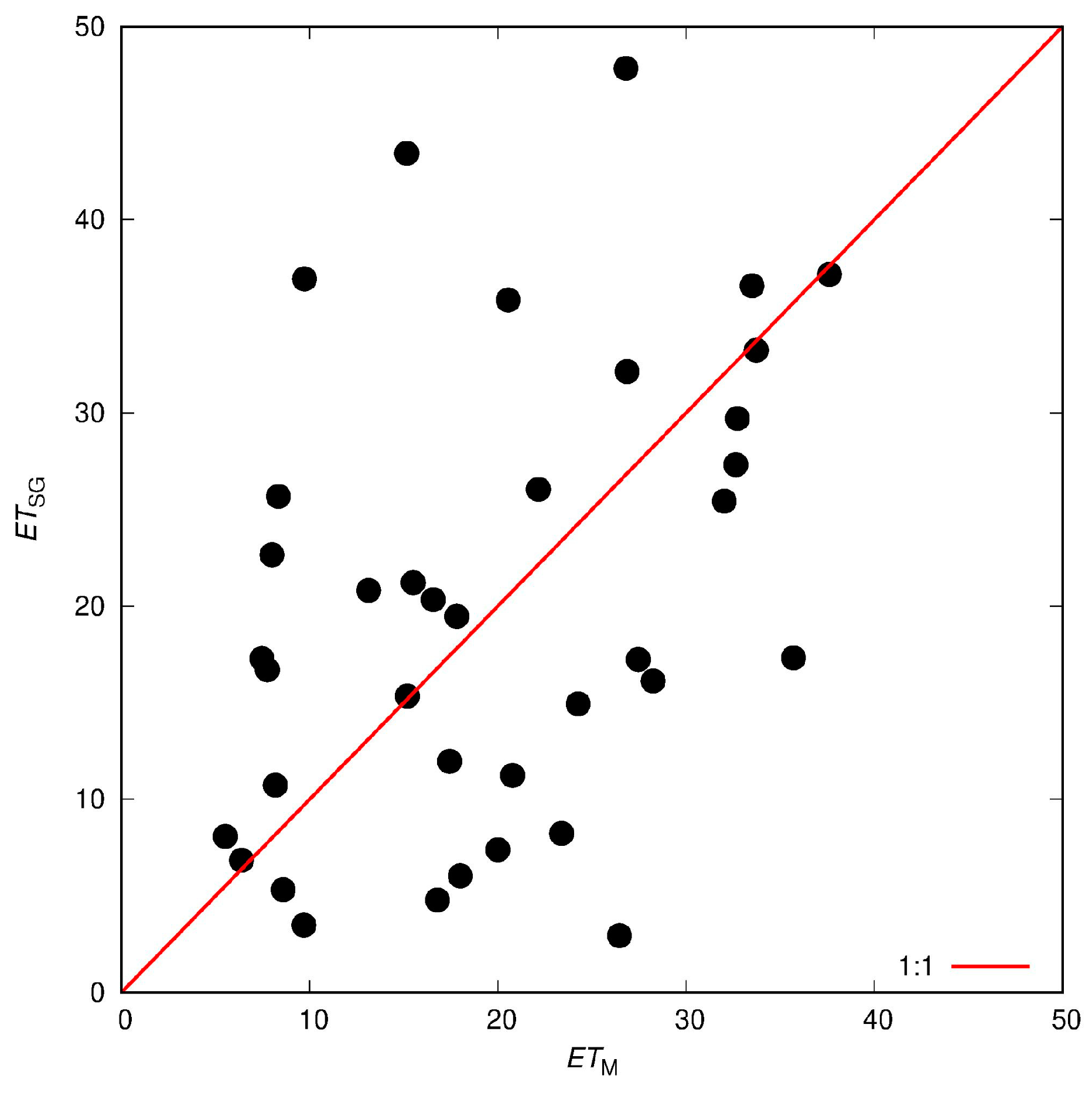
In order to visualise the dispersion between ET series, a crossplot of ETSG and ETM is shown in Figure 6. The discrepancies between the ET series could be attributed to a non-hydrological signal with a period of approximately 14 days observed in gravity data (Figure 4). This periodical signal on the gravimetric residuals may be associated with the global non-tidal oceanic and atmospheric loading effect, which was probably not completely removed in the gravity signal processing stage. At timescales longer than 14 days this signal is expected to attenuate. In the next section, ET estimated by both methods at monthly timescale are compared.

3.2. Estimation of Monthly ET

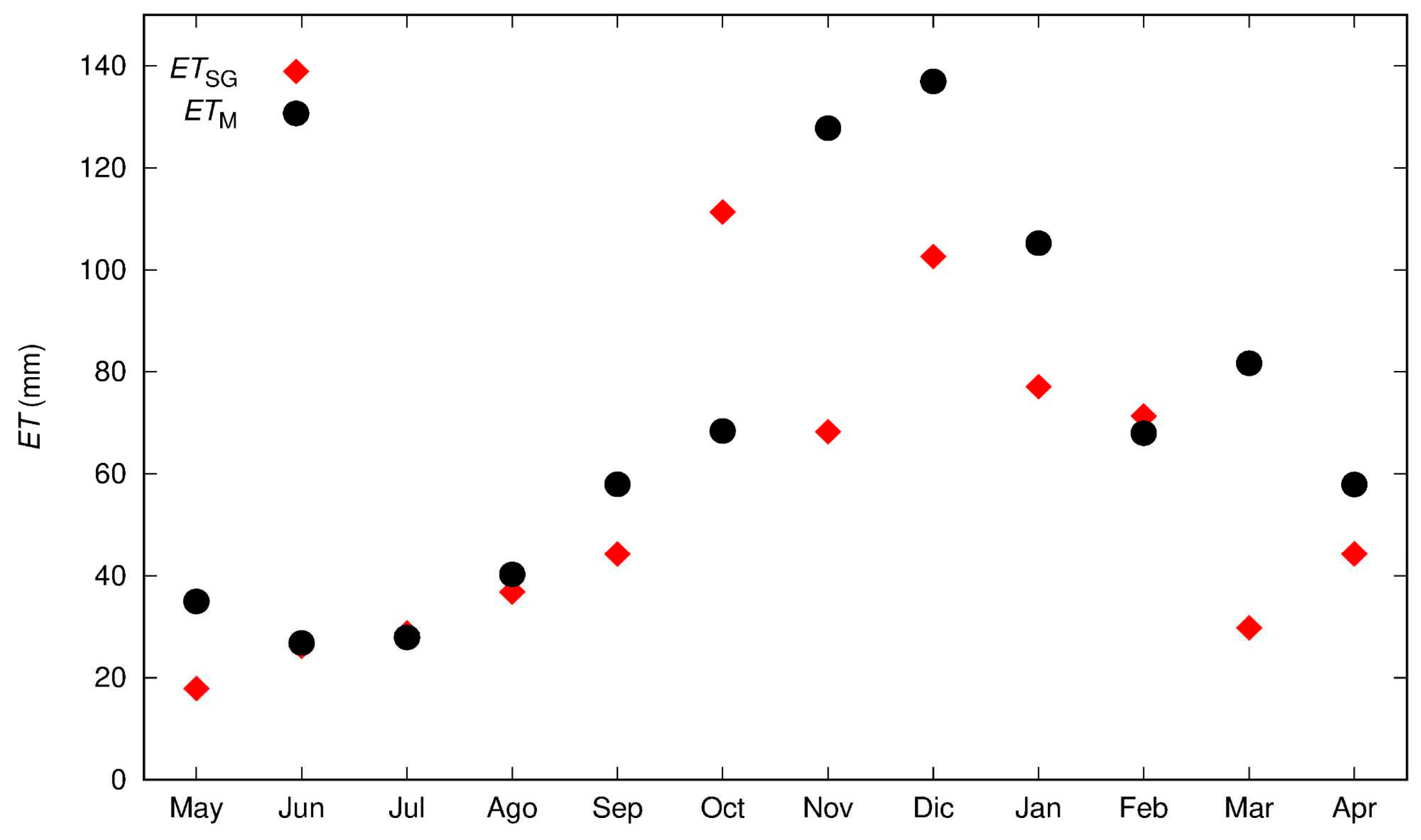
In this section, ETSG is estimated from the Equation (6) using cumulative precipitation and gravity residuals data with a monthly period of time Δt. To obtain MOD16A2 ET values at a monthly timescale, a temporal upscaling approach is applied to ETM at an 8-day. Figure 7 shows monthly values of ETSG and ETM and now no dispersion is observed. The ET estimated by both methods show a seasonal pattern where minimum and maximum values are observed in winter and summer, respectively. Note that ET estimates are similar for the winter season. The largest discrepancies between ET gravity-based approach and ETM are observed in the spring-summer period whose values ranging from 42 to 59 mm. In addition, ETM values tend to be higher than ET values. This period coincides with the beginning of a marked drop in water storage observed in the soil moisture sensors located in AGGO and which can also be inferred from the gravimetric residuals shown in Figure 4. The differences between ETSG and ETM can be mainly attributed to the MOD16A2 algorithm. Specifically, the MOD16A2 algorithm does not directly consider soil moisture variations when estimating ET. Instead, it is constrained by daily vapour pressure deficit, relative humidity, and minimum air temperature [37]. This approach is based on the assumption of congruence between near surface atmosphere and soil moisture conditions at coarser spatio-temporal scales [44,45].
At the monthly timescale, the values of all statistical metrics improve. Certainly, MAE (24.5 mm = 0.8 mm day-1) and RMSE (32.6 mm = 1.1 mm day-1) values are reduced compared to those obtained at 8-day timescale (see Table 1). Besides, a higher value of the Pearson correlation coefficient r = 0.7 is obtained, indicating a positive monotonic relationship between ETM and ETSG.
To verify the effect of the time scale on ET gravity-based approach estimates, an additional comparison between ETSG and ETM at 16 days is also performed. The comparison of both data sets gives values of MAE = 13.5 mm (0.8 mm day-1), RMSE = 19.6 mm (1.2 mm day-1) and r = 0.58. Note that these statistical values ​​improve in relation to those obtained for 8 days, but are worse than those of the monthly scale (see Table 1). These results confirm that, as the time scale increases, a better agreement is observed between the ET series.

4. Conclusions

This study proposes a novel methodology to validate remote sensing estimates of evapotranspiration (ET) using ground-truth ET data obtained from a superconducting gravimeter at mesoscale. This validation is consistent since the radius of influence of the superconducting gravimeters (50 to 4000 m) is similar with the horizontal resolution of several satellite observations (e.g., Soil Moisture Active Passive, Global Land Evaporation Amsterdam and Priestley-Taylor Jet Propulsion Laboratory Model). In particular the MOD16A2 products used in this study have a spatial resolution of 500 m, which provides good representativeness on a global scale.
The gravity-based technique estimates ET as a residual of the classical water balance equation using precipitation and superconducting gravimeter data. ET gravity-based approach is used for validating the global ET products MOD16A2 in a study site located in Buenos Aires Province for one year from May 2017 to April 2018. This analysis is performed at two different time scales: 8 days and one month. At 8-day scale, a greater dispersion is observed between ET time series, with RMSE values of 11.9 mm (1.5 mm day-1) and correlation coefficient r = 0.4. The discrepancies observed could be associated with the persistence of a 14-day non-hydrological periodical signal in the gravity residuals. This effect impacts directly on ET data resulting in some unrealistic values.
At the monthly timescale, both ET time series show similar seasonal patterns. The estimated RMSE value for this analysis is 32.6 mm month-1 (1.1 mm day-1) which is within the expected range for satellite products. Moreover, a better correlation is observed between ET gravity-based approach and satellite data (r = 0.7) since the 14-day periodic signal is attenuated by temporal upscaling. This result shows the potential of gravity-based approach as a ground truth ET data at a monthly timescale and spatial mesoscale, which represents a major step forward in the field of remote sensing validation.
The current state of the art for gravimetric data processing can only guarantee good ET estimates at monthly scales. For short time periods, gravity reductions need to be available with high accuracy to asses ET patterns. However, it is expected that with the increasing use of superconducting gravimetry, data reduction models will improve, leading to better results at smaller time scales.

5. Patents

Author Contributions

“Conceptualization, Rivas, R. and Guarracino, L.; methodology, Pendiuk, J. and Degano M. F.; software, Pendiuk, J.; validation, Pendiuk, J. and Degano M. F.; formal analysis, Pendiuk, J., Degano M. F., Guarracino, L. and Rivas, R.; investigation, Pendiuk, J., Degano M. F., Guarracino, L. and Rivas, R.; resources, Pendiuk, J., Degano M. F. and Guarracino, L.; data curation, Pendiuk, J. and Degano M. F.; writing—original draft preparation, Pendiuk, J. and Guarracino, L.; writing—review and editing, Degano M. F.; visualization, Pendiuk, J., Degano M. F.; supervision, Rivas, R. and Guarracino, L.; project administration, Pendiuk, J., Degano M. F., Guarracino, L. and Rivas, R.; funding acquisition, Pendiuk, J., Degano M. F., Guarracino, L. and Rivas, R. All authors have read and agreed to the published version of the manuscript.”

Funding

This research received no external funding.

Data Availability Statement

SG data published in [31] https://dataservices.gfz-potsdam.de/panmetaworks/showshort.php?id=escidoc:3748903. MOD16 data, obtained to Google Earth Engine https://developers.google.com/earth-engine/datasets/catalog/MODIS_006_MOD16A2

Acknowledgments

The authors would like to thank the Instituto de Hidrología de Llanuras "Dr. Eduardo Jorge Usunoff", the Consejo Nacional de Investigaciones Científicas Técnicas, the Facultad de Ciencias Astronómicas y Geofísicas and the Comisión de Investigaciones Científicas de la provincia de Buenos Aires.

Conflicts of Interest

“The authors declare no conflict of interest.”

References

  1. Zhang, K. , Kimball, J. S., Running, S.W. A review of remote sensing based actual evapotranspiration estimation. Wiley Interdisc. Rev.: Water 2016, 3, 834–853. [Google Scholar] [CrossRef]
  2. Güntner, A. , Reich, M., Mikolaj, M., Creutzfeldt, B., Schroeder, S., Wziontek, H. Landscape-scale water balance monitoring with an iGrav superconducting gravimeter in a field enclosure. Hydrol. Earth Syst. Sci. 2017, 21, 3167–3182. [Google Scholar] [CrossRef]
  3. Schrader, F. , Durner, W., Fank, J., Gebler, S., Pütz, T., Hannes, M., Wollschläger, U. Estimating Precipitation and Actual Evapotranspiration from Precision Lysimeter Measurements. Procedia Env. Sci. 2013, 19, 543–552. [Google Scholar] [CrossRef]
  4. Rana, G. , Katerji, N. Measurement and estimation of actual evapotranspiration in the field under Mediterranean climate: a review, Eur. Jour. of Agr. 2000, 13, 125–153. [Google Scholar] [CrossRef]
  5. Creutzfeldt, B. , Güntner, A , Wziontek, H., Merz, B. Reducing local hydrology from high precision gravity measurements: A lysimeter-based approach, Geophys. J. Int. 2010, 183, 178–187. [Google Scholar] [CrossRef]
  6. Huo, S. , Jin, M., Liang, X. et al. Estimating impacts of water-table depth on groundwater evaporation and recharge using lysimeter measurement data and bromide tracer. Hydrogeol J. 2020, 28, 955–971. [Google Scholar] [CrossRef]
  7. Tapley, B.D. , Watkins M.M., Flechtner F., Reigber C., Bettadpur S. et al. Contributions of GRACE to understanding climate change. Nat Clim Chang. 2019, 9, 358–369. [Google Scholar] [CrossRef] [PubMed]
  8. Long, D. , Longuevergne, L., Scanlon, B. R. Global analysis ofapproaches for deriving total waterstorage changes from GRACE satellites, Water Resour. Res. 2015, 51, 2574–2594. [Google Scholar] [CrossRef]
  9. Rodell, M. , Velicogna, I., Famiglietti, J.S. Satellite-based estimates of groundwater depletion in India. Nature 2009, 460, 999–1002. [Google Scholar] [CrossRef]
  10. Ciracì, E. , Velicogna, I., Swenson, S. Continuity of the mass loss of the world's glaciers and ice caps from the GRACE and GRACE Follow-On missions. Geophy. Res. Let. 2020, 47, e2019GL086926. [Google Scholar] [CrossRef]
  11. Cesanelli, A. , Guarracino, L., Estimation of regional evapotranspiration in the extended Salado Basin (Argentina) from satellite gravity measurements. Hydrogeol. J. 2011, 19, 629–639. [Google Scholar] [CrossRef]
  12. Swenson, S. , Wahr, J., Milly, P.C.D. Estimated accuracies of regional water storage variations inferred from the Gravity Recovery and Climate Experiment (GRACE). Water Resour. Res. 2003, 39, 1121–1134. [Google Scholar] [CrossRef]
  13. Sriwongsitanon, N. , Suwawong, T., Thianpopirug, S., Williams, J., Jia, L., Bastiaanssen, W. Validation of seven global remotely sensed ET products across Thailand using water balance measurements and land use classifications. J. Hydrol.: Regional Studies 2020, 30, 100709. [Google Scholar] [CrossRef]
  14. Dile, Y. , Ayana E., Worqlul, A., Xie, H., Srinivasan, R., Lefore, N., You, L., Clarke N. Evaluating satellite-based evapotranspiration estimates for hydrological applications in data-scarce regions: A case in Ethiopia. Sci. Tot. Env. 2020, 743, 140702. [Google Scholar] [CrossRef]
  15. Luo, Z. , Shao, Q., Wan, W., Li, H., Chen, X., Zhu, S., Ding, X. A new method for assessing satellite-based hydrological data products using water budget closure. J. Hydrol. 2021, 594, 125927. [Google Scholar] [CrossRef]
  16. Creutzfeldt, B. , Güntner, A, Vorogushyn, S., Merz, B. The benefits of gravimeter observations for modelling water storage changes at the field scale, Hydrol. Earth Syst. Sci. 2010, 14, 1715–1730. [Google Scholar] [CrossRef]
  17. Naujoks, M. , Kroner, C, Weise, A., Jahr, T., Krause, P., Eisner, S. Evaluating local hydrological modelling by temporal gravity observations and a gravimetric three-dimensional model, Geophys. J. Int., 2010, 182, 233–249. [Google Scholar] [CrossRef]
  18. Kennedy, J. , Ferré, TP.A., Creutzfeld, B. Time-lapse gravity data for monitoring and modeling artificial recharge through a thick unsaturated zone, Water Resour. Res. 2016, 52, 7244–7261. [Google Scholar] [CrossRef]
  19. Pendiuk, J.E. , Guarracino, L., Reich, M., Brunini, C., Güntner, A. Estimating the specific yield of the Pampeano aquifer, Argentina, using superconducting gravimeter data, Hydrogeology J. 2020, l, 28, 2303–2313. [CrossRef]
  20. Van Camp, M. , de Viron, O, Pajot-Métivier, G., Casenave, F., Watlet, A., Dassargues, A., Vanclooster, M. Direct measurement of evapotranspiration from a forest using a superconducting gravimeter, Geophys. Res. Lett. 2016, 43, 10225–10231. [Google Scholar] [CrossRef]
  21. Carrière, S.D. , Loiseau, B., Champollion, C., Ollivier, C., Martin-StPaul, N. K., Lesparre, N., et al. The first evidence of correlation between evapotranspiration and gravity at a daily time scale from two vertically spaced superconducting gravimeters. Geophy. Res. Lett. 2021, 48, e2021GL096579. [Google Scholar] [CrossRef]
  22. Pendiuk, J. Modelado y análisis de problemas hidrogravimétricos Ph.D. Thesis. National University of La Plata, 2022. [Google Scholar]
  23. Tasumi, M. Estimating evapotranspiration using METRIC model and Landsat data for better understandings of regional hydrology in the western Urmia Lake Basin. Agric. Water Manag. 2019, 226, 105805. [Google Scholar] [CrossRef]
  24. Xiang, K. , Li, Y., Horton, R., Feng, H. Similarity and difference of potential evapotranspiration and reference crop evapotranspiration–a review. Agric. Water Manag. 2020, 232, 106043. [Google Scholar] [CrossRef]
  25. Degano, M.F., Carmona, F., Olivera-Rodríguez, P., Faramiñán, A., Rivas, R., Bayala, M., Niclòs-Corts, R. Analysis of Priestley-Taylor method in different environments and coverages. In XIX Workshop on Information Processing and Control (RPIC) (pp. 1-6). IEEE. 2021. [CrossRef]
  26. Degano, M.F. , Rivas, R.E., Carmona, F., Niclòs, R., Sánchez, J.M. Evaluation of the MOD16A2 evapotranspiration product in an agricultural area of Argentina, the Pampas region, The Egyptian Journal of Remote Sensing and Space Sciences, 2020, 24, 319–328. [Google Scholar] [CrossRef]
  27. Wziontek, H. , Wolf, P., Häfner, M., Hase, H., Nowak, I., Rülke, A., Wilmes, H., Brunini, C. Superconducting Gravimeter Data from AGGO/ La Plata - Level 1 GFZ Data Services, 2017. [CrossRef]
  28. Mikolaj, M. , Güntner, A., Brunini, C., Wziontek, H., Gende, M., Schröder, S., Pasquaré, A., Cassino, A.M., Reich, M., Hartmann, A., Oreiro, F.A., Pendiuk, J., Antokoletz, E.D., Guarracino, L. Hydrometeorological and gravity data from the Argentine-German Geodetic Observatory in La Plata, GFZ Data Services, 2018. [Google Scholar] [CrossRef]
  29. Nossetto, M.D. , Paez, R.A., Ballesteros, S.I., Jobbágy, E.G. Higher water-table and flooding risk under grain vs. livestock production systems in the subhumid plains of the Pampas, Agriculture, Ecosystems and Environment, 2015, 206, 60–70. [Google Scholar] [CrossRef]
  30. Hinderer, J. , Crossley D., Warburton, R.J. Superconducting Gravimetry, in Treatise on Geophysics, 2nd edn, 3 Geodesy, pp. 59 – 115., ed.Herring T., Schubert G., (editor-in-chief), Elsevier, 2015. [CrossRef]
  31. Hector, B. , Hinderer, J., Séguis, L., Boy, J-P., Calvo, M., Descloitres, M., Rosat, S., Galle, S., Riccardi, U. Hydro-gravimetry in West-Africa: First results from the Djougou (Benin) superconducting gravimeter, J.l of Geodynamics, 2014, 80, 34–49. [Google Scholar] [CrossRef]
  32. Telford, W.M. , Geldart, L.P., Sheriff, R.E. Applied geophysics, 2nd edn. Cambridge University Press, New York, 1992.
  33. Van Camp, M. , de Viron, O., Watlet A., Meurers, B., Francis, O., Caudron, C. Geophysics from terrestrial time-variable gravity measurements. Rev. of Geoph. 2017, 55, 938–992. [Google Scholar] [CrossRef]
  34. Voigt, C. , Schulz, K., Koch, F., Wetzel, K.-F., Timmen, L., Rehm, T., Pflug, H., Stolarczuk, N., Förste, C., and Flechtner, F. Technical note: Introduction of a superconducting gravimeter as novel hydrological sensor for the Alpine research catchment Zugspitze. , Hydrol. Earth Syst. Sci. 2021, 25, 5047–5064. [Google Scholar] [CrossRef]
  35. Reich, M. , Mikolaj, M., Blume, T., Güntner, A. Reducing gravity data for the influence of water storage variations beneath observatory buildings. Geophysics. 2019, 84, EN15-EN31. [CrossRef]
  36. Mikolaj, M. , Güntner, A., Brunini, C., Wziontek, H., Gende, M., Schröder, S.,Cassino, A.M., Pasquaré, A., Reich, M., Hartmann, A., Oreiro, F.A., Pendiuk, J., Guarracino, L., Antokoletz, E.D. Hydrometerological and gravity signals at the Argentine-German Geodetic Observatory (AGGO) in La Plata. Earth Syst Sci Data Discuss 2019, 11, 1501–1513. [Google Scholar] [CrossRef]
  37. Mu, Q.Z. , Zhao, M.S., Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Rem. Sens. Env. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
  38. Ruhoff, A. L. , Paz, A. R., Aragao, L. E. O. C., Mu, Q., Malhi, Y., Collischonn, W. Assessment of the MODIS global evapotranspiration algorithm using eddy covariance measurements and hydrological modelling in the Rio Grande basin. Hydrological Sciences Journal, 2013, 58, 1658–1676. [Google Scholar] [CrossRef]
  39. Hu, G. , Jia, L., & Menenti, M. Comparison of MOD16 and LSA-SAF MSG evapotranspiration products over Europe for 2011. Remote Sensing of Environment, 2015, 156, 510–526. [Google Scholar] [CrossRef]
  40. Kim, H. W. , Hwang, K., Mu, Q., Lee, S. O., & Choi, M. Validation of MODIS 16 global terrestrial evapotranspiration products in various climates and land cover types in Asia. KSCE Journal of Civil Engineering, 2012, 16, 229–238. [Google Scholar] [CrossRef]
  41. Monteith, J. , Unsworth, M. Principles of Environmental Physics. Edward Arnold (ed.), London, 1990, 291 pp.
  42. Mu, Q.Z. , Heinsch, F.A., Zhao, M.S., Running, S.W. Development of a global evapotranspiration algorithm based MODIS and global meteorology data. Remote Sensing of Environment. 2007, 111, 519–536. [Google Scholar] [CrossRef]
  43. Running, S.W. , Mu, Q.Z., Zhao, M.S. MOD16A2 MODIS/Terra Net evapotranspiration 8-Day L4 Global 500m SIN Grid V006 [Data set] NASA EOSDIS Land Processes DAAC, 2017. [CrossRef]
  44. Fisher, J.B. , Tu, K.P., Baldocchi, D.D. Global estimates of the land–atmosphere water flux based on monthly AVHRR and ISLSCP-II data, validated at 16 FLUXNET sites. Rem. Sens. of Env. 2008, 112, 901–919. [Google Scholar] [CrossRef]
  45. Brust, C. , Kimball, J.S., Maneta, M.P., Jencso, K., He, M., Reichle, R.H. Using SMAP Level-4 soil moisture to constrain MOD16 evapotranspiration over the contiguous USA. Rem. Sens. of Env. 2021, 255, 112277. [Google Scholar] [CrossRef]
Preprints 74977 g001
Figure 1. Location of AGGO in Buenos Aires province, Argentina.
Figure 1. Location of AGGO in Buenos Aires province, Argentina.
Preprints 74977 g001
Preprints 74977 g002
Figure 2. Gravimetric modelling of water storage changes at depth z below the SG using an infinite horizontal layer and a vertical cylinder of radius R.
Figure 2. Gravimetric modelling of water storage changes at depth z below the SG using an infinite horizontal layer and a vertical cylinder of radius R.
Preprints 74977 g002
Preprints 74977 g003
Figure 3. Gravity effect (Δg) of a vertical cylinder with a thickness of 1 mm and variable radius at different depths (2 to 18 m). The dashed line indicates the gravity effect of an infinite horizontal layer of water of 1 mm thickness (water admittance).
Figure 3. Gravity effect (Δg) of a vertical cylinder with a thickness of 1 mm and variable radius at different depths (2 to 18 m). The dashed line indicates the gravity effect of an infinite horizontal layer of water of 1 mm thickness (water admittance).
Preprints 74977 g003
Preprints 74977 g004
Figure 4. Gravity residuals (Δg) and precipitation (P) time series.
Figure 4. Gravity residuals (Δg) and precipitation (P) time series.
Preprints 74977 g004
Preprints 74977 g005
Figure 5. ET gravity-based approach (ETSG) and MOD16A2 (ETM) at an 8-day scale time series.
Figure 5. ET gravity-based approach (ETSG) and MOD16A2 (ETM) at an 8-day scale time series.
Preprints 74977 g005
Preprints 74977 g006
Figure 6. Crossplot between MOD16A2 ET (ETM) and ET gravity-based approach (ETSG) at 8-day timescale.
Figure 6. Crossplot between MOD16A2 ET (ETM) and ET gravity-based approach (ETSG) at 8-day timescale.
Preprints 74977 g006
Preprints 74977 g007
Figure 7. Comparison between ET gravity-based approach and MOD16A2 at monthly scale.
Figure 7. Comparison between ET gravity-based approach and MOD16A2 at monthly scale.
Preprints 74977 g007
Table 1. Estimated statistical metrics at 8-day and monthly scales.
Table 1. Estimated statistical metrics at 8-day and monthly scales.
Coefficient (units) Value at 8-day scale Value at monthly scale
MAE (mm) 9.32 24.5
RMSE (mm) 11.9 32.6
r (-) 0.4 0.7
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated