Prerpints.org logo
Preprint
Article

This version is not peer-reviewed.

Characteristics of Convective Parameters Derived from Rawinsonde and ERA5 Data Associated with Hailstorms in North-eastern Romania

A peer-reviewed version of this preprint was published in:
Meteorology 2023, 2(3), 387-402. https://doi.org/10.3390/meteorology2030023

Submitted:

29 May 2023

Posted:

30 May 2023

You are already at the latest version

Abstract
Using a database of 378 hail days between 20981 and 2020, the climatic characteristics of 23 convective parameters from sounding data and ERA5 data were statistically analyzed. The goal of this work is to evaluate the usefulness and representativeness of convective parameters derived from sounding data and reanalysis data for the operational forecast of the hail phenomenon. As a result, average values from 12:00 UTC were 433J / Kg for CAPE in the case of data from ERA5 and 505 J/kg from rawinsonde respectively. The Spearman correlation coefficients matrix between the values of the parameters indicates high correlations between the parameters calculated based on the parcel theory, the humidity indices, and the complex indices. The probability for large hail maximizes with high low level and boundary layer moisture, high CAPE, and a high lifted condensation level height.
Keywords: 
hailstorm
;  
convective environment
;  
statistical correlation
;  
hail forecasting
Subject: 
Environmental and Earth Sciences  -   Atmospheric Science and Meteorology

1. Introduction

Regardless of its regional trends, hail represents one of the most extreme weather phenomena determined by severe convective storms [1]. Therefore, improving the capacity to forecast this extreme weather phenomenon represents one of the main available tools for the mitigation of its impact.
In the beginning early hail forecasting methods had limited success, using small statistical samples and developing empirical relationships between hail size and Convective Available Potential Energy (CAPE) or temperature values at different levels [2,3,4,5,6]. Because they involved in the analysis only convection energy available, estimated directly from CAPE, or indirectly from temperature values at different levels, these methods tended to forecast unrealistic hail sizes or had poor ability to distinguish between hail formation conditions of small and large dimensions respectively [7].
Thermodynamic parameters that are closely related to the magnitude of the updraft have been proven almost the same popular in Europe and the USA. For example, CAPE or the thermal gradient in the middle troposphere causes the increase of the updraft and implicitly the increase of hailstones [8,9,10,11,12,13,14,15,16,17,18]. In Europe, the Lifted Index also has been shown to be useful for hail forecasting [12]. Specialists within the hail control system from the former Soviet republics carried out complex hail forecasting procedures also. The most important thermodynamic parameters used in operational hail forecasting, are those related to updraft speed, humidity at different levels, and middle tropospheric flow [19,20,21,22].
ther representative parameters highly relevant include the vertical gradient of air pressure, causing strong updrafts and hail, known as generators of highly organized convective storms. In the case of supercells, in most cases associated with large-size hail falls, several parameters have been developed that are used to help forecast them. The most relevant among them can be considered the wind shear between the surface and the 6 km level (DLS), or the storm relative helicity [13,15,16,23,24,25,26,27,28,29,30].
Potential predictors could come from the optimum hail growth zone estimation represented by a layer above the 00C isotherm. The height at which the frost level is above the ground is also used for the same purpose. [13,31,32]. The amount of moisture available below the freezing level or in the boundary layer also has an influence on the density and growth rate of hailstones [13,32]. Recent research from Europe has suggested that the level of updraft condensation can become a useful predictor [15,28,29], this one can be correlated with lifted condensation level and convective temperature and the cloud base, which in turn their influences the speed of the updraft [33]. These results are similar to other studies [24,34].
Alternative forecast techniques such as one-dimensional and convective cloud models (HAILCAST) to estimate potential hail size based on the vertical profile of the atmosphere [35,36]. Other models use cloud microphysical properties to forecast hail size by simulating an updraft [37,38]. Although not yet widely applied in operational forecasting, both approaches provide a reasonable estimate of hail size [36,37,38].
Machine learning applications became another current direction of development for the parameters analysis useful for hail forecasting. They can assimilate a larger number of variables that can be considered, including simulated model updates, hail microphysical characteristics, environmental parameters, and weather radar observations [37,39,40,41].
This topic in Romania is rather poorly represented in studies. Bălescu and Militaru [42] carry out a study describing convective favorable conditions to hail falls. Some studies have addressed the forecast of instability, in general, or of storms using instability indices [43,44,45]. For hailstorms, a convective environment appears as a case study of exceptional events [46,47,48,49]. The efficiency of some instability indices derived from sounding data for hail forecasting was tested for the Romania territory. The lifted Index linked with the values of temperature laps in the middle troposphere proved a good ability to forecast hail [50,51].
This paperwork is intended to be an approach that brings a contribution to the most detailed knowledge of short-term hail forecasting methods in the north eastern part of Romania. Numerous areas with a high hail risk [52] determined the implementation of some hail suppression technologies in the study area. The need and opportunity to improve knowledge related to the prognosis and manifestation of this phenomenon thus intervened.

2. Materials and Methods

2.1. Study Area and Hail Climatology

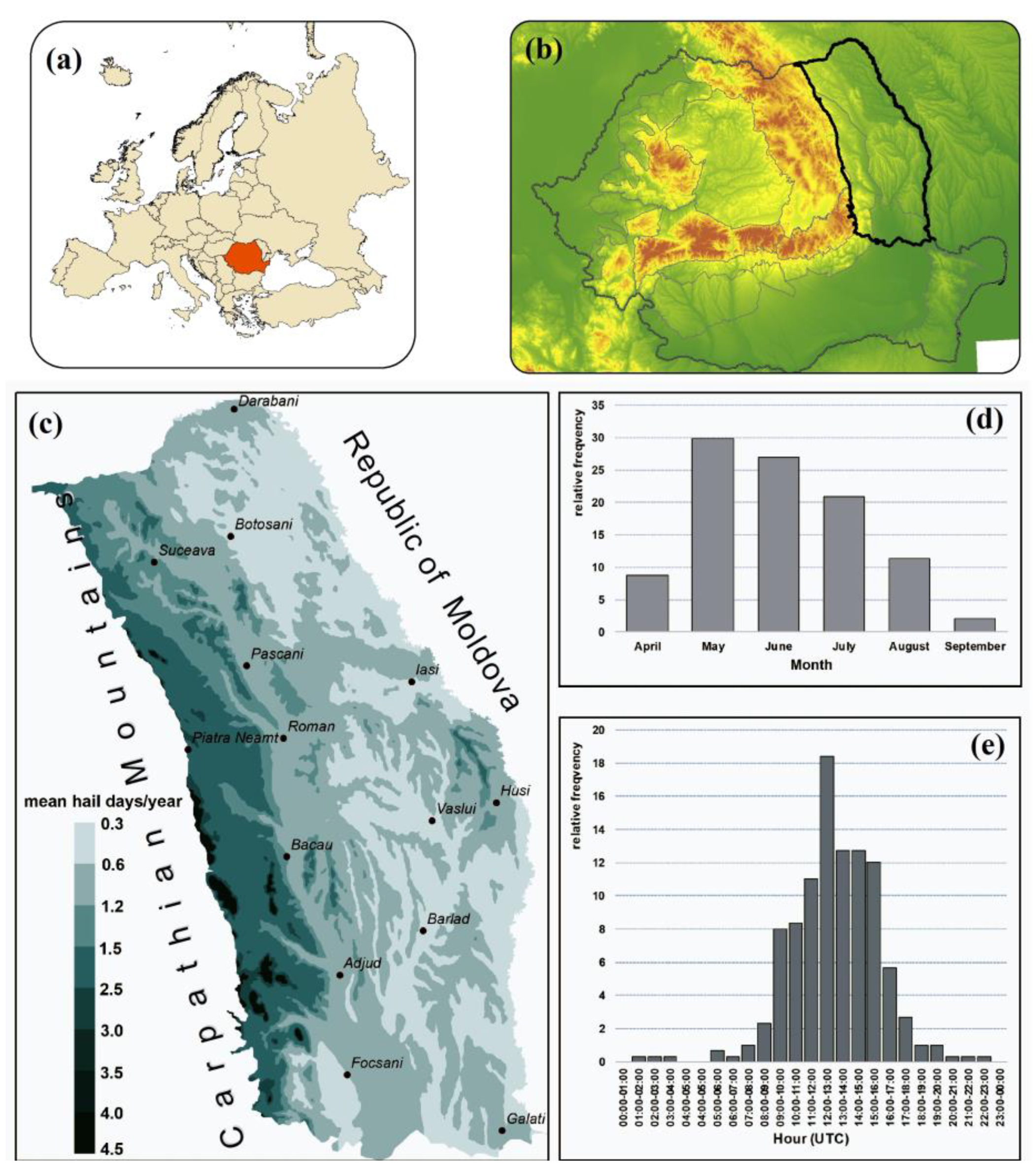
The study area represents the north-eastern part of Romania (Figure 1(a)), corresponding with the western part of Moldova historical region (Figure 1(b)).
The mountain area was excluded due to the lack of significant hail falls data. Although the number of days with hail is higher in the mountain area [53], the characteristics of the economic activities determine a very low impact of damage in this area in connection with strong hailstorms [54,55]. The studied area hypsometry is between 10 m in the extreme south and over 900 meters in the hilly area in the west. The region it is sheltered in the western part by the Carpathian Mt., which induces a series of peculiarities. [56].
The average number of days with hail, drops from 3 days/year on the highest peaks of the Moldavian Subcarpathian and the Curved Subcarpathian, to below 0.6 days/year in the southern Moldavian Plain, the Bârlad valley and most of the valley Prut [53]. Many hailfall events (78%) occur in the afternoon and evening hours, between 10:00 and 18:00 UTC, while the rest of the hail events (22%) occur in the interval 19:00–10:00 UTC.

2.2. Hail data.

Reported hail falls, used in this study was used in previous studies [52,57], and comes from three different sources, namely: Romanian National Meteorological Administration (RNMA), ESWD (European Severe Weather Database) and media and local newspaper . The dataset from RNMA represents a total of 242 hail days from 18 weather stations from 1979-2017. 29 hail days were taken from ESWD reports, the database used in studies at the continental level [28,29,58] as well as at the regional level [59,60]. The third data source is represented by large hail reports from the local newspapers archive. These types of meteorological phenomena reports, including data from past centuries, have been used in climatological studies that have been carried out [61,62,63].
Preprints 75045 g001
Figure 1. Geographical position of north-eastern Romania at continental (a) and country (b) scale; spatial distribution of the mean hail days per year (c), monthly distribution of the hail events (d), and hourly distribution of the hail events (c) for 1981–2020.
Figure 1. Geographical position of north-eastern Romania at continental (a) and country (b) scale; spatial distribution of the mean hail days per year (c), monthly distribution of the hail events (d), and hourly distribution of the hail events (c) for 1981–2020.
Preprints 75045 g001

2.3. Convective Parameters

The convective environment of hail storms was studied using 23 instability parameters from two data sources. Data from sounding stations in the vicinity of the studied area, namely Bucharest-Băneasa, Cluj-Napoca, Cernăuți and Odesa, as well were used reanalysis data from ERA5. Sounding data were downloaded from the web server of the University of Wyoming [64] The spatial density of air sounding stations from the studied territory is very low, and the atmosphere sounding is carried out at most twice a day. The use of aerial survey data was done according to the criterion of proximity. Data from the sounding station closest to the place where the hail phenomenon was reported were thus used. For a comparison the convective parameters, was used ERA5 database [65]. From ERA5 was used a number of 14 instability indices such as CAPE, CIN, TT, KI and the values of temperature, relative humidity, dew point and wind speed and direction at 850 hPa, 800 hPa, 700 hPa and 500 hPa levels. Convective parameter values for 378 hail days were analyzed at 00:00 UTC and 12:00 UTC. The 23 instability indices used are divided into five categories, namely particle theory indices, moisture indices, temperature indices, kinematic indices, and complex indices. They are presented synthetically in tab no. 1.
Statistical analyses were run only for the convective period during which the hail occurs, namely from April to October and for the 00:00 (03:00 AM local time) and 12:00 PM GMT (12:00 PM local time) of the day. Analysis of parameters values at 00:00 was made to evaluate the condition prevailing hailstorm development. Parameters values at 12:00 PM were considered those that characterize the convective environment during the manifestation of the phenomenon trying to capture the convective developments in the afternoon, the classical daytime period for hail occurrence.
Table 1. Parameters used in study.
Table 1. Parameters used in study.
Group Index Name Acronym Unit of Measure
1 Parcel
parameters		 Convective available potential energy CAPE J/kg
2 Convective Inhibition CIN J/kg
3 Lifted index LI -
4 Showalter index SI °C
5 Lifted condensation level LCL m
6 Equlibrum level EL m
7 Cloud vertical extent H_Cl m
8 Parcel’s max vertical velocity (square root of 2 X CAPE) Wmax m/s
9 Temperature
indices		 Freezing level FL m
10 2 m - 700 hPa lapse rate LR_0-7 °C/km
11 800 - 500 hPa lapse rate LR_5-8 °C/km
12 Moisture
indices		 Relative humidity at 850 hPa pressure level RH850 %
13 Relative humidity at 700 hPa pressure level RH 700 %
14 Relative humidity at 500 hPa pressure level RH 500 %
15 Mean mixed layer MIXR (average MIXR in the lowest 500 m) MLMIXR g/kg
16 Precipitable water PW mm
17 Kinematic
indices		 0-6-km AGL wind shear - deep-layer shear DLS m/s
18 Velocity of the main stream Vw Km/h
19 Compositeindices K index KI K
20 Total totals TT K
21 Bulk-Richardson Number BRN -
22 Severe Weather Threat Index SWEAT -
23 DLS x Wmax WMAXSHEAR m2/s2

3. Results

3.1. Convective Parameters Values

3.1.1. Parcel Parameters

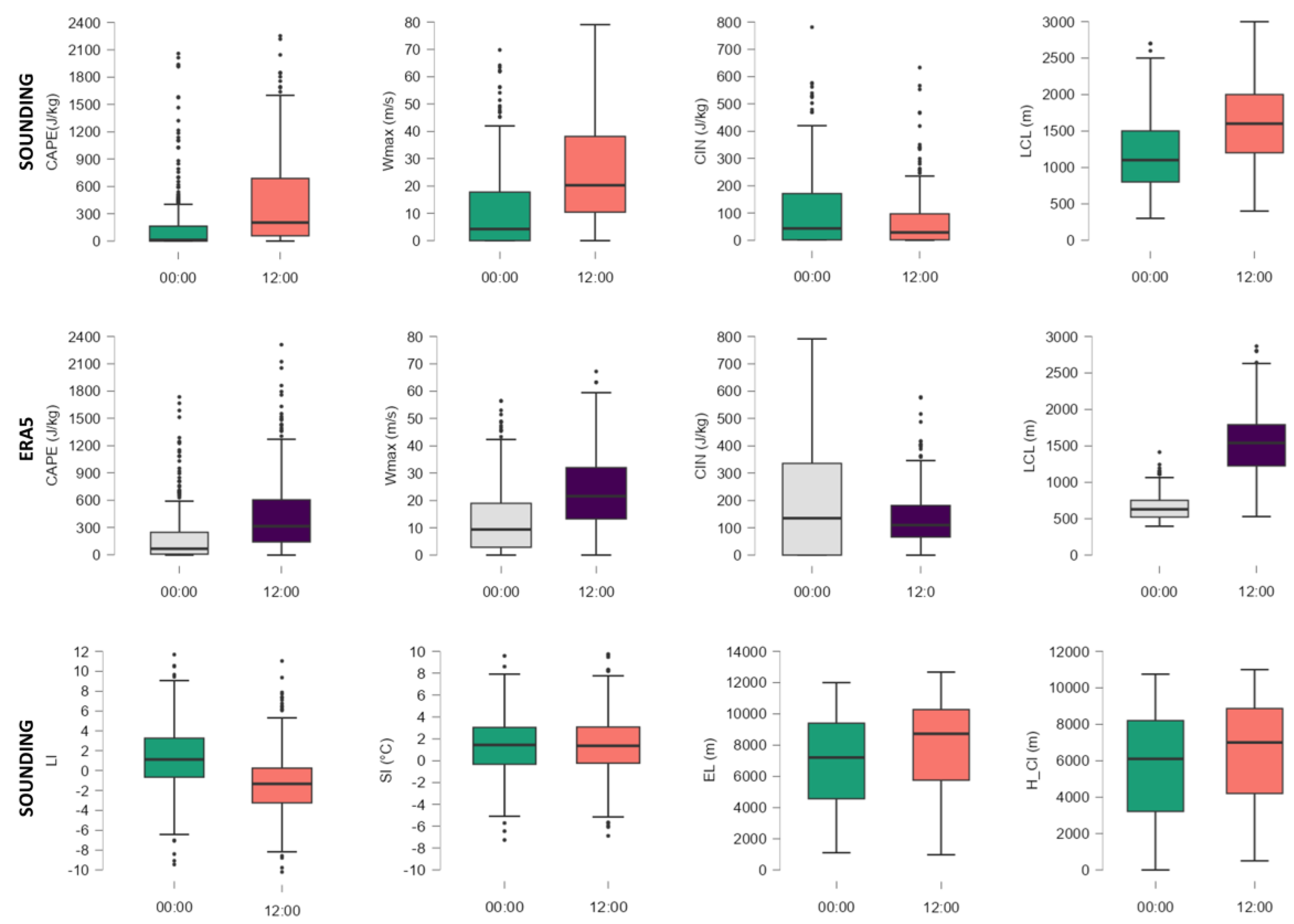
CAPE mean values from the two databases are approximately 200 J/kg (Figure 2). The median values are about 433 J/kg in the case of ERA5 and 505 J/kg for the asounding data. These are comparable to those of small hail size days in central and western Europe obtained in other studies [15,27]. In Switzerland, for the cases with weak and isolated convective storms, the average value of CAPE from the 12 UTC sounding data was 400 J/kg, and in the Czech Republic, in the case of strong convective storms in more than 80% of the cases, the value was 322 J /kg [66]. Can be seen a difference , especially for higher values than the median quartile, between ERA5 and sounding data. The 75th and 90th percentile values from sounding are about 100 J/kg lower than those calculated with ERA5 data. CAPE maximum values recorded in sounding data was 4351 J/kg on 24.06.1987 and from ERA5 it was 3918 J/kg on 18.06.2016. The parameter Wmax being obtained from taking the square root of the double CAPE, is characterized by the same statistical distribution of values and also by a similar spatial distribution.
Half of CIN values from air sounding stations are close to 0, those from ERA5 have a median value of 70 J/Kg and extreme values exceeding 300 J/kg. We can aproximate this value of convective inhibition on hail days as available convective energy once it has been overcome. The lifting condensation level (LCL) at 12:00 UTC calculated from sounding and ERA5 data, which can be associated with cloud base, located at altitudes higher than 900 m for 90% of the analyzed hail days . In the case of the data from 00:00, the LCL was located at altitudes higher than 800 m for 75% of the analyzed hail days.
LI and SI values ​​being calculated in a similar way also have similar statistical distribution. The difference between the two indices lies in the lower values ​​of LI compared to SI. The values ​​of the lower quartiles of LI lower than -2 that characterize a moderately and strongly unstable environment denote the existence of a moist, unstable layer in the layer at the soil surface. We can associate the higher SI values ​​with a much lower frequency of an unstable, moist layer at altitude corresponding to the 850 hPa level.
The EL values, with much greater variability compared into those of the LCL, also greatly influence the height of the clouds (H_Cl). In most cases the vertical cloud extent was recorded between 3500 and 8000 meters at 00 UTC and 4000 and 9000 m at 12 UTC. Being calculated only from air sounding data, some values of EL and H_Cl are close to 0, as a fact due to the large distance of the stations of aerial sounding toward of hailstorm location.
Preprints 75045 g002
Figure 2. Box-and-whisker plots for parcel theory parameters The median is represented as a horizontal line inside the box, the edges of the box represent the 25th and 75th percentiles, while whiskers represent the 10th and 90th percentiles.
Figure 2. Box-and-whisker plots for parcel theory parameters The median is represented as a horizontal line inside the box, the edges of the box represent the 25th and 75th percentiles, while whiskers represent the 10th and 90th percentiles.
Preprints 75045 g002

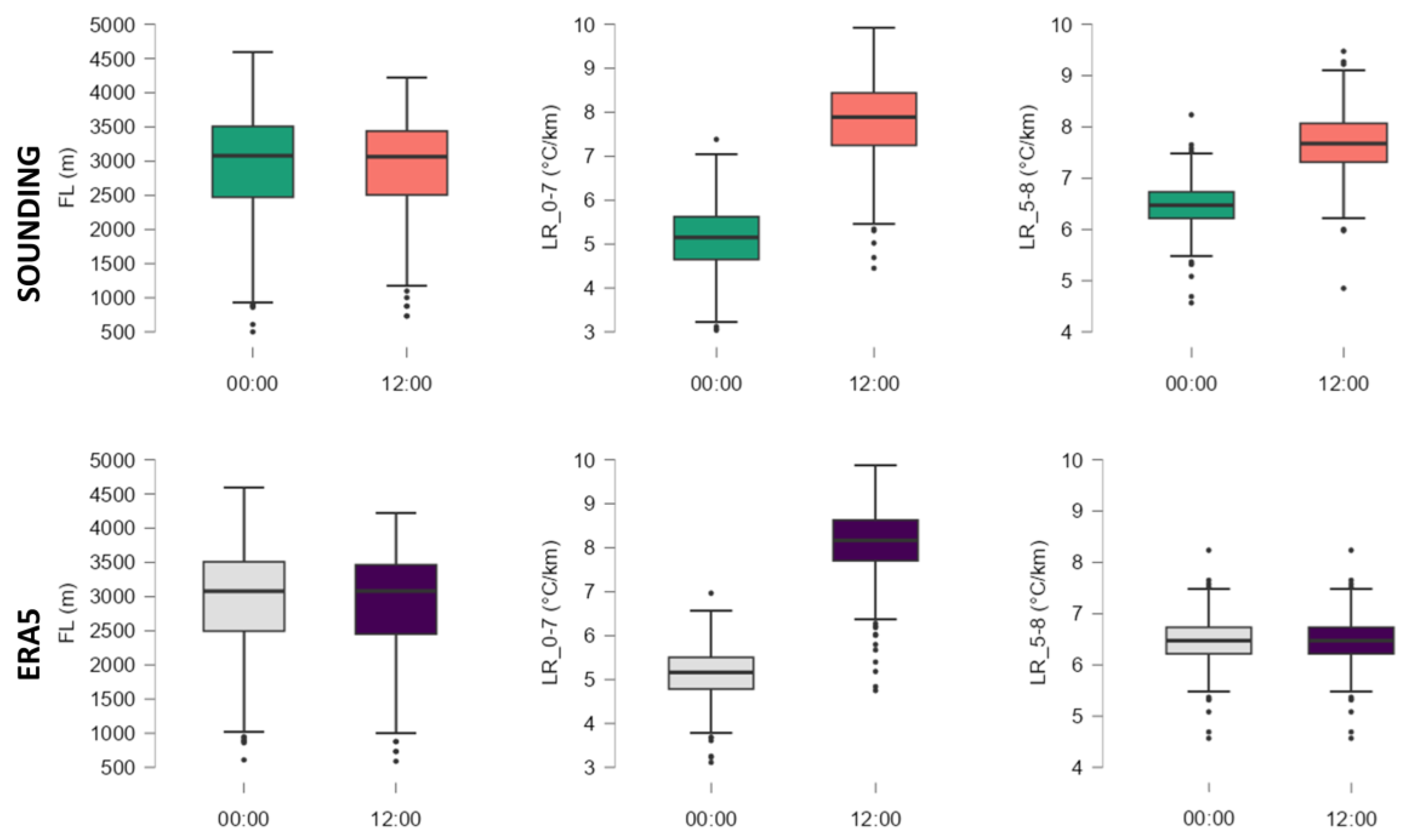
3.1.2. Temperature Parameters

The vertical profile of temperature distribution in the atmosphere on hail days brings essential information on the 'hail growth zone'. The freezing level is correlated, with the size of hail recorded on the ground [67,68,69,70]. This parameter has the advantage of having a spatial and temporal homogeneity of values, especially for small regions like the studied area. Generally, the FL value on hail days was between 2500 and 3500 m (Figure 3). At the beginning of the convective season, values lower than 2500 m can be recorded in April and values higher than 3500 m in July and August. The other two indices in this category LR_0-7 and LR_5-8 provide an image of some thermal and humidity characteristics of the low troposphere, respectively of the middle troposphere (Figure 3). LR_0-7 represents, from this point of view, in general the situation in the first 3 km of the troposphere. Its values from 12 UTC, in the case of both data sources, are between 6.5 and 9.5 0C/Km indicating the presence of an amount of moisture located below the planetary boundary layer.

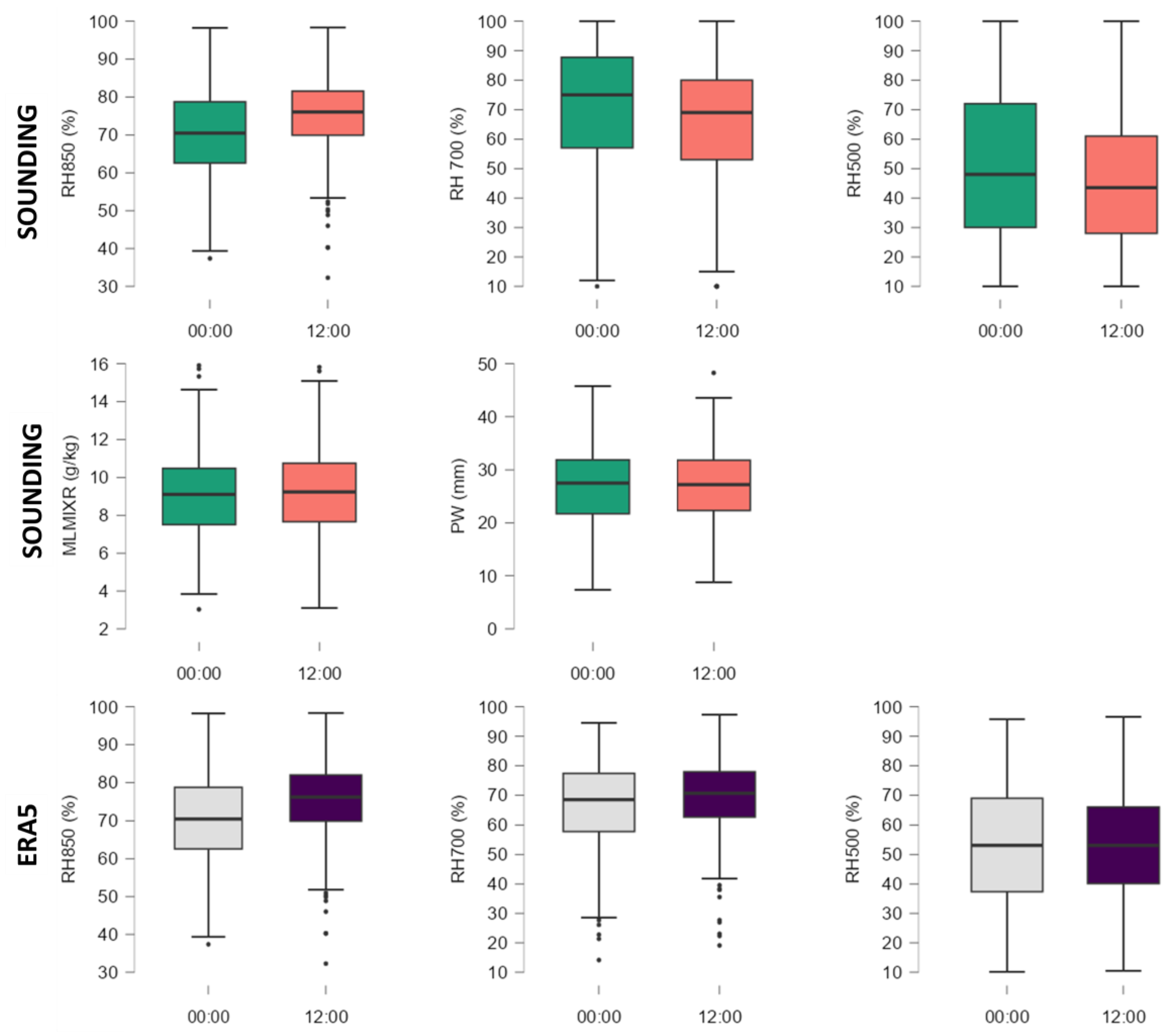
3.1.3. Moisture Parameters

The humidity parameters have a similar distribution in the case of both data sources, especially in the case of RH 850 and RH 500 (Figure 4). Differences showup in the case of RH700 where the interquartile values calculated from the ERA5 data are lower. The average value of these parameters calculated for all hail days analyzed begine from 75% in the case of RH850 till 50% in the case of RH500. Values distribution for MLMXR and PW are similar the two time intervals studied. Mean value around 9 kg/g for MLMXR is also specific for large hail cases in western Europe [27]. Over 75% from hail cases in the dataset used had PW values exceeding 22 mm, with a median value of 27 mm.

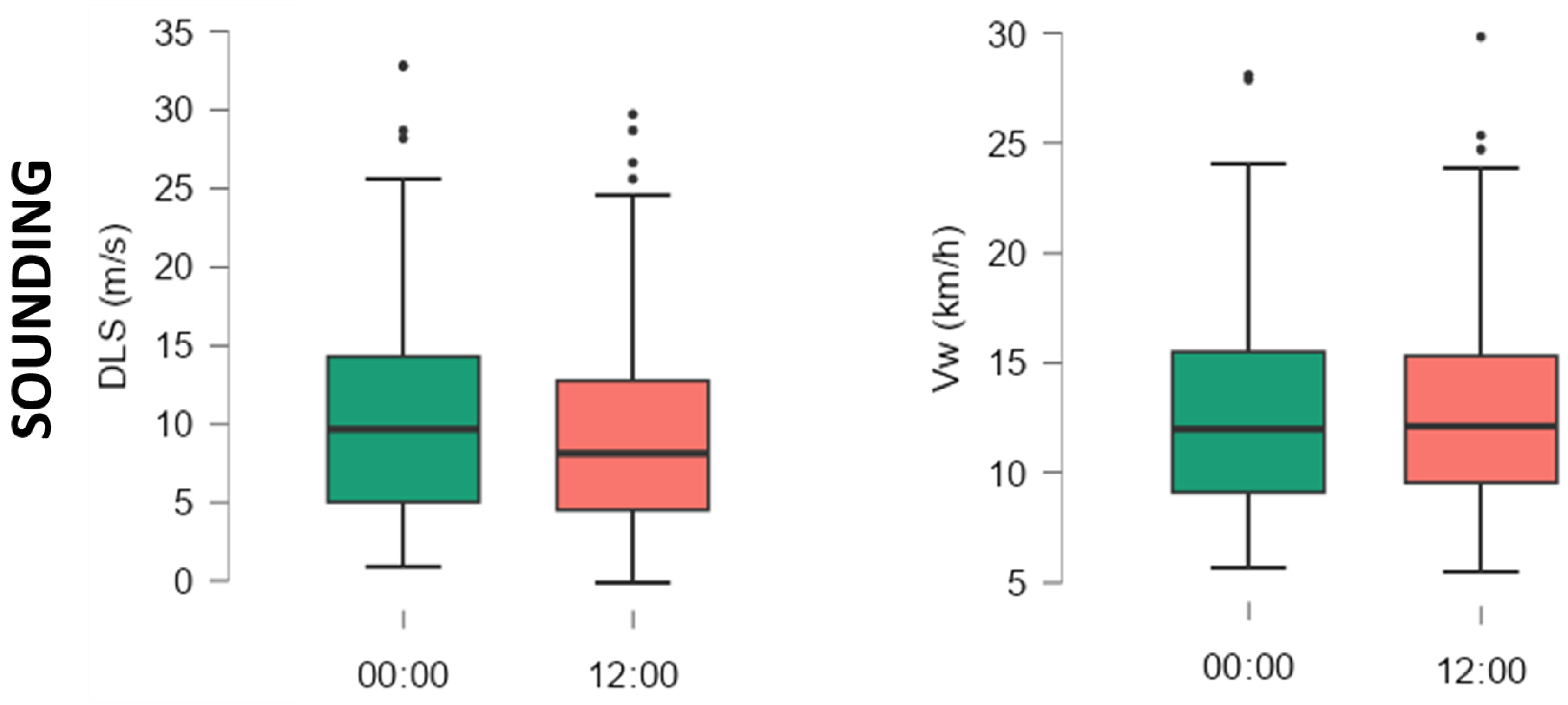
3.1.4. Kinematic Parameters

For all analyzed hail cases, DLS mean value is around 10 m/s for sounding data from 00 UTC and 8 m/s for those from 12UTC (Figure 5). The similar values are found in central and western Europe [15,27] and greater (around 15 m/s) for the hailstorm in USA [29,71]. DLS upper quartile values exceed 10 m/s and maximum 20 m/s. Vw has values between 7 and 19 km/h, being a very useful index for determining the movement of convective clouds. Its values can be correlated with the speeds of air masses that cause atmospheric instability in the studied territory or with relief and microclimate conditions in the case of local convections.

3.1.5. Composite Parameters

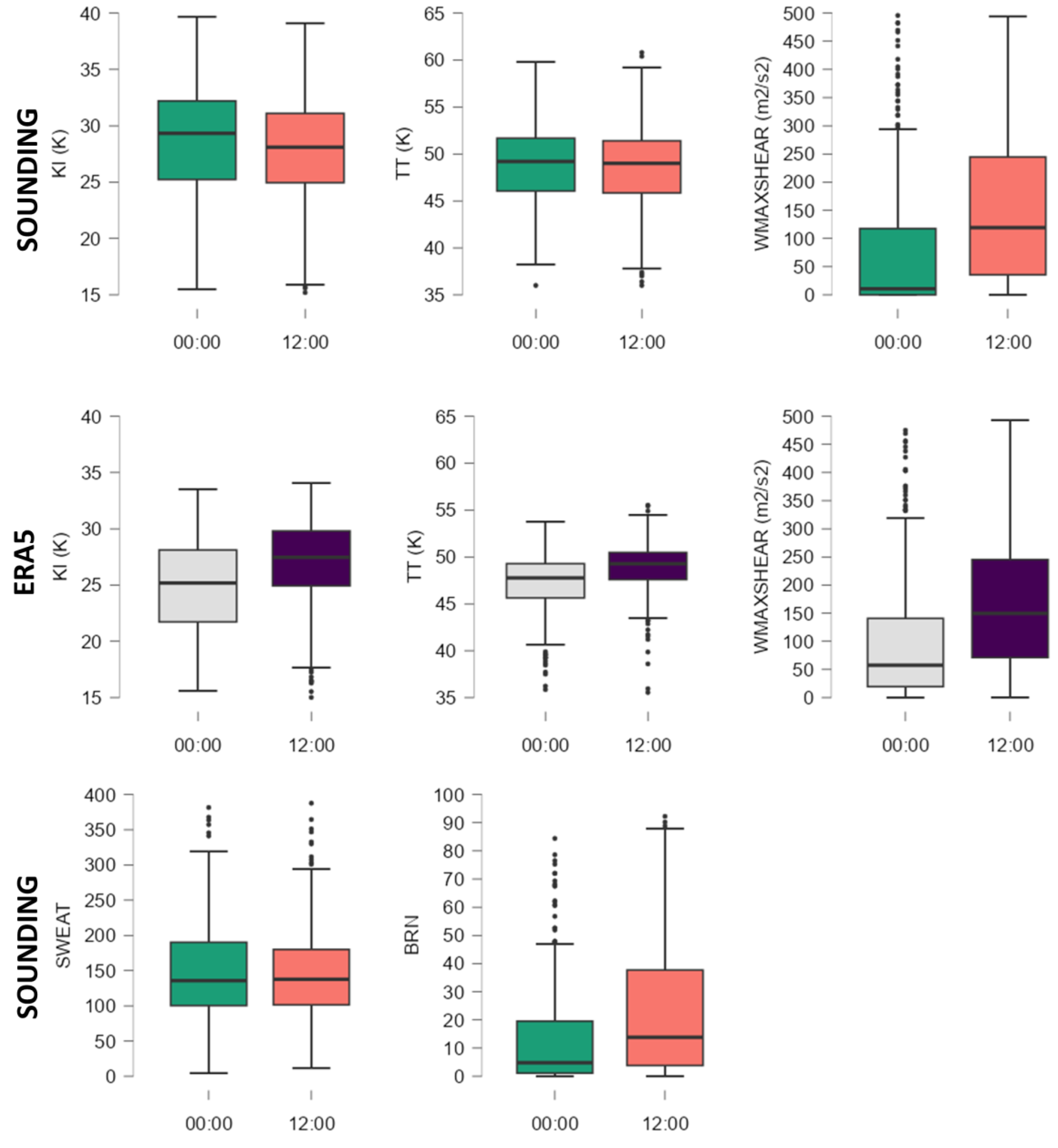
The TT and KI values indicates a moderately unstable environment with the probability of producing strong convective storms in limited areas (Figure 6). The values of these two indices calculated from ERA5 are lower than those calculated from sounding data. KI does not stand out with values higher than 40. Values above 50 in the upper quartile of TT can highlight situations in the first part of the warm semester when the instability was caused by cold air cores located at altitude (at the level of 500 hPa ). WMAXSHEAR is a composite index that has shown a good potential to forecast strong atmospheric instability but also to differentiate the degree of severity of convective phenomena [15,27]. The distribution of WMAXSHEAR values is closely related to that of CAPE from which the updraft velocity is estimated. It is noted that the values calculated from ERA5 are higher than those from the sounding are. For 00UTC only in 25% of cases, WMAXSHEAR indicates the possibility of some convection. Much more suggestive are the data from 12UTC (from both data sources) which have a mean value of 150 m2/s2. Thus, values indicated the presence of an environment with increased instability in 50% of cases.
Other two composite indices calculated from air sounding data, namely SWEAT and BRN have values that indicate the existence of a convective environment favourable to the development of potential hail just for only part of the cases analyzed in the study. In the case of SWEAT, the upper quartile values are between 150 and 300 (Figure 6). These values indicate a reduced probability of the occurrence of strong storms, but it must be considered that in its calculation parameters of moisture from the low levels of the atmosphere, parameters of instability, but also data related to the direction and speed of the vertical wind are used. Values in the lower quartile indicate an environment favorable to strong convection. The upper quartile includes values over 45 that characterize a weakly unstable environment.
Preprints 75045 g006
Figure 6. Box-and-whisker plots for composites parameters. The median is represented as a horizontal line inside the box, the edges of the box represent the 25th and 75th percentiles, while whiskers represent the 10th and 90th percentiles.
Figure 6. Box-and-whisker plots for composites parameters. The median is represented as a horizontal line inside the box, the edges of the box represent the 25th and 75th percentiles, while whiskers represent the 10th and 90th percentiles.
Preprints 75045 g006

3.2. Correlations among Parameters

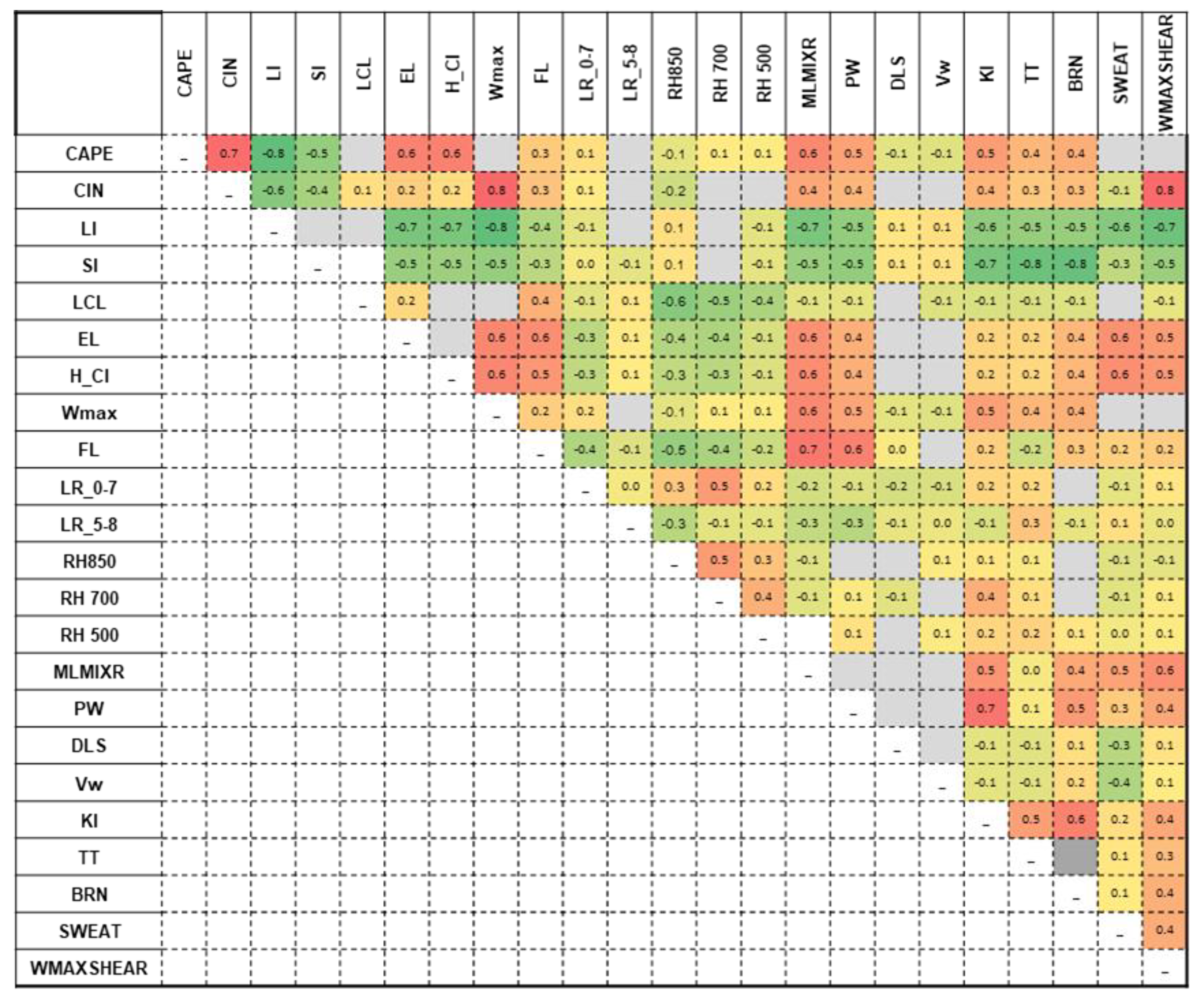
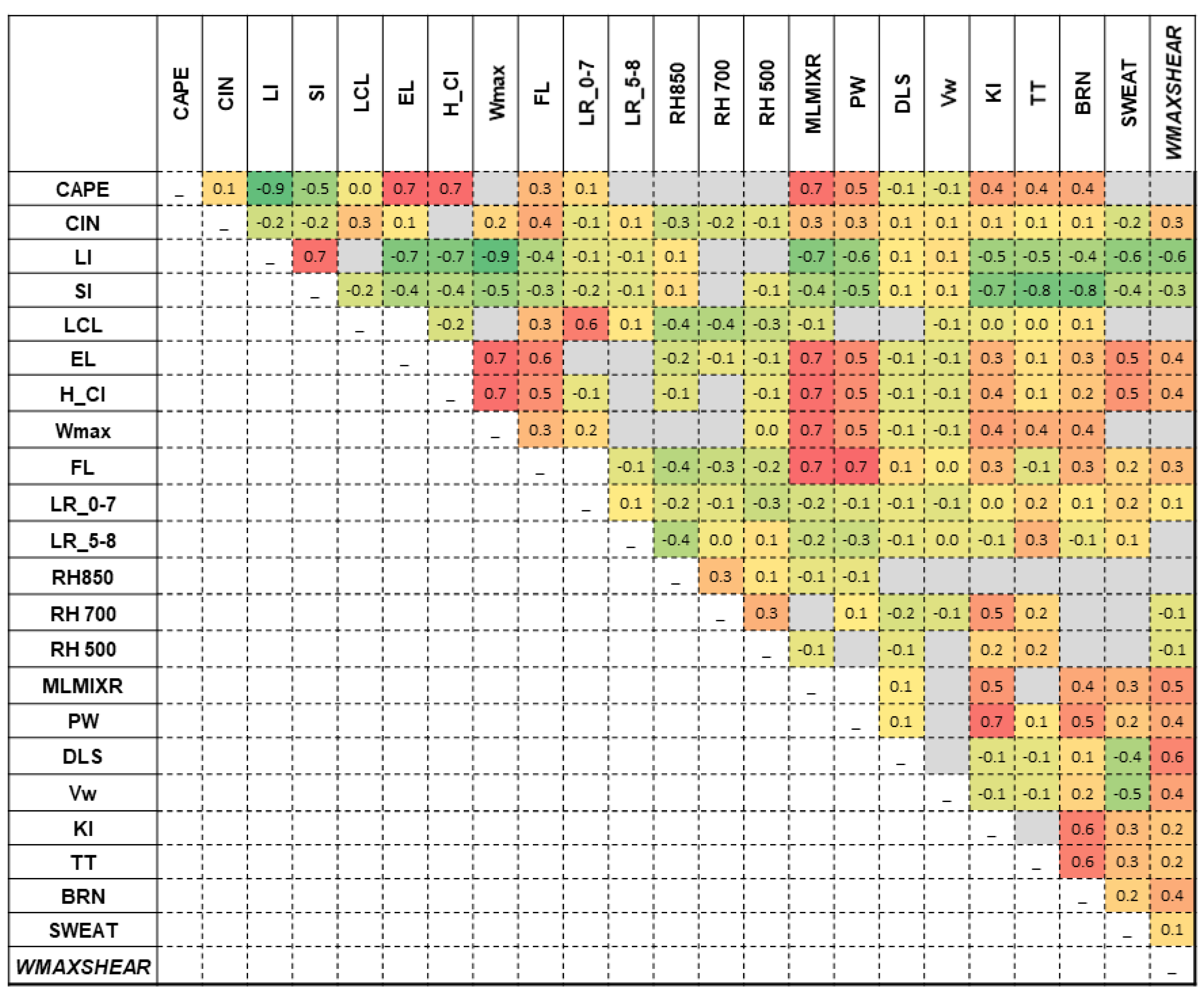
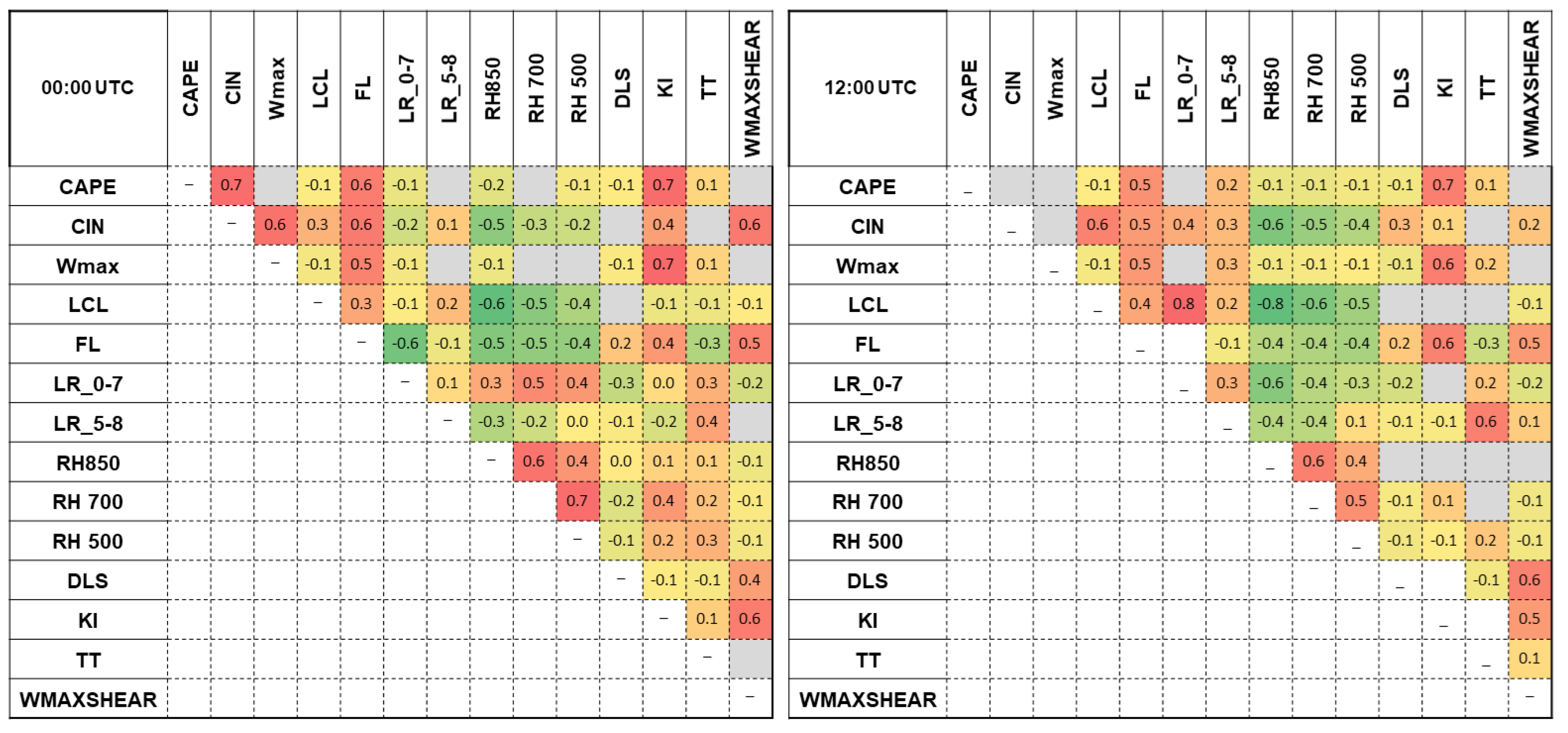
Derivate indices from correlation matrix from sounding data at 00:00 UTC, show up a very strong correlations between indices of the same type or from different "families". Coefficient values of 0.9 or higher are actually autocorrelations occurring between indices that are calculated with the same thermodynamic variables. In this situation there are correlations betwin CAPE – BRN, LI –SI, KI – TT or PW – MLMIXR. Other autocorrelations are recorded between CAPE and indices calculated using its value: Wmax, WMAXSHEAR. Good correlations were considered those with values of rs greater than 0.5. The correlation matrix show two concentration with integer coefficients values over 0.5. The most obvious are the high correlations between the indices calculated based on the particle theory and those between them and the moisture parameters, respectively the composite parameters. Correlations with coefficient values close to 0.5 also show up between the MLMIXR and the composite indices.
Strong negative correlations are recorded between LI, SI and the other indicators due to the negative characteristic values of these two parameters. Other negative correlations such as those between EL and RH850 or FL and RH850 can be explained in terms of thermodynamic laws governing energy exchange in the lower and middle troposphere.
The correlation matrix between parameters calculated from sounding data at 12:00 UTC (Figure 8) shows the same pattern of rs coefficient values. The major difference lies in the higher correlation coefficient values between the particle theory-derived and moisture indices compared to the 00:00 UTC data. The index values at this time are the significant ones that characterize the convective environment, being the closest to the interval in which most of the hail falls occurred.
Correlation matrix for ERA5 parameters stand out significant correlations between the same types of thermo-dynamic parameters as indices derived from air sounding (Figure 9). Between CAPE and CIN exists a strong correlation only at 00:00 UTC observations. The correlation between night time CIN and CAPE and its lack at midday indicates that daytime heating and dynamical factors can convert convective inhibition into available energy for the development of convective hailstorms. At the case of the EL and LR_0-7 indices, a positive correlation present only from 12:00 UTC may be caused by cases where there is a reduced amount of moisture in the early troposphere. This situation involves the increase of the thermal gradient and implicitly of the air saturation deficit, which in turn causes the EL to increase.
Other good correlations are recorded between the relative humidity values at the three pressure levels, 850 hPa, 700 hPa and 500 hPa respectively. These indicate the presence of moist air layers in the lower and middle troposphere.
Preprints 75045 g007
Figure 7. Correlation matrix for 23 instability indices derived from sounding data at 00:00 UTC. Spearman correlation coefficient (rs) values indicating strong correlations are marked with the darkest shades of red and green. Significance level α=0.05. Autocorrelations and insignificant correlations less than ║0.1║ are marked in gray.
Figure 7. Correlation matrix for 23 instability indices derived from sounding data at 00:00 UTC. Spearman correlation coefficient (rs) values indicating strong correlations are marked with the darkest shades of red and green. Significance level α=0.05. Autocorrelations and insignificant correlations less than ║0.1║ are marked in gray.
Preprints 75045 g007

4. Discussions

The highest values of the linear correlation coefficient rs were summarized in Table 2 according to the groups in which the instability indices were classified. Correlations within the particle theory indices are recorded between LI or CAPE (Wmax) and the other indices. The decrease LI value and the increase CAPE value correlate very well with the LCL and H_Cl increase indicating that the unstable layer can rise to very high altitudes in the troposphere in the presence of a strong vertical flow. A strong correlation also exists between LI and CAPE. The LI negative value indicates that the planetary boundary layer is unstable in relation to the middle troposphere, and the high value of CAPE indicates a large amount of latent energy released following the condensation of water vapour. Generaly, LI values lower than -4 correspond to CAPE values above 1000 J/kg. For the same region [57] found that highest MUCAPE characterizing the north-easterly anticyclonic. There are numerous situations where LI values indicate moderate instability but CAPE low stability which can be attributed to the existence of temperature inversions or an inhibitory layer. Istrate et al. [51] obtained similar results for 140 hail days recorded in Romania between 2007 and 2018.
The first category of indices also correlate very well with the amount of moisture in the lower troposphere, expressed by MLMIXR and RH850. Therefore, a higher amount of moisture in the lower troposphere causes a lower temperature gradient and increases the cloud base height approximated by the LCL index. Some research [9,15,24,34,72] also found LCL values to be higher on hail days compared to convective storm days with no hail. The negative correlation between LCL and UR850 can be explained by the presence of the moist-unstable layer at about 1500 m in the lower troposphere.
A larger amount of available water in the lower and middle troposphere to be ascended at negative temperatures in the hail growth zone, indicated by the CAPE-MLMIXR, LI - MLMIXR, LI – PW, or Wmax- MLMIXR correlations.
Among the temperature indices, FL has the best correlations with EL and H_Cl. The increase in the value of FL is associated with a stronger heating of the first part of the troposphere, which causes the increase of EL and including H_Cl under conditions of instability.
Indices that capture the single-level instability of the atmosphere, LI and SI are well correlated with KI, TT and SWEAT values. However, they indicate stronger correlations between SI and the three indices mentioned. Those between SI –KI and SI-TT indicate that there is a thick layer of warm, moist air in the lower to middle troposphere and a layer of cold air aloft. One of the correlations that can help to improve the forecast of hail is that between SI and SWEAT index. SI indicates the increase of the convective potential in the case of the approach of cold air masses that descend below the level of 850 mb. SWEAT takes into account several important parameters such as moisture in the lower troposphere, instability and wind shear. Thus, under the conditions of a cold atmospheric front, accretion of hail grelons is faster when the updraft contains a large amount of liquid water. The large amount of liquid water is determined by the high values of relative humidity in the lower troposphere.
High coefficients value correlation are found between FL and moisture parameters, such as MLMXR, RH850 and PW. In the summer months when the lower troposphere is warmer and richer in moisture, strong positive correlations could be find between FL - MLMXR and FL – PW. The negative coefficient between FL and RH850 can be explained by the influence that moisture in the lower troposphere, at 1500 meters, (approximate altitude at which the 850 hPa level is usually found) has on the vertical thermal gradient.
An important limitation of our approach is the potential unrepresentativeness of the sounding. Sounding stations are located hundreds of kilometers apart and are taken only every 12 h, so that a relaxed criterion for proximity measurement was chosen in order to extract parameters data for all hail reports used. In addition, there are seasonal differences in parameters values, which must be discussed. For future, we plan to use several parameters from ERA5, analyze them on a monthly basis and establish of a minimum forecast threshold like 25th percentile, used by [73].
Table 2. Strong linear correlations between index values derived from sounding and ERA5 at 00:00 UTC and 12:00 UTC of the 378 hail fall days analyzed.
Table 2. Strong linear correlations between index values derived from sounding and ERA5 at 00:00 UTC and 12:00 UTC of the 378 hail fall days analyzed.
Parameters Couples Spearman Corelation Coeficient (rs)
00:00 UTC 12:00 UTC
Between parcel parameters CAPE-LI -0,80 -0,90
CAPE-LCL 0,60 0,70
CAPE-H_Cl 0,60 0,69
LI-LCL -0,70 -0,70
LI- H_Cl -0,70 -0,70
LI-Wmax -0,80 -0,90
LCL – LR_0-7 0,60 0,70
LCL- Wmax 0,60 0,70
Between parcel parameters and moisture parameters CAPE-MLMIXR 0,60 0,70
LI- MLMXR -0,70 -0,70
EL- MLMIXR 0,60 0,70
H_Cl - MLMIXR 0,60 0,70
Wmax- MLMIXR 0,60 0,70
Wmax-PW 0,50 0,50
Between parcel parameters and temperature parameters LCL-FL 0,60 0,60
H_Cl - FL 0,60 0,50
Between parcel parameters and composite parameters SI-KI -0,70 -0,70
SI-TT -0,80 -0,80
SI-SWEAT -0,80 -0,80
Wmax-KI 0,50 0,30
Between temperature parameters and moisture parameters FL - MLMIXR 0,70 0,70
FL - PW 0,60 0,70
Between composite parameters and moisture parameters KI- PW 0,70 0,70
WMAXSHEAR- MLMIXR 0,60 0,50

5. Conclusion

Based on the multi-source hail reports data, sounding data and ERA5 reanalysis data in north-eastern Romania from 1981 to 2020, this paper statistically analyzes the climatic characteristics of some convective parameters. The convective environment of hail storms was studied using 23 instability parameters divided into five categories, namely particle theory indices, moisture indices, temperature indices, kinematic indices, and complex indices.
Statistical analysis of instability parameters used indicates a significant difference in their values between 00:00 UTC and 12:00 UTC. The values of the indices at 12:00 UTC are much higher, some of them characterizing the convective environment very well. The most used parameter, CAPE, have average values, at 12:00 UTC around 430J/kg in the case of data from ERA5, respectively 505J/kg in the case of data from sounding data. The average values at 00:00 UTC of this index are much lower, being below 200 J/kg and in about 50% of the cases they were very close to 0 or even 0. Moreover, forecasts of convective hazards are more difficult in situations of modest CAPE (<1000 J /kg) than large CAPE (>1000 J/kg).
Verification of the existence of some statistical correlations between the analyzed indices was carried out using the Spearman correlation coefficient (rs). Using correlation matrix of the derived indices from sounding data and ERA5 data at the 00UTC and 12UTC, are distinguished very strong correlations between indices of the same or different categories. Good correlations were considered those with rs values greater than 0.5. The most obvious are the high correlations between the indices calculated based on the particle theory and those between them and the moisture indices, respectively the composite indices. The mail conclusion is that probability for large hail maximizes with high low level and boundary layer moisture, high CAPE, and a high LCL height. We cannot specify exactly which of the convective parameters are the most useful in hail forecasting. Following this analysis as well as the research in the field, it turns out that certain parameters are more important depending on the synoptic and local conditions. Furtermore, we consider it necessary to continue the research for the studied area and establish some minimum thresholds values ​​to be used in the operational hail forecast.

Author Contributions

Conceptualization, V.I. and D.P.; methodology, V.I., D.A.S. software, V.I., D.A.S. and E.P. validation, E.S. and D.D.P.; data curation, V.I.; writing—original draft preparation, V.I. and D.P.; writing—review and editing, V.I. and D.P; visualization, E.S. and D.D.P.; All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

ERA5 datasets used in this study are openly available and were downloaded from the European Centre for Medium- Range Weather Forecasts (ECMWF), Copernicus Climate Change Service (C3S) available at https://cds.climate.copernicus.eu/. Sounding data were downloaded from the web server of the University of Wyoming.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Hoeppe, P. Trends in weather related disasters – Consequences for insurers and society, Weather Clim. Extrem. 2016, 11, 70-79. [CrossRef]
  2. Fawbush, E.J.; Miller, R.C. A method for forecasting hailstone size at the earth’s surface, Bull Am Meteorol Soc. 1953, 34, 235–244. https://www.jstor.org/stable/26242128.
  3. Foster, D.S.; Bates F. C. A hail size forecasting technique, Bull. Am. Meteor. Soc., 1956, 37, 135–141. [CrossRef]
  4. Miller, R.C. Notes on Analysis and Severe-Storm Forecasting Procedures of the Air Force Global Weather Central, Technical Report no 200, 1972. https://apps.dtic.mil/dtic/tr/fulltext/u2/744042.pdf.
  5. Renick, J. H.; Maxwell, J. B. Forecasting Hailfall in Alberta. In Hail: a review of hail science and hail suppression, Foote, G.B., Knight C., Eds.; American Meteorological Society: Boston, MA, USA, 1977; 16, 145-154. [CrossRef]
  6. Moore, J.T.; Pino, J.P. An interactive method for estimating maximum hailstone size from forecast soundings, Wea. Forecasting, 1990 5(3), 508–525. [CrossRef]
  7. Doswell, C. Thermodynamic analysis procedures at the national severe storms forecast center, in Conference on Weather Forecasting and Analysis, 9 th, Seattle, WA, USA, 27 June – 1 July 1982.
  8. Manzato, A. The use of sounding-derived indices for a neural network short-term thunderstorm forecast, Wea. Forecasting, 2005, 20(6), 896–917. [CrossRef]
  9. Groenemeijer, P. H.; van Delden, A. Sounding-derived parameters associated with large hail and tornadoes in the Netherlands, Atmos. Res., 2007, 83, 473–487. [CrossRef]
  10. Kunz, M. The skill of convective parameters and indices to predict isolated and severe thunderstorms, Nat. Hazards Earth Sys. Sci., 2007, 7, 327–342. [CrossRef]
  11. Sanchez, L.; Gil-Robles, B.; Dessens, J.; Martin, E.; López, L.; Marcos, J.; Berthe, C.; Fernández, J. T.; García-Ortega, E. Characterization of hailstone size spectra in hailpad networks in France, Spain, and Argentina, Atmos. Res, 2009, 93 (1–3), 641 – 654. [CrossRef]
  12. Mohr, S.; Kunz, M. Recent trends and variabilities of convective parameters relevant for hail events in Germany and Europe, Atmos. Res. 2013, 123, 211–228. [CrossRef]
  13. Johnson, A.W.; Sugden K.E. Evaluation of sounding-derived thermodynamic and wind-related parameters associated with large hail events, Electron. J. Severe Storms Meteorol. 2014, 9(5), 1-42. https://www.ejssm.org/ojs/idex.php/ejssm/article/view/137/101.
  14. Merino, A.; Wu, X.; Gascón, E.; Berthet, C.; García-Ortega, E.; Dessens, J. Hailstorms in southwestern France: incidence and atmospheric characterization, Atmos. Res. 2014, 140, 61–75. [CrossRef]
  15. Púčik, T.; Groenemeijer, P.; Rýv, D.; Kolář, M. Proximity Soundings of Severe and Nonsevere Thunderstorms in Central Europe, Mon Weather Rev. 2015, 143(12), 4805-4821. https://journals.ametsoc.org/view/journals/mwre/143/12/mwr-d-15-0104.1.xml.
  16. Tuovinen, J.P.; Rauhala, J.; Schultz, D.M. Significant-hail-producing storms in Finland: Convective-storm environment and mode, Wea. Forecasting 2015 30(4), 1064–1076. [CrossRef]
  17. Sanchez, J.L.; Merino, A.; Melcón, P.; García-Ortega, E.; Fernández-González, S.; Berthe, C.; Dessens, J. Are meteorological conditions favouring hail precipitation change in Southern Europe? Analysis of the period 1948–2015, Atmos. Res. 2017, 198, 1–10. [CrossRef]
  18. Lkhamjav, J.; Jin, H.-G.; Lee, H.; Baik, J.-J. A hail climatology in Mongolia, Asia-Pacific J. Atmos. Sci. 2017, 53(4), pp. 501–509. [CrossRef]
  19. Abshaev, M.T.; Goral, G.G.; Malbakhova, N.M. Hail type forecast. Geophysical Institute in Nalicic 1965 67, 72-79.
  20. Fedchenko, L.M.; Belentsova, V.A; Berova, M.A. Forecast of intensive hail processes in the North Caucasus, Geophysical Institute in Nalicic 1981, 50, 21-35.
  21. Goral, G.G.; Barekova, M.V. Potential atmospheric instability and hail forecast in Armenia, Geophysical Institute in Nalicic, 1986, 63, pp. 48-57.
  22. Fedchenko, G.L.M.; Goral, G.G.; Malbakhova, N.M. Detailed methods of hail forecast, Atmos. Res. 1992, 28, 375-384. [CrossRef]
  23. Weisman, M.L.; Klemp, J.B. The dependence of numerically simulated convective storms on vertical wind shear and buoyancy, Mon. Wea. Rev. 1982, 110(6), 504–520. [CrossRef]
  24. Rasmussen, E.N.; Blanchard, D.O. A baseline climatology of sounding derived supercell and tornado forecast parameters, Wea. Forecasting. 1998, 13, 1148–1164. [CrossRef]
  25. Thompson, R.L.; Edward, R.; Hart, J.A.; Elmore, K.L.; Markowski, P. Close proximity soundings within supercell environments obtained from the Rapid Update Cycle, Wea. Forecasting, 2003, 18, pp. 1243–1261. [CrossRef]
  26. Dennis, E.J.; Kumjian, M. R. The impact of vertical wind shear on hail growth in simulated supercells, J. Atmos. Sci. 2017, 74(3), 641–663. [CrossRef]
  27. Taszarek, M.; Brooks, H.E.; Czernecki, B.; Sounding-Derived Parameters Associated with Convective Hazards in Europe, Mon Weather Rev. 2017, 145(4), 1511-1528. [CrossRef]
  28. Taszarek, M.; Allen, J.T.; Groenemeijer, P.; Edwards, R.; Brooks, H.E.; Chmielewsk, V.; Enno S. Severe convective storms across Europe and the United States. Part 1: Climatology of lightning, large hail, severe wind and tornadoes, J. Climate. 2020, 33(23), 10239-1026. [CrossRef]
  29. Taszarek, M.; Allen, J.T.; Púčik, T.; Hoogewind, K.A.; Brooks, H.E,. Severe Convective Storms across Europe and the United States. Part II: ERA5 Environments Associated with Lightning, Large Hail, Severe Wind, and Tornadoes J. Climate. 2020, 33(23), 10263-10286. [CrossRef]
  30. Kunz, M.; Wandel, J.; Fluck, E.; Baumstark, S.; Mohr, S.; Schemm, S. Ambient conditions prevailing during hail events in central Europe, Nat. Hazards Earth Syst. Sci. 2020, 20, pp. 1867–1887. [CrossRef]
  31. Edwards, R.; Thompson, R.L. Nationwide comparisons of hail size with WSR-88D vertically integrated liquid water and derived thermodynamics sounding data, Wea. Forecasting. 1998, 13, 277–285. [CrossRef]
  32. Allen, J.T.; Tippett, M.K.; Sobel, A.H. An empirical model relating U.S. monthly hail occurrence to large-scale meteorological environment, J. Adv. Model. Earth Syst. 2015, 7, pp. 226–243. [CrossRef]
  33. McCaul, J.; Cohen, C. The impact on simulated storm structure and intensity of variations in the mixed layer and moist layer depths, Mon. Wea. Rev. 2022, 130(7), 2527, 1722–1748. [CrossRef]
  34. Grams, J.S.; Thompson, R.L.; Snively ,D.V.; Prentice, J.A.; Hodges, G.M.; Reames, L.J.A climatology and comparison of parameters for significant tornado events in the United States, Wea. Forecasting. 2012, 27(1),106–123.
  35. Brimelow, J.C.; Reuter, G.W.; Goodson, R.; Krauss, T.W. Spatial forecasts of maximum hail size using prognostic model soundings and HAILCAST, Wea. Forecast. 2006, 21(2), 206–219. [CrossRef]
  36. Jewell, R.; Brimelow, J. Evaluation of Alberta hail growth model using severe hail proximity soundings from the United States, Wea. Forecasting. 2009, 24(6), 1592–1609. [CrossRef]
  37. Gagne, D.J.; McGovern, A.; Haupt, S.E.; Sobash, R.A.; Williams, J.K.; Xue, M. Storm-based probabilistic hail forecasting with machine learning applied to convection-allowing ensembles, Wea. Forecasting. 2017, 32(5), 1819–1840. [CrossRef]
  38. Labriola, J.; Snook, N.; Jung, Y.; Xue, M. Explicit ensemble prediction of hail in 19 may 2013 Oklahoma City thunderstorms and analysis of hail growth processes with several multi-moment microphysics schemes, Mon. Wea. Rev. 2019, 147, 1193-1213. [CrossRef]
  39. McGovern, A.; Elmore, K.L.; Gagne, D.J.; Haupt, S.E.; Karstens, C.D.; Lagerquist, R.; Smith, T.; Williams, J.K. Using artificial intelligence to improve real-time decision-making for high-impact weather, Bull. Am. Meteor. Soc. 2017, 98(10), 2073–2090. [CrossRef]
  40. Czernecki, B.; Taszarek, M.; Marosz ,M.; Półrolniczak, M.; Kolendowicz, L.; Wyszogrodzki, A.; Szturc, J. Application of machine learning to large hail prediction-the importance of radar reflectivity, lightning occurrence and convective pa rameters derived from ERA5, Atmos. Res. 2019, 227, 249–262. [CrossRef]
  41. Gagne, D.J.; Haupt, S.E.; Nychka, D.W.; Thompson, G. Interpretable deep learning for spatial analysis of severe hailstorms, Mon. Wea. Rev. 2019. 147, 2827-2845. [CrossRef]
  42. Bălescu, O.I.; Militaru, F. Aerological study of hail falls, Collection of papers of the Meteorological Institute. 1967, 24, 73-85.
  43. Grama, M. Methods for forecasting Cumulonimbus clouds and thunderstorms at Bucharest-Băneasa airport, Collection of papers of the Meteorological Institute 1969, 26, 153-160.
  44. Ionescu-Nișcov, Ș. Forecast of stormy phenomena within the mass applying some of the methods of mathematical statistics, Studies and research. Part I. Meteorology. 1978, 283-294.
  45. Sfîcă, L.; Apostol, L.; Istrate, V.; Lesenciuc, D.; Necula, M.F. Instability indices as predictors of atmospheric lightning - Moldova region study case, SGEM 2015 Conference Proceedings. 387 – 394. [CrossRef]
  46. Stan-Sion, A.; Antonescu, B. Mesocyclones in Romania –characteristics and environments, In Proceedings of 23rd Conference on Severe Local Storms, 6–10 November 2006, St. Louis, MO. American Meteorological Society: Boston, MA.
  47. Hauer, E.; Nichita, C. The Mesoscale Convective System from 24.07.2010, Riscuri și Catastrofe. 2011, 10(9), 121-131.
  48. Istrate, V.; Axinte, A.D.; Florea, D.; Bărcăcianu, F.; Apostol L. Characteristics and impacts of the severe hailstorms on 18 June 2016 in northern Moldavia, Romania, 19th International SGEM 2019 Conference Proceedings. 2019, 19(4.1), 899-906. [CrossRef]
  49. Ilie, N.; Apostol, L.; Axinte, A.D. The way to determine the approximately hail's dimensions, Present Environment and Sustainable Development. 2020, 14(1), 209 – 219. [CrossRef]
  50. Istrate, V.; Apostol, L.; Sfîcă, L.; Iordache, I.; Bărcăcianu, F. The status of atmospheric instability indices associated with hail events throughout Moldova, Air and Water - Components of the Environment Conference Proceedings. 2015, 7, 323–331. [CrossRef]
  51. Istrate, V.; Dobri, R.V.; Bărcăcianu, F.; Ciobanu, R.A.; Apostol, L. Sounding-derived parameters associated with severe hail events in Romania, Időjárás. 2021, 125(1), 39-52. [CrossRef]
  52. Istrate, V.; Jitariu V.; Ichim P.; Machidon O.M.; Apostol, L. Hailstorm risk assessment for crop areas in Moldova Region (Romania), Present Environement and Sustainable Development. 2021, 15 (2), 55-67. [CrossRef]
  53. Burcea, S.; Cică R.; Bojariu, R. Hail Climatology and Trends in Romania: 1961–2014, Mon. Wea. Rev. 2016, 144, 4289–4299. [CrossRef]
  54. Popovici ,E.A.; Balteanu, D.; Kucsicsa, G. Assessment of changes in land-use and land-cover pattern in Romania using Corine land cover database, Carpath. J. Earth Environ. Sci. 2013, 8, 195–208.
  55. Rusu, A.; Ursu, A.; Stoleriu, C.C.; Groza, O.; Niacșu, L.; Sfîcă, L.; Minea, I.; Stoleriu O.M. Structural Changes in the Romanian Economy Reflected through Corine Land Cover Datasets. Remote Sens. 2020, 12(8), 1323. [CrossRef]
  56. Apostol, L.; Sfîcă, L. Thermal differentiations induced by the Carpathian Mountains on the Romanian territory. Carpath. J. Earth Environ. Sci. 2013, 8, 215–221.
  57. Sfîcă, L.; Istrate, V.; Hrițac, R.; Machidon, O. The continental and regional synoptic background favorable for hailstorms occurrence in North-Eastern Romania. Prog. Phys. Geogr.: Earth and Environment, 2023, 47(1), 3–31. [CrossRef]
  58. Púčik, T.; Castellano, C.; Groenemeijer, P.; Kühne, T.; Rädler Anja, T.; Antonescu, B.; Faust, E., Large hail incidence and its economic and societal impacts across Europe, Mon. Wea. Rev. 2019 147, 3901–3916. [CrossRef]
  59. Dotzek, N.; Forster C. Quantitative comparison of METEOSAT thunderstorm detection and nowcasting with in situ reports in the European Severe Weather Database (ESWD), Atmos Res. 2011, 100(4), 511–522. [CrossRef]
  60. Istrate, V.; Dobri, R.V.; Bărcăcianu, F.; Ciobanu, R.A; Apostol, L. A ten years hail climatology based on ESWD hail reports in Romania, 2007-2016, Geographia Technica. 2017, 12, 110-118. [CrossRef]
  61. Añel, J.A.; Sáenz, G.; Ramírez-González, I.A.; Polychroniadou, E.; Vidal-Mina, R.; Gimeno, L.; de la Torre, L. Obtaining meteorological data from historical newspapers: La Integridad. Weather, 2017, 72 (12), pp. 366–371. [CrossRef]
  62. Munro, D.; Fowler, A. Testing the credibility of historical newspaper reporting of extreme climate and weather events, New Zealand Geographer, 2014, 70(3), pp. 153–164. [CrossRef]
  63. Cheval, S.; Haliuc, A.; Antonescu, B; et al., Enriching the historical meteorological information using Romanian language newspaper reports: A database from 1880 to 1900. Int J Climatol. 2021, 41 (Suppl. 1), E548– E562. [CrossRef]
  64. University of Wyoming Sounding data. Available online: http://www.weather.uwyo.edu/upperair/sounding.html. (Accessed 20 September 2020).
  65. Hersbach, H.; Bell, B.; Berrisford, P.; et al. The ERA5 global reanalysis. Q J R Meteorol Soc. 2020, 146, pp. 1999– 2049. [CrossRef]
  66. Pešice, P.; Sulan, J.; Řezáčová, D. Convection precursors in the Czech territory. Atmos. Res. 2003, 67-68, 523-532. [CrossRef]
  67. Palencia, C.; Giaiotti, D.; Stel, F.; Castro, A.; Fraile, R. Maximum hailstone size: relationship with meteorological variables, Atmos. Res. 2010, 96, 256–265. [CrossRef]
  68. Kunz, M.; Sander J.; Kottmeier C.Recent trends of thunderstorm and hailstorm frequency and their relation to atmospheric characteristics in southwest Germany. Int. J. Climatol. 2009, 29, 2283–2297. [CrossRef]
  69. Manzato ,A. Hail in Northeast Italy: climatology and bivariate analysis with the sounding-derived indices, J. Appl. Meteorol. Climatol. 2012, 51, 449–467. [CrossRef]
  70. Dessens, J.; Berthet, C.; Sanchez, J.L. Change in hailstone size distributions with an increase in the melting level height, Atmos. Res. 2015, 158–159, 245-253, ISSN 0169-8095. [CrossRef]
  71. Craven, J. P.; Brooks H.E. Baseline climatology of sounding derived parameters associated with deep moist convection. Natl. Wea. Dig. 2004, 28, 13–24.
  72. Kaltenböck, R.; Diendorfer, G.; Dotzek, N. Evaluation of thunderstorm indices from ECMWF analyses, lightning data and severe storm reports, Atmos. Res. 2009, 93, 381–396. [CrossRef]
  73. Tang, J.; Xu, L.; Yao, R.; Ou, X.; Long, Q.; Wang, X. Characteristics of Environmental Parameters of Compound and Single Type Severe Convection in Hunan. Atmosphere 2022, 13, 1870. [CrossRef]
Preprints 75045 g003
Figure 3. Box-and-whisker plots for temperature parameters. The median is represented as a horizontal line inside the box, the edges of the box represent the 25th and 75th percentiles, while whiskers represent the 10th and 90th percentiles.
Figure 3. Box-and-whisker plots for temperature parameters. The median is represented as a horizontal line inside the box, the edges of the box represent the 25th and 75th percentiles, while whiskers represent the 10th and 90th percentiles.
Preprints 75045 g003
Preprints 75045 g004
Figure 4. Box-and-whisker plots for moisture parameters. The median is represented as a horizontal line inside the box, the edges of the box represent the 25th and 75th percentiles, while whiskers represent the 10th and 90th percentiles.
Figure 4. Box-and-whisker plots for moisture parameters. The median is represented as a horizontal line inside the box, the edges of the box represent the 25th and 75th percentiles, while whiskers represent the 10th and 90th percentiles.
Preprints 75045 g004
Preprints 75045 g005
Figure 5. Box-and-whisker plots for kinematic parameters. The median is represented as a horizontal line inside the box, the edges of the box represent the 25th and 75th percentiles, while whiskers represent the 10th and 90th percentiles.
Figure 5. Box-and-whisker plots for kinematic parameters. The median is represented as a horizontal line inside the box, the edges of the box represent the 25th and 75th percentiles, while whiskers represent the 10th and 90th percentiles.
Preprints 75045 g005
Preprints 75045 g008
Figure 8. Correlation matrix for 23 instability indices derived from sounding data at 12:00 UTC. Spearman correlation coefficient (rs) values indicating strong correlations are marked with the darkest shades of red and green. Significance level α=0.05. Autocorrelations and insignificant correlations less than ║0.1║ are marked in gray.
Figure 8. Correlation matrix for 23 instability indices derived from sounding data at 12:00 UTC. Spearman correlation coefficient (rs) values indicating strong correlations are marked with the darkest shades of red and green. Significance level α=0.05. Autocorrelations and insignificant correlations less than ║0.1║ are marked in gray.
Preprints 75045 g008
Preprints 75045 g009
Figure 9. Correlation matrix for 14 mean instability indices values derived from ERA5 data at 00:00 UTC and 12:00 UTC. Spearman correlation coefficient (rs) values indicating strong correlations (darkest shades of red and green marked). Significance level α=0.05. Autocorrelations and insignificant correlations smaller than ║0.1║gray marked.
Figure 9. Correlation matrix for 14 mean instability indices values derived from ERA5 data at 00:00 UTC and 12:00 UTC. Spearman correlation coefficient (rs) values indicating strong correlations (darkest shades of red and green marked). Significance level α=0.05. Autocorrelations and insignificant correlations smaller than ║0.1║gray marked.
Preprints 75045 g009
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
bsky
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

Privacy Settings

© 2026 MDPI (Basel, Switzerland) unless otherwise stated