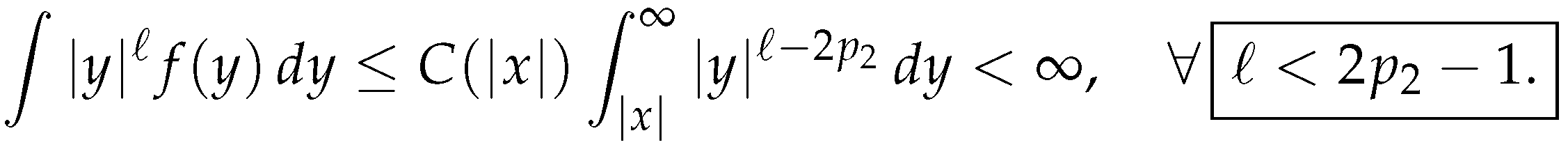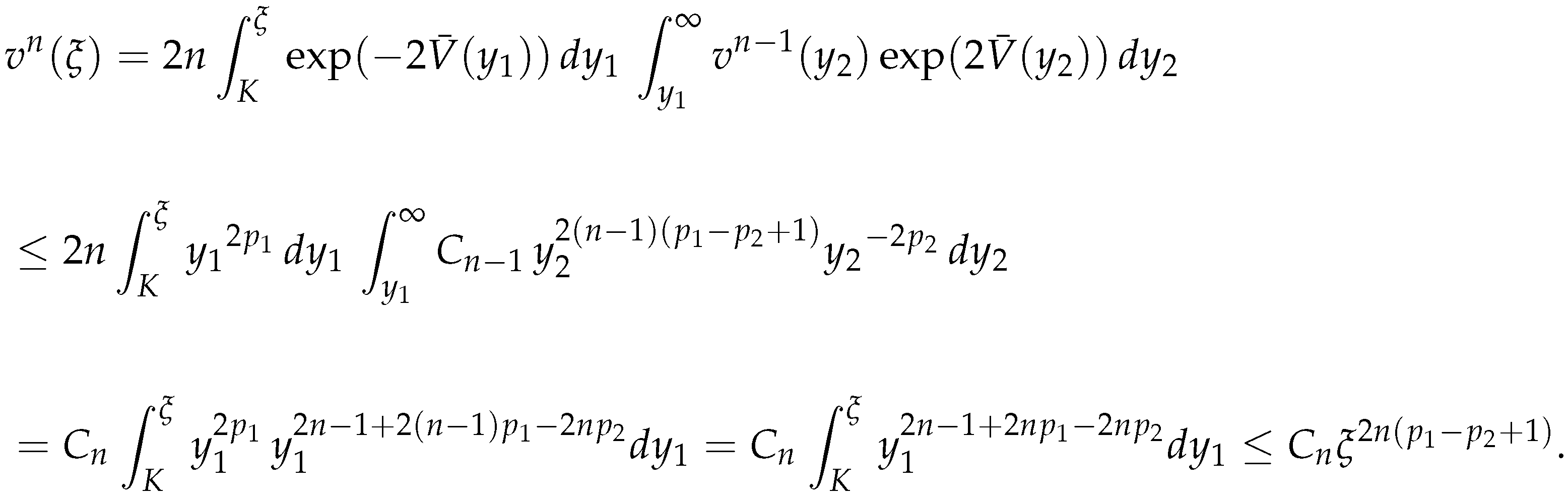1. Introduction
Let us consider a stochastic differential equation in
with initial data
Here
is a
d-dimensional Brownian motion,
takes values in
,
U is a
symmetric non-positive function,
and
. This function
U is assumed to be locally bounded and locally in
. The aim of this paper is to establish recurrence properties of the Markov process
, which are the usual preliminary steps to ergodicity, existence and uniqueness of its invariant probability measure, and to the bounds in the Law of Large Numbers type theorems, as well as to the bounds for the beta-mixing rate (cf. [
21]). In this paper the goal is to establish some polynomial bound for the hitting time to some compact in
by the process
X and the moment bounds for the marginal distribution of the process
itself; the issues related to the invariant measure are left till further studies. This hitting time bound would not depend on the first derivatives of the function
U, even though the drift in the SDE is of the gradient type. This may look a bit unusual because the drift in the SDE (
1) is of the form
. Such a problem – about bounds not depending explicitly on
– was posed and in some particular case solved in [
22]. Earlier, some other results in this area of SDEs with a gradient type drift were established by S.Ya. Makhno in his articles [
13,
14] and in the monograph [
15]; more precisely, in [
13,
14,
15] the drift is of the usual form, but the assumptions are stated for the integrated drift, which does correspond to our setting after an easy reformulation. Here we extend, and relax, and also correct some of the assumptions from [
22], with the main aim to replace the assumptions of the limit type (see (
7) in what follows) to the asymptotic inequalities (see (
9) in what follows).
It is known that the rate of convergence to the invariant distribution as well as the rates for certain mixing coefficients may be derived from the estimates of the type
along with
for some
,
, where
for some
, see, e.g., [
8,
20], et al. Here the value of
m in (
3) and in the left hand side of (
4) should be the same. In particular, for SDEs (
1) it may be derived from (
3) and (
4) that
with some
and with some polynomial function
P, at least, with a
bounded function
. Moreover, similar bounds may be established for the beta-mixing coefficient on the basis of the recurrence properties; this is known to be quite useful in various limit theorems (cf. [
7]) as well as in the extreme value theory, cf. [
11]. However, we do not pursue this goal here; certain applications will be studied in a separate paper.
The bounds like (
3) under various assumptions were obtained for various classes of processes by many authors, see, in particular, [
1,
8,
10,
17,
21], et al., and the references therein; yet, for SDEs all assumptions were usually – except the paper [
22] – stated in terms of
. See also [
4,
16] where stronger sub-exponential bounds were established under another standing assumption. In [
20] and [
21] a recurrence condition
was used to get bounds like (
5) and naturally these bounds also depend on some norm of
. Here the problem was to find some analogue of the latter condition in terms of the limiting behaviour of the function
U itself, as in [
22] but under further relaxed assumptions.
In general, it seems to a be a rare case where recurrence bounds may be established without using Lyapunov functions. Moreover, it is even not clear how to construct them for SDEs of such a type. Of course,
after the first moment bound is established (the inequality (
12) in what follows), it provides itself a Lyapunov function, but the most standard way of using them is the opposite, and here it is apparently not applicable.
The paper consists of three sections: this introduction; the main results split in two parts, the earlier results and the new ones; and the proofs.
3. Proof of theorem 1
1. Comparison to a solution for a 1D equation with reflection. Similarly to [
22], after an application of Itô’s formula to
and due to the comparison theorems for SDEs with reflection as, for example, in [
9, Proofs] one gets,
where
is a 1-dimensional Wiener process, and
is a (strong and pathwise unique) solution of the SDEs above with a non-sticky boundary condition at (any) point
so that
for all
t,
is its local time at
K,
for
; in other words, we let
Notice that the condition (
9) may be rewritten in the form
Indeed, let us show (
14): by Itô’s formula for
, denoting for convenience
we have,
Therefore, still for
,
and so,
Thus, where
, its stochastic differential has the same form as the stochastic differential of
, but unlike
, the process
with positive probability takes the values less than
K. By well-known comparison theorems,
NB: Here it is important that both solutions are strong.
2. Invariant density and its moments. The invariant density
of the process
is well known: it has a form
. Indeed, we may check the invariance equation
:
Further, for any finite dimension
we have,
The last integral converges iff
, that is,
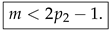
Recall that the uniqueness of the invariant measure is not emphasized here, but see remark 3. The value of m may be integer, or non-integer here.
3. An upper bound for the normalizing constant. The invariant density
of the process
on the half-line
with the reflection barrier
has a form
which can be easily verified by a direct computation of the stationarity equation
that follows in a standard way from Itô’s formula with expectations for any
for
(with a compact support and with
), where
is the generator of
and
is its adjoint with respect to Lebesgue’s measure. Notice that at this stage it is irrelevant weather or not this invariant distribution of the process
is unique (in fact, it is, although, we do not use it and, hence, do not pursue this goal).
The normalizing identity implies the estimation from above under the condition
(it coincides with
just for
),
for the values of
where the assumptions (
16) are valid. For smaller values of
below
K, convergence of the integral
cannot be destroyed because in any finite neighbourhood of zero the function
is assumed bounded by one, see the condition (
6). Naturally, the integral
increases when
decreases, so that for smaller values of
we have also smaller values of
. Hence, in all cases
with some finite
. Also note for the sequel that due to the assumption (
9), the density
admits the bound
for
and, hence, integrates some power function: namely, under the condition
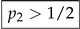
we have,
Note that the range for possible values of
ℓ here coincides with that for
ℓ in (
13). This prompts that if we had no explicit formulae for the invariant distribution of the process
but only for the dominating one
, then still the right order for its finite moments could have been obtained using the technique based on Harris – Khasminskii’s metod.
4. The inequality (10) with any real value
and with
(where
is not necessarily integer either) follows from a direct calculation: since by the comparison theorem the process
with
large enough does not exceed the stationary version of the Markov process satisfying the same non-sticky reflection SDE with the reflection barrier at
, then
(here the constants
C and
may be different on different lines and even on the same line), which is true for any
x large enough, due to comparison theorems for the processes
with different initial data
, see, e.g., [
19] for bounded coefficients; this result naturally generalizes to the locally bounded ones in the situation where there is no explosion for
. For
any – not necessarily small – this implies the bound (
4), as required. Note that the drift in [
19] was assumed bounded, or, at most, satisfying a linear growth condition; however, given that all solutions are strong and that they are defined on the infinite interval of time without explosion, this assumption can be dropped and replaced by a local boundedness of
outside zero. Important is that the values or norms of the drift
do not contribute to the constants in the final bound where only features of the function
U itself will be used.
5. The inequality (12). This is the crucial part of the statement of the theorem. Denote
for any integer
,
;
. Recall that
denotes the generator of
, that is,
where
,
. By virtue of the identity
it follows,
for any
q such that the integral in the right hand side converges. In turn, by Itô’s or Dynkin’s formula this implies an equation
(cf. with [
2, theorem 13.17] where the equation is explained differently and under a stronger assumption which guarantees some exponential moment of
). Evidently, one boundary value for the latter equation is
. Concerning the “second boundary value” usual for a PDE of the second order, it is seemingly missing here. The justification of the formula for solution below can be done by the limiting procedure as follows. Let
be the second boundary (later on
N would go to infinity). Let
for any integer
,
, where the process
is a solution of the equation similar to (15) but with another non-sticky reflection at
N. Recall that all solutions are strong and, hence, may be constructed on the same probability space; see, e.g., [
19] for SDEs with one boundary, and results from this paper are easily extended for the case with two finite boundaries. Apparently,
for any
t and
N, and
as
. So, by the monotone convergence,
for all values of
q, no matter whether or not the limit
is finite. Then the sequence of the functions
satisfies the equations (
21) with boundary conditions
The formula for solution of such an equation reads,
which may be verified by a direct calculation. Indeed, substituting
, we get
, and by taking the derivative, we can see that
The equation itself follows from a little calculus as follows:
as required. Uniqueness of solution for a linear ODE system is well-known.
Hence, by induction, the function
satisfies a representation using the function
,
By another induction this implies the inequalities (recall that
):
which is finite under the condition that
(otherwise the inner integral diverges). Further,
where in the calculus it was assumed that
, that is, that
, otherwise the inner integral in the calculus diverges. Since from the beginning
, for the value of
this means that compulsory
.
It looks plausible that the general bound for a (finite)
is provided by the formula
The base being already established, let us show the induction step. Assume that for
the formula is valid with some constant
, that is,
Then for
, as long as the integrals in the calculus below converge, we have,
Hence, indeed, by induction the formula (
24) is established.
The values of
q for which all the integrals in the calculus above converge for each
must satisfy the bound
that is,
Recall that in this paper only integer values of q are used; however, introduced above is not necessarily integer, but in any case the inequality is equivalent to , which is necessary and sufficient for the finiteness of the first . This proves the last statement of the theorem. QED
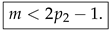
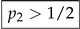 we have,
we have,