Analysis of Arbitrarily Loaded Rectangular Thin Plates with Two Opposite Edges Supported, One or Both of them Clamped, Using the Flexibility Method and a Modified Lévy Solution

Preprint

Article

Analysis of Arbitrarily Loaded Rectangular Thin Plates with Two Opposite Edges Supported, One or Both of them Clamped, Using the Flexibility Method and a Modified Lévy Solution

Altmetrics

Downloads

163

Views

905

Comments

Supplementary Material

supplementary.rar (373.37KB )

Valentin Fogang^*

This version is not peer-reviewed

Submitted:

12 June 2023

Posted:

12 June 2023

You are already at the latest version

Alerts

Abstract

This paper aims to analyze arbitrarily loaded isotropic rectangular thin plates with two opposite edges supported (simply supported or clamped), from which one or both are clamped, and the other edges have arbitrary support conditions. Rectangular thin plates with two opposite edges simply supported are routinely analyzed using for the deflection the simple trigonometric series of Lévy or the double trigonometric series of Navier, while the loads are expanded in Fourier series. In this paper the flexibility method (or force method) of the linear beam theory was applied whereby the unknowns were the bending moments along the opposite edges; in this regard, the primary system was the plate simply supported along the above-mentioned opposite edges and subjected to the external loads, system solved using the Lévy solution, and the redundant system was the plate simply supported along the opposite edges and subjected to bending moments along those edges. In the redundant system, a modified Lévy solution was introduced to account for the edge moments. The compatibility equations (vanishing of the slopes at selected positions of the opposite edges) were set to determine the unknowns and so the efforts in the plate. The results obtained were in good agreement with the exact results.

Keywords:

Subject: Engineering - Civil Engineering

1. Introduction

The Kirchhoff–Love plate theory (KLPT) was developed in 1888 by Love using assumptions proposed by Kirchhoff [1]. The KLPT is governed by the Germain−Lagrange plate equation; this equation was first derived by Lagrange in December 1811 in correcting the work of Germain [2] who provided the basis of the theory. For rectangular plates, Navier [3] in 1820 introduced a simple method for the analysis when a plate is simply supported along all edges; the applied load and the deflection were expressed in terms of Fourier components and double trigonometric series, respectively. Another approach was proposed by Lévy [4] in 1899 for rectangular plates simply supported along two opposite edges; the applied load and the deflection were expressed in terms of Fourier components and simple trigonometric series, respectively. Many exact solutions for isotropic linear elastic thin plates have been developed by Timoshenko [5]; the simple trigonometric series of Lévy was mostly considered. Mama et al. [6] presented the single finite Fourier sine integral transform method for the flexural analysis of rectangular Kirchhoff plate with opposite edges simply supported, and the other edges clamped for the case of triangular load distribution on the plate domain. Sayyad et al. [7] assessed a trigonometric plate theory for the static bending analysis of plates resting on Winkler elastic foundation; the theory considered the effects of transverse shear and normal strains. Xu et al. [8] got exact solutions for rectangular anisotropic plates with four clamped edges through the state space method whereby the Fourier series in exponential form were adopted. Khan et al. [9] used the variational approach to investigate a clamped rectangular plate under a uniform load; the minimum total potential energy approach was considered. Onyia et al. [10] presented the elastic buckling analysis of rectangular thin plates using the single finite Fourier sine integral transform method. Pisacic et al. [11] developed a procedure of calculating deflection of rectangular plate using a finite difference method, programmed in Wolfram Mathematica; the system of equations was built using the mapping function and solved with solve function. Delyavskyy et al. [12] developed an approach to analyze thin isotropic symmetrical plates using combined analytical and numerical methods. Imrak et al. [14] presented an exact solution for a rectangular plate clamped along all edges in which each term of the series is trigonometric and hyperbolic, and identically satisfies the boundary conditions on all four edges.

In this paper, arbitrarily loaded rectangular plates with two opposite edges supported, from which one or both are clamped, and the other edges with arbitrary support conditions are analyzed. The plate is modeled as the superposition of two systems: 1) the plate simply supported along the opposite edges and subjected to the external loads, this system being solved using the Lévy solution, 2) the plate simply supported along the opposite edges and subjected to edge moment loading. Given that the Lévy solution is not able to model plate edges subjected to a moment loading, a modified Lévy solution will be introduced to account for the edge moments. Then, the flexibility method can be applied.

2. Materials and methods

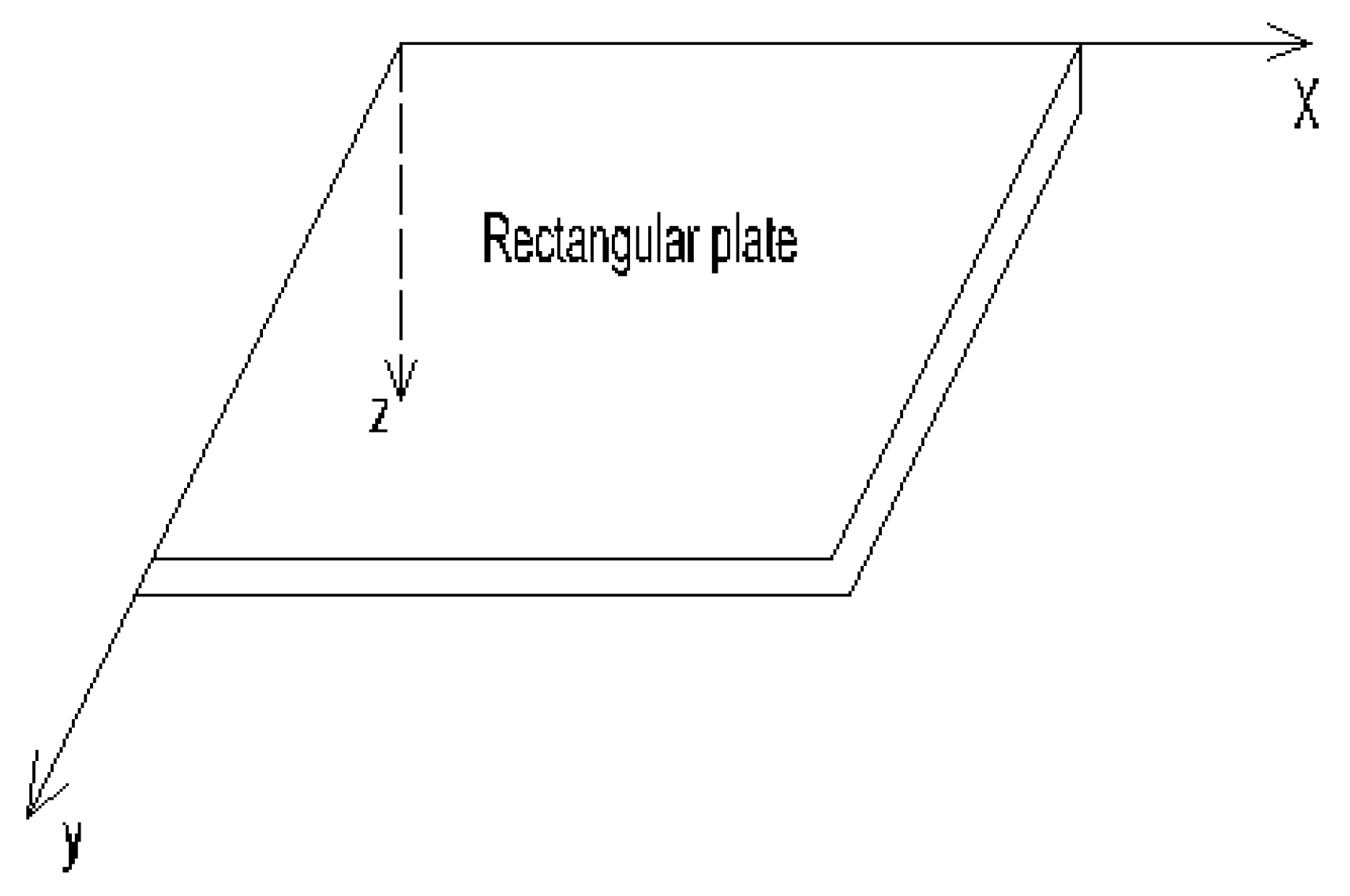
2.1. Governing equations of the plate

The Kirchhoff–Love plate theory (KLPT) [1] is used for thin plates whereby shear deformations are not considered. The spatial axis convention (X, Y, Z) is represented in Figure 1 below.

The equations of the present section are related to the KLPT. The governing equation of the isotropic Kirchhoff plate, derived by Lagrange, is given by

(1)

where w(x,y,z) is the displacement in z-direction, q(x,y) the applied transverse load per unit area, and D the flexural rigidity of the plate.

The bending moments per unit length m_xx and m_yy, and the twisting moments per unit length m_xy are given by

(2a–d)

The Kirchhoff shear forces per unit length combine shear forces and twisting moments, and can be expressed as follows:

V_{x} = - D \times (\frac{\partial^{3} w}{\partial x^{3}} + (2 - ν) \frac{\partial^{3} w}{\partial x \partial y^{2}}), \begin{matrix} V_{y} = - D \times (\frac{\partial^{3} w}{\partial y^{3}} + (2 - ν) \frac{\partial^{3} w}{\partial x^{2} \partial y}) \end{matrix} .

(3a–b)

In these equations, E is the elastic modulus of the plate material, h is the plate thickness, and ν is the Poisson’s ratio.

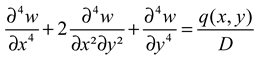
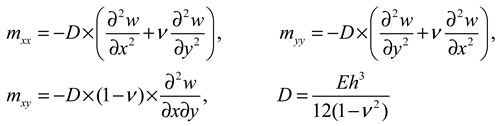
2.2. Rectangular isotropic plate clamped along two opposite edges

The analyzed rectangular plate is assumed clamped along two opposite edges. The flexibility method (or force method) of the linear beam theory was applied in this analysis whereby the unknowns were the bending moments along the opposite edges. In this regard the primary system was the plate simply supported along the above-mentioned opposite edges and subjected to the external loads, and the redundant system was the plate simply supported along the opposite edges and subjected to bending moments along those edges. The compatibility equations (vanishing of the slopes along the opposite edges) will be used to determine the unknowns.

2.2.1. Primary problem: plate simply supported along two opposite edges

The plate dimensions in x- and y-direction are denoted by a and b, respectively. The rectangular plate is assumed simply supported along the edges x = 0 and x = a. The solution by Lévy [4] that satisfies the boundary conditions at these edges is considered for the deflection curve w(x,y) as follows:

w (x, y) = \frac{1}{D} \sum_{m} F_{m} (y) \sin \frac{m π x}{a} .

(4)

The Fourier sine series of the transverse applied load is given by

q (x, y) = \sum_{m} q_{m} (y) \sin \frac{m π x}{a}

(5)

Substituting Equations (4) and (5) into (1) yields the differential equation

\frac{d^{4} F_{m} (y)}{d y^{4}} - 2 {(\frac{m π}{a})}^{2} \frac{d^{2} F_{m} (y)}{d y^{2}} + {(\frac{m π}{a})}^{4} F_{m} (y) = q_{m} (y)

(6)

The solution to Equation (6) is as follows:

\begin{array}{l} F_{m} (y) = A_{m} \cosh α_{m} y + B_{m} α_{m} y \sinh α_{m} y + C_{m} \sinh α_{m} y + D_{m} α_{m} y \cosh α_{m} y + F_{m p} (y) \\ \begin{matrix} α_{m} = \frac{m π}{a} \end{matrix} \end{array}

(7)

where the coefficients A_m, B_m, C_m, and D_m are determined by satisfying the boundary and continuity conditions in y-direction, and F_mp(y) is a particular solution to the differential equation.

Substituting Equation (4) into (2a-c) yields the equations of bending moments and twisting moments as follows:

\begin{array}{l} m_{x x} = - \sum_{m} [- α_{m}^{2} F_{m} (y) + ν \frac{d^{2} F_{m} (y)}{d y^{2}}] \sin α_{m} x, \\ m_{y y} = - \sum_{m} [\frac{d^{2} F_{m} (y)}{d y^{2}} - ν α_{m}^{2} F_{m} (y)] \sin α_{m} x, \\ m_{x y} = - (1 - ν) \times \sum_{m} α_{m} \frac{d F_{m} (y)}{d y} \cos α_{m} x . \end{array}

(8a–c)

With regard to the boundary conditions at y = 0 and y = b the equations for the slope ∂w/∂y and the bending moment myy are set using Equations (4), (7), and (8b) as follows

\begin{array}{l} \frac{\partial w (x, y)}{\partial y} = \frac{1}{D} \sum_{m} \frac{d F_{m} (y)}{d y} \sin α_{m} x \\ \begin{matrix}  \end{matrix} = \frac{1}{D} \sum_{m} α_{m} [\begin{array}{l} A_{m} \sinh α_{m} y + B_{m} (\sinh α_{m} y + α_{m} y \cosh α_{m} y) + \\ C_{m} \cosh α_{m} y + D_{m} (\cosh α_{m} y + α_{m} y \sinh α_{m} y) + \frac{1}{α_{m}} \frac{d F_{m p} (y)}{d y} \end{array}] \sin α_{m} x \end{array}

(9a)

m_{y y} = - \sum_{m} α_{m}^{2} (1 - ν) [\begin{array}{l} A_{m} \cosh α_{m} y + B_{m} (\frac{2}{1 - ν} \cosh α_{m} y + α_{m} y \sinh α_{m} y) + \\ C_{m} \sinh α_{m} y + D_{m} (\frac{2}{1 - ν} \sinh α_{m} y + α_{m} y \cosh α_{m} y) + \\ \frac{1}{α_{m}^{2} (1 - ν)} [\frac{d^{2} F_{m p} (y)}{d y^{2}} - ν α_{m}^{2} F_{m p} (y)] \end{array}] \sin

(9b)

Furthermore, with regard to the boundary conditions at y = 0 and y = b the Kirchhoff shear force V_y is calculated by substituting Equations (4) and (7) into (3b) as follows:

\begin{array}{l} V_{y} = - \sum_{m} [\frac{d^{3} F_{m} (y)}{d y^{3}} - (2 - ν) α_{m}^{2} \frac{d F_{m} (y)}{d y}] \sin α_{m} x \\ \begin{matrix}  \end{matrix} = - \sum_{m} α_{m}^{3} (ν - 1) [\begin{array}{l} A_{m} \sinh α_{m} y + B_{m} (\frac{ν + 1}{ν - 1} \sinh α_{m} y + α_{m} y \cosh α_{m} y) + \\ C_{m} \cosh α_{m} y + D_{m} (\frac{ν + 1}{ν - 1} \cosh α_{m} y + α_{m} y \sinh α_{m} y) + \\ \frac{1}{α_{m}^{3} (ν - 1)} [\frac{d^{3} F_{m p} (y)}{d y^{3}} - (2 - ν) α_{m}^{2} \frac{d F_{m p} (y)}{d y}] \end{array}] \sin α_{m} x \end{array}

(9c)

In summary, the boundary conditions at y = 0 and y = b needed to determine the coefficients A_m, B_m, C_m, and D_m.are expressed using the equations for the deflection (Equations (4) and (7)), the slope ∂w/∂y (Equation (9a)), the bending moment myy (Equation (9b)), and the Kirchhoff shear force Vyy (Equation (9c)).

The flexibilities δ_j0 (slopes at positions j (xj, yj) of the opposite edges where the compatibility equations will be set) for the primary problem are calculated using Equations (4) and (7) as follows:

δ_{j 0} = {\frac{\partial w (x, y)}{\partial x} |}_{\begin{array}{l} x = x_{j} \\ y = y_{j} \end{array}} = \frac{1}{D} \sum_{m} α_{m} [\begin{array}{l} A_{m} \cosh α_{m} y_{j} + B_{m} α_{m} y_{j} \sinh α_{m} y_{j} + C_{m} \sinh α_{m} y_{j} \\ + D_{m} α_{m} y_{j} \cosh α_{m} y_{j} + F_{m p} (y_{j}) \end{array}] \cos α_{m} x_{j}

(10)

For the primary problem the bending moments myy are calculated using Equations (9b), and the bending moments mxx and twisting moments mxy are calculated using Equations (7) and (8a,c) as follows

(11a–b)

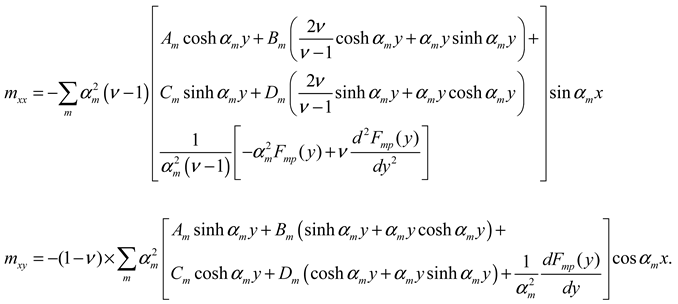
2.2.2. Redundant problem: plate subjected to a distributed bending moment along the edge x = 0

The distribution of the bending moments X(y) along the clamped edge x = 0 depends on the support conditions along the edges y = 0 and y = b, namely supported (simply supported or clamped) or free.

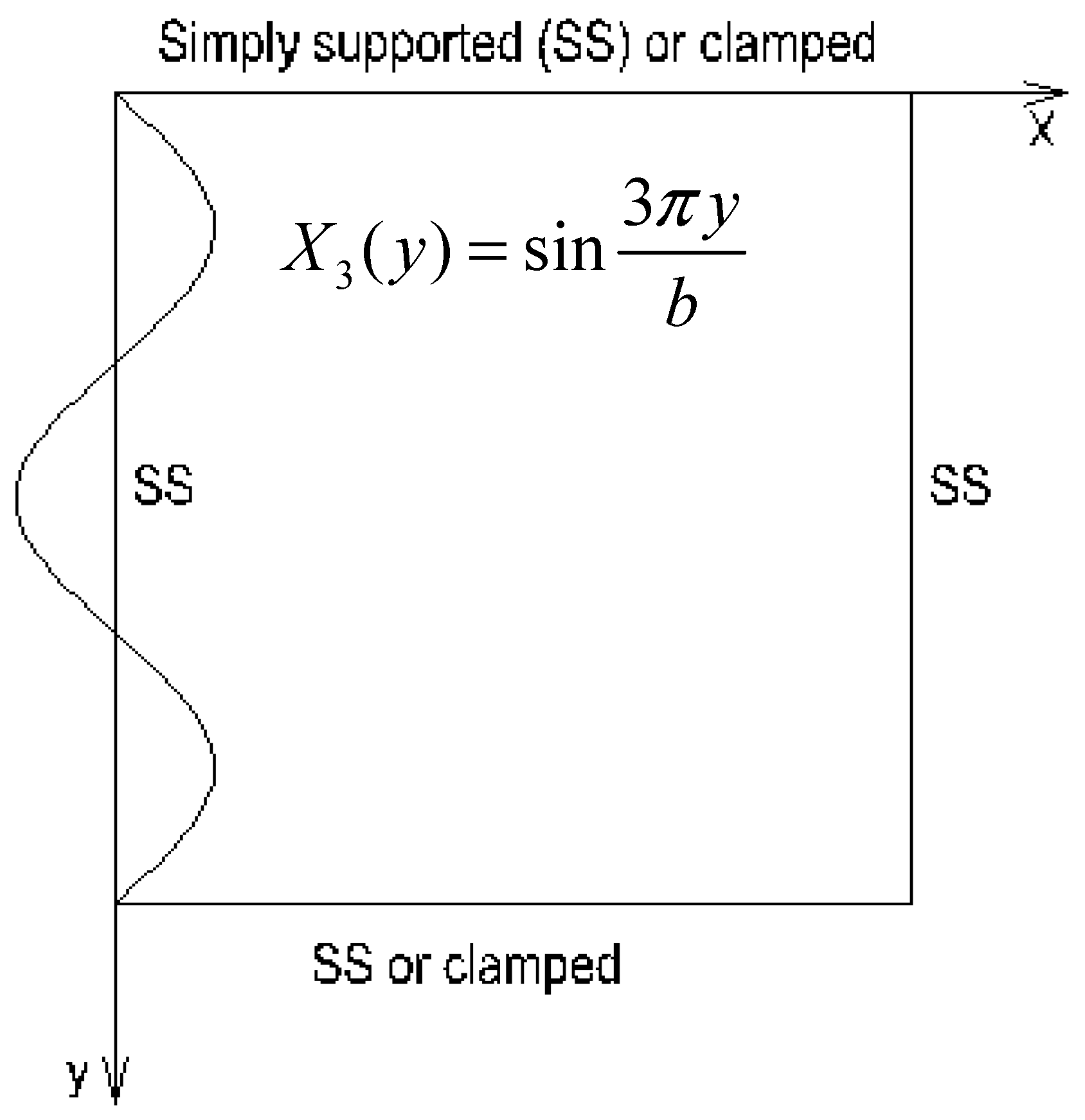
2.2.2.1. Edges y = 0 and y = b simply supported or clamped

Redundant problem Xi = 1

The edges y = 0 and y = b are assumed simply supported or clamped. Observing that the bending moments vanish at angles supported in two directions (in this case at y= 0 and y = b), the distribution of the bending moments X(y) along the clamped edge x = 0 can be described with the following trigonometric series

X (y) = \sum_{i = 1, 2...}^{n} X_{i} \sin \frac{i π y}{b}

(12)

Here, the redundant effort is a distributed bending moment sin (iπy/b) along the edge x = 0 according to Equation (12), as represented in Figure 2 for i = 3.

It is observed that in case of system and loading symmetrical with respect to axis y = b/2 only odd values of i need be considered, the redundants being zero for even values; and in case of system symmetrical and loading anti symmetrical with respect to axis y = b/2 only even values of i need be considered, the redundants being zero for odd values.

To account for the edge moments the solution by Lévy [4] for the transverse displacement can be modified as follows

w_{i} (x, y) = \frac{1}{D} \sum_{m} F_{m i} (y) \sin α_{m} x + \frac{a^{2}}{6 D} [1 - \frac{x}{a} - {(1 - \frac{x}{a})}^{3}] \sin \frac{i π y}{b}

(13)

The second term on the right-hand side of Equation (13) is the displacement function of a plate strip simply supported at its ends and subjected at the edge x = 0 to a distributed moment sin (iπy/b). It is noted that Equation (13) satisfies the boundary conditions at edges x = 0 and x = a. Substituting Equation (13) into (1) yields

\begin{array}{l} \frac{1}{D} \sum_{m} [\frac{d^{4} F_{m i} (y)}{d y^{4}} - 2 α_{m}^{2} \frac{d^{2} F_{m i} (y)}{d y^{2}} + α_{m}^{4} F_{m i} (y)] \sin α_{m} x + \\ + \frac{2}{D} {(\frac{i π}{b})}^{2} (1 - \frac{x}{a}) \sin \frac{i π y}{b} + \frac{a^{2}}{6 D} {(\frac{i π}{b})}^{4} [1 - \frac{x}{a} - {(1 - \frac{x}{a})}^{3}] \sin \frac{i π y}{b} = 0 \end{array}

(14)

The following functions contained in Equation (14) are expanded in Fourier sine series

1 - \frac{x}{a} = \sum_{m} \frac{2}{m π} \sin α_{m} x, \begin{matrix} 1 - \frac{x}{a} - {(1 - \frac{x}{a})}^{3} = \end{matrix} \sum_{m} \frac{12}{m^{3} π^{3}} \sin α_{m} x

(15)

Substituting Equations (15) into (14) yields

\begin{array}{l} \sum_{m} [\frac{d^{4} F_{m i} (y)}{d y^{4}} - 2 α_{m}^{2} \frac{d^{2} F_{m i} (y)}{d y^{2}} + α_{m}^{4} F_{m i} (y)] \sin α_{m} x + \\ + \sum_{m} [\frac{4 π}{m} {(\frac{i}{b})}^{2} + \frac{2 π a^{2}}{m^{3}} {(\frac{i}{b})}^{4}] \sin \frac{i π y}{b} \sin α_{m} x = 0 \end{array}

(16)

Given that Equation (16) holds for any value of x, it results the following differential equation

\frac{d^{4} F_{m i} (y)}{d y^{4}} - 2 α_{m}^{2} \frac{d^{2} F_{m i} (y)}{d y^{2}} + α_{m}^{4} F_{m i} (y) = - [\frac{4 π}{m} {(\frac{i}{b})}^{2} + \frac{2 π a^{2}}{m^{3}} {(\frac{i}{b})}^{4}] \sin \frac{i π y}{b}

(17)

The solution to Equation (17) is identical to Equation (7) whereby the particular solution is given by

F_{m p i} (y) = k_{m i} \sin \frac{i π y}{b} \begin{matrix} k_{m i} = - \frac{[\frac{4}{m} {(\frac{i}{b})}^{2} + \frac{2 a^{2}}{m^{3}} {(\frac{i}{b})}^{4}]}{π^{3} {[{(\frac{i}{b})}^{2} + {(\frac{m}{a})}^{2}]}^{2}} \end{matrix}

(18)

Combining Equations (7), (13) and (18) yields the transverse displacement function as follows

\begin{array}{l} w_{i} (x, y) = \frac{1}{D} \sum_{m} [\begin{array}{l} A_{m i} \cosh α_{m} y + B_{m i} α_{m} y \sinh α_{m} y + C_{m i} \sinh α_{m} y + \\ D_{m i} α_{m} y \cosh α_{m} y + k_{m i} \sin \frac{i π y}{b} \end{array}] \sin α_{m} x + \\ \begin{matrix}  \end{matrix} \frac{a^{2}}{6 D} [1 - \frac{x}{a} - {(1 - \frac{x}{a})}^{3}] \sin \frac{i π y}{b} \end{array}

(19)

To satisfy the boundary conditions at y = 0 and y = b, the Fourier series of Equation (15) is used; Equation (19) becomes

(20)

With resect to the boundary conditions at y = 0 and y = b the equations for the slope ∂w/∂y and the bending moment myy are set using Equations (9a-b) and (20) as follows

\frac{\partial w (x, y)}{\partial y} = \frac{1}{D} \sum_{m} α_{m} [\begin{array}{l} A_{m i} \sinh α_{m} y + B_{m i} (\sinh α_{m} y + α_{m} y \cosh α_{m} y) + \\ C_{m i} \cosh α_{m} y + D_{m i} (\cosh α_{m} y + α_{m} y \sinh α_{m} y) + \\ \frac{i a}{m b} k_{m i}^{*} \cos \frac{i π y}{b} \end{array}] \sin α_{m} x

(21a)

m_{y y} = - \sum_{m} α_{m}^{2} (1 - ν) [\begin{array}{l} A_{m i} \cosh α_{m} y + B_{m i} (\frac{2}{1 - ν} \cosh α_{m} y + α_{m} y \sinh α_{m} y) + \\ C_{m i} \sinh α_{m} y + D_{m i} (\frac{2}{1 - ν} \sinh α_{m} y + α_{m} y \cosh α_{m} y) \\ - \frac{π^{2}}{α_{m}^{2} (1 - ν)} [{(\frac{i}{b})}^{2} + ν {(\frac{m}{a})}^{2}] k_{m i}^{*} \sin \frac{i π y}{b} \end{array}] \sin α_{m} x

(21b)

In summary, the boundary conditions at y = 0 and y = b needed to determine the coefficients A_mi, B_mi, C_mi, and D_mi.are expressed using Equations (20) and (21a-b)

The flexibilities δ_ji (slopes at relevant positions j (xj, yj) of the opposite edges where the compatibility equations will be set) for the redundant problem X_i = 1 are calculated using Equation (19); it yields

\begin{array}{l} δ_{j i} = {\frac{\partial w (x, y)}{\partial x} |}_{\begin{array}{l} x = x_{j} \\ y = y_{j} \end{array}} = \frac{1}{D} \sum_{m} α_{m} [\begin{array}{l} A_{m i} \cosh α_{m} y_{j} + B_{m i} α_{m} y_{j} \sinh α_{m} y_{j} + C_{m i} \sinh α_{m} y_{j} + \\ D_{m i} α_{m} y_{j} \cosh α_{m} y_{j} + k_{m i} \sin \frac{i π y_{j}}{b} \end{array}] \cos α_{m} x_{j} \\ \begin{matrix}  \end{matrix} + \frac{a}{6 D} [- 1 + 3 {(1 - \frac{x_{j}}{a})}^{2}] \sin \frac{i π y_{j}}{b} \end{array}

(22)

The positions j must be chosen such as to be regularly distributed along the clamped edge. Keeping in mind that there should be as many redundants as compatibility equations, for an edge with n redundants considered the positions y_j = k×b/ (n + 1) with k = 1, 2, 3 …n as represented in Figure 3a can be taken.

It is recalled that in case of system and loading symmetrical with respect to axis y = b/2 only odd values of i need be considered and in case of system symmetrical and loading anti symmetrical with respect to the same axis only even values of i need be considered. In both cases, the flexibilities and compatibility equations can be set in half of the structure in y–direction. Given the half edge with n redundants, the positions y_j = k×b/2n with k = 1, 2, 3 …n as represented in Figure 3b can be taken.

For the redundant problem X_i = 1 the bending moments m_xx and m_yy , and the twisting moments m_xy are calculated using Equations (2a-c) and (19) as follows

\begin{array}{l} m_{x x, i} = - \sum_{m} α_{m}^{2} (ν - 1) [\begin{array}{l} A_{m i} \cosh α_{m} y + B_{m i} (\frac{2 ν}{ν - 1} \cosh α_{m} y + α_{m} y \sinh α_{m} y) + \\ C_{m i} \sinh α_{m} y + D_{m i} (\frac{2 ν}{ν - 1} \sinh α_{m} y + α_{m} y \cosh α_{m} y) \\ - \frac{π^{2}}{α_{m}^{2} (ν - 1)} [{(\frac{m}{a})}^{2} + ν {(\frac{i}{b})}^{2}] k_{m i} \sin \frac{i π y}{b} \end{array}] \sin α_{m} x + \\ \begin{matrix} + \end{matrix} (1 - \frac{x}{a}) \sin \frac{i π y}{b} + \frac{ν a^{2}}{6} {(\frac{i π}{b})}^{2} [1 - \frac{x}{a} - {(1 - \frac{x}{a})}^{3}] \sin \frac{i π y}{b} \end{array}

(23a)

\begin{array}{l} m_{y y, i} = - \sum_{m} α_{m}^{2} (1 - ν) [\begin{array}{l} A_{m i} \cosh α_{m} y + B_{m i} (\frac{2}{1 - ν} \cosh α_{m} y + α_{m} y \sinh α_{m} y) + \\ C_{m i} \sinh α_{m} y + D_{m i} (\frac{2}{1 - ν} \sinh α_{m} y + α_{m} y \cosh α_{m} y) \\ - \frac{π^{2}}{α_{m}^{2} (1 - ν)} [{(\frac{i}{b})}^{2} + ν {(\frac{m}{a})}^{2}] k_{m i} \sin \frac{i π y}{b} \end{array}] \sin α_{m} x \\ \begin{matrix} + \frac{a^{2}}{6} {(\frac{i π}{b})}^{2} [1 - \frac{x}{a} - {(1 - \frac{x}{a})}^{3}] \sin \frac{i π y}{b} + \end{matrix} ν (1 - \frac{x}{a}) \sin \frac{i π y}{b} \end{array}

(23b)

\begin{array}{l} m_{x y, i} = - (1 - ν) \times \sum_{m} α_{m}^{2} [\begin{array}{l} A_{m i} \sinh α_{m} y + B_{m i} (\sinh α_{m} y + α_{m} y \cosh α_{m} y) + C_{m i} \cosh α_{m} y \\ + D_{m i} (\cosh α_{m} y + α_{m} y \sinh α_{m} y) + \frac{i a^{2}}{π m^{2} b} k_{m i} \cos \frac{i π y}{b} \end{array}] \cos α_{m} x \\ \begin{matrix} + \end{matrix} \frac{a (1 - ν)}{6} \frac{i π}{b} [1 - 3 {(1 - \frac{x}{a})}^{2}] \cos \frac{i π y}{b} \end{array}

(23c)

According to the flexibility method of the theory of elasticity, the compatibility equations are set so as to restore the geometric boundary conditions of the clamped edges (vanishing of slopes ∂w/∂x at selected positions of the edge). Assuming a plate with n redundants, the compatibility equations for the position j (xj, yj) can be expressed as follows

\sum_{i = 1}^{n} X_{i} δ_{j i} + δ_{j 0} = 0

(24)

δ_j0 and δ_ji being the flexibilities in the primary problem and in the redundant problems, respectively. Equation (24) is set at selected positions j and so the redundant efforts are determined. The efforts in the plate are then calculated as follows

S = S_{0} + \sum_{i = 1}^{n} X_{i} S_{i}

(25)

S₀ and S_i being the efforts in the primary problem and in the redundant problems, respectively.

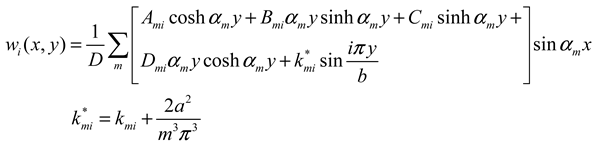
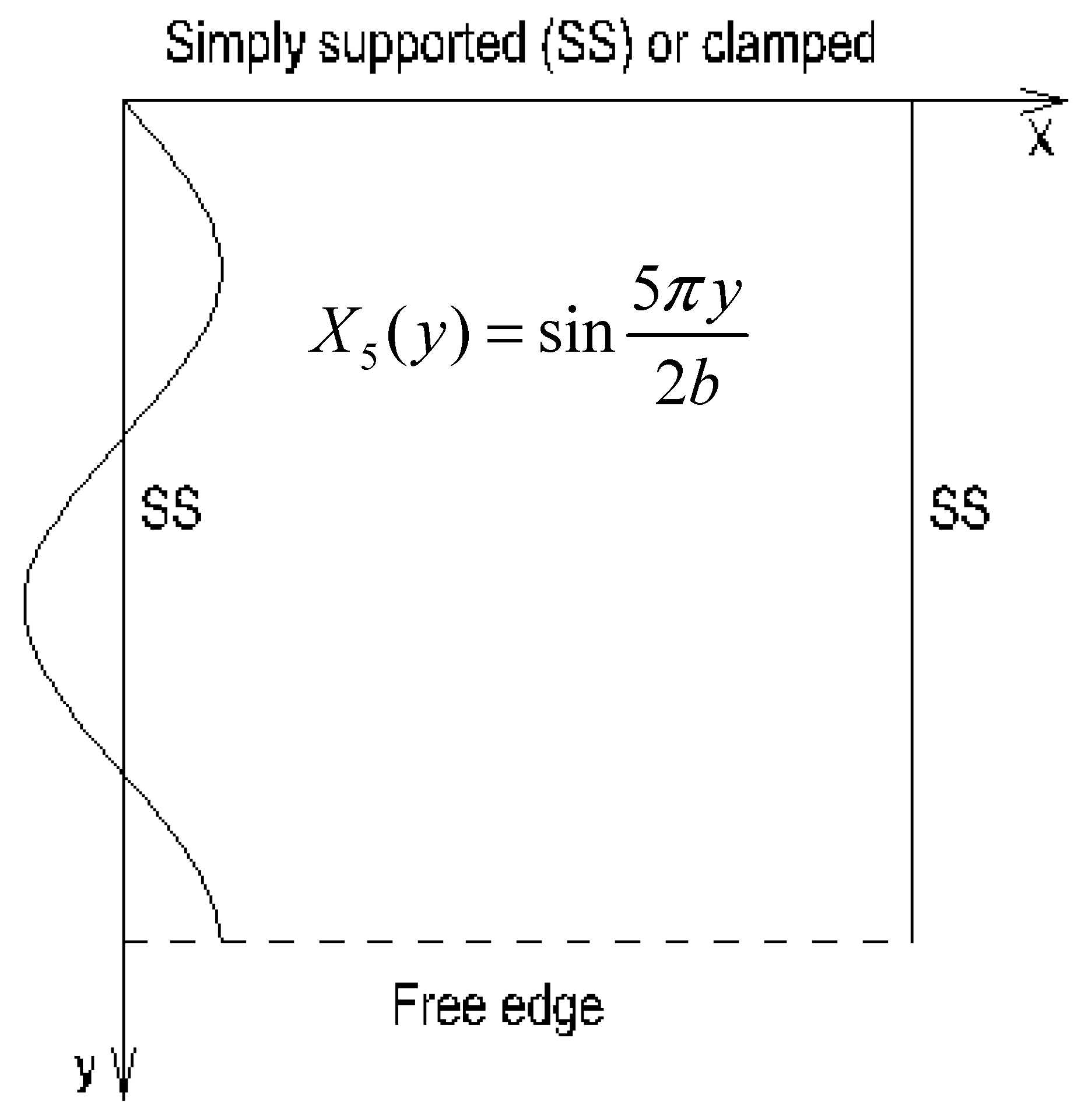
2.2.2.2. Edge y = 0 simply supported or clamped, and edge y = b free

Redundant problem Xi = 1

Here the edge y = 0 is simply supported or clamped and y = b is free. The analysis in this section holds further if the edge y = 0 is free and y = b is simply supported or clamped; the plate must simply be rotated by 180°.

Observing that the bending moments X(y) vanish at y = 0 (angle supported in two directions), their distribution along the clamped edge x = 0 can be described with the following trigonometric series

X (y) = \sum_{i = 1, 3, 5...}^{n} X_{i} \sin \frac{i π y}{2 b}

(26)

i being an odd number . The redundant effort is a distributed bending moment sin (iπy/2b) along the edge x = 0 according to Equation (26), as represented in Figure 4 for i = 5.

To account for the edge moments the solution by Lévy [4] for the transverse displacement can be modified as follows

w_{i} (x, y) = \frac{1}{D} \sum_{m} F_{m i} (y) \sin α_{m} x + \frac{a^{2}}{6 D} [1 - \frac{x}{a} - {(1 - \frac{x}{a})}^{3}] \sin \frac{i π y}{2 b}

(27)

The analysis continues similarly to Section 2.2.2.1. The differential equation (Equation (17)) becomes

\frac{d^{4} F_{m i} (y)}{d y^{4}} - 2 α_{m}^{2} \frac{d^{2} F_{m i} (y)}{d y^{2}} + α_{m}^{4} F_{m i} (y) = - [\frac{4 π}{m} {(\frac{i}{2 b})}^{2} + \frac{2 π a^{2}}{m^{3}} {(\frac{i}{2 b})}^{4}] \sin \frac{i π y}{2 b}

(28)

The solution to Equation (28) is identical to Equation (7) whereby the particular solution is given by

F_{m p i} (y) = k_{m i} \sin \frac{i π y}{2 b} \begin{matrix} k_{m i} = - \frac{[\frac{1}{m} {(\frac{i}{b})}^{2} + \frac{a^{2}}{8 m^{3}} {(\frac{i}{b})}^{4}]}{π^{3} {[{(\frac{i}{2 b})}^{2} + {(\frac{m}{a})}^{2}]}^{2}} \end{matrix}

(29)

Therefore the transverse displacement function is as follows

\begin{array}{l} w_{i} (x, y) = \frac{1}{D} \sum_{m} [\begin{array}{l} A_{m i} \cosh α_{m} y + B_{m i} α_{m} y \sinh α_{m} y + C_{m i} \sinh α_{m} y + \\ D_{m i} α_{m} y \cosh α_{m} y + k_{m i} \sin \frac{i π y}{2 b} \end{array}] \sin α_{m} x \\ \begin{matrix}  \end{matrix} + \frac{a^{2}}{6 D} [1 - \frac{x}{a} - {(1 - \frac{x}{a})}^{3}] \sin \frac{i π y}{2 b} \end{array}

(30)

To satisfy the boundary conditions at y = 0 and y = b, the Fourier series of Equation (15) is used; Equation (30) becomes

\begin{array}{l} w_{i} (x, y) = \frac{1}{D} \sum_{m} [\begin{array}{l} A_{m i} \cosh α_{m} y + B_{m i} α_{m} y \sinh α_{m} y + C_{m i} \sinh α_{m} y + \\ D_{m i} α_{m} y \cosh α_{m} y + k_{m i}^{*} \sin \frac{i π y}{2 b} \end{array}] \sin α_{m} x \\ \begin{matrix}  \end{matrix} k_{m i}^{*} = k_{m i} + \frac{2 a^{2}}{m^{3} π^{3}} \end{array}

(31)

With respect to the boundary conditions at y = 0 and y = b the equations for the slope ∂w/∂y and the bending moment myy are set using Equations (8b) and (31) as follows

\frac{\partial w (x, y)}{\partial y} = \frac{1}{D} \sum_{m} α_{m} [\begin{array}{l} A_{m i} \sinh α_{m} y + B_{m i} (\sinh α_{m} y + α_{m} y \cosh α_{m} y) + \\ C_{m i} \cosh α_{m} y + D_{m i} (\cosh α_{m} y + α_{m} y \sinh α_{m} y) + \\ \frac{i a}{2 m b} k_{m i}^{*} \cos \frac{i π y}{2 b} \end{array}] \sin α_{m} x

(32a)

m_{y y} = - \sum_{m} α_{m}^{2} (1 - ν) [\begin{array}{l} A_{m i} \cosh α_{m} y + B_{m i} (\frac{2}{1 - ν} \cosh α_{m} y + α_{m} y \sinh α_{m} y) + \\ C_{m i} \sinh α_{m} y + D_{m i} (\frac{2}{1 - ν} \sinh α_{m} y + α_{m} y \cosh α_{m} y) \\ - \frac{π^{2}}{α_{m}^{2} (1 - ν)} [{(\frac{i}{2 b})}^{2} + ν {(\frac{m}{a})}^{2}] k_{m i}^{*} \sin \frac{i π y}{2 b} \end{array}] \sin α_{m} x

(32b)

Furthermore, with regard to the boundary conditions at y = b the Kirchhoff shear force is calculated using Equations (31) and (9c). Observing that the first and third derivatives with respect to y of the term with sin (iπy/2b) contain cos (iπy/2b) which vanishes at y = b, it results

{V_{y} |}_{y = b} = - \sum_{m} α_{m}^{3} (ν - 1) [\begin{array}{l} A_{m i} \sinh α_{m} b + B_{m i} (\frac{ν + 1}{ν - 1} \sinh α_{m} b + α_{m} b \cosh α_{m} b) + \\ C_{m i} \cosh α_{m} b + D_{m i} (\frac{ν + 1}{ν - 1} \cosh α_{m} b + α_{m} b \sinh α_{m} b) \end{array}] \sin α_{m} x

(33)

In summary, the boundary conditions at y = 0 and y = b are expressed using Equations (31), (32a-b), and (33); they permit to determine the coefficients A_mi, B_mi, C_mi, and D_mi.

\begin{array}{l} δ_{j i} = {\frac{\partial w (x, y)}{\partial x} |}_{\begin{array}{l} x = x_{j} \\ y = y_{j} \end{array}} = \frac{1}{D} \sum_{m} α_{m} [\begin{array}{l} A_{m i} \cosh α_{m} y_{j} + B_{m i} α_{m} y_{j} \sinh α_{m} y_{j} + C_{m i} \sinh α_{m} y_{j} + \\ D_{m i} α_{m} y_{j} \cosh α_{m} y_{j} + k_{m i} \sin \frac{i π y_{j}}{2 b} \end{array}] \cos α_{m} x_{j} \\ \begin{matrix}  \end{matrix} + \frac{a}{6 D} [- 1 + 3 {(1 - \frac{x_{j}}{a})}^{2}] \sin \frac{i π y_{j}}{2 b} \end{array}

(34)

Given n redundants considered, the positions y_j = k×b/n with k = 1, 2, 3 …n as represented in Figure 5 can be taken.

For the redundant problem the bending moments m_xx and m_yy and the twisting moments m_xy are calculated using Equations (2a-c) and (30):

\begin{array}{l} m_{x x, i} = - \sum_{m} α_{m}^{2} (ν - 1) [\begin{array}{l} A_{m i} \cosh α_{m} y + B_{m i} (\frac{2 ν}{ν - 1} \cosh α_{m} y + α_{m} y \sinh α_{m} y) + \\ C_{m i} \sinh α_{m} y + D_{m i} (\frac{2 ν}{ν - 1} \sinh α_{m} y + α_{m} y \cosh α_{m} y) \\ - \frac{π^{2}}{α_{m}^{2} (ν - 1)} [{(\frac{m}{a})}^{2} + ν {(\frac{i}{2 b})}^{2}] k_{m i} \sin \frac{i π y}{2 b} \end{array}] \sin α_{m} x + \\ \begin{matrix} + \end{matrix} (1 - \frac{x}{a}) \sin \frac{i π y}{2 b} + \frac{ν a^{2}}{6} {(\frac{i π}{2 b})}^{2} [1 - \frac{x}{a} - {(1 - \frac{x}{a})}^{3}] \sin \frac{i π y}{2 b} \end{array}

(35a)

\begin{array}{l} m_{y y, i} = - \sum_{m} α_{m}^{2} (1 - ν) [\begin{array}{l} A_{m i} \cosh α_{m} y + B_{m i} (\frac{2}{1 - ν} \cosh α_{m} y + α_{m} y \sinh α_{m} y) + \\ C_{m i} \sinh α_{m} y + D_{m i} (\frac{2}{1 - ν} \sinh α_{m} y + α_{m} y \cosh α_{m} y) \\ - \frac{π^{2}}{α_{m}^{2} (1 - ν)} [{(\frac{i}{2 b})}^{2} + ν {(\frac{m}{a})}^{2}] k_{m i} \sin \frac{i π y}{2 b} \end{array}] \sin α_{m} x + \\ \begin{matrix} + \frac{a^{2}}{6} {(\frac{i π}{2 b})}^{2} [1 - \frac{x}{a} - {(1 - \frac{x}{a})}^{3}] \sin \frac{i π y}{2 b} + \end{matrix} ν (1 - \frac{x}{a}) \sin \frac{i π y}{2 b} \end{array}

(35b)

\begin{array}{l} m_{x y, i} = - (1 - ν) \times \sum_{m} α_{m}^{2} [\begin{array}{l} A_{m i} \sinh α_{m} y + B_{m i} (\sinh α_{m} y + α_{m} y \cosh α_{m} y) + C_{m i} \cosh α_{m} y \\ + D_{m i} (\cosh α_{m} y + α_{m} y \sinh α_{m} y) + \frac{i a^{2}}{2 π m^{2} b} k_{m i} \cos \frac{i π y}{2 b} \end{array}] \cos α_{m} x + \\ \begin{matrix} + \end{matrix} \frac{a (1 - ν)}{6} \frac{i π}{2 b} [1 - 3 {(1 - \frac{x}{a})}^{2}] \cos \frac{i π y}{2 b} \end{array}

(35c)

The compatibility equations and the efforts in the plate are calculated using Equations (24) and (25).

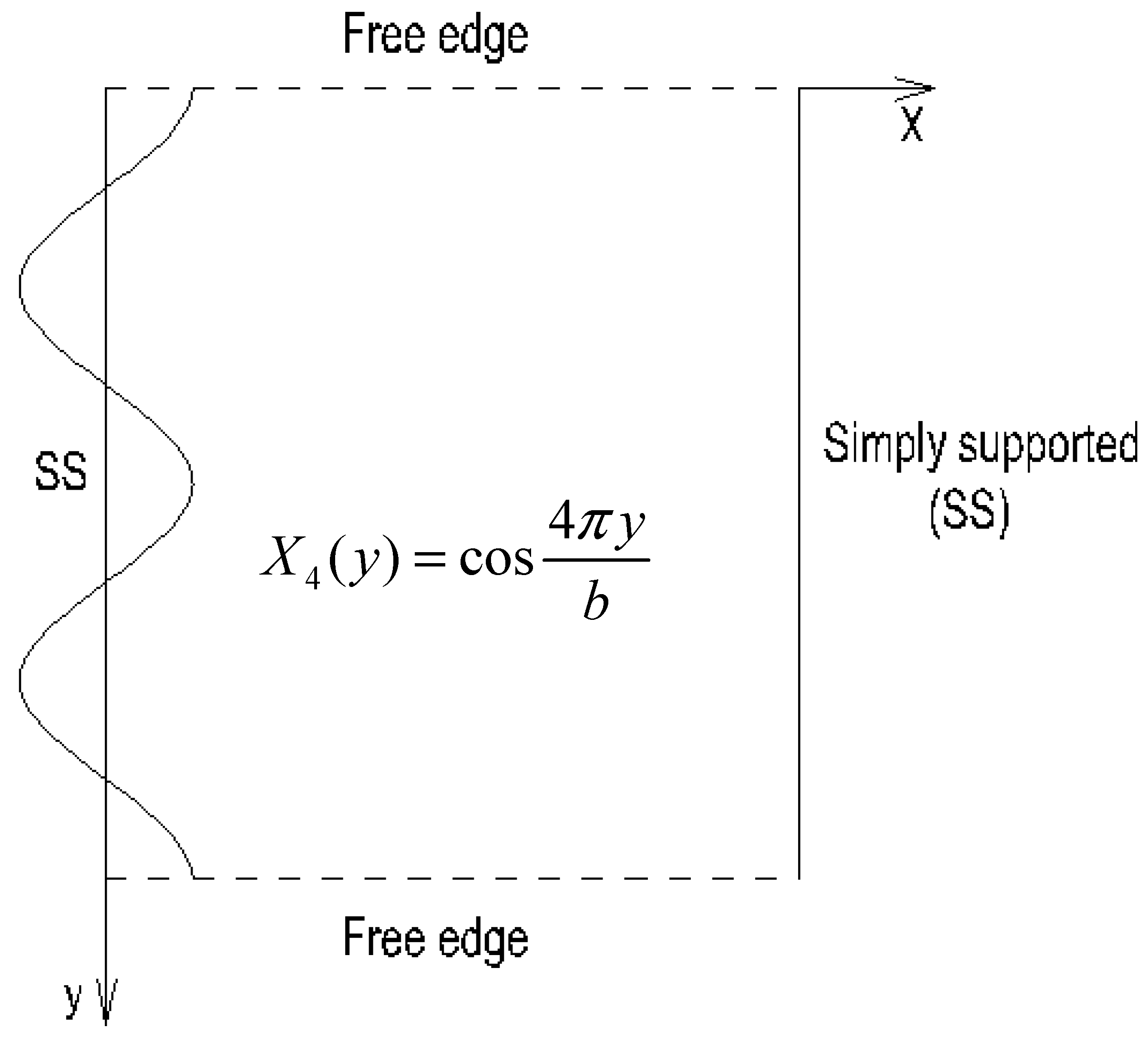
2.2.2.3. Edges y = 0 and y = b free

Redundant problem Xi = 1

The edges y = 0 and y = b are free. Observing that the bending moments X(y) have non zero values at the angles, their distribution along the clamped edge x = 0 can be described with the following trigonometric series

X (y) = \sum_{i = 0, 1, 2...}^{n} X_{i} \cos \frac{i π y}{b}

(36)

The redundant effort is a distributed bending moment cos (iπy/b) along the edge x = 0 according to Equation (36), as represented in Figure 6 for i = 4.

It is observed that in case of loading symmetrical with respect to axis y = b/2 only even values of i need be considered, the redundants being zero for odd values; and in case of loading anti symmetrical with respect to the same axis only odd values of i need be considered, the redundants being zero for even values.

To account for the edge moments the solution by Lévy [4] for the transverse displacement can be modified as follows

w_{i} (x, y) = \frac{1}{D} \sum_{m} F_{m i} (y) \sin α_{m} x + \frac{a^{2}}{6 D} [1 - \frac{x}{a} - {(1 - \frac{x}{a})}^{3}] \cos \frac{i π y}{b}

(37)

The analysis continues similarly to Section 2.2.2.1. The differential equation (Equation (17)) becomes

\frac{d^{4} F_{m i} (y)}{d y^{4}} - 2 α_{m}^{2} \frac{d^{2} F_{m i} (y)}{d y^{2}} + α_{m}^{4} F_{m i} (y) = - [\frac{4 π}{m} {(\frac{i}{b})}^{2} + \frac{2 π a^{2}}{m^{3}} {(\frac{i}{b})}^{4}] \cos \frac{i π y}{b}

(38)

The solution to Equation (38) is identical to Equation (7) whereby the particular solution is given by

F_{m p i} (y) = k_{m i} \cos \frac{i π y}{b} \begin{matrix} k_{m i} = - \frac{[\frac{4}{m} {(\frac{i}{b})}^{2} + \frac{2 a^{2}}{m^{3}} {(\frac{i}{b})}^{4}]}{π^{3} {[{(\frac{i}{b})}^{2} + {(\frac{m}{a})}^{2}]}^{2}} \end{matrix}

(39)

Therefore, the transverse displacement function is as follows

\begin{array}{l} w_{i} (x, y) = \frac{1}{D} \sum_{m} [\begin{array}{l} A_{m i} \cosh α_{m} y + B_{m i} α_{m} y \sinh α_{m} y + C_{m i} \sinh α_{m} y + \\ D_{m i} α_{m} y \cosh α_{m} y + k_{m i} \cos \frac{i π y}{b} \end{array}] \sin α_{m} x \\ \begin{matrix}  \end{matrix} + \frac{a^{2}}{6 D} [1 - \frac{x}{a} - {(1 - \frac{x}{a})}^{3}] \cos \frac{i π y}{b} \end{array}

(40)

To satisfy the boundary conditions at y = 0 and y = b, the Fourier series of Equation (15) is used; Equation (40) becomes

\begin{array}{l} w_{i} (x, y) = \frac{1}{D} \sum_{m} [\begin{array}{l} A_{m i} \cosh α_{m} y + B_{m i} α_{m} y \sinh α_{m} y + C_{m i} \sinh α_{m} y + \\ D_{m i} α_{m} y \cosh α_{m} y + k_{m i}^{*} \cos \frac{i π y}{b} \end{array}] \sin α_{m} x \\ \begin{matrix}  \end{matrix} k_{m i}^{*} = k_{m i} + \frac{2 a^{2}}{m^{3} π^{3}} \end{array}

(41)

With regard to the boundary conditions at y = 0 and y = b the equation for the bending moment myy is set using Equations (8b) and (41) as follows

m_{y y} = - \sum_{m} α_{m}^{2} (1 - ν) [\begin{array}{l} A_{m i} \cosh α_{m} y + B_{m i} (\frac{2}{1 - ν} \cosh α_{m} y + α_{m} y \sinh α_{m} y) + \\ C_{m i} \sinh α_{m} y + D_{m i} (\frac{2}{1 - ν} \sinh α_{m} y + α_{m} y \cosh α_{m} y) \\ - \frac{π^{2}}{α_{m}^{2} (1 - ν)} [{(\frac{i}{b})}^{2} + ν {(\frac{m}{a})}^{2}] k_{m i}^{*} \cos \frac{i π y}{b} \end{array}] \sin α_{m} x

(42)

Furthermore, with regard to the boundary conditions at y = 0 and y = b the Kirchhoff shear force is calculated using Equations (41) and (9c). Observing that the first and third derivatives with respect to y of the term with cos (iπy/b) contain sin (iπy/b) which vanishes at y = 0 and y = b, it results at y = 0 and y = b

V_{y} = - \sum_{m} α_{m}^{3} (ν - 1) [\begin{array}{l} A_{m i} \sinh α_{m} y + B_{m i} (\frac{ν + 1}{ν - 1} \sinh α_{m} y + α_{m} y \cosh α_{m} y) + \\ C_{m i} \cosh α_{m} y + D_{m i} (\frac{ν + 1}{ν - 1} \cosh α_{m} y + α_{m} y \sinh α_{m} y) \end{array}] \sin α_{m} x

(43)

In summary the boundary conditions at y = 0 and y = b are formulated using Equations (42) and (43); they permit to determine the coefficients A_mi, B_mi, C_mi, and D_mi.

\begin{array}{l} δ_{j i} = {\frac{\partial w (x, y)}{\partial x} |}_{\begin{array}{l} x = x_{j} \\ y = y_{j} \end{array}} = \frac{1}{D} \sum_{m} α_{m} [\begin{array}{l} A_{m i} \cosh α_{m} y_{j} + B_{m i} α_{m} y_{j} \sinh α_{m} y_{j} + C_{m i} \sinh α_{m} y_{j} + \\ D_{m i} α_{m} y_{j} \cosh α_{m} y_{j} + k_{m i} \cos \frac{i π y_{j}}{b} \end{array}] \cos α_{m} x_{j} \\ \begin{matrix}  \end{matrix} + \frac{a}{6 D} [- 1 + 3 {(1 - \frac{x_{j}}{a})}^{2}] \cos \frac{i π y_{j}}{b} \end{array}

(44)

For n redundants considered, the positions y_j = k×b/(n – 1) with k = 0, 1, 2 …n - 1 as shown in Figure 7a can be taken.

It is reminded that in case of loading symmetrical with respect to axis y = b/2 only even values of i need be considered and in case of loading anti symmetrical with respect to the same axis only odd values of i need be considered. In both cases, the flexibilities and compatibility equations can be set in half of the structure in y–direction. Given the half edge with n redundants, the positions y_j = k×b/2(n – 1) with k = 0, 1, 2, 3 …n - 1 as represented in Figure 7b can be taken.

However, in case of loading anti symmetrical with respect to axis y = b/2 compatibility equations should not be set at position y_j = b/2 since the slopes vanish there in the redundant problems as well as in the primary problem; by considering this position the flexibility matrix becomes singular.

For the redundant problem X_i = 1 the bending moments m_xx and m_yy and the twisting moments m_xy are calculated using Equations (2a-c) and (40):

\begin{array}{l} m_{x x, i} = - \sum_{m} α_{m}^{2} (ν - 1) [\begin{array}{l} A_{m i} \cosh α_{m} y + B_{m i} (\frac{2 ν}{ν - 1} \cosh α_{m} y + α_{m} y \sinh α_{m} y) + \\ C_{m i} \sinh α_{m} y + D_{m i} (\frac{2 ν}{ν - 1} \sinh α_{m} y + α_{m} y \cosh α_{m} y) \\ - \frac{π^{2}}{α_{m}^{2} (ν - 1)} [{(\frac{m}{a})}^{2} + ν {(\frac{i}{b})}^{2}] k_{m i} \cos \frac{i π y}{b} \end{array}] \sin α_{m} x + \\ \begin{matrix} + \end{matrix} (1 - \frac{x}{a}) \cos \frac{i π y}{b} + \frac{ν a^{2}}{6} {(\frac{i π}{b})}^{2} [1 - \frac{x}{a} - {(1 - \frac{x}{a})}^{3}] \cos \frac{i π y}{b} \end{array}

(45a)

\begin{array}{l} m_{y y, i} = - \sum_{m} α_{m}^{2} (1 - ν) [\begin{array}{l} A_{m i} \cosh α_{m} y + B_{m i} (\frac{2}{1 - ν} \cosh α_{m} y + α_{m} y \sinh α_{m} y) + \\ C_{m i} \sinh α_{m} y + D_{m i} (\frac{2}{1 - ν} \sinh α_{m} y + α_{m} y \cosh α_{m} y) \\ - \frac{π^{2}}{α_{m}^{2} (1 - ν)} [{(\frac{i}{b})}^{2} + ν {(\frac{m}{a})}^{2}] k_{m i} \cos \frac{i π y}{b} \end{array}] \sin α_{m} x + \\ \begin{matrix} + \frac{a^{2}}{6} {(\frac{i π}{b})}^{2} [1 - \frac{x}{a} - {(1 - \frac{x}{a})}^{3}] \cos \frac{i π y}{b} + \end{matrix} ν (1 - \frac{x}{a}) \cos \frac{i π y}{b} \end{array}

(45b)

\begin{array}{l} m_{x y, i} = - (1 - ν) \times \sum_{m} α_{m}^{2} [\begin{array}{l} A_{m i} \sinh α_{m} y + B_{m i} (\sinh α_{m} y + α_{m} y \cosh α_{m} y) + C_{m i} \cosh α_{m} y \\ + D_{m i} (\cosh α_{m} y + α_{m} y \sinh α_{m} y) - \frac{i a^{2}}{π m^{2} b} k_{m i} \sin \frac{i π y}{b} \end{array}] \cos α_{m} x + \\ \begin{matrix} - \end{matrix} \frac{a (1 - ν)}{6} \frac{i π}{b} [1 - 3 {(1 - \frac{x}{a})}^{2}] \sin \frac{i π y}{b} \end{array}

(45c)

The compatibility equations and the efforts in the plate are calculated using Equations (24) and (25).

2.2.3. Redundant problem: plate subjected to a distributed bending moment along the edge x = a

The edges x = 0 and x = a are assumed clamped. Given then the symmetrical nature of the plate with respect to the axis x = a/2, the positions along the edge x = a where the compatibility equations are set will be taken identical to those of the edge x = 0. Therefore, for redundant problems the bending moments mxx and myy and the twisting moments mxy will be the same as in Section 2.2.2; however, given that the flexibilities are defined as slopes in this study, the values for the case of bending moments acting along the edge x = a are obtained by affecting a minus sign to the corresponding values for the case of bending moments acting along the edge x = 0.

Else, the analysis could be conducted similarly to Section 2.2.2, whereby the modified Lévy solution for edges y = 0 and y = b supported e.g. would be given by

w_{i} (x, y) = \frac{1}{D} \sum_{m} F_{m i} (y) \sin α_{m} x + \frac{a^{2}}{6 D} [\frac{x}{a} - {(\frac{x}{a})}^{3}] \sin \frac{i π y}{b}

(46)

Following Fourier sine series expansions are useful in the analysis

\frac{x}{a} = \sum_{m} \frac{2 {(- 1)}^{m + 1}}{m π} \sin α_{m} x, \begin{matrix} \frac{x}{a} - {(\frac{x}{a})}^{3} = \end{matrix} \sum_{m} \frac{12 {(- 1)}^{m + 1}}{m^{3} π^{3}} \sin α_{m} x

(47)

3. Results and discussion

3.1. Plate clamped along the edges x = 0, y = 0, and y = b and simply supported along x = a

The analysis of a rectangular plate clamped along the edges x = 0, y = 0, and y = b and simply supported along the edge x = a and subjected to a uniformly distributed load q was conducted whereby the Poisson’s ratio was not considered. The plate dimensions in x- and y-directions were denoted by a and b, respectively. The bending moments at the middle of the clamped edge x = 0 are m_x,cl = -qa²/N_x,cl and those at the middle of the plate m_xm = qa²/N_xm and m_ym = qa²/N_ym. Detailed results are presented in the Supplementary Material “Rectangular plate clamped and simply supported.” Table 1 lists the results, depending on the ratio b/a, obtained using the Czerny tables [14] (exact results) and those obtained in the present study whereby one redundant (i = 1 for the position y_j = b/2), three redundants (i = 1, 3, and 5 for the positions y_j = b/10, 3b/10, and b/2), and five redundants (i = 1, 3, 5, 7, and 9 for the positions y_j = b/10, b/5, 3b/10, 2b/5, and b/2) were considered. It is recalled that only half of the structure in y–direction and odd values of i are taken since the system and loading are symmetrical with respect to axis y = b/2.

As Table 1 shows, the results of the present study show good agreement with the exact results. The accuracy should be increased by considering more redundants (more values of i) since the geometric boundary conditions of the original structure (vanishing of the slopes along the opposite edges) should be restored all over the clamped edge and not only at selected positions. In this example, accuracies more than 99% were already obtained by taking three redundants.

3.2. Rectangular plate clamped along all edges

A rectangular plate clamped along all edges and subjected to a uniformly distributed load q was analyzed whereby the Poisson’s ratio was not considered. The plate dimensions in x- and y-directions are denoted by a and b, respectively. The bending moments at the middle of the clamped edges x = 0 and x = a and at the middle of the clamped edges y = 0 and y = b are m_x,cl = -qa²/N_x,cl and m_y,cl = -qa²/N_y,cl , respectively, and those at the middle of the plate are m_xm = qa²/N_xm and m_ym = qa²/N_ym. Detailed results are presented in the Supplementary Material “Rectangular plate clamped along all edges.” Table 2 displays the results, depending on the ratio b/a, obtained using the Czerny tables [14] (exact results) and those obtained in the present study whereby at edges x = 0 and x = a one redundant (i = 1 for the position y_j = b/2) and three redundants (i = 1, 3, and 5 for the positions y_j = b/10, 3b/10, and b/2) were considered. It is recalled that only half of the structure in y–direction and odd values of i are taken since the system and loading are symmetrical with respect to axis y = b/2.

As Table 2 shows, the results of the present study show good agreement with the exact results. The accuracy should be increased by considering more redundants (more values of i). In this example, accuracies more than 99% were already obtained by taking three redundants at each edge.

3.3. Rectangular plate clamped along x = 0, simply supported along x = a and y = 0, and free along y = b

The analysis of a plate clamped along the edge x = 0, simply supported along x = a and y = 0, and free along y = b and subjected to a uniformly distributed load q was conducted whereby the Poisson’s ratio was not considered. The plate dimensions in x- and y-directions are denoted by a and b, respectively. The bending moments are m_x,fre = -qb²/N_x,fre at the end of the clamped edge x = 0, m_x,frm = qb²/N_x,frm in the middle of the free edge, and m_xm = qb²/N_xm and m_ym = qb²/N_ym in the middle of the plate. Details of the results are presented in the Supplementary Material “Rectangular plate clamped simply supported and free.” Table 3 lists the results, depending on the ratio b/a, obtained using the Czerny tables [14] (exact results) and those obtained in the present study whereby one redundant (i = 1 for the position y_j = b), three redundants (i = 1, 3, and 5 for the positions y_j = b/5, 3b/5, and b), and five redundants (i = 1, 3, 5, 7, and 9 for the positions y_j = b/5, 2b/5, 3b/5, 4b/5, and b) were considered.

As Table 3 shows, the results of the present study show good agreement with the exact results. The accuracy is increased by considering more redundants. In this example, accuracies more than 99% were already obtained by taking three redundants.

3.4. Rectangular plate clamped along the edges x = 0 and x = a, free along the edges y = 0 and y = b and subjected to an anti-symmetrical loading

A rectangular plate clamped along the edges x = 0 and x = a, free along y = 0 and y = b and subjected to an anti-symmetrical loading p = p(1 – 2y/b) was analyzed whereby the Poisson’s ratio was not considered. The plate dimensions in x- and y-directions are denoted by a and b, respectively. The bending moments are m_x,fre = -qa²/N_x,fre at the end of the clamped edge x = 0 and m_x,frm = qa²/N_x,frm in the middle of the free edge. Details of the results are presented in the Supplementary Material “Rectangular plate clamped and free.” Table 4 displays the results, depending on the ratio b/a, obtained using the Finite element method (FEM) and those obtained in the present study. On the one hand, the finite element analysis was carried out by taking a 20 × 20 mesh for the ratio b/a = 1.0, a 20 × 25 mesh for the ratio b/a = 1.25, and a 20 × 30 mesh for the ratio b/a = 1.5. On the other hand, we considered in the present study at edges x = 0 and x = a one redundant (i = 1 for the position y_j = 0), three redundants (i = 1, 3, and 5 for the positions y_j = 0, b/5, and 2b/5), and five redundants (i = 1, 3, 5, 7, and 9 for the positions y_j = 0, b/10, b/5, 3b/10, and 2b/5). It is recalled that compatibility equations should not be set at positions y = b/2 since the slopes vanish in the redundant problems.

As Table 4 shows, the results of the present study show reasonable agreement with the FEM results.

4. Conclusions

In this paper, arbitrarily loaded isotropic rectangular thin plates supported (simply supported or clamped) along two opposite edges, from which one or both are clamped, and the other edges with arbitrary support conditions were analyzed. The flexibility method (or force method) of the linear beam theory was applied whereby the unknowns were the bending moments along the opposite edges; in this regard the primary system was the plate simply supported along the above-mentioned opposite edges and subjected to the external loads and the redundant system was the plate simply supported along the opposite edges and subjected to edge moments. We showed that the solution by Lévy [4] commonly used in the case of simply supported opposite edges can be extended, with some adjustment, to simply supported opposite edges subjected to edge moment loading. The compatibility equations (vanishing of the slopes at selected positions of the clamped edge) were set to determine the unknowns and so the efforts in the plate. Numerical results were presented and showed good agreement with the exact results.

The following aspect was not addressed in this study but could be analyzed in future research: Rectangular anisotropic plate

However, the following study limitation should be acknowledged: the vanishing of the slopes at the clamped edge (the compatibility equation) is set at selected positions and not all over the edge as it should be. Hence, more redundants must be considered to increase the accuracy.

Supplementary Materials

The following files were uploaded during submission:

“Rectangular plate clamped and simply supported”
“Rectangular plate clamped along all edges”
“Rectangular plate clamped simply supported and free”
“Rectangular plate clamped and free.”

Conflicts of Interest

The author declares no conflict of interest.

References

Kirchhoff, G. Über das Gleichgewicht und die Bewegung einer elastischen Scheibe. J. für die Reine und Angew. Math.; vol. 18, no. 40, pp. 51-88, 1850. [CrossRef]
Germain, S. Remarques sur la nature, les bornes et l’étendue de la question des surfaces élastiques et équation générale de ces surfaces. impr. de Huzard-Courcier, paris, 1826.
Navier, C.L. Extrait des recherches sur la flexion des plaques élastiques. Bull. des Sci. Société Philomath, Paris, vol. 10, no. 1, pp. 92–102, 1823.
Lévy, M. Sur l’équilibre élastique d’une plaque rectangulaire. Comptes rendus l’Académie des Sci. Paris, vol. 129, no. 1, pp. 535-539, 1899.
Timoshenko, S., Woinowsky-Krieger, S. Theory of plates and shells. Second ed., McGraw Hill, New York (1959).
Mama, B.O., Oguaghamba, O.A., Ike, C.C. Single Finite Fourier Sine Integral Transform Method for the Flexural Analysis of Rectangular Kirchhoff Plate with Opposite Edges Simply Supported, Other Edges Clamped for the Case of Triangular Load Distribution. IJERT, Vol. 13, 7 (2020), pp. 1802-1813. [CrossRef]
Sayyad, A.S., Ghugal Y.M. Bending of shear deformable plates resting on Winkler foundations according to trigonometric plate theory. J. Appl. Comput. Mech., 4(3) (2018) 187-201. [CrossRef]
Xu, Y., Wu, Zhangjan. Exact solutions for rectangular anisotropic plates with four clamped edges. Mechanics of Advanced Materials and Structures, Volume 29, 2022 - Issue 12. [CrossRef]
Khan, Y., Tiwari, P., Ali, R. Application of variational methods to a rectangular clamped plate problem. Computers & Mathematics with Applications. Volume 63, Issue 4, February 2012, Pages 862-869. [CrossRef]
Onyia, M.E., Rowland-Lato, E.O., Ike, C.C. Elastic buckling analysis of SSCF and SSSS rectangular thin plates using the single finite Fourier sine integral transform method. IJERT, Vol 13, No 6, pp 1147 – 1158, july 2020. [CrossRef]
Pisacic, K., Horvat, M., Botak, Z. Finite Difference Solution of Plate Bending Using Wolfram Mathematica. Tehnicki Glasnik 13, 3(2019), 241-247. [CrossRef]
Delyavskyy, M., Rosinski, K. The New Approach to Analysis of Thin Isotropic Symmetrical Plates. Appl. Sci. 2020, 10, 5931. [CrossRef]
Imrak, C.E., Gerdemeli, I. An Exact Solution for the Deflection of a Clamped Rectangular Plate under Uniform Load. Applied Mathematical Sciences, Vol. 1, 2007, no. 43, 2129 - 2137.
Czerny, F. Tafeln für vierseitig und dreiseitig gelagerte Rechteckplatten (Tables for rectangular plates supported along four and along three edges). Beton-Kalender 1982, Teil 1. Verlag Von Wilhelm, Ernst & Sohn Berlin, München S. 397-474. In German.

Figure 1. Spatial axis convention X, Y, Z.

Figure 2. Redundant problem X3 = 1: Edge x = 0 subjected to bending moment loading sin (3πy/b).

Figure 3. a) Positions y_i (●) in general b) Positions y_i (●) for system symmetrical and loading symmetrical or anti symmetrical with respect to axis y = b/2.

Figure 4. Redundant problem X5 = 1: Edge x = 0 subjected to bending moment loading sin (5πy/2b).

Figure 5. Positions y_i (●) for edges y = 0 supported and y = b free.

Figure 6. Redundant problem X4 = 1: Edge x = 0 subjected to bending moment loading cos (4πy/b).

Figure 7. a) Positions y_i (●) in general b) Positions y_i (●) for loading symmetrical or anti symmetrical with respect to axis y = b/2.

Table 1. Coefficients of bending moments at the middle of the clamped edge and middle of the plate.

b/a	1.00			1.25
	N_x,cl	N_xm	N_ym	N_x,cl	N_xm	N_ym
	Czerny tables [14] (exact results)
	18.3	59.5	44.1	12.7	34.2	45.8
	Present study
1 redundant	18.82	59.30	44.20	13.29	34.48	45.81
3 redundants	18.29	59.31	44.03	13.03	34.34	45.74
5 redundants	18.19	59.30	44.02	12.96	34.34	45.71

Table 2. Coefficients of bending moments at the middle of the clamped edge and middle of the plate.

b/a	1.00				1.25
	N_x,cl	N_y,cl	N_xm	N_ym	N_x,cl	N_y,cl	N_xm	N_ym
	Czerny tables [14] (exact results)
	19.4	19.4	56.8	56.8	14.9	17.7	37.0	69.4
	Present study
2 redundant	20.10	19.72	56.49	57.13	15.33	18.15	36.98	69.42
6 redundants	19.61	19.45	56.71	55.80	15.15	17.86	36.82	67.36

Table 3. Coefficients of bending moments at the clamped edge, at the free edge and at the middle of the plate.

b/a	1.00				1.20
	N_xm	N_ym	N_x,frm	N_x,fre	N_xm	N_ym	N_x,frm	N_x,fre
	Czerny tables [14] (exact results)
	21.42	79.85	16.60	7.89	27.91	143.64	23.29	11.40
	Present study
1 redundant	20.92	70.85	16.21	7.69	26.56	116.24	22.44	10.85
3 redundants	21.42	79.89	16.61	7.97	27.89	144.74	23.28	11.41
5 redundants	21.40	79.77	16.59	7.90	27.87	143.53	23.27	11.40

Table 4. Coefficients of bending moments at the end of the clamped edge and at the middle of the free edge.

b/a	1.00		1.25		1.50
	N_x,fre	N_xfrm	N_x,fre	N_xfrm	N_x,fre	N_xfrm
	FEM results
	16.58	42.42	15.32	36.52	14.61	33.35
	Present study
2 redundant	18.59	45.40	17.13	39.22	16.28	35.94
6 redundants	16.40	44.15	15.44	37.89	14.88	34.52
10 redundants	15.51	44.05	14.73	37.78	14.29	34.42

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Analysis of Arbitrarily Loaded Rectangular Thin Plates with Two Opposite Edges Supported, One or Both of them Clamped, Using the Flexibility Method and a Modified Lévy Solution

Abstract

1. Introduction

2. Materials and methods

2.1. Governing equations of the plate

2.2. Rectangular isotropic plate clamped along two opposite edges

2.2.1. Primary problem: plate simply supported along two opposite edges

2.2.2. Redundant problem: plate subjected to a distributed bending moment along the edge x = 0

2.2.2.1. Edges y = 0 and y = b simply supported or clamped

2.2.2.2. Edge y = 0 simply supported or clamped, and edge y = b free

2.2.2.3. Edges y = 0 and y = b free

2.2.3. Redundant problem: plate subjected to a distributed bending moment along the edge x = a

3. Results and discussion

3.1. Plate clamped along the edges x = 0, y = 0, and y = b and simply supported along x = a

3.2. Rectangular plate clamped along all edges

3.3. Rectangular plate clamped along x = 0, simply supported along x = a and y = 0, and free along y = b

3.4. Rectangular plate clamped along the edges x = 0 and x = a, free along the edges y = 0 and y = b and subjected to an anti-symmetrical loading

4. Conclusions

Supplementary Materials

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe