A Class of Models That Support a Maximum Entropy Principle for Age Structure

Preprint

Article

A Class of Models That Support a Maximum Entropy Principle for Age Structure

Altmetrics

Downloads

Views

Comments

Henri Laurie^*

This version is not peer-reviewed

Submitted:

30 May 2023

Posted:

30 May 2023

You are already at the latest version

Alerts

Abstract

Models with age as a variable but actual dynamics invariant under age structure allow use of MaxEnt to predict uniform age structure. Interpretations include a major role for accepting randomness as a causal principle in ecology (in the face of ignorance, in a further interpretative stance).

Keywords:

Subject: Biology and Life Sciences - Ecology, Evolution, Behavior and Systematics

1. Introduction

It seems both important and difficult to develop a purely thermodynamic view of theoretical ecology [1,2]. The concept of entropy has received recent attention, in theoretical work such as [3,4] as well observational work such as [5,6,7].

Many open questions remain, for example whether to adopt one of the many proposals of minimum and maximum principles of entropy production [3,8] and indeed whether entropy is a single unified concept [9] or a group concepts only superficially related by very similar formalisms [10].

Perhaps progress can be made if as many of these difficulties as possible are avoided. Population dynamics is well suited to that aim. It can model both steady and transient states, and it spans the gamut from extremely simple to extremely complex models. At the simple end, full analysis is possible while at the complex end the models are capable of expression extreme realism.

It is true that population models do not obviously have thermodynamic meaning. But all are based on birth, growth and death (albeit often merely implicitly), and these involve flows of matter and energy and therefore can and should be understood thermodynamically.

In this paper, I consider a set of models of a simple chemostat with only one population of microbes. This can be viewed as an ecosystem in that it contains many living individuals that are kept alive by a flow of energy and matter. Of course chemostat models can include more and more populations, competing and interacting and constituting several trophic levels. Such models might represent wild ecosystems better and better, but the point here is to have a system that has a manageably small amount of structure.

The only departure from standard chemostat modelling is that growth dynamics is segregated from birth and death dynamics.

2. Models

The models are intentionally as simple as possible.

I first present the base case: a chemostat with a population of n microbes each of mass m, exponential dynamics, constant dilution rate and parameters adjusted to keep biomass constant. Each microbe undergoes binary fission when its initial size has doubled. The only loss of biomass is due to elution, so upon binary fission the two new microbes each has the same biomass as the initial biomass of their parent.

I then present a periodic case: the base case but with a diapause in growth during which binary fission occurs.

Finally, I present the simplest realistic case, with nutrient replenished by the inflow concentration and depleted by the microbe uptake which follows Monod dynamics.

To conclude this section, I briefly discuss age structure, and point out that although the models do not explicitly model age structure, there is a clear sense in which they imply age structure.

Simplicity first: the base case

Microbe mass m grows at the rate r, microbe number is reduced only by dilution at the rate s; initial values are

m_{0}, n_{0}

t = 0

\begin{matrix} \dot{m} & = r m \\ \dot{n} & = - s n . \end{matrix}

Obviously, we have

m (t) = m_{0} exp (r t)

and

n (t) = n_{0} exp (- s t)

so that biomass b as a function of time is

b (t) = m (t) n (t) = m_{0} n_{0} exp ((r - s) t)

Assume that

t = 0

coincides with binary fission, so that age a is equal to t. Then

m (a) = m (t)

gives microbe size at age a, and binary fission happens at

t^{*}

given by

m_{0} exp (r t) = 2 m_{0}

. In this paper,

t^{*}

denotes the generation time, that is, the time from one binary fission to the next, and for this model

t^{*} = log (2) / r

The base case + non-zero time for binary fission

Recall that binary fission must happen when

m (t) = 2 m_{0}

. It is realistic that this process is not instantaneous, and a simple way to model the duration of fission is simply to have growth stop for a while. This leads to the following modification of the base model:

\begin{matrix} \dot{m} & = \{\begin{matrix} r m & if m < 2 m_{0} \\ 0 & otherwise \end{matrix} \\ \dot{n} & = - s n . \end{matrix}

In this case, the generation time is

t^{*} = \tilde{t} + t^{\circ}

, where

t^{\circ}

is the duration of binary fission and

\tilde{t} = log (2) / r

. Since the equations do not include the process of binary fission, for the numerical solution a direct implementation of the duration

t^{\circ}

is necessary.

Minimally realistic: constant resource supply, Monod-like uptake dynamics

Assume nutrient concentration x with uptake rate

ν \frac{x}{K + x}

per microbe at and inflow concentration i. The size growth rate per microbe is proportional to the uptake rate. Then the base model is modified to the following.

\begin{matrix} \dot{x} & = i - ν \frac{x m n}{K + x} - s x \end{matrix}

(1)

\begin{matrix} \dot{m} & = c ν \frac{x m}{K + x} \end{matrix}

(2)

\begin{matrix} \dot{n} & = - s n . \end{matrix}

(3)

This model is minimally realistic for two reasons.

(1) The constant inflow of nutrient provides a realistic (albeit simplistic) model for a driver of the growth of the microbes and thus a source of the energy required to maintain this system in a steady state far from thermodynamic equilibrium. Such a source is necessary for any biological model to qualify as realistic.

(2) The uptake per individual saturates and becomes constant as nutrient concentration increases. This is another requirement for realism, deriving from the fact that nutrient flow into an organism must be constrained by the finite extent of surface area which is able to conduct such a flow.

But the model is not fully realistic (for example, it excludes the non-zero time for binary fission of the previous model). The claim is not that the model meets, in some minimal way, all the requirements of realism but rather that the two requirements it does meet are essential for any model that aims at realism.

Population structure in the three models above

Although the models do not have any parameters that depend on age nor any mechanisms that vary by age, every individual microbe has an age in the sense of the time it has lived since it came into being by binary fission. So every individual has an age, and the population as a whole has an age structure. Since size is a function of age, population structure also includes age structure.

One can describe the population structure in terms of cohorts (here, a cohort is the set of all individuals of a given age). The models above are formulated as if there is only one cohort, but can be extended to multiple cohorts, as follows.

Assume that at

t = 0

there are k cohorts with ages, individual mass and number denoted by

a_{i}

m_{i}

and

n_{i}

, where

i = 1, 2, \dots, k

. To study the evolution of this cohort structure, it will be convenient to use the cohort biomasses

b_{i} (t) = m_{i} (t) n_{i} (t)

and the total biomass

b = \sum_{i} b_{i}

. To avoid confusion, the initial biomass is always written as

b (0)

In the first two models, the cohorts do not interact at all and each have exactly the same dynamics. In the last model, the cohorts interact indirectly by sharing the nutrient supply. But we shall see that there is a critical level of biomass at the cohort dynamics effectively decouple.

3. Results

In what follows, the term “steadily cyclic state” denotes a system state where m and n are periodic and

b = m n

is either periodic or constant.

The diagrams illustrating the results require numerical values to be chosen for the parameters and initial values. For convenience, these are chosen to so that mass varies approximately from 1 to 2 and the period is not too far from 1. Clearly, this implies a unit of mass of a few nano- or micrograms, a similarly arbitrary unit of for the number of perhaps a few millions or billions and careful adjustment of parameters.

The steadily cyclic states of the three models

For the base case,

b (t) = m_{0} n_{0} exp ((r - s) t)

. So if and only

r = s

do we have the steady state

b (t) = m_{0} n_{0}

, and this applies to every cohort. Denoting the initial state of the i-th cohort by

m_{0 i}, n_{0 i}

, we have

b (t) = \sum_{i} m_{i} (t) n (t) = m_{0 i} n_{0 i} = b (0)

. On the other hand,

m (t), n (t)

are periodic with period

t^{*}

as defined above, see Figure 1.

In model two, the base case + pause for fission, size doubles in time

\tilde{t}

and then growth stops for time

t^{\circ}

while binary fission takes place. Generation time

t^{*} = \tilde{t} + t^{\circ}

and for a steady state this must be the time it takes for the population number to be halved by dilution. Hence

s = log (2) / t^{*}

in the steady state. During the pause in size growth, biomass declines as there is no pause in dilution. But since

m (t) = 2 m_{0}

during the pause, after binary fission we have

m (t) = m_{0}

so the individual size is

m_{0}

at the start of each new period of size growth. As a result, although biomass

b (t)

is not constant, it is periodic, see Figure 2.

Population structure is more complicated than in the base case, as each cohort biomass has periods of increase and decrease. However, the changes in structure are themselves periodic and in that sense population structure is persistent.

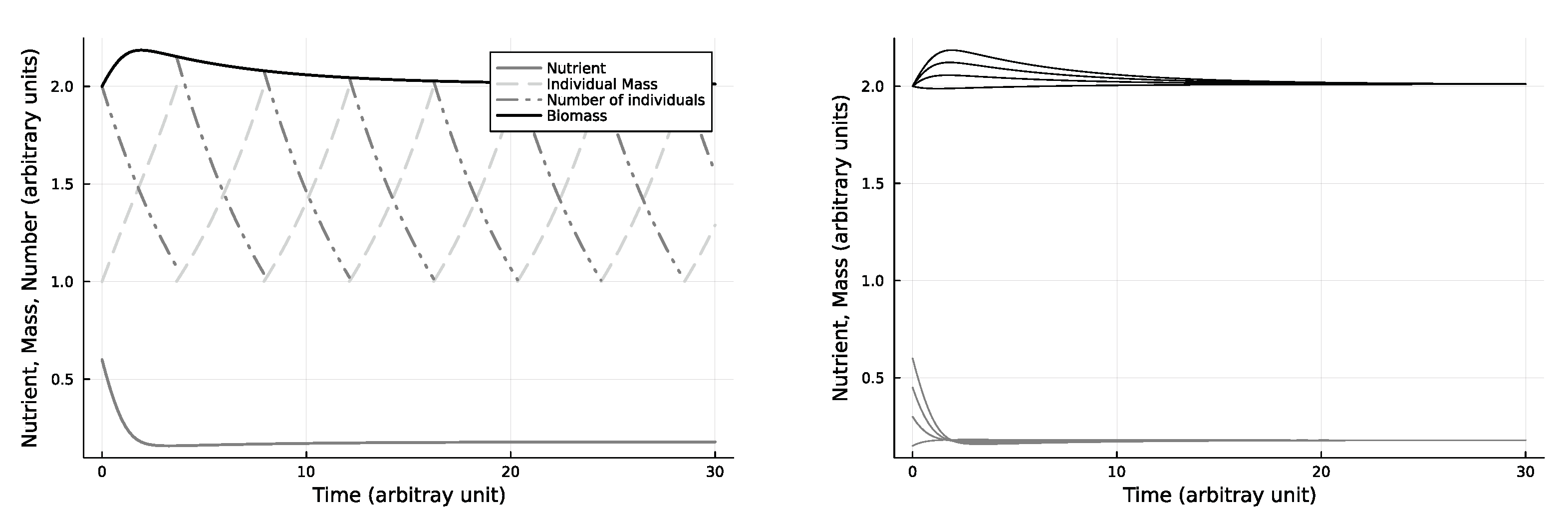
For model three, the minimally realistic case, the biomass

x^{*}

and nutrient concentration

x^{*}

of the steadily cycling state can be found by solving

\dot{x}, \dot{b} = 0

simultaneously. Noting that

\dot{b} = \dot{m} n + m \dot{n} = m n (\frac{c ν x}{K + x} - s m n)

we deduce that for

b > 0

\dot{b} = 0

if and only if

x = x^{*} = \frac{s K}{c ν - s}

. Applying this to

\dot{x} = 0

we obtain

b^{*} = (i K + x^{*} (i - s K) - s {(x^{*})}^{2}) / ν x^{*}

. Then size growth is at the rate

r^{*} = c ν x^{*} / (K + x^{*})

, and solving

x^{*} = s K / (c ν - s)

we obtain

s = c ν x^{*} / (K + x^{*})

, so that

r^{*} = s

and the doubling time for size growth equals the halving time for in population number due to dilution. Thus

m, n

are periodic with generation time

t^{*} = log (2) / s

. This is illustrated in Figure 3, which also shows that the steadily cycling state is a limit cycle.

Now for the question of age structure. Unlike the previous two, in the minimally realistic case the different cohorts interact (albeit indirectly) because they share the nutrient supply. However, when steadily cycling, the nutrient level is constant at

x = x^{*}

and the parameter values

r^{*}, s

are the same for all cohorts. Therefore in this case, as in the previous two, age structure is persistent.

Entropy production in the steadily cycling states

Every metabolically active organism produces entropy (see [11] for a discussion of entropy production in a model of the life cycle of an aerobic organism). Thus the size growth in each of the three models in this paper implies entropy production. As noted above, entropy production in non-linear thermodynamics is a very active area of research and many issues remain to be resolved. However, if we restrict our attention to the steadily cycling case of each model, then the rate of entropy production is periodic and we can for the moment ignore the causal role of entropy in how that state was reached. All that matters is that entropy production is guaranteed by individual growth.

However, entropy production is not necessarily constant throughout the life cycle of a microbe. In these models, under steady cycling, this difficulty is avoided quite simply: each microbe grows from

m_{0}

2 m_{0}

before fission occurs

t^{\circ}

later (where

t^{\circ} = 0

for the base model and the minimally realistic model) and at a constant rate. Therefore all microbes produce the same amount of entropy during their lifetimes; in fact, entropy production for a single microbe over a period equal to the generation time is a constant, no matter at what size it starts (that is, this includes the growth pattern

m_{1}

2 m_{0}

followed by

m_{0}

m_{1}

). Summing over all cohorts the entropy produced over a single generation time is therefore therefore a constant, whatever time the interval starts.

Moreover, this applies to any age distribution, as follows. Consider the interval

t \in [0, t^{*}]

and a cohort of size

m_{1}

initially. This cohort will grow to size

2 m_{0}

, then double in number and halve in size and grow back to size

m_{1}

at the end of the interval. All this time the undergo dilution such that the enumerated size of the cohort at

t = 0

is equal to its size at

t = t^{*}

. Therefore cohort i exports the entropy that corresponds to an overall mass gain of

n_{0 i} m_{0 i}

for all i, irrespective of initial indivdidual size.

In other words, in these models the entropy produced by the metabolism of the microbes is decoupled from the age structure—entropy production over an interval of length

t^{*}

is the same for all age structures.

4. Discussion

These results illuminate the following question: do changes to ecosystem structure result in changes to entropy production? For the models presented above, the answer is no: no matter what the age structure, the population is steadily cycling and the entropy production per cycle is invariant. It seems possible that some aspects of ecosystem structure may escape from entropic constraint.

How far might these results generalise?

Many models could be written analogously to the ones above. All that is needed is for biomass b to be decomposed into

b = \sum_{i} m_{i} n_{i}

, with models that imply births and deaths such that solutions for b are the same for all age structures.

Moreover, introducing a death rate

λ

would not change the results. Simply replace the dilution rate s with the loss rate

s + λ

. The individuals in a given cohort will still have the same age (by definition), so that deaths actually do not influence the age structure. Neither to they influence the production of entropy, which (in these models, anyway) is due solely to the metabolism of living individuals.

Might non-deterministic dynamics be used? Certainly. Let’s interpret the dynamics as expected values of stochastic processes. Then the expected biomass is still a steadily cycling variable, and hence the expected rate of entropy export is constant, irrespective of age distribution. However, the strict synchrony of individuals in a cohort would be lost, and some sort of drift in age distribution would result.

It seems plausible that other structures might also allow for escape from entropic constraint. For a spatial example, consider cattle in a pasture. Suppose that over longish time intervals, they spatial distribution of grazing pressure is constant. This can obviously be achieved in many different spatial arrangements. For example, a tight herd could move steadily around the paddock, or individuals could move randomly, independently and ergodically.

However, it seems less easy to construct examples for intra- and interspecific interactions, because as mass m changes with age, these interactions could not plausibly have unchanged effects.

What about genetics? Could it be that some changes in genetic structure have no implications for entropy production? Again, yes. For example, this follows from the genetic code itself, whereby a give amino acid is coded for by several different codons, so that there are genetic changes which do not result in any changes to the resulting protein.

A role for information entropy?

It seems unlikely that cohorts can maintain synchrony over many generations; some version of drift in age structure dynamics seems far more likely. As noted above, this does not preclude steady cycling and constant entropy production per cycle. However, it does allow for the possibility that some age structures are more likely than others.

Here, Jayne’s principle of maximum entropy seems applicable. Age structure is a probability distribution. In the models as stated, the only constraint on probability of an individual having age a is

0 \leq a \geq t^{*}

, which in turn implies that the uniform age distribution is the one with maximum entropy. Inferring any other age distribution is equivalent to applying further constraints—that is, to a claim of knowledge about the age distribution that we have assumed we do not have.

One should note that the entropy in question here is information entropy, and the causal role of maximum information entropy is far from settled [10]. However, one need not adduce a causal role, one could merely state that without information beyond a maximum age, the best prediction is to expect the uniform age distribution.

The best inference for spatial distribution is not as simple. The known constraints go beyond physical limits such as island shores, they should include effects of low density (such as reduced reproductive success) and of high density (such as resource depletion). The resulting maximum entropy distribution would need to find the best trade-off among these contradictory tendencies.

Funding

This research received no external funding.

Conflicts of Interest

The author declares no conflict of interest.

References

Jørgensen, S.E.; Fath, B.D. Application of thermodynamic principles in ecology. Ecological Complexity 2004, 1, 267–280. [Google Scholar] [CrossRef]
Nielsen, S.N.; Müller, F.; Marques, J.C.; Bastianoni, s.; Jørgensen, S.E. Thermodynamics in Ecology — An Introductory Review. Entropy 2020, 22, 820. [Google Scholar] [PubMed]
Endres, R.G. Thermodynamics of switching in multistable non-equilibrium systems. Nature Scientific Reports 2017, 7, 14437. [Google Scholar]
Roach, T.N.F. Use and abuse of entropy in biology: a case for caliber. Entropy 2020, 22, 1335. [Google Scholar] [PubMed]
Meysman, F.J.R.; Bruers, S. Ecosystem functioning and maximum entropy production: a quantitative test of hypotheses. Phil. Trans. R. Soc. B 2010, 365, 1405–1416. [Google Scholar] [CrossRef]
Ludovisi, A. Effectiveness of entropy-based functions in the analysis of ecosystem state and development. Ecological Indicators 2014, 36, 617–623. [Google Scholar]
Worrall, F. ; Morrison, R; Evans, C. ; Kaduk, J.; Page, S.; Cumming, A.; Rayment, M.; Kettridge, N. Are peatlands in different states with respect to their thermodynamic behaviour? A simple test of peatland energy and entropy budgets. Hydrological Processes 2021, 35(12), e14431. [Google Scholar]
Di Vita, A. The Garden of Forking Paths. In Non-equilibrium Thermodynamics. Lecture Notes in Physics; Springer: Switzerland, 2022; Volume 1007, pp. 201–212. [Google Scholar]
Jaynes, E.T. Information theory and statistical mechanics. Physical Review 2002, 106, 620–630. [Google Scholar]
Popović, M. E. Research in Entropy Wonderland: A Review of the Entropy Concept. Thermal Science 2018, 22, 1163–1178. [Google Scholar] [CrossRef]
Jusup, M.; Sousa, T.; Domingos, T.; Labinac, V.; Marn, N.; Wang, Z.; Klanjšček, T. Physics of metabolic organization. Physics of Life Reviews 2017, 20, 1–39. [Google Scholar] [CrossRef]
Michaelian, K.; Cano Mateo, R.E. A Photon Force and Flow for Dissipative Structuring: Application to Pigments, Plants and Ecosystems. Entropy 2022, 24, 76. [Google Scholar] [CrossRef] [PubMed]
Schrödinger, E. What is life? Cambridge University Press: London, 1944. [Google Scholar]
Demetrius, L.; Gundlach, V. Directionality Theory and the Entropic Principle of Natural Selection, Entropy 2014 16, 5428–5522.

Figure 1. Base case, one cohort, steadily cycling state. This figure shows how binary fission causes periodic behaviour of individual size growth and population number dilution. In this case they compensate each other exactly, so that biomass is constant.

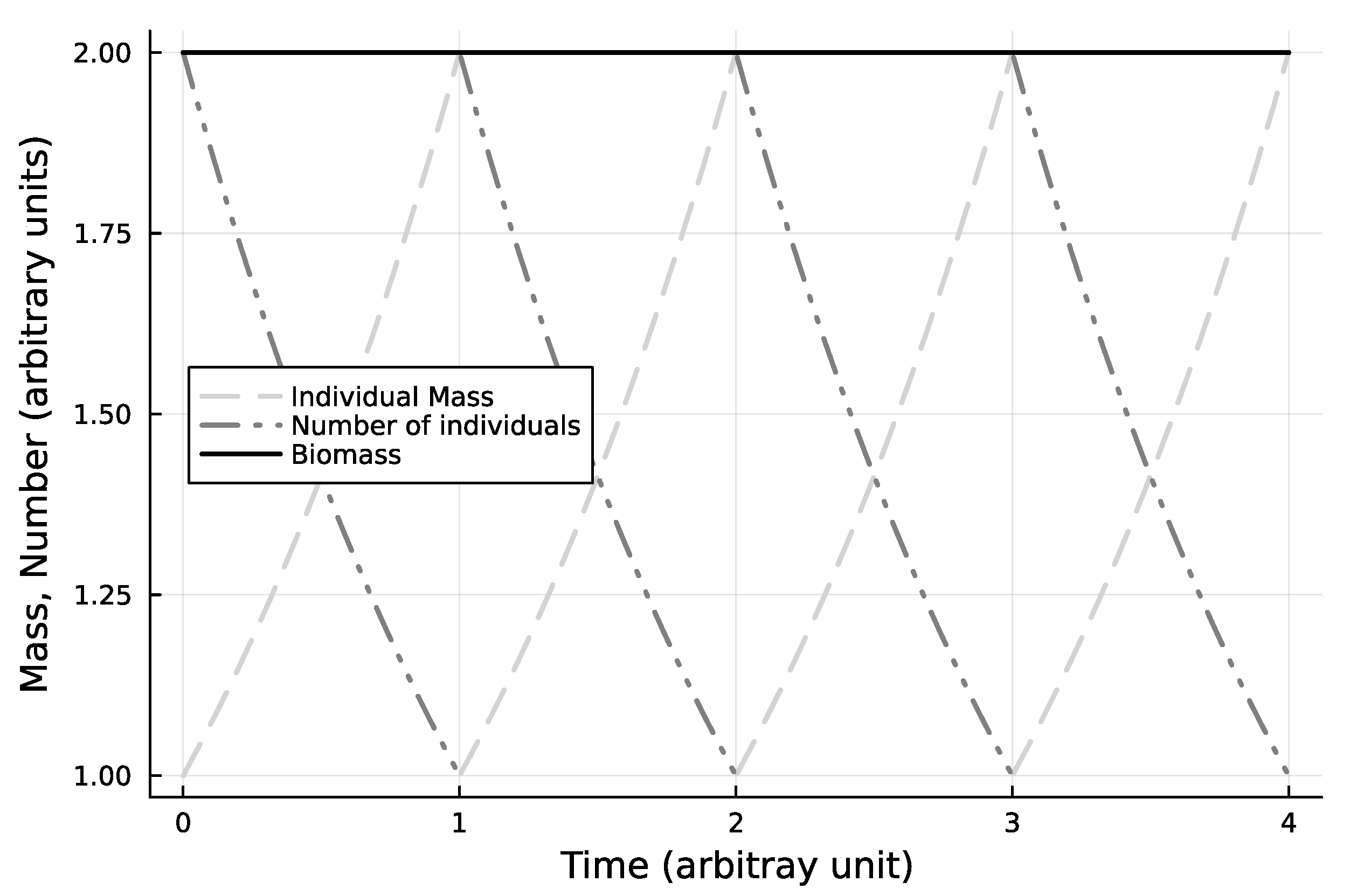
Figure 2. Base + pause for fission case, one cohort, steadily cycling state. In this case, the biomass is periodic.

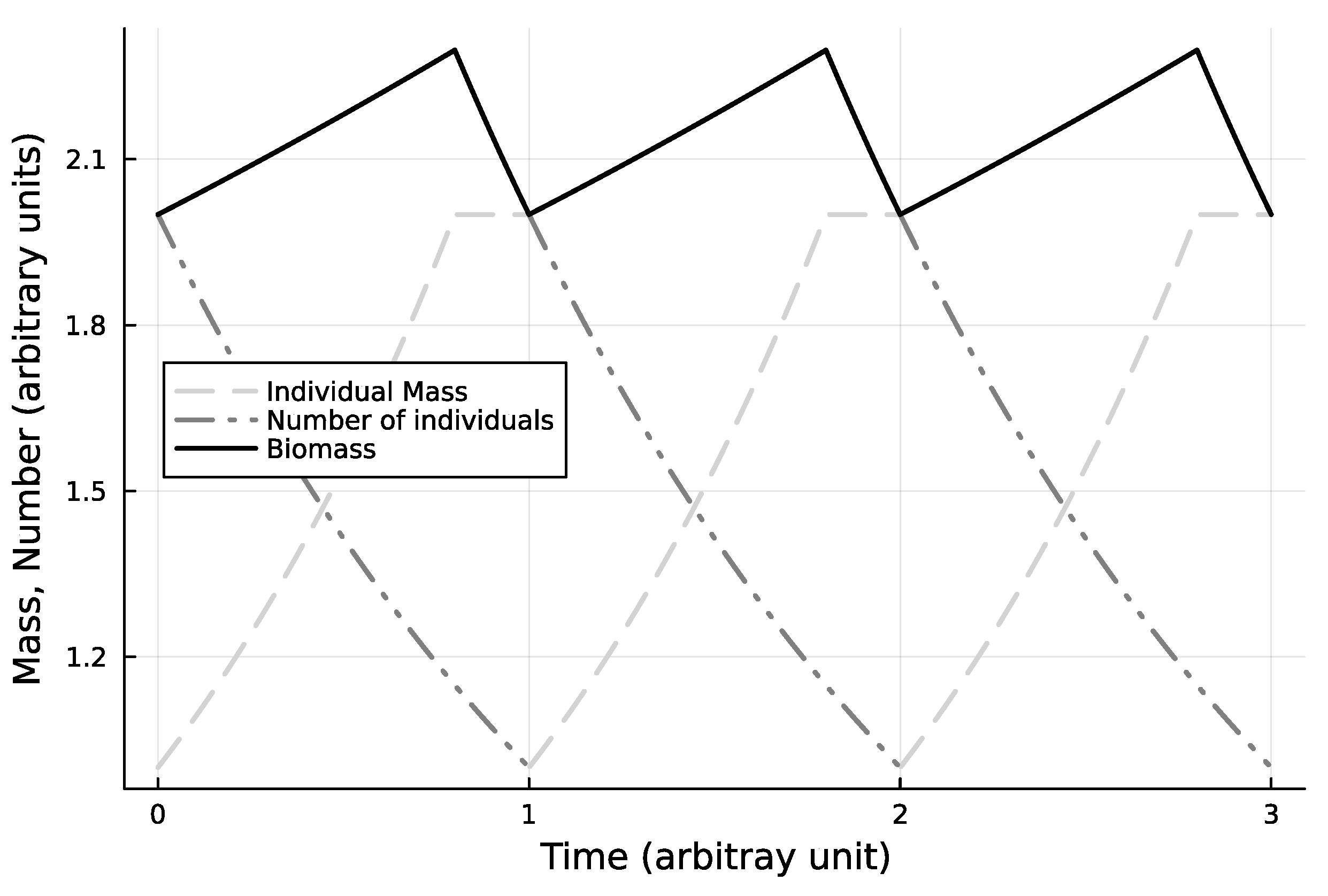
Figure 3. Minimally realistic case, one cohort, convergence to steadily state. The figure on the left shows all four components of for one set of intial values; on the right shows biomass and nutreints only, for four different initial values of nutrient.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Class of Models That Support a Maximum Entropy Principle for Age Structure

Abstract

1. Introduction

2. Models

Simplicity first: the base case

The base case + non-zero time for binary fission

Minimally realistic: constant resource supply, Monod-like uptake dynamics

Population structure in the three models above

3. Results

The steadily cyclic states of the three models

Entropy production in the steadily cycling states

4. Discussion

How far might these results generalise?

A role for information entropy?

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe