Prerpints.org logo
Preprint
Article

Wavelet Analysis of Respiratory Muscle sEMG Signals During the Physiological Breakpoint of Static Dry End-Expiratory Breath-Holding in Naive Apneists: A Pilot Study

Altmetrics

Downloads

116

Views

99

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

29 May 2023

Posted:

31 May 2023

You are already at the latest version

Alerts
Abstract
The wavelet spectral characteristics of three respiratory muscle signals (Scalenus (SC), Parasternal intercostal (IC) and Rectus abdominis (RA)) and one locomotor muscle Brachioradialis (BR) were analyzed in the time-frequency (T-F) domain during breath-holding (BH). Study was performed for an end-expiratory BH maneuver on twelve healthy, physically active, naive apneists (6 professional athletes; 6 recreational athletes, two in the post-COVID-19 period) using surface electromyography (sEMG). We observe individual effects dependent on muscle oxygenation and person’s fitness, consistent with the mechanism of motor unit (MU) recruitment and the transition of slow-twitch oxidative (type 1) to fast-twitch (oxidative) glycolytic (type 2) muscle fibers. Professional athletes had longer BH duration (BHD) and strong hypercapnic response on expiratory RA, which is activated abruptly at higher BHDs in a person-specific range below 250 Hz and dependent on BHD. This is in contrast with recreational athletes, who had strong hypoxic response on inspiratory IC, which is activated faster and gradually in the frequency range of 250-450 Hz (independent of the apneist and BHD). This pilot study preliminarily indicates that it is possible to non-invasively assess the physiological characteristics of skeletal muscles, especially oxygenation, and improve physical fitness tests by determining T-F features of elevated myoelectric IC and RA activity during BH.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

The theoretical limits of human voluntary breath-holding (apnea) are defined primarily by the metabolic and mechanical limitations of cardiorespiratory physiology. The metabolic limit is the loss of consciousness due to the extreme hypoxemia and hypercapnia, while the mechanical limits are the lung compression and intrathoracic vascular distension [1,2,3]. These limits are reached only by highly trained apneists due to a powerful involuntary breakpoint mechanism of prolonged apnea [1], which is activated significantly below these extreme physiologic limits. Understanding of the precise mechanism and threshold for breakpoint activation is still insufficient due to complex and integrated cardiorespiratory physiology, while the persistence of sinus arrhythmia during apnea indicates the probable continuity of the central respiratory rhythm and thus the impossibility of its voluntary stopping [1,4]. Decades of apnea research through the design of different breath-hold (BH) maneuvers have unequivocally shown large variations in the physiological response, showing the continuous and robust adaptation capability of the respiratory system to changes in the internal and external environment, indicating its integrative nature [1,2,5,6,7,8,9]. Moreover, the correlation of intracellular mitochondrial respiratory metabolic processes with respiration in real time, as well as changes in membrane potential with inhalation and exhalation [10], suggest that respiration is one of the most integrated physiological processes.
Contemporary extensive, although incomplete, knowledge about the function and control of the physiological response to apnea has been acquired by studying a number of BH maneuvers under different conditions: wet/dry, normobaric/hyperbaric, static/dynamic, repetitive/nonrepetitive, end-expiratory/end-inspiratory, with/without prior hyperventilation and/or oxygenation, with/without manipulation of perception etc., as well as for different body positions: sitting, supine, arms up, prone, and lateral, and on different populations: trained/naive, healthy/unhealthy, younger/older, human, animal etc. Despite these great variations in the human physiological response to apnea, also ascribed to the mammalian dive reflex, its critical function is oxygen conservation to maintain cerebral functioning, while its central processes are sympathetically mediated peripheral vasoconstriction connected with initial hypertension and vagally mediated bradycardia connected with the cardiac output reduction [2,5,8]. This initial increase in mean arterial pressure (MAP) coincides with a probably also sympathetically mediated spleen contraction, and thus the ejection of fresh blood, which all together apparently have a beneficial effect on the apnea onset [11].
During the apneic response, it distinguishes two basic phases – the ”easy-going” phase and the ”struggle” phase, and their demarcation point represents the physiological breakpoint which is commonly considered as the first involuntary breathing movement (IBM) – the powerful contractions of the respiratory muscles during which a motivated but naive apneist will break breath hold and reinstate [1,8]. The occurrence frequency and intensity of IBMs increase towards the end of apnea, which indicates that IBM has an additional beneficial impact along with other mechanisms, although its role is obscured by the fact that some elite apneists do not experience an IBM maintained apnea [12]. IBMs induce short-lasting increases in MAP accompanied by positively correlated oscillations in cerebral blood volume and oxygenated hemoglobin concentration, and are probably a consequence of chemoreceptor stimulation and consequent efferent respiratory motor output [12,13]. IBMs also coincide with splenic volume reduction and restoration of hemodynamics, which probably facilitates the use of the last oxygen reserves before apnea cessation [11].
Understanding the physiological responses associated with apnea has the potential to provide models that illustrate cardiorespiratory interactions as well as more integrated physiological processes, and thereby improve physical fitness tests and training [14,15,16].
In terms of improving clinical management through (early) diagnosis of general and specific pathogenesis, various breath-holding tests provide a clinical test for health risk assessment and stratification, starting with breath-holding duration (BHD) for different breath-hold maneuvers as the simplest objective measure [17,18] or integrated with other measures. Of particular interest is the early diagnosis of obstructive sleep apnea-hypopnea syndrome (OSAHS), as a common sleep disorder characterized by episodes of intermittent airway obstruction during sleep with a complete (apnea) or partial (hypopnea) reduction in airflow. OSAHS leads to sleep fragmentation and intermittent hypoxia during sleep, while in the long term it has also been reported to be part of age-related diseases and to accelerate aging mechanisms [19], as well as other disorders and diseases [20,21]. OSAHS is still an underdiagnosed condition, but recent studies have not only shown that OSA can be identified using simple breath-holding maneuvers performed during wakefulness [22], but some research approaches suggest that it can be modeled using prolonged breath-holding [23], which highlights the importance of reliable identification and characterization of IBMs.
Based on our previous study [24], the first goal here was to investigate the electrophysiological behaviour of three specific respiratory muscles during IBMs (for comparison, one locomotor muscle was also included), particularly
  • to find out which muscle is most appropriate for IBM detection and characterization,
  • to test the reproducibility of physiological responses of respiratory muscles, and
  • to investigate an improved time-frequency (T-F) analysis method for studying respiratory muscle sEMG signals to non-invasively assess skeletal muscle oxygenation and improve physical fitness tests.
Research results in the literature have demonstrated that the wavelet transform (WT) is one of the most promising method for T-F analysis, given that it very accurately extracts features from biomedical signals. It is widely used for the analysis and classification of EEG recordings, while for muscle sEMG signals it has been shown to be a good tool for identifying muscle fatigue [25]. This paper is one of the few in which a wavelet-based multiresolution analysis has been performed for respiratory muscle sEMG signals.
Our long-term goal is to define reliable machine learning features and a robust analysis method for noninvasive apnea/hypopnea detection (similar to [26]) and to improve physical fitness tests by establishing a closer relationship between physical condition with BHD and sEMG spectral characteristics.

2. Database

This descriptive and exploratory study was conducted in Belgrade, Serbia. The study was performed in accordance with appropriate data protection legislation, the Declaration of Helsinki, and has been approved by the Research Ethics Committee at the Faculty of Sports and Physical Education, University of Belgrade, Serbia.

2.1. Participants and Procedure

All participants in this study were regularly athletically/physically active non-smokers, had a fully preserved locomotor and nervous system, had no lasting damage to the lungs, airways and associated musculature, and were not taking any prescription medications. Participants in this study beforehand received the necessary explanations and instructions, and then stated in writing that they understood the goals and procedures of the study and that they agreed to participate in the study.
A schematic representation of the BH maneuver with its tasks, phases and durations is given in Figure 1. Breath-holding began after spontaneous exhalation to functional residual capacity (FRC), with the suggestion of refraining from preparatory hyperventilation, and ended with spontaneous inhalation. Subjects completed a shortened form of the BH maneuver as a preparatory exercise before the experimental breath-holding, which consisted of the first three phases (three-minute spontaneous breathing, breath holding, three-minute spontaneous breathing). All preparatory exercises were performed in a full experimental setting and were recorded, but not included in the analysis. In both cases, preparatory and experimental exercise, with participants having a 5-minute rest period between preparatory and experimental exercises.
A total of 12 healthy, physically active, naive apneists (breath holders) participated voluntarily, divided into two equal number groups according to the level of sports participation – professional and amateur level. For self-assessment, participants noted their sport, age, gender, height and weight, as well as their status as a professional or amateur athlete and their main sport discipline/activity (Table 1). The table additionally contains their resulting BHD during the first and second voluntary apnea defined by the BH maneuver (BHD1 and BHD2 in Figure 1).

2.2. Measurement and Preprocessing

Participants performed the entire experimental test in an upright sitting position,without lumbar support, and in a quiet environment with occasional and timely notification of the remaining time until the onset of breath-holding. Subjects were instructed to breathe through the nose, especially in the entry and exit phases of breath-holding. They were suggested to completely relax their respiratory musculature during the early BH period, and allow respiratory contractions to develop ’’naturally’’ towards the end of breath-holding. For the entire experimental setup, the choice of the right body-side for acquisition was dictated by minimizing the interferences of cardiac activity signals which are more pronounced on the left body side (see Figure 2). In addition, the subjects were instructed to avoid activating their peripheral muscles, except when they should mark the beginning and ending of breath-holding, which was also a sign to the operator to put and remove the nose-clip. This sign was given with a slight lifting of the index finger of the left hand, to further avoid right body side activity during the critical measurement phases (start and end of the BH maneuver).
Surface EMG data collection was performed by the research-orientated high-performance Trignotm Wireless EMG System (DelSys Inc., MA, USA), using four hybrid EMG/Movement Trigno sensors for the selected muscles described and depicted in Figure 2 (the recorded electromyogram signals are EMGSC, EMGIC (electr. pos.: 2nd right IC space at the parasternal line), EMGRA, and EMGBR, respectively). The sensors were applied simultaneously according to the manufacturer’s instructions and SENIAM recommendations [27,28]. Proper skin preparation was performed by shaving (hair removal), cleaning by mild scrubbing with 70 % isopropyl alcohol, and then allowing the alcohol to vaporize before the sensor positioning. An arrow-shaped top of the sensor was orientated parallel to the muscle fiber direction and placed over the muscle mid-belly (Figure 2). Prior to sensor affixing, its precise position was determined by optimizing the signal quality during the muscle contractions using the real-time Signal Quality Tool included in the Delsys EMGworks® Acquisition software. The sensors were affixed with original Trigno Adhesive Skin Interfaces, enabling a robust interface between the sensor and the skin without needing additional gels.
The sensor design as a double-differential bar sensor (four bipolar Ag/AgCl bar electrode: bar size, 5 × 1 mm; inter-electrode spacing, fixed 10 mm; Common Mode Rejection Ratio, CMRR > 80 dB) ensures reliability and consistency across all data collection, reduces the crosstalk signals from adjacent muscles and suppress movement artifacts, as well as any common signal from distant sources as power lines [29]. The data at the sensor level were filtered with the AC-coupling (DC-blocking) filter by 7 Hz highpass FIR filter based on the LS algorithm and a Hamming window and with a second-order Butterworth bandpass filter between 20 ± 5 Hz and 450 ± 50 Hz to increase the signal-to-noise ratio, similar as explained in [30]. Data were collected at a sampling frequency of 1926 Hz using a 16-bit A/D converter. In addition to hardware filtering, software filtering was performed on the raw data with Root Mean Square (RMS) filter. RMS envelope calculation was performed with fully overlapped windows, so that the sampling rate of the RMS is identical to the sampling rate of acquired data. Muscle movement artifacts are manually removed from the signal by visual inspection. All data analyses was subsequently performed in MatLab (MathWorks Inc., MA, USA).

3. Research Objectives and Methods

Following the set objectives of the research previously stated in the Introduction, here we present the underlying rationale and methods with the technical procedures undertaken to conduct the research process.
Most biomedical signals being a non-stationary and transient phenomena are often a research topic, as in the case of IBM in this study. The analysis of non-stationary and transient signals demands their localization in both frequency and time. The uncertainty principle inherent in the Fourier transform, called the Heisenberg-Gabor limit, implies that localization in a time-frequency (T-F) domain is a non-trivial problem and that there is always a tradeoff between their localization. This inherent coupling between time resolution and frequency resolution in the T-F plane is represented by the minimum area of the so-called Heisenberg box with a lower bound of 1 2 . Optimizing the T-F resolution is based on representing signals as linear superpositions of a family of functions built from translations and modulations of the generating function. This decomposition of the signals over a family of functions, called T-F atoms, is the basis of sparse representation theory. Depending on the choice of T-F atoms that define the basis set of the sparse transform, the decomposition can have very different properties and thus different T-F resolution (Heisenberg boxes; Figure 3, left). Since a large and redundant basis set accompanies high T-F resolution, adapting the transform framework to the signal properties and the needs of further signal analysis is one of the key steps. The wavelet transform (WT) provides a high frequency resolution at low frequencies and a high time resolution at high frequencies, making it a convenient and powerful tool for T-F analysis in biomedical applications.
The WT is a sparse signal decomposition using strictly local time-frequency waveform functions – the wavelet family (Appendix A). Depending on the construction of compactly supported wavelets and the scaling and translating parameters, the WT provides a flexible time-frequency resolution – from high to critical resolution representation. This distinguishes two main classes of WTs, namely the continuous wavelet transform (CWT; Appendix A.1) with high resolution but also high redundancy due to the large overlap in the frequency and time domains, and the discrete wavelet transform (DWT; Appendix A.2) with critical resolution but nonredundancy and therefore easily invertible (for a comparison of CWT and DWT resolutions, see Figure 2 & 4–6 in [31]). The orthogonal basis expansion methods provide a minimal set that can yield a sparse representation and thus a critical resolution, which in the case of WT gives a perfect T-F plane tiling for DWT (Figure 3, left). The concept of multiresolution analysis (MRA) combines continuous time wavelet theory and discrete filter banks [32]. The multiresolution theory of orthogonal wavelets can be implemented by a cascade of so-called conjugate mirror filters, which also gives a fast DWT (fDWT; Figure 3, right). Corresponding DWT, fDWT and MRA are equivalent in decomposition and all provide the same expansion coefficients, but DWT-based MRA provides in addition the reconstructed signal components of scales (frequency bands).
Regarding the advantages and disadvantages of CWT and DWT implementations, the general opinion is that CWT has excellent capabilities and performances in signal analysis but not in signal synthesis due to its numerical instability, while the reverse is true for DWT. All this motivated the modifications of both WT methods (e.g., [31,33]), so that in addition to CWT and DWT, several forms of redundant DWT have also been developed in order to optimally combine the advantages of both WTs. In this paper, we use the maximal overlap DWT (MODWT [33]; Section 3.2.1 and Appendix A.2) with good wavelet analysis and synthesis properties, in which translation and dilatation parameters correspond to integer sequence as in discretized CWT and dyadic scaling as in DWT, respectively. The MODWT enables suitable analysis because it does not average the frequencies contained in the signal, but the averaging takes place only in the time domain, additionally stabilizing the signal by filtering (removing) high-frequency components that represent a form of noise.
Since most real-world signals are available as discrete-time samples and their processing is regularly implemented in a computational environment, as is the case here, the discretized WT versions is further considered.

3.1. Transient Localization and Scalograms

The CWT uses a near-continuous discretization ((A6) in Appendix A.1) that transforms the time-domain waveform into the time-scale domain, where the scale can be converted to frequency, thus transforming the 1D-signal into the T-F plane. The absolute value of the CWT coefficients of the signal in this T-F plane gives a visual representation of the CWT, known as a scalogram. Similarly to the spectrogram, the scalogram can be interpreted as an energy density of the signal in the T-F plane. In this way, the scalogram offers a high-resolution and smoothly varying representation of the T–F domain, which enables high-fidelity signal analysis with accurate localization of transients, characterization of oscillatory behavior, etc. The CWT is used here to generate the scalograms for visual detection of transient phenomena in respiratory muscle sEMG signals, as well as oscillatory cardiac (QRS) activity and their precise T-F localization. The part of the scalogram where edge effects become significant (COI; Appendix A.1) is mostly avoided and is located at the very margins of the signal by setting the lower frequency limit to 2 Hz and also does not affect the BH1&BH2 areas.

3.2. MODWT-based Multiresolution Analysis

The MODWT is naturally defined for each signal sample, giving it significant advantages over DWT, including the possibility of its application to sequences of arbitrary length and translation invariance (overcoming the problem of effects attributable to the choice of a starting point for analysis in DWT). Since MODWT enables a reliable comparison of specific short-term signal intervals of interest, this WT technique is imposed as the minimum necessary for analyzing the dynamic patterns in the signals studied here.
In the MODWT method, a real-valued uniformly-sampled time series x = { x n } n = 1 N is decomposed using wavelet family
ψ j , k [ n ] = 1 2 j ψ n − k 2 j ,
where j , k ∈ N index the scale/octave and the shift, respectively. Comparing with the wavelet families in (1), (A6) and (A7), it follows that scales have the octave range as in DWT, which means that there are no intermediate scales in the octave range as in CWT and no downsampling by 2 j with scaling as in DWT.
The DWT (MODWT) of a function x is expressed by the following sum
X w ( j , k ) = ∑ j = 1 J ∑ k = 1 N d j , k ψ j , k + ∑ k = 1 N s J , k φ J , k ,
where for each scale j, D j = { d j , k } k = 1 N and S J = { s J , k } k = 1 N respectively represent the wavelet (detail coefficients) and the scaling (smooth coefficients) of the MODWT for corresponding mother (wavelet) functions Ψ j = { ψ j , k } k = 1 N and father (scaling) functions Φ J = { φ J , k } k = 1 N (more details in Appendix A.2).
The standard MODWT algorithm implements circular convolution between the signal and the filters that must satisfy the conditions for an orthogonal wavelet. The MODWT decomposes the input signal x, sampled at a frequency f s , into J + 1 coefficient sequences { D j } j = 1 J and S J within J logarithmically evenly spaced frequency intervals for
scale j ( D j ) : [ 2 − ( j + 1 ) f s , 2 − j f s ] , j = 1 , 2 , . . . , J , scale J ( S J ) : [ 0 , 2 − ( J + 1 ) f s ] .
The MODWT is generally used to analyze the MODWT partitions of signal energy and variance.

3.2.1. Wavelet Energy Spectrum (WES)

Unlike the DWT, which is an orthonormal WT that preserves signal energy (variance), the MODWT preserves energy (variance) by normalizing the MODWT filter energy to 2 − j at the jth level (instead of the DWT filters that have unit energy). The discrete form of (A1) gives the MODWT partitions of the total signal energy at each decomposition level as
∥ x ∥ 2 = E = ∑ j = 1 J ∥ D j ∥ 2 + ∥ S j ∥ 2 = ∑ j = 1 J E j d + E J s ≠ ∑ j = 1 J ∥ D ˜ j ∥ 2 + ∥ S ˜ J ∥ 2 .
The magnitude square of a wavelet coefficient, d j , k 2 , or a smooth coefficient, s j , k 2 , in (4) represent a local T-F energy density, and their sequence shows a time evolution of the energy density in a bandwidth corresponding to the scaling level j. Their sums by individual frequency components, { E j d } j = 1 J and E J s , characterize the signal energy distribution at different frequency subbands and represent a wavelet energy spectrum (WES).
The total normalized energy, obtained by dividing (4) by E, reflects the relative energy contribution
ε j = E j / E
of each frequency interval to the total signal energy (description also known as the relative wavelet energy (RWE) in [34]). These normalized energy spectra P ( w ) ≡ { { ε j d } j = 1 J , ε J s } of respiratory signals EMGSC, EMGIC, and EMGRA were used to analyze the correlation of the BH1 and BH2 maneuvers, shown by scatter plots with marginal histograms in Section 4.2.3.

3.2.2. Wavelet Variance

The wavelet variance provides a scale-based analysis of variance, i.e., decomposes the variance of a time series into components related to different scales [35]. The variance is the mean squared difference from the mean, so the MODWT-based estimate of the time-independent wavelet variance is
σ 2 ( x ) = x 2 ¯ − x ¯ 2 = 1 N ∑ j = 1 J ∥ D j ∥ 2 + 1 N ∥ S j ∥ 2 − x ¯ 2 = ∑ j = 1 J E j d N + E J s N − x ¯ 2 .
If the signal has a mean value of zero, x ¯ 2 = 0 , the wavelet variance is related to the scale-averaged WES of the signal x, i.e., to the wavelet power spectrum (WPS). Given that the selection of the optimal number of decomposition levels J also implies the selection of a set of scales that significantly contribute to the signal variance, the variance of the J-level smooth (approximate) coefficients usually is not of interest, and the wavelet variance at scale j can be estimated by the variance of the j-level detail coefficients, σ j 2 ( x ) = 1 N ∥ D j ∥ 2 .

3.2.3. MRA Component Correlation

Linked to our long-term goal of a robust analysis method for detecting OSAHS and improving physical fitness tests, we would like to test the reproducibility of physiological responses of respiratory muscles. We will perform reproducibility and correlation analysis by comparing normalized WES of BH1 and BH2 phases. If we establish the actual equivalence of physiological responses as measured by normalized WES, we are able to combine BH1 and BH2 data for increased statistical significance of our conclusions.

3.3. Research Objectives and Steps

In the forthcoming analysis, we will use wavelet coefficients to describe the signals in the T-F domain by means of scalograms, as well as to define the (relative) energies of the signal MODWT components and derive metrics such as WES and moving average variance. For this purpose, we will use wavelets and related methodologies, in some cases correlated with BHD, through the key steps of study as follows:
Step 1. Defining frequency ranges and time intervals important for sEMG signal analysis using the occupied bandwidth (OBW) estimates of power spectral density (PSD) for signal decomposition within MODWT and MODWT-based MRA.
Step 2. Calculation of the (normalized) WES, i.e., the (relative) energies of MODWT components for the total BH period and its initial and final stages with their further use for quantitative analysis of muscle response (related to Steps 4 and 5). Finding the correlation of WESs classified according to different criteria (subject type, types of muscles and MODWT components) in order to determine the reproducibility of the IBM phenomenon, studying the response specificities of different muscle types.
Step 3. Studying the trends of muscle activity changes in different frequency ranges and corresponding self-adaptive mechanisms of response to BH in order to better understand the physiological response to the diving reflex. This is achieved by variance calculation using the moving window method of MRA components, as a useful research tool for identifying important scales and detecting energy/power inhomogeneities.
Step 4. Determining the reproducibility of the time-frequency response of the respiratory muscles by correlating the energy components of the sEMG signals for all signal classifications through the comparison of BH1 and BH2 phases (related to the long-term goal).
Step 5. Better understanding of mechanisms that are included in apneic response for inspiratory and expiratory muscles, with the purpose of improving a general fitness test that includes tissue oxygenation assessment. We define the muscle and the frequency range in which the largest energy change occurs globally through studying the energy change between the initial and final stages of BH phases.

4. Results and Discussion

This section presents our research results, which are accompanied by a corresponding discussion. Although subjects with similar interindividual characteristics within each of the two groups were recruited for this study, they showed significant inter- and intraindividual variability in physiological muscle responses to the designed BH maneuver (Figure 1), thereby reducing the statistical consistency of the results. To draw valid conclusions from these highly variable data, we focused on understanding the correlation between physiological responses and physical fitness/training within individuals. Hence, the paper is based on a qualitative case study research with discussion of physiological implications and presentation of quantitative indicators with statistical significance. Physiological implications were analyzed and interpreted mainly in the context of hypoxic and/or hypercapnic stimulation on one hand, and the neuromuscular junction of muscle fiber subtypes on the other hand.
The two main sets of results presented in this paper are: (1) a primary one related to the sEMG time-frequency features during involuntary breathing movements (IBMs) and (2) a secondary one related to breath-hold durations (BHDs). Both result sets are generally modulated by many factors. Beside individual factors such as sex, age, body size, chest shape, diaphragm position, thoracic blood volume, blood hemoglobin content, metabolic rate, obesity, disease etc., other common factors such as initial lung volume and posture have significant influence on sEMG and BHD results [36]. Considering that in this study we mainly limited the research objectives to the sEMG response of respiratory muscles to hypoxic and/or hypercapnic stimuli, the mentioned common factors were chosen to minimize their effects on EMG activity. This is achieved by reducing additional unwanted elastic forces in the respiratory muscles and changes in lung volume, thus reducing unwanted stimulation of the respiratory center control. Namely, most breath-holding studies are based on breath-holding from fully inflated lung or total lung capacity (TLC), but such an initial lung volume generates tension in all respiratory muscles to overcome increased inspiratory resistance and pulmonary pressure. This produces the inflation reflex and also increases the impact of mentioned individual factors [37]. Overcoming these factors can be achieved by the breath-holding onset during totally relaxed respiratory muscles, which is characteristic of the lung volume at the end of a normal exhalation, i.e., functional residual capacity (FRC). In terms of posture, supine position increases the pressure of abdominal contents on the diaphragm, preventing the diaphragm from being fully relaxed at end-expiration and significantly reducing thoracic volumes and, thus, the resting end-expiratory lung volume FRC. Compared to the upright sitting position, the supine position has the diminished elasticity of the ribcage and diaphragm, as well as the reduction of the rib cage compliance by 30% and the total static compliance of the respiratory system by 60% [36]. All the stated reasons led us to experiment design with BH maneuver during upright sitting. Additionally, the BH onset from FRC and the upright sitting posture both reduce pulmonary blood flow resistance and volume, preventing or reducing unwanted receptor stimulation.
Furthermore, we have also selected subjects who are physically active, either professionally or recreationally, and have normal body weight and fat as indicated by body-mass index (BMI) being in the range of 21.8-25.3 kg / m 2 (Table 1). The biggest deviation in terms of population coherence is the fact that two subjects, BHr7 and BHr12, were in the post-COVID-19 period with six and four weeks after recovery, respectively. Given that the development of post-COVID-19 syndrome is associated with the persistence of some symptoms such as silent hypoxia and muscle weakness [38], we wanted to compare the potential influence of silent hypoxia on the respiratory muscle response to BH.

4.1. Breath-Hold Duration

All the subjects classified into groups of professional and amateur/recreational athletes successfully completed the experimental protocol. Their resulting BHDs during the first and second voluntary apnea BHD1 and BHD2 are given in Table 1 through individual values, as well as mean values μ and standard deviations σ (both per group and for all participants in total).
In this study, BHD is of secondary interest as a parameter that allows us to better interpret the primary interest – the sEMG spectral characteristics. Population-wide BHD values fit a normal distribution with 43.5 ± 15.8 s ( μ ± σ in seconds) and the values less than σ away from the mean include 8 out of 12 apneists, i.e., only 2 apneists (BHr4 and BHr6) with the highest and 2 apneists (BHr12 and BHr1) with the lowest BHD are outside the σ interval. However, by comparing the spectral characteristics of sEMG signals, it is more reasonable to rank them into sub-groups according to μ ± σ / 2 (more details in Section 4.2), so that:
  • BHD rank #1 - BHr4 (72.5 p/m), BHr6 (63.0 p/m), BHr5 (54.5 p/m), BHr3 (52.0 p/m),
  • BHD rank #2 - BHr10 (48.5 a/m), BHr8 (47.5 a/m), BHr11 (42.5 a/m), BHr9 (35.5 a/m),
  • BHD rank #3 - BHr2 (29.5 p/f), BHr7 (28.0 a/m), BHr1 (25.5 p/f), BHr12 (22.5 a/m),
where the average of BHD1 and BHD2 values in seconds is shown in parentheses, and the abbreviations indicate the following terms: p – professional, a – amateur, m – male, f – female.

4.2. Respiratory Muscle EMG Response

Illustrations of muscle sEMG recordings during the BH maneuver are shown for two typcial classes of response, represented by an apneists BHr3 (BHD rank #1) in Figure 4 and BHr4 (BHD rank #1) in Figure 5. Visual analysis of these sEMG time series reveals some characteristic signal patterns for different muscle types.
Consistent with findings of other researchers, the periodic increase and decrease in the magnitude of EMGSC signal during three-minute periods of spontaneous breathing is associated with the changes in SC activity during repeated inhalation and exhalation, respectively, whereby this periodicity is absent during BH (see BHr3.SC in Figure 4 and BHr4.SC in Figure 5). The periodic activity on EMGSC is more pronounced for BHr4, while an additional increase before apnea indicates hyperventilation (it does not fit the design of the BH maneuver, but it was a mild hyperventilation that was not observed during the measurement), which is one of the factors that contributed to this subject having highest BHD score. In addition, more intense hypoxia causes the resumption of breathing with an intense and sometimes abnormal pattern, which all together allowed us to use EMGSC to fine tune the time marker Tstop, when possible due to significant interindividual specificity in the SC response.
The low-frequency, high-amplitude peaks in EMGIC and EMGRA (BHr3.IC & BHr3.RA in Figure 4 and BHr4.IC & BHr4.RA in Figure 5) during spontaneous breathing represent the R peaks of the cardiac QRS complex and are associated with the well-known general cardiac interference in respiratory EMG recordings.
In the pre-BH periods in BHr4, comparing the envelopes of EMGSC and EMGRA (to a lesser extent EMGIC), as well as changes in the RR interval (time between successive heartbeats), a correlation is observed that corresponds to respiratory sinus arrhythmia – a normal change in heart rhythm during breathing.
Also, the EMGIC and EMGRA signals of apneist BHr4 in the advanced stage of BH show an increase in the RR interval corresponding to the slowing of the heart rate. During BH phases, especially in its final stages, these ECG readings are mixed with respiratory EMG responses, particularly for EMGRA in BHD rank #1 group. The impact of this signal mixing is additionally shown in Section 4.2.1, where it can be observed especially for the final BH stages of EMGRA that the distribution of bandlimited power spectrum across apneists showed both increasing and decreasing power depending on the dominance of these two independent sources and their response to BH. The separation of components from this linear mixture of signals of different origin was performed using CWT and MODWT in Section 4.2.2, Section 4.2.3, and Section 4.2.4 when possible.
Signal patterns related to cardiac activities are not observable in EMGSC and EMGBR (BHr3.BR in Figure 4 and BHr4.BR in Figure 5), as they may have some limited ECG interference.
The main observed effects of prolonged BH for these two representative cases are different. For BHr3, it consists in a gradual increase of the sEMG magnitudes of the inspiratory muscle signals starting from the second half of the BH periods. This is noticeable for EMGSC, but significantly more pronounced for EMGIC. For BHr4, we observe a somewhat opposite effect – the abrupt changes in the magnitudes of the expiratory muscle RA.
The observed difference in the response of inspiratory and expiratory muscles to BH in BHr3 and BHr4 led to our main hypothesis that this difference is caused by different mechanisms. In order to test this hypothesis, we will correlate certain wavelet spectral characteristics with BHD, which will be given in more detail in the Section 4.2.4, and especially in the Table 2.
Other significant individual variations in respiratory neuromuscular control resulted in a different muscular response to the BH maneuver are analyzed and discussed in more detail in Section 4.2.2 and Section 4.2.4.

4.2.1. Power Spectral Analysis

sEMG signals in the time domain show us different types of response to breath-holding. In order to understand in more detail how frequencies and power of the signal change over time, we will compare response in the initial and final stages of BH. To study change in the frequency response, we will calculate the occupied bandwidth (OBW), which gives a frequency range of the signal containing 99% of the total integrated power of its spectrum. The OBW is the frequency difference between points where the integrated power crosses 0.5% and 99.5% of the total power in the spectrum. To determine the OBW, we first estimate a periodogram power spectral density using a rectangular window and then integrate the estimate using the Riemann sum (midpoint rule). The time intervals for which the OBW are calculated is 3 seconds, while the locations of the time intervals are shifted by 2 seconds inwards from the BH phase boundaries, i.e., the BH Initial stage is calculated from Tstart+2 to Tstart+5 (in seconds), while the BH Final stage from Tstop-5 to Tstop-2 (in seconds) (Figure 6).
In Figure 6, we show comparison of the occupied bandwidth (OBW) characteristics of the initial and final stages of BH (combined for BH1 and BH2) of muscle sEMG signals for the case of the combined 12 naive apneists. Each column represents the OBW of individual muscle sEMG signals of SC, IC, RA, and BR, in order from left to right, which corresponds to the order of sensors from top to bottom in Figure 2. We can observe that the lower bounds approximately stay the same, while the upper bounds increase for SC, IC and RA signal. As a result, the width of the OBW increases for these three signals, and stays the same for BR signal. Occupied band power which represents the signal power within the OBW slightly increases for IC signal, whereas it is not visibly changed for other signals. We have noticed that combined effect of heart rate drop takes place together with increased response of muscle sEMG signals, which is not easily discerned in these combined graphs. This motivates more detailed signal analysis in both time and frequency, so that we can better see various influences that overlap each other and how signals change their frequency and energy over time.

4.2.2. Frequency Range of Muscle Response Using Scalograms

Our study uses the Daubechies (db) wavelets family, specifically db8 (of order eight) as one of the most suitable mother wavelets for the sEMG signal analysis according to [39]. In line with the recommendation [33], higher order wavelets were used in order to achieve the lowest possible interactions between the decomposed components. Mother wavelets db8 [39] and sym8 [33] were compared, however db8 slightly better concentrates energy into active components, while their asymmetry does not affects the translation of the signal due to the high sampling frequency f s = 1926 Hz. Hence, our WMRA splits sEMG signals in the frequency bands D1-D8 and S8, as follows: D1 (481-963 Hz), D2 (241-481 Hz), D3 (120-241 Hz), D4 (60-120 Hz), D5 (30-60 Hz), D6 (15-30 Hz), D7 (7-15 Hz) D8 (4-7 Hz) and S8 (0-4 Hz).
For visual detection and the T-F localization of transient phenomena in respiratory muscle sEMG signals, as well as in interfered oscillatory cardiac (QRS) activity, first we will use scalograms (Section 3.1). CWT and MODWT analysis show that for the selected group of respiratory muscles in this study, the dominant muscle response and thus the physiological break point in all subjects occurs on two respiratory muscles - either the inspiratory IC or the expiratory RA. The scalograms of two representative cases for these two types of muscle responses are given as follows:
  • Figure 7 shows results for apneist BHr3 (BHD rank #1) with dominant response at the inspiratory IC (see sEMG time series for BHr3 in Figure 4),
  • Figure 8 shows results for apneist BHr4 (BHD rank #1, highest BHD score) with dominant response at the expiratory RA (see sEMG time series for BHr4 in Figure 5).
In order to analyze the contribution of higher and lower frequencies to sEMG signals, it is worth noting that the sEMG frequency spectrum lies between 20 Hz (or lower) and 500 Hz, and that for respiratory muscles the high frequency range is defined at 130-250 Hz and the low frequency range at 30-50 Hz [40]. In accordance with these standards, here we will assume the following division of frequency bands (FB): very high FB – VHFB (250-500 Hz), high FB – HFB (130-250 Hz), medium FB – MFB (50-130 Hz), and low FB – LFB (30-50 Hz). Comparing WMRA and standard FB division, we can determine the following approximate correlation: D2∼VHFB, D3∼HFB, D4∼MFB, and D5∼LFB.
For BHr3, the most pronounced muscle activity related to the apneic response is at IC in D2/VHFB and less in D3/HFB, characterized by a progressive increase in EMGIC energy density centered around 300 Hz starting approximately in the middle of the BH and ending abruptly immediately after breath reinstatement. Very slight correlated changes in the same FBs are also observed for EMGSC. In contrast, for BHr4, no obvious increased sEMG activity is observed on the inspiratory muscles SC and IC, but the abrupt activation of the expiratory muscle RA in D3/HFB and less in D4/MFB, and therefore in a lower FB than for the inspiratory muscles.
Muscle activation accompanied by changes in sEMG amplitude and energy/power spectral density is generally achieved by varying the combination of motor unit (MU) recruitment and modulation of the firing rate. The MU morphological features such as the number, spatial distributions (cross-sectional area) and composition of muscle fibers are the major determinants of MU potential. Based on previous studies [41,42,43], these three partially dependent factors contribute differently to the variation of the motor unit action potential (MUAP) waveform, and thus to the electromyographic activity and force generation, so that the geometric factors have a greater influence on the amplitude of the sEMG signal, while the fiber type has a greater influence on its spectral characteristics.
Three types of fibers are known to exist in human skeletal muscles, each with specific contractile and biochemical characteristics, so that different composition of fibers in a muscle is adapted to muscle function in the body. The main biochemical characteristics of fibers are related to metabolic pathways for energy supply and oxidative capacity. According to contractile properties and oxidative capacity, fibers are commonly categorized into slow oxidative (type 1), fast-twitch oxidative glycolytic (2A), and fast-twitch glycolytic fibers (2X). Type 1 fibers use mainly oxidative phosphorylation, which makes them resistant to fatigue, and hence are mainly involved in aerobic activities and endurance exercises. In contrast, type 2 fibers rely mainly on glycolytic metabolic pathways for energy supply, have faster contraction velocities than type 1 fibers, and are not fatigue-resistant. These types of fibers are predominant in the skeletal muscles of adult humans, but in addition to them, muscles of specific functions may contain other types, as well as ’’hybrid’’ types of fibers [44].
The recruitment pattern of MUs usually follows the principle of orderly recruitment according to their motor neuron size. Because MUs with slow type 1 fibers have smaller motor neurons and those with fast-twitch type 2 fibers have larger ones, the order of recruitment is also related to MU fiber type composition. Hence, skeletal muscle contraction involves progressive recruitment in an additive manner and in the following order: type 1 → type 2 A → type 2 X [44]. Since an interference signal of all generated MUAPs defines the properties of sEMG, the MU recruitment pattern reflects the spectral characteristics of muscle activity, such that fast fibers generate higher frequencies within the myoelectric spectrum than slow fibers [41]. Hypoxia-induced progressive activation of larger MUs with faster fibers during apnea can significantly explain the pattern of gradual changes in EMGSC and EMGIC spectral characteristics on inspiratory muscles in BHr3 [9,45], but unsatisfactory for the case of apneist BHr4 (Figure 8).
Although the generated MUAPs mainly depend on the MU recruitment pattern, other specific factors can significantly influence the modulation of the firing rate of MUAPs. In addition to hypercapnia induced by prolonged apnea, muscle contractions cause an increase in the concentration of lactic acid and other metabolic products, which leads to a decrease in intracellular pH and consequently to a decrease in muscle fiber conduction velocity [41,42,43]. The compensatory mechanism in maintaining or increasing the muscle contractile force despite the decrease in fiber conduction velocity induces a direct change in the shape of the MUAP waveform, which leads to an increase in various parameters of the waveform (duration, area, amplitude, etc.). Thus, these changes in MUAP characteristics induced by pH reduction directly influence greater electromyographic responses, but do not imply correspondingly greater MU recruitment and muscle activation. In the case of BHr4 apneist, as well as other apneists that held their breath for about 1 minute at FRC (which at TLC could correspond to approximately twice as long BHD [37]), we suggest that the sudden activation of the RA is primarily the result of hypercapnic stimulation.
Observed differences in the response of respiratory muscles to apnea-induced hypoxia and hypercapnia for apneists BHr3 and BHr4 are supported by well-known differences in the response of respiratory muscles to hyperventilation. Namely, for the equivalent minute volume, hypoxia stimulates mainly inspiratory muscles, while hypercapnia stimulates both inspiratory and expiratory groups [36]. Moreover, while diaphragmatic EMG activity increases in response to both hypercapnia and hypoxia, expiratory muscle activity increases almost exclusively during hypercapnic hyperventilation [36]. Abdominal muscles are generally expiratory, and RA, one of the important abdominal expiratory muscles, is known to play an important respiratory role during exercise and hypercapnia [36].
It was thought that hypoxia and hypercapnia were simply additive in their effects, but due to complexity, a hybrid model of integration of possible additive, hyperadditive and hypoadditive interactions between central and peripheral chemoreceptors in relation to systemic P CO 2 was proposed, where the form of interaction generally depends on the behavior and/or metabolism of the individual [46,47]. In this regard, the case of apneist BHr12 (BHD rank #3, the lowest BHD score) is particularly indicative, where we can observe two phenomena by comparing the scalograms for EMGSC and EMGIC shown in Figure 9. First, we observe a correlation of neuromuscular activity for SC and IC inspiratory muscles in the approximate frequency range 120-480 Hz , the same characteristic D2/VHFB and D3/HFB that were present in the IC and partially SC muscle response to apnea in BHr3 (scalograms were adopted to assess muscle co-contraction [48]). This correlation could be partly attributed to the intercostal-scalene reflex related to the phrenic nerve [49]. Second, there is a disproportionate increase in IC electromyographic activity compared to breath-hold duration (average BHD is 22 seconds, a period in which BHr3 and BHr4 had no response). The explanation may be in the mentioned ’silent’ or ’apathetic’ hypoxia and respiratory muscle weakness as the consequences of the previously acquired disease of COVID-19, while it is also known that COVID-19 can induce lactic acid production accompanied by uncompensated respiratory acidosis, decreased plasma pH, hypercapnia, and more [38]. This can be linked to the previous comment regarding a decrease in muscle fiber conduction velocity and an increase in sEMG activity without a proportional increase in muscle activity. Similarly, some other respiratory diseases can lead to a disproportionate increase in neural respiratory drive directed towards the respiratory muscles [42,43]. The correlation of respiratory muscles with physical performance/training is also indicated by respiratory muscle training [50,51].
Large interindividual variations in the physiological response to hypoxic and/or hypercapnic stimulation during apnea could be explained by a heterogeneous tissue of human skeletal muscle, as well as metabolic, energetic and neuromuscular differences. Our analysis showed that among the selected muscles, the individual specificities of the neuromuscular coupling in the participants are most pronounced on the SC, as demonstrated in the case of the apneist BHr6 (BHD rank #1) who is a professional diver (Figure 10).
The claims we made in this section could be partially confirmed if a relationship could be established between the spectral features of sEMG activity and BHD, so we will first examine the reproducibility of the spectral features of sEMG activity during BH1 and BH2, using wavelet MRA (WMRA).

4.2.3. Muscle Response Reproducibility Analyses Using WMRA

In order to analyze the relationship between two groups of data – the distributions of the relative energies ε j of the WMRA components during BH1 and BH2, and thus muscle-activation reproducibility, the scatter plots with marginal histograms are presented in Figure 11 and Figure 12. They show the distributions of relative energies of the respiratory signals EMGSC, EMGIC and EMGRA, which were determined using a probability density estimate based on the normal kernel function. To avoid a strong bias in the distributions, we exclude D1, D8 and S8 scales, as these components have very small relative energies compared to the other scales, and would otherwise create large peaks in the distribution around zero. In this way, we focus on the frequency components D2-D7 in the range from about 7 Hz to 500 Hz.
In Figure 11, data of all participants from both BH periods is used (x-axis: BH1 and y-axis: BH2) and distributions are shown for three types of data grouping: professionals vs. amateurs (left), respiratory muscle signal type (middle), and WMRA components (right). We can notice that the energy distribution of professionals and amateurs is approximately the same (see Figure 11, left), which means that on average the populations of different subjects behave similarly. At the same time, a strong correlation was observed between BH1 and BH2 since the coefficient of the linear regression model is approximately 1, which provides the basis for integral analysis of BH1 and BH2.
Observing the maximum values of probability density for relative energies in Figure 11 (middle) indicates some biases between different muscles. RA is characterized by large number of components with low relative energy and a small number of components with a larger range of high relative energies, which mostly exceed the relative energy values of components SC and IC. On the contrary, SC has the narrowest distribution and the maximum shifted most to the right, which means that the relative energies by components are most evenly distributed (similar energies for all D2-D7 spectral components) and with higher values compared to RA and IC. The characteristics of IC are somewhat in between SC and RA, with two peaks of accumulation of relative energies. Comparing with Figure 11 (right), we can conclude that high relative energies mostly originate from D6 signal component (15-30 Hz), which has an interference with cardiac electromyographic activity that pushes energies towards higher values, especially for EMGRA and then for EMGIC (corresponds to the second distribution peak with a smaller number of components of higher relative energies). This general distribution of relative energy across the respiratory muscles is consistent with the energy density distribution in the T-F plane of their corresponding scalograms (Figure 7 and Figure 8).
Additionally, Figure 11 (right) shows that the relative energies at all scales have similar behavior, except for D5 and D6. While we gave an explanation for D6, the distribution of D5 most closely corresponds to the distribution of SC, especially for high relative energies, which indicate the negligible influence of D6 and D7 components. The narrow distribution of D5 is a result of an accumulation of components of approximately similar relative energies that originate from different muscles and subjects - this indicates that it corresponds to a frequency range of SC that is not significantly involved in apnea-induced muscle activity.
Since one of our goals is to find out which muscle is the most appropriate for IBM detection and characterization, we will perform an analysis of separate distributions of each of the respiratory muscles for grouping by sporting activity – professionals vs. amateurs (Figure 12). As there is also a partial correlation with BHD (Section 4.1) for this type of grouping, we will give an interpretation of some results in that context as well.
A consistent overlap of the distribution curves for professionals and amateurs is noticeable only for IC, while for RA and especially SC they differ (Figure 12). Since the IC distribution is very similar for widely varying values of BHD (from ∼ 20 to ∼ 80 seconds), it follows that the apneic response of IC is largely universal in the healthy population. In contrast, there is a significant difference in the distributions for SC: wide distribution for professionals points to a strong energy redistribution for longer BH. Finally, for RA muscle in professional population there is a redistribution of energy from components with high relative energies to components with medium energies, which is not noticeable for amateurs (this can be more clearly seen in Table 2, for rank #1 subjects). This can be explained by the more pronounced heart rate drop accompanying longer periods of BH for professionals.

4.2.4. Correlation Analyses of Muscle-Activation and BH Duration Using WMRA

In the Section 4.2.3, we analyzed the relative energies of the wavelet MRA components for the entire interval of BH duration, but our goal now is to visualize and quantify the changes in relative energies during the development of the apneic response. We will use the moving variance to visualize the transient process (as explained in Section 3.2.2), while the absolute difference of the normalized wavelet energy spectra (Section 3.2.1) between the BH Final stage and BH Initial stage was used to quantify energy changes during IBM.
The moving variance is a common tool for detecting short-term fluctuations and long-term trends or cycles in a time series. Since the moving variance is a type of convolution (nonlinear filter), it is calculated using the sliding window method. Here, it is applied to the WMRA components by a centered window of 1.5 seconds (2889 samples), where the window length is chosen to contain approximately two cardiac RR intervals. Figure 13 shows a representative case of subject BHr3 (BHD rank #1) for the IC muscle, where the upper part of the figure contains the WMRA components of the entire EMGIC signal, and the lower part the corresponding filtered components using the centered moving variances.
From Figure 13, two synchronized processes are visible that occur as a result of the apneic response (both start around the middle of BH1 and BH2): the first refers to a gradual increase in power for the high-frequency range D2/VHFB – D3/HFB (120-481 Hz) and to a lesser extent D4/MFB, and the second refers to a gradual decrease in power for the frequency range D6-D7 (7-30 Hz) and to a lesser extent D5/LFB.
In order to quantify the changes of relative energy across the scales related to the first IBM during BHs, we will compare the normalized wavelet energy spectra P ( ε ) ≡ { { ε j d } j = 1 J , ε J s } (Section 3.2.1) at the BH Initial stage, P Int ( ε ) , and the BH Final stage, P Fin ( ε ) . We calculate this change as the absolute difference between P Fin ( ε ) and P Int ( ε ) , so that for each component we obtain △ P ( ε ) = P Fin ( ε ) - P Int ( ε ) . The time intervals for calculating △ P ( ε ) are 3 seconds with a shift of 2 seconds inwards from the BH phase boundaries as in the case of OBW in Figure 6.
The distributions of △ P ( ε ) of all participants across the scales, grouped by muscles, is presented by boxplots in Figure 14. We can observe that the most pronounced increase in activity for IC is primarily in the D2/VHFB component, followed by D3/HFB, which are also the only increased components whose lower quartile is above zero. It is also indicative that a similar trend is present in the same components of SC, so that the apneic response of IC and SC is generally consistent in the frequency range above 120 Hz (D3 and D2 components). This correlated muscle activity of inspiratory IC and SC muscles in the higher frequency range during apnea has been previously observed in scalograms of EMGSC and EMGIC for several individual apneists and is very apparent for apneist BHr12 (rank #3; Figure 9), not only during apneic periods, but also during spontaneous breathing in the inspiratory phases.
At the same time, D6 component of IC has the largest energy drop similar to D6 component of RA, which can be attributed to heart rate drop (SC and BR do not follow this trend due to the absence or limited electromyographic contributions from the cardiac).
For BR muscle a slight frequency redistribution of muscle activity from medium to high frequency band can also be observed, especially a slight shift from D5 to D4 frequency range. This can be explained by the limitation of blood flow to the limbs, not only as a consequence of the apneic response (sympathetically mediated peripheral vasoconstriction) but also of the metaboreflex (redistribution of blood flow to the respiratory muscles during their fatigue followed by a consequent restriction of blood flow to the locomotor muscles).
To understand which frequency bands have significant change of energy in SC, IC and RA muscles, we calculate a change of relative energies across all the subjects and wavelet scales, per muscle (see left side of Table 2 encompassing 12 subjects labeled as professionals and amateurs). According to a central limit theorem, distribution of values for each random process can be approximated with a Gaussian normal distribution for large enough sample. As we are calculating a relative energy change for each person which implies normalization, we obtain a process with zero mean value for each person, but also for all components of each muscle. Looking at Table 2, in many cases only a small relative change is observable, which can be attributed to a random process. In order to isolate components with significant energy change, we can calculate a 95% Confidence Interval (CI) which in this case encompasses majority of values where no significant change is observable. Values that are outside of this 95% CI are significantly different from the majority of population and are the components of interest. In the right side of Table 2, with Average change of significant components, we average per rank all the relative energies of a particular wavelet scale that are outside of 95% CI, and hence which represent components with significant change. For example, value 3.09% for D2 component of Rank #1 subgroup represents an average value of significantly changed D2 components of SC muscle for that subgroup.
Distributions of △ P ( ε ) of the average values per scale for the total population and the BHD rank groups confirm the insights and conclusions given for Figure 14, and also provide new ones in the context of BHD.
According to the average values (Table 2, columns Total and Rank #1, #2, and #3), relative energy increase of EMGSC of the main two components D2 and D3 calculated for the entire population is 88%, while for the three BHD rank groups are 91%, 89%, and 78%, respectively. The corresponding average D2 and D3 values of EMGIC constitute 87% of the total energy increase, while separated by the ranks they are 93%, 81% and 88%, respectively. The consistent contribution of D2 and D3 components in the total energy increase of EMGSC and EMGIC again indicates their correlated muscle activity in the higher frequency range, which we mentioned in the context of the results from Figure 9 and Figure 14. By comparing the joint percentage increase of these two components by BHD ranks #1, #2, and #3 for SC which are 6.17%, 6.03% and 14.65%, respectively, we conclude that it is the most pronounced for BHD rank # 3 group, especially with BHr12 apneist, which can be related to a possible post-COVID hypoxic state.
From Table 2, two sharp transitions of energy decrease and increase between adjacent components can be observed: first, between D3 and D4 of EMGSC, visible for subjects with BHD ranks #1 and #3 and, second, between D5 and D6 of EMGRA, visible only for subjects with BHD rank #1. It is particularly indicative that these most pronounced changes are correlated with BHD rank groups: for SC, it is for apneists for which hypoxia is more pronounced either due to a significantly prolonged BH (BHD rank #1) or due to the partial influence of possible chronic hypoxia and accompanied by uncompensated hypercapnia due to the post-COVID state (BHD rank #3), while for RA, it is for apneists for which hypercapnia is more pronounced due to prolonged BH (BHD rank #1). We consider that this phenomenon could be explained by MU recruitment: a change in recruited MUs during the time evolution of the apneic response from smaller MUs of slow-twitch oxidative type 1 fibers to larger MUs of fast-twitch (oxidative) glycolytic type 2 fibers.
Finally, Table 2 provides us with one of the most significant results that follows from the comparison of the distribution of energy changes for EMGRA in correlation with BHD, where it is shown that the increase in activity in D3-D5 components refers only to apnests from rank 1, more precisely BHr4 and BHr5, whose BHDs lasted about 1 minute. This observation is consistent with [36] according to which RA responds almost exclusively to hypercapnia.
The observed links between sEMG activity and BHD, as well as their interpretation in the context of MU recruitment in relation to the respiratory muscles response to hypoxia/hypercapnia, are also supported by a recent study [52] in which an sEMG-NIRS correlation analysis was performed. Namely, using near-infrared spectroscopy (NIRS), as a standard method of measuring local tissue oxygenation, in correlation with sEMG activity of the locomotor muscle, a higher correlation between EMG and NIRS signals was observed in participants with a more active lifestyle. It was also shown that subjects with the least active lifestyle had the lowest correlation. Reduced EMG-NIRS correlation indicates the influence of factors other than oxygenation, such as metabolic, energetic and neuromuscular factors, which may be particularly pronounced in persons with a specific health condition, as in the case of BHr12 in the post-COVID state (more details in Section 4.2.2, Figure 9). All this gives us an additional argument that by using the sEMG signals we can evaluate oxygenation, even in cases when a disproportion between sEMG activity and muscle response is observed.
Considering all these findings, we conclude that our setup allows assessment of skeletal muscle oxygen storage and current fitness level: subjects with higher BHD and a primarily hypercapnic response on expiratory RA are more fit than subjects with shorter BHD and primarily hypoxic response on inspiratory IC.
This study has limitations that should be taken into account when validating the final conclusions related to the mentioned relationships between the spectral characteristics of respiratory muscles, their fiber activation and metabolism during the apneic response. Future studies should include bigger population, more respiratory muscles, especially the diaphragm, and use sEMG in combination with advanced techniques to assess blood flow and tissue oxygenation (NIRS) in order to obtain more accurate quantitative estimators of physical fitness.

5. Conclusions

Voluntary breath-holding (apnea) serves as a model for studying various physiological concepts/principles and testing various physical/clinical conditions. Breath holding and involuntary breathing movements during the ”struggle” phase of BH have been investigated extensively, but relatively few studies have been related to skeletal muscle characteristics in that context (e.g., muscle fiber type, fiber oxidative capacity, and fiber size). In this paper we focus on the spectral characteristics of respiratory muscle electromyography (sEMG) signals during breath-holding to find out the most appropriate muscle for IBM detection and characterization, as well as to assess tissue hypoxia and/or hypercapnia response in healthy, physically active adults (professional and recreational athletes). The sEMG signals of three respiratory muscles Scalenus (SC), Parasternal intercostal (IC), Rectus abdominis (RA), and one locomotor muscle Brachioradialis (BR) were analyzed in the time-frequency (T-F) domain using the continuous and discrete wavelet transform (CWT & MODWT). Our investigation demonstrates that the dominant respiratory muscle response related to the physiological breakpoint (the first IBM) can be detected either on the inspiratory IC or the expiratory RA.
This pilot study preliminarily indicates high reproducibility of physiological responses of respiratory muscles. We have observed that professional athletes had higher BHD and a stronger hypercapnic response on expiratory RA than recreational athletes, who had a stronger hypoxic response on inspiratory IC. The hypoxic sensitive inspiratory IC is activated faster and gradually in the frequency range of 250-450 Hz for recreational athletes (independent of the apneist and BHD). This is in contrast to the hypercapnic-sensitive expiratory RA, which is activated for professional athletes only at higher BHDs, but abruptly and in a person-specific range below 250 Hz (dependent of the apneist and BHD), which in some individuals may partially overlap with cardiac activity ranges. Comparison of BHD and T-F features of sEMG signals shows changes consistent with the mechanism of motor unit (MU) recruitment and the transition of slow-twitch oxidative (type 1) to fast-twitch (low oxidative) glycolytic (type 2) muscle fibers.
With this, we are able to assess skeletal muscle oxygen storage and see a potential to improve physical fitness tests by establishing a closer relationship between physical condition with breath-hold duration (BHD) and sEMG spectral characteristics of elevated myoelectric IC and RA activity during BH.

Author Contributions

Conceptualization, N.Ž.M. and M.O.; methodology, N.Ž.M., M.O. and P.M.; software, N.Ž.M. and S.C.; validation, N.Ž.M., M.O. and A.K.P.; formal analysis, N.Ž.M. and S.C.; investigation, N.Ž.M., M.O., P.M., and Z.A.; resources, Z.A., Đ.S. and M.O.; data curation, M.O., Z.A. and N.Ž.M.; writing—original draft preparation, N.Ž.M., S.C. and M.O.; writing—review and editing, N.Ž.M., S.C., M.O., P.M. and Đ.S.; visualization, N.Ž.M. and S.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Ministry of Education, Science and Technological Development of the Republic of Serbia, Grants No. 451-03-68/2023-14/200066, 451-03-47/2023-01/200114, and 451-03-47/2023-01/200154.

Institutional Review Board Statement

The study was conducted in accordance with the Declaration of Helsinki for experiments on humans, and the protocol was approved by the Ethics Committee of Faculty of Sport and Physical Education, University of Belgrade, Belgrade, Serbia (protocol no. 580/22-2 dated April 5, 2022).

Informed Consent Statement

Informed written consent was obtained from all subjects involved in the study.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author, N.Ž.M., upon reasonable request.

Acknowledgments

The authors would like to thank all participants who took part in this study for their patience and commitment.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

Abbreviations

The following abbreviations are used in this manuscript:
BH             Breath-hold
BHD Breath-hold duration
BR M. brachioradialis
CWT Continuous wavelet transform
DWT Discrete wavelet transform
FB Frequency band
FRC Functional residual capacity
IBM Involuntary breathing movement
IC M. parasternal intercostal
LFB Low frequency band
LS Least-square
MAP Mean arterial pressure
MFB Medium frequency band
MODWT Maximal overlap discrete wavelet transform
MRA Multiresolution analysis
MU Motor unit
MUAP Motor unit action potential
OBW Occupied bandwidth
OSAHS Obstructive sleep apnea-hypopnea syndrome
QRS Ventricular depolarization and contraction (ventricular systole)
RA M. rectus abdominis
RMS Root mean square
RWE Relative wavelet energy
SC M. scalenus anterior at medium
sEMG Surface electromyography
TLC Total lung capacity
WES Wavelet energy spectrum
WMRA Wavelet multiresolution analysis
WPS Wavelet power spectrum
WT Wavelet transform

Appendix A. Wavelet Transform (WT)

The WT theory is well known (one of the most comprehensive monographs on the subject to date is [32]), but here we present the basics for familiarity with our notations and a precise definition of the signal processing techniques we used.

Appendix A.1. Continuous Wavelet Transform (CWT)

The WT decomposes a finite energy time signal x ∈ L 2 ( R d ) into a linear combination of dilated/scaled and translated versions of a fixed prototype time function, called mother wavelet ψ ∈ L 2 ( R d ) . For d = 1 , the CWT transforms a time-domain waveform into a time-scale domain, where the scale can be converted to frequency, thus transforming the 1D-signal into the T-F plane.
Since signal x belongs to the space of square-integrable functions, L 2 ( R ) , the square norm of the signal, also called the energy of the signal (the Parseval–Plancherel identity), is induced as an inner product
∥ x ( t ) ∥ 2 = 〈 x , x 〉 = ∫ R | x ( t ) | 2 d t = ∫ R x ( t ) x ¯ ( t ) d t < ∞ ,
where the overline represents an operation of the complex conjugate.
In the CWT, the mother wavelet dilated and translated versions give the wavelet family, sometimes called the child wavelets,
ψ a , b ( t ) = 1 a ψ t − b a ,
where a ∈ R + defines dilation and also the scale or, so called, the octave band [ 1 a , 2 a ] , while b ∈ R defines translation. The term a − 1 / 2 ensures that the norm of ψ a , b ( t ) is equal to one (a unit-norm or unit energy). The wavelet family (A6) can be more compactly expressed using translation operator T b ψ ( t ) = ψ ( t − b ) and dilation operator D a ψ ( t ) = a − 1 / 2 ψ ( t / a ) , so that equivalently to (A6),
ψ a , b ( t ) = T b D a ψ ( t ) .
The CWT, analogous to (A1), is the inner product of the input signal x ( t ) and the wavelet family ψ a , b ( t ) , giving for the complex case the wavelet coefficients
X w ( a , b ) = 〈 x , ψ a , b 〉 = ∫ R x ( t ) 1 a ψ ¯ t − b a d t .
In special case x , h a ∈ L 1 ( R ) (continuous functions with compact support), the convolution can be written as an inner product, i.e., ( x * h a ) ( t ) = 〈 x , T b h a ˜ 〉 , where h a ˜ ( t ) = h a ¯ ( − t ) is the involution [53]. From (A3) and (A4) follow
h a ( t ) = D a ψ ¯ ( − t ) ⟹ X w ( a , b ) = ( x * h a ) ( t ) ,
i.e., the CWT can be interpreted as a continuous time convolution [53]. Since the filtering operation is also a convolution, the CWT is mathematically equivalent to passing the input signal x ( t ) through a series of wavelet filters h a ( t ) that are a reflected, conjugated, dilated and normalized version of the mother wavelet ψ ( t ) .
Since CWT does not have an analytical solution for most functions and can only be calculated numerically, and since most real-world signals are available as discrete-time samples and their analytical form is generally unavailable, a discretized version of the CWT is implemented in a computational environment. A discretized CWT, like other types of WT, uses discretizing of the time axis by samples n ∈ Z and the scale axis in a dyadic (octave band) configuration ( a = 2 ), so that the discretized wavelet family has form
ψ j , k [ n ] = 1 2 j / ν ψ n − k 2 j / ν ,
where j , k ∈ Z index the scale/octave and the shift, respectively, and ν ∈ N > 1 is the number of intermediated scales in an octave, which defines approximately the number of wavelet bandpass filters per octave (the filterbank). Using the filterbank generated by (A6), the CWT with the additional specification of the mother wavelet and the sampling frequency f s , returning the scale-to-frequency conversions. The absolute value of the CWT plotted as a function of time and frequency in a semi-log graph represents the scalogram. The scalogram can be interpreted, similarly to the spectrogram, as an energy density of a signal in the T-F plane [53]. The part of the scalogram where edge effects become significant is defined as the cone of influence (COI), and is the result of convolution near the signal boundaries where it performs wavelet multiplication with undefined data outside the signal.
Although CWT typically results in high-fidelity signal analysis, signal reconstruction from the coefficients (A4) using the inverse CWT is much less stable due to the high redundancy of the CWT (large shift and scale overlap).

Appendix A.2. Discrete Wavelet Transform (DWT)

The discrete wavelet transform (DWT), like the CWT, can be applied to a continuous-time signal or a discrete-time signal (a real-valued uniformly-sampled time series). The discreteness of DWT is based on discrete shift and scale parameters that ensure signal reconstruction with minimum redundancy and loss of information. Since shift and scale parameters are correlated, the DWT is generated on a fine-tuned time-scale lattice (instead of a time-scale plane as for the CWT).
In a special case, a signal description by the minimal number of wavelet coefficients possible can be obtained when the scaled and shifted wavelets form a multiresolution analysis (MRA), i.e., when the (mother) wavelet functions { ψ j , k [ n ] : j , k ∈ Z } and the newly introduced (father) scaling functions { φ j , k [ n ] : j , k ∈ Z } form an orthonormal basis of L 2 ( R ) , so they are both orthogonal and normalized. This applies when the mother and father functions have a similar form with the same shift and dilate/scale parameters, while the mother functions are as in (A6) for ν = 1 and k ⟼ k 2 j ,
ψ j , k [ n ] = 1 2 j ψ n − k 2 j 2 j ,
which means that there are no intermediate scales in the octave range and there is a downsampling by 2 j with scaling.
However, a redundant representation offers a higher-fidelity signal analysis, as in the time (or shift) invariant and highly redundant DWT with no downsampling, called the maximal overlap discrete wavelet transform (MODWT) [33]. The MODWT uses values removed from DWT by downsampling and has form as in (A6) for ν = 1 , so the mother functions are rescaled or dilated by powers of two as in DWT and translated by integers as in CWT, and thus it is defined for all samples sizes (any signal length).
Similar to DWT, it can perform MRA, where MODWT-based MRA is more reliable and provides a high-accuracy reconstruction of discrete-time signal x = { x n } n = 1 N as
x = ∑ j = 1 J ∑ k = 1 N d j , k ψ ˜ j , k + ∑ k = 1 N s J , k φ ˜ J , k = ∑ j = 1 J D ˜ j + S ˜ J ,
where d j , k = 〈 x , ψ j , k 〉 are the wavelet or detail coefficients and s j , k = 〈 x , φ j , k 〉 are the scaling or smooth coefficients of the MODWT, while ψ ˜ and φ ˜ are the dual functions of ψ and φ , respectively. Orthogonal projections of detail coefficients at scale/level j yield a sequence D ˜ j that defines the jth level MODWT-based MRA signal detail, and analogously S ˜ J is the Jth level signal smooth (approximation). Adding the jth level signal detail to the jth level signal smooth gives the ( j − 1 ) th signal smooth, i.e., the signal approximation at an increased resolution. The relation (A8) also represents the inverse MODWT (iMODWT) and differs from iDWT by the summation’s upper limit for k where is N ⟼ N / 2 j due to downsampling in the DWT signal decomposition. Hence, for DWT the lowest resolution J is bounded by 2 J ≯ N , in contrast to the MODWT pyramidal algorithm which always yields N scaling coefficients for the next level and thus J is unbounded. The MODWT is generally used to analyze the MODWT partitions of signal energy and variance.
A time-redundancy of the MODWT enables accurate time-alignment of the original signal features and the features of its decomposition coefficients d j , k 2 and s j , k 2 at each level, but it induces a certain degree of correlation among these coefficients. As a consequence, although the MODWT-based MRA components D ˜ j and S ˜ j accurately reveal the content of the original signal within the frequency bands, they do not preserve energy as indicated by equation (4). Using wider filters, i.e., those with a larger number of vanishing moments can result in an approximate uncorrelatedness between wavelet coefficients across scales for certain time series [33].
Using filters, DWT/MODWT results in a recursive relationship between the filter coefficients and the scaling and wavelet functions: the lowpass halfband filter determine the scaling functions and produces s j , k , while the highpass halfband filter determine the wavelet functions and produces d j , k . Dyadic signal decomposition (analysis) and perfect reconstruction (synthesis) are fulfilled when two pairs of filters satisfy the conjugate quadrature filter (CQF) relationship, which means that the corresponding lowpass and highpass filters are orthogonal, while the corresponding analysis and synthesis filters are time-reversed.

References

  1. Parkes, M.J. Breath-holding and its breakpoint. Experimental Physiology 2006, 91, 1–15. [Google Scholar] [CrossRef]
  2. Lindholm, P.; Lundgren, C.E. The physiology and pathophysiology of human breath-hold diving. Journal of Applied Physiology 2009, 106, 284–292. [Google Scholar] [CrossRef] [PubMed]
  3. Bain, A.R.; Ainslie, P.N.; Barak, O.F.; Hoiland, R.L.; Drvis, I.; Mijacika, T.; Bailey, D.M.; Santoro, A.; DeMasi, D.K.; Dujic, Z.; et al. Hypercapnia is essential to reduce the cerebral oxidative metabolism during extreme apnea in humans. Journal of Cerebral Blood Flow & Metabolism 2017, 37, 3231–3242. [Google Scholar] [CrossRef]
  4. Cooper, H.E.; Parkes, M.J.; Clutton-Brock, T.H. CO2-dependent components of sinus arrhythmia from the start of breath holding in humans. American Journal of Physiology-Heart and Circulatory Physiology 2003, 285, H841–H848. [Google Scholar] [CrossRef] [PubMed]
  5. Foster, G.E.; Sheel, A.W. The human diving response, its function, and its control. Scandinavian Journal of Medicine & Science in Sports 2005, 15, 3–12. [Google Scholar] [CrossRef]
  6. Dujic, Z.; Breskovic, T. Impact of breath holding on cardiovascular respiratory and cerebrovascular health. Sports Medicine 2012, 42, 459–472. [Google Scholar] [CrossRef] [PubMed]
  7. Skow, R.J.; Day, T.A.; Fuller, J.E.; Bruce, C.D.; Steinback, C.D. The ins and outs of breath holding: simple demonstrations of complex respiratory physiology. Advances in Physiology Education 2015, 39, 223–231. [Google Scholar] [CrossRef]
  8. Bain, A.R.; Drvis, I.; Dujic, Z.; MacLeod, D.B.; Ainslie, P.N. Physiology of static breath holding in elite apneists. Experimental Physiology 2018, 103, 635–651. [Google Scholar] [CrossRef]
  9. Elia, A.; Gennser, M.; Harlow, P.S.; Lees, M.J. Physiology, pathophysiology and (mal)adaptations to chronic apnoeic training: a state-of-the-art review. European Journal of Applied Physiology 2021, 121, 1543–1566. [Google Scholar] [CrossRef]
  10. Jerath, R.; Crawford, M.W.; Barnes, V.A.; Harden, K. Widespread depolarization during expiration: A source of respiratory drive? Medical Hypotheses 2015, 84, 31–37. [Google Scholar] [CrossRef]
  11. Palada, I.; Bakovic, D.; Valic, Z.; Obad, A.; Ivancev, V.; Eterovic, D.; Shoemaker, J.K.; Dujic, Z. Restoration of hemodynamics in apnea struggle phase in association with involuntary breathing movements. Respiratory Physiology & Neurobiology 2008, 161, 174–181. [Google Scholar] [CrossRef]
  12. Willie, C.K.; Ainslie, P.N.; Drvis, I.; MacLeod, D.B.; Bain, A.R.; Madden, D.; Maslov, P.Z.; Dujic, Z. Regulation of Brain Blood Flow and Oxygen Delivery in Elite Breath-Hold Divers. Journal of Cerebral Blood Flow & Metabolism 2015, 35, 66–73. [Google Scholar] [CrossRef]
  13. Cross, T.J.; Kavanagh, J.J.; Breskovic, T.; Zubin Maslov, P.; Lojpur, M.; Johnson, B.D.; Dujic, Z. The Effects of Involuntary Respiratory Contractions on Cerebral Blood Flow during Maximal Apnoea in Trained Divers. PLOS ONE 2013, 8, 1–10. [Google Scholar] [CrossRef] [PubMed]
  14. Joulia, F.; Steinberg, J.G.; Faucher, M.; Jamin, T.; Ulmer, C.; Kipson, N.; Jammes, Y. Breath-hold training of humans reduces oxidative stress and blood acidosis after static and dynamic apnea. Respiratory Physiology & Neurobiology 2003, 137, 19–27. [Google Scholar] [CrossRef]
  15. Trembach, N.; Zabolotskikh, I. Breath-holding test in evaluation of peripheral chemoreflex sensitivity in healthy subjects. Respiratory Physiology & Neurobiology 2017, 235, 79–82. [Google Scholar] [CrossRef]
  16. Trembach, N.; Zabolotskikh, I. The influence of age on interaction between breath-holding test and single-breath carbon dioxide test. Biomed Res. Int. 2017, 2017, 1010289. [Google Scholar] [CrossRef]
  17. Barnai, M.; Laki, I.; Gyurkovits, K.; Angyan, L.; Horvath, G. Relationship between breath-hold time and physical performance in patients with cystic fibrosis. European Journal of Applied Physiology 2005, 95, 172–178. [Google Scholar] [CrossRef]
  18. Yeo, J.; Kim, J.Y.; Kim, M.H.; Park, J.W.; Park, J.K.; Lee, E.B. Utility of the breath-holding test in patients with systemic sclerosis. Rheumatology 2022, 61, 4113–4118. [Google Scholar] [CrossRef]
  19. Li, Y.; Wang, Y. Obstructive Sleep Apnea-hypopnea Syndrome as a Novel Potential Risk for Aging. Aging and Disease 2021, 12, 586–596. [Google Scholar] [CrossRef]
  20. Drager, L.F.; Togeiro, S.M.; Polotsky, V.Y.; Lorenzi-Filho, G. Obstructive Sleep Apnea: A Cardiometabolic Risk in Obesity and the Metabolic Syndrome. Journal of the American College of Cardiology 2013, 62, 569–576. [Google Scholar] [CrossRef]
  21. Athayde, R.A.B.; Oliveira Filho, J.R.B.; Lorenzi Filho, G.; Genta, P.R. Obesity hypoventilation syndrome: a current review. Jornal Brasileiro de Pneumologia 2018, 44. [Google Scholar] [CrossRef] [PubMed]
  22. Messineo, L.; Taranto-Montemurro, L.; Azarbarzin, A.; Oliveira Marques, M.D.; Calianese, N.; White, D.P.; Wellman, A.; Sands, S.A. Breath-holding as a means to estimate the loop gain contribution to obstructive sleep apnoea. The Journal of Physiology 2018, 596, 4043–4056. [Google Scholar] [CrossRef] [PubMed]
  23. Stewart, M.; Bain, A.R. Assessment of respiratory effort with EMG extracted from ECG recordings during prolonged breath holds: Insights into obstructive apnea and extreme physiology. Physiological Reports 2021, 9, e14873. [Google Scholar] [CrossRef] [PubMed]
  24. Ostojić, M.; Milosavljević, M.; Kovačević, A.; Stokić, M.; Stefanović, D.; Mandić-Gajić, G.; Jeličić, L. Changes in power of surface electromyogram during breath-holding. Srpski arhiv za celokupno lekarstvo 2020, 148, 440–446. [Google Scholar] [CrossRef]
  25. Fidalgo-Herrera, A.; Miangolarra-Page, J.; Carratalá-Tejada, M. Electromyographic traces of motor unit synchronization of fatigued lower limb muscles during gait. Human Movement Science 2021, 75, 102750. [Google Scholar] [CrossRef]
  26. Barroso-García, V.; Gutiérrez-Tobal, G.C.; Gozal, D.; Vaquerizo-Villar, F.; Álvarez, D.; del Campo, F.; Kheirandish-Gozal, L.; Hornero, R. Wavelet Analysis of Overnight Airflow to Detect Obstructive Sleep Apnea in Children. Sensors 2021, 21, 1491. [Google Scholar] [CrossRef]
  27. Hermens, H.J.; Freriks, B.; Disselhorst-Klug, C.; Rau, G. Development of recommendations for SEMG sensors and sensor placement procedures. Journal of Electromyography and Kinesiology 2000, 10, 361–374. [Google Scholar] [CrossRef]
  28. Merletti, R.; Muceli, S. Tutorial. Surface EMG detection in space and time: Best practices. Journal of Electromyography and Kinesiology 2019, 49, 102363. [Google Scholar] [CrossRef]
  29. De Luca, C.J.; Kuznetsov, M.; Gilmore, L.D.; Roy, S.H. Inter-electrode spacing of surface EMG sensors: Reduction of crosstalk contamination during voluntary contractions. Journal of Biomechanics 2012, 45, 555–561. [Google Scholar] [CrossRef]
  30. Boyer, M.; Bouyer, L.; Roy, J.S.; Campeau-Lecours, A. Reducing Noise, Artifacts and Interference in Single-Channel EMG Signals: A Review. Sensors 2023, 23, 2927. [Google Scholar] [CrossRef]
  31. Arts, L.P.A.; van den Broek, E.L. The fast continuous wavelet transformation (fCWT) for real-time, high-quality, noise-resistant time–frequency analysis. Nature Computational Science 2022, 2, 47–58. [Google Scholar] [CrossRef] [PubMed]
  32. Mallat, S. A Wavelet Tour of Signal Processing: The Sparse Way, 3rd ed.; Academic Press: Boston, 2009. [Google Scholar]
  33. Percival, D.B.; Walden, A.T. The Maximal Overlap Discrete Wavelet Transform. In Wavelet Methods for Time Series Analysis; Cambridge Series in Statistical and Probabilistic Mathematics; Cambridge University Press, 2000; pp. 159–205. [Google Scholar] [CrossRef]
  34. Rosso, O.; Martin, M.; Figliola, A.; Keller, K.; Plastino, A. EEG analysis using wavelet-based information tools. Journal of Neuroscience Methods 2006, 153, 163–182. [Google Scholar] [CrossRef] [PubMed]
  35. Percival, D.B.; Walden, A.T., The Wavelet Variance. In Wavelet Methods for Time Series Analysis; Cambridge Series in Statistical and Probabilistic Mathematics, Cambridge University Press, 2000; pp. 295–339. [CrossRef]
  36. Lumb, A.B. Chapter 2 - Elastic Forces and Lung Volumes. In Nunn’s Applied Respiratory Physiology, 8th ed.; Lumb, A.B., Ed.; Elsevier, 2017; pp. 17–32. [CrossRef]
  37. McCulloch, P.F.; Gebhart, B.W.; Schroer, J.A. Large Lung Volumes Delay the Onset of the Physiological Breaking Point During Simulated Diving. Frontiers in Physiology 2021, 12. [Google Scholar] [CrossRef]
  38. Rahman, A.; Tabassum, T.; Araf, Y.; Al Nahid, A.; Ullah, M.A.; Hosen, M.J. Silent hypoxia in COVID-19: pathomechanism and possible management strategy. Molecular Biology Reports 2021, 48, 3863–3869. [Google Scholar] [CrossRef]
  39. Kilby, J.; Gholam Hosseini, H. Wavelet analysis of surface electromyography signals. In Proceedings of the The 26th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vol. 1; 2004; pp. 384–387. [Google Scholar] [CrossRef]
  40. ATS/ERS Statement on Respiratory Muscle Testing. American Journal of Respiratory and Critical Care Medicine 2002, 166, 518–624. [CrossRef]
  41. Wakeling, J.M.; Uehli, K.; Rozitis, A.I. Muscle fibre recruitment can respond to the mechanics of the muscle contraction. Journal of The Royal Society Interface 2006, 3, 533–544. [Google Scholar] [CrossRef] [PubMed]
  42. Duiverman, M.; de Boer, E.; van Eykern, L.; de Greef, M.; Jansen, D.; Wempe, J.; Kerstjens, H.; Wijkstra, P. Respiratory muscle activity and dyspnea during exercise in chronic obstructive pulmonary disease. Respiratory Physiology & Neurobiology 2009, 167, 195–200. [Google Scholar] [CrossRef]
  43. Cavalcanti, J.D.; Fregonezi, G.A.F.; Sarmento, A.J.; Bezerra, T.; Gualdi, L.P.; Pennati, F.; Aliverti, A.; Resqueti, V.R. Electrical activity and fatigue of respiratory and locomotor muscles in obstructive respiratory diseases during field walking test. PLoS One 2022, 17, e0266365. [Google Scholar] [CrossRef]
  44. Schiaffino, S.; Reggiani, C. Fiber Types in Mammalian Skeletal Muscles. Physiological Reviews 2011, 91, 1447–1531. [Google Scholar] [CrossRef]
  45. Elia, A.; Wilson, O.J.; Lees, M.; Parker, P.J.; Barlow, M.J.; Cocks, M.; O’Hara, J.P. Skeletal muscle, haematological and splenic volume characteristics of elite breath-hold divers. European Journal of Applied Physiology 2019, 119, 2499–2511. [Google Scholar] [CrossRef]
  46. Wilson, R.J.A.; Day, T.A. CrossTalk opposing view: Peripheral and central chemoreceptors have hypoadditive effects on respiratory motor output. The Journal of Physiology 2013, 591, 4355–4357. [Google Scholar] [CrossRef] [PubMed]
  47. Teppema, L.J.; Smith, C.A. CrossTalk opposing view: Peripheral and central chemoreceptors have hyperadditive effects on respiratory motor control. The Journal of Physiology 2013, 591, 4359–4361. [Google Scholar] [CrossRef] [PubMed]
  48. Di Nardo, F.; Morano, M.; Strazza, A.; Fioretti, S. Muscle Co-Contraction Detection in the Time-Frequency Domain. Sensors 2022, 22, 4886. [Google Scholar] [CrossRef] [PubMed]
  49. Butler, J.E.; McKenzie, D.K.; Gandevia, S.C. Reflex inhibition of human inspiratory muscles in response to contralateral phrenic nerve stimulation. Respiratory Physiology & Neurobiology 2003, 138, 87–96. [Google Scholar] [CrossRef]
  50. Cirino, C.; Marostegan, A.B.; Hartz, C.S.; Moreno, M.A.; Gobatto, C.A.; Manchado-Gobatto, F.B. Effects of Inspiratory Muscle Warm-Up on Physical Exercise: A Systematic Review. Biology 2023, 12, 333. [Google Scholar] [CrossRef]
  51. Manchado-Gobatto, F.B.; Torres, R.S.; Marostegan, A.B.; Rasteiro, F.M.; Hartz, C.S.; Moreno, M.A.; Pinto, A.S.; Gobatto, C.A. Complex Network Model Reveals the Impact of Inspiratory Muscle Pre-Activation on Interactions among Physiological Responses and Muscle Oxygenation during Running and Passive Recovery. Biology 2022, 11, 963. [Google Scholar] [CrossRef]
  52. Daniel, N.; Sybilski, K.; Kaczmarek, W.; Siemiaszko, D.; Małachowski, J. Relationship between EMG and fNIRS during Dynamic Movements. Sensors 2023, 23, 5004. [Google Scholar] [CrossRef]
  53. Gröchenig, K. , MA, 2001; pp. 3–20. https://doi.org/10.1007/978-1-4612-0003-1_2.Analysis. In Foundations of Time-Frequency Analysis; Birkhäuser Boston: Boston, MA, 2001; pp. 3–20. [Google Scholar] [CrossRef]
Preprints 75025 g001
Figure 1. Breathing pattern of BH maneuver. BH began after completion of spontaneous exhalation to functional residual capacity and ended with spontaneous inhalation to normal lung capacity. The T1start/T1stop and T2start/T2stop markers define the beginning/ending of the first and second exhalation BH, respectively (the time markers are displayed on all signal plots, whether in the time or wavelet domain, while their colors correspond to the sensor colors in Figure 2).
Figure 1. Breathing pattern of BH maneuver. BH began after completion of spontaneous exhalation to functional residual capacity and ended with spontaneous inhalation to normal lung capacity. The T1start/T1stop and T2start/T2stop markers define the beginning/ending of the first and second exhalation BH, respectively (the time markers are displayed on all signal plots, whether in the time or wavelet domain, while their colors correspond to the sensor colors in Figure 2).
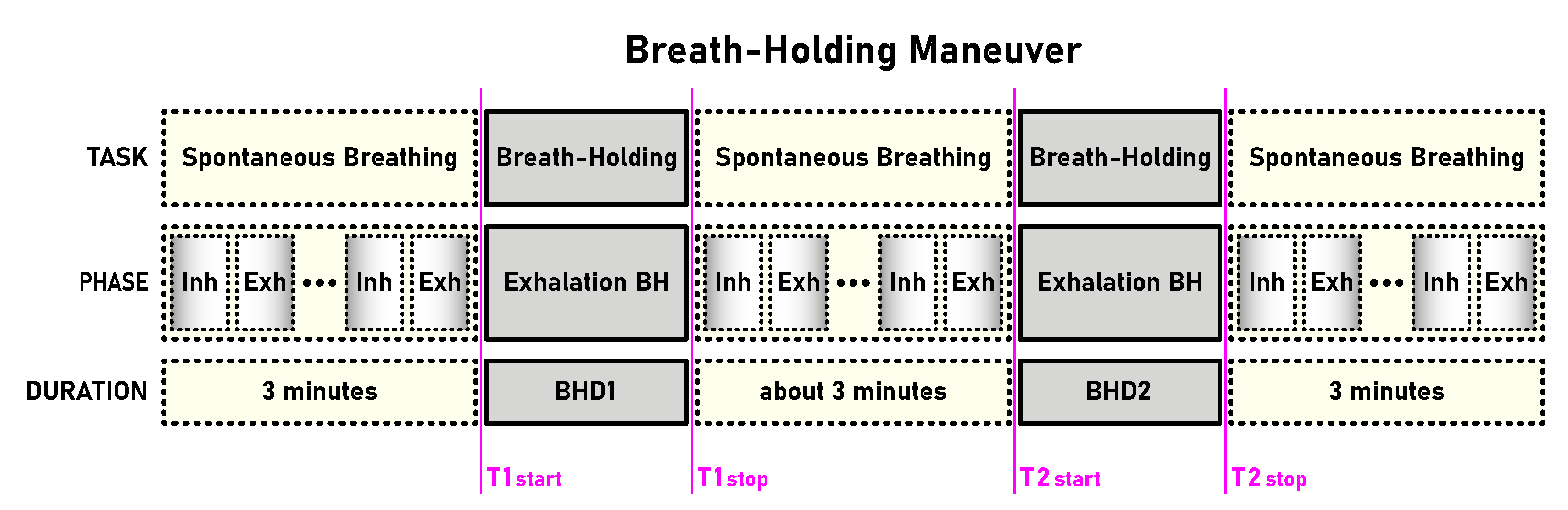
Preprints 75025 g001
Preprints 75025 g002
Figure 2. Placement of Delsys Trigno wireless sensors for unilateral right-sided body data collection of the myoelectric activity for the three respiratory muscles – the accessory inspiratory muscles Scalenus anterior at medium (SC; green), the primary inspiratory muscle Parasternal intercostal (IC; magenta) and the accessory expiratory muscle Rectus abdominis (RA; cyan), as well as for the locomotor muscle Brachioradialis (BR; black). The colors of the sensors correspond to the colors of the time markers (T1start/T1stop and T2start/T2stop, Figure 1) on all signal plots in the time domain.
Figure 2. Placement of Delsys Trigno wireless sensors for unilateral right-sided body data collection of the myoelectric activity for the three respiratory muscles – the accessory inspiratory muscles Scalenus anterior at medium (SC; green), the primary inspiratory muscle Parasternal intercostal (IC; magenta) and the accessory expiratory muscle Rectus abdominis (RA; cyan), as well as for the locomotor muscle Brachioradialis (BR; black). The colors of the sensors correspond to the colors of the time markers (T1start/T1stop and T2start/T2stop, Figure 1) on all signal plots in the time domain.
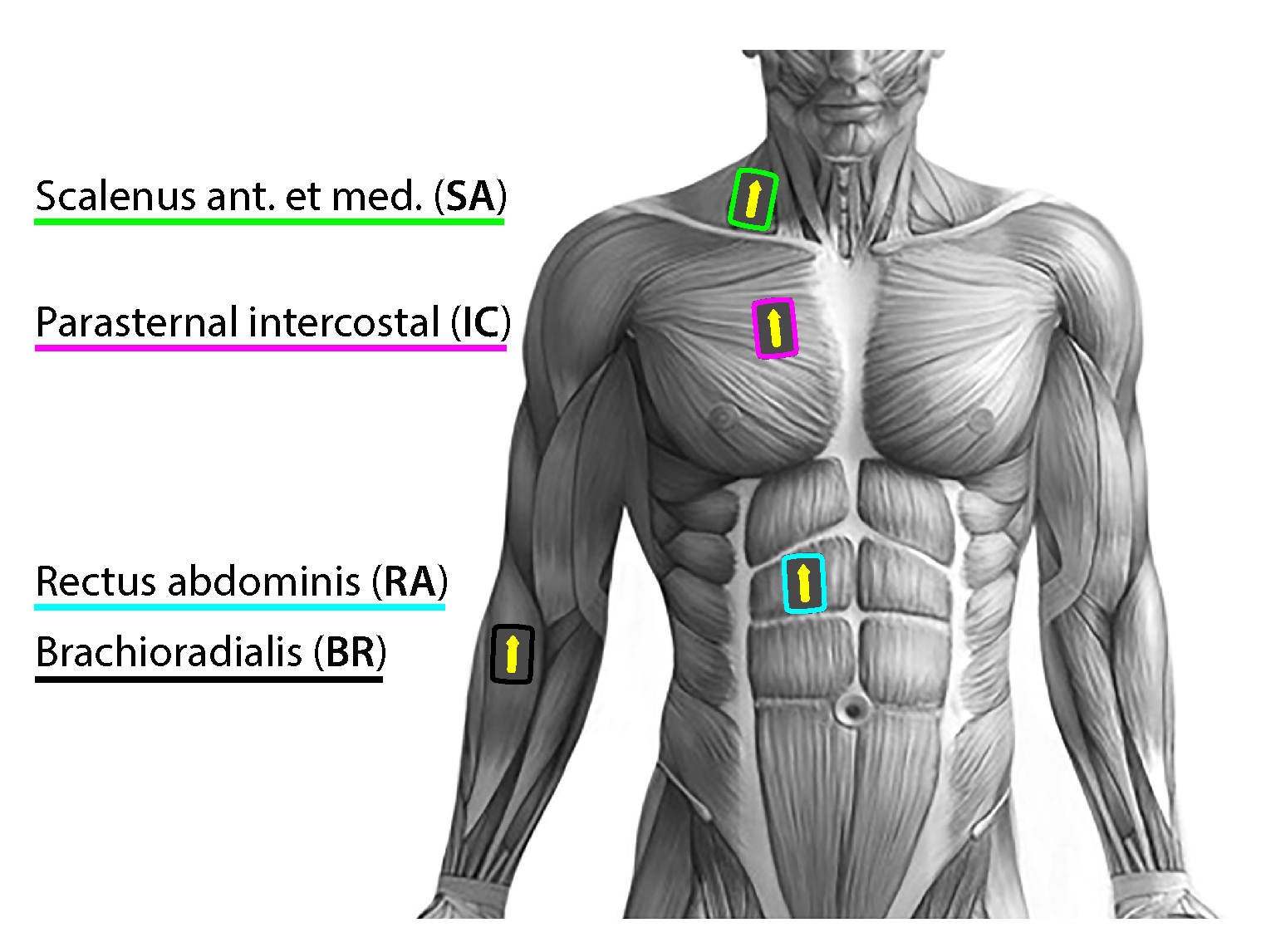
Preprints 75025 g002
Preprints 75025 g003
Figure 3. The equivalence of processing for a discrete-time signal x = { x n } n = 1 N between DWT using wavelet and scaling functions ( { Ψ j } j = 1 5 and Φ 5 ) and the corresponding fDWT using lowpass and highpass filters (L and H). Left: A perfect T-F plane tiling for DWT in dyadic (octave range) configuration, resulting in Heisenberg boxes with the same constant area. With successive downscaling, the wavelet is scaled by 2 − 1 and translated by 2. Right: The corresponding fDWT bandwidth division using the cascade in the form of a tree structure of half-band filters and subsampling by 2 results in filterbank with a constant relative bandwidth. Such filtering followed by sampling at the respective Nyquist frequency f s / 2 gives same wavelet and smooth coefficients ( { D j } j = 1 5 and S 5 ) as for DWT. More detailed explanations in the main text.
Figure 3. The equivalence of processing for a discrete-time signal x = { x n } n = 1 N between DWT using wavelet and scaling functions ( { Ψ j } j = 1 5 and Φ 5 ) and the corresponding fDWT using lowpass and highpass filters (L and H). Left: A perfect T-F plane tiling for DWT in dyadic (octave range) configuration, resulting in Heisenberg boxes with the same constant area. With successive downscaling, the wavelet is scaled by 2 − 1 and translated by 2. Right: The corresponding fDWT bandwidth division using the cascade in the form of a tree structure of half-band filters and subsampling by 2 results in filterbank with a constant relative bandwidth. Such filtering followed by sampling at the respective Nyquist frequency f s / 2 gives same wavelet and smooth coefficients ( { D j } j = 1 5 and S 5 ) as for DWT. More detailed explanations in the main text.
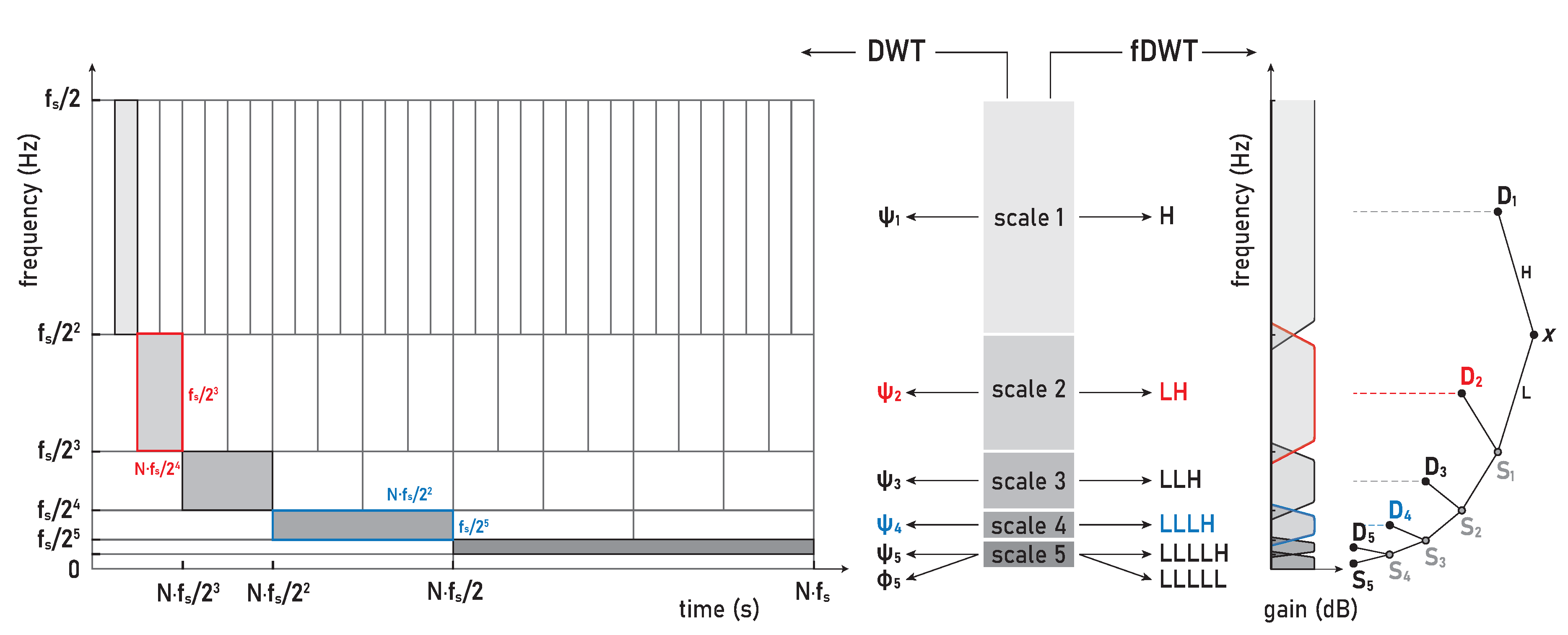
Preprints 75025 g003
Preprints 75025 g004
Figure 4. Time series of sEMG signals for three respiratory muscles, EMGSC, EMGIC, and EMGRA, and one non-respiratory muscle, EMGBR, respectively from top to bottom, given for a representative apneist BHr3(BHD rank #1; Table 1). The first and second BH phases (BH1 and BH2) are marked with time markers (T1start/T1stop and T2start/T2stop, Figure 1) and colored rectangles, while their colors correspond to the sensor colors in Figure 2. In the final stages of BH, a gradual increase in the magnitudes of EMGSC, and especially EMGIC, is noticeable in both BH1 and BH2 periods.
Figure 4. Time series of sEMG signals for three respiratory muscles, EMGSC, EMGIC, and EMGRA, and one non-respiratory muscle, EMGBR, respectively from top to bottom, given for a representative apneist BHr3(BHD rank #1; Table 1). The first and second BH phases (BH1 and BH2) are marked with time markers (T1start/T1stop and T2start/T2stop, Figure 1) and colored rectangles, while their colors correspond to the sensor colors in Figure 2. In the final stages of BH, a gradual increase in the magnitudes of EMGSC, and especially EMGIC, is noticeable in both BH1 and BH2 periods.
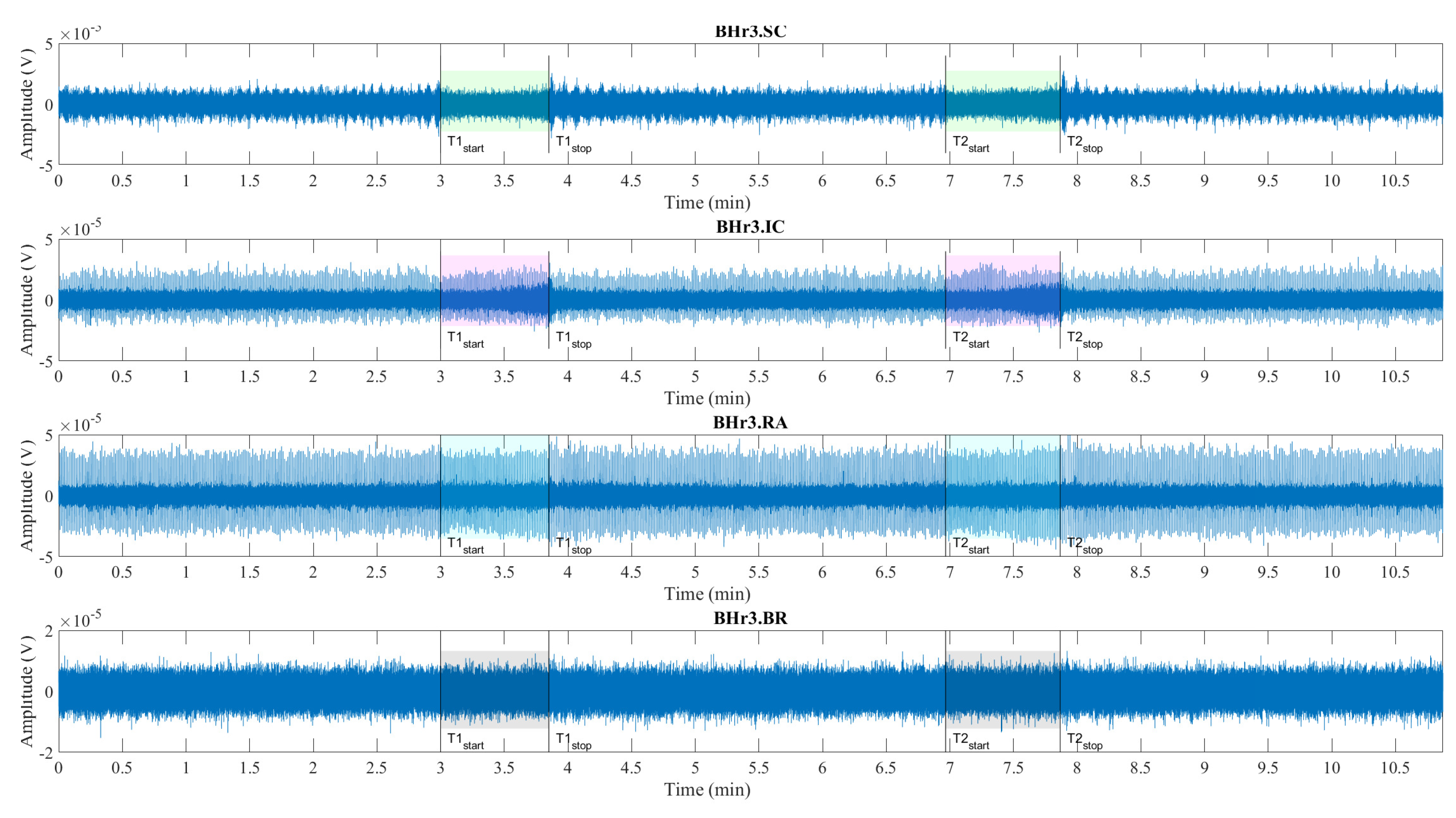
Preprints 75025 g004
Preprints 75025 g005
Figure 5. Time series of EMGSC, EMGIC, and EMGRA, and EMGBR, respectively from top to bottom, given for a representative apneist BHr4 (BHD rank #1, highest BHD score; Table 1). Other descriptive notes as in the caption for Figure 4. In contrast to BHr3, limited or no changes were observed in EMGSC and EMGIC, however abrupt changes in EMGRA magnitudes are present in the final stages of BH2, indicating a different BH response mechanism.
Figure 5. Time series of EMGSC, EMGIC, and EMGRA, and EMGBR, respectively from top to bottom, given for a representative apneist BHr4 (BHD rank #1, highest BHD score; Table 1). Other descriptive notes as in the caption for Figure 4. In contrast to BHr3, limited or no changes were observed in EMGSC and EMGIC, however abrupt changes in EMGRA magnitudes are present in the final stages of BH2, indicating a different BH response mechanism.
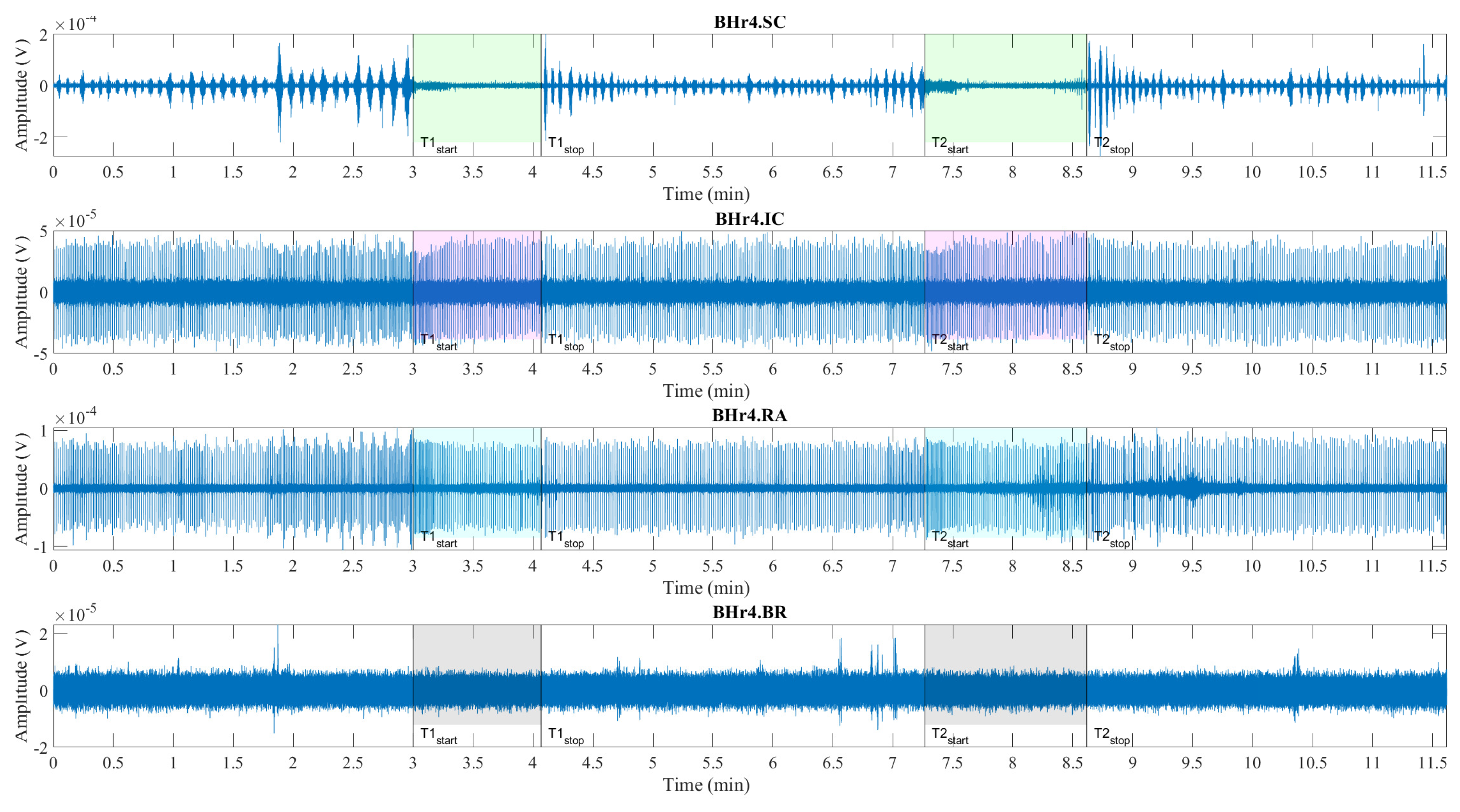
Preprints 75025 g005
Preprints 75025 g006
Figure 6. Comparison of the occupied bandwidth (OBW) estimates (the width of the frequency band that contains 99% of the power of the signal, the lower and upper bounds of the band and the power in the band), of the muscle sEMG signals in the initial and final phase of breath-holding (during BH1 and BH2). The lower bounds are about 7 Hz, as the consequence of an AC-coupling filtering with 7 Hz highpass filter that strongly attenuates lower frequencies in the sEMG signals. As a consequence, the upper bounds are similar to the occupied bandwidth. The increase in occupied bandwidth is most pronounced for IC, followed by SC. The occupied band power is the highest for RA and the lowest for BR, which indicates that it is necessary to normalize the power in order to be able to compare the change of the initial and final BH phase for different muscles.
Figure 6. Comparison of the occupied bandwidth (OBW) estimates (the width of the frequency band that contains 99% of the power of the signal, the lower and upper bounds of the band and the power in the band), of the muscle sEMG signals in the initial and final phase of breath-holding (during BH1 and BH2). The lower bounds are about 7 Hz, as the consequence of an AC-coupling filtering with 7 Hz highpass filter that strongly attenuates lower frequencies in the sEMG signals. As a consequence, the upper bounds are similar to the occupied bandwidth. The increase in occupied bandwidth is most pronounced for IC, followed by SC. The occupied band power is the highest for RA and the lowest for BR, which indicates that it is necessary to normalize the power in order to be able to compare the change of the initial and final BH phase for different muscles.
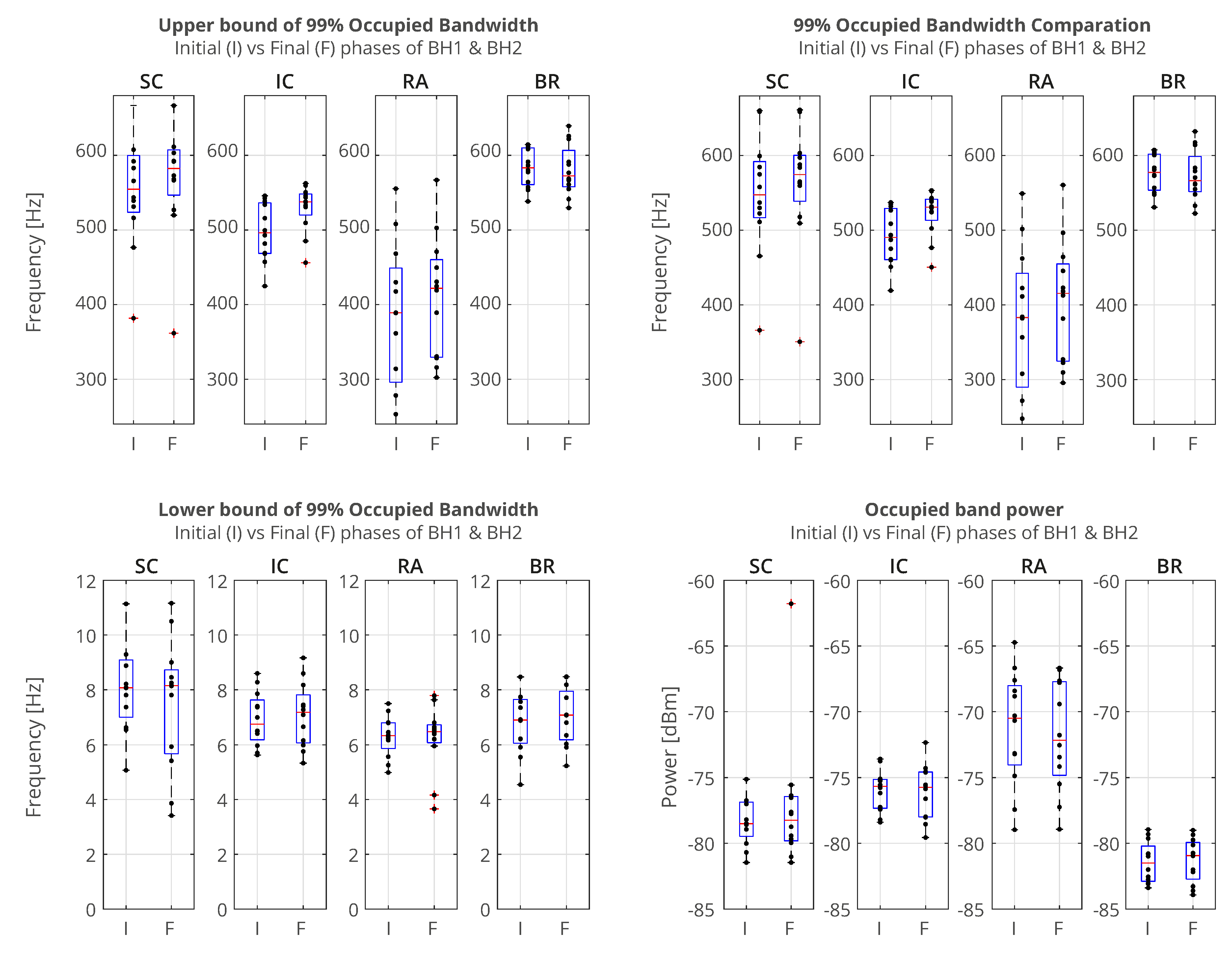
Preprints 75025 g006
Preprints 75025 g007
Figure 7. Scalograms of all four sEMG signals given for a representative apneist BHr3 (BHD rank #1) (description of signals and time markers are the same as in Figure 4). Two specific frequency bands are observed: the first, for EMGIC and EMGRA in the approximate frequency band (FB) of 9-30 Hz, which normally corresponds to cardiac activity (the QRS wave), and the second, for EMGSC and EMGIC in the approximate FB of 120-480 Hz (D3/HFB & D2/VHFB), which occurred in the final stage of BH and is related to the physiological breakpoint.
Figure 7. Scalograms of all four sEMG signals given for a representative apneist BHr3 (BHD rank #1) (description of signals and time markers are the same as in Figure 4). Two specific frequency bands are observed: the first, for EMGIC and EMGRA in the approximate frequency band (FB) of 9-30 Hz, which normally corresponds to cardiac activity (the QRS wave), and the second, for EMGSC and EMGIC in the approximate FB of 120-480 Hz (D3/HFB & D2/VHFB), which occurred in the final stage of BH and is related to the physiological breakpoint.
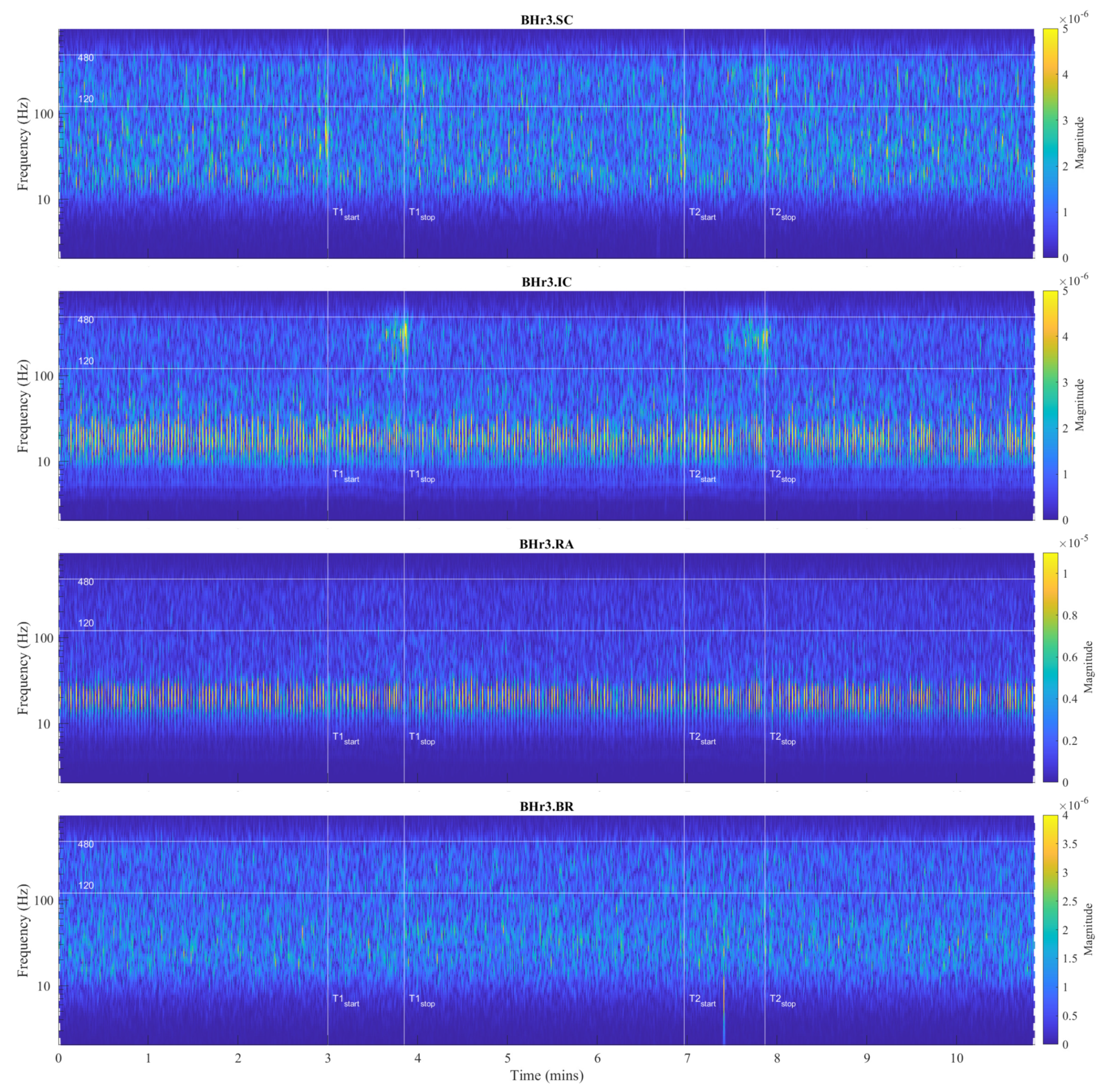
Preprints 75025 g007
Preprints 75025 g008
Figure 8. Scalograms of all four sEMG signals given for a representative apneist BHr4 (BHD rank #1, highest BHD score) (description of signals and time markers are given in Figure 5). Similar to BHr3 (Figure 7), the same frequency range is observed for EMGIC and EMGRA related to cardiac activity. But in contrast to BHr3, limited or no changes were observed in EMGSC and EMGIC, however abrupt changes in EMGRA in FB of 80-300 Hz (dominantly in D4/MFB & D3/HFB) during the final stages of BH2, indicating a different BH response mechanism (compare with the caption on Figure 5).
Figure 8. Scalograms of all four sEMG signals given for a representative apneist BHr4 (BHD rank #1, highest BHD score) (description of signals and time markers are given in Figure 5). Similar to BHr3 (Figure 7), the same frequency range is observed for EMGIC and EMGRA related to cardiac activity. But in contrast to BHr3, limited or no changes were observed in EMGSC and EMGIC, however abrupt changes in EMGRA in FB of 80-300 Hz (dominantly in D4/MFB & D3/HFB) during the final stages of BH2, indicating a different BH response mechanism (compare with the caption on Figure 5).
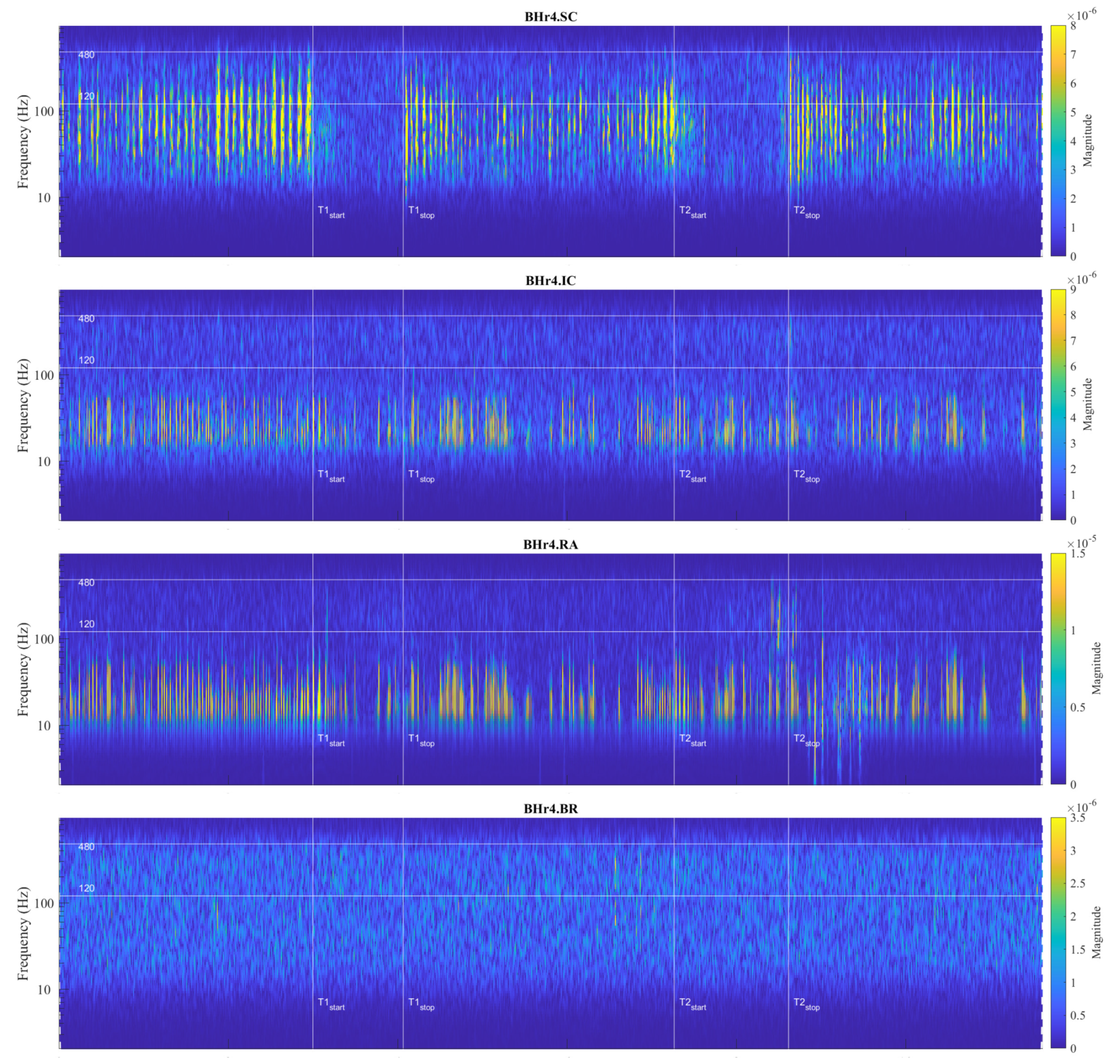
Preprints 75025 g008
Preprints 75025 g009
Figure 9. Correlations of neuromuscular coupling for inspiratory muscles SC and IC were demonstrated by comparing scalograms for EMGSC and EMGIC of naive apneist BHr12 (BHD rank #3). Correlation of areas of high energy density for EMGSC and EMGIC in the T-F plane are characteristic for the approximate FB of 120-480 Hz. This is the same FB for the increased energy density of the BH final stages for EMGIC in both BHr12 and BHr3, as shown in Figure 7, indicating that this FB is characteristic of increased IC electromyographic activity regardless of the primary stimulus.
Figure 9. Correlations of neuromuscular coupling for inspiratory muscles SC and IC were demonstrated by comparing scalograms for EMGSC and EMGIC of naive apneist BHr12 (BHD rank #3). Correlation of areas of high energy density for EMGSC and EMGIC in the T-F plane are characteristic for the approximate FB of 120-480 Hz. This is the same FB for the increased energy density of the BH final stages for EMGIC in both BHr12 and BHr3, as shown in Figure 7, indicating that this FB is characteristic of increased IC electromyographic activity regardless of the primary stimulus.
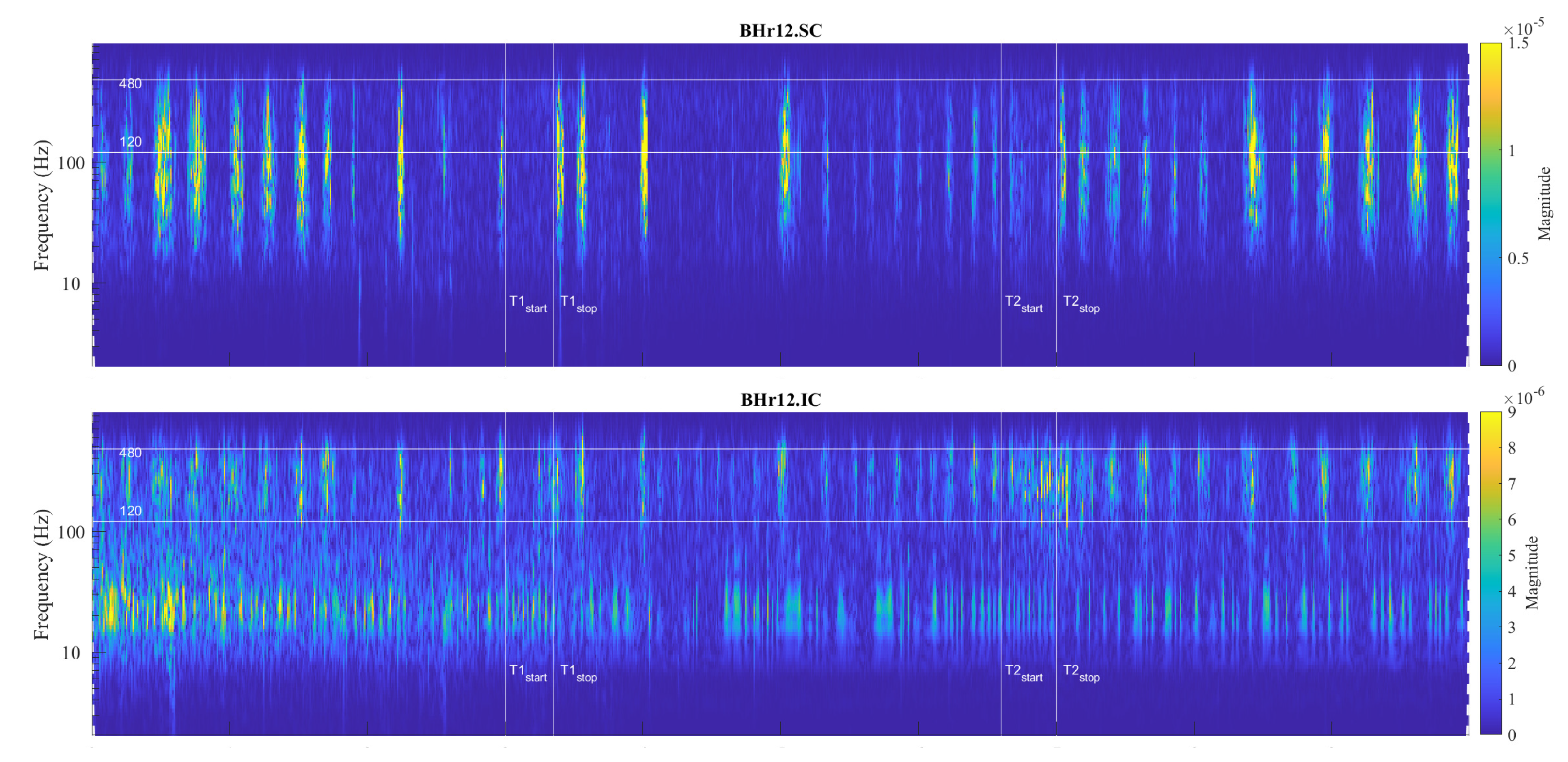
Preprints 75025 g009
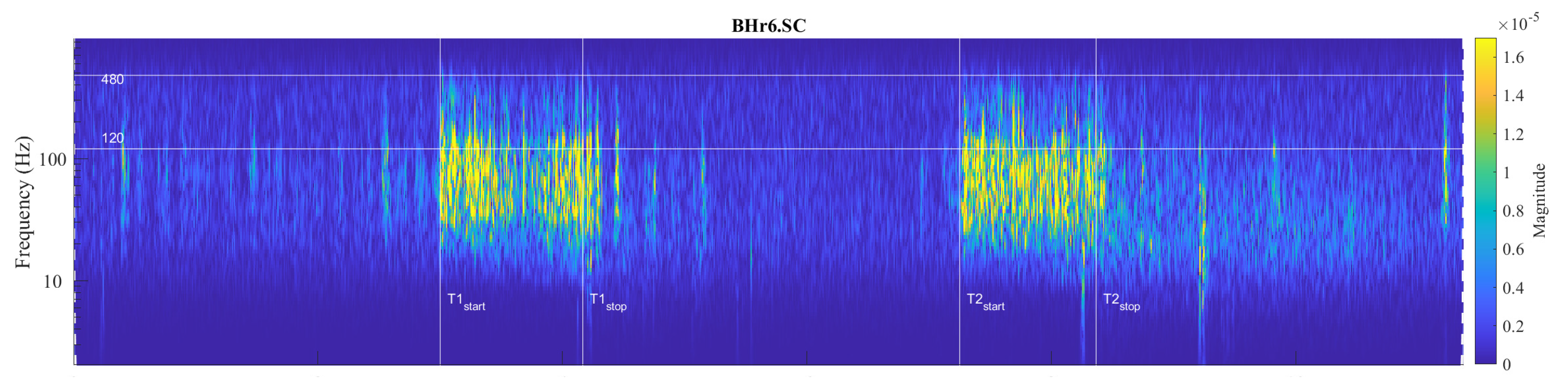
Preprints 75025 g010
Figure 10. Individual specificities of neuromuscular coupling in participants for SC were demonstrated by comparing the scalograms for EMGSC of apneist BHr6 (BHD rank #1) with BHr4 (BHD rank #1, presented in Figure 8). During the BH maneuver, participant BHr4 (rower) showed higher SC activity during spontaneous breathing (areas of high energy density for EMGSC in the T-F plane are related to inspiration), while BHr6 (diver) showed greater SC activity during breath-holding.
Figure 10. Individual specificities of neuromuscular coupling in participants for SC were demonstrated by comparing the scalograms for EMGSC of apneist BHr6 (BHD rank #1) with BHr4 (BHD rank #1, presented in Figure 8). During the BH maneuver, participant BHr4 (rower) showed higher SC activity during spontaneous breathing (areas of high energy density for EMGSC in the T-F plane are related to inspiration), while BHr6 (diver) showed greater SC activity during breath-holding.
Preprints 75025 g010
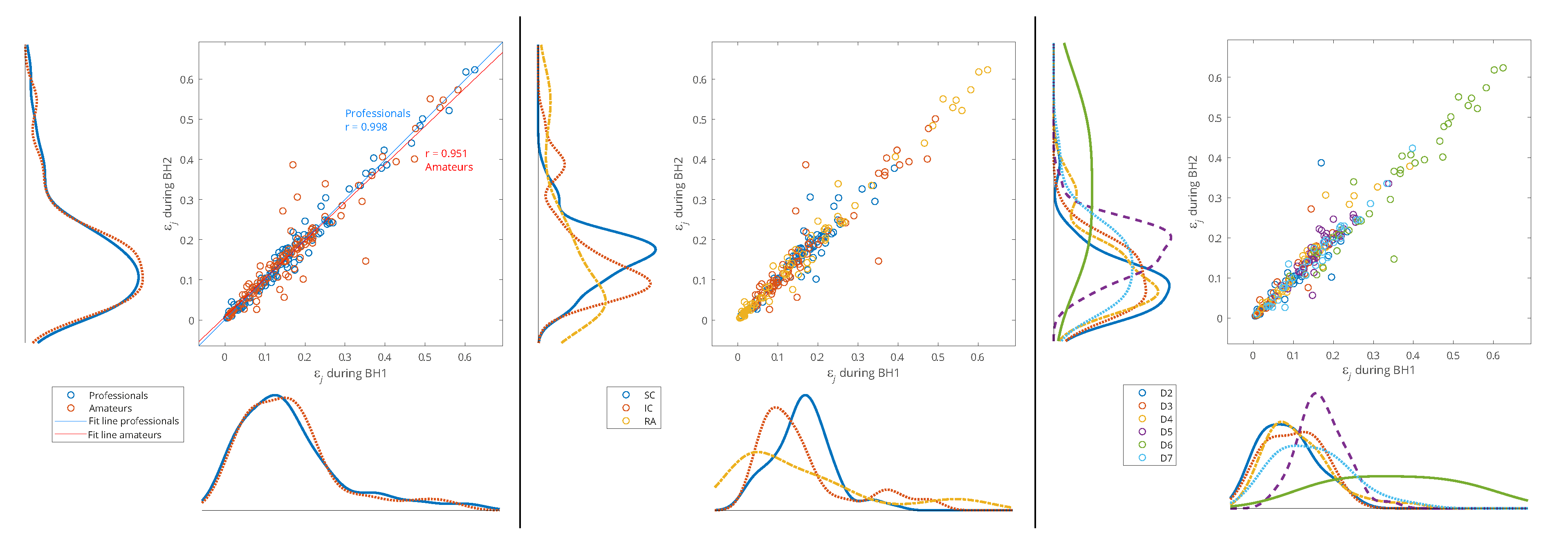
Preprints 75025 g011
Figure 11. Joint distribution of relative energies of WMRA components of respiratory signals EMGSC, EMGIC and EMGRA of all participants for three types of data grouping: professional/amateur (left), respiratory signal type (middle), and MRA components (right). The distributions were determined using a probability density estimate based on a normal kernel function.
Figure 11. Joint distribution of relative energies of WMRA components of respiratory signals EMGSC, EMGIC and EMGRA of all participants for three types of data grouping: professional/amateur (left), respiratory signal type (middle), and MRA components (right). The distributions were determined using a probability density estimate based on a normal kernel function.
Preprints 75025 g011
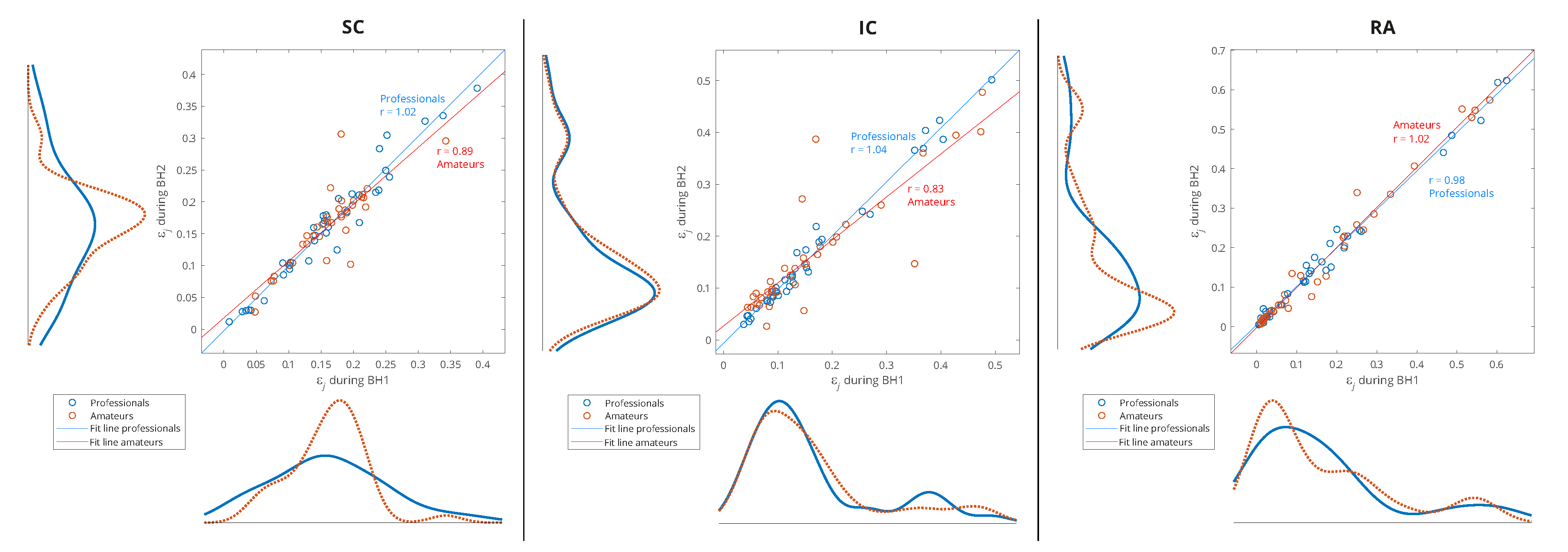
Preprints 75025 g012
Figure 12. Separated distributions of relative energies of WMRA components of respiratory signals EMGSC, EMGIC and EMGRA of all participants for professional/amateur grouping. A comparison of the distribution curves for professionals and amateurs shows that they most closely match for IC.
Figure 12. Separated distributions of relative energies of WMRA components of respiratory signals EMGSC, EMGIC and EMGRA of all participants for professional/amateur grouping. A comparison of the distribution curves for professionals and amateurs shows that they most closely match for IC.
Preprints 75025 g012
Preprints 75025 g013
Figure 13. Wavelet MRA components of EMGIC for BHr3 (above) and their centered moving variances (below). The moving window has a time interval of 1.5 seconds – approximately 2 times the cardiac interbeat (RR) interval. BHD of BHr3 was 52 seconds in average, while energy increase started around middle of BH period and lasted till the end, in total 27 seconds. Greyed-out areas correspond to frequency bands with highest relative energy change.
Figure 13. Wavelet MRA components of EMGIC for BHr3 (above) and their centered moving variances (below). The moving window has a time interval of 1.5 seconds – approximately 2 times the cardiac interbeat (RR) interval. BHD of BHr3 was 52 seconds in average, while energy increase started around middle of BH period and lasted till the end, in total 27 seconds. Greyed-out areas correspond to frequency bands with highest relative energy change.
Preprints 75025 g013
Preprints 75025 g014
Figure 14. Changes of relative energy across the scales related to IBM between the Initial and Final stages calculated for both BH1 and BH2 periods is most pronounced for IC.
Figure 14. Changes of relative energy across the scales related to IBM between the Initial and Final stages calculated for both BH1 and BH2 periods is most pronounced for IC.
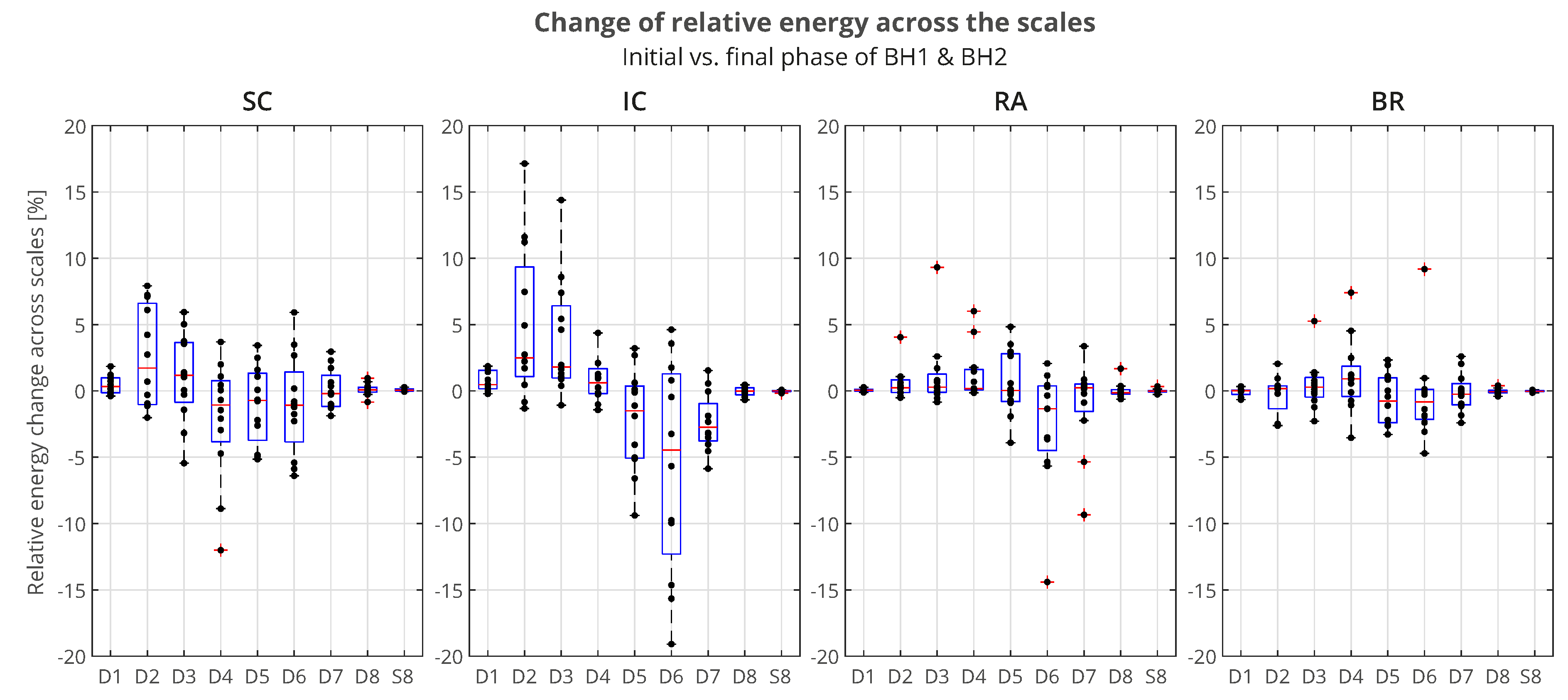
Preprints 75025 g014
Table 1. Sports-related, demographic and anthropometric data of naive breath-holders (BHr), together with their resulting breath-hold duration (BHD) during the first and second voluntary apnea (BHD1 and BHD2). All data are classified into professional and amateur groups according to sport discipline/activity, and given through individual values, mean values and standard deviations, both for groups and for all participants in total.
Table 1. Sports-related, demographic and anthropometric data of naive breath-holders (BHr), together with their resulting breath-hold duration (BHD) during the first and second voluntary apnea (BHD1 and BHD2). All data are classified into professional and amateur groups according to sport discipline/activity, and given through individual values, mean values and standard deviations, both for groups and for all participants in total.
Age Height Weight BMI BHD1 BHD2
Sports Participation Sport/Activity Gender (years) (cm) (kg) ( kg / m 2 ) (min:sec) (min:sec)
BHr1 Professional Swimming Female 20.9 168 63 22.3 0:24 0:27
BHr2 Professional Rowing Female 29.4 180 75 23.2 0:31 0:28
BHr3 Professional Rowing Male 30.5 195 92 24.2 0:51 0:53
BHr4 Professional Rowing Male 26.9 197 90 23.2 1:04 1:21
BHr5 Professional Athletics Male 25.1 192 85 23.1 0:57 0:52
BHr6 Professional Scuba diving Male 27.2 186 80 23.1 1:10 1:06
MEAN 26.7 186.3 80.8 23.2 0:49 0:51
PROFESSIONALS SD 3.1 10.0 9.8 0.5 0:17 0:19
BHr7 Amateur Volleyball Male 20.6 204 95 22.8 0:27 0:29
BHr8 Amateur Jujutsu Male 36.7 185 76 22.2 0:43 0:52
BHr9 Amateur Jujutsu Male 19.2 178 69 21.8 0:34 0:37
BHr10 Amateur Jujutsu Male 44.9 180 80 24.7 0:40 0:57
BHr11 Amateur Jujutsu Male 40.1 180 82 25.3 0:36 0:49
BHr12 Amateur Yoga Male 45.0 197 93 24.0 0:21 0:24
MEAN 34.4 187.3 82.5 23.5 0:33 0:41
AMATEURS SD 11.7 10.7 10.0 1.4 0:08 0:12
MEAN 30.5 186.8 81.7 23.3 0:41 0:45
TOTAL SD 9.1 10.3 9.9 1.0 0:12 0:14
Table 2. Changes of relative energy across the scales △ P ( ε ) between the BH Final and Initial stages (left) and corresponding average values per scale for the total population and grouped by ranks (right). Scales with a significant positive change are displayed in boldface, and with negative change are italic (all values are expressed in percentages). Gradual highlighting from negative (blue) to positive (red) values is performed at the level of one muscle. Average values show the largest energy increase for D2 and D3 scales of EMGIC and EMGSC regardless of the rank, as well as D3, D4 and D5 scales of EMGRA, but only for the rank #1 group.
Table 2. Changes of relative energy across the scales △ P ( ε ) between the BH Final and Initial stages (left) and corresponding average values per scale for the total population and grouped by ranks (right). Scales with a significant positive change are displayed in boldface, and with negative change are italic (all values are expressed in percentages). Gradual highlighting from negative (blue) to positive (red) values is performed at the level of one muscle. Average values show the largest energy increase for D2 and D3 scales of EMGIC and EMGSC regardless of the rank, as well as D3, D4 and D5 scales of EMGRA, but only for the rank #1 group.
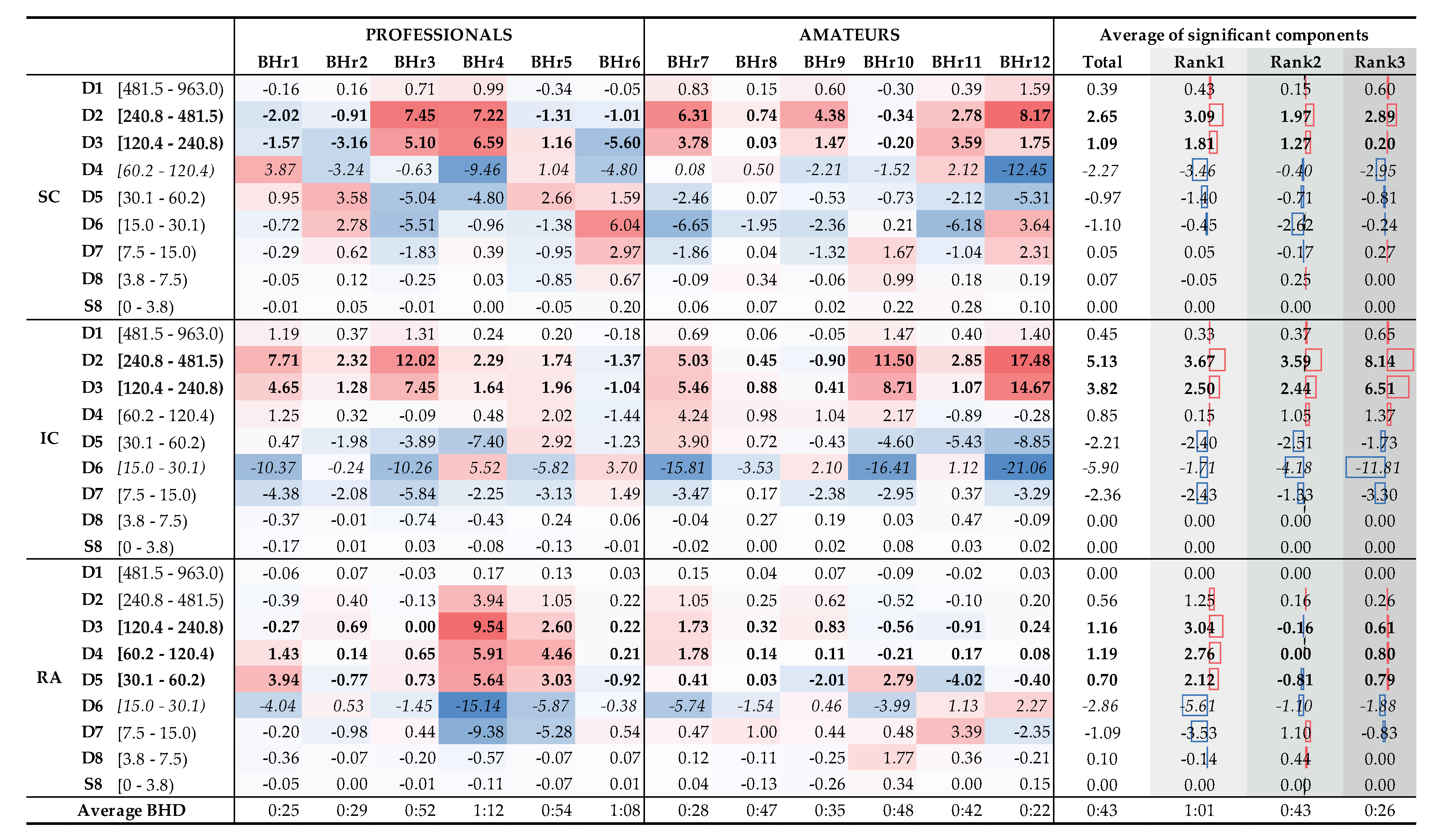
Preprints 75025 i001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated