Prerpints.org logo
Preprint
Review

A Review of Machine Vision Pose Measurement

Altmetrics

Downloads

218

Views

108

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

29 May 2023

Posted:

31 May 2023

You are already at the latest version

Alerts
Abstract
This review paper provides a comprehensive overview of machine vision pose measurement algorithms. The paper focuses on the state-of-the-art algorithms and their applications. The paper is structured as follows: The introduction in Section 1 provides a brief overview of the field of machine vision pose measurement. Section 2 describes the commonly used algorithms for machine vision pose measurement. Section 3 discusses the factors that affect the accuracy and reliability of machine vision pose measurement algorithms. Section 4 presents the applications of machine vision pose measurement in various fields. The paper provides specific examples of how machine vision pose measurement is used in each of these fields. Finally, Section 5 summarizes the paper and provides future research directions. The paper highlights the need for more robust and accurate algorithms that can handle varying lighting conditions and occlusion. It also suggests that the integration of machine learning techniques may improve the performance of machine vision pose measurement algorithms. Overall, this review paper provides a comprehensive overview of machine vision pose measurement algorithms, their applications, and the factors that affect their accuracy and reliability. It provides a valuable resource for researchers and practitioners working in the field of computer vision.
Keywords: 
Subject: Computer Science and Mathematics  -   Analysis

1. Introduction

Pose measurement is a technique used to determine the position and orientation of an object in three-dimensional space [1]. Traditional methods of pose measurement involve the use of sensors, but they suffer from low precision, high cost, and poor real-time performance, which make it difficult to meet the current demands for high precision, low cost, and real-time performance in the industrial and technological sectors [2]. To address these issues, researchers have turned to computer vision technology and introduced the concept of visual pose measurement [3].
Visual pose measurement is a method that uses computer vision technology to perform pose measurement, typically employing a camera as a sensor [4]. The target object's position and direction are determined by capturing scene images and performing image processing and calculations. Compared to traditional methods, visual pose measurement offers advantages such as non-contact operation, high precision, high speed, and low cost [5]. It is widely used in fields such as robotics [6], autonomous driving [7], virtual reality [8], and aerospace [9].
The research focus in visual pose measurement includes the development of accurate scene models [10], robust image processing and matching algorithms [11], and real-time pose measurement [12]. Building an accurate scene model is a significant challenge since it serves as the foundation for matching real images with theoretical models and extracting pose information [10]. Maintaining high-precision pose measurements in the presence of interference from motion blur, illumination changes, and noise is another significant challenge [13]. To address these issues, visual pose measurement researchers are working to improve the algorithm's accuracy and stability, develop new image processing and matching algorithms, and enhance the system's real-time and robustness.
To build an accurate scene model, visual pose measurement researchers use a variety of techniques and methods, such as structured light [14] and lidar sensors [15] to obtain scene information and combine it with camera images. Additionally, 3D reconstruction techniques, such as stereo matching using multiple images [16] or semantic segmentation [17] and 3D reconstruction using deep learning models [18], can be used to generate scene models.
In response to factors such as illumination changes, researchers have developed a variety of image processing and matching algorithms based on features such as color [19], texture [20], and shape [21]. Multiple images captured under different lighting conditions can be used to reconstruct the target object in 3D [22], thereby reducing the impact of illumination changes on pose measurement. To reduce the effects of motion blur, researchers have proposed pose estimation algorithms based on motion models [23] and filtering methods such as the Kalman filter [24], particle filter [25], and extended Kalman filter [26]. The multi-target tracking algorithm [26] can be used to track and estimate the pose of moving objects, improving the accuracy and stability of pose measurement.
To improve the real-time and robustness of the system, researchers have adopted various hardware and software technologies [27], such as high-speed cameras [27], parallel computing [28], GPUs [29], deep learning [30], and neural networks [31], to optimize the pose measurement algorithm and accelerate the calculation speed of image processing and pose estimation algorithms.
In conclusion, the field of visual pose measurement has made significant progress in addressing challenges such as illumination changes [32], motion blur [33], and noise [34]. The accuracy, speed, and stability of the visual pose measurement algorithm will continue to improve as computer vision technology advances, further advancing the promotion and development of visual pose measurement in practical applications.

2. The Commonly used machine vision pose measurement algorithms

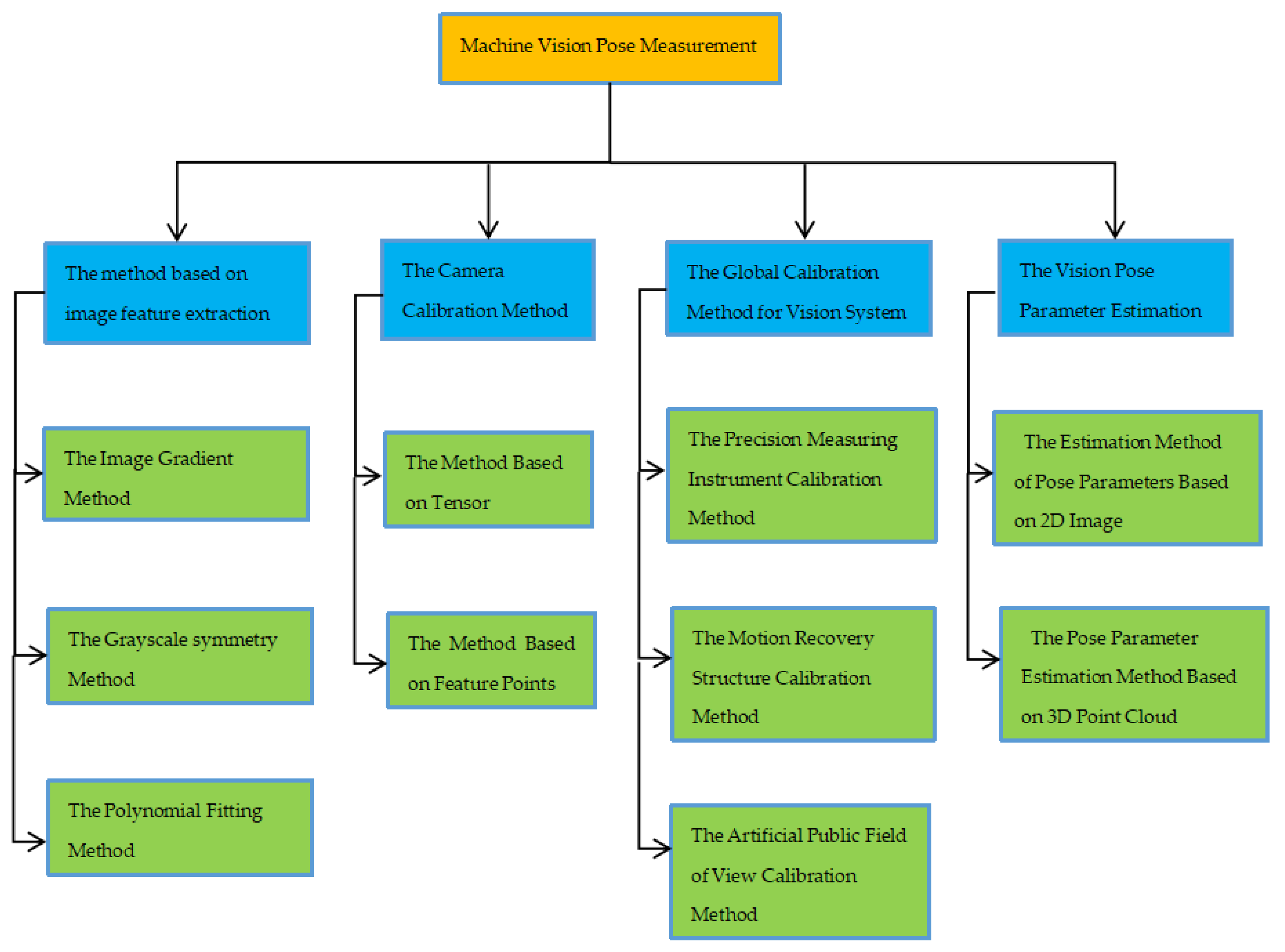
This paper presents a detailed algorithm for machine vision pose measurement, as shown in Figure 1. It encompasses four main aspects: image feature extraction method, camera calibration method, vision system global calibration method, and visual pose parameter estimation. Each category contains commonly used algorithms that are further introduced and explained in this article.

2.1. The method based on image feature extraction

Image feature extraction is a critical step in machine vision pose measurement, as it involves identifying and extracting key points, lines, surfaces, and other features from an image to enable object recognition and pose estimation [35]. Commonly used image features in machine vision include edges, corners, SIFT features, SURF features, ORB features, and more. These features are often invariant, repeatable, and discriminative, making them ideal for matching and identification. Table 1 is an introduction to the advantages and disadvantages of these commonly used methods.
In feature-based pose estimation, feature points of the target object are extracted from the input image, and the pose of the object is calculated by matching these feature points with the corresponding points in the target model. Matching methods like nearest neighbor matching, nearest neighbor distance ratio matching, and RANSAC are commonly used, but the accuracy and robustness of matching can be affected by noise, occlusion, deformation, and other factors, which must be addressed for optimal performance [36].
Deep learning-based image feature extraction methods, such as those based on convolutional neural networks (CNNs), can also be used to improve the accuracy of object recognition and pose estimation. These methods learn feature expressions from input images through deep learning, leading to more accurate and effective pose estimation [37].

2.1.1. The Image Gradient Method

The image gradient method is a widely used method for pose estimation in machine vision [38]. This method calculates the pose of an object by using the gray value change rate at the edge of the object in the image. To use this method, the image needs to be processed first to extract the edge information, which is then used to calculate the pose of the object. The first-order derivative and second-order derivative information of the image are used to calculate the pose of the object, which correspond to the gray-scale gradient and gray-scale Laplacian of the image, respectively [38]. The commonly used image gradient methods include the Canny operator, Sobel operator, Prewitt operator, and more, which can smooth the image to different degrees to reduce the influence of noise, calculate the gradient value and direction information of each pixel in the image, and finally determine the pose of the object through statistical analysis of the gradient information [39]. However, this method has high requirements on image quality and continuity of the edges of objects in the image. Additionally, since the image gradient method can only calculate the pose of the object, but cannot determine its position, it usually needs to be used in combination with other methods [40].
Sroba, et al. [41] presents a corner sub-pixel extraction method that utilizes image gradients. This method exploits the characteristic that the vector pointing to any nearby pixel from a corner point is perpendicular to the gradient direction between the corner point and the pixel point. It selects the neighborhood of the pixel-level corner point as the region of interest and employs a series of mathematical processing methods and optimization techniques to iteratively obtain the sub-pixel localization of the corners. In the iterative process, the sub-pixel positioning coordinates of the corner points obtained in the previous operation are used as the center of the region of interest in the next operation. The iteration stops when the center coordinates converge and remain within the preset range. Bok, et al. [42] proposes a sub-pixel corner extraction method based on the Harris operator. The method starts iterative calculation from a given initial corner position, and uses the structural tensor principle of block sampling for optimization. The goal of the method is to obtain the location of the maximum gradient value and locate the sub-pixel corners. The method adopts direct gradient interpolation, which significantly improves the calculation efficiency compared with the traditional method that performs image interpolation first and then performs gradient calculation.

2.1.2. The Grayscale symmetry Method

Gray-scale symmetry is a widely used pose measurement method in industrial manufacturing processes, which uses image gray-scale information to calculate the pose information of objects with high precision, robustness, and adaptability [50]. The method involves obtaining the grayscale image of the target object and using image processing techniques to extract the grayscale symmetry line on its surface. The grayscale symmetry line is a line on the object surface where the gray-scale values on both sides are equal or nearly equal. By using the properties of the grayscale symmetry line, the position and rotation angle of the object on the plane can be determined, and its pose information can be obtained [51].
In previous studies, researchers have proposed various methods to improve the accuracy and robustness of the grayscale symmetry algorithm [52,53]. Moreover, the grayscale symmetry method has been combined with other techniques, such as stereo vision[54] and contour features [55], to further enhance its performance in pose estimation. Zhao, et al. [56] employs a method that directly utilizes the grayscale symmetry of the area surrounding corners for sub-pixel localization. As the center of the square pixel block approaches the corner, the gray symmetry increases. Therefore, the algorithm defines a region of interest with a fixed window radius around the pixel-level corner. Within this region, a square pixel block is extracted with each pixel as the center, and its gray-scale symmetry degree is calculated as the gray-scale symmetry factor. By using the gray symmetry factors of all pixels as weights, the coordinates are then weighted to obtain the sub-pixel positioning coordinates of the corner points.
The gray-scale symmetry method has been widely studied and applied in the field of industrial manufacturing due to its high precision, robustness, and adaptability. Moreover, the gray-scale symmetry method can be combined with other pose measurement methods, such as the point cloud registration method [57] and the structured light method [58], to improve the accuracy and reliability of the pose measurement.

2.1.3. The Polynomial Fitting Method

The polynomial fitting method is a widely used approach for attitude measurement, which involves fitting the attitude angle curve to obtain the object's attitude information [59]. The basic principle of the polynomial fitting method is to collect the object's attitude angle data during its movement, fit it into a polynomial function, and then solve for the object's attitude information. In practice, quadratic or cubic polynomials are typically used since they can better approximate the real attitude angle curve. The polynomial fitting method offers several advantages, including high precision and reliability, and its applicability to various object attitude measurement problems. Moreover, since the polynomial fitting method only requires fitting the attitude angle curve, it has a small calculation amount and operates at high speeds. However, this method also has some disadvantages, such as the need for high-quality attitude angle curve data, and the potential for overfitting or underfitting in some cases [60].
One of the advantages of the polynomial fitting method is its high precision and reliability. This method has been applied successfully in various attitude measurement problems, such as the control of a quadrotor UAV [61], the measurement of satellite attitude [62], and the estimation of vehicle dynamics [63]. Another advantage of this method is its high computational efficiency since only fitting the attitude angle curve is required. As a result, this method is suitable for real-time applications that require a fast response.
However, the polynomial fitting method also has some limitations. One major limitation is the requirement for high-quality attitude angle curve data. The accuracy of the attitude estimation heavily relies on the accuracy and quality of the collected data. Therefore, the noise and bias in the data can lead to significant errors in the estimated attitude information. Another limitation is the potential for overfitting or underfitting, which can cause the polynomial function to fit the noise instead of the actual attitude angle curve. Various regularization techniques, such as L1 and L2 regularization, have been proposed to address this issue [64].

2.2. The Camera Calibration Method

The camera calibration method is a technique used for pose measurement, enabling the conversion from the camera image to the actual three-dimensional space of the object by calibrating the internal and external parameters of the camera [70]. To perform pose measurement, it is necessary to know the camera's internal parameters, such as focal length and pixel size, and the camera's external parameters, namely, its position and orientation relative to the object.
The process of camera calibration usually involves using a specific calibration plate or calibration point, placing it at different positions and angles, and taking multiple images. In the image, calibration plates or calibration points must be accurately positioned to calculate the intrinsic and extrinsic parameters of the camera. The calibration plate can be a plane with special patterns or marks, or a three-dimensional object with a specific spatial structure. The calibration point can be a marker of a special shape or a point of a specific color. The most commonly used methods for camera calibration are tensor-based methods and feature-point-based methods. Table 2 is an introduction to the advantages and disadvantages of these commonly used methods.

2.2.1. The Method Based on Tensor

The tensor-based camera calibration method is a camera calibration method that estimates the intrinsic and extrinsic parameters of the camera by using corresponding points in multiple views and tensor decomposition. The method requires at least two different viewpoints, and performs feature matching on images in these viewpoints to obtain corresponding point pairs. Then, the intrinsic and extrinsic parameters of the camera are computed using the tensor decomposition of these corresponding points [71].
The basic idea of this method is to represent the 3D coordinates of corresponding points as a function of the camera intrinsic parameter matrix and extrinsic parameters (ie rotation and translation vectors). These 3D coordinates are then represented as a product of tensors, using the tensor decomposition technique of corresponding points, where one tensor is the camera intrinsic parameter matrix and the other tensor is a vector containing the 3D coordinates of each corresponding point. Then, by decomposing the tensor, the intrinsic and extrinsic parameters of the camera can be estimated simultaneously [72].
Tensor-based camera calibration methods have the advantages of high accuracy and robustness, and can handle multiple images from different viewing angles. Furthermore, the method is able to eliminate calibration errors due to feature matching errors and can be used for various types of cameras, including nonlinear ones. The disadvantage of this method is that it is computationally intensive and therefore requires powerful computers and optimization algorithms [73].

2.2.2. The Method Based on Feature Points

The camera calibration method based on feature points is a widely used and effective approach for camera calibration [74]. It involves extracting feature points from images taken at different viewing angles and calculating the internal and external parameters of the camera based on the correspondence between these feature points. The basic idea of this method is to project known 3D points onto the image plane using the camera projection model and match them with their corresponding 2D feature points. By solving the matching point pairs, the internal and external parameters of the camera can be determined.
The most commonly used feature point extraction algorithms in this method are Scale-Invariant Feature Transform (SIFT) [46] and Speeded Up Robust Features (SURF) [46], among others [75]. Zhang [74] proposes a new technique for camera calibration using a chessboard pattern. It presents a closed-form solution that allows the estimation of both the intrinsic and extrinsic parameters of a camera. The proposed method is simple, efficient, and requires only a few images taken from different viewpoints. Hartley and Zisserman [71] provides a comprehensive introduction to the principles and techniques of multiple view geometry in computer vision. It covers various aspects of camera calibration, including the camera projection model, intrinsic and extrinsic parameters, and stereo calibration. These algorithms are able to extract feature points that are invariant to rotation, scaling, and brightness changes, and can be used to extract the same feature points under different viewing angles. During camera calibration, these feature points must be accurately matched, and an optimization algorithm is used to estimate the internal and external parameters.
The feature point-based camera calibration method has several advantages, including its ease of implementation and high accuracy, which makes it a fundamental tool for many computer vision tasks, such as 3D reconstruction [76], object detection [77], and tracking [78]. However, this method also has some limitations. For example, it may produce matching errors in low-texture areas or under large illumination changes. Furthermore, it requires a large amount of computing resources to achieve high-precision calibration. Thus, it is important to weigh the advantages and disadvantages of this method and choose an appropriate calibration method based on specific application requirements.

2.3. The Global Calibration Method for Vision System

The global calibration of a vision system is a process of obtaining its internal and external parameters by capturing images of multiple objects in different positions and orientations [79]. This calibration requires the use of multiple calibration boards or calibration points. By capturing images of these calibration objects at different positions and angles, the camera's internal and external parameters can be determined, including its focal length, distortion, rotation, and translation. Internal parameters are camera-specific and independent of the scene being captured, while external parameters are scene-specific and related to the camera's position and direction. The accuracy and stability of pose measurement largely depend on the results of global calibration, which makes it crucial for practical applications. Therefore, choosing appropriate calibration objects, methods, and algorithms is essential for achieving the desired accuracy and stability in different scenarios. Table 3 is an introduction to the advantages and disadvantages of these commonly used methods.

2.3.1. The Precision Measuring Instrument Calibration Method

The calibration method of precision measuring instruments refers to the method of determining the measurement error of the instrument and correcting its measurement results by comparing a set of standard objects of known size or position with the measured instrument [84]. It is a key step to ensure the measurement accuracy and reliability of the instrument. The calibration method of precision measuring instruments usually includes the following steps: first, select a suitable standard object and measure its exact size or position; then, collect multiple sets of data at different positions and angles; Analyze and process, calculate the internal error and external error of the instrument; finally, correct according to the error value to improve the measurement accuracy and stability of the instrument. In [79], a dual-camera system with no common field of view is globally calibrated using a high-precision photoelectric theodolite and a moving target. Once the calibration data collection is completed, the calibration algorithm is employed to determine the relative pose between the two cameras. Similarly, in [85], a global calibration is performed using a laser rangefinder and a planar target. This method involves adjusting the target pose to ensure the laser rangefinder's emitted light spot precisely falls on the target working surface, facilitating distance data measurement. Simultaneously, it guarantees that the light spot is fully captured by a specific sub-camera in the multi-camera system. By acquiring multiple sets of distance data and spot center image coordinate data, the relative pose relationship between the sub-cameras can be deduced based on the collinearity and distance constraints of the laser spot center. These approaches achieve high calibration accuracy; however, they rely on costly and complex-to-operate precision measuring instruments. Additionally, feature localization relies on optical information extraction, making it vulnerable to interference from noise present in industrial environments.

2.3.2. The Motion Recovery Structure Calibration Method

Motion recovery structure calibration, also known as multi-view geometric calibration, is a 3D reconstruction and pose recovery method that relies on the geometric relationship between multiple views. This method typically requires multiple cameras to simultaneously capture multiple views of the same object and extract common feature points or feature lines. By matching these features, the internal and external parameters of the camera can be recovered to determine the position and orientation of the camera. Additionally, performing 3D reconstruction on these features allows for the extraction of 3D structure information of the observed object. The motion recovery structure calibration method is widely used in applications such as 3D modeling, computer vision, and robotics. In [86], the proposed method aims to achieve global calibration by leveraging a freely moving light point to construct a 3D control point cloud. It employs the RANSCA algorithm and fourth-order matrix factorization to robustly recover motion and estimate the projected structure. Moreover, a hierarchical algorithm with geometric constraints is introduced to further enhance the accuracy and robustness of the calibration, ultimately obtaining global calibration parameters. Conversely, in [87], a movable auxiliary camera is utilized to collect landmarks within the multi-camera system's global field of view. By calculating the three-dimensional coordinates of these landmarks, the global calibration is accomplished. This method also demonstrates practical effectiveness. While both methods enable global calibration, it should be noted that the approach presented in [86] achieves higher calibration accuracy and robustness through the use of freely moving light points and a hierarchical algorithm with geometric constraints. On the other hand, the method described in [87] offers relative ease of operation by employing a movable auxiliary camera for landmark collection. Choosing an appropriate method for global calibration is crucial, considering specific requirements and conditions.

2.3.3. The Artificial Public Field of View Calibration Method

Artificial public field of view calibration is a technique used in computer vision and computer graphics to determine the intrinsic and extrinsic parameters of a camera in order to transform an object from a three-dimensional space into a two-dimensional image [74]. These parameters include the camera's focal length, field of view angle, pixel size, image distortion, and more. Kumar, et al. [88] proposes a method for global calibration of multi-camera systems without a common field of view, using planar mirror groups. In this method, a target object is placed in the field of view of the main camera, and the mirror position of the target object in the sub-camera is directly imaged and processed by adjusting the mirror. This generates a virtual camera. The method first calculates the pose relationship between the target object, the main camera, and the virtual camera, and then solves the global parameters using the mirror image relationship between the virtual camera and the sub-camera. Agrawal [89] presents a global calibration method that utilizes a spherical mirror of known curvature. This method is capable of simultaneously solving for the position of the spherical mirror and the external parameters of the camera using a mathematical model, which eliminates the need for precise estimation of the mirror position beforehand. Additionally, the method incorporates a three-dimensional reference point that allows for effective calibration even when the edge of the spherical mirror is not fully imaged. While this method has advantages when calibrating a small baseline system, it may not be suitable for multi-camera systems with large inter-camera distances, where it is challenging to ensure that all cameras can observe the complete target either directly or indirectly through the use of artificial fields of view.
The artificial public field of view calibration method uses a special calibration object, usually an object such as a checkerboard or a sphere of known geometry and size. By placing these objects in different positions and angles, the internal and external parameters of the camera can be determined, thereby calibrating the camera [90]. When using the artificial public field of view calibration method, it is necessary to take multiple images and analyze these images to calculate the camera parameters. These parameters can be used for applications such as correcting image distortion [91] and performing 3D reconstruction [76].

2.4. The Vision Pose Parameter Estimation

Machine vision pose parameter estimation is the process of obtaining the pose information of an object in three-dimensional space by processing image or point cloud data in computer vision [92]. This process includes two approaches: 2D image-based pose parameter estimation and 3D point cloud-based pose parameter estimation. Table 4 is an introduction to the advantages and disadvantages of these commonly used methods.

2.4.1. The Estimation Method of Pose Parameters Based on 2D Image

The methods for estimating pose parameters based on two-dimensional images can be broadly categorized into feature point matching methods and deep learning methods.
Feature point matching is a traditional approach where robust feature points are extracted from two images and the pose parameters are computed by matching these points [97]. The most widely used feature point algorithms include SIFT [98], SURF [99], and ORB [100]. These algorithms extract feature points from images, which are then matched to compute the pose parameters.
Deep learning methods are a newer approach where deep neural networks are used to directly estimate the pose parameters from input images [101]. This method bypasses the feature point matching process and requires a large amount of labeled data and computing resources. However, in some scenarios, such as object detection, deep learning methods can be more robust and accurate than traditional methods.
In addition to these two basic methods, there are some derivative methods, such as direct methods [102] and depth map methods [103], which use depth information to estimate pose parameters.

2.4.2. The Pose Parameter Estimation Method Based on 3D Point Cloud

3D point cloud-based pose parameter estimation involves estimating camera pose by matching a known 3D model with the 3D point cloud [104]. It mainly includes the iterative closest point (ICP) algorithm [105] and methods based on deep learning [106].The ICP algorithm is a classic point cloud registration algorithm that matches point clouds by iteratively finding the transformation matrix that minimizes the sum of squared distances between point clouds. Specifically, the ICP algorithm aligns the point cloud set to be matched with the reference point cloud set. Through continuous iterations, it gradually adjusts the pose parameters so that the distance between the two point clouds decreases, finally obtaining the camera's pose parameters. Deep learning-based point cloud matching methods have gained extensive attention in recent years. They directly estimate camera poses from point cloud data using deep neural networks. In this method, an encoder is usually used to map point cloud data into a low-dimensional feature space, and then a decoder converts the information in the feature space into pose parameters. Although this method requires a large amount of labeled data and computing resources, it can achieve higher accuracy and robustness in scenarios such as real-time localization and map construction.

3. The Factors Affecting the Accuracy of Machine Vision Pose Measurement Algorithms

Machine vision pose measurement algorithm is one of the very important technologies in modern industry. It can realize the attitude measurement and positioning of objects through image processing and computer vision algorithms, and provides basic technical support for automated production. However, the accuracy of machine vision pose measurement algorithms is affected by various factors. Understanding these influencing factors is of great significance for improving and optimizing the algorithm and improving the accuracy and reliability of attitude measurement.

3.1. Image Quality

Image quality is an important factor affecting the accuracy of machine vision pose measurement algorithms. The quality of the image directly affects the accuracy of attitude measurement. When the image quality is not good, there may be problems such as noise, blur, distortion, etc., which will lead to an increase in the error of the pose measurement. Therefore, when performing machine vision pose measurement, images with better image quality should be selected and the influence of image quality problems should be minimized.

3.2. Camera Distortion

The distortion of the camera refers to the difference between the shape and position of the pixels in the image when the camera is imaging and the shape and position of the actual object [107]. Camera distortion is mainly divided into radial distortion and tangential distortion. Radial distortion refers to the distortion caused by irregularities in the shape of the lens, while tangential distortion is the distortion caused by the deflection of the camera lens. These distortions affect the actual size and position of objects in the image, which in turn affects the accuracy of pose measurement.
In order to reduce the distortion effect of the camera, it can be eliminated by the method of camera calibration. Camera calibration refers to the process of determining the internal and external parameters of the camera, mainly including the determination of the internal parameters of the camera (such as focal length, optical center, etc.) and the external parameters of the camera (such as the relative position and direction between the camera and the target object, etc.). After calibration, the image can be corrected by using the method of de-distortion, so as to improve the accuracy of pose measurement.

3.3. Camera Parameters

Camera parameters are one of the key factors affecting the accuracy of machine vision pose measurement. Camera parameters include camera intrinsic parameters and camera extrinsic parameters. Camera intrinsic parameters refer to the inherent parameters of the camera itself, including focal length, principal point coordinates, etc.; camera extrinsic parameters refer to the pose information of the camera in the world coordinate system, including the position and direction of the camera in space. The accuracy of camera parameters has a significant impact on the accuracy of pose measurements. Therefore, before attitude measurement, camera parameters need to be calibrated to ensure the accuracy of camera parameters. At present, commonly used camera parameter calibration methods include Zhang Zhengyou calibration method [108], Tsai calibration method [109].

3.4. Surface Properties

The properties of an object's surface can also affect the accuracy of machine vision pose measurements. For example, the reflectivity, texture, color and other characteristics of the surface of the object will have an impact on the accuracy of attitude measurement. The reflectivity of the surface of the object will cause the reflection of light, which will produce artifacts and affect the accuracy of the measurement. The texture and color characteristics of the object surface will affect the extraction and matching of feature points, thereby affecting the accuracy of pose measurement. Therefore, when performing machine vision attitude measurement, objects with relatively stable surface properties should be selected as much as possible, and the surface of the object should be fully processed to reduce the impact of surface properties on measurement accuracy.

3.5. Selection and Extraction of Feature Points

In machine vision attitude measurement, the selection and extraction of feature points have an important impact on the measurement accuracy. In general, selecting feature points with stable features and easier to be extracted can improve the accuracy of attitude measurement. In the process of feature point extraction, it is necessary to pay attention to the preprocessing of the image, including grayscale stretching, filtering, binarization, etc. At the same time, for different application scenarios, different feature points need to be selected to meet actual needs.

3.6. Attitude Calculation Algorithm

Attitude calculation algorithm is the core part of machine vision attitude measurement, which has a decisive impact on measurement accuracy. At present, commonly used attitude calculation algorithms include three-point algorithm [110], quaternion-based algorithm [111], and rotation vector-based algorithm [112]. Different algorithms have different precision and computational complexity, so they need to be selected according to specific needs in practical applications.

4. The Application of Machine Vision Pose Measurement in Various Fields

Machine vision pose measurement technology is to obtain the position and attitude information of the target object through image processing and analysis of the target object. With the continuous development and improvement of computer vision technology, machine vision pose measurement technology is more and more widely used in various fields. This article will introduce the application of machine vision pose measurement technology in various fields.

4.1. The Field of Robotics

The rapid development of robot technology provides a broad space for the application of machine vision pose measurement technology in the field of robots. The specific application is illustrated in Figure 2. Leica T-cam and T-Mac are advanced space coordinate measuring instruments that integrate laser trackers and visual measurement systems [113]. They enable the acquisition of precise six-degree-of-freedom pose information for cooperative targets by employing spatial intersection measurements conducted by a rotatable camera embedded in the laser tracker's head. Machine vision pose measurement technology has played an important role in autonomous navigation, positioning and attitude control of robots. Machine vision pose measurement technology can be used for autonomous navigation of robots in different environments, so that robots can accurately identify the environment and obstacles, plan appropriate paths and travel postures, and thus realize autonomous navigation. In addition, machine vision pose measurement technology can also be used for positioning and attitude control of robots to ensure the accuracy and stability of robots when performing tasks.

4.2. The Industrial Manufacturing Field

In the field of industrial manufacturing, machine vision pose measurement technology is widely used in the positioning, tracking, detection, assembly and quality control of industrial robots. The specific application is shown in Figure 3: OKUMA's MULTUS B300 CNC machine tool has an anti-collision system and is equipped with an attitude measurement function for real-time monitoring and measurement of the attitude state of the machine tool. Machine vision pose measurement technology can realize automatic positioning and attitude control of industrial robots, so that industrial robots can efficiently complete various assembly tasks. In addition, machine vision pose measurement technology can also be used for parts inspection and quality control in industrial manufacturing to ensure product quality and stability.

4.3. The Intelligent Transportation Field

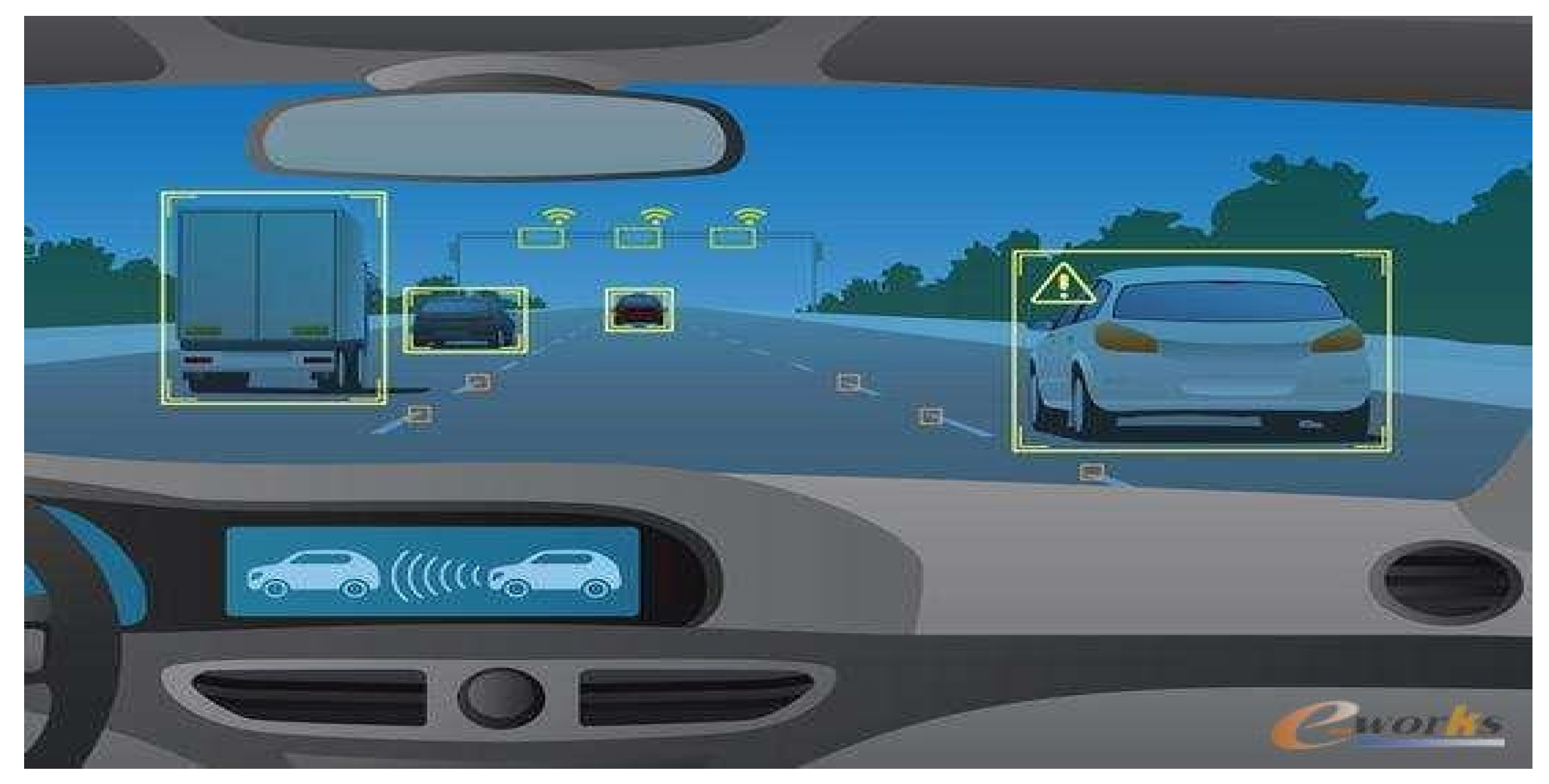
The application of machine vision pose measurement technology in the field of intelligent transportation is also becoming more and more extensive. The specific application is shown in Figure 4: Pose measurement can provide real-time vehicle or pedestrian position and orientation information, enabling real-time navigation and path planning. Machine vision pose measurement technology can be used to identify and track vehicles and pedestrians in intelligent transportation systems, thereby realizing the automatic control of intelligent transportation systems. In addition, machine vision pose measurement technology can also be used for the detection and recognition of road edges, road signs and lane lines, improving the driving safety of drivers.

4.4. The Healthcare Field

Machine vision pose measurement technology is also widely used in the field of medical and health. The specific application is shown in Figure 5: Human motion posture estimation can be used to analyze and capture human motion. This is important for fields such as exercise science, physical training, sports medicine and rehabilitation. In terms of surgical robots, machine vision pose measurement can accurately measure the position and attitude of surgical instruments to ensure the accuracy and safety of surgery. In medical image processing, machine vision pose measurement can be used for segmentation and registration of medical images to achieve precise positioning and analysis of lesion areas.

4.5. The Aerospace Field

Machine vision pose measurement technology also has important applications in the aerospace field. The specific application is shown in Figure 6: for Advanced Video Guidance Sensitive (AVGS), a laser diode is used to illuminate the reflector on the target spacecraft, and after detecting the reflected light, the digital signal processor is used to convert the video information into the relative position and attitude information of the target [114]. Machine vision pose measurement can be used in the assembly and maintenance of aircraft components, and the attitude control of satellites. In the assembly and maintenance of aircraft components, machine vision pose measurement can measure the position and attitude of aircraft components to ensure their correct installation and operation. In terms of satellite attitude control, machine vision pose measurement can realize attitude measurement and control of satellites to ensure their normal operation and task completion.

5. Conclusions

Machine vision pose measurement is a rapidly growing field that has become increasingly important in many industries, such as robotics, autonomous vehicles, and augmented reality. This review paper provides an in-depth overview of the field, with a focus on the state-of-the-art algorithms and their applications.
Section 1 provides an introduction to the field of machine vision pose measurement, including its history and significance. The authors explain that the goal of machine vision pose measurement is to determine the position and orientation of objects in three-dimensional space using digital images. This section also highlights the importance of accurate pose measurement in a variety of industries, including manufacturing, medical imaging, and entertainment. In Section 2, the authors describe the commonly used algorithms for machine vision pose measurement. They discuss different methods for detecting and tracking objects, such as feature-based, model-based, and template matching techniques. They also explain how machine learning algorithms, such as convolutional neural networks (CNNs), can be used to improve the accuracy of pose estimation. Section 3 focuses on the factors that affect the accuracy and reliability of machine vision pose measurement algorithms. The authors discuss various sources of error, including lighting conditions, occlusion, and camera calibration. They also explain how noise reduction techniques and sensor fusion can be used to improve the accuracy of pose measurement. In Section 4, the authors present the applications of machine vision pose measurement in various fields, such as robotics, augmented reality, and sports analysis. They highlight the importance of accurate pose measurement in these industries, and provide examples of how it has been used to improve efficiency and safety.
In conclusion, this review paper provides a comprehensive overview of the field of machine vision pose measurement, including the state-of-the-art algorithms and their applications. The authors highlight the importance of accurate pose measurement in various industries and provide insights into the factors that affect its accuracy and reliability. This paper is a valuable resource for researchers, engineers, and practitioners interested in the field of machine vision pose measurement.

Author Contributions

Supervision, N.S.B; conceptualization, all the authors; writing, W.X.X; All authors have read and agreed to the published version of the manuscript.

Funding

No funding was received for this paper.

Informed Consent Statement

The informed consent of all authors was obtained.

Data Availability Statement

The data used to support the study are available upon request.

Conflicts of Interest

The author declares that there is no conflict of interest with any institution or individual regarding the publication of this paper.

References

  1. Linnainmaa, S.; Harwood, D.; Davis, L.S. Pose determination of a three-dimensional object using triangle pairs. IEEE Transactions on Pattern Analysis and Machine Intelligence 1988, 10, 634–647. [Google Scholar] [CrossRef]
  2. Peng, J.; Xu, W.; Yan, L.; Pan, E.; Liang, B.; Wu, A.-G. A pose measurement method of a space noncooperative target based on maximum outer contour recognition. IEEE Transactions on Aerospace and Electronic Systems 2019, 56, 512–526. [Google Scholar] [CrossRef]
  3. Keim, D.; Andrienko, G.; Fekete, J.-D.; Görg, C.; Kohlhammer, J.; Melançon, G. Visual analytics: Definition, process, and challenges; Springer: 2008.
  4. Taketomi, T.; Uchiyama, H.; Ikeda, S. Visual SLAM algorithms: A survey from 2010 to 2016. IPSJ Transactions on Computer Vision and Applications 2017, 9, 1–11. [Google Scholar] [CrossRef]
  5. Wang, Y.-s.; Liu, J.-y.; Zeng, Q.-h.; Liu, S. Visual pose measurement based on structured light for MAVs in non-cooperative environments. Optik 2015, 126, 5444–5451. [Google Scholar] [CrossRef]
  6. Liu, B.; Zhang, F.; Qu, X. A method for improving the pose accuracy of a robot manipulator based on multi-sensor combined measurement and data fusion. Sensors 2015, 15, 7933–7952. [Google Scholar] [CrossRef] [PubMed]
  7. Merfels, C.; Stachniss, C. Pose fusion with chain pose graphs for automated driving. Proceedings of 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS); pp. 3116–3123.
  8. Murphy-Chutorian, E.; Trivedi, M.M. Head pose estimation and augmented reality tracking: An integrated system and evaluation for monitoring driver awareness. IEEE Transactions on intelligent transportation systems 2010, 11, 300–311. [Google Scholar] [CrossRef]
  9. Liu, Y.; Zhou, J.; Li, Y.; Zhang, Y.; He, Y.; Wang, J. A high-accuracy pose measurement system for robotic automated assembly in large-scale space. Measurement 2022, 188, 110426. [Google Scholar] [CrossRef]
  10. Zhang, Z.; Deriche, R.; Faugeras, O.; Luong, Q.-T. A robust technique for matching two uncalibrated images through the recovery of the unknown epipolar geometry. Artificial intelligence 1995, 78, 87–119. [Google Scholar] [CrossRef]
  11. Szeliski, R. Computer vision: algorithms and applications; Springer Nature: 2022.
  12. Fischler, M.A.; Bolles, R.C. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography. Communications of the ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
  13. Lowe, D.G. Distinctive image features from scale-invariant keypoints. International journal of computer vision 2004, 60, 91–110. [Google Scholar] [CrossRef]
  14. Tomasi, C.; Kanade, T. Shape and motion from image streams: a factorization method. Proceedings of the National Academy of Sciences 1993, 90, 9795–9802. [Google Scholar] [CrossRef] [PubMed]
  15. Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. Proceedings of Sensor fusion IV: control paradigms and data structures; pp. 586–606.
  16. Scharstein, D.; Szeliski, R. A taxonomy and evaluation of dense two-frame stereo correspondence algorithms. International journal of computer vision 2002, 47, 7–42. [Google Scholar] [CrossRef]
  17. Chen, L.-C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE transactions on pattern analysis and machine intelligence 2017, 40, 834–848. [Google Scholar] [CrossRef] [PubMed]
  18. Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of Proceedings of the IEEE conference on computer vision and pattern recognition; pp. 652–660.
  19. Li, Y.; Wang, S.; Tian, Q.; Ding, X. A survey of recent advances in visual feature detection. Neurocomputing 2015, 149, 736–751. [Google Scholar] [CrossRef]
  20. Kaur, N.; Nazir, N. A Review of Local Binary Pattern Based texture feature extraction. In Proceedings of 2021 9th International Conference on Reliability, Infocom Technologies and Optimization (Trends and Future Directions)(ICRITO); pp. 1–4.
  21. Belongie, S.; Malik, J.; Puzicha, J. Shape matching and object recognition using shape contexts. IEEE transactions on pattern analysis and machine intelligence 2002, 24, 509–522. [Google Scholar] [CrossRef]
  22. Furukawa, Y.; Ponce, J. Accurate, dense, and robust multi-view stereopsis (pmvs). In Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition.
  23. Son, H.; Lee, J.; Lee, J.; Cho, S.; Lee, S. Recurrent video deblurring with blur-invariant motion estimation and pixel volumes. ACM Transactions on Graphics (TOG) 2021, 40, 1–18. [Google Scholar] [CrossRef]
  24. Welch, G.; Bishop, G. An introduction to the Kalman filter. 1995.
  25. Arulampalam, M.S.; Maskell, S.; Gordon, N.; Clapp, T. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Transactions on signal processing 2002, 50, 174–188. [Google Scholar] [CrossRef]
  26. Julier, S.J.; Uhlmann, J.K. New extension of the Kalman filter to nonlinear systems. In Proceedings of Signal processing, sensor fusion, and target recognition VI; pp. 182–193.
  27. Zhang, J.; Tan, T. Brief review of invariant texture analysis methods. Pattern recognition 2002, 35, 735–747. [Google Scholar] [CrossRef]
  28. Harris, C.; Stephens, M. A combined corner and edge detector. Proceedings of Alvey vision conference; pp. 10–5244.
  29. Lippmann, R. An introduction to computing with neural nets. IEEE Assp magazine 1987, 4, 4–22. [Google Scholar] [CrossRef]
  30. LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
  31. Goodfellow, I.; Bengio, Y.; Courville, A. Deep learning; MIT press, 2016. [Google Scholar]
  32. Rambach, J.R.; Tewari, A.; Pagani, A.; Stricker, D. Learning to fuse: A deep learning approach to visual-inertial camera pose estimation. Proceedings of 2016 IEEE International Symposium on Mixed and Augmented Reality (ISMAR); pp. 71–76.
  33. Kalaitzakis, M.; Cain, B.; Carroll, S.; Ambrosi, A.; Whitehead, C.; Vitzilaios, N. Fiducial markers for pose estimation: Overview, applications and experimental comparison of the artag, apriltag, aruco and stag markers. Journal of Intelligent & Robotic Systems 2021, 101, 1–26. [Google Scholar]
  34. Ryberg, A.; Christiansson, A.-K.; Eriksson, K. Accuracy Investigation of a vision based system for pose measurements. Proceedings of 2006 9th International Conference on Control, Automation, Robotics and Vision; pp. 1–6.
  35. Tsai, C.-Y.; Tsai, S.-H. Simultaneous 3D object recognition and pose estimation based on RGB-D images. IEEE Access 2018, 6, 28859–28869. [Google Scholar] [CrossRef]
  36. Lin, H.-Y.; Liang, S.-C.; Chen, Y.-K. Robotic grasping with multi-view image acquisition and model-based pose estimation. IEEE Sensors Journal 2020, 21, 11870–11878. [Google Scholar] [CrossRef]
  37. Lin, M. Deep learning-based approaches for depth and 6-DoF pose estimation. Massachusetts Institute of Technology, 2020.
  38. Canny, J. A computational approach to edge detection. IEEE Transactions on pattern analysis and machine intelligence 1986, 679–698. [Google Scholar] [CrossRef]
  39. Prewitt, J. Object enhancement and extraction picture processing and psychopictorics. 1970. A.
  40. Cui, F.-y.; Zou, L.-j.; Song, B. Edge feature extraction based on digital image processing techniques. Proceedings of 2008 IEEE International Conference on Automation and Logistics; pp. 2320–2324.
  41. Sroba, L.; Ravas, R.; Grman, J. The influence of subpixel corner detection to determine the camera displacement. Procedia Engineering 2015, 100, 834–840. [Google Scholar] [CrossRef]
  42. Bok, Y.; Ha, H.; Kweon, I.S. Automated checkerboard detection and indexing using circular boundaries. Pattern Recognition Letters 2016, 71, 66–72. [Google Scholar] [CrossRef]
  43. Derpanis, K.G. The harris corner detector. York University 2004, 2, 1–2. [Google Scholar]
  44. Bansal, M.; Kumar, M.; Kumar, M.; Kumar, K. An efficient technique for object recognition using Shi-Tomasi corner detection algorithm. Soft Computing 2021, 25, 4423–4432. [Google Scholar] [CrossRef]
  45. Vairalkar, M.K.; Nimbhorkar, S. Edge detection of images using Sobel operator. International Journal of Emerging Technology and Advanced Engineering 2012, 2, 291–293. [Google Scholar]
  46. Lindeberg, T. Scale invariant feature transform. 2012.
  47. Alcantarilla, P.F.; Bergasa, L.M.; Davison, A.J. Gauge-SURF descriptors. Image and vision computing 2013, 31, 103–116. [Google Scholar] [CrossRef]
  48. Liao, K.; Liu, G.; Hui, Y. An improvement to the SIFT descriptor for image representation and matching. Pattern Recognition Letters 2013, 34, 1211–1220. [Google Scholar] [CrossRef]
  49. Tatu, A.; Lauze, F.; Nielsen, M.; Kimia, B. Exploring the representation capabilities of the HOG descriptor. Proceedings of 2011 IEEE international conference on computer vision workshops (ICCV Workshops); pp. 1410–1417.
  50. Guan, X.; Jian, S.; Hongda, P.; Zhiguo, Z.; Haibin, G. A novel corner point detector for calibration target images based on grayscale symmetry. Proceedings of 2009 Second International Symposium on Computational Intelligence and Design; pp. 64–67.
  51. Yu, Z.; Yang, Z. Method of remote sensing image detail encryption based on symmetry algorithm. Journal of Ambient Intelligence and Humanized Computing 2021, 1–9. [Google Scholar] [CrossRef]
  52. Tsogkas, S.; Kokkinos, I. Tsogkas, S.; Kokkinos, I. Learning-based symmetry detection in natural images. In Proceedings of Computer Vision–ECCV 2012: 12th European Conference on Computer Vision, Florence, Italy, October 7-13, 2012, Proceedings, Part VII 12; pp. 41–54.
  53. Wang, L.; Pavlidis, T. Direct gray-scale extraction of features for character recognition. IEEE transactions on pattern analysis and machine intelligence 1993, 15, 1053–1067. [Google Scholar] [CrossRef]
  54. Lazaros, N.; Sirakoulis, G.C.; Gasteratos, A. Review of stereo vision algorithms: from software to hardware. International Journal of Optomechatronics 2008, 2, 435–462. [Google Scholar] [CrossRef]
  55. Li, W.; Huang, Q.; Srivastava, G. Contour feature extraction of medical image based on multi-threshold optimization. Mobile Networks and Applications 2021, 26, 381–389. [Google Scholar] [CrossRef]
  56. Zhao, Q.; Chen, Z.; Yang, T.; Zhao, Y. Detection of sub-pixel chessboard corners based on gray symmetry factor. Proceedings of Ninth International Symposium on Precision Engineering Measurement and Instrumentation; pp. 1186–1192.
  57. Huang, X.; Mei, G.; Zhang, J.; Abbas, R. A comprehensive survey on point cloud registration. arXiv preprint arXiv:2103.02690 2021. arXiv:2103.02690 2021.
  58. Zhang, S. High-speed 3D shape measurement with structured light methods: A review. Optics and lasers in engineering 2018, 106, 119–131. [Google Scholar] [CrossRef]
  59. Atefi, E.; Mann Jr, J.A.; Tavana, H. A robust polynomial fitting approach for contact angle measurements. Langmuir 2013, 29, 5677–5688. [Google Scholar] [CrossRef] [PubMed]
  60. Schwarz, N. Attitude measurement. Attitudes and attitude change 2008, 3, 41–60. [Google Scholar]
  61. Liu, Y.; Chen, L.; Fan, S.; Zhang, Y. Design of Gas Monitoring Terminal Based on Quadrotor UAV. Sensors 2022, 22, 5350. [Google Scholar] [CrossRef]
  62. Reichert, A.K.; Axelrad, P. Carrier-phase multipath corrections for GPS-based satellite attitude determination. Navigation 2001, 48, 76–88. [Google Scholar] [CrossRef]
  63. Jung, H.-K.; Kim, S.-S.; Shim, J.-S.; Kim, C.-W. Development of Vehicle Dynamics Model for Real-Time ECU Evaluation System. Proceedings of AVEC; pp. 555–560.
  64. Ding, S.X. Model-based fault diagnosis techniques: design schemes, algorithms, and tools; Springer Science & Business Media: 2008.
  65. Yu, W.; Xie, J.; Wu, X.; Liu, K. Research of improved Zhang's calibration method. Proceedings of 2017 Chinese Automation Congress (CAC); pp. 1423–1427.
  66. Li, W.; Gee, T.; Friedrich, H.; Delmas, P. A practical comparison between zhang's and tsai's calibration approaches. In Proceedings of Proceedings of the 29th International Conference on Image and Vision Computing New Zealand; pp. 166–171.
  67. Shapiro, R. Direct linear transformation method for three-dimensional cinematography. Research Quarterly. American Alliance for Health, Physical Education and Recreation 1978, 49, 197–205. [Google Scholar] [CrossRef]
  68. Lv, X.Z.; Wang, M.T.; Qi, Y.F.; Zhao, X.M.; Dong, H. Research on ranging method based on binocular stereo vision. Proceedings of Advanced Materials Research; pp. 2075–2081.
  69. Abu-Rahmah, A.; Arnott, W.; Moosmüller, H. Integrating nephelometer with a low truncation angle and an extended calibration scheme. Measurement Science and Technology 2006, 17, 1723. [Google Scholar] [CrossRef]
  70. Tsai, R. A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses. IEEE Journal on Robotics and Automation 1987, 3, 323–344. [Google Scholar] [CrossRef]
  71. Hartley, R.; Zisserman, A. Multiple view geometry in computer vision; Cambridge university press: 2003.
  72. Triggs, B.; McLauchlan, P.F.; Hartley, R.I.; Fitzgibbon, A.W. Bundle adjustment—a modern synthesis. In Proceedings of Vision Algorithms: Theory and Practice: International Workshop on Vision Algorithms Corfu, Greece, September 21–22, 1999 Proceedings; pp. 298–372.
  73. Shen, J.; Gans, N. A trifocal tensor based camera-projector system for robot-human interaction. Proceedings of 2012 IEEE International Conference on Robotics and Biomimetics (ROBIO); pp. 1110–1116.
  74. Zhang, Z. A flexible new technique for camera calibration. IEEE Transactions on pattern analysis and machine intelligence 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
  75. Bay, H.; Tuytelaars, T.; Van Gool, L. Surf: Speeded up robust features. Lecture notes in computer science 2006, 3951, 404–417. [Google Scholar]
  76. Pedersen, M.; Hein Bengtson, S.; Gade, R.; Madsen, N.; Moeslund, T.B. Camera calibration for underwater 3D reconstruction based on ray tracing using Snell's law. In Proceedings of Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops; pp. 1410–1417.
  77. Jung, J.; Yoon, I.; Lee, S.; Paik, J. Object detection and tracking-based camera calibration for normalized human height estimation. Journal of Sensors 2016, 2016. [Google Scholar] [CrossRef]
  78. Porikli, F.; Divakaran, A. Multi-camera calibration, object tracking and query generation. In Proceedings of 2003 International Conference on Multimedia and Expo. ICME'03. Proceedings (Cat. No. 03TH8698); pp. I–653.
  79. Lu, R.; Li, Y. A global calibration method for large-scale multi-sensor visual measurement systems. Sensors and Actuators A: Physical 2004, 116, 384–393. [Google Scholar] [CrossRef]
  80. Munaro, M.; Basso, F.; Menegatti, E. OpenPTrack: Open source multi-camera calibration and people tracking for RGB-D camera networks. Robotics and Autonomous Systems 2016, 75, 525–538. [Google Scholar] [CrossRef]
  81. Kassir, A.; Peynot, T. Reliable automatic camera-laser calibration. In Proceedings of Australasian Conference on Robotics and Automation.
  82. Gu, C.; Cong, Y.; Sun, G. Environment driven underwater camera-IMU calibration for monocular visual-inertial SLAM. Proceedings of 2019 International Conference on Robotics and Automation (ICRA); pp. 2405–2411.
  83. Rosero, L.A.; Osório, F.S. Calibration and multi-sensor fusion for on-road obstacle detection. Proceedings of 2017 Latin American Robotics Symposium (LARS) and 2017 Brazilian Symposium on Robotics (SBR); pp. 1–6.
  84. Qiao, X.; Ding, G.; Chen, X.; Cai, P.; Shao, L. Comparison of 3-D Self-Calibration Methods for High-Precision Measurement Instruments. IEEE Transactions on Instrumentation and Measurement 2022, 71, 1–9. [Google Scholar] [CrossRef]
  85. Liu, Z.; Li, F.; Zhang, G. An external parameter calibration method for multiple cameras based on laser rangefinder. Measurement 2014, 47, 954–962. [Google Scholar] [CrossRef]
  86. Svoboda, T.; Martinec, D.; Pajdla, T. A convenient multicamera self-calibration for virtual environments. Presence: Teleoperators & virtual environments 2005, 14, 407–422. [Google Scholar]
  87. Mouragnon, E.; Lhuillier, M.; Dhome, M.; Dekeyser, F.; Sayd, P. 3D reconstruction of complex structures with bundle adjustment: an incremental approach. In Proceedings of Proceedings 2006 IEEE International Conference on Robotics and Automation, 2006. ICRA 2006.; pp. 3055–3061.
  88. Kumar, R.K.; Ilie, A.; Frahm, J.-M.; Pollefeys, M. Simple calibration of non-overlapping cameras with a mirror. Proceedings of 2008 IEEE Conference on Computer Vision and Pattern Recognition; pp. 1–7.
  89. Agrawal, A. Extrinsic camera calibration without a direct view using spherical mirror. In Proceedings of Proceedings of the IEEE International Conference on Computer Vision; pp. 2368–2375.
  90. Lébraly, P.; Deymier, C.; Ait-Aider, O.; Royer, E.; Dhome, M. Flexible extrinsic calibration of non-overlapping cameras using a planar mirror: Application to vision-based robotics. Proceedings of 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems; pp. 5640–5647.
  91. Melo, R.; Barreto, J.P.; Falcao, G. A new solution for camera calibration and real-time image distortion correction in medical endoscopy–initial technical evaluation. IEEE Transactions on Biomedical Engineering 2011, 59, 634–644. [Google Scholar] [CrossRef]
  92. Erol, A.; Bebis, G.; Nicolescu, M.; Boyle, R.D.; Twombly, X. Vision-based hand pose estimation: A review. Computer Vision and Image Understanding 2007, 108, 52–73. [Google Scholar] [CrossRef]
  93. Li, S.; Xu, C.; Xie, M. A robust O (n) solution to the perspective-n-point problem. IEEE transactions on pattern analysis and machine intelligence 2012, 34, 1444–1450. [Google Scholar] [CrossRef] [PubMed]
  94. Irani, M.; Anandan, P. About direct methods. In Proceedings of Vision Algorithms: Theory and Practice: International Workshop on Vision Algorithms Corfu, Greece, September 21–22, 1999 Proceedings; pp. 267–277.
  95. Markley, F.L.; Crassidis, J.; Cheng, Y. Nonlinear attitude filtering methods. Proceedings of AIAA guidance, navigation, and control conference and exhibit; p. 5927.
  96. Liu, X.; Yu, S.-y.; Flierman, N.A.; Loyola, S.; Kamermans, M.; Hoogland, T.M.; De Zeeuw, C.I. OptiFlex: Multi-frame animal pose estimation combining deep learning with optical flow. Frontiers in Cellular Neuroscience 2021, 15, 621252. [Google Scholar] [CrossRef] [PubMed]
  97. Roessle, B.; Nießner, M. End2end multi-view feature matching using differentiable pose optimization. arXiv preprint arXiv:2205.01694 2022. arXiv:2205.01694 2022.
  98. Zhong, B.; Li, Y. Image feature point matching based on improved SIFT algorithm. In Proceedings of 2019 IEEE 4th International Conference on Image, Vision and Computing (ICIVC); pp. 489–493.
  99. Bakheet, S.; Al-Hamadi, A.; Youssef, R. A fingerprint-based verification framework using Harris and SURF feature detection algorithms. Applied Sciences 2022, 12, 2028. [Google Scholar] [CrossRef]
  100. Qin, Y.; Xu, H.; Chen, H. Image feature points matching via improved ORB. Proceedings of 2014 IEEE International Conference on Progress in Informatics and Computing; pp. 204–208.
  101. Gamra, M.B.; Akhloufi, M.A. A review of deep learning techniques for 2D and 3D human pose estimation. Image and Vision Computing 2021, 114, 104282. [Google Scholar] [CrossRef]
  102. Kondori, F.A.; Yousefit, S.; Ostovar, A.; Liu, L.; Li, H. A direct method for 3d hand pose recovery. Proceedings of 2014 22nd International Conference on Pattern Recognition; pp. 345–350.
  103. Marin-Jimenez, M.J.; Romero-Ramirez, F.J.; Munoz-Salinas, R.; Medina-Carnicer, R. 3D human pose estimation from depth maps using a deep combination of poses. Journal of Visual Communication and Image Representation 2018, 55, 627–639. [Google Scholar] [CrossRef]
  104. Xu, T.; An, D.; Jia, Y.; Yue, Y. A review: Point cloud-based 3d human joints estimation. Sensors 2021, 21, 1684. [Google Scholar] [CrossRef]
  105. Zhang, J.; Yao, Y.; Deng, B. Fast and robust iterative closest point. IEEE Transactions on Pattern Analysis and Machine Intelligence 2021, 44, 3450–3466. [Google Scholar] [CrossRef]
  106. Guo, Y.; Wang, H.; Hu, Q.; Liu, H.; Liu, L.; Bennamoun, M. Deep learning for 3d point clouds: A survey. IEEE transactions on pattern analysis and machine intelligence 2020, 43, 4338–4364. [Google Scholar] [CrossRef] [PubMed]
  107. Tang, Z.; Von Gioi, R.G.; Monasse, P.; Morel, J.-M. A precision analysis of camera distortion models. IEEE Transactions on Image Processing 2017, 26, 2694–2704. [Google Scholar] [CrossRef] [PubMed]
  108. Lu, P.; Liu, Q.; Guo, J. Camera calibration implementation based on Zhang Zhengyou plane method. In Proceedings of Proceedings of the 2015 Chinese Intelligent Systems Conference: Volume 1; pp. 29–40.
  109. Samper, D.; Santolaria, J.; Brosed, F.J.; Majarena, A.C.; Aguilar, J.J. Analysis of Tsai calibration method using two-and three-dimensional calibration objects. Machine vision and applications 2013, 24, 117–131. [Google Scholar] [CrossRef]
  110. Yakimenko, O.; Kaminer, I.; Lentz, W. A three point algorithm for attitude and range determination using vision. In Proceedings of Proceedings of the 2000 American Control Conference. ACC (IEEE Cat. No. 00CH36334); pp. 1705–1709.
  111. Feng, K.; Li, J.; Zhang, X.; Shen, C.; Bi, Y.; Zheng, T.; Liu, J. A new quaternion-based Kalman filter for real-time attitude estimation using the two-step geometrically-intuitive correction algorithm. Sensors 2017, 17, 2146. [Google Scholar] [CrossRef]
  112. Wang, M.; Wu, W.; He, X.; Yang, G.; Yu, H. Higher-order rotation vector attitude updating algorithm. The Journal of Navigation 2019, 72, 721–740. [Google Scholar] [CrossRef]
  113. Krebs, F.; Larsen, L.; Braun, G.; Dudenhausen, W. Design of a multifunctional cell for aerospace CFRP production. The International Journal of Advanced Manufacturing Technology 2016, 85, 17–24. [Google Scholar] [CrossRef]
  114. Howard, R.T.; Johnston, A.S.; Bryan, T.C.; Book, M.L. Advanced video guidance sensor (AVGS) development testing. Proceedings of Spaceborne Sensors; pp. 50–60.
Preprints 75016 g001
Figure 1. This is a figure. Schemes follow the same formatting.
Figure 1. This is a figure. Schemes follow the same formatting.
Preprints 75016 g001
Preprints 75016 g002
Figure 2. (a) Leica T-cam, (b) T-Mac.
Figure 2. (a) Leica T-cam, (b) T-Mac.
Preprints 75016 g002
Preprints 75016 g003
Figure 3. MULTUS B300 CNC machine tool from OKUMA.
Figure 3. MULTUS B300 CNC machine tool from OKUMA.
Preprints 75016 g003
Preprints 75016 g004
Figure 4. The vehicle navigation based on machine vision pose measurement.
Figure 4. The vehicle navigation based on machine vision pose measurement.
Preprints 75016 g004
Preprints 75016 g005
Figure 5. T-Mac.The motion pose estimation.
Figure 5. T-Mac.The motion pose estimation.
Preprints 75016 g005
Preprints 75016 g006
Figure 6. TAVGS navigation system: (a) illustration of the short-range navigation process, (b) cooperative targets in the experiment.
Figure 6. TAVGS navigation system: (a) illustration of the short-range navigation process, (b) cooperative targets in the experiment.
Preprints 75016 g006
Table 1. The advantages and disadvantages of commonly used machine vision pose measurement methods based on image feature extraction.
Table 1. The advantages and disadvantages of commonly used machine vision pose measurement methods based on image feature extraction.
Method Advantage Diadvantage
Harris corner detection [43] (1) Robustness
(2) Scale invariance
(3) Independence		 (1) Insensitive to rotation changes
(2) Sensitive to scale changes
(3) Computational complexity
(4) Sensitive to noise
Shi-Tomasi corner detection [44] (1) Ranking of corner responsivity
(2) Robustness
(3) Scale invariance
(4) Suitable for tracking		 (1) Insensitive to rotation changes
(2) Sensitive to scale changes
(3) Computational complexity
(4) Sensitive to noise
Sobel operator [45] (1) Simple and efficient
(2) Edge positioning is accurate
(3) Direction Sensitivity
(4) Noise suppression		 (1) Gray level smoothness is poor
(2) The gradient boundary response is discontinuous
(3) Sensitive to edge width
(4) Applicable only to grayscale images
Canny edge detection (1) Accurate edge positioning
(2) Single edge response
(3) Low error rate
(4) Multi-scale processing		 (1) Computational complexity
(2) Parameter selection
(3) Sensitive to noise
(4) slower speed
Scale-Invariant Feature Transform (SIFT) [46] (1) Scale invariance
(2) Uniqueness
(3) Not affected by light changes
(4) Efficiency		 (1) Computational complexity
(2) Scale space extremum selection
(3) Sensitive to image distortion
SURF descriptor [47] (1) Fast performance
(2) Scale invariance
(3) Rotation invariance
(4) Robustness		 (1) Poor spatial invariance
(2) The feature expression ability is relatively weak
(3) Sensitive to light changes
(4) Parameter selection
SIFT descriptor [48] (1) Scale invariance
(2) Rotation invariance
(3) Uniqueness and distinguishability
(4) Robustness		 (1) Computational complexity
(2) Parameter selection
(3) Sensitive to light changes
(4) Higher feature dimension
HOG descriptor [49] (1) Invariance
(2) Robustness to illumination changes
(3) Local texture features
(4) Low-dimensional representation		 (1) Sensitive to viewing angle changes and deformation
(2) Requires explicit target labeling
(3) Low-level feature representation
(4) Sensitive to noise
Table 2. The advantages and disadvantages of commonly used machine vision pose measurement methods based on camera calibration.
Table 2. The advantages and disadvantages of commonly used machine vision pose measurement methods based on camera calibration.
Method Advantage Shortcoming
Zhang's calibration [65] (1) High precision
(2) Easy to use
(3) Scalability
(4) Open source code		 (1) Higher requirements on the calibration board
(2) There are more requirements for calibration images
(3) High requirements for computing resources
(4) Strong assumptions about the distortion model
Tsai's calibration [66] (1) High precision
(2) Scalability
(3) Intuitive mathematical model
(4) Wide application		 (1) Higher requirements on the calibration board
(2) A large number of calibration images are required
(3) High requirements for computing resources
(4) Strong assumptions about the camera model
Direct Linear Transform (DLT) [67] (1) Simple and easy to implement
(2) Wide application range
(3) Scalability
(4) Based on geometric relationship		 (1) Higher requirements for calibration data
(2) Sensitive to noise and errors
(3) Restrictions on the distortion model
(4) Does not consider the distribution of camera parameters
Bouguet's stereo calibration [68] (1) High precision
(2) Scalability
(3) Comprehensive multiple calibration parameters
(4) Open source code		 (1) Higher requirements on the calibration board
(2) A large number of calibration images are required.
Extended Calibration Method [69] (1) High precision
(2) Polynomial distortion model
(3) Adaptive optimization
(4) Scalability		 (1) Complex calculation and data processing
(2) Higher requirements for calibration boards and images
(3) Complicated calibration process
(4) Calibration accuracy is limited
Table 3. The advantages and disadvantages of commonly used machine vision pose measurement methods based on global calibration.
Table 3. The advantages and disadvantages of commonly used machine vision pose measurement methods based on global calibration.
Method Advantage Shortcoming
Multi-Camera Calibration [80] (1) Accurate camera alignment
(2) 3D reconstruction and stereo vision
(3) Flexible multi-camera configuration
(4) Wide application		 (1) The calibration process is complicated
(2) A large amount of calibration data is required
(3) Higher requirements for calibration boards and images
(4) High computational complexity
Camera-Laser Calibration [81] (1) High precision
(2) Non-contact calibration
(3) Real-time
(4) Scalability		 (1) High equipment requirements
(2) The calibration device is complex
(3) Higher requirements on the scene
(4) Affected by environmental factors
Camera-Inertial Measurement Unit [82] (1) High-precision attitude estimation
(2) Real-time
(3) Environmental adaptability
(4) Multiple applications		 (1) Cumulative error
(2) Sensing range limitation
(3) Equipment complexity and cost
Multi-Sensor Fusion Calibration [83] (1) High precision and accuracy
(2) Diversity and redundancy
(3) Environmental adaptability
(4) Wide application		 (1) Computational complexity
(2) Data inconsistency
(3) Sensor selection and configuration
(4) Calibration data requirements
Table 4. The advantages and disadvantages of commonly used vision pose parameter estimation.
Table 4. The advantages and disadvantages of commonly used vision pose parameter estimation.
Method Advantage Shortcoming

Perspective-n-Point [93]		 (1) Efficiency
(2) High accuracy
(3) Does not depend on the scene structure
(4) Suitable for various camera configurations		 (1) Sensitive to noise and mismatch
(2) Sub-pixel precision limitation
(3) Complex scene challenges
(4) Lack of scale information
Direct Methods [94] (1) High precision
(2) Global consistency
(3) Real-time
(4) Scale consistency		 (1) Robustness challenges
(2) Computational complexity
(3) Memory requirements
(4) Limited by texture
Filtering Methods [95] (1) Robustness
(2) Data association
(3) System modeling
(4) State estimation		 (1) Computational complexity
(2) Data association problem
(3) Accumulation of errors
(4) Selection of parameters
Optical Flow Methods [96] (1) Motion continuity
(2) Speed estimation
(3) Real-time
(4) No need for feature points		 (1) Lighting changes
(2) Occlusion problem
(3) Multi-scale problem
(4) Cumulative error
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated