Prerpints.org logo
Preprint
Article

Research on Formation Pressure Prediction Method for Ultra-Deep Tight Sandstone Based on Collocated Cokriging

Altmetrics

Downloads

114

Views

16

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

29 May 2023

Posted:

31 May 2023

You are already at the latest version

Alerts
Abstract
Comparison with conventional reservoirs, the prediction of pressure in ultra-deep tight sandstone formations is difficult. The prediction of seismic pressure is more challenging than well logging pressure prediction. The main methods for seismic pressure prediction include equivalent depth method, Eaton method, Fillippone formula, and its modified versions. Among them, the Eaton method is widely used and has good effectiveness. However, this method relies on difficult-to-obtain normal compaction trend line, which leads to low prediction accuracy in space. To address this issue, a method combining the Eaton method and Collocated cokriging is proposed. The Eaton formula is used to predict formation pressure at the well, with compressional wave velocity as the covariate for predicting the main variable, formation pressure. By simulating the shear wave velocity based on seismic compressional wave velocity, the influence of various parameters on the prediction results is analyzed, and the accuracy of this method is verified by comparing it with other methods. The proposed method is then applied to predict formation pressure in the ultra-deep formations of the Junggar Basin. The simulation results show that the Collocated cokriging method achieves higher planar accuracy and better matches the experimental expectations in terms of prediction results. The application results also demonstrate the scientific effectiveness of the combined method, which has achieved good results in practical production applications.
Keywords: 
Subject: Environmental and Earth Sciences  -   Geophysics and Geology

1. Introduction

In the process of petroleum exploration and development, accurate prediction of formation pressure has always been an extremely important aspect. In the petroleum industry, there are many methods used to predict formation pressure, which can be broadly divided into two categories: pre-drilling prediction based on seismic exploration data and post-drilling detection using well logging data.
Currently, in China, the seismic layer velocity obtained from seismic exploration and the logging data obtained after drilling are commonly used as the basis for establishing a system that can quickly understand the geological environment at the drilling site [1]. However, research on how to predict formation pressure more accurately has been conducted both domestically and internationally. In terms of well logging, Zhao, et al. [2] improved the prediction accuracy by using cluster analysis to separate shale from other lithologies and obtain normal trend line velocities. Xie, et al. [3] effectively calculated formation pore pressure by combining dipole sonic and other conventional well logging data, achieving good application results. Li, et al. [4] found that the Dc index method and the time difference of sonic waves are suitable for calculating formation pressure in Block A of the Bohai Sea, with a maximum error of 5%, which meets engineering requirements and is of practical significance for on-site drilling operations. Fan, et al. [5] proposed and modified a formation pressure prediction model based on the Eaton method, taking into account the geological influences of the actual area. They established three pressure profiles for the formations in that area, providing important support for subsequent drilling. In terms of seismic exploration, pre-drilling pressure prediction mainly involves calculating formation pore pressure using seismic layer velocity data. Wang, et al. [6] introduced the effective stress principle in porous media to develop a new method for calculating pore fluid pressure in unconventional reservoirs, achieving good application results. Zhang, et al. [7] used the DIX formula to obtain layer velocities based on velocity spectrum data and predicted formation pressure using seismic layer velocities. Yang, et al. [8] combined seismic and well logging data to establish pressure prediction profiles for deep formations and conducted in-depth analysis of the drilling geological conditions in the study area. Ma [9] used an improved Fillippone method to predict formation pressure ahead of the drill bit, and the results showed that the method is scientifically effective and meets the requirements of actual field applications. Qian, et al. [10] applied the equivalent medium theory to determine the upper and lower limits of rock velocities in the Fillippone formula, obtaining more reasonable estimation results. So far, the methods for predicting formation pressure based on seismic data can be broadly classified into two categories. One category relies on seismic velocity spectrum data and uses the Fillippone formula and its modified versions to predict formation pressure. The advantage is the ability to establish the spatial distribution of formation pressure in the underground three-dimensional space. However, this method relies on seismic layer velocities, which are often difficult to obtain accurately. Moreover, when predicting formation pressure, it requires the establishment of an empirical equation between velocity and pressure, resulting in insufficient prediction accuracy of formation pressure in the entire three-dimensional space. The other category involves predicting formation pressure using seismic data under well constraints, including the equivalent depth method and the Eaton formula [11]. The advantage of using sonic time difference to predict formation pressure at the well is its high accuracy. However, this method relies on normal compaction trend line, and the relationship between compaction trend line and well spatial positions varies, leading to a decrease in the accuracy of predicting formation pressure in spatial terms.
In recent years, the introduction of geostatistical stochastic simulation methods has provided effective tools for reservoir prediction. In particular, the Collocated cokriging has strong advantages in integrating well logging information and effectively utilizing precise well location data. Gao [12] used three different kriging methods to interpolate the sandstone formation in Yuncheng City. The fitting effect of the exponential model in the variogram fitting was the best, and the results showed that the ordinary kriging method could more accurately reflect the spatial distribution of sandstone formation elevation in Yuncheng City. Ma, et al. [13] combined functional data analysis and kriging interpolation techniques to improve the accuracy and reliability of oil and gas well productivity prediction. Li et al. [14] addressed the “banding effect” that occurs during kriging interpolation by using distance constraint to correct the weights obtained from kriging estimation, making the kriging interpolation method more stable. However, whether it is simple kriging or ordinary kriging, the interpolation effect decreases rapidly when the data points are sparse, and the interpolated results do not meet expectations. Cokriging technology has wider applications. Under the constraint of secondary data that has a certain correlation with the primary data, it conducts collaborative simulation on a small amount of sparse and irregularly distributed primary data, and the simulation results are similar to the spatial distribution pattern of the secondary data. Wang, et al. [15] used Cokriging interpolation to predict the spatial distribution trend of low-pressure pipeline networks in suburban and rural areas. The results showed that the prediction model performed well, with average error and root mean square error within the acceptable range. Du, et al. [16] used Cokriging method to predict coal seam thickness, and the results showed that the method was effective, with small errors and improved accuracy. Geng, et al. [17] applied Cokriging method to three-dimensional inversion of gravity gradient tensor data, reducing the ambiguity of inversion and improving the resolution of inversion results. Yu, et al. [18] proposed a cokriging porosity prediction method under facies control based on Cokriging. Through comparative analysis, the estimated results had smaller errors and the predicted results were more realistic. However, cokriging is relatively complex in computation, with a large amount of calculation, and the actual values of primary data at the same location cannot be consistent, which limits the development environment of cokriging. Collocated cokriging technique simplifies the complexity of cokriging in computation and matches well with the known data points and actual parameters. Chen, et al. [19] integrated seismic, well logging, geological, and other information to predict the distribution and variation of channel sand bodies using collocated cokriging, achieving significant improvement in prediction accuracy compared to traditional methods. Wang, et al. [20] improved the prediction accuracy of seismic inversion by combining collocated cokriging method to effectively utilize information from horizontal sections. Zhang, et al. [21] applied sequential Gaussian collocated cokriging method to predict reservoirs by incorporating other seismic parameter data, demonstrating high prediction accuracy and effective reduction of drilling risks. Niu, et al. [22] estimated the variogram function by filtering the expected values of co-variates using primary variable observations, and proposed and derived a new collocated cokriging method.
Considering the above research status, the Eaton formula method is widely used and has high accuracy. However, its predictive accuracy is not high in entire spatial domain. Geostatistical stochastic simulation methods, including the collocated cokriging method, serve as effective tools to improve accuracy by integrating well logging information in spatial analysis. Combining the Eaton formula method with the isochronous co-simulation kriging method is expected to enhance the accuracy of formation pressure prediction in the plane. Numerical simulations of seismic P-wave and S-wave velocities are conducted to analyze the experimental variogram of P-wave velocity and fit it using a spherical model. Anisotropy of the formation is considered, and elliptical anisotropic model is established to make the simulation results better match the actual formation. By comparing with simple kriging and cokriging methods, the accuracy of the collocated cokriging method is validated. The effects of range, azimuth, and number of reference points on the simulation results are analyzed, and appropriate parameters are selected. Finally, the Eaton formula method combined with the collocated cokriging method is applied to predict formation pressure in the ultra-deep rock formations of the Junggar Basin.

2. Principle and Process of Formation Pressure Prediction Based on Collocated Cokriging

2.1. Principle of Formation Pressure Prediction

The Eaton method predicts formation pressure by establishing a normal compaction trend line. The calculation formula is as follows:
P p = P o b − ( P o b − P h ) ( V V n ) N
In the above, P p represents formation pressure; P o b represents overburden pressure; P h represents normal hydrostatic pressure; V represents actual formation velocity, which is obtained from sonic log data or stacking velocity; V n represents the normal trend line velocity, mainly obtained by fitting the velocity of mudstone; N represents the Eaton index, which is a coefficient related to the formation. The value of the Eaton index varies for different geological periods and regions.
In the formula, P h hydrostatic pressure increases with the increase of depth; at the same depth, its value increases with the increase in formation water density:
P h = ∫ 0 D 0 ρ ( z ) g d D
In the formula, P o b overburden pressure is an important factor in generating underground pressure. Its driving force is mainly a combination of sedimentary and compaction effects of the formation. This pressure is a fundamental parameter in the process of predicting formation pressure. In the detection of formation pressure, its value is determined first.
G o i = ρ ω h ω + ρ 0 h 0 + ∑ i = 1 n ρ b i Δ h h ω + h 0 + ∑ i = 0 n Δ h i  
In the formula, G o i represents the gradient of overburden pressure at a certain depth; ρ ω represents seawater density; h ω represents seawater depth; ρ 0 represents the average density of the upper density-free logging formation section; h 0 represents the thickness of the upper density-free logging formation section; ρ b i represents density scatter data at a certain depth; h i represents depth interval. The calculation of overburden pressure involves multiple data and is a tedious process.

2.2. Cokriging Principle

When there are two or more characteristic parameters in the interpolation area, and there is a significant correlation between the main variable and covariates to be interpolated within that area, Co-Kriging method can be used. This method belongs to multivariate geostatistics and involves analyzing multiple parameters in the study area, studying the linear and nonlinear relationships between these parameters, and understanding the spatial differences of different parameters to achieve a certain level of precision in estimating the main variable.
The Cokriging estimation is formulated as follows:
Z * ( u 0 ) = ∑ i = 1 n λ z i Z ( u z i ) + ∑ k = 1 m λ y k Y ( u y k )
In the equation, Z * ( u 0 ) represents the estimated value at the estimation point u 0 ; Z ( u z i ) represents the actual attribute value of the main variable at point u z i ; Y ( u y k ) represents the actual attribute value of the covariate at point u y k ; λ z i and λ y k are the weight coefficients corresponding to the main variable and covariate, respectively.
The Co-Kriging estimation is defined as a linear combination of available samples. Similar to ordinary Kriging, Co-Kriging estimation requires unbiasedness and minimum error variance.
E [ Z ( u 0 ) − Z * ( u 0 ) ] = 0
V a r [ Z ( u 0 ) − Z * ( u 0 ) ] = min
By incorporating the minimum variance condition with weight constraints, each considered random variable introduces Lagrange multipliers during the minimization process. By taking partial derivatives of each weight λ z i , λ x j , and λ y k and setting the results to zero, the minimum variance can be determined. After expanding and processing the variance, derivative calculations yield the Cokriging equations:
∑ i = 1 n λ z i C z z Z ( u z i ) , Z ( u I ) + + ∑ k = 1 m λ y k C z y Y ( u y k ) , Z ( u I ) + ξ 1 = C z z Z ( u 0 ) − Z ( u I ) Ι = 1 , 2 , … n
∑ i = 1 n λ z i C z y Z ( u x i ) , Y ( u K ) + ∑ k = 1 m λ y k C y y Y ( u y k ) , Y ( u K ) + ξ 2 = C z y Z ( u 0 ) − Y ( u K ) Κ = 1 , 2 , … m
∑ i = 1 n λ z i = 1 ； ∑ k = 1 m λ y k = 0
In the equations, C z z represents the auto-covariance of the main variable; C y y represents the auto-covariance of the covariate; C z y represents the cross-covariance between the main variable and covariate. ξ 1 and ξ 2 are Lagrange factors.
The covariance function can be obtained from the variogram function, but calculating the cross-covariance or cross-variogram requires a significant amount of computation and involves complex derivation, which severely reduces the interpolation efficiency of Co-Kriging. Even if the cross-variogram function is obtained, solving the equations can lead to a singular, resulting in situations where the estimation point has no solution.

2.3. Collocated Cokriging Principle

Collocated cokriging is a simplified form of Cokriging that greatly reduces the computational burden on the equation system. In Cokriging, a considerable number of covariates need to be selected for calculation. However, collocated cokriging only requires the covariates at the same positions as the estimation point. The covariates around the estimation point will be masked by the covariance in the same position. This also requires that there are corresponding covariates for each estimation location.
In collocated cokriging, only three functions are needed: the auto-covariance function of the main variable, the cross-covariance function between the main variable and covariates, and the latter can be derived from the Markov model, significantly improving the computational speed of collocated cokriging.
The estimation value in collocated cokriging is given by the equation:
Z * ( u 0 ) = ∑ i = 1 n λ x i Z ( u x i ) + β 1 X u 0
In the equation, Z * ( u 0 ) represents the estimated value at the estimation point u 0 , and Z ( u z i ) represents the actual attribute value of the main variable at point u z i . Since there is only one secondary data used for calculation, the weight for the secondary data has only one value.
Then, by incorporating the condition of unbiasedness and minimum error variance:
E [ Z ( u 0 ) − Z * ( u 0 ) ] = 0
V a r [ Z ( u 0 ) − Z * ( u 0 ) ] = min
A series of mathematical operations lead to the collocated cokriging equation matrix:
C z z ( u x 1 , u x 1 ) ⋯ C z z ( u x 1 , u x n ) C z x ( u x 1 , u 0 ) 1 ⋮ ⋮ ⋮ 1 C z z ( u x n , u x 1 ) ⋯ C z z ( u x n , u x n ) C z x ( u x n , u 0 ) 1 C x z ( u u 0 , u x 1 ) ⋯ C x z ( u 0 , u x n ) C x x ( u 0 , u 0 ) 1 1 ⋯ 1 1 0 × λ x 1 ⋮ λ x n β 1 μ = C z z ( μ 0 , μ x 1 )                 ⋮ C z z ( μ 0 , μ x n ) C z x ( μ 0 , μ 0 )                 1

2.4. Workflow of Collocated Cokriging Method for Prediction

The Eaton method is used to calculate the formation pressure at well locations. In collocated cokriging, the assumption is that the variogram function of the secondary variable is the same as that of the primary variable. Therefore, only fitting the secondary variable is required. A spherical model is used for fitting, and the parameters are obtained using the least squares method to determine the range. An elliptical model is established to improve the interpolation accuracy. The covariance and cross-covariance functions of the primary and secondary variables are calculated using the variogram function. A certain number of primary data points are selected around the estimation point, and their weights, along with the weights of the corresponding secondary data points, are obtained by solving the equation matrix for estimation.
Preprints 75020 g001
Figure 1. Collocated Cokriging Prediction Process Diagram.
Figure 1. Collocated Cokriging Prediction Process Diagram.
Preprints 75020 g001

3. Data Overview and Numerical Simulation of collocated cokriging Method

3.1. Fitting Experimental Model Variogram Functions

In a certain oilfield work area, seismic data for compressional wave velocity (Vp) and shear wave velocity (Vs) are available. The numerical simulation uses Vp as the covariate to constrain the interpolation of the main variable, Vs. To simulate the distribution of actual well points, six randomly sampled data points of Vs are chosen as the primary data, as shown in Figure 2.
The Markov MM1 model assumes that the covariance function of the covariate is the same as that of the primary data, so only the experimental variogram function of the covariate needs to be discussed. Variogram functions exhibit directional characteristics in anisotropic media, with the azimuth of the variogram function being consistent with its opposite direction. An angle tolerance of 30° is chosen, and the variogram functions of the covariate in the six directions on the plane are analyzed within 30° intervals, as shown in Figure 3. The length of the range is defined in terms of the number of grid cells, and this definition size is used for all ranges in the experimental model.
From the experimental variogram function graph (Figure 3) and the fitted range ellipse graph (Figure 4), it can be observed that the maximum range occurs in the northeast-southwest direction (21°) and is equal to 71.704 grid units in length. This direction represents the maximum extension of the compressional wave velocity, indicating good continuity of the compressional wave velocity in that direction.
Figure 4 is the ellipse variogram function graph on the plane of the compressional wave velocity. From this function, it can be observed that the variogram function structure type within the work area is an ellipse model. The maximum range in all directions is 71.704 grid units in length, with an azimuth of 21°. The minimum range is 36.872 grid units in length, with an azimuth of 111°. The ratio of the short axis to the long axis of the range ellipse is approximately 0.514, indicating a strong directional distribution of compressional wave velocity Vp within the work area, and its distribution on the plane is not uniform.
After determining the range size and direction, with the maximum range being 71.704 grid units and the minimum range being 36.872, and the direction being 21°, the variogram function of the covariate is established using the range ellipse model. According to the assumption of the Markov MM1 model:
ρ y ( h ) = ρ z ( h ) ρ z y ( h ) = ρ z y ( 0 ) ⋅ ρ z ( h )
where ρ z ( h ) and ρ y ( h ) are the standardized autocovariance functions or autocorrelation plots of the main and covariate variables, ρ z y ( h ) is the cross-covariance function or cross-correlation plot between the main and covariate variables, and ρ z y ( 0 ) is the linear correlation coefficient derived from the co-located main and covariate variables.
The MMI model does not require the covariance function of the covariate variable because of the following assumptions:
It is assumed that ρ z y ( h ) and ρ z ( h ) have the same shape and continuity, and by adjusting the covariate variable y(u) with the main variable z(u) located at the same position, the influence of any more distant main variables can be eliminated. If z(u) is defined on the same or larger volume than y(u), then MM1 is a reasonable model.

3.2. Kriging Method Selection

In the case of limited primary data points, the simple kriging, cokriging, and collocated cokriging methods are sequentially applied to simulate and predict the S-wave velocity, as shown in Figure 5. The simple kriging method only uses the primary variable in the interpolation process, and since no secondary data is used, the predicted distribution map generated by simple kriging has limited practical reference value in the current situation. When introducing secondary data with certain correlation coefficients, the predicted distribution map simulated by cokriging approximately aligns with the spatial distribution of the secondary data. The influence of the primary data on the estimated values in the surrounding area is limited, and the predicted distribution map is mostly determined by the secondary data. On one hand, the scarcity of primary data points results in a limited influence range. On the other hand, because the prediction grid is based on the distribution of secondary data, when searching for data points around the estimated point, the secondary data points are closer and more densely distributed. According to the variogram function model, the closer the lag distance, the larger the covariance value. Therefore, in the process of solving the equation system, the weights corresponding to the secondary data are larger, which leads to the dominance of the secondary data in the prediction when the primary data points are relatively sparse. The predicted results of collocated cokriging show a spatial distribution that is roughly consistent with the distribution of the secondary data. However, compared to cokriging, the weight of the secondary data in collocated cokriging depends on the correlation coefficient between the primary and secondary data, and the influence of the primary data on the estimated values in the surrounding area is enhanced, while still preserving the information from the primary data.
In comparing the three kriging methods, it is found that simple kriging has limited practical reference value when interpolating with few data points. When the number of primary data points is small and the secondary data is densely distributed, cokriging relies more on the secondary data, with less influence from the primary data during interpolation. Collocated cokriging only uses the secondary data located at the same position as the estimated point, and the calculated weights are dependent on the correlation coefficients. Cokriging requires a significant amount of computation in calculating the cross-covariance or cross-variogram functions, and its computational efficiency is significantly slower compared to collocated cokriging.

3.3. Parameter Optimization for Collocated Cokriging

The variogram function is an important input parameter in the collocated cokriging method, and therefore, the characteristic parameters of the variogram function will inevitably have certain effects on the results.

3.3.1. Influence of Range on Experimental Results

Figure 6 shows the impact of range variation on simulated predictions. Since an elliptical variogram model is established, two ranges in different directions are needed to correspond to the major and minor axes of the ellipse, reflecting the elliptical influence of the primary data points on the surrounding data in the prediction. Decreasing the range reduces the affected area by the primary data, while increasing the range expands its influence. The magnitude of the range represents the extent of the influence of the primary data points. When there is a strong correlation between the primary and secondary data, the strong correlation weakens the influence of the primary data on the surrounding estimated points. Strong correlation plays an important role in collocated cokriging, and it can weaken the influence of fewer primary data points.

3.3.2. Influence of Anisotropy on Experimental Results

Anisotropy includes azimuth and anisotropy ratio. The azimuth is based on the positive direction of the X-axis, rotating clockwise as the positive direction. Changing the azimuth to 0°, 60°, and 120°, the collocated cokriging is simulated for the primary data. When different azimuths are set, the simulated prediction distribution map shows evident directional characteristics around the existing primary data points, and the data outside the range, i.e., beyond the influence of the primary data, is not significantly affected by the primary data. Similar to the range, when there is a strong correlation between the primary and secondary data, the strong correlation weakens the influence of the primary data on the estimated points within the range.

3.3.3. Influence of Number of Conditioning Points on Experimental Results

In the simulation experiment, if there are too many conditioning points involved in the estimation, it will result in complex calculations for the equation matrix, severely affecting the execution speed of the algorithm. On the other hand, a certain number of conditioning points are needed for the estimation, as an insufficient number of conditioning points will lead to interpolated results that do not reflect the true distribution of reservoir parameters. Therefore, the selection of the number of conditioning points is crucial.
In the simulation experiment, the primary and secondary data have a strong correlation. To better illustrate the influence of the number of conditioning points on the results, the same set of data is used, and the correlation coefficient between the primary and secondary data is artificially changed. The collocated cokriging simulation experiments under different numbers of conditioning points are shown in Figure 8. When performing interpolation on the estimated points using collocated cokriging, only the surrounding primary data points are considered. From the images, it can be observed that when there are too few primary data points involved in the estimation, the interpolated images have distinct abrupt boundaries. On one hand, this is due to the scarcity and uneven distribution of primary data points; on the other hand, the significant differences in parameter values among different primary data points lead to large variations between different regions. Therefore, the number of conditioning points should be reasonably selected based on the actual situation.

4. Pressure Prediction of Actual Strata

The Eaton formula was originally established as an empirical relationship based on data from the Gulf of Mexico region and remains the most widely used method for predicting pore pressure in practical applications. This method establishes a normal compaction trend line based on consolidation theory, effective stress theory, and equilibrium theory. It predicts strata pressure by establishing a relationship between formation pressure and acoustic time difference.
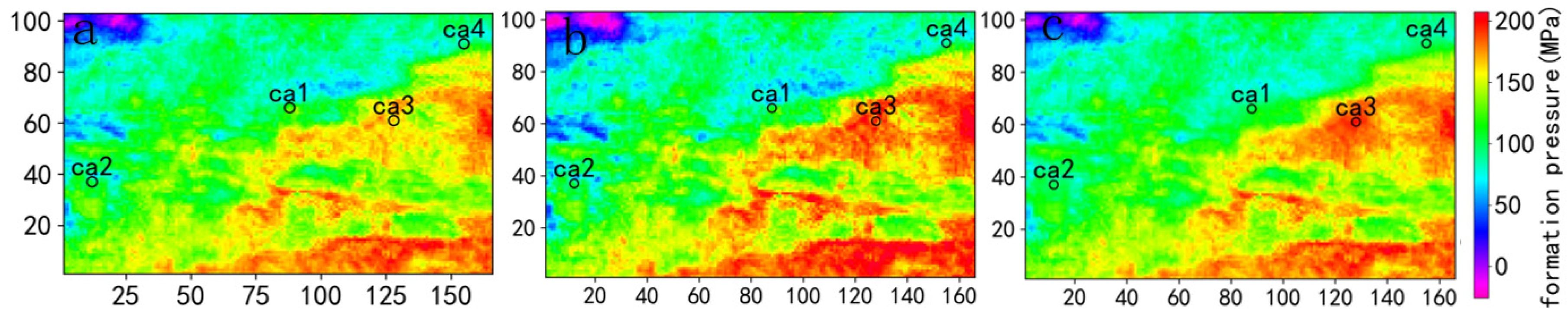
In the ultra-deep rock formations of the Junggar Basin, the well points are distributed within the measured compressional wave velocity region, namely ca1, ca2, ca3, and ca4. The exponent N in the Eaton formula varies in different regions, and multiple trial calculations have shown that an N value of 5.0 is more suitable for the work area. The normal acoustic time difference is calculated using the fitted trend of normal acoustic time difference from wells ca1, ca2, ca3, and ca4. The formation pressures at the same depth calculated by the Eaton formula for these wells are 98.761 MPa, 99.372 MPa, 93.12 MPa, and 98.714 MPa, respectively. Figure 9 shows the overburden pressure, hydrostatic pressure, and formation pressure at the same depth for well ca2 calculated using the Eaton formula.
In the actual calculation process, calculating the formation pressure for individual wells is cumbersome, and obtaining the normal compaction velocity is not straightforward. Analyzing the Eaton formula reveals that there is a certain relationship between formation pressure and measured velocity, and the calculated formation pressure from the Eaton formula and the measured compressional wave velocity exhibit a linear correlation with a correlation coefficient of 0.8034. Therefore, collocated cokriging and ordinary cokriging are simultaneously used to predict formation pressure.
Analyzing Figure 10 shows that, consistent with the results of simulation testing, using fewer primary data points for cokriging interpolation aligns more with the distribution trend of secondary data, but it fails to match the existing data at known point locations, resulting in the loss of existing data. On the other hand, collocated cokriging, while maintaining the existing data, assigns appropriate weights to surrounding data points, resulting in predicted results that better align with expectations. Compared to the Eaton formula for predicting formation pressure, which inevitably introduces errors in the process of obtaining normal compaction velocity, the collocated cokriging method predicts formation pressure using measured layer velocities that have a certain correlation with formation pressure, thereby avoiding the difficulty of obtaining normal compaction velocity.

5. Conclusions

  • The numerical simulation prediction results show that among different kriging methods, collocated cokriging method, while ensuring the known data, effectively utilizes secondary data for plane prediction, resulting in prediction results that better align with experimental expectations.
  • The calculation and fitting of the variogram function directly affect the prediction results. When performing calculations, geological knowledge should be considered, appropriate models should be selected, and relevant parameters should be obtained reasonably to avoid using variogram functions that do not match the reality, thereby reducing errors.
  • Combining the Eaton formula with the collocated cokriging method for predicting formation pressure demonstrates feasibility. This method can be combined with seismic data, and the predicted results align with expectations, providing guidance for exploration and development in actual work areas.

References

  1. Zu, F., Zhang Z.L, Feng Q.H; et al. ABNORMAL FORMATION PRESSURE MONITORING AND PREDICTING METHOD. Oil Drilling & Production Technology 2004, 26, 035–038. [CrossRef]
  2. Zhao M., Wei C.J., Wang S.H. Algorithm Research and Realization of Formation Pressure Prediction Based on Eaton Method. Journal of Qingdao university (Natural Science Edition) 2017, 30, 86–88.
  3. Xie Y., Li X.Y., Zhai Y.. Establishing formation pressure profiles and guiding adjacent wells balanced drilling in new area by logging data. Petroleum Instruments, 2011, 25, 46–48.
  4. Li H., Yu Z.T., Yuan H.S., He P.F.. Application of formation pressure prediction technology in drilling in Bozhong A block. Petrochemical Industry Application, 2018, 37, 33–36.
  5. Fan X.Z., Li X., Wu Y.C.; et al. A formation pressure prediction method for well drilling in the Arctic permafrost region. Natural Gas Industry 2022, 42, 99–105.
  6. Wang B., Yong X.S., Pan J.G., Yin L., Xu D.N., Kong X., Qu J.H., Tan K.J., Huang Y.. A new method to predecit pore pressure in low permeability reservoirs and its application. Progress in Geophysics, 2015, 30, 695–699. [CrossRef]
  7. Zhang Q., Zhi Y.P.. Applying Seismic Velocity to Predicting Formation Pressure. Chinese Journal Of Engineering Geophysics, 2015, 30, 695–699. [CrossRef]
  8. Yang H., Zhou P.G., Sun W.G., Shi J.G., Chen W.F.. Using Seismic Data to Predict Formation Pressure in Piedmont Structures at the Southern Margin of Junggar Basin. Xinjiang Petroleum Geology 2017, 38, 347–351.
  9. Ma, H. Pore Pressure Prediction with Seismic Interval Velocity by the Modified Fillippone Method. Petroleum Drilling Techniques 2012, 40, 56–61. [Google Scholar] [CrossRef]
  10. Qian L.P., Wang X., Li F., LI J.H., Wang J., Qu Y.W.. Formation pore pressure prediction using Fillipone formula combined with equivalent medium theory. Oil Geophysical Prospecting, 2018, 53, 224–229.
  11. Shi M.X., Liu Z.D., Yang X.F., Yang J.R., Chen X.J., Liu H.Z., Cao J.L.. Review and prospect prediction technology for formation pore pressure by geophysical well logging. Progress in Geophysics 2020, 35, 1845–1853. [CrossRef]
  12. Gao, R.n. Study on Sandstone Distribution in Yuncheng Based on Geostatistics. Shanxi Science Technology 2020, 35, 37–41. [Google Scholar]
  13. Ma W.L., Deng S.Z.. Application of Functional Kriging on the Well Productivity Prediction. Inner Mongolia Petrochemical Industry, 2021, 47, 92–96.
  14. Li S.H., Wang Y.B., Li J., Liu X.T., Wang J., Gong W.Q.. Correcting the string effect of Kriging. OGP 2012, 47, 978–983.
  15. Wang C.Y., Qu Y., Shuai Y.M.. Prediction of the Spatial Distribution of Gas Pipe Network Using Cokriging Method Based on ArcGIS Technologies. Geomatics & Spatial information technology, 2022, 45, 28–32.
  16. Du W.F., Peng S.P.. COALSEAM THICKNESS PREDICTION WITH GEOSTATISTICS. Chinese Journal of Rock Mechanics and Engineering, 2010, 29, 2762–2767.
  17. Geng M.X., Huang D.N., Yu P., Yang Q.J.. Three-dimensional constrained inversion of full tensor gradiometer data based on cokriging method. Chinese Journal of Geophysics (in Chinese), 2016, 59, 1849–1860. [CrossRef]
  18. Yu, Z.J., Dong D.D., Song W.Q., Gao Y.K., Wu S.G.. Porosity prediction with co-Kriging method controlled by sedimentary facies. Progress in Geophysics, 2012, 1581-1587. [CrossRef]
  19. Chen, J.Y., Yu X.H., Li S.L., Hou G.W.. Application and Method of Predicting Reservoir by Collocated Seismic Attributes. Inner Mongolia Petrochemical Industry, 2007, 1-3.
  20. Wang D.D., Yang X.F., Zhou Y.B., Ma Z.Z., Liu Y.M.. Improving the accuracy of seismic inversion using the horizontal well data. Progress in Geophysics, 2019, 34, 185–190. [CrossRef]
  21. Zhang S.P., Yu X.H.. THE APPLICATION OF COLLOCATED CO-KRIGING STOCHASTIC MODELING IN RESERVOIR DESCRIPTION. Natural Gas Geoscience, 2006, 17, 378–381.
  22. Niu W.J., Meng X.H., Li J.G.. A new estimation method of collocated CoKing combined with soft data. COAL GEOLOGY & EXPLORATION, 2011, 39, 13–17. [CrossRef]
Preprints 75020 g002
Figure 2. Distribution map of Vp (a), Vs (b), and primary data (c).
Figure 2. Distribution map of Vp (a), Vs (b), and primary data (c).
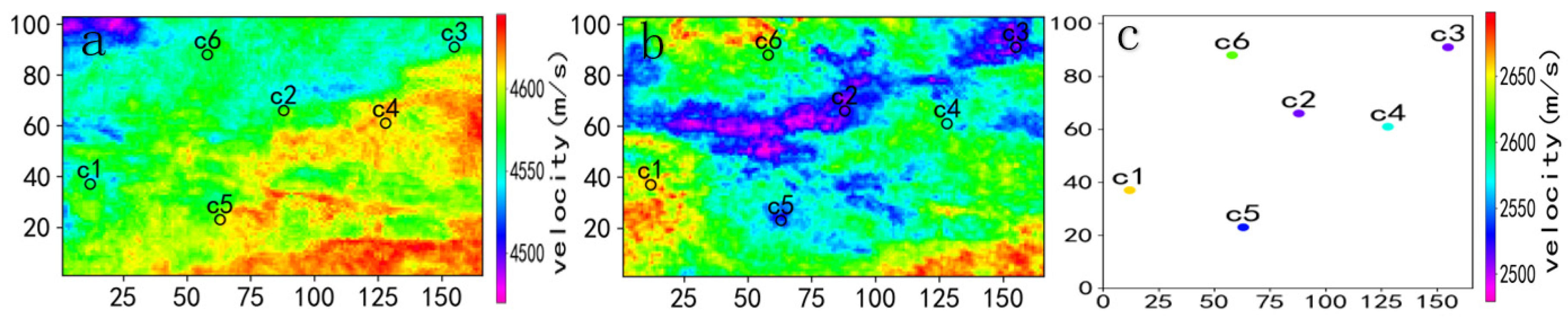
Preprints 75020 g002
Preprints 75020 g003
Figure 3. Experimental variogram of Vp in six directions.
Figure 3. Experimental variogram of Vp in six directions.
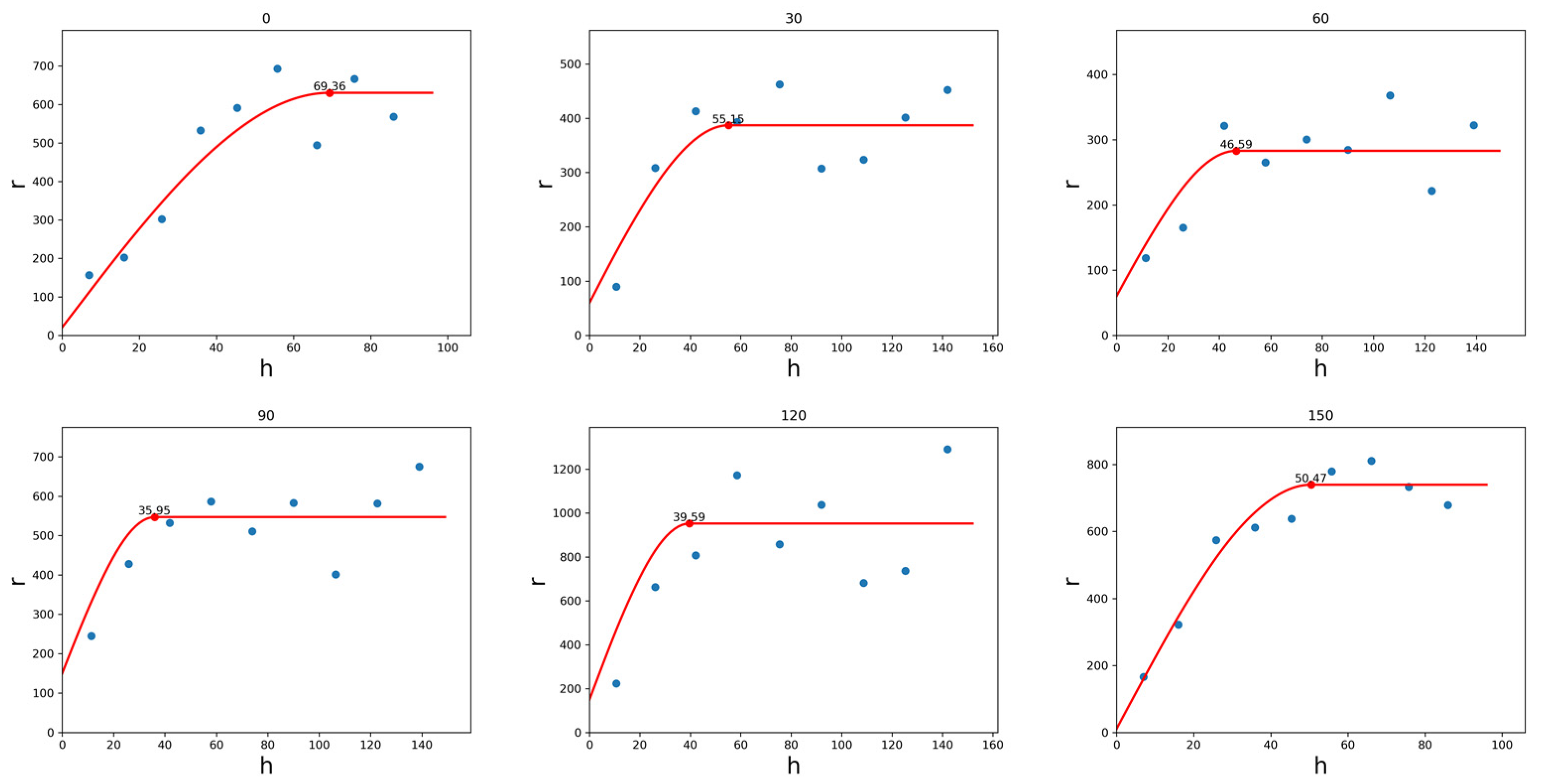
Preprints 75020 g003
Preprints 75020 g004
Figure 4. Elliptic variogram.
Figure 4. Elliptic variogram.
Preprints 75020 g004
Preprints 75020 g005
Figure 5. Simulated prediction maps using simple kriging (a), cokriging (b), and collocated cokriging (c) (red circles indicate the locations of the primary data points).
Figure 5. Simulated prediction maps using simple kriging (a), cokriging (b), and collocated cokriging (c) (red circles indicate the locations of the primary data points).
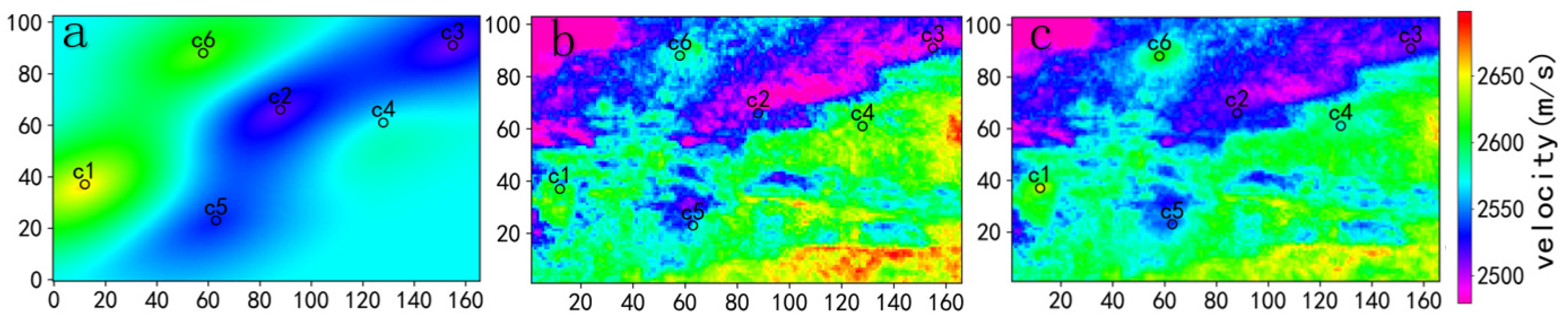
Preprints 75020 g005
Preprints 75020 g006
Figure 6. The maximum range and minimum range are 40 and 20 (a); 60 and 30 (b); 80 and 40 (c).
Figure 6. The maximum range and minimum range are 40 and 20 (a); 60 and 30 (b); 80 and 40 (c).
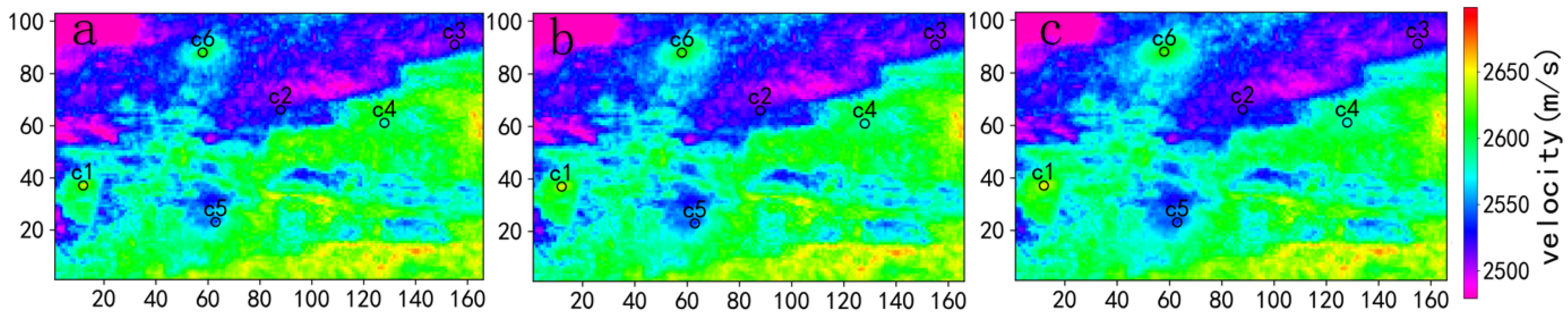
Preprints 75020 g006
Preprints 75020 g007
Figure 7. The angles are 0° (a), 60° (b), and 120° (c).
Figure 7. The angles are 0° (a), 60° (b), and 120° (c).
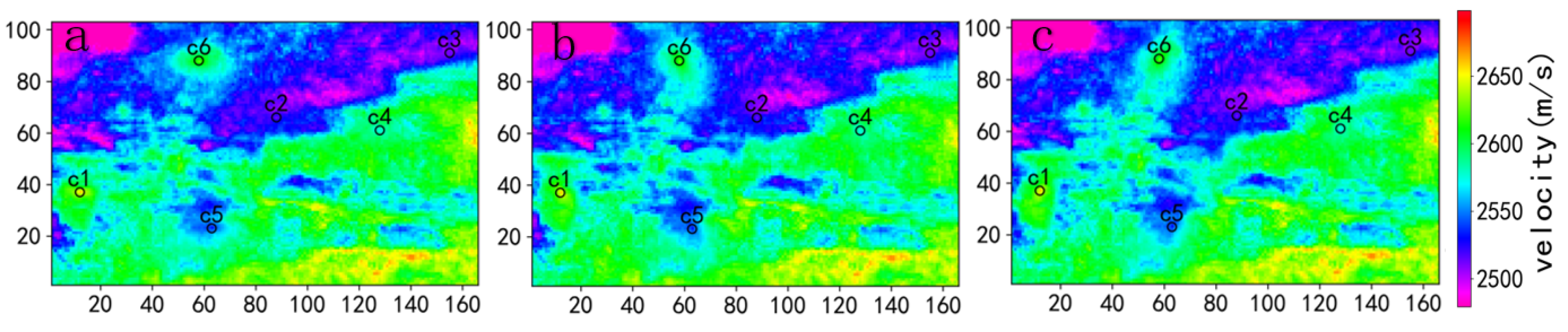
Preprints 75020 g007
Preprints 75020 g008
Figure 8. Number of conditioning points are 2 (a), 3 (b) and 4 (c).
Figure 8. Number of conditioning points are 2 (a), 3 (b) and 4 (c).
Preprints 75020 g008
Preprints 75020 g009
Figure 9. Formation pressure calculated by the Eaton formula for well ca2.
Figure 9. Formation pressure calculated by the Eaton formula for well ca2.
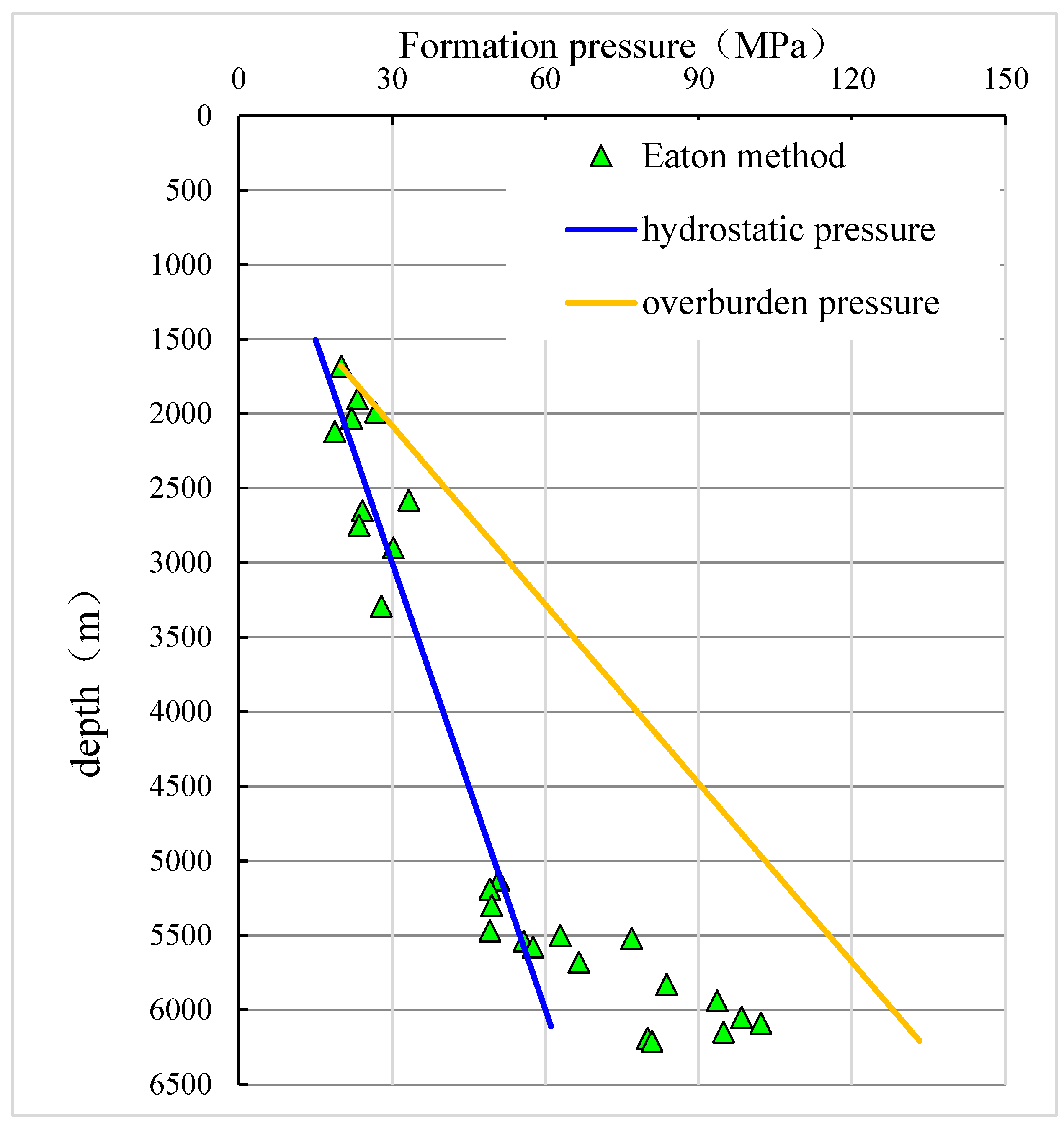
Preprints 75020 g009
Preprints 75020 g010
Figure 10. Well point distribution and vp distribution map (a), Formation pressure map is obtained by Cokriging method (b) and Collocated cokriging method (c).
Figure 10. Well point distribution and vp distribution map (a), Formation pressure map is obtained by Cokriging method (b) and Collocated cokriging method (c).
Preprints 75020 g010
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated