Prerpints.org logo
Preprint
Article

Predicting the Effect of Surface Waviness on Fatigue Life of a Wire + Arc Additive Manufactured Ti-6Al-4V Alloy

Altmetrics

Downloads

233

Views

79

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

29 May 2023

Posted:

31 May 2023

You are already at the latest version

Alerts
Abstract
This paper reports the effect of as-deposited surface condition on the fatigue strength in an additive manufactured titanium alloy Ti-6Al-4V (WAAM Ti64). First, local stress concentration caused by the surface waviness was quantified by a metrology technique followed by numerical modelling. Fatigue tests were conducted under bending load with the as-deposited surface being under tensile cyclic stress. The applicability of two predictive methods was studied and compared with the fatigue test results. The traditional notch stress method overestimated the fatigue strength by a factor of 1.5 at a given life; the poor agreement with the test is attributed to the crack propagation from the waviness being dominant in the bending test, i.e., the crack initiation stage was short, hence the local stress method is unsuitable. The fracture mechanics approach has delivered good predictions at every applied stress levels. The method treats a waviness trough as an initial crack. This approach is suitable for predicting the fatigue life in materials built by wire based directed energy deposition processes.
Keywords: 
Subject: Engineering  -   Aerospace Engineering

1. Introduction

Wire and arc additive manufacturing (WAAM) is a directed energy deposition (DED) AM process that is capable of producing near net shape and large scale metallic structures, at low manufacturing cost, high deposition rates and virtually no porosity defects in high strength titanium parts [1,2,3]. Amongst all the materials studied by WAAM and other AM processes, titanium alloy Ti6Al4V (Ti64) has been extensively studied because of its high manufacturing cost using conventional routes and its wider applications in the aerospace, biomedical and energy sectors [1,2,3]. When considered the mechanical properties, yield and ultimate tensile strengths of WAAM Ti64 are comparable with conventional wrought and considerably higher than the cast materials. Moreover, these properties meet the minimum requirements for tensile loads as outlined by ASTM F2924 for AM-built Ti64 [4]. However, WAAM Ti64 showed approximately 42% lower elongation at failure compared to its wrought counterpart due to presence of columnar grains as the result of repeated thermal cycles and fine α lath width due to faster cooling rates in AM processes [4]. Under cyclic loads, WAMM Ti64 has similar fatigue strength as wrought at 107 cycles and higher strength than the cast materials [4]. Despite the enormous advantages and comparable mechanical performance as the conventional materials, one of the remaining challenges faced by WAAM process is the poor surface finish in the as deposited materials. Due to the large layer height in the WAAM process, an obvious stairstep occurs between two layers resulting in higher surface roughness, which is referred as surface waviness in this paper for WAAM, compared to the powder-based AM processes.
Load bearing parts produced by AM built Ti64 are subjected to cyclic loading in service. Therefore, fatigue performance is one of the most important design criteria. Although AM provides near net shape parts, the nature of layer wise deposition causes unfavourable surface roughness or waviness which will act as stress concentration zones and lead to fatigue life reduction. Considerable efforts have been made to understand the influence of as built surface on the fatigue performance of AM Ti64, particularly in the high cycle fatigue regime [5,6,7,8,9,10]. In powder bed AM, surface roughness in Ti64 resulted in three times lower fatigue strength at a given life compared to machined and polished surface [8]. At the same applied stress, increase in surface roughness led to an approximately 75% reduction in fatigue strength [8]. Initial studies have correlated the surface parameters with fatigue life and found that roughness parameters i.e., average roughness (Ra) and maximum height of the profile (Rt) gave a correlation to high cycle fatigue (HCF) life where increased Ra and Rt caused decreased fatigue life as these features replicated as micro-notches on the as built surface leading to early crack initiation thereby premature failure [9,10,11]. Similar observations were made in another study [12] where influence of as-built surface roughness parameters on the HCF performance of Ti64 manufactured via electron beam (EBLBF) and laser powder fusion (LPBF) processes and found 35% decrease in fatigue strength (at 107 cycles) for a 50% increase in the Ra and Rt values. Nevertheless, such correlation between Ra, Rt and fatigue life was not found in other materials such as nickel-based alloys [13]. A more holistic approach by Sanaei et al.[14] found a good correlation between parameters such as maximum profile peak height and maximum profile trough depth across various materials. Kahlin et. al [15] studied the fatigue behaviour of purposely built notched as built Ti64 built by LPBF and EBPBF processes. Presence of surface roughness was the single most severe factor for fatigue life reduction resulting in a fatigue notch factor having a rougher surface.
Efforts have also been devoted to fatigue life prediction. They are the notch stress method [6,16,17] and fracture mechanics based method [18,19,20,21]. Dinh et al.[17] applied the notch stress method and finite element analysis to study the synergistic effects of gas pores and surface roughness on the fatigue life of powder bed fusion Ti64. Vayssette et. al. [22] used a fracture mechanics based numerical model, in which surface roughness profiles were measured using optical light interferometer and the result was used to build a realistic finite element model. However, the fatigue strength was not well predicted since the micro-notches associated with the as built surface were not well described. Peng and Jones et al. [18,19] treated the surface waviness profile as a series of small cracks to predict the durability of specimens made of 18Ni 250 maraging steel and Ti64 based on the crack growth life.
With regard to the surface waviness of WAAM materials, limited research is available in open literature. Dirisu et. al. [23] studied the influence of as built waviness on the tensile and fatigue strength of WAAM ER70S-6 structural steel. Thicker layer deposition associated with WAAM process caused stair steps between the layers and resulted in surface waviness of 0.18 mm between peak and trough [23]. A surface waviness of 0.08 mm and 0.18 mm caused approximately 75% fatigue strength reduction for a given life compared to samples with machined surfaces. In a similar study on ER50-6 steel the as built surface waviness was about 0.136 mm between peak and trough [24]. To the author’s knowledge, there is no published data available on the influence of as built surface waviness on the fatigue performance of WAAM built Ti64. Although, surface waviness can be reduced by subsequent machining process, with an increasing emphasis on sustainability and reducing the buy-to-fly ratios, it is vital to reduce the materials waste, particularly for metals which are either expensive to purchase or hard to machine. On the other hand, it is not always possible to remove the surface roughness, or the presence of minimal surface roughness is acceptable in certain applications where the service loads are moderate or low. In such scenarios, it is important to understand the acceptable surface waviness and to propose a methodology for fatigue life prediction in the presence of surface waviness.
Therefore, the work reported in this paper aims to investigate the influence of as-built surface waviness on the fatigue life of WAAM Ti64. Fatigue tests were conducted under bending loads. Two different predictive methods were used; one is based on the traditional notch stress method treating a waviness trough as a micro-notch; the other is based on the fracture mechanics treating a waviness trough as an initial crack. The modified Hartman-Schijve equation and small crack growth data were employed. The fatigue life of as-built WAAM was then computed and was compared with the experimental data.

2. Materials and Methods

For extracting fatigue test specimens, a wall was built on a 12 mm thick forged Ti64 plate by the WAAM process with a single bead deposition strategy. The grade-5 Ti64 wire of 1.2 mm diameter was used as feed stock. Plasma arc was used as a heat source and Argon gas of 99.99% purity was directed precisely at the melt pool to prevent oxidation. The dimension of the wall was 300 x 150 x 10 mm3 as shown in Figure 1a.
After the deposition, the wall was cut off from the substrate and used for extracting fatigue testing samples of rectangular shape by wire electric discharge machining (W-EDM) as shown in Figure 1b & 1c. To investigate the influence of surface waviness on fatigue life, two types of samples were prepared, i.e., 22 with the as-deposited surface (no machining) and 14 with machined and polished surface. For the samples with as-deposited surface, one side of the sample was machined to facilitate sample mounting on the bending test frame. In order to observe the crack propagation path during the fatigue testing, some of the as-deposited samples were ground and polished on the ND-TD plane (Figure 1b) using SiC paper, polished using 0.06 µm silica suspension and subsequently etched using Kroll’s reagent for approx. 45 seconds. For samples with the machined surfaces, the as-deposited surface was removed using high precision milling machine, and subsequently ground incrementally and polished to achieve an average surface roughness of 0.2 µm as recommended by ASTM E466 [25]. In the following text, samples with as-deposited surface are called as-deposited samples, and samples with machined and polished surfaces are called machined samples.

2.1. Characterisation of surface waviness

The as-deposited surface was characterised using a metrology tool called Formtracer, which is a type of contact mode surface measurement technique where the probe touches and scans the surface (Figure 2a and 2b). The Mitutoyo FT SV-C3200/4500 series with an arm containing a diamond tip stylus of 4 µm diameter was used. A load of 5 mN was applied to keep the stylus in contact with the sample surface as illustrated schematically in Figure 2b. The scanned data was recorded and analysed using the SurfAnalysis software. Here the term “surface roughness” is used to quantify the following representative parameters employing commonly used equations, i.e., Ra being the arithmetical mean height, Ry the maximum depth of troughs, and Rz is the average of 10-point surface roughness where y i max and y i m in are the 5 higher local maxima and lower local minima respectively [20,26], see Figure 2c. These surface roughness parameters are defined by eqs. 1-3.
R a = 1 n ∑ i = 1 n | y i |
R y = y max - y min
R z = 1 5 ∑ i = 1 5 y i max + ∑ j = 1 5 y i min
However, the conventional surface roughness parameters do not correlate well with the fatigue life of bending specimens as the surface waviness at sample’s mid-span plays a more dominant role than owing to the maximum bending stress and stress gradient through the specimen’s height. Therefore, the commonly used surface roughness parameters (Ra, Ry and Rz) are only used for characterisation of surface waviness of the as-built material. For fatigue analysis, a “notch” profile (Figure 3a) representing typical surface waviness profile was further characterised in terms of the notch depth (d), notch mouth opening angle (θ), and notch base radius (r) as shown in Figure 3b. Parameter r is calculated by a polynomial equation generated from the spline created by the data points obtained by the Formtracer, which was used to compute the first and second derivatives, f /(z), f // (z) , used in eq. 4 [27].
r = ( 1 + f   ′ z 2 ) 3 2 f   ″ ( z )

2.2. Fatigue testing

Three-point bending (3-point-bending) fatigue test was performed under constant amplitude load-controlled condition on a 10 kN Instron servo-hydraulic test machine using a standard sinusoidal waveform with a cyclic load ratio R = 0.1 and loading frequency 10 Hz. The experimental setup of an as-deposited sample is shown in Figure 4. The maximum nominal tensile stress acting on specimen’s bottom surface was calculated using eq. 5 [28].
S max = 3 PL 2 W t 2
where Smax is the maximum tensile stress on sample bottom surface at mid-span, P the applied load, L the distance between the supporting rollers (beam sample span length = 60 mm), W and t the width and thickness of the sample, respectively.

2.3. Life prediction methods

Two different methods are used for predicting the fatigue life of bending fatigue test specimens. One is based on the traditional method for durability analysis using the material’s S-N data in conjunction with the notch stress concentration factor (Kt) arising from the surface waviness; the other is based on the fracture mechanics approach treating the notch as a crack and using the stress intensity factor range (ΔK) and the material’s fatigue crack propagation rate property. The analyses of Kt and ΔK are presented in Section 3.
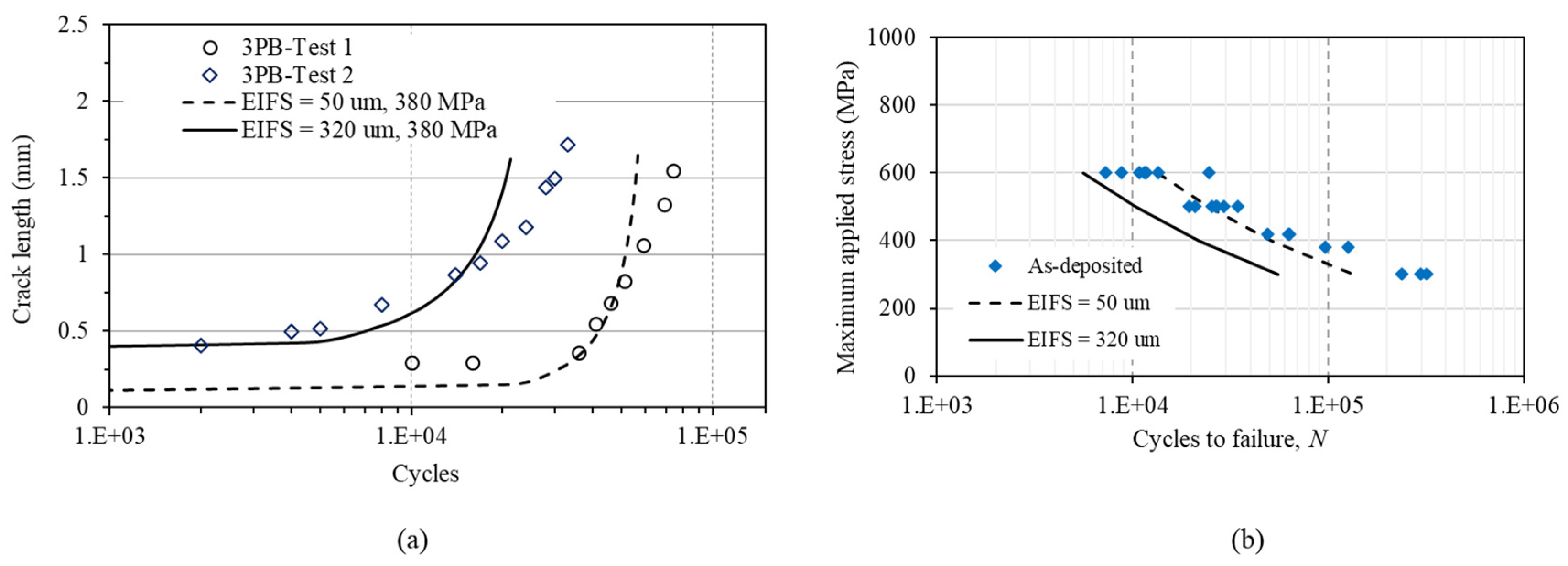
For the fracture mechanics method, small crack growth rate data is used based on our previous work [29], where the crack growth rates of small and long cracks were obtained for the same material are used in this study, which is shown in Figure 5. The result indicates that small cracks exhibited higher crack growth rates than long cracks under the same applied ΔK. The observed difference in crack growth rates can be attributed to the difference in constraints imposed by the elastic material surrounding the crack, which can vary in the case of small cracks [30]. The constraints experienced by small cracks that initiate from or grow on a free surface of smooth samples differ from those experienced by through-thickness long cracks in the same material [31]. Consequently, even when the loading conditions and crack sizes follow the requirements of Linear Elastic Fracture Mechanics (LEFM), the physically small cracks exhibited faster crack growth rates. Furthermore, long cracks usually have longer plastic wake that reduce the crack growth rate due to the crack closure effect [30].
The modified Hartman-Schijve equation [32,33,34,35,36], eq. 6, was used to represent the small crack growth rate as shown in Figure 5.
d a d N = D ∆ K - ∆ K thr 1 - K max / A p
where, Kmax is the maximum stress intensity factor, ∆K the stress intensity factor range, A the cyclic fracture toughness, D and p are material constants. Term ∆Kthr is the effective threshold of stress intensity factor range for small cracks. For long cracks, threshold ∆Kth is the value of applied ∆K corresponding to a crack growth rate of 10-10 m/cycle according to the ASTM E647 standard.
Work in [37,38,39,40,41] has demonstrated that the variability in crack growth rates can be modelled using the modified Hartman-Schijve equation. In this work, eq. 6 was used to compute the variability in the crack growth rates in WAAM Ti64 where the material constants D and p were obtained from long crack test data [29]. The values suggested by [33,42] may be suitable for microstructurally small cracks but may be impractical for physically small cracks initiated from defects found in WAAM Ti64, as work in [43,44] found higher ΔKthr values for small cracks in Ti64 as 1.8–3.0 MPa m . In this study, ΔKthr = 2 MPa m was used in eq. 6 for predicting the small crack growth behaviour in the material; the prediction curve is shown in Figure 5.

3. FE analysis of stress concentration factor and stress intensity factor

3.1. Stress concentration factor (Kt)

The Ra, Ry and Rz values measured from the as-deposited surface were 26.8±2.8 µm, 245±29 µm and 152±15 µm, respectively. These values represent the overall waviness of the specimens.
A unit of periodically repeating surface waviness is called a notch in this paper, which was characterised by three parameters, radius of curvature (r), depth of the notch (d) and notch mouth opening angle (θ) that were obtained from the Formtracer measurement data (Figure 3a). Corresponding to their definitions in Figure 3b, parameters r, d, and θ can fully characterise the profile of a waviness trough or a notch. In the stress analysis and fatigue life prediction the notch at the mid-span is used. Typical value ranges were r = 90-200 µm, d = 50-320 µm and θ = 167°-175°.
In the literature, it is observed that when the ratio r/t is below 0.03 and ratio t/(t-d) is below 1.05, the notch mouth angle θ becomes the dominant factor on the Kt, hence termed as Ktθ from here onwards [28]. Similar trend was also found in this study that Ktθ decreases as θ increases (with r/t and t/(t-d) kept constant) until θ reaches 180° (Kt = 1).
In the FE analysis, stress concentration factor Ktθ was calculated by the ratio of the maximum local stress at the notch root to the applied bending stress at the lower surface of the beam mid-span. The as-deposited surface profile from metrology data was imported into the ABAQUS software using the data points from Formtracer, and the value of Ktθ was calculated as shown in Figure 6. It was observed that due to the asymmetric nature of the notch, the difference between a symmetric V-notch and the actual notch was within ~7%. Nevertheless, the Ktθ value is still dependent on the θ angle. To reduce the computational time, the 60,000 data points obtained from Formtracer in a single scan were reduced to 6000 by removing intermediate points without affecting the Ktθ values. The data points were converted into splines which were then converted to 2D geometry models using the software package CATIA V5. The profile was then used as a surface model to generate the finite element geometry in ABAQUS. A linear elastic material model was considered with the plane strain condition. An element size of 0.02 mm was taken near the notch root, which gradually increased in size to 0.5 mm away from the notch. The element size was selected after mesh sensitivity analysis for solution convergence. The load and boundary conditions applied are shown in Figure 6.
To verify the finite element analysis, eq. 7 from [28] is used:
K t θ = 1.11 K t - - 0.0159 + 0.2243 θ 150 - 0.4293 θ 150 2 + 0.3609 θ 150 3 K t 2
where Ktθ is the notch stress concentration factor taking account of the notch mouth angle θ, and Kt is stress concentration factor of a straight sided U notch with semi-circular base.
For a typical notch in the as-deposited surface Ktθ was found between 1.25-1.85 from FE analysis. The difference between the FEA and the analytical solution from eq. 7 is below 5%.

3.2. Stress intensity factor in mode-I loading (KI)

For analysis based on fracture mechanics, the mid-span notch is treated as a crack as shown in Figure 7a. To verify the FE model of stress intensity factor, analytical solution for standard single edge notch specimen under bending, i.e., the SEN(B) configuration, was used [45,46]. ABAQUS code was used for FE analysis. The SEN(B) sample was modelled using two-dimensional model as shown in Figure 7b. The width of the sample was 8 mm. Fracture surface analysis shown in Figure 8, of as-deposited samples show no significant variation of the crack front across the width of the sample. Therefore, it is reasonable to assume a uniform crack front and analyse the crack propagation problem with 2D plane strain elements (CPE4R). The benchmark sample is considered symmetrical about the crack depth, so the symmetrical boundary condition was applied with half the beam being modelled (Figure 7b). The applied load on the half model was P/2 and applied on the top surface as a point load. Using eq. 5, the tensile stress acting on the lower surface of the beam was calculated as 380 MPa. Since the notch at mid-span has the highest stress concentration and almost all the samples failed at the middle of the sample, only the centre notch was modelled. The actual profile was then modelled with an initial notch depth of 0.05 mm and a crack length of 0.1 mm, as shown in Figure 7b. The element size at the crack front was 0.006 mm which was progressively increased to 0.5 mm for both models and was selected after mesh convergence study (with an accepted margin of error, < 3%). Linear elastic material properties were used for this analysis as well, and the displacement extrapolation method was adopted for calculating K ahead of the crack tip.
The modelling result was verified with an analytical solution for three different crack lengths in Figure 7b. The difference between the analytical solutions and FE analysis was below 3%. Therefore, eq. 8 from [45] was used in this study.
K = PL Wt 3 2 2.9 a t 1 2 -   4.6 a t 3 2 + 21.8 a t 5 2 -   37.6 a t 7 2 + 38.7 a t 9 2
where P is the applied load, L the distance between the supporting rollers, W the width of the sample, t the thickness of the sample, and a the crack length.

4. Experimental test results

The stress vs. life (S-N) data of as-deposited and machined specimens under bending fatigue load is presented in Figure 9. It shows a large reduction in fatigue strength at a given life; the worst case being 50% decrease in strength at 300,000 load cycles. Fatigue life was significantly reduced under the same applied stress, e.g., life was reduced by 10 times at applied stress 600 MPa. These were owing to the stress concentration arising from the surface waviness resulting in premature crack initiation at the notch roots. In this study, fatigue cracks always initiated from a single ‘notch-like’ feature that experienced the maximum tensile stress in the bending test.
As mentioned in [28], the three parameters r, d and θ determine the notch profile and the stress concentration factor value for the specimen. Therefore, after sample failure, the crack initiating notch was identified and traced using recorded surface measurement. This has enabled the determination of r, d and θ of the crack initiating notch in all the as-deposited samples.
Figure 9 also shows that the scatter in test data varied at different applied stress levels. In the machined samples, scatter was the smallest at 800 MPa applied bending stress as the stress level is closer to the yield strength of the material. The scatter increased as the applied stress decreased. This is because at the higher stress levels the surface condition was less likely to influence crack nucleation as micro-cracks were formed much earlier in the fatigue life, which was followed by crack growth as shown for axially loaded samples in [47]. This could be the reason for lower scatter in all the samples tested at 800 MPa. At lower applied stress levels, the surface condition became more relevant, and crack initiation depends on the surface irregularities which vary among the test samples, hence larger scatter was observed for the machined samples tested at 600 MPa. For the as-deposited samples, the scatter was smaller at 600 MPa than the machined samples because the as-deposited samples were dominated by crack growth from the centre notch as a result of the surface waviness, whereas the machined sample fatigue life was dominated by the crack initiation stage.

5. Fatigue Life Prediction

5.1. Notch fatigue approach

The first prediction method was based on the traditional notch reduction factor approach based on the following assumptions: a) the as-built surface waviness can be considered as a series of individual notches that act as stress raisers; b) the predicted fatigue life represents the crack initiation life, and the subsequent crack propagation life is neglected for the small laboratory samples.
In the prediction, the applied maximum bending stress, Smax, was reduced by a factor of Ktθ which had a value range from 1.25 to 1.85 according to the FE analysis in Section 4. Figure 10 shows the predicted range of life for the as-deposited specimens based on the Ktθ value range.
Using the most severe notch, Ktθ=1.85, life prediction agrees with test only at the highest applied bending stress (600 MPa). Life is overestimated for lower stresses and the overestimation is by one magnitude at 400 MPa. The slops of the prediction curves are shallower than the test data. The poor agreement between the test and prediction can be explained as follows. The Kt based method works better if the crack initiation life is dominant, i.e., large portion of the total life is spent in crack initiation stage from a notch root. In bending test, the notch tip is under much higher mode-I stress than in axial loading, hence the crack initiation life is much shorter, or negligible, and crack propagation stage is dominating. In our research, we investigated the behaviour of crack growth that is shown in Figure 11, which illustrates a portion of the specimen height and earlier part of crack length that were measured during the tests. Based on the definition that the total life (Nt) is the sum of the crack initiation life (Ni) and the subsequent crack propagation life (Np), we found that the crack initiation life occupied approximately 2-8% of the total life. The cycle numbers displayed in Figure 11 represent the accumulated cycle numbers from the first cycle at the corresponding crack length measurements.

5.2. Fracture mechanics approach

The second prediction method was based on the fracture mechanics approach treating a notch (a waviness trough) as a small crack that will propagate under cyclic loads. Fatigue crack growth rate was calculated using eq. 6, using the material constants obtained in [29] as D = 1×10-10, p = 2.5, ΔKthr=2 and A=90 (in unit of MPa, m). The fatigue life for a given crack length was then calculated by integrating the crack growth rates. The prediction starts from an equivalent initial flaw size (EIFS) which is the notch depth d and finishes at a critical crack length based on the fracture toughness of the material. The final critical crack length was also established from examining fracture surfaces as shown in Figure 8b which was estimated to be around 4 mm, about half of the sample thickness. Figure 11 shows the flowchart for fatigue life prediction based on fracture mechanics.
Crack growth from surface waviness was also monitored during the fatigue test (Figure 11), which was then plotted as crack length (a) vs. load cycle number (N) relation in Figure 13a. Under the same applied load, the Test-1 lasted longer than the Test-2 owing to different values of maximum applied bending stress, however, the crack growth rate was similar as indicated by similar slopes of the two a vs. N curves.
Preprints 75079 g012
Figure 12. Flowchart for fatigue life prediction used in this study.
Figure 12. Flowchart for fatigue life prediction used in this study.
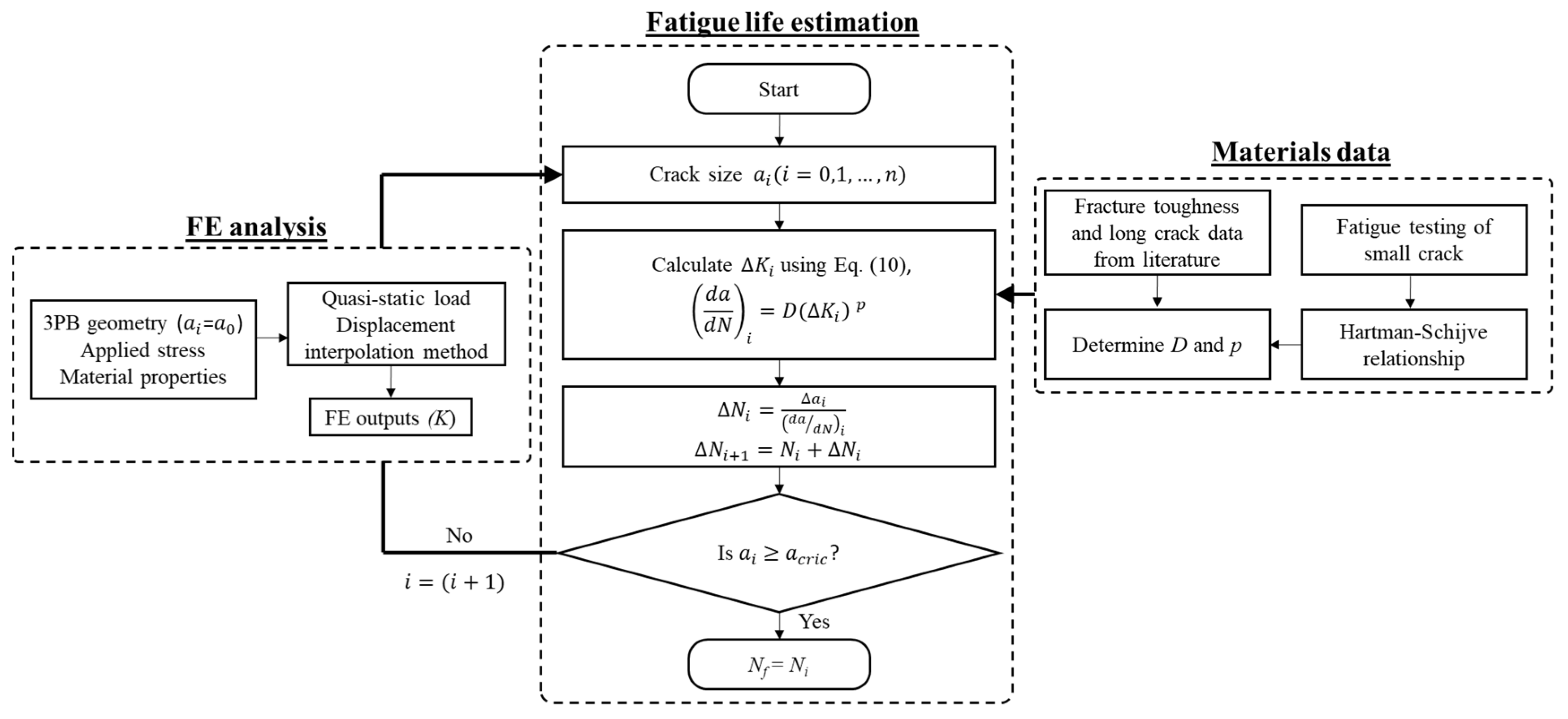
Preprints 75079 g012
Preprints 75079 g013
Figure 13. (a) Crack length vs number of cycles for 3-point-bending -Test 1 (σmax=380 MPa, Nf = 74,000) and 3-point-bending -Test 2 (σmax=380 MPa, Nf = 33,000) and predicted fatigue life for beam specimen with as-deposited surface condition based on the small crack growth approach, (b) S-N curve showing experimental data of as-deposited WAAM Ti64 and durability prediction based on the modified Hartman-Schijve equation.
Figure 13. (a) Crack length vs number of cycles for 3-point-bending -Test 1 (σmax=380 MPa, Nf = 74,000) and 3-point-bending -Test 2 (σmax=380 MPa, Nf = 33,000) and predicted fatigue life for beam specimen with as-deposited surface condition based on the small crack growth approach, (b) S-N curve showing experimental data of as-deposited WAAM Ti64 and durability prediction based on the modified Hartman-Schijve equation.
Preprints 75079 g013
The prediction is also presented in terms of an S-N graph in Figure 12b. Using two different initial crack lengths representing the depths of the shallowest notch (50 µm) and the deepest notch (320 µm), the predicted life forms an upper bound and a lower bound of the fatigue test data, showing that the prediction has encompassed the range of the experimental test data, hence can be considered as a good prediction.

6. Conclusions

This research aims to quantify the effect of surface waviness on the fatigue life in a wire + arc additive manufactured titanium alloy Ti-6Al-4V (WAAM Ti64). Two different predictive methods were used based on the notch-stress or fracture mechanics approaches. Three-point bending tests were conducted to validate the prediction. Following conclusions have been drawn:
  • Surface waviness in WAAM materials can be treated as a series of individual micro notches that can be characterised by three parameters: notch depth (d), notch base radius (r), and notch mouth opening angle (θ).
  • The traditional notch stress method overestimated the fatigue life up to a factor of 1.5 at lower applied stresses. Poor agreement with the test is attributed to the crack propagation dominance owing to the troughs from surface waviness.
  • The fracture mechanics approach has given good prediction by treating the centre trough as an initial crack and using the material’s crack growth rate property obtained by testing short and long cracks.

Author Contributions

Conceptualization, M.S., A.K.S. and X.Z.; methodology, M.S., A.K.S., W.S., and X.Z.; software, M.S.; validation, M.S.; formal analysis, M.S.; resources, X.Z.; data curation, M.S.; writing, original draft preparation, M.S., A.K.S. and X.Z.; writing—review and editing, M.S., A.K.S. and X.Z.; visualization, M.S.; supervision, A.K.S. and X.Z.; project administration, X.Z.; funding acquisition, X.Z. All authors have read and agreed to the published version of the manuscript.

Funding

PhD studentship to M.S. was jointly funded by the WAAMMat programme and Coventry University.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data will be provided based on request.

Acknowledgments

The authors thank Cranfield University for providing testing materials. MS also thanks the WAAMMat programme and Coventry University for PhD studentship. XZ thanks the Engineering and Physical Science Research Council (EPSRC) for supporting this research through the NEWAM programme grant (EP/R027218/1). .

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. S.W. Williams, F. Martina, A.C. Addison, J. Ding, G. Pardal, P. Colegrove, Wire + Arc additive manufacturing, Materials Science and Technology (United Kingdom). 32 (2016) 641–647. [CrossRef]
  2. D. Jafari, T.H.J. Vaneker, I. Gibson, Wire and arc additive manufacturing : Opportunities and challenges to control the quality and accuracy of manufactured parts, Materials & Design. 202 (2021) 109471. [CrossRef]
  3. N. Kumar, H. Bhavsar, P.V.S. Mahesh, A.K. Srivastava, B.J. Bora, A. Saxena, A.R. Dixit, Wire Arc Additive Manufacturing – A revolutionary method in additive manufacturing, Materials Chemistry and Physics. 285 (2022) 126144. [CrossRef]
  4. A.K. Syed, X. Zhang, A. Caballero, M. Shamir, S. Williams, Influence of deposition strategies on tensile and fatigue properties in a wire + arc additive manufactured Ti-6Al-4V, International Journal of Fatigue. 149 (2021) 106268. [CrossRef]
  5. D. Arola, C.L. Williams, Estimating the fatigue stress concentration factor of machined surfaces, International Journal of Fatigue. 24 (2002) 923–930. [CrossRef]
  6. J. Pegues, M. Roach, R. Scott Williamson, N. Shamsaei, Surface roughness effects on the fatigue strength of additively manufactured Ti-6Al-4V, International Journal of Fatigue. 116 (2018) 543–552. [CrossRef]
  7. J. Zhang, A. Fatemi, Surface roughness effect on multiaxial fatigue behavior of additive manufactured metals and its modeling, Theoretical and Applied Fracture Mechanics. 103 (2019) 102260. [CrossRef]
  8. L. Ednie, R.J. Lancaster, A.A. Antonysamy, F. Zelenka, A. Scarpellini, L. Parimi, R. Maddalena, N.C. Barnard, P. Efthymiadis, The effects of surface finish on the fatigue performance of electron beam melted Ti–6Al–4V, Materials Science and Engineering: A. 857 (2022) 144050. [CrossRef]
  9. D. Greitemeier, C. Dalle Donne, F. Syassen, J. Eufinger, T. Melz, Effect of surface roughness on fatigue performance of additive manufactured Ti–6Al–4V, Materials Science and Technology. 32 (2016) 629–634. [CrossRef]
  10. J. Gockel, L. Sheridan, B. Koerper, B. Whip, The influence of additive manufacturing processing parameters on surface roughness and fatigue life, International Journal of Fatigue. 124 (2019) 380–388. [CrossRef]
  11. S. Lee, Z. Ahmadi, J.W. Pegues, M. Mahjouri-Samani, N. Shamsaei, Laser polishing for improving fatigue performance of additive manufactured Ti-6Al-4V parts, Optics & Laser Technology. 134 (2021) 106639. [CrossRef]
  12. D. Greitemeier, F. Palm, F. Syassen, T. Melz, Fatigue performance of additive manufactured TiAl6V4 using electron and laser beam melting, International Journal of Fatigue. 94 (2017) 211–217. [CrossRef]
  13. H. Javadi, W. Jomaa, D. Texier, M. Brochu, P. Bocher, Surface roughness effects on the fatigue behavior of as-Machined Inconel718, Solid State Phenomena. 258 (2016) 306–309. [CrossRef]
  14. N. Sanaei, A. Fatemi, Progress in Materials Science Defects in additive manufactured metals and their effect on fatigue performance : A state-of-the-art review, Progress in Materials Science. (2020) 100724. [CrossRef]
  15. M. Kahlin, H. Ansell, J.J. Moverare, Fatigue behaviour of notched additive manufactured Ti6Al4V with as-built surfaces, International Journal of Fatigue. 101 (2017) 51–60. [CrossRef]
  16. S.K. Ås, B. Skallerud, B.W. Tveiten, Surface roughness characterization for fatigue life predictions using finite element analysis, International Journal of Fatigue. 30 (2008) 2200–2209. [CrossRef]
  17. T.D. Dinh, J. Vanwalleghem, H. Xiang, H. Erdelyi, T. Craeghs, W. Van Paepegem, A unified approach to model the effect of porosity and high surface roughness on the fatigue properties of additively manufactured Ti6-Al4-V alloys, Additive Manufacturing. 33 (2020) 101139. [CrossRef]
  18. D. Peng, R. Jones, A.S.M. Ang, V. Champagne, A. Birt, A. Michelson, A Numerical Study into the Effect of Machining on the Interaction between Surface Roughness and Surface Breaking Defects on the Durability of WAAM Ti-6Al-4V Parts, (2022). [CrossRef]
  19. D. Peng, R. Jones, A. Alankar, R.R.K. Singh, Computing the durability of WAAM 18Ni 250 maraging steel specimens, (2022) 3535–3545. [CrossRef]
  20. M. Suraratchai, J. Limido, C. Mabru, R. Chieragatti, Modelling the influence of machined surface roughness on the fatigue life of aluminium alloy, International Journal of Fatigue. 30 (2008) 2119–2126. [CrossRef]
  21. H. Masuo, Y. Tanaka, S. Morokoshi, H. Yagura, T. Uchida, Y. Yamamoto, Y. Murakami, Influence of defects, surface roughness and HIP on the fatigue strength of Ti-6Al-4V manufactured by additive manufacturing, International Journal of Fatigue. 117 (2018) 163–179. [CrossRef]
  22. B. Vayssette, N. Saintier, C. Brugger, M. El May, E. Pessard, Numerical modelling of surface roughness effect on the fatigue behavior of Ti-6Al-4V obtained by additive manufacturing, International Journal of Fatigue. 123 (2019) 180–195. [CrossRef]
  23. P. Dirisu, G. Supriyo, F. Martina, X. Xu, S. Williams, Wire plus arc additive manufactured functional steel surfaces enhanced by rolling, International Journal of Fatigue. 130 (2020). [CrossRef]
  24. J. Xiong, Y.-J. Li, Z.-Q. Yin, H. Chen, Determination of surface roughness in wire and arc additive manufacturing based on laser vision sensing, Chinese Journal of Mechanical Engineering. 31 (2018) 74. [CrossRef]
  25. ASTM-E466, Standard practice for conducting force controlled constant amplitude axial fatigue tests of metallic materials, i (2018) 1–6. [CrossRef]
  26. Formtracer SV-C3200 / 4500 Series Hybrid Measuring Instrument for Surface, 2016.
  27. M. Kline, Calculus: An intuitive and Physical Approach, Second, Courier Corporation, 1998.
  28. W.D. Pilkey, D.F. Pilkey, Peterson’s Stress Concentration Factors, Third, 2008.
  29. M. Shamir, X. Zhang, A.K. Syed, Characterising and representing small crack growth in an additive manufactured titanium alloy, Engineering Fracture Mechanics. 253 (2021) 107876. [CrossRef]
  30. S. Suresh, Chapter 15: Small fatigue cracks, in: Fatigue of Materials, Second, Cambridge University Press, New York, 1998.
  31. Y. Xie, M. Gong, Z. Luo, Q. Li, M. Gao, F. Wang, X. Zeng, G. Wang, Effect of microstructure on short fatigue crack growth of wire arc additive manufactured Ti-6Al-4V, Materials Characterization. (2021) 104743. [CrossRef]
  32. L. Molent, R. Jones, The influence of cyclic stress intensity threshold on fatigue life scatter, International Journal of Fatigue. 82 (2016) 748–756. [CrossRef]
  33. R. Jones, R.K.S. Raman, A.P. Iliopoulos, J.G. Michopoulos, N. Phan, D. Peng, Additively manufactured Ti-6Al-4V replacement parts for military aircraft, International Journal of Fatigue. 124 (2019) 227–235. [CrossRef]
  34. Iliopoulos, R. Jones, J. Michopoulos, N. Phan, R. Singh Raman, Crack growth in a range of additively Manufactured aerospace structural materials, Aerospace. 5 (2018) 118. [CrossRef]
  35. R. Jones, L. Molent, K. Walker, Fatigue crack growth in a diverse range of materials, 40 (2012) 43–50. [CrossRef]
  36. R. Jones, L. Molent, K. Walker, Fatigue crack growth in a diverse range of materials, International Journal of Fatigue. 40 (2012) 43–50. [CrossRef]
  37. R. Jones, J.G. Michopoulos, A.P. Iliopoulos, R.K. Singh Raman, N. Phan, T. Nguyen, Representing crack growth in additively manufactured Ti-6Al-4V, International Journal of Fatigue. 116 (2018) 610–622. [CrossRef]
  38. R. Jones, Fatigue crack growth and damage tolerance, Fatigue and Fracture of Engineering Materials and Structures. 37 (2014) 463–483. [CrossRef]
  39. D. Peng, V.K. Champagne, A.S.M. Ang, A. Birt, A. Michelson, S. Pinches, Computing the Durability of WAAM 18Ni-250 Maraging Steel Specimens with Surface Breaking Porosity, (2023) 1–18. [CrossRef]
  40. D. Peng, R. Jones, A.S.M. Ang, A. Michelson, V. Champagne, A. Birt, S. Pinches, S. Kundu, A. Alankar, R.R.K. Singh, Computing the durability of WAAM 18Ni 250 maraging steel specimens, Fatigue and Fracture of Engineering Materials and Structures. 45 (2022) 3535–3545. [CrossRef]
  41. R. Jones, C. Rans, A.P. Iliopoulos, J.G. Michopoulos, N. Phan, D. Peng, Modelling the variability and the anisotropic behaviour of crack growth in slm ti-6al-4v, Materials. 14 (2021). [CrossRef]
  42. A.P. Iliopoulos, R. Jones, J.G. Michopoulos, N. Phan, C. Rans, Further studies into crack growth in additively manufactured materials, Materials. 13 (2020) 5–10. [CrossRef]
  43. M.J. Caton, R. John, W.J. Porter, M.E. Burba, Stress ratio effects on small fatigue crack growth in Ti-6Al-4V, International Journal of Fatigue. 38 (2012) 36–45. [CrossRef]
  44. R.O. Ritchie, B.L. Boyce, J.P. Campbell, O. Roder, A.W. Thompson, W.W. Milligan, Thresholds for high-cycle fatigue in a turbine engine Ti-6Al-4V alloy, International Journal of Fatigue. 21 (1999) 653–662. [CrossRef]
  45. D. Broek, J.R. Rice, Chapter 3: The elastic crack-tip stress field, in: Elementary Engineering Fracture Mechanics, Third, Martinus Nijhoff, Hague, 1982. [CrossRef]
  46. ASTM E1820: Standard Test Method for Measurement of Fracture Toughness 1, (2019) 1–65. [CrossRef]
  47. J. Schijve, ed., Chapter 12-Fatigue and Scatter BT - Fatigue of Structures and Materials, Springer Netherlands, Dordrecht, 2009. [CrossRef]
Preprints 75079 g001
Figure 1. (a) Photo of a WAAM Ti64 wall built by single-pass deposition method, (b) schematic of sample extraction plan, (c) geometry and dimensions of as-deposited bending test samples (unit: mm); WD = weld torch movement direction, TD = transverse direction, ND = normal direction.
Figure 1. (a) Photo of a WAAM Ti64 wall built by single-pass deposition method, (b) schematic of sample extraction plan, (c) geometry and dimensions of as-deposited bending test samples (unit: mm); WD = weld torch movement direction, TD = transverse direction, ND = normal direction.
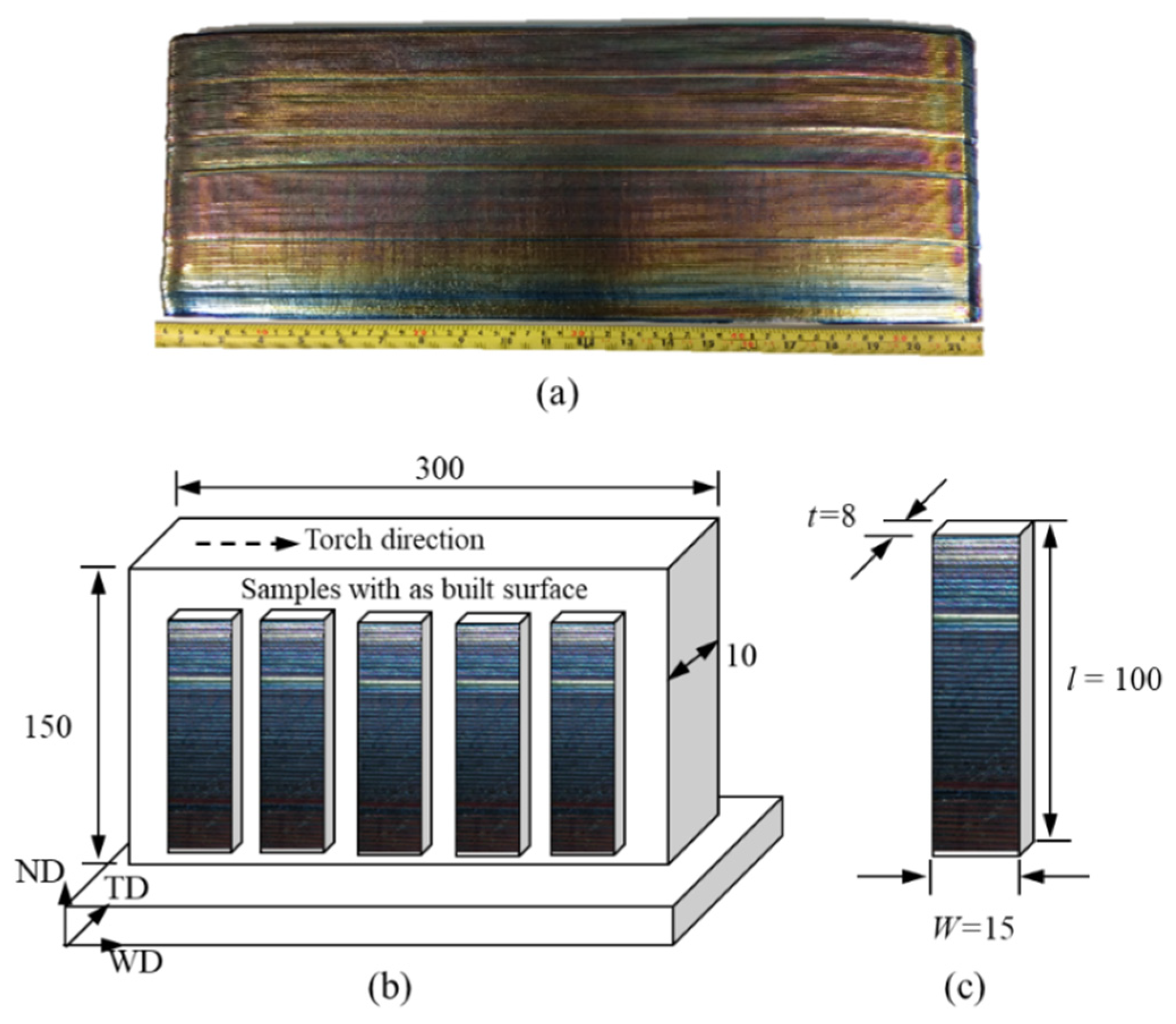
Preprints 75079 g001
Preprints 75079 g002
Figure 2. (a) Photograph of fatigue samples with as-deposited surface waviness, (b) schematic of as-deposited surface waviness using a Formtracer, (c) schematic of surface waviness parameters.
Figure 2. (a) Photograph of fatigue samples with as-deposited surface waviness, (b) schematic of as-deposited surface waviness using a Formtracer, (c) schematic of surface waviness parameters.
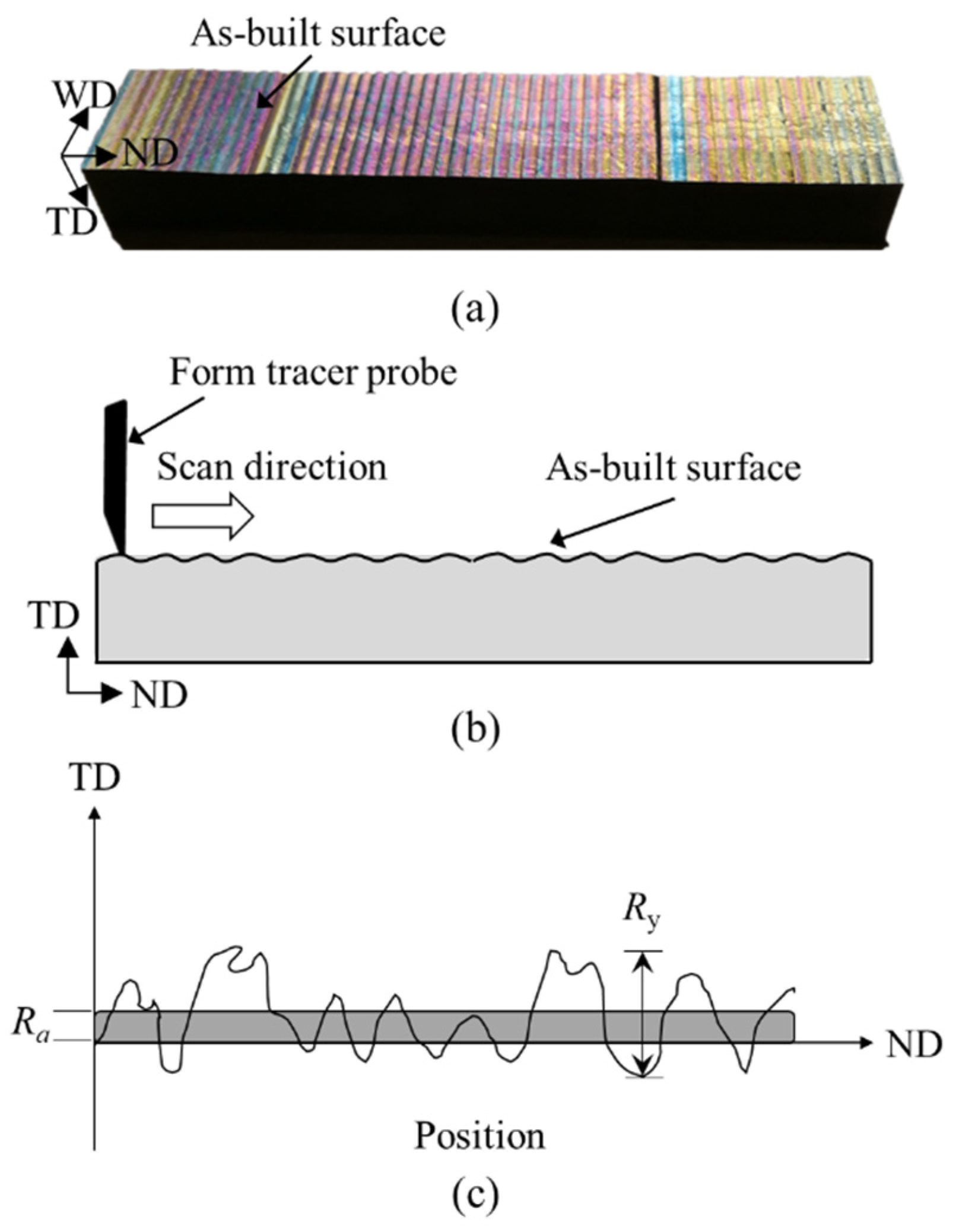
Preprints 75079 g002
Preprints 75079 g003
Figure 3. (a) A high-resolution Formtracer data overlaid onto an optical microscopic image of a single waviness (referred as a “notch”) for depiction of the notch profile, (b) schematic of notch base radius (r), notch depth (d), and notch mouth opening angle (θ).
Figure 3. (a) A high-resolution Formtracer data overlaid onto an optical microscopic image of a single waviness (referred as a “notch”) for depiction of the notch profile, (b) schematic of notch base radius (r), notch depth (d), and notch mouth opening angle (θ).
Preprints 75079 g003
Preprints 75079 g004
Figure 4. Setup of 3-point bending fatigue test showing the positions of the loading and supporting rollers with the as-deposited surface waviness facing downwards (unit: mm).
Figure 4. Setup of 3-point bending fatigue test showing the positions of the loading and supporting rollers with the as-deposited surface waviness facing downwards (unit: mm).
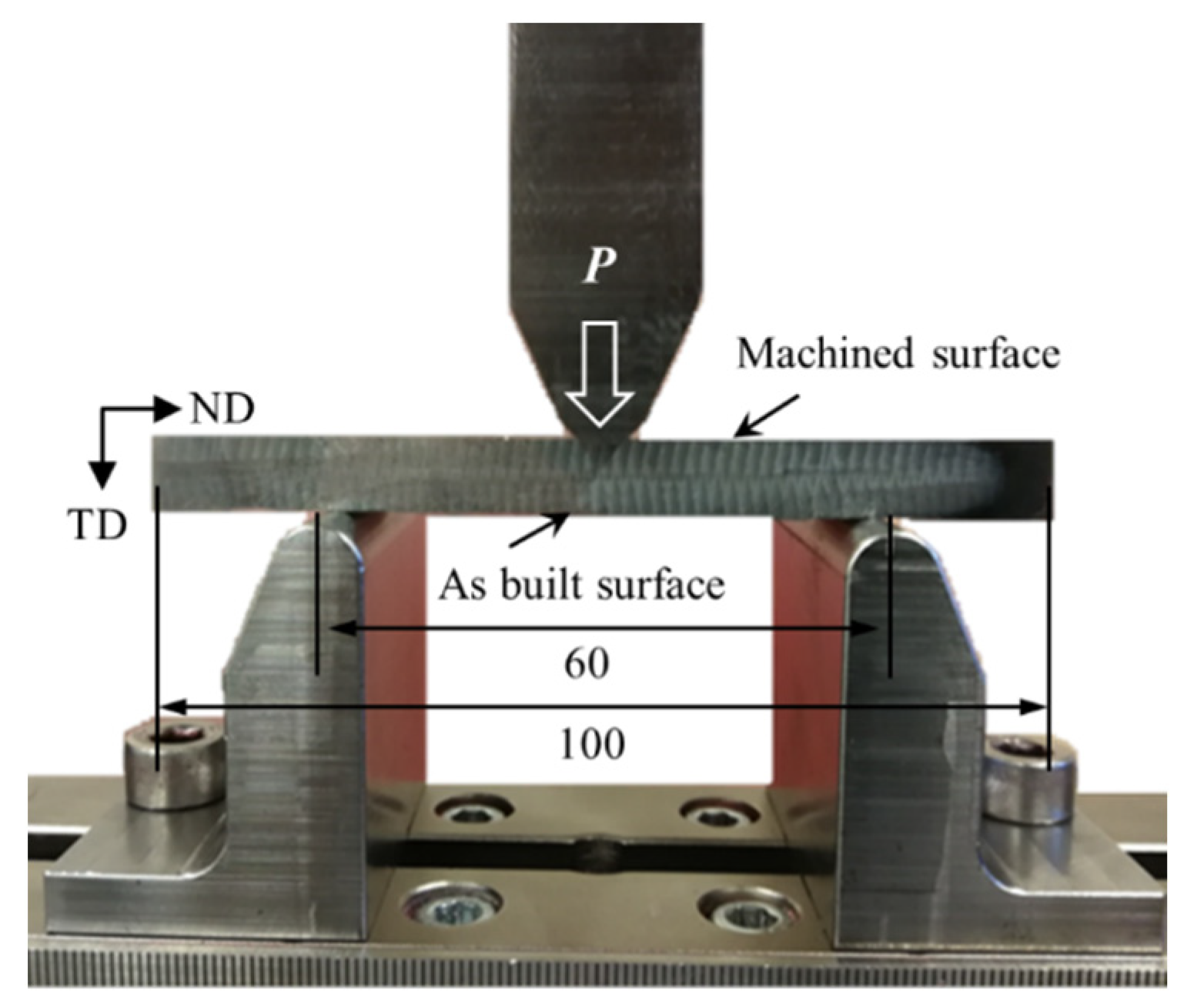
Preprints 75079 g004
Preprints 75079 g005
Figure 5. Curve representing the modified Hartman-Schijve equation fitted by long crack test data and predicted crack growth curve for small crack growth rate using long crack data with ΔKthr = 2 MPa m , A = 90 MPa m (LC = long crack, SC = small crack).
Figure 5. Curve representing the modified Hartman-Schijve equation fitted by long crack test data and predicted crack growth curve for small crack growth rate using long crack data with ΔKthr = 2 MPa m , A = 90 MPa m (LC = long crack, SC = small crack).
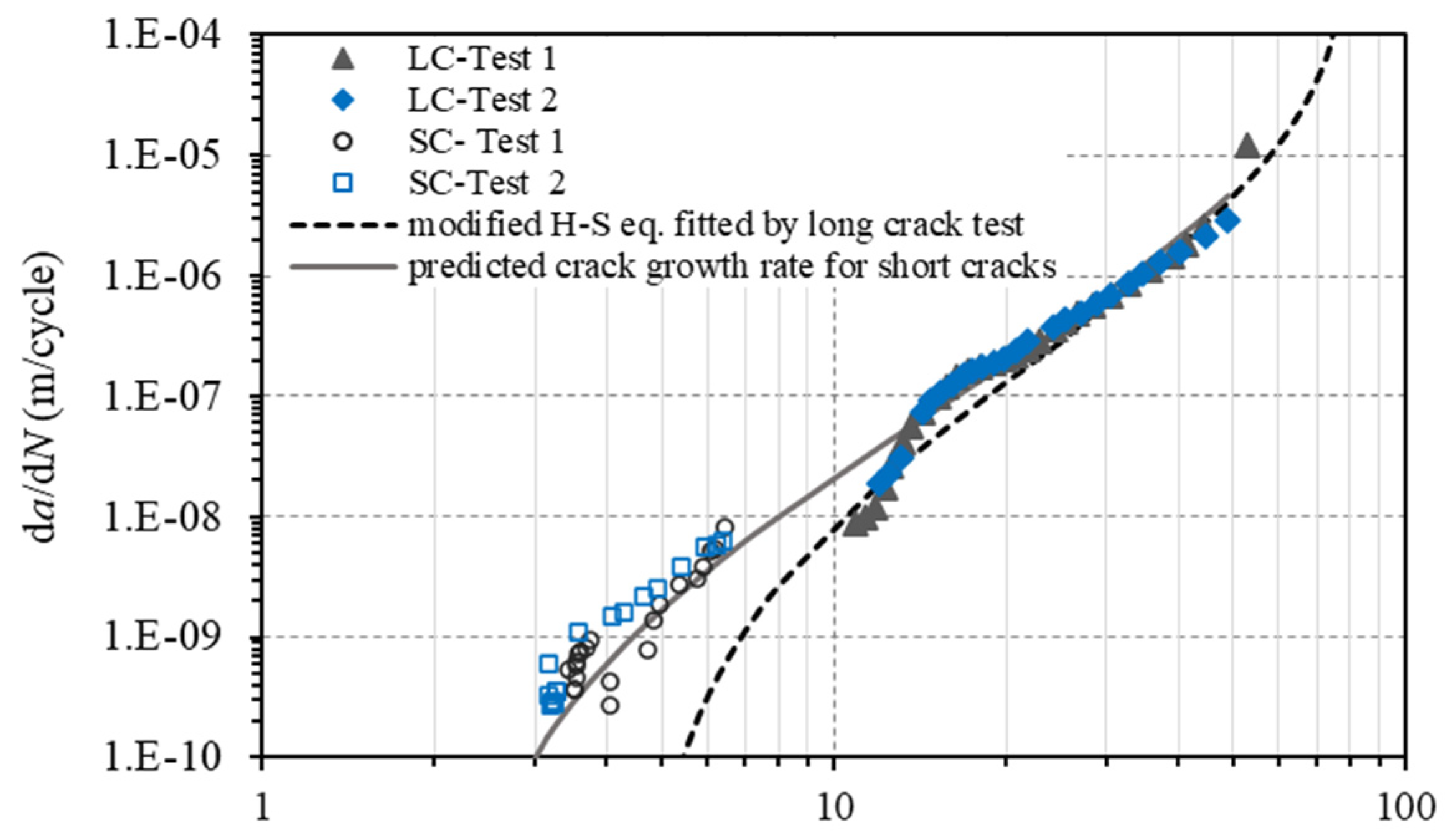
Preprints 75079 g005
Preprints 75079 g006
Figure 6. A finite element model for the sample subjected to 3-point-bending testing, and a zoomed view of a single notch.
Figure 6. A finite element model for the sample subjected to 3-point-bending testing, and a zoomed view of a single notch.
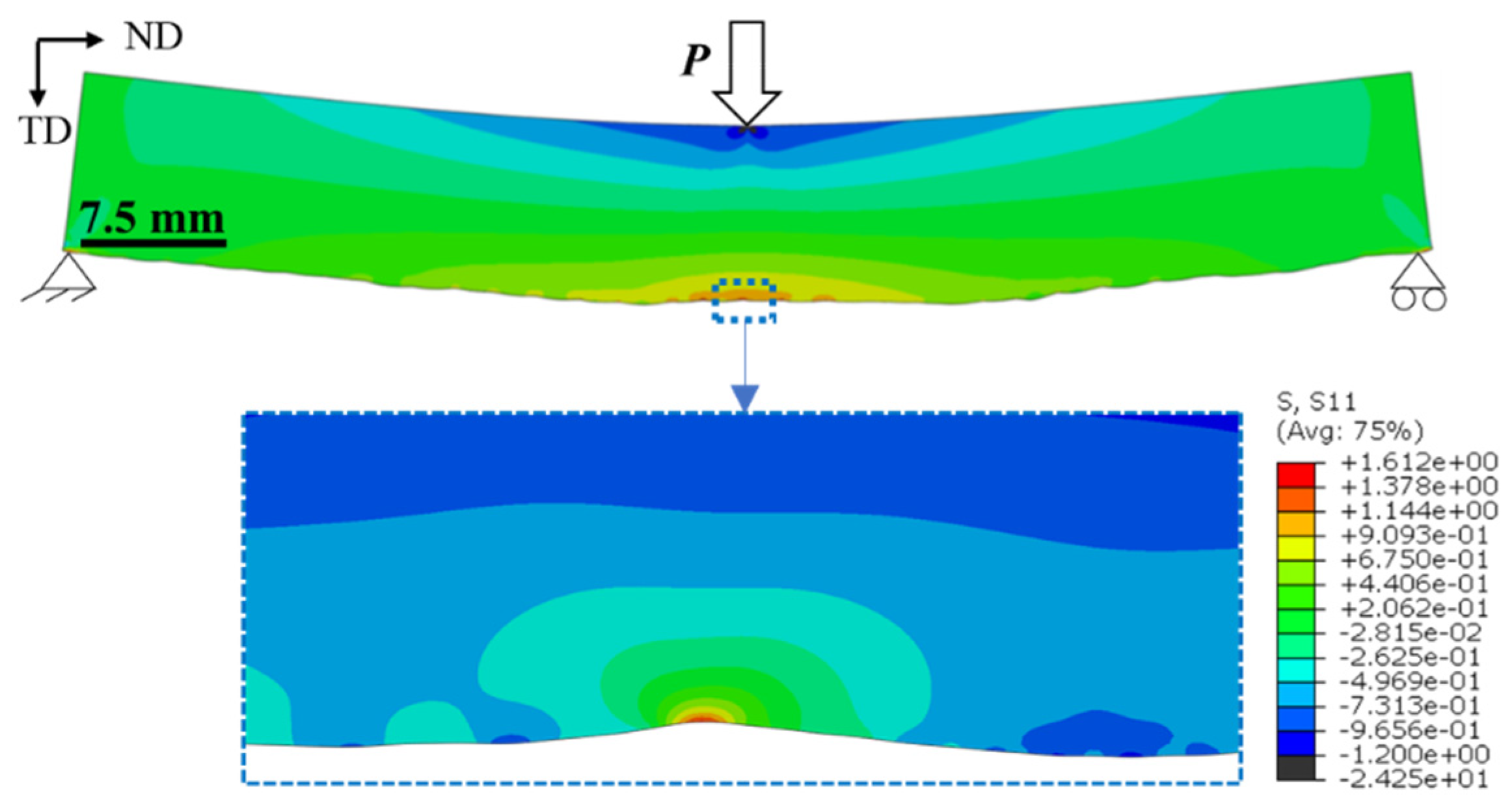
Preprints 75079 g006
Preprints 75079 g007
Figure 7. (a) Schematic representation and finite element model to calculate stress intensity factor of a notch at mid-span representing a typical surface waviness profile, (b) comparison of stress intensity factor values between finite element model and analytical solution [45].
Figure 7. (a) Schematic representation and finite element model to calculate stress intensity factor of a notch at mid-span representing a typical surface waviness profile, (b) comparison of stress intensity factor values between finite element model and analytical solution [45].
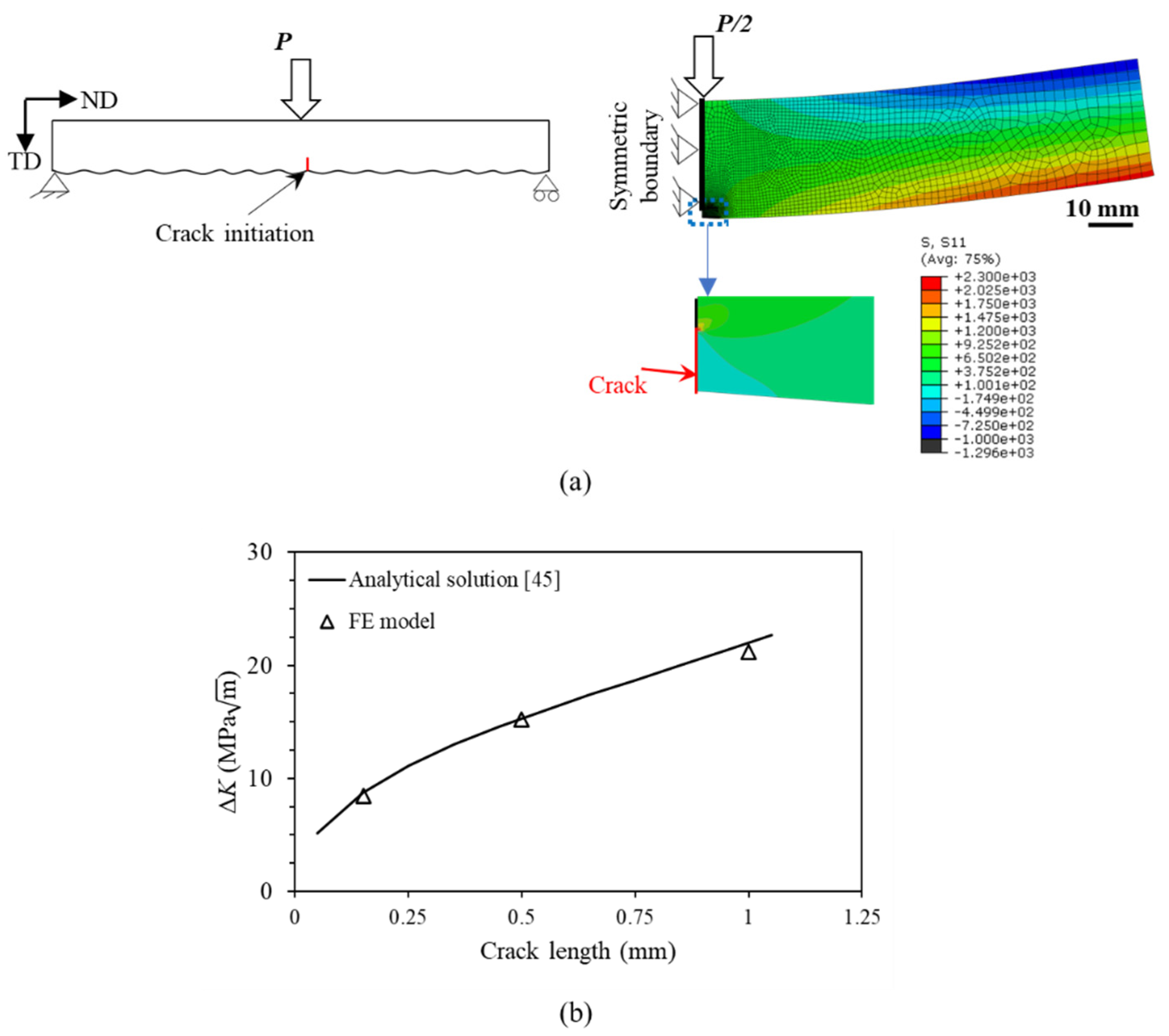
Preprints 75079 g007
Preprints 75079 g008
Figure 8. (a) a specimen with as-built surface showing fracture failure at the mid-span, (b) fracture surface showing stable crack growth stage (Region I) and fast fracture (Region II).
Figure 8. (a) a specimen with as-built surface showing fracture failure at the mid-span, (b) fracture surface showing stable crack growth stage (Region I) and fast fracture (Region II).
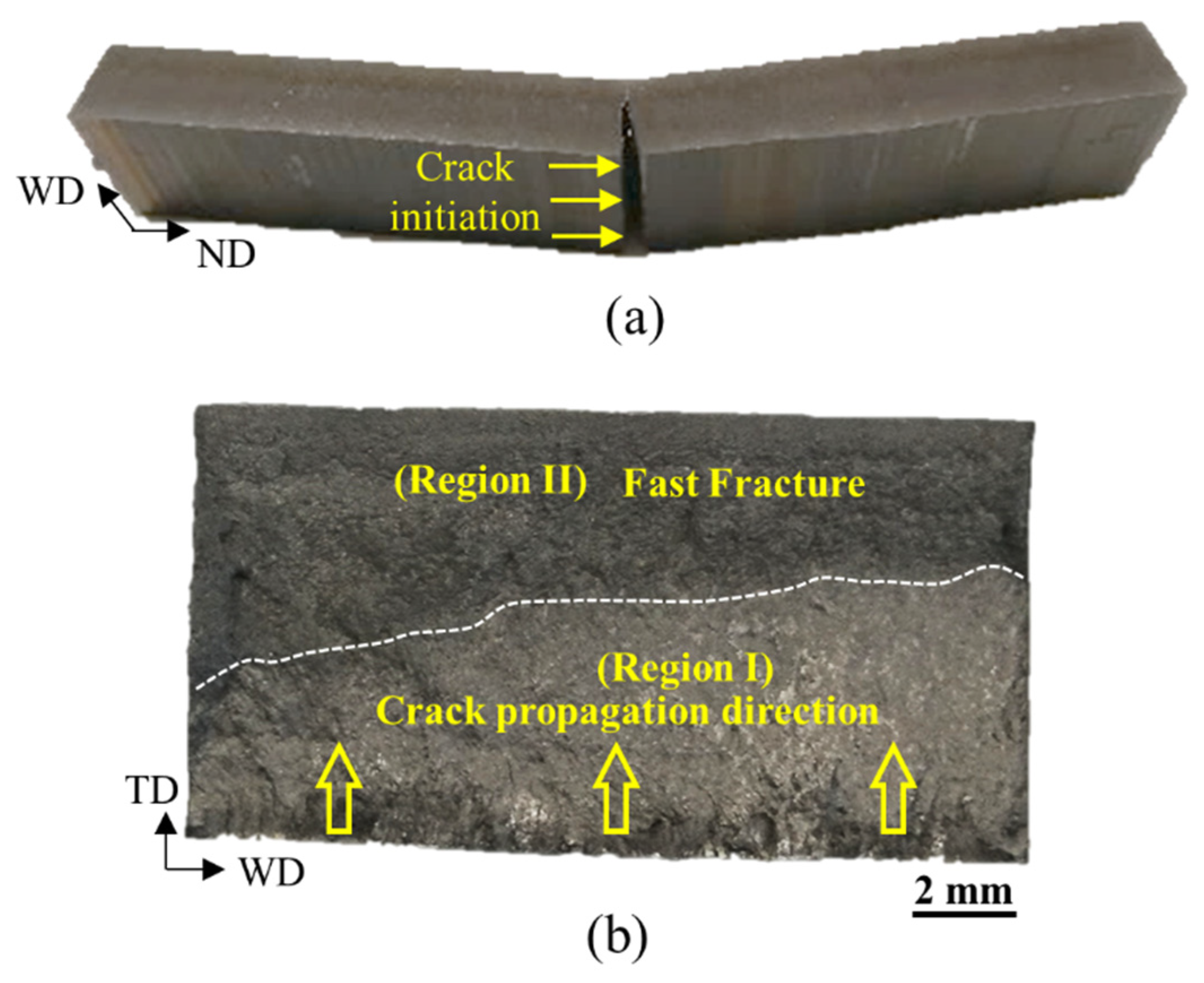
Preprints 75079 g008
Preprints 75079 g009
Figure 9. S-N data of 3-point-bending fatigue tests for machined and as-deposited WAAM Ti64 samples. The y-axis represents the maximum bending stress on the beam lower surface at the mid-span.
Figure 9. S-N data of 3-point-bending fatigue tests for machined and as-deposited WAAM Ti64 samples. The y-axis represents the maximum bending stress on the beam lower surface at the mid-span.
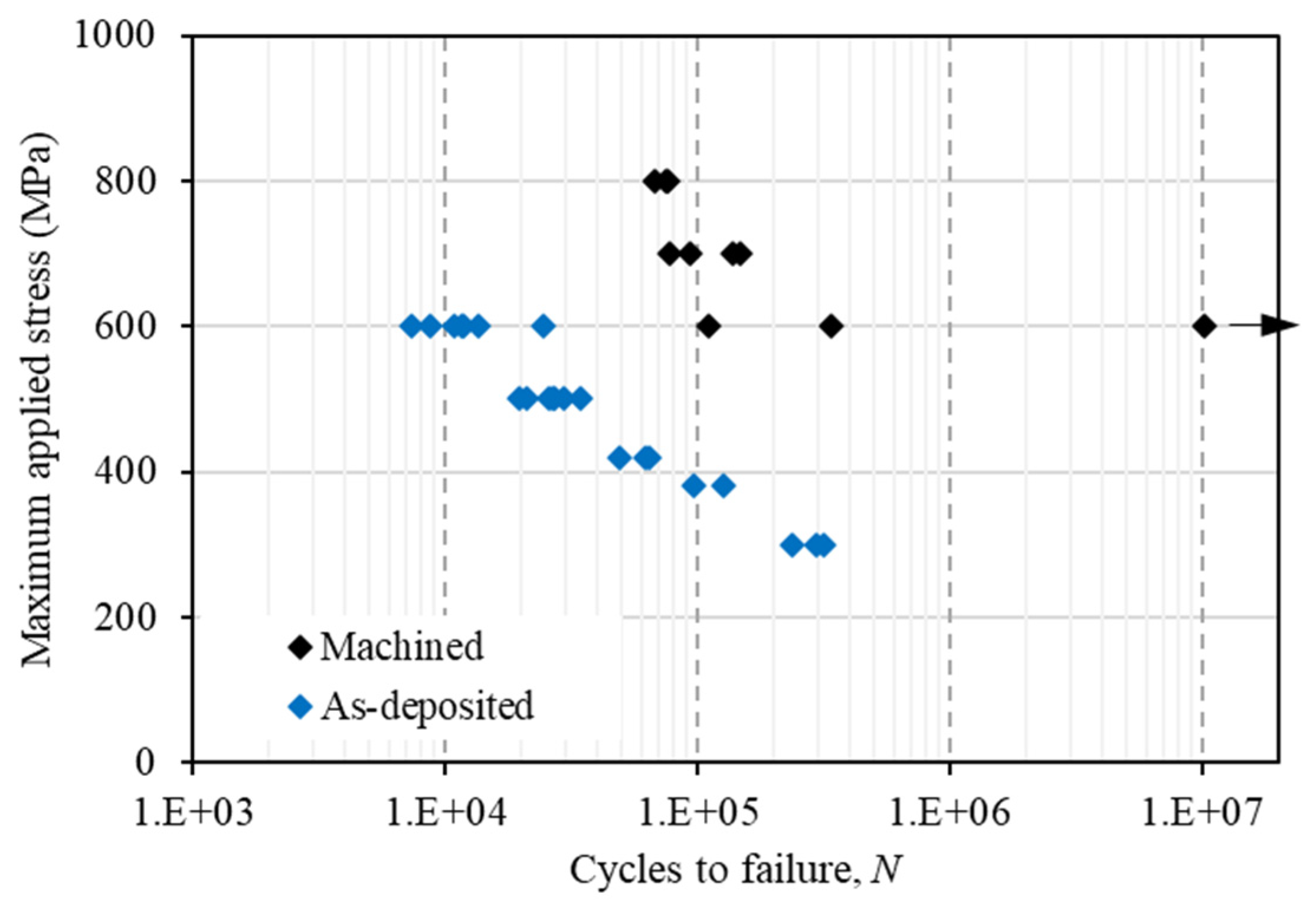
Preprints 75079 g009
Preprints 75079 g010
Figure 10. Fatigue life prediction for as-deposited specimens using the notch stress approach.
Figure 10. Fatigue life prediction for as-deposited specimens using the notch stress approach.
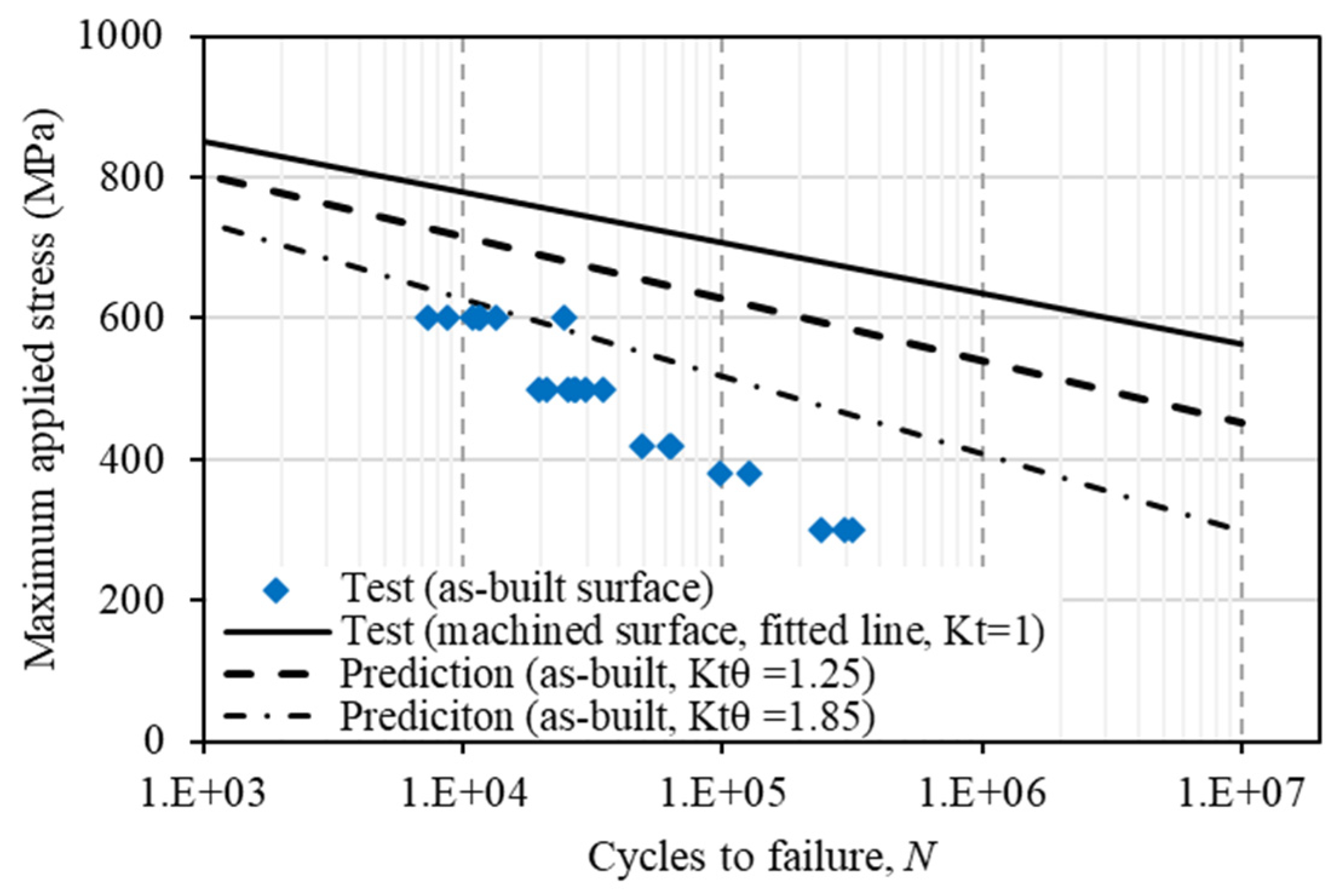
Preprints 75079 g010
Preprints 75079 g011
Figure 11. Macroscopic images of the crack propagation trajectories with indicators of accumulated load cycle numbers at crack measurement points for (a) 3PB-Test 1 (σmax=380 MPa, Ni = 31,000, Np = 74,000 and Nt = 126,737), (b) 3PB-Test 2 (σmax=380 MPa, Ni = 3,000, Np = 33,000 and Nt = 96,875), where Ni denotes the crack initiation life corresponding to initiation of a 0.5 mm crack, Np the crack propagation life from 0.5 mm to around 1.5 mm, and Nt the total life from the first cycle to fracture. The images only captured part of the specimens’ height.
Figure 11. Macroscopic images of the crack propagation trajectories with indicators of accumulated load cycle numbers at crack measurement points for (a) 3PB-Test 1 (σmax=380 MPa, Ni = 31,000, Np = 74,000 and Nt = 126,737), (b) 3PB-Test 2 (σmax=380 MPa, Ni = 3,000, Np = 33,000 and Nt = 96,875), where Ni denotes the crack initiation life corresponding to initiation of a 0.5 mm crack, Np the crack propagation life from 0.5 mm to around 1.5 mm, and Nt the total life from the first cycle to fracture. The images only captured part of the specimens’ height.
Preprints 75079 g011
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated