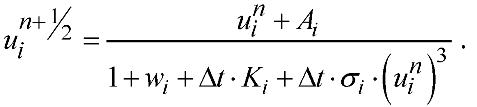1. Introduction
In nature and technologies, transport processes are essential because they drive an important number of phenomena [
1]. One of them is diffusion, where energy or particles are transported in a specific way [
2,
3]. The phenomenon of spreading in the universe occur on a large scale from atoms to stars [
4,
5].
In the case of the models of two-dimensional diffusion, an important step has been realized by Machta and Zwanzig in Lorentz gas [
6]. This work was followed by further simulations in Lorentz gas regarding the connection of diffusivity to certain phase space parameters [
7] or to entropy [
8]. Diffusion on surfaces is also a relevant topic. In the case when the surface may cause a chaotic dynamic, the phenomena has been studied in Refs. [
9,
10,
11].
Recently, exciting results have been obtained regarding diffusion with large spatial extension, which covers important analytical and computational results [
12,
13,
14,
15,
16]. However, the studied geometry of the system is either one-dimensional or if two-dimensional, then the Cartesian coordinate system is used. In reality, the geometry of the studied system often drives the researcher to use other coordinate systems, most importantly spherical and cylindrical. A typical example is the case when a piece of ice is melting in water [
17]. In nuclear physics, neutron diffusion occurs in finite spherical reactors [
18]. Reactive diffusion through triple layers in spherical geometry was studied by Erdélyi and Schmitz [
19] experimentally as well as numerically by the finite volume method. Cylindrical geometry was used to study diffusion in nanowires and nanorods by Roussel et al. [
20]. The classic textbook [
21] and [
22] covers the theory of heat conduction in solids and that of diffusion and reaction in permeable catalysts, respectively, including spherically symmetric cases.
Heat conduction and similar problems are routinely solved by well-established numerical methods. However, in our view, these are far from being the optimal ones since they have serious drawbacks. Conventional explicit finite difference schemes are unstable when the applied time step size exceeds the so-called Courant–Friedrichs–Lewy (CFL) limit, which is usually rather low. This is the main reason that implicit algorithms, which possess much better stability properties, are often used to tackle these equations [
23,
24,
25,
26]. These methods involve the solution of an algebraic equation system with the whole system matrix, which can be very large, especially if the number of spatial dimensions is larger than one. This is often time- and computer memory consuming and cannot be straightforwardly parallelized.
In the last years, our research team developed some explicit methods that are stable for the heat conduction equation for arbitrary time step sizes in any number of spatial dimensions [
27,
28]. The algorithms were examined in several systems with homogeneous and inhomogeneous material parameters. They are orders of magnitude faster than the conventional solvers, including the standard Runge-Kutta schemes and the common MATLAB 'ode' solvers. However, all of these tests were performed in Cartesian coordinate systems, and now it is high time to perform them in cylindrical and spherical systems.
In the next section, we derive the studied equation and present its discretization. It is followed by the derivation of the analytical solution, which is valid in both cylindrical and spherical cases.
Section 4 is devoted to the description of the numerical algorithms, while
Section 5 is about the verification of the methods using the analytical solution. Then we turn our attention to examining the performance of the methods in reproducing experimental results: first, the circumstances are described, and then the numerical results of the Ansys software and our code are presented. Finally, the last section summarizes our conclusions.
2. The Studied Problem
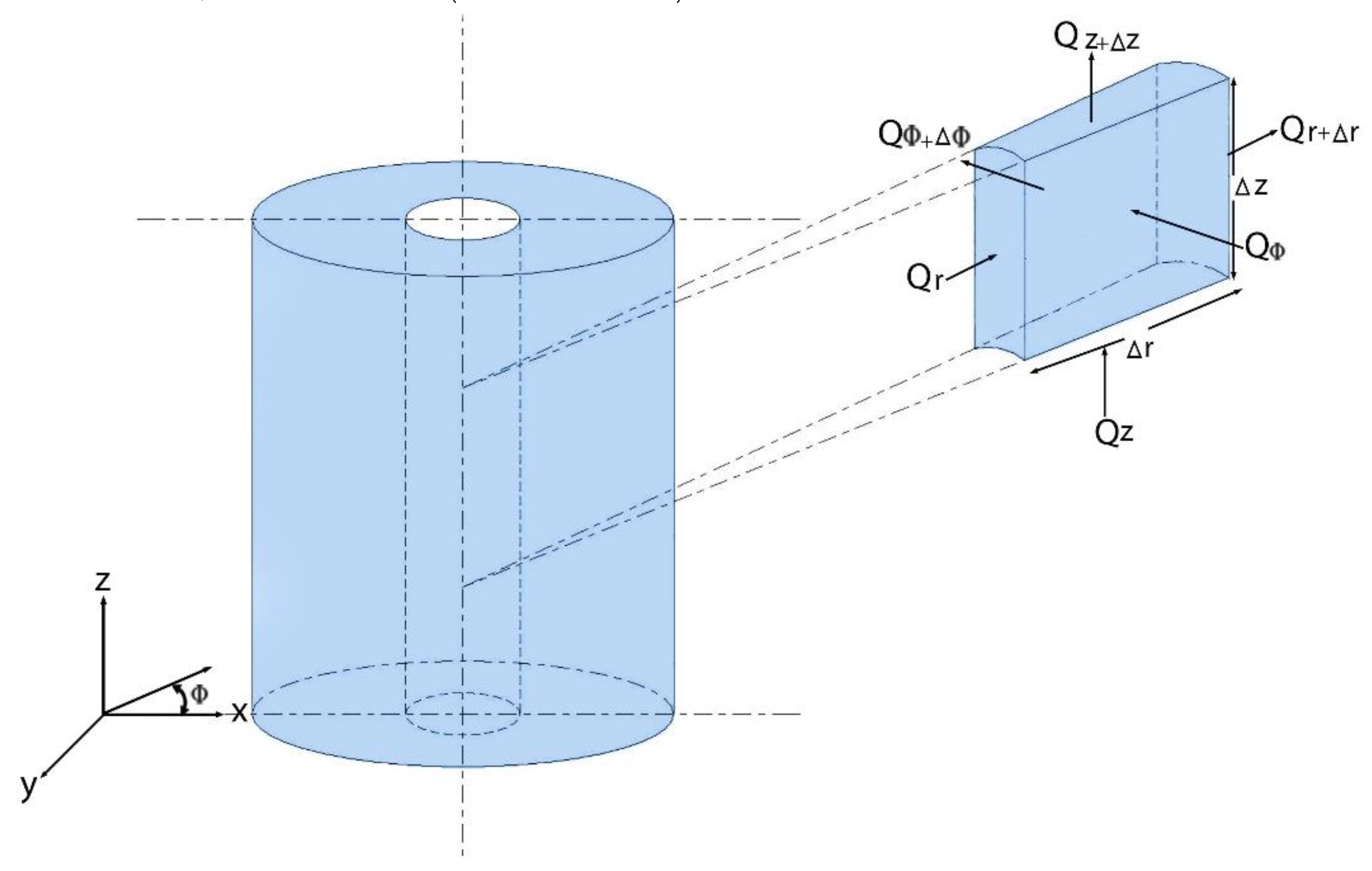
We derive the heat transfer equation (conduction, convection, and radiation) in cylindrical and spherical coordinates based on energy balance. Firstly, in cylindrical coordinates, consider a small 3D cylindrical element. In the case of full cylindrical symmetry, it is better to choose a full ring-shaped element, which yields .
Figure 1.
Visualization of a cylindrical element.
Figure 1.
Visualization of a cylindrical element.
We assume that physical quantities, including the temperature, are not changing in the
ϕ -direction. It means we deal only with two-dimensional problems from the mathematical point of view, as shown in Fig. 1. The energy balance in this element during a time interval can be expressed as:
or briefly,
To fill Eq. (1) with concrete formulas, the following three well-known laws are used.
Fourier’s law of heat conduction:
In the given equation, represents the temperature, represents the thermal conductivity of the material, and S represents the surface area through which the heat flows.
Newton's law of heat convection can be stated as follows:
in the given equation, the symbol
h denotes the convection heat transfer coefficient. The ambient temperature
is independent of the temperature u of the body under examination. Hence, the term
is included in the heat generation term to account for this effect.
Stefan-Boltzmann law governs the incoming and outgoing heat radiation, and its expression is as follows:
In the given context
, the universal Stefan-Boltzmann constant
needs to be multiplied by
the emissivity constant to account for the surface not being a black body. The incoming radiation
is also considered in the heat source term
q as the
absorptivity term. Consequently, the change in energy of an element over a specific time interval
can be expressed as.
where
,
are the density and the specific heat, respectively.
From these equations one can derive the heat-transport equation in a 3D cylindrical coordinate system, which can be written as:
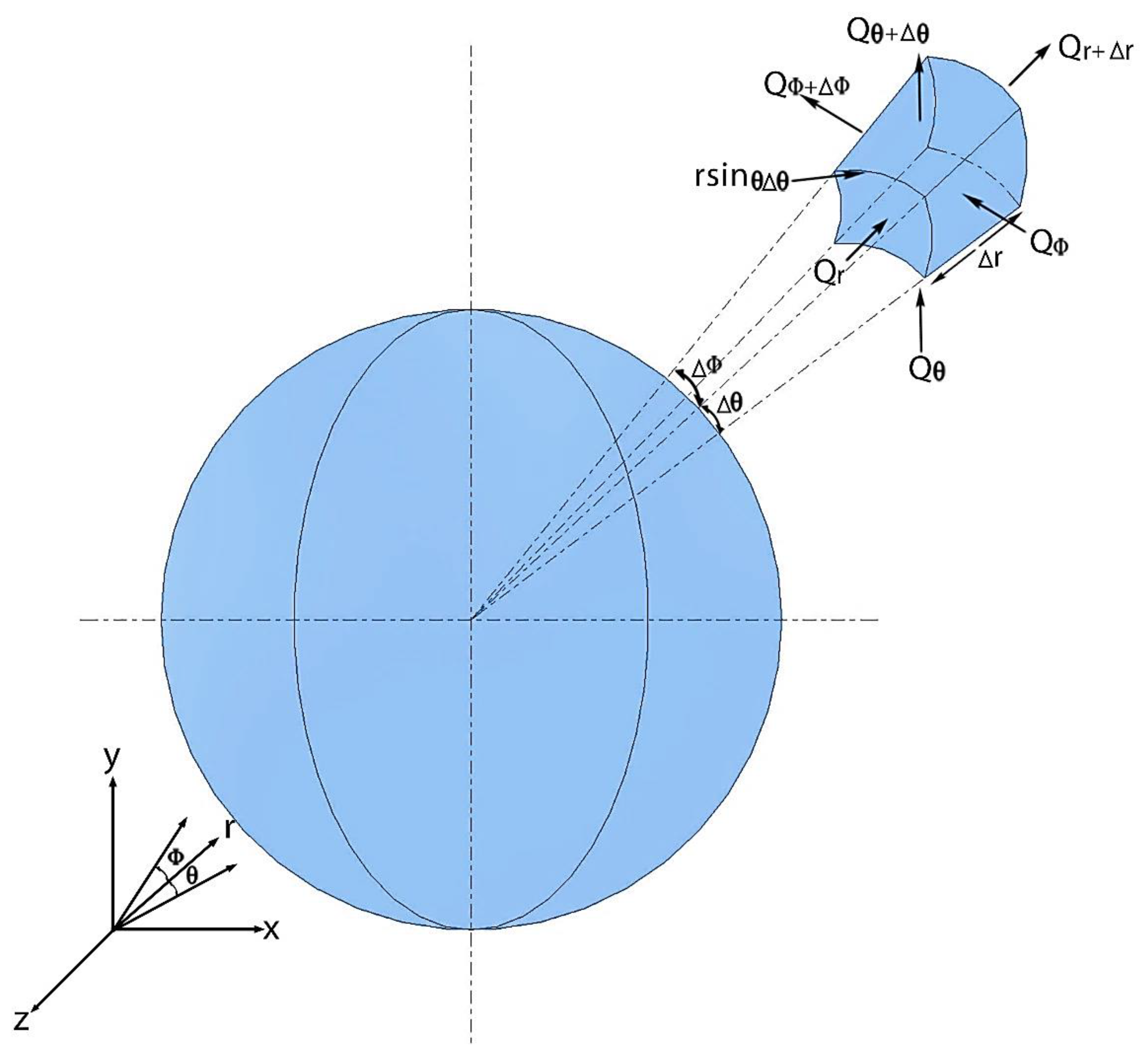
In the case of spherical coordinates, a small 3D spherical element can be seen in Fig. 2. The heat-transport equation for this case can be expressed as follows:
Figure 2.
Visualization of a spherical element.
Figure 2.
Visualization of a spherical element.
If one does not consider the convection, radiation and source terms in Eq. (6) and assume that the material properties are homogeneous, one obtains the form of the heat conduction equation in cylindrical and spherical coordinate systems. We study only symmetrical systems, which means no relevant physical quantities depend on coordinate
in the cylindrical and on coordinates
and
in the spherical case. If we – temporarily – also assume that nothing depends on the
z coordinate in the cylindrical case, only the radius
r remains as a spatial variable, which yields
where
n=0, 1, and 2, which mean Cartesian, cylindrical and spherical coordinates respectively, while
is the diffusivity. Eq. (7) is also used for particle-diffusion, where the diffusivity is usually denoted by
D.
2.1. The spatial discretization of the problem
Instead of directly discretizing PDEs (6) or (7), we use an equivalent resistance-capacitance model. In the case of cylindrical geometry, we consider tube-shaped cells with height and thickness . For spheres the cells have spherical-shell shapes with thickness again. The temperature is considered at the middle of the cell-layer, where the radial distance from the origin (the mean radius of the cells) is denoted by , while the subsequent radius of the cell border is denoted by .
The cells’ heat capacity in the cylindrical and in the spherical case is approximated as , and , respectively.
Let us denote the area of the cylindrical cell-surface perpendicular to
r with
, which can be given as
. Now the thermal resistance in
r-direction, the approximate formula
is used. For the thermal resistance in the
z-direction, the approximate formula
is used, where the cell
i+Nr is below the cell
i.
In the spherical case,
can be given as
. Using this, the thermal resistance is calculated similarly as in the cylindrical case, but now the integration yields
. From Eq. (2) and (5) it is easy to obtain the ODE system
to determine the time-evolution of the cell temperatures. Here
S is the area of the surface on which the convection and radiation occurs, which will be the outer surface of the cylinder in
Section 7. In publications [
29,
30] the interested readers can find more details about this treatment of heat conduction. If one neglects the higher powers of
, one can easily derive that
in both cases. Let us use the following notations:
Inserting these into (9) we can write Eq. (9) into a simpler form:
which will be solved numerically in
Section 5 and
Section 7.
3. The analytical solution
In this section we outline how the radial solutions of Eq. (7) look like for both cylindrical and spherical coordinate systems. The self-similar Ansatz we use:
Substituting the first and second derivative of the Ansatz into the original Eq. (2), we arrive at an ordinary differential equation (ODE) for
with the constraint that
a is an arbitrary real number. The software Maple12 gives the following solution to this ODE:
Unfortunately, for unclear reasons substituting the
n = 0 we cannot get back the original Cartesian solution, some factor is missing. Luckily, Eq. (12) describes well the cylindrical and spherical symmetric solutions. Note that unlike the Cartesian case, here all the solutions have the even property. In our former theoretical publications [
12,
31] we analyzed the possible different kind of solutions. Depending on the numerical values of parameter
a, four species of solution curves exist. It is generally true for Cartesian, cylindrical and spherical systems as well, the only difference is just the numerical values of
a.
So for large negative a values, the solutions show an exploding behavior at infinite temporal and spatial values, which obviously violates energy conservation or thermodynamics. When a is close to zero, we get solutions which have a finite non-zero numerical value at large times and special points. For small positive a values, the solution has a maximum at zero and has a similar decay to zero as the fundamental Gaussian solution. Finally, for large positive a values, the solutions have a power law explosion in the origin (at zero time and zero spatial coordinate) with a drastic decay accompanied by additional oscillations. So, the solutions become negative at some values. These are the general new features of these kinds of solutions for Cartesian, cylindrical and spherical systems as well.
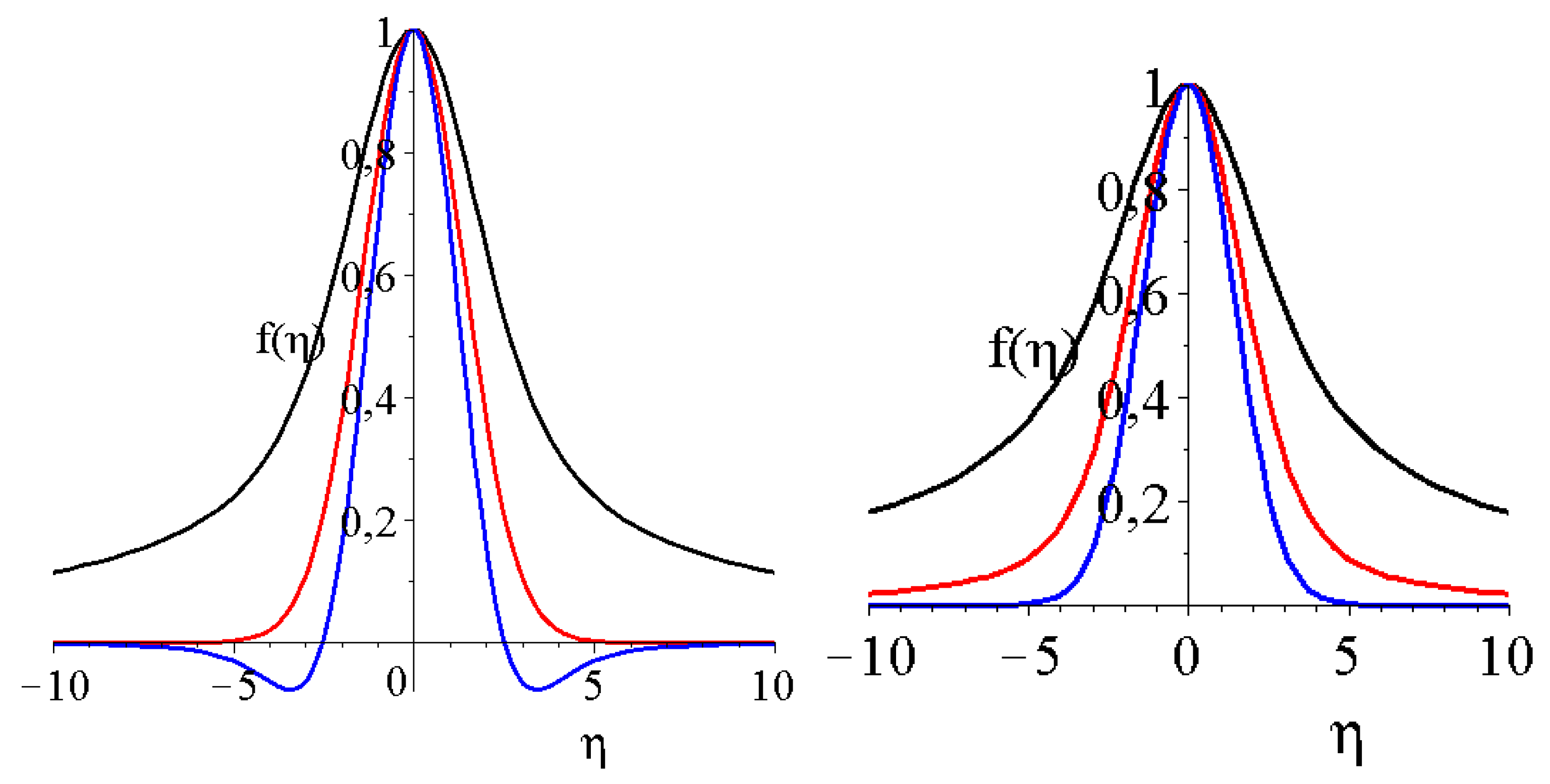
Figure 3.
The Kummer's M shape functions f(η) from Eq. 9 for the cylindrical (left figure) and spherical (right) symmetry for three different self-similar exponents a. The black, red and blue lines are for a = 1/2, 1 and 3/2. The diffusion coefficient α was set to unity for all cases.
Figure 3.
The Kummer's M shape functions f(η) from Eq. 9 for the cylindrical (left figure) and spherical (right) symmetry for three different self-similar exponents a. The black, red and blue lines are for a = 1/2, 1 and 3/2. The diffusion coefficient α was set to unity for all cases.
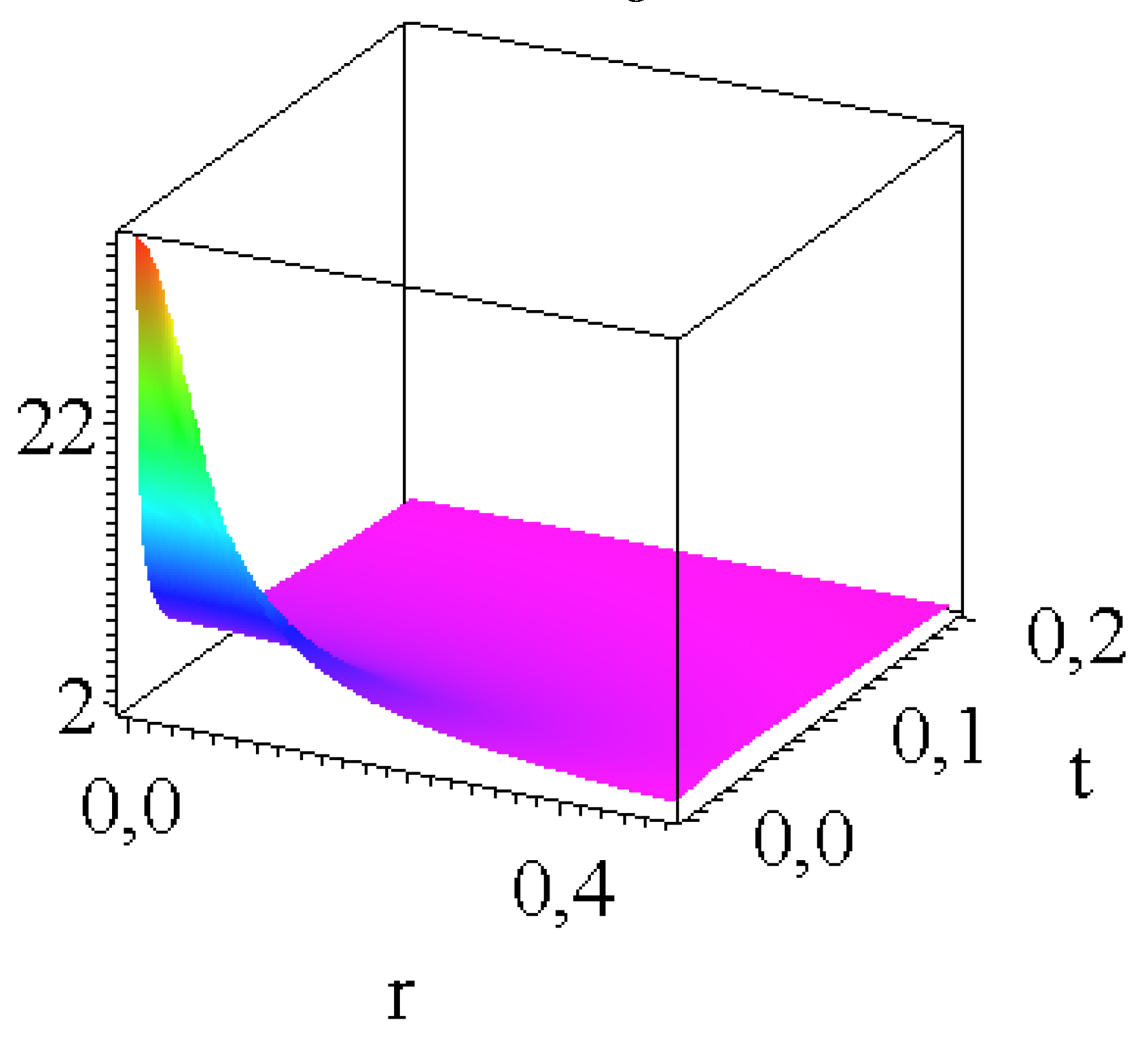
For our forthcoming numerical analysis, instead of the solution (12) of the ODE (11), we need the final form of the solution of the PDE (7), which reads as follows:
Figure 4 presents the
solution for Kummer's M function for cylindrical symmetry. One can observe certain similarities with the regular Gaussian.
4. The applied numerical methods
We present the numerical schemes adapted for Equation (10). We always use equidistant discretization of the time variable with time step size
, and the temperature of cell
i at the time
is denoted by
. The following quantities will be extensively used:
The quantity w is the generalization of the so-called mesh-ratio (which has the expression), but it now depends on the cell index. The aggregated quantity A, on the other hand, responsible for the conductive heat exchange with the neighbors of cell i as well as the source term.
1. The UPFD (unconditionally positive finite difference) method was proposed in [
32] for the diffusion-advection-reaction equation a decade ago. We recently adapted it [
28] to Eq. (10) as follows:
2. The pseudo-implicit (PI) method [
28] has the following two stages:
3. A two-stage version of the Rational Runge-Kutta methods [
33] will be applied as follows. First, a full step is taken by the standard FTCS (explicit Euler) scheme to calculate the predictor values:
where the increment
is calculated as
Using these predictor values, the increment in the second stage is
Now the new values of the variable are as follows
where the following scalar products are used:
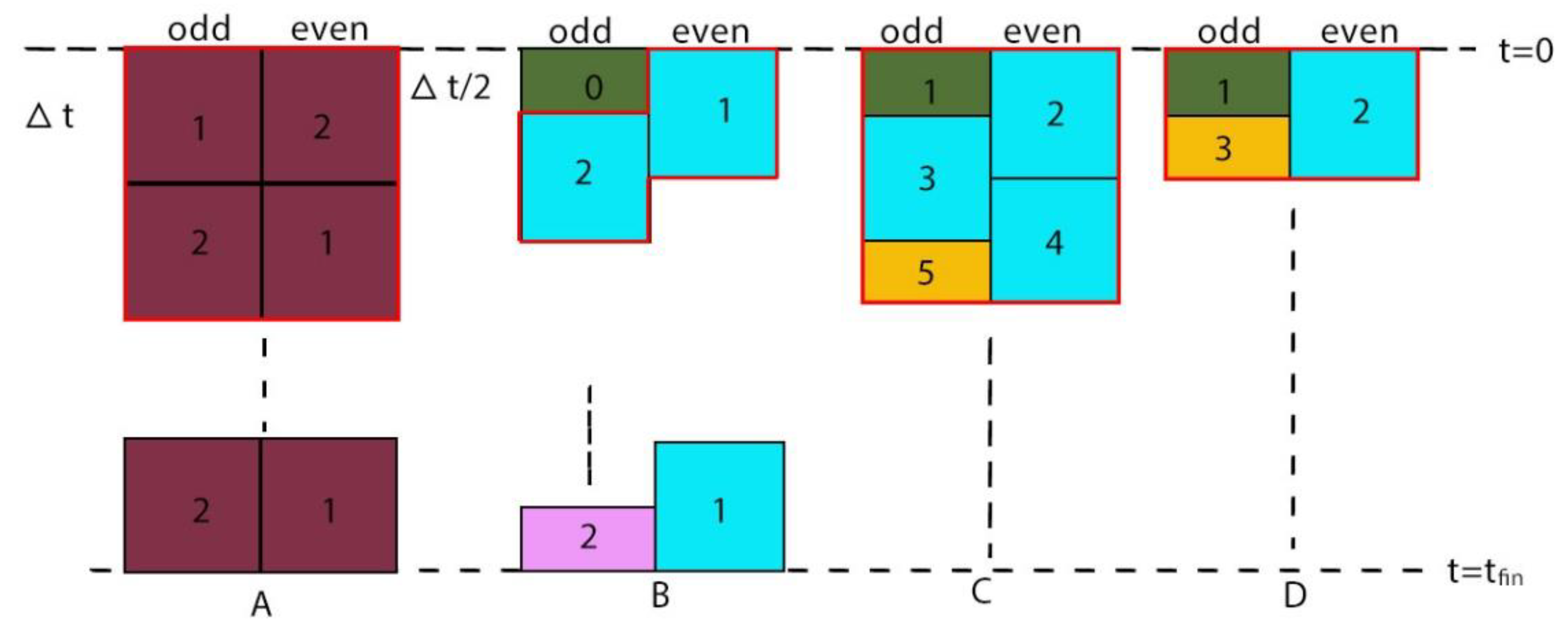
A special, checkerboard-like spatial grid must be constructed if someone wants to use any version of the odd-even hopscotch methods [
34]. The cells of this grid are labeled as odd and even, with the requirement that all the nearest neighbors of the even cells are odd and vice versa. In the case of the original version (denoted by OOEH here), the odd-even labels must be interchanged after each time step as it is displayed in
Figure 5A. The standard FTCS formula is modified in the first stage to make it slightly more stable [
30] by treating the convection and radiation terms in an “implicit” way:
The implicit (Euler) scheme in the second stage is as follows:
It is important that in the second stage, similarly to the other odd-even hopscotch scheme below, always the latest available values of the neighbors are used when the new values of u are calculated. Due to this, the values in the implicit formula have been just obtained at Stage 1, which makes it effectively explicit.
5. In the case of the shifted-hopscotch (SH) algorithm [
29], five stages constitute a two-step long repeating block. Two of the stages are half- and the remaining three of them are full-length steps, see in
Figure 5 (C). The first stage is for the odd cells only and symbolized by a dark green box with the number 1 in the figure. It uses the formula
Then, a full-time step with formula
for the even, the odd, and the even cells come again (blue rectangles in the figure). The superscript
µ equals
n for the even and
n+1 for the odd cells. Finally, a half-length time step (pink box with number 5 inside) for the odd cells closes the calculation with the formula
6. The asymmetric hopscotch (ASH) algorithm is almost the same as the SH one, but the repeating block is only one-time step long as one can see in Fig 5D. It contains only three stages instead of five which use the same formulas (14), (15) and (16), respectively.
7. The procedure of the leapfrog-hopscotch (LH) algorithm [
27] begins and ends by a half-length stage, but then all other stages have full time step length (blue boxes in Fig. 5B). At the first and intermediate stages, it uses formulas (14) and (15). However, at the last stage (pink rectangle) it uses (15) again, but
must be divided by 2, including their appearances in the quantities
w and
A.
8. Although the Dufort–Frankel (DF) method [
35] is a known explicit and unconditionally stable algorithm for the linear heat equation, it is rarely used. The formula adapted for the case of Eq. (10) is:
It is a two-step scheme which is not self-starter, thus we apply the UPFD formula of point 1 to start the DF method.
9. One of the most common algorithms to solve the heat conduction equation is the explicit-Euler based FTCS (forward time central space) algorithm. It can be adapted to our case in the standard way as follows:
5. Verification using the analytical solution
In this section, we take the height of the cylinder as well as
unity. It means that computationally there is one space dimension only in both the cylindrical and the spherical case. The solution parameters are:
Here N represents the total number of cells, while and are the radial coordinates of the center of the first and last cells. The initial condition obtained by substituting the initial t and boundary r values into the analytical solution, respectively. The Dirichlet boundary conditions on the right side (the circumference of cylinder and sphere) obtained simply by substituting the radius into the analytical solution and calculate the function value at each time step. On the left side (the cylinder and sphere center, ), zero-Neumann boundary applied, since no heat can disappear from the center of the cylinder or the sphere. This boundary actually exists only computationally but not physically. We remind the reader that the analytical solutions are constructed for Eq. (7), and here we accurately reproduce them by solving the apparently different Eq. (10) numerically.
We calculate the so-called maximum error:
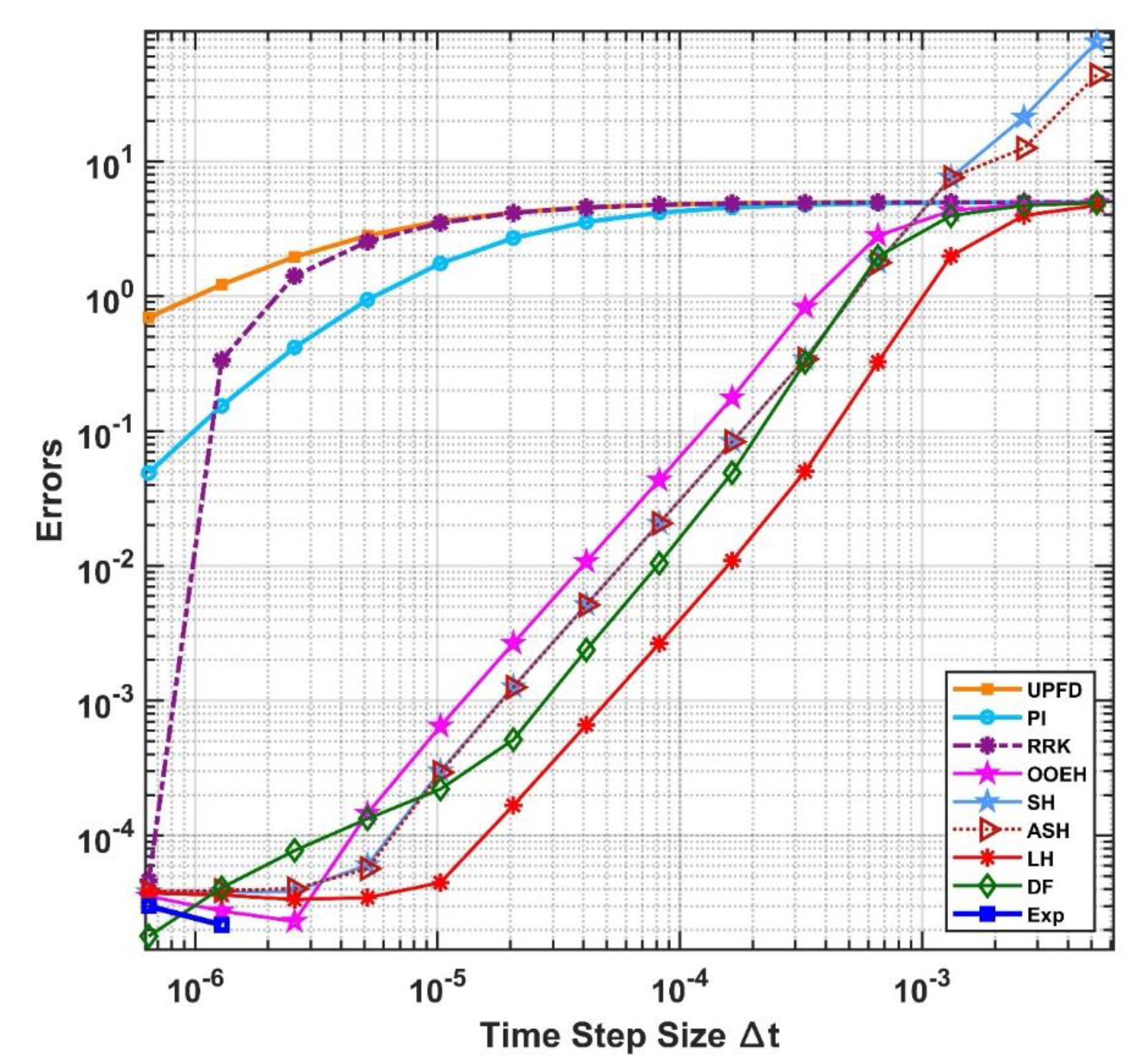
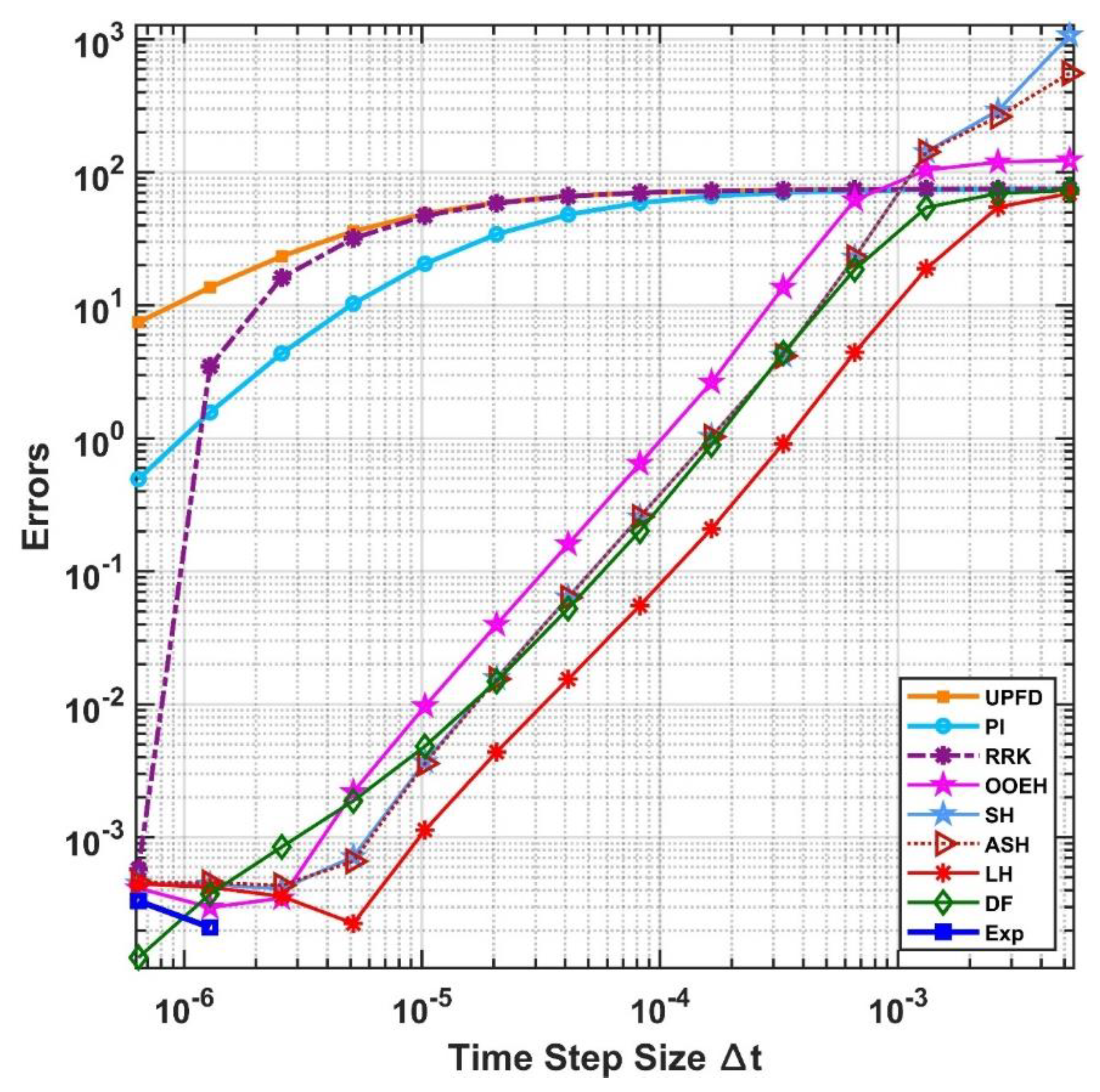
The obtained maximum errors are displayed as a function of the time step size in Fig. 6 and 7 for two values of parameter
a in cylindrical coordinates.
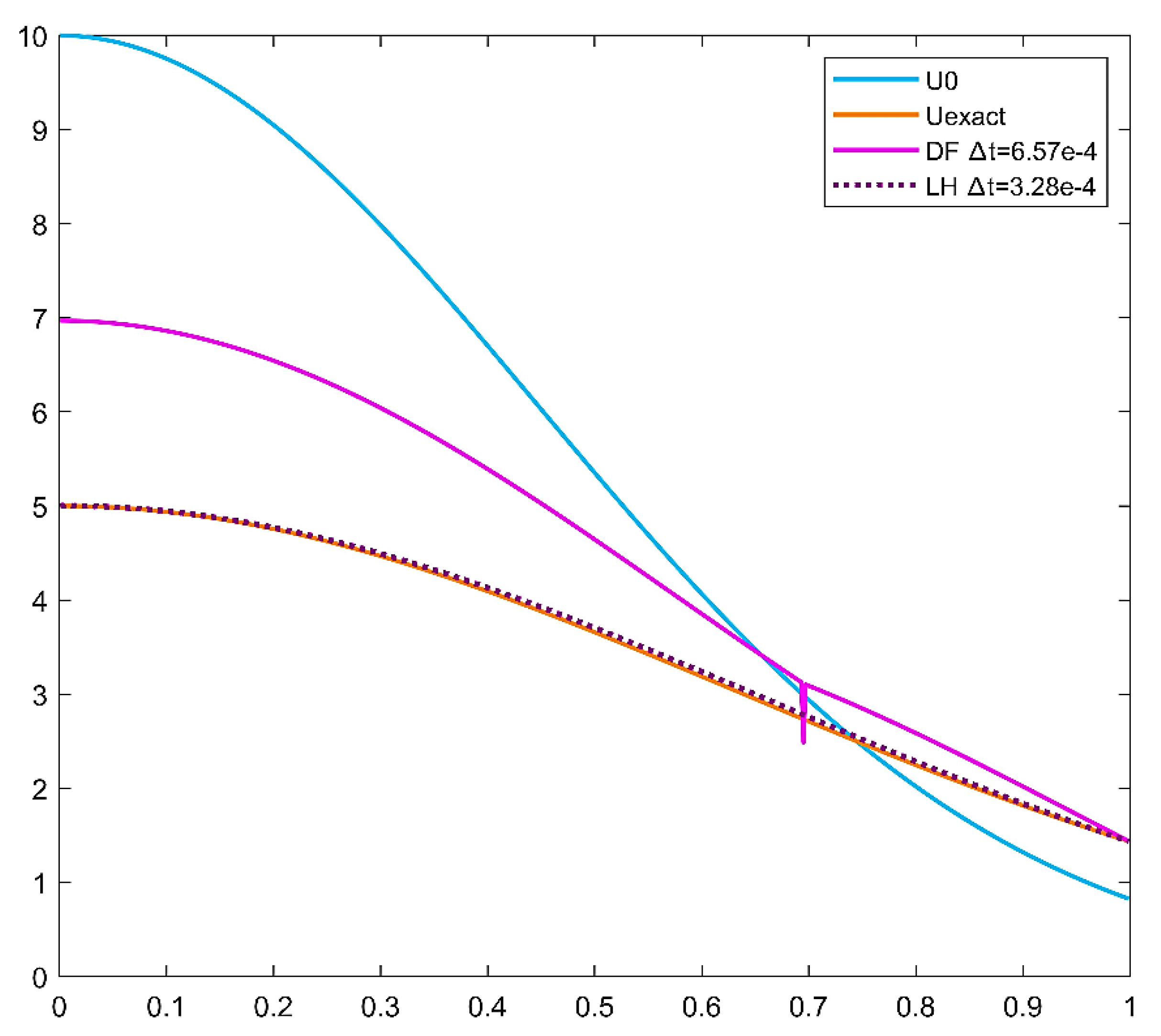
Figure 8 presents the temperature value as a function of
r. For the case of spherical coordinates,
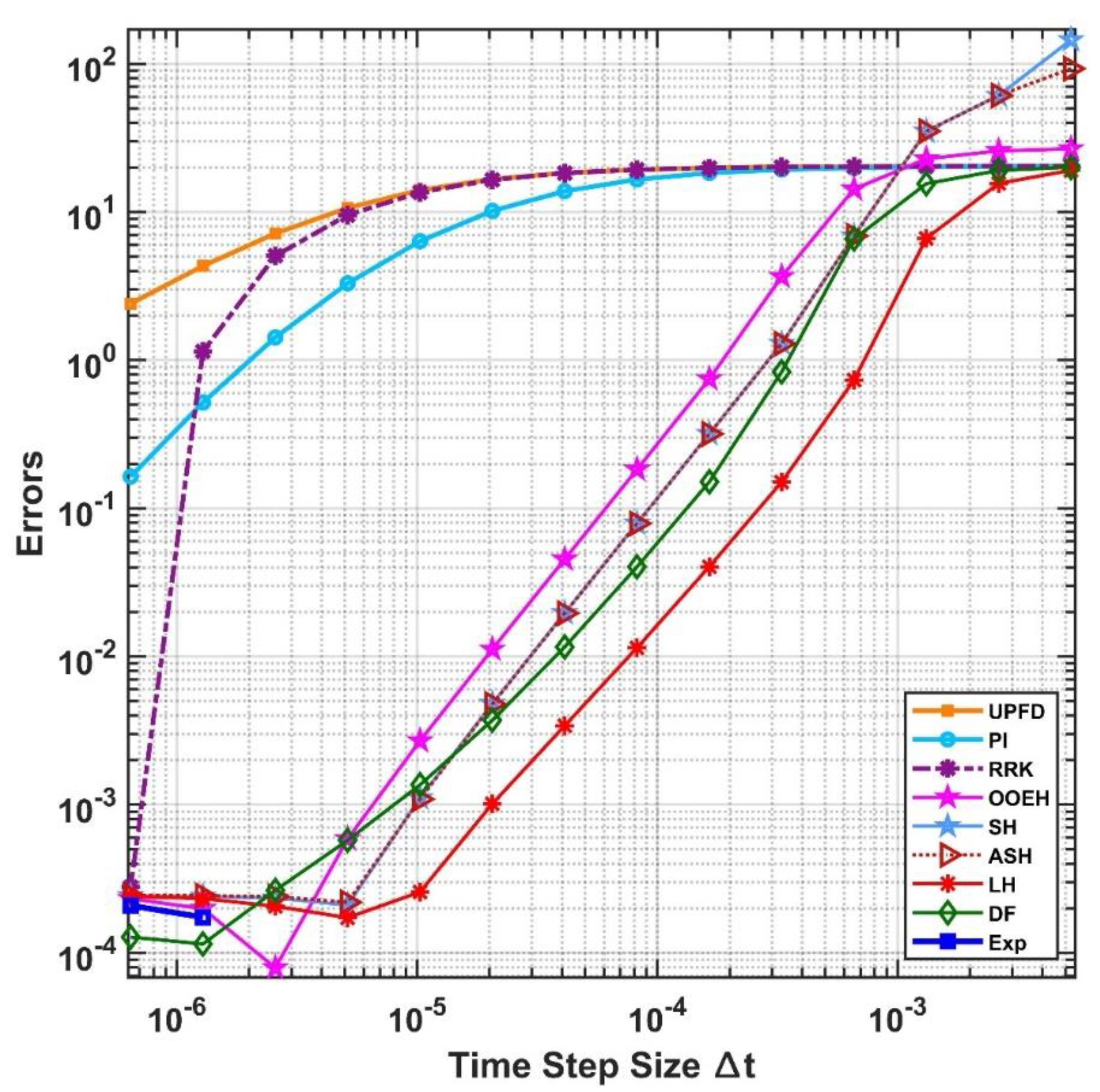
Figure 9 shows the maximum error as a function of the time step, and
Figure 10 presents the temperature as a function of
r. The fact that we obtain very small errors in all cases verifies not only the numerical algorithms, but the equivalence of the two mathematical treatments of the physical problem.
Figure 6.
The maximum errors as a function of the time step size for the 9 numerical methods in case of cylindrical coordinates for a=1.
Figure 6.
The maximum errors as a function of the time step size for the 9 numerical methods in case of cylindrical coordinates for a=1.
Figure 7.
The maximum errors as a function of the time step size for the 9 numerical methods in case of cylindrical coordinate for a=2.
Figure 7.
The maximum errors as a function of the time step size for the 9 numerical methods in case of cylindrical coordinate for a=2.
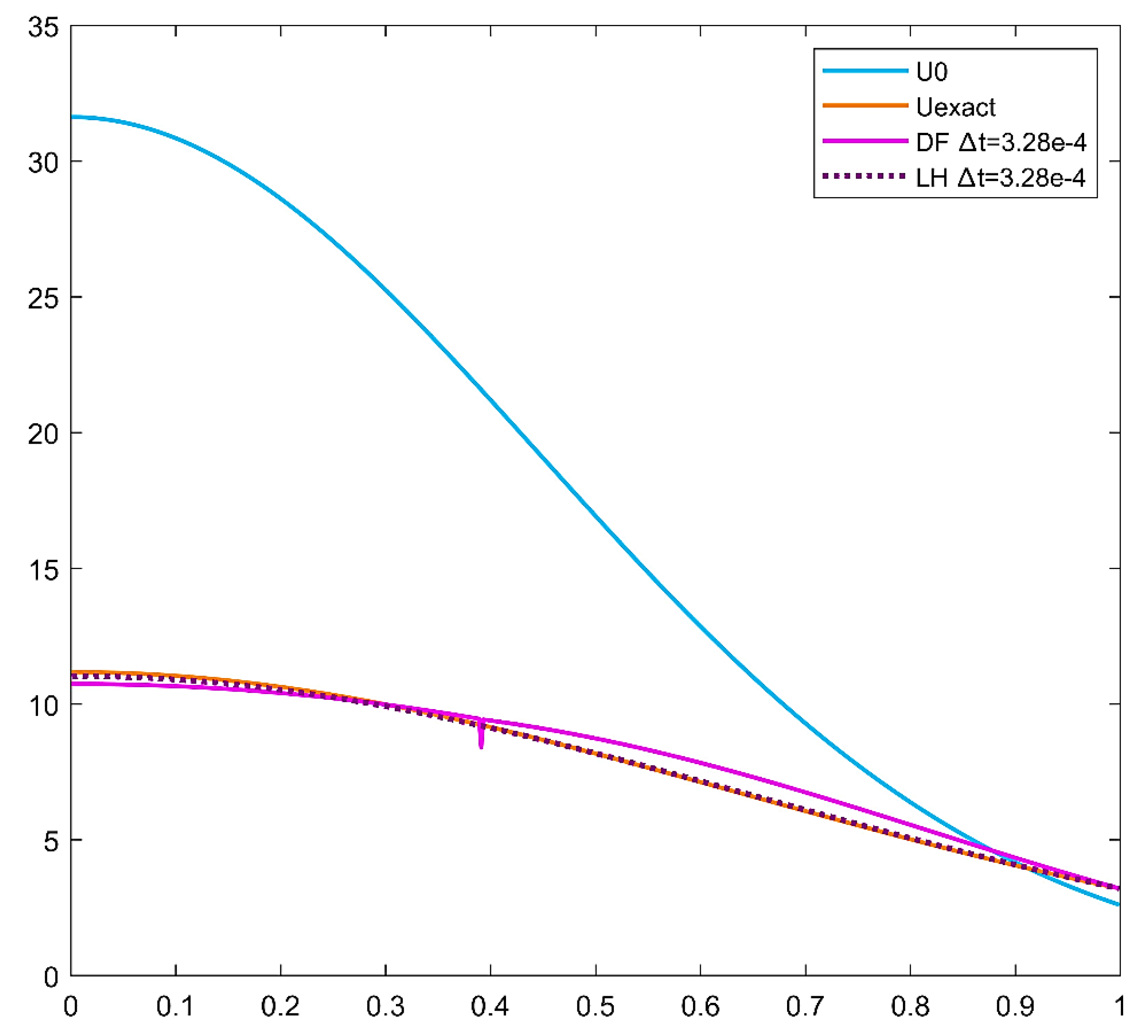
Figure 8.
The values of temperature as a function of variable r in case of the initial function u0, the analytical solution Uexact, the DF method and the LH method in case of cylindrical coordinate for a=1. .
Figure 8.
The values of temperature as a function of variable r in case of the initial function u0, the analytical solution Uexact, the DF method and the LH method in case of cylindrical coordinate for a=1. .
Figure 9.
The maximum errors as a function of the time step size for the 9 numerical methods in case of spherical coordinates for a=1.2.
Figure 9.
The maximum errors as a function of the time step size for the 9 numerical methods in case of spherical coordinates for a=1.2.
Figure 10.
The values of temperature as a function of r variable in case of the initial function u0, the analytical solution Uexact, the DF method and the LH method in case of spherical coordinate for a=1.2.
Figure 10.
The values of temperature as a function of r variable in case of the initial function u0, the analytical solution Uexact, the DF method and the LH method in case of spherical coordinate for a=1.2.
6. Setup of the reproduction of the experimental results
6.1. Material properties
We are going to reproduce the experimental results of Cabezas et al. [
36], where heat transfer is studied in a steel C45 cylinder with properties shown in
Table 1 below.
The volume of the cylinder segment is
,while
. In our approximation, physical quantities are not changing in the
ϕ-direction, thus that dimension is irrelevant and computationally we deal with a two-dimensional problem. The total area of the meshes is 0.0174 m
2 in the
r direction, and
in the
z direction. The number of the cells along the
r axis and
z axis are set to
Nr = 15 and
Nz = 100, thus the total number of the cells in the system is
. We emphasize that we use the same code as in
Section 5, only some parameters such as
Nz are different.
6.2. The initial and the boundary conditions
We use a constant initial condition in all cases.
As in
Section 4, we use different boundary conditions on different sides. On the left side, the center of the cylinder, we applied Neumann boundary condition in all cases, which don’t allow conductive heat transfer at the boundary,
On the right and upper boundaries, we use two types of boundary conditions. The first one is zero-Neumann, when there is no heat exchange with the environment. The second one when there is a heat exchange with the environment by convection and radiation, considering the heat convection coefficient
, and the emissivity constant as 0.85 to obtain realistic values for
. On the lower boundary, we applied the constant heat flux with
P=1500 W for all cases to follow the experimental setup in the paper [
36].
The heat generation contains a fraction of the ambient temperature radiation. The ambient temperature of the air is taken with three values depending on the experimental measurments (30.7,31.1, and 31.7 C). The term q contains also the convective heat gain due to the nonzero temperature of the air (in Kelvin). The convective and radiative energy transfer is perpendicular to the surface. The interior elements cannot gain or lose heat by the heat source, heat convection, or radiation.
7. Simulation results
In this section, the end of the examined time interval is defined as. To ensure that the errors of the numerical algorithms are small, we used a reference solution of the spatially discretized Eq. (9) obtained by the ode15s solver in MATLAB with a small tolerance. This reference solution is utilized in Eq. (20) to determine the maximum error of the time integration, which does not contain the error of the mathematical model and that of the space discretization.
7.1. Results of the numerical methods
For the simulation, we have chosen the top 5 algorithms, namely DF, OOEH, LH, SH, and ASH.
Figure 11present the maximum error results obtained from these selected algorithms.
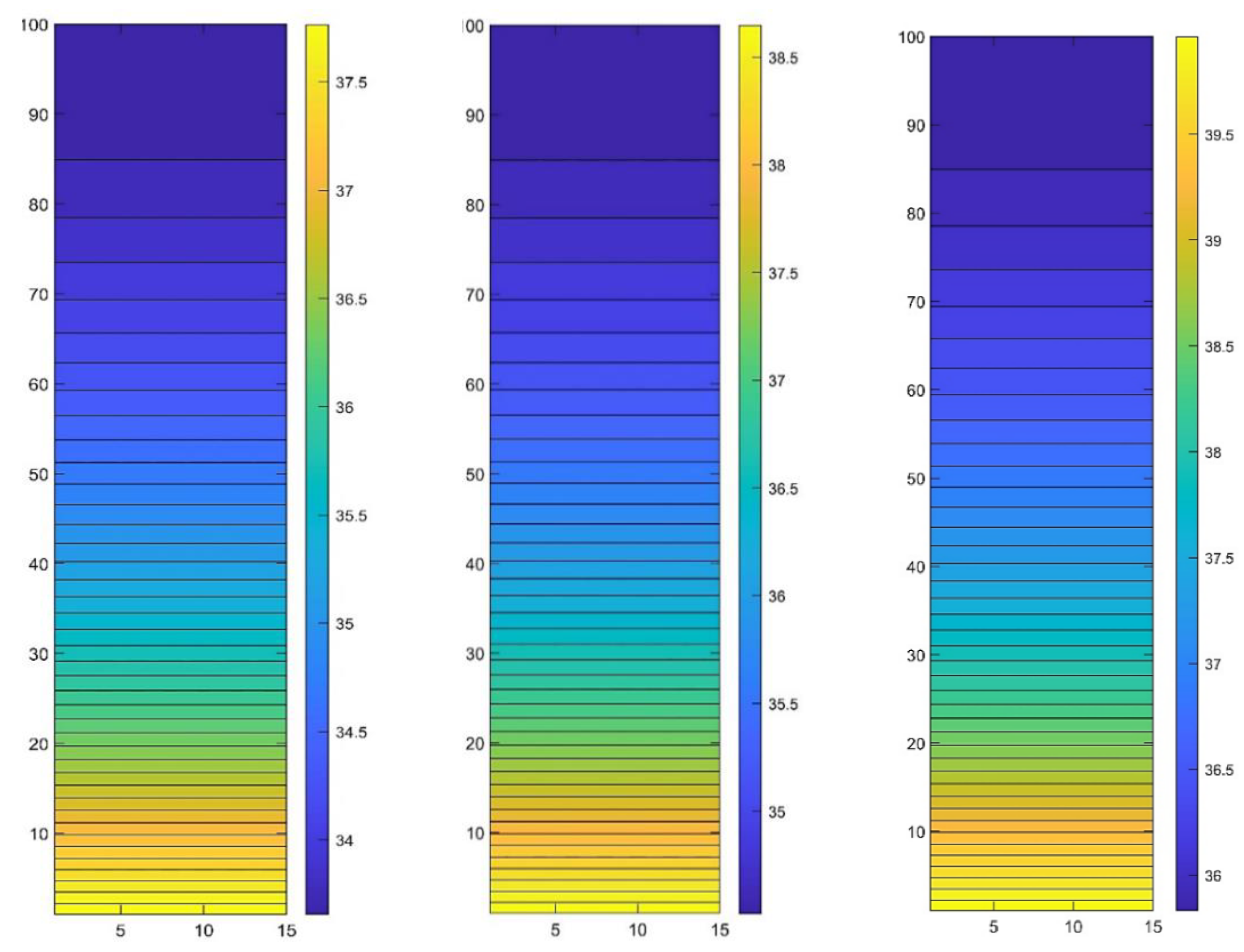
The simulation of a steel C45 cylinder was conducted using the selected algorithms, considering different boundary conditions as previously mentioned. Among these algorithms, the shifted-hopscotch method was chosen to visualize the temperature contour due to its high accuracy at small time step size. Figs 12-13 display the final temperature distribution obtained from this method.
Figure 12.
The final temperature distribution contour for different time values (t=20, 24, and 30 min, respectively from left to right) presented by the SH method when there is no heat exchange with the environment.
Figure 12.
The final temperature distribution contour for different time values (t=20, 24, and 30 min, respectively from left to right) presented by the SH method when there is no heat exchange with the environment.
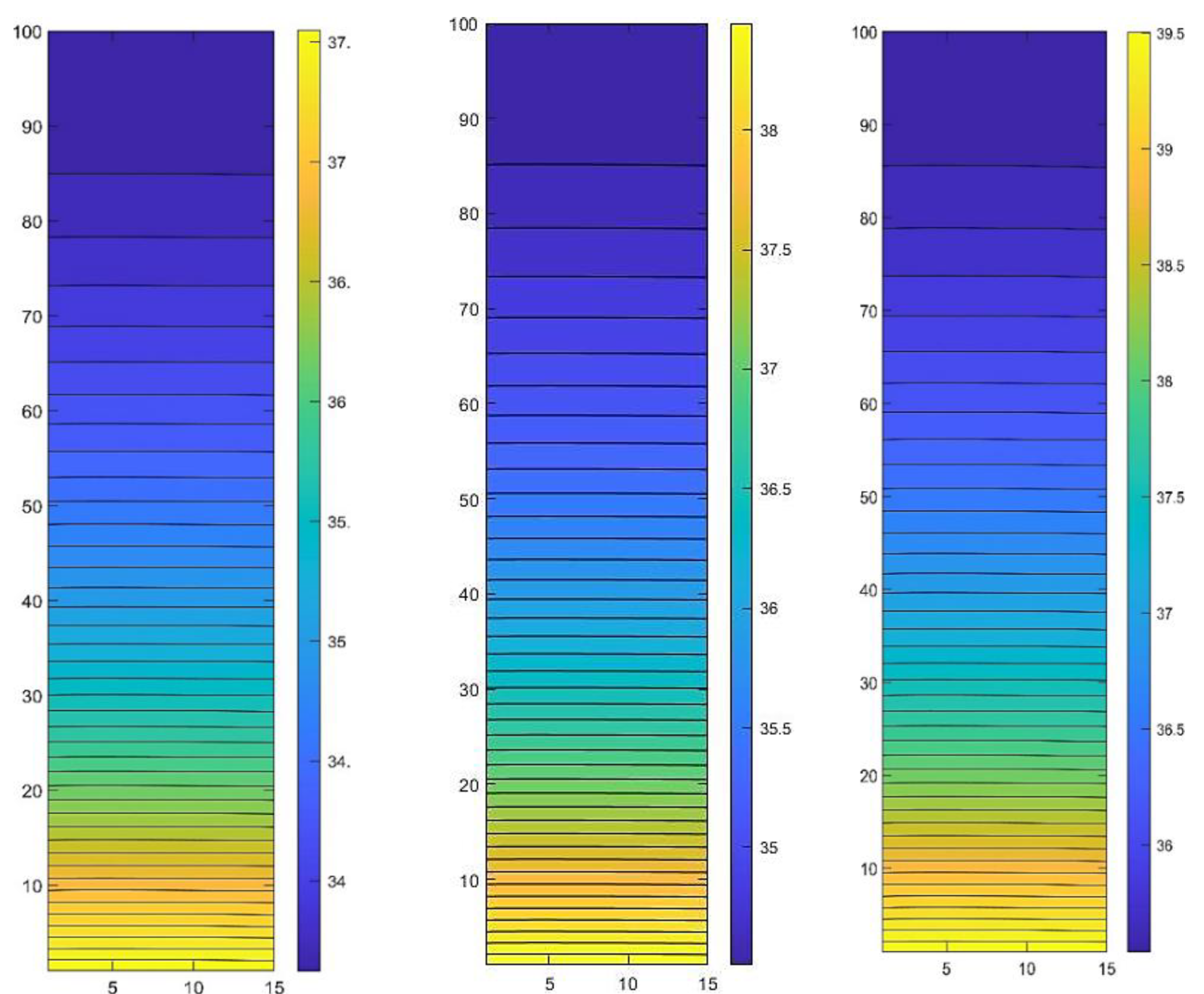
Figure 13.
The temperature distribution contour for different time values (t=20, 24, and 30 min) presented by the SH method when there is heat exchange with the environment by convection and radiation.
Figure 13.
The temperature distribution contour for different time values (t=20, 24, and 30 min) presented by the SH method when there is heat exchange with the environment by convection and radiation.
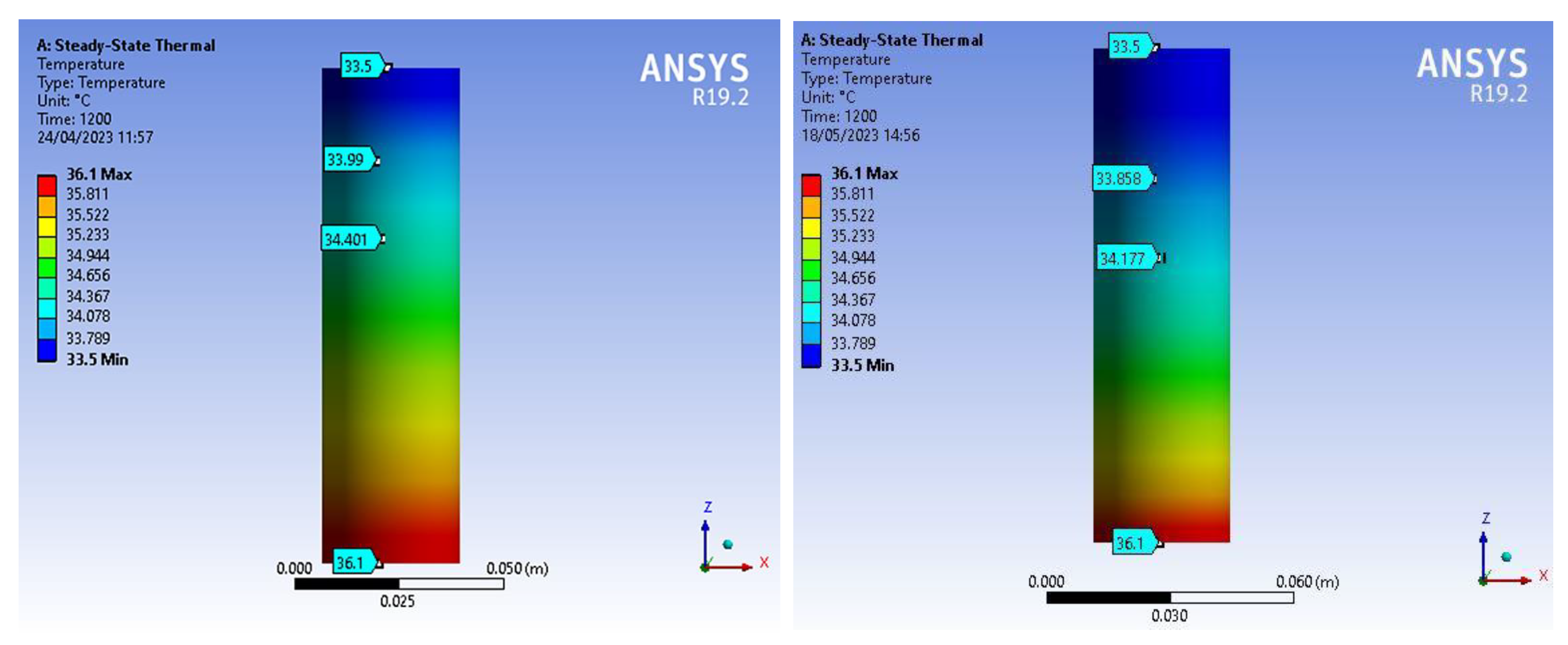
7.2. Ansys Simulation Results
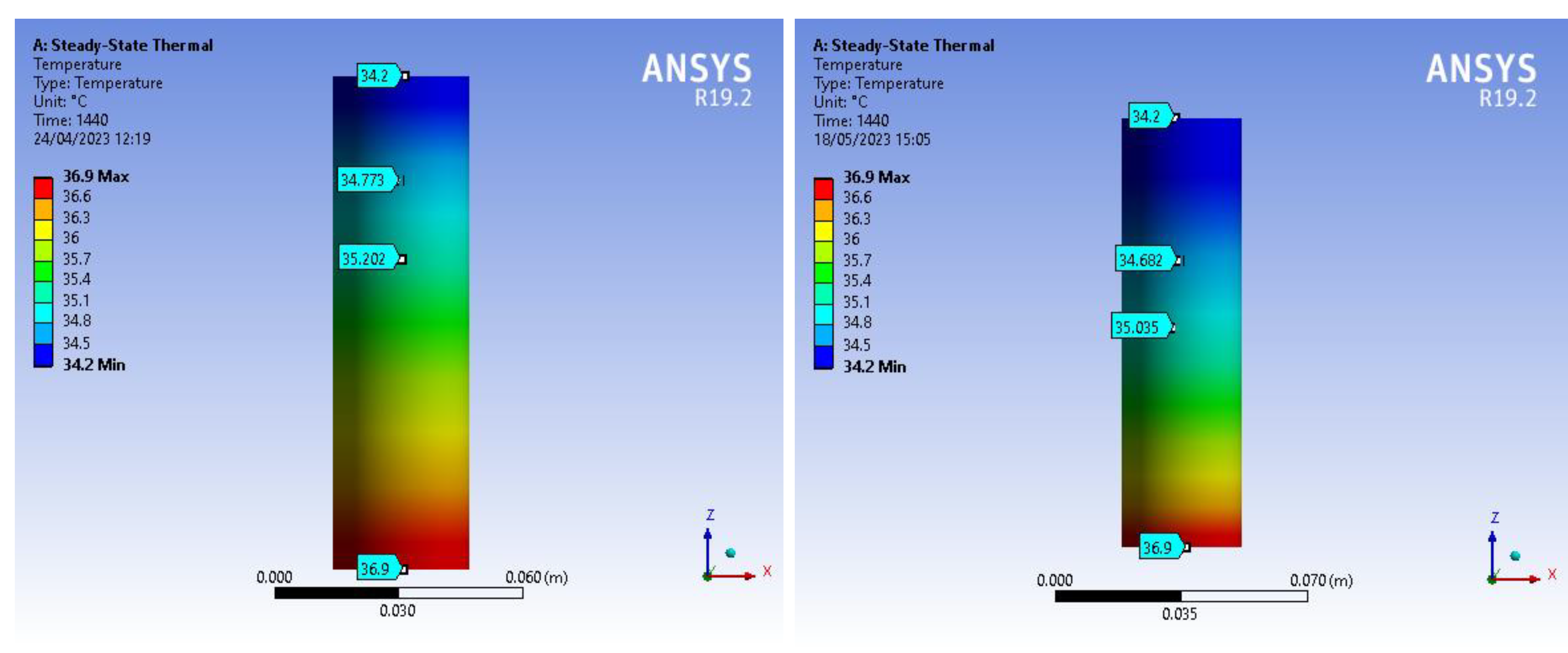
Ansys workbench steady state thermal analysis, with Mechanical APDL solver was used to simulate the steel C45 cylinder. The mesh size was , the total number of elements was 197183, since it was a computationally 3D problem. In Figs. 14-16 we present the final temperature distribution at three measurement times.
Figure 14.
The temperature contour at time (t=20 min) presented by Ansys workbench 19.2 when there is no heat exchange with the environment (left side of the figure) and when there is a heat exchange (right side of the figure).
Figure 14.
The temperature contour at time (t=20 min) presented by Ansys workbench 19.2 when there is no heat exchange with the environment (left side of the figure) and when there is a heat exchange (right side of the figure).
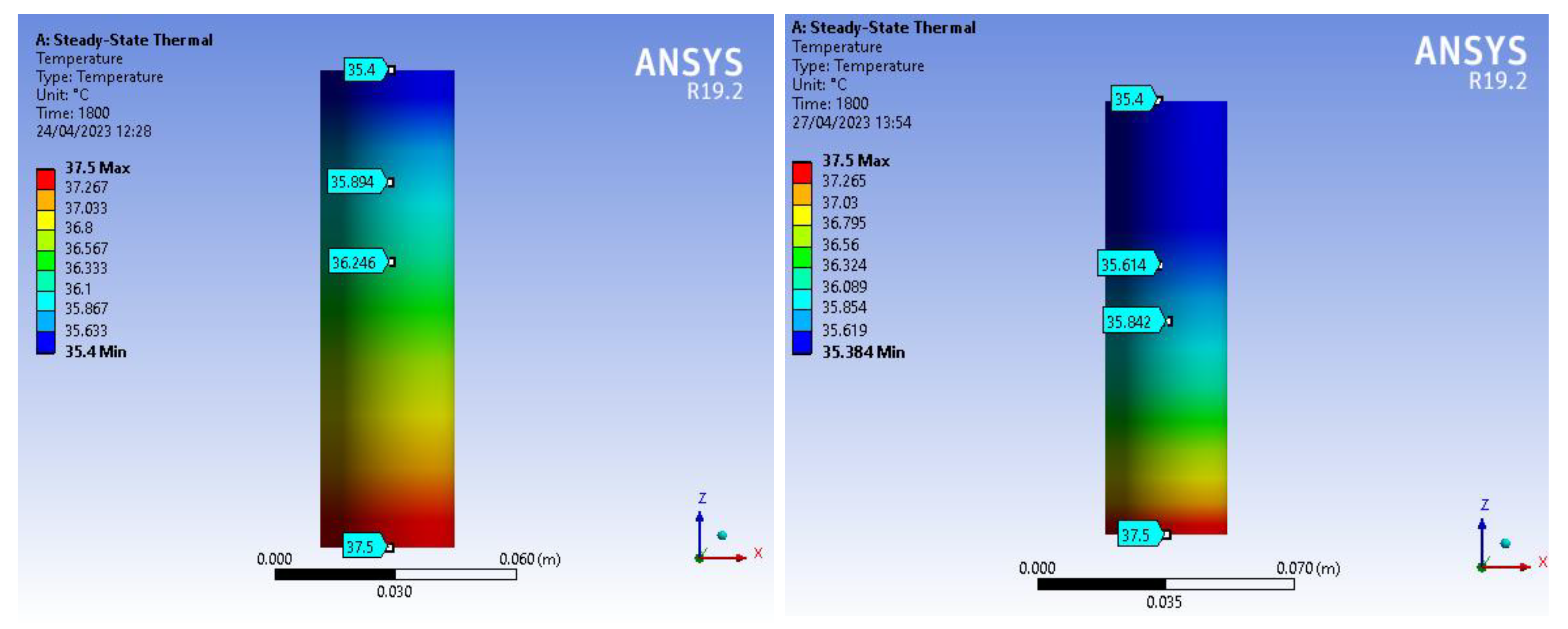
Figure 15.
The temperature contour at time (t=24 min) presented by Ansys workbench 19.2 when there is no heat exchange with the environment (left side of the figure) and when there is a heat exchange (right side of the figure).
Figure 15.
The temperature contour at time (t=24 min) presented by Ansys workbench 19.2 when there is no heat exchange with the environment (left side of the figure) and when there is a heat exchange (right side of the figure).
Figure 16.
The temperature contour at time (t=30 min) presented by Ansys workbench 19.2 when there is no heat exchange with the environment (left side of the figure) and when there is a heat exchange (right side of the figure).
Figure 16.
The temperature contour at time (t=30 min) presented by Ansys workbench 19.2 when there is no heat exchange with the environment (left side of the figure) and when there is a heat exchange (right side of the figure).
7.3. Comparsion of the results
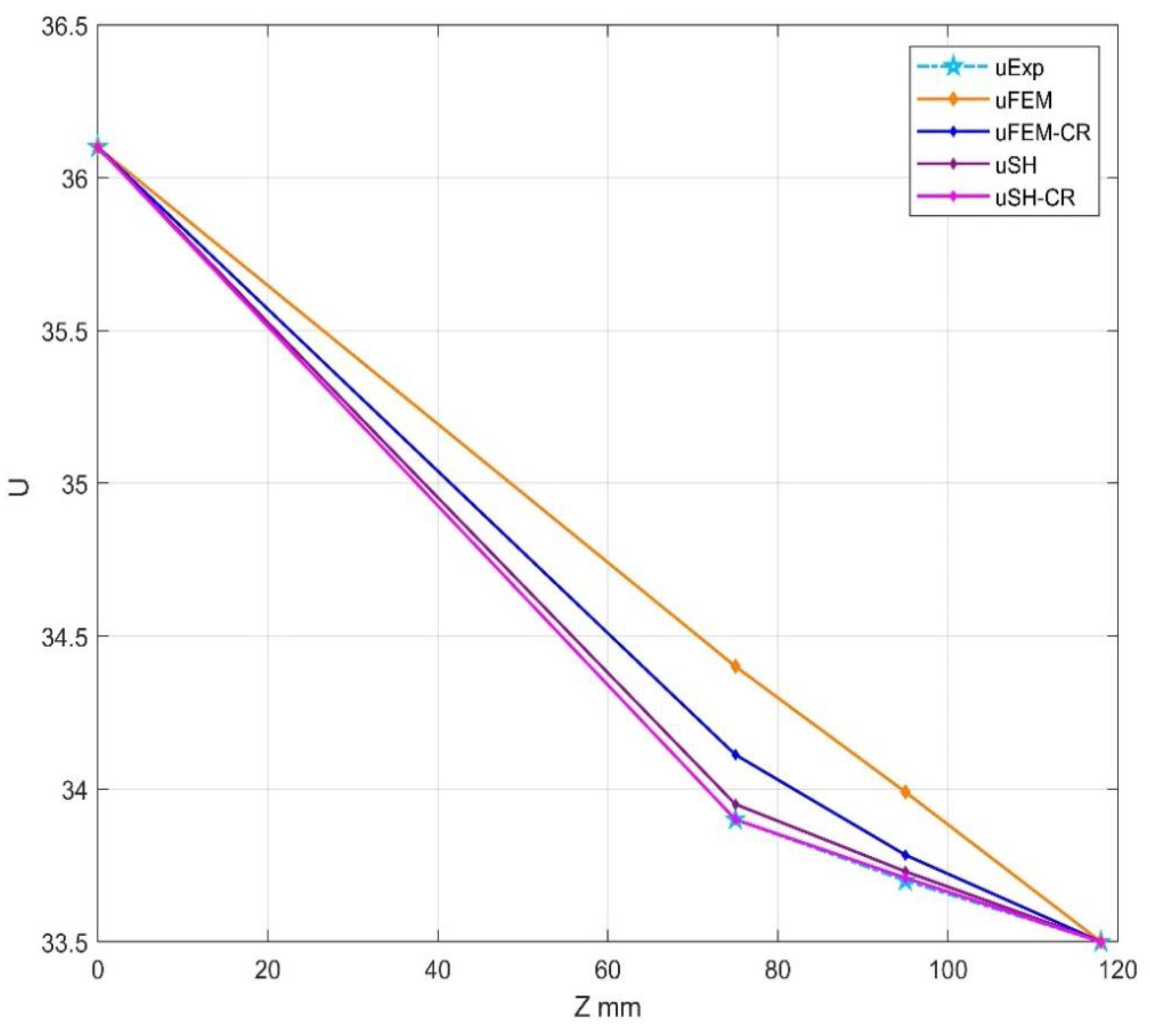
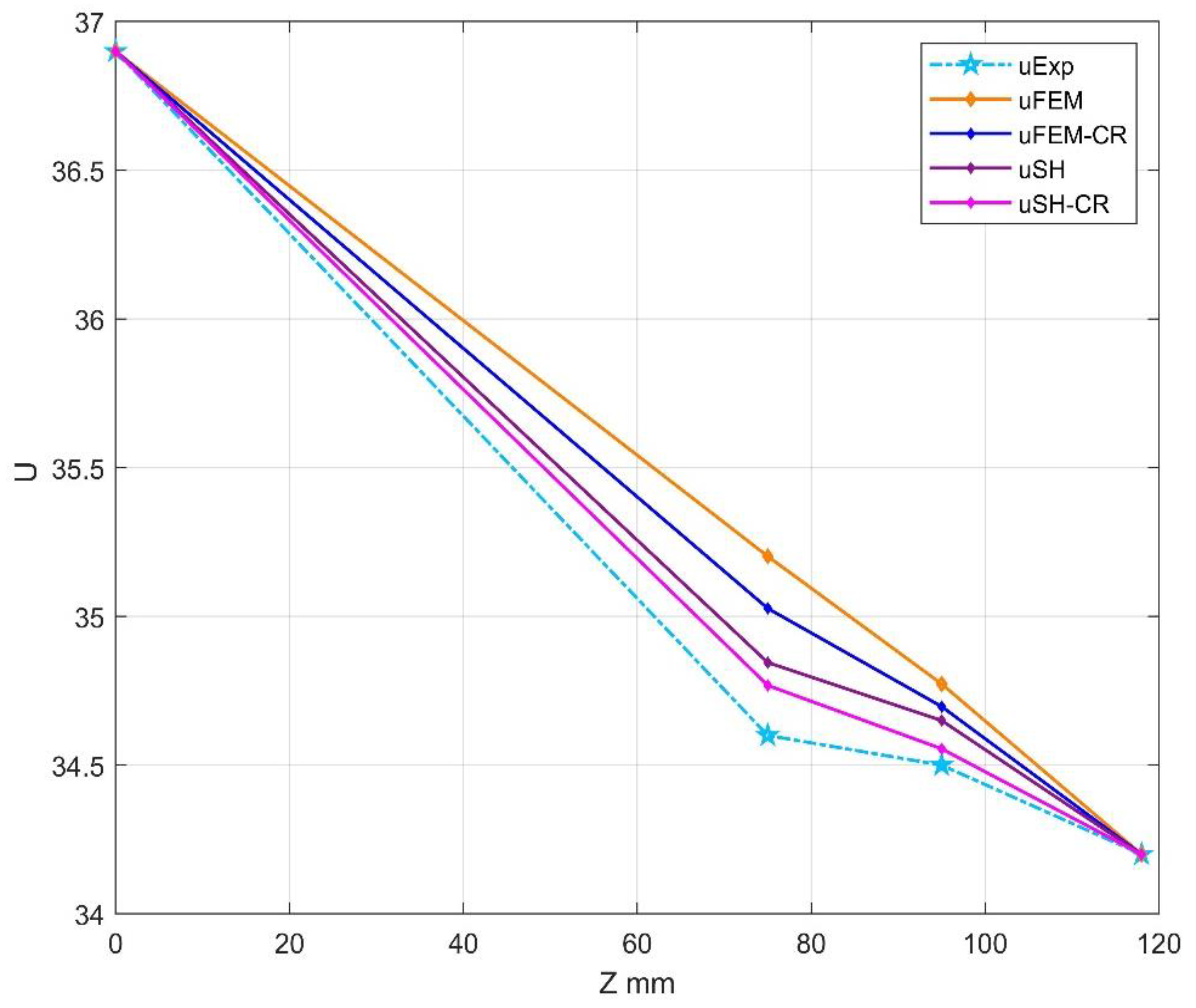
The results of the experimental measurements, the finite element method (FEM) using Ansys Workbench, and the explicit numerical methods (exemplified by the shifted hopscotch method) were compared. Both FEM and SH were subjected to two types of tests, one considering convection and radiation effects, and the other excluding them. In
Table 1 and 2 the comparison was conducted at two specific spatial points, and the results were measured at three different time moments. The temperatures are compared at four space points via plots in
Figure 17,
Figure 18 and
Figure 19.
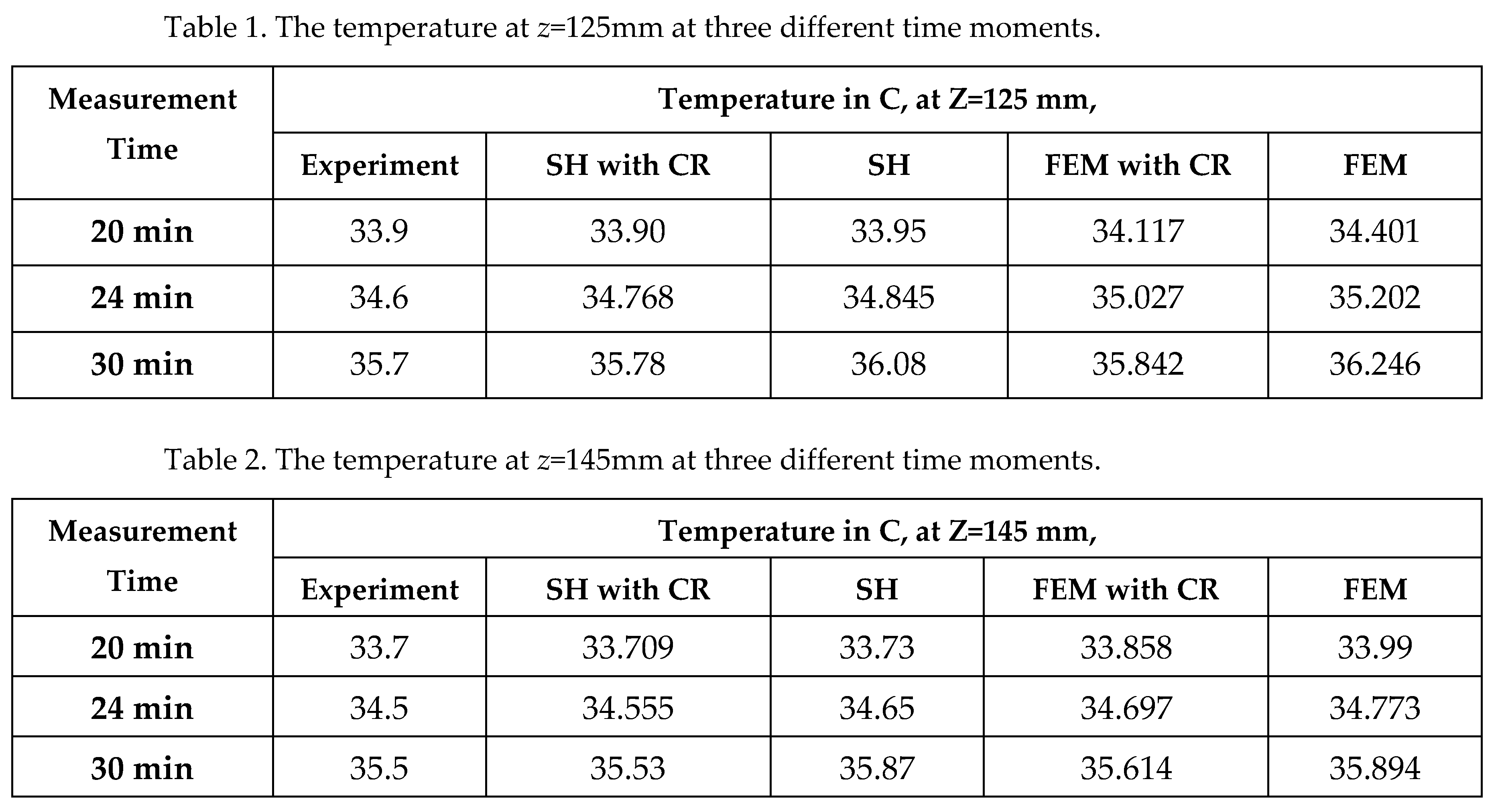
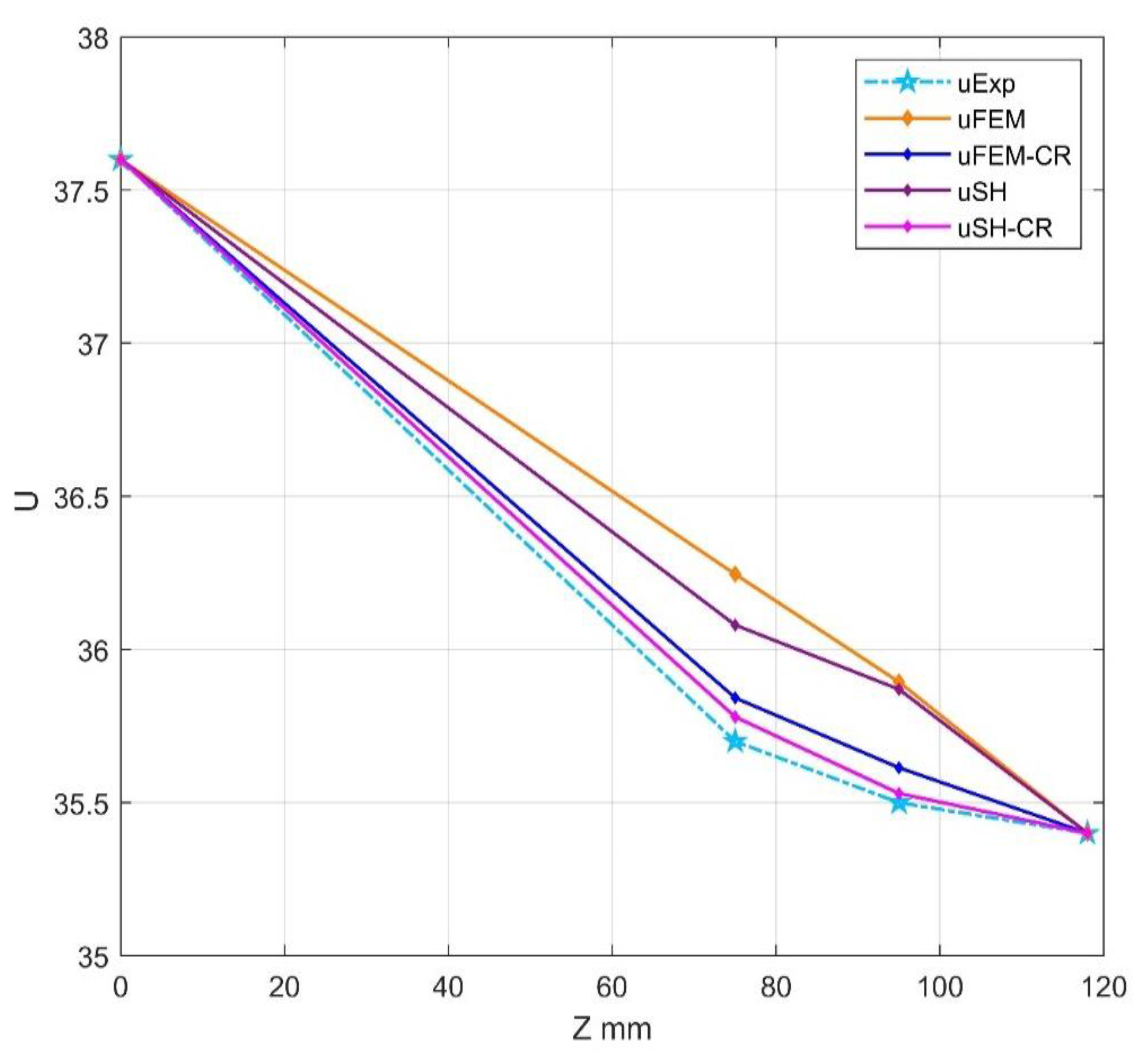
Figure 17.
The temperature at the selected 4 measurement points in z at time t=20min.
Figure 17.
The temperature at the selected 4 measurement points in z at time t=20min.
Figure 18.
The temperature at the selected 4 measurement points in z at time t=24min.
Figure 18.
The temperature at the selected 4 measurement points in z at time t=24min.
Figure 19.
The temperature at the selected 4 measurement points in z at time t=30min.
Figure 19.
The temperature at the selected 4 measurement points in z at time t=30min.
8. Discussion and Summary
This work was devoted to solving heat transfer problems in cylindrical and spherical geometries. Using the self-similar Ansatz, novel analytical solutions of the heat-conduction PDE were constructed, which contain the Kummer functions. Nine numerical algorithms were presented, most of which are recently introduced unconditionally stable explicit methods. To perform the verification, the analytical solutions are reproduced by these methods.
After these, experimental work is considered from the literature where a cylinder is heated from below, and the results are attempted to be reproduced by the Ansys commercial software, but without considering convection and radiation on the surface of the cylinder. In contrast to that, we reproduced the experimental results by considering convection and radiation as well by not only the Ansys but the explicit methods as well. Since in reality, convection and radiation are present, taking them into account makes the results closer to the experimental ones. Moreover, the explicit and stable schemes were more accurate and effective than the finite element software in all cases.
Author Contributions
Conceptualization and methodology, E. K. and I. F. B.; supervision and resources, E. K.; analytical investigation and the related visualization, I. F. B., L. M.; software, E. K. and H. K. J., numerical investigation and the related visualization, H. K. J.; FEM investigation, H. K. J.; writing—original draft preparation, H. K. J.; writing—review and editing, E. K., H. K. J and L. M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no funding.
Data availability statement
Data available on request from the first author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- T. Bennett, Transport by Advection and Diffusion. New York: Wiley, 2012.
- R. Ghez, Diffusion Phenomena: Cases and Studies. Dover Publications Inc, 2001.
- F. Pasquill and F. B. Smith, Atmospheric Diffusion. West Sussex: Ellis Horwood Limited, 1883.
- P. Heitjans and J. Kärger, Diffusion in condensed matter: Methods, materials, models. Berlin Heidelberg: Springer, 2005.
- G. Michaud, G. Alecian, and J. Richer, Atomic Diffusion in Stars. Cham: Springer International Publishing, 2015.
- J. Machta and R. Zwanzig, “Diffusion in a periodic lorentz gas,” Phys. Rev. Lett., vol. 50, no. 25, pp. 1959–1962, Jun. 1983. [CrossRef]
- W. G. Hoover, Time Reversibility, Computer Simulation, and Chaos, vol. 13. WORLD SCIENTIFIC, 1999.
- L. Mátyás, T. Tél, and J. Vollmer, “Coarse-grained entropy and information dimension of dynamical systems: The driven Lorentz gas,” Phys. Rev. E - Stat. Physics, Plasmas, Fluids, Relat. Interdiscip. Top., vol. 69, no. 1, p. 8, Jan. 2004. [CrossRef]
- L. Mátyás and R. Klages, “Irregular diffusion in the bouncing ball billiard,” in Physica D: Nonlinear Phenomena, 2004, vol. 187, no. 1–4, pp. 165–183. [CrossRef]
- R. Klages, I. F. Barna, and L. Mátyás, “Spiral modes in the diffusion of a single granular particle on a vibrating surface,” Phys. Lett. Sect. A Gen. At. Solid State Phys., vol. 333, no. 1–2, pp. 79–84, Nov. 2004. [CrossRef]
- L. Mátyás and I. F. Barna, “Geometrical origin of chaoticity in the bouncing ball billiard,” Chaos, Solitons and Fractals, vol. 44, no. 12, pp. 1111–1116, Dec. 2011. [CrossRef]
- I. F. Barna and L. Mátyás, “Advanced Analytic Self-Similar Solutions of Regular and Irregular Diffusion Equations,” Mathematics, vol. 10, no. 18, p. 3281, Sep. 2022. [CrossRef]
- M. Saleh, E. Kovács, I. F. Barna, and L. Mátyás, “New Analytical Results and Comparison of 14 Numerical Schemes for the Diffusion Equation with Space-Dependent Diffusion Coefficient,” Mathematics, vol. 10, no. 15, p. 2813, Aug. 2022. [CrossRef]
- M. K. Kolev, M. N. Koleva, and L. G. Vulkov, “An Unconditional Positivity-Preserving Difference Scheme for Models of Cancer Migration and Invasion,” Mathematics, vol. 10, no. 1, pp. pp. 1–22, 2022. [CrossRef]
- C. K. Mbayi, J. B. Munyakazi, and K. C. Patidar, “Layer resolving fitted mesh method for parabolic convection-diffusion problems with a variable diffusion,” J. Appl. Math. Comput., vol. 68, no. 2, pp. 1245–1270, Apr. 2022. [CrossRef]
- M. Saleh, E. Kovács, and I. F. Barna, “Analytical and Numerical Results for the Transient Diffusion Equation with Diffusion Coefficient Depending on Both Space and Time,” Algorithms, vol. 16, no. 4, p. 184, Mar. 2023. [CrossRef]
- J. R. Cannon, The One-Dimensional Heat Equation. Cambridge: Cambridge University Press, 1984.
- W. S. C. Williams, Nuclear and Particle Physics. Oxford: Clarendon Press, 1991.
- Z. Erdélyi and G. Schmitz, “Reactive diffusion and stresses in spherical geometry,” Acta Mater., vol. 60, no. 4, pp. 1807–1817, Feb. 2012. [CrossRef]
- M. Roussel, Z. Erdélyi, and G. Schmitz, “Reactive diffusion and stresses in nanowires or nanorods,” Acta Mater., vol. 131, pp. 315–322, Jun. 2017. [CrossRef]
- H. S. Carslaw and J. C. Jaeger, Conduction of Heat in Solids. Oxford: Oxford Science Publications, 1986.
- Rutherford Aris, The Mathematical Theory of Diffusion and Reaction in Permeable Catalysts. Oxford: Oxford University Press Inc, 1975.
- N. A. Mbroh and J. B. Munyakazi, “A robust numerical scheme for singularly perturbed parabolic reaction-diffusion problems via the method of lines,” Int. J. Comput. Math., no. May, 2021,. [CrossRef]
- M. Fteiti, M. Ghalambaz, M. Sheremet, and M. Ghalambaz, “The impact of random porosity distribution on the composite metal foam-phase change heat transfer for thermal energy storage,” J. Energy Storage, vol. 60, p. 106586, Apr. 2023. [CrossRef]
- V. Kumar, K. Chandan, K. V. Nagaraja, and M. V. Reddy, “Heat Conduction with Krylov Subspace Method Using FEniCSx,” Energies, vol. 15, no. 21, p. 8077, Oct. 2022. [CrossRef]
- N. Ndou, P. Dlamini, and B. A. Jacobs, “Enhanced Unconditionally Positive Finite Difference Method for Advection–Diffusion–Reaction Equations,” Mathematics, vol. 10, no. 15, p. 2639, Jul. 2022. [CrossRef]
- Á. Nagy, I. Omle, H. Kareem, E. Kovács, I. F. Barna, and G. Bognar, “Stable, Explicit, Leapfrog-Hopscotch Algorithms for the Diffusion Equation,” Computation, vol. 9, no. 8, p. 92, 2021.
- H. K. Jalghaf, E. Kovács, J. Majár, Á. Nagy, and A. H. Askar, “Explicit stable finite difference methods for diffusion-reaction type equations,” Mathematics, vol. 9, no. 24, 2021. [CrossRef]
- Á. Nagy, M. Saleh, I. Omle, H. Kareem, and E. Kovács, “New stable, explicit, shifted-hopscotch algorithms for the heat equation,” Math. Comput. Appl., vol. 26, no. 61, 2021.
- H. K. Jalghaf, E. Kovács, and B. Bolló, “Comparison of Old and New Stable Explicit Methods for Heat Conduction, Convection, and Radiation in an Insulated Wall with Thermal Bridging,” Buildings, vol. 12, no. 9, p. 1365, Sep. 2022. [CrossRef]
- L. Mátyás and I. F. Barna, “General Self-Similar Solutions of Diffusion Equation and Related Constructions,” Rom. J. Phys., vol. 67, p. 101, 2022.
- B. M. Chen-Charpentier and H. V. Kojouharov, “An unconditionally positivity preserving scheme for advection-diffusion reaction equations,” Math. Comput. Model., vol. 57, pp. 2177– 2185, 2013. [CrossRef]
- G. Sottas, “Rational Runge-Kutta methods are not suitable for stiff systems of ODEs,” J. Comput. Appl. Math., vol. 10, pp. 169–174, 1984.
- A. R. Gourlay and G. R. McGuire, “General Hopscotch Algorithm for the Numerical Solution of Partial Differential Equations,” IMA J. Appl. Math., vol. 7, no. 2, pp. 216–227, 1971.
- Hirsch, Numerical computation of internal and external flows, volume 1: Fundamentals of numerical discretization. Wiley, 1988.
- S. Cabezas, G. Hegedűs, and P. Bencs, “Thermal experimental and numerical heat transfer analysis of a solid cylinder in longitudinal direction,” Analecta Tech. Szeged., vol. 17, no. 1, pp. 16–27, 2023. [CrossRef]
- J.P. Holman, Heat Transfer: Tenth Edition. New York: McGraw-Hill Education, 2009.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).