Prerpints.org logo
Preprint
Article

A New Data Balancing Approach based Generative Adversarial Network for Network Intrusion Detection System

Altmetrics

Downloads

269

Views

123

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

30 May 2023

Posted:

31 May 2023

You are already at the latest version

Alerts
Abstract
The IDS serves as a security system that maintains constant surveillance over network traffic and host systems in order to identify any security breaches or potentially concerning activities. Recently. the rise in cyber-attacks has driven the necessity for the development of automated and intelligent network intrusion detection systems. These systems are designed to learn the typical patterns of network traffic, allowing them to identify any deviations from normal behaviour, which can be classified as anomalous or malicious. Machine learning methods are widely used to exhibit a satisfactory effectiveness in detecting malicious payloads in the network traffic. While the volume of the data generated from IDS is increasing exponentially results in the emergence of substantial security risks, it highlighted the imperative to strengthen network security. The performance of traditional machine learning methods depends on the dataset and the data balance distribution in it. while most of IDS datasets suffer from unbalancing, this limits the performance of the machine learning method used in the system and results in missed detections and false alarms in the conventional IDSs. To address this issue, this paper presents a new model-based Generative Adversarial Network (GAN) called TDCGAN to enhance the detection rate of less of minor class in the dataset while maintaining efficiency. The proposed model consists of one generator and three discriminators with an election layer at the end of architecture. The UGR’16 data set is used for evaluation purposes. In order to demonstrate the efficacy of our proposed model, various machine learning algorithms have been utilized for comparison. The experimental findings have determined that TDCGAN presents an efficient resolution for addressing imbalanced intrusion detection and surpasses the performance of other oversampling machine learning methods.
Keywords: 
Subject: Computer Science and Mathematics  -   Security Systems

1. Introduction

The process of data science comprises multiple stages, commencing with the collection of a dataset, followed by its preparation and exploration, and eventually modelling the data to yield solutions. However, since different problem domains have varying datasets, the data gathering process may uncover various issues within the dataset that must be addressed and rectified before proceeding to data modelling. Successfully handling these problems can significantly impact the model’s accuracy.
One application where machine learning methods are widely used is Intrusion Detection System (IDS) [1]. IDS is employed to monitor the network traffic and identify any unauthorized efforts to access a network through the analysis of incoming and outgoing actions, with the aim of detecting indications of potentially harmful actions [2].
Machine learning (ML) methods, such as supervised network intrusion detection, have demonstrated satisfactory effectiveness in identifying malicious payloads within network traffic datasets that are annotated with accurate labelling. Nevertheless, the substantial growth in network scale and the proliferation of applications processed by network nodes have led to an overwhelming volume of data being shared and transmitted across the network. Consequently, this has given rise to significant security threats and underscored the urgency to enhance network security. As a result, numerous researchers have focused their efforts on enhancing intrusion detection systems (IDS) by improving the detection rate for both novel and known attacks, while concurrently reducing the occurrence of false alarms (False Alarm Rate or FAR) [1]. Unsupervised intrusion detection techniques have emerged as a solution that eliminates the need for labelled data [3]. These methods can effectively train using samples from a single class, typically normal samples, to identify patterns that deviate from the training observations. However, the accuracy of these unsupervised learning approaches tends to decline when faced with imbalanced classes, where the number of samples in one class significantly exceeds or falls short of the number of samples in other classes.
To tackle the issue of imbalanced datasets, oversampling techniques are frequently employed. Traditional approaches utilize interpolation to generate samples among the nearest neighbours, such as the Synthetic Minority Oversampling Technique (SMOTE) [4] and the Adaptive Synthetic Sampling Technique (ADASYN) [5]. However, a novel generative model called Generative Adversarial Network (GAN) has emerged, providing a fresh framework for sample generation [6]. GAN allows the generator to effectively learn data features by engaging in a game-like interaction with the discriminator to simulate data distributions. GAN has demonstrated remarkable advancements in generating images, sounds, and texts [7,8,9]. As a result, researchers from various domains are increasingly incorporating this method into their research endeavours.
This paper proposes a new oversampling technique based on GAN applied for IDS considering the viewpoint of imbalanced data. The new model is called Triple Discriminator Conditional Generative Adversarial Networks (TDCGAN). The new model consists of one generator and three discriminators with an added layer at the end for election. The dataset used in this paper to evaluate and test our model is UGR’16 dataset. There are many datasets for IDS such as KDD CUP 99-1998, CICIDS2017, DARPA-1998 and more [10], we chose UGR’16 which is built with real traffic and up-to-date attacks.
This paper makes two main contributions. Firstly, it addresses the issue of high-class imbalance by analysing the UGR’16 dataset. Secondly, it conducts evaluations on this dataset using several commonly used machine learning algorithms for balancing dataset.
The rest of this paper is organised as follows: Section 2 presents some of the relevant studies. Section 3 gives an overview about IDS and UGR’16 dataset. Section 4 proposes the TDCGAN model. The design, execution and results are given in Section 5. Finally, Section 6 gives the conclusion and future works.

2. Related Works

The impact of data in-sampling on machine learning model performance has been examined in multiple studies, and this issue can result in diminished predictive capabilities of the model.
The concept of employing GAN models to address the class imbalance problem is introduced by the author in reference [11]. GAN, an unsupervised learning technique rooted in deep learning, generates synthetic data that closely resembles the existing data. By explicitly defining the desired rare class, the GAN effectively tackles fitting issues, class overlaps, and noise through the process of resampling. To evaluate the classifier’s performance, the re-sampled data is trained using the widely adopted machine learning technique called random forest (RF). The proposed solution demonstrates superior performance compared to the methods currently utilized. The author in the study referenced in [12] utilizes swarm intelligence optimization heuristics, specifically Artificial Fish Swarm (AFS) and Bee Colony Optimization (BCO), for the anomaly detection process. The detection approach proposed in this research focuses on reducing the subset of characteristics.
The study referenced in [13] presents a novel solution that applies an optimum allocation technique to efficiently manage large datasets by selecting the most representative samples. This approach aims to develop a new network intrusion detection system (NIDS) based on the least support vector machine (LSVM). The samples are arranged based on the desired confidence interval and the number of observations. Additionally, alternative solutions for NIDS were proposed. The authors in [14] aim to tackle the problem arising from the increasing quantity and diversity of network attacks, which leads to insufficient data during the training phase of machine learning-based intrusion detection systems (IDS). The author addresses this issue by examining a considerable number of network datasets from recent years. Each dataset’s limitations, such as a shortage of attack instances and other issues, are identified. As a result, Finlay proposed a new dataset that aims to resolve, or at least alleviate, the encountered problem. Another solution was proposed in [15].
The authors introduce a new IDS system designed to address five common conventional attacks. In this solution, the author constructs a new dataset that surpasses the UNSW-NB15 dataset. A misuse-based strategy is employed to create a fresh dataset, and a gain information technique is applied to collect features from the original UNSW-NB15 dataset.
Another IDS solution based on GAN was proposed in the study cited in [16]. Due to the limited number of known attack signatures for vehicle networks, the author employs the concept of generating unknown attacks during the training process to enable the IDS to effectively handle various types of attacks. In the context of vehicle IDS, accuracy is of utmost importance to ensure driver safety, as any false-positive error could have serious consequences. Traditional IDS approaches are inadequate in dealing with numerous new and undiscovered attacks that may arise. The proposed GAN-based IDS solution successfully detects four previously unknown attacks. The authors in [17] propose a novel approach by combining ADASYN and RENN techniques. This approach aims to tackle the imbalances between negative and positive instances in the initial dataset, as well as address the issue of feature redundancy. The RF algorithm and Pearson correlation analysis are employed to select the most relevant features.

3. Background

3.1. Intrusion Detection System

In an IDS (Intrusion Detection System), the term "intrusion" refers to any unauthorized attempt by users to access information within computer network systems with the intention of compromising its integrity, confidentiality, or availability [18]. Detection, on the other hand, is a security method deployed to identify and capture such illicit activities. Thus, an IDS serves as a security system that continually monitors both network traffic and host systems to detect any security violations or suspicious behaviours. When an intrusion is detected, the IDS generates alerts and takes appropriate actions in response to such behaviour [19]. Typically, IDSs are deployed in proximity to network nodes to effectively monitor network hosts and enable network traffic to pass through the system. IDS can be classified either by detection method to anomaly detection-based IDS and signature-based IDS or by deployed method into host-based IDS and network-based IDS. Different types of IDS are widely implemented by using machine learning algorithms. For anomaly detection of image data, AnoGan was applied and evaluated on diseased medical image data [20]. In AnoGAN, the generator used feature matching to produce a fake instance in the case of anomaly data. The KDD-99 network intrusion dataset was used for evaluation purposes. IDSGAN is another model which used NSL-KDD dataset to produce an authenticity score for the instance that belongs to the real dataset. The ISD was simulated using six machine learning algorithms: support-vector machine, Naive Bayes, linear programming, logistic regression, random forest, and K-nearest neighbours [21]. attackGAN is another IDS based GAN techniques which used a new loss function to achieve effective detection functionality [22]. Within the framework of GANs, the discriminator model plays a crucial role in discerning between the generated sample and the authentic sample. Simultaneously, the generator model is trained to deceive the discriminator model by causing it to incorrectly classify the generated sample as an authentic one. In view of adversarial attack against network intrusion detection system, the traffic data belongs to the discrete data. How to produce imperceptible and effective adversarial samples is a challenge that effect on the model performance accuracy.

3.2. UGR’ 16 Dataset

In this paper, UGR’ 16 dataset [23] is used to test performance of the proposed model and achieve data balancing. The entire dataset comprises two distinct sets: a calibration set and a testing set. The calibration set is used in constructing and adjusting machine learning model, this set contains no attacks and data that was recorded between March and June 2016 and contains inbound and outward ISP network traffic. While testing set acquired in July and August of 2016 is used to evaluate the model in the detection process. Table 1 contains the list of different attacks with their corresponding labels in the UGR’ 16 dataset.
The UGR’ 16 is created based on packet and flow data. It contains 16900,000,000 anonymous network traffic flows that were gathered over the period of four months at the facilities of an Internet service provider (ISP) in Spain. The UGR’16 dataset was divided into 23 compressed files, each of which was assigned to a particular week. Based on this, 16 of the files were assigned to the calibration class of datasets, and the remaining 6 to the test class. The size of each file is around 14GB as compressed format and they can be downloaded as csv format.

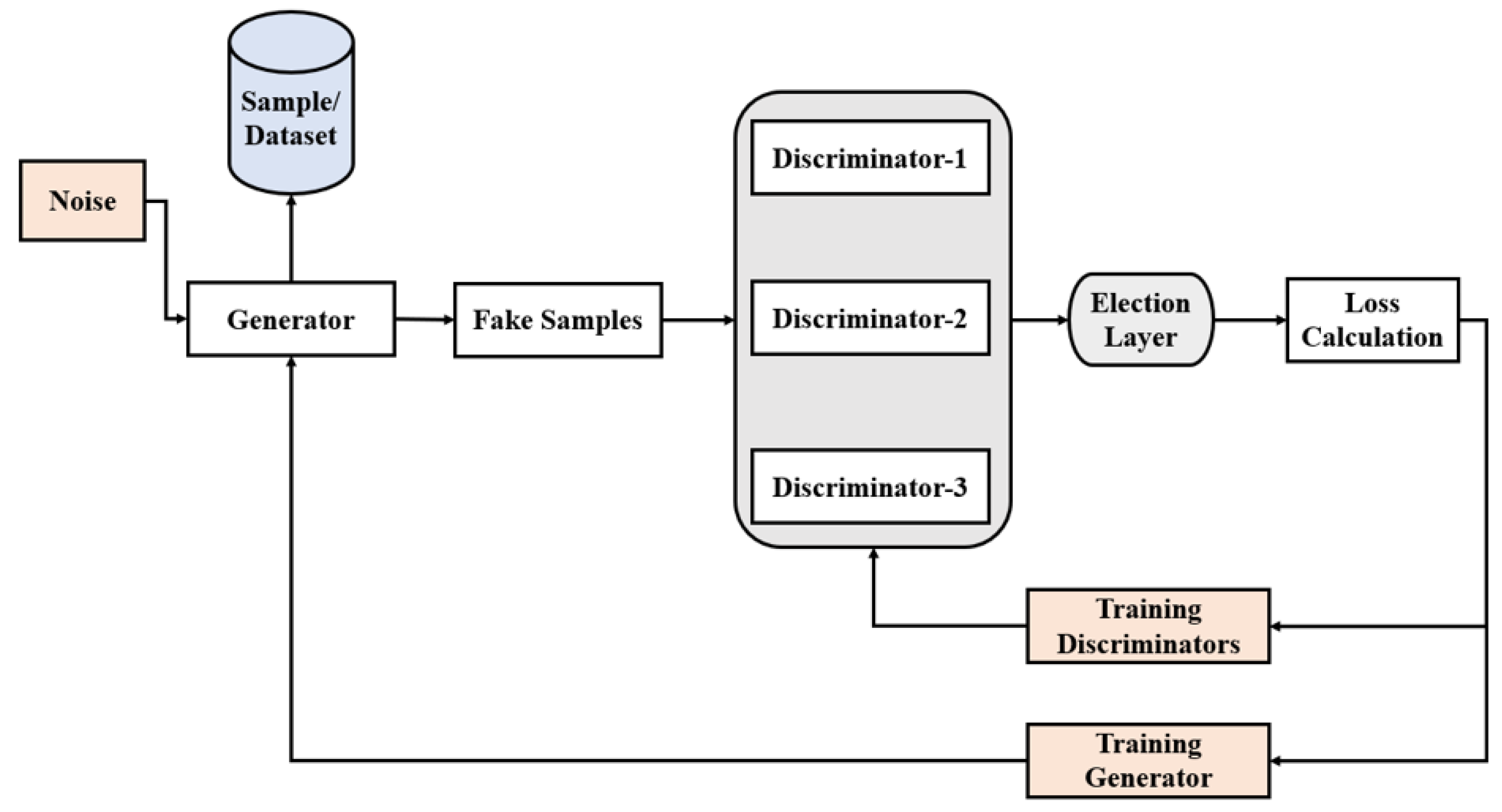
4. Proposed Model

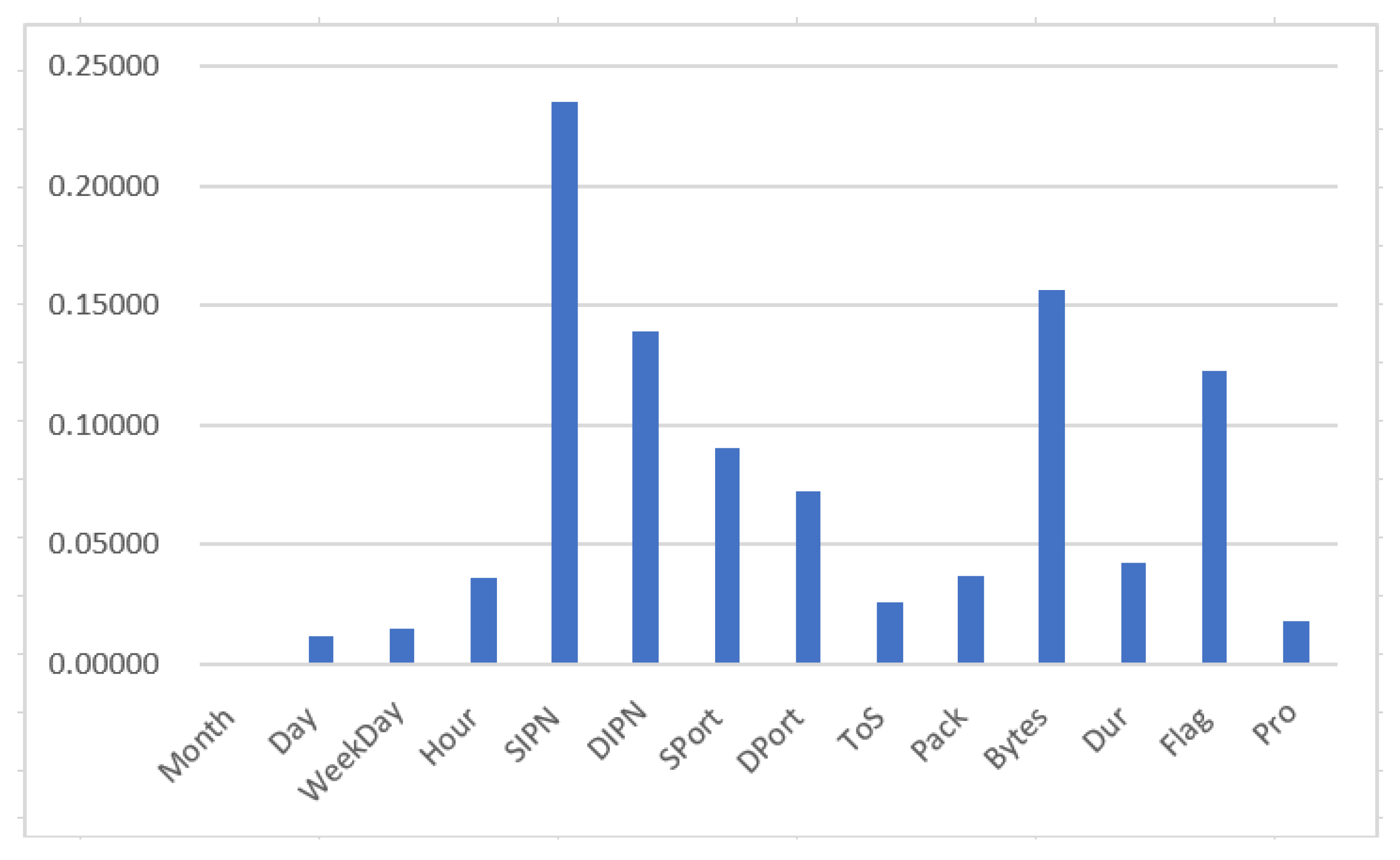
4.1. Data Preparation

The UGR-16 dataset used in this paper contains 16.9 billion records. While the deep learning algorithms require high hardware resources such as CPU, memory and GPU for data processing and training, a subset of data points that cover all types of normal and anomalous traffic from UGR’16 dataset was selected. The selected subset was then pre-processed which includes cleaning it from the missing values and remove the duplicate instances. The details of the selected subset are shown in Table 2.
Within the context of network security, normal traffic tends to occur more often than malicious traffic, leading to imbalanced class proportions and an imbalanced dataset [24]. This poses a challenge for machine learning, as learning from imbalanced data is a common issue. In order to address this problem, one potential solution is to either under-sample the majority class or over-sample the minority class.
In this paper, dataset records with class label equals to background is major. The other class labels are over sampled to obtain a balanced subset of the UGR’16 dataset. The original number of records and classes of the selected subset is given in Table 2.
Since machine learning algorithms works with numerical data, some features in the dataset need to be encoded which are: Protocol, Source IP, Destination IP and Class Label. One-hot encoded is used to encode these features. The dataset is then scaled using MinMaxScaler from Scikit-learn library to scale the values from zero to one.
The Random Forest classifier is used to explore the features importance based on Mean Decrease in Impurity (MDI). The calculation for a given feature’s importance involves summing the number of splits that incorporate the feature across all trees, proportionally to the number of samples that it splits. Figure 1 shows the highest numerical features of the UGR’16 dataset based on the Mean Decrease in Impurity (MDI). In the proposed model, all the features are included in the process where the most important feature is the Source_IP.

4.2. Setup of Proposed Model

Generative Adversarial Network (GAN) is a machine learning based deep learning methods used to generate new data. It is an unsupervised learning task that involve learning from input data to produce new samples from the original dataset. GAN is used in the literature in many applications such as computer vision [25], Time-series applications [26], health [27] and more making a significant advancement and outperformance in the data generation. As many improvements and versions for the GAN are proposed in order to fit it with the application domain and increase the performance and model accuracy [28,29], this paper proposes a new version of GAN called Triple Discriminator Conditional Generative Adversarial Networks (TDCGAN) as an augmentation tool to generate new data for the UGR’16 dataset with the aim to restore balance in the dataset by increasing minor attack classes.
In the TDCGAN, the architecture consists of one generator and three discriminators. Generator takes random noise from a latent space as input and generates raw data that closely resembles the real data, aiming to avoid detection by discriminators. Each discriminator is a deep neural network with different architecture and different parameters setting. Each discriminator’s role is to extract features from the output of the generator and classify the data with varying levels of accuracy for each discriminator. An Election layer is added to the end of TDCGAN architecture that gets the output from the three discriminators and perform an election procedure to get the best result with highest classification accuracy in a form of ensemble method. The model aims to classify data into two groups: normal flows for the background flow with 0 representation and anomaly flows for the attack data with 1 representation. Also, in the case of anomaly flow, the model classifies it to its specific class type. Figure 2 shows the workflow of the proposed TDCGAN model. The setting details of generator and each discriminator are given below.
The model of the generator is a Deep Multi-layer Perceptron (MLP) composed of Input layer, output layer and four hidden layers. Initially, the generator takes a point from latent space to generate new data. The latent space is a multi-dimensional hypersphere normal distributed points where each variable drawn from the distribution of the data in the dataset. An embedded layer in the generator creates a vector representation for the generated point. Through training, the generator learns to map point from the latent space into a specific output data which will different each time the model is trained. Taken a step further, new data are then generated using random points in the latent space. So, the points in the latent space are used to generate a specific data. The discriminator distinguished the new data generated by the generator from the true data distribution.
GAN is unsupervised learning model. Both the generator and discriminator models are trained simultaneously [30]. The generator produces a batch of samples, which, along with real examples from the domain, are fed to the discriminator. The discriminator then classifies them as either real or fake. Subsequently, the discriminator undergoes updates to improve its ability to distinguish between real and fake samples in the subsequent round. Additionally, the generator receives updates based on its success or failure in deceiving the discriminator with its generated samples.
In this manner, the two models engage in a competitive relationship, exhibiting adversarial behaviour in the context of game theory. In this scenario, the concept of zero-sum implies that when the discriminator effectively distinguishes between real and fake samples, it receives a reward or no adjustments are made to its model parameters. Conversely, the generator is penalized with significant updates to its model parameters.
Alternatively, when the generator successfully deceives the discriminator, it receives a reward or no modifications are made to its model parameters. However, the discriminator is penalized and its model parameters are updated. This is the generis GAN approach.
In the proposed TDCGAN model, the generator takes as input the point from the latent space and produce a data to a data distribution of the real data in the dataset. This is done through a fully connected layers with 4-hidden layers, one input layer and one output layer. The discriminators try to classify data into its corresponding class which is done through a fully connected MLP network.
MLP has gained widespread popularity as a preferred choice among neural networks [31,32]. This is primarily attributed to its fast computational speed, straightforward implementation, and ability to achieve satisfactory performance with relatively smaller training datasets.
In this paper, the generator model will learn how to generate new data similar to the minor class in the URG’16 dataset, while discriminators will try to distinguish between real data from the dataset and new one generated by generator. During the training process, both the generator and discriminator models are conditioned on the class label. This conditioning enables the generator model, when utilized independently, to generate minor class data within the domain that correspond to a specific class label. TGCGAN model can be formulated by integrating both the generator and three discriminators’ models into a single, larger model.
The discriminator models undergo separate training, where each model weights are designated as non-trainable within the TDCGAN model. This ensures that solely the weights of the generator model are updated during the training process. This trainability modification specifically applies when training the TDCGAN model, not when training the discriminator independently. So, TDCGAN model is employed to train the generator’s model weights by utilizing the output and error computed by the discriminator models.
A point in the latent space is provided as input to TDCGAN model. The generator model generates the data based on this input, which is subsequently fed into the discriminator model. The discriminator then outputs a classification, determining whether the data is real or fake and in case of fake data, the model classify it to its corresponding class.
The generator takes a batch of vectors (z) which are randomly drown from Gaussian distribution, and map them to G(z) which have the same dimension of the dataset. The discriminators take the output from the generator and tris to classify it. The loss is then evaluated between the observed data and the predicted data and is used to update the weights of the generator only to ensure that only generator weights are updated. The difference between observed data and the predicted data is estimated using cross-entropy loss function which is expressed in the following equation.
L O S S C E = − 1 / N ∑ n = 1 N y i . l o g ( p ( y i ) ) + ( 1 − y i ) . l o g ( 1 − p ( y i ) )
where y i is the true label (1 for malicious traffic and 0 for normal traffic) and p( y i ) is the predicted probability of the observation (i) calculated by the sigmoid activation function. N is the number of observations in the batch.
The generator model has 4-hidden layers. The first hidden layer composed of 256 neurons with a Rectified Linear Unit (ReLU) activation function. An embedded layer is used between hidden layers to efficiently maps input data from high-dimension to lower dimension space. This allows network to learn data relationship and process it efficiently. The second hidden layer compromise of 128 neurons, the third have 64 neurons and the last one has 32 neurons with ReLU activation function used with them all and a regularization dropout of 20% is added to avoid overfitting. The output layer is activated using Softmax activation function with 14-neurons as the number of features in the dataset.
After defining the generator, we will define the architecture of each discriminator in the proposed model. Each discriminator is a MLP model with different number of hidden layers, different number of neurons and different dropout percentage. The first discriminator composed of 3 hidden layers with 100 neurons for each and 10% dropout regularization. The second have five hidden layers with 64, 128, 256, 512, 1024 neurons for each layer respectively. The dropout percentage is 40%. The last discriminator has 4 hidden layers with 512, 256, 128, 64 neurons for each layer and 20% dropout percentage. The LeakyReLU(alpha=0.2) is used as an activation function for the hidden layers in the discriminators. Two output layers are used for each discriminator with Softmax function as an activation function for one output layer and Sigmoid activation function for the second output layer. The model trained with two loss functions, binary cross entropy for the first output layer, and categorical cross-entropy loss for the second output layer. The output is extracted from each discriminator and are then fed to the last layer in the model where the election is performed to get the best result.
The TDCGAN model can be defined that combines both generator model and the three discriminator models into one large model. This large model will be used to train the weights in the generator model, using the output and error calculated of discriminators. Discriminators are trained separately by taking a real input from the dataset.
The model is then trained for 1000 epochs with batch size of 128. The optimizer is Adam with learning rate equal to 0.0001. The proposed model allows generator to train until it produces a new set of data samples that resembles the real distribution of the original dataset.
Nevertheless, this training strategy frequently fails to function effectively in various application scenarios. This is due to the necessity of preserving the relationships within the feature sets of the generated dataset by the generator, while the dataset used by the discriminator may differ from it. This disparity often leads to instability during the training of the generator.
In numerous instances, the discriminator quickly converges during the initial stages of training, thereby preventing the generator from reaching its optimal state. To tackle this challenge in network intrusion detection tasks, we adopt a modified training strategy where three discriminators with different architecture are used. This approach helps prevent an early emergence of an optimal discriminator, ensuring a more balanced training process between the generator and discriminator.

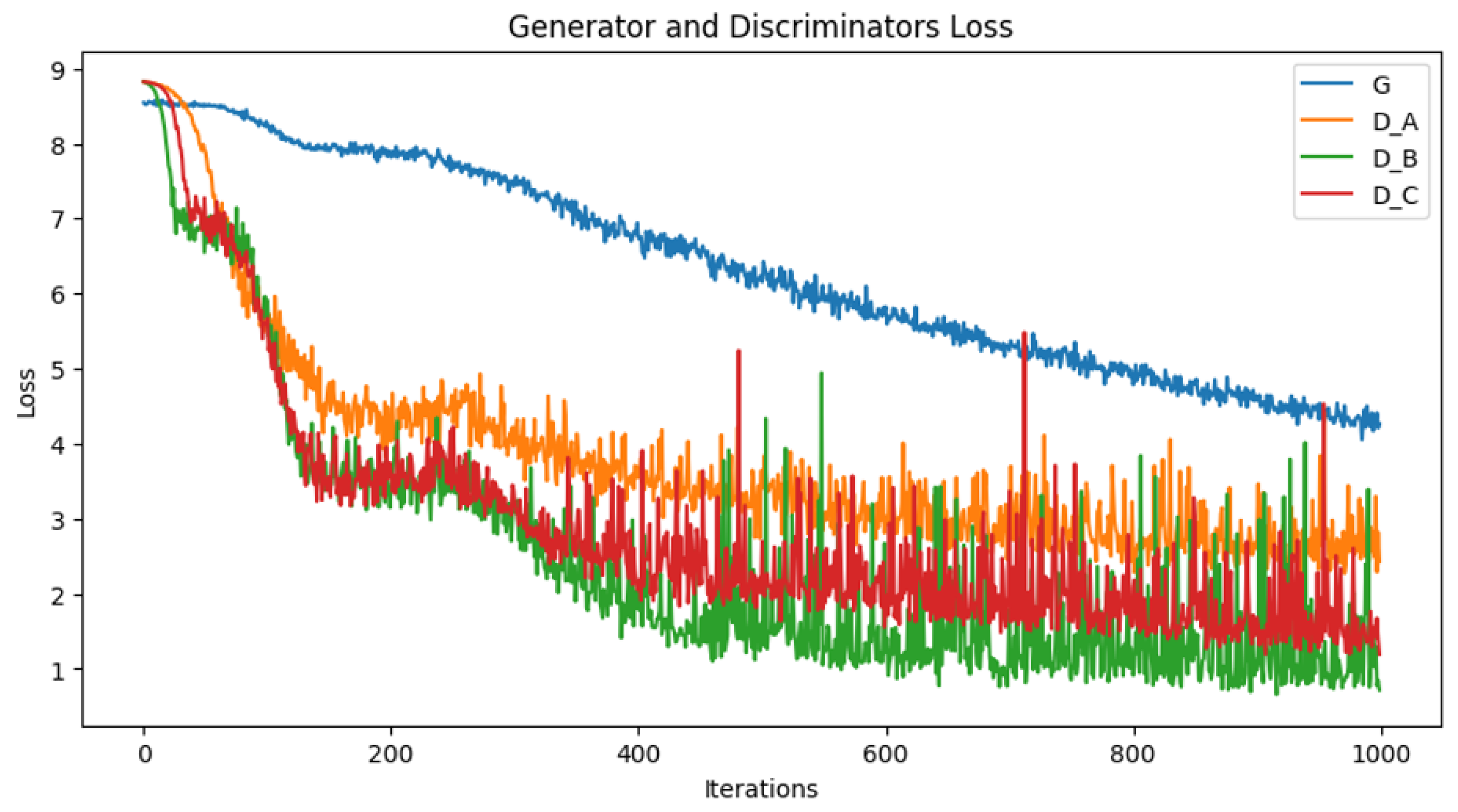
4.3. Training Phase

The primary objective of the training methodology employed in a GAN framework is for generator to generate fake data that closely resembles real data, and the discriminator has acquired sufficient knowledge to differentiate between real and fake samples. Both generator and discriminator trained until discriminator can no longer distinguish real data from fake data. This mean that the generated network can estimate data sample’s distribution and achieve Nash equilibrium.
In order to assess the performance of our model with precision, it is customary to divide the data into training and test sets to produce accurate predictions on unseen data. The training set is utilized for model fitting, while the test set is employed to measure the predictive precision of the trained model. The dataset was split into 70% for training and validation and 30% for testing. The training set is divided into minor class data and other class data. The TDCGAN model used minor class to generate data. The generator is trained to model the distribution of anomaly data (minor class) while fixing the discriminator. The output from generator is fed as input to discriminator to predict it. The error is estimated and the generator’s weight are then updated. The training continues until discriminator cannot distinguish is the input data comes from generator’s output or from the real anomaly dataset. In the training process, we make sure that all architectures undergo an equal number of epochs and that the weights from the final epoch are selected to generate artificial attack samples.
Begin by adhering to this iterative training procedure, and ultimately utilize the generator to produce attack samples. Eventually, incorporate the generated attack samples into the training set.
By this, we oversample minor classes in the dataset during the training phase. The test dataset is then used to test the model performance.

5. Experimental Results

Within this section, we methodically plan and execute a sequence of experiments, and subsequently analyse the obtained results.

5.1. Experimental Setup

Our experiments were carried out on Python Colab Jupyter notebook that run in the browser with the integrated free GPUs and freely installed Python libraries. The system setup is shown in Table 3.

5.2. Performance Metrics

To assess the effectiveness of our proposed model, we employ performance metrics such as classification accuracy, precision, recall, and F1 score.
We utilize the metric of Accuracy (Acc) to quantify the correct classification of data samples, considering all predictions made by the model, as measured by the following equation.
A c c = ( T P + T N ) / ( T P + T N + F P + F N )
where TP is the True Positive which represents the number of truly predicted anomalies. TN is the True Negative which indicated the number of truly predicted normal instances. FP is the False Positive indicator that denotes the number of normal instances that are incorrectly classified as anomalies. FN is the False Negative indicator that indicates the number of the number of anomalies that are misclassified as normal.
Precision is employed to assess the accuracy of correct predictions, calculated as the ratio of accurately predicted samples to the total number of predicted samples for a specific class as given in the following equation.
P e r c i s i o n = T P / ( T P + F P )
Recall, which is known as True Positive Rate (TPR), is used to determine the ratio of correctly predicted samples of a particular class to the total number of instances within the same class, as given by the following equation.
T P R ( R e c a l l ) = T P / ( T P + F N )
Finally, the F1-Score computes the balance between precision and recall, evaluating the trade-off between the two metrics as given in the following equation.
F 1 = 2 X ( ( P r e c i s i o n X R e c a l l ) / ( P r e c i s i o n + R e c a l l ) )

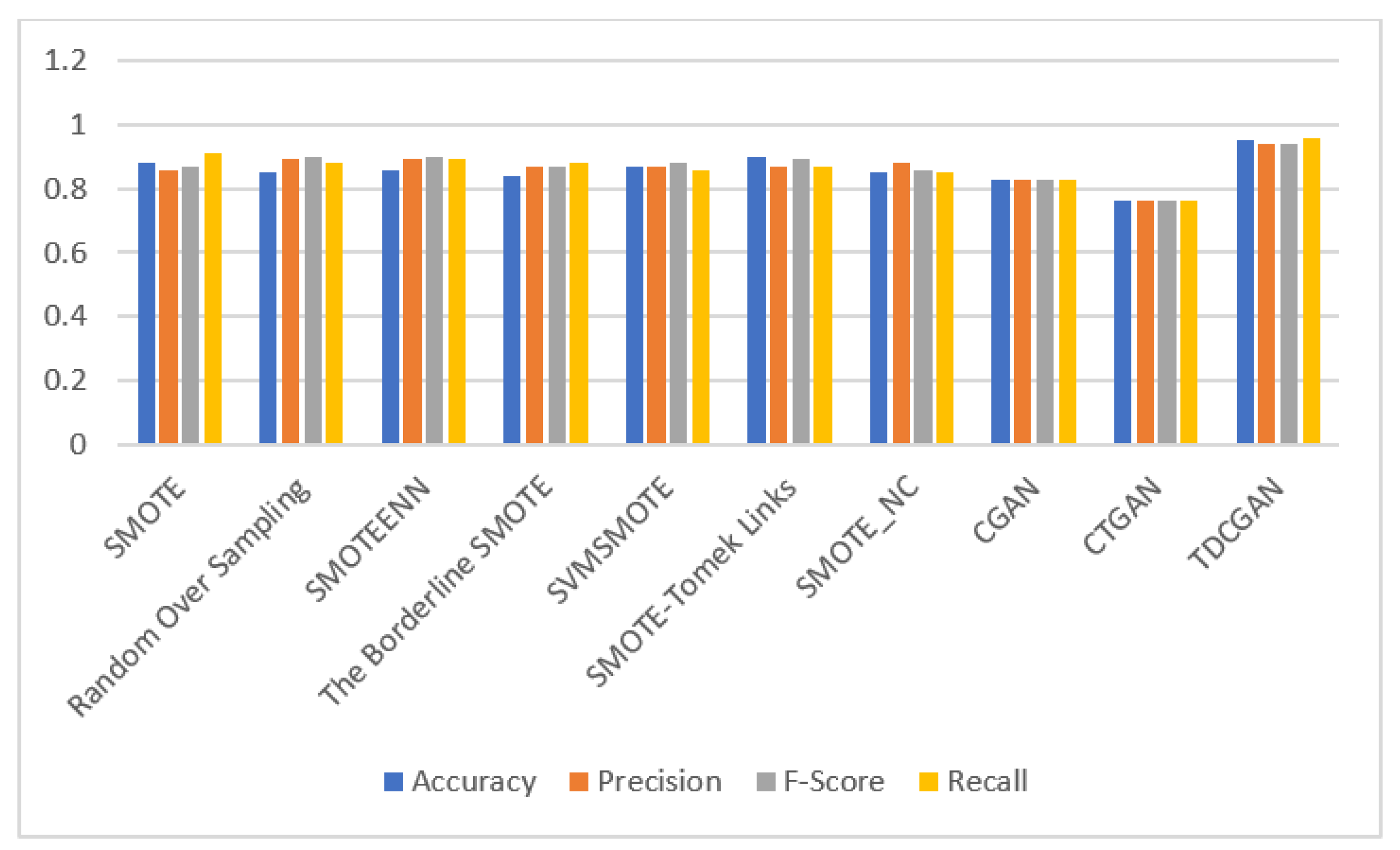
5.3. Experimental Results and Analysis

The performance of TDCGAN model is evaluated on the testing dataset. The previous metrics were used to evaluate and compare the results. The results after training TDCGAN model for URG’16 dataset balancing is given in Table 4.
Figure 3 shows the loss function while training the model for different number of epochs: 200, 400, 600, 800 and 1000.
We compared the performance of TDCGAN model for data balancing on testing dataset with some machine learning methods. The methods are: (1) Synthetic Minority Oversampling Technique (SMOTE), which is a method for oversampling that produces artificial instances from the minor class. Its purpose is to create a training set that is either synthetically balanced or close to balance in terms of class distribution, which is subsequently utilized for classifier training. We used the implementations provided in the imbalanced-learn python library which provide a range of resample techniques that can be combined for evaluation comparison. (2) Random over sampling is used that randomly duplicate the instances from the minor class. (3) Then we combined SMOTE with Edited Nearest Neighbour (ENN) SMOTEENN. (4) The Borderline SMOTE (Over-sample technique using Borderline-SMOTE) where the minority instances which are near the borderline are over sampled. (5) The SVMSMOTE that combines Support Vector Machine (SVM) with SOMTE. (6) Oversample using SMOTE-Tomek Links. Tomek Links denotes a technique used to detect pairs of closest neighbours within a dataset that exhibit dissimilar classes. Eliminating either one or both instances from these pairs, particularly those from the majority class, results in a reduction of noise or ambiguity within the decision boundary of the training dataset. (7) SMOTE_NC (Synthetic Minority Over-sampling Technique for Nominal and Continuous) which is used to over sample data with categorical features. (8) CGAN (conditional generative adversarial networks which is a conditional GAN that generates data under a conditional generation. And lastly, (9) CTGAN (conditional tabular generative adversarial networks) which models tabular data using CGAN. The results are listed in Table 5 and shown in Figure 4.
After conducting extensive experiments on UGR’16 dataset, our proposed model showcases its remarkable effectiveness in generating synthetic network traffic datasets, which in turn aids in the identification of anomalous network traffic. Through benchmarking, our model has surpassed other similar generative models, achieving an impressive accuracy of over 0.95%.

6. Conclusions and Future Works

The imbalanced condition of attacks in historical network traffic poses a challenge for machine learning methods commonly utilized in intrusion detection research. These methods often exhibit limited effectiveness in addressing this issue. This paper proposes a new technique-based GAN technology named TDCGAN to solve the imbalance learning problem in the IDS dataset. The proposed model consists of one generator with three discriminators which are all implemented based MLP network. To enhance the TDCGAN architecture, an extra layer is incorporated at the end of the network to carefully choose the optimal outcome from the outputs generated by the three discriminators. The UGR’16 dataset for IDS is used for testing and evaluation. The experiment is carried out by taking a subset from the dataset which is divided into training and testing sets. The experimental outcomes demonstrate that the proposed method delivers exceptional performance across various evaluation metrics, including Accuracy, F1 score, AUC (Area Under the Curve), and Recall and comparing with other oversampling machine learning techniques. For future works, the proposed model will be applied in an IDS in a VANET environment to detect unknown attacks.

Author Contributions

Conceptualization, O.S., M.K. and M.J.; methodology, O.S., M.K. and M.J.; software, M.J.; validation, O.S., M.K., M.J. and A.G.; formal analysis, O.S., M.K., M.J. and A.G.; investigation, O.S.; resources, M.J.; data curation, M.J.; writing original draft preparation, O.S. and M.K.; writing review and editing, O.S. and M.K.; visualization, O.S., M.K. and M.J.; supervision, A.G.; project administration, O.S., M.K. and M.J.; funding acquisition, M.J. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Deanship of Scientific Research at Princess Sumaya University for Technology.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Surakhi, O.M.; García, A.M.; Jamoos, M.; Alkhanafseh, M.Y. A Comprehensive Survey for Machine Learning and Deep Learning Applications for Detecting Intrusion Detection. 2021 22nd International Arab Conference on Information Technology (ACIT). IEEE, 2021, pp. 1–13. [CrossRef]
  2. Susilo, B.; Sari, R.F. Intrusion detection in IoT networks using deep learning algorithm. Information 2020, 11, 279. [Google Scholar] [CrossRef]
  3. Schlegl, T.; Seeböck, P.; Waldstein, S.M.; Schmidt-Erfurth, U.; Langs, G. Unsupervised anomaly detection with generative adversarial networks to guide marker discovery. Information Processing in Medical Imaging: 25th International Conference, IPMI 2017, Boone, NC, USA, June 25-30, 2017, Proceedings. Springer, 2017, pp. 146–157. 25 June. [CrossRef]
  4. Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. Journal of artificial intelligence research 2002, 16, 321–357. [Google Scholar] [CrossRef]
  5. He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. 2008 IEEE international joint conference on neural networks (IEEE world congress on computational intelligence). IEEE, 2008, pp. 1322–1328. [CrossRef]
  6. Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets Advances in neural information processing systems. arXiv 2014, arXiv:1406.2661 2014. [Google Scholar]
  7. Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 4681–4690.
  8. Su, H.; Shen, X.; Hu, P.; Li, W.; Chen, Y. Dialogue generation with gan. Proceedings of the AAAI Conference on Artificial Intelligence, 2018, Vol. 32. [CrossRef]
  9. Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. Proceedings of the IEEE international conference on computer vision, 2017, pp. 2223–2232.
  10. Abdulrahman, A.A.; Ibrahem, M.K. Toward constructing a balanced intrusion detection dataset based on CICIDS2017. Samarra Journal of Pure and Applied Science 2020, 2, 132–142. [Google Scholar]
  11. Lee, J.; Park, K. GAN-based imbalanced data intrusion detection system. Personal and Ubiquitous Computing 2021, 25, 121–128. [Google Scholar] [CrossRef]
  12. Hajisalem, V.; Babaie, S. A hybrid intrusion detection system based on ABC-AFS algorithm for misuse and anomaly detection. Computer Networks 2018, 136, 37–50. [Google Scholar] [CrossRef]
  13. Kabir, E.; Hu, J.; Wang, H.; Zhuo, G. A novel statistical technique for intrusion detection systems. Future Generation Computer Systems 2018, 79, 303–318. [Google Scholar] [CrossRef]
  14. Sharafaldin, I.; Lashkari, A.H.; Ghorbani, A.A. Toward generating a new intrusion detection dataset and intrusion traffic characterization. ICISSp 2018, 1, 108–116. [Google Scholar]
  15. Kumar, V.; Sinha, D.; Das, A.K.; Pandey, S.C.; Goswami, R.T. An integrated rule based intrusion detection system: Analysis on UNSW-NB15 data set and the real time online dataset. Cluster Computing 2020, 23, 1397–1418. [Google Scholar] [CrossRef]
  16. Seo, E.; Song, H.M.; Kim, H.K. GIDS: GAN based intrusion detection system for in-vehicle network. 2018 16th Annual Conference on Privacy, Security and Trust (PST). IEEE, 2018, pp. 1–6. [CrossRef]
  17. Cao, B.; Li, C.; Song, Y.; Qin, Y.; Chen, C. Network Intrusion Detection Model Based on CNN and GRU. Applied Sciences 2022, 12, 4184. [Google Scholar] [CrossRef]
  18. AlKhanafseh, M.Y.; Surakhi, O.M. VANET Intrusion Investigation Based Forensics Technology: A New Framework. 2022 International Conference on Emerging Trends in Computing and Engineering Applications (ETCEA). IEEE, 2022, pp. 1–7. [CrossRef]
  19. Denning, D.E. An intrusion-detection model. IEEE Transactions on software engineering 1987, 222–232. [Google Scholar] [CrossRef]
  20. Di Mattia, F.; Galeone, P.; De Simoni, M.; Ghelfi, E. A survey on gans for anomaly detection. arXiv 2019, arXiv:1906.11632 2019. [Google Scholar]
  21. Lin, Z.; Shi, Y.; Xue, Z. Idsgan: Generative adversarial networks for attack generation against intrusion detection. Advances in Knowledge Discovery and Data Mining: 26th Pacific-Asia Conference, PAKDD 2022, Chengdu, China, May 16–19, 2022, Proceedings, Part III. Springer, 2022, pp. 79–91. 16 May. [CrossRef]
  22. Zhao, S.; Li, J.; Wang, J.; Zhang, Z.; Zhu, L.; Zhang, Y. attackgan: Adversarial attack against black-box ids using generative adversarial networks. Procedia Computer Science 2021, 187, 128–133. [Google Scholar] [CrossRef]
  23. Maciá-Fernández, G.; Camacho, J.; Magán-Carrión, R.; García-Teodoro, P.; Therón, R. UGR ‘16: A new dataset for the evaluation of cyclostationarity-based network IDSs. Computers & Security 2018, 73, 411–424. [Google Scholar]
  24. Ndichu, S.; Ban, T.; Takahashi, T.; Inoue, D. AI-Assisted Security Alert Data Analysis with Imbalanced Learning Methods. Applied Sciences 2023, 13, 1977. [Google Scholar] [CrossRef]
  25. Wang, Z.; She, Q.; Ward, T.E. Generative adversarial networks in computer vision: A survey and taxonomy. ACM Computing Surveys (CSUR) 2021, 54, 1–38. [Google Scholar] [CrossRef]
  26. Jiang, W.; Hong, Y.; Zhou, B.; He, X.; Cheng, C. A GAN-based anomaly detection approach for imbalanced industrial time series. IEEE Access 2019, 7, 143608–143619. [Google Scholar] [CrossRef]
  27. Yang, Y.; Nan, F.; Yang, P.; Meng, Q.; Xie, Y.; Zhang, D.; Muhammad, K. GAN-based semi-supervised learning approach for clinical decision support in health-IoT platform. Ieee Access 2019, 7, 8048–8057. [Google Scholar] [CrossRef]
  28. Wang, X.; Guo, H.; Hu, S.; Chang, M.C.; Lyu, S. Gan-generated faces detection: A survey and new perspectives. arXiv 2022, arXiv:2202.07145 2022. [Google Scholar]
  29. Xia, X.; Pan, X.; Li, N.; He, X.; Ma, L.; Zhang, X.; Ding, N. GAN-based anomaly detection: A review. Neurocomputing 2022. [Google Scholar] [CrossRef]
  30. Durgadevi, M. Generative Adversarial Network (GAN): A general review on different variants of GAN and applications. 2021 6th International Conference on Communication and Electronics Systems (ICCES). IEEE, 2021, pp. 1–8. [CrossRef]
  31. Zaidan, M.A.; Surakhi, O.; Fung, P.L.; Hussein, T. Sensitivity Analysis for Predicting Sub-Micron Aerosol Concentrations Based on Meteorological Parameters. Sensors 2020, 20, 2876. [Google Scholar] [CrossRef] [PubMed]
  32. Surakhi, O.; Serhan, S.; Salah, I. On the ensemble of recurrent neural network for air pollution forecasting: Issues and challenges. Adv. Sci. Technol. Eng. Syst. J 2020, 5, 512–526. [Google Scholar] [CrossRef]
Preprints 75123 g001
Figure 1. The highest numerical features of the UGR’16 dataset based on the Mean Decrease in Impurity (MDI).
Figure 1. The highest numerical features of the UGR’16 dataset based on the Mean Decrease in Impurity (MDI).
Preprints 75123 g001
Preprints 75123 g002
Figure 2. Workflow of TDCGAN model.
Figure 2. Workflow of TDCGAN model.
Preprints 75123 g002
Preprints 75123 g003
Figure 3. The loss function of G: Generator, D_A: First Discriminator, D_B: Second Discriminator and D_C: Third Discriminator in the TDCGAN model.
Figure 3. The loss function of G: Generator, D_A: First Discriminator, D_B: Second Discriminator and D_C: Third Discriminator in the TDCGAN model.
Preprints 75123 g003
Preprints 75123 g004
Figure 4. Performance evaluation metrics score for TDCGAN model and other machine learning methods.
Figure 4. Performance evaluation metrics score for TDCGAN model and other machine learning methods.
Preprints 75123 g004
Table 1. List of attacks in UGR’16 dataset.
Table 1. List of attacks in UGR’16 dataset.
Attack Label
DoS11 DoS
DoS53s DoS
DoS53a DoS
Scan11 Scan11
Scan44 Scan14
Botnet Nerisbotnet
IP in blacklist Blacklist
UDP Scan Anomaly-udpscan
SSH Scan Anomaly-sshscan
SPAM Anomaly-spam
Table 2. UGR’16 subset details.
Table 2. UGR’16 subset details.
From To Class Label Counts Percentage
07/27/2016 07/31/2016 background 197185 98.5%
07/27/2016 07/31/2016 dos 1169 0.6%
07/27/2016 07/31/2016 scan44 578 0.3%
07/27/2016 07/31/2016 blacklist 545 0.3%
07/27/2016 07/31/2016 nerisbotnet 227 0.1%
07/27/2016 07/31/2016 anomaly-spam 170 0.1%
07/27/2016 07/31/2016 scan11 126 0.1%
Table 3. System environment specifications.
Table 3. System environment specifications.
Unit Description
Processor Intel® Xeon®
CPU 2.30GHz with No.CPUs 2
RAM 12GB
OS
Packages TensorFlow 2.6.0
Table 4. Performance evaluation metrics score for TDCGAN model.
Table 4. Performance evaluation metrics score for TDCGAN model.
Accuracy Precision F1 Score Recall
0.95 0.94 0.94 0.96
Table 5. Performance evaluation metrics score for TDCGAN model and other machine learning methods.
Table 5. Performance evaluation metrics score for TDCGAN model and other machine learning methods.
Model Accuracy Precision F1 Score Recall
SMOTE 0.88 0.86 0.87 0.91
Random Over Sampling 0.85 0.89 0.90 0.88
SMOTEENN 0.86 0.89 0.90 0.89
The Borderline SMOTE 0.84 0.87 0.87 0.88
SVMSMOTE 0.89 0.90 0.91 0.89
SMOTE-Tomek Links 0.90 0.87 0.89 0.87
SMOTE_NC 0.85 0.88 0.86 0.85
CGAN 0.83 0.83 0.83 0.83
CTGAN 0.76 0.76 0.76 0.76
TDCGAN 0.95 0.94 0.94 0.96
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated