Preprint

Article

A Practical Type System for Formal Verification CPS &Amp; IoT C/C++ Programs

Altmetrics

Downloads

232

Views

Comments

This version is not peer-reviewed

Submitted:

30 May 2023

Posted:

31 May 2023

You are already at the latest version

Alerts

Abstract

Misuse of measurement units and orientations leads to errors in scientific applications, Cyber Physical Systems (CPS), and IoT C/C++ programs. Standard type system are inadequate in preventing such errors. Although dimensional and orientational analysis in physics can manually detect these errors in equations, analyzing complex code with intricate physical computations is impractical. To overcome this challenge, we propose an advanced type system that incorporates units and orientations as integral components within a specialized type library. Our enhanced type system automatically detects potential errors during compile time by representing physical quantities as types and utilizing dimensional analysis, orientational analysis, and metaprogramming techniques. Our improved type system enables formal verification of C++ software, successfully verifying programs with extensive codebases. We also employ it for runtime verification of dynamic linking and pointer operations in C++ programs. The integration of compile-time verification, dimensional analysis, orientational analysis, and advanced type system enhances the robustness and accuracy of scientific applications, CPS, and IoT C/C++ programs. By leveraging these approaches, we ensure precise calculations and prevent errors related to measurement units and orientations, resulting in substantial improvements in reliability and accuracy.

Keywords:

Subject: Computer Science and Mathematics - Software

1. Introduction

CPS [1] and IoT applications, as well as scientific applications, heavily rely on the use of measurement units such as meters, seconds, kilograms, and more (as specified in the SI system). The misuse of measurement units in these applications can lead to catastrophic consequences. One notable example is the loss of the Mars Climate Orbiter, where data denominated in the English system was mistakenly input into the navigation system, which expected metric units [2]. This incident highlights the importance of correctly managing measurement units in order to obtain accurate computational results.

However, in modern applications, it is common to encounter scenarios where multiple variables have the same dimension but different orientations. This adds an additional layer of complexity. Therefore, it is crucial to ensure the validation of both the physical dimensional units and the physical orientations in order to achieve correct computational results.

Unfortunately, standard type system do not enforce the proper use of physical dimensions and orientations, leaving room for potential errors and inconsistencies. To address this challenge, physicists and engineers often employ dimensional analysis [3] to verify the dimensional unit correctness of quantities in equations. Dimensional analysis assumes that each physical quantity has a well-defined, fixed unit of measure, and it requires the units on both sides of an equation to match. While dimensional analysis is a useful tool, it can be challenging, particularly for non-physicists. Many physical equations involve complex computations, making it difficult to accurately track the flow of units throughout the calculations. The manual application of dimensional analysis to programs that involve such equations can further exacerbate the complexity.

There are several libraries and frameworks available that provide built-in support for units and dimensions in software development. Some popular ones include:

NumPy [4]: NumPy is a powerful Python library for numerical computing. Although it doesn′t have built-in support for units and dimensions, it provides a flexible multi-dimensional array object that allows you to attach metadata to the arrays, such as units;
Pint [5]: Pint is a Python library specifically designed for handling physical quantities and units;
SciPy [6]: SciPy is a scientific computing library for Python. While it doesn′t offer direct support for units and dimensions, it works seamlessly with NumPy and Pint. By combining SciPy with Pint, you can leverage SciPy′s mathematical and scientific functionality while preserving the units and dimensions of your data;
Boost.Units [7]: Boost.Units is a C++ library that provides a comprehensive framework for handling physical quantities and units. It offers compile-time dimensional analysis, type-safe unit conversions, and arithmetic operations on quantities with different units. Boost.Units allows you to create custom unit systems and perform calculations while ensuring dimensional consistency;
UDUNITS [8]: UDUNITS is a widely used library in scientific and meteorological applications. It provides a flexible and extensive database of physical units and supports unit conversions, arithmetic operations, and parsing of unit expressions. UDUNITS is written in C and has bindings for various programming languages, including Python and Java;
Units.NET [9]: Units.NET is a C# library that offers a comprehensive set of units and dimensional analysis features. It supports unit conversions, arithmetic operations, and provides a user-friendly API for handling physical quantities. Units.NET allows you to work with units and dimensions in a strongly-typed manner.

Similarly, orientational analysis [10,11] assumes that each physical quantity has a meaningful, fixed orientation in space, and it requires the orientations on both sides of an equation to align [12]. Like dimensional analysis, orientational analysis can be challenging, especially for individuals without a strong physics background. Complex computations in physical equations make it difficult to accurately trace the flow of units and orientations. Therefore, manually applying both dimensional and orientational analysis to programs that involve such equations can be an even more daunting task.

In summary, ensuring the correctness of physical dimensional units and orientations is essential for CPS, IoT, and scientific applications. The limitations of standard type system in enforcing these constraints make it necessary to incorporate methods like dimensional analysis and orientational analysis. However, manually applying these analyses to programs that involve complex equations can be intricate and time-consuming, highlighting the need for more efficient and automated approaches to ensure the accuracy and reliability of these applications.

This paper presents a novel specialized type library (TL) designed to facilitate the formal verification of C++ software at both compile time and run-time. By leveraging this library, developers can enhance the reliability and correctness of their C++ programs through rigorous verification techniques.

Benefits of the proposed library:

Extensibility: The library allows for easy expansion to accommodate new domains and physical quantities;
Addition of orientation to quantities: The library enables the inclusion of orientation information for the quantities;
Adaptive use of prefixes: The library allows for the adaptive utilization of prefixes for units, enabling flexibility in expressing quantities.

The TL introduces a set of specialized types that enforce specific constraints and properties during program execution. These types enable compile-time verification by utilizing static analysis techniques to detect potential errors and inconsistencies in the code before it is executed. By catching these issues early on, developers can prevent runtime errors and enhance the overall robustness of their software.

Furthermore, the TL extends its functionality to run-time verification. During program execution, the library dynamically checks the validity of the program′s state and behavior against the defined constraints. This dynamic verification process acts as an additional safety net, ensuring that the software adheres to the intended specifications and behaves as expected.

The library′s formal verification capabilities enable developers to reason about their C++ programs in a more rigorous and systematic manner. By providing a higher level of assurance, it becomes possible to detect and prevent various types of errors, including type mismatches, undefined behavior, and violations of specified invariants. This significantly reduces the risk of bugs, improves code quality, and enhances the overall reliability of the software.

In addition to its verification features, the TL integrates seamlessly into the C++ development workflow. It provides clear and expressive interfaces that allow developers to specify constraints and properties in a concise and readable manner. The library also offers extensive documentation and support, making it accessible to developers with varying levels of expertise in formal verification.

Through the adoption of this TL, C++ developers can elevate the quality of their software by incorporating formal verification techniques into their development process. By combining the advantages of compile-time and run-time verification, the library offers a comprehensive approach to ensure the correctness and robustness of C++ software, ultimately leading to increased confidence in its reliability and improved software quality.

2. Key Principles of the Type Library

The International System of Units (SI) consists of seven base units: the amount of substance, current, length, luminous intensity, mass, time, and thermodynamic temperature and dimensionless symbol. Each base unit is associated with a unit symbol and a dimension symbol. According to the Siano convention [10,11], length is commonly understood to possess a fixed orientation in space, categorized as orientless, x-oriented, y-oriented, or z-oriented. This orientation is defined by the symbol "O" (see Table 1).

In the International System of Units (SI), each physical quantity is defined as a product of base units raised to certain powers. These base units serve as the fundamental building blocks for expressing various measurements.

When using SI units, physical values are associated with specific subject areas (SA). In cases where a dimension has an orientation, the corresponding value can have one of the following directions: {0, X, Y, Z}. A value of 0 indicates an orientationless quantity, while X, Y, and Z denote values oriented in the respective directions. For instance, quantities like force and acceleration fall into this category. On the other hand, certain physical values, including mass and current, are considered orientationless. This means they do not possess a specific direction associated with them

Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9 and Table 10 offer a comprehensive compilation of common units of measurement utilized across diverse subject areas. These tables serve as valuable references, allowing users to conveniently access and apply the appropriate units in their respective fields of study or work. The subject areas covered encompass Chemistry, Density & Concentration, Electricity & Magnetism, Flow, Geometry, Optics and Photometry, Physics, and Thermodynamics. Importantly, these tables should be considered as a foundation, providing a starting point for users to expand upon based on their specific requirements and subject areas of interest. Users are encouraged to augment the list as needed to accommodate their unique needs and ensure comprehensive coverage within their chosen domain.

According to Table 1 -Table 10, we have more than 80 different orientationless physical quantities and more than 60 oriented physical quantities.

In order to implement compile-time software formal verification, we need to create a total of 320 (80 + 60 x 4) different C++ classes. Considering both dimension homogeneity and orientation homogeneity, we are required to create overloading operators for product and division between these 320 classes, resulting in a total of 320 x 320 x 2 operators. When dealing with expressions that involve the product of multiple values (n-values), it is necessary to overload the product and division operators to accommodate the varying number of operands. In total, there will be 2 x 320ⁿ overloads required for these operators. Clearly, such a TL would be considerably complex and substantial in size. However, the advantage of having this TL is that it enables the execution of formal verification during compile time.

A common approach to representing units is by utilizing exponent vectors based on base units (as shown in Table 1) and unit factors [12]. For instance, the dimension of an orientationless unit of force is T^-2L¹M¹, which can be represented as [-2, 1, 1, 0, 0, 0, 0] using exponent vectors. On the other hand, an oriented force has the dimension T^-2L¹M¹O, where O can take values of lx, ly, or lz, representing the orientation in the x, y, or z direction, respectively, for example exponent vector = [-2, 1, 1, 0, 0, 0, 0, 1] for x-oriented force. By employing both orientational and dimensional analysis, we can distinguish between quantities that have the same dimension but different orientations. For example, energy [N x m] and torque [N x m].

Thus, arithmetic operations on units can be simplified to vector additions, subtractions, or comparisons. These operations can be performed only on physical quantities that have the same dimension or correspond to vectors with identical coordinates. In other words, units with matching exponent vectors can be directly added, subtracted, or compared using these operations.

However, complications arise when dealing with the product and division of physical quantities. For orientationless quantities, we can simply add or subtract their corresponding exponent vectors to obtain the resulting vector. However, for orientated quantities, determining the resulting vector requires more than just adding or subtracting the exponent vectors. We also need to consider the rules of Siano, which help define the orientation of the resulting vector [10,11]. Siano demonstrated that orientational symbols have an algebra defined by the multiplication table for the orientation symbols, which is as follows:

\begin{matrix} l_{0} & l_{x} & \begin{matrix} l_{y} & l_{z} \end{matrix} \\ l_{0} & l_{0} & l_{x} & \begin{matrix} l_{y} & l_{z} \end{matrix} \\ l_{x} & l_{x} & l_{0} & \begin{matrix} l_{z} & l_{y} \end{matrix} \\ \begin{matrix} l_{y} \\ l_{z} \end{matrix} & \begin{matrix} l_{y} \\ l_{z} \end{matrix} & \begin{matrix} l_{z} \\ l_{y} \end{matrix} & \begin{matrix} \begin{matrix} l_{0} \\ l_{x} \end{matrix} & \begin{matrix} l_{x} \\ l_{0} \end{matrix} \end{matrix} \end{matrix} and rules : \begin{matrix} l_{o} = \frac{1}{l_{o}} & l_{x} = \frac{1}{l_{x}} \\ l_{y} = \frac{1}{l_{y}} & l_{z} = \frac{1}{l_{z}} \end{matrix}

Based on the above, the product of two orientated physical quantities has an orientation as follows:

l_{o} l_{x} = l_{x} l_{o} = l_{x}

l_{o} l_{y} = l_{y} l_{o} = l_{y}

l_{o} l_{z} = l_{z} l_{o} = l_{z}

l_{x} l_{x} = l_{y} l_{y} = l_{z} l_{z} = l_{0}

But a common approach to representing units is by utilizing exponent vectors based on base units and unit factors has some constraint: we may realize software formal verification only in run time.

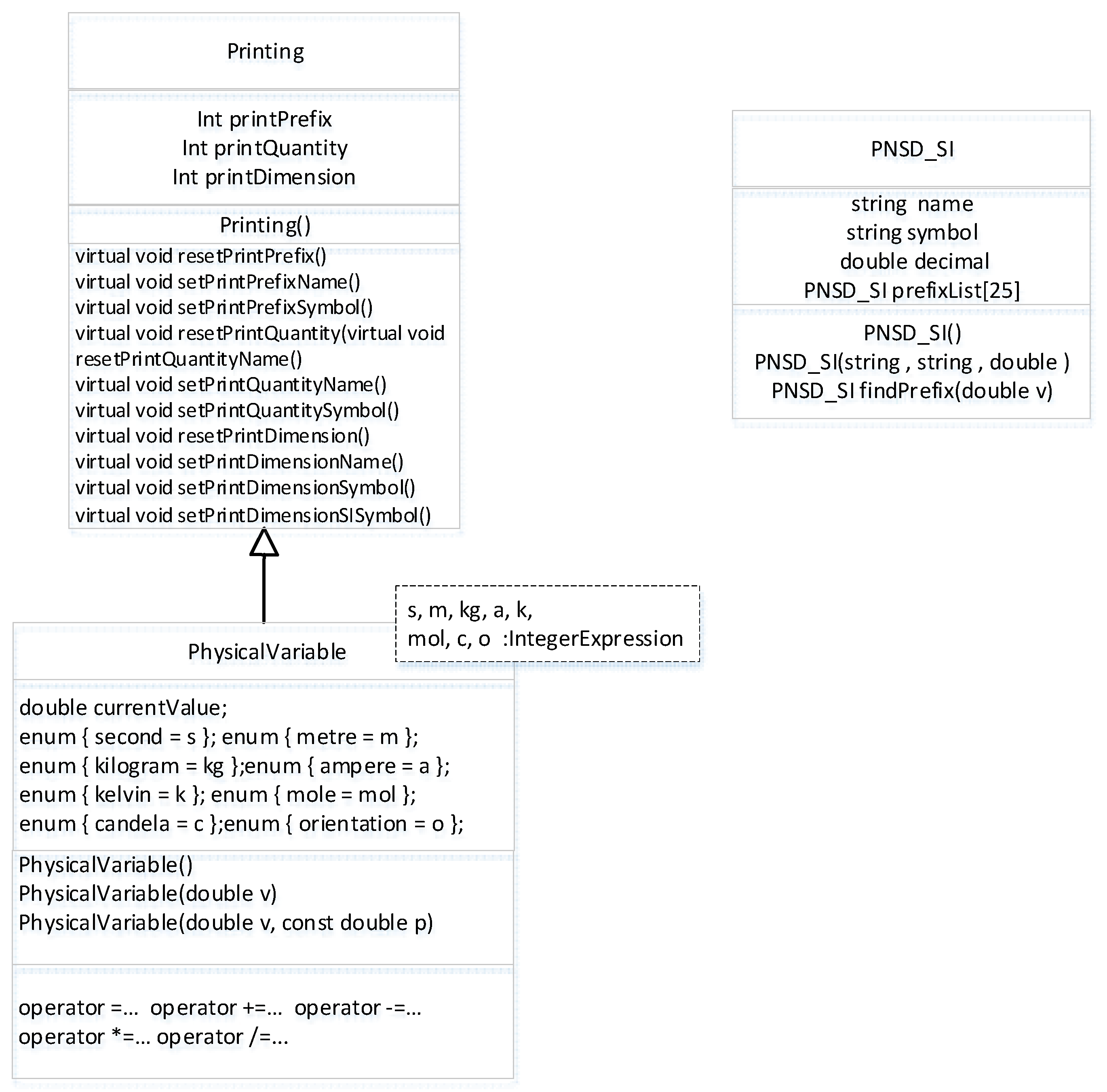
To enable the utilization of compile-time formal verification, we present the TL that encompasses key components designed to enhance the verification process. The TL comprises several essential classes, including the "PNSD_SI" class for facilitating operations with SI prefixes (e.g., nano, milli, giga, etc.). This class enables seamless handling of units with different magnitudes.

Another integral component of the TL is the "Printing" class, which provides comprehensive control over output formatting. This class empowers developers to customize the display of results, ensuring clear and informative representation of data.

Additionally, the TL incorporates a template class called "PhysicalVariable" that plays a vital role in dimensional analysis and orientational analysis operations. This class allows for precise handling of physical quantities, taking into account both their dimensions and orientations. Moreover, the "PhysicalVariable" class inherits essential functions from the "Printing" class, enabling seamless integration of output control capabilities.

The architecture of the TL is depicted in Figure 1, showcasing the relationships and dependencies between the classes.

By leveraging this TL, developers can harness the power of compile-time formal verification while benefiting from the flexibility and functionality provided by the "PNSD_SI," "Printing," and "PhysicalVariable" classes. These components collectively contribute to the accuracy, reliability, and ease of use in verifying C++ software.

The template class "PhysicalVariable" serves as a powerful tool for creating various C++ classes that correspond to specific physical quantities (Table 1 - Table 10) [13]. This template class, combined with metaprogramming [14] techniques, forms the foundation of a library that enables the generation of new types at compile time [15,16,17].

To simplify the creation of these classes, the library provides special preprocessor macros that leverage the "PhysicalVariable" template. These macros facilitate the generation of C++ classes during the compilation process. Using these macros is straightforward: developers define the desired quantity name, unit name, unit symbol, and a vector representing the dimensions based on the basis dimensions T (time), L (length), M (mass), I (electric current), θ (thermodynamic temperature), N (amount of substance), and J (luminous intensity) (see Table 1).

For instance, the following macro invocation creates a class named "Density" representing the physical quantity of density:

createSomeUnit(Density, "kilogram per cubic metre", "kg / m3", 0, -3, 1, 0, 0, 0, 0)

This macro generates the necessary code to define the "Density" class with the specified unit name and symbol.

To create oriented physical quantities, a different macro is used:

createSomeUnit0XYZ(Area, "square metre", "m2", 0, 2, 0, 0, 0, 0, 0)

This macro results in the creation of four C++ classes: "Area" (representing orientless quantities), "AreaX" (representing x-oriented quantities), "AreaY" (representing y-oriented quantities), and "AreaZ" (representing z-oriented quantities).

By employing these macros in the development process, developers can easily generate the necessary C++ classes for their desired physical quantities. This streamlined approach leverages the power of metaprogramming and compile-time generation to create a comprehensive library of types that accurately represent physical quantities and their orientations.

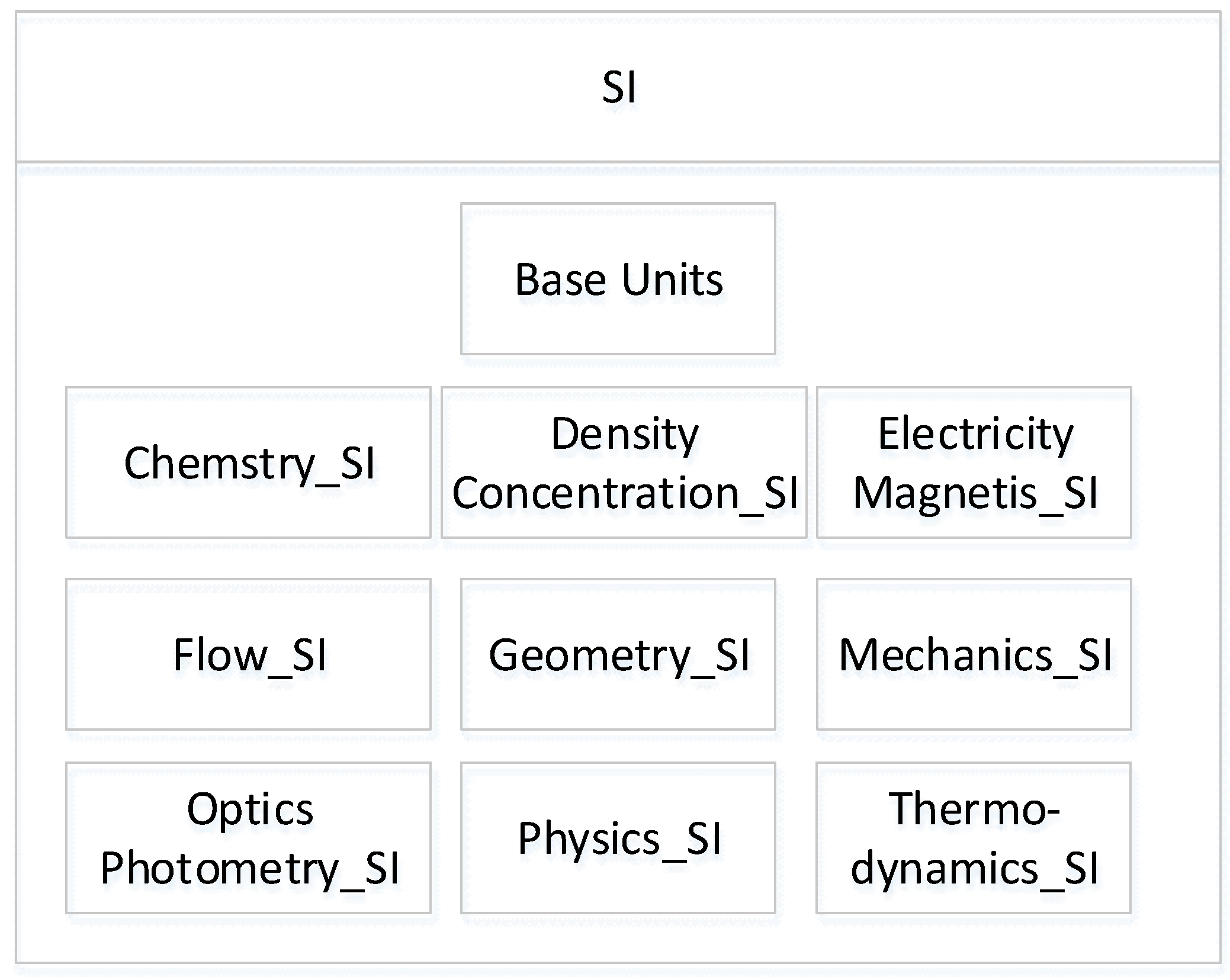
According to Table 1 - Table 10, each generated class is mapped to a specific subject area. Each subject area is associated with a C++ namespace. All of these namespaces are included within the SI namespace (see Figure 2).

The mapping of each generated class to a specific subject area, as described in Table 1 - Table 10, is achieved through the association with a dedicated C++ namespace. This approach ensures that classes related to Chemistry, Density & Concentration, Electricity & Magnetism, Flow, Geometry, Optics and Photometry, Physics, and Thermodynamics are organized and grouped accordingly. To maintain a well-structured codebase, all of these subject-specific namespaces are encapsulated within the SI (System International) namespace. This hierarchical structure promotes modularity, clarity, and ease of navigation within the codebase, facilitating efficient development and maintenance of the library. Please refer to Figure 2 for a visual representation of this namespace arrangement. Importantly, these namespaces should be considered as a foundation, providing a starting point for users to expand upon based on their specific requirements and subject areas of interest.

3. Implementation of Operators and Function Wrappers Using Templates

The proposed library adheres to the principles of homogeneity in both physical dimensions and orientations by ensuring that the left and right operands have equal dimensions and orientations. The assignment operators (=, +=, -=) are defined as function-members within the template class.

For the conditional operators (>, >=, ==, !=, <=,<) as well as the addition (+) and subtraction (-) operators, template functions are employed with template class arguments. These operators utilize the Seano conventions (see expressions 1 and 2) to ensure consistency and accuracy.

The multiplication and division operators are also defined as template functions, utilizing template class arguments and adhering to the Seano conventions. These operators enable proper handling of physical quantities during calculations.

The compound assignment operators (*=, /=) require a dimensionless and orientationless right operand. To preserve the dimension and orientation of the result, these operators are defined as template function-members with dimensionless and orientationless right operands.

The implementation of this library provides a significant advantage in terms of unit testing, integration testing, and regression testing. The effectiveness of static checking during compilation reduces the time required for these testing activities. By catching errors and inconsistencies at compile-time, developers can identify and address issues early in the development process, resulting in improved software quality and reduced debugging efforts.

Overall, the proposed library ensures consistency, accuracy, and efficiency by enforcing homogeneity of physical dimensions and orientations, and by leveraging static checking during compilation.

To accommodate the dimensionless and orientationless arguments of the exp and log functions, wrapper functions are utilized with template arguments that have zero values. The purpose of these wrapper functions is to ensure that the correct version of the exp and log functions is called for the PhysicalVariable instances. Here are the improved versions of the wrapper functions:

double exp(PhysicalVariable <0, 0, 0, 0, 0, 0, 0, 0>pv){ return ::exp(pv.value()); }

double log(PhysicalVariable <0, 0, 0, 0, 0, 0, 0, 0>pv){ return ::log(pv.value()); }

By specifying the template argument <0, 0, 0, 0, 0, 0, 0, 0>, the wrappers ensure that only dimensionless and orientationless instances of PhysicalVariable can be passed as arguments to the exp and log functions. This way, the correct mathematical operations can be applied to these specific instances, guaranteeing the accuracy and integrity of the calculations.

These wrapper functions play a crucial role in maintaining the consistency and correctness of operations involving dimensionless and orientationless quantities within the proposed library.

To handle the square root function (sqrt) within the template framework, we can create a wrapper function that correctly handles the dimensions of the result.

template < int T, int L, int M, int I, int θ, int N, int J>

PhysicalVariable < T/2, L/2, M/2, I/, θ /2, N/2, J/2, 0, 0> sqrt(

PhysicalVariable < T, L, M, I, K, N, J, 0> p)

{ return PhysicalVariable < T/2, L/2, M/2, I/, K/2, N/2, J/2, 0>(::sqrt(p.value())); }

This wrapper function takes a PhysicalVariable instance as an argument, where the dimensions are represented by the template parameters T, L, M, I, θ, N, J, and O. The sqrt function calculates the square root of the value stored in the PhysicalVariable instance and creates a new PhysicalVariable instance with dimensions halved for each base unit.

To create a function wrapper for xⁿ or pow(x, n), where x represents a dimensioned and orientationed value and n is an integral number, the following struct template, function template, and macro can be used:

template <int num>

struct powN

{ enum { np = num }; };

template < int T, int L, int M, int I, int θ, int N, int J, int O, int n>

PhysicalVariable< T*n, L*n, M*n, I*n, θ*n, N*n, J*n, (O*n)%2>

powPhysicalVariable(PhysicalVariable < T, L, M, I, θ, N, J, O > left, powN< n>)

{ return PhysicalVariable < T*n, L*n, M*n, I*n, θ*n, N*n, J*n, (O*n)%2>(::pow(left.value(), n)); }

#define pow(x,y)powPhysicalVariable( x, powN<y>())

This implementation allows you to calculate the power of a dimensioned and orientationed value (x) raised to an integral exponent (n).

To handle trigonometric functions (sine, cosine, tangent, arcsine, arccosine) within the template framework, we have created wrapper functions that correctly handle the dimensions of the result.

#define X SI::Geometry_SI::PlaneAngleX

#define Y SI::Geometry_SI::PlaneAngleY

#define Z SI::Geometry_SI::PlaneAngleZ

#define cosXYZ(L) double cos(L pv) { return ::cos(pv.value());}

cosXYZ(X) cosXYZ(Y) cosXYZ(Z)

#define FXYZ(F,L)\

Dimensionless##L F(SI::Geometry_SI::PlaneAngle##L pv)\

{ return Dimensionless##L (::F(pv.value())) ;}

FXYZ(sin, X) FXYZ(sin, Y) FXYZ(sin, Z)

FXYZ(tan, X) FXYZ(tan, Y) FXYZ(tan, Z)

double acos(Dimensionless pv){ return ::acos(pv.value()); }

X asinx(double v){ return X(::asin(v)); }

Y asiny(double v){ return Y(::asin(v)); }

Z asinz(double v){ return Z(::asin(v)); }

X asinx(Dimensionless v) { return X(::asin(v.value())); }

Y asiny(Dimensionless v) { return Y(::asin(v.value())); }

Z asinz(Dimensionless v) { return Z(::asin(v.value())); }

4. Using the Type Library

Using the TL is a straightforward process. In your C++ file, you need to include the necessary namespaces to access the desired subject areas. Here is an example of including the SI (System International) namespace and its subnamespaces:

using namespace SI;

using namespace SI::Optics_Photometry_SI;

using namespace SI::Electricity_Magnetism_SI;

using namespace SI::Thermodynamics_SI;

By including these namespaces, you gain access to the classes and functionality related to each subject area. It allows you to use the units, perform calculations, and leverage the features provided by the TL.

Furthermore, the subnamespaces can be extended separately in different blocks or even different files. For example:

// SomeUnit.h file

namespace SI::Electricity_Magnetism_SI {

class SomeUnit { /* Class implementation*/ };

}

// OtherUnit.h file

namespace SI::Electricity_Magnetism_SI {

class OtherUnit { /* Class implementation*/ };

}

// app.cpp

int main() {

SI::Electricity_Magnetism_SI::SomeUnit someUnit;

SI::Electricity_Magnetism_SI::OtherUnit otherUnit;

// Use the classes as needed

return 0;

}

We can create an alias for a long or nested namespace using the namespace aliasing feature:

namespace ZSI = SI::Electricity_Magnetism_SI;

int main() {

ZSI::Capacitance c;

// Use the alias to access the classes within the namespace

return 0;

}

This modular approach provides users with the flexibility to extend and organize subnamespaces in a structured manner, resulting in enhanced code reusability and maintainability.

By dividing the functionality into subnamespaces, developers can logically group related classes and functions, making it easier to locate and reuse code across different projects. Additionally, it promotes a modular design where each subnamespace can be independently extended or modified without affecting other parts of the codebase.

Furthermore, this approach enhances code organization, making it more intuitive and comprehensible. Developers can navigate through the codebase more efficiently, understanding the purpose and scope of each subnamespace.

Overall, this modular approach fosters better code management, encourages code reuse, and facilitates future modifications and enhancements. It is a powerful technique for structuring and maintaining complex projects effectively.

5. Verification of the Type Library

To verify the functionality of the TL, dedicated C++ units were created for each subnamespace. In this section, we will focus on the verification of the Geometry_SI namespace as an example.

Let′s consider the operations with the Area class within the Geometry_SI namespace:

Area area(100); //[square metre == m2 l=0]

AreaX areax(10); //[square metre == m2 l=x]

AreaY areay(10); //[square metre == m2 l=y]

AreaZ areaz(10); //[square metre == m2 l=z]

area = length0 * length0; areax = lengthy * lengthz;

areay = lengthx * lengthz; areaz = lengthx * lengthy;

double k = 10;

areaz *= k; areay /= k;

In the above code, we create instances of the Area class, along with AreaX, AreaY, and AreaZ classes, representing areas with different orientations.

We perform various operations to verify the correct behavior of the TL:

By performing these verification operations, we can validate the proper implementation of the Geometry_SI namespace within the TL;
In the second verification, we will examine operations involving the Curvature class within the Geometry_SI namespace.

Curvature curvarure(1); //[reciprocal metre == 1/m l=0]

CurvatureX curvarurex(1);//[reciprocal metre == 1/m l=x]

CurvatureY curvarurey(2);//[reciprocal metre == 1/m l=y]

CurvatureZ curvarurez(3);//[reciprocal metre == 1/m l=z]

// curvaturex = length0 / lengthx; error

curvarurex = 1.0 / lengthx; lengthx = 1.0 * lengthx;

In the provided code, we create instances of the Curvature class, along with CurvatureX, CurvatureY, and CurvatureZ classes, representing curvatures with different orientations.

We perform the following operations to verify the behavior of the TL.

Initially, we attempt to assign the result of length0 / lengthx to the curvaturex variable. However, this operation is invalid because the TL enforces the homogeneity of dimensions and orientations for valid mathematical operations. Since length0 has a dimension of [L^0], it cannot be divided by lengthx with a dimension of [L^x], resulting in an error.

Next, we assign the inverse of lengthx (1.0 / lengthx) to the curvaturex variable, demonstrating the ability of the TL to handle dimensionally consistent operations.

Finally, we perform a valid operation where lengthx is multiplied by 1.0, ensuring that the TL correctly handles scalar multiplication with a dimensioned quantity.

By verifying these operations and ensuring the expected outcomes, we can confirm the proper implementation of the Curvature class and its orientation-specific counterparts within the Geometry_SI namespace of the TL.

Now let′s proceed with the verification of trigonometric functions within the TL:

double lcosd = cos(1.25), dlx=0.5 , dly=0.6, dlz=0.7, dl=0.8;

PlaneAngleX planeAnglex(0.5);

PlaneAngleY planeAngley(0.4);

PlaneAngleZ planeAnglez(0.3);

Dimensionless lcosx = cos(planeAnglex);

Dimensionless lcosy = cos(planeAngley);

Dimensionless lcosz = cos(planeAnglez);

double lsind = sin(1.25);

DimensionlessX lsinx = sin(planeAnglex);

DimensionlessY lsiny = sin(planeAngley);

DimensionlessZ lsinz = sin(planeAnglez);

double ltan = tan(1.25);

DimensionlessX ltanx = tan(planeAnglex);

DimensionlessY ltany = tan(planeAngley);

DimensionlessZ ltanz = tan(planeAnglez);

double acosd = acos(0.5);

PlaneAngleX acosx = acos(dlx);

PlaneAngleY acosy = acos(dly);

PlaneAngleZ acosz = acos(dlz);

double asind = asin(0.5);

PlaneAngleX asinxd = asinx(dl);

PlaneAngleY asinyd = asiny(dl);

PlaneAngleZ asinzd = asinz(dl);

// double d0 = sin(planeAngle); errors!!! OK

// double dx = sin(planeAnglex);

// double dy = sin(planeAngley);

// double dz = sin(planeAnglez);

The provided code snippet focused on the verification of specific classes within the Geometry_SI namespace. However, similar checks were conducted for all other classes and operations within the TL to ensure their correctness and adherence to the defined rules and principles.

SI defines some set of prefixes of physical values. The provided code defines a list of prefixes used in the SI to denote physical values. Each prefix is associated with a name, symbol, and a corresponding decimal factor:

const PNSD_SI prefixList[24] = {

{"quetta","Q", 1e30 }, {"ronna", "R", 1e27}, {"yotta", "Y", 1e24},

{"zetta", "Z", 1e21 }, {"exa", "E", 1e18}, {"peta", "P", 1e15 }, {"tera", "T", 1e12 },

{"giga", "G", 1e9 }, {"mega", "M", 1e6 }, {"kilo", "k", 1e3 }, {"hecto", "h", 1e2},

{"deca", "da", 10 }, {"deci", "d", 1e-1 }, {"centi", "c", 1e-2 },

{"milli", "m", 1e-3 }, {"micro", "u", 1e-6 }, {"nano", "n", 1e-9 },

{"pico", "p", 1e-12 }, {"femto", "f", 1e-15}, {"atto", "a", 1e-18},

{"zepto", "z", 1e-21}, {"yocto", "y", 1e-24}, {"ronto", "r", 1e-27}, {"quecto", "q", 1e-30} };

In the following code example, you can observe the utilization of prefixes for initializing physical quantities:

Mass m(15., prefix::micro), m2(20.,nano), m3(1);

Current currentI1(2.), currentI2(2., prefix::nano), currentI3(2., prefix::kilo);

Volume w0(23, prefix::milli), w;

Current i1(100);

Based on the provided code, the following interpretations can be made:

For mass (m), the value is 15 * 10^-6 kg (15 milli grams);
For currentI1, the value is 2 A (amperes);
For currentI2, the value is 2 * 10^-9 A (2 nano amperes);
For currentI3, the value is 2000 A (2 kilo amperes).

It′s important to note that the code example assumes the availability of appropriate class definitions for Mass, Current, and Volume, which handle the incorporation of prefixes for physical quantities.

In the following code snippet, we can observe the configuration and utilization of print settings for physical quantities:

i1.setPrintPrefixSymbol();

i1.setPrintQuantitySymbol();

cout << "i1=" << i1;

currentI2.setPrintPrefixName();

currentI2.setPrintQuantityName();

currentI2.setPrintDimensionSymbol();

cout << "i2=" << currentI2 << endl;

currentI2 *= 2;

cout << "i2=" << currentI2 << endl;

currentI2 = currentI2 * 2.1 + i1;

cout << "i2=" << currentI2 << endl;

Code sets the print options:

For i1 to display the prefix symbol and the quantity symbol. Then, it prints the value of i1;
For currentI2 to show the prefix name, quantity name, and dimension symbol. Afterward, it prints the value of currentI2;
Multiplies currentI2 by 2 and prints the updated value;
Performs calculations on currentI2, multiplying it by 2.1 and adding i1. Finally, it prints the final value of currentI2.

In the following Figure 3, you can observe the output of physical quantities with different settings: printing prefixes (without prefix, name, symbol), printing quantities (without quantity, name, symbol), and printing dimensions (without dimension and dimension vector).

In the above figure:

i1 = 100 A (or 1 hA or 1 hecto A);
i2 = 2 nA, vector [0, 0, 0, 1, 0, 0, 0];
edf = 1.2 coulomb per square meter;
r1 = 1 kΩ, vector [-3, 2, 1, -2, 0, 0, 0].

This comprehensive output process ensures the reliability verification of the CPS embedded software.

The proposed TL was developed with the assistance of Microsoft Visual Studio Community 2022 Version 17.1.2. This widely-used development environment played a crucial role in the elaboration and creation of the TL, ensuring compatibility and leveraging the powerful features and tools provided by Visual Studio for efficient development and implementation.

The thorough verification process ensures the reliability, accuracy, and effectiveness of the TL implementation across diverse subject areas and namespaces. This process instills confidence in the TL′s functionality and usability, making it a dependable tool for software development and related tasks.

6. SW verification model

After successfully verifying the TL, we proceeded to utilize it for formal verification of embedded software. By incorporating TL into the development process, we leveraged its capabilities to ensure the correctness and reliability of the software′s behavior and interactions with the physical world. The TL′s ability to handle physical dimensions, units, and orientations provided a powerful tool for static checking and validation, minimizing the risk of errors and improving the overall quality of the embedded software.

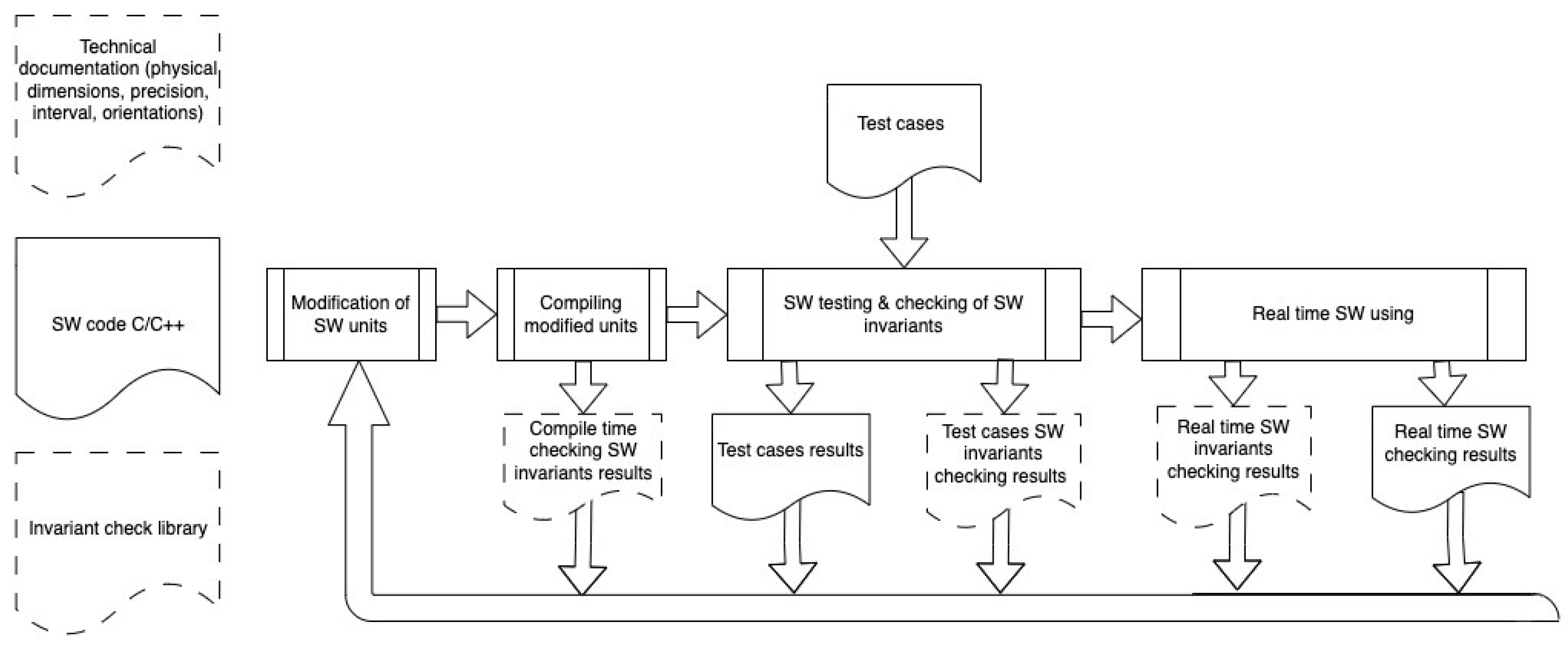
The software verification model employs invariants checking to ensure dimension and orientation homogeneity (see Figure 4). By enforcing these invariants, the model validates that the software components and operations maintain consistent physical dimensions and orientations throughout their execution. This approach guarantees the integrity of calculations and prevents incompatible combinations of quantities, resulting in more reliable and accurate software behavior. The TL plays a crucial role in supporting this verification process, providing the necessary tools and mechanisms to enforce and validate dimension and orientation consistency.

The software verification process involves several steps. The first step is to set the physical dimension, orientation, interval, and precision of input and output SW variables based on the technical documentation. This is done by using the source code of every function as the body of a method of a special testing class.

The second step involves modifying the C++ source code by overriding standard data types to match the physical dimensions and orientation of the input and output variables.

In the third step, a standard compiler is used to detect SW defects, such as violations of dimensional and/or orientational homogeneity. After modifying the SW units, the modified units are compiled again.

In the fourth step, after compiling and linking editing, test cases are used for software testing. Negative results of the test cases indicate the presence of violations of dimensional and/or orientational homogeneity. This allows for modification of the source code to correct any detected issues. The test cases also allow for the checking of the correctness of different pointer operations during dynamic linking in C++.

In the fifth and final step, after software verification, invariants checking can be used in real-time to ensure the software is operating correctly.

Overall, this software verification process provides a reliable and effective method for detecting and correcting dimensional and orientational homogeneity violations in C++ code, ensuring high-quality and reliable software.

7. Discussion

The proposed type library, which incorporates dimensional analysis and orientational analysis, demonstrates promising effectiveness in detecting software defects. Its ability to identify over 60% of software defects [18], including those resulting from incorrect usage of variables, operations, and functions, is remarkable. This suggests that the library could serve as a valuable tool in software development.

However, it is essential to acknowledge that no type library can detect all types of software defects. Therefore, while the proposed library based on the SI exhibits potential, it should be thoroughly evaluated and compared to other type libraries that are based on different system units.

An imminent task is to utilize the proposed type library for the formal verification of CPS and IoT software, both during compile time and runtime.

8. Conclusions

This article introduces a novel type library (TL) for software formal verification based on software invariants. The proposed TL leverages both dimensional and orientational analysis to enhance software quality. By employing two independent formal software verification methods, it offers diverse and robust verification capabilities, leading to improved software quality.

The proposed software verification model relies on the utilization of software invariants. While this approach has certain drawbacks, such as the requirement to determine physical dimensions and orientation of variables during compile-time and increased compilation time, it still provides significant advantages over manual error detection by humans. The TL empowers compilers to efficiently identify errors, making it a valuable tool in software development.

On the other hand, the proposed model brings several notable advantages. It enhances programmer productivity by eliminating the need to spend time troubleshooting dimensional and orientational errors during runtime. The TL enables comprehensive analysis of dimensional and orientational correctness of software, covering both compile-time and run-time phases. It ensures the correct usage of software variables and operations, as well as verifies the arguments of functions and procedures.

Designed specifically for integration with C/C++ languages, the proposed TL seamlessly integrates with existing compilers for formal compile-time software verification. It enhances software reliability by introducing additional checks during dynamic linking, and it also facilitates real-time formal verification.

Through the analysis of real-world software for unmanned aerial vehicles (drones) on GitHub, the effectiveness of the proposed TL was demonstrated. It successfully detected 90% of incorrect uses of software variables and over 50% of incorrect operations, resulting in an overall conditional probability of defect detection of 60% [18]. These results highlight the efficacy of the proposed software verification model in identifying software defects and reinforcing software reliability.

Author Contributions

Conceptualization, Y.M.; methodology, Y.M., Y.S.; software, Y.M., Y.S.; validation, Y.M., Y.S.; formal analysis, Y.M., Y.S.; resources, Y.M., Y.S.; data curation, Y.M.; writing—original draft preparation, Y.M., Y.S.; writing—review and editing, Y.M., Y.S.; visualization, Y.M., Y.S.; supervision, Y.M.; project administration, Y.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Data is contained within this article.

Conflicts of Interest

The authors declare no conflict of interest.

References

Cyber-Physical Systems (CPS). Available online: https://www.nsf.gov/publications/pub_summ.jsp?ods_key=nsf21551&org=NSF (accessed on 11 January 2021).
Novak, G. S. Conversion of units of measurement. IEEE Transactions on Software Engineering 1995, Volume 21, Issue 8, pp. 651-661. [CrossRef]
Mahoney, J. F., Yeralan, S. Dimensional Analysis. Procedia Manufacturing 2019, Volume 38, pp. 694-701. [CrossRef]
NumPy. Available online: https://numpy.org/ (accessed on 10 May 2023).
Pint. Available online: https://pypi.org/project/Pint/ (accessed on 25 May 2023).
SciPy. Available online: https://scipy.org/ (accessed on 10 May 2023).
Boost ++ Library. Available online: https://www.boost.org (accessed on 14 April 2023).
UDUNITS. Available online: https://www.unidata.ucar.edu/software/udunits/ (accessed on 28 December 2020).
Units.NET. Available online: https://sourceforge.net/projects/units-net.mirror/ (accessed on 9 June 2022).
Siano, D. B. Orientational analysis—a supplement to dimensional analysis. Journal of the Franklin Institute 1985, Volume 320, Issue 6, pp. 267-283.
Siano, D. B. Orientational analysis, tensor analysis and the group properties of the SI supplementary units. Journal of the Franklin Institute 1985, Volume 320, Issue 6, pp. 285-302. [CrossRef]
Santos, Luiza & Conde de Freitas, Alessandra. Orientational Analysis of the Vesic’s Bearing Capacity of Shallow Foundations. Soils and Rocks 2020, Volume 43, pp. 3-9. [CrossRef]
Sutter, H. Metaclasses: Generative C++. Available online: http://www.open-std.org/jtc1/sc22/wg21/docs/papers/2018/p0707r3.pdf (accessed on 11 February 2018).
Sutton, A. Metaprogramming. https://www.open-std.org/jtc1/sc22/wg21/docs/papers/2020/p2237r0.pdf (accessed on 15 October 2020).
Alligand, E., Falcou J. Practical C++ Metaprogramming, 1st ed.; O’Reilly Media, Inc., 2016; 44 p.
Monnon, J. Type functions and beyond. An exploration of type functions and concept functions. Available online: 2018-02-26 https://www.open-std.org/jtc1/sc22/wg21/docs/papers/2018/p0844r0.html (accessed on 26 February 2018).
Working Draft, Standard for Programming Language C++. Available online: https://isocpp.org/files/papers/N4928.pdf (accessed on 22 May 2023).
Manzhos, Y.; Sokolova, Y. A Software Verification Method for Internet of Things and Cyber-Physical Systems. Preprints.org 2023, 2023050118. [CrossRef]

Figure 1. Architecture of the Specialized Type Library.

Figure 2. Namespace structure.

Figure 3. Fragment physical quantities output.

Figure 4. A functional model of SW formal verification.

Table 1. Base Units of SI & Dimensionless Unit.

SI unit	Unit [Symbol]	Dimension symbol
Amount Of Substance	[mol]	N
Current	[A]	I
Length	[m]	LO
Luminous Intensity	[cd]	J
Mass	[kg]	M
Time	[s]	T
Thermodynamic Temperature	[K]	Θ
Dimensionless	[1]	1O

Table 2. Units of Measurement for Quantities in the Subject Area of "Geometry".

Quantity	Unit [Symbol], Dimension
Area	[m²], L², O
Aspect Ratio	[1], 1
Curvature	[1/m], L^-1O
Perimeter	[m], L
Plane Angle	[rad], 1 O
Solid Angle	[Sr], 1
Surface Area	[m²] L², O
Volume	[m³], L³

Table 3. Units of Measurement for Quantities in the Subject Area of "Optics and Photometry".

Quantity	Unit [Symbol], Dimension
Illuminance	[lx], L^-2JO
Luminance	[cd/m²], L^-2JO
Luminous Efficacy	[lm /W], T³L^-4M^-1J
Luminous Energy	[lm s], TJ
Luminous Exposure	[lx s], TL^-2JO
luminous flux or luminous power	[cd sr], J
Optical Power	[1/m], L^-1O
Refractive Index	[1], 1O

Table 4. Units of Measurement for Quantities in the Subject Area of "Density & Concentration".

Quantity	Unit [Symbol], Dimension
Density	[kg/m³], L^-3M¹
Energy Density	[J/m³], T^-2L^-1M¹
Mass Concentration	[kg/m³], L^-3M¹
Mass Fraction	[kg/kg], 1
Specific Volume	[m³/kg], L³M^-1
Surface Density	[kg/m²], L^-2M¹O
Linear Mass Density	[kg/m], L^-1M¹

Table 5. Units of Measurement for Quantities in the Subject Area of "Chemistry".

Quantity	Unit [Symbol], Dimension
Catalytic Activity	[kat], T^-1N¹
Catalytic Efficiency	[m³/(mol s)], T^-1L³N^-1
Catalytic Activity Concentration	[kat / m³], T^-1L^-3N¹
Concentration	[mol/m³], L^-3N¹
Molar Conductivity	[s m²/mol], T³M^-1A²N^-1O
Molar Flow Rate	[mol/s], T^-1N¹
Molar Mass	[kg/mol], M¹N^-1
Molarity	[mol/kg], M^-1N¹
Molar Volume	[m³/mol], L³N^-1
Mole Fraction	[mol/mol,1], 1
pH	[1], 1
Rate Of Reaction	[mol/(m³·s)], T^-1L^-3N¹

Table 6. Units of Measurement for Quantities in the Subject Area of "Flow".

Quantity	Unit [Symbol], Dimension
Energy Flow Rate	[J/s], T^-3L²M¹O
Heat Flux Density	[W/m²], T^-3M¹O
Irradiance	[J/(m²s)], T^-3M¹O
Mass Flow Rate	[kg/s], T^-1M¹O
Mass Flux	[kg /(m²s)], T^-1 L²M¹O
Spectral flux	[W/Hz], T^-2L²M¹O
Reynolds Number	Dimensionless
Turbulent Kinetic Energy	[J/kg], T^-2L²
Turbulent Dissipation Rate	[W/kg], T^-3L²
Volumetric Flow Rate or or volume velocity	[m³/s], T^-1L³ O

Table 7. Units of Measurement for Quantities in the Subject Area of "Physics".

Quantity	Unit [Symbol], Dimension
Absorbed Dose	[Gy], T^-2L²
Absorbed Dose Rate	[Gy / s], T^-3L²
Exposure	[C/kg], T¹M^-1I¹
Equivalent Dose	[Sv], T^-2L²
Radiance	[W/(m² sr)], T^-3M¹ O
Radioactivity	[Bq], T^-1
Radiant Intensity	[W / sr], T^-3L²M¹
Specific Energy	[J/kg], T^-2L²
Spectral Intensity	[W/(sr m)], T^-3L¹M¹
Spectral Power	[W/Hz], T^-3L¹M¹
Spectral Radiance	[W/(sr m³)], T^-3L^-1M¹
Stefan Boltzmann Constant	[W/(m² K^-4)], T^-3M¹Θ^-4
Wave Length	[m], L¹
Wave number	[1/m], L^-1

Table 8. Units of Measurement for Quantities in the Subject Area of "Mechanic".

Quantity	Unit [Symbol], Dimension
Acceleration	[m/s²], T^-2L¹ O
Action	[J s], T^-1L²M1
Angular Acceleration	[rad/s²], T^-2 O
Angular Momentum	[N m s], T^-1L²M¹ O
Angular Velocity	[rad/s], T^-1 O
Bulk Modulus	[Pa N/m²], T^-2L^-1M¹
Kinetic Energy	[J], T^-2L²M¹
Compressibility	[1/Pa], T²L¹M^-1
Diffusivity	[m²/s], T^-1L² O
Dynamic Viscosity	[N s/m²], T^-1L^-1M¹
Energy	[J], T^-2L²M¹
Force	[N], T^-2L¹M¹ O
Gravitational Potential	[J/kg], T^-2L² O
Impulse	[N s], T^-1L¹M¹ O
Jerk -the change in acceleration	[m/s³], T^-3L¹ O
Jounce – the change in jerk	[m/s⁴], T^-4L¹O
Kinematic Viscosity	[m²/s], T^-1L² O
Moment Of Force	[N m], T^-2L²M¹ O
Moment Of Inertia	[kg m²], L²M¹ O
Momentum	[N s], T^-1L¹M¹ O
Power	[W], T^-3L²M¹
Potential Viscosity	[m²/s], T^-1L² O
Pressure	[Pa], T^-2L^-1M¹
Speed	[m/s], T^-1L¹ O
Stiffness	[N/m], T^-2M¹ O
Stress	[Pa], T^-2L^-1M¹
Surface Tension	[N/m], T^-2M¹ O
Torque	[N m], T^-2L²M¹ O
Velocity	[m/s], T^-1L¹ O
Weight	[N], T^-2L¹M¹ O
Work	[J], T^-2L²M¹
Young Modulus	[Pa], T^-2L^-1M¹

Table 9. Units of Measurement for Quantities in the Subject Area of "Physics".

Quantity	Unit [Symbol], Dimension
Absorbed Dose	[Gy], T^-2L²
Absorbed Dose Rate	[Gy / s], T^-3L²
Exposure	[C/kg], T¹M^-1I¹
Equivalent Dose	[Sv], T^-2L²
Radiance	[W/(m² sr)], T^-3M¹ O
Radioactivity	[Bq], T^-1
Radiant Intensity	[W / sr], T^-3L²M¹
Specific Energy	[J/kg], T^-2L²
Spectral Intensity	[W/(sr m)], T^-3L¹M¹
Spectral Power	[W/Hz], T^-3L¹M¹
Spectral Radiance	[W/(sr m³)], T^-3L^-1M¹
Stefan Boltzmann Constant	[W/(m² K^-4)], T^-3M¹Θ^-4
Wave Length	[m], L¹

Table 10. Units of Measurement for Quantities in the Subject Area of " Electricity & Magnetism".

Quantity	Unit [Symbol], Dimension
Capacitance	[F], T⁴L^-2M^-1I²
Current Density	[A/m²], L^-2I¹ O
Electric Charge	[C], T¹I¹
Electric Charge Density	[C/m³], T¹L^-3I¹
Electrical Conductance	[S], T³L^-2M^-1I²
Electric Displacement Field	[C/m], T¹L^-2I¹ O
Electric Field Strength	[V/m], T^-3L¹M¹I^-1 O
Electric Flux Density	[C/m²], T¹L^-2I¹ O
Frequency	[Hz], T^-1
Frequency Drift	[1/s²], T^-2
Impedance	[Ohm], T^-3L²M¹I^-2
Inductance	[H], T^-2L²M¹I^-2
Linear Charge Density	[C/m], T¹L^-1I¹ O
Magnetic Dipole Moment	[J/T], L²I¹ O
Magnetic Field Strength	[A/m], L^-1I¹ O
Magnetic Flux	[Wb], T^-2L²M¹I^-1 O
Magnetic Flux Density	[T], T^-2M¹I^-1 O
Magnetic induction	[T], T^-2M¹I^-1 O
Magnetic Moment	[Wb m], T^-2L³M¹I^-1 O
Magnetic Permeability	[H/m], T^-2L¹M¹I^-2O
Magnetic Rigidity	[T m], T^-2L¹M¹I^-1 O
Magnetic Reluctance	[H^-1], T²L^-2M^-1I²
Magnetomotive Force	[A rad], I¹ O
Permittivity	[F/m], T⁴L^-3M^-1I²
Resistance	[Ohm], T^-3L²M¹I^-2
Resistivity	[Ohm m], T^-3L³M¹I^-2
Surface Charge Density	[C/m²], T¹L^-2I¹ O
Voltage	[V], T^-3L²M¹I^-1

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.