Preprint
Article
Rlc Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann’s Constant in Curved Space-Time
Altmetrics
Downloads
600
Views
1944
Comments
3
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
03 August 2023
Posted:
08 August 2023
You are already at the latest version
Alerts
Abstract
Here we mathematically model black holes and the early universe following dynamics similar to RLC electrical models, focusing on their similarities at the singularity. We use this mathematically modelling to hypothesize the evolution of an expanding universe as the result of a black hole collapse followed by its evaporation. Or model consists of several steps defined by: (1) the formation of a black hole following general relativity equations; (2) growth of the black hole modelled as a resistance-capacitance-like electrical circuit; (3) expansion of space-time following the disintegration of the black hole, modelled by RLC-like dynamics. In updating this article, version 2, we will expand by presenting three additional examples related to the theory of the generalization Boltzmann's constant in curved space-time and the theory of general and especial relativity. We will calculate the critical mass to produce a black hole in the LHC, the existence of a high temperature Bose-Einstein condensate and finally we will demonstrate the existence of a tangential force to the repulsion force in the disintegration of subatomic particles. In the update of this article, version 3, we will expand to develop two examples. First, we will present the relationship between M-theory, extra dimensions with the theory of the generalization of Boltzmann's constant in curved space-time. Secondly, we will propose the idea of updating the Lambda-CDM model, considering the primordial gravitational waves to correctly describe the evolution of the universe.
Keywords:
Subject: Physical Sciences - Astronomy and Astrophysics
1. RC electrical model for a black hole
If considering electric charge and
mass as fundamental properties of matter.
From the point of view of electric
charge, we know that a capacitor stores electrical energy
and we can represent it as an RC circuit.
Analogously,
from the mass point of view, we can consider a black hole as a capacitor that
stores gravitational potential energy.
Continuing
with the analogy, the space-time that surrounds a black hole can be represented
as the inductance L.
from this
simple conceptual idea was born RLC electrical modelling of black hole and
early universe.
RC
electrical model for a Black Hole:
Here we
put forward the hypothesis of a black hole growth in analogy to an RC
electrical circuit that grows according to a constant Tau being defined as:
First, we
will consider the total mass of a black hole to consist of the sum of baryonic
mass and dark matter mass (equation 2), considering dark matter as an imaginary
number.
Where M
is the total mass of a black hole, m is the baryonic mass;
corresponds to dark matter and I is the
irrational number
. This
equation is in analogy to impedance of an RC circuit.
Where z
represents impedance; R represents resistance and Xc represents reactance.
If proper
accelerations for the masses are introduced in equation (2) we obtain the following:
Where F
is the total force, f is the force associated to baryonic mass, and i
is the force associated to dark mass. In
analogy to a phasor diagram for an RC circuit, in which the reactance phasor
lags the resistance phasor R by
, we can
represent the two forces associated to barionic matter and dark matter as two
orthogonal vectors (Figure 1).
Vector diagram of forces in a
black hole for circular motion with constant acceleration:
taking
into account Newton’s equation of universal gravitation:
F = - (G M1 M2)/r2
The sign
(-) of the equation means that the force Fc is at 180 degrees with respect to
the resistance R and the force Ft is also at 180 degrees from the reactance Xc.
It is important to make clear the
physical interpretation of the imaginary mass, it is simply telling us that the
force Ft due to the mass δ lag the force fc by 90 degrees, that lag is
represented by the imaginary number i.
Later we will determine that the mass
δ, is the result of v > c inside a black hole.
Where v is the speed of a massless
particle and c is the speed of light in a vacuum.
Figure 1
is represented for a circular motion with constant acceleration
simply because the tangential velocity of a particle is proportional to the
radius from the centre of the black hole multiplied by the average angular
frequency.
Vt = rω
The
contribution of (Ft, Vt) is what makes the speed of the galaxy remain constant
as the radius of the galaxy grows.
Where Vt
represents the tangential velocity of a galaxy, r is the radius from the
galaxy, and
ω
is the average angular velocity of the
rotation of the galaxy.
Circular
motion with constant acceleration tells us that the mass input into a black
hole is negligible with respect to the black hole’s own mass.
The growth of a black hole
according to the tau constant is an intrinsic property of a black hole and is
independent of the amount of matter that enters a black hole.
To calculate the total energy associated
to the black hole, we can introduce its total mass (equation 2) into:
Where E
is energy; c represents the speed of light and m represents the mass. This lead
to:
We can
assume that during the big bang inflation phase baryonic matter was
overrepresented compared to dark matter together with an infinitesimal
momentum, which would give us from equation (6) the following:
As
expected, this result corresponds to the total energy of the universe at the
big bang if we consider it to be made of dark matter represented as a reactance
in an RC circuit.
The
positive value of E is determined by matter, there is no antimatter inside a
black hole.
If we
consider charge as a fundamental property of matter,
,
represents the amount of relativistic dark matter inside the black hole at the
time of disintegration.
If we
consider mass as a fundamental property of matter,
,
represents the amount of relativistic dark matter inside a black hole, which
exerts a repulsive gravitational force at the moment of disintegration. This
repulsive gravitational force is what generates the dark energy after the Big
Bang.
At time
T0, when the black hole disintegrates and the Big Bang occurs, roughly all
matter was dark matter.
We could
also consider a universe at infinity proper time in which baryonic matter is
dominant over dark matter, which would transform equation (6) back into
equation (5) but with baryonic matter.
2. RLC electrical model of the universe
We will
analyse the Dirac delta function &(t).
&(t) = {∞, t = 0} ^ {0, t ≠ 0}
If we
perform the Fourier transform of the function &(t) and analyse the
amplitude spectrum, we observe that the frequency content is infinite.
If we
perform the Fourier transform of the function &(t) and analyse the phase
spectrum, we observe that the phase spectrum is zero for all frequencies.
We say
that it is a non-causal zero phase system.
The most
important thing to emphasize in this system is that an infinite impulse has an
infinite frequency content.
When we
work in seismic prospecting looking for gas or oil, using explosives, the
detonations produce an energy peak that generates a frequency spectrum that
propagates in the layers of the earth. The energy produced in the detonation is
not instantly transferred to the ground, a time delay occurs, it is said to be
causal system of minimum phase.
In
analogy, we are going to suppose that the Big Bang also behaves like a causal
system of minimum phase.
Here we
put forward the hypothesis that the big bang is the convolution of the energy
released by disintegration of the black hole with the space-time surrounding
the black hole, being defined as:
Where is the total mass of a black hole, Ɛ is the space-time surrounding the black hole and * is the convolution symbol.
Equation (9) can be simplified and considered analogous to an RLC circuit.
Where RC represents a black hole and L represents the space-time around a black hole
the resolution of the quadratic equation of the RLC circuit will determine how space-time will expand after the Big Bang and the bandwidth of the equation will give us the spectrum of gravitational waves that originated during the Big Bang.
3. Cosmic inflation
From the following equation:
We will analyse the Schwarzschild solution for a punctual object in which mass and gravity are introduced.
Where M is the mass of a black hole, c is the speed of light, and G is the gravitational constant.
if we consider dθ = 0; and dφ = 0; that is, we move in the direction of dR.
R = Rs, ds = 0, let’s analyse this specific situation.
Replacing the conditions given in (13), (14) and (15) in equation (12), we have:
(dR / dt) ² = v² = c² (1 - (2MG/Rc²) ²
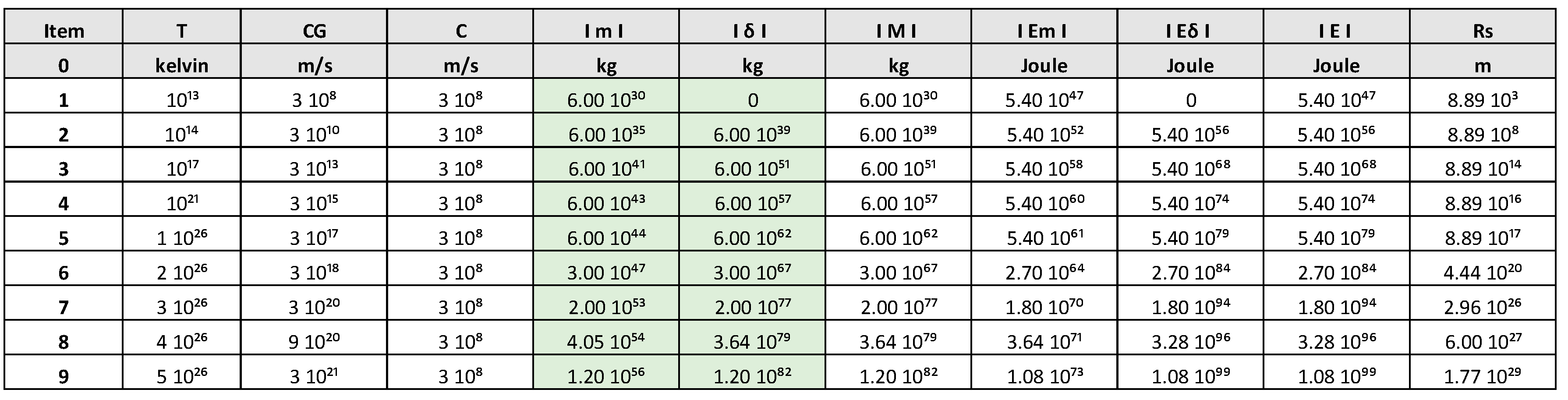
R = Rs, v = 0; ds² = 0; Rs is the Schwarzschild’s radius.
R > Rs, v < c; ds < 0, time type trajectory.
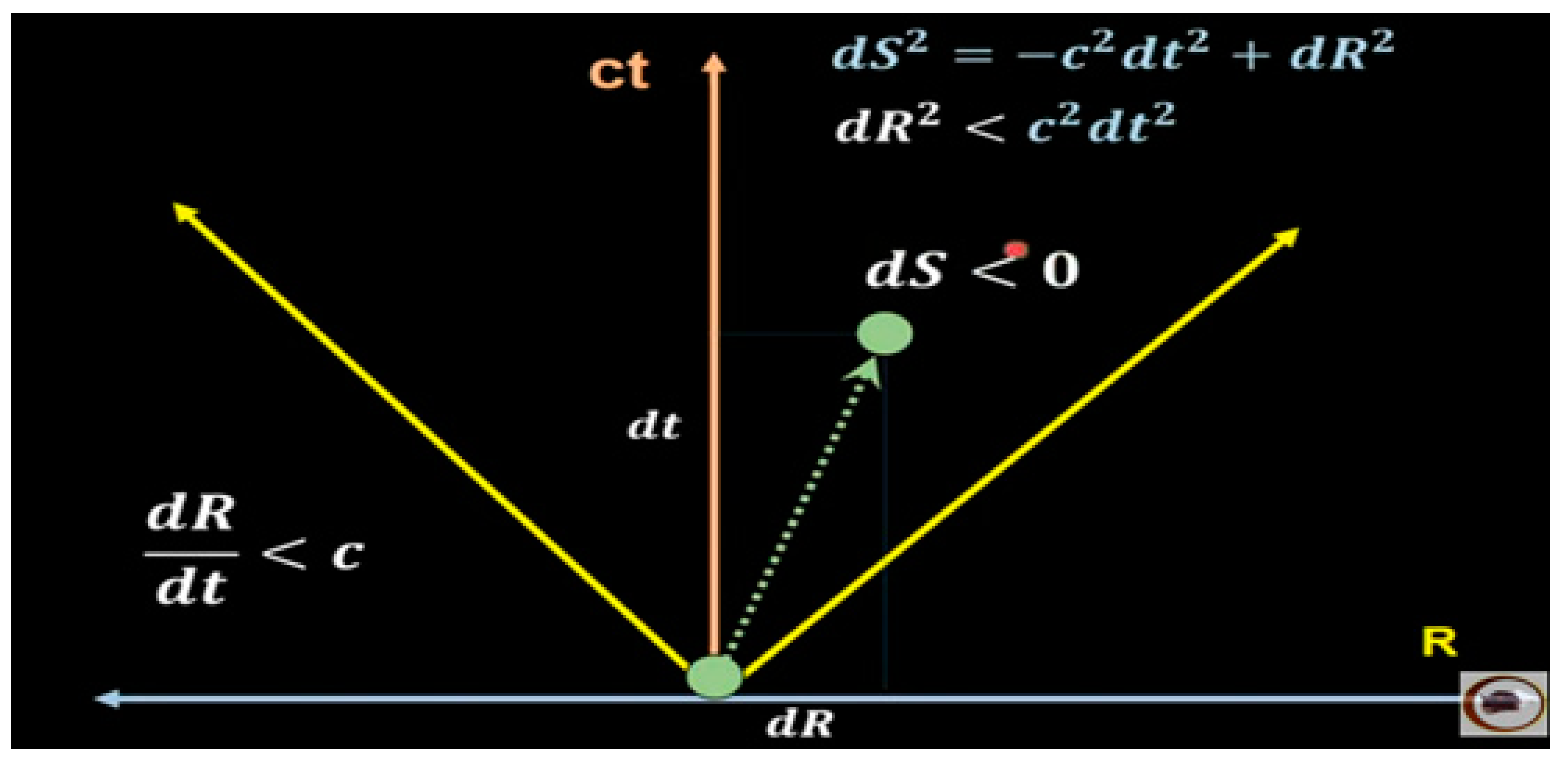
R < Rs, v > c; ds > 0, space type trajectory.
Condition (18) is very important because to the extent that R < Rs, v > c is fulfilled, it is precisely this speed difference that generates the imaginary mass in a black hole given by Planck length equation:
where h is Planck’s constant, G is the gravitational constant, and c is the speed of light.
If we consider condition (18) and equation (19), to the extent that R < Rs and v > c, are fulfilled, we deduce that the Planck length decreases in value.
We define the following:
Lpɛ = Lp = 1.616199 10⁻³⁵ m; electromagnetic Planck length.
Lpɢ = gravitational Planck length.
Always holds:
Lpɢ < Lpɛ
Here we put forward the hypothesis that cosmic inflation is the expansion of space-time that is given by Lpɢ that tends to reach its normal value Lpɛ after a black hole disintegrates.
If we consider the Planck length Lpɛ, the minimum length of space-time, like a spring and due to the action of v > c (300,000 km/s), this length decreases in values of Lpɢ, that is, Lpɢ < Lpɛ, allowing us to imagine the immense forces involved in compressing space-time of length Lpɛ into smaller values of space-time Lpɢ. The immense energy stored and released in the spring of length Lpɢ, to recover its initial length Lpɛ, is the cause of the exponential expansion of space-time in the first moments of the Big Bang.
At time T0, when the black hole disintegrates and the Big Bang occurs, roughly all matter was dark matter, relativistic dark matter.
4. Generalization of the Boltzmann’s constant in curved space-time
Equation of state of an ideal gas as a function of the Boltzmann constant.
Where, P is the absolute pressure, V is the volume, N is the number of particles, KB is Boltzmann’s constant, and T is the absolute temperature.
Boltzmann’s constant is defined for 1 mole of carbon 12 and corresponds to 6.0221 10²³ atoms.
Equation (20) applies for atoms, molecules and for normal conditions of pressure, volume and temperature.
We will analyse what happens with equation (20) when we work in a degenerate state of matter.
We will consider an ideal neutron star, only for neutrons.
We will analyse the condition:
This condition tells us that the number of particles remains constant, under normal conditions of pressure, volume and temperature
However, in an ideal neutron star, the smallest units of particles are neutrons and not atoms.
This leads us to suppose that number of neutrons would fit in the volume of a carbon 12 atom, this amount can be represented by the symbol Dn.
In an ideal neutron star,
Where Dn represents the number of neutrons in a carbon 12 atom.
However, equation (22) is not constant, with respect to equation (21), the number of particles increased by a factor Dn, to make it constant again, I must divide it by the factor Dn.
Where N’ = (Dn N), is the new number of particles if we take neutrons into account and not atoms as the fundamental unit.
Where KB’ = (KB / Dn), is the new Boltzmann’s constant if we take neutrons into account and not atoms as the fundamental unit.
We can say that equation (21) is equal to equation (24), equal to a constant
Generalizing, it is the state in which matter is found that will determine Boltzmann’s constant.
A white dwarf star a will have a Boltzmann’s constant KBe, a neutron star will have a Boltzmann’s constant KBn, and a black hole will have a Boltzmann’s constant KBq.
There is a Boltzmann’s constant KB that we all know for normal conditions of pressure, volume and temperature, for a flat space-time.
There is an effective Boltzmann’s constant, which will depend on the state of matter, for curved space-time.
The theory of general relativity tells us that in the presence of mass or energy space-time curves but it does not tell us how to quantify the curvature of space-time.
Here we put forward the hypothesis that there is an effective Boltzmann’ constant that depends on the state of matter and through the value that the Boltzmann’ constant takes we can measure or quantify the curvature of space-time.
Quantifying space-time, considering the variable Boltzmann constant, is also quantizing gravitational waves and, as with the electromagnetic spectrum, we will determine that there is a spectrum of gravitational waves.
These analogies to represent the gravitational and electromagnetic wave equations are achieved thanks to the ADS/CFT correspondence.
We can determine the equations of electromagnetic and gravitational waves as shown below.
Electromagnetic wave spectrum for flat space-time:
Eε = h x fε
Cε = λε x fε
Eε = h x Cε / λε
Eε = Kʙε x Tε
Kʙɛ = 1.38 10⁻²³ J/K
Gravitational wave spectrum for curved spacetime:
Eɢ = h x fɢ
Cɢ = λɢ x fɢ
Eɢ = h x Cɢ / λɢ
Eɢ = Kʙɢ x Tɢ
Kʙɢ = 1.38 10⁻²³ J/K to 1.78 10⁻⁴³ J/K.
Where the subscript ε means electromagnetic and the subscript ɢ means gravitational.
It can be seen that there is an electromagnetic and a gravitational frequency as well as an electromagnetic and a gravitational temperature.
The maximum curvature of space-time occurs for an effective Boltzmann’s constant of KB = 1.78 10⁻⁴³ J/K, given by the ADS/CFT correspondence in which a black hole is equivalent to the plasma of quarks and gluons to calculate the viscosity of the plasma of quarks and gluons.
Once a black hole is formed and the maximum curvature of space-time is reached, as a black hole grows following the tau growth law analogous to an RC circuit, as v grows fulfilling the relationship v > c, it happens that the gravitational Planck length becomes less than the electromagnetic Planck length, it holds that Lpɢ < Lpɛ.
5. Black hole’s radiation
Equation (2) defines the mass of a black hole, as shown below:
Where M is the total mass of a black hole, m is the baryonic mass; corresponds to dark matter and i is the irrational number .
Also, here we put forward the hypothesis of a black hole growth in analogy to an RC electrical circuit that grows according to a constant Tau being defined as:
If we consider the black hole’s radiation that produces pairs of particles and antiparticles at the event horizon.
Here we put forward the hypothesis:
the HR (matter) particle, with frequency ω and energy hω, falls into the black hole and adds to m and δ increasing the mass of the black hole, that is, it adds mass.
This is defined with the assumption that a black hole grows according to the tau constant just like an RC circuit.
The P particle (antimatter), with frequency ω and energy -hω, moves away from the black hole in the form of a gravitational wave.
According to the proposed hypothesis, a black hole always grows, following the curve of the tau constant in analogy to an RC electrical circuit.
For a black hole of 3 solar masses, the stationary frequency would be approximately 2.6 10³ Hz.
6. Application of the model and results
6.1. Additional calculations. Growth of a black hole in analogy to the tau growth curve of an RC circuit
In the ADS/CFT correspondence to calculate the viscosity of quark-gluon plasma, the following assumption is used, a black hole is equivalent to quark-gluon plasma.
We consider the temperature of a black hole equal to the temperature of the quark-gluon plasma, equal to T = 10¹³ K.
Another way of interpreting it is as follows:
When a star collapses, a white dwarf star, a neutron star, or a black hole is formed.
A white dwarf star has a temperature of about 10⁶ K, a neutron star has a temperature of about 10¹¹ K. If we consider that a black hole is a plasma of quarks and gluons, its temperature is expected to be higher than 10¹¹ K.
Hypothesis: the temperature of a black hole is 10¹³ K.
We will make the following approximation:
T = 0.0000000000001τ, T = 10⁻¹³τ
τ = 10²⁶ K
Cɢ(T) = Cɢmax (1 - e⁻(ᵀ/τ))
Cɢ(T) = Cɢmax (1 - e ⁻ ⁰·⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰¹(τ/τ))
Cɢ(T) = Cɢmax (1 - e ⁻ ⁰·⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰¹)
Cɢ(T) = Cɢmax (1 - e ⁻ (¹ / 10¹³)
Cɢ(T) = Cɢmax (1 - 1 / e (¹/ 10¹³))
Cɢ(T) = Cɢmax (1 – 0.9999999999999)
Cɢ(T) = Cɢmax x 10⁻¹³
Cɢmax = Cɢ(T) / 10⁻¹³ = 3 10⁸ m/s x 10¹³
Cɢmax ≡ 3 10²¹ m/s.
Where T is the absolute temperature, τ represents the growth constant tau, Cɢ = v represents the speed of a massless particle greater than the speed of light and Cɢmax represents the maximum speed that Cɢ can take.
Parametric equations:
Cɢ (T) = Cɢmax (1 – e ⁻(ᵀ/τ)
T (kelvin) = {(ɦ c³) / (8 x ᴨ x Kʙ x G x M)}, Hawking’s equation for the temperature of a black hole.
Rs = (2 x G x M) / c², Schwarzschild’s radius.
IMI = K ImI, where K is a constant.
IMI = I δ I
Kʙq = 1.78 10⁻⁴³ J/K, Boltzmann ‘s constant for black hole.
- a)
- In item 1 of the Table 1, for the following parameters, T = 10¹³ K, Cɢ = C = 310⁸ m/s, calculating we get the following values:
m = 6 10³⁰ kg, baryonic mass.
δ = 0, dark matter mass.
M = m = 6 10³⁰ kg
Rs = 8,89 10³ m, Schwarzschild radius.
- b)
- In item 9 of the Table 1, for the following parameters, T = 5 10²⁶ K, Cɢ = 3 10²¹ m/s, C = 310⁸ m/s, calculating we get the following values:
m = 1.20 10⁵⁶ kg, baryonic mass.
δ = 1.20 10⁸² kg, dark matter mass.
M = δ = 1.20 10⁸² kg
Rs = 1.77 10²⁹ m, Schwarzschild radius.
- c)
- It is important to emphasize, for the time t equal to 5τ, at the moment the disintegration of the black hole occurs, the big bang originates, the total baryonic mass of the universe corresponds to m = 10⁵⁶ kg.
- d)
- Figure 2 shows the growth of the tau (τ) constant, as a function of speed vs. temperature.
6.2. Calculation of the amount of dark matter that exists in the Milky Way
Mass and Schwarzschild’s radius of the Sagittarius A* black hole:
m = 4.5 10⁶ Ms = 4.5 x 10⁶ x 1.98 10³⁰ kg
Where Ms is the mass of the sun.
m = 8.1 x 10³⁶ kg
Rs = 6 million kilometres
Where Rs is the Schwarzschild’s radius of the Sagittarius A*.
Rs = 6 x 10⁹ m
If we look at Figure 2, for m = 8.1 x 10³⁶ kg and Rs = 6 x 10⁹ m, extrapolating we have approximately that T = 3 10¹⁴ K.
To calculate the speed Cɢ we are going to use the Hawking temperature equation:
T = hc³ / (8ᴨ x KB x G x M)
Where h is Boltzmann’s constant, c is the speed inside a black hole, KB is Boltzmann’s constant, G is the universal constant of gravity, and M is the mass of the black hole.
Substituting the values and calculating the value of C we have:
Cɢ = 10.30 10¹⁰ m/s
If we look at Figure 3, we see that this value corresponds approximately to the calculated value.
With the value of Cɢ we calculate δ and M:
E = M C²
Where E is energy, M is mass, and C is the speed of light.
Eɢ = M Cɢ
Eɢ = K M C²
Cɢ ² = k C²
Where K is a constant.
Calculation of the constant K:
C = 3 10⁸ m/s,
Cɢ = 10.30 10¹⁰ m/s,
M = 8.1 10³⁶ kg
E = 8.1 10³⁶ kg x 9 10¹⁶ m²/s²
Eɢ = 8.1 10³⁶ x (10.30 10¹⁰) ² = 8.1 10³⁶ x 106 10²⁰
Eɢ = (106 / 9) 10⁴ x 8.1 10³⁶ x 9 10¹⁶
Eɢ = K E
K = 11.77 10⁴
Calculation of the total mass M:
M = K m
M = (11.77 10⁴) x (8.1 10³⁶ kg)
M = 9.54 10⁴¹ kg, Total mass of black hole Sagittarius A*
m = 8.1 x 10³⁶ kg, total baryonic mass inside the black hole Sagittarius A*
Calculation of the mass of dark matter δ:
M = δ
δ = 9.54 10⁴¹ kg, total dark matter inside the black hole Sagittarius A*
Calculation of the ratio of the mass of dark matter and the mass of the Milky Way
Mvl = 1.7 10⁴¹ kg, mass of the milky way
δ = 9.54 10⁴¹ kg, total dark matter inside the black hole Sagittarius A*
δ / Mvl = (9.54 10⁴¹ kg / 1.7 10⁴¹ kg)
δ / Mvl = 5.61, ratio of the mass of dark matter and the mass of the Milky Way
δ = 5.61 Mvl
The total dark matter δ is 5.61 times greater than the measured amount of baryonic mass of the Milky Way Mvl.
6.3. Calculation of the variations of the Planck length, Planck time and Planck temperature as a consequence of the fact that the velocity v varies from 310⁸ m/s to 3 10²¹ m/s
We define the following:
Cε < Cɢ < Cɢmax
Where ε stands for electromagnetic, ɢ stands for gravitational, and max stands for maximum.
Planck’s length equation:
Planck’s time equation:
Planck’s temperature equation:
Where Lp represents the Planck’s length, tp represents the Planck’s time, and Tp represents the Planck’s temperature.
Where h stands for Planck’s constant, C for the speed of light, G for the universal constant of gravity, and KB for Boltzmann’s constant.
Substituting the values of (27) and (28) in equations (29), (30) and (31) we obtain:
Electromagnetic Planck constants:
Cɛ = 3 x 10⁸ m/s
Lpɛ = 1.61 10⁻³⁵ m
tpɛ = 5.39 10⁻⁴⁴ s
Tpɛ = 1.41 10³² K
Gravitational Planck constants:
Cɢ = 3 x 10⁸ m/s to 3 x 10²¹ m/s
Lp = 1.61 10⁻³⁵ m to 1.28 10⁻⁵⁴ m
tp = 5.39 10⁻⁴⁴ s to 0.426 10⁻⁷⁵ s
Tp = 1.41 10³² K to 0.62 10⁹⁰ K
6.4. The observation of the 1919 solar eclipse in Brazil and Africa provided the first experimental proof of the validity of Albert Einstein’s theory of relativity. We will calculate the Boltzmann constant for the sun and show how it adjusts to the deviation found.
No solar eclipse has had as much impact in the history of science as that of May 29, 1919, photographed and analysed at the same time by two teams of British astronomers. One of them was sent to the city of Sobral, Brazil, in the interior of Ceará; the other to the island of Principe, then a Portuguese territory off the coast of West Africa. The goal was to see if the path of starlight would deviate when passing through a region with a strong gravitational field, in this case the surroundings of the Sun, and by how much this change would be if the phenomenon was measured.
Einstein introduced the idea that gravity was not a force exchanged between matter, as Newton said, but a kind of secondary effect of a property of energy: that of deforming space-time and everything that propagates over it, including waves like light. “For Newton, space was flat. For Einstein, with general relativity, it curves near bodies with great energy or mass”, comments physicist George Matsas, from the Institute of Theoretical Physics of the São Paulo State University (IFT-Unesp). With curved space-time, Einstein’s calculated value of light deflection nearly doubled, reaching 1.75 arcseconds.
The greatest weight should be given to those obtained with the 4-inch lens in Sobral. The result was a deflection of 1.61 arc seconds, with a margin of error of 0.30 arc seconds, slightly less than Einstein’s prediction.
Demonstration:
- i)
- Let us calculate the Boltzmann’s constant for the Sun, Kʙs, curved spacetime.
Hawking’s temperature equation:
Where Kʙs is the Boltzmann constant for the sun, Ts is the temperature of the sun’s core, G is the universal constant of gravity, and Ms is the mass of the sun.
Kʙs = (6.62 10⁻³⁴ x 27 10²⁴) / (8 x 3.14 x 1.5 10⁷ x 6.67 10⁻¹¹ x 1.98 10³⁰)
Kʙs = 3.59 10⁻³⁷ J/K, Boltzmann’s constant of the sun.
We use the following equation:
Es = Kʙs x Ts
Es = 3.59 10⁻³⁷ x 1.5 10⁷
Es = 5.38 10⁻³⁰ J/K
We use the following equation:
Es = h x fs
fs = Es / h
fs = 5.38 10⁻³⁰ / 6.62 10⁻³⁴ = 0.81 10⁴ = 8.1 10³ Hz
fs = 8.1 10³ Hz
We use the following equation:
c = λs x fs
λs = c / fs
λs = 3 10⁸ / 8.1 10³
λs = 3.7 10⁴ m
We use the following equation:
Degree = λs / 360
Degree =102.77 m
We use the following equation:
Arcsecond = degree / 3600
Arcsecond = 102.77 m / 3600 = 0.0285 m
1.61 arcsecond = 0.0458 m
1 inch = 0.0254 m
4 inch = 0.1016 m
With a 4-inch lens, we can measure the deflection produced by the 1.61 arcsecond curvature of space-time, which was predicted by Albert Einstein’s theory of general relativity, and corresponds to a wavelength λs = 3.7 10⁴ m, a frequency fs = 8.1 10³ Hz, for an effective Boltzmann constant of the sun Kʙs = 3.59 10⁻³⁷ J/K.
- ii)
- We will carry out the same calculations for Kʙ = 1.38 10⁻²³ J/K, flat space-time.
Kʙ = 1.38 10⁻²³ J/K
We use the following equation:
E = Kʙ x Ts
E = 1.38 10⁻²³ x 1.5 10⁷
E = 2.07 10⁻¹⁶ J/K
We use the following equation:
E = h x f
f = E / h = 2.07 10⁻¹⁶ / 6.62 10⁻³⁴
f = 3.12 10¹⁷ Hz
We use the following equation:
c = λ x f
λ = c / f
λ = 3 10⁸ / 0.312 10¹⁸
λ = 9.61 10⁻¹⁰ m
We use the following equation:
Degree = λ / 360
Degree = 0.02669 10⁻¹⁰ m
We use the following equation:
Arcsecond = degree / 3600
Arcsecond = 7.41 10⁻¹⁶ m
Using the Boltzmann constant Kʙ = 1.38 10⁻²³ J/K, we cannot correctly predict by mathematical calculations the deflection of light given by Albert Einstein’s general theory of relativity, to be measured in the telescope at Sobral.
Through the example given, we can conclude that the Boltzmann’s constant Kʙs = 3.59 10⁻³⁷ J/K fits the calculations of the deflection of light in curved space-time.
6.5. Dark energy and its relationship with the wave equation of the universe produced by the big bang and the generalization of Boltzmann’s constant for curved space-time.
a) Calculation of the wave equation of the universe for the time T0 when the Big Bang occurs:
we will use the Table 1.
Table 1 – Represents values of ImI, baryonic mass; IδI, dark matter mass; IMI, mass of baryonic matter plus the mass of dark matter; IEmI, energy of baryonic matter; IEδI, dark matter energy; IEI, Sum of the energy of baryonic matter plus the energy of dark matter and Rs, Schwarzschild’s radius, as a function of, c, speed of light; Cɢ, speed greater than the speed of light; T, temperature in Kelvin; using the parametric equations.
We are going to consider that at the instant t=0¯, the black hole is about to disintegrate.
Calculation of gravitational waves for a damped parallel RLC circuit (α > ωo).
Initial conditions:
V(0)¯ = 1.08 10⁷³ V, V is equivalent to E
I(0)r = I(0)c = 3 10²¹ A, I is equivalent to C
Calculation of the value of the wavelength lambda λ.
λ = 1.000.000 light years = 10⁶ x 9.46 10¹⁵ m
λ = 9.46 10²¹ m
Calculation of the value of the frequency f:
C = λ x f
f = C / λ
f = 3 10²¹ / 9,46 10²¹
f = 0.317 Hz
Calculation of the value of the angular frequency ω:
ω = 2 ᴨ f
ω = 2.00 rad/s
Calculation of the value of the resistor R:
V (0) = I (0) x R
R = V (0) / I (0) = 1.08 10⁷³ / 3 10²¹
R = 3.60 10⁵¹ Ohms
Calculation of the number of seconds in 380,000 years:
t = 11.81 10¹² s
Let’s consider α = 55 10⁹ ωo
α = 110 10⁹
let’s define:
ω = ωo = 2.00 rad/s; the fundamental frequency is equal to the resonant frequency.
α = 1 / 2RC
Calculation of the value of capacitance C:
C = 1 / 2Rα
C = 1 / (2 x 3.60 10⁵¹ x 110 10⁹)
C = 1.26 10⁻⁶³ F
Calculation of the value of inductance L:
ωo² = 1/LC
L = 1/ (ωo² x C) = 1 / (4 x 1.26 10⁻⁶³)
L = 1.98 10^62 Hy
Calculation of the value of S1:
S1 = -α + √ (α² - ωo²)
S1 = - 1.81 10⁻¹¹
Calculation of the value of S2:
S2 = -α - √ (α² - Wo²)
S2 = -2.19 10¹¹
With these calculated values we have the following equation:
Calculations of the constant A1 and A2:
First condition V(0):
V(t) = A1 e^ (-1.81 10⁻¹¹t) + A2 e^ (-2.19 x 10¹¹t)
V (0) = A1 + A2 = 0
Second condition dV(0) / dt:
V(t) = A1 e^ (-1.81 10⁻¹¹t) + A2 e^ (-2.19 x 10¹¹t)
d V(t) / dt = d (A1 e^ (-1.81 10⁻¹¹t) + A2 e^ (-2.19 x 10¹¹t))
dV(t)/dt = - 1.81 10⁻¹¹ x A1 x e^-1.81 10⁻¹¹t - 2.19 10¹¹ x A2 x e^-2.19 10¹¹t
Let’s calculate dV(0)/dt = ?
Third condition:
IR + IC + IL = 0; but for t = 0, IL = 0 then it remains
V/R + CdV(t)/dt =0
dV(0)/dt = V/RC
Combining the equations (33), (34) and (35) we obtain the following values for A1 and A2:
A1 = + 1.086 10⁷³
A2 = - 1.086 10⁷³
Substituting the values of A1 and A2 in equation (32) we obtain the equation of gravitational waves of the Big Bang for the time T0.
Where E(t) represents the energy of gravitational waves and E0 represents the energy that corresponds to the temperature of 2.7K.
The spectrum of amplitude and phase as a function of frequency (Figure 3) is the Fourier transform from ideal similar equation (36).
The amplitude spectrum shows us the frequency content as a function of the magnitude.
The phase spectrum shows the frequency content as a function of the angle, but we have to remember by Fourier that the angle is a function of time, therefore a variation of angle implies a variation in displacement and it is precisely this very important characteristic, which we can relate to dark energy.
Here we put forward the hypothesis that dark energy is the expansion of space-time that is produced by a spectrum of gravitational waves whose produced frequencies are a function of time, when the disintegration of a black hole (big bang) occurs.
Here we put forward the hypothesis that dark energy is the result of relativistic dark matter that propagates when the black hole disintegrates (Big Bang).
Therefore, dark energy is the result of the combination of the spectrum of gravitational waves whose frequency content is a function of time added to the relativistic dark matter, both propagate with the disintegration of the black hole (Big Bang).
Additional calculations
Calculation of the temperature of the universe for a time t = 380,000 years:
Let’s calculate E (t) for t = 11.81 10¹² s, (380,000 years)
E (t) = 1.08 10⁷³ {e^ - (1.81 10⁻¹¹t)} – 1.08 10⁷³ {e^ - (2.19 10¹¹t)}
E (t) = 1.08 10⁷³ {e⁻²¹³}
E (t) = 0.33 10⁻¹⁹ Joules
T = E/KB
T = 2390 k
Approximately the temperature of the cosmic microwave background.
Calculation of the time t for when the universe stabilizes and reaches the temperature of 2.7 K
Substituting (37) in equation (36) we have:
3.72 10⁻²³ = 1.08 10⁷³ e ˉ (1.81 10⁻¹¹t)
e ^ (1,81 10⁻¹¹t) = 0.290 10⁹⁶
1.81 10⁻¹¹t = ln (0.290 10⁹⁶)
t = 1.22 10¹³ s
In that time t the space-time travels the following distance:
e = v x t
Where e is space, v is velocity, and t is time.
e = 3 10²¹ m/s x 1.22 10¹³ s
If we calculate the Fourier transform of equation (32), that is, E (ω).
All the frequencies that make up the frequency spectrum have to travel the distance given by equation (38), that is, 3.66 10³⁴ m.
Therefore, the influence of the spectrum of gravitational waves in the expansion of space-time will be twice as long, that is, 2.44 10²⁶ s
If we divide by power of 10, logarithmic scale, we have approximately 26 steps.
Let’s calculate the time t today.
t= 4.35 10¹⁷ s, correspond to 17 steps.
(17,5 / 26) x 100 = 67.3%, this is similar to the dark energy content of the universe.
100% - 67.3 = 32.7 %, this is similar to the dark matter content of the universe.
Calculation of the number of seconds in 380,000 years:
Calculation of the number of seconds for when the universe stabilizes and reaches the temperature of 2.7 K
We divide the time t, given by (39) by the time t, in (40), we get:
(11.81 10¹² s / 1.22 10¹³ s) x 100 = 96.72 %
100% - 96,72% = 3.28%, this is similar to the baryonic matter content in the universe.
The true interpretation of this result is the following, the fundamental wavelength that corresponds to λ = 1,000,000 light years, represents the fundamental peak of the CMB sound spectrum, has convolved 96% with the space-time of the universe and still needs to be convolved 4%.
All these calculations are referenced to a time t = 11.81 10¹² s, which correspond to the CMB.
b) Dark energy and the relationship that exists with the generalization theory of Boltzmann’s constant and curved space-time
The formation of a black hole produces a contraction of space-time.
For the sun, the contraction would be in the following order:
R= 696,340 km, Sun radius.
Rs = 3 km, Schwarzschild’s radius of the sun.
Equation of volume of a sphere:
(4/3) π R³
Calculation of the volume of the sun:
V = (4/3) π R³
V = (4/3) x 3.14 x (6.9610⁸) ³
V = 1411.54 10²⁴
Calculation of the volume of the equivalent black hole of the sun:
Vs = (4/3) π Rs³
Vs = (4/3) x 3.14 x (3 10³) ³
Vs = 113.04 10⁹
Calculation of the V / Vs ratio:
V / Vs = 1411.54 10²⁴ / 113.04 10⁹
V / Vs = 12.48 10¹⁵
In three dimensions the space-time contraction factor is 10¹⁵ times.
In one dimension the space-time contraction factor is 10⁵ times.
We can call it the contraction factor of space-time or the compactification factor of matter.
Another way to calculate the factor of contraction of space-time or compactification of matter is the following:
Boltzmann’s constant for flat space-time, is defined for 1 mole of carbon 12 and corresponds to 6.0221 10²³ atoms.
We assume the ratio of the quark given by the German accelerator HERA (Hadron-Elektron-Ringanlage) in the year of 2016, whose article is published following the right of the internet (21).
Rc12 = 0.75 10⁻¹⁰ m, Radius of the atom carbon 12
Rq = 0.43 10⁻¹⁸ m, radius of the quark
Equation of volume of a sphere:
(4/3) π R³
Where R is the radius of the sphere.
Calculation of the volume of the atom carbon 12:
VaC12 = (4/3) x 3.14 x (0.75 10^-10⁻¹⁰) ³
VaC12 = 1.76 10⁻³⁰ m³, volume of C12 atom.
Calculate the volume of a quark:
Rq = 0.43 10⁻¹⁸ m, radius of the quark
Vq = (4/3) x 3.14 x (0.43 10⁻¹⁸) ³
Vq = 0.33 10⁻⁵⁴ m³
Calculation of the contraction factor Vac12 / Vq:
Vac12 / Vq = 1.76 10⁻³⁰ m³ / 0.33 10⁻⁵⁴ m³
Vac12 / Vq = 5.33 10²⁴
In three dimensions the space-time contraction factor is 10²⁴ times.
In one dimension the space-time contraction factor is 10⁸ times.
In both examples, we can relate the contraction of space-time to the Boltzmann’s constant as follows:
There is a Boltzmann’s constant KB that we all know for normal conditions of pressure, volume and temperature, for a flat space-time.
There is an effective Boltzmann’s constant, which will depend on the state of matter, for curved space-time.
Knowing that Boltzmann’s constant is defined between the following limits
1.38 10⁻²³ J/K > KB > 1.78 10⁻⁴³ J/K
Through the variation of the Boltzmann’s constant we can quantify the curvature of space-time.
Analysing we can conclude the following:
In both examples, there is a contraction of spacetime which is related to the curvature of space-time.
According to our theory, the Big Bang is born from the disintegration of a black hole.
Generalizing, let’s define dark energy:
Here we put forward the hypothesis that dark energy is the expansion of space-time that is produced by a spectrum of gravitational waves whose produced frequencies are a function of time, when the disintegration of a black hole (big bang) occurs.
Here we put forward the hypothesis that dark energy is the result of relativistic dark matter that propagates when the black hole disintegrates (Big Bang).
Here we put forward the hypothesis that dark energy is the expansion of space-time produced by a curved space-time (KB = 1.78 10⁻⁴³ J/K) that tends to reach its normal state, flat space-time (KB = 1.38 10⁻²³ J/K)
Therefore, dark energy is the result of the combination of the spectrum of gravitational waves whose frequency content is a function of time, added to the relativistic dark matter, both propagate with the disintegration of the black hole (Big Bang); added to the expansion of space-time produced by a curved space-time (KB = 1.78 10⁻⁴³ J/K) that tends to reach its normal state, flat space-time (KB = 1.38 10⁻²³ J/K).
Dark energy is a combination of events already mentioned, which determine the expansion of space-time in our universe.
6.6. Calculation of the density parameter of the universe Ωᴍ,o
- I)
- Calculation of Ωᴍ,o
Ωᴍ,o: relationship of density of the universe today
Ωᴍ,o = ρo / ρcr,o
ρo, density of the universe today
ρcr,o, critical density of the universe today, UFSC data.
ρcr,o = 3.84 10⁻²⁹ g/cm³
Today, a time t = 4.35 10¹⁷ s, is considered.
In the following table:
Table 1 – Represents values of ImI, baryonic mass; IδI, dark matter mass; IMI, mass of baryonic matter plus the mass of dark matter; IEmI, energy of baryonic matter; IEδI, dark matter energy; IEI, Sum of the energy of baryonic matter plus the energy of dark matter and Rs, Schwarzschild’s radius, as a function of, c, speed of light; Cɢ, speed greater than the speed of light; T, temperature in Kelvin; using the parametric equations.

m = 1.20 10⁵⁶ kg, total baryonic mass
δ = 1.20 10⁸² kg, total mass of dark matter
It is very important to make it clear, the expansion of the universe is a function of frequency, each frequency has a certain expansion.
The calculations that we are going to carry out are referenced to the fundamental frequency.
In the spectrum of sound waves of the CMB, the fundamental frequency corresponds to the peak of greatest amplitude or first peak.
ω = 2.0 rad/s, fundamental angular frequency
f = 0.317 Hz, fundamental frequency
λ = 1.000.000 light years
λ = 9.46 10²¹ m
c1 = 3 10²¹ m/s
t1 = 1.22 10¹³ s
Calculation of the expansion of space-time to today:
Distance travelled 1:
where e1 is the distance travelled 1, c1 = 3 10²¹ m/s and t 1= 1.22 10¹³ s:
e1 = c1 x t1
e1 = 3 10²¹ m/s x t = 1.22 10¹³ s
e1 = 3.66 10³⁴ m
Distance travelled 2:
where e2 is the distance travelled 2, c2 = 3 10⁸ m/s and t 2= 4.35 10¹⁷ s:
e2 = c2 x t2
e2 = 3 10⁸ m/s x 4.35 10¹⁷ s
e2 = 1.30 10²⁶ m
Total distance travelled:
e = e1 + e2
e = 3.66 10³⁴ m + 1.30 10²⁶ m
We know that the bandwidth of the spectrum goes from 10⁻¹³ s to approximately 10¹³s.
If we consider the time 10⁻¹ s, close to the fundamental frequency, important for its contribution, we can increase the space e, a power of 10.
Figure 4 represents the sound spectrum of the CMB, the fundamental frequency is defined by the first peak or the peak with the highest amplitude.
Although we have considered the contribution of the first peak to the right, we note that it is important to consider the contribution of the first peak to the left, that is why we consider the frequency content 10⁻¹ s before the fundamental frequency.
Therefore, the total distance covered will be:
e = 3.66 10³⁵ m
In one dimension, the universe will have the following radius:
Ru, radius of the universe:
Ru = 3.66 10³⁵ m
1 light-year = 9.46 10¹⁵ m
Ru = 3.66 10³⁵ / 9.46 10¹⁵
Ru = 3.86 10¹⁹ light-year
Knowing the radius of the universe, we will calculate the density.
Density equation:
ρ = m / v
Where ρ is density, m is mass, and v is volume.
v = 4/3 x π x R³
ρ = m / (4/3 x π x R³)
ρ = 1.20 10⁸² / (1.33 x 3.14 x 49.02 10¹⁰⁵)
ρ = 5.86 10⁻²⁶ kg/mᶾ
Density of the universe today.
ρo = 5.86 10⁻²⁹ g/cm³
Critical density of the universe today.
ρcr,o = 3.84 10⁻²⁹ g/cm3
Calculation of Ωᴍ,o:
Ωᴍ,o = ρo / ρcr,o
Ωᴍ,o = 5.86 10⁻²⁹ / 3.84 10⁻²⁹
According to the calculations:
Ωᴍ,o = 1.52; most probable value.
- II)
- Another way to calculate Ωᴍ,o:
Ωᴍ,o = ρo / ρcr,o
ρo, density of the universe today
ρcr,o; critical density of the universe today
ρcr,o = 3.84 10⁻²⁹ g/cm³, UFSC data.
look at figure 7
In item 9, the Schwarzschild’s radius corresponds to:
Rs = 1.77 10²⁹ m
We can call it the contraction factor of space-time or the compactification factor of matter.
Rc12 = 0.75 10⁻¹⁰ m, Radius of the atom carbon 12
Rq = 0.43 10⁻¹⁶ m, 100 times the radius of the quark.
Equation of volume of a sphere:
(4/3) π R³
Where R is the radius of the sphere.
Calculation of the volume of the atom carbon 12:
VaC12 = (4/3) x 3.14 x (0.75 10^-10⁻¹⁰) ³
VaC12 = 1.76 10⁻³⁰ m³, volume of C12 atom.
Calculate the volume of a 100-quark:
Rq = 0.43 10⁻¹⁶ m, 100 times the radius of the quark
Vq = (4/3) x 3.14 x (0.43 10⁻¹⁶) ³
Vq = 0.33 10⁻⁴⁸ m³
Calculation of the contraction factor Vac12 / Vq:
Vac12 / Vq = 1.76 10⁻³⁰ m³ / 0.33 10⁻⁴⁸ m³
Vac12 / Vq = 5.33 10¹⁸
In three dimensions the space-time contraction factor is 5.33 10¹⁸ times.
In one dimension the space-time contraction factor is 1.74 10⁶ times.
Fc = 1.74 10⁶
The approximate expansion of space-time will be equal to the Schwarzschild radius multiplied the contraction factor of space-time in one dimension.
In one dimension, the universe will have the following radius:
Ru, radius of the universe:
Ru = Rs x Fc
Rs, Schwarzschild radius.
Fc, contraction factor of space-time in one dimension.
Ru = 1.77 10²⁹ m x 1.74 10⁶ m
Ru = 3.09 10³⁵ m
Knowing the radius of the universe, we will calculate the density.
Density equation:
ρ = m / v
Where ρ is density, m is mass, and v is volume.
v = 4/3 x π x R³
ρ = m / (4/3 x π x R³)
ρ = 0.00971 10⁻²³
ρ = 9.71 10⁻²⁶ kg/m³
ρ = 9.71 10⁻²⁹ g/cm³
Density of the universe today.
ρo = 9.71 10⁻²⁹ g/cm³
Critical density of the universe today.
ρcr,o = 3.84 10⁻²⁹ g/cm3
Calculation of Ωᴍ,o:
Ωᴍ,o = ρo / ρcr,o
Ωᴍ,o = 9.71 10⁻²⁹ g/cm3/ 3.84 10⁻²⁹ g/cm3
According to the calculations:
Ωᴍ,o = 2.52
- III)
- Calculate Ωᴍ,∞; for t → ∞:
Ωᴍ,∞ = ρ∞ / ρcr,o
ρ,∞; density of the universe for t → ∞
ρcr,o; critical density of the universe today
ρcr,o = 3.84 10⁻²⁹ g/cm³, UFSC data.
look at figure 7
In item 9, the Schwarzschild’s radius corresponds to:
Rs = 1.77 10²⁹ m
We can call it the contraction factor of space-time or the compactification factor of matter.
Boltzmann’s constant for flat space-time, is defined for 1 mole of carbon 12 and corresponds to 6.0221 10²³ atoms.
We assume the ratio of the quark given by the German accelerator HERA (Hadron-Elektron-Ringanlage) in the year of 2016, whose article is published following the right of the internet (21).
Rc12 = 0.75 10⁻¹⁰ m, Radius of the atom carbon 12
Rq = 0.43 10⁻¹⁸ m, radius of the quark
Equation of volume of a sphere:
(4/3) π R³
Where R is the radius of the sphere.
Calculation of the volume of the atom carbon 12:
VaC12 = (4/3) x 3.14 x (0.75 10^-10⁻¹⁰) ³
VaC12 = 1.76 10⁻³⁰ m³, volume of C12 atom.
Calculate the volume of a quark:
Rq = 0.43 10⁻¹⁸ m, radius of the quark
Vq = (4/3) x 3.14 x (0.43 10⁻¹⁸) ³
Vq = 0.33 10⁻⁵⁴ m³
Calculation of the contraction factor Vac12 / Vq:
Vac12 / Vq = 1.76 10⁻³⁰ m³ / 0.33 10⁻⁵⁴ m³
Vac12 / Vq = 5.33 10²⁴
In three dimensions the space-time contraction factor is 5.33 10²⁴ times.
In one dimension the space-time contraction factor is 1.74 10⁸ times.
Fc = 1.74 10⁸
The approximate expansion of space-time will be equal to the Schwarzschild radius multiplied the contraction factor of space-time in one dimension.
In one dimension, the universe will have the following radius:
Ru, radius of the universe:
Ru = Rs x Fc
Rs, Schwarzschild radius.
Fc, contraction factor of space-time in one dimension.
Ru = 1.77 10²⁹ m x 1.74 10⁸ m
Ru = 3.07 10³⁷ m
Knowing the radius of the universe, we will calculate the density.
Density equation:
ρ = m / v
Where ρ is density, m is mass, and v is volume.
v = 4/3 x π x R³
ρ,∞= m / (4/3 x π x R³)
ρ,∞ = 0.00971 10⁻²⁹
ρ,∞ = 9.71 10⁻³² kg/m³
ρ,∞ = 9.71 10⁻³⁵ g/cm³
Density of the universe for t → ∞.
ρ,∞ = 9.71 10⁻³⁵ g/cm³
Critical density of the universe today.
ρcr,o = 3.84 10⁻²⁹ g/cm3
Calculation of Ωᴍ,∞:
Ωᴍ,∞ = ρ,∞ / ρcr,o
Ωᴍ,∞ = 9.71 10⁻³⁵ g/cm3/ 3.84 10⁻²⁹ g/cm3
According to the calculations:
Ωᴍ,∞ = 2.52 10⁻⁶ for t → ∞
6.7. We will demonstrate how the expansion of space-time as a function of frequency is asymmetry, that is, a variation in time gives us a variation in displacement.
In the damped RLC model, the fundamental frequency is the resonant frequency.
λ = λ0 = 1,000,000 light years
λ = λ0 = 9.46 10²¹m
ω = ω0 = 2 rad /s.
f0 = 0.31 Hz
low cut-off frequency calculation
ω1 = 1.81 10⁻¹¹ rad/s
f1 = 2.88 10⁻¹¹ Hz; low cut-off frequency
λ1 = 1.08 10³³ m
High cut-off frequency calculation:
ω2 = 2.19 10¹¹ rad/s
f2 = 0.348 10¹¹ Hz; high cut-off frequency
λ2 = 8.60 10¹⁰ m
For the low cut-off frequency, it is fulfilled:
If we replace (41) in (42)
0.707 = 1 / e ⁻ (1.81 10⁻¹¹t)
t = ln (1.41) / 1.81 10⁻¹¹
t = 0.3467 / 1.81 10⁻¹¹
t1 = 1.915 10¹⁰ s
For the high cut-off frequency, it is fulfilled:
If we replace (43) in (42)
0.707 = 1 / e - (2.19 10¹¹t)
t = ln (1.41) / 2.19 10¹¹
t = 0.3467 / 2.19 10¹¹
t2 = 0.158 ⁻¹¹ s
Observe Figure 5, we are going to calculate the time variation IΔtI between the frequency ω2 and ω1.
IΔtI = I t2 – t1I
IΔtI = I 0.158 ⁻¹¹ s - (- 1.915 10¹⁰ s) I
Consider that t1 originates much earlier than t2
IΔtI = 1.915 10¹⁰ s
This variation of time occurs within the interval of expansion of space-time, inside the bandwidth of the equation of gravitational waves, therefore its speed corresponds to 3 10²¹ m/s.
We will calculate the displacement variation IΔXI for a variation of IΔtI = 1.915 10¹⁰ s.
IΔXI = v x t
IΔXI = 3 10²¹ x 1.915 10¹⁰
IΔXI = 5.745 10³¹ m.
For the instant at which ω2 occurs, ω1 advances ω2 by 90 degrees and this corresponds to a time difference IΔtI = 1.915 10¹⁰ s, and a difference in displacement IΔXI = 5.745 10³¹ m.
We show how space-time, as a function of frequency, expands asymmetrically.
6.8. Calculation of the critical mass to produce a black hole in the LHC applying the theory of the generalization of Boltzmann constant in curved spacetime
Method No. 1:
let us consider the average thermal energy equal to the gravitational potential energy of a black hole of radius Rs.
Eε, Average thermal energy of the plasma of quarks and gluons.
Epg, Gravitational potential energy of a black hole of three solar masses and radius Rs = 8.89 10³ m.
Where N, number of elementary particles; Kʙ, Boltzmann ‘constant; Tε, electromagnetic temperature; G, gravitational constant; M, mass of a black hole of three solar masses; M1, unit mass and Rs, Schwarzschild’s radius.
We consider the mass M1 as a unitary body of mass 1 kg that orbits around a black hole of mass M and radius Rs.
Where M is the mass of a volume V and m, the amount of mass of a particle in the volume V.
We divide everything by the volume V in do
We consider on both sides that the densities ρ = M/V are equal in (47):
Critical mass equation to create a black hole in the LHC
Calculation of the value of the critical mass mc:
Kʙ = 1.78 10⁻⁴³ J/K
Tε = 10¹³ K
Rs = 8.89 10³ m
G = 6.67 10⁻¹¹ Nm²/kg
M1 = 1 kg
replacing in (49), we have:
mc = 2.37 10⁻¹⁶ kg
mc = 13.33 10¹⁰ GeV/C²
Method No. 2:
Let’s start from the following assumption:
Where Em, energy of the mass at rest and Epg, gravitational potential energy of a black hole of mass M and radius Rs.
Where m, mass corresponding to a volume V; c, speed of light; G, gravitational constant; M, mass of a black hole of three solar masses; M1, unit mass and Rs, Schwarzschild’s radius.
Remember that energy is also defined as follows:
For a photon of wavelength λ,
Where E, energy of a photon; h, Planck’s constant; c, speed of light and λ, wavelength of a photon.
replacing we have:
where N is the number of photons
If we consider the following conditions:
We get the following equation:
M is the mass of a volume V.
m, the amount of unit mass equivalent in volume V.
replacing we have:
We divide everything by the volume V, we have:
If we consider that the density (M/V) is the same on both members, we obtain:
Planck’s critical mass equation
Calculation of the value of the critical mass mc:
c = 3 10⁸ m/s
G = 6.67 10⁻¹¹ Nm²/kg
M1 = 1 kg
h = 6.62 10⁻³⁴ J.s
replacing in (60), we have:
mc = 2.37 10⁻¹⁶ kg
mc = 13.33 10¹⁰ GeV/C²
We have verified that both methods to calculate the critical mass to produce a black hole in the LHC reach the same result.
- Planck’s mass mp = 1.2 10¹⁹ GeV/C²; it is not the limit to form a black hole in a particle accelerator.
- 13.33 10¹⁰ GeV/C². It should be considered a critical or limit value and we should not work with higher values in the LHC.
Using two different methods, we must emphasize how the results of the equations shown below are practically the same for Kʙ = 1.78 10⁻⁴³ J/K.
Here we put forward the hypothesis that there is a critical mass mc to produce a black hole at the LHC, given by the following equations:
- mc = (Kʙ x Tε x Rs) / G x M1; mc = 13.33 10¹⁰ GeV/C².
- mc = h x c / (2π x G x M1); mc = 13.33 10¹⁰ GeV/C².
- This equality is given for Kʙ = 1.78 10⁻⁴³ J/K
Example:
Currently, the CERN particle accelerator is working with energies of the order of 14 TeV.
If we consider that the LHC works with proton packages of 100,000 10⁶ protons (22), we have:
Mp = 100,000 10⁶ x mp
Where Mp, total mass of the collision and mp, proton mass.
Mp = 10¹¹ x 1.672 10⁻²⁷ kg = 1.672 10⁻¹⁶ kg
Mp = 1.672 10⁻¹⁶ kg
Mp ≈ mc, we are working on the order of the critical mass to produce a black hole at the LHC.
Note that in the RLC electrical theory of the universe, black holes always grow until they disintegrate.
6.9. Calculation of the critical temperature Tc of the high-temperature Bose-Einstein Condensate applying the theory of the generalization of Boltzmann’s constant in curved space-time.
Bose-Einstein Condensate:
In quantum mechanics, all particles have an associated wave and at normal temperature this wave is very small, much smaller than the typical distance between atoms in a gas, but as the temperature decreases the wavelength increases.
Below a critical temperature, the particle waves begin to overlap and interact, interfering and forming a joint wave. This is what is called a Bose-Einstein condensate, a state where atoms act together, coherently, with a single wave function for all atoms, where the quantum wave properties of matter are visible, we can’t talk about individual atoms, but of the whole as a single atom; like a big atom.
This can be understood as follows:
In a physical system, particles can be established at various energy levels, discrete levels, at a certain temperature, atoms are randomly distributed among all available energy levels. Now, if I decrease the temperature, the discrete levels of energy available go down, so the lowest energy levels are taken. If the temperature is too low, passing a critical threshold, only the minimum level of energy, the fundamental level, is available. Here we clarify that the Bosons are all characterized by being able to occupy the same energy level, the fundamental one; then they become indistinguishable, they behave like a single atom, a big atom, and their quantum properties become macroscopic, visible.
Plasma of quarks and gluons – confinement:
Quark-gluon plasma is created in RHIC or LHC particle collisions, colliding gold or lead particles at relativistic speeds with energies on the order of Tera electron-volts. The quark-gluon plasma is a perfect liquid and its temperature is of the order of 10¹² kelvin.
The temperature generated in these collisions is so high that the quarks and gluons that were confined within the protons and neutrons in atomic nuclei break apart, and for a short time, move freely.
Quarks and gluons have a property called confinement, and under normal temperature conditions, they form protons and neutrons (baryons). This means that if we consider the color of the quarks (red, green or blue), they must always form states of white color and cannot escape from the ball of neutrons or protons, that is, they are confined.
White color states can also be formed with a quark and an antiquark, called mesons.
The confinement tells us that the force of interaction experienced by the quarks is a function of energy. At very high energy, the interaction between quarks and gluons is very weak, a weak coupling. At low energy the interaction is strong, quarks cannot escape from confinement because the interaction of quarks and gluons is strong, a strong coupling.
Analysis of an isolated quark
Let’s see what happens if we drop a quark into the quantum vacuum. We know that gluons have charges, they are charged colored dipoles, they are carriers of the strong force.
Now, if we throw a quark and a gluon into the quantum vacuum, we observe that the gluon is oriented with the same color charge in the direction of the quarks, this is called antiscreening, this causes the quark’s strength to increase.
So, when we drop a quark into a vacuum, the gluons start accumulating, forming an infinite cascade with infinite energy. An isolated quark has infinite energy.
This would explain why in nature quarks are not found in an isolated state, except inside a black hole.
Here we put forward the hypothesis that, when the baryons that make up the matter we know reach a limit of temperature and energy density, the Hagedorn temperature, a phase change occurs in the matter, the quarks and gluons inside it no longer belong to the nuclei of protons and neutrons, begin to move freely, isolated, they are no longer confined, forming a plasma of quarks and gluons. If we continue to increase the temperature and energy density, we reach another critical threshold Tc, at which the plasma of quarks and gluons, a superfluid as a whole, behaves like a single quark whose gluons begin to stack up in an orderly fashion, forming a cascade of infinite energy, that is, a black hole is created, which makes it the most energetic state of existing matter, with almost infinite energy.
Calculation of the critical temperature Tc of the high-temperature Bose-Einstein Condensate:
Equation that defines Tc for a Bose-Einstein condensate

According to the information of (24), Cauê Muraro - Agência USP - 10/30/2007, the temperature of a Bose-Einstein condensate for 100,000 rubidium atoms corresponds to Tcmin = 180 nK.
Where Tcmin, low temperature Bose-Einstein condensate.
For KB = 1.38 10⁻²³ J/K and rubidium atoms corresponds:
Tcmin = 180 nk
Approximate critical temperature of the Bose-Einstein condensate for low temperatures, with rubidium atoms.
Let’s calculate Tcmax, for KB = 1.78 10⁻⁴³ J/K
Where Tcmax, High temperature Bose-Einstein condensate.
Tcmax, we are going to calculate considering the relationship between the Boltzmann constant KB = 1.38 10⁻²³ J/K, for flat space-time and KB = 1.78 10⁻⁴³ J/K for curved space-time.
For KB = 1.78 10⁻⁴³ J/K and rubidium atoms corresponds:
Tcmax = 180 nk / 1,78 10⁻²⁰ = 1,01 10¹³ K
Tcmax = 1.01 10¹³ K
Critical temperature of the Bose-Einstein condensate for high temperatures with rubidium atoms.
Here we put forward the hypothesis that for an effective Boltzmann’s constant KB = 1.78 10⁻⁴³ J/K, there is a temperature Tcmax, that corresponds to a high temperature Bose Einstein condensate.
For a temperature of approximately 1.01 10¹³ K, in a plasma of quarks and gluons, a phase transition occurs that gives rise to a Bosonic-Fermionic condensate, at high temperatures, which is characterized by being very energetic.
We can interpret it as follows, when a star collapses and a black hole is formed, we can affirm that a high-temperature Bode-Einstein condensate exists inside a black hole.
In analogy with the properties of materials at very low temperatures, super fluids and superconductivity; quark-gluon plasma achieves similar exotic properties, but not with atoms and molecules as we normally know; these properties are achieved for the quark-gluon plasma, a superfluid or super solid, the main property of which makes this liquid or solid behave like isolated quarks, allowing the gluons to stack up neatly in an infinite cascade of energy, making it the most energetic matter in the universe. We also said that quarks are fermions and gluons are bosons, but in black holes, by analogy with what happens with superconducting materials, and super fluids and super solids, the plasma of quarks and gluons as a whole act as a Bose-Einstein condensate, as a single atom whose macroscopic properties are unique.
6.10. Intuitively we will demonstrate the existence of a tangential force to the repulsive force in subatomic decays analogous to the tangential force ft that lags the force fc by 90 degrees inside black holes.
We will analyse the following equation:
where E is energy, m is mass, and c is the speed of light in a vacuum.
If we consider 0 the moment P of a particle, P = 0, we have:
E² = m²c⁴
E = (+/-) mc²
If we consider mass as a fundamental property of matter we have:
E = + mc², positive energy, (+ m), gravity attracts.
E = - mc², negative energy (- m), gravity repels.
According to the equation E = (+/-) mc², we have that gravity acts in two ways, (+m) as an attractive force or (-m) as a repulsive force.
METRIC FOR TIME TYPE TRAJECTORIES.
Figure 6.
Time-like trajectory, light cone, ds < 0.
Let’s write the metric:
This metric is defined for speeds less than light, v < c.
We skip the mathematical steps and with this metric we calculate the moment P and the energy E.
If we analyse the energy, we see that when the particle is at rest the energy corresponds to E = mc²; when the speed tends to c, the energy tends to infinity.
v = 0, E = mc²
v → c, E → ∞
Now we are going to perform the following mathematical trick, although the metric does not allow us to do this because it is not defined for speeds greater than light, v > c, we are going to see the consequences of the following mathematical operation.
E = mc² / √-1 √(v²/c²) – 1
multiplying the numerator and denominator by the imaginary number i:
we see that the terms – i appear.
If we compare with the mass of a black hole:
, baryonic mass.
= , for v > c; mass of dark matter.
How can we interpret this, what meaning does it have?
Although the metric we use is not defined for particles that move at a speed greater than that of light, there are massless, tachyonic particles that can cross this barrier and travel at a speed greater than that of light.
These tachyonic particles produce a tangential force Ft to the attractive force Fc of gravity and as the speed increases with respect to the speed of light, they generate dark matter. It must be made clear that these particles are inside the black hole.
METRIC FOR SPACE TYPE TRAJECTORIES
Figure 7.
Space-like trajectory, light cone, ds > 0.
Let’s write the metric:
We skip the mathematical steps and with this metric we calculate the moment P and the energy E.
These equations for momentum P and energy E are valid for speeds greater than light and can never reach speeds of light.
v → ∞, E = 0
v → c, E = -∞
How can we interpret this, what does it mean?
We are going to relate the equations of P and E with the electrical model RLC of the universe, at the moment that the black hole explodes, let us remember that the space-time that was compressed begins to expand and generates a well of gravitational potential of negative energy analogous to the equation E = - mc² / √(v²/c²) – 1, in other words, a spectrum of gravitational waves is produced that produce a repulsive force that gives rise to the expansion of space-time. In this case, tachyons are related to gravitons, in which, during the period of cosmic inflation, they travel at a speed greater than that of light.
Now we are going to perform the following mathematical trick, although the metric does not allow us to do this because it is not defined for speeds less than light, v < c, we are going to see what happens if a particle exceeds the limit for speeds less than c.
E = - mc² / √(v²/c²) – 1
E = - mc² / √-1 √ (1 - v²/c²)
Multiplying and dividing by the imaginary number i.
If we compare with the mass of a black hole:
, baryonic mass.
The subatomic disintegrations that occur in particle accelerators represent a clear example.
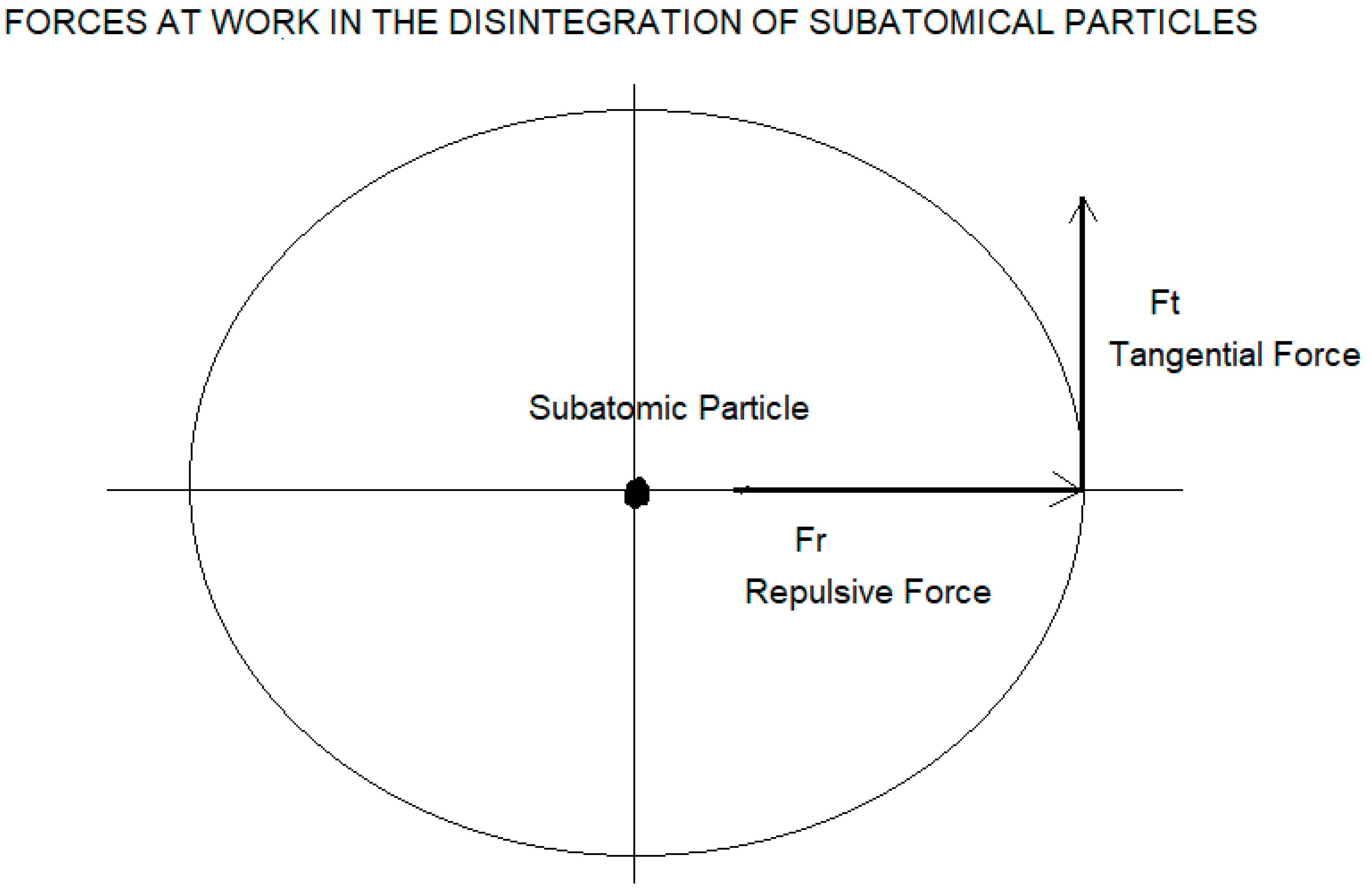
Here we put forward the hypothesis that, for v < c, there is an additional force that corresponds to the mass that leads 90 degrees to the force given by the mass , in other words, when the subatomic disintegration of particles occurs, two forces act, a repulsive force given by the mass and a tangential force that leads 90 degrees to the force given by , resulting from the mass .
In the following tables we will define the statement.
Table 3.
From left to right represented by the numbers 1,2 and 3; We describe the forces that act on matter. In phase 1, for v < c, only an attractive force acts; in phase 2, for v = c, only an attractive force acts; in phase 3, for v > c, inside a black hole, we can see that two forces act, an attractive force and a tangential force that delays the attractive force by 90 degrees.
Table 3.
From left to right represented by the numbers 1,2 and 3; We describe the forces that act on matter. In phase 1, for v < c, only an attractive force acts; in phase 2, for v = c, only an attractive force acts; in phase 3, for v > c, inside a black hole, we can see that two forces act, an attractive force and a tangential force that delays the attractive force by 90 degrees.
| TIME TYPE PATH | LIGHT TYPE PATH | SPACE TYPE PATH |
|---|---|---|
| 1 | 2 | 3 |
| ds < 0 | ds = 0 | ds > 0 |
| v < c | v = c | v > c |
| attraction | attraction | attraction |
| Lp = Lpɛ | Lpɢ = Lpɛ = Lp | Lpɢ < Lpɛ |
| E = c² / √1 - (v²/c²) | Phase change | E = - i c² / √(v²/c²) – 1 |
Table 4.
From right to left, represented by the numbers 1,2 and 3, we will describe the forces that act on matter. In phase 1, for v > c, we see that a repulsive force acts, in phase 2, for v = c, we see that a repulsive force acts; in phase 3, for v < c, we see that two forces act, a repulsive force and a tangential force that leads the repulsive force by 90 degrees.
Table 4.
From right to left, represented by the numbers 1,2 and 3, we will describe the forces that act on matter. In phase 1, for v > c, we see that a repulsive force acts, in phase 2, for v = c, we see that a repulsive force acts; in phase 3, for v < c, we see that two forces act, a repulsive force and a tangential force that leads the repulsive force by 90 degrees.
| TIME TYPE PATH | LIGHT TYPE PATH | SPACE TYPE PATH |
|---|---|---|
| 3 | 2 | 1 |
| ds < 0 | ds = 0 | ds > 0 |
| v < c | v = c | v > c |
| Repulsion | Repulsion | Repulsion |
| Lp = Lpɛ | Lpɢ = Lpɛ = Lp | Lpɢ < Lpɛ |
| E = c² / √1 - (v²/c²) | Phase change | E = - m c² / √(v²/c²) – 1 |
Figure 8.
Diagram of forces that act in the disintegration of subatomic particles.
6.11. M-theory, extra dimensions and the theory of the generalization of Boltzmann’s constant in curved spacetime
In this section, we will use the information from the IFT UAM, as a guide and technical-scientific support.
In string theory, the fundamental degrees of freedom are extended one-dimensional objects, strings that live in 10-dimensional space-time; 9 for space and 1 for time. These strings can interact by division-recombination, and the strength of this interaction is measured by a parameter gs, the string coupling constant, which can range from 0 to infinity. When the coupling constant is small, it is called a perturbative regime; when the coupling constant is large, it is called a non-perturbative regime.
In the non-perturbative regime, new components appear, the P-Branes, which are extensive and have P extended spatial dimensions; the strings no longer play an essential role, they are on an equal footing with all those branes and all these objects of different extensive dimensions coexist.
When gs is small, the regime is perturbative. This regime is dominated by a single object, the strings, and in this regime the energy required to create a brane is greatly increased. In this regime, string theory is well explained, well formulated, and well defined.
Figure 9.
Perturbative regime, dominated by strings, small gs.
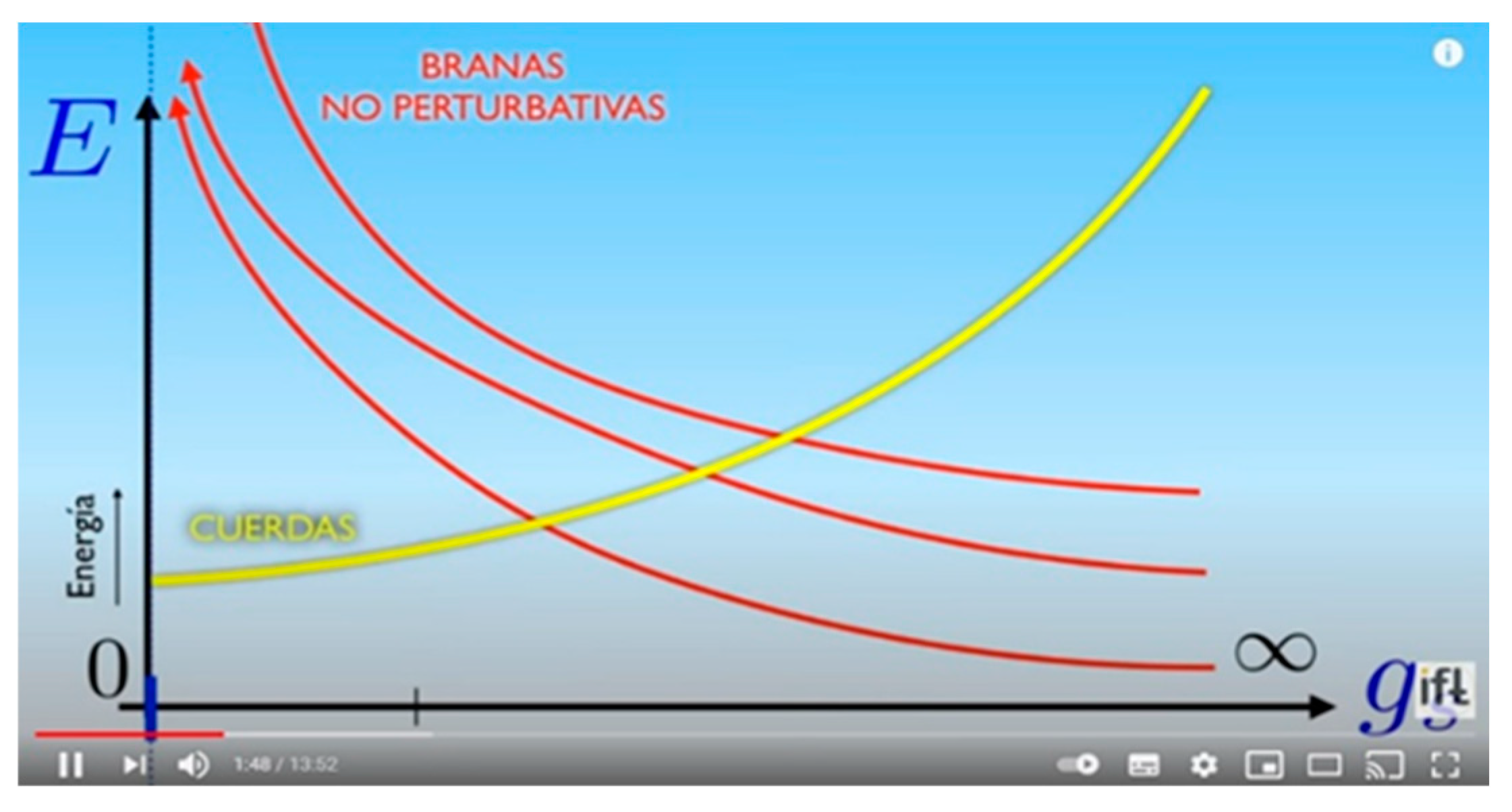
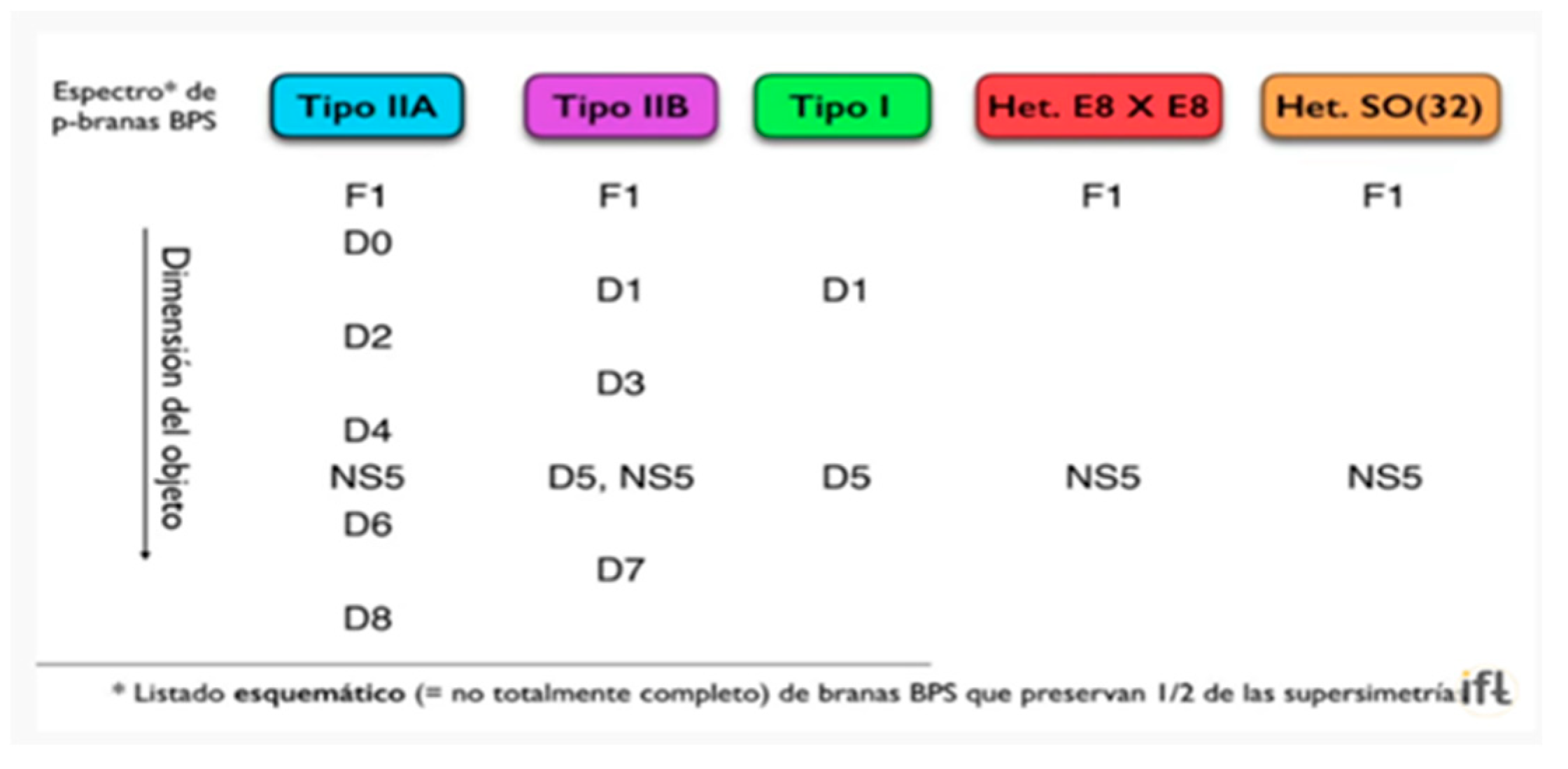
There are 5 different types of supersymmetric string theory in 10 dimensions namely: TYPE IIA, TYPE IIB, TYPE I, HETEROTIC E8 X E8 AND HETEROTIC SO (32). These theories are very different from each other, they have different particle contents, different interactions, different supersymmetries, different symmetry groups, and they also have different P-Brane contents.
Figure 10.
TYPE IIA, TYPE IIB, TYPE I, HETEROTIC E8 X E8 AND HETEROTIC SO (32).
To study how branes behave as gs approaches infinity, it is important to specify which particular string theory we are going to study. For our case we are going to study the TYPE IIA theory, a theory that lives in 10 dimensions and has a perturbative content corresponding to the graviton and its companions, as well as a non-perturbative content of P-Branes. D0 branes are objects without extended dimension, they are like point particles.
Figure 11.
Non-perturbative regime, dominated by D0 branes, gs infinite.
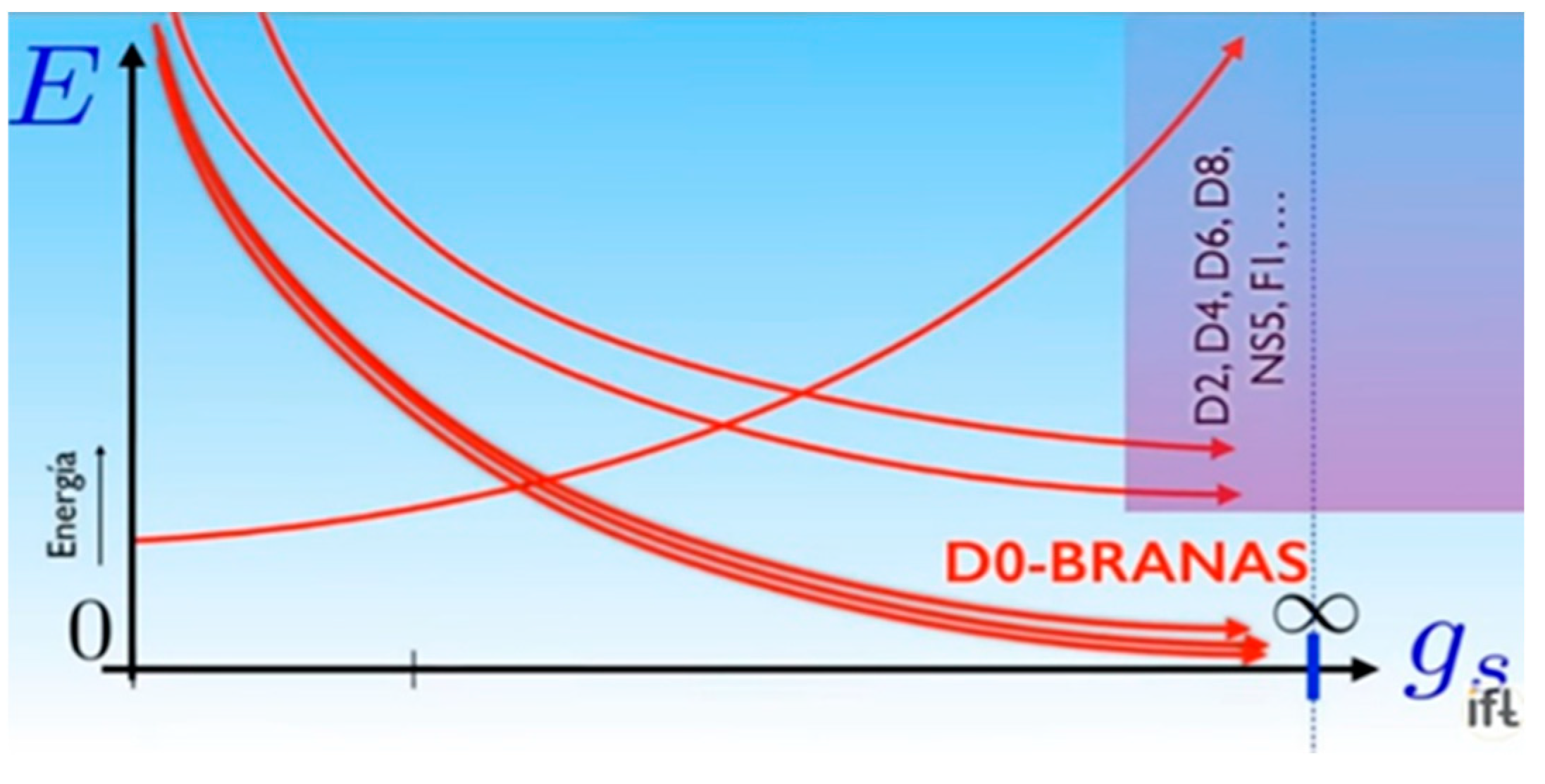
It is observed that the limit when the coupling tends to infinity is dominated by the D0-branes. This is very interesting, it is a single object that dominates all dynamics and they are not strings, they are point particles and it is a theory that quantum gravity has.
In the case of D0-Branes, the binding energy is zero (0), basically because these branes are BPS supersymmetry (state with certain properties protected by supersymmetry). Supersymmetry causes the cancellation of many quantities, specifically the binding energy between D0-Brans.
Figure 12.
mass of a set of particles in a bound state is M* = k / gs.
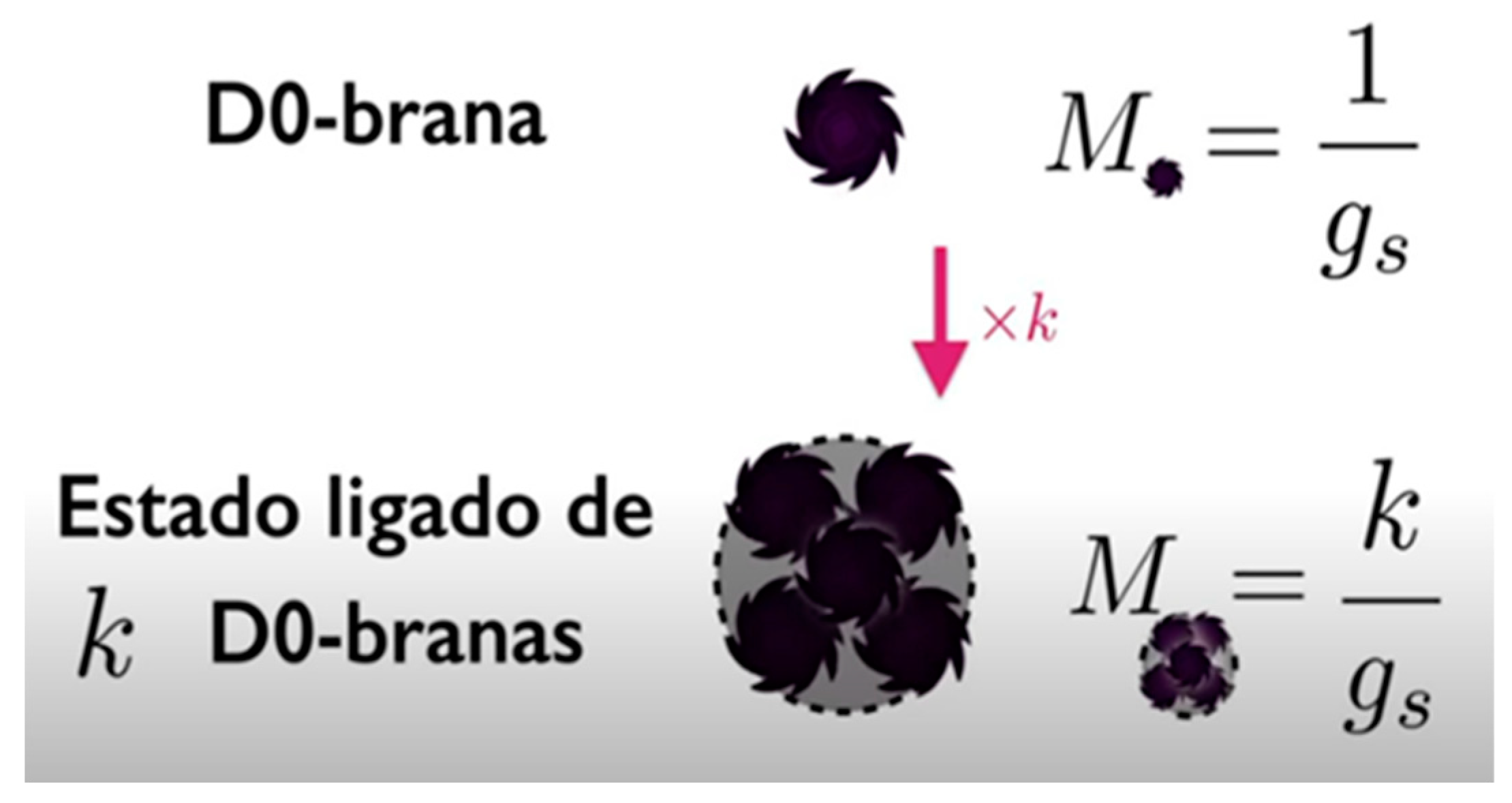
Therefore, the mass of a particle is equal to M = 1/gs and the mass of a set of particles in a bound state is M* = k / gs. With that we have that the different states for the different values of k, the different sets of non-perturbative particles, would form a tower whose masses would be x-spaced by the value 1/gs.
Now, if we make gs go to infinity, that is, an infinitely strong coupling, all the particles in that tower will have mass equal to zero (0); there would be an infinite number of particles with mass zero (0).
How do you discover an extra dimension? We have seen that if you have a theory in which there is an extra dimension packed into a circle of radius R, the way this extra dimension manifests are that a tower of state appears with masses spaced 1/R apart; and that is exactly what we are seeing in our TYPE IIA theory in strong coupling. That is, the theory has a hidden extra dimension with a radius R controlled by the coupling constant gs. The D0-Branas are the Kaluza-Klain replicas of the states of the theory in 10 dimensions, that is, of the graviton.
So, we have an 11-dimensional theory, where one of the dimensions is packed into a radius of size R that is related to the coupling constant gs. When R is small, gs is also small, that is, we recover a loosely coupled 10-dimensional theory that exactly matches the TYPE IIA, perturbative theory we started with.
When we go to the strong coupling, in the limit where R and gs tend to infinity, the circle of dimension 11 is decompressed, that is, we recover a theory in 11 dimensions.
M-theory is the 11-dimensional theory that is recovered when the circle that is hidden in the extra dimension of TYPO IIA theory is decompressed.
Let’s give an example explaining what it means when we talk about a perturbative regime and a non-perturbative regime.
We can explain the meaning of a perturbative regime, through a hydrodynamic analogy, saying, if we consider a lake with calm waters and we throw a small stone, small waves are produced that propagate in the water; we say that we are in a perturbative regime and it would be analogous to space-time in which small significant disturbances occur.
When we talk about a non-perturbative regime, hydrodynamically, we refer as an example to very rough seas, giant waves; in the space-time regime it would be analogous, for example, to black holes, neutron stars; large disturbances in space-time, very large space-time curvature.
After having explained the perturbative and non-perturbative regime, let’s try to explain M-theory with its 11 dimensions by comparing it with the generalization theory of Boltzmann’s constant in curved space-time.
Three spatial dimensions plus one temporal (3 + 1), these are the dimensions in which we live every day, the ones that our senses perceive. Next, we have the theory of superstrings consisting of 10 dimensions, in addition to the 4 dimensions, 6 more dimensions are added. Finally, we have an additional dimension that when decompressed creates the 11 dimensions of M-theory.
the theory of the generalization of Boltzmann’s constant in curved space-time, has 3 stages. The first stage corresponds to the regime in which the Boltzmann constant is equal to Kʙ = 1.38 10⁻²³ J/K, for a flat space-time; the second stage corresponds to the regime in which the Boltzmann constant varies from 1.38 10⁻²³J/K > Kʙ >1.78 10⁻⁴³ J/K, for a curved space-time; the third stage corresponds to the regime where the Boltzmann constant is maximum, equal to Kʙ = 1.78 10⁻⁴³ J/K, maximum curvature of space-time.
Considering these two theories, the M-theory and the theory of the generalization of Boltzmann’s constant in curved space-time, we will make the following comparison, in 3 stages.
Here we put forward the following hypothesis:
First stage: Corresponds to the (3 + 1) dimensions in which we live, the three spatial dimensions plus time. In the theory of the generalization of the Boltzmann constant in curved space-time, it corresponds to the regime in which the Boltzmann constant is equal to Kʙ = 1.38 10⁻²³ J/K. We are in a perturbative regime, that is, small gs, dominated by the strings. This regime is characterized by the fact that the space-time structure does not undergo modifications, flat space-time.
Second stage: matter undergoes the first compaction process. This would be represented by the 10-dimensional superstring theory, that is, by the dimensions (3 + 1) plus 6 additional dimensions that arise from the first compaction process. In the theory of the generalization of the Boltzmann constant in curved space-time, this regime would be characterized because the Boltzmann constant varies between 1.38 10⁻²³ J/K > Kʙ > 1.78 10⁻⁴³ J/K. We are in a perturbative to non-perturbative transition regime, that is, gs tends to a large value. This regime is characterized by the fact that the structure of space-time undergoes modifications. An example of this regime would be white dwarf stars and neutron stars. This is a regime in which spacetime is curved.
Third stage: In this stage of M-Theory, the second compaction process occurs, that is, the decompression of dimension 11 occurs, the radius R becomes infinitely large. In the theory of the generalization of the Boltzmann constant in curved space-time, in this regime, the Boltzmann constant assumes the value of Kʙ = 1.78 10⁻⁴³ J/k. We are in the non-perturbative regime, that is, gs is infinite. In this regime, the structure of space-time undergoes great changes, a concrete example would be the creation of black holes. The decompression of dimension 11 in M-theory is equivalent to creating a black hole. In this stage the maximum curvature of space-time occurs. At this stage, as the black hole grows, inside a black hole, it is true that the gravitational Planck length Lpɢ is less than the electromagnetic Planck length Lpɛ.
Decompression of dimension 11
It is important to understand that the concept of dimension depends on the scale of energies or distances. We are used to the four dimensions of everyday life (x, y, z, t), now when we work at high energies in the LHC, at small distances we introduce 6 more dimensions, that is, we would be working in 10 dimensions, which is the case of the plasma of quarks and gluons. In the theory of the generalization of the Boltzmann constant in curved spacetime, we can represent this by varying the Boltzmann constant in the range of 1.38 10⁻²³ J/K > Kʙ > 1.78 10⁻⁴³ J/ K.
If we imagine dimension 11 as a circle, unroll the circle to represent it as an interval, then all particles have a wave function in on that interval, which must be periodic. This type of wave is characterized by a number K and we can represent it as follows, k = 0, (+/-) 1, (+/-) 2, (+/-) 3, etc.
The momentum or energy that the particles possess does not reside in the 10 dimensions, it is hidden in the 11 dimensions. This internal energy manifests as additional mass in the 11 dimensions.
Using equations, we can represent it as follows:
λ = (2 π R) / K
λ = h / p
p = (h k) / 2 π R = m c
The energy can be written as:
E = √ {(m² c⁴) + (Px² + Py² +Pz²) C² + (h k / 2 π R) ² C²}
Where the rest mass seen by an observer is equal to:
M² = m² + (h k / 2 π R c) ²
This is the general formula that tells us how to detect an extra dimension.
We define that the mass of a black hole is equal to:
Where represents the imaginary mass of a black hole that results from decompression of dimension 11 of the M theory and m represents the baryonic mass.
All the development stated, we can complement it with the analysis carried out in section 3. COSMIC INFLATION.
Specifically, in (18):
R < Rs, v > c; ds > 0, space type trajectory.
Condition (18) is very important because to the extent that R < Rs, v > c is fulfilled, it is precisely this speed difference that generates the imaginary mass in a black hole given by -iδ.
ADS/CFT correspondence and the theory of the generalization of Boltzmann’s constant in curved spacetime
When analysing M-theory and the theory of the generalization of the Boltzmann constant in curved space-time, it is inevitable to make a comparison with the ADS/CFT correspondence.
According to the analysis carried out in M-theory and the theory of the generalization of Boltzmann’s constant in curved space-time, in a non-perturbative regime, when gs is infinitely large, we can equate a theory of gravity in anti-de Sitter space ADS n+1-dimensional, with a field theory according to CFT n-dimensional.
Do we not ask why we can do this? And the answer lies in the value that Boltzmann’s constant takes.
We will give the answer with an example where the plasma viscosity of quarks and gluons is calculated. For the non-perturbative regime, for very large gs tending to infinity, we are comparing two theories in which the Boltzmann constants are approximately equal.
For the case of the 11-dimensional ADS theory, where we introduce a black hole, Boltzmann’s constant is equal to Kʙ = 1.38 10⁻⁴³ J/K. For the 10-dimensional CFT theory, in which we want to calculate the plasma viscosity of quarks and gluons, the Boltzmann constant is of the order of 0.76 10⁻⁴¹ J/K > Kʙ > 1.78 10⁻⁴³ J/ K.
This tells us that we can use the ADS and CFT theories to calculate the plasma viscosity of quarks and gluons because both theories work in an almost identical non-perturbative regime, which is why whichever of the theories we use to calculate the answer will be practically the same.
In strong coupling, in the limit where gs tends to infinity, that is, in the non-perturbative regime, we can reduce superstring theory to general relativity and with that we can simply use a theory of gravity in anti-de Sitter space ADS, to describe the strong coupling regime of a particle theory, we call dual QCD. This becomes a very useful duality.
In other words, whenever we use a CFT theory that works with a Boltzmann constant close to Kʙ = 1.78 10⁻⁴³ J/K, we can say that the duality ADS = CFT is fulfilled.
Generalization of the electromagnetic spectrum
In QED theory, in 10 dimensions, considering the non-perturbative regime, the value of gs tending to infinity and the Boltzmann constant very close to Kʙ = 1.78 10⁻⁴³ J/K, the following must be fulfilled:
ADS = CFT
Gravity = QED
spectrum of gravitational waves = spectrum of electromagnetic waves
Let us consider the QED theory in a 10-dimensional space-time. An example of this case would be neutron stars, very large gs and also the disturbance of space-time.
In physics, we know that there is a spectrum of electromagnetic frequencies. In quantum electrodynamics (QED), photons are the intermediary particles of electromagnetic interaction and are the fundamental building blocks of electromagnetic waves at the quantum level.
We will describe simple equations that represent the electromagnetic spectrum.
Eε = h x fε
Cε = λε x fε
Eε = h x Cε / λε
Eε = Kʙε x Tε
Kʙε = 1,38 10⁻²³ J/K
Let us consider the theory of gravity in an 11-dimensional space-time.
With the discovery of gravitational waves, we can infer that there is also a spectrum of gravitational waves that would represent vibrations in the structure of space-time. In this context, gravitons would be analogous to photons in the electromagnetic case and would be the mediators of gravitational waves. Therefore, gravitons would be the fundamental building blocks of gravitational waves at the quantum level.
We must remember that both electromagnetic and gravitational waves are transverse waves.
A gravitational wave is a disturbance of the structure of space-time that manifests itself in the following way, contraction, stretching or simply undulation of space-time; while an electromagnetic wave manifests itself as the propagation of electric and magnetic fields in the same space-time without affecting the structure of space-time.
Taking into account the ADS/CFT correspondence, we will describe gravity using the same QED equations, considering all 10 dimensions. This would be expressed by introducing the theory of the generalization of Boltzmann’s constant in curved space-time.
We can express this in the following way:
Eɢ = h x fɢ
Cɢ = λɢ x fɢ
Eɢ = h x Cɢ / λɢ
Eɢ = Kʙɢ x Tɢ
Kʙɢ = 1,38 10⁻²³ J/K > Kв ef > 1,78 10⁻⁴³ J/K
So far, following an intuitive path, we have shown that we can describe gravitational waves using the same QED equations, but with the consideration of using the effective Boltzmann constant.
As a consequence of this set of equations that describe the spectrum of electromagnetic and gravitational waves with different values for the Boltzmann constant, the concept of electromagnetic temperature Tε and gravitational temperature Tɢ arose.
Here we put forward the following hypothesis, let us define that the electromagnetic temperature is different from the gravitational temperature, that is:
Tε ≠ Tɢ
We can also infer that electromagnetic energy will be different from gravitational energy:
Eε ≠ Eɢ
Our question is: why the difference between the temperature Tε and the temperature Tɢ?
My answer is the following, it is the very nature of electromagnetic and gravitational waves that determines the difference between the temperatures Tε and Tɢ; as long as there are no changes in the structure of space-time, the temperature of a system will be determined by the electromagnetic temperature Tε.
In a black hole, where there are no electromagnetic and weak force fields, the temperature will be determined by the gravitational temperature Tɢ.
The value that the effective Boltzmann constant takes would tell us if we are measuring a purely electromagnetic temperature, a purely gravitational temperature, or the interaction of electromagnetic and gravitational temperatures.
When a black hole forms, Kʙ = 1.78 10⁻⁴³ J/K.
Eε = Kʙε x Tε
Eɢ = Kʙɢ x Tɢ
If we look at the equations, taking into account the Boltzmann constants Kʙε = 1.38 10⁻²³ J/K, which corresponds to the domain of the four fundamental forces, and Kʙɢ = 1.78 10⁻⁴³ J/K, which corresponds to the domain of the strong force and gravitational fields inside a black hole; it is determined that there is a difference of 10²⁰ in order of magnitude between the energy Eε and Eɢ, that is, if we make Tε = Tɢ, we have that Eε = 10²⁰ Eɢ.
This factor 10²⁰ is very important, it is telling us the energy level that exists between the photon and the graviton, it is telling us that the graviton has an energy of the order of 10²⁰ times less than the photon.
Example:
If we consider white dwarf stars (electron degeneracy pressure) and neutron stars (neutron degeneracy pressure), these systems have a disturbance that modifies the space-time structure and are in a space-time transition process, because their Boltzmann’s constant lies at intermediate values between the extremes Kʙ = 1.38 10⁻²³ J/K and Kʙ = 1.78 10⁻⁴³ J/K.
White dwarf stars and neutron stars are two examples of systems where there are changes in the fabric of space-time. Knowing Boltzmann’s constant, we can calculate the temperature in these systems using the Hawking radiation equation.
When we calculate the temperature of a black hole using the Hawking radiation equation and the Boltzmann constant Kʙɢ = 1.78 10⁻⁴³ J/K, this gives us that the temperature is Tɢ = 10¹³ K and that temperature is given by the gravitational effects of space-time and not by electromagnetic effects.
To finish this example, we will determine the temperature of a stellar black hole of three solar masses, using the Boltzmann constants given by Kʙε and Kʙɢ.
Tʙʜ = Tε + Tɢ, temperature of a black hole.
Tε = hc³ / (8 x ᴨ x Kʙε x G x M) = 9.9 10⁻¹⁶ K
Tɢ = hc³ / (8 x ᴨ x Kʙɢ x G x M) = 10¹³ K
Tʙʜ = Tε + Tɢ = 0 K + 10¹³ K
Tʙʜ = Tɢ = 10¹³ K
We show that the temperature of a black hole is 10¹³ K, it is a gravitational temperature, not an electromagnetic one.
Finally, we are going to define the following:
• In the absence of a disturbance that modifies the structure of space-time, the temperature of a system T will be determined by the electromagnetic temperature Tε, that is, the gravitational temperature Tɢ = 0. This is true in the domain of the four fundamental forces. We consider that the Boltzmann constant for this system is equal to Kʙε = 1.38 10⁻²³ J/K.
• Inside a black hole, in the domain of the strong and gravitational force field, the temperature will be determined by the gravitational temperature Tɢ, that is, the electromagnetic temperature Tε = 0. In this context, Boltzmann’s constant will be Kʙɢ = 1.78 10 ⁻⁴³ J/K.
• There is an intermediate condition, in the domain of the four fundamental forces, in which there are variations in the structure of space-time, which is manifested by the variation of the amplitude of the Boltzmann constant that goes from Kʙε = 1.38 10⁻ ²³ J/K to Kʙɢ = 1.78 10⁻⁴³ J/K. In this condition, the temperature of the system will be determined by the interaction of the electromagnetic temperature and the gravitational temperature, T = Tε + Tɢ.
Equivalent mass of the photon and its relationship with the graviton
Do photons really have an experimentally verifiable equivalent mass? The answer was given by the American physicist Arthur Compton in 1922, who, when carrying out experiments to make X-rays collide with electrons, the deviation in the trajectory of the latter corresponded to a collision with a particle of equivalent mass calculated for the photon with the following formula.
M(photon) = E / C² = h x C / λ x C² = h / (λ x C)
M(photon) = h / (λε x Cε)
Example:
(Photon-mass)680 = 6.62 10ˉ³⁴ Js / (6.80 10ˉ⁷ m x 2.99 10⁸ m/s) = 3.25 10ˉ³⁶ kg
(Photon-mass)0,1 = 6.62 10ˉ³⁴ Js / (0.1 10ˉ⁹ m x 2.99 10⁸ m/s) = 2.21 10ˉ³² kg
(Photon-mass)0,001 = 6.62 10ˉ³⁴ Js / (0,001 10ˉ⁹ m x 2,99·10⁸ m/s) = 2.21 10ˉ³⁰ kg
Compared to the mass of the electron (9.10939 10⁻³¹ kg), the mass of the photon is smaller, but in the case of gamma rays (0.001 10⁻⁹ nm) the masses are of the same order and slightly higher!
If we consider the following equation:
Eε = 10²⁰ Eɢ
M(graviton) = h / (λɢ x Cɢ)
This tells us that electromagnetic energy is on the order of 10²⁰ times greater than gravitational energy, so we can infer the following:
M(photon) = 10²⁰ M(graviton)
M(graviton) = M(photon) / 10²⁰
With this we show that the equivalent mass of the graviton is variable, in analogy with the photon and depends on its wavelength λ (remember that there is a spectrum of gravitational waves).
Let’s use the following equations; Let’s do a parallelism to see the energy and temperature differences for the electromagnetic and gravitational spectra.
Eε = h x fε
Cε = λε x fε
Eε = h x Cε / λε
Eε = Kʙε x Tε
Eɢ = h x fɢ
Cɢ = λɢ x fɢ
Eɢ = h x Cɢ / λɢ
Eɢ = Kʙɢ x Tɢ
- We are going to work with gamma ray frequencies.
fε = 10²⁴ Hz
Eε = h x fε = 6.62 10⁻³⁴ x 10²⁴ = 6.62 10⁻¹⁰ J
Eε = 6.62 10⁻¹⁰ J
Eε = Kʙε x Tε; Tε = Eε / Kʙε = 6.62 10⁻¹⁰ / 1.38 10⁻²³ = 4.79 10¹³
Tε = 4.79 10¹³ K
fɢ = 10²⁴ Hz
Eɢ = h x fɢ = 6.62 10⁻³⁴ x 10²⁴ = 6.62 10⁻¹⁰ J
Eɢ = 6.62 10⁻¹⁰ J
Eɢ = Kʙɢ x Tɢ; Tɢ = Eɢ / Kʙɢ = 6.62 10⁻¹⁰ / 1.78 10⁻⁴³ = 3.71 10³³ K
Tɢ = 3.71 10³³ K
- We will work with long wave radio frequencies.
fε = 1 Hz
Eε = h x fε = 6.62 10⁻³⁴ x 1 = 6.62 10⁻³⁴ J
Eε = 6.62 10⁻³⁴ J
Eε = Kʙε x Tε; Tε = Eε / Kʙε = 6.62 10⁻³⁴ / 1.38 10⁻²³ = 4.79 10⁻¹¹ K
Tε = 4.79 10⁻¹¹ K
fɢ = 1 Hz
Eɢ = h x fɢ = 6.62 10⁻³⁴ x 1 = 6.62 10⁻³⁴ J
Eɢ = 6.62 10⁻³⁴ J
Eɢ = Kʙɢ x Tɢ; Tɢ = Eɢ / Kʙɢ = 6.62 10⁻³⁴ / 1.78 10⁻⁴³ = 3.71 10⁹ K
Tɢ = 3.71 10⁹ K
- We will work with radio frequency.
fε = 10⁴ Hz = 10.000 Hz
Eε = h x fε = 6.62 10⁻³⁴ x 10⁴ = 6.62 10⁻³⁰ J
Eε = 6.62 10⁻³⁰ J
Eε = Kʙε x Tε; Tε = Eε / Kʙε = 6.62 10⁻³⁰ / 1.38 10⁻²³ = 4.79 10⁻⁷ K
Tε = 4.79 10⁻⁷ K
fɢ = 10⁴ = 10,000 Hz
Eɢ = h x fɢ = 6.62 10⁻³⁴ x 10⁴ = 6.62 10⁻³⁰ J
Eɢ = 6.62 10⁻³⁰ J
Eɢ = Kʙɢ x Tɢ; Tɢ = Eɢ / Kʙɢ = 6.62 10⁻³⁰ / 1.78 10⁻⁴³ = 3.71 10¹³ K
Tɢ = 3.71 10¹³ K
- Consider the formation temperature of a BH of three solar masses.
T = 10¹³ K
Eε = Kʙε x Tε = 1.38 10⁻²³ x 10¹³ = 1.38 10⁻¹⁰ J
Eε = 1.38 10⁻¹⁰ J
Eε = 8.61 10⁸ eV
Eε = h x fε; fε = Eε / h = 1.38 10⁻¹⁰ / 6.62 10⁻³⁴ = 0.20 10²⁴
fε = 0.20 10²⁴ Hz
M(Photon) = h / (λε x Cε); λε = 15 10⁻¹⁶ m
M(Photon) = 6.62 10⁻³⁴ / (15 10⁻¹⁶ x 3 10⁸) = 6.62 10⁻³⁴ / 45 10⁻⁸ = 0.14 10⁻²⁶
M(Photon) = 1.4 10⁻²⁷ kg
Eɢ = Kʙɢ x Tɢ = 1.78 10⁻⁴³ x 10¹³ = 1.78 10⁻³⁰ J
Eɢ = 1.78 10⁻³⁰ J
Eɢ = 1.11 10⁻¹¹ eV
Eɢ = h x fɢ; fɢ = Eɢ / h = 1.78 10⁻³⁰ / 6.62 10⁻³⁴ = 0.26 10⁴ = 2,6 10³ Hz
fɢ = 2600Hz; λɢ = 1,15 10⁵ m
M(graviton) = h / (λɢ x Cɢ), λɢ = 1.15 10⁵ m
M(graviton) = 6.62 10⁻³⁴ / (1.15 10⁵ x 3 10⁸) = 6.62 10⁻³⁴ / 3.46 10¹³
M(graviton) = 1.91 10⁻⁴⁷ kg
- Consider the temperature of 3000 K.
T = 3 10³ K
Eε = Kʙε x Tε = 1.38 10⁻²³ x 3 10³ = 4.14 10⁻²⁰ J
Eε = 4.14 10⁻²⁰ J
Eε = 0.25 eV
Eε = h x fε; fε = Eε / h = 4.14 10⁻²⁰ / 6.62 10⁻³⁴ = 0.62 10¹⁴
fε = 0.62 10¹⁴ Hz
M(Photon) = h / (λε x Cε); λε = 4.83 10⁻⁶ m
M(Photon) = 6.62 10⁻³⁴ / (4.83 10⁻⁶ x 3 10⁸) = 0.45 10⁻³⁶
M(Photon) = 4.5 10⁻³⁷ kg
Eɢ = Kʙɢ x Tɢ = 1.78 10⁻⁴³ x 3 10³ = 5.34 10⁻⁴⁰ J
Eɢ = 5.34 10⁻⁴⁰ J
Eɢ = 3.33 10⁻²¹ eV
Eɢ = h x fɢ; fɢ = Eɢ / h = 5.34 10⁻⁴⁰ / 6.62 10⁻³⁴ = 0.80 10⁻⁶
fɢ = 0.80 10⁻⁶ Hz
M(graviton) = h / (λɢ x Cɢ), λɢ = 3.75 10¹⁴ m
M(graviton) = 6.62 10⁻³⁴ / (3.75 10¹⁴ x 3 10⁸) = 6.62 10⁻³⁴ / 11.25 10²²
M(graviton) = 5.8 10⁻⁵⁷ kg
6.12. Why is it necessary to consider gravitational waves to correctly describe the expansion of the universe?
The collision of two stellar black holes with an average mass of 40 solar masses, detected by the LIGO and Virgo observatory, confirmed the existence of gravitational waves.
Now, if we take this to the Big Bang, to the inflationary period, the immense energy released would be expected to generate a spectrum of gravitational waves; This affirmation is very important and based on this we are going to work.
Let us define the impulse function &(t) or also called the Dirac delta function.
&(t) = {∞, t = 0 ^ 0, t ≠ 0}
Graphical representation of the impulse function:
Figure 13.
impulse function.
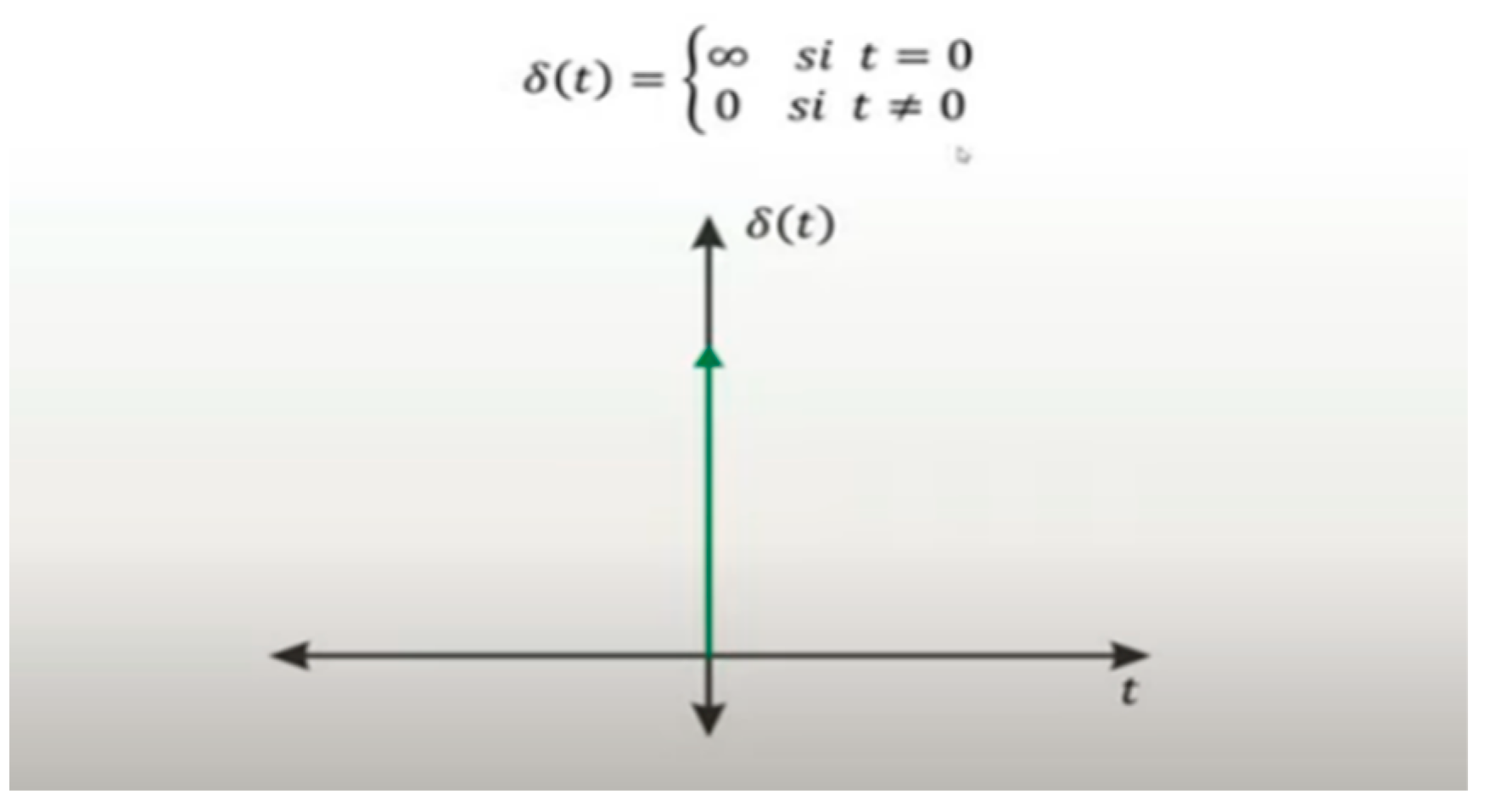
We see that for t = 0 the value of the impulse function tends to infinity and that for t ≠ 0 the value is 0. Based on what has been said, we can make an analogy with the expansion of the Big Bang and say that at time t = 0, its expansion would behave like a pulse of infinite energy.
If we analyse the amplitude and phase spectrum of the Fourier transform of the impulse function, we see that the amplitude spectrum is equal to a constant K for all frequencies and the phase spectrum is equal to 0 for all frequencies.
Again, making an analogy between the impulse and the burst of energy of the Big Bang released at time t = 0, we can say that for all frequencies the amplitude spectrum is constant and the phase spectrum is zero.
Figure 14.
Amplitude spectrum of the function &(t) in the frequency domain.
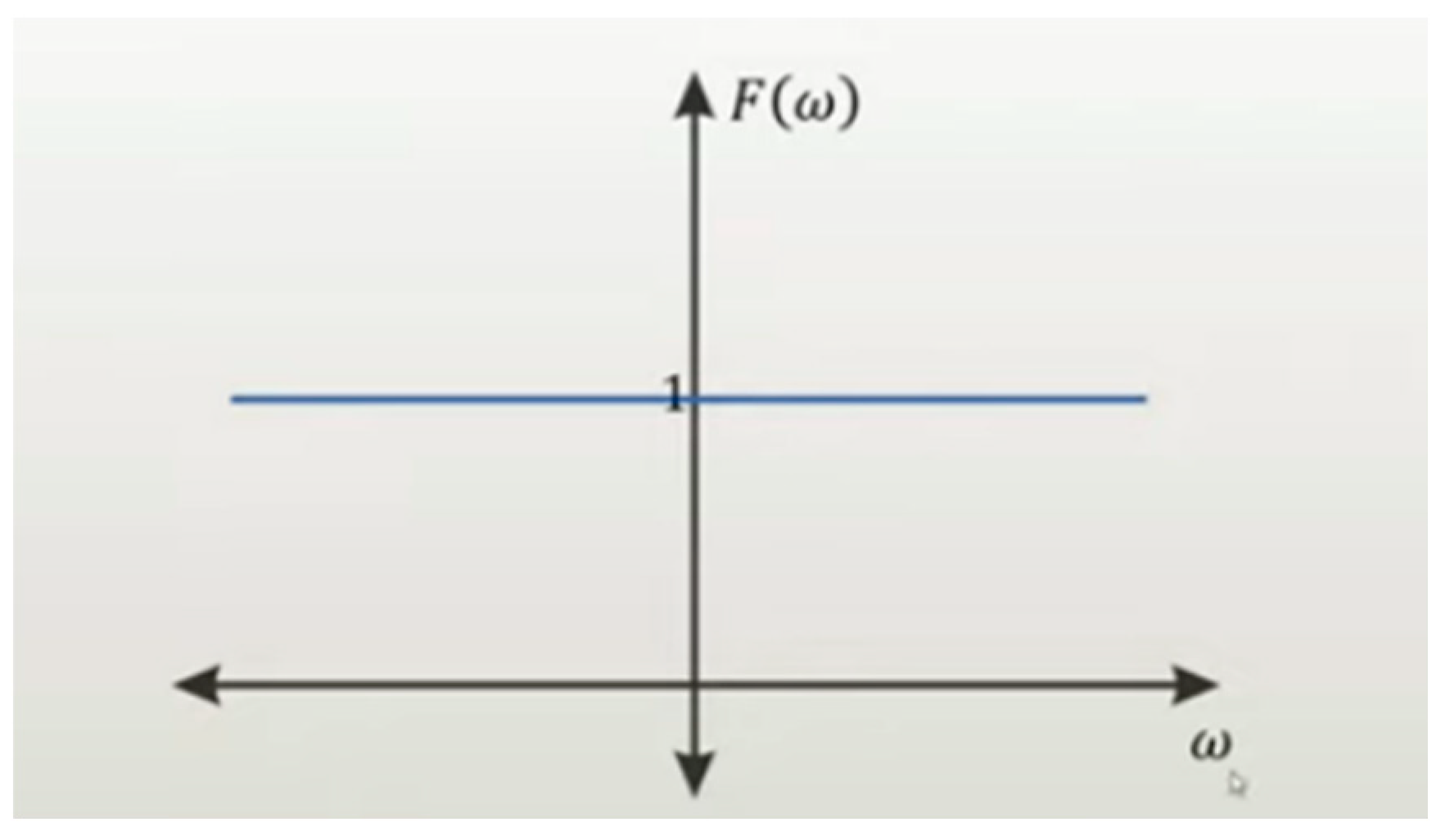
Figure 15.
phase spectrum of the function &(t) in the frequency domain.
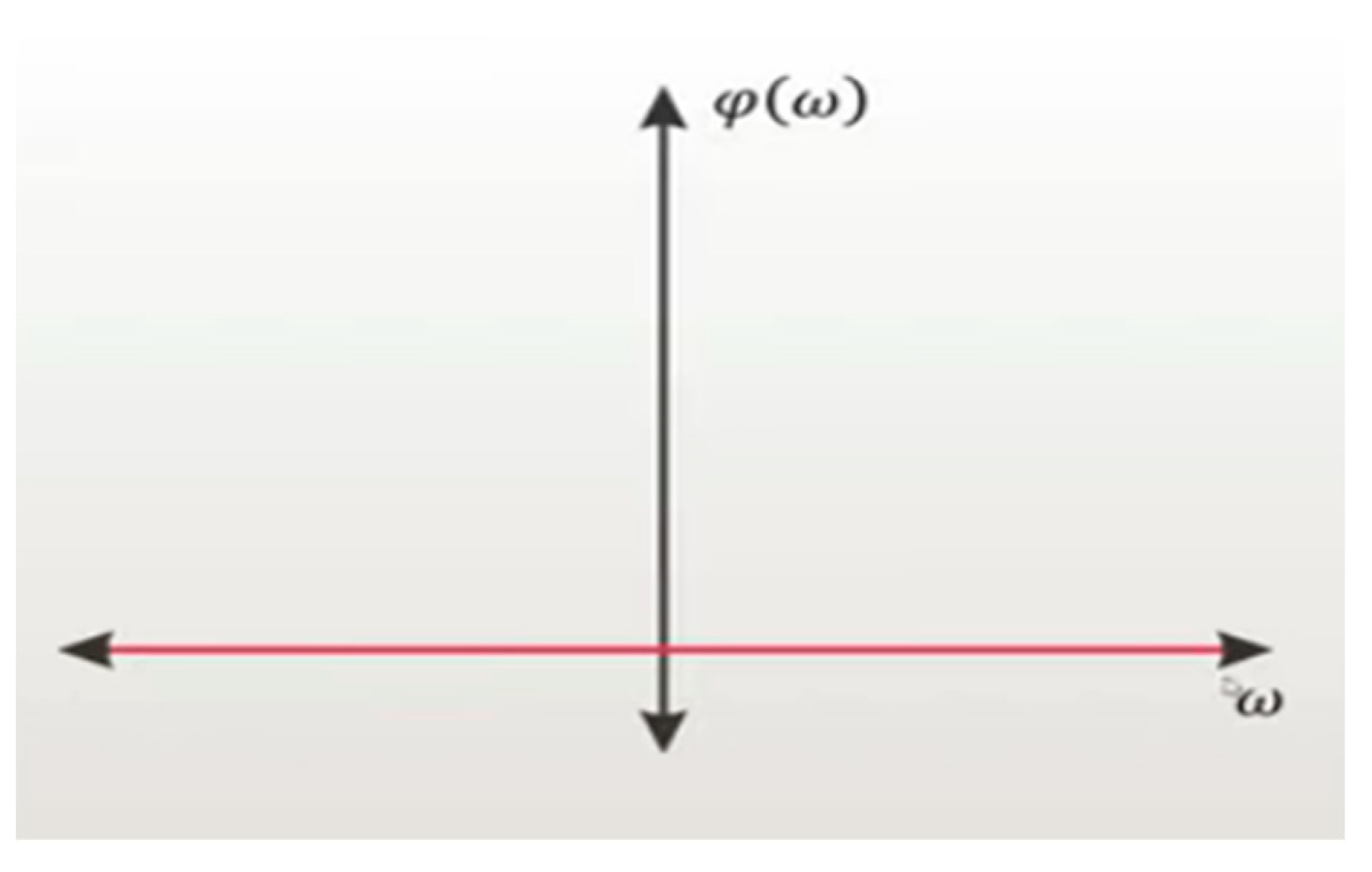
Let’s try to clarify what has been explained and let’s say that at t = 0, at the moment of the Big Bang explosion, the enormous amount of energy released generates infinite waves of energy (infinite frequency spectrum) that will propagate through space in all directions, each wave with the same amplitude and the same phase.
For the amplitude spectrum to be constant and the phase spectrum to be zero, we will infer that it is a zero-phase system.
We will introduce the concept of convolution and for this we will make the following analogy. When we do seismic exploration studies to look for gas or oil and use dynamite as a source of energy, the signal that we pick up on our seismic sensors is the result of the energy released by exploding the dynamite that mixes or convolves with the physical characteristics of the earth. If we analyse the signals captured by geophones in the frequency domain, we see that the amplitude and phase spectra depend on the physical characteristics of the earth. We are dealing with a causal type minimal phase system.
Likewise, we will consider the explosion of the dynamite as the explosion of a black hole and the physical characteristics of the Earth analogous to the physical characteristics of the space-time of our universe that surrounds the black hole. According to the above, we can say that the energy released and produced by the Big Bang mixes or convolves with the physical characteristics of the existing universe to produce infinite waves of energy that propagate through space-time (gravitational wave spectrum), whose spectrum of amplitude and phase in the frequency domain, will depend on the physical characteristics of space-time at the moment of the explosion in analogy with the physical characteristics of the Earth. In other words, we can consider the Big Bang as a minimum phase causal system.
Figure 16.
wavelet with minimum phase in the upper graph and a wavelet with zero phase in the lower graph.
Figure 16.
wavelet with minimum phase in the upper graph and a wavelet with zero phase in the lower graph.
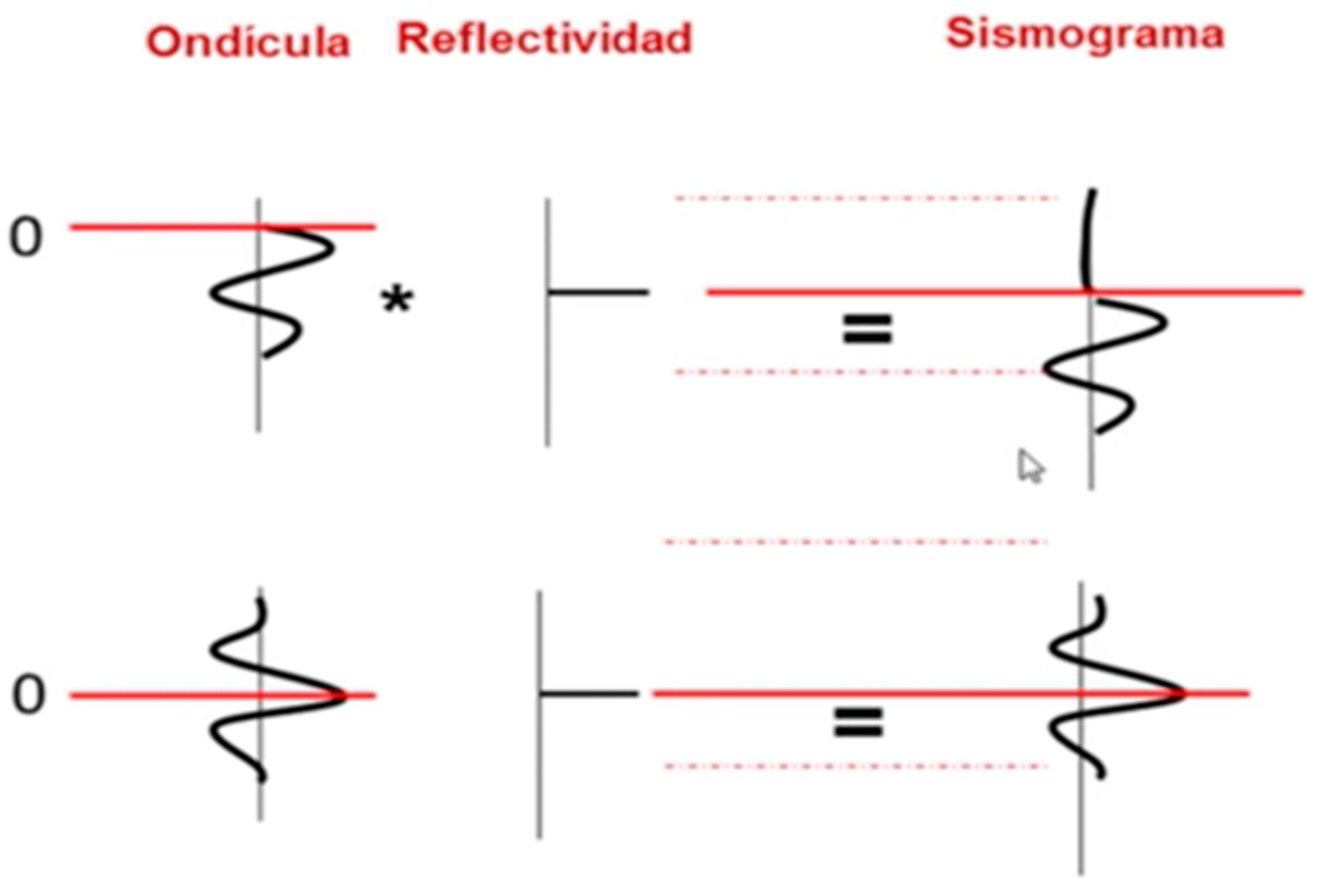
The Lambda-CDM model and the FLRW metric are indicating that the expansion period of the universe, called inflation, behaves as an approximation of the Dirac function for t = 0, the energy released is infinite, spectrum of constant magnitude and spectrum of phase 0.
What would happen if we consider the causal system, minimum phase and anisotropic? that is, that the energy released during inflation is not transmitted instantaneously and that the expansion of gravitational waves (space-time) during inflation is a function of time. Possibly these considerations could end or solve the problem of dark energy generated by an incorrect conjecture when considering the isotropic universe, that is, we would be affirming that Einstein’s field equations would not be adequate to analyse the evolution of the universe or would eventually be needing of a fine adjustment.
I propose that the space-time expansion of the inflationary era of the Big Bang behaves as a system causal, of minimum phase, in which the released energy is transmitted with a minimum delay and the propagation of the generated gravitational waves depend on the characteristics of the space, physical environment. An example of this behaviour is analogous to the seismic exploration method with explosives, in which the entire system is of minimum phase (causal) and the waves generated by the explosion are transmitted to an anisotropic medium, that is, with different refractive and reflection coefficients.
Bearing this in mind, we will carry out the following analysis:
Figure 17.
Hubble’s constant and the isotropic principle.
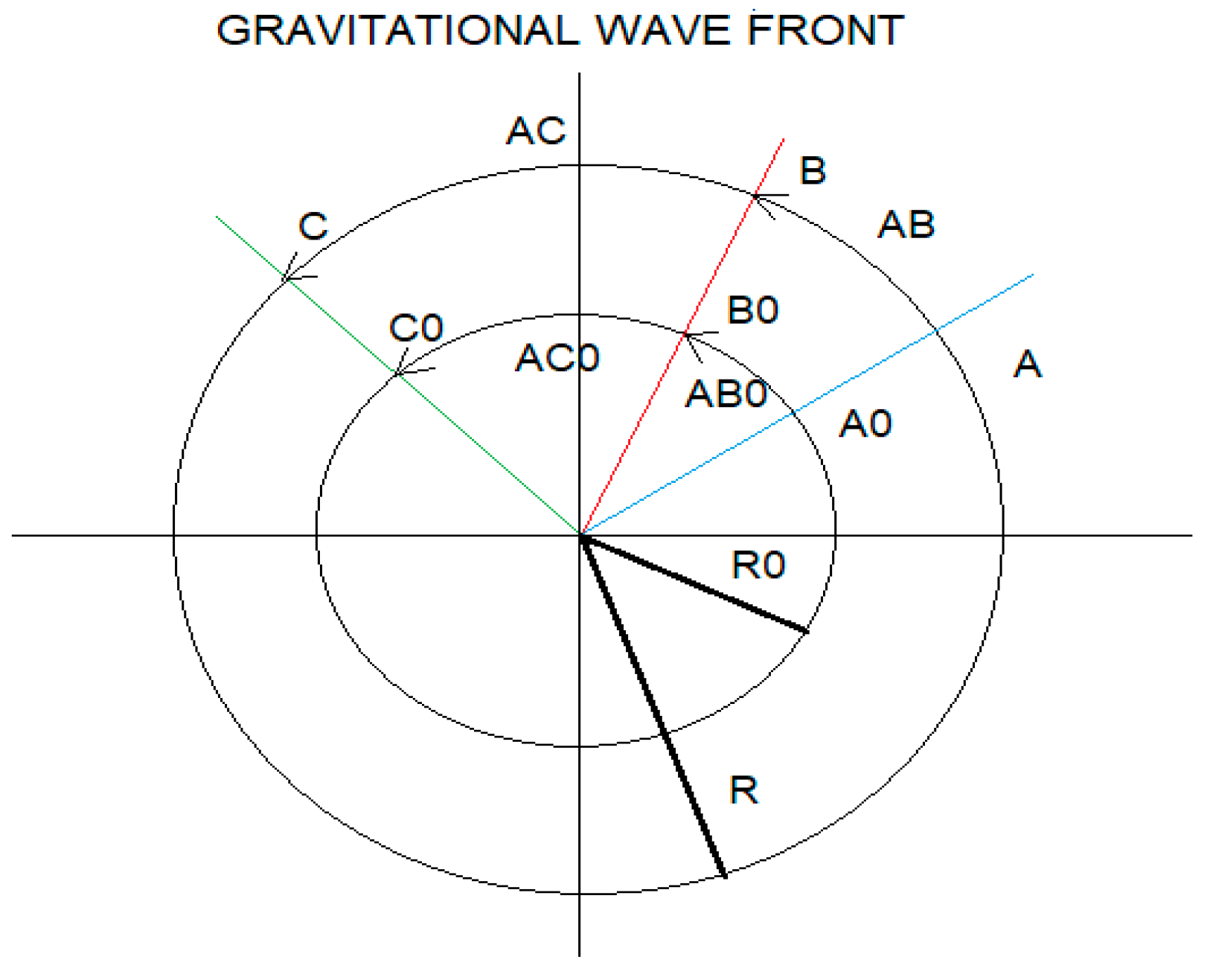
We are going to give a mathematical interpretation to the gravitational wave front:
D(ABo) = Ro α(ABo)
D(ACo) = Ro α(ACo)
D(AB) = R α(AB)
D(AC) = R α(AC)
Deriving with respect to time we have:
V(AB) = (d/dt) D(AB) = (d/dt) R α(AB)
V(AB) = R’α(AB)
in the same way it is fulfilled:
V(AC) = R`α(AC)
Working mathematically, we have:
D(AB) = R α(AB)
V(AB) = R’α(AB)
V(AB) = (R’/R) D(AB)
H(t) = R`/R
V(AB) = H(t) D(AB)
V = H D, Hubble’s law
H = R’/ R, Hubble’s constant
Mathematically we can deduce that the propagation of a single gravitational wave front, in an isotropic medium, produces a single Hubble constant.
Now we return to our hypothesis that in the inflationary era a spectrum of gravitational waves is produced.
Suppose that in this spectrum, the main waves that have the highest energy are the fundamental frequency, the first and second harmonics.
If we consider the first wave front, that is, the fundamental frequency, it is to be expected that for this wave front there is a Hubble constant.
Now let us consider the second wave front or first harmonic, it is to be expected, with the arrival of the energy impulse of the first harmonic the Hubble constant will vary.
Now let’s consider the third wave front or second harmonic, again with the arrival of this pulse of energy it is to be expected that the Hubble constant will vary again.
In short, for a spectrum of gravitational waves produced in the inflationary era, it is to be expected that with the arrival of each of the gravitational waves a variation in the Hubble constant is produced.
Now, we will consider the geometric interpretation, as shown below, and relate each graph as a propagation of a gravitational wavefront with energy E, wavelength λ, time t, velocity C, and temperature T.
E1, λ1, t1, C, T1
Figure 18.
fundamental wavefront.
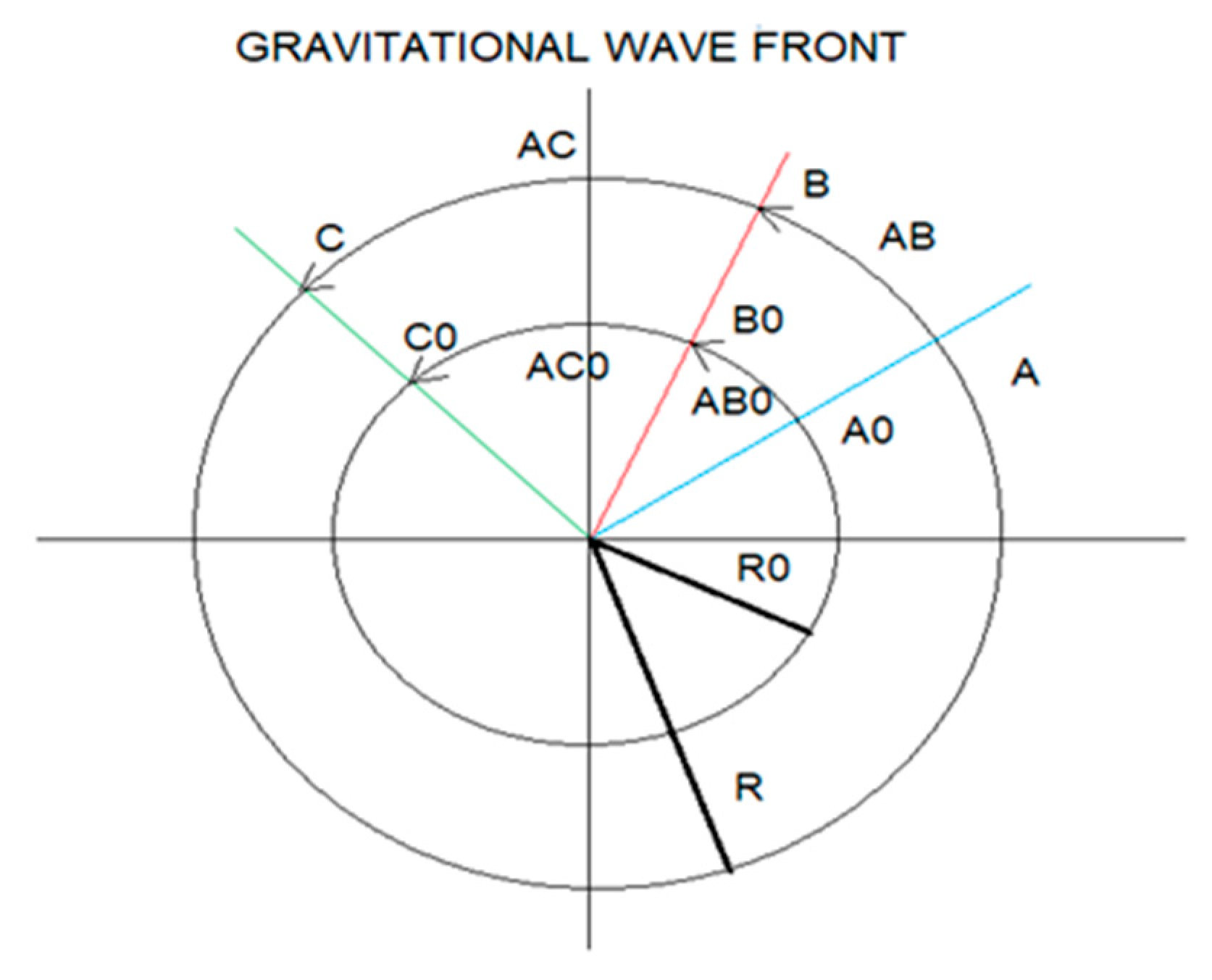
E2, λ2, t2, C, T2
Figure 19.
first harmonic wavefront.
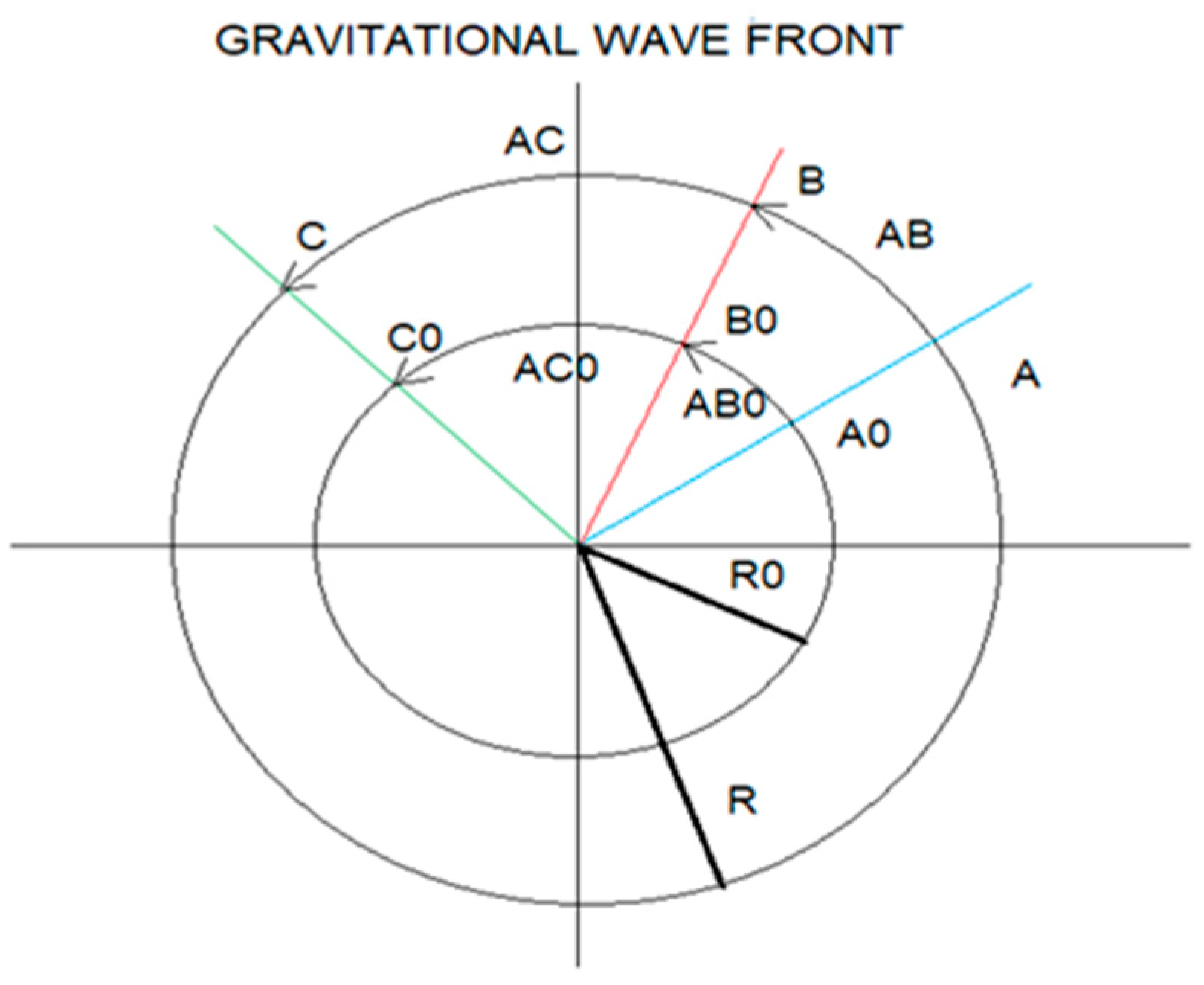
E3, λ3, t3, C, T3
Figure 19.
second harmonic wavefront.
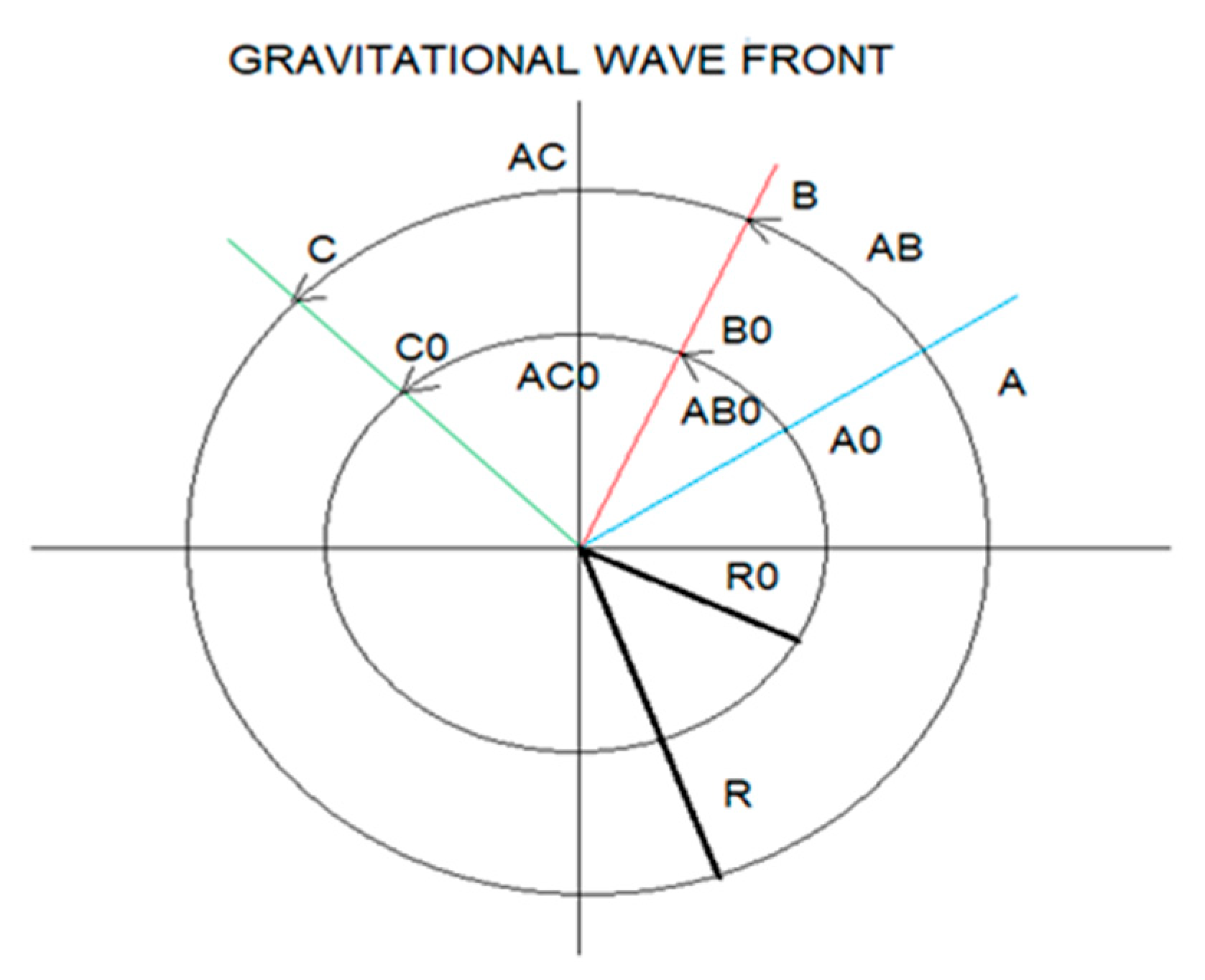
Let’s consider the power spectrum of the CMB acoustic waves, and relate it to the 3 graphs, shown above.
We can see in the graph of Figure 20, which corresponds to the power spectrum of acoustic waves, they have 3 well-defined peaks that are related to the graphs of Figure 17, Figure 18 and Figure 19, this would correspond to three wave fronts, that are They propagate through space-time with different energies E , wavelength λ, out of phase at time t, with the speed C and different temperatures T.
This can be interpreted as follows:
- E1, λ1, t1, C, T1: characteristics of the gravitational wavefront for the fundamental frequency.
- E2, λ2, t2, C, T2: characteristics of the gravitational wavefront for the first harmonic frequency.
- E3, λ3, t3, C, T3: characteristics of the gravitational wavefront for the second harmonic frequency.
- En, λn, tn, C, Tn: characteristics of the gravitational wavefront for the harmonic of the nth frequency
In conclusion, the Hubble’s constant H will depend on the characteristics of the spectrum of the gravitational wavefront H (En, λn, tn, C, Tn) and will be independent of our chosen model.
For example, for the first peak of the power spectrum, this gravitational energy E1 will define the wavefront λ1 +Δλ, and this will occur at time t1; this wavefront will define the Hubble constant H1 (E1, λ1, t1, C, T1). Finally, we must consider the contributions of all wavefronts; with this criterion we must update our Lambda-CDM model. It is also to be expected that whenever there is a gravitational wavefront with an energy E, it will surely result from a variation in the Hubble constant.
Remember that in the expansion of the universe there are two phases:
- Phase 1, takes place during the inflationary era, where the speed of propagation of gravitational waves is caused by the expansion of the structure of space-time itself, and will be greater than c = 300,000 km/s; will depend on the characteristics of the gravitational wavefront (E, λ, t, C, T). In this phase, the expansion of space-time that is given by Lpɢ that tends to reach its normal value Lpɛ after a black hole disintegrates.
- Phase 2, occurs when the propagation speed of gravitational waves is equal to c = 300,000 km/s, as in the events detected by LIGO and Virgo. In this phase the universe stabilizes. In this phase, the Boltzmann constant Kʙ = 1.78 10⁻⁴³ J/K (curved space time) tends to reach the value of Kʙ = 1.38 10⁻²³ J/K (flat space time).
We will analyse the following equation:
E (t) = 1.08 10⁷³ {e ⁻ (1.81 10⁻¹¹ t)} – 1.08 10⁷³ {e ⁻ (2.19 10¹¹ t)} + E0
Where E0 corresponds to the temperature of 2.7 K
This equation represents the gravitational wave equation of the universe.
λ = 1.000.000 Light years = 10⁶ x 9.46 10¹⁵ m
where λ is the fundamental wavelength
λ is a data provided by the IFT UAM.
λ = 9.46 10²¹ m
c = λ x f, f = c/λ, f = 3 10²¹ / 9.46 10²¹ = 0.317 Hz
f = 0.317 Hz
where f is the fundamental frequency
ω = 2.ᴨ.f = 2 x 3.14 x 0.317 = 2
ω = 2.00 rad/s
Where ω is the fundamental angular frequency
We will perform the calculations of ω0, B, ω1 and ω2 for our RLC circuit.
R = 3.60 10⁵¹ Ohms
L = 1.98 10⁶² Hy
C = 1.26 10⁻⁶³ F
ω0 = 1 / √ LC rad/s
ω0 = 1 / √ LC = 1 / √ (1.98 10⁶² Hy x 1.26 10⁻⁶³ F) = 1 / √2.49 x 10⁻¹
ω0 = 2.00 rad/s
Where ω0, is the resonance frequency or fundamental angular frequency.
Calculation of the high cut-off frequency
ω2 = + 1 / 2RC + √ (1 / 2RC) ² - (1 / LC)
S2 = - α - √ (α) ² - (ω0) ²
ω2 = 11.00 10¹⁰ + √ (121.00 10²⁰ - 4)
ω2 = 2.19 10¹¹ rad/s
ω2 is the high cut-off frequency
ω2 = 2.19 10¹¹ rad/s
f2 = ω2 / 2π = 2.19 10¹¹ / 2 x 3.14 = 0.348 10¹¹
f2 = 0.348 10¹¹ Hz
λ2 = C / f2 = 3 10²¹ / 0.348 10¹¹ = 8.60 10¹⁰
λ2 = 8.60 10¹⁰ m
Calculation of the low cut-off frequency
ω1 = -1 / 2RC + √ (1 / 2RC) ² + (1 / LC)
S1 = - α + √ ((α)² - (ω0) ²)
ω1 = -11.00 10¹⁰ + √ (121.00 10²⁰ - 4)
ω1 = 1.81 10⁻¹¹ rad/s
where ω1 is the low cut-off frequency
ω1 = 1.81 10⁻¹¹ rad/s
f1 = ω1 / 2π = 1,81 10⁻¹¹ rad/s / 2 x 3.14 = 2.88 10⁻¹²
f1 = 2.88 10⁻¹² Hz
λ1 = C / f1 = 3 10²¹ / 2.88 10⁻¹² = 1.08 10³³
λ1 = 1.08 10³³ m
Bandwidth Calculation
B = ω2 - ω1
B = 2.2 10¹¹ rad/s
B is the bandwidth
Remember that the energy stabilizes when the space reaches 2.7 K, which corresponds to 3.72 10⁻²³ J.
3.72 10⁻²³ = 1.08 10⁷³ e⁻ (1.81 10⁻¹¹ t)
e⁻ (1.81 10⁻¹¹ t) = 0.290 10⁹⁶
1,81 10⁻¹¹ t = ln (0.290 10⁹⁶)
t = ln (0.290 10⁹⁶) / 1.81 10⁻¹¹ = 219.84 / 1.81 10⁻¹¹ = 121.46 10¹¹
t = 1.22 10¹³ s
Where t is the time in which the equation E(t) reaches 2.7 K
At t = 1.22 10¹³ s, space-time has expanded by a factor of:
e = v x t
e = 1.22 10¹³ s x 3 10²¹ m/s = 3.66 10³⁴ m.
e = 3.66 10³⁴ m
Calculation of the number of seconds in 380,000 years:
t = 11.81 10¹² s
We will analyse Figure 21:
- low cut-off frequency, ω1 = 1.81 10⁻¹¹ rad/s
- High cut-off frequency, ω2 = 2.19 10¹¹ rad/s
- Fundamental or resonant frequency, ω0 = 2.00 rad/s
- Bandwidth, B =2.2 10¹¹ rad/s
- Space travelled that corresponds to the total bandwidth: e = 3.66 10³⁴ m
- Minimum time, approximately t = 10ˉ¹³ s
- Maximum time, t = 1.22 10¹³ s
Now we are going to analyse something very important that will help us understand the origin of dark energy.
We said, to form a black hole, the Boltzmann constant changes from KB = 1.38 10ˉ²³ J/K (flat space-time) to KB = 1.78 10ˉ⁴³ J/K (curved space-time). once the black hole forms the Boltzmann constant remains constant at KB = 1.78 10ˉ⁴³ J/K. As the black hole grows, the Planck length varies from Lp = 1.61 10⁻³⁵ m to 1.28 10⁻⁵⁴ m. When it reaches the Planck length Lp = 1.28 10⁻⁵⁴ m, the speed of massless particles inside a black hole is c = 10²¹ m/s.
How can we relate the statement to the Big Bang? Let’s try to interpret this as follows:
If we consider Planck’s constant as a spring, as a black hole grows, Planck’s constant decreases, that is, the spring decreases in size, increasing its potential energy.
When the disintegration of the black hole occurs and causes the Big Bang, Planck’s constant that was at the value of Lp = 1.28 10⁻⁵⁴ m tries to reach its normal or stable value of Lp = 1.61 10⁻³⁵ m, expanding to a speed of c = 10²¹ m/s, generating the period of cosmic inflation.
This implies, in the first instance, each generated frequency, shown in the bandpass circuit in Figure 21, must travel a distance e = 3.66 10³⁴ m, which brings the total time to 10²⁶ s. Example, the fundamental frequency that originates in 1 sec goes up to 1.22 10¹³ s, the last frequency that originates in 1.22 10¹³ s goes up to 10²⁶ s, where each of the frequencies of the spectrum travels a distance e = 3.66 10³⁴ m.
This is the first event that contributes to the origin of dark energy, where each generated gravitational wave travels at a speed c = 10²¹ m/s and travels a space of e = 3.66 10³⁴ m.
Now we are going to analyse the second event that will help us understand dark energy even more.
The second important event is related to the Boltzmann constant, in this process the Boltzmann constant KB = 1.78 10ˉ⁴³ J/K (curved space-time) must reach the value of KB = 1.38 10ˉ²³ J/K (flat space-time), In this process each gravitational wave travels at the speed of light c = 3 10⁸ m/s
In the second event, we will propose that the shape of the CMB power spectrum will determine the shape of the gravitational wave contribution.
Both events contribute and give origin to dark energy.
Finally, considering the statement above, in the following graph we will try to represent the energy (E(t) vs t(s)) and (H(t) vs t(s)).
In Figure 22 and Figure 23, the X axis is represented to scale, the y axis is not represented to scale.
In Figure 22, I try to represent the contribution of the energy of gravitational waves up to a time t = 10²⁶ s.
In Figure 23, I try to represent the variation of the Hubble constant up to a time t = 10²⁶ s, considering the energy contribution of gravitational waves.
Observing Figure 23, we see that from t = 10¹² s, there is an inflection point in which the Hubble constant goes from negative to positive slope, this is due to the gravitational wave front, which has the shape of the frequency spectrum distributed in time, Figure 22, which adds energy, causing the universe to go from decelerated expansion to accelerated expansion. This is manifested by a variable Hubble constant as shown in Figure 23.
We also observe for t = 10²⁶ s, Figure 23, another inflection point occurs due to the absence of gravitational waves, as shown in Figure 22, in which the slope is zero (horizontal).
It is very important to make clear that the accelerated expansion of the universe has a limit and it is given for t = 10²⁶ s, after that time, space-time stabilizes.
When we measure the Hubble constant using the IA supernova method, it gives us H = 74 km/s/Mpc.
When we measure the Hubble constant, using the CMB microwave radiation background, it gives us H = 67 km/s/Mpc.
When we measure the Hubble constant using merged neutron stars, using the electromagnetic spectrum and gravitational waves, it gives us H = 66.2 km/s/Mpc.
When we measure the Hubble constant using an IA supernova and gravitational lensing, it gives us H = 64 km/s/Mpc.
Which of all these values is correct? Or are they all correct values?
Possibly the values of the Hubble constants determined by the four different methods are correct and the difference between the calculated values for the Hubble constants is due to the fact that the expansion of space-time is different in each place where the measurements are carried out, because the measurements were made in different time periods of the expansion of the space-time of the universe, as shown in Figure 23, which represents the variation of the Hubble’s constant H vs t.
Example 1:
According to Figure 23, if we divide by power of 10, logarithmic scale, we have approximately 26 steps, neglecting negative exponent stages.
Let’s calculate the time t today.
t = 4.35 10¹⁷ s, correspond to 17 steps.
(17,5 / 26) x 100 = 67.3%
This is similar to the dark energy content of the universe.
100% - 67.3 = 32.7 %
This is similar to the dark matter content of the universe.
Calculation of the number of seconds in 380,000 years:
t = 11.81 10¹² s
Calculation of the number of seconds for when the universe stabilizes and reaches the temperature of 2.7 K
t = 1.22 10¹³ s
We divide the time t, we get:
(11.81 10¹² s / 1.22 10¹³ s) x 100 = 96.72 %
100% - 96,72% = 3.28%
This is similar to the baryonic matter content in the universe.
The true interpretation of this result is the following, the fundamental wavelength that corresponds to λ = 1,000,000 light years, represents the highest amplitude peak of the CMB power spectrum, has convolved 96% with the space-time of the universe and still needs to be convolved 4%.
The following values:
Dark energy = 67.3%
Dark matter = 29.42 %
Baryonic matter = 3.28 %
They represent the proportions of dark energy, dark matter and baryonic matter of the fundamental frequency referenced to the moment of time t that corresponds to the CMB.
As we consider the contribution of frequencies that make up the power spectrum, the percentage values for dark energy, dark matter, and baryonic matter should change.
Example 2:
Comment:
At present, the new discoveries of the James Webb telescope have raised a controversy in the astronomical scientific community. The new galaxies discovered 500 million years after the Big Bang appear smooth (well defined), old and numerous; have cast doubt on the Big Bang theory of evolution.
Galaxies formed similar to the Milky Way, well defined whose size exceeds our galaxy as well as discovered black holes with sizes up to 10 Millon solar masses, break the Big Bang theory of evolution.
Now, if we consider the theory of the RLC electrical model of the universe, in which RC represents a black hole that grows in a universe represented by L; in this approach, it is to be expected until the moment T0 in which the black hole disintegrates, that around the black hole, we can find perfectly developed galaxies similar to the Milky Way, it is also to be expected to find large numbers of galaxies as well as supermassive black holes; which would imply that the RLC electrical model of the universe does not contradict the recent discoveries of the James Webb telescope and would be in line.
Therefore, the RLC electrical model of the universe does not contradict the new discoveries of the James Webb telescope.
7. Conclusions
Through the calculations and analysis carried out in item 6), it is possible to demonstrate that the theory proposed in items 1) to 5), is a theory that complements the Lambda-CDM model, in which several of the important calculations that predict the theory of the RLC electric model of the universe conforms to the predictions of the Lambda CDM model.
It was also possible to demonstrate, how the curvature of space-time is measured, by means of the theory of the generalization of space-time for curved space-time, fundamental, for the theory of the RLC electrical model of the universe to work.
The RLC electric model theory of the universe generalizes the Lambda-CDM model theory and predicts the origin of the universe, the origin of cosmic inflation, the origin of dark matter and the origin of dark energy. It also solves the horizon problem and demonstrates how the universe is flat and uniform.
In the update of this article, version 2, we calculated the existence of the critical mass to produce a black hole in the LHC and proved the existence of a high-temperature Bose-Einstein condensate, applying the theory of generalization of the constant Boltzmann in curved spacetime.
We also show intuitively that in the disintegrations of subatomic particles, two forces act, a repulsive force whose direction is opposite to the attractive force and a tangential force that leads the repulsive force by 90 degrees. If we manage to demonstrate the existence of this tangential force in subatomic disintegrations, we can infer the existence of the tangential force inside black holes.
In the update of this article, version 3, we propose the relationship between M-theory and effective Boltzmann’s constant in three stages and demonstrate how dimension number 11 is generated inside a black hole. We also analyse, how the energy contribution of the gravitational waves generated in the Big Bang as a function of time, determines the variation of the Hubble constant as a function of time.
About the author
HECTOR GERARDO FLORES (ARGENTINA, 1971). I studied Electrical Engineering with an electronic orientation at UNT (Argentina); I worked and continue to work in oil companies looking for gas and oil for more than 25 years, as a maintenance engineer for seismic equipment in companies such as Western Atlas, Baker Hughes, Schlumberger, Geokinetics, etc. Since 2010, I study theoretical physics in a self-taught way. In the years 2020 and 2021, during the pandemic, I participated in the course and watched all the online videos of Cosmology I and Cosmology II taught by the Federal University of Santa Catarina UFSC (graduate level).
Conflicts of Interest
The author declares that there are no conflicts of interest.
References
- Gival Pordeus da Silva Neto. Estimando parâmetros cosmológicos a partir de dados observacionais. Departamento de Física Teórica e Experimental, Universidade Federal do Rio Grande do Norte. file:///C:/Users/Hecto/Downloads/Estimando_parametros_cosmologicos_a_partir_de_dado.pdf.
- Aurelio Carnero Rosell, Director Eusebio Sánchez Álvaro, Madrid, 2011. Determinación de parámetros cosmológicos usando oscilaciones acústicas de bariones en cartografiados fotométricos de galáxias. TESIS DOCTORAL, UNIVERSIDAD COMPLUTENSE DE MADRID https://eprints.ucm.es/13761/1/T33317.pdf.
- Anderson Luiz Brandão de Souza, Orientador: Pedro Cunha de Holanda. Oscilações Acústica Bariõnicas. TESIS DE MESTRADO, Universidade Estadual de Campinas, Instituto de Física “Gleb Wataghin”, Campinas 2018. https://sites.ifi.unicamp.br/sobreira/files/2018/07/mestrado-tanderson.pdf.
- JEFF STEIHAUER. Observation of quantum Hawking radiation and its entanglement in an analogue black hole. https://arxiv.org/abs/1510.00621.
- JEFF STEIHAUER. Spontaneous Hawking radiation and beyond: Observing the time evolution of an analogue black hole https://arxiv.org/abs/1910.09363.
- Quando a Luz se curvou. https://revistapesquisa.fapesp.br/quando-a-luz-se-curvou/.
- J.S.Farnes. A Unifying Theory of Dark Energy and Dark Matter: Negative Masses and Matter Creation within a Modified ΛCDM Framework. https://arxiv.org/abs/1712.07962.
- Alberto Casas, Profesor de Investigación IFT, CSIC/UAM. La luz y el origen de la materia. https://www.youtube.com/watch?v=CTrX_JBNEnU.
- Eisberg Resnick, Física Cuántica.
- Eyvind, H. Wichmann. Física cuántica.
- Sears – Zemansky. Física Universitaria con Física Moderna Vol II.
- Iván García Brao. Ecuación de campo de Einstein, Universidad de Murcia, Facultad de Matemáticas. Trabajo de grado año 2018. https://www.um.es/documents/118351/9850492/Garc%C3%ADa+Brao+TF_77837970.pdf/debaa03b-605b-420d-b3ac-85549b6622c0.
- Luis Felipe de Oliveira Guimarães, Orientadora Maria Emilia Xavier Guimarães. Soluciones de buracos negros na relatividade general, Universidad federal Fluminense, Bacherelado em Física. Trabajo de grado 2015. https://app.uff.br/riuff/bitstream/handle/1/5977/Luiz%20Filipe%20Guimaraes.pdf;jsessionid=4EAAF6CB7A4B776D04C9E6E6573D5919?sequence=1.
- Kostas kokkotas, Field Theory.
- James, B. Hartle, Gravity and introduction to Einstein’s General Relativity.
- Charles, W. Misner, Kip S. Thorne and Jhon Archibald Wheelher, Gravitation.
- Benito Marcote, Cosmologia Cuantica y creacion del universe.
- Carlos Rovelli, Quantum Gravity.
- Vinicius Miranda Bragança, Singularidades em teorias f(r) da gravitação. http://arcos.if.ufrj.br/teses/mestrado_vinicius_miranda.pdf.
- Laurent Pitre ∗, Mark D. Plimmer, Fernando Sparasci, Marc E. Himbert; 2019. Determinations of the Boltzmann constant. https://hal.science/hal-02166573/file/1-s2.0-S1631070518301348-main.pdf.
- ZEUS Collaboration, 2016. Limits on the effective quark radius from inclusive ep scattering at HERA. Accepted for publication in Physics Letters B. https://arxiv.org/pdf/1604.01280.pdf.
- María José Herrero, Física de Partículas, el acelerador LHC y el bosón de Higgs.
- Wikipedia, Bose-Einstein condensate. https://en.wikipedia.org/wiki/Bose%E2%80%93Einstein_condensate.
- Cauê Muraro - Agência USP - 30/10/2007. Cientistas brasileiros criam átomo artificial. https://www.inovacaotecnologica.com.br/noticias/noticia.php?artigo=010160071030&id=010160071030.
- J. S. Farnes - Received 22 February 2018 / Accepted 20 October 2018. A unifying theory of dark energy and dark matter: Negative masses and matter creation within a modified ΛCDM framework. [CrossRef]
- Bernard Carr, and Florian Kühnel - Annual Review of Nuclear and Particle Science. Primordial Black Holes as Dark Matter: Recent Developments. https://www.annualreviews.org/doi/10.1146/annurev-nucl-050520-125911.
- D. T. Son - University of Washington. AdS/CFT correspondence and the Quark-Gluon Plasma. https://www.phenix.bnl.gov/WWW/publish/jfrantz/ou_nucl_lunch/DamTSon_lectures.pdf.
- Marc Kamionkowski and Adam, G. Riess. The Hubble tension and Early Dark Energy. https://arxiv.org/pdf/2211.04492.pdf.
- Luis Anchordoqui, Carlos Nuñez and Kasper Olsen. Quantum cosmology and AdS/CFT. https://arxiv.org/abs/hep-th/0007064.
Figure 1.
Vector representation of the forces in a black hole. Fc = f, represents the force towards the interior of the black hole generated by the mass m and Ft = -iφ, is a tangential force that retards Fc by 90 degrees, generated by the mass δ.
Figure 1.
Vector representation of the forces in a black hole. Fc = f, represents the force towards the interior of the black hole generated by the mass m and Ft = -iφ, is a tangential force that retards Fc by 90 degrees, generated by the mass δ.
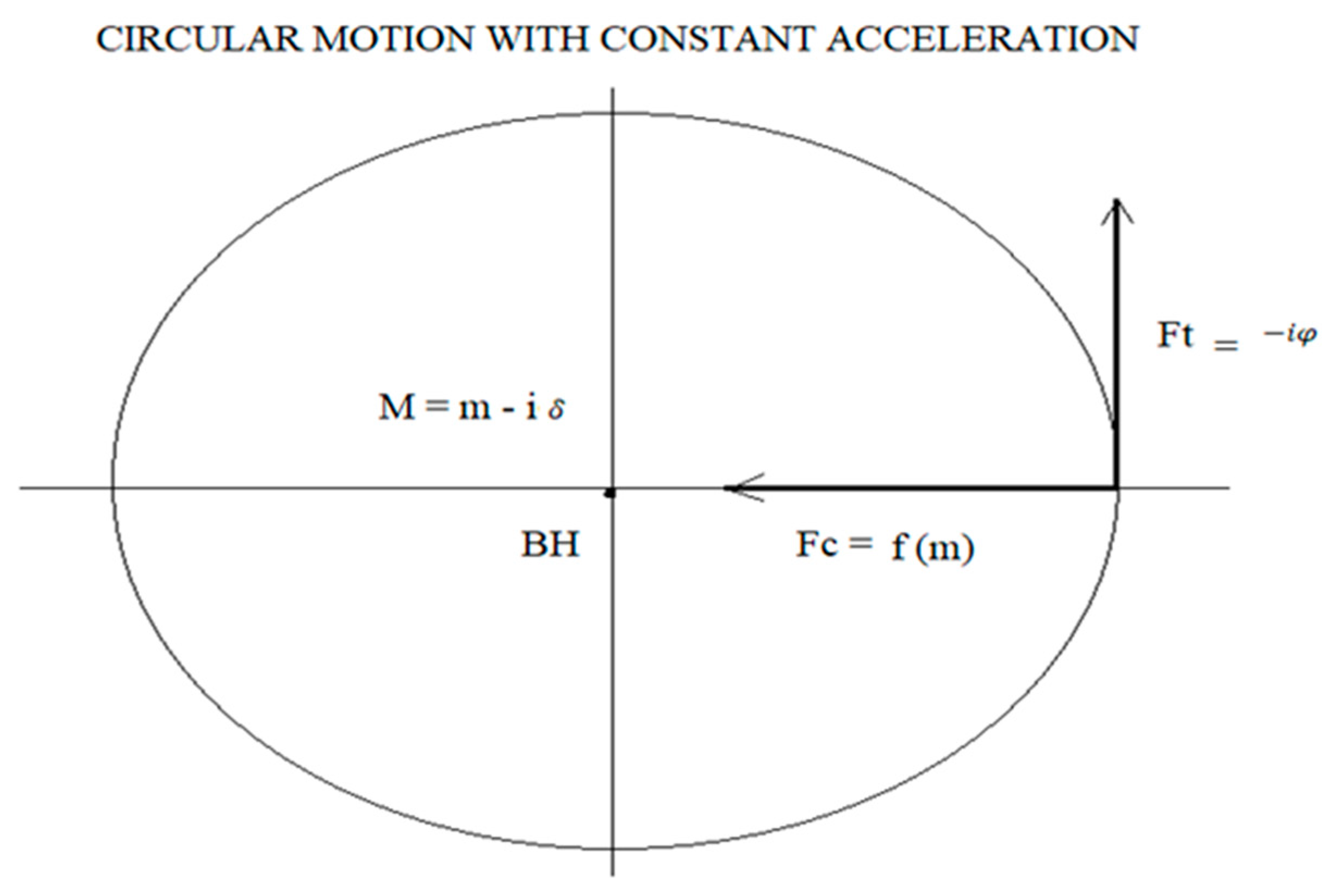
Figure 2.
Represents the variation of speed Cɢ, as a function of temperature T, inside a black hole.
Figure 2.
Represents the variation of speed Cɢ, as a function of temperature T, inside a black hole.
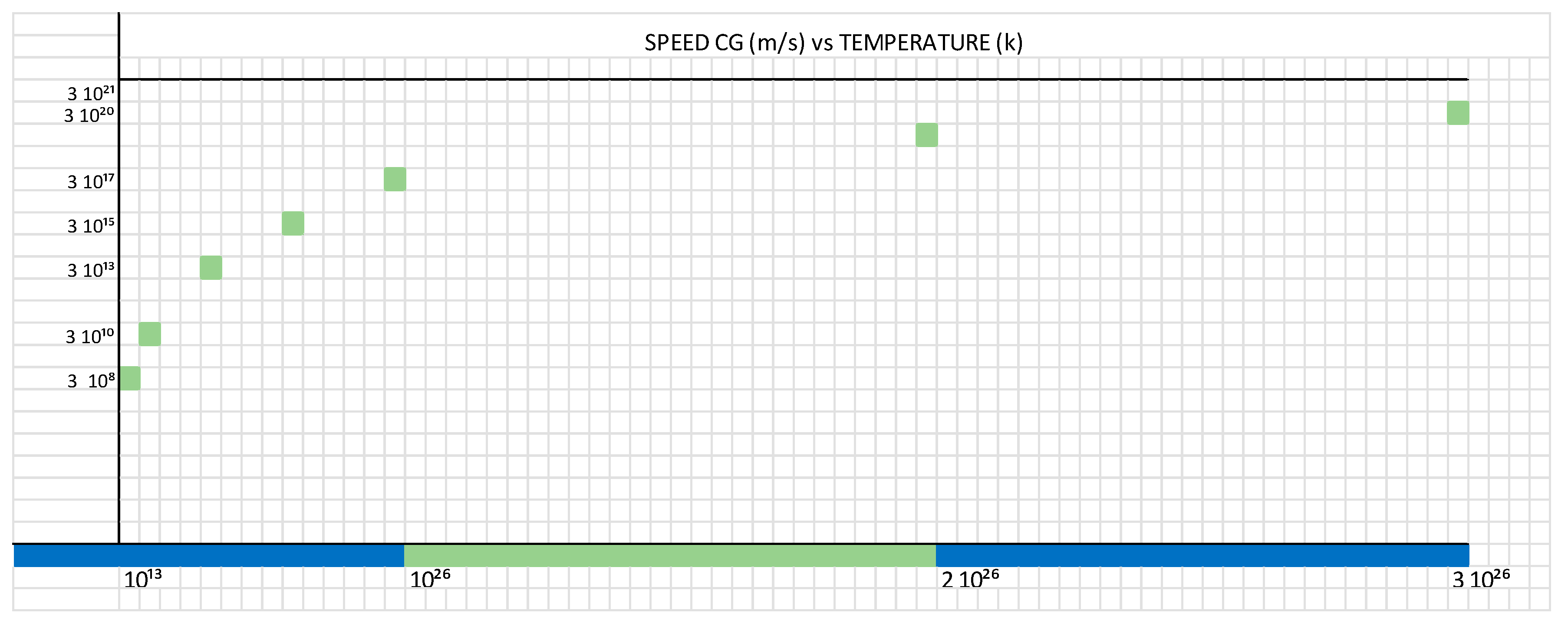
Figure 3.
shows the amplitude spectrum as a function of frequency at the top and the phase spectrum as a function of frequency at the bottom.
Figure 3.
shows the amplitude spectrum as a function of frequency at the top and the phase spectrum as a function of frequency at the bottom.
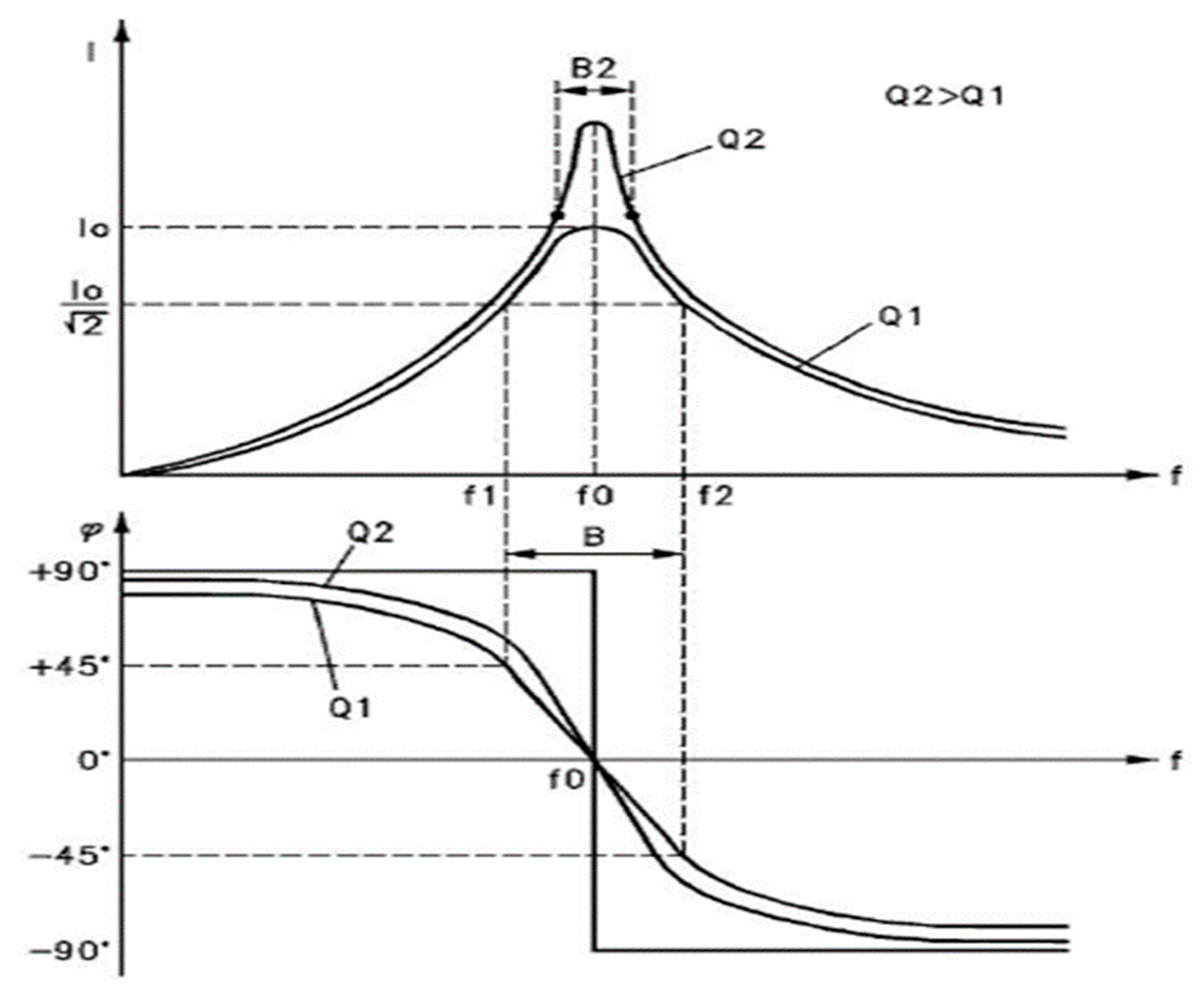
Figure 4.
CMB Power Spectrum.
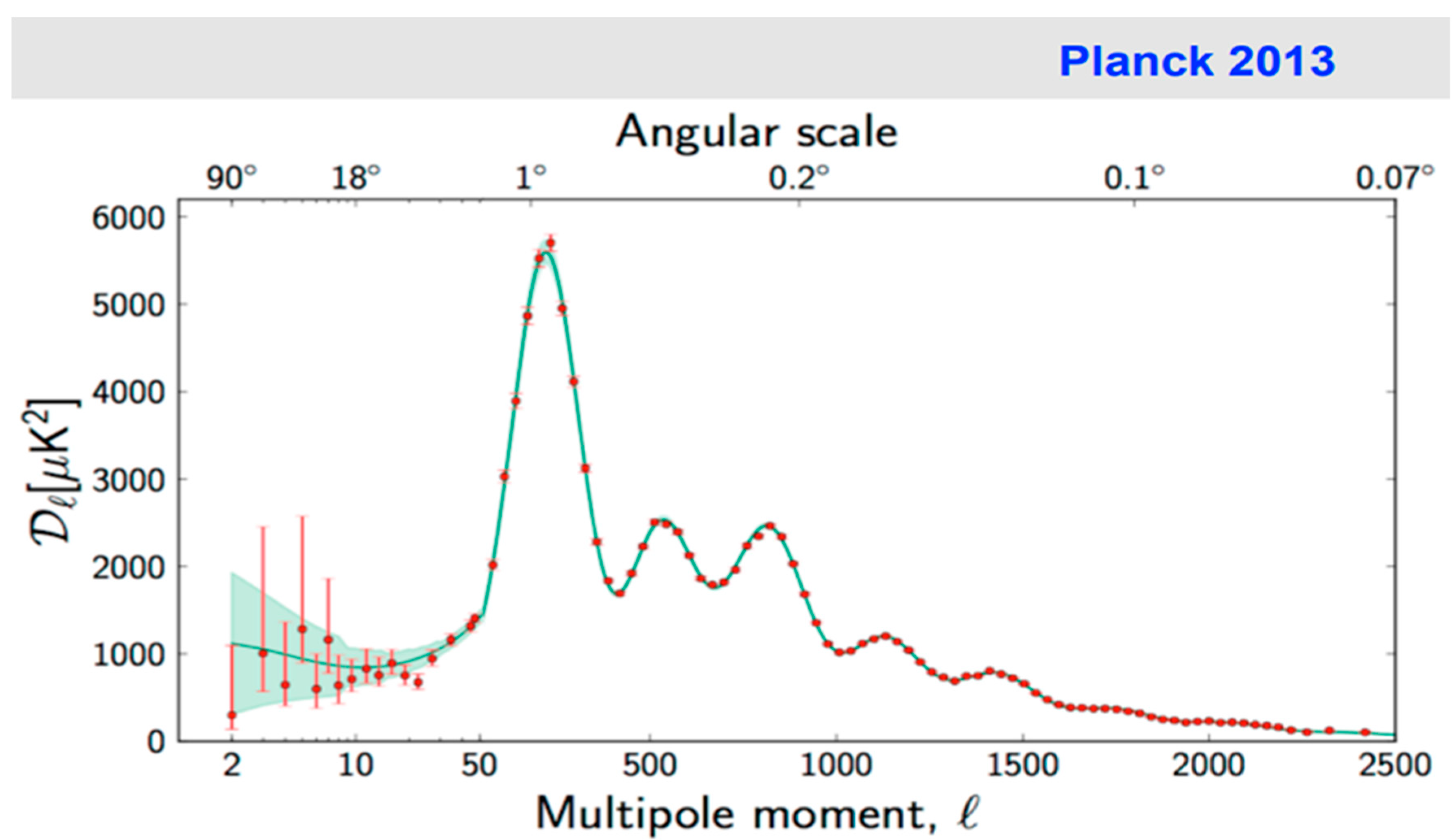
Figure 5.
For a frequency difference given by ω2 and ω1, we can observe that there is a phase difference, a time difference and therefore a displacement difference IΔtI.
Figure 5.
For a frequency difference given by ω2 and ω1, we can observe that there is a phase difference, a time difference and therefore a displacement difference IΔtI.
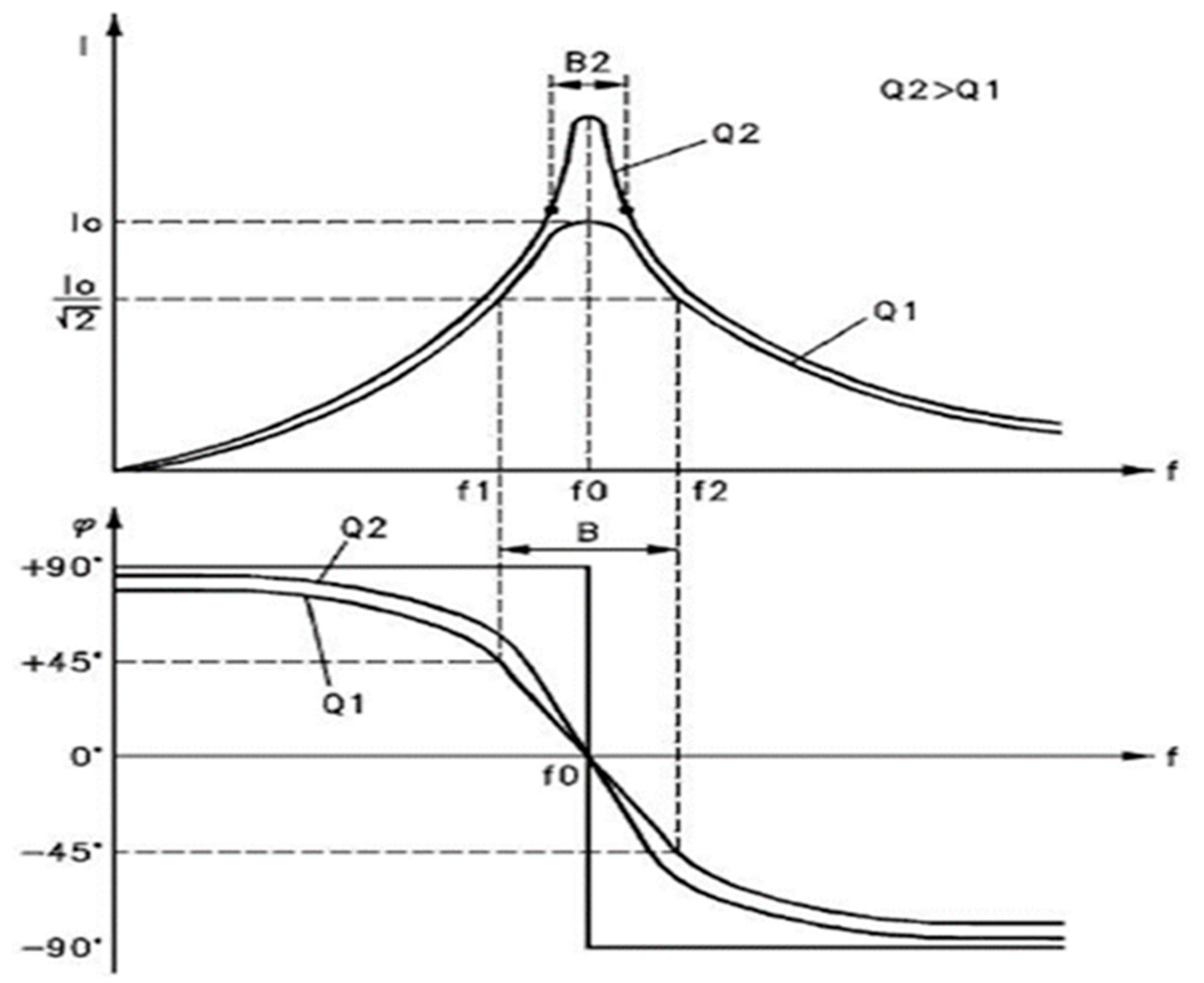
Figure 20.
The power spectrum of the CMB acoustic waves.
Figure 21.
Spectrum of gravitational waves produced in the era of cosmic inflation, ω0 is the resonant or fundamental frequency, ω1 is the low cut-off frequency and ω2 is the high cut-off frequency. The time t corresponds to the moment when the amplitude spectrum reaches 2.7 K.
Figure 21.
Spectrum of gravitational waves produced in the era of cosmic inflation, ω0 is the resonant or fundamental frequency, ω1 is the low cut-off frequency and ω2 is the high cut-off frequency. The time t corresponds to the moment when the amplitude spectrum reaches 2.7 K.
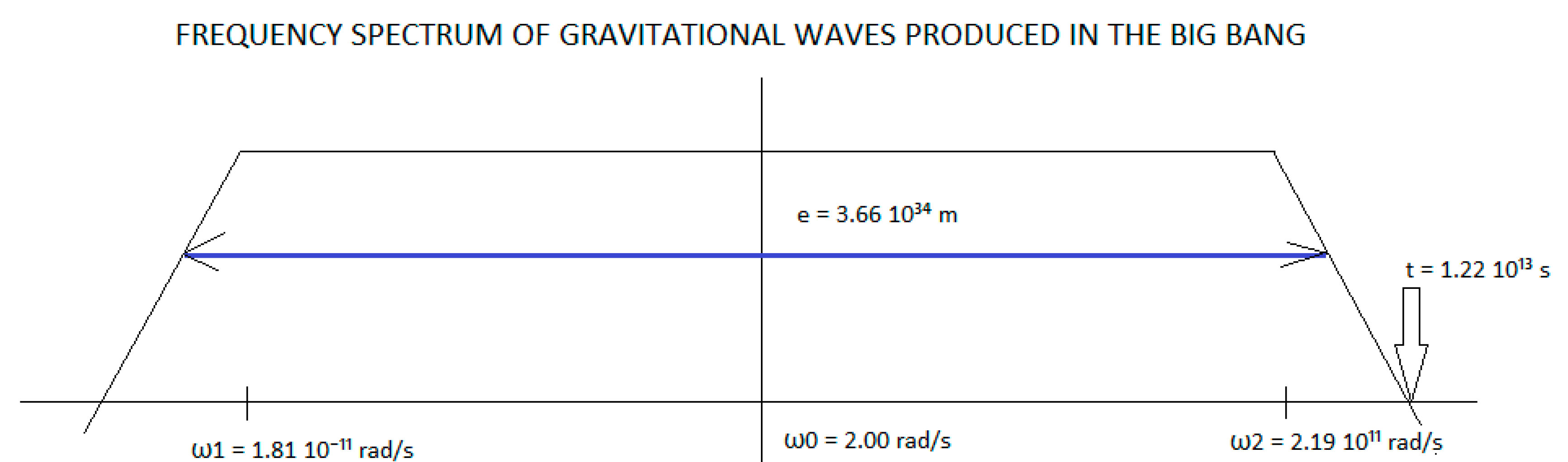
Figure 22.
In blue, it represents the energy contribution of gravitational waves as a function of time, it is observed for t = 10²⁶ s, the energy contribution of gravitational waves becomes zero (0).
Figure 22.
In blue, it represents the energy contribution of gravitational waves as a function of time, it is observed for t = 10²⁶ s, the energy contribution of gravitational waves becomes zero (0).
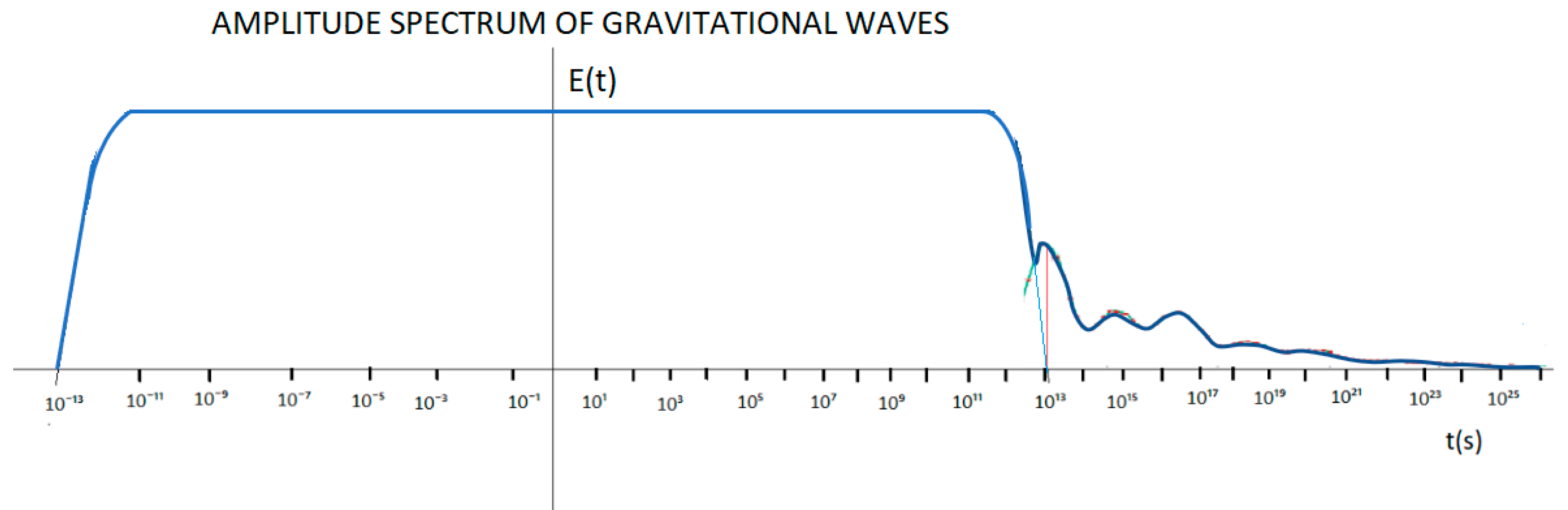
Figure 23.
In orange, it represents the variation of the Hubble’s constant as a function of time, for t = 10²⁶ s, the Hubble’s constant becomes zero (0).
Figure 23.
In orange, it represents the variation of the Hubble’s constant as a function of time, for t = 10²⁶ s, the Hubble’s constant becomes zero (0).
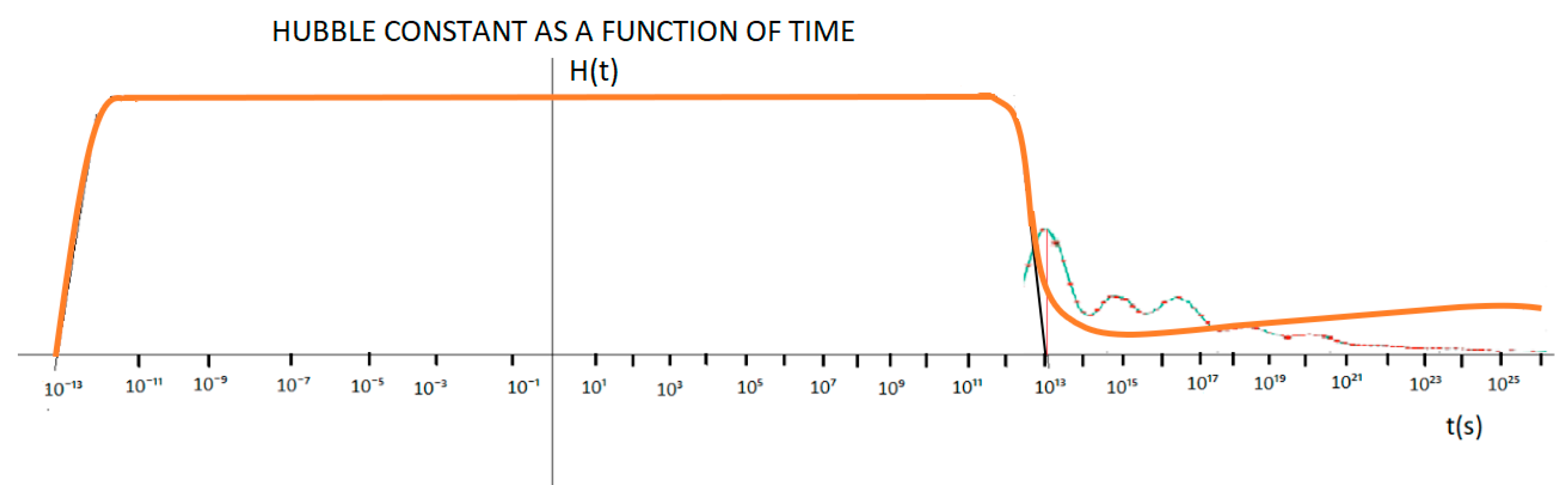
Table 1.
Represents values of ImI, baryonic mass; IδI, dark matter mass; IMI, mass of baryonic matter plus the mass of dark matter; IEmI, energy of baryonic matter; IEδI, dark matter energy; IEI, Sum of the energy of baryonic matter plus the energy of dark matter and Rs, Schwarzschild’s radius, as a function of, c, speed of light; Cɢ, speed greater than the speed of light; T, temperature in Kelvin; using the parametric equations.
Table 1.
Represents values of ImI, baryonic mass; IδI, dark matter mass; IMI, mass of baryonic matter plus the mass of dark matter; IEmI, energy of baryonic matter; IEδI, dark matter energy; IEI, Sum of the energy of baryonic matter plus the energy of dark matter and Rs, Schwarzschild’s radius, as a function of, c, speed of light; Cɢ, speed greater than the speed of light; T, temperature in Kelvin; using the parametric equations.

Table 2.
we represent the range of variation of the velocity C, the Planck’s length, the Planck’s time and the Planck’s temperature.
Table 2.
we represent the range of variation of the velocity C, the Planck’s length, the Planck’s time and the Planck’s temperature.
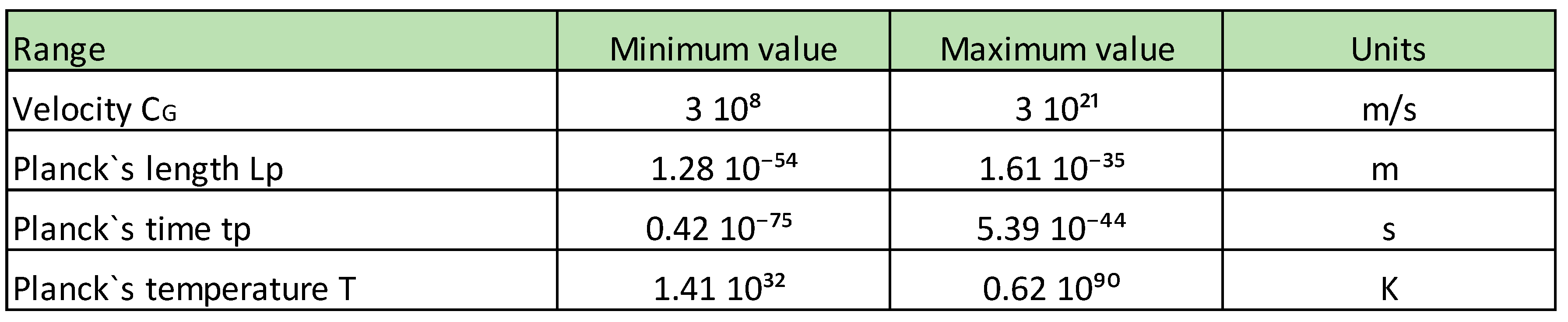
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





