Prerpints.org logo
Preprint
Article

End-to-end 3D Human Pose Estimation using Dual Decoders

Altmetrics

Downloads

200

Views

48

Comments

0

This version is not peer-reviewed

Submitted:

31 May 2023

Posted:

01 June 2023

You are already at the latest version

Alerts
Abstract
Existing methods for 3D human pose estimation mainly divide the task into two stages. The first stage identifies the 2D coordinates of the human joints in the input image, namely the 2D human joint coordinates. The second stage uses the results from the first stage as input to recover the depth information of human joints from the 2D human joint coordinates to achieve 3D human pose estimation. However, the recognition accuracy of the two-stage method relies heavily on the results of the first stage and includes too many redundant processing steps, which reduces the inference efficiency of the network. To address these issues, we propose the EDD, a fully End-to-end 3D human pose estimation method based on transformer architecture with Dual Decoders. By learning multiple human poses, the model can directly infer all 3D human poses in the image using a pose decoder, and then further optimize the recognition result using a joint decoder based on the kinematic relations between joints. With the attention mechanism, this method can adaptively focus on the most relevant features to the target joint, effectively overcoming the feature misalignment problem in the human pose estimation task and greatly improving the model performance. Any complex post-processing step, such as non-maximum suppression, is eliminated, further improving the efficiency of the model. The results show that the method achieves an accuracy of 87.4% on the MuPoTS-3D dataset, significantly improving the accuracy of end-to-end 3D human pose estimation methods.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Vision and Graphics

1. Introduction

3D human pose estimation aims to estimate the coordinates of human joints in 3D space by inputting an image or video. It is an important task in the field of computer vision and artificial intelligence, and is widely used in areas such as action recognition [1,2,3], robotics [4,5,6], and animation [7,8,9], and can also provide information for other computer vision tasks. Currently, 3D human pose estimation methods can be broadly divided into two categories: two-stage 3D human pose estimation method and end-to-end 3D human pose estimation method.
The two-stage method splits the overall procedure into two stages. The first stage is to recover the coordinates of human joints in the 2D plane from the input image, which is a 2D human pose estimation task. The second stage takes the results of the first stage as input and recovers the human joint coordinates in 3D space from the 2D human joint coordinates. The two-stage method can reduce the overall task complexity. The task of mapping the joint coordinates from 2D to 3D is relatively easy. It can not only use the currently well-established 2D human pose estimation method in the first stage, but also introduce semi-supervised learning via back-projection in the second stage. The idea of the two-stage method was first proposed by Chen [10] in 2017. They consider 3D human pose estimation as two parts: 2D human pose estimation and 2D human pose matching to 3D human pose. They first used CPM (Convolutional Pose Machine) for 2D human pose estimation and then used the nearest neighbor matching method to find the closest 3D human pose in the training set. This method can achieve good accuracy only when the training set is sufficiently large and contains a rich variety of actions. However, in the two-stage method, the lack of raw image input in the second stage may lead to the loss of spatial information related to the image, which is unfavorable for the recovery of coherent content such as joint depth, and may affect the accuracy of the recognition results. Moreover, the error in the 2D pose estimation in the first stage can be further amplified in the second stage.
The end-to-end method mainly takes the image as the network input and predicts the coordinates of human body joints directly in the three-dimensional plane through a neural network model. Compared with the two-stage method, the end-to-end method can consider the rich spatial information in the original image, which is beneficial to improving the recognition accuracy of the output results. However, it loses the supervision information brought by the 2D joint coordinates, making the overall prediction more difficult. Inspired by the hourglass network structure used in 2D human pose estimation, [11] proposed to represent human pose in 3D space using heatmaps of the keypoints. To reduce the memory consumption associated with storing 3D data, a method was adopted to gradually increase the resolution in the depth dimension. However, existing end-to-end method mainly use traditional convolutional neural networks for 3D human pose estimation, which cannot consider global depth information, resulting in poor recognition accuracy. The recognition accuracy is lower than that of two-stage 3D human pose estimation method, and there are too many redundant post-processing steps, which cannot achieve a completely end-to-end method.
We propose a Transformer-based end-to-end 3D human pose estimation framework using dual decoders to address the issues in existing method. By combining human pose prediction with fine-grained body joint localization and exploiting the attention mechanism, we leverage the global spatial information of the image to improve the accuracy of the recognition results. Given multiple randomly initialized human poses, we extract human features from the image using a feature extraction network and feature encoder, and use a pose decoder to infer multiple human object perception instances, i.e., 3D human joint coordinates, based on the image’s human features and spatial information. Then, through a joint decoder, we explore the kinematic relationships between different joints belonging to the same object instance for more refined optimization. Moreover, this framework does not rely on existing 2D human pose models and does not contain any redundant post-processing steps to achieve fully end-to-end 3D human pose estimation.
Our contributions are summarized as follows.
  • We introduce the pelvic point as the root node and predict the relative depth of the other nodes with respect to the root node to reduce the prediction difficulty. Moreover, we design multiple encoder-decoder modules to gradually improve the prediction accuracy of point depth.
  • We introduce the Transformer architecture to achieve complete end-to-end processing without any redundant post-processing. In addition, we propose dual decoders to gradually improve the recognition accuracy of the network.
  • To the best of our knowledge, our method outperforms all known end-to-end methods and most two-stage methods in predicting the relative depth of 3D human joint points on the MuPoTs-3D dataset.

2. Related Work

2.1. 3D Human Posture Estimation

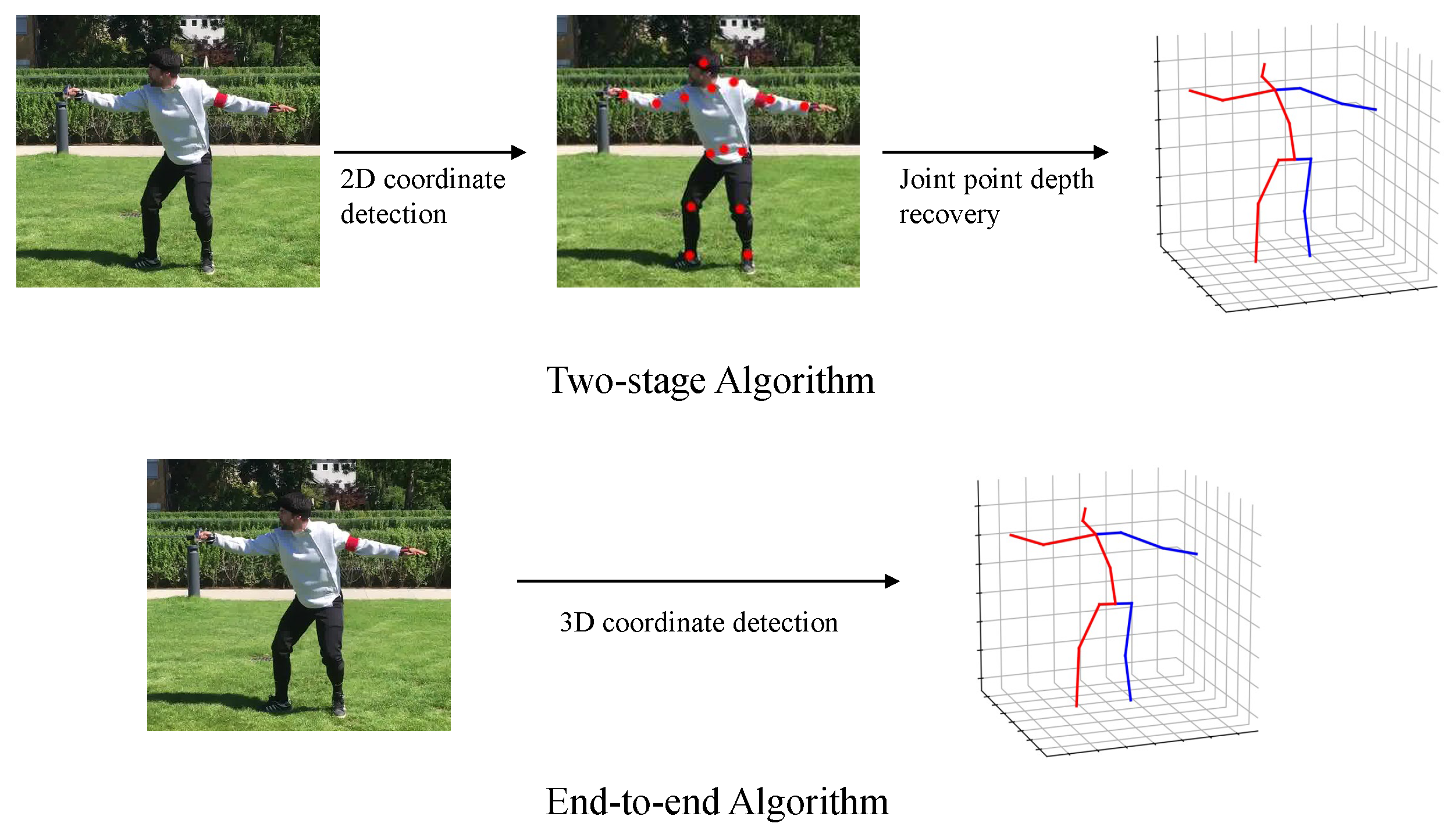
A comparison of two common methods for 3D human pose estimation is shown in Figure 1.
Two-stage Method. The two-stage method uses the existing 2D human pose estimation as the first stage, and then lifts the 2D human pose estimation results to 3D pose as the second stage. [12] proposed a simple but effective fully connected residual network structure based on regressing 3D joint coordinates from 2D joint coordinates, demonstrating that the 2D-3D stage is the main problem of 3D human pose regression. Despite achieving state-of-the-art results at the time, over-reliance on 2D pose detectors may result in blurry reconstructions. [13] proposed a pose grammar to solve the 3D human pose estimation problem. The network model includes a basic network that effectively captures pose alignment features and a top-level bidirectional RNN (recurrent neural network) hierarchy that takes 2D poses as input and incorporates knowledge about human configurations (kinematics, symmetry, motion coordination) to learn a generalized 2D-3D mapping function.
Due to the excellent performance of existing 2D human pose detectors, the results of two-stage methods are generally better than those of end-to-end methods. However, due to the high reliance on the first stage prediction result, which is the 2D human pose estimation, any errors or mistakes in the first stage will become more apparent in the second stage. Another issue is that some information in the original image, such as spatial information, may be lost after the first stage, which may lead to inaccurate predictions in the second stage.
End-to-end Method. The end-to-end method takes the image as input data for the model and directly predicts the coordinates of the human keypoints in 3D space. Li [14] first proposed a deep convolutional neural network for 3D human pose estimation from monocular images in 2014. Using a joint training and pre-training strategy, they predict the 3D spatial coordinates of human keypoints directly from RGB images. Pavlakos [15] proposed an end-to-end framework for estimating 3D human pose and shape from monochrome images, by introducing the SMPL (Skinned Multi-Person Linear) model to accurately represent human poses in 3D space with fewer parameters, which is beneficial for network training. However, this method includes redundant post-processing steps and does not achieve a full end-to-end implementation.

2.2. Transformer in Vision

Transformer is an attention mechanism based encoder-decoder model that was initially applied with great success in fields such as natural language processing. In recent years, many works have attempted to apply the Transformer architecture to computer vision tasks, showing good performance and demonstrating its effectiveness in the three fundamental tasks of computer vision (classification, detection, and segmentation) as well as with multi-sensor data ,such as images, point clouds, and vision-language data.
ViT [16] applies the Transformer architecture to encode sequences of image patches for image classification, with a simple and effective model and strong scalability, demonstrating that Transformer architecture outperforms CNN(Convolutional Neural Network) when enough data is available for pre-training. DETR [17] and Deformable DETR [18] adopt the Transformer architecture, combined with the Hungarian method and bipartite matching, to achieve end-to-end object detection. SOIT [19] uses the Transformer architecture and a decoder to directly predict a series of binary masks, effectively eliminating the need for many hand-crafted components. Building on the power and effectiveness of the Transformer architecture, we propose a fully end-to-end 3D human pose estimation method by combining the Transformer structures using Dual Decoders.

3. Methodology

3.1. Overall Architecture

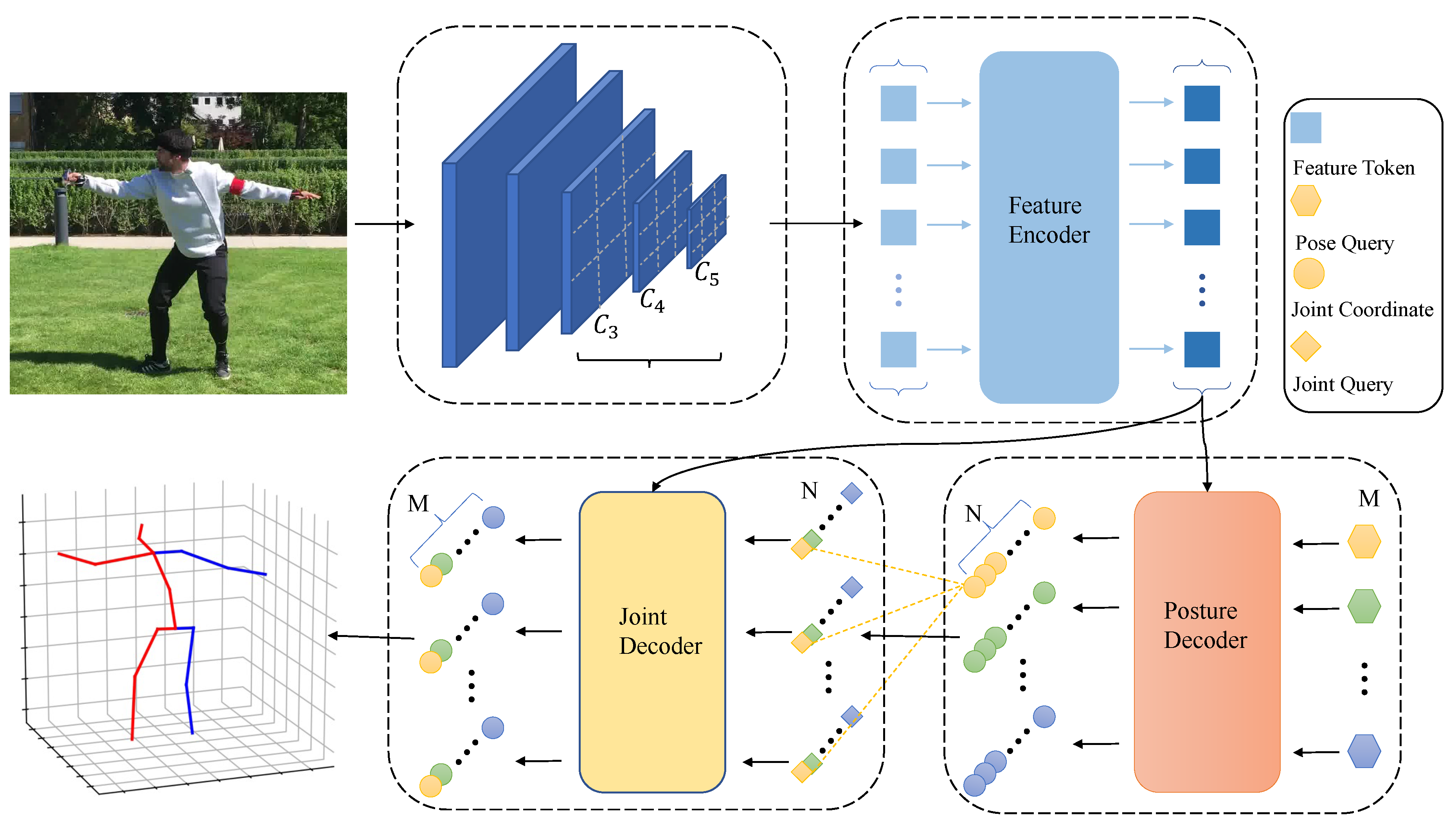
As shown in Figure 2, the framework proposed in this paper consists of four main parts: feature extraction network, feature encoder, posture decoder, and joint decoder. The feature extraction network is used to extract multi-scale feature maps from the image, the feature encoder is used to refine the multi-scale feature maps, the pose encoder is used to directly predict the 3D joint coordinates of the human object contained in the image, and the joint decoder is used to further refine the human pose obtained before at the joint level.
With an image as network input, the feature extraction network, i.e., backbone network, is used to extract multi-scale features from the image. The extracted feature maps are scaled to the same number of channels through fully connected layers and 1 × 1 convolutional layers, followed by flattening and concatenation. Then, the concatenated features are fed into the feature encoder, which outputs further refined features without changing the size and number of channels of the feature maps. Afterwards, multiple randomly initialized human poses and the refined features are given as input to the pose decoder, which outputs the 3D joint coordinates of multiple inferred human instances and their corresponding confidence scores. Finally, each human instance is treated as a whole and fed into the joint decoder for further optimization of each human pose.
We select ResNet-50 [20] as the feature extraction network, give an image I ∈ R H × W × 3 , extract multi-scale feature maps C 3 , C 4 and C 5 from the last three stages of backbone, whose dimensions are 1 8 , 1 16 and 1 32 , respectively. Then, the channel number of each feature map is uniformly mapped to 256 through the full connection layer and the 1 × 1 convolution layer, and then the flattening process is performed to obtain the feature tokens C 3 ′ , C 4 ′ and C 5 ′ . The shape of feature tokens C l ˙ ′ i ∈ 3 , 4 , 5 is L i × 256 ( L i = H 2 i × W 2 i ) , respectively. Next, we perform the stitching operation to obtain the input F of the feature encoder, whose shape is ∑ i = 3 5 L i × 256 .

3.2. Feature Encoder

For object detection and recognition tasks, high-resolution and multi-scale feature maps are particularly important. However, increasing the resolution affects the computational complexity and inference performance of the model and requires more memory. For typical multi-head self-attention mechanisms, their computational and memory complexity increases quadratically with the input feature map size. In [18], a deformable attention module was proposed that takes advantage of the sparse spatial sampling capability of deformable convolution [21] and the correlation modeling ability of the Transformer architecture. This module can accelerate network convergence, reduce computational complexity, and improve the ability to detect small objects. Therefore, in this paper, deformable attention modules are used as the basic units in the encoder and decoder.
As shown in Figure 3, the feature encoder consists of six identical encoder layers stacked in sequence, and each encoder layer mainly includes deformable multi-head self-attention module and feedforward neural network. The input and output of the encoder are multi-scale feature maps with the same resolution. For the deformable attention module, the input consists of three parts: query, key, and value. Both the query and the key are pixels in the multi-scale feature map, and for each pixel in the query, its reference point is itself.
Due to the flattening and concatenation process, hierarchical embeddings are added in addition to the position embeddings in order to identify the level of the feature map where each pixel is located. For position embeddings with fixed encoding, layer embeddings are randomly initialized and jointly trained with the network.

3.3. Posture Decoder

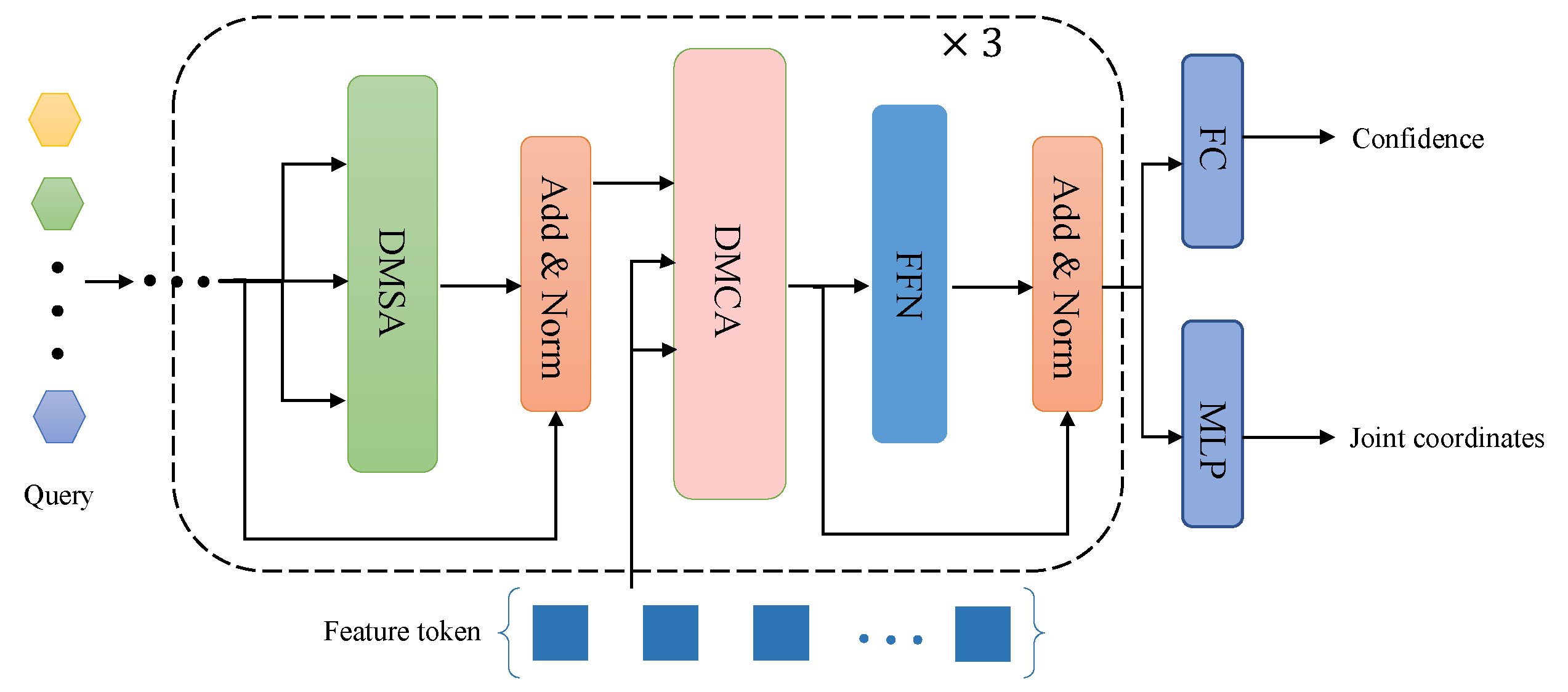
The pose decoder takes the refined features and M randomly initialized human poses as inputs and outputs the predicted keypoint coordinates of M human instances detected by the model. Since the number of human instances in an image is unknown and cannot be pre-defined, the output of the model includes a confidence score for each detected instance, indicating the reliability of the prediction. The predicted predictions are filtered out by setting a confidence score threshold. M denotes the maximum number of possible human instances in an image, which is set to 100 during training for computational efficiency. Similar to the feature encoder, the pose decoder also utilizes deformable attention module to construct the network, which helps to reduce the computational complexity.
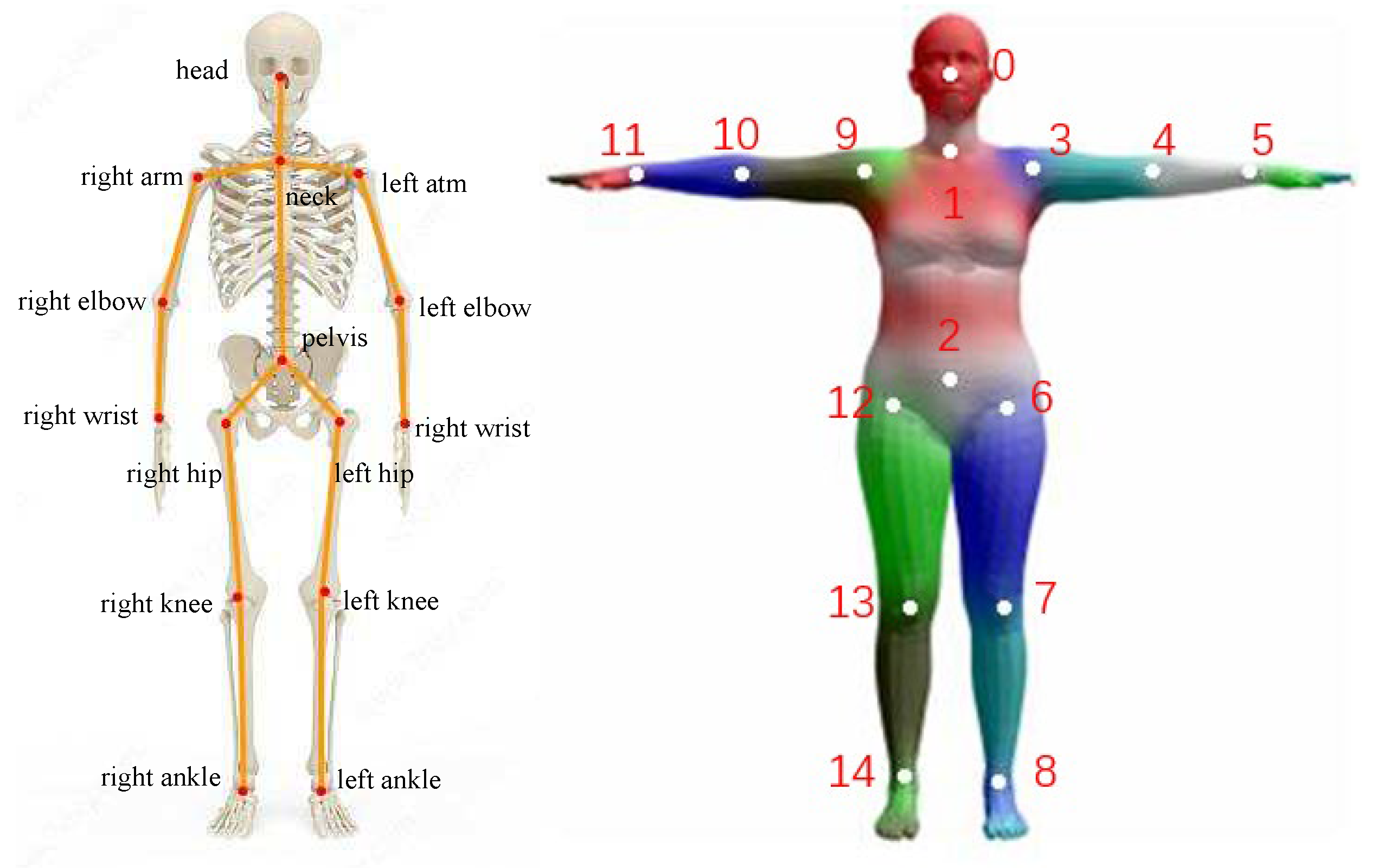
The specific details are shown in Figure 4, where the input consists of M randomly initialized query, Q p o s e ∈ R M × D , Where D represents the dimension of the query. The output of the pose encoder is represented as M groups of human body joint coordinates, denoted as p i i = 1 M ∈ R M × 3 k , and p i = x i j , y i j , Z i j j = 1 m represents the coordinate x , y and joint point depth Z of the m-th joint point of the i-th person in two-dimensional space. During the training process, an N = 15 point skeleton model was selected to represent the human posture, and the pelvis point was selected as the root node, with a constant depth of zero. The depth of the remaining nodes is relative to the pelvis point. The skeleton model is shown in Figure 5.
According to 2D coordinates and joint point depth, 3D posture can be restored through perspective camera models.
X , Y , Z T = Z K − 1 x , y , 1 T ,
where X , Y , Z T and x , y T represent the coordinates of joint points in three-dimensional and two-dimensional space, respectively, and K is the camera internal parameter matrix.The K is formulated as follows.
K = f 0 0 0 f 0 0 0 1 ,
where f represents the camera focal length, which is provided by the dataset during training. For Internet images with unknown focal length, the pixel width of the input image is used to represent the camera focal length since the choice of focal length does not affect the predicted relative depth relation between people.
The pose decoder consists of three identical decoder layers stacked together, each encoder layer consisting of a deformable auto-attention module, a deformable cross-attention module, and a feed-forward network. Self-attention modules are used to interact with each other’s features, and cross-attention modules are used to extract features from multiple features.The query features output by the decoder layer are fed into multiple regression branches. In, the pose prediction regression branch uses a multi-layer perceptron with channel number 256 to predict the relative offset and corresponding depth of N reference points, and the classification prediction regression branch predicts the confidence score of each object through a fully connected layer.
Inspired by the [18], Instead of using a decoder of the final layer to predict the final coordinates of keypoints, we estimate the coordinates of keypoints gradually by using multiple decoder layers. Specifically, each layer refines the pose based on the prediction of the previous layer. Assuming that the output posture of the decoder in layer d − 1 is P d − 1 , the optimized output of the d-th decoder layer is formulated as follows.
P d = σ σ − 1 P d − 1 + Δ P d ,
where Δ P d represents the offset predicted by the d-th decoder layer, σ and σ − 1 represents the sigmoid activation function and the inverse sigmoid activation function, respectively, used to constrain the parameter range during network training. In this way, P d − 1 serves as a new reference point for the cross attention module of the d-th decoder layer. Initial reference point P 0 is a randomly initialized coordinate that is updated with model parameters during training. Therefore, the progressive deformable cross attention module can focus on the visual features most relevant to the target key points, overcoming the feature misalignment problem.

3.4. Joint Decoder

Joint decoder is used to explore the structured relationships between joints and further refine the overall posture at the joint level. Deformable attention modules are also used to construct joint decoder. Given N randomly initialized query, Q j o i n t = R N × D , where D represents the dimension of the query, and the joint decoder obtains each full body posture predicted by the posture decoder as an initial reference point, and then further refines the joint point coordinates.
The specific details of the joint decoder are shown in Figure 6. Similar to the pose decoder, the self-attention module is used to interact features with each other, and the cross-attention module is used to extract features from multi-scale features. Subsequently, the joint prediction regression branch uses a multi-layer perceptron to predict the displacement of the joint. Also adopting a step-by-step prediction method, assuming J d − 1 is the normalized prediction result of the d − 1 decoder layer, the prediction result of the d-th decoder layer is formulated as follows.
J d = σ σ − 1 J d − 1 + Δ d .

3.5. Training and Inference

To accelerate the convergence speed of the network during training, various loss functions are used to constrain the model. To ensure that each true pose has a unique predicted value corresponding to it during the training process, Hungarian matching [18] is used for constraint.
Heatmap Loss During training, intermediate supervision is performed using heatmap loss, which only constructs heatmaps for the coordinates of human keypoints in two-dimensional space. The ultimate task of keypoint detection is still to output the coordinates of predicted keypoints. However, directly optimizing the network to output two-dimensional coordinates is a nonlinear process, and the constraint of the loss function on the weights is relatively weak. By constructing heatmap loss, the network can be guided to learn better.
Similarly, the deformable attention module is used to construct the heatmap branch. The feature map C 3 is selected and restored to its original size, and the final predicted heatmap size is F 3 ϵ R H 8 × W 8 × D .Then, a variation of the focal loss function proposed by [22] is used to calculate the loss between the true value and the predicted value, which is denoted by L h m .
Linear Regression Loss Each decoder layer’s output in the pose decoder and joint decoder is constrained using L1 loss, including the coordinates and depth of keypoints. The difference between the predicted values and the true values is calculated, denoted by L r e g , with the formula expressed as follows.
L r e g = ∑ i = 1 N V P r e d − V t r u t h N ,
where N represents the number of human joint points, set to 15 during training, V P r e d represents the predicted value of the network, V t r u t h represents the groundtruth of the joint point coordinates and depth.
OKS Loss The most commonly used L1 loss has different scales for small and large poses, meaning that the loss calculation for large poses results in a larger value with the same relative error. To alleviate this issue, the OKS (object keypoint similarity) loss is used simultaneously for the coordinates of keypoints. The result is denoted by L o k s , with the formula expressed as:
The most commonly used L1 loss has different scales for small and large attitudes, meaning that with the same relative error, the loss calculation results for large attitudes are greater. To alleviate this problem, the similarity loss of object key points is used simultaneously for joint point coordinates. Result in L o k s represents, and the formula is formulated as follows.
L o k s = ∑ i = 1 N exp − V i − V i * / 2 s 2 k i 2 δ v i > 0 ∑ i = 1 N δ v i > 0 ,
among them, V i − V i * is the Euclidean distance between the predicted value and the groundtruth of the i i joint point, v i is a sign of whether the true value is visible, s is the area of the human instance, and k i is a constant coefficient that controls the weights of different joint points. The loss of similarity between object key points comprehensively considers the area of human instances and the importance of different joint points.
Overall Loss The overall loss function of the model is formulated as follows.
L = λ 1 L h m + λ 2 L r e g + λ 3 L o k s ,
where λ 1 , λ 2 and λ 3 represents the weight of different losses respectively.
During inference, given an image, the backbone network extracts features from the image and uses the feature encoder to obtain feature tokens. Then, the pose decoder predicts M-person object instances. In the inference process, M = 100 is set, and then joint decoding is used to further refine each person object instance. Based on the confidence level, the 2D human keypoint coordinates and depth information are taken for each keypoint of the first 10 human object instances, and the final 3D human pose keypoint coordinates are obtained using the camera coordinate formula and the final result is output.

4. Experimental

To fully train the network, a method of mixed dataset is used during training, referring to SMAP [23]. Specifically, the COCO [24] dataset and the MuCo-3DHP [25] dataset are mixed together and unified in format. Since the COCO dataset is a 2D human pose annotation dataset and does not include 3D keypoint coordinates and camera intrinsics, the depth-related loss is set to zero when calculating the loss if the image comes from the COCO dataset. During testing, the MuPoTS-3D [25] dataset is used.
Dataset. The MuCo-3DHP (Multiperson Composited 3D Human Pose) dataset is a large-scale training dataset of complex and realistic images containing multiple person interactions and occlusions, synthesized artificially. MuCo-3DHP uses single-person image data of real people from the MPI-INF-3DHP [26] dataset and employs a series of synthesis and enhancement measures to synthesize corresponding multiple-person interaction images, covering a range of simulated scenarios such as overlapping and activities between people, and comes with complete 3D pose annotations.
The MuPoTs-3D (Multiperson Pose Test Set in 3D) dataset is a 3D human pose dataset consisting of over 8,000 frames of images from 20 real-world scenarios (5 indoor and 15 outdoor), with up to three subjects in each image. This dataset is specifically used for testing and does not participate in the network training process.
Evaluating Indicator. The standard evaluation metric is based on 3DPCK (3D Percentage of Correct Keypoints) [27], which is an extension of the PCK (Percentage of Correct Keypoints) metric commonly used in 2D human pose estimation. If the predicted value of a keypoint coordinate is within a sphere with the true value as the center and a specific threshold (15 cm in the experiment) as the radius, it is considered as a correct prediction. The final prediction result is the mean value of all keypoint prediction results. P C K r e l measures the relative pose accuracy with root alignment.
Training Details. The implementation of the model’s code is based on the open-source mmdetection [28] framework. Image augmentation includes changing the contrast, brightness, randomly cropping, flipping, and scaling the images (short side >= 400 pixels, long side <= 1400 pixels). The model uses Adam (Adaptive Moment Estimation) as the optimizer, with a base learning rate of 2 × 10 − 4 , a momentum of 0.9, and a weight decay of 1 × 10 − 4 . During training, 8 NVIDIA Tesla V100 GPUs are used, with a batch size of 16 and a total of 20 training epochs. The initial learning rate is reduced by a factor of 10 at the 10th and 15th epochs.
Testing Details. During the test, the input image size is adjusted to have a short side of 800 pixels and a long side of less than or equal to 1,333 pixels, followed by random flipping and padding. The model’s test results and test time are measured using a single NVIDIA Tesla V100 GPU.

5. Results

5.1. Result on Dataset

We compare our model with other two-stage methods and end-to-end methods on the MuPoTs-3D dataset. As shown in Table 1, when using the same backbone network as the feature extractor, our method surpasses all existing end-to-end methods and most two-stage methods, achieving a recognition rate of 87.4 on the MuPoTs-3D dataset.
Comparison with State-of-the-Art methods. Our end-to-end method achieve 87.4 P C K r e l . Compared with the existing two-stage methods, it surpasses the vast majority of existing two-stage methods, including Lcr-net [29], XNect [30], CDMP [27], Pi-net [31], etc., and is only two percentage points lower than 3DPose [25], which is the state-of-the-art two-stage method. Note that our method is NMS-free which make it more efficient compared with these two-stage methods. Compared with the existing end-to-end methods, our method significantly outperforms existing end-to-end methods, such as Metha [25] and DRM [33]. The performance of our method is three points higher compared with DRM.
Analysis of experimental results. From the experimental results, it can be seen that the recognition is favorable for human keypoints with obvious features such as head and wrist, which is also attributed to the training method using the mixed dataset. However, the recognition of keypoints such as Hip and Neck is not as good as other existing methods.

5.2. Ablation Study

We perform multiple ablation experiments to analyze the effectiveness of the network structure and loss function on the MuPoTS-3D dataset.
Analysis of the Pelvis joint point. As described in Sec. Section 3.4, we use the pelvis point as the root node, where the depth of the root joint point is zero and denoted by the coordinate ( X p e l v i s , Y p e l v i s , Z p e l v i s = 0 ) , and the other joints are computed with respect to the root joint point to obtain the relative depth of all the joints. We perform an ablative analysis to explore the superiority of such representations.
We use 14 joint points (excluding pelvic points) for training, and directly calculate the relative depth of each key point, based on the relative depth provided by the MuCo-3DHP dataset. The experimental results are shown in Table 2, where it can be seen that the accuracy of the results decreases. The reason for the decrease in accuracy is the lack of a uniform point representation with zero depth, so we propose to use pelvis joint points as root nodes for prediction. On the one hand, it specifies that the depth of the plane in which the pelvic joint is located is zero, and on the other hand, using the pelvic joint as the root node can improve the accuracy of the recognition result due to the high accuracy of pelvic joint recognition. Therefore, we have demonstrated the rationality of using pelvic points as root nodes, which significantly improves the accuracy and stability of the prediction results.
Analysis of the Depth reasoning methods. As described in Sec. Section 3.3 and Section 3.4, According to [18], we use a step-by-step optimization method for each layer to progressively predict the 2D coordinates of the human joint points, but for depth we still employ a direct prediction method for each layer instead of a layer-by-layer optimization method. We perform an ablative analysis to explain the design rationale.
We also employ an iterative prediction method and prediction depth for training, as shown in the Table 2, it can be seen that there is no gain, but rather an increase in computational complexity and inference time. We use an iterative prediction method to predict 2D human joint points, since the prediction results of each decoder layer are correlated. Through optimization, we can better consider the features around the keypoints in the 2D plane and then locally optimize the coordinates of the keypoints. However, the depth correlation is not as good as the 2D keypoints and the optimization is limited.The range of depth variation is large and using an optimization method will actually limit the prediction results of the network. This is why we adopt a direct prediction method for depth, while using a progressive prediction method for 2D human keypoint coordinates.
Analysis of Other Designs. We also performed experimental analysis on other ideas, including using a model to directly predict the 3D coordinates of the human body instead of predicting the 2D coordinates and depth of the human body, and then using a camera coordinate system for the conversion. However, directly predicting the 3D joint point coordinates of the human body is less effective, and learning 3D features of the human body through images is more difficult than learning 2D joint point features of the human body. So in the end, we still adopt a method that predicts both the 2D human keypoints and the depth, which is different from the two-stage method, since the two-stage method first predicts the 2D human keypoints and predicts the depth of the joint points based on the prediction results. Therefore, our method remains end-to-end.

5.3. Visualization results

The results of our model are demonstrated in Figure 7. We selected images with different human poses to demonstrate the accuracy of the recognition results. It can be seen that our model can still fully recover the 3D spatial pose of the human body for different types of kinematic poses. It can also achieve good recognition results for certain complex poses, such as sit cross-legged.

6. Conclusion

In this paper, we propose a new 3D human pose estimation method named EDD based on the Transformer architecture and experimentally validate it. Using dual decoders during design to improve recognition accuracy. Considering the problems of existing two-stage methods and end-to-end methods, the Transformer architecture and self-attention mechanism are used to capture features of long-range dependencies, fully account for global spatial information, improve the recognition accuracy of the network, and remove redundant processing steps to achieve a fully end-to-end 3D human pose estimation model.

Funding

This research was funded by National Nature Fund No.62102039.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Pham, H.H.; Khoudour, L.; Crouzil, A.; Zegers, P.; Velastin, S.A. Skeletal movement to color map: A novel representation for 3D action recognition with inception residual networks. 2018 25th IEEE International Conference on Image Processing (ICIP). IEEE, 2018, pp. 3483–3487.
  2. Hassan, M.; Choutas, V.; Tzionas, D.; Black, M.J. Resolving 3D human pose ambiguities with 3D scene constraints. Proceedings of the IEEE/CVF international conference on computer vision, 2019, pp. 2282–2292.
  3. Sigal, L.; Isard, M.; Haussecker, H.; Black, M.J. Loose-limbed people: Estimating 3D human pose and motion using non-parametric belief propagation. International journal of computer vision 2012, 98, 15–48. [Google Scholar] [CrossRef]
  4. Yazdani, A.; Novin, R.S.; Merryweather, A.; Hermans, T. Occlusion-Robust Multi-Sensory Posture Estimation in Physical Human-Robot Interaction. arXiv preprint 2022, arXiv:2208.06494 2022. [Google Scholar]
  5. Zimmermann, C.; Welschehold, T.; Dornhege, C.; Burgard, W.; Brox, T. 3d human pose estimation in rgbd images for robotic task learning. 2018 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2018, pp. 1986–1992.
  6. Clever, H.M.; Kapusta, A.; Park, D.; Erickson, Z.; Chitalia, Y.; Kemp, C.C. 3d human pose estimation on a configurable bed from a pressure image. 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2018, pp. 54–61.
  7. Tsoli, A.; Mahmood, N.; Black, M.J. Breathing life into shape: Capturing, modeling and animating 3D human breathing. ACM Transactions on graphics (TOG) 2014, 33, 1–11. [Google Scholar] [CrossRef]
  8. Hasler, N.; Stoll, C.; Sunkel, M.; Rosenhahn, B.; Seidel, H.P. A statistical model of human pose and body shape. Computer graphics forum. Wiley Online Library, 2009, Vol. 28, pp. 337–346.
  9. Trumble, M.; Gilbert, A.; Malleson, C.; Hilton, A.; Collomosse, J. Total capture: 3d human pose estimation fusing video and inertial sensors. Proceedings of 28th British Machine Vision Conference, 2017, pp. 1–13.
  10. Chen, C.H.; Ramanan, D. 3d human pose estimation= 2d pose estimation+ matching. Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 7035–7043.
  11. Pavlakos, G.; Zhou, X.; Derpanis, K.G.; Daniilidis, K. Coarse-to-fine volumetric prediction for single-image 3D human pose. Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 7025–7034.
  12. Martinez, J.; Hossain, R.; Romero, J.; Little, J.J. A simple yet effective baseline for 3d human pose estimation. Proceedings of the IEEE international conference on computer vision, 2017, pp. 2640–2649.
  13. Fang, H.S.; Xu, Y.; Wang, W.; Liu, X.; Zhu, S.C. Learning pose grammar to encode human body configuration for 3d pose estimation. Proceedings of the AAAI conference on artificial intelligence, 2018, Vol. 32.
  14. Reddy, N.D.; Guigues, L.; Pishchulin, L.; Eledath, J.; Narasimhan, S.G. Tessetrack: End-to-end learnable multi-person articulated 3d pose tracking. Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2021, pp. 15190–15200.
  15. Pavlakos, G.; Zhu, L.; Zhou, X.; Daniilidis, K. Learning to estimate 3D human pose and shape from a single color image. Proceedings of the IEEE conference on computer vision and pattern recognition, 2018, pp. 459–468.
  16. Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S. ; others. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv preprint arXiv:2010.11929, arXiv:2010.11929 2020.
  17. Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-end object detection with transformers. Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, –28, 2020, Proceedings, Part I 16. Springer, 2020, pp. 213–229. 23 August.
  18. Zhu, X.; Su, W.; Lu, L.; Li, B.; Wang, X.; Dai, J. Deformable detr: Deformable transformers for end-to-end object detection. arXiv preprint arXiv:2010.04159, arXiv:2010.04159 2020.
  19. Cheng, B.; Schwing, A.; Kirillov, A. Per-pixel classification is not all you need for semantic segmentation. Advances in Neural Information Processing Systems 2021, 34, 17864–17875. [Google Scholar]
  20. He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778.
  21. Dai, J.; Qi, H.; Xiong, Y.; Li, Y.; Zhang, G.; Hu, H.; Wei, Y. Deformable convolutional networks. Proceedings of the IEEE international conference on computer vision, 2017, pp. 764–773.
  22. Li, S.; Chan, A.B. 3d human pose estimation from monocular images with deep convolutional neural network. Computer Vision–ACCV 2014: 12th Asian Conference on Computer Vision, Singapore, Singapore, -5, 2014, Revised Selected Papers, Part II 12. Springer, 2015, pp. 332–347. 1 November.
  23. Zhen, J.; Fang, Q.; Sun, J.; Liu, W.; Jiang, W.; Bao, H.; Zhou, X. Smap: Single-shot multi-person absolute 3d pose estimation. Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, –28, 2020, Proceedings, Part XV 16. Springer, 2020, pp. 550–566. 23 August.
  24. Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft coco: Common objects in context. Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, -12, 2014, Proceedings, Part V 13. Springer, 2014, pp. 740–755. 6 September.
  25. Mehta, D.; Sotnychenko, O.; Mueller, F.; Xu, W.; Sridhar, S.; Pons-Moll, G.; Theobalt, C. Single-shot multi-person 3d pose estimation from monocular rgb. 2018 International Conference on 3D Vision (3DV). IEEE, 2018, pp. 120–130.
  26. Mehta, D.; Rhodin, H.; Casas, D.; Fua, P.; Sotnychenko, O.; Xu, W.; Theobalt, C. Monocular 3d human pose estimation in the wild using improved cnn supervision. 2017 international conference on 3D vision (3DV). IEEE, 2017, pp. 506–516.
  27. Moon, G.; Chang, J.Y.; Lee, K.M. Camera distance-aware top-down approach for 3d multi-person pose estimation from a single rgb image. Proceedings of the IEEE/CVF international conference on computer vision, 2019, pp. 10133–10142.
  28. Chen, K.; Wang, J.; Pang, J.; Cao, Y.; Xiong, Y.; Li, X.; Sun, S.; Feng, W.; Liu, Z.; Xu, J. ; others. MMDetection: Open mmlab detection toolbox and benchmark. arXiv preprint arXiv:1906.07155, arXiv:1906.07155 2019.
  29. Rogez, G.; Weinzaepfel, P.; Schmid, C. Lcr-net: Localization-classification-regression for human pose. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017, pp. 3433–3441.
  30. Mehta, D.; Sotnychenko, O.; Mueller, F.; Xu, W.; Elgharib, M.; Fua, P.; Seidel, H.P.; Rhodin, H.; Pons-Moll, G.; Theobalt, C. XNect: Real-time multi-person 3D motion capture with a single RGB camera. Acm Transactions On Graphics (TOG) 2020, 39, 82–1. [Google Scholar] [CrossRef]
  31. Guo, W.; Corona, E.; Moreno-Noguer, F.; Alameda-Pineda, X. Pi-net: Pose interacting network for multi-person monocular 3d pose estimation. Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, 2021, pp. 2796–2806.
  32. Jin, L.; Xu, C.; Wang, X.; Xiao, Y.; Guo, Y.; Nie, X.; Zhao, J. Single-stage is enough: Multi-person absolute 3D pose estimation. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2022, pp. 13086–13095.
  33. Cheng, Y.; Wang, B.; Yang, B.; Tan, R.T. Monocular 3D multi-person pose estimation by integrating top-down and bottom-up networks. Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2021, pp. 7649–7659.
  34. von Marcard, T.; Henschel, R.; Black, M.; Rosenhahn, B.; Pons-Moll, G. Recovering Accurate 3D Human Pose in The Wild Using IMUs and a Moving Camera. European Conference on Computer Vision (ECCV), 2018.
Preprints 75231 g001
Figure 1. Comparison of two common methods for 3D human pose. The two-stage method identifies the 2D joint coordinates of the human body in the first stage and recovers the joint depth from the 2D joint coordinates in the second stage to obtain the 3D joint coordinates of the human body. An end-to-end method for directly obtaining 3D joint coordinates of the human body.
Figure 1. Comparison of two common methods for 3D human pose. The two-stage method identifies the 2D joint coordinates of the human body in the first stage and recovers the joint depth from the 2D joint coordinates in the second stage to obtain the 3D joint coordinates of the human body. An end-to-end method for directly obtaining 3D joint coordinates of the human body.
Preprints 75231 g001
Preprints 75231 g002
Figure 2. Overall framework of our model. Multi-scale feature maps extracted from the backbone network, and used as the input of the feature encoder after flattening and splicing, and further refine. Given M pose queries and refined multi-scale features as the input, the posture decoder predicts M human posture instances, including 2D joint point coordinates and joint point depth. After that, an additional joint decoder takes each scattered pose as its reference points and outputs the refined pose as final results. N is the number of keypoint for each instance.
Figure 2. Overall framework of our model. Multi-scale feature maps extracted from the backbone network, and used as the input of the feature encoder after flattening and splicing, and further refine. Given M pose queries and refined multi-scale features as the input, the posture decoder predicts M human posture instances, including 2D joint point coordinates and joint point depth. After that, an additional joint decoder takes each scattered pose as its reference points and outputs the refined pose as final results. N is the number of keypoint for each instance.
Preprints 75231 g002
Preprints 75231 g003
Figure 3. Detailed structure of the feature encoder. The feature encoder takes as input the feature token, which is processed by flattening and concatenating multi-scale features, and outputs the refined features. Each encoder layer mainly includes DMSA (Deformable Multi-head Self-Attention module) and FFN (Feedforward Neural Network).
Figure 3. Detailed structure of the feature encoder. The feature encoder takes as input the feature token, which is processed by flattening and concatenating multi-scale features, and outputs the refined features. Each encoder layer mainly includes DMSA (Deformable Multi-head Self-Attention module) and FFN (Feedforward Neural Network).
Preprints 75231 g003
Preprints 75231 g004
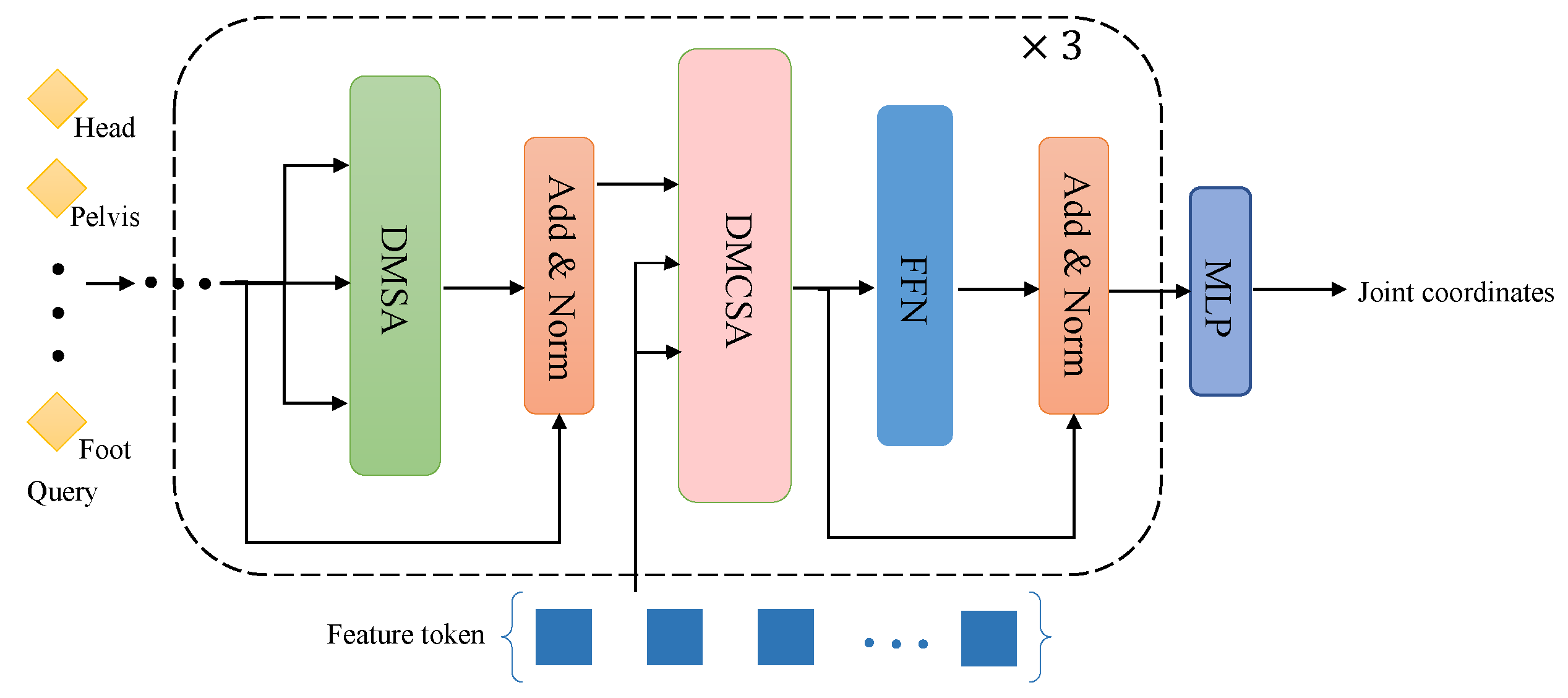
Figure 4. Detailed structure of the pose decoder. Given M pose queries, the pose decoder outputs M instance-aware full-body poses, including joint coordinates and joint depths. In addition to Deformable Multi-head Self-Attention module and Feedforward Neural Network, each decoder layer also includes DMCA (Deformable Multi-head Cross-Attention module) , used to focus on visual features most relevant to target keypoints.
Figure 4. Detailed structure of the pose decoder. Given M pose queries, the pose decoder outputs M instance-aware full-body poses, including joint coordinates and joint depths. In addition to Deformable Multi-head Self-Attention module and Feedforward Neural Network, each decoder layer also includes DMCA (Deformable Multi-head Cross-Attention module) , used to focus on visual features most relevant to target keypoints.
Preprints 75231 g004
Preprints 75231 g005
Figure 5. Skeleton model. During training, select a skeleton model with N=15, where the pelvis point is selected as the root node. The sequence of numbered human joint points during training is shown in Fig.
Figure 5. Skeleton model. During training, select a skeleton model with N=15, where the pelvis point is selected as the root node. The sequence of numbered human joint points during training is shown in Fig.
Preprints 75231 g005
Preprints 75231 g006
Figure 6. Detailed structure of the joint decoder. The input to the joint decoder is different types of joint coordinates, and its structure is similar to the Pose decoder, including Deformable Multi-head Self-Attention module, Feedforward Neural Network, and Deformable Multi-head Cross-Attention module.
Figure 6. Detailed structure of the joint decoder. The input to the joint decoder is different types of joint coordinates, and its structure is similar to the Pose decoder, including Deformable Multi-head Self-Attention module, Feedforward Neural Network, and Deformable Multi-head Cross-Attention module.
Preprints 75231 g006
Preprints 75231 g007
Figure 7. Visualize the results of different types of actions. The test images are all from the 3DPW [34] dataset.
Figure 7. Visualize the results of different types of actions. The test images are all from the 3DPW [34] dataset.
Preprints 75231 g007
Table 1. Joint-wise 3 D P C K r e l comparison with state-of-the-art methods on the MuPoTS-3D dataset. All groundtruths are used for evaluation.
Table 1. Joint-wise 3 D P C K r e l comparison with state-of-the-art methods on the MuPoTS-3D dataset. All groundtruths are used for evaluation.
Method 3 D P C K r e l
Head Neck Shoulder Elbow Wrist Hip Knee Ankle Avg
Two-stage
Lcr-net [29] 49.4 67.4 57.1 51.4 41.3 84.6 56.3 36.3 53.8
XNect [30] - - 81.4 67.2 53.2 - 75.8 54.3 72.1
CDMP [27] 79.1 92.6 85.1 79.4 67.0 96.6 85.7 73.1 81.8
Pi-net [31] 78.3 91.8 87.8 81.9 68.5 94.2 85.3 74.8 82.5
3DPose [25] - - - - - - - - 89.6
End-to-end
Metha [26] 62.1 81.2 77.9 57.7 47.2 97.3 66.3 47.6 66.0
DRM [32] 94.1 78.6 83.0 72.1 94.5 78.6 73.0 98.7 84.3
EDD (Ours) 93.8 78.5 86.4 76.9 95.5 86.0 79.6 98.5 87.4
Table 2. Results of the ablation experiments. Root Point represents whether to use the pelvic point as the root node, Iterative inference depth represents whether to use iterative prediction methods to predict depth.
Table 2. Results of the ablation experiments. Root Point represents whether to use the pelvic point as the root node, Iterative inference depth represents whether to use iterative prediction methods to predict depth.
Root Point Iterative inference depth 3 D P C K r e l
Pelvis Head Shoulder Elbow Avg
✓ 91.7 92.7 82.7 72.6 84.6
✓ 91.6 92.3 84 73.6 85.6
✓ ✓ 93.5 93.8 86.4 76.9 87.4
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated