Submitted:
31 May 2023
Posted:
01 June 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Theoretical Basis
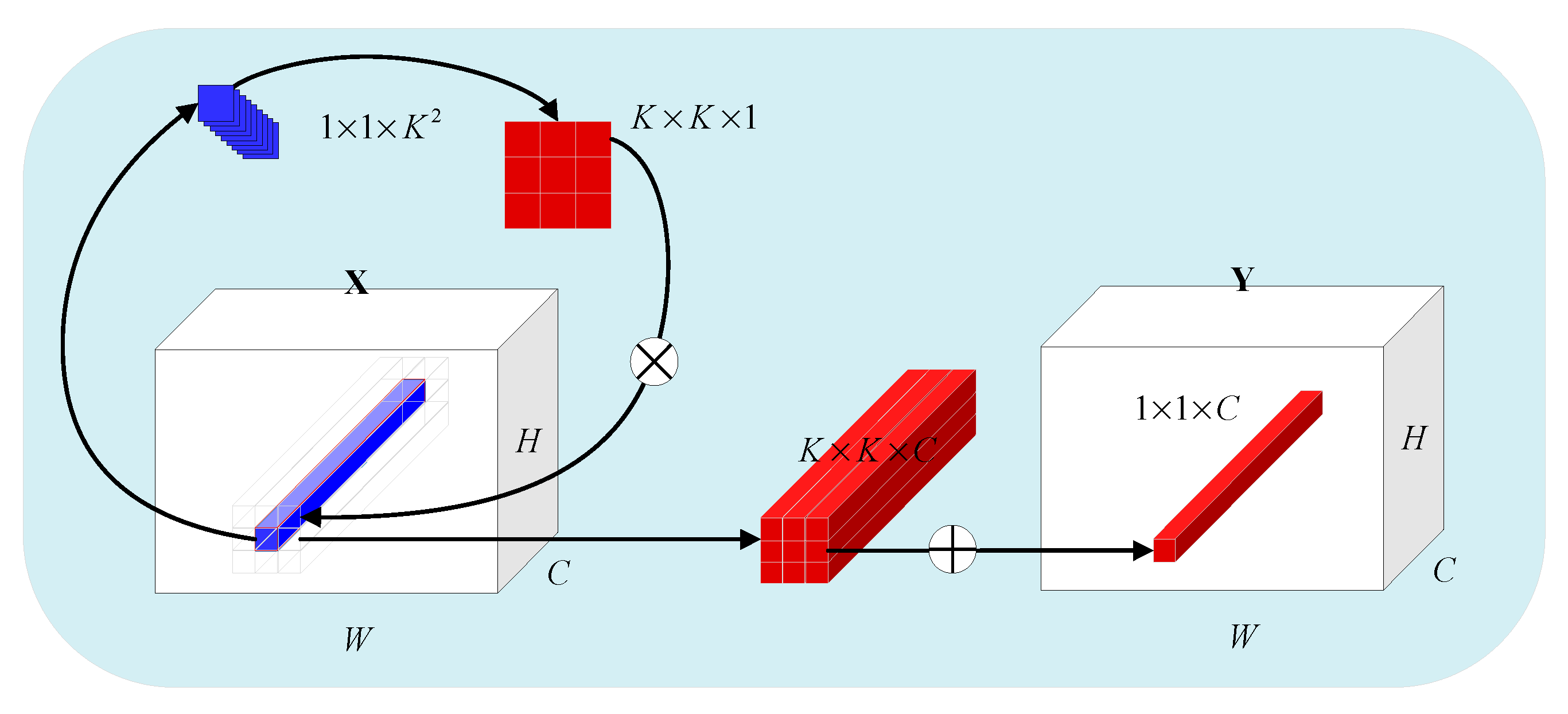
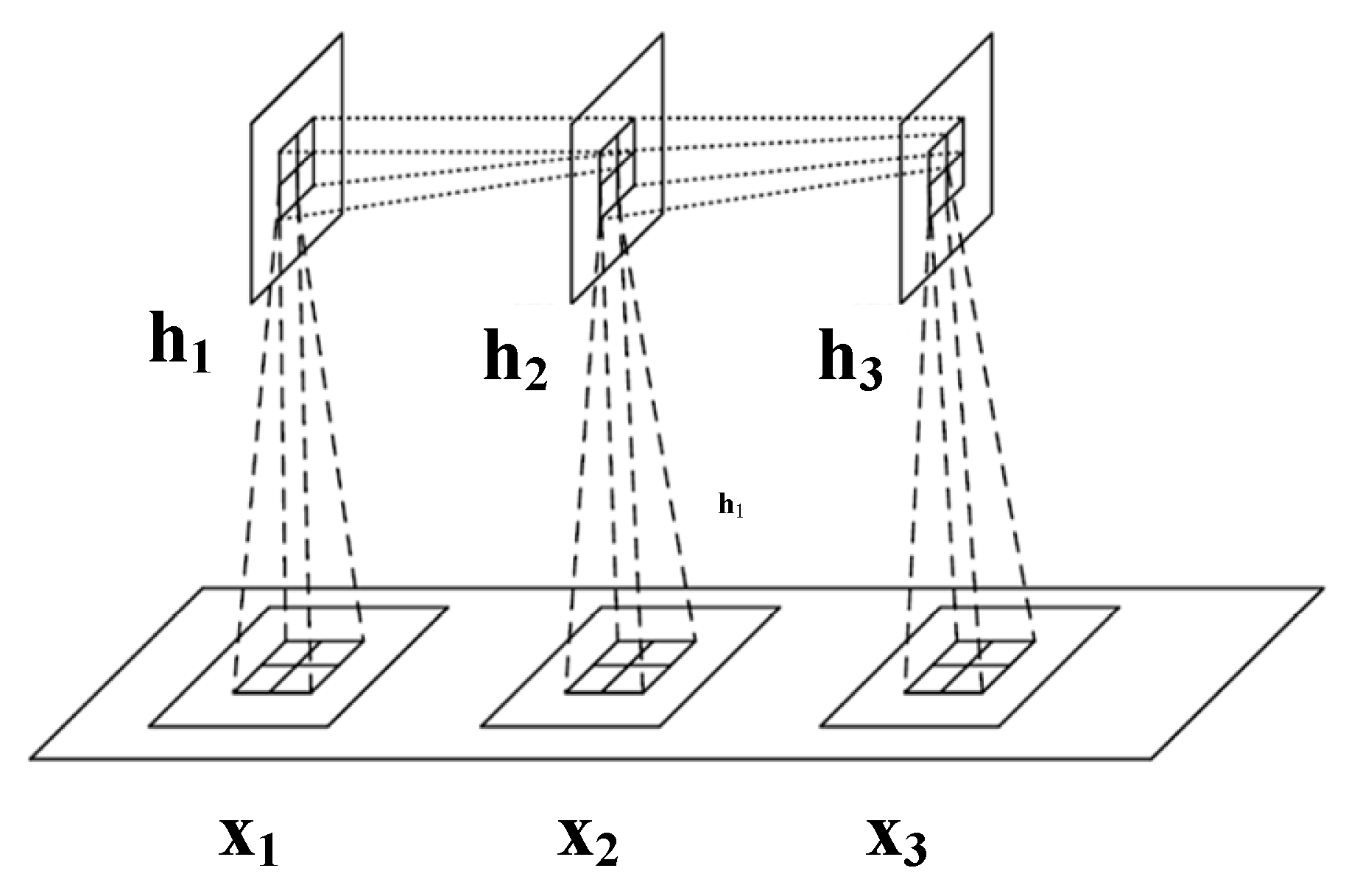
2.1. Inverse Convolution
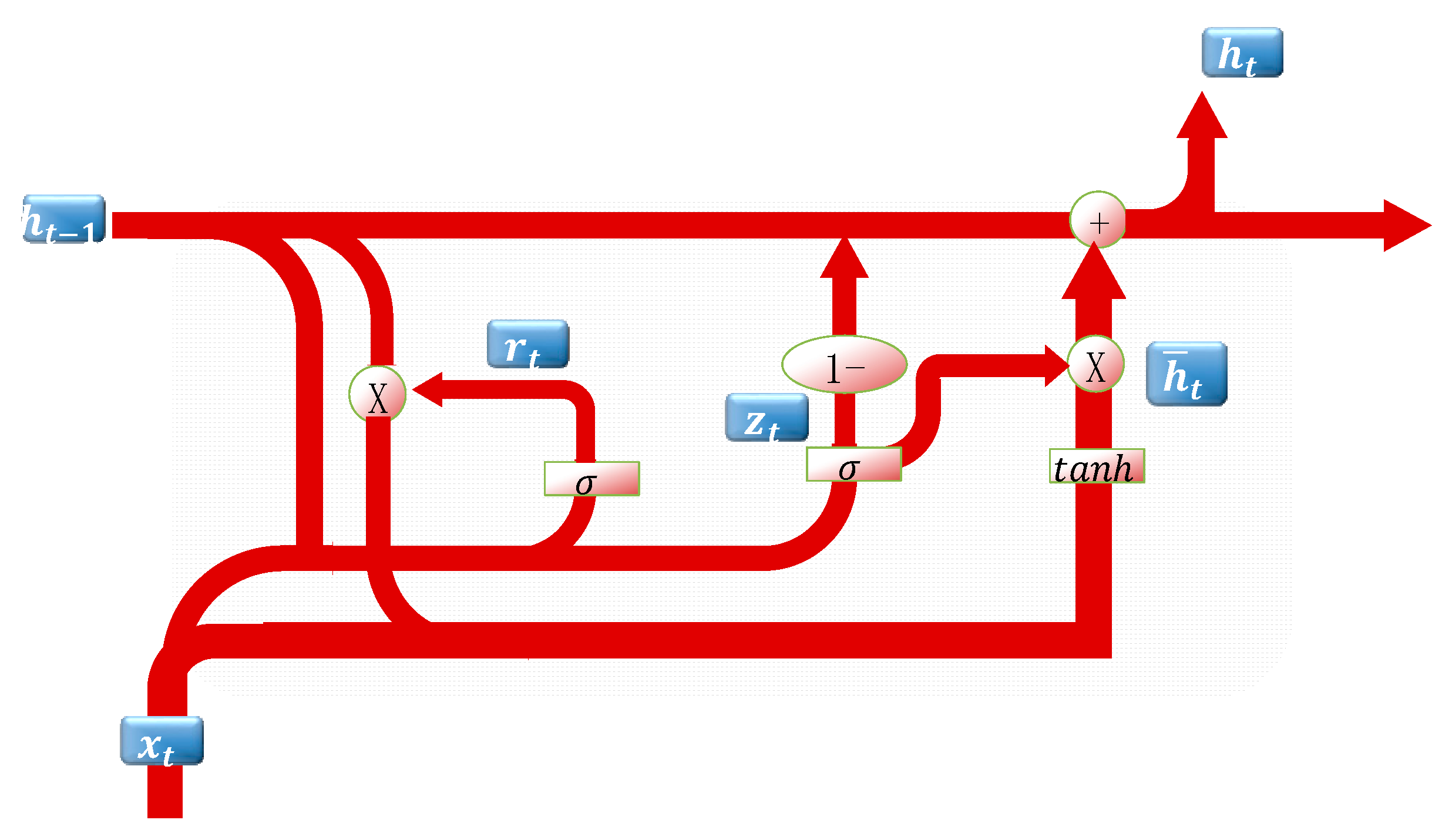
2.2. GRU
3. Proposed Methodology
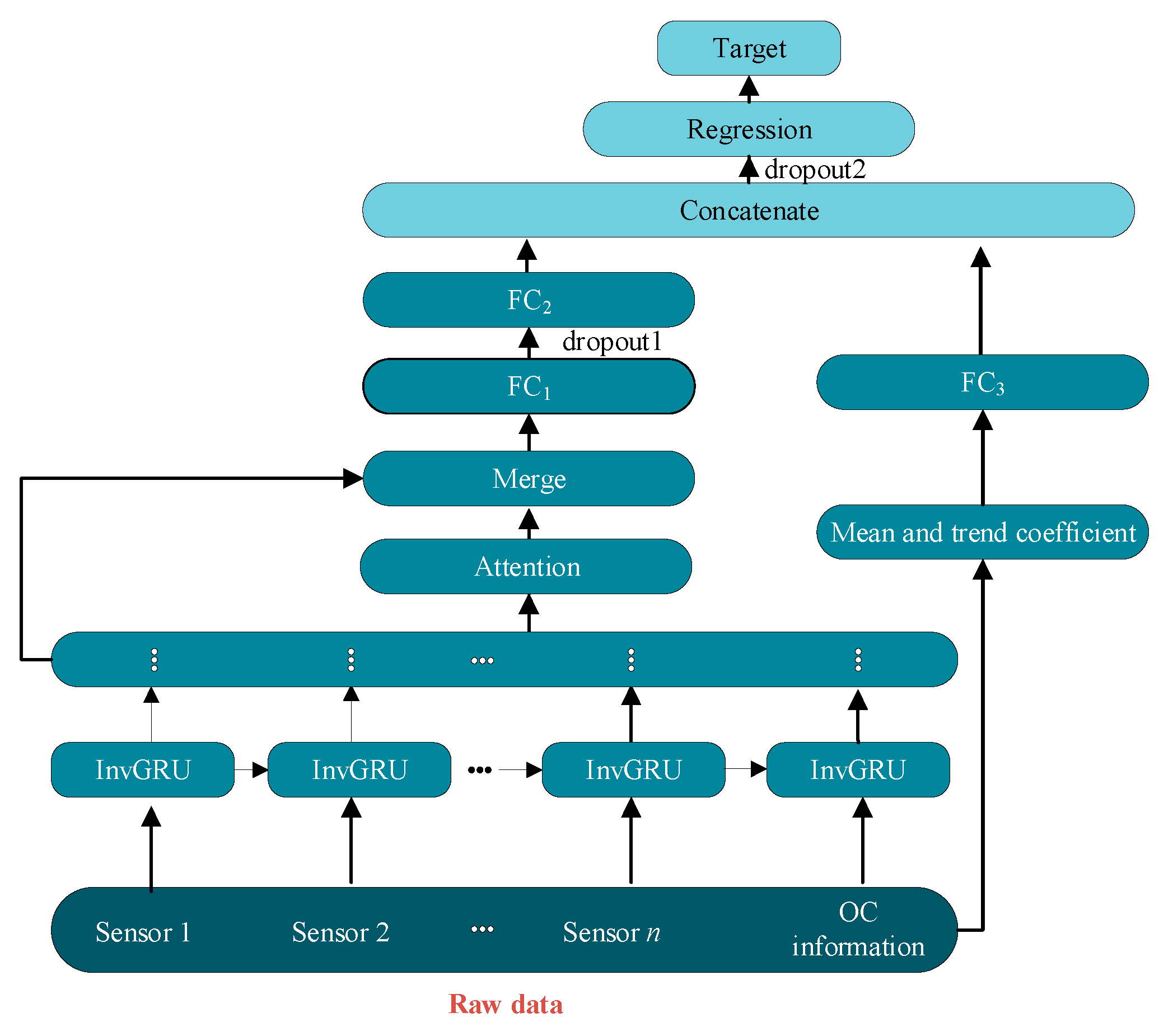
3.1. Proposed InvGRU
3.2. The adopted DL Framework
4. Experimental Analysis
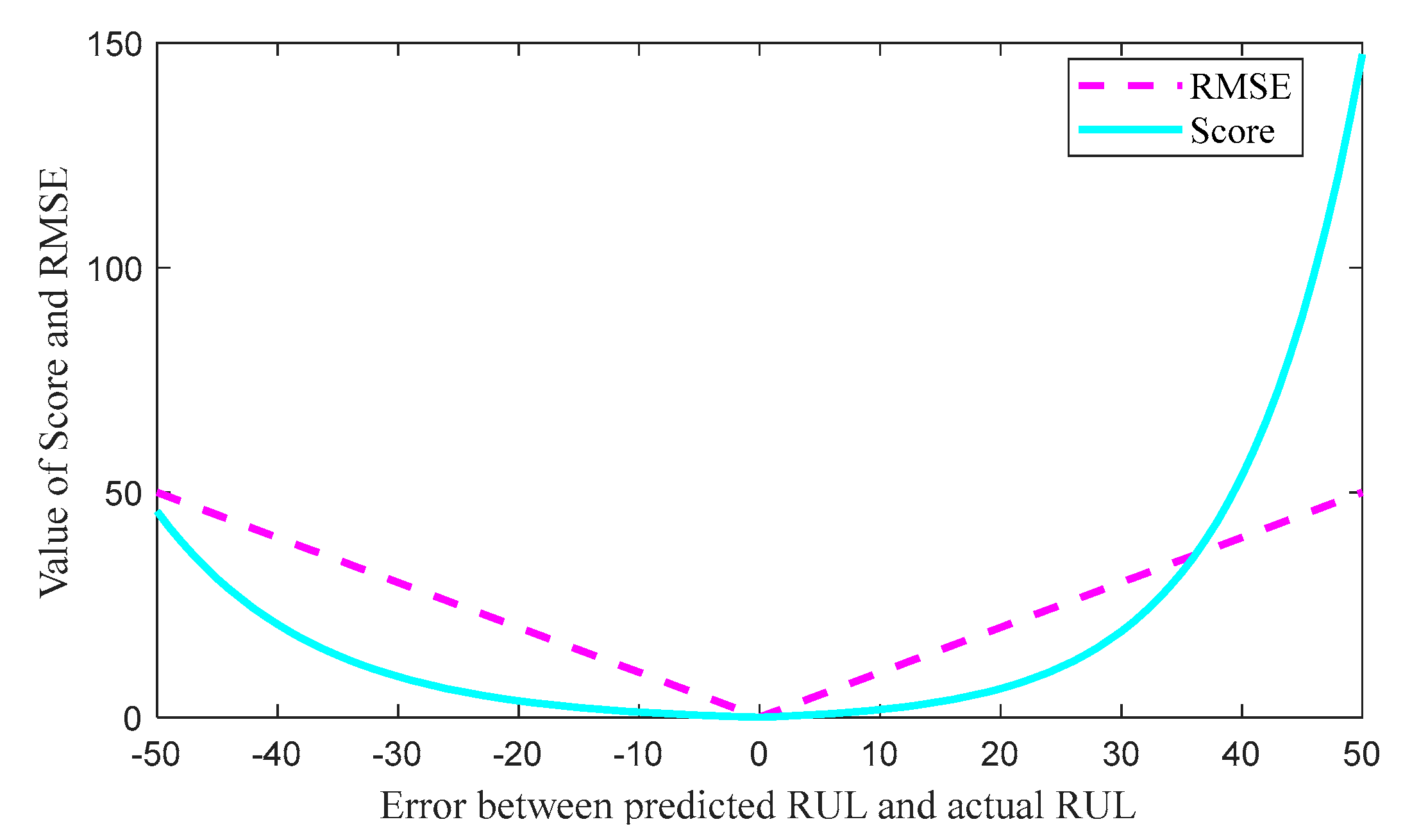
4.1. Evaluation Indexes
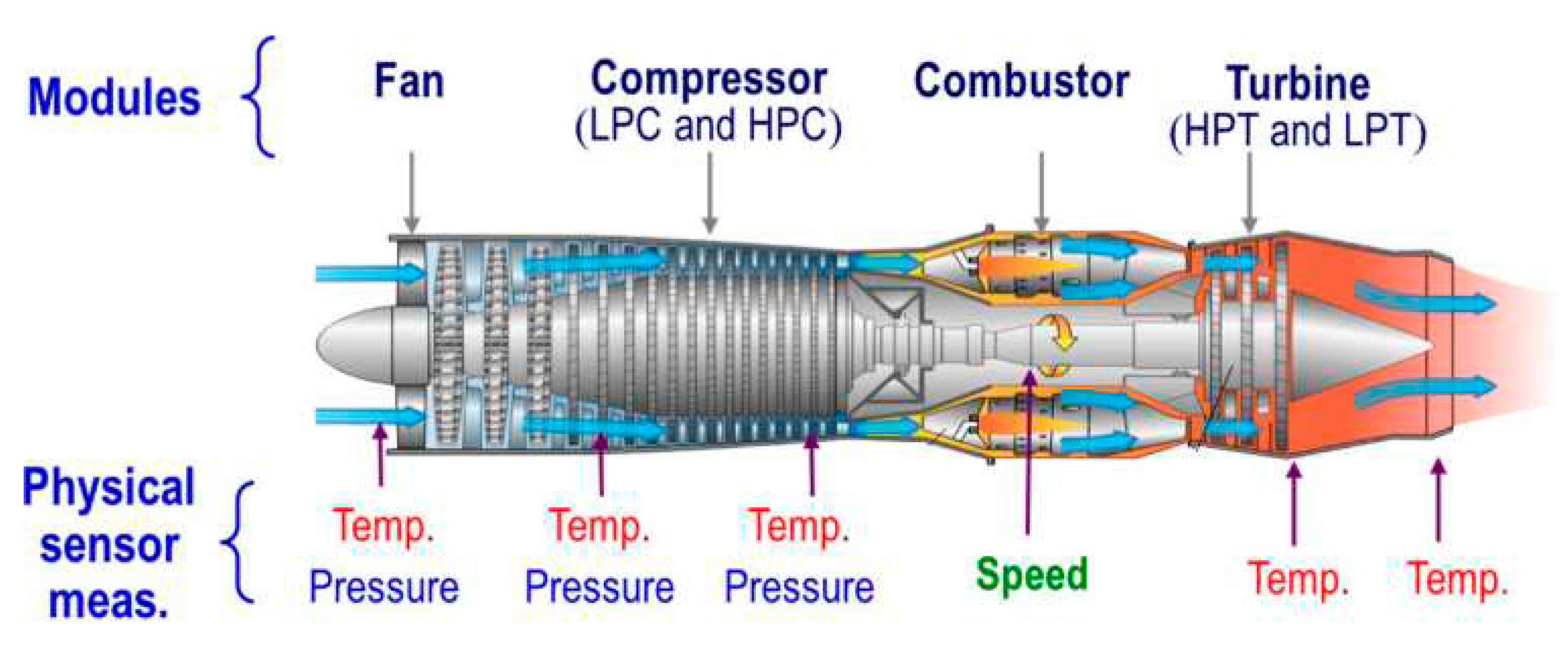
4.2. The Details of C-MAPSS Dataset
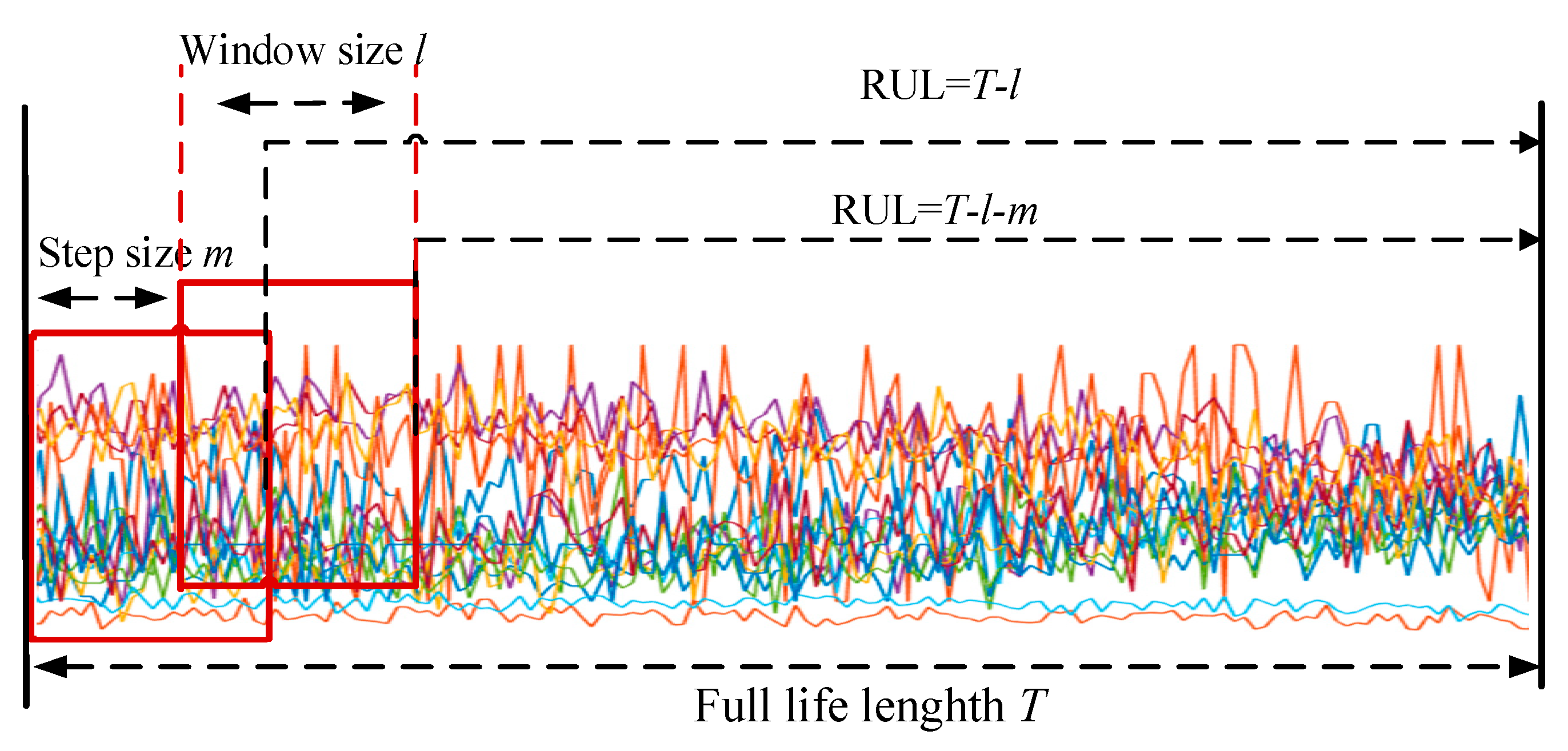
4.3. Data Preprocessing
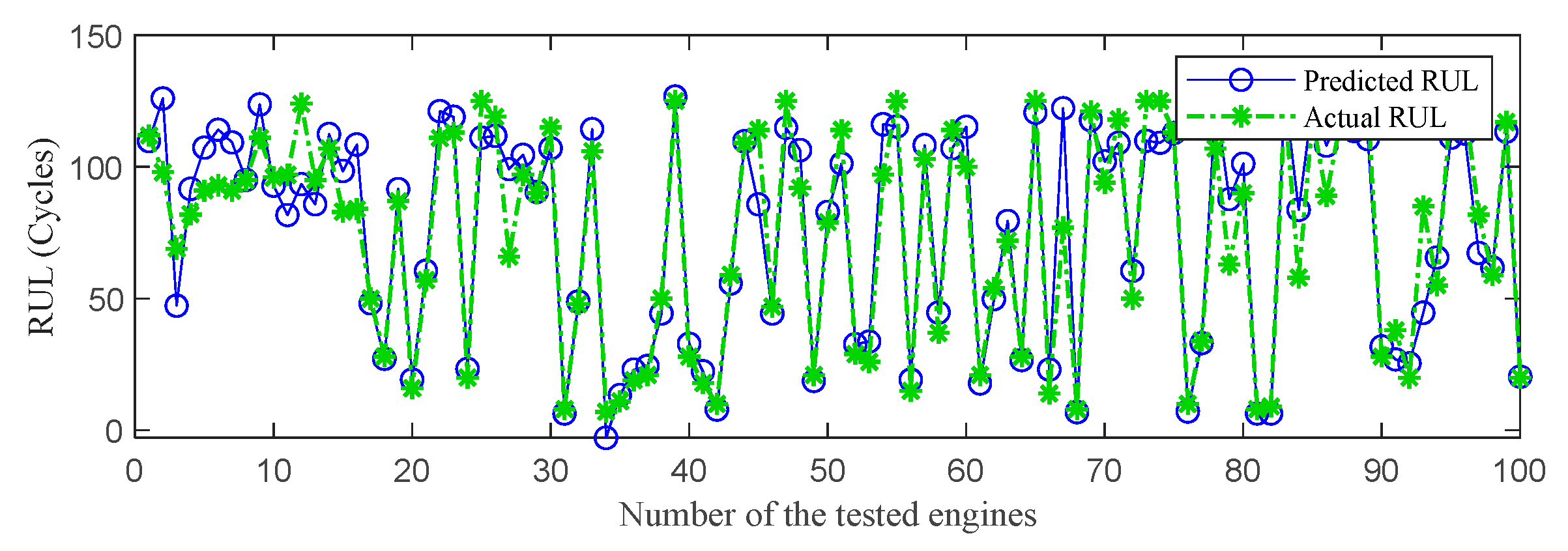
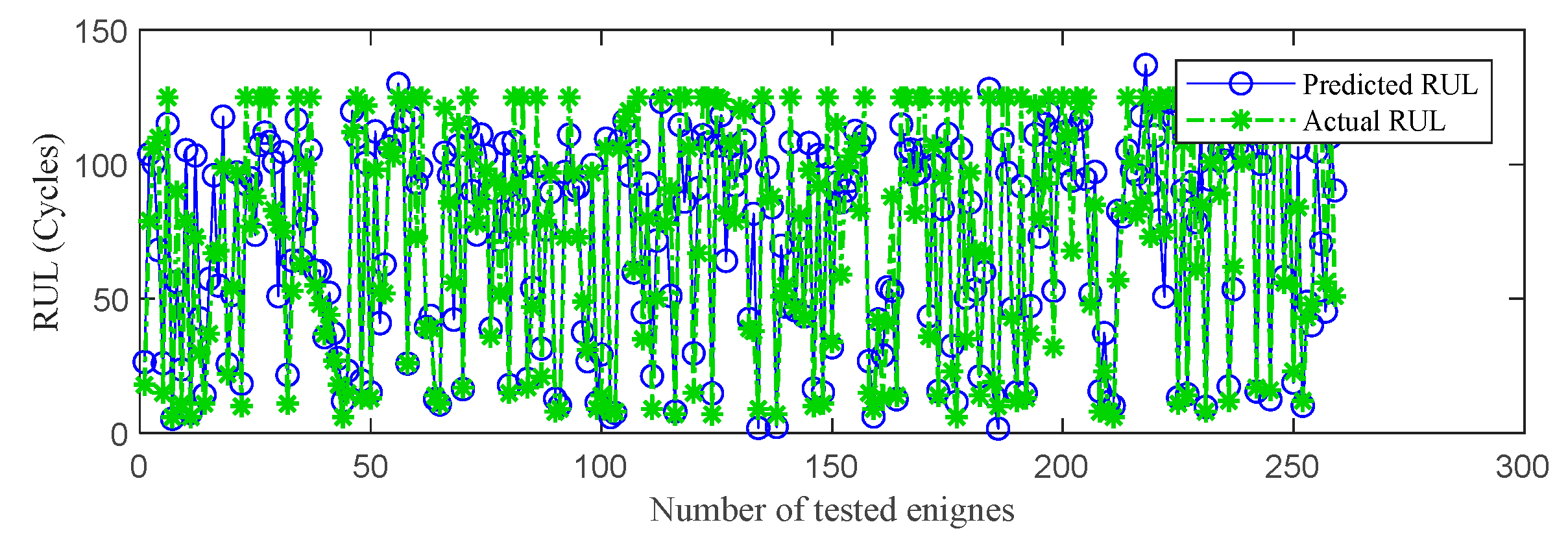
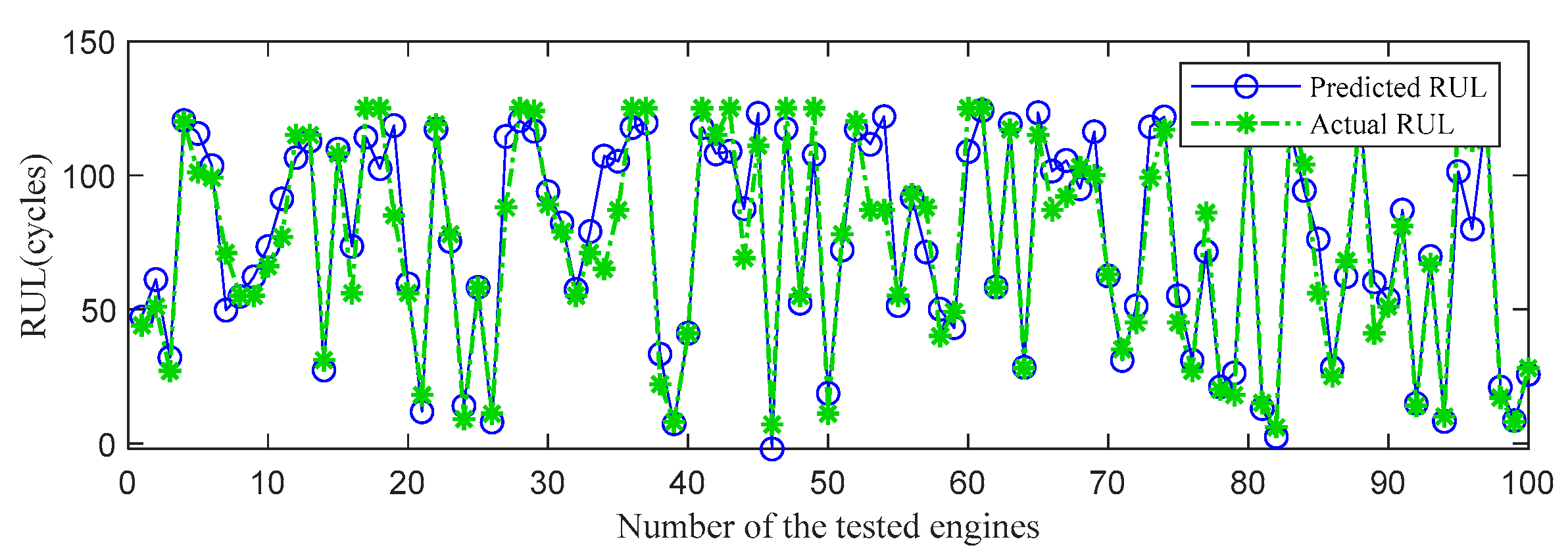
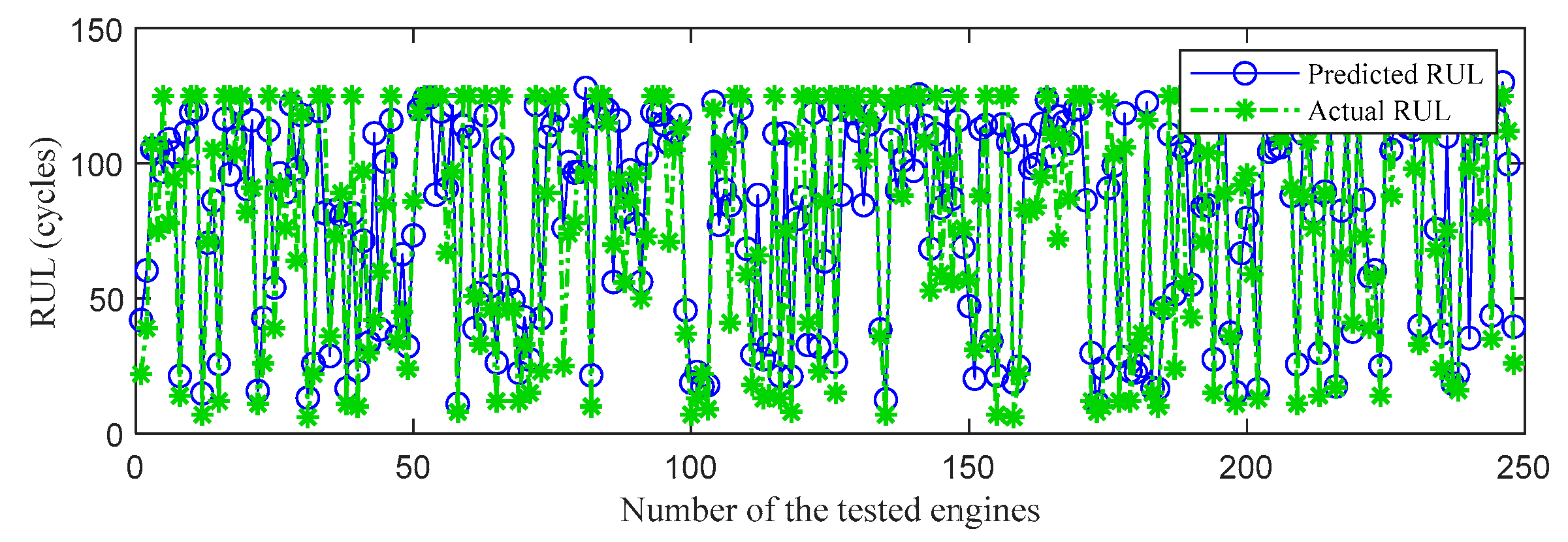
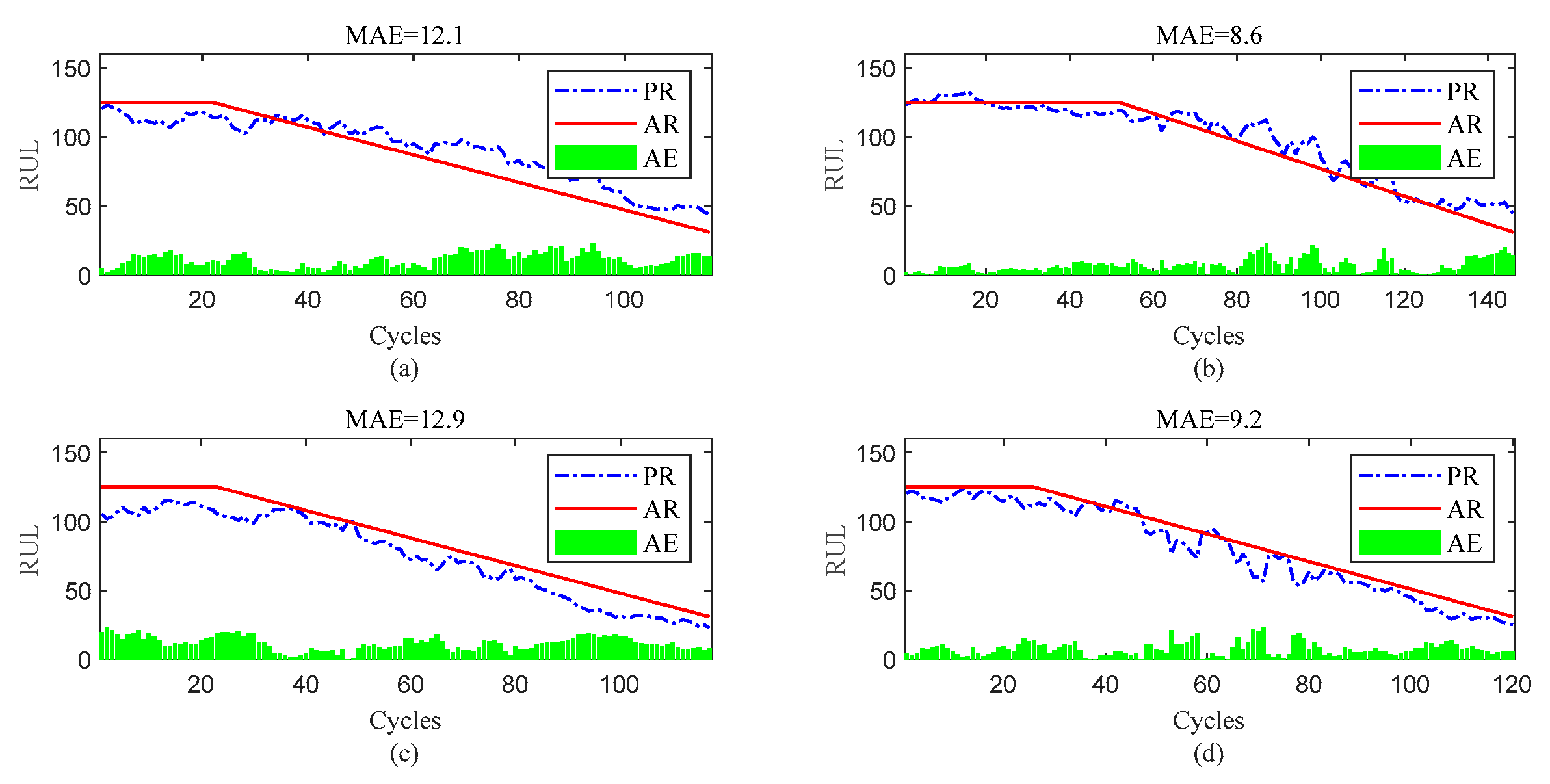
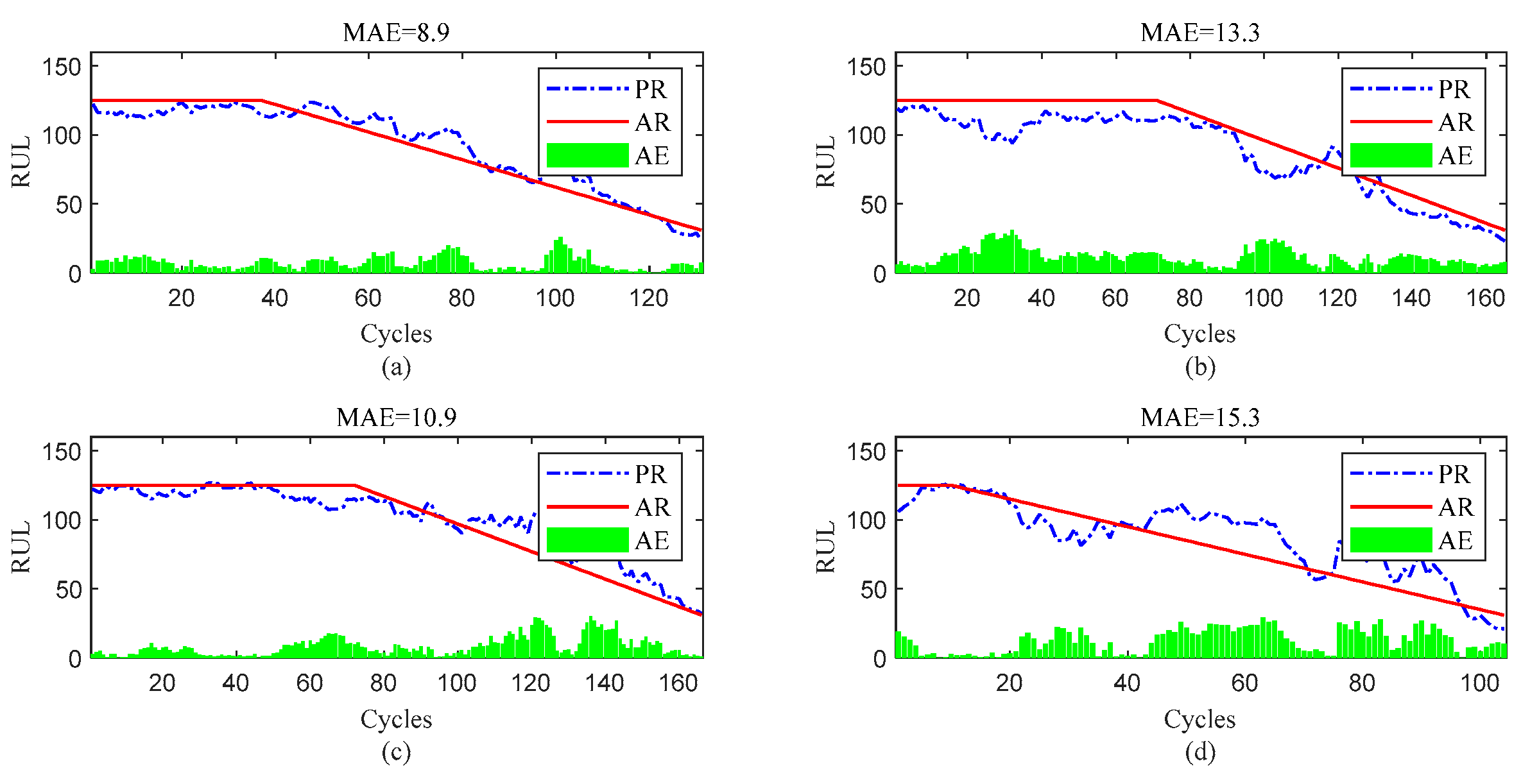
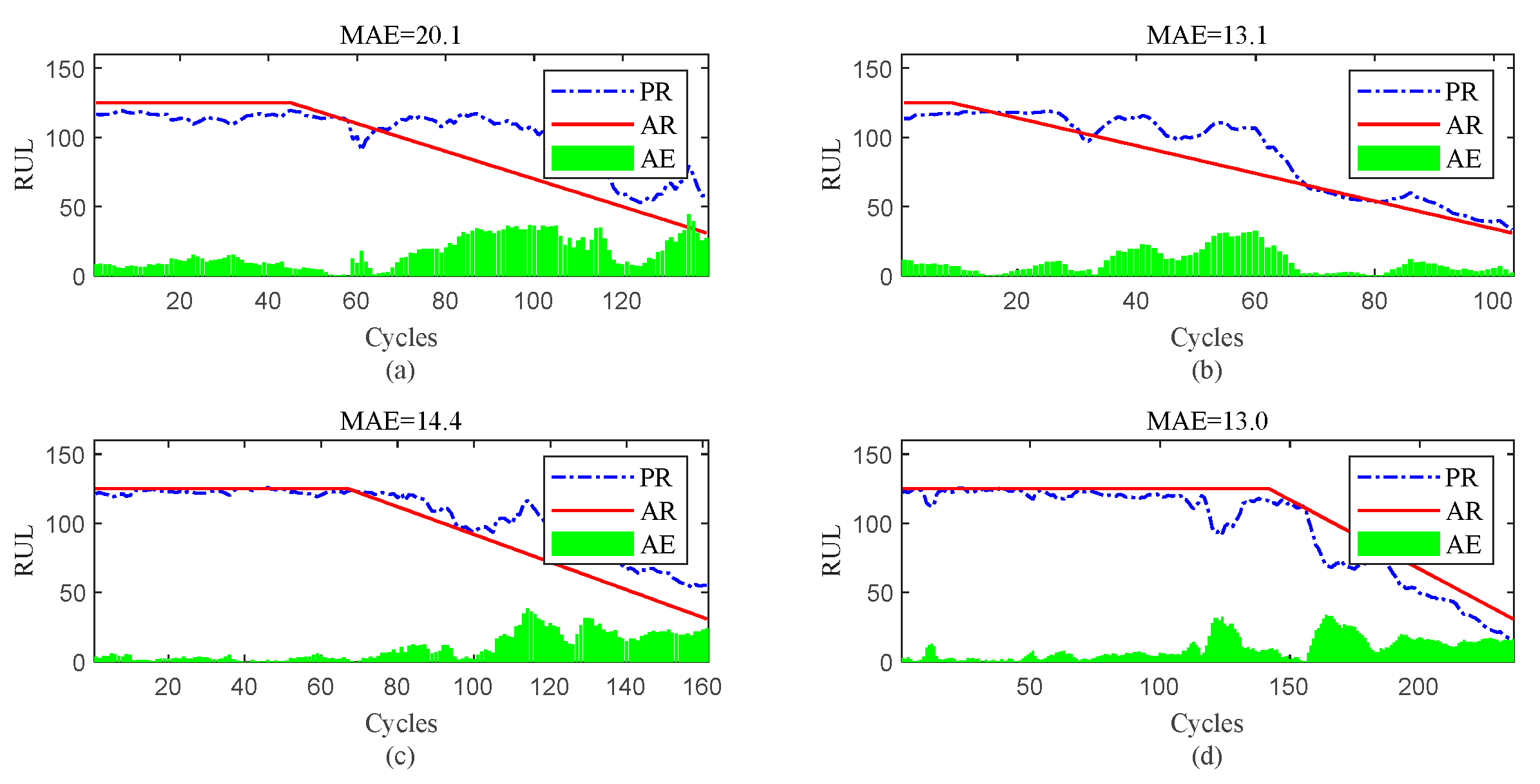
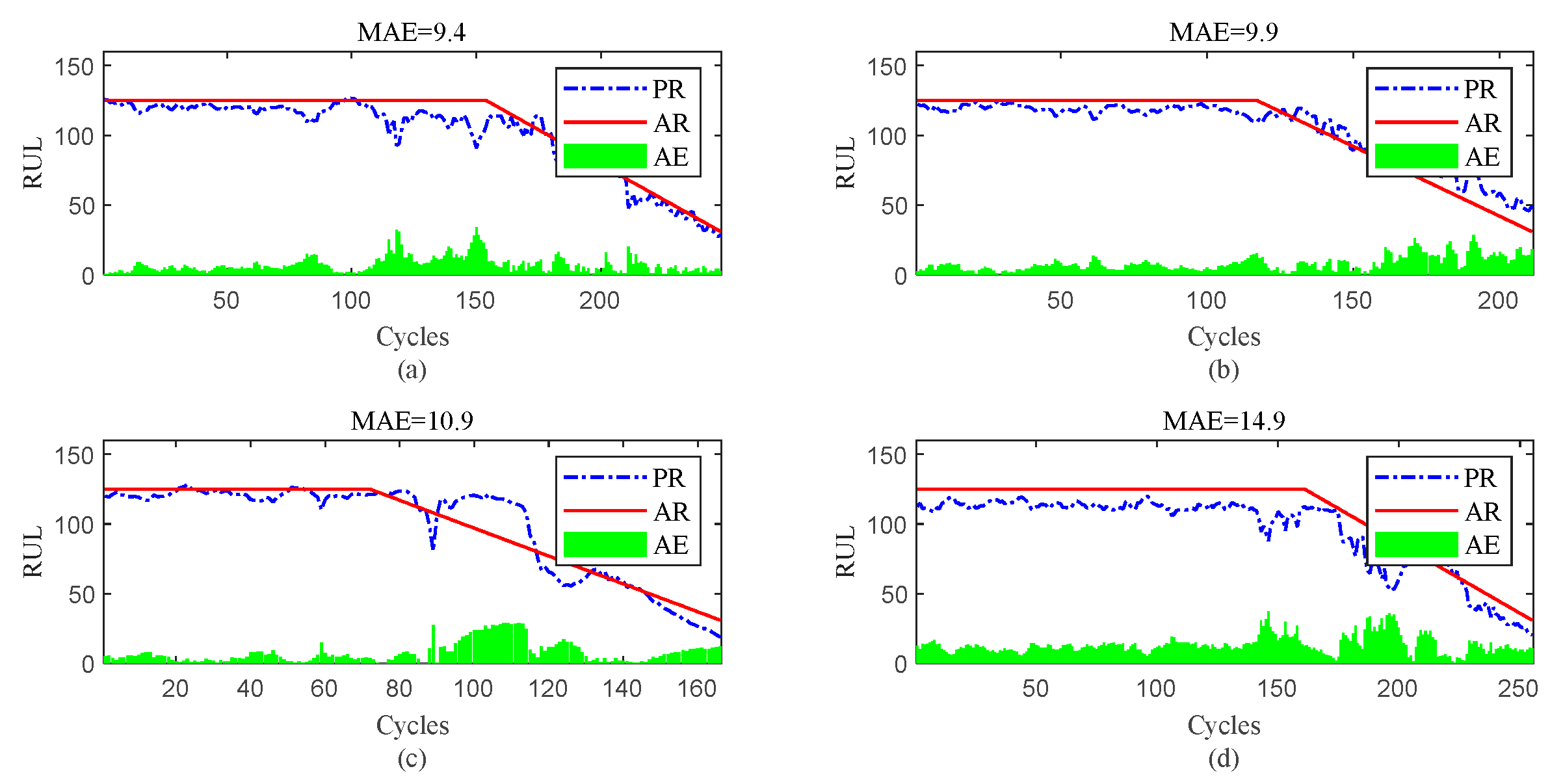
4.4. The Analysis and Comparison of RUL Prediction Results
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Zhao, R.; Yan, R.; Chen, Z.; Mao, K.; Wang, P.; Gao, R.X. Deep learning and its applications to machine health monitoring. Mech Syst Signal Process 2019, 115, 213–237. [Google Scholar] [CrossRef]
- Khan, S.; Yairi, T. A review on the application of deep learning in system health management. Mech Syst Signal Process 2018, 107, 241–265. [Google Scholar] [CrossRef]
- Lei, Y.; Li, N.; Guo, L.; Li, N.; Yan, T.; Lin, J. Machinery health prognostics: A systematic review from data acquisition to RUL prediction. Mech Syst Signal Process 2018, 104, 799–834. [Google Scholar] [CrossRef]
- Xiang, S.; Qin, Y.; Luo, J.; Pu, H.; Tang, B. Multicellular LSTM-based deep learning model for aero-engine remaining useful life prediction. Reliab. Eng. Syst. Saf. 2021, 216, 107927. [Google Scholar] [CrossRef]
- Gebraeel, N.; Lawley, M.; Liu, R.; Parmeshwaran, V. Residual life predictions from vibration-based degradation signals: A neural network approach. IEEE Trans. Ind. Electron. 2004, 51, 694–700. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, T.; Zhao, Z.; Sun, C.; Chen, X.; Yan, R.; Jia, J. Time-varying trajectory modeling via dynamic governing network for remaining useful life prediction. Mech Syst Signal Process 2023, 182, 109610. [Google Scholar] [CrossRef]
- Herzog, M.A.; Marwala, T.; Heyns, P.S. Machine and component residual life estimation through the application of neural networks. Reliab. Eng. Syst. Saf. 2009, 94, 479–489. [Google Scholar] [CrossRef]
- Ren, L.; Cui, J.; Sun, Y.; Cheng, X. Multi-bearing remaining useful life collaborative prediction: A deep learning approach. J Manuf Syst 2017, 43, 248–256. [Google Scholar] [CrossRef]
- Guo, L.; Li, N.; Jia, F.; Lei, Y.; Lin, J. A recurrent neural network based health indicator for remaining useful life prediction of bearings. Neurocomputing 2017, 240, 98–109. [Google Scholar] [CrossRef]
- Yu, W.; Kim, I.Y.; Mechefske, C. An improved similarity-based prognostic algorithm for RUL estimation using an RNN autoencoder scheme. Reliab. Eng. Syst. Saf. 2020, 199, 106926. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans Neural Netw 1994, 5, 157–166. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural computation 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Xiang, S.; Qin, Y.; Liu, F.; Gryllias, K. Automatic multi-differential deep learning and its application to machine remaining useful life prediction. Reliab. Eng. Syst. Saf. 2022, 223, 108531. [Google Scholar] [CrossRef]
- Xiang, S.; Qin, Y.; Luo, J.; Pu, H. Spatiotemporally multidifferential processing deep neural network and its application to equipment remaining useful life prediction. IEEE Trans Industr Inform 2021, 18, 7230–7239. [Google Scholar] [CrossRef]
- Yuan, M.; Wu, Y.; Lin, L. In Fault diagnosis and remaining useful life estimation of aero engine using LSTM neural network, 2016 IEEE international conference on aircraft utility systems (AUS), 2016; IEEE: 2016; pp 135-140.
- Wang, J.; Peng, B.; Zhang, X. Using a stacked residual LSTM model for sentiment intensity prediction. Neurocomputing 2018, 322, 93–101. [Google Scholar] [CrossRef]
- Zhao, R.; Wang, J.; Yan, R.; Mao, K. In Machine health monitoring with LSTM networks, 2016 10th international conference on sensing technology (ICST), 2016; IEEE: 2016; pp 1-6.
- Wu, J.; Hu, K.; Cheng, Y.; Zhu, H.; Shao, X.; Wang, Y. Data-driven remaining useful life prediction via multiple sensor signals and deep long short-term memory neural network. ISA Trans 2020, 97, 241–250. [Google Scholar] [CrossRef] [PubMed]
- Guo, L.; Li, N.; Jia, F.; Lei, Y.; Lin, J. A recurrent neural network based health indicator for remaining useful life prediction of bearings. Neurocomputing 2017, 240, 98–109. [Google Scholar] [CrossRef]
- Zhao, R.; Wang, D.; Yan, R.; Mao, K.; Shen, F.; Wang, J. Machine health monitoring using local feature-based gated recurrent unit networks. IEEE Trans. Ind. Electron. 2017, 65, 1539–1548. [Google Scholar] [CrossRef]
- Zhou, J.; Qin, Y.; Chen, D.; Liu, F.; Qian, Q. Remaining useful life prediction of bearings by a new reinforced memory GRU network. Adv. Eng. Inform. 2022, 53, 101682. [Google Scholar] [CrossRef]
- He, X.; Wang, Z.; Li, Y.; Khazhina, S.; Du, W.; Wang, J.; Wang, W. Joint decision-making of parallel machine scheduling restricted in job-machine release time and preventive maintenance with remaining useful life constraints. Reliab. Eng. Syst. Saf. 2022, 222, 108429. [Google Scholar] [CrossRef]
- Que, Z.; Jin, X.; Xu, Z. Remaining useful life prediction for bearings based on a gated recurrent unit. IEEE Trans Instrum Meas 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Li, X.; Jiang, H.; Liu, Y.; Wang, T.; Li, Z. An integrated deep multiscale feature fusion network for aeroengine remaining useful life prediction with multisensor data. Knowl Based Syst 2022, 235, 107652. [Google Scholar] [CrossRef]
- Ni, Q.; Ji, J.; Feng, K. Data-driven prognostic scheme for bearings based on a novel health indicator and gated recurrent unit network. IEEE Trans Industr Inform 2022, 19, 1301–1311. [Google Scholar] [CrossRef]
- Zhang, Y.; Xin, Y.; Liu, Z.-w.; Chi, M.; Ma, G. Health status assessment and remaining useful life prediction of aero-engine based on BiGRU and MMoE. Reliab. Eng. Syst. Saf. 2022, 220, 108263. [Google Scholar] [CrossRef]
- Ma, M.; Mao, Z. Deep wavelet sequence-based gated recurrent units for the prognosis of rotating machinery. Structural Health Monitoring 2021, 20, 1794–1804. [Google Scholar] [CrossRef]
- Zhao, M.; Zhong, S.; Fu, X.; Tang, B.; Dong, S.; Pecht, M. Deep residual networks with adaptively parametric rectifier linear units for fault diagnosis. IEEE Trans. Ind. Electron. 2020, 68, 2587–2597. [Google Scholar] [CrossRef]
- Ren, L.; Dong, J.; Wang, X.; Meng, Z.; Zhao, L.; Deen, M.J. A data-driven auto-CNN-LSTM prediction model for lithium-ion battery remaining useful life. IEEE Trans Industr Inform 2020, 17, 3478–3487. [Google Scholar] [CrossRef]
- Zhao, C.; Huang, X.; Li, Y.; Yousaf Iqbal, M. A double-channel hybrid deep neural network based on CNN and BiLSTM for remaining useful life prediction. Sensors 2020, 20, 7109. [Google Scholar] [CrossRef]
- Wang, B.; Lei, Y.; Yan, T.; Li, N.; Guo, L. Recurrent convolutional neural network: A new framework for remaining useful life prediction of machinery. Neurocomputing 2020, 379, 117–129. [Google Scholar] [CrossRef]
- Ma, M.; Mao, Z. Deep-convolution-based LSTM network for remaining useful life prediction. IEEE Trans Industr Inform 2020, 17, 1658–1667. [Google Scholar] [CrossRef]
- Li, B.; Tang, B.; Deng, L.; Zhao, M. Self-attention ConvLSTM and its application in RUL prediction of rolling bearings. IEEE Trans Instrum Meas 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Cheng, Y.; Hu, K.; Wu, J.; Zhu, H.; Shao, X. Autoencoder quasi-recurrent neural networks for remaining useful life prediction of engineering systems. IEEE ASME Trans Mechatron 2021, 27, 1081–1092. [Google Scholar] [CrossRef]
- Al-Dulaimi, A.; Zabihi, S.; Asif, A.; Mohammadi, A. A multimodal and hybrid deep neural network model for remaining useful life estimation. Comput Ind 2019, 108, 186–196. [Google Scholar] [CrossRef]
- Xia, T.; Song, Y.; Zheng, Y.; Pan, E.; Xi, L. An ensemble framework based on convolutional bi-directional LSTM with multiple time windows for remaining useful life estimation. Comput Ind 2020, 115, 103182. [Google Scholar] [CrossRef]
- Xue, B.; Xu, Z.-b.; Huang, X.; Nie, P.-c. Data-driven prognostics method for turbofan engine degradation using hybrid deep neural network. J. Mech. Sci. Technol 2021, 35, 5371–5387. [Google Scholar] [CrossRef]
- Li, D.; Hu, J.; Wang, C.; Li, X.; She, Q.; Zhu, L.; Zhang, T.; Chen, Q. In Involution: Inverting the inherence of convolution for visual recognition, Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2021; 2021; pp 12321-12330.
- Chen, Z.; Wu, M.; Zhao, R.; Guretno, F.; Yan, R.; Li, X. Machine remaining useful life prediction via an attention-based deep learning approach. IEEE Trans. Ind. Electron. 2020, 68, 2521–2531. [Google Scholar] [CrossRef]
- Sateesh Babu, G.; Zhao, P.; Li, X.-L. In Deep convolutional neural network based regression approach for estimation of remaining useful life, Database Systems for Advanced Applications: 21st International Conference, DASFAA 2016, Dallas, TX, USA, -19, 2016, Proceedings, Part I 21, 2016; Springer: 2016; pp 214-228. 16 April.
- Zhang, C.; Lim, P.; Qin, A.K.; Tan, K.C. Multiobjective deep belief networks ensemble for remaining useful life estimation in prognostics. IEEE Trans Neural Netw Learn Syst 2016, 28, 2306–2318. [Google Scholar] [CrossRef]
- Zheng, S.; Ristovski, K.; Farahat, A.; Gupta, C. In Long short-term memory network for remaining useful life estimation, 2017 IEEE international conference on prognostics and health management (ICPHM), 2017; IEEE: 2017; pp 88-95.
- Li, J.; Li, X.; He, D. A directed acyclic graph network combined with CNN and LSTM for remaining useful life prediction. IEEE Access 2019, 7, 75464–75475. [Google Scholar] [CrossRef]
| Sub layer | Hyperparameter value | Sub layer | Hyperparameter value |
|---|---|---|---|
| InvGRU | 70 | Regression (Linear) | 1 |
| FC1 (Relu) | 30 | Learning rate | 0.005 |
| FC2 (Relu) | 30 | Dropout1 | 0.5 |
| FC3 (Relu) | 10 | Dropout2 | 0.3 |
| Subset | FD001 | FD002 | FD003 | FD004 |
|---|---|---|---|---|
| Total number of engines | 100 | 260 | 100 | 249 |
| Operating condition | 1 | 6 | 1 | 6 |
| Type of fault | 1 | 1 | 2 | 2 |
| Maximum cycles | 362 | 378 | 525 | 543 |
| Minimum cycles | 128 | 128 | 145 | 128 |
| number | symbol | description | unit | trend | number | symbol | description | unit | trend |
|---|---|---|---|---|---|---|---|---|---|
| 1 | T2 | Total fan inlet temperature | ºR | ~ | 12 | Phi | Fuel flow ratio to Ps30 | pps/psi | ↓ |
| 2 | T24 | Total exit temperature of LPC | ºR | ↑ | 13 | NRf | Corrected fan speed | rpm | ↑ |
| 3 | T30 | HPC Total outlet temperature | ºR | ↑ | 14 | NRc | Modified core velocity | rpm | ↓ |
| 4 | T50 | Total LPT outlet temperature | ºR | ↑ | 15 | BPR | bypass ratio | -- | ↑ |
| 5 | P2 | Fan inlet pressure | psia | ~ | 16 | farB | Burner gas ratio | -- | ~ |
| 6 | P15 | Total pressure of culvert pipe | psia | ~ | 17 | htBleed | Exhaust enthalpy | -- | ↑ |
| 7 | P30 | Total outlet pressure of HPC | psia | ↓ | 18 | NF_dmd | Required fan speed | rpm | ~ |
| 8 | Nf | Physical fan speed | rpm | ↑ | 19 | PCNR_dmd | Modify required fan speed | rpm | ~ |
| 9 | Nc | Physical core velocity | rpm | ↑ | 20 | W31 | HPT coolant flow rate | lbm/s | ↓ |
| 10 | Epr | Engine pressure ratio | -- | ~ | 21 | W32 | LPT coolant flow rate | lbm/s | ↓ |
| 11 | Ps30 | HPC outlet static pressure | psia | ↑ |
| Model | FD001 | FD002 | ||
|---|---|---|---|---|
| Score | RMSE | Score | RMSE | |
| Cox’s regression [34] | 28616 | 45.10 | N/A | N/A |
| SVR [39] | 1382 | 20.96 | 58990 | 41.99 |
| RVR [39] | 1503 | 23.86 | 17423 | 31.29 |
| RF [39] | 480 | 17.91 | 70456 | 29.59 |
| CNN [40] | 1287 | 18.45 | 17423 | 30.29 |
| LSTM [42] | 338 | 16.14 | 4450 | 24.49 |
| DBN [41] | 418 | 15.21 | 9032 | 27.12 |
| MONBNE [41] | 334 | 15.04 | 5590 | 25.05 |
| LSTM+attention+handscraft feature [20] | 322 | 14.53 | N/A | N/A |
| Acyclic Graph Network [43] | 229 | 11.96 | 2730 | 20.34 |
| AEQRNN [34] | N/A | N/A | 3220 | 19.10 |
| MCLSTM-based[4] | 260 | 13.21 | 1354 | 19.82 |
| SMDN [14] | 240 | 13.72 | 1464 | 16.77 |
| Proposed | 238 | 12.34 | 1205 | 15.59 |
| Model | FD003 | FD004 | ||
|---|---|---|---|---|
| Score | RMSE | Score | RMSE | |
| Cox’s regression [34] | N/A | N/A | 1164590 | 54.29 |
| SVR [39] | 1598 | 21.04 | 371140 | 45.35 |
| RVR [39] | 17423 | 22.36 | 26509 | 34.34 |
| RF [39] | 711 | 20.27 | 46568 | 31.12 |
| CNN [40] | 1431 | 19.81 | 7886 | 29.16 |
| LSTM [42] | 852 | 16.18 | 5550 | 28.17 |
| DBN [41] | 442 | 14.71 | 7955 | 29.88 |
| MONBNE [41] | 422 | 12.51 | 6558 | 28.66 |
| LSTM+attention+handscraft feature [20] | N/A | N/A | 5649 | 27.08 |
| Acyclic Graph Network [43] | 535 | 12.46 | 3370 | 22.43 |
| AEQRNN [34] | N/A | N/A | 4597 | 20.60 |
| MCLSTM-based[4] | 327 | 13.45 | 2926 | 22.10 |
| SMDN [14] | 305 | 12.70 | 1591 | 18.24 |
| Proposed | 292 | 13.12 | 1020 | 13.25 |
| Model | Mean performance | |
|---|---|---|
| RMSE | Score | |
| Cox’s regression [34] | 49.70 | 596603 |
| SVR [39] | 32.335 | 108277 |
| RVR [39] | 27.96 | 11716 |
| RF [39] | 24.72 | 29553 |
| CNN [40] | 24.42 | 7006 |
| LSTM [42] | 21.25 | 2797 |
| DBN [41] | 21.73 | 4461 |
| MONBNE [41] | 20.32 | 3225 |
| LSTM+attention+handscraft feature [20] | 20.80 | 2985 |
| Acyclic Graph Network [43] | 16.80 | 1716 |
| AEQRNN [34] | 19.85 | 3908 |
| MCLSTM-based[4] | 17.40 | 1216 |
| SMDN [14] | 15.36 | 900 |
| Proposed | 13.58 | 689 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




