Temporal Estimation of Non-Rigid Dynamic Point Cloud Sequence using 3D Skeleton-based Deformation for Compression

This paper proposes an algorithm for transmitting and reconstructing the estimated point cloud using temporally estimating a dynamic point cloud sequence. When a non-rigid 3D point cloud sequence (PCS) is input, the sequence is divided into groups of point cloud frames (PCF), and a key PCF is selected. After the 3D skeleton is predicted through 3D pose estimation, the motion of the skeleton is estimated by analyzing the joints and bones of the 3D skeleton. For the deformation of the non-rigid human PC, the 3D PC model is transformed into a mesh model, and the key PCF is rigged using the 3D skeleton. After deforming the key PCF into the target PCF utilizing the motion vector of the estimated skeleton, the residual PC between the motion compensation PCF and the target PCF is generated. If there is a key PCF, the motion vector of the target PCF, and a residual PC, the target PCF can be reconstructed. Just as compression is performed using pixel correlation between frames in a 2D video, this paper compresses 3D PCF by estimating the non-rigid 3D motion of a 3D object in a 3D PC. The proposed algorithm can be regarded as an extension of the 2D motion estimation of a rigid local region in a 2D plane to the 3D motion estimation of a non-rigid object (human) in 3D space. Experimental results show that the proposed method can successfully compress 3D PC sequences. If it is used together with a PC compression technique such as MPEG PCC (point cloud compression) in the future, a system with high compression efficiency may be configured.

Keywords:

Subject: Computer Science and Mathematics - Computer Vision and Graphics

1. Introduction

With the recent development of virtual reality (VR) and augmented reality (AR) technologies, 3D volumetric content technology that provides a realistic experience from a free point of view has been actively developed [1]. 3D volumetric content can be applied to various applications such as games, video services, medical care, and education. When a 3D volumetric model is consumed through a device, like other contents, coding-related technology for efficient transmission and data storage is emerging as an important issue [2]. A point cloud (PC), which expresses the surface of an object in the form of a point, is typically used to express volumetric 3D data [1]. This data contains 3D coordinates and texture color for each point, and additional information such as shape, normal vectors, and maps is included depending on the application field. This data requires a more massive amount of bits than a 2D image because it uses hundreds of thousands or millions of points for visualization. Therefore, coding is essential for 3D PC [3].

We introduce some previous research to compress 3D PC [3]. The first is a method to compress 2D images projected from a 3D PC. First, the virtual cubic box, including an object, is defined in 3D space to map an object into a virtual cubic box. Then, the points of an object are projected into corresponding planes using their normal vectors. This process is regarded as making patches by clustering 3D PC. Finally, each patch is cast into the nearest virtual plane and placed in a rectangular atlas [4,5]. Two images with geometry and texture information are output for each frame, and a video codec compresses the resultant sequence.

There was a method to compress the point cloud using the octree. The sparse voxel octree was first used to express the geometry of a 3D object [6,7], but it was also used to compress the point cloud using octree serialization [8]. In the intra-coding, the data can be reduced by removing the spatially overlapped point clouds [9]. In the inter-coding, the temporally repeated point clouds are removed using the XOR arithmetic of the octree serialization between frames [10,11].

The motion estimation and compensation algorithm for enhancing the coding efficiency of a video sequence can be applied to the compression of the point cloud. The motion estimation of the point cloud divides the point cloud into voxel blocks and finds the motion vector of each voxel block [12]. Another method draws vertex graphs of 3D coordinates and texture of point cloud and estimates the motion vector of vertices using spectral graph wavelet descriptors [13].

In this paper, we propose a method of compressing the point cloud sequence by extracting the 3D skeleton of the point cloud. The skeleton is generated based on OpenPose, a deep learning model for 2D pose estimation. Since the quality of the extracted 3D skeleton significantly affects the point cloud compression performance, a 3D skeleton with high precision is required. Point cloud compression is performed by deforming the key frame point cloud using the motion vector of each joint of the skeleton of the non-key frame and removing overlapping points between the deformed key frame and the point cloud of the target frame. For point cloud deformation, key frame point clouds are converted to mesh models for rigging. The interval at which the key frame is determined depends on the target compression rate.

This paper is structured as follows. Section 2 explains the process of acquiring a point cloud sequence based on reality. Section 3 describes the 3D pose estimation technique, and a point cloud sequence compression algorithm is proposed. Section 4 shows the compression result by the proposed algorithm, and section 5 concludes this paper.

2. Dynamic Point Cloud Sequence

In this section, we explain the 3D point cloud sequence. First, we describe the point cloud structure and the method to capture the 3D point cloud. Next, we introduce a way to precisely estimate 3D human pose estimation using a 3D point cloud.

2.1. Dynamic Point Cloud

To generate and express 3D space or objects, volumetric visual data capable of expressing geometric information is essential. This information may include geometric shapes and additional information such as color, transparency, and normal vectors. Furthermore, according to the time sequence, if this information is to be expressed in time, information about every moment (individual capture instance) or action is required. Therefore, the temporal expression method may include a method of separately storing information about each moment and recording an object’s movement as a function of time. The former is similar to creating a video by saving still images, and the latter is similar to animating a graphics model. In general, a point cloud is mainly used to express such information.

A point cloud is a set of independent 3D points. Each 3D point contains a 3D position, color, and surface normal. A point cloud can express non-manifold geometry, so it is a more flexible expression method than a polygonal mesh and has the advantage of being processed in real time.

3D point cloud data is used in a wide variety of fields. The MPEG PCC standardization activity deals with three categories of point cloud data. The first is a static point cloud, and the second is a dynamic point cloud with temporal information. The third is a dynamically acquired point cloud. MPEG PCC standardization discusses techniques for compressing these point cloud data. These data have

(x, y, z)

coordinates, and each point has reflectivity and RGB properties.

We deal with human data among dynamic point clouds corresponding to the second data type in MPEG PCC. Just as a temporal sequence of a two-dimensional still image is defined as a video, a dynamic point cloud video is defined as a temporal sequence of a point cloud. We introduce a technique for analyzing human motion and predicting correlation using skeleton information in each frame to compress the point cloud.

2.2. Dynamic Point Cloud Capture

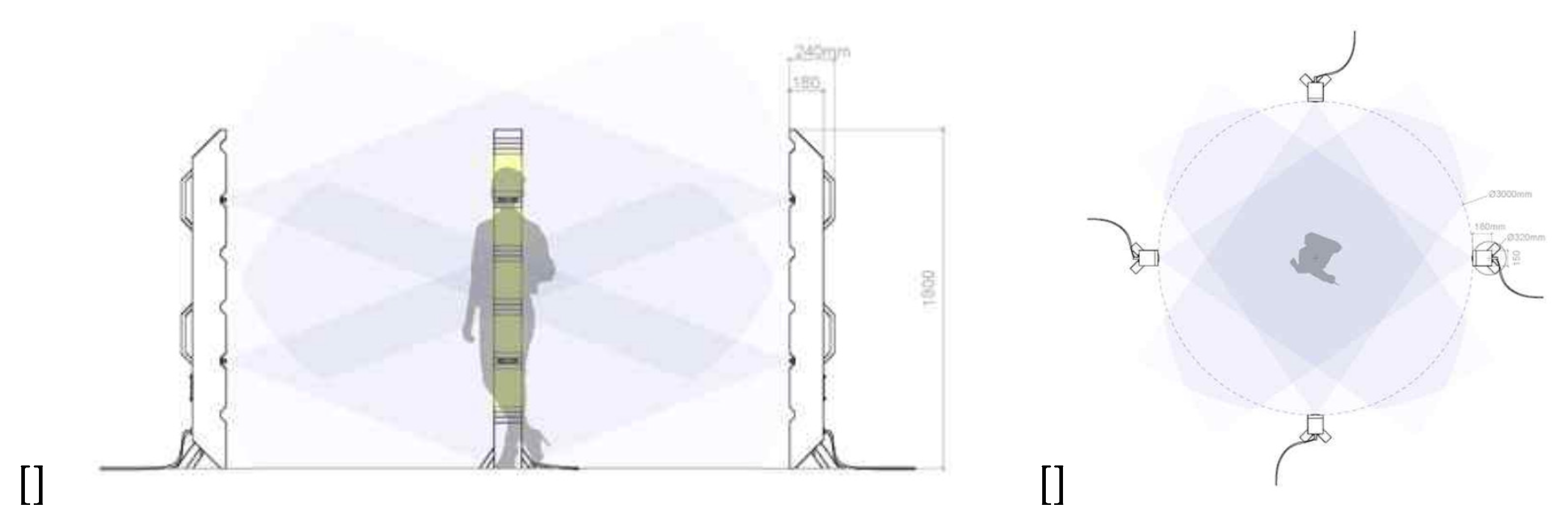
An RGB-D camera equipped with depth and RGB sensors is used to acquire dynamic point cloud sequences. Since the goal is to generate a volumetric 3D model, eight RGB-D cameras are installed at different viewpoints. Before registering the 3D model, the point cloud is acquired using the depth and RGB images taken through the RGB-D camera. Eight RGB-D cameras are installed on the camera stand. Four sets of stands are placed in the front, back, and side of four directions to capture the object from all directions. Figure 1 shows the camera system to be used in this paper.

To calibrate the point cloud captured by multi-view cameras, we minimize errors between feature points of each image. We use the Charuco board to find exact matching points [14] and the gradient descent for transformation parameter optimization [15].

The coordinates for parameter optimization correspond to the internal corner coordinates of the Charuco board. The transformation matrix includes six parameters for rotation and translation about the x, y, and z axes.

X_{r e f}

is the coordinate of the reference camera, and

X_{i}

is the coordinate of the others.

R_{i \to r e f}

and

t_{i \to r e f}

is the rotation and translation matrices respectively and they are initialized at start. The transforming relationship from

X_{i}

X_{i}^{'}

is defined as Eq. (1).

X_{i}^{'} = R_{i \to r e f} X_{i} + t_{i \to r e f}

(1)

The loss function used in the parameter optimization is the average value of the squared Euclidean distance between

X_{r e f}

and

X_{i}^{'}

. The update process of parameters by the gradient descent is defined as Eq. (2) [14,15].

α

is a constant value for learning rate and we use 0.1 which was decided in the experiment.

P_{n + 1} = P_{n} - α \frac{\partial}{\partial P_{n}} (\frac{1}{N} \sum_{j = 0}^{N} ∥ X_{r e f (j)} - X_{i}^{'} (j) ∥_{2}^{2})

(2)

The calibration requires multiple RGB and depth images captured from multi-view RGB-D cameras. The RGB images are used for finding feature points using the Charuco board, and the depth images are used for acquiring the 3D coordinates of the RGB feature points.

2.3. 3D Pose Estimation

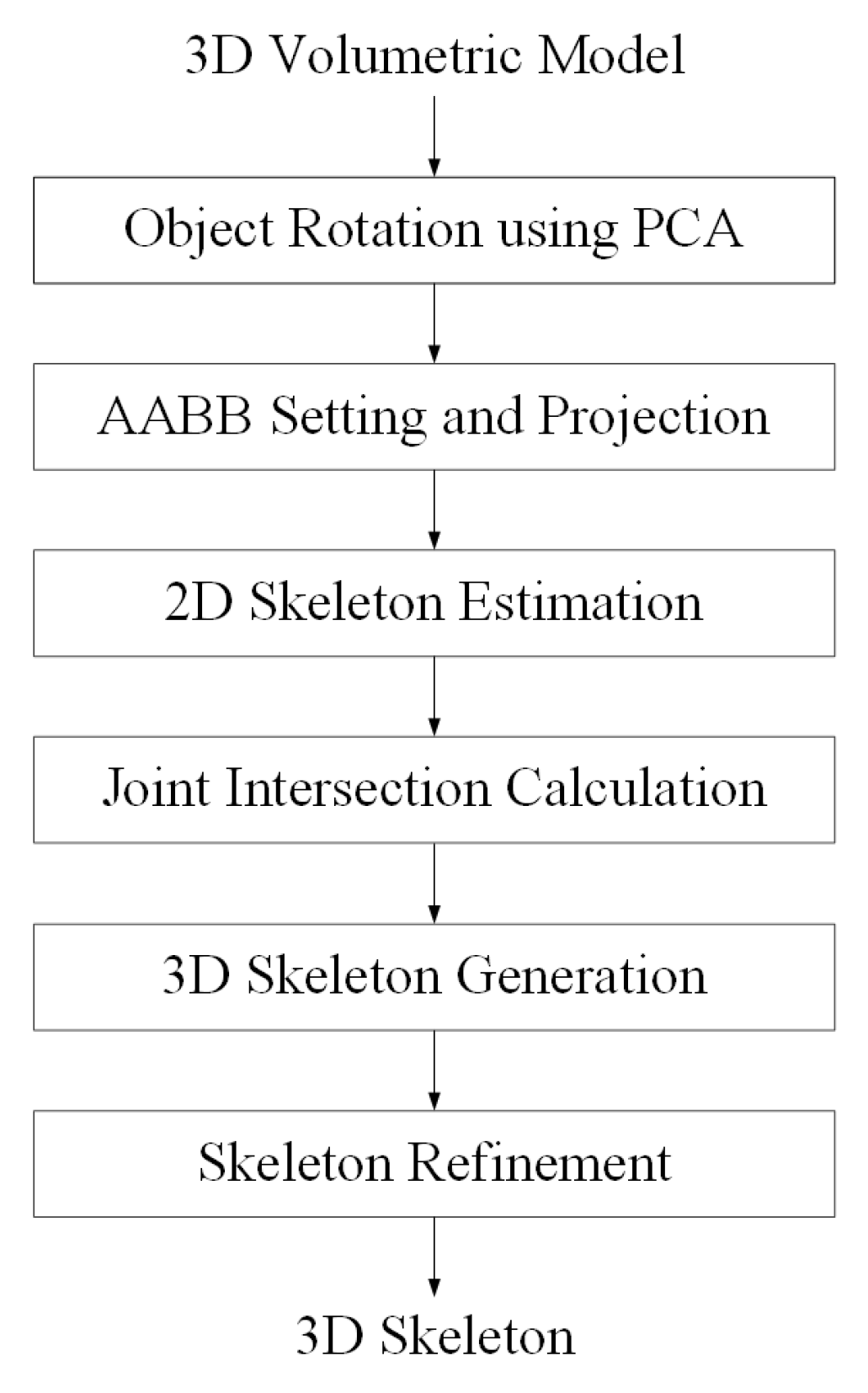
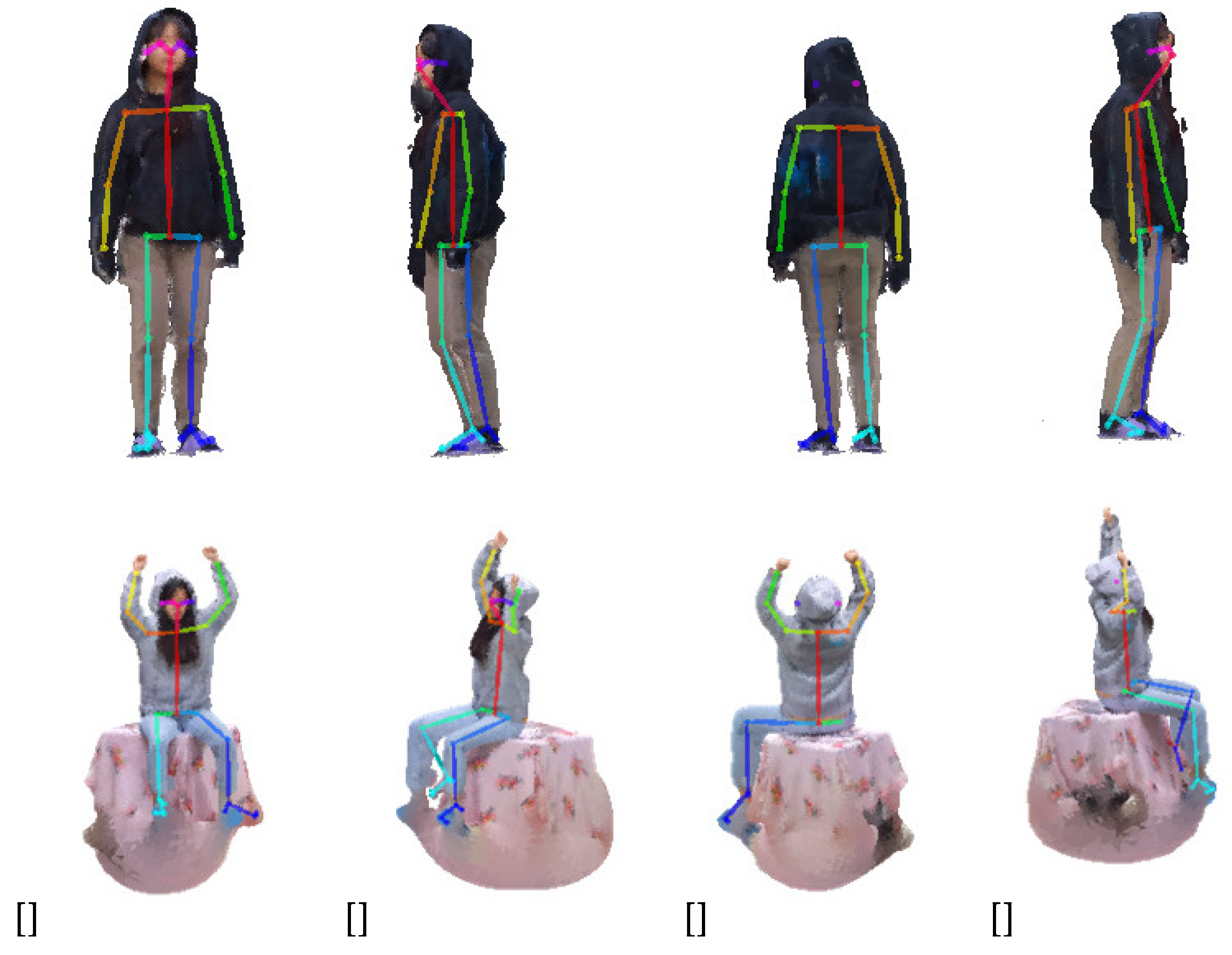
When a point cloud is captured through multi-view RGB-D cameras, projection images are generated on four virtual planes for 3D skeleton extraction. Next, the 2D skeleton of the projected image is extracted using the OpenPose library, and the intersection points for the joints in space are calculated for the 3D skeleton operation. In this paper, we use OpenPose, but it does not matter which method is used to extract the 2D skeleton. Finally, a refinement process for high-precision 3D skeleton extraction is performed. Figure 2 summarizes the algorithm for skeleton extraction.

Since we propose an new algorithm to estimate motion of the 3D point cloud for compression, we already have 3D reconstruction result. Therefore we estimate 3D human pose in the 3D point cloud domain.

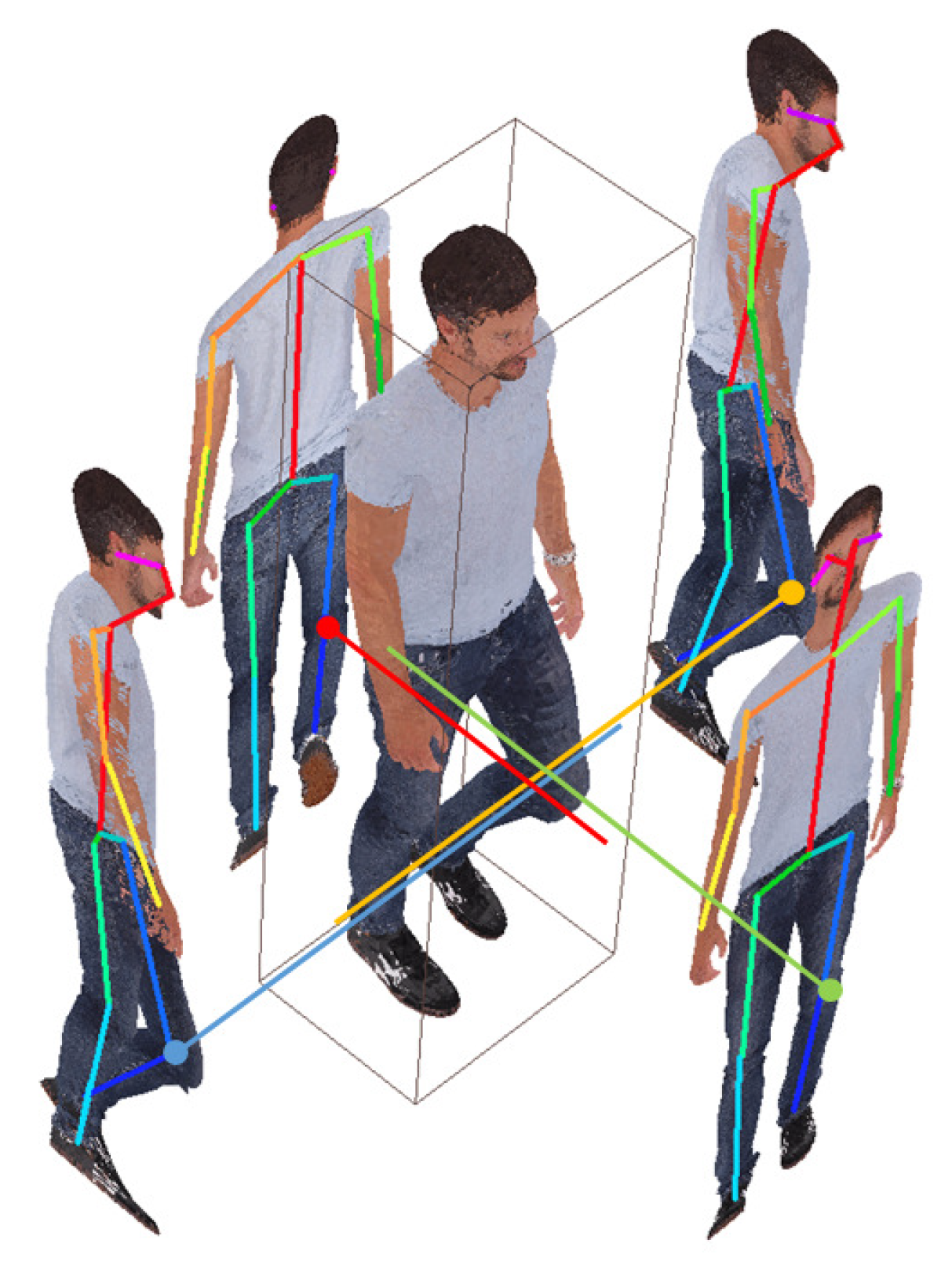
When a 2D skeleton is extracted from the image projected by the point cloud using the OpenPose network, the skeleton extracted from the image projected in the front direction has the highest accuracy. Therefore, the front of the object is found by analyzing the distribution of the point cloud in 3D space, and the front direction of the 3D point cloud is rotated so that it is parallel to the Z-axis direction. Principal component analysis (PCA) is used to find the frontal direction [16]. The primary component analysis is used to find the principal components of distributed data. After finding the front of the object, set the AABB (Axis-aligned Bounding Box) to determine the projection plane in space [17]. Projecting from the 3D to 2D plane uses the MVP (Model View Projection) matrix, which is a 4×4 matrix. Using this matrix, the 3D point cloud defined in the 3D world coordinate system is transformed into coordinates on the 2D projection plane. When four projection images are generated, 2D skeletons are extracted using OpenPose [18]. When the skeleton’s 2D coordinate system is restored back to the 3D coordinate system, the joint coordinates extracted on the four projection planes located in space are calculated. If you connect matching coordinates on four planes, you get four coordinates intersecting in space. Among these four coordinates, the coordinates having a distance of 3 cm or more from other coordinates are determined as coordinates with errors and removed. In addition to this method, various methods for 3D pose estimation have been introduced, and it does not matter which way is used as long as the accuracy is high. The accuracy of 3D pose estimation increases the residual point cloud between the two frames (key frame, target frame) point clouds, so the compression efficiency can be lowered.

3. Temporal Prediction of Dynamic Point Cloud

This section describes our method to temporally estimate the point cloud sequence.

3.1. Prediction and Reconstruction

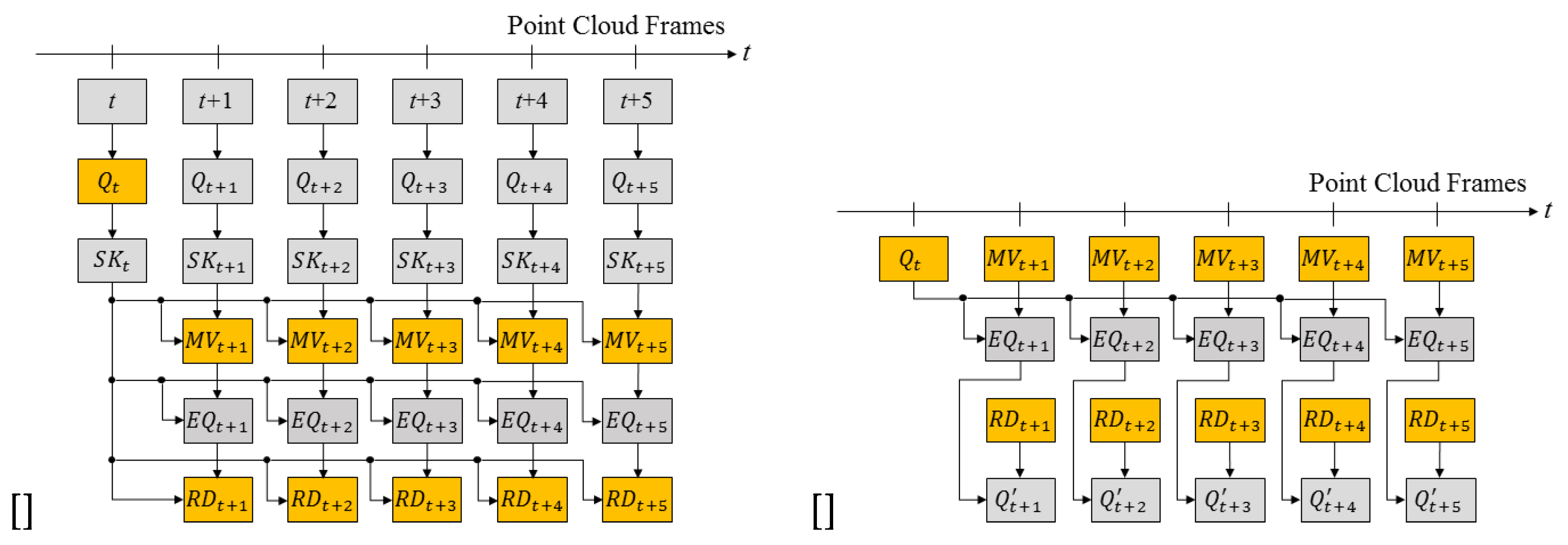
We propose a temporal prediction algorithm for point cloud sequences considering the trade-off relationship between maximizing visual quality and minimizing compressed data to transmit and store a large amount of point cloud sequence.

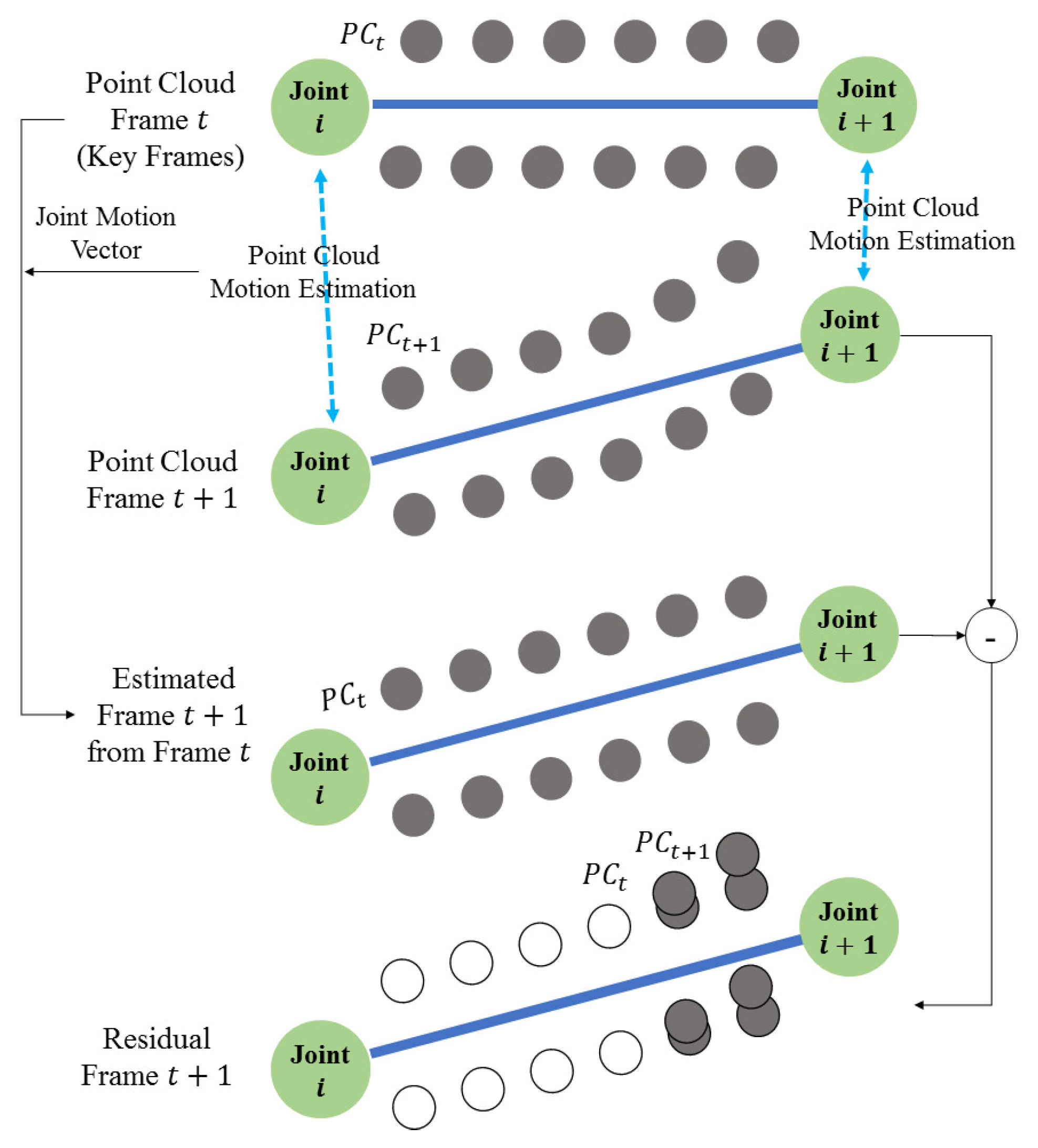
The point cloud sequence (or dynamic point cloud) is a set of point cloud captured at every frames. The 3D skeleton

S K_{t}

is obtained applying the pose estimation to the point cloud

Q_{t}

of a frame. The motion vector

M V_{t + 1}

is estimated between the skeletons (

S K_{t}

S K_{t + 1}

) of the current and next frames. The motion vector is defined as the Euclidian distance between two relative joints with the same number in the hierachical structure of the skeleton. After the 3D point cloud

Q_{t + 1}

t + 1

frame is compensated using the motion vector

M V_{t + 1}

and the 3D point cloud , the deformed point cloud

E Q_{t + 1}

is obtained. Using the deformation result

E Q_{t + 1}

and the 3D point cloud

Q_{t + 1}

, the residual point cloud

R D_{t + 1}

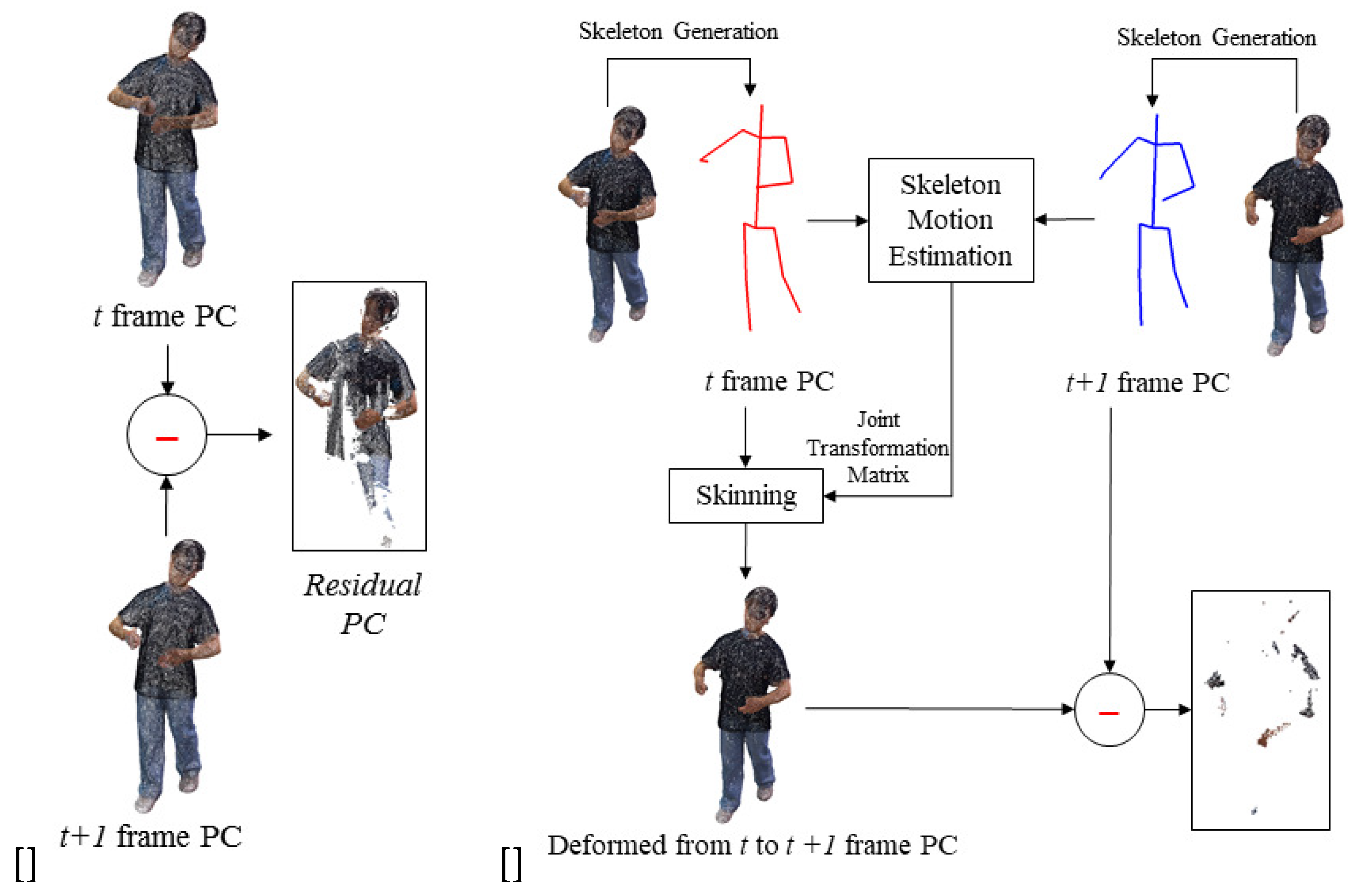
is calculated. The point cloud or residual point cloud can be compressed using various point cloud coding methods such as MPEG PCC, but developing an optimal codec for compressing the residual point cloud is beyond the scope of this paper. We focus the temporal prediction of 3D point cloud sequence. Finally, the key frame, the motion vector, and the residual point cloud are transferred. The prediction process is depicted in Figure 4

After deforming the key frame

Q_{t}

using the motion vector

M V_{t + 1}

, the deformed model

E Q_{t + 1}

is calculated. Next, the transferred residual data

R D_{t + 1}

is added to

E Q_{t + 1}

and the original 3D point cloud is reconstructed.

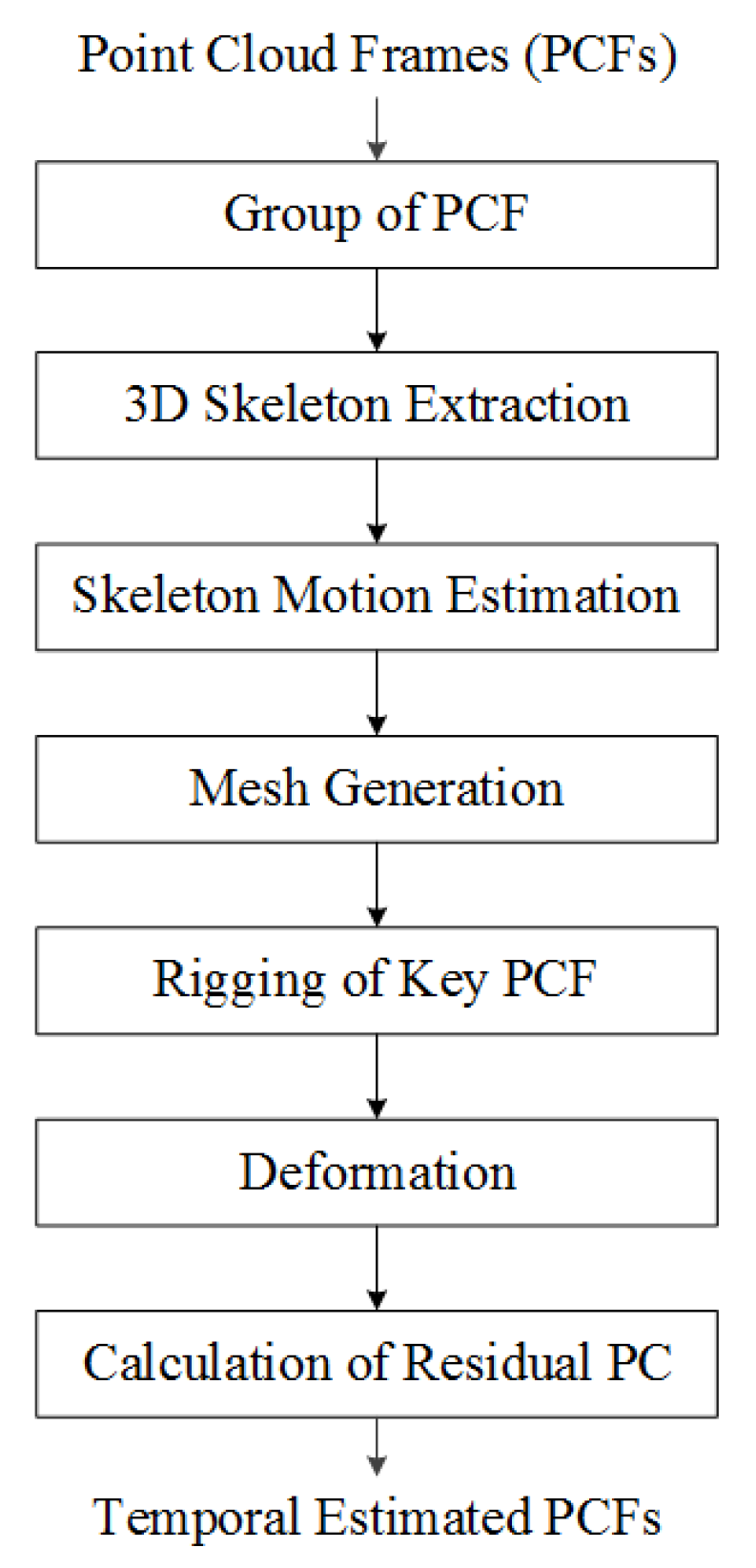
Figure 5 summarizes the flow chart for coding the proposed point cloud sequence. When a point cloud sequence is an input, the keyframe interval is determined according to the compression rate. Next, 3D skeletons are extracted from key frames and non-key frames using the proposed algorithm. After that, the keyframe is converted into a mesh for deformation, and the mesh model is deformed using the motion of the skeleton of the non-keyframe. Finally, find the residual between the point cloud composing the deformed mesh and the point cloud of the non-key frame.

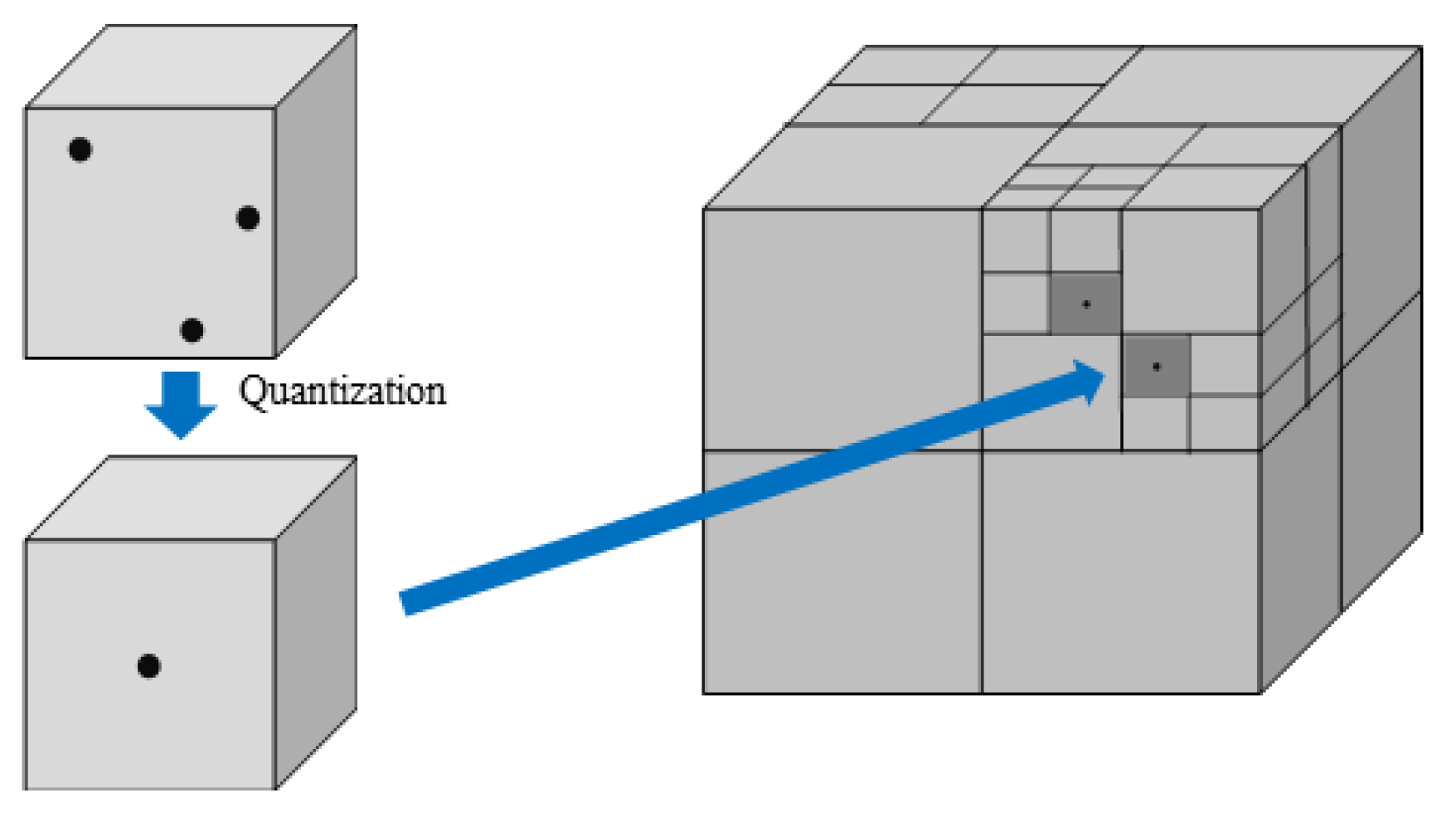
3.2. Point Cloud Quantization

When calculating the residual of the point cloud, quantization of the coordinate value of the floating point is required because it is necessary to find the location where the coordinates match. An octree, a 3D extended form of a quadtree, has a hierarchical tree structure and a structure in which a parent node is connected to eight child nodes. This paper uses the octree algorithm for quantization [6]. Quantization using the octree structure also affects compression because overlapping points in the 3D model are removed [6]. The minimum unit of voxels is set to. Figure 6 is an example of a quantization method using an octree structure. As shown in Figure 6, when voxels are divided, all point clouds inside the voxels are converted to the center coordinates of the voxels.

3.3. Skeleton Motion Estimation

Figure 7 shows the proposed point cloud estimation algorithm. First, the skeleton of the rigged keyframe is moved to the location of the skeleton of the non-key frame and deformed in the form of the point cloud of the non-key frame [19]. After deformation, the residual between the original point cloud of the non-key frame and the point cloud with the deformed key frame is obtained. The data transmitted through this process are the initial point cloud of the key frame, the skeleton information of each frame, and data about the point cloud residual of the non-key frame.

3.4. Deformation of 3D Point Cloud

Before estimating the motion of the point cloud sequence, the threshold for the number of the residual point cloud is required to decide the key frame. The number of key frames can be changed according to the compression ratio. If a frame has the residual point cloud over the threshold for others frames, the frame can be a key frame. The other frames, except the key frames transfer the motion vector of the 3D skeleton and the residual point cloud. If the threshold is larger, the interval of key frames is larger. If the key frame increases in a sequence, the compression ratio decreases, and the visual quality increases.

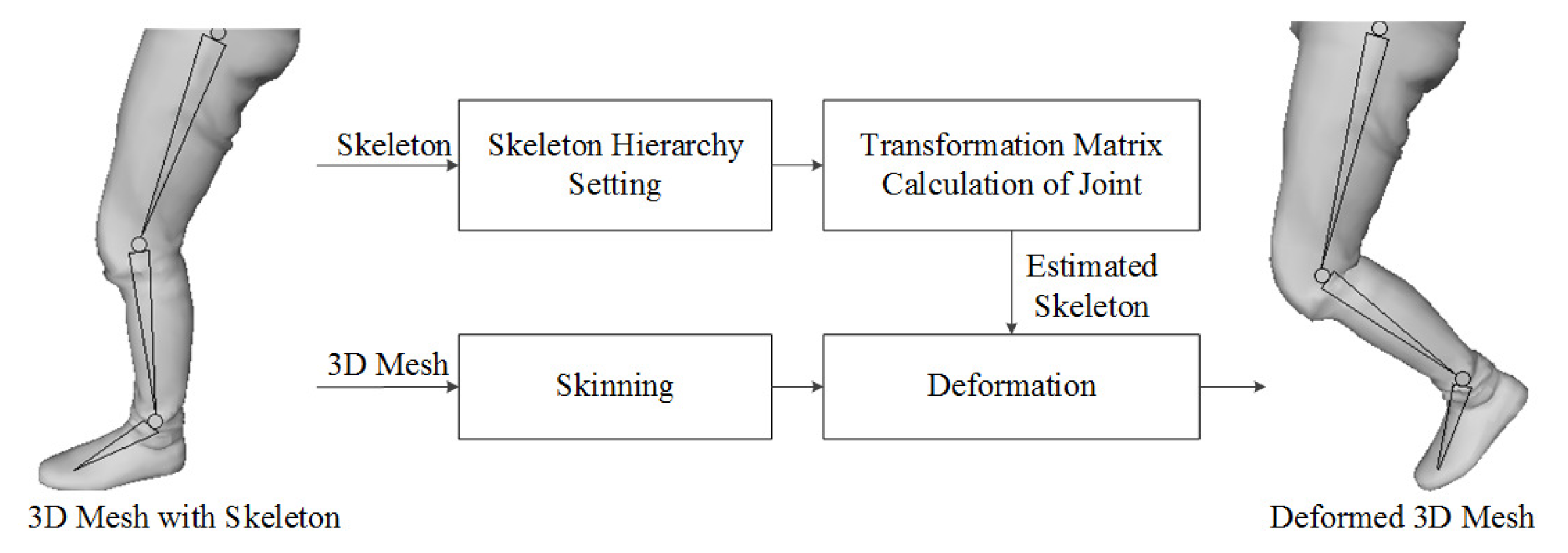
Next, we explain the deformation step for motion compensation. To compensate for the 3D PC, after deforming the 3D key PCF using the estimated motion vector by the 3D pose estimation, the overlapped PC between the key and target PCFs is removed using the motion-compensated 3D key PCF. Next, the 3D PC is converted to the mesh model for deformation, where we use Poisson surface reconstruction [20]. Figure 8 is a flow for the mesh deformation to convert mesh using the 3D mesh and skeleton. After generating the 3D mesh, skinning, which attaches the skin to bones using the estimated skeleton, is conducted. The transformation matrix is also required to deform the 3D key PCF, which calculates the 3D distance and direction between the joints of the key PCF and target PCF. The matrix and estimating method are the same types as Eq. (1). The key PCF is deformed to the target PCF using the transformation matrices of the joints and the skinned 3D model.

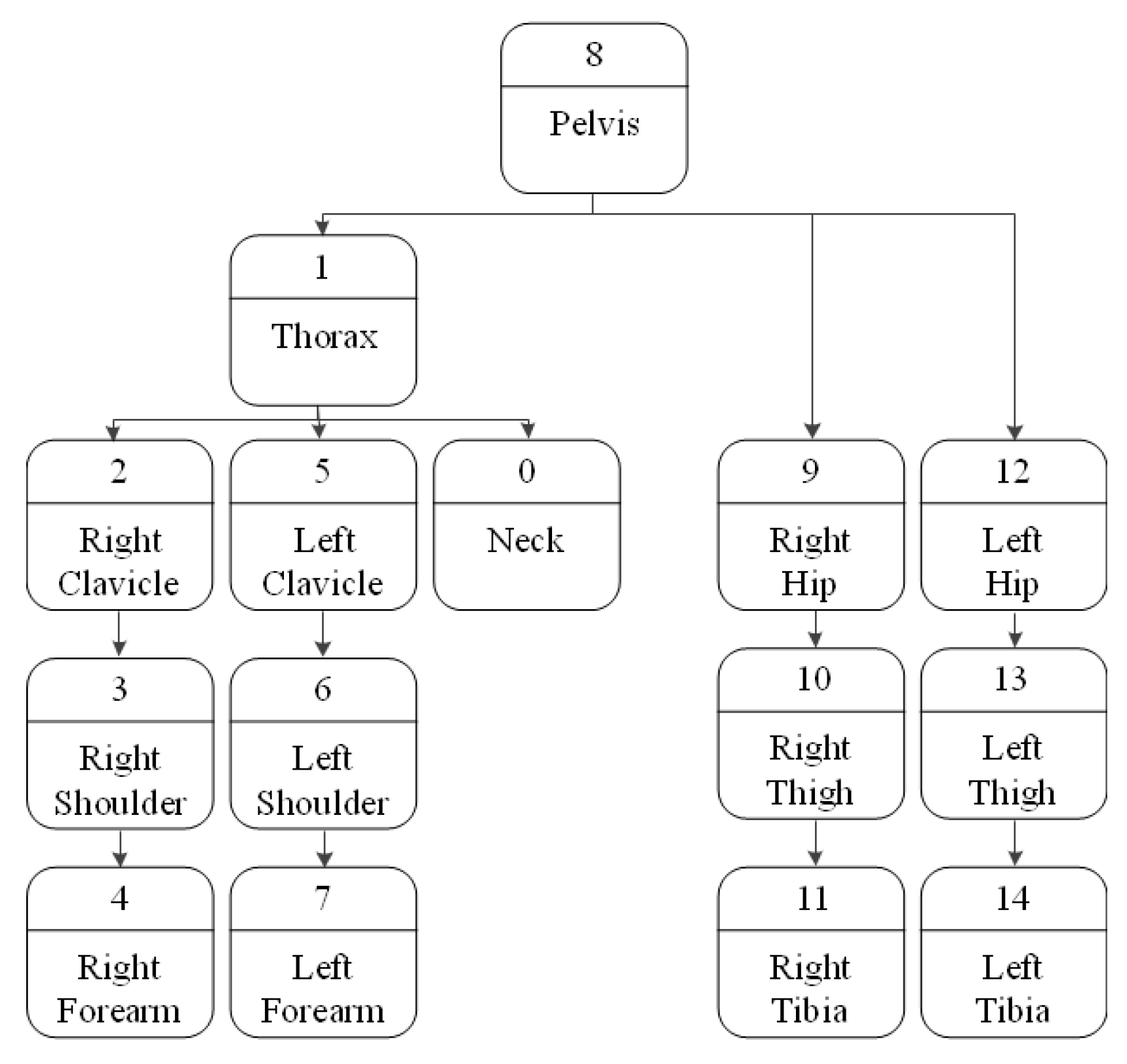
When a person moves, the movement of one part may or may not affect the movement of another part. For example, if you move your thigh up, your calves will be affected by the movement of your thigh and move up together. However, just because the calf moves, the thigh doesn’t necessarily move with it. A hierarchical structure is set in the 3D model to reflect this influence so that the lower nodes work together with the movement of the upper nodes. In the skeleton hierarchy, the pelvis corresponding to the core is the highest node, and the closer it is to the pelvis, the higher the node is. Figure 9 shows the skeleton hierarchy used in this paper [20].

After setting the hierarchy, skinning is performed from the skeleton of the lower hierarchy. We use the bisector of the two bones. First, a mesh is assigned to the bones located on the left and right with respect to the plane passing through the bisector. However, if the mesh is divided simply like this, the mesh may be separated when it is moved. Therefore, skinning weight is used to express natural movement [21,22]. Since the degree of skin stretching can vary depending on the distance away from the joint, this part is expressed using skinning weights. 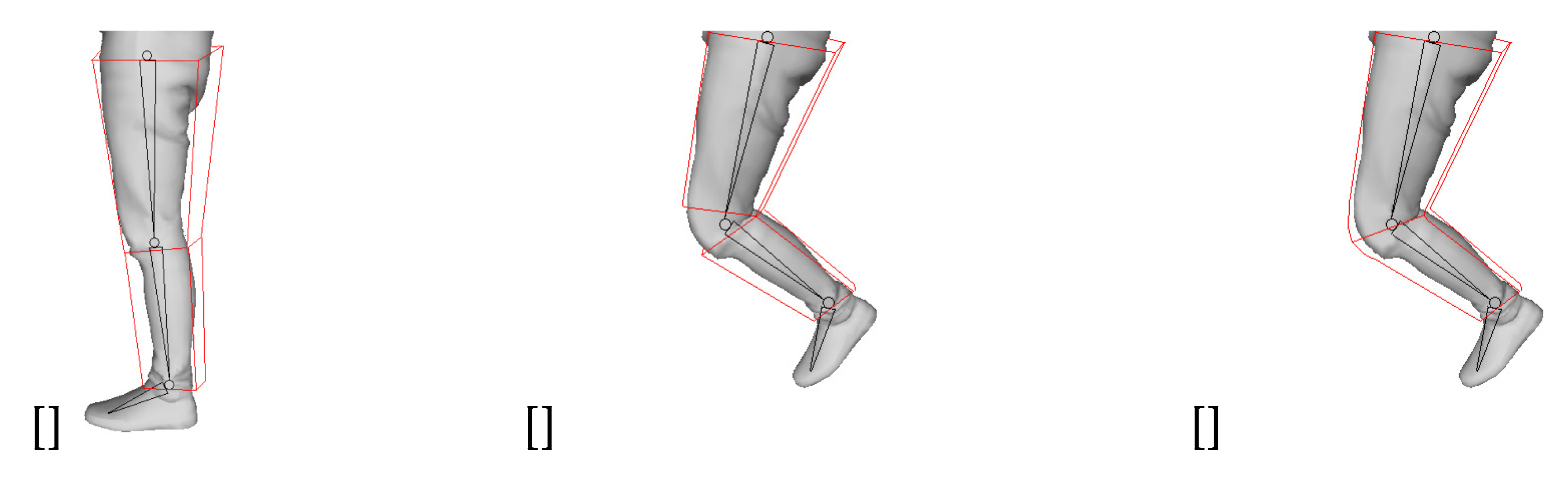Figure 10 is an example of the movement of the mesh before and after applying the skinning weight. Figure 10a is a key frame mesh and skeleton to be transformed, Figure 10b is a non-key frame mesh and a keyframe mesh transformed without weight, Figure 10c is a non-key frame mesh, and a key frame mesh with weights applied. This is an example of deformation when applied. From this figure, you can see that the joint is deformed unnaturally if no weight is applied. The weight has a value between 0 and 1, and the closer it is to the center of the bone, the closer it gets to 1, and the closer it gets to the joint, the closer it gets to 0 [22].

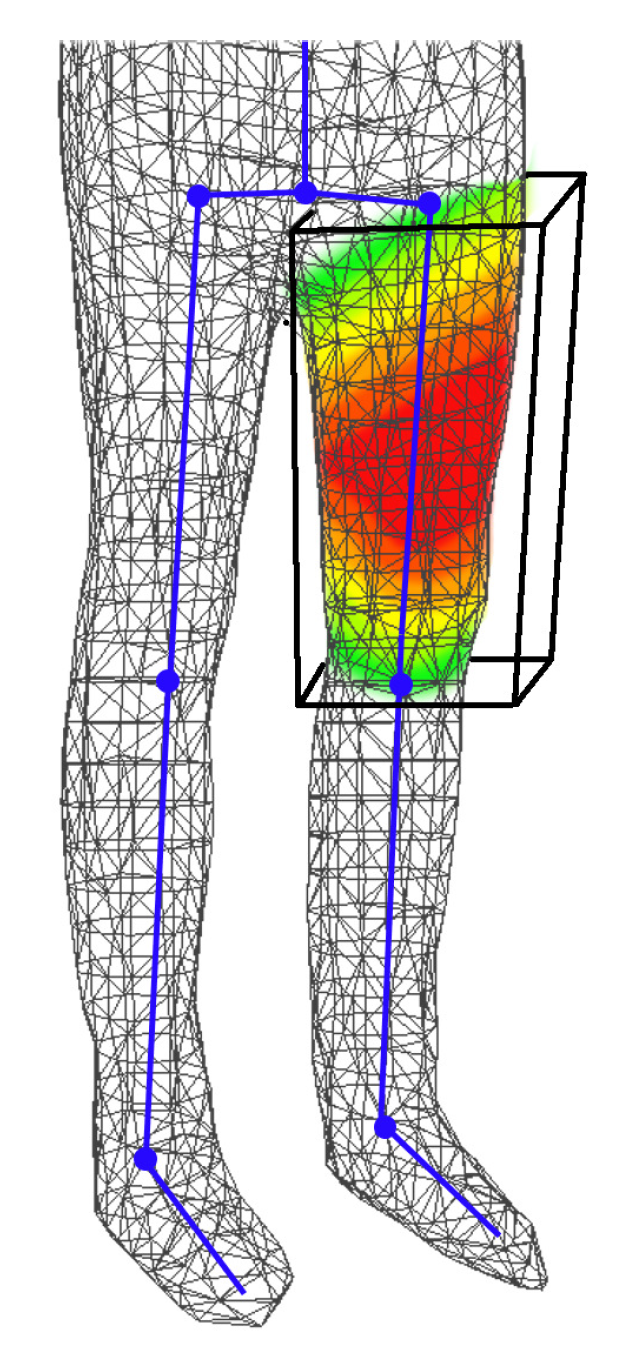
Figure 11 shows the mesh with skinning weight applied. The closer it is to the red color, the closer it is to 1, and the closer it is to blue, the closer it is to 0. When only the mesh for the left thigh is considered, all of the left thigh bones have non-zero values, and the farther from the middle of the bone, the closer to the green color.

Next, we explain calculation of the transformation matrix (

R | T

) for the joint. The movement of a bone from the frame t to the frame t+1 is shown in Figure 12, j1, j2 and j2 represent joints.

t (\vec{a})

is the direction vector from j2 to j1 in the frame t and

t + 1 (\vec{b})

is the direction vector from j2 to j1 in the frame t+1.

θ

is an angle between

t (\vec{a})

and

t + 1 (\vec{b})

, and

\vec{u}

is an axis of rotation.

The transformation matrix (T) is derived from the joint movement defined as Eq. (3).

T = j 2_{t + 1} - j 2_{t}

(3)

The rotation matrix (R) can be estimated from the angle and axis of rotation. In Figure 12, the 3D coordinate of j2 is fixed in t and t+1, but it can be changed. After assuming that

j 2_{t + 1}

and

j 2_{t}

are located in the same position, the rotation matrix is calculated. The axis of rotation (

\vec{u}

) is calculated as the cross product of

t (\vec{a})

and

t + 1 (\vec{b})

as shown in Eq. (4).

\vec{u} = t + 1 (\vec{b}) \times t (\vec{a})

(4)

The angle of rotation is calculated by the arccosine of the inner product of

t (\vec{a})

and

t + 1 (\vec{b})

as Eq. (5).

θ = a cos (t + 1 (\vec{b}) • t (\vec{a}))

(5)

The rotation matrix is defined as Eq. (1) using the axis and angle of rotation.

R = [\begin{matrix} cos θ + u_{x}^{2} (1 - cos θ) - 11 m u & - 11 m u u_{x} u_{y} (1 - cos θ) - u_{z} sin θ - 11 m u & - 11 m u u_{x} u_{z} (1 - cos θ) + u_{y} sin θ \\ u_{y} u_{x} (1 - cos θ) + u_{z} sin θ - 11 m u & - 11 m u cos θ + u_{y}^{2} (1 - cos θ) - 11 m u & - 11 m u u_{y} u_{z} (1 - cos θ) - u_{x} sin θ \\ u_{x} u_{z} (1 - cos θ) - u_{y} sin θ - 11 m u & - 11 m u u_{y} u_{z} (1 - cos θ) + u_{x} sin θ - 11 m u & - 11 m u cos θ + u_{z}^{2} (1 - cos θ) \end{matrix}]

(6)

The mesh (or point cloud) is deformed with the skinning weight and the transformation matrix. The mesh is deformed with Eq. (7), where W is the skinning weight, and X and

X^{'}

are the coordinates after and before deformation, respectively.

X^{'} = W (R (X - j 2_{t}) + j 2_{t + 1})

(7)

3.5. Residual Point Cloud

This section describes the process of finding the residuals. In the previous chapter, the mesh was used for the convenience of skinning. Since we are dealing with a point cloud, we return the vertices of the mesh to the point cloud. The vertices of the mesh model are treated as the same information as the 3D PC. The mesh model can be viewed as the same as the 3D PC model. Using the method described in the previous section, the deformed target PCF is calculated using the key PCF and the target PCF, and the residual between the original target PCF and the deformed target PCF is calculated. Figure 13 conceptually shows how to calculate the residual of the point cloud before and after pose estimation and deformation. In the case of calculation, as shown in Figure 13a, most of the upper body remains residual. However, as shown in Figure 13b, the number of residual point clouds can be reduced by more than three times by using the proposed method. In addition, lossless compression, such as binary encoding, is applied to the residual point cloud. If various compression codecs, including methods such as MPEG PCC, are applied to the residual, a higher compression rate can be obtained. However, since we conducted a study to reduce the number of point clouds themselves, this paper needs to discuss such compression techniques in detail. Also, how such a compression technique can affect our proposed method is not covered, as it is beyond the focus of this paper.

4. Experimental Result

In this section, the experimental environment and experimental results are explained.

4.1. Experimental Environment

In this paper, 8 Microsoft Kinect Azure cameras were used. The camera arrangement follows the shooting system, as shown in Figure 14. Four units were installed at 0.7m from the ground, and the remaining four units were placed at 1.5m from the floor to photograph the top of the object. A threshold value was set for the depth value to obtain a point cloud for objects within 0.1m to 1.5m. Figure 14 is a photograph of the configured camera system.

Figure 15 shows projection images of the two 3D point cloud sequences used in the experiment and the result of extracting the 2D skeleton from the projection images. The upper 3D point cloud sequence has a walking motion, and the lower 3D point cloud sequence is stationary and sitting. The upper sequence features most of the body visible from all sides, while the lower sequence features an occlusion where parts of the legs are not visible from the back. As shown in Figure 15, the skeleton extraction is more accurate on the front than on the other side.

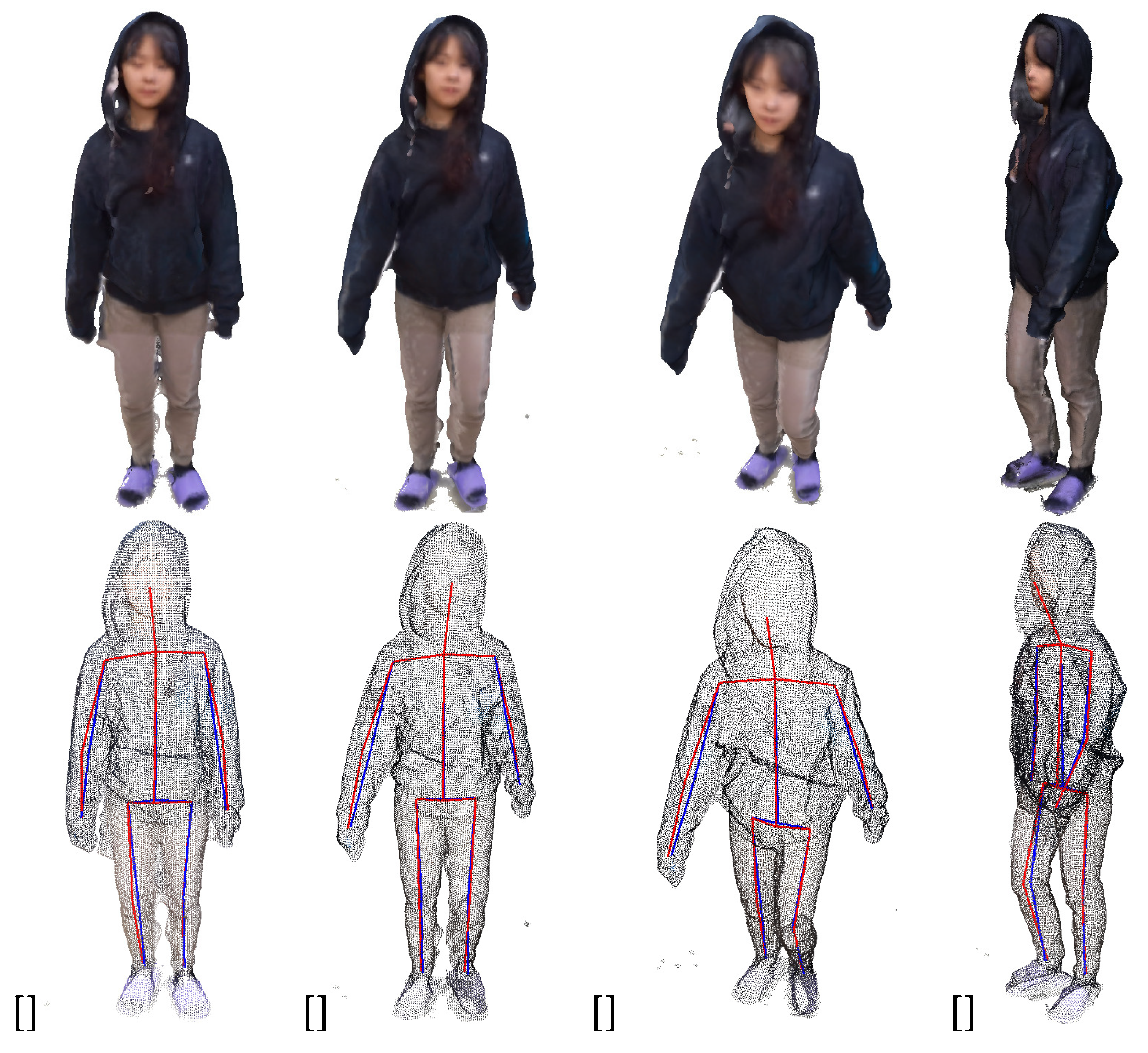
Figure 16 shows four frames from the first 3D point cloud sequence in Figure 15. In Figure 16, the first row represents the texture of the 3D model, and the second row represents the point cloud. The result of estimating the 3D skeleton from the four extracted frames is shown. If you check the estimated 3D skeleton, you can visually confirm that all joints and bones are accurately located inside the point cloud distribution of the model.

Compression was performed on five frames of directly acquired point cloud data. The first frame was keyframed, and the rest were compressed. Figure 17 is the compression result of five frames. Figure 17a is the mesh before compression, Figure 17b is the deformed mesh after skinning, Figure 17c is the point cloud residual obtained without motion compensation, Figure 17d is the point cloud residual after motion compensation, And Figure 17e is the restored point cloud result. Figure 17 shows that the compression effect improves as the sequence increases.

Table 1 shows the number of vertices and data size between the original and compressed data after applying octree quantization, the proposed compression algorithm, and the binary encoding of each frame. To the results of this table, the compression rate before and after applying motion compensation increased more than three times.

For performance evaluation, a tool called cloud compare was used to measure the error’s mean distance and standard deviation between the original point cloud and the restored point cloud after compression. Table 2 is the Mean Distance and Standard Deviation measurement results using Cloud Compare. The mean distance of all frames is within ±0.1, and the standard deviation is less than 0.05, which does not differ significantly from the original data [23].

5. Conclusions

In this paper, we propose a system from acquiring a photo-realistic-based point cloud sequence at 30 fps through an RGB-D camera system to extracting a 3D skeleton and compressing it. To extract the skeleton, create a projection plane for the four sides of the object and extract the 2D skeleton using the Openpose library, a deep learning model. Then, post-processing is performed for high-precision skeleton extraction. The 3D skeleton for the entire point cloud of the extracted sequence is used for compression. Compression is carried out in the form of moving the rigged keyframe to the skeleton movement of the non-keyframe, predicting the movement, removing overlapping points, and transmitting only the residual.

Using 8 RGB-D cameras, it was possible to acquire point cloud data based on real-life images in all directions. In addition, it was possible to create an integrated point cloud with an error of less than 5 mm through the camera calibration process by applying the optimization algorithm. In addition, it was possible to extract a high-precision 3D skeleton without additional motion capture equipment using the generated point cloud sequence. A stable skeleton with half the standard deviation was extracted through a post-processing algorithm to compensate for the instability of the deep learning network. In addition, using this skeleton, the number of residual point clouds can be reduced by about 12 times by predicting motion between point clouds and removing temporally overlapping points. In addition, motion compensation increased the compression rate three times, and the compression effect improved as the sequence increased. In addition, the restored data after compression through Cloud Compare was similar to the original, with a mean distance of ±0.1 and a standard deviation of less than 0.05.

Author Contributions

Conceptualization and methodology, S.L. and Y.-H.S.; software and hardware, S.L.; data curation, J.-K.K. and Y.-W.J.; writing–review and editing, E.S.H.; project administration and funding acquisition, Y.-H.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research is supported Year 2021 Culture Technology R&D Program by Ministry of Culture, Sports and Tourism and Korea Creative Content Agency (Project Name: Development of social XR showroom technology for the distribution of cultural products by one-person enterprises and small business owners, Project Number: R2021070007). The present Research has been conducted by the Research Grant of Kwangwoon University in 2023.

Conflicts of Interest

The authors declare no conflict of interest.

References

Pavez, E.; Chou, P.A.; De Queiroz, R.L.; Ortega, A. Dynamic polygon clouds: representation and compression for VR/AR. APSIPA Transactions on Signal and Information Processing 2018, 7, e15. [Google Scholar] [CrossRef]
Kammerl, J.; Blodow, N.; Rusu, R.B.; Gedikli, S.; Beetz, M.; Steinbach, E. Real-time compression of point cloud streams. 2012 IEEE international conference on robotics and automation. IEEE, 2012, pp. 778–785.
Schwarz, S.; Preda, M.; Baroncini, V.; Budagavi, M.; Cesar, P.; Chou, P.A.; Cohen, R.A.; Krivokuća, M.; Lasserre, S.; Li, Z.; others. Emerging MPEG standards for point cloud compression. IEEE Journal on Emerging and Selected Topics in Circuits and Systems 2018, 9, 133–148. [Google Scholar] [CrossRef]
Briceno, H.M.; Sander, P.V.; McMillan, L.; Gortler, S.; Hoppe, H. Geometry videos: a new representation for 3D animations. Proceedings of the 2003 ACM SIGGRAPH/Eurographics symposium on Computer animation, 2003, pp. 136–146.
Collet, A.; Chuang, M.; Sweeney, P.; Gillett, D.; Evseev, D.; Calabrese, D.; Hoppe, H.; Kirk, A.; Sullivan, S. High-quality streamable free-viewpoint video. ACM Transactions on Graphics (ToG) 2015, 34, 1–13. [Google Scholar] [CrossRef]
Jackins, C.L.; Tanimoto, S.L. Oct-trees and their use in representing three-dimensional objects. Computer Graphics and Image Processing 1980, 14, 249–270. [Google Scholar] [CrossRef]
Meagher, D. Geometric modeling using octree encoding. Computer graphics and image processing 1982, 19, 129–147. [Google Scholar] [CrossRef]
Schnabel, R.; Klein, R. Octree-based Point-Cloud Compression. PBG@ SIGGRAPH 2006, 3. [Google Scholar]
Pathak, K.; Birk, A.; Poppinga, J.; Schwertfeger, S. 3D forward sensor modeling and application to occupancy grid based sensor fusion. 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems. IEEE, 2007, pp. 2059–2064.
Rusu, R.B.; Cousins, S. 3d is here: Point cloud library (pcl). 2011 IEEE international conference on robotics and automation. IEEE, 2011, pp. 1–4.
Mekuria, R.; Blom, K.; Cesar, P. Design, implementation, and evaluation of a point cloud codec for tele-immersive video. IEEE Transactions on Circuits and Systems for Video Technology 2016, 27, 828–842. [Google Scholar] [CrossRef]
Thanou, D.; Chou, P.A.; Frossard, P. Graph-based compression of dynamic 3D point cloud sequences. IEEE Transactions on Image Processing 2016, 25, 1765–1778. [Google Scholar] [CrossRef] [PubMed]
Kim, K.J.; Park, B.S.; Kim, J.K.; Kim, D.W.; Seo, Y.H. Holographic augmented reality based on three-dimensional volumetric imaging for a photorealistic scene. Optics Express 2020, 28, 35972–35985. [Google Scholar] [CrossRef] [PubMed]
Lee, S. Convergence rate of optimization algorithms for a non-strictly convex function. Institute of Control Robotics and Systems, 2019; 349–350. [Google Scholar]
Kim, K.J.; Park, B.S.; Kim, D.W.; Kwon, S.C.; Seo, Y.H. Real-time 3D Volumetric Model Generation using Multiview RGB-D Camera. Journal of broadcast engineering 2020, 25, 439–448. [Google Scholar]
Shlens, J. A tutorial on principal component analysis. arXiv preprint arXiv:1404.1100, arXiv:1404.1100 2014.
Barequet, G.; Har-Peled, S. Efficiently approximating the minimum-volume bounding box of a point set in three dimensions. Journal of Algorithms 2001, 38, 91–109. [Google Scholar] [CrossRef]
Cao, Z.; Simon, T.; Wei, S.E.; Sheikh, Y. Realtime multi-person 2d pose estimation using part affinity fields. Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 7291–7299.
Pan, H.; Huo, H.; Cui, G.; Chen, S. Modeling for deformable body and motion analysis: A review. Mathematical Problems in Engineering 2013, 2013. [Google Scholar] [CrossRef]
Kwolek, B.; Rymut, B. Reconstruction of 3D human motion in real-time using particle swarm optimization with GPU-accelerated fitness function. Journal of Real-Time Image Processing 2020, 17, 821–838. [Google Scholar] [CrossRef]
Kazhdan, M.; Hoppe, H. Screened poisson surface reconstruction. ACM Transactions on Graphics (ToG) 2013, 32, 1–13. [Google Scholar] [CrossRef]
Bang, S.; Lee, S.H. Computation of skinning weight using spline interface. In ACM SIGGRAPH 2018 Posters; 2018; pp. 1–2.
Cushman, R. Open source rigging in Blender: A modular approach. PhD thesis, Clemson University, 2011.

Figure 1. Capturing system of the 3D point cloud sequence (a) side, (b) top view

Figure 2. Work flow for 3D skeleton extraction

Figure 3. Example of point cloud’s left shoulder 3D joint extraction

Figure 4. The procedure of the temporal prediction and reconstruction of the point cloud sequence

Figure 5. Workflow of proposed point cloud compression algorithm

Figure 6. Example of quantization using octree structure

Figure 7. Example of the proposed point cloud compression algorithm

Figure 8. Mesh deformation workflow

Figure 9. keleton Hierarchy

Figure 10. Skinning example (a) keyframe mesh and skeleton that has been skinned, (b) keyframe mesh and skeleton before and (c) after skinning weight is applied

Figure 11. Skinning result of the left thigh

Figure 12. Examples of Skeleton Coordinate Transformation

Figure 13. 3D point cloud compression process using skeleton estimation (a) frame-by-frame residual calculation method, (b) proposed method

Figure 14. Camera system environment used

Figure 15. Extraction of the 2D skeleton of the projected image (a) front, (b) right, (c) rear, and (d) left.

Figure 16. For the 4 frames acquired directly, (a) the first frame, (b) the second frame, (c) the third frame, (d)the mesh of the fourth frame and the skeleton before and after post-processing

Figure 17. Compression and reconstruction result, (a) original pointcloud, (b) mesh deformation result, (c) residual result to which estimation was not applied, (d) residual result to which estimation was applied, (e) restoration result

Table 1. Number of vertices and data amount before and after compression for each frame

Item	Frame	Key frame	Non-Key Frame	Ratio
Original	Number of Point Cloud	348,597	341,334	100.00%
Original	Data size (KB)	17,699	16,427	100.00%
Residual	Number of Point Cloud	348,597	26,473	7.76%
Residual	Data size (KB)	17,699	1,061	6.46%
Residual with Deformation	Number of Point Cloud	348,597	2,190	0.64%
Residual with Deformation	Data size (KB)	6,923	35	0.01%

Table 2. Mean Distance and Standard Deviation measurement results using Cloud compare

Frame	t+1	t+2	t+3	t+4
Mean Distance (m)	0.004571	0.006422	0.009824	0.014579
Standard Deviation (m)	0.002758	0.00506	0.007838	0.009799

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer