Prerpints.org logo
Preprint
Article

Predicting Commercial Building Energy Consumption Using a Multivariate Multilayered Long-Short Term Memory Time-Series Model

Altmetrics

Downloads

177

Views

118

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

31 May 2023

Posted:

02 June 2023

You are already at the latest version

Alerts
Abstract
The global demand for energy has been steadily increasing due to population growth, urbanization, and industrialization. Numerous researchers worldwide are striving to create precise forecasting models for predicting energy consumption to manage supply and demand effectively. In this research, a time-series forecasting model based on multivariate multilayered long short-term memory (LSTM) is proposed for forecasting energy consumption and tested using data obtained from commercial buildings in Melbourne, Australia: the Advanced Technologies Center, Advanced Manufacturing and Design Center, and Knox Innovation, Opportunity, and Sustainability Center buildings. This research specifically identifies the best forecasting method for subtropical conditions and evaluates its performance by comparing it with the most used methods at present, including LSTM, bidirectional LSTM, and linear regression. The proposed multivariate multilayered LSTM model was assessed by comparing mean average error (MAE), root-mean-square error (RMSE), and mean absolute percentage error (MAPE) values with and without labeled time. Results indicate that the proposed model exhibits optimal performance with improved precision and accuracy. Specifically, the proposed LSTM model achieved a decrease in MAE by 30%, RMSE by 25%, and MAPE by 20% compared to the LSTM method. Moreover, it outperformed the bidirectional LSTM method with a reduction in MAE by 10%, RMSE by 20%, and MAPE by 18%. Furthermore, the proposed model surpassed linear regression with a decrease in MAE by 2%, RMSE by 7%, and MAPE by 10%. These findings highlight the significant performance increase achieved by the proposed multivariate multilayered LSTM model in energy consumption forecasting.
Keywords: 
Subject: Engineering  -   Energy and Fuel Technology

1. Introduction

Energy consumption refers to the amount of energy used over a certain period of time, usually measured in units such as kilowatt-hours (kWh) or British thermal units (BTUs). It is an important metric for assessing energy usage and efficiency, and for understanding the overall energy needs of a region or country [1]. According to the International Energy Agency (IEA) [2], global energy consumption is expected to continue to increase in the coming decades, driven by population growth, urbanization, and industrialization in developing countries.
However, most of the current research has focused on forecasting in countries or regions [3,4]. However, only a limited number of studies exist that specifically focus on forecasting for individual buildings. Energy consumption in buildings encompasses the precise measurement of energy utilized for specific purposes such as heating, cooling, lighting, and other essential functions within residential, commercial, and institutional structures. In China and India, buildings account for a 37% [5] and 35% [6] of global energy consumption, making it an important area for energy efficiency and sustainability efforts [7].
In this study, we propose the forecasting model for energy consumption for various commercial buildings, such as Hawthorn Campus - ATC Building, Hawthorn Campus - AMDC Building, Wantirna Campus - KIOSC Building. In the study, the proposed model, along with its trained data preprocessing method, demonstrates superior performance compared to other popular models, particularly when there is a sufficient amount of training data available or when there is a lack of training data. The results indicate that the proposed method and model can be used to accurately predict energy consumption in commercial buildings, which is crucial for energy management and conservation. In addition, the proposed method can be easily applied to other commercial buildings with similar energy consumption patterns, providing a practical solution for energy management in the commercial building sector.
The rest of this study is organized as follows. Section 2 delivers the background of the research. Section 4 provides the details of the proposed model. Section 5 describes some popular bench-marking models. Section 6 presents the experiment to evaluate the efficiency of the models in different datasets. Finally, the conclusion of this study is given in Section 7.

2. Background

2.1. Forecasting Models

A forecasting model is a mathematical algorithm or statistical tool used to predict future trends, values, or events based on historical data and patterns. A forecasting model M that analyzes the historical values from the current time t to return the predicted future value at time t + 1 (denoted as y ^ t + 1 ) is built. The objective of the forecasting model is to minimize the discrepancy between the estimated value y ^ t + 1 and the actual value y t + 1 by seeking the closest approximation. To achieve this in a temporal context where data points are indexed in time order, a specific type of forecasting model is often used.
A time series forecasting model is a predictive algorithm that utilizes historical time-series data to anticipate future trends or patterns in data over time. Two techniques are available for building the model M to obtain this objective, i.e., (i) univariate and (ii) multivariate time-series (TS) [8,9,10]. In univariate TS, only a 1D sequence of energy consumption value y t = { y t − ( k − 1 ) , y t − ( k − 2 ) , . . . , y t − 1 , y t } is utilized to produce the estimated value y ^ t + 1 , where k is a period of time from the current time t [11,12]. By contrast, for multivariate TS, we could employ one or more other historical features in addition to the energy consumption for training model M [13]. They can be time field or other specific sources. Therefore, the input for multivariate TS is a multi-dimensional sequence X t = { x t − ( k − 1 ) , x t − ( k − 2 ) , . . . , x t − 1 , x t } , with x i ∈ R n is a vector of dimension n). In forecasting new values, the model could be enhanced if related available features are taken into account. The additional information could help to model capture the dependencies or correlations between features and target variable. Therefore, the model could better understand the context, mitigate the impact of missing values, and make more precise predictions. Therefore, multivariate TS are frequently employed for building the forecasting model recently [14].

2.2. Energy Consumption Forecasting

Energy consumption forecasting refers to predicting a particular region’s future energy consumption based on historical consumption and other relevant factors [1]. Accurate energy consumption forecasting is essential for proper energy planning, pricing, and management. It plays a significant role in the transition toward a more sustainable energy future. There have been numerous studies on energy consumption forecasting, and various models have been proposed for this purpose [15]. As shown in Figure 1, in the literature, forecasting models often fall into two categories: (i) Conventional Models and (ii) Artificial Intelligence (AI) Models. Table 1 shows different forecasting models for commercial buildings. It shows the name of forecasting techniques, location, and performance evaluation indexes with the best accuracy.
Conventional models used in energy consumption forecasting commonly include Stochastic time series (TS) models [16], regression models (RMs) [17], and gray models (GMs) [18,19]. These models typically require historical energy consumption data as input and use various statistical and mathematical techniques to make future energy consumption predictions. However, these models may not be able to capture complex nonlinear relationships and may require manual feature engineering, making them less efficient and scalable compared to AI-based models. AI-based models have become increasingly popular in the field of energy forecasting due to their ability to learn patterns and relationships in complex data [32,33,34]. The use of AI in energy forecasting has the potential to reduce energy costs, optimize energy production, and enhance energy security. Especially, LSTM models are able to capture both short-term and long-term dependencies in TS data. They are also capable of handling non-linear relationships between input and output variables, which is important in energy forecasting where the relationships may be complex. Finally, LSTMs could process sequential data of varying lengths, which is useful for handling variable-length TS data in energy forecasting.

3. Data Used in this Study

3.1. Data Collection

Data collected from three buildings in different regions are employed to evaluate the models, i.e Hawthorn Campus - ATC Building (denoted as DatasetS 1 ), Hawthorn Campus - AMDC Building (denoted as DatasetS 2 ), and Wantirna Campus - KIOSC Building (denoted as DatasetS 3 ) is incredibly valuable as it provides real-time insights into the building’s performance, energy consumption, and operational efficiencies, allowing for the swift response to potential issues. This real-time data not only enhance decision-making capabilities for building management, maintenance, and optimization but also provides a basis for developing more accurate forecasting models. Furthermore, it can guide strategic energy management, potentially leading to significant cost savings, improved sustainability, and increased occupant comfort over time. The two datasets DatasetS 1 and DatasetS 2 contain the energy consumption from 2017 to 2019 and the dataset DatasetS 3 contains the energy consumption from 2018 to 2019. The prediction value is the difference between the previous and the intermediate next time in using energy, or the cumulation of energy. The historical value is 96 data in every 15 minutes to predict the next value.
Preprints 75240 g002
Figure 2. Location of Hawthorn Campus and Wantirna Campus in Metropolitan Melbourne, Victoria, Australia.
Figure 2. Location of Hawthorn Campus and Wantirna Campus in Metropolitan Melbourne, Victoria, Australia.
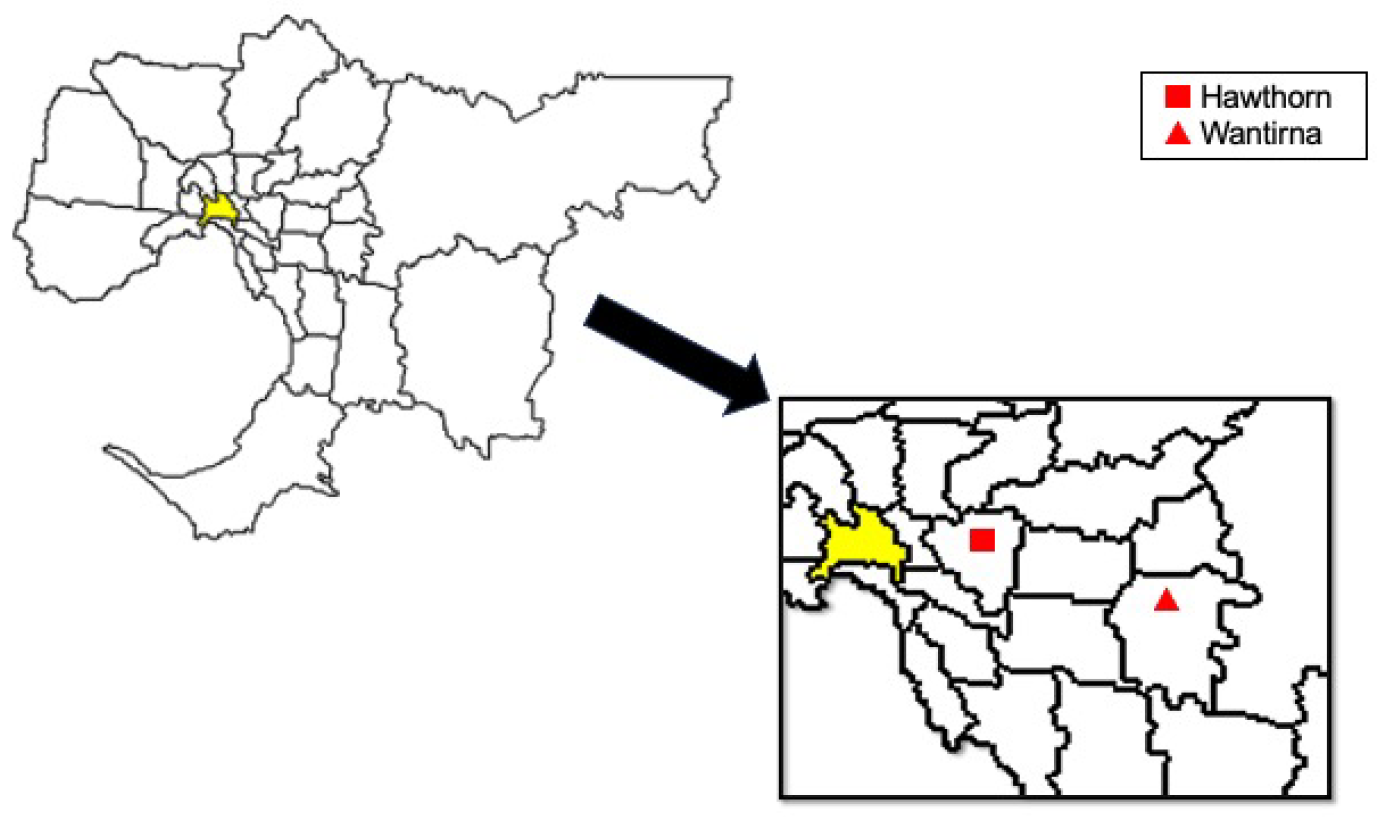
Preprints 75240 g002
Preprints 75240 g003
Figure 3. Electricity accumulation in every 15 minutes at Hawthorn Campus - ATC Building.
Figure 3. Electricity accumulation in every 15 minutes at Hawthorn Campus - ATC Building.
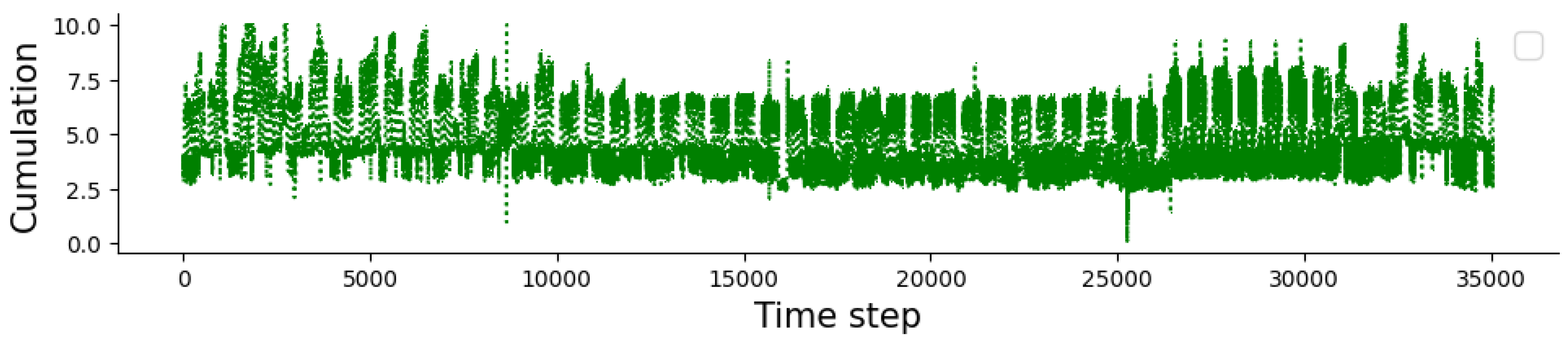
Preprints 75240 g003
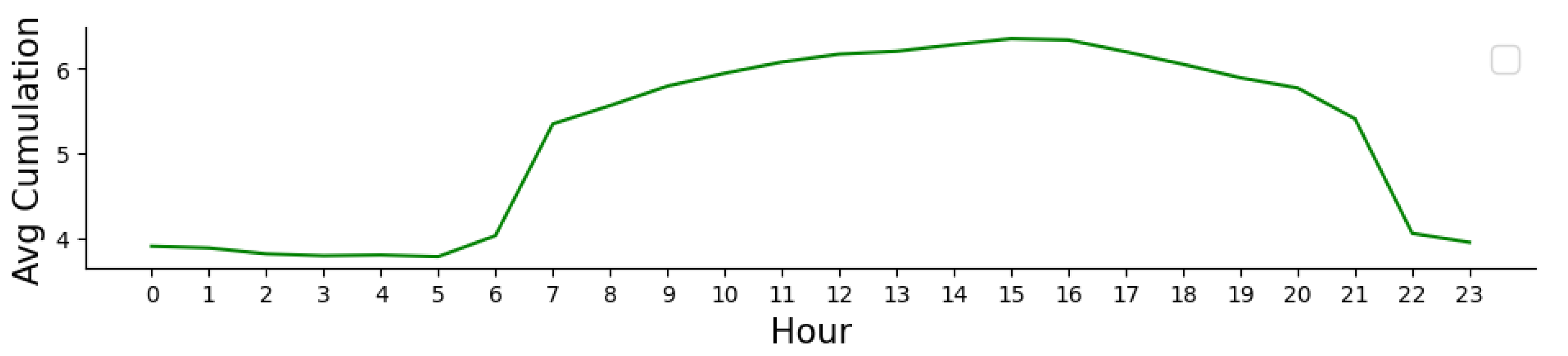
Preprints 75240 g004
Figure 4. Average electricity accumulation in every 1 hour at Hawthorn Campus - ATC Building in 2018. As can be seen, electricity consumption peaks between 8 a.m. and 21 p.m.
Figure 4. Average electricity accumulation in every 1 hour at Hawthorn Campus - ATC Building in 2018. As can be seen, electricity consumption peaks between 8 a.m. and 21 p.m.
Preprints 75240 g004

3.2. Data Setup

Dataset. In this experiment, three datasets from three buildings in different regions are employed to evaluate the models, i.e Hawthorn Campus - ATC Building (denoted as DatasetS 1 ), Hawthorn Campus - AMDC Building (denoted as DatasetS 2 ), and Wantirna Campus - KIOSC Building (denoted as DatasetS 3 ). The two datasets DatasetS 1 and DatasetS 2 contain the energy consumption from 2017 to 2019 and the dataset DatasetS 3 contains the energy consumption from 2018 to 2019. The prediction value is the difference between the previous and the intermediate next time in using energy, or the cumulation of energy. The historical value is 96 data in every 15 minutes to predict the next value.
Configuration of proposed model. The proposed model, M − LSTM , consists of a succession of one input layer, two LSTM layers, and one dense layer at the end. The input layer contains two input types as described in Section 4.1. In the following, the first LSTM layer wraps eight LSTM units and the second wraps four units. The last dense layer has one unit for predicting energy consumption.
Configuration of bench-marking models. As mentioned earlier, three competitive models are used for comparison: LSTM, Bi-LSTM, and LR. The LSTM model consists of one single layer with one unit, followed by a Dense layer for prediction. The Bi-LSTM consists of one single Bi-Directional LSTM layer of one unit, followed by a Dense layer for prediction as the LSTM model. The LR model trains with one dense layer.
Training Configuration. Both M − LSTM , LSTM, Bi-LSTM, LR models are trained using the same training set, and evaluated on the same test set. In DatasetS 1 and DatasetS 2 , the models are trained on the data in 2017 and 2018. In DatasetS 3 , the models are trained on the data in 2018 to demonstrate the ability of models with a lack of training data.

4. Methodology

In this section, we propose the forecasting model (Multivariate Multilayered LSTM), which is referred to as M − LSTM . The overview of the proposed method is illustrated in Figure 5. There are three phases, i.e. data preprocessing, model training and evaluation.

4.1. Data Preprocessing

Two major techniques are used in the data preprocessing phase, i.e. (i) data differencing and (ii) time labelling. Additionally, there are two other techniques, i.t (iii) concatenation and (iv) window slicing.
In regard to data differencing, due to a large amount of energy consumption and the value is not commonly stationary, the difference between the data value and its previous data value is taken into account. By removing these patterns through data differencing, the resulting stationary TS can be more easily modelled and forecasted. This technique is often required for many forecasting models [35].
In time labelling, the amount of energy consumption during peak time points is typically greater than that during non-peak time. Consequently, the labelling convention assigns a value of 1 to peak time and 0 to non-peak time. [36] These labelled time periods serve as valuable features for training the forecasting model. In the concatenation phase, the data from data differencing and labelled time are concatenated and then sliced into vectors with a length of k during the window-slicing phase.

4.2. Forecasting Model - Multivariate Multilayered LSTM

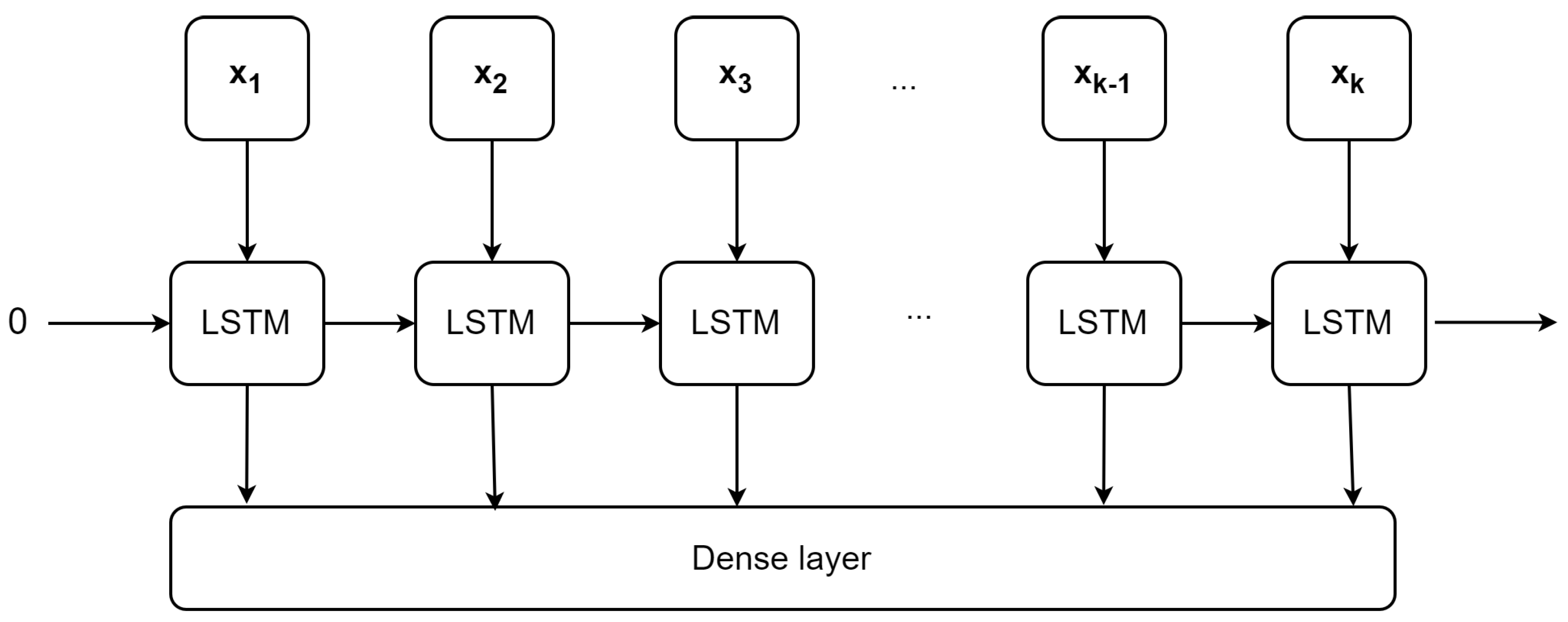
M − LSTM is an extension of the LSTM model, which is a type of recurrent neural network (RNN) architecture used for sequential data processing tasks such as TS forecasting. There are h sub-layers In the hidden layer. The M − LSTM model consists of multiple LSTM layers, with each layer having its own set of neurons that process the input variables independently. The output of each layer is then fed into the next layer, allowing the model to capture more complex and abstract relationships between the input variables. There are some additional layers such as the dropout layer, normalization layer, etc in the hidden part for training the model efficiently.
As shown in Figure 6, the memory cell is responsible for storing information about the long-term dependencies and patterns in the input sequence, while the gates control the flow of information into and out of the cell. The gates are composed of sigmoid neural network layers and a point-wise multiplication operation, that allows the network to learn which information to keep or discard. In particular, each i t h cell at the layer m, denoted as C i m , has three inputs, i.e the hidden state h i − 1 m , cell state c i − 1 m of the previous cell, and the hidden state h i m − 1 of the cell i at the previous layer m − 1 . The cell C i m has two recurrent features, i.e., hidden state h i m , and cell state c i m . C i m is a mathematical function as Equation 1, that takes three inputs and returns two outputs. Both outputs leave the cell at time i and are fed into that same cell at time i + 1 , and the input sequence x i + 1 is also fed into the cell. In the first layer ( m = 1 ), the hidden state h i m − 1 is the input x i .
( h i m , c i m ) = C ( h i − 1 m , c i − 1 m , h i m − 1 )
Inside the i t h cell, the previous hidden state h i − 1 m and input vector x i are fed into three gates. i.e input gate ( i g i m ), forget gate ( f g i m ), output gate ( o g i m ). They are s i g m o i d functions ( σ ), each of which produces a scalar value as described in Equations 2, 3, 4 respectively.
i g i m ( h i − 1 m , h i m − 1 ) = σ ( w i g , m − 1 h i m − 1 + w i g , m h i − 1 m + b i g )
f g i m ( h i − 1 m , h i m − 1 ) = σ ( w f g , m − 1 h i m − 1 + w f g , m h i − 1 m + b f g )
o g i m ( h i − 1 m , h i m − 1 ) = σ ( w o g , m − 1 h i m − 1 + w o g , m h i − 1 m + b o g )
where w i g , m − 1 , w h g , m − 1 , w o g , m − 1 ∈ R n and w i g , m , w h g , m , w o g , m , b i g , b f g , b o g ∈ R denote weight, which is the parameter that should be updated during the training of the cell. Another scalar function, called the update function (denoted as u g ) has a t a n h activation function as described in Equation 5.
u g i ( h i − 1 m , h i m − 1 ) = t a n h ( w u g , x h i m − 1 + w u g , h h i − 1 m + b u g )
where w i g , x ∈ R and w u g , h ∈ R are further weighted to be learned. The returned cell state ( c i m ) and hidden state ( h i ) are formulated in Equations 6, 7 respectively.
c i m = f g i m · c i − 1 m + i g i m · u g i
h i m = o g i m · t a n h ( c i m )
In energy forecasting, loss optimization is an important step to improve the accuracy of the model [37]. One common technique for loss optimization is using the Adam optimizer, which is a stochastic gradient descent optimizer that uses moving averages of the parameters to adapt the learning rate. The Adam optimizer computes individual adaptive learning rates for different parameters from estimates of the first and second moments of the gradients. This makes it suitable for optimizing the loss function in models where there are a large number of parameters. By using the Adam optimizer, the model can efficiently learn and update the weights of the neurons in each time step, resulting in better prediction accuracy.

5. Bench-Marking Models

In this study, we compare the proposed model with three well-known models, i.e., linear regression (LR), long-short-term memory (LSTM), and bidirectional long-short-term memory (Bi-LSTM).

5.1. Linear Regression

LR allows knowing the relationship between the response variable (energy consumption) and the return variables (the other variables). As a causative technique, regression analysis predicts energy demand from one or more reasons (independent variables), which might include things like the day of the week, energy prices, the availability of housing, or other variables. When there is a clear pattern in the previous forecast data, the LR method is applied. Due to this, its simple application has been used in numerous works related to the prediction of electricity consumption. Bianco V et al. (2009) used a LR model to conduct a study on the projection of Italy’s electricity consumption [38] while Saab C et al. (2001) looked into various univariate modelling approaches to project Lebanon’s monthly electric energy usage [39]. With the help of our statistical model, this research has produced fantastic outcomes.
The LR model works by fitting a line to a set of data points, with the goal of minimizing the sum of the squared differences between the predicted and actual values of the dependent variable. The slope of the line represents the relationship between the dependent and independent variables, while the intercept represents the value of the dependent variable when the independent variable is equal to zero. The LR model describes the linear relationship between the previous values y t and the estimated future value y ^ t + 1 , formulated as follow:
y ^ t + 1 = ∑ i = t − ( k − 1 ) t w i · y i

5.2. LSTM

The LSTM technique is a type of Recurrent Neural Network (RNN). The RNNs [40] are capable of processing data sequences, or data that must be read together in a precise order to have meaning, in contrast to standard neural networks. This ability is made possible by the RNNs’ architectural design, which enables them to receive input specific to each instant of time in addition to the value of the activation from the previous instant. Given their ability to preserve data from earlier actions, these earlier temporal instants provide for a certain amount of “memory”. Consequently, they possess a memory cell, which maintains the state throughout time [41].
Preprints 75240 g007
Figure 7. Overview of the LSTM model.
Figure 7. Overview of the LSTM model.
Preprints 75240 g007
As noted in Section 4, LSTM [42] model have ability to remove or add information to decide what information need to go through the network from the cell state [42]. Different from M − LSTM model, LSTM model has just one LSTM layer with the input is the input sequence x . Therefore, the hidden state (h) and cell state (c) for the i t h LSTM cell are calculated as Equation 9.
( h i , c i ) = C ( h i − 1 , c i − 1 , x i )
In the experiment, we compare the performance of the proposed model with the univariate and multivariate LSTM model. The univariate LSTM takes the first input (i) described in Section 4.1 and the multivariate LSTM takes both those inputs.

5.3. Bidirectional LSTM

Bi-LSTM is also an RNN. It utilizes information in both the previous and the following directions in training phase [43]. The fundamental principle of the Bi-LSTM model is that it examines a specific sequence from both the front and back. Which uses one LSTM layer for forward processing and the other for backward processing. The network would be able to record the evolution of energy that would power both its history and its future [44]. This bidirectional processing is achieved by duplicating the hidden layers of the LSTM, where one set of layers processes the input sequence in the forward direction and another set of layers processes the input sequence in the reverse direction. As illustrated in Figure 8, the hidden state ( h i f ) and the cell state ( c i f ) in the i t h forward LSTM cell are calculated as similar as the Equation 9. On the contrary, each LSTM cell in the backward LSTM takes the following hidden state ( h i + 1 b ), and following cell state ( c i + 1 b ), and x i as input. Therefore, the hidden state ( h i b ) and cell state ( c i b ) of the i t h backward LSTM cell are calculated as Equation 10.
( h i b , c i b ) = C ( h i + 1 b , c i + 1 b , x i )
After the calculations of both forward and backward LSTM cells, the hidden states of two directions could be concatenated or combined in some way to obtain the output. The common combination is the sigmoid function as noted in Figure 8. The output is fed into the Dense layer to obtain the final prediction. Similar to the LSTM model, we also compare the proposed model with univariate and multivariate Bi-LSTM models.

6. Experiment

6.1. Metric

To better evaluate the performance, a model is tested by making a set of predictions y ^ = { y ^ 1 , y ^ 2 , . . . , y ^ D } and then comparing it with a set of known actual values Y = { y 1 , y 2 , . . . , y D } , where D is the size of the test set. Three common metrics are used to compare the overall distance of these two sets, i.e. mean average error ( M A E ), root mean square error ( R M S E ), and mean absolute percentage error ( M A P E ).
MAE As shown in Equation 11, MAE is calculated by taking the absolute difference between the predicted and actual values and averaging them. This calculation results in a single number that represents the average magnitude of the errors in the predictions made by the model.
MAE = ∑ i = 1 D | y ^ i − y i |
RMSE As shown in Equation 12, RMSE is calculated by taking the square root of the mean of the squared differences between the predicted and actual values. This calculation results in a single number that represents the typical magnitude of the errors in the predictions made by the model.
RMSE = ( 1 D ) ∑ i = 1 D ( y ^ i − y i ) 2
MAPE As shown in Equation 13, MAPE is calculated by taking the absolute difference between the predicted and actual values, dividing it by the actual value, and then taking the average of these values over the entire dataset. This calculation results in a single number that represents the average percentage difference between the predicted and actual values.
MAPE = 100 % D ∑ i = 1 D y ^ i − y i y i

6.2. Result and Discussion

This study aims to experimentally address the effectiveness of the proposed model by answering the following research inquiries: the general performance of training the proposed model and the comparative performance analysis against other competitive models.

6.2.1. General Performance

In the first part of the experiments, M − LSTM is trained and evaluated with two types of data preprocessing strategies, i.e., with a labelled time field and without a labelled time field. Figure 9 shows the results in the test set in DatasetS 1 , DatasetS 2 , and DatasetS 3 . In this question, there are two results, (i) result in the sufficient training set and (ii) result in the lack of training set.
For the first result (i), the model is sufficiently trained with data in 2017, and 2018 and evaluated in 2019 from DatasetS 1 and DatasetS 2 . Figure 9 shows that the model achieves better performance in all three metrics with the labelled time field. The results are similar under the same setting for the other models. The details are provided in Table 2 and the line plot in Figure 10. Therefore, the models can learn and extract more valued features if they are trained with the appropriate data preprocessing strategy.
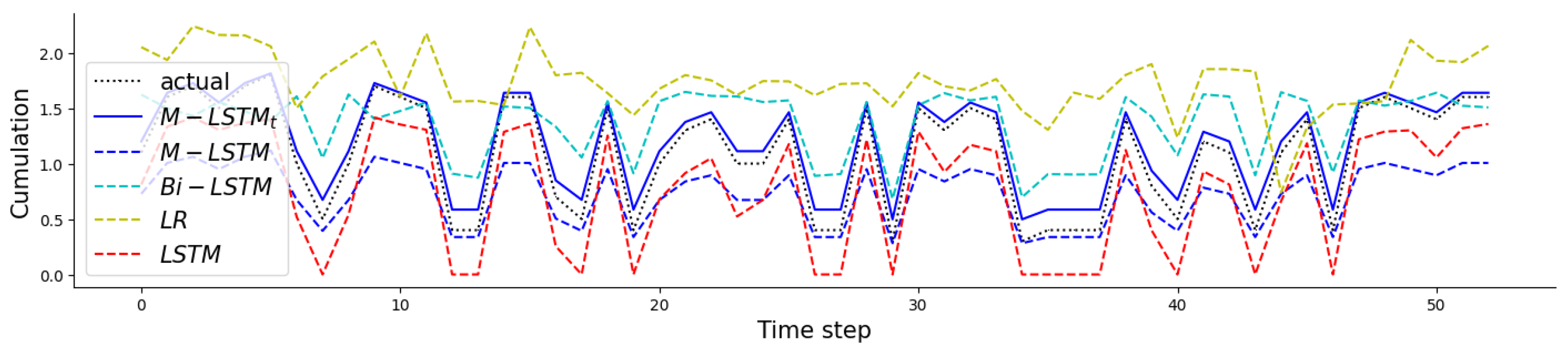
For the second result (ii), the model is only trained with data in 2018 and evaluated in 2019 from DatasetS 3 . Figure 10 shows that the model performed well in predicting and matching the actual values, as evidenced by its superior fit line compared with the other models in Figure 9 and Figure 10. These findings suggest that the proposed preprocessing method is effective, particularly in situations with a limited amount of training data available for model training.
Preprints 75240 g010
Figure 10. Comparison of M − LSTM with labelled time ( M − LSTM t ) with M − LSTM without labelled time, and other models in case of lack of training data ( DatasetS 3 in 2019). The time step is 7 days.
Figure 10. Comparison of M − LSTM with labelled time ( M − LSTM t ) with M − LSTM without labelled time, and other models in case of lack of training data ( DatasetS 3 in 2019). The time step is 7 days.
Preprints 75240 g010

6.2.2. Experience Different Models

In the second part of the experiments, we compare the performance evaluation results of M − LSTM to other competitive models (LSTM, Bi-LSTM, LR models) on three datasets in terms of three metrics. Two sets of performance metrics are presented, one set includes time label information (MAE_t, RMSE_t, and MAPE_t), whereas the other set does not include time label information (MAE, RMSE, and MAPE). Table 2 presents the performance evaluation results of M − LSTM and LSTM, Bi-LSTM, and LR models on three datasets in terms of three metrics. Figure 11 shows the MAPE error of models with and without labelled time.
Table 2. Comparison of M − LSTM with competitive models with and without labelled time. MAE_t, RMSE_t and MPAE_t are denoted metrics for model trained with labelled time. MAE, RMSE and MPAE are denoted metrics for model trained without labelled time. MPAE_t and MPAE are rescale to the range from 0 to 1. Better values are marked in bold.
Table 2. Comparison of M − LSTM with competitive models with and without labelled time. MAE_t, RMSE_t and MPAE_t are denoted metrics for model trained with labelled time. MAE, RMSE and MPAE are denoted metrics for model trained without labelled time. MPAE_t and MPAE are rescale to the range from 0 to 1. Better values are marked in bold.
with labelled time without labelled time
Dataset Model MAE_t RMSE_t MAPE_t MAE RMSE MAPE
DatasetS 1 M − LSTM 0.75 1.15 0.16 1.08 1.37 0.26
LSTM 1.30 1.47 0.32 1.35 1.58 0.34
Bi-LSTM 1.46 1.85 0.24 1.53 1.63 0.31
Linear Regression 1.40 1.53 0.29 1.40 1.50 0.27
DatasetS 2 M − LSTM 0.49 0.74 0.14 0.84 0.96 0.18
LSTM 1.47 1.66 0.39 1.89 2.00 0.50
Bi-LSTM 1.45 1.16 0.22 1.89 2.06 0.48
Linear Regression 0.60 0.75 0.17 1.21 1.52 0.34
DatasetS 3 M − LSTM 0.66 0.85 0.07 0.69 0.87 0.10
LSTM 0.79 0.95 0.18 0.67 0.94 0.43
Bi-LSTM 1.61 2.15 0.40 1.23 1.92 0.81
Linear Regression 0.84 1.18 0.27 0.73 0.90 0.73
Preprints 75240 g011
Figure 11. Bart chart in the comparison of M − LSTM with labelled time ( M − LSTM t ) with M − LSTM without labelled time, and other models with and without labelled time in case of lack of training data ( DatasetS 3 in 2019).
Figure 11. Bart chart in the comparison of M − LSTM with labelled time ( M − LSTM t ) with M − LSTM without labelled time, and other models with and without labelled time in case of lack of training data ( DatasetS 3 in 2019).
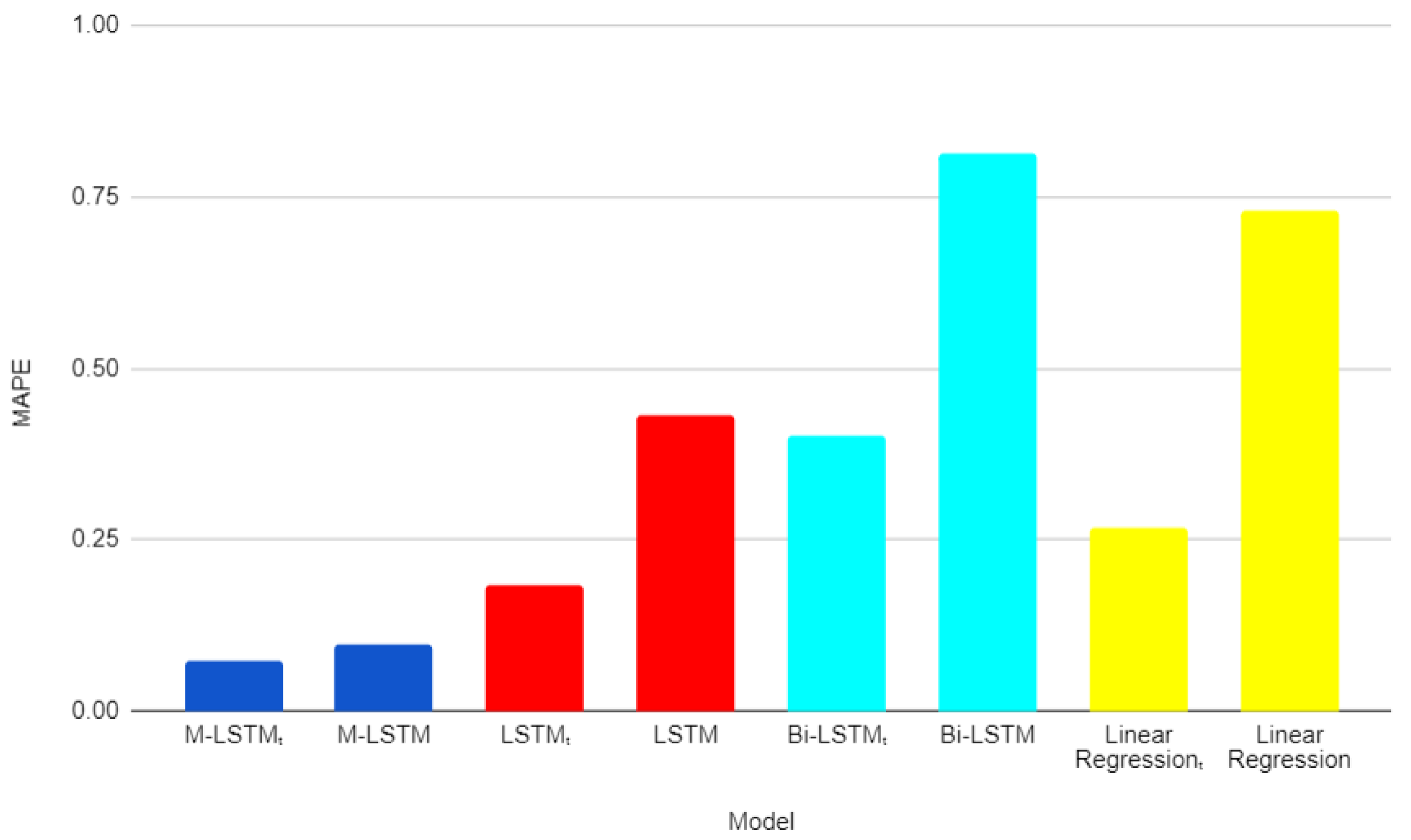
Preprints 75240 g011
In general, the results indicate that models using labelled time information tend to perform better than those that do not use labelled time information in the same setting. For example, on DatasetS 1 , the four models get the lower values, while the same models have higher error values. On the other hand, among the different models, the model M − LSTM using the labelled time information tends to perform the best overall with the lowest MAE_t, RMSE_t, and MAPE_t in most cases. To summarize, using the proposed preprocessing method with time information tends to improve the performance of the models. The M − LSTM model using time label information performs the best in general. The labelled time field provides useful information for predicting energy consumption in peak and non-peak periods. These findings suggest that considering time information can help in accurately predicting the target variable in the studied datasets.

7. Conclusions

In conclusion, this work presents a method for pre-processing data and a model for accurately predicting energy consumption in commercial buildings, specifically focusing on buildings in the Hawthorn and Wantirna campuses. The proposed pre-processing method effectively improves the accuracy of energy consumption prediction, even when training data are limited. The results demonstrate the applicability of the proposed method and model for accurately predicting energy consumption in various commercial buildings.
The proposed model, denoted as M − LSTM , achieved the lowest MAE values of 0.75, 0.49, and 0.66 for DatasetS 1 , DatasetS 2 , and DatasetS 3 , respectively. This achievement is crucial for effective energy management and conservation in commercial buildings. The practicality of this approach extends to other commercial buildings with similar energy consumption patterns, making it a viable solution for energy management in the commercial building sector. Visualizations were also provided to aid in understanding data patterns and trends in the model predictions.
Considering the impact of the COVID-19 pandemic on energy consumption patterns, it is essential to develop forecasting models that account for these changes in demand across sectors. Additionally, further research can explore the effectiveness of the proposed pre-processing method and models in predicting energy consumption for different types of buildings or larger datasets. Exploring alternative techniques, such as seasonal decomposition or time series analysis, for incorporating time information into the models could also yield valuable insights. These advancements in energy consumption forecasting contribute to significant cost savings and environmental benefits in commercial buildings.

References

  1. Khalil, M.; McGough, A.S.; Pourmirza, Z.; Pazhoohesh, M.; Walker, S. Machine learning, deep learning and statistical analysis for forecasting building energy consumption — a systematic review. Engineering Applications of Artificial Intelligence. 2022, 115, 105287. [Google Scholar] [CrossRef]
  2. IEA. Clean energy transitions in emerging and developing economies. 2021. [Google Scholar]
  3. Shin, S.-Y.; Woo, H.-G. Energy consumption forecasting in korea using machine learning algorithms. Energies 2022, 15, 4880. [Google Scholar] [CrossRef]
  4. Özbay, H.; Dalcalı, A. Effects of covid-19 on electric energy consumption in turkey and ann-based short-term forecasting. Turkish Journal of Electrical Engineering Computer Sciences 2021, 29, 78–97. [Google Scholar] [CrossRef]
  5. Ji, Y.; Lomas, K.J.; Cook, M.J. Hybrid ventilation for low energy building design in south China. Building and Environment 2009, 44, 2245–2255. [Google Scholar] [CrossRef]
  6. Manu, S.; Shukla, Y.; Rawal, R.; Thomas, L.E.; De Dear, R. Field studies of thermal comfort across multiple climate zones for the subcontinent: India Model for Adaptive Comfort (IMAC). Building and Environment 2016, 98, 55–70. [Google Scholar] [CrossRef]
  7. Delzendeh, E.; Wu, S.; Lee, A.; Zhou, Y. The impact of occupants’ behaviours on building energy analysis: A research review. Renewable and Sustainable Energy Reviews 2017, 80, 1061–1071. [Google Scholar] [CrossRef]
  8. Itzhak, N.; Tal, S.; Cohen, H.; Daniel, O.; Kopylov, R.; Moskovitch, R. Classification of univariate time series via temporal abstraction and deep learning. In Proceedings of the 2022 IEEE International Conference on Big Data (Big Data); IEEE, 2022; pp. 1260–1265. [Google Scholar]
  9. Ibrahim, M.; Badran, K.M.; Hussien, A.E. Artificial intelligence-based approach for univariate time-series anomaly detection using hybrid cnn-bilstm model. In Proceedings of the 2022 13th International Conference on Electrical Engineering (ICEENG); IEEE, 2022; pp. 129–133. [Google Scholar]
  10. Hu, M.; Ji, Z.; Yan, K.; Guo, Y.; Feng, X.; Gong, J.; Zhao, X.; Dong, L. Detecting anomalies in time series data via a meta-feature based approach. IEEE Access 2018, 6, 27760–27776. [Google Scholar] [CrossRef]
  11. Niu, Z.; Yu, K.; Wu, X. Lstm-based vae-gan for time-series anomaly detection. Sensors 2020, 20, 3738. [Google Scholar] [CrossRef]
  12. Warrick, P.; Homsi, M.N. Cardiac arrhythmia detection from ecg combining convolutional and long short-term memory networks. In 2017 Computing in Cardiology (CinC); IEEE, 2017; pp. 1–4. [Google Scholar]
  13. Karim, F.; Majumdar, S.; Darabi, H.; Harford, S. Multivariate lstm-fcns for time series classification. Neural networks 2019, 116, 237–245. [Google Scholar] [CrossRef]
  14. Gasparin, A.; Lukovic, S.; Alippi, C. Deep learning for time series forecasting: The electric load case. CAAI Transactions on Intelligence Technology 2021, 7. [Google Scholar] [CrossRef]
  15. Wei, N.; Li, C.; Peng, X.; Zeng, F.; Lu, X. Conventional models and artificial intelligence-based models for energy consumption forecasting: A review. Journal of Petroleum Science and Engineering 2019, 181, 106187. [Google Scholar] [CrossRef]
  16. Divina, F.; Garcia Torres, M.; Gomez Vela, F.A.; Vazquez Noguera, J.L. A comparative study of time series forecasting methods for short term electric energy consumption prediction in smart buildings. Energies 2019, 12, 1934. [Google Scholar] [CrossRef]
  17. Johannesen, N.J.; Kolhe, M.; Goodwin, M. Relative evaluation of regression tools for urban area electrical energy demand forecasting. Journal of cleaner production 2019, 218, 555–564. [Google Scholar] [CrossRef]
  18. Singhal, R.; Choudhary, N.; Singh, N. Short-Term Load Forecasting Using Hybrid ARIMA and Artificial Neural Network Model. 2020, 01, 935–947. [Google Scholar]
  19. Li, K.; Zhang, T. Forecasting electricity consumption using an improved grey prediction model. Information 2018, 9, 204. [Google Scholar] [CrossRef]
  20. Kim, Y.; Son, H.G.; Kim, S. Short term electricity load forecasting for institutional buildings. Energy Reports 2019, 5, 1270–1280. [Google Scholar] [CrossRef]
  21. Chitalia, G.; Pipattanasomporn, M.; Garg, V.; Rahman, S. Robust short-term electrical load forecasting framework for commercial buildings using deep recurrent neural networks. Applied Energy 2020, 278, 115410. [Google Scholar] [CrossRef]
  22. Pinto, T.; Praça, I.; Vale, Z.; Silva, J. Ensemble learning for electricity consumption forecasting in office buildings. Neurocomputing 2021, 423, 747–755. [Google Scholar] [CrossRef]
  23. Pallonetto, F.; Jin, C.; Mangina, E. Forecast electricity demand in commercial building with machine learning models to enable demand response programs. Energy and AI 2022, 7, 100121. [Google Scholar] [CrossRef]
  24. Skomski, E.; Lee, J.Y.; Kim, W.; Chandan, V.; Katipamula, S.; Hutchinson, B. Sequence-to-sequence neural networks for short-term electrical load forecasting in commercial office buildings. Energy and Buildings 2020, 226, 110350. [Google Scholar] [CrossRef]
  25. Dagdougui, H.; Bagheri, F.; Le, H.; Dessaint, L. Neural network model for short-term and very-short-term load forecasting in district buildings. Energy and Buildings 2019, 203, 109408. [Google Scholar] [CrossRef]
  26. Khan, Z.A.; Hussain, T.; Ullah, A.; Rho, S.; Lee, M.; Baik, S.W. Towards efficient electricity forecasting in residential and commercial buildings: A novel hybrid CNN with a LSTM-AE based framework. Sensors 2020, 20, 1399. [Google Scholar] [CrossRef]
  27. Karijadi, I.; Chou, S.Y. A hybrid RF-LSTM based on CEEMDAN for improving the accuracy of building energy consumption prediction. Energy and Buildings 2022, 259, 111908. [Google Scholar] [CrossRef]
  28. Hwang, J.; Suh, D.; Otto, M.O. Forecasting electricity consumption in commercial buildings using a machine learning approach. Energies 2020, 13, 5885. [Google Scholar] [CrossRef]
  29. Fernández-Martínez, D.; Jaramillo-Morán, M.A. Multi-Step Hourly Power Consumption Forecasting in a Healthcare Building with Recurrent Neural Networks and Empirical Mode Decomposition. Sensors 2022, 22, 3664. [Google Scholar] [CrossRef] [PubMed]
  30. Jozi, A.; Pinto, T.; Marreiros, G.; Vale, Z. Electricity consumption forecasting in office buildings: an artificial intelligence approach. In 2019 IEEE Milan PowerTech; 2019; pp. 1–6. [Google Scholar]
  31. Mariano-Hernández, D.; Hernández-Callejo, L.; Solís, M.; Zorita-Lamadrid, A.; Duque-Pérez, O.; Gonzalez-Morales, L.; Alonso-Gómez, V.; Jaramillo-Duque, A.; Santos García, F. Comparative study of continuous hourly energy consumption forecasting strategies with small data sets to support demand management decisions in buildings. Energy Science & Engineering 2022, 10, 4694–4707. [Google Scholar]
  32. del Real, A.J.; Dorado, F.; Duran, J. Energy demand forecasting using deep learning: Applications for the french grid. Energies 2020, 13, 2242. [Google Scholar] [CrossRef]
  33. Fathi, S.; Srinivasan, R.S.; Kibert, C.J.; Steiner, R.L.; Demirezen, E. AI-based campus energy use prediction for assessing the effects of climate change. Sustainability 2020, 12, 3223. [Google Scholar] [CrossRef]
  34. Khan, S.U.; Khan, N.; Ullah, F.U.M.; Kim, M.J.; Lee, M.Y.; Baik, S.W. Towards intelligent building energy management: AI-based framework for power consumption and generation forecasting. Energy and Buildings 2023, 279, 112705. [Google Scholar] [CrossRef]
  35. Athiyarath, S.; Paul, M.; Krishnaswamy, S. A comparative study and analysis of time series forecasting techniques. SN Computer Science 2020, 1. [Google Scholar] [CrossRef]
  36. Noor, R.M.; Yik, N.S.; Kolandaisamy, R.; Ahmedy, I.; Hossain, M.A.; Yau, K.L.A.; Shah, W.M.; Nandy, T. Predict Arrival Time by Using Machine Learning Algorithm to Promote Utilization of Urban Smart Bus. 2020. [Google Scholar]
  37. Ciampiconi, L.; Elwood, A.; Leonardi, M.; Mohamed, A.; Rozza, A. A survey and taxonomy of loss functions in machine learning. 2023. [Google Scholar]
  38. Bianco, V.; Manca, O.; Nardini, S. Electricity consumption forecasting in italy using linear regression models. Energy 2009, 34, 1413–1421. [Google Scholar] [CrossRef]
  39. Saab, S.; Badr, E.; Nasr, G. Univariate modeling and forecasting of energy consumption: the case of electricity in lebanon. Energy 2001, 26, 1–14. [Google Scholar] [CrossRef]
  40. Yuan, X.; Li, L.; Wang, Y. Nonlinear dynamic soft sensor modeling with supervised long short-term memory network. IEEE transactions on industrial informatics 2019, 16, 3168–3176. [Google Scholar] [CrossRef]
  41. Durand, D.; Aguilar, J.; R-Moreno, M.D. An analysis of the energy consumption forecasting problem in smart buildings using lstm. Sustainability 2022, 14, 13358. [Google Scholar] [CrossRef]
  42. Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural computation 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
  43. Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional lstm and other neural network architectures. Neural networks 2005, 18, 602–610. [Google Scholar] [CrossRef] [PubMed]
  44. Le, T.; Vo, M.T.; Vo, B.; Hwang, E.; Rho, S.; Baik, S.W. Improving electric energy consumption prediction using cnn and bi-lstm. Applied Sciences 2019, 9, 4237. [Google Scholar] [CrossRef]
Preprints 75240 g001
Figure 1. Common categories of Forecasting model in the literature.
Figure 1. Common categories of Forecasting model in the literature.
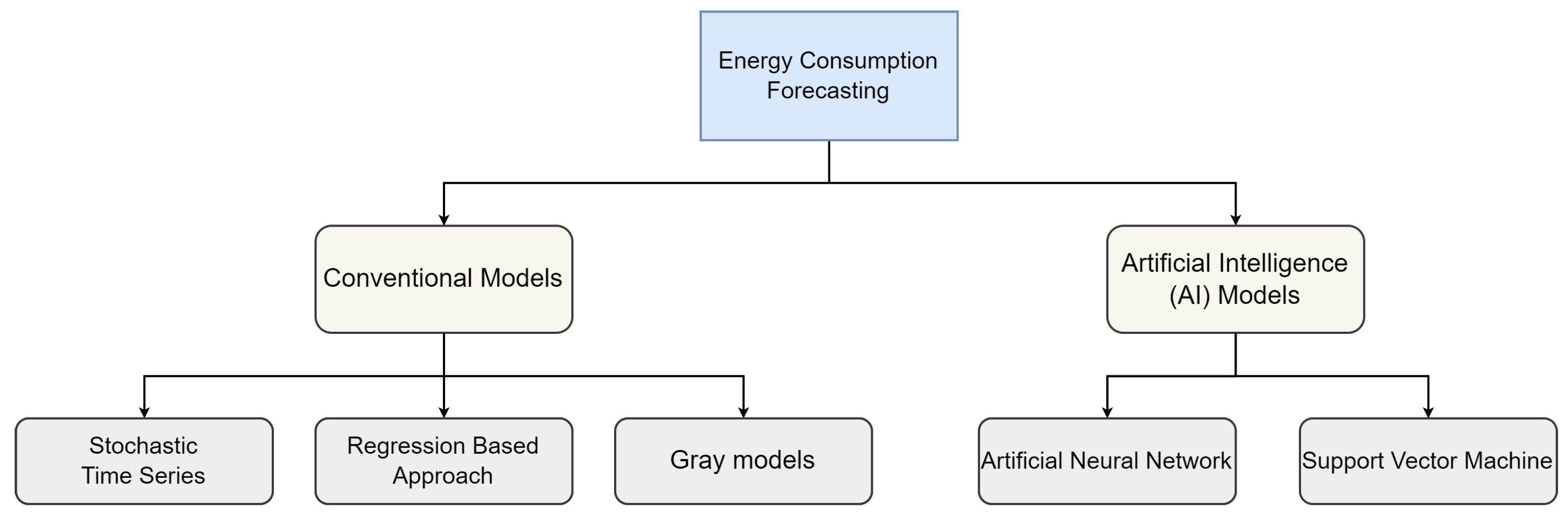
Preprints 75240 g001
Preprints 75240 g005
Figure 5. Workflow of the proposed model.
Figure 5. Workflow of the proposed model.
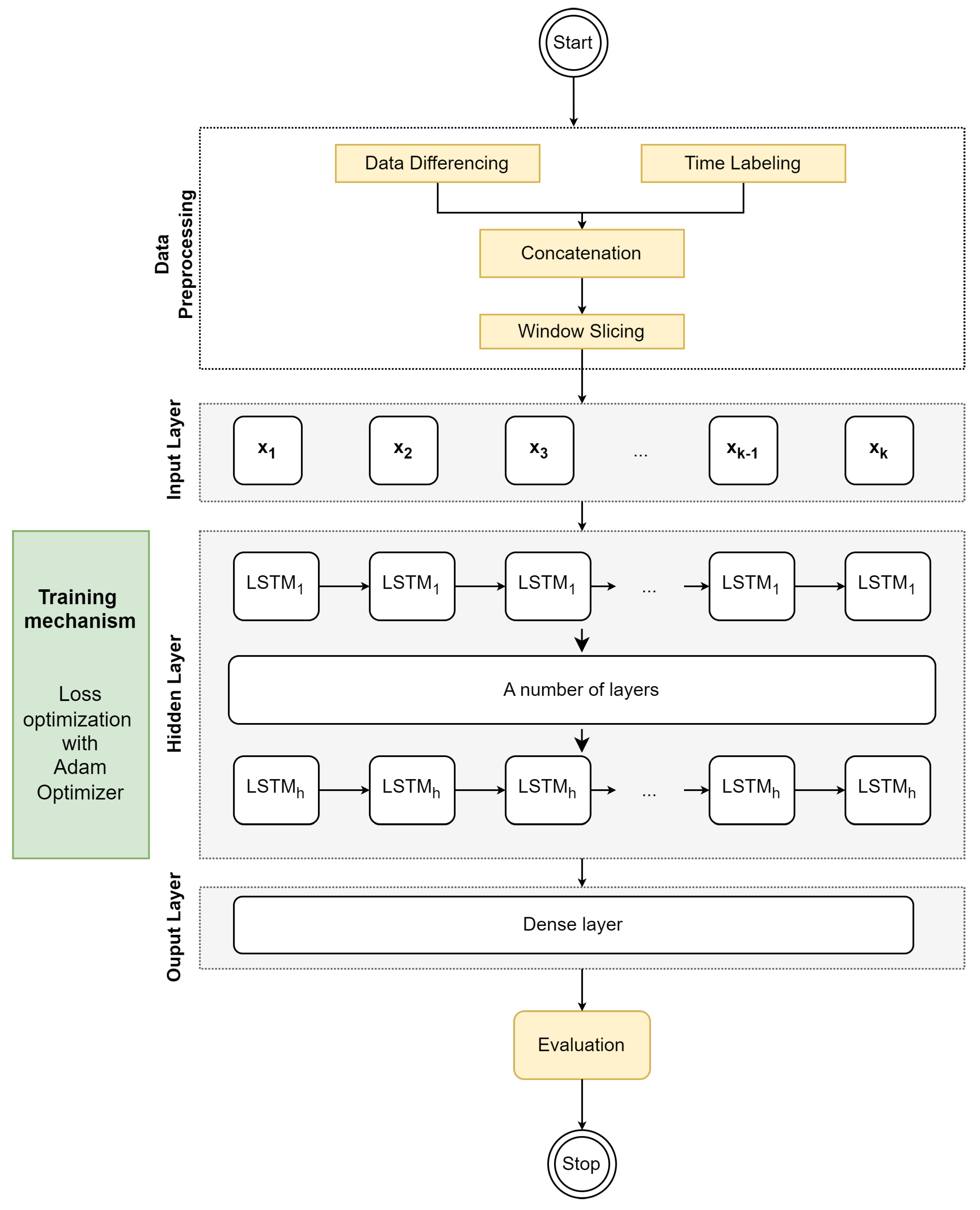
Preprints 75240 g005
Preprints 75240 g006
Figure 6. Illustration of the i t h LSTM cell at the layer m.
Figure 6. Illustration of the i t h LSTM cell at the layer m.
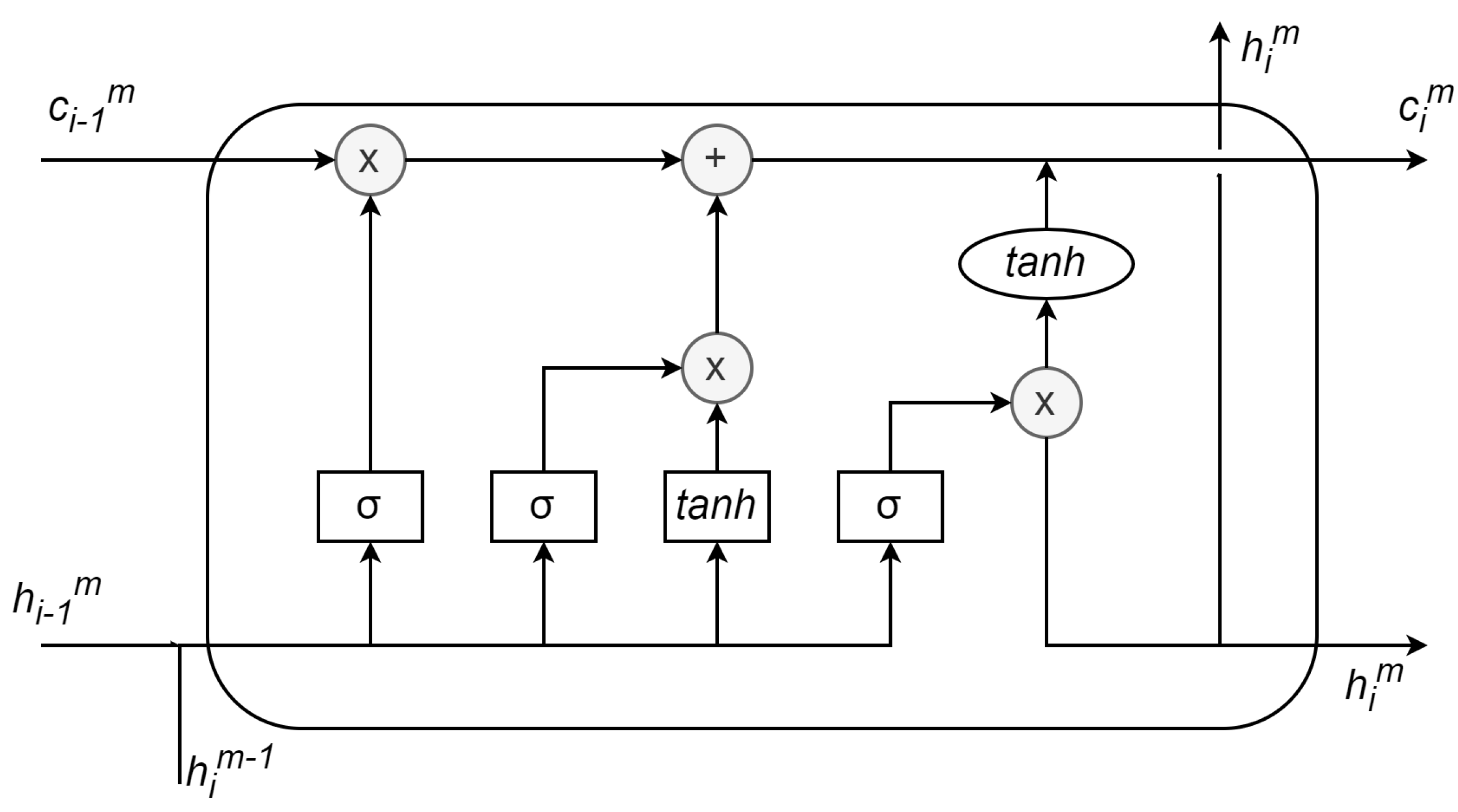
Preprints 75240 g006
Preprints 75240 g008
Figure 8. Overview of the Bi-LSTM model.
Figure 8. Overview of the Bi-LSTM model.
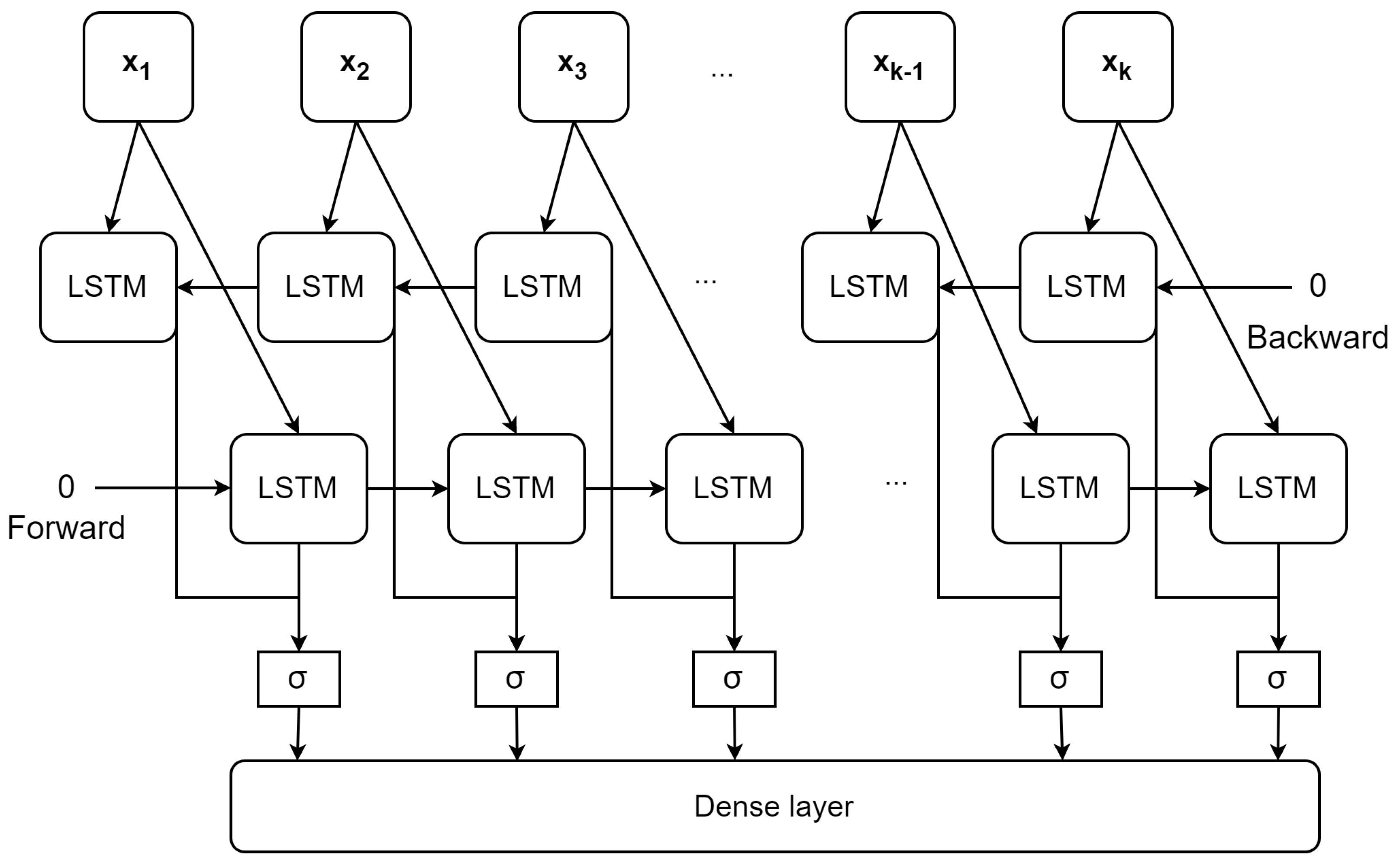
Preprints 75240 g008
Preprints 75240 g009
Figure 9. Comparison of M − LSTM trained with labelled time and without labelled time. (a) MAE error, (b) RMSE error, (c) MPAE error in the scale of (0, 1).
Figure 9. Comparison of M − LSTM trained with labelled time and without labelled time. (a) MAE error, (b) RMSE error, (c) MPAE error in the scale of (0, 1).
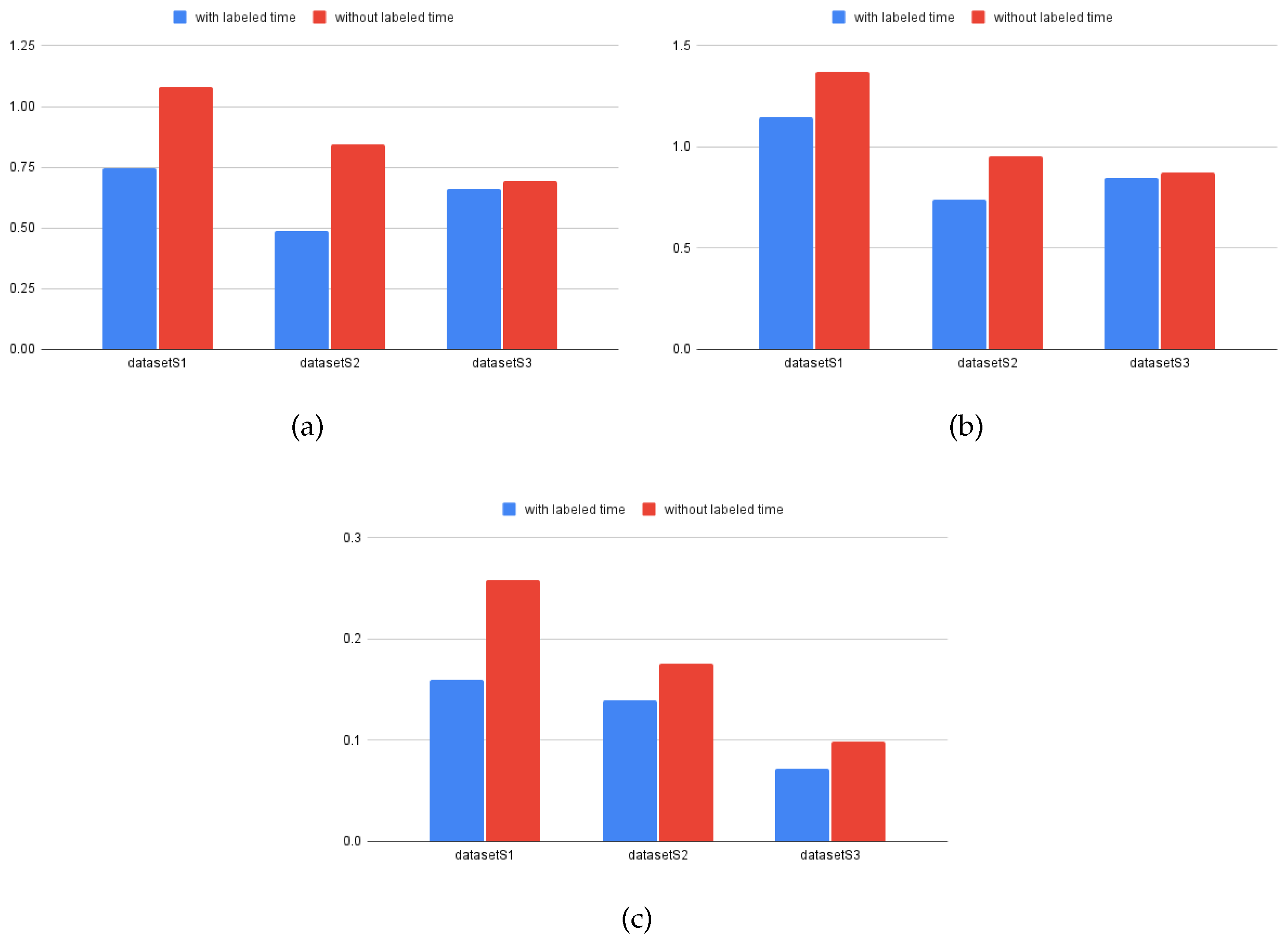
Preprints 75240 g009
Table 1. Summary of different forecasting models for commercial buildings.
Table 1. Summary of different forecasting models for commercial buildings.
No Forecasting Model Year Country Forecast Horizon Ref Accuracy
MAPE RMSE MAE
1 ANN model with external variables (NARX) 2019 Korea hour ahead [20] 1.69% 85.44
2 Long Short-term Memory Networks with attention (LSTM) 2020 USA hour ahead [21] 5.96% 7.21
3 AdaBoost.R2 2021 Portugal hour ahead [22] 5.34%
4 Support Vector Machine (SVM) 2022 Ireland hour ahead [23] 5.3% 3.82 11.94 kW
5 Seq2seq RNN 2020 USA hour ahead [24] 3.74 kW
6 Bayesian regularized (BR) (12 inputs) 2019 Canada hour ahead [25] 1.83% 105.03 kW
Levenberg Macquardt (LM) (12 inputs) 2019 Canada hour ahead 1.82% 104.21 kW
7 Hybrid convolutional neural network (CNN) 2020 Korea hour ahead [26] 0.76% 0.47 0.31
with an LSTM autoencoder (LSTM-AE)
8 Hybrid method of Random Forest (RF) and Long Short-Term 2022 USA hour ahead [27] 5.33% 0.57 0.43
Memory (LSTM) based on Complete Ensemble Empirical
Mode Decomposition with Adaptive Noise (CEEMDA)
9 Seasonal autoregressive integrated moving average (SARIMAX) 2020 Korea day ahead [28] 27.15% 557.6 kW
10 Gated Recurrent Unit (GRU) 2022 Spain day ahead [29] 7.86% 156.11
11 Hybrid Neural Fuzzy Interface System (HyFIS) 2019 Portugal day ahead [30] 8.71%
Wang and Mendel’s Fuzzy Rule Learning Method (WM) 2019 Portugal day ahead 8.58%
A genetic fuzzy system for fuzzy rule learning 2019 Portugal day ahead 9.87%
based on the MOGUL methodology (GFS.FR.MOGUL)
12 XGBoost 2022 Spain day ahead [31] 8.83
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated