Prerpints.org logo
Preprint
Article

On Scalability of FDD-based Cell-Free Massive MIMO Framework

Altmetrics

Downloads

163

Views

92

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

02 June 2023

Posted:

02 June 2023

You are already at the latest version

Alerts
Abstract
Cell-free massive multiple input multiple output (MIMO) has the potential of providing joint services including joint initial access, efficient clustering of access points (APs) and pilot allocation to user equipments (UEs) over large coverage area with reduced interference. In cell-free massive MIMO, large coverage area corresponds to provision and maintenance of scalable quality of service requirements for infinitely large number of UEs. The research in cell free massive MIMO is mostly focused on time division duplex mode due to availability of channel reciprocity which aids in avoiding feedback overhead. However, frequency division duplex (FDD) protocol still dominates the current wireless standards and the provision of angle reciprocity aids in reducing this overhead. The challenge of providing a scalable cell-free massive MIMO system in FDD setting is also prevalent, since computational complexity regarding signal processing tasks such as channel estimation, precoding/combining and power allocation, becomes prohibitively high with increase in number of UEs. In this work, we consider an FDD based scalable cell-free network with angular reciprocity and dynamic cooperation clustering approach. We have proposed scalability for our FDD cell-free and perform comparative analysis with reference to channel estimation, power allocation and precoding/combining techniques. We present expressions for scalable spectral efficiency, angle based precoding/combining schemes and provide comparison of overhead between conventional and scalable angle based estimation as well as combining schemes. Simulations confirm that the proposed scalable cell-free network based on FDD scheme outperforms the conventional matched filtering scheme based on non-scalable precoding/combiming schemes. The angle based LP-MMSE in FDD cell-free network provides 14.3% improvement in spectral efficiency and 11.11% improvement in energy efficiency compared to non-scalable MF scheme.
Keywords: 
Subject: Engineering  -   Telecommunications

1. Introduction

The fifth generation systems promise to provide data rates as much as ten times higher compared to the previous generations of wireless communication, and that too at a faster pace [1,2]. The utilization of millimeter wave bands makes it possible to achieve the goals set in terms of data rate and latency. However, there are some challenges in the way to fulfilling these demands. These include harsh channel conditions in millimeter wave, need for high performance but estimation schemes with lower computational complexity as well as efficient interference management and optimal choice of duplexing scheme. Possible solutions may include utilization of massive MIMO, use of suitable cooperation mechanism, such as cell-free framework and deployment of optimal estimation and precoding/combining schemes [3–5].
The concept of cell-free massive MIMO has the potential to greatly reduce interference issue of cellular networks. Since, cell-free frameworks have large coverage area, they are inherently equipped with diversity gains, thus providing immunity against fading and shadowing effects. However, cell-free framework requires huge amount of control signaling with core network and increased backhaul requirements. The key feature of cell-free is to create a network, where all the APs cooperate in order to jointly serve the UEs and eliminate inter-cell interference. At the core of the network, there is a central processing unit (CPU) and all APs in the network are connected to it through the backhaul link [6–10].
Performance of cell-free framework relies on acquisition of accurate channel state information (CSI) statistics. These CSI estimates are required for precoding during transmission and interference mitigation in spatial domain. Acquiring these estimates requires sending/receiving pilots, that subsequently incurs greater overhead as well as computational complexity. Channel estimation techniques may result in high computational complexity for cell-free framework. Since, utilization of channel reciprocity in time division duplexing (TDD) requires only estimating CSI in the uplink, therefore, pilot overhead and estimation cost are reduced. Frequency division duplex (FDD) is another duplexing mode that can offer equal improvement in terms of reduced pilot overhead and computational complexity. Although, FDD does not possess channel reciprocity, yet, it has angular reciprocity where angles of departure (AoDs) are the same in both uplink and downlink. Utilization of TDD protocol is suitable in sub-6GHz band, due to time reciprocity. However, FDD can leverage from millimeter wave frequency band since angular reciprocity is valid for larger frequency range [4]. In addition, FDD based wireless systems still dominate the wireless communication due to their lower cost and better coverage compared to their TDD counterparts.
The scalability of FDD cell-free network is another challenge that is based on AP’s ability of data processing and sharing in a computationally efficient manner. The complexity of these tasks increases linearly with the increase in number of UEs. To overcome this issue in an FDD cell-free framework, it is imperative to acquire some kind of adaptive cooperative clustering scheme that can provide a scalable network operation. In addition, an appropriate algorithm for power control is also required in a cell-free network to address the scalablility with increasing number of users joining the network. It is worth mentioning here that all APs make independent power allocation decisions, not knowing the power allocation at the neighboring APs, therefore, scalable solutions are difficult to devise. A heuristic approach to the power allocation challenge can prove useful as suggested in [4]. Max-min power control and equal power allocation are also two popular choices for power control [4,5] and will be analysed in this work for scalable FDD cell-free.
In essence, it is significant for a cell-free framework to be scalable with respect to the increase in number of users joining the network [10]. For an FDD based cell-free framework to be scalable, there are two important conditions 1) propagation channel must be sufficiently sparse to benefit from angular reciprocity, a feature that is inherent in millimeter wave massive MIMO, and 2) number of pilots should be independent of number of UEs. The second condition is the focus of our current work, where, we utilize a millimeter wave cell-free massive MIMO framework with FDD protocol.

1.1. Paper Contribution and Organization

This work focuses on a scalable cell-free framework, where APs operate in FDD mode with angle reciprocity, in which no feedback is needed from UEs. The utilization of angular reciprocity aids in the acquisition of multipath components from the uplink pilots using combining schemes. The contributions of this paper are as follows:
  • This paper addressed the scalability conditions linked with angle-based FDD system and also identifies the relationship of the number of orthogonal pilots with UEs.
  • A complete mathematical model for scalable angle-based FDD cell-free system is presented while considering a dynamic and cooperative clustering technique.
  • The proposed scalable angle-based FDD system is evaluated thoroughly via simulations. The results demonstrate significant performance gains with respect to energy efficiency, spectral efficiency, and computational complexity.
The rest of the paper is organized as follows: Section 1 describe cell-free network for massive MIMO, Section 2 deals with scalability analysis of FDD-based cell-free massive MIMO, Section 3 is dedicated to modeling and analysis of spectral and energy efficiency, Section 4 presents derivation of power control algorithm for scalable cell-free, Section 5 provides results and discussion and Section 6 concludes the research work.

1.2. Related Work

The cell-free framework has evolved from its original form of network MIMO or coordinated multipoint (CoMP) implementation. In network MIMO, all the APs were assumed to have the knowledge of CSI for the whole network and were supposed to transmit this knowledge to all the users. However, this form of cell-free, although theoretically preferred, was practically not possible, since, the signalling overhead for training and data transmission would increase immensely [11,12]. An improvement was suggested by [13], where local channel state information (CSI) sharing is encouraged at the cost of network’s ability to jointly mitigate the interference. However, the interference mitigation is still better compared to non-cooperative cellular networks. The approach is to serve a single UE by only a subset of APs, therefore, performing fronthaul signaling for cooperation as well as data transmission at a local level, each UE with its neighboring APs only. There are two approaches for this kind of network operation: network-centric, where APs over the whole coverage area are divided into non-contagious clusters to serve the UEs inside each cluster by providing the CSI estimates and payload data [14–17]. This technique, although better than network MIMO, provides only slight performance improvement with reference to interference mitigation. A refinement to network-centric is user-centric approach, where, the whole coverage area is divided into overlapping clusters, and clustering is based on the ability of APs to serve the UEs with strong channel conditions, as shown in Figure 1 [18–20]. A user-centric cooperation approach is suggested in [19] and is named "dynamic cooperation clustering (DCC)" [21].
The research in the area of cell-free massive MIMO is usually centered on TDD protocol as cited by authors in [22–25,10] and its scalability is also analyzed in [4]. An FDD based cell-free massive MIMO system is considered in [26] with angle reciprocity and authors provide simulation results to confirm that the angle reciprocity based FDD performs better compared to the subspace-based scheme and in addition, the cell-free framework provides significant improvement in energy efficiency. An FDD cell-free network is proposed in [27] that utilizes compressive sensing estimation scheme for channel gains and simulation results confirm that the suggested estimation scheme provides reduced pilot overhead and improved energy efficiency. Authors in [5] suggest angular reciprocity based precoding/beamforming schemes and provide spectral and energy efficiency expressions for an FDD cell-free network. The research work cited in [5] presents detailed numerical simulations for the mathematical model of angle based FDD cell-free framework, however, the number of users is kept equal to the number of utilized orthogonal pilots. Therefore, the suggested system is not scalable for large number of users, since, the number of orthogonal pilots is limited.
Table 1 presents the comparison of existing literature and highlights the differences between the proposed scalable angle based cell-free massive MIMO network and the current literature. In the light of this discussion, scalability analysis of FDD cell-free is needed, and therefore, in this work we present scalability analysis of FDD cell-free with efficient precoding/combining schemes. The work in [4] details scalable TDD cell free, however, the coverage of FDD scheme is better compared to TDD due to inherent interference mitigation, as uplink and downlink frequencies are separated. Therefore, the comparative analysis of the impact of large K in the FDD cell free framework is crucial for future wireless communication. In addition, optimal number of APs required in the intended geographical area for a scalable FDD cell-free can also be established with large number of UEs connecting to the network. Unlike [4], this work considers FDD based cell-free framework in the context of scalability. In addition, this work suggests angle based precoding for both minimum mean squared error (MMSE) and matched filtering (MF), presents results based on comparative analysis of MF and MMSE by considering multiple antenna’s per AP, since FDD scheme leverages from the antenna gains and provides improvement in spectral efficiency.
The concept of angle based estimation has been considered in subspace based schemes, [28,29], for cellular wireless networks including multiple signal classification (MUSIC) algorithm and estimation of signal parameters by rotational in-variance technique (ESPRIT) [30]. Interested readers can read more on ESPRIT and MUSIC algorithm in [31–34]. However, these schemes are not scalable due to their higher computational cost and therefore, are not suitable for cell-free massive MIMO framework [4]. This research work presents a solution based on scalability of FDD based massive MIMO network and paper contributions are described in the following subsection.

2. Cell-free Network for Massive MIMO

This work considers a frequency division duplex (FDD) based cell-free massive MIMO setting with K single antenna users and N APs equipped with M antennas. All the APs are randomly distributed over the intended geographical area and are connected to a central processing unit (CPU). The UEs are distributed uniformly and independently in the entire coverage area [35]. Cell-free mMIMO network ensures joint coherent transmission and reception to the users over the whole coverage area. We assume that even for a large value of K such that K → ∞ , N ≥ K [4]. The cell-free network here is based on FDD protocol with angular reciprocity, where there is a pilot transmission phase for training and estimation purposes followed by a payload data transmission phase. The coherence time τ c in angular domain is much greater than its time domain counterpart [35]. We consider a fairly large τ c such that τ c is always greater than the number of UEs being served, and τ p represents number of pilot symbols that are mutually orthogonal. τ p is assumed to be a constant, that is independent of K [35,36].
The channel model is assumed to be geometric with L propagation paths [26,28]. FDD based system has partial reciprocity in angle domain [5,35]. Therefore, we can assume that angles of arrival (AoAs) in the uplink and angles of departure in the downlink are almost equal. Similarly, the large scale fading coefficients for both the up/downlink are similar. Since the FDD protocol shows partial reciprocity, small-scale fading coefficients vary with the uplink and downlink frequencies [5]. We denote the channel between n t h AP and k t h UE as h k n ∈ C M . Let P = M N represent the number of antennas in the whole coverage area. The realization of Rayleigh fading channel in a coherence block is given as h k n ∼ N ( 0 , R k n ) such that R k n ∈ C M × M represents the spatial correlation matrix [4,5,26,28]. Considering this, the M × 1 channel vector is represented as,
h = 1 L ∑ j = 1 L q ( ϕ j ) β j α j
where, q ( ϕ j ) is the array steering vector, α j represents the complex path gain, such that α j ∼ C N ( 0 , 1 ) is the small scale fading, whereas β j represent large scale fading coefficients including shadowing, path loss and spatial correlation for the j t h path [4,5,35]. All the APs in cell-free framework are independently distributed and therefore, perform the estimation of multipath components in a distributed manner and channel vectors for i t h AP with j t h AP gives, E { h k i h k j * } = 0 ∀ i ≠ j . Therefore, the channel vector is represented in the matrix form as,
H = 1 L Q B α
where, Q M × L = [ q ( ϕ 1 ) , . . . , q ( ϕ L ) ] , B L × L = d i a g ( β 1 , . . . , β L ) and α L × 1 = [ α 1 , . . , α L ] T .
It is worth mentioning here that the small scale fading parameter given in α vector are frequency dependent whereas, the large scale fading coefficients β j in B are independent of frequency for an angle coherence interval τ c . The system model in this work follows from [5,21,37] with partial reciprocity in FDD protocol, where multipath components for both up/downlink are assumed to be independent and identically distributed (i.i.d.) random variables.
In the following Section, we build the FDD cell-free massive MIMO system model (more details can be found in [39,40]) and analyze its scalability for a large number of UEs K joining the network such that K → ∞ .

3. Scalability Analysis for FDD-based Cell-Free Massive MIMO

A cell-free massive MIMO framework is deemed scalable if increase in number of users such that K → ∞ does not impact the implementation of the following [4]:
  • computation of estimates of wireless channel for K UEs
  • combining/beamforming computation for up/downlink
  • control signaling for fronthaul (data and feedback)
  • optimization of power control.
In a scalable system, the complexity of implementation and requirement for resources must remain finite for all APs, even with large number of UEs joining the network [4,8]. In FDD based systems with angular reciprocity, increase in number of UEs such that K → ∞ requires an equal increase in system resources like number of N Aps and M antenna elements per AP. Therefore, the dependence of implementation complexity shifts from K to the product M N which is much larger than K. However, the solution is the localized cell-free framework, where APs are equipped with their own processors and connection with the fronthaul. The APs only exchange local CSI estimates among each other and network wide CSI exchange is not utilized in cell-free networks [5]. In addition, our FDD based cell-free framework can leverage from the dynamic cooperation clustering (DCC) scheme that allows APs to communicate with only a subset of UEs A n instead of all K UEs [4,21,38]. To check the scalability of our FDD-based cell-free framework, we further assume that set A n comprises of UEs served by at least one antenna of the n t h AP, as,
A n = k : t r ( D n k ) ≥ 1 , k ∈ 1 , 2 , . . . , K .
Let D k n ϵ C N × N be defined as a set of matrices, each a diagonal one, to represent the communication from n t h AP to k t h UE. The corresponding diagonal element of D k n is asserted to 1 if AP n wishes to transmit to UE k, and is 0 otherwise i.e.
D k n = { I M k ∈ A n 0 M k ∉ A n .

3.1. Uplink Pilot Training and Channel Estimation

As explained in Section 1, τ c represents the angular coherence time such that τ c = τ p + τ d , with τ p pilot symbols and τ d data symbols. Each pilot sequence comprises of pilot length τ p and has unit norm. In FDD cell-free network with angular reciprocity, the value of τ c is comparatively large, thus, pilot sequences are assumed as mutually orthogonal. When UEs join the coverage area of our cell-free network, they are assigned pilots according to the algorithm suggested in [4]. It is worth mentioning here that the estimation of multipath components is performed by each AP independently by utilizing the pilot sequences . The n t h AP ∈ M k ⊂ { 1 , 2 , . . . , N } is required to perform multipath component estimation locally, for its neighboring A n UEs such that A n ⊂ { 1 , 2 , . . . , K } . There is no cooperation or sharing of information among the APs for estimation of multipath components. We assume τ p pilot symbols, utilizing (2), the received signal Y n ∈ C M × τ p at the n t h AP, for FDD protocol, is presented in matrix form as [5],
Y n k = ρ L Q n k B n k α n k τ p + U n k
where, ρ is the transmit power for k t h UE and U n k ∼ ( 0 , σ n 2 ) is the AWGN matrix such that U n k ∈ C M × τ c .
The estimation of FDD based cell-free massive MIMO framework is performed by first utilizing the DFT-based angle of arrival estimation after acquiring the multipath components estimates directly via uplink training and then applying this angle information to estimate the large scale fading coefficients. The overall complexity of angle based estimation is reduced when beamforming/combining schemes are applied that are based on estimation of both of these components. The AoA estimation in [5] has better accuracy due to utilization of angle rotation technique, whereby, a phase shift is introduced into the initial estimates, resulting in accurate peak elements. Therefore, the estimated AoA matrix is given as;
Q ^ n k = [ q ( ϕ ^ 1 , n k ) , q ( ϕ ^ 2 , n k ) , . . . , q ( ϕ ^ L , n k ) ]
Next, these AoA estimates Q ^ n k are used for computing large scale fading coefficients β n k . The covariance matrix R ^ n k , z is related to β L , n k and therefore, large scale fading coefficients can be obtained, as suggested in [5],
β ^ n k = d i a g ( β 1 , n k , β 2 , n k , . . . , β L , n k ) = R ^ n k , z
The estimation algorithm is run over the search grid V for all paths L and all antennas M that incorporates the complexity of DFT operation as well as angle rotation procedure, Δ ϕ l ∈ [ − π M , π M ] , where Δ ϕ l is defined as the angle rotation parameter [5,33]. The purpose of this grid parameter V is to establish the accuracy and computational complexity of the angle based estimation algorithm [5]. Table 1 shows the comparison of complexity of estimation for angle based, MUSIC and ESPRIT algorithms, U i is the search grid parameter for ESPRIT algorithm, such that, U i > > V i .
It is worth mentioning that the performance of the angle based FDD estimation degrades slightly for a large grid size V . It is also evident that the estimated values of β ^ and Q ^ remain fixed for the coherence interval and therefore, only estimated once during the entire communication. Authors in [4] suggest to pre-compute the channel statistics at n t h AP and perform the channel estimation for each UE based on that pre-computed statistics matrix, thus requiring less number of complex multiplications.

3.2. Data Transmission Phase for Downlink

For the downlink data transmission to K users, APs use precoding vector w ^ n k of length M × 1 . There is no exchange of information among APs regarding the precoding vectors. The downlink signal of n t h AP to k t h UE, x n is represented as,
x n = ρ d ∑ k = 1 K w ^ n k s k d
where, s k d represents the data symbol and ρ d depicts the maximum transmit power for k t h user.

3.3. Angle Based Beamforming

The precoding/beamforming is performed to suppress the noise and interference in an efficient manner. The angle based precoding vector for matched filtering is given as,
w ^ n k = G ^ n k | | G ^ n k | | Υ n k
where, Υ n k represents the complex normalized weight of the k-th user, such that E [ | Υ n k | 2 ] = 1 where Υ n k = [ Υ n k , 1 , . . . , Υ n k , L ] T and G ^ n k = [ g ^ n k , 1 , g ^ n k , 2 , . . . , g ^ n k , L ] T .
Matched filtering is a simple precoding technique that only requires estimates of AoA and large scale fading coefficients for the channel between n t h AP and k t h UE. G ^ n k is the angle based precoding matrix and for matched filtering it can be represented as,
G ^ n k m f = Q ^ n k B ^ n k
Finally, angle based MMSE, given as G ^ n k a − m m s e , provides precoding with efficient performance against interference and noise suppression as well as estimation error. G ^ n k a − m m s e is given as,
G ^ n k a − m m s e = ∑ k = 1 K ( Q ^ n k B ^ n k Q ^ n k H B ^ n k H + ı n k ) + σ m 2 I M − 1 × Q ^ n k B ^ n k
where, ı n k depends on the variance of difference among up/downlink multipath components ( υ n a n d β l ) [5].
For the downlink, we utilize DCC and modify the received signal at k t h UE as;
y k = ∑ n = 1 N h k n H ∑ k = 1 K D n k w ^ n k ρ d + U n = h k H ∑ k = 1 K D k w ^ k ρ d + U n
where, U n ∼ N C ( 0 , σ 2 ) is the noise at the receiver. It is apparent from eq. (12) that n t h AP will transmit to k t h UE if D n k w ^ n k = w ^ n k or when D n k ≠ 0 .
We argue that if the number of users K increases such that K → ∞ , but the cardinality | A n | remains finite for all n = 1 , 2 , . . . , N then the FDD based cell-free network is scalable (proof follows from [4]). We utilize the algorithm suggested by [4] for the tasks like initial joint access, clustering and pilot allocation. Based on the assumption that every AP serves a maximum of one UE for one pilot sequence, and all M antennas of that AP will be utilized to serve all those UEs, eq. (4) describes the communication among n t h AP and k t h UE.
Previously, we assumed τ p to be independent of K, this combined with the argument of A n having constant cardinality provides sufficient conditions for scalability of FDD-based cell-free framework. The algorithm for clustering, joint initial access and pilot allocation is scalable because the complexity of the tasks of estimation and precoding is independent of K and only depends on k ∈ A n that is a maximum of one pilot per UE.

3.4. Data Transmission Phase for Uplink

All K UEs send payload in the uplink at the same time. The data symbols s k u , such that E [ | s k u | 2 ] = 1 , are sent towards the APs and received signal is represented as,
y n u = ρ u ∑ k = 1 K h n k s k u + U n u
where, ρ u is the transmit power in the uplink and n n u represents the noise added at n t h AP, such that n n u N ( 0 , σ n 2 ) . At n t h AP, the signal is multiplied by the M × 1 combining vector v n k . Finally, the signal is sent for detection to the CPU via fronthaul link. The received signal at CPU is expressed as,
r k u = ∑ k = 1 K ∑ n = 1 N ρ u v n k H h n k s k u + ∑ n = 1 N v n k H U n u
The original cell-free concept employs network-wide decoding of the uplink, where, n-th AP chooses the combining vector v n k ∈ C N for k-th UE and performs local computations. For cell-free network with DCC, the APs acquire the CSI estimates locally during pilot transmission. Although all APs will receive the signal from all K UEs, yet, only a subset of these APs perform signal detection, therefore, the estimated R ^ k = ∑ n = 1 N v n k H D k n y n u is modified as,
R ^ k = v k H D k h k s k u + ∑ j = 1 , j ≠ k K v k H D k h j s j u + v k H D k U n u
where, v k = [ v k , 1 T , v k , 2 T , . . . , v k , N T ] T ∈ C N represents the overall combining vector for all APs and U n represents the combination of all noise vectors, U n = [ U 1 T , . . . U N T ] T ∈ C N . given that, D k = d i a g ( D k 1 , . . . , D k N ) ∈ C N × N represents a block diagonal matrix and only the APs for which D j n ≠ 0 M will apply combining vector at the received signal. Two cooperation mechanisms are available for APs: centralized combining and distributed combining. In centralized combining based cooperation, APs send the pilot and data signals to the CPU via fronthaul link. The CPU performs channel estimation and signal detection in a centralized manner. For every coherence time, n t h AP is required to send approximately τ p M complex values for pilot as well as τ p u M complex values for received signal. In distributed combining, n-th AP chooses vector v k n based on local channel estimates ∀ [ h ^ j n : j ∈ A n ] and performs the computation of local estimates as R ^ k n = v k n H y n u . The n t h AP is required to compute only the local estimates of | A n | users and τ p u | A n | complex values are sent every coherence interval to CPU, which are independent of K and therefore, make the combining scalable. It maybe noted that for distributed combining case, CPU has no knowledge of channel estimates making it unlikely to obtain the expression for spectral efficiency in the uplink. A popular solution is "use-and-then-forget bound" in cell-free massive MIMO systems, details are given in [4,39], for a choice of combining vector v k n such that D j = I N ∀ j . We utilize this approach for the signal received, given by eq. (15) and angle based combining as represented in the following subsection.

3.5. Angle-based Combining

The received signal combining vector of n t h AP and k t h UE is given as [5],
v n k = ∑ j = 1 L γ n k , j c ^ n k , j = C ^ n k γ n k
where, C ^ n k = [ c ^ n k , 1 , . . . , c ^ n k , L ] , γ n k , j = 1 L and γ n k = [ γ n k , 1 , . . . , γ n k , L ] .
We utilize the uplink-downlink duality to obtain the combining vector expressions for angle based matched filtering and angle based MMSE combining as presented in (10) and (11). This duality implies that C ^ n k = G ^ n k .

4. Analysis of Spectral and Energy Efficiency

Based on the beamforming and combining results obtained so far, we analyze the performance of this scalable cell-free massive MIMO framework for per UE spectral and energy efficiency in this section.

4.1. Spectral Efficiency of FDD-based Cell-Free

The per user spectral efficiency in the downlink is computed by utilizing the precoding scheme and is represented as [5],
S E k d = l o g 2 [ 1 + S I N R k d ] ≃ l o g 2 1 + ρ d R k d ρ d I j k d + ρ d F k d + σ d l 2
where, R k d denotes the desired signal strength for cell-free framework, I j k d is the interference term due to j-th UE and F k d is the uncertainty in the beamforming gain defined as zero mean random variable [5].
Therefore, for the proposed, sclalable cell-free framework, S I N R k d is expressed as,
S I N R k d = l o g 2 ρ d E [ | | h ^ k H D k w ^ k | | 2 ] ρ j d E [ | | h k H D j w ^ j | | 2 ] + ρ d E [ | | h ˜ k H D k w ^ k | | 2 ] + σ d l 2
The per user spectral efficiency for combining schemes in the uplink can be deduced from the downlink case by substituting w ^ j with v j and is presented as;
S E k u ≃ l o g 2 ( 1 + ρ u E [ | | h ^ k H D k v k | | 2 ] ρ j u E [ | | h k H D j v j | | 2 ] + ρ u E [ | | h ˜ k H D k v k | | 2 ] + σ d l 2 | | v k | | 2 )

4.2. Scalability Analysis of Spectral Efficiency for Uplink

Considering the SINR expressions for the uplink combining scheme with v n k , where, k ∈ D n k , the n-th AP is required to choose the combining vector based on the h ^ j n = Q ^ j n B ^ j n such that { h ^ j n : j ∈ A n } with no knowledge of CSI estimates at other APs. Any of the combining schemes mentioned before (angle based MF and angle based MMSE) can be utilized to compute the SINR for spectral efficiency. The most simple is angle based matched filtering combining scheme. Angle based MMSE combining gives performance improvement, however, it is not a scalable option. A local partial MMSE combining scheme is suggested in [4] that is inspired from the partial MMSE (P-MMSE) scheme [22] and is given as,
v n k l p − m m s e = ∑ j ∈ A ( h ^ j n h ^ j n H + ı j n ) + σ u l 2 I M − 1 h ^ j n
where, ı j n is the collective estimation error between the variances of the uplink and downlink multipath components [5]. The difference in eq. (11) and (20) is that, LP-MMSE in (20) is only considering the estimates of UEs that are served by j APs ( ∀ j ∈ A n ) , since, | A n | < τ p and τ p is assumed independent of K, the LP-MMSE becomes a scalable scheme even for K → ∞ . The complexity of LP-MMSE is lower compared to the centralized P-MMSE [4]. In addition, the computational order of LP-MMSE remains finite even for K → ∞ due to finite number of multiplications required. The spectral efficiency of LP-MMSE is obtained easily through Monte Carlo simulations.

4.3. Scalability Analysis of Spectral Efficiency for Downlink

The spectral efficiency of downlink can be obtained from the uplink-downlink duality by considering the uplink combining vector given as [ v j : j = 1 , 2 , . . . , K ] with power of each UE as [ ρ i u : i = 1 , 2 , . . . , K ] . We use the uplink-downlink duality by first expressing beamforming per UE w ¯ j as,
w ¯ j = v j E [ v j H D j v j ]
by utilizing an appropriate power control algorithm in the downlink, where,
∑ j = 1 K ρ j σ n , d l 2 = ∑ j = 1 K ρ j σ n , u l 2
such that for k-th UE, S I N R d = S I N R u for all k.
The two cooperation mechanisms for precoding are: centralized precoding and distributed precoding. In centralized precoding, estimates for downlink are obtained by using the uplink-downlink duality. Once the estimates are computed, we deduce precoding matrix from eq. (21) and next, CPU constructs the downlink signal,
x n d = ∑ j = 1 K ρ j D j n w ¯ j n ζ j
and sends it to the AP through fronthaul, where ζ j corresponds to the data signal for downlink. In every coherence interval, n t h AP has to send τ p M complex values to the CPU and receive τ p M values from CPU.
In distributed precoding, n t h AP chooses the precoding vector w ¯ j by using only the local channel estimates [ h ^ j n : j ∈ A n ] for scalable cell-free framework. Therefore, in every coherence block, τ d A n complex values are exchanged among n t h AP and CPU. This work utilizes distributed precoding mechanism. It is worth mentioning here that only angle based matched filtering and angle based LP-MMSE precoding schemes are scalable, like in the combining schemes case.

4.4. Overhead of Scalable Angle based Scheme in FDD cell-free

Table 3 provides the comparison of angle based MMSE (non-scalable) with scalable angle based LP-MMSE and MF schemes. The total order of complexity for original angle based MMSE is the sum of DFT operations performed for multipath components estimation M l o g M , order of angle rotation performed over the search grid V M L and number of complex scalers transmitted to CPU for decoding of signal in each coherence block, which are M τ p for centralized scheme and | A n | τ u for the distributed case. This complexity increases linearly with increase in number of users joining the network. It is evident from Table 3 that angle based MMSE without utilizing DCC is not scalable for large K due to its linear dependence on the number of UEs. The LP-MMSE scheme, however, is scalable due to its dependence on M k instead of K since M k ⊂ K and does not scales linearly with K.

4.5. Energy Efficiency

Energy efficiency is a good measure for performance evaluation of FDD based system and is defined as the ratio of throughput in bits/s to the total power consumed in Watts. It is measured in bit/joule. It is given as,
η = E ∑ k = 1 K ⋋ S E k u P t
where, ⋋ = 1 − τ p τ c . The total power consumed is the sum of power consumption at AP and the power utilized over the backhaul and control signaling [4,40]. As mentioned already, we assume τ p to be independent of K. The power consumption of n t h AP depends on angle based beamforming vector and number of antennas M. Therefore, increase in number of UEs K will not effect the energy efficiency.

5. Power Control Algorithm for Scalable Cell-Free

Some works in literature suggest to perform power control at the CPU for scalable cell-free massive MIMO [4,5]. For angle based schemes, coherence time is greater, therefore, low signaling overhead is incurred. Authors in [5] utilize user centric AP selection approach for power control that results in increased energy efficiency. Work in [4] proposes trial and error approach towards power control. In this work, a network-wide power allocation is studied for centralized as well as distributed beamforming cooperation. The two approaches help APs to ensure conformity to the power constraint by serving maximum number of users equal to the number of pilots with equal power per user. For equal power allocation with centralized precoding in the uplink, the power allocated to an i t h UE is, ρ i = ρ n τ p , where, ρ n is power of n t h AP in the network [4]. We assume that in the uplink, all users transmit with maximum power P to enhance the spectral efficiency for all UEs, strong or weak, such that, p i = P , f o r i = 1 , 2 , . . . , K .
In this research work, we also analyze the performance of distributed approach for power control in the FDD cell-free network. The aim is to ensure that every user will be served by at least one AP and therefore, will have non-zero spectral efficiency.The power control task in distributed scenario is more complicated. In distributed scenario, AP has to assign power to all the UEs being served by it. Two most common approaches for power control are equal power allocation and max-min power control algorithms [4]. Out of these two, the max-min power/weight control approach works very well in FDD cell-free network even if some users are far away from the serving AP [5]. For the users that are located far away from AP, the joint initial access algorithm ensures that such a user is served by at least one AP which will allocate the UE a certain amount of transmission power and thus its spectral efficiency will also be non-zero. The max-min power control algorithm is discussed in the following subsection for FDD cell-free massive MIMO network.

5.1. Max-Min Power Allocation for Downlink

After the large scale fading coefficients and array angle steering vectors have been obtained, the coefficients Υ n k for n t h AP to k t h UE are utilized for max-min power control [5],
m a x m i n S E k d { Υ n k , j } k = 1 , . . . , K g i v e n t h a t , ∑ k = 1 K G ^ n k | | G ^ n k | | Υ n k ≤ 1 , ∀ m = 1 , . . . , M
where, S E k d is the downlink spectral efficiency for k t h UE, and Υ n k ≥ 0 ∀ n , k a n d j , i.e. the algorithm will ensure to maximize the minimum data rate for UEs in the downlink. The best case scenario is that all UEs will achieve the same maximum data rate, and in the worst case scenario, UEs with weak channel conditions will be allocated lower power compared to the UEs with stronger channel link (based on Υ n k ). The original form of this algorithm is not scalable for large number of UEs in cell-free network. However, for cell-free network with scalable precoding/combining, the power distribution among the APs in distributed precoding based system is determined by the unit norm precoding vector w j ¯ . The max-min power control algorithm is utilized to compute w ¯ j , based on the Υ n k coefficients. All the APs ensure adhering to the power constraint by serving a maximum of τ p users and a maximum of ρ n τ p power per user is allocated. Therefore, the maximum power control algorithm is scalable because the number of variables to be optimized are now independent of K.

6. Simulation Results

We provide numerical results for an FDD based cell-free massive MIMO network and compared the performance of scalable angle based precoding and combining schemes in terms of their spectral and energy efficiencies.

6.1. Simulation Setup

In this work we use monte-carlo simulations for an FDD cell-free network. As literature suggests that FDD cell-free networks require less number of APs to provide same coverage area compared to TDD based cell-free networks, the interference in FDD based network will be inherently limited due to separation in the up/downlink frequencies [5]. In addition, the higher number of antennas per AP achieve spatial diversity gain for angle based FDD scheme. Therefore, FDD is expected to provide improved performance for centralized scenario ( N = 100 , M = 8 ) compared to the performance in case of distributed scenario ( N = 200 , M = 4 ). We consider an area of 2 × 2 K m 2 and a wrap-around scenario is assumed to mimic a very large network with randomly distributed APs [4] and 200 antennas per K m 2 . Number of UEs is considered to be K = 100 with uniform and independent distribution over the coverage area. Two scenarios are simulated: i ) N = 100 and M = 8 , i i ) N = 200 and M = 4 , therefore, total number of serving antennas in the network remains the same i.e. N M = 800 .
Initially, τ p UEs connect with the FDD based cell-free massive MIMO network. UEs are assigned random pilots from a set of orthogonal pilot sequences. We utilize the channel model as presented in [5], where APs are placed 10m above the UEs such that a minimum distance between n t h AP and k t h UE is maintained. Rest of the simulation parameters are listed in Table 4.

6.2. Results and Discussion

First, we analyze the performance of max-min power control algorithm in both the uplink and downlink. Figure 2 shows the performance on the basis of downlink spectral efficiency by utilizing max-min power control versus equal power allocation. Figure 3 compares the performance of the uplink spectral efficiency with max-min power control versus equal power allocation. It is apparent from these results that max-min power control algorithm provides better spectral efficiency compared with equal power allocation in both the uplink and downlink. In addition, the LP-MMSE with max-min power control provides significant performance improvement over angle based MF and MMSE schemes with max-min power control. For the results presented of the downlink case, the spectral efficiency of LP-MMSE with max-min power control at 24 dBs is 800 bits/s/Hz, whereas, with equal power allocation it is at 650 bits/s/Hz. Likewise, in the uplink, the spectral efficiency of LP-MMSE with max-min power control at 24 dBs is 690 bits/s/Hz, whereas, with equal power allocation it is at 625 bits/s/Hz, therefore, LP-MMSE with max-min power allocation reports 10.4 % increase in spectral efficiency over equal power allocation.
Next, we analyze the performance of the uplink per user spectral efficiency, by using the expression in eq.(19). The cumulative distribution function (CDF) of DCC with angle based precoding schemes including MF, MMSE and scalable LP-MMSE are compared for the two scenarios and are shown in Figure 4 and Figure 5. In our case, the angle based MF scheme shows improved performance over simple MF, however, its performance is still not at par with the angle based LP-MMSE scheme. It is evident from Figure 4, that the scalable LP-MMSE outperforms both MF and MMSE schemes. The LP-MMSE scheme gives significant improvement in spectral efficiency for 97 % of the UEs, and its performance for rest 3 % weak channel condition users is still better compared to MF counterpart. In addition, it is also shown in Figure 4 that FDD based cell-free provides improved spectral efficiency in the scenario where number of antennas per AP is higher, N = 100 , M = 8 compared to N = 200 , M = 4 case in Figure 5, because of the increase in spatial diversity gains with angle based beamforming. The gap in the performances of MF vs LP-MMSE and MMSE vs LP-MMSE is significant, where latter is even greater, which endorses that our proposed scalable LP-MMSE scheme is the better choice for FDD cell-free network. In Figure 5, this performance gap reduces for N = 200 , M = 4 with the decrease in number of antennas per AP.
The performance of downlink spectral efficiency is analyzed in Figure 6 and Figure 7, where, we compare the performance of scalable, angle based MF, MMSE and scalable LP-MMSE at a fixed SNR level with DCC. The spectral efficiency of LP-MMSE is improved in comparison with the rest of the two schemes. The performances are compared in the downlink by utilizing max-min power control algorithm. As was the case with the uplink, for distributed scenario, N = 200 , M = 4 , performance gap in spectral efficiency of MMSE Vs LP-MMSE and MF vs LP-MMSE is decreased i.e. LP-MMSE performance is slightly compromised against the MF and MMSE counterparts, whereas, the gap is increased in case of centralized scenario N = 100 , M = 8 . It is due to increase in number of antennas per AP, resulting in array gain. Its worth mentioning here that this array gain saturates at M ≥ 32 , as suggested in [5]. It is also evident from Figure 6 and Figure 7 that performance gap between angle based estimation schemes (LP-MMSE and MMSE) is not as high as in the uplink in both centralized ( N = 100 , M = 8 ) as well as distributed ( N = 200 , M = 4 ) scenarios. This is due to the fact that the higher power in downlink signal gives leverage to MMSE and its performance improves, however, spectral efficiency in MMSE is still lower than than LP-MMSE.
The energy efficiency versus number of APs for FDD based cell-free network is compared and presented in Figure 8. We only consider the energy efficiency for scalable angle based MF and LP-MMSE schemes with max-min power allocation versus equal power allocation algorithm. It is shown in Figure 8 that max-min power allocation algorithm gives significant improvement in energy efficiency in both angle based MF and angle based LP-MMSE schemes. With the increase in number of APs, there is a decrease in number of antennas per AP, to keep M N constant over the coverage area. As a result, the energy efficiency starts to increase due to increase in number of APs per unit area. However, further increase in number of APs will result in further reduction in number of antennas per APs, causing spatial gain to decrease. Therefore, the energy efficiency degrades for higher number of AP deployment in cell-free framework due to an increase in backhaul power consumption, on the same lines as indicated by the results shown in [5]. It can be seen in the graph that for a given number of APs e.g. N = 100 , max-min power control provides better energy efficiency, i.e. 520 M b i t s / J o u l e for K = 100 UEs, whereas, equal power algorithm gives 220 M b i t s / J o u l e . The LP-MMSE with max-min power control shows best performance, i.e. 580 M b i t s / J o u l e vs 280 M b i t s / J o u l e with equal power allocation algorithm. It is worth mentioning here that increase in number of UEs such that k → ∞ will not effect the downlink energy efficiency as long as the combining/precoding vectors have finite complexity, which is true in our analysis of angle based scalable MF and LP-MMSE schemes.

7. Conclusions

This work presents a scalable FDD based cell-free massive MIMO system. Utilization of FDD in a cell-free setting can achieve reliable communication with low latency in applications with real-time communication. However, there are a few challenges associated with FDD utilization such as higher computational complexity compared to TDD counterpart. In addition, FDD based systems do not include channel reciprocity, however, these systems encompass angular reciprocity, where AoA and AoD are the same in the uplink and downlink. We exploit this angular reciprocity to obtain the expressions for scalable angle based beamforming and combining schemes in FDD based cell-free network. We utilize the concept of dynamic cooperation clustering for computation of efficient and scalable beamforming and combining vector expressions. The DCC is applied to angle based MF, angle based LP-MMSE and angle based MMSE expressions. The performance of angle based MF is compared with angle based MMSE and angle based LP-MMSE in terms of spectral and energy efficiency. The comparative analysis shows that LP-MMSE outperforms the MF and provides best performance compared to the rest of the schemes. Future research directions may include implementation of more efficient algorithms for joint initial access, AP clustering and power control in an FDD cell-free framework.

References

  1. Hassan B., et al.; et al. A Survey of FDD-Based Channel Estimation Schemes With Coordinated Multipoint. IEEE Systems Journal 2022, 16, 4563–4573. [Google Scholar] [CrossRef]
  2. Riviello, D.G. et. al. Implementation of Deep-Learning-Based CSI Feedback Reporting on 5G NR-Compliant Link-Level Simulator. Sensors 2023, 23. [Google Scholar] [CrossRef] [PubMed]
  3. Kang, X. et. al. Deep Learning for Joint Pilot Design and Channel Estimation in MIMO-OFDM Systems. Sensors 2022, 22. [Google Scholar] [CrossRef] [PubMed]
  4. Bjornson E., et. al. Scalable Cell-Free Massive MIMO Systems. IEEE Transactions on Communications 2020, 7, 4247–4261.
  5. Abdallah Asma, et. al. Efficient Angle-Domain Processing for FDD-Based Cell-Free Massive MIMO Systems. IEEE Transactions on Communications 2020, 4, 2188–2203. [Google Scholar] [CrossRef]
  6. Enyu Shi, et. al. Spatially Correlated Reconfigurable Intelligent Surfaces-Aided Cell-Free Massive MIMO Systems. IEEE Transactions on Vehicular Technology 2022, 71, 9073–9077. [Google Scholar]
  7. Garg Navneet, et. al. Generalized Superimposed Training Scheme in IRS-Assisted Cell-Free Massive MIMO Systems. IEEE Journal of Selected Topics in Signal Processing 2022, 16, 1157–1171. [Google Scholar] [CrossRef]
  8. Mahmoud Zaher, et. al. Learning-Based Downlink Power Allocation in Cell-Free Massive MIMO Systems. IEEE Transactions on Wireless Communications 2023, 22, 174–188. [Google Scholar] [CrossRef]
  9. S. Elhoushy et. al., Cell-Free Massive MIMO: A Survey. IEEE Communications Surveys & Tutorials 2022, 24, 492–523.
  10. Shuaifei Chen, Jiayi Zhang, Jing Zhang, Emil Bjornson and Bo Ai, A survey on user-centric cell-free massive MIMO systems. Digital Communications and Networks 2022, 8, 695–719. [CrossRef]
  11. S. Venkatesan, A. Lozano, R. Valenzuela Network MIMO: Overcoming Intercell Interference in Indoor Wireless Systems, 2007 Conference Record of the Forty-First Asilomar Conference on Signals, Systems and Computers, 2007, 83-87.
  12. D. Gesbert, S. Hanly, H. Huang, Shamai Shitz, S. Shlomo, Osvaldo and Wei Yu Multi-Cell MIMO Cooperative Networks: A New Look at Interference. IEEE Journal on Selected Areas in Communications 2010, 28, 1380–1408. [CrossRef]
  13. E. Bjornson, R. Zakhour, D. Gesbert, B. Ottersten Cooperative Multicell Precoding: Rate Region Characterization and Distributed Strategies With Instantaneous and Statistical CSI. IEEE Transactions on Signal Processing 2010, 58, 4298–4310. [CrossRef]
  14. P. Marsch, G. Fettweis On multicell cooperative transmission in backhaul-constrained cellular systems. Annales des Telecommunications 2008, 63, 253–269. [CrossRef]
  15. J. Zhang, R. Chen et. al. Networked MIMO with clustered linear precoding. IEEE Transactions on Wireless Communications 2009, 8, 1910–1921. [CrossRef]
  16. H. Huang, M. Trivellato, A. Hottinen, M. Shafi, P. Smith, Peter J. and R. Valenzuela Increasing downlink cellular throughput with limited network MIMO coordination. IEEE Transactions on Wireless Communications 2009, 8, 2983–2989. [CrossRef]
  17. Osseiran, Afif et. al. 5G Mobile and Wireless Communications Technology, 2016.
  18. A. Tolli, M. Codreanu, M. Juntti Cooperative MIMO-OFDM Cellular System with Soft Handover Between Distributed Base Station Antennas. IEEE Transactions on Wireless Communications 2008, 7, 1428–1440. [CrossRef]
  19. Emil B. et., al. Optimality Properties, Distributed Strategies, and Measurement-Based Evaluation of Coordinated Multicell OFDMA Transmission. IEEE Transactions on Signal Processing 2011, 59, 6086–6101. [Google Scholar]
  20. S. Kaviani, O. Simeone, W. Krzymien, Shlomo Shamai Linear Precoding and Equalization for Network MIMO With Partial Cooperation. IEEE Transactions on Vehicular Technology 2012, 61, 2083–2096. [CrossRef]
  21. Emil Bjornson, Eduard Jorswieck Optimal Resource Allocation in Coordinated Multi-Cell Systems, Now Publishers, 2013.
  22. Emil Bjornson and Luca Sanguinetti Making Cell-Free Massive MIMO Competitive With MMSE Processing and Centralized Implementation. IEEE Transactions on Wireless Communications 2020, 19, 77–90. [CrossRef]
  23. J. Zheng, Jiayi Zhang, Emil Bjornson, Zhetao Li, Bo Ai Cell-Free Massive MIMO-OFDM for High-Speed Train Communications. IEEE Journal on Selected Areas in Communications 2022, 40, 2823–2839. [CrossRef]
  24. Shuto Fukue, Hiroki Iimori, Giuseppe De Abreu, Koji Ishibashi Joint Access Configuration and Beamforming for Cell-Free Massive MIMO Systems With Dynamic TDD. IEEE Access 2022, 10, 40130–40149. [CrossRef]
  25. Lorenzo Miretti, Emil Bjornson, David Gesbert Team MMSE Precoding With Applications to Cell-Free Massive MIMO. IEEE Transactions on Wireless Communications 2022, 21, 6242–6255. [CrossRef]
  26. S. Kim, B. Shim FDD-Based Cell-Free Massive MIMO Systems. 2018 IEEE 19th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), 2018, 1-5.
  27. Tongzhou Han, Danfeng Zhao Downlink channel estimation in FDD cell-free massive MIMO. Physical Communication 2022, 52.
  28. H. Xie, F. Gao, Shun Zhang, Shi Jin A Unified Transmission Strategy for TDD/FDD Massive MIMO Systems With Spatial Basis Expansion Model. IEEE Transactions on Vehicular Technology 2017, 66, 3170–3184. [CrossRef]
  29. Lei Cheng, Yik-Chung Wu, J. Zhang, L. Liu Subspace Identification for DOA Estimation in Massive/Full-Dimension MIMO Systems: Bad Data Mitigation and Automatic Source Enumeration. IEEE Transactions on Signal Processing 2015, 63, 5897–5909. [CrossRef]
  30. A. Hu, T. Lv, Hui Gao, Zhang Zhang, Shaoshi Yang An ESPRIT-Based Approach for 2-D Localization of Incoherently Distributed Sources in Massive MIMO Systems. IEEE Journal of Selected Topics in Signal Processing 2014, 8, 996–1011. [CrossRef]
  31. Ting Wang, Bo Ai, Ruisi He, Z. Zhong Two-Dimension Direction-of-Arrival Estimation for Massive MIMO Systems. IEEE Access 2015, 3, 2122–2128. [Google Scholar] [CrossRef]
  32. R. Shafin, L. Liu, J. Zhang, Y. Wu DoA Estimation and Capacity Analysis for 3-D Millimeter Wave Massive-MIMO/FD-MIMO OFDM Systems. IEEE Transactions on Wireless Communications 2016, 15, 6963–6978. [CrossRef]
  33. D. Fan et. al. Training Based DOA Estimation in Hybrid mmWave Massive MIMO Systems. GLOBECOM 2017 - 2017 IEEE Global Communications Conference, 2017, 1-6.
  34. D. Fan et. al. Angle Domain Channel Estimation in Hybrid Millimeter Wave Massive MIMO Systems. IEEE Transactions on Wireless Communications 2018, 17, 8165–8179. [CrossRef]
  35. Zikum Liu, G. Singh, C. Xu, D. Vasisht FIRE: Enabling Reciprocity for FDD MIMO Systems. Proceedings of the 27th Annual International Conference on Mobile Computing and Networking, 2021, 68, 628–641. [Google Scholar]
  36. Vutha Va, Junil Choi, R. Heath The Impact of Beamwidth on Temporal Channel Variation in Vehicular Channels and Its Implications. IEEE Transactions on Vehicular Technology 2017, 66, 5014–5029. [Google Scholar] [CrossRef]
  37. K. Hugl et. al., Spatial reciprocity of uplink and downlink radio channels in FDD systems. Proc. COST 2002, 273, p–066.
  38. Emil Bjornson, Niklas Jalden, Mats Bengtsson, Bjorn Ottersten Optimality Properties, Distributed Strategies, and Measurement-Based Evaluation of Coordinated Multicell OFDMA Transmission. IEEE Transactions on Signal Processing 2011, 59, 6086–6101. [CrossRef]
  39. Emil Bjornson et. al., Massive MIMO Networks: Spectral, Energy, and Hardware Efficiency. Now Publishers 2017, Now Publishers.
  40. Hien Ngo, Le-Nam Tran, Trung Duong, M. Matthaiou, Erik Larsson On the Total Energy Efficiency of Cell-Free Massive MIMO. IEEE Transactions on Green Communications and Networking 2018, 2, 25–39. [Google Scholar] [CrossRef]
Preprints 75448 g001
Figure 1. DCC framework for overlapping Clustering Scheme.
Figure 1. DCC framework for overlapping Clustering Scheme.
Preprints 75448 g001
Preprints 75448 g002
Figure 2. Comparison of Downlink Power Control for angle based MF, LP-MMSE and MMSE Schemes.
Figure 2. Comparison of Downlink Power Control for angle based MF, LP-MMSE and MMSE Schemes.
Preprints 75448 g002
Preprints 75448 g003
Figure 3. Comparison of Uplink Power Control for angle based MF, LP-MMSE and MMSE Schemes.
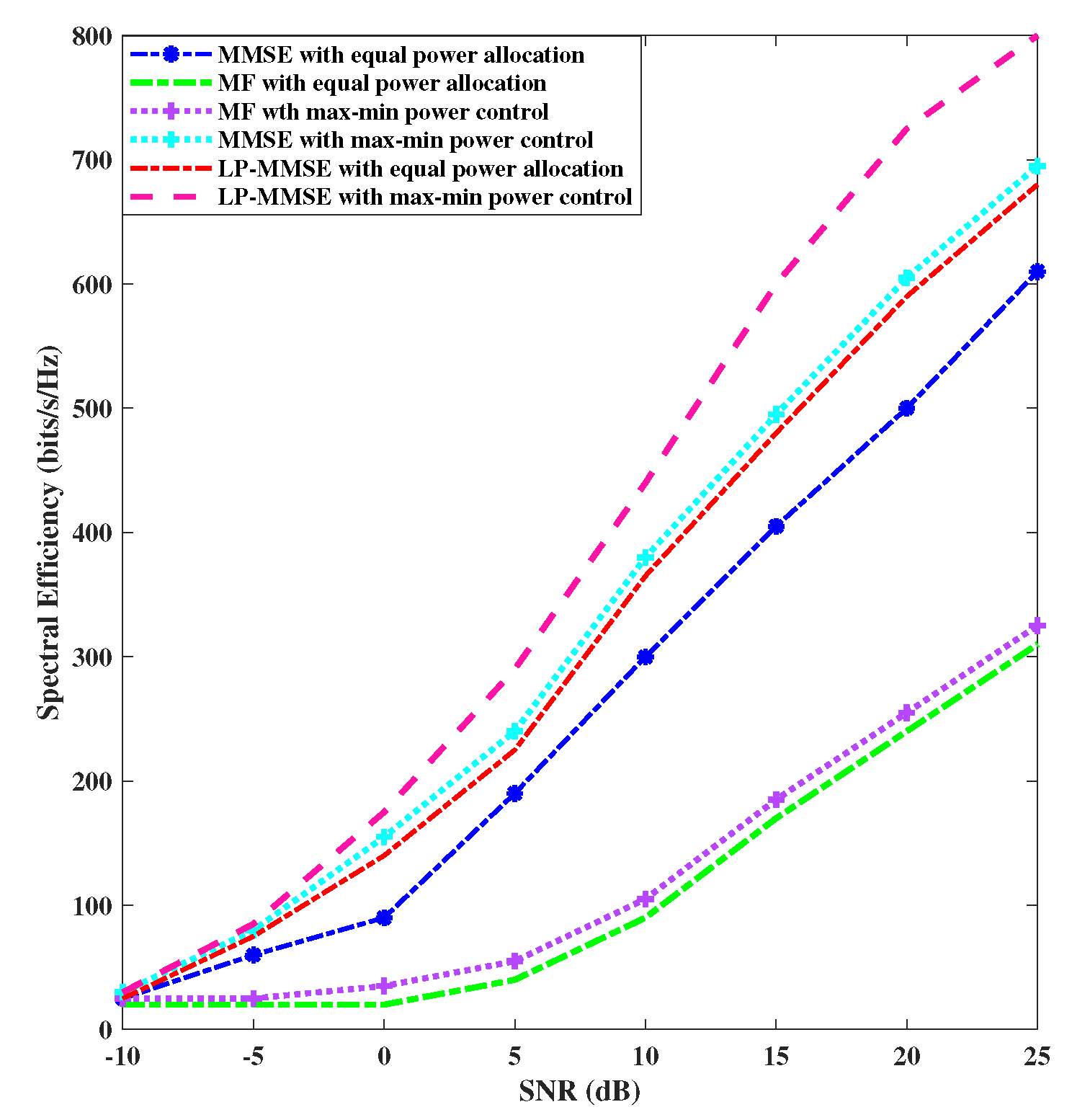
Figure 3. Comparison of Uplink Power Control for angle based MF, LP-MMSE and MMSE Schemes.
Preprints 75448 g003
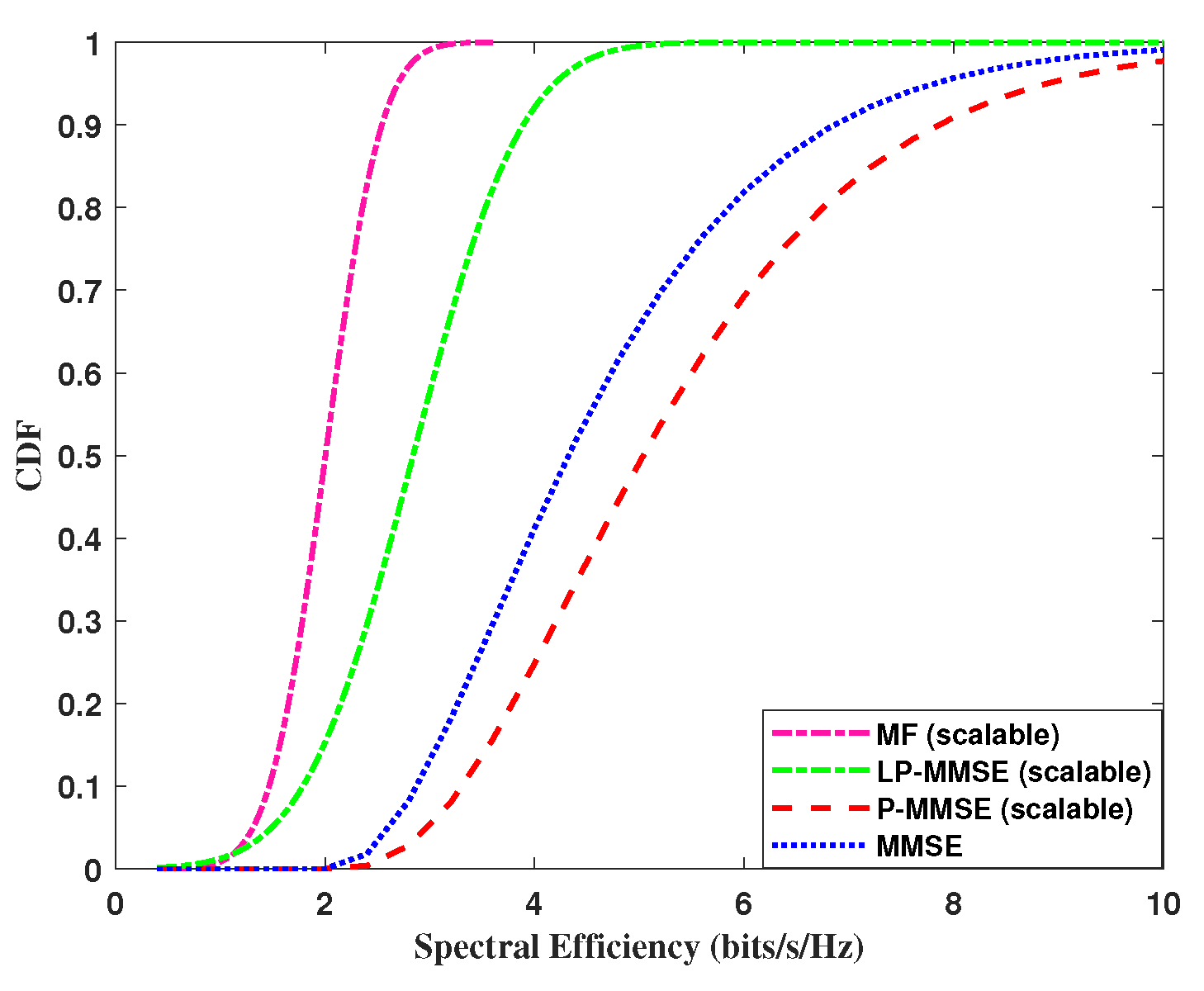
Preprints 75448 g004
Figure 4. CDF of Spectral Efficiency for Uplink, 100 APs and M=8 antennas/AP.
Figure 4. CDF of Spectral Efficiency for Uplink, 100 APs and M=8 antennas/AP.
Preprints 75448 g004
Preprints 75448 g005
Figure 5. CDF of Spectral Efficiency for Uplink, N=200 APs and M=4 antennas/AP.
Figure 5. CDF of Spectral Efficiency for Uplink, N=200 APs and M=4 antennas/AP.
Preprints 75448 g005
Preprints 75448 g006
Figure 6. CDF of Spectral Efficiency for Downlink, N=100 APs and M=8 antennas/AP.
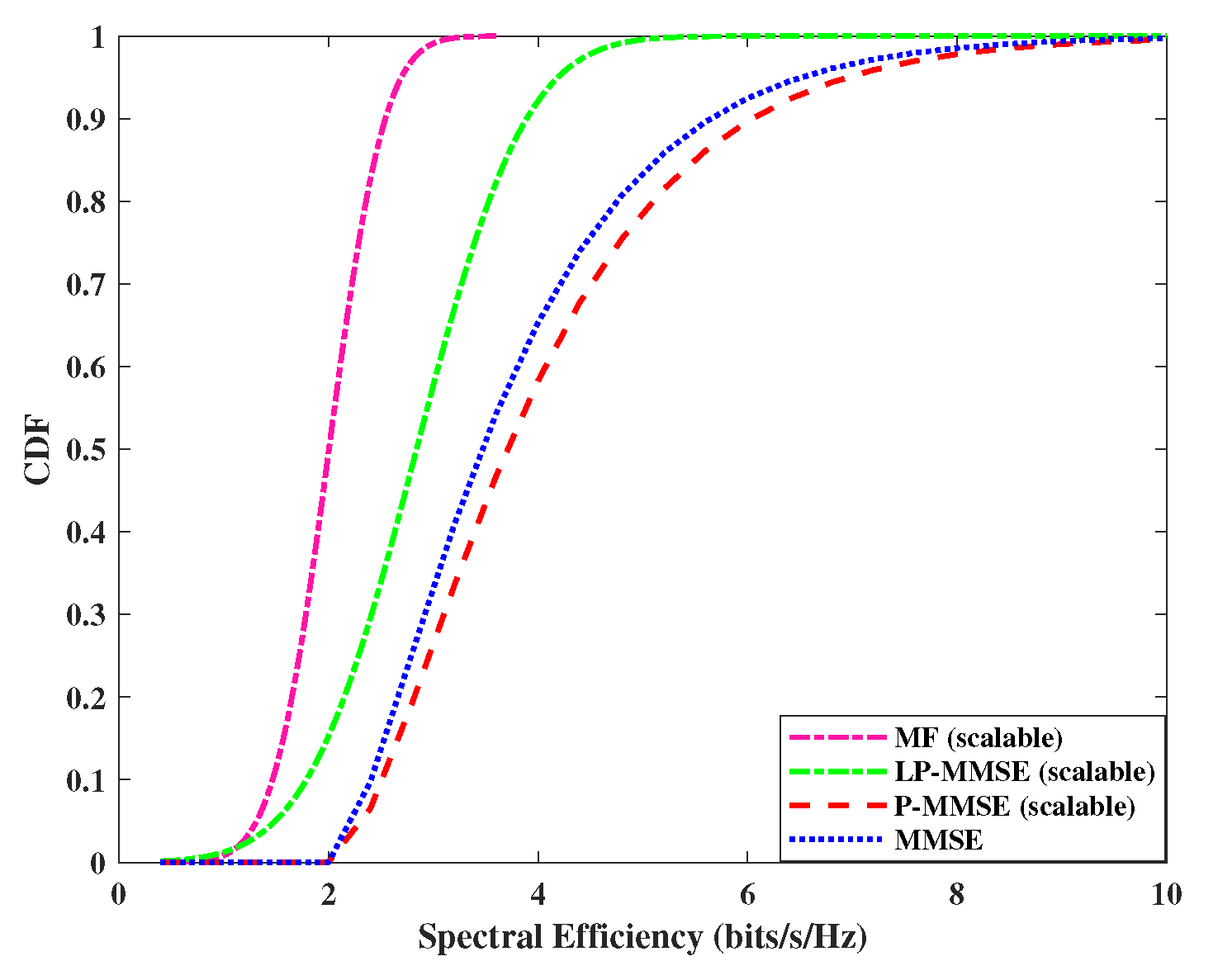
Figure 6. CDF of Spectral Efficiency for Downlink, N=100 APs and M=8 antennas/AP.
Preprints 75448 g006
Preprints 75448 g007
Figure 7. CDF of Spectral Efficiency for Downlink, N=200 APs and M=4 antennas/AP.
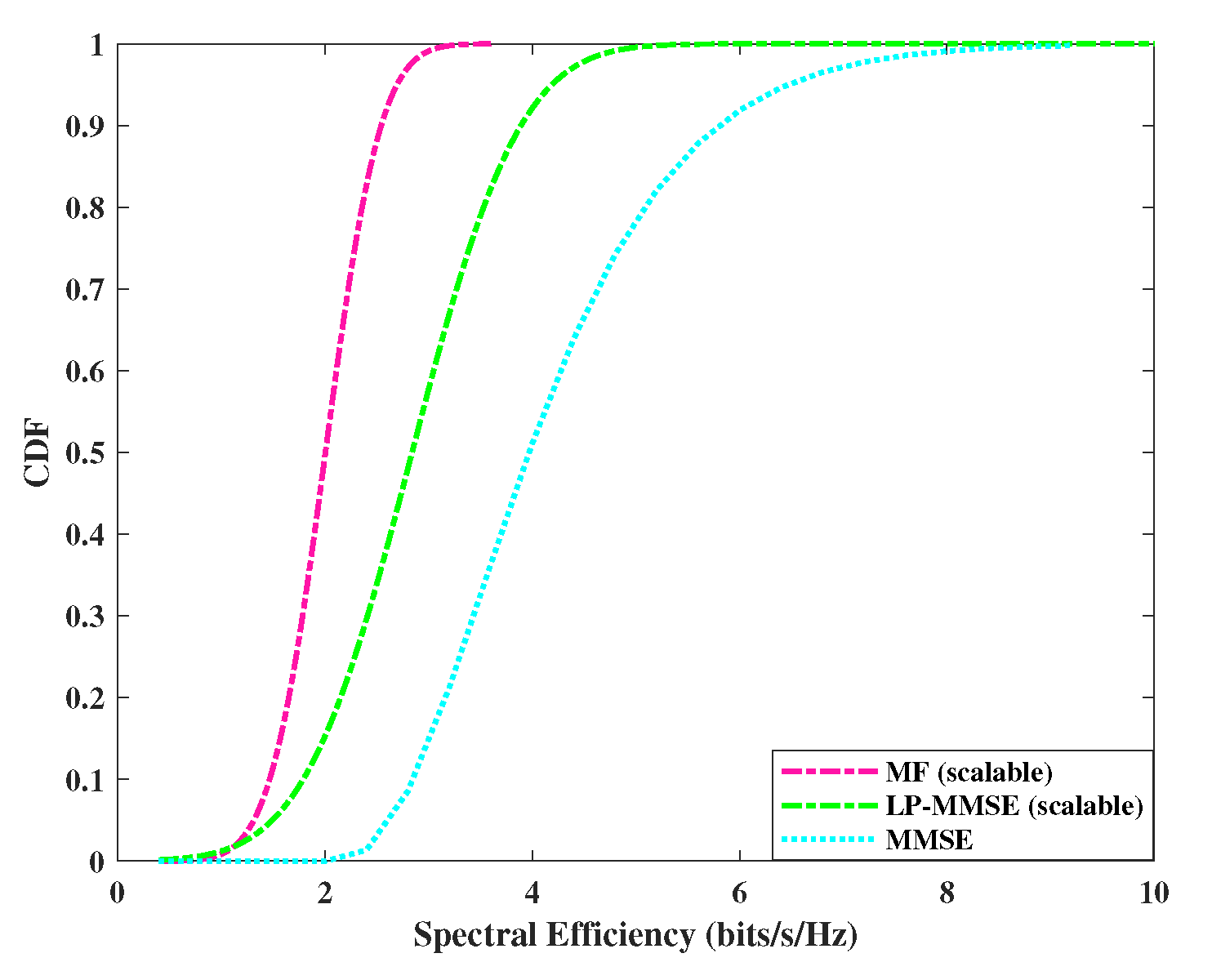
Figure 7. CDF of Spectral Efficiency for Downlink, N=200 APs and M=4 antennas/AP.
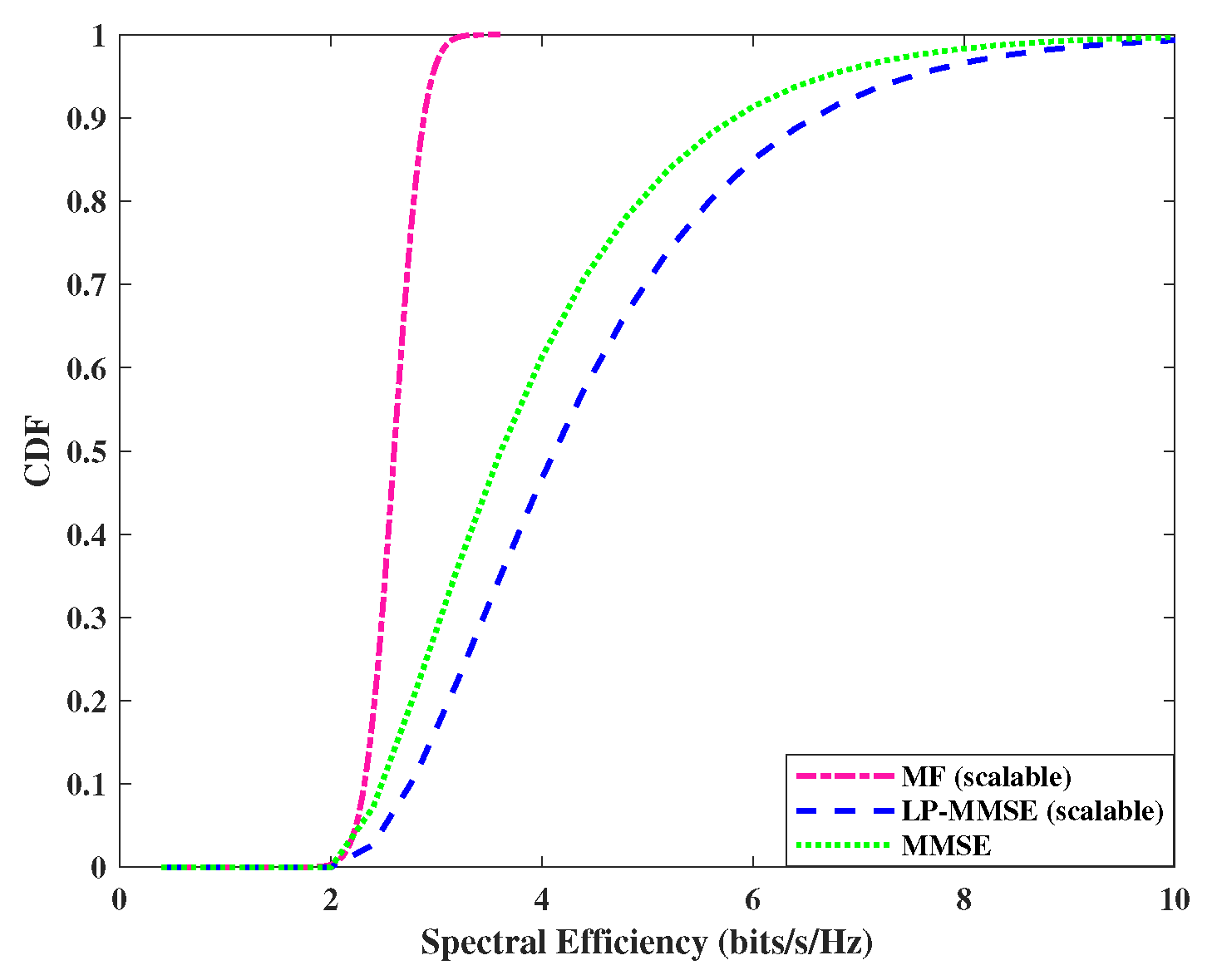
Preprints 75448 g007
Preprints 75448 g008
Figure 8. Comparison of Energy Efficiency for angle based MF and angle based LP-MMSE.
Figure 8. Comparison of Energy Efficiency for angle based MF and angle based LP-MMSE.
Preprints 75448 g008
Table 1. Comparison of Proposed Scalable Angle based FDD Scheme with Existing Techniques.
Table 1. Comparison of Proposed Scalable Angle based FDD Scheme with Existing Techniques.
Article Scalable Duplexing Mode Precoding / Combining Power Allocation Spectral Efficiency Energy Efficiency
[4] TDD LP-MMSE, MMSE, MR equal power ✗
[5] ✗ FDD Angle based MMSE, MF and ZF max-min, equal power
[22] ✗ TDD L-MMSE ✗ ✗
Proposed FDD Angle based LP-MMSE, MMSE and MF max-min, equal power
Table 2. Comparison of Computational Complexity for Estimation Techniques.
Table 2. Comparison of Computational Complexity for Estimation Techniques.
Estimation Technique Complexity of Estimation
Angle based M l o g ( M ) + V M L
ESPRIT M 3 + U i N 3
MUSIC ( N 3 M 3 + K 3 )
Table 3. Comparison of Computational Complexity for Estimation and Combining Schemes.
Table 3. Comparison of Computational Complexity for Estimation and Combining Schemes.
Technique Complexity of Channel Estimation Complexity of Precoding/Combining
Angle based MMSE ( M l o g ( M ) + V M L + M τ p ) K   | M k | M | M | k l o g ( M | M k | ) + M | M k | 2 K + M | M k | l o g ( M | M k | ) + ( M | M k | ) 3 − M | M k | 2
Angle based LP-MMSE ( M l o g ( M ) + V M L + M τ p ) ∑ n ∈ M k | A n | M l o g ( M ) + M 2 ∑ n ∈ M k | A n | + ( M 3 − M 3 + M l o g ( M ) ) | M k |
Angle based MF M l o g ( M ) + V M L + M τ p ) | M k | -
Table 4. Simulation Parameters for FDD based Cell-Free Framework.
Table 4. Simulation Parameters for FDD based Cell-Free Framework.
System Parameters Value
Coverage Area 2 × 2 K m 2
Bandwidth 100 MHz
Up/Downlink Frequency 49.8 / 50 GHZ
Transmit Power for uplink pilot 200 mW
Transmit Power of Payload in Uplink 200 mW
Transmit Power of Payload in Downlink 1 W
Angle Coherence Interval 200 samples
Number of Monte-Carlo Simulations 1000
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated