Prerpints.org logo
Preprint
Article

Modern Optimization Algorithm for Improved Performance of Maximum Power Point Tracker of Partially Shaded PV Systems

Altmetrics

Downloads

124

Views

39

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

29 May 2023

Posted:

02 June 2023

You are already at the latest version

Alerts
Abstract
Because of the rapid advancement in the use of photovoltaic (PV) energy systems, it has become critical to look for ways to improve the energy generated by them. The extracted power from the PV modules is proportional to the output voltage. The relationship between output power and array voltage has only one peak under uniform irradiance, whereas it has multiple peaks under partial shade circumstances (PSC). There is only one global peak (GP) and many local peaks (LPs), where the typical maximum power point trackers (MPPT) may become locked in one of the LPs, significantly reducing the PV system's generated power and efficiency. The metaheuristic optimization algorithms (MOAs) solved this problem, albeit at the expense of the convergence time, which is one of these algorithms' key shortcomings. Most MOAs attempt to lower the convergence time at the cost of the failure rate and the accuracy of the findings because these two factors are interdependent. To address these issues, this work introduces the dandelion optimization algorithm (DOA), a novel optimization algorithm. The DOA's convergence time and failure rate are compared to other modern MOAs in critical scenarios of partial shade PV systems to demonstrate the DOA's superiority. The results obtained from this study showed substantial performance improvement compared to other MOAs, where the convergence time is reduced to 0.4 s with zero failure rate compared to 0.9 s, 1.25 s, and 0.43 s for other MOAs under study. The optimal number of search agents in the swarm, optimal initialization of search agents, and optimal design of the dc-dc converter is introduced for optimal MPPT performance.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

With the continuous increase in the need for electrical energy and the continuous shortage of fossil fuels and the impact of geopolitical problems on energy supplies and the environmental impact of excessive use, the need for renewable energies, especially the energy generated from PV cells, has increased. Most of the world’s nations realize this problem and started ambitus programs to completely rely on renewable energy sources by 2050 [1]. Statistics indicate a significant rise in the use of PV in the production of electric energy, as the worldwide capacity of PV cells increased to 1300 megawatts, exceeding the capacity generated from wind energy by 400 megawatts [2]. With the rapid progress in modern energy storage systems (ESS) and smart grid systems [3,4], the problem of intermittency in the generated power as a result of climate change has been overcome. The ESS can save the extra energy greater than the load needs and serve this stored energy when there is a deficiency in the extracted power from renewable energy sources (RES) compared to the power of the load. Moreover, the smart grid system can control the loads by different smart grid concepts to a level near the available generation from RES.
The PV systems are used to directly generate electricity from sunlight. The extracted power from the PV array is directly proportional to the light intensity, operating temperature, and the output voltage of the PV array. Connecting many modules in series and parallel are required to increase the voltage and current of the PV array. The relation between the generated power and the terminal voltage is nonlinear and it has only one peak at about 0.8 of the open circuit voltage (Voc) of the PV array in case of uniform irradiance. In case of non-uniform irradiance falling on the PV modules, different generated power will be generated from these PV modules. For extracting the maximum power from these modules, each module should work with its optimal voltage and current which is not the case in real PV systems because modules are connected in series and parallel. This means that the current in each series branch is the same in all series modules, meanwhile, the terminal voltage of each module is different. A negative voltage may be generated at the terminal of some modules in some severe partial shading conditions (PSC). The negative voltage of shaded modules occurs when these modules act as a load on other modules due to PSC. The occurrence of the negative voltage on some of the shaded modules generates heat inside the module which may destroy it. This phenomenon is called the hot-spot phenomenon [5]. For this reason, a bypass diode should be added in parallel with each module for hotspot protection. When the shunt diode is activated, the generated power from these modules is wasted, and the PV system loses this quantity of energy. Because of the PSC and shunt diodes, the P-V characteristics of the PV array will have fewer than or equal to the number of series modules in the PV array that have varying irradiances. The global peak (GP) is having the highest power among these peaks, whereas the other local peaks (LPs) have lower power than the GP. Several ways have been developed to track the maximum power point (MPP) during real-time operation with various PSCs. Several strategies have been introduced to track the MPP during their real-time operation with different PSCs. As a result, a dc-dc converter was utilized to track the MPP of PV systems by manipulating the power electronics switches with logic created by maximum power point tracker (MPPT) approaches. As illustrated in Figure 1, MPPT techniques are utilized to extract the maximum power provided by a PV system by managing the on/off times of power electronic switch/switches. Some typical procedures employed the incremental change in voltage to track the MPP, such as hill climbing (HC), perturb and observe (P&O), and incremental conductance (In.Con.) [6]. Other smart techniques, such as using fuzzy logic controllers [7] and artificial neural networks [8], have been used as an MPPT of PV systems, but all of these strategies fall into the conventional strategies category because they cannot track the GP and they may stick at one of the LPs in the event of PSC. As a result, typical MPPT techniques are not suggested for usage with PSC-equipped PV systems. The metaheuristic optimization algorithms (MOAs) can follow the GP and prevent the PV system from becoming caught in one of the LPs. Several MOA techniques, including particle swarm optimization (PSO) [9], bat algorithm (BA) [10], grey wolf optimization (GWO) [11], and musical chairs algorithm (MCA) [12], among others, have been employed as MPPT of PV systems. All of these MOAs have several problems, including extended convergence times, premature convergence, and particle stagnation at one of the LPs. The majority of recent studies on this subject have been proposed to overcome these challenges [13,14,15,16,17,18]. Still, additional efforts are needed in this sector to lower convergence time while maintaining GP tracking accuracy.
Various strategies have been used in the literature to overcome the long convergence time problem. The majority of these studies are centered on making changes to current MOAs to capture the GP quicker [13,14,15,16,17,18]. To overcome the random aspect of the PSO in tracking the MPP of PV systems, a deterministic approach was used to modify it [13,14]. The fundamental concept behind this approach is to replace the random values that should be multiplied by the acceleration factors to estimate particle velocity. The accelerated parameters are replaced by 1.0 in this investigation, and the random numbers are deleted. As a result, just the inertia weight parameter has to be adjusted. This strategy has been compared with conventional PSO and shows better performance [13]. The main shortcoming of this optimization algorithm is the random initialization which may cause premature convergence to one of the LPs and a long convergence time that can be avoided with better initialization algorithms [19,20]. The strategy used in [14] improved the random initialization of particles by initializing these particles at the predicted position of peaks. Moreover, it reduced the swarm size to reduce the convergence time. This strategy is reduced the convergence time but it should be trained for different operating voltages due to the particles using the terminal voltage, not the duty ratio [14]. The predicted positions of peaks used in this strategy are based on the anticipated peaks placed at 0.8 Voc which is not accurate as has been discussed in [20]. Another technique employed a linear drop in inertia weight value from 0.9 to 0.4 to increase global search at the start of optimization and improve local search at the end [21]. This method lowered the convergence time and steady-state oscillations, but it still has to be improved. Another strategy suggested the variation of the inertia weight from 0.8 to 0.1 [15] for the same purpose. Some other studies introduced a dynamic inertia weight in which the value of inertial weight will change based on the convergence performance [16,17,18]. Another approach for linearly adjusting the acceleration parameters and inertia weight is provided [22,23]. All these modifications are implemented based on try-and-error bases without an optimal determination of the MOAs’ control parameters. To circumvent the use of trial and error procedures in obtaining the control parameters of MOAs, an intriguing strategy for calculating these optimal control parameters for PSO [9] and BA [24] is presented. In this technique, two nested optimization loops are used: the inner one to track the MPP of the PV system, and the outer one to optimize the control parameters for the internal one for the shortest time of convergence and zero failure rate. These MOAs have been used with photovoltaic systems with varying number of peaks to identify the ideal swarm size, inertia weight, and acceleration parameters. These strategies significantly enhance performance while maintaining a quick time of convergence and great accuracy.
The success of catching the GP and the convergence time will rise as the number of particles increases, and vice versa. This suggests that the time of convergence and failure rate are related to the swarm size. As a result, it is critical to choose the number of particles that provides the quickest time of convergence and zero failure rate. Some solutions employed three search agents [25,26], five search agents [27], and six search agents [28], among others. Other algorithms calculated the appropriate number of particles based on the number of peaks for the shortest time of convergence and zero failure rate [28].
Another strategy is used to reduce the time of convergence while maintaining a zero failure rate using hybrid MPPT techniques (HMTs) [29,30,31,32,33,34,35]. The idea behind the use of HMTs is the use of an effective GP searching strategy to determine its position at the beginning of the optimization, then use the fast local search and low ripple technique to accurately capture the GP. Some hybrid strategies used MOA at the beginning of optimization and conventional MPPT after that [29,30,31,32,33]. There are other HMTs used two MOAs such as [34,35]. A detailed discussion of the HMT techniques is introduced in [36].
In terms of the time of convergence and failure rate, the MPPT's success depends on the initial placements of search agents in all MOAs. For the search agents, the majority of the MOAs employed random position initialization [13]. Random initialization raises the failure rate and increases the time of convergence and should be avoided in MPPT applications. Several strategies are used to replace the random initialization by dividing the search area (voltage or duty ratio) to equal distances and initializing the search agents at these distances [19]. This strategy is better than random initialization but still, the convergence time can be further reduced using initialization at predicated positions of peaks [20]. This strategy has the fastest time of convergence and the lowest rate of failure than random initialization, but the swarm size should be equal to the number of peaks which may limit the flexibility of the MPPT algorithms. This point can be avoided by selecting a swarm size equal to the peaks and the rest of the particles can be randomly distributed.
Another strategy using the skipping model algorithm to reduce the time of convergence while maintaining a zero failure rate is introduced [37,38,39,40,41]. The idea of this strategy is to avoid the search within certain values and concentrate on other areas that probably contain the GP. This strategy reduced the convergence time but it increased the calculation time which may limit the operating frequency and sampling time which consequently increases the convergence time. A detailed discussion of these algorithms is shown in [42].
Another issue that all MOAs have when utilized as an MPPT of a PV system is termed search agent stagnation in one of the local peaks. This issue was resolved by initializing the search agents whenever the change in extracted power exceeded the present tolerance, as stated in Eqn. (1). The high value of the predefined tolerance may cause the system to be insensitive to critical changes in shading patterns and leave the search agents at one of the LPs and lose the GP, especially in gradual changes in shading patterns. Meanwhile, a low value of the specified tolerance may lead the system to reinitialize without necessity, increasing the oscillations of the PV system waveforms. The predefined tolerance is used between 5% [43] to 10% [44]. Some strategies avoid the dependency of re-initialization based on Eqn. (1) by re-initialization of the search agents every certain time [45] or by using scanning search agents re-initialization at certain periods [46,47,48].
| P i − P i − 1 P i − 1 | > ε
where, Pi and Pi-1 are the extracted power from the photovoltaic system at iteration i and i-1, respectively, ε is a predetermined tolerance.

1.1. Motivation

Because of the long convergence time associated with the usage of MOAs in MPPT of photovoltaic energy systems applications, researchers sought to employ novel MOAs or improve current ones. Nonetheless, the long time of convergence and high rate of failure necessitates greater work due to their relevance in PV system functioning. As a result, it is critical to assess and compare some of the most current MOAs in MPPT PV system applications with previous ones. Due to this, the dandelion optimization algorithm (DOA), a recently developed and promising optimization algorithm [49] is introduced in this paper to evaluate its performance compared to superior MOAs used before for this purpose such as PSO [9], GWO [11], and MCA [12]. Moreover, optimum initialization, optimal design of the dc-dc converter, optimal swarm size, and avoidance of search agent stagnation in LPs are tactics used to optimize the performance of MOAs when employed as an MPPT of PV systems.

1.2. Innovation and Contribution

Several MOAs have been employed in PV system MPPT applications. Several of these MOAs have shown greater performance, but additional efforts should be made to test novel MOAs to further reduce the time of convergence and rate of failure, which may be translated into an improvement in extracted power and efficiency of photovoltaic systems. As a result, the recently developed dandelion optimization algorithm (DOA) [49] has been employed for the first time in the MPPT of PV systems. This research also provides a unique strategy for significantly reducing convergence time and avoiding search agent stagnation in LPs. The innovation and contribution involved in this paper are listed below:
  • Evaluation of the application of the DOA in a photovoltaic MPPT as a function of conversion time and failure rate.
  • Calculate the best swarm size to achieve the shortest time of convergence maintaining zero failure rate.
  • Evaluating the performance of the MPPT with different initialization strategies.
  • Using a novel strategy for avoiding the stagnation of search agents in LPs.

1.3. Paper Outlines

The remainder of this study provides a full discussion of the PV array modeling in Section 2. Section 3 has a full overview of the DOA and how it may be employed in the MPPT of photovoltaic energy applications. Section 4 introduces the simulation experiments that were performed to compare the proposed DOA MPPT algorithm to alternative MOAs techniques. Section 5 introduces the experimental work performed to validate the simulated results. Section 6 introduces the findings of this investigation.

2. PV Array Modelling

The photovoltaic cell, which is composed of two semiconductor layers (P-N layers), is the smallest component of the PV array. The sunlight falls on the N-layer which has free electrons in its atom’s outer layer that can be easily moved from its atom if it has enough energy to move. The photon energy has adequate energy that can give this free electron the energy to move from the N-layer to the P-layer which has a free hole. The N-layer atoms turn into positive ions as the electron goes from the N-layer to the P-layer, while the P-layer atoms turn into negative ions, which might result in a voltage difference. The produced energy from the PV cell may be transmitted from the PV cell to the load after the load is linked between the P and N-layers. The PV cells should be arranged in parallel and series to get the required current and voltage of the PV modules. For the same objective, the modules should also be linked in parallel and in series. The simplest photovoltaic cell model is called the single diode model (SDM), which is the simplest way to represent the PV cell performance, is depicted in Figure 2 [50] which is used to represent the PV cell used in this study. Another model with higher accuracy when more than one diode shunt to the first diode to well represent the charge diffusion and recombination components charge of the PV cell [51]. Some other studies recommend using three diodes in the PV cell model to get more accurate results [52]. The main problem of increasing the number of diodes will increase the calculation burden of the model without a substantial improvement in the accuracy compared to the SDM [53]. The SDM is providing adequate accuracy with a reasonable calculation burden and for this reason it is used in the modeling of this study.
From the above discussion, the PV cell can be modeled as a current generator in a shunt with a diode. The PV cell output current can be obtained from Eqn. (2) [53].
I = I g − I 0 ( e q ( V + R s I ) a K T − 1 ) − V + R s I R s h
Where, Ig is the current source value, K is the Boltzmann constant, a is the diode ideality constant (a=0.95194), T is the temperature of PV cells (oK). I and V are the terminal current and voltage of the PV modules, respectively, Rsh and Rs are the shunt and series resistances of the photovoltaic cell model, respectively.
The current is used to represent one PV cell shown in Eqn. (2) should be modified to model the current in the PV array as expressed in Eqn. (3).
I = N p I g − N p I 0 ( e q ( V + R s ( N s N p ) I ) N s     a K T − 1 ) − V + ( N s N p ) R s I ( N s N p ) R s h
Where, Np and Ns are the number of PV cells in each branch and the number of series PV cells in each branch, respectively.
The current of the source current is directly proportional to the solar irradiation and also functions in the operating temperature of the PV cell, as shown in Eqn. (4).
I g = ( I g n + K I ( T − T n ) ) G G n
Where, Ign is the light-generated current, Tn and Gn are the standard test temperature (25oC) and standard solar irradiance (1000 W/m2), respectively, and KI is the current temperature coefficient (0.12499 %/oC).
The diode saturation current Io can be obtained from Eqn. (5).
I 0 = I 0 n ( T n T ) 3   e ( q E g a K ( 1 T n − 1 T ) )
Where, Eg is the semiconductor’s band-gap energy, and I0n is the rated saturation current at standard test condition which can be obtained from Eqn. (6)
I 0 n = I s c n /   e ( q V o c n a K T − 1 )
From Eqn. (5) and (6), the diode saturation current can be obtained from Eqn. (7).
I 0 = ( I s c n + K I .   Δ T ) /   e ( q ( V o c n + K V Δ T ) a K T − 1 )
Where, KV is the voltage temperature coefficient (-0.349 %/oC).

3. Dandelion Optimization Algorithm

Modern optimization methods must be utilized in conjunction with PV system MPPT to precisely predict the GP in a short time. The dandelion optimization algorithm (DOA) has been used in several applications, including Extreme Learning Machine (ELM) for biomedical classification problems [49,54], traffic flow prediction [55], parameter estimation of PEMFCs' models [56], the speed reducer problem of a mechanical device [57], AVR-LFC architecture for a multi-area power system employing hybrid fractional-order PI and PIDD controllers [58], and reactive power dispatch optimization with DG unit uncertainty [59], and credit card fraud detection [60]. Because the DOA performs well in these applications, it has been employed in the MPPT of photovoltaic energy systems in this research. The DOA, which was launched in 2017, was inspired by the life cycles of dandelion plants [49]. The dandelion seeds can be spread for a long distance by wind. The structure of the seed enables it to travel with the wind that can carry the seeds due to the vortexes above it which can lift the dandelion seeds (DSs) in the rising stage. Once the rain occurs or the humidity increases, the DSs gain more weight and land in different locations. The landed seeds may be able to plant again and some others cannot plant again. The plants can plant again and will be used to generate a new generation. The same concept may be used to track the best solution to many optimization challenges. The DOA is divided into three stages: ascending, mutation, and selection. The objective is to model these three steps and apply them to find optimum solutions to optimization issues, as detailed in the following subsections. As indicated in Eqn. (8), the optimization technique is utilized to maximize the power supplied by the photovoltaic system by regulating the dc-dc converter’s duty ratio.
d o p t = max ( P ( d ) )
Where dopt is the duty ratio corresponding to maximum power, d is the duty ratio, P is the extracted power from the photovoltaic energy system.
Dandelions are classified into two categories: core (CDs) and assistant dandelions (ADs). The CD has the greatest amount of power (Pmax), meanwhile, the ADs are the rest of the dandelions.
The mathematical modeling for the breeding cycle of the DSs is shown in the following subsections:

3.1. Rising Stage

Due to the vortices above the DSs, the lift force is created and it can carry the seeds for a distance depending on the wind speed and the humidity. The radius of sowing of the CD is representing the radius of the dandelions and it can be obtained from Eqn. (9).
R C D i t = { ( U − L ) / 2 R C i t − 1 .   e R C i t − 1 .   g     t = 1 a = 1 a ≠ 1
Where U and L are the upper and lower duty ratio values, respectively, and e and g are the fade and growth factors, respectively, and a is a factor termed the cross trend that may be calculated from Eqn. (10) [60].
a = P max t + ε P max t − 1 + ε
Where, P max t − 1 and P max t are the maximum power at previous and current iterations, respectively. Meanwhile, ε is a specified tolerance to prevent a denominator value of zero.
The sowing radius of the DAs is given in Eqn. (11).
R A D i t = { ( U − L ) / 2 t = 1 ω   .   R A D i t − 1 + ‖ d C D t ‖ − ‖ d A D t ‖ E l s e w h e r
Where, d C D t and d A D t are the position of CD and AD of search agent i at iteration t, respectively. ω is the weight factor used to enhance the stability of the search agents and it can be obtained from Eqn. (12) [60].
ω = 1 − P E P E max
Where, PE is the ratio of the number of calls to the goal function to the total number of calls. The total number of calling the objective function is not known since the optimization continuously works in real time. For this reason, similar values are used in [49]. The value of the inertia factor is shown in Eqn. (12) starts with 1.0 and gradually reduced to zero when PE=PEmax and stays at zero till the end of the simulation. The re-initialization of search agents of the optimization algorithm is setting the inertia factor with 1.0 again and reducing it again with the progress of the optimization. The inertia factor enhances the effect of the previous radius of the ADs on the current radius and gradually reduces this effect and makes it depending on the difference between the positions of the CD and AD as shown in Eqn. (11).

3.2. Mutation Sowing

The ADs search particles will move toward the CD search agent and it will search for GP during their journey. A mutation approach should be employed with the CD to prevent early convergence or the ability of the search agents to become caught in one of the local peaks. This mutation strategy is done based on the Levy flight as shown in Eqn. (13).
d C D t = d C D t ( 1 + L e v y ( ) )
Where, Where Levy() is a random duty ratio value derived from the Levy flight distribution with 𝛽 = 1.5 [60].

3.3. Selection Stage

The search agents should be evaluated in terms of their fitness value in comparison to the other search agent's fitness values. Based on this assessment, a selection strategy is used to select the seeds (search agents) that will be used in the next iteration and the seeds will be removed from the search agents' swarm size. The probability of the fitness value of a certain search agent compared to the other search agents is shown in Eqn. (14), or it can be calculated from the difference between the fitness value and the average value as shown in Eqn. (15).
p i t =   P i t ∑ n = 1 S S t P n t
P i t = | P i t − P a v g t |
Reference [49] proposes selecting search agents with low and high probabilities and removing search agents with medium probabilities to improve the DOA's exploration performance and avoid becoming caught in one of the local peaks. This technique is extremely effective at the beginning of the optimization to improve exploration, but after capturing the position of the GP, it should eliminate the search agent with a low probability to improve the exploitation of the DOA utilized in this study.

3.4. Improved DOA for MPPT of PV Systems

The suggested approach in this study is designed to improve DOA exploration and exploitation. Several solutions have been proposed in the literature to increase the exploitation performance of the MOAs, including:
1- Reducing the swarm size gradually [61,62,63], where the MOA is started with a high number of search agents to increase the exploration and gradually reduces the search agents to enhance exploitation.
2- Enhancing local search pressure in which an adaptive scale factor for local search is introduced to enhance the differential evaluation’s local search [64,65].
3- Hybrid optimization methods utilize MOA with high exploration at the start of the optimization and MOA with strong exploitation at the end to improve exploitation performance. This method has been used with differential evolution [55,66,67].
4- Dynamic variation of the control parameter, where the control parameters change during the optimization iterations [9,21,24,68,69,70].
The above improvement strategies have been used with the modified strategy called a guided probability-based DOA (GDOA) [55]. In this strategy, a learning factor is introduced to learn from the CD based on the fitness value in which the highest fitness value will get a higher enhanced learning factor to enhance the exploitation performance of the DOA. Moreover, the middle search agents will be removed at the start of the optimization to improve exploration; however, after each iteration, the worst AD search agent (the one with the lowest generated power) will be removed from the swarm size in each iteration to improve the proposed algorithm's exploitation performance. The swarm size that started the simulation is called SSmax and the minimum value of swarm size is called SSmin. The logic used in the proposed algorism is shown in Figure 3. The position of each search agent should be selected and the fitness values of these search agents will be determined. Moreover, the best power generated from the PV system should be compared with the previous one based on Eqn. (1). In case the condition is shown in Eqn. (1) is validated, the DOA should be reinitialized and the optimization started again due to the substantial change (ε >0.1) in the shading patterns. Meanwhile, in case the condition is shown in Eqn. (1) is not verified, the search agents' positions should be adjusted depending on the fitness values given by the previous iteration.
The swarm size changes throughout optimization, and it can be calculated using Eqn. (16).
S S t = [ S S max . P max t − P min t + ε P max − P min + ε S S t > S S min S S min S S t ≤ S S min

4. Simulation Work

The simulation of this study is done using Matlab/Simulink software with an array having 4 modules in series and three branches. The module used in the simulation and experimental study is SOLTON Power SPI-185M with performance parameters shown in Figure 4. The available modules in the lab have been selected to be similar to the one in the simulation to ease the comparison between the simulation and experimental results.

4.1. Optimal Design of the Boost Converter

The design of the dc-dc converter is critical to the MPPT's performance. This converter should handle the MPPT instructions (duty ratios) quickly and accurately. The time it takes the dc-dc converter to achieve the steady-state condition should be used to calculate the sampling time. So, the steady-state time should be shortened as much as we can. The boost converter's steady-state time is determined by its inductance, capacitance, switching frequency, and processed current. The boost converter is the ideal solution since it increases the dc-link voltage rather than the PV array's terminal voltage. Many studies introduced to design the boost converter for shorter steady state time and consequently short sampling time [62]. In this work, the optimum design technique utilized to develop the boost converter shown in [62] is applied. Eqn. (17) and Eqn. (18) may be used to calculate the capacitance and inductance of a boost converter with a switching frequency of 20 kHz. The average duty ratio is chosen to be 0.5, the Vdc=220V. With a 1% ripple factor, Vr, then based on Eqn. (17), the capacitor of the boost converter is calculated (C=5.5 mF). The maximum dc-current (Idc) is obtained by dividing the rated power of the PV array (185*12=2220W) by the dc-link voltage (220V)=10.1 A. The inductance of the boost converter conductor can be obtained from Eqn. (18) which is equal to 68.1 μH.
C = d f s .   V d c V r
L = d ( 1 − d ) 2 2 f s .   V d c I d c
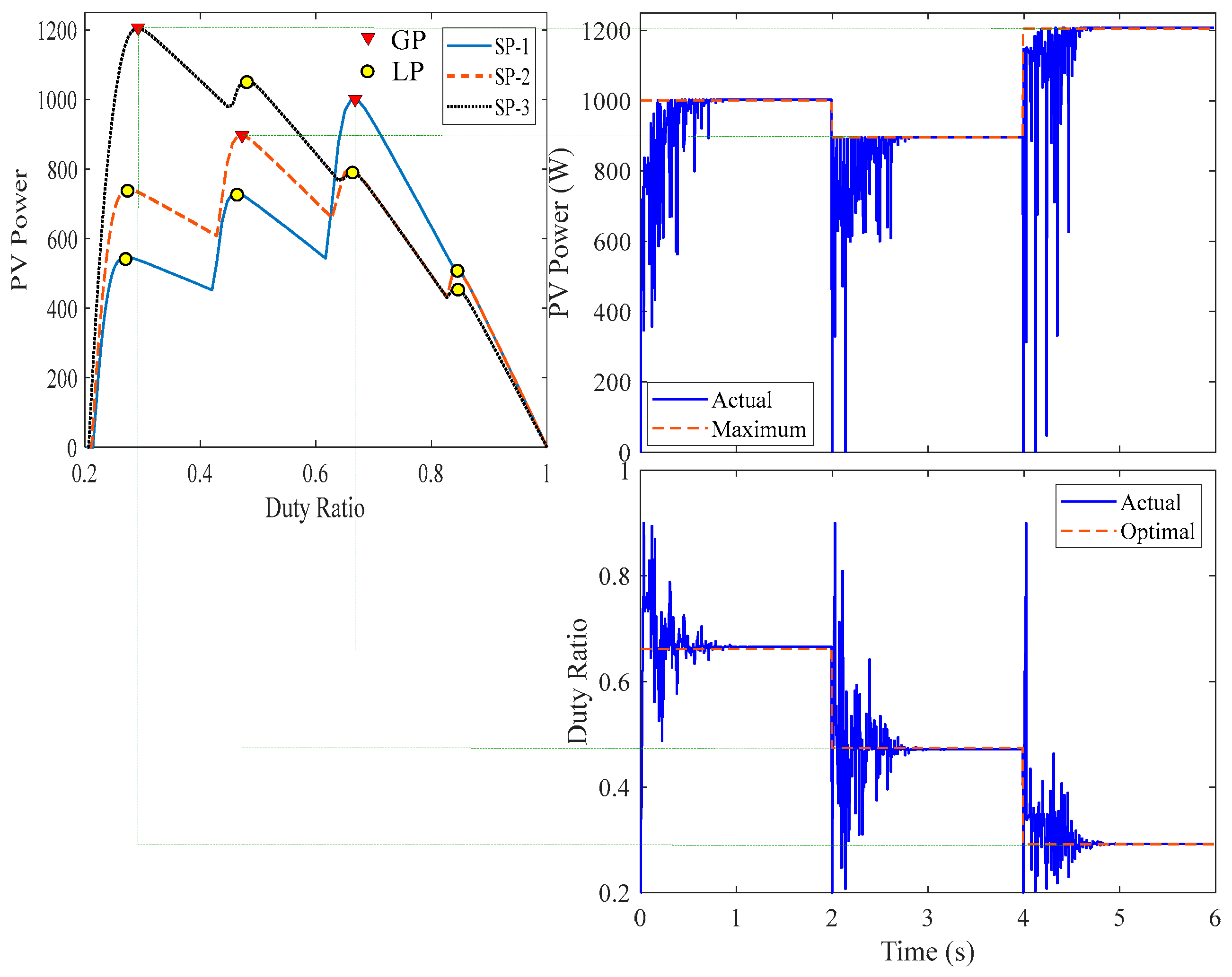
The three-phase inverter is linked to the grid using a space vector control approach [47] to keep the dc-link voltage constant at 220V and to decouple active and reactive power regulation. In the computational and experimental investigations indicated in Table 1, three distinct shading patterns were employed, where G1 to G4 are the solar irradiance levels that fall on various modules in W/m2. The simulation technique employs three distinct shading patterns: Sp-1, SP-2, and SP-3. The PV array's P-V and P-d characteristics for the aforementioned SPs are depicted in Figures 5 (a) and (b), respectively.
Preprints 75032 g005
Figure 5. The operating performance of the photovoltaic system under study.
Figure 5. The operating performance of the photovoltaic system under study.
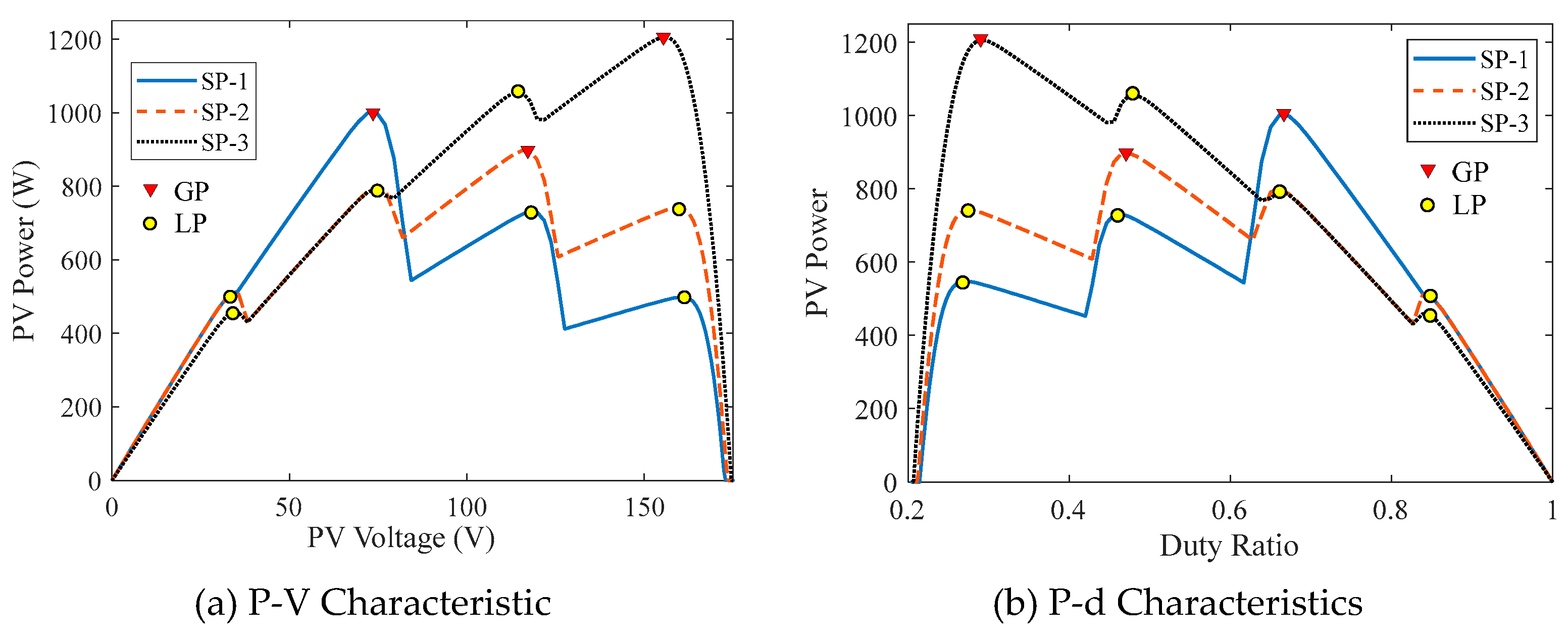
Preprints 75032 g005
Three different simulation studies are performed in this article. The first simulation study is to select the best initial position (duty ratio) of search agents among three different strategies. The second simulation study is to estimate the optimal swarm size for DOA. The third simulation study is to compare the simulation performances of the DOA with MCA, PSO, and GWO. These studies are discussed in the following subsections:

4.2. Optimal Initialization

In this study, three distinct initialization procedures are explored to determine which one will be used in the final simulation study. The time of convergence and rate of failure are used to assess each initialization approach. To prevent the random character of the MOAs, each approach runs 100 times with random amounts of sun irradiances to estimate the rate of failure and average time of convergence. The swarm size used in this study is 6 search agents. The first study is done using random positions (duty ratios) of the search agents limited between 0.2 to 0.9 as indicated in Figure 5 (b). Table 2 displays the average time of convergence and rate of failure. The data in Table 2 clearly reveal that this approach is linked with the longest convergence time and the only method with a failure rate larger than zero. For these reasons, it is not recommended to use this strategy in the initialization of any MOA. The second strategy is done by using equal distance for the initial position of search agents between 0.2 to 0.9 where these values are 0.20, 0.34, 0.48, 0.62, 0.76, and 0.90 which can be obtained from Eqn. (19). The results obtained from this strategy showed that the convergence time is 0.41 s with zero failure rate which is substantially better than the random initialization strategy. The third technique involves starting the search agents at the expected peak location, which may be calculated using Eqn. (20). This technique produced somewhat shorter convergence times with a 0% failure rate than the initialization with equal distance. This technique is the best based on the convergence time and failure rate, but it has no flexibility to adjust the swarm size since it must equal the number of peaks; so, the second study will be employed in further simulation and experimental research.
d k 0 = d min + k . ( d max − d min ) / ( S S − 1 )
d k = 1 − ( S S − k + 1 )     k v     S S V o c V D C
Where, k is the search agent order inside the swarm, kV is a constant equal to 0.79 [20].

4.3. Optimal Swarm Size

The swarm size has a substantial influence on the MPPT performance of the photovoltaic energy system regarding the time of convergence and the rate of failure. The larger the swarm size, the longer the time of convergence and the lower the rate of failure; conversely, the smaller the swarm size, the faster the time of convergence and the higher the rate of failure. As a result, it is advised to choose the ideal swarm size by setting their values to zero failure rate and shortest time of convergence. This study is performed by selecting several search agents varying between 10 to 3 with initialization at equal distance strategy as explained above in section 4.2. To prevent the random character of the outcomes of these optimization methods, this initialization technique is done 1000 times for the DOA, MCA, PSO, and GWO. Table 3 depicts the relationship between swarm size, time of convergence, and failure of rate for several optimization techniques. This table clearly shows that the time of convergence increases with the swarm size in all MOAs under consideration. Meanwhile, as the swarm size in the swarm grows, the rate of failure decreases. The most interesting result from this table is that all the MOAs under study are getting a zero failure rate when the swarm size is above or equal to 6. Moreover, the best time of convergence is associated with the DOA and MCA with 0.41 s and 0.43 s convergence times, respectively. So, it is recommended to use the DOA with 6 search agents in the swarm for the shortest conversion time at zero failure rate.

4.4. Real-Time Simulation Results

This study's simulation is carried out using Matlab/Simulink for the three distinct shading patterns presented in Table 1 and Figure 5 for 6 s, where each shading pattern is used for 2 s. Based on the recommended value from the study shown above in subsection 4.3, the swarm size used in this study is 6 for the shortest time of convergence and zero failure rate. The initial position of search agents for DOA used in this study is based on an equal distance between each search agent from 0.2 to 0.9 duty ratio with duty ratios equal to 0.20, 0.34, 0.48, 0.62, 0.76, and 0.90 using Eqn. (19). The simulation is performed with the use of re-initialization based on Eqn. (1) as shown in Figure 6 to Figure 9 for DOA, MCA, PSO, and GWO, respectively. This image clearly shows that the DOA recorded the GP of the first shading pattern (SP-1) in a short amount of time (0.4 s). Meanwhile, the MCA, PSO, and GWO won the GP in 0.43 seconds, 1.2 seconds, and 0.9 seconds, respectively. This demonstrates the DOA and MCA's advantages over the other MOAs employed in this study.
In case of shading pattern changes, the search agents will be stagnated around the previous GP and will not have the ability to escape from this position in all the optimization algorithms unless the reinitialization occurs based on the condition shown in Eqn. (1). This critical condition aids in avoiding the stalling of search agents at one of the LPs, which can result in a significant increase in extracted power and system efficiency of the photovoltaic energy systems.
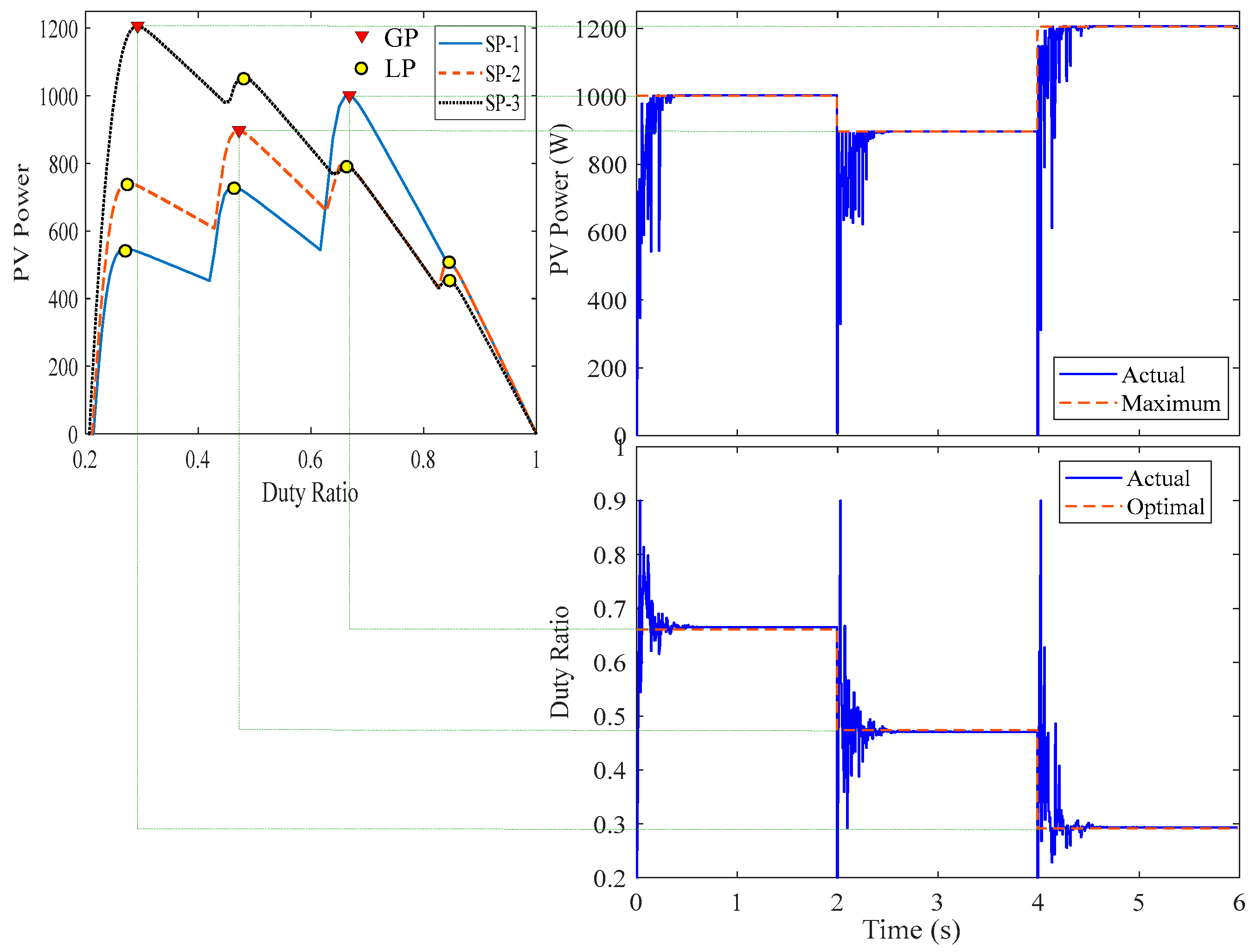
Preprints 75032 g006
Figure 6. The simulation results of DOA MPPT for different PSC.
Figure 6. The simulation results of DOA MPPT for different PSC.
Preprints 75032 g006
Preprints 75032 g007
Figure 7. The simulation results of MCA MPPT for different PSC.
Figure 7. The simulation results of MCA MPPT for different PSC.
Preprints 75032 g007
Preprints 75032 g008
Figure 8. The simulation results of PSO MPPT for different PSC.
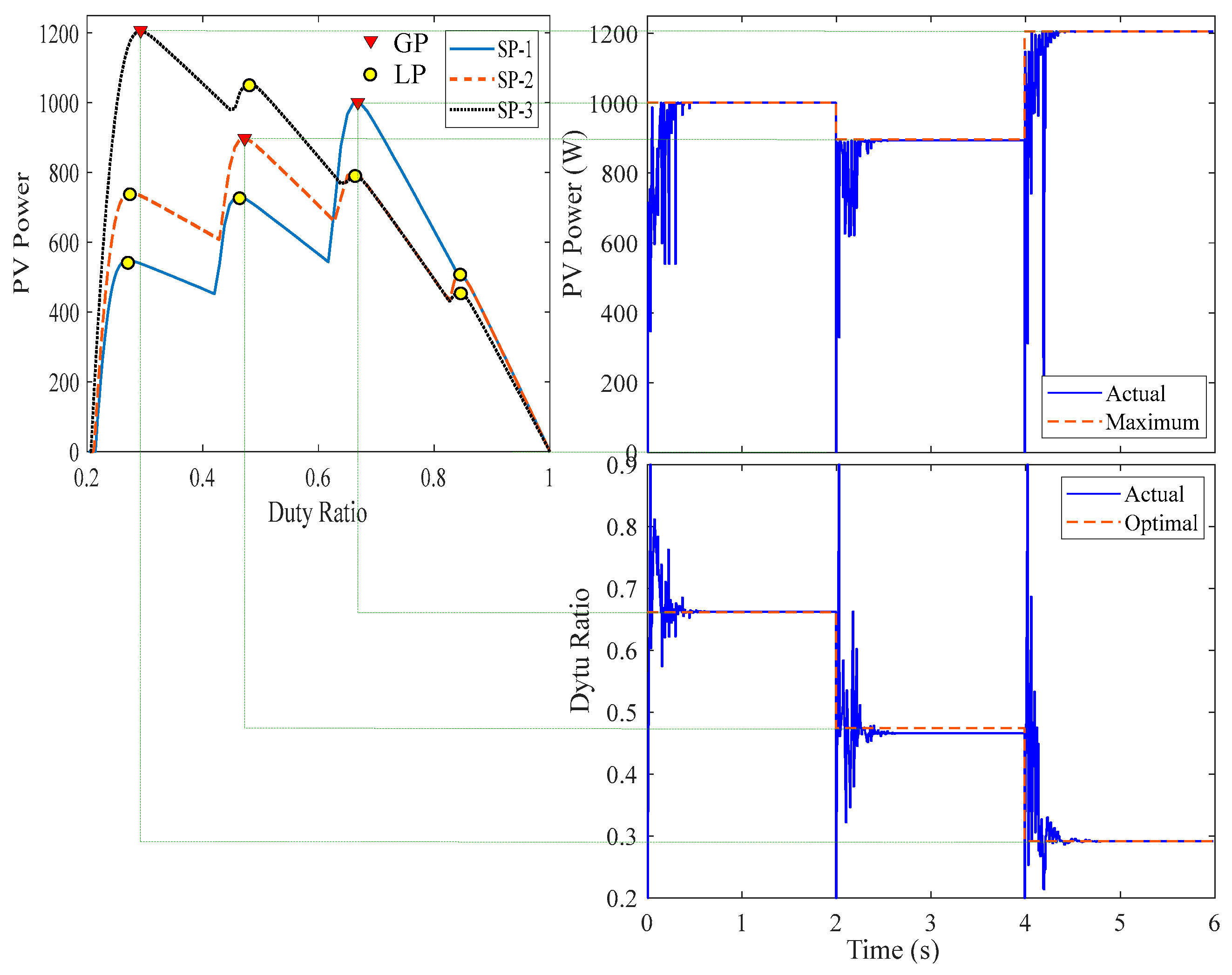
Figure 8. The simulation results of PSO MPPT for different PSC.
Preprints 75032 g008
Preprints 75032 g009
Figure 9. The simulation results of GWO MPPT for different PSC.
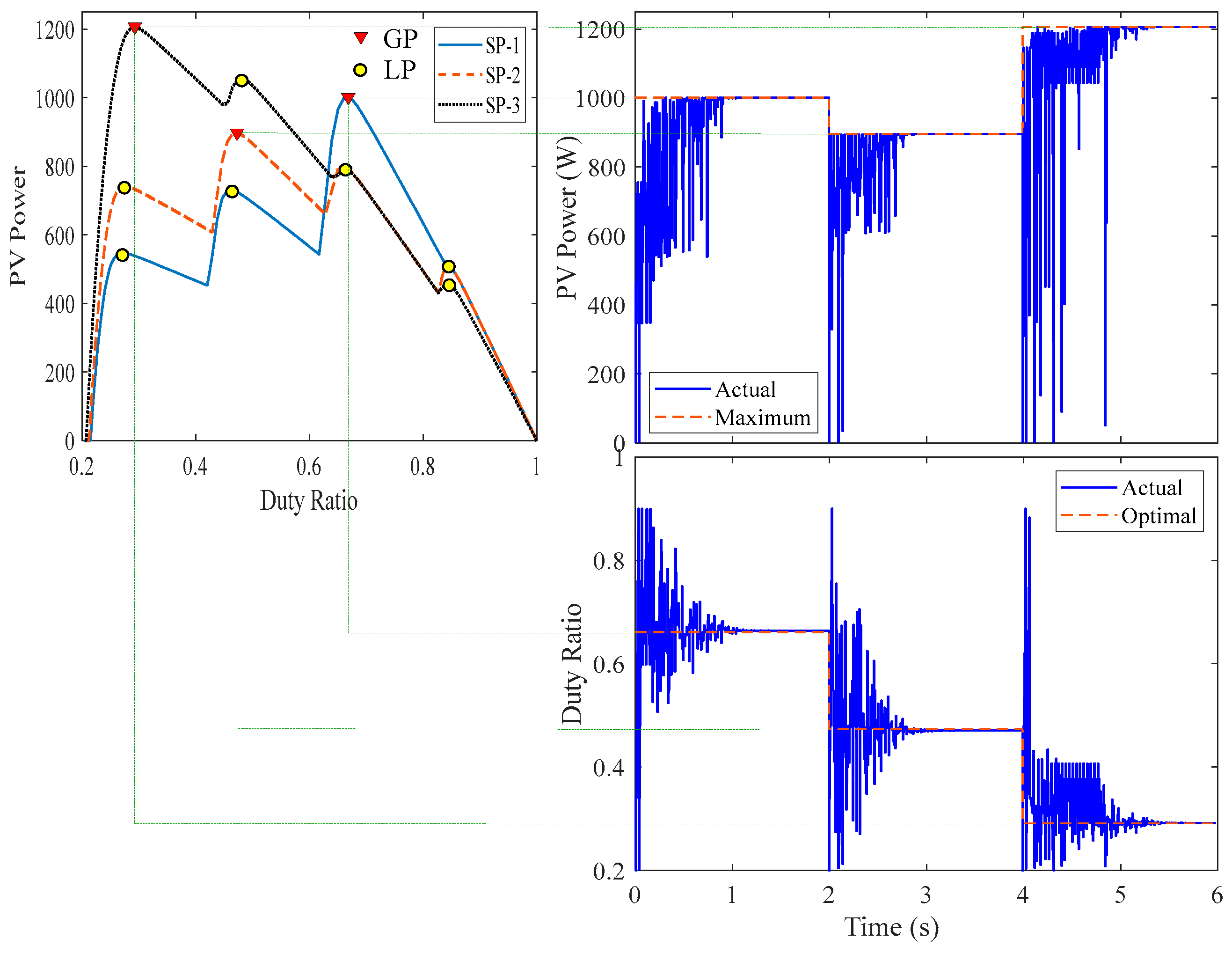
Figure 9. The simulation results of GWO MPPT for different PSC.
Preprints 75032 g009

5. Experimental Work

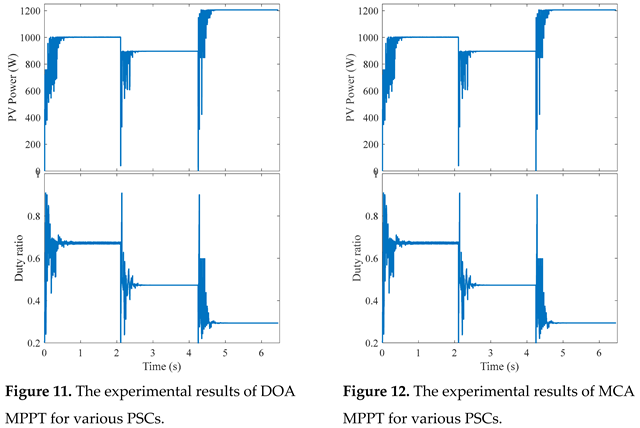
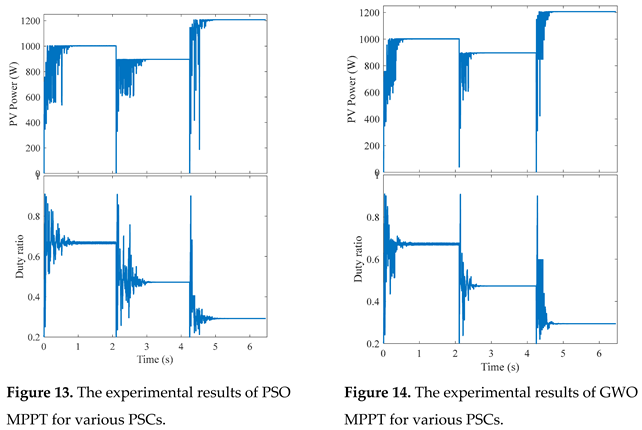
To validate the simulation results, the identical configuration as described in the simulation study is used in the lab. The system is divided into three branches, each with four series modules. As illustrated in Figure 10, the radiation is regulated by an automatic controllable light source. The PV system includes a boost converter with the same specifications as presented in the simulation study, as well as a three-phase inverter controlled by sliding mode control to keep the dc-link voltage constant at 220V under various operating situations. The dc-dc converter (boost converter) is controlled using different MPPT algorithms with 20 kHz switching frequency and 0.01 s sampling time. The switching signal generated from the Matlab/Simulink is interfaced with the boost converter through dSPACE MicroLabBox. The waveforms are collected through Control Desk Graphical Interface (CDGI) software as shown in Figure 10. Six search agents are used in all MOAs. The experimental work PV power and duty ratio results are displayed in Figures 11 to 14 for the DOA, MCA, PSO, and GWO algorithms, respectively. These results show that all of the MOAs employed in this investigation caught the GP for all shading patterns at varying time of convergence. Meanwhile, the time of convergence for DOA, MCA, PSO, and GWO are 0.4, 0.43, 1.2, and 0.9 s, respectively. The practical findings are quite close to the same values obtained from simulation, validating the improved performance of the DOA when utilized as an MPPT of PV systems compared to alternative optimization techniques used in this study.
Preprints 75032 g010
Figure 10. The experimental prototype.
Figure 10. The experimental prototype.
Preprints 75032 g010
Preprints 75032 i001
Preprints 75032 i002

6. Conclusions

The P-V properties of the PV array exhibit nonlinear relationships. In the event of uniform irradiance, this connection has just one peak, making traditional maximum power point tracker (MPPT) approaches suitable for tracking their maximum power. In the meanwhile, in the situation of non-uniform irradiance (partial shade), this relation has extra peaks, which may lead traditional MPPT approaches to become stuck at one of the local peaks. To address this issue, metaheuristic optimization algorithms (MOAs) are a better choice. The primary disadvantages of these algorithms are their long time of convergence time and sometimes high failure rate. As a result, a recently developed dandelion optimization algorithm (DOA) is employed to lower the time of convergence and failure rate of PV system MPPT. When compared to other MOAs such as MCA, PSO, and GWO, the DOA has the quickest time of convergence of 0.4 s compared to 1.2 s for PSO. Furthermore, using an identical distance between the search agents' beginning positions significantly lowered the convergence time. Due to the cross-relationship between swarm size and time of convergence and failure rate, an optimal swarm size determination for all MOAs under consideration is provided, in which 6 search agents in the swarm are chosen. These superior findings demonstrated the DOA's supremacy in MPPT of PV systems when compared to other optimization techniques.

References

  1. K. Hansen, C. Breyer and H. Lund, "Status and perspectives on 100% renewable energy systems," Energy, 175, pp.471-480., 2019. [CrossRef]
  2. "Renewable Energy," PowerWeb, a Forecast International Inc, [Online]. Available: http://www.fi-powerweb.com/Renewable-Energy.html.
  3. A. Eltamaly, M. Alotaibi, A. Alolah and M. Ahmed, "A Novel Demand Response Strategy for Sizing of Hybrid Energy System with Smart Grid Concepts," IEEE Access, 2021.
  4. M. Alotaibi and A. Eltamaly, "A smart strategy for sizing of hybrid renewable energy system to supply remote loads in Saudi Arabia," Energies, 14(21), p.7069., 2021. [CrossRef]
  5. A. Eltamaly, "Performance of MPPT techniques of photovoltaic systems under normal and partial shading conditions," In Advances in renewable energies and power technologies (pp. 115-161). Elsevier., 2018.
  6. H. Rezk and A. M. Eltamaly, "A comprehensive comparison of different MPPT techniques for photovoltaic systems," Solar energy, 112, pp.1-11., 2015. [CrossRef]
  7. A. Eltamaly, "February. Modeling of fuzzy logic controller for photovoltaic maximum power point tracker," In Solar Future 2010 Conference, Istanbul, Turkey., 2010.
  8. S. Messalti, A. Harrag and A. Loukriz, "A new variable step size neural networks MPPT controller: Review, simulation and hardware implementation," Renewable and Sustainable Energy Reviews, 68, pp.221-233., 2017.
  9. A. Eltamaly, "A novel particle swarm optimization optimal control parameter determination strategy for maximum power point trackers of partially shaded photovoltaic systems," Engineering Optimization, 54(4), pp.634-650., 2022. [CrossRef]
  10. A. Eltamaly, M. Al-Saud and A. Abokhalil, "A novel bat algorithm strategy for maximum power point tracker of photovoltaic energy systems under dynamic partial shading," IEEE Access, vol. 8, pp. 10048-10060, 2020. [CrossRef]
  11. S. Mohanty, B. Subudhi and P. Ray, "A new MPPT design using grey wolf optimization technique for photovoltaic system under partial shading conditions," IEEE Transactions on Sustainable Energy, 7(1), pp.181-188., 2015. [CrossRef]
  12. A. Eltamaly, "A novel musical chairs algorithm applied for MPPT of PV systems," Renewable and Sustainable Energy Reviews, 146, p.111135., 2021. [CrossRef]
  13. K. Ishaque and Z. Salam, "A deterministic particle swarm optimization maximum power point tracker for photovoltaic system under partial shading condition," IEEE transactions on industrial electronics, 60(8), pp.3195-3206., 2012. [CrossRef]
  14. T. Imtiaz, B. Khan and N. Khanam, "Fast and improved PSO (FIPSO)-based deterministic and adaptive MPPT technique under partial shading conditions," IET Renewable Power Generation, 14(16), pp.3164-3171., 2020. [CrossRef]
  15. M. Merchaoui, A. Sakly and M. Mimouni, "March. Improved fast particle swarm optimization based PV MPPT," In 2018 9th international renewable energy congress (IREC) (pp. 1-7). IEEE., 2018.
  16. A. Jordehi, "Time varying acceleration coefficients particle swarm optimisation (TVACPSO): A new optimisation algorithm for estimating parameters of PV cells and modules," Energy Conversion and Management, 129, pp.262-274., 2016. [CrossRef]
  17. Y. Shi and R. Eberhart, "A modified particle swarm optimizer," In 1998 IEEE international conference on evolutionary computation proceedings, IEEE world congress on computational intelligence (Cat. No. 98TH8360) (pp. 69-73). IEEE., 1998.
  18. B. Jiao, Z. Lian and X. Gu, "A dynamic inertia weight particle swarm optimization algorithm," Chaos, Solitons & Fractals, 37(3), pp.698-705., 2008. [CrossRef]
  19. A. M. Eltamaly, H. M. Farh and A. G. Abokhalil, "A novel PSO strategy for improving dynamic change partial shading photovoltaic maximum power point tracker," Energy Sources, Part A: Recovery, Utilization, and Environmental Effects, pp. 1-15, 2020. [CrossRef]
  20. A. Eltamaly, M. Al-Saud, A. Abokhalil and H. Farh, "Photovoltaic maximum power point tracking under dynamic partial shading changes by novel adaptive particle swarm optimization strategy," Transactions of the Institute of Measurement and Control 42.1 (2020): 104-115., 2020. [CrossRef]
  21. A. Chatterjee and P. Siarry, "Nonlinear inertia weight variation for dynamic adaptation in particle swarm optimization," Computers & operations research, 33(3), pp.859-871., 2006. [CrossRef]
  22. M. Abdulkadir, A. H. M. Yatim and S. T. Yusuf, "An improved PSO-based MPPT control strategy for photovoltaic systems," International Journal of Photoenergy 2014 (2014)., 2014. [CrossRef]
  23. K. Sundareswaran, S. Peddapati and S. Palani, "MPPT of PV systems under partial shaded conditions through a colony of flashing fireflies," IEEE transactions on energy conversion 29, no. 2 (2014): 463-472., 2014. [CrossRef]
  24. A. Eltamaly, "Optimal control parameters for bat algorithm in maximum power point tracker of photovoltaic energy systems," International Transactions on Electrical Energy Systems, 31(4), p.e12839., 2021. [CrossRef]
  25. Y. Liu, S. Huang, J. Huang and W. Liang, "A particle swarm optimization-based maximum power point tracking algorithm for PV systems operating under partially shaded conditions," IEEE transactions on energy conversion, 27(4), pp.1027-1035., 2012. [CrossRef]
  26. H. Chaieb and A. Sakly, "Comparison between P&O and PSO methods based MPPT algorithm for photovoltaic systems," In 2015 16th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA) (pp. 694-6, 2015.
  27. K. Sundareswaran and S. Palani, "Application of a combined particle swarm optimization and perturb and observe method for MPPT in PV systems under partial shading conditions," Renewable Energy, 75, pp.308-317., 2015. [CrossRef]
  28. A. Eltamaly, "An Improved Cuckoo Search Algorithm for Maximum Power Point Tracking of Photovoltaic Systems under Partial Shading Conditions," Energies, vol. 14, no. 4, p. 953, 2021. [CrossRef]
  29. M. da Rocha, L. Sampaio and S. da Silva, "Comparative analysis of MPPT algorithms based on Bat algorithm for PV systems under partial shading condition," Sustainable Energy Technologies and Assessments, 2020.
  30. S. Mohanty, B. Subudhi and R. PK., "A grey wolf-assisted perturb & observe MPPT algorithm for a PV system," IEEE Trans Energy Convers. 2017;32(1):340-347., 2017.
  31. C.C. Ahmed, M. Cherkaoui and M. Mokhlis, "PSO-SMC Controller Based GMPPT Technique for Photovoltaic Panel Under Partial Shading Effect," International Journal of Intelligent Engineering and Systems 13.2 (2020): 307-316., 2020. [CrossRef]
  32. N. Kamal, A. Azar, G. Elbasuony, K. Almustafa and Almakhles, "PSO-based adaptive perturb and observe MPPT technique for photovoltaic systems." International Conference on Advanced Intelligent Systems and Informatics," Springer, Cham, 2019., 2019.
  33. A. M. Eltamaly and H. M. Farh., "Dynamic global maximum power point tracking of the PV systems under variant partial shading using hybrid GWO-FLC," Solar Energy 177 (2019): 306-316., 2019. [CrossRef]
  34. F. Davoodkhani, S. Arabi Nowdeh, A. Abdelaziz, S. Mansoori, S. Nasri and M. Alijani, "A new hybrid method based on gray wolf optimizer-crow search algorithm for maximum power point tracking of photovoltaic energy system," Modern Maximum Power Point Tracking Techniques for Photovoltaic Energy Systems. Springer,, 2020.
  35. M. Seyedmahmoudian, R. Rahmani, S. O. A. Mekhilef, A. Stojcevski, T. Soon and A. Ghandhari, "Simulation and hardware implementation of new maximum power point tracking technique for partially shaded PV system using hybrid DEPSO method," IEEE transactions on sustainable energy 6.3 (2015): 850-862. [CrossRef]
  36. A. Eltamaly, "Photovoltaic Maximum Power Point Trackers: An Overview," Advanced Technologies for Solar Photovoltaics Energy Systems, pp.117-200., 2021.
  37. A. M. S. Furtado, F. Bradaschia, M. C. Cavalcanti and L. R. Limongi, "A Reduced Voltage Range Global Maximum Power Point Tracking Algorithm for Photovoltaic Systems Under Partial Shading Conditions," IEEE Transactions on Industrial Electronics, vol. 65,, 2018. [CrossRef]
  38. S. Xu, Y. Gao, G. Zhou and G. Mao, "A Global Maximum Power Point Tracking Algorithm for Photovoltaic Systems Under Partially Shaded Conditions Using Modified Maximum Power Trapezium Method," IEEE Transactions on Industrial Electronics, pp. 1-1, 2020. [CrossRef]
  39. M. Kermadi, Z. Salam, J. Ahmed and E. M. Berkouk, "A High-Performance Global Maximum Power Point Tracker of PV System for Rapidly Changing Partial Shading Condition," IEEE Transactions on Industrial Electronics, pp. 1-1, 2020., 2020. [CrossRef]
  40. M. Boztepe, F. Guinjoan, G. Velasco-Quesada, S. Silvestre, A. Chouder and E. Karatepe, "Global MPPT Scheme for Photovoltaic String Inverters Based on Restricted Voltage Window Search Algorithm," IEEE Transactions on Industrial Electronics, vol. 61, no. 7. [CrossRef]
  41. M. Kermadi, Z. Salam, J. Ahmed and E. M. Berkouk, "An Effective Hybrid Maximum Power Point Tracker of Photovoltaic Arrays for Complex Partial Shading Conditions," IEEE Transactions on Industrial Electronics, vol. 66, no. 9, pp. 6990-7000, 2019., 2019. [CrossRef]
  42. M. Kermadi, Z. Salam, A. Eltamaly, J. Ahmed, S. Mekhilef, C. Larbes and E. Berkouk, "Recent Developments of MPPT Techniques for PV Systems under Partial Shading Conditions: A Critical Review and Performance Evaluation," IET Renewable Power Generation, 2020. [CrossRef]
  43. A. M. Eltamaly, M. S. Al-Saud and A. G. Abokhalil, "A novel scanning bat algorithm strategy for maximum power point tracker of partially shaded photovoltaic energy systems," Ain Shams Engineering Journal (2020).‏, 2020. [CrossRef]
  44. J. Ahmed and Z. Salam, "A Maximum Power Point Tracking (MPPT) for PV system using Cuckoo Search with partial shading capability," Applied Energy 119 (2014): 118-130., 2014. [CrossRef]
  45. A.M. Eltamaly, H. M. Farh and M. S. A. Saud, "Impact of PSO reinitialization on the accuracy of dynamic global maximum power detection of variant partially shaded PV systems," Sustainability, vol. 11, no. 7, p. 2091, 2019. [CrossRef]
  46. A.M. Eltamaly, M. S. Al-Saud and A. G. Abokhalil, "A novel scanning bat algorithm strategy for maximum power point tracker of partially shaded photovoltaic energy systems," Ain Shams Engineering Journal, 2020. [CrossRef]
  47. A.M. Eltamaly, M. S. Al-Saud and A. G. Abo-Khalil, "Performance Improvement of PV Systems’ Maximum Power Point Tracker Based on a Scanning PSO Particle Strategy," Sustainability, vol. 12, no. 3, p. 1185, 2020. [CrossRef]
  48. R. Celikel, M. Yilmaz and A. Gundogdu, "A voltage scanning-based MPPT method for PV power systems under complex partial shading conditions," Renewable Energy, 184, pp.361-373., 2022. [CrossRef]
  49. X. Li, S. Han, L. Zhao, C. Gong and X. Liu, "New dandelion algorithm optimizes extreme learning machine for biomedical classification problems," Computational intelligence and neuroscience, 2017. [CrossRef]
  50. A.M. Eltamaly, "Performance of smart maximum power point tracker under partial shading conditions of photovoltaic systems," Journal of Renewable and Sustainable Energy, vol. 7, no. 4, p. 043141, 2015. [CrossRef]
  51. D. Cotfas, P. Cotfas and S. Kaplanis, "Methods to determine the dc parameters of solar cells: a critical review," Renewable and Sustainable Energy Reviews 28 (2013): 588-596., 2013. [CrossRef]
  52. V. Khanna, B. Das, D. Bisht and P. Singh, "A three diode model for industrial solar cells and estimation of solar cell parameters using PSO algorithm," Renewable Energy, 78, pp.105-113., 2015. [CrossRef]
  53. A. Eltamaly, "Musical chairs algorithm for parameters estimation of PV cells," Solar Energy, 241, pp.601-620., 2022. [CrossRef]
  54. C. Gong, S. Han, X. Li, L. Zhao and X. Liu, "A new dandelion algorithm and optimization for extreme learning machine," Journal of ExpErimEntal & thEorEtical artificial intElligEncE, 30(1), pp.39-52., 2018. [CrossRef]
  55. X. Liu and X. Qin, "A probability-based core dandelion guided dandelion algorithm and application to traffic flow prediction," Engineering Applications of Artificial Intelligence, 96, p.103922., 2020. [CrossRef]
  56. R. Abbassi, S. Saidi, A. Abbassi, H. Jerbi, M. Kchaou and B. Alhasnawi, "Accurate Key Parameters Estimation of PEMFCs’ Models Based on Dandelion Optimization Algorithm," Mathematics, 11(6), p.1298., 2023. [CrossRef]
  57. S. Zhao, T. Zhang, S. Ma and M. Chen, "Dandelion Optimizer: A nature-inspired metaheuristic algorithm for engineering applications," Engineering Applications of Artificial Intelligence, 114, p.105075., 2022. [CrossRef]
  58. M. Alharbi, M. Ragab, K. AboRas, H. Kotb, M. Dashtdar, M. Shouran and E. Elgamli, "Innovative AVR-LFC design for a multi-area power system using hybrid fractional-order PI and PIDD2 controllers based on dandelion optimizer," Mathematics, 11(6), p.1387., 2023. [CrossRef]
  59. M. Ali, A. Soliman and A. Adel, "Optimization of Reactive Power Dispatch Considering DG Units Uncertainty By Dandelion Optimizer Algorithm," International Journal of Renewable Energy Research (IJRER), 12(4), pp.1805-1818., 2022. [CrossRef]
  60. H. Zhu, G. Liu, M. Zhou, Y. Xie, A. Abusorrah and Q. Kang, "Optimizing weighted extreme learning machines for imbalanced classification and application to credit card fraud detection," Neurocomputing, 407, pp.50-62., 2020. [CrossRef]
  61. A. Zamuda, J. Brest and E. Mezura-Montes, "Structured population size reduction differential evolution with multiple mutation strategies on CEC 2013 real parameter optimization," In 2013 IEEE congress on evolutionary computation (pp. 1925-1931). IEEE., 2013. [CrossRef]
  62. A.M. Eltamaly and A. Hamdy, "Novel musical chairs," IEEE, vol. 3, no. 5, pp. 20-27, 2020.
  63. J. Brest and M. Sepesy Maučec, "Population size reduction for the differential evolution algorithm," Applied Intelligence, 29, pp.228-247., 2008. [CrossRef]
  64. N. Noman and H. Iba, "Accelerating differential evolution using an adaptive local search," IEEE Transactions on evolutionary Computation, 12(1), pp.107-125., 2008. [CrossRef]
  65. F. Neri and V. Tirronen, "Scale factor local search in differential evolution," Memetic Computing, 1, pp.153-171., 2009. [CrossRef]
  66. F. Neri, G. Iacca and E. Mininno, "Disturbed exploitation compact differential evolution for limited memory optimization problems," Information Sciences, 181(12), pp.2469-2487., 2011. [CrossRef]
  67. F. Caraffini, G. Iacca, F. Neri, L. Picinali and E. Mininno, "A CMA-ES super-fit scheme for the re-sampled inheritance search," In 2013 IEEE Congress on Evolutionary Computation (pp. 1123-1130). IEEE., 2013.
  68. A. Eltamaly, "Performance of MPPT techniques of photovoltaic systems under normal and partial shading conditions," In Advances in renewable energies and power technologies (pp. 115-161). Elsevier., 2018.
  69. A. M. Eltamaly and H. M. Farh, "Dynamic global maximum power point tracking of the PV systems under variant partial shading using hybrid GWO-FLC," Solar Energy 177 (2019): 306-316., 2019. [CrossRef]
  70. M. Abdulkadir, A. Yatim and S. Yusuf, "An improved PSO-based MPPT control strategy for photovoltaic systems," International Journal of Photoenergy, 2014. [CrossRef]
Preprints 75032 g001
Figure 1. Grid-connected PV energy system with MPPT.
Figure 1. Grid-connected PV energy system with MPPT.
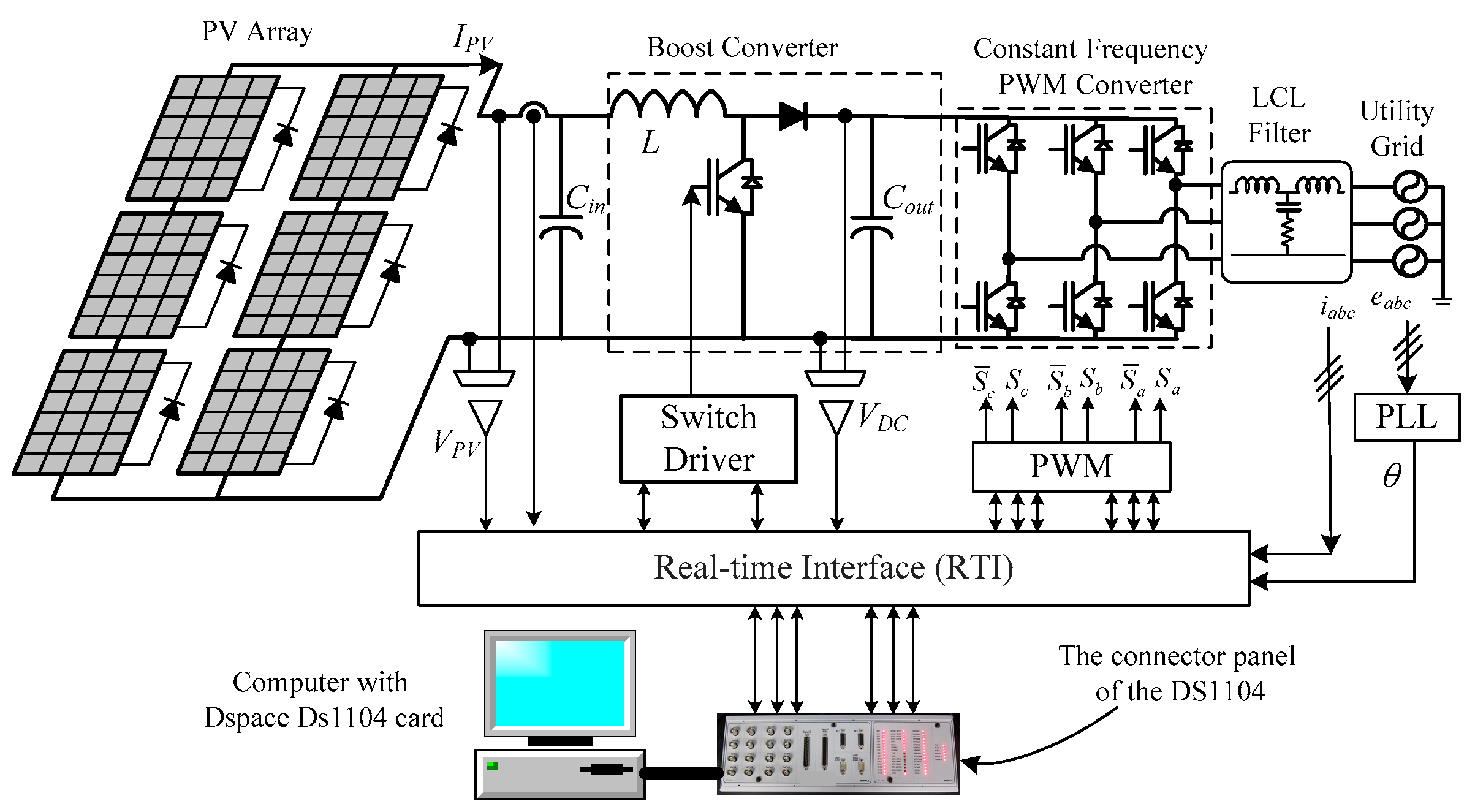
Preprints 75032 g001
Preprints 75032 g002
Figure 2. The schematic of the single diode model of the photovoltaic cell.
Figure 2. The schematic of the single diode model of the photovoltaic cell.
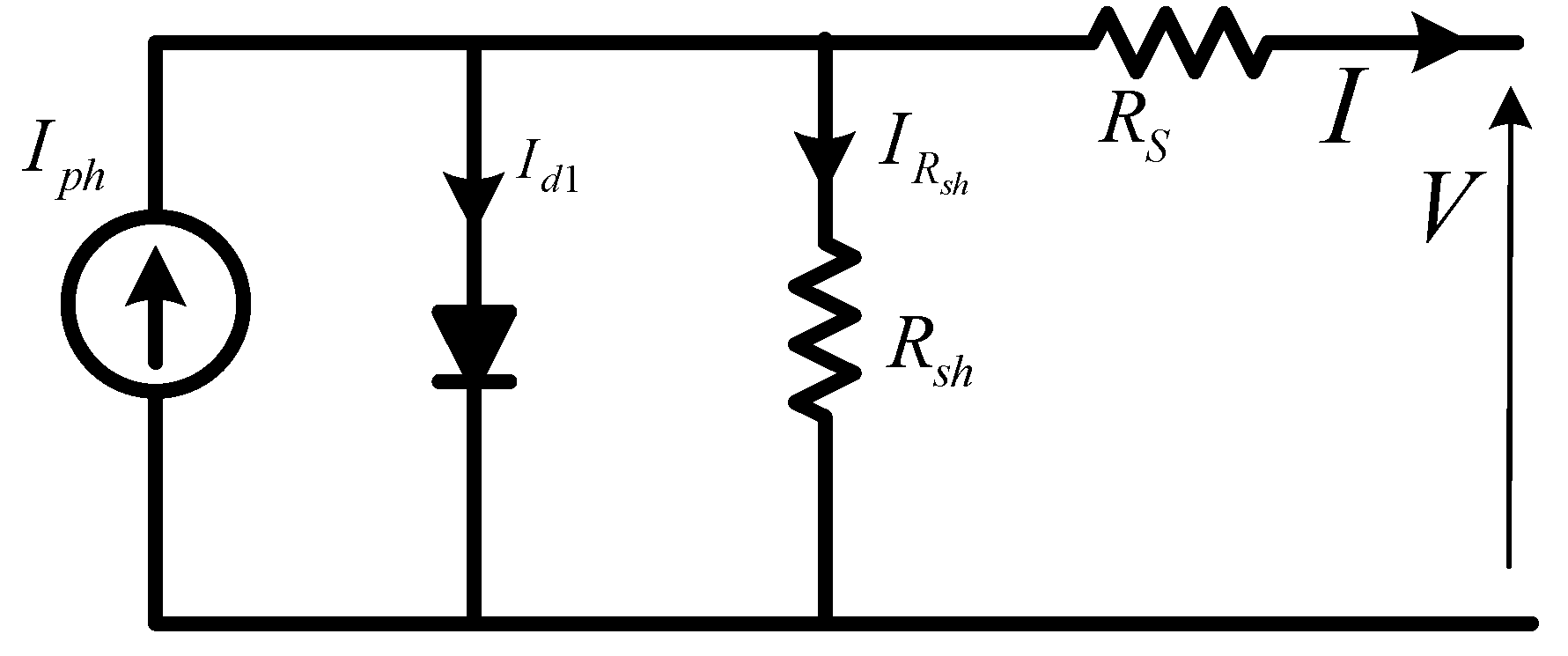
Preprints 75032 g002
Preprints 75032 g003
Figure 3. The framework of the use of the DOA as an MPPT of PV systems.
Figure 3. The framework of the use of the DOA as an MPPT of PV systems.
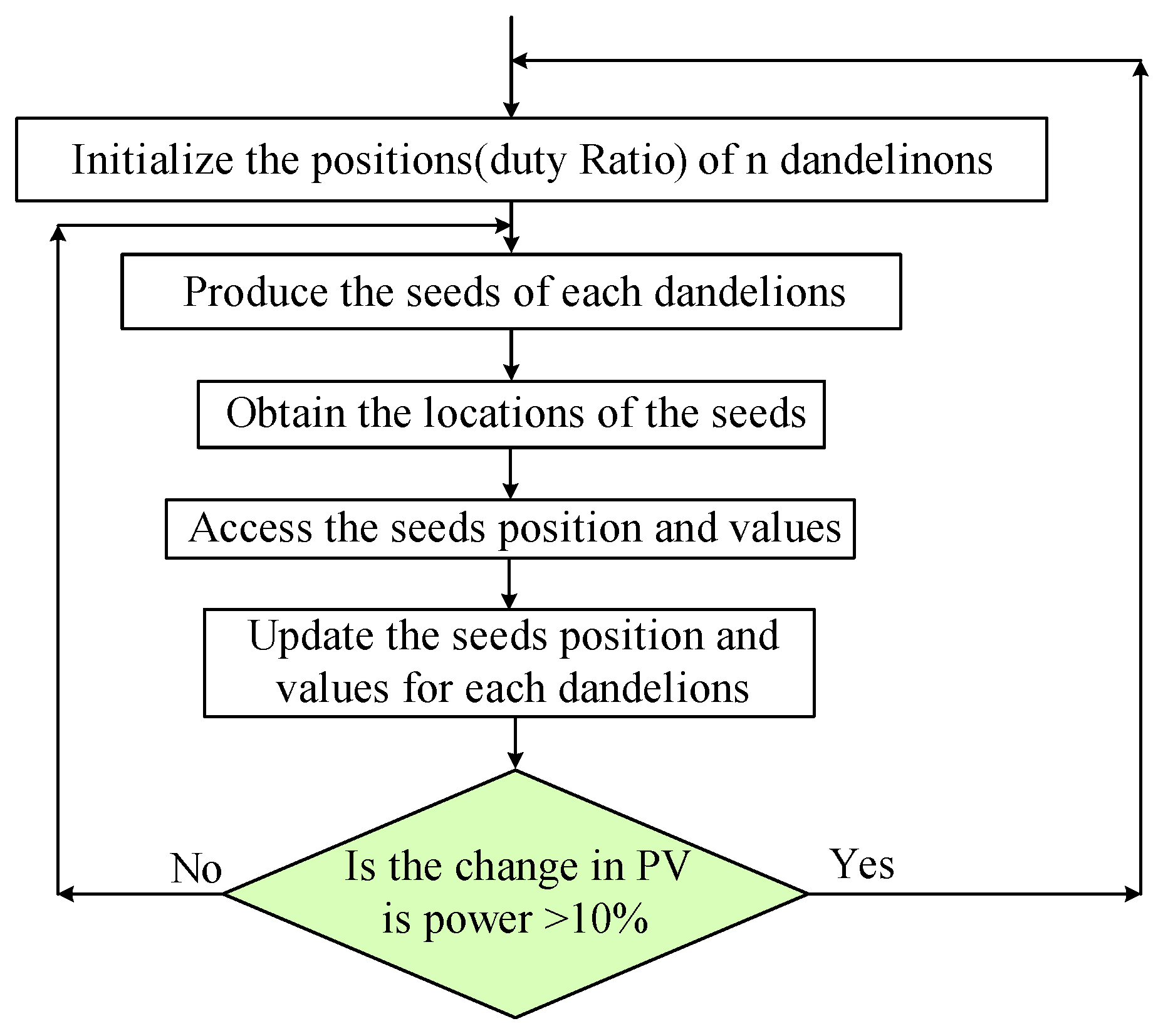
Preprints 75032 g003
Preprints 75032 g004
Figure 4. Specification of photovoltaic module used in this study.
Figure 4. Specification of photovoltaic module used in this study.
Preprints 75032 g004
Table 1. The specifications of the shading patterns under study.
Table 1. The specifications of the shading patterns under study.
Name Solar Irradiances (W/m2) GP Parameters
G1 G2 G3 G4 d V (V) P (W)
SP-1 1000 900 400 200 0.6613 74.51140 1001.4
SP-2 1000 700 500 300 0.4740 115.7296 897.32
SP-3 900 700 600 500 0.2912 155.9261 1205.8
Table 2. The comparison between each initialization strategy used with the DOA.
Table 2. The comparison between each initialization strategy used with the DOA.
Initialization Strategy Convergence Time (s) Failure Rate (%)
Random Duty Ratio 0.49 2
Equal Distance 0.41 0
Anticipated Position of Peaks 0.40 0
Table 3. The performance of each MOA under study for different swarm size.
Table 3. The performance of each MOA under study for different swarm size.
Swarm size Convergence Time (s) Failure Rate (%)
DOA MCA PSO GWO DOA MCA PSO GWO
3 0.35 0.38 0.68 0.49 6.5 8.1 11.7 8.8
4 0.39 0.40 0.82 0.61 3.3 4.5 5.8 4.5
5 0.40 0.41 1.07 0.78 1.1 2.1 3.5 2.2
6 0.41 0.43 1.25 0.92 0 0 0 0
7 0.48 0.51 1.36 1.06 0 0 0 0
8 0.57 0.57 1.44 1.15 0 0 0 0
9 0.62 0.61 1.52 1.21 0 0 0 0
10 0.65 0.62 1.58 1.29 0 0 0 0
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated