Prerpints.org logo
Preprint
Article

Effect of Jet Nozzle Position on Mixing Time in Large Tanks

Altmetrics

Downloads

230

Views

146

Comments

3

A peer-reviewed article of this preprint also exists.

Submitted:

21 July 2023

Posted:

26 July 2023

You are already at the latest version

Alerts
Abstract
The present investigation focuses on the impact of jet nozzle orientation on mixing time in a cylindrical tank. The aim is to identify nozzle positions that improve mixing performance and to elucidate the governing parameters that influence it. A water tank was employed for the experiment. The vertical inclination angle (α) and the horizontal inclination angle (β) of the jet nozzle determined the nozzle positions. Mixing time was determined using an inert tracer and spectrophotometry measurements. The findings show that the mixing time is significantly influenced by the position of the jet nozzle position. The accuracy of existing jet turbulence and the circulation models for the prediction of mixing time was evaluated for the different nozzle positions. Our results indicate that both models provide accurate predictions for the conventional centrally aligned (β = 0°), upward-pointing jet nozzle positions only (α > 0). For the other nozzle positions where β > 0° and at varying α, the data follow the same trends as the jet turbulence and circulation models, however, the proportionality constants vary. Shorter mixing times can be attributed principally to longer jet path lengths and therefore higher fluid entrainment and circulation, as well as higher dissipation rates per jet length squared. However, it is suspected that the 3-dimensional nature of the flow pattern generated in the tank also plays a non-negligible role since mixing is hindered when the nozzle points more towards the tank wall.
Keywords: 
Subject: Engineering  -   Chemical Engineering

1. Introduction

Jet mixing is a widely used process that utilises kinetic energy from a pumped stream to blend miscible fluids in tanks or reactors [1,2]. It is particularly effective for large storage tanks where mechanical agitation is difficult to implement [3,4]. The process entails the recirculation of tank fluid in the form of a jet stream, which is directed through a nozzle and reintroduced into the bulk fluid of the tank. Jet-mixed tanks can be designed with an axial (i.e. vertical) jet or a side-entry jet that is inclined vertically as shown in Figure 1; the jets can be either upwards- or downwards-pointing. Revill [5] recommended that the jet be positioned such that it spans the longest tank dimension; this is across the liquid height, H for an axial jet and across the diagonal for a side-entry jet.
The submerged jet has specific characteristics along its length, starting from the nozzle inlet up until several hundred nozzle diameters, dj. A jet typically forms a conical shape with a universal opening angle of approximately 11.80°, regardless of the fluid type, nozzle diameter, and injection speed, uj [6]. The shear flow between a turbulent jet fluid and the surrounding ambient fluid can be divided into three regions [6,7]. The initial region consists of the potential core, which is a small conical-shaped zone formed by mixing the jet and ambient fluid. The potential core possesses the flow characteristics of the nozzle inlet, i.e. the centreline velocity is equal to the velocity at the nozzle, and spans a length of approximately six nozzle diameters. The transition region occurs where turbulent eddies start to form in the shear layer and the centreline velocity starts to decay. This process starts at approximately a distance of 6dj until 30dj after the jet nozzle and facilitates mixing and entrainment of the ambient fluid. Lastly, the fully-developed region, which typically commences at about 30dj along the jet axis, is characterised by high turbulence and self-similar velocity profiles [5,19].
The velocity of the fluid at the centreline of a turbulent jet reduces rapidly as it moves downstream due to mixing with the surrounding fluid, and this decay rate depends on factors such as initial velocity, fluid properties, jet geometry, and distance from the source. Rajaratnam [21] provides an approximation for the centreline jet velocity (uz) in the fully-developed region for a turbulent jet as follows:
u z    =   6   u j d j z  
where uj is the jet velocity at the nozzle, and z is the distance from the nozzle along the jet axis. From Equation 1 it can be seen that at a distance of 100dj from the nozzle, the centreline velocity decreases to 6% of the jet inlet velocity. It is typically considered that the effectiveness of the turbulent jet for mixing becomes negligible beyond a distance of roughly 400dj [7]. It is important to note that the jet also loses its characteristic properties upon impact with the tank wall, bottom, or liquid surface [6,7].

1.1. Mixing Time

Steady jets have been used for industrial mixing applications for many years, mainly for mixing low-viscosity, single-phase liquids. Mixing time, tm, is a fundamental performance indicator used to evaluate the efficiency of mixing operations, signifying the duration needed to achieve a satisfactory level of homogeneity [4,8,9]. In the context of jet mixing, various empirical equations have been presented in the literature to estimate mixing time. Wasewar [3] provides an overview of multiple correlations linking diverse jet mixing parameters with the mixing time, as documented in the existing literature. Amongst these, one of the earliest correlations is that proposed by Fosset [20] given in Equation 2, which only includes tank diameter, jet velocity and nozzle diameter. The correlation is only for the turbulent flow regime and it suggests that mixing time is independent of jet Reynolds number.
t m = 4.5 T ² u j d j
The correlations presented by Fox and Gex [10] in Equation 3 show a strong dependence of mixing time on Reynolds number in the laminar regime but less so in the turbulent regime (Reynolds numbers ≥ 2000. Like the previous correlation, the applicability and accuracy of these correlations is limited due to their empirical nature and the fact that the physical processes involved in mixing are not considered. Consequently, these correlations may not always provide accurate mixing time predictions, especially in other tank geometries. Okita and Oyama [11] aimed to address this issue, and they reported correlations of mixing time for vertical and inclined side entry nozzle configurations (Equations 4 and 5). They concluded that mixing time is independent of Reynolds number for values above 5000 in the turbulent jet regime.
t m = δ T H u j d j ( d j H ) 0.5
δ = 7.8 × 10 5 F r 0.17 R e j 1.33   for   250 < R e j < 2000 δ = 120 F r 0.17 R e j 0.17 ,   for   2000 < R e j < 1.6 × 10 5
t m = 2.8 × 10 ⁴ R e j   T 1.5 H 0.5 u j d j , for   1000 < R e j < 5000
t m = 5.5 T 1.5 H 0.5 u j d j for   5000 < R e j < 80000
In addition to the numerous empirical correlations that exist for the prediction of mixing time, two more physically-based models exist for the design jet-mixed vessels. These are the circulation and the turbulent jet models.

1.1.1. Circulation Model

The circulation model employed in jet mixing tanks relies on the concept of fluid circulation, which occurs through the entrainment of bulk fluid by the jet stream. The total volumetric flow rate, QT, is expressed by the sum of the flow rate through the nozzle, Q and the maximum entrained flow rate, Q E ( z m a x ) , which occurs at the maximum jet path length, z m a x . This is the distance from the nozzle to the point where the jet impinges on the tank wall, base or liquid surface. The mean circulation time can be expressed in terms of the liquid volume (V) contained within the tank and the total volumetric flow rate of bulk liquid, QT as given by Equation 6.
t C = V   Q T  
Rajaratnam [22] has shown through a momentum balance that the ratio of the total flow rate in the jet to the flow rate at this nozzle increases with the distance from the nozzle:
Q T Q =   k z d j
where k is an experimental coefficient. The total flow rate at the end of the jet (at a distance zmax from the nozzle) can therefore expressed as:
Q T Q =   k z m a x d j
Ricou and Spalding [23] reported a value of k equal to 0.32 for a free jet. However, Maruyama et al. [12] presented k values ranging from 0.48 to 1, depending on nozzle clearance, liquid height, and inclination angle. The variation in the value of k is attributed to the distortion of the conical shape of the jet stream [12], which leads to smaller circulation times compared with that of a free jet. This suggests that the jet in a tank is confined to some extent, depending on the jet orientation. In addition, k was found to strongly depend on the Reynolds number of the jet (Rej) within the range of 100 to 2000 [5]. However, as Rej exceeds 2000, the correlation between k and Rej weakens [5].
Maruyama et al. [12] presented the circulation model by expressing equation (8), in terms of circulation time, tc and mean residence time, tR:
t c t R / d j z m a x ≅   1 k    = C o n s t a n t
which can be written as Equation (10) when expressing tR in terms of tank geometry and the flow velocity:
t C   = T 2 H k u j d j z m a x
Mixing time has been shown to be directly proportional to circulation time [11] [12], which can be written as:
t m = φ T 2 H   u j d j z m a x
Grenville & Tilton [13] reported φ equal to 9.34 for vertical nozzle inclinations, α > 15°, and 13.8 for α < 15° when β = 0° and 0.4 ≤  H/T ≤ 1. It is worth noting that irrespective of the specific value of k selected, φ remains constant for a given jet configuration.

1.1.2. Jet Turbulence Model

Using another physical representation, Corrsin [24] demonstrated that the mixing time for a passive scalar in a low-viscosity fluid is a function of the integral scale of concentration fluctuations (L) and the turbulent kinetic energy dissipation rate (ε). Using this, Grenville and Tilton [14] introduced the jet turbulence model (JTM) and showed that mixing time in jet-mixed vessels is determined by the rate of turbulent energy dissipation at the end of the free jet path length:
t m ∝ ε z m a x z m a x 2 − 1 / 3
where the turbulent kinetic energy dissipation rate at the end of free jet path length, ε z m a x , is:
ε z m a x ∝   u z m a x 3 / d z m a x  
They conducted experiments using tanks with aspect ratios (H/T) ranging between 0.2 and 3.0 and for jet nozzle positions such that the jet path spanned the diagonal of tank. By substituting Equations (1) and (12) into Equation (11) and using the conservation of momentum ( u j d j = u z m a x d z m a x ) they showed that dimensionless mixing time in all vessels could be expressed as:
t m u j d j = 2.97 d j z m a x 2
Whilst the constant in Equation (14) is obtained empirically from the large set of experimental data, the correlation is based on a physical model where local energy dissipation rate at the end of the jet controls mixing in the vessel.
Despite the abundance of literature on jet mixing of Newtonian fluids in vessels and the existing general design guidelines for jet-mixed tanks, there is a lack of clear understanding of the impact of nozzle orientation on mixing. Indeed, most studies have explored mixing for upwards-pointing jets that span the diagonal of the tank and are oriented across the tank diameter. The case of downwards-pointing nozzles has rarely been dealt with, although important for mixing stratified systems. Side-entry nozzles that are oriented horizontally towards the wall have also been given little attention although they have shown potential for effective mixing in wastewater treatment [15]. This study therefore focuses on the impact of nozzle orientation – both vertical and horizontal inclination – on single phase low-viscosity jet mixing in a tank. The effectiveness of different nozzle positions is evaluated by measuring mixing time using an inert tracer. The results obtained are discussed on the basis of existing correlations and physical models.

2. Materials and Methods

2.1. Experimental setup and operating conditions

Figure 2 presents the schematic diagram of the vessel, which consists of a cylindrical tank made of transparent plexiglass with a flat base and a diameter of 0.78 m. The aspect ratio, i.e. liquid height-to-tank diameter (H/T) is equal to 0.5. The nozzle is situated in the tank at 0.05 m from the tank bottom and 0.085 m from the side wall. Three nozzle diameters were tested: 3 mm, 5 mm, and 7.5 mm. The vertical (α) and the horizontal (β) inclination angles of the nozzle are illustrated in Figure 3. The angles were varied as given in Table 1; positive values of α correspond to an upward-pointing jet, whilst negative value correspond to a downwards-pointing jet. When α and β equal zero, the jet spans across the diameter of the tank. Figure 4 presents a schematic diagram showing various impingement zones resulting from the vertical inclinations of the nozzle. When α exceeds the upper critical angle of   α U L , the jet impinges on the liquid surface (Zone A). For α L L < α < α U L , the jet impinges on the tank side wall (Zone B). Finally, when α is less than the lower critical angle of α L L , the jet impinges on the tank bottom (Zone C). The values of αLLand αULare dependent on β.
Water at ambient conditions is the working fluid. The flow rate at the nozzle (Q) varied between 5.3 L/min and 14 L/min, giving with the residence times ranging from 843 – 7157 seconds. These flow rates correspond to jet velocities at the nozzle ranging from 2 m/s to 16.7 m/s and jet Reynolds numbers from 15,000 to 62,300 indicating a turbulent jet. Note that the liquid is pumped through the nozzle and tank in a closed circuit in order to maintain the liquid level at constant. However, the mean residence time for all tested conditions was sufficiently long compared with the mixing time, such that liquid recirculation had no impact on the mixing process.

2.2. Mixing time measurements

Mixing time is measured by monitoring the decay of the normalised concentration variance of an inert tracer, as given by Equation 15 [16]. 80 mL of an aqueous fluorescein solution (0.0166 mol/L) was introduced into the tank on the centre of the free liquid surface. A spectrophotometer with three T300-RT-UV/VIS dip probes (Ocean Insight) was used to take absorbance measurements over time at three different positions in the tank as shown in Figure 1 (b); (p0: 0, − 0.29, 0.15 m; p1: 0, 0, 0.34 m; p2: 0.305, 0.085, 0.15 m). The response time of the probes was 250 ms. The absorbance values were within the range to maintain the linearity of Beer-lambert’s law and therefore they are directly proportional to the tracer concentration in the tank. Mixing time is defined as the time required to reach 95% of the perfectly mixed state and occurs when log (σ2) < − 2.6. The mixing time for each experimental configuration is determined a minimum of two times, and the average value is taken. The percent deviation in mixing time between two repeats is equal to or less than 9%, a magnitude that falls within an admissible range when considering the reproducibility of experimental outcomes.
l o g σ 2 = l o g ∑ M = 1 M C i − C ∞ 2 M C ∞ 2
In addition, in order to better understand the impact of the nozzle position on the mixing time, the fluctuations of the concentration response curve of probes have been measured after the addition of the tracer at the liquid surface, above the position of p0.

3. Results and Discussion

3.1. Comparison of experimental mixing time with different models

Figure 5 and Figure 6 present comparisons of the mixing times measured experimentally for different nozzle positions and the mixing times calculated by previous models/correlations as a function of jet Reynolds number. Results indicate that both the Maruyama [12] circulation model (Equation 11) and the jet turbulence model presented by Grenville and Tilton [14] provide a good fit with the experimental data for upwards pointing nozzles with 0° ≤ α ≤ 35° and β = 0°. The other correlations examined did not agree well with the current data. The coefficients for the circulation model presented by Grenville and Tilton [13] are found to be completely out of range for the data obtained in this study. Notably, the value of the proportionality constant is contingent upon the specific tank geometry employed making these correlations poorly adapted to other geometries.
Figure 6 shows however that none of the correlations fit the experimental data for the downward-pointing nozzle position of α = − 30° and β = 60°. This is due to the fact that previous literature on jet mixing has focused on centrally aligned, upwards-pointing nozzle positions. These setups certainly exhibit dissimilar mixing mechanisms and flow patterns to those with the nozzle position at α = − 30°, and β = 60°.

3.2. Correlating experimental data using jet turbulent model

The present study investigates the mixing performance of the different jet nozzle configurations by analysing the mixing time t95 as a function of ε z m a x z m a x 2 at the end of the maximum free jet path length. The results presented in Figure 7 indicate a reduction in mixing time with ε z m a x z m a x 2 for all nozzle positions, however, a clear separation in the data is observed between upward and downward-pointing nozzles. The downwards-pointing jets require significantly higher turbulence energy dissipation rates per jet length squared to achieve equivalent mixing times as the upwards pointing jets. Indeed, mixing is not affected the turbulence energy dissipation generated at the nozzle; equivalent flow rates do not give equivalent mixing times for all nozzle positions. This affirms the proposition put forth by Grenville and Tilton [14] that the mixing time is influenced by energy dissipation rate, ε in a region located far from the jet nozzle, where velocities and turbulence intensity are considerably lower rather than energy dissipation rate at the nozzle, εj. It can also be seen that for upwards-pointing nozzles with a horizontal angle β = 0°, where the jet spans across the tank diameter, the vertical inclination angle α has no impact and all the data collapse. On the other hand, the horizontal angle of the nozzle clearly has an influence and different mixing times can be obtained for equal ε z m a x z m a x 2 . In such cases he mixing time increases as the horizontal inclination angle of the nozzle increases, i.e. as the nozzle is directed increasingly towards the side wall of the tank.
A regression analysis was conducted on the data for upwards-pointing jets with 0° < α < 35° and β = 0° and for the downwards-pointing jet with α = − 30° and β = 60° and the results are Equations 16 and 17. The power exponent for both equations is very close to –1/3 as expected by Corrsin’s [24] model. On the other hand, the proportionality constants are very different. A lower value of the proportionality constant corresponds to a more efficient mixing process. The data thus indicates that the mixing process is much more efficient with the upwards-pointing nozzles. For the upwards-pointing nozzles, the proportionality constant is similar to the value of 32.4 reported by Grenville and Tilton [14] for upwards-pointing nozzles that orient the jet centrally and across the diagonal of the tank.
When the horizontal angle of the nozzle is varied, the data appear to correlate with a similar slope close to –1/3, however the proportionality coefficient increases with increasing horizontal angle even though the data have the same value of ε z m a x z m a x 2 for equal jet velocity at the nozzle. This indicates that the constant of proportionality in Equations 16 and 17 may depend not only on ε z m a x z m a x 2 but also on the flow pattern created by the jet with different the nozzle positions.
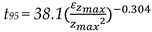Preprints 80247 i001
with a correlation coefficient, R2, of 0.895 for 0° ≤ α ≤ 35°, β = 0°
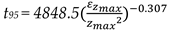Preprints 80247 i002
with a correlation coefficient, R2, of 0.978 for α = − 30°, β = 60°

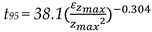
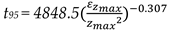
3.3. Correlating experimental data using the circulation model

The experimental mixing time data was also correlated using the circulation model, which consists in plotting mixing time against circulation time. Circulation time was measured for downwards- and upwards-pointing nozzles with α = − 30° or 15° and varied values of β using the method described by Maruyama et al. [12]. This method involves calculating tc as the time interval between successive oscillations in concentration measurements in order to obtain a value of coefficient 1/k appearing in Equation (9). For the other nozzle positions, values provided in Maruyama et al. [12] were used. The values are provided in Table 2.
Figure 8 displays the mixing time for various nozzle positions as a function of fluid circulation time. For all nozzle positions, the mixing time increases with circulation time. A regression analysis was conducted on the t95 mixing time and the t C for nozzle positions at β = 0°, 0° ≤ α ≤ 35° and that of α = − 30° and 15°, β = 60°, yielding the following relationships for the upwards- and downwards-pointing nozzles, respectively.
Preprints 80247 i003
with a correlation coefficient, R2, of 0.97 for 0° ≤ α ≤ 35°, β = 0°
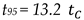Preprints 80247 i004
with a correlation coefficient, R2, of 0.99 for α = − 30°, β = 60°
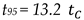
From Equations 18 and 19, it follows that for nozzle positions at β = 0°, 0° ≤ α ≤ 35° the mixing is achieved when the fluid has circulated approximately two and a half times in the tank, whilst more than 13 tank turnovers are required to mix the tank when a downwards-pointing jet (α = − 30° and 15°, β = 60°) is used. Indeed, in the latter case the length of the jet is very short (< 20 dj), which means that less fluid is entrained, thereby resulting in less fluid circulation. In addition, it is expected that conical shape and characteristic properties of the jet are modified by the proximity of the tank base and as a result, fluid entrainment may be hindered [12,17]. It can also be seen from Figure 8 that for both downwards- and upwards-pointing jets, the proportionality constant between mixing time and circulation time strongly depends on the horizonal orientation β. In the case of upwards-pointing jets, the jet points more and more towards the side tank wall as β increases, becoming shorter at the same time, and more tank turn overs are required to achieve mixing. For downwards-pointing jets, however, the jet length is not modified with a change in β. Therefore the increase in mixing time for these cannot only be attributed to a lack of fluid entrainment and consequently fluid circulation in the tank. On the other hand, it is suspected that as β increases for both downwards- and upwards-pointing jets, the tangential component of the flow increases, whilst the radial and axial components decrease, thereby hindering mixing.
Using the mixing time circulation model presented in Equation 11, the value of the proportionality constant φ found for the various jet configurations in this study ranges from 3 to 4.7 for 0° ≤ α ≤ 35°, β = 0°, and for the downwards-pointing jet with α = − 30°, β = 60°, φ = 2.2. For the centrally aligned nozzle where α = 15° and β = 0°, φ = 4.7, which agrees well with the value of 5 reported by Maruyama et al. [12] (as noted by Perona et al. [17]) in tanks with aspect ratios (H/T ) ranging from 0.5 to 1.0. However, Grenville and Tilton [13] reported a value φ = 9.34 for α > 15°, β = 0°, and 13.8 for α < 15°, β = 0° for jets that span the tank diagonal in tanks with H/T from 0.4 to 1, which are similar conditions to those of Maruyama et al. [12]. A plausible explanation for this inconsistency lies in the choice of the k value, which is governed by the nozzle installation positions relative to the tank geometry and the relative confinement. Indeed, Maruyama et al. [12] showed experimentally that k is dependent on the orientation of the nozzle and found values ranging from 0.48 to 1.0, while Grenville and Tilton [13] employed a fixed value of 0.25.

3.4. Impact of the horizontal position of the jet nozzle

Figure 9 (a) shows the relationship between the coefficient 1/k appearing in Equation (9) and the horizontal inclination of the jet nozzle (β) for two specific values of α: 15° and − 30°. 1/k appears to be more sensitive to β for the upwards-pointing nozzle with α = 15°, than for the downwards-pointing nozzle with α = − 30°. In the case of α = 15°, 1/k decreases from 2.06 to 0.7 (by 66%) as β is varied from 15° to 60°. On the other hand, when α = − 30° 1/k decreases from 0.31 to 0.16 (i.e. by 48%) when β increases from 15° to 60°. Since 1/k and circulation time are directly related, this data shows that fluid circulation is hindered (being slower) as β increases. As mentioned previously, the increase in circulation time can possibly be attributed to (i) less flow entrainment because the jet length decreases as β increases and/or (ii) an increased tangential velocity component in the flow. For the upwards-pointing jet, it is expected that both (i) and (ii) contribute to the increased circulation time, whilst for the downwards-pointing jet, only (ii) contributes since the jet length does not vary with β. Indeed, 1/k only varies slightly for the downwards-pointing jet, thereby showing that the jet length is the prime factor in flow entrainment and mixing. The indirect impact of 1/k and fluid circulation on mixing time is shown in Figure 9 (b) for α values of 15° and − 30°, and β values ranging from 0° to 60°. As expected, mixing time increases as β increases since circulation is hindered.

3.5. Impact of the vertical inclination of the nozzle

Figure 10 shows the effect of the vertical inclination of the nozzle α on the mixing time t 95 at two different jet Reynolds numbers (24900 and 49900), with a nozzle diameter of 0.005 m and horizontal orientation β = 0. As expected, mixing is faster at higher Reynolds numbers, which is attributed to the increased entrainment rates of the bulk fluid. At Rej = 49900, there is little impact of α on mixing time. However, at Rej of 24900, mixing time is significantly affected by α. Indeed, mixing is slower when the jet is oriented towards the tank bottom or across the tank diameter compared with when it is upwards-pointing.
The results at Rej =24900 indicate that when the jet impacts the free liquid surface (Zone A), the mixing time is similar regardless of the inclination angle α. In contrast, when the jet impacts the side wall of the tank (Zone B), mixing time decreases with increasing α. When the jet impacts the tank bottom (Zone C), the mixing time is relatively high compared with upwards-pointing nozzle configurations. Previous researches [13,14,18] proposed that the most effective vertical inclination of the jet was when the free jet path length spans the diagonal of the tank volume. In the current setup, this corresponds to α = 26°. However, this study found that similar mixing times can be achieved for all vertical inclination angles of the nozzle, except for horizontal and downwards-pointing nozzles at the lower Reynolds number (Rej = 24900).

3.6. Impact of the free jet path length on mixing time

The mixing time as a function of the free jet path length, which ranges from 0.0925 m to 0.72 m, is presented in Figure 11 for jet Reynolds numbers of 24900 and 49900. For both Reynolds numbers, an increase in the free jet path length leads to a decrease in mixing time for jet configurations where the jet impacts the side wall of the tank (blue symbols; Zone B). This shows that the mixing process is mainly influenced by the entrained flow of the bulk fluid, which is proportional to the jet length. For jet installation positions with α = − 30° where the jet impacts the tank bottom (green symbols; Zone C), the free jet path length is the same for all horizontal orientations (β values equal to 0°, 15°, 30°, 45°, and 60°). Like shown previously, as β increases – and the nozzle points further towards the side tank wall, mixing time increases. This shows that the free jet path length – and consequently circulation flow rate – is not the only factor controlling mixing time in jet mixed vessels. It is believed that the flow patterns in the tank are significantly modified by the horizontal orientation of the jet nozzle, inducing a dominant tangential component of the flow as β increases and reducing the 3-dimensional nature of the flow that is required for effective mixing. When the jet impinges on the liquid surface (red symbols; Zone A) at angles α = 26°, 30°, 35° and β = 0° the free jet path length decreases but there is no significant impact on mixing time.
Returning back to Grenville and Tilton's [14] jet turbulence model, it can be shown that for α = − 30°, the jet free path length remains constant (z = 0.0925 m) regardless of β value and for given flow conditions, ε z m a x z m a x 2 at the end of the jet path length is the same for all the values of β. However, Figure 7 shows that the mixing time varies significantly even with identical ε z m a x z m a x 2 . This again demonstrates that the constant of proportionality in Equations 16 and 17 may depend not only on the ratio ε z m a x z m a x 2 , but also on the flow pattern induced by the nozzle orientation. This observation may also hold for circulation models which are based on the fluid entrainment rate into the jet spread along the jet path length, considering the differences in mixing time across jet nozzle positions with equal free jet path length (α = − 30°and β = 0°, 15°, 30°, 45°, and 60°). The flow pattern induced by the nozzle orientation may affect the proportionality constant in Equations 18 and 19; the proportionality constant increases principally as β increases, while the vertical inclination of the nozzle has a relatively minor impact on this constant.

3.7. Impact of the jet nozzle diameter and jet inlet velocity on mixing time

Figure 12 (a) shows how the nozzle diameter and the inlet velocity affect mixing time t 95 . It is not surprising that an increase in the velocity reduces mixing time for all nozzle diameters since Reynolds number is increased. Additionally, at a fixed velocity, mixing time is shown to decrease as nozzle diameter increases. The data show a three-fold increase in mixing time for a 0.003 m nozzle compared with a 0.0075 m nozzle at identical fluid velocities. Increased fluid circulation and mixing, as well as turbulence at higher velocities likely explain the trend of decreasing mixing time. Improvements in mixing performance at constant velocity for different nozzle diameters are mostly due to increased flow rate as the nozzle diameter increases [8]. Figure 12 (b) shows the mixing time obtained from various nozzle orientations as a function of jet fluid Reynolds number and it can be seen that mixing time is inversely proportional to jet Reynolds number. Like observed in previous analyses, the mixing time data collapse for all upwards-pointing orientations when the jet spans the tank diameter, i.e. β = 0°. However there is a shift in the data to longer mixing times at equivalent Reynolds number as the jet is oriented towards the side tank wall or the tank bottom. This is clearly seen by the values of the proportionality constants Equations 20 and 21 that indicate that a larger Reynolds number is required for the downwards-pointing nozzle with α = − 30°, β = 60° to achieve an equivalent mixing time to that obtained with upwards-pointing nozzles with 0° ≤ α ≤ 35°, β = 0°.
t 95 = 1.51 × 10 6 R e j
t 95 = 5.10 × 10 6 R e j

3.8. Correlation of mixing time with power input and flow momentum

Figure 13 (a) presents mixing time obtained with different nozzle diameters and orientations as a function of power per unit mass (Pj), as given by Equation 22. A power-law relationship is observed between t95 and Pj resulting in Equations 23 and 24 for the nozzle configurations 0° ≤ α ≤ 35°, β = 0° and α = − 30°, β = 60°.
P j = π 4 d j 2   u j 1 2 ρ u j 2 ρ V = π 8 d j 2   u j 3 V
t 95 = 1.50   P j − 0.32
t 95 = 4.84   P j − 0.32
The proportionality coefficients in Equations 23 and 24 reveal that a higher power per unit mass is required to mix in a tank with a downwards-pointing nozzle oriented at α = − 30°, β = 60° compared with centrally aligned upwards-pointing nozzles (0° ≤ α ≤ 35°, β = 0°). Indeed, from the ensemble of data in Figure 13 (a), increased power per unit mass is require when the nozzle points downwards or further towards the side-tank wall. This may stem from factors such as free jet path length, limited bulk fluid entrainment, and the flow pattern associated with the nozzle orientation, which have been discussed in previous sections of this article.
Of particular interest is the observation that the exponent on Pj in Equations 23 and 24 is approximately equal to –1/3, which is the same as that in Equations 16 and 17. This similarity arises because an increase in power per unit mass of the jet results in increased rates of turbulent energy dissipation.
Figure 13 (b) shows mixing time as a function of jet flow momentum (G) as given by Equation 25 for all nozzle orientations. From Equations 26 (for nozzles with 0° ≤ α ≤ 35°, β = 0°) and Equation 27 (for nozzles with α = − 30°, β = 60°), it can be seen that mixing time is proportional to the inverse square root of jet flow momentum.
G = ρ u j 2 π d j 2 4
t 95 = 46.75 G − 0.5
t 95 = 157.67 G − 0.5
Like seen previously, the data for the centrally aligned upwards-pointing nozzles collapse but higher momentum is required for downwards-pointing nozzles and for nozzles oriented towards the side-wall of the tank.

4. Conclusions

This experimental study focuses on the impact of nozzle orientation – both vertical and horizontal inclination – on single phase low-viscosity jet mixing in a tank. The effectiveness of different nozzle positions is evaluated by measuring mixing time using an inert tracer.
For upwards-pointing jets positioned across the tank diameter, mixing time was found to follow the jet turbulence model by Grenville and Tilton [14] and scales with ε z m a x z m a x 2 . The proportionality constant is in agreement with that found by Grenville and Tilton [14] for a range of vessel sizes and jets spanning the diagonal of the tank. If the horizontal inclination of the nozzle β is increased or the nozzle is downwards-pointing, mixing time was still found to correlate with ε z m a x z m a x 2 but the proportionality constant is modified. Mixing is typically worse with a downwards-pointing nozzle or as the nozzle is oriented further towards the side wall of the tank.
Based on analyses using the circulation model by Marayuma et al. [12], mixing time was also found to scale with circulation time for upwards-pointing jets positioned across the tank diameter and the proportionality constant is in agreement with that found by Marayuma et al. [12]. Like for the jet turbulence model, if the horizontal inclination of the nozzle β is increased or the nozzle is downwards-pointing, mixing time still correlates with circulation time but the proportionality constant is modified. A larger number of turnovers of the fluid in the tank are required to mix the contents when the nozzle points further towards the side wall of the tank.
Shorter mixing times can be attributed principally to longer jet path lengths and therefore higher fluid entrainment and circulation, as well as higher dissipation rates per jet length squared. Generally, centrally aligned upwards-pointing nozzles provide faster and more efficient mixing. Mixing performance is less effective and efficient with downwards-pointing nozzles and when nozzles are oriented towards the side-wall of the tank.
There appear to be several ways to correlate mixing time data – ε z m a x z m a x 2 , circulation time, jet Reynolds number, power per unit mass and momentum. Mixing times for all centrally aligned upwards-pointing nozzles were found to collapse with all of the above variables but did not for other nozzle configurations (downwards-pointing and wall oriented jets). It is suspected that the 3-dimensional nature of the flow pattern is significantly modified in the latter cases, thereby impacting the dominance of tangential flow and the mixing mechanism.

Author Contributions

Conceptualization, C.X., M.P., J. A. and T. A. O.; methodology, T.A.O; validation T.A.O., J.A. and M.P.; formal analysis, T.A.O; investigation, T.A.O.; data curation, T.A.O.; writing—original draft preparation, T.A.O.; writing—review and editing, T.A.O., J.A., M.P.; supervision, C.X., J. A., and M.P.; project administration, M. P.; funding acquisition, C.X. and T.A.O. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by PETROLEUM TECHNOLOGY DEVELOPMENT FUND, Nigeria, and Laboratoire de Génie Chimique, Toulouse.

Acknowledgments

This project has received funding from Petroleum Technology Development Fund, Nigeria.

Conflicts of Interest

The authors declare no conflict of interest.

Nomenclature

Ci Initial Concentration (Moldm-3)
C ∞ Final Concentration (Moldm-3)
dj Jet nozzle diameter (m)
dz Jet spread diameter at z (m)
f frequency (s-1)
Fr Froude number Fr = = u j 2 d j g
G Jet flow momentum (N)
g Gravitational force (m/s2)
H Liquid height (m)
hN Nozzle clearance from tank bottom (m)
ho Outlet Clearance from tank bottom (m)
k Entrainment rate model constant
L integral scale of concentration fluctuations (m)
Pj Jet power per unit volume (Watts/kg)
Q Jet nozzle discharge flow rate (m3/s)
QE(zmax) Jet entrainment Rate within the jet spread across the free jet path length (m3/s)
QT Total volumetric flow rate of the bulk volume (m3/s)
Rej Jet fluid Reynolds number Rej = ρ u j d j μ
tm Mixing time (s)
tc Mean circulation time due to entrainment within the jet spread around zmax (s)
tR Bulk fluid residence time (s)
t95 95% mixing time (s)
T Tank diameter (m)
uj Jet inlet velocity (m/s)
uz Jet velocity at z (m/s)
V Bulk fluid volume (m3)
XN Jet nozzle clearance from the side wall (m)
z Distance from the nozzle in the axis of the jet (m)
zmax Free jet path length as the jet impinges on the liquid surface, side tank wall, or tank bottom (m)
Greek Symbols
εj Turbulent energy dissipation rate at the jet inlet (m2/s3)
ε z m a x Turbulent energy dissipation rate at z m a x (m2/s3)
ρ Density (kg/m3)
µ Viscosity (Pa.s)
α Jet nozzle vertical inclination (°)
αuL Jet nozzle vertical inclination upper limit (°)
αLL Jet nozzle vertical inclination lower limit (°)
β Jet nozzle horizontal position (°)
δ Fox and Gex correlation constant
φ Circulation model constant

References

  1. K. L. Wasewar and J. V. Sarathi, ‘CFD Modelling and Simulation of Jet Mixed Tanks’, Engineering Applications of Computational Fluid Mechanics, vol. 2, no. 2, pp. 155–171, Jan. 2008. [CrossRef]
  2. P. S. Randive, D. D. P. Singh, D. V. Varghese, and D. A. M. Badar, ‘Study of Jet Mixing in Flocculation Process’, IJIRMPS vol. 6, no. 4, p. 10, 2018.
  3. K. L. Wasewar, ‘A Design of Jet Mixed Tank’, Chem. Biochem. Eng. Q., p. 17, 2006.
  4. W. Patwardhan and A. R. Thatte, ‘Process Design Aspects of Jet Mixers’, Can. J. Chem. Eng., vol. 82, no. 1, pp. 198–205, May 2008. [CrossRef]
  5. K. Revill, ‘Chapter 9 - Jet mixing’, in Mixing in the Process Industries, N. Harnby, M. F. Edwards, and A. W. Nienow, Eds., Oxford: Butterworth-Heinemann, 1992, pp. 159–183. [CrossRef]
  6. Abdel-Rahman, ‘A Review of Effects of Initial and Boundary Conditions on Turbulent Jets’, WSEAS Tr. vol. 5, no. 4, p. 20, 2010.
  7. J. N. Tilton, Perry’s Chemical Engineers’ Handbook: Fluid and Particle Dynamics. McGraw-Hill, 2008.
  8. W. Patwardhan and S. G. Gaikwad, ‘Mixing in Tanks Agitated by Jets’, Chem Engr Res. Design vol. 81, no. 2, pp. 211-220, 2003.
  9. F. Cabaret, C. Rivera, L. Fradette, M. Heniche, and P. A. Tanguy, ‘Hydrodynamics performance of a dual shaft mixer with viscous Newtonian liquids’, Chemical Engineering Research and Design, vol. 85, no. 5, pp. 583–590, 2007.
  10. E. A. Fox and V. E. Gex, ‘Single-phase blending of liquids’, AIChE J., vol. 2, no. 4, pp. 539–544, Dec. 1956. [CrossRef]
  11. Okita N. and Oyama Y., ‘Mixing Characteristics in Jet Mixing’, Chemical engineering, vol. 27, no. 4, pp. 252–260, 1963. [CrossRef]
  12. T. Maruyama, Y. Ban, and T. Mizushina, ‘Jet mixing of fluids in tanks.’, J. Chem. Eng. Japan / JCEJ, vol. 15, no. 5, pp. 342–348, 1982. [CrossRef]
  13. R. Grenville and J. N. Tilton, ‘Turbulence for flow as a predictor of blend time in turbulent jet mixed vessels’, in Nineth European Conference on Mixing, France, 1997, pp. 67–74.
  14. R. K. Grenville and J. N. Tilton, ‘A new theory improves the correlation of blend time data from turbulent jet mixed vessels’, Chemical engineering research & design, vol. 74, no. 3, pp. 390–396, 1996.
  15. T. Sotiriadis, T. Firmansyah, and Dawson, ‘Mixing of Sludges with Liquid Jets’, Journal of the Chartered Institution of Water and Environmental Management, Nov. 2006.
  16. E. L. Paul, V. A. Atiemo-Obeng, and S. M. Kresta, Eds., Handbook of industrial mixing: science and practice. Hoboken, N.J: Wiley-Interscience, 2004.
  17. J. J. Perona, T. D. Hylton, E. L. Youngblood, and R. L. Cummins, ‘Jet Mixing of Liquids in Long Horizontal Cylindrical Tanks’, Ind. Eng. Chem. Res., vol. 37, no. 4, pp. 1478–1482, Apr. 1998. [CrossRef]
  18. R. K. Grenville and J. N. Tilton, ‘Jet mixing in tall tanks: Comparison of methods for predicting blend times’, Chemical Engineering Research and Design, vol. 89, no. 12, pp. 2501–2506, Dec. 2011. [CrossRef]
  19. H.E. Fielder, ‘Control of free turbulent shear flows’ In M.G. El-Hak, A. Pollard. J. P. Bonnet (Eds), Flow Control: Fundamentals and Practices, Springer-Verlag, Germany, pp.335-429, 1998.
  20. H. Fosset, Mech. E, M. I., Tran. Inst. Chem Engrs. Vol. 29. p 322, 1951.
  21. N. Rajaratnam, ‘Turbulent mixing and diffusion of Jets’ Cheremisinoff (Ed.), Encyclopedia Fluid of Mechanics, vol. 2. Gulf Publishing, Houston, (Chapter USA 15). pp 391-404, 1986.
  22. N. Rajaratnam, ‘Turbulent Jets’ Elsevier Scientific Publishing Co., Amsterdam. The Netherlands, 1976.
  23. F. P. Ricou and D. B. Spalding: J. Fluid Mech., Vol. 11, no. 21, 1961.
  24. S. Corrsin, ‘The isotopic turbulent mixer: part II’ Arbitrary Schmidt number, AICHEJ., Vol. 10, no. (6), pp. 870-877, 1964.
Preprints 80247 g001
Figure 1. Jet paths for (a) an axial jet and (b) a side-entry jet with vertical inclination angle α.
Figure 1. Jet paths for (a) an axial jet and (b) a side-entry jet with vertical inclination angle α.
Preprints 80247 g001
Preprints 80247 g002
Figure 2. Schematic diagram of the cylindrical tank, the nozzle position and the position of the spectrophotometry probes (p0, p1, p2). (a) Side view (b) Top view.
Figure 2. Schematic diagram of the cylindrical tank, the nozzle position and the position of the spectrophotometry probes (p0, p1, p2). (a) Side view (b) Top view.
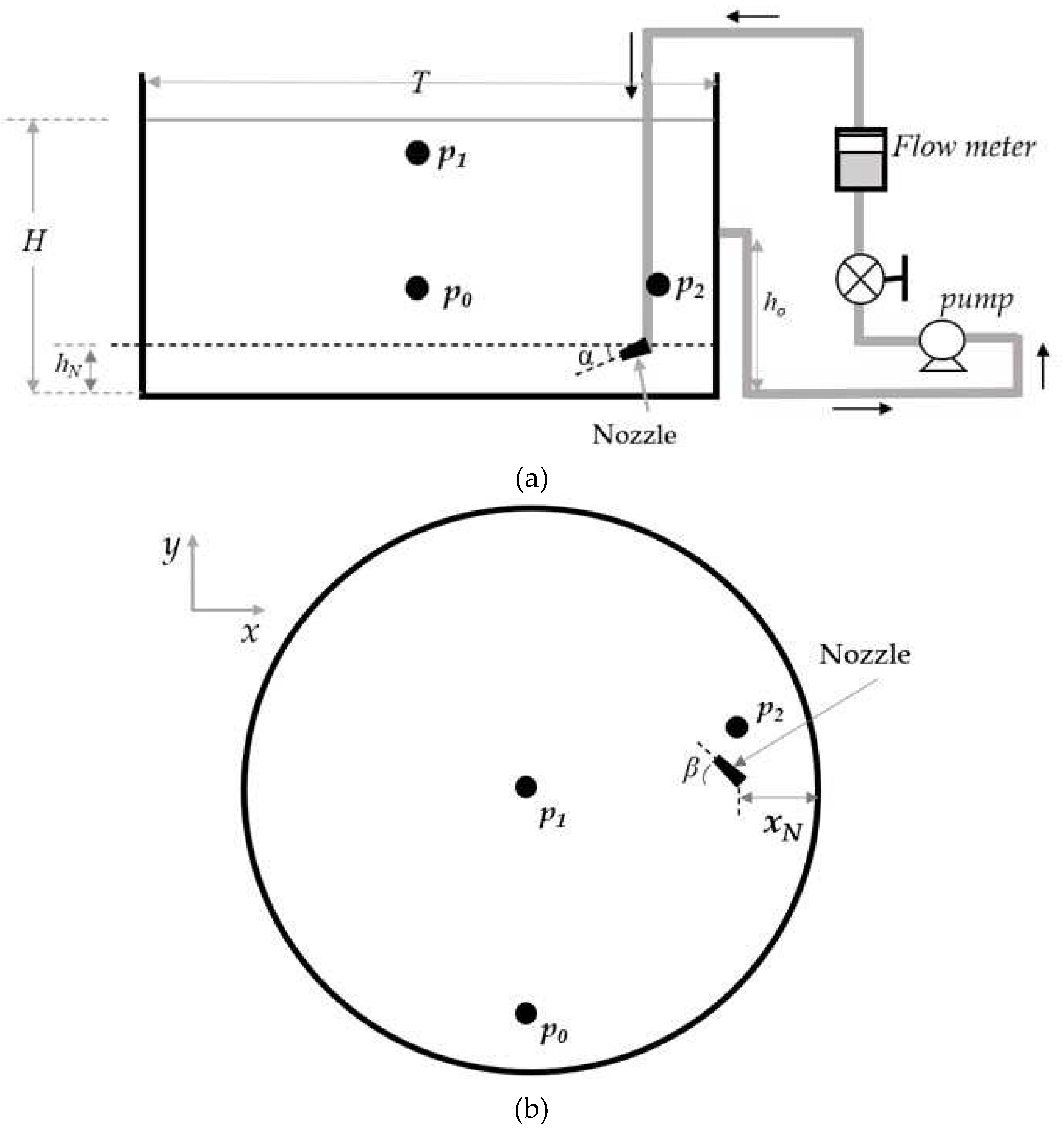
Preprints 80247 g002
Preprints 80247 g003
Figure 3. Jet nozzle orientations (a) vertical inclination, α (positive α corresponds to an upwards-pointing nozzle and negative α corresponds to a downwards-pointing nozzle), and (b) horizontal orientation angle (β) (the nozzle points across the tank diameter when β = 0° and points towards the side wall when β > 0°).
Figure 3. Jet nozzle orientations (a) vertical inclination, α (positive α corresponds to an upwards-pointing nozzle and negative α corresponds to a downwards-pointing nozzle), and (b) horizontal orientation angle (β) (the nozzle points across the tank diameter when β = 0° and points towards the side wall when β > 0°).
Preprints 80247 g003
Preprints 80247 g004
Figure 4. Schematic diagram of the jet path length for different vertical jet nozzle inclinations.
Figure 4. Schematic diagram of the jet path length for different vertical jet nozzle inclinations.
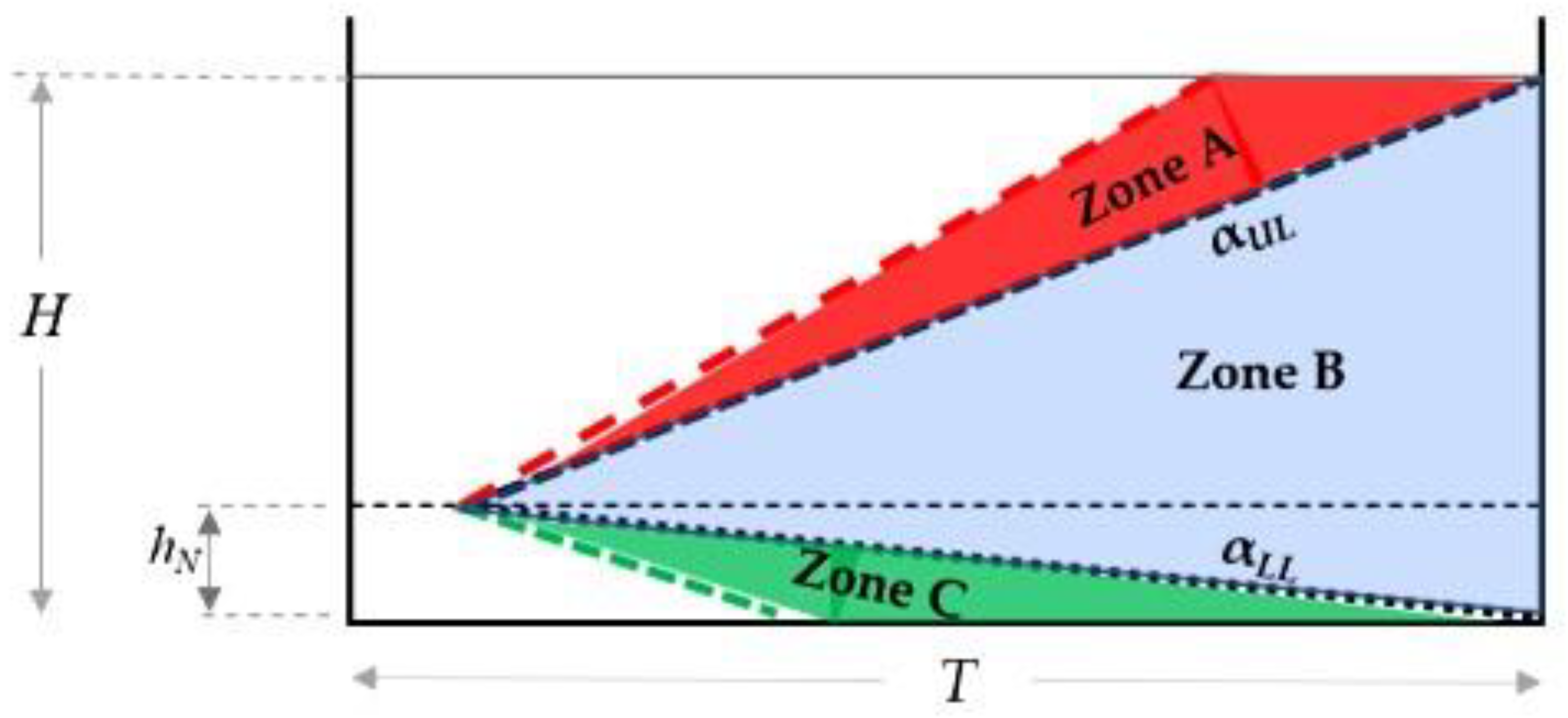
Preprints 80247 g004
Preprints 80247 g005
Figure 5. Comparison of experimental mixing time data for upwards-pointing nozzles (0° ≤ α ≤ 35° and β = 0°) with mixing time calculated by the previous correlations and models.
Figure 5. Comparison of experimental mixing time data for upwards-pointing nozzles (0° ≤ α ≤ 35° and β = 0°) with mixing time calculated by the previous correlations and models.
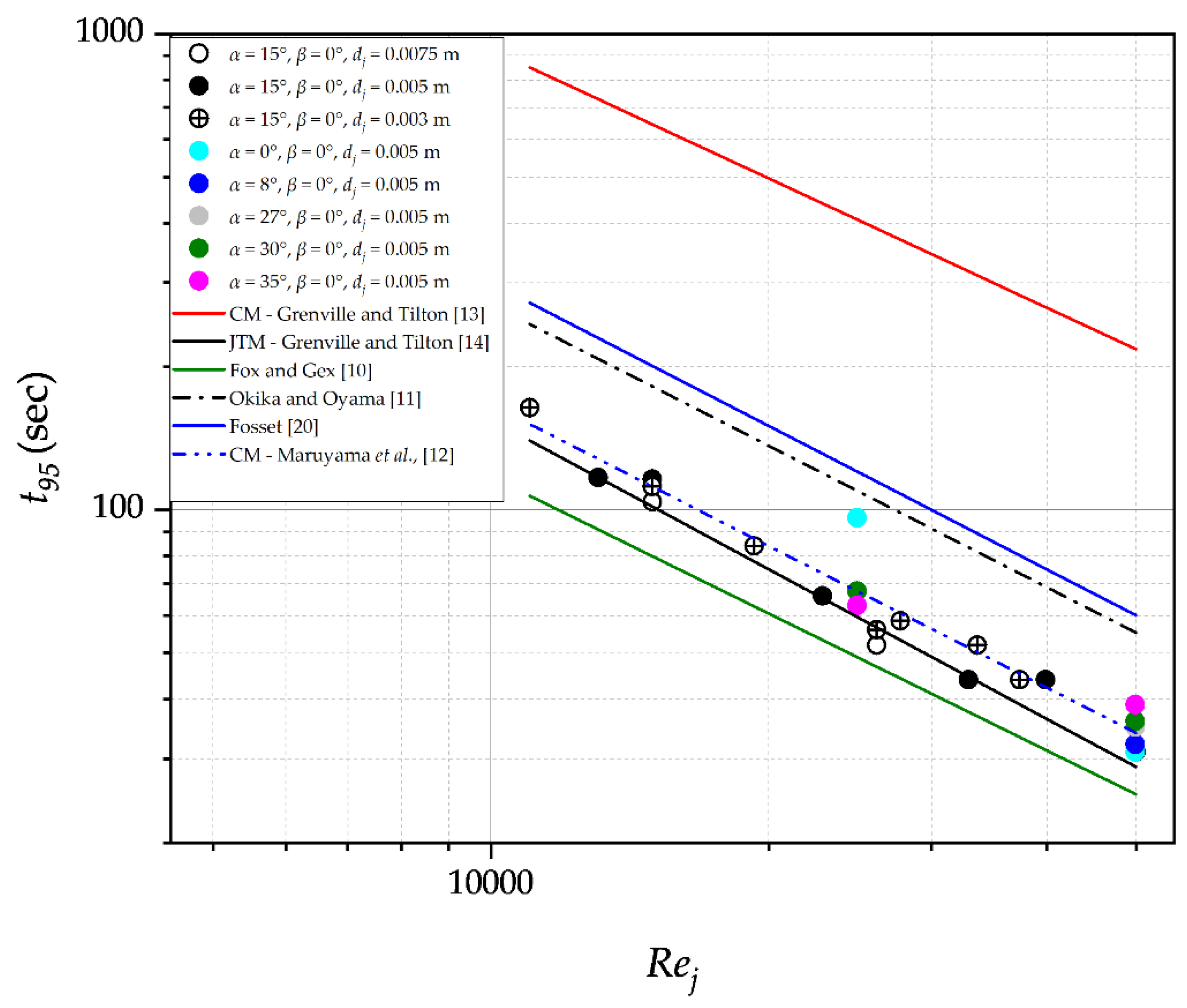
Preprints 80247 g005
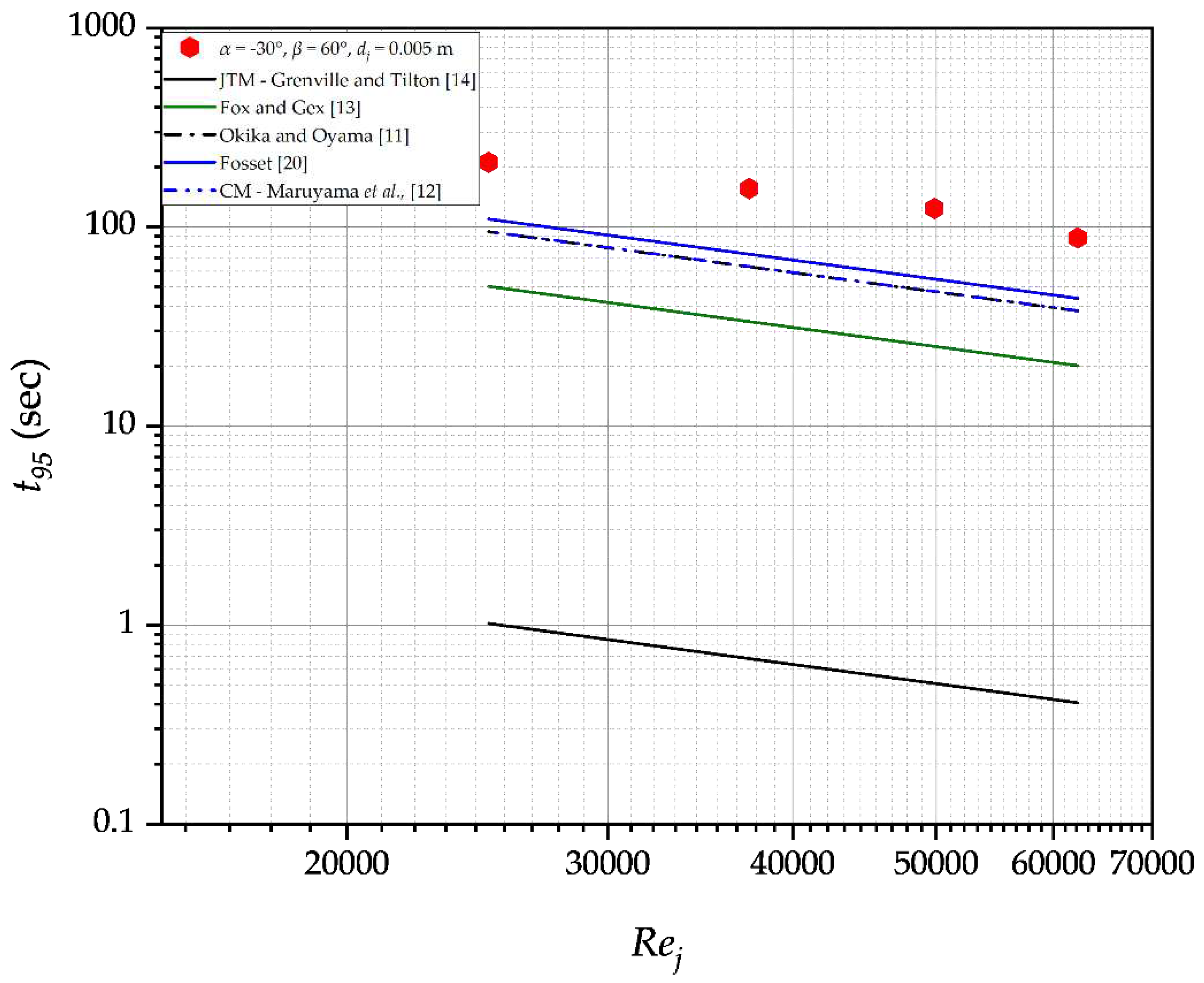
Preprints 80247 g006
Figure 6. Comparison of experimental mixing time data for a downwards-pointing nozzle (α = − 30° and β = 60°) with mixing time calculated by the previous correlations and models.
Figure 6. Comparison of experimental mixing time data for a downwards-pointing nozzle (α = − 30° and β = 60°) with mixing time calculated by the previous correlations and models.
Preprints 80247 g006
Preprints 80247 g007
Figure 7. Mixing time (t95) versus ε z m a x z m a x 2 for Rej = 15000 to 62000.
Figure 7. Mixing time (t95) versus ε z m a x z m a x 2 for Rej = 15000 to 62000.
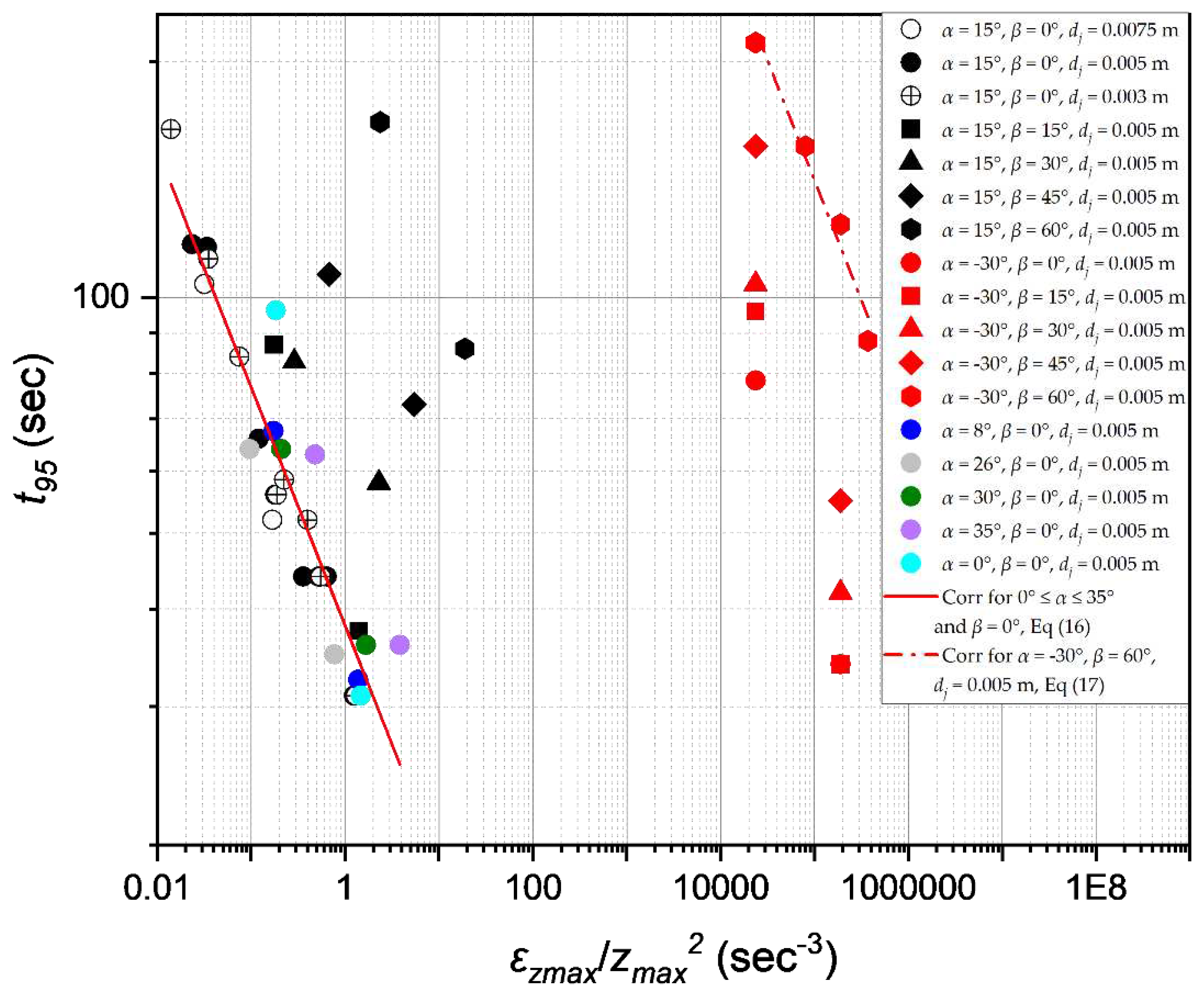
Preprints 80247 g007
Preprints 80247 g008
Figure 8. Mixing time (t95) as a function of circulation time ( t C ) at Rej = 15000 – 62300.
Figure 8. Mixing time (t95) as a function of circulation time ( t C ) at Rej = 15000 – 62300.
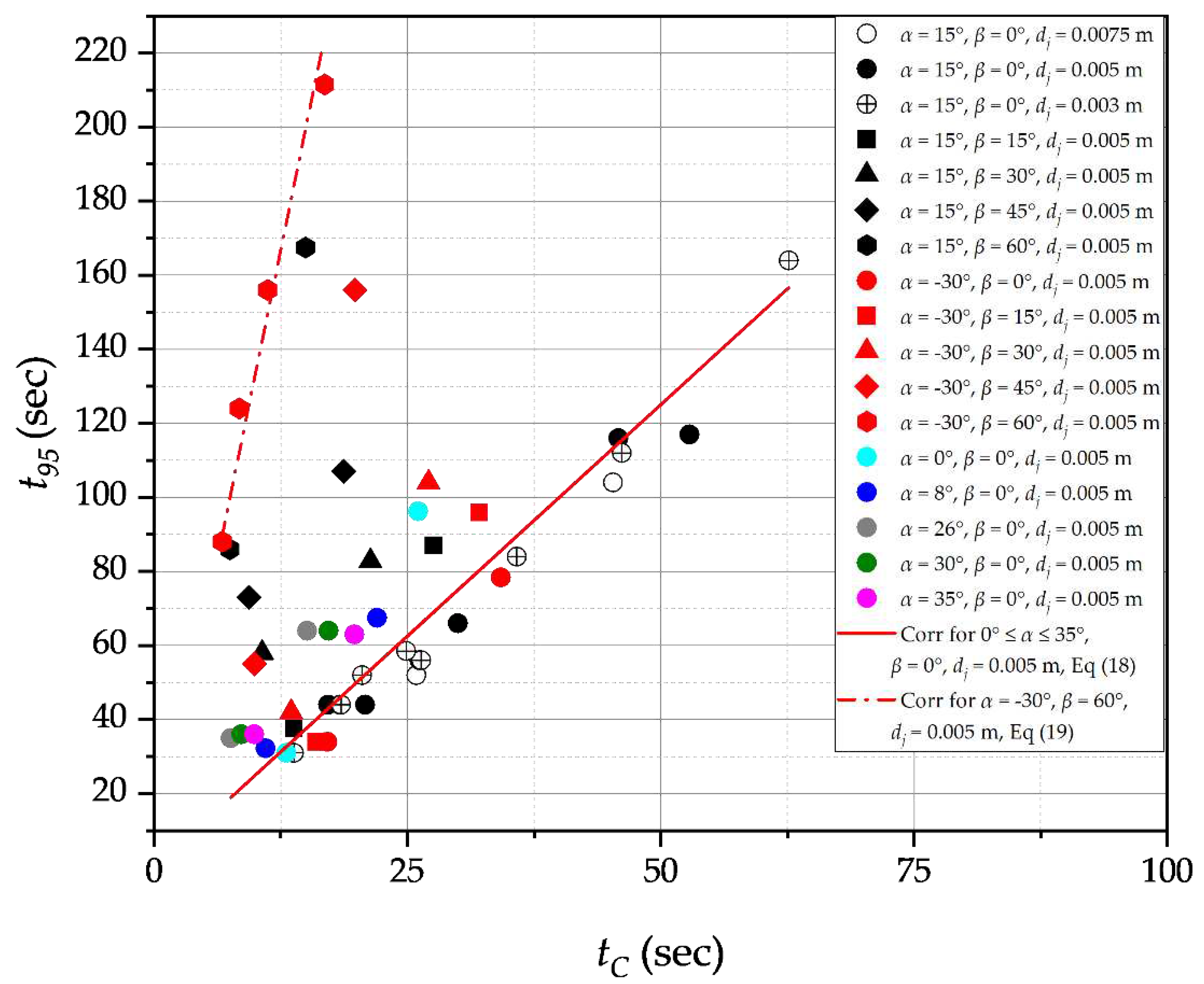
Preprints 80247 g008
Preprints 80247 g009
Figure 9. (a) Value of coefficient 1/k as a function of the horizontal orientation β of the nozzle; (b) Impact of the horizontal orientation β of the nozzle on mixing time t95.
Figure 9. (a) Value of coefficient 1/k as a function of the horizontal orientation β of the nozzle; (b) Impact of the horizontal orientation β of the nozzle on mixing time t95.
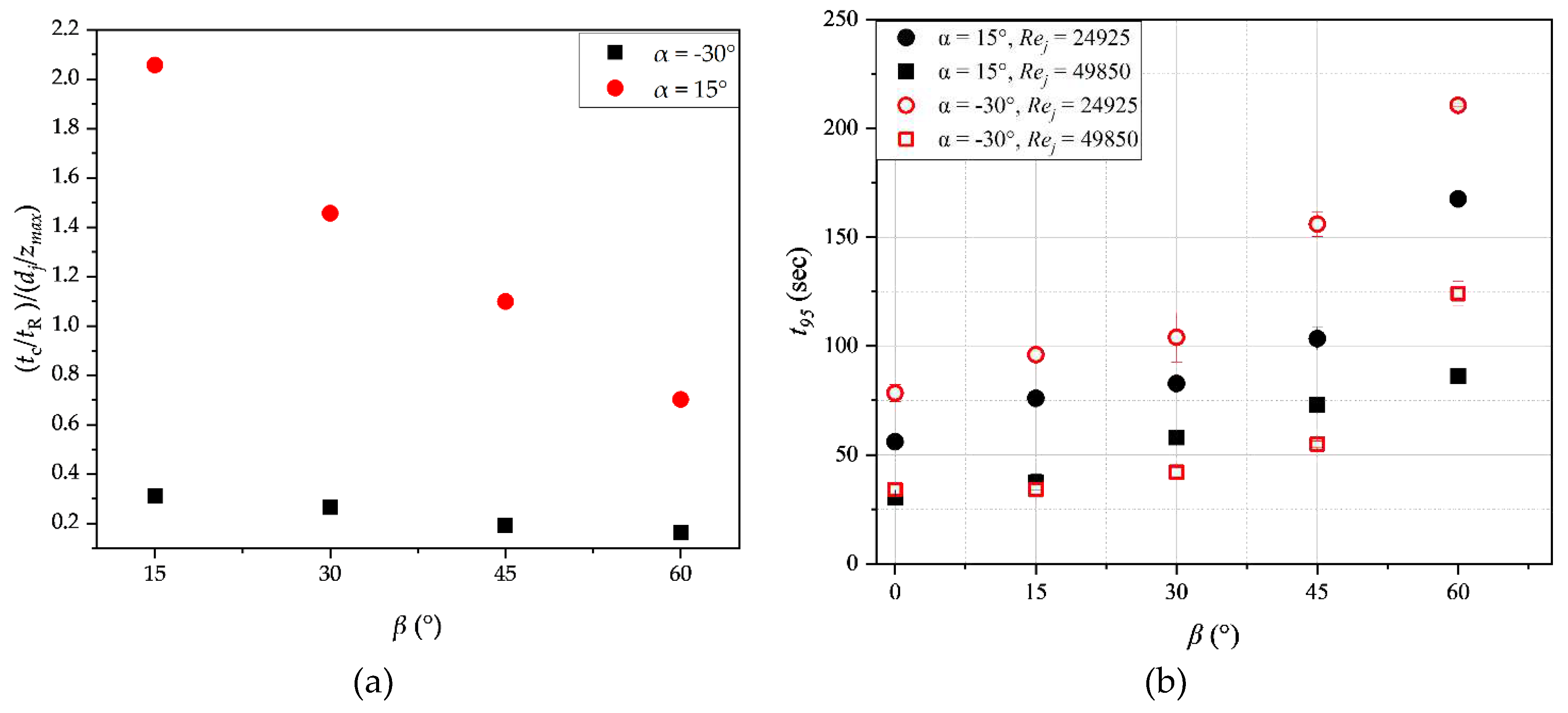
Preprints 80247 g009
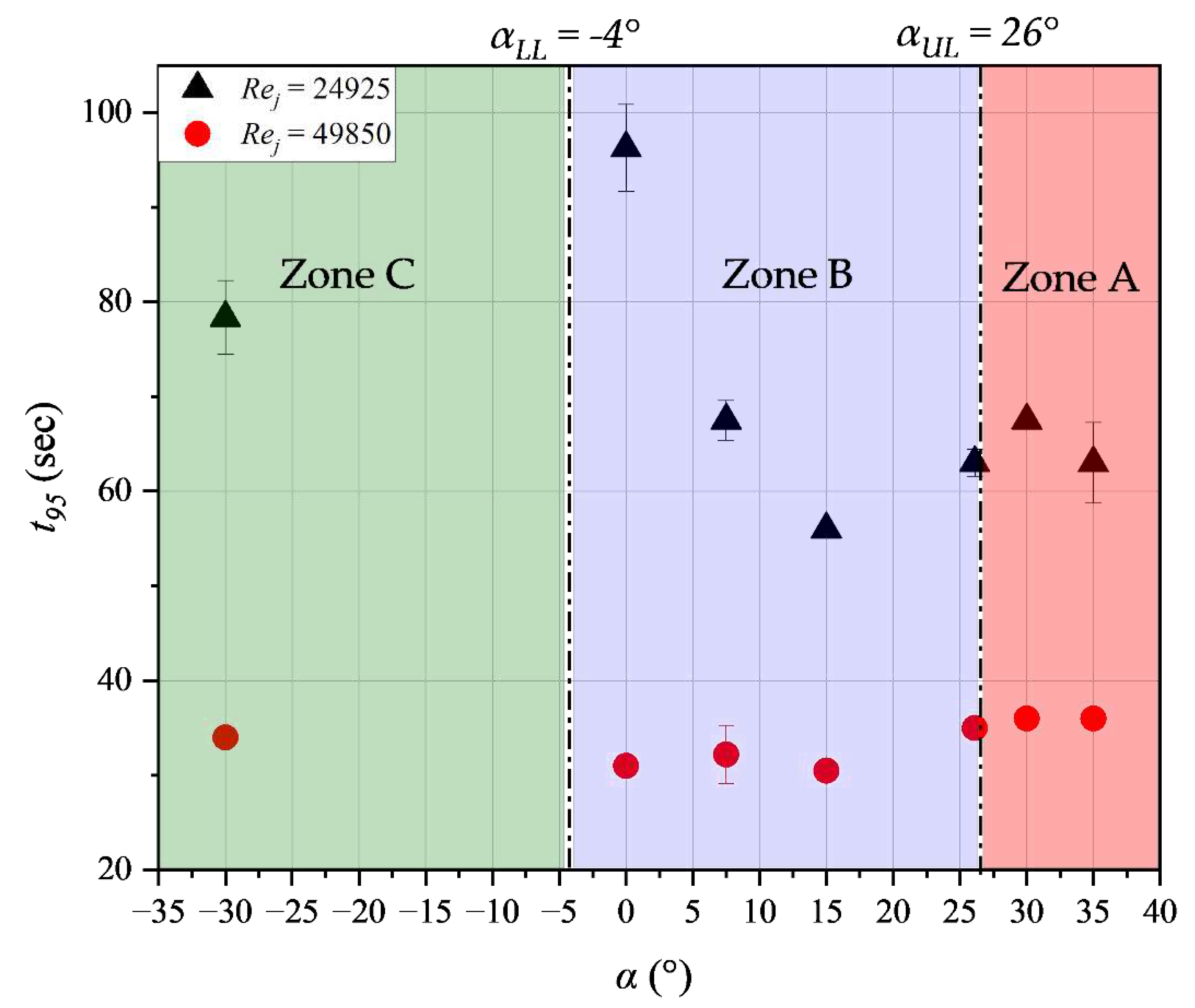
Preprints 80247 g010
Figure 10. Impact of the vertical inclination of the jet nozzle (α) on mixing time (t95) at fixed horizontal orientation (β = 0) for dj = 0.005 m.
Figure 10. Impact of the vertical inclination of the jet nozzle (α) on mixing time (t95) at fixed horizontal orientation (β = 0) for dj = 0.005 m.
Preprints 80247 g010
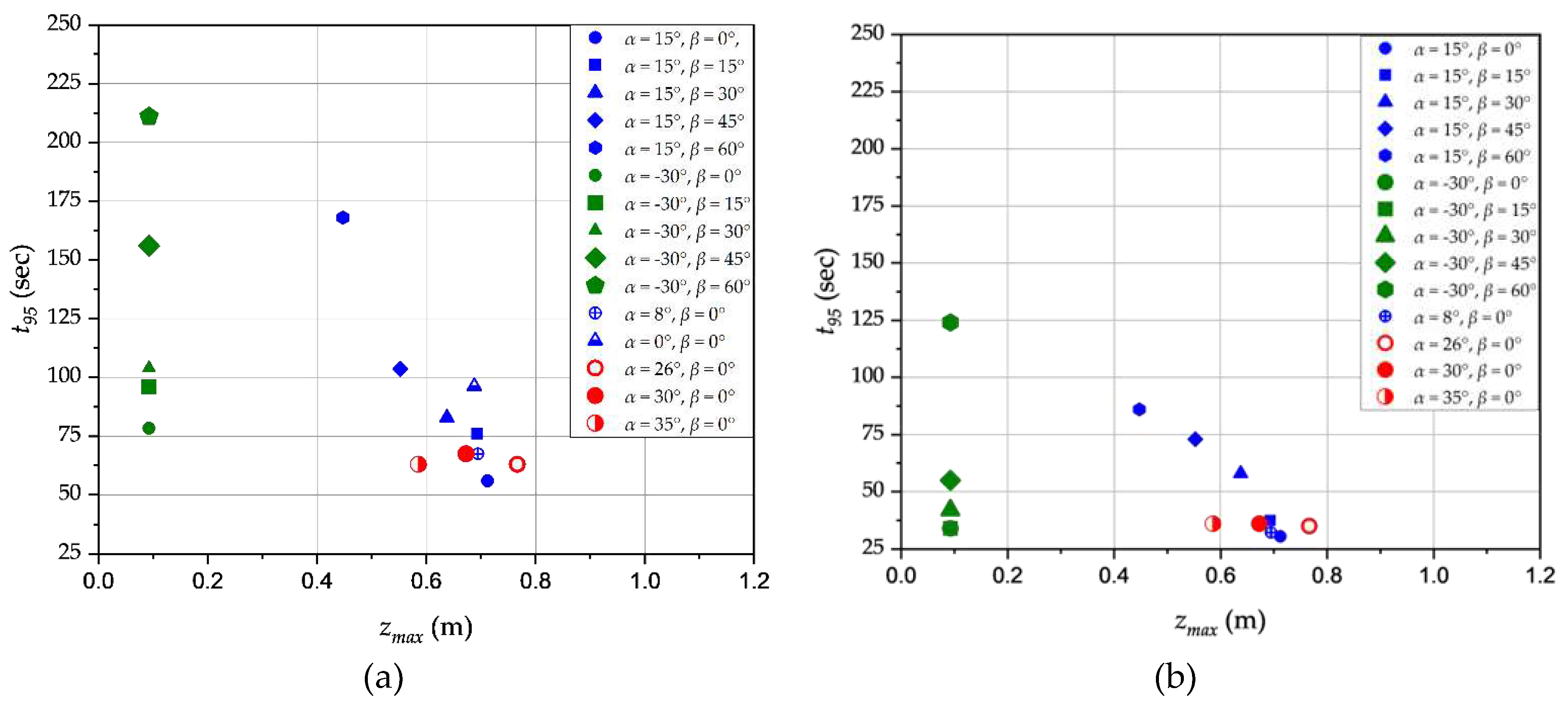
Preprints 80247 g011
Figure 11. Mixing time (t95) as a function of maximun jet length for dj = 0.005 m and for various nozzle positions at (a) Rej = 24900 and (b) Rej = 49900.
Figure 11. Mixing time (t95) as a function of maximun jet length for dj = 0.005 m and for various nozzle positions at (a) Rej = 24900 and (b) Rej = 49900.
Preprints 80247 g011
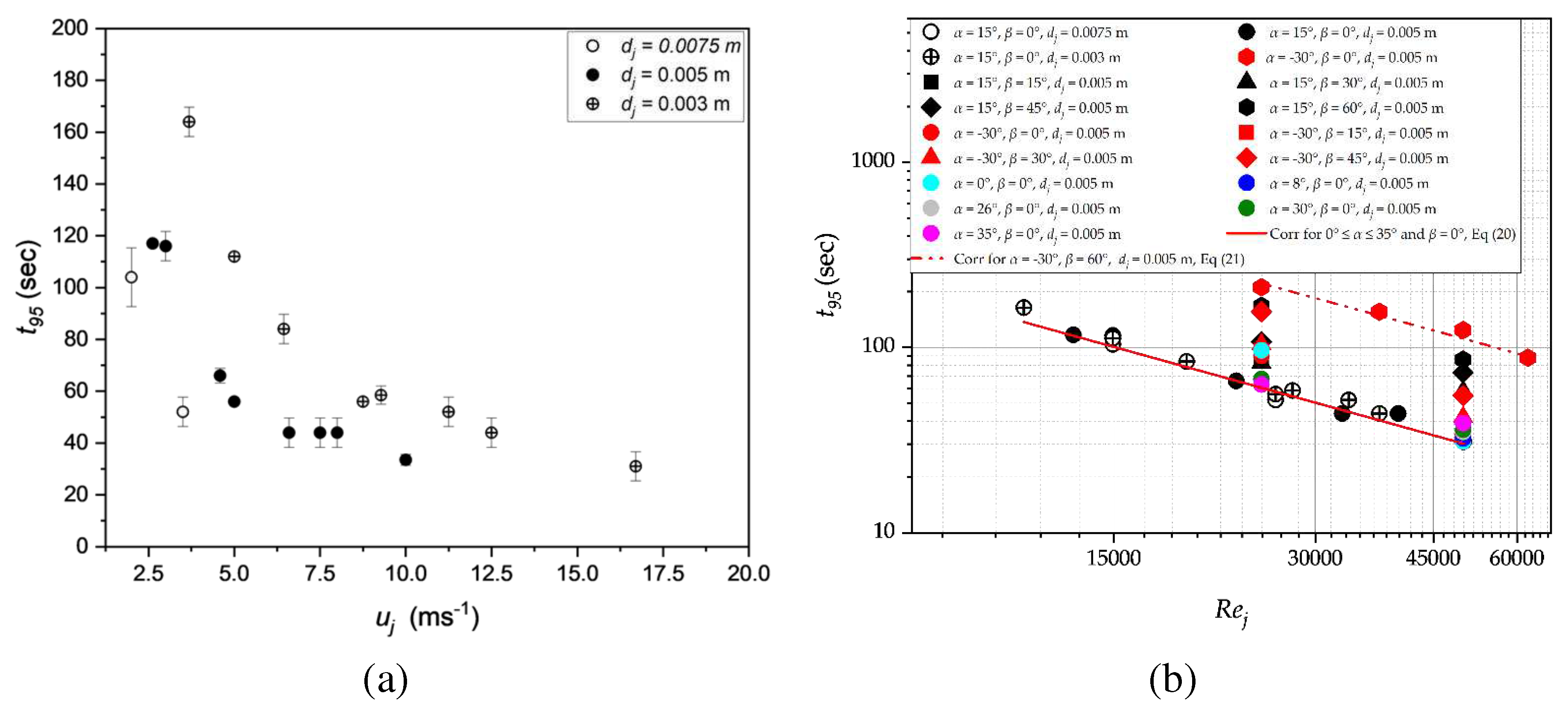
Preprints 80247 g012
Figure 12. Mixing time t95 (a) as a function of jet velocities for dj = 0.003 m, 0.005 m, and 0.0075 m with nozzle orientations of α = 15° and β = 0° (b) as a function of Rej: (15000 ≤ Rej  ≤ 62000).
Figure 12. Mixing time t95 (a) as a function of jet velocities for dj = 0.003 m, 0.005 m, and 0.0075 m with nozzle orientations of α = 15° and β = 0° (b) as a function of Rej: (15000 ≤ Rej  ≤ 62000).
Preprints 80247 g012
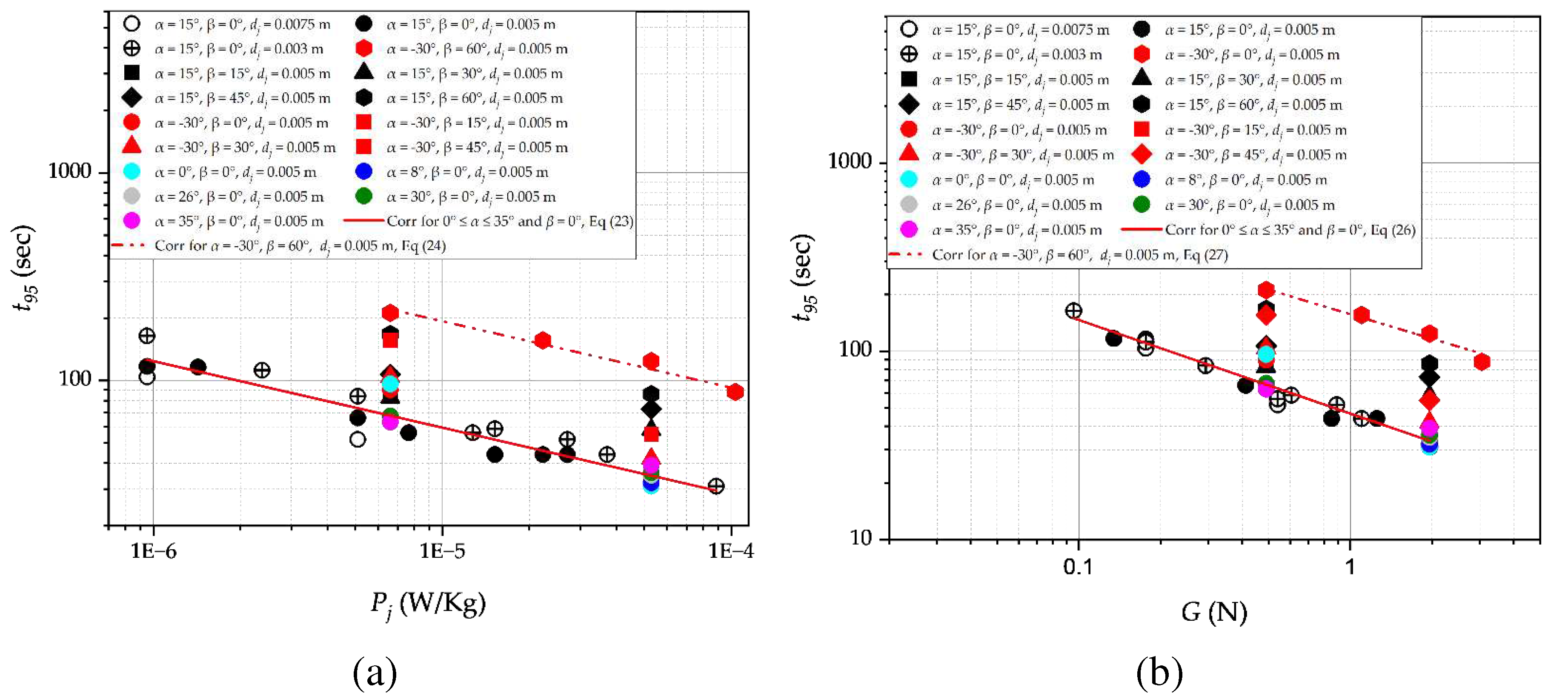
Preprints 80247 g013
Figure 13. Mixing time t95 as a function of (a) specific power input, and (b) jet flow momentum.
Figure 13. Mixing time t95 as a function of (a) specific power input, and (b) jet flow momentum.
Preprints 80247 g013
Table 1. Dimensions of the tank and nozzle for the experimental setup.
Table 1. Dimensions of the tank and nozzle for the experimental setup.
Parameter Symbol Value (m)
Tank diameter T 0.780
Liquid height H 0.390
Nozzle diameter dj 0.003, 0.005, 0.0075
Nozzle clearance from side wall XN 0.085
Nozzle clearance from tank bottom hN 0.050
Outlet clearance hO 0.192
Vertical inclination of nozzle α 35°, 30°, 26°, 15°, 8°, 0°, − 30°
Horizontal inclination of nozzle β 0°, 15°, 30°, 45°, 60°
Table 2. Values of 1/k used in the circulation model for various nozzle positions.
Table 2. Values of 1/k used in the circulation model for various nozzle positions.
A (°) β (°) dj (m) zmax (m) t c t R d j z m a x = 1 / k
− 30 0 0.005 0.093 0.32
15 0.005 0.093 0.31
30 0.005 0.093 0.264
45 0.005 0.093 0.193
60 0.005 0.093 0.164
15 0 0.0075 0.720 2.06
0 0.005 0.712 2.06
0 0.003 0.707 2.06
15 0.005 0.6930 2.06
30 0.005 0.638 1.46
45 0.005 0.552 1.10
60 0.005 0.447 0.70
0 0 0.005 0.688 1.88
8 0 0.005 0.694 1.61
26 0 0.005 0.766 1.22*
30 0 0.005 0.673 1.22*
35 0 0.005 0.585 1.22*
* Averaged k value from similar tank geometries and nozzle positions from Maruyama et al[12].
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated