Preprint
Article
Film Boiling Around a Finite Size Cylindrical Apecimen - A Transient Conjugate Heat Transfer Approach
Altmetrics
Downloads
128
Views
54
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
01 June 2023
Posted:
02 June 2023
You are already at the latest version
Alerts
Abstract
The DNS of film boiling requires strong computational resources that are difficult to obtain for a daily CFD use by the practitioners of the industrial R&D experts. On the other hand, the film boiling experiments are associated with the usage of the expensive and highly sophisticated apparatus, and the research to this end is found to be relatively difficult due to high heat flow rates that are present in the process itself. When combined with a transient heat conduction in a solid, the problem becomes significantly difficult. Therefore, a novel method in computation of conjugate heat transfer during film boiling in a quiescent liquid has been proposed in this paper. The method relies on the solution of mass, momentum and energy conservation equations in a two-fluid framework, supplemented with the appropriate closures. Furthermore, the turbulent flow has been found as an important parameter in obtaining the accurate solution of the temperature field evolution in a solid specimen, via the proper modeling of turbulent kinetic energy (TKE) value, that has been imposed as a constant value, i.e., the frozen turbulence approach. It was found, in addition, that the appropriate TKE value can be obtained by use of Kelvin-Helmholtz instability theory in conjunction with the boundary layer theory. The obtained results show excellent agreement with the experimental data within the first 15 s of the experiment, i.e., the first ca. 10 % of the total duration of the film boiling mode of heat transfer. Furthermore, the heat transfer coefficient has matched the error bands prescribed by the authors of the paper that has presented the correlations, whilst the averaged values are far beyond this band, i.e., are slightly more than 30 % higher. The further inspection has revealed a measure of similarity between the computational result of the volume fraction field distribution and the experiment, thus confirming the capability of the method to obtain realistic interface evolution in time. The method has shown full capability for further pursuing the industrial-scale film boiling problems that involve turbulent flow and the conjugate heat transfer approach.
Keywords:
Subject: Engineering - Mechanical Engineering
1. Introduction
The sustainable development of the world’s leading economies is strongly linked with optimized power engineering and metal processing industries. However, it is less known that these two industrial branches require well-optimized processes that involve boiling phenomena, to operate smoothly. Thus, the nucleate boiling regime is preferred among thermal power plants, since it allows for the removal of high heat fluxes with relatively small temperature differences at the heat transfer surface. Exceeding this limit, i.e., by surface overheating, may lead to a failure of the system with catastrophic consequences. This is the so-called film boiling regime. However, this unfavorable boiling mode in power plants is very common in the metallurgical quenching process, that is, the rapid cooling of a metal object to achieve certain microstructure that yields desired mechanical properties of the same, for example, hardness. To this end, a comprehensive set of experimental data is needed to achieve the safe and environmentally friendly work of these plants. But this experimental work is very costly and should be preceded by comprehensive theoretical and computational studies to extract the benefit from it. However, the computational studies of boiling incorporate very resource-demanding interface tracking methods (ITMs), that require very fine grid resolutions to model the interfacial phenomena; well known as the single-fluid methods, such as, for example, Volume-of-Fluid (VOF), coupled with Direct Numerical Simulation (DNS) of interface motion, in which the volume fraction of vapor/liquid is tracked by solving the advection equation. On the other hand, two-fluid methods can overcome this but require adequate closure models. Compared to the aforementioned single-fluid models, a two-fluid model is considered to be able to predict more accurate results on coarser mesh owing to the necessity of resolving the interface geometry/shape, though two sets of momentum and energy equations must be solved. However, due to the averaging process in the formulation of the governing equations, the shape, and area of the liquid-vapor interface are lost, and the dynamics related to the interface, e.g., surface tension and interphase forces, cannot be directly computed.
The relevant fundamental studies refer to the investigations that are focused more on microscopic phenomena and can be used for validation or verification purposes. The mass transfer model based on energy jump condition at the interface can be found in the study by Nichita [1]. The model is implemented within ANSYS Fluent as a part of coupled Level-set and Volume-Of-Fluid (CLSVOF) approach in the set of governing equations method via the source term in mass and energy conservation equations. A slug flow in a microchannel has been studied in Magnini [2]. The considered cases include isothermal flows; flows with heat transfer and flows with phase change, that is, the evaporative flows. The commercial software ANSYS Fluent has been extended in the direction of curvature calculation in the computation of surface tension body force in a single-fluid VOF model. To this end, a height function algorithm has been implemented within the software and validated against the already available interface reconstruction algorithm in the software. Furthermore, an evaporation model has been also included; however, since the method is aimed at micro-scale simulations, the assumption of thermodynamics equilibrium at the interface does not hold anymore, that is, the temperature of the interface differs from the saturation temperature. Another modified formulation of the energy jump mass transfer model and its application in film boiling relevant studies is proposed by Sun et al. [3]. The model is applied in solution to a one-dimensional Stefan problem and a film boiling on a horizontal surface, assuming thereby co-existence of saturated and unsaturated phases in the domain. A mass conservative method for the computation of phase change processes using a sharp interface representation is proposed by Sato and Ničeno [4]. The mass transfer rate is computed directly from the heat flux at the interface, thus allowing for the sharp distribution of the dominant mass transfer rate in the interface region; the interface thereby being denoted as an iso-surface (iso-line in 2 D) of the phase indicator (color function) equal to 0.5, and the cells bisected by this surface being marked as the interface cells. In the evaluation of temperature gradients, the orthogonal distances between the center of the interface cell and the interface are used. The study on film boiling in the vicinity of a sphere immersed in saturated water at atmospheric pressure, considering also the case with the involved radiation heat transfer, is carried out by Arévalo et al. [5]. The film boiling is studied for various solid surface temperatures, and the obtained heat flux values were compared with the results obtained using different correlations. Furthermore, an estimation of radiation coupling factors is done using numerical simulation. A comprehensive review of the computational models for the simulation of boiling and condensation phenomena is presented in Kharangate and Mudawar [6]. Among the reviewed models three distinct mass transfer models were outlined, namely: the energy jump, Schrage, and Lee model, and their characteristics are summarized in a tabular form. A study of the pool boiling process in which the film boiling regime is achieved as a consequence of exceeding the critical heat flux (CHF) limit is carried out in Sato and Ničeno [7]. The authors use the aforementioned approach [4] for handling multiphase flow with a phase change in an Eulerian framework, that is, using a single set of governing equations with a color function as an interface indicator, but adapting it to turbulent flow modeling using a large eddy simulation (LES) approach. More recently, the simulation of the dispersed flow film boiling (DFFB) regime using the level-set method (LSM) in conjunction with Direct Numerical Simulation (DNS) of turbulence is presented in Saini and Bolotnov [8]. This adiabatic flow study is carried out using “in-house” computational software PHASTA, based on stabilized finite-element method, with the conditions at the inlet obtained from single-phase computation.
In summary, the fundamental studies have revealed the main issues regarding the mass transfer modeling; and demonstrated the main mass transfer models; among them, the energy balance model has been identified as the most prominent, since it does not rely on empirical constants and stems from pure energy balance at the interface between the fluids. The two main issues in successful resolving of the film boiling during immersion quenching using this model are:
- The reconstruction of the temperature gradient at the vapor-liquid interface in the mass transfer model.
- The adequate turbulence modeling.
The necessary prerequisite to this end (first item) is the existence of the identifiable interface between the phases, such that the mass transfer may take place at the interface. This is due to the gradient of volume fraction incorporated in the computation of interfacial area density. Furthermore, an additional remark has to be pointed out on turbulence modeling (second item); since the turbulent heat flux is defined by consideration of the effective thermal conductivity and has to be computed accurately in order to estimate the transient temperature distribution in a solid object correctly. Hence, a more elaborate turbulence modeling has to be carried out, since there is a complex interaction between the vapor and liquid phase in the process. However, these approaches are mostly assigned to one-fluid formulations, such as VOF or LSM, wherein a single set of governing equations is solved for both phases, and hence the individual phase modeling instead of mixture, becomes difficult to handle.
Therefore, in this paper, a novel method for estimation of the mass transfer across the interface in a thermally driven phase change process is presented. The method is implemented within the two-fluid VOF formulation (available in the commercial CFD software ANSYS Fluent). It consolidates the benefits of the two multiscale multiphase modeling approaches: the low resolution meshes and large time steps from the two-fluid formulation; whilst preserving the sharp interface treatment using geometrical reconstruction algorithm, that is, a property of the pure VOF method, used generally for DNS of interface motion.
2. Materials and Methods
2.1. Description of the experiment
A film boiling experiment in the case of saturated and subcooled bath medium is reported in Momoki et al. [9], and used as a validation study in this work. The specimens of different sizes were submerged into liquid coolant and the temperature distribution was measured in the specimen center. The specimens were made of silver, thus, due to small Biot number, that is, 0 < Bi < 0.1, a lumped transient heat conduction model is relevant for estimation of solid temperature due to inexistence of significant temperature gradients with respect to space coordinates in the solid body. A sheathed K-type thermocouple was placed in the center of the specimen, and the sampling time was 0.25 s.
In the context of present work, a cylinder specimen with dimensions 45 mm in diameter and 45 mm in length, for which the transient temperature distribution is available, is used as a validation benchmark. The specimens that are made of materials without structural transformation during the process are used in determination of cooling characteristics of a quenchant medium.
2.2. Mathematical modeling
The mathematical model that underlies the proposed computational method is composed of mass, momentum and energy conservation equations, written on a per-phase basis, and supplemented with adequate closure models. The full description of the governing equation set, and appropriate closures is given in [10], whilst special attention regarding the heat transfer modeling at the interface has been presented herein. The goal is to invoke the kind of asymptotic-like behavior of a two-fluid model, in a sense that a sharp interface is maintained between the phases, whilst preserving all the features of a two-fluid model, i.e., the relatively small mesh resolutions with relatively high time steps. In what follows, a brief overview of the heat transfer aspect of the model is presented together with the turbulence modeling issues.
2.2.1. Interphase heat transfer
Since the saturation temperature liquid is assumed at this point, i.e., , and the heat flow rate from the interface to the liquid phase reduces to , the volumetric heat flow rate from the interface to the vapor phase reads:
where hv is the heat transfer coefficient at the vapor side of the interface, h’ is the specific enthalpy of a saturated liquid at the system pressure, is the interfacial area density, is the temperature difference between the interface and the vapor phase, is the volumetric mass transfer rate for a vapor-liquid phase pair in a phase change process, h’’ is the enthalpy of the saturated vapor at the system pressure. It is noteworthy that a heat balance between the phases exists, i.e., ∣Φv∣ = ∣Φl∣. The heat transfer coefficient at the vapor phase of the interface has a fictitious function in a sense that is used to involve the approximated distance between the neighboring cell’s center to the interface and thus to approximate the temperature gradient in the vicinity of an interface.
2.2.2. Turbulent flow
By insertion of an average turbulent kinetic energy in all the cells except the ones in the immediate neighborhood of the heat transfer surface, i. e. the specimen surface’s adjacent cells, one may enhance the heat extraction from the solid and thus achieve better agreement with the experimental data. This is due to the enhanced heat flux at the interface that reads [7]:
where λ is molecular thermal conductivity, λt is the turbulent thermal conductivity, and is the temperature gradient in the normal direction to the interface. Joining together molecular and turbulent thermal conductivity gives effective thermal conductivity:
In the validation case, the flow is considered as turbulent, although the turbulence transport equations are not being solved; yet the turbulent kinetic energy (TKE) is prescribed in all the cells of the computational domain, thus affecting the turbulent dynamic viscosity, μt, and, correspondingly, the turbulent thermal conductivity.
This approach can be referred to as the “frozen turbulence” approach, since the governing equations of turbulent transport are not being solved, yet the turbulent kinetic energy contributions to the effective thermal conductivity, and thus the heat flow rate extraction from the solid specimen, are considered by prescription of TKE values thorough the domain.
Furthermore, a dispersed formulation of a realizable k-ε turbulence model has been chosen for the computations herein. Thus, only the bulk phase turbulence is modeled with transport equations, while the dispersed phase turbulence modeling is carried out using the Tchen correlation [11], as per [12].
2.2.3. The “frozen turbulence” approach
The one half of the sum of principal stresses in a non-linear Reynolds stress tensor, that appears in momentum conservation equation after the Reynolds averaging of dependent variables is applied due to fluctuations of these quantities in a wide spectrum of wavelengths and frequencies, forms the turbulent kinetic energy, see e. g. in Markatos [13], as follows:
where is the fluctuating velocity component in the i-th direction (index notation). Hence, the turbulent kinetic energy is strongly interlinked with another flow variable, the turbulent viscosity, νt, that is relevant only for turbulent flow. Since it appears in the effective thermal conductivity term, it is thus plausible for heat rejection from a cylinder specimen. An analogy between film flow and free jet flow near the nozzle exit can be made, since the initial core with a laminar flow inside precedes the disturbed flow. The disturbance that appears in a downstream direction is a Kelvin-Helmholtz instability and is, according to Hoppe and Breurer [14], consequence of different tangential velocities across the interface between two fluids; the disturbance of this type is due to surface instabilities, and is noticeable in the case of large bubbles wherein the significant influence has the surface tension in contrast to small bubbles of small radii. The turbulent kinetic energy is, furthermore, in close relationship with turbulence intensity, another measure of turbulent flow. The experimental work by Philip [15] has revealed that in the case of annular jet flow, the peaks of turbulence intensities appear in the shear layers; thus, as claimed by the author, the turbulence occurs in the shear layers. The study by Kimber [16] has revealed that turbulence intensity profile closely follows the TKE distribution in a single jet flow. It is the bubble induced turbulence (BIT), studied in Ničeno et al. [17], wherein the liquid flow is turbulent, whilst the flow inside the vapor phase is laminar. Another analogy is with the flow of breaking sea waves in the surf zone; the studies of Kashima et al. [18] and Mori et al. [19] provide more detail in this regard; while the numerical assessment of this topic has been presented in the simulation in Makris et al. [20]. The authors conducted a detailed study using a Lagrangian method that corresponds to the LES approach.
As per Cascioli et al. [21], in a co-flow of a jet, a strong shear between the jet and surrounding fluid domain contributes to turbulent kinetic production; on the other hand, the overall heat transfer rate, extracted from the solid object and transferred to the vapor-liquid interface, is significantly dependent on flow condition, i. e., the shear force driving the flow of liquid in the immediate neighborhood of the interface, as can be concluded from theoretical exposure given in Sakurai et al. [22].
As in the case of the jet or liquid film flow, in film boiling around a vertical cylinder two distinct zones are defined according to Momoki et al. [9]: the zone of smooth interface and the zone where the interface is wavy. In contrast to flow of liquid film, that can be represented as Couette flow, as shown in Javed et al. [23], or a flow film boiling, where the maximum velocity, regarding the film, is in the vicinity of the upper part of the film; in this case, i. e., the film boiling in a liquid pool, a more convenient approximation is a pipe flow, that is, a non-slip condition at the outer surface of the film.
2.2.4. The estimation of the turbulent kinetic energy value
It is interesting to note, however, that these values correspond to a great extend to the ones obtained with the equation for turbulent kinetic energy proposed in Hillier et al. [24] that, in the context of the present research, read:
where is the mixture density, Δwrel is the relative velocity difference across the layer and Fv and Fl are the ratios between the density of vapor or liquid, respectively, and the sum of phase densities. The mixture density, , is defined as:
whilst density ratios, Fv and Fl read:
The velocity profile in the case of immersion quenching has, at least to a certain extent, a parabolic like profile, thus an assumption of Poiseuille's flow may be applied in obtaining the velocity distribution across the vapor layer, assuming thereby that the flow inside the layer is laminar, that is, λeff = λ. This assumption is justified that, in the case of pool film boiling around a vertical surface of a cylinder, non-slip conditions at the interface between vapor and liquid, and the stationary wall of the cylinder. Hence, a parabolic-like, as in the case of pipe flow velocity profile may be considered.
The relative velocity, that is, the velocity input in the above expression has to reflect the velocities in both the phases; hence, we assume that liquid velocity is zero, due to pool boiling conditions, thus the stationary interface between the phases may be assumed, the so-called “no-slip” condition. Consequently, inside the vapor film, a parabolic velocity profile may be assumed, that spreads over the vapor layer of thickness δ; hence, an averaged velocity through the vapor film is used in estimation of TKE, calculated from the continuity equation, that is, the mass conservation law as follows:
where qm is the mass flow rate per unit circumference is vapor phase density, and is an average thickness of the vapor layer, calculated as shown in Appendix A.
The computational model for analysis of the heat transfer phenomena during film boiling on a vertical surface is proposed in Yamada et al. [25], being derived for the case of film boiling at the vertical plane surface. Hence, a rectification of the unit width is conducted here by multiplication with π, when a cross-section of fluid element perpendicular to the flow direction is considered in obtaining the average velocity, Equation (10). The authors in the aforementioned article distinguish four different cases at the vapor-liquid interface, considering thereby the conditions at the bottom horizontal surface of the cylinder; hence, a no-slip condition at both, the vapor layer beneath the cylinder and at the vertical surface is taken into account in this study, due to the pool boiling conditions that are present in the flow.
The mass flow rate is defined analogously to Nusselt’s film condensation theory, from the momentum balance on the fluid element, with the exception of multiplication by 1/12 instead of 1/31
where local layer thickness, that is present in the original model, is replaced with the averaged one, computed as shown in Appendix A.
The assumption of laminar flow inside the vapor layer may be approved with calculation of Reynolds number:
where is the mean velocity of the vapor phase, deqv is the equivalent diameter, and νv is the vapor phase’s kinematic viscosity. The equivalent diameter is calculated as a difference between the outer diameter of the vapor film, i. e., Dv = d + 2δ, and diameter of cylinder, d = 0,045 m; or the equivalent diameter can be calculated as deqv = 4A/O = 2δ. This yields a value of 33.3, and thus confirms the accepted assumption of laminar flow inside the vapor film.
2.3. Computational modeling
2.3.1. Description of the case and geometry
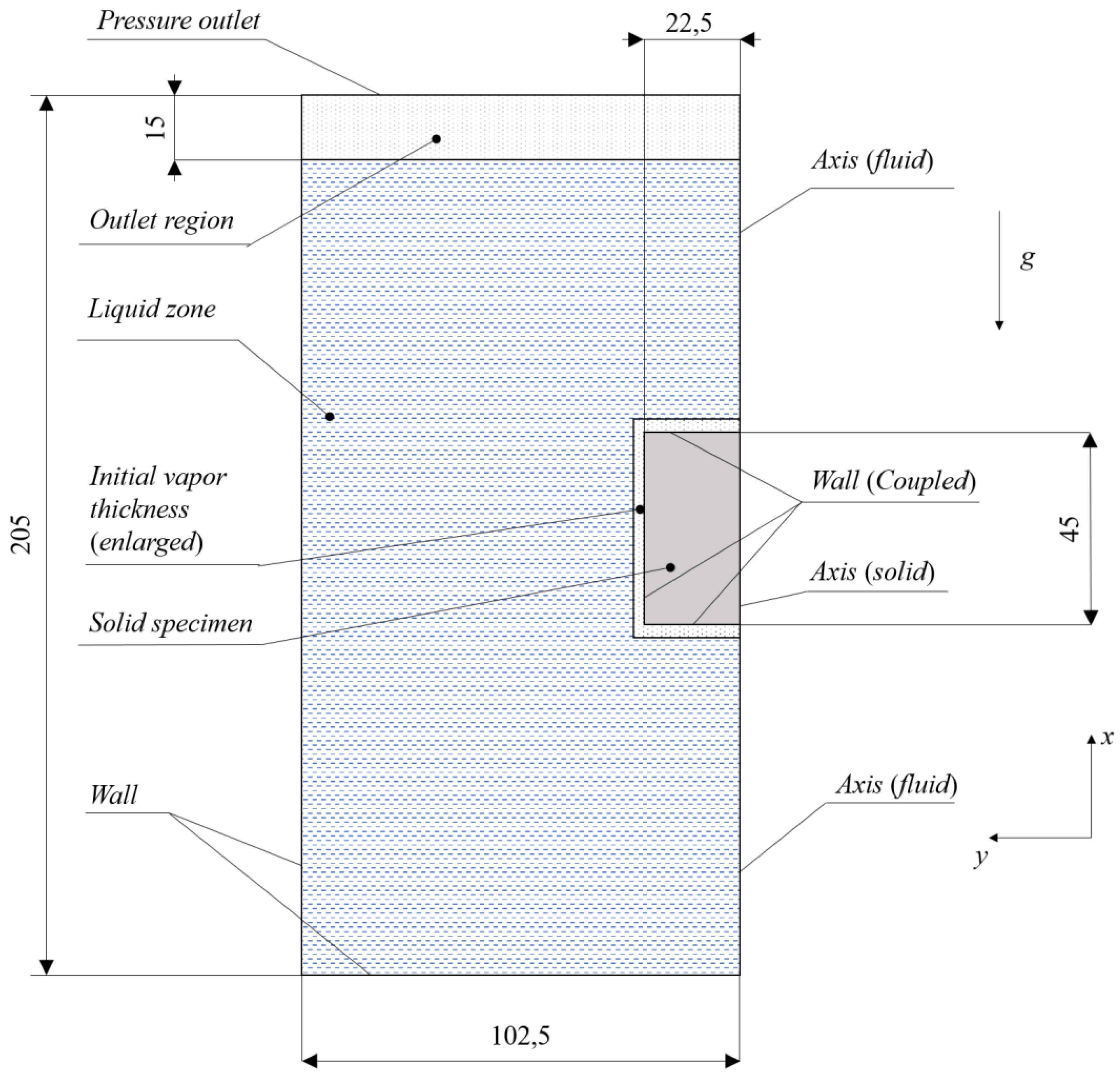
An axis-symmetric domain is constructed with the cylinder specimen placed in the middle of the domain height, as shown in Figure 1. The computational domain spans over the area x ∈ [-1.025e-1, 1.025e-1] m × y ∈ [0, 1,025e-1] m, and is composed of fluid and solid part, separated via the fluid-solid interface. At the domain top, a 15 mm high outlet region is prescribed, containing the vapor phase. In the vicinity of the solid specimen, a one-cell vapor layer is initially placed, with a thickness of 0.61 mm, required for the mass transfer model in order to induce the mass transfer. In Figure 1, the vapor blanked is, for the sake of simplicity, enlarged.
Figure 1.
A schematic representation of the validation model with the boundary conditions in two dimensional axisymmetric coordinate system. The dimensions are in mm.
Figure 1.
A schematic representation of the validation model with the boundary conditions in two dimensional axisymmetric coordinate system. The dimensions are in mm.
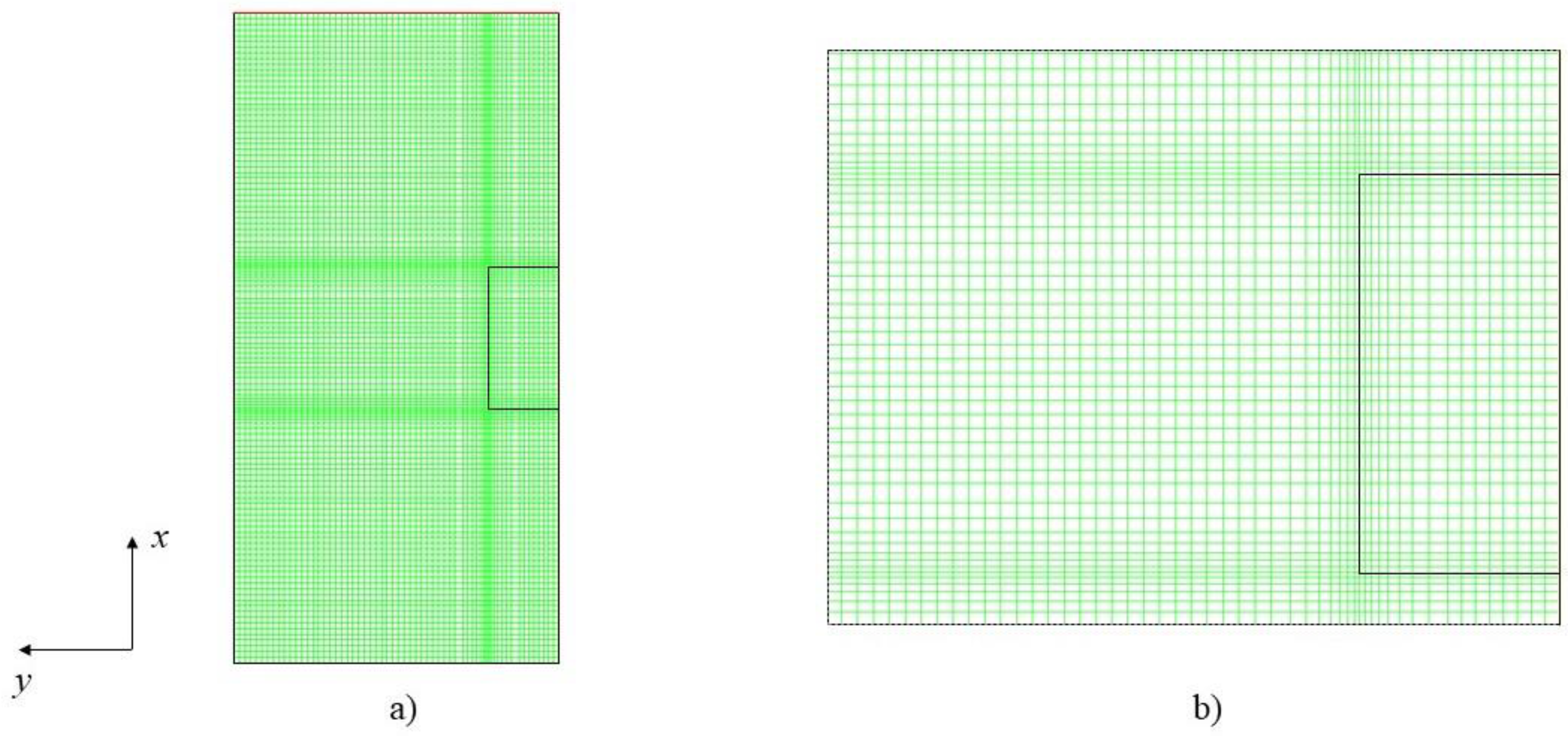
The domain is composed of 7938 quadrilateral cells (Figure 2a), with the refined cell zone adjacent to the specimen surface (Figure 2b). The specimen is made of silver and has equal diameter and height, 45 mm.
Figure 2.
(a) The entire computational mesh; (b) A magnified view in the vicinity of the fluid-solid boundary.
Figure 2.
(a) The entire computational mesh; (b) A magnified view in the vicinity of the fluid-solid boundary.
2.3.2. Boundary conditions
The boundary conditions are assigned to the domain’s top, bottom, and left side surface for both the phases, whilst the domain symmetry axis is defined as “axis” in the applied software. Thus, the top of the domain is set to pressure outlet condition, with prescribed outlet temperature 100 oC for both phases and the unit backflow vapor volume fraction. The bottom and left surface are defined as solid walls. The specimen surface is composed of three walls that interact with the fluid region via “coupled” condition.
2.3.3. Initial conditions
The initial conditions involve the initial distributions of phase volume fractions, temperatures and velocities, supplemented with the initial profile of turbulent kinetic energy that is, in contrast to other aforementioned dependent variables, maintained constant through the simulation, since the turbulence equations are not being solved - so-called „frozen turbulence” approach. The velocity fields of both phases were initially set to zero elsewhere in the domain, although the turbulent kinetic energy is initially set to a non-zero value everywhere except the initial vapor layer.
The initial temperature of a solid specimen is set to 600 oC, as per experiment in Momoki et al. [9]. The liquid and outlet zone were set to the initial temperature of 100 oC. Inside the vapor layer, an initial temperature field is prescribed as follows (see Figure 3 and Figure 4).
Figure 3.
A schematic representation of initial temperature field distribution: (a) In radial direction, in vicinity of the vertical surface; (b) In the immediate neighborhood of top and bottom horizontal surface.
Figure 3.
A schematic representation of initial temperature field distribution: (a) In radial direction, in vicinity of the vertical surface; (b) In the immediate neighborhood of top and bottom horizontal surface.
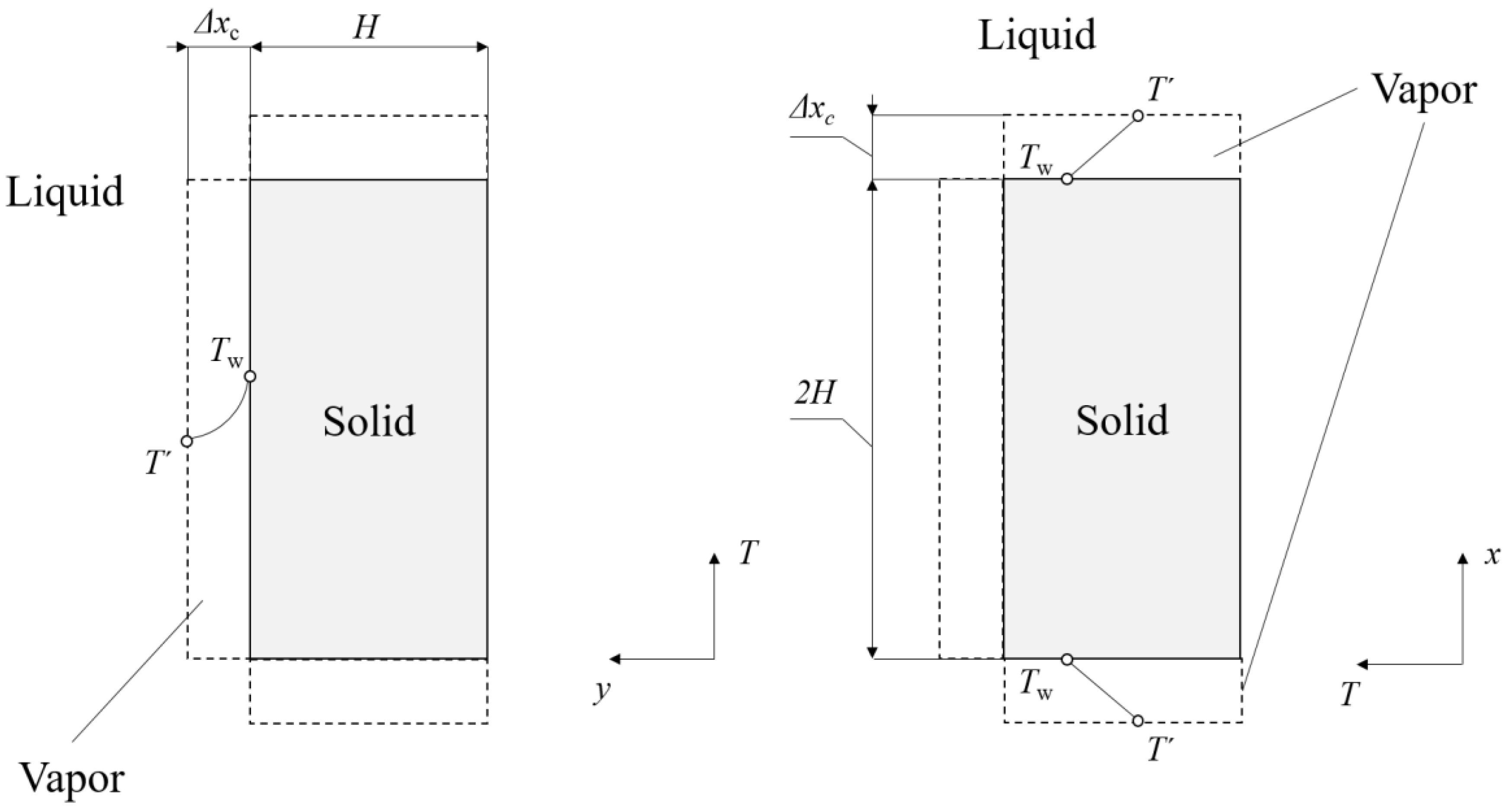
Figure 4.
A conceptual sketch on determination of initial temperature in the edge control volume: (a) The position of the control volume; (b) The neighboring cell center values used in computation.
Figure 4.
A conceptual sketch on determination of initial temperature in the edge control volume: (a) The position of the control volume; (b) The neighboring cell center values used in computation.

In radial direction along the cylinder height, due to the analytical solution of the heat conduction equation in the radial direction of a cylindrical coordinate system (see Figure 3a for a qualitative description), a logarithmic temperature profile is imposed as follows:
whilst in the axial direction, at top and bottom surfaces, respectively, it follows the linear law due to the same reason as in the former case (the analytical solution to heat conduction PDE in the axial directions of the cylindrical coordinate system; see Figure 3b for a qualitative description):
The edge element, however, is filled with the initial temperature computed as (Figure 4):
that stems from an energy balance on a knot in the cell center assuming thereby that the face temperatures of neighboring cells are those of their respective cell centers. This yields, however, the initial temperature in the edge control volume (CV) that is lower than these other two temperatures, due to cooling contributions from two sides that remain at, significantly lower, saturation temperature.
2.3.4. Time stepping procedure applied in the simulation
The time step applied in simulation is divided into two parts. Firstly, ten time steps with a size of 1e-6 s were carried out. Then, a 2e-4 s time step size has been applied in the remainder of the simulation. Extensive study on the applied time-step size, and a brief comment on the applied equation- discretization techniques can be found in [10].
3. Results
3.1. Temperature distribution
The temperature distribution in a solid specimen agrees well with the experimental data by Momoki et al. [9] in approximately ten percent of total film boiling period2, as shown in Figure 5.
Figure 5.
The temperature evolution in a solid specimen during approximately the first 15 s of the simulation; the data is compared to the experimental results from Momoki et al. [9], extracted using [26]. The dashed line denotes ± 2 % error band.
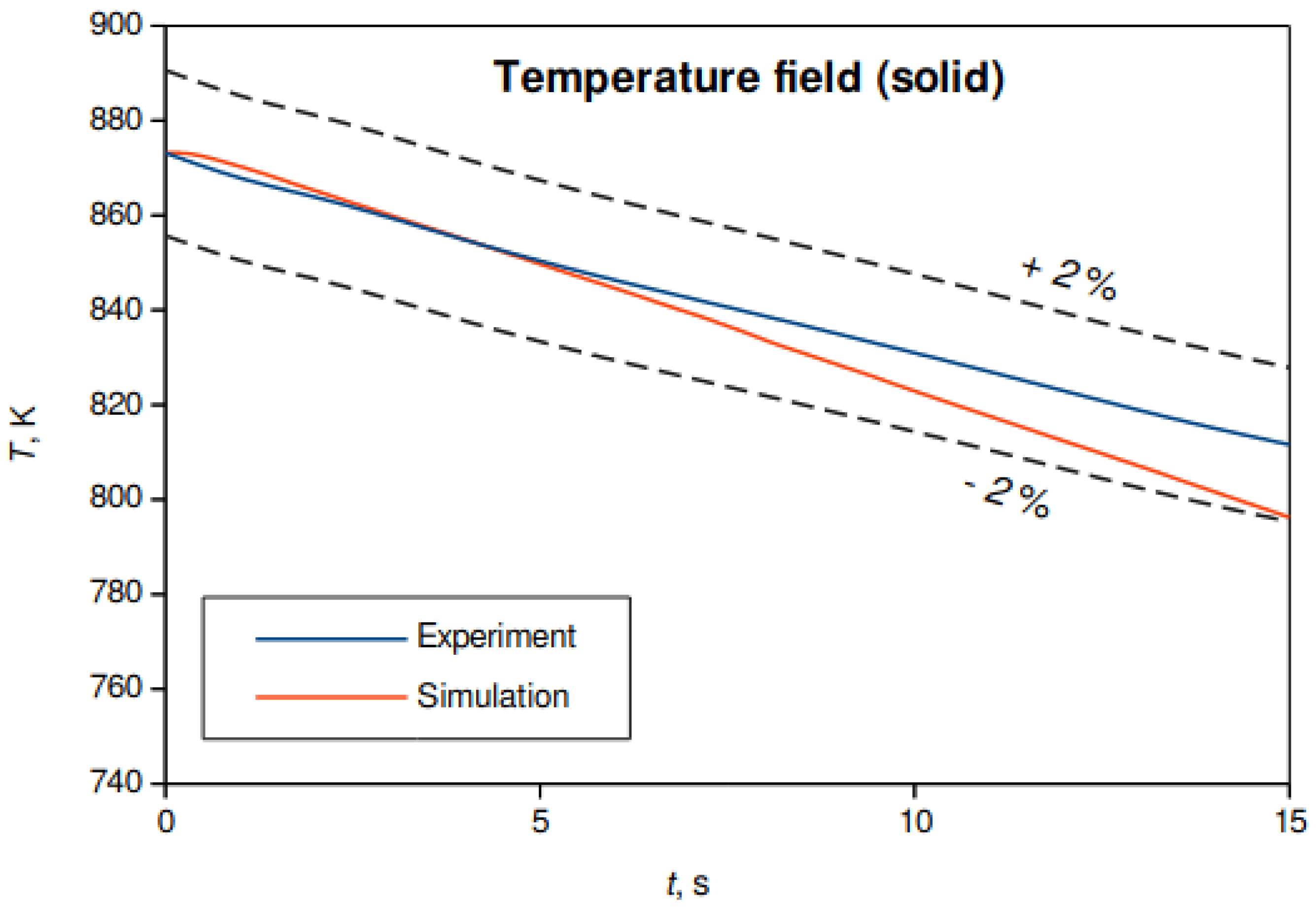
The time shift is accomplished using initial vapor thickness as shown in [10], since there is no known analytical solution to Stefan problem in cylindrical coordinates, as outlined by Galović [27]; yet there is a quasi-steady approximate solution that is valid for low Stefan number, Ste = cp(Tw – T’)/r0, that is, in the case of the low wall superheat.
3.2. Comparison of calculated heat transfer coefficients
The area weighted average heat transfer coefficients were extracted using the graphical-user interface; the data is stored approximately every 0.2 s. The calculated heat transfer coefficient, h, in the performed numerical simulation stems from the Newton’s cooling law:
where qw is the heat flux at the specimen wall, Tw and T∞ are the wall and free stream temperature, respectively. The area-weighted heat transfer coefficient is calculated as a post-process, considering thereby the heat transfer rates at bottom, top and vertical (circumferential) surface of the cylinder; that is, the overall heat transfer coefficient is taken into account; instead of separate, per-surface heat transfer. The analytical solution to average overall heat transfer coefficient is presented in Momoki et al. [9] and reads:
where and are, respectively, the average heat transfer coefficient at the bottom and top horizontal surface of the cylinder; and are the heat transfer coefficients at the vertical surface in the region of smooth and wavy vapor-liquid interfaces, respectively, whilst L and LB1 denote the total and smooth interface length, respectively; D is the diameter of the cylinder. In their study, the authors impose the ± 15 % error bandwidth on the estimated average heat transfer coefficient results. Hence, we will stick here to the value obtained using the Equation (18), and the result is shown in Figure 6.
Figure 6.
The calculated heat transfer coefficients using numerical simulation in comparison to ones obtained using Equation (18).
Figure 6.
The calculated heat transfer coefficients using numerical simulation in comparison to ones obtained using Equation (18).
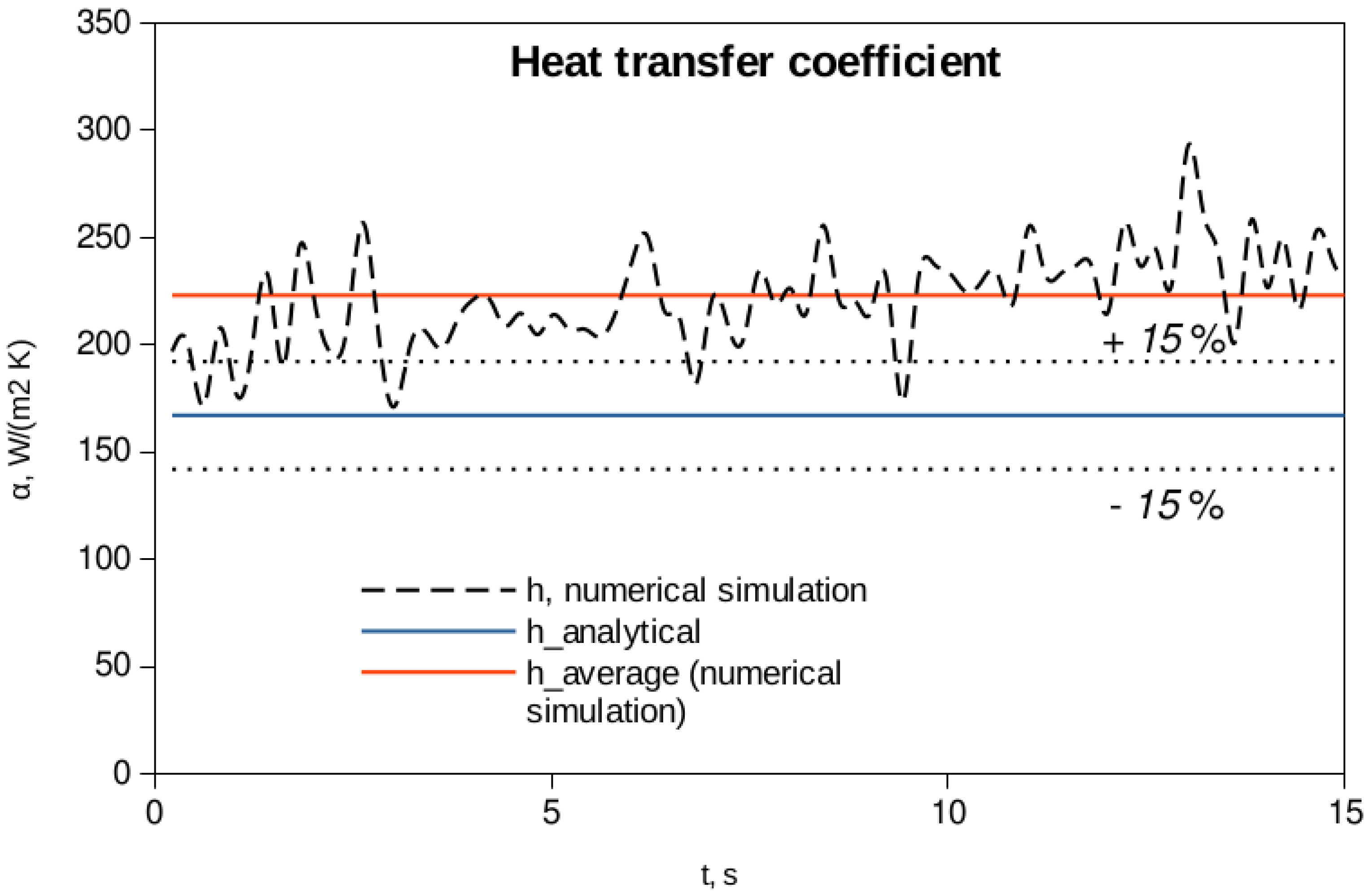
In the formulae for average heat transfer coefficient during film boiling around a finite length cylinder specimen, Equation (18), the contributions from each heat transfer surface via its own heat transfer coefficient noted above, the vapor phase is considered and superheated and thus the thermal properties of the vapor phase were taken for mean temperature, ϑm = (ϑw + ϑ’)/2, from [28] using the linear interpolation technique, and are listed in Table 1.
Table 1.
The thermal properties of superheated vapor are used in estimation of film boiling heat transfer coefficient at the temperature 350 oC.
Table 1.
The thermal properties of superheated vapor are used in estimation of film boiling heat transfer coefficient at the temperature 350 oC.
| Phase | , kg/m3 | cp, kJ/(kg K) | λ, W/(m K) | Pr, - |
| Vapor | 0.35 | 2.04 | 0.041 | 0.91 |
The liquid (water) is considered as saturated, hence among the thermal properties of the water, only the density is used, = 958.41 kg/m3, also taken from [28].
The discrepancy is found to be slightly more than 30 % in the present numerical simulation. The average heat transfer coefficient from the numerical simulation is calculated as:
where, refers to a calculated heat transfer coefficient using numerical simulation, is the time segment used for the averaging of heat transfer coefficient, and is the total simulation time, ~15 s.
In Figure 6, furthermore, one can observe the cyclic behavior of the heat transfer coefficient. This is due to cyclic behavior of the vapor-liquid interface during the film boiling process, that has been also noted in study by Tsui et al. [29]. The heat transfer coefficient, obtained via the numerical simulation, enters the upper limit of the error band, that is 15 %, prescribed by the authors of the correlation.
The vapor evolves from the top horizontal surface and is being advected due to buoyancy to the free surface of water, as shown in Figure 7; forming thereby the vapor jet, as observed also in other studies. Similar flow patterns were observed with photographic study in Tsui et al. [29] and Jurić and Tryggvason [30]; both being calculated for film boiling on a horizontal surface.
Figure 7.
Transient behavior of: (a) vapor film, (b) temperature in the vapor phase and (c) temperature in the liquid phase.
Figure 7.
Transient behavior of: (a) vapor film, (b) temperature in the vapor phase and (c) temperature in the liquid phase.

The temperature field, on the other hand, exhibits slightly overheating above the top of the cylinder, while being uniform elsewhere. The superheats may be found comparable, at least quantitatively, to those in the film boiling study by Sato and Ničeno [7]. The uniform temperature distribution in a solid is due to its small Biot number and, therefore, the inexistence of spatial temperature gradients in a solid. Since the vapor temperature doesn’t differ significantly from the liquid temperature, the latter would be studied any further in this text.
An analysis of a single bubble using Newton’s second law, that is, the momentum conservation equation, shows how the bubble shape is influenced by inertia, buoyancy, viscous and surface tension forces. The study by Yamada [31] reveals the true behavior during film boiling of a cylinder specimen studied here, but with different dimensions. It is rather difficult to make a direct comparison with the experimental observation, but at least qualitatively one may obey the similarity between the performed simulation and the experiment that is conducted using silver specimens of similar dimensions and wall superheat.
In Table 2, a comparison of the flow fields obtained in the numerical simulation and the one in experiment is made. The influence of surface tension is in the tendency to minimize the contact area between the bulk fluid and a vapor phase, i. e., the surface tension force acts on the vapor, and tends to minimize the shape of the vapor bubble.
Table 2.
Joint comparison of experimental and the flow fields (volume fraction) obtained with usage of numerical simulation.
Table 2.
Joint comparison of experimental and the flow fields (volume fraction) obtained with usage of numerical simulation.
| Quantity | Simulation; d × L = 45 × 45 mm | Experiment [31]; d × L = 32 × 32 mm |
| Flow field |  |
 |
| t, s | 10.22 | 15 |
| ΔTw, K | 444.9 | ~345 |
3.3. The applied turbulent kinetic energy value
The effective thermal conductivity in a liquid phase, as outlined before, has been found to be crucial in appropriate modeling of heat extraction from a solid specimen. Hence, since the molecular thermal conductivity of the liquid phase remains constant thorough the computation, one should affect the turbulent part of the effective thermal conductivity; which, on the other hand, is a function of a turbulent viscosity since the turbulent Prandtl number is assumed as constant. The turbulent viscosity, from the viewpoint of truly relevant dependent variables, is a function of turbulent kinetic energy, although there is also a factor Cμ, that in the case of the selected two-equation turbulence model is a variable, that is, it has not its default value 0.09 as in standard and RNG instances of the model. However, we will now focus on turbulent kinetic energy as the key parameter in turbulence modeling; similar has been also pointed out in the thesis by Subhash [32]. Within the framework of the present work, the TKE value has been obtained using a parametric investigation. A parametric study has been carried out in order to determine the TKE value for which the temperature evolution would agree with the experimental result. In this case it was 0.25 m2/s2. This value, however, may be obtained from Equation (6) if the velocity input is taken from numerical simulation; the volume-weighted average velocity magnitude field of the vapor phase in the boundary layer in vicinity of the vertical surface of the cylinder. In doing so, the one-cell boundary layer thickness may be found as appropriate since the two-fluid model is used, and the mesh resolution does not play an important role in obtaining the accurate solution, as shown in study by Gauss et al. [33]. In addition, the usage of fine mesh resolution is regarded as inappropriate in the framework of Euler-Eulerian modeling, as noted in the study by Liu and Pointer [34]. Figure 8 compares the calculated TKE values using Equation (6) and the one obtained with parametric study and used in this validation case.
Figure 8.
The comparison of the applied TKE value, obtained by use of a parametric analysis, and the ones obtained using Equation (6).
Figure 8.
The comparison of the applied TKE value, obtained by use of a parametric analysis, and the ones obtained using Equation (6).
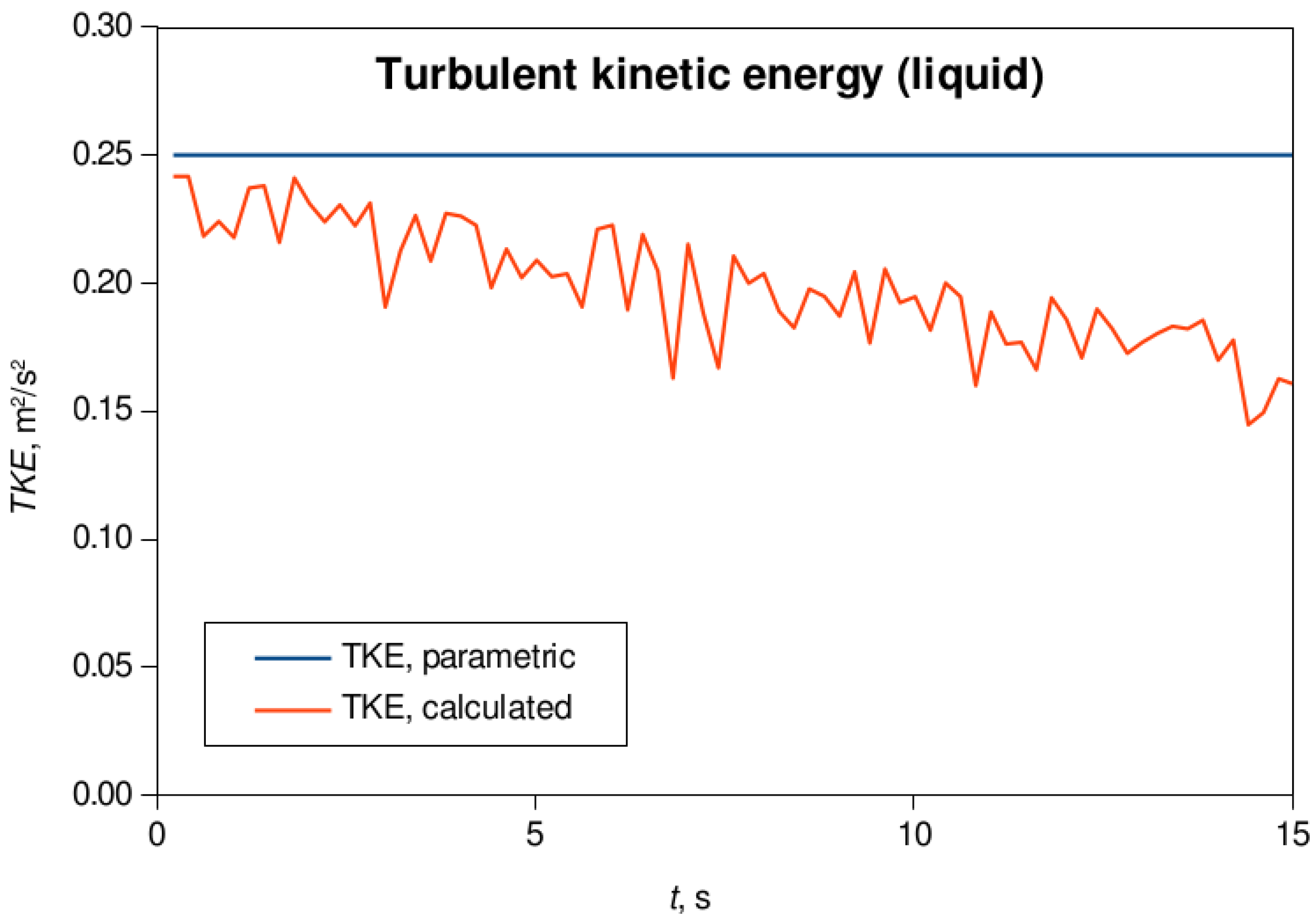
It is, however, obvious that the applied TKE value obtained using the parametric investigation is slightly overestimated in the very beginning of the film boiling process (first 5 s of the process), whilst being completely overestimated in the later section of the process; when compared to calculated values using Equation (6).
This range of TKE values, say, ~ 0.15 m2/s2 to ~ 0.25 m2/s2, could be related to the studies that follow. The study by Kashima et al. [18] brings us the study from Svendsen [35], in whose model, if the TKE values in the range from 0.05 m2/s2 to 0.15 m2/s2 are used together with a certain turbulent length scale, one may obey the energy dissipation rate, in the context of breaking surf zone wave analysis. It is interesting to note that these values coincide with the TKE values obtained in instability of a stable vapor flow study presented in Zimmer and Bolotnov [36]. In their study, the authors found 0.15 m2/s2 value of TKE as the threshold value in causing the instability of the stable slug flow. Also, the authors have proposed the correlation for which average value of TKE the instability may occur. Furthermore, these findings, obtained in the present research, are in close correspondence with the TKE value obtained in an analysis of a single jet flow in Kimber [16], wherein a 0.2 m2/s2 is obtained slightly beneath the jet core.
On the other hand, the TKE value of 0.25 m2/s2 has been chosen as the highest TKE input value in the simulation of dispersed two-phase flow using LES method in the context of atmospheric turbulent boundary layer modeling in Vinković et al. [37]. Contrasting the temperature field in a solid specimen (Figure 5) with the calculated TKE values (Figure 8) may reveal that the constant TKE value resulted in too strong cooling after initial say 5 s of the process; yet the variable TKE value should be considered in further studies.
The visual observation of turbulent viscosity and corresponding vapor volume fraction fields shown in Figure 9., reveals how the former closely follow the pattern of the latter. This may be addressed to the selected mode of the applied turbulence model, i. e., the dispersed mode, wherein the turbulence is being modeled only in the continuous phase, whilst Tchen correlation has been used in the dispersed phase. In addition to this, there is also a changeable turbulent viscosity coefficient, Cμ, that is present in the selected, although not solved, turbulence model. This may be found relevant in obtaining the turbulent viscosity adjacent to the interface, in the liquid phase; the transition values from zero to a constant value that is in the bulk, since the k is assumed as a constant. Hence, it is obvious that a laminar flow is concerned within the vapor phase, implying the existence of the BIT in the performed numerical simulation. Speaking in terms of analogy with a turbulent jet flow, the realizable k-epsilon turbulence model is recommended for such flows.
Figure 9.
The distributions of (a) turbulent viscosity and (b) volume fraction of vapor in two different time instances.
Figure 9.
The distributions of (a) turbulent viscosity and (b) volume fraction of vapor in two different time instances.
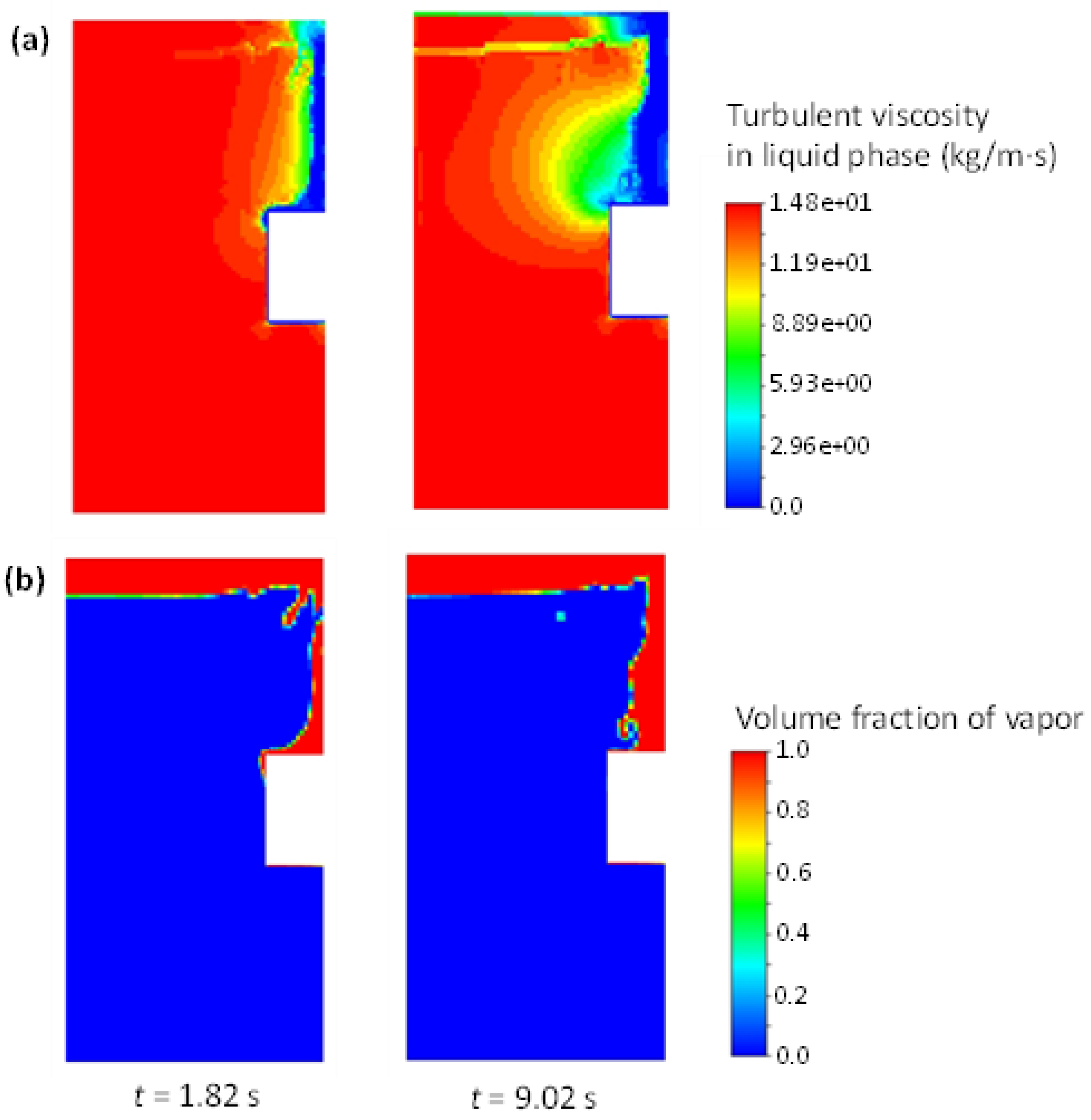
In the present case, the Cμ is a function of strain rate, that is, the non-diagonal elements of a strain rate tensor (momentum equation) that can be found in standard continuum mechanics or fluid mechanics textbooks and reads [38]:
where i and j are indexes of spatial coordinates in index notation (i, j = 1, 2, 3; meaning: x-, y- and z-coordinate), with u as the fluid velocity in the i-th direction and correspond to tangential stresses (friction). Hence, the distribution of the turbulent viscosity exhibits the pattern shown before in Figure 9; it experiences smooth transition in the areas in the liquid that are occupied with a vapor-liquid interface. This friction is further transferred into the liquid in the nearby zone to the interface between the phases. Once more, we prove, at least quantitatively, the necessity of the application of such an instance of the selected turbulence model (realizable) in modeling such a phenomenon (film boiling).
A joint view of velocity magnitude of the vapor phase and its strain rate shows how the friction is about to occur at the interface nearby zone, say, the “shear layer” in the context of the turbulent jet flow, Figure 10, where velocity gradients are the highest. A discussion on the application of this model in the context of jet flow in a confined space is available in Heschl [39].
Figure 10.
An observation in vapor phase distributions of (a) velocity magnitude and (b) strain rate. The strain rate follows closely the interface shape, indicating the presence of friction at the interface between the phases.
Figure 10.
An observation in vapor phase distributions of (a) velocity magnitude and (b) strain rate. The strain rate follows closely the interface shape, indicating the presence of friction at the interface between the phases.

4. Conclusions
In this paper, a novel method calculating mass transfer for two-phase flows with phase change has been proposed. The method is based on a two-fluid VOF formulation, and involves two asymptotic-like behaviors, i. e., the equality of the velocities and temperatures of the phases involved at the interface; thus, mimicking the pure VOF calculation. The method is previously verified using an analytical solution to Stefan problem, using thereby the computational meshes of three different cell types, namely: quadrilateral, stretched and hybrid cell type meshes. Furthermore, in this paper, the method is validated using the experimental data for pool film boiling during cooling of a silver specimen, available in Momoki et al. [9]. The silver specimen has been subjected to a liquid medium, water, at saturation temperature; hence, the vapor film thickness is mostly pronounced. To accomplish this by use of numerical simulation, additional treatment of turbulent kinetic energy has been carried out in order to extract the, at least to a commensurate level of accuracy, the heat flux from the specimen, and, therefore, to accurately estimate the temperature field in a solid specimen; a transient CHT approach has been used in the simulation of the film boiling, and the accuracy of the model has been evaluated from the viewpoint of temporal distribution of the solid temperature in the vicinity of a particular point in a solid body.
The TKE value has been obtained by using a parametric study, i. e., it was varied until a sufficiently correct estimate of a solid temperature was obtained. The TKE value of 0.25 m2/s2 has been found as a reasonably accurate, i. e., a ± 2 % accurate temperature distribution in the immediate neighborhood of the specimen center was obtained in ~ 10 % of the total duration of stable film boiling.
Hence, a transient CHT film boiling simulation in axis-symmetric coordinate system has been carried out within the validation part of the work, and the following conclusions may be drawn:
- The shared velocity field values at the interface have accurately represented the interface behavior also in the case of more complex interface evolution.
- The application of the dispersed turbulence model is necessary in order to correctly estimate the temperature distribution in a solid; that is, the BIT may be assumed in the present context of the pool film boiling.
- The application of Kelvin-Helmholtz instability theory in estimation of TKE magnitudes has been found to be very straightforward when used in conjunction with the boundary layer theory in estimation of the necessary velocity input.
- The obtained heat transfer coefficient values exhibit a cyclic character, the same as the evolution of vapor-liquid interface, as shown by the other authors.
- The obtained heat transfer coefficients only locally enter the prescribed error bandwidth of ± 15 %, whilst the average value is slightly above 30 %.
- The temperature distribution in a solid material has agreed with the measured values in, say, ~ 10 % of total duration of film boiling phase.
- The selected turbulence model has exhibited a realistic value of turbulent viscosity inside the vapor film, which may be addressed to usage of Cμ factor that, among other variables, depends on strain rate.
Finally, a zero-equation-like turbulence modeling approach has been found appropriate; in addition to the proposed mass transfer model. Thus, all the prerequisites for conduction of a real quenching case that is industrially relevant have been completed and are a matter of the subsequent publication.
Further investigations may also address the occurrence of selective radiation of gases. Since the vapor is participating in radiation heat transfer, involvement of selective radiation of gases may have some content in the future research. added if there are patents resulting from the work reported in this manuscript.
Author Contributions
Conceptualization, A.C. and Y.S.; methodology, A.C.; software, Y.S., and B.N; validation, A.C.,; investigation, A.C.; resources, I.B.; data curation, A.C.; writing—original draft preparation, A.C.; writing—review and editing, Y.S., and I.B; visualization, A.C.; supervision, I.B.; project administration, I.B., and B.N; funding acquisition, I.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data is available upon request from the corresponding author.
Acknowledgements
The first author would like to express his sincere gratitude to Assistant Professor Severino Krizmanić, PhD, who proposed the “frozen turbulence” modeling approach. Furthermore, the help received from Mr. Danijel Zadravec in obtaining the equation for the initial temperature in the edge control volume has been gratefully acknowledged. The discussion with Dr. Robert Keser on the application of a suitable time advancement procedure has been also appreciated. The inputs received by Professor Antun Galović are also kindly appreciated. The help from Mr. Taku Yonemoto, The University of Tokyo, has been also gratefully acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
In what follows a boundary layer theory analysis, according to Yamada et al.[25] has been performed in order to study the vapor film thickness. The average vapor film thickness reads:
where is the average dimensionless film thickness, L is the specimen length (height in the case of vertical, upward oriented, cylinder, expressed in m), GrB is the Grashoff number for this natural convection case and Sp is the degree of wall superheat. The average dimensionless vapor layer thickness, , is calculated as:
where is the dimensionless vapor layer thickness profile, given by the expression derived in Yamada et al. [25].
After integration the profile equation reads:
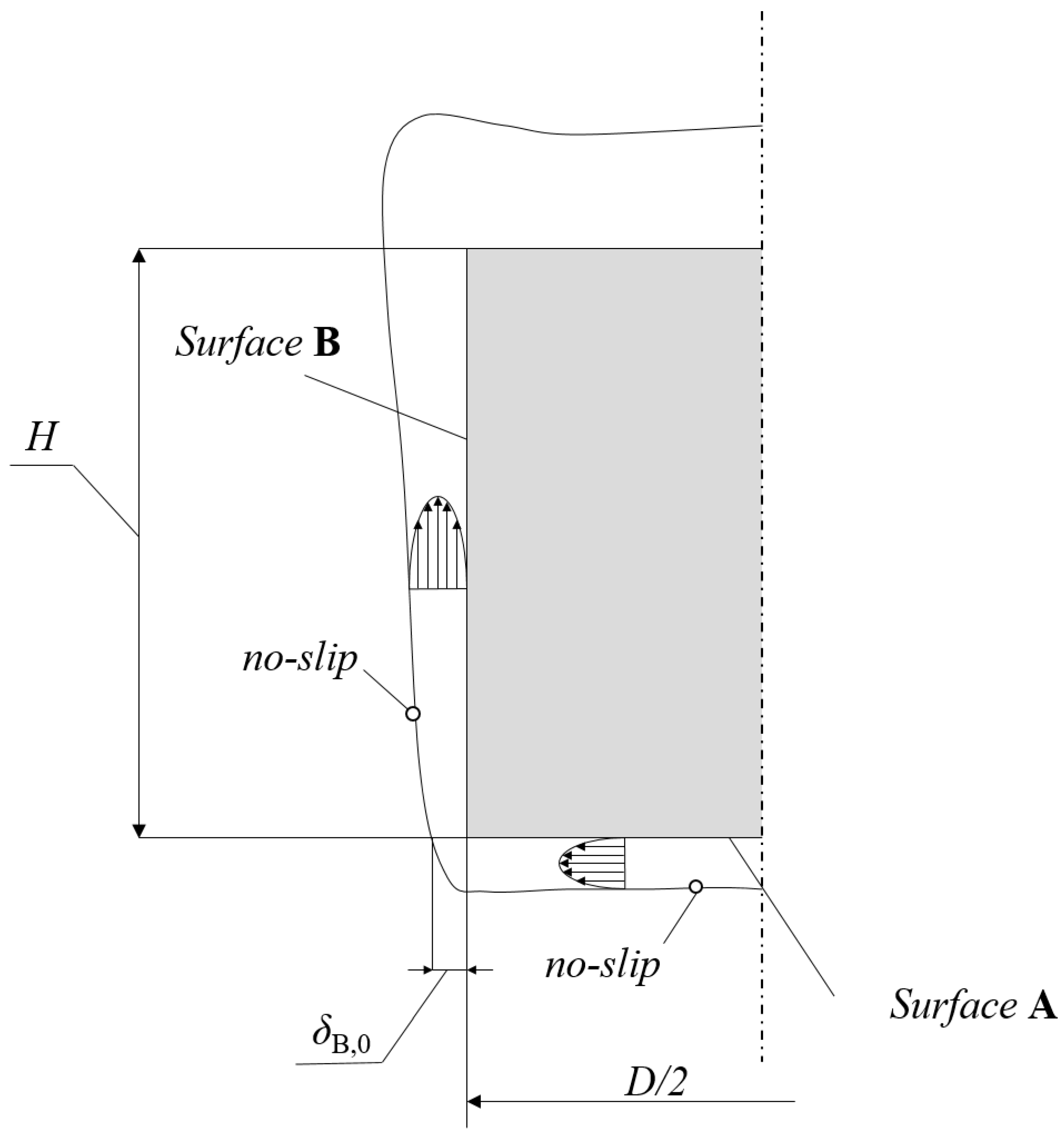
where is the dimensionless initial layer thickness due to the inflow from the vapor layer beneath the bottom surface of the cylinder and is dependent on the flow conditions, i. e., the momentum equation boundary conditions at the vapor-liquid interface at the horizontal bottom and vertical surface of the cylinder specimen. Hence, for the no-slip (see Figure A1) conditions at both the interfaces, Yamada et al. [25] arrive at the following expression for computation of the initial film layer:
where D and L are cylinder’s diameter and length (height!), respectively; whilst Sp and GrB are respectively the degree of wall superheat and the cylinder side surface’s Grashoff number.
Figure A1.
A conceptual sketch of the boundary conditions applied in the theoretical according to Yamada et al. [25], and used in obtaining the average velocity for determination of TKE here.
Figure A1.
A conceptual sketch of the boundary conditions applied in the theoretical according to Yamada et al. [25], and used in obtaining the average velocity for determination of TKE here.
References
- Nichita, B.A. An Improved CFD Tool to Simulate Adiabatic and Diabatic Two-Phase Flows, EPFL, 2010.
- Magnini, M. <1982> CFD Modeling of Two-Phase Boiling Flows in the Slug Flow Regime with an Interface Capturing Technique. Doctoral Thesis, Alma Mater Studiorum - Università di Bologna, 2012.
- Sun, D.-L.; Xu, J.-L.; Wang, L. Development of a Vapor–Liquid Phase Change Model for Volume-of-Fluid Method in FLUENT. Int. Commun. Heat Mass Transf. 2012, 39, 1101–1106. [Google Scholar] [CrossRef]
- Sato, Y.; Ničeno, B. A Sharp-Interface Phase Change Model for a Mass-Conservative Interface Tracking Method. J. Comput. Phys. 2013, 249, 127–161. [Google Scholar] [CrossRef]
- Arévalo, R.; Antúnez, D.; Rebollo, L.; Abánades, A. Estimation of Radiation Coupling Factors in Film Boiling around Spheres by Mean of Computational Fluid Dynamics (CFD) Tools. Int. J. Heat Mass Transf. 2014, 78, 84–89. [Google Scholar] [CrossRef]
- Kharangate, C.R.; Mudawar, I. Review of Computational Studies on Boiling and Condensation. Int. J. Heat Mass Transf. 2017, 108, 1164–1196. [Google Scholar] [CrossRef]
- Sato, Y.; Niceno, B. Pool Boiling Simulation Using an Interface Tracking Method: From Nucleate Boiling to Film Boiling Regime through Critical Heat Flux. Int. J. Heat Mass Transf. 2018, 125, 876–890. [Google Scholar] [CrossRef]
- Saini, N.; Bolotnov, I.A. Two-Phase Turbulence Statistics from High Fidelity Dispersed Droplet Flow Simulations in a Pressurized Water Reactor (PWR) Sub-Channel with Mixing Vanes. Fluids 2021, 6, 72. [Google Scholar] [CrossRef]
- Momoki, S.; Yamada, T.; Shigechi, T.; Kanemaru, K.; Yamaguchi, T. Film Boiling Around a Vertical Cylinder With Top and Bottom Horizontal Surfaces.; American Society of Mechanical Engineers Digital Collection, August 24 2009; pp. 611–619. 24 August.
- Cukrov, A.; Sato, Y.; Boras, I.; Ničeno, B. A Solution to Stefan Problem Using Eulerian Two-Fluid VOF Model. Brodogr. Teor. Praksa Brodogr. Pomor. Teh. 2021, 72, 141–164. [Google Scholar] [CrossRef]
- Hinze, J.O. Turbulence; McGraw-Hill, 1975; ISBN 978-0-07-029037-2. [Google Scholar]
- nsys® Fluent ANSYS Fluent Theory Guide, Release 19.2, Help System. 2018.
- Markatos, N.C. The Mathematical Modelling of Turbulent Flows. Appl. Math. Model. 1986, 10, 190–220. [Google Scholar] [CrossRef]
- Hoppe, F.; Breuer, M. A Deterministic Breakup Model for Euler–Lagrange Simulations of Turbulent Microbubble-Laden Flows. Int. J. Multiph. Flow 2020, 123, 103119. [Google Scholar] [CrossRef]
- Philip, G. Measurement of Turbulence in an Annular Jet, University of Missouri--Rolla, 1972.
- Kimber, M.; Brigham, J.; Jana, A. Experimentally Validated Numerical Models of Non-Isothermal Turbulent Mixing in High Temperature Reactors; Univ. of Pittsburgh, PA (United States), 2018. [Google Scholar]
- Ničeno, B.; Dhotre, M.T.; Deen, N.G. One-Equation Sub-Grid Scale (SGS) Modelling for Euler–Euler Large Eddy Simulation (EELES) of Dispersed Bubbly Flow. Chem. Eng. Sci. 2008, 63, 3923–3931. [Google Scholar] [CrossRef]
- Kashima, H.; Mori, N.; Mizutani, N. Visualization on Air Bubble Characteristics of the Surf Zone Breaking Waves. Proc. Coast. Eng. Jsce 2007, 54, 56–60. [Google Scholar] [CrossRef]
- Mori, N.; Suzuki, T.; Kakuno, S. Experimental Study of Air Bubbles and Turbulence Characteristics in the Surf Zone. J. Geophys. Res. Oceans 2007, 112. [Google Scholar] [CrossRef]
- Makris, C.V.; Memos, C.D.; Krestenitis, Y.N. Numerical Modeling of Surf Zone Dynamics under Weakly Plunging Breakers with SPH Method. Ocean Model. 2016, 98, 12–35. [Google Scholar] [CrossRef]
- Cascioli, E.; Buckingham, S.; Keijers, S.; Tichelen, K.V.; Kenjeres, S. Numerical and Experimental Analysis of a Planar Jet with Heated Co-Flow at Medium and Low Prandtl-Number Values. Nucl. Eng. Des. 2020, 361. [Google Scholar] [CrossRef]
- Sakurai, A.; Shiotsu, M.; Hata, K. A General Correlation for Pool Film Boiling Heat Transfer From a Horizontal Cylinder to Subcooled Liquid: Part 1—A Theoretical Pool Film Boiling Heat Transfer Model Including Radiation Contributions and Its Analytical Solution. J. Heat Transf. 1990, 112, 430–440. [Google Scholar] [CrossRef]
- Javed, B.; Watanabe, T.; Himeno, T.; Uzawa, S. Experimental Investigation on Characteristics of Liquid Film at Different Angle of Attack. Int. J. Gas Turbine Propuls. Power Syst. 2017, 9, 22–31. [Google Scholar] [CrossRef]
- Hillier, A.; Doorsselaere, T.V.; Karampelas, K. Estimating the Energy Dissipation from Kelvin–Helmholtz Instability Induced Turbulence in Oscillating Coronal Loops. Astrophys. J. Lett. 2020, 897, L13. [Google Scholar] [CrossRef]
- Yamada, T.; Shigechi, T.; Momoki, S.; Kanemaru, K. An Analysis of Film Boiling around a Vertical Finite-Length Cylinder. 長崎大学工学部研究報告 Rep. Fac. Eng. Nagasaki Univ. 2001, 31, 1–11. [Google Scholar]
- Rohatgi, A. Webplotdigitizer: Version 4. 5 2021.
- Galović, A. A selected chapters from conduction 2003.
- Halasz, B.; Galović, A.; Boras, I. Toplinske Tablice; FSB: Zagreb, 2013. [Google Scholar]
- Tsui, Y.-Y.; Lin, S.-W.; Lai, Y.-N.; Wu, F.-C. Phase Change Calculations for Film Boiling Flows. Int. J. Heat Mass Transf. 2014, 70, 745–757. [Google Scholar] [CrossRef]
- Juric, D.; Tryggvason, G. Computations of Boiling Flows. Int. J. Multiph. Flow 1998, 24, 387–410. [Google Scholar] [CrossRef]
- Yamada, T. Study on Film Boiling Heat Transfer around a Vertical Cylinder with Top and Bottom Horizontal Surfaces, Nagasaki University, 2007.
- Maharshi, S. Computational Modelling of Liquid Jet Impingement onto Heated Surface. Ph.D. Thesis, Technische Universität: Darmstadt, 2017.
- Gauss, F.; Lucas, D.; Krepper, E. Grid Studies for the Simulation of Resolved Structures in an Eulerian Two-Fluid Framework. Nucl. Eng. Des. 2016, 305, 371–377. [Google Scholar] [CrossRef]
- Liu, Y.; Pointer, W.D. Eulerian Two-Fluid RANS-Based CFD Simulations of a Helical Coil Steam Generator Boiling Tube; Oak Ridge National Lab. (ORNL), Oak Ridge, TN (United States), 2017. [Google Scholar]
- Svendsen, I.A. Analysis of Surf Zone Turbulence. J. Geophys. Res. Oceans 1987, 92, 5115–5124. [Google Scholar]
- Zimmer, M.D.; Bolotnov, I.A. Exploring Two-Phase Flow Regime Transition Mechanisms Using High-Resolution Virtual Experiments. Nucl. Sci. Eng. 2020, 194, 708–720. [Google Scholar] [CrossRef]
- Vinkovic, I.; Aguirre, C.; Simoëns, S.; Gorokhovski, M. Large Eddy Simulation of Droplet Dispersion for Inhomogeneous Turbulent Wall Flow. Int. J. Multiph. Flow 2006, 32, 344–364. [Google Scholar] [CrossRef]
- Herman, K. Teorija elastičnosti i plastičnosti; Udžbenici Sveučilišta u Zagrebu = Manualia Universitatis studiorum Zagrabiensis; 1. izd.; Element: Zagreb, 2009; ISBN 978-953-197-682-4. [Google Scholar]
- Heschl, C. Ein Beitrag zur numerischen Berechnung turbulenter Raumluftströmungen, 2010.
| 1 | The multiplication of the r.h.s. terms with 1/3 is also in the case with film boiling when slip, i.e., zero velocity gradient, is present at the top of the boundary layer, as shown in Yamada et al. [25]. |
| 2 | The inflection point may be regarded as t ∼ 140 s in [9], in the case of stable film boiling at the saturation temperature. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






