Prerpints.org logo
Preprint
Article

Forecasting PM Levels Using Machine Learning Models in the Arctic: A Comparative Study

This version is not peer-reviewed.

Submitted:

03 June 2023

Posted:

05 June 2023

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
In this study, we present a statistical forecasting framework and assess its efficacy using a range of established machine learning algorithms for predicting Particulate Matter (PM) concentrations in the Arctic, specifically in Pallas (FI), Reykjavik (IS), and Tromso (NO). Our framework leverages historical ground measures and 24-hour predictions from 9 models provided by the Copernicus Atmosphere Monitoring Service (CAMS) to provide PM predictions for the following 24 hours. Furthermore, we compare the performance of various memory cells based on artificial neural networks (ANN), including recurrent neural networks (RNNs), gated recurrent units (GRUs), long short-term memory networks (LSTMs), echo state networks (ESNs), and windowed multi-layer perceptrons (MLPs), which are commonly employed in time series forecasting tasks. Irrespective of the chosen memory cell type, our results demonstrate that the proposed framework consistently outperforms the CAM models in terms of mean squared error (MSE), with average improvements ranging from 25% to 40%. Additionally, we investigate the impact of outliers on the overall model performance.
Keywords: 
Subject: 
Environmental and Earth Sciences  -   Pollution

1. Introduction

The Arctic is warming at a faster rate compared to other areas of the Earth [1]. Environmental changes due to warming promote economic activities which increase anthropogenic emissions while population growth amplifies the exposure to pollution [1]. Rising temperatures in the Arctic augment the risk of wildfires [2] representing a major natural source of atmospheric pollution. In the European Arctic, atmospheric pollution levels and exposure are lower compared to highly populated urban areas at middle latitudes [3]. Nevertheless, recent studies raised concerns about the health effects of atmospheric pollution on the local population, generating an issue for public health and policymakers [1,4]. A limited number of atmospheric pollution monitoring stations are available in the Arctic to record concentrations at a hourly frequency. One of the most commonly measured parameters at those stations that has a significant impact on human health is the concentration of particulate matter (PM10) with an equivalent diameter less than 10 µm. PM10 is a mixture of solid particles and liquid droplets present in the air, emitted from anthropogenic and natural sources. In the Arctic region, PM10 can originate from local sources, but it can also be transported from mid-latitudes by winds [5]. Looking ahead, the opening of new shipping routes, the expected rise in forest fire frequency, the intensified extraction of resources, and the subsequent expansion of infrastructure are likely to result in increased PM10 emissions in the Arctic [1].
PM10 concentration behavior can be simulated via deterministic or statistical models with varying degrees of reliability [6]. The Copernicus Atmospheric Monitoring Service (Several studies demonstrated that statistical models based on Machine Learning algorithms may improve the PM10 concentration forecasts for a specific geographic point [8,9,10,11,12]. In particular, Artificial Neural Networks (ANN) have proven to be quite efficient in dealing with complex nonlinear interactions; generically speaking, ANN can have various architectures, from simple Multi-Layer Perceptrons [13,14,15] to more sophisticated Deep Learning structures [16,17], or even Hybrid solutions [18], [19,20,21]. Among the various macro-families of neural networks, Recurrent Neural Networks (RNNs) are particularly well-suited for analyzing time series, such as atmospheric data. RNNs manage to outperform Regression Models and Feed-Forward Networks by carrying information about previous states and using it to make predictions together with current inputs [12]. When dealing with long-term dependencies, ANN such as Long Short-Term Memory Networks (LSTM) provide effective time series forecasting: LSTMs arise as an enhanced version of Recurrent Neural Networks (RNNs) specifically designed to address the vanishing and exploding gradient problems that can occur during training [22]. LSTMs incorporate additional processing units, known as memory and forget blocks, which enable the network to selectively retain or discard information over multiple time steps. Gated Recurrent Unit Networks (GRUs) are another variant of Recurrent Neural Networks (RNNs) that offer a simplified structure compared to LSTMs. GRUs aim to address some of the computational complexities of LSTMs while still maintaining the ability to capture long-term dependencies in sequential data.
In a GRU, the simplified structure is achieved by combining the update gate and the reset gate into a single gate called the "update gate". This gate controls the flow of information and helps determine how much of the previous hidden state should be updated with the current input [17].
Numerous studies have been conducted using the aforementioned neural network algorithms in the context of urban and metropolitan areas. In [12], for instance, a Standard Recurrent Neural Network model is compared to a multiple linear regression and a Feed-Forward Network to predict concentrations of PM10 showing that the former algorithm provides better performance. As another example, in [10] the authors compare the performances of a Multi-Layer Perceptron with the ones of a Long Short-Term Memory Network in predicting concentrations of PM10 based on data acquired from five monitoring stations in Lima. Results show that both methods are quite accurate in short-term prediction, especially in average meteorological conditions. For more extreme values, on the other hand, the LSTM model results in better forecasts. More evidence can also be found in [23] and [11], where convolutional models for LSTM are considered, and in [24], where different approaches to defining the best hyperparameters for an LSTM are analyzed. Similarly, in [17] the authors develop architectures based on RNN, LSTM, and GRU, putting together air quality indices from 1498 monitoring stations with meteorological data from the Global Forecasting System to predict concentrations of PM10: results confirm that the examined networks are effective in handling long-term dependencies. Specifically, the GRU model outperforms both the RNN and LSTM networks.
Another neural methodology used in this study is the Echo State Networks (ESN). The architecture of ESNs follows a recursive structure where the hidden layer, known as the dynamical reservoir, is composed of a large number of sparsely and recursively connected units. The weights of these units are initialized randomly and remain constant throughout the iterations. The weights for the input and output layers are the ones trained within the learning process. In [25], an ESN predicts values of PM2.5 concentration based on the correlation between average daily concentrations and night-time light images from the National Geophysical Data Center. Hybrid models can also be considered to improve the performance of an ESN model as in [26] where is performed an integration with Particle Swarm Optimisation, and in [27] where the authors manage to further optimize computational speed.
In conclusion, Neural Networks appear to be a viable approach for obtaining reliable forecasts of pollutant concentrations. However, the performance of the network often depends on architectural features as well as the quality of the acquired data.
In the upcoming sections, we evaluate the performance of six distinct memory cells (models). Our study utilizes two components as input time series: i) measurements of PM10 concentration recorded at 00:00 UTC from six stations situated in the Arctic polar region within the AMAP area, and ii) PM10 forecasts generated by CAMS models at 00:00 UTC for the subsequent day. The resulting output is a new forecast for 00:00 UTC of the following day.
In Section 2, we provide an overview of data acquisition and processing, describe the structure underlying the architecture, including details of each ANN design, and outline the technical aspects of implementation.
In Section 3, we present the results and compare the performance of the aforementioned architectures.

2. Materials and Methods

2.1. Station Data

In the framework of this study, we selected six air quality monitoring stations of the European Environmental Agency (EEA) and Finnish Meteorological Institute (FMI) collecting hourly measurements of PM10 concentrations ( μ g / m 3 ). The chosen stations are located inside and close to the Arctic Monitoring and Assessment Program (AMAP) area, which defines the physical-geographical and political boundaries of the Arctic [28]. The AMAP area includes terrestrial and marine regions north of the Arctic Circle (66°32’N) modified to cover the marine areas north of the Aleutian chain, Hudson Bay, and covers parts of the North Atlantic Ocean including the Labrador Sea.
We selected the Arctic monitoring stations which measured PM10 concentrations at hourly frequency during the period January 2020-December 2022 and produced time series with only scarce and short temporal gaps (Table 1, Figure 1). The completeness of the PM10 time series represents a fundamental condition for our prediction experiments since missing data could degrade the performance of the ANN [29]. Other stations are located in the AMAP area, but the measured PM10 concentration records were not sufficiently long and complete for the application of the ANN. From the time series produced by the chosen monitoring stations, we extracted the concentrations measured at 00:00 UTC for each day. This choice allowed to provide the ANN with PM10 measurements performed at the same time as the CAMS models forecast at 00:00 UTC basetime. The six selected stations are situated in areas with different environmental conditions and emission sources; for this reason, they can be considered representatives of different Arctic contexts. Stations in Grundartangi Gröf, Kópavogur Dalsmári (Iceland), Oulu (Finland) and Tromso (Norway) are located in urban areas and close to the Atlantic Ocean coast, while the station in Muonio (Finland) is positioned in a remote area far from the ocean, representative of background pollution levels. Two stations in Oulu (Finland) located south of the border of the AMAP area are chosen to additionally validate the methodology.

2.2. Model Data

CAMS provides forecasts of the main atmospheric pollutant concentrations over Europe [30]. They are produced once a day by eleven state-of-the-art numerical air quality models employed at different research institutions and weather services in Europe. Forecasts produced by different models are interpolated on the regular latitude-longitude grid with the horizontal resolution of 0.1°×0.1° and are available from the Copernicus European Air Quality service 1. Only nine Copernicus models provide air quality forecasts between January 2020 and December 2022 with only short temporal gaps. Models differ from each other by applying distinct theoretical solutions for estimating the spreading of pollutants and chemical reactions in the atmosphere and have several horizontal and vertical resolutions. Analyses by all models combine information from model forecasts and measures, but they use different observational data sets and techniques for data assimilation [31]. Table 2 lists the major characteristics of models used in the study.

2.3. Definition of Input Vector for the ANN

The input vectors of Machine Learning Algorithms used to predict PM levels are usually data sets derived either from concentrations measured at monitoring stations [11,32] or from single or ensemble models forecasts [8,33]. In this study, we apply a novel approach that consists in providing the ANN with the input vector including both PM10 in-situ measure available at the starting time of the forecast, and an ensemble of 24h PM10 model forecasts. CAMS generate forecasts at 0h, 24h, and 48h. While the 0h forecasts are most accurate, the 24h forecast aligns with our model’s prediction time. To reconcile this, we measured the Mean Squared Error (MSE) and found that using the CAMS forecast at 24h is the optimal choice (Figure 2).

2.4. Data Preprocessing

To address the technical difficulties resulting in the data gaps mentioned earlier, preprocessing of the input data is necessary to ensure temporal continuity. If the data gaps span multiple time points, the dataset is adjusted by cropping it to avoid such large gaps. In cases where only a single time point is missing, the missing data is interpolated using linear interpolation based on the previous and subsequent data points. Furthermore, prior to being fed into the classification pipeline, the input data is normalized, and after processing, it is de-normalized. This normalization step helps ensure consistent scaling across the features. To confirm the stationarity of all measurement series, an Augmented Dickey-Fuller test is conducted. This test is performed to assess the presence of trends or unit roots that may affect the analysis and modeling process.

2.5. General Architecture

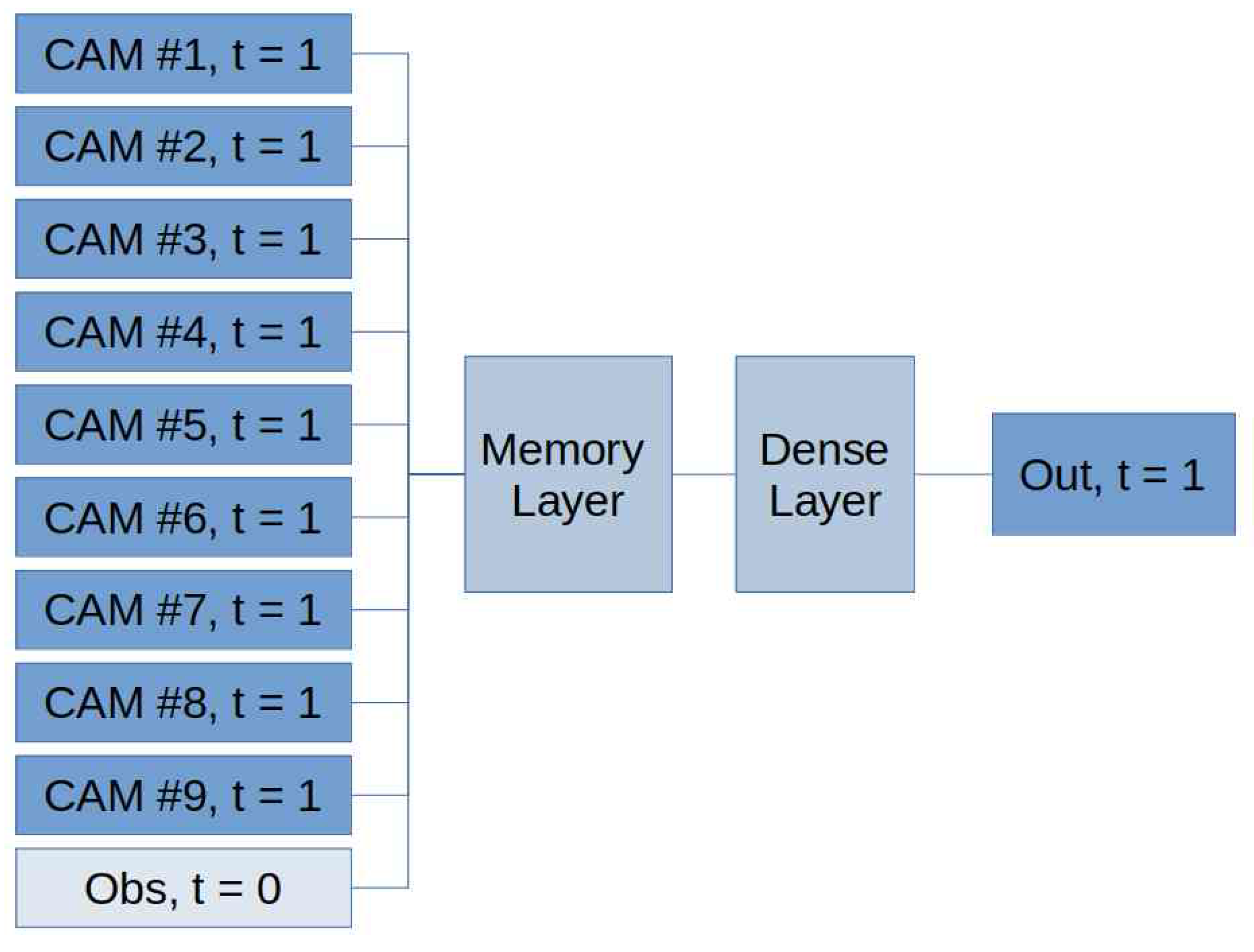
In this study, we propose a design that comprises an input layer, a memory layer, a dense layer, and an output layer (see Figure 4). The input consists of nine sets of measures provided by the CAMS, and with one set of measures. To enhance the accuracy of the predictions, we incorporate 24-hour CAMS (referred as time t = 1 in Figure 4). As stated in the earlier sections, this architectural decision yields improved results in terms of mean squared error (MSE).
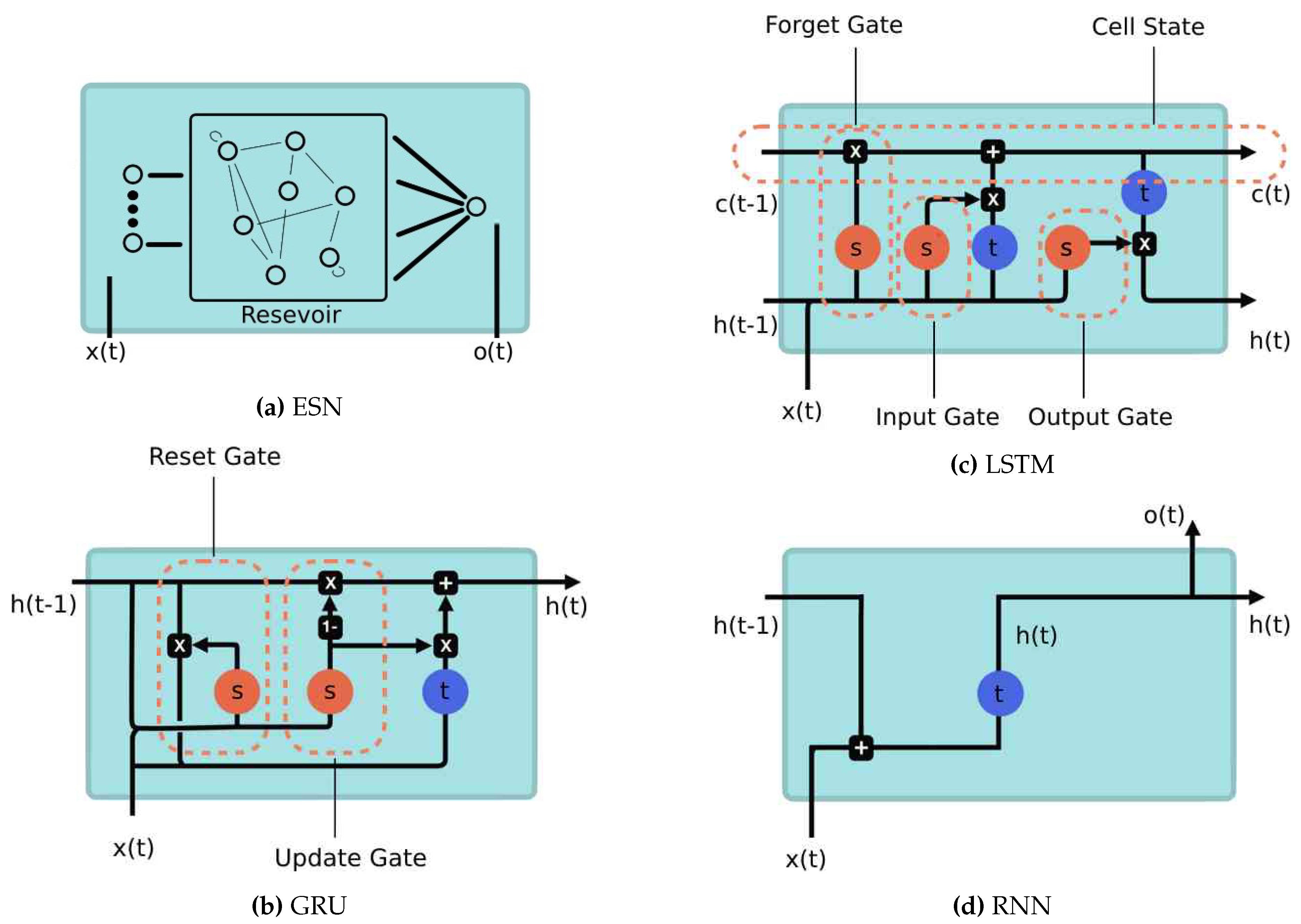
The memory cell in our architecture is implemented using various specifications, i.e. Echo State Networks (ESN), Long Short-Term Memory Networks (LSTM), Gated Recurrent Units (GRU), Standard Recurrent Neural Networks (RNN), and windowed multi-perceptron (with time window sizes of 4 and 1 time steps). We briefly provide some details on these different specifications below. In addition to the approach described in Figure 4, where a single time instant is considered for both the input and output, we also explored alternative designs where both the input and output are treated as sequences. We also experimented with multiple memory layers and multiple memory cells per layer. However, these attempts did not yield any performance benefits or provide additional insights for the cross-comparison of the different approaches.

2.5.1. Memory Layer

The Memory Layer plays a crucial role in storing the temporal information present in the input sequence. In our study, we explored six popular solutions.

Echo state Networks

The ESN approach (Figure 3) [34] sets the weights of the recurrent layer, called "reservoir," in such a way that the recurrent hidden units effectively capture the history of past inputs, while only the weights of the output layer are trained. The key question in this case is how to choose the weights of the recurrent layer. First, connections among the recurring units should be sparse, resulting in a sparse square weight matrix. Additionally, the spectral radius of the matrix should be kept low, ideally less than 1 (as in our implementation), to contribute to the echo state property as described in [35]2. However, in combination with carefully chosen activation functions such as tanh(), it can be allowed to exceed 1. This mechanism enables the propagation of information through time. Proper tuning of hyperparameters is essential for generating echoes that accurately reflect the input content, and tools provided in [37] and [35] can aid in this process. We train our ESN using gradient descent, similar to the algorithms presented in [38].

Long Short-Term Memory

Standard RNN cells (see Section 2.5.1.4) suffer from well-known limitations, including vanishing and exploding gradients during training with back-propagation. To address these issues, Long Short-Term Memory (LSTM) cells were developed, offering a more sophisticated approach to managing the hidden state. Figure 3 illustrates its structure. The rectangular boxes represent activation functions applied prior to matrix multiplications (not depicted in the figure). The circular spots indicate element-wise operations. The variables x t , h t , and c t denote the input, hidden state, and cell activation vector, respectively. The function σ represents the sigmoid activation function. The cell output is computed by applying a sigmoid activation function to a weighted sum of x t , h t − 1 , and a bias term. Figure 3 also highlights the internal architecture of LSTM, which incorporates Input, Forget, and Output Gates. Confluences in the figure represent concatenations, while bifurcations denote element-wise copying. Taking into account these details and referring to the illustrated diagram (Figure 3), it is possible to derive the corresponding equations.

Gated Recurrent Units

GRU cells are a simplified version of LSTM, offering comparable performance for modeling tasks. They are particularly advantageous with small datasets since they have a smaller parameter count. Figure 3 depicts the overall structure of a GRU cell, emphasizing the presence of the Reset and Update Gates.

Recurrent Neural Networks

The Standard RNN is based on the original recurrent approach (see Figure 3). It operates by combining an input x(t) with the previous hidden state h(t-1), which is then passed through an elementwise tanh() cell (depicted as the rounded block labeled with t). The resulting output is stored as the next hidden state h(t) and also serves as the output o(t). In the figure, bifurcations represent component-wise copies before being multiplied by weight matrices and added with biases. Operations such as addition (+) are applied prior to multiplying with weight matrices and adding biases. This recurrent scheme was historically the first proposal capable of storing variable-length information from a time series.

Multi-Layer Perceptron

In this study, a multi-layer perceptron (MLP) with a configuration of 5 units in the hidden layer and 1 unit in the output layer is employed. Two different implementations of the MLP are considered: one utilizes 4 time steps from the input data sequence, while the other utilizes only 1 time step.
Preprints 75599 g003
Figure 3. Various Alternatives for the Memory Layer
Figure 3. Various Alternatives for the Memory Layer
Preprints 75599 g003

2.5.2. Implementation Details

Our implementation relies on keras for RNN, LSTM, GRU, WMP, WMP4 and on tensorflow for ESN. The hyperparameters of the algorithms were carefully selected to ensure a fair comparison among the four methods, as outlined in Table 4, Table 5, and Table 6. These hyperparameters were determined based on the stations listed in Table 3, which were subsequently excluded from the validation process. Furthermore, loss (Minimum Absolute Error) and optimizer (Adam) have been used in all cases. This choice was subsequently applied to the data from all other stations, which should be regarded as validation sets. For each station, validation is performed over 365 time steps (covering a whole year).
Preprints 75599 g004
Figure 4. General Architecture.
Figure 4. General Architecture.
Preprints 75599 g004

3. Results

In this section, we present the results obtained using measure and CAM forecast data from January 2020 to December 2022. The data is divided into training (730 steps) and test (365 steps). In the case of potential single data gaps, linear interpolation was utilized to fill in the missing values. However, if the missing data resulted in larger gaps, the training data set was cropped to exclude these gaps. The initial time step for each station is provided in Table 7.

3.1. Original Data

In the following subsections, we present our results. Measures and CAM forecasts are used as input of our architecture without any pre-processing steps applied.

3.1.1. MSE Results

The convexity of the MSE function and the application of Jensen’s inequality guarantee that the MSE of the average of the models is always lower than or equal to the average MSE of the individual models. Hence, in addition to presenting the results of each model, we also provide the MSE of their average. This average can be viewed as an ensemble forecast and can be utilized in practical applications. Our MSE results are reported in Figure 5.
Figure 5 demonstrates that there is no large difference among the memory cells. All the implemented solutions show that the model MSE is less or equal the best available CAM forecast. Notably, in three instances (e.g., Figure 5, Figure 5, and Figure 5), the model produces significantly more accurate results compared to the CAMS’ forecasts.

3.1.2. Forecast Results

In Figure 6, we present the forecasting results. To ensure clarity, we have depicted the graph of the memory cell that achieved the best performance in terms of MSE, along with the corresponding measure data. The time interval considered in the plot spans the entire year of 2022.
To further evaluate the performance of the algorithms, we provide a closer examination of the forecasting results for the time interval from the 200th to the 260th day of the year 2022. Figure 7 displays the results obtained from all the memory cells. The shaded area in Figure 7 represents the standard deviation of the forecasted values from the different memory cells relative to their average, indicating variations in the predictions among the different models.
Finally in Figure 8, we present a comparison between the CAMS forecast, our model, and the measure data for station with code 15609. The last row of the graph represents our model’s forecast, while the rows above display the CAMS forecasts.

3.2. Filtering the Input Data

While Figure 5 illustrates that our model either matches (Figure 5, Figure 5, and Figure 5) or clearly outperforms (Figure 5, Figure 5, and Figure 5) the best CAMS, Figure 7 reveals variations in the performance of our architecture depending on the specific station under consideration. Notably, there is a stark contrast in forecast quality between Figure 7 and Figure 7, with the latter displaying significant differences (shaded area) among the utilized memory cells (also apparent in Figure 5).
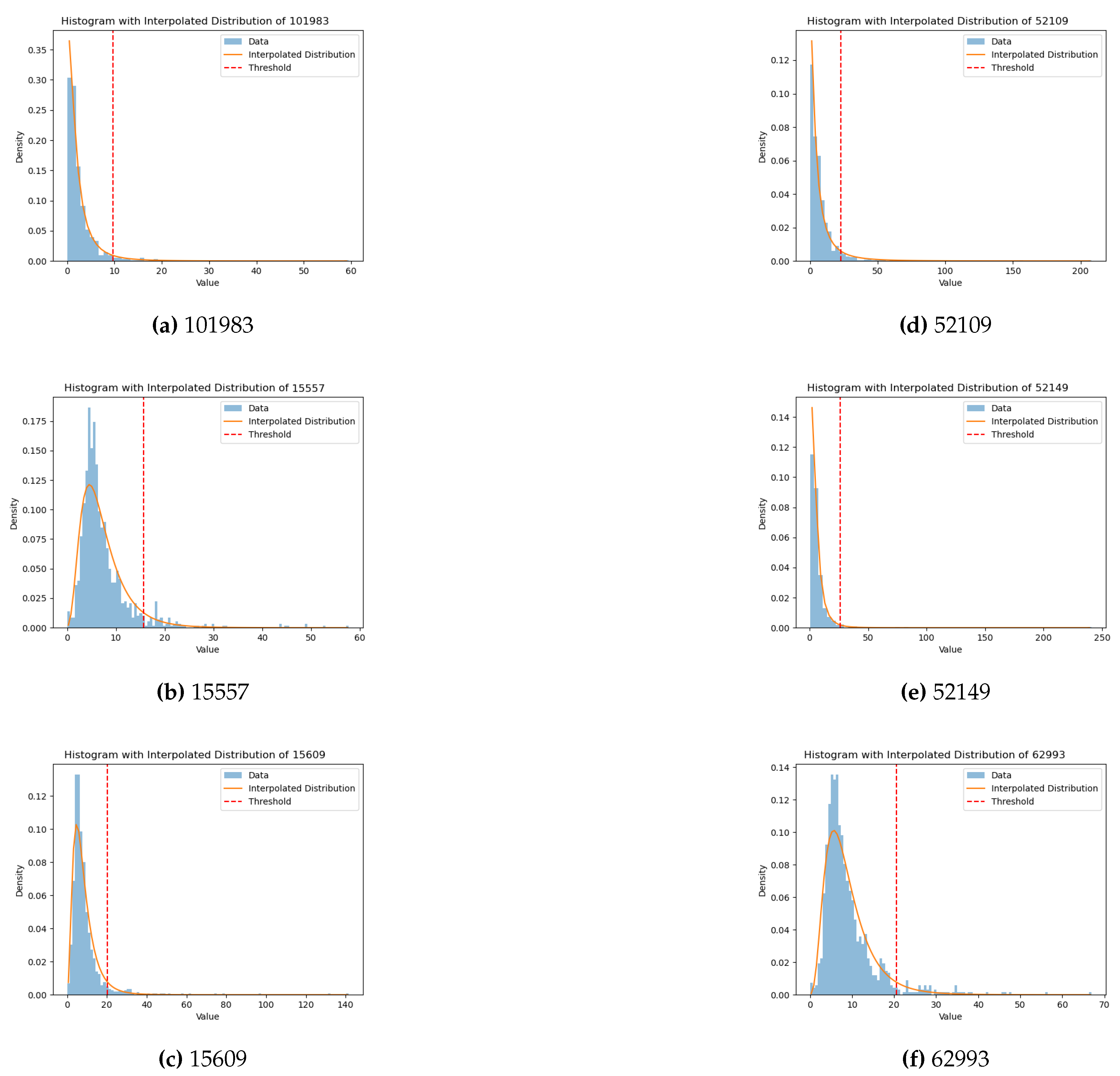
In the literature ([39,40,41,42]), it is common practice to utilize a log-normal distribution for interpolating PM data histograms. In our study, we adopt this assumption to handle outliers in our dataset by replacing them with the temporally nearest data points. This is consistent with the analysis of the station measures, which shows isolated spikes probably due to experimental errors. The algorithm used for this purpose is provided in Appendix A.1. In Figure 9, the data points to be removed are indicated by the region on the right-hand side of the vertical dashed line (colored dark/red). Appendix A.2 displays the histograms and the cutting thresholds of all the stations listed in Table 1.

3.3. Filtered Data

In the following subsections, we present our results using outlier-filtered input data, evaluating both the mean squared error (MSE) and the forecasting performance.

3.3.1. MSE Results

In the following we report our results in terms of MSE (Figure 10) and forecasting (Figure 6).

3.3.2. Forecast Results

Figure 11 illustrates the forecast details for the time interval from the 200th to the 260th day. Specifically, Figure 12 focuses on the case of station 52109. In the scenario without data filtering, the Echo State Network (ESN) model exhibits the highest Mean Squared Error (MSE), while the Long Short-Term Memory (LSTM) model performs the best. However, when the data is filtered, both the ESN and LSTM models show improved performance and have similar MSE values. Removing outliers from the data significantly enhances the forecast quality of both memory cell models. Notably, the mentioned significant difference in terms of MSE between the ESN and LSTM models (as observed in Figure 5) corresponds to the noticeable difference in their forecasting, as depicted in Figure 12. The ESN memory cell appears to be more affected by outliers compared to the LSTM.
On the other hand, filtering measures with high pollution concentration further improves the prediction performance of the Artificial Neural Network (ANN) in terms of MSE compared to the CAMS model forecasts and the persistence model (Figure 10). When using the filtered dataset, the persistence model demonstrates better prediction performance than any of the CAMS model forecasts (Figure 10), while with unfiltered measures, the CAMS model forecasts outperform the persistence model (Figure 5). This indicates that, in comparison to persistence, also the CAMS forecasts improve when spikes are removed. However, regardless of whether the measures are filtered or not, the predictions of the Artificial Neural Network (ANN) consistently show significantly higher accuracy.

4. Discussion

In this study, we conduct an in-depth analysis of a 24-hour forecasting design that leverages both present P M 10 measures and 24-hour forecasts generated by CAMS models. Central to the design are the memory cells, which serve as alternative options for modeling the data and improving forecasting accuracy. Specifically, we explore the utilization of Echo State Networks (ESN), Long Short-term Memory (LSTM), GRU (Gated Recurrent Unit), Recurrent Neural Networks (RNN), as well as 4-steps and 1-step temporally windowed Multi-Perceptron.
Our architecture exhibits remarkable performance by effectively capturing the strengths of either the CAMS or measures, regardless of the specific memory cell employed. It consistently outperforms the CAMS, resulting in significant average improvements ranging from 25% to 40% in terms of mean squared error (MSE). This demonstrates the effectiveness of the design in harnessing the predictive capabilities of the alternative memory cells.
However, it is important to note that the choice of the memory cell has a substantial impact on the forecasting capability of the design, particularly when dealing with data series characterized by intricate behavior.
Furthermore, we investigated the impact of outliers as a potential source of error and assessed how their removal significantly affects the forecasting capability of our model.
Looking ahead, future research endeavors can explore the integration and fusion of the distinct strengths exhibited by different memory cells, going beyond the conventional approach of simply averaging their results. By developing an ensemble design that selectively leverages the best options based on the specific characteristics of the data series to be forecast, we can further enhance the overall forecasting performance and reliability of the system.
In conclusion, our comprehensive analysis highlights the effectiveness of the alternative memory cells in improving forecasting accuracy within the context of the 24-hour forecasting design. By describing the individual strengths and characteristics of each memory cell and addressing the impact of outliers, we present a promising avenue for advancing forecasting methodologies in a variety of domains and applications.

Author Contributions

Conceptualization, Dobricic., Fazzini and Pasini; methodology, Fazzini.; software, Fazzini; validation, Dobricic, Fazzini, Montuori, and Pasini ; formal analysis, Dobricic, Fazzini, Montuori; investigation, Fazzini; resources, Campana, Petracchini; data curation, Dobricic, Crotti, Fazzini; writing—original draft preparation, Crotti, Cuzzucoli Fazzini, Dobricic ; writing—review & editing all authors; visualization, Fazzini; supervision, Montuori; project administration, Fazzini; funding acquisition, Campana, Pasini, Petracchini All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the Arctic PASSION project under the European Union’s Horizon 2020 research and innovation programme grant agreement No. 101003472.

Data Availability Statement

Input in-situ observations are available from EEA and FMI, while model forecasts are available from Copernicus (see Materials and methods section). Data produced in the study are available from the authors upon request.

Conflicts of Interest

The authors declare no conflict of interest.

Sample Availability

Samples of the compounds ... are available from the authors.

Appendix A.

Appendix A.1

In the algorithm, the function c a l c u l a t e _ o p t i m a l _ t h r e s h o l d is based on the assumption that the expected data distribution should fit the log-normal. This assumption translates to replace the outliers with the temporally nearest data: the algorithm finds the optimal threshold to correspondingly cut the histogram. The position of this threshold is calculated to minimize the MSE between the histogram of the new data and the corresponding log-normal distribution.

Appendix A.2

In the following, Algorithm 1 results are plotted in Figure A1.
Algorithm 1:ComputeOptimalThsh
Preprints 75599 i001
Preprints 75599 g0a1
Figure A1. Simulation Results (Filtered-MSE). See Table 1 for code reference.
Figure A1. Simulation Results (Filtered-MSE). See Table 1 for code reference.
Preprints 75599 g0a1

References

  1. AMAP. AMAP, 2021. Arctic Climate Change Update 2021: Key Trends and Impacts, 2021.
  2. Descals, A.; Gaveau, D.L.; Verger, A.; Sheil, D.; Naito, D.; Peñuelas, J. Unprecedented fire activity above the Arctic Circle linked to rising temperatures. Science 2022, 378, 532–537. [Google Scholar] [CrossRef] [PubMed]
  3. EEA. Air quality in Europe 2022. Technical report, European Environmental Agency, 2022. [CrossRef]
  4. Schmale, J.; Arnold, S.R.; Law, K.S.; Thorp, T.; Anenberg, S.; Simpson, W.R.; Mao, J.; Pratt, K.A. Local Arctic Air Pollution: A Neglected but Serious Problem. Earth’s Future 2018, 6, 1385–1412. [Google Scholar] [CrossRef]
  5. Law, K.S.; Roiger, A.; Thomas, J.L.; Marelle, L.; Raut, J.C.; Dalsøren, S.; Fuglestvedt, J.; Tuccella, P.; Weinzierl, B.; Schlager, H. Local Arctic air pollution: Sources and impacts. Ambio 2017, 46, 453–463. [Google Scholar] [CrossRef]
  6. Zhang, Y.; Bocquet, M.; Mallet, V.; Seigneur, C.; Baklanov, A. Real-time air quality forecasting, part I: History, techniques, and current status. Atmospheric Environment 2012, 60, 632–655. [Google Scholar] [CrossRef]
  7. Basart, H. J., S.; Benedictow, A.; Bennouna, Y.; Blechschmidt, A.M.; Chabrillat, S.; Cuevas, E.; El-Yazidi, A.; Flentje, H.; Fritzsche, P.; Hansen, K.; Im, U.; Kapsomenakis, J.; B.Langerock.; Richter, A.; Su, N.; Zerefos, C. Validation report of the CAMS near-real time global atmospheric composition service Period December 2019 – February 2020. Copernicus Atmosphere Monitoring Service (CAMS) report 2020.
  8. Gregório, J.; Gouveia-Caridade, C.; Caridade, P. Modeling PM2.5 and PM10 Using a Robust Simplified Linear Regression Machine Learning Algorithm. Atmosphere 2022, 13, 1–13. [Google Scholar] [CrossRef]
  9. Bertrand, J.M.; Meleux, F.; Ung, A.; Descombes, G.; Colette, A. Technical note: Improving the European air quality forecast of Copernicus Atmosphere Monitoring Service using machine learning techniques. Atmospheric Chemistry and Physics Discussions 2022, pp. 1–28.
  10. Cordova, C.H.; Portocarrero, M.N.L.; Salas, R.; Torres, R.; Rodrigues, P.C.; López-Gonzales, J.L. Air quality assessment and pollution forecasting using artificial neural networks in Metropolitan Lima-Peru. Scientific Reports 2021, 11, 1–19. [Google Scholar] [CrossRef]
  11. Wang, W.; Mao, W.; Tong, X.; Xu, G. A novel recursive model based on a convolutional long short-term memory neural network for air pollution prediction. Remote Sensing 2021, 13. [Google Scholar] [CrossRef]
  12. Biancofiore, F.; Busilacchio, M.; Verdecchia, M.; Tomassetti, B.; Aruffo, E.; Bianco, S.; Di Tommaso, S.; Colangeli, C.; Rosatelli, G.; Di Carlo, P. Recursive neural network model for analysis and forecast of PM10 and PM2.5. Atmospheric Pollution Research 2017, 8, 652–659. [Google Scholar] [CrossRef]
  13. Kurt, A.; Oktay, A.B. Forecasting air pollutant indicator levels with geographic models 3 days in advance using neural networks. Expert Systems with Applications 2010, 37, 7986–7992. [Google Scholar] [CrossRef]
  14. De Gennaro, G.; Trizio, L.; Di Gilio, A.; Pey, J.; Pérez, N.; Cusack, M.; Alastuey, A.; Querol, X. Neural network model for the prediction of PM10 daily concentrations in two sites in the Western Mediterranean. Science of the Total Environment 2013, 463-464, 875–883. [Google Scholar] [CrossRef]
  15. Jiang, D.; Zhang, Y.; Hu, X.; Zeng, Y.; Tan, J.; Shao, D. Progress in developing an ANN model for air pollution index forecast. Atmospheric Environment 2004, 38, 7055–7064. [Google Scholar] [CrossRef]
  16. Li, X.; Peng, L.; Hu, Y.; Shao, J.; Chi, T. Deep learning architecture for air quality predictions. Environmental Science and Pollution Research 2016, 23, 22408–22417. [Google Scholar] [CrossRef] [PubMed]
  17. Athira, V.; Geetha, P.; Vinayakumar, R.; Soman, K.P. DeepAirNet: Applying Recurrent Networks for Air Quality Prediction. Procedia Computer Science 2018, 132, 1394–1403. [Google Scholar] [CrossRef]
  18. Cheng, Y.; Zhang, H.; Liu, Z.; Chen, L.; Wang, P. Hybrid algorithm for short-term forecasting of PM2.5 in China. Atmospheric Environment 2019, 200, 264–279. [Google Scholar] [CrossRef]
  19. Díaz-Robles, L.A.; Ortega, J.C.; Fu, J.S.; Reed, G.D.; Chow, J.C.; Watson, J.G.; Moncada-Herrera, J.A. A hybrid ARIMA and artificial neural networks model to forecast particulate matter in urban areas: The case of Temuco, Chile. Atmospheric Environment 2008, 42, 8331–8340. [Google Scholar] [CrossRef]
  20. Elangasinghe, M.A.; Singhal, N.; Dirks, K.N.; Salmond, J.A.; Samarasinghe, S. Complex time series analysis of PM 10 and PM 2 . 5 for a coastal site using arti fi cial neural network modelling and k-means clustering. Atmospheric Environment 2014, 94, 106–116. [Google Scholar] [CrossRef]
  21. Ausati, S.; Amanollahi, J. Assessing the accuracy of ANFIS , EEMD-GRNN , PCR , and MLR models in predicting PM 2 . 5. Atmospheric Environment 2016, 142, 465–474. [Google Scholar] [CrossRef]
  22. Li, X.; Peng, L.; Yao, X.; Cui, S.; Hu, Y.; You, C. Long short-term memory neural network for air pollutant concentration predictions : Method development and evaluation. Environmental Pollution 2017, 231, 997–1004. [Google Scholar] [CrossRef]
  23. Zhang, G.; Lu, H.; Dong, J.; Poslad, S.; Li, R.; Zhang, X.; Rui, X. A Framework to Predict High-Resolution Spatiotemporal PM 2 . 5 Distributions Using a Deep-Learning Model : A Case Study of. Remote Sensing 2020, 12, 1–33. [Google Scholar] [CrossRef]
  24. Drewil, G.I.; Al-Bahadili, R.J. Air pollution prediction using LSTM deep learning and metaheuristics algorithms. Measurement: Sensors 2022, 24, 100546. [Google Scholar] [CrossRef]
  25. Xu, Z.; Xia, X.; Liu, X.; Qian, Z. Combining DMSP/OLS nighttime light with echo state network for prediction of daily PM2.5 average concentrations in Shanghai, China. Atmosphere 2015, 6, 1507–1520. [Google Scholar] [CrossRef]
  26. Xu, X.; Ren, W. Application of a hybrid model based on echo state network and improved particle swarm optimization in PM2.5 concentration forecasting: A case study of Beijing, China. Sustainability 2019, 11. [Google Scholar] [CrossRef]
  27. Xu, X.; Ren, W. Prediction of Air Pollution Concentration Based on mRMR and Echo State Network. Applied Sciences 2019, 9. [Google Scholar] [CrossRef]
  28. Murray, J.L.; Hacquebord, L.; Gregor, D.J.; Loeng, H. Physical - Geographical Characteristics of the Arctic. In AMAP Assessment Report; Murray, J.L., Ed.; AMAP, 1998; pp. 9–23. [CrossRef]
  29. Yuan, H.; Xu, G.; Yao, Z.; Jia, J.; Zhang, Y. Imputation of missing data in time series for air pollutants using long short-term memory recurrent neural networks. UbiComp/ISWC 2018 - Adjunct Proceedings of the 2018 ACM International Joint Conference on Pervasive and Ubiquitous Computing and Proceedings of the 2018 ACM International Symposium on Wearable Computers; , 2018; pp. 1293–1300. [CrossRef]
  30. Marécal, V.; Peuch, V.H.; Andersson, C.; Andersson, S.; Arteta, J.; Beekmann, M.; Benedictow, A.; Bergström, R.; Bessagnet, B.; Cansado, A.; Chéroux, F.; Colette, A.; Coman, A.; Curier, R.L.; Van Der Gon, H.A.; Drouin, A.; Elbern, H.; Emili, E.; Engelen, R.J.; Eskes, H.J.; Foret, G.; Friese, E.; Gauss, M.; Giannaros, C.; Guth, J.; Joly, M.; Jaumouillé, E.; Josse, B.; Kadygrov, N.; Kaiser, J.W.; Krajsek, K.; Kuenen, J.; Kumar, U.; Liora, N.; Lopez, E.; Malherbe, L.; Martinez, I.; Melas, D.; Meleux, F.; Menut, L.; Moinat, P.; Morales, T.; Parmentier, J.; Piacentini, A.; Plu, M.; Poupkou, A.; Queguiner, S.; Robertson, L.; Rouïl, L.; Schaap, M.; Segers, A.; Sofiev, M.; Tarasson, L.; Thomas, M.; Timmermans, R.; Valdebenito. ; Van Velthoven, P.; Van Versendaal, R.; Vira, J.; Ung, A. A regional air quality forecasting system over Europe: The MACC-II daily ensemble production. Geoscientific Model Development 2015, 8, 2777–2813. [Google Scholar] [CrossRef]
  31. Collin, G. Regional Production, Updated documentation covering all Regional operational systems and the ENSEMBLE. Copernicus Atmosphere Monitoring Service 2020. [Google Scholar]
  32. Jia, M.; Cheng, X.; Zhao, T.; Yin, C.; Zhang, X.; Wu, X.; Wang, L.; Zhang, R. Regional air quality forecast using a machine learning method and the WRF model over the yangtze river delta, east China. Aerosol and Air Quality Research 2019, 19, 1602–1613. [Google Scholar] [CrossRef]
  33. Li, T.; Chen, Y.; Zhang, T.; Ren, Y. Multi-model ensemble forecast of pm2.5 concentration based on the improved wavelet neural networks. Journal of Imaging Science and Technology 2019, 63, 1–11. [Google Scholar] [CrossRef]
  34. Jaeger, H. The" echo state" approach to analysing and training recurrent neural networks-with an erratum note’. Bonn, Germany: German National Research Center for Information Technology GMD Technical Report 2001, 148. [Google Scholar]
  35. Lukoševičius, M. A Practical Guide to Applying Echo State Networks. In Neural Networks: Tricks of the Trade: Second Edition; Springer Berlin Heidelberg: Berlin, Heidelberg, 2012; pp. 659–686. [CrossRef]
  36. Nakajima, K.; Fischer, I. Reservoir Computing: Theory, Physical Implementations, and Applications; Natural Computing Series, Springer Nature Singapore, 2021.
  37. Jaeger, H. Tutorial on training recurrent neural networks, covering BPPT, RTRL, EKF and the echo state network approach. GMD-Forschungszentrum Informationstechnik, 2002. 2002, 5. [Google Scholar]
  38. Subramoney, A.; Scherr, F.; Maass, W. Reservoirs Learn to Learn. In Reservoir Computing: Theory, Physical Implementations, and Applications; Nakajima, K.; Fischer, I., Eds.; Springer Singapore: Singapore, 2021; pp. 59–76. [CrossRef]
  39. Lu, H.C. The statistical characters of PM10 concentration in Taiwan area. Atmospheric Environment 2002, 36, 491–502, Seventh Internatioonal Conference on Atmospheric Science and Appl ications to Air Quality (ASAAQ). [Google Scholar] [CrossRef]
  40. Papanastasiou, D.; Melas, D. Application of PM10’s Statistical Distribution to Air Quality Management—A Case Study in Central Greece. Water, Air, and Soil Pollution 2009, 207, 115–122. [Google Scholar] [CrossRef]
  41. abdul hamid, H.; Yahaya, A.S.; Ramli, N.; Ul-Saufie, A.Z. Finding the Best Statistical Distribution Model in PM10 Concentration Modeling by using Lognormal Distribution. Journal of Applied Sciences 2013, 13, 294–300. [Google Scholar] [CrossRef]
  42. Md Yusof, N.F.F.; Ramli, N.; Yahaya, A.S.; Sansuddin, N.; Ghazali, N.A.; Al Madhoun, W. Monsoonal differences and probability distribution of PM10 concentration. Environmental Monitoring and Assessment 2010, 163, 655–667. [Google Scholar] [CrossRef] [PubMed]
1
https://www.regional.atmosphere.copernicus.eu/
2
in [36] it is stated that a spectral radius less than 1 is neither sufficient nor necessary for the echo state property
Preprints 75599 g001
Figure 1. Geographical positions of the monitoring stations selected for hyper-parameter tuning (represented by stars) and for model training and testing (represented by dots) are located in proximity to the AMAP area, indicated by a thick line. The shaded region represents the area covered by the CAMS models.
Figure 1. Geographical positions of the monitoring stations selected for hyper-parameter tuning (represented by stars) and for model training and testing (represented by dots) are located in proximity to the AMAP area, indicated by a thick line. The shaded region represents the area covered by the CAMS models.
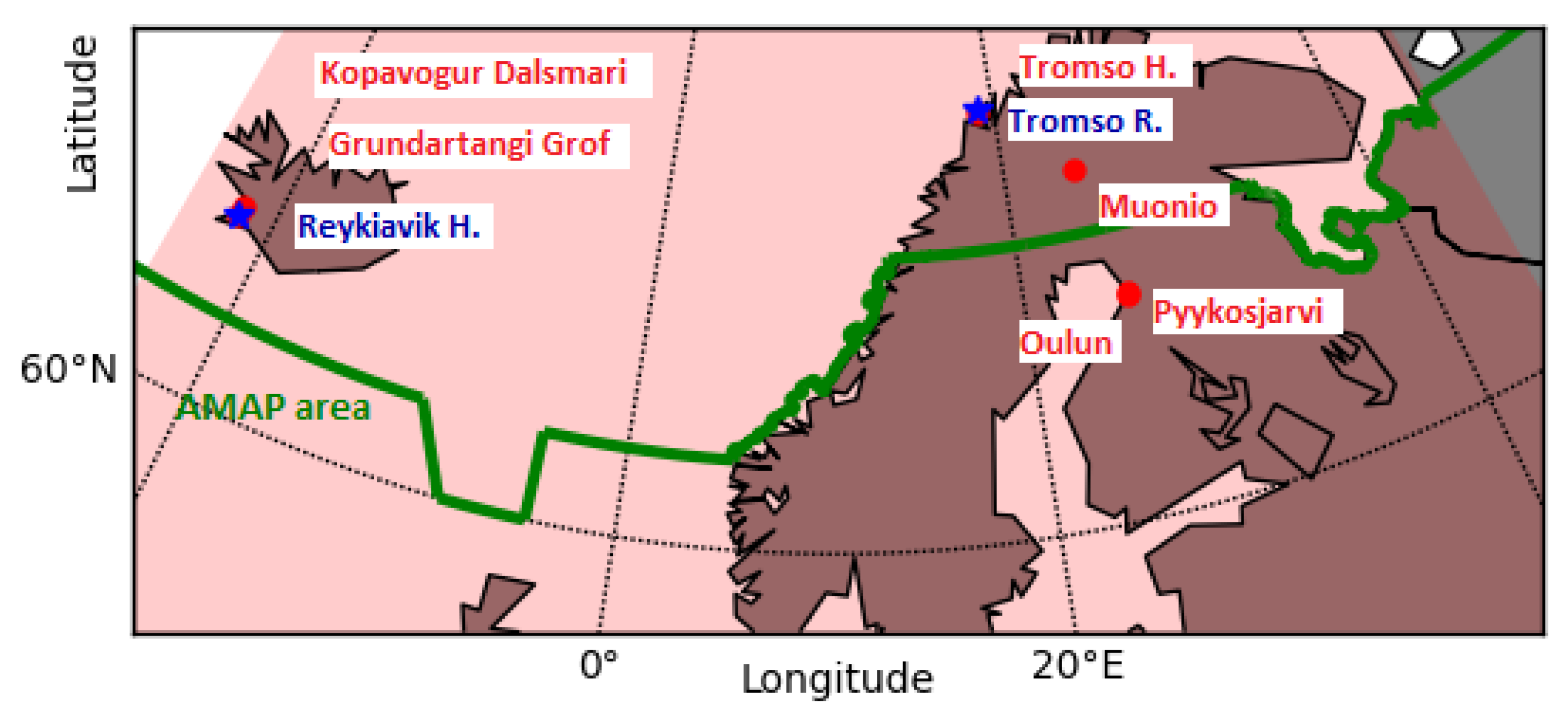
Preprints 75599 g001
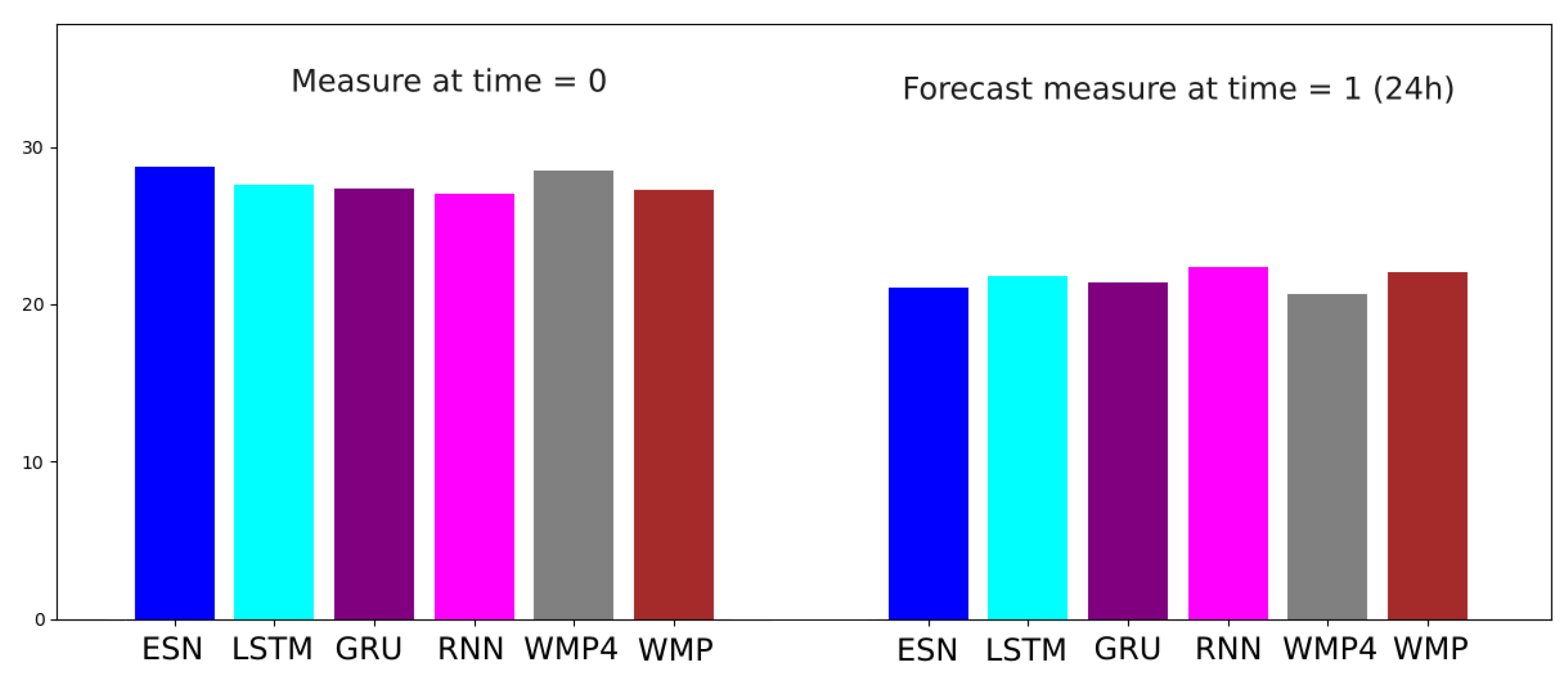
Preprints 75599 g002
Figure 2. The mean squared error (MSE) results of the adopted algorithms (details provided in the subsequent sections) are presented for two scenarios: exploiting CAM forecast prediction at 24 hours (left) or CAM forecast prediction at the present time (right) for station 15557. Similar outcomes were observed for the other stations in our analysis.
Figure 2. The mean squared error (MSE) results of the adopted algorithms (details provided in the subsequent sections) are presented for two scenarios: exploiting CAM forecast prediction at 24 hours (left) or CAM forecast prediction at the present time (right) for station 15557. Similar outcomes were observed for the other stations in our analysis.
Preprints 75599 g002
Preprints 75599 g005
Figure 5. Simulation Results (MSE, from left to right): CAMS 1 to 9; Pers: Persistence; Models: ESN, LSTM, GRU, RNN, WMP4, WMP; AVE: average of the models. See Table 1 for station code reference.
Figure 5. Simulation Results (MSE, from left to right): CAMS 1 to 9; Pers: Persistence; Models: ESN, LSTM, GRU, RNN, WMP4, WMP; AVE: average of the models. See Table 1 for station code reference.
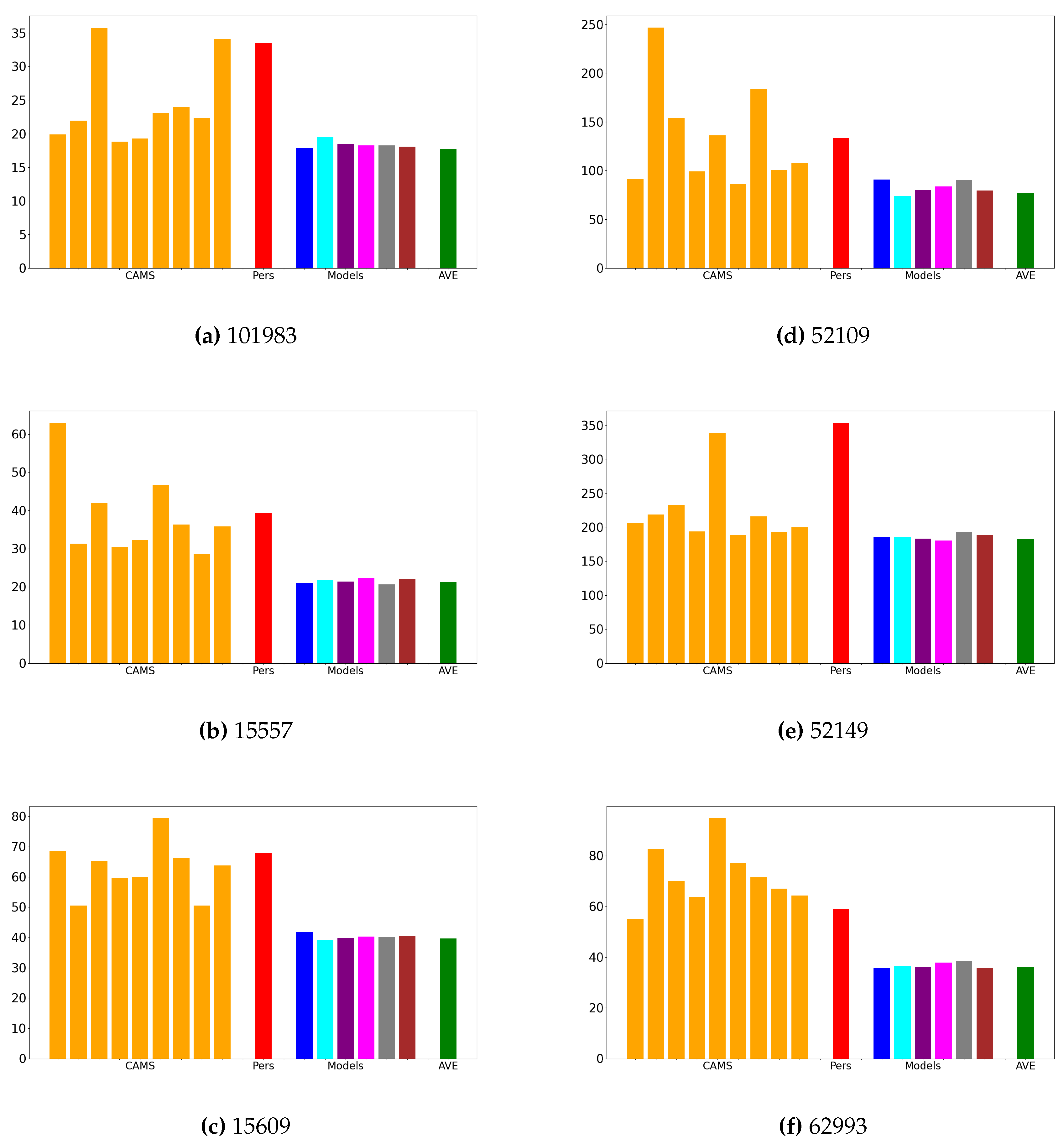
Preprints 75599 g005
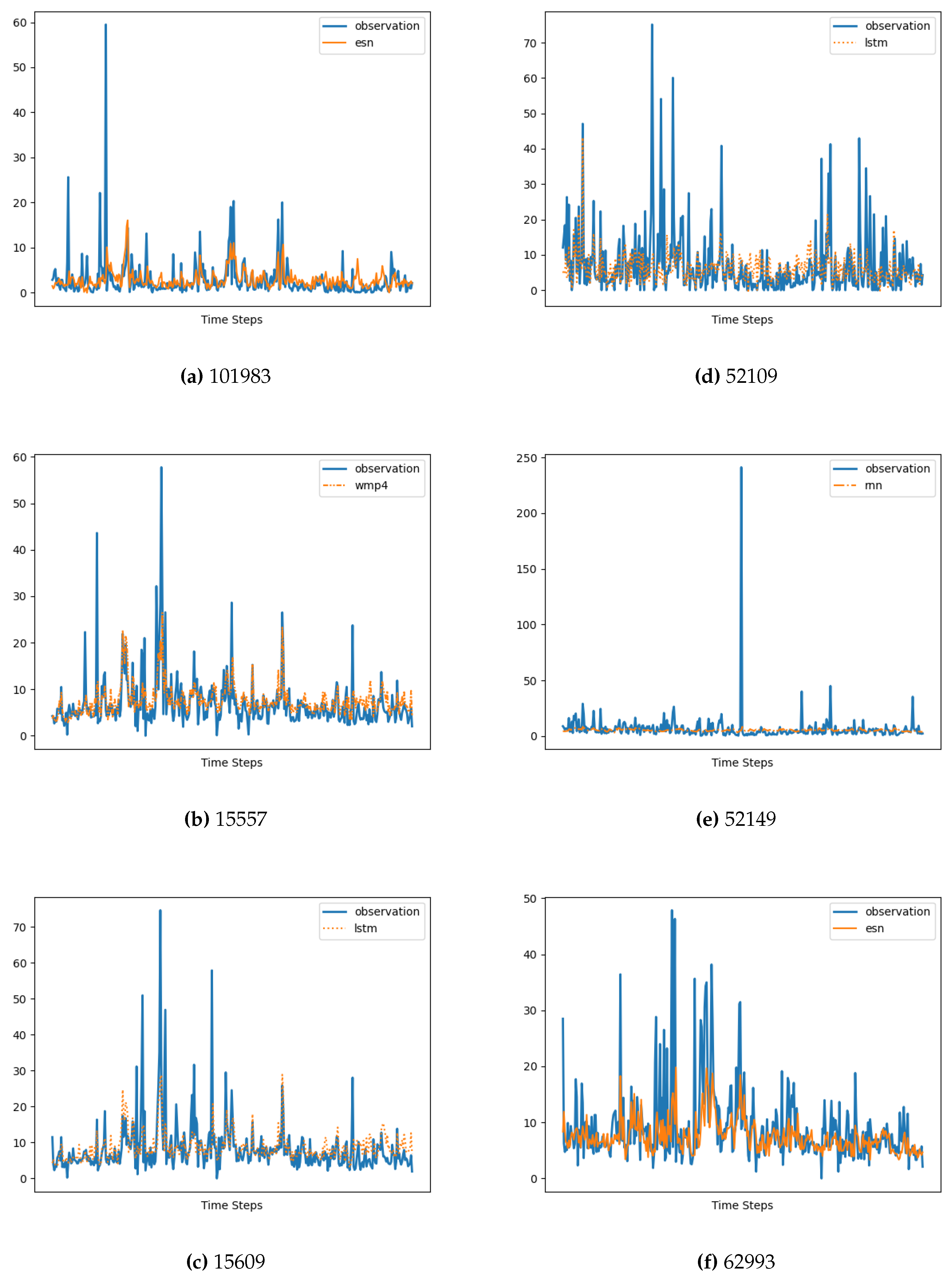
Preprints 75599 g006
Figure 6. Simulation Results (Forecasting). Only the most performing memory cell is graphed. See Table 1 for code reference.
Figure 6. Simulation Results (Forecasting). Only the most performing memory cell is graphed. See Table 1 for code reference.
Preprints 75599 g006
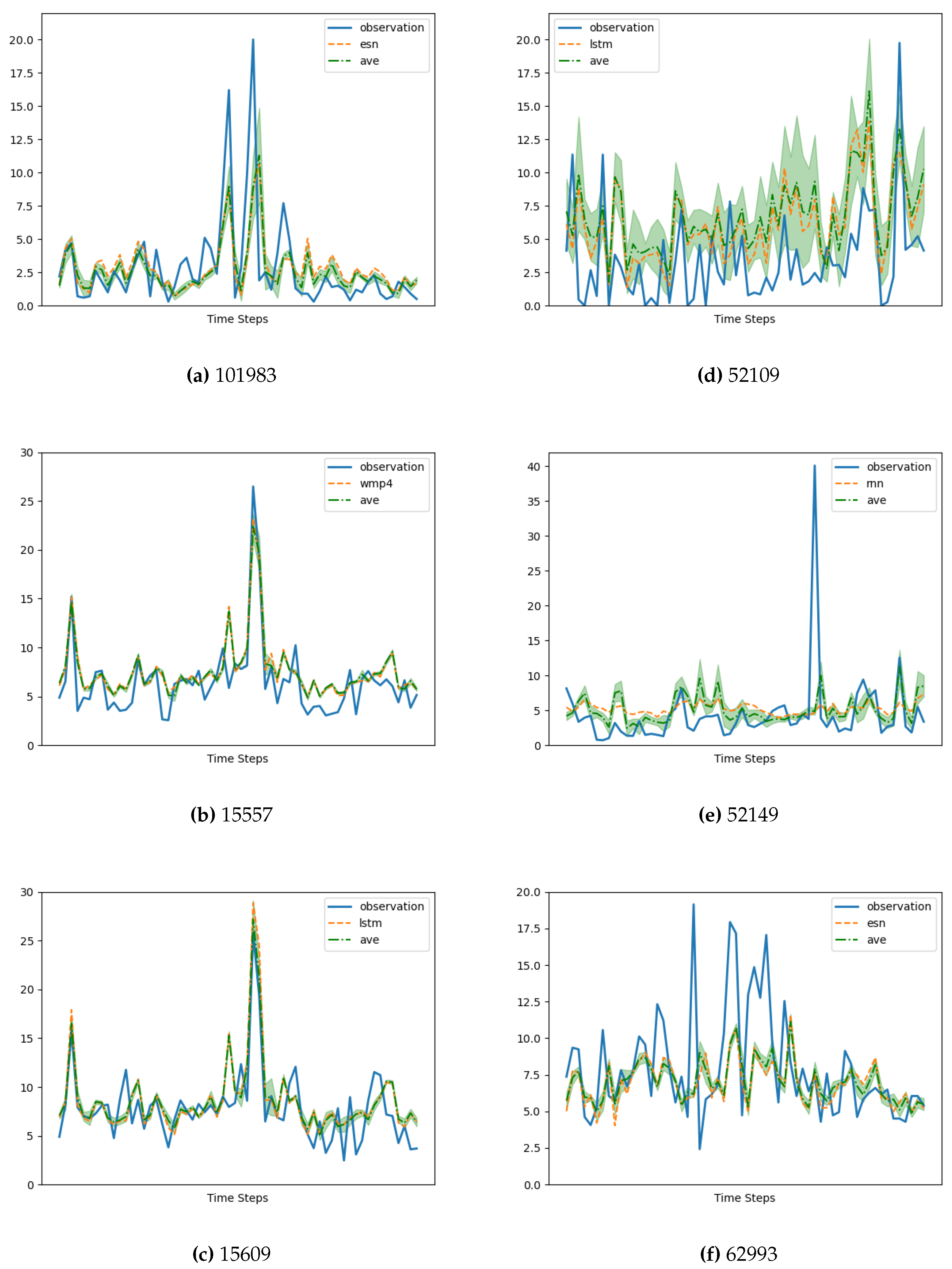
Preprints 75599 g007
Figure 7. Simulation Results (Forecasting Detail). Only the most performing memory cell is graphed, along with the average of all the models. See Table 1 for code reference.
Figure 7. Simulation Results (Forecasting Detail). Only the most performing memory cell is graphed, along with the average of all the models. See Table 1 for code reference.
Preprints 75599 g007
Preprints 75599 g008
Figure 8. CAMS (rows from one to ten, green/dark color) and our model (eleventh row, blue/dark color) are compared with measure (orange/light color). The x axis shows the time steps.
Figure 8. CAMS (rows from one to ten, green/dark color) and our model (eleventh row, blue/dark color) are compared with measure (orange/light color). The x axis shows the time steps.
Preprints 75599 g008
Preprints 75599 g009
Figure 9. Histogram (light/cyan shade, log-normal distribution (solid line) and threshold (dashed vertical line. The data on the right hand side of the vertical dashed line are removed from the dataset and linearly interpolated.
Figure 9. Histogram (light/cyan shade, log-normal distribution (solid line) and threshold (dashed vertical line. The data on the right hand side of the vertical dashed line are removed from the dataset and linearly interpolated.
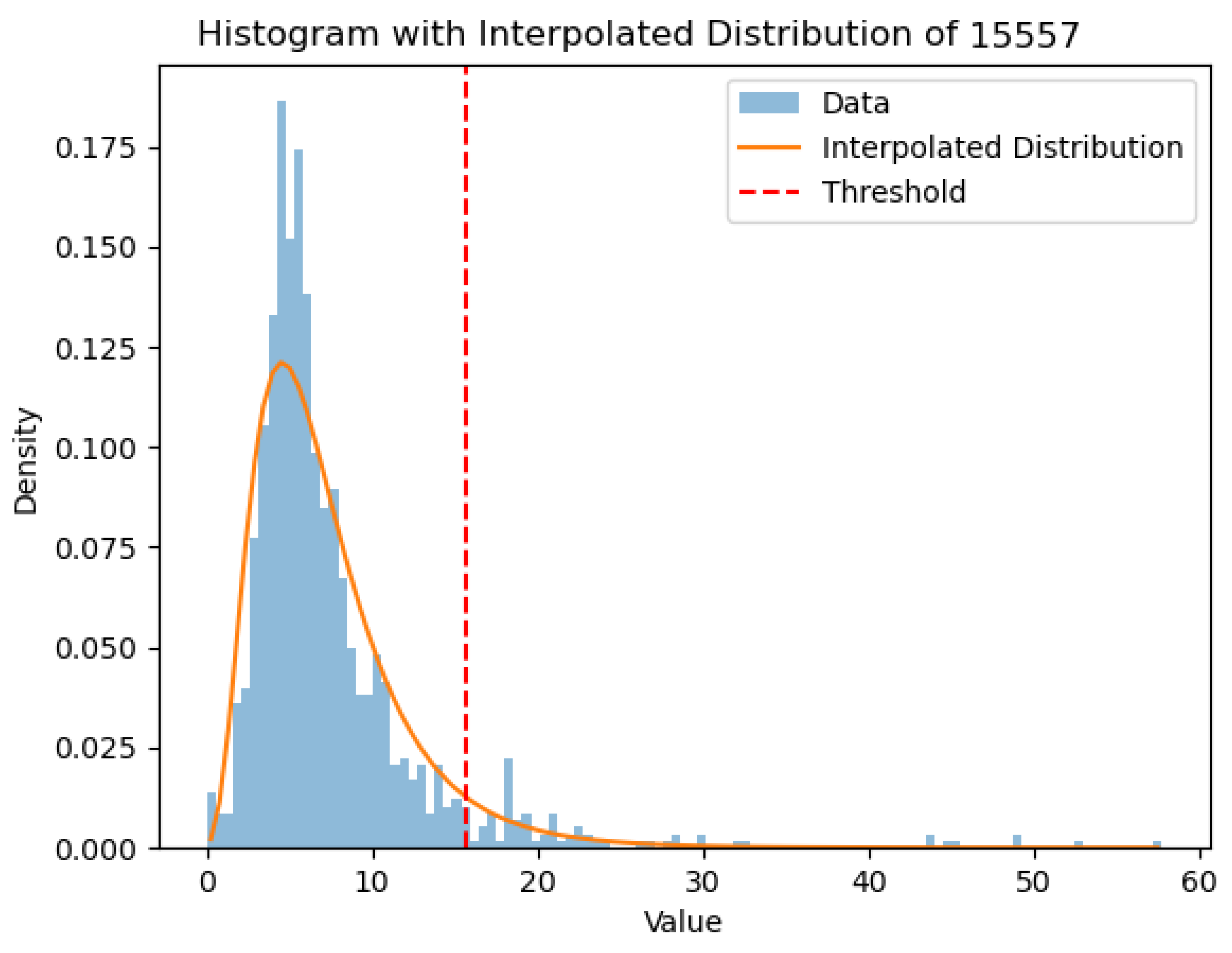
Preprints 75599 g009
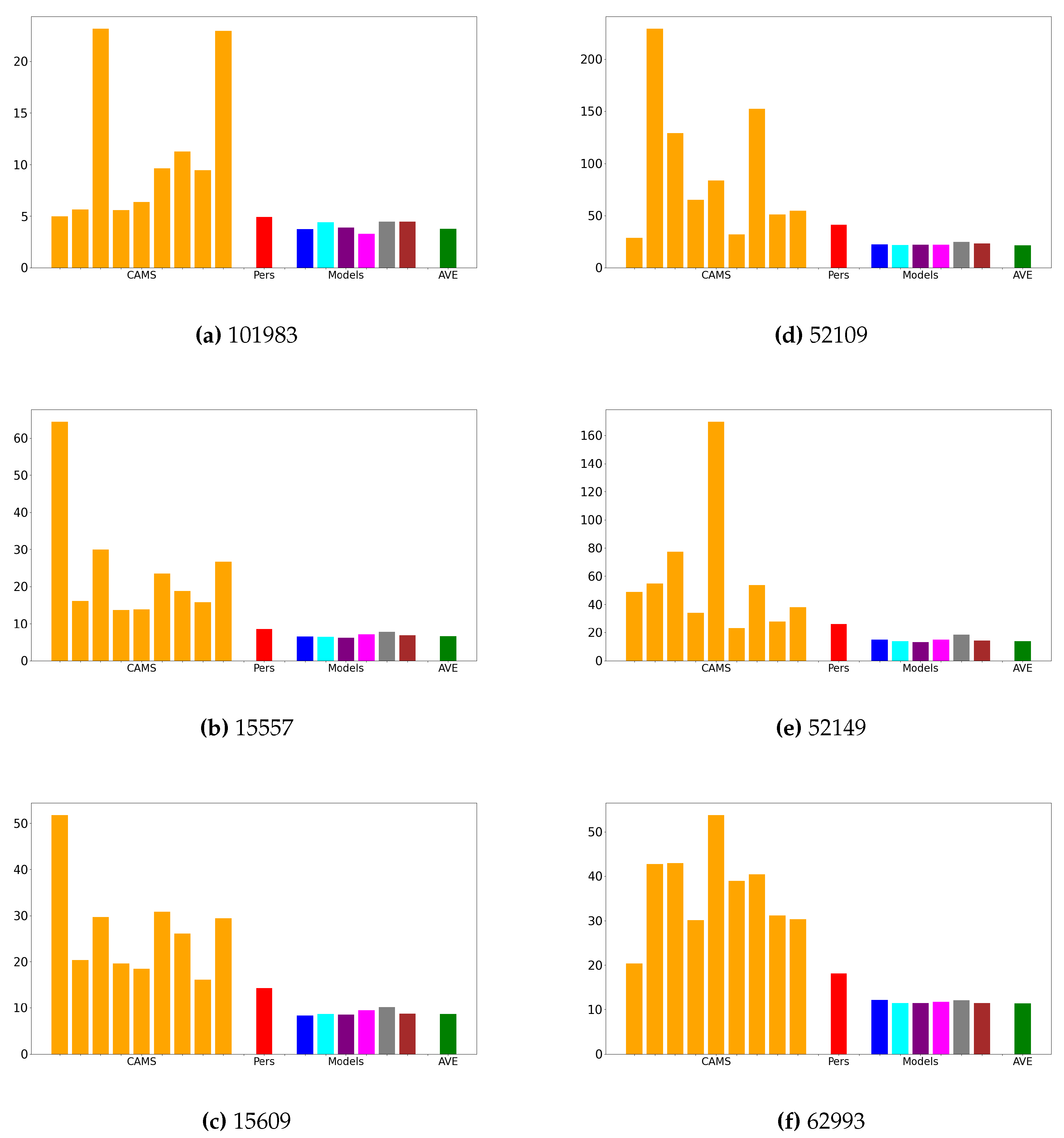
Preprints 75599 g010
Figure 10. Simulation Results of filtered data (MSE, from left to right): CAMS 1 to 9; Pers: Persistence; Models: ESN, LSTM, GRU, RNN, WMP4, WMP; AVE: average of the models. See Table 1 for station code reference.
Figure 10. Simulation Results of filtered data (MSE, from left to right): CAMS 1 to 9; Pers: Persistence; Models: ESN, LSTM, GRU, RNN, WMP4, WMP; AVE: average of the models. See Table 1 for station code reference.
Preprints 75599 g010
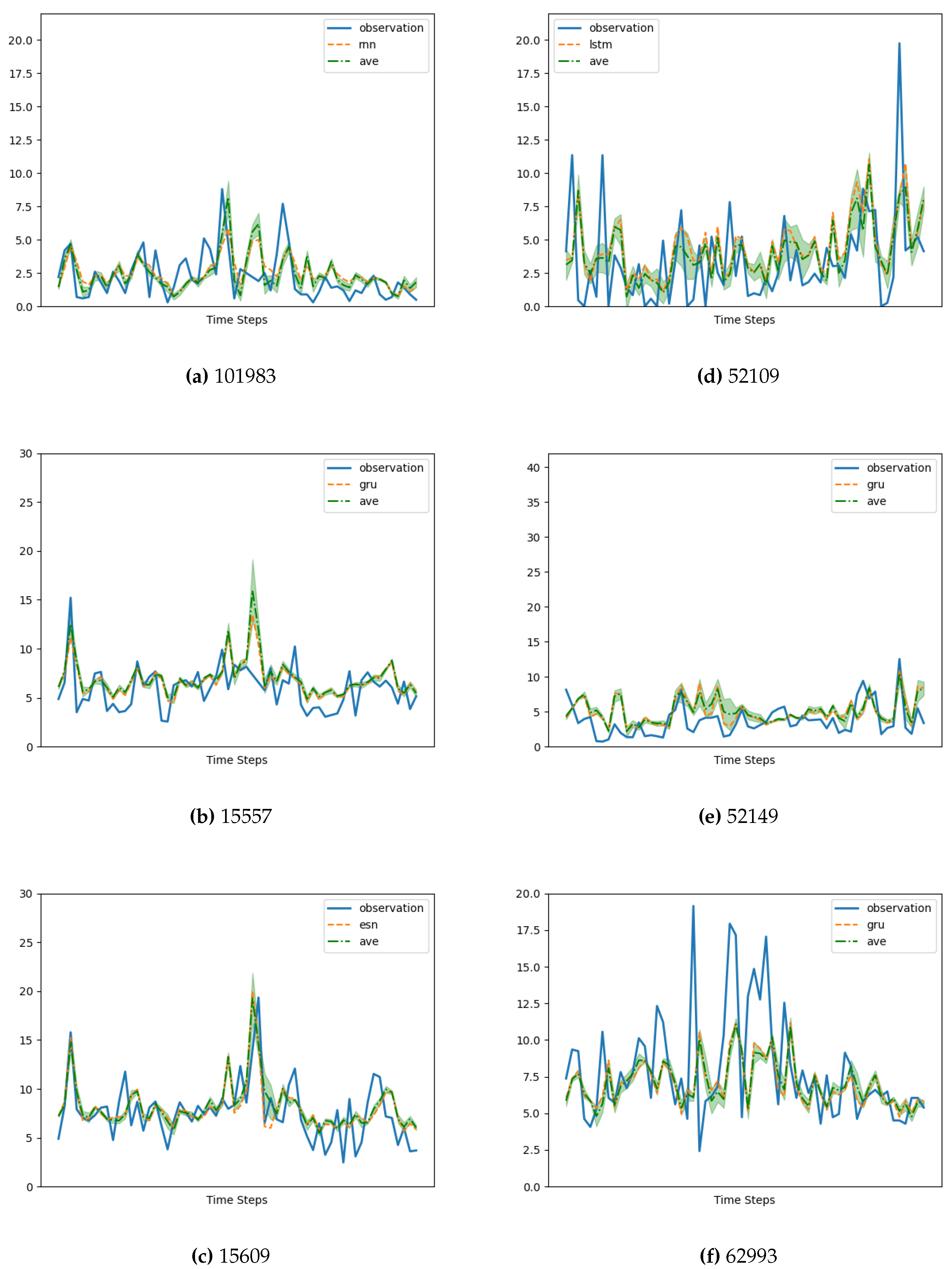
Preprints 75599 g011
Figure 11. Simulation Results (Forecasting) of filtered data. Only the most performing memory cell is graphed, along with the average of all the models. See Table 1 for code reference.
Figure 11. Simulation Results (Forecasting) of filtered data. Only the most performing memory cell is graphed, along with the average of all the models. See Table 1 for code reference.
Preprints 75599 g011
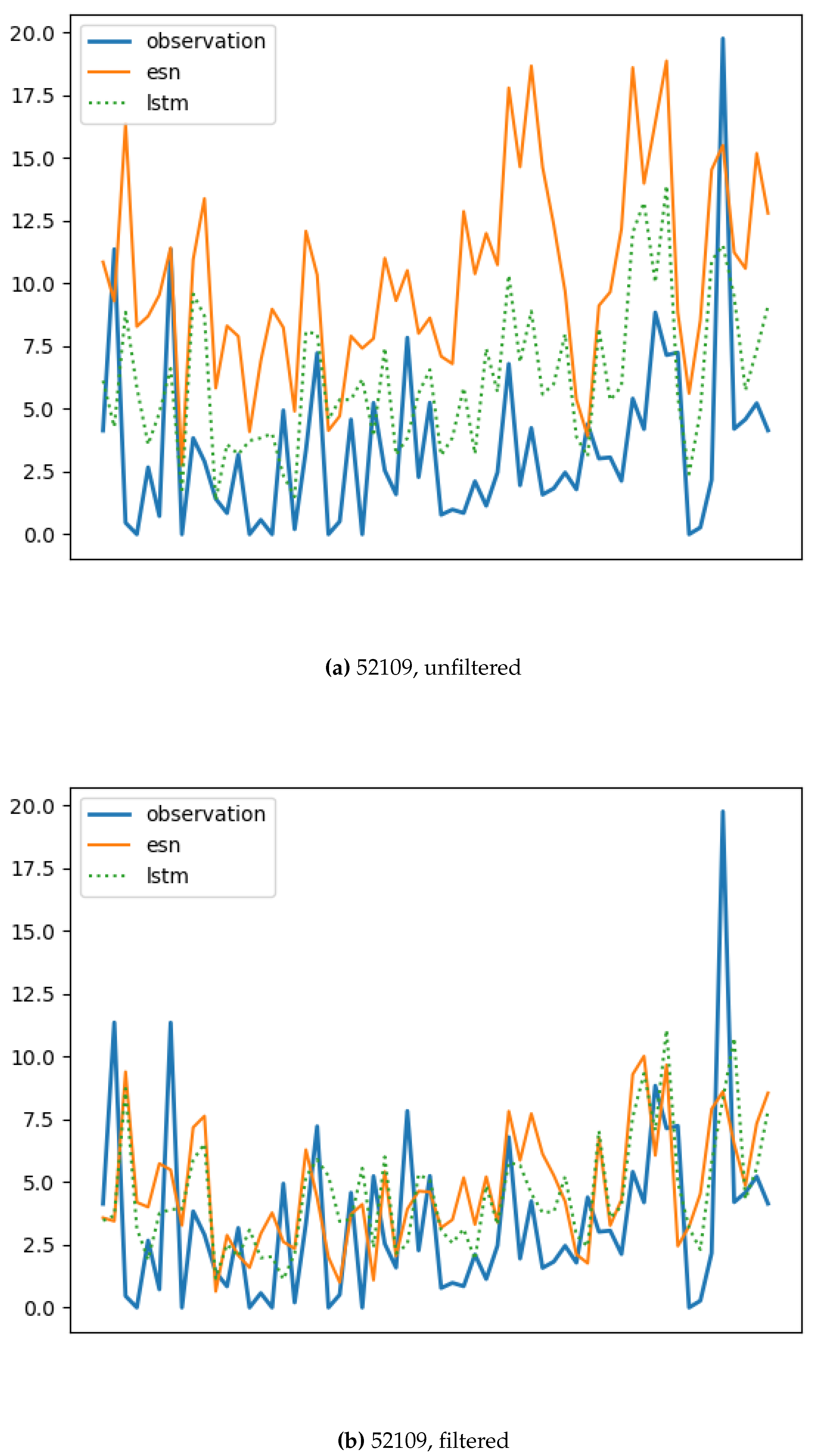
Preprints 75599 g012
Figure 12. Comparison between unfiltered (above) and filtered (below) forecast from 52109 station data) using the ESN and LSTM memory cells. See Table 1 for code reference.
Figure 12. Comparison between unfiltered (above) and filtered (below) forecast from 52109 station data) using the ESN and LSTM memory cells. See Table 1 for code reference.
Preprints 75599 g012
Table 1. Air quality monitoring stations selected for this forecasting study with their geographical positions and PM10 measurements techniques.
Table 1. Air quality monitoring stations selected for this forecasting study with their geographical positions and PM10 measurements techniques.
Station Country Latitude Longitude Measure Source Code
Muonio Sammaltunturi Finland 67.97 24.12 TEOM1 FMI 101983
Kópavogur Dalsmári Iceland 64.10 -21.89 BAN2 EEA 52109
Grundartangi Gröf Iceland 64.33 -21.83 BAN2 EEA 52149
Pyykösjärvi (Oulu) Finland 65.04 25.50 TEOM3 EEA 15557
Tromso Rambergan Norway 69.65 18.96 TEOM1 EEA 62993
Oulun keskusta 2 (Oulu) Finland 65.01 25.47 TEOM1 EEA 15609
14.1cm 1 Tapered Element Oscillating Microbalance. 2 Beta Attenuation and Nephelometry. 3 Beta Attenuation by a two beam compensation method.
Table 2. Main characteristics of the air quality regional models used by CAMS [30,31]
Table 2. Main characteristics of the air quality regional models used by CAMS [30,31]
Model Institution Horizontal Resolution Vertical Resolution Assimilated measures
]1*CHIMERE INERIS1 0.1ºx0.1º 8 levels, top at 500 hPa O3 and PM10 from surface stations
]1*EMEP MET Norway2 0.25ºx0.125º 20 levels, top at 100 hPa NO2 columns from OMI/Aura remote sensing and NO2 from surface stations
]1*EURAD-IM RIU UK3 15 km, Lambert conformal projection 23 levels, top at 100 hPa O3, NO, NO2, SO2, CO, PM10, PM2.5 from surface stations, NO2 from remote sensing column retrievals, CO profiles
]1*LOTOS-EUROS KNMI4 0.25ºx0.125º 34 levels, top at 3.5 km O3 from surface stations
]1*MATCH SMHI5 0.2ºx0.2º 52 levels top at 300 hPa O3, NO2, CO, PM10, PM2.5 from surface stations
]1*MOCHAGE Météo France 0.2ºx0.2º 47 levels, top at 5 hPa O3 from surface stations
]1*SILAM FMI6 0.15ºx0.15º 8 levels, top at 6.7 km O3, NO2 and SO2 from surface stations
]1*GEMA-Q IEP-NRI7 0.1ºx0.1º 28 levels, top at 10 hPa O3, NO2, CO, SO2, PM10, PM2.5 from surface stations
]1*DEHM AARHUS UNIVERSITY Denmark 18 km, polar streographic projection 29 layers, top at 100 hPa O3 and NO2from surface stations, PM10 and PM2.5 from global CAMS forecast
14.1cm 1 Institut National de l’Environnement Industriel et des Risques. 2 Meteorologisk institutt, Norway. 3 Rheinisches Institut Für Umweltforschung an der Universität zu Köln E. V., Germany. 4 Koninklijk Nederlands Meteorologisch Instituut, the Netherlands. 5 Sveriges Meteorologiska och Hydrologiska Institut, Sweden. 6 Ilmatieteen Laitos, Finland. 7 Institute of Environmental Protection, Poland.
Table 3. Air quality monitoring stations selected for this study with their geographical positions and PM10 measurements techniques.
Table 3. Air quality monitoring stations selected for this study with their geographical positions and PM10 measurements techniques.
Station Country Latitude Longitude Measure Source Code
Reykjavik Husdyragardurinn Iceland 64.14 -21.87 BA2BC3 EEA 45497
Tromso Hansjordnesbukta Norway 69.66 18.96 TEOM1 EEA 28816
14.1cm 1 Tapered Element Oscillating Microbalance. 2 Beta Attenuation and Nephelometry. 3 Beta Attenuation by a two beam compensation method.
Table 4. RNN Hyperparameters
Table 4. RNN Hyperparameters
Hyperparameter Specification Description
activation (dense layer) linear activation function in the dense layer
act. func. (recurrent output) t a n h ( ) activation function in the recurrent layer output
units 1 dimensionality of the output space
dropout no fraction of the units to drop for the linear transformation of the inputs and the recurrent states
bias yes layer bias
kernel initializer glorot uniform weights matrix, used for the linear transformation of the inputs
recurrent initializer orthogonal weights matrix, used for the linear transformation of the recurrent state
bias initializer 0 initializer for the bias vector
Table 5. LSTM and GRU Hyperparameters
Table 5. LSTM and GRU Hyperparameters
Hyperparameter Specification Description
act. func. (dense layer) linear activation function in the dense layer
act. func. (rec. output) t a n h ( ) activation function in the recurrent layer output
act. func. (recurrent) hard sigmoid activation function in the recurrent layer
units 1 dimensionality of the output space
dropout no fraction of the units to drop for the linear transformation of the inputs and the recurrent states
bias yes layer bias
kernel initializer glorot uniform weights matrix, used for the linear transformation of the inputs
recurrent initializer orthogonal weights matrix, used for the linear transformation of the recurrent state
bias initializer 0 initializer for the bias vector
Table 6. ESN Hyperparameters
Table 6. ESN Hyperparameters
Hyperparameter Specification Description
act. func. (dense layer) linear activation function in the dense layer
act. func. (resevoir) t a n h ( ) activation function in the resevoir
units 30 dimensionality of the resevoir
dropout no fraction of the units to drop for the linear transformation of the inputs and the recurrent states
connectivity 0.1 connection probability between two reservoir units
leaky 1 Leaking rate of the reservoir; ’1’ means no leaky integration
spectral radius 0.9 desired spectral radius of recurrent weight matrix
bias yes layer bias
kernel initializer glorot uniform weights matrix, used for the linear transformation of the inputs
recurrent initializer glorot uniform weights matrix, used for the linear transformation of the recurrent state
bias initializer 0 initializer for the bias vector
Table 7. Starting time step for each station, depending on contiguous missing data.
Table 7. Starting time step for each station, depending on contiguous missing data.
Station Code Starting time step
101983 469
52109 0
52149 0
15557 0
62993 308
15609 432
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated