Prerpints.org logo
Preprint
Article

Fracture Electromagnetic Radiation Induced by a Seismic Active Zone (in the Vicinity of Eilat City, Southern Israel)

Altmetrics

Downloads

166

Views

30

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

03 June 2023

Posted:

05 June 2023

You are already at the latest version

Alerts
Abstract
This paper deals with the quantitative analysis of measured fracture-induced electromagnetic radiation (FEMR) in the vicinity of the Dead Sea Transform using the Angel-M1 instrument, which enables the recording of FEMR signals in a 3D manner. Results show both the possibility of estimating the sizes of micro-fractures that are the sources of the radiation, and of assessing the direction of their location to the measuring device and the range of magnitude Mw of the impending "events" (EQ's) associated with the present FEMR measurements. Moreover, the relation between the measured FEMR activity (the number of FEMR hits per unit time) and the FEMR event magnitudes shows consistency with the Gutenberg-Richter relationship for the region. Such measurements could therefore constitute a preliminary 'field reinforcement' towards an EMR valid method for a real earthquake forecast, which would provide much earlier warnings than the seismic ones. Obviously, the present observed FEMR measurements can only be used as an assessment of the stress concentration and micro-fracturing in the region since they relate to the very initial nucleation phase of a "virtual" (extremely low Richter scale value) earthquake, but they do provide the necessary feasibility test for a prediction method since all lab-measured FEMR features were confirmed also in the field.
Keywords: 
Subject: Environmental and Earth Sciences  -   Geophysics and Geology

1. Introduction

It is well known that the Eastern Mediterranean and the Near East have experienced a great many earthquakes (EQs) over hundreds of thousands of years [1]. For example, the cities of Jerusalem, Jericho, Ramle, Tiberias, and Nablus were heavily damaged in 1927: about 300 houses collapsed or were damaged as well as the Church of the Holy Sepulcher and the al-Aqsa Mosque. Written records of EQs in China and Japan date as far back as 3000 and 1600 years, respectively [2]. On average 10,000 people die worldwide each year from earthquakes [3]. Only during the period of one year (30.3.22-30.3.23), the Mediterranean region and its close vicinity were shaken by 7 EQs of magnitude 6.0 or above (the biggest EQ of magnitude 7.8 took place in Central Turkey on 6.2.23).
The view that “understanding how earthquakes occur is one of the most challenging questions in fault and earthquake mechanics” [4] is not an overstatement. Despite intensive research activity including the study of the acoustic emission process associated with micro-fracturing [5,6,7,8,9], many aspects of these phenomena are still unknown. It is debated whether EQs begin as small dynamic instabilities that develop into larger fractures (“cascade” model), or as a slow but accelerating aseismic slip that eventually reaches a critical size and then develops into a failure (“pre-slip” model), or their combination [10,11].
So far, no reliable method of early EQ forecasting has been found [12,13] by the commonly used seismic measurements. It is established that such a real early forecast cannot be achieved based only on seismic measurements due to the high attenuation of the high-frequency seismic waves emitted at this stage [14]. The two "so-called" existing types of seismic forecast are either statistical ones, providing only probabilistic predictions, or "alarm systems", starting to operate only when the EQs have already started. The latter systems are based on the dual seismic waves emitted when an actual EQ process is already full blown. These two waves have different speeds. The first (longitudinal) P-wave, which causes no harm, moves at a velocity of ~3-6 km/s while the damage-causing transverse S-wave is slower (its velocity is around ~2-3 km/s) depending on the rock’s mechanical properties. Thus, an alarm signal is obtained by measuring the P-wave arrival before that of the S-wave. Since the difference in the velocities depends on the Poisson ratio (~0.15-0.45), such an alarm is inherently brief and depends on the receiver distance from the hypocenter as to its pre-catastrophic appearance. For example, using the velocity values typical for granite rock (Vp≈5 km/s and Vs≈2.7 km/s), the difference between the first arrivals of these waves will be K=(Vp-Vs)/(Vp*Vs)≈0.17s/km. Hence, people located 5 km from the hypocenter would have an approximately 0.85s foreknowledge of the disaster, while even at 50 km, only a meager 8.5s alarm is possible.
In order to build a reliable early EQ forecast, many precursors of an EQ were targeted over the past several decades, e.g., [15,16]. It has recently been accepted that one of these precursors, i.e., electromagnetic (EM) phenomena, does occur before an EQs, e.g., [17,18], and does allow for real-time monitoring of fracture evolution during mechanical loading, from incredibly early stages of failure nucleation [19,20]. For example, the distribution of fracture electromagnetic radiation (FEMR) signals was found to match the Gutenberg-Richter and Benioff relationships, like the acoustic emission relationships [21,22]. Here we carry out FEMR measurements "in the field", in order to establish feasibility proof of such measurements, on the road to creating an FEMR EQ forecasting scheme.

1.1. FEMR state of art

FEMR measurements have been carried out in a wide variety of laboratory studies and in a wide frequency spectrum (from the kHz band to the MHz band), e.g., [21,22,23,24,25,26,27,28,29,30,31,32,33,34]. Results of studies performed till 2021 are reviewed in [35]. On the geophysical scale, FEMR was recorded prior to significant EQs [36,37,38,39,40,41,42]. The timely increase of FEMR intensity was shown to be a common characteristic both in the lab medium and on the geophysical scale. For example, the application of the FEMR method was shown to be incredibly useful for assessing the intensity of stress levels [43,44,45,46,47,48,49,50] and stress directions in underground openings [51], and for locating landslide-prone zones [52]. Studies of FEMR for defining stress field orientations are quite rare [52,53,54,55,56,57] though they are highly interesting for understanding features of neotectonics and seismic activity in the vicinity of active faults. It was shown [52,53,54,55,56,57] that the FEMR direction accurately reflects stress distribution near active reverse-type faults. However, no measurements of the combined features of fault fracturing and its location in the field do exist. Here we present FEMR measurements conducted at the southern part of a strike-slip fault of the Syrian African transform (the Dead Sea Transform) focused on the possibility of extracting both fracture and field properties from the sole description of the EMR pulses. This region was selected for the study as being the most seismically active in Israel and even in relation to the entire Syrian-African Transform [58,59,60,61,62].

1.2. Eilat region - geology, faults, and the location of measurement stations

The measurements were conducted at three locations near the most Southern Israeli city of Eilat (Figure 1). As noted above, this vicinity is one of the most active seismic regions in Israel (Figure 2, [59]). The major geological structure in the Eilat area was developed as a result of the tectonic activity associated with the rifting of the Red Sea and the Dead Sea Transforms [63]. The main faults, their branches, and the stress field in the region are thoroughly described in various studies, e.g., [63,64,65,66].
The EQs in this region are mainly associated with the southern part of the Syrian African Transform fault and its active branches which are shown schematically by dashed lines in Figure 1.

2. FEMR measurements methodology in the Eilat region

2.1. The Instrument and Method

The measurements were conducted using an ANGEL-M1 instrument manufactured by OAO VNIMI, Russia, which is an upgraded version of the ANGEL-M apparatus described in detail in [55,56,68]. It is a portable measuring device for FEMR recording in situ as well as in underground conditions in the frequency range from 5-150 kHz. The difference between the upgraded version and that used in references [55,56,57], is the upgraded version’s ability to perform 3D measurements using three antennas simultaneously. Figure 3 shows an example of a measurement using the upgraded version of the instrument in Timna Park.
Before each measurement, the antennae were oriented to Up (channel 1), North (channel 2), and East (channel 3) directions. The duration of each measurement was 10 s, and 20 measurements were carried out at each location. The measured data was saved on the instrument's hard disk and then downloaded to a PC for further processing. The original software package Angel-Works was used for data filtering while the data processing was done using the Origin software.

3. Results

We use our acquired analyzing lab methods [14,20,21,68,69,70,72] to obtain several results about the fracturing process and its location. Sec. 3.1 presents the obtained measurements themselves, while the inferred results are presented in sections 3.2-3.6.

3.1. The results of the FEMR measurements

Figure 4 portray an example of the 10 s sequence of FEMR pulses after bandpass filtering (5-50kHz) at Timna Park (Figure 1). It is seen that the signal-to-noise ratio of each FEMR signal is high enough for further signal analysis. The amplitudes of FEMR pulses recorded in situ by the Angel-M1 instrument is of the order of 10-20 µVolt, being consistent with former FEMR results measured in similar regions of tectonic faults [55,56,57]. Such FEMR amplitudes were shown to be caused by rock micro-fracturing [55,56,57]. Figure 5 portrays a zoom-in example of a single FEMR pulse while Figure 6 shows its frequency spectrum. It is worthwhile to emphasize that the shape of the FEMR signal is identical to those described in our previous laboratory studies (e.g., [69]) proving the consistency of the present study with those performed in the laboratory.
Note that the number of FEMR pulses shown in Figure 4 is about 9 (depending on the amplitude’s threshold). A part of these pulses coincides in time in the Eastern and Northern channels (4) while some (5) do not do so. This observation obviously means that while the fracturing events inducing the pulses were located differently, they occurred mostly in a northeasterly direction (see below). The average rate of FEMR pulses (calculated on the basis of 20 records in each region) were 6.4±2.8, 8.2±3.3, 12.3±10.9 pulses/10 s, in Timna Park, Shlomo Wadi, and the Park of Birds, respectively.

3.2. The source amplitude of the electromagnetic field of the FEMR signals

Following [70] the source electric field amplitude inducing the EMR signals reaching the antenna from granite samples when the antenna is in a close vicinity to the source is given by:
E = 3 × 10 9 f 0.99 ± 0.04
where E is the EMR field amplitude in mV/m and f is the EMR frequency in Hz.
The measured EMR frequency of all the obtained EMR pulses (e.g., Figure 6) in the Eilat region is of the order of 15-20 kHz, yielding source electric field amplitudes between 150 and 200V/m. Since the amplitudes of electric E0 and magnetic H0 fields are related via the following expression:
E 0 = H 0 μ 0 ε 0
Where μ0 and ε0 are the values of magnetic and dielectric permittivity of the free space, the magnetic field amplitudes at the source are: H0≈0.4-0.5 A/m.

3.3. Sources’ distances

3.3.1. Attenuation factor

The EMR field amplitude attenuation is given by [27]:
E = E 0 e − α R
Where the attenuation coefficient, α ,   is given by:
α = ω μ ε 2 − 1 + ( 1 + ( σ ω ε ) 2
where:
ω = 2 π f
μ = μ 0 1 + κ = 4 π × 10 − 7 1 + κ H / m
ε = ε 0 ε r = 8.84 × 10 − 12 ε r F / m
and where   κ   is the value of magnetic susceptibility, σ is the value of the electrical conductivity, and ε r   is the value of dielectric permittivity. The measured values of these parameters in the Eilat region are as follows: κ = 25 , σ = 10 − 5 S m , ε r = 5 , Yielding α = 3.2 × 10 − 3 1/m.

3.3.2. FEMR amplitudes at the input of the measuring instrument and the antenna factor

As we noted above, the electric field amplitudes of FEMR pulses recorded in situ by the Angel-M1 instrument are of the order of 10-20 μVolt. The gain of the instrument is 18000, hence the FEMR amplitudes reaching the instrument’s input from the antenna is of the order of (5-10)x10-4 μV = (5-10) x10-10V.
The Antenna Factor (or correction factor, A F ) is defined as the ratio of the incident Electromagnetic Field E a n t _ i n p u t to the output voltage V from the antenna and the output connector and is given by [71]:
A F = 20 L o g E a n t _ i n p u t V a n t   v o l t   o u t p u t = 19.8 − G d B − 20 L o g λ = 19.8 − G d B − 20 L o g c f ε r ≈ − 80 d B / m
Where G d B is the antenna gain, λ is the length of the EM wave, c is the speed of light, f is the frequency of the FEMR signal and ε r is the dielectric permittivity.
Eq. 5 yields: E a n t _ i n p u t = 10 − 4 V = ~ 5 − 10 × 10 − 14 V m . And, according to Eq. 3, R = ( 1 / α ) L n ( E 0 E a n t i n p u t ) ≈ 5 k m Note that this estimation was performed for FEMR signals that are propagating through granite rock.

3.4. Crack dimensions

The crack length and crack width are related to the FEMR signal parameters via two relationships [27,69,70] as follows:
b = V R 2 f l = V c r × T '
where l and b are the crack length and width respectively (m), V c r and V R are the crack and Rayleigh wave speeds, respectively (m/s), T ' is the time from the FEMR origin till the maximum of the FEMR signal envelope.
Using the values of the Rayleigh wave and the crack speeds of the order of 2600 m/s and 2340 m/s [72] respectively, yields the value of crack width: b = 5 − 10 c m and of crack length (based on the estimated value of T' of the order of 50-150 μs) : l = 10 − 35 c m .
Our previous estimation [72] shows that such crack dimensions correspond to seismic moment values of M0 ≈105 Nm and based on the diagram developed in Ref. [73] – the seismic moment magnitude of the (virtual) impending EQ is of the order of Mw ≈(-3) to (-4).

3.5. The FEMR source direction

The 3D electric field emitted by the crack source of the FEMR is given by:
E = E 1 x ^ + E 2 y ^ + E 3 z ^ .
Its amplitude is:
E = ( E 1 2 + E 2 2 + E 3 2 )
The amplitude is measured by the Angel-M1 instrument, while the indexes 1,2,3 here mean North, East and Up directions, respectively.
Define:
c o s α = E 1 E ,   c o s β = E 2 E ,   c o s γ = E 3 E
The values of these cosines are calculated from the amplitudes obtained respectively by the three antennas, according to Eq. (7.2), yielding the following directions from the different source locations to the measuring devices calculated on the basis of the average of 20 records in each measurement position:
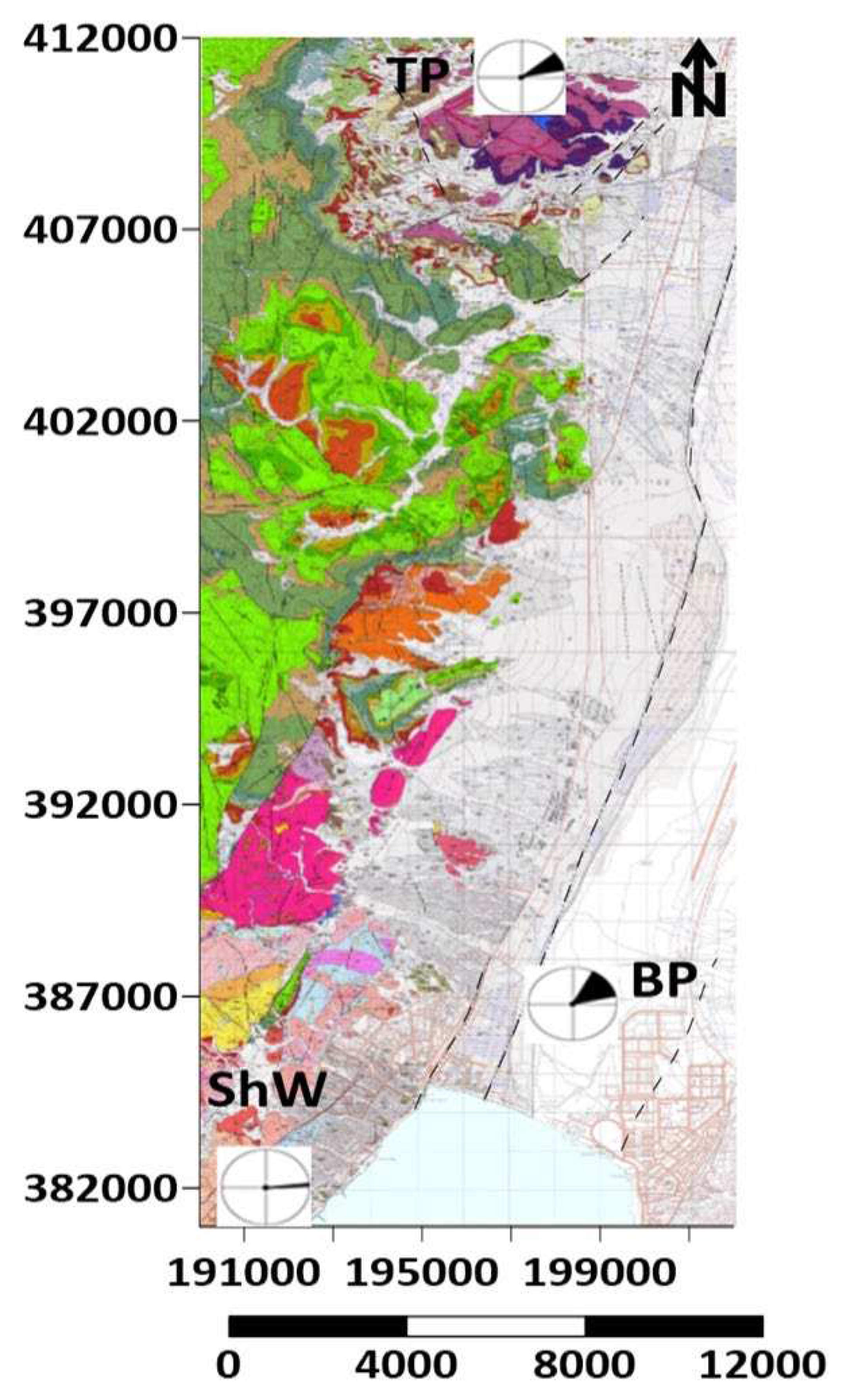
  • Wadi Shlomo: 4-7° from the East and 83-86° from the North
  • The Birds Park: 14-62° from the East and 28-76° from the North
  • The Timna Park: 10-40° from the East and 60-80° from the North
Figure 7 shows the locations of the measurement points with superimposed diagrams of the FEMR directions to the signals’ sources.
It is seen that the directions to the FEMR sources clearly correspond to the location of the main active faults in the region (Figure 7). The amplitude of the FEMR signals in the Up-Down antennas are quite low indicating that the radiations from all locations is in the horizontal plane.
In summary, it is seen that the FEMR records in all three locations point in the direction of the Syrian-African fault.

3.6. The FEMR activity

The FEMR activity is generally defined as the number of FEMR signals per unit time [68]. As noted above, the measurements were carried out during 10 s intervals and the estimated magnitudes of FEMR signals were of the order of Mw≈ (-3) to (-4). It is known [60] that during a period of 30 years in Israel there have occurred 15856 EQs with magnitudes Mw≈0.5, implying about 500 EQs per year with the magnitudes larger than 0.5. Considering that changes in magnitude of 1 unit means a change in number of events by a factor of 10, it can be estimated that the number of events with a magnitude of the order
Mw≈ (-3) -(-4) can be of the order of 1.5x(106-107) per year or 0.5-5 events each 10 s. The analysis of the FEMR data shows that the average FEMR activity (calculated on the basis of 20 records in each region) measured by the Angel-M1 instrument each 10 s of recording, are 6.4±2.8, 8.2±3.3, 12.3±10.9 pulses/10sec, in Timna Park, Shlomo Wadi, and the Park of Birds, respectively. The measured values agree with the above estimates. Note that the minimal FEMR activity was measured in Timna Park which is located about 3 km from the Syrian African transform while the largest activity was measured in the Park of Birds located within the boundaries of the Transform itself.

4. Discussion

Seismic global methods, such as the MOWLAS (Monitoring of Waves on Land and Seafloor) in Japan [74], are valuable assets for monitoring and understanding the nature of earthquakes and tsunamis. They can also be used for statistical estimates of EQ forecasting. Such statistical methods are termed "Probabilistic earthquake forecasts" [75]. Other schemes, e.g., Machine learning (ML) methods on experimental monitoring of water-level variations in wells and on geomagnetic and tidal time series [76] are also used in such forecasts. However, only probabilities but no warnings before an actual catastrophe can be gathered from them.
Some recent FEMR signals were measured before EQs mainly in the Athens Basin, Greece [77,78,79,80]. Baron et al [81] conducted a six months operation to measure FEMR signals in the Obir Cave in the eastern Alps to try to extract the relevant signals to EQ prediction from them.
The methods using multidisciplinary precursors [82] or AI approaches of learning the relevant signals (see e.g., [83]), have been promoted. These procedures which can be very valuable in EQ prediction may possibly use the present pulse shapes based on the cracks’ features as guiding elements.
We advocate the use of an FEMR method for real warnings, and the present measurements constitute a step forward in validating this technique, showing both the feasibility of these measurements and the ability of extracting a myriad of quantitative facts (see enumeration a-f below) regarding the stress and possible pre-quake fault situation. Note that measurements of FEMR phenomena carried out previously only focused on the magnitude and frequency of the pulses' appearance while the present study is the first one to use our lab experience, based on the actual shape of the pulses, to extract all these features.
The FEMR measurements were conducted in the vicinity of Eilat city, a region that is one of the most active seismic regions in Israel. Seismicity there is mainly associated with the activity of the Dead Sea transformation and its branches. The investigation was carried out using 3D antennae (in the frequency range 5-150 kHz) in three locations. Obtained results, based on our lab developed analyzing methods, showed that:
  • the range of micro-fractures lengths associated with the FEMR parameters is between 5-30 cm,
  • the amplitude of the FEMR field at the source (micro-fracture) is assessed to be of the order of 150-200 V/m (0.4-0.5 A/m),
  • the amplitude of the FEMR field at the input of the recording antennae is estimated to be of the order of ≈10-13-10-14V/m (H≈10-16A/m),
  • the distance between the antennae and the FEMR signals' sources is assessed to be of the order of 5 km, while their azimuth of ≈5-60° to the East indicate that the sources of FEMR are indeed within the zone of the Dead Sea transform,
  • the range of Mw magnitudes of the impending "EQ's" associated with the micro-fractures is shown to be of the order of -4 to -3, implying that they were created during an early period of a micro-earthquake nucleation,
  • conclusion e. is also confirmed by the comparison of the FEMR activities (the number of FEMR hits per unit time) and the associated FEMR magnitudes, with the Gutenberg-Richter relationship in the region.

5. Conclusions

The results of this study are entirely consistent with our previous laboratory studies and show the feasibility of using FEMR measurements for early earthquake forecast. Rock fracture characteristics are easily obtainable from the detailed features and shapes of the measured signals and, specifically, the magnitudes of approaching EQ's. Obviously, this feasibility signals and, specifically in establishing such a forecasting method. More field experiments are necessary for complete validation, especially experiments preceding actual large EQs.

References

  1. Nur, A. Apocalypse. Earthquakes, Archaeology, and the wrath of God. Princeton University Press Princeton and Oxford, 2008.
  2. Kramer, S.L. Geotechnical Earth Engineering. Prentice Hall, 1996.
  3. Bolt, B.A.; Horn, W.L.; Macdonald, G.A.; Scott, R.F. Geological Hazards. Springer-Verlag 1977.
  4. Kazama, M.; Noda, T. Damage statistics (Summary of the 2011 off the Pacific Coast of Tohoku Earthquake damage). Soils Found. 2012, 52, 780–792. [Google Scholar] [CrossRef]
  5. Ishida, T.; Kanagawa, T.; Kanaori, Y. Source distribution of acoustic emissions during an in-situ direct shear test: Implications for an analog model of seismogenic faulting in an inhomogeneous rock mass. Eng. Geol. 2010, 110, 66–76. [Google Scholar] [CrossRef]
  6. Cheon, D.-S.; Jung, Y.-B.; Park, E.-S.; Song, W.-K.; Jang, H.-I. Evaluation of damage level for rock slopes using acoustic emission technique with waveguides. Eng. Geol. 2011, 121, 75–88. [Google Scholar] [CrossRef]
  7. Deng, L.; Yuan, H.; Chen, J.; Sun, Z.; Fu, M.; Zhou, Y.; Yan, S.; Zhang, Z.; Chen, T. Experimental investigation on progressive deformation of soil slope using acoustic emission monitoring. Eng. Geol. 2019, 261, 105295. [Google Scholar] [CrossRef]
  8. Mei, C.; Fang, Z.; Wu, W. Slip transition of rock fractures due to chemical corrosion. Eng. Geol. 2022, 308. [Google Scholar] [CrossRef]
  9. Meng, F.; Wong, L.N.Y.; Zhou, H.; Wang, Z. Comparative study on dynamic shear behavior and failure mechanism of two types of granite joint. Eng. Geol. 2018, 245, 356–369. [Google Scholar] [CrossRef]
  10. McLaskey, G.C.; Lockner, D.A. Preslip and cascade processes initiating laboratory stick slip. J. Geophys. Res. Solid Earth 2014, 119, 6323–6336. [Google Scholar] [CrossRef]
  11. Noda, H.; Nakatani, M. Hori, T. Large nucleation before large earthquakes is sometimes skipped due to cascade-up—Implications from a rate and state simulation of faults with hierarchical asperities, J. Geophys. Res. Solid Earth, 2013, 118, 2924–2952. [Google Scholar]
  12. Rikitake, T. Predictions and precursors of major earthquakes: The Science of Macro-Anomaly Precursory to an Earthquake. Terra Scientific Publishing Company, Tokyo, 2001.
  13. Bormann, P. From Earthquake Prediction Research to Time-Variable Seismic Hazard Assessment Applications. Pure Appl. Geophys. 2010, 168, 329–366. [Google Scholar] [CrossRef]
  14. Rabinovitch, A.; Frid, V.; Bahat, D. Use of electromagnetic radiation to predict earthquakes. Geological Magazine. 2018, 155, 992–996. [Google Scholar] [CrossRef]
  15. Shimamoto, T.; Togo, T. Earthquakes in the Lab. Science 2012, 338, 54–55. [Google Scholar] [CrossRef] [PubMed]
  16. Hayakawa, M. Earthquake Prediction with Radio Techniques; Wiley: Hoboken, NJ, United States, 2015; ISBN 9781118770160. [Google Scholar]
  17. Hayakawa, M. Earthquake prediction studies: seismo electromagnetics. Terrapub, Tokyo, 2013.
  18. Uyeda, S.; Nagao, T.; Kamogawa, M. Short-term earthquake prediction: Current status of seismo-electromagnetics. Tectonophysics 2009, 470, 205–213. [Google Scholar] [CrossRef]
  19. Liu, Y.; Li, X.; Li, Z.; Chen, P.; Yang, T. Experimental study of the surface potential characteristics of coal containing gas under different loading modes (uniaxial, cyclic and graded). Eng. Geol. 2018, 249, 102–111. [Google Scholar] [CrossRef]
  20. Das, S.; Mallik, J.; Deb, T.; Das, D. Quantification of principal horizontal stresses inside a tunnel: An application of Fracture induced Electromagnetic Radiation (FEMR) technique in the Darjeeling-Sikkim Himalayas. Eng. Geol. 2020, 279, 105882. [Google Scholar] [CrossRef]
  21. Rabinovitch, A.; Frid, V.; Bahat, D. Gutenberg-Richter-type relation for laboratory fracture-induced electromagnetic radiation. Phys. Rev. E 2001, 65, 011401. [Google Scholar] [CrossRef] [PubMed]
  22. Frid, V.; Goldbaum, J.; Rabinovitch, A.; Bahat, D. Time-dependent Benioff strain release diagrams. Philos. Mag. 2011, 91, 1693–1704. [Google Scholar] [CrossRef]
  23. Baddari, K.; Frolov, A.D.; Tourtchine, V.; Rahmoune, F. An Integrated Study of the Dynamics of Electromagnetic and Acoustic Regimes During Failure of Complex Macrosystems Using Rock Blocks. Rock Mech. Rock Eng. 2010, 44, 269–280. [Google Scholar] [CrossRef]
  24. Lacidogna, G.; Carpinteri, A.; Manuello, A.; Durin, G.; Schiavi, A.; Niccolini, G.; Agosto, A. Acoustic and Electromagnetic Emissions as Precursor Phenomena in Failure Processes. Strain 2011, 47, 144–152. [Google Scholar] [CrossRef]
  25. Hadjicontis, V.; Mavromatou, C.; Mastrogiannis, D.; Antsygina, T.N.; Chishko, K.A. Relationship between electromagnetic and acoustic emissions during plastic deformation of gamma-irradiated LiF monocrystals. J. Appl. Phys. 2011, 110. [Google Scholar] [CrossRef]
  26. Carpinteri, A.; Lacidogna, G.; Manuello, A.; Niccolini, G.; Schiavi, A.; Agosto, A. Mechanical and Electromagnetic Emissions Related to Stress-Induced Cracks. Exp. Tech. 2011, 36, 53–64. [Google Scholar] [CrossRef]
  27. Rabinovitch, A.; Frid, V.; Bahat, D. Directionality of electromagnetic radiation from fractures. Int. J. Fract. 2017, 204, 239–244. [Google Scholar] [CrossRef]
  28. Liu, X.; Zhang, Z.; Wang, E.; Wang, X.; Yang, B.; Wang, H. Characteristics of electromagnetic radiation signal of coal and rock under uniaxial compression and its field application. J. Earth Syst. Sci. 2019, 129, 1–11. [Google Scholar] [CrossRef]
  29. Song, D.; Wang, E.; Song, X.; Jin, P.; Qiu, L. Changes in Frequency of Electromagnetic Radiation from Loaded Coal Rock. Rock Mech. Rock Eng. 2015, 49, 291–302. [Google Scholar] [CrossRef]
  30. Lou, Q.; Song, D.; He, X.; Li, Z.; Qiu, L.; Wei, M.; He, S. Correlations between acoustic and electromagnetic emissions and stress drop induced by burst-prone coal and rock fracture. Saf. Sci. 2019, 115, 310–319. [Google Scholar] [CrossRef]
  31. Wang, W.; Song, D.; He, X.; Liu, Q.; Li, Z.; Qiu, L.; Mei, G. Dynamic Propagation and Electro-Mechanical Characteristics of New Microcracks in Notched Coal Samples Studied by the Three-Point Bending Test System and AFM. Minerals 2022, 12, 582. [Google Scholar] [CrossRef]
  32. Qiu, L.; Zhu, Y.; Song, D.; He, X.; Wang, W.; Liu, Y.; Xiao, Y.; Wei, M.; Yin, S.; Liu, Q. Study on the Nonlinear Characteristics of EMR and AE during Coal Splitting Tests. Minerals 2022, 12, 108. [Google Scholar] [CrossRef]
  33. Zang, Z.; Li, Z.; Niu, Y.; Tian, H.; Zhang, X.; Li, X.; Ali, M. Energy Dissipation and Electromagnetic Radiation Response of Sandstone Samples with a Pre-Existing Crack of Various Inclinations under an Impact Load. Minerals 2021, 11, 1363. [Google Scholar] [CrossRef]
  34. Potirakis, S.; Mastrogiannis, D. Critical features revealed in acoustic and electromagnetic emissions during fracture experiments on LiF. Phys. A: Stat. Mech. its Appl. 2017, 485, 11–22. [Google Scholar] [CrossRef]
  35. Sharma, S.K.; Chauhan, V.S.; Sinapius, M. A review on deformation-induced electromagnetic radiation detection: history and current status of the technique. J. Mater. Sci. 2020, 56, 4500–4551. [Google Scholar] [CrossRef]
  36. Hayakawa M, Fujinawa Y Electromagnetic Phenomena Related to Earthquake Prediction. Terrapub, Tokyo.1994.
  37. Qian, S.; Yian, J.; Cao, H.; Shi, S.; Lu, Z.; Li, J.; Ren, K. Results of the observations on seismo-electromagnetic waves at two earthquake areas in China. In: Hayakawa M, Fujinawa Y (Eds) Electromagnetic Phenomena Related to Earthquake Prediction. Terrapub, Tokyo, pp. 205–211. 1994.
  38. Kapiris, P.G.; Eftaxias, K.A.; Chelidze, T.L. Electromagnetic Signature of Prefracture Criticality in Heterogeneous Media. Phys. Rev. Lett. 2004, 92, 065702. [Google Scholar] [CrossRef]
  39. Contoyiannis, Y.F.; Eftaxias, K. Tsallis and Levy statistics in the preparation of an earthquake. Nonlinear Process. Geophys. 2008, 15, 379–388. [Google Scholar] [CrossRef]
  40. Contoyiannis, Y.; Kapiris, P.G.; Eftaxias, K. A Monitoring of a pre-seismic phase from its electromagnetic precursors. Phys. Rev. E. 2005, 71, 066123. [Google Scholar] [CrossRef]
  41. Contoyiannis, Y.; Potirakis, S.M. Signatures of the symmetry breaking phenomenon in pre-seismic electromagnetic emissions. J. Stat. Mech. Theory Exp. 2018, 2018, 083208. [Google Scholar] [CrossRef]
  42. Potirakis, S.M.; Minadakis, G.; Nomicos, C.D.; Eftaxias, K. A multidisciplinary analysis for traces of the last state of earthquake generation in preseismic electromagnetic emissions. Nat. Hazards Earth Syst. Sci. 2011, 11, 2859–2879. [Google Scholar] [CrossRef]
  43. Frid, V. Electromagnetic radiation method water-infusion control in rockburst-prone strata. J. Appl. Geophys. 2000, 43, 5–13. [Google Scholar] [CrossRef]
  44. Frid, V.; Vozoff, K. Electromagnetic radiation induced by mining rock failure. Int. J. Coal Geol. 2005, 64, 57–65. [Google Scholar] [CrossRef]
  45. Liu, X.; Zhang, Z.; Wang, E.; Wang, X.; Yang, B.; Wang, H. Characteristics of electromagnetic radiation signal of coal and rock under uniaxial compression and its field application. J. Earth Syst. Sci. 2019, 129, 1–11. [Google Scholar] [CrossRef]
  46. Qiu, L.; Li, Z.; Wang, E.; Liu, Z.; Ou, J.; Li, X.; Ali, M.; Zhang, Y.; Xia, S. Characteristics and precursor information of electromagnetic signals of mining-induced coal and gas outburst. J. Loss Prev. Process. Ind. 2018, 54, 206–215. [Google Scholar] [CrossRef]
  47. Liu, X.; Wang, E. Study on characteristics of EMR signals induced from fracture of rock samples and their application in rockburst prediction in copper mine. J. Geophys. Eng. 2017, 15, 909–920. [Google Scholar] [CrossRef]
  48. Qiu, L.; Wang, E.; Song, D.; Liu, Z.; Shen, R.; Lv, G.; Xu, Z. Measurement of the stress field of a tunnel through its rock EMR. J. Geophys. Eng. 2017, 14, 949–959. [Google Scholar] [CrossRef]
  49. Li, B.; Li, Z.; Wang, E.; Li, N.; Huang, J.; Ji, Y.; Niu, Y. Discrimination of Different AE and EMR Signals during Excavation of Coal Roadway Based on Wavelet Transform. Minerals 2022, 12, 63. [Google Scholar] [CrossRef]
  50. He, S.; Qin, M.; Qiu, L.; Song, D.; Zhang, X. Early warning of coal dynamic disaster by precursor of AE and EMR "quiet period". Int. J. Coal Sci. Technol. 2022, 9, 1–14. [Google Scholar] [CrossRef]
  51. Lichtenberger, M. Underground Measurements of Electromagnetic Radiation Related to Stress-induced Fractures in the Odenwald Mountains (Germany). Pure Appl. Geophys. 2006, 163, 1661–1677. [Google Scholar] [CrossRef]
  52. Das, S.; Mallik, J.; Dhankhar, S.; Suthar, N.; Singh, A.K.; Dutta, V.; Gupta, U.; Kumar, G.; Singh, R. Application of Fracture Induced Electromagnetic Radiation (FEMR) technique to detect landslide-prone slip planes. Nat. Hazards 2020, 101, 505–535. [Google Scholar] [CrossRef]
  53. Mallik, J.; Mathew, G.; Angerer, T.; Greiling, R.O. Determination of directions of horizontal principal stress and identification of active faults in Kachchh (India) by electromagnetic radiation (EMR). J. Geodyn. 2008, 45, 234–245. [Google Scholar] [CrossRef]
  54. Greiling, R.O.; Obermeyer, H. Natural electromagnetic radiation (EMR) and its application in structural geology and neotectonics. J. Geol. Soc. India 2010, 75, 278–288. [Google Scholar] [CrossRef]
  55. Das, S.; Mallik, J.; Bandyopadhyay, K.; Das, A. Evaluation of maximum horizontal near-surface stress (SHmax) azimuth and its distribution along Narmada-Son Lineament, India by geogenic Electromagnetic Radiation (EMR) technique. J. Geodyn. 2019, 133, 101672. [Google Scholar] [CrossRef]
  56. Das, S.; Mallik, J.; Deb, T.; Das, D. Quantification of principal horizontal stresses inside a tunnel: An application of Fracture induced Electromagnetic Radiation (FEMR) technique in the Darjeeling-Sikkim Himalayas. Eng. Geol. 2020, 279, 105882. [Google Scholar] [CrossRef]
  57. Das, D.; Mallik, J.; Das, S.; Deb, T.; Das, A.; Bandyopadhyay, K. Active thrust induced realignment of recent near-surface stresses in the Darjeeling-Sikkim Himalayas: Reasons and implications. J. Struct. Geol. 2021, 145. [Google Scholar] [CrossRef]
  58. https://eq.gsi.gov.il/en/earthquake/eqsOnMapLF.php.
  59. Sharon, M.; Sagy, A.; Kurzon, I.; Marco, S.; Rosensaft, M. Assessment of seismic sources and capable faults through hierarchic tectonic criteria: implications for seismic hazard in the Levant. Nat. Hazards Earth Syst. Sci. 2020, 20, 125–148. [Google Scholar] [CrossRef]
  60. Wetzler, N.; Kurzon, I. The Earthquake Activity of Israel: Revisiting 30 Years of Local and Regional Seismic Records along the Dead Sea Transform. Seism. Res. Lett. 2016, 87, 47–58. [Google Scholar] [CrossRef]
  61. Hofstetter, A.; Thio, H.K.; Shamir, M. Source mechanism of the 22/11/1995 Gulf of Aqaba earthquake and its aftershock sequence. Journal of Seismology 2003, 7, 99–114. [Google Scholar] [CrossRef]
  62. Hofstetter, A. Seismic observations of the 22/11/1995 Gulf of Aqaba earthquake sequence. Tectonophysics 2003, 369, 21–36. [Google Scholar] [CrossRef]
  63. Beth, M.; Eyal, Y.; Garfunkel, Z. The geology of the Eilat Sheet, explanatory notes. GSI report 2013, 22. [Google Scholar]
  64. Hartman, G.; Niemi, T. M.; Tibor, G.; Ben-Avraham, Z.; Al-Zoubi, A.; Makovsky, Y.; Akawwi, E.; Abueladas, A.-R.; Al-Ruzouq, R. Quaternary tectonic evolution of the Northern Gulf of Eilat/Aqaba along the Dead Sea Transform, J. Geophys. Res. Solid Earth, 2014, 119, 1–23. [Google Scholar] [CrossRef]
  65. Zilberman, E.; Amit, R.; Porat, N.; Enzel, Y.; Avner, U. Surface ruptures induced by the devastating 1068 AD earthquake in the southern Arava valley, Dead Sea Rift, Israel. Tectonophysics 2005, 408, 79–99. [Google Scholar] [CrossRef]
  66. Shamir, G. The active structure of the Dead Sea Depression, in Enzel, Y. , Agnon, A., and Stein, M., eds., New frontiers in Dead Sea paleoenvironmental research. Geological Society of America Special Paper 2006, 401, 15–32. [Google Scholar]
  67. Geological map of Israel 1:50000, Be'er Ora sheet 25-IV (1999), and Eilat sheet 26-I,II 2012. GSI.
  68. Frid, V.; Wang, E.Y.; Mulev, S.N.; Li, D.X. The Fracture Induced Electromagnetic Radiation: Approach and Protocol for the Stress State Assessment for Mining. Geotech. Geol. Eng. 2021, 39, 3285–3291. [Google Scholar] [CrossRef]
  69. Rabinovitch, A.; Frid, V.; Bahat, D. Surface oscillations — A possible source of fracture induced electromagnetic radiation. Tectonophysics 2007, 431, 15–21. [Google Scholar] [CrossRef]
  70. Rabinovitch, A.; Frid, V.; Bahat, D. A note on the amplitude - frequency relation of electromagnetic radiation pulses induced by material failure, Phil. Mag. Lett. 1999, 79, 195–200. [Google Scholar] [CrossRef]
  71. https://www.ahsystems.com/articles/Antenna-Factor-Calculations.php.
  72. Frid, V.; Rabinovitch, A.; Bahat, D. Earthquake forecast based on its nucleation stages and the ensuing electromagnetic radiations. Phys. Lett. A 2019, 384, 126102. [Google Scholar] [CrossRef]
  73. Goodfellow, S.D.; Young, R.P. A laboratory acoustic emission experiment under in situ conditions. Geophys. Res. Lett. 2014, 41, 3422–3430. [Google Scholar] [CrossRef]
  74. Aoi, S.; Asano, Y.; Kunugi, T.; Kimura, T.; Uehira, K.; Takahashi, N.; Ueda, H.; Shiomi, K.; Matsumoto, T.; Fujiwara, H. MOWLAS: NIED observation network for earthquake, tsunami and volcano. Earth, Planets Space 2020, 72, 1–31. [Google Scholar] [CrossRef]
  75. Serafini, F.; Naylor, M.; Lindgren, F.; Werner, M.J.; Main, I. Ranking earthquake forecasts using proper scoring rules: binary events in a low probability environment. Geophys. J. Int. 2022, 230, 1419–1440. [Google Scholar] [CrossRef]
  76. Chelidze, T.; Kiria, T.; Melikadze, G.; Jimsheladze, T.; Kobzev, G. Earthquake Forecast as a Machine Learning Problem for Imbalanced Datasets: Example of Georgia, Caucasus. Front. Earth Sci. 2022, 10. [Google Scholar] [CrossRef]
  77. Kapiris, P.; Nomicos, K.; Antonopoulos, G.; Polygiannakis, J.; Karamanos, K.; Kopanas, J.; Zissos, A.; Peratzakis, A.; Eftaxias, K. Distinguished seismological and electromagnetic features of the impending global failure: Did the 7/9/1999 M5.9 Athens earthquake come with a warning? Earth, Planets Space 2005, 57, 215–230. [Google Scholar] [CrossRef]
  78. Eftaxias, K.; Panin, V.; Deryugin, Y. Evolution-EM signals before earthquakes in terms of mesomechanics and complexity. Tectonophysics 2007, 431, 273–300. [Google Scholar] [CrossRef]
  79. Potirakis, S.; Minadakis, G.; Eftaxias, K. , Relation between seismicity and pre-earthquake electromagnetic emissions in terms of energy, information and entropy content. Nat. Hazards Earth Syst. Sci. 2012, 12, 1179–1183. [Google Scholar] [CrossRef]
  80. Donner, R.; Potirakis, S.; Balasis, G.; Eftaxias, K; Kurths, J. Temporal correlation patterns in pre-seismic electromagnetic emissions reveal distinct complexity profiles prior to major earthquakes. Phys. Chem. Earth 2015, 85–86, 44–55. [Google Scholar] [CrossRef]
  81. Baroň, I.; Koktavý, P.; Trčka, T.; Rowberry, M.; Stemberk, J.; Balek, J.; Plan, L.; Melichar, R.; Diendorfer, G.; Macků, R.; et al. Differentiating between artificial and natural sources of electromagnetic radiation at a seismogenic fault. Eng. Geol. 2022, 311. [Google Scholar] [CrossRef]
  82. Zhuang, J.; Matsu’ura, M.; Han, P. Critical zone of the branching crack model for earthquakes: Inherent randomness, earthquake predictability, and precursor modelling. Eur. Phys. J. Spéc. Top. 2021, 230, 409–424. [Google Scholar] [CrossRef]
  83. Petrescu, L.; Moldovan, I.-A. Prospective Neural Network Model for Seismic Precursory Signal Detection in Geomagnetic Field Records. Mach. Learn. Knowl. Extr. 2022, 4, 912–923. [Google Scholar] [CrossRef]
Preprints 75600 g001
Figure 1. The three locations of FEMR measurements in the vicinity of Eilat city superimposed on the combined fragments of the Geological maps of Timna (sheet, 25-IV) and Eilat (sheet 26-I, II) regions [67]. The dashed lines show the locations of the main strike-slip faults [63]. TP, ShW, and BP mark the location of the three measurement stations in Timna Park, Shlomo Wadi, and the Park of Birds, respectively.
Figure 1. The three locations of FEMR measurements in the vicinity of Eilat city superimposed on the combined fragments of the Geological maps of Timna (sheet, 25-IV) and Eilat (sheet 26-I, II) regions [67]. The dashed lines show the locations of the main strike-slip faults [63]. TP, ShW, and BP mark the location of the three measurement stations in Timna Park, Shlomo Wadi, and the Park of Birds, respectively.
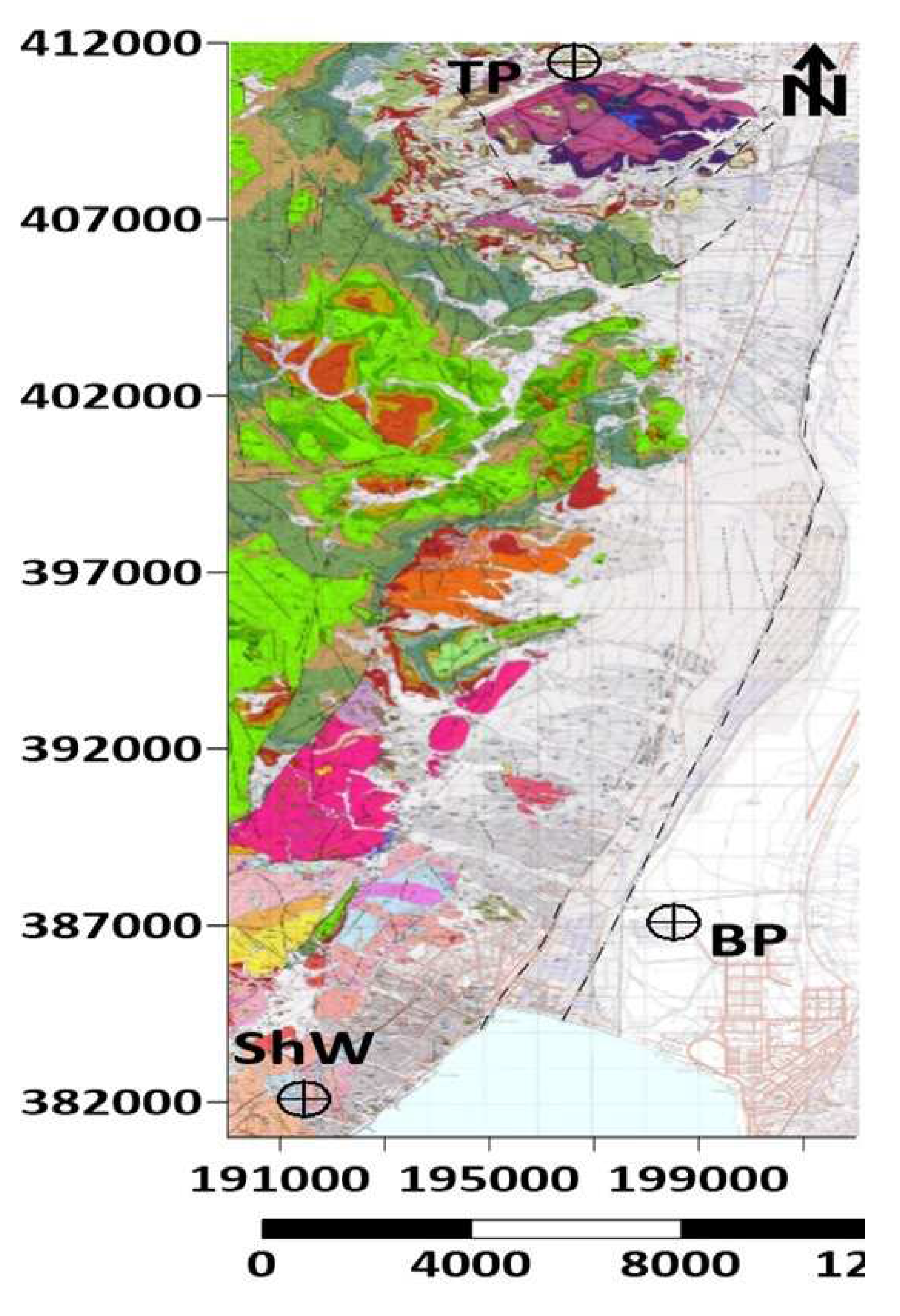
Preprints 75600 g001
Preprints 75600 g002
Figure 2. EQs epicenters in the vicinity of Eilat city – modified from [59].
Figure 2. EQs epicenters in the vicinity of Eilat city – modified from [59].
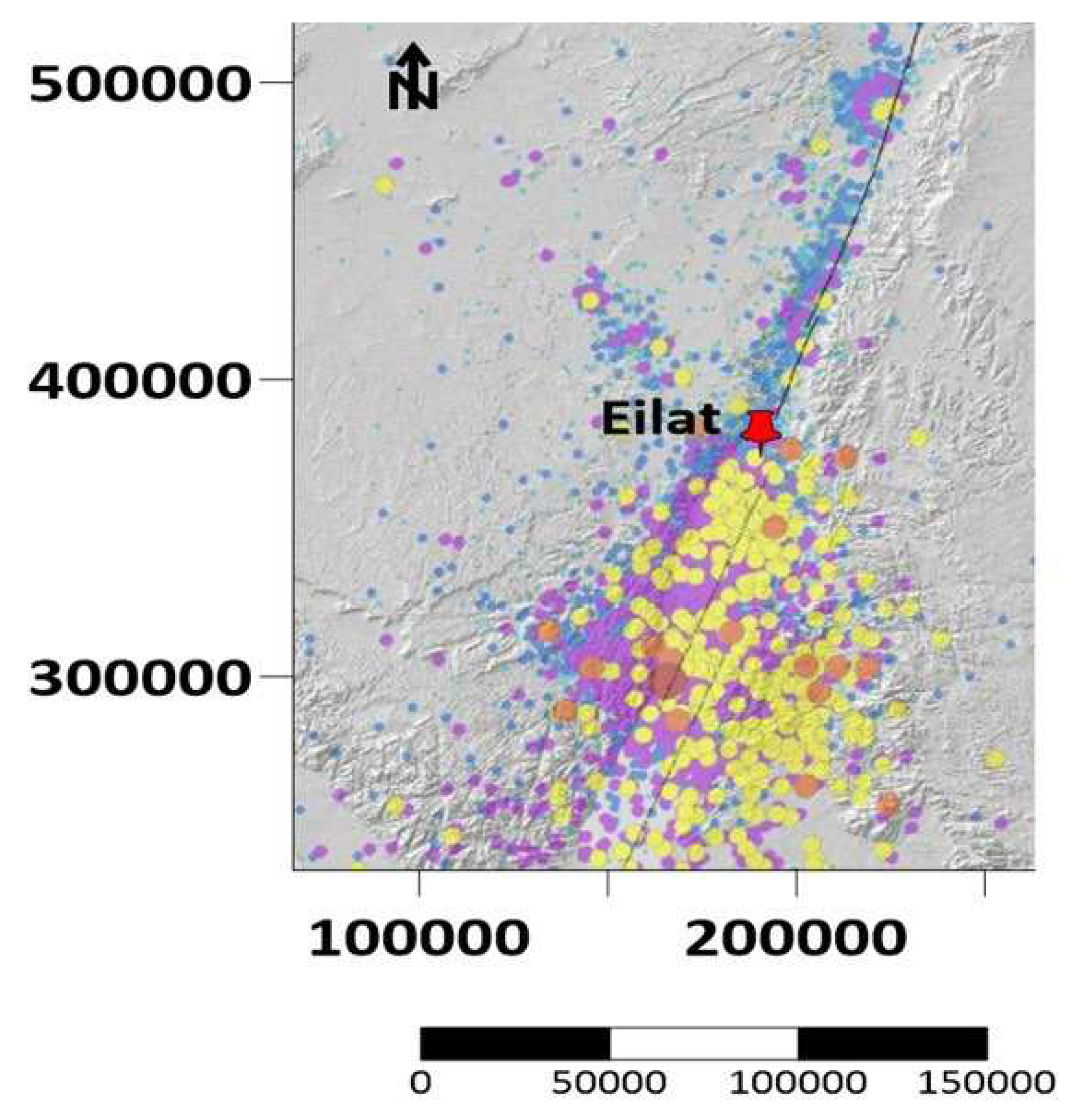
Preprints 75600 g002
Preprints 75600 g003
Figure 3. FEMR acquisition in Timna Park.
Figure 3. FEMR acquisition in Timna Park.
Preprints 75600 g003
Preprints 75600 g004
Figure 4. The FEMR pulse sequence recorded in Timna Park (a) The East direction, (b) The North direction, (c) The Up direction.
Figure 4. The FEMR pulse sequence recorded in Timna Park (a) The East direction, (b) The North direction, (c) The Up direction.
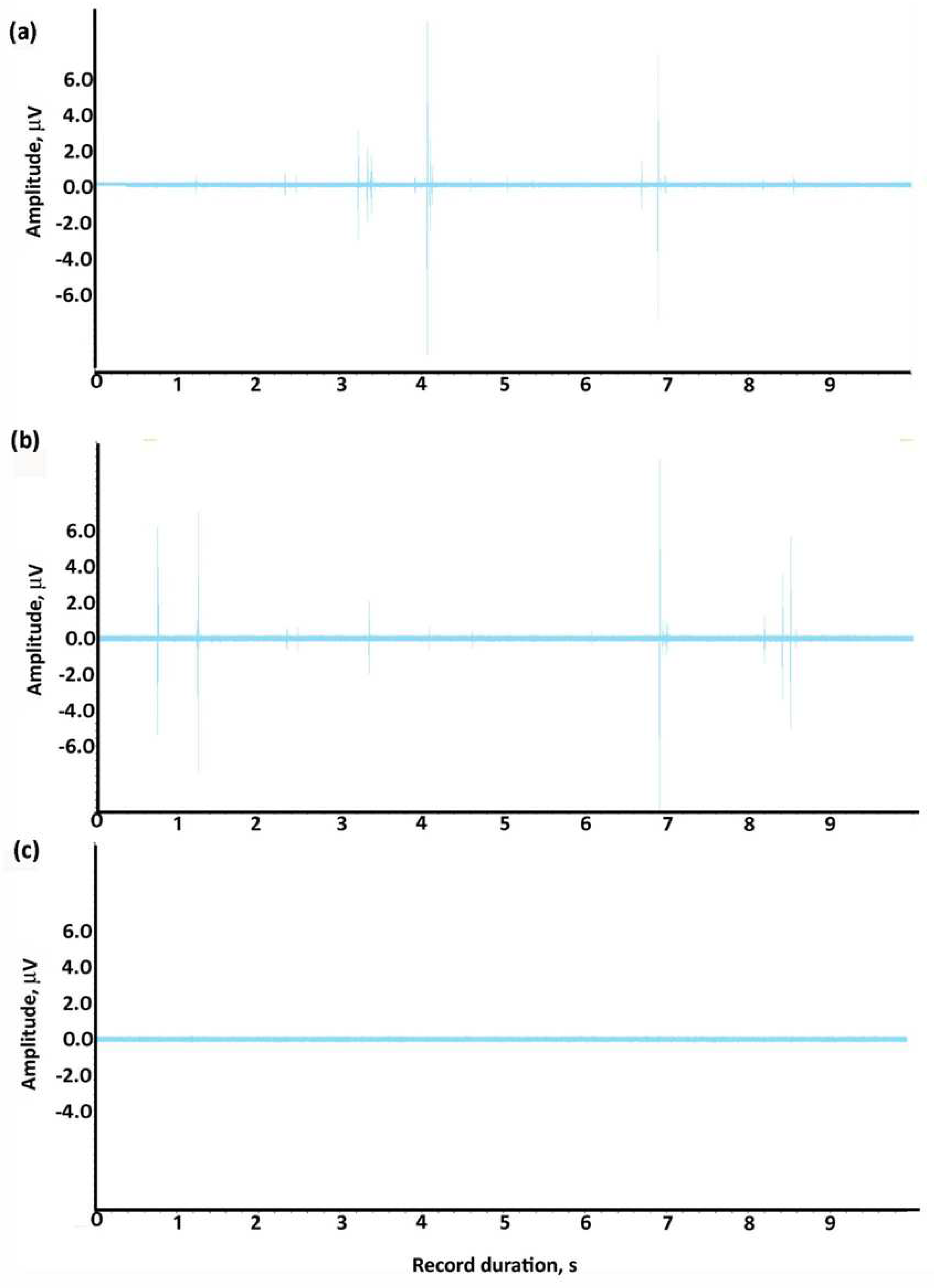
Preprints 75600 g004
Preprints 75600 g005
Figure 5. An example of a single FEMR pulse measured in the vicinity of Eilat city.
Figure 5. An example of a single FEMR pulse measured in the vicinity of Eilat city.
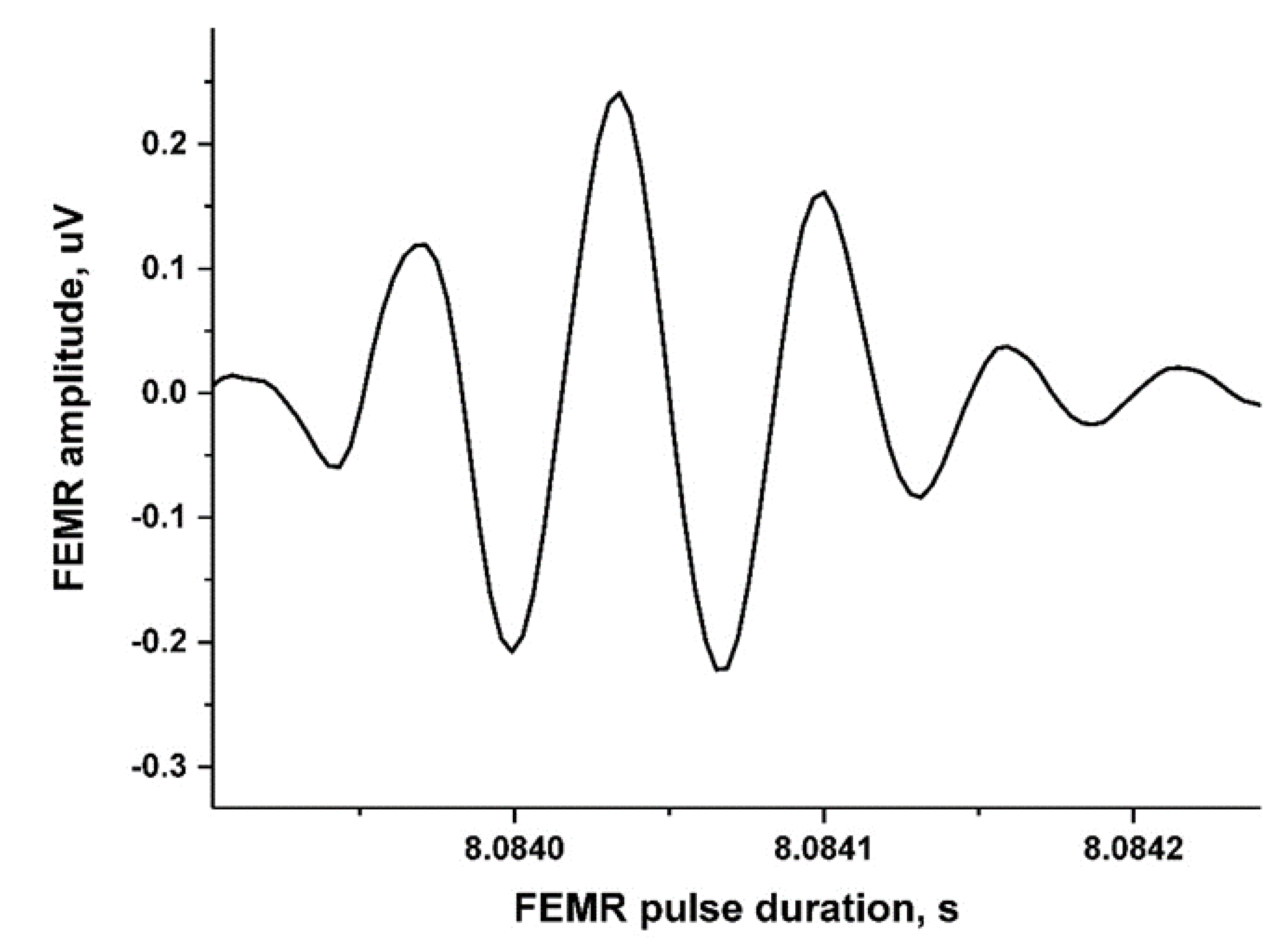
Preprints 75600 g005
Preprints 75600 g006
Figure 6. The spectrum amplitude of the FEMR pulse is shown in Figure 5.
Figure 6. The spectrum amplitude of the FEMR pulse is shown in Figure 5.
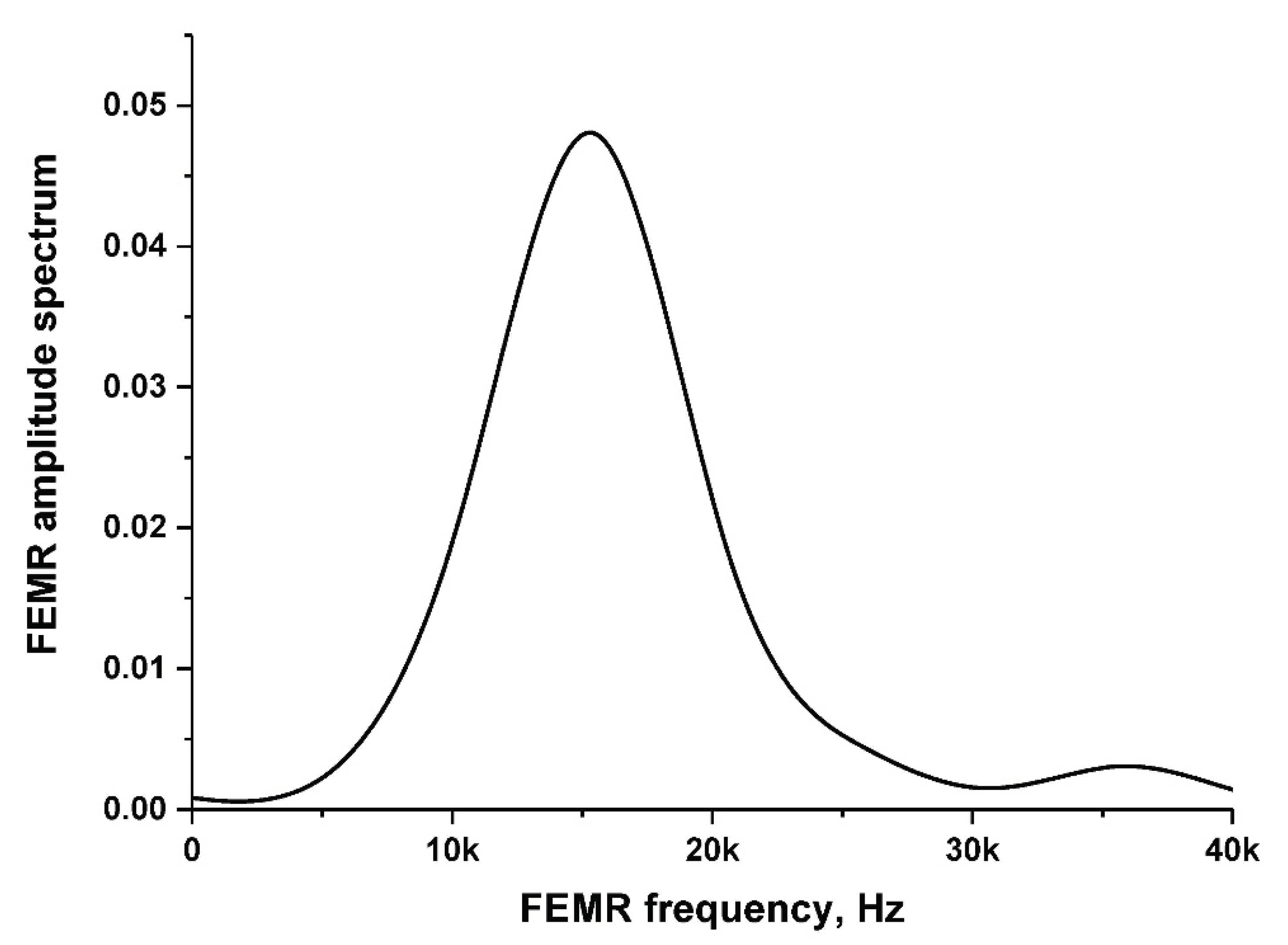
Preprints 75600 g006
Preprints 75600 g007
Figure 7. The directions to the FEMR sources.
Figure 7. The directions to the FEMR sources.
Preprints 75600 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated