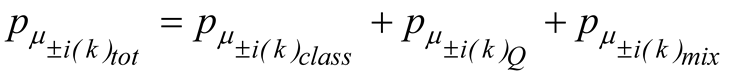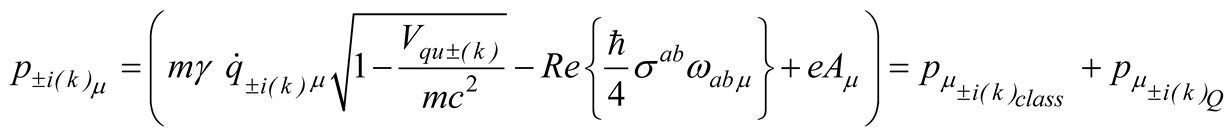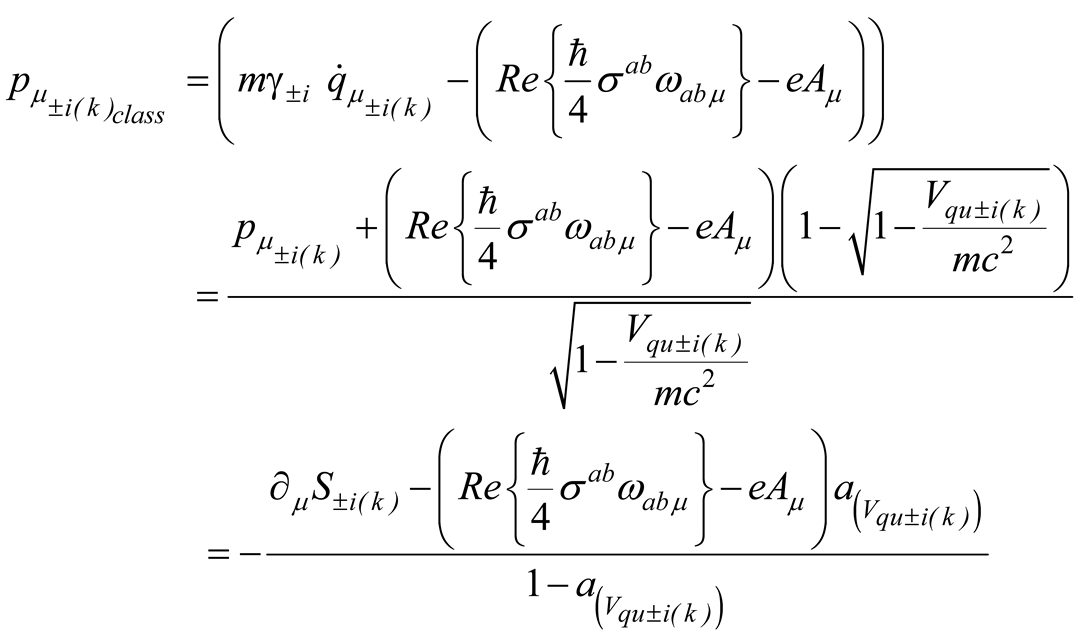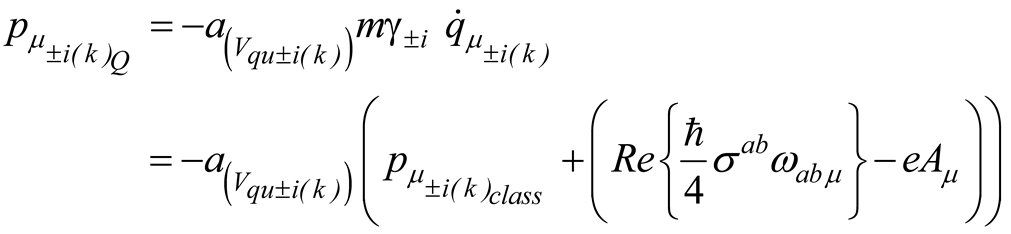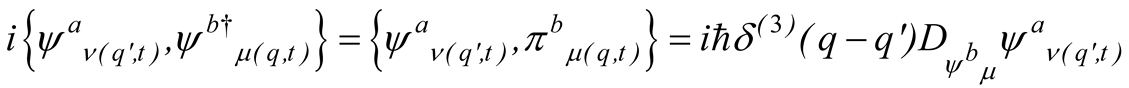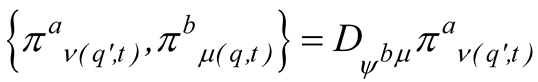Preprint
Article
Quantum Spacetime Geometrization in QED and Beyond: Towards the Standard Model
Altmetrics
Downloads
94
Views
25
Comments
0
This version is not peer-reviewed
Submitted:
03 June 2023
Posted:
05 June 2023
You are already at the latest version
Alerts
Abstract
In this work the author utilizes the quantum geometrization of spacetime for describing the gravitational interaction within the framework of quantum theory. This approach allows for the development of an equation of gravity that is mathematically connected to the fermion and boson fields. This achievement is accomplished by incorporating two fundamental principles: covariance of the quantum field equations and the principle of least action. By considering these principles, a theory is established that enables the calculation of gravitational corrections to Quantum Electrodynamics, and potentially, to the standard model of particle physics as well. The theory also provides an explanation for two phenomena: the existence of a cosmological pressure density similar to quintessence, that is compatible with the small value of the observed cosmological constant, and the breaking of matter-antimatter symmetry at high energies offering insights into why there is an imbalance between the two in the early universe.
In the cosmological modeling of the theory, there exists a proposal to account for the formation of supermassive black holes that are accompanied by their own surrounding galaxies, without relying on the process of mass accretion. The model, in accordance with recent observations conducted by the James Webb Space Telescope, supports the notion that galactic configurations were established relatively early in the history of the universe, shortly after the occurrence of the Big Bang.
Keywords:
Subject: Physical Sciences - Particle and Field Physics
1. Introduction
Physics faces a major challenge in unifying general relativity and quantum theory, which are fundamentally different in their approaches. General relativity explains gravity as the curvature of spacetime due to matter and energy, while quantum theory describes the behavior of matter and energy at very small scales. However, attempts to merge these two theories have been unsuccessful so far. There have been various proposals for reconciling general relativity and quantum theory, such as string theory [1,2,3], loop quantum gravity [4,5,6], and causal dynamical triangulation [7,8,9], but none have yet been confirmed by experimental evidence. The search for a unified theory of physics remains an active area of research in theoretical physics.
The standard model faces various challenges when dealing with curved spacetime, one of which is that it is not a renormalizable theory in this context. This means that the theory predicts divergent results for certain physical quantities, making it impossible to obtain finite and meaningful predictions.
Moreover, the standard model predicts that the vacuum state of the universe, which is the lowest energy state, may not be stable in curved spacetime. This instability can lead to the creation of particles out of vacuum, a phenomenon known as vacuum decay.
Furthermore, the standard model is based on the principle of gauge invariance, which means that the theory should be independent of the choice of gauge. However, in curved spacetime, it is not clear how to define a consistent gauge choice, leading to problems in the formulation of the theory.
On the other hand, there are several problems of general relativity with respect to the quantum nature of the matter, which is believed to be inadequate in fully explaining some observed phenomena in the universe. Observations indicate the existence of non-luminous matter in the universe, known as dark matter, which accounts for about 27% of the total mass of the universe. General relativity is unable to explain the nature of dark matter, as it does not emit electromagnetic radiation and does not interact with radiation.
Observations also suggest the existence of another form of energy, known as dark energy, which is responsible for the accelerating expansion of the universe. General relativity cannot explain the origin and nature of dark energy.
Besides, general relativity predicts that the universe began with a singularity, where the laws of physics break down. This prediction raises questions about the validity of the theory in such extreme conditions.
In recent studies [10,11], the author showcased that by postulating the covariance of quantum field equations and employing their classical-like quantum hydrodynamic portrayal, it becomes feasible to delineate the spacetime geometry via a gravity equation that encompasses quantum mechanics. This accomplishment is realized by employing a generalized least action principle, yielding a set of equations that characterizes the evolution of quantum-gravitational interactions. The resulting system intertwines the gravity equation with the quantum equation of bosonic or fermionic fields.
The theoretical investigation put forth in this paper holds the promise of advancing Quantum Electrodynamics (QED) for high-energy fermionic states and exploring gravitational corrections to Minkowskian theory. The theory reveals symmetry breaking in gravitational fermion-antifermion interactions, as well as the potential discrepancy in the magnetic moments of leptons and antileptons, which could serve as a possible test for the theory.
2. The Charged Fermion Field Coupled to the Gravity Equation
In recent papers [10,11], the author demonstrated that it is possible to define the geometry of the spacetime induced by fermion and boson fields by utilizing the covariance condition. This achievement is accomplished by employing the Madelung quantum hydrodynamic description, where the field equation for the complex field
where
where , and , are the vielbein and the inverse vielbein, respectively, and is the Christoffel matrix that reads
by utilizing the substitution
where , is transformed into a system of four differential equations in terms of the real variables , , and [11].
By assuming the covariant derivative for affine and spinor connections
Equation (2.1) more simply reads
that by utilizing (2.5) leads to
from which the covariant hydrodynamic form of the Dirac equation reads
that, after some manipulation, leads to [11]
Moreover, by equating the real and imaginary parts, respectively, of (2.11), the four hydrodynamic quantum equations are obtained. The real part leads to the Hamilton-Jacobi hydrodynamic motion equation in curved space-time that reads [11]
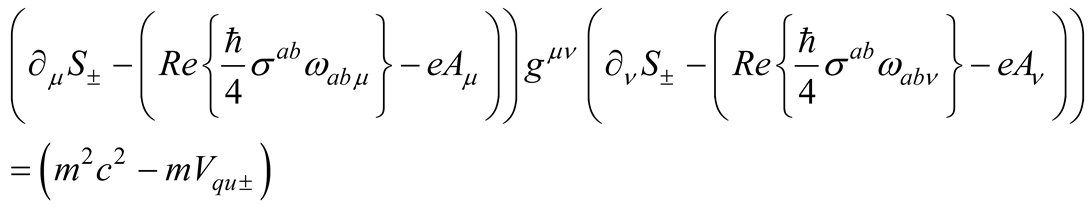 where the quantum potential reads [11]
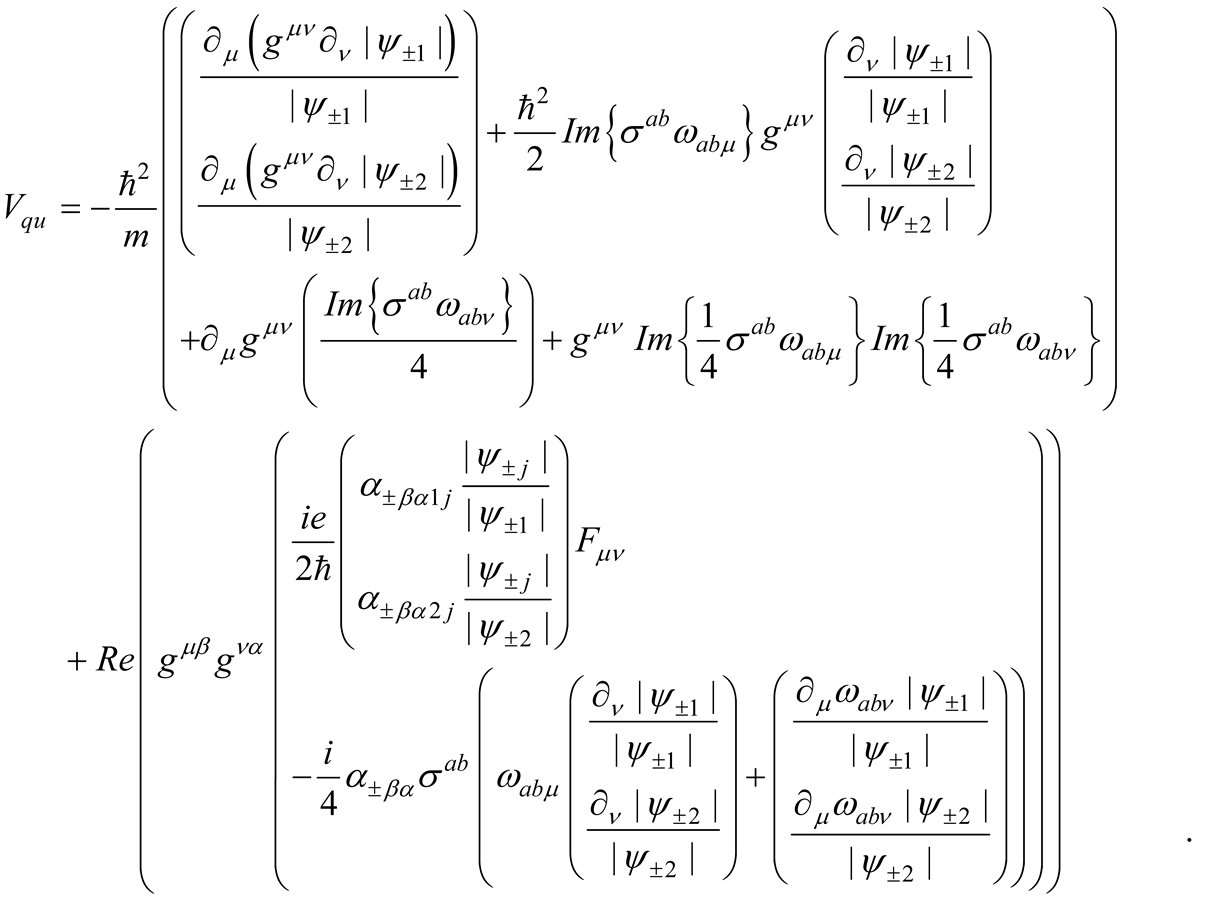
where the quantum potential reads [11]
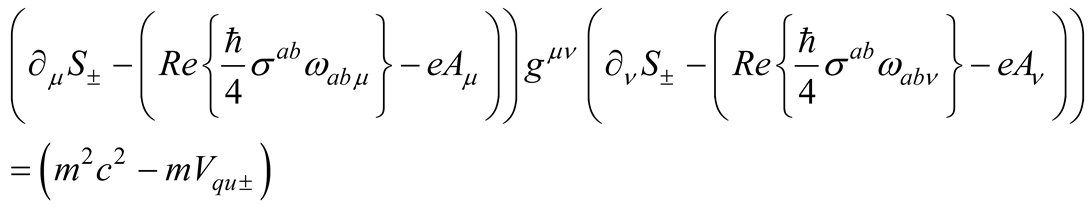

Afterward, the equation of gravity
is obtained by employing the principle of least action within the framework of quantum hydrodynamics [11], applied to the motion Equation (2.12) governing the quantum mass densities.
By following this methodology, the set of equations for gravitationally-coupled quantum electrodynamics (G-QED) is accomplished with the equations [10,11]
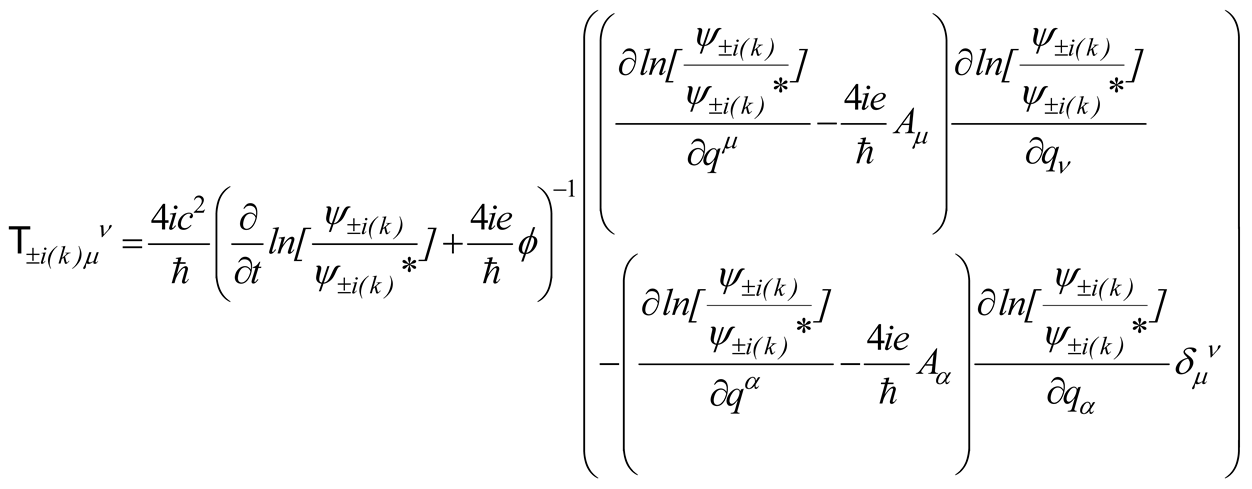
where is the electromagnetic tensor and the related vector potential. The term in (2.14) is the energy implulse tensor of the fermion field (2.11) [11] whose detail is given in Appendix A.
2.1. The Least Action Principle in the Quantum Hydrodynamic Formalism
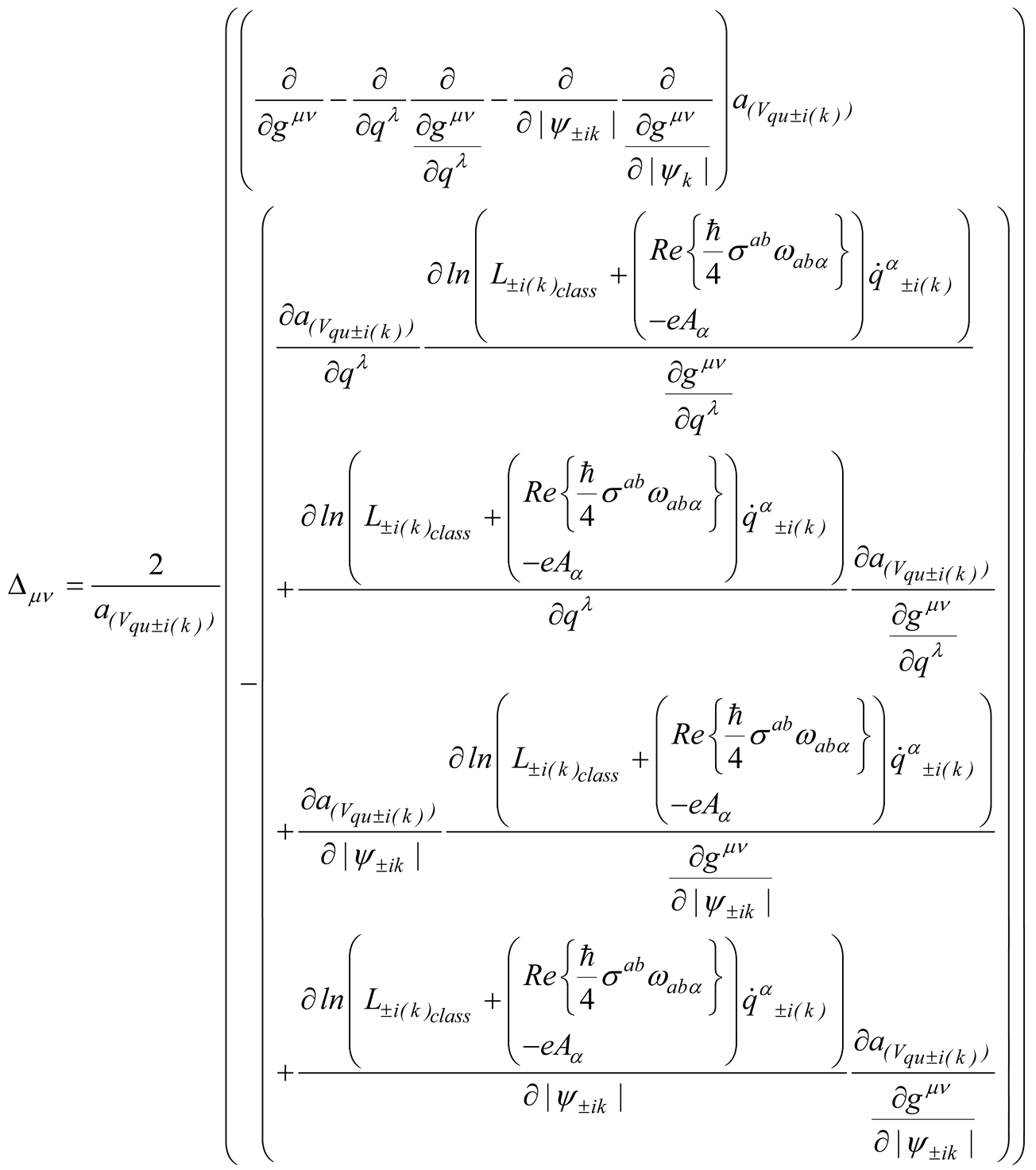
Since the hydrodynamic Lagrangian depends on both and (i.e., the mass density and the quantum potential), the challenge of defining the equation of motion can be addressed by employing the set of variables. Therefore, the variation of the hydrodynamic action , where , (between the fixed starting and end points, , respectively) can be expressed as follows [11]
Given that the quantum motion equations for eigenstates (1.30-1.31) satisfy the condition
(that explicitly defines ) the variation of the action for the k-th eigenstate reads
where the variation of the action due to the quantum potential contained within the hydrodynamic Lagrangian results in a quantum generation.
Thence, the least action principle can be redefined for the quantum hydrodynamic evolution of the eigenstates as follows:
It is noteworthy that (2.23) coherently leads to the least action principle of the classical mechanics since for (and ) it holds that:
and hence that
Besides, generally speaking, by using (1.37) for the superposition of states (1.17), the variation of the action reads
where the additional contribution due to the mixing originated by the superposition of state reads
and where
Thence, the least action principle in the general case can be expressed by the identity
Moreover, it is worth mentioning that being , but
the condition it is not enough to obtain the classical least action principle for which also the decoherence is necessary. In fact
From Equation (2.32), it can be inferred that quantum decoherence is theoretically required in order to derive classical mechanics from the least action principle.
2.2. Classical and Quantum Spacetime Geometrization
If we assume that the ST (Space-Time) follows the classical equation of motion, without the presence of a quantum potential, we can distribute mass density locally within it, attributing classical characteristics to ST. Conversely, if we assume that the mass distribution in ST is influenced by the quantum potential force, it becomes impossible to freely distribute mass locally, as it becomes coupled to the mass present in the surrounding area, resulting in a quantum mechanical ST. Thus, the properties of ST are determined by the governing law of mass density motion within it.
These definitions are not absolute as they rely on the observational characteristics of mass distribution motion. Specifically, classical ST refers to a vacuum state observed in the Newtonian regime, characterized by low gravity, far beyond the gravitational radius of black holes. In this context, classical behavior can manifest at the macroscopic scale [12,13]. Based on this physical description, ST is considered classical.
However, when the physical length scale is smaller than the De Broglie wavelength, the classical equation of motion must be supplemented with the quantum potential, and the mass distribution cannot be freely localized or exhibit local motion. In such cases, ST exhibits quantum mechanical properties.
Since the quantum potential energy contributes to the determination of the curvature of ST, the geometry of ST associated with a mass density distribution relies also on it, which is defined by the corresponding equation of evolution.
The equation of motion defines the properties of ST and, through the covariance condition, the equation of gravity. Thus, since the classical and quantum equations of motion for photons are identical, classical and quantum general relativity coincide in this scenario. This particular characteristic of the electromagnetic field enables the explicit coupling of the photon field to the equation of gravity within the framework of classical general relativity.
Table 1.
| SPACETIME CHARACTERISTICS | BASIC EQUATIONS OF EVOLUTION | QUANTUM MECHANICAL EVOLUTION |
SECOND QUANTIZATION |
|---|---|---|---|
|
FAT CLASSICAL SPACETIME (*) |
Relativistic classical mechanics |
Relativistic quantum Mechanics (by quantization of classical mechanics) Deterministic evolution. |
Second quantization of boson and fermion fields in Minkowskian ST |
| CURVED CLASSICAL SPACETIME | General relativity (equivalence principle and least action condition) |
Quantum Mechanics in curved ST; Relativistic quantum mechanical equations in assigned curved ST (Unknown gravitational coupling with fields of massive particle). |
Second quantization of fields and classical Einstein’s gravity equation. (No coupling with particle fields (except for the photon field)). |
| FLAT QUANTUM MECHANICAL SPACETIME (*) | Relativistic quantum mechanics |
Relativistic quantum mechanics (classical mechanics emergent on macroscopic scale by decoherence in weakly bounded system) |
Second quantization of bosonic and fermion fields in Minkowskian ST |
| CURVED QUANTUM MECHANICAL SPACETIME |
Quantum General Relativity (covariant principle and least action condition) |
General relativity and gravitation of quantum mechanical fields (Boson and fermion fields in curved ST gravitationally coupled. General Relativity as classical decoherent limit) |
Second quantization of boson and fermion fields gravitationally coupled (high energy QFT) |
This passage explores the distinctions between the treatment of fields in classical and quantum mechanical space-time (ST). At the scale of elementary particles, quantum mechanics dictates that fields cannot be treated as continuous variables, and their quantization becomes necessary. Consequently, in quantum mechanical ST, a second quantization of the fields differs from the treatment in classical ST.
When massive particles are present, quantum mechanical space-time (ST) gives rise to a gravity equation that interacts with the boson and fermion fields of these particles. This gravity equation differs from the classical one due to the inclusion of new effects arising from the presence of the quantum potential.
These effects can encompass several phenomena, such as the absence of a point-like mass density within a black hole, the emergence of a repulsive gravitational force at cosmological distances from a black hole, and the existence of a physically stable vacuum [14].The presence of cosmological pressure density offers the potential to explain the observed cosmological constant as an indication of the quantum mechanical characteristics of the vacuum, eliminating the need to introduce it as an arbitrary parameter in classical general relativity. Consequently, the cosmological constant lies beyond the classical framework of general relativity, and its existence can be attributed to the quantum mechanical properties of the vacuum.
3. First Order Gravitationally-Coupled QED
The above system of G-QED equations is extremely difficult to handle, but for the specific physical scenario of interest (which involves mass densities far from the Planckian mass densities), a simplifying perturbative approach can be employed.
The zero order gravity QGE (minkowskian spacetime) leads to the ordinary QED. The first order G-QED reads [11]
where the weak gravity perturbation to the Minkowskian metric tensor
is given by the solution of the first order GE
where the Christoffel symbols [11] reads
where
where comes from the solution of zero order Dirac equation
where
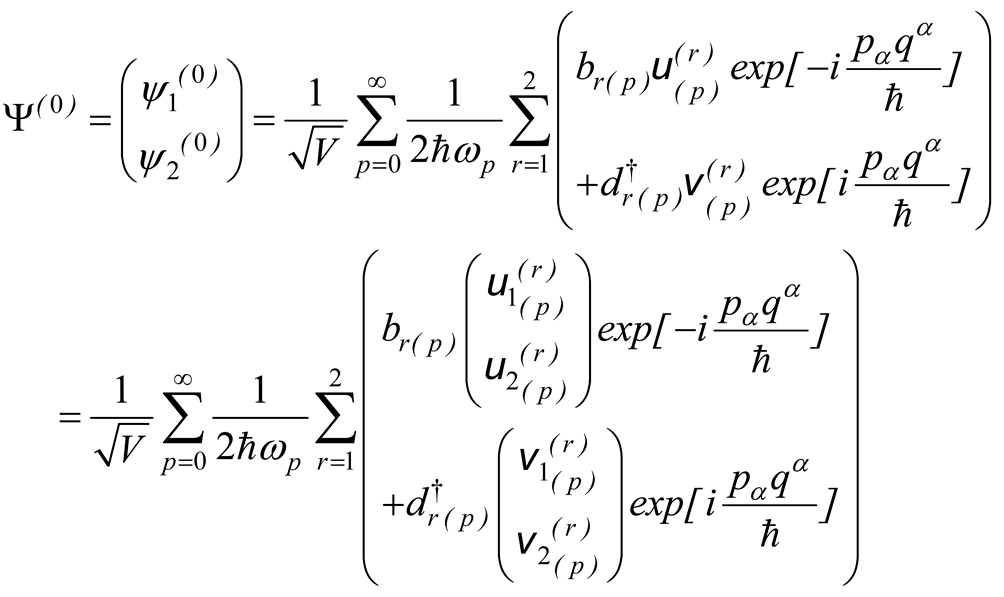
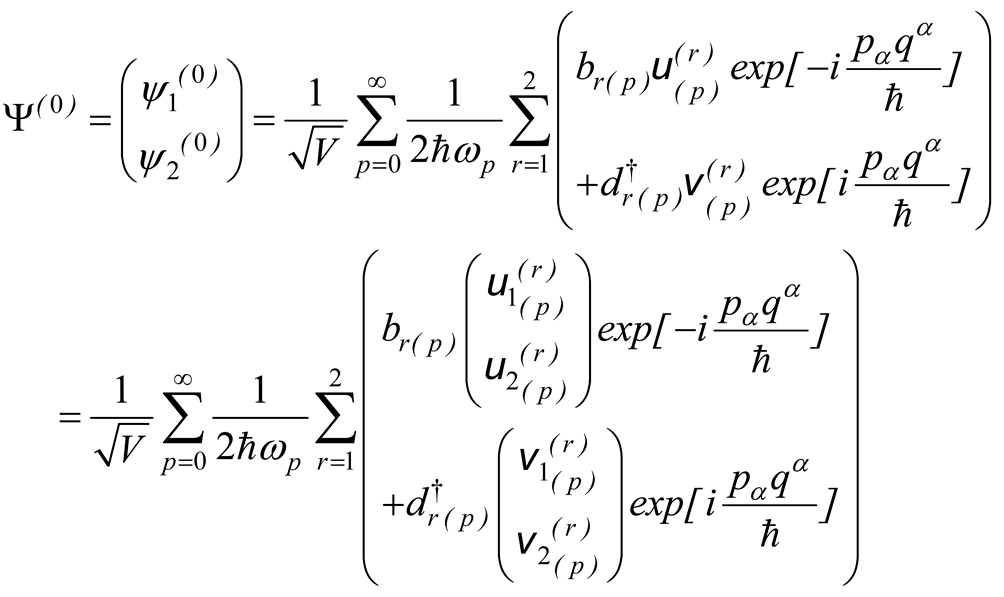
and thence,
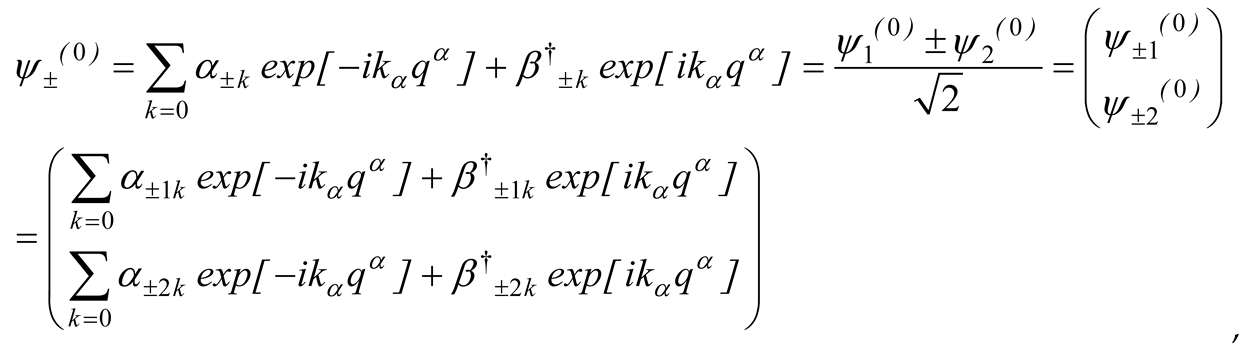
with
where

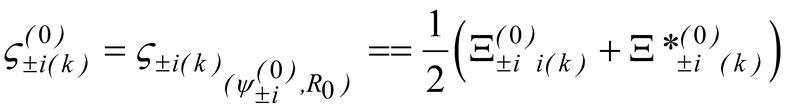
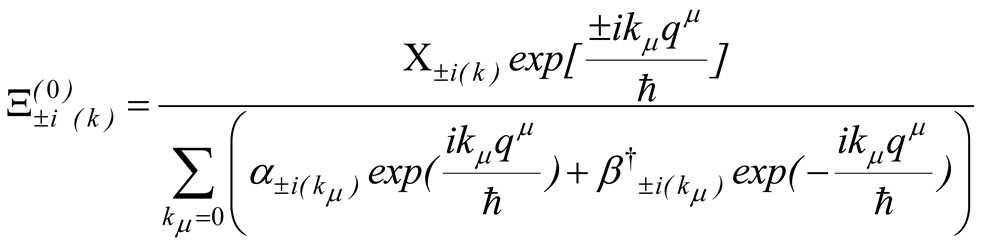
where
4. Towards the Gravitationally-Coupled Standard Model: The Perturbative Approach
The field Lagrangian of the Standard Model (SM) containing the coupling with the gravity equation
constitutes a strongly non-linear system of differential equations and have tout-court a limited usefulness.
Nonetheless, in the quasi-Minkowskian ST, for light particles with mass/energy densities far from Planckian order of magnitude (and/or under weak gravity outside the gravitational radius of SMBHs), the description of the gravitational coupling for the standard model can be obtained in a perturbative form.
This can be achieved by introducing the weak limit of the curvature tensor (2.79) in the covariant form of the SM field Lagrangian that synthetically at zero order reads
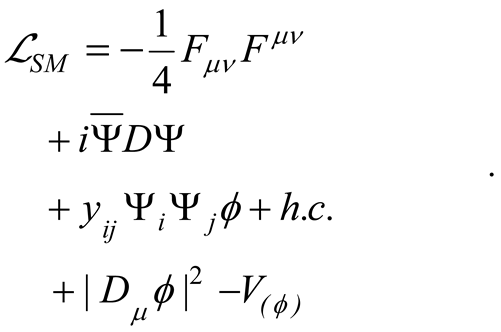
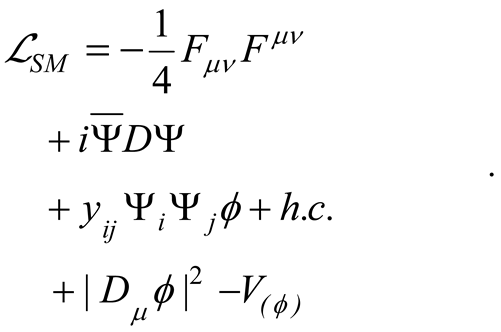
By doing that, the first order Lagrangian of SM can be synthetically schematized in the form
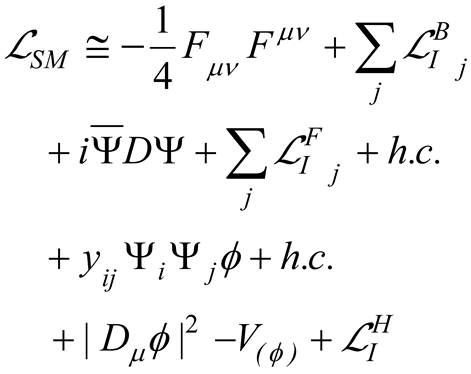
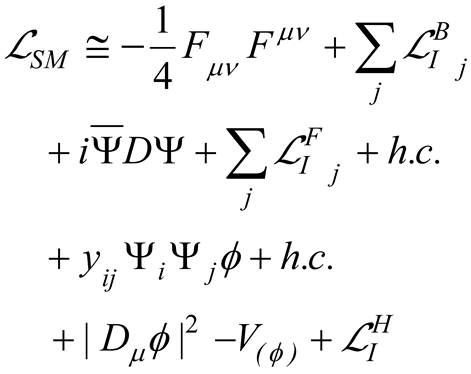
where , and describe the weak gravity coupling of bosons, fermions and Higgs boson, respectively.
For instance, the expression for the particular cases of the free charged bosons , (see Appendix B) the coupling lagrangian reads
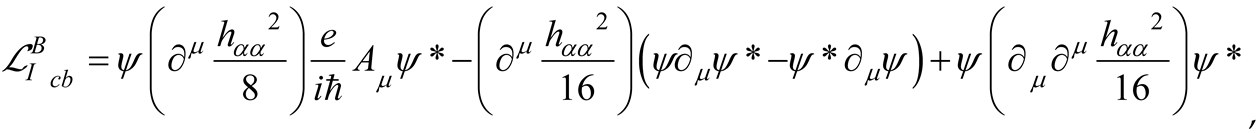
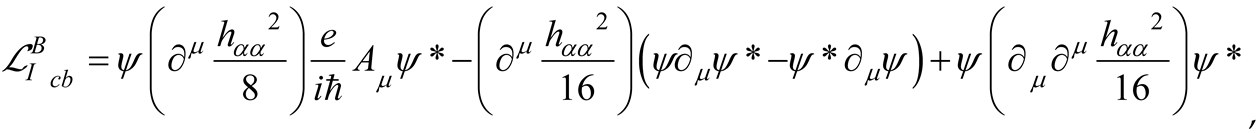
while, for the uncharged free vector boson , we obtain (see Appendix B)
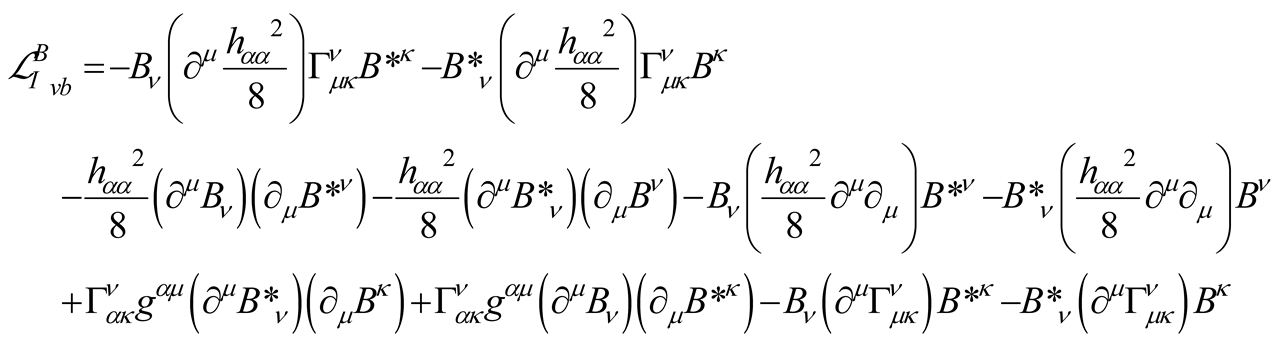
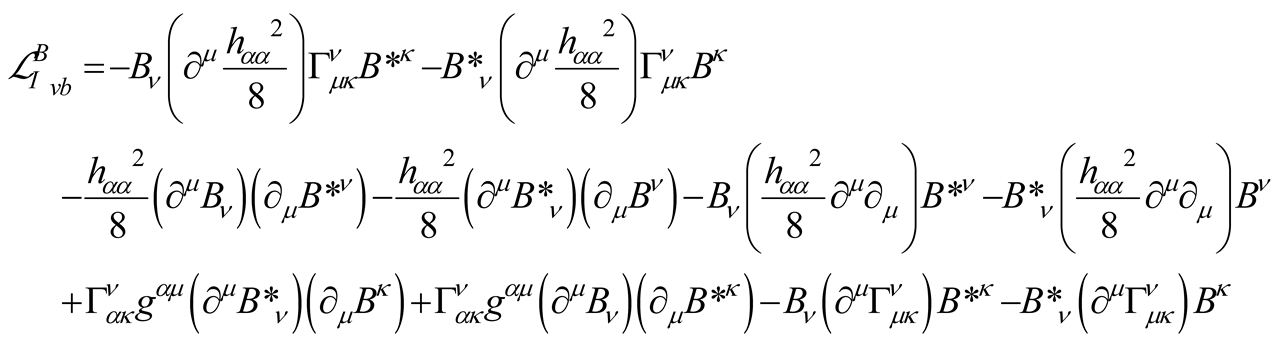
For free fermions, the perturbative field Lagrangian reads
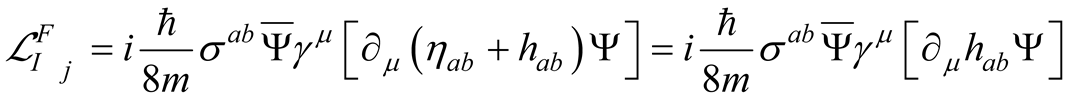
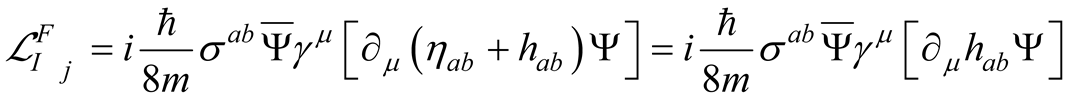
that in the limit of weak gravity at first order (being antisymmetric) gives
Thus, the fermion non-zero perturbative contribution is at the second order in becoming relevat at higher energy and ST curvature.
Moreover, even if the mass terms do not give contributions in the first order gravity coupling (both for bosons and fermions) the mass-coupling parameters may comprehend gravitational contributions.
The field lagrangian for the free uncharged scalar boson with fourth-order self-interacting field [15] reads
Generally speaking, additional gravitational contributions arise from the particle interaction in the SM field equations.
So far, we haven’t yet utilized the quantum mechanical geometrization of the ST but only the covariance of the field equations. The QGE becomes necessary in order to determine the perturbative metric tensor as a function of the SM fields. To this end, at first order, the perturbative QGE reads
where , and are the fermions, gauge bosons and the Higgs boson (with mutual interacting terms) EITDs respectively and where
In the QGE (4.9) the superscript refers to the zero order fields of the SM in flat ST ().
4.1. Second Quantization of Fields in Quantum General Relativity
If we intend to formulate Quantum Field Theory within the framework of curved space-time, building upon the system of equations of the Quantum Gravitational Equation (QGE)-Standard Model (SM) (primarily applicable to high energy states), we have only tackled half of the challenge thus far.
This is due to the fact that in order to proceed with second quantization, quantization rules specific to curved ST are necessary.
Generally, when transitioning from a specific case to a more general one, multiple potential outcomes arise. To resolve this indeterminacy, A. Einstein utilized the equivalence principle, which establishes a connection between inertial and gravitational mass, in formulating General Relativity. Similarly, in the quantum geometrization of space-time, the requirement of covariance in the quantum equations has been employed to address this concern.
The mentioned coincidence is not coincidental, as the equivalence between inertial and gravitational mass corresponds to the covariance of the classical equation of motion within curved spacetime (see Appendix C). From this standpoint, we can interpret the Quantum Gravitational Equation (QGE) as the quantum mechanical counterpart of General Relativity.
Thus, akin to the covariant formulation of charged fields rooted in Gauge invariance, the covariance of quantum equations within curved spacetime emerges as a potent and straightforward criterion for generalization. Expanding upon this foundation, the covariance of the commutation and anticommutation relations becomes a valuable consideration (see Appendix D). However, in this scenario, we must contend with heightened complexity, as these rules become dependent on the local curvature of spacetime.
5. Discussion. Semi-Quantitative Analysis: Matter-Antimatter Symmetry-Breaking, Quantum Decoherence, Primordial Black Hole Fragmentation and Mass Expulsion
In the realm of the Quantum Gravitational Equation, the existence of a singularity within a black hole is rendered impossible, making the concept of a point-like mass density invalid. Consequently, the initial universe system must have possessed a finite initial volume. However, due to the high concentration of mass, it would have given rise to a massive black hole referred to as the Pre-Big Bang Black Hole (PBBH). The PBBH state was not stationary, and the quantum arrow of time, exemplified by matter-antimatter asymmetry, was in effect, leading to an irreversible relaxation process that ultimately culminated in the Big Bang.
In the subsequent analysis, we investigate the progression of the Pre-Big Bang Black Hole (PBBH) utilizing the Quantum Gravitational Equation (QGE) coupled with the boson and fermion fields.
5.1. CPT inversion and Lepton-Antilepton Symmetry-Breaking in Curved ST
If we consider the Dirac equation for the fermion field, it is well known that the CPT transformation leads to the same Dirac equation for the field of the antiparticle . The formal invariance of the Dirac equation, under CPT inversion, expresses the matter-antimatter symmetry in the Minkowskian space-time.
If we analyse the gravitational interaction described by the Lagrangian (4.6) we can see that under the CPT inversion (for which it holds and ) the fermion current transforms as
(while the electromagnetic (EM) one remains unchanged) so that the gravity interaction Lagrangian under CPT inversion changes as
and weakly breaks the matter-antimatter symmetry. It is worth noting that, at the first order (light particles and Newtonian gravity), the correction to the fermion field due to gravity (4.6) and the breaking of CPT symmetry is practically null. Therefore, the difference in mass/energy between a fermion and its antiparticle becomes significant only for very heavy fermions, which are sources of strong gravitational fields (such as those present in PBBH) with masses of the order of the Planck mass or even bigger.
Furthermore, since the magnetic moment of leptons is dependent on their masses, it follows that the slight difference in the magnetic moment of a lepton and its corresponding antiparticle becomes increasingly larger as the mass of the lepton increases. This provides a potential means of testing the theory.
When considering only the dynamics of electro-gravity, in which only gravity and electromagnetic forces are considered, the presence of the electro-gravity coupling term (5.2) requires us to consider the theoretical possibility that a graviton (which is very light) may be released/absorbed in the process of lepton-antilepton annihilation, as well as in the inverse process. This is necessary in order to account for the difference in gravitational mass between fermions and antifermions.
The matter-antimatter (fermion-antifermion) asymmetry induced by gravity allows the formulation of a mechanism for the realization of baryonic asymmetry in the early universe. Generally speaking, the gravitational generation of baryonic asymmetry in the high-energy states of PBBH is produced by the gravitational interaction with all the fields of bosons and fermions.
The physical imbalance between matter and antimatter in the quantum PBBH immediately leads to the breaking of time inversion symmetry in the QGE-fermion-boson fields system of equations. Consequently, the highly ordered quantum configuration of PBBH undergoes a time-directional irreversible evolution towards a less ordered conformation, leading to the appearance of the quantum arrow of time and the irreversible randomization of energy that generates the Big Bang. The production of many residual light particles, which constitute the mass difference in the annihilation of high-energy matter-antimatter states, makes the inverse process highly unlikely, requiring the simultaneous grouping of many product particles.
5.2. Cosmological Constant, Fermion-Antifermion Annihilation and Matter-Antimatter Asymmetry
As illustrated by (2.14), particles possessing rest mass exhibit a non-zero cosmological pressure density (CPD) . Consequently, when a fermion and its corresponding antiparticle annihilate, the gravitational field undergoes a transition from one characterized by a non-zero CPD to one featuring a zero CPD, since the emitted photons possess a zero CTD. The absence of a CPD for photons can be attributed to the fact that in the QGE governing the electromagnetic photon field simplifies to the classical expression found in general relativity.
Conversely, when a photon generates an electron-positron pair, the gravitational field associated with the resulting massive particle and antiparticle is formed. If the photon possesses a null scalar Ricci curvature R [16] and CPD, then the scalar curvature of the electron and positron's gravitational field is non-zero, along with a non-zero CPD.
The formation of an electron-positron pair and the subsequent alteration of the gravitational field lead to an energy change, attributing a gravitational contribution to the masses of both the particle and the antiparticle. Hence, during their annihilation, it is anticipated that a low-energy graviton will be emitted.
Furthermore, considering that the energy (as indicated in Equation (5.2)) has opposite signs for particles and antiparticles, there exists a slight disparity in their masses.
For light fermions, the disparity in mass mentioned earlier is insignificant since they serve as sources for the Newtonian gravity field. As we approach the Minkowskian limit, the symmetry between matter and antimatter becomes asymptotically established. Consequently, the discrepancy in mass between particles and antiparticles diminishes progressively as we transition from heavier to lighter particles within each particle family.
This pattern of behavior implies that the asymmetry between matter and antimatter could have been notable in the vacuum states of extremely high energy prior to the Big Bang. Within the pre-Big Bang horizon, the high energy fermion state, surpassing the Planck mass, comprised black holes formed by fermions and antifermions. Through their annihilation, these black holes emitted a burst of lighter fermions that accounted for the disparity in mass between them.
If we consider, by assuming a contrary position, that the matter-antimatter symmetry was preserved within the PBBH, it would imply that the subsequent universe following the Big Bang would possess a cosmological constant of zero. This is because in the absence of massive particles (given that photons have a cosmological pressure tensor density of zero), there would be no contribution to the cosmological constant and the vacuum state would have collapsed into the polymer branched phase [17].
Nevertheless, according to the Quantum Gravity Equation, the existence of a non-zero cosmological constant, that we observe in the present-day universe, serves as evidence for the matter-antimatter asymmetry within the initial PBBH and the quantum properties of space-time gravity. In this context, the Cosmological Pressure Density represents a quantum contribution to the gravitational field.
5.3. High Temperature Quantum Decoherence, PBBH Fragmentation and Mass Expulsion
The annihilation of very heavy PBBH massive vacuum states (consisting of high-energy fermions and massive bosons) with their respective non-symmetric antimatter states during the Big Bang should have resulted in:
- The emission of gravitational boson waves, which contribute to the content of dark energy in the present universe.
- The production of fragments of SMBHs from the initial PBBH.
- The release of residual low-energy fermions, which constitute the baryonic and dark matter of the present universe.
All of these leftover parts can be considered as the "ashes of the Big Bang".
Since the matter-antimatter annihilation is irreversible (meaning the backward process of fermion-antifermion formation is not as likely as annihilation due to the very large number of products), the energy, associated to the products of the annihilation, undergoes randomization. This results in an increase of fluctuations amplitude up to a temperature
at which the quantum potential force is deeply perturbed and the quantum coherence breaks down [18] ( and are the gravitational radius of the PBBH and its mass, respectively, is the Boltzman constant, the temperature, the Planck constant and the inverse of the quantum friction coefficient [18]) .
Thus, as the PBBH experiences quantum decoherence and transitions into a classical entity, it breaks apart and releases supermassive black hole (SMBH) snippets with the surplus matter around them.
The fragmentation of the PBBH and the ejection of mass into the expanded spacetime with low curvature outside the gravitational radius of each SMBH are two interconnected stages of a unified process.As the temperature of the PBBH increases due to matter-antimatter annihilation, the expanding force of the quantum potential
supported by the thermal expansive force due to the thermodynamic potential
produces the mass expansion (with the decrease of its mean density inside the sphere of the PBBH gravitational radius) far below the critical value
producing expulsion of mass (in form of SMH) and in the low gravity space between the fragments of SMBH.
As each fragment of a SMBH possesses a lower gravitational pull compared to the original PBBH, the mass within each fragment continues to disperse further. Throughout this progression, the gravitational radius of each SMBH diminishes, resulting in more mass being located outside of it. This external mass then undergoes rotational motion within the gravitational well of the SMBH.
The process of SMBHs contracting in size, accompanied by mass expulsion, concludes when a new state of equilibrium is achieved between the gravitational force and the repulsive quantum force. This equilibrium is attained due to the decrease in temperature caused by the expulsion of matter.
This process gives rise to SMBHs harboring external mass that orbits within their gravitational wells, thereby providing an explanation for the formation of observed galaxies. Additionally, it elucidates how SMBHs represent a prevalent cosmological configuration and how they could form without the need for mass accretion.
6. Conclusions
The quantum spacetime geometrization has the capability to give rise to a gravity equation that is analytically coupled to the fermion and boson fields. This achievement is made possible by incorporating two fundamental principles in the process of generalization: covariance and the least action. This theory enables the calculation of gravitational corrections to QED and potentially to the standard model as well.
Furthermore, it offers an explanation for the presence of the quintessence-like cosmological pressure density and the breaking of matter-antimatter symmetry at high energies.
In the cosmological model, there is also a proposal to explain the formation of supermassive black holes, surrounded by its own galaxy, without the need for mass accretion. This model also aligns with the recent observations made by the James Webb Space Telescope [19], which provide support for the early formation of galactic configurations shortly after the Big Bang.
It is noteworthy to observe that, similarly to classical General Relativity, which couples with the electromagnetic field and is formally unified in the context of five-dimensional gravity, as proposed by Theodor Kaluza [20], the system of equations for the Quantum Gravity Extension of the Standard Model establishes the mathematical groundwork for developing a unique, multi-dimensional gravity-like equation which encompasses the description of fundamental interactions and particle fields.
Appendix A
The Energy Implulse Tensor of the Fermion Field
The Energy Implulse Tensor of the Fermion Field
The matrices , and , whose trace gives the energy implulse tensor in (2.14), are given in ref. [11] and read
where

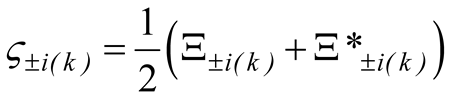
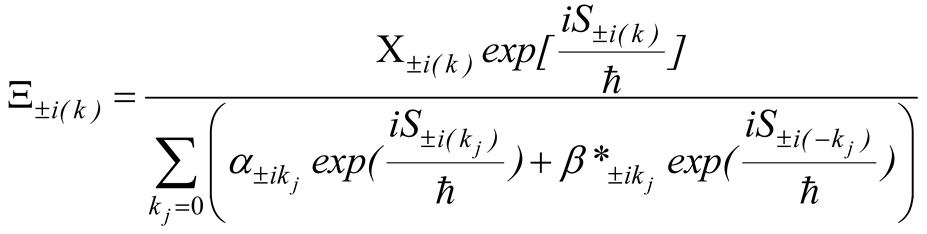


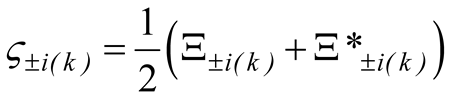
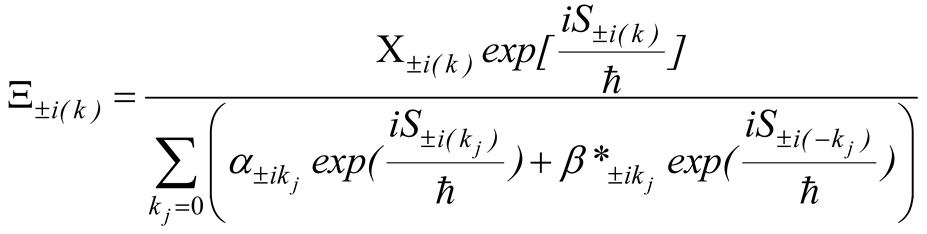
where
where
where
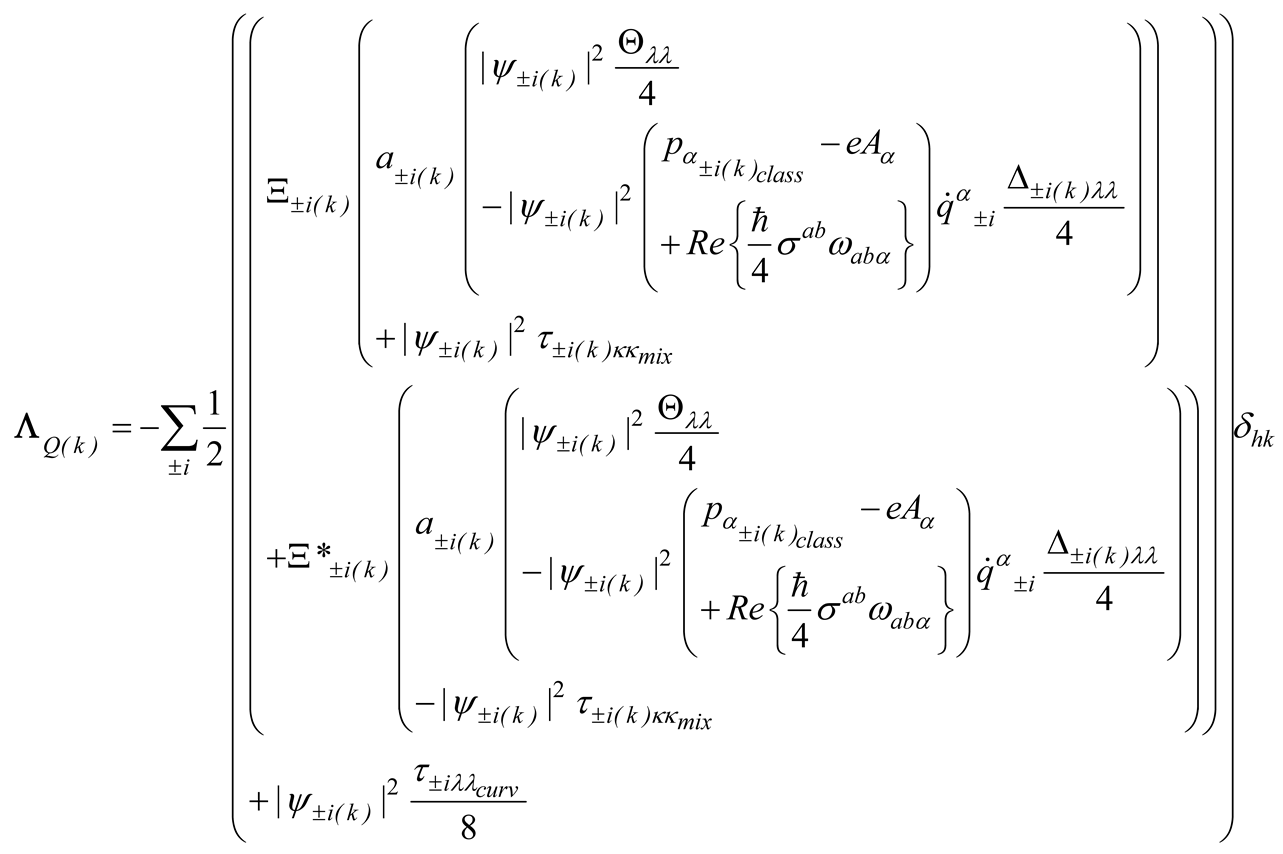

where
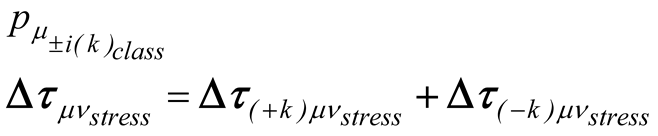
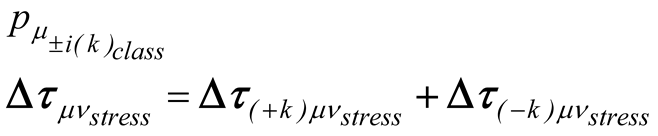
where
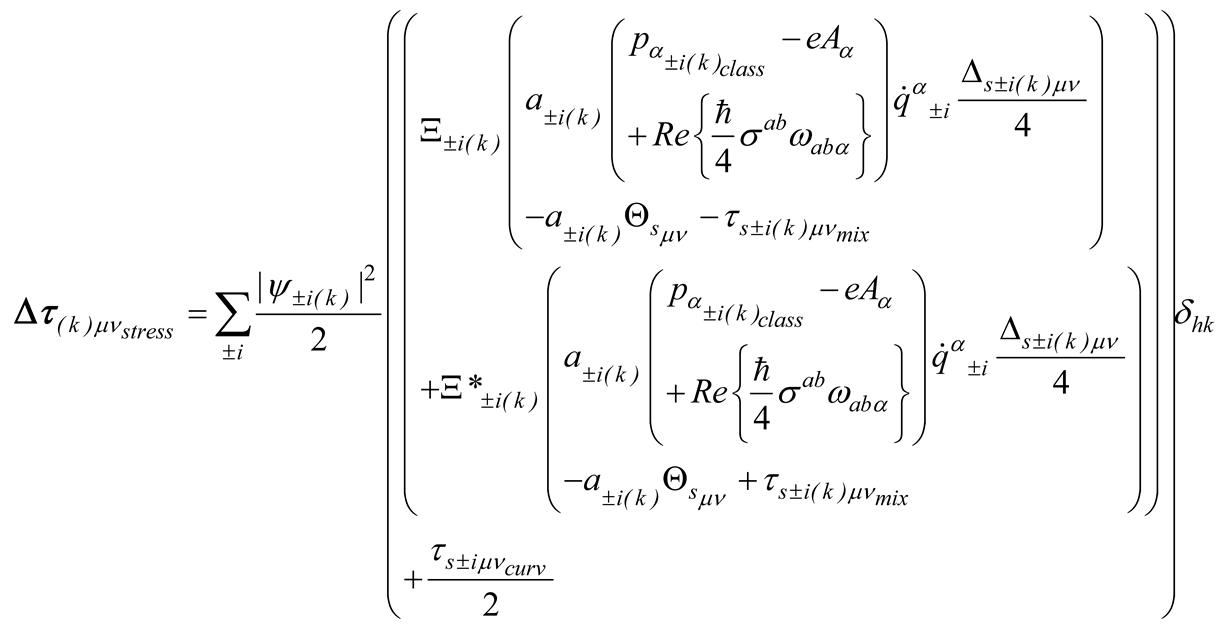

where
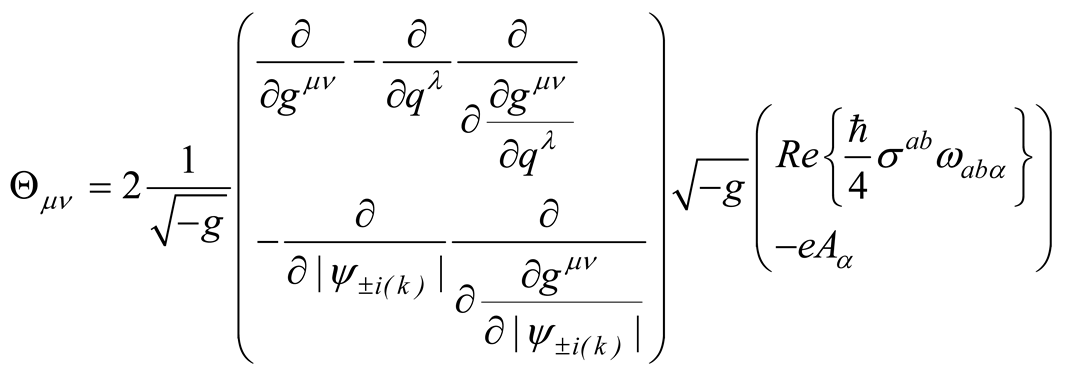
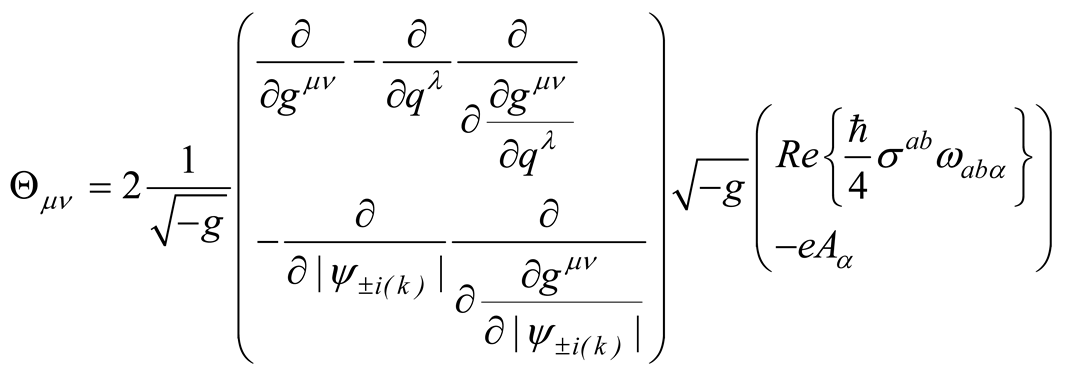

where
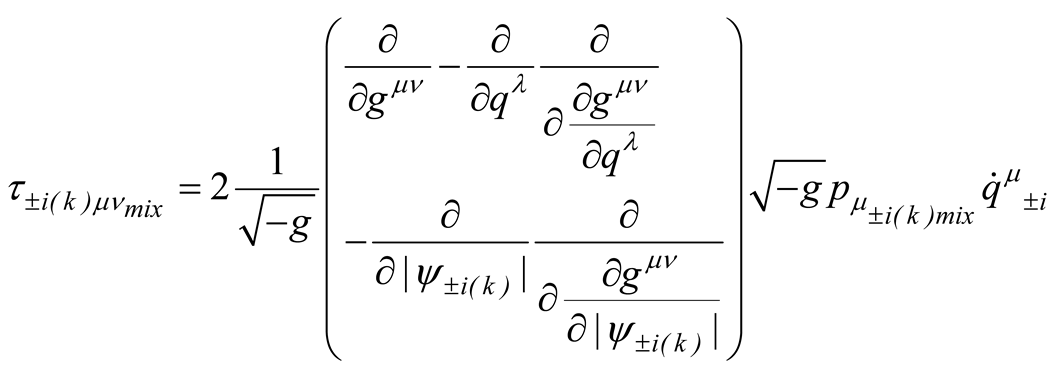
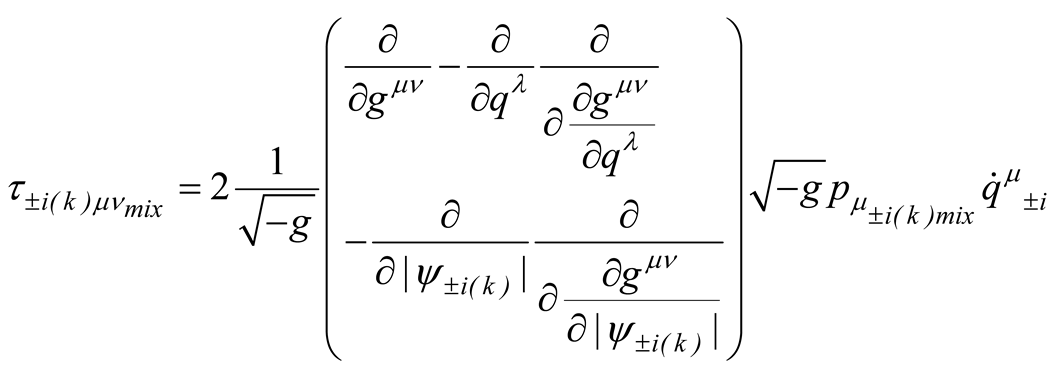
and [11]
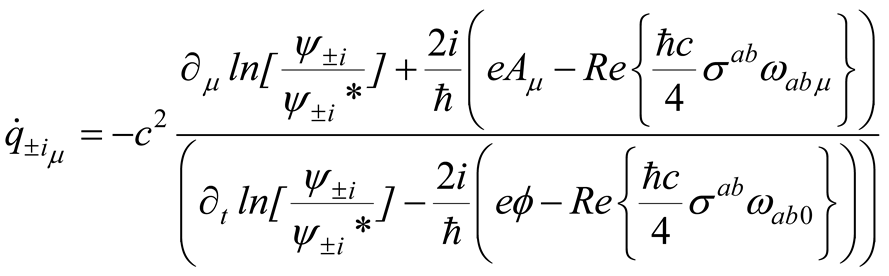
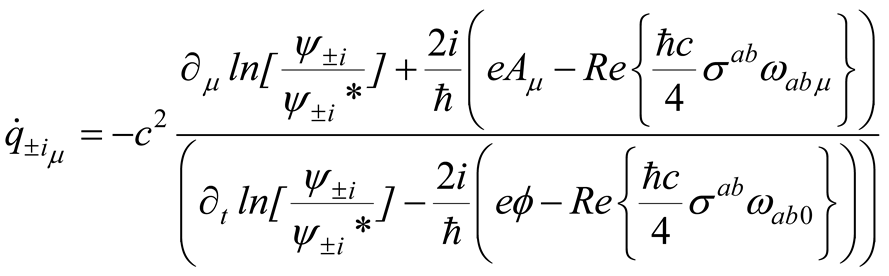
Besides, reads
where
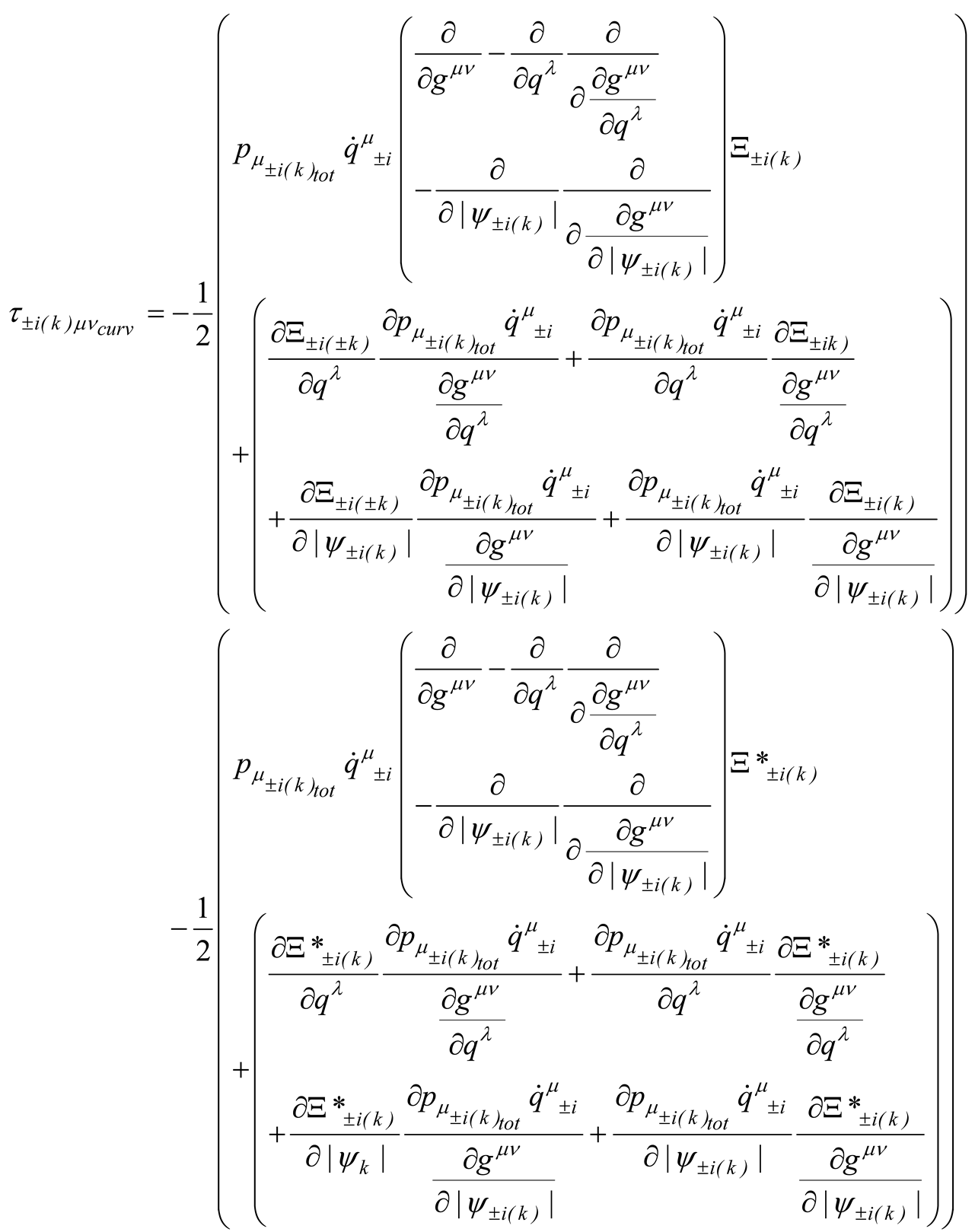

and
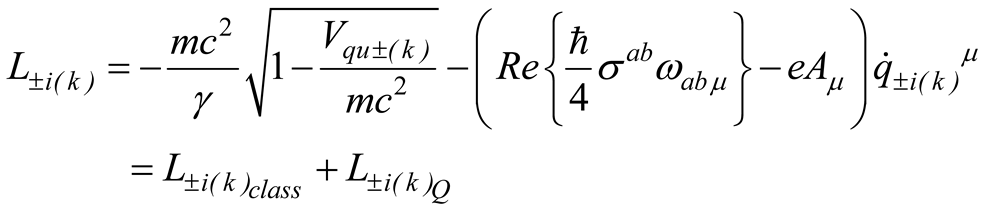
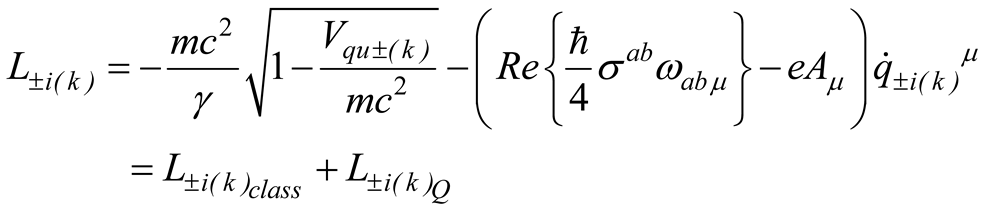
where
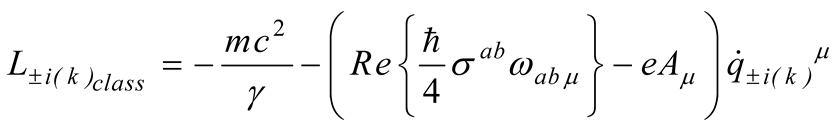
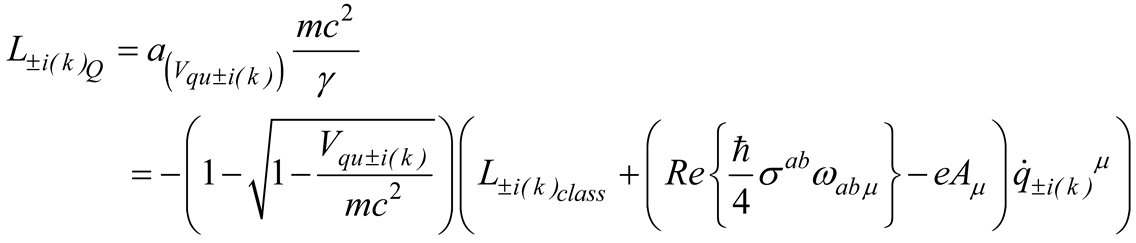
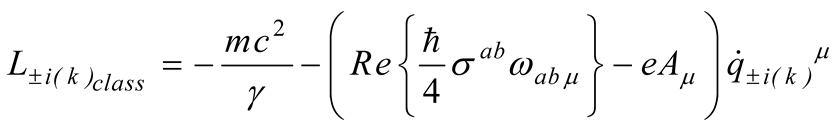
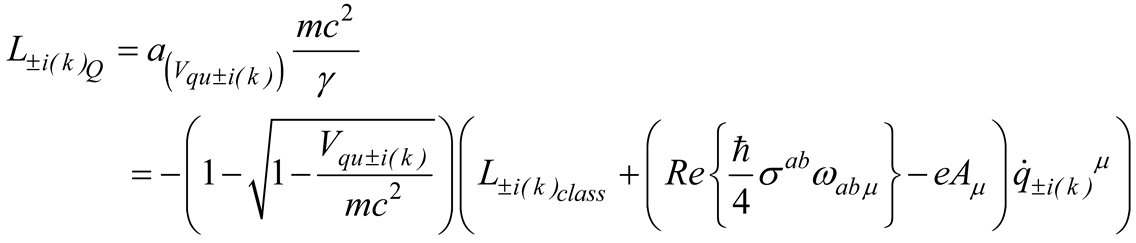
Appendix B
Weak Gravity Coupling of Boson Fields
As shown in [11] in the limit of weak curvature
where
and, disregarding the quantum contributions from the CPT and (that at first order are null), the metric tensor reads [18]
where
and is the Newton potential.
Charged boson
Given the KGE in flat ST
it covariantly transforms as
Moreover, by assuming that the out-diagonal terms of the weak-gravity metric tensor can be disregarded we obtain the following identities
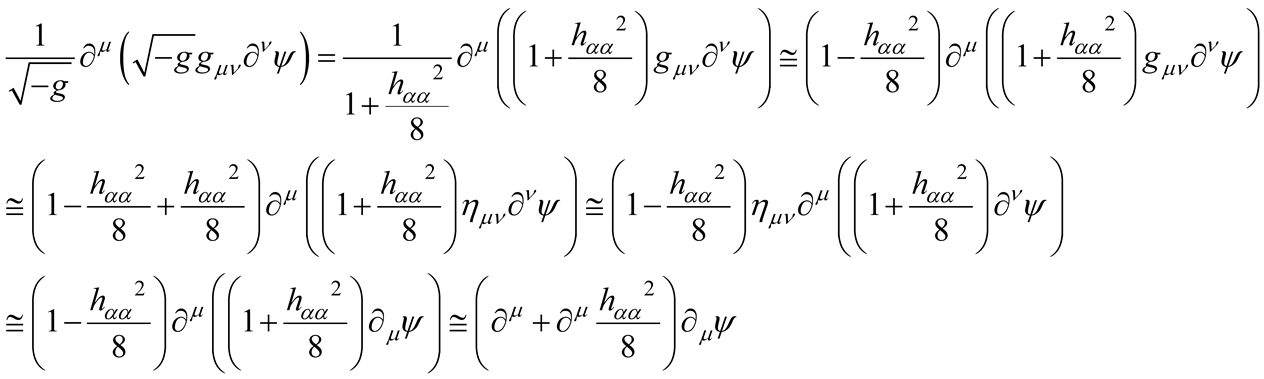

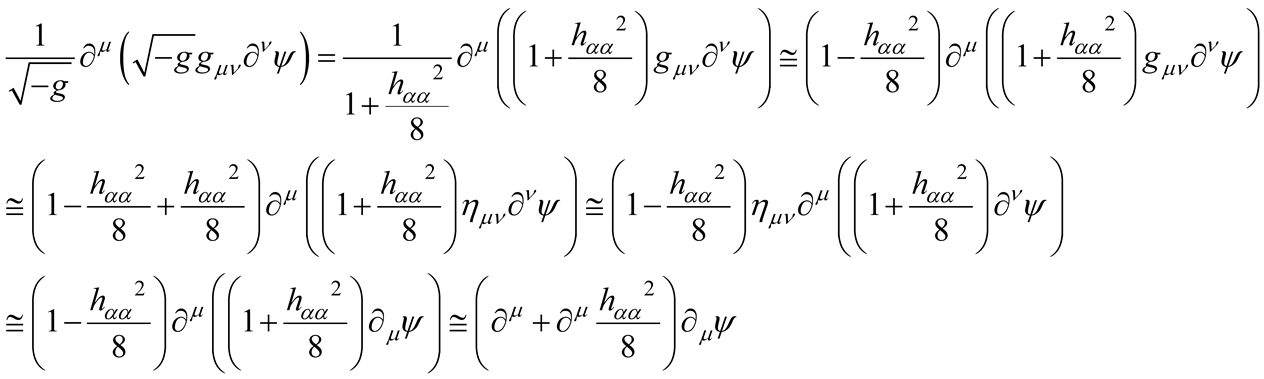

it follows that Equation (B.7) reads
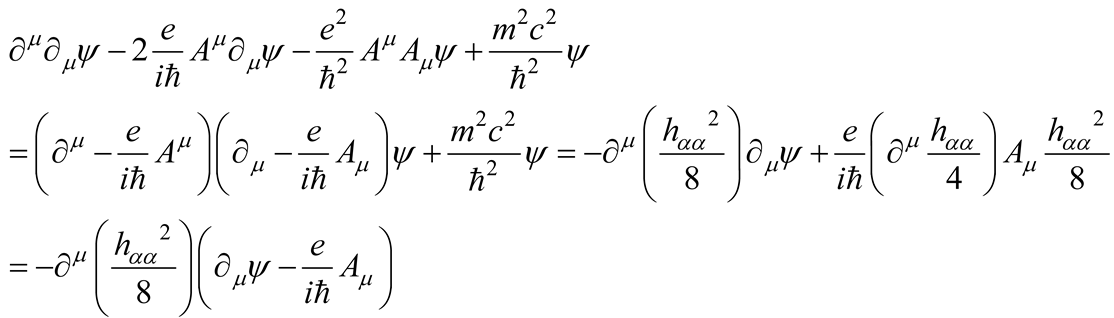
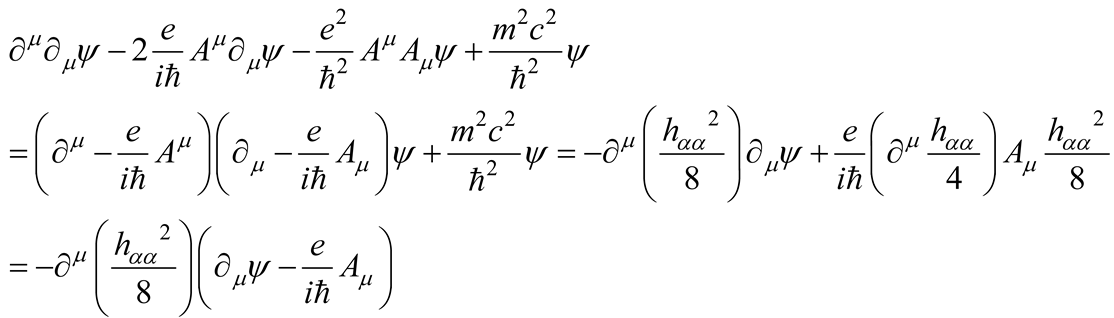
Furthermore, given the EM charged KGE
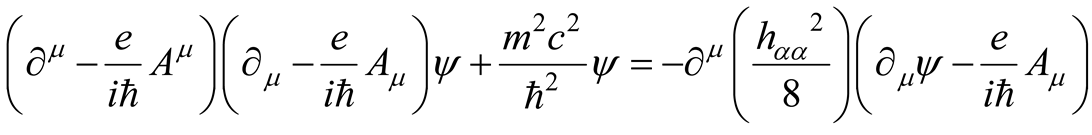
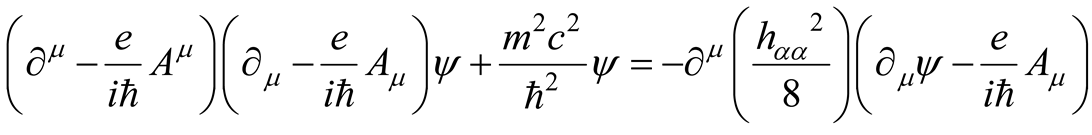
with the zero-order field Lagrangian
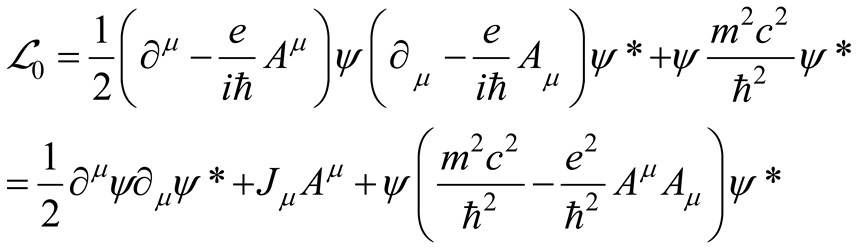
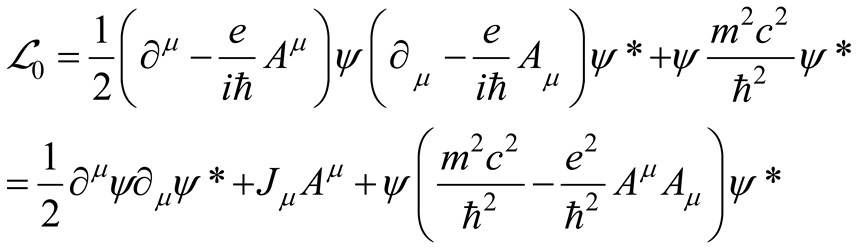
we can obtain the perturbative field Lagrangian for the gravity interaction by direct calculation since it cannot be covariantly obtained from .
Assuming at first order of approximation the flat ST Lagrangian equation of motion for the field
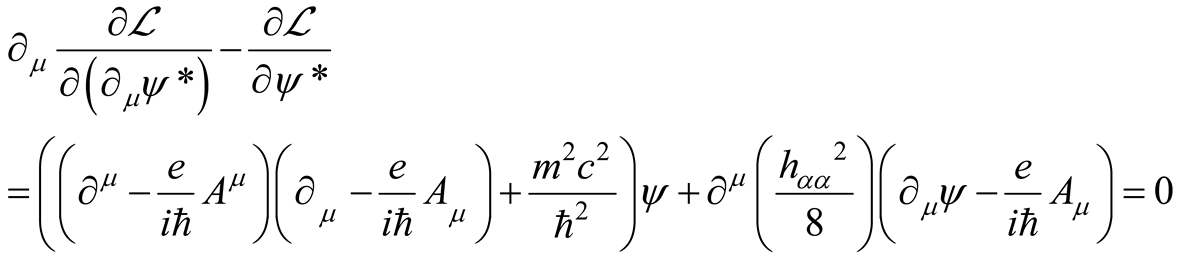
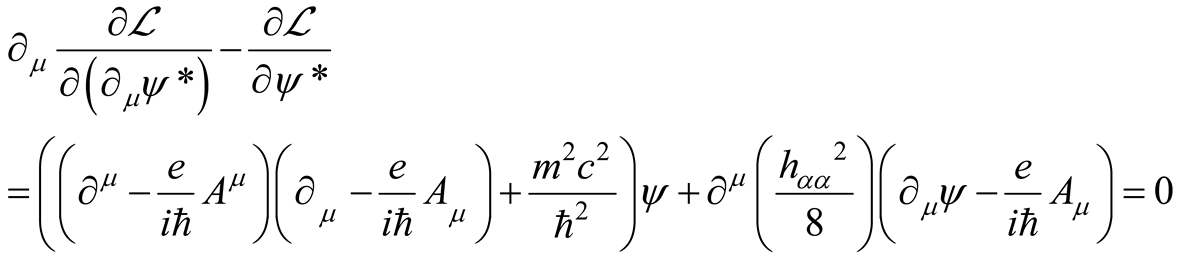
and its conjugate
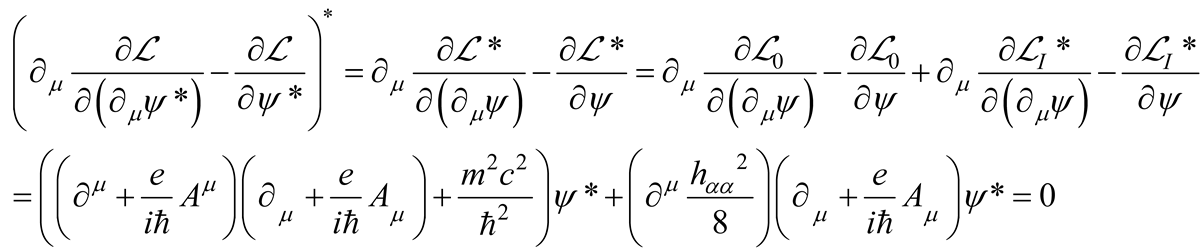
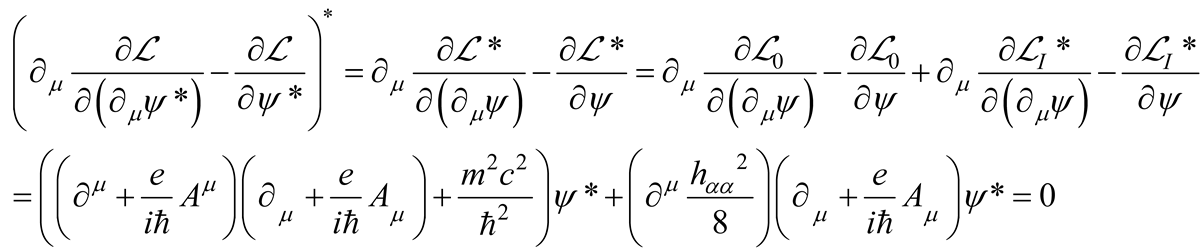
the weak-gravity interaction Lagrangian reads
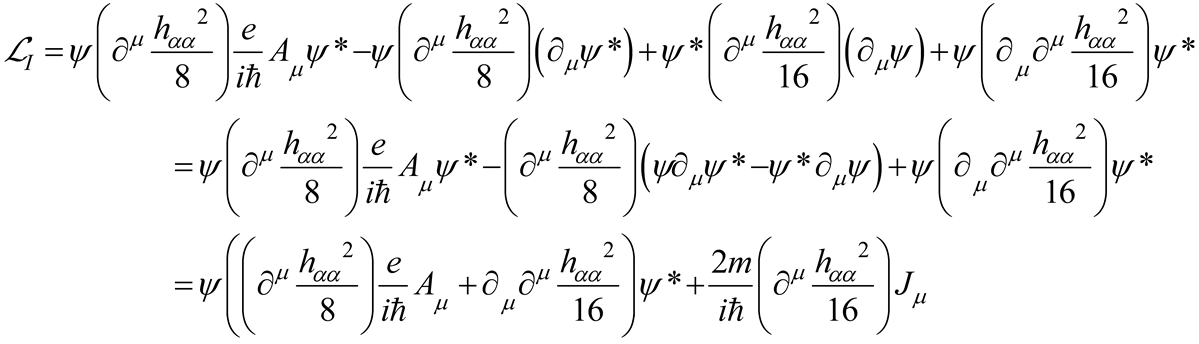
where.
For uncharged scalar boson (B.18) reduces to
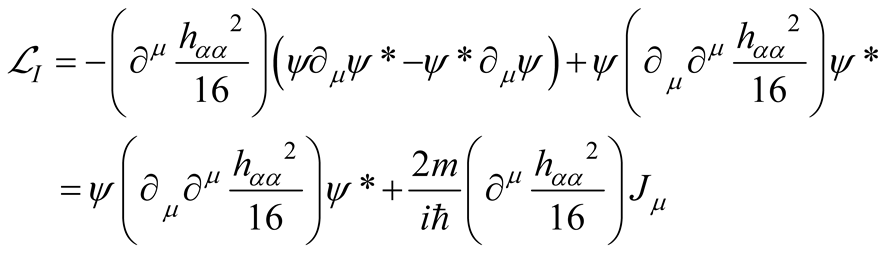
As far as it concerns the Higgs boson, the fourth order self-interacting field term does not bring contribution to the gravity coupling.
Uncharged Vector Boson
Given the Proca equation for vector boson in flat ST
whose field Lagrangian reads
when (and the current is conserved) with the Lorenz gauge condition, the KGE follows
In this case, in curved ST the covariant expression reads
that by using the identity
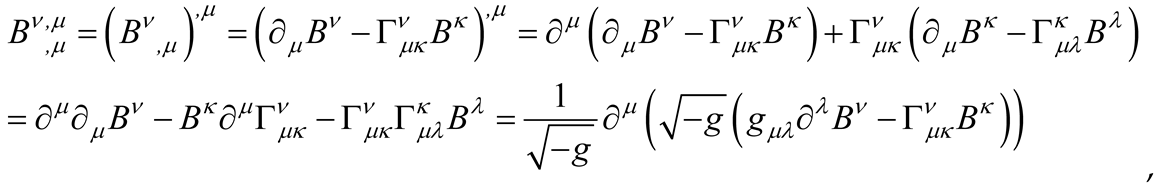
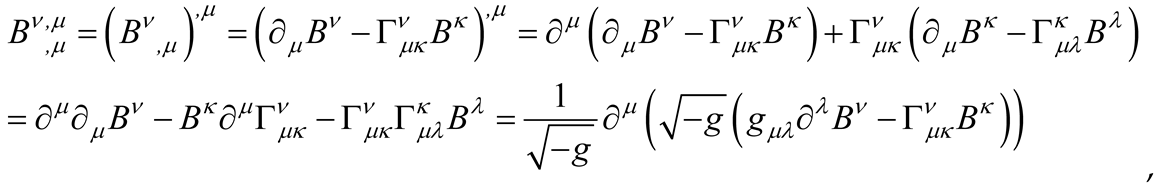
leads to
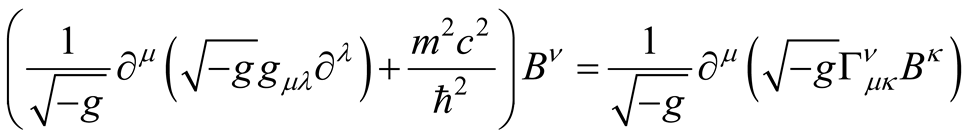
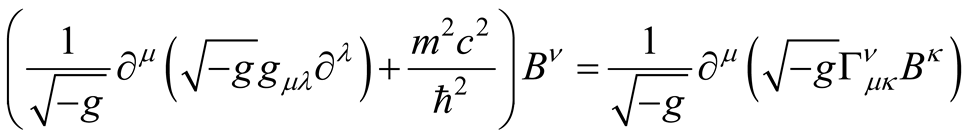
For the weak curvature limit
by using the identity
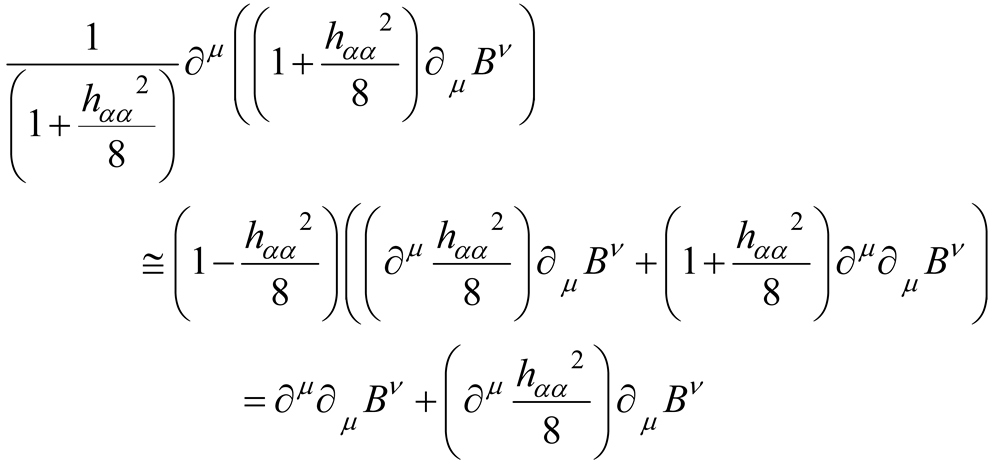
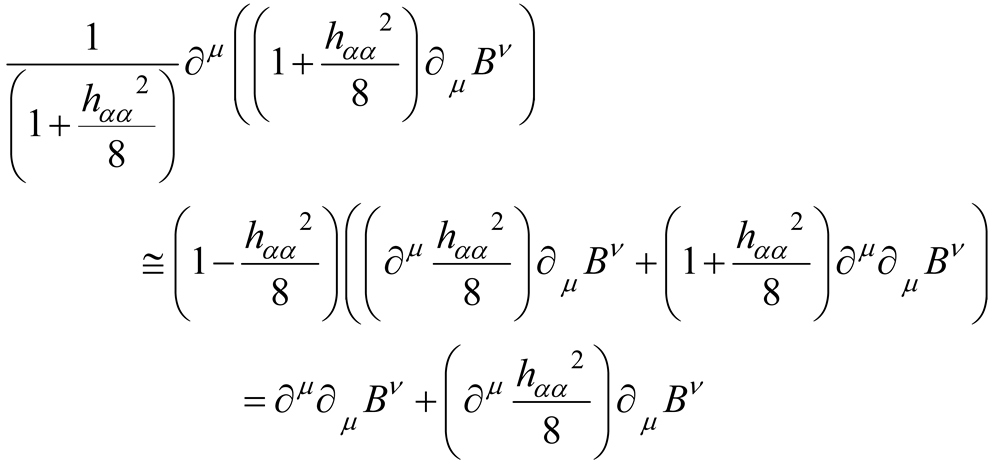
the perturbative KGE for uncharged vector boson (with conserved current) at first order reads
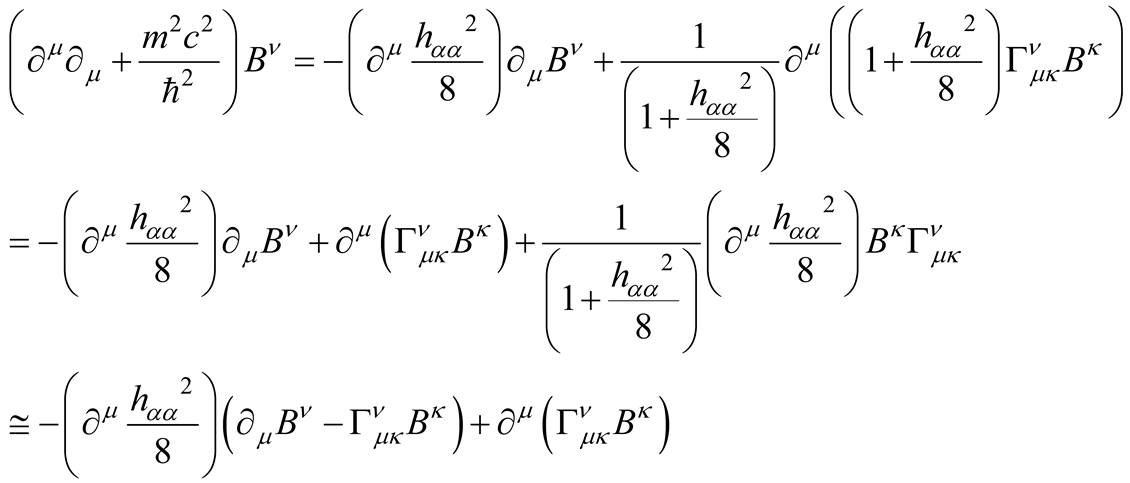

Perturbative Lagrangian of Uncharged Vector Boson (with Conserved Current)
Given the flat ST motion equation
Given that
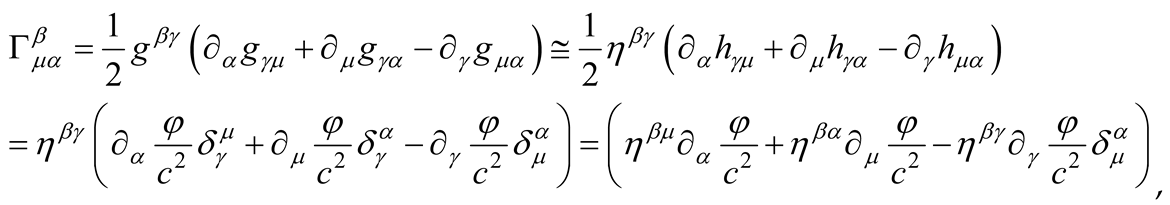
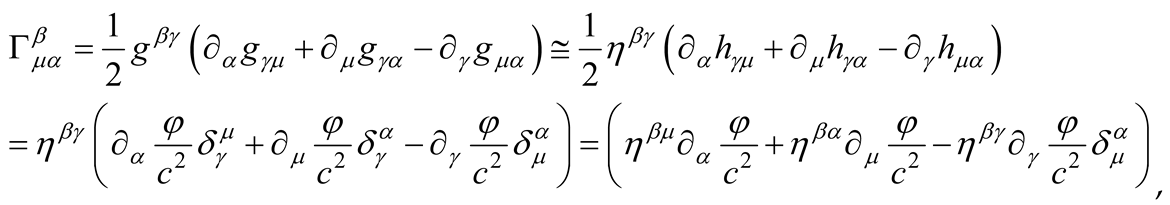
it follows that
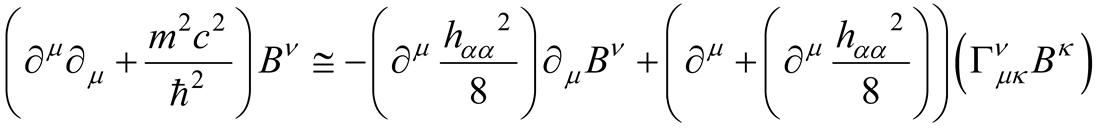
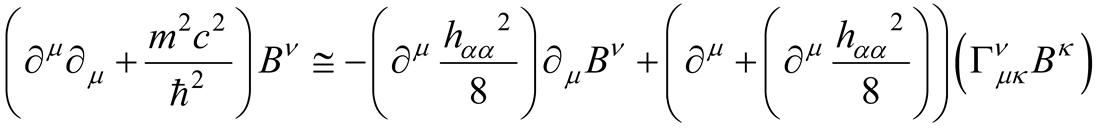
whose field Lagrangian for the left side reads
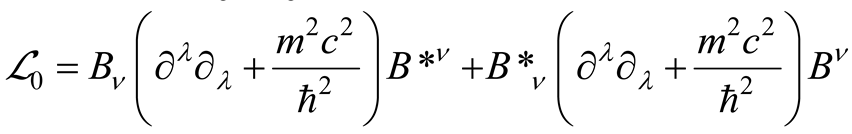
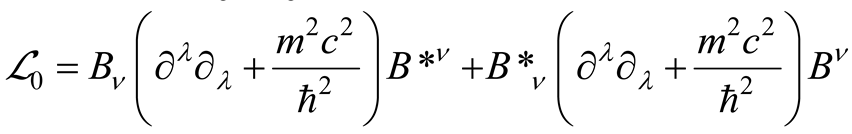
while the perturbative gravity coupling on the right side reads
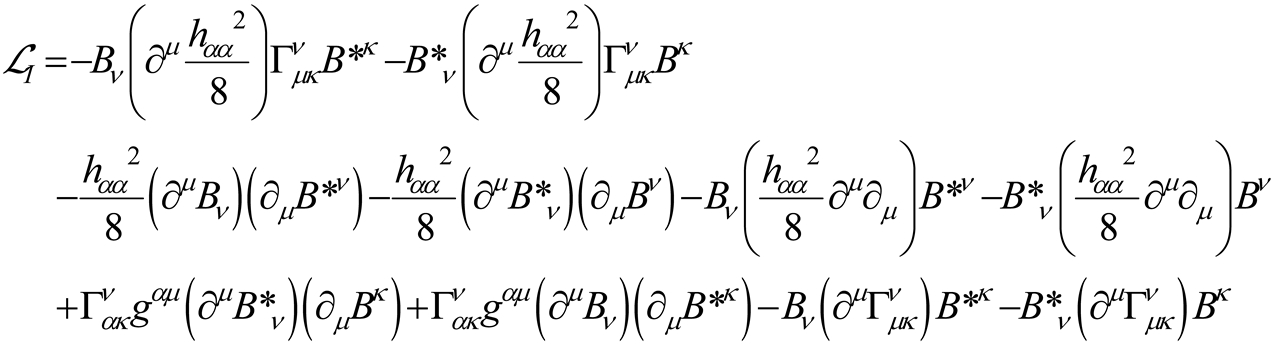
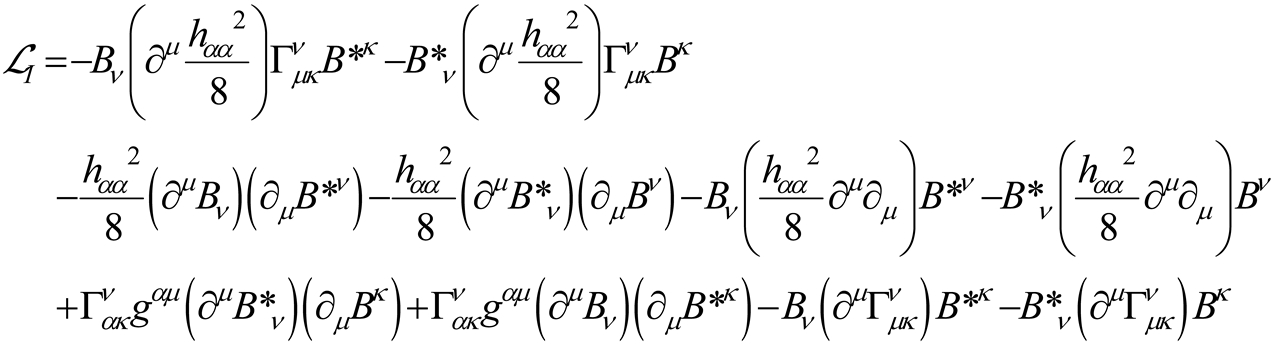
Since contains the gravity field at first order, for weak-gravity field (with small gradients), (B.34) at second order reads
and (B.36) simplifies to
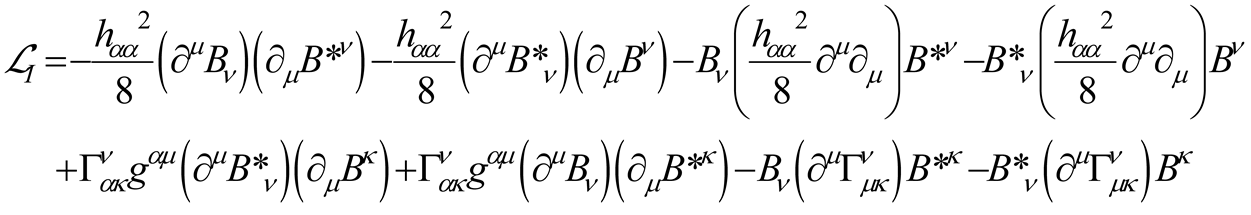
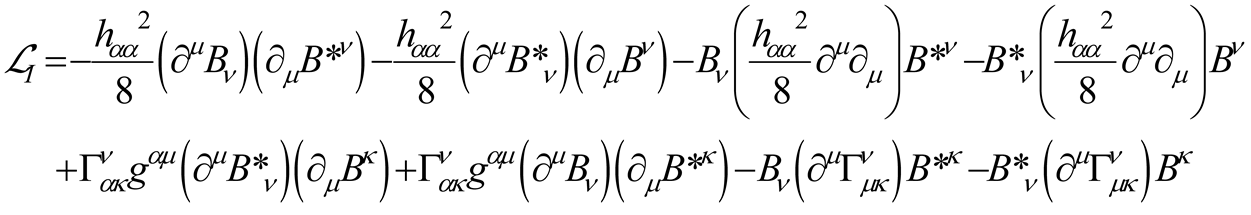
On the same foot, the gravity coupling for the Proca or the Stueckelberg action can be obtained.
Appendix C
Covariance of Classical Law of Motion from the Equivalence of Inertial and Gravitational Mass
The covariant form of the equation of motion (4.8) in the classical limit (i.e., ) for non-stationary state (i.e., ) reads [11,18]
and in low velocity limit (i,e., and ) reduces to
where on the right side there is the effect of the geometry of the space-time that generates the gravitational force.
If there is a difference between gravitational mass and inertial one (C.2) reads
that in the limit of weak gravity [18], where
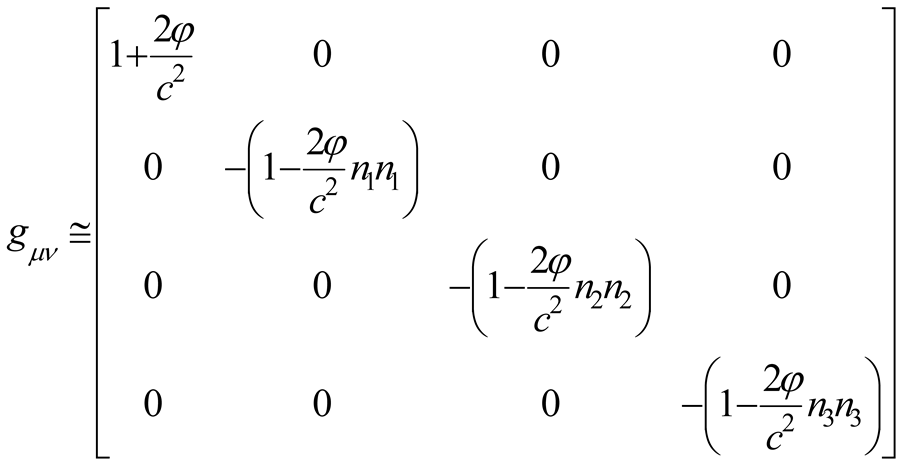
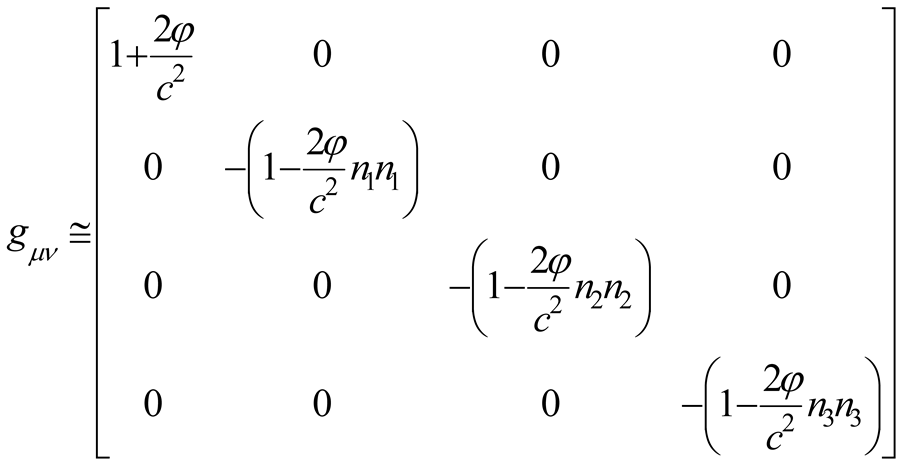
where [18], leads to
that, at the generic instant of time, in the reference system where leads to
and to
that for the radial direction leads to
If we introduce the equivalence between the inertial and gravitational mass , (C.8) becomes independent by the mass of the body, leading to the classical expression
In this way, the acceleration in (C.2), as well as the gravity, can be described as phenomena that depend only by geometry of the space. The covariance of classical motion Equation (4.8) makes the geometry of the space a background property that the observer does not perceive directly but as the presence of a field force.
Equation (C.8) shows that the covariance of the motion equation leading to (C.2) implies the equivalence of inertial and gravitational mass in the classical limit.
Appendix D
Covariant Anti-Commutation Rules for Fermions
By applying the covariance to the anti-commuting rules for the fermion field
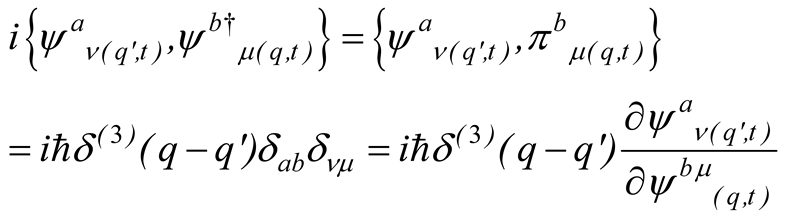
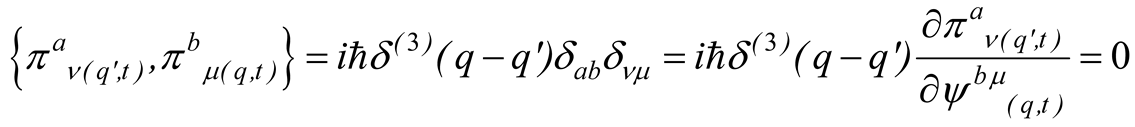
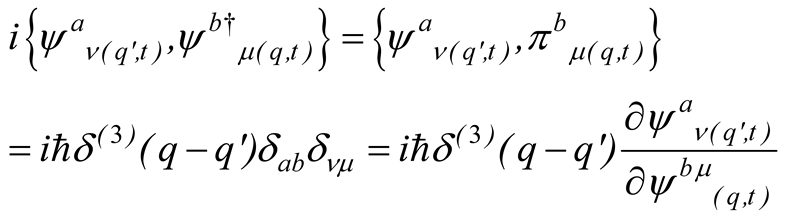
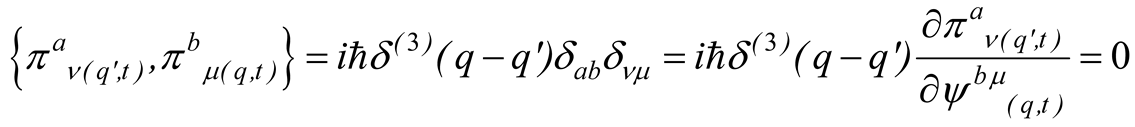
where
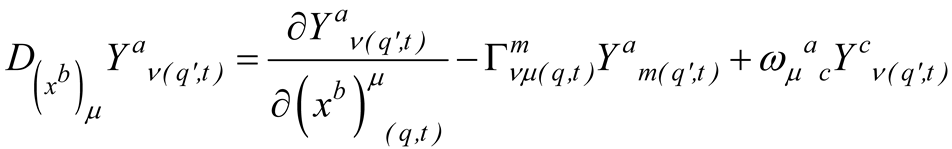
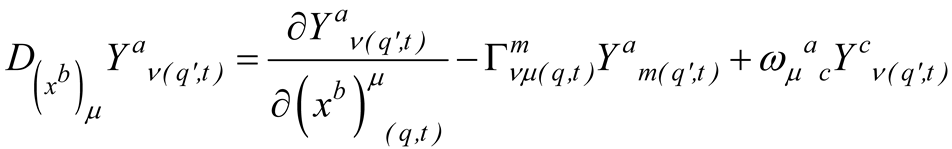
is the covariant derivative for affine and spinor connections that, for vector bi-spinor
, leads to the expression
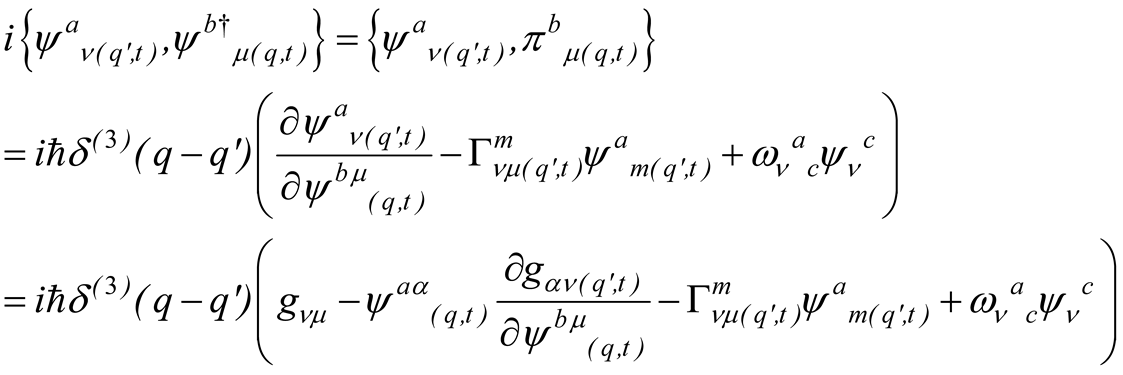
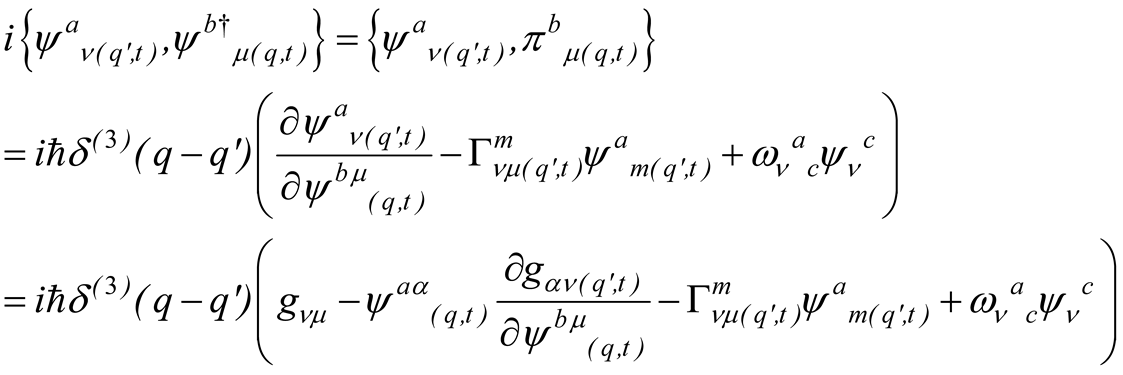
In the case of the Dirac spinor , (D.3-5) read
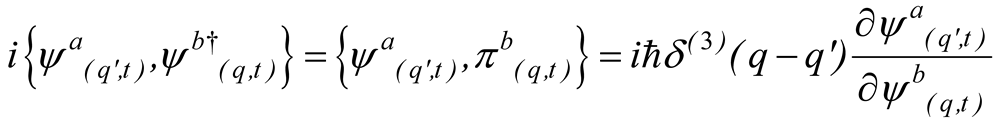
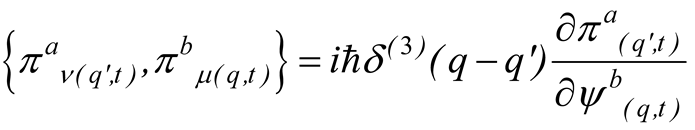
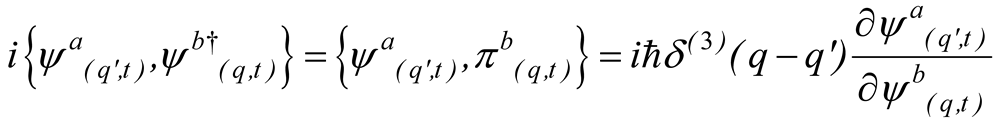
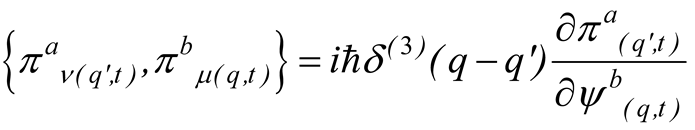
that by using the identity
with the help of (D.2), in the weak gravity limit, leads to
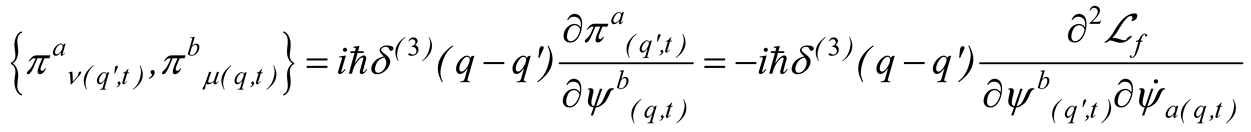
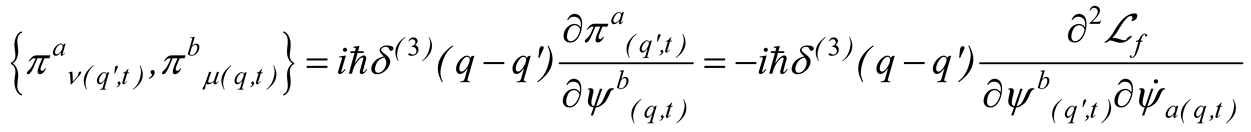
It worth noting that, the second quantization under the covariant commutations/anticommutations relations brings additional perturbative contributions into the interaction Hamiltonian.
References
- Green, M., B., John H. Schwarz, and Edward Witten. Superstring theory: Volume 1, Introduction. Cambridge University Press, 1987.
- Polchinski, J., String theory: Volume 1, An introduction to the bosonic string, Cambridge University Press, 2005.
- Becker, Katrin, Melanie Becker, and John H. Schwarz. String theory and M-theory: A modern introduction, Cambridge University Press, 2007.
- Rovelli, C. Loop quantum gravity, Living Reviews in Relativity 1, no. 1 (1998): 1. [CrossRef]
- Thiemann, T. Modern canonical quantum general relativity, Cambridge University Press, 2007.
- Ashtekar, Abhay, and Jerzy Lewandowski, Background independent quantum gravity: A status report, Classical and Quantum Gravity 21, R53.
- Ambjorn, J. , Jerzy Jurkiewicz, and Renate Loll. Reconstructing the universe. Physical Review D 2005, 72, 064014. [Google Scholar]
- Loll, R. Discrete approaches to quantum gravity in four dimensions, Living Reviews in Relativity 1, no. 1 (1998): 13.
- Ambjorn, J. Aleksei Gorlich, Jerzy Jurkiewicz, and Renate Loll. The nonperturbative quantum gravity. . arXiv:1203.3591. [CrossRef]
- Chiarelli, P. The Gravity of the Classical Klein-Gordon Field. Symmetry 2019, 11, 322. [Google Scholar] [CrossRef]
- Chiarelli, P. The Spinor-Tensor Gravity of the Classical Dirac Field. Symmetry 2020, 12, 1124. [Google Scholar] [CrossRef]
- Chiarelli, P. , Quantum to Classical Transition in the Stochastic Hydrodynamic Analogy: The Explanation of the Lindemann Relation and the Analogies Between the Maximum of Density at He Lambda Point and that One at Water-Ice Phase Transition. Phys. Rev. Res. Int. 2013, 3, 348–366. [Google Scholar]
- Chiarelli, P. The quantum potential: The missing interaction in the density maximum of He4 at the lambda point? Am. J. Phys. Chem. 2014, 2, 122–131. [Google Scholar] [CrossRef]
- Chiarelli, P. Beyond General Relativity: Exploring Quantum Geometrization of Spacetime, BP International, 2023, in Press.
- Chiarelli, P. The Non-Euclidean Hydrodynamic Klein–Gordon Equation with Perturbative Self-Interacting Field, Technologies 2017, 5, 63. [CrossRef]
- Landau L., D.; Lifšits, E.M. Course of Theoretical Physics Italian Edition. Mir Mosca Editori Riuniti 1976, 335–63. [Google Scholar]
- Hamber, H.W. Vacuum Condensate Picture of Quantum Gravity. Symmetry 2019, 11, 87. [Google Scholar] [CrossRef]
- Chiarelli, S.; Chiarelli, P. Stochastic Quantum Hydrodynamic Model from the Dark Matter of Vacuum Fluctuations: The Langevin-Schrödinger Equation and the Large-Scale Classical Limit. Open Access Library Journal 2020, 7, e6659. [Google Scholar] [CrossRef]
- Boylan-Kolchin, M. Stress testing ΛCDM with high-redshift galaxy candidates. Nat Astron 2023. [Google Scholar] [CrossRef] [PubMed]
- Kaluza, Th. , On the Unification Problem in Physics. Int. J. Mod. Phys. 2018, 27(14). [Google Scholar] [CrossRef]
- Ibid [13], pp. 386-396.
- M. Le Bellac, Quantum and Statistical Field Theory; Oxford Science pubblication, Oxford, ISBN 19 853929 0, 1991, pp. 315–337.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated