Quantum Effects in General Relativity: Investigating Repulsive Gravity of Black Holes at Large Distances

Preprint

Article

Quantum Effects in General Relativity: Investigating Repulsive Gravity of Black Holes at Large Distances

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Piero Chiarelli^*

This version is not peer-reviewed

Submitted:

03 June 2023

Posted:

05 June 2023

You are already at the latest version

Alerts

Abstract

The paper proposes a theoretical study that investigates the quantum effects on the gravity of black holes. The study utilizes a gravitational model that incorporates quantum mechanics derived from the classical-like quantum hydrodynamic representation. The research calculates the mass density distribution of quantum black holes, specifically in the case of central symmetry. The gravity of the quantum black hole shows contributions coming from the quantum potential energy, which is also sensitive to the presence of the background of gravitational noise. The additional energy, stored in the quantum potential fluctuations and constituting a form of dark energy, leads to a repulsive gravity in the weak gravity limit. This repulsive gravity overcomes the attractive classical Newtonian force at large distances of order of the intergalactic length.

Keywords:

Subject: Physical Sciences - Astronomy and Astrophysics

1. Introduction

One of the biggest challenges in physics today is the unification of general relativity and quantum theory. General relativity provides a description of gravity as the curvature of spacetime caused by the presence of matter and energy, while quantum theory describes the behavior of matter and energy at the smallest scales.

The problem is that these two theories are fundamentally different in their approach, and attempts to merge them have so far been unsuccessful. One of the key challenges is the existence of singularities, such as those found in black holes, which arise from the application of general relativity at very small scales.

Another issue is the conflict between the principles of quantum mechanics and general relativity, such as the principle of locality, which states that information cannot travel faster than the speed of light, and the principle of unitarity, which requires that the total probability of all possible outcomes of an experiment add up to one.

There have been various proposals for reconciling general relativity and quantum theory, such as string theory [1,2,3], loop quantum gravity [4,5,6], and causal dynamical triangulation [7,8,9], but none have yet been confirmed by experimental evidence, and the search for a unified theory remains an active area of research in theoretical physics.

Since the discovery of the universe's accelerated expansion, scientists have been trying to determine what is driving this acceleration. However, despite the many attempts to explain it, the current observational data cannot conclusively identify the source.

Recently, the author demonstrated [10,11] that by assuming the covariance of quantum field equations and utilizing their classical-like quantum hydrodynamic representation, it is possible to define the geometry of space-time through a gravity equation that incorporate the quantum mechanics. This is achieved through the use of a generalized least action principle, resulting in a system of equations that describes the quantum-gravitational evolution. This system couples the gravity equation with the quantum equation of boson or fermion fields.

The theoretical study proposed in this paper is centered on the quantum mechanical state of black holes and the resulting gravity in spacetime, where a background of gravitational noise is present. The findings of this study have the potential to confirm observational evidence such as the existence of dark energy and the repulsive nature of gravity at large distances.

2. Cosmological Scalar Boson Mass under Self-Gravity

During the collapse of a black hole, the mass distribution becomes highly concentrated, but the repulsive force of the quantum potential may become strong enough to counteract the gravitational force and prevent the collapse. This can result in the formation of stationary mass distributions. The uncertainty principle ensures that the repulsive quantum non-local potential grows sufficiently to overcome the gravitational force, thereby preventing a point-like collapse.

When the mass distribution of a scalar uncharged boson becomes extremely concentrated in space, its gravitational force can generate stable self-bonded states. These states are the quantum mechanical analogue of black hole predicted by General Relativity.

In this section, the author investigates whether the quantum potential force can stop the gravitational collapse when the mass distribution approaches the classical point singularity.

In order to obtain quantum mechanical stationary black hole configurations on a cosmological scale with large mass distributions, we make the assumption that the mass field can be represented as a classical scalar variable. This simplified model of scalar black hole mass serves as a "macroscopic" viewpoint that is acceptable for studying the gravitational behavior of black holes on a cosmological scale. T

The distribution of mass in the space-time (ST) is attributed to the formation of vacuum states resulting from the quantization of spinor and massive boson fields. This mass distribution in the ST is not only non-continuous, but also exhibits physical phenomena arising from the other three fundamental interactions. Hence, the focus is solely on the configuration of an eternal black hole, and the process of black hole evaporation and the production of Hawking radiation are out the description.

2.1. Stationary Scalar Mass Distribution

In the case of scalar mass field obeying to the Klein-Gordon equation, the gravitationally coupled system of motion equation reads [11]

R_{ν μ} - \frac{1}{2} g_{ν μ} R_{α}^{α} = \frac{8 π G}{c^{4}} T_{ν μ_{}}

(2.1)

\partial^{μ} ψ_{; μ} = \frac{1}{\sqrt{- g}} \partial^{μ} \sqrt{- g} (g^{μ ν} \partial_{ν} ψ) = - \frac{m^{2} c^{2}}{ℏ^{2}} ψ

(2.2)

with

T_{μ ν} = - \frac{m c^{2} | ψ_{\pm} |^{2}}{γ} [\begin{array}{l} (\sqrt{1 - \frac{V_{q u}}{m c^{2}}} - 1) g_{μ ν} \\ + {\sqrt{1 - \frac{V_{q u}}{m c^{2}}}}^{- 1} {(\frac{ℏ}{2 m c})}^{2} \frac{\partial \ln [\frac{ψ}{ψ *}]}{\partial q^{μ}} \frac{\partial \ln [\frac{ψ}{ψ *}]}{\partial q_{λ}} g_{λ ν} \end{array}]

(2.3)

where

γ = \frac{1}{\sqrt{\frac{g_{μ ν} {\dot{q}}^{ν} {\dot{q}}^{μ}}{c^{2}}}} = \frac{1}{c \sqrt{\partial_{0} S g_{μ ν} \partial^{ν} S \partial^{μ} S}} = \frac{2}{ℏ^{3 / 2} c \sqrt{i \partial_{0} \ln [\frac{ψ}{ψ *}] g_{μ ν} \partial^{ν} \ln [\frac{ψ}{ψ *}] \partial^{μ} \ln [\frac{ψ}{ψ *}]}}

(2.4)

and where the quantum potential reads

V_{q u} = - \frac{ℏ {}^{2}}{m} \frac{1}{| ψ | \sqrt{- g}} \partial_{μ} \sqrt{- g} (g^{μ ν} \partial_{ν} | ψ |)

(2.5)

The KGE (2.2) in the hydrodynamic notation, as a function of the real variables

| ψ |

and

\partial_{μ} S

, reads

g_{μ ν} \partial^{ν} S \partial^{μ} S - ℏ {}_{2}{\frac{1}{| ψ | \sqrt{- g}}} \partial_{μ} \sqrt{- g} (g^{μ ν} \partial_{ν} | ψ |) - m^{2} c^{2} = 0

(2.6)

\frac{1}{\sqrt{- g}} \partial_{μ} \sqrt{- g} (g^{μ ν} | ψ |^{2} \partial_{ν} S) = 0

(2.7)

Given the covariant approach of the theory, the motion equation (2.6) for eigenstates, reads

D_{q_{0}} p_{(k)}_{μ} = - \frac{1}{c} \frac{\partial L_{(k)}}{\partial q^{μ}} = \frac{m c}{γ_{(k)}} \frac{\partial}{\partial q^{μ}} \sqrt{1 - \frac{V_{q u (k)}}{m c^{2}}}

(2.8)

where

c D_{q_{0}}

is the curvilinear covariant total time derivative, and

p_{(k)}_{μ}

reads

p_{(k)}_{μ} = - \partial_{μ} S_{(k)} = (\pm) m γ_{(k)} {\dot{q}}_{{(k)}_{μ}} \sqrt{1 - \frac{V_{q u}_{(k)}}{m c^{2}}} = (\pm) m c u_{{(k)}_{μ}} \sqrt{1 - \frac{V_{q u}_{(k)}}{m c^{2}}}

(2.9)

. (2.9)

Developing equation (2.8) it follows that

\begin{array}{l} D_{q_{0}} (u_{{(k)}_{μ}} \sqrt{1 - \frac{V_{q u}_{(k)}}{m c^{2}}}) \\ = \sqrt{1 - \frac{V_{q u}_{(k)}}{m c^{2}}} D_{q_{0}} u_{{(k)}_{μ}} + u_{{(k)}_{μ}} D_{q_{0}} \sqrt{1 - \frac{V_{q u}_{(k)}}{m c^{2}}} = (\pm) \frac{1}{γ_{(k)}} \frac{\partial}{\partial q^{μ}} \sqrt{1 - \frac{V_{q u (k)}}{m c^{2}}} \end{array}

(2.10)

and, by utilizing the relation

D_{q_{0}} u_{μ} = \frac{d u_{μ}}{d q_{0}} - \frac{1}{γ} Γ_{_{μ ν}}^{α} u_{α} u^{ν}

(2.11)

The motion equation, to which the stationary condition

\frac{d u_{μ}}{d t} = 0

must be applied, reads

\begin{array}{l} \frac{d u_{μ}}{d t} - \frac{c}{γ} Γ_{_{μ ν}}^{α} u_{α} u^{ν} = - u_{μ} \frac{d}{d t} (\ln \sqrt{1 - \frac{V_{q u}}{m c^{2}}}) \pm \frac{1}{γ_{(k)}} \frac{\partial}{\partial q^{μ}} (\ln \sqrt{1 - \frac{V_{q u}}{m c^{2}}}) \\ = - u_{μ} \frac{d}{d t} (\ln \sqrt{1 + {(\frac{ℏ}{m c})}^{2} \frac{1}{| ψ | \sqrt{- g}} \partial_{μ} \sqrt{- g} (g^{μ ν} \partial_{ν} | ψ |)}) \\ \pm \frac{c}{γ_{(k)}} \frac{\partial}{\partial q^{μ}} (\ln \sqrt{1 + {(\frac{ℏ}{m c})}^{2} \frac{1}{| ψ | \sqrt{- g}} \partial_{μ} \sqrt{- g} (g^{μ ν} \partial_{ν} | ψ |)}) \end{array}

(2.12)

2.2. The Mass Distribution in Central Symmetric Scalar Uncharged Black Hole

In classical General Relativity, the collapse in a central gravitational field results in a final point-like mass density, approached with increasing velocity. However, in the quantum case, the quantum potential generates an expansive force

\partial_{μ} \ln \sqrt{1 - \frac{V_{q u}}{m c^{2}}}

(2.13)

that counteracts gravity, leading to deceleration and potentially halting the collapse. As a result, stable stationary configurations may exist at an equilibrium point. This suggests that the interplay between quantum effects and gravity can lead to different outcomes than those predicted by classical General Relativity.

From a general standpoint, the stationary mass distribution, as described by equation (2.12), depends on the metric tensor defined by the Quantum Einstein Gravity (QGE) equations (2.1), and vice versa. Although the general solution of these coupled equations is quite complex, the simplifying assumption of central symmetry can be introduced to extract useful information. This assumption leads to the quantum analogue of the Schwarzschild black hole, where the metric tensor satisfies a particular condition [13].

d s^{2} = e^{ν} c^{2} d t^{2} - r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}) - e^{λ} d r^{2}

(2.14)

where

q_{μ} = (c t, r, θ, ϕ)

and

g_{00} = e^{ν}; g_{11} = - e^{λ}; g_{22} = - r^{2}; g_{33} = - r^{2} \sin^{2} θ; \sqrt{- g} = | e^{\frac{λ + ν}{2}} r^{2} \sin^{2} θ |^{- 1};

(2.15)

that inserted into the gravity equation leads to the relations [13]

\frac{8 π G}{c^{4}} T_{1}^{1} = - e^{- λ} (\frac{ν'}{r} + \frac{1}{r^{2}}) + \frac{1}{r^{2}}

(2.16)

\frac{8 π G}{c^{4}} T_{0}^{0} = - e^{- λ} (\frac{1}{r^{2}} - \frac{λ'}{r}) + \frac{1}{r^{2}}

(2.17)

\frac{8 π G}{c^{4}} T_{0}^{1} = - e^{- λ} \frac{\dot{λ}}{r}

(2.18)

with

γ = \frac{1}{\sqrt{\frac{g_{μ ν} {\dot{q}}_{_{}}^{ν} {\dot{q}}_{_{}}^{μ}}{c^{2}}}}

(2.19)

and

V_{q u} = - \frac{ℏ {}_{2}}{m} \frac{1}{| ψ | \sqrt{- g}} \partial^{1} \sqrt{- g} (e^{- λ} \partial_{1} | ψ |)

(2.20)

where the apex and the dot over the letters mean derivation respect to r and ct, respectively.

Assuming that in the stationary distributions the mass is enclosed in a sphere of radius

R_{0}

, for

r > R_{0}

we can use the approximated gravitational relations [13]

- e^{- λ} (\frac{ν'}{r} + \frac{1}{r^{2}}) + \frac{1}{r^{2}} ≅ 0

(2.21)

- e^{- λ} (\frac{1}{r^{2}} - \frac{λ'}{r}) + \frac{1}{r^{2}} ≅ 0

(2.22)

- e^{- λ} \frac{\dot{λ}}{r} ≅ 0

(2.23)

whose solutions read

λ + ν = 0

(2.24)

g_{11} = - e^{λ} = - e^{- ν} ≅ - {(1 - \frac{R_{g}}{r})}^{- 1} \frac{r}{R_{g}} ≫ 1

(2.25)

g = - \frac{1}{r^{4} \sin^{4} θ}

(2.26)

e^{λ} = \frac{r}{r - R_{g}} = \frac{1}{g_{00}}

(2.27)

from which the quantum potential reads [14]

V_{q u} = - \frac{ℏ {}_{2}}{m} \frac{1}{| ψ | \sqrt{- g}} \partial^{1} \sqrt{- g} (e^{- λ} \partial_{1} | ψ |)

(2.28)

By introducing the relations (2.24-28) into the motion equation, it follows that

\begin{array}{l} \frac{d u_{μ}}{c d t} - \frac{1}{γ} Γ_{_{μ ν}}^{α} u_{α} u^{ν} = - u_{μ} \frac{1}{c} \frac{d}{d t} (\ln \sqrt{1 + {(\frac{ℏ}{m c})}^{2} \frac{1}{| ψ | \sqrt{- g}} \partial^{1} \sqrt{- g} (e^{- λ} \partial_{1} | ψ |)}) \\ + \frac{1}{γ} \frac{\partial}{\partial q^{μ}} (\ln \sqrt{1 + {(\frac{ℏ}{m c})}^{2} \frac{1}{| ψ | \sqrt{- g}} \partial^{1} \sqrt{- g} (e^{- λ} \partial_{1} | ψ |)}) \\ = - u_{μ} \frac{1}{c} \frac{\partial}{\partial q^{ν}} (\ln \sqrt{1 + {(\frac{ℏ}{m c})}^{2} \frac{1}{| ψ | \sqrt{- g}} \partial^{1} \sqrt{- g} (e^{- λ} \partial_{1} | ψ |)}) {\dot{q}}^{ν} \\ + \frac{1}{γ} \frac{\partial}{\partial q^{μ}} (\ln \sqrt{1 + {(\frac{ℏ}{m c})}^{2} \frac{1}{| ψ | \sqrt{- g}} \partial^{1} \sqrt{- g} (e^{- λ} \partial_{1} | ψ |)}) \\ = 0 + \frac{1}{γ} \frac{\partial}{\partial q^{μ}} (\ln \sqrt{1 + {(\frac{ℏ}{m c})}^{2} \frac{1}{| ψ | \sqrt{- g}} \partial^{1} \sqrt{- g} (e^{- λ} \partial_{1} | ψ |)}) \end{array}

(2.29)

and, by the stationary condition in the BH system of reference at large distance

u_{μ} = \lim_{\frac{r}{R_{g}} \to \infty} (γ, 0, 0, 0) = \lim_{\frac{r}{R_{g}} \to \infty} (\frac{1}{\sqrt{g^{00}}}, 0, 0, 0) = (1, 0, 0, 0)

(2.30)

and

u^{μ} = \lim_{\frac{r}{R_{g}} \to \infty} (g^{00} γ, 0, 0, 0) = \lim_{\frac{r}{R_{g}} \to \infty} (\sqrt{g^{00}}, 0, 0, 0) ≅ (1, 0, 0, 0)

(2.31)

we obtain

\begin{array}{l} Γ_{_{μ ν}}^{α} u_{α} u^{ν} = Γ_{_{10}}^{0} u_{0} u^{0} = \frac{1}{2} u_{0} u^{0} g^{00} \partial_{1} g_{00} = u^{0} u^{0} \partial_{1} g_{00} ≅ \partial_{1} g_{00} \\ = - \partial_{1} (\ln (1 + {(\frac{ℏ}{m c})}^{2} \frac{1}{| ψ | \sqrt{- g}} \partial^{1} \sqrt{- g} (e^{- λ} \partial_{1} | ψ |))) \end{array}

(2.32)

\partial_{1} \frac{r - R_{g}}{r} = \partial_{1} (\ln (1 - {(\frac{ℏ}{m c})}^{2} \frac{1}{| ψ | r^{- 2}} \partial^{1} r^{- 2} (\frac{r - R_{g}}{r} \partial_{1} | ψ |)))

(2.33)

where

R_{g}

is the gravitational radius of the BH and

R_{c}

the Compton’s length, leading to the BH mass density at large distances (see Appendix) following the law

\lim_{r \to \infty} | ψ | = G_{0} e^{- ς \frac{r}{R_{c}}}

(2.34)

The constants

G_{0}

is defined by the normalization condition.

2.3. The mass Distribution near the Center of Schwarzschild Black Hole

In the classical case the BH mass collapses into a point, in the quantum case, for the uncertainty principle (see 2.44), the maximum concentration is inside a sphere whose radius is of order of magnitude of Compton’s length

R_{c}

. Thence, for macroscopically massive BH, with condition

R_{g} ≫ R_{c}

(for BH of mass

m \sim 10 {}_{35}k g

\frac{R_{g}}{R_{c}} \sim 10 {}_{85}

,), we can assume with a good approximation that in the limit

\frac{r}{R_{g}} \to 0

(at least

\frac{r}{R_{g}} ≫ 10 {}_{- 85}

) there is no mass for

R_{c} ≪ r < R_{g}

. Thus, by observing that

\lim_{\frac{r}{R_{g}} \to 0} λ = \lim_{\frac{r}{R_{g}} \to 0} \ln \frac{r}{r - R_{g}} ≅ - \frac{r}{R_{g}} = 0

(2.35)

and that

\frac{8 π G}{c^{4}} T_{1}^{1} = - e^{- λ} (\frac{ν'}{r} + \frac{1}{r^{2}}) + \frac{1}{r^{2}} ≅ - (\frac{ν'}{r} + \frac{1}{r^{2}}) + \frac{1}{r^{2}} ≅ 0

(2.36)

\frac{8 π G}{c^{4}} T_{0}^{0} = - e^{- λ} (\frac{1}{r^{2}} - \frac{λ'}{r}) + \frac{1}{r^{2}} ≅ - (\frac{1}{r^{2}} - \frac{λ'}{r}) + \frac{1}{r^{2}} ≅ 0

(2.37)

e^{λ} \frac{8 π G}{c^{4}} T_{0}^{1} = - \frac{\dot{λ}}{r} = 0

(2.38)

equation (A.9), in Appendix, can be also retained for

x = \frac{r}{R_{g}} \to 0

Thus, providing that at small distance from the BH center it holds

\lim_{x \to 0} | {\tilde{y}}^{2}_{(x)} | < < | {\tilde{y}}_{(x)} |

(2.39)

We obtain the differential equation

\lim_{x \to 0} \tilde{y}'_{(x)} = R_{g} y'_{(r)} = {\tilde{y}}_{(x)} (\frac{3}{x} - \frac{1}{x - 1}) + \frac{R_{g}^{2}}{R_{c}^{2}} \frac{x}{x - 1} (1 - C_{0} e^{\ln (\frac{x - 1}{x})})

(2.40)

whose solution, given in Appendix, reads

\lim_{\frac{r}{R_{g}} \to 0} | ψ | ≅ G_{0} e^{- \frac{1 - ς^{2}}{e} \frac{R_{g}}{R_{c}} z} r ≫ R_{c}, R_{g} ≫ R_{c}

(2.41)

The output (2.41) shows that, for large mass BHs (e.g.,

m \sim 10 {}_{35}k g

) the mass density is practically null outside the sphere of Compton’s radius at the center of the BH (e.g., for

r = 10 R_{c}

| ψ | \sim G_{0} e^{- \frac{1 - ς^{2}}{e} 10^{86}} \sim G_{0} e^{- \frac{1}{e} 10^{86}}

( see Appendix).

This output in agreement with the uncertainty principle leads to a piece of information about the minimum mass for the formation of BHs. In fact, in order that the BH energy due to its localization does not exceed the value

m c^{2}

(otherwise a new BH it is formed), by the uncertainty principle it follows that

Δ E = \frac{ℏ}{2 Δ t} = \frac{v ℏ}{2 Δ x} \leq m c^{2}

(2.42)

where

v \geq Δ v = \frac{Δ p}{m} = \frac{ℏ}{2 m Δ x}

(2.43)

that leads to

m c^{2} > \frac{ℏ^{2}}{4 m Δ x^{2}}

and, finally, to

Δ x > \frac{ℏ}{2 m c} = \frac{R_{c}}{2}

(2.44)

Besides, since in order to form a BH all the mass must be inside the gravitational radius, we must have that

R_{g} = \frac{2 G m}{c^{2}} > \frac{Δ x}{2} = r_{\min} = \frac{R_{c}}{4}

(2.45)

and, thence, that

\frac{R_{c}}{4 R_{g}} = \frac{ℏ}{8 m c R_{g}} = \frac{ℏ c}{8 m^{2} G} = π \frac{m_{p}^{2}}{m^{2}} < 1

(2.46)

leading to the condition for the black hole mass

m

m > π^{1 / 2} m_{p}

(2.47)

where

m_{p} = \sqrt{\frac{ℏ c}{8 π G}}

is the reduced Planck mass.

For small masses when

m \to 0

(quantum case) the gravitational radius

R_{g}

tends to zero, while the Compton’s radius

R_{c}

goes to infinity so that it exists the minimum mass (2.47) for the formation of the black hole (

R_{g} = \frac{R_{c}}{4}

). This condition is safe for our universe since low energy elementary particles cannot form BHs.

On the other hand, it is noteworthy to observe that for very large mass

m \to \infty

V_{q u} \propto \frac{1}{m} \to 0

(classical limit) the BH Compton’s radius

R_{c}

goes to zero and the point singularity of the classical general relativity is asymptotically approached.

Additionally, as black holes with a Planck mass cannot be divided into two smaller black holes, they represent the lightest possible configuration of scalar uncharged mass density that can be achieved solely through gravitational interaction. Moreover, since the condition expressed in equation (2.47) also applies to quantized fields, the fundamental lowest state of a quantum black hole is heavier than

π^{1 / 2} m_{p}

It is worth noting that the mass density output of macroscopic black holes enclosed within a sphere with a radius smaller than the Planck length and on the order of the Compton wavelength is typically derived from a continuous (classical) description of the fields and may undergo modifications in the context of quantized fields.

3. Gravitational Field of Black Holes at Large Distance in Spacetime with Background Fluctuations

In this paragraph, we derive the weak gravitational force of black holes over long distances. The large distance approximation is used because the gravitational radius of a black hole is much smaller than the cosmological physical scale, allowing us to treat the mass distribution of the black hole as point-like.

fact, given the mass distribution of BH (2.34) arranged in the form

| ψ |^{2} = | ψ_{0} |^{2} {(\frac{ς}{2 \sqrt{π} R_{c}})}^{2} B_{(r)} \frac{ς}{2 R_{c}} e^{- ς \frac{r}{R_{c}}}

(3.1)

at large distance reads

\begin{array}{l} \lim_{\frac{r}{R_{c}} \to \infty} | ψ_{0} |^{2} {(\frac{ς}{2 \sqrt{π} R_{c}})}^{2} B_{(r)} \frac{ς}{2 R_{c}} e^{- ς \frac{r}{R_{c}}} \\ = \lim_{\frac{r}{R_{c}} \to \infty} = \frac{B_{(r)}}{\int B_{(r)} {(\frac{ς}{2 \sqrt{π} R_{c}})}^{2} \frac{ς}{2 R_{c}} e^{- ς \frac{r}{R_{c}}} d^{3} Ω} {(\frac{ς}{2 \sqrt{π} R_{c}})}^{2} \frac{ς}{2 R_{c}} e^{- ς \frac{r}{R_{c}}} \\ = \lim_{R_{c} \to 0} \frac{B_{(r)}}{\int B_{(r)} {(\frac{ς}{2 \sqrt{π} R_{c}})}^{3} e^{- ς \frac{r^{2}}{4 R_{c}^{2}}} d^{3} Ω} {(\frac{ς}{2 \sqrt{π} R_{c}})}^{3} e^{- ς \frac{r^{2}}{4 R_{c}^{2}}} \\ = \frac{B_{(r)}}{\int B_{(r)} δ^{3}_{(r)} d^{3} Ω} δ^{3}_{(r)} = \frac{B_{(r = 0)}}{B_{(r = 0)}} δ^{3}_{(r)} = δ^{3}_{(r)} \end{array}

(3.2)

where the normalization condition

\int | ψ |^{2} d^{3} Ω = 1

has been used.

It must be noted that at temperature bigger than the absolute zero, the BH quantum potential undergoes fluctuation

δ {\bar{E}}_{q u}

[15,16,17] that brings the equivalent additional mass density

m_{B H} | δ ψ_{0} |^{2} = \frac{δ {\bar{E}}_{q u}}{c^{2}}

(3.3)

Being so, for cosmological problems (i.e.,

R_{c} \to 0

), we assume that the total mass density of the BH field in the spacetime with fluctuating background reads

\lim_{r \to \infty} | ψ |^{2} ≃ δ^{3}_{(r)} + | δ ψ_{0} |^{2}

(3.4)

Furthermore, as black holes are quantum objects with a significant quantum potential energy (as described in the appendix), we anticipate that their gravity over long distances may result in quantum effects contributing to the Newtonian law.

The contribution coming from the quantum potential, contained into the energy density tensor of the QGE, reads

\begin{array}{l} R_{ν μ} - \frac{1}{2} g_{ν μ} R_{α}^{α} = \frac{8 π G}{c^{4}} \frac{m c^{2} | ψ_{\pm} |^{2}}{γ} ((\sqrt{1 - \frac{V_{q u}}{m c^{2}}} - 1) g_{μ ν} + {\sqrt{1 - \frac{V_{q u}}{m c^{2}}}}^{- 1} {(\frac{ℏ}{2 m c})}^{2} \frac{\partial \ln [\frac{ψ}{ψ *}]}{\partial q^{μ}} \frac{\partial \ln [\frac{ψ}{ψ *}]}{\partial q^{ν}}) \\ = \frac{8 π G}{c^{4}} \frac{m c^{2} | ψ_{\pm} |^{2}}{γ} ((\sqrt{1 - \frac{V_{q u}}{m c^{2}}} - 1) g_{μ ν} + \sqrt{1 - \frac{V_{q u}}{m c^{2}}} u_{μ} u_{ν}) \end{array}

(3.5)

where it has been used the identity . Moreover, given that

V_{q u} = - \frac{ℏ {}_{2}}{m} \frac{1}{| ψ | \sqrt{- g}} \partial^{1} \sqrt{- g} (e^{- λ} \partial_{1} | ψ |)

(3.6)

g = - \frac{1}{r^{4} \sin^{4} θ}

(3.7)

e^{λ} = \frac{r}{r - R_{g}} = \frac{1}{g_{00}} = - g_{11}

(3.8)

γ = \frac{1}{\sqrt{1 - \frac{{\dot{q}}^{2}}{c^{2}}}} = \frac{1}{\sqrt{\frac{g^{μ ν} {\dot{q}}_{_{ν}}^{} {\dot{q}}_{_{μ}}^{}}{c^{2}}}} = \frac{1}{\sqrt{g^{00}}}

(3.9)

\lim_{r \to \infty} | ψ | = G_{0} e^{- ς \frac{r}{R_{c}}}

(3.10)

it follows that

\begin{array}{l} \lim_{r ≫ R_{g}} V_{q u} = \lim_{r ≫ R_{g}} - \frac{ℏ {}_{2}}{m} \frac{1}{e^{- ς x}} r^{2} \partial^{r} r^{- 2} (e^{- λ} \partial_{r} e^{- ς z}) \\ = \lim_{r ≫ R_{g}} \frac{ℏ {}_{2}}{m} (\frac{ς}{R_{c}}) \frac{1}{e^{- ς x}} r^{2} \partial^{r} r^{- 2} ((1 - \frac{R_{g}}{r}) e^{- ς x}) \\ = \lim_{r ≫ R_{g}} \frac{ℏ {}_{2}}{m} \frac{ς}{R_{c}} (- 2 r^{- 1} (1 - \frac{R_{g}}{r}) + (\frac{ς}{R_{c}} (1 - \frac{R_{g}}{r}) + \frac{R_{g}}{r^{2}})) \\ = \lim_{r ≫ R_{g}} - \frac{ℏ {}_{2}}{m} \frac{ς}{R_{c}} (2 r^{- 1} - \frac{ς}{R_{c}}) = \frac{ℏ {}_{2}}{m} \frac{ς {}_{2}}{R_{c} {}_{2}} = m c^{2} ς {}_{2} \end{array}

(3.10)

Thence, the gravitational equation (3.5) in the mixed form reads

R_{μ}^{ν} - \frac{1}{2} δ_{μ}^{ν} R_{α}^{α} = \frac{8 π G}{c^{4}} \frac{m c^{2} | ψ_{\pm} |^{2}}{γ} (\begin{array}{l} (\sqrt{1 + ς^{2}} - 1) δ_{μ}^{ν} \\ + \sqrt{1 + ς^{2}} u_{μ} u^{ν} \end{array})

(3.11)

leading to the equation for the trace of the Ricci tensor

R_{α}^{α} = - \frac{8 π G}{c^{4}} \frac{m c^{2} | ψ_{\pm} |^{2}}{γ} (\begin{array}{l} 4 (\sqrt{1 + ς^{2}} - 1) \\ + \sqrt{1 + ς^{2}} u_{α} u^{α} \end{array})

(3.12)

and to

R_{0}^{0} = \frac{8 π G}{c^{4}} \frac{m c^{2} (δ_{(r - r_{B H})} + | δ ψ_{0} |^{2})}{γ} (\begin{array}{l} (\sqrt{1 + ς^{2}} - 1) (δ_{0}^{0} - 2) \\ + \frac{\sqrt{1 + ς^{2}}}{2} u_{0} u^{0} \end{array})

(3.13)

Given that at large distance we can use the approximations

l i m_{r \to \infty} u_{0} = 1

(3.14)

g_{00} = \frac{r - R_{g}}{r} = (1 - \frac{R_{g}}{r})

(3.15)

(3.13) reads

\begin{array}{l} R_{0}^{0} = \frac{8 π G}{c^{2}} \frac{m (δ_{(r - r_{B H})} + | δ ψ_{0} |^{2})}{γ} \lim_{r \to \infty} (\begin{array}{l} (\sqrt{1 + ς^{2}} - 1) (δ_{0}^{0} - 2) \\ + \frac{\sqrt{1 + ς^{2}}}{2 g_{00}} \end{array}) \\ = \frac{8 π G}{c^{2}} \frac{m (δ_{(r - r_{B H})} + | δ ψ_{0} |^{2})}{γ} \lim_{r \to \infty} (1 + (\frac{1}{g_{00}} - 2) \frac{\sqrt{1 + ς^{2}}}{2}) \\ = \frac{8 π G}{c^{2}} \frac{m (δ_{(r - r_{B H})} + | δ ψ_{0} |^{2})}{γ} \lim_{r \to \infty} (1 + (\frac{\frac{r}{R_{g}} + 2}{1 - \frac{r}{R_{g}}}) \frac{\sqrt{1 + ς^{2}}}{2}) \\ ≅ \frac{8 π G}{c^{2}} \frac{m (δ_{(r - r_{B H})} + | δ ψ_{0} |^{2})}{γ} (1 - \frac{\sqrt{1 + ς^{2}}}{2}) \end{array}

(3.16)

leading to the identity

R_{0}^{0} = R_{00} = \frac{1}{c^{2}} \frac{\partial}{\partial q^{α}} \frac{\partial ϕ}{\partial q^{α}} ≅ \frac{4 π G}{c^{2}} m (δ_{(r - r_{B H})} + | ψ_{0} |^{2}) (1 - \frac{\sqrt{1 + ς^{2}}}{2})

(3.17)

By integrating the flux of the gravitational force

\frac{\partial ϕ}{\partial q^{α}}

on the sphere of radius

r - r_{B H}

it follows that

∭ \frac{\partial}{\partial q^{α}} \frac{\partial ϕ}{\partial q^{α}} d V = ∯ \frac{\partial ϕ}{\partial q^{α}} \cdot d S^{α} = \frac{\partial ϕ}{\partial r} 4 π {(r - r_{B H})}^{2} = 4 π G m ∭ (δ_{(r - r_{B H})} + | δ ψ_{0} |^{2}) (1 - \frac{\sqrt{1 + ς^{2}}}{2}) d V

(3.18)

By the

δ

-shape approximation of the BH mass distribution it can be posed

V_{q u_{(r - r_{B H} = 0)}} = 0

so that the BH gravitational field at large distance reads

\begin{array}{l} \frac{\partial ϕ}{\partial r} = G m (\frac{1 - π \sqrt{1 + ς^{2}} | δ ψ_{0} |^{2} ∭ {(r - r_{B H})}^{2} \frac{d r}{R_{c}}}{{(r - r_{B H})}^{2}}) \\ = G m (\frac{1}{{(r - r_{B H})}^{2}} - \frac{1}{3} \frac{π \sqrt{1 + ς^{2}} | δ ψ_{0} |^{2}}{R_{c}} (r - r_{B H})) \end{array}

(3.19)

where the repulsive force

- G m \frac{1}{3} \frac{π \sqrt{1 + ς^{2}} | δ ψ_{0} |^{2}}{R_{c}} (r - r_{B H})

(3.20)

overcomes the attractive one when

{(r - r_{B H})}^{3} \geq \frac{3 R_{c}}{π \sqrt{1 + ς^{2}} | δ ψ_{0} |^{2}}

(3.21)

From (3.11) we can observe that the cosmological pressure density originating by the BH at large distance is constant and reads

\lim_{r \to \infty} Λ_{_{_{Q}}}^{B H} = (\sqrt{1 + ς^{2}} - 1) ≅ \frac{ς^{2}}{2}

(3.22)

and that the repulsive gravity is generated by the presence of the dark energy/mass density

| δ ψ_{0} |

of the background fluctuations.

From (3.22) it is also interesting to note that the large distance mass density of the BH (2.34) acquire the form

\lim_{r \to \infty} | ψ |^{2} = G_{0} e^{- \sqrt{8 Λ_{Q}^{B H}} (r / R_{c})}

(3.23)

3.1. Quantum Potential Fluctuations Generated by the Background Fluctuations

To determine the parameter

| δ ψ_{0} |^{2}

, we must move beyond the static vacuum solution and consider that the vacuum is filled with stochastic gravitational waves. These waves originate from various sources, including relic gravitational waves from the Big Bang and other sources [18].

Taking into account the vacuum fluctuations in the background, it becomes possible to define the stochastic generalization of the quantum-hydrodynamic equations [19] that for the wave function

ψ = | ψ | e^{- \frac{i S}{ℏ}}

, in the low velocity limit, are given by the equations

\frac{\partial}{\partial t} | ψ |^{2} + \frac{\partial}{\partial q_{i}} (| ψ |^{2} {\dot{q}}_{i}) = 0

(3.24)

{\dot{q}}_{i} = \frac{p_{i}}{m} = \frac{1}{m} \frac{\partial S_{(q, t)}}{\partial q_{i}}

(3.25)

{\dot{p}}_{i} = - \frac{\partial (H + V_{q u})}{\partial q_{i}}

(3.26)

where

S_{(q, t)} = - \frac{ℏ}{2} \ln \frac{ψ}{ψ *}

, where

H

is the Hamiltonian of the system and where

V_{q u}

is given by the low velocity limit of (2.5).

The ripples of the vacuum curvature are assumed to manifest themselves by an additional fluctuating mass density

δ n_{_{v a c}}

into the vacuum so that

n_{_{t o t}} \equiv n ¯ + δ n_{_{v a c}}

(3.27)

where

n ¯

is linked to

n

by the relation

\lim_{δ n_{_{v a c}} \to 0} n ¯ = n

, that, introduced into the quantum potential

V_{q u_{(n_{_{t o t}})}} = - \frac{ℏ^{2}}{2 m} n_{_{t o t}}^{- 1 / 2} \frac{\partial^{2} n_{t o t}^{1 / 2}}{\partial q_{i} \partial q_{i}}

(3.28)

leads to the quantum fluctuating force [19]

- \frac{\partial V_{q u_{(n)}}}{\partial q_{i}}

we are going to determine.

Being the energy/mass density

δ n_{_{v a c}}

defined positive, the mean vacuum fluctuations give rise to non-zero additional (dark) energy density into the vacuum.

Being the energy/mass density

δ n_{_{v a c}}

defined positive, this paragraph describes the assumption that the mean vacuum fluctuations

< δ n_{_{v a c}} >

give rise to an additional dark energy density into the vacuum. The assumption is made that this vacuum dark energy/matter does not interact with the physical system under consideration, and therefore, the gravity interaction is disregarded in the Hamiltonian

H

in (3.26). The evolution of the total dark energy is assumed to depend on cosmological dynamics and that it has reached an equilibrium configuration.

Thence, we assume

< δ n_{_{v a c}} >

locally uniformly distributed with zero mean fluctuations

δ n_{(q, t)}

such as

δ n_{_{v a c}} ≅ < δ n_{_{v a c}} > + δ n_{(q, t)}

(3.29)

3.2. Spectrum and Correlation Function of Mass Density Noise in Quantum Spacetime with Curvature Fluctuations

When determining the features of the fluctuations of the quantum potential, which consequently produce the force noise, we employ the stipulation that:

The fluctuations of the vacuum curvature are described by the wave function

ψ_{v a c}

with density

δ n_{_{v a c}} = | ψ_{v a c} |^{2}

They do not have Hamiltonian interaction with the physical system (gravitational interaction is disregarded).

In this case the wave function of the overall system

ψ_{t o t}

reads

ψ_{t o t} ≅ ψ ψ_{v a c}

(3.30)

Moreover, by assuming that, the equivalent mass of the dark energy is much smaller than the mass of the system (i.e.,

m_{t o t} = m_{d a r k} + m ≅ m

), the overall quantum potential (2.5) reads

\begin{array}{l} V_{q u_{(n_{t o t})}} = - \frac{ℏ^{2}}{2 m_{t o t}} | ψ |^{- 1} | ψ_{v a c} |^{- 1} \frac{\partial^{2} | ψ | | ψ_{v a c} |}{\partial q_{i} \partial q_{i}} = \\ = - \frac{ℏ^{2}}{2 m} (| ψ |^{- 1} \frac{\partial^{2} | ψ |}{\partial q_{i} \partial q_{i}} + | ψ_{v a c} |^{- 1} \frac{\partial^{2} | ψ_{v a c} |}{\partial q_{i} \partial q_{i}} + | ψ |^{- 1} | ψ_{v a c} |^{- 1} \frac{\partial | ψ_{v a c} |}{\partial q_{i}} \frac{\partial | ψ |}{\partial q_{i}}) \end{array}

(3.31)

Moreover, given the vacuum mass density noise of wave-length

λ

δ n_{v a c (λ)} = | ψ_{v a c (λ)} |^{2} \propto \cos^{2} \frac{2 π}{λ} q

(3.32)

associated to the fluctuation wave-function

ψ_{v a c} \propto \pm \cos \frac{2 π}{λ} q

(3.33)

It follows that the quantum potential energy fluctuations read

(3.34)

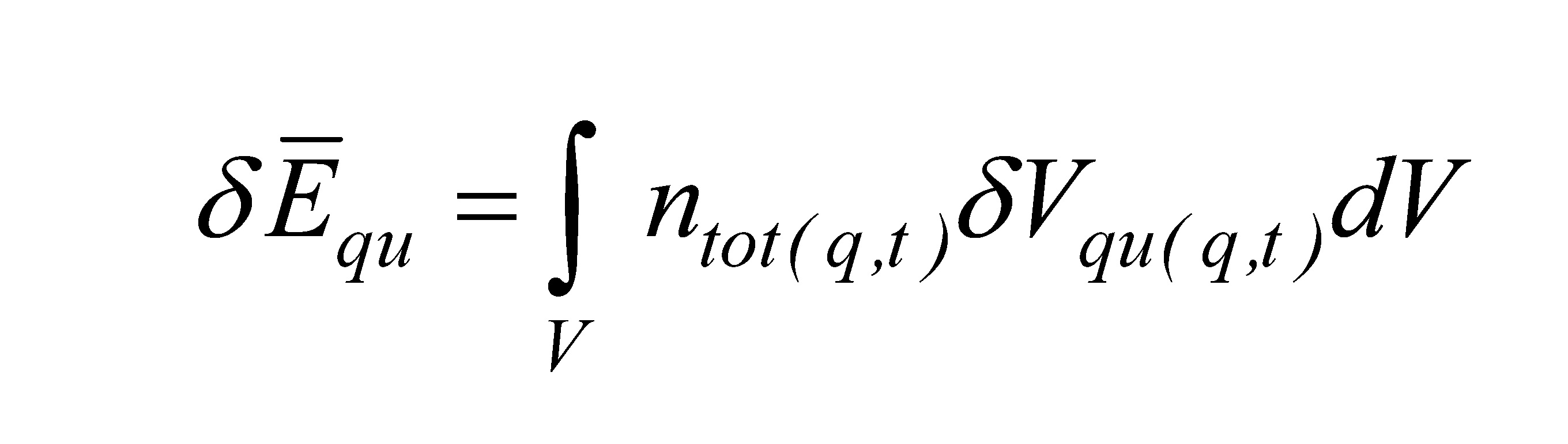where

\begin{array}{l} δ V_{q u (q, t)} = - \frac{ℏ^{2}}{2 m} (| ψ_{v a c} |^{- 1} \frac{\partial^{2} | ψ_{v a c} |}{\partial q_{i} \partial q_{i}} + | ψ |^{- 1} | ψ_{v a c} |^{- 1} \frac{\partial | ψ_{v a c} |}{\partial q_{i}} \frac{\partial | ψ |}{\partial q_{i}}) \\ = \frac{ℏ^{2}}{2 m} ({(\frac{2 π}{λ})}^{2} + | ψ |^{- 1} \frac{\partial | ψ |}{\partial q_{i}} {(\pm \cos \frac{2 π}{λ} q)}^{- 1} (\pm \sin \frac{2 π}{λ} q)) \\ = \frac{ℏ^{2}}{2 m} ({(\frac{2 π}{λ})}^{2} + | ψ |^{- 1} \frac{\partial | ψ |}{\partial q_{i}} \tan \frac{2 π}{λ} q) \end{array}

(3.35)

For

V \to \infty

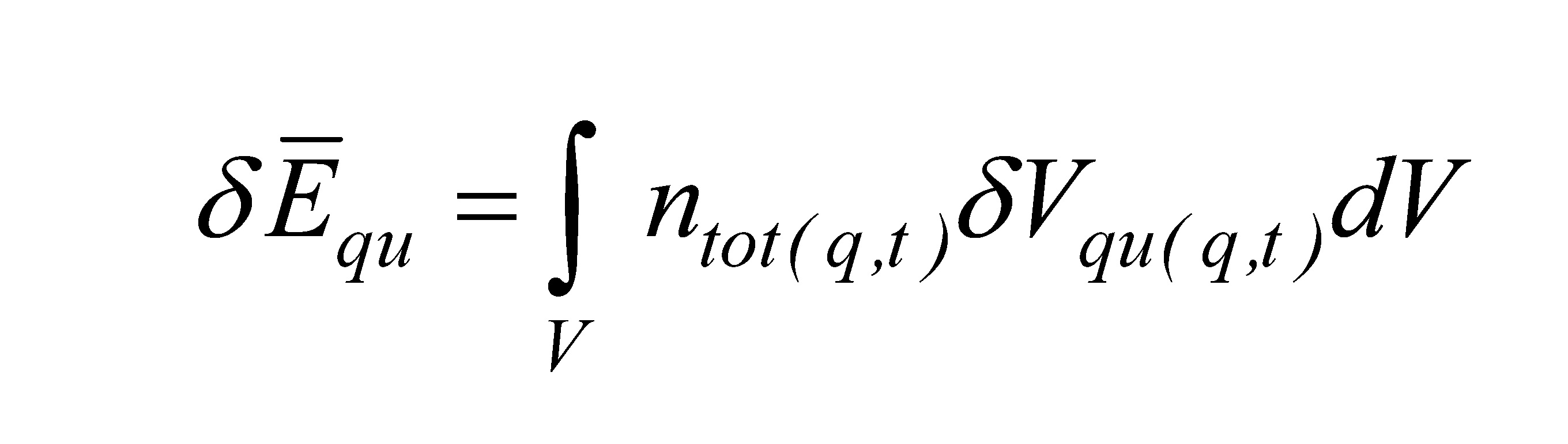
, the unidimensional case leads to

\begin{array}{l} δ {\bar{E}}_{q u (λ)} = \frac{1}{{\bar{n}}_{t o t} V} \frac{ℏ^{2}}{2 m} \int_{V}^{} n_{t o t}_{(q, t)} ({(\frac{2 π}{λ})}^{2} + | ψ |^{- 1} \frac{\partial | ψ |}{\partial q_{i}} \tan \frac{2 π}{λ} q) d q \\ = \frac{1}{{\bar{n}}_{t o t} V} \frac{ℏ^{2}}{2 m} ({(\frac{2 π}{λ})}^{2} \int_{V}^{} n_{t o t}_{(q, t)} d q + \int_{V}^{} n_{t o t}_{(q, t)} (| ψ |^{- 1} \frac{\partial | ψ |}{\partial q_{i}} \tan \frac{2 π}{λ} q) d q) ≅ \frac{ℏ^{2}}{2 m} {(\frac{2 π}{λ})}^{2} \end{array}

(3.36)

In (3.36) it has been used the normalization condition

\int_{V}^{} n_{t o t}_{(q, t)} d q = {\bar{n}}_{t o t} V

and, on large volume (

V ≫ λ_{c}^{3}

see (3.39)), it has been used the approximation

\lim_{λ \to 0} \int_{- \infty}^{\infty} n_{t o t}_{(q, t)} (| ψ |^{- 1} \frac{\partial | ψ |}{\partial q_{i}} \tan \frac{2 π}{λ} q) d q ≪ {\bar{n}}_{t o t} V {(\frac{2 π}{λ})}^{2}

For the three-dimensional case (3.36) leads to

δ {\bar{E}}_{q u (λ)} ≅ \frac{ℏ^{2}}{2 m} \sum_{i} {(k_{i})}^{2} = \frac{ℏ^{2}}{2 m} | k |^{2}

(3.37)

The equation (3.37) reveals that the energy arising from the mass density fluctuations of the vacuum becomes greater as the square of the inverse of

λ

. Thus, the corresponding fluctuations in the quantum potential may produce extremely large energy fluctuations, even for very small noise amplitudes (i.e.,

T \to 0

) when

λ

approaches zero), at very short distances.

To ensure that the convergence to the deterministic limit of quantum mechanic (5.24-26) is achieved for

T \to 0

, a further condition is required on the spatial correlation function of the quantum potential noise as

λ \to 0

One way to obtain the shape of the spatial correlation function

G (λ)

is through a stochastic calculation, which can be quite complex [20]. However, a simpler approach to obtain

G (λ)

this function can be achieved by considering the spectrum of the fluctuations, as described in [19].

Since each component of spatial frequency

k = \frac{2 π}{λ}

brings the quantum potential energy contribution (3.36), its probability of happening, reads

\begin{array}{l} p_{(λ)} \propto \exp [- \frac{δ {\bar{E}}_{q u}}{k T}] \\ = \exp [- \frac{\frac{ℏ^{2}}{2 m} {(\frac{2 π}{λ})}^{2}}{k T}] = \exp [- {(\frac{π λ_{c}}{λ})}^{2}] \end{array}

(3.38)

where

λ_{c} = 2 \frac{ℏ}{{(2 m k T)}^{1 / 2}}

(3.39)

is the De Broglie length.

From (3.38) it comes out that the spectrum

S (k)

of the spatial frequency

S (k) \propto p (\frac{2 π}{λ}) = \exp [- {(\frac{π λ_{c}}{λ})}^{2}] = \exp [- {(\frac{k λ_{c}}{2})}^{2}]

(3.40)

is not white and the components with wave-length

λ

smaller than

λ_{c}

go quickly to zero.

Besides, from (3.40) the spatial shape

G (λ)

reads

\begin{array}{l} G_{(λ)} \propto \int_{- \infty}^{+ \infty} \exp [i k λ] S_{(k)} d k \propto \int_{- \infty}^{+ \infty} \exp [i k λ] \exp [- {(k \frac{λ_{c}}{2})}^{2}] d k \\ \propto \frac{π^{1 / 2}}{λ_{c}} \exp [- {(\frac{λ}{λ_{c}})}^{2}] \end{array}

(3.31)

One can see from equation (3.41) that the quantum potential progressively suppresses uncorrelated MDD fluctuations on shorter and shorter distance scales, which in turn allows for the realization of deterministic quantum mechanics in systems whose physical length is much smaller than the De Broglie length.

The assumption for sufficiently general case is that the mass density noise correlation function is Gaussian, with zero correlation time, isotropic in space, and independent among different coordinates. Under these assumptions, it can be expressed as:

< δ n_{(q_{α}, t)}, δ n_{(q_{β} + λ, t + τ)} > = < δ n_{(q_{α})}, δ n_{(q_{β})} >_{(T)} G (λ) δ (τ) δ_{α β}

(3.42)

3.3. The (Dark) Energy Density of Quantum Potential Fluctuations

The energy associated with the quantum potential noise of a body with mass m can be evaluated using the probability energy fluctuation function

p_{(E_{(λ)})} = A \exp [- \frac{\frac{ℏ^{2}}{2 m} {(\frac{2 π}{λ})}^{2}}{k T}]

(3.43)

where

\begin{array}{l} A = \frac{1}{\int_{0}^{λ_{\max}} \exp [- \frac{\frac{ℏ^{2}}{2 m} {(\frac{2 π}{λ})}^{2}}{k T}] d λ} = \frac{1}{\int_{0}^{N λ_{c}} \exp [- \frac{\frac{ℏ^{2}}{2 m} {(\frac{2 π}{λ})}^{2}}{k T}] d λ + \int_{N λ_{c}}^{λ_{\max}} \exp [- \frac{\frac{ℏ^{2}}{2 m} {(\frac{2 π}{λ})}^{2}}{k T}] d λ} \\ = \frac{1}{\int_{0}^{N λ_{c}} \exp [- \frac{\frac{ℏ^{2}}{2 m} {(\frac{2 π}{λ})}^{2}}{k T}] d λ + \int_{N λ_{c}}^{λ_{\max}} d λ} = \frac{1}{\int_{0}^{N λ_{c}} \exp [- {(\frac{π λ_{c}}{λ})}^{2}] d λ + (λ_{\max} - N λ_{c})} \end{array}

(3.44)

where

λ_{c} = \sqrt{2} \frac{ℏ}{\sqrt{m k T}}

and N >> 1.

In this case, the energy density of quantum potential fluctuation reads

\begin{array}{l} m c^{2} | δ ψ_{0} |^{2} {}_{(r)}= \frac{\int δ {\bar{E}}_{q u (λ)} p_{(λ)} d λ}{\int p_{(λ)} d λ} = \frac{\int_{0}^{λ_{\max}} \frac{ℏ^{2}}{2 m} {(\frac{2 π}{λ})}^{2} p_{(λ)} d λ}{\int_{0}^{λ_{\max}} p_{(λ)} d λ} ≅ \int_{0}^{λ_{\max}} \frac{ℏ^{2}}{2 m} {(\frac{2 π}{λ})}^{2} p_{(λ)} d λ \\ = \frac{1}{λ_{\max}} \int_{0}^{λ \max} \frac{ℏ^{2}}{2 m} {(\frac{2 π}{λ})}^{2} \exp [- \frac{\frac{ℏ^{2}}{2 m} {(\frac{2 π}{λ})}^{2}}{k T}] d λ \end{array}

(3.45)

where for (3.37) in the three-dimensional case

λ = | k |

and where

m | δ ψ_{0} |^{2}

is the additional mass density in the vacuum that the body of mass m acquires due to the background fluctuations. Besides, it can be posed

λ_{\max} = l_{u} \approx 10^{27} m

(3.46)

where

l_{u}

is the diameter of the universe.

Moreover, since, for SMBHs (of order of Sagittarius A* of mass of about of

10^{38}

kg) at

1 ° K

λ_{c} = 2 \frac{ℏ}{{(2 m k T)}^{1 / 2}} \approx \frac{1, 41 \times 10^{- 34}}{{(3 \times 10^{38} 10^{- 23})}^{1 / 2}} \approx 3 \times 10^{- 41} m \approx 0

(3.47)

it follows that

A = \frac{1}{l_{u}}

(3.48)

and that

\begin{array}{l} m c^{2} | δ ψ_{0} |^{2} = \frac{1}{l_{u}} \frac{ℏ^{2}}{2 m} \int_{0}^{l_{u}} {(\frac{2 π}{λ})}^{2} \exp [- \frac{\frac{ℏ^{2}}{2 m} {(\frac{2 π}{λ})}^{2}}{k T}] d λ \\ = \frac{1}{l_{u}} \frac{ℏ^{2}}{2 m} \int_{\infty}^{2 π l_{u}^{- 1}} \exp [- \frac{\frac{ℏ^{2}}{2 m}}{k T} | k |^{2}] d | k | = \frac{ℏ}{2 l_{u}} \sqrt{\frac{π k T}{2 m}} \end{array}

(3.49)

leading to

| δ ψ_{0} |^{2}_{(r)} \approx \frac{1}{l_{u}} \frac{ℏ}{2 m c} \sqrt{\frac{π k T}{2 m c^{2}}}

(3.50)

3.4. Repulsive Gravity at Large Distance

By introducing (3.50) into (3.21), the repulsive Newtonian gravity overcomes the attractive one at the distance

{(r - r_{B H})}_{r e p} \approx {(\frac{3 R_{c}}{π \sqrt{1 + ς^{2}} | δ ψ_{0} |^{2}})}^{1 / 3} = {(\frac{3 R_{c}}{π (1 + Λ_{Q}^{B H}) | δ ψ_{0} |^{2}})}^{1 / 3} \sim {(l_{u} \sqrt{\frac{2 m c^{2}}{π k T}})}^{1 / 3}

(3.51)

that for SMBHs mass of order of

10^{38 \div 41} K g

ς ≪ 1

, reads

{(r - r_{B H})}_{r e p} > \approx 10^{21} m

(3.52)

The gravitational force between galaxies becomes repulsive at intergalactic distances, which is on the same order of magnitude as the typical radius of galaxies ( ). This may affect the external part of the galactic disc. However, the amplitude of the background fluctuations decreases with the expansion of the radius

l_{u}

of the universe since

\lim_{t \to \infty} | δ ψ_{0} |^{2}_{(r)} \sim \frac{1}{l_{u}} \frac{ℏ}{2 m c} \sqrt{\frac{π k T}{2 m c^{2}}} \to 0

), and the repulsive force asymptotically approaches zero, leading to a final static universe. The decrease in temperature with

T \to 0

due to expansion results in a perfectly quantum final stationary state with

λ_{c} \to \infty

and

λ_{q u} \to \infty

3.5. The Energy Density of Quantum Potential Fluctuations of a Classical Body

On the other hand, it is interesting to calculate the dark energy associated to the quantum potential fluctuations of ordinary macroscopic (classical) bodies.

In the quasi-Minkowskian space-time, constituted by atoms interacting by Lennard Jones potential [15,21] for which the quantum non-local range of interaction

λ_{q u}

is limited to microscopic distance of order of

λ_{c}

so that

λ_{q u} ≅ λ_{c}

(3.54)

it follows that

\begin{array}{l} m c^{2} | δ ψ_{0} |^{2} ≅ \frac{\int_{0}^{λ_{c}} δ {\bar{E}}_{q u (λ)} p_{(λ)} d λ}{\int_{0}^{λ_{c}} p_{(λ)} d λ} ≅ \frac{\frac{ℏ^{2}}{2 m}}{l_{u}} \int_{0}^{λ_{c}} {(\frac{2 π}{λ})}^{2} \exp [- \frac{\frac{ℏ^{2}}{2 m} {(\frac{2 π}{λ})}^{2}}{k T}] d λ \\ ≅ \frac{1}{l_{u}} ℏ \sqrt{\frac{k T}{2 m}} \int_{1}^{\infty} \exp [- x^{2}] d x \end{array}

(3.55)

| δ ψ_{0} |^{2} \approx \frac{1}{l_{u}} ℏ \sqrt{\frac{k T}{2 m}} \frac{1}{m c^{2}} \int_{1}^{\infty} \exp [- x^{2}] d x . 0 < r < λ_{c}

(3.56)

| δ ψ_{0} |^{2} = 0 . r > λ_{c}

(3.57)

The output (3.56) leads to the Newtonian force (3.19)

\frac{\partial ϕ}{\partial r} = G m (\frac{1 + \frac{| δ ψ_{0} |^{2}}{R_{c}} λ_{c}^{4}}{{(r - r_{B H})}^{2}}) ≅ - G m (\frac{1 + 4 \frac{| δ ψ_{0} |^{2}}{m c} \frac{ℏ^{3}}{{(k T)}^{2}}}{{(r - r_{B H})}^{2}})

(3.58)

In the case of the proton at 1°K (3.58) reads

\frac{\partial ϕ}{\partial r} = \frac{G m}{{(r - r_{B H})}^{2}} (1 + \sim 10^{- 76})

(3.59)

The equation (3.59) implies that the dark energy produced by the background fluctuations for classical macroscopic bodies is negligible because the range of the quantum potential is short.

This suggests that the repulsive gravitational force causing the expansion of the universe is mainly attributed to black holes and supermassive black holes due to the quantum nature of space-time with a fluctuating background metric.

The correction to the Newtonian gravity that arises from the energy of the quantum potential in massive bodies such as BHs and SMBHs is similar in some way to the concept of Modified Newtonian Dynamics (MOND) theories [22], which suggest a modification of the Newtonian gravity for very low accelerations in order to account for the observed motion of galaxies.

The current model proposes that the modification of Newtonian gravity at large distances is explained as coming from the gravitational effects of the energy of the quantum potential in huge massive bodies such as BHs and SMBHs.

4. Conclusions

The work shows that quantum black holes with central symmetry have a mass density distribution that is not point-like but concentrated in a sphere of radius approximately equal to its Compton wavelength.

Due to the significant quantum potential energy, there exists an isotropic pressure density term in the gravity equation, resulting in an additional contribution to the gravity force at weak limit.

In the presence of fluctuations of the space-time background metric, this contribution leads to a repulsive gravitational force that dominates over the Newtonian force at distances typical of intergalactic space.

Appendix

Schwarzschild black hole mass distribution

The differential equation (2.33) can be solved by posing

{(\frac{ℏ}{m c})}^{2} \frac{r^{2}}{| ψ |} \partial^{1} r^{- 2} (\frac{r - R_{g}}{r} \partial_{1} | ψ |) = 1 - A_{0} e^{f_{(r)}}

(A.1)

from which it follows that

(\partial_{1} \frac{r - R_{g}}{r}) A_{0} e^{f_{(r)}} = (\partial_{1} f_{(r)}) A_{0} e^{f_{(r)}}

(A.2)

leading to the solution

f_{(r)} = (\frac{r - R_{g}}{r} + C)

(A.3)

Furthermore, by posing

| ψ | = G_{0} e^{g_{(r)}}

(A.4)

it follows that

\begin{array}{l} {(\frac{ℏ}{m c})}^{2} r^{2} G_{0}^{- 1} e^{- g_{(r)}} \partial^{1} r^{- 2} (\frac{r - R_{g}}{r} g'_{(r)} G_{0} e^{g_{(r)}}) = 1 - A_{0} e^{f_{(r)}} \end{array}

(A.5)

and thence,

\begin{array}{l} {(\frac{ℏ}{m c})}^{2} r^{2} G_{0}^{- 1} e^{- g_{(r)}} (g'_{(r)} G_{0} e^{g_{(r)}} \partial^{1} (r^{- 2} \frac{r - R_{g}}{r}) + r^{- 2} \frac{r - R_{g}}{r} \partial^{1} (g'_{(r)} G_{0} e^{g_{(r)}})) = \\ {(\frac{ℏ}{m c})}^{2} (r^{2} g'_{(r)} \partial^{1} r^{- 3} (r - R_{g}) + \frac{r - R_{g}}{r} (g'^{2}_{(r)} + g''_{(r)})) = \\ {(\frac{ℏ}{m c})}^{2} (g'_{(r)} (\frac{1}{r} - \frac{3 (r - R_{g})}{r^{2}}) + \frac{r - R_{g}}{r} (g'^{2}_{(r)} + g''_{(r)})) = 1 - A_{0} e^{f_{(r)}} \end{array}

(A.6)

that by posing

g'_{(r)} = y_{(r)}

(A.7)

leads to the Riccati’s differential equation

y'_{(r)} = y_{(r)} (\frac{3}{r} - \frac{1}{r - R_{g}}) - y^{2}_{(r)} + {(\frac{m c}{ℏ})}^{2} \frac{r}{r - R_{g}} (1 - C_{0} e^{\frac{r - R_{g}}{r}})

(A.8)

where

C_{0} = A_{0} e^{- C}

Moreover, by using the adimensional variable

x = \frac{r}{R_{g}}

it follows that

{\tilde{y}}^{|}_{(x)} = R_{g} y'_{(r)} = {\tilde{y}}_{(x)} (\frac{3}{x} - \frac{1}{x - 1}) - R_{g} {\tilde{y}}^{2}_{(x)} + \frac{R_{g}}{R_{c}^{2}} \frac{x}{x - 1} (1 - C_{0} e^{\frac{x - 1}{x}})

(A.9)

where

R_{c} = \frac{ℏ}{m c}

The condition of mass density at infinity

\lim_{r \to \infty} | ψ | = \lim_{r \to \infty} G_{0} e^{g_{(r)}} = 0

(A.10)

\lim_{r \to \infty} | ψ |' = \lim_{r \to \infty} G_{0} g'_{(r)} e^{g_{(r)}} = 0

(A.11)

leads to the condition on

g_{(r)}

l i m_{r \to \infty} g_{(r)} = - \infty

(A.12)

Large distance BH mass density distribution

On the condition that

\lim_{x \to \infty} | {\tilde{y}}^{2}_{(x)} | ≫ \frac{| {\tilde{y}}_{(x)} |}{x}

(to be checked at the end) and by choosing

c = 1

so that

C_{0} = \frac{A_{0}}{e}

, equation (A.9) simplifies to

\lim_{x \to \infty} {\tilde{y}}^{|}_{(x)} ≅ - R_{g} {\tilde{y}}^{2}_{(x)} + \frac{R_{g}}{R_{c}^{2}} (1 - A_{0})

(A.13)

that by posing

{\tilde{y}}_{(x)} = \frac{u'}{R_{g} u}

(A.14)

leads to

\lim_{x \to \infty} {(\frac{u'}{R_{g} u})}^{'} = \lim_{x \to \infty} (\frac{u''}{R_{g} u} - \frac{u'^{2}}{R_{g} u^{2}}) ≅ - \frac{u'^{2}}{R_{g} u^{2}} + \frac{R_{g}}{R_{c}^{2}} (1 - A_{0})

(A.15)

\lim_{x \to \infty} u'' ≅ u \frac{R_{g}^{2}}{R_{c}^{2}} (1 - A_{0})

(A.16)

owing the solution

u = u_{0} e^{\pm \frac{R_{g}}{R_{c}} {(1 - A_{0})}^{1 / 2} x}

(A.17)

leading to

{\tilde{y}}_{(x)} = \pm \frac{R_{g}}{R_{c}} {(1 - A_{0})}^{1 / 2}

(A.18)

and to

\begin{array}{l} \lim_{x \to \infty} | ψ | = \lim_{x \to \infty} G_{0} e^{\int_{}^{} g'_{(r)} d r} = G_{0} e^{\int_{}^{} R_{g} {\tilde{y}}_{(x)} d x} \\ = G_{0} e^{- \frac{R_{g}}{R_{c}} {(1 - A_{0})}^{1 / 2} x} = G_{0} e^{- ς \frac{r}{R_{c}}} \end{array}

(A.19)

where

ς = {(1 - A_{0})}^{1 / 2}

and where the condition

\lim_{r \to \infty} g_{(r)} = - \infty

requires to consider the negative solution of

{\tilde{y}}_{(x)}

In order to evaluate the numerical constant

ζ

, we observe that the ratio between the total mass of the BH and the part outside the gravitational radius due to the quantum mass distribution (with unitary normalization

\int_{0}^{\infty} | ψ |^{2} = 1

) reads

\frac{Δ m_{o u t}}{m} = \frac{\int_{r = R_{g}}^{\infty} | ψ |^{2}}{\int_{0}^{\infty} | ψ |^{2}} = \int_{r = R_{g}}^{\infty} | ψ |^{2}

(A.20)

and it is vanishing small for cosmological BHs (e.g., for BHs of mass of order

10^{38} k g

,assuming unitary outside mass (1 kg) it results

\int_{r = R_{g}}^{\infty} | ψ |^{2} \approx 10^{- 38}

). Moreover, by utilizing the expression (2.2)

\lim_{\frac{r}{R_{c}} \to \infty} | ψ |^{2} = δ^{3}_{(r)} ≅ \lim_{R_{c} \to 0} {(\frac{ς}{2 \sqrt{π} R_{c}})}^{3} e^{- ς \frac{r^{2}}{4 R_{c}^{2}}}

(A.21)

It follows that

\begin{array}{l} \int_{r = R_{g}}^{\infty} | ψ |^{2} d V = \frac{1}{π^{3 / 2}} {(\frac{ς}{2})}^{3} \int_{r = R_{g}}^{\infty} {(\frac{r}{R_{c}})}^{2} e^{- ς \frac{r^{2}}{4 R_{c}^{2}}} d \frac{r}{R_{c}} \\ = \frac{1}{π^{3 / 2}} {(\frac{ς}{2})}^{3} \int_{t = \frac{R_{g}}{R_{c}}}^{\infty} t^{2} e^{- ς \frac{t^{2}}{4}} d t = \frac{1}{π^{3 / 2}} {(\frac{ς}{2})}^{3} \int_{t = \frac{R_{g}}{R_{c}}}^{\frac{_{l_{u}}}{R_{c}}} t^{2} e^{- ς \frac{t^{2}}{4}} d t = \frac{Δ m_{o u t}}{m} \end{array}

(A.22)

F that for BH of

10^{38} k g

, a kg of

Δ m_{o u t}

gives the contribution

\frac{1}{π^{3 / 2}} {(\frac{ς}{2})}^{3} \int_{t = \frac{R_{g}}{R_{c}}}^{\infty} t^{2} e^{- ς \frac{t^{2}}{4}} d t = \frac{1}{π^{3 / 2}} {(\frac{ς}{2})}^{3} \int_{10^{85}}^{\infty} t^{2} e^{- ς \frac{t^{2}}{4}} d t = 10^{- 38} < \frac{1}{π^{3 / 2}} {(\frac{ς}{2})}^{3} 10^{170} e^{- ς \frac{10^{170}}{4}} 10^{102}

(A.23)

and that

\frac{1}{π^{3 / 2}} {(\frac{ς}{2})}^{3} 10^{170} e^{- ς \frac{10^{170}}{4}} 10^{102} > 10^{- 38}

(A.24)

{(\frac{ς}{2})}^{3} e^{- ς \frac{10^{170}}{4}} = {(\frac{ς}{2})}^{3} 10^{^{- ς \frac{10^{170}}{4} \lg_{10} e}} > \sim 10^{- 310}

(A.25)

that by posing

ς = 10^{- n}

leads to

10^{^{- \frac{10^{170 - 3 n}}{4} \lg_{10} e}} > \sim 10^{- 309 + 3 n}

(A.26)

10^{170 - 3 n} > 4 \frac{309 - 3 n}{\lg_{10} e} \sim 10^{2}

(A.27)

and to

0 < ζ < \sim 10^{- 56}

(A.28)

Even for larger values of

\frac{Δ m_{o u t}}{m} \sim 10^{- 9}

the order of magnitude (A.28) remains practically the same. This because the ratio

\frac{R_{c}}{R_{g}}

determines

ζ

Thus, BHs with small mass, close to the Planck one with

R_{c} \sim R_{g}

, can lead to higher values of

ζ

. As a consequence of this, smaller the BHs larger the contribution to the repulsive gravity (2.20) and to the cosmological constant (2.22).

Mass distribution at short distance (

r ≪ R_{g}

)

Near the center for

x ≪ 1

we must use the relation

Γ_{_{μ ν}}^{α} u_{α} u^{ν} = u^{0} u^{0} \partial_{1} g_{00} = g^{00} \partial_{1} g_{00} = \frac{1}{g_{00}} \partial_{1} g_{00} ≅ \partial_{1} \ln g_{00}

(A.29)

That leads to the equation

(\partial_{1} \ln (\frac{r - R_{g}}{r})) = (\partial_{1} f_{(r)})

(A.30)

with the solution

f_{(r)} = (\ln (\frac{r - R_{g}}{r}) + C)

(A.31)

and the equation

{\tilde{y}}^{|}_{(x)} = R_{g} y'_{(r)} = {\tilde{y}}_{(x)} (\frac{3}{x} - \frac{1}{x - 1}) - R_{g} {\tilde{y}}^{2}_{(x)} + \frac{R_{g}}{R_{c}^{2}} \frac{x}{x - 1} (1 - C_{0} e^{\ln (\frac{x - 1}{x})})

(A.32)

Furthermore, on the condition that

\lim_{x \to 0} | {\tilde{y}}^{2}_{(x)} | < < \frac{| {\tilde{y}}_{(x)} |}{x}

(to be checked at the end) Equation (A.9) simplifies to

{\tilde{y}}^{|}_{(x)} = {\tilde{y}}_{(x)} (\frac{3}{x} - \frac{1}{x - 1}) + \frac{R_{g}}{R_{c}^{2}} \frac{x}{x - 1} (1 - C_{0} \frac{x - 1}{x}) = {\tilde{y}}_{(x)} (\frac{3}{x} - \frac{1}{x - 1}) - C_{0} \frac{R_{g}}{R_{c}^{2}}

(A.33)

where

x ≪ 1

and

{\tilde{y}}_{(x)} = \frac{u'}{R_{g} u}

, leading to the solution

\begin{array}{l} y_{(x)} = (e^{\int_{}^{} \frac{R_{g}}{R_{c}^{2}} C_{0} e^{- \int_{}^{} (\frac{3}{x} - \frac{1}{x - 1}) d x} d r}) e^{\int_{}^{} (\frac{3}{x} - \frac{1}{x - 1}) d x} \\ = (e^{\int_{}^{} \frac{R_{g} {_{c}}^{2}}{R_{c}^{2}} C_{0} e^{- \int_{}^{} \frac{2}{x} d x} d x} + C) e^{\int_{}^{} \frac{2}{x} d x} \\ ≅ (e^{- C_{0} \frac{R_{g}^{2}}{R_{c}^{2}} \frac{1}{x^{2}}} + C) x^{2} = g'_{(r)} = \frac{1}{R_{g}} g'_{(x)} \end{array}

(A.34)

and, thence, for

\begin{array}{l} \lim_{x \to 0} | ψ | = \lim_{x \to 0} G_{0} e^{\int_{}^{} (e^{- C_{0} \frac{R_{g}^{2}}{R_{c}^{2}} \frac{1}{x^{2}}} + C) x^{2} d x} = \lim_{x \to 0} G_{0} e^{\int_{}^{} (1 - C_{0} \frac{R_{g}^{2}}{R_{c}^{2}} \frac{1}{x^{2}} + C) x^{2} d x} \\ = \lim_{x \to 0} G_{0} e^{\frac{(1 + C)}{3} x^{3} - C_{0} \frac{R_{g}^{2}}{R_{c}^{2}} x} ≅ G_{0} e^{- C_{0} \frac{R_{g}^{2}}{R_{c}^{2}} x} ≅ G_{0} e^{- \frac{1 - ς^{2}}{e} \frac{R_{g}}{R_{c}} z} \end{array}

(A.35)

where it has been used the identity

C_{0} = \frac{1 - ς^{2}}{e} ≅ e^{- 1}

References

Green, M.B.; John, H. Schwarz, and Edward Witten. Superstring theory: Volume 1, Introduction; Cambridge University Press: 1987.
Polchinski, J. String theory: Volume 1, An introduction to the bosonic string; Cambridge University Press: 2005.
Becker, Katrin, Melanie Becker, and John H. Schwarz. String theory and M-theory: A modern introduction; Cambridge University Press: 2007.
Rovelli, C. Loop Quantum Gravity. Living Rev. Relativ. 1998, 1, 1–69. [Google Scholar] [CrossRef] [PubMed]
Thiemann, T. Modern Canonical Quantum General Relativity; Cambridge University Press (CUP): Cambridge, United Kingdom, 2007; ISBN 9780511755682. [Google Scholar]
Ashtekar, A.; Lewandowski, J. Background independent quantum gravity: a status report. Class. Quantum Gravity 2004, 21, R53–R152. [Google Scholar] [CrossRef]
Ambjorn, J. , Jerzy Jurkiewicz, and Renate Loll. "Reconstructing the universe." Physical Review D 2005, 72, 064014.
Loll, R. Discrete Approaches to Quantum Gravity in Four Dimensions. Living Rev. Relativ. 1998, 1, 1–53. [Google Scholar] [CrossRef] [PubMed]
Ambjørn, J.; Görlich, A.; Jurkiewicz, J.; Loll, R. Nonperturbative quantum gravity. Phys. Rep. 2012, 519, 127–210. [Google Scholar] [CrossRef]
Chiarelli, P. The Gravity of the Classical Klein-Gordon Field. Symmetry 2019, 11, 322. [Google Scholar] [CrossRef]
Chiarelli, P. The Spinor-Tensor Gravity of the Classical Dirac Field. Symmetry 2020, 12, 1124. [Google Scholar] [CrossRef]
Landau L., D.; Lifšits, E.M. Course of Theoretical Physics Italian Edition. Mir Mosca Editori Riuniti 1976, 403–9. [Google Scholar]
Ibid [12], pp. 386-96.
Chiarelli, P. The Mass Lowest Limit of a Black Hole: The Hydrodynamic Approach to Quantum Gravity. Phys. Sci. Int. J. 2016, 9, 1–25. [Google Scholar] [CrossRef]
Chiarelli, P. , Quantum to Classical Transition in the Stochastic Hydrodynamic Analogy: The Explanation of the Lindemann Relation and the Analogies Between the Maximum of Density at He Lambda Point and that One at Water-Ice Phase Transition. Physical Review & Research International 2013, 3, 348–366.
Chiarelli, P.; Chiarelli, S. Stability of Quantum Eigenstates and Collapse of Superposition of States in a Fluctuating environment: The Madelung Hydrodynamic Approach. Eur. J. Appl. Phys. 2021, 3, 11–28. [Google Scholar] [CrossRef]
Chiarelli, P. , Classical Mechanics from Stochastic Quantum Dynamics. Advances and Trends in Physical Science Research Vol. 2(3). [CrossRef]
Nelson, C. , 2019 Rep. Prog. Phys. 82 01 6903. [CrossRef]
Chiarelli, S.; Chiarelli, P. Stochastic Quantum Hydrodynamic Model from the Dark Matter of Vacuum Fluctuations: The Langevin-Schr？dinger Equation and the Large-Scale Classical Limit. Open Access Library Journal 2020, 7, e6659. [Google Scholar] [CrossRef]
Chiarelli, P. Can fluctuating quantum states acquire the classical behavior on large scale? J. Adv. Phys. 2013, 2, 139–163. [Google Scholar]
Chiarelli, P. The Quantum Potential: The Missing Interaction in the Density Maximum of He4 at the Lambda Point. Am. J. Phys. Chem. 2014, 2, 122. [Google Scholar] [CrossRef]
Arraut, I. Can a nonlocal model of gravity reproduce Dark Matter effects in agreement with MOND? Int. J. Mod. Phys. D 2014, 23, 1450008. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Quantum Effects in General Relativity: Investigating Repulsive Gravity of Black Holes at Large Distances

Abstract

1. Introduction

2. Cosmological Scalar Boson Mass under Self-Gravity

2.1. Stationary Scalar Mass Distribution

2.2. The Mass Distribution in Central Symmetric Scalar Uncharged Black Hole

2.3. The mass Distribution near the Center of Schwarzschild Black Hole

3. Gravitational Field of Black Holes at Large Distance in Spacetime with Background Fluctuations

3.1. Quantum Potential Fluctuations Generated by the Background Fluctuations

3.2. Spectrum and Correlation Function of Mass Density Noise in Quantum Spacetime with Curvature Fluctuations

3.3. The (Dark) Energy Density of Quantum Potential Fluctuations

3.4. Repulsive Gravity at Large Distance

3.5. The Energy Density of Quantum Potential Fluctuations of a Classical Body

4. Conclusions

Appendix

References

MDPI Initiatives

Important Links

Subscribe