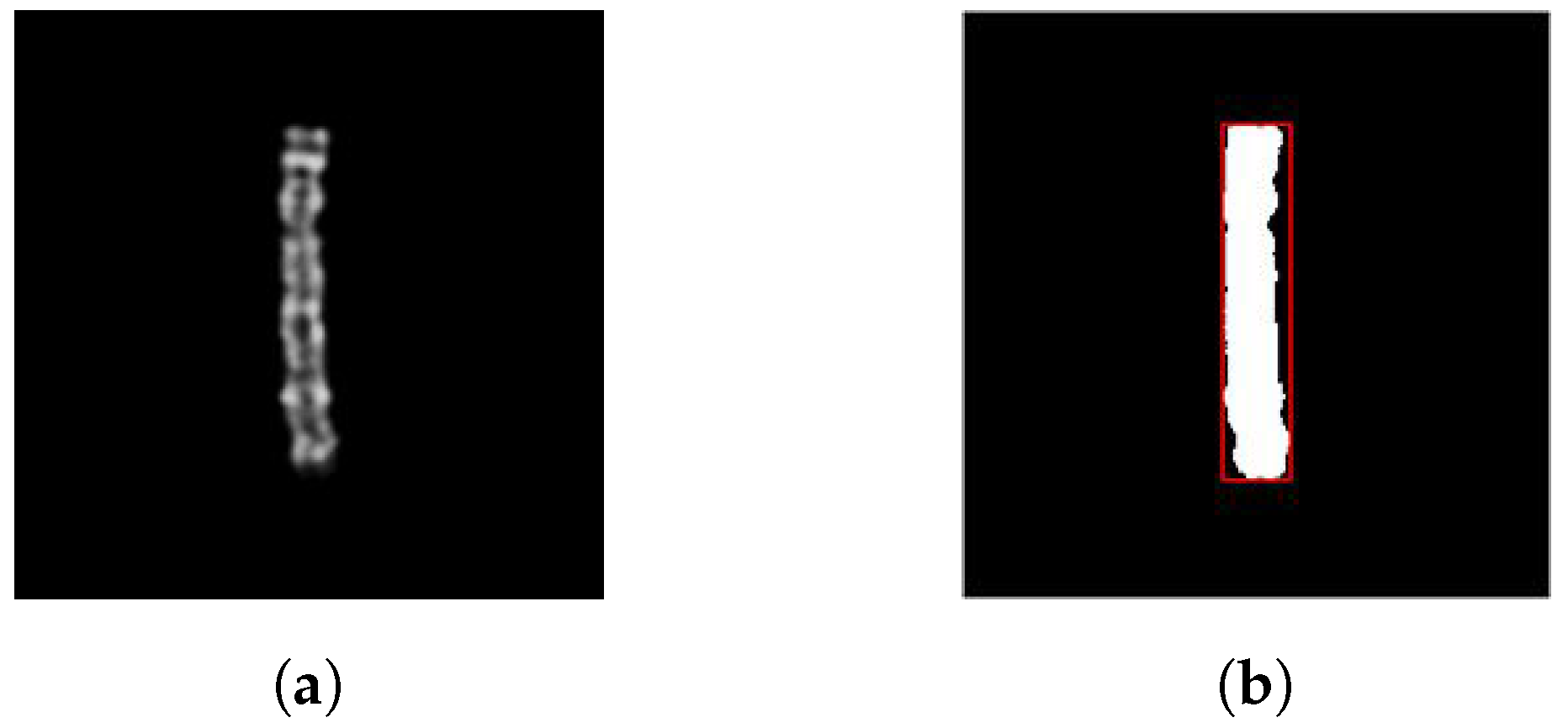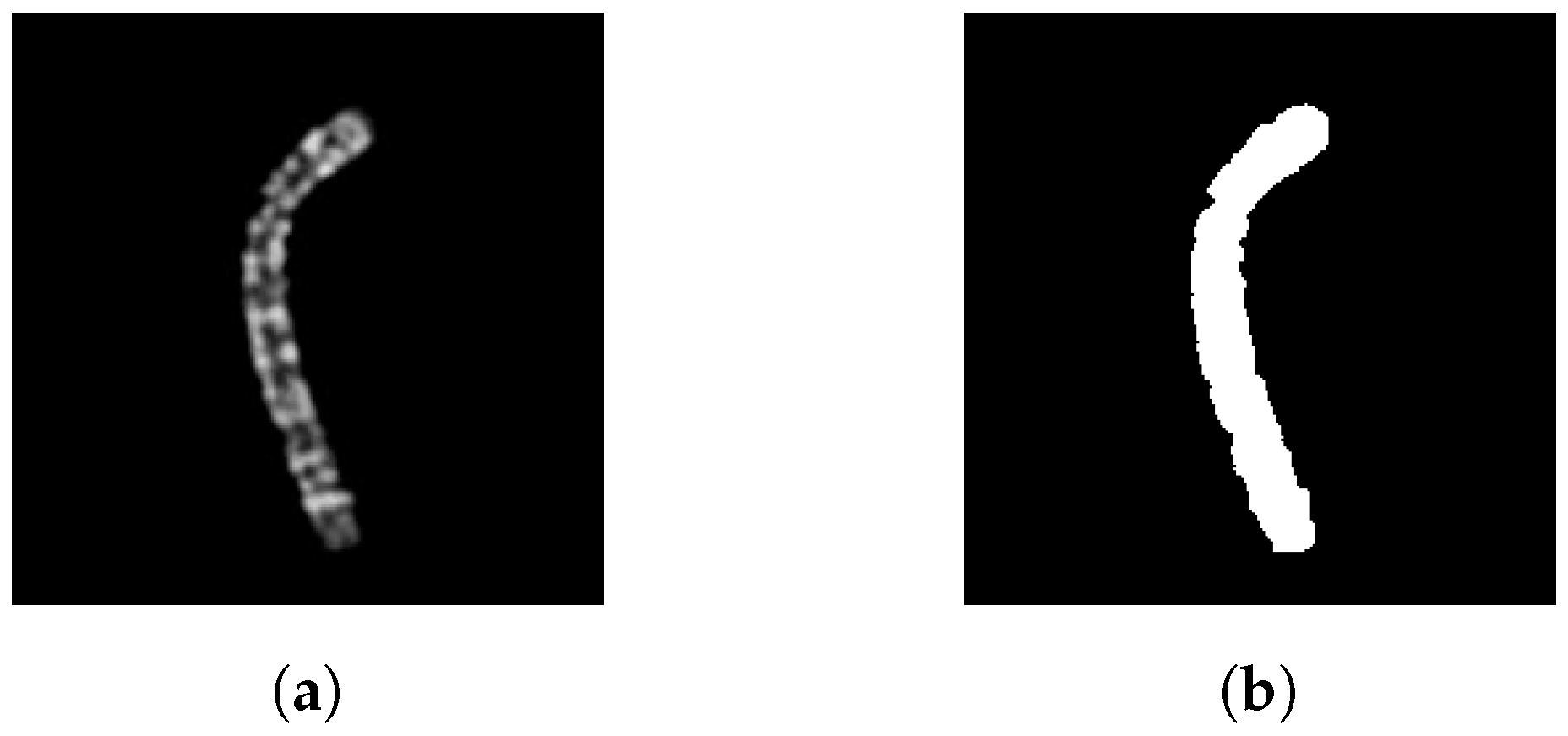Deep Learning-Based Human Chromosome Classification: Data Augmentation and Ensemble

Preprint

Article

Deep Learning-Based Human Chromosome Classification: Data Augmentation and Ensemble

Altmetrics

Downloads

205

Views

101

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

02 June 2023

Posted:

05 June 2023

You are already at the latest version

Alerts

Abstract

Object classification is a crucial task in deep learning, which involves the identification and categorization of objects in images or videos. Although humans can easily recognize common objects, such as cars, animals, or plants, performing this task on a large scale can be time-consuming and error-prone. Therefore, automating this process using neural networks can save time and effort while achieving higher accuracy. Our study focuses on the classification step of human chromosome karyotyping, an important medical procedure that helps diagnose genetic disorders. Traditionally, this task is performed manually by expert cytologists, which is a time-consuming process that requires specialized medical skills. Therefore, automating it through deep learning can be immensely useful. To accomplish this, we implemented and adapted existing preprocessing and data augmentation techniques to prepare the chromosome images for classification. We used ResNet-50 convolutional neural networks and an ensemble approach to classify the chromosomes, obtaining state-of-the-art performance in the tested dataset.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

Karyotyping is the laboratory medical procedure that allows to individuate the karyotype, which is an organism’s complete set of chromosomes. Studying the size, number, and shape of chromosomes is important to diagnose cancers and genetic disorders, such as monosomy, trisomy or deletions at an early stage [1].

Chromosomes consist of DNA molecules containing genetic information. In a healthy human cell there are 46 chromosomes [2], organized into 23 pairs. They include 22 pairs of autosomes and a pair of sex chromosomes (X and Y in male cells and double X in female cells). In order to study them, cytologists perform karyotyping by first taking cells from the patient and culturing them in vitro. During the metaphase stage of mitosis, chromosomes become distinguishable and hence the cells are arrested. Subsequently, a staining technique is employed to highlight the morphological features of the chromosomes, such as bands, by applying a specific dye. One commonly used staining procedure is G banding, which utilizes Giemsa staining to color the chromosomes, enhancing dark and light bands [3].

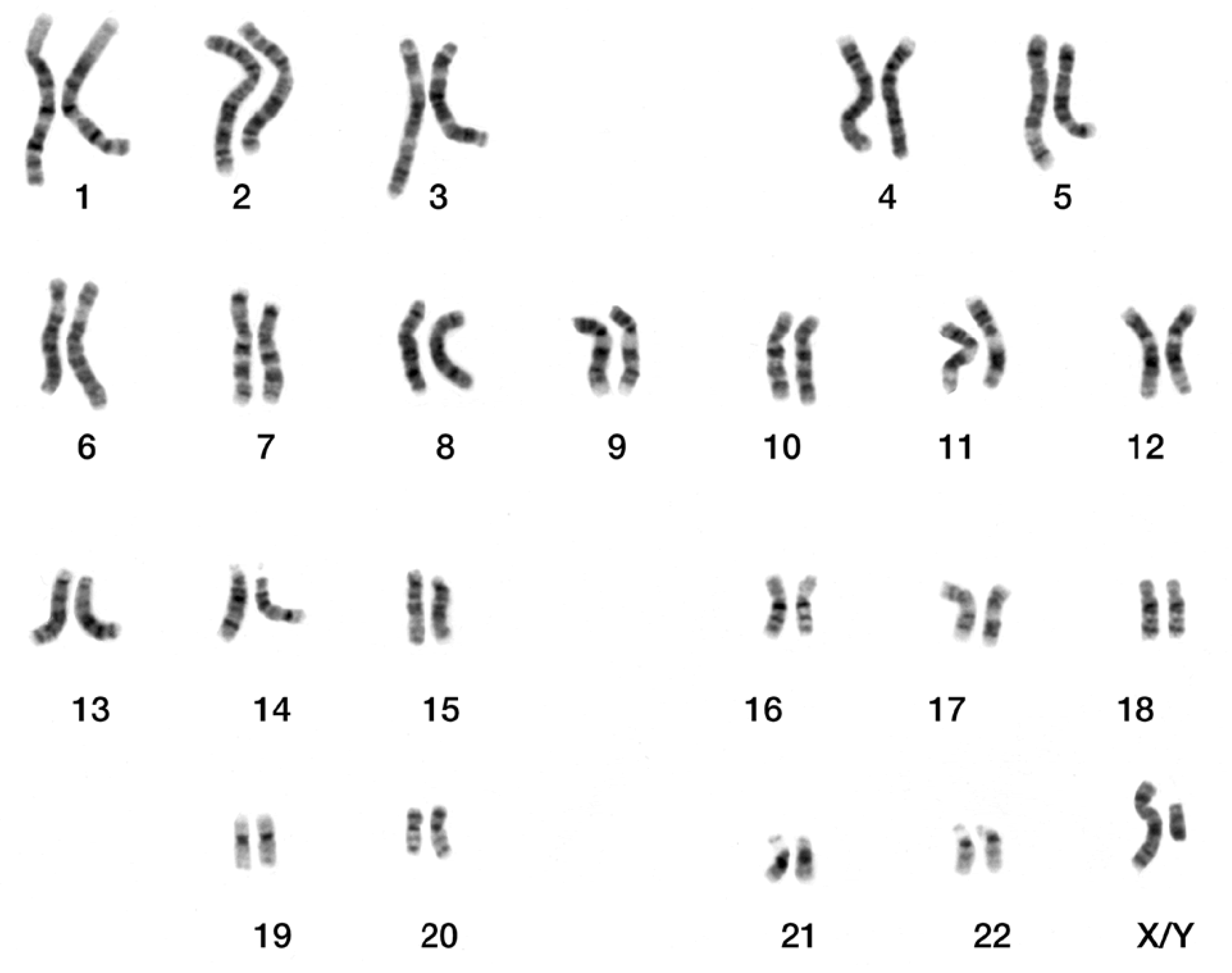
Through a microscope, a chromosome picture is taken, producing a micrograph. Cytologists visually inspect this image, examining chromosome features such as size, shape, banding pattern, centromere position. By organizing and pairing chromosomes according to these characteristics, karyotyping generates a graphical representation called a karyogram, illustrated in Figure 1.

While karyotyping is an essential procedure, it is also time-consuming and requires skilled cytologists to work manually on cells. As a result, researchers have developed computational techniques [4,5,6,7] to automate it.

The two main challenges of automated karyotyping are chromosome segmentation and chromosome classification. The first consists in analyzing a micrograph and extracting, through segmentation techniques, the chromosome instances. These are randomly located within the image and often overlap and adhere together. By defining chromosome geometric features such as area, bounding box, axis length and using specific algorithms, including those based on machine learning, it is possible to extract chromosome instances from the image and subsequently classify them [8].

The second important stage in the karyotyping procedure is the classification of chromosomes into 24 different types, i.e., they are labeled from 1 to 22 and X, Y. This process can be performed through convolutional neural networks (CNNs) trained on large datasets of labeled chromosome images. However, collecting such datasets from medical institutions can be challenging due to privacy-related constraints. Additionally, due to their non-rigid body, chromosomes can be bent or oriented in different ways, which makes their classification more difficult [9]. Differences in cell cultivation techniques and micrograph productions increase the problem [10]. To address these issues, data augmentation and straightening techniques can be employed.

Our work focused on chromosome classification. We implemented a data augmentation technique proposed by Lin et al. [11], as well as a common straightening procedure [12] improved by Sharma et al. [13]. We introduced some modifications and improvements to the baseline methods. Finally, we applied three different image processing techniques based on the Features Transform (Fourier and Discrete cosine). The combination of them and the use of the ResNet-50 for the classification show better results than some previous works.

The paper is organized as follows: in Section 2 we present the dataset used in this work, as well as the methods used for data augmentation and classification. In Section 3, we describe the performed experiments; moreover, we discuss the reported performance. In Section 4 the conclusion and some proposals for future research are given.

The MATLAB source code of the methods here reported is freely available at:

https://github.com/LorisNanni/.

2. Materials and Methods

This section provides a complete description of the dataset used and the image processing techniques mentioned above. In particular, Section 2.1 introduces convolutional neural networks to better understand the context of this work, Section 2.2 describes the dataset, Section 2.3 describes the data augmentation technique, Section 2.4 describes the straightening procedure and Section 2.5 describes the feature transform-based techniques.

2.1. A Brief Introduction to CNNs

Convolutional Neural Networks (CNNs) are powerful deep learning models commonly used for image detection and classification tasks. They are designed to replicate how our brain recognizes images, by extracting relevant features from them.

One of the key advantages of CNNs is their ability to be invariant to certain changes in the image. For example, a CNN can still recognize a cat even if the image is resized, rotated, or exposed to different lighting conditions if it has learned what features are important for identifying a cat. To achieve this level of performance, CNNs are trained on large datasets of images, with multiple samples of the same object to ensure that the network learns the relevant features and can generalize to new, unseen, images.

A CNN is typically composed of some convolutional blocks used for feature extraction, followed by fully connected layers used for classification. The network input is either a grayscale image or an RGB image and the output is the class prediction.

A convolutional block is composed of one or more convolutional layers and a pooling layer. Convolutional layers apply one or more filters to their input, performing a convolution operation. This allows the network to learn relevant features from the image, producing a feature map. After one or more convolutional layers, it is common to include a pooling layer: its purpose is to reduce the spatial size of the feature maps, which also reduces the number of parameters and computation required in the network.

Finally, fully connected layers classify the image by mapping the learned features to the output classes, i.e., they produce an output vector representing the predicted class probabilities for the input image.

2.1.1. ResNet-50

The ResNet-50 is a type of CNN architecture with 50 layers, introduced in 2015 by a team of researchers at Microsoft Research [14].

In general, residual neural networks (ResNet) were introduced to solve the “vanishing gradient problem”, a phenomenon that can occur during the training of deep neural networks with many layers and makes it difficult to obtain accurate predictions.

ResNet-50 has been pretrained on the large ImageNet dataset and therefore can classify objects up to 1000 different categories [15].

2.2. The dataset

The dataset used in this study was obtained from Lin et al.’s GitHub repository (https://github.com/CloudDataLab/CIR-Net) and it contains 2986 G-band chromosome images. They represent 65 different karyotypes, of which 32 are male and 33 are female; in particular, the dataset consists of 130 chromosomes per label from 1 to 22, except for labels 8, 12, 16, and 19, which are associated with only 129 chromosomes. Sex chromosomes are composed of 98 type X chromosomes labeled to 23, and 32 type Y chromosomes labeled to 24. The images are grayscale with 8-bit color depth, which means pixels have an intensity range from 0 (black) to 255 (white). The size is 224x224 pixels, with the background being black and the chromosome composed of shades of gray. Figure 2 (a) illustrates an image of a type 8 chromosome from the dataset.

We also looked for other datasets that might be useful for testing purposes. For convenience, we report here the papers and links to each of the datasets found: BioImLab dataset for segmentation [16] and BioImLab dataset for classification [17]; Passau Chromosome Image Data (Pki-3) [18]; Guangdong Women and Children Hospital dataset [19]. The first dataset contains 162 PAL-resolution quinacrine (Q)-banded prometaphase images and 117 manual karyograms; the second dataset consists of 5.474 Q-band single chromosome images; Pki-3 contains tiff-images of 612 human metaphase cells and the associated karyograms using Giemsa staining; the Guangdong Women and Children Hospital dataset contains tiff-images of 528 chromosome instances and 105 chromosome clusters using Giemsa staining.

2.3. Data Augmentation

Data augmentation refers to a set of techniques used to manipulate and transform existing data in order to artificially increase the number of samples in a dataset. The primary goal of data augmentation is to improve the performance of deep learning models and prevent overfitting. This procedure is commonly applied to image datasets, where it involves using various methods such as geometric transformations, color space augmentations, and random erasing [20].

The dataset described in Section 2.2 is relatively small and will bring to a not accurate classification. In their work, Lin et al. [11] proposed a data augmentation algorithm called CDA (Chromosome Data Augmentation), which generates additional data samples from the original dataset: the algorithm introduces random variations in the position and orientation of chromosomes within the images.

The key step of the CDA algorithm is to apply affine transformations to the original chromosome images, which are grayscale. In computing, a grayscale image is represented as a matrix of pixels. Its size is expressed as height and width, which are the number of rows and columns of pixels, respectively. Affine transformations are commonly used on such images to scale, rotate, or reflect them.

In the CDA algorithm, the images are rotated by a specific angle

θ

and then translated by a randomly determined offset. Equation (1) formalizes the process:

x^{'} = A (θ) x + b

(1)

A (θ) = [\begin{matrix} c o s (θ) & - s i n (θ) \\ s i n (θ) & c o s (θ) \end{matrix}]

(2)

b = [\begin{matrix} r_{o f f s e t} \\ c_{o f f s e t} \end{matrix}]

(3)

In Equation (1), x denotes the original image;

A (θ)

is a rotation matrix formalized in Equation (2); b is a translation vector formalized in Equation (3), where

r_{o f f s e t}

and

c_{o f f s e t}

denote the pixel offset in rows and columns.

x^{'}

denotes the augmented image.

As said before, the translation offsets are randomly determined. It’s important to choose them so the chromosomes are always within the boundaries of the images, or there would be a loss of pixels. Therefore, we used the built-in MATLAB function regionprops, which can return the position and the size of the smallest box containing the region, i.e., the chromosome. Using this information, we can constrain the offsets to a specific range so that shifting the chromosome horizontally or vertically ensures that it remains within the image boundaries.

In some cases, multiple bounding boxes are returned for certain images in the dataset due to the presence of artifacts such as non-black pixels outside the chromosome region. To address this, we select only the largest bounding box from the set of bounding boxes, as it corresponds to the rectangle that encloses the chromosome region.

The regionprops function requires a binary image that consists of pixels either 0 (black) or 1 (white). In the dataset used, common binarization techniques like Otsu’s method did not yield satisfactory results. This is because some parts of the chromosome, such as the bands, have similar shades of color to the black background, leading to loss of chromosome borders as they are mistaken for the background. Therefore, we opted for a simple binarization method where every pixel with a value greater than 0 is set to 1. This approach separates the chromosome well from the background, coloring it white and making it possible to apply the regionprops function (Figure 2 (b)). Note that if background pixel values are modified by other image processing techniques, this binarization method may not be optimal. In such cases, alternative segmentation approaches may be necessary.

Algorithm 1 describes the data augmentation operation.

Algorithm 1 Chromosome Data Augmentation

Input:: A chromosome image x

The chromosome label y corresponding to x
Output:: $The set of augmented images$
1:: $a u g m e n t e d_s e t \leftarrow {}$
2:: for $θ \leftarrow 15$ to 345 step 15 do
3:: $x_{θ} \leftarrow A (θ) x$
4:: $x_{b w} \leftarrow$ binarize $x_{θ}$
5:: $b o u n d i n g_b o x \leftarrow$ find largest chromosome bounding box using $x_{b w}$
6:: $r_{o f f s e t} \leftarrow$ calculate random vertical offset according to $b o u n d i n g_b o x$
7:: $c_{o f f s e t} \leftarrow$ calculate random horizontal offset according to $b o u n d i n g_b o x$
8:: $b \leftarrow [\begin{matrix} r_{o f f s e t} \\ c_{o f f s e t} \end{matrix}]$
9:: $x^{'} \leftarrow x_{θ} + b$
10:: $a u g m e n t e d_s e t \leftarrow a u g m e n t e d_s e t \cup {(x^{'}, y)}$
11:: end for
12:: return $a u g m e n t e d_s e t$

We apply Algorithm 1 for each image in the dataset and we generate a set composed of original and augmented images.

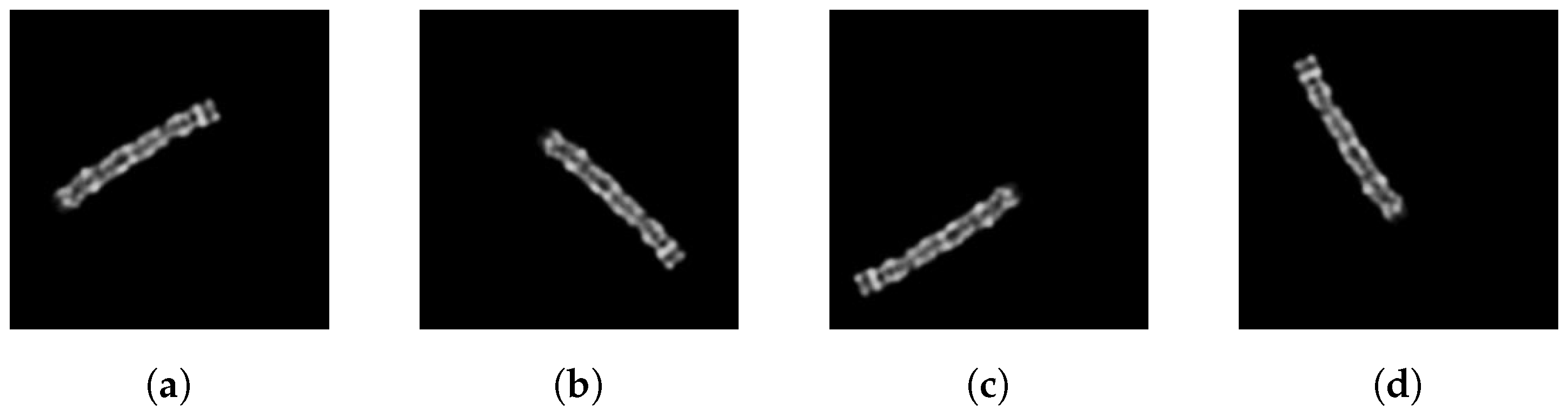
As specified by Lin et al., we rotate each chromosome by 15 to 345 degrees in steps of 15 degrees. Some examples are shown in Figure 3. As a result, each image generates a total of 23 augmented images. The data augmentation is applied only to the training images.

2.4. Straightening

The straightening procedure is a preprocessing step (i.e., something done before training the neural network) aimed at removing the random curves and orientation of a chromosome by making it straight and vertical within the image. This allows the neural network classifier to focus on other important features and refrain from learning to discriminate based on curves and orientation, as seen in the CDA algorithm.

We implemented in MATLAB a known straightening algorithm proposed in 2008 [12], with improvements from a 2017 work [13], and some personal adaptations for improving it.

The algorithm finds the bending centre of a curved chromosome, i.e., the point where the latter is bent, and uses this information to straighten the chromosome. Here we provide the description of the procedure.

2.4.1. Chromosome Image Binarization and Bending Centre Locating

First, the chromosome grayscale image needs to be binarized. For the dataset in use, we adopted the same binarization technique described in the data augmentation section, so all the pixels greater than 0 are set to 1. The resulting binary image has a black background and a white chromosome, as shown in Figure 4. Then, it is cropped to retain only the chromosome.

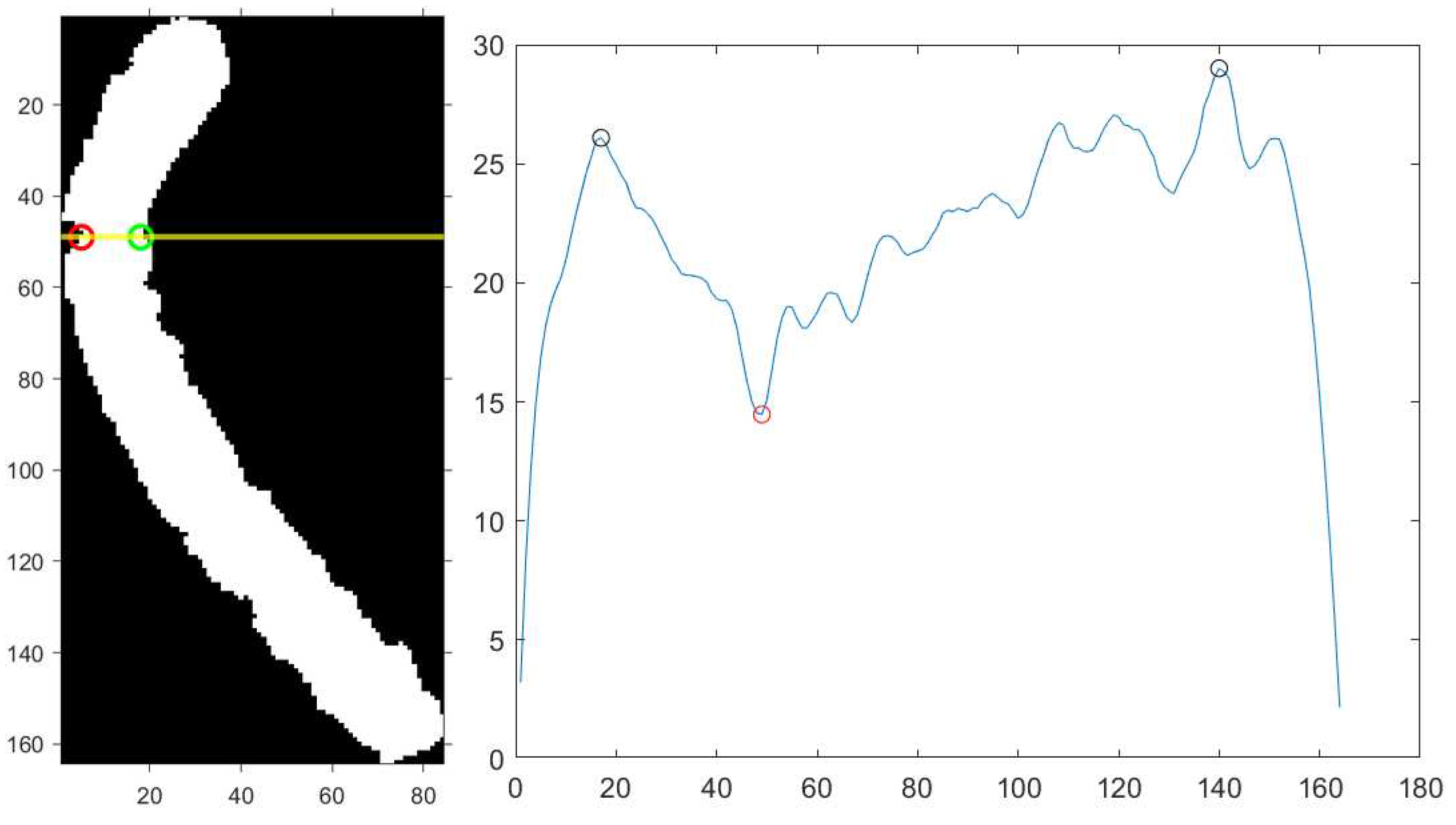
Next, the algorithm calculates the horizontal projection vector of the binary image by summing up the pixel values on each row. The horizontal projection contains the morphological information of the chromosome. Analyzing its extrema, it is possible to find the bending centre as explained below (to minimize the effects of small deflections on the location of the extrema, we applied a Savitzky-Golay filter using the built-in MATLAB function sgolayfilt, which smooths out the horizontal projection).

For a straight chromosome, the global minimum point in the horizontal projection vector corresponds to the centromere, the thinner part of a chromosome [21]. This point often corresponds to the bending centre of a curved chromosome. However, since the horizontal projection vector is strongly dependent on the position of the chromosome and its degree of bending, locating just the global minimum point would not be effective. To overcome this, the algorithm rotates the binary image from 0° to 180° by steps of 10° and analyzes the corresponding projection vectors. It is found that the actual bending centre corresponds to the global minimum point between two locally global maxima with similar amplitudes. Since there is a projection vector for each rotated image, the correct bending centre is selected in the image that presents the minimum rotation score S, defined in Equation (4):

S = w_{1} \times R_{1} + w_{2} \times R_{2}

(4)

R_{1} = \frac{|P_{1} - P_{2}|}{P_{1} + P_{2}}

(5)

R_{2} = \frac{P_{3}}{P_{1} + P_{2}}

(6)

In Equations (5) and (6),

P_{1}

and

P_{2}

represent the values of the two locally global maxima, while

P_{3}

represents the value of the global minimum located between them.

R_{1}

describes the relation between the two maxima: if they have similar amplitudes, then

R_{1}

will be smaller.

R_{2}

describes the relative amplitude of the global minimum between the two maxima. In Equation (4),

w_{1}

and

w_{2}

are the tuning parameters whose selection influences the location of the bending centre. The location of the global minimum point

P_{3}

in the horizontal projection vector identifies the bending axis of the chromosome, i.e., a horizontal line which divides the chromosome into two arms; the outermost point of intersection between the chromosome and the bending axis is the actual bending centre of the chromosome. The opposite point, i.e., the last chromosome pixel along the same bending axis with respect to the bending centre, we called unjoined point and will be used in a further process. An idea of the process explained above is presented in Algorithm 2.

Algorithm 2 Rotation Score Calculation

Figure 5 illustrates the smoothed horizontal projection, the corresponding bending axis and the bending centre. The chromosome shown has been rotated counterclockwise by 20°, which corresponds to the lowest rotation score S in this case.

A point on the tuning parameters

w_{1}

w_{2}

described in Equation (4): these weights affect the performance of the straightening procedure; they can be chosen by visually analyzing the bending axis in the chromosome images. We found that setting

w_{1}

to 0.67 and

w_{2}

to 0.33 produced good results.

2.4.2. Chromosome Arms Straightening and Final Image Creation

The chromosome image is now divided along the bending axis into two sub-images, each containing an arm of the chromosome (upper and lower). Both sub-images are rotated from -90° to 90° by steps of 10° using a rotation matrix. For each rotation, the vertical projection vector is calculated by summing up the pixel values on each column. The vertical projection vector with minimum width is associated with the arm in a vertical position within the image (see Algorithm 3). The coordinates of the bending centre and the unjoined point in both sub-images are recalculated in the vertical image after the rotation.

Algorithm 3 Chromosome Arm Straightening

As can be seen in Algorithm 3, the operation is applied to both the binary image and the grayscale image. The two sub-images are then cropped to retain only the chromosome arms; this will be useful in the alignment procedure. Figure 6 shows the result.

Finally, the two arms must be aligned and connected. Thinking of the image pixels to be in a Cartesian plane, with the origin in the upper left corner and the horizontal axis toward the right, we compute the difference between the x-coordinate of the bending centre in the upper and lower arm, resulting in a horizontal shift called

s h i f t x

. Then, we need to move to the right the image with the leftmost bending centre: to avoid losing arm pixels, the selected image’s right border is padded with

| s h i f t x |

black pixel columns and it is moved by

| s h i f t x |

. This ensures that the two arms are perfectly aligned along the x-coordinate of the bending centre. The coordinates of the points are then updated to always refer to the same pixels.

Now, we can just copy all the pixels of the two sub-images in a new image that corresponds to the straightened version of the original chromosome. Obviously, in the upper part of the image there will be the upper arm, and in the lower part of the image there will be the lower arm (Figure 7).

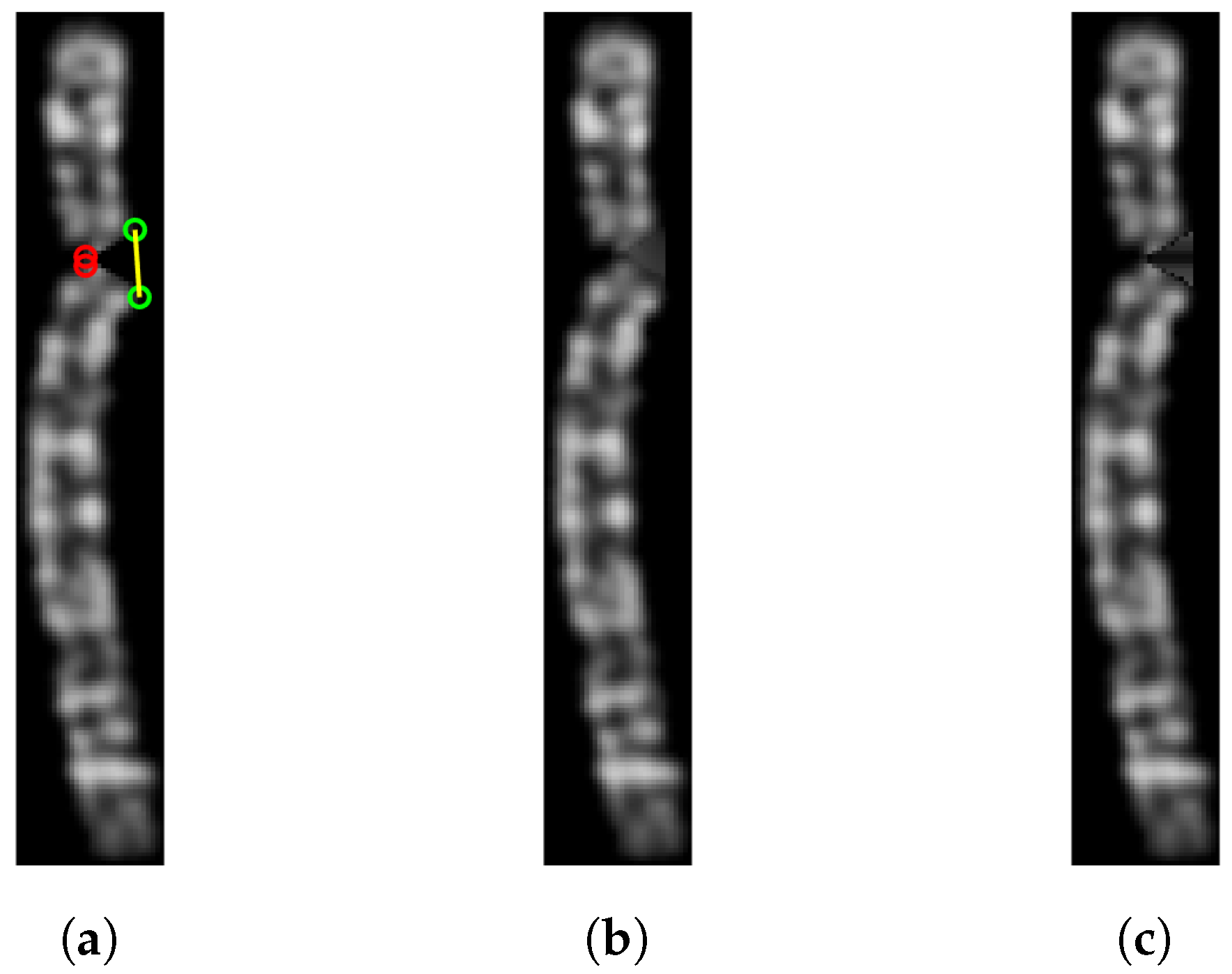
The last step of the algorithm, proposed by Sharma et al. [13], involves reconstructing the area of the chromosome lost during the straightening. This is performed on the grayscale image by connecting the unjoined points through a straight line and filling the enclosed area with the mean value of the non-black pixels at the same horizontal level. This reconstructs the missing part and preserves the horizontal bands of the chromosome. However, this procedure doesn’t give optimal results with the binarization technique we used: chromosome border pixels are dark but not completely black and therefore are included in the binarization; when reconstructing the missing area, they lower the mean resulting in an overall color that is darker than it should be; moreover, they result in a non-homogeneous shade of color, as shown in Figure 8 (c). To produce a more uniform color, each pixel value in the area enclosed by the bending centre points and the unjoined points (upper and lower) is replaced with the mean of the surrounding non-black pixels (using a radius of 1), resulting in a smoother color that still preserves the shade of the chromosome bands (Figure 8 (b)).

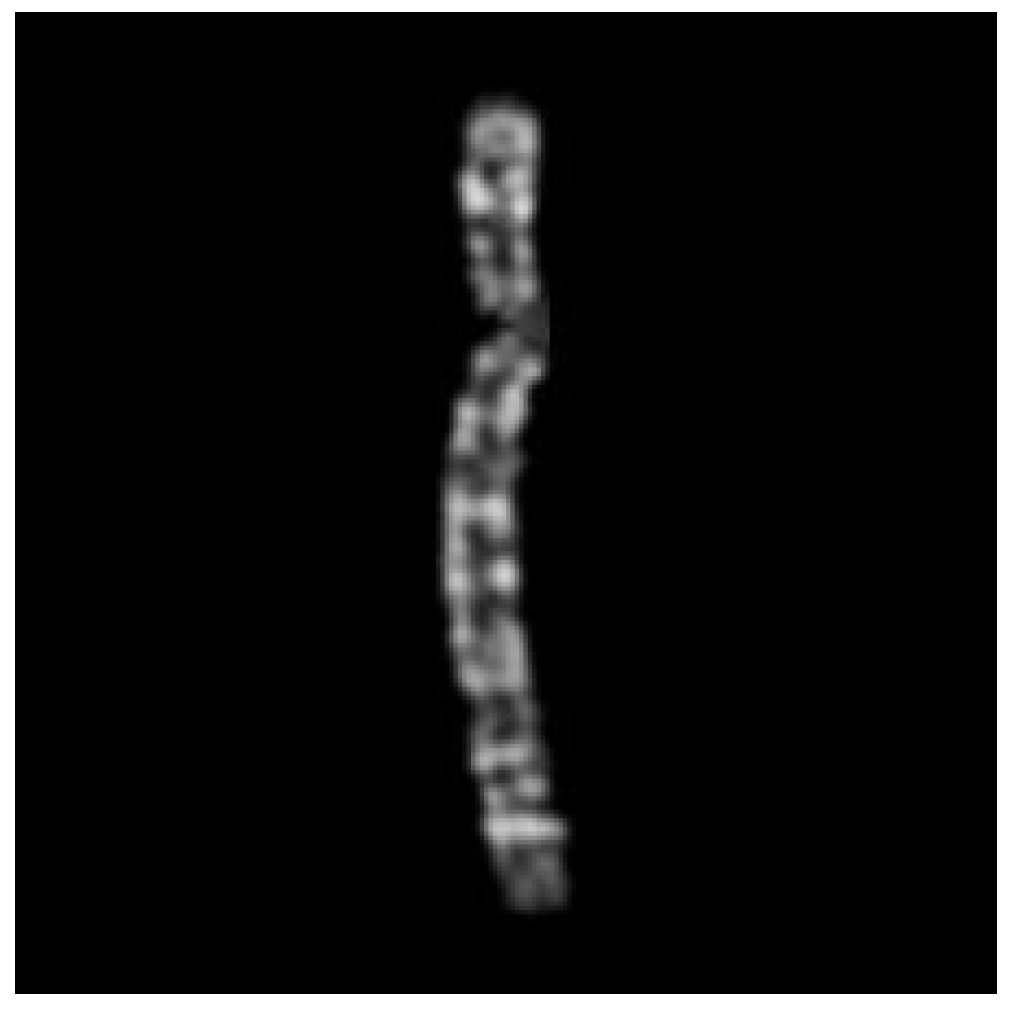
Finally, the algorithm pads the borders of the straightened image with black pixels to resize it to the same size as the original image, before returning it as the final output, illustrated in Figure 9.

2.4.3. Algorithm Improvements

The effectiveness of the straightening procedure can be enhanced by applying it only to the bent chromosomes. Since the upright tightest fitting rectangle for a straight chromosome contains fewer black pixels compared to a bent one, it is possible to automatically determine whether a chromosome is bent or straight. We applied this idea by manually selecting 1014 visibly straightest chromosomes from the original dataset of 2986 images, i.e., those chromosomes with arms forming an angle of approximately 180°. Then, we binarized each image and calculated the whiteness value W [13], defined as the ratio of the sum of white pixels and the area of the tightest fitting rectangle of the chromosome. The closer W is to 1, the straighter the chromosome is. We used the MATLAB function regionprops to find the rectangle, i.e., the bounding box. We selected a whiteness threshold

W_{T}

of 0.667, meaning that only chromosomes with

W < W_{T}

are considered bent and therefore are sent for further straightening. Using this method, we identified 1472 bent chromosomes from the original dataset.

To improve classification accuracy, we added some check conditions to the straightening algorithm: not all bent chromosomes can be effectively straightened due to their particular shapes and the effects of the weights

w_{1}

and

w_{2}

in Equation (4). In general, we consider an effective straightening to be one in which the chromosome arms are vertical and oriented correctly (i.e., not upside down). Thus, we check the relative location of the bending center and the unjoined point in both the upper and lower arm images: if these conditions are not met, the algorithm stops and returns the original chromosome image. This approach avoids incorrectly straightening 447 chromosomes, resulting in a more robust dataset composed of original and well-straightened images.

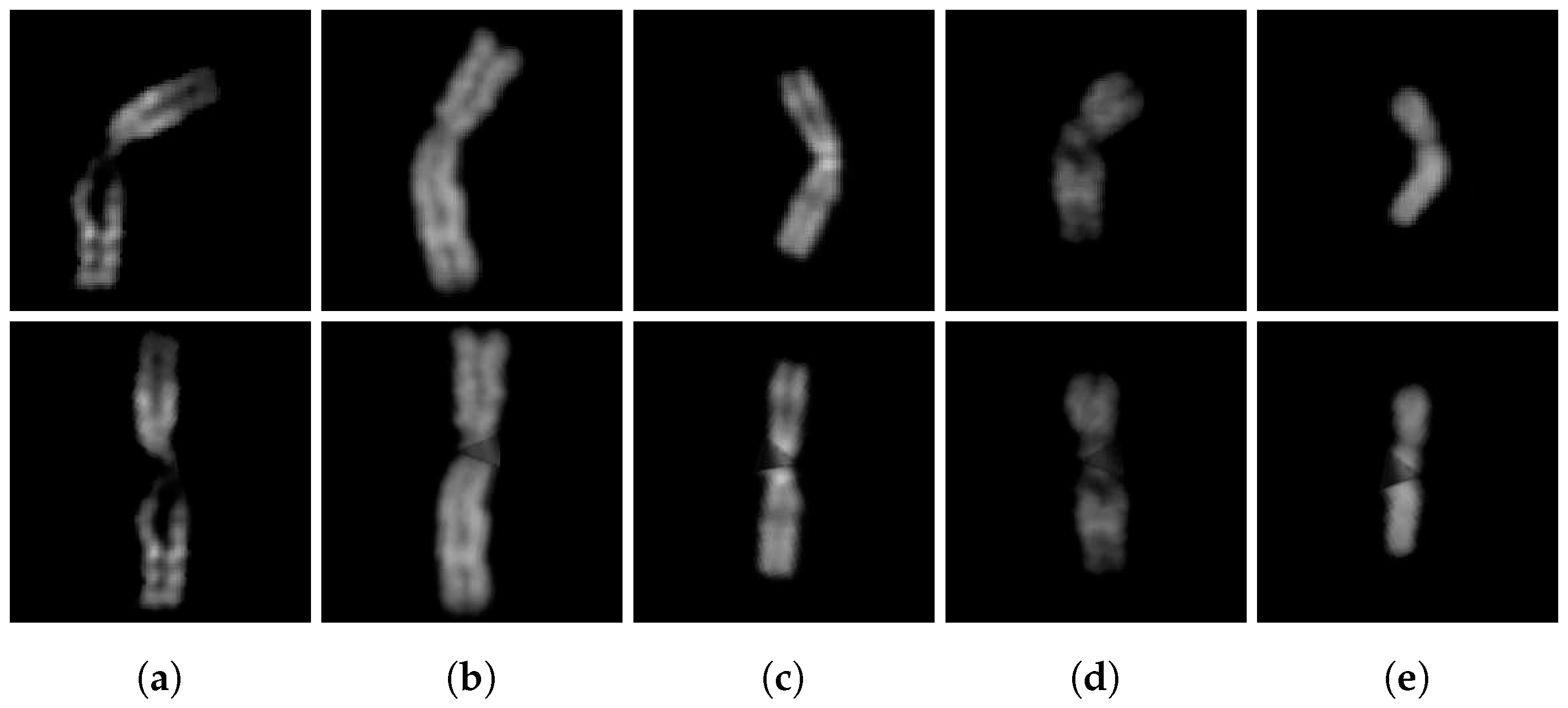
2.4.4. Additional Tests

We evaluated the effectiveness of the proposed straightening technique by applying it to some chromosome images from two different datasets [16,18]. The first dataset contains Q-band chromosome images with a black background, while the second contains G-band chromosome images with a white background. As the binarization technique described in the previous sections works better with black backgrounds, we modified it to handle white backgrounds as well. We achieved this by computing the complement of the white background image, which turns the background black. We apply the straightening procedure to this modified image and finally, we restore its original color by computing the complement again. The straightening procedure worked well on the chromosome images from both datasets, as shown in Figure 10 and Figure 11.

2.5. Feature Transform-Based Techniques

To enhance the contrast, blur, and add noise to the chromosome images, three image processing methods are utilized. These involve the use of a 2-D Fast Fourier Transform (FFT) for the first two techniques and a 2-D Discrete Cosine Transform (DCT) for the third one. For each image, three new images are created.

These techniques are applied to grayscale images. If necessary, input RGB images are converted to grayscale and restored to RGB after processing. The methods are described in the following steps:

I.

First technique

1.: Apply FFT to the grayscale chromosome image.
2.: Shift the zero frequency component to the center of the frequency-domain.
3.: Create a mask made of 1s with the same dimensions as the transformed and frequency-shifted image; this will preserve only selected frequencies in step 7.
4.: Create two 2-D grids to represent the x and y coordinates.
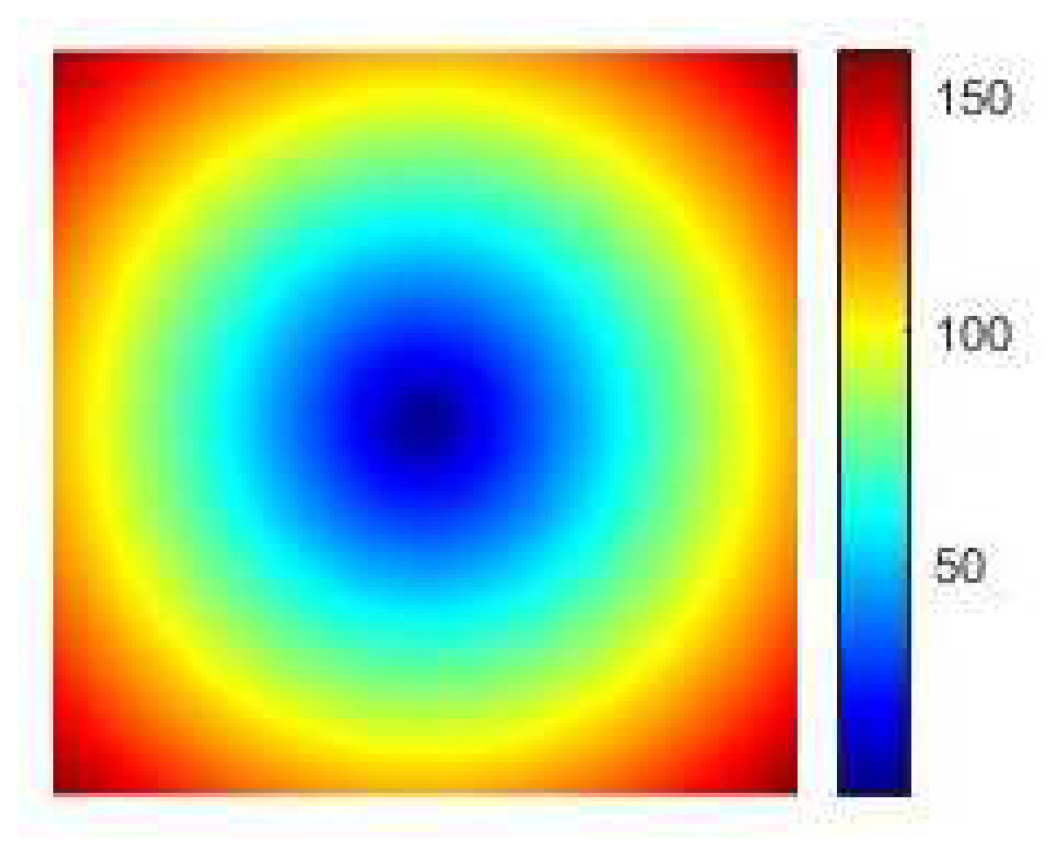
5.: Use the grids to compute the euclidean distance and get a colored distance matrix R (see Figure 12).
6.: Select a radius (threshold) $r = 2$ and set to zero the values of the mask inside this radius using the values of distance matrix R as coordinates.
7.: Apply the mask to the transformed image.
8.: Apply the inverse Fourier Transform (iFFT) to get the blurred grayscale image, visible in Figure 13 (b).

II.

Second technique

This technique is similar to the previous one, except that the zero frequency is not shifted:

1.: Apply FFT to the grayscale image.
2.: Sort and store in an array the elements (IDs) of the transformed image by their intensity values.
3.: Select a value $p = 0.5$ that represents the percentage of points in the transformed image that will be set to zero.
4.: Randomize the IDs array and set a portion of the elements corresponding to the selected percentage p to zero in the transformed image.
5.: Apply the inverse Fourier Transform (iFFT) to recover the filtered grayscale image. The result is shown in Figure 13 (c).

III.

Third technique

This method uses the Discrete Cosine Transform (DCT) for image processing instead of the Fourier Transform:

1.: Convert the input RGB image to grayscale.
2.: Apply the DCT to the grayscale image to obtain its frequency components.
3.: Set to zero a low frequency range, which is a 10x10 square in this case.
4.: Apply the inverse DCT (iDCT) to obtain the processed grayscale image (Figure 13 (d)).

3. Results

This section describes the evaluation metrics, the experiment settings and the experimental results on the methods presented.

3.1. Metrics

We evaluated the performance of the ResNet-50 using typical metrics: precision, recall, accuracy,

F_{1} s c o r e

(

F_{1}

), which can be compared to the ones obtained by other studies. In the context of multi-class classification, precision is defined as Equation (7), recall as Equation (8), accuracy as Equation (9),

F_{1}

as Equation (10).

p r e c i s i o n = \frac{1}{M} \sum_{i = 1}^{M} \frac{T P_{i}}{T P_{i} + F P_{i}}

(7)

r e c a l l = \frac{1}{M} \sum_{i = 1}^{M} \frac{T P_{i}}{T P_{i} + F N_{i}}

(8)

a c c u r a c y = \frac{1}{N} \sum_{i = 1}^{M} T P_{i}

(9)

F_{1} = \frac{1}{M} \sum_{i = 1}^{M} \frac{2 \times T P_{i}}{2 \times T P_{i} + F N_{i} + F P_{i}}

(10)

In the above equations,

T P_{i}

stands for True Positives, i.e., chromosomes of type i are correctly classified as type i;

F P_{i}

stands for False Positives, i.e., chromosomes of type i are incorrectly classified as type j;

F N_{i}

stands for False Negatives, i.e., chromosomes of type i are incorrectly classified as type j (

\forall i \neq j

). M is the number of chromosome types and N is the number of chromosome images in the test set.

3.2. Experiment settings

To classify the chromosomes, we utilized the ResNet-50 pre-trained on ImageNet. In line with transfer learning, we fine-tuned the pre-trained network by replacing its last three layers, responsible for image classification, with a fully connected layer, a softmax layer, and a classification layer adapted to handle the number of chromosome classes.

We trained the network with the following hyperparameters: mini-batch of 30, epochs of 20, and a learning rate of 0.001. The 5-fold cross-validation is used as a test protocol.

3.3. Experimental results

This section presents the performance achieved by the ensemble proposed in our study and those from some previous research, all tested on the same dataset with the same testing protocol. The experimental results are presented in Table 1.

METHOD(n) means the use of a ResNet-50 ensemble; in particular, n stands for the number of neural networks used. Their predictions are fused by sum rule. A(n)+B(n) means that we combine by sum rule the ensemble A(n) and B(n).

None refers to the use of a ResNet-50 without any data augmentation technique. CDA is the Chromosome Data Augmentation algorithm detailed in Section 2.3; STR is the straightening procedure described in Section 2.4, using this approach we apply straightening procedure to both training and test images, moreover, after the straightening procedure we apply CDA to the training set; while FT refers to the use of the Feature Transform-based techniques presented in Section 2.5, we apply this method to one image out of every three images in the training set, adding the new images to the original training set, then we apply CDA to the expanded training set.

From the results reported in Table 1 we can get the following conclusions:

None(1) achieves significantly lower performance than the network trained using an expanded training set. None(10) outperforms None(1), but its performance is not comparable to that achieved by CDA(10). It is clear that in this application data augmentation is a very important step.
CDA(10) clearly outperforms CDA(1).
The best performance, considering a single data augmentation approach, is obtained by STR(10).
The ensemble trained with different augmentation methods can outperform each of its components, e.g., CDA(3) + STR(3) + FT(3) outperforms STR(10).
The best result is obtained by CDA(3) + STR(3) + FT(3), which achieved an accuracy of 98.56%.

The primary drawback of the suggested ensemble is the longer computation time it requires. While the preprocessing methods are not computationally intensive, the main computational demand lies in performing inferences with the set of CNNs. Nonetheless, using a Titan RTX 24 GB, it is possible to classify using ResNet-50 a batch of one thousand images in just 1.945 seconds (therefore, an ensemble of 10 ResNet-50 networks can classify 100 images in ~2 seconds).

4. Conclusions

In this study, we focused on automating the karyotyping procedure, specifically the classification of human chromosome images. We provided an overview of the context and an in-depth analysis of three image processing and data augmentation techniques that we adopted to achieve state-of-the-art performance:

A data augmentation algorithm called CDA was used to generate additional samples from the original dataset. This algorithm introduces different spatial orientations to the chromosomes, effectively diversifying the training data.
We implemented a straightening procedure that utilizes projection vectors to straighten the chromosomes. This step removes curves from the subjects, allowing the neural network to learn other important features.
In the end, we employed three feature transform-based techniques to create more images and alter their appearance through manipulations such as blur and contrast adjustments. These techniques contributed to further enhancing the diversity and variability of the training data.

To evaluate the effectiveness of our methods, we conducted experiments on a dataset comprising 2986 human chromosome images. The dataset was used to create five folds for training and testing purposes. Furthermore, we partially used two additional datasets to evaluate the effectiveness of the straightening procedure.

For the classification, we utilized a ResNet-50 neural network combined with an ensemble approach. This method allows for high accuracy and robust predictions, resulting in state-of-the-art performance.

As future work, we plan to conduct tests on other datasets. The overall performance could be improved by processing the unstraightened curved chromosomes, this can be achieved by finding new tuning parameters or employing different algorithms. Additionally, it would be interesting to examine the impact of reducing or increasing the number of data samples generated through the data augmentation techniques discussed in this work. Furthermore, considering alternative neural network architectures or ensembles could further improve performance.

All the code was written in MATLAB, and it is freely available on GitHub at

https://github.com/LorisNanni/, ensuring accessibility for the research community.

Author Contributions

“Conceptualization, M.D. and L.N.; methodology, M.D. and L.N.; software, M.D. and L.N.; writing—original draft preparation, M.D. and L.N.. All authors have read and agreed to the published version of the manuscript.”

Funding

“This research received no external funding.”

Institutional Review Board Statement

“Not applicable.”

Data Availability Statement

dataset is available at https://github.com/CloudDataLab/CIR-Net.

Acknowledgments

We would like to acknowledge the support that NVIDIA provided us through the GPU Grant Program. We used a donated TitanX GPU to train the neural networks discussed in this work. Special thanks to Nicolas Guglielmo for performing/implementing some FT-based methods in partial fulfillment of his degree requirements.

Conflicts of Interest

“The authors declare no conflict of interest.”

References

Wang, X.; Zheng, B.; Li, S.; Mulvihill, J.J.; Liu, H. A rule-based computer scheme for centromere identification and polarity assignment of metaphase chromosomes. Computer Methods and Programs in Biomedicine 2008, 89, 33–42. [CrossRef]
Tjio, J.H.; Levan, A. The Chromosome Number in Man. Hereditas 2010, 42, 1 – 6. [CrossRef]
Remani Sathyan, R.; Chandrasekhara Menon, G.; S, H.; Thampi, R.; Duraisamy, J.H. Traditional and deep-based techniques for end-to-end automated karyotyping: A review. Expert Systems 2022, 39, e12799. [CrossRef]
Agam, G.; Dinstein, I. Geometric separation of partially overlapping nonrigid objects applied to automatic chromosome classification. IEEE Transactions on Pattern Analysis and Machine Intelligence 1997, 19, 1212–1222. [CrossRef]
Errington, P.A.; Graham, J. Application of artificial neural networks to chromosome classification. Cytometry 1993, 14, 627–639. [CrossRef]
Zhang, W.; Song, S.; Bai, T.; Zhao, Y.; Ma, F.; Su, J.; Yu, L. Chromosome Classification with Convolutional Neural Network Based Deep Learning. 2018 11th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), 2018, pp. 1–5. [CrossRef]
Swati.; Gupta, G.; Yadav, M.; Sharma, M.; Vig, L. Siamese Networks for Chromosome Classification. 2017 IEEE International Conference on Computer Vision Workshops (ICCVW), 2017, pp. 72–81. [CrossRef]
Huang, K.; Lin, C.; Huang, R.; Zhao, G.; Yin, A.; Chen, H.; Guo, L.; Shan, C.; Nie, R.; Li, S. A novel chromosome instance segmentation method based on geometry and deep learning. 2021 International Joint Conference on Neural Networks (IJCNN), 2021, pp. 1–8. [CrossRef]
Abid, F.; Hamami, L. A survey of neural network based automated systems for human chromosome classification. Artificial Intelligence Review 2018, 49, 41–56. [CrossRef]
Anh, L.Q.; Thanh, V.D.; Son, N.H.H.; Phuong, D.T.K.; Anh, L.T.L.; Ram, D.T.; Minh, N.T.B.; Tung, T.H.; Thinh, N.H.; Ha, L.V.; Ha, L.M. Efficient Type and Polarity Classification of Chromosome Images using CNNs: a Primary Evaluation on Multiple Datasets. 2022 IEEE Ninth International Conference on Communications and Electronics (ICCE), 2022, pp. 400–405. [CrossRef]
Lin, C.; Zhao, G.; Yang, Z.; Yin, A.; Wang, X.; Guo, L.; Chen, H.; Ma, Z.; Zhao, L.; Luo, H.; Wang, T.; Ding, B.; Pang, X.; Chen, Q. CIR-Net: Automatic Classification of Human Chromosome Based on Inception-ResNet Architecture. IEEE/ACM Transactions on Computational Biology and Bioinformatics 2022, 19, 1285–1293. [CrossRef]
Javan Roshtkhari, M.; Setarehdan, K. A novel algorithm for straightening highly curved images of human chromosome. Pattern Recognition Letters 2008, 29, 1208–1217. [CrossRef]
Sharma, M.; Saha, O.; Sriraman, A.; Hebbalaguppe, R.; Vig, L.; Karande, S. Crowdsourcing for Chromosome Segmentation and Deep Classification. 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), 2017, pp. 786–793. [CrossRef]
He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016, pp. 770–778. [CrossRef]
MathWorks. ResNet-50 convolutional neural network - MATLAB resnet50 - MathWorks. https://it.mathworks.com/help/deeplearning/ref/resnet50.html?lang=en, n.d. Accessed: April 27, 2023.
Grisan, E.; Poletti, E.; Ruggeri, A. Automatic Segmentation and Disentangling of Chromosomes in Q-Band Prometaphase Images. IEEE Transactions on Information Technology in Biomedicine 2009, 13, 575–581. [CrossRef]
Poletti, E.; Grisan, E.; Ruggeri, A. Automatic classification of chromosomes in Q-band images. 2008 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, 2008, pp. 1911–1914. [CrossRef]
Ritter, G.; Gao, L. Automatic segmentation of metaphase cells based on global context and variant analysis. Pattern Recognition 2008, 41, 38–55. [CrossRef]
Lin, C.; Yin, A.; Wu, Q.; Chen, H.; Guo, L.; Zhao, G.; Fan, X.; Luo, H.; Tang, H. Chromosome Cluster Identification Framework Based on Geometric Features and Machine Learning Algorithms. 2020 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), 2020, pp. 2357–2363. [CrossRef]
Shorten, C.; Khoshgoftaar, T.M. A survey on Image Data Augmentation for Deep Learning. Journal of Big Data 2019, 6. [CrossRef]
Moradi, M.; Setarehdan, S.; Ghaffari, S. Automatic locating the centromere on human chromosome pictures. 16th IEEE Symposium Computer-Based Medical Systems, 2003. Proceedings., 2003, pp. 56–61. [CrossRef]

Figure 1. Micrographic karyogram of human male using Giemsa staining.

Figure 2. (a) Grayscale image of a type 8 chromosome and (b) its binary version, including the chromosome bounding box.

Figure 3. Chromosome images rotated clockwise by (a) 60°, (b) 135°, (c) 240°, (d) 330° and horizontally and vertically randomly shifted.

Figure 4. (a) Grayscale image of a type 5 chromosome and (b) its binary version.

Figure 5. From the left: type 5 chromosome image rotated counterclockwise by 20° (yellow line: bending axis; red circle: bending centre; green circle: unjoined point), the corresponding smoothed horizontal projection (black circles: maxima points; red circle: minimum point identifying the bending axis).

Figure 6. (a), (b) Straightened upper arm and (c), (d) lower arm. Red circle: bending centre; green circle: unjoined point.

Figure 7. (a) Binary and (b) grayscale image of the straightened chromosome.

Figure 8. (a) The straightened chromosome image with reference points. (b) The corresponding filled version. (c) The same chromosome but using the mean value of the non-black pixels to reconstruct the missing area.

Figure 9. The final straightened chromosome image.

Figure 10. Type (a) 1, (b) 2, (c) 3, (d) 11, (e) 23 Q-band chromosome images and their straightened version.

Figure 11. Type (a) 3, (b) 4, (c) 6, (d) 11, (e) 23 G-band chromosome images and their straightened version.

Figure 12. The distance matrix R.

Figure 13. (a) Type 6 chromosome image and the corresponding results after applying (b) first technique, (c) second technique and (d) third technique.

Table 1. Experimental results.

Method	Precision	Recall	Accuracy	F1
Vanilla-CNN [6]	0.8800	0.8600	0.8644	0.8700
SiameseNet [7]	0.8800	0.8700	0.8763	0.8700
CIR-Net [11]	0.9600	0.9600	0.9598	0.9600
ResNet-50
None(1)	0.8834	0.8767	0.8808	0.8775
None(10)	0.9246	0.9157	0.9216	0.9157
CDA(1)	0.9765	0.9743	0.9759	0.9749
CDA(10)	0.9822	0.9748	0.9812	0.9772
STR(10)	0.9834	0.9787	0.9822	0.9803
FT(10)	0.9846	0.9810	0.9836	0.9822
CDA(5) + STR(5)	0.9858	0.9814	0.9849	0.9831
CDA(3) + STR(3) + FT(3)	0.9864	0.9831	0.9856	0.9843

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Deep Learning-Based Human Chromosome Classification: Data Augmentation and Ensemble

Abstract

1. Introduction

2. Materials and Methods

2.1. A Brief Introduction to CNNs

2.1.1. ResNet-50

2.2. The dataset

2.3. Data Augmentation

2.4. Straightening

2.4.1. Chromosome Image Binarization and Bending Centre Locating

2.4.2. Chromosome Arms Straightening and Final Image Creation

2.4.3. Algorithm Improvements

2.4.4. Additional Tests

2.5. Feature Transform-Based Techniques

3. Results

3.1. Metrics

3.2. Experiment settings

3.3. Experimental results

4. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe