Prerpints.org logo
Preprint
Article

Strain Modulation of Electronic Properties in Monolayer SnP2S6 and GeP2S6

Altmetrics

Downloads

127

Views

89

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

03 June 2023

Posted:

05 June 2023

You are already at the latest version

Alerts
Abstract
In recent years, two-dimensional (2D) materials have attracted significant attention due to their distinctive properties, including exceptional mechanical flexibility and tunable electronic properties. Via the first-principles calculation, we investigate the effect of strain on the electronic properties of monolayer SnP2S6 and GeP2S6. We find that monolayer SnP2S6 is an indirect band gap semiconductor, while monolayer GeP2S6 is a direct band gap semiconductor. Notably, under uniform biaxial strains, SnP2S6 undergoes an indirect-to-direct band gap transition at 4.0% biaxial compressive strains, while GeP2S6 exhibits a direct-to-indirect transition at 2.0% biaxial tensile strain. The changes of the conduction band edge can be attributed to the high-symmetry point Γ being more sensitive to strain than K. Thus, the relocation of the conduction-band and valence-band edges in monolayer SnP2S6 and GeP2S6 induces a direct-to-indirect and indirect-to-direct band-gap transition respectively. Consequently, the strain is an effective band engineering scheme which is crucial for the design and development of next-generation nanoelectronic and optoelectronic devices.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

Two-dimensional (2D) materials, such as graphene [1,2] have attracted immense interest because of the exotic physical properties and potential application in nanoelectronic and optoelectronic devices [3]. However, graphene is a semimetal with zero band gap [4], and the absence of bandgap will limit its application in nanoscale optoelectronic and next-generation ultra-high-speed electronic devices [5]. Hence, searching for two-dimensional (2D) materials with suitable bandgap is significant for device applications. The transition metal dichalcogenides (TMDs) [6], hexagonal boron nitride (b-BN) [7], germanene (2D germanium) [8], metal halogenides [9,10] and so on, have received a lot of attention in the fields of materials science, microelectronics, physics, etc. Among these promising candidates, 2D nanoporous metal chalcogen phosphates MP2S6 (M = metal, X = S, Se) also gained considerable attention because of their moderate bandgap [11]. Moreover, the metal chalcogen phosphates MP2X6 have rich properties, such as topological magnetism [12], ferroelectric ordering [13], photocatalytic properties [14], H2 storage and Li intercalation for batteries [15], etc. For example, SnP2S6 is a promising 2D photocatalyst for water splitting as well as a good candidate for thin film electronics and photoelectronics [16]. The novel physical properties of 2D nanoporous metal chalcogen phosphates material have the potential to expand the range of applications in nanoelectronics. [17]
The development of two-dimensional (2D) materials has gained significant attention due to their distinctive properties, such as high surface-to-volume ratio and tunable electronic properties. Strain is a promising avenue for tuning the electric properties of 2D materials [18,19]. Theoretical studies have shown that transition metal dichalcogenides (TMDs) are quite sensitive to tensile strain [20], and strain engineering can shift the conduction band minima (CBM) and valence band maxima (VBM) [20,21,22,23]. For instance, it has been reported that the bandgap of MoS2 can be narrowed under tensile strain in monolayer system [24,25,26]. Moreover, the direct-to-indirect bandgap transition can occur in monolayer MoS2 as the tensile strain increases [27]. The strain-induced band-gap transition in 2D materials has significant implications for the development of next-generation nanoelectronic and optoelectronic devices [28,29,30]. The metal chalcogen phosphates MP2X6 with intrinsic nanoporous structure is expected to be able to effectively tune the electronic properties under strain [31].
In this study, the electronic properties of monolayer metal chalcogen phosphates SnP2S6 and GeP2S6 are explored through first-principles calculations. Monolayer SnP2S6 is found be indirect band-gap type semiconductors with gaps of 1.35eV in equilibrium. While monolayer GeP2S6 is a direct band-gap type semiconductor with a gap of 1.06 eV. The electronic properties of monolayer semiconductors can be effectively engineered by strain with direct-to-indirect or indirect-to-direct band-gap transition. For example, monolayer SnP2S6 undergoes an indirect-to-direct band-gap transition at 4.0% of biaxial compressive (BC) strains. While monolayer GeP2S6 exhibits a direct-to-indirect transition at 2.0% biaxial tensile (BT) strain. These results provide valuable insights into the strain engineering in tunning the electronic structures of the monolayer systems.

2. Calculation method

Density functional theory (DFT) [32] calculation was performed to investigate the electronic properties of monolayer metal chalcogen phosphates of SnP2S6 and GeP2S6 using the Vienna ab-initio simulation package (VASP) [33]. The projector-augmented wave method was adopted with a cutoff energy of 450 eV [33]. The Perdew-Burke-Ernzerhof (PBE) [34] exchange-correlation functional within the generalized gradient approximation (GGA) was utilized. To minimize interactions between vertically periodic layers, a vacuum layer of 25 Å was set in the z direction for the monolayer structures. A 15×15×1 Monkhorst-Pack k-grid mesh was employed for Brillouin zone sampling. Atomic positions were fully optimized until all the Hellmann-Feynman forces on all atoms were less than 0.01 eV/Å.

3. Result and discussion

SnP2S6 and GeP2S6 are members of the family of novel 2D metal thiophosphates. These monolayers are characterized by space group P312 and contain one metal cation (Sn or Ge) and one anionic [P2S6]4- unit as illustrated in Figure 1(a) and (b) [31]. The metal cation is coordinated with six S atoms to form a hexahedron, while each P atom is coordinated with three S atoms in a tetrahedral arrangement as depicted in Figure 1(b). The optimized lattice parameters are 6.13 and 5.99 Å for monolayer SnP2S6 and GeP2S6, respectively, which is consistent with the previous result [35].
The biaxial strain is applied to explore the strain effect on the electronic properties of monolayer SnP2S6 and GeP2S6. The biaxial strain is defined as
δ = Δ a a 0  
where a0 represents the optimized lattice constant when the structure is unstrained and Δa represents the change of the lattice constant after applying a certain strain in the xy plane. Electronic property calculations are presented within a range of δ=−6% to δ=+6%. The negative value of δ denotes compressive strain whereas the positive sign refers to tensile strain.
The electronic band structures of monolayer SnP2S6 and GeP2S6 structures under biaxial strain are investigated. Our calculations reveal that the total energy of the system exhibits a weak dependence on the applied biaxial strain as depicted in Figure 2. The total energy of the relaxed monolayer structures SnP2S6 and GeP2S6 is found to be -42.6808 eV and-42.4794806 eV, respectively. The maximum change of total energy is only around 0.5eV and 0.6eV within the considered strain range. Even though the total energy change may be minimal as the strain is applied, it can still have a substantial impact on the material properties.
The electronic band structure of the unstrained SnP2S6 is presented in Figure 3(a), where the VBM and CBM are located at the K and Γ points, respectively, with an indirect band gap of 1.346 eV. The contribution of different orbitals to the VBM and CBM are investigated by calculating the orbitals resolved density of states. S-p orbitals contribute mostly to the VBM, while Sn-s orbitals have the highest contribution to the CBM, along with a minor contribution from S-p orbitals, as illustrated in Figure 3(a). We investigate the impact of applying homogeneous biaxial strain on the electronic structure of SnP2S6. At 4.0% BC strain, the CBM shifts from the Γ point to the K point, while the VBM remains at the K point, leading to an indirect-to-direct band-gap transition as shown in Figure 3(b).
Similarly, we investigated the electronic structure of the unstrained GeP2S6 and strained system as illustrated in Figure 3(c) and 3(d). Notably, one can notice that both the VBM and CBM are located at the K points for unstrained GeP2S6 monolayer, indicating a direct bandgap semiconductor. As depicted in Figure 3(c), the majority of the orbital contribution to the VBM sources from S-p orbitals, whereas Ge-s orbital dominates the CBM along with a minor contribution from S-p orbitals. Under a 2.0% biaxial tension (BT) strain, we observed a shift of the CBM from the K point to the Γ point, while the VBM remains at the K point. Hence a direct-to-indirect band-gap transition emerges under 2.0% biaxial tension (BT) strain.
To gain further insights into the orbital contributions to the band structure, we evaluate the projected band structure without strain. It is clear that the conduction band edge of system SnP2S6 is primarily contributed by Sn-s orbitals, with additional small contributions from S-pz orbitals and a small contribution from S-px/py orbitals, while the valence band edge is mainly contributed by S-px orbital with a small contribution from S-py orbital in Figure 4(a-d). Similarly, the conduction band edge of the GeP2S6 monolayer is mainly contributed by the Ge-s orbital, while the valence band edge is mainly contributed by the S-px orbital with a small contribution from S-pz orbitals as depicted in Figure 5(a-d).
According to Figure 3(a-d), the transition from indirect to direct bandgap for monolayer SnP2S6 and the transition from direct to indirect bandgap for monolayer GeP2S6 is primarily caused by the shift of the conduction band minimum. To further investigate this phenomenon, we plotted the variation of the energy of the conduction band edge state at the Γ point (CB-Γ) and at the K point (CB-K) as a function of strain as depicted in Figure 6(a)and(b). One can find that both systems exhibit an approximately linear decrease between the energy and strain for both Γ and K points, decreasing with increasing tensile strain and increasing with increasing compressive strain. The high-symmetry point Γ exhibits a higher rate under strain as compared to the K point, indicating the band edge near Γ point is more sensitive to strain. Hence the relative position of the energy bands at Γ and K points reverses under certain strain. In the case of system SnP2S6, when the applied strain is less than -4%, ECB-Γ is smaller than ECB-K with located at K. when the applied strain exceeds -4% ECB-Γ is larger than ECB-K with the CBM is located at the Γ point. In contrast, when the strain is less than 1%, ECB-Γ is larger than ECB-K for monolayer GeP2S6 with the CBM located at the K point. When the strain exceeds 2%, ECB-Γ becomes smaller than ECB-K, and the CBM shifts to the Γ point.
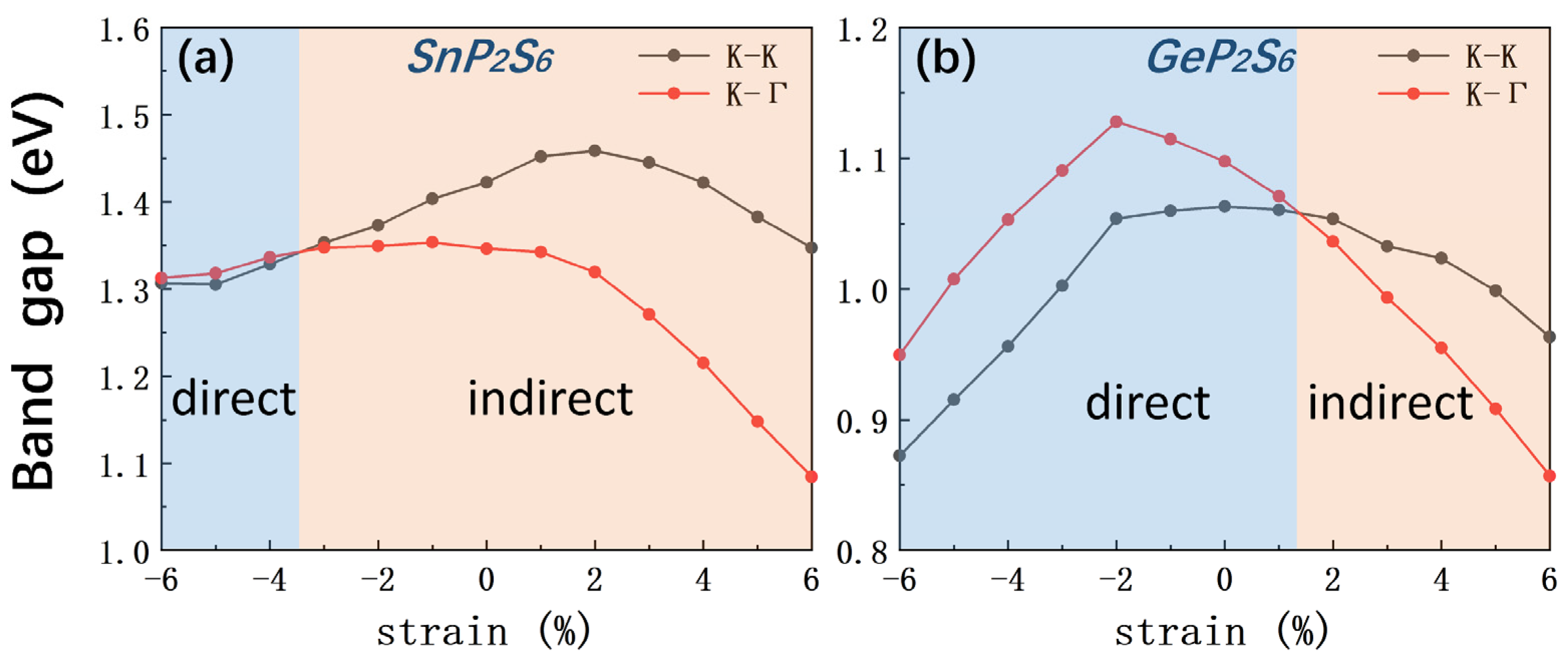
We also studied the variation in the band gap along the different symmetry directions K-K and K-Γ with the strain. The band gaps of SnP2S6 along the symmetric directions K-K and K-Γ direction are very close when the strain is less than -4%, and the difference between the two distinct band gaps along K-K and K-Γ becomes larger when the strain is greater than -4% as illustrated in Figure 7(a). The bandgap changes slightly with compressive strain and significantly with tensile strain. Differently, the difference of bandgap is relatively larger between K-K and K-Γ for monolayer GeP2S6 under compressive strain as compared with that of monolayer SnP2S6. The bandgap changes significantly with both compressive strain and tensile strain as shown in Figure 7(b). These findings provide valuable insights into the design and optimization of 2D materials for electronic and optoelectronic applications.

4. Conclusion

In summary, we have conducted a comprehensive investigation on the electrical properties of monolayer SnP2S6 and GeP2S6 under biaxial strain. The results demonstrate that the monolayer SnP2S6 with an indirect bandgap of 1.346 eV exhibit an indirect-to-direct band-gap transition under 4.0% uniform biaxial compressive (BC) strain. Additionally, we report a direct-to-indirect band-gap transition in the monolayer semiconductor GeP2S6 under a uniform BT strain of 2.0%. The transition occurs because the high-symmetry point Γ is more sensitive to strain than K. Our findings suggest that biaxial strain can effectively tune the electrical properties of monolayer systems which is a promising approach for designing high-performance ultra-fast nanoelectronic and optoelectronic devices based on these materials.

Author Contributions

Conceptualization, J.-L.Z.; methodology, Y.-Z.G.; validation, Y.-EX. and F.Q.; formal analysis, J.-L.Z. and Y.-Z.G.; investigation, J.-L.Z. and Y.-Z.G.; resources, J.-J.H.; data curation, J.-L. Z.; writing—original draft, J. L. Z. and J. R. Y.; writing—review and editing, S. -K.W., Y.-S.L. and Y. B.Z; supervision, J. R.Y., Y.-S.L. and Y. B.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (Nos. 62264010, 12264026, 12004142, 62201268), the Natural Science Foundation of Jiangxi Province, China (Nos. 20212BAB211023, 20224BAB211013) and the Innovation and Entrepreneurship Leading Talent Plan of Jiangxi Province (Nos. Jxsq2023101068).

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
  2. Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A. Two-dimensional gas of massless Dirac fermions in graphene. Nature. 2005, 438, 197–200. [Google Scholar] [CrossRef] [PubMed]
  3. Tang, Q.; Zhou, Z.; Chen, Z. Innovation and discovery of graphene-like materials via density-functional theory computations. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2015, 5, 360–379. [Google Scholar] [CrossRef]
  4. Neto, A.C.; Guinea, F.; Peres, N.M.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef]
  5. Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.E.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science. 2004, 306, 666–669. [Google Scholar] [CrossRef]
  6. Kanoun, M.B.; Goumri-Said, S. Tailoring optoelectronic properties of monolayer transition metal dichalcogenide through alloying. Materialia. 2020, 12, 100708. [Google Scholar] [CrossRef]
  7. Chettri, B.; Patra, P.K.; Verma, S.; Rao, B.K.; Verma, M.L.; Thakur, V.; Kumar, N.; Hieu, N.N.; Rai, D.P. Induced magnetic states upon electron–hole injection at B and N sites of hexagonal boron nitride bilayer: A density functional theory study. Int J Quantum Chem. 2021, 121, e26680. [Google Scholar] [CrossRef]
  8. Raya, S.S.; Ansari, A.S.; Shong, B. Adsorption of gas molecules on graphene, silicene, and germanene: A comparative first-principles study. Surf. Interfaces. 2021, 24, 101054. [Google Scholar] [CrossRef]
  9. Lu, F.; Wang, W.; Luo, X.; Xie, X.; Cheng, Y.; Dong, H.; Liu, H.; Wang, W.H. A class of monolayer metal halogenides MX2: electronic structures and band alignments. Appl. Phys. Lett. 2016, 108, 132104. [Google Scholar] [CrossRef]
  10. Liu, P.; Lu, F.; Wu, M.; Luo, X.; Cheng, Y.; Wang, X.W.; Wang, W.; Wang, W.H.; Liu, H.; Cho, K. Electronic structures and band alignments of monolayer metal trihalide semiconductors MX 3. J. Mater. Chem. C. 2017, 5, 9066–9071. [Google Scholar] [CrossRef]
  11. Susner, M.A.; Chyasnavichyus, M.; McGuire, M.A.; Ganesh, P.; Maksymovych, P. Metal thio-and selenophosphates as multifunctional van der Waals layered materials. Adv. Mater. 2017, 29, 1602852. [Google Scholar] [CrossRef] [PubMed]
  12. Sugita, Y.; Miyake, T.; Motome, Y. Multiple dirac cones and topological magnetism in honeycomb-monolayer transition metal trichalcogenides. Phys. Rev. B. 2018, 97, 035125. [Google Scholar] [CrossRef]
  13. Chyasnavichyus, M.; Susner, M.A.; Ievlev, A.V.; Eliseev, E.A.; Kalinin, S.V.; Balke, N.; Morozovska, A.N.; McGuire, M.A.; Maksymovych, P. Size-effect in layered ferrielectric CuInP2S6. Appl. Phys. Lett. 2016, 109, 172901. [Google Scholar] [CrossRef]
  14. Zhang, X.; Zhao, X.; Wu, D.; Jing, Y.; Zhou, Z. MnPSe3 monolayer: a promising 2d visible-light photohydrolytic catalyst with high carrier mobility. Adv. Sci. 2016, 3, 1600062. [Google Scholar] [CrossRef] [PubMed]
  15. Susner, M.A.; Chyasnavichyus, M.; McGuire, M.A.; Ganesh, P.; Maksymovych, P. Metal thio-and selenophosphates as multifunctional van der Waals layered materials. Adv. Mater. 2017, 29, 1602852. [Google Scholar] [CrossRef] [PubMed]
  16. Jing, Y.; Zhou, Z.; Zhang, J.; Huang, C.; Li, Y.; Wang, F. SnP 2 S 6 monolayer: a promising 2D semiconductor for photocatalytic water splitting. Phys. Chem. Chem. Phys. 2019, 21, 21064–21069. [Google Scholar] [CrossRef]
  17. Susner, M.A.; Chyasnavichyus, M.; McGuire, M.A.; Ganesh, P.; Maksymovych, P. Metal thio-and selenophosphates as multifunctional van der Waals layered materials. Adv. Mater. 2017, 29, 1602852. [Google Scholar] [CrossRef]
  18. Jacobsen, R.S.; Andersen, K.N.; Borel, P.I.; Fage-Pedersen, J.; Frandsen, L.H.; Hansen, O.; Kristensen, M.; Lavrinenko, A.V.; Moulin, G.; Ou, H.; et al. Strained silicon as a new electro-optic material. Nature. 2006, 441, 199–202. [Google Scholar] [CrossRef]
  19. Falvo, M.R.; Clary, G.J.; Taylor, R. 2.; Chi, V.; Brooks Jr, F.P.; Washburn, S.; Superfine, R. Bending and buckling of carbon nanotubes under large strain. Nature. 1997, 389, 582–584. [Google Scholar] [CrossRef]
  20. Johari, P.; Shenoy, V.B. Tuning the electronic properties of semiconducting transition metal dichalcogenides by applying mechanical strains. ACS Nano. 2012, 6, 5449–5456. [Google Scholar] [CrossRef]
  21. Shi, H.; Pan, H.; Zhang, Y.W.; Yakobson, B.I. Quasiparticle band structures and optical properties of strained monolayer MoS 2 and WS 2. Phys. Rev. B. 2013, 87, 155304. [Google Scholar] [CrossRef]
  22. Horzum, S.; Sahin, H.; Cahangirov, S.; Cudazzo, P.; Rubio, A.; Serin, T.; Peeters, F.M. Phonon softening and direct to indirect band gap crossover in strained single-layer MoSe 2. Phys. Rev. B. 2013, 87, 125415. [Google Scholar] [CrossRef]
  23. Lee, Y.; Cho, S.B.; Chung, Y.C. Tunable indirect to direct band gap transition of monolayer Sc2CO2 by the strain effect. ACS Appl. Mater. Interfaces. 2014, 6, 14724–14728. [Google Scholar] [CrossRef]
  24. Falvo, M.R.; Clary, G.J.; Taylor, R.2.; Chi, V.; Brooks Jr, F.P.; Washburn, S.; Superfine, R. Bending and buckling of carbon nanotubes under large strain. Nature. 1997, 389, 582–584. [Google Scholar] [CrossRef]
  25. He, K.; Poole, C.; Mak, K.F.; Shan, J. Experimental demonstration of continuous electronic structure tuning via strain in atomically thin MoS2. Nano Lett. 2013, 13, 2931–2936. [Google Scholar] [CrossRef]
  26. Conley, H.J.; Wang, B.; Ziegler, J.I.; Haglund Jr, R.F.; Pantelides, S.T.; Bolotin, K.I. Bandgap engineering of strained monolayer and bilayer MoS2. Nano Lett. 2013, 13, 3626–3630. [Google Scholar] [CrossRef]
  27. Yun, W.S.; Han, S.W.; Hong, S.C.; Kim, I.G.; Lee, J.D. Thickness and strain effects on electronic structures of transition metal dichalcogenides: 2H-M X 2 semiconductors (M= Mo, W. X= S, Se, Te). Phys. Rev. B. 2012, 85, 033305. [Google Scholar] [CrossRef]
  28. Zhong, F.; Wang, H.; Wang, Z.; Wang, Y.; He, T.; Wu, P.; Peng, M.; Wang, H.; Xu, T.; Wang, F.; et al. Recent progress and challenges on two-dimensional material photodetectors from the perspective of advanced characterization technologies. Nano Res. 2021, 14, 1840–1862. [Google Scholar] [CrossRef]
  29. Wang, L.; Boutilier, M.S.; Kidambi, P.R.; Jang, D.; Hadjiconstantinou, N.G.; Karnik, R. Fundamental transport mechanisms, fabrication and potential applications of nanoporous atomically thin membranes. Nat. Nanotechnol. 2017, 12, 509–522. [Google Scholar] [CrossRef] [PubMed]
  30. Zhao, J.; Ma, D.; Wang, C.; Guo, Z.; Zhang, B.; Li, J.; Nie, G.; Xie, N.; Zhang, H. Recent advances in anisotropic two-dimensional materials and device applications. Nano Res. 2021, 14, 897–919. [Google Scholar] [CrossRef]
  31. Lin, M.; Liu, P.; Wu, M.; Cheng, Y.; Liu, H.; Cho, K.; Wang, W.H.; Lu, F. Two-dimensional nanoporous metal chalcogenophosphates MP2X6 with high electron mobilities. Appl. Surf. Sci. 2019, 2019 493, 1334–1339. [Google Scholar] [CrossRef]
  32. Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
  33. Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B. 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
  34. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
  35. Whangbo, M.H.; Brec, R.; Ouvrard, G.; Rouxel, J. Reduction sites of transition-metal phosphorus trichalcogenides MPX3. Inorg. Chem. 1985, 24, 2459–2461. [Google Scholar] [CrossRef]
Preprints 75614 g001
Figure 1. (a) Top and (b) side views of monolayer MP2S6. Blue, green, and yellow spheres represent M (M = Sn, Ge) atoms, P atoms, and S atoms, respectively.
Figure 1. (a) Top and (b) side views of monolayer MP2S6. Blue, green, and yellow spheres represent M (M = Sn, Ge) atoms, P atoms, and S atoms, respectively.
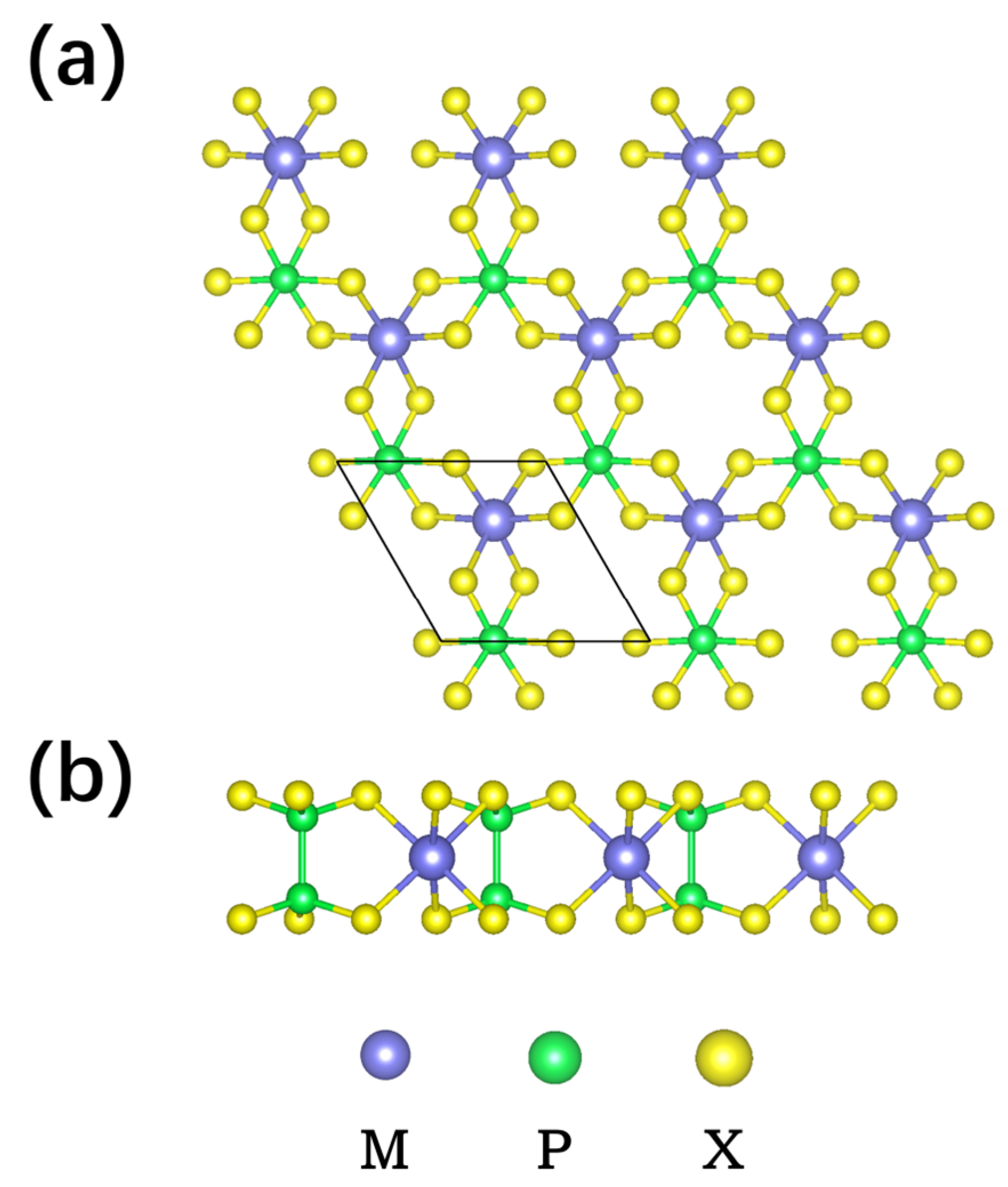
Preprints 75614 g001
Preprints 75614 g002
Figure 2. (a) Total energy vs. strain in monolayer SnP2S6, (b) Total energy vs. strain in monolayer GeP2S6.
Figure 2. (a) Total energy vs. strain in monolayer SnP2S6, (b) Total energy vs. strain in monolayer GeP2S6.
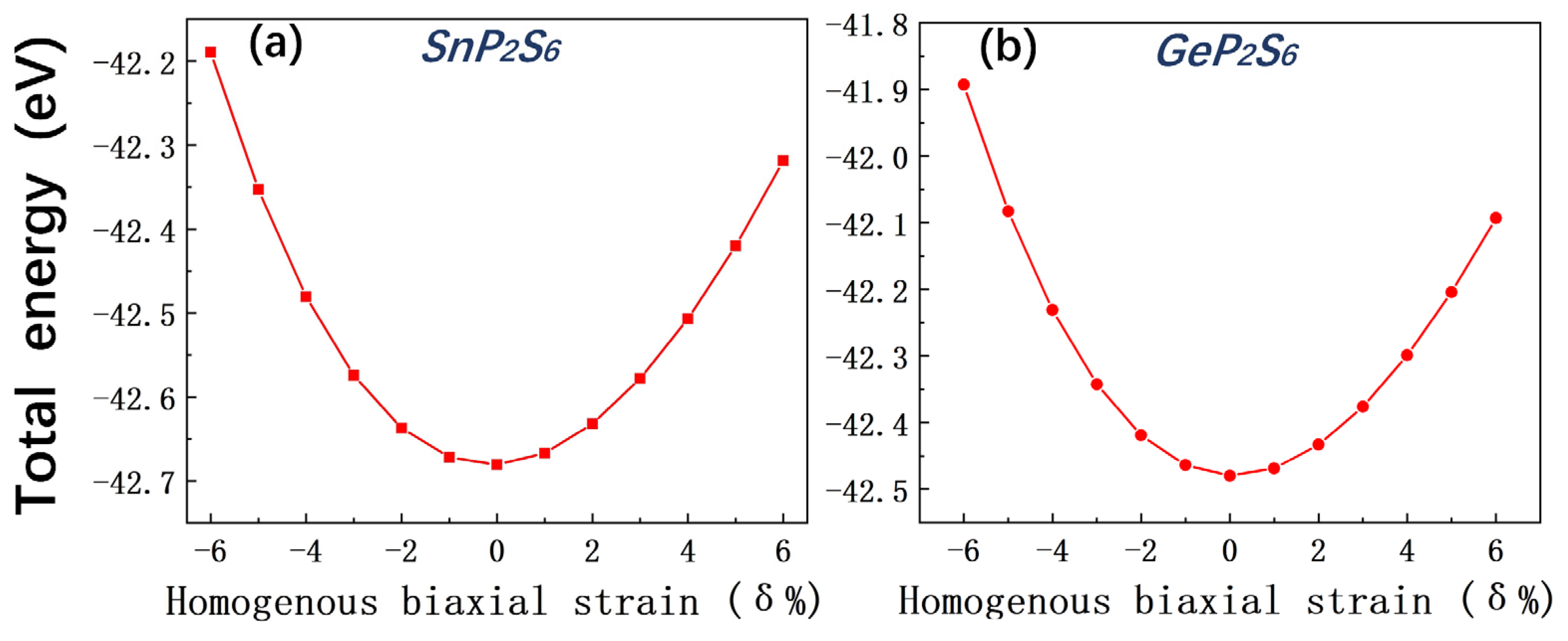
Preprints 75614 g002
Preprints 75614 g003
Figure 3. (a,b) Monolayer SnP2S6 electronic band structure and angular-momentum resolved density of states at 0.0% and 4.0% BC strain, respectively. (c,d) The monolayer GeP2S6 at 0.0% and 2.0% BT strain.
Figure 3. (a,b) Monolayer SnP2S6 electronic band structure and angular-momentum resolved density of states at 0.0% and 4.0% BC strain, respectively. (c,d) The monolayer GeP2S6 at 0.0% and 2.0% BT strain.
Preprints 75614 g003
Preprints 75614 g004
Figure 4. Orbital-resolved band structure in the case of no strain and strain of SnP2S6. Red circles represent the corresponding VBM and CBM in the band structures.
Figure 4. Orbital-resolved band structure in the case of no strain and strain of SnP2S6. Red circles represent the corresponding VBM and CBM in the band structures.
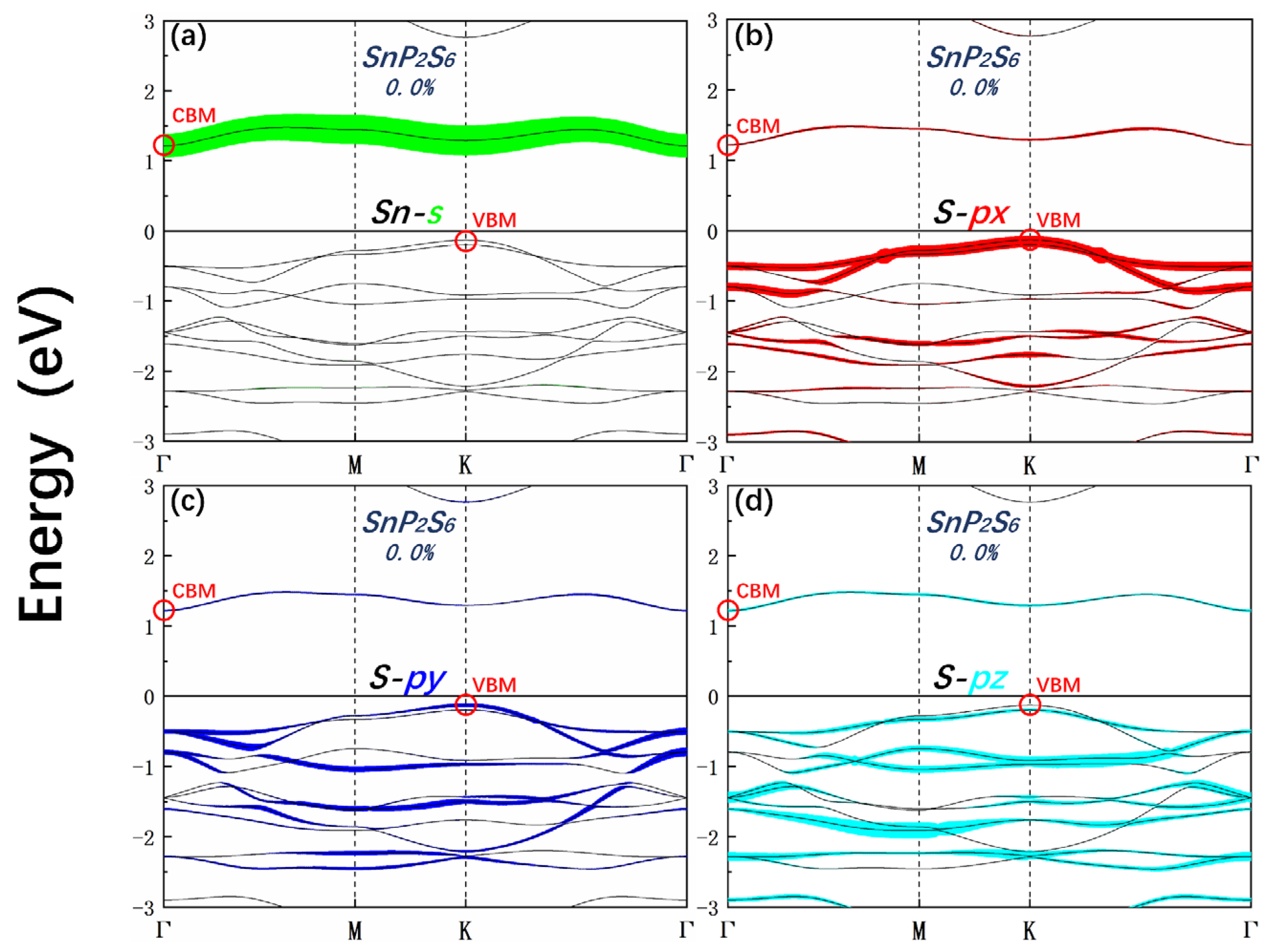
Preprints 75614 g004
Preprints 75614 g005
Figure 5. Orbital-resolved band structure in the case of no strain and strain of GeP2S6. Red circles represent the corresponding VBM and CBM in the band structures.
Figure 5. Orbital-resolved band structure in the case of no strain and strain of GeP2S6. Red circles represent the corresponding VBM and CBM in the band structures.
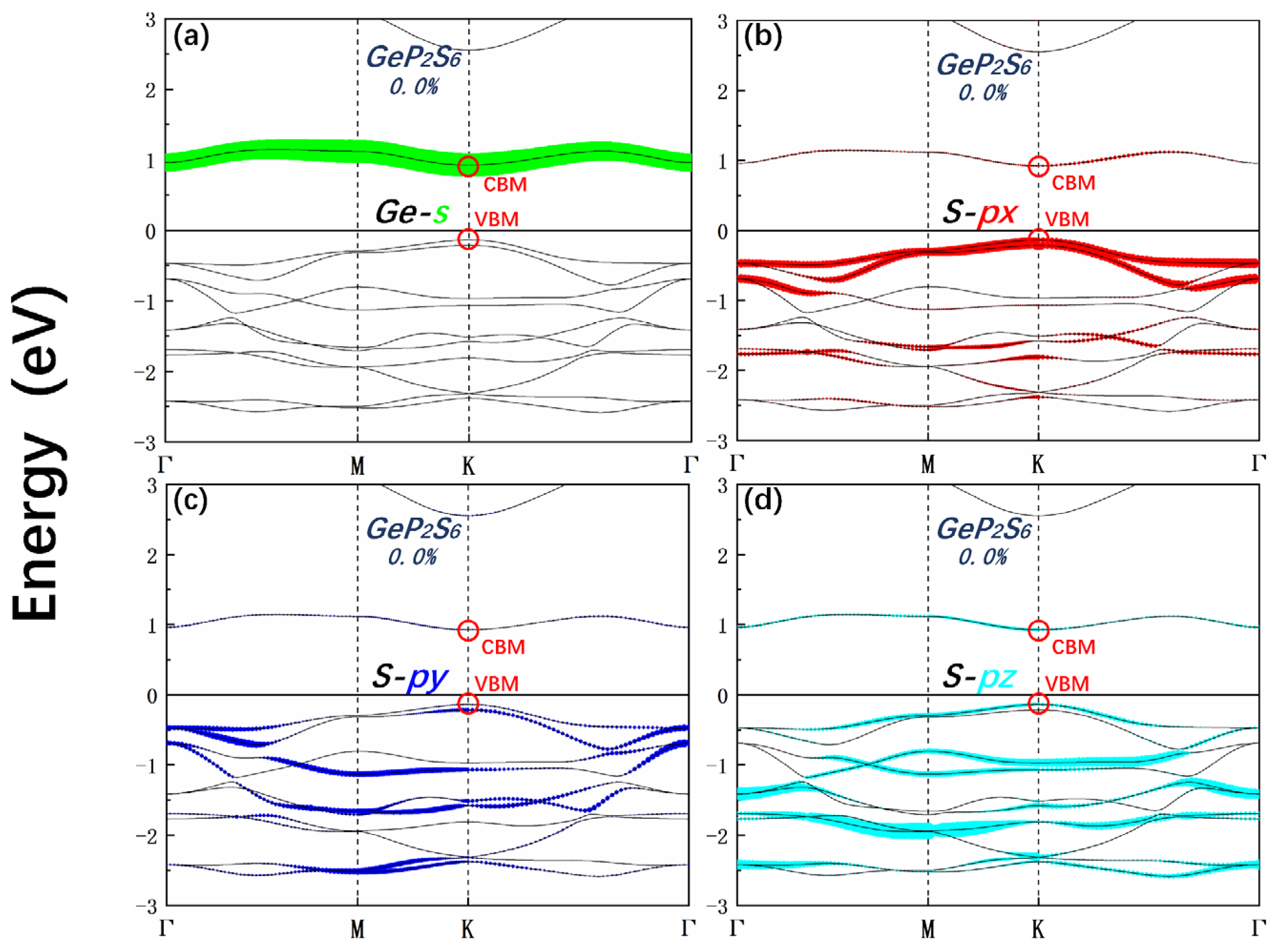
Preprints 75614 g005
Preprints 75614 g006
Figure 6. The variation of CBM energy at the Γ point (CB-Γ) and at the K point (CB-K) with strain for SnP2S6 (a) and GeP2S6 (b).
Figure 6. The variation of CBM energy at the Γ point (CB-Γ) and at the K point (CB-K) with strain for SnP2S6 (a) and GeP2S6 (b).
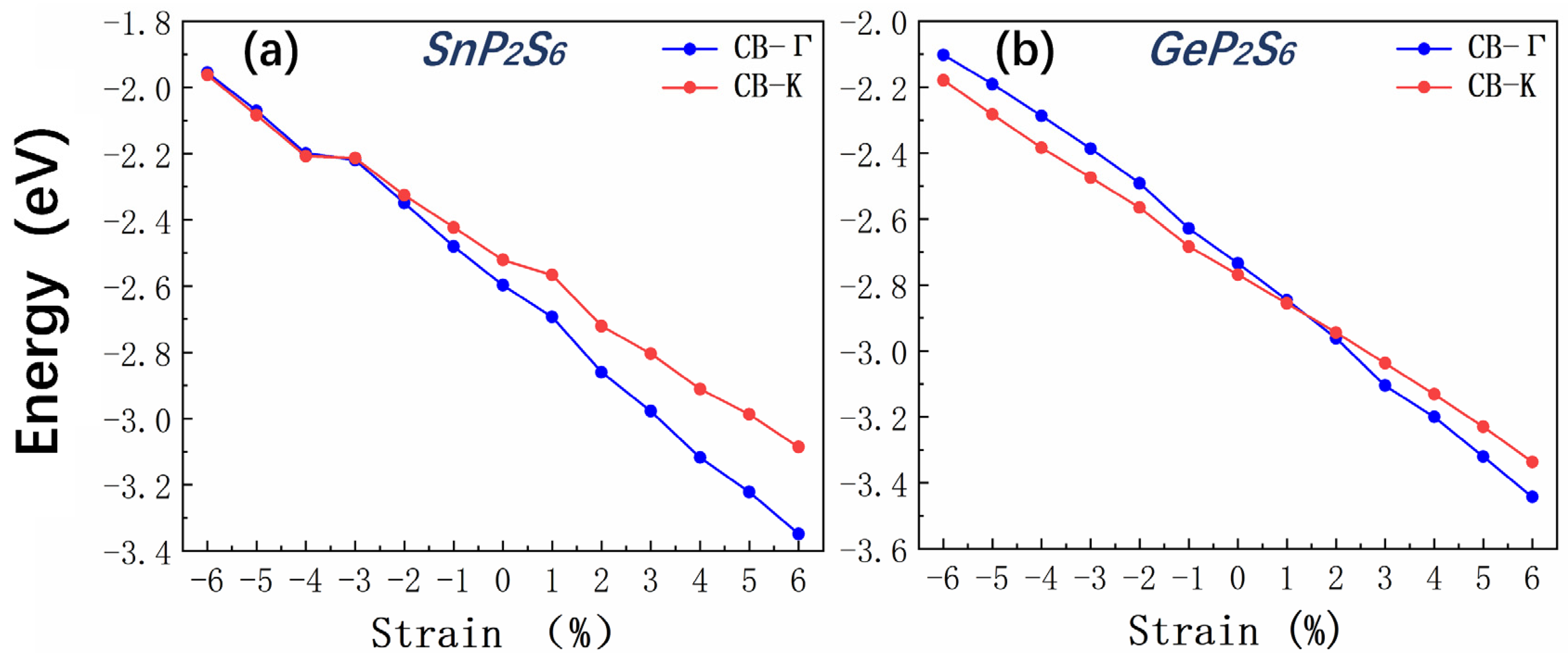
Preprints 75614 g006
Preprints 75614 g007
Figure 7. (a) Band-gap variations along the symmetric directions K-K and K-Γ in SnP2S6, (b) Band-gap variations along the symmetric directions K-K and K-Γ in GeP2S6.
Figure 7. (a) Band-gap variations along the symmetric directions K-K and K-Γ in SnP2S6, (b) Band-gap variations along the symmetric directions K-K and K-Γ in GeP2S6.
Preprints 75614 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated