Prerpints.org logo
Preprint
Article

A Deep Neural Network Regression of the Cahn–Hilliard Single-Particle Thermal Model for LiFePO4 Batteries

Altmetrics

Downloads

267

Views

104

Comments

0

Submitted:

04 June 2023

Posted:

05 June 2023

You are already at the latest version

Alerts
Abstract
Lithium-ion batteries serve as the primary sources of power for electric vehicles (EVs) and hybrid electric vehicles (HEVs). For vehicle applications, battery management systems (BMSs) are nec-essary to protect lithium-ion batteries from overheating and to ensure optimum vehicle perfor-mance. Our approach to developing a BMS was based on recent advances in the application of phase field models for lithium-ion batteries. In particular, our reduced-order model (ROM) uti-lized a dataset generated from the COMSOL® Multiphysics simulation of the Cahn–Hilliard equation for a single particle of a lithium iron phosphate (LiFePO4) cathode: an example of using a reduced-order model (ROM) based on a single-particle model (SPM). The main innovation of our ROM is that the SPM is fully coupled to a heat transfer model at the battery cell level. We utilized principal component analysis to identify a lower-order model that could reproduce the battery’s voltage and temperature response for ambient temperatures ranging from 253 to 298 K and for discharge rates ranging from 1 C to 20.5 C. The reduced-order dataset was then fitted to the ex-perimental data for an A123 Systems 26650 2.3 Ah cylindrical battery using deep neural network (DNN) regression.
Keywords: 
Subject: Engineering  -   Chemical Engineering

1. Introduction

Global oil resources will eventually dry up and fossil-fueled vehicles are a major source of greenhouse emissions. There is an ongoing global trend of electrifying transportation, and as a result, intensive research is being conducted into electric vehicles and hybrid electric vehicles (EVs and HEVs) [1,2]. Lithium-ion batteries have become the most promising choice for EVs due to their high energy density and long cycle life [3,4]. For EV applications, battery management systems (BMSs) are necessary to prevent Li-ion batteries from overheating and overcharging and avoid potential thermal runaway. Currently, BMSs cannot store and process large amounts of data while managing the battery’s state of charge (SOC), voltage, and temperature in real time [5,6,7]. To address this shortcoming, additional research is needed to develop reduced-order models (ROM) that can both model complex battery mechanisms and provide real-time management data. Applications of machine learning (ML) and artificial intelligence (AI) are fertile areas for eventual solutions to this problem.
Models that describe battery dynamic processes at all levels are not feasible. Therefore, mechanistic battery models, referred to as full-order models (FOMs), need to be tailored to specific purposes that require a deep understanding of a particular aspect of the battery’s operation and performance. Many mechanistic models have been developed specifically to describe battery thermal behavior [8,9,10,11,12]. In general, models for analysis and diagnosis purposes employ detailed simulations of the battery’s physics and, thus, are often multidimensional, multiphysics models and are computationally slow. Models for control and optimization applications are usually computationally fast, but provide a limited description of the underlying physics. The most commonly used mechanistic model for single-battery cells is a lumped parameter simplification of a FOM called the pseudo-two-dimensional (P2D) model. Even given P2D simplifications of battery homogeneity and a constant electrode thickness, P2D models still use more than fifteen parameters specific to a particular battery and their computational cost is still too high for control and optimization applications. On the other hand, P2M parameters are too lumped to provide much insight into the underlying phenomena [13,14]. Decades of research have been conducted to develop reduced-order models (ROMs) that adequately retain the robustness of FOMs without excessive computational complexity. The state of the art for the various methods of achieving Li-ion battery ROMs has recently been reviewed in the literature [15,16]. We limit our following discussion of such methods to equivalent circuit models (ECMs), their model-based extensions, and the single-particle model approximation. These methods are most pertinent since our ROM, developed in the following sections, is a single-particle application and is most likely to be used instead of or alongside an ECM.
ECMs that do not consider fundamental physics have been extensively used to imitate the relationships between battery input and output systems while offering real-time computation [17,18,19,20,21,22]. ECMs use electrical circuits to simulate lithium-ion cells utilizing capacitors to shape the battery capacity, while variable resistors and controlled-voltage sources shape the temperature effect or SOC variations. Black-box modeling is another extensively applied method to provide real-time computation. It relies on developing an equivalent transform function with different inputs and outputs. Like ECMs, this method depends on experimental data for a specified battery [23]. ECMs and transform functions are generally implemented in a “mixed approach” along with thermal and aging models, as shown in Figure 1 [24].
Model-based methods have been developed that have greatly enhanced the basic ECM. Some of the predominant model-based methods have been recently reviewed in the literature including the Luenberger, sliding mode, Kalman filter, and proportional integral (PIO) methods [25,26,27,28,29,30]. Model-based methods have a battery model at their core that uses measured current and voltage signals to provide a closed-loop estimation method. These methods typically use static models where model parameters are applied offline and assumed to not change over time. However, these models often do not ensure sufficient accuracy over a broad range of operation conditions and long time frames. In light of this, efforts have been made towards online model adaptation methods, including population-based optimization, dual filtering, and least squares (LS)-based methods such as moving window LS, continuous-time LS, and recursive least squares (RLS) [31,32,33].
Lithium iron phosphate (LiFePO4) is the most frequently used phosphate-based cathode material in Li-ion batteries. LiFePO4 has a strong tendency to separate into solid high-Li+-concentration and low-Li+-concentration phases, leading to the battery’s characteristic broad voltage plateau at room temperature [34,35,36,37,38,39]. Traditionally, mathematical models of intercalation dynamics in LiFePO4 cathodes were based on spherical diffusion or the shrinking core concept [40,41,42]. However, recent experimental and theoretical progress suggests that a more realistic SPM should encompass a phase field model for equilibrium and nonequilibrium solid-solution transformations [43,44,45,46,47]. A phase-field model is a computational method for modeling morphological and microstructure evolution in materials. They have been proposed for solid-state phase transformations, grain growth and coarsening, microstructure evolution in thin films, and crack propagation [48,49,50,51]. Research is currently underway that seeks to bridge the gap between phase-field mesoscale models and macro battery properties. For example, (Yuan et al. [52], 2021) recently used a phase field modeling approach to develop a physics-based, fully coupled model that bridges dendrite and crack propagation at the micro level with macrostate battery charging and discharging [53]. Another application (Zeng & Bazant [54], 2013) demonstrated a method for estimating the voltage plateau of LiFePO4 batteries based on the Cahn–Hilliard phase field model solution for a single cathode particle. Our ROM was motivated by (Zeng & Bazant, 2013), and the spatial mass transfer elements of our 3-D COMSOL® Multiphysics finite element solution are similar to their 1-D, isotropic, and isothermal solution. The major enhancement of our single-particle model (SPM) is that it is a multiphysics thermal model that fully couples the battery cell’s heat transfer model. Statistically, we relate the SPM simulation to battery cell property estimation. Specifically, the plateauing effect of the battery’s voltage response at higher ambient temperatures and the apparent diffusion-controlled behavior at lower temperatures are related to the SPM by statistical inference. Our SPM is a specific example of a widely used method for order reduction in P2D based on a single-particle model that aims to enhance computational run time while retaining elements of the underlying physics, as opposed to an ESM [55,56]. In the single-particle thermal model preparation, the local potential and concentration gradients in the electrolyte phase were ignored and accounted for by utilizing a lumped solution resistance term. Likewise, the potential gradient in the solid phase of the electrodes was dismissed, and the porous electrode was considered as a large number of individual particles, all subjected to the same conditions. These assumptions are generally only valid under relatively low current rates and the SPM is not recommended for high-power applications, such as fast EV charging and operations involving high-power pulses, but it is well-suited to daily EV driving, where the operating ranges are less extreme. These shortcomings of the SPM are not prohibitive for our ROM since we did not attempt to model the battery voltage response by directly scaling up the SPM, but sought to only retain enough information from the SPM to make statistical inferences concerning the macro battery properties. The ROM was realized by subjecting the raw simulation results from the COMSOL® Multiphysics simulation data to principal component analysis (PCA) to determine the lowest-order simulation dataset capable of fitting the experimental data using deep neural network (DNN) regression. We validated our SPM based on available experimental data for the A123 Systems 26650 2.3 Ah battery [57].

2. Methods and Materials

The scope of our modelling effort is as follows
  • Use experimental charge/discharge and heat transfer data for the A123 Systems 26650, 2.3 Ah lithium-ion battery to estimate the parameters of our SPM.
  • Use the simulation results from the SPM and experimental data to train and test a DNN.
  • Train and test the same DNN with a similar data set except it is derived from real time operation data for the extreme road test: Up Mount Sano in Huntsville, AL
We are stating this here to avoid confusion by our discussion of the implementation of the SPM and DNN in an actual BMS in the following sections.

2.1. COMSOL Simulation of the Cahn–Hilliard Single-Particle Model

Our SPM poses the Cahn–Hilliard equation in COMSOL® Multiphysics’ standard PDF format as two coupled second-order PDEs in ion concentration and chemical potential, respectively. Details of the model variables along with all parameter magnitudes and units from the following equations are given below in the nomenclature section. We assumed the particles to be spherical and isotropic. The model equations are given below, where the overbar denotes dimensionless parameters and variables. We provide only the main points of the derivation of the Cahn–Hilliard equation and refer the reader to (Zeng & Bazant, 2013) for more details. The diffusional chemical potential based on the regular solution model and acquired from the Cahn–Hilliard free energy functional is
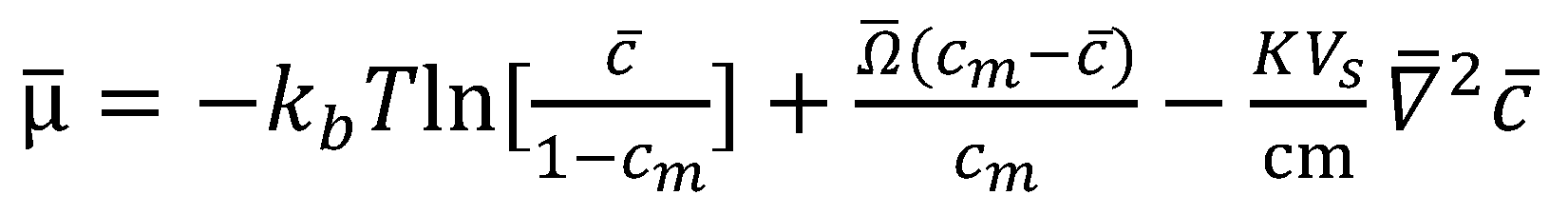
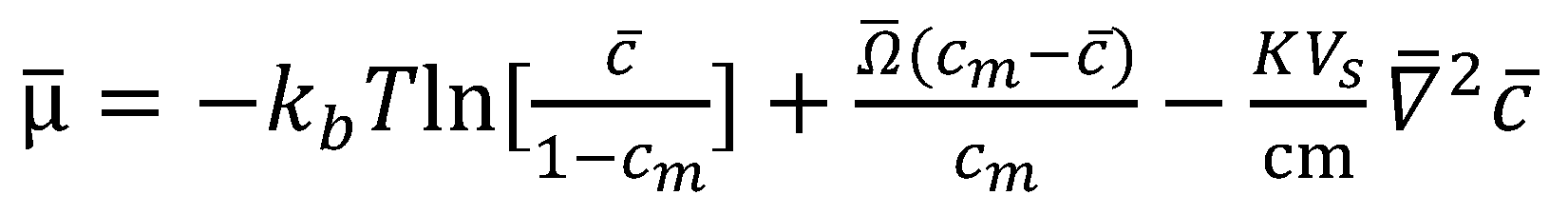
Preprints 75636 i001
The basic equation of evolution for mass conservation is
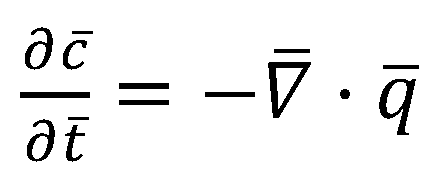
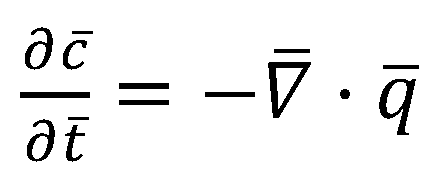
Preprints 75636 i002
The ion flux is driven by the gradient of the diffusional chemical potential as
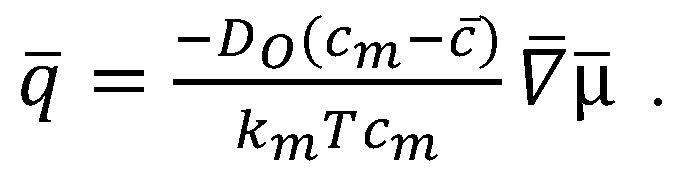
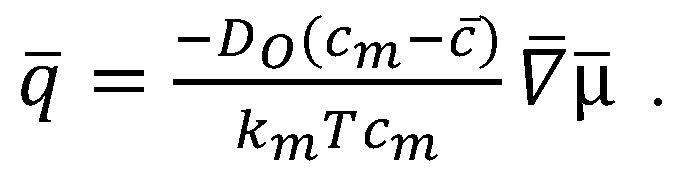
Preprints 75636 i003
Voltage enters the Cahn–Hilliard SPM through Butler–Volmer kinetics obtained from transition state theory for concentrated solutions as
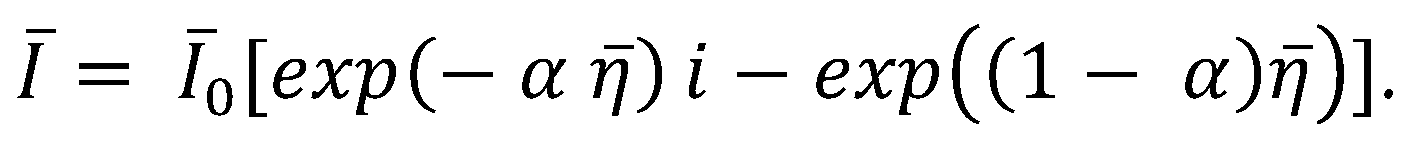Preprints 75636 i004
where α is the electron transfer symmetry factor, η = Δϕ − Δϕeq is the surface overpotential because of the activation polarization, Δϕ is the local voltage drop across the interface, and Δϕeq is the Nernst equilibrium voltage. The boundary conditions we implemented in the dimensionless form are
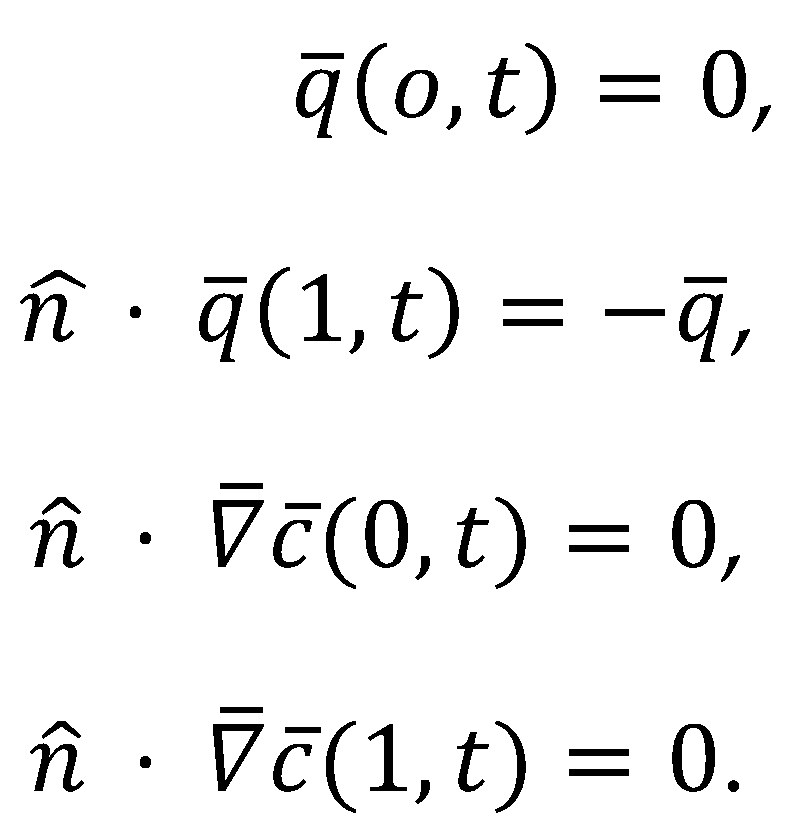
Preprints 75636 i005

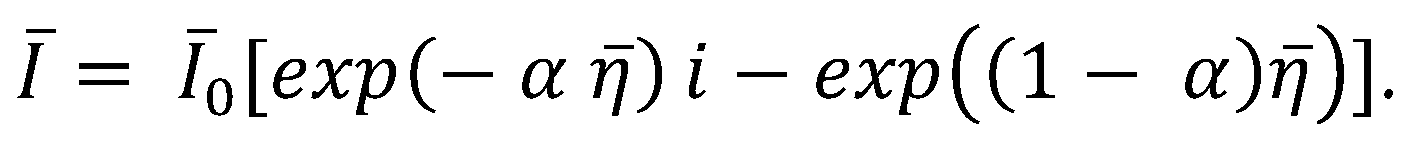
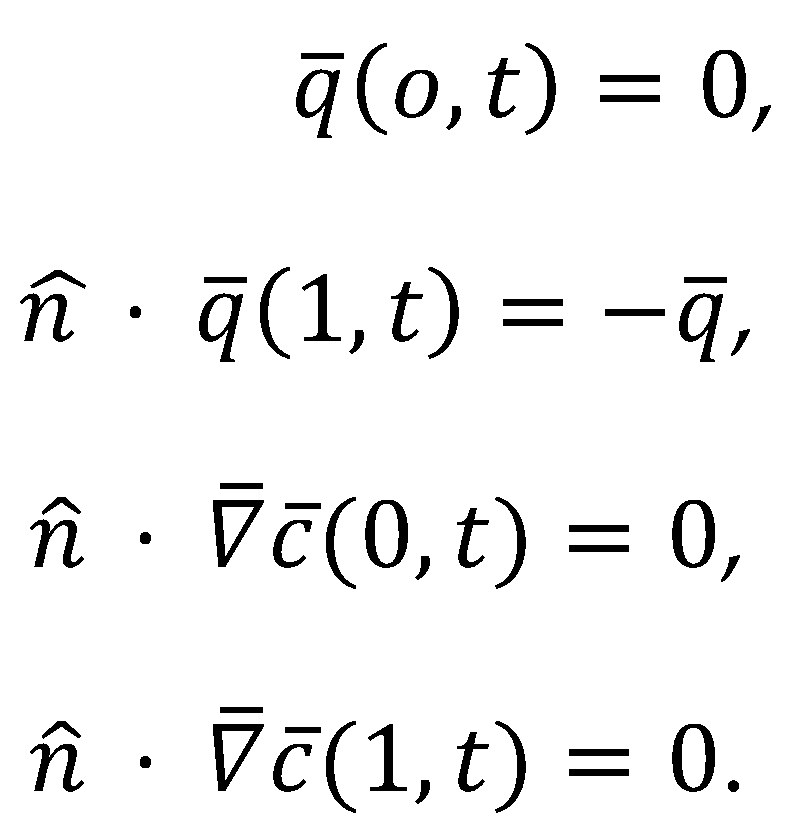
2.2. Coupling the Heat Transfer Model to the Cahn–Hilliard Equation

Transient temperature response and thermal power conservation were incorporated into the ROM by an enthalpy balance on the bulk battery. An A123 Systems 26650 2.3 Ah cylindrical battery was selected because it is extensively studied and property data are readily available. The battery specifications are shown in Table 1.
A cylindrical Li-ion battery is constructed by rolling a stack of cathode/separator/anode layers. The individual layered sheets are thin, and lumped parameters are used. Therefore, material properties such as thermal conductivity, density, and specific heat capacity are presumed to be constant in a homogeneous and isotropic body. In the axial direction, the thermal conductivity is one or two orders of magnitude higher than in the radial direction, leading to a relatively uniform temperature distribution in the axial direction [58,59]. Additionally, considering natural convection, the heat transfer at the surface is much smaller than the internal heat transfer by conduction, leading to negligible temperature gradients inside the battery. Based on these assumptions, the energy balance equation in the battery can be expressed by one bulk volume-averaged temperature. To estimate the thermal response of the battery, we utilized a simplified energy balance equation for the enthalpy change for electrochemical reactions [60]. Assuming a constant system volume and pressure and neglecting heat generation because of enthalpy of mixing, the energy balance equation is presented as
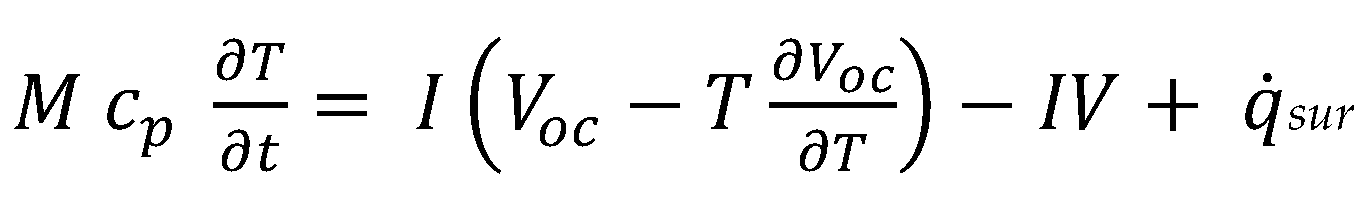
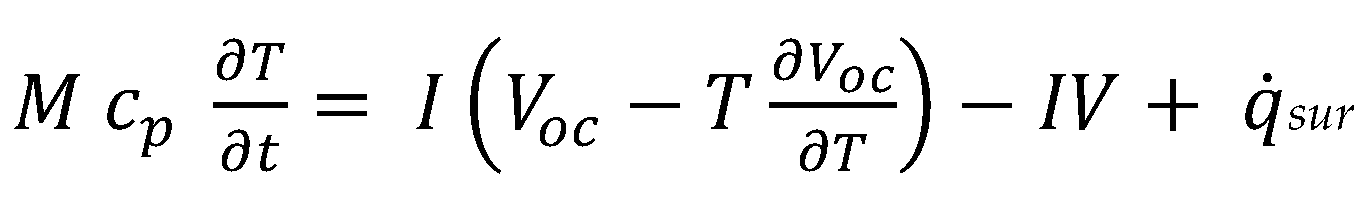
Preprints 75636 i006
The term T ∂ V o c ∂ T stands for reversible heat generation and can be calculated from the entropy of the reaction [61]. In this study, this reversible heat generation was ignored for simplicity. This simplification is justified since it is insignificant for the LiFePO4 chemistry [62,63]. Assuming this simplification, the OCV becomes a function of SOC only, and Equation (5) was solved exactly for the battery’s temperature response.
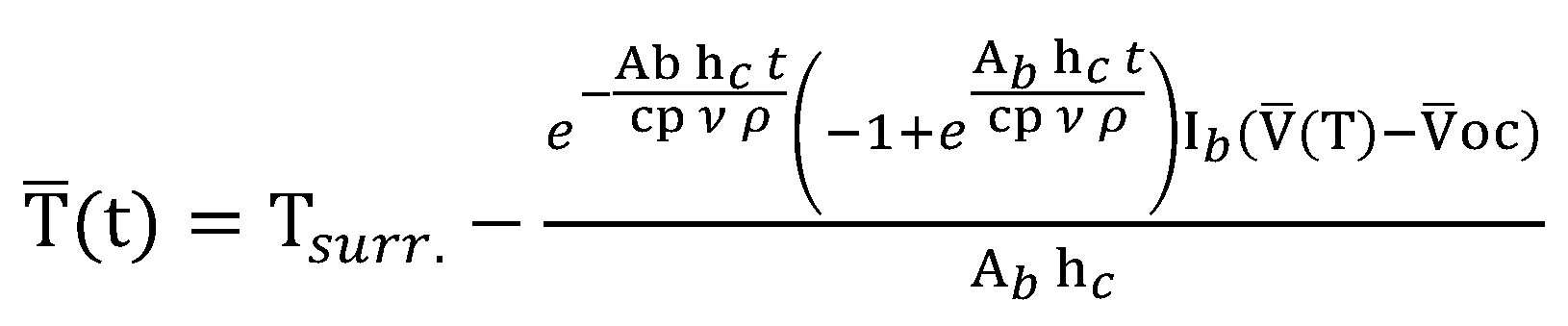
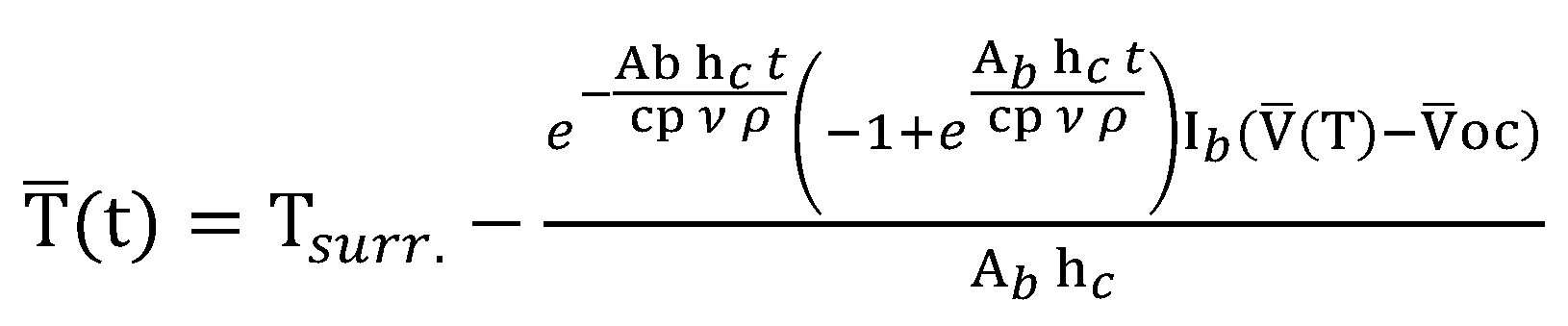
Preprints 75636 i007
The temperature enters the Cahn–Hilliard model via Equation (1) as
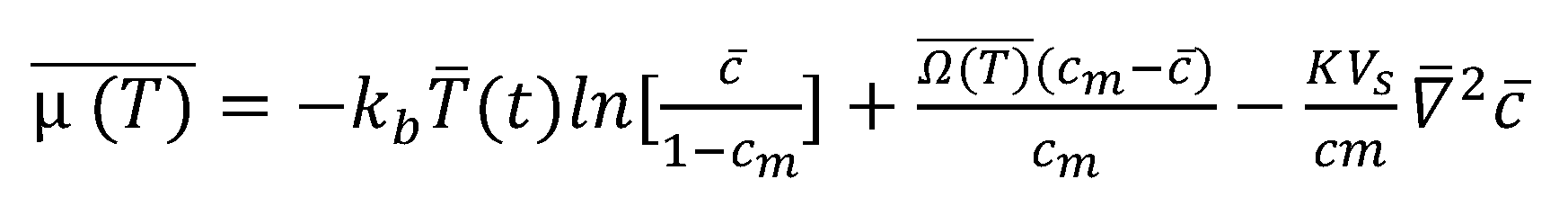
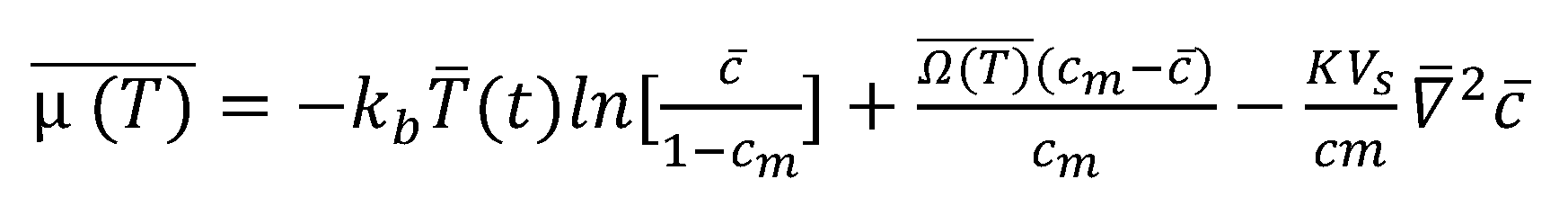
Preprints 75636 i008
Assuming that the ion activity in the electrolyte adjacent to the particle (based on the dimensionless ion concentration) is 1.0, Δϕeq = −µ/e. This provides the voltage profile for the single-particle battery V = V θ + η − µ / e , where Vθ is the standard potential defined by the half-cell voltage (3.42 V vs. Li metal). The solution for η gives the voltage response of the single-particle battery as
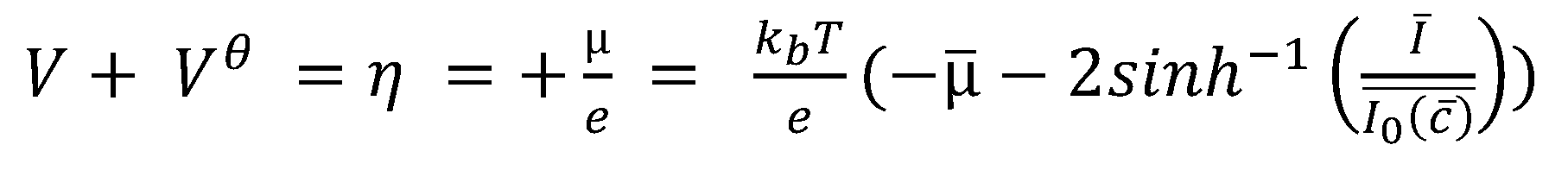
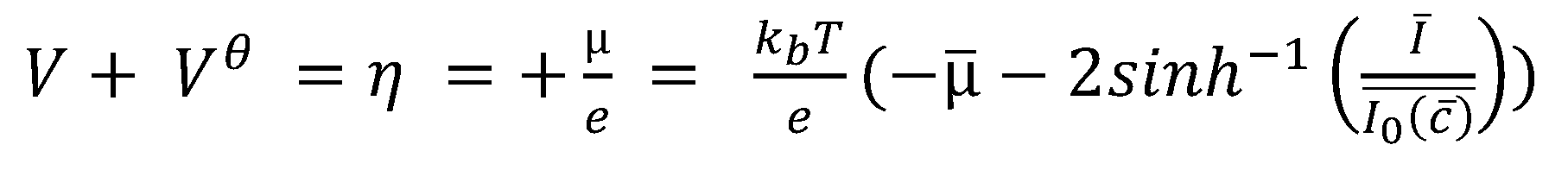
Preprints 75636 i009

2.3. Digital Twin Configuration of BMS

In this section we describe how our SPM and DNN fit into an actual BMS. This is necessary because both components must have on-board and off-board configurations The value of our approach is realized in conjunction with a digital-twin (DT) configuration with an offboard COMSOL® Multiphysics SPM simulation and training of the DNN, allowing the ROM to be periodically updated by retraining the DNN for aging batteries and actual operating conditions. In this configuration, only the trained DNN predictor function is onboard and in real time. Our approach to implementing a DT for lithium-ion batteries follows the process of (Singh et al. [61], 2021). There is some ambiguity as to what constitutes a DT and it may be more appropriate to refer to our process as a part of the DT for the entire EV but the main focus is to designate on-board and off-board components and the flow of information between the components. At a minimum the DT configuration for a BMS, as shown schematically in Figure 2, shows the role of the SPM and the DNN. In Figure 2 we refer to the COMSOL® Multiphysics finite element simulation of the SPM in the terminology of (Singh et al., 2021) as a heavyweight model because it has a relatively larger number of parameters that are related to the actual underlying physics of the battery. The SPM is computationally slow and must be run off-board. Also, in Figure 2 we refer to the on-board trained DNN predictor function that replaces the traditional ECM as the lightweight model because it is computationally fast and efficient and does not reflect the underlying physics. We envision the DNN predictor function as the only component of our ROM that resides on-board and in real time. The SPM calculates electrical, chemical, and electrochemical phenomena to predict the battery’s performance and lifespan. Thus, providing for a deeper understanding of aging mechanisms, accurately predicting battery performance by considering the material characteristics, mass, heat and energy transfer and the electrode design.
In the initial step of developing the COMSOL® Multiphysics SPM, accurate datasets and manufactures’ data was used to develop estimates of the SPM physical parameters. This initial data is not EV operational data and tends to be collected in carefully controlled experimental conditions on individual cells or packs. This initial data having served its purpose for parameter estimation cannot be treated statically because the battery’s response changes over the lifetime of the battery. Battery cells and packs cannot be pulled from the EV and lab tested so updating of the SPM must rely on operational data or off-board experiments that mimic EV operation. In our BMS we assume that operational data with sufficient quality and or filtering is available for updating the SPM. The on-board DNN predictor function, however, is updated using real time operation data. As Figure 2 indicates, the DNN updates both the on-board trained DNN predictor function for on-board battery management and the SPM. During normal operation, model parameter update estimation will periodically retrain the onboard DNN predictor function and update the SPM. There is only one DNN but its training inputs come from two sources; the SPM and EV real time operation data. The methodology for obtaining the training data is given in Section 2.4. We do not address the medium by which the components of the BMS acquire the information that we prescribe. Suffice it to say that research and applications are underway into IoT devices, 4G and 5G networks, cloud computing, and artificial intelligence that can augment our model.

2.4. Generating the Dataset from the COMSOL® Multiphysics Simulation

To create the simulation dataset over a large range of conditions, we ran the COMSOL® MULTIPHYSICS simulation for temperatures ranging from 253 to 298 K. Each run of the COMSOL® MULTIPHYSICS simulation created a vector of length 100, consisting of the right-hand side of Equation (8). All the vectors were stacked column-wise into an array to form the matrix shown in Figure 3.
We then stacked the experimental voltage responses for the A123 Systems 26650 cylindrical 2.3 Ah cell column-wise to form the matrix shown in Figure 4.
As shown in Figure 2, the training parameters for the DNN come from two sources, the SPM and from the EV’s on-board sensors and computer. The DNN training parameters from the SPM simulation before and after PCA are shown in Figure 5. The resulting input from the SPM is a rank five array of column vectors. The input parameters for training the DNN to update the on-board DNN predictor function for battery management and updating the SPM are estimates of the same SPM parameters derived from the EV’s sensor data. These inputs are also shown in Figure 5. We relate c ¯ to SOC as a fraction the same as (Zeng & Bazant, 2013) and the temperature T s and the current   ( I s ) are EV sensor data. The voltage plateau for the half-filled particle ( V c ( 1 2 ) e s t ) is scaled to   I s and k b T e µ ¯ e s t is estimated from Equation (7) by setting the penalty function coefficient ( Κ ) to zero. All of these parameters are defined below in the nomenclature section.

2.4. Developing the DNN

The DNN was coded in the Wolfram language as a Mathematica® notebook. Sufficient detail is given in Figure 6 to duplicate our results given a simulation dataset.

3. Results and Discussion

As shown in Figure 7, the DNN is a simple feed forward neural network (FNN) with nine hidden layers, consisting of five linear layers and four elementwise scaled exponential linear layers (SELU). The DNN has a rank five vector input for training and a scaler output. The residual plot and error report for the predicted and experimental values are also shown in Figure 7. The important things to note in the error report for the trained DNN predictor function is the regression correlation coefficient and the speed of the processing of examples in this case on a desktop computer CPU. We tested and verified the DNN for a 1 C discharge rate for ambient temperatures ranging from 253 to 298 K, as shown in Figure 9. Also, in Figure 9, the model results are compared to the experimental results for discharge rates ranging from 6.8 to 20.5 C for an ambient temperature of 298 K [65].
We tested the DNN predictor function using the road test: Up Mount Sano in Huntsville, AL [66]. This is an extreme road test and we had to input a moving average of the current data. Figure 10 shows the DNN fit for the road test data for 15, 30, and 60 second update times for the moving average. Longer update time on the order of 60 seconds would be necessary for updating the SPM. If shorter than 15 seconds updating is necessary it would be necessary to modify the DNN at the expense of computation complexity perhaps requiring on-board GPU capability.
Preprints 75636 g009
Figure 9. (Top): Voltage response of DNN for temperature range 253–298 K and 1 C discharge. (Bottom): Thermal model validation for fast discharge at ambient temperature of 298 K.
Figure 9. (Top): Voltage response of DNN for temperature range 253–298 K and 1 C discharge. (Bottom): Thermal model validation for fast discharge at ambient temperature of 298 K.
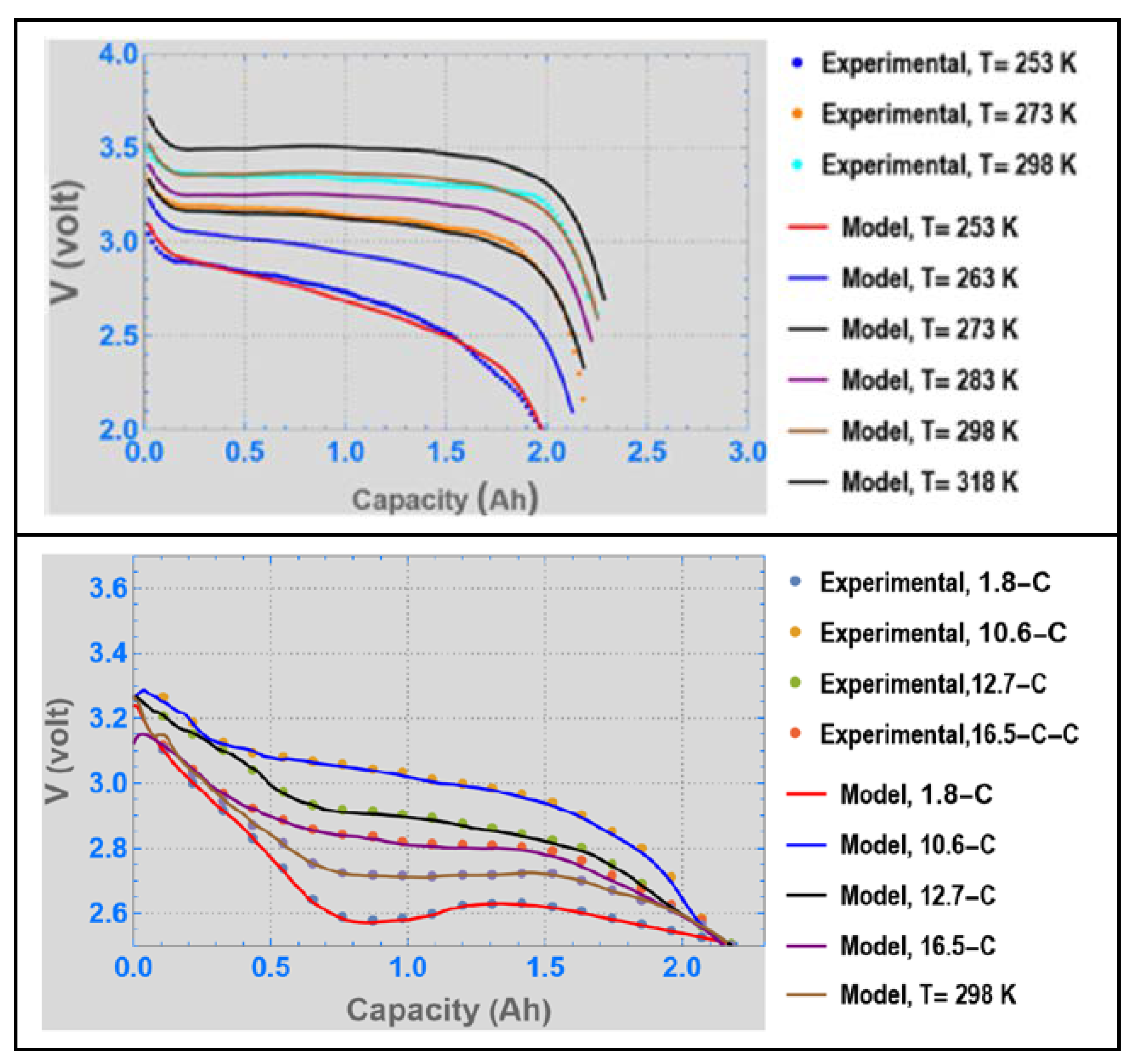
Preprints 75636 g009
Preprints 75636 g010
Figure 10. Onboard DNN predictor function testing for road test: “Up Mount Sano in Huntsville, AL” for 15, 30 and 60 second updating.
Figure 10. Onboard DNN predictor function testing for road test: “Up Mount Sano in Huntsville, AL” for 15, 30 and 60 second updating.
Preprints 75636 g010

4. Conclusions

Our ROM was motivated by (Zeng & Bazant, 2013) and the spatial mass transfer elements of our 3-D COMSOL® Multiphysics finite element simulation are similar to their 1-D isotropic and isothermal solution. The major enhancement of our single-particle model (SPM) is that it is a multiphysics, thermal model that fully couples the battery cell’s heat transfer model. The battery cell level thermal model is a robust macro enthalpy balance for the battery despite the simplifying assumptions. The OCV in Equation (5) provides an approximation of the voltage profile of the limiting reversible cycle and allows for an explicit estimation of the cell’s temperature profile based on the updated voltage. We relate the SPM simulation statistically to the battery cell voltage and temperature responses. Specifically, the plateauing effect of the battery’s voltage response at higher ambient temperatures and the apparent diffusion-controlled behavior at lower temperatures are related by statistical inference to the SPM. The ROM was realized by subjecting the raw simulation results from the COMSOL® Multiphysics simulation data to PCA to determine the lowest-order simulation dataset capable of fitting the experimental data. The reduced-order dataset was then fitted using DNN regression. The model was validated for discharge rates ranging from 1 C to 20.5 C and for ambient temperatures ranging from 253 to 298 K by comparison with the manufacturer’s experimental data.
Aside from the SPM providing a robust thermal model the other significant outcome of our model has to do with the statistical inference we drew from the SPM for the initial training of the DNN and then retraining the DNN to reproduce the drive test data from: “Up Mount Sano in Huntsville, AL” with a simple FNN with only nine hidden layers. We believe this is evidence of a significant correlation between the meso-scale and macro-scale properties. In particular we associate this to the strong correlation between the single particle voltage for the half-filed particle and the macro cell voltage at 50% SOC where the chemical potential is at or near zero.

Author Contributions

Conceptualization, R. Painter; methodology, R. Parthasarathy, R. Painter; formal analysis, R. Painter.; investigation, R. Painter; resources, L. LI, L. Sharpe, S., Keith Hargrove data curation, R. Painter; writing—original draft preparation, R. Painter; writing—review and editing, R. Parthasarathy, R. Painter; visualization, R. Painter.; supervision, L. Li, L. Sharpe, S. Keith Hargrove; project administration, L. Li, L. Sharpe, S. Keith Hargrove.; funding acquisition, L. Li, L. Sharpe, S. Keith Hargrove. All authors have read and agreed to the published version of the manuscript.

Funding

Funding was provided by Massie Chair of Excellence at Tennessee State University and The Office of Dean of College of Engineering at Tennessee State University.

Data Availability Statement

All data and computer code are available upon request to rpainter@tnstate.edu

Conflicts of Interest

The authors declare no conflicts of interest.

Nomenclature

Ab Battery surface area Parameter 4.12 × 10−2 [m2]
c Concentration Variable [mol m−3]
c ¯ Dimensionless concentration Variable c c m
cm Maximum concentration Parameter 1.379 × 1028 [m−3]
cp Specific heat coefficient Parameter 825 J [kg−1 K−1]
hc Convection heat transfer coefficient Parameter 5.0 [W m−2 K−1]
I Current Variable [A]
I ¯ Dimensionless current Variable R p c m n e D 0 I
I0 Current density Parameter 1.6 × 10−4 [A m−2]
I 0 ¯ Dimensionless current density Parameter R p c m n e D 0 I 0
Is Current from online sensors Variable [A]
kb Boltzmann constant Constant 3.13 × 109 [eV K−1]
q Radial flux Variable [s−1 m−2]
q ¯ Dimensionless radial flux Variable R p c m D 0 q
q s u r r . ˙ Heat loss to surroundings Variable [W ]
Rp Particle diameter Parameter 1 × 10−7 [m]
T Temperature Variable [K[
Tsurrr. Surroundings temperature Parameter (253–298) [K]
Ts Temperature from on-board sensor Variable [K]
V Voltage Variable [V]
V ¯ Dimensionless voltage Variable e V k b T
V c 1 2 Single particle voltage for half-filled particle Variable [V]
V c 1 2 e s t ) Cell voltage at 50 % SOC Variable [V]
Vθ Reference voltage Constant 3.42 [V]
VCH Voltage simulated by the SPM Variable [V]
V θ ¯ Dimensionless reference voltage Constant e V θ k b T
α Electron transfer symmetry factor Parameter 0.5
η Activation potential Variable -
η ¯ Dimensionless activation potential Variable e k b T η
Δϕeq Near-equilibrium voltage Variable [V]
μ Chemical potential Variable [eV]
μ ¯ Dimensionless chemical potential Variable μ k b T
k b T e μ Potential energy term from the SPM Variable -
k b T e µ ¯ e s t Potential energy estimated from Equation with 7 Variable -
VOC Open circuit voltage
ν Battery volume Parameter 3.42 × 10−5 [m3]
ρ Battery density Parameter 1824 [kg m−3]
Ω Enthalpy of mixing Parameter 0.115 [eV]
Ω ¯ Dimensionless enthalpy of mixing Parameter Ω k b T

References

  1. Tian, J.; Xiong, R.; Shen, W. Electrode aging estimation and open circuit voltage reconstruction for lithium-ion batteries. Energy Storage Mater. 2021, 37, 283–295. [Google Scholar] [CrossRef]
  2. Tian, J.; Xiong, R.; Shen, W.; Lu, J. State-of-charge estimation of LiFePO4 batteries in electric vehicles: A deep-learning enabled approach. Appl. Energy 2021, 291, 116812. [Google Scholar] [CrossRef]
  3. Etacheri, V.; Marom, R.; Elazari, R.; Salitra, G.; Aurbach, D. Challenges in the development of advanced Li-ion batteries: A review. Energy Environ. Sci. 2011, 4, 3243–3262. [Google Scholar] [CrossRef]
  4. Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]
  5. Dai, H.; Jiang, B.; Hu, X.; Lin, X.; Wei, X.; Pecht, M. Advanced battery management strategies for a sustainable energy future: Multilayer design concepts and research trends. Renew. Sustain. Energy Rev. 2021, 138, 110480. [Google Scholar] [CrossRef]
  6. Wang, Y.; Tian, J.; Sun, Z.; Wang, L.; Xu, R.; Li, M.; Chen, Z. A comprehensive review of battery modeling and state estimation approaches for advanced battery management systems. Renew. Sustain. Energy Rev. 2020, 131, 110015. [Google Scholar] [CrossRef]
  7. Scrosati, B.; Garche, J. Lithium Batteries: Status, Prospects and Future. J. Power Sources 2010, 195, 2419–2430. [Google Scholar] [CrossRef]
  8. Fergus, J. Recent Developments in Cathode Materials for Lithium Ion Batteries. J. Power Sources 2010, 195, 939–954. [Google Scholar] [CrossRef]
  9. Shim, J. Electrochemical analysis for cycle performance and capacity fading of a lithium-ion battery cycled at elevated temperature. J. Power Sources 2002, 112, 222–230. [Google Scholar] [CrossRef]
  10. Ning, G.; Popov, B. Cycle Life Modeling of Lithium-Ion Batteries. J. Electrochem. Soc. 2004, 151, A1584. [Google Scholar] [CrossRef]
  11. Spotnitz, R.; Franklin, J. Abuse behavior of high-power, lithium-ion cells. J. Power Sources 2003, 113, 81–100. [Google Scholar] [CrossRef]
  12. Wang, Y.; Dan, D.; Zhang, Y.; Qian, Y.; Panchal, S.; Fowler, M.; Li, W.; Tran, M.; Xie, Y. A novel heat dissipation structure based on flat heat pipe for battery thermal management system. Int. J. Energy Res. 2022, 46, 15961–15980. [Google Scholar] [CrossRef]
  13. Yalçın, S.; Panchal, S.; Herdem, M.-S. A CNN-ABC model for estimation and optimization of heat generation rate and voltage distributions of lithium-ion batteries for electric vehicles. Int. J. Heat Mass Transf. 2022, 199, 123486. [Google Scholar] [CrossRef]
  14. Mevawalla, A.; Shabeer, Y.; Tran, M.K.; Panchal, S.; Fowler, M.; Fraser, R. Thermal Modelling Utilizing Multiple Experimentally Measurable Parameters. Batteries 2022, 8, 147. [Google Scholar] [CrossRef]
  15. Guo, M.; Sikha, G.; White, R. Single-Particle Model for A Lithium-Ion Cell: Thermal Behavior. Electrochem. Soc. 2011, 158, A122, Erratum in: J. Electrochem. Soc. 2011, 158, S11. [Google Scholar] [CrossRef]
  16. Cai, L.; White, R. Mathematical Modeling of a Lithium Ion Battery with Thermal Effects in COMSOL® Inc. Multiphysics (MP) Software. J. Power Sources 2011, 196, 5985–5989. [Google Scholar] [CrossRef]
  17. Krewer, U.; Roder, F.; Harinath, E.; Braatz, R.; Bedurftig, B.; Findeisen, R. Review—Dynamic Models of Li-Ion Batteries for Diagnosis and Operation: A Review and Perspective. J. Electrochem. Soc. 2018, 165, A3656–A3673. [Google Scholar] [CrossRef]
  18. Li, Y.; Wei, Z.; Xiong, B.; Vilathgamuwa, D. Adaptive ensemble-based electrochemical–thermal degradation state estimation of lithium-ion batteries. IEEE Trans. Ind. Electron. 2021, 69, 6984–6996. [Google Scholar] [CrossRef]
  19. Li, Y.; Karunathilake, D.; Vilathgamuwa, D.M.; Mishra, Y.; Farrell, T.W.; Zou, C. Model Order Reduction Techniques for Physics-Based Lithium-Ion Battery Management. IEEE Ind. Electron. Mag. 2022, 16, 36–51. [Google Scholar] [CrossRef]
  20. Sakar, S.; Halim, Z.; El-Halwagi, M.; Khan, F. Electrochemical models: Methods and applications for safer lithium-ion battery operation. J. Electrochem. Soc. 2022, 169, 100501. [Google Scholar] [CrossRef]
  21. Yannliaw, B. Modeling of lithium ion cells? A simple equivalent-circuit model approach. Solid State Ion. 2004, 175, 835–839. [Google Scholar] [CrossRef]
  22. Xie, Y.; Li, W.; Hu, X.; Tran, M.K.; Panchal, S.; Fowler, M.; Liu, K. Co-estimation of SOC and three dimensional SOT for lithium-ion batteries based on distributed spatial-temporal online correction. IEEE Trans. Ind. Electron. 2022, 70, 5937–5948. [Google Scholar] [CrossRef]
  23. Sekhar, R.; Shah, P.; Panchal, S.; Fowler, M.; Fraser, R. Distance to empty soft sensor for ford escape electric vehicle. Results Control. Optim. 2022, 9, 100168. [Google Scholar] [CrossRef]
  24. Verbrugge, M. Adaptive, multi-parameter battery state estimator with optimized time-weighting factors. J. Appl. Electrochem. 2007, 37, 605–616. [Google Scholar] [CrossRef]
  25. Hu, Y.; Yurkovich, S.; Guezennec, Y.; Yurkovich, B. Electro-thermal battery model identification for automotive applications. J. Power Sources 2011, 196, 449–457. [Google Scholar] [CrossRef]
  26. Perez, H.E.; Siegel, J.B.; Lin, X.; Stefanopoulou, A.G.; Ding, Y.; Castanier, M.P. Parameterization and Validation of an Integrated Electro-Thermal Cylindrical LFP Battery Model. In Renewable Energy Systems; Robotics; Robust Control; Single Track Vehicle Dynamics and Control; Stochastic Models, Control and Algorithms in Robotics; Structure Dynamics and Smart Structures; ASME 2012 5th Annual Dynamic Systems and Control Conference: Fort Lauderdale, Florida, USA, 2012; Volume 3. [Google Scholar]
  27. Torabi, F.; Ahmadi, P. Simulation Of Battery Systems; Academic Press: London, UK, 2019. [Google Scholar]
  28. Barreras, J.; Schaltz, E.; Andreasen, S. Datasheet-Based Modeling of Li-Ion Batteries. In Proceedings of the 2012 IEEE Vehicle Power and Propulsion Conference, Seoul, Republic of Korea, 9–12 October 2012. [Google Scholar]
  29. Zou, Z.; Xu, J.; Mi, C.; Cao, B.; Chen, Z. Evaluation of Model Based State of Charge Estimation Methods for Lithium-Ion Batteries. Energies 2014, 7, 5065–5082. [Google Scholar] [CrossRef]
  30. Wei, Z.; Hu, J.; He, H.; Yu, Y.; Marco, J. Embedded distributed temperature sensing enabled multistate joint observation of smart lithium-ion battery. IEEE Trans. Ind. Electron. 2022, 70, 555–565. [Google Scholar] [CrossRef]
  31. Hu, X.; Sun, F.; Zou, Y. Estimation of state of charge of a lithium-ion battery pack for electric vehicles using an adaptive Luenberger observer. Energies 2010, 3, 1586–1603. [Google Scholar] [CrossRef]
  32. Kim, I. The novel state of charge estimation method for lithium battery using sliding mode observer. J. Power Sources 2006, 163, 584–590. [Google Scholar] [CrossRef]
  33. Sun, F.; Xiong, R.; He, H.; Li, W.; Aussems, J. Model-based dynamic multi-parameter method for peak power estimation of lithium-ion batteries. Appl. Energy 2012, 96, 378–386. [Google Scholar] [CrossRef]
  34. Xu, J.; Mi, C.; Cao, B.; Deng, J.; Chen, Z.; Li, S. The state of charge estimation of lithium-ion batteries based on a proportional integral observer. IEEE Trans. Veh. Technol. 2014, 63, 1614–1621. [Google Scholar]
  35. Wei, Z.; Dong, G.; Zhang, X.; Pou, J.; Quan, Z.; He, H. Noise-immune model identification and state-of-charge estimation for lithium-ion battery using bilinear parameterization. IEEE Trans. Ind. Electron. 2021, 68, 312–323. [Google Scholar] [CrossRef]
  36. Dong, G.; Wei, J.; Zhang, C.; Chen, Z. Online state of charge estimation and open circuit voltage hysteresis modeling of LiFePO4 battery using invariant imbedding method. Appl. Energy 2016, 162, 163–171. [Google Scholar] [CrossRef]
  37. Zhang, Y.; Xiong, R.; He, H.; Shen, W. A lithium-ion battery pack state of charge and state of energy estimation algorithms using a hardware-in the-loop validation. IEEE Trans. Power Electron. 2017, 32, 4421–4431. [Google Scholar] [CrossRef]
  38. Padhi, A.K. Phospho-olivines as Positive-Electrode Materials for Rechargeable Lithium Batteries. J. Electrochem. Soc. 1997, 144, 1188. [Google Scholar] [CrossRef]
  39. Yamada, A.; Chung, S.C.; Hinokuma, K. ChemInform Abstract: Optimized LiFePO4 for Lithium Battery Cathodes. ChemInform 2010, 32. [Google Scholar]
  40. Huang, H.; Yin, S.; Nazar, L.F. Approaching Theoretical Capacity of LiFePO4 at Room Temperature at High Rates. Electrochem. Solid-State Lett. 2001, 4, A170. [Google Scholar] [CrossRef]
  41. Ravet, N.; Chouinard, Y.; Magnan, J.; Besner, S.; Gauthier, M.; Armand, M. Electroactivity of natural and synthetic triphylite. J. Power Sources 2001, 97–98, 503–507. [Google Scholar] [CrossRef]
  42. Chung, S.; Bloking, J.T.; Chiang, Y. Electronically conductive phospho-olivines as lithium storage electrodes. Nat. Mater. 2002, 1, 123–128. [Google Scholar] [CrossRef]
  43. Johns, P.A.; Roberts, M.R.; Wakizaka, Y.; Sanders, J.H.; Owen, J.R. How the electrolyte limits fast discharge in nanostructured batteries and supercapacitors. Electrochem. Commun. 2009, 11, 2089–2092. [Google Scholar] [CrossRef]
  44. Newman, J.; Tiedemann, W. Porous-Electrode Theory with Battery Applications. AIChE J. 1975, 21, 25–41. [Google Scholar] [CrossRef]
  45. Doyle, M. Modeling of Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell. J. Electrochem. Soc. 1993, 140, 1526. [Google Scholar] [CrossRef]
  46. Bazant, M. Theory of Chemical Kinetics and Charge Transfer Based on Nonequilibrium Thermodynamics. Acc. Chem. Res. 2013, 46, 1144–1160. [Google Scholar] [CrossRef] [PubMed]
  47. Singh, G.; Ceder; Bazant, M. Intercalation dynamics in rechargeable battery materials: General theory and phase-transformation waves in LiFePO4. Electrochim. Acta 2008, 53, 7599–7613. [Google Scholar] [CrossRef]
  48. Painter, R.; Embry, I.; Sharpe, L.; Hargrove, S.K. A Reduced Order Thermal Model for Lithium Ion Batteries Derived from the Cahn-Hilliard Equation. In Proceedings of the 2020 COMSOL® Conference, Boston, MA, USA, 7–8 October 2020. [Google Scholar]
  49. Bai, P.; Cogswell, D.; Bazant, M.Z. Suppression of phase separation in LiFePO4 nanoparticles during battery discharge. Nano Lett. 2011, 11, 4890–4896. [Google Scholar] [CrossRef]
  50. Malik, R.; Abdellahi, A.; Ceder, G. A Critical Review of the Li Insertion Mechanisms in LiFePO4 Electrodes. J. Electrochem. Soc. 2013, 160, A3179–A3197. [Google Scholar] [CrossRef]
  51. Chen, L. Phase-Field Models for Microstructure Evolution, Annu. Rev. Mater. Res. 2002, 32, 113–140. [Google Scholar] [CrossRef]
  52. Yuan, C.; Gao, X.; Jia, Y.; Zhang, W.; Wu, Q.; Xu, J. Coupled crack propagation and dendrite growth in solid electrolyte of all-solid-state battery. Nano Energy 2021, 86, 106057. [Google Scholar] [CrossRef]
  53. Yuan, C.; Lu, W.; Xu, J. Unlocking the electrochemical–mechanical coupling behaviors of dendrite growth and crack propagation in all-solid-state batteries. Adv. Energy Mater. 2021, 11, 2101807. [Google Scholar] [CrossRef]
  54. Zeng, Y.; Bazant, M. Cahn-Hilliard Reaction Model for Isotropic Li-Ion Battery Particles. MRS Proc. 2013, 1542, 0201. [Google Scholar] [CrossRef]
  55. Painter, R.; Berryhill, B.; Sharpe, L.; Hargrove, S.K. A Single Particle Thermal Model for Lithium Ion Batteries. In Proceedings of the 2012 COMSOL® Conference, Boston, MA, USA, 3–5 October 2020. [Google Scholar]
  56. Painter, R.; Sharpe, L.; Hargrove, S.K. A Phase Field Model for Lithium Batteries. In Proceedings of the 2012 COMSOL® Conference, Boston, MA, USA, 3–5 October 2020. [Google Scholar]
  57. Sullivan, U.V. Published 2019. Available online: http://www.sullivanuv.com/wp-content/uploads/2014/06/A123-Cell-Datasheet-2008-08.pdf (accessed on 1 December 2019).
  58. Maleki, H. Thermal Properties of Lithium-Ion Battery and Components. J Electrochem Soc. 1999, 146, 947. [Google Scholar] [CrossRef]
  59. Chen, Y. Thermal Analysis of Lithium-Ion Batteries. J Electrochem Soc. 1996, 143, 2708. [Google Scholar] [CrossRef]
  60. Onda, K.; Ohshima, T.; Nakayama, M.; Fukuda, K.; Araki, T. Thermal behavior of small lithium-ion battery during rapid charge and discharge cycles. J Power Sources. 2006, 158, 535–542. [Google Scholar] [CrossRef]
  61. Thomas, K.; Newman, J. Thermal Modeling of Porous Insertion Electrodes. J. Electrochem. Soc. 2003, 150, A176. [Google Scholar] [CrossRef]
  62. Forgez, C.; Vinh Do, D.; Friedrich, G.; Morcrette, M.; Delacourt, C. Thermal modeling of a cylindrical LiFePO4/graphite lithium-ion battery. J. Power Sources 2010, 195, 2961–2968. [Google Scholar] [CrossRef]
  63. Youngki, K. Power Capability Estimation Accounting for Thermal and Electrical Constraints for Lithium-Ion Batteries. Ph.D. Thesis, University of Michigan, Midsize city, MI, USA, 2014. [Google Scholar]
  64. Singh, S.; Weeber, M.; Birke, K. Implementation of digital twin: Approach, Functionaliyies and Benefits, Batteries; MDPI, 2021. [Google Scholar]
  65. Available online: https://docplayer.net/20772679-Managing-a123-cells-with-fma-cell-balancing-technologies.html (accessed on 1 March 2022).
  66. Pivelait, B.; Rentel, C.; Plett, G.; Marcel, M.; Carmen, D. An advanced battery management system for lithium-ion batteries, 2011 NDIA Ground Vehicle Systems Engineering and Technology Symposium; Power and Mobility (P&M) Mini-Symposium August 9-11 Dearborn Michigan.
Preprints 75636 g001
Figure 1. Equivalent-Circuit-Model-Based Battery Management System.
Figure 1. Equivalent-Circuit-Model-Based Battery Management System.
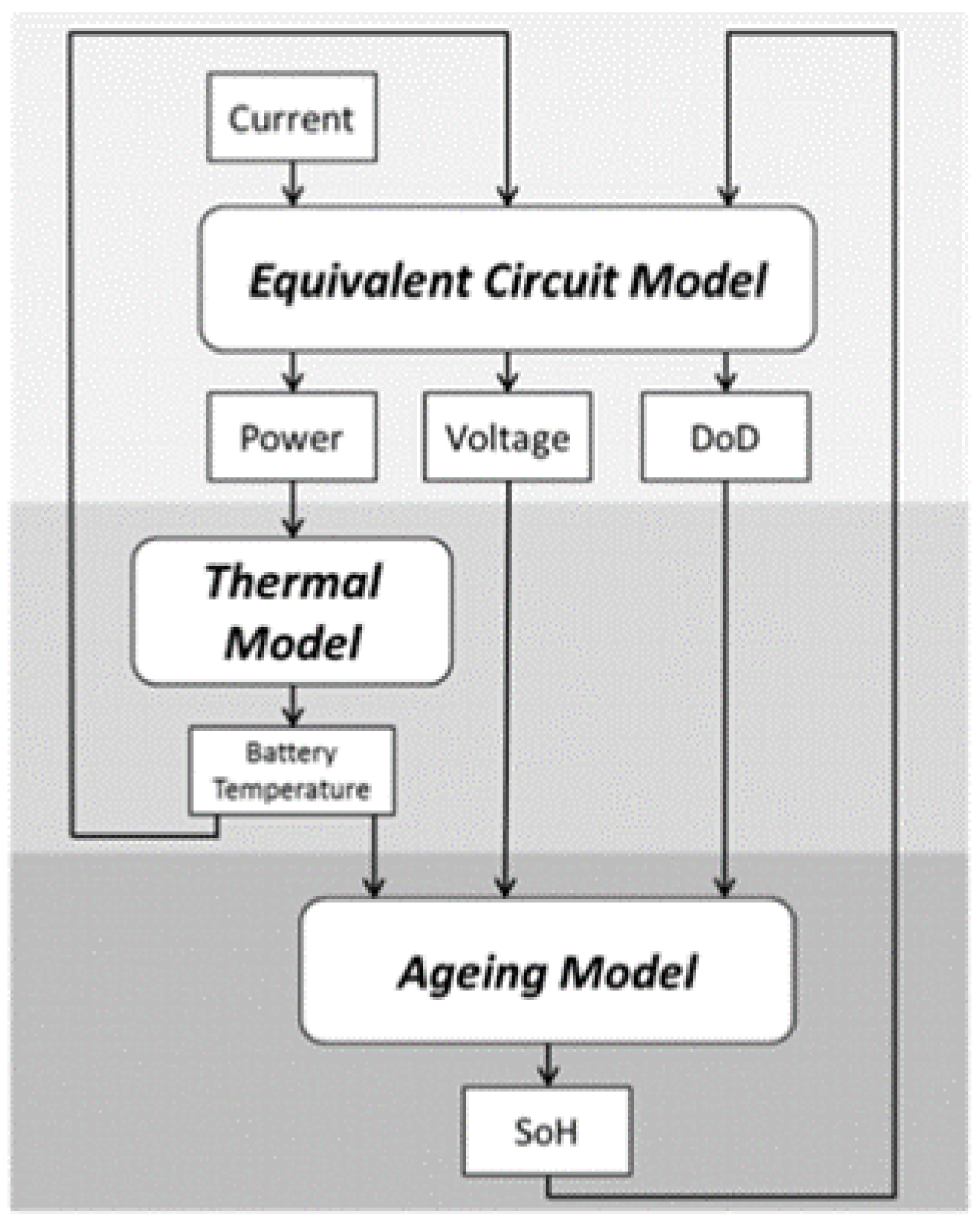
Preprints 75636 g001
Preprints 75636 g002
Figure 2. DT configuration showing the role of the DNN and SPM according to the process of Singh et al., 2021.
Figure 2. DT configuration showing the role of the DNN and SPM according to the process of Singh et al., 2021.
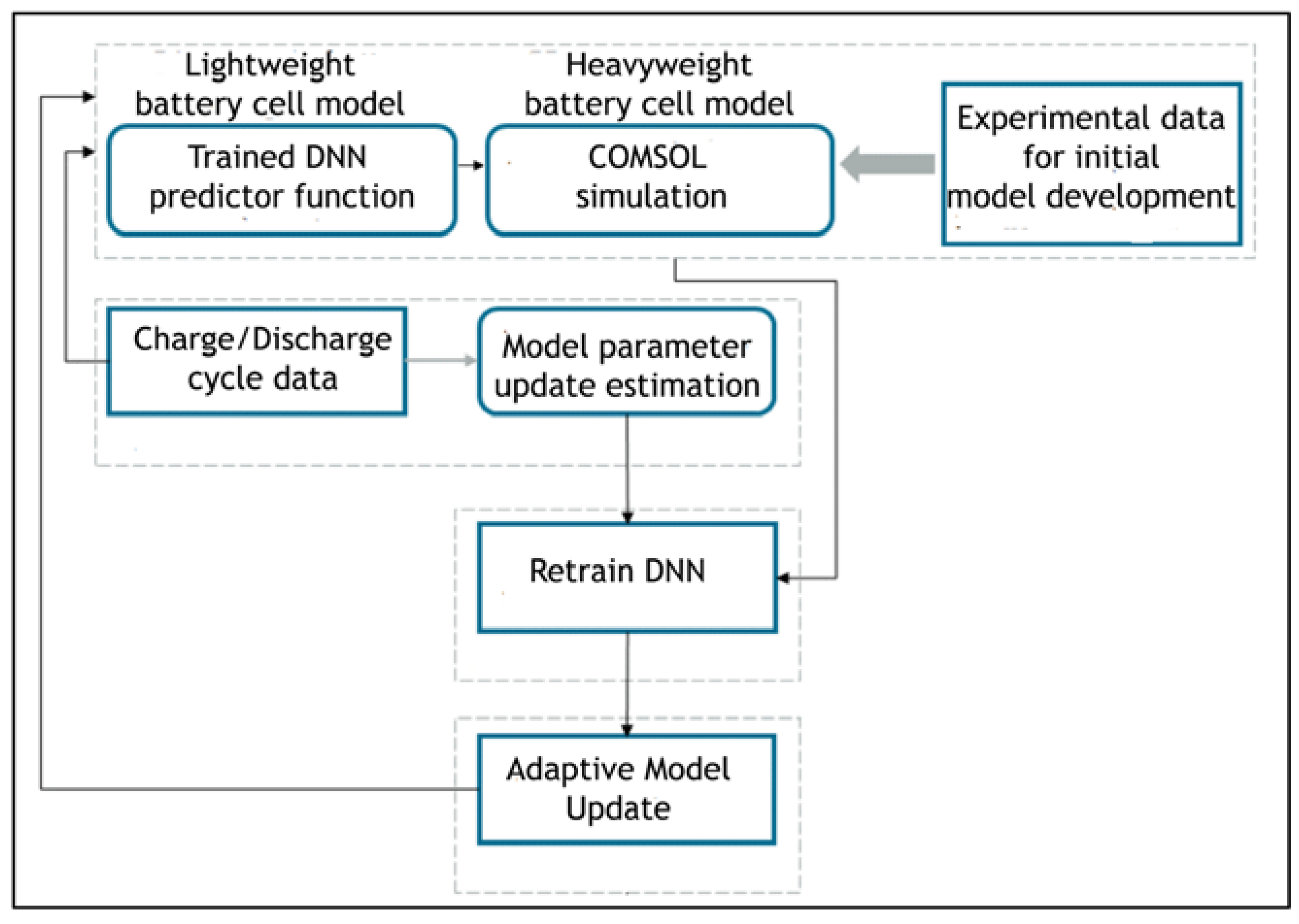
Preprints 75636 g002
Preprints 75636 g003
Figure 3. Schematic of the COMSOL®-simulated data for the Systems A123 2.3 Ah lithium-ion battery.
Figure 3. Schematic of the COMSOL®-simulated data for the Systems A123 2.3 Ah lithium-ion battery.
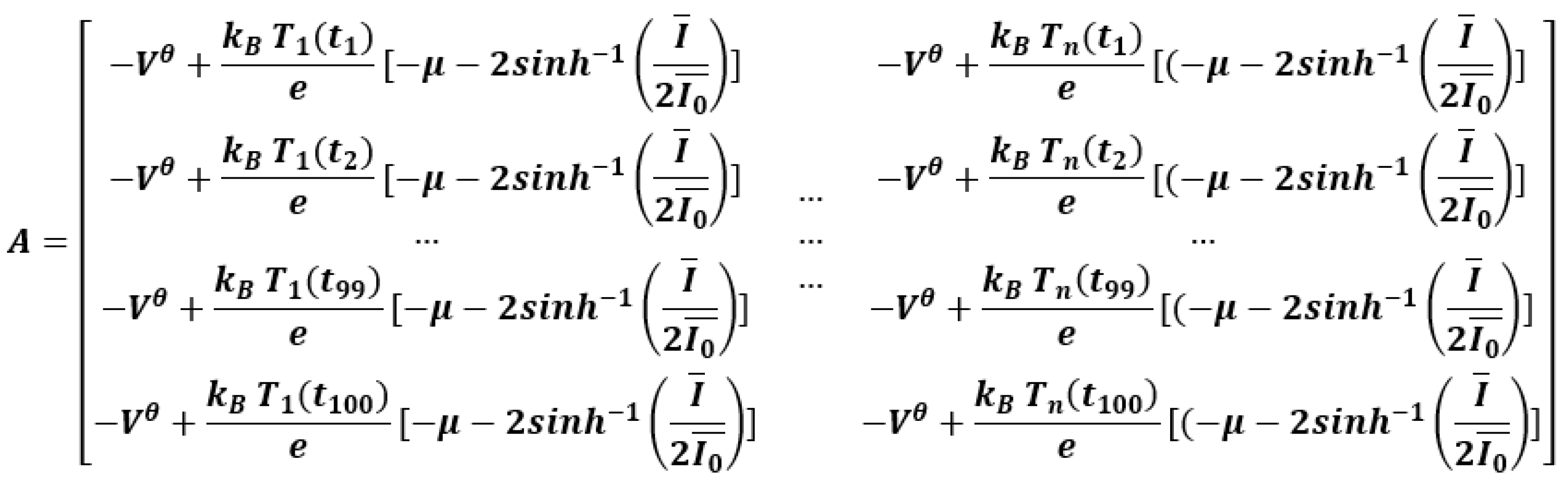
Preprints 75636 g003
Preprints 75636 g004
Figure 4. Schematic of the experimental voltage data.
Figure 4. Schematic of the experimental voltage data.
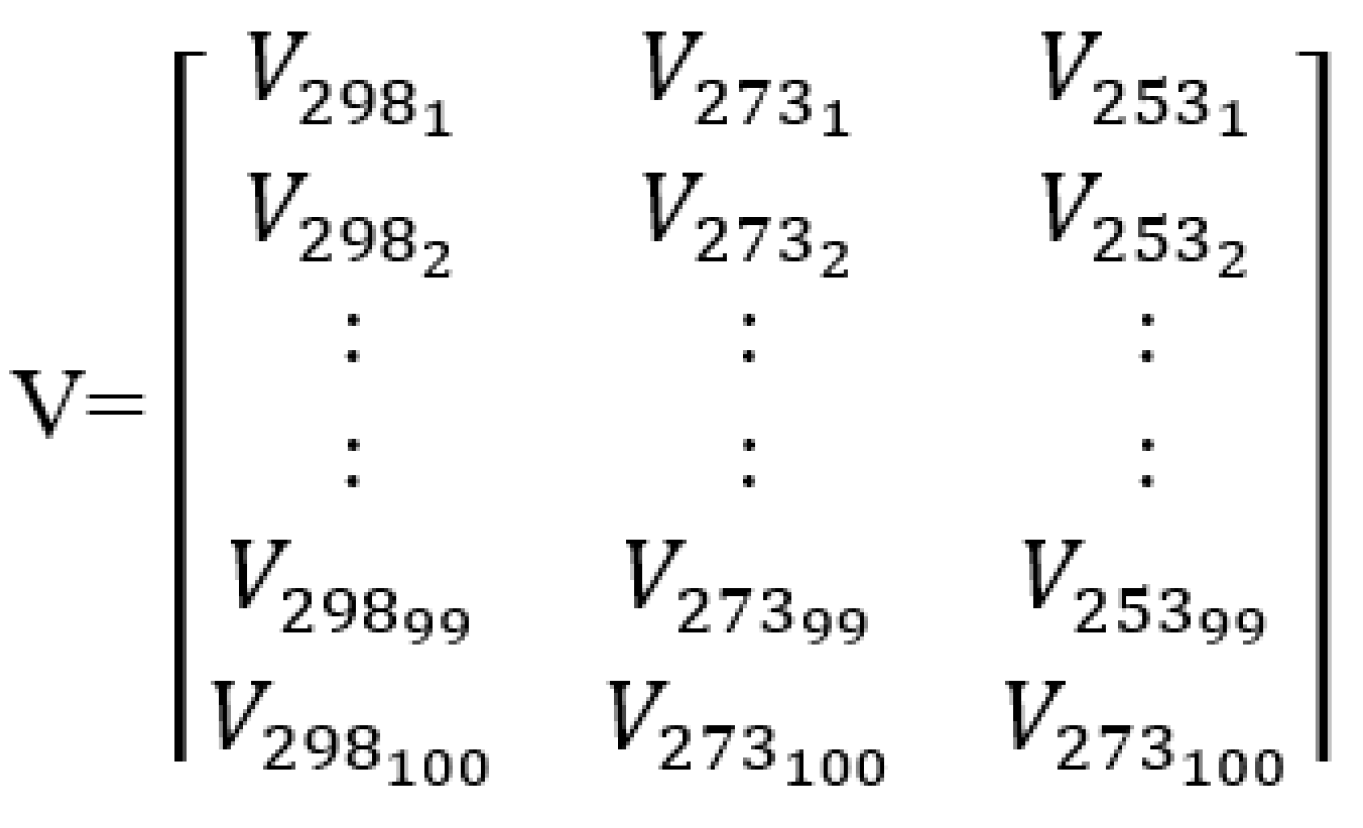
Preprints 75636 g004
Preprints 75636 g005
Figure 5. (Left) DNN training input from SPM before and after PCA; (Right) Estimated parameters and EV sensor data.
Figure 5. (Left) DNN training input from SPM before and after PCA; (Right) Estimated parameters and EV sensor data.
Preprints 75636 g005
Preprints 75636 g006
Figure 6. Mathematica code for the DNN; (a) We used PCA to determine the minimum number of features for the ROM from the simulation dataset (A, Figure 3) that adequately fit the experimental data (V, Figure 4); (b) Eighty percent of the reduced-order dataset was randomly selected for training and twenty percent for testing; (c) The training data were then normalized to mean = 1.0 and standard deviation of 0.0 and the test data were standardized relative to the mean and standard deviation of the training data; (d) The DNN was constructed and trained using a mean absolute loss layer and RMS propagation for gradient descent.
Figure 6. Mathematica code for the DNN; (a) We used PCA to determine the minimum number of features for the ROM from the simulation dataset (A, Figure 3) that adequately fit the experimental data (V, Figure 4); (b) Eighty percent of the reduced-order dataset was randomly selected for training and twenty percent for testing; (c) The training data were then normalized to mean = 1.0 and standard deviation of 0.0 and the test data were standardized relative to the mean and standard deviation of the training data; (d) The DNN was constructed and trained using a mean absolute loss layer and RMS propagation for gradient descent.
Preprints 75636 g006
Preprints 75636 g007
Figure 7. (Left)): Layer details of the DNN. (Right): Error report for DNN testing and comparison plot (blue circles are actual predictions and the dashed line are perfect predictions).
Figure 7. (Left)): Layer details of the DNN. (Right): Error report for DNN testing and comparison plot (blue circles are actual predictions and the dashed line are perfect predictions).
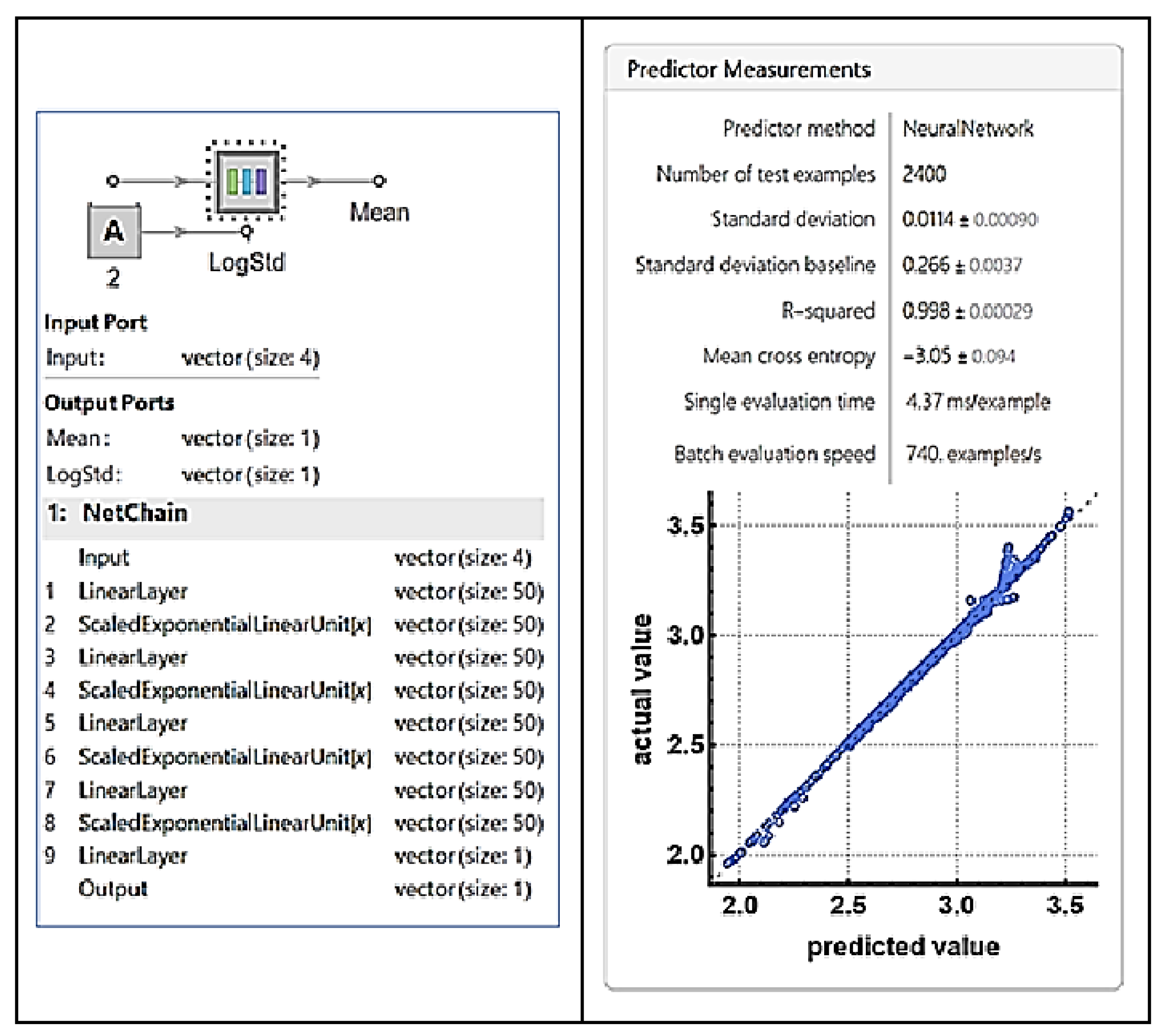
Preprints 75636 g007
Table 1. Specifications for Systems A123 2.3 Ah Lithium-ion Battery.
Table 1. Specifications for Systems A123 2.3 Ah Lithium-ion Battery.
Nominal capacity and voltage 2.3 Ah, 3.3 V
Internal impedance (1 kHz AC) 8 mΩ typical
Internal resistance 10 A, 1 s DC 10 mΩ typical
Recommended charge method 3 A to 3.6 V CCCV, 45 min
Recommended fast charge current 10 A to 3.6 CCCV
Maximum continuous discharge 70 A
Pulse discharge at 10 s 120 A
Cycle life at 10 C discharge Over 1000 cycles
Recommended pulse charge/discharge cutoff 3.8 V to 1.6 V
Operating temperature range 243 K to 333 K
Core cell weight 70 g
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated