Prerpints.org logo
Preprint
Article

Automatic River Planform Recognition Tested on Chilean Rivers

Altmetrics

Downloads

113

Views

49

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

04 June 2023

Posted:

05 June 2023

You are already at the latest version

Alerts
Abstract
This paper addresses the issue of the automatic identification of river reaches and their planform type, given the (observed) set of geomorphic elements and units. It introduces further advances with respect to the original proposal by Nardini and Brierley. And it explores explicitly the ability of the algorithm and associated tools to work properly on significantly different rivers while adopting a given same parametrization. This was indeed an envisaged ability speculated as a challenging conclusion of the previous work. The Duqueco, Laja and Biobío rivers (Chile) are analyzed for this purpose. The conclusion is definitely positive, what opens future promising application horizons.
Keywords: 
Subject: Environmental and Earth Sciences  -   Water Science and Technology

1. Introduction

One of the key characters of a river is its “planform”, i.e., its spatial configuration in terms of path, sinuosity, number of channels, their width, and the assemblage of in channel geomorphic units. It is also the core of several geomorphic classification schemes (e.g., Kondolf et al., [1]; Buffington and Montgomery, [2]; Brierley and Fryirs, [3]). Nardini et al. [4] adopted planform as one of the key attributes to segment a river into meaningful stretches.
Curiously, in the literature several attempts can be found to automatically identify the geomorphic elements (valley bottom, active channel) and units (e.g., bars, islands, water channels) from remote sensed data (e.g., Parker et al., [5]; Piégay et al., [6]; Ouellet et al., [7]; Demarchi et al., [8]; Bernard et al., [9]; Jézéquel et al., [10]). But we have not found attempts to identify the planform typology automatically once such elements are given from a direct observation on the territory (be it through a manual, expert based procedure, or an automatic one). The only work directly addressing this challenge is that of Nardini and Brierley, [11].
Similar exercises utilized supervised Machine Learning (ML) algorithms to identify the planform based on some “predictors” (causal factors), in order to extrapolate then to broad territories (e.g. Frasson et al., [12]; Beechie and Imaki, [13]; Beechie et al., [14] Rabanaque et al., [15]); but, although some predictors are very close to some of the geomorphic attributes describing planform, they mainly refer to different things and in any case they are not conceived to directly constitute the set of planform descriptors. Also, the belonging to a given planform category is performed manually on an expert judgment, rather than an automatic procedure. Other attempts (e.g. Bertrand et al., [16]; Guillon et al., [17]; Horacio et al.,[18]) are rather based on unsupervised ML algorithms, where reaches are described by a set of attributes (quantified by indicators) and then grouped into clusters of similar elements finally assigned, again based on expert judgment, to the different planform typologies; there, attributes are calculated on pre-defined stretches, although the finals reaches may not coincide with them (what may create a discrepancy). Conceptually similar, although implemented through a different technique, namely the Self-Organizing Maps (SOM), is the experience of Bizzi and Lerner [19], working again on pre-defined stretches. Perhaps, an exercise more similar to the one we address here is the attempt to recognize the type of drainage network (terrestrial or even extraterrestrial), again through supervised ML but this time fed by (remote sensed) images (Donadio et al., [20]). This is however a global judgment over a whole network and lies clearly far from our problem both for the (lacking) detail of the attributes considered, and because it does not address the difficult associated problem of recognizing jointly with the type also the spatial reach where it applies. Additionally, the idea of applying a supervised ML algorithm to a set of images (the assemblage of geomorphic elements and units directly observed for a river) faces the harsh difficulty of counting with a (very) large number of examples classified…manually (analogously to the exercise of the “River Zoo” http://dame.oacn.inaf.it/riverzoo.html).
Nardini and Brierley, [11] defined a set of planform archetypes, then chose a set of attributes to characterize them according to explicit criteria, together with suitable indicators computed for each one of the river “slices” produced by a discretization process (according to the Fluvial Corridor Toolbox scheme, Alber and Piégay, [21]). These indicators are then transformed by suitable scalar Value Functions-VF (fully defined by a set of parameters to be specified) which translate the value of each indicator into a judgment of adherence to a given criterion. For each archetype, a collage of such VFs is defined which composes a specific multi-attribute VF: them all are evaluated in parallel for each slice and the archetype for which the corresponding multi-attribute VF assumes the highest score is the “winner”, i.e., is assigned to that slice. This process is permeated by the idea of evaluating the attributes over a moving window centered on the current slice i, where such a window has a length proportional to the local Active Channel (AC) width so to always guarantee a suitable holistic view, rather than a reductionist one, while adapting to a spatially changing river. This algorithm was applied to the Baker River (Southern Chile) with promising results [4]. This Excel® spreadsheet (programmed), implementing the algorithm described here, is referred to as the “Tool”.
A fundamental doubt was however raised, i.e., whether the chosen parametrization (the set of values assigned to the parameters) for the Baker River would serve well also for other, significantly different rivers, or, in other words, whether the nice performance was due to an overfitting of the parameters. This paper is fruit of a research explicitly aimed at exploring the truthfulness of this thesis by applying the same Tool, with the same given parametrization, to a set of three rivers very different in terms of size and characteristics, although all located in the VIII Region (south-central area) in Chile.

2. Methodology

The methodology adopted here is the same already described in Nardini and Brierley, [11], already synthesized above, but it includes some further progresses described in what follows.

2.1. Ability to Deal with Rivers with Highly Variable AC Width

Some of the rivers considered here display a peculiarity: their width greatly and suddenly varies along the river, as can be seen for example in the Duqueco case in the segment between slices 1000-1500 (Figure 1). This constitutes a hard challenge for the Planform algorithm that is based on the concept of significant length because, while in the narrow segment it is quite short, as soon as a wide segment is touched, it suddenly becomes very large and as such it tends to ignore the character of the widened, but proportionally short, segment.
To address this issue, we introduced a step to smooth out this width variability. To achieve that, the idea is first identifying macro segments over which to determine a local average AC width; this is used to determine the length of a moving window (for all the slices falling within that macro segment) over which the actual average AC width is determined (denoted as “smoothed”); this is in turn used to determine the local LC(i) with which the moving window is created. The macro segments can be identified manually or via the AGO creation criterion introduced by Alber and Piégay [21] based on the Hubert test (Hubert, [22]); clearly, this includes an arbitrary step because the user has to specify how many diverse segments are to be to obtain, as the Hubert test just finds where they are. But reasonable low numbers (like 3 or 5) work well. This new part of the overall algorithm is depicted in the following Figure 1; in case only one Hubert segment is adopted together with a unity inflation factor, LC is the whole river and w(j(i)) is the average river width.

2.2. Improvement of Some Indicators and Value Functions (VF)

In the original Baker exercise described in Nardini and Brierley [11] some archetypes, though considered in the algorithm, had not been called into play because they were not present in that river. As such, they had not been tested. Other posterior applications showed that some of the attributes/indicators adopted were not adequate or somehow redundant. The applications described in this paper involved a broader number of archetypes with a broader spectrum of situations that evidenced some limits of the previous implementation. For this reason, several small adjustments have been undertaken in the current version (9.1).
As already set in the original formulation, sinuosity is the only attribute that conceptually deserves an iteration, as it needs reaches to be specified before it is computed, and these are unknown at the beginning. As an operational solution, at a first approximation stage, such reaches are assumed to coincide (as suggested within the FCT framework) by the segments connecting the flexus point of the AC axis (once smoothed to eliminate the “noise” introduced by the irregularities of the axis polyline). An improvement has been introduced now with a process to eliminate those segments (output of this geometric procedure) resulting shorter than the local significant length and then recalculating the sinuosity degree over the ensemble of the adjacent joined segments (a correction procedure that may require iterations as well and can be conducted through a new Excel tool developed ad hoc). Once reaches are identified by the couple Planform-Holistic, the sinuosity should hence be recalculated over them, and the Planform-Holistic cycle rerun (see below about Holistic).
In the original version, aside the sinuosity degree, the indicator sinuosity type had been adopted which the aim to identify in particular the Constrained sinuosity reaches. The assumption was that it would be possible to determine such an indicator by comparing the position of the AC axis with respect to the VB (i.e., whether the axis occurred to be external to it), while in the Baker application it has been estimated based on expert judgment. Formalizing an automatic procedure to this aim proved however to be less straightforward than expected. Hence, a new, much simpler solution has been now introduced: Constrained sinuosity is a typology associated only with the Single channel family and it appears only when the entrenchment indicator (ratio between AC width and VB width) passes a given threshold (parameter).
Another innovation has been the adoption of multiplicative scalar Value Functions (VF) as an attempt to better discern amongst typologies (e.g., where a slice shows multiple channels, it should not belong to the Single channel family). This idea proved to bring in some improvements, but, as shown particularly in the Biobío case, also introduced some “hysteria” of the Planform algorithm (implemented in an Excel® Tool).
More important, it implies the necessity to work in couple with the Holistic categorical Tool; this is a kind of heuristic filter that smooths out too frequent variations and ensures that no final reach be shorter than the local significant length, so fulfilling the requirement imposed to ensure a holistic view of the river. The output of Planform is hence input into the Holistic and its output is the final product.
The Holistic categorical algorithm (implemented in another Excel® Tool) deals with indicators that can assume values within a discrete set, where the elements have no ordinal relationships (categorical indicators). Its philosophy is very simple: do not leave windows shorter than LM and assign to each stretch the prevailing value in it.
It implements the algorithm whose main traits are described as follows:
Holistic I round:
−
identify the discontinuities of Planform type (output of Planform)
−
then proceed from upstream towards downstream considering each generic slice i, and:
−
Where there is no discontinuity, it keeps the value of the preceding slice (that in the following rounds may have been modified by Holistic itself).
Instead, where there is a discontinuity:
−
it determines the “distance of constancy D(i)”, i.e., the number of slices along which the previous type (now changed) kept constant within half of the significant length centered in the current slice; this distance, by construction, progressively reduces while moving to slices ahead of a discontinuity
−
"prevailing type K steps forward window": the algorithm here identifies the most frequent type occurring within the K slices ahead
−
"prevailing type in the D residual forward window ": analogous task, but in a reduced window of just K – D(i) -1 slices ahead: this is a moving window ahead within a K horizon whose start is anchored to the previous discontinuity (it is changed when the algorithm processes the next discontinuity) and that progressively gets shorter. Its purpose is to consider which value is prevailing in the vicinity in front of the current slice and so avoid concluding that a certain type is prevailing in the K window ahead when it indeed is, but leaving “a hole” (i.e., different types are present) in the most proximal slices:
  • when the prevailing type in this window is the same than before the (last) discontinuity → current type was a “local hole” and therefore the previous value is kept instead
  • when it is "not detectable" it is kept
  • otherwise, the prevailing type within the K forward window is adopted.
Holistic II round:
Here the algorithm tries to solve the cases of reaches shorter than the local significant distance. The criterion is for the moment quite brutal: the type in these too short reaches is just uniformed to the adjacent (preceding or following depending on the user choice set at the beginning amongst the algorithm characteristics) reach type. So, the algorithm proceeds as follows:
−
it identifies discontinuities in the sequence of types just determined by Holistic I round;
−
where there is no discontinuity, it keeps the already computed value;
−
where there is a discontinuity: if the distance D(i) from the last discontinuity is D(i) < K, it adopts the value type occurring upstream of the discontinuity; otherwise, it keeps current one.

3. Case Study

3.1. Study Area

The study area is located within the Biobío River basin (Figure 2). The Biobío River basin, located in the Biobío region (VIII Region) of Chile, is the second largest in the country, with a surface area of 24,273 km2. Located between parallels 36º 45' - 38º 49' S and meridians 71º - 73º 20' W. This basin has a mixed regime and originates in the majestic Andes Mountains. As it passes through the central plain, it meanders through diverse landscapes until it finally merges with the Pacific Ocean south of Hualpén. Composed of 15 distinct sub-basins, this river system is characterized by a series of geographic and environmental conditions that contribute to its remarkable variability along its extensive course [23]. The Biobío River and the Laja River, which are its main tributaries, contribute to the general drainage of this basin.
Originating on the eastern shore of the Gualletué Lagoon in the Andes Mountains, the Biobío River extends for approximately 380 km until it reaches its mouth [24]. For the purposes of this study, owing to the information availability, a specific long stretch of the river was selected, starting from the Angostura dam, Quillaco, and running approximately 198 km to the mouth.
The Laja River, the main tributary of the Biobío River, has an area of 4,667 km2. Its headwaters are in the Andes Mountains, east of the Antuco Volcano and south of the “Nevados de Chillán”. This river system not only drains the Laja Lagoon, but also crosses the Central Depression. Lastly, the Laja river joins with the Biobío River, marking an important confluence point [25]. Finally, the Duqueco River, which also originates in the Andes Mountains, specifically to the southwest of the Sierra Velluda, flows towards the Biobío River, eventually converging near the town of Negrete. With a hydrographic basin of 1,550.8 km2 and an approximate length of 102 km (evaluated in this study), the Duqueco River has remarkable size. Its tributaries are the Canicura, Quillaco and Llerquenco streams, with the Coreo River as its main tributary [26]. Table 1 reports additional data on the morphometric characteristics of these rivers.

3.2. Data and Methods

In this study we utilized a high-resolution 10 m TanDEM-X radar interferometric digital elevation model sourced from the DRL (Deutsches Zentrum für Luft- und Raumfahrt - German Aerospace Center) in Germany. Complementing this dataset, satellite images from the RapidEYE and Planet Scope nanosatellite constellations were employed, offering pixel resolutions of 5 m and 3 m, respectively.
The processing of satellite images allowed the generation of Unitary Geographic Objects (UGO) relevant to the analysis, with greater efficiency than that of a manual exercise; these UGO (or geomorphic elements) are: the active channels in high waters, bars, islands, and fluvial elements of the floodplain. To this aim, in the ENVI-IDL 5.x software, a multispectral mosaic was created using RapidEYE and Planet Scope images [for the years 2009 (Duqueco), 2019 (Laja) and 2020 (Biobío)], representing both high water and low water conditions within the basin. The Normalized Difference Water Index (NDWI) [27] was then computed, enabling the identification of areas with water; this distinction is achieved through spectral separation techniques specific to these materials. The geographic difference (Difference tool of QGIS) allows to identify those areas comprising dry soil and vegetation contained within the former, i.e., island or bars. Subsequently, images captured on different dates, reflecting varying water conditions, were processed, and merged to enhance the identification of islands and bars within the active channel. It has to be noted, however, that this method is reliable for large rivers where hydrological changes are quite slow and hold for significant periods; for rivers like ours (either relatively small and/or affected by reservoir management) this method may lead to imperfect results because it is not ensured that the images -and the recorder hydrological daily data- captured really high and low flows.
To generate the floodplain or valley bottom, we used the TanDEM-X DEM at a resolution of 10 m through the V-BET (Valley Bottom Extraction Tool) program, as described in the workflow presented by Gilbert et al., [28]. V-BET is a tool that allows for the extraction and mapping of the valley bottom from a Digital Elevation Model (DEM). Its driving idea is to identify depressed areas in a landscape by looking at changes in slope within sections of DEM transverse to the main flow direction.
Additionally, we utilized the South Rivers Toolbox tool within the QGIS 3.x interface [26] to enhance our analysis. We employed the segmentation tool offered by the "River Skeleton" module to segment the active channel and its envelope. This process involves utilizing the centerline of each UGO. It is crucial to note anyway that the sequencing of the centerline is essential to maintain a consistent order in the coding of the segments (DGOs - Disaggregated Geographic Objects) from upstream to downstream or vice versa.
The geomorphic elements and units (GUs) finally obtained through a manual exercise (conducted by students) are: the Valley Bottom (VB), the Active Channels (ACs), the bars (bank attached -left/right or point bar; mid channel), the islands, and the AC envelope.
For planform analysis, the algorithm developed by Nardini and Brierley [11] was employed, offering an automated approach to identify planform characteristics. The adopted archetypes are a variant of those originally proposed by Kleinhans and Van den Berg [29]. The data eventually input into the Planform Tool are (for each slice i):
−
ID of the slice or DGO (i)
−
length of discretization slice (all slices equal; 50 m has been adopted for the three rivers)
−
length LH(j) of the Hubert segment j(i) corresponding to slice i (several slices are associated with the same segment j); reference moving window length L(i) = f* LH(j(i)) over which the reference width w(j(i)) is calculated, with f inflation factor (f ≥1) → corresponding significant length (smoothed) LS(i) = K*w(j(i)) with K characteristic parameter. Notice hence that w(j(i)) in general does not coincide with the local slice width w(i) which may be much more variable along the river: w(j(i)) is a filtered out relative of w(i);
−
AC envelope area (or width)
−
VB area (or width)
−
Area of left, right, point bank attached bars; area of mid channel bars
−
number of active channels
−
max, min, average water channel width of channels
−
max and average distance between two channels (when multi-channel)
−
max whole length of water channel crossing slice i (from its departure from main channel until its joining downstream)
−
area of wetlands within the VB (for slice i)
−
sinuosity of reach in which slice i falls (see discussion above on sinuosity iteration).
Figure 3 visually presents in a comprehensive fashion the exercise conducted and the essential steps required to automatically identify the dominant archetypes governing the planform of the river within the GIS and Excel environment.

4. Results and Discussion

We do not present an expert judgment identification of Planform typology to be compared with the Tool output because the former should be the fruit of a wide exercise, involving several independent experts, what has not been conducted yet. Rather, for each river we present the original geomorphic elements and units (those adopted as basic information to input into the Planform Tool), the corresponding Planform output and the final output of Holistic. From such elements the reader can verify and judge the performance of the algorithm. Comments are however provided to ease the analysis.
The important point is that all of them have been obtained by using the same parametrization of Planform; the only difference lies in the key parameter K defining the significant length which is set to the default value 1 for the Duqueco and Laja cases, while it is 1.5 for the Biobio case (and consistently the T1 parameter of Holistic is set to 50): this is fruit of a couple of attempts.
The spatial discretization (segmentation) step was fixed at 50 m which approximates the average AC envelop width of Duqueco with the idea to achieve a finer description of the units. Of course, this is an arbitrary choice that can be varied and is discussed later on.

4.1. Duqueco River

Here (Figure 4) Planform and Holistic provide the same identical answer which is very well suited according to the geomorphic units identified. It can be noted that some quite short reaches appear; they however still respect the condition of being no shorter than the local (slice i) significant length LS(i) as can be appreciated from Figure 5.
Here (Figure 6) Planform recognizes correctly a number of archetypes, including the Swallowing and the Alternate bars types, both belonging to the Transitional family, being the Swallowing a significant enlargement, with a big fluvial island inside, within a prevailing single channel reach, with no significant width difference between the two channels aside the island, and no bars presence; while the Alternate bars type requires to display a lateral bar on one side and then the opposite in an alternate fashion moving along the river, without an excessive distance between any two of them (i.e. less than the significant length), and with no other bars or islands present (and hence with just a single channel), nor evident enlargement.
Holistic, however, only keeps the first of the two Swallowing reaches (Figure 6): this is the effect of a special functionality introduced to avoid to skip such reaches as Swallowing reaches are typically shorter than the significant length as they are a kind of anomaly, but nevertheless deserve to be identified: therefore, as soon as at least two consecutive Swallowing slices are found, it adds a short queue before and after such nucleus to ensure it acquires a sufficient consistency. In this case, this happens only in the upstream Swallowing reach because it is born sufficiently long (more than just one slice), while this is not the case for the other reach which hence disappears.
The Alternate bars reaches are correctly identified, but they prove to be too short according to the local significant length criterion and hence they are overcome by the prevailing local type. An analogous destiny is given to other too short reaches identified by Planform and un politely, but correctly, merged with “the mainstream” by Holistic.
Here (Figure 7) again Planform correctly recognizes several archetypes, including the Swallowing and the Alternate bar types. Holistic respects them, except for the too short reaches which include, in particular the ALT bars ones that hence disappear; but the Swallowing one is correctly kept (according to the criteria illustrated above), although an excessive queue has been added. It can also be noticed that two Single channel reaches in the middle (between slices 461-481) are differentiated, because the downstream one of the two is a Constrained sinuosity one, according to the criteria adopted.
Here (Figure 8) too Holistic shows its utility by eliminating a few too short reaches. It conserves on the other side the ALT bar reach, though it arbitrarily extends it a bit outside of the actual reach delimited by alternating bars (notice that the downstream bar is small and not well visible in this image, but…is well present).
Here (Figure 9) the behavior is very similar to the previous case with some imperfections in the position of the start and end of the ALT bar reaches that nevertheless are correctly identified.
Here (Figure 10) the function of Holistic is more evident and the result well acceptable. A new type correctly appears, although just for two reaches (1532-1536 and 1567-1587): the Single Meandering archetype. Also, the stretch 1455-1474 might seem meandering, but the widespread presence of bars and islands correctly leads it to the Trans Wandering category; additionally, sinuosity does not achieve the 1.5 threshold.
Here (Figure 11) Planform correctly identifies several archetypes, including a Swallowing reach, although there is some imprecision in the ALT bars ones. Holistic fulfils its duty by eliminating too short reaches and adds some further correction, although it adds an excessive queue to the Swallowing.

4.2. Laja River

Here (Figure 12) Planform correctly distinguishes the Single, Low sinuosity, the Constrained sinuosity, and the Single, Straight reaches, while Holistic correctly eliminates some very short reaches.
This (Figure 13) is a quite varied stretch where Planform sees several types alternating where probably several choices might appear somehow questionable, like in particular the Swallowing one (because there is not a very much marked enlargement while there is a rather significant difference in the width of the two channels). Holistic correctly eliminates some very short reaches (all those kept indeed are longer than their local significant length) and, consistently with its criteria, keeps the Swallowing reach, being probably this the only questionable final choice. In other words, it improves greatly Planform response.
This stretch (Figure 14) includes very different situations, also because of the presence of a reservoir (grey zone) in large part responsible of the dramatic widening occurring upstream of it. Of the many reaches identified by Planform, Holistic keeps a reasonable selection, including the Trans, Swallowing one. This latter at first sight might seem unjustified; but at a closer view indeed it is justified by the significant enlargement although mainly with respect to the downstream reach (the algorithm currently does not check, as it should, that the enlargement does occur in both sides) and the presence of a two almost equally wide branches. Both Tools split the stretch upstream of the reservoir in a first (downstream) part Multi, Anabranching according to the presence of very large lateral branches and a significant enlargement, while more upstream, a second part is classified as Multi, Island braided, because the characteristics just mentioned are there smoothed. The ALT bars reach has been canceled, while the Swallowing one (consistently) kept, although an excessive queue is attached.
It is worth noting that here the algorithm was applied without splitting the river although the presence of the reservoir would suggest doing so, so it certainly gets a bit confused by the grey area that inputs misleading information.
This stretch (Figure 15), according to Planform, includes several different types, including Multi, Island braided; Single, Low sinuosity, Straight, Meandering Regular, and Constrained Sinuosity; Trans, Wandering and ALT bars (two reaches). The presence of a (quite rare) Meandering reach is justified (according to the criteria specified in the algorithm) by the presence of a point bar (that, rigorously speaking, can be highly questionable, but is what was given in input to the algorithm, so it is out of discussion here) and a sufficient value of the sinuosity itself (higher than 1.5).
Holistic significantly reduces this geomorphic diversity and probably most of the readers will be in favor of its choices. Indeed, several are too short and as such eliminated, like the first (upstream) ALT, while the second is kept and enlarged a bit (possibly unduly).
Here again (Figure 16), the river presents a significant enlargement just upstream of a bottle neck, here naturally imposed. A significant Single, Constrained sinuosity reach is correctly identified by both Planform and Holistic, while, upstream and downstream of it, Multi channels reaches are present. The reach upstream of the bottle neck is identified as Anabranching, according to the criteria specified, i.e., a significant enlargement (particularly with respect to the following reach), very large side channels, a significant difference in width amongst the multiple channels, absence (or negligible presence) of bars.

4.3. Biobío River

Notice: in this case, the numbering of slices starts from the most downstream slice, contrary to the other cases.
Here (Figure 17), the sporadic presence of relatively small islands does not suffice to switch to the multichannel family. The reach on the right is correctly identified as Constrained sinuosity (although it improperly involves few slices on the left that are not: 3876-3858). Although a Swallowing slice appears in Planform, being isolated it is then correctly ignored by Holistic. The differentiation between the last two reaches, both single channels, is correctly based on the value of sinuosity.
Here (Figure 18) the algorithm performs modestly as it correctly captures the main typologies, but imprecisely defines the position of the reaches: in particular, the Single, Low sinuosity reach (of about 3.2 km length) should start earlier (slice 3506, while it starts at 3485, that is about a kilometer after) and end earlier (slice 3448, rather than slice 3426, i.e., 1.1 km earlier). This is evidently a mistake of Holistic and is associated with a non-optimal choice of the significant length factor K. The key factor distinguishing the Anabranching from the Island braided archetype is the presence, in the former, of a channel of significant length, the marked presence of a main channel as well as the presence of an enlargement of the Active Channel envelope.
Here (Figure 19) the algorithm performs well as it correctly captures the main typologies and defines sufficiently correctly the position of the reaches. It is apparent its key role of filtering out the uncertainties (or hysteria) of Planform that is definitely exaggerate (at least with respect to previous versions of the Tool we experienced). This suggests that the use of multiplicative VF should be rethought and at least moderated.
Again, here (Figure 20) the algorithm performs quite well, despite the hysteria of Planform. The only mistake is the identification of a Swallowing reach, but this is due to a technical detail as discussed later.
Here (Figure 21) the output is consistent with the geomorphic evidence (the Swallowing reach is the same noted above and commented later on), although it can be questionable where it is appropriate to identify Anabranching reaches: here Holistic only retains two of the multiple smaller reaches identified by Planform because only those constitute a significant length and indeed present all the due characteristics (already reminded previously). The new Wandering transitional archetype appears at the downstream end (top, left) as several latera bars appear which deny the Island braided typology.
Here (Figure 22) the algorithm must deal with the difficult task of interpreting the assemblages of multiple small islands and bars. Planform, although with a significant uncertainty, correctly identifies specific sub reaches with Braided, Wandering, Island braided (and even, very locally, Constrained sinuosity) archetypes. Holistic, under the compelling requirement to eliminate reaches shorter than the significant length merges two Braided sub reaches by incorporating an island zone that, at first sight, should not be part of it. However, taken from another point of view, that island sub reach is too short to deserve existence as an actual reach, and no other archetype would fit better to the unified reach: so, the choice of Holistic is hardly improvable.

General Considerations

It is worth observing that the ability of the algorithm is identifying the most suited archetype, but also deciding the reach to be assigned to a given archetype. This is not a trivial task, and the algorithm seems to perform well, although certainly it is not perfect. Several dams are present along the considered rivers; but this fact has been ignored in this application (introducing so a certain bias in the results). A practical, although approximate, recipe to avoid this type of difficulty is however easy: just break the river into (two) stretches at each dam site and proceed with each one separately.
Figure 23 shows a statistical summary of the percentage of total length of each river according to the dominant planform archetypes for the three rivers.
The Biobío case is quite challenging. It indeed presents a somehow confused physical configuration amongst multiple, small islands and bars, probably owing to anthropogenic alterations linked to deforestation in its catchment. On the other side, the width along the whole river varies greatly (compare for instance slices 3810 in Figure 17 and 2767 in Figure 19) and this indeed rises a quite difficult challenge for the algorithm: in order to discretize with a sufficient resolution the narrowest segments, a slice length of 50 m has been suitably adopted, but this proves to be very tiny when moving downstream. In fact, the too thin character of the slices, jointly with the multiplicative Value Functions adopted, introduces a marked hysteria of the algorithm as consecutive slices find, apparently, very different situations. In addition, a problem arises with the Swallowing archetype: as already explained, the algorithm has hence a special functionality to preserve such reaches (which are not very much long, by definition): it adds a short queue before and after the nucleus found; in the Biobío case (Figure 24) a couple of such adjacent slices are indeed found just because slices are very thin, otherwise just one would show up: this fact ends up with a Swallowing reach identified where it should not.
Also, the Duqueco case too is quite challenging because it presents sudden, significant enlargements and a quite large number of archetypes; nevertheless, the algorithm basically captures them all. In that case, however, a weakness of Holistic appears: as at the end of Round I still few reaches are present which are shorter than the significant length, it goes through Round II and applies a last option rule with which it assigns to the too short reach the same typology of the following one: this produces the undue preceding queue classified as Swallowing, which should not be (and can be corrected in future versions).
Very rarely the meandering type appears, while visually one would like perhaps to see it more often; but this is consistent with the criterion that a meandering requires a sinuosity not less than 1.5.

5. Conclusions

The proposed Tool, indeed, the Planform-Holistic couple, performs quite satisfactorily and the exercise has proven what had been theorized in the discussion section by Nardini and Brierley [11], i.e., that a given parametrization holds for different rivers because all the differences are captured explicitly by the attributes considered. Only the key parameter K determining the significant length (and its associated minimum length parameter T1 of the Holistic) deserves possibly an adaptation given a specific case study; but a couple of attempts can be sufficient.
The algorithm can however still be improved: better sets of attributes and corresponding indicators can be adopted; more precise identification of start and end for the ALT bars type can be set; improved Value Functions can be introduced; and particularly the role of the multiplicative ones rediscussed and marginalized to avoid the unpleasant hysteria it introduces. In Holistic, the way the special case of Swallowing type is dealt with can be improved to avoid too long queues to appear; and the appearance (although quite unusual) of reaches not fulfilling the significant length constraint should be avoided (perhaps by iterating once more the same algorithm). It must be considered however that the imprecisions or mistakes, when related to the whole river length, are quite minor indeed.
Another line of improvement refers to the introduction of new archetypes. This is certainly possible; however, addressing very large rivers (e.g., Amazon, Magdalena, Ob, Mackenzie, Congo and Orinoco rivers, described in Ashworth and Lewin, [30]) would raise new demanding challenges because each one of multiple channels may require a specific identification with specific geomorphic units.
An interesting experiment would be to receive several different expert identification of planform reaches/types and to compare their consistency with the algorithm answer.
Another experiment would be the use of ML algorithm, fed by the same information basis (the indicators values associated with the spatial discretization), to ascertain what their answer would be in the unsupervised mode (analogous to the one adopted here) and then in the supervised mode (once expert judgments were available).
Although the Planform and Holistic Tools are now developed on an Excel® support, the whole package has been conceived to be potentially fully automatized, once the basic geomorphic elements and units are provided (a task that itself can potentially be conducted in an automatized way, on the line for instance of [8,19,26]). Difficulties are however present, like the ability to determine, for each discretization slice, the length of the water channels intercepted; or the initial estimation of the sinuosity (which requires itself an iterative procedure).
From an operational point of view, it is recommendable to split the cases with too marked width differences along the river into two (or more) long stretches and adopt a proportional discretization length (i.e., in particular for the Biobío River, a length greater than the 50 m now adopted); the same recommendation holds when an artificial structure (like a dam) is present.
The exercise has an intrinsic value in making explicit the criteria to classify reaches amongst the available archetypes. It ensures a consistent application of such criteria, a property (consistency) that can hardly be ensured by expert judgment. Its direct usefulness lies however in:
−
the ability to characterize large river networks
−
the possibility to carry out a regular, systematic monitoring of a river network to detect possible typological changes as clear indicators of (natural or anthropogenic) alterations occurred.

Author Contributions

“Conceptualization, AN and SY; methodology, AN and SY; software, FS, NV, ZC and RR; validation, AN and SY; formal analysis, FS, NV, ZC and RR; investigation, AN and FS; resources, SY; data curation, AN and SY; writing—original draft preparation, AN and FS; writing—review and editing, SY, FS and AN; visualization, ZC; supervision, SY, AN and JV; project administration, SY; funding acquisition, SY and JV. All authors have read and agreed to the published version of the manuscript.”.

Funding

South Rivers Toolbox project (19BP-117424) funded by CORFO.

Data Availability Statement

All raw data can be provided by the corresponding authors upon request.

Acknowledgments

We would like to thank Planet for providing the RapidEYE and Planet Scope (nanosatellite) images used in this study free of charge. Also, to the TanDEM-X DEM GEOL08450 project for providing the high spatial resolution terrain elevation model.

Conflicts of Interest

“The authors declare no conflict of interest.”.

References

  1. Kondolf, G.M.; Piégay, H.; Schmitt, L.; Montgomery, D.R. Geomorphic classification of rivers and streams. Tools in fluvial geomorphology 2016, 133–158. [Google Scholar] [CrossRef]
  2. Buffington, J.; Montgomery, D. Geomorphic classification of rivers. 2013.
  3. Fryirs, K.; Brierley, G. Practical applications of River Styles Framework as a tool for catchment-wide river management: A case study from Bega Catchment New South Wales. Auckland, NZ: MacQuirie University 2005.
  4. Nardini, A.; Yépez, S.; Mazzorana, B.; Ulloa, H.; Bejarano, M.D.; Laraque, A. A systematic, automated approach for river segmentation tested on the Magdalena River (Colombia) and the Baker River (Chile). Water 2020, 12, 2827. [Google Scholar] [CrossRef]
  5. Parker, C.; Clifford, N.J.; Thorne, C.R. Automatic delineation of functional river reach boundaries for river research and applications. River Research and Applications 2012, 28, 1708–1725. [Google Scholar] [CrossRef]
  6. Piégay, H.; Arnaud, F.; Belletti, B.; Bertrand, M.; Bizzi, S.; Carbonneau, P.; Dufour, S.; Liébault, F.; Ruiz-Villanueva, V.; Slater, L. Remotely sensed rivers in the Anthropocene: State of the art and prospects. Earth Surface Processes and Landforms 2020, 45, 157–188. [Google Scholar] [CrossRef]
  7. Dallaire, O.C. Ouellet Dallaire, B.; Lehner, R.; Sayre, M. Thieme A multidisciplinary framework to derive global river reach classifications at high spatial resolution. Environ. Res. Lett. 2018, 14, 024003. [Google Scholar] [CrossRef]
  8. Demarchi, L.; Bizzi, S.; Piégay, H. Hierarchical object-based mapping of riverscape units and in-stream mesohabitats using LiDAR and VHR imagery. Remote Sensing 2016, 8, 97. [Google Scholar] [CrossRef]
  9. Bernard, T.G.; Davy, P.; Lague, D. Hydro-geomorphic metrics for high resolution fluvial landscape analysis. Journal of Geophysical Research: Earth Surface 2022, 127, e2021JF006535. [Google Scholar] [CrossRef]
  10. Jézéquel, C.; Oberdorff, T.; Tedesco, P.A.; Schmitt, L. Geomorphological diversity of rivers in the Amazon Basin. Geomorphology 2022, 400, 108078. [Google Scholar] [CrossRef]
  11. Nardini, A.; Brierley, G. Automatic river planform identification by a logical-heuristic algorithm. Geomorphology 2021, 375, 107558. [Google Scholar] [CrossRef]
  12. Frasson, R.P.d.M.; Pavelsky, T.M.; Fonstad, M.A.; Durand, M.T.; Allen, G.H.; Schumann, G.; Lion, C.; Beighley, R.E.; Yang, X. Global relationships between river width, slope, catchment area, meander wavelength, sinuosity, and discharge. Geophysical Research Letters 2019, 46, 3252–3262. [Google Scholar] [CrossRef]
  13. Beechie, T.; Imaki, H. Predicting natural channel patterns based on landscape and geomorphic controls in the Columbia River basin, USA. Water Resources Research 2014, 50, 39–57. [Google Scholar] [CrossRef]
  14. Beechie, T.J.; Liermann, M.; Pollock, M.M.; Baker, S.; Davies, J. Channel pattern and river-floodplain dynamics in forested mountain river systems. Geomorphology 2006, 78, 124–141. [Google Scholar] [CrossRef]
  15. Rabanaque, M.P.; Martínez-Fernández, V.; Calle, M.; Benito, G. Basin-wide hydromorphological analysis of ephemeral streams using machine learning algorithms. Earth Surface Processes and Landforms 2022, 47, 328–344. [Google Scholar] [CrossRef]
  16. Bertrand, M.; Piégay, H.; Pont, D.; Liébault, F.; Sauquet, E. Sensitivity analysis of environmental changes associated with riverscape evolutions following sediment reintroduction: Geomatic approach on the Drôme River network, France. International journal of river basin management 2013, 11, 19–32. [Google Scholar] [CrossRef]
  17. Guillon, H.; Byrne, C.F.; Lane, B.A.; Sandoval Solis, S.; Pasternack, G.B. Machine learning predicts reach-scale channel types from coarse-scale geospatial data in a large river basin. Water Resources Research 2020, 56, e2019WR026691. [Google Scholar] [CrossRef]
  18. Horacio, J.; Ollero, A.; Pérez-Alberti, A. Geomorphic classification of rivers: A new methodology applied in an Atlantic Region (Galicia, NW Iberian Peninsula). Environmental Earth Sciences 2017, 76, 1–20. [Google Scholar] [CrossRef]
  19. Bizzi, S.; Lerner, D.N. Characterizing physical habitats in rivers using map-derived drivers of fluvial geomorphic processes. Geomorphology 2012, 169, 64–73. [Google Scholar] [CrossRef]
  20. Donadio, C.; Brescia, M.; Riccardo, A.; Angora, G.; Veneri, M.D.; Riccio, G. A novel approach to the classification of terrestrial drainage networks based on deep learning and preliminary results on solar system bodies. Scientific Reports 2021, 11, 1–13. [Google Scholar] [CrossRef]
  21. Alber, A.; Piégay, H. Spatial disaggregation and aggregation procedures for characterizing fluvial features at the network-scale: Application to the Rhône basin (France). Geomorphology 2011, 125, 343–360. [Google Scholar] [CrossRef]
  22. Hubert, P. The segmentation procedure as a tool for discrete modeling of hydrometeorological regimes. Stochastic Environmental Research and Risk Assessment 2000, 14, 297–304. [Google Scholar] [CrossRef]
  23. Caamaño, D. Caracterización de cambios morfológicos en la parte media del río Biobío. Universidad Católica de la Santísima Concepción, 2019.
  24. Niemeyer, H. Hoyas hidrográficas de Chile: 8a. Región del Bío-Bío, 9a. Región de la Araucanía, 10a. Región de Los Lagos. 1980.
  25. Mardones, M.; Vargas, J. Efectos hidrológicos de los usos eléctrico y agrícola en la cuenca del río Laja (Chile centro-sur). Revista de Geografía Norte Grande 2005, 89–102. [Google Scholar]
  26. Yépez, S.; Salas, F.; Nardini, A.; Valenzuela, N.; Osores, V.; Vargas, J.; Rodriguez, R.; Piégay, H. Semi-automated morphological characterization using South Rivers Toolbox. Proc. IAHS 2023, 100, 1–8. [Google Scholar] [CrossRef]
  27. McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. International journal of remote sensing 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
  28. Gilbert, J.T.; Macfarlane, W.W.; Wheaton, J.M. The Valley Bottom Extraction Tool (V-BET): A GIS tool for delineating valley bottoms across entire drainage networks. Computers & Geosciences 2016, 97, 1–14. [Google Scholar] [CrossRef]
  29. Kleinhans, M.G.; van den Berg, J.H. River channel and bar patterns explained and predicted by an empirical and a physics-based method. Earth Surface Processes and Landforms 2011, 36, 721–738. [Google Scholar] [CrossRef]
  30. Ashworth, P.J.; Lewin, J. How do big rivers come to be different? Earth-Science Reviews 2012, 114, 84–107. [Google Scholar] [CrossRef]
Preprints 75627 g001
Figure 1. The algorithm introduced to manage highly varying AC width situations. This example (Duqueco River) shows how this process works: the grey line identifies macro segments (4 from Hubert test) and determines their width w(j); the orange line is the original AC width (varying very much); the blue line is the output width: it is quite smoothed, although still sensitive to AC width variations.
Figure 1. The algorithm introduced to manage highly varying AC width situations. This example (Duqueco River) shows how this process works: the grey line identifies macro segments (4 from Hubert test) and determines their width w(j); the orange line is the original AC width (varying very much); the blue line is the output width: it is quite smoothed, although still sensitive to AC width variations.
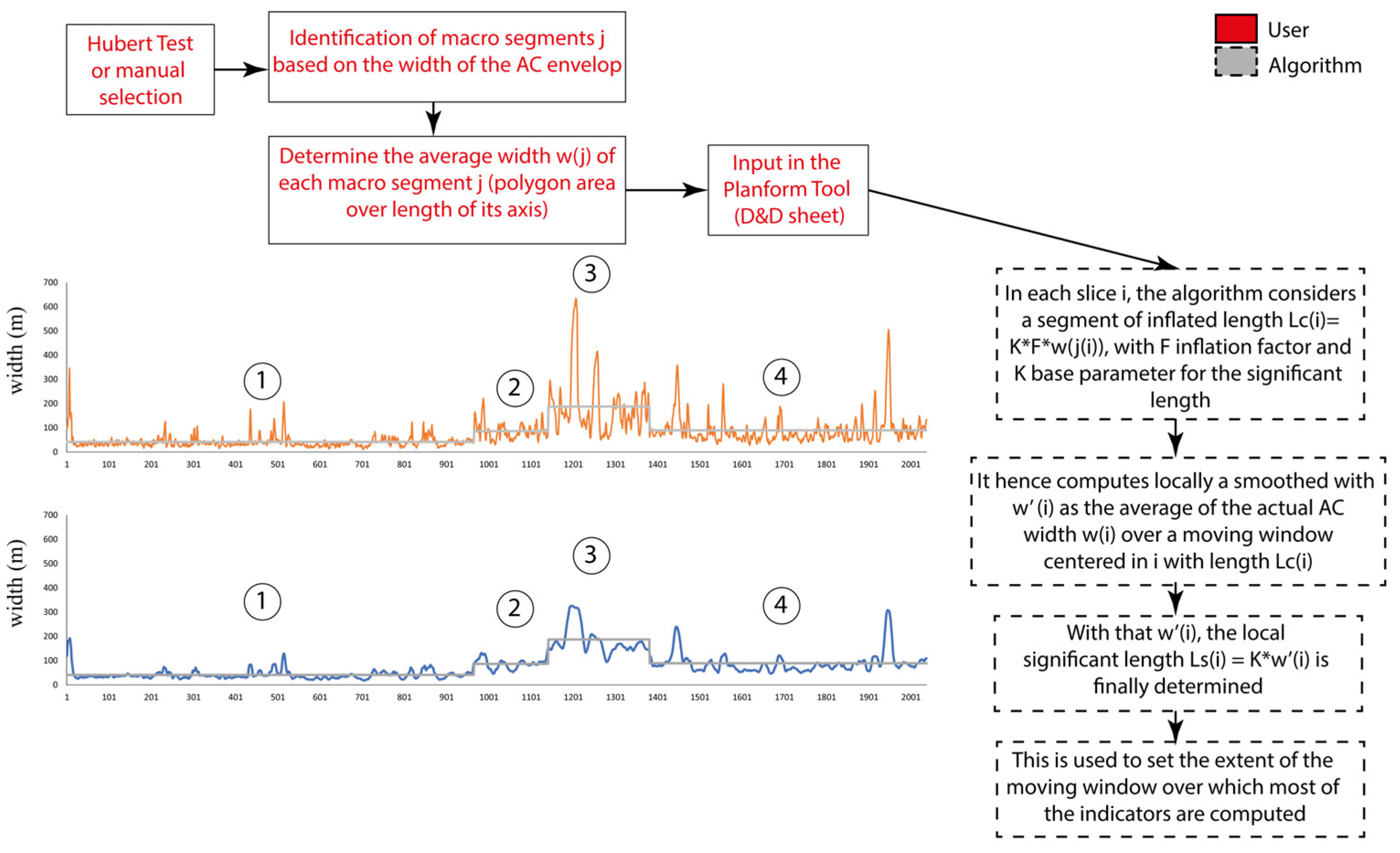
Preprints 75627 g001
Preprints 75627 g002
Figure 2. Study Area in Biobío Basin.
Figure 2. Study Area in Biobío Basin.
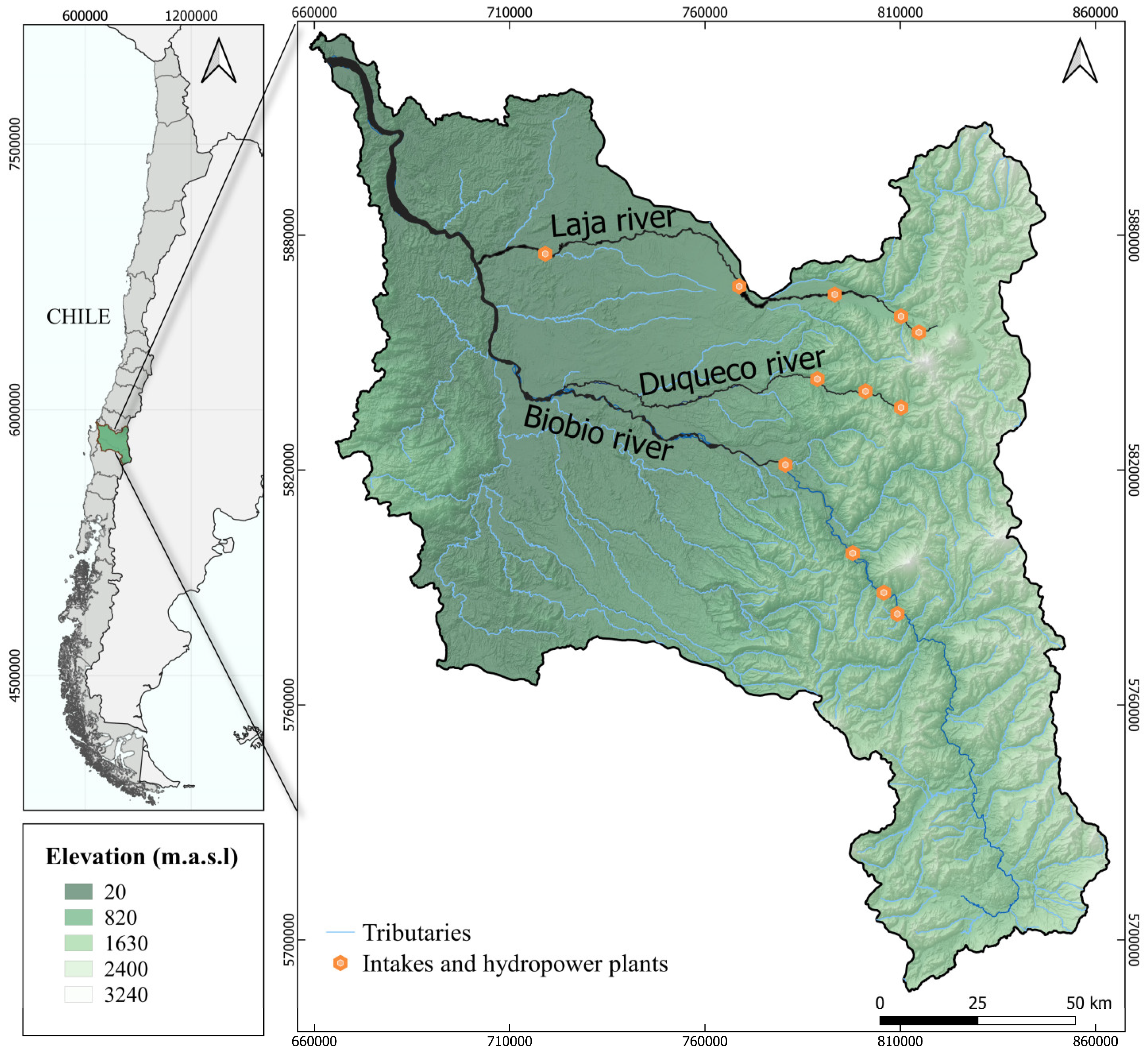
Preprints 75627 g002
Preprints 75627 g003
Figure 3. Workflow for calculating Planform.
Figure 3. Workflow for calculating Planform.
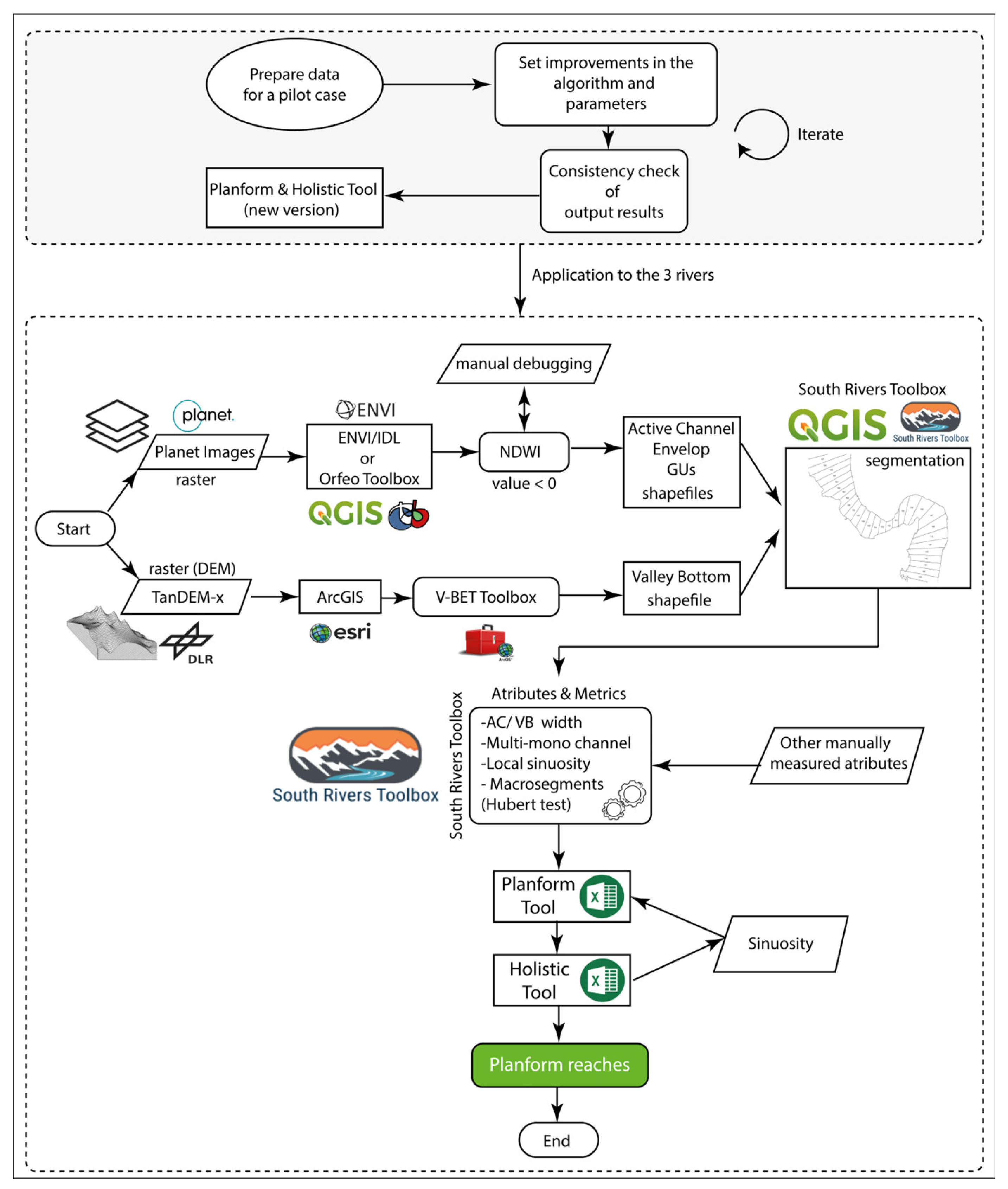
Preprints 75627 g003
Preprints 75627 g004
Figure 4. Upstream segment of the Duqueco River (slices: 15-205; slices 1-14 belong to a reservoir).
Figure 4. Upstream segment of the Duqueco River (slices: 15-205; slices 1-14 belong to a reservoir).
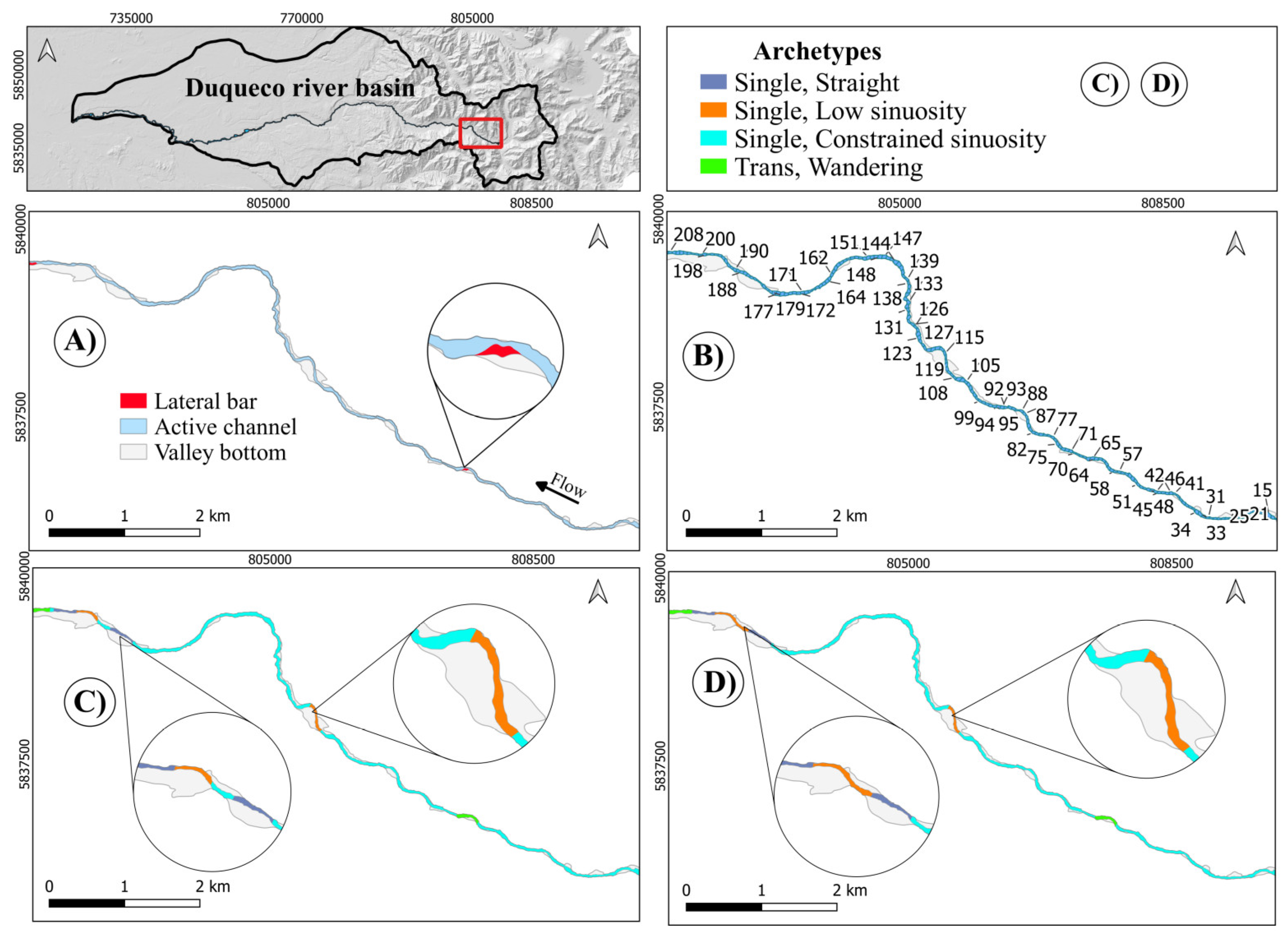
Preprints 75627 g004
Preprints 75627 g005
Figure 5. A zoom into the short reach 61-66: still it is longer than the local significant length Ls(i) (about 300 m), being the average width around 30 m and the K factor adopted 10. Notice that, by definition, only the archetypes from the Single family can be classified as Constrained sinuosity.
Figure 5. A zoom into the short reach 61-66: still it is longer than the local significant length Ls(i) (about 300 m), being the average width around 30 m and the K factor adopted 10. Notice that, by definition, only the archetypes from the Single family can be classified as Constrained sinuosity.
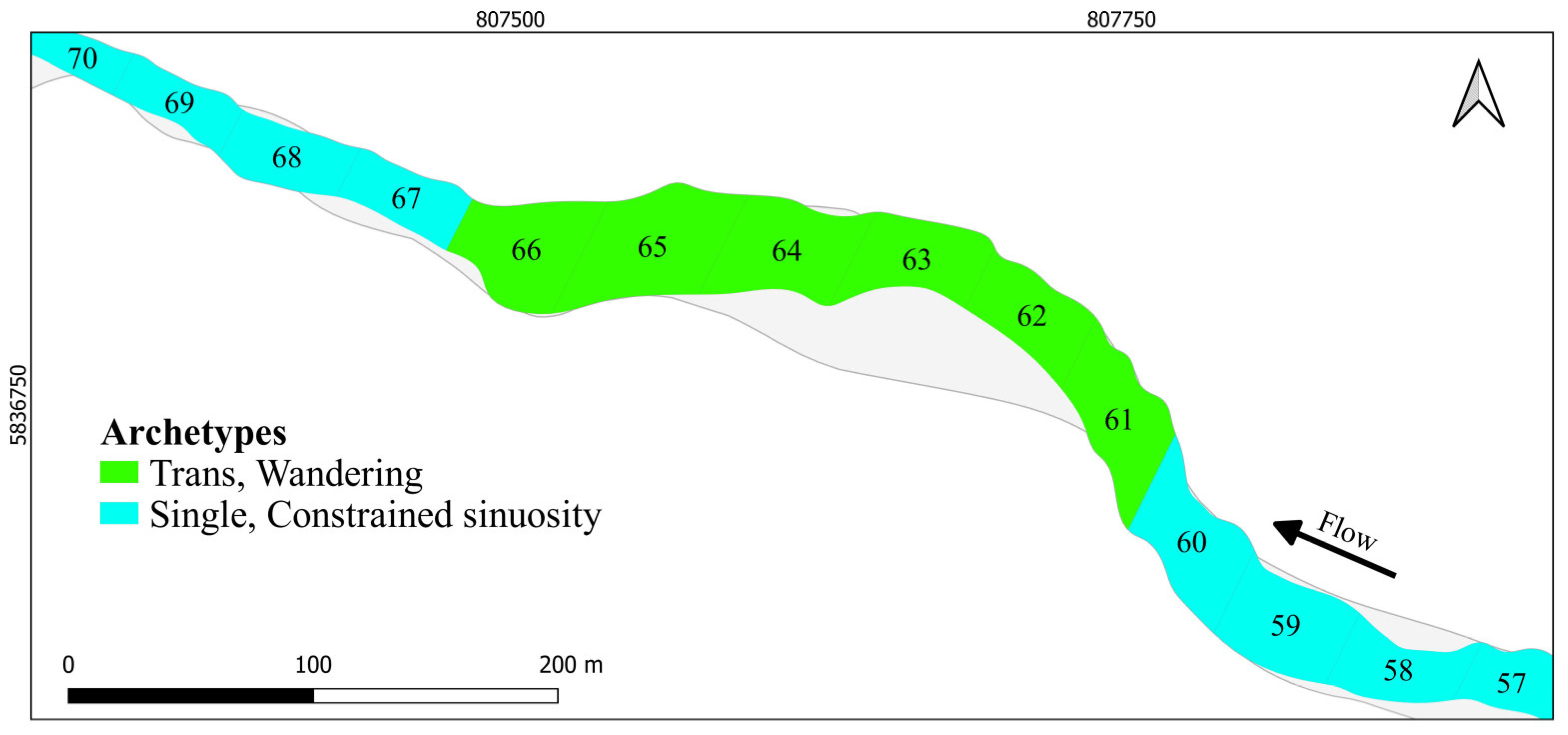
Preprints 75627 g005
Preprints 75627 g006
Figure 6. A stretch of the Duqueco River (slices: 205-370).
Figure 6. A stretch of the Duqueco River (slices: 205-370).
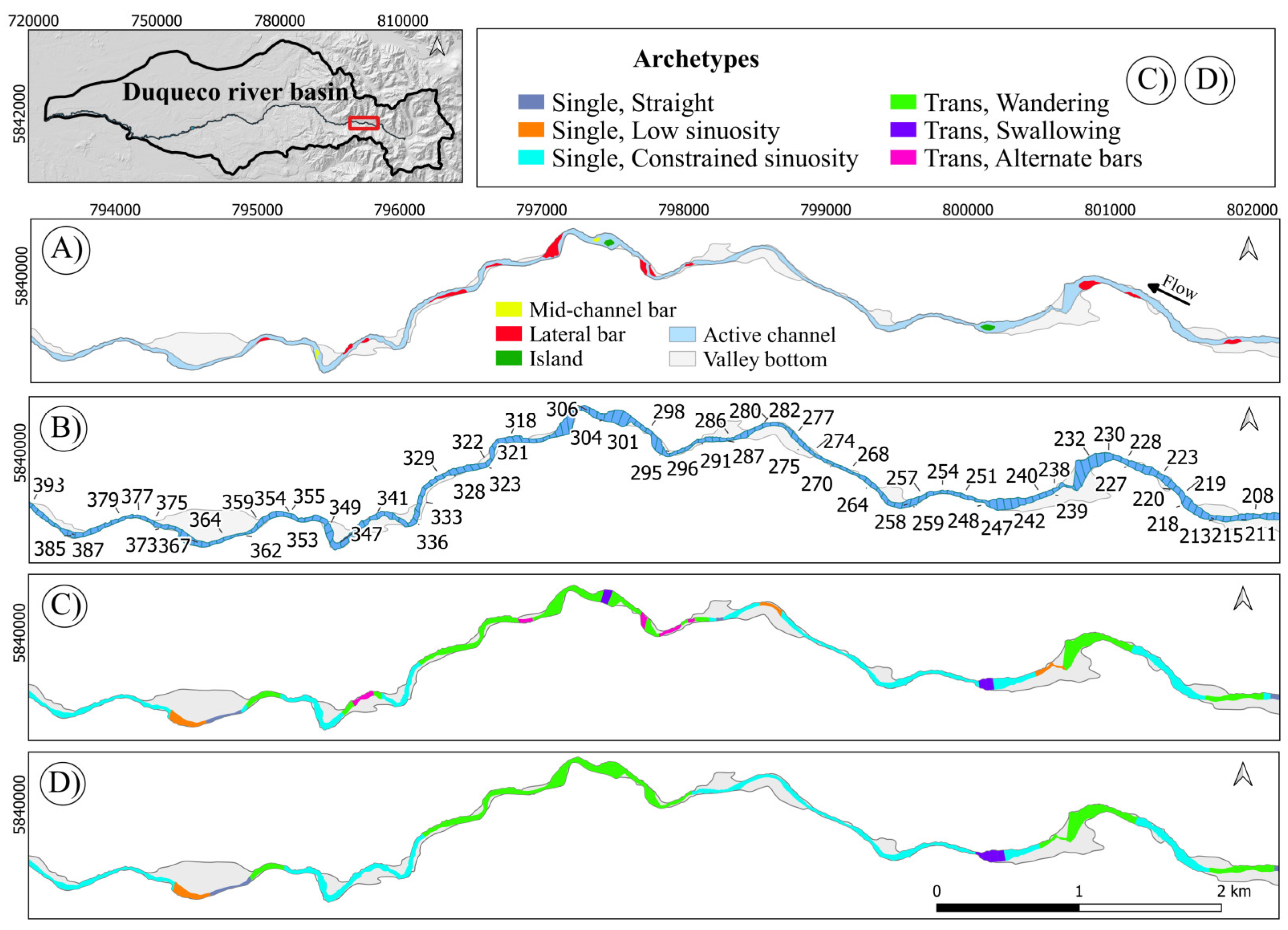
Preprints 75627 g006
Preprints 75627 g007
Figure 7. A stretch of the Duqueco River (slices: 370-562).
Figure 7. A stretch of the Duqueco River (slices: 370-562).
Preprints 75627 g007
Preprints 75627 g008
Figure 8. A stretch of the Duqueco River (slices: 725-926); notice that an upstream stretch has been omitted because banal (fully Constrained sinuosity).
Figure 8. A stretch of the Duqueco River (slices: 725-926); notice that an upstream stretch has been omitted because banal (fully Constrained sinuosity).
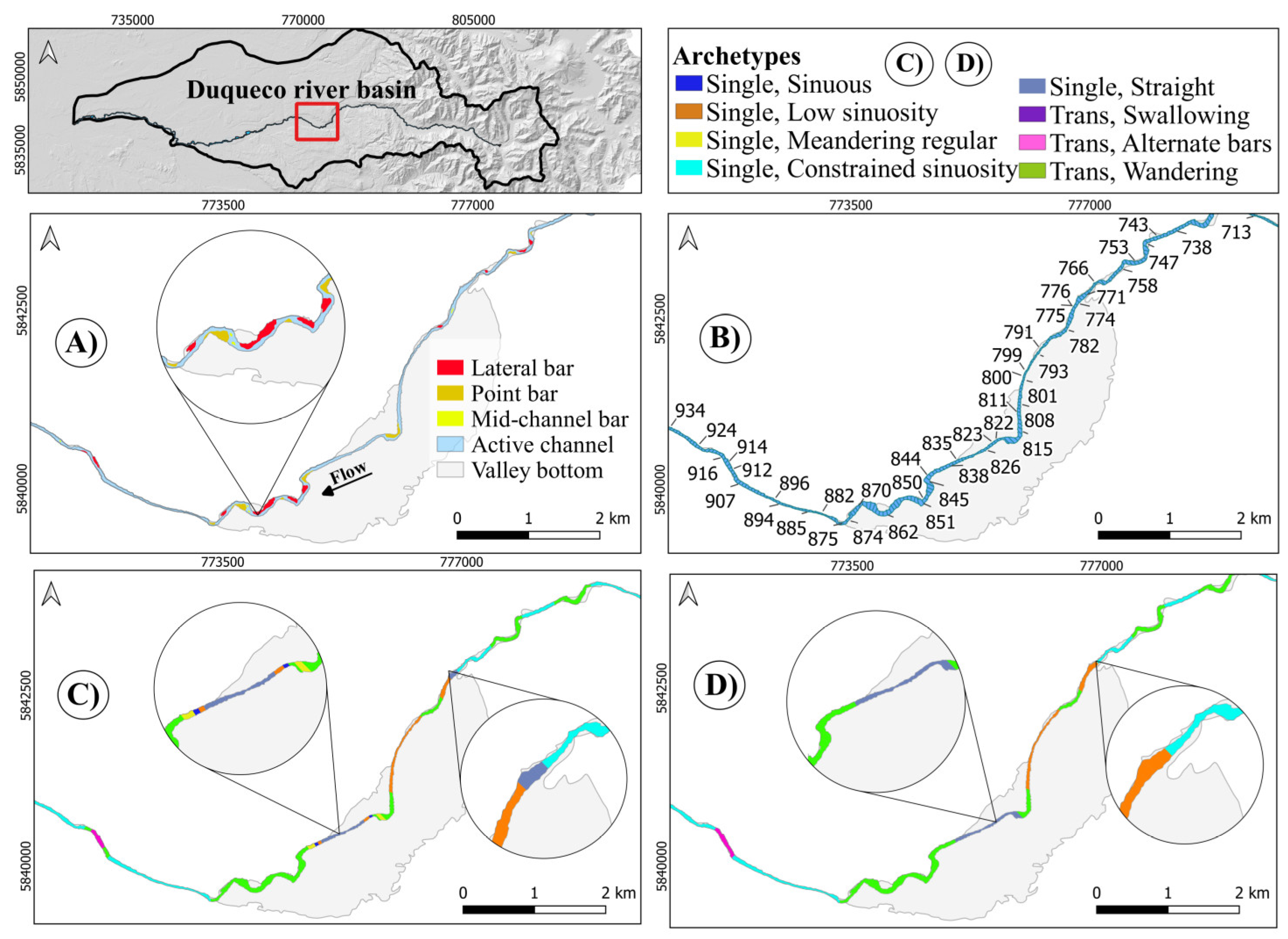
Preprints 75627 g008
Preprints 75627 g009
Figure 9. A stretch of the Duqueco River (slices: 982-1151).
Figure 9. A stretch of the Duqueco River (slices: 982-1151).
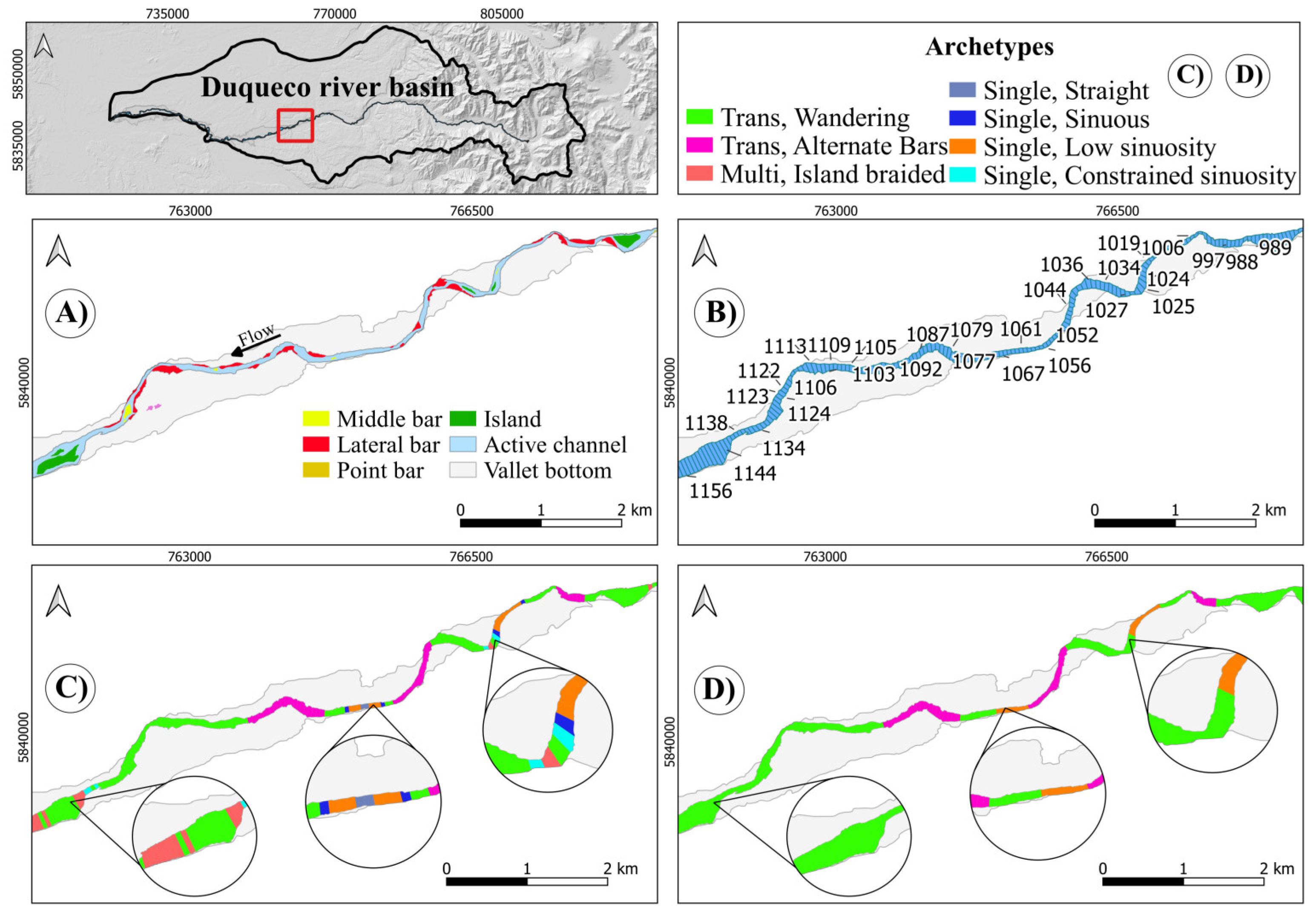
Preprints 75627 g009
Preprints 75627 g010
Figure 10. A stretch of the Duqueco River (slices: 1440-1657), after a long Trans Wandering reach correctly identified.
Figure 10. A stretch of the Duqueco River (slices: 1440-1657), after a long Trans Wandering reach correctly identified.
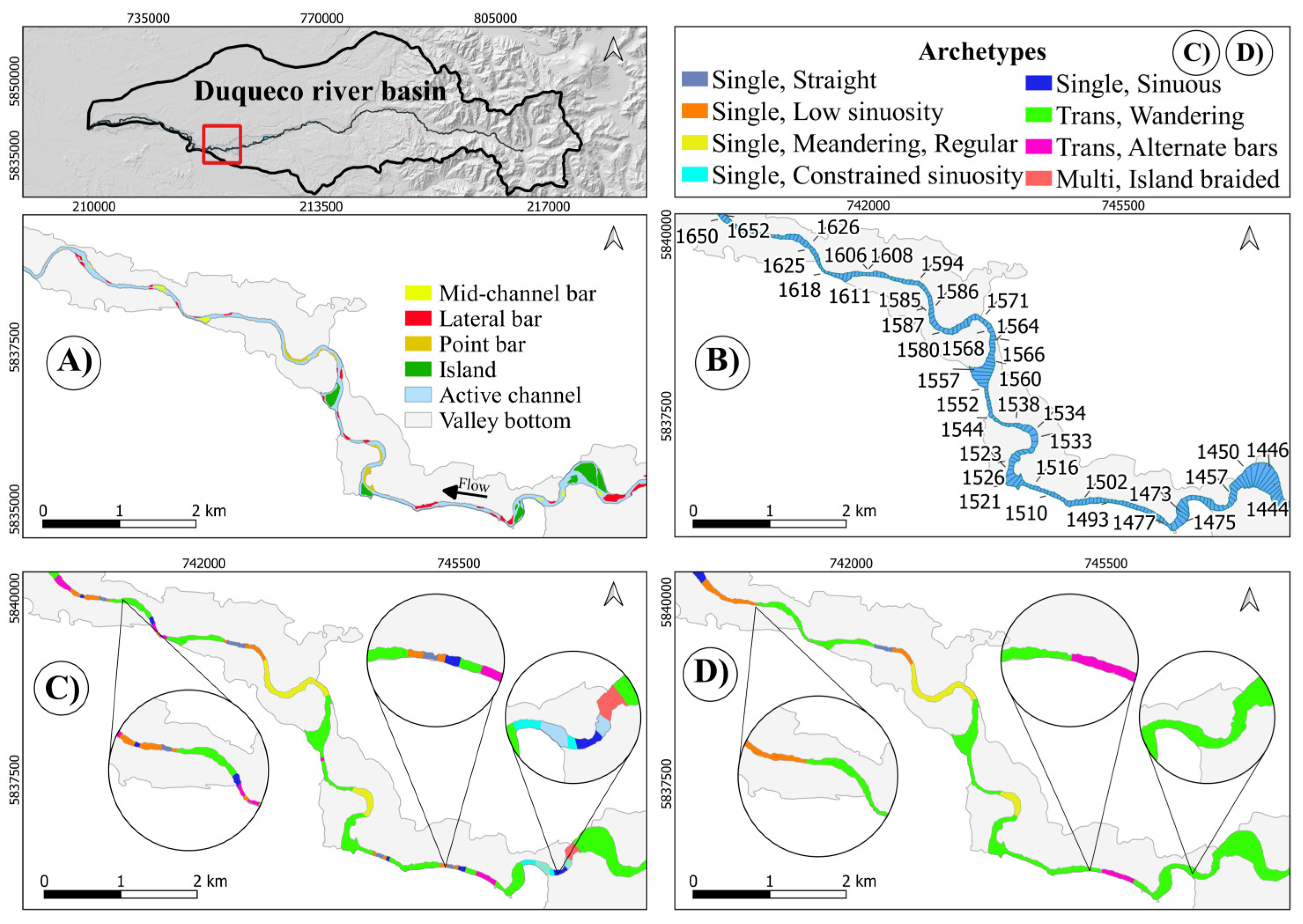
Preprints 75627 g010
Preprints 75627 g011
Figure 11. The final stretch of the Duqueco River (slices: 1834-2016).
Figure 11. The final stretch of the Duqueco River (slices: 1834-2016).
Preprints 75627 g011
Preprints 75627 g012
Figure 12. The first upstream stretch of the Laja River (slices: 10-194).
Figure 12. The first upstream stretch of the Laja River (slices: 10-194).
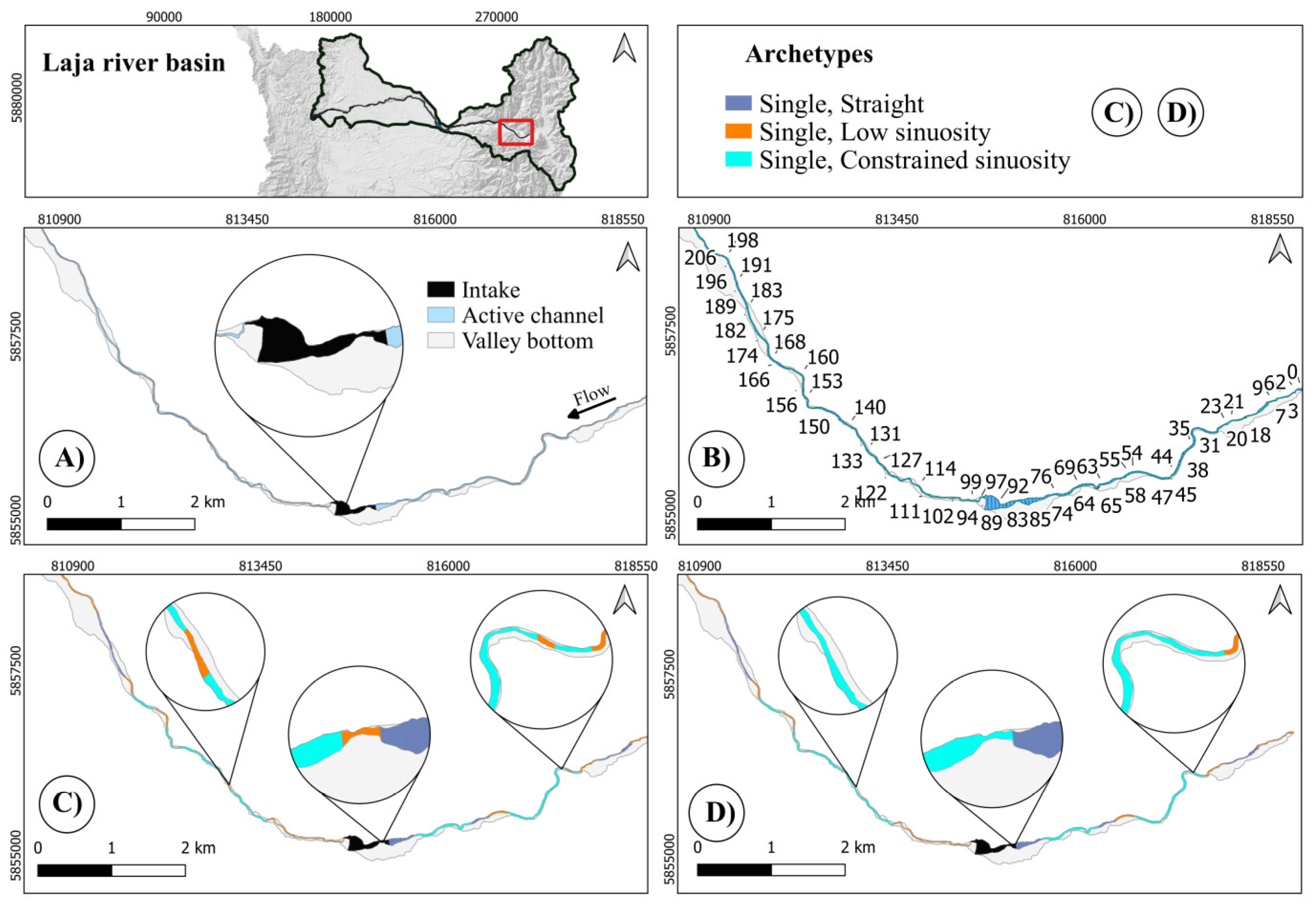
Preprints 75627 g012
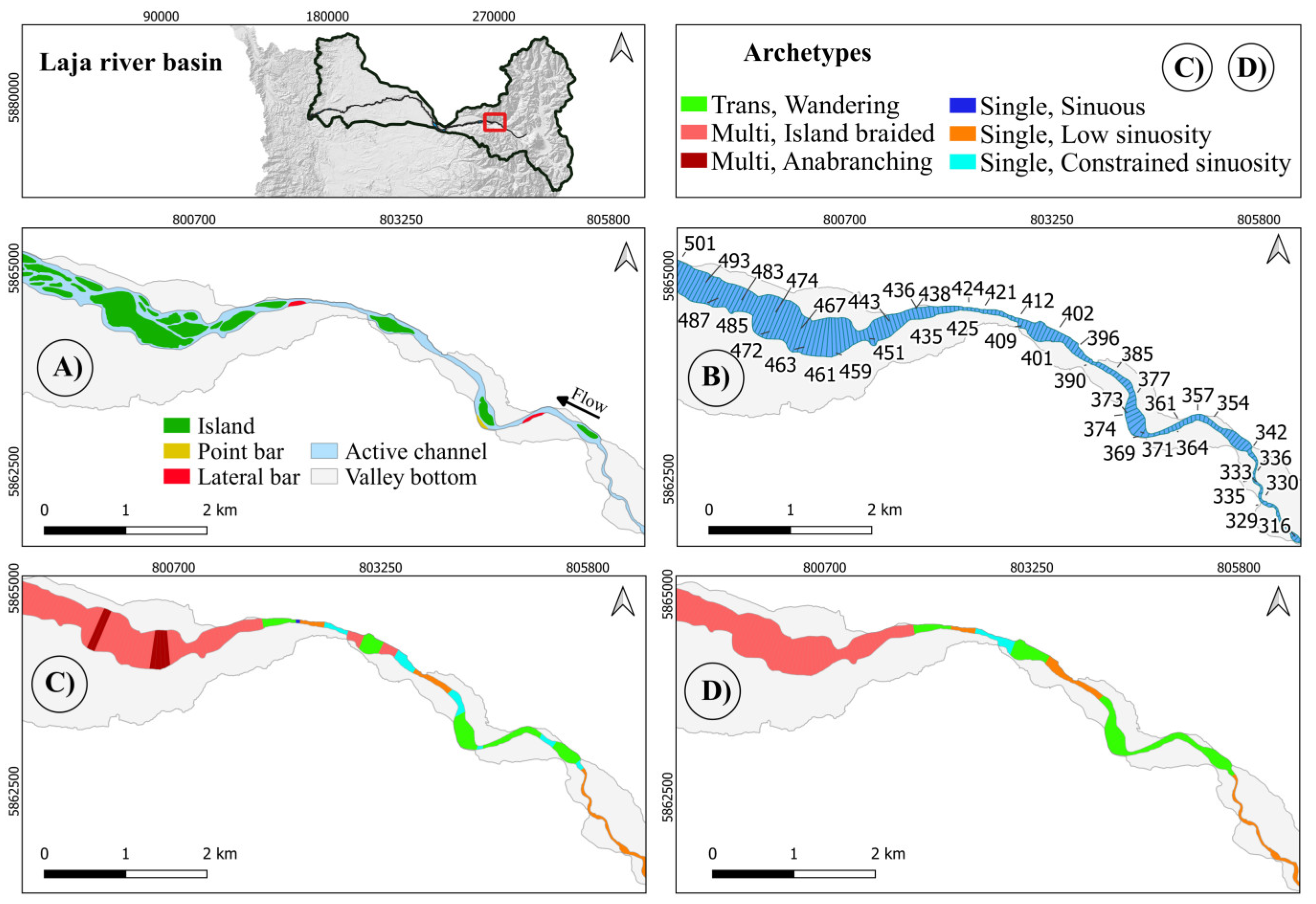
Preprints 75627 g013
Figure 13. Another stretch of the Laja River (slices: 318-499), skipping an intermediate stretch very similar to the previous one.
Figure 13. Another stretch of the Laja River (slices: 318-499), skipping an intermediate stretch very similar to the previous one.
Preprints 75627 g013
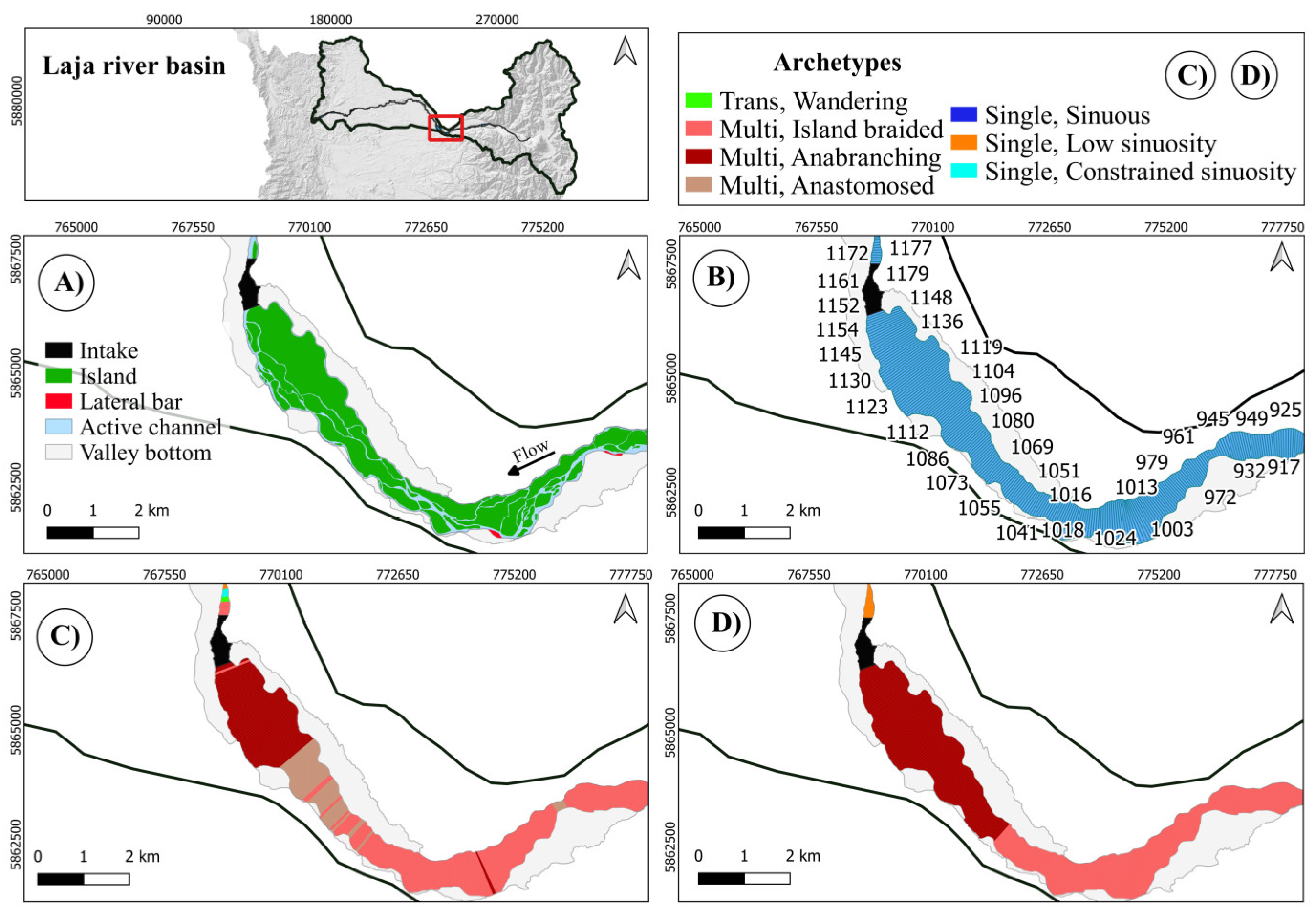
Preprints 75627 g014
Figure 14. Another stretch of the Laja River (slices: 947-1263), skipping an intermediate stretch quite uniform, mainly Multi, Island braided.
Figure 14. Another stretch of the Laja River (slices: 947-1263), skipping an intermediate stretch quite uniform, mainly Multi, Island braided.
Preprints 75627 g014
Preprints 75627 g015
Figure 15. A quite varied stretch of the Laja River (slices: 1634-1921), skipping an intermediate stretch much more regular and well represented.
Figure 15. A quite varied stretch of the Laja River (slices: 1634-1921), skipping an intermediate stretch much more regular and well represented.
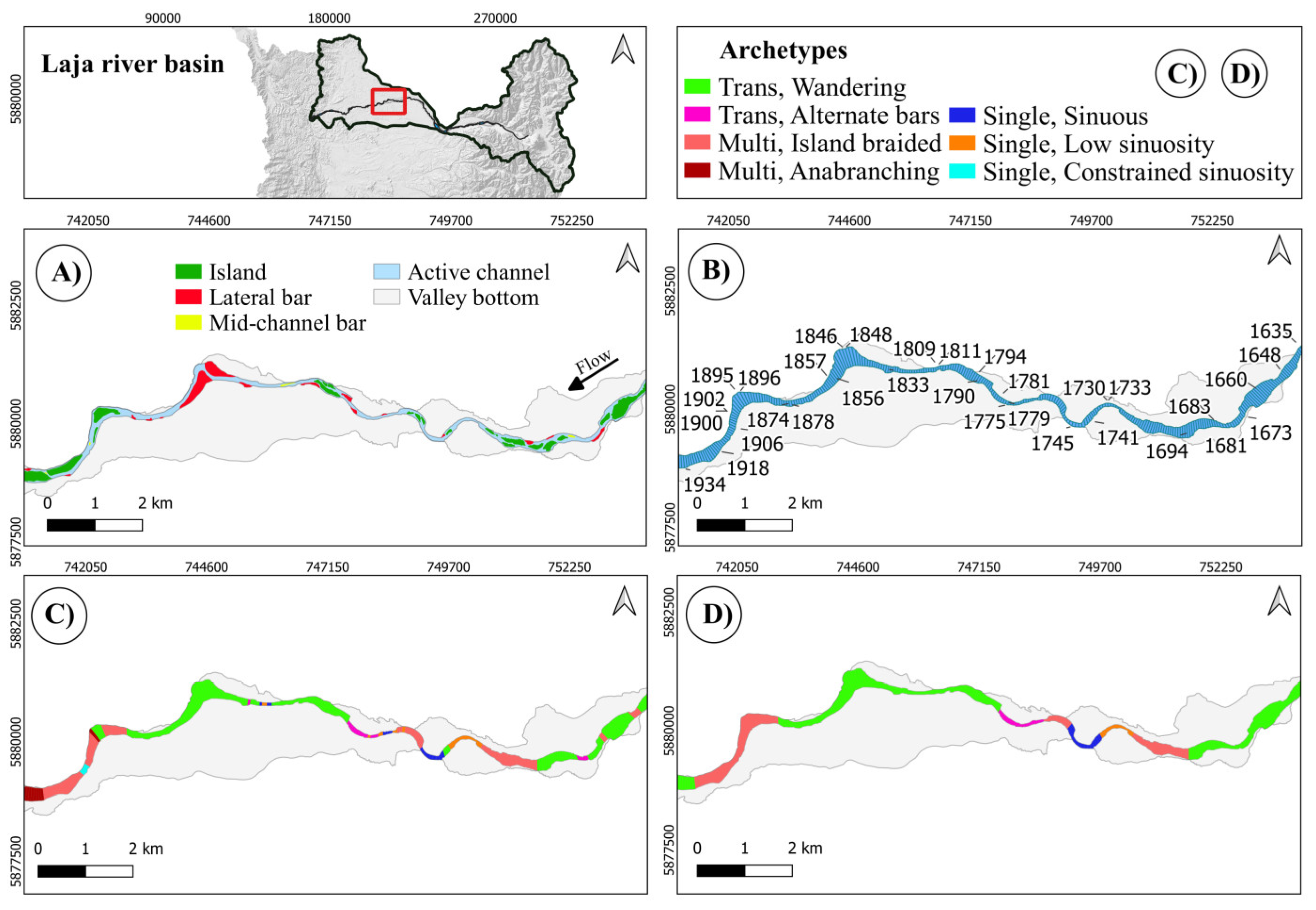
Preprints 75627 g015
Preprints 75627 g016
Figure 16. The last interesting stretch of the Laja River (slices: 1982-2225).
Figure 16. The last interesting stretch of the Laja River (slices: 1982-2225).
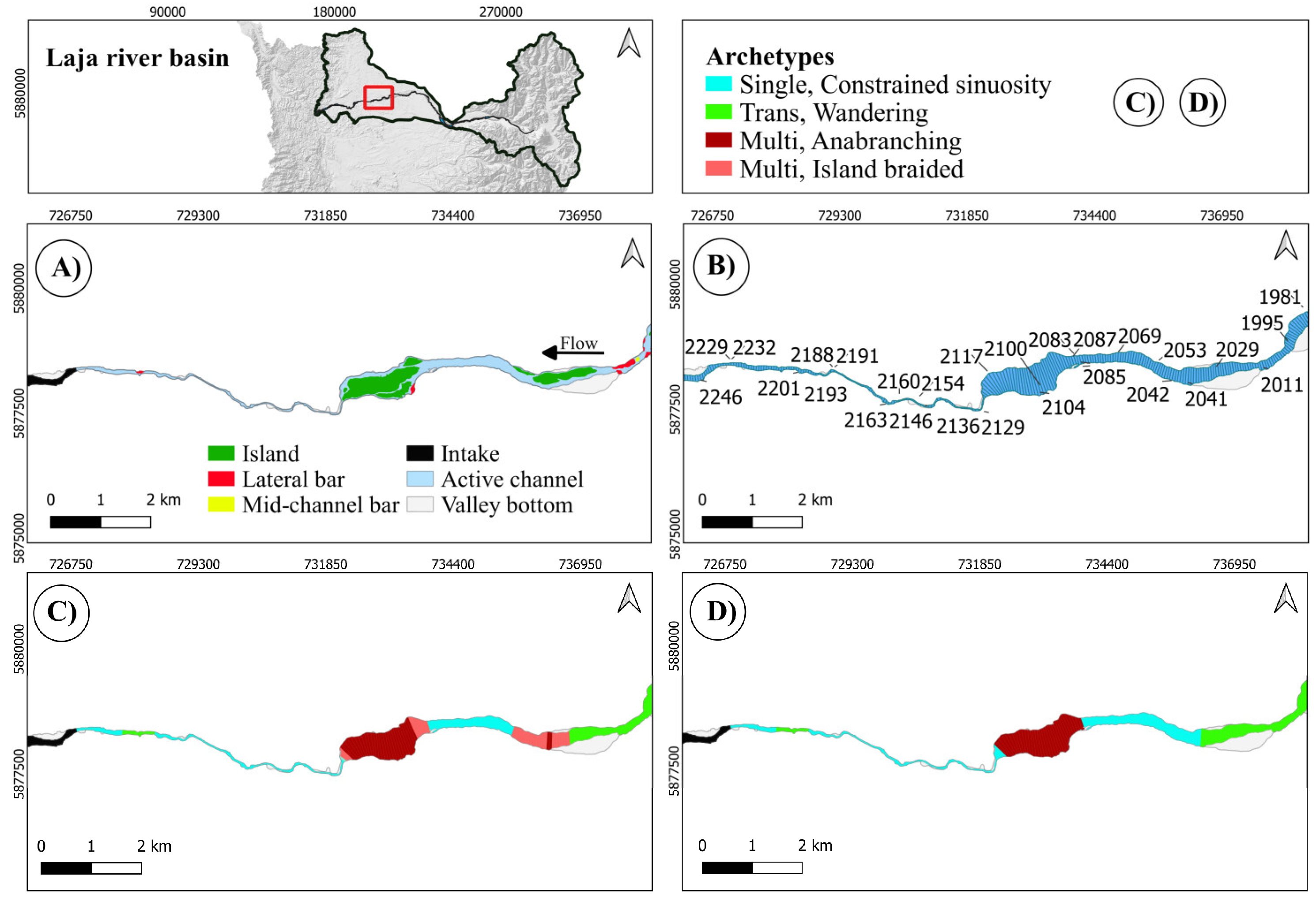
Preprints 75627 g016
Preprints 75627 g017
Figure 17. Upstream segment of the Biobío River (slices: 3950-3779; notice that in this case the numbering of slices starts from the most downstream slice, contrary to the other cases).
Figure 17. Upstream segment of the Biobío River (slices: 3950-3779; notice that in this case the numbering of slices starts from the most downstream slice, contrary to the other cases).
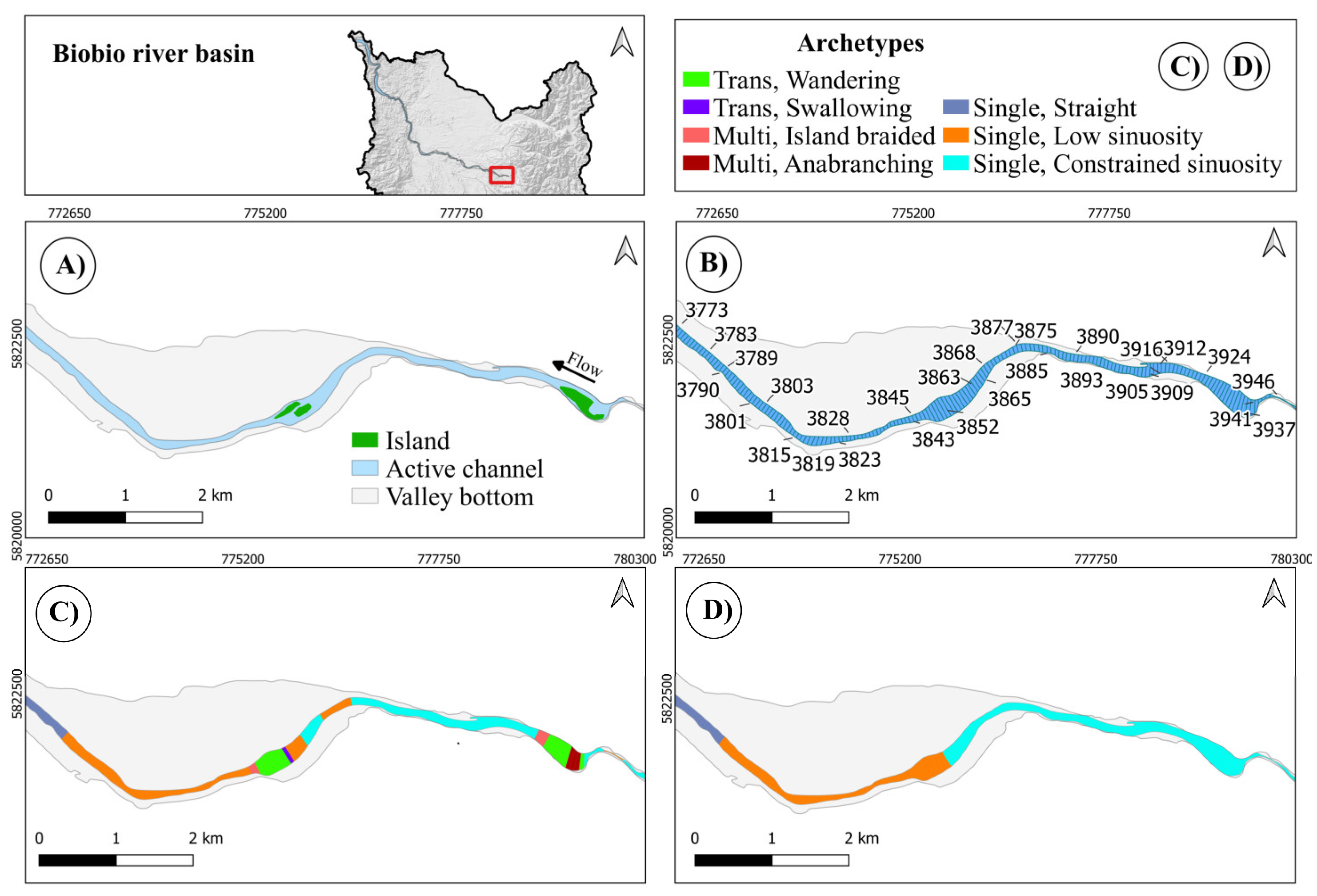
Preprints 75627 g017
Preprints 75627 g018
Figure 18. Biobío River (slices: 3554-3373).
Figure 18. Biobío River (slices: 3554-3373).
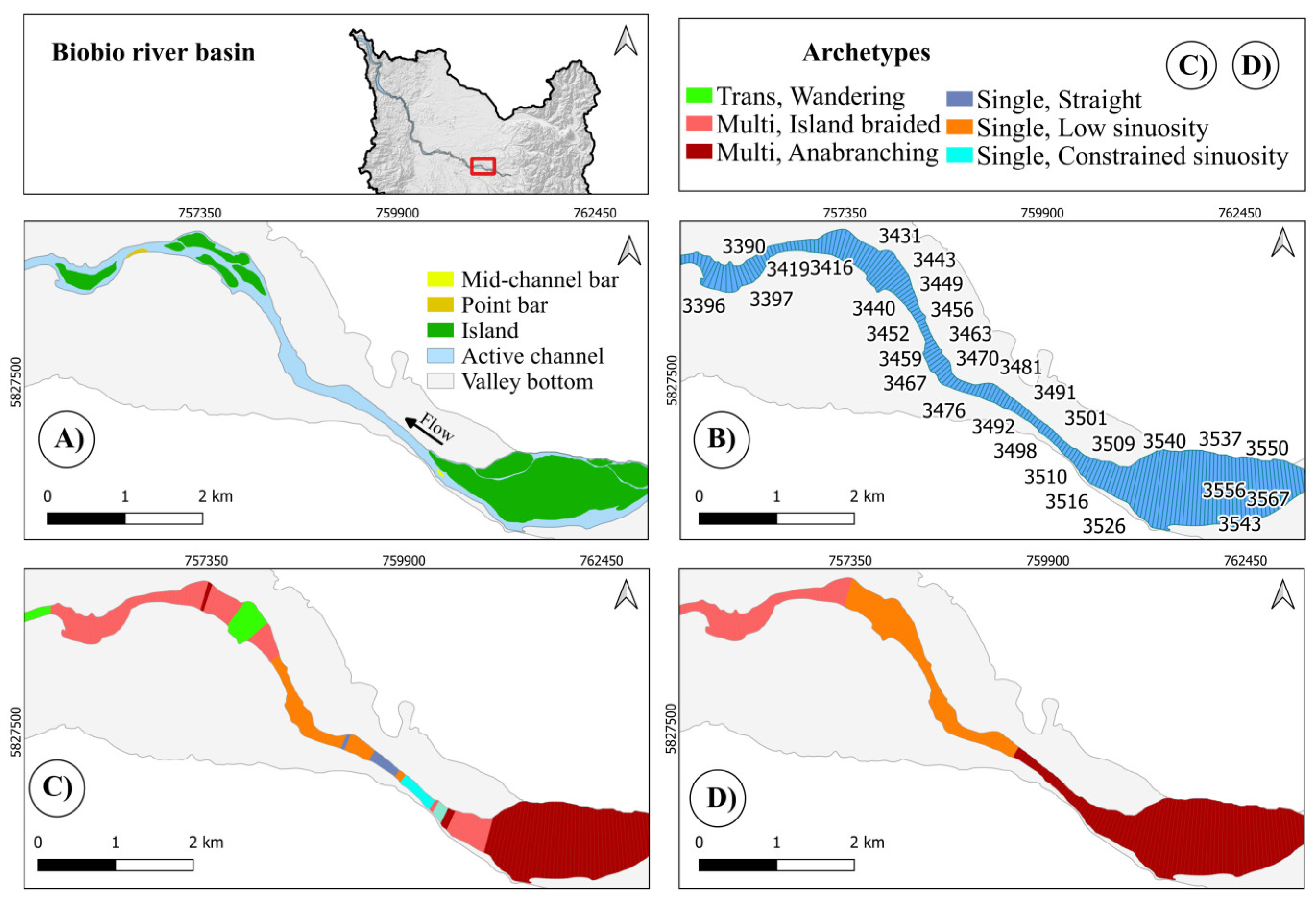
Preprints 75627 g018
Preprints 75627 g019
Figure 19. Biobío River (slices: 3056-2756).
Figure 19. Biobío River (slices: 3056-2756).
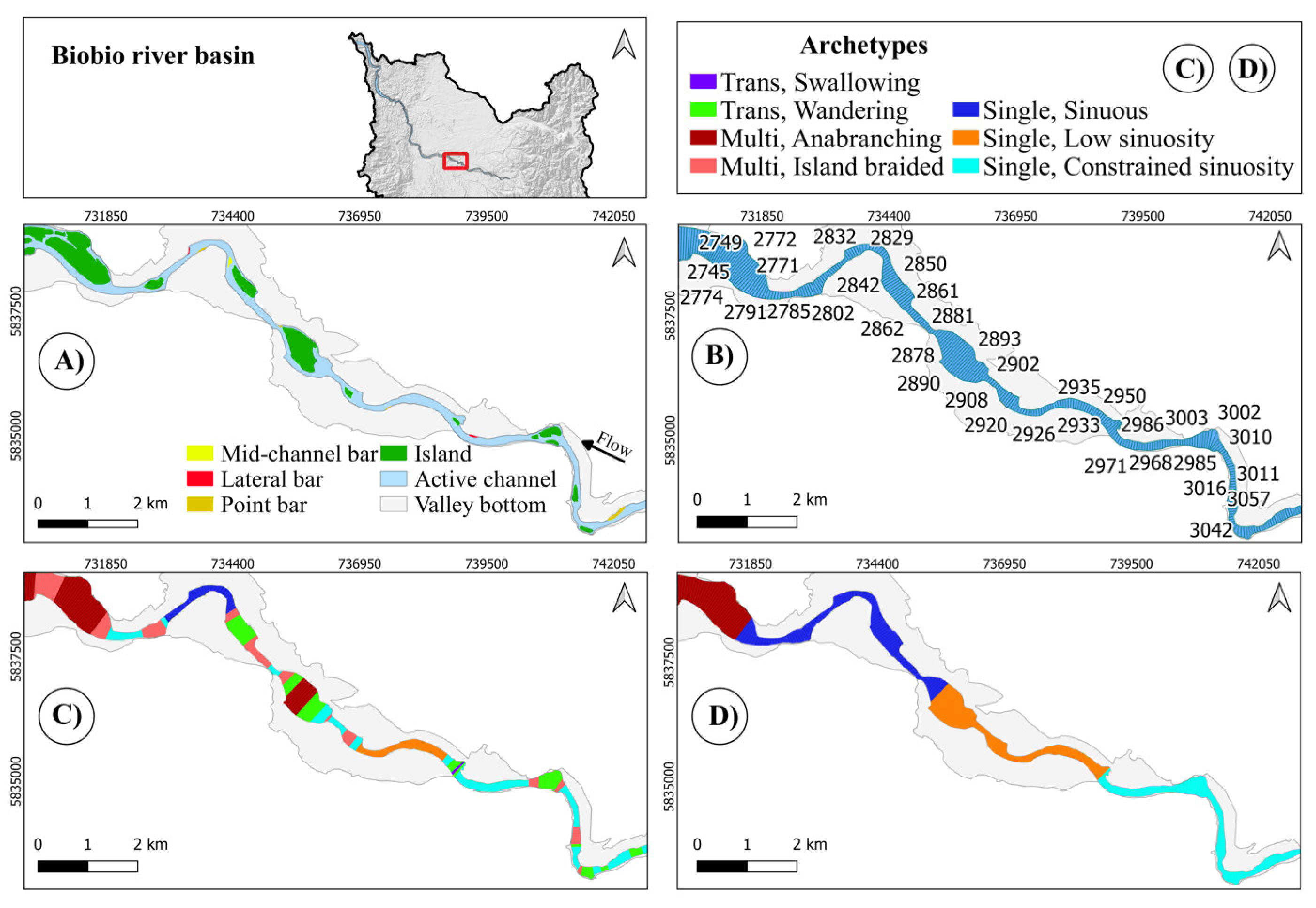
Preprints 75627 g019
Preprints 75627 g020
Figure 20. Biobío River (slices: 2790-2617).
Figure 20. Biobío River (slices: 2790-2617).
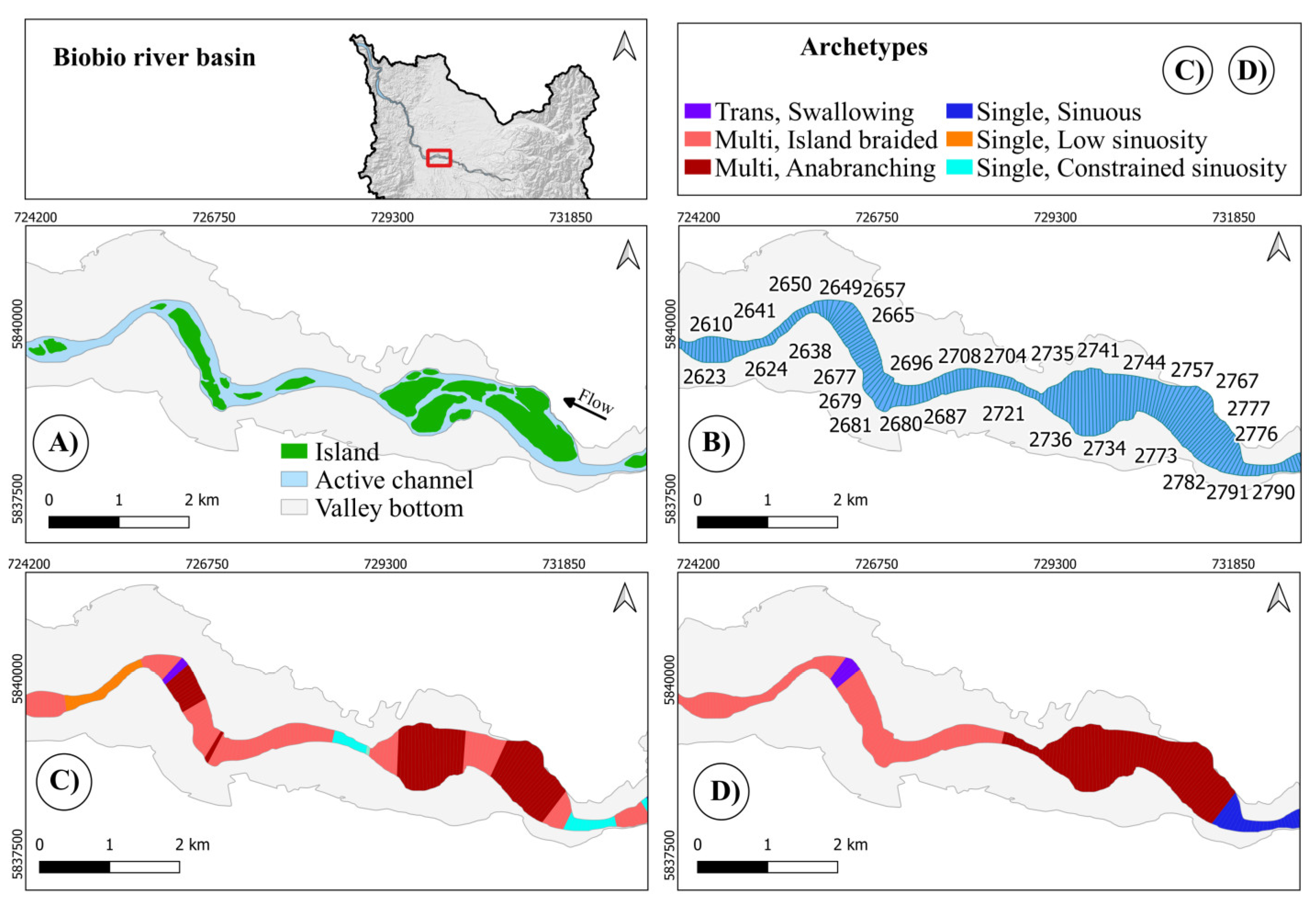
Preprints 75627 g020
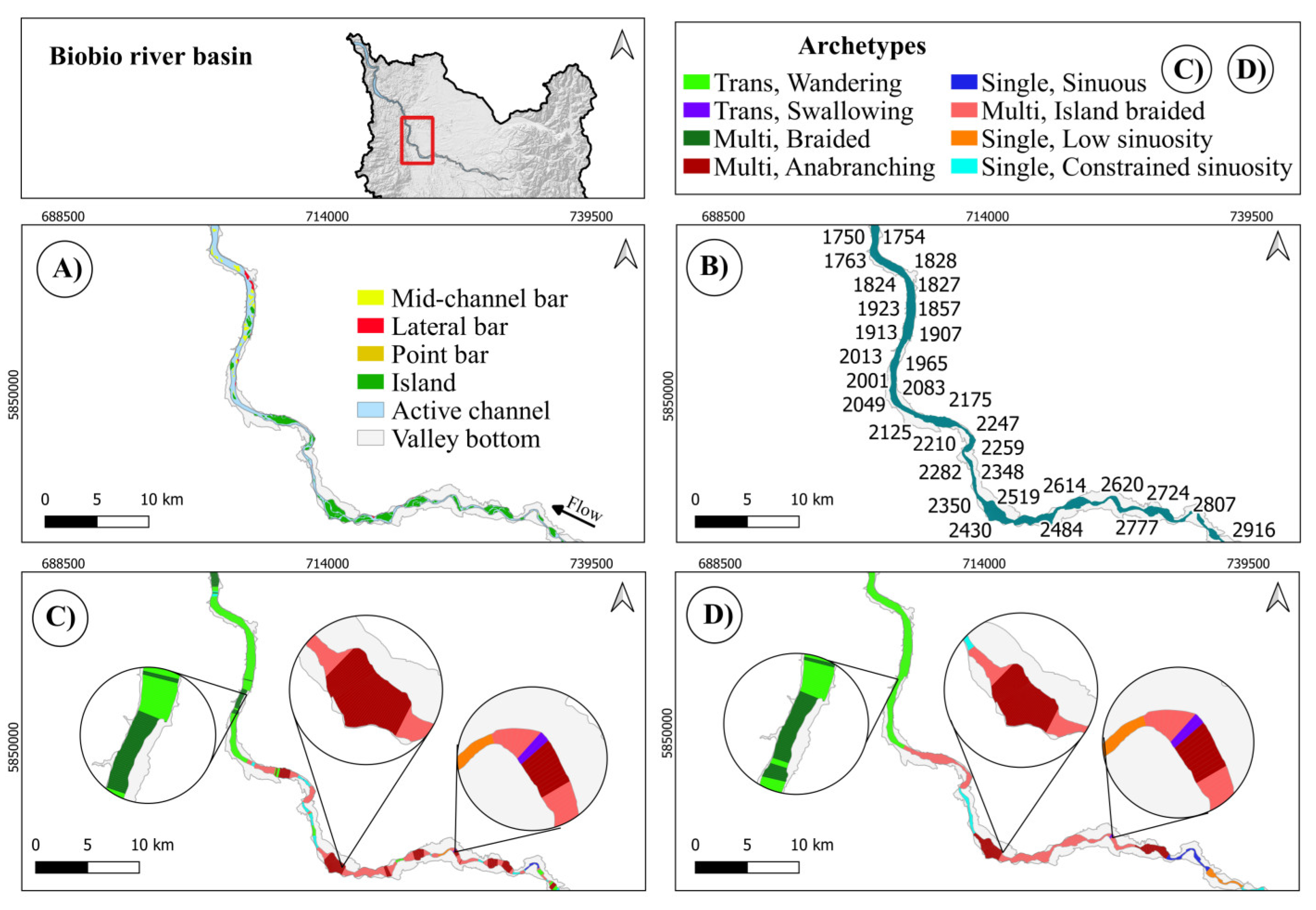
Preprints 75627 g021
Figure 21. Biobío River (slices: 2880-1751). This is a view at a smaller scale to better appreciate the response of the algorithm on a longer distance.
Figure 21. Biobío River (slices: 2880-1751). This is a view at a smaller scale to better appreciate the response of the algorithm on a longer distance.
Preprints 75627 g021
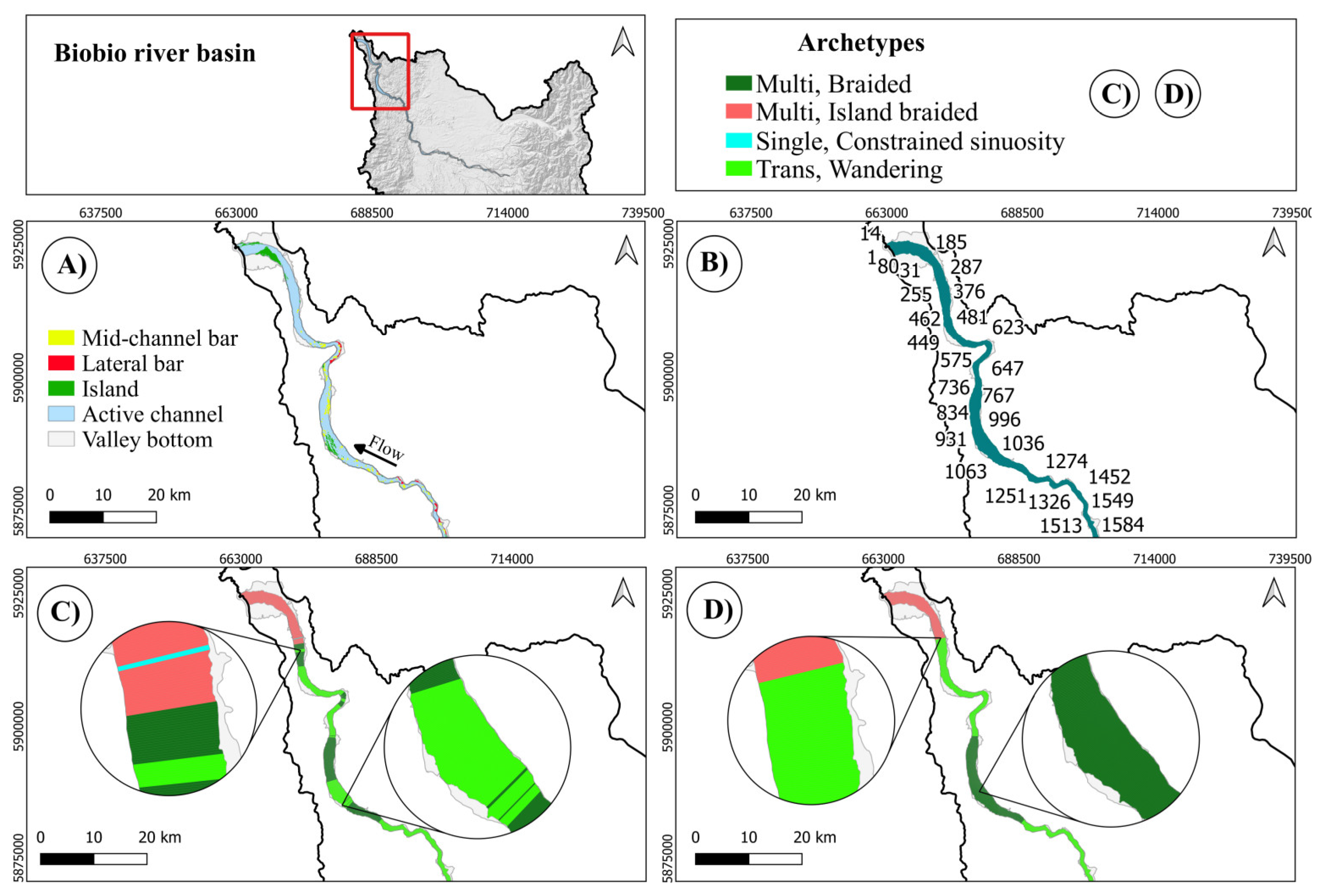
Preprints 75627 g022
Figure 22. Biobio River (slices: 1542-0001): another view at a smaller scale as variations here are less frequent.
Figure 22. Biobio River (slices: 1542-0001): another view at a smaller scale as variations here are less frequent.
Preprints 75627 g022
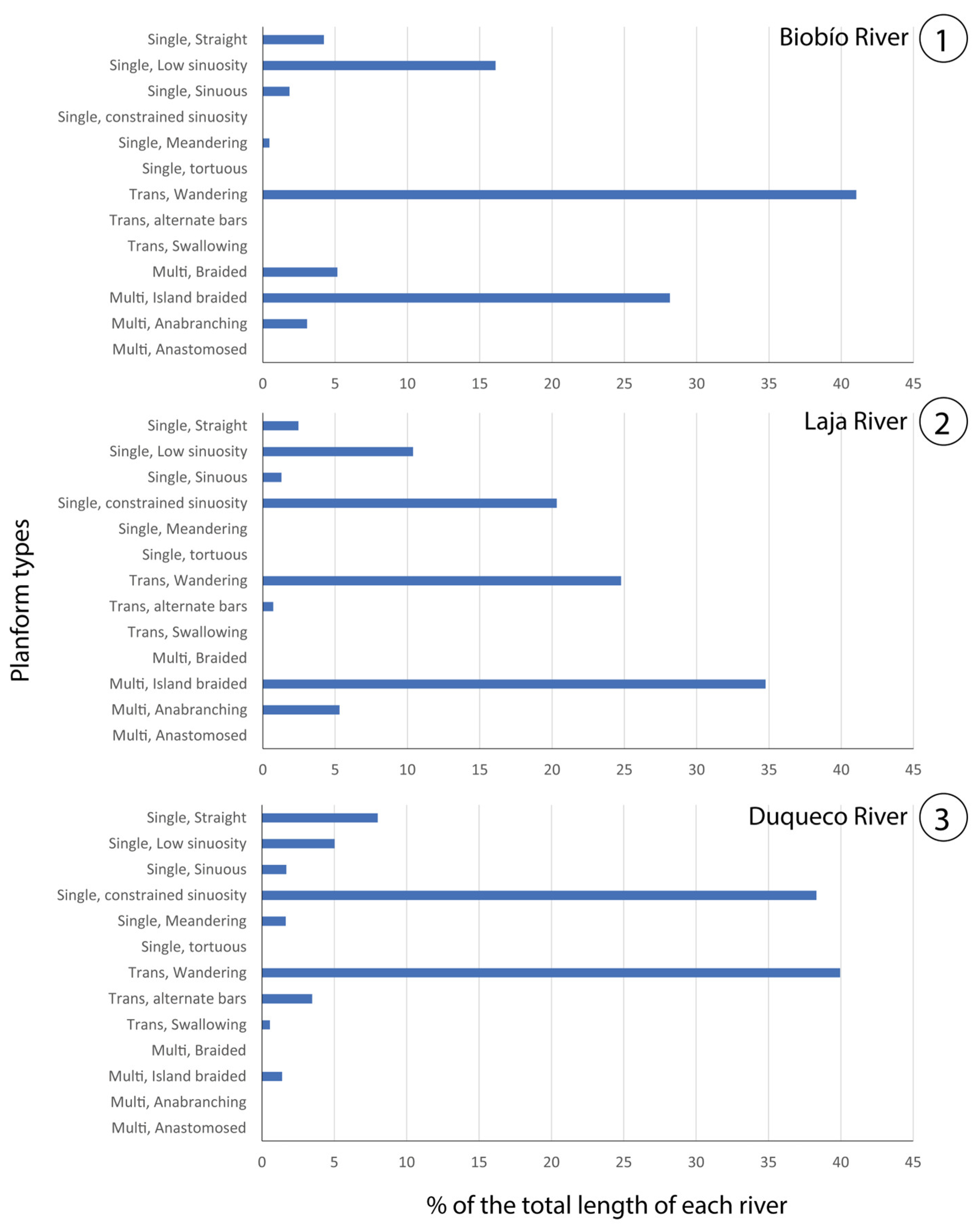
Preprints 75627 g023
Figure 23. Main planform archetypes determined with the automated methodology, including the use of holistic analysis in Excel: (1) Biobío River; (2) Laja River and (3) Duqueco River.
Figure 23. Main planform archetypes determined with the automated methodology, including the use of holistic analysis in Excel: (1) Biobío River; (2) Laja River and (3) Duqueco River.
Preprints 75627 g023
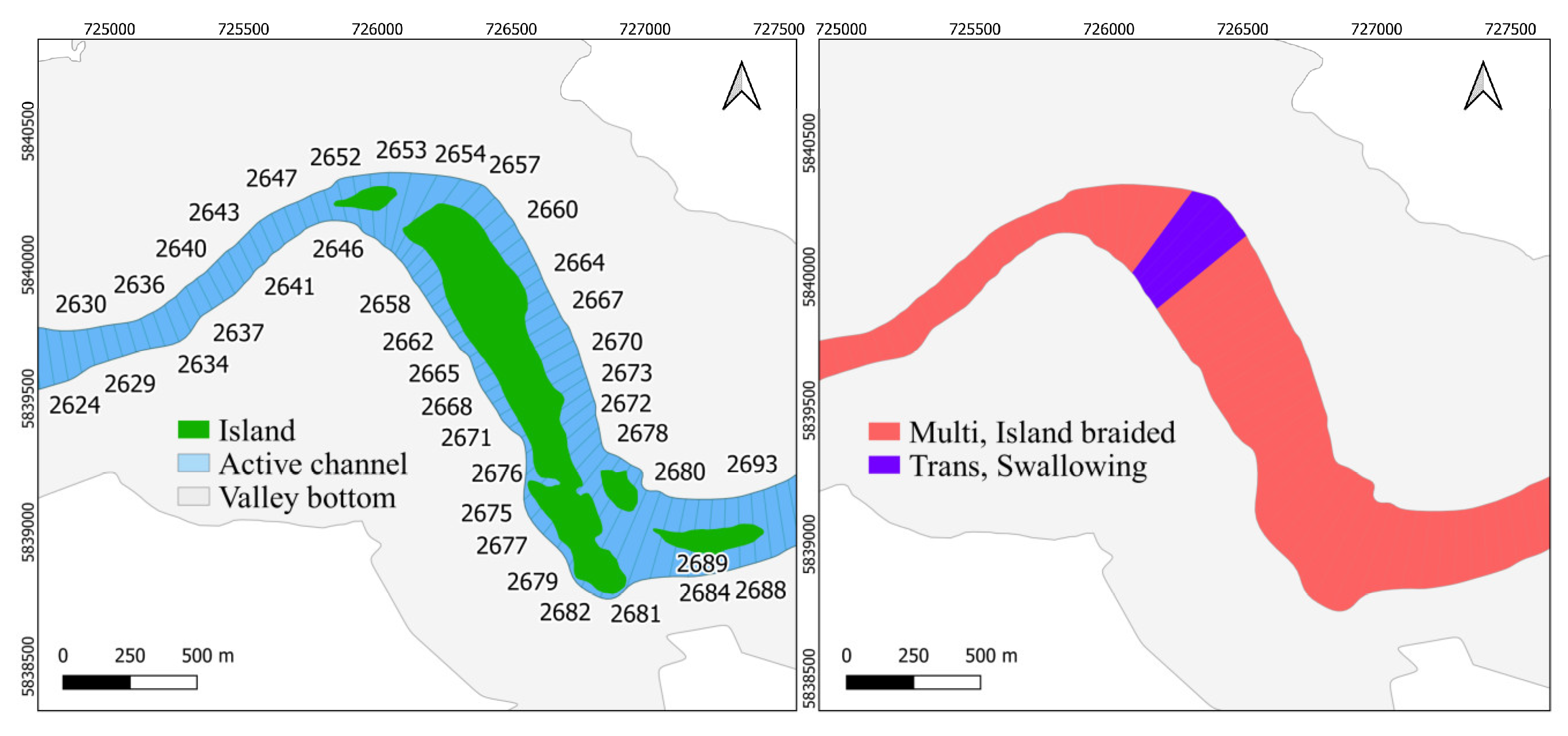
Preprints 75627 g024
Figure 24. False identification of a Swallowing reach in the Biobío River (slices: 2656-2659).
Figure 24. False identification of a Swallowing reach in the Biobío River (slices: 2656-2659).
Preprints 75627 g024
Table 1. Main characteristics of the rivers studied.
Table 1. Main characteristics of the rivers studied.
N River Year L
[km]		 wmax
[m]		 wmin
[m]		 A. Basin
[km2]		 Qav
[m3/s]		 N.
Macrosegments
1 Duqueco 2009 102 634 11 1,551 127 4
2 Laja 2019 140 44 5 4667 59 5
3 Biobío 2020 198 (*) 2,649 15 24,273 2,020 5
(*) The length "L" of the Biobío River was analyzed from the mouth to the first dam called "Angostura"(see Figure 2). The symbol w denotes the width of the Active Channel envelop; “A. Basin”: is the area of the basin; “Qav” is the avergae flowrate.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated