Prerpints.org logo
Preprint
Article

Dynamic Output Feedback and Neural Network Control of a Non-Holonomic Mobile Robot

Altmetrics

Downloads

171

Views

52

Comments

0

A peer-reviewed article of this preprint also exists.

  ‡ These authors contributed equally to the work.

This version is not peer-reviewed

Submitted:

03 June 2023

Posted:

05 June 2023

You are already at the latest version

Alerts
Abstract
In this paper is presented the design and syntheis of a dynamic output feedback neural network controller for a non-holonomic mobile robot. First the dynamic model of a non-holonomic mobile robot is presented, in which these constraints are considered for the mathematical derivation of a feasable representation for this kind of robot. Then two control strategies are provided based on kinematic control for this kind of robot. The first control strategy is based on driftless control, this means, that considering that the velocity vector of the mobile robot is orthogonal to its restriction a dynamic output feedback and neural network controller is designed in order that the control action would be zero only when the velocity of the mobile robot is zero. The Lyapunov stability theorem is implemented in order to find a suitable control law. Then another control strategy is designed for trajectory tracking purposes, which similar to the driftless controller, a kinematic control scheme is provided but suitable to implement in more sophisticated hardware. In both control strategy a dynamic control law is provided along with a feedforward neural network controller, so in this way, by the Lyapunov theory the stability and convergence to the origin of the mobile robot position coordinates is ensured. Finally, two numerical experiment are presented in order to validate the theoretical results synthetized in this research study. Discussions and conclusions are provided in order to analyze the results found in this research study.
Keywords: 
Subject: Computer Science and Mathematics  -   Robotics

1. Introduction

Mobile robots have been implemented since several decades ago due to the vast applications of this kinds of robots. It is important to mention also that mobile robots have been implemented for several tasks in military and civil missions. For these reasons is important to design and synthetize several kinds of control strategies for these robots taking into consideration that is imperative for trajectory tracking, path following, leader follower missions etc. Due to the simplcity of the mobile robot dynamics and the implementation in hardware platforms for this kind of robots, it is important to remark that kinematic control is abundant for these kind of robots. The control strategies for robots are diverse, among these control strategies are the strategies based on robust control, sliding mode control, fuzzy control, neural control among others. Restriction in the dynamics of mobile robots which are found commonly are of non-holonomic type. These kind of restrictions are based considering the kinematic and dynamics properties of the mobile robot. That is why these restrictions provide a way to develop driftless control strategies in order to provide an easy way to implement these control approaches.
Taking into consideration that the dynamic modeling of mobile robots is very important to this research study, it is crucial to mention the following research papers in which this topic is considered. So for example, in papers like [1] the dynamic modeling with its uncertainties is evinced in this paper. Then in [2] a non-holonomic wheeled mobile robot with unknown dynamics is represented mathematically for control purposes. Then in [3] a non-holonomic mobile robot is modeled with unknown dynamics. In [4] is a remarkable paper whihc is very important for this research study considering that a analysis of the dynamics of a lightweight mobile robot for longitudinal motion is presented. Meanwhile in [5] the dynamic modeling and sliding mode control of a tractor mobile robot is presented. Then in [6] a complete book chapter about the dynamic modeling of mobile robots is presented considering the longitudinal and lateral slip. In all these research studies are considered the dynamic modeling of mobile robot, but it is important to mention, that in general the dynamics of mobile robots is quite simple, but sometimes in order to obtain the mathematical representation of mobile robot’s dynamics is important to considered unmodelled and unknown dynamics, something that in this research study are not took into consideration clarifying that the dynamic controllers and neural controllers are sufficiently robust for kinds of mobile robots.
Holonomic constraints are crucial to mention in this research study taking into consideration that these kinds of constratints, especially the non-holonomic constraints, are found in mobile robots. These constraints are related to the velocity vector field of the mobile robot and the mathematical explanation of these kind of constraints are mentioned in the content of this research paper. For these reasons it is important to mention the following research papers found in the literature, so for example in papers like, [7] non-holonomic constraints for geometric control theory are explained. Meanwhile in [8] an interesting research paper about the singularities of holonomic and non-holonomic robotic systems are presented. In [9] are studied holonomic and non-holonomic deformations in the AB equations are shown in which these equations are useful for atmospheric fluid modeling. Then in [10] are presented the dynamical invariant based quantum gates. In [11,12] are presented the model predictive control of a holonomic mobile robot and a adaptive robust controller ofr mechanical systems with non-holonomic trajectories are provided in this paper respectively.
Mobile robot’s dynamic models constraints allow us a way to obtain efficient control strategies by the driftless control method. The driftless control method consists into obtaining a zero control effort only if the velocity of the mobile robot is equal to zero. In the literature there are different driftless control techniques for different kinds of robots or mechanisms, so for example, in [13] the calculation of control effort of two input driftless control system is presented. Then in [14] the switched driftless control of a kind of non-holonomic system is shown. Meanwhile in [15] a driftless oscillation control for nonlinear systems is provided. Then in [16] is studied the controllability of driftless nonlinear time delayed system. In [17,18] the involutive flows of a nonlinear driftless control system and the asymptotic control for wheeled mobile robot with driftless constraints are evinced respectivelly.
One of the most important theoretical fundamentals for this research study are basically the design and implementation of dynamic output feedback controllers, taking into consideration that an hybrid control strategy based on dynamic output feedback control is implemented for this kind of mobile robots. In papers like [19] a dynamic output feedback control for switched affined system based on L − ∞ control is presented. It is important to mention the following papers [20,21] in which the dynamic output feedback control of a networked control system is presented and a mixed dynamic output feedback control for an active suspension system with actuator saturation and time delays are presented respectivelly. It is important to mention that in the second one paper an hybrid control strategy with dynamic output feedback and fuzzy type-2 controllers are implemented, taking into consideration that this control strategy provide an optimal framework for the present research study. In [22] the dynamic output feedback control of a Luré system is proposed. Then in [23,24] the consensus of a linear multi-agent system by reduced order dynamic output feedback and the robust stabilization for an uncertain singular Markovian-jump system via dynamic output feedback control is achieved.
It is important to mention that neural control is a suitable control strategy taking into consideration that an hybrid control strategy for a mobile non-holonomic robot is presented. For example, in [25] a neural fault-tolerant controller with input constraints for an output manipulator with output constraints is presented. Meanwhile in [26] an indirect neural control for unmanned surface vessel are presented considering injection and deception attacks. Then in [27,28] a quasi-optimal neural control for solar thermal systems and neural based fixed optimal control for attitude tracking of an space vehicle with output constraints are evinced respectivelly. Finally in [29,30] a space manipulator neural output constrained control for space manipulator using Lyapunov tan-barrier functional and the neural network control of nuclear plants are evinced respectivelly.
In this paper is presented the implementation of an hybrid control strategy which consists of a neural and dynamic output feedback controller for a non-holonomic mobile robot. In this paper are shown two control strategies, the first one is a driftless control system based on the dynamic output feedback and neural controller, and the second one, is a full controller based also in neural and feedback output control. The dynamic output feedback and neural control are designed implementing a Lyapunov functional suitable to obtain the control law in both cases. The neural network implemented in this research study is a feedforward neural network in order to facilitate the controller design. The two control strategies ensures the stability for trajectory tracking purposes and the convergence to zero for the error variable which comprise the difference between the desired trajectory and the measured trajectory. It is important to mention that two numerical experiments are provided in order to validate the theoretical results of this research study. Discussion and conclusions are provided at the end of this research study.

2. Related Work

In this section some related work that is worthy to mention in this research study is presented. This literature review consists in the following items related to non-holonomic mobile robots and its control:
  • Kinematics of mobile robots.
  • Non-holonomic mobile robots.
  • Dynamic output feedback of mobile robots.
  • Neural control of mobile robots.
  • Miscellaneous control strategies for mobile robots.
It is important to mention the following references related to kinematics of mobile robots because they are crucial for this research study. For example in [31] a kinematic Lyapunov based controller is presented for mobile robots. Then in [32] a kinematic based control strategy for a spherical mobile robot driven by a 2-D pendulum is shown. Meanwhile in [33] a singularity free kinematic model of a degenerated mobile robot is obtained. Meanwhile in the following references [34,35,36] the kinematic control and two kinematic models of mobile robots are presented.
In this section it is important to mention the following research study taking into consideration that non-holonomic mobile robots kinematic and dynamic model design is important for this research study. Among these research studies we found the following, in [37] a distance based control of non-holomic mobile robots swarm is presented. Meanwhile in [38] the motion and force control of mobile robots is presented by means of a fuzzy wavelet neural network controller. Then in [39] the distributed formation control for a swarm of mobile robots is presented taking into consideration the velocity constraints and iterative learning. Meanwhile in [11,40] a model predictive path following control strategy for holonomic mobile robots and the real time identification of different types of non holonomic mobile robots are presented respectivelly. In [41] the trajectory tracking of a non holonomic mobile robot is presented by means of sliding mode control with disturbances.
Dynamic output feedback control has been implemented in specific for mobile robots. For this reason is important to mention the following control strategies which are found in the literature considering the importance that they have for this research study. In [42,43] are mentioned the cooperative output control of a mobile flexible manipulator and also the distributed output feedback control of non-holonomic mobile robots with only the leader’s position measurement. Then in [44,45] an output trajectory tracking of mobile robots and an adaptive tracking control by means of output feedback for mobile robots are presented respectivelly. Then in [46] an output tracking of a non-holonomic mobile robot with fractional order visual feedback is evinced. In [47] a finite time output feedback tracking control of a non-holonomic mobile robot is presented.
It is important to mention in this research study some neural robot control strategies which are found in the literature. So for example in papers like [48] a vision approach with deep neural networks to control autonomous mobile robots is presented. Meanwhile in [49] the kinematics of a cable driven parallel robot is achieved by the implementation of neural networks. Then in [50] the trajectory tracking of a self balancing robot by adaptive neural networks is performed. Then in [51] a fault diagnosis for the harmonic reducer of industrial robots is achieved by means of neural networks. Other examples of the implementation of neural networks are found in [52,53] in which in the first case, the integrated consensus control of multi-robots using neural model predictive control is done, Meanwhile, in the second reference a neural control for a robotic manipulator with input deadzone is presented.
To finalize this section the following references are related to miscellaneous robot control strategies related in any or other way to mobile robot control. In papers like [54,55] model predictive and model control are implemented for the control of different kinds of robots. Then in [56,57] two control strategies are presented for trajectory tracking of mobile robots. Finally in [11,58] model predictive and adaptive full state constrained tracking control for mobile robots are presented respectivelly.

3. Problem Formulation

In this section the kinematic model of the mobile robot is presented. It is important to mention that only a generic mobile robot is implemented in this research study. The intention is to drive the robot according to a pre-specified trajectory. The kinematics of the mobile robot is given by the following equations:
s i n ( θ ) x ˙ − c o s ( θ ) y ˙ = 0 s i n ( θ + ϕ ) x ˙ − c o s ( θ + ϕ ) y ˙ = 0
In which as can be noticed in Figure 1 the coordinates and mobile robot length are defined as appears in the figure. In order to facilitate the mathematical tractability of this kinematic model in order to obtain the proposed control strategies the following equivalent kinematic model is obtained as appears in [59]. Consider the following change of variable q = [ x , y , θ , ϕ ] T , so (1) can be obtained as:
〈 ω 1 , q ˙ 〉 = s i n ( θ ) c o s ( θ ) 0 0 q ˙ = 0 〈 ω 2 , q ˙ 〉 = s i n ( θ + ϕ ) − c o s ( θ + ϕ ) − d c o s ( ϕ ) 0 q ˙ = 0
In order to verify the holonomy of the previous mentioned system the following definition is needed [59]:
Definition 1.
Consider two vector fields given by f ∈ R n and g ∈ R n so the Lie bracket between this two vectors are given by:
f , g = ∂ g ∂ x f − ∂ f ∂ x g
In which x = [ x 1 , x 2 , . . . , x n ] T in which:
∂ f ∂ x = ∂ f 1 ∂ x 1 . . . ∂ f 1 ∂ x n ⋮ ⋱ ⋮ ∂ f n ∂ x 1 . . . ∂ f n ∂ x n
So by defining the following vector fields:
g 1 = 0 0 0 1 g 2 = − c o s ( ϕ ) − s i n ( ϕ ) − 1 d s i n ( θ ) c o s ( θ ) 0
Somehow the Lie bracket of g 1 and g 2 is given by:
g 1 , g 2 = − s i n ( ϕ ) − c o s ( ϕ ) − 1 d c o s ( θ ) s i n ( ϕ ) c o t a n ( ϕ )
So the previous Lie bracket does not span the set of g 1 and g 2 and the system is non-holonomic [59].

4. Control Strategies Definitions

In this section are defined the two control strategies proposed in this research study. So this section is divided into the following subsections in order to evince the main theoretical results:
  • Neural controller definition.
  • Driftless control strategy.
  • Non-Driftless control strategy.

4.1. Neural Controller Structure

The neural controller structure consists into the following components:
y ˜ j = ∑ i = 1 n w j i σ ( p + θ i ) + θ j
In which w j i are the hidden units weights of the neural network, θ i are the input weights, θ j are the bias of the neural network, and σ ( . ) is the activation function, that in this case is a sigmoidal function, and p = ∑ r = 1 k q r for the inputs q r and the j output. The neural network (7) can be written in vector matrix form as follow:
y ˜ = ∑ i = 1 n w 1 i w 2 i ︸ w i σ ( p + θ i ) + θ 1 θ 2 ︸ θ y ˜ = ∑ i = 1 n w i σ ( p + θ i ) + θ
In which w i ∈ R 2 is the hidden unit weights and θ ∈ R 2 is the bias vector.

4.2. Driftless Control of the Mobile Robot

For the dynamic neural network control of the mobile robot consider the following dynamic neural controller:
x ˙ c = K 1 e + K 2 x c + ∑ i = 1 n w i σ ( p + θ i ) + θ
In which x c ∈ R 2 is the controller variable, K 1 ∈ R 2 × 2 and K 2 ∈ R 2 × 2 are the gain matrices and p is the neural network controller input. In order to establish the driftless control system the following scheme is implemented:
q ˙ = g 1 u 1 + g 2 u 2 = g 1 g 2 ︸ G u 1 u 2 ︸ U
In the following theorem is defined the driftless control law for the mobile robot:
Theorem 1.
The driftless dynamic system (10) is stabilized by the following control law:
U = − G − 1 q α ∥ q ∥ 2 η x c T K 1 e − G − 1 q α ∥ q ∥ 2 η x c T K 2 x c − q α ∥ q ∥ 2 η x c T ∑ i n w i σ ( p + θ i ) + θ − G − 1 q
in which η ∈ R + and α η ∈ R + are positive gain constants and e = q d − q is the error variable in which q d is the desired trajectory of the mobile robot.
Proof. 
Consider the following Lyapunov function:
V = η 2 x c T x c + α 2 q T q
Obtaining the first time derivative of the previous Lyapunov function yields:
V ˙ = η x c T x ˙ c + α q T q ˙
Now by making the required substitution in the previous equation yields:
V ˙ = η x c T K 1 e + η x c T K 2 x c + η x c T ∑ i n w i σ ( p + θ i ) + θ + α q T G U
So by making the required substitutions of (11) into the previous equation yields:
V ˙ = − α q T q < 0
and the proof is completed. □

4.3. Non Driftless Control of the Mobile Robot

To achieve this it is necessary to define the dynamic model of the mobile robot in the following way:
s i n ( θ ) − c o s ( θ ) 0 0 s i n ( θ + ϕ ) − c o s ( θ + ϕ ) − d c o s ( ϕ ) 0 ︸ G x ˙ y ˙ θ ˙ ϕ ˙ ︸ q ˙ = u 1 u 2 ︸ U
in which U ∈ R 2 is the control input. Now consider the following neural dynamic controller:
x ˙ c = K 1 e + K 2 x c + ∑ i = 1 n w i σ ( p + θ i ) + θ
In which K 1 ∈ R 4 and K 2 ∈ R 4 are appropriate gain matrices. Meanwhile e ˙ = q ˙ d − q ˙ is the error dynamics with q d ∈ R 4 is the desired trajectory of the mobile robot. The following theorem evince how can the dynamics of the mobile robot can be stabilized.
Theorem 2.
The dynamic system of the mobile robot (16) is stabilized by the following control law as shown in:
U = G q ˙ d − G e β ∥ e ∥ 2 ρ x c T K 1 e − G e β ∥ e ∥ 2 ρ x c T K 2 x c − G e β ∥ e ∥ 2 ρ x c T ∑ i = 1 n w i σ ( p + θ i ) + θ + G e
In which ρ ∈ R + and β ∈ R + are appropiate control parameters.
Proof. 
Consider the following Lyapunov functional:
V = ρ 2 x c T x c + β 2 e T e
So by taking the derivative of the previous Lyapunov function and making the appropriate substitutions yields:
V ˙ = ρ x c T K 1 e + K 2 x c + ∑ i = 1 n w i σ ( p + θ i ) + θ + β e T q ˙ d − G − 1 U
Now by substituting (18) into the previous equation yields:
V ˙ = − β e T e < 0
So the system is globally stable and the proof is complete. □

5. Numerical Experiments

In this section two numerical experiments are performed to test and validate the theoretical results found in this research study. The numerical experiments conducted in this research study are intended to verify the following performance indicators:
  • Minimization of the tracking error.
  • Speed of response of the controller.
  • Improvement in comparison with other control strategies.
The experiments performed in this research study are the following:
  • Driftless control strategy.
  • Non-driftless control strategy.
The conditions in which these experiments are performed is basically d = 0.5 m taking into consideration that these control strategies are intended for kinematic control purposes.

5.1. Numerical Experiment 1

For this experiment the following gain constants are implemented; η = 1 × 10 − 6 , α = 1 × 10 − 6 . Now consider the neural network parameters defined as:
W i = 0.084825 0.087038 0.073776 0.098989 θ i = 0.071581 0.096176 0.026009 0.086780 0.048502 0.041201 0.083732 0.015706 0.044176 0.037104 0.033042 0.024069 0.081635 0.010157 0.035023 0.089209 θ = 0.080926 0.066993 0.044356 0.046736
The experiment consist into driving the position variables x and y to the origin starting from an initial condition in order to obtain the maximum accuracy until the final desired value must be reached to obtain the maximum performance.
In Figure 2 and Figure 3 is presented the evolution in time of the mobile robot when it is driven from the initial condition to the origin in finite time. It is important to notice that the action of the controller drive these variables to the origin in approximately 1 s proving that the controller is effective despite the conditions in which the experiment is performed.
Meanwhile in Figure 4 and Figure 5 are evinced the evolution in time of the angles of the mobile robot in order to drive the position variables x and y to the desired final value in finite time. The action of the neural controller and the dynamic surface controller are demonstrated to be fast and accurate in order to follow a predifined trajectory.
Meanwhile in Figure 6 it can be noticed the trajectory of the mobile robot in 3D. It is corroborated in this figure how the trajectory is done considering not only the position of the mobile robot, therefore it is considered by evincing the orientation of the mobile robot.
Finally in Figure 7 and Figure 8 are evinced the evolution in time of the control inputs U 1 and U 2 . It is verified that a small control input is necessary to drive the position and orientation of the mobile robot in finite time.

5.2. Numerical Experiment 2

In this numerical experiment is tested and validated the theoretical results regarding the synthesis of a non-driftless control of a mobile robot. This strategy, similar to the first experiment, consists into designing a neural-dynamic controller for trajectory tracking purposes. In this experiment the proposed control strategy is compared with the following strategies:
  • Neural controller.
  • Neural proportional-derivative PD controller.
The simulation parameters are the following; ρ = 0.1 , β = 0.1 , K 1 = 1 × 10 − 1 , K 2 = 1 × 10 − 8 . Meanwhile the neural controller component has the following weights:
W i = 1.1557 × 10 − 2 7.6815 × 10 − 3 7.8527 × 10 − 2 7.4791 × 10 − 2 θ i = 0.083379 0.02538 0.051005 0.092401 0.018102 0.090383 0.044346 0.067841 0.063258 0.062726 0.079339 0.090871 0.0421146 0.01078 0.006508 0.0038533 θ = 0.044756 0.083565 0.041632 0.076618
In Figure 9 and Figure 10 are evinced the evolution in time of the position variables x and y of the mobile robot. It is evinced that the controller synthetized with the proposed control strategy, is more accurate in comparison with the neural and neural PD controllers. The proposed control strategy is more accurate in comparison with the strategies used as a comparative benchmark. The reason is because of the addition of a dynamic controller component that makes this control strategy more accurate and faster than the other control strategies.
Meanwhile in Figure 11 and Figure 12 it is corroborated how the error variables reach the origin in finite time. As evinced in the previous figures, it is verified that the error variables yielded by the proposed control strategies reach the origin faster and more accurate than the neural and neural PD control strategies.
Then in Figure 13 the trajectory of the mobile robot in 3D is presented. It is evinced that the trajectory tracked by proposed controller is significantly better than the neural and neural PD controllers.
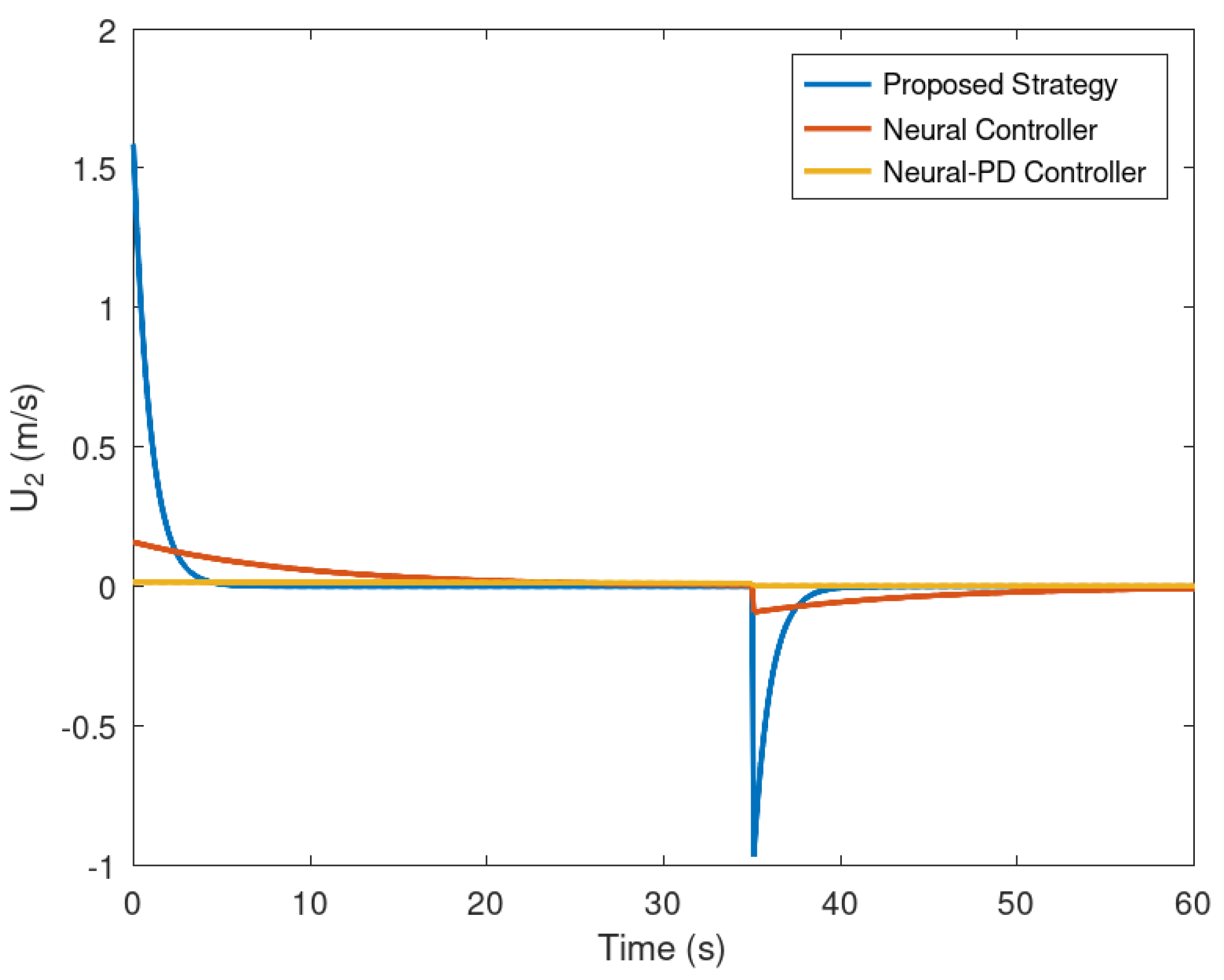
Finally in Figure 14 and Figure 15 are evinced the evolution in time of the control efforts for the variables U 1 and U 2 . It is important to notice that the control effort for both control inputs is significantly smaller in comparison with the control effort generated by the neural and neural PD control strategies. This is an advantage when the controller is implemented in a real experimental setup. If the control effort is smaller then unwanted effects like saturation are avoided.

6. Discussion

According to the theoretical and experimental results of this research paper, it is important to mention and discuss some important results and findings obtained. First, considering that the driftless control strategies with neural networks have not been reported extensively in the literature, in this research study is proposed a combined neural network and dynamic controller for the trajectory tracking of mobile robots. As it is verified the driftless control strategy is less costly in terms of control effort in comparison with other control strategies. Besides, the driftless control strategy presented in this research paper is useful for non-holonomic dynamics, that in this case, is a mobile robot.
In this paper it is demonstrated that the driftless control strategy provide an efficient mobile robot navigation estrategy, by considering that is fast, reliable and accurate. It is worthy to mention that the neural network component of the proposed strategy provides an adequate control strategy that can be implemented and tuned relatively easily. The weights of the neural network do not need to be tuned offline by training methods like the Newton or Gaussian method, but it is important to remark that the neural networks used in this research study can be tuned by different optimization algorithms, with less computational effort. The stable trajectory tracking of the mobile robot by implementing the neural network controller component ensured a precise stabilization by meeting the appropriate weight requirements, so several training and optimization algorithms can be implemented.
The dynamic controller part ensures that the stability of the driftless controller must be accurate and fast by meeting the adequate requirements of closed loop global stability. The controller synthesis by selecting an appropriate Lyapunov function and obtaining the adequate control law. It is important to remark that the controller was carefully designed in order to be implemented in hardware easily, so the proposed control approach was done by making it relatively simple considering also that the dynamics of the mobile robot is relativelly simple, but recognizing the complexity of non-holonomy of the mobile robot dynamics. This control strategy provides a smaller computational effort taking into consideration that the proposed controller is compact and the neural network controller only requires matricial and vectorial operations.
Meanwhile the non-driftless controller, is also reliable, accurate and fast, taking into consideration that this dynamic controller provides a more robust but with slightly higher control effort than the driftless control system, but it is even more adequate for trajectory tracking in comparison with the driftless control system. It is important to notice that depending on the application of the mobile robot one of these two control strategies are suitable. For this reason in this research study both strategies are investigated taking into consideration the control effort than in some cases is required to be smaller to avoid some effects like saturation that can produce unwanted effects. In case that the required hardware is available, the non-driftless control strategy is more adequate, so the driftless control strategy result to be suitable with no need of adequate hardware.

7. Conclusions

In this research paper is presented a driftless and non-driftless control strategy based on neural dynamic controllers for trajectory tracking of a mobile robot. Considering the non-holonomic characteristics of the mobile robot dynamics, an appropriate, relatively simple and implementable control strategy is provided in order that these results would be implementable in real time hardware. The Lyapunov stability theorem is implemented for the design of the two control approach in order to obtain a globally closed loop stable system. Numerical examples validate the theoretical results obtained in this research study, proving that the theoretical results yields an appropriate performance of the mobile robot in order to track a predefined trajectory. References

References

  1. Zhao, L.; Li, J.; Li, H.; Liu, B. Double-loop tracking control for a wheeled mobile robot with unmodeled dynamics along right angle roads. ISA Trans. 2022. [Google Scholar] [CrossRef]
  2. Wu, Y.; Wang, Y.; Fang, H. Full-state constrained neural control and learning for the nonholonomic wheeled mobile robot with unknown dynamics. ISA Trans. 2022, 125, 22–30. [Google Scholar] [CrossRef]
  3. Yoo, S.J.; Park, B.S. Quantized feedback control strategy for tracking performance guarantee of nonholonomic mobile robots with uncertain nonlinear dynamics. Appl. Math. Comput. 2021, 407, 126349. [Google Scholar] [CrossRef]
  4. Trojnacki, M.; Dąbek, P. Studies of dynamics of a lightweight wheeled mobile robot during longitudinal motion on soft ground. Mech. Res. Commun. 2017, 82, 36–42, SI: Advances/Dynamics. [Google Scholar] [CrossRef]
  5. Alipour, K.; Robat, A.B.; Tarvirdizadeh, B. Dynamics modeling and sliding mode control of tractor-trailer wheeled mobile robots subject to wheels slip. Mech. Mach. Theory 2019, 138, 16–37. [Google Scholar] [CrossRef]
  6. Tzafestas, S.G. 3 - Mobile Robot Dynamics. In Introduction to Mobile Robot Control; Tzafestas, S.G., Ed.; Elsevier: Oxford, 2014; pp. 69–99. [Google Scholar]
  7. Gover, A.R.; Slovák, J. Non-holonomic equations for the normal extremals in geometric control theory. J. Geom. Phys. 2022, 171, 104395. [Google Scholar] [CrossRef]
  8. Tchoń, K.; Ratajczak, J. Singularities of holonomic and non-holonomic robotic systems: A normal form approach. J. Frankl. Inst. 2021, 358, 7698–7713. [Google Scholar] [CrossRef]
  9. Abhinav, K.; Mukherjee, I.; Guha, P. Non-holonomic and quasi-integrable deformations of the AB equations. Phys. D Nonlinear Phenom. 2022, 433, 133186. [Google Scholar] [CrossRef]
  10. Li, Y.; Xin, T.; Qiu, C.; Li, K.; Liu, G.; Li, J.; Wan, Y.; Lu, D. Dynamical-invariant-based holonomic quantum gates: Theory and experiment. Fundam. Res. 2022. [Google Scholar] [CrossRef]
  11. Cenerini, J.; Mehrez, M.W.; woo Han, J.; Jeon, S.; Melek, W. Model Predictive Path Following Control without terminal constraints for holonomic mobile robots. Control. Eng. Pract. 2023, 132, 105406. [Google Scholar] [CrossRef]
  12. Chen, X.; Liang, W.; Zhao, H.; Al Mamun, A. Adaptive robust controller using intelligent uncertainty observer for mechanical systems under non-holonomic reference trajectories. ISA Trans. 2022, 122, 79–87. [Google Scholar] [CrossRef] [PubMed]
  13. LI, S.J.; RESPONDER, W. Describing and Calculating Flat Outputs of Two-input Driftless Control Systems. IFAC Proc. Vol. 2010, 43, 683–688, 8th IFAC Symposium on Nonlinear Control Systems. [Google Scholar] [CrossRef]
  14. Ishikawa, M. Switched Feedback Control for a class of First-order Nonholonomic Driftless Systems. IFAC Proc. Vol. 2008, 41, 4761–4766, 17th IFAC World Congress. [Google Scholar] [CrossRef]
  15. Zuyev, A.; Grushkovskaya, V. Obstacle Avoidance Problem for Driftless Nonlinear Systems with Oscillating Controls. IFAC-PapersOnLine 2017, 50, 10476–10481, 20th IFAC World Congress. [Google Scholar] [CrossRef]
  16. Califano, C.; Li, S.; Moog, C.H. Controllability of driftless nonlinear time-delay systems. Syst. Control. Lett. 2013, 62, 294–301. [Google Scholar] [CrossRef]
  17. Altafini, C. Involutive flows and discretization errors for nonlinear driftless control systems. Syst. Control. Lett. 2017, 110, 29–37. [Google Scholar] [CrossRef]
  18. Shim, H.S.; Sung, Y.G. Asymptotic control for wheeled mobile robots with driftless constraints. Robot. Auton. Syst. 2003, 43, 29–37. [Google Scholar] [CrossRef]
  19. Xie, H.; Zong, G.; Yang, D.; Chen, Y.; Shi, K. Dynamic output feedback L-Infinity control of switched affine systems: An event-triggered mechanism. Nonlinear Anal. Hybrid Syst. 2023, 47, 101278. [Google Scholar] [CrossRef]
  20. Zhang, D.; Zhang, L.; Yu, Z.; Li, H.; Shu, L. Dynamic output feedback control for networked control systems: A sum-based discrete event-triggered approach. IFAC-PapersOnLine 2022, 55, 61–66, 16th IFAC Symposium on Large Scale Complex Systems: Theory and Applications LSS 2022. [Google Scholar] [CrossRef]
  21. Xie, Z.; Wang, D.; Wong, P.K.; Li, W.; Zhao, J. Dynamic-output-feedback based interval type-2 fuzzy control for nonlinear active suspension systems with actuator saturation and delay. Inf. Sci. 2022, 607, 1174–1194. [Google Scholar] [CrossRef]
  22. Bertolin, A.L.; Oliveira, R.C.; Valmorbida, G.; Peres, P.L. Dynamic output-feedback control of continuous-time Lur’e systems using Zames-Falb multipliers by means of an LMI-based algorithm. IFAC-PapersOnLine 2022, 55, 109–114, 10th IFAC Symposium on Robust Control Design ROCOND 2022. [Google Scholar] [CrossRef]
  23. Silva, B.M.; Ishihara, J.Y.; Tognetti, E.S. LMI-based consensus of linear multi-agent systems by reduced-order dynamic output feedback. ISA Trans. 2022, 129, 121–129. [Google Scholar] [CrossRef]
  24. Chen, W.; Gao, F.; Xu, S.; Li, Y.; Chu, Y. Robust stabilization for uncertain singular Markovian jump systems via dynamic output-feedback control. Syst. Control. Lett. 2023, 171, 105433. [Google Scholar] [CrossRef]
  25. Yao, Q. Fixed-time neural adaptive fault-tolerant control for space manipulator under output constraints. Acta Astronaut. 2023, 203, 483–494. [Google Scholar] [CrossRef]
  26. Wu, C.; Zhu, G.; Lu, J. Indirect adaptive neural tracking control of USVs under injection and deception attacks. Ocean. Eng. 2023, 270, 113641. [Google Scholar] [CrossRef]
  27. Friese, J.; Brandt, N.; Schulte, A.; Kirches, C.; Tegethoff, W.; Köhler, J. Quasi-optimal control of a solar thermal system via neural networks. Energy AI 2023, 100232. [Google Scholar] [CrossRef]
  28. Alsaade, F.W.; Yao, Q.; Al-zahrani, M.S.; Alzahrani, A.S.; Jahanshahi, H. Neural-based fixed-time attitude tracking control for space vehicle subject to constrained outputs. Adv. Space Res. 2022. [Google Scholar] [CrossRef]
  29. Jahanshahi, H.; Yao, Q.; Ijaz Khan, M.; Moroz, I. Unified neural output-constrained control for space manipulator using tan-type barrier Lyapunov function. Adv. Space Res. 2022. [Google Scholar] [CrossRef]
  30. Zhou, G.; Tan, D. Review of nuclear power plant control research: Neural network-based methods. Ann. Nucl. Energy 2023, 181, 109513. [Google Scholar] [CrossRef]
  31. Panahandeh, P.; Alipour, K.; Tarvirdizadeh, B.; Hadi, A. A kinematic Lyapunov-based controller to posture stabilization of wheeled mobile robots. Mech. Syst. Signal Process. 2019, 134, 106319. [Google Scholar] [CrossRef]
  32. LI, W.; ZHAN, Q. Kinematics-based four-state trajectory tracking control of a spherical mobile robot driven by a 2-DOF pendulum. Chin. J. Aeronaut. 2019, 32, 1530–1540. [Google Scholar] [CrossRef]
  33. LiBretto, M.; Qiu, Y.; Kim, E.; Pluckter, K.; Yuk, N.S.; Ueda, J. Singularity-free solutions for inverse kinematics of degenerate mobile robots. Mech. Mach. Theory 2020, 153, 103988. [Google Scholar] [CrossRef]
  34. Zhao, L.; Jin, J.; Gong, J. Robust zeroing neural network for fixed-time kinematic control of wheeled mobile robot in noise-polluted environment. Math. Comput. Simul. 2021, 185, 289–307. [Google Scholar] [CrossRef]
  35. Jilek, T.; Burian, F.; Kriz, V. Kinematic Models for Odometry of a Six-Wheeled Mobile Robot. IFAC-PapersOnLine 2016, 49, 305–310, 14th IFAC Conference on Programmable Devices and Embedded Systems PDES 2016. [Google Scholar] [CrossRef]
  36. Jiang, H.; Xu, G.; Zeng, W.; Gao, F. Design and kinematic modeling of a passively-actively transformable mobile robot. Mech. Mach. Theory 2019, 142, 103591. [Google Scholar] [CrossRef]
  37. Hernández-León, P.; Dávila, J.; Salazar, S.; Ping, X. Distance-Based Formation Maneuvering of Non-Holonomic Wheeled Mobile Robot Multi-Agent System. IFAC-PapersOnLine 2020, 53, 5665–5670, 21st IFACWorld Congress. [Google Scholar] [CrossRef]
  38. Wang, Y.; Mai, T.; Mao, J. Adaptive motion/force control strategy for non-holonomic mobile manipulator robot using recurrent fuzzy wavelet neural networks. Eng. Appl. Artif. Intell. 2014, 34, 137–153. [Google Scholar] [CrossRef]
  39. Hou, R.; Cui, L.; Bu, X.; Yang, J. Distributed formation control for multiple non-holonomic wheeled mobile robots with velocity constraint by using improved data-driven iterative learning. Appl. Math. Comput. 2021, 395, 125829. [Google Scholar] [CrossRef]
  40. Ma, Y.; Zheng, G.; Perruquetti, W. Real-time Identification of different types of non-holonomic mobile robots. IFAC Proc. Vol. 2013, 46, 791–796, 9th IFAC Symposium on Nonlinear Control Systems. [Google Scholar] [CrossRef]
  41. Goswami, N.K.; Padhy, P.K. Sliding mode controller design for trajectory tracking of a non-holonomic mobile robot with disturbance. Computers Electrical Engineering 2018, 72, 307–323. [Google Scholar] [CrossRef]
  42. Zhang, S.; Wu, Y.; He, X. Cooperative output feedback control of a mobile dual flexible manipulator. J. Frankl. Inst. 2021, 358, 6941–6961. [Google Scholar] [CrossRef]
  43. Zou, Y.; Deng, C.; Dong, L.; Ding, L.; Lu, M. Distributed output feedback consensus tracking control of multiple nonholonomic mobile robots with only position information of leader. Appl. Math. Comput. 2022, 422, 126962. [Google Scholar] [CrossRef]
  44. Andreev, A.S.; Peregudova, O.A. On Output Feedback Trajectory Tracking Control of an Omni-Mobile Robot⁎⁎This work was financially supported by the Ministry of Education and Science of Russia under Grant [9.5994.2017/BP] and Russian Foundation for Basic Research under Grant [19-01-00791 ]. IFAC-PapersOnLine 2019, 52, 37–42, 10th IFAC Symposium on Intelligent Autonomous Vehicles IAV 2019. [Google Scholar] [CrossRef]
  45. Huang, J.; Wen, C.; Wang, W.; Jiang, Z.P. Adaptive output feedback tracking control of a nonholonomic mobile robot. Automatica 2014, 50, 821–831. [Google Scholar] [CrossRef]
  46. Chen, H.; Chen, Y.; Chen, W.; Yang, F. Output Tracking of Nonholonomic Mobile Robots with a Model-free Fractional-order Visual Feedback. IFAC-PapersOnLine 2016, 49, 736–741, 10th IFAC Symposium on Nonlinear Control Systems NOLCOS 2016. [Google Scholar] [CrossRef]
  47. Wu, D.; Cheng, Y.; Du, H.; Zhu, W.; Zhu, M. Finite-time output feedback tracking control for a nonholonomic wheeled mobile robot. Aerosp. Sci. Technol. 2018, 78, 574–579. [Google Scholar] [CrossRef]
  48. Sleaman, W.K.; Hameed, A.A.; Jamil, A. Monocular vision with deep neural networks for autonomous mobile robots navigation. Optik 2023, 272, 170162. [Google Scholar] [CrossRef]
  49. Chawla, I.; Pathak, P.; Notash, L.; Samantaray, A.; Li, Q.; Sharma, U. Inverse and Forward Kineto-Static Solution of a Large-Scale Cable-Driven Parallel Robot using Neural Networks. Mech. Mach. Theory 2023, 179, 105107. [Google Scholar] [CrossRef]
  50. Gandarilla, I.; Montoya-Cháirez, J.; Santibáñez, V.; Aguilar-Avelar, C.; Moreno-Valenzuela, J. Trajectory tracking control of a self-balancing robot via adaptive neural networks. Eng. Sci. Technol. Int. J. 2022, 35, 101259. [Google Scholar] [CrossRef]
  51. He, Y.; Chen, J.; Zhou, X.; Huang, S. In-situ fault diagnosis for the harmonic reducer of industrial robots via multi-scale mixed convolutional neural networks. J. Manuf. Syst. 2023, 66, 233–247. [Google Scholar] [CrossRef]
  52. Xiao, H.; Chen, C.P.; Lai, G.; Yu, D.; Zhang, Y. Integrated nonholonomic multi-robot consensus tracking formation using neural-network-optimized distributed model predictive control strategy. Neurocomputing 2023, 518, 282–293. [Google Scholar] [CrossRef]
  53. Wu, Y.; Niu, W.; Kong, L.; Yu, X.; He, W. Fixed-time neural network control of a robotic manipulator with input deadzone. ISA Trans. 2022. [Google Scholar] [CrossRef] [PubMed]
  54. Mai, T.; Tran, H. An adaptive robust backstepping improved control scheme for mobile manipulators robot. ISA Trans. 2023. [Google Scholar] [CrossRef] [PubMed]
  55. Raikwar, S.; Fehrmann, J.; Herlitzius, T. Navigation and control development for a four-wheel-steered mobile orchard robot using model-based design. Comput. Electron. Agric. 2022, 202, 107410. [Google Scholar] [CrossRef]
  56. Rosenfelder, M.; Ebel, H.; Eberhard, P. Cooperative distributed nonlinear model predictive control of a formation of differentially-driven mobile robots. Robot. Auton. Syst. 2022, 150, 103993. [Google Scholar] [CrossRef]
  57. Zhang, J.; Li, S.; Meng, H.; Li, Z.; Sun, Z. Variable gain based composite trajectory tracking control for 4-wheel skid-steering mobile robots with unknown disturbances. Control. Eng. Pract. 2023, 132, 105428. [Google Scholar] [CrossRef]
  58. Luo, X.; Mu, D.; Wang, Z.; Ning, P.; Hua, C. Adaptive full-state constrained tracking control for mobile robotic system with unknown dead-zone input. Neurocomputing 2023, 524, 31–42. [Google Scholar] [CrossRef]
  59. Spong, M.W.; Hutchinson, S.; Vidyasagar, M. Robot Modeling and Control; John Wiley and Sons, 2006. [Google Scholar]
Preprints 75579 g001
Figure 1. Schematic drawing of the mobile robot used in this research study.
Figure 1. Schematic drawing of the mobile robot used in this research study.
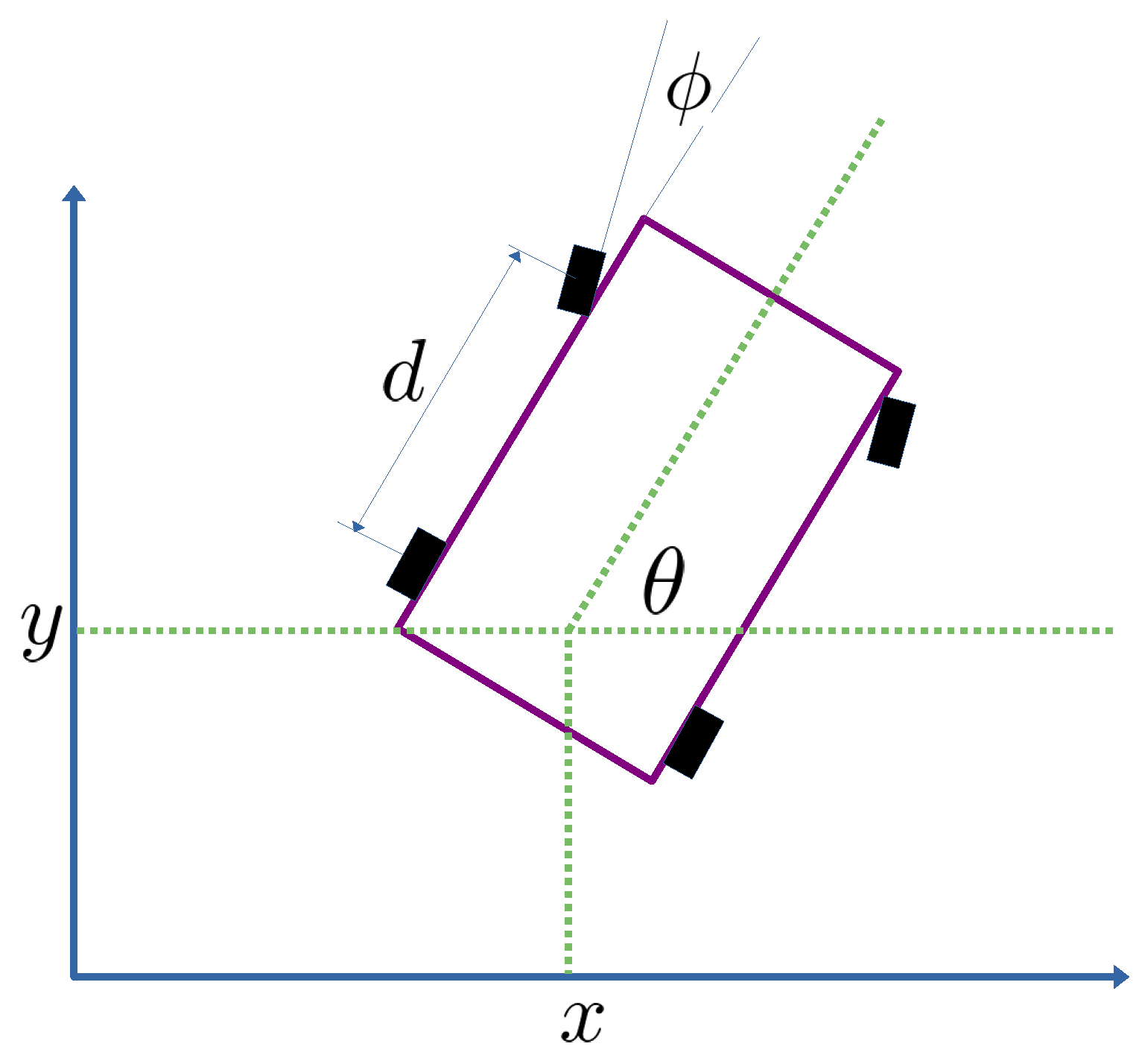
Preprints 75579 g001
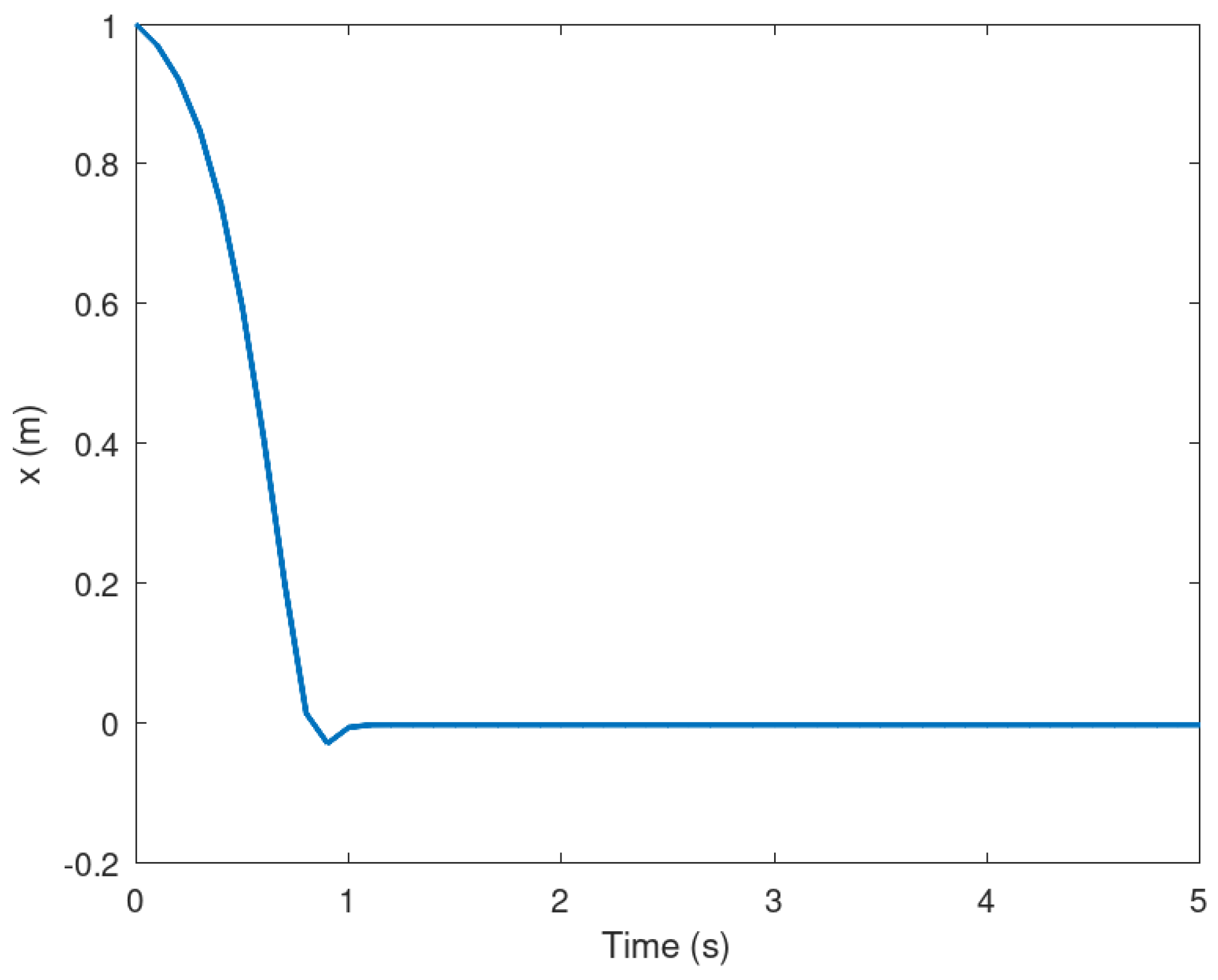
Preprints 75579 g002
Figure 2. Position of the mobile robot in the x frame.
Figure 2. Position of the mobile robot in the x frame.
Preprints 75579 g002
Preprints 75579 g003
Figure 3. Position of the mobile robot in the y frame.
Figure 3. Position of the mobile robot in the y frame.
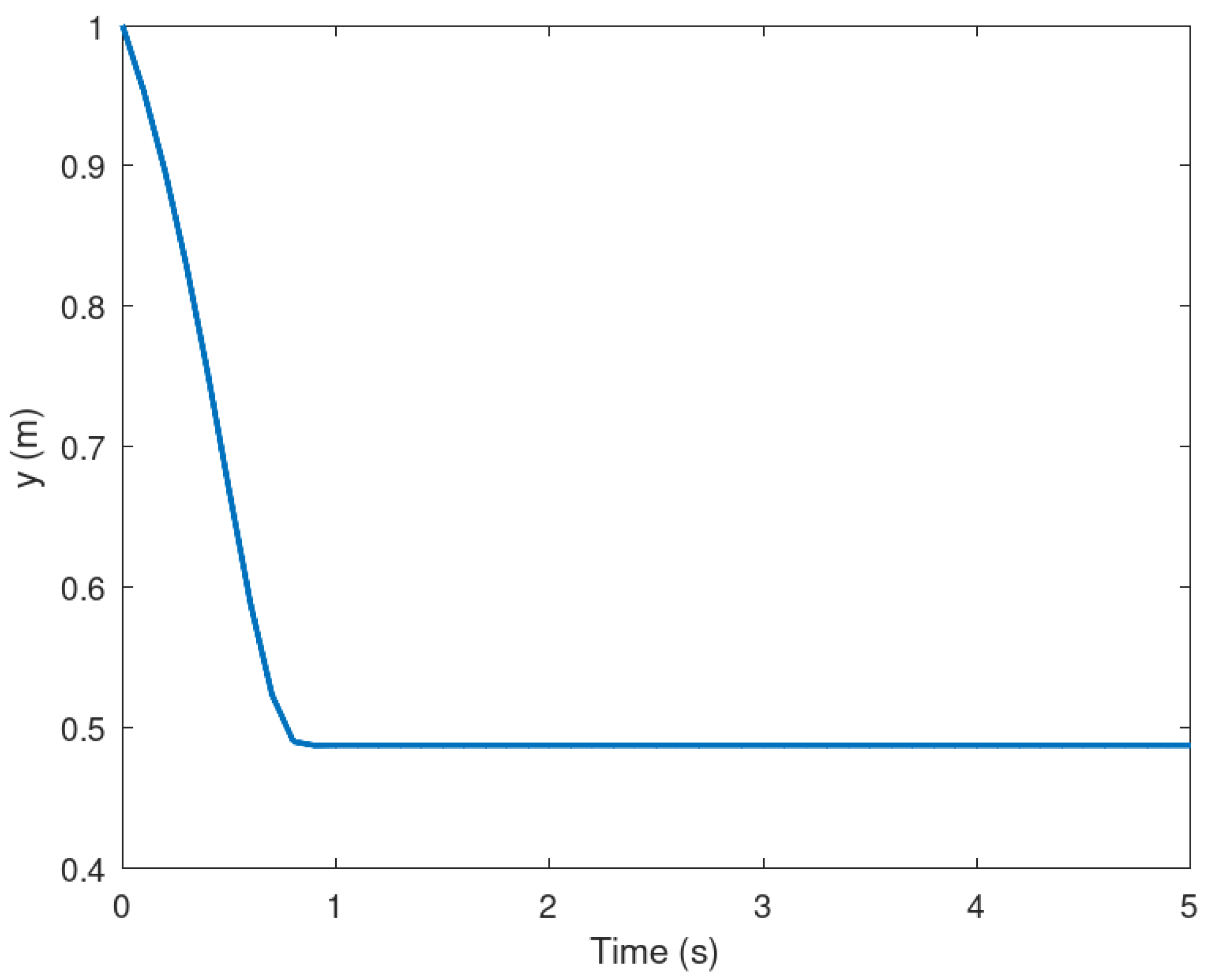
Preprints 75579 g003
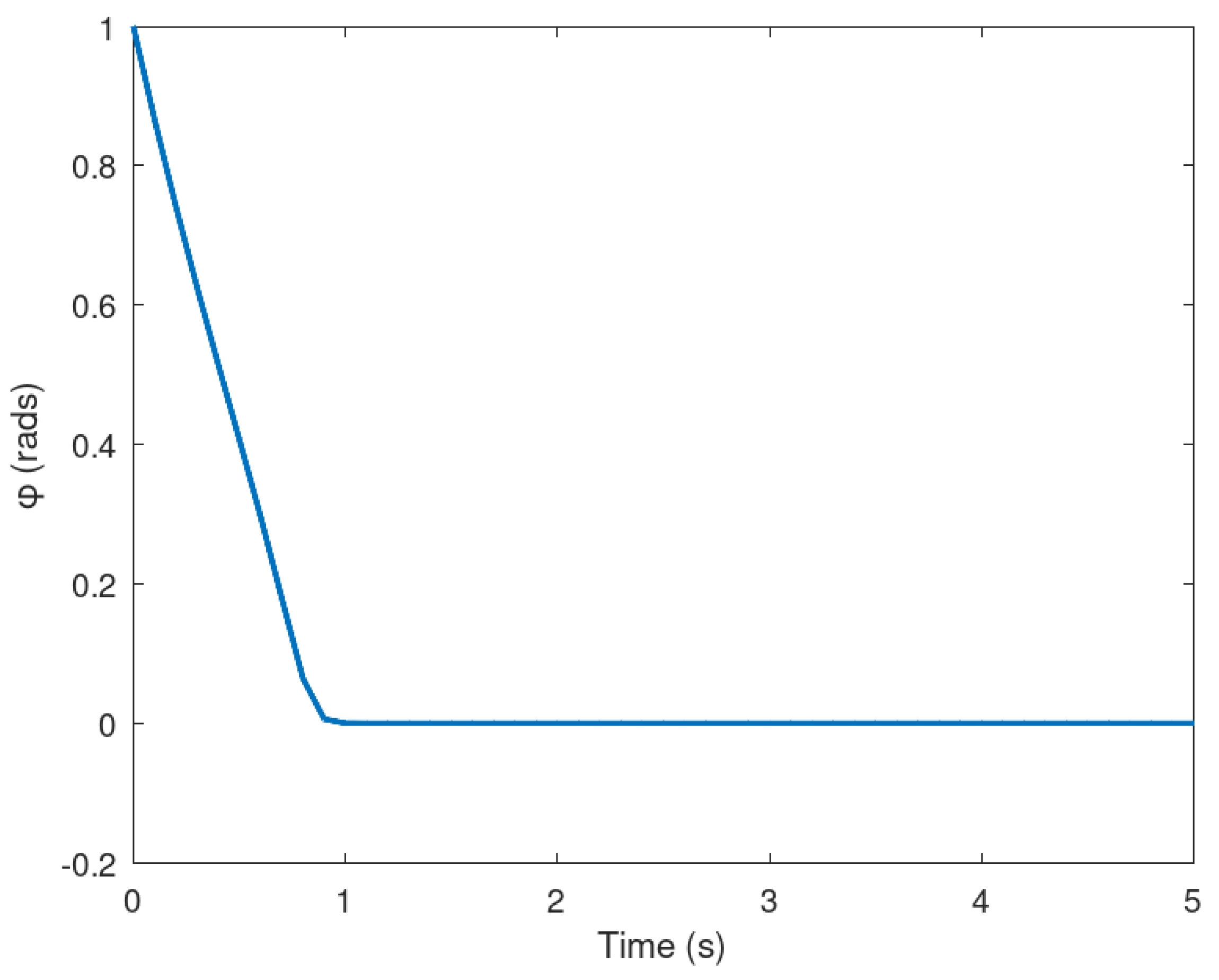
Preprints 75579 g004
Figure 4. Evolution in time of the variable ϕ .
Figure 4. Evolution in time of the variable ϕ .
Preprints 75579 g004
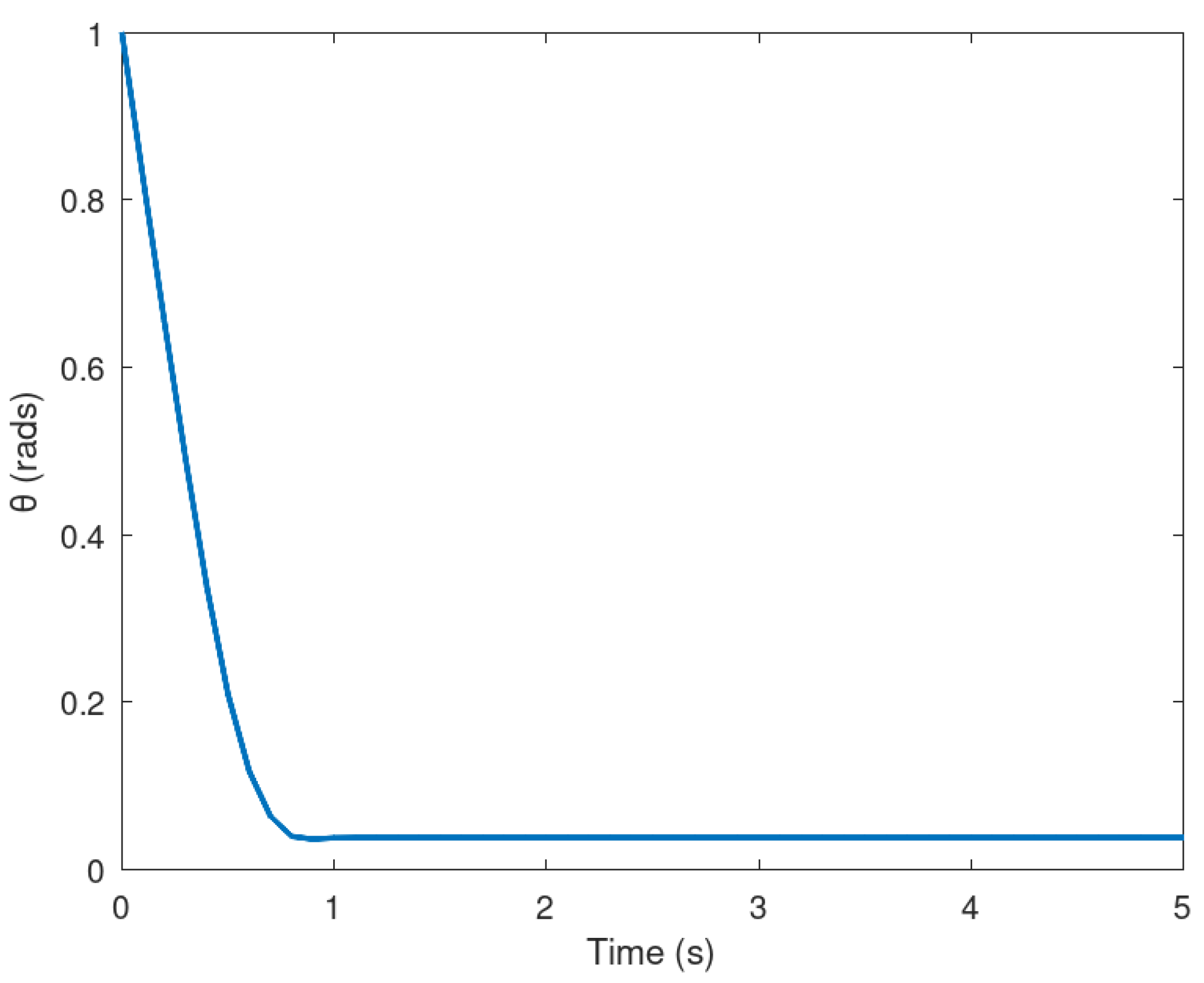
Preprints 75579 g005
Figure 5. Evolution in time of the variable θ .
Figure 5. Evolution in time of the variable θ .
Preprints 75579 g005
Preprints 75579 g006
Figure 6. Evolution in time of the mobile robot trajectory.
Figure 6. Evolution in time of the mobile robot trajectory.
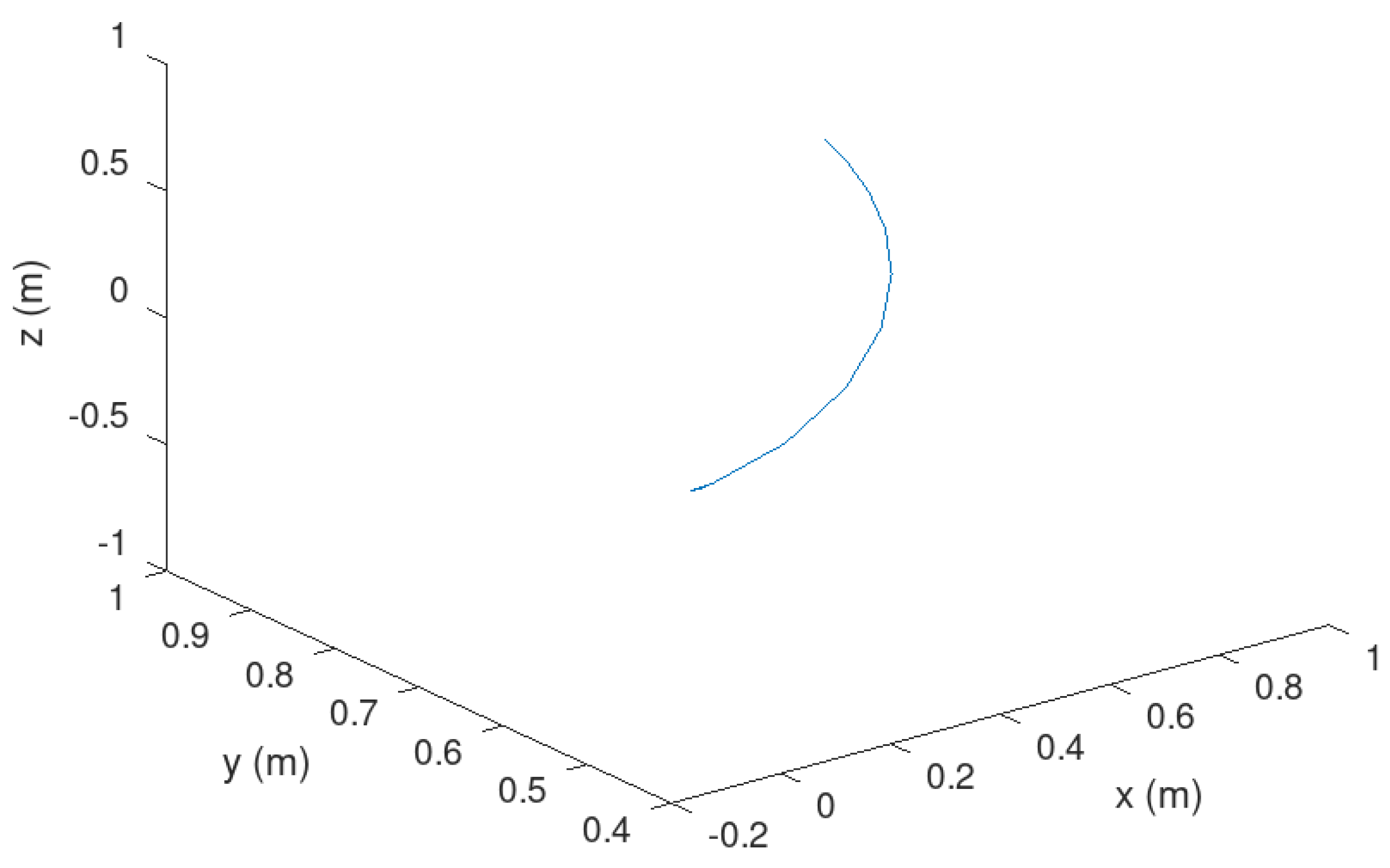
Preprints 75579 g006
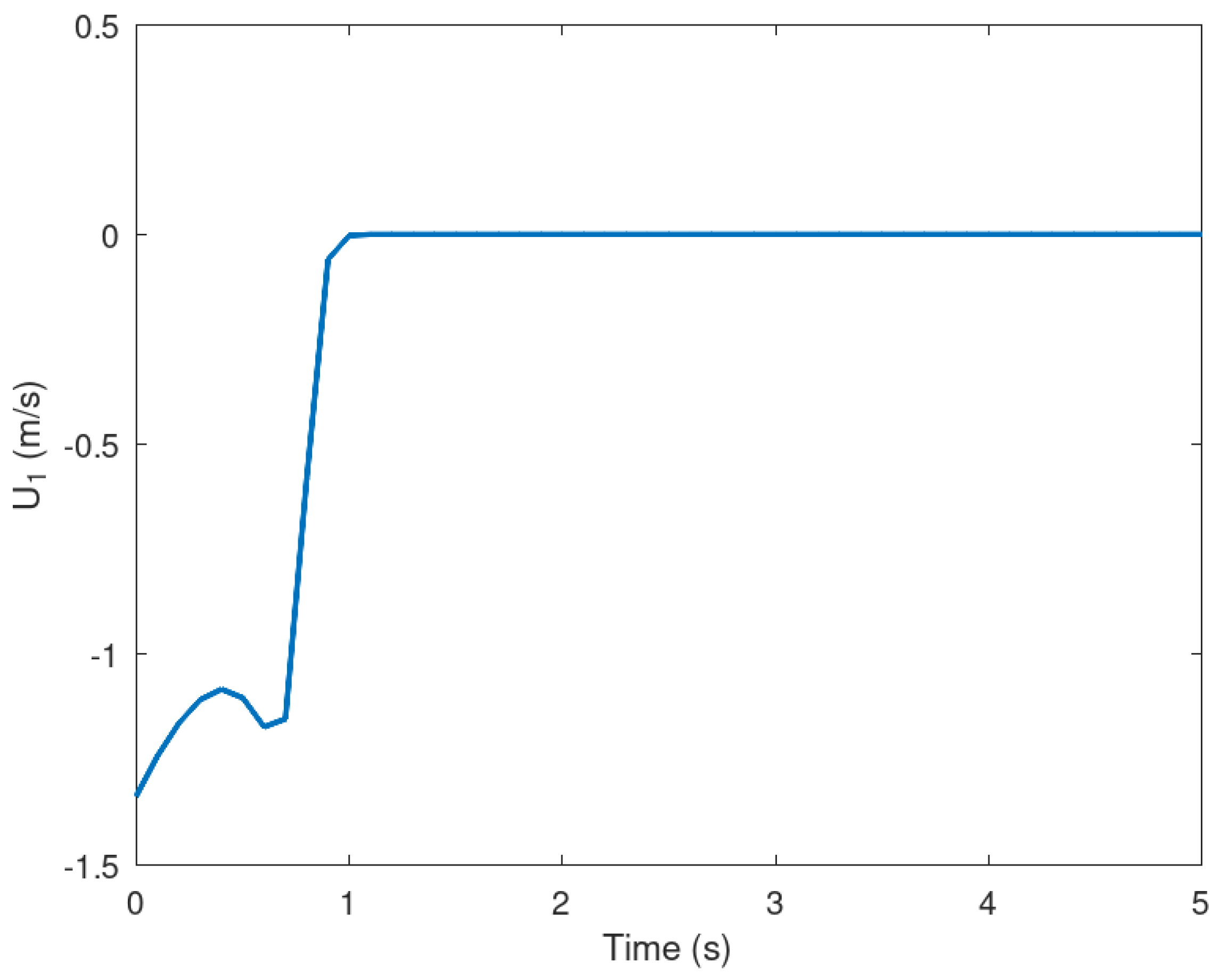
Preprints 75579 g007
Figure 7. Evolution in time of the variable U 1 .
Figure 7. Evolution in time of the variable U 1 .
Preprints 75579 g007
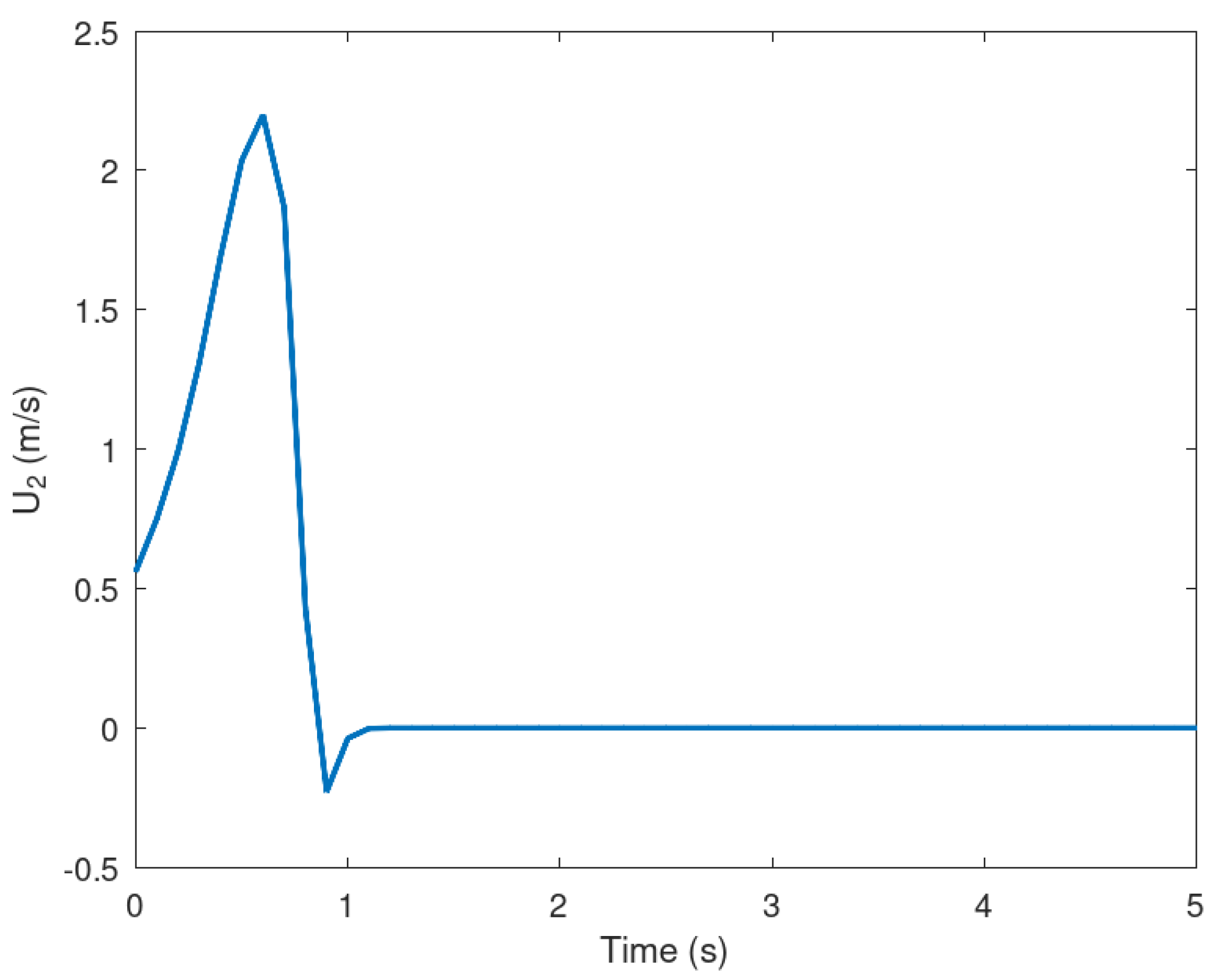
Preprints 75579 g008
Figure 8. Evolution in time of the variable U 2 .
Figure 8. Evolution in time of the variable U 2 .
Preprints 75579 g008
Preprints 75579 g009
Figure 9. Position of the mobile robot in the x frame.
Figure 9. Position of the mobile robot in the x frame.
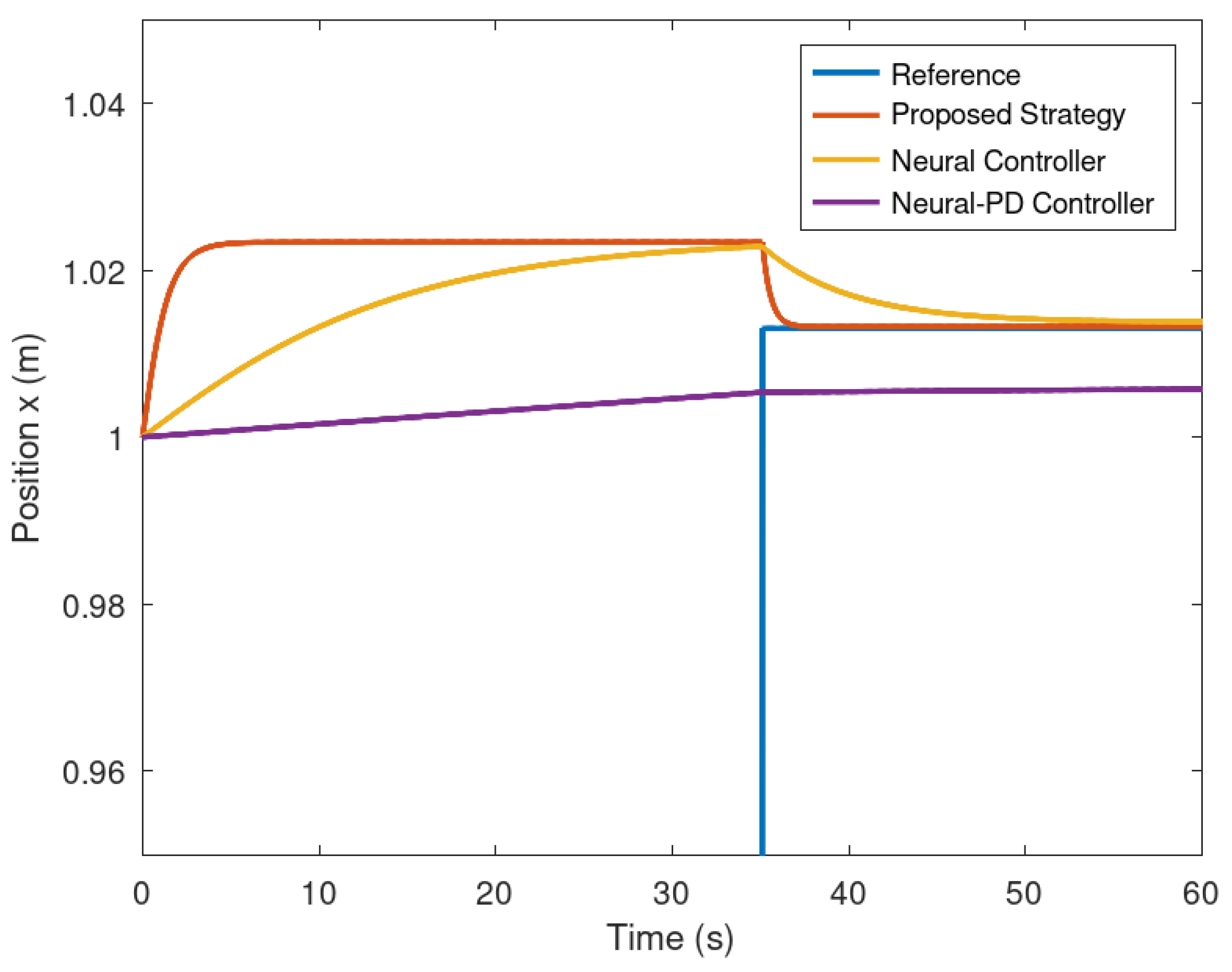
Preprints 75579 g009
Preprints 75579 g010
Figure 10. Position of the mobile robot in the y frame.
Figure 10. Position of the mobile robot in the y frame.
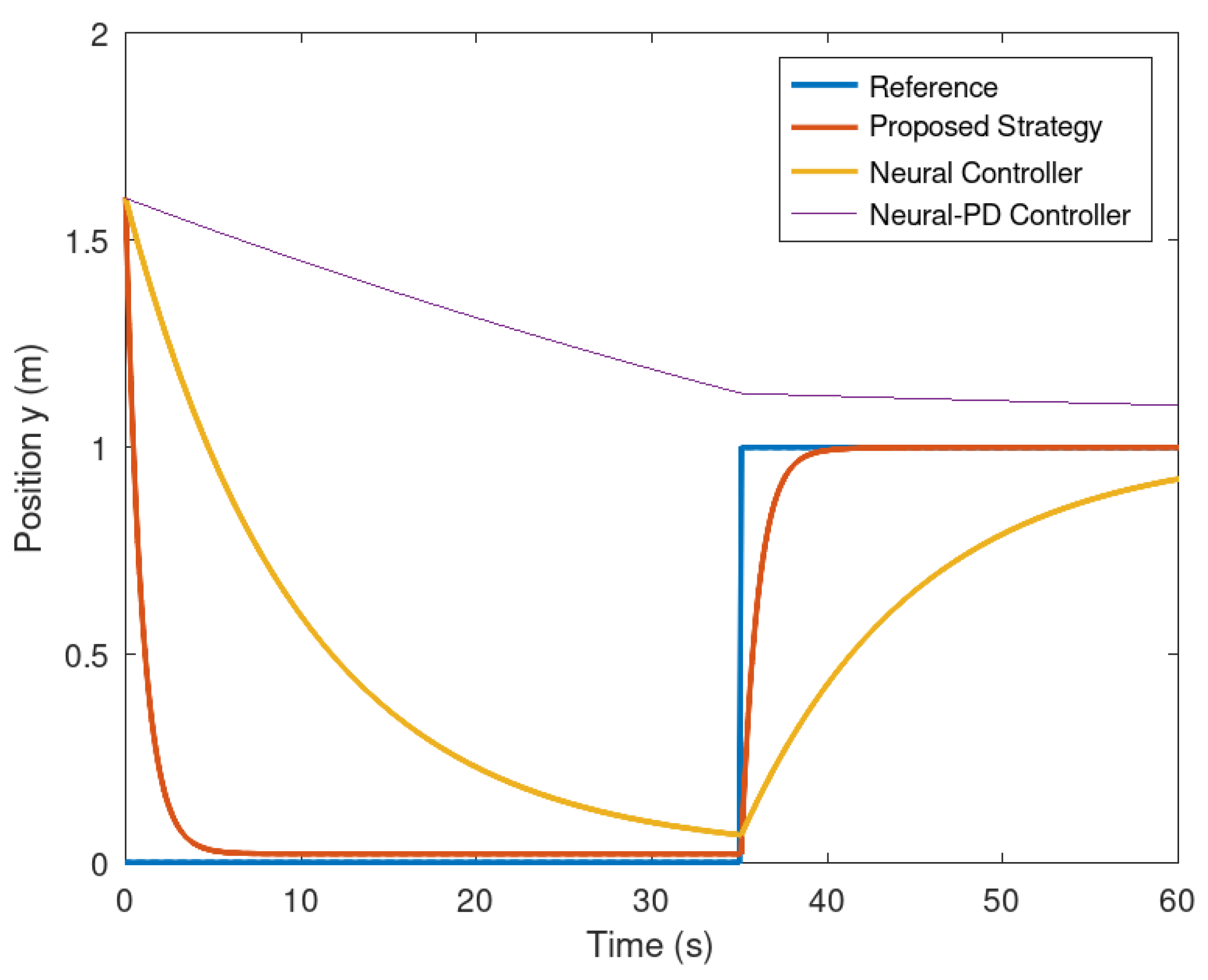
Preprints 75579 g010
Preprints 75579 g011
Figure 11. Evolution in time of the error variable e 1 .
Figure 11. Evolution in time of the error variable e 1 .
Preprints 75579 g011
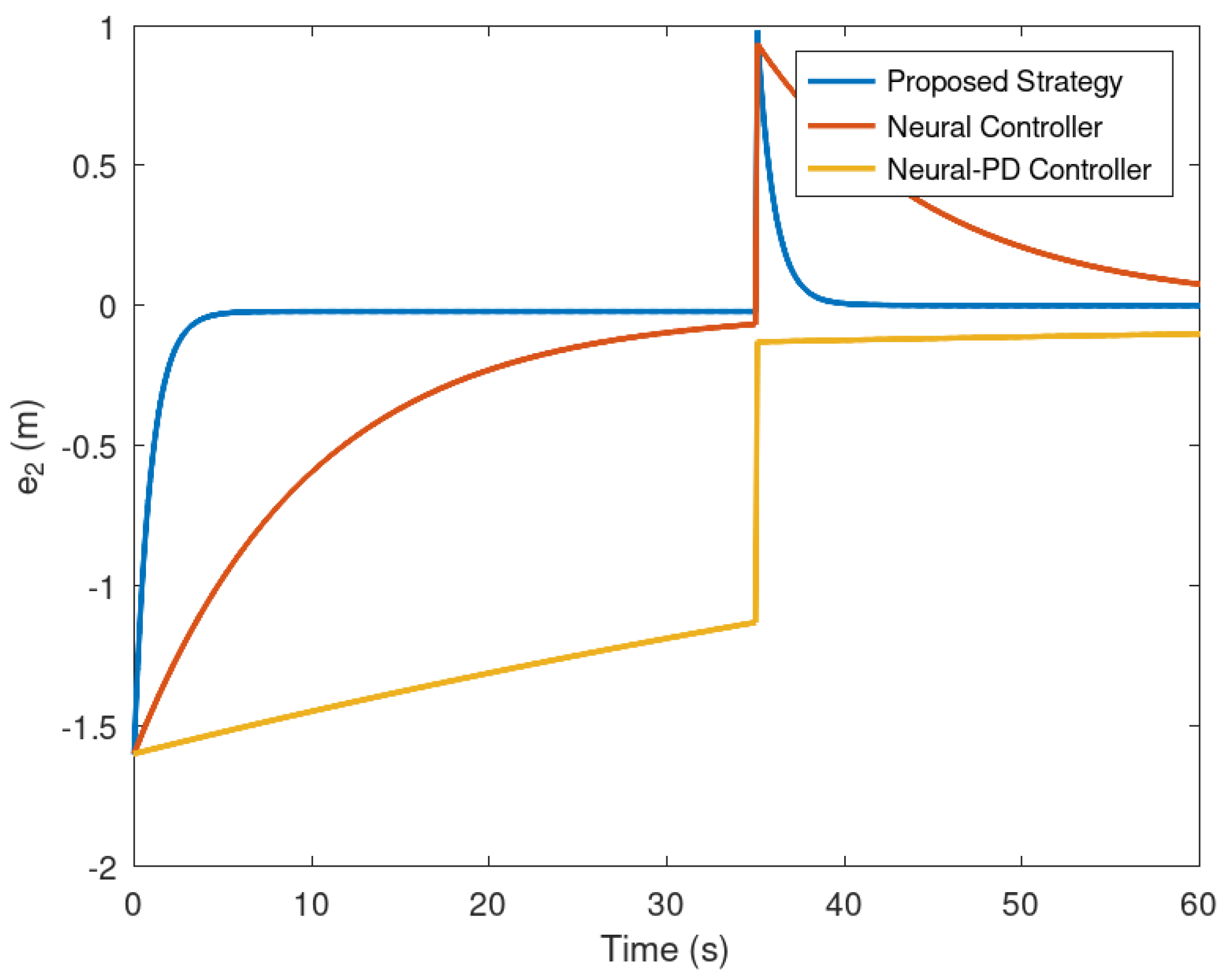
Preprints 75579 g012
Figure 12. Evolution in time of the error variable e 2 .
Figure 12. Evolution in time of the error variable e 2 .
Preprints 75579 g012
Preprints 75579 g013
Figure 13. Evolution in time of the mobile robot trajectory.
Figure 13. Evolution in time of the mobile robot trajectory.
Preprints 75579 g013
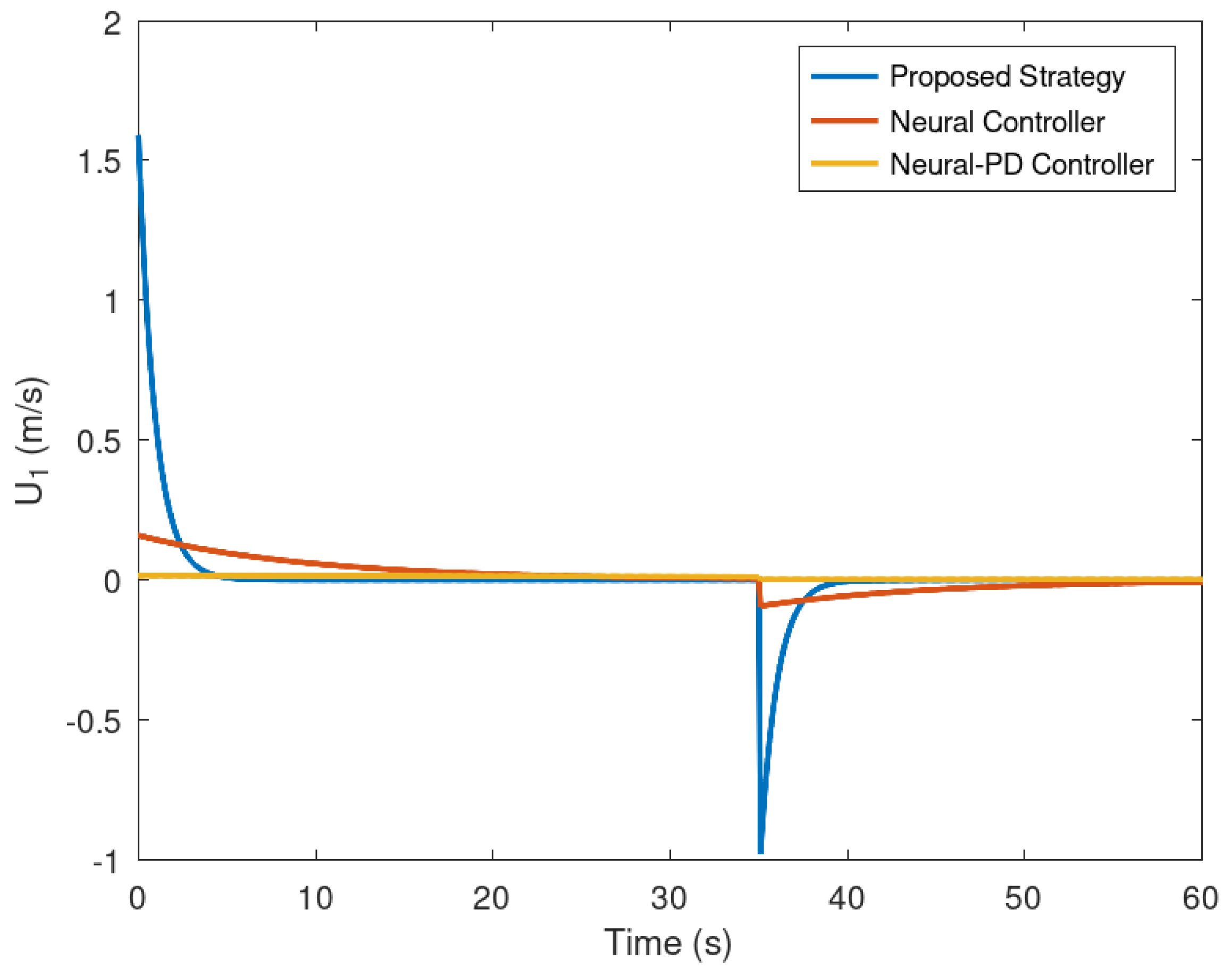
Preprints 75579 g014
Figure 14. Evolution in time of the variable U 1 .
Figure 14. Evolution in time of the variable U 1 .
Preprints 75579 g014
Preprints 75579 g015
Figure 15. Evolution in time of the variable U 2 .
Figure 15. Evolution in time of the variable U 2 .
Preprints 75579 g015
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated