Prerpints.org logo
Preprint
Article

Pattern-Multiplicative Average of Nonnegative Matrices Revisited: Eigenvalue Approximation Is the Best of Versatile Optimization Tools

Altmetrics

Downloads

100

Views

14

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

05 June 2023

Posted:

06 June 2023

You are already at the latest version

Alerts
Abstract
Given several nonnegative matrices with a single pattern of allocation among their zero/nonzero elements, the average matrix should have the same pattern, too. This is the first tenet of the pattern-multiplicative average (PMA) concept, while the second one suggests the multiplicative (or geometric) nature of averaging. The original concept of PMA was motivated by the practice of matrix population models as a tool to assess the population viability from long-term monitoring data. The task has reduced to searching for an approximate solution to an overdetermined system of polynomial equations for unknown elements of the average matrix (G), hence to a nonlinear constrained minimization problem for the matrix norm. Former practical solutions faced certain technical problems, which required sophisticated algorithms but returned acceptable estimates. Fresh idea to use the eigenvalue approximation ensues also from the basic equation of averaging, which determines the exact value of λ1(G), the dominant eigenvalue of matrix G, too, and the corre-sponding eigenvector. These are bound by the well-known linear equations, which reduce the task to a standard problem of linear programing (LP). The LP approach is realized for 13 fixed-pattern matrices gained in a case study of Androsace albana, an alpine short-lived perennial, monitored on permanent plots during 14 years. A standard software routine reveals the unique exact solution, rather than an approximate one, to the PMA problem, which turns the LP approach into ‘’the best of versatile optimization tools”. The exact solution turns out to be peculiar in reaching zero bounds for certain nonnegative entries of G, which deserves a modified problem formulation separating the lower bounds from zero.
Keywords: 
Subject: Computer Science and Mathematics  -   Applied Mathematics

MSC:  15B48; 90C08; 90C26; 92D25; 92-10

1. Introduction

Pattern-multiplicative average (PMA) of nonnegative matrices is a concept motivated in the field of Matrix Population Models by the need to assess the viability of a local population from the outcome of its long-term monitoring. Matrix Population Models represent a wide and rapidly growing area of applications [CA23, CP23], where the theory of nonnegative matrices applies to population dynamics [BP94]. When biologists study a population of a plant or animal species and observe the population at discrete time moments, they classify individuals according to an observable trait such as age, body size, ontogenetic stage, etc., and divide the entire range of trait values into certain discrete classes, thus dealing with a discrete population structure [Cas01]. It is expressed mathematically as a vector x(t) ϵ R + n (n ≥ 2) representing the (absolute or relative) abundances of n class-specific groups of individuals, whereafter the Matrix Population Model is a system of first-order difference equations,
x(t + 1) = L(t) x(t), t = 0, 1, 2, …,
linking the population vector at the next moment, t + 1, to that at the current one, t.
Matrix L(t) is therefore called the population projection matrix (PPM) [Cas01], despite the projection term has quite another meaning in matrix algebra [HoJ90]. All the matrix entries are nonnegative and called vital rates as they have certain demographic sense [Cas01]. The pattern of how zero/nonzero elements are arranged within the matrix is associated, in a unique way, to what is called the life cycle graph (ibidem) as it bears the biological knowledge of how the individuals grow/develop for one time step and provide for the population recruitment.
Being nonnegative, the PPM becomes a legal target for the Perron–Frobenius Theorem [Gan59, HoJ90], whereby a rich repertoire of model properties and population characteristics can be obtained after the PPM having been calibrated from data [Cas01, LSG21]. In particular, the dominant eigenvalue, λ1 > 0, of matrix L(t) serves as a “measure of how the local population is adapted to the environment where and when the data have been mined to calibrate the PPM” [L19] (p.1). When the data are of the ‘identified individuals’ type [Cas01], a great advantage of MPMs is that the calibration can be done just from two successive observations, thus meeting Eq.(1) and yielding a time-dependent L(t). Correspondingly, the adaptation measure, λ1, inherits the time dependence, and the great advantage turns dialectically into a great trouble or challenge when the task is to assess the adaptation from a time series of observation data, hence from a finite set of one-step PPMs.
The historically first response to the challenge was grounded on the theory of random sequences of vectors L(t)x(t), t → ∞ [Co79, TuO80, Tu86, Tu90], and it has led to what is now called the stochastic growth rate of a population in a randomly changing environment (see [Cas01] and refs therein). Another, more recent approach reverts the task just to averaging a given number, say M (M ≥ 2), of one-step PPMs and calculating the dominant eigenvalue, λ1(G), of the average matrix G. Letter “G” here bears a hint to the geometric (or multiplicative) nature of averaging, and the hint will be revealed further in Section 2.2. This approach has led to a concept that was proposed 5 years ago with regard to matrix population models [L18], and the task of averaging was reduced to a constrained nonlinear minimization problem for the matrix norm [L19, L18] (see Section 2.3). The norm has however not appeared quite fit for global optimization, but required versatile optimization tools [PZL22] to solve the problem.
This paper aims at expanding those “versatile optimization tools” with another target of optimization, namely, the deviation of λ1(Gopt) from the ideal calculable λ1(G) (Section 2.4). The approach originates from the fact the ideal λ1(G) is known:
λ1(G) = (Prod)1/M,
where Prod denotes the product of M one-step PPMs. This leads to a problem that appears to be formalizable as a standard problem of linear programming (LP), hence solvable by standard routines. The solution is exemplified by a case study of monitoring a local population of an alpine short-lived perennial for 13 years [Let23] (Section 2.1). Sections 2.3 and 2.4 contain respectively a short presentation of the published “versatile optimization tools” and an in-depth one of the original LP approach. The outcomes of the both are presented in Section 3, enabling the comparison of results, which reveals a surprising contrast and induces some comments (Section 4), in particular, on how general the proposed LP technique might be. Section   5 contains some ensuing conclusions.

2. Materials and Methods

2.1. Case Study

A local population of Androsace albana, an alpine short-lived perennial plant species, was monitored on permanent sample plots once a year [Let23] during 14 years (2009–2022). Although A. albana reproduces actually by seeds, the stage of dormant seeds was deliberately excluded from the life cycle graph by ontogenetic stages as the seed-related vital rates cannot be reliably estimated in the field [LKBO18]. Later on, we proved such an exclusion to be correct within the integer-valued formalism [LKO20], which can always be applied for the ‘identified individuals’ data. The life cycle graph looks correspondingly as shown in Figure 1, with the “virtual” rather than real recruitment arcs. These three arcs ingo respectively to three early stages since the newly recruited plants can be observed in any of them at the moment of observation.
Now, we have x(t) ϵ R + 5 , and the natural order of components in x(t) leads to the following PPM pattern:
L = 0 0 d 0 0 0 0 0 a b e f 0 0 h 0 k l c 0 0 0 0 m 0 ;   a ,   b ,   … ,   l ,   m ≥ 0 ,
with 10 vital rates to be calibrated. The calibration for 13 successive pairs of observation years results in 13 annual PPMs, L(t) = [lij(t)], presented in Table 1. Each of them obeys Eq. (1). There are 6 annual PPMs with λ1(L(t)) > 1 and 7 of those with λ1(L(t)) < 1, so that even an “educated guess” of what should be λ1(G), the dominant eigenvalue of the average matrix, remains uncertain.

2.2. Pattern-Multiplicative Average of Annual PPMs

The logic of PMA ensues from the following apparent observation: given the 13 annual PPMs calibrated according to Eq. (1) (Table 1), we have the initial population structure projected to the terminal one,
x(2022) = L(2021) L(2020) . . .L(2009) x(2009),
by
Prod = L(2021) L(2020) . . . L(2009),
the product of 13 annual PPMS in the chronological order.
x(2022) = Prod x(2009).
Since the average matrix ought to do absolutely the same when raised to the 13th power, we have the following basic equation of averaging:
G13 = Prod,
which justifies Eq. (2) of the Introduction. As is noted ibidem, a routine extraction of the 13th root from a given, even positive, Prod can hardly return a nonnegative matrix, nor guarantee the fixed pattern (3) for the root.
A workaround leads to solving matrix equation (6) as a system of scalar polynomial equations for unknown matrix elements. In fact, there are 5×5 – 10 = 15 elements that are prescribed to be zero by pattern (3), while the corresponding 15 scalar equations bind the unknown elements too, in addition to the 10 equations for the 10 unknowns. It means that Eq. (6) is overdetermined as a system of scalar equations, hence it may have an exact solution only under special relations between the equations depriving those extra 15 ones of their independence. No reason however to seek this kind of relation among the PPMs, so that Eq. (6), the basic equation of averaging has no solution over the set of pattern (3) PPMs.
The simple and clear logic of PPM averaging thus faces a principal obstacle in matrix algebra, and a workaround comes to an approximate solution.

2.3. Approximate PMA as a Nonlinear Constraned Minimization Problem

Any approximation invokes the question of how close is the approximate solution to the exact one. Although the latter is unknown, the equivalent form of Eq, (6):
G13– Prod = 0,
just illustrates the ideal, yet unreachable, closeness as a 5×5 matrix of zeros. Retaining the same notation G = [gij] for the approximate average matrix, we can see the elements of G13 as certain polynomials of the 5×13 = 65th degree. If we consider the quality of approximation to be a scalar value, then it should be the error of approximation. The error can be measured as the (squared) matrix norm, whereby we come to the following nonlinear minimization problem:
Φ ( G ) → min B ⁡ Φ ( G ) = | | G 13 – P r o d | | 2 .
Here B ⊏ R + 10 defines the problem to be a constrained one as it represents the constraints that ensue from the logics of averaging: the average vital rates should not be less, nor greater than those fixed in observations. In matrix terms, it means that each entry of the annual PPM has to lay within the bounds defined by the minimal value and the maximal one among the 13 annual values of that entry. In formal terms,
min t ⁡ l i j ( t ) ≤ g i j ≤ max t ⁡ l i j t ,       i ,   j = 1 , … ,   5
(see Table 2).
So, we come to the constrained nonlinear minimization problem (8–9), where the bounds
of B are defined in Table 2. Both standard routines for global optimization [MW23G] and more sophisticated ones [PZL22] can be applied for solving problem (8–9).

2.4. Approximate PMA as an Eigenvalue Constrained Optimization Problem

Noted in the Introduction, expression (2) is actually a simple algebraic consequence of (6), the basic equation of averaging, that would be true if the exact solution existed. Since it does not exist, another measure of approximation quality can be found by the following speculations.
Suppose v to be a dominant eigenvector of the average matrix G, i.e., we have
G v = λ1(G) v.
Acting by operator G successively on the both sides of Eq. (10), we get
(G)2 v = λ1(G)2 v,
(G)3 v = λ1(G)3 v,
…,
(G)13 v = λ1(G)13 v.
In combination with the averaging Eq.(6), Eq.(11) signifies that v is a dominant eigenvector of the matrix product, Prod, too. Hereby, the other measure of approximation error is
|λ1(G) – ρ0|, where ρ0 = ρ(Prod)
can be calculated from the data presented in Table 1. The optimal solution should be searched for among those matrices G that has the same eigenvector v. To exemplify how matrices of a single pattern with different eigenvalues may have the same dominant eigenvector is a student level exercise (A hint to solution in Appendix A).
To be unique, this eigenvector, v*, can, for instance, be expressed in percent and calculated like the vectors x* presented in Table 1. It can thereafter serve as a constraint in the search of approximation among various λ1 values associated with a single v*. (To give an example of matrix eigenvalue being nonlinear as a function of matrix elements is another exercise.) Hence, we have a nonlinear minimization problem again. However, the change of variables, a beloved mathematical trick,
y = |λ1(G) – ρ0|,
turns the problem into a linear one. More specifically, it turns the task into the following two linear problems: to maximize the λ1(G) when ρ0 ≥ λ1(G) and to minimize it when λ1(G) ≥ ρ0.
Moreover, vector v* = [v1, v2, …, v5], the known positive eigenvector of G, and its dominant eigenvalue λ1(G) are bound by definition to the matrix equation
Gv* = λ1(G)v*.
With due regard to the fixed pattern (3) and with omitting subscript 1 at λ1, this matrix equation reduces to the five scalar linear equations for a, b, …, l, m, λ, the ten unknown entries of G and the 11th formal variable λ:
av5 – λv1 = 0,
bv5 + dv1 – λv2 = 0,
cv5 + ev1+ fv2+ hv3 – λv3 = 0,
kv3 + lv4 – λv4 = 0,
mv4 – λv5 = 0.
The 11th variable has its own bounds: as the dominant eigenvalue of the average matrix, the unknown λ has to locate within the following bounds:
λ ∈ min t ⁡ λ 1 L t ,   max t ⁡ λ 1 L t ,   t = 2009 ,   … ,   2021 ,
to be determined from Table 1. The two specific problems specify these bounds further:
λ ∈ min t ⁡ λ 1 ( L t ) ,   ρ 0   i f   λ ≤ ρ 0 ; ρ 0 , min t ⁡ λ 1 ( L t )   i f   λ ≥ ρ 0 .
Finally, we have the following problem formulation:
y → min p ⁡ y p   p = 1 ,   2 ; y p → min x ∈ B p ⁡ y p x ,
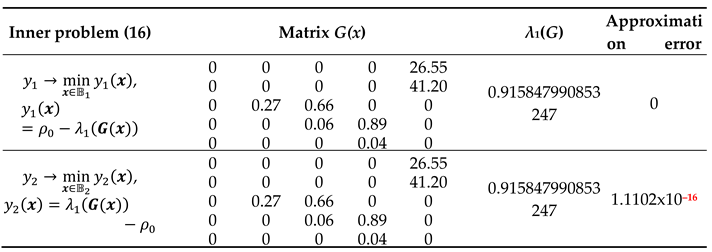
where x = [a, b, …, l, m, λ]T, while the polygons B p ⊂ R + 11   (p = 1, 2) are defined in (15) and the equality-type constraints (14). The two inner problems (16) represent the standard LP ones to be solved by standard software routines, such as function linprog in MATLAB® [MW23L] (technical details in Appendix B).

3. Results

3.1. Case Study Outcome

Calibrated with the absolute accuracy, 13 annual PPMs for A. albana are presented in Table 1 with their dominant eigenvalues and corresponding eigenvectors.

3.2. Pattern-Multiplicative Averaging as an Approxiation Problem

The logics of approximate PMA have been implemented as problem settings in Subsections 2.3 and 2.4. Matrix Prod (4), the product of 13 annual PPMs, is too cumbersome to be presented here in its original rational form. Its numerical form up to the 15th significant digit is shown in Table 3 together with the dominant eigenvalue and the corresponding eigenvector.

3.3. Minimizing the Approximation Error as a Matrix Norm.

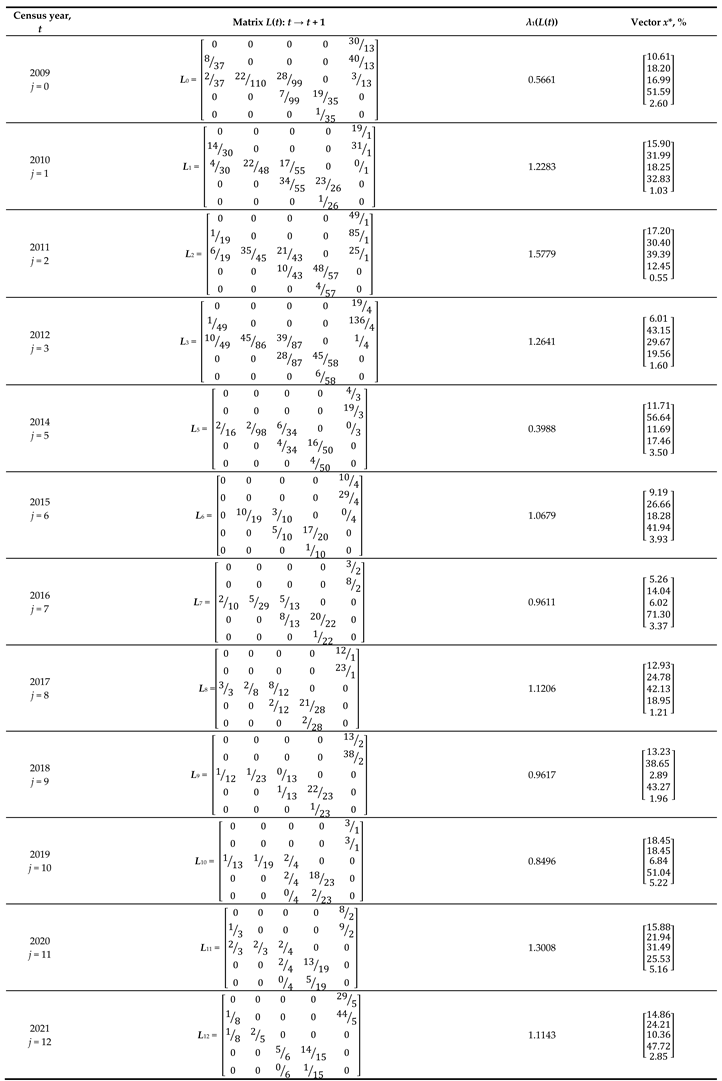
Solution to the constraint minimization problem (8) has been obtained in [PZL22] by the “versatile optimization tools” (Table 4) for the case of 12 annual PPMs. The quality of approximation ranges from 0.002374 to 0.002379 as a function of the optimization method (ibidem). In the format of Table 1, the obtained average matrices are presented in Table 4.

3.4. Eigenvalue Constrained Optimization Problem

Solutions to the problem (14–16) are shown in Table 5.
The solutions to the two optimization problems look indistinguishable within the publication format allowed, and they are really different at the 16th decimal digit alone, which may well be attributed to the computer round-off errors. It means that both problems have the same unique optimal solution, i.e., the corresponding vertex is in common of the polygons B1 and B 2.

4. Discussion and Conclusions

The case study practice has not motivated any logics of PMA beyond the population structure projection from the initial vector to the terminal one, i.e., Eqs. (4-5). Therefore, we deal here with single-objective problems alone (in the terminology of [DRH21]). Once having been formulated in mathematical terms [L18], this objective comes immediately to the difference norm as the distance between two matrices following the fundamental of real analysis [K22]. However, even the squared matrix norm has required “versatile optimization tools” [PZL22] to achieve even moderate approximation quality in the corresponding nonlinear constrained minimization problem (Table 4).
Beside of the moderate approximation quality, the basin-hopping global search, as an essential part of the “versatile optimization tools”, leaves no chance for the results being quantitatively reproducible as it is essentially stochastic [RC04]. In contrast, the LP approach is essentially deterministic [Lu73], hence the results of Section 3.4 can be reproduced any number of times.
What does not contrast the LP approach to the PMA task is the eigenvalue optimization problem being nonlinear, too. Since the matrix eigenvalue in general and the dominant eigenvalue in particular is not linear as a function of matrix elements (see Appendix A), the use of linear programming seems paradoxical at the first glance. However, beside of the trick with change of variables (11), the very nature of eigenvalue–eigenvector relations is linear, resulting in the linear relationships among matrix elements and the linear equality-type constraints in the LP setting. The trick has nevertheless failed to cheat a software routine formality, namely, to express the loss function as a linear combination of formal variables at fixed coefficients (see Appendix B). The reason is quite evident: function (11) is not a linear function, albeit consisting of two linear parts.
These two parts have logically resulted in the two adjacent LP problems differing in the range (15) of the lambda alone. The both yield a single solution surprisingly coincident with the ideal λ1(G) (Table 5). On the one hand, the theory of linear programming is known to admit nonunique solutions [Lu73]. On the other, different matrices might well have the same dominant eigenvector (see Appendix A) in our practical case, too. Fortunately, the solution returned by the routine has turned out unique, hence the unique best solution to the averaging problem.
Moreover, this best solution is absolutely accurate (Table 5), thus turning a solution to the approximate PMA problem into the exact one and suggesting the best alternative to our former ecological practice [L19, Let23, LKBO18]. Therefore, it makes no sense to quantitatively compare the outcomes of the “versatile optimization tools” and the LP approach – the comparison should rather be qualitative, with an obvious conclusion.
this best solution is absolutely accurate (Table 5), thus turning a solution to the approximate PMA problem into the exact one and suggesting the best alternative to our former ecological practice [L19, Let23, LKBO18]. Therefore, it makes no sense to quantitatively compare the outcomes of the “versatile optimization tools” and the LP approach – the comparison should rather be qualitative, with an obvious conclusion, thus denying any possible reproaches to comparing the case of 12 annual PPMs [PZL22] with the current case of 13 PPMs.
The only “spoon of tar” in this “barrel of honey” is due to certain zeros in the optimal solution, i.e., zero entries to the average matrix G. While there are totally 4 vital rates that have zero minimal values among the 13 annual ones (Table 2), three of them, namely, for c, d, e, (Figure 1), are reached by the “ideal” solution (Table 5). The shares of c = 0, d = 0, and d = 0, in the set of 13 annual PPMs (Table 1) are equal respectively to 9/13, 7/14 and 1/13 (Appendix C). Whether the average matrix should take into account the most frequent zeros or all of them is a dialectical issue. The paradigm of biological diversity in general and the concept of polyvariant ontogeny [Zh86,95] in particular dictate retaining all the links in the life cycle graph (Figure1), hence the absence of occasional zeros in the average matrix.
Therefore, an optimistic mathematical hypothesis is that the same absolute result can be obtained in the eigenvalue constrained optimization problem when we substitute the minimal positive bounds for the zero ones. Testing this hypothesis might be an object of further studies.
Note also that the LP technique presented in Section 2.4 for a specific case study is general enough to be applied for any finite set of irreducible nonnegative fixed-pattern matrices, the specificity being only confined to the bounds and equality-type constraints. While the task is always to find the best approximation, a supertask is to motivate younger mathematicians for giving a theoretical explanation of why the best approximation turns into the exact solution.

Funding

This research was supported by the Russian Scientific Foundation, grant number 22–24–00628.

Acknowledgments

Author thanks Vladimir Yu. Protasov for the idea to formulate the PMA task as an LP problem. Programming and calculations were implemented in MATLAB® R2021b.

Conflicts of Interest

The author declares no conflict of interest with himself. The funder had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

Appendix A

Exercise 1. Exemplify how matrices with a fixed pattern and different eigenvalues may have the same dominant eigenvector. Hint: Consider an imprimitive Leslie matrix with the pattern of
L = 0 0 c a 0 0 0 b 0
and double it.
Exercise 2. Exemplify the matrix eigenvalue being nonlinear as a function of matrix elements. Hint: See matrix (A1).

Appendix B

Using MATLAB®, we have logically to reformulate the LP problem in matrix terms and in the terms of problem (14–16). The corresponding solver linprog [MW23L] finds the minimum in a problem specified by
min x ⁡ y T x   s u c h   t h a t A · x ≤ b , A e q · x = b e q , l b ≤ x ≤ u b .
Here vectors x , y ∈ R + 11 are defined as
x = [a, b, …, l, m, λ]T, yT = [0, 0, …, 0, 1];
matrix A and vector b represent the inequality-type constraints (empty in our case), Aeq and beq the equality-type constraints:
Preprints 75769 i004
vectors lb and ub, the lower and upper bounds respectively for x, are given in Table 2 lacking them for the last component λ. Extracted from Table 1, these bounds for λ1(G) are
0.3988 ≤ λ ≤ 1.5779.
Specified in accordance with (15), these bounds split to
0.3988 ≤ λ ≤ ρ0 and ρ0 ≤ λ ≤ 1.5779,
where ρ0 is given in Table 3. Correspondingly, the pair of lb and ub split to the following ones:
lb, ub1 and lb2, ub
where
ub111 = lb211 = ρ0.
Following (B1–B6) and the syntax of linprog [MW23L], we input the following two calls:
[xopt1, yval1] = linprog(y1, [], [], Aeq, beq, lb, ub1);
[xopt2, yval2] = linprog(y2, [], [], Aeq, beq, lb2, ub),
which return what is shown in Table 5.

Appendix С

To determine how many zeros are there among particular entries into a fixed place, say (3, 5), at all the 13 given matrices, we first arrange them as a 3D MATLAB® array [MW23D] All13L. Second, we calculate the frequency of zeros at that place by means of the built-in MATLAB® function nnz [MW23N] and the following line:
>> sym(13 - nnz(All13L(3, 5, :)))/13,
ans = 9/13.
Similar lines for the places of (2, 1) and (3, 1) return respectively 7/13 and 1/13.

References

  1. CA23 COMADRE, https://compadre-db.org/Data/Comadre (accessed on 30 05 2023).
  2. CP23 COMPADRE, https://compadre-db.org/Data/Compadre (accessed on 30 05 2023).
  3. BP94 Berman, A.; Plemmons, R.J. Nonnegative Matrices in the Mathematical Sciences. Philadelphia, Pennsylvania, USA.: Society for Industrial and Applied Mathematics, 1994.
  4. Cas01 Caswell, H. Matrix Population Models: Construction, Analysis and Interpretation, 2nd ed. Sinauer Associates: Sunderland, Mass., USA., 2001.
  5. HoJ90 Horn, R. A.; Johnson, C. R. Matrix Analysis; Cambridge University Press: Cambridge, 1990.
  6. Gan59 Gantmacher, F.R.. Matrix Theory; Chelsea Publ.: New York, NY, 1959.
  7. LSG21 Logofet, D.O.; Salguero-Gómez, R. Novel challenges and opportunities in the theory and practice of matrix population modelling: An editorial for the special feature “Theory and Practice in Matrix Population Modelling”. Ecological Modelling, 2021, 443, 109457. [CrossRef]
  8. L19 Logofet, D.O. Does averaging overestimate or underestimate population growth? It depends. Ecological Modelling, 2019, 411, 108744. [CrossRef]
  9. L18 Logofet, D.O. Averaging the population projection matrices: heuristics against uncertainty and nonexistence. Ecol. Complexity, 2018, 33(1), 66–74. [CrossRef]
  10. PZL22 Protasov, V.Yu.; Zaitseva, T.I.; Logofet, D.O. Pattern-multiplicative average of nonnegative matrices: When a constrained minimization problem requires versatile optimization tools. Mathematics, 2022, 10, 4417. [CrossRef]
  11. Co79 Cohen, J.E. Comparative statics and stochastic dynamics of age-structured populations Theor. Popul. Biol., 1979, 16 (2), 159–171. [CrossRef]
  12. TuO80, Tuljapurkar, S.D.; Orzack, S.H. Population dynamics in variable environments I. Long-run growth rates and extinction. Theor. Popul. Biol., 1980, 18 (3), 314–342. [CrossRef]
  13. Tu86. Tuljapurkar, S.D. Demography in stochastic environments. II. Growth and convergence rates. J. Math.Biol. 1986, 24, 569–581. [CrossRef]
  14. Tu90 Tuljapurkar, S.D. Population Dynamics in Variable Environments. Springer, Berlin, (Lecture Notes in Biomathematics, 85). [CrossRef]
  15. MW23G MathWorks, Documentation, https://www.mathworks.com/help/gads/globalsearch.html?s_tid=doc_ta (accessed on 30 05 2023).
  16. Let23 Logofet, D.O.; Golubyatnikov, L.L.; Kazantseva, E. S.; Belova, I.N., and Ulanova, N.G. Thirteen years of monitoring an alpine short-lived perennial: Novel methods disprove the former assessment of population viability. Ecol. Model., 2023, 477, 110208. [CrossRef]
  17. McD14 McDonald, J.J; Paparella, P.; Tsatsomeros, M.J. Matrix roots of eventually positive matrices. Linear Algebra and its Applications, 2014, 426, 122–137. [CrossRef]
  18. Aet04 Ando, T.; Li, C.-K.; Mathias, R. Geometric means. Linear Algebra Appl., 2004, 385, 305–334. [CrossRef]
  19. BH06 Bhatia, R.; Holbrook, J. Noncommutative geometric means. Math. Intell., 2006, 28 (1), 32–39. [CrossRef]
  20. dAr10 De Abreu, B.; Raydan, M. Residual methods for the large-scale matrix pth root and some related problems. Applied Mathematics and Computation, 2010, 217 (2), 650–660. [CrossRef]
  21. PP15 Politi, T.; Popolizio, M. On stochasticity preserving methods for the computation of the matrix pth root. Math. Comput. Simul., 2015, 100, 53–68. [CrossRef]
  22. Gu22 Guerry, M.-A. Algorithms for the matrix pth root. Special Matrices, 2022, . [CrossRef]
  23. Bi05 Bini, D. A.; Higham, N. J.; Meini, B. Algorithms for the matrix pth root. Numerical Algorithms, 2005, 39, 349–378. [CrossRef]
  24. LKBO18 Logofet, D.O.; Kazantseva, E.S.; Belova, I.N.; Onipchenko, V.G. How long does a short-lived perennial live? A modelling approach. Biol. Bul. Rev. 2018, 8 (5), 406–420.
  25. LKO20 Logofet, D.O.; Kazantseva, E.S., and Onipchenko, V.G. Seed bank as a persistent problem in matrix population models: from uncertainty to certain bounds. Ecol. Modell., 2020, 438, 109284. [CrossRef]
  26. Lu73 Luenberger, D. G. Introduction to Linear and Non-linear Programming, Reading, MA: Addison-Wesley, 1973.
  27. Zh86 Zhukova, L.A. Polyvariance of the meadow plants, in Zhiznennye formy v ekologii i sistematike rastenii (Life Forms in Plant Ecology and Systematics); Mosk. Gos. Pedagog. Inst.: Moscow, Russia, 1986; pp. 104–114.
  28. Zh95 Zhukova, L.A. Populyatsionnaya zhizn’ lugovykh rastenii (Population Life of Meadow Plants); Lanar: Yoshkar-Ola, Russia, 1995.
  29. MW23L MathWorks, Documentation, https://www.mathworks.com/help/optim/ug/linprog.html?s_tid=doc_ta (accessed on 30 05 2023).
  30. DRH21 Deb, K.; Roy, P.C.; Hussein, R. Surrogate modeling approaches for multiobjective optimization: Methods, taxonomy, and results. Math. Comput. Appl. 2021, 26(1), 5; [CrossRef]
  31. K22 Krantz, S.G. Real Analysis and Foundations, 5th ed.; Chapman & Hall: Publisher Location, 2022; pp. 325–413.
  32. RC04 Robert, C. P.; Casella, G. Monte Carlo Statistical Methods, 2nd ed. Springer, 2004. http://dx.doi.org/10.1007/978-1-4757-4145-2.
  33. MW23M MathWorks, Documentation, https://www.mathworks.com/help/matlab/math/multidimensional-arrays.html (accessed on 30 05 2023).
  34. MW23N MathWorks, Documentation, https://www.mathworks.com/help/matlab/ref/nnz.html?s_tid=doc_ta (accessed on 30 05 2023).
Preprints 75769 g001
Figure 1. A. albana life cycle graph by ontogenetic stages: pl, plantules; j, juvenile plants; im, immature plants; v, adult vegetative plants, and g, generative plants; dashed arrows correspond to “virtual” reproduction (adapted from [LKBO18]).
Figure 1. A. albana life cycle graph by ontogenetic stages: pl, plantules; j, juvenile plants; im, immature plants; v, adult vegetative plants, and g, generative plants; dashed arrows correspond to “virtual” reproduction (adapted from [LKBO18]).
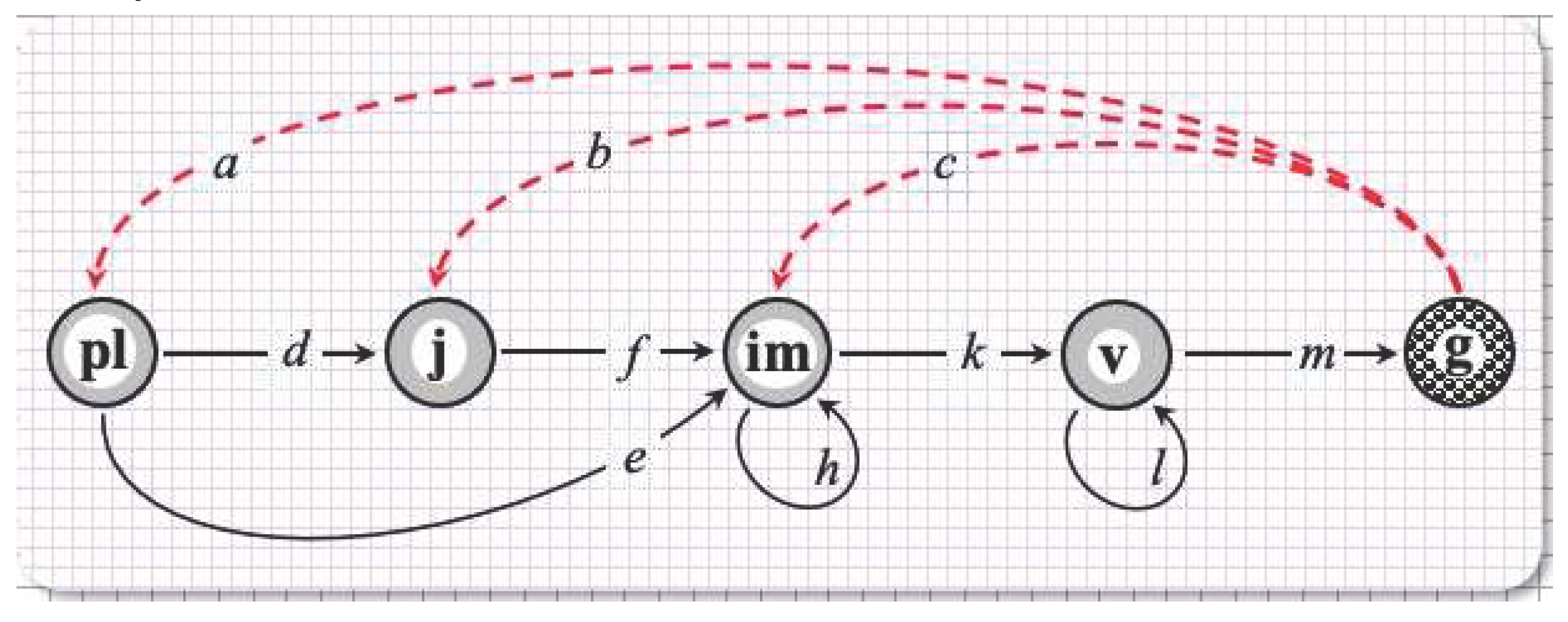
Preprints 75769 g001
Table 1. Outcome of PPM calibration for A. albana based on 2009–2022 data (updating Table 2 from [Let23]).
Table 1. Outcome of PPM calibration for A. albana based on 2009–2022 data (updating Table 2 from [Let23]).
Preprints 75769 i001
* To be explained in Subsection 2.4.
Table 2. Bounds for the 10 unknown variables ensuing from 13 annual PPMs (Table 1).
Table 2. Bounds for the 10 unknown variables ensuing from 13 annual PPMs (Table 1).
Minimal Vital rate Maximal
4/3 a 49
3 b 85
0 c 25
0 d 7/15
0 e 1
1/49 f 7/9
0 h 2/3
6/95 k 5/6
8/25 l 22/23
1/35 m 5/15
Table 3. Numerical inputs for the optimization problems.
Table 3. Numerical inputs for the optimization problems.
Matrix Prod λ1(G13),
ρ0 		Vector v*, %
0.021185585295608 0.039538528446472 0.086369212318887 0.321576284325812 0.312397941844407
0.032875920640909 0.061354070510449 0.134019914355007 0.498983075380778 0.484789540051083
0.003661007803335 0.006824023057585 0.014887199373520 0.055368303504470 0.054013601100565
0.013845526439184 0.025919668563603 0.056669501627721 0.210813605518226 0.203676548113200
0.000729124010650 0.001363464687049 0.002980796589266 0.011096313418442 0.010736266465211		 0.31893645391
0.91584799085		 29.2923
45.4532
5.0480
19.1962
1.0103
Table 4. Solutions to the PMA problem by various optimization techniques (adapted from [PZL22]).
Table 4. Solutions to the PMA problem by various optimization techniques (adapted from [PZL22]).
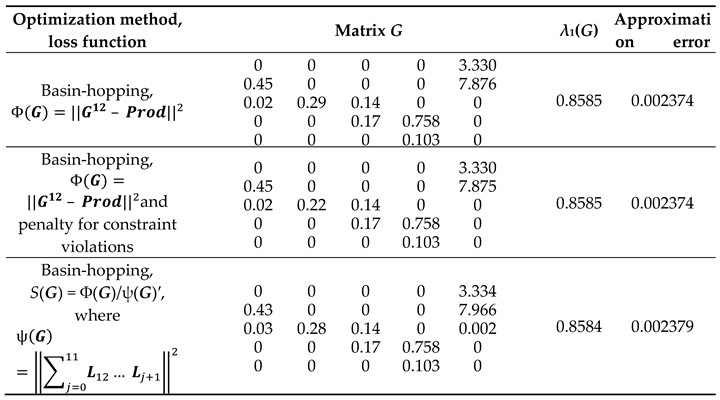
Preprints 75769 i002
Table 5. Solutions to the PMA problem by the LP technique.
Table 5. Solutions to the PMA problem by the LP technique.
Preprints 75769 i003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated