Prerpints.org logo
Preprint
Article

Neuromorphic Dendritic Computation with Silent Synapses for Visual Motion Perception

Altmetrics

Downloads

467

Views

432

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

05 June 2023

Posted:

06 June 2023

You are already at the latest version

Alerts
Abstract
Most neuromorphic technologies use a point-neuron model, missing the spatiotemporal nature of neuronal computation performed in dendrites. Dendritic morphology and synaptic organization are structurally tailored for spatiotemporal information processing, enabling various computations like visual perception. Here, we report on a neuromorphic computational model termed ‘dendristor’, which integrates functional synaptic organization with dendritic tree-like morphology computation. The dendristor presents bioplausible nonlinear integration of excitatory and inhibitory synaptic inputs with silent synapses and diverse spatial distribution dependency. We show that the dendristor can emulate direction selectivity, which is the feature to react robustly to a preferred signal direction on the dendrite. We discover that silent synapses can remarkably enhance direction selectivity, turning out to be a crucial player in dendritic computation processing. Finally, we develop neuromorphic dendritic neural circuits that can emulate a cognitive function such as motion perception in the retina. Using dendritic morphology, we achieve visual perception of motion in 3D space by various mapping of spatial information on different dendritic branches. This neuromorphic dendritic computation innovates beyond current neuromorphic computation and provides solutions to explore new skylines in artificial intelligence, neurocomputation, and brain-inspired computing.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

INTRODUCTION

Neuromorphic research aims to develop artificial intelligence (AI) [1] and to analyse neuroscience using neuromorphic architectures [2,3,4]. These architectures emulate particular neuroscientific operations like synaptic plasticity [5], or neuronal nonlinearity [6] (Figure 1a(i-ii)), and their learning algorithm is inspired by brain, but mainly driven by artificial neural network (ANN) and spike neural network (SNN). However, the point neuron model [7,8] used in these architectures is a loose schematization of a biological neuron. There is still a large gap between the neuromorphic models and the nervous systems due to the morphological and the computational complexity of neuron’s subcellular components [9,10], such as dendrites and synapses, and their connectivity [11,12,13,14,15]. Therefore, researchers included dendritic computation [7,16] in a master plan for neuromorphic research [17,18], discussing its potential for AI problem-solving
Dendritic computation is a neuronal signal process that occurs in dendrites and involves the integration of synaptic inputs to control the somatic membrane potential. The morphology of the dendritic tree [19,20,21] and the distribution of synapses on dendritic branches [22,23] are critical factors in determining the nonlinearity of the dendritic computation, which enables complicated computational tasks by functional segregation and selectivity of branches (Figure 1b). The dendritic arborization (tree-like branching out, Figure 1a(ii)) increases the complexity of the computation in the neuronal system to enhance learning [24] and computational efficiency [25,26]. The spatial distribution of synapses on a dendritic branch drives core features of the dendritic computation such as encoding the spatiotemporal synaptic input signals [8,27,28] and the direction selectivity [21,29,30], which is particularly important in the sensory neural circuits to encode spatiotemporal input signals [21,30,31,32,33,34,35] and implement memory and learning [36,37,38,39,40]. Direction selectivity of a dendrite is the feature to react robustly to a preferred signal direction on the dendrite (for instance, sequentially arriving synaptic inputs from distal to proximal to soma) and to react weakly in the opposite direction [21,29,30]. Excitatory and inhibitory integrations within a dendrite have been studied last decade [8,19,22,41], but the role of a ‘silent synapse’ [42,43,44], which is dormant and wake up only under certain dendritic (post-synaptic) circumstances to leverage the dendritic integration, has not yet been fully understood.
Dendritic computation provides essential functionalities in the neurocomputation, and is intrinsically ideal for spatiotemporal processing [18], but it is not widely studied in the neuromorphic field. There have been attempts to include the dendritic functions in neuromorphic devices and architectures including memristors [45,46,47] (Figure 1a(i)). However, those architecture can be considered as an extension of the point neuron model (c.f. linear summation of weighted synaptic inputs enters into a neuronal body with nonlinear transfer function) with added nonlinear function of the dendrite to increase the learning efficiency. For effective modelling of neuromorphic dendritic computation, a computational framework of dendritic computation (i.e., neuronal unit model) is required to emulate electrical dynamics and the spatial morphology of dendrites. A ‘neurotransistor’ was recently reported, which uses a field-effect transistor (FET) coated with an ion-doped sol-gel dielectric film [48] to emulate neuronal intrinsic membrane plasticity. This device can perform a new form of the computation by implementing the nonlinear dynamic signal integration property occurring in the dendritic branch.
Here, we introduce a novel type of dendritic computation model called a ‘dendristor’ using neurotransistors [48] with dendrite-like spatial morphological characteristics and synaptic organization. The dendristor performs nonlinear integration of various synapses based on their distribution on a dendritic branch (Figure 1a(iii)). We investigate the role of the spatial distribution of diverse types of synapses in dendritic nonlinear integration, including excitatory, inhibitory, and silent synapses. The direction selectivity of a dendirstor branch is successfully demonstrated, which exhibits a greater response to a preferred direction of a sequentially incoming input signal. We adopt the modelling of silent synapses in dendritic computation, which is essential for enhancing the direction selectivity. We propose a neuromorphic dendritic neural circuit (NDNC) which maps the spatial information from the receptors on a one-dimensional array to the dendritic branches. Then, combining multiple NDNCs, we model a network of multiple dendritic neurons for spatiotemporal processing that allows visual motion perception in 3D space. Our work offers a novel bioplausible neuromorphic computation and a simulation environment to predict and elucidate the biocomputational phenomena that are currently challenging to study in in-vitro or in-vivo neuroscientific experiments.
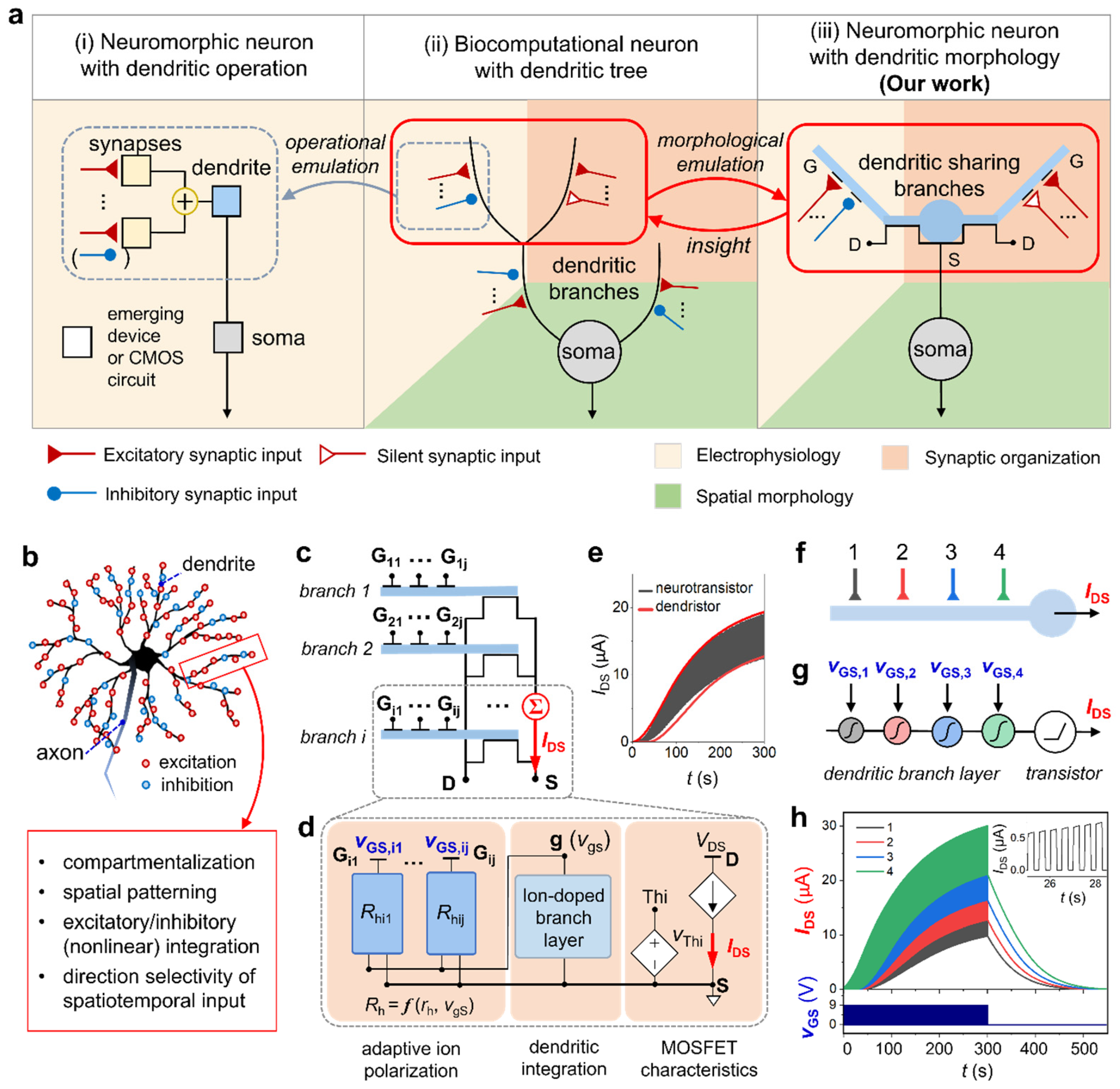
Preprints 75693 g001
Figure 1. Neuromorphic dendrite model representation. (a) Schematics of (i) a neuromorphic neuron model with dendritic operation which is driven by an operational rationale which is typical of engineering, (ii) a biocomputational neuron model composed of the dendritic trees with synaptic inputs, and (iii) a proposed neuromorphic neuron model with dendritic spatial morphology, so-called ‘dendristor’, composed of the first layer of the dendritic bunch, which driven by spatial morphology of the biosystem. (b) Illustration of biological dendrites in a neuron and their functions. (c) Schematic diagram of multi-branch dendristor with multiple gate inputs and the source-drain output. (d) Circuit modeling of the dendristor with one branch. (e) Output comparison between the neurotransistor device and dendristor model with single input. (f) Simplified illustration of a dendritic branch with four inputs with different distances from the dendritic output (IDS). (g) Schematics of nonlinear signal integration of four synaptic gate inputs (vGS,1-4) within a dendritic branch. (h) The output current (IDS, black, red, blue and green curves) responding to input pulse-train (vGS, dark blue) applying on synaptic gate inputs (Gj, where j:1-4) of the dendristor (vGS pulse period: 500 ms, pulse width: 250ms, pulse amplitude: 9 V). The inset shows the enlarged IDS response to pulses.
Figure 1. Neuromorphic dendrite model representation. (a) Schematics of (i) a neuromorphic neuron model with dendritic operation which is driven by an operational rationale which is typical of engineering, (ii) a biocomputational neuron model composed of the dendritic trees with synaptic inputs, and (iii) a proposed neuromorphic neuron model with dendritic spatial morphology, so-called ‘dendristor’, composed of the first layer of the dendritic bunch, which driven by spatial morphology of the biosystem. (b) Illustration of biological dendrites in a neuron and their functions. (c) Schematic diagram of multi-branch dendristor with multiple gate inputs and the source-drain output. (d) Circuit modeling of the dendristor with one branch. (e) Output comparison between the neurotransistor device and dendristor model with single input. (f) Simplified illustration of a dendritic branch with four inputs with different distances from the dendritic output (IDS). (g) Schematics of nonlinear signal integration of four synaptic gate inputs (vGS,1-4) within a dendritic branch. (h) The output current (IDS, black, red, blue and green curves) responding to input pulse-train (vGS, dark blue) applying on synaptic gate inputs (Gj, where j:1-4) of the dendristor (vGS pulse period: 500 ms, pulse width: 250ms, pulse amplitude: 9 V). The inset shows the enlarged IDS response to pulses.
Preprints 75693 g001

RESULTS

Neuromorphic Dendritic Neuron and Its Output Dynamics

We form the neuromorphic dendritic neuron model (Figure 1c,d) based on the physics of the neurotransistor [48] (Figure 1e), so we call it ‘dendristor.’ We selected the existing neuromorphic hardware platform that can stably and closely mimic dendritic properties, and therefore, is able to show various spatiotemporal performances of the dendritic computation. The Si-based transistor provides stable current dynamics and good controllability as a device compared to other types of electronic devices. The connection of the multiple specular transistors (Figure 1c) provides a summated source-drain current like the dendritic signal summation at the point where the dendritic branches are combined. The dendristor model is formed based on the physical phenomena of metal-oxide-semiconductor field-effect transistors (MOSFETs) covered with ion-doped soft dielectric material, which includes mobile ions to mimic the neuronal membrane’s ion diffusion in the neuronal membrane [48]. The synaptic inputs are applied as gate voltage (vGS,ij, where i is the number of dendritic branches and j is the number of the synaptic inputs) to metal electrodes, Gij (Figure 1c) on the dendritic branch and transforms to output current, IDS. The physical design and properties of the device model are explained in Supplementary Information S1. Figure 1d illustrates the simplified LT-SPICE circuit model, which illustrates a single dendristor branch formed with the large-signal MOSFET model and the sub-circuit of the ion-doped sol-gel dielectric film. The circuit model has three functional parts: (i) a circuit for the adaptive polarization of ions occurring in the film triggered by each gate, (ii) a combined RC circuit of the dendritic integration film contacting Si nanowire oxide that provides effective gate voltage to the transistor channel, and (iii) the MOSFET large-signal circuit (Figure 1d). The mathematical model and corresponding phenomena on a neurotransistor [48] are explained in Supplementary Information S2. The description of the circuit elements and their parameters are summarized in Methods. The current output dynamics of the neurotransistor and the dendristor model with single gate input in Figure 1e demonstrates how closely the model simulates the device physics. Most important element in the dendritic computation is the variable resistance, Rhj, which identifies each synaptic input’s location related to the length between the synaptic input and the dendritic integration center (i.e., the channel of the transistor). Rhj is updated by the present gate input (vGS,j) and the internal state of the film, which can be defined as an effective gate voltage (vgS, the voltage between node g and node S) of the transistor, and their relation is described in the following equation:
R h j = r h j · v G S , j − v g S / V A , j
where rhj is a constant resistance parameter (unit: Ω) of the film between the jth gate input and the conductive channel output, and VA,j is a voltage amplitude of vGS,j. As the resistance is relevant to the length of the ionic migration path, rhj is the distance-correlated factor based on the film distance from the nanowire channel to the gate. Hence, each synaptic input signal is differently weighted by rhj in a single dendritic branch to map the spatial information. The effective gate voltage, vgS, is another critical value since it defines Rhj and IDS (Figure 1d). The built-in potential in the film (vgS) evolves nonlinearly with respect to vGS,j. In sum, the dendritic integration of multiple inputs in a dendritic branch is obtained as a combined process of the time-varying nonlinear vgS change and the nonlinear vgS-to-IDS transfer function of a MOSFET. All results below are obtained from the LT-SPICE circuit simulation.
Figure 1f is a schematic diagram of a dendritic branch that receives four synaptic inputs entering from different locations. Since a distal input requires a longer film length than a proximal input, rh of the distal input is higher than the proximal input, such as rh1 = 1.25 kΩ, rh2 = 1 kΩ, rh3 = 0.75 kΩ and rh4 = 0.5kΩ. The first dendritic integration occurs locally near the interface of the film, which is strongly affected by the position of the synaptic input and influences to the other synaptic input integration (the serial connection of nonlinear integration in the dendritic branch layer in Figure 1g). Global integration is done by the field-effect of the transistor (the transistor integration in Figure 1g). Figure 1h shows the nonlinear current output dynamics of the dendristor (IDS, by repeated input pulses, VGS) when the voltage pulsed-train is applied on the gate inputs, and each current dynamics are depending on the position of the synaptic inputs in a single dendritic branch. The excitatory input voltage pulse (amplitude, VA: 9V, pulse period: 500 ms, and pulse width: 250 ms) is applied for 300 seconds and stopped. IDS increases along the sigmoidal trajectory by input pulses. The current increase implies that the device has a short-term memory function as maintaining the electric potential in the film when the pulse is removed. Relevant memory phenomenon in IDS-VGS curve and its comparison between the dendirstor model and the neurotransistor measurement are explained in Supplementary Information S3. The distal input induces stronger IDS increase than the proximal input does. Under the absence of the input pulses, IDS reduces exponentially.

Comparing the Nonlinear Integration of Biological Dendrite and the Dendristor

We compared the coincident input signal integration rule of the biological dendrite and the dendristor (Figure 2). The important aspect in this result is the different integration rules of coincident inputs within a single dendritic branch (Figure 2a(i)) and between different dendritic branches (Figure 2a(ii)). Figure 2b(i) shows in-vivo measurement of excitatory postsynaptic potential (EPSP) of pyramidal neuron cells [49]. The EPSP was measured in a soma when two different synaptic inputs are coincidently applied on a dendritic branch. The arithmetic sum of two individual EPSPs (blue) is different from the combined EPSP (orange) when two inputs are coincidently applied. The relation between the expected peak EPSP, which is the arithmetic sum of two individual EPSPs, and the measured peak EPSP is summarized in Figure 2c(i) [49]. The measured peaks between branches (green dots) show an almost identical trend (i.e., linear) with the expected peak EPSP (black dot line). However, the measured peaks within a branch (coloured dots) show a supralinear curve regarding the expective peak EPSP, which is a dominant phenomenon in the dendrite [27]. This biological result shows the different integration rule of the dendrite (within branch condition) and the soma (between branch condition).
Likewise, the analogous experiments are conducted in a dendristor (Figure 2b(ii),c(ii)). Two synaptic inputs on the different locations within a branch (coloured dots) and on separated branches (green squares) are defined as different rh values, such as 0.5, 0.75, 1, and 1.25 kΩ, which are represented as the location 4, 3, 2 and 1 respectively (Figure 2a). The bottom envelope of the IDS (IDS,baseline) was extracted to show the conductivity change in the absence of the input voltage (Figure 2b(ii)). The integration of two synaptic inputs within a dendritic branch of the dendristor shows the different dynamic responses from the arithmetic sum of individual IDS,baseline, depending on the strength of the input pulses. For example, the medium amplitude of the input pulses (VA = 9 V) induces a stronger IDS increase in a dendritic branch than the arithmetic sum, but the stronger input (VA = 20 V) induces a lower output peak than the arithmetic sum. This nonlinear relation between the integration within a branch and the expected sum is demonstrated in Figure 2c(ii). IDS,peak measured within a branch shows supralinearity to the arithmetic sum of individual current. IDS,peak from two different branches (green squares) was identical to the arithmetic sum of individual current (dashed line) like in the biological dendrite. The location of the synaptic inputs on a dendristor branch influences nonlinearity. The supralinearity of the integrated current is more prominent with distal input (1,2). The contributions of various synaptic input locations, input voltage intensity, and frequency on the nonlinearity are summarized in Supplementary Information S4. A biological neuron cell in Figure 2c(i) shows the large degree of nonlinear signal integration within a dendritic branch, compared to the dendristor in Figure 2c(ii). The lower degree of the nonlinearity of the dendristor is due to the electrical property of the major component, the FET, of the dendristor model: IDS of the FET increases by vgS after turning on (vgS > Vth) without saturation.
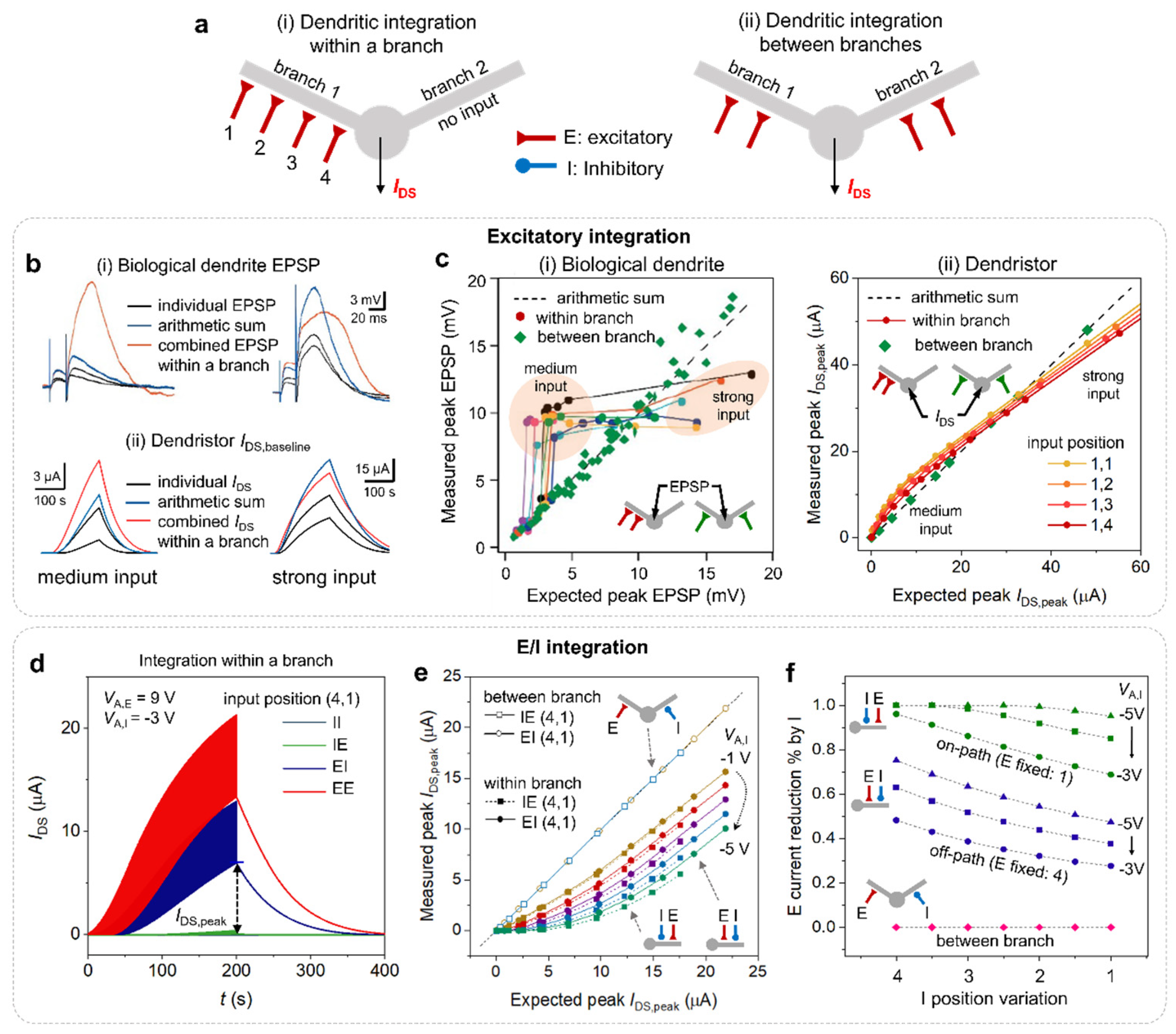
Preprints 75693 g002
Figure 2. Nonlinear synaptic integration in dendrites and the dendristor. (a) Illustration of synaptic organizations (i) within a dendritic branch and (ii) between dendritic branches. (synapse position 1: rh1 = 1.25 kΩ, 2: rh2 = 1 kΩ, 3: rh3 = 0.75 kΩ, 4: rh4 = 0.5 kΩ) (b) comparison between (i) the neuronal output response (EPSP) to two excitatory synaptic inputs49 and (ii) the dendristor output current, IDS,baseline (the bottom envelop of IDS) with two coincident excitatory synaptic inputs (rh of two inputs: 0.75kΩ, 1 kΩ) within a branch. (c) Plot of the dendritic integration within a branch and between branches of (i) biological dendrite49 and (ii) dendristor. Data in the plot corresponds to the peak measurement in (b). Plot shows the relationship between measured peak (EPSP or peak current (IDS,peak at t = 200 s), coloured dots) and expected peak (an arithmetic sum of two individual EPSP outputs or IDS,peak, dashed line). (b(i), c(i)) are reproduced by courtesy of 49. (d-e) Excitatory and inhibitory integration of the dendristor. (d) The IDS responses of the dendristor with various combinations of excitatory, E, and inhibitory, I, synapses on a dendritic branch. (e) Dendritic integration of I and E inputs within a dendritic branch and between two different branches. (Synaptic inputs positioned on 1 and 4 for (d, e).) (f) The inhibitory efficacy (excitatory IDS reduction percentage by inhibitory signal) under coincident E and I inputs activation depending on I position. (rh,I is varied from 1 to 4) while E position is fixed (E :1 for on-path case, E:4 for off-path case) (VA,E is varied from 3 to 12 V for (e) and VA,E = 9 V for (f), Pulse period: 500 ms, pulse width: 250 ms for (c-f)).
Figure 2. Nonlinear synaptic integration in dendrites and the dendristor. (a) Illustration of synaptic organizations (i) within a dendritic branch and (ii) between dendritic branches. (synapse position 1: rh1 = 1.25 kΩ, 2: rh2 = 1 kΩ, 3: rh3 = 0.75 kΩ, 4: rh4 = 0.5 kΩ) (b) comparison between (i) the neuronal output response (EPSP) to two excitatory synaptic inputs49 and (ii) the dendristor output current, IDS,baseline (the bottom envelop of IDS) with two coincident excitatory synaptic inputs (rh of two inputs: 0.75kΩ, 1 kΩ) within a branch. (c) Plot of the dendritic integration within a branch and between branches of (i) biological dendrite49 and (ii) dendristor. Data in the plot corresponds to the peak measurement in (b). Plot shows the relationship between measured peak (EPSP or peak current (IDS,peak at t = 200 s), coloured dots) and expected peak (an arithmetic sum of two individual EPSP outputs or IDS,peak, dashed line). (b(i), c(i)) are reproduced by courtesy of 49. (d-e) Excitatory and inhibitory integration of the dendristor. (d) The IDS responses of the dendristor with various combinations of excitatory, E, and inhibitory, I, synapses on a dendritic branch. (e) Dendritic integration of I and E inputs within a dendritic branch and between two different branches. (Synaptic inputs positioned on 1 and 4 for (d, e).) (f) The inhibitory efficacy (excitatory IDS reduction percentage by inhibitory signal) under coincident E and I inputs activation depending on I position. (rh,I is varied from 1 to 4) while E position is fixed (E :1 for on-path case, E:4 for off-path case) (VA,E is varied from 3 to 12 V for (e) and VA,E = 9 V for (f), Pulse period: 500 ms, pulse width: 250 ms for (c-f)).
Preprints 75693 g002

Inhibitory Integration in the Dendristor

The dendristor can emulate the integration of the excitatory and inhibitory synaptic inputs. We applied positive and negative voltage pulses as excitatory and inhibitory synaptic inputs, respectively. Figure 2d shows the IDS response when the excitatory (E) and inhibitory (I) inputs coincidentally enter into the distal (D) and proximal (P) gates. While the excitatory synapses-only inputs (EE, red curve) induce strong IDS increase, inhibitory synapse-only inputs (II, black line) are unable to induce the increase. The proximal inhibitory inputs (IE, green curve) are more effective than the distal (EI, navy curve) to suppress IDS. The inhibitory suppression in dendritic integration as a function of inhibitory voltage amplitude is shown in Supplementary information S5. The integration of excitatory and inhibitory synapses within a branch shows sublinearity (Figure 2e, filled square and dots), which is relevant to the biological inhibitory integration [50]. For this analysis, the same analytical technique as Figure 2c was used (Expected peak IDS,peak means the arithmetic sum of each output current from single E and I activation, and measured peak IDS, peak is the integrated current from both E and I are activated). Noteworthily, the amplitude of inhibitory input signal strongly affects the nonlinearity (Supplementary information S5). This trend is fascinating since the nonlinearity of excitatory inputs integration within a branch (EE, Supplementary Information S4e) shows weak dependency on the input voltage variation, but it depends on the intrinsic dendrite structure. In contrast, inhibitory synapses can strongly modulate the nonlinearity of dendritic integration (i.e., non-static nonlinearity), which relies on computational variables like input intensity and locations. The different features of nonlinearities in EE and IE integration show how the neuronal system uses different nonlinear integration, which can be used as a theoretical hypothesis for new biocomputational studies.
Figure 2f reports the result of the dendristor experiment where the excitatory input E is fixed at distal (green) and proximal (navy) positions, and the position of inhibitory input I is shifted over the dendritic branch, considering both within and between branch settings. The inhibitory efficacy (E current reduction percentage by I) within a branch is linearly changed by the position of the inhibitory synapse when the inhibitory input voltage is small, like -3 V. However, when the inhibitory input signal becomes larger (-4 and -5 V), the inhibitory efficacy of the ‘on-path (IE)’ cases reaches the saturation and shows nonlinear trend. On the other hand, in the between branch setting, the inhibitory synapse is unable to regulate the excitatory inputs regardless of its position. This observation is partially corresponding to the in vivo measurement of local dendritic response [51]. Note, since neurons in a different part of the brain area show different signalling based on their functionality [52] and our results agree with this biological study [51].

Dendritic Direction Selectivity

The direction selectivity of a spatiotemporal input signal is a landmark pattern recognition process for information pre-processing in sensory neural circuits, and it is one of the most investigated phenomena in biological studies on dendritic signal integration [21,23,30,31,32,33,34,35]. Replication of direction selectivity in neuromorphic computing is a crucial step toward complex dendritic computation for visual motion perception. A dendrite of a cortical neuron and the EPSP measured at the soma with spatiotemporal input sequences are shown in Figure 3a [53]. The direction of the input signal entering from the distal- to proximal relative to the soma is called the IN direction (IN-D, Figure 3a red arrow), and the opposite input signal direction is the OUT direction (OUT-D, Figure 3a blue arrow). The larger amplitude of EPSP is observed when the input signal moves in IN-D. Similarly, we perform an experiment where the synaptic inputs of the dendristor is sequentially activated with the excitatory pulses in IN-D and OUT-D from the dendristor channel (Figure 3b). The excitatory pulses are applied on one input gate for 100 seconds and then passed to the following input gate. The direction of the sequentially arrived input signal is encoded as the dynamics of the IDS. IN-D response shows a higher current peak amplitude (IDS,peak) and a longer time to reach the peak (tpeak) than the OUT-D response. This result is comparable to the directional selectivity of the biological dendrite in Figure 3a. In the biological dendrite study, tpeak difference between the directions was not clearly observed, but computational modelling studies of the dendrite showed a similar tpeak difference to our study [21,29]. The burst level in Figure 3b is chosen to design a direction-selective neural circuit (Figure 4a) in which a neuron with the single dendritic branch bursts when IDS exceeds the burst level like in a biological neuron, which will be discussed in the following section.
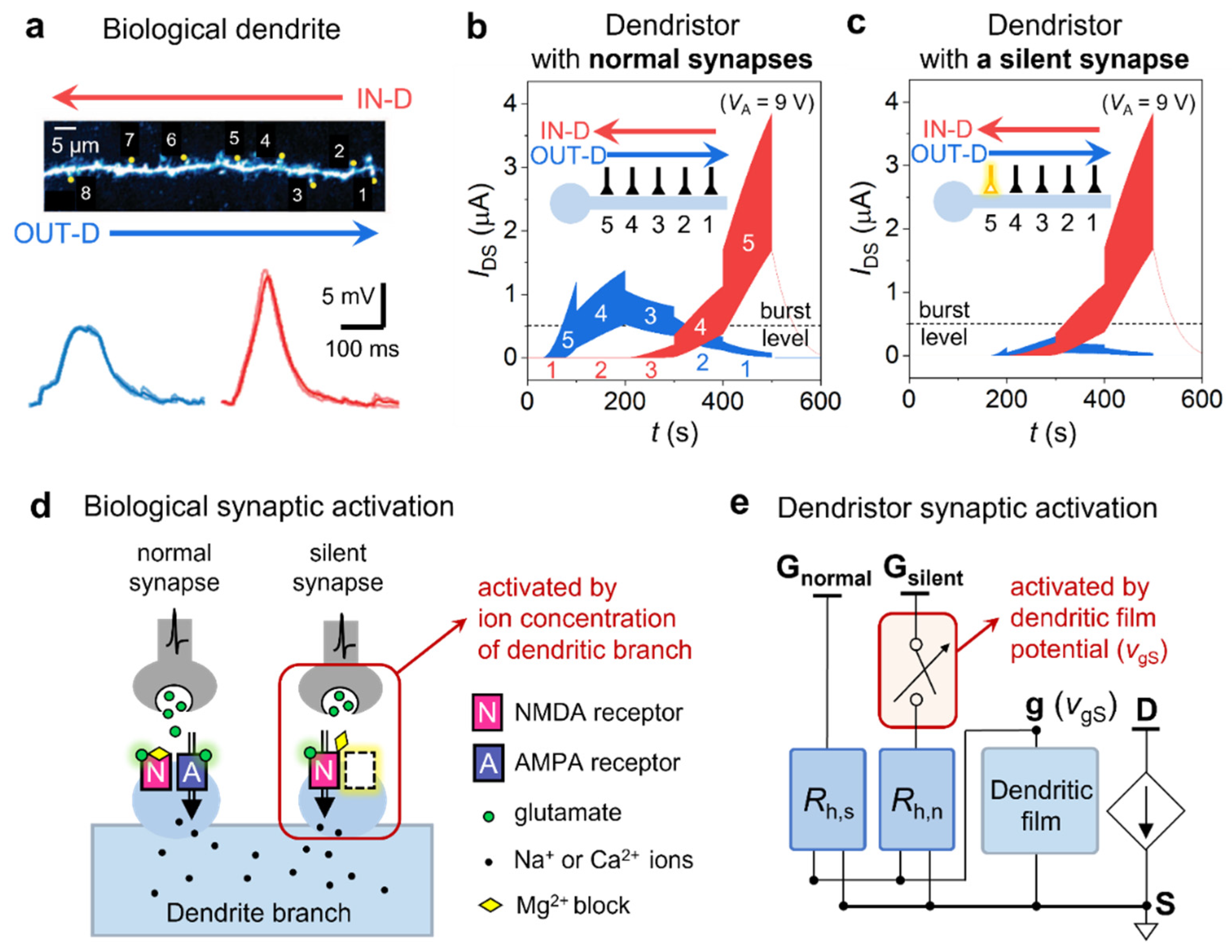
Preprints 75693 g003
Figure 3. Direction selectivity of the dendristor and the effect of a silent synapse. (a) Biological dendrite with synaptic inputs (numbers) and the direction selectivity shown as EPSP induced by sequentially entering inputs in IN-D (red) and OUT-D (blue) directions (reproduced by courtesy of 53). (b) Direction selectivity of the dendristor with normal synapses shown as IDS, the sequential response of the voltage pulses applied to the synaptic input gates. Numbers on the curve indicate the activated gate at the corresponding time period. (c) Direction selectivity of dendristors with a silent synapse (yellow) (IN-D: from G1 to G5, OUT-D: from G5 to G1, where rh1 = 1.5 kΩ, rh2 = 1.25 kΩ, rh3 = 1 kΩ, rh4 = 0.75 kΩ and rh5 = 0.5 kΩ for (b,c)) (d) Schematics of the synaptic transmission of normal and silent synapses on a biological dendrite. (e) The circuit modelling of the synaptic transmission of normal and silent synapses.
Figure 3. Direction selectivity of the dendristor and the effect of a silent synapse. (a) Biological dendrite with synaptic inputs (numbers) and the direction selectivity shown as EPSP induced by sequentially entering inputs in IN-D (red) and OUT-D (blue) directions (reproduced by courtesy of 53). (b) Direction selectivity of the dendristor with normal synapses shown as IDS, the sequential response of the voltage pulses applied to the synaptic input gates. Numbers on the curve indicate the activated gate at the corresponding time period. (c) Direction selectivity of dendristors with a silent synapse (yellow) (IN-D: from G1 to G5, OUT-D: from G5 to G1, where rh1 = 1.5 kΩ, rh2 = 1.25 kΩ, rh3 = 1 kΩ, rh4 = 0.75 kΩ and rh5 = 0.5 kΩ for (b,c)) (d) Schematics of the synaptic transmission of normal and silent synapses on a biological dendrite. (e) The circuit modelling of the synaptic transmission of normal and silent synapses.
Preprints 75693 g003

Role of A Silent Synapse in Direction Selectivity

This section reports the results related to a pivotal innovation introduced in our study. Biological postsynaptic neurons have AMPA and NMDA receptors which receive glutamates (one type of neurotransmitters) to modulate cell excitability (Figure 3d). NMDA receptor-only excitatory synapses are called ‘silent synapses’ since NMDA receptors alone cannot activate the neuronal membrane potential [42,43]. Activation of silent synapses (transition from silent to normal synapse) requires correlated pre-, and postsynaptic activities, which are (i) NMDA activation by pre-synaptic neurotransmission and (ii) rising ion concentration in postsynaptic neuron [54,55](red rectangle of Figure 3d). Activation of silent synapses is critical for the early development of the neuron and brain by increasing plasticity since the brain selects frequently activated connections by activation of silent synapses and eliminates unimportant connections; that is one of the reasons the brain can learn so efficiently [55]. In this context, we modelled the NMDA receptor-only silent synapse that requires both pre- and postsynaptic activation conditions and implanted the silent synapse in the dendristor to figure out the role of the silent synapse in neuromorphic dendritic computation. In the dendristor, the silent synapse keeps silent when the pre-synaptic condition (which is the input signal, VA), and the postsynaptic condition (which is the effective gate voltage, vgS (the dendritic film potential)) are lower than a certain threshold level and the silent synapse is activated when both conditions exceed the threshold level (red rectangle of Figure 3e). The detailed circuit structure of the silent synapse and the activation mechanism are described in Supplementary Information S6. Since the inhibitory synapses are mediated by another synaptic receptors (e.g., GABA receptor) and the silent inhibitory synapse has not been reported in literatures, here we only focus on modelling the silence of excitatory synapses.
We measure the degree of direction selectivity by the difference between peak current of IN-D and OUT-D signals (ΔIDS,peak = IDS,peak,IN-D - IDS,peak,OUT-D). The dendristor with a proximal silent synapse (Figure 3c, yellow synaptic input) shows enhanced direction selectivity since the proximal silent synapse suppresses OUT-D current (Figure 3c, blue curve) by silencing the fifth input signal. However, IN-D current level (Figure 3c, red curve) is equal to that of the dendristor without silent synapse (Figure 3b, red curve) since the fifth silent synapse is activated by a high membrane potential induced by serial activation of previous (1st to 4th) synaptic inputs. Therefore, ΔIDS,peak becomes larger in the dendristor with a silent synapse, which implies enhanced direction selectivity. The further analysis of the silent synapse compared with the case of the disabled synapse and its position on a dendritic branch is shown in Supplementary Information S7.
The result that the most proximal silent synapses induce remarkably higher direction selectivity, is inspiring since the early brain and young neurons have more silent synapses than mature ones, and it exploits them to establish new synaptic connection and form specific neuronal assemblies [54,56]. Hence, we speculate that the increase of signal selectivity triggered by silent synapses could make young neurons react to the stimulations more efficiently.

Neuromorphic Dendritic Neural Circuit for Various Motion Detections

In sensory nerve systems, direction and motion detection is implemented as biocomputation by functional neural circuits that generate spike outputs (i.e., burst). Although in a dendristor branch, the signal direction can be classified as the intensity of the IDS, this is not straightforward as an output of a biologically plausible system. To achieve easy readout, a circuit with two different and specific outputs - one that indicates IN-D and the other that indicates OUT-D - is fundamental to designing a network. Hence, we develop a direction-selective neuromorphic dendritic neural circuit (NDNC) by connecting together three single-dendritic-branch neurons (Figure 4a) which includes also silent and inhibitory synapses. Each neuron performs dendritic computation such as spatiotemporal integration for the direction selectivity (N1 and N2′) and inhibitory integration (N2). When the directional input signal is applied simultaneously on N1 and N2′ as if they are connected to receptor cells, the internal current outputs (IDS,Ni) of the neurons are shown in the red curves in Figure 4b. To emulate the neuronal action potential generation when the internal membrane potential reaches a certain threshold in a neuron, we connected a burst circuit to each neuronal output (Supplementary Information S8). When IDS,Ni exceeds the burst level (Figure 3b,c), the dendristor neuron generates voltage pulses, so-called “burst” (VB,Ni in Figure 4b). The logic tables of the NDNC outputs (Supplementary Information S9) show the burst output depending on the directions. N1 bursts only with IN-D signal because of the silent synapse. N2′ without silent synapse bursts for both directions. N2 bursts only with OUT-D signal, since IN-D signal activate the inhibitory synapse from N1 and supress the N2 signal. Therefore, the NDNC generates two independent burst outputs depending on the signal direction and works as direction indicators. NDNC with the normal synapse or the disabled synapse in N1 failed to detect the directions (Supplementary Information S9). The selectivity enhancement of the silent synapse plays a crucial role in NDNC detection. To prove the general dendritic computation capacity of spatiotemporal signal integration and the effect of the morphology of the dendritic branch, we extend the one-dimensional receptor to the two-dimensional receptive field of the artificial retina using the basic principle of the NDNC formation (Figure 4c). The 5x5 cells are mapped on 4 neurons (NS, NN’, NE, NW’) with five dendritic branches. Each dendritic branch of NS and NN maps each column [a to e] and the dendritic branch of NE and NW maps each row [1,2,3,4,5]. There are two NDNCs that detect North and South directions and East and West directions. Figure 4e shows a table of input direction (the first row) across the 2-dimensional (2D) receptive field versus output voltage of 4 output neurons (NS, NN, NE, NW). The neurons respond only to the corresponding directions of the signal movement. Apart from the directional movement, another important visual process of retina is to recognize the depth movement of object. There are several principles of depth perception [57], we used the detection of the size change depending on the movement along the depth. When the object is coming close, the large area of the receptive cells (all the coloured circles) is activated (dark brown area of Figure 4d) and when the object is moving far, the activating area becomes small (only light brown area of Figure 4d). Based on the centre area of the receptive field, the radiating cells are mapped on dendritic branches. The dendritic morphology should be also like the radiating shape to enhance the mapping efficiency. When object is coming close, the neuron should be more activated, but not be overshoot because of all-input activation. Therefore, here the mapping is not straightforward; the centre cells (all-time activating) are mapped on distal synapses and the edge cells (activating when coming close) are mapped on proximal synapses to strongly enhance the neuronal signal. The topology of the receptive cells and the synapses on dendrites is opposite based on the centre. Neuronal connection in NDNC is formed similarly with previous examples, but here three silent synapses are used to make the asymmetry between Nclose and Nfar. Since many synapses are activating together and longer, the more silent synapses are necessary to make the significant current difference between close and far direction. Figure 4f shows the output pulses from Nclose and Nfar which are selectively activated with corresponding movement. The circuit details of Figure 4c,d are described in Supplementary Information S10. This result proves that NDNC is capable to recognize crucial movement using dendritic computation and shows a neuromorphic circuit design principle using spatial mapping and various synaptic regulations, which is introduced for the first time in this study.
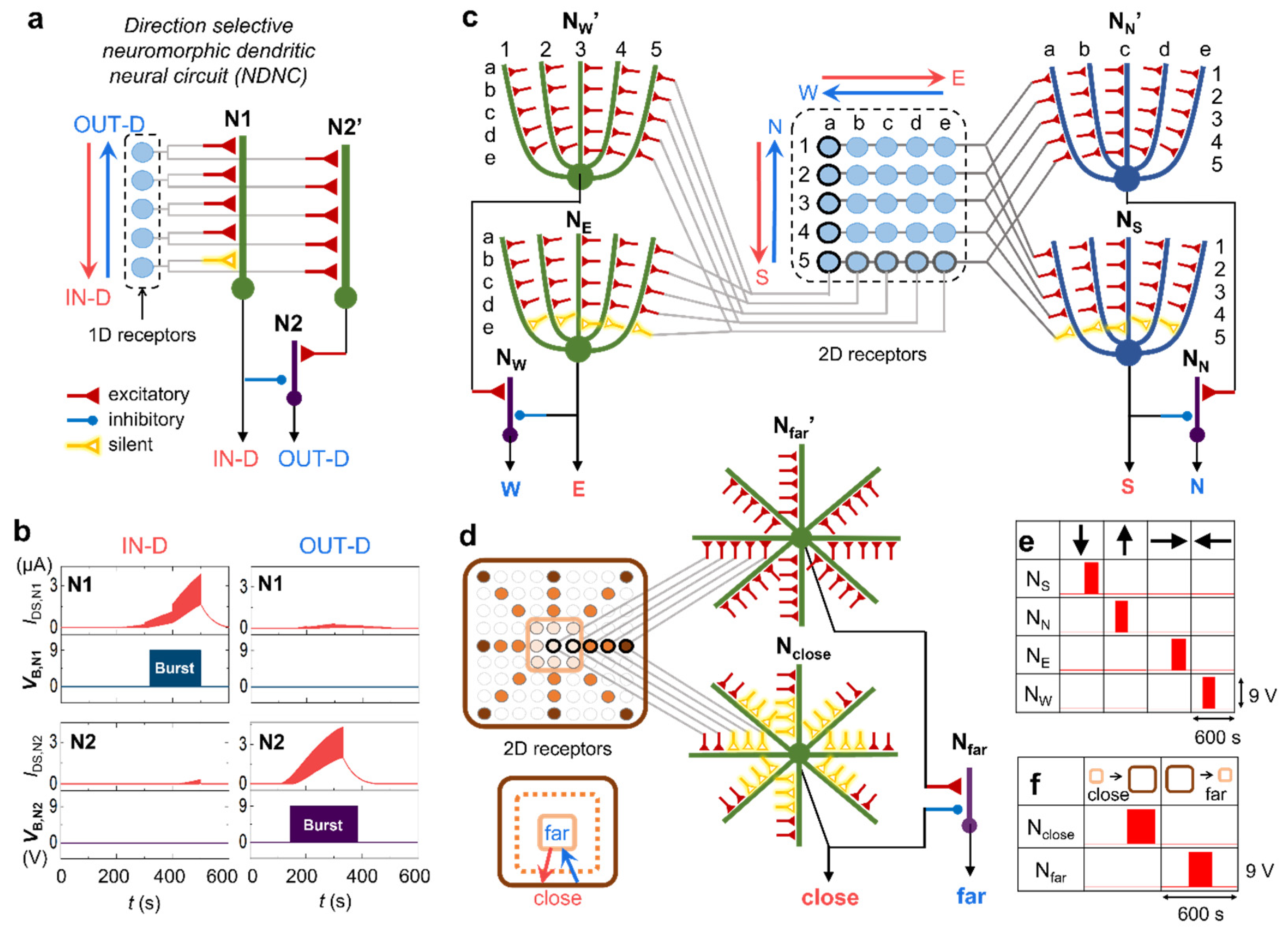
Preprints 75693 g004
Figure 4. Neuromorphic neural circuit for direction selectivity and morphological variation of dendrites. (a) Direction selective neuromorphic dendritic neural circuit (NDNC) design. (b) The current and voltage pulse output of N1 and N2 in the neuromorphic neural circuit of (a), depending on the input signal directions. Excitatory burst amplitude is 9 V and inhibitive burst amplitude is -3 V. (c) 2-dimensional direction detecting NDNC. The receptive cells (blue circles) are mapped on 4 neurons with 5 dendritic branches. (d) NDNC and dendritic mapping of the receptors that detect the movement of object which is moving close or far. Based on the center position of the receptor, the receptive cells (coloured circles) on the radiating line are mapped on a dendritic branch. The same-coloured receptive cell and the synapse are connected. (e) 2-dimentional direction output pulses of each neuron of (c). (f) Close and far output pulses of each neuron of (d). The first row is the input direction and the first column is the output neuron for (e,f).
Figure 4. Neuromorphic neural circuit for direction selectivity and morphological variation of dendrites. (a) Direction selective neuromorphic dendritic neural circuit (NDNC) design. (b) The current and voltage pulse output of N1 and N2 in the neuromorphic neural circuit of (a), depending on the input signal directions. Excitatory burst amplitude is 9 V and inhibitive burst amplitude is -3 V. (c) 2-dimensional direction detecting NDNC. The receptive cells (blue circles) are mapped on 4 neurons with 5 dendritic branches. (d) NDNC and dendritic mapping of the receptors that detect the movement of object which is moving close or far. Based on the center position of the receptor, the receptive cells (coloured circles) on the radiating line are mapped on a dendritic branch. The same-coloured receptive cell and the synapse are connected. (e) 2-dimentional direction output pulses of each neuron of (c). (f) Close and far output pulses of each neuron of (d). The first row is the input direction and the first column is the output neuron for (e,f).
Preprints 75693 g004

Neuromorphic Visual Perception of Motion in 3D Space

We further investigated neuromorphic motion perception in three-dimensional (3D) environment. In 3D space, x and y axes represent 2D directions and the z axis is linked to the motion depth. We designed 2D retina receptors (Figure 5a) with two functional layers: a receptor layer detecting 2D movement directions (Figure 5b, which is identical to Figure 4c) and a receptor layer detecting depth movement (Figure 5c). A single receptive cell on the 2D direction layer (a yellow dot, Figure 5b) and a receptors’ unit of depth layer (the 2D depth receptors in Figure 4d) are overlapped, so that, in the unit time period, the 2D retina can detect the location on the 2D x-y plane and the size of object together. Since a depth NDNC detect the size changes of the object moving along the x (or y) direction, all depth receptive cells on the x (or y) axis (orange rectangle in Figure 5c) are connected to the mapping neurons (Nz and N-z’) of the NDNC. The detailed connection between the receptors and the NDNCs is shown in Supplementary Information S11. For the 3D motion perception test, the butterfly’s motion in 3D space (Figure 5d) is projected on the 2D retina receptors over time (Figure 5e). The 2D receptor inputs activates 3D perceptive-NDNCs that generates six different neuronal output pulses ( v ± x , v ± y , and v ± z ) (Figure 5f). We reconstructed the neuronal pulse outputs onto 3D space as the unit directions (coloured dashed arrows in Figure 5g) and the order in which the arrows are arranged corresponds to the order of pulse outputs. Then, we did vector summation when the x/y directional neurons burst simultaneously with z directional neurons (red dashed rectangle in Figure 5f and black arrows in Figure 5g). The reconstructed directions with final black arrows on 3D space are identical to the original movement of butterfly.
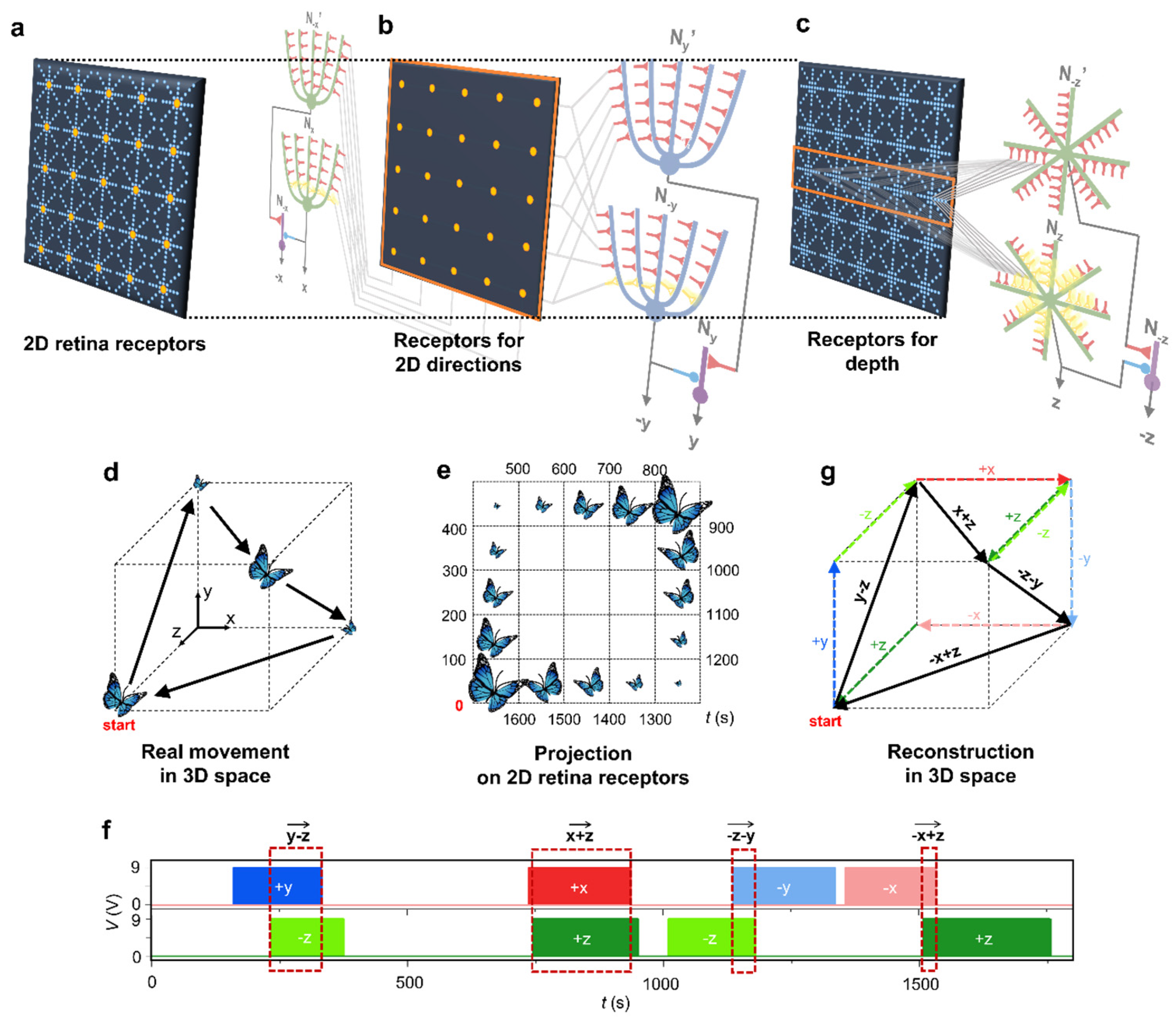
Preprints 75693 g005
Figure 5. neuromorphic visual perception of motion in 3D environment. (a) The embedded 2D retina receptor. The receptor layer for the 2D directions and the depth are combined into the embedded receptor. (b) The receptor layer for 2D directions, which is linked to the NDNC responsible for detecting 2-dimentional motion. (c) The receptor layer for depth, which is linked to the NDNC responsible for detecting depth movement. (d) Illustration of a butterfly’s test movement of in 3D space. (e) The projection of the butterfly’s motion in 3D space onto 2D receptors. (f) The pulses produced by each directional neuron. Different directional neuronal outputs are represented by different colors. (g) The visual perception of the motion in 3D environment, which is reconstructed from the neuronal pulse outputs in (f).
Figure 5. neuromorphic visual perception of motion in 3D environment. (a) The embedded 2D retina receptor. The receptor layer for the 2D directions and the depth are combined into the embedded receptor. (b) The receptor layer for 2D directions, which is linked to the NDNC responsible for detecting 2-dimentional motion. (c) The receptor layer for depth, which is linked to the NDNC responsible for detecting depth movement. (d) Illustration of a butterfly’s test movement of in 3D space. (e) The projection of the butterfly’s motion in 3D space onto 2D receptors. (f) The pulses produced by each directional neuron. Different directional neuronal outputs are represented by different colors. (g) The visual perception of the motion in 3D environment, which is reconstructed from the neuronal pulse outputs in (f).
Preprints 75693 g005

Discussion

In this study, we pave the way towards a new direction in neuromorphic research that is particularly specialized to process spatiotemporal visual patterns using dendritic computation. We offer engineering rationale in this new direction by designing a neuromorphic computational model, ‘dendristor’ exploiting the intrinsic plasticity of neurotransistor [48]. The dendristor model mimics the segmented dendritic branch morphology and its nonlinear signal integration which provides branch-specific plasticity. The dendirstor exhibits dendritic supralinearity [27,58] that is commonly observed in the somatosensory operation of neurons, such as orientation/angular tuning or detection of sensory stimuli [59,60], and therefore, the supralinearity of the dendristor serves as a measure of the neuronal computation capacity in sensory operation. Also, the dendristor branch encodes spatiotemporal sequence of the inputs and generates different output based on the direction on signal arrivals on a branch, so-called direction selectivity. The direction selectivity of the dendristor can be considered as intrinsic spatiotemporal adaptation that is not obtainable in a point-neuron model that uses synaptic adaptation. Interestingly and importantly, our study demonstrates how the silent synapse (NMDA-only synapse) participates in dendritic computation to enhance the direction selectivity by actively diminishing insignificant signals. The activation of the silent synapse is a result of the postsynaptic dendritic integration while in conventional synaptic function without dendrites, presynaptic activity predominates.
We expand the direction selectivity of a dendristor branch to build neuromorphic sensory neural circuits that is the first neuromorphic demonstration of morphological neural circuits performing bioplausible dendritic computation for direction selectivity [35]. Neuronal units in NDNC do not process inputs in batches like in a typical ANN, but do computations according to branch-by-branch mapping and inhibitory integration. The silent synapses contribute to forming the asymmetry in direction sensitive neurons in the NDNC, which shows critical similarity with the asymmetric morphology and the inhibition control in retinal direction-selective ganglion cells [32]. Various cognition examples in 2D shows that dendritic morphology plays as a mapping platform of the spatial inputs, and the tailored mapping optimizes the spatiotemporal process. Also, we use neuromorphic dendritic engineering to investigate the basis of perception and the representation of the movement in 3D space. Our study demonstrated a brain-inspired working model of NDNC in 3D, though the mechanism of visual perception of motion in 3D space combining 2D directions and depth movement has not yet been fully understood in cognitive neuroscience [61].
It was reported that to model the input-output behaviour of a cortical neuron it is necessary a deep neural network with 5 to 8 hidden layers with up to 256 channels [62]. However, when NMDA receptors are not included in the model the equivalent deep neural network requires only one hidden layer. This implies that the depth of the neural network arises from the modelling of the interaction between NMDA receptors and dendritic morphology [62]. Our study provides evidence in the same direction because we can achieve visual motion perception by a neuromorphic system of 36 neurons leveraging NMDA-only synapses and dendritic morphology. The dendritic visual process is less computationally intensive because the NDNC perception does not require training and deep layer process like existing convolutional neural network (CNN)-based motion detection does [63]. The visual perception of the NDNC is qualitative representation of movement, which is related to how the encoded signal is reconstructed and recognized like in the brain and this is distinct from quantitative detection.
Neuromorphic research and neuroscientific research might share insights about neuro-inspired computational principles based on the similarity of spatial morphology of the system and that allow computational neurobiologists to explore and formulate a new hypothesis and neuromorphic engineers to create intelligent systems. In this study, we provide biocomputational insights regarding the inhibitory integration role depending on the strength (Supplementary Information S5) and the enhancement function of the silent synapse in direction selectivity. In general, in vivo study of the synapses is technically challenging to be realized, for example, most silent synapses naturally disappear after the critical period. This result may give a hint into why neuronal signalling should go through the stage of silent synapses in early neural circuit development.
The final remark is that we selected the neurotransistor model [48] for dendritic computation among many existing neuromorphic devices such as memristors since the neurotransistor has a structure that shares a single material layer as a neuronal membrane with multiple input gates and its electrodynamics are more controllable. This material sharing structure is the core of dendristor modeling since this single material branch can store accumulated history generated from different inputs as localized polarization which influences the global branch. We strongly encourage developing neuromorphic devices with various material types performing the dendritic computation for spatiotemporal processing.

Supplementary Materials

Methods and Supplementary Information are made available to the public after the research is accepted.

Author Contributions

E.B. and C.V.C. developed the concept of the dendristor and the neuromorphic visual motion perception system. C.V.C. devised the role of the silent synapses and the visual motion perception in dendritic computation. E.B. developed the neuromorphic dendritic neural circuits. S.S. clarified the silent synaptic function for modelling and advised for the biocomputational emulation. E.B. and C.V.C. designed the computational experiments and E.B. realized the electrical circuit and the computational experiments using LT-SPICE. All authors analysed the data and results. E.B., R.Z., L.S., and C.V.C. designed the figures and E.B. realized them. E.B. R.Z., L.S. and C.V.C. wrote the manuscript and all authors reviewed it. C.V.C. and L.S. supervised the project.

Acknowledgments

This work was partly supported by the National Nature Science Foundation of China (No. 61836004, No. 62088102); National Key R&D Program of China 2018YFE0200200, a grant from Guoqiang Institute of Tsinghua University. C.V.C is funded by the Zhou Yahui Chair Professorship award of Tsinghua University, the starting funding of the Tsinghua Laboratory of Brain and Intelligence (THBI) and the National High-Level Talent Program of the Ministry of Science and Technology of China. C.V.C thanks professor Antonio Malgaroli for introducing and inspiring his research on silent synapses when he was a master student.

Conflicts of Interests

Authors declare that they have no competing interests.

References

  1. Zhang, W. et al. Neuro-inspired computing chips. Nat Electron 3, 371–382 (2020). [CrossRef]
  2. Furber, S. B., Galluppi, F., Temple, S. & Plana, L. A. The SpiNNaker project. Proceedings of the IEEE 102, 652–665 (2014). [CrossRef]
  3. Sen-Bhattacharya, B. et al. Building a Spiking Neural Network Model of the Basal Ganglia on SpiNNaker. IEEE Trans Cogn Dev Syst 10, 823–836 (2018). [CrossRef]
  4. Casanueva-Morato, D., Ayuso-Martinez, A., Dominguez-Morales, J. P., Jimenez-Fernandez, A. & Jimenez-Moreno, G. Spike-based computational models of bio-inspired memories in the hippocampal CA3 region on SpiNNaker. in 2022 International Joint Conference on Neural Networks (IJCNN) 1–9 (2022). [CrossRef]
  5. Boybat, I. et al. Neuromorphic computing with multi-memristive synapses. Nat Commun 9, 2514 (2018). [CrossRef]
  6. Yi, W. et al. Biological plausibility and stochasticity in scalable VO2 active memristor neurons. Nature Communications 2018 9:1 9, 1–10 (2018). [CrossRef]
  7. Poirazi, P. & Papoutsi, A. Illuminating dendritic function with computational models. Nat Rev Neurosci 21, 303–321 (2020). [CrossRef]
  8. Ujfalussy, B. B., Makara, J. K., Lengyel, M. & Branco, T. Global and Multiplexed Dendritic Computations under In Vivo-like Conditions. Neuron 100, 579-592.e5 (2018). [CrossRef]
  9. Sidiropoulou, K., Pissadaki, E. K. & Poirazi, P. Inside the brain of a neuron. EMBO Reports vol. 7 886–892 (2006). [CrossRef]
  10. Bhalla, U. S. Molecular computation in neurons: A modeling perspective. Current Opinion in Neurobiology vol. 25 31–37 (2014). [CrossRef]
  11. Marković, D., Mizrahi, A., Querlioz, D. & Grollier, J. Physics for neuromorphic computing. Nature Reviews Physics 2, 499–510 (2020). [CrossRef]
  12. Zenke, F. et al. Visualizing a joint future of neuroscience and neuromorphic engineering. Neuron 109, 571–575 (2021). [CrossRef]
  13. Sinz, F. H., Pitkow, X., Reimer, J., Bethge, M. & Tolias, A. S. Engineering a Less Artificial Intelligence. Neuron 103, 967–979 (2019). [CrossRef]
  14. Cannistraci, C. V., Alanis-Lobato, G. & Ravasi, T. From link-prediction in brain connectomes and protein interactomes to the local-community-paradigm in complex networks. Scientific Reports 2013 3:1 3, 1–14 (2013). [CrossRef]
  15. Cannistraci, C. V. Modelling Self-Organization in Complex Networks Via a Brain-Inspired Network Automata Theory Improves Link Reliability in Protein Interactomes. Scientific Reports 2018 8:1 8, 1–16 (2018). [CrossRef]
  16. London, M. & Häusser, M. Dendritic Computation. Annu. Rev. Neurosci 28, 503–535 (2005). [CrossRef]
  17. Mehonic, A. & Kenyon, A. J. Brain-inspired computing needs a master plan. Nature 604, 255–260 (2022). [CrossRef]
  18. Boahen, K. Dendrocentric learning for synthetic intelligence. Nature vol. 612 43–50 (2022). [CrossRef]
  19. Wybo, W. A. M., Torben-Nielsen, B., Nevian, T. & Gewaltig, M. O. Electrical Compartmentalization in Neurons. Cell Rep 26, 1759-1773.e7 (2019). [CrossRef]
  20. Jarvis, S., Nikolic, K. & Schultz, S. R. Neuronal gain modulability is determined by dendritic morphology: A computational optogenetic study. PLoS Comput Biol 14, 1–21 (2018). [CrossRef]
  21. Vlasits, A. L. et al. A Role for Synaptic Input Distribution in a Dendritic Computation of Motion Direction in the Retina. Neuron 89, 1317–1330 (2016). [CrossRef]
  22. Iascone, D. M. et al. Whole-Neuron Synaptic Mapping Reveals Spatially Precise Excitatory/Inhibitory Balance Limiting Dendritic and Somatic Spiking. Neuron 106, 566-578.e8 (2020). [CrossRef]
  23. Ju, N. et al. Spatiotemporal functional organization of excitatory synaptic inputs onto macaque V1 neurons. Nature Communications 2020 11:1 11, 1–11 (2020). [CrossRef]
  24. Jones, I. S. & Kording, K. P. Might a single neuron solve interesting machine learning problems through successive computations on its dendritic tree? Neural Comput 33, 1554–1571 (2021). [CrossRef]
  25. Guerguiev, J., Lillicrap, T. P. & Richards, B. A. Towards deep learning with segregated dendrites. Elife 6, 1–37 (2017). [CrossRef]
  26. Ujfalussy, B. B., Makara, J. K., Branco, T. & Lengyel, M. Dendritic nonlinearities are tuned for efficient spike-based computations in cortical circuits. Elife 4, 1–51 (2015). [CrossRef]
  27. Tran-Van-Minh, A. et al. Contribution of sublinear and supralinear dendritic integration to neuronal computations. Front Cell Neurosci 9, 1–15 (2015). [CrossRef]
  28. Tzilivaki, A., Kastellakis, G. & Poirazi, P. Challenging the point neuron dogma: FS basket cells as 2-stage nonlinear integrators. Nat Commun 10, (2019). [CrossRef]
  29. Li, S. et al. Dendritic computations captured by an effective point neuron model. Proc Natl Acad Sci U S A 116, 15244–15252 (2019). [CrossRef]
  30. Goetz, L., Roth, A. & Häusser, M. Active dendrites enable strong but sparse inputs to determine orientation selectivity. Proceedings of the National Academy of Sciences 118, (2021). [CrossRef]
  31. Takahashi, N., Oertner, T. G., Hegemann, P. & Larkum, M. E. Active cortical dendrites modulate perception. Science (1979) 354, 1587–1590 (2016). [CrossRef]
  32. Vaney, D. I., Sivyer, B. & Taylor, W. R. Direction selectivity in the retina: Symmetry and asymmetry in structure and function. Nat Rev Neurosci 13, 194–208 (2012). [CrossRef]
  33. Jia, H., Rochefort, N. L., Chen, X. & Konnerth, A. Dendritic organization of sensory input to cortical neurons in vivo. Nature 464, 1307–1312 (2010). [CrossRef]
  34. Taylor, W. R., He, S., Levick, W. R. & Vaney, D. I. Dendritic Computation of Direction Selectivity by Retinal Ganglion Cells. Science (1979) 289, 2347–2350 (2000). [CrossRef]
  35. Mauss, A. S., Vlasits, A., Borst, A. & Feller, M. Visual Circuits for Direction Selectivity. Annu Rev Neurosci 40, 211–230 (2017). [CrossRef]
  36. Wu, X., Mel, G. C., Strouse, D. J. & Mel, B. W. How dendrites affect online recognition memory. PLoS Computational Biology vol. 15 (2019). [CrossRef]
  37. Frank, A. C. et al. Hotspots of dendritic spine turnover facilitate clustered spine addition and learning and memory. Nat Commun 9, 1–11 (2018). [CrossRef]
  38. Kaifosh, P. & Losonczy, A. Mnemonic Functions for Nonlinear Dendritic Integration in Hippocampal Pyramidal Circuits. Neuron 90, 622–634 (2016). [CrossRef]
  39. Kastellakis, G., Silva, A. J. & Poirazi, P. Linking Memories across Time via Neuronal and Dendritic Overlaps in Model Neurons with Active Dendrites. Cell Rep 17, 1491–1504 (2016). [CrossRef]
  40. Poirazi, P. & Mel, B. W. Impact of active dendrites and structural plasticity on the memory capacity of neural tissue. Neuron 29, 779–796 (2001). [CrossRef]
  41. Gidon, A. & Segev, I. Principles Governing the Operation of Synaptic Inhibition in Dendrites. Neuron 75, 330–341 (2012). [CrossRef]
  42. Malgaroli, A. Silent synapses: I can’t hear you! Could you please speak aloud? Nat Neurosci 2, 3–5 (1999). [CrossRef]
  43. Kerchner, G. A. & Nicoll, R. A. Silent synapses and the emergence of a postsynaptic mechanism for LTP. Nat Rev Neurosci 9, 813–825 (2008). [CrossRef]
  44. Vincent-Lamarre, P., Lynn, M. & Béïque, J. C. The Eloquent Silent Synapse. Trends Neurosci 41, 557–559 (2018). [CrossRef]
  45. Kaiser, J. et al. Emulating Dendritic Computing Paradigms on Analog Neuromorphic Hardware. Neuroscience 489, 290–300 (2022). [CrossRef]
  46. Cartiglia, M. et al. Stochastic dendrites enable online learning in mixed-signal neuromorphic processing systems. (2022). [CrossRef]
  47. Li, X. et al. Power-efficient neural network with artificial dendrites. Nat Nanotechnol 15, 776–782 (2020). [CrossRef]
  48. Baek, E. et al. Intrinsic plasticity of silicon nanowire neurotransistors for dynamic memory and learning functions. Nat Electron 3, 398–408 (2020). [CrossRef]
  49. Polsky, A., Mel, B. W. & Schiller, J. Computational subunits in thin dendrites of pyramidal cells. Nat Neurosci 7, 621–627 (2004). [CrossRef]
  50. Vervaeke, K., Lorincz, A., Nusser, Z. & Silver, R. A. Gap junctions compensate for sublinear dendritic integration in an inhibitory network. Science (1979) 335, 1624–1628 (2012). [CrossRef]
  51. Liu, G. Local structural balance and functional interaction of excitatory and inhibitory synapses in hippocampal dendrites. Nat Neurosci 7, 373–379 (2004). [CrossRef]
  52. Grienberger, C., Chen, X. & Konnerth, A. Dendritic function in vivo. Trends Neurosci 38, 45–54 (2015). [CrossRef]
  53. Branco, T., Clark, B. A. & Häusser, M. Dendritic discrimination of temporal input sequences in cortical neurons. Science (1979) 329, 1671–1675 (2010). [CrossRef]
  54. Hanse, E., Seth, H. & Riebe, I. AMPA-silent synapses in brain development and pathology. Nat Rev Neurosci 14, 839–850 (2013). [CrossRef]
  55. Xu, W., Löwel, S. & Schlüter, O. M. Silent Synapse-Based Mechanisms of Critical Period Plasticity. Front Cell Neurosci 14, 1–27 (2020). [CrossRef]
  56. Li, L. et al. Silent synapses generate sparse and orthogonal action potential firing in adult-born hippocampal granule cells. Elife 6, 1–23 (2017). [CrossRef]
  57. Welchman, A. E. The Human Brain in Depth: How We See in 3D. Annual review of vision science vol. 2 345–376 (2016). [CrossRef]
  58. Schmidt-Hieber, C. et al. Active dendritic integration as a mechanism for robust and precise grid cell firing. Nat Neurosci 20, 1114–1121 (2017). [CrossRef]
  59. Lavzin, M., Rapoport, S., Polsky, A., Garion, L. & Schiller, J. Nonlinear dendritic processing determines angular tuning of barrel cortex neurons in vivo. Nature 490, 397–401 (2012). [CrossRef]
  60. Smith, S. L., Smith, I. T., Branco, T. & Häusser, M. Dendritic spikes enhance stimulus selectivity in cortical neurons in vivo. Nature 503, 115–120 (2013). [CrossRef]
  61. Whritner, J. A. Visual Perception of Motion in the 3D Environment. (The University of Texas at Austin, 2022). [CrossRef]
  62. Beniaguev, D., Segev, I. & London, M. Single cortical neurons as deep artificial neural networks. Neuron 109, 2727-2739.e3 (2021). [CrossRef]
  63. Dominguez-Sanchez, A., Cazorla, M. & Orts-Escolano, S. Pedestrian Movement Direction Recognition Using Convolutional Neural Networks. IEEE Transactions on Intelligent Transportation Systems 18, 3540–3548 (2017). [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Neuromorphic Dendritic Computation with Silent Synapses for Visual Motion Perception

Eunhye Baek

et al.

,

2023

A Computational Model of Dendritic Growth Dynamics: Exploring Exponential and Logarithmic Scales in Neural Development

Richard Murdoch Montgomery

,

2024

Towards Random Walks Underlying Neuronal Spikes

Arturo Tozzi

et al.

,

2019

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated