Prerpints.org logo
Preprint
Article

Towards Resonantly Enhanced Acoustic Phonon-Exchange Magnon Interactions at THz Frequencies

Altmetrics

Downloads

128

Views

59

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

05 June 2023

Posted:

06 June 2023

You are already at the latest version

Alerts
Abstract
Using valid experimental parameters we quantify the magnitude of resonantly phonon-driven precession of exchange magnons in freestanding ferromagnetic nickel thin films on their thickness L. Analytical solutions of acoustically driven equations for magnon oscillators display a nonmonotonous dependence of the peak magnetization precession on the film thickness. It is explained by different L-dependence of multiple prefactors entering in the expression for the total magnetization dynamics. Depending on the ratio of acoustic and magnetic (Gilbert) damping constants, the magnetization precession is shown to be amplified by a Q-factor of either the phonon or the magnon resonance. The increase of the phonon mode amplitude for thinner membranes is also found to be significant. Focusing on the magnetization dynamics excited by the two first acoustic eigenmodes with p=1 and p=2 we predict the optimum thicknesses of nickel membranes to achieve large amplitude magnetization precession at multi 100 GHz frequencies at reasonably low values of an external magnetic field.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

Ultrafast magneto-acoustics investigates peculiarities of ultrafast magnetization dynamics driven by ultrashort, fs-laser-excited acoustic transients [1,2,3,4,5]. In most cases the physical interpretation of magneto-elastic interactions roots back to numerically solving the Landau-Lifshitz-Gilbert equations for ferromagnetic resonance (FMR) precession driven by time- and space-dependent magneto-elastic fields. This approach is well justified when the characteristic time scales of the magnetization precession are much longer than the duration of magneto-elastic driving impact. Such simplified approach has been successfully used to describe the phenomenon of ultrafast magnetization switching in magnetostrictive thin films [6] and nanomagnets [7]. However, a closer look at the experimental data for magnetic semiconductors deposited on semi-infinite substrates [8] evidenced some more complicated magnetization dynamics and revealed contributions of the spatially inhomogeneous mod magnetization precession due to perpendicular standing spin wave modes (PSSWs, to be called magnons throughout this paper). The investigated GaMnAs ferromagnetic thin film with a thickness L=200 nm was too thick for individual modes (to be called magnons) to be spectrally resolved. Another complication was that the acoustic excitation in form of ultrashort acoustic pulses, injected in the GaMnAs layer from a semi-infinite GaAs substrate, was characterized by a continuous acoustic spectrum.
Several steps have been undertaken to get access to and quantify individual phonon-magnon interactions. First, reducing the thickness L of a ferromagnetic layer below a few tens of nanometers allowed the magnon modes to be well separated in frequency domain [9,10]. Under these conditions, the injection of an ultrashort laser pulse from a semi-infinite substrate results in the excitation of multiple spectrally isolated magnon modes within the continuous frequency spectrum of ultrashort acoustic pulses [11].
Second, Kim and Bigot have conceived and conducted an ultrafast optical experiment in a L = 300 nm thin freestanding nickel membrane acting as an acoustic cavity [12]. In this experiment the modes of longitudinal acoustic phonons could be well resolved, each of them interacting with several spectrally overlapping magnon modes. Nevertheless, it was possible to partially discriminate distinct phonon-magnon resonances based on the selection rules for phonon and magnon modes of same/different parity [13].
Third, a recent purely theoretical study by Vernik et al. discussed the details of resonant phonon-magnon interactions based for freestanding bi-layer and trilayer structures, based on some model parameters for acoustic and magnetic damping.
In the present manuscript we apply the results of quantitative analysis from Ghita et al. [13], using the extracted frequency-dependent acoustic damping factor β ∝ ω and magnetic Gilbert damping parameter α = 0.04 , to inspect the dynamics of resonantly enhanced phonon-magnon interactions in the ultrahigh frequency range as a function of nickel thickness L. The purpose of this work is to check the feasibility of experimental observation of this effect in the highest frequencies reaching the THz frequencies, i.e. the range important for studies in fundamental magnetism [10,14,15,16].

2. Theoretical description of ultrafast magneto-acoustics in freestanding magnetostrictive thin films

Absorption of an ultrashort acoustic pulse excitation in a freestanding nickel membrane results in a nearly instantaneous (on acoustic time scales) spatially inhomogeneous heating profile, which can be approximated by an exponential function Δ T ( z ) ∝ exp ( − z / h ) , see Figure 1a. The characteristic heating depth h typically exceed the optical penetration depth of laser light due to the diffusion of hot electrons during the picosecond electron-phonon relaxation time [17,18]. Since the electron-phonon relaxation time depends on the excitation conditions [19], the effective heating depth h becomes experiment-specific and is treated as a fitting parameter [13,20]. Throughout this manuscript, we are going to use the value h = 60 nm obtained from the comprehensive modeling of recent magneto-acoustic experiments [13].
Once impulsively heated, the film starts vibrating due to the thermal expansion and the spatio-temporal dynamics of the acoustic strain ε z z ( z , t ) can be represented as a superposition of acoustic eigenmodes according to
ε z z ( z , t ) = ∑ p = 1 ∞ ε z z ( p ) ( z ) e − γ p t cos ( ω p t + φ p ) .
We assume acoustic eigenmodes to oscillate at frequencies ω p = c s k p and decay with damping constants γ p ; φ p denote their initial phases. In a freestanding film, the acoustic eigenmodes obey the free boundary conditions for the acoustic displacement (corresponding to zero strains at both Ni/air interfaces) resulting in
ε z z ( p ) ( z ) = a p sin k p z ,
where k p = π p / L is the wavevector of the p-th acoustic eigenmode.
According to Ghita et al. [13], in the frequency range 0 - 80 GHz, the damping coefficient γ p = β p ω p scaled as ∝ ω p 2 . As this is coherent with a model of damping due to phonon-phonon scattering processes, we will extrapolate this scaling to frequencies up to 200 GHz, which is the highest frequency of a fundamental mode involved in our study.
In the same study, it was revealed that assuming an exponential heating profile, with penetration depth h = 60 nm, offers a satisfactory description of the mode amplitudes extracted from the experiment of Kim and Bigot. Assuming that for z ∈ [ 0 , L ] , the initial strain in the film is given by ε z z ( z , 0 ) = A 0 e − z / h , the individual mode amplitudes read
a p ( L ) = A 0 L ∫ 0 L e − z / h sin k p z d z = A 0 π p π 2 p 2 + ( L / h ) 2 1 − ( − 1 ) p e − L / h .
In the following, we will assume that the amplitude A 0 and the characteristic length scale h of the strain are constant and do not depend on the thickness L of the freestanding thin film. This assumption neglects thin-film effects in light absorption and reflection of heat at the back nickel-air interface. Possible (minor) corrections due to the aforementioned effects do not change the conclusions in this manuscript.
With this in mind, we can examine the dependence of the first three mode amplitudes on the film thickness L. It can be seen that, when going down to thinner films, the first acoustic mode becomes over-represented with respect to the higher-order harmonics. As shown in panel (d) of Figure 2, the evolution of the strain amplitude of modes p = 1 and p = 3 is monotonous with respect to the increase of thickness L. On the contrary, the acoustic mode p = 2 displays a maximum at L = 141 nm. While these modes start with comparable values around L = 300 nm, the first mode steeper increase than the others respect as L decreases. Therefore, it is reasonable to assume that at lower film thicknesses, interactions governed by the first acoustic mode will dominate.
In a thin film of thickness L the general form of the spatially inhomogeneous magnetization precession m ( z , t ) = m 0 + s ( z , t ) can be represented as a superposition in magnetic eigenmodes, i.e. PSSWs or exchange magnons superimposed on the FMR-precession (see Figure 1a,c):
s ( z , t ) = ∑ n = 0 ∞ s ( n ) ( t ) cos ( k n z ) ,
for n = 0 , 1 , 2 , . . . across the film with quantized wave vectors k n = π n / L and eigenfrequencies
ω n = γ μ 0 H cos ξ − M ˜ − D ˜ k n 2 cos θ 2 + H sin ξ + D ˜ k n 2 sin θ H sin ξ + M ˜ + D ˜ k n 2 sin θ
where D ˜ = D * / ( ℏ γ μ 0 ) is the exchange stiffness (the numerical value D * =430 [meV Å 2 ] for Ni is taken from Ref. [9]), γ stands for the gyromagnetic ratio, μ 0 is vacuum permeability and ℏ is the Planck’s constant.
It has been shown recently [11,21] that in the linear approximation when the acoustic strains are small, the magneto-elastically driven dynamics for each magnon mode satisfy the equation of a damped driven harmonic oscillator,
d 2 s z ( n ) d t 2 + 2 α ω n d s z ( n ) d t + ω n 2 s z ( n ) = f n ( t ) .
The external magneto-elastic driving force
f n ( t ) = P n ( H ) ∫ 0 L ε z z ( z , t ) cos k n z d z ,
is proportional to the overlap integral between the magnon eigenmode with the acoustic strain pulse ε z z ( z , t ) . For our experimental geometry the prefactor
P n ( H , L ) = μ 0 γ 2 b 1 sin ( 2 θ ) M 0 D ˜ k n 2 sin θ + H sin ξ
is proportional to the magnetostriction coefficient b 1 and depends both on the magnitude and orientation of an external magnetic field H .
Using the decomposition of the acoustic strain in its respective eigenmodes, the expression of the magneto-elastic driving force becomes
f n ( t ) = P n ( H ) ∑ p = 1 ∞ I n p a p e − γ p t cos ( ω p t + φ p ) .
Here we have introduced the overlap integral [21]
I n p = 1 L ∫ 0 L cos k n z sin k p z d z = 2 p π ( p 2 − n 2 ) for odd n + p 0 for even n + p
between the n-th magnetic and p-th acoustic eigenmodes.
Therefore, the theoretical modeling in ultrafast magnetoacoustics is reduced to solving Eq. (6) driven by a superposition of acoustic eigenmodes. The latter are quantified by amplitudes a p ( L ) , frequencies ω p ( L ) = c s π p / L and damping constants β p ( L ) = G ω p ( L ) . In order to evaluate the overall efficiency of magneto-elastic interactions it is sufficient to inspect the analytical solutions for each magnon mode n driven by an individual phonon mode with index p, as a function of nickel thickness L. For the purposes of numerical simulations, we use the valid experimental parameters used in [13], namely μ 0 M 0 = 0.6 T, c s = 6.04 · 10 3 m/s and G = 8.5 · 10 − 14 GHz − 1 .
We note that the change in thickness of the film leads to a shift of acoustic frequencies with respect to the magnon modes, thus drifting away from the resonant regime. In order to preserve the resonant behavior, one needs to adjust the magnetic field H . In the following, we will preserve the orientation of H at an angle ξ = 45 ∘ with respect to the normal, while varying its modulus. Furthermore, we will focus in our numerical studies on the interactions of the p = 1 and p = 3 acoustic mode with the n = 0 and n = 2 magnon modes, as well as that of p = 2 acoustic mode with n = 1 and n = 3 magnon modes.
This resonant tuning of H to the acoustic frequencies induces a change in the prefactor P n ( H ) , which in turn changes the driving force amplitude.
In the case of resonant interaction between a phonon and a magnon mode ( ω n = ω p ), the precession of magnetization in time is given by
s z ( t ) = A 2 ω p 2 ( α − β p ) [ e − β p ω p t − e − α ω p t ] sin ( ω p t + ϕ p )
The expression for the maximum amplitude of magnetization precession of the nth magnon mode resonantly driven by the pth acoustic mode reads:
s z , m a x ( n p ) ( L ) = a p ( L ) I n p P n ( H n p , L ) ω p ( L ) 2 A m a x ( α , β p ( L ) ) .
The damping-dependent factor
A m a x ( α , β p ) = 1 2 α α β p − β p α − β p .
can be understood in terms of the quality factors Q m = 1 / ( 2 α ) and Q p = 1 / ( 2 β p ) for magnon and phonon modes, respectively:
A m a x ( α , β p ) = Q m Q p Q m 1 1 − Q p / Q m ≃ Q p for Q m ≫ Q p Q m for Q m ≪ Q p .
Therefore we conclude that resonant phonon-magnon interactions are enhanced by the smaller Q-factor.
Mathematical derivation of equations (11-13) is provided in the Appendix A. The rest of the manuscript will be devoted to their numerical analysis for nickel membranes of arbitrary thickness L.

3. Numerical results for acoustically driven magnetization dynamics and their discussion

In this section, we show the numerical results obtained through the prism of the above-mentioned theoretical treatment. Figure 3 shows the results for driven magnon oscillator equations, for the n = 0 , p = 1 and n = 1 , p = 2 magnon-phonon pairs, respectively. The expected behavior of the rise and subsequent decay is recovered. We notice that both of the rise and decay time scales are decreasing as the film thickness decreases. Naturally, the frequency of these excitations increases, reaching values of up to 160 GHz.
We can already notice that in case of the n = 0 FMR-mode driven by the p = 1 phonon mode, the maximal magnetization displays the non-monotonous dependence on the film thickness L. Furthermore, the magnetic field needed to achieve this resonance increases with the decreasing thickness. For the considered values of the thickness ( L = 300 nm, L = 150 nm, L = 75 nm, L = 50 nm and L = 37.5 nm), there is no clear conclusion on the dependence of this maximal magnetization in the case of the n = 1 magnon mode driven by the p = 2 phonon mode. As such, it is interesting to study the dependence of the maximal magnetization achieved, as well as the magnetic field needed for the resonant interaction, as a function of the film thickness L.
Figure 4 shows the thickness dependence of the resonant magnetic field (lower panel) and the maximal magnetization (upper panel) for six distinct phonon-magnon resonances. We start our discussion from two phonon-magnon resonances observed in the Kim & Bigot experiment performed for L = 300 nm [13]: the p = 1 -excited n = 0 FMR precession and the p = 2 -excited n = 1 magnon. In the first case, one can see that for L = 65 nm the FMR precession can be amplified by a factor of 10 as compared with Kim & Bigot experiment. Meanwhile, for the driving of n = 1 mode, a peak precession amplitude is achieved for L = 180 nm, but the increase in precession with respect to the Kim-Bigot experiment is marginal (only a factor of 1.25).
One can furthermore see that these two low-order phonon-magnon resonances are the ones with the largest amplitudes when going towards smaller thicknesses. Furthermore, in terms of the required resonant magnetic fields, for film thicknesses L > 50 nm the fields stay in the range below 10 T (and below 5 T for low-order resonances). These experimentally achievable magnetic fields suggest that for this range of thicknesses, resonant phonon-magnon interaction can be observed and measured. The problem arises when considering the behaviour at very small film thicknesses (or, equivalently, at very high frequencies, exceeding 100 GHz). One notices that the required resonant required magnetic fields diverge to unreasonably high values. However, for certain phonon-magnon pairs (evidenced with dotted lines in Figure 4), there is a sharp decrease toward zero of these required magnetic fields. As such, at certain very low thicknesses, one can again find high-frequency phonon-magnon resonances at experimentally reasonable magnetic fields.
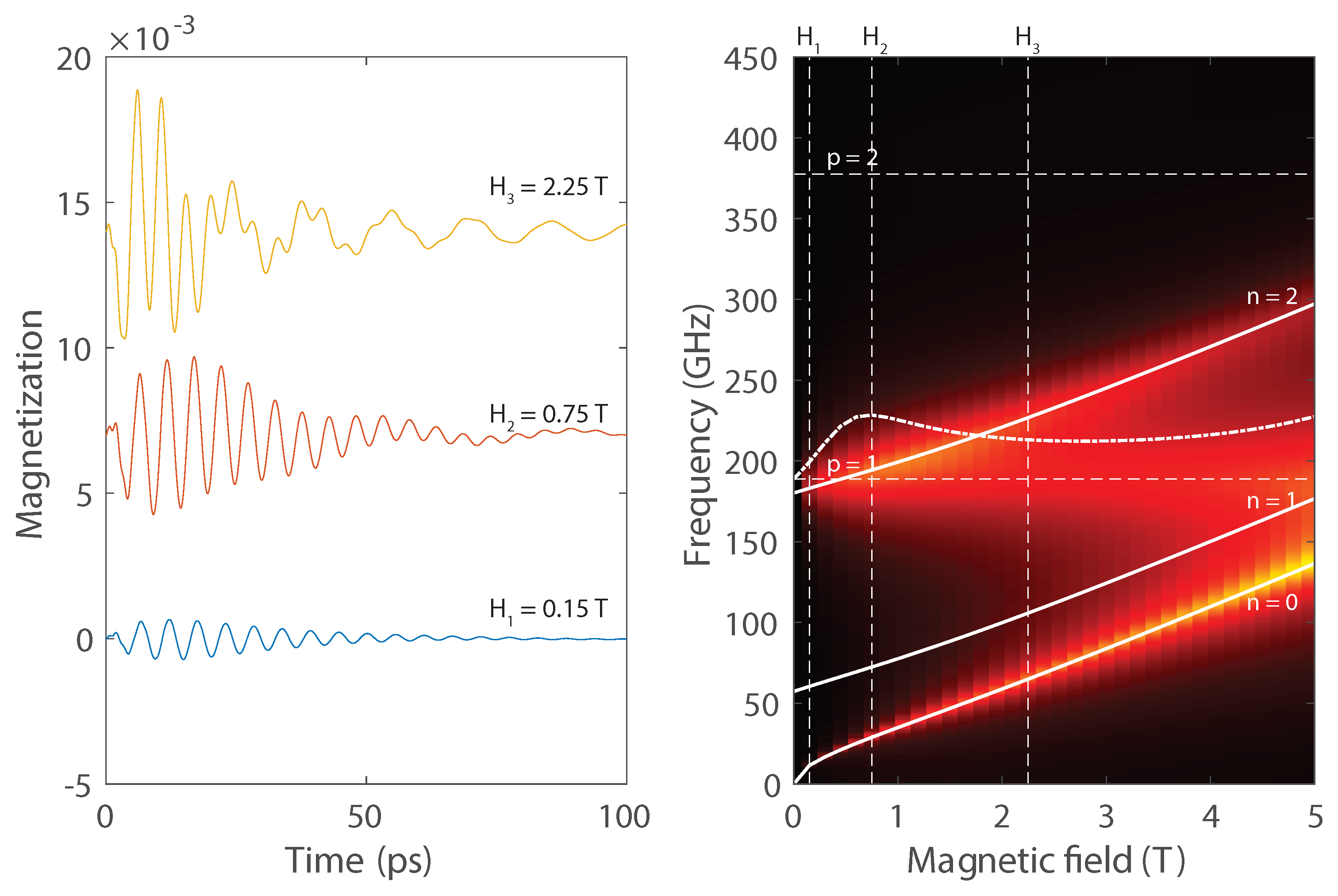
We will focus our analysis on one of these cases, namely, that of a L = 16 nm film thickness. Figure 5b shows the magneto-acoustic interaction landscape, given by the dependence of the magnitude of the Fourier transform of s z ( t ) on the external magnetic field. One notices a rather faint, yet visible trace of resonant behavior at the intersection of the p = 1 and n = 2 phonon and magnon curves. This resonant enhancement is achieved for the external magnetic field value H = 0.75 T, at a frequency of approximately 200 GHz. Numerical simulation of magnetization dynamics at this set of experimental parameters shows indeed a behaviour as expected, with the typical rise and decay time being evident on the magnetization dynamics. As such we have achieved the main goal of this paper to demonstrate that previously anticipated higher-order phonon-magnon resonances in hybrid metal-ferromagnet membranes [21] can be indeed achieved using realistic parameters [13] in much simpler structures, i.e. thin nickel membranes.
It is worth mentioning that the resonant curve is described by the analytical expression Eq. 12. As such, Eq. 12 represents a powerful tool to engineer arbitrary phonon-magnon resonances as a function of magnetic and acoustic material parameters. For example, experiments with magnetic dielectrics BiYIG [15,22,23,24,25], characterized by orders-of-magnitude lower values of the Gilbert damping parameter α ∼ 10 − 4 , may seem better candidates to observe large-amplitude phonon-magnon interactions at first glance. However, in the limit α ≪ β p Eq. 14 converges towards Q p indicating the crucial role of the acoustic damping β p in this case. This rather straightforward example demonstrates that the choice of an optimum combination of membrane’s material and thickness represents a rather nontrivial multiparameter optimization problem.

4. Conclusions

We have performed extensive analytical calculations for resonantly enhanced phonon-magnon interactions in freestanding nickel films in fs-laser-excited magnetostrictive membranes of arbitrary thickness L. Solutions of driven harmonic oscillator equations for each magnon modes demonstrate the complex nonlinear dependence on multiple physical parameters highlighting the role of magnetic and acoustic damping factors as well as the heat penetration depth and acoustic mode amplitudes to achieve the maximum peak precession amplitude. The application of this modeling freestanding ferromagnetic nickel membranes suggest that experimental observations of elastically driven multi-100 GHz exchange magnon resonances in ultrathin nickel membranes can be observed at moderate values of the external magnetic field below 1 Tesla. Apart from ferromagnetic metals, our analytical results can be adopted to describe ultrafast magneto-acoustics in ferromagnetic semiconductors [1,8] and dielectrics [22,24,25].

Author Contributions

Conceptualization, V.T.; methodology, T.M., A.G., V.T.; software, A.G, T.M.; investigation, T.M. and A.G.; writing—original draft preparation, T.M and A.G.; writing—review and editing, T.M., A.G., V.T.; supervision, V.T.; project administration, V.T. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Acknowledgments

The support of the Physics Department of École Polytechnique and Institut Polytechnique de Paris within the framework of a Projet de Recherche en Laboratoire and by the ANR-21-MRS1-0015-01 "IRON-MAG" is gratefully acknowledged.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
PSSW Perpendicular standing spin waves
FMR ferromagnetic resonance

Appendix A

In this appendix, we present a derivation of equations 12 and 13, starting from equations 6-10. We consider the resonant interaction regime between any two phonon-magnon modes p and n, ie. when the driving force frequency ω p is equal to the magnon frequency ω n , thus we neglect the contribution of any other phonon-magnon pair. In this case, the driving force is simply given by
f n ( t ) = A e − β p ω p t cos ω p t = A 2 e ( − β p + i ) ω t + A 2 e ( − β p − i ) ω p t
Where the driving force amplitude is A = P n ( H ) I n p a p . The standard approach is to find first a driven solution of equation 6, then superpose with an eigensolution of the associated homogeneous equation such that the total solution obeys the initial time conditions s z ( 0 ) = 0 and d s z d t ( 0 ) = 0 . Let us find the driven solution associated to each term. For the first term, let us seek a solution of the form s z 1 = B e ( − β p + i ) ω p t . Plugging this back into equation 6, we find the following condition on B:
[ 2 i ( α − β p ) + β p 2 − 2 α β p ] ω p 2 B = A 2
Given the typical values of α and β p , on the order of 10 − 2 , we can distinguish two different regimes. When the difference between α and β p is large, as is the case for most experimental applications, the terms β p 2 and 2 α β p can be neglected. On the other hand, the case where α ≈ β p yields qualitatively different behavior. We will start with the analysis of the first case. The amplitude of the driven solution s z 1 is given by
B = A 4 i ω p 2 ( α − β p )
By following a similar approach for the second term in the driving force, the total driven solution of equation 6 can be expressed as
s z , d = A 2 ω p 2 ( α − β p ) e − β p ω p t sin ω p t
Keeping in mind the initial conditions on s z and its time derivative, we find the following suitable eigensolution of equation 6.
s z , e = − A 2 ω p 2 ( α − β p ) e − α ω p t sin ω p t
Finally, the solution of the driven magnon oscillator reads
s z = A 2 ω p 2 ( α − β p ) [ e − β p ω p t − e − α ω p t ] sin ω p t
We note that the above equation contains a sinusoidal oscillation, with an amplitude depending on time as e − β p ω p t − e − α ω p t . Given that the oscillation is usually significantly faster than the time scales of amplitude evolution, we can assume that the maximum of s z is given by the maximum of the amplitude envelope, whose expression is
s z , m a x ( n p ) ( L ) = A ω p 2 A m a x ( α , β p ) ,
Here, the factor A m a x ( α , β p ) captures the maximal value of the envelope, given by
A m a x ( α , β p ) = 1 2 α α β p − β p α − β p .
Which finishes our proof.
From an experimental point of view, the value of the parameter β p can be varied by changing the film thickness L, given the quadratic dependency of the acoustic damping γ p on the acoustic frequencies ω p . Indeed, the frequency of the p acoustic mode scales inversely proportional to the film thickness L, according to
ω p ( L ) = c s π p L
Assuming a quadratic dependence of γ p on ω p , given by γ p = G ω p 2 , we get that the damping coefficient β p corresponding to mode p also scales inversely proportional to the film thickness
β p ( L ) = G ω p ( L )
Finally, we note that even though the derivation assumes that there is a large difference between α and β p , we note that the solution is extendable by continuity around α = β p . A numerical study showed that there is no peculiar behavior in this region, such that the solution can still be considered as valid.

References

  1. Scherbakov, A.V.; Salasyuk, A.S.; Akimov, A.V.; Liu, X.; Bombeck, M.; Brüggemann, C.; Yakovlev, D.R.; Sapega, V.F.; Furdyna, J.K.; Bayer, M. Coherent Magnetization Precession in Ferromagnetic (Ga,Mn)As Induced by Picosecond Acoustic Pulses. Phys. Rev. Lett. 2010, 105, 117204. [Google Scholar] [CrossRef]
  2. Thevenard, L.; Peronne, E.; Gourdon, C.; Testelin, C.; Cubukcu, M.; Charron, E.; Vincent, S.; Lemaître, A.; Perrin, B. Effect of picosecond strain pulses on thin layers of the ferromagnetic semiconductor (Ga,Mn)(As,P). Phys. Rev. B 2010, 82, 104422. [Google Scholar] [CrossRef]
  3. Kim, J.W.; Vomir, M.; Bigot, J.Y. Ultrafast magnetoacoustics in nickel films. Phys. Rev. Lett. 2012, 109, 166601. [Google Scholar] [CrossRef] [PubMed]
  4. Yang, W.G.; Schmidt, H. Acoustic control of magnetism toward energy-efficient applications. Applied Physics Reviews 2021, 8, 021304. [Google Scholar] [CrossRef]
  5. Vlasov, V.S.; Golov, A.V.; Kotov, L.N.; Shcheglov, V.I.; Lomonosov, A.M.; Temnov, V.V. The modern problems of ultrafast magnetoacoustics (Review). Acoustical Physics 2022, 68, 18–47. [Google Scholar] [CrossRef]
  6. Kovalenko, O.; Pezeril, T.; Temnov, V.V. New concept for magnetization switching by ultrafast acoustic pulses. Phys. Rev. Lett. 2013, 110, 266602. [Google Scholar] [CrossRef]
  7. Vlasov, V.S.; Lomonosov, A.M.; Golov, A.V.; Kotov, L.N.; Besse, V.; Alekhin, A.; Kuzmin, D.A.; Bychkov, I.V.; Temnov, V.V. Magnetization switching in bistable nanomagnets by picosecond pulses of surface acoustic waves. Phys. Rev. B 2020, 101, 024425. [Google Scholar] [CrossRef]
  8. Bombeck, M.; Salasyuk, A.S.; Glavin, B.A.; Scherbakov, A.V.; Brüggemann, C.; Yakovlev, D.R.; Sapega, V.F.; Liu, X.; Furdyna, J.K.; Akimov, A.V.; Bayer, M. Excitation of spin waves in ferromagnetic (Ga,Mn)As layers by picosecond strain pulses. Phys. Rev. B 2012, 85, 195324. [Google Scholar] [CrossRef]
  9. Van Kampen, M.; Jozsa, C.; Kohlhepp, J.; LeClair, P.; Lagae, L.; De Jonge, W.; Koopmans, B. All-optical probe of coherent spin waves. Phys. Rev. Lett. 2002, 88, 227201. [Google Scholar] [CrossRef] [PubMed]
  10. Razdolski, I.; Alekhin, A.; Ilin, N.; Meyburg, J.P.; Roddatis, V.; Diesing, D.; Bovensiepen, U.; Melnikov, A. Nanoscale interface confinement of ultrafast spin transfer torque driving non-uniform spin dynamics. Nature communications 2017, 8, 15007. [Google Scholar] [CrossRef]
  11. Besse, V.; Golov, A.V.; Vlasov, V.S.; Alekhin, A.; Kuzmin, D.; Bychkov, I.V.; Kotov, L.N.; Temnov, V.V. Generation of exchange magnons in thin ferromagnetic films by ultrashort acoustic pulses. J. Magn. Magn. Mater. 2020, 502, 166320. [Google Scholar] [CrossRef]
  12. Kim, J.W.; Bigot, J.Y. Magnetization precession induced by picosecond acoustic pulses in a freestanding film acting as an acoustic cavity. Phys. Rev. B 2017, 95, 144422. [Google Scholar] [CrossRef]
  13. Ghita, A.; Mocioi, T.G.; Lomonosov, A.M.; Kim, J.; Kovalenko, O.; Vavassori, P.; Temnov, V.V. Anatomy of ultrafast quantitative magnetoacoustics in freestanding nickel thin films. Phys. Rev. B 2023, 107, 134419. [Google Scholar] [CrossRef]
  14. Lomonosov, A.M.; Temnov, V.V.; Wegrowe, J.E. Anatomy of inertial magnons in ferromagnetic nanostructures. Physical Review B 2021, 104, 054425. [Google Scholar] [CrossRef]
  15. Kimel, A.; Zvezdin, A.; Sharma, S.; Shallcross, S.; De Sousa, N.; García-Martín, A.; Salvan, G.; Hamrle, J.; Stejskal, O.; McCord, J.; et al. The 2022 magneto-optics roadmap. Journal of Physics D: Applied Physics 2022, 55, 463003. [Google Scholar] [CrossRef]
  16. Li, J.; Yang, C.J.; Mondal, R.; Tzschaschel, C.; Pal, S. A perspective on nonlinearities in coherent magnetization dynamics. Applied Physics Letters 2022, 120, 050501. [Google Scholar] [CrossRef]
  17. Tas, G.; Maris, H.J. Electron diffusion in metals studied by picosecond ultrasonics. Physical Review B 1994, 49, 15046. [Google Scholar] [CrossRef]
  18. Temnov, V.V. Ultrafast acousto-magneto-plasmonics. Nature Photonics 2012, 6, 728–736. [Google Scholar] [CrossRef]
  19. Lin, Z.; Zhigilei, L.V.; Celli, V. Electron-phonon coupling and electron heat capacity of metals under conditions of strong electron-phonon nonequilibrium. Physical Review B 2008, 77, 075133. [Google Scholar] [CrossRef]
  20. Saito, T.; Matsuda, O.; Wright, O. Picosecond acoustic phonon pulse generation in nickel and chromium. Physical Review B 2003, 67, 205421. [Google Scholar] [CrossRef]
  21. Vernik, U.; Lomonosov, A.M.; Vlasov, V.S.; Kotov, L.N.; Kuzmin, D.A.; Bychkov, I.V.; Vavassori, P.; Temnov, V.V. Resonant phonon-magnon interactions in free-standing metal-ferromagnet multilayer structures. Physical Review B 2022, 106, 144420. [Google Scholar] [CrossRef]
  22. Deb, M.; Popova, E.; Hehn, M.; Keller, N.; Mangin, S.; Malinowski, G. Picosecond acoustic-excitation-driven ultrafast magnetization dynamics in dielectric Bi-substituted yttrium iron garnet. Phys. Rev. B 2018, 98, 174407. [Google Scholar] [CrossRef]
  23. Soumah, L.; Beaulieu, N.; Qassym, L.; Carrétéro, C.; Jacquet, E.; Lebourgeois, R.; Ben Youssef, J.; Bortolotti, P.; Cros, V.; Anane, A. Ultra-low damping insulating magnetic thin films get perpendicular. Nature communications 2018, 9, 3355. [Google Scholar] [CrossRef]
  24. An, K.; Litvinenko, A.N.; Kohno, R.; Fuad, A.A.; Naletov, V.V.; Vila, L.; Ebels, U.; de Loubens, G.; Hurdequint, H.; Beaulieu, N.; et al. Coherent long-range transfer of angular momentum between magnon Kittel modes by phonons. Physical Review B 2020, 101, 060407. [Google Scholar] [CrossRef]
  25. An, K.; Kohno, R.; Litvinenko, A.N.; Seeger, R.L.; Naletov, V.V.; Vila, L.; de Loubens, G.; Youssef, J.B.; Vukadinovic, N.; Bauer, G.E.; et al. Bright and dark states of two distant macrospins strongly coupled by phonons. Physical Review X 2022, 12, 011060. [Google Scholar] [CrossRef]
Preprints 75764 g001
Figure 1. (a) Femtosecond laser excitation of a freestanding nickel membrane generates the thermal strain ∝ exp − z / h launching acoustic pulses and precessional magnetization dynamics. Both dynamics can be decomposed in (b) acoustic phonon modes and (c) magnon modes.
Figure 1. (a) Femtosecond laser excitation of a freestanding nickel membrane generates the thermal strain ∝ exp − z / h launching acoustic pulses and precessional magnetization dynamics. Both dynamics can be decomposed in (b) acoustic phonon modes and (c) magnon modes.
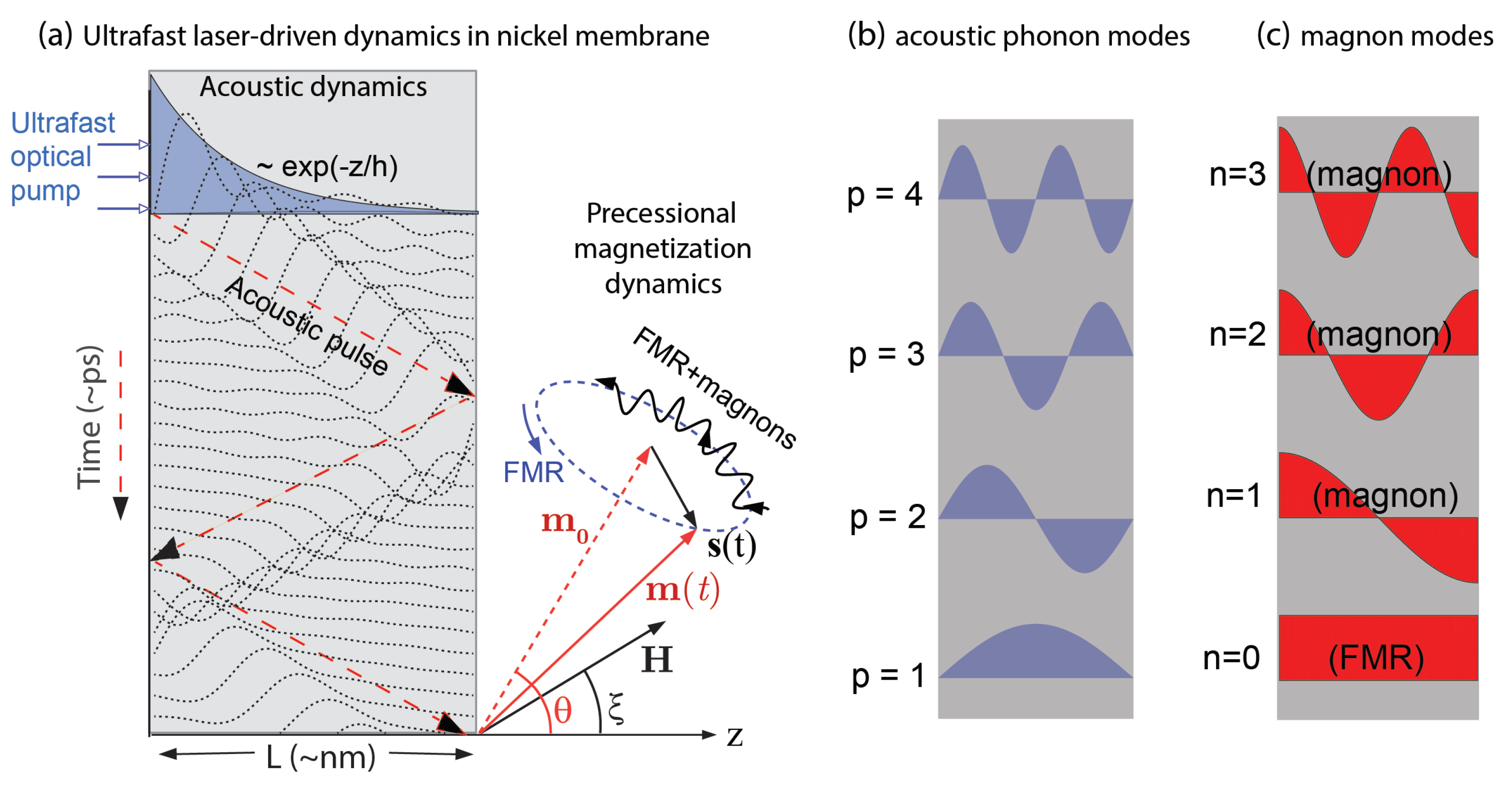
Preprints 75764 g001
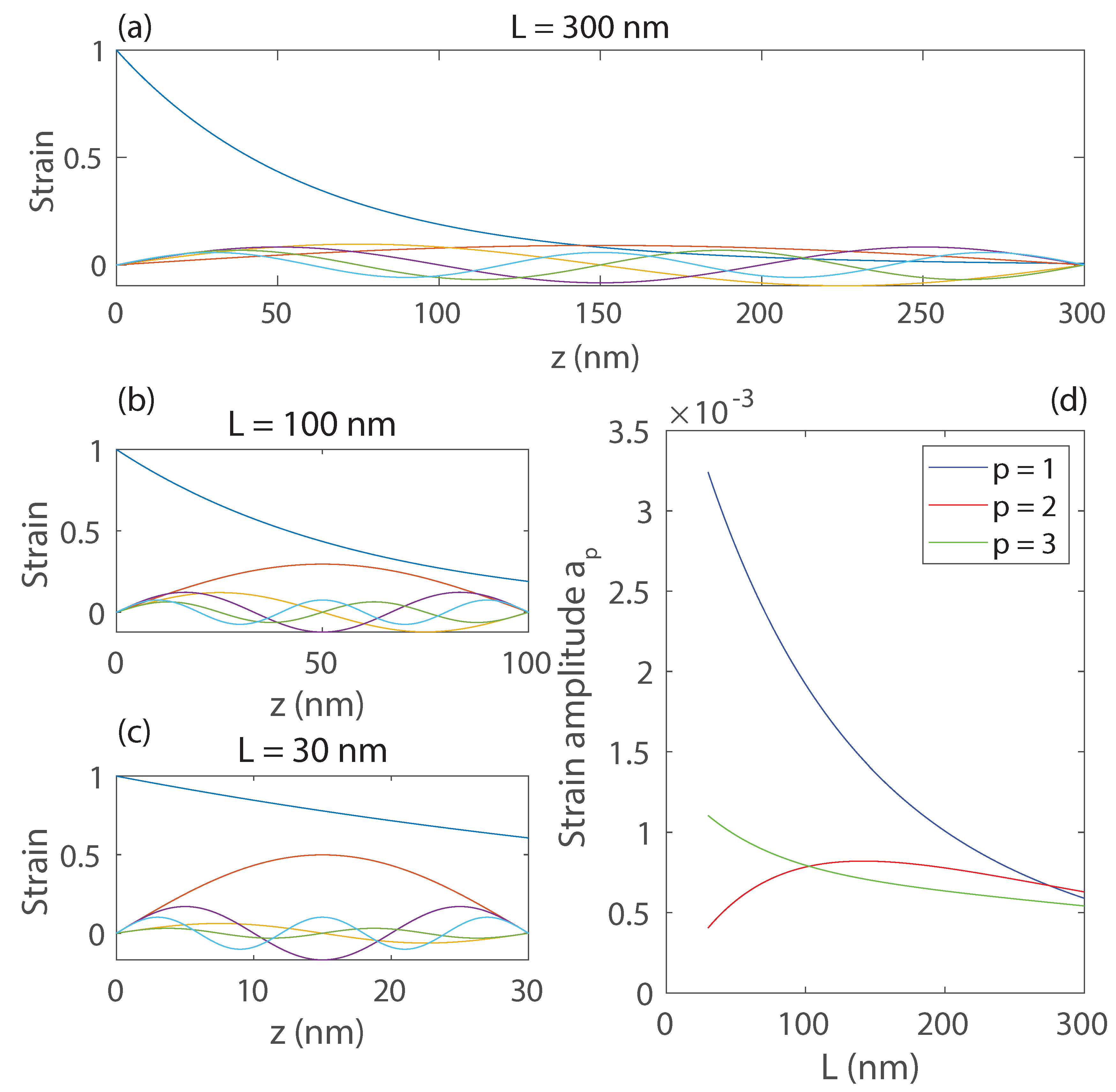
Preprints 75764 g002
Figure 2. Illustration of the first few acoustic eigenmode profiles (normalized) for (a) L = 300 nm, (b) L = 100 nm and (c) L = 30 nm. (d) Strain amplitudes a p ( L ) , for the first three modes p = 1 , 2 , 3 .
Figure 2. Illustration of the first few acoustic eigenmode profiles (normalized) for (a) L = 300 nm, (b) L = 100 nm and (c) L = 30 nm. (d) Strain amplitudes a p ( L ) , for the first three modes p = 1 , 2 , 3 .
Preprints 75764 g002
Preprints 75764 g003
Figure 3. Magneto-acoustic resonances of different acoustic order p and magnetic order n behave differently as the thickness of a freestanding nickel layer decreases. Acoustically-driven magnetization precession of p = 1 -driven n = 0 (FMR) and p = 2 -driven n = 1 (magnon) precession, for different values of film thickness L ( L = 300 nm, L = 150 nm, L = 75 nm, L = 50 nm and L = 37.5 nm). The required magnetic field values are indicated next to each curve.
Figure 3. Magneto-acoustic resonances of different acoustic order p and magnetic order n behave differently as the thickness of a freestanding nickel layer decreases. Acoustically-driven magnetization precession of p = 1 -driven n = 0 (FMR) and p = 2 -driven n = 1 (magnon) precession, for different values of film thickness L ( L = 300 nm, L = 150 nm, L = 75 nm, L = 50 nm and L = 37.5 nm). The required magnetic field values are indicated next to each curve.
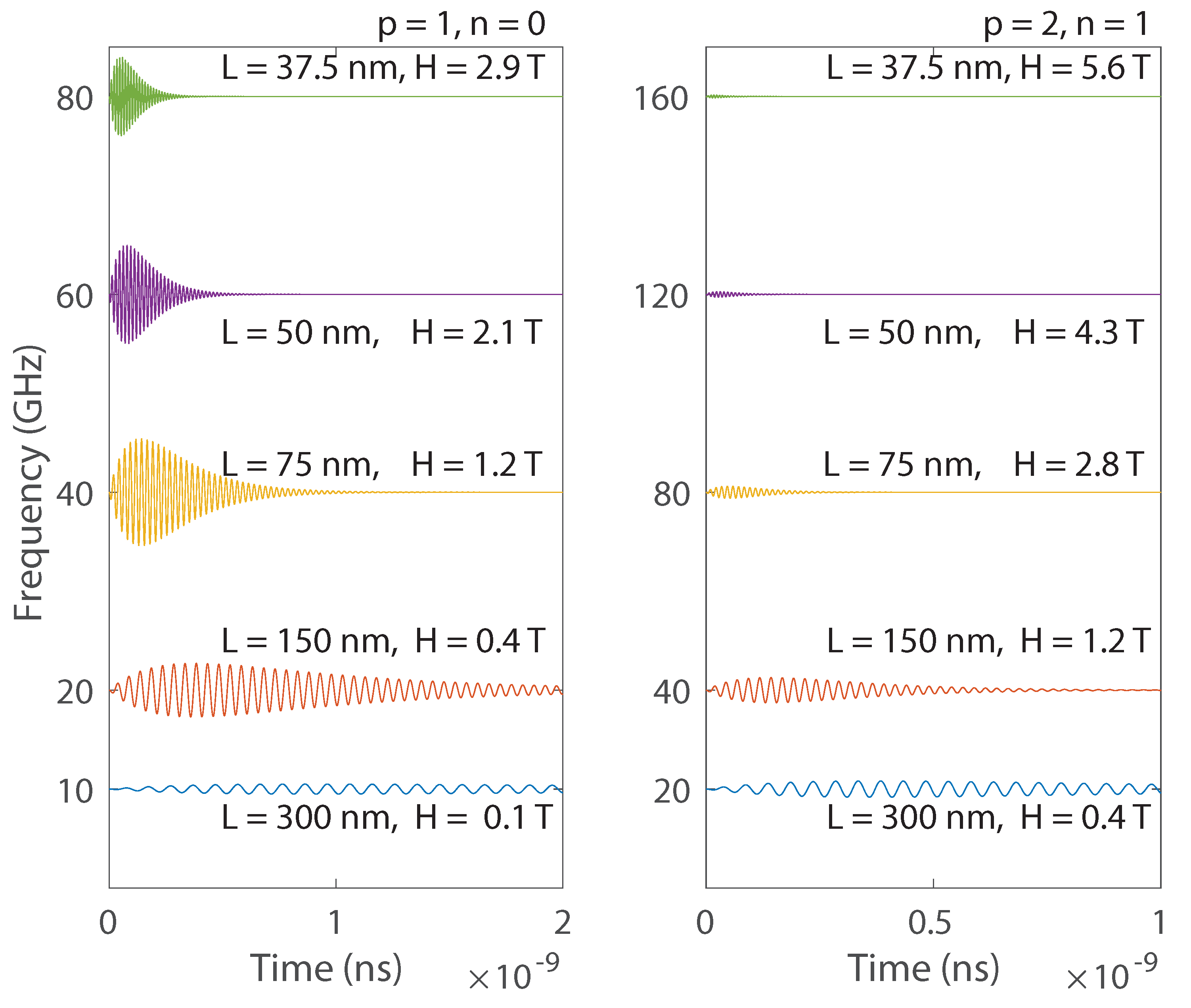
Preprints 75764 g003
Preprints 75764 g004
Figure 4. (a) Peak magnetization amplitudes dependence on film thickness, for different phonon-magnon pairs ( p , n ). (b) Magnetic field necessary for resonant interaction versus film thickness, for different phonon-magnon pairs ( p , n ). The inset shows the same graph, restricted to experimentally feasible magnetic fields in the range 0 T - 2 T and to film thicknesses between 0 - 50 nm. A prominent feature is the sudden fall to zero of the magnetic field necessary to achieve a magnon resonance, for film thicknesses of 16 nm ( p = 1 , n = 0 and p = 2 , n = 1 ) and 3 nm respectively ( p = 3 , n = 0 ).
Figure 4. (a) Peak magnetization amplitudes dependence on film thickness, for different phonon-magnon pairs ( p , n ). (b) Magnetic field necessary for resonant interaction versus film thickness, for different phonon-magnon pairs ( p , n ). The inset shows the same graph, restricted to experimentally feasible magnetic fields in the range 0 T - 2 T and to film thicknesses between 0 - 50 nm. A prominent feature is the sudden fall to zero of the magnetic field necessary to achieve a magnon resonance, for film thicknesses of 16 nm ( p = 1 , n = 0 and p = 2 , n = 1 ) and 3 nm respectively ( p = 3 , n = 0 ).
Preprints 75764 g004
Preprints 75764 g005
Figure 5. (a) Magnetization dynamics for L = 16 nm thick film, under the magnetic fields H 1 = 0.15 T, H 2 = 0.75 T and H 3 = 2.15 T. The magnetization precession at H 2 presents all the characteristic features of the above-discussed resonant behavior. The precession under the field H 1 is very weak, while the precession at H 3 displays a sharp, strong initial excitation, that quickly dies out and decays into an irregular beating pattern. (b) The absolute value of the Fourier transform of s z ( t ) displays the magneto-acoustic resonant landscape for L = 16 nm. Dashed white lines show acoustic frequencies and solid white lines show magnon dispersion according to Eq. (5). The solid blue line displays cross section at the p = 1 acoustic frequency and is interpreted as the magnetic field dependence of the n = 2 resonance driven by the acoustic p = 1 -mode.
Figure 5. (a) Magnetization dynamics for L = 16 nm thick film, under the magnetic fields H 1 = 0.15 T, H 2 = 0.75 T and H 3 = 2.15 T. The magnetization precession at H 2 presents all the characteristic features of the above-discussed resonant behavior. The precession under the field H 1 is very weak, while the precession at H 3 displays a sharp, strong initial excitation, that quickly dies out and decays into an irregular beating pattern. (b) The absolute value of the Fourier transform of s z ( t ) displays the magneto-acoustic resonant landscape for L = 16 nm. Dashed white lines show acoustic frequencies and solid white lines show magnon dispersion according to Eq. (5). The solid blue line displays cross section at the p = 1 acoustic frequency and is interpreted as the magnetic field dependence of the n = 2 resonance driven by the acoustic p = 1 -mode.
Preprints 75764 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated