Prerpints.org logo
Preprint
Article

Further Explanation on the Excitation Mechanism of Stay Cable Vibration in Dry Conditions

Altmetrics

Downloads

101

Views

20

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

06 June 2023

Posted:

07 June 2023

You are already at the latest version

Alerts
Abstract
This article presents a study conducted within a wind tunnel to enhance understanding of the excitation mechanism of stay cable vibration under arid conditions. Numerous wind tunnel tests were meticulously analyzed. Initially, the vibration of the stay cable was measured under steady flow conditions at a flow angle of 45 degrees and an inclination of 25 degrees, while varying wind velocities were applied. Additionally, an investigation into the flow field surrounding the stay cable was conducted in both vertical and horizontal directions. By utilizing two hot wire anemometers in the cable wake, an extensive database of flow field measurements was obtained. The experimental results revealed that the vibration characteristics of the stay cable under the arid conditions considered in this study aligned with findings reported in existing literature. Notably, a deeper comprehension of the excitation mechanism of a stay cable in a dry state was attained. This mechanism is closely associated with the inhibition of Karman vortices and the development of low-frequency vortices. At low wind speeds, Karman vortices predominated, resulting in small-amplitude vibrations. However, as the wind speed increased, the influence of Karman vortices diminished progressively, while the low-frequency vortices grew stronger. These low-frequency vortices exhibited high energy and a significant correlation with shedding along the stay cable, thereby inducing cable vibration in a dry environment.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Stay cable vibration due to wind can be divided into several categories. The critical wind speed range, cable angles, rain volume, magnitude of vibration, and dynamic properties of the cable are just a few variables that may have an impact on the excitation of stay cables. Dry-state galloping (DSG) is a recent phenomenon that causes dangerous cable vibration in arid environments [1,2,3,4,5]. DSG is a wind-induced vibration phenomenon characterized by significant amplitude. This phenomenon is typically observed during dry weather conditions and is often associated with high wind speeds. Despite the observation of significant amplitude in cable vibrations in various field studies [4,5,6,7,8], no on-site measurements were conducted to comprehensively comprehend the underlying cause. The phenomenon in question has been demonstrated through recent research utilizing both field observations and wind tunnel testing. The complete comprehension of its qualities poses a challenge. The study conducted in the wind tunnel has also determined the presence of DSG (dynamic stall generation) in the stay cable, as reported in references [9,10,11,12,13,14,15]. Hence, it is imperative to acknowledge its occurrence on stay-cable bridges. In DSG, it is possible to differentiate between two distinct types of cable vibration. The initial type of vibration is denoted as possessing a restricted amplitude and is denominated "limited amplitude vibration". The second type of galloping is known as divergent galloping, which pertains to the erratic oscillation of a cable. The occurrence of divergent galloping is conjoined with the presence of adverse aerodynamic damping. When the magnitude of damping is significant enough to exceed the positive structural damping, it leads to a negative effective damping of the cable. As a result, the amplitude of the oscillation will experience a significant increase, resulting in a motion that demonstrates divergence. Consequently, the quantification of the aerodynamic damping of a stay cable could serve as a valuable approach for comprehending the mechanics of DSG. The evaluation of the aerodynamic dampening of a vibration cable subjected to wind forces is frequently conducted through the utilization of the conventional Den-Hartog criteria [16]. Macdonald et al. [17] extended the conventional Den Hartog theory to enable its application to a cylindrical structure undergoing vibration in any direction perpendicular to its axis and possessing any cross-sectional shape. In addition, Piccardo et al. [18] proposed a dynamic model of inclined full-scale stay-cables under the effect of yawed steady wind, which is able to induce DSG. Nevertheless, Qingkuan Liu et al. [19] conducted a study to investigate the impact of modifications in the cross-sectional configuration of stay cables. Specifically, they compared the performance of micro-elliptical sections with that of circular cylinders. The results of their study revealed that the regions of galloping that were anticipated based on the quasi-steady hypothesis did not demonstrate a satisfactory correlation with the actual vibrations that were observed. Consequently, the utilization of the quasi-steady assumption as a prediction method is unsuitable for precise prognostication of the detected vibrations.
Parallel to this, Nakamura et al. [20] proposed that the phenomenon of galloping can be explained by the interference of the separation flows around a bluff body, leading to a balance of pressure on both the upper and lower surfaces of the cable due to the interaction of these distinct flows. Matsumoto et al. [4] conducted wind tunnel experiments to clarify the function of axial flow in galloping instability by introducing natural and artificial axial flow in the wake of the cable. The empirical results unambiguously indicate that the existence of axial flow in the wake has the potential to trigger galloping. Matsumoto et al. [21] have previously reported the identification of axial flow in physical bridge configurations through the use of light strings as representations of prototype stay cables. Nonetheless, the fundamental concepts that regulate axial flow are not yet fully comprehended. The study conducted by Nikitas et al. [14] revealed that the flow pattern's transitional behavior in the critical Reynolds number range, along with its interaction with wind turbulence and inclination angle, has a notable impact on the incidence of dry galloping. The occurrence of an unusual dynamic response necessitates a blend of quasi-steady features and unsteadiness, like the wake-induced vibration phenomenon. Significant findings include abrupt alterations in movement, inconsistent temporal gaps between loading and movement, and a wind-generated force element displaying traits similar to rigidity. McTavish et al. [22] conducted a wind tunnel experiment to examine the aerodynamic characteristics of stay cables with varying surface geometries in a dry environment. Nevertheless, the precise mechanism underlying the action of DSG remains incompletely comprehended.
Prior research has offered limited understanding regarding the attributes of DSG, utilizing diverse approaches to examine this occurrence. However, comprehension of the excitation mechanism that is responsible for the vibration of circular cylinders induced by wind in arid conditions is still restricted. Moreover, the flow regime encompassing the cable in the context of Deep Sea Gravity (DSG) events is predominantly obscure. The aim of this investigation is to improve our understanding of the excitation mechanism in DSG, with a particular focus on circular cables.

2. Experimental setting up

2.1. Wind tunnel and cable model

The wind tunnel employed in this investigation is an open-circuit wind tunnel that incorporates a working section with measurements of 1.3 meters in width and 1.3 meters in height. The apparatus possesses the capacity to perform experiments while maintaining consistent flow conditions, characterized by elevated flow velocities of up to 20 meters per second. The present study involved the vertical plane support of a circular cylinder with a single degree of freedom. The assessment of turbulence intensity was conducted within the wind tunnel to ensure the homogeneity of the flow field.
The manipulation of the suspended cable frame through two distinct angles, namely the inclined angle () and the horizontal angle (), can enable the simulation of cable orientation. The predetermined angle of 25° was conjoined with a horizontal angle of 45°. A standard practice in the design of cable-stayed bridges involves selecting an inclined angle of 25° to accommodate the inclination of the stay cables that are situated at the apex of the tower.
Preprints 75854 g001
Figure 1. Cable model in wind tunnel.
Figure 1. Cable model in wind tunnel.
Preprints 75854 g001

2.2. Wind flow profile

The analysis of turbulence intensity was conducted within the wind tunnel to ascertain the homogeneity of the flow field. The flow conditions were assessed by means of a hot wire anemometer located at the position of the cylinder prototype. Based on the findings of the measurements, a range of turbulence levels around 0.5%-0.6% were detected across various wind velocities, as presented in Table 1. Wind speed measurements were obtained at each site using a hot wire apparatus, as depicted in Figure 2. This allowed for the verification of the wind speed differential between the wind tunnel entrance, where the cable model was positioned, and the interior of the wind tunnel, where the Pitot tube was situated. Table 2 presents a comparison of wind speeds at different locations, indicating that wind speeds at two distinct sites are generally similar. The wind speed ratio (U1/U2) at the cable position has been estimated to be approximately 1.03, based on the analysis of wind speeds spanning from 3 to 20 meters per second.

2.3. Experimental parameters

Table 2 provides a detailed overview of the experimental parameters, including the cable diameters measuring 158mm and the effective model length of 1.5m. In both instances, the aspect ratio measures 9.5. The logarithmic decrement denotes that the damping exhibits variability within the range of around 0.5% to 1.6%. The empirical data indicates that the customary magnitude of factual stay cables implies that the inherent frequency falls within the range of roughly 0.8 to 1 Hz. The maximum wind speed attainable is 20 meters per second, which is equivalent to a Reynolds number of approximately 2.1 x 105.
The phenomenon of DSG reproduction in a wind tunnel for stay cables is depicted in Figure 3. The stay cable exhibited oscillations of restricted magnitude at lower wind velocities. Nevertheless, once the wind velocity attained a critical value of 10 meters per second, the cable exhibited a phenomenon commonly referred to as divergent galloping, wherein the amplitude escalates despite the constant wind speed. At a wind velocity of approximately 12 m/s, a maximum vibration amplitude of roughly 22cm was observed. It is noteworthy that the present cable model underwent testing with a significantly low damping ratio. Subsequently, the Dual-Clutch Transmission System (DSG) continues to operate at elevated wind velocities. The discovery mentioned above is consistent with prior research conducted by scholars [1,2,4].

3. Excitation mechanism of wind induced circular cylinder vibration

The flow pattern around the cable wake will be investigated to shed light on the galloping mechanism of a circular cylinder. The wavelet analysis on the vertical wind fluctuation component (w-component) and along the wind fluctuation component (u-component) will be performed to reveal the flow field pattern surrounding the cable wake.

3.1. Wake flow measurements

On the model, the fluctuating wind velocity after the inclined cable was measured. The vertical component of wind (w) and the horizontal component of wind in the direction of motion (u) will be taken into account. Cylindrical structures featuring a horizontal angle of 45 degrees and an inclination of 25 degrees were implemented within the wind tunnel. As illustrated in Figure 4, the hot wire anemometer sensor was situated at a distance of 2D from the cable discharge (Figure 4a) and at a distance of 0.5D from the cable axis (Figure 4b). The hot wire anemometer sensor was relocated from the upper side to the lower side of the cable at distances ranging from 2D to 7D. This setup enables the examination of the spatiotemporal fluctuations of wind velocity across different wind speeds.

3.2. Excitation mechanism of DSG

3.2.1. Wavelet-analysis on vertical-wind fluctuation component (w-component)

The Morlet wavelet function was utilized as the fundamental basis for the wavelet analysis conducted to examine the temporal fluctuations of wind velocity and the associated excitation mechanism. The wavelet analysis of fluctuating vertical-wind velocity near the discharge along the cable orientation is illustrated in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10. The wind tunnel maintains a constant mean wind speed of 5, 10, 15, and 20 meters per second. The wavelet analysis of fluctuating wind velocity in the vertical direction near the cable discharge for case 45-25 is illustrated in Figure 5, where the wind speed ranges from 5 meters per second to 20 meters per second. The graphical representation depicted in Figure 5a exhibits frequency peaks characterized by notably diminished periods. The conventional Karman vortex-induced vibration may be inferred from the calculated reduced velocity range of U/fvD = 5–10 for these peaks. According to observation, the Karman vortex only showed a very small amplitude of vibration for the stay cable. At a wind speed of U = 10 meters per second (as depicted in Figure 5b), it appears that the Karman vortex underwent a reduction while low-frequency vortices began to shed.
Figure 5c,d show that this type of pattern is also more apparent. When wind speed increased to 15 to 20 meters per second, Karman vortex scattering disappeared, and low-frequency vortices became dominant at the same time. In addition, the dominant vortex corresponds to reduced wind speed (U/fvD) around 110, which was likely driven by the wind-induced circular cylinder vibration phenomenon identified in earlier investigations [1,4]. This result is consistent with the large amplitude range illustrated in Figure 3. In addition, this trend was also observed in the discharge location from 3D to 7D (Figure 6–10). In brief, wake flow perturbation with extremely low-frequency vortices plays a crucial role in the mechanism that excites circular cylinder galloping. It is apparent that a significant quantity of low frequencies is present at high wind speeds. Furthermore, these low-frequency components exhibit high energy at high wind speeds. The phenomenon of circular cylinder vibration induced by wind can be succinctly described as follows: under low wind speeds, the dominant mechanism is the vibration induced by Karman vortex shedding. The Karman vortex is then eliminated as wind speed increases, and low-frequency vortices with high energy manifest. These low-frequency vortices continue to dissipate at higher wind speeds; the circular cylinder will be stimulated.

3.2.2. Wavelet-analysis on along-wind fluctuation component (u-component)

To gain a more comprehensive understanding of the flow field surrounding the circular cyl-inder, an examination of along-wind fluctuation (u-component) was undertaken. Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 illustrate the wavelet-analysis performed on the u-component at locations ranging from 2D to 7D. Remarkably, a similar mechanism was observed in the along-wind direction, indicating that the excitation of low-frequency vortices manifests in both the vertical and horizontal directions. Spe-cifically, it was observed that Karman vortex shedding occurred at low wind speeds in conjunction with low-frequency vortices (as depicted in Figure 11a,b), which dissipated as wind speeds increased. Conversely, low-frequency vortices commenced shedding at a certain wind speed threshold (as shown in Figure 11b,c,d).

3.3. Shedding correlation of wind flow in cable wake

Two hot wire anemometers were used to measure the wake flow along the cable to better understand the shedding correlation between wind flow near cable wake. The cross-spectral density's non-dimensional form of coherence, Coh2, is shown by:
C o h u 1 u 2 2 ( f ) = C u 1 u 2 ( f ) 2 C u 1 u 1 ( f ) × C u 2 u 2 ( f ) ≤ 1
The decay properties of the autocorrelation and cross-correlation coefficients are consistent with those of the corresponding functions. Moreover, the cross-spectral density and cross-covariance functions in the frequency domain exhibit equivalence. The identical description of the correlation, frequency content, and relative phases of the same frequencies between the two signals is apparent. The concept of coherence can be employed to determine a specific point at which the two signals exhibit a significant level of correlation [23].
Figure 17 depicts the correlation among wake flow fluctuations at distinct positions for different wind speeds. Obviously, the correlation at wind speeds between 5 and 10 meters per second is very high at reduced frequencies (fD/U) of approximately 0.2, which coincides with the Karman vortex shedding frequency. At 10 and 15 meters per second, the correlation of low-frequency flow gradually increased. At 20 meters per second, the correlation of the Karman vortex is already suppressed, while the low frequency becomes very high. The highest correlation at 20 meters per second is around 0.65 for locations 2D–7D. The results align with the wavelet analysis discussed in the previous section. The frequency range of fD/U, which was limited to 0.005-0.01, demonstrated a strong correlation with coherence levels exceeding 0.5 across different locations at a wind velocity of 20 meters per second. Furthermore, the correlation coefficient observed at the frequency of vortex-induced vibration is approximately 0.2 at a wind speed of 20 meters per second. To sum up, the variability in wind velocity characterized by low band frequency, high energy, and high correlation has the potential to generate significant excitation force, thereby triggering the galloping phenomenon in a circular cylinder. This observation is in accordance with the behavior of DSG's stay cable.

4. Conclusions

This research endeavor aims to enhance our comprehension of the excitation mechanism underlying wind-induced galloping of circular cylinders in dry environments. To achieve this objective, numerous tests have been conducted and extensively discussed to gain insights into the galloping phenomenon driven by wind. The current study presents the following key conclusions:
  • The study successfully reproduces both limited response and divergent galloping, which are characteristic responses of wind-induced vibration in dry conditions in circular cylinders.
  • Comprehensive measurements of the wake flow around the cylinders have been conducted, capturing both the vertical and horizontal wind fluctuation components. Additionally, wavelet analysis and coherence analysis have been employed to elucidate the flow field characteristics in the vicinity of the cylinder wake.
  • Under dry conditions, the formation of low-frequency dominant vortices and the suppression of Karman vortex shedding in the cylinder wake are closely associated with the process of wind-induced circular cylinder galloping.
  • At high wind speeds, there is a significant increase in the shedding correlation of low-frequency vortices. Conversely, as wind speed increased, the shedding correlation of the Karman vortex was progressively attenuated.
  • The low-frequency vortices exhibit high energy levels and demonstrate a strong temporal shedding correlation. Consequently, they have a significant excitation effect on the cylinder, contributing to its strong vibration response.

Author Contributions

Conceptualization, D.T. Nguyen (Duy Thao Nguyen) and D.H. Vo (Duy Hung Vo); methodology, D.H. Vo; software, D.T. Nguyen; validation, D.H. Vo; formal analysis, D.H. Vo; investigation, D.T. Nguyen and D.H. Vo; resources, D.H. Vo; data curation, D.T. Nguyen.; writing—original draft preparation, D.T. Nguyen and D.H. Vo; writing—review and editing, D.H. Vo; visualization, D.T. Nguyen; supervision, D.H. Vo.; project administration, D.H. Vo; funding acquisition, D.T. Nguyen and D.H. Vo. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by The University of Danang, University of Science and Technology, code number of project: T2022-02-24.

Data Availability Statement

The data presented in this study are available on request from the corresponding author. The data is not publicly available due to privacy considerations. Please contact the corresponding author before use.

Acknowledgments

The data presented in this study are available on request from the corresponding author. The data is not publicly available due to privacy considerations. Please contact the corresponding author before use.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Vo, H.D.; Katsuchi, H.; Yamada, H.; Nishio, M. A wind tunnel study on control methods for cable dry-galloping. Front. Struct. Civ. Eng. 2015, 10, 72–80. [Google Scholar] [CrossRef]
  2. Vo-Duy, H.; Nguyen, C.H. Mitigating Large Vibrations of Stayed Cables in Wind and Rain Hazards. Shock. Vib. 2020, 2020, 5845712. [Google Scholar] [CrossRef]
  3. J.B. Jakobsen, et al., Wind-induced response and excitation, characteristic of an inclined cable model in the critical Reynolds number range. J. Wind Eng. Ind. Aerodyn., 2012. 110: p. 100-112.
  4. Matsumoto, M.; Yagi, T.; Hatsuda, H.; Shima, T.; Tanaka, M.; Naito, H. Dry galloping characteristics and its mechanism of inclined/yawed cables. J. Wind. Eng. Ind. Aerodyn. 2010, 98, 317–327. [Google Scholar] [CrossRef]
  5. Ni, Y.; Wang, X.; Chen, Z.; Ko, J. Field observations of rain-wind-induced cable vibration in cable-stayed Dongting Lake Bridge. J. Wind. Eng. Ind. Aerodyn. 2007, 95, 303–328. [Google Scholar] [CrossRef]
  6. Zuo, D. and J.P. Jones, Interpretation of field observations of wind- and rain-wind-induced stay cable vibrations. J. Wind Eng. Ind. Aerodyn. 2010, 98(2): p. 73-87.
  7. Kumarasena, S. , et al., Wind Induced Vibration of Stay Cables, in Report No. FHWA-HRT-05-083, 2007, Federal Highway Administration: McLean, Virginia.
  8. Kusuhara, S. , Vibration and countermeasures for cable structure of Honshu-Shikoku bridges. The International Symposium on Flutter and its Application 2016, 2016. 1: p. CD Room.
  9. Saito, T., M. Matsumoto, and M. Kitazawa. Rain-wind Excitation of Cables on Cable-stayed Higashi-Kobe Bridge and Cable Vibration Control. in Proc. of Cable-stayed and Suspension Bridges. 1994.
  10. Honda, A. , et al. Wind tunnel test on rain-induced vibration of the stay cable. in Proceedings of International Symposium on Cable Dynamics. 1995. Lie`ge, Belgium.
  11. Miyata, T., H. Yamada, and T. Hojo. Aerodynamic response of PE stay cables with pattern-indented surface. In the International Conference on Cable-Stayed and Suspension Bridges (AFPC). 1994. Deauville, France.
  12. Cheng, S.; Larose, G.L.; Savage, M.G.; Tanaka, H.; Irwin, P.A. Experimental study on the wind-induced vibration of a dry inclined cable—Part I: Phenomena. J. Wind. Eng. Ind. Aerodyn. 2008, 96, 2231–2253. [Google Scholar] [CrossRef]
  13. J.B. Jakobsen, et al., Wind-induced response and excitation, characteristic of an inclined cable model in the critical Reynolds number range. J. Wind Eng. Ind. Aerodyn., 2012. 110: p. 100-112.
  14. Nikitas, N.; Macdonald, J. Aerodynamic forcing characteristics of dry cable galloping at critical Reynolds numbers. Eur. J. Mech. - B/Fluids 2015, 49, 243–249. [Google Scholar] [CrossRef]
  15. Kleissl, K.; Georgakis, C. Comparison of the aerodynamics of bridge cables with helical fillets and a pattern-indented surface. J. Wind. Eng. Ind. Aerodyn. 2012, 104-106, 166–175. [Google Scholar] [CrossRef]
  16. Den Hartog, J.P. , Mechanical Vibrations, 4th ed. 1956: McGraw-Hill, New York.
  17. Macdonald, J.; Larose, G. A unified approach to aerodynamic damping and drag/lift instabilities, and its application to dry inclined cable galloping. J. Fluids Struct. 2006, 22, 229–252. [Google Scholar] [CrossRef]
  18. Piccardo, G.; Zulli, D.; Luongo, A. Dry galloping in inclined cables: linear stability analysis. Procedia Eng. 2017, 199, 3164–3169. [Google Scholar] [CrossRef]
  19. Liu, Q.; Sun, Y.; Jia, Y.; Ma, W.; Xiao, B. Study on the characteristics and mechanisms of the wind-induced vibration of micro-elliptical section stay cables. J. Wind. Eng. Ind. Aerodyn. 2020, 206, 104355. [Google Scholar] [CrossRef]
  20. Nakamura, Y.; Hirata, K.; Urabe, T. Galloping of rectangular cylinders inthe presence of a splitter plate. J. Fluids Struct. 1991, 5, 521–549. [Google Scholar] [CrossRef]
  21. Matsumoto, M. , et al. Aerodynamic Behavior of Inclined Circular Cylinders Cable Aerodynamics. International Colloquium on Bluff Bodies Aerodynamics and Applications, 1990.
  22. McTavish, S.; D’auteuil, A.; Raeesi, A. Effect of cable surface characteristics and flow turbulence on the aerodynamic behaviour of stay cables in dry conditions. J. Wind. Eng. Ind. Aerodyn. 2020, 207, 104414. [Google Scholar] [CrossRef]
  23. Barltrop, N.D.P.; Adams, A.J. Dynamics of Fixed Marine Structures, 3rd ed.; Butterworth Heinemann: Oxford, UK, 1991. [Google Scholar]
Preprints 75854 g002
Figure 2. Wind speed calibration.
Figure 2. Wind speed calibration.
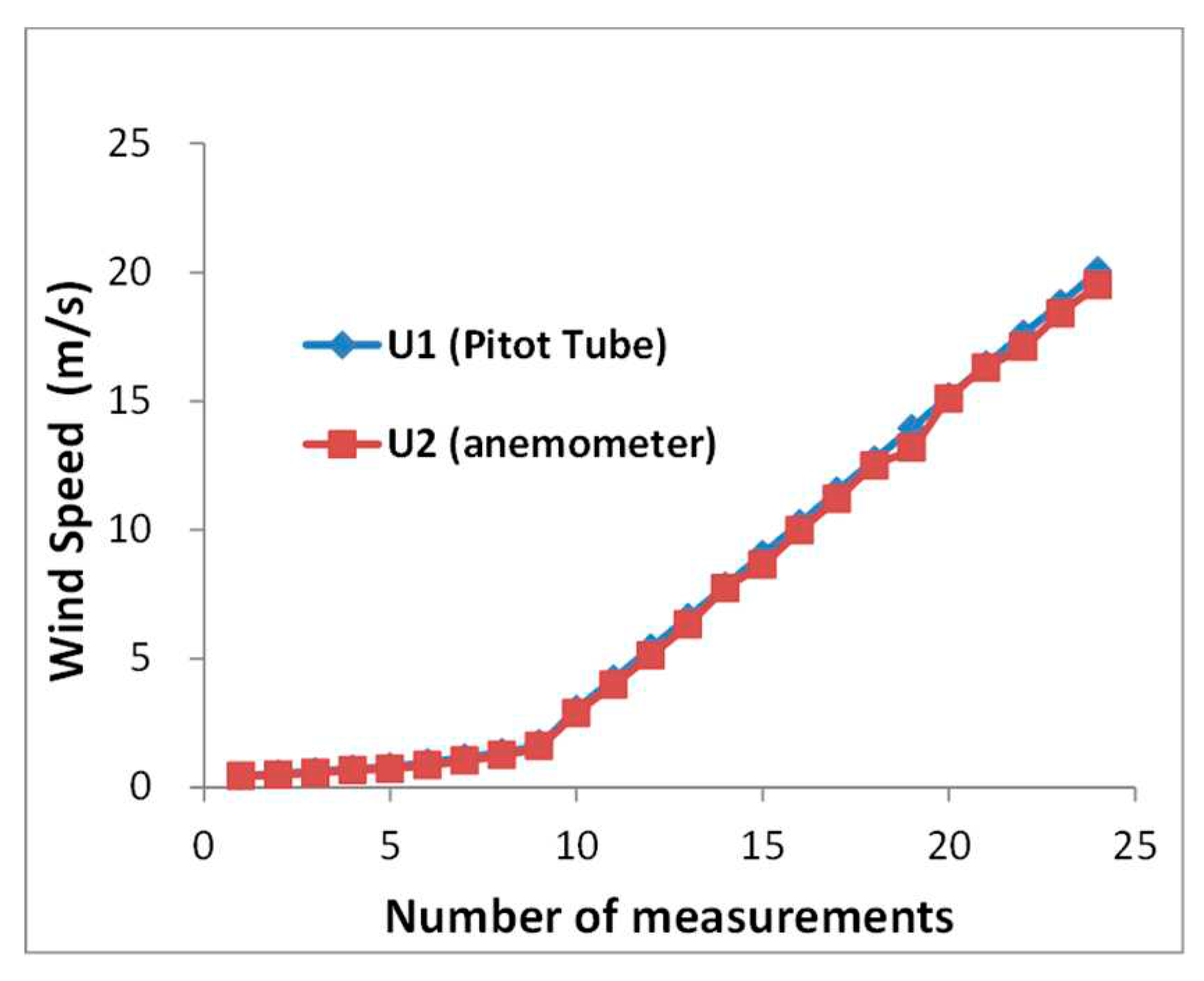
Preprints 75854 g002
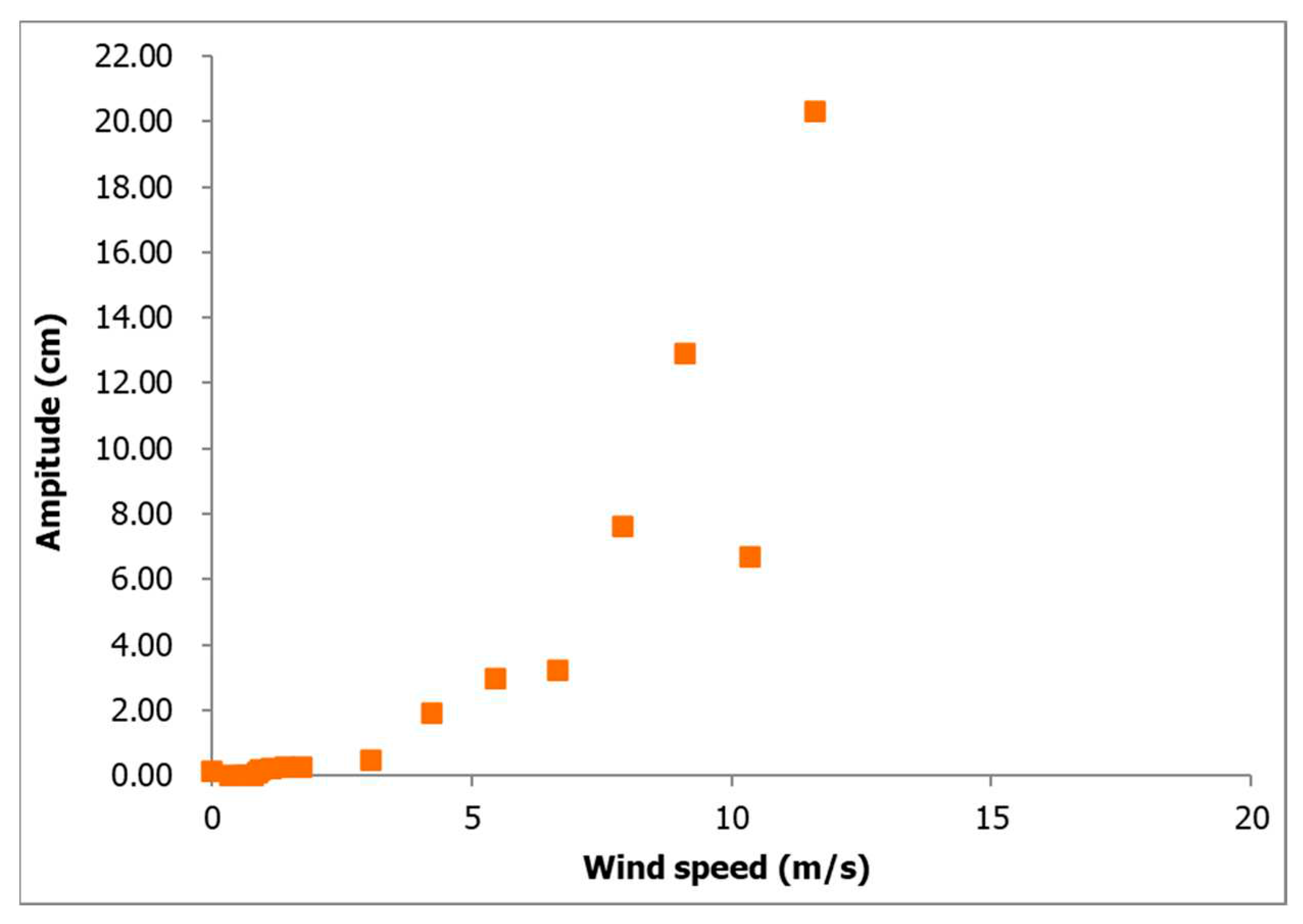
Preprints 75854 g003
Figure 3. Reproduction of DSG for stay cable in wind tunnel.
Figure 3. Reproduction of DSG for stay cable in wind tunnel.
Preprints 75854 g003
Preprints 75854 g004
Figure 4. Measurement of the flow field near cylinder wake.
Figure 4. Measurement of the flow field near cylinder wake.
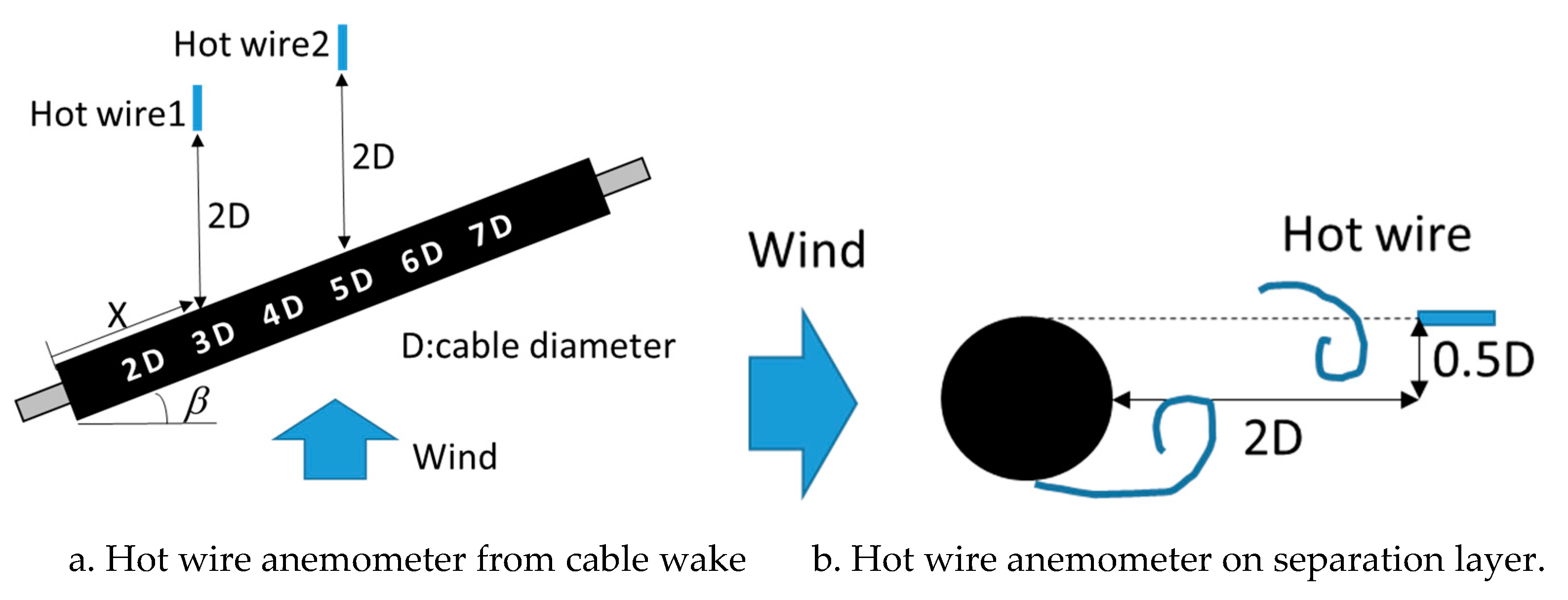
Preprints 75854 g004
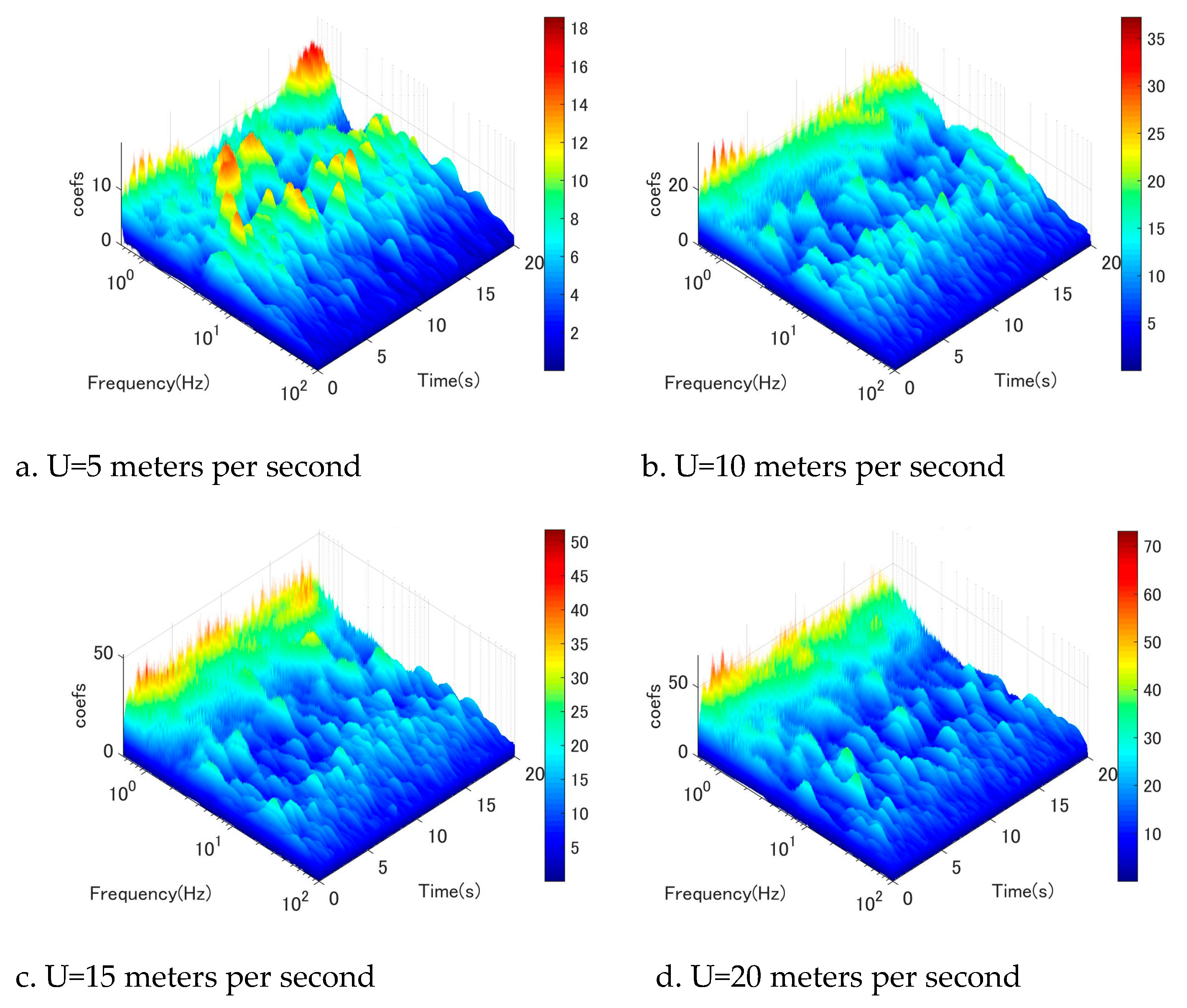
Preprints 75854 g005
Figure 5. Wavelet-analysis of wind velocity fluctuation at location 2D, w-component.
Figure 5. Wavelet-analysis of wind velocity fluctuation at location 2D, w-component.
Preprints 75854 g005
Preprints 75854 g006
Figure 6. Wavelet-analysis of wind velocity fluctuation at location 3D, w- component.
Figure 6. Wavelet-analysis of wind velocity fluctuation at location 3D, w- component.
Preprints 75854 g006
Preprints 75854 g007
Figure 7. Wavelet-analysis of fluctuating wind velocity at location 4D, w- component.
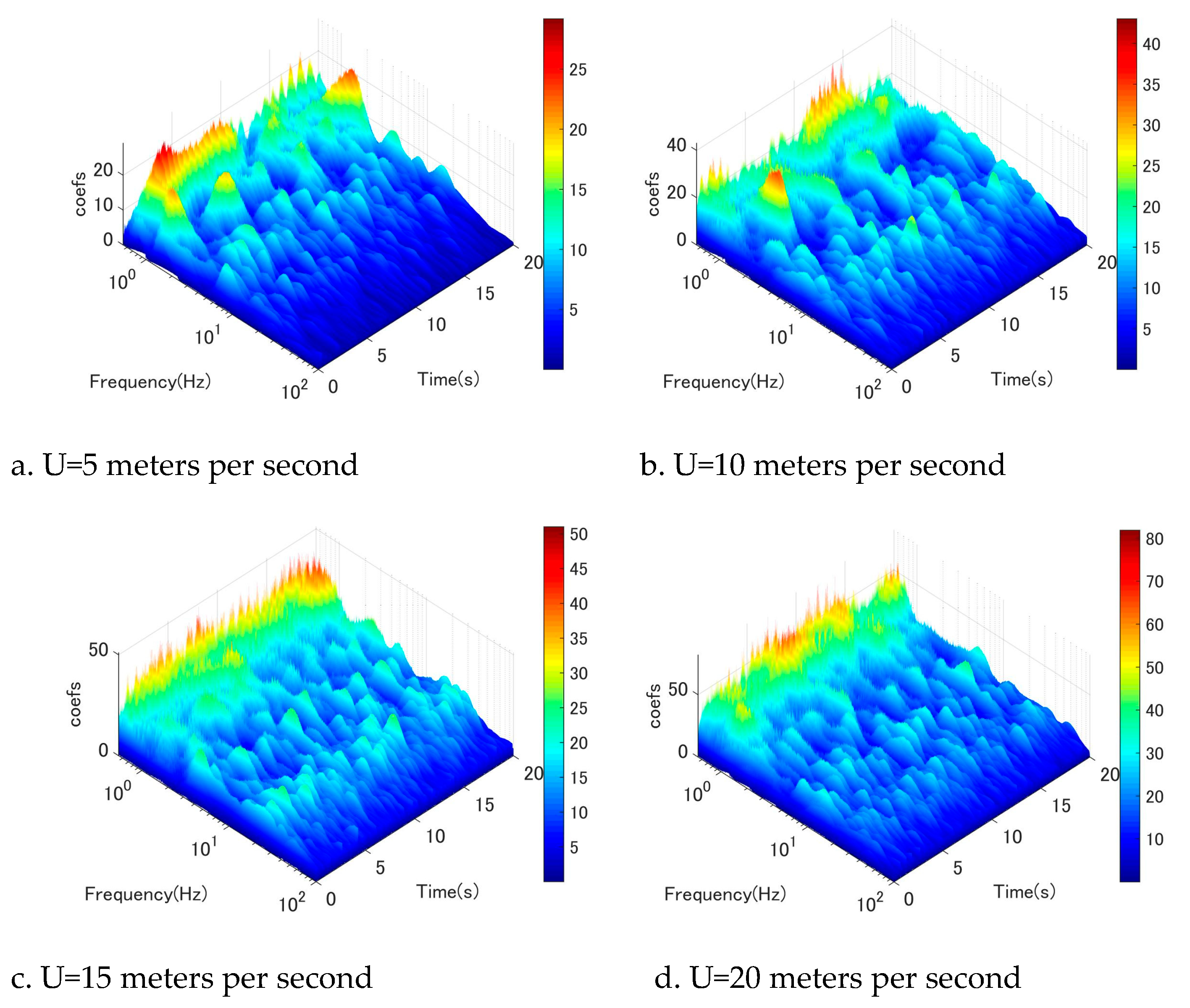
Figure 7. Wavelet-analysis of fluctuating wind velocity at location 4D, w- component.
Preprints 75854 g007
Preprints 75854 g008
Figure 8. Wavelet-analysis of fluctuating wind velocity at location 5D, w- component.
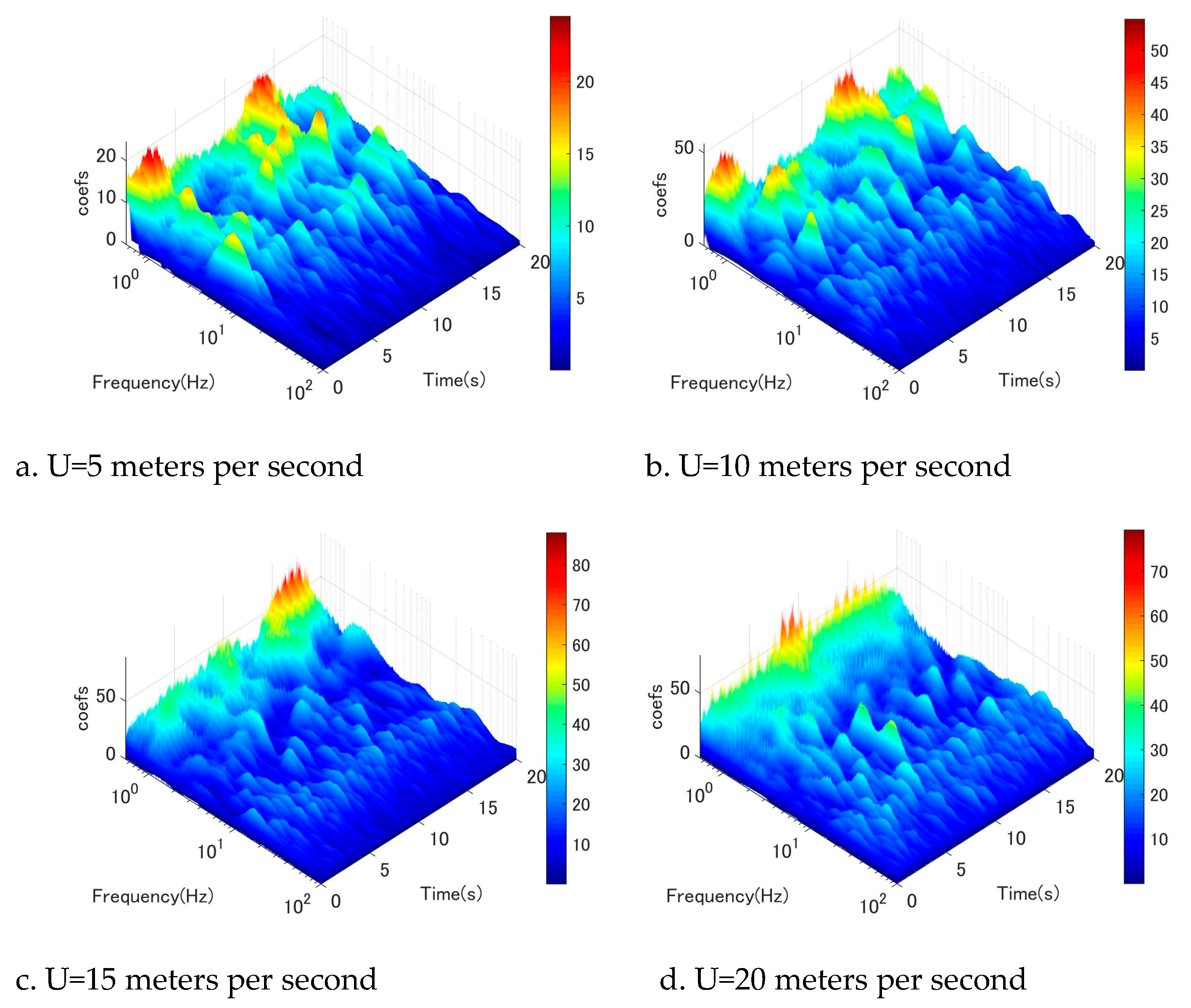
Figure 8. Wavelet-analysis of fluctuating wind velocity at location 5D, w- component.
Preprints 75854 g008
Preprints 75854 g009
Figure 9. Wavelet-analysis of fluctuating wind velocity at location 6D, w- component.
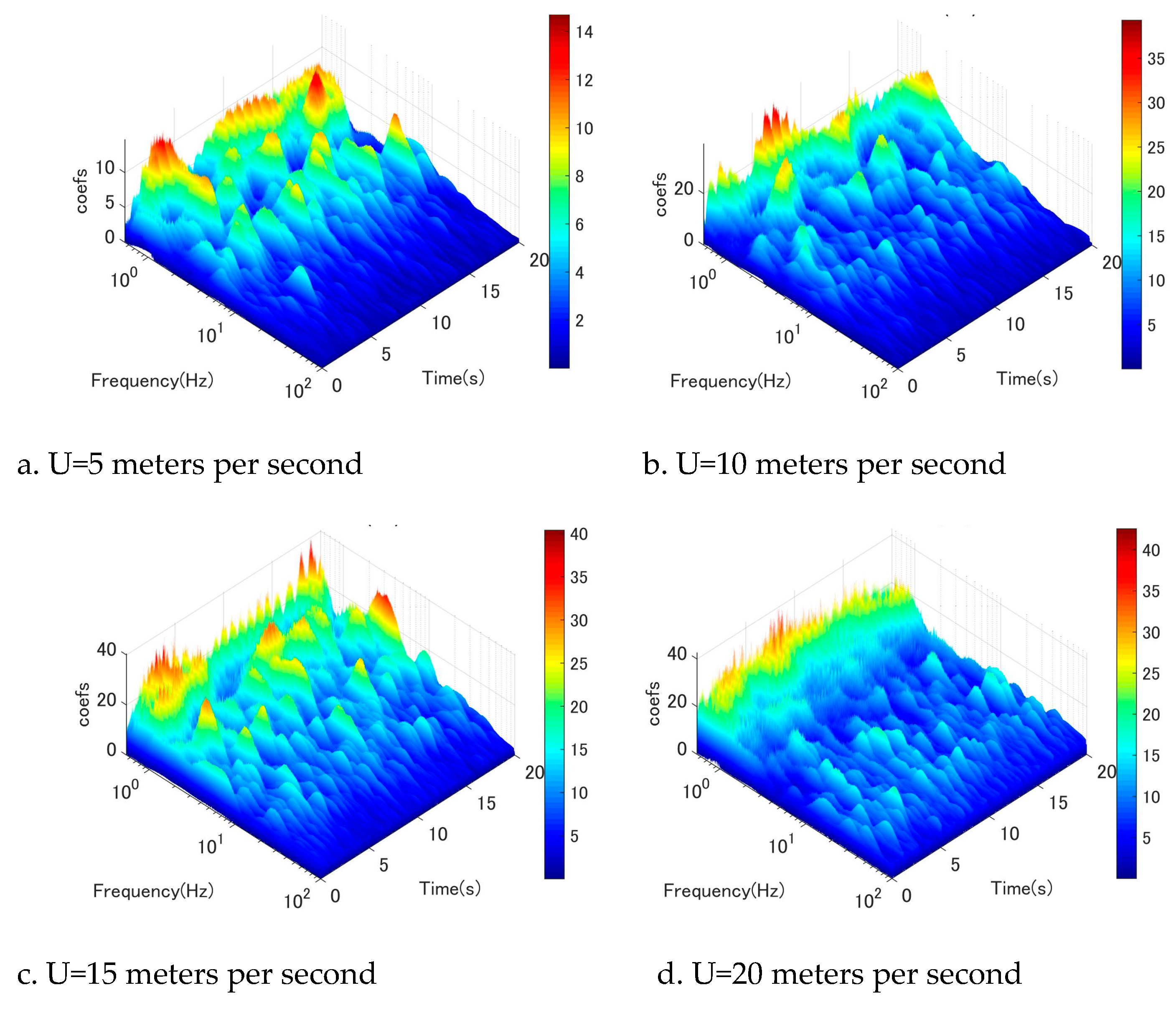
Figure 9. Wavelet-analysis of fluctuating wind velocity at location 6D, w- component.
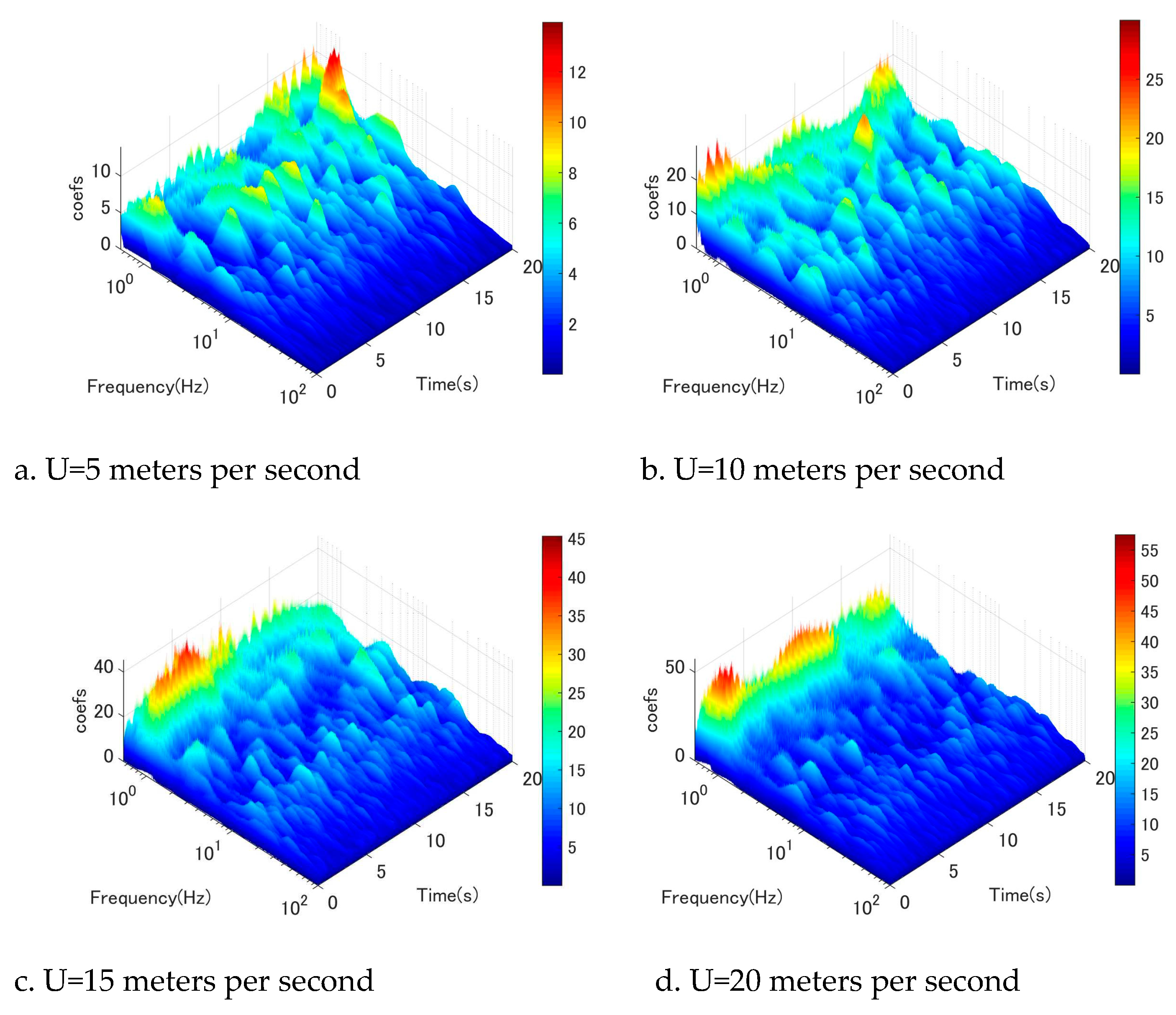
Preprints 75854 g009
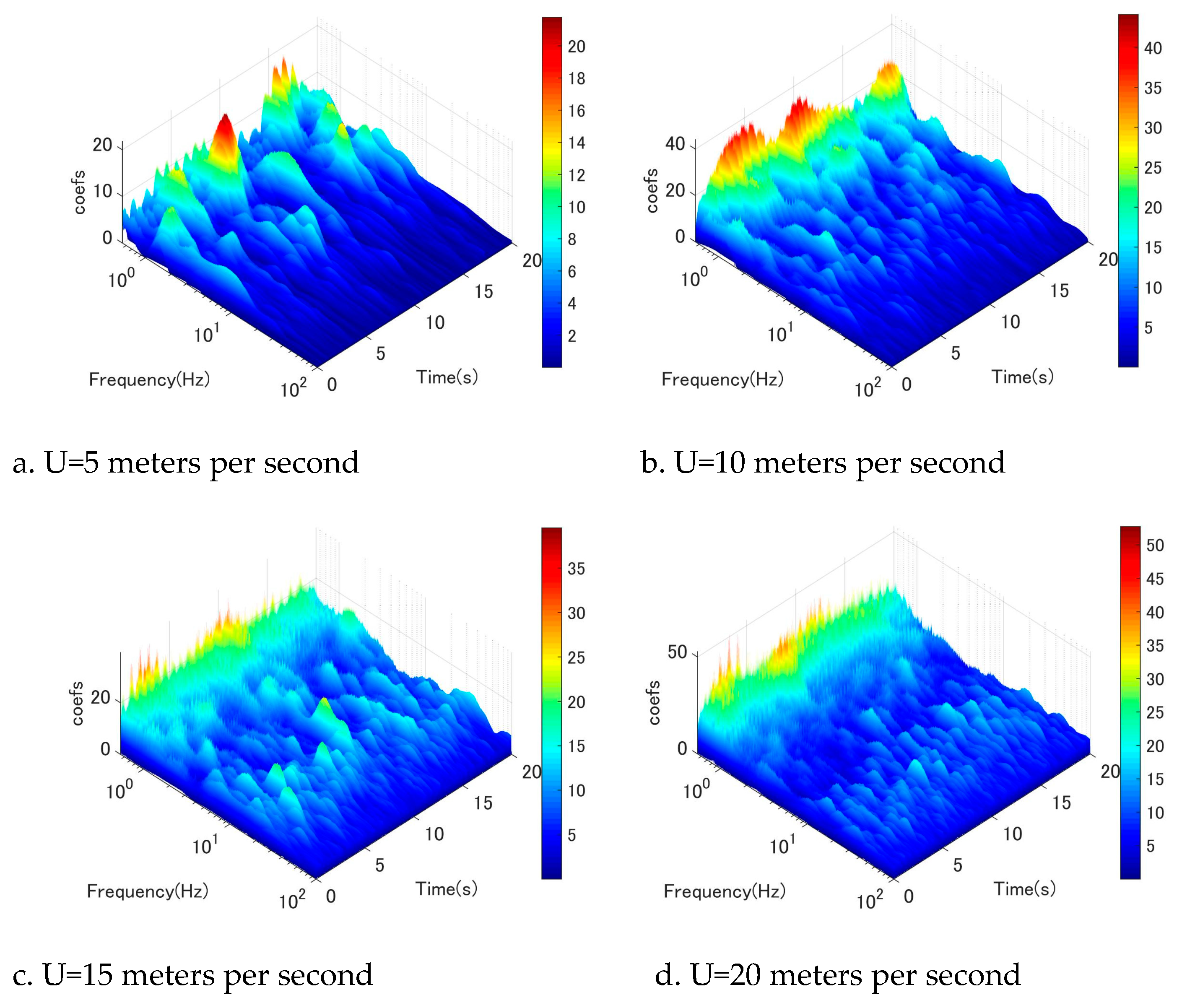
Preprints 75854 g010
Figure 10. Wavelet-analysis of fluctuating wind velocity at location 7D, w-component.
Figure 10. Wavelet-analysis of fluctuating wind velocity at location 7D, w-component.
Preprints 75854 g010
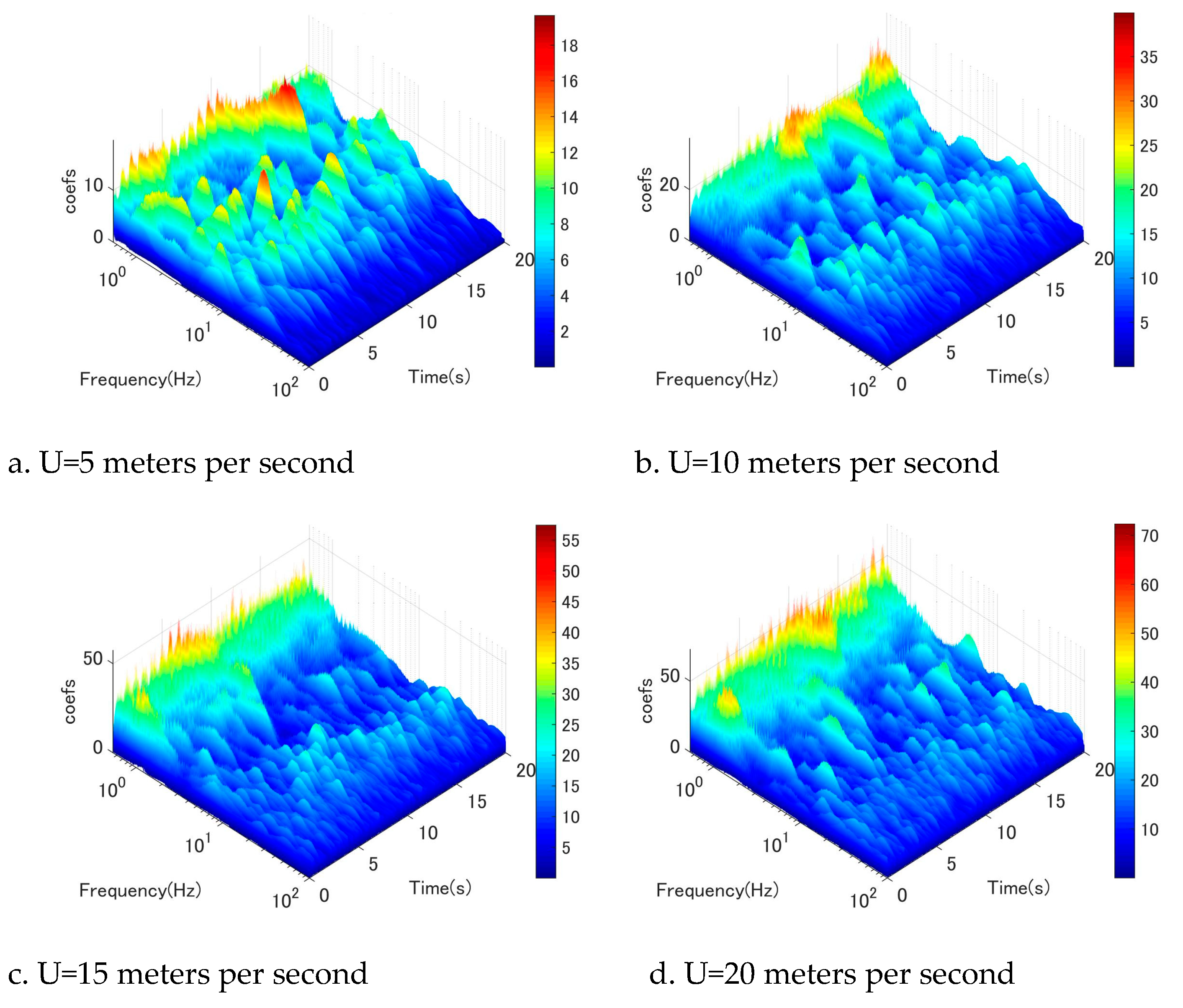
Preprints 75854 g011
Figure 11. Wavelet-analysis of fluctuating wind velocity at location 2D, u component.
Figure 11. Wavelet-analysis of fluctuating wind velocity at location 2D, u component.
Preprints 75854 g011
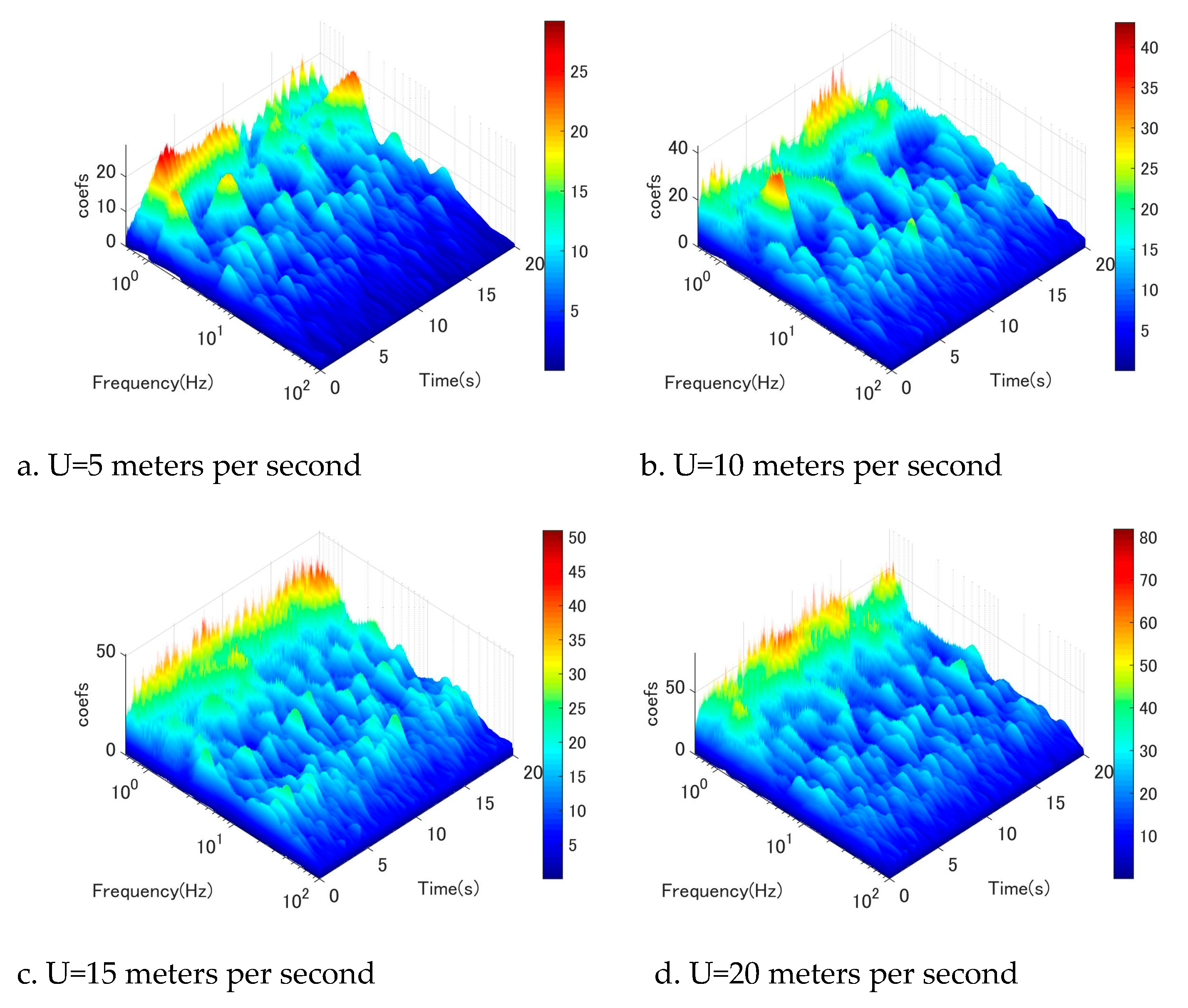
Preprints 75854 g012
Figure 12. Wavelet-analysis of fluctuating wind velocity at location 3D, u-component.
Figure 12. Wavelet-analysis of fluctuating wind velocity at location 3D, u-component.
Preprints 75854 g012
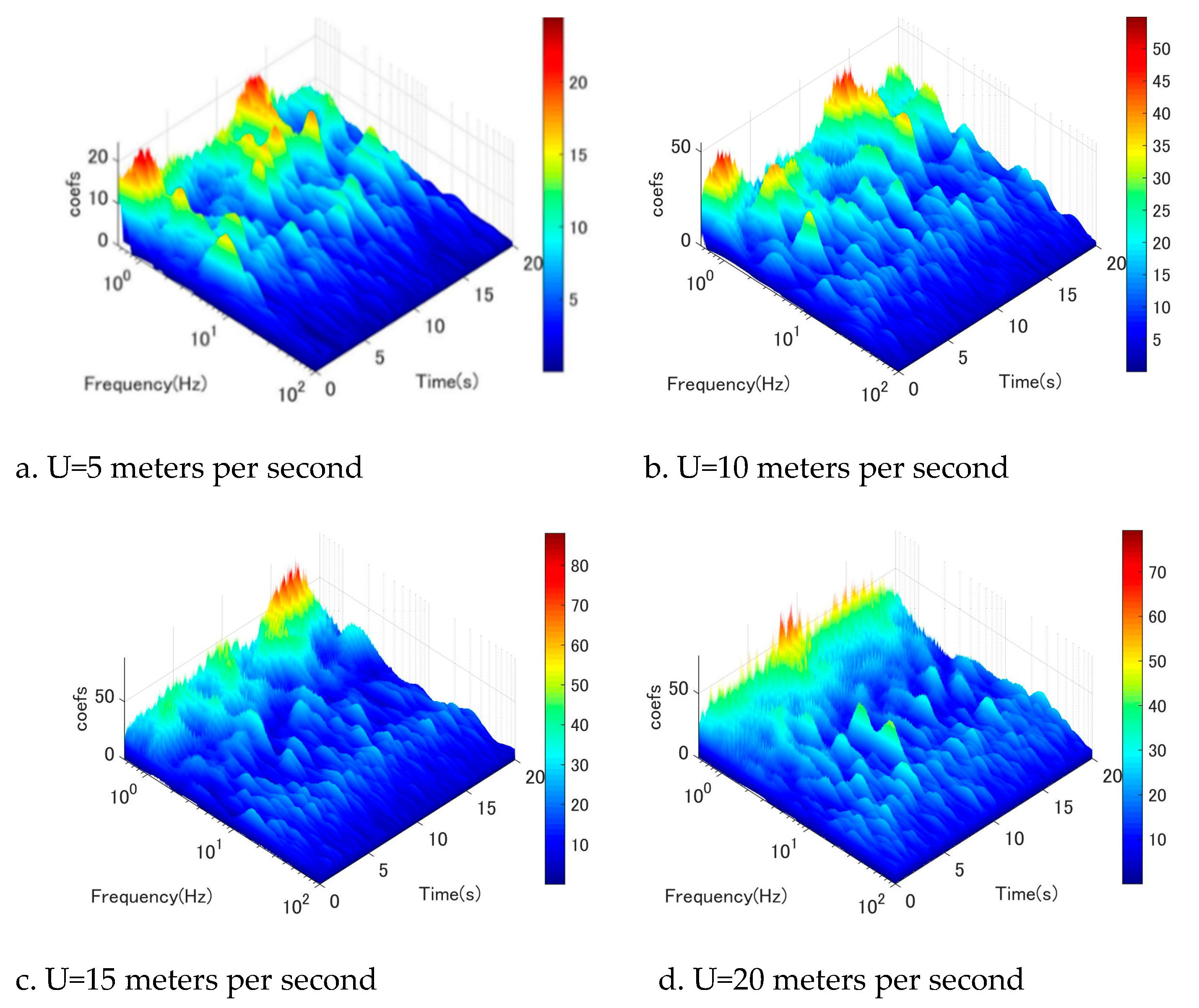
Preprints 75854 g013
Figure 13. Wavelet-analysis of fluctuating wind velocity at location 4D, u-component.
Figure 13. Wavelet-analysis of fluctuating wind velocity at location 4D, u-component.
Preprints 75854 g013
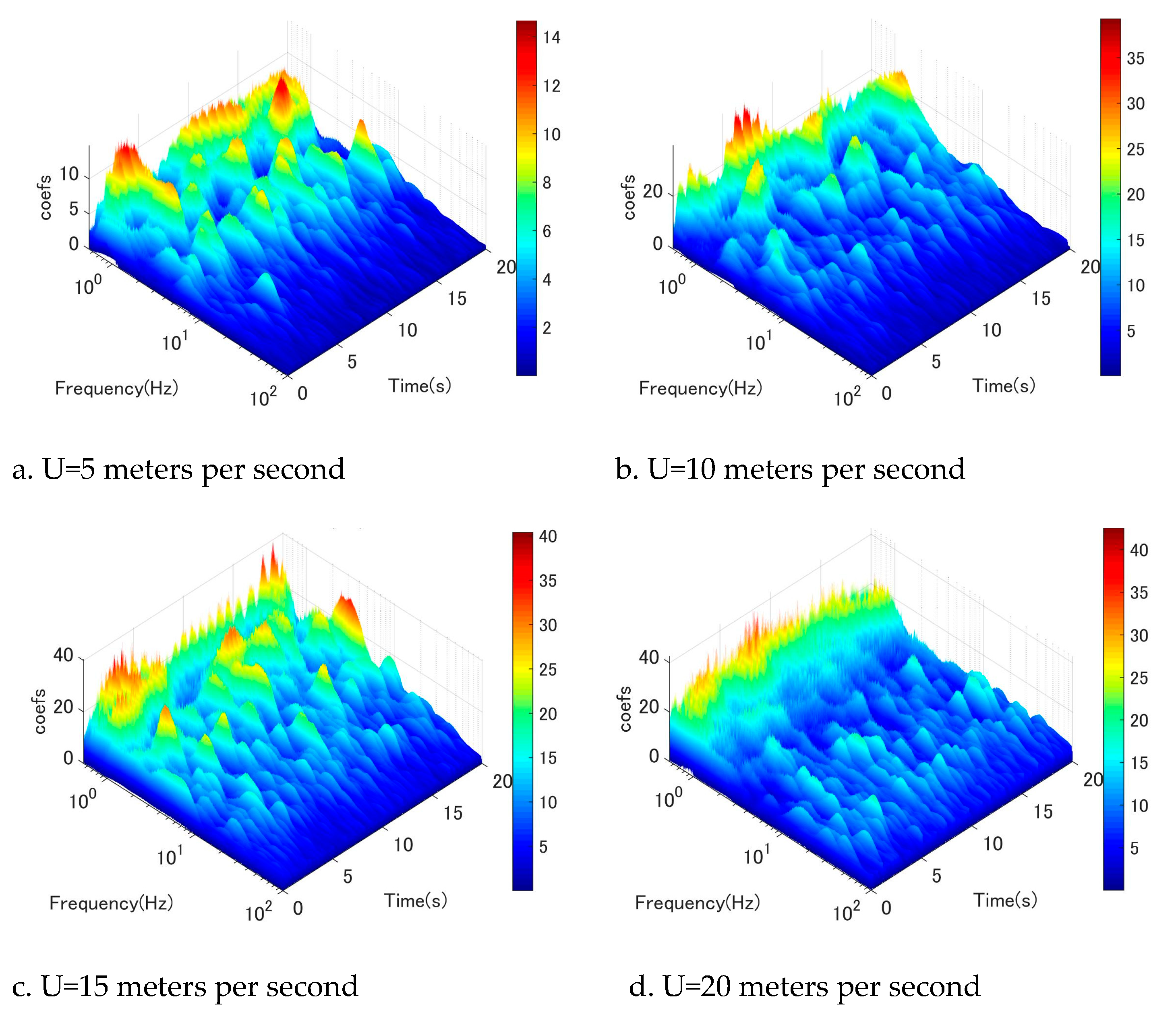
Preprints 75854 g014
Figure 14. Wavelet-analysis of fluctuating wind velocity at location 5D, u-component.
Figure 14. Wavelet-analysis of fluctuating wind velocity at location 5D, u-component.
Preprints 75854 g014
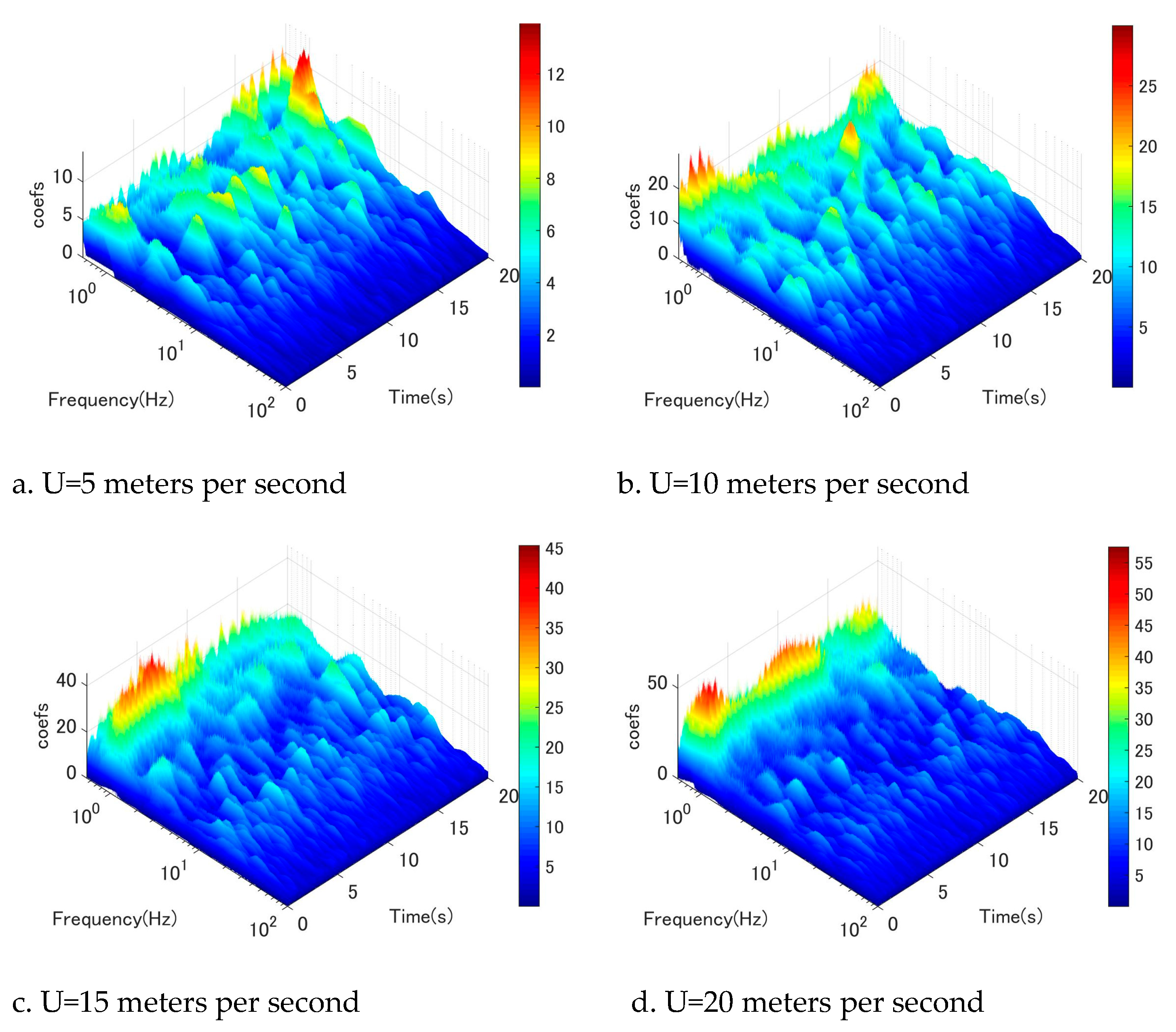
Preprints 75854 g015
Figure 15. Wavelet-analysis of fluctuating wind velocity at location 6D, u-component.
Figure 15. Wavelet-analysis of fluctuating wind velocity at location 6D, u-component.
Preprints 75854 g015
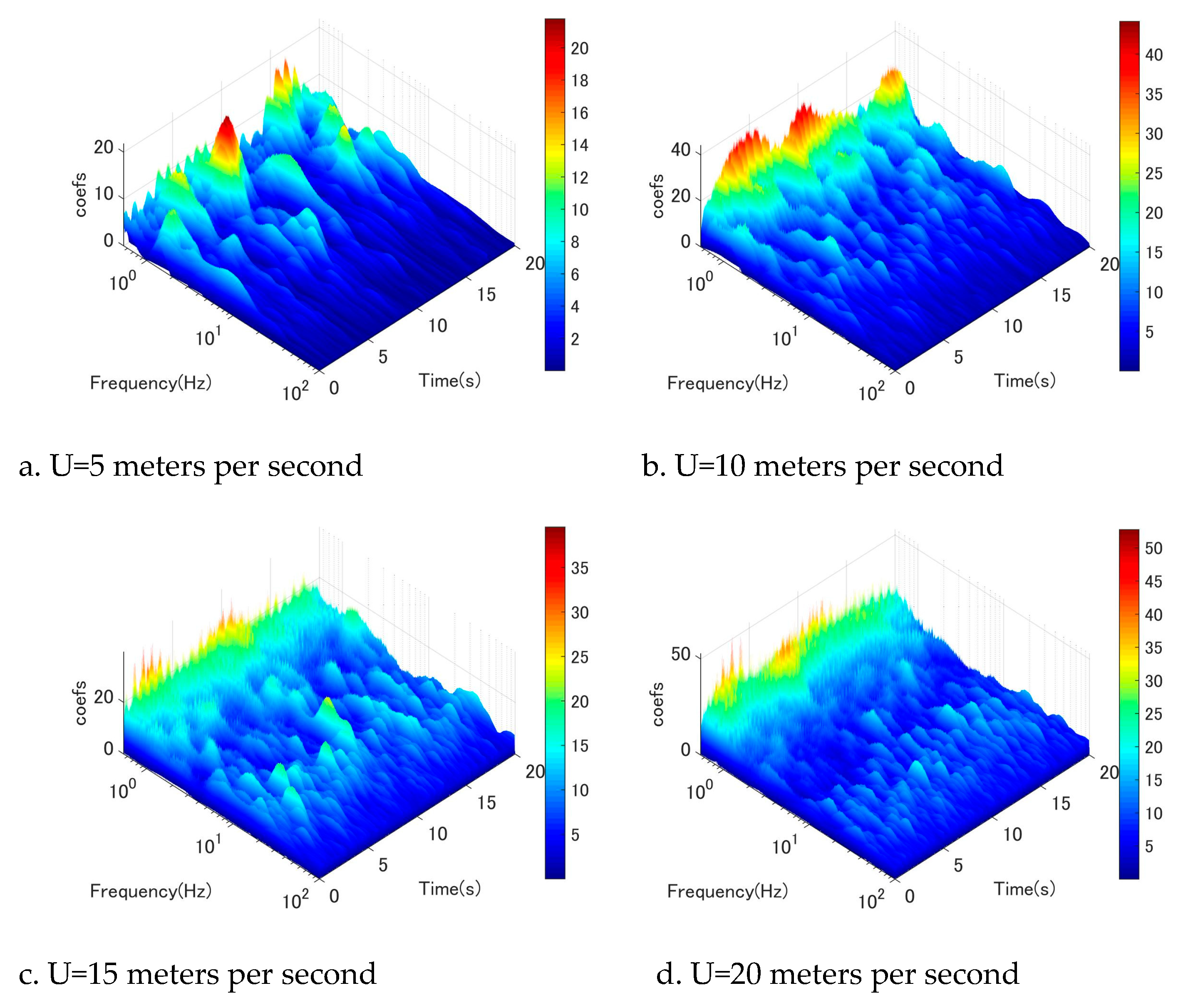
Preprints 75854 g016
Figure 16. Wavelet-analysis of fluctuating wind velocity at location 7D, u-component.
Figure 16. Wavelet-analysis of fluctuating wind velocity at location 7D, u-component.
Preprints 75854 g016
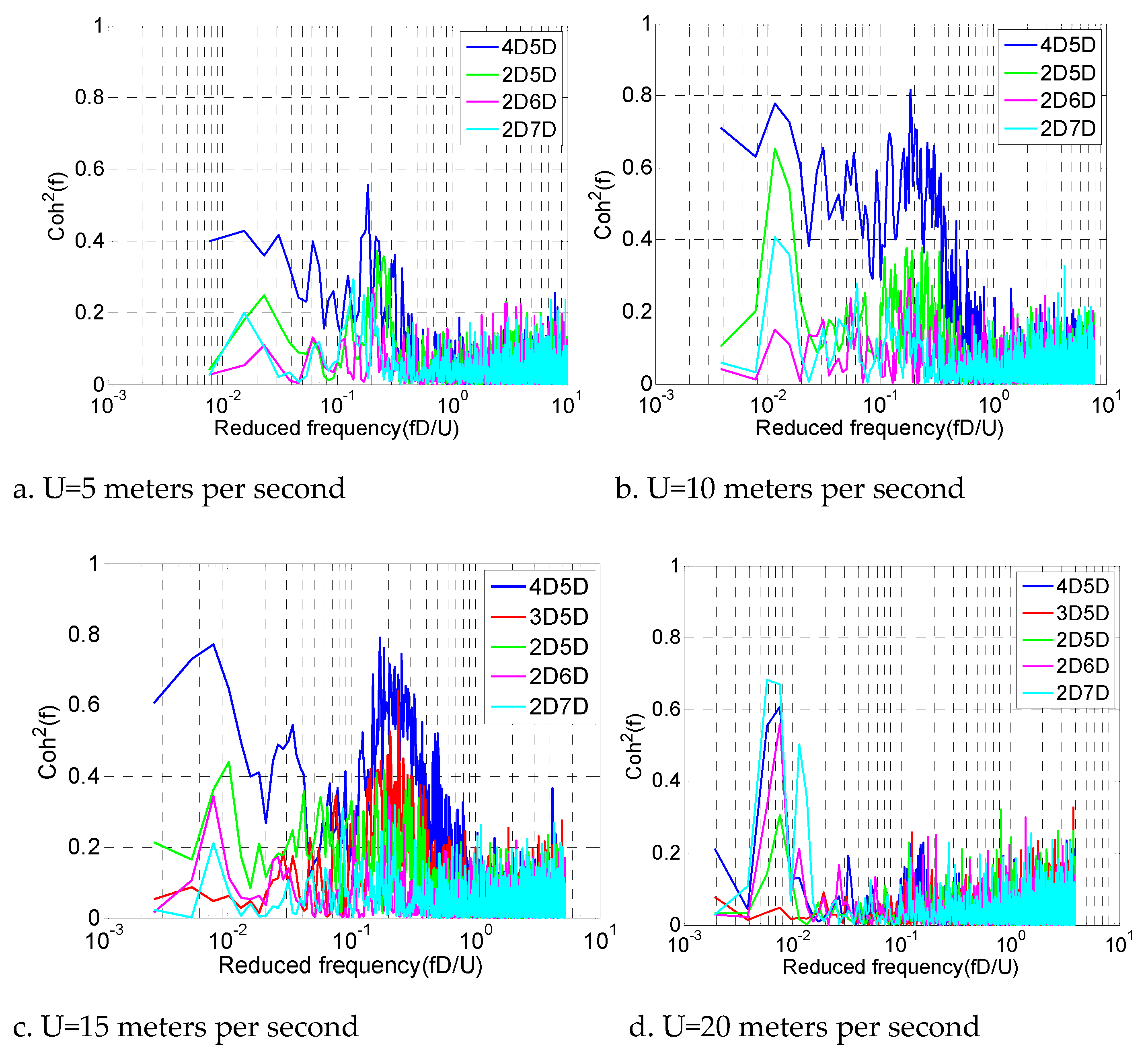
Preprints 75854 g017
Figure 17. Coherence analysis, circular cylinder, U=20meters per second.
Figure 17. Coherence analysis, circular cylinder, U=20meters per second.
Preprints 75854 g017
Table 1. Turbulence intensity.
Table 1. Turbulence intensity.
No. Mean U (m/s) Iu Iw
1 6.71 0.59% 0.60%
2 9.20 0.59% 0.62%
3 11.68 0.56% 0.59%
4 14.15 0.60% 0.61%
5 19.06 0.48% 0.62%
Table 2. Wind speed ratio.
Table 2. Wind speed ratio.
No. U1 (m/s)
At pitot tube		 U2 (m/s)
At model position		 U1/U2
1 0.45 0.44 1.024
2 0.54 0.49 1.095
3 0.62 0.56 1.114
4 0.72 0.67 1.081
5 0.80 0.73 1.099
6 0.96 0.87 1.109
7 1.16 1.03 1.123
8 1.38 1.26 1.093
9 1.72 1.62 1.059
10 3.04 2.89 1.051
11 4.21 3.99 1.055
12 5.41 5.13 1.055
13 6.60 6.32 1.045
14 7.82 7.73 1.012
15 9.06 8.66 1.046
16 10.25 9.97 1.028
17 11.51 11.20 1.028
18 12.73 12.50 1.018
19 13.95 13.20 1.057
20 15.18 15.10 1.005
21 16.42 16.30 1.007
22 17.62 17.10 1.030
23 18.79 18.40 1.021
24 20.07 19.50 1.029
Table 2. Experimental parameters.
Table 2. Experimental parameters.
Parameters Value
Stay cable diameter: D 158mm
Model length 1,500mm
Mass per unit 14.00 - 16.00 kg/m
Frequency 0.80 – 1.00 Hz
Logarithm decrement (δ) 0. 5% - 1.6%
Reynolds number ~ 2.1×105
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated