Prerpints.org logo
Preprint
Article

Influence of Frustration Effects on the Critical Current of DC SQUID

Altmetrics

Downloads

76

Views

14

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

06 June 2023

Posted:

07 June 2023

You are already at the latest version

Alerts
Abstract
Here we present calculation of the critical current of DC SQUID based on the Josephson junction on multi-band superconductor with frustration effect. It is shown that the changing of the critical current of DC SQUID with small geometrical inductance is determined by the ratio of supercurrent amplitude in different channels and the external magnetic field. In the a case of DC SQUID with high inductance frustration effects can be ignored.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

Introduction

Direct Current (DC) Superconducting Quantum Interference Device-SQUID consists of two Josephson junction including to superconducting loop in parallel (Figure 1). Foundation of DC SQUID on conventional superconductor based Josephson junctions were presented in Ref. [1,2]. In the calculation of DC SQUID characteristics and dynamical effects, the sinusoidal current-phase relation of Josephson junctions [1,2] was used. For low-temperature superconductor based junctions the relationship I = I c 0 sin φ is fulfilled with high accuracy [3]. In the case of Josephson junctions between single- and multi-band superconductors, the phase dynamics are influenced by the frustration effects. The influence of frustration effects on the characteristics of Josephson systems should be taken into account [4,5]. In particular, the presence of frustrated ground state in multi-band superconductors causes ϕ -junction peculiarity [4]. The a frustration effects in many-band superconductors and Josephson junctions based on them are described in papers [6–11]. The influence of frustration effects in multiband superconductors on escape rate in Josephson junctions was considered in Refs. [12,13]. Theoretical analysis of the escape rate for the AC SQUID based on the junction with nonharmonic current-phase relation was conducted in the study [14].
In this study, we carried out the calculation of the critical current of the DC SQUID on the Josephson junction based on many-band superconductors with frustration effects.

Basic Equations

It is well known that, the dynamics of DC SQUID in general cases described by the system of equations
I 1 + I 2 = I e
Φ = Φ e − L 1 I 1 + L 2 I 2
φ = φ e − 2 π L + I L Φ 0 ; I L = ( L 1 I 1 − L 2 I 2 ) / ( L 1 + L 2 )
where Φ 0 is the quantum of magnetic flux, Φ e external magnetic flux. It is also well known that [1], in the case of DC SQUID, the small total inductance of the loop L 1 I 1 , L 2 I 2 < < Φ 0 , l = 2 π L I c Φ 0 < < 1 (total inductance is the sum of left and right inductances L=L1+L2) and with sinusoidal current-phase relation is equivalent to single Josephson junction with effective critical current
I e = I m sin χ
and with effective phase
χ = φ 1 + η = φ 2 + η − φ e
where
η = − 2 I c 1 tan ( φ e / 2 ) I c 1 + I c 2 + ( I c 1 − I c 2 ) tan 2 ( φ e / 2 )
In Equation (3) effective critical current can be calculated as
I m 2 = I c 1 2 + I c 2 2 + 2 I c 1 I c 2 cos φ e
where Ic1,Ic2 is the critical currents of the junctions in DC SQUID (Figure 1).
For the study of frustration effects in DC SQUID we consider left junction has a single-/single-band and right junction a single-/multi-band character (see Figure 1) For the Josephson junctions between single- and multi-band superconductors (in single-band/single-band case I = I c sin χ ), the supercurrent is the sum of different tunneling channel currents [14–16]
I = I c 1 sin χ + I c 2 sin ( χ + φ ) + I c 3 sin ( χ + θ ) + ....
where I c 1 , 2 , 3 , .. is the different channel critical currents, φ , θ ,…. the phase differences between order parameters in a frustrated state of multi-band superconductor. In single-band superconductor with the zeroes phase we have Ψ 0 = | Ψ 0 | exp ( 0 ) . For the multi-band superconductor it is true the following expressions: Ψ 1 = | Ψ 1 | exp ( χ ) , Ψ 2 = | Ψ 2 | exp ( χ + φ ) , Ψ 3 = | Ψ 3 | exp ( χ + θ ) , …… The Ginzburg-Landau free energy functional of the multiband character of superconducting state can be written as [19–21]
F = ∫ d 3 r ( ∑ i j ( F i i − F i j + H 2 8 π )
where
F i i = ℏ 2 4 m i | ( ∇ − 2 π i A ⇀ Φ 0 ) Ψ i | 2 + α i ( T ) | Ψ i | 2 + β i | Ψ i | 4 / 2
F i j = ε i j ( Ψ i * Ψ j + c . c . ) + ε 1 i j { ( ∇ + 2 π i A → Φ 0 ) Ψ i * ( ∇ − 2 π i A → Φ 0 ) Ψ j + c . c . }
mi are the effective masses of the electrons in different bands, (i = 1-3); αi= γi(T – Tci) are the quantities linearly dependent on temperature T; βi and γiare constants; εij = εji and ε1ij = ε1ji describe the interaction between order parameters and their gradients in different bands, respectively, H is the magnetic field applied superconductor and Φ0 is the magnetic flux quantum. In the case of single- and two-band junction, for the phase differences φ of order parameters, we have effective critical current as [14]
I c e f f = ( I c 1 + I c 2 ) for φ = 0
I c e f f = ( I c 1 − I c 2 ) for φ = π
For single-/three-band junctions, in the case of identical and positive interband interaction term εij = εji=ε>0, one of the phase differences is zero and other phase differences in frustration states are given as ( φ θ ) = ( 2 π / 3 − 2 π / 3 ) and ( φ θ ) = ( − 2 π / 3 2 π / 3 ) [15]. Another frustration state corresponds to phase differences ( φ θ ) = ( 0 π ) ; ( π 0 ) and ( φ θ ) = ( π π ) . From the expression for potential energy for single-/three-band junctions under external current I e = I e 1 + I e 2 + I e 3 , we can get for effective critical current
I c e f f = I c 1 ( ( 1 − I c 2 2 I c 1 − I c 3 2 I c 1 ) 2 + ( I c 3 I c 1 − I c 2 I c 1 ) 2 ) 1 / 2
In the derivation of Eq. (13), we use that Josephson junction reveal ϕ -junction peculiarity I = I c e f f sin ( φ − ϕ ) , with ϕ = arctan I c 3 − I c 2 I c 1 − I c 2 2 − I c 3 2 . In the other frustration state ( φ θ ) = ( − 2 π / 3 2 π / 3 ) , the terms Ic2 and Ic3 in Eq. (12) replaced by the places. The frustration case ( φ θ ) = ( 0 π ) corresponds to the effective critical current
I c e f f = ( I c 1 + I c 2 − I c 3 )
In the state ( φ θ ) = ( π π ) for effective critical current is true the expression
I c e f f = ( I c 1 − I c 2 − I c 3 )

Results

The inclusion of frustration effects in current-phase relation (See Eqs. 12 and 13) leads to the renormalization of the critical current of DC SQUID Im in comparison without similar effects. The normalized critical current of a DC SQUID with a frustrated Josephson junction is a maximum value of the superconducting current that can be written as
i m = ( 1 + i c 2 2 ) 1 / 2 ( 1 + A cos φ e ) 1 / 2
where modulation function A is calculated as
A = 2 i c 2 ( 1 + i c 2 2 )
The calculated critical current I m of DC SQUID on SB/two-band Josephson junction with frustrated state 0 and π using Eqs. (12) presented in Figure 2. In calculations without restriction of generality, we consider Ic1=1. Corresponding normalization of critical currents in Eq. (12) we also use the same scale. It is clear monotonic increasing and decreasing character of critical current 0 and π cases correspondingly. In Figure 3 we plot the result of calculations modulation coefficient A in DC SQUID based on SB/two-band Josephson junction. It is clearly crucial changing of this parameter in the frustrated π case. For the high ratio parameter ic2/ic1 close to 1, the sensitivity of DC SQUID to the external magnetic field becomes very small.
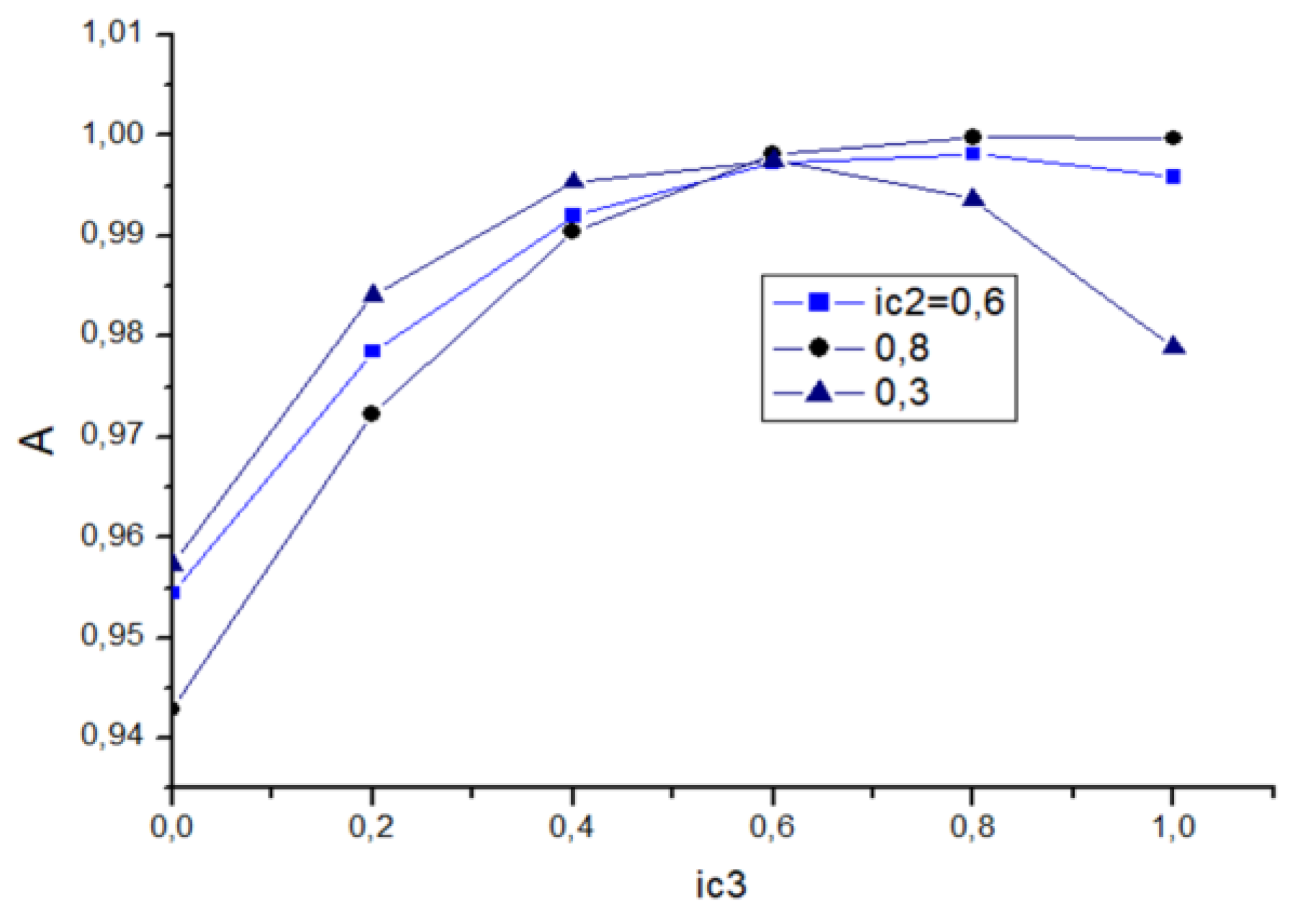
In Figure 4 we present the results of calculations critical current of DC SQUID based on SB/Three-band junctions for different ratios ic2 versus ic3. It is a clear appearance of minimum in the dependence of im(ic3) at small ic2 in contrast to the SB/two-band case. Another important moment related to the changing of critical current in restricted regions close to 1. In Figure 5 presented the modulation coefficient A in DC SQUID on SB/three-band Josephson junction. It means that sensitivity in the case of DC SQUID on the SB/three-band Josephson junction is higher than in SB/two-band case.
For the small values of geometrical inductance l < < 1 , the calculations show, that in all cases of current-phase relation, the changing of the inductance of DC SQUID has a small impact on the presented results on Figure 2, Figure 3, Figure 4 and Figure 5. For the high values of inductance of DC SQUID l>>1, the Josephson inductance of junctions can be ignored in consideration of dynamical effects [1]. As a result the phase of Josephson junctions on the superconducting loop of DC SQUID (Figure 1) changes independently and in this limit is a true system of linear equations for currents [1]
i 1 = i e 2 + φ e l
i 2 = i e 2 − φ e l
It means that in DC SQUID with hlgh geometrical inductance l>>1, the frustrated effects in current-phase relation can be neglected.

Conclusions

Finally, in this paper, the influence of the frustration effect in the many-band superconductor on the critical current Im of DC SQUID was investigated. The renormalization of critical current in such frustrated junctions under an external magnetic field was taken into account in the limit of the small geometrical inductance of DC SQUID. In the opposite case of high geometrical inductance l>>1, the influence of frustration effects in current-phase relation is negligibly small.

Author Contributions

All statements conducted by Askerzade I. N.

Funding

This study is partially supported by TÜBİTAK grant No 118F093.

Data Availability Statement

Not applicable

Conflicts of Interest

The author declare no conflict of interest.

References

  1. Likharev, K.K. , Introduction into Dynamics of Josephson junctions and circuits, New York, Gordon Breach, 586 p. 1986. [Google Scholar]
  2. Askerzade, I. , Bozbey A., Canturk M., 2017. Modern aspects of Josephson Dynamics and superconductivity electronics, (Springer, Berlin). 2017. [Google Scholar]
  3. Il’ichev E. et al, Review of Scientific Instruments. 72,1882(2001).
  4. Yerin, Y. et al., Frustration phenomena in Josephson point contacts between single-band and three-band superconductors, Low Temp. Phys., 2014, 40, 943–949. [Google Scholar] [CrossRef]
  5. Askerzade, I. , Unconventional Superconductors: anisotropy and multiband effects, (Springer, Berlin), 177 p. 2012. [Google Scholar]
  6. Yerin, Y. , et al, DC SQUID based on a three-band superconductor with broken time-reversal symmetry, Supercond. Sci. Technol., 2015, 28, 095006. [Google Scholar] [CrossRef]
  7. Ng, T. , Nagaosa, N. , Broken time-reversal symmetry in Josephson junction involving two-band superconductors, EPL, 2009, 87, 17003. [Google Scholar] [CrossRef]
  8. Stanev, V. , Tešanović Z., Three-band superconductivity and the order parameter that breaks time-reversal symmetry, 2010, Phys. Rev. B 81 (2010)134522. [CrossRef]
  9. Dias, R. , Marques A. , Frustrated multiband superconductivity, Supercond. Sci. Technol., 2011, 24, 085009. [Google Scholar] [CrossRef]
  10. Lin, S.-Z. , Josephson effect between a two-band superconductor with s++ or s± pairing symmetry and a conventional s-wave superconductor, Phys. Rev. B, 2012, 86, 014510. [Google Scholar] [CrossRef]
  11. Bojesen, T. , Babaev E. ,Sudbø, A., Time reversal symmetry breakdown in normal and superconducting states in frustrated three-band systems, Phys. Rev. B, 2013, 88, 220511(R). [Google Scholar] [CrossRef]
  12. Askerzade, I.N. Escape rate in Josephson junctions between single -band and two -band superconductors, Physica C,2020, 374,1353647. [CrossRef]
  13. Askerzade, I.N. , Aydın A. , Frustration effect on escape rate in Josephson junctions between single-band and three-band superconductors in the macroscopic quantum tunneling regime, Low Temperature Physics, 2021, 47, 282–286. [Google Scholar] [CrossRef]
  14. Askerzade, I.N. , Askerbeyli R. , Ulku I., Effect of unconventional current-phase relation of Josephson junction on escape rate in ac SQUID, Physica C, 2022, 598, 1354068. [Google Scholar] [CrossRef]
  15. Askerzade, I.N. , Influence of Anharmonic and Frustration Effects on Josephson Phase Qubit Characteristics, Condensed Matter, 2023, 8(1),20. [CrossRef]
  16. Askerzade, I.N. ,Gencer A., Guclu N., On the Ginzburg-Landau analysis of upper critical field Hc2 of MgB2, Superconductor Science and Technology 15 (2), L13,2002, https://iopscience.iop.org/article/10. 1088. [Google Scholar] [CrossRef]
  17. Askerzade, I.N. , Gencer A., Guclu N., Kilic A., Two-band Ginzburg–Landau theory for the lower critical field Hc1 in MgB2, Superconductor Science and Technology 15 (2), L17,2002. [CrossRef]
  18. Askerzade, I.N. , Ginzburg - Landau theory: The case of two-band superconductors,Physics Uspekhi, 2006, https://www.researchgate.net/journal/Physics-Uspekhi-1468-4780.
Preprints 75812 g001
Figure 1. Schematic presentation of a DC SQUID.
Figure 1. Schematic presentation of a DC SQUID.
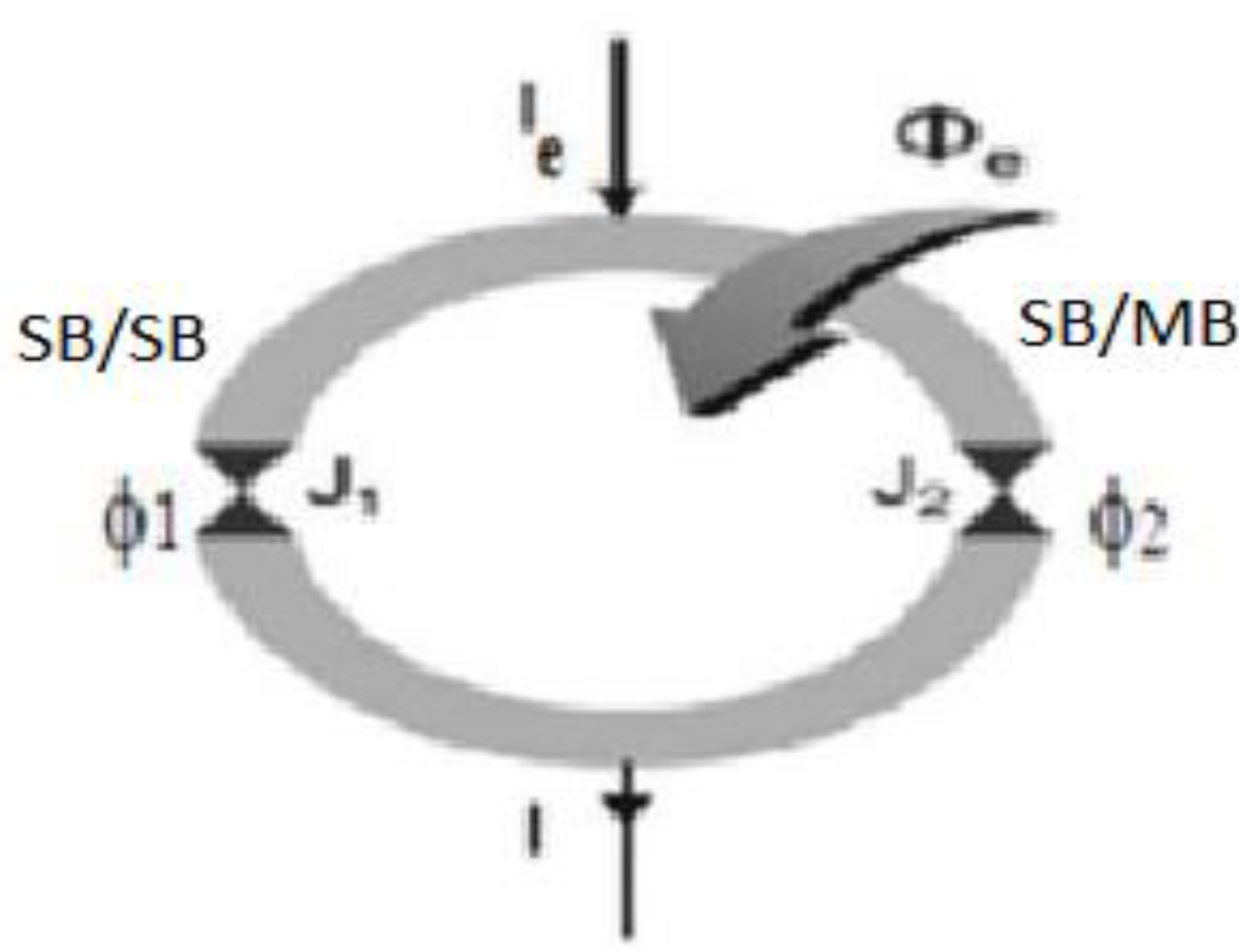
Preprints 75812 g001
Preprints 75812 g002
Figure 2. Critical current of DC SQUID with small inductance l for SB/TB junction case.
Figure 2. Critical current of DC SQUID with small inductance l for SB/TB junction case.
Preprints 75812 g002
Preprints 75812 g003
Figure 3. Modulation coefficient of DC SQUID with small inductance l for SB/TB junction case.
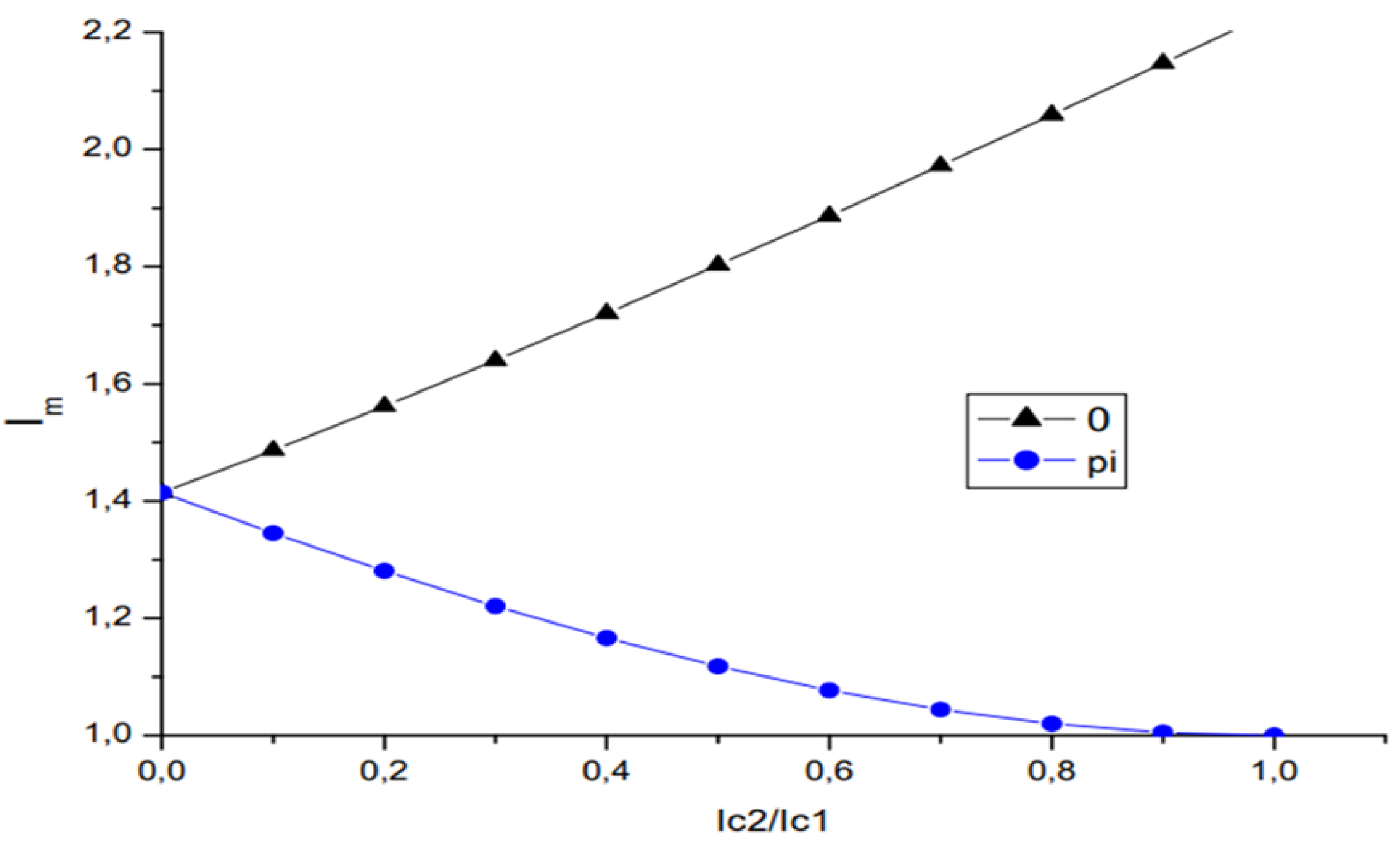
Figure 3. Modulation coefficient of DC SQUID with small inductance l for SB/TB junction case.
Preprints 75812 g003
Preprints 75812 g004
Figure 4. Critical current of DC SQUID with small inductance l for SB/ThreeB junction case.
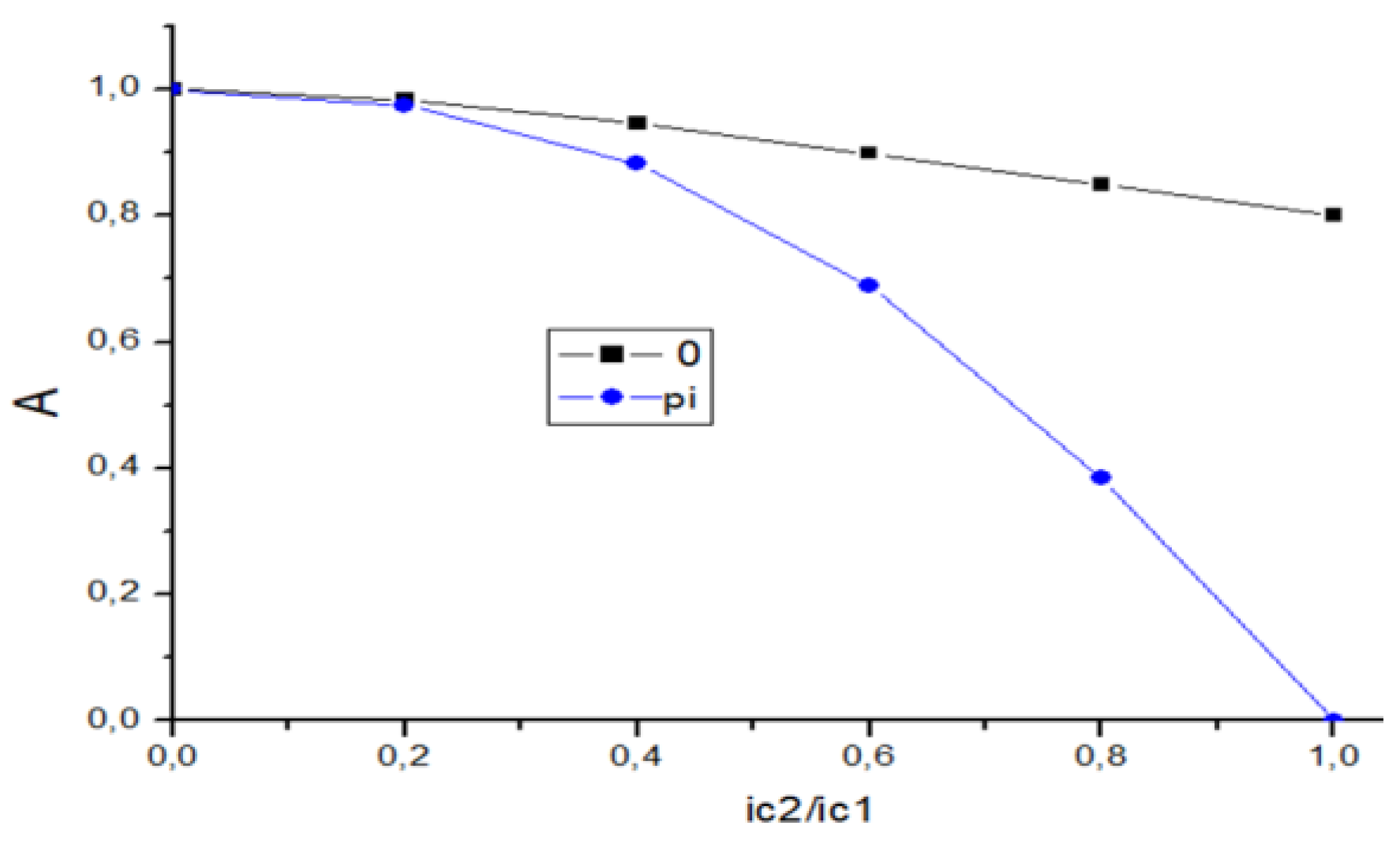
Figure 4. Critical current of DC SQUID with small inductance l for SB/ThreeB junction case.
Preprints 75812 g004
Preprints 75812 g005
Figure 5. Modulation coefficient of DC SQUID with small inductance l for SB/ThreeB junction case.
Figure 5. Modulation coefficient of DC SQUID with small inductance l for SB/ThreeB junction case.
Preprints 75812 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated