Hydraulic Response and Overtopping Performance of Single-Layer Double-Cube Unit Armored Mound Breakwater

The newly developed friction-interlocking armor unit, called ‘Double cube’ (DC), has been designed to improve the performance of the concrete armor unit used in river/marine structures against currents/waves actions. DC unit, is an octagonal-shaped block, made up of two parts: an upper cube set on a lower base that is either square or octagonal in shape. The innovative design aims to provide a good performance in terms of stability, high tolerance placement with various contact points and ease of placement. DC’s shape and placement enhance the stability by bringing the center of gravity closer to the underlayer and providing a large contact surfaces with surrounding blocks that reduce the chance of extraction and limit movements (rocking, lifting) via "keystone" effect. The characteristics of this new unit provides a relatively high hydraulic stability number for the armor layer (NS=2.9), a favorable hydraulic performance due to energy dissipation from turbulence and aeration, as well as a high roughness coefficient (γf≈0.46) helping to reduce the overtopping.

Keywords:

Subject: Engineering - Marine Engineering

1. Introduction

In a context of climate change and significant sea level rise, coastal engineers and scientists are still conducting extensive research on developing new types of artificial armor units to improve their performance meanwhile reducing the amount of concrete but also limiting the visual and environmental impacts.

Key considerations for an artificial unit are:

Hydraulic stability;
Good performance in terms of run-up and overtopping;
Structural robustness;
Ease and speed of placement with sufficient tolerances, ease of handling and simplicity of lifting;
Easy prefabrication with a simple mold composed of limited parts;
Ease of storage.

In recent decades, there has been a resurgence of interest in structurally robust forms: Accropode^®I, Coreloc^®, Xbloc^® (CIRIA [11]), Crablock (Salauddin et al. [37,38]) and particularly for simpler shapes (Cubipod^® (Gómez-Martín and Medina [17,18])), C-ROC (Perrin et al. [31]). It is also worth mentioning that during recent years, many new regular placed armor blocks have been introduced in the studies, like Xbloc^® Plus (Reedijk et al. [32]), Chi (Park et al. [29]), Starblock (Safari et al. [33,34,35]) and TB-CUBE (Peng et al. [30]).

Stability of concrete armor units against waves is achieved through their own weight, friction, and interlocking. Setting aside the hollowed units, which are placed in a tight regular pattern side by side and rather confined to revetments, the best performing units, in terms of hydraulic stability, are those that mobilize strong interlocking, for example the Dolos. But, since the failure of the Sines breakwater, engineers are being cautious with using slender units which are thought to be structurally fragile (Bakker et al. [3,4]). Bulky units such as Accropode^®I appear to be more preferred by coastal structure designers. For the same reason, the significance of the structural integrity of armor blocks, some of the most basic armor blocks, such as cubes, are frequently employed in the design of breakwaters. Concrete armor blocks may be placed in one or two layers according to a random or a regular pattern (Van Gent and Luis [47]).

Nowadays the most commonly used armor blocks are double layer cube shaped blocks and Interlocking type armor blocks. Interlocking type armor blocks can be placed in single layer or double layer placements. Single layer Interlocking armor blocks are particularly interesting due to economic reasons and cost efficiency (CIRIA [11]).

The objective of this group was in priority to propose optimized shapes leading to high strength and high stability on the one hand, and secondly to reduce overtopping. These characteristics were resulting in a high-interlocking units with more empty spaces between units leading to an increased porosity of the armor layer. The major drawback regarding the placement of these types of units, can strongly affect the hydraulic stability of the armor layer. The random placement method, used in most of single layer blocks, is constrained by several rules governing blocks orientation as well as positioning or number of contacts. The latest affect the placement process and thus the cost of the entire project (CIRIA [11]).

This is one of reasons that authors such as Bhageloe [6], d'Angremond et al. [2], Van Gent et al. [45,46], Van Buchem [40], Van Gent and Luis [47], Van der Lem et al. [41], Van Gent and van der Werf [49], Vieira et al. [51,52,53] proposed that single layer placed cubes could be an economically interesting alternative solution for construction of the armor layer.

However, simple single layer cubes are suffering a huge disadvantage, as they tend to fit face to face during storms. (Medina et al. [24]). In such cases, the placement tends to form a heterogeneous porous armor layer, with areas of high cube concentration to the detriment of other parts with less protective cover (Figure 1).

Low porosity cubes, arranged closely together, are likely to experience excessive pore pressure inside the breakwater, which is unfavorable for stability. Consequently, a damaged armor layer cannot not provide sufficient cover for exposed under-layers, therefore it would increase the risk of material extraction. A single armor layer of cubes, unless with a very low porosity, is likely to experience significant settlement. Moreover, the edges and sharp corners of the cube will be subjected to localized breakages, not only during placement but also throughout the life of the structure (Safari [33]).

Therefore, even if the hydraulic stability performance is acceptable, the outer surface of the armor is rather smooth as the units are parallel to the breakwater’s slope, thus enhancing the overtopping rates.

In general, cubes placed in a single layer exhibit a stability number (N_s) between 2 and 3 depending on the packing density of armor layer (Van Gent et al. [45,46]). Regarding overtopping, the roughness coefficient is close to 0.5 for the single layer cube armor layer, whereas it decreases to 0.47 for the cubes in two layers, resulting in an unexpectedly small gap (CIRIA [11]).

The Cubipod^® recently developed by the laboratory PCUPV (Ports and Coasts of the University of Valencia Polytecnic) also illustrates the strong interest in the simple cube shape. This unit is based on a cube shape with a protrusion (half pyramid) located on each face. In order to avoid face-to-face contact, the cubes are moved away from one another, protrusions have been used. This is done in order to obtain a greater, more uniform porosity. (Gómez-Martín and Medina [17,18]). Nevertheless, this unit does not provide a higher stability in single layer compared to other existing irregularly placed armor units. (Salauddin et al. [37]).

This demonstrates that a more effective concrete armor can be proposed with a simple shape while yet assuring an easy placement method and construction. As a general point of view, stability is closely related to interlocking. In contrast, a strong interlocking result in a low surface porosity and permeability, leading to unsatisfactory hydraulic responses (Safari et al. [35]). This contradiction, between stability and overtopping, is an incentive to look for innovative unit forms able to reach an optimal compromise.

The main purpose of this research is to develop a new artificial unit, namely ‘Double Cube’ or DC, for breakwater protection against wave action. DC is comprised of a cubic base with chamfered corners and an upper half with a cubic shape that has a smaller cross section than the base part. The basic design idea consists in developing a bulky armor unit (Dupray and Roberts [13]) such that fulfil the following main criteria:

placed in a single layer on a 3V: 4H slope;
A homogeneous porosity;
Easy to place, it might be an advantage that the unit could be placed on a filter made of rather small size elements to avoid surface irregularities;
High hydraulic stability (expected N_S (K_D)≈2.9 (18));
High rough surface armoring (γ_f≈0.46).

All physical modeling tests were performed in 2D wave flume, the units being placed on a uniform slope and subjected to irregular waves.

In future studies, DC will be studied in a wave basin in order to examine primarily its behaviors under the action of oblique waves, and secondly to analyze the stability of the roundhead of the structure.

Furthermore, these 2D experiments were focused only on one size of armor unit. In the laboratory, it is easy to place units in their assigned position. However, it may not be the case for placing the blocks in prototype conditions; this can be the case especially for blocks under the water level while undergoing wave agitation. It is therefore necessary to consider placement tolerances and anticipate the influence of displacement of some blocks on the stability of armor layer.

2. Logic of the new designed geometry

It is well known that the stability of an armor layer increases with increasing packing density and decreases with decreasing porosity. (Medina et al. [24]). It has also proven that a decrease in porosity leads to unfavorable increase in overtopping (Safari et al. [34]). DC’s goal is taking advantage of these functions by combining two parts into one unit.

DC is consisting of a cubic base with chamfered corners (hexagonal form), topped by a cubic form of reduced cross-sectional area in comparison with the base part (Figure 2) The upper part and lower part are connected with a short transition part to reduce the structural tensions.

The rough pattern created by high porosity of upper part of the block, increases the dissipation of wave energy. The upper part, which can be of different shapes such as square or octagonal, creates a rough outer layer able to dissipate energy of the flows close to the armor layer. The upper part also offers a grip for clamps and cranes due to the large gaps around the upper part of units.

The lower part of the new unit contributes most to the blocks weight as well as frictional forces, therefore ensuring the stability of the block. The unit’s base has been chamfered to ensure a minimum porosity, even with a tight placement or different orientations of the units. The transition zone eliminates the sharp corners that are most exposed to contact. Chamfers also provide better quality supports and contact surface for the blocks.

The chamfers also offer the possibility of a number of different regular placement with a homogeneous porosity over the entire surface without the risk of uneven settlement of the armor layer (surface porosity).

Dimensions of chamfered DC were standardized on the following ratios based on the characteristic dimension "D", the side length of the unit in which the element fits (Figure 3):

The volume of an individual unit, as a function of characteristic dimension can be given by:

V = 0.698 D^{3} = D_{n}^{3}

(1)

Where D_n is the nominal diameter of the unit and D the ‘primary or characteristic’ length of unit.

2. Placement method

One of the most important features of every block is the ease of placement, as a difficult or complicated placement method can be time consuming and therefore increase the final cost of the project. To assess the possible placement configurations and their properties. 3D virtual models have been used for this purpose.

Different placements have been modelled to find the best performing configuration regarding following criteria:
Interlocking of the units: taking into account block’s geometry to avoid loose connections;

optimal porosity of the armor layer: to increase wave dissipation and minimizes the run-up as well as uplift pressure.

In this study, the packing density coefficient (ϕ) and the armor layer porosity (n_v) is defined by the following equation (CIRIA [11]):

ø = \frac{N_{a}}{A} {D_{n}}^{2} = t_{a} (1 - n_{v}) / {D_{n}}^{2}

(2)

where N_a the total number of armor units in the studied area, A the surface area of armor layer parallel to the slope, D_n the nominal diameter of armor unit, t_a armor layer thickness.

In the following sections, two proposed placements for the DC units, ‘Direct placement’ and ‘Random placement, will be discussed.

3.1. Direct Placement (DP)

This placement method can be described as a regular placement. All units are placed uniformly in one direction (Figure 4). In the first line, all units are placed with the bases inclined at 0° to the line of greatest slope of the embankment.

In the second row, the units are secured between two units on the row below, so the chamfers of the unit are in contact the two chamfered parts of the lower units. The placement of the following lines will be carried out similarly to the two previous lines up to the crest of the structure. In this pattern, the theoretical horizontal (D_x) and upslope (D_y) distances are 1.550D and 0.775D, respectively. Therefore, a theoretical packing density coefficient of (1.550 D*0.775 D)^-1=0.832 D^-2 (0.655 D_n^-2) would be resulted.

Similar to other blocks with regular placement, the main disadvantage of such placements is the needed precession and low tolerance for errors. It has been observed during the small-scale modelling for the DC that the correct placement of the first line is very important for the accurate placement of the next lines. Since the unit’s positions must be very precise; any inaccuracy will be transmitted and exacerbated in higher lines.

3.2. Random Placement (RP)

In the Random Placement (RP) the units are placed randomly line by line. The pattern does not follow any strict rules or specific orientations. (Figure 5).

For the first line, the units are placed with various orientation. There is no pre-determined orientation for the units and the units are placed in various positions. For the second line, the units are placed between the lower units and their orientation can vary, without any specific rule.

Both placements have shown a strong Interlocking, and it is difficult to withdraw a unit without dislodging the surrounding units.

In this configuration, the horizontal distance of the blocks is the only factor that should be controlled. the less horizontal distance, the more upslope distance (the upslope distance decrease as the horizontal distance increase), although the total packing density remains constant.

The horizontal placing distance varies between 1.50 D < D_x < 1.70 D and the upslope spacing varies between 0.625 D < D_y < 0.750 D. As previously stated, the theoretical total packing density coefficient remains constant at around 0.893 D^-2 (0.702 D_n^-2).

4. Hydraulic model tests

4.1. Experimental set-up

The physical mode tests were carried out in the wave flume of the Coastal and Continental Morphodynamics laboratory of the University of Caen.

This wave flume has a length of 22 m, a width of 0.8 m and a depth of 1.0 m, as shown in Figure 6. The flume has an Edinburgh Designs piston wave generator that enables to generate regular and irregular waves with active wave reflection compensation system. The wave-maker can produce a significant wave height of about 0.1 m with a period of 1 to 3 seconds (Edesign.co.uk. [14]). All tests were conducted on a flat bottom.

The sidewalls of the flume are made of glass, allowing visual observations and optical measurement of wave-structure interactions (Figure 6).

The sketch of the breakwater cross-section, as well as, material characteristics used in this model, are presented in Figure 7. The 2D model was built with a Froude scaling (model to prototype) of 1:57.

The armor layer is built using DC with an average mass of 0.072 kg, and a nominal diameter of 0.0355 m. It must be noted that the mean mass density of unit is 1620 kgm^-3, lower than the normal concrete elements (2400 kgm^-3). The reason for this was that the dimensions of the model were constrained by the capabilities of the wave generator (significant wave height and period). Nevertheless, the major dominant forces are reproduced in correct proportion (Hughes [20]) at the initiation of damages. This is relevant to estimate the armor stability. The same techniques (using light units) have been validated and used successfully by Gόmez-Martín and Medina [17] to study a highly stable unit (Cubipod) and Safari et al. [35] on Starbloc unit.

There are methods to estimate scale effects in core permeability such as Burcharth et al. [9], Vanneste and Troch [50], and Wolters et al. [54]. In this study, the dimension of core materials has been determined according to the method proposed by Burcharth et al. [9]. In this method, an empirical model is based on pore pressure calculations, leading to the hydraulic gradient of pore velocity, which is used for Reynolds comparisons. Burcharth et al. [9] proposed using time and space averaged interstitial velocity for the calculation of the Reynolds number. For the evaluation of the interstitial velocity in the core, the extended Forchheimer formulation was used. Finally, the core nominal diameter (D_n50) is equal to 0.010 m.

To calculate the dimension of the filter material, the methods recommended by CERC [10] are used. The filter support consists of narrow grading of natural rocks with a median nominal diameter and a mass density of 0.015 m and 0.009 kg, respectively. The thickness of the underlayer was about 2D_n50=0.030 m.

The properties of the materials used in the breakwater are listed in Table 1. The tests are carried out for varying wave parameters such as the wave height and wave period, as well as properties of the armor layer such as placement, packing density, freeboard position. The test matrix is summarized in Table 2. The water depth at the toe of the slope was 0.455 m, the crown height R_c was 0.18 m (stability and overtopping tests) or 0.08 m (for additional overtopping tests). The crown width is equal to the length of 3 rows of units.

4.2. Wave measurements

Two groups of three resistance-type wave gauges, with a precision of ±2%, are used to measure the water surface elevations in the flume (Figure 6).

The first group was positioned 1.5 m seaward of the structure toe and the second group was placed 10 m away from the wave-maker. Incident and reflected waves are analyzed using the least-squares method proposed by Mansard and Funke [22].

Each test was performed with a target mean peak period and an Iribarren number, ξ, varied from one test to another:

ξ = t a n α / {(\frac{H_{s}}{L_{0}})}^{1 / 2}

(3)

Where H_s is the significant wave height at the toe of the structure and L₀ = gT_p²/2π, T_p is the peak wave period and α is the armor slope angle. Here, the significant wave height H_m0 (= H_s) and T_p (peak wave period) are obtained using the frequency domain analysis.

Each test starts with a lower wave height than the target wave to induce the initial settlement. Subsequently, the wave height is increased (with a constant wave period) incrementally up to a wave height resulting in a damage (failure). Therefore, each test series consisted of 5 to 6 steps with increasing wave height. with T_p being fixed and H_s variable during each series, the Iribarren number changes within the same series. This approach is therefore different from the one adopted in Medina et al. [25], where the Iribarren number was kept constant. All tests were conducted in a non-breaking waves condition (Table 2).

All tests are conducted using irregular waves with a JONSWAP spectrum (γ = 3.3). The stability test for each wave height is performed for fixed acquisition duration, from 1024 s to 2048 s. This corresponds from 1000 to 1700 waves depending on the tested wave period. Wave statistic significance is already achieved for 1000 waves. The measurement data are obtained using a sample frequency of 32 Hz. In order to obtain the accurate generations of wave, all wave conditions were calibrated through a transfer function with the model in place. Before starting each test, the wave gauges were calibrated in still water through three fixed positions.

4.3. Damage analysis

Armor damage measurement in this study is done by visual observations of the displacements of the units of the armor layer. Photographs of the armor layer are taken after each series of tests to measure the evolution of the damage (before, during and after the test).

To improve visualization of displacement and the orientation change of the units during damage, each row is colored differently.

In this study, three different levels of damages were considered (CIRIA [11):

Start of damage;
Intermediate damage;
Failure.

Start of damage is corresponded to no damage or no movement of units. Intermediate damage is corresponded to the first significant movements detected on an armor layer and finally, with increasing wave height, the failure of the armor layer is reached when removal of a number of units leads to the exposure of the filter layer or the core. Damages were not repaired during succeeding test series. In this way the cumulative damage during the test series was determined. The armor layer is reconstructed, if necessary, only after completion of each test series.

The damage level is corresponding to the value of N_od which is the number of displaced armor unit to a width (along the longitudinal axis of the breakwater) of one nominal diameter D_n. The value of (accepted) N_od is affected by unit type (massive, interlocking) as well as number of layers. For example, the allowed N_od for a single layer cube armor layer is N_od=0.0 for start of damage and N_od=0.2 for failure. The N_od for failure level in Double layer cube armor layer increases to about N_od=2 (Van Gent and Luis [47]).

Moreover, the stability of the armor units can be represented using the dimensionless parameters, such as the stability number N_s (Van de Meer [42]), against the Iribarren number (ξ_p):

N_{s} = \frac{H_{s}}{∆ D_{n}} = {(K_{D} \cot α)}^{\frac{1}{3}}

(4)

where N_s= stability number;

K_D= stability coefficient (introduced by Hudson [19]);

H_m0=H_s= significant wave height in front of the structure;

Δ= (ρ_a/ρ_w-1);

ρ_a= mass density of the armor unit;

ρ_w= mass density of the water;

D_n= nominal diameter of the unit = (m/ρ_a)^1/3;

m = mass of the armor unit;

α= slope angle.

3.1. Overtopping measurement

Breakwater’s overtopping is affected by different parameters such as slope geometry, crest level, presence of a crown wall etc. Overtopping has been investigated in various studies (Bradbury et al. [5]; Owen [28]; Van der Meer and Stam [44]; Aminti and Franco [1]; Van Gent et al. [48]; Bruce et al. [7,8]; Molines and Medina [26]; EurOtop [15,16]).

In this study, the mean overtopping rate is measured for all tests, using the same standard method described by researchers such as Möller et al. [27]. The overtopping discharge (m3/s/m) is measured using a collection container placed behind the breakwater model as shown in Figure 6. This container is made of 10-mm-thick PVC plates, with dimensions of 0.795 m x 0.785 m x 0.360 m (length x width x height).

The post analysis allows us to calculate the average overtopping rate, i.e., the quantity of collected water in the container during a sequence of N incident waves (a storm or period considered), per unit length of breakwater's width.

For this purpose, the discharge, q, is calculated according to the following formula:

q = \frac{V}{t B}

(5)

where q: mean overtopping discharge;

V: accumulated wave overtopping volume;

t: test duration;

B: width of wave flume.

For tests with high overtopping rates, water is pumped into the leeward part of the wave flume during the test run to maintain a constant level of water in the front of the structure.

The accuracy of overtopping measurement is:

a container with an uncertainty of 1.3% (calibration with given input water volumes);
a chronometer with an operational accuracy precision of 1 s;
a digital scale balance with an accuracy of 5 g (test weights);
wave gauges with a precision of 2% (calibration in still water).

5. Hydraulic stability results

Among the great variety of factors affecting the design of a breakwater, hydraulic stability is one of the key design criteria that should be carefully investigated, particularly in one-layer system. The goal was to find the hydraulic stability of the single armor layer for the two placement methods that mentioned earlier.

The ‘Direct placement’ has a theoretical packing density of about 0.83 D^-2 (0.65 D_n^-2). However, due to the irregularities of the under-layer, the final packing density has been decreased to 0.81 D^-2 (0.64 D_n^-2). Similarly, for ‘Random placement’ the theoretical packing density of 0.89 D^-2 (0.70 D_n^-2) decreased to 0.86 D^-2 (0.68 D_n^-2).

Figure 8 presents the value of stability number N_s versus the Iribarren number (ξ_p) for the two studied placements.

The resulted packing densities in experiments were 0.68 for random placement and 0.64 for direct placement. These tests were repeated at least two times in order to assess the reliability of the results.

The square sign represents the stability numbers related to the ‘Direct placement’ method (DP); the diamond sign corresponds to the ‘Random placement’ method (RP). Center crossed- signs are corresponded to the start of the damage and full white and half black symbols are corresponded to the intermediate damage and failure of the armor layer, respectively. As previously mentioned, the start of damage is accordance to the standard practice of ‘no damage’, as defined for randomly placed armor units in a single layer (CIRIA [11]).

In the ‘Random placement’ tests, the start of damage was observed at the N_s close to 4.0 and the failure have reached at the Ns values between 5.7-5.9.

During the ‘Direct placement’ method, the start of damage occurred at the N_s close to 5.6-6.2, the failure happened at the stability number in the range of 6.4-7.2.

As it can be seen in Figure 8, higher values of N_s have been obtained for ‘Direct placement’ than the random placement in all tests for the three levels of damages.

5.1. Discussion

Figure 9 demonstrates the damage level as a function of stability number for the two studied placements. It is noticeable that the behavior of this unit is comparable to other single armor units. In general, for a single layer armor, it is expected to observe failure of the structure after occurrence of the first damage in the armor layer. In view of this, it is concluded that the criterion of failure and the start of damage are very close (Van der Meer [42]).

According to observations made from both placements, only minor changes in the damage progression process has been noted. A more gradual damage progress of armor layer and a wider gap between ‘no damage’ and ‘failure’ criteria has been observed (intermediate damage). Indeed, gradual extraction of more units from the initial damaged zone leads to failure. Moreover, it has been noticed that one unit can be extracted without affecting the stability of the adjacent units. In fact, the armor layer can remain stable after occurrence of the first damage and failure of the armor layer may be started from a different region in the following of the test. In this case, it can be considered that such a block was initially badly positioned with its neighbors during the placement, and that it suffers, as a results, from an increased vulnerability. It can also be assumed that this lack of support can lead to redistribution of specific forces for the neighboring units by mechanisms similar to ‘arching effect’. In fact, placement and specific shape of this unit (base hexagonal) lead to ‘Keystone’ feature allowing to keep the stability of the units adjacent to a unit extracted from the armor layer. There is no ‘unravelling’ effect as observed on any single layer interlocking units.

Reedjik et al. [32] are also stated that the irregularities in the surface of the underlayer might cause mispositions of some units that leads to lower stability.

Also, vertical settlement of the units parallel to the slope, particularly with a direct placement, was observed to occur. Vertical settlement of units can be extended toward the crest. This phenomenon tends to increase the packing density on the lower rows of the armor layer and reduce the packing density in the higher areas (Figure 10).

By analyses of the test results, the following formulas were derived for the start of the damage and failure (CIRIA et al. [11]):

\frac{H_{s}}{{∆ D}_{n}} = 4.0 Start of damage \emptyset = 0.68

(6)

\frac{H_{s}}{{∆ D}_{n}} = 5.7 Failure \emptyset = 0.68

(7)

These formulas are related to the ‘random placement’ with a packing density of 0.68 and 3.4 < ξ_p < 4.5

Medina and Gómez-Martín [23] and Jacobs et al. [21] stated that a safety factor in the case of single armor layer should be considered.

As above values are close to other single armor unit such as Accropode (N_s=3.7) or Coreloc (N_s= 4.2), it is recommended to use a safety factor of 1.5 on the (H_s/Δ D_n) (CIRIA [11]). As the design stability criteria is referred to the start of damage, the following equation could be proposed as the design rule for DC unit:

\frac{H_{s}}{{∆ D}_{n}} = 2.7 (K_{D} = 15) F o r d e s i g n

(8)

5.2. Influence of slope angle on stability

A steeper slope provides a better economical solution for breakwater construction (reduced number of armor units and less material). Figure 11 shows test results for an armor layer with random placement with two different slopes cotα=3/4 and cotα=2/3. For the two slopes, the packing densities of armor layer were ø=0.68.

It is evident that the stability number Ns for the start of damage for the two slopes was nearly the same. However, the failure level for the 2V:3H slope was slightly higher than the 3V:4H slope. This result is in agreement with the many others researches that investigated the effect of the slope steepness (Reedijk et al. [32]).

5.3. Comparison tests with cubes

In order to investigate the reliability of the previous tests and the influence of the scale effects, similar experimental tests with cubes as a single layer armor has been conducted. The characteristics of tests were exactly the same with previous tests (number of waves, specific mass of units, etc.).

The Cubes had a nominal diameter of 0.0355 m and were placed with an irregular pattern on a 4H:3V slope as described by Van Gent and Luis [47]. The cube tests have been placed on an underlayer of quarry stone with a D_n50 = 0.015 m, with a theoretical packing density of 0.70.

Figure 12 shows the results for stability number obtained from tests with DC in a random placement and tests with cubes in a single top layer placement.

For these single top-layers of cubes, stability results show a N_s 30% higher than values given in the CIRIA [11] and the stability values close to those of Van Gent and Luis [47] and Vieira et al. [52]. Stability number N_s obtained from tests with DC, demonstrate a considerable improvement of 30% for all criterions of damage in comparison to the Cubes.

It is well known that porosity play an important role in armor stability. considering that packing density and volume porosity were almost the same for both cases, the differences in stability number can be regarded as the effect of unit shape and surface porosity of the armor layer described by Safari et al. [34]. The ratio of porous area in any section is critically compared to the more common global main armor porosity. It is then demonstrated that the minimum section porosity should be the critical retained parameter. DC shape, provides a nonhomogeneous porosity within the amour’s section. This feature can enhance energy dissipation characteristics of an armor block through pressure differentials (Safari et al. [35]).

5.4. Comparison with other types of armor units

To compare the Double-cube with other single layer units, the following table demonstrate the data related to the stability, packing density and concrete consumption (Table 3).

The packing density is optimized through the new design, allowing an effective use of concrete for the breakwater armor unit. ‘Double cube’ performance is comparable to the units available on the market, and the tests indicate that in term of concrete consumption there will be no significant increases in the total concrete volume. Regarding concrete consumption, Xbloc^®, Accropode^® and DC (random placement), use less concrete than cube and Cubipod^®. It should be noted that the proposed design N_s is as a preliminary result and that it should be confirmed by complementary tests.

To compare and summarize the performance aspects of some the most common single layer armor blocks with DC, the following table is presented (Table 4).

This assessment has been done considering following points:

Easy placement of new unit without strict rules or specific positioning;
In comparison to simple units, complex-shaped units typically require a more complicated handling, building, and storage processes;
Regarding structural integrity, simple-shaped units (massive units) are more robust than complex-shaped units (slender units).

6. Analysis of wave overtopping

Overtopping tests were conducted following the conventional method described by TAW [39] to estimate the unit’s performance in terms of roughness. In the basic proposed equations, it is assumed that the overtopping rate can be estimated based on the relative crest freeboard Rc /Hs, Rc being the crest height of the structure above still water level.

Van de Meer and Janssen [43] provided an empirical overtopping formula, in case of non-breaking waves (ξ_m-1,0 > ≈ 2):

Q = \frac{q}{\sqrt{g H_{m 0}^{3}}} = 0.2 e x p (- 2.6 \frac{R_{c}}{H_{m 0}} \frac{1}{γ_{f}})

(9)

where q is the average specific overtopping discharge, R_c the elevation of crest above SWL (m), H_m0 spectral wave height at the toe of the structure, ξ_m-1,0 the local surf similarity parameter, and γ_f the reduction factor for the effect of slope roughness.

In total more than 100 tests were conducted with a structure armored with DC. The ranges of all parameters used in the tests are given in Table 5.

The water level for all tests was adjusted prior to each test. Depending upon the wave period, the tests had a duration of 1024s to 2048s, corresponding to 850-1365 waves, respectively.

Figure 13 shows the results for the dimensionless mean overtopping discharge as a function of crest relative height. The square symbol corresponds to direct placement and the polygon symbol corresponds to random placement. All the tests were conducted using the non-breaking wave conditions, which means that the surf-similarity parameter is greater than 2 (ξ_m-1,0 > ≈ 2). The graph shows an almost identical trend for both placement patterns, a decrease in overtopping with increasing R_c/H_m0.

Furthermore, for the test with ‘direct’ placement results show a little wider dispersion than the tests with random placement.

6.1. Effect of filter layer on overtopping

As discussed in a previous section, we have studied the effect of different filter layers on the stability of the armor layer. In order to complete these series of tests, we have also investigated the effect of filter materials on overtopping.

In Figure 14, all overtopping results from a random placement are illustrated as a relative mean overtopping rate against the relative freeboard R_c/H_m0. In this figure, results for a smooth slope are also illustrated.

From this figure, the following points are evident:

Among different studied filter layers, results obtained from the tests with D_n50= 0.0150 m have a larger scattering compared to those of other sizes.
the response for the two underlayers D_n50= 0.0150 m and 0.0100 m is similar, but less overtopping has been collected for the underlayer D_n50=0.0125 m.

6.2. Comparison with other units

The model profile used in this study, particularly the crest of the structure (small freeboard), is similar to the designs that has been used in the CLASH program. CLASH program intended to provide roughness coefficients for natural stones and various types of artificial units (Bruce et al. [7,8]).

Table 6 gives some recent roughness coefficients for single armor units, extracted from the CLASH program (Bruce et al. [8]), Reedijk et al. [32] and Perrin et al. [31].

As stated by Bakker et al. [3], it is difficult to compare different results obtained from different laboratories, due to the effect of different parameters such as crest width, packing density of the armor layer, geometric characteristics of underlayer and the core and also the scale effects (Safari et al. [35]).

Therefore, in order to not confront the same problems as that encountered during the tests in Delft Hydraulics for the Xbloc® (Bakker et al. [3]), it was necessary to realize on our model new series of tests on a reference unit which have been experienced during the CLASH program studies. This is the simple cube placed in monolayer was chosen by reason of similarity in its configuration to that of new unit and also easy casting of cube in our laboratory.

The overtopping volume was measured for a single layer regular cube placed on a slope of 3V:4H following with packing density of 70% (Figure 15). the test resulted in a roughness coefficient of γr=0.51 instead of the expected 0.50. In this study, the roughness coefficient for the DC unit was determined to be 0.46, a 10% decrease when compared to the one-layer regular placed cubes.

Additional tests have been done on a 2V:3H slope for the single layer regular cube and DC (Figure 16). In the tests with cube armor layer, the results deduced a roughness coefficient of approximately 0.48, a 6% decrease when compared to the slope of 3V:4H.

The roughness coefficient measured for the DC was approximately 0.43, meaning a decrease of about 7% compared to slope of 3V:4H (Table 4).

The tests conducted with a 2V:3H slope also confirm that DC provides an approximately 10% lower roughness coefficient compared to one-layer regular placed cube.

7. Conclusions

The Double cube, a new friction-type bulky armor unit, designed to protect breakwaters, shorelines and riverbanks. DC is composed of two cubic parts joined by a transition section. Inspired by the simplicity and effectiveness of the Cube, the new design is aimed to address some of its performance flaws.

The innovative design seeks an optimized shape leading to high structural integrity, high hydraulic stability and a low concrete consumption while providing an easy placement method.

Another object was to increase the roughness coefficient of armor layer and subsequently to reduce the overtopping.

The following findings can be drawn from the 2D hydraulic laboratory investigations:
The Double cube allows for simple random placement with no special requirements for the toe or the filter layer;
The hydraulic stability of the DC is comparable to that of a single armor layer like Accropode^®I or Xbloc^®;
In terms of hydraulic performance, the DC has a roughness parameter that is roughly 10% lower than the single layer regular placed cube. The new block's roughness parameter is comparable to that of Xbloc^® or Accropode^®I.
Regarding concrete consumption, it is comparable to that of the most efficient units, such as the Xbloc^® or the Accropode^®I;
Because of the new innovative form, fewer units can be used in a single layer. This will reduce the time and cost of manufacturing, storing, and placing units;
Greater hydraulic stability allows for the use of smaller cranes.

Promising results has been observed testing the newly developed block. This can be regarded as a start to further studies and optimizations on the proposed block.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The study was carried out as part of the research project of Iman Safari in the framework of a research fellowship program. The authors gratefully acknowledge the laboratory of Continental and Coastal Morphodynamics of the University of Caen, for the use of research facilities. Financial support for this study was granted to the INOUCO Company.

Conflicts of Interest

The authors declare no conflict of interest.

References

Aminti, P.; Franco, L. Wave overtopping on rubble mound breakwaters. Coastal Eng. Proc. 1988, 1, 770–781. [Google Scholar] [CrossRef]
d'Angremond, K.; Berendsen, E.; Bhageloe, G.S.; Van Gent, M.R.A.; Van der Meer, J.W. Breakwaters with a single armour layer. In Proceedings of the Int. Conf. on Coast. and Port Eng. in Developing Countries; 1999; pp. 1441–1449. [Google Scholar]
Bakker, P.; Klabbers, M.; Muttray, M.; Van den Berge, A. Hydraulic performance of Xbloc armour units. In Proceedings of the 1st Int. Conf. on Coast. Zone Management and Eng. in the Middle East Conference Paper, Dubai, UAE; 2006. [Google Scholar]
Bakker, P.; Van den Berge, A.; Hakenberg, R.; Klabbers, M.; Muttray, M.; Reedijk, B.; Rovers, I. Development of concrete breakwater armour blocks. In 1st Coastal, Estuary and Offshore Eng. In Proceedings of the Specialty Conference of the Canadian Society for Civil Engineering, Moncton, Canada; 2003. [Google Scholar]
Bradbury, A.P.; Allsop, N.W.H.; Stephens, R.V. Hydraulic performance of breakwater crown walls; Report SR146; H.R. Wallingford, 1988. [Google Scholar]
Bhageloe, G.S. Breakwaters with a single toplayer (In Dutch: Golfbrekers met een enkele toplaag). MSc-Thesis, Delft University of Technology, Delft, 1998. [Google Scholar]
Bruce, T.; Van der Meer, J.W.; Franco, L.; Pearson, J.M. A comparison of overtopping performance of different rubble mound breakwater armours. In Proceedings of the 30th Int. Conf. on Coast. Eng. 2006; Volume 5, pp. 4567–4579. [Google Scholar]
Bruce, T.; Van der Meer, J.W.; Franco, L.; Pearson, J.M. Overtopping performance of different armour blocks for rubble mound breakwaters. Coast. Eng. 2009, 56, 166–179. [Google Scholar] [CrossRef]
Burcharth, H.F.; Liu, Z.; Troch, P. Scaling of core material in rubble mound breakwater model tests. In Proceedings of the 5th Int. Conf. on Coastal and Port Engineering in Developing Countries (COPEDEC V), Cape Town, South Africa; 1999. [Google Scholar]
CERC. Shore protection manual [SPM], 4th edition; Coast. Eng. Research Center, US Army Corps of Engineers: Vicksburg, MS, 1984. [Google Scholar]
CIRIA/CUR/CETMEF. The Rock Manual. The use of rock in hydraulic engineering, 2nd ed.; CIRIA: London, UK, 2007; 1267p. [Google Scholar]
de Rover, R.; Verhagen, H.J.; Van den Berge, A.; Reedijk, J.S. Breakwater stability with damaged single layer armour blocks. In Proceedings of the 31th Int. Conf. on Coast. Engineering, Hambourg, Germany; 2008. [Google Scholar]
Dupray, S.; Roberts, J. Review of the use of concrete in the manufacture of concrete armour units. In Proceedings of the Int. Conf. of Coasts, Marine Structures and Breakwaters; 2009; Volume 1, pp. 245–259. [Google Scholar]
Edesign.co.uk. Piston coastal wave generators | Edinburgh Designs. 2016. Available online: http://www.edesign.co.uk/product/piston-wave-generators.
EurOtop. Overtopping Manual, Wave Overtopping of sea defences and related Structures: Assessment Manual. Pullen, T.; Allsop, N.W.H.; Bruce, T.; Kortenhaus, A.; Schüttrumpf, H.; Van der Meer, J.W., 2007.
EurOtop. Manual on wave overtopping of sea defences and related structures. An overtopping manual largely based on European research, but for worldwide application. Van der Meer, J.W.; Allsop, N.W.H.; Bruce, T.; De Rouck, J.; Kortenhaus, A.; Pullen, T.; Schüttrumpf, H.; Troch, P.; Zanuttigh, B., 2018.
Gómez-Martín, M.E.; Medina, J.R. Cubipod concrete armour block and heterogeneous packing. In Proceedings of the 5th Coastal Structures Int. Conf., World Scientific; 2007; pp. 140–151. [Google Scholar]
Gómez-Martín, M.E.; Medina, J.R. Erosion of cubes and Cubipods armour layers under wave attack. In Proceedings of the 30th Int. Conf. on Coastal Eng., ASCE; 2008; pp. 3461–3473. [Google Scholar]
Hudson, R.Y. Laboratory investigations of rubble mound breakwaters. J. waterw. Harb. Div. 1959, 93–121. [Google Scholar] [CrossRef]
Hughes, S.A. Physical models and laboratory techniques in coastal engineering; Advanced Series on Ocean Engineering; World Scientific, 1993; Volume 7. [Google Scholar]
Jacobs, R.; Bakker, P.; Vos-Rovers, I.; Reedijk, B. Xbloc-plus development of a regular placed interlocking armour unit. Coast. Eng. Proc. 2018, 36. [Google Scholar] [CrossRef]
Mansard, E.P.D.; Funke, E.R. The measurement of incident and reflected spectra using a least squares method. In Proceedings of the 17th Int. Conf. on Coast. Eng., ASCE, Sydney, Australia; 1980; Volume 1, pp. 154–172. [Google Scholar]
Medina, J.R.; Gómez-Martín, M.E. KD and safety factors of concrete armour blocks. In Proceedings of the 33nd Int. Conf. on Coast. Eng., ASCE; 2012; Volume 1, p. 29. [Google Scholar]
Medina, J.R.; Gómez-Martín, M.E.; Corredor, A. Influence of armour unit placement on armour porosity and hydraulic stability. In Proceedings of the 32nd Int. Conf. on Coast. Eng., ASCE; 2010. [Google Scholar]
Medina, J.R.; Molines, J.; Gómez-Martín, M.E. Influence of armour porosity on the hydraulic stability of cube armour layers. J. Ocean Eng. 2014, 88, 289–297. [Google Scholar] [CrossRef]
Molines, J.; Medina, J.R. Calibration of overtopping roughness factors for concrete armor units in non-breaking conditions using the CLASH database. Coast. Eng. 2015, 96, 62–70. [Google Scholar] [CrossRef]
Mӧller, J.; Kortenhaus, A.; Oumeraci, H.; de Rouck, J.; Medina, J.R. Wave run-up and wave overtopping on a rubble mound breakwater-Comparison of prototype and laboratory investigations. Coastal Structures 2003, 456–468. [Google Scholar]
Owen, M.W. Design of seawalls allowing for wave overtopping; Report 924; H.R. Wallingford, 1980. [Google Scholar]
Park, Y.H.; Oh, Y.-M.; Ahn, S.M.; Han, T.H.; Kim, Y.-T.; Suh, K.-D.; Won, D. Development of a new concrete armor unit for high waves. J. of Coastal Research 2019, 35, 719–728. [Google Scholar] [CrossRef]
Peng, C.; Wang, H.; Zhang, H.; Chen, H. Parametric design and numerical investigation of hydrodynamic characteristics of a new type of armour block TB-CUBE based on SPH method. J. Mar. Sci. Eng. 2022, 10, 1116. [Google Scholar] [CrossRef]
Perrin, S.; Collinsworth, S.; Giraudel, C.; Melby, J.; Perrin, S.; Giraudel, C.; Collinsworth, S.; Melby, J. Hydraulic response & placement methods for a new single-layer concrete armour unit called C-ROC™. Marine structures and breakwaters 2017, 321–330. [Google Scholar]
Reedijk, B.; Eggeling, T.; Bakker, P.; Jacobs, R.; Muttray, M. Hydraulic stability and overtopping performance of a new type of regular placed armor unit. In Proceedings of the 36th Int. Conf. on Coast. Eng., Baltimore, Maryland; 2018; Volume 1. [Google Scholar]
Safari, I. Analyse de la performance hydraulique d’un nouveau type de bloc artificiel utilisé pour la protection côtière. Ph.D. Thesis, University of Caen, 2011. [Google Scholar]
Safari, I.; Mouazé, D.; Ropert, F.; Haquin, S.; Ezersky, A. Influence du plan de pose sur les distributions de porosité au sein d'une carapace de digue à talus. In Proceedings of the XIIèmes Journée Nationales Génie Côtière-Génie Civil; 2012; pp. 791–798. [Google Scholar]
Safari, I.; Mouazé, D.; Ropert, F.; Haquin, S.; Ezersky, A. Hydraulic stability and wave overtopping of Starbloc ® armored mound breakwaters. Ocean. Eng. 2018, 151, 268–275. [Google Scholar] [CrossRef]
Safari, I.; Mouazé, D.; Ropert, F.; Haquin, S.; Ezersky, A. Experimental study to determine forces acting on starbloc armor units and velocities occurring in a single-layer rubble mound breakwater. J. Waterway, Port, Coastal and Ocean Eng. 2022, 148. [Google Scholar] [CrossRef]
Salauddin, M.; Broere, A.; Van Der Meer, J.W.; Verhagen, H.J.; Bijl, E. First tests on the symmetrical breakwater armor unit crablock. J. Coast. Eng. 2017, 59, 1–33. [Google Scholar] [CrossRef]
Salauddin, M.; Broere, A.; Van Der Meer, J.W.; Verhagen, H.J.; Bijl, E. A new symmetrical unit for breakwater armour: First Tests. In Proceedings of the Coast. Structures & Solutions to Coastal Disasters; 2015. [Google Scholar]
TAW. Technical report wave run-up and wave overtopping at dikes; Technical report; Technical Advisory Committee on Flood Defence, 2002. [Google Scholar]
Van Buchem, R.V. Stability of a single top layer of cubes. MSc-Thesis, Delft University of Technology, Delft, 2009. [Google Scholar]
Van der Lem, C.; Stive, R.; Van Gent, M.R.A. Sal Rei breakwaters with single layer cubes. In Proceedings of the PIANC-Copedec, Rio de Janeiro; 2016. [Google Scholar]
Van der Meer, J.W. Design of concrete armour layers. In Proceedings of the Coast. Structures 99, Santander, Spain; 1999; pp. 213–221. [Google Scholar]
Van der Meer, J.W.; Janssen, J.P.F.M. Wave Run-up and Wave Overtopping at Dikes; Delft Hydraulics, 1985; No. 485. [Google Scholar]
Van der Meer, J.W.; Stam, C.J.M. Wave run-up on smooth and rock slopes of coastal structures. J. Waterway, Port, Coastal and Ocean Eng. 1992, 118, 534–550. [Google Scholar] [CrossRef]
Van Gent, M.R.A.; Spaan, G.B.H.; Plate, S.E.; Berendson, E.; Van der Meer, J.W.; d'Angremond, K. Single-layer rubble mound breakwaters. In Proceedings of the 3th Int. Conf. Coast. Structures; 2000; Volume 1, pp. 231–239. [Google Scholar]
Van Gent, M.R.A.; d'Angremond, K.; Triemstra, R. Rubble mound breakwaters: single armour layers and high-density blocks. In Proceedings of the Coastlines, Structures and Breakwaters, ICE, London; 2001. [Google Scholar]
Van Gent, M.R.A.; Luis, L. Application of cubes in a single layer. Proceedings of 6th Conference on Applied Coastal Research (SCACR), Lisbon; 2013. [Google Scholar]
Van Gent, M.R.A.; Van den Boogaard, H.F.P.; Pozueta, B.; Medina, J.R. Neural network modelling of wave overtopping at coastal structures. Coast. Eng. 2007, 54, 586–593. [Google Scholar] [CrossRef]
Van Gent, M.R.A.; Van der Werf, I.M. Single layer cubes in a berm. Proceedings of Applied Coast. Research, Santander; 2017. [Google Scholar]
Vanneste, D.; Troch, P. An improved calculation model for the wave induced pore pressure distribution in a rubble-mound breakwater core. Coast. Eng. 2012, 66. [Google Scholar] [CrossRef]
Vieira, F.; Taveira-Pinto, F.; Rosa-Santos, P. Single-layer cube armoured breakwaters: Critical review and technical challenges. Ocean Eng. 2020, 216. [Google Scholar] [CrossRef]
Vieira, F.; Taveira-Pinto, F.; Rosa-Santos, P. Damage evolution in single-layer cube armoured breakwaters with a regular placement pattern. Coast. Eng. 2021, 169. [Google Scholar] [CrossRef]
Vieira, F.; Taveira-Pinto, F.; Rosa-Santos, P. New developments in assessment of wave overtopping on single-layer cube armoured breakwaters based on laboratory experiments. Coast. Eng. 2021, 166. [Google Scholar] [CrossRef]
Wolters, G.; Van Gent, M.R.A.; Hofland, B.; Wellens, P. Wave damping and permeability scaling in rubble mound breakwaters. In Proceedings of the Coastlab, Varna, Bulgaria; 2014. [Google Scholar]

Figure 1. Disarrangement of cube placement (Safari [33]).

Figure 2. Plan view of Double-Cube unit.

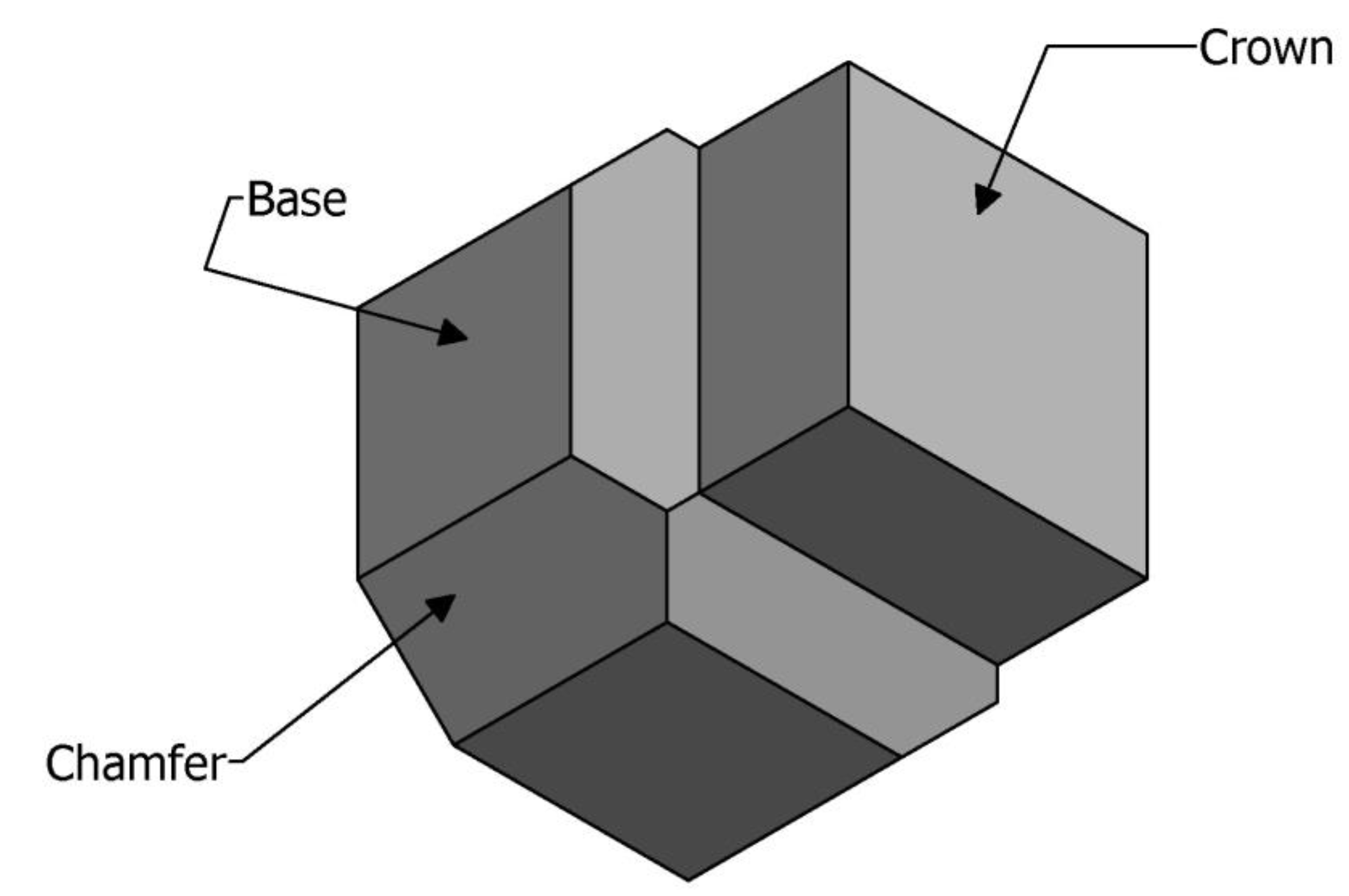
Figure 3. DC unit geometry.

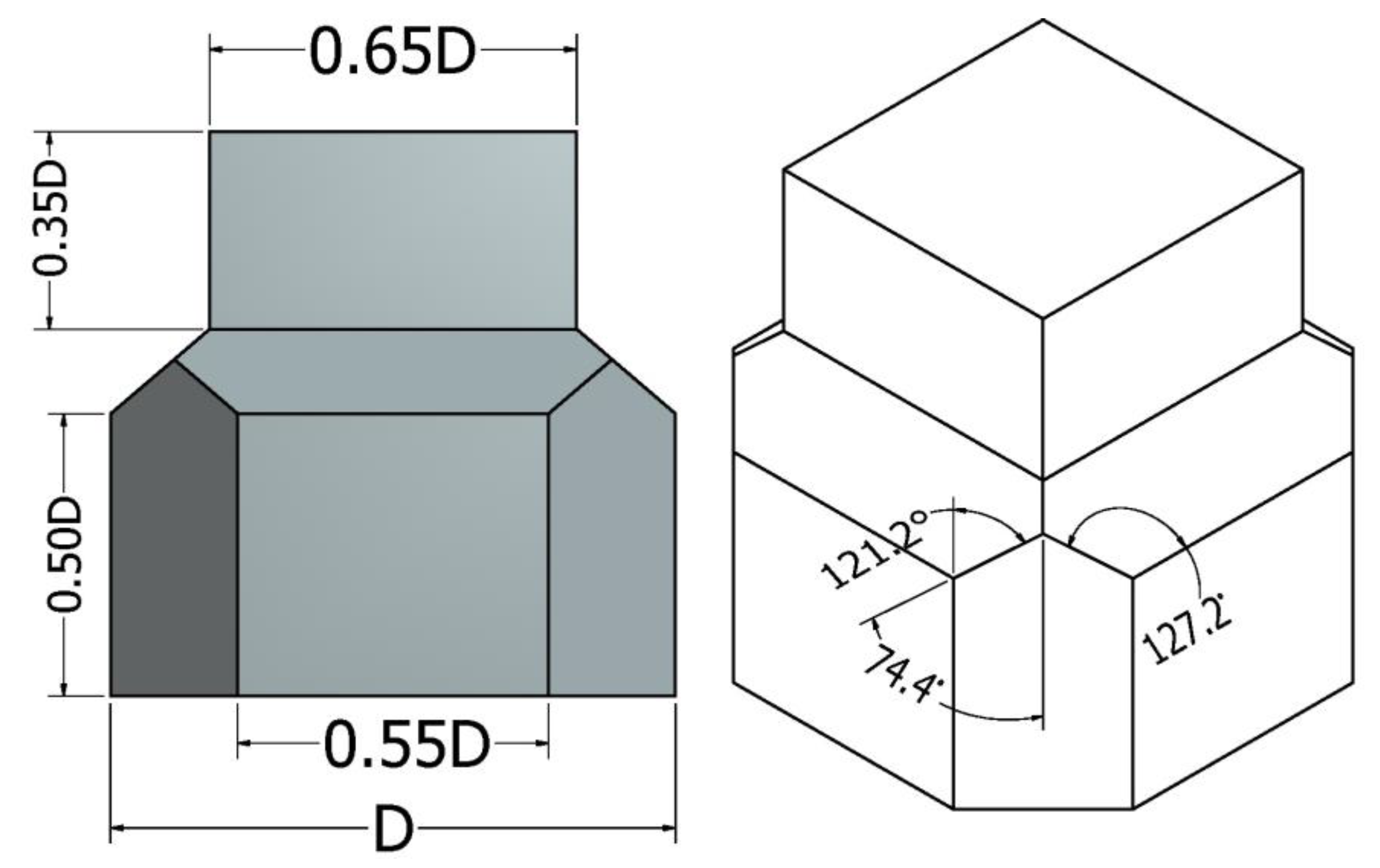
Figure 4. Schematic of Direct placement method (DP).

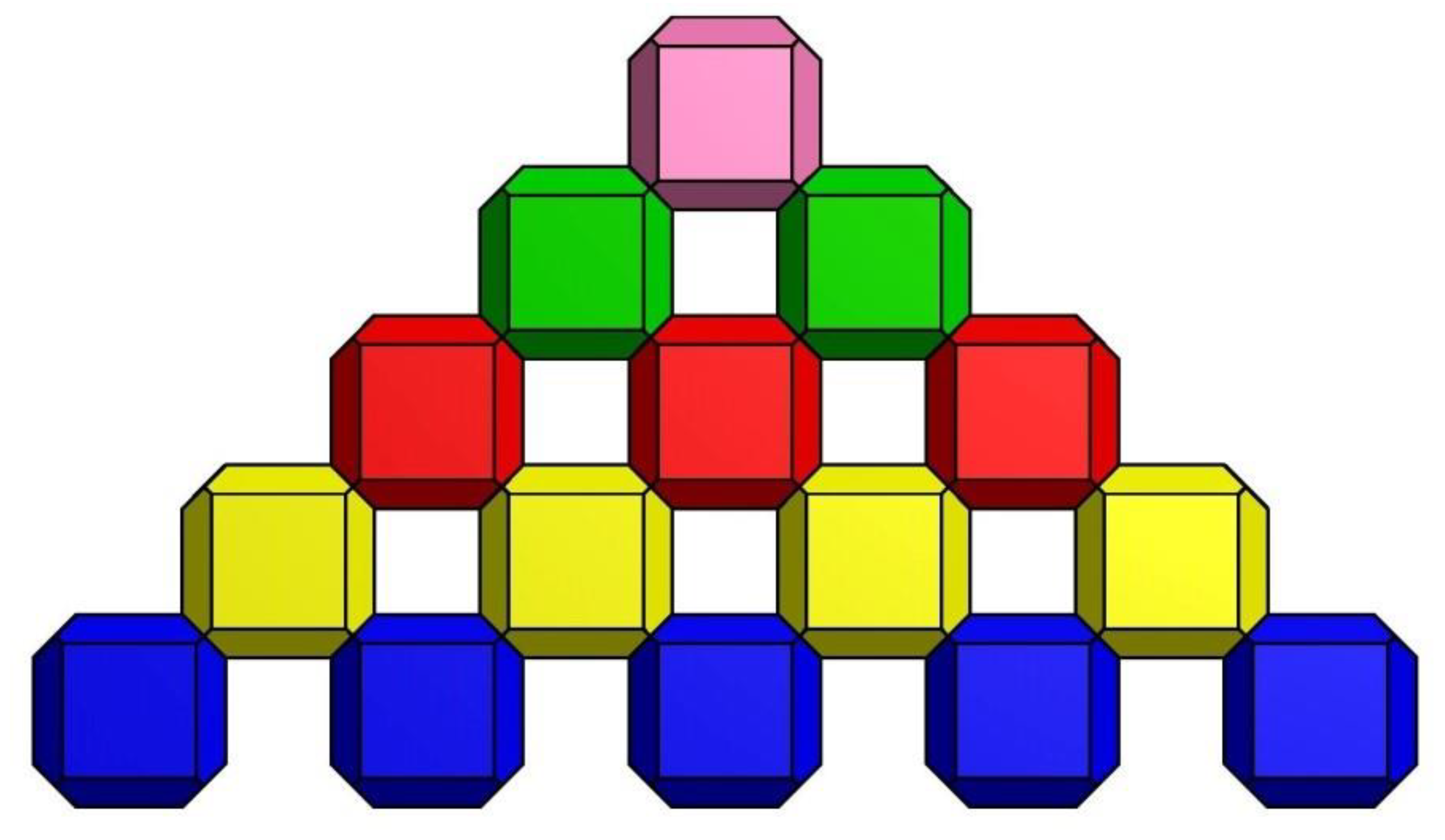
Figure 5. Schematic of Random placement method (RP).

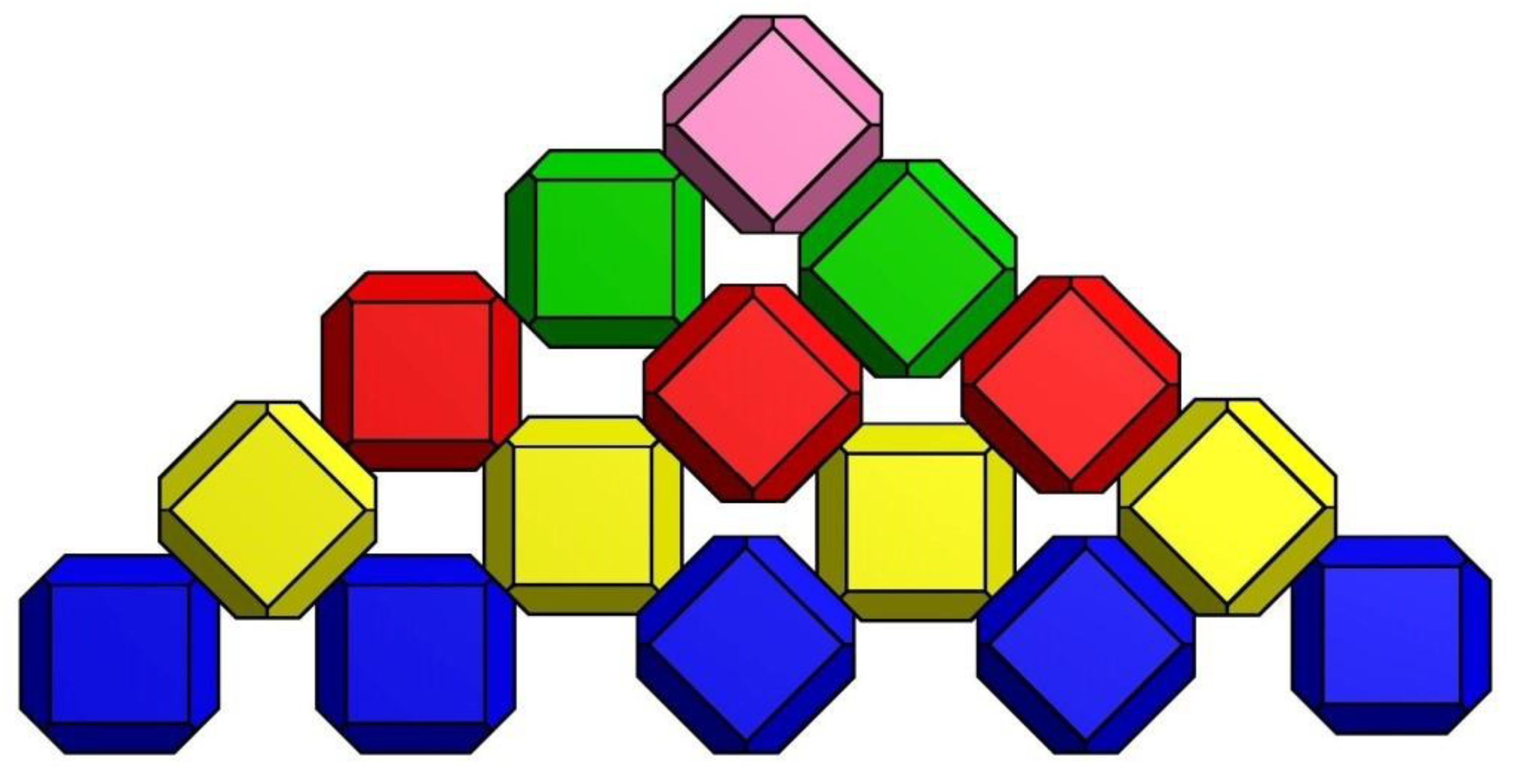
Figure 6. Schematic diagram of wave flume and instrumentation.

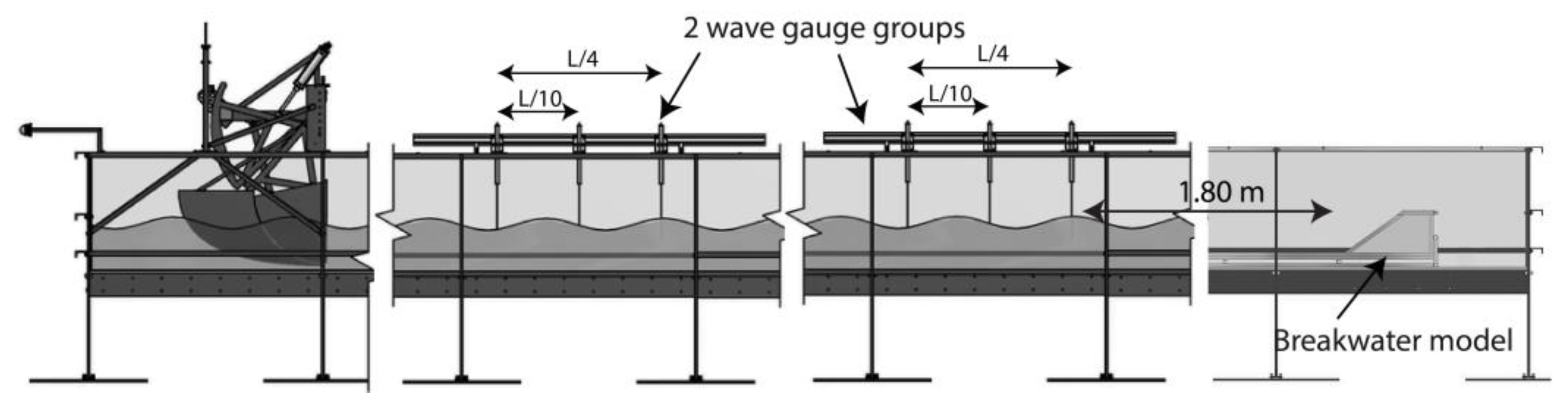
Figure 7. Cross section of the rubble mound breakwater (all dimensions in m)

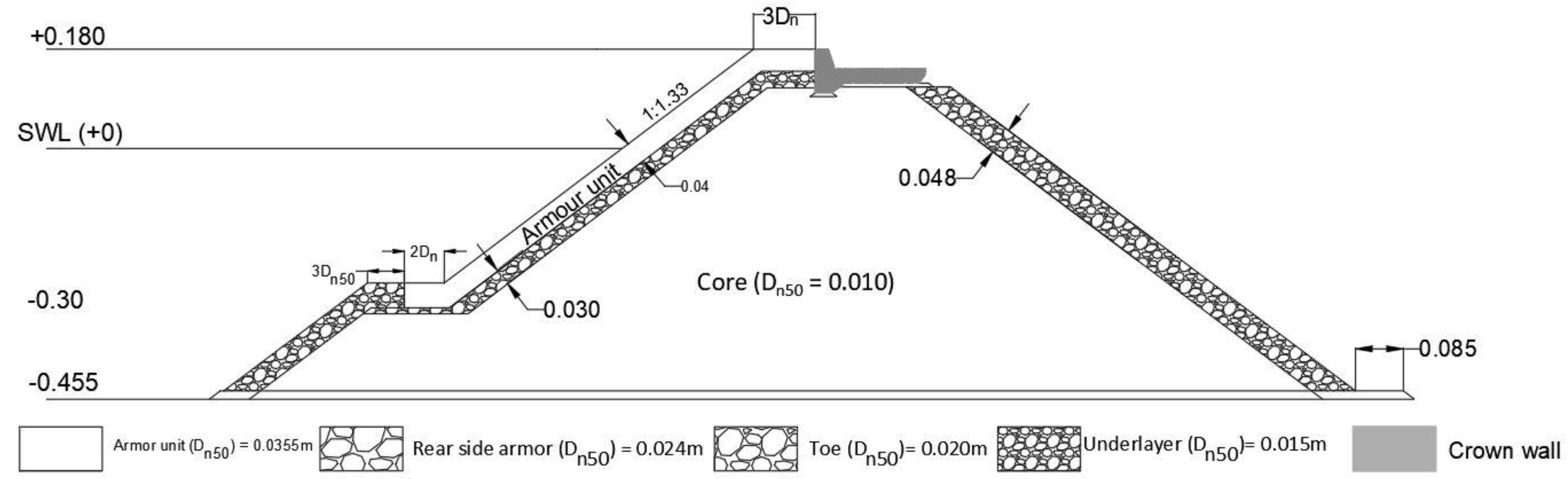
Figure 8. Stability test results (Filter D_n50 = 0.015 m)

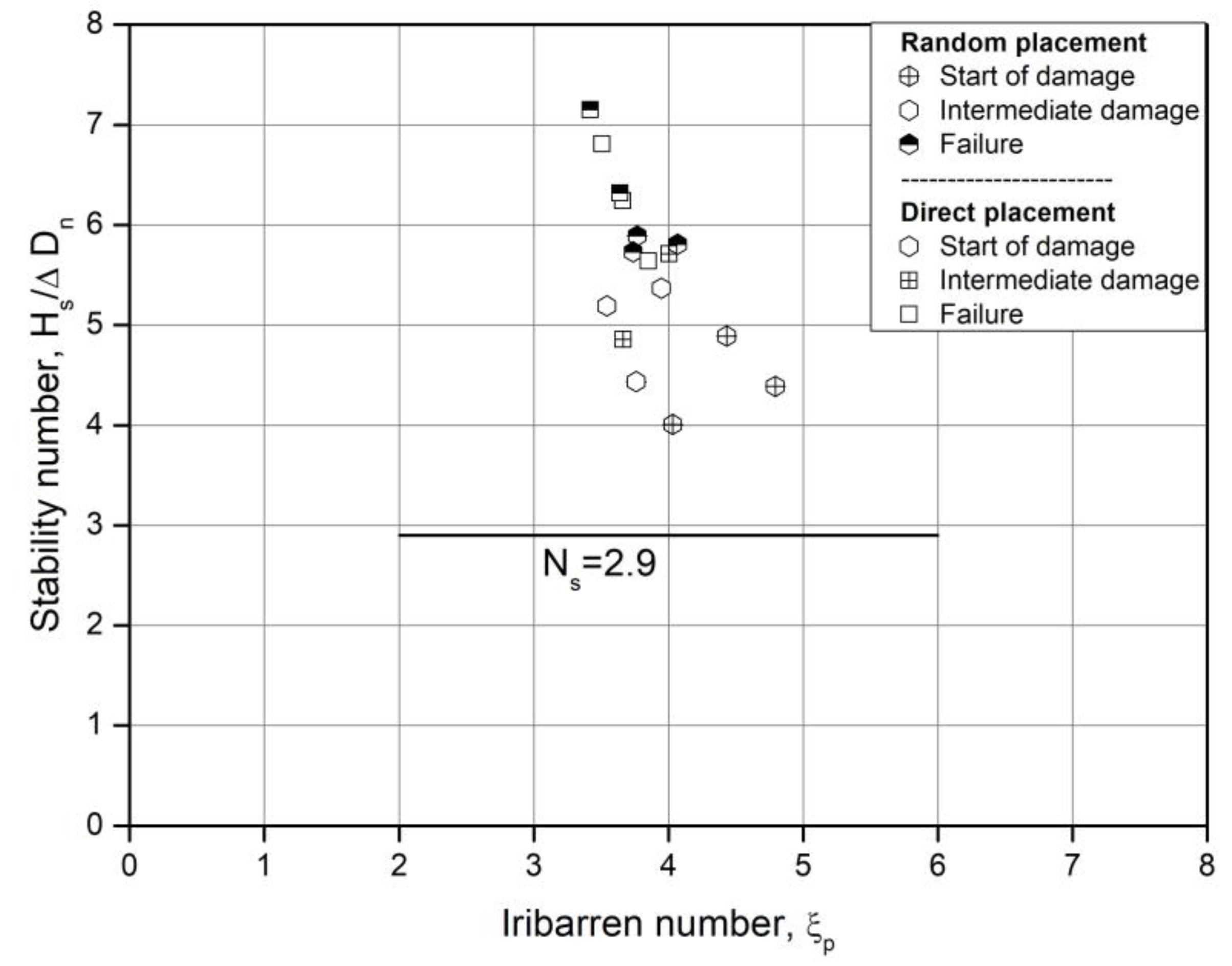
Figure 9. Relation between Nod and H_s/ΔD_n

Figure 10. Vertical settlement of upper armor layer : (a) before test; (b) after some tests.

Figure 11. Influence of the slope angle on stability on a ‘Random placement’ with a packing density of 0.68

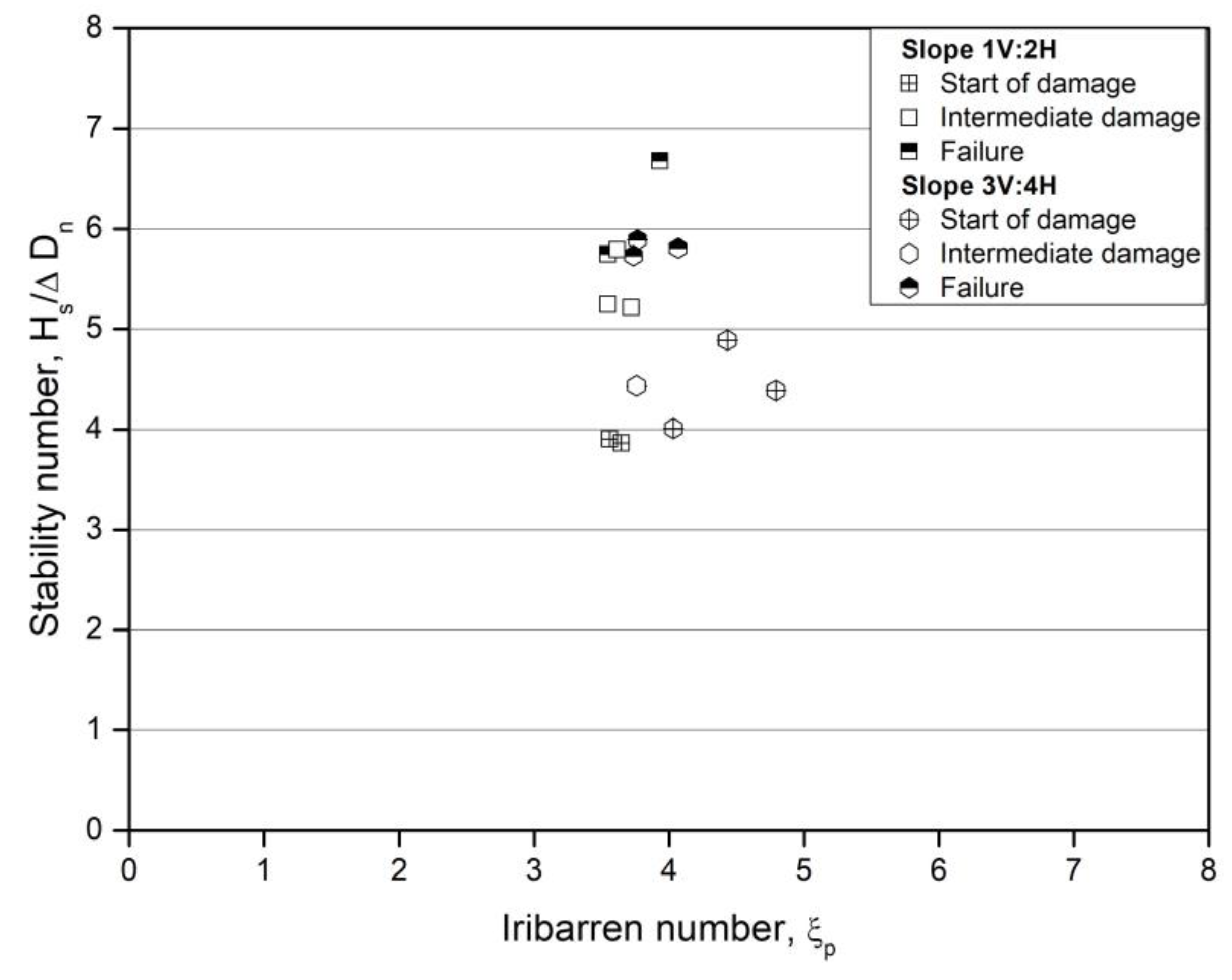
Figure 12. Comparison of stability test results for Double cube unit with a single layer cube

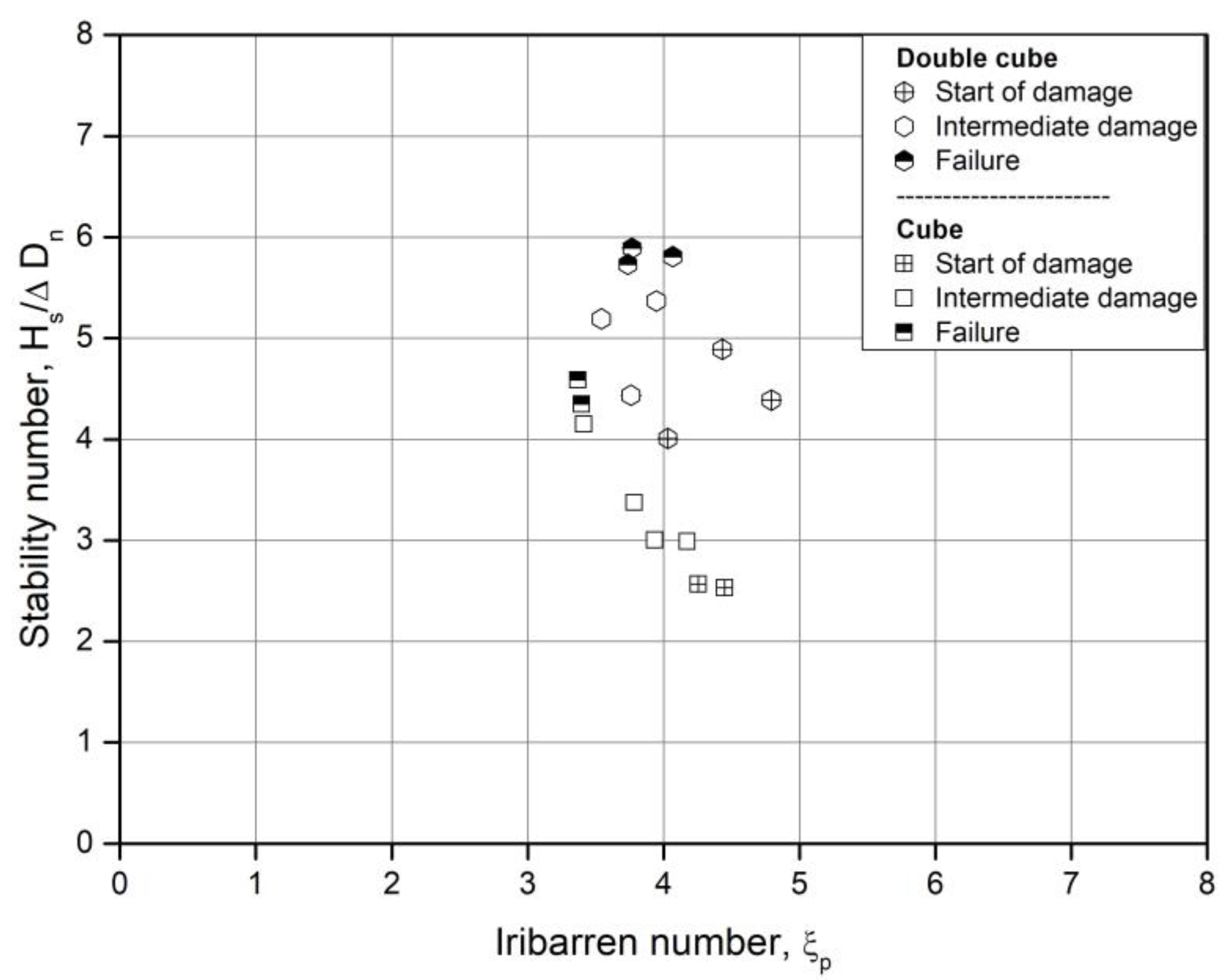
Figure 13. Dimensionless plot of overtopping tests for two studied placements

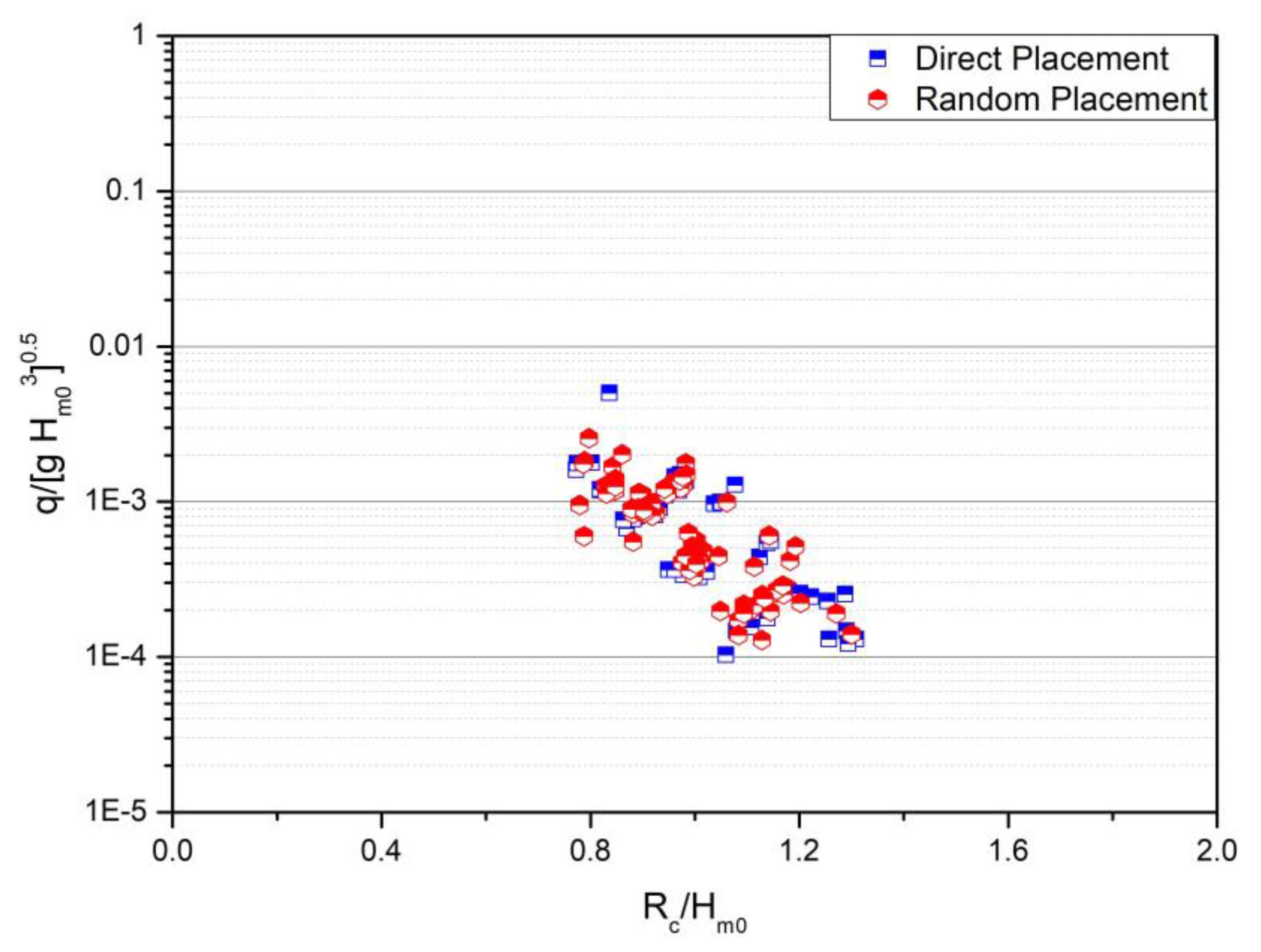
Figure 14. Comparison of tests results for three under layers

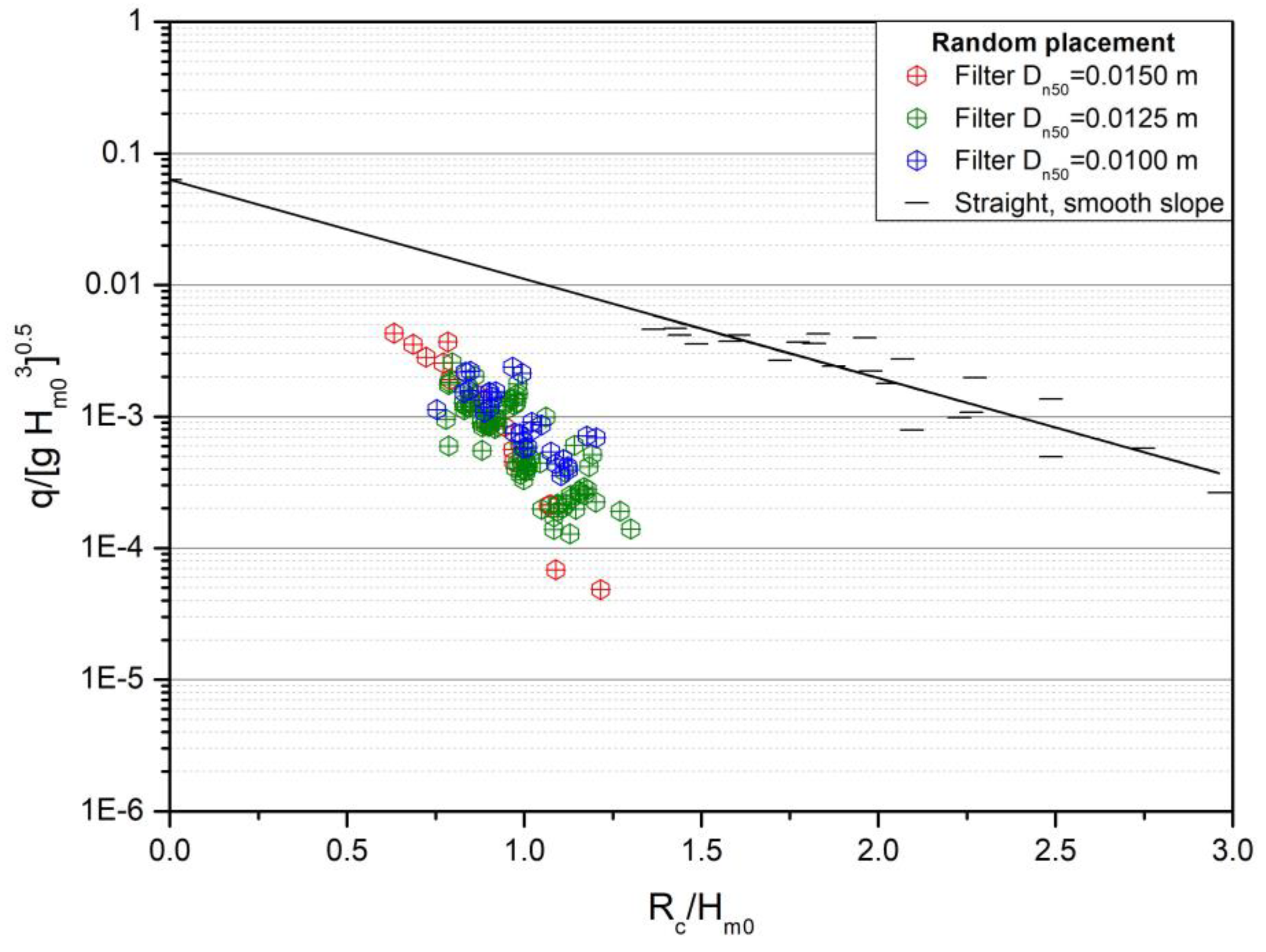
Figure 15. Comparison of measured wave overtopping for two units (3V:4H)

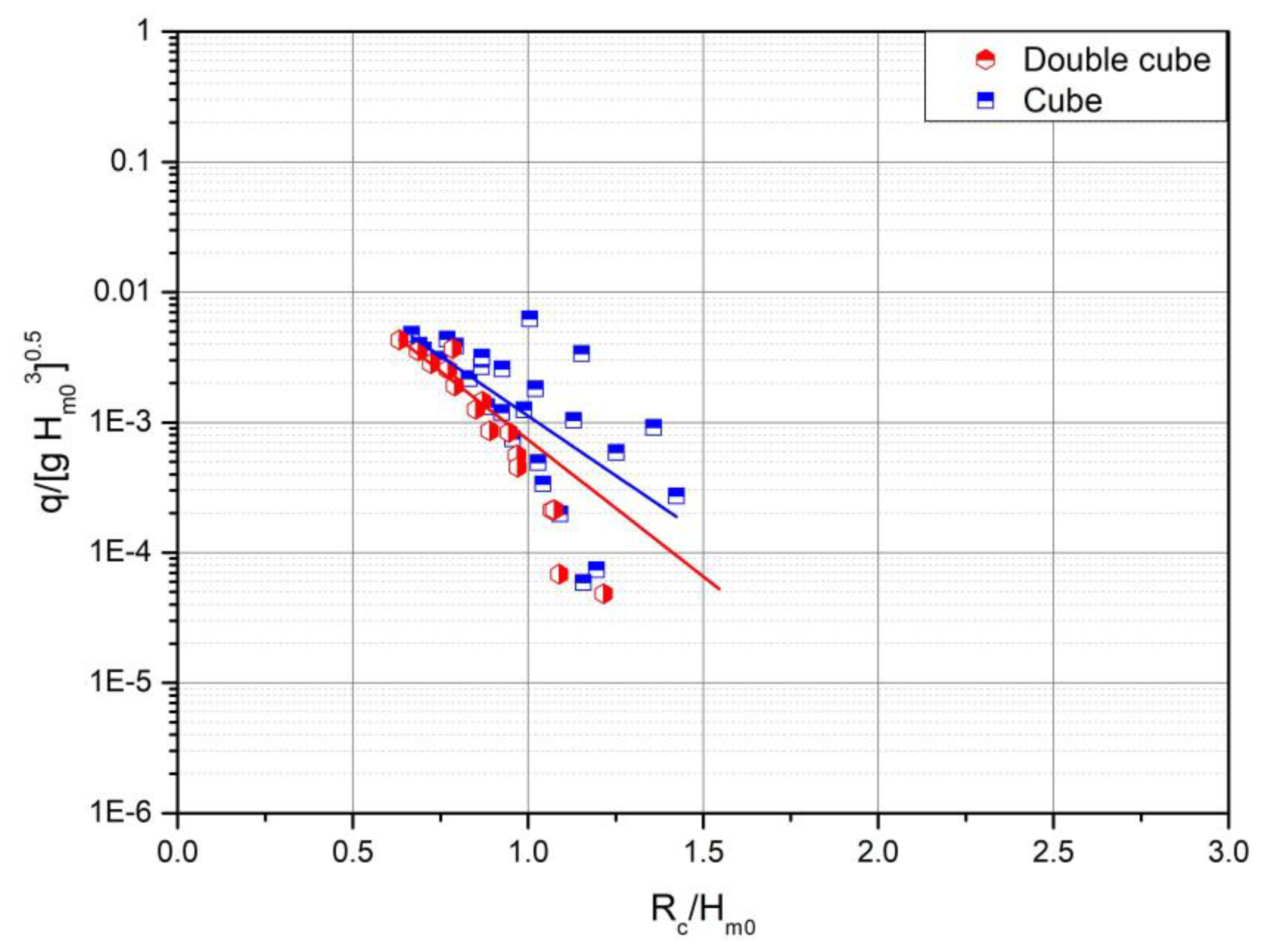
Figure 16. Comparison of measured wave overtopping for Cubes and DC (2V:3H)

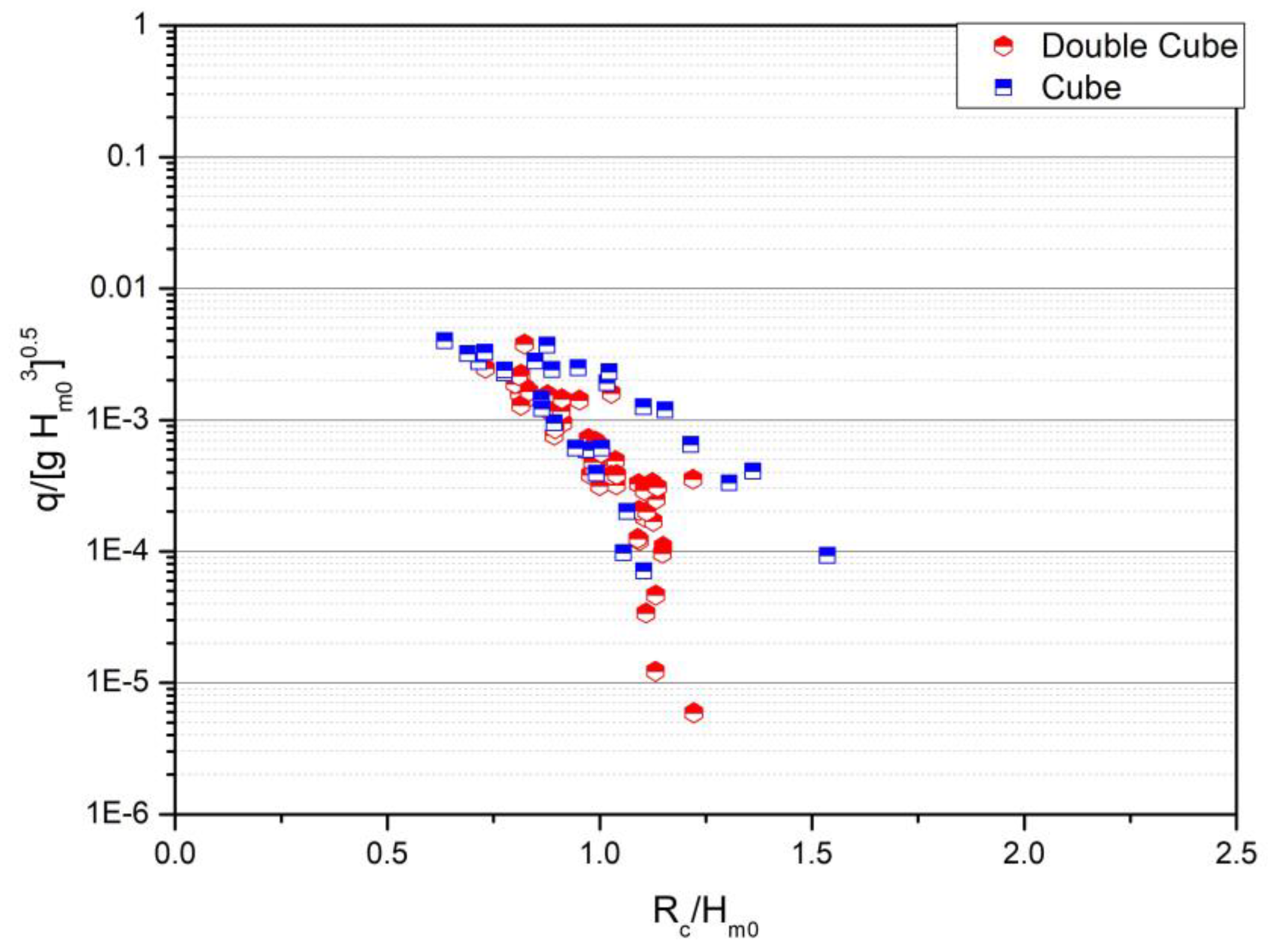
Table 1. Properties of unit and model parameters.

Elements	D_n-D_n50 (m)	ρ_s (kgm^-3)	M₅₀ [kg]
Armor layer	0.0355	1620	0.0725
Underlayer	0.0150	2650	0.0090
Core	0.0100	2650	0.0026
Rear-side armor	0.0240	2650	0.0360
Toe	0.0200	2650	0.0210

Table 2. Summary of hydraulic stability wave conditions.

Armour layer	Filter layer Dn50 (m)	Slope angle	Placement pattern	Tp (s)	No. of tests	Rc (m)	Packing density
Double cube	0.0100	3V:4H	Random	1.2	16	0.08	0.68
				1.5	8	0.08
				1.5	6	0.11
	0.0125	3V:4H	Direct	1.2	8	0.08	0.64
				1.5	4	0.08
				1.5	3	0.11
			Random	1	8	0.08	0.68
				1.2	40	0.08
				1.2	16	0.11
				1.5	20	0.08
				1.5	27	0.11
	0.0150	3V:4H	Random	1	6	0.07	0.68
				1	3	0.105
				1.2	11	0.07
				1.2	18	0.105
				1.5	4	0.09
				1.5	12	0.105
			Direct	1	1	0.105	0.64
				1.2	5	0.105
				1.5	4	0.105
		2V:3H	Random	1	10	0.08	0.68
				1.2	42	0.08
				1.5	6	0.08
			Direct	1	4	0.07	0.64
				1.2	22	0.07
				1.5	2	0.07

Table 3. Comparative table for hydraulic stability and consumption of concrete for different units.

	Accropode^® I	X-bloc^®	Cubipod^®	Cube 1 layer	DC
Placement pattern	Random	Random	Random	Random	Random	Direct
Breakwater slope	3V:4H	3V:4H	2V:3H	2V:3H	3V:4H	3V:4H
N_s no damage	3.7¹	3.3-5.5²	33	2.9-3.0¹	4.0-5.4	4.9-5.7
N_s failure	4.1¹	3.7-6.0²	3.7³	3.5-3.75¹	5.7-5.9	6.3-7.2
N_s project	2.7¹	2.8¹	2.6³	2.2¹	2.9	3.1
Min N_s/N_s project	1.37	1.18	1.15	1.32	1.38	1.58
Packing density	0.62	0.58	0.65	0.7	0.67	0.63
Consumption of concrete unit related to a cubic shape	72.2	65.1	78.6	100	72.6	64.9

¹ Ref. CIRIA [11]. ¹ Ref. Bakker et al. [3]. ¹ Ref. Medina and Gómez-Martín [23].

Table 4. Comparative table for hydraulic stability and consumption of concrete for different units.

	Cube¹	Cubipod®	Accropode^® I	DC	Xbloc®	Core-loc®
Number of layers	1	1	1	1	1	1
Hydraulic stability	+-²	+	++	++	++	++
Overtopping	+-	+	+	+	+	+
Structural Integrity	+	+	+-	+	+-	+-
Porosity	-	+	+	+	+	+
Ease of placement	+-	+-	--	+	+-	--
Ease of build	++	+	--	+	--	--
Storage	++	+	-	+	-	+-
Safety	+	+-	+-	+	+-	+-
Economy	-	+	+-	+	+-	+-

¹ Cubes are considered as the basis of the comparison. ¹ The +- sign means that we did not make a determination either because of too much variation in the criterion within the group, or because of insufficient available data (economy), or because of the strong dependency on other criteria (safety).

Table 5. Summary of overtopping test conditions.

Armour layer	Under layer D_n50 (m)	Slope angle	Placement pattern	T_p (s)	No. of tests	R_c (m)	Packing density
DC	0.0100	3V:4H	Random	1.2	16	0.08	0.68
				1.5	8	0.08
				1.5	6	0.11
	0.0125	3V:4H	Direct	1.2	8	0.08	0.64
				1.5	4	0.08
				1.5	3	0.11
			Random	1	8	0.08	0.68
				1.2	40	0.08
				1.2	16	0.11
				1.5	20	0.08
				1.5	27	0.11
	0.0150	3V:4H	Random	1	6	0.07	0.68
				1	3	0.105
				1.2	11	0.07
				1.2	18	0.105
				1.5	4	0.09
				1.5	12	0.105
			Direct	1	1	0.105	0.64
				1.2	5	0.105
				1.5	4	0.105
		2V:3H	Random	1	10	0.08	0.68
				1.2	42	0.08
				1.5	6	0.08
			Direct	1	4	0.07	0.64
				1.2	22	0.07
				1.5	2	0.07
Cube	0.0100	3V:4H	Simple	1.2	10	0.08	0.69
	0.0100			1.5	8	0.08
	0.0150			1	6	0.07
				1.2	11	0.07
				1.2	6	0.105
				1.5	3	0.09
		2V:3H		1	7	0.07
				1.2	19	0.07
				1.2	6	0.105
				1.5	3	0.07
				1.5	4	0.105

Table 6. Roughness coefficient for single placed armor layer, from synthesis of new data and other comparable tests (Bruce et al. [8]; Reedijk et al [32]; Perrin et al. [31]; Safari et al. [35]).

Type of armour	No. of layers	Slope angle	γ_r	γ_r	γ_r
			Mean	95% CI, low	95% CI, high
Smooth	-	1.5	1
Rock (permeable core)	1	1.5	0.45
Cube	1	1.5	0.49	0.46	0.52
Accropode I	1	1.5	0.46	0.43	0.48
Core-Loc	1	1.5	0.44	0.41	0.47
Xbloc	1	1.5	0.44	0.41	0.46
Xbloc^PLUS	1	1.5	0.45
Starbloc	1	1.5	0.45	0.43	0.47
C-ROC	1	1.5/1.33	0.67
DC	1	1.33	0.46	0.43	0.48
DC	1	1.5	0.43	0.40	0.45

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Hydraulic Response and Overtopping Performance of Single-Layer Double-Cube Unit Armored Mound Breakwater

Abstract

1. Introduction

2. Logic of the new designed geometry

2. Placement method

3.1. Direct Placement (DP)

3.2. Random Placement (RP)

4. Hydraulic model tests

4.1. Experimental set-up

4.2. Wave measurements

4.3. Damage analysis

3.1. Overtopping measurement

5. Hydraulic stability results

5.1. Discussion

5.2. Influence of slope angle on stability

5.3. Comparison tests with cubes

5.4. Comparison with other types of armor units

6. Analysis of wave overtopping

6.1. Effect of filter layer on overtopping

6.2. Comparison with other units

7. Conclusions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe